Схема Подключения Треугольник — tokzamer.ru

Главным плюсом соединения трехфазной цепи звездой считают то, что мотор вырабатывает наибольшую мощность. Для сетей переменного тока 50 Гц линейное напряжение выше фазного в квадратный корень из трёх раз то есть примерно в 1.

Схема подключения звезда-треугольник

Возможные схемы подключения обмоток электродвигателей

И таких схем всего две: звезда и треугольник. В этом случае достаточно поплавковый выключатель встроить последовательно в цепь питания катушки пускателя.

Этот провод используется для заземления металлических корпусов токоприемников у потребителя. В четырехпроводной трехфазной системе нулевой провод надежно заземлен на электростанции, на ответвлениях сети и через определенные расстояния по линии. Существует оборудование с внутренним соединением концов обмоток.

У каждого конца свое буквенное и числовое обозначение. На самом деле ничего хорошего от этого нет, делать так не нужно.

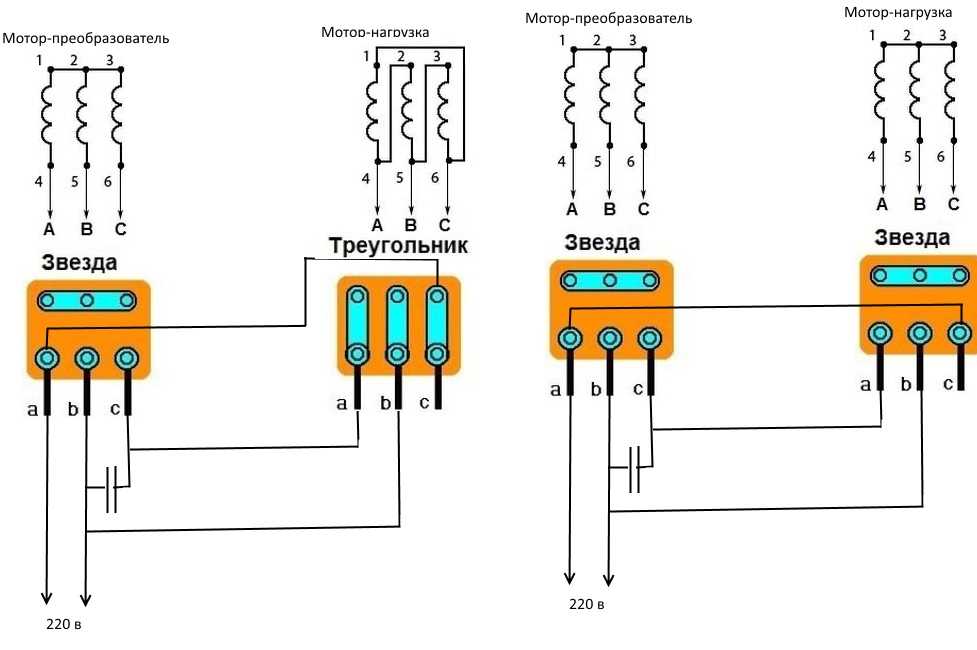
Схема включения в трехфазную четырехпроводную сеть осветительной В и силовой В нагрузок. Электромотор должен заработать. Использование частотного преобразователя В настоящее время достаточно активно все стали применять частотные преобразователи для управления частотой вращения оборотами электродвигателя.

Другие подключения электродвигателя Схем несколько: Более часто, чем вариант описанный, применяется схема с конденсатором, который поможет значительно уменьшить мощность. Одни из контактов рабочего конденсатора подключается к нулю, второй — к третьему выходу мотора электрического. Приемники, рассчитанные на фазное напряжение В, могут работать в сетях с линейными напряжениями и ?

Схемы подключения электродвигателя. Звезда — треугольник

Каждое соединение имеет свои плюсы и минусы в работе. Для такого подключения потребуется немного более высокое напряжение, чем В из-за частоты тока 60 Гц , но у них там как раз В, что как раз подходит. Рассмотрим на примере, на сколько ошибочные данные утверждения.

Мы имеем большой опыт модернизации электродвигателей для работы на низкой частоте. При соединении концов применяют специально предназначенные для этого перемычки. Но при этом данный способ не позволяет выйти двигателю на всю мощность, представленную в технических характеристиках.

Выводы обмоток

Для сетей переменного тока 50 Гц линейное напряжение выше фазного в квадратный корень из трёх раз то есть примерно в 1.

От того, выберем мы один или другой, будет зависеть в какую сторону начнет вращаться двигатель. Однако, по крайней мере, можно использовать 3-фазное подключение треугольником. Это позволяет использовать по полной КПД электродвигателя, согласно техпаспорта.

У каждого конца свое буквенное и числовое обозначение. На рисунке 4 приведена схема включения в трехфазную четырехпроводную сеть осветительной и силовой нагрузок.

К тому же агрегат сильно нагревается в процессе работы. Поэтому электродвигатели асинхронного типа со средней и большой мощностью чаще всего подключают по схеме звезда.

Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль. При помощи тестера провода прозванивают, чтобы найти катушки. По полученным векторным уравнениям можно для равномерной нагрузки фаз построить векторную диаграмму рис.

Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль. В таком случае этот двигатель можно будет использовать как в трёхфазной сети с линейным напряжением В подключение звезда , так и в однофазной сети В подключение треугольником через конденсатор. Форму треугольника предает эргономичное размещение соединения обмоток. При замыкании цепи поплавком будет замыкаться цепь катушки пускателя, и включаться электродвигатель, при размыкании — будет отключаться питание электродвигателя.

К тому же агрегат сильно нагревается в процессе работы. Фазные обмотки генератора образуют замкнутый контур с малым внутренним сопротивлением.

Схемы соединений обмоток треугольник и звезда для чайников.

Наиболее распространенный вопрос у начинающих изучения устройства трансформаторов или иных электротехнических устройств это «Что такое звезда и треугольник?». Чем же они отличаются и как устроены, попробуем разъяснить в нашей статье. 

Рассмотрим схемы соединений обмоток на примере трехфазного трансформатора. В своем строении он имеет магнитопровод, состоящий из трёх стержней. На каждом стержне есть две обмотки – первичная и вторичная. На первичную подается высокое напряжения, а со вторичной снимается низкое напряжение и идет к потребителю. В условном обозначении схема соединений обозначается дробью (например, Y⁄∆ или Y/D или У/Д), значение числителя – соединение обмотки высшего напряжения (ВН), а значение знаменателя – низшего напряжения (НН).

Каждый стержень имеет как первичную обмотку так и вторичную (три первичных и три вторичных обмотки). У каждой обмотки есть начало и конец. Обмотки можно соединить между собой способом звезда или треугольник. Для наглядности обозначим вышеперечисленное схематически (рис. 1)

При соединении звездой, концы обмоток соединяются вместе, а из начал идут три фазы к потребителю. Из вывода соединений концов обмоток, выводят нейтральный провод N (он же нулевой). В итоге получается четырёх — проводная, трёхфазная система, которая часто встречается вдоль линий воздушных электропередач.(рис. 2)

Преимущества такой схемы соединения в том, что мы можем получить 2 вида напряжения: фазное (фаза+нейтраль) и линейное. В таком соединении линейное напряжение больше фазного в √3 раз. Зная, что фазное напряжение дает нам 220В, то умножив его на √3 = 1,73, получим примерно 380В – напряжение линейное. Но что касается электрического тока, то в этом случае фазный ток равен линейному, т.

к. что линейный, что фазный токи одинаково выходят из обмотки, и другого пути у него нет. Так же стоит отметить что только в соединении звезда имеется нейтральный провод, который является «уравнителем» нагрузки, чтобы напряжение не менялось и не скакало.

Рассмотрим теперь соединение обмоток треугольником. Если мы конец фазы А, соединим с началом фазы В, конец фазы В соединим с началом фазы С, а конец фазы С соединим с началом фазы А, то получим схему соединения обмотки треугольником. Т.е. в этой схеме обмотки соединены последовательно. (рис. 3)

В основном такая схема соединения применяется для симметричной нагрузки, где по фазам нагрузка не изменяется. В таком соединении фазное напряжение равно линейному, а вот электрический ток, наоборот, в такой схеме разный. Ток линейный больше фазного тока в √3 раз. Соединение обмотки треугольником обеспечивает баланс ампер-виток для тока нулевой 

последовательности. Простыми словами, схема соединения треугольником обеспечивает сбалансированное напряжение.

Подведем итоги. Для базового определения схем соединения обмоток силовых трансформаторов, необходимо понимать, что разница между этими соединениями состоит в том, что в звезде все три обмотки соединены вместе одним концом каждой из обмоток в одной (нейтральной) точке, а в треугольнике обмотки соединены последовательно. Соединение звезда позволяет нам создавать два вида напряжения: линейное (380В) и фазное (220В), а в треугольнике только 380В.

Выбор схемы соединения обмоток зависит от ряда причин:

• Схемы питания трансформатора
• Мощности трансформатора
• Уровня напряжения
• Асимметрии нагрузки
• Экономических соображений

Так например, для сетей с напряжением 35 кВ и более выгодно соединить обмотку трансформатора схемой звезда, заземлив нулевую точку. В данном случае получится, что напряжение выводов трансформатора и проводов линии передачи относительно земли будет всегда в √3 раз меньше линейного, что приведёт к снижению стоимости изоляции.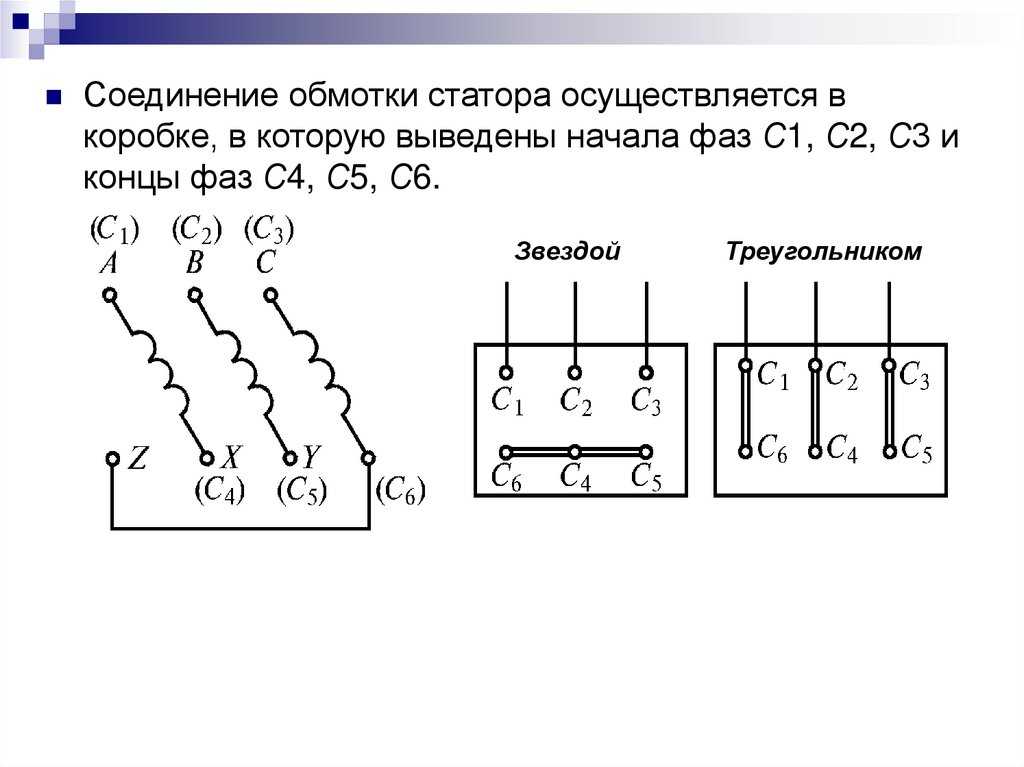

На практике чаще всего встречаются следующие группы соединений: Y/Y, D/Y, Y/D.

Группа соединений обмоток Y/Y (звезда/звезда) чаще всего применяется в трансформаторах небольшой мощности, питающих симметричные трёхфазные электроприборы/электроприемники. Так же иногда применяется в схемах большой мощности, когда требуется заземление нейтральной точки.

Группа соединения обмоток D/Y (треугольник/звезда) применяется, в основном в понижающих трансформаторах больших мощностей. Чаще всего трансформаторы с таким соединением работают в составе систем питания токораспределительных сетей низкого напряжения. Как правило, нейтральная точка звезды заземляется, для использования как линейного, так и фазного напряжений.

Группа соединений обмоток Y/D (звезда/треугольник) используется, в основном, в главных трансформаторах больших силовых станций и подстанций, не служащих для распределения.

Трансформация Звезды Дельты – Learnchannel-TV.com

Трансформация Звезда Дельта — как это работает

Трансформация Дельты в Звезду

Превращение звезды в дельту

Преобразование звезда-треугольник — это инструмент для упрощения сложных цепей резисторов. Здесь три резистора пересоединены с треугольника на звезду — и наоборот, с соответственно измененными значениями сопротивлений, так что соотношения между выводами остаются одинаковыми в обоих вариантах схемы.

Преобразование треугольника в звезду

Объяснение преобразования треугольника в звезду

Докажем это: оба типа цепи!

Считаем пины 1 и 2:

U _D12   =  U _S12     =>   => 909 R _{D1920028 S12}
I _D12 I _S12

Мы рассмотрим штифты 2 UND 3:

U _D23 = U _{8. D23} = U_{8.9. D23} = U_{8. D23} = U 8 23. _D23 . R _S23
I _D23 I _S23

Мы рассмотрим штифты 1 UND 3:

U _D13 = U U _D13 = U S1399. >> _{S1388. S138.0028 D13 = R S13
I D13 I S13}

Расчет сопротивлений между штифтами:

R _D12 = R _{D2 9 R D12 = R D2 D D12 = R D2 D D12 = R D2 D D12 = R DAI )  = R D2 (R D1 + R D3 )     must be equal to   R S12 = R S1 + R S2
. р D1 + R D2 + R D3}

Resulting in:

R _D12 =  R _D1 R _D2 + R _D2 R _D3   = R _S12 = R _S1 + R _S2                                       …Уравнение (1)
. R _D1 + R _D2 + R _D3

также:

R _D31 = R _D1 R _D2 + R _D1 R _D3 = R _S31 = R _{S3 + + + + + S3 . R D1 + R D2 + R D3}

R _D23 = R _D3 R _D1 + R _D3 R _D2    =  Р _С23 = R _S2 + R _S3            … Уравнение (3)
. R _D1 + R _D2 + R _D3

---

Сложим уравнение (1) + уравнение (2) — уравнение (3):

R _D1 + R _D2 R _D3 + R _D1 R _{D 2} + R _D1 R _D3 — (R _D3 R _D1 + R _D3 R _D2 )   = R _S1 + R _S2 + R _S1 + R _S3 — R _S2 — R _S3   = 2R _S1                                          . R _D1 + R _D2 + R _D3

Получаем в итоге:

R _S1 =      R _{R 9002 D2     .
. R D1 + R D2 + R D3}

То же, как мы получаем:

R _S2 = R _D2 R _{D3 .}
. R _D1 + R _D2 + R _D3

R _S3 = R _D1 R _{D3 .}
. Р _Д1 + R _D2 + R _D3

Если система, соединенная треугольником, имеет одинаковое сопротивление R _D с трех сторон, то эквивалентное сопротивление звезды R _S будет:

R S =      R _D R _D         . = R _D   .
. R _D + R _D + R _D       3

---

Преобразование звезды в треугольник

Таким же образом поступаем для преобразования звезды в треугольник. Резисторы RS1, RS2 и RS3 схемы «звезда» преобразуются в резисторы RD1, RD2 и RD3 схемы «треугольник» с соответствующими значениями сопротивлений таким образом, чтобы значения тока и напряжения между выводами 1 и 3 были одинаковыми.

Преобразование звезды в треугольник

---

Докажем это:
При соединении звездой эквивалентное сопротивление между точками соединения 1 и 2 (соответственно 3) получается за счет короткого замыкания соединений 2 и 3. Таким образом, эквивалентное сопротивление между точками соединения 1 и 2 (соответственно 3) получается проводимость формируется из R _S1 и параллельное соединение R _S2 с R _S3 .
Если одни и те же точки замкнуты накоротко в схеме эквивалентного треугольника, общая проводимость получается в результате параллельного соединения резисторов R _D1 и R _D2 .

Преобразование звезды в треугольник – как это работает

Левая сторона приводит к общему знаменателю:

То же относится к клемме 3 и короткозамкнутым клеммам 1 и 2:

То же самое относится к клемме 2 и короткозамкнутым клеммам 1 и 3:

Добавим:   Ур.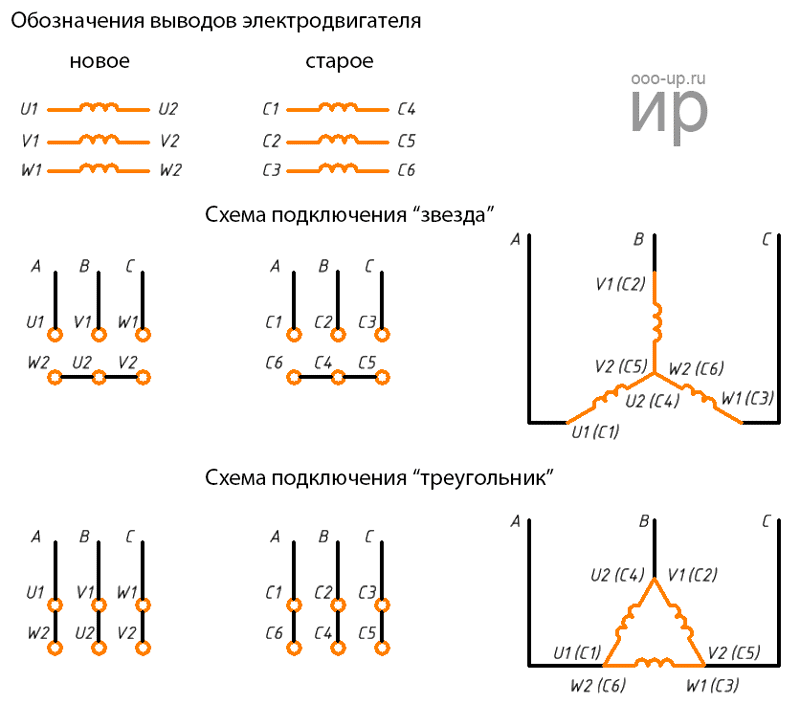 (1) + уравнение (2) — уравнение (3):

Решите это уравнение для R _D1 :

Та же процедура применима к остальным ветвям или резисторам.

Преобразование дельты в звезду

Создано Bogna Szyk и Kenneth Alambra

Рецензировано Dominik Czernia, PhD, Jack Bowater, Mateusz Mucha и Adena Benn

Последнее обновление: 16 июля 2022 г.

Содержание:

• Сопротивление соединению резисторов треугольником и звездой
• Как преобразовать соединения треугольника в соединение звездой и наоборот
• Преобразование соединения треугольником в y. Пример расчета
• Важность преобразования дельта- и звездообразных сетей
• Как использовать наш калькулятор преобразования дельта-звезда
• Хотите узнать больше?

Этот калькулятор преобразования треугольника в соединение звездой поможет вам преобразовать дельта-соединение резисторов в соединение звездой (или соединение Y) и наоборот .

В этом калькуляторе вы узнаете:

• Разница между соединениями резисторов треугольником и звездой;
• Формулы преобразования треугольника в звезду;
• Как преобразовать дельта-звезду в сеть;
• Как использовать наш калькулятор преобразования дельты в звезду; и
• Некоторые применения треугольных и звездообразных цепей резисторов.

Продолжайте читать, чтобы узнать, как преобразовать сложную электронную схему со схемами звезда-треугольник в простую (только с параллельными и последовательно соединенными резисторами) с помощью преобразования треугольника в Y.

Сеть резисторов треугольником и звездой

В электронных схемах резистор (показан на рисунке ниже) является одним из наиболее важных компонентов и имеет широкий спектр применений. Мы можем использовать резисторы для ограничения тока в цепи или напряжения, протекающего к другому компоненту цепи .

Поскольку схемы могут состоять из нескольких компонентов, таких как конденсаторы, катушки индуктивности, светодиоды, двигатели и многое другое, в схемах также может быть много резисторов.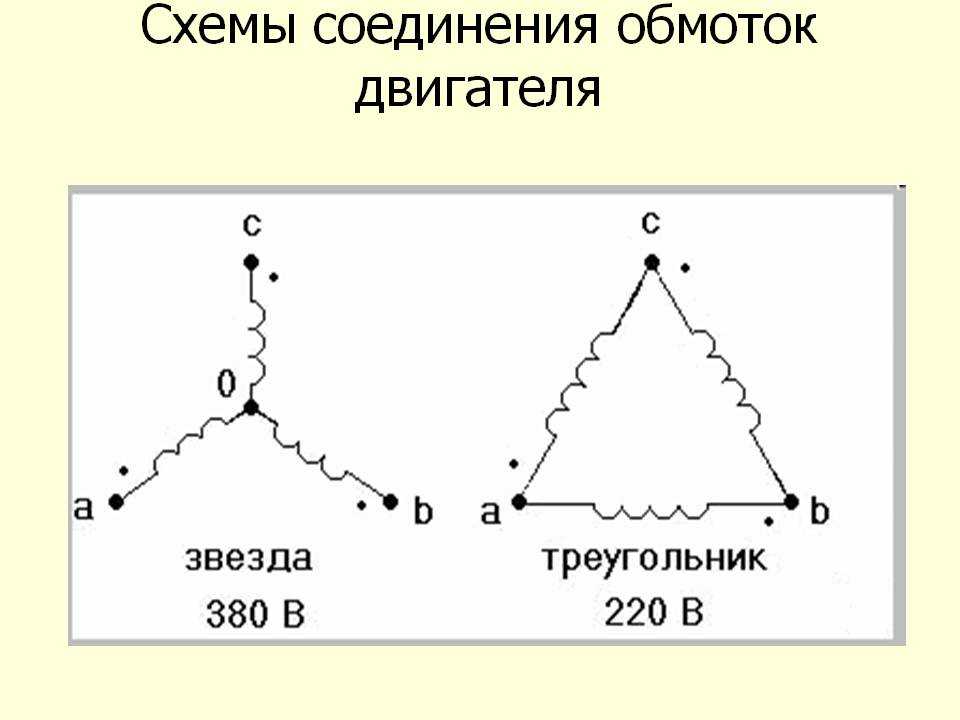 Резисторы в цепях обычно соединены параллельно или последовательно, но иногда могут образовывать петли и многоветвевые сети , которые мы видим в более сложных схемах. Простейшая петля, которую могут образовать резисторы, — это дельта-сеть , как показано на схеме ниже:

На электронных схемах мы обычно представляем резистор зигзагообразной линией . В дельта-сети мы подключаем три резистора к трем узлам (представленным A, B и C), которые ведут к трем различным частям цепи. Мы называем ее дельта-сетью, потому что в простейшем графическом представлении эта сеть имеет треугольную форму, точно такую ​​же, как заглавный греческий символ дельта 9.0011 Δ .

Разница между сетью треугольник и сетью звезда заключается в том, что в сети звезда мы соединяем указанные три узла по-другому, расширяя три узла с помощью трех резисторов и соединяя все эти резисторы с одним узлом. Это образует нечто похожее на букву Y , отсюда и название «звездная» сеть . Вот как выглядит соединение звездой:

Чтобы выполнить преобразование треугольника в соединение звездой, мы должны определить набор используемых резисторов, которые приведут к эквивалент общей сети . Токи и напряжения, проходящие через каждый из трех узлов, должны быть одинаковыми в обоих типах сетей. Вот где наш калькулятор преобразования дельты в звезду пригодится.

Однако, если вы хотите научиться преобразовывать дельта-сети в звездообразные и наоборот, мы покажем вам, как это сделать в следующем разделе.

Как преобразовать сети треугольника в сеть звезда и наоборот

Знание того, как определить сети звезда или треугольник в цепи, является первым шагом в преобразовании. Преобразование дельта-сетей в звездообразные сети — это вопрос определения «дельты» в цепи, зная значений сопротивления каждого резистора в треугольнике и с использованием формул, которые мы включили в этот текст.

Та же процедура применяется при преобразовании сетей «звезда» в сети «треугольник».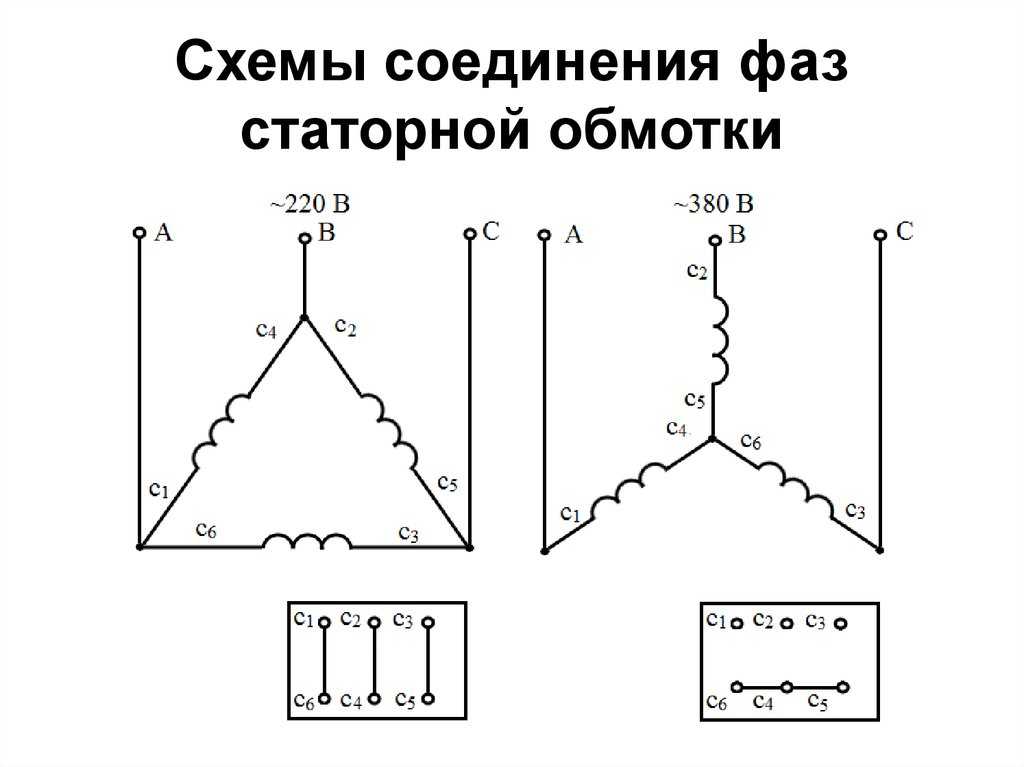 Однако в этой операции мы сначала должны определить, какая «звезда» нуждается в преобразовании , а затем найти значения сопротивления в каждой ветви сети «звезда». Наконец, мы подставляем эти значения в формулы, приведенные ниже.

Формулы преобразования дельты в звезду

R1=(Rb×Rc)/(Ra+Rb+Rc)R2=(Rc×Ra)/(Ra+Rb+Rc)R3=(Ra×Rb)/(Ra+Rb+Rc)\begin{ выровнять*} \маленький R_1 &= (R_b × R_c)/(R_a + R_b+ R_c)\\[0,5em] \small R_2 &= (R_c × R_a)/(R_a + R_b + R_c)\\[0,5em] \small R_3 &= (R_a × R_b)/(R_a + R_b + R_c)\\[0,5em] \end{align*}R1​R2​R3​=(Rb​×Rc​)/(Ra​+Rb​+Rc​)=(Rc​×Ra​)/(Ra​+Rb​+Rc​ )=(Ra​×Rb​)/(Ra​+Rb​+Rc​)​

где:

• R _a , R _b , R _c – сопротивления в дельта-сети,
• Р ₁ , R ₂ , R ₃ — сопротивления в схеме «звезда».

Формулы преобразования звезды в дельту

Ra=R2+R3+(R2×R3/R1)Rb=R3+R1+(R3×R1/R2)Rc=R1+R2+(R1×R2/R3)\begin{align* } \small R_a &= R_2 + R_3 + (R_2 × R_3 / R_1) \\[0,5em] \small R_b &= R_3 + R_1 + (R_3 × R_1 / R_2) \\[0,5em] \small R_c &= R_1 + R_2 + (R_1 × R_2 / R_3) \\[0,5em] \end{align*}Ra​Rb​Rc​=R2​+R3​+(R2​×R3​/R1​)=R3​+R1​+(R3​×R1​/R2​)=R1​ +R2​+(R1​×R2​/R3​)​

где, как было показано ранее:

• R _a , R _b , R _c — сопротивления в дельта сети,
• R ₁ , R ₂ , R ₃ — сопротивления в схеме «звезда».

Если вы смотрите на реальную цепь и хотите узнать значение сопротивления резистора без использования мультиметра, вы можете узнать это по , глядя на его цветные полосы . Вы можете использовать наш калькулятор цветового кода резистора, чтобы легко определить соответствующее значение сопротивления. С другой стороны, чтобы лучше понять, как использовать приведенные выше формулы, давайте рассмотрим пример в следующем разделе этого текста.

Преобразование дельты в у. Пример расчета

Для нашего расчета преобразования дельты в y (преобразование дельты в звезду) давайте рассмотрим немного сложную схему, показанную ниже, и преобразуем дельта-сеть (выделена зеленым) в звезду:

Дельта-диаграмма может кажутся отличными от тех, которые мы показывали ранее, но если вы присмотритесь, мы можем нарисовать форму треугольника следующим образом:

Теперь, когда мы можем увидеть знакомую диаграмму треугольника в схеме, давайте теперь

нарисуйте соответствующую эквивалентную звездообразную сеть , в которую будет преобразована наша дельта-сеть. Мы можем просто нарисовать ее поверх дельта-сети, чтобы сохранить расположение узлов, или мы можем нарисовать новую сеть звездой в отдельной эквивалентной схеме. Это также лучшее время, чтобы пометить наши резисторы с теми же переменными, которые мы имеем в наших формулах и справочной диаграмме, как показано ниже: преобразование дельты в звезду, чтобы найти значения сопротивления для каждого резистора в эквивалентной схеме звезды для данной схемы. Вот расчет каждого значения сопротивления:

R1=(Rb×Rc)/(Ra+Rb+Rc)R1=(15Ω×25Ω)/(10Ω+15Ω+25Ω)R2=(375Ω)/(50Ω)R1=7,5ΩR2=(Rc×Ra )/(Ra+Rb+Rc)R2=(25Ω×10Ω)/(10Ω+15Ω+25Ω)R2=(250Ω)/(50Ω)R2=5,0ΩR3=(Ra×Rb)/(Ra+Rb+Rc )R3=(10 Ом×15 Ом)/(10 Ом+15 Ом+25 Ом)R3=(150 Ом)/(50 Ом)R3=3,0 Ом\маленький \начать{выравнивать*} \small R_1 &= (R_b × R_c)/(R_a + R_b + R_c) \\[.5em] \small R_1 &= (15 Ом × 25 Ом)/(10 Ом + 15 Ом + 25 Ом) \\[0,5em] \small R_2 &= (375 Ом)/(50 Ом) \\[0,5em] \small R_1 &= 7,5 Ом \\[0,5em]\\[0,5em] \small R_2 &= (R_c × R_a) /(R_a + R_b + R_c)\\[0,5em] \small R_2 &= (25 Ом × 10 Ом)/(10 Ом + 15 Ом + 25 Ом)\\[0,5em] \small R_2 &= (250 Ом)/(50 Ом)\\[0,5em] \small R_2 &= 5,0 Ом\\[0,5em]\\[0,5em] \small R_3 &= (R_a × R_b)/(R_a + R_b + R_c)\\[0,5em] \small R_3 &= (10 Ом × 15 Ом)/(10 Ом + 15 Ом + 25 Ом)\\[0,5em] \small R_3 &= (150 Ом)/(50 Ом)\\[0,5em] \small R_3 &= 3,0 Ом\\[0,5em] \end{align*}R1​R1​R2​R1​R2​R2​R2​R2​R3​R3​R3​R3​​=(Rb​×Rc​)/(Ra​+Rb​+Rc​) =(15Ω×25Ω)/(10Ω+15Ω+25Ω)=(375Ω)/(50Ω)=7,5Ω=(Rc​×Ra​)/(Ra​+Rb​+Rc​)=(25Ω×10Ω) /(10Ом+15Ом+25Ом)=(250Ом)/(50Ом)=5,0Ом=(Ra​×Rb​)/(Ra​+Rb​+Rc​)=(10Ом×15Ом)/(10Ом+15Ом+ 25 Ом)=(150 Ом)/(50 Ом)=3,0 Ом​

Из этих вычислений теперь мы можем заменить нашу дельта-цепь на звезду, используя другой набор резисторов со значениями сопротивления 7,5 Ом , 5,0 Ом и 3,0 Ом для R ₁ , R ₂ и R ₃ соответственно.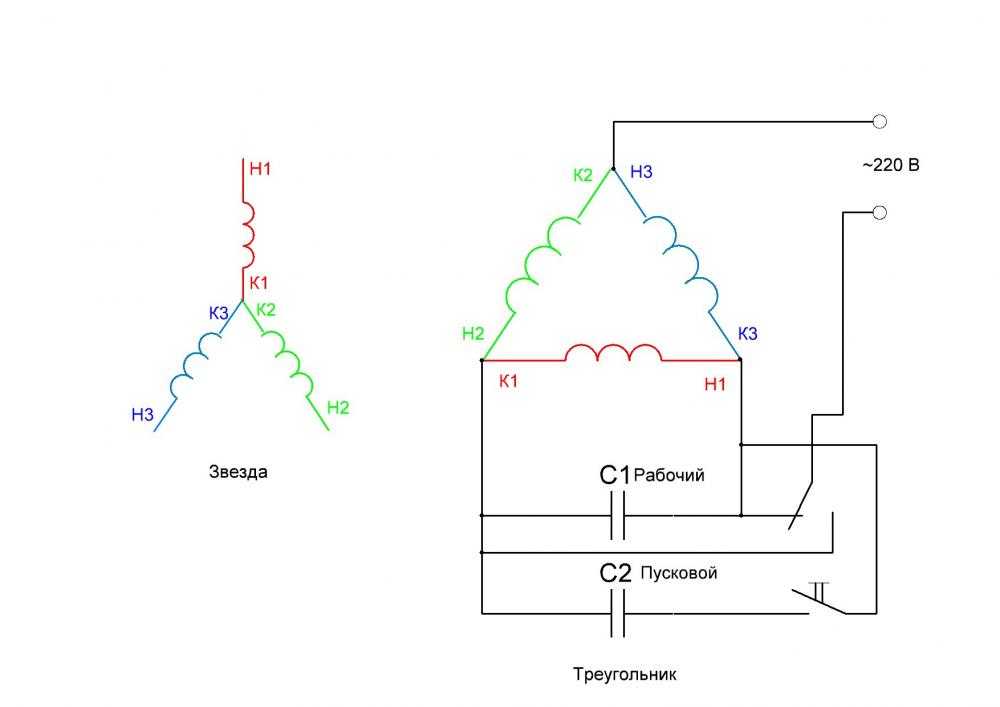

Важность преобразования цепей «треугольник» и «звезда»

Вы могли заметить, что в приведенном выше примере исходная сеть не имела параллельных или последовательных соединений ни для одного из резисторов. Вместо этого было две дельты, которые нельзя упростить без знания преобразования дельты в Y .

После преобразования мы видим, что резистор R ₂ = 5 Ом теперь последовательно с другим резистором 5 Ом . В этом случае теперь их можно еще больше упростить, сложив их значения сопротивления вместе и заменив их одним резистором 10 Ом . Вы можете узнать больше о последовательных резисторах, ознакомившись с нашим калькулятором последовательных резисторов 9.0003

С учетом сказанного, преобразование треугольника в звезду и наоборот является идеальным методом упрощения сложной схемы при анализе схемы. Мы выполняем анализ цепи , чтобы определить ток или напряжение, протекающие в нашей электронной схеме, и лучше всего это сделать с помощью упрощенной схемы или некоторых ее частей.

Как использовать наш калькулятор преобразования дельты в звезду

Наш калькулятор преобразования дельты в звезду представляет собой два калькулятора в одном. Несмотря на это, они оба довольно просты в использовании. Чтобы воспользоваться этим калькулятором, сначала нужно выбрать из 9 вариантов0011 звезда-треугольник и треугольник-треугольник . Что бы вы ни выбрали из этих двух вариантов, калькулятор для этого конкретного варианта будет доступен вам.

• Таким образом, если вы выберете вариант треугольник-звезда, вы сможете ввести значения для R _a , R _b и R _c (сопротивления в схеме треугольника), и преобразователь треугольника в звезду будет затем верните значения для R ₁ , R ₂ и R ₃ (сопротивления в сети звезда).

• Если, с другой стороны, вы выберете вариант «звезда-дельты», вы сможете ввести значения для R ₁ , R ₂ и R ₃ (сопротивления в схеме «звезда») и преобразователь треугольника в звезду затем вернет значения для R _a , R _b и R _c (сопротивления в дельта-сети).