Vektornaya_algebra
Векторная алгебра
163. Задание {{ 163 }} ТЗ № 168
Введите пропущенное слово
Число, равное квадратному корню из суммы квадратов проекций вектора на оси координат, называется … вектора
Правильные варианты ответа: модуль; модулем; длина; длиной;
164. Задание {{ 164 }} ТЗ № 169
Введите пропущенное слово
Два вектора называются …, если лежат на одной прямой или параллельных прямых
Правильные варианты ответа: коллинеарные; коллинеарными; колинеарные; колинеарными;
165. Задание {{ 165 }} ТЗ № 170
Введите пропущенное слово
Если скалярное произведение двух ненулевых векторов равно нулю, то такие векторы являются …
Правильные варианты ответа: перпенди#$#; перпенди#$# вектор#$#; нормальн#$#; нормальн#$# вектор#$#;
166. Задание {{ 166 }} ТЗ № 171
Введите пропущенное слово
Если векторное произведение двух ненулевых векторов равно нулю, то такие векторы являются …
Правильные варианты ответа: коллинеарными; коллинеарные; колинеарными; колинеарные; коллин#$#; коллин#$# вектор#$#;
167. Задание {{ 167 }} ТЗ № 172
Введите пропущенное слово
Число, равное произведению модулей двух векторов на косинус угла между ними, называется … произведением этих векторов
Правильные варианты ответа: скалярным; скалярное;
168. Задание {{ 168 }} ТЗ № 173
Введите пропущенное слово
Два ненулевых вектора перпендикулярны тогда и только тогда, когда их … произведение равно нулю
Правильные варианты ответа: скалярное;
169. Задание {{ 169 }} ТЗ № 174
Введите пропущенное слово
Произведение модулей двух векторов на синус угла между ними равно модулю … произведения этих векторов
Правильные варианты ответа: векторного; векторное;
170. Задание {{ 170 }} ТЗ № 175
Введите пропущенное слово
Скалярное произведение двух векторов равно … произведений их одноименных координат
Правильные варианты ответа: сумме; сумма;
171. Задание {{ 171 }} ТЗ № 176
Введите пропущенное слово
Если смешанное произведение трех ненулевых векторов равно нулю,
то такие векторы являются …
Правильные варианты ответа: компланарные; компланарными;
172. Задание {{ 172 }} ТЗ № 177
Введите пропущенное слово
Три вектора образуют правую тройку, если их … произведение больше нуля
Правильные варианты ответа: смешанное; смешан#$#;
173. Задание {{ 173 }} ТЗ № 178
Введите пропущенное слово
Три вектора образуют левую тройку, если их … произведение отрицательно
Правильные варианты ответа: смешанное; смешан#$#;
174. Задание {{ 174 }} ТЗ № 179
Введите пропущенное слово
Площадь треугольника, построенного на двух векторах, можно вычислить при помощи … произведения этих векторов
Правильные варианты ответа: векторного; векторное;
175. Задание {{ 175 }} ТЗ № 180
Введите пропущенное слово
Смешанное произведение векторов при перестановке двух любых сомножителей меняет свой …
Правильные варианты ответа: знак;
176. Задание {{ 176 }} ТЗ № 340
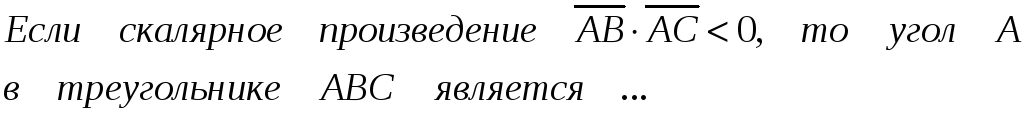
Правильные варианты ответа:
177. Задание {{ 177 }} ТЗ № 341
 Правильные
варианты ответа: трапеци#$#;
Правильные
варианты ответа: трапеци#$#;
178. Задание {{ 178 }} ТЗ № 342
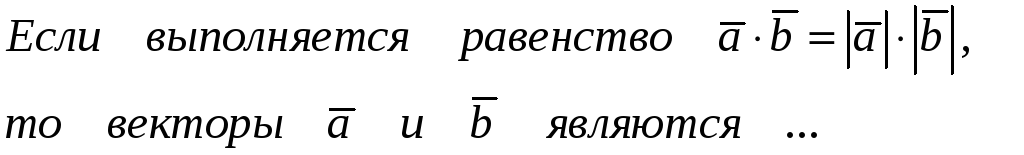
Правильные варианты ответа: колинеар#$#; коллинеар#$#; паралл#$#;
179. Задание {{ 179 }} ТЗ № 803

Правильные варианты ответа: острым;
180. Задание {{ 180 }} ТЗ № 804

Правильные варианты ответа: ортогональными; перпендикулярными;
181. Задание {{ 181 }} ТЗ № 805
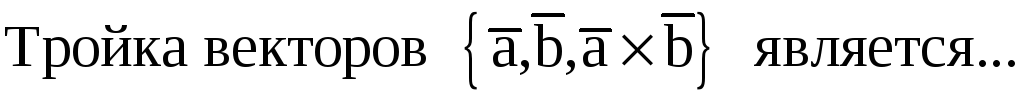
Правильные варианты ответа: правой;
182. Задание {{ 182 }} ТЗ № 806
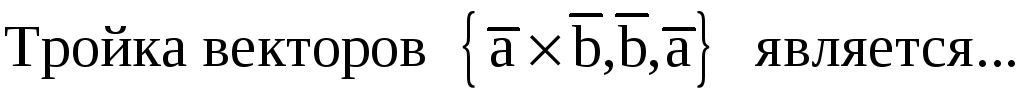
Правильные варианты ответа: левой;
183. Задание {{ 183 }} ТЗ № 807
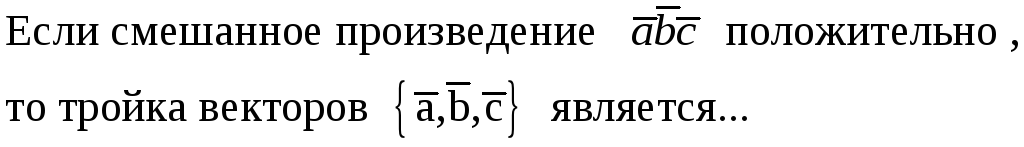
Правильные варианты ответа:
184. Задание {{ 184 }} ТЗ № 808
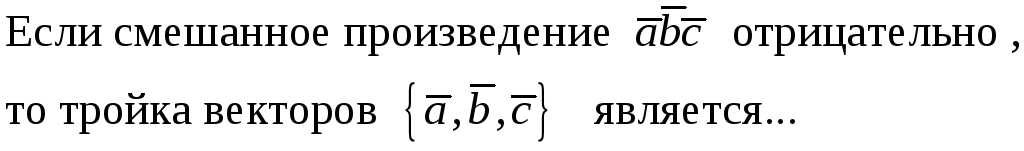
Правильные варианты ответа: левой;
185. Задание {{ 185 }} ТЗ № 809
 Правильные
варианты ответа: смешанным;
Правильные
варианты ответа: смешанным;
186. Задание {{ 186 }} ТЗ № 317
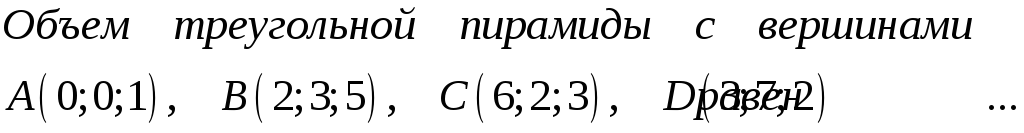
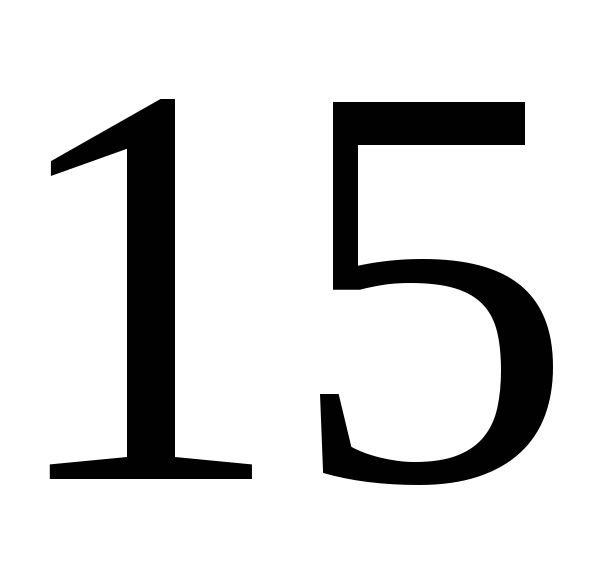
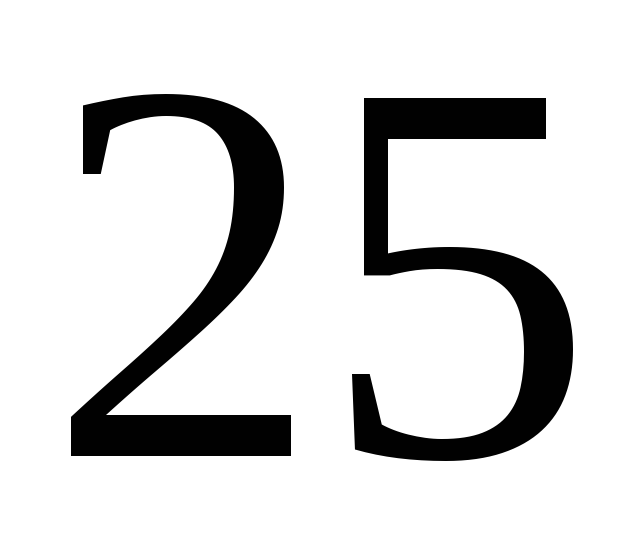
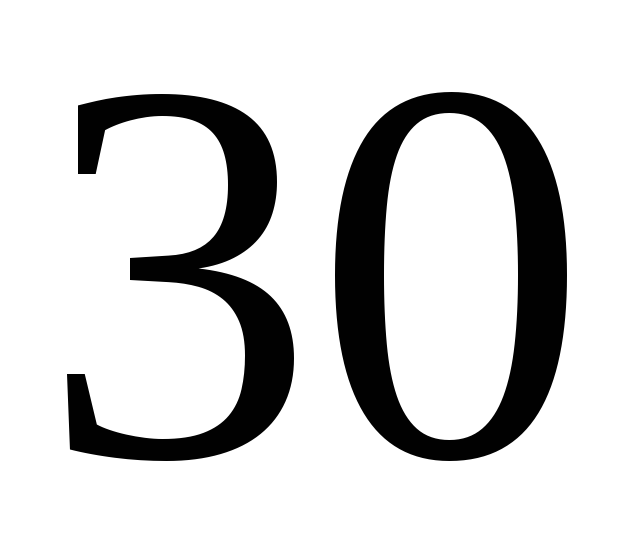
187. Задание {{ 187 }} ТЗ № 751
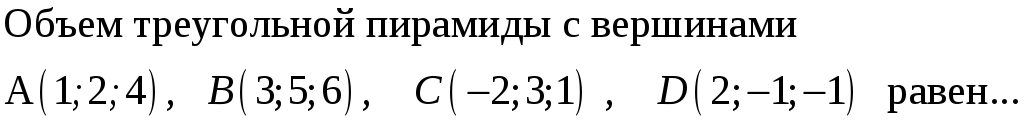
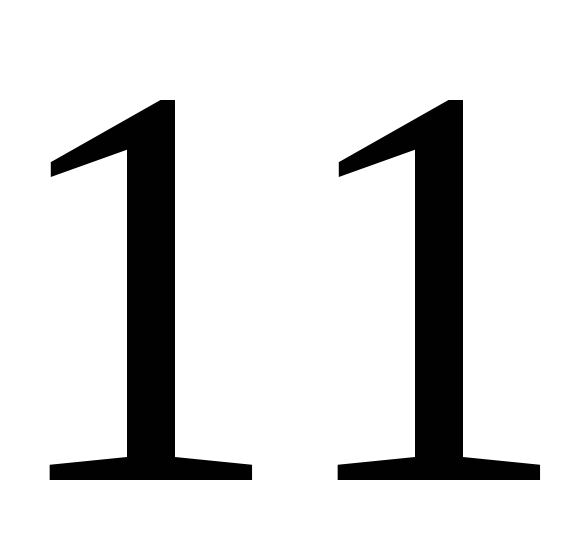
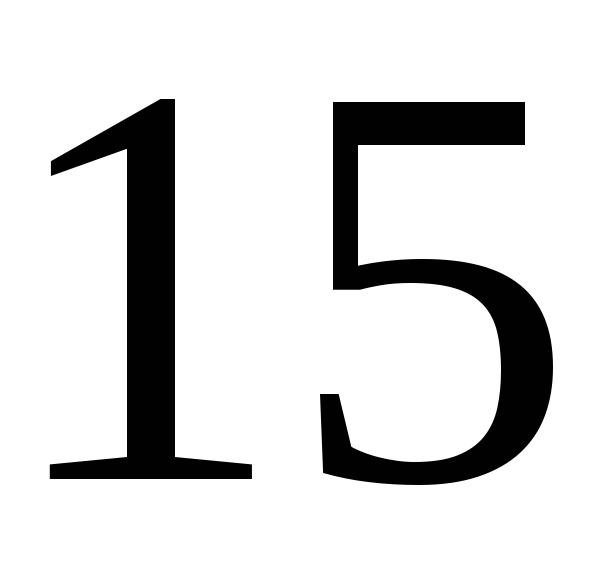
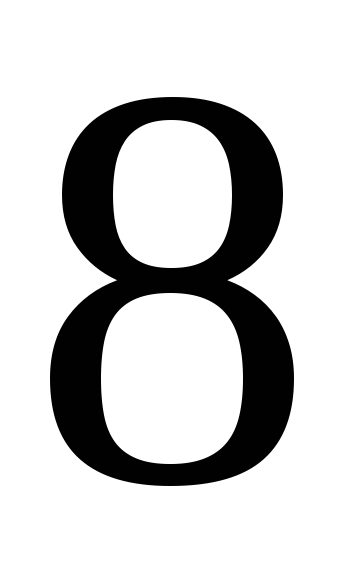

188. Задание {{ 188 }} ТЗ № 752
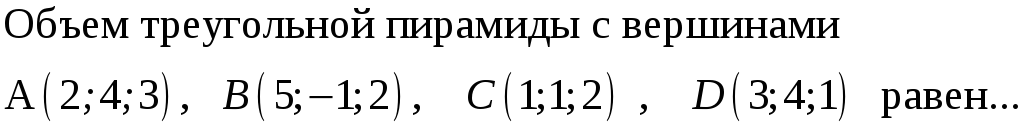

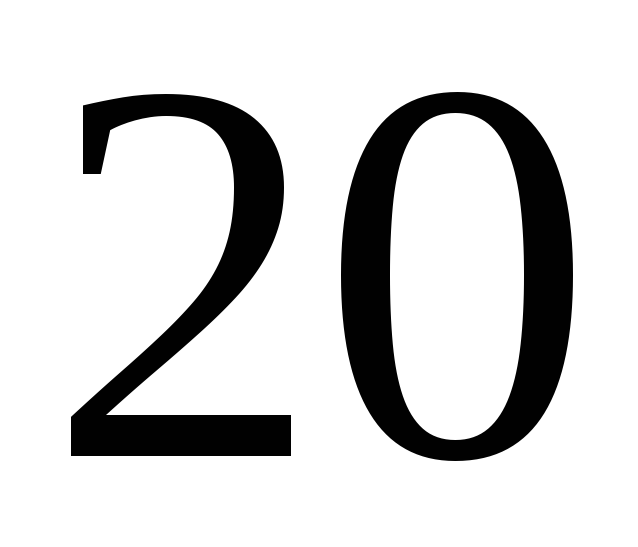
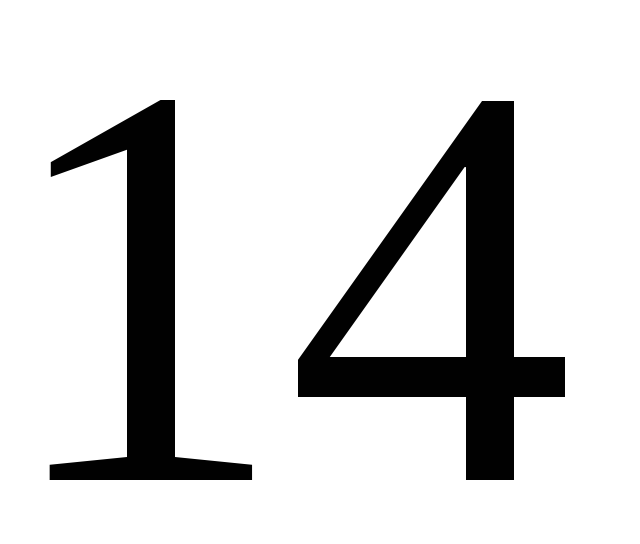

189. Задание {{ 189 }} ТЗ № 753
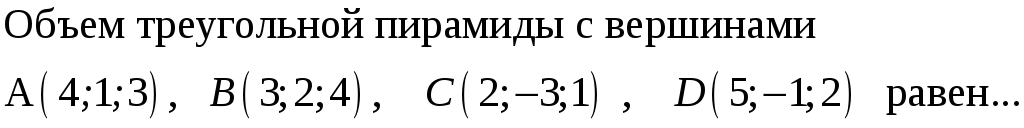
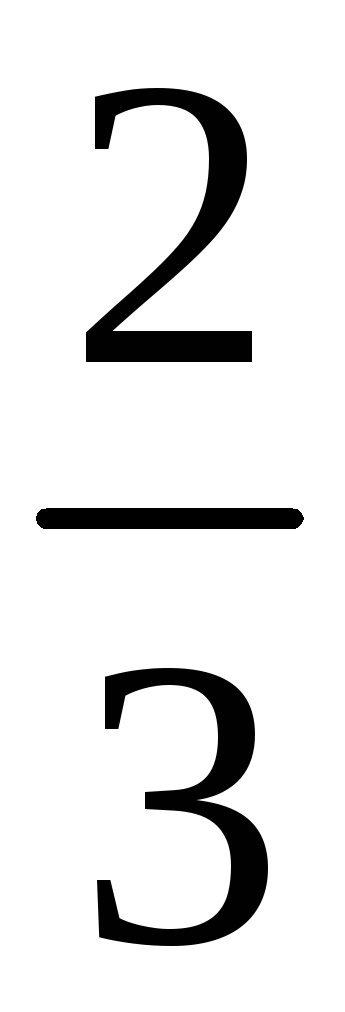

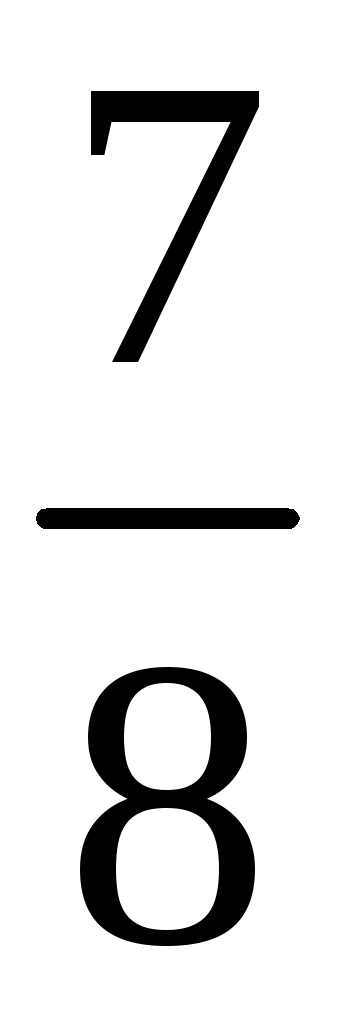
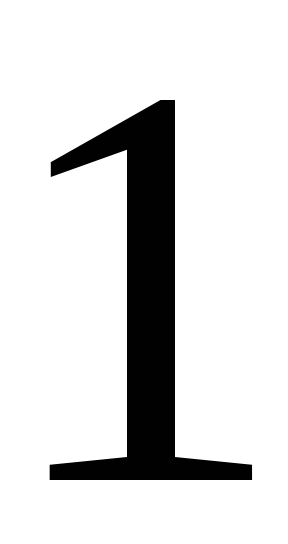
190. Задание {{ 190 }} ТЗ № 754
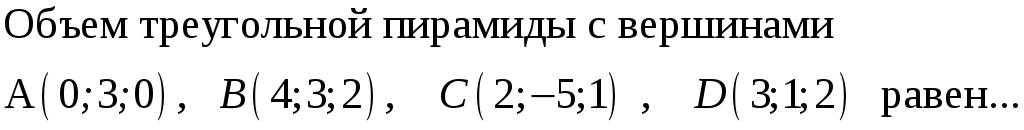

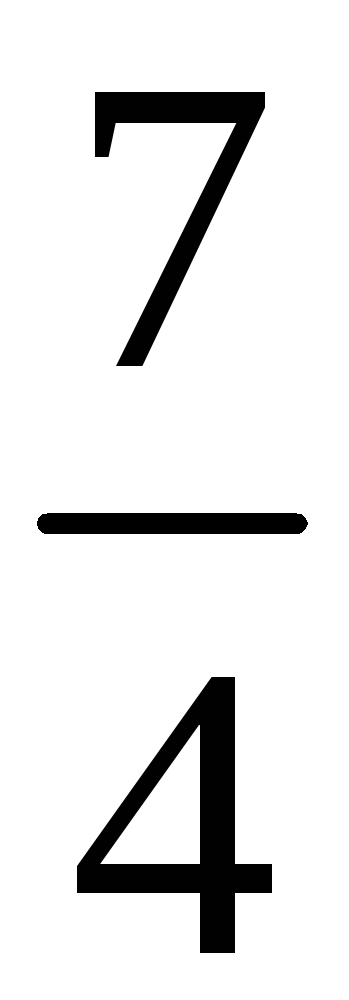

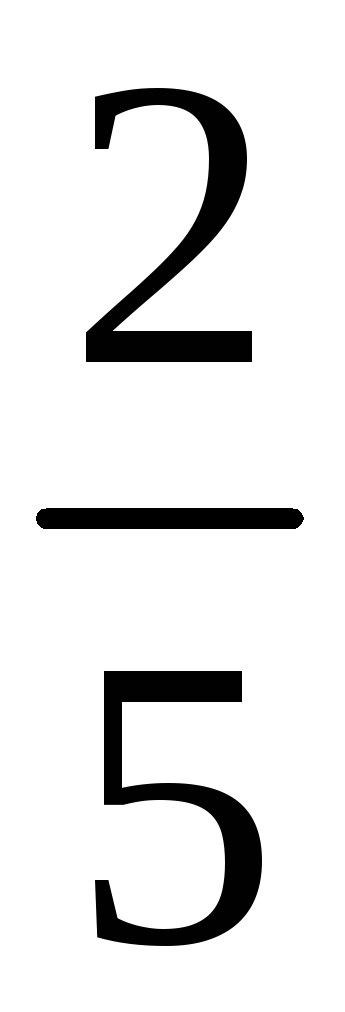
191. Задание {{ 191 }} ТЗ № 755
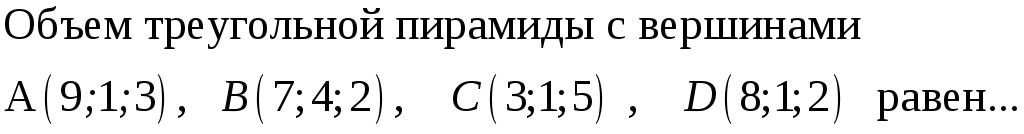

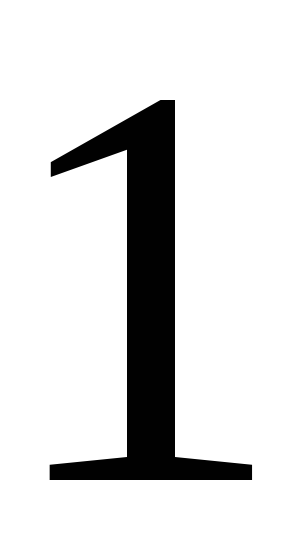
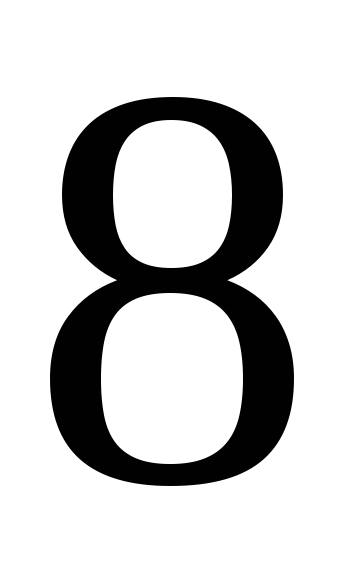
192. Задание {{ 192 }} ТЗ № 756
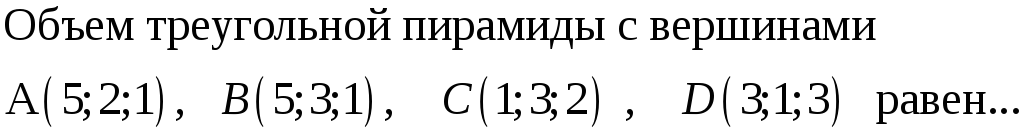

193. Задание {{ 193 }} ТЗ № 757

194. Задание {{ 194 }} ТЗ № 758
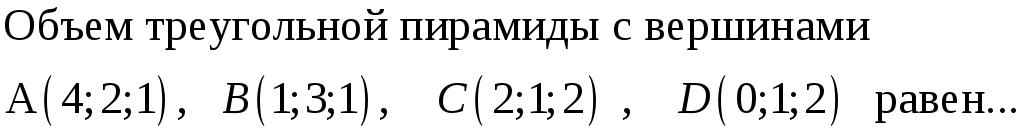


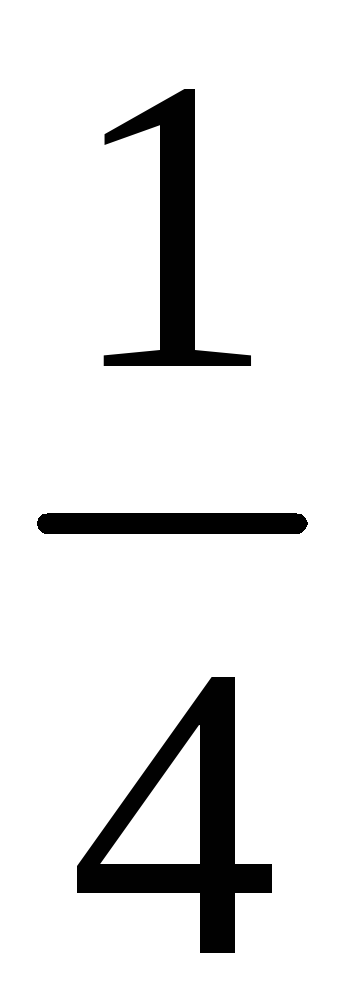
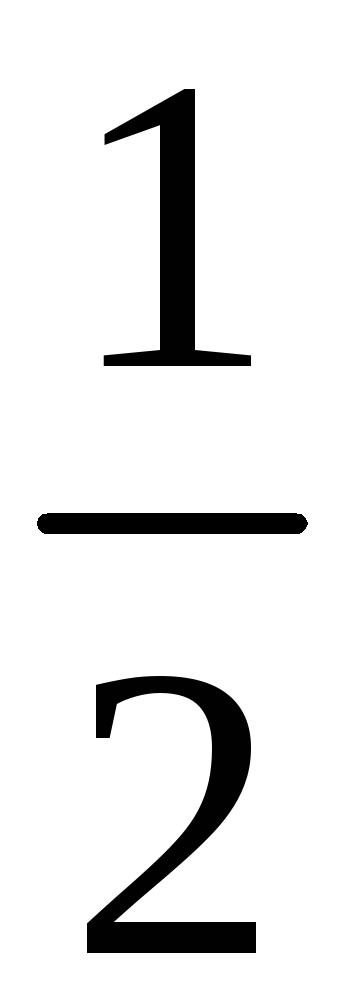
195. Задание {{ 195 }} ТЗ № 759
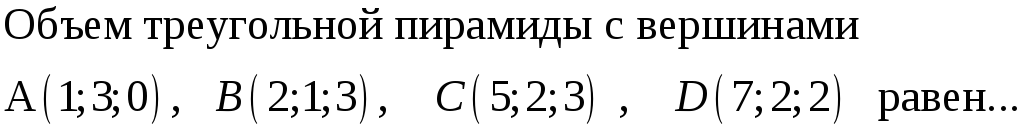
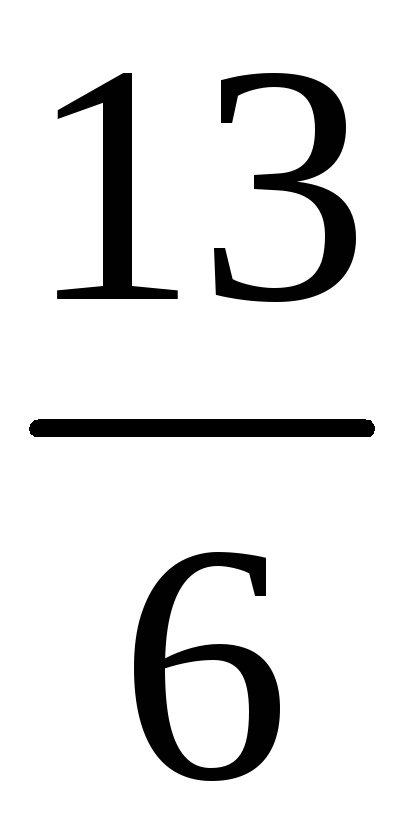
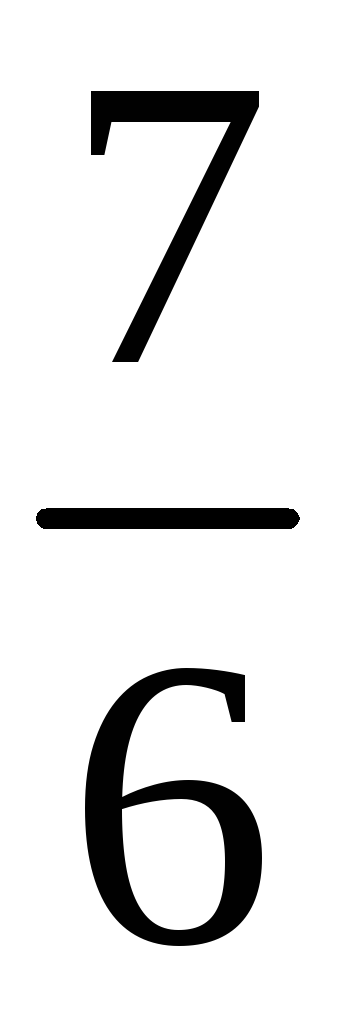
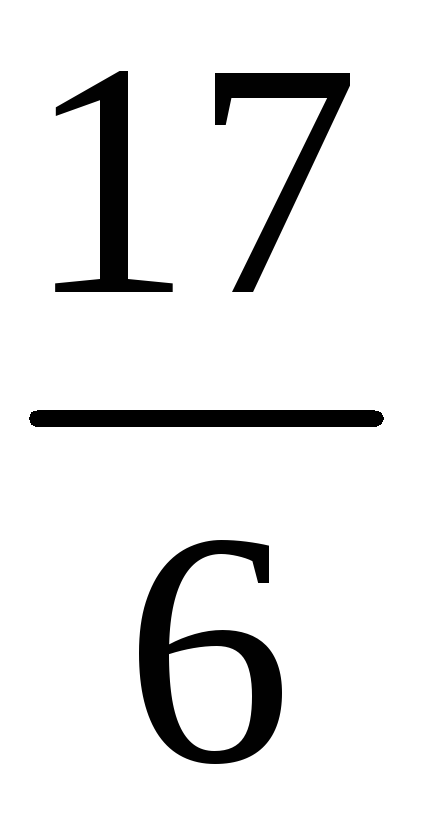
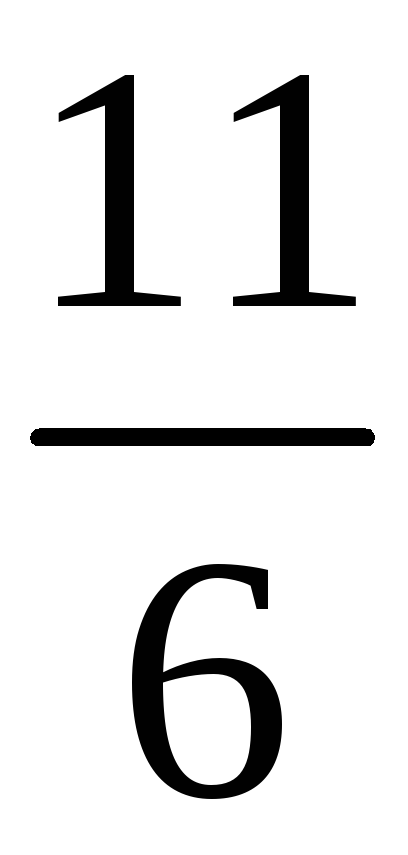
196. Задание {{ 196 }} ТЗ № 108
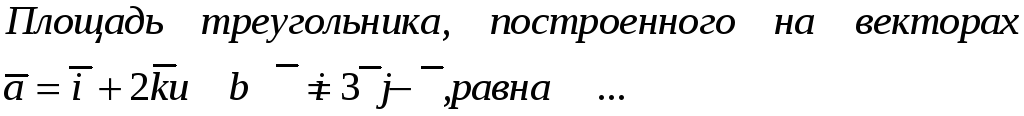
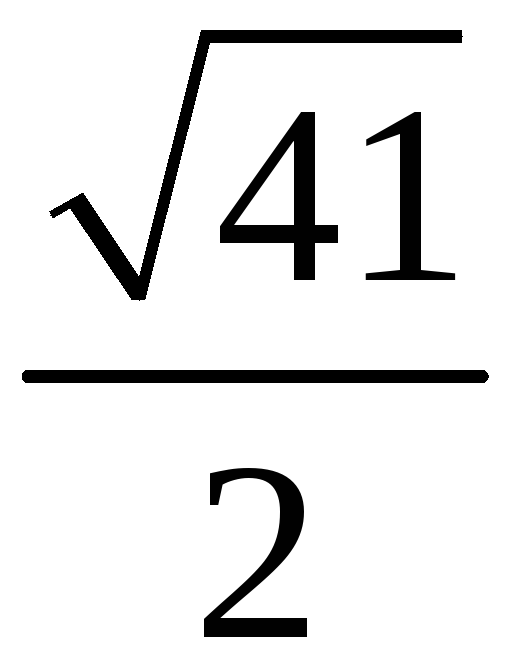
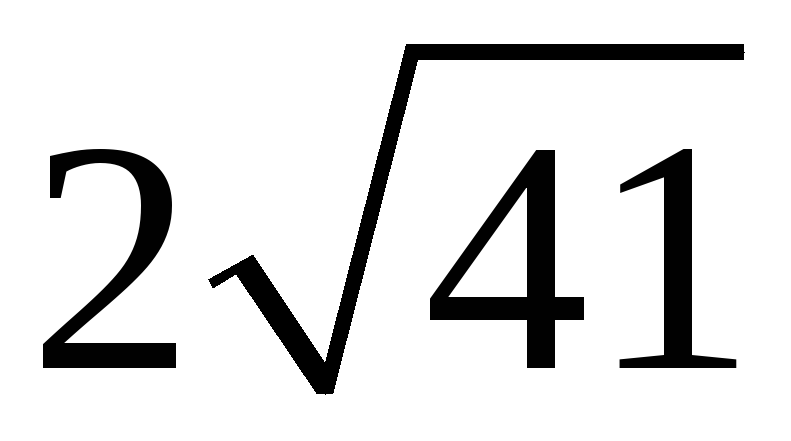
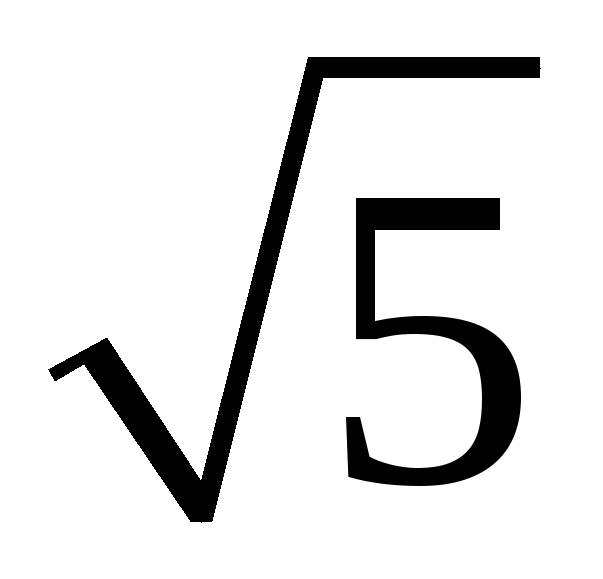
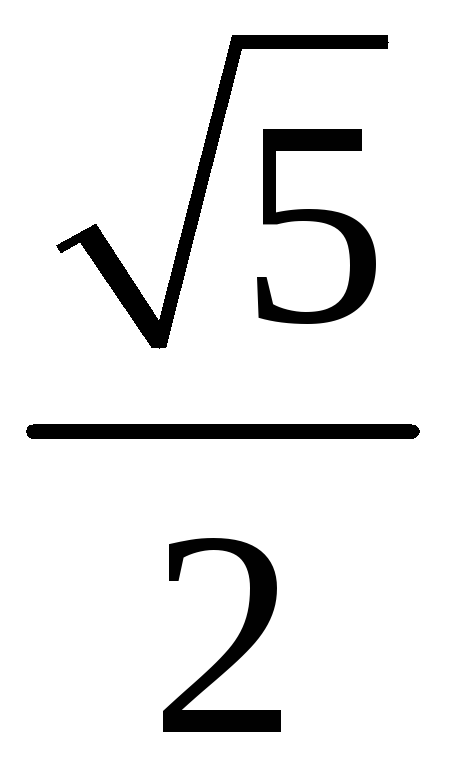
197. Задание {{ 197 }} ТЗ № 109

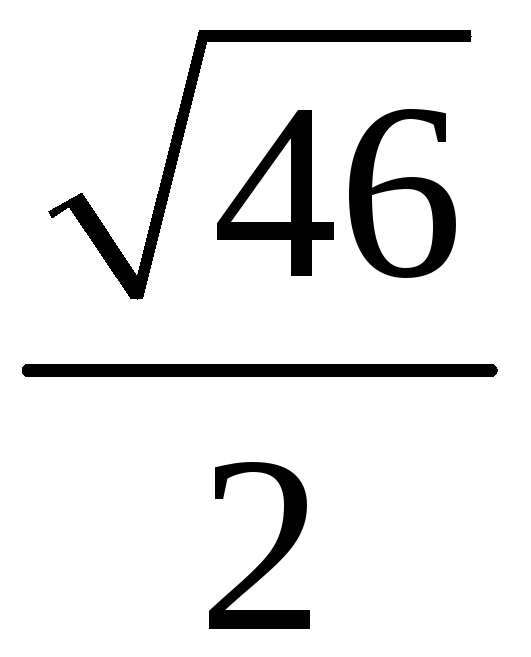
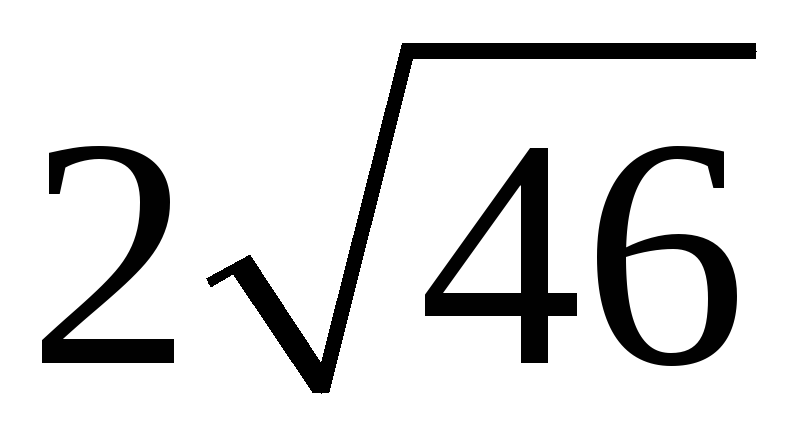
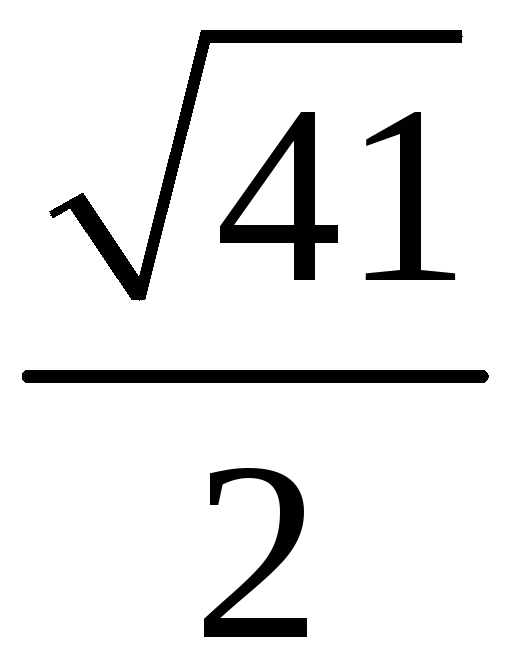
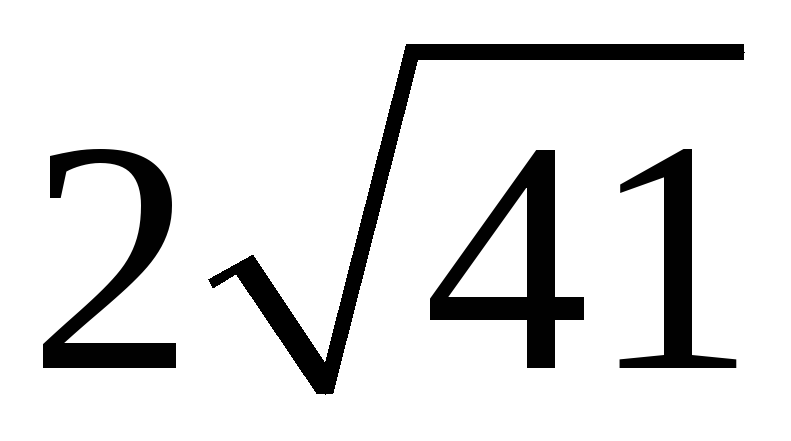
198. Задание {{ 198 }} ТЗ № 110
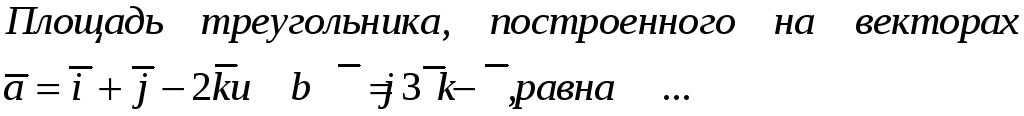
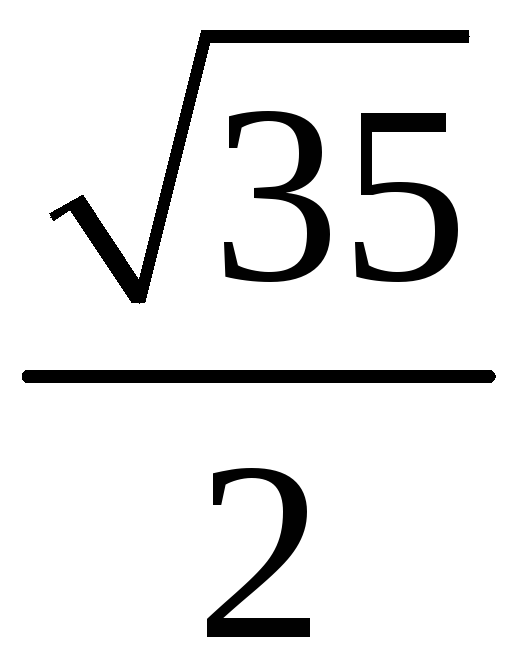
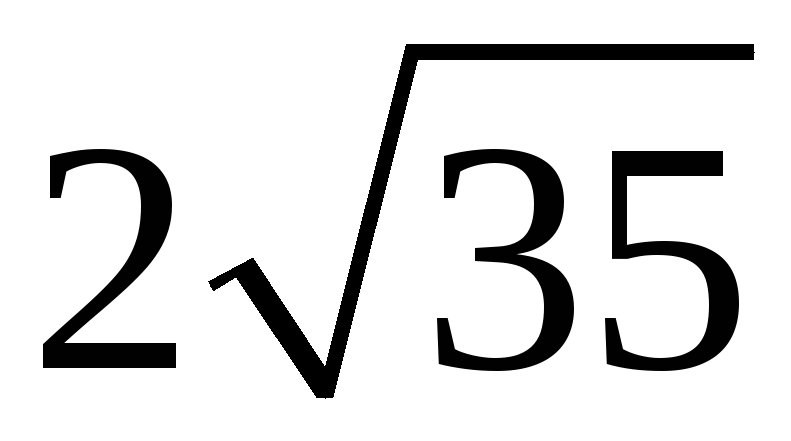
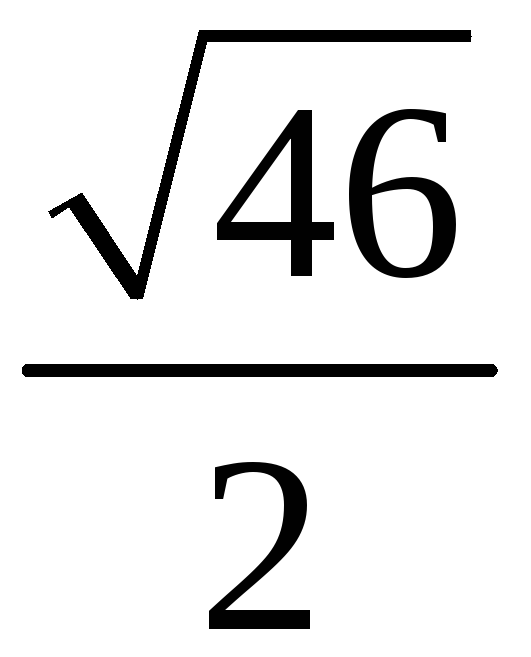
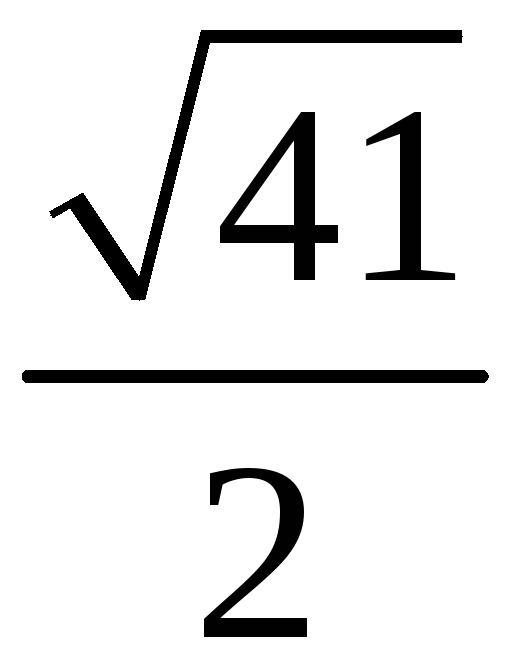
199. Задание {{ 199 }} ТЗ № 111
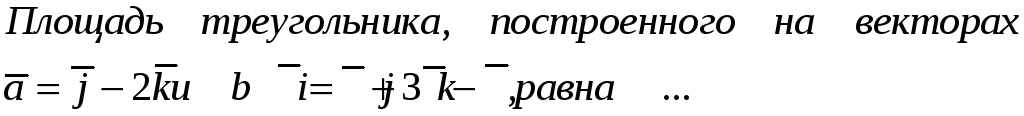
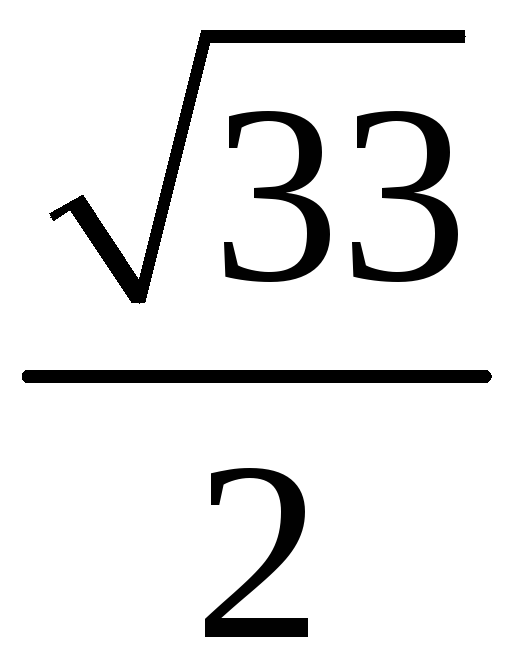
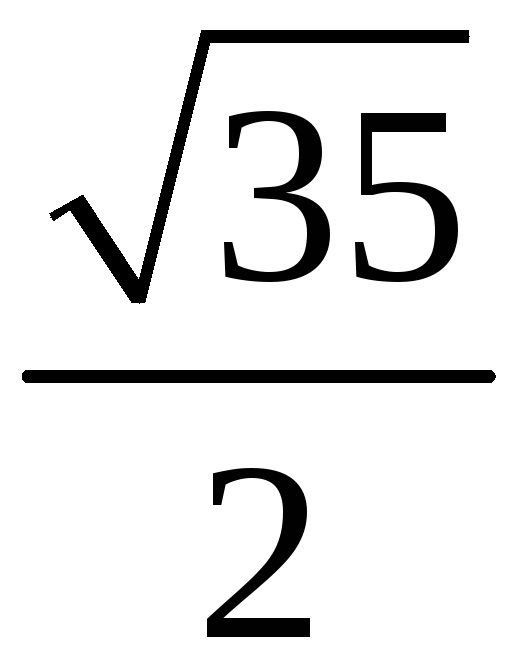

200. Задание {{ 200 }} ТЗ № 112
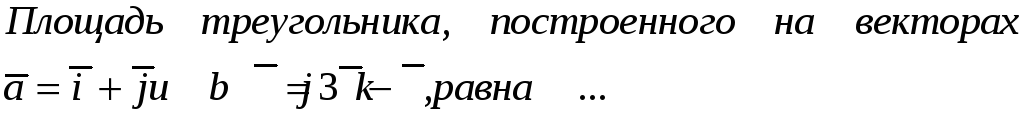
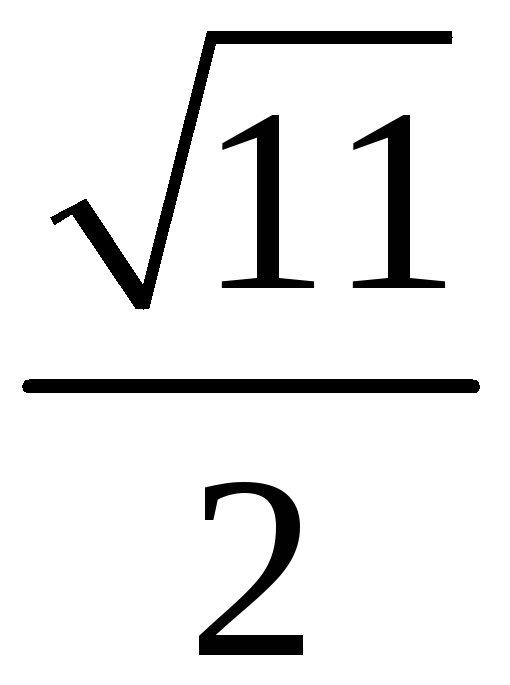
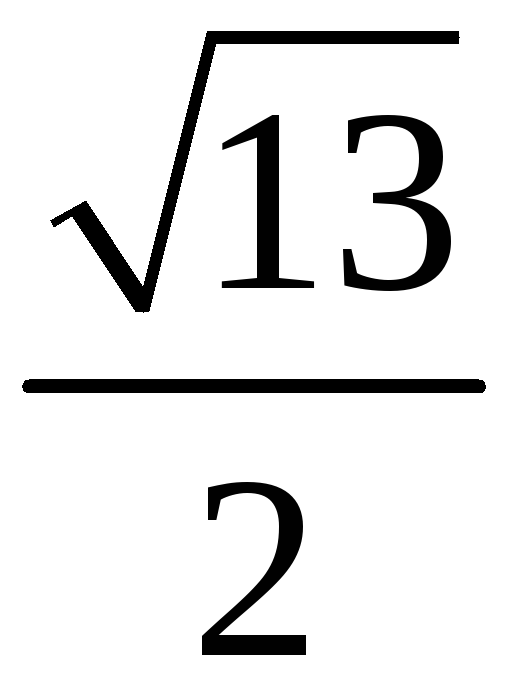
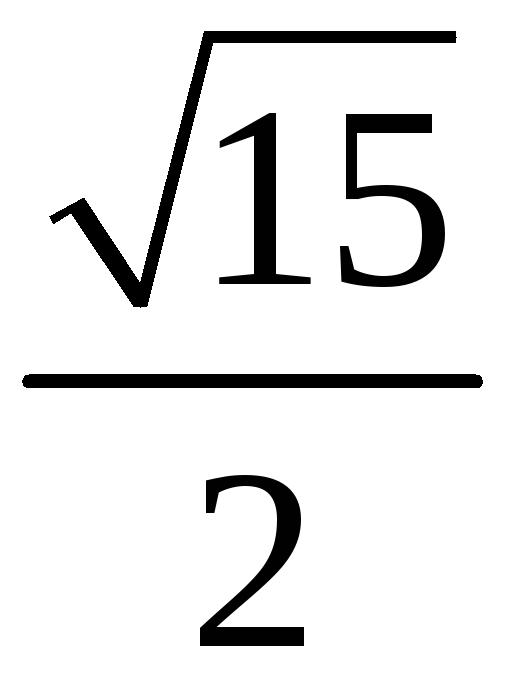
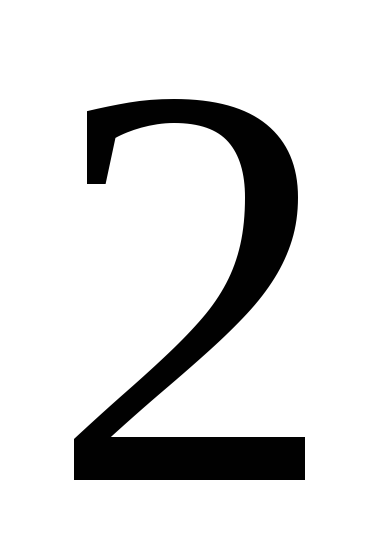
201. Задание {{ 201 }} ТЗ № 760
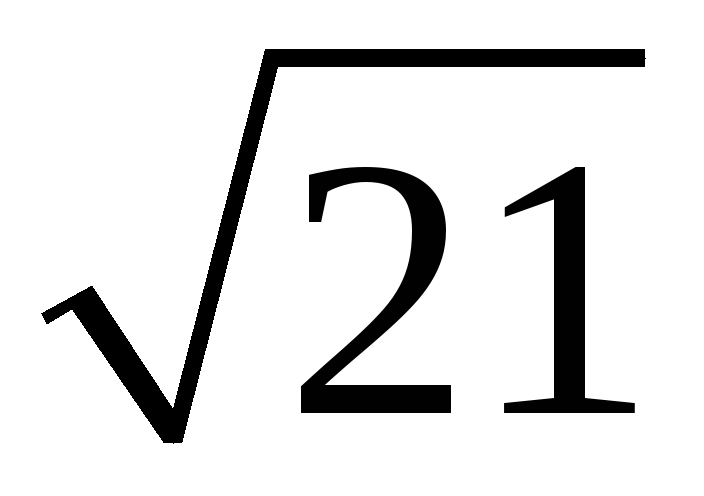
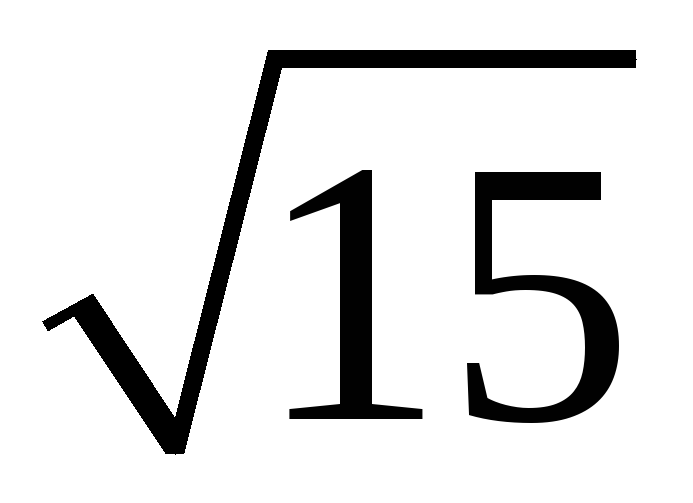
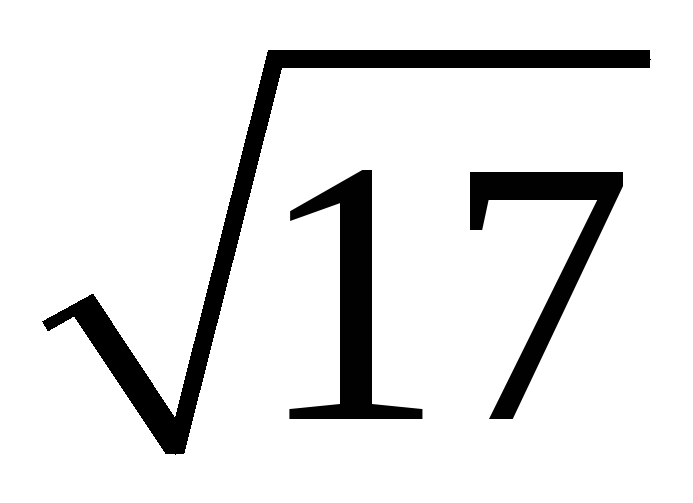
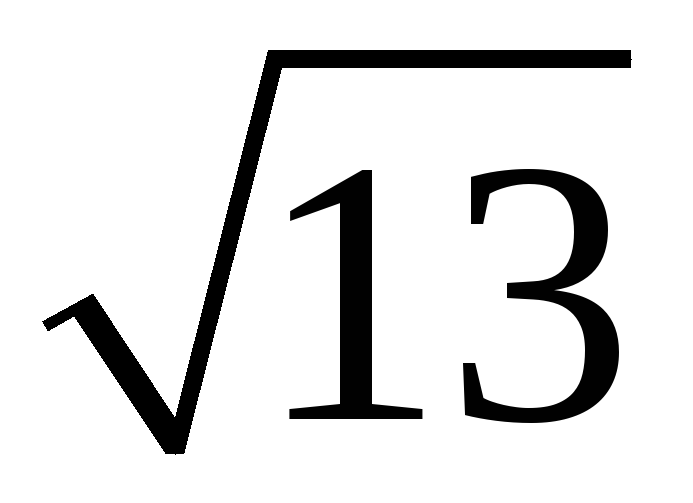
202. Задание {{ 202 }} ТЗ № 761
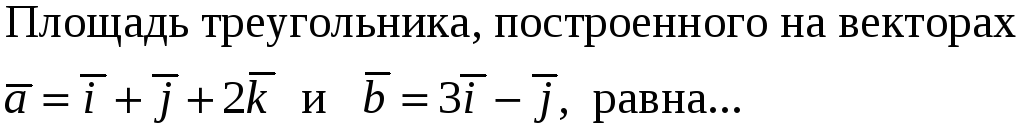
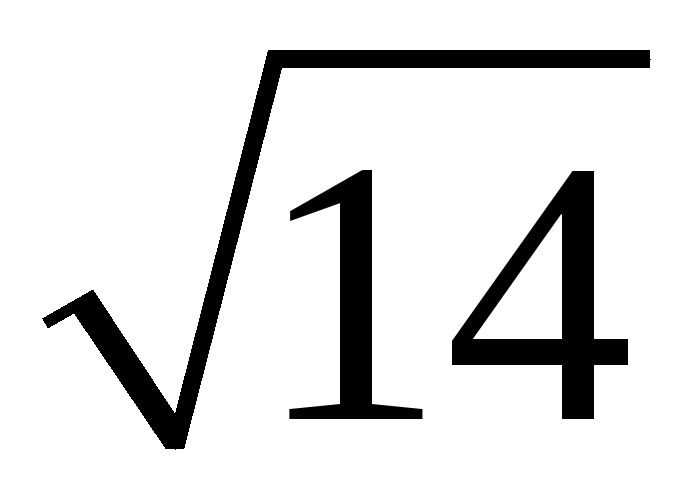
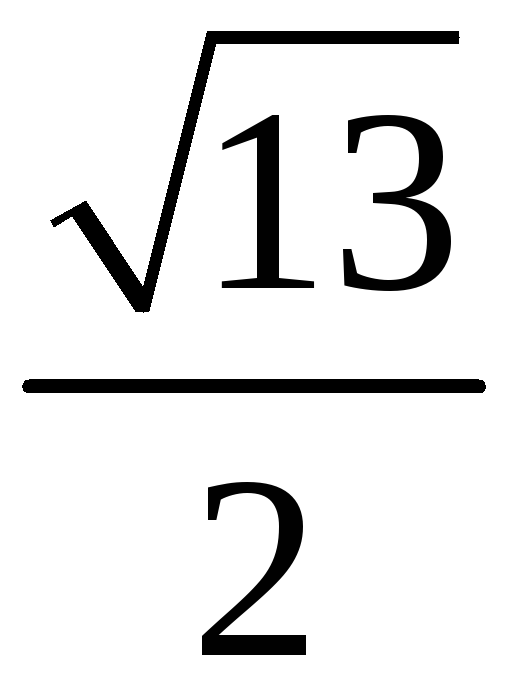
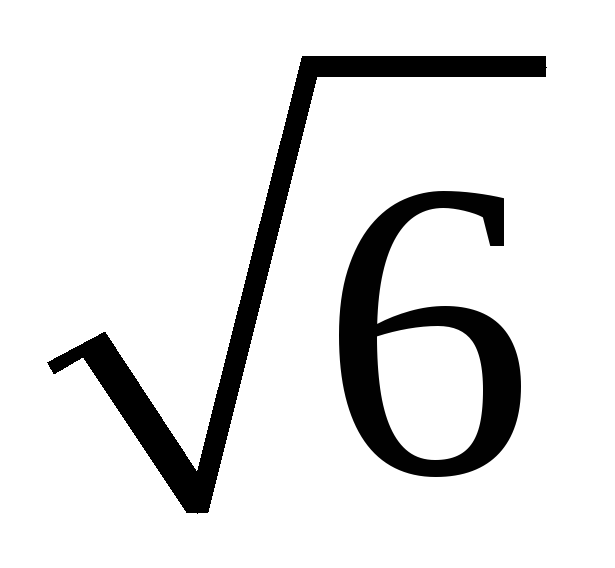
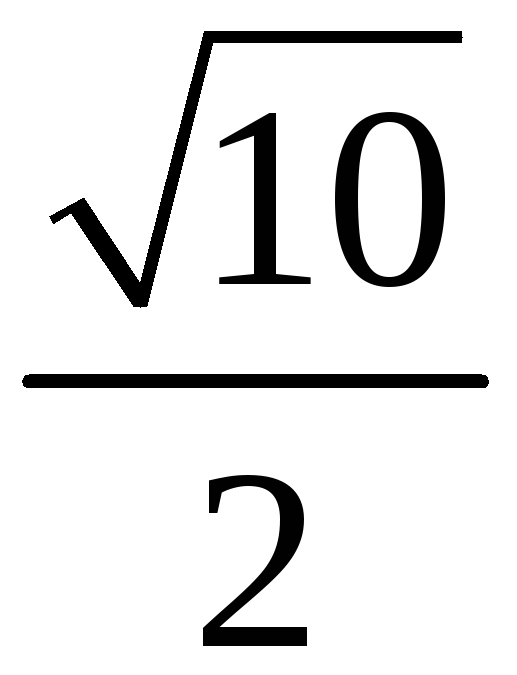
203. Задание {{ 203 }} ТЗ № 762


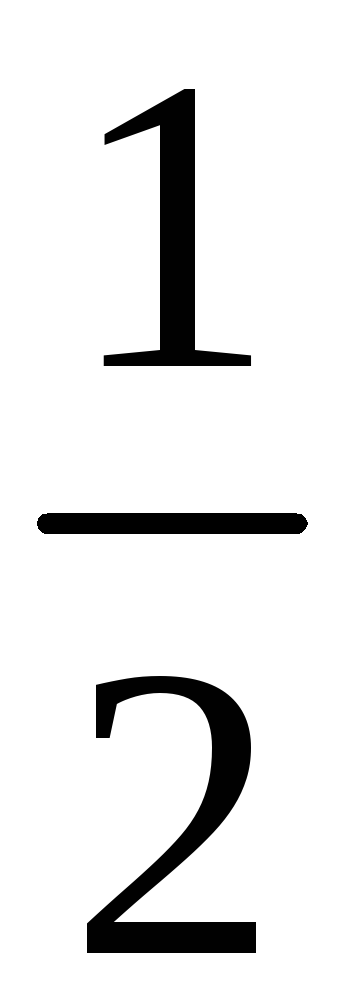
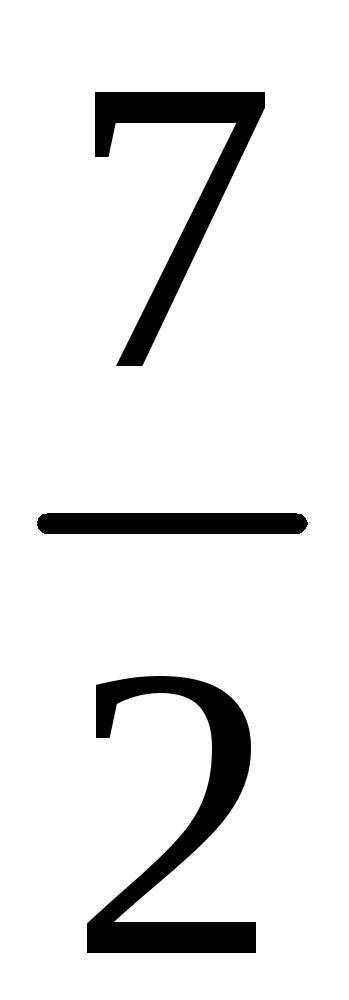
204. Задание {{ 204 }} ТЗ № 763
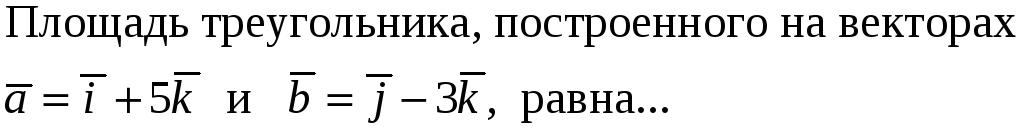
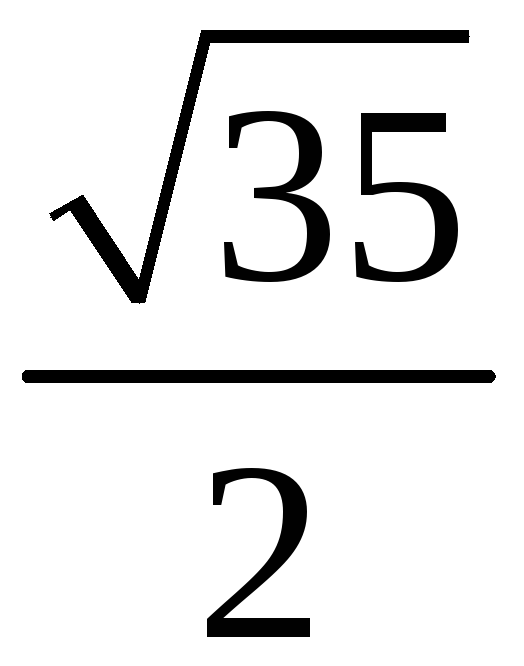
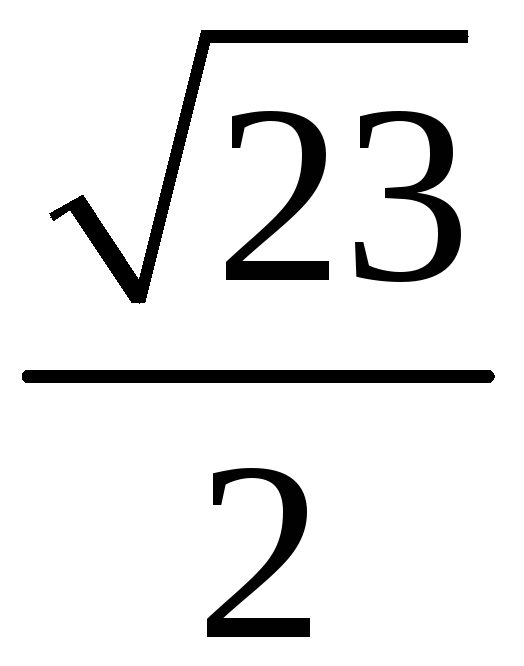
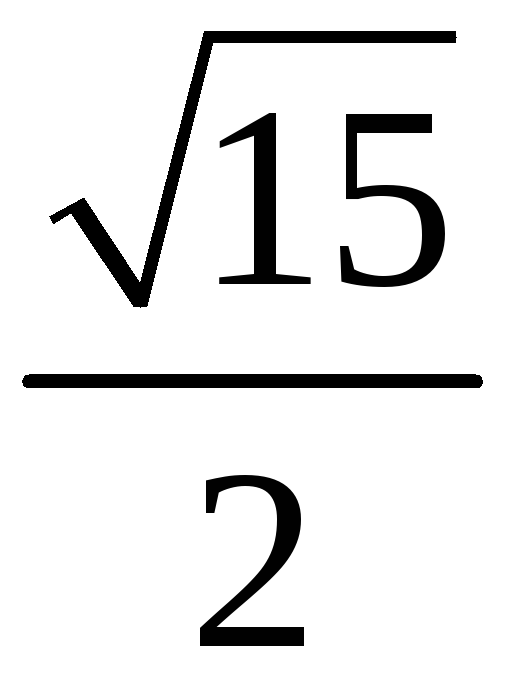
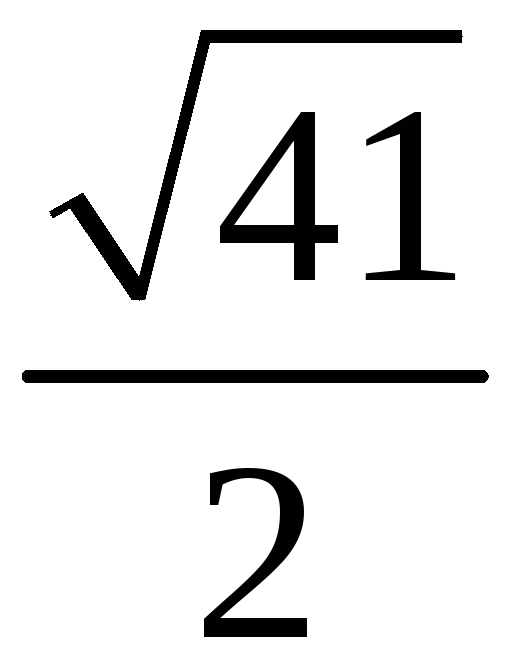
205. Задание {{ 205 }} ТЗ № 764
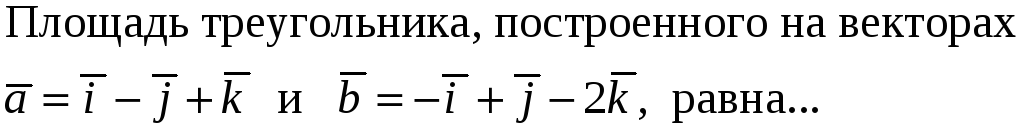
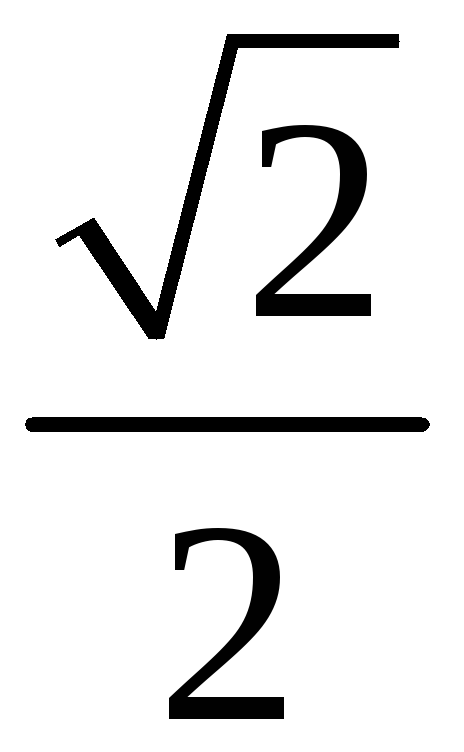
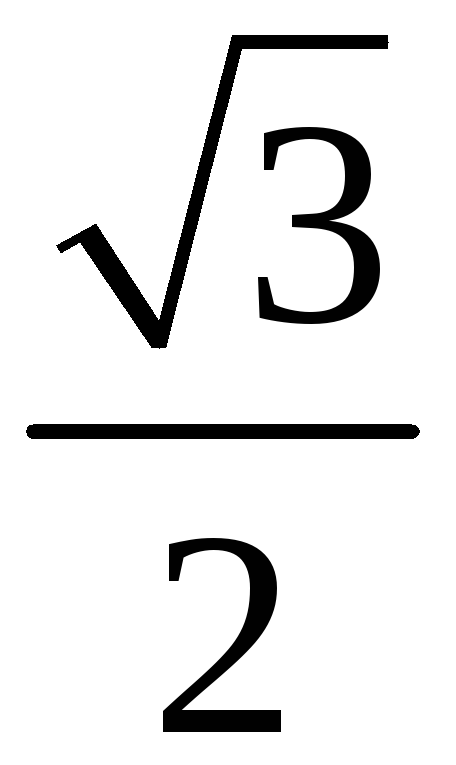
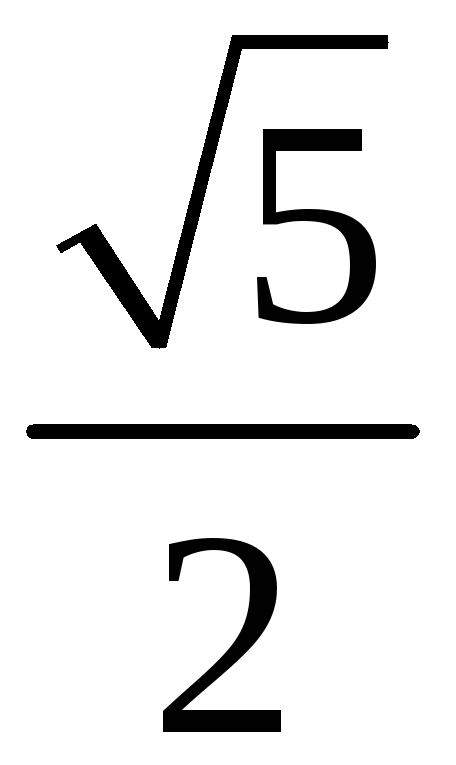
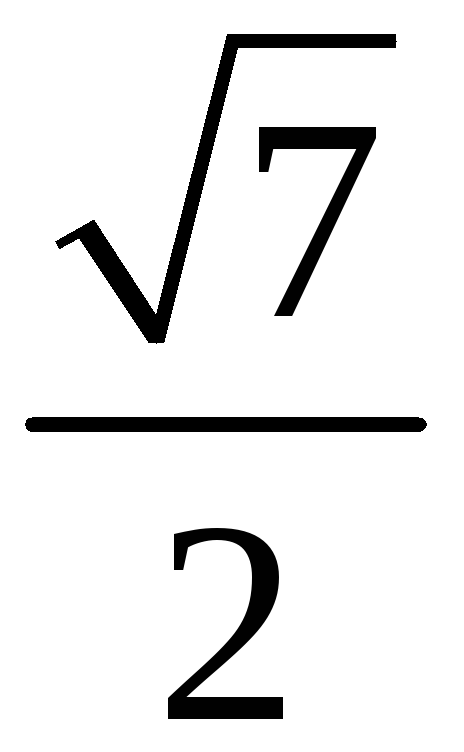
206. Задание {{ 206 }} ТЗ № 32
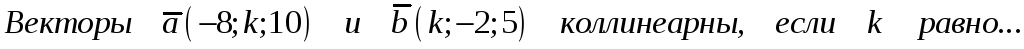
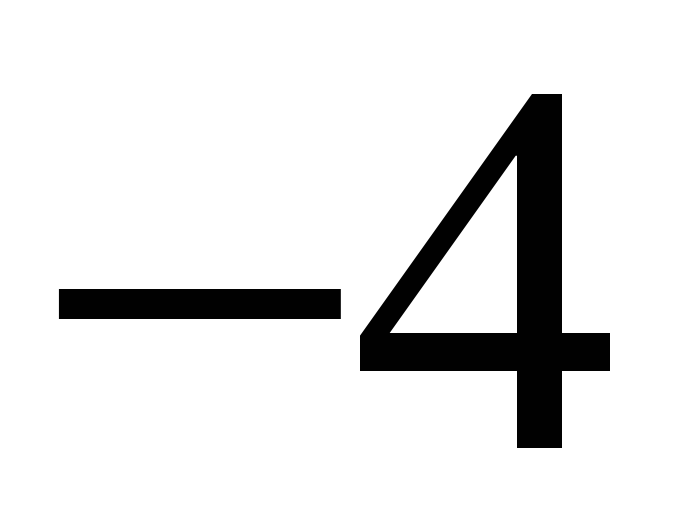
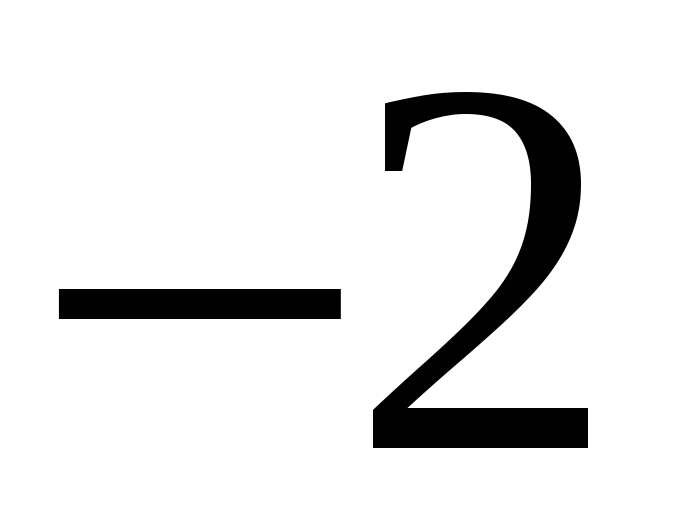

207. Задание {{ 207 }} ТЗ № 35
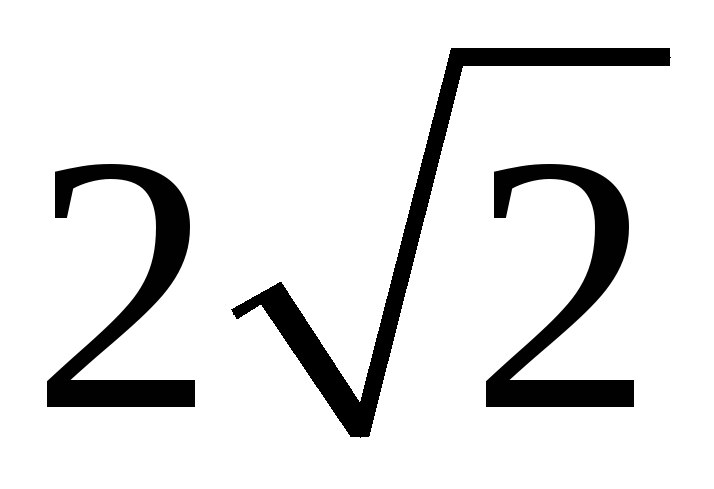
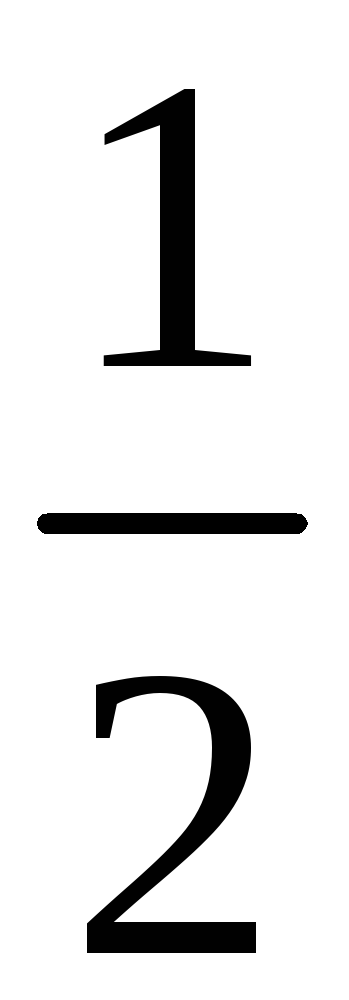
208. Задание {{ 208 }} ТЗ № 38
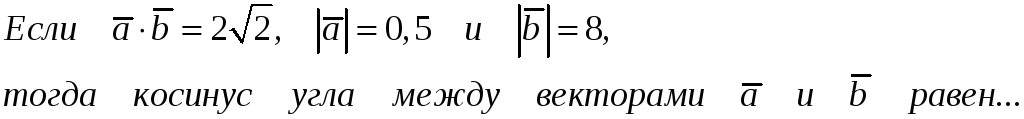
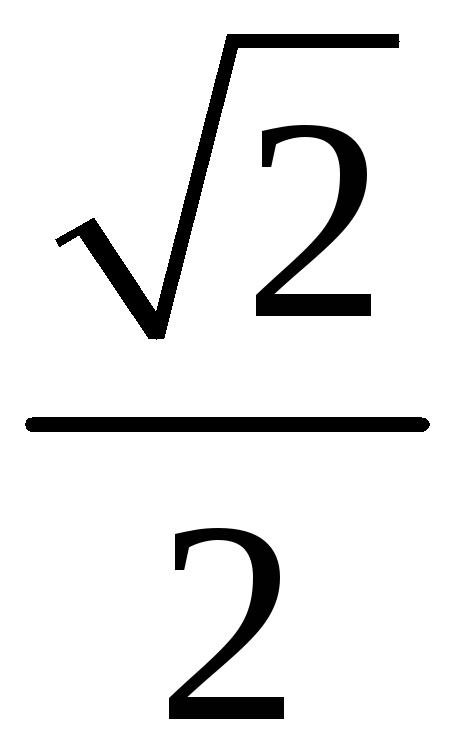
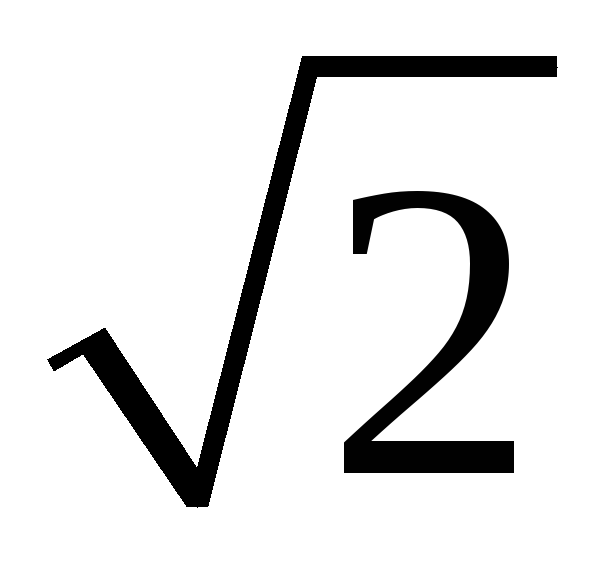
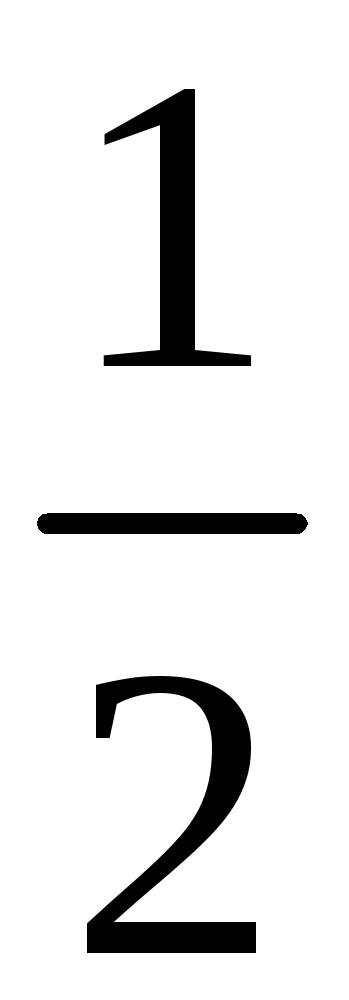
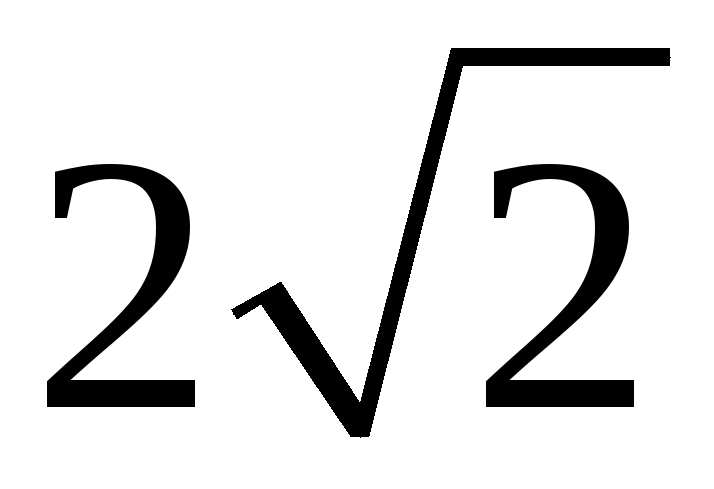
209. Задание {{ 209 }} ТЗ № 106
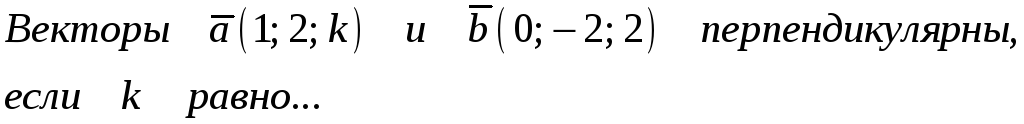
-1 -2 1 2
210. Задание {{ 210 }} ТЗ № 107
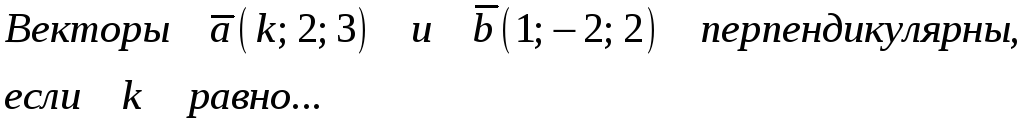
-1 -2 1 2
211. Задание {{ 211 }} ТЗ № 765
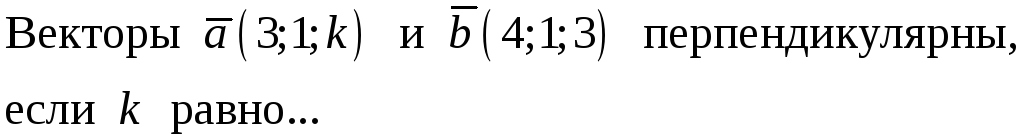
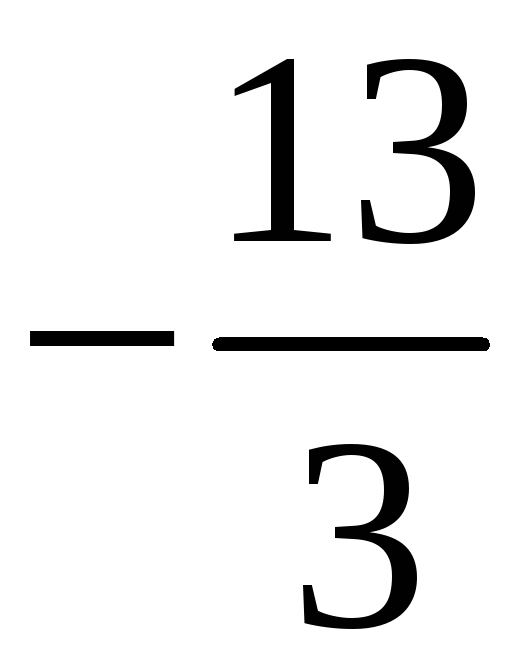
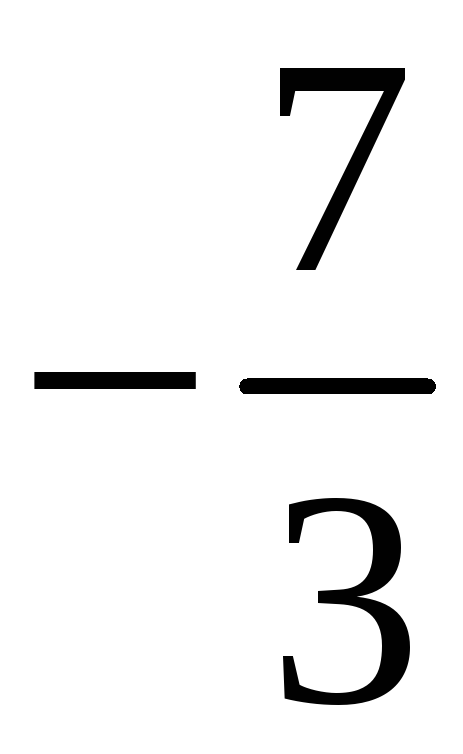


212. Задание {{ 212 }} ТЗ № 766
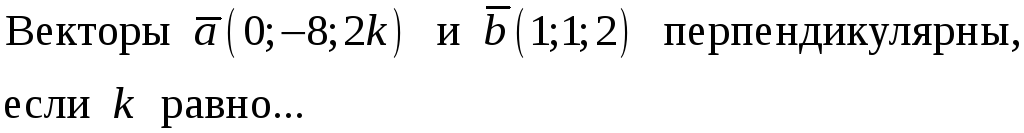


213. Задание {{ 213 }} ТЗ № 767
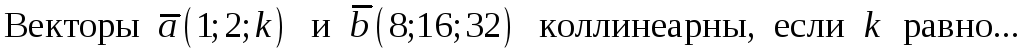




214. Задание {{ 214 }} ТЗ № 768
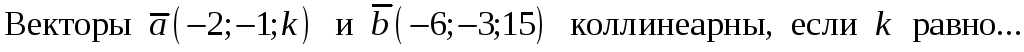



 215.
Задание {{ 215 }} ТЗ № 769
215.
Задание {{ 215 }} ТЗ № 769
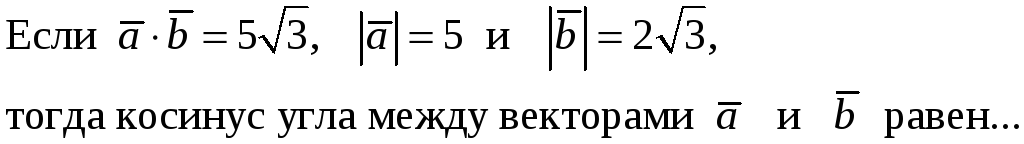
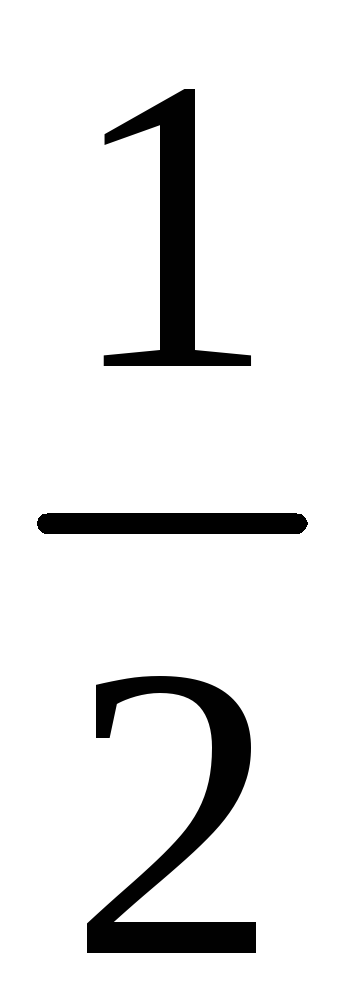
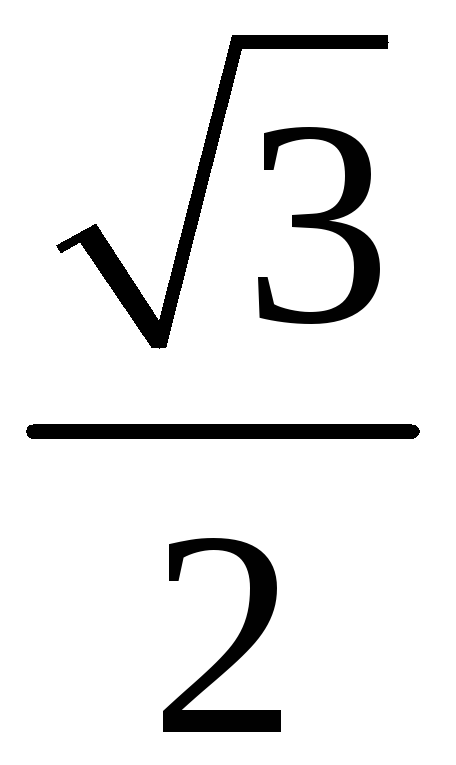
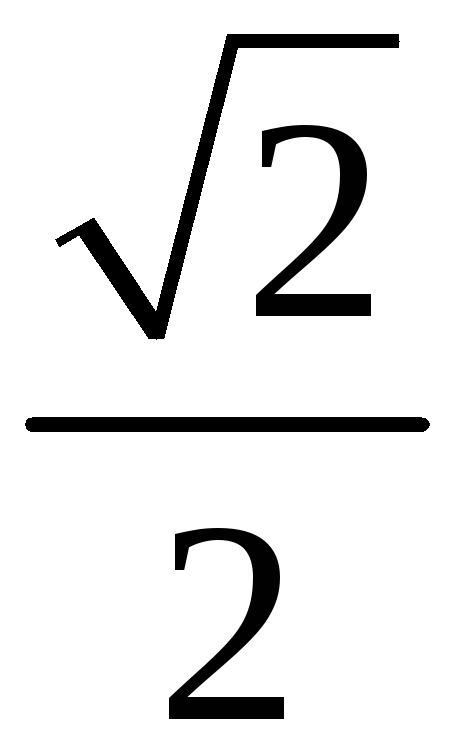

216. Задание {{ 216 }} ТЗ № 315
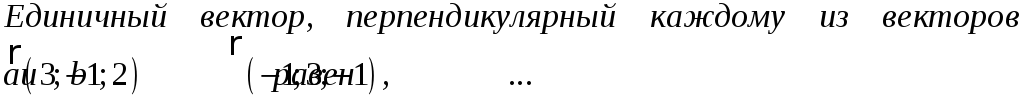
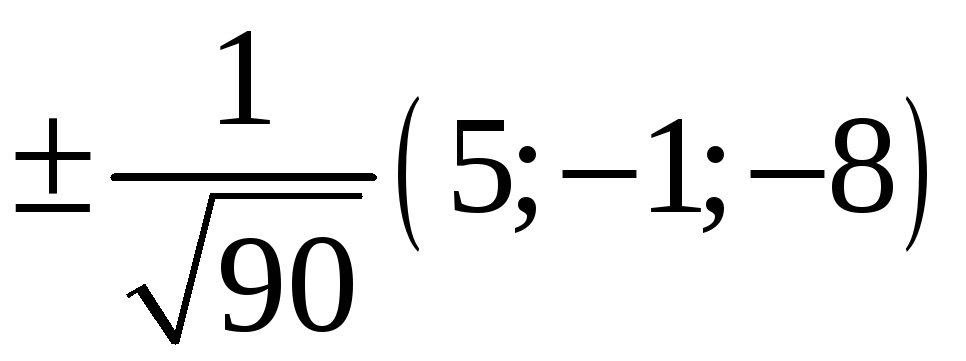
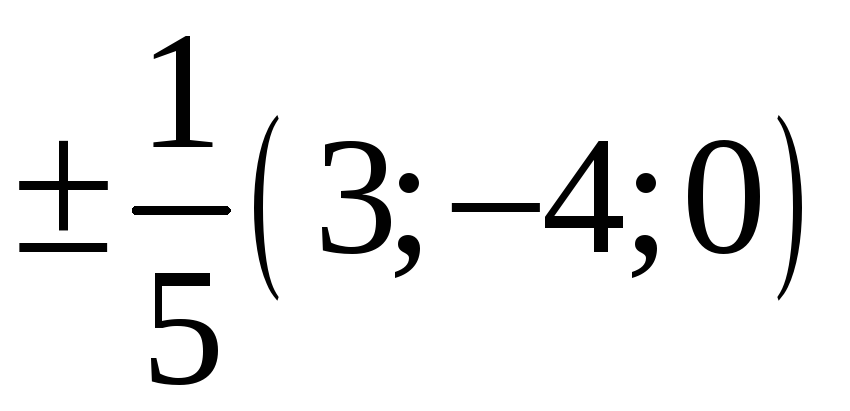
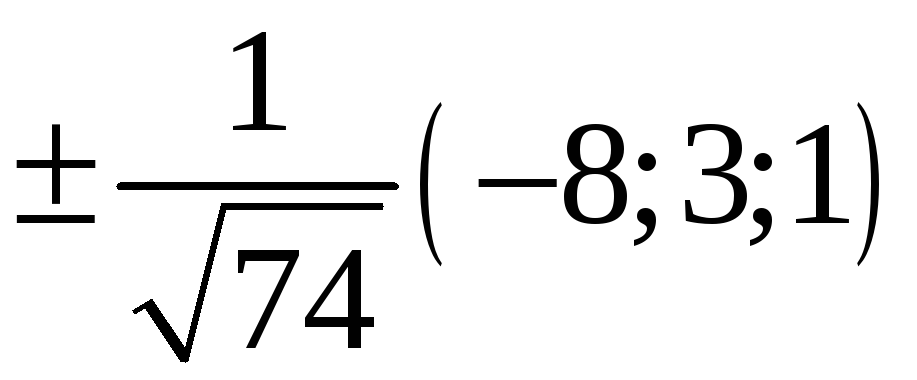
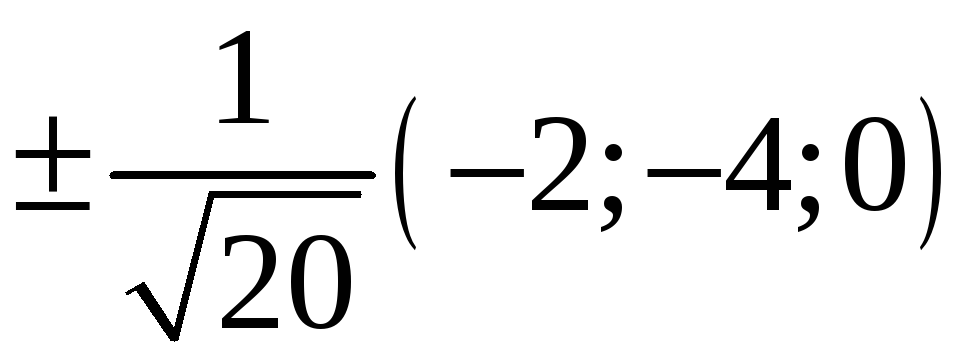
217. Задание {{ 217 }} ТЗ № 733
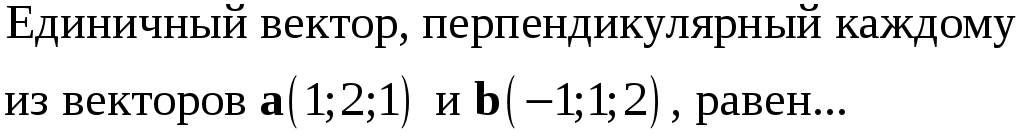
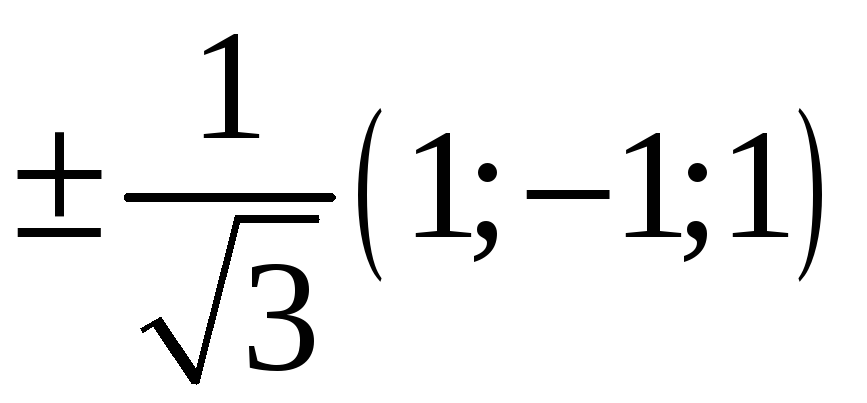
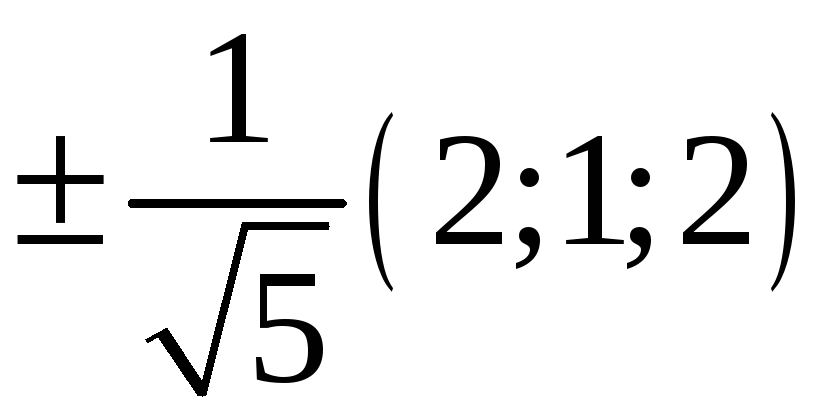
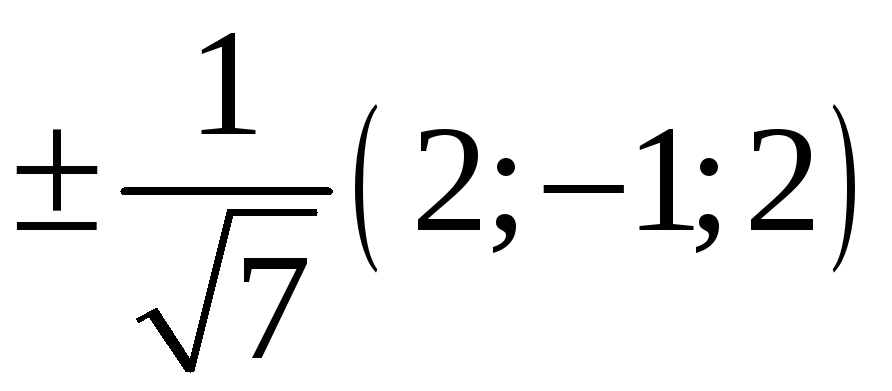
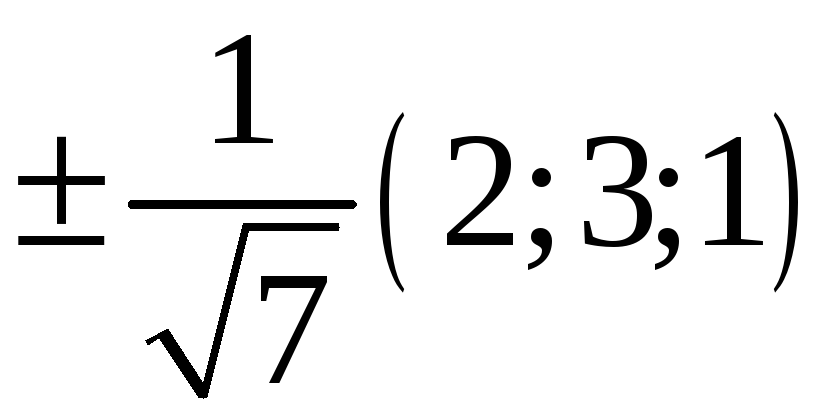
218. Задание {{ 218 }} ТЗ № 734

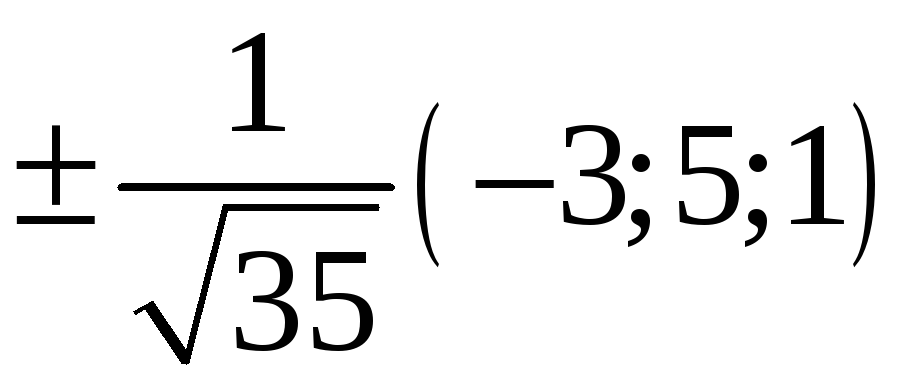
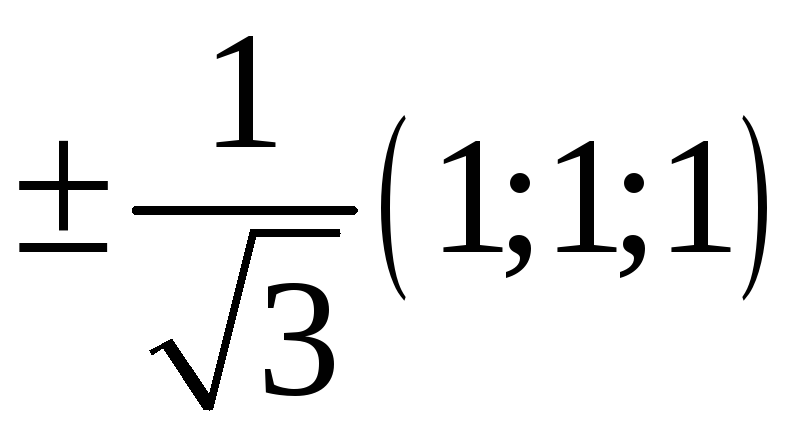
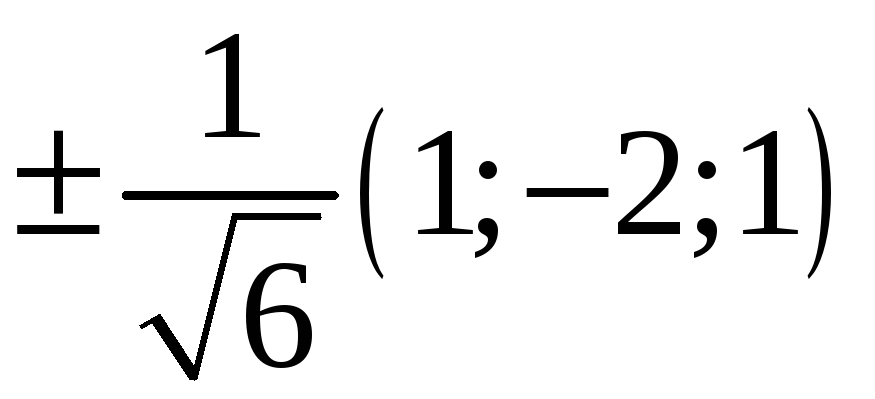
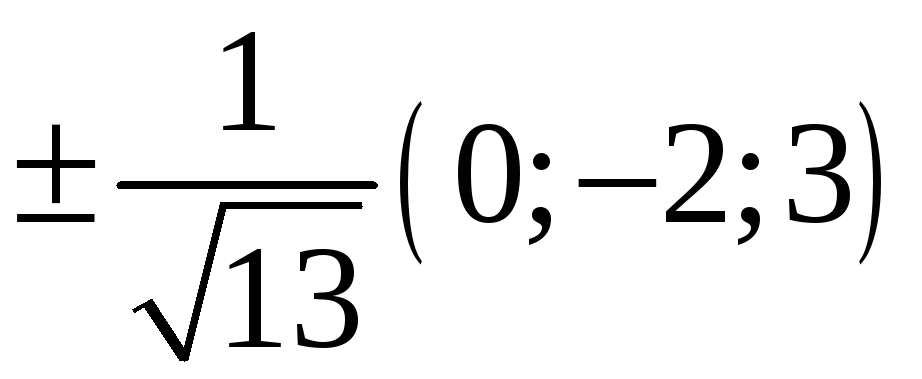
219. Задание {{ 219 }} ТЗ № 735
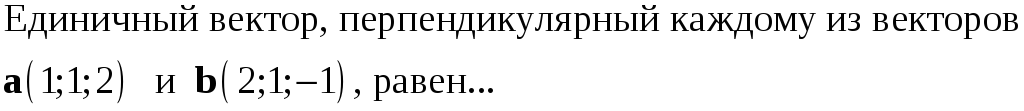
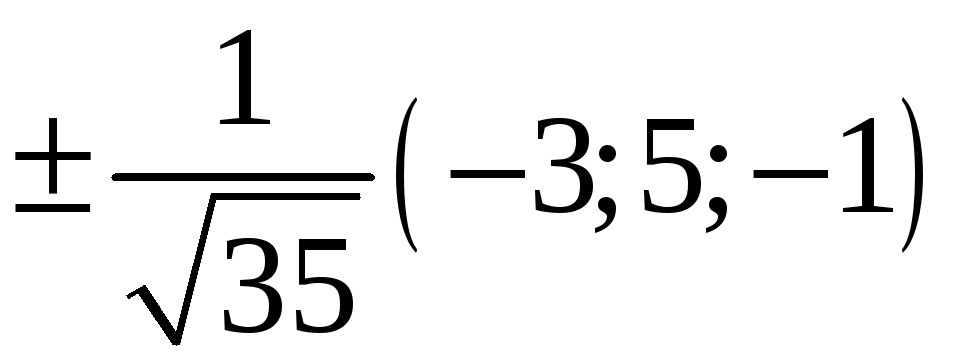
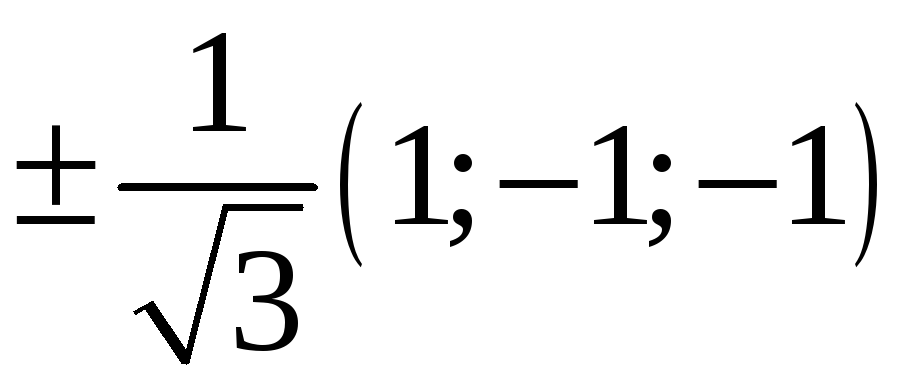
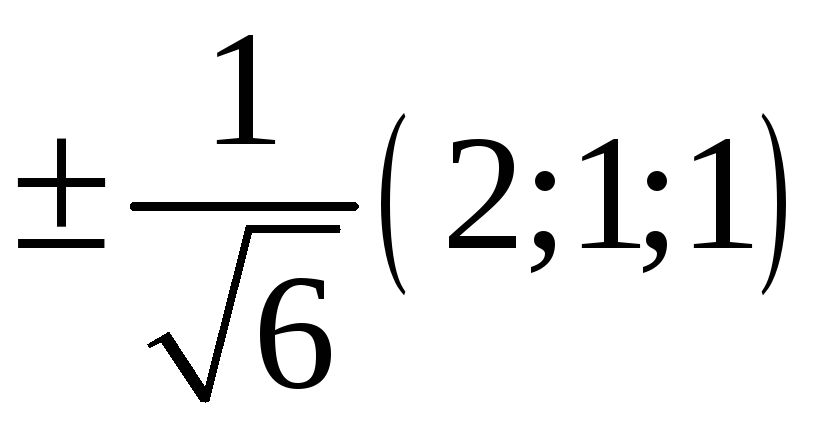
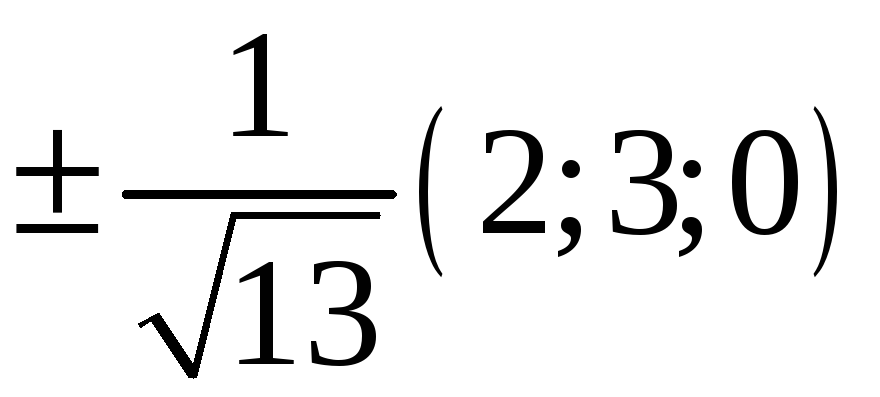
220. Задание {{ 220 }} ТЗ № 736
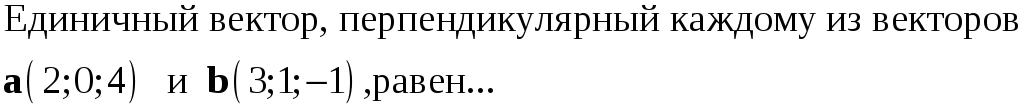
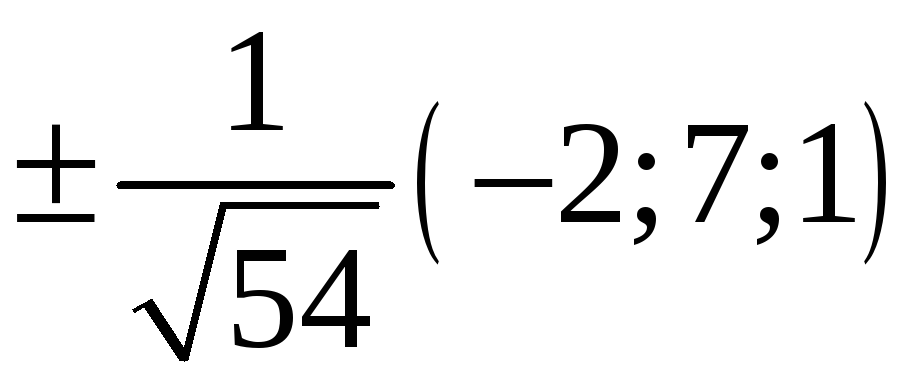
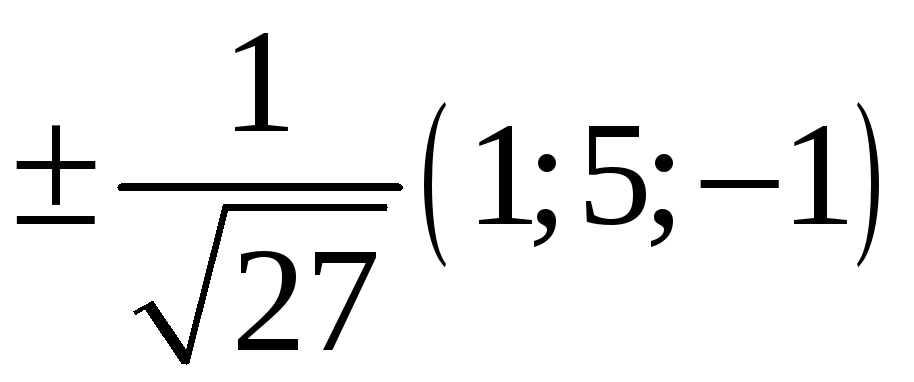
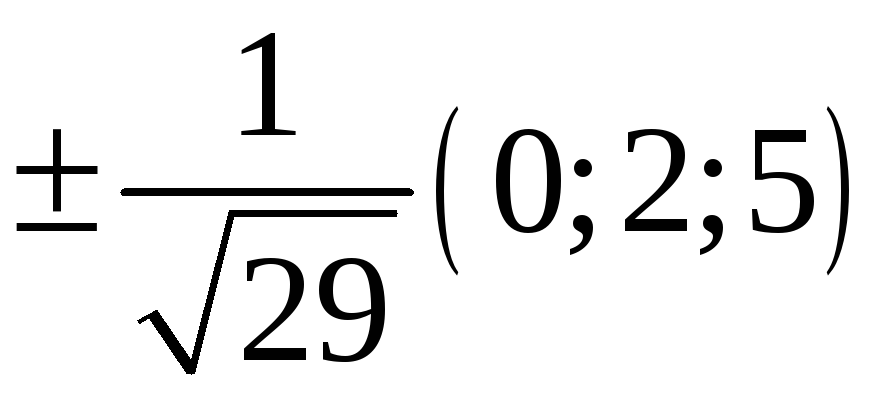
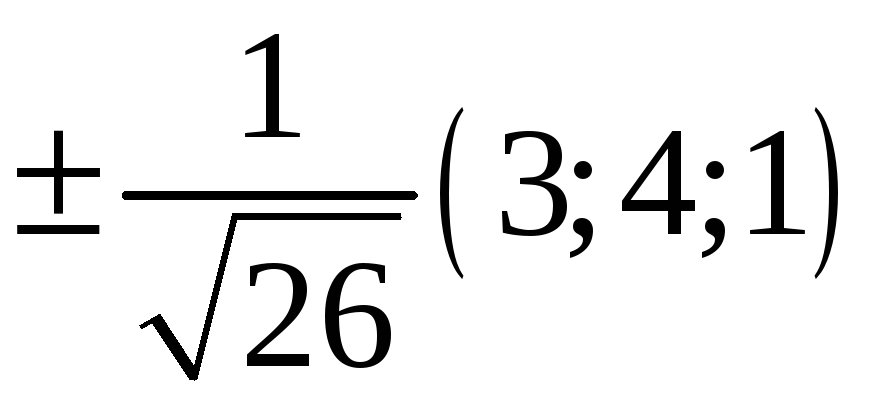
221. Задание {{ 221 }} ТЗ № 737

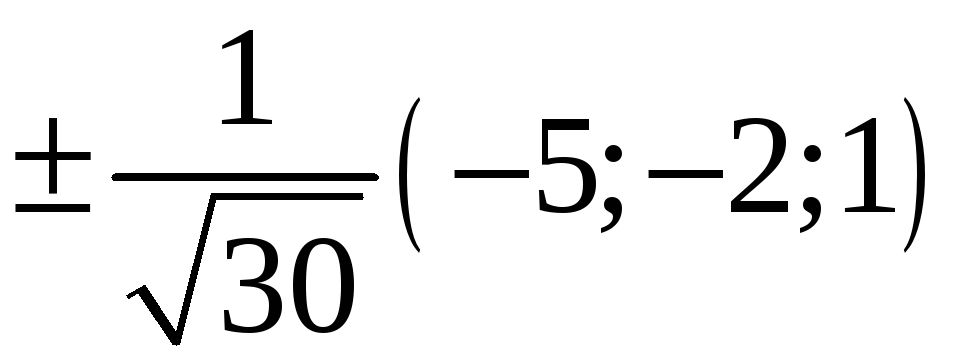
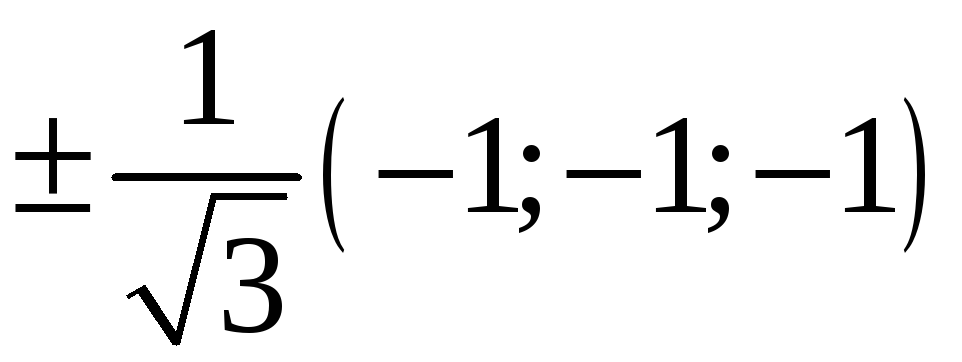
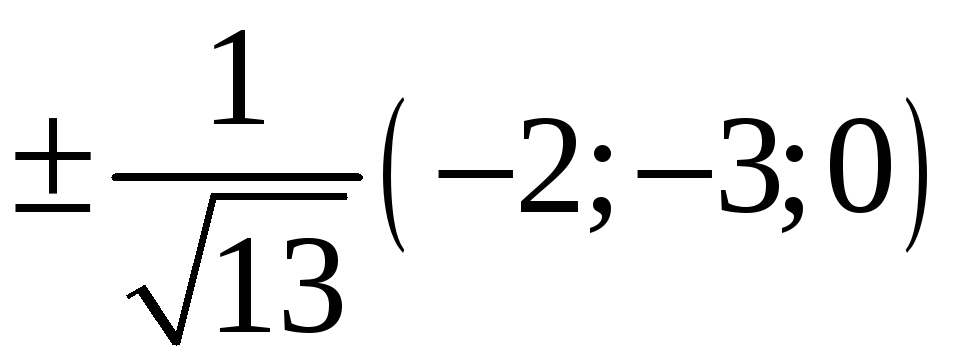
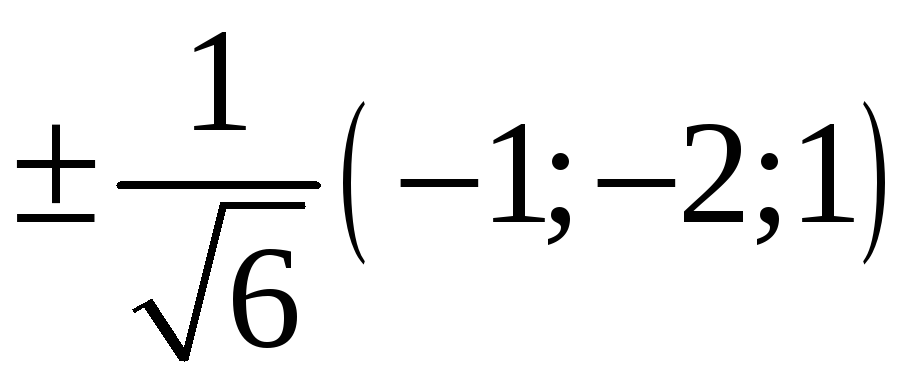
222. Задание {{ 222 }} ТЗ № 738
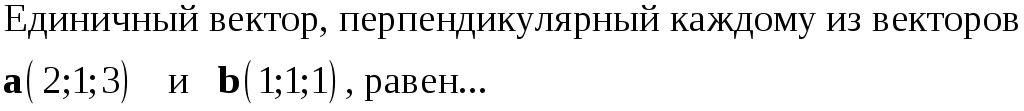
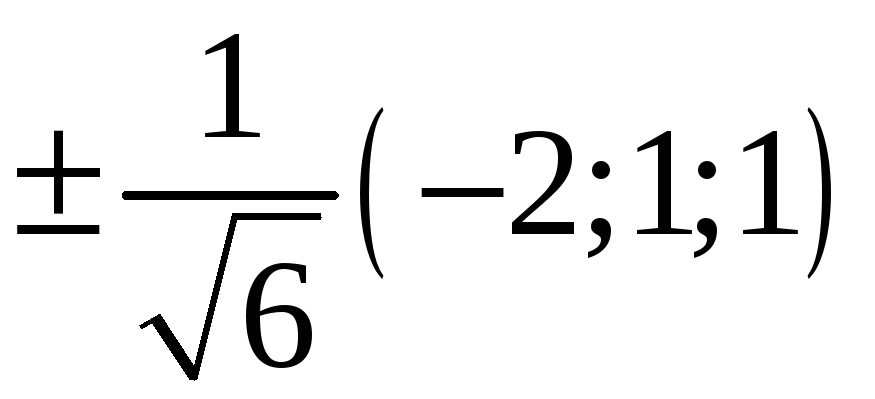
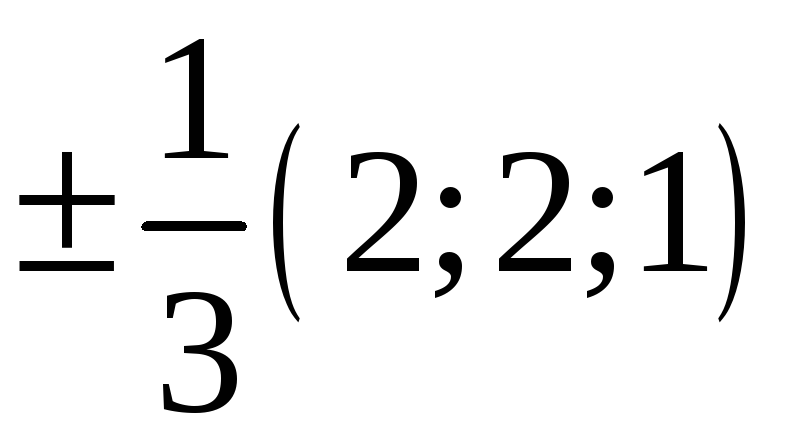
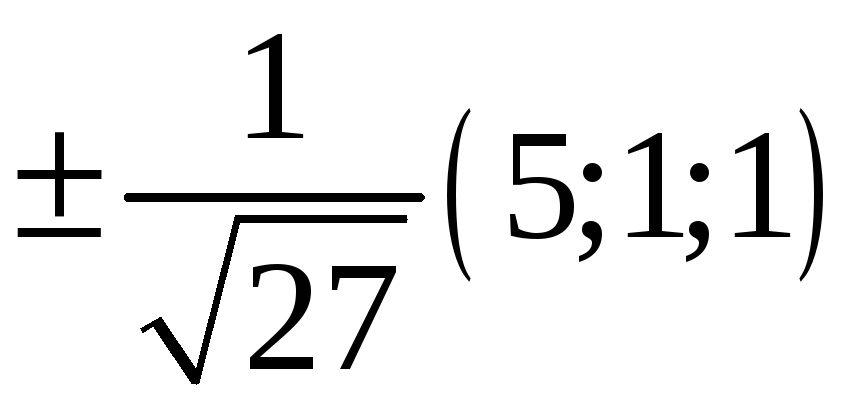
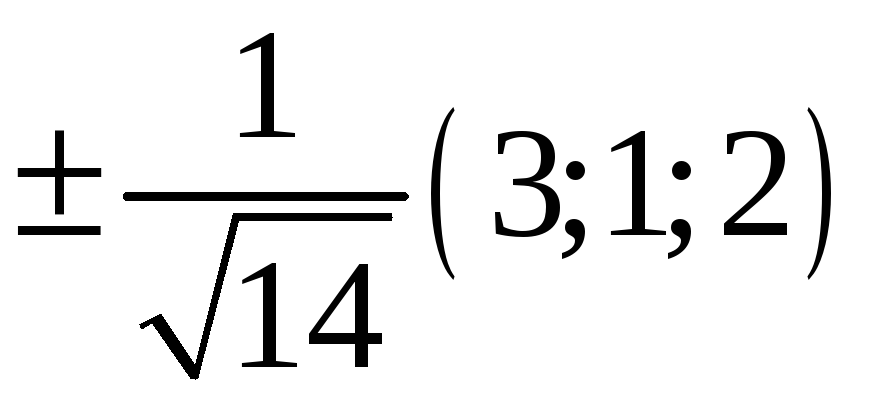
223. Задание {{ 223 }} ТЗ № 739

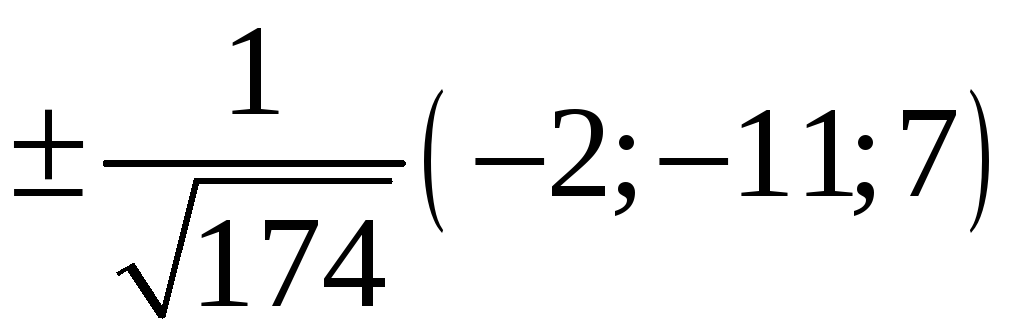
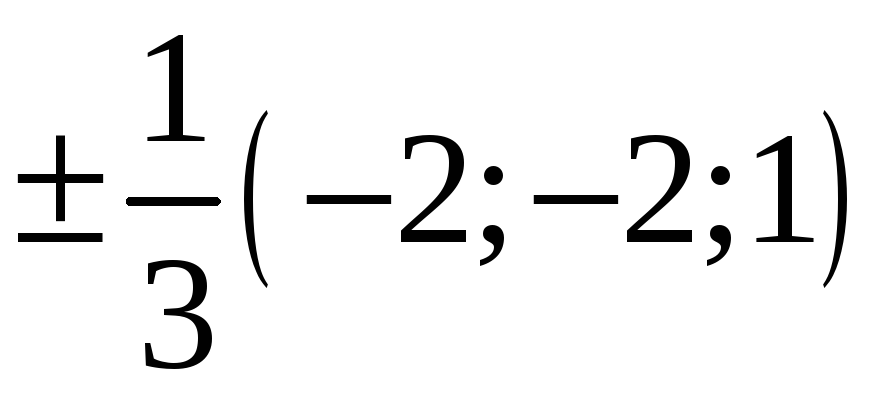
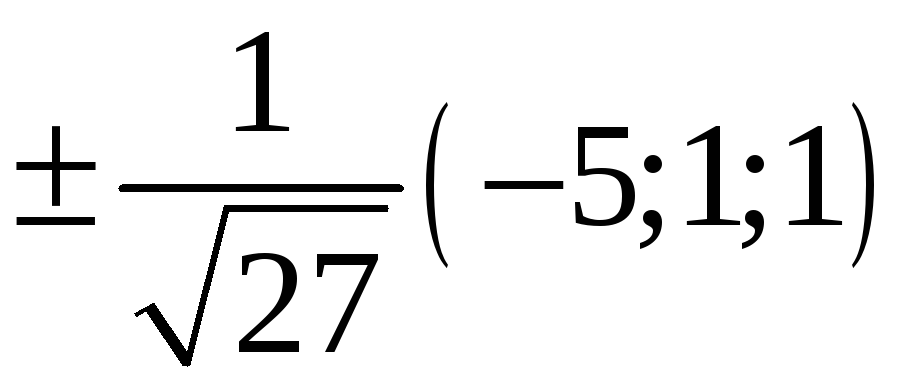
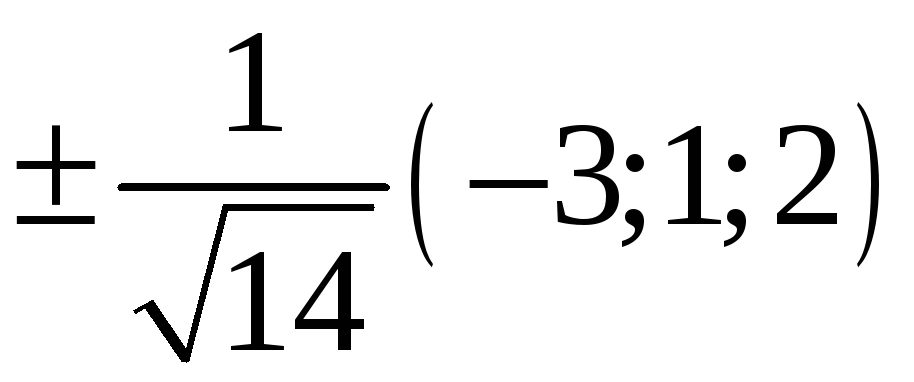
224. Задание {{ 224 }} ТЗ № 740
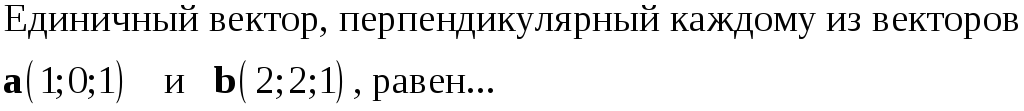
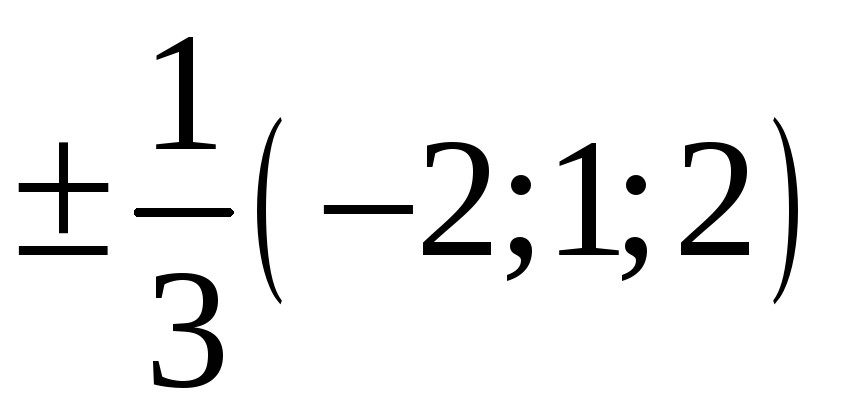
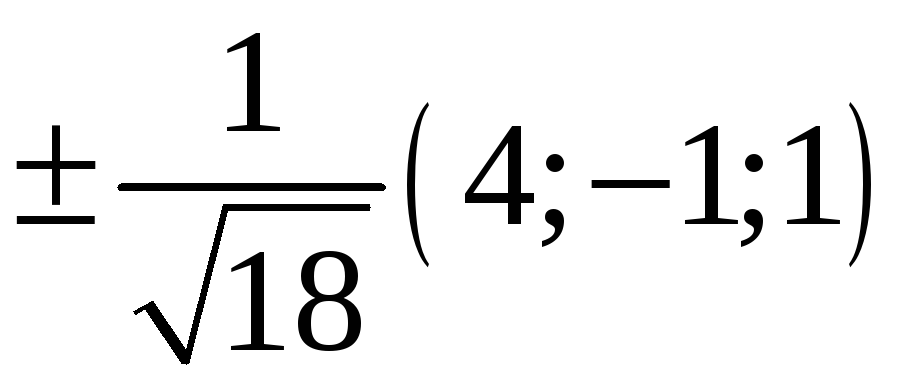
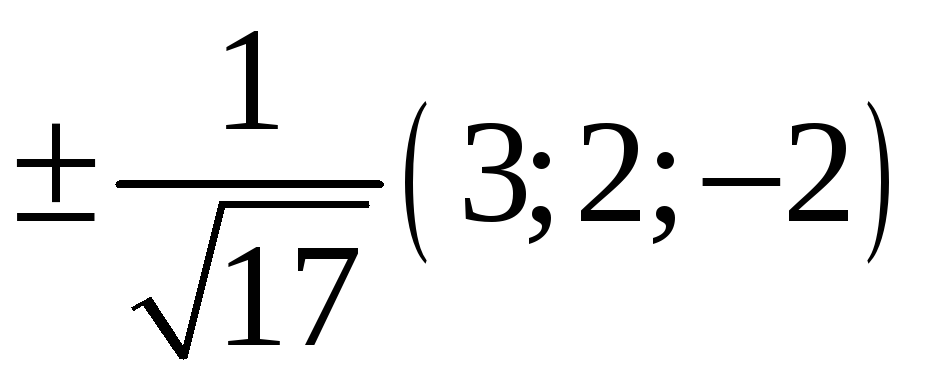
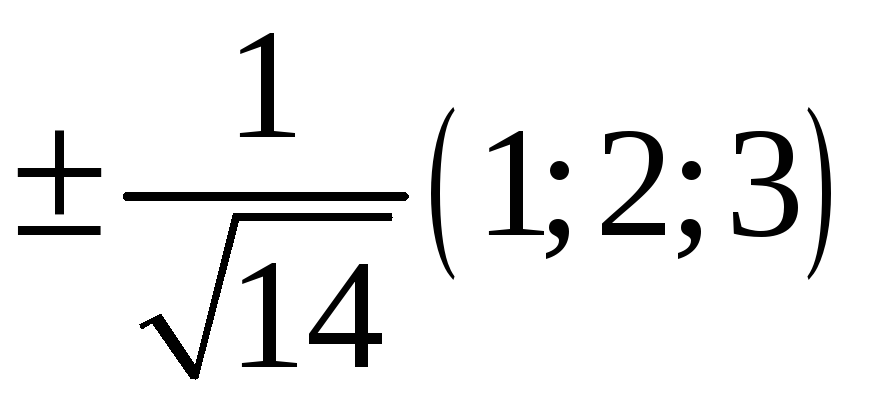
225. Задание {{ 225 }} ТЗ № 741
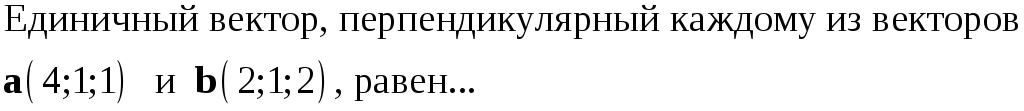
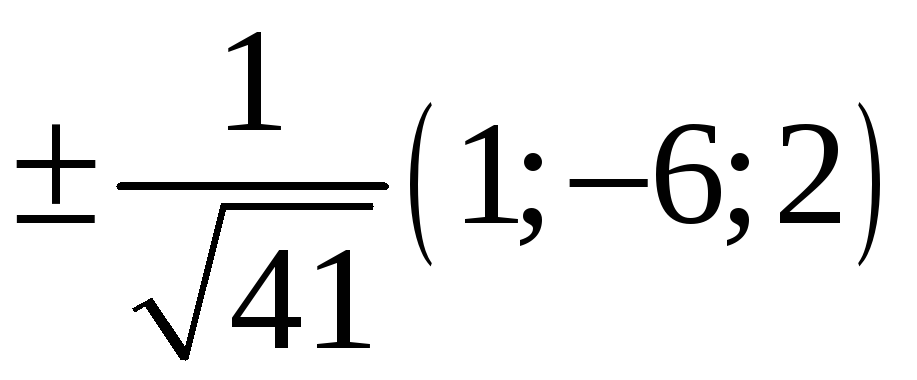
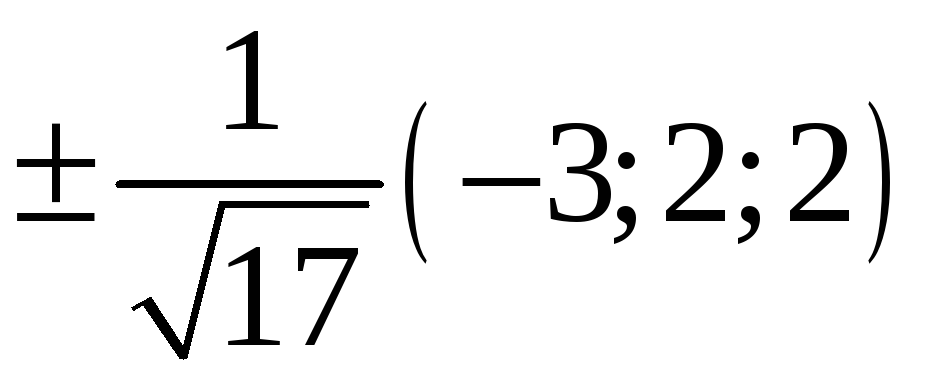
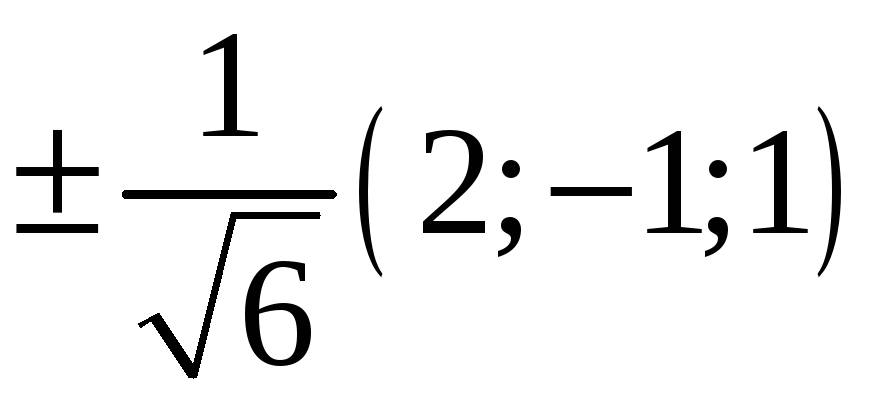
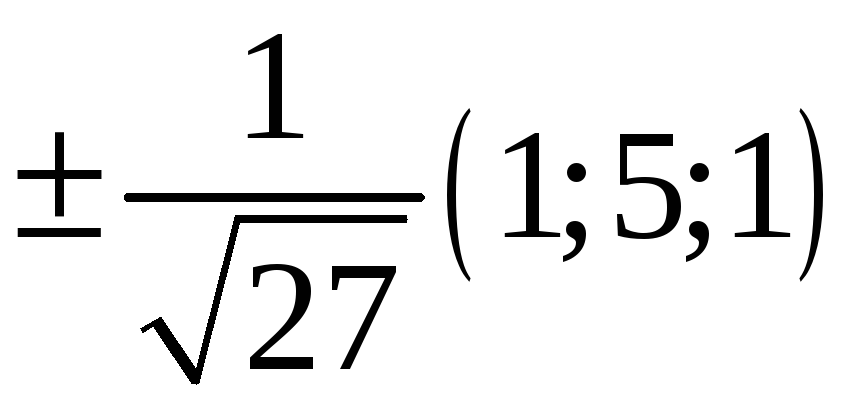
226. Задание {{ 226 }} ТЗ № 316
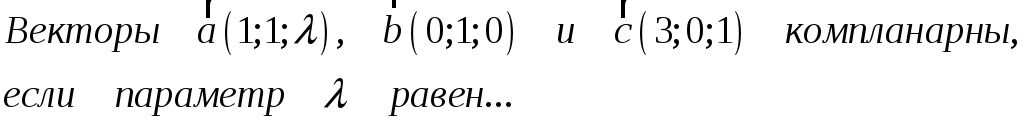


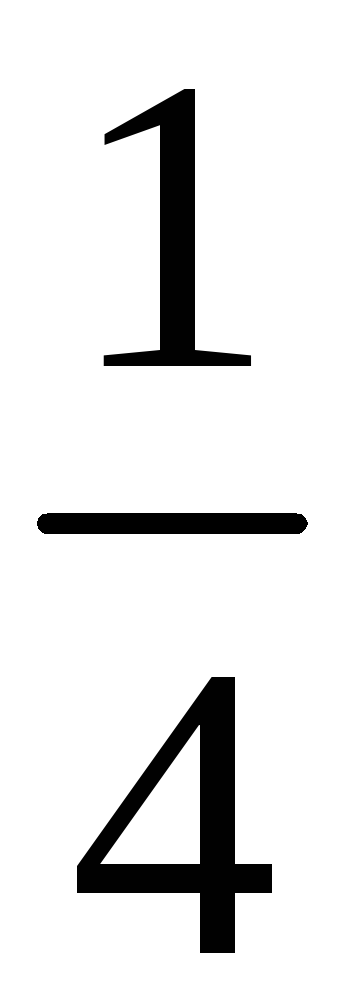

227. Задание {{ 227 }} ТЗ № 742
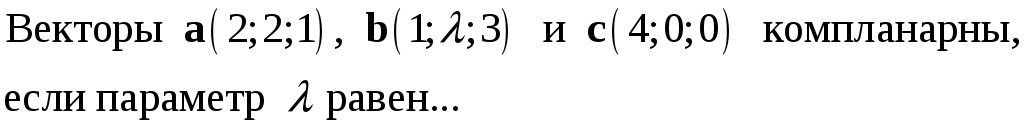


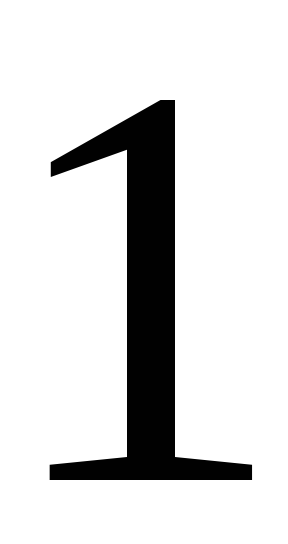

228. Задание {{ 228 }} ТЗ № 743
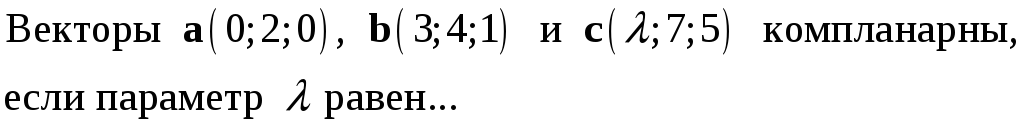
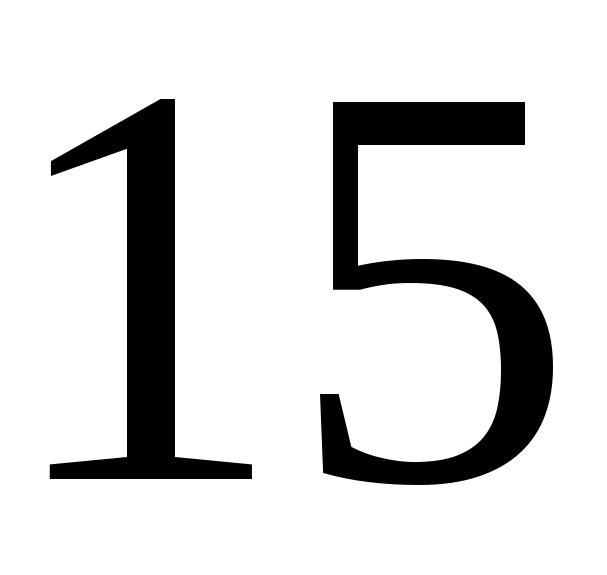



229. Задание {{ 229 }} ТЗ № 744
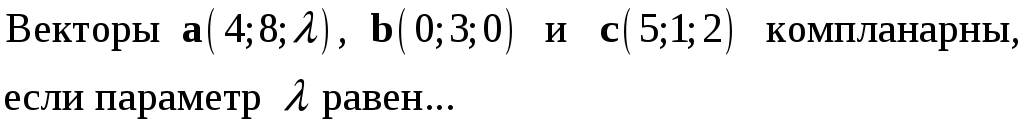


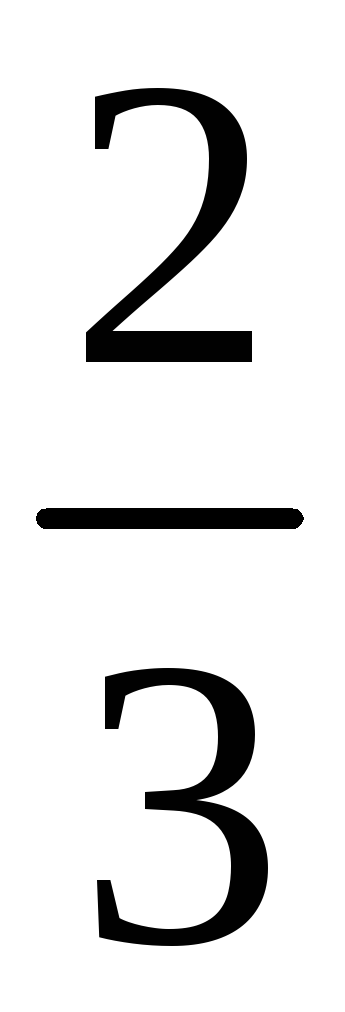

230. Задание {{ 230 }} ТЗ № 745
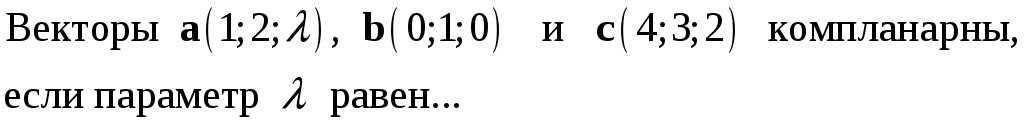
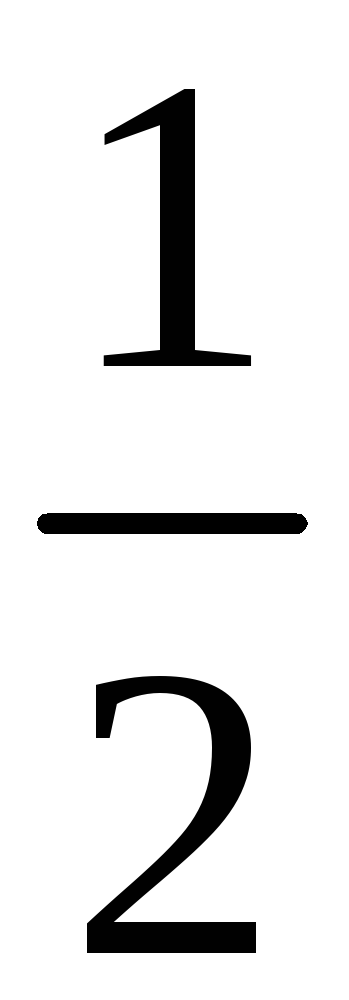
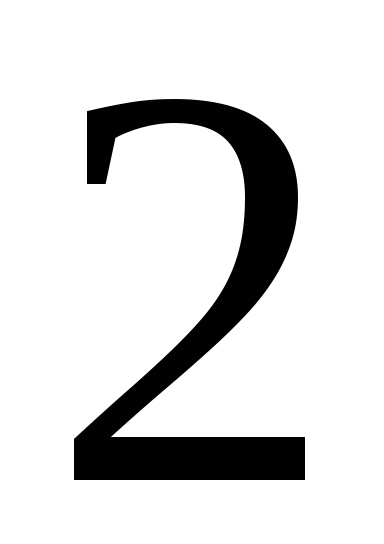
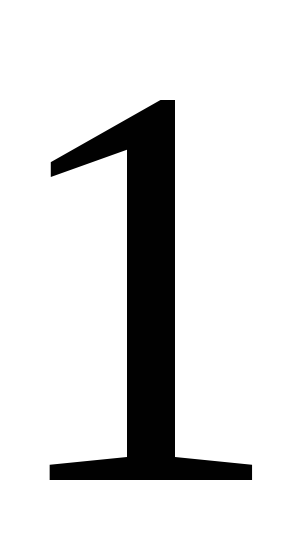

231. Задание {{ 231 }} ТЗ № 746
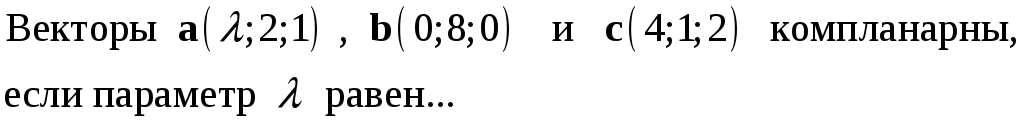
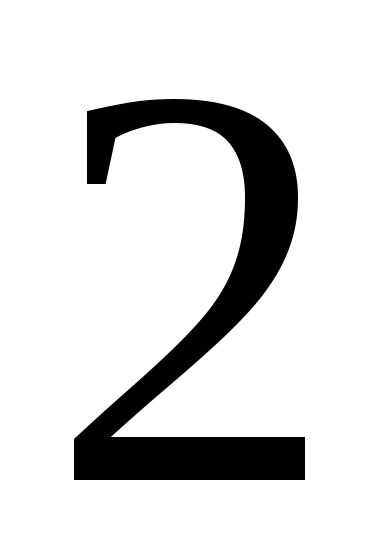
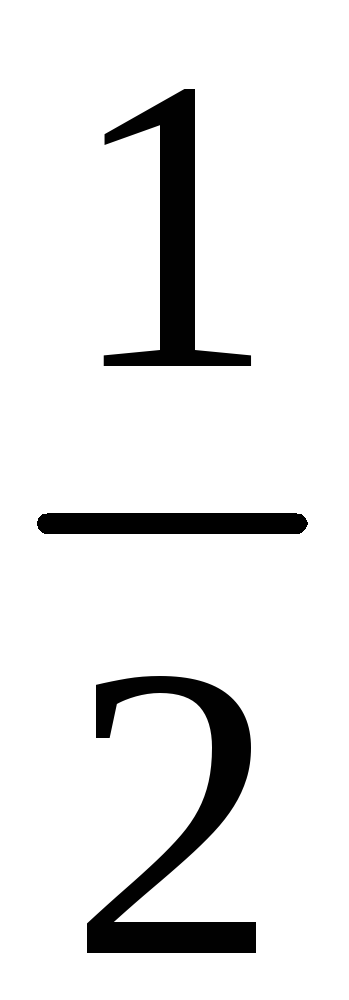

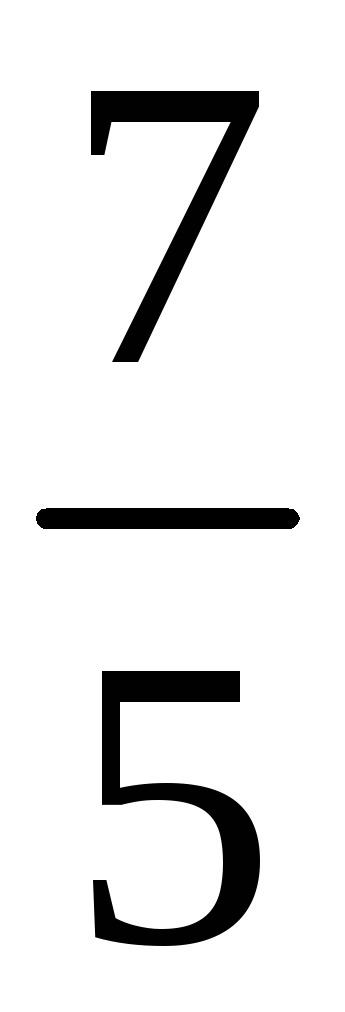
232. Задание {{ 232 }} ТЗ № 747
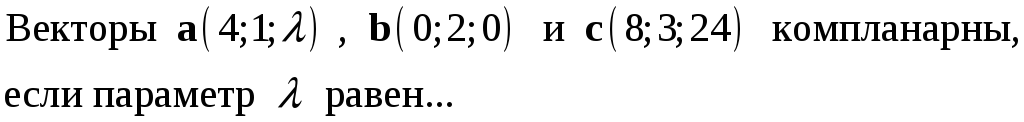
233. Задание {{ 233 }} ТЗ № 748
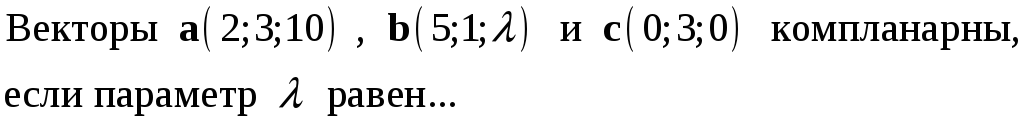
234. Задание {{ 234 }} ТЗ № 749
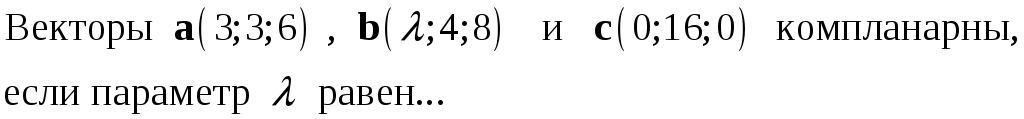

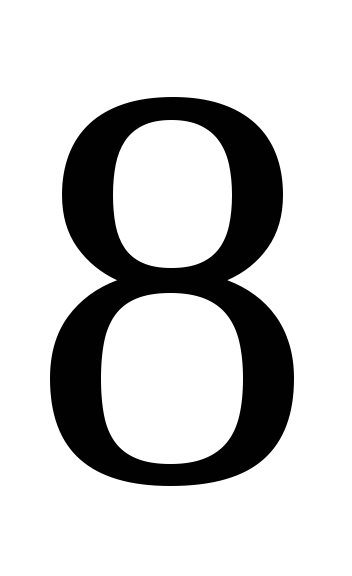

235. Задание {{ 235 }} ТЗ № 750
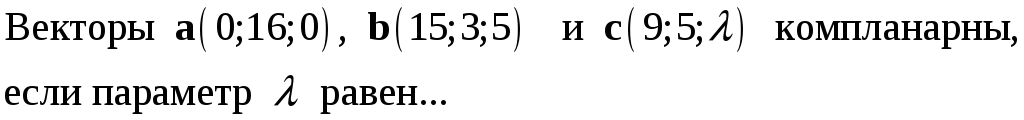

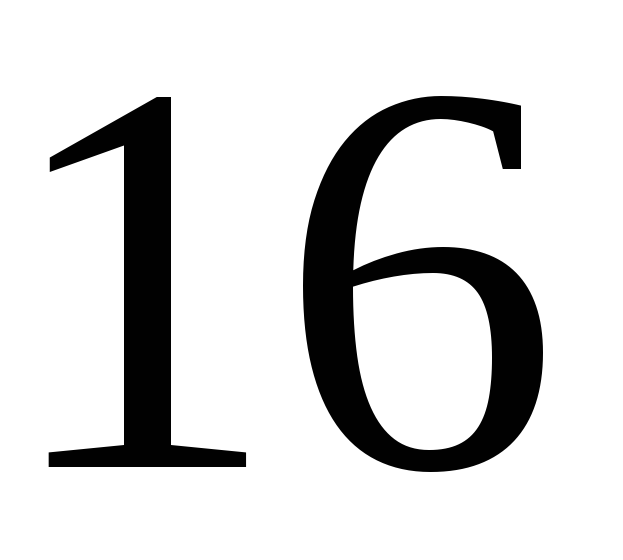

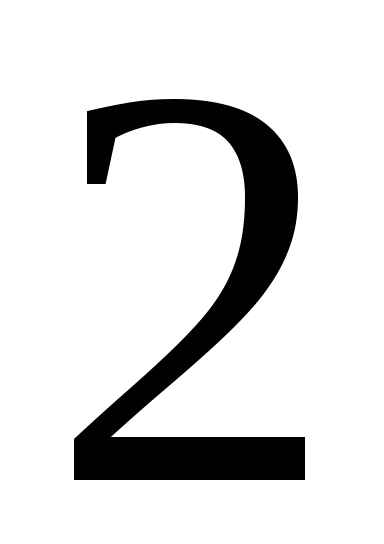
11
2.5. Скалярное произведение векторов
П р и м е р 23. Даны векторы 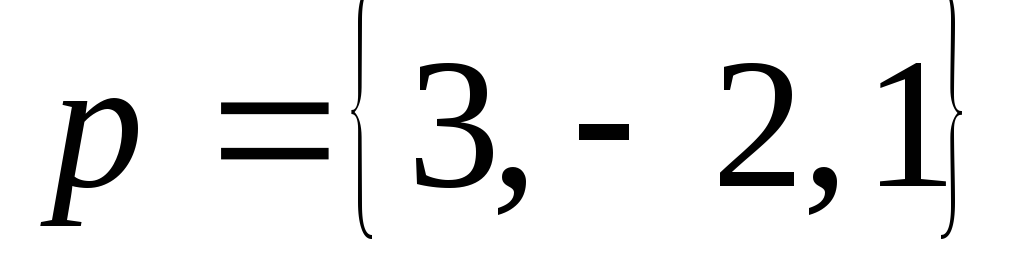 ,
,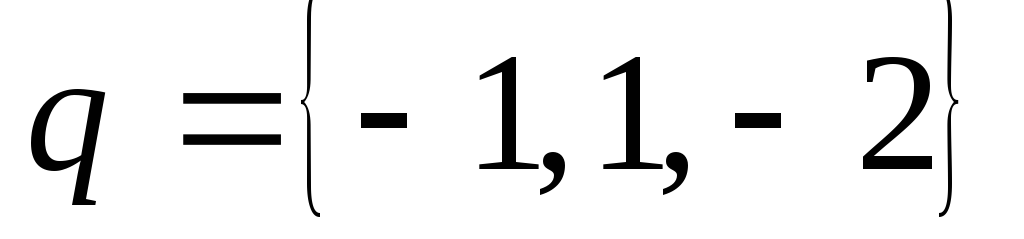 ,
,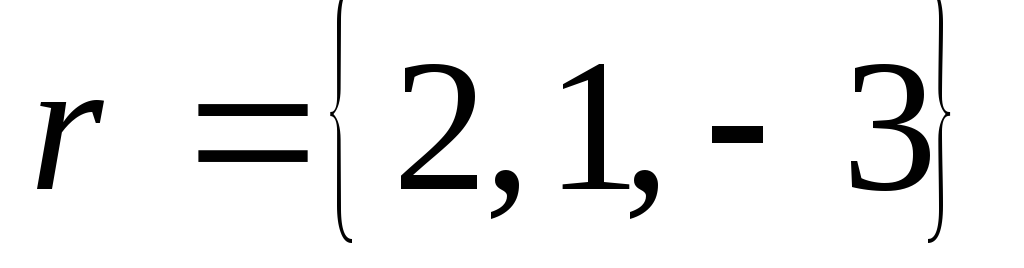 .
Найти разложение вектора
.
Найти разложение вектора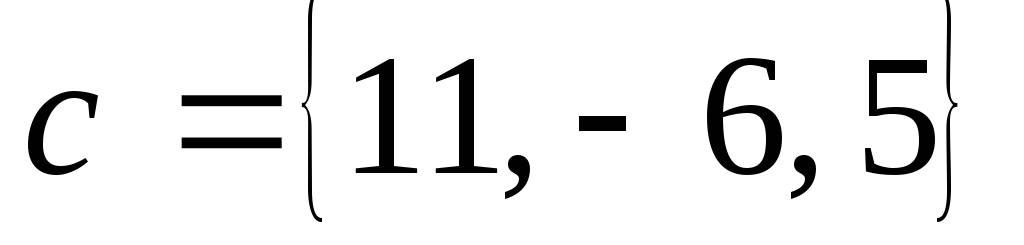 по базису
по базису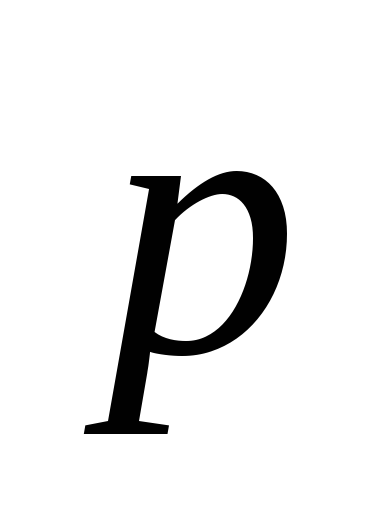 ,
, ,
,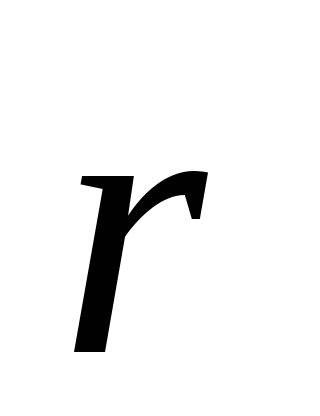 .
.
Решение.
Для разложение вектора  по базису
по базису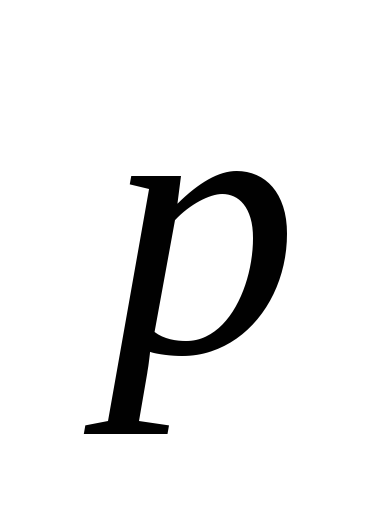 ,
, ,
,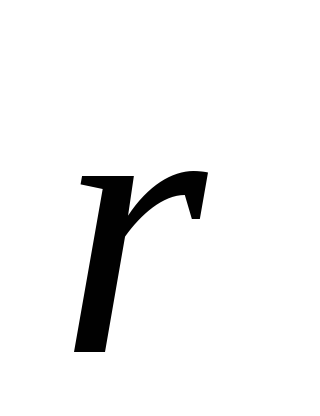 необходимо найти такие числа
необходимо найти такие числа ,
, и
и ,
чтобы выполнялось равенство
,
чтобы выполнялось равенство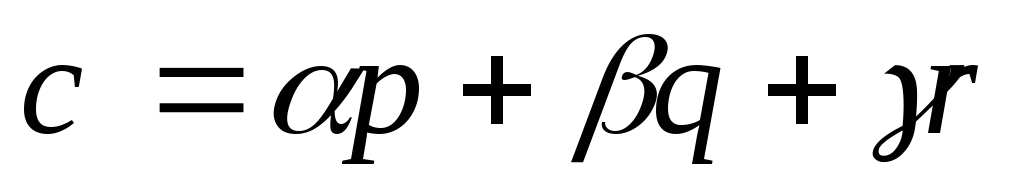 .
Если два вектора равны, то равны и их
соответствующие координаты, поэтому
относительно
.
Если два вектора равны, то равны и их
соответствующие координаты, поэтому
относительно ,
, и
и имеем систему уравнений
имеем систему уравнений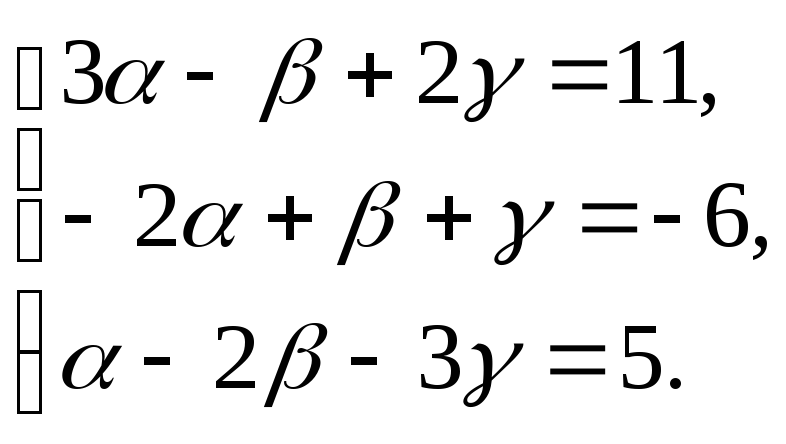 Векторы
Векторы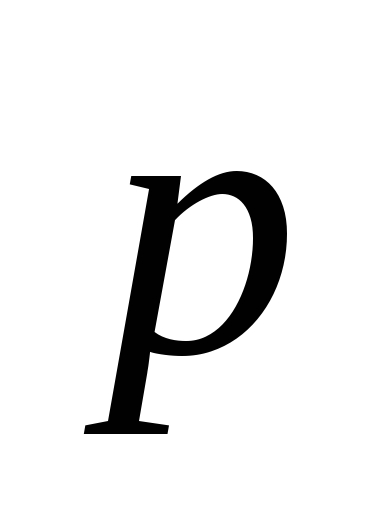 ,
, ,
,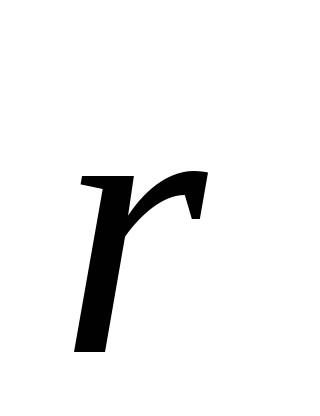 по условию задачи образуют базис, поэтому
главный определитель системы отличен
от нуля и по теореме Крамера она имеет
единственное решение:
по условию задачи образуют базис, поэтому
главный определитель системы отличен
от нуля и по теореме Крамера она имеет
единственное решение: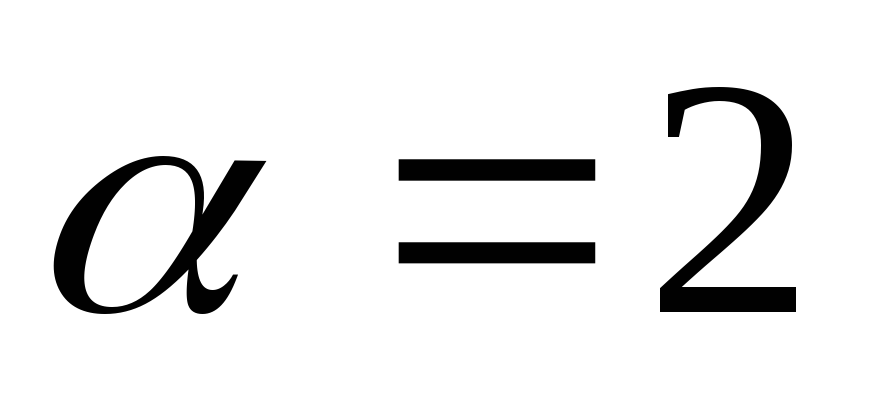 ,
,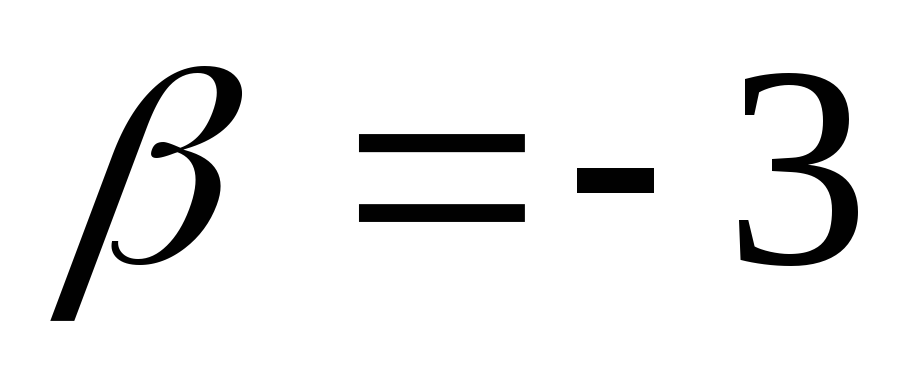 ,
,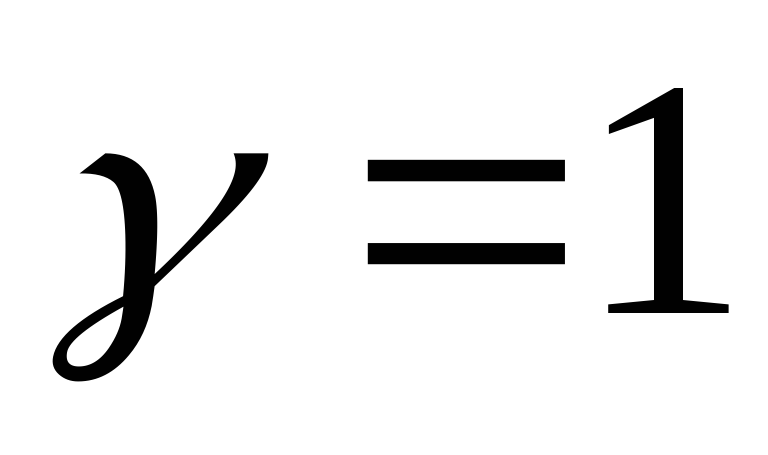 .
Таким образом,
.
Таким образом,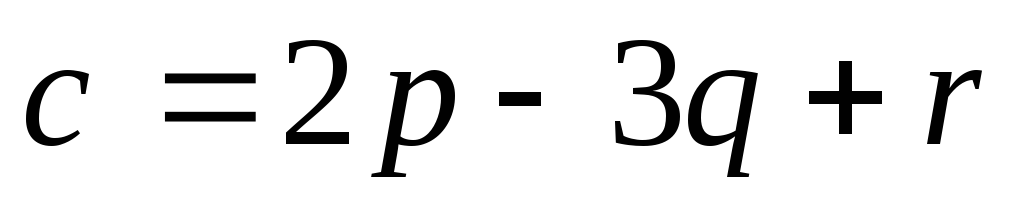 .
.
Определение. Скалярным произведениемдвух
ненулевых векторов  и
и 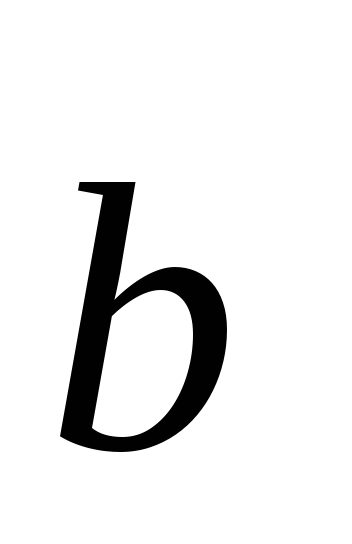 называется число (скаляр), равное
произведению длин этих векторов на
косинус угла между ними, т. е.
называется число (скаляр), равное
произведению длин этих векторов на
косинус угла между ними, т. е.
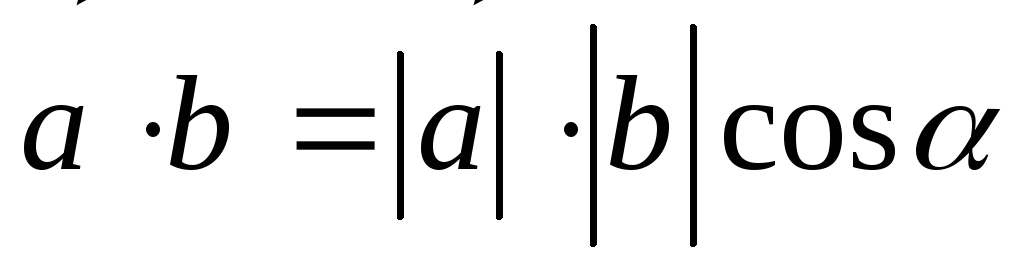 ,
(2.16)
,
(2.16)
где 
угол между векторами
угол между векторами  и
и 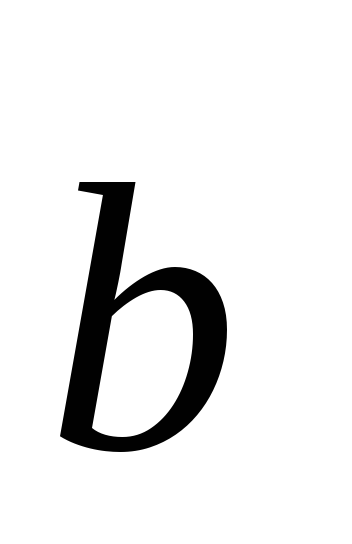 .
.
Если
хотя бы один из векторов  или
или 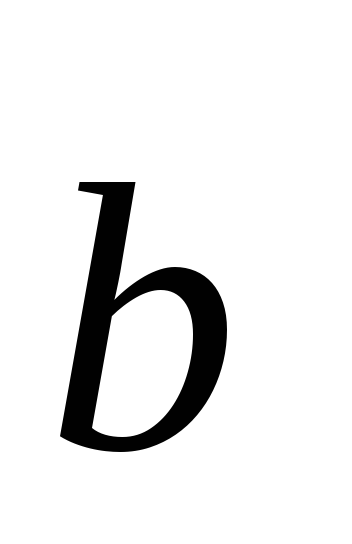
нулевой, то угол между векторами не
определен, и скалярное произведение
полагается равным нулю.
нулевой, то угол между векторами не
определен, и скалярное произведение
полагается равным нулю.
Проекцию
вектора 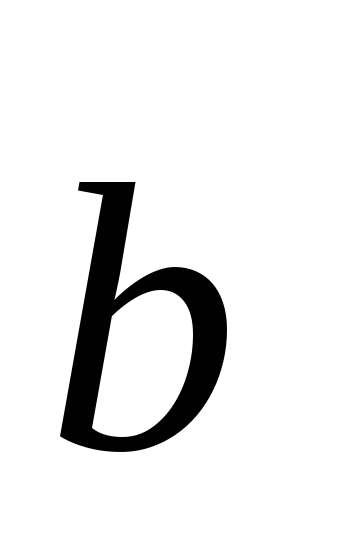 на ось, определяемую вектором
на ось, определяемую вектором  ,
обозначим
,
обозначим 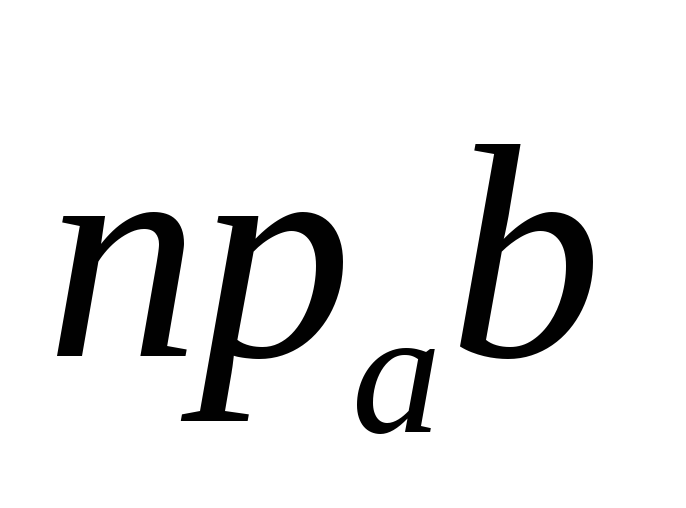 .
По определению проекции вектора на ось
имеем:
.
По определению проекции вектора на ось
имеем: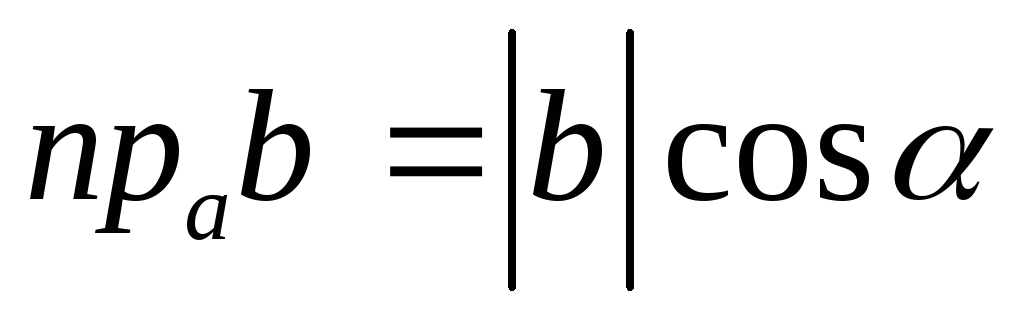 .
Тогда скалярное произведение двух
ненулевых векторов
.
Тогда скалярное произведение двух
ненулевых векторов  и
и 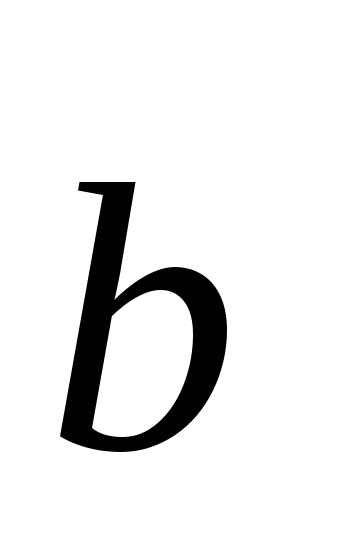 определяется формулой
определяется формулой
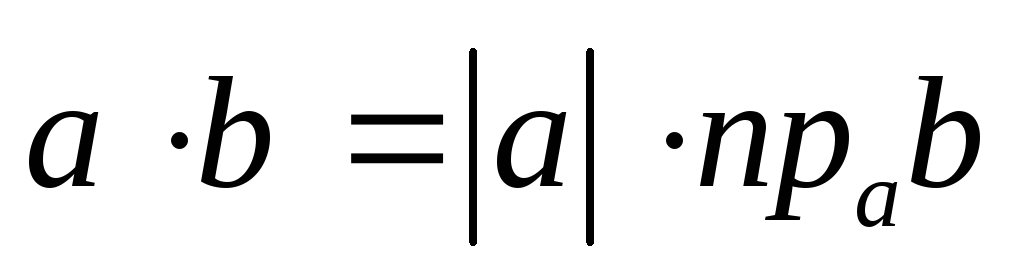 .
(2.17)
.
(2.17)
Учитывая,
что в определении скалярного произведения
векторы  и
и 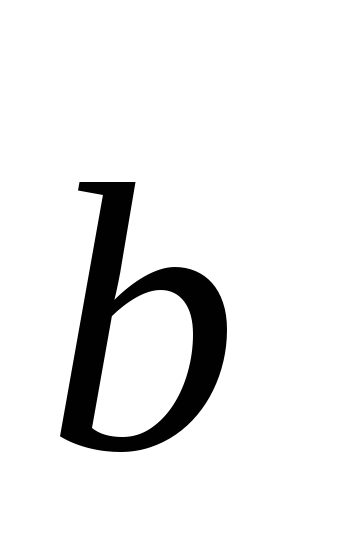 взаимозаменяемые, его можно представить
в виде
взаимозаменяемые, его можно представить
в виде
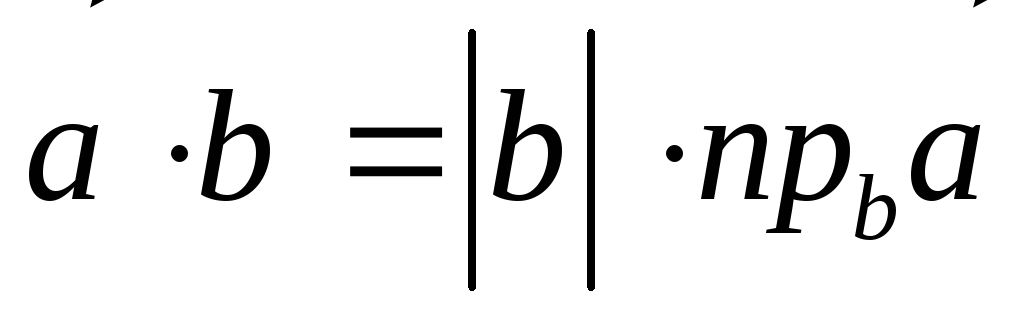 .
(2.18)
.
(2.18)
Соотношения (2.17) и (2.18) позволяют сформулировать другое определение скалярного произведения.
Определение. Скалярным произведениемдвух
ненулевых векторов  и
и 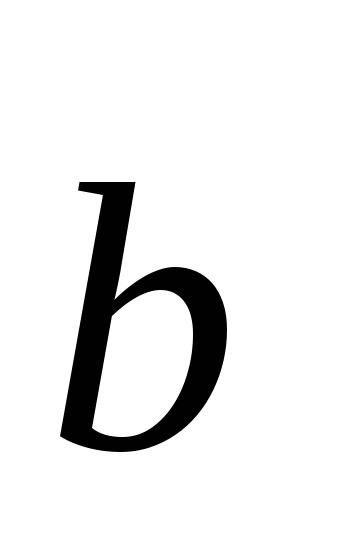 называется число (скаляр), равное
произведению длины одного из этих
векторов на проекцию другого вектора
на ось, определяемую первым из указанных
векторов.
называется число (скаляр), равное
произведению длины одного из этих
векторов на проекцию другого вектора
на ось, определяемую первым из указанных
векторов.
Физический
смысл скалярного произведения заключается
в следующем: если точка приложения силы,
задаваемой постоянным вектором 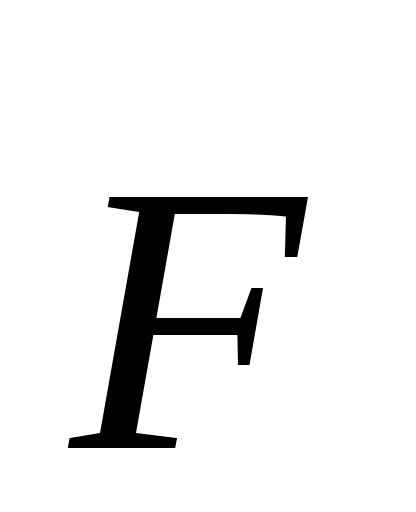 ,
перемещается вдоль вектора
,
перемещается вдоль вектора  ,
то работа этой силы определяется
равенством
,
то работа этой силы определяется
равенством 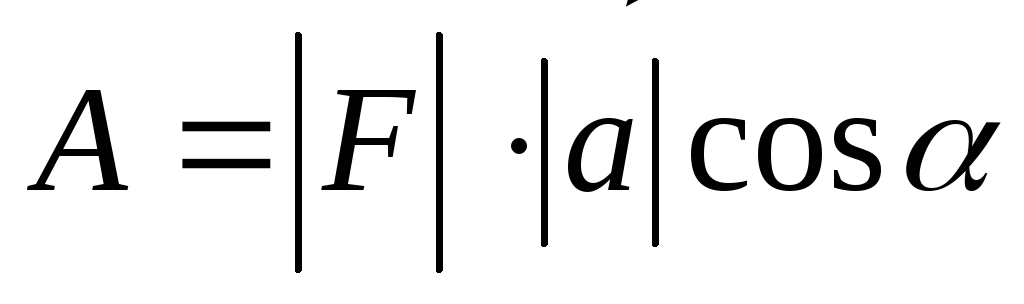 ,
где
,
где
угол между векторами
угол между векторами  и
и 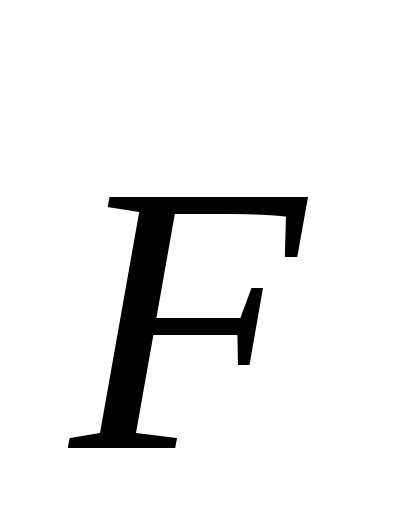 ,
т. е. работа равна скалярному произведению
векторов
,
т. е. работа равна скалярному произведению
векторов  и
и 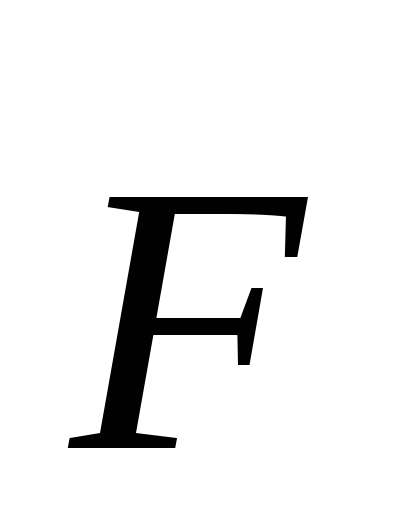 .
.
Теорема 8. Необходимым и достаточным условием ортогональности (перпендикулярности) двух векторов является равенство нулю их скалярного произведения.
Доказательство.
Необходимость. Пусть
векторы  и
и 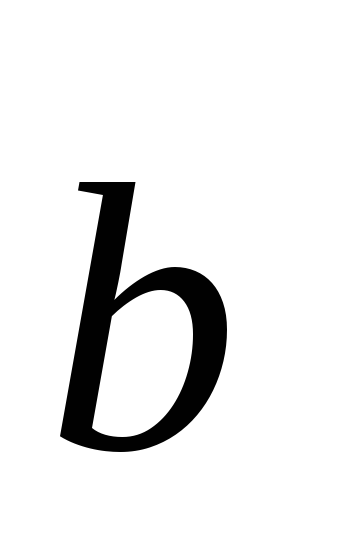 ортогональны,
ортогональны,
угол между ними, тогда
угол между ними, тогда 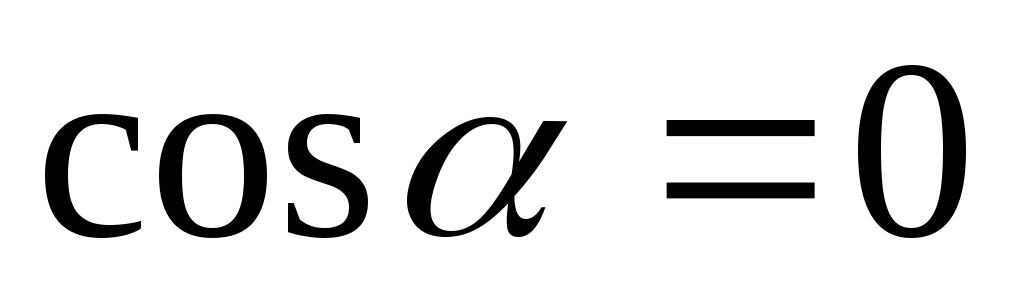 ,
и в силу формулы (2.16)
,
и в силу формулы (2.16)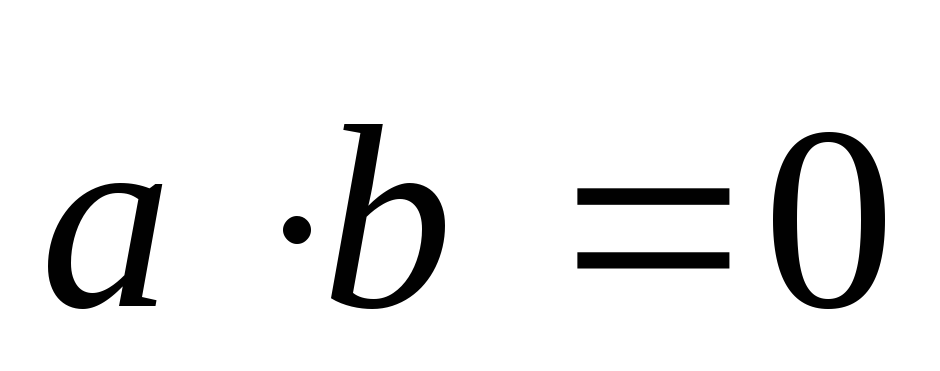 .
.
Достаточность. Пусть 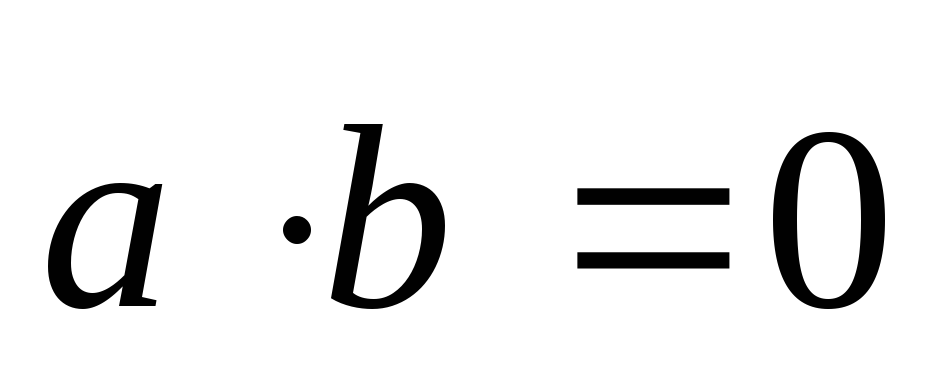 .
Докажем, что векторы
.
Докажем, что векторы  и
и 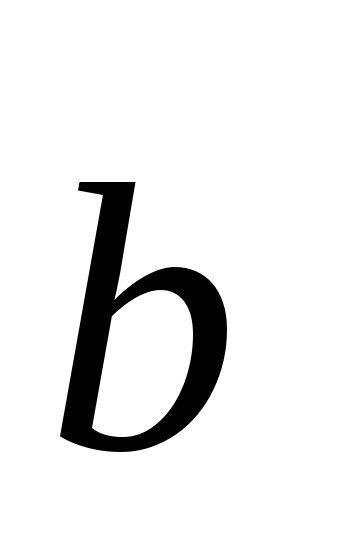 ортогональны. Если хотя бы один из
векторов равен нулевому вектору, то он
имеет неопределенное направление, и
можно считать, что векторы ортогональны.
Если оба вектора
ортогональны. Если хотя бы один из
векторов равен нулевому вектору, то он
имеет неопределенное направление, и
можно считать, что векторы ортогональны.
Если оба вектора  и
и 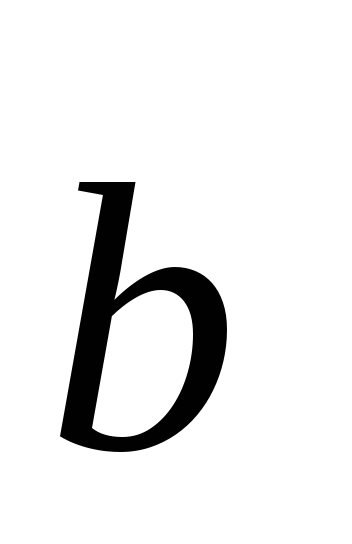 ненулевые, то
ненулевые, то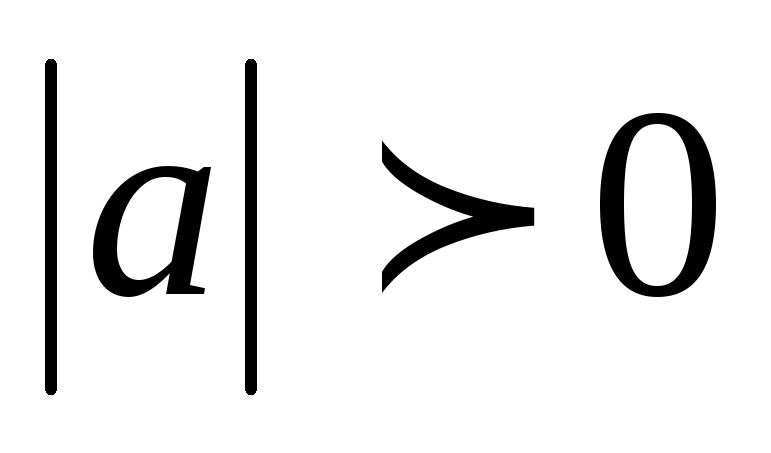 ,
,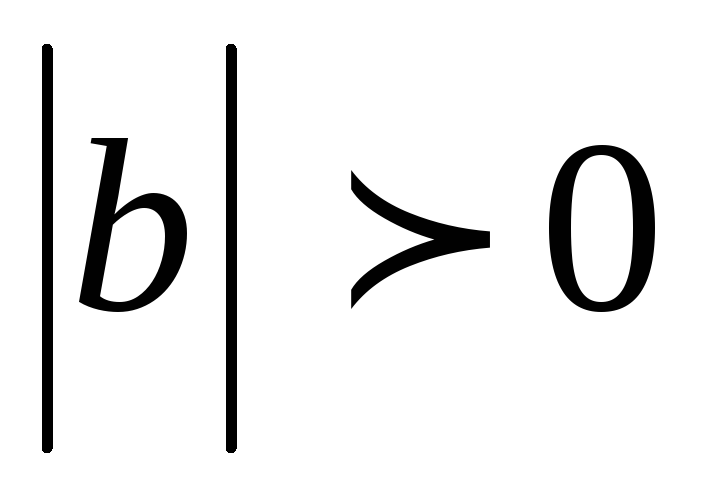 ,
поэтому из (2.16) следует, что
,
поэтому из (2.16) следует, что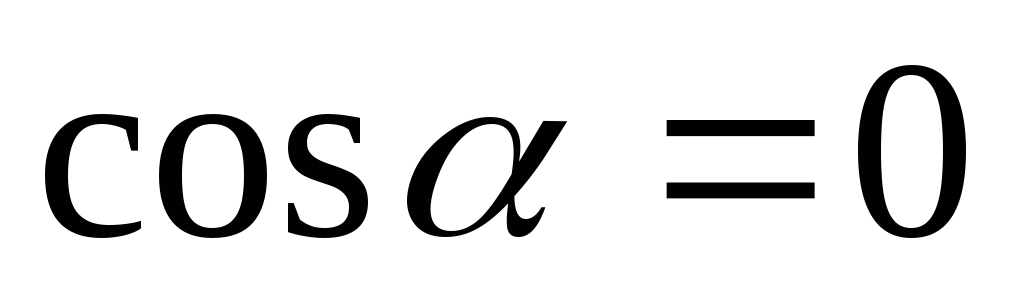 ,
т, е. векторы
,
т, е. векторы  и
и 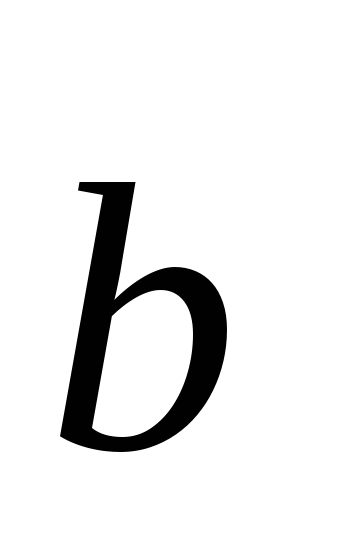 ортогональны. Теорема доказана.
ортогональны. Теорема доказана.
Если
два вектора привести к общему началу,
то в качестве угла  между этими векторами можно взять любой
из углов
между этими векторами можно взять любой
из углов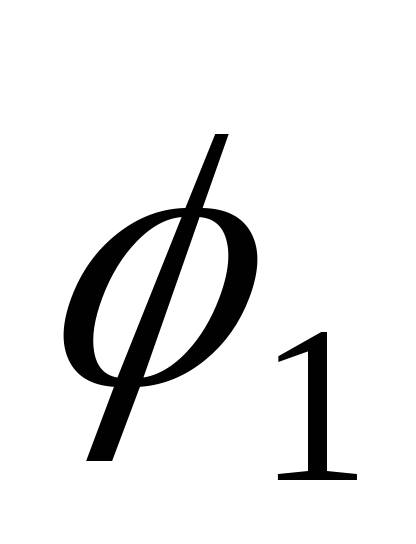 или
или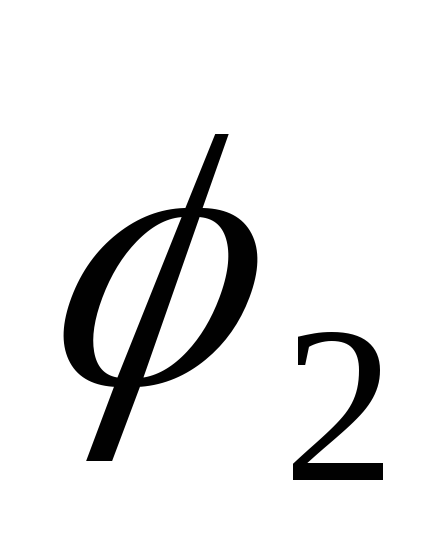 .
.
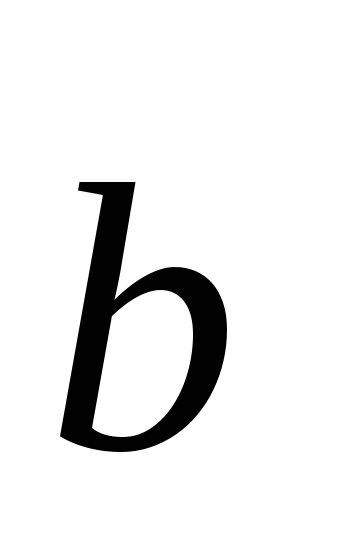
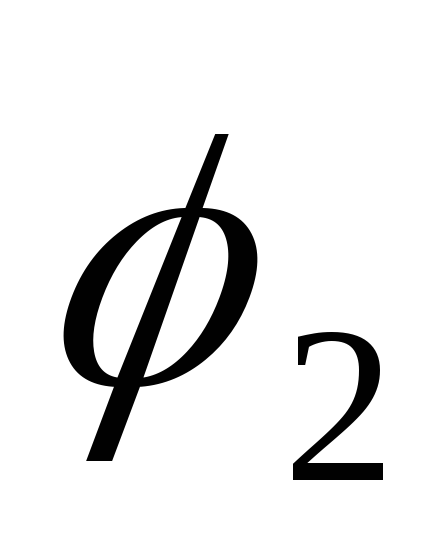

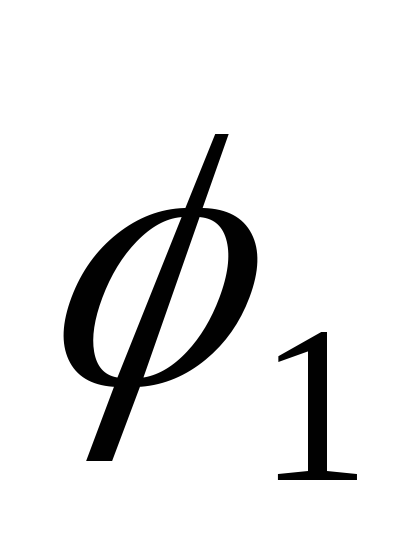



Действительно,
сумма углов 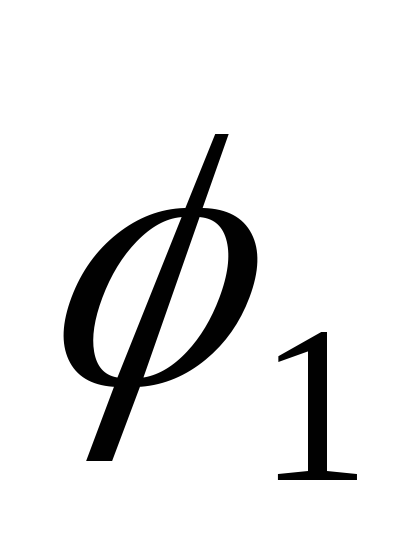 и
и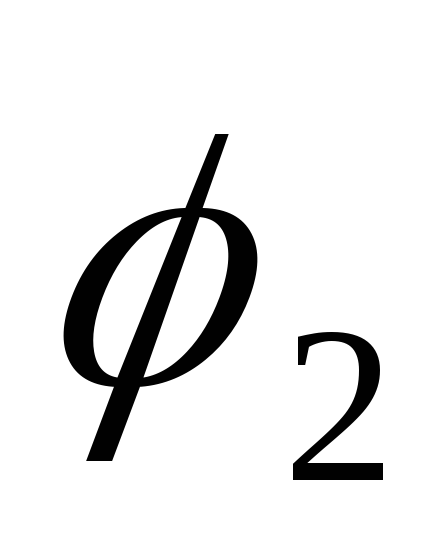 равна
равна ,
поэтому
,
поэтому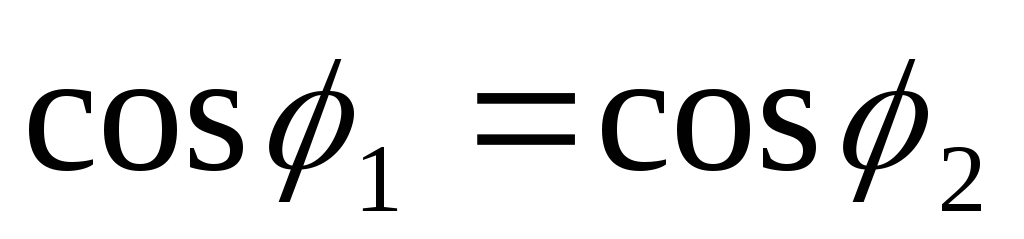 .
В определение скалярного произведения
входит сомножителем только косинус
угла между векторами. Из двух углов
.
В определение скалярного произведения
входит сомножителем только косинус
угла между векторами. Из двух углов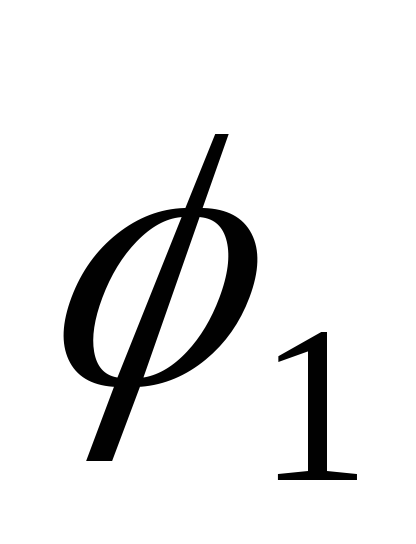 и
и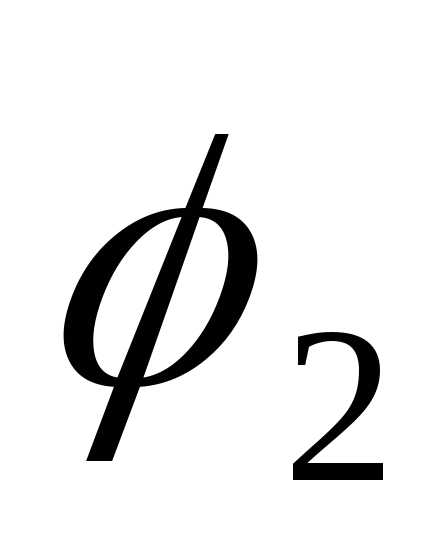 между векторами один всегда не более
между векторами один всегда не более .
За угол
.
За угол между векторами принимается наименьший
из углов
между векторами принимается наименьший
из углов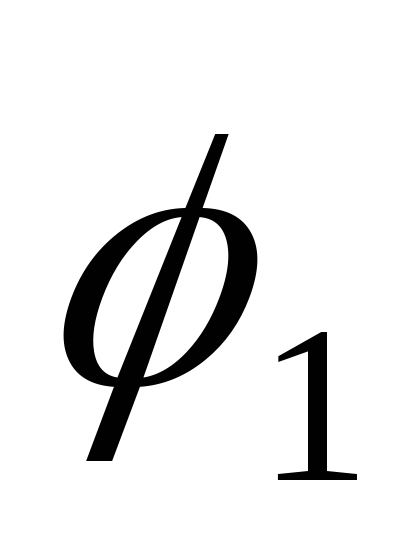 и
и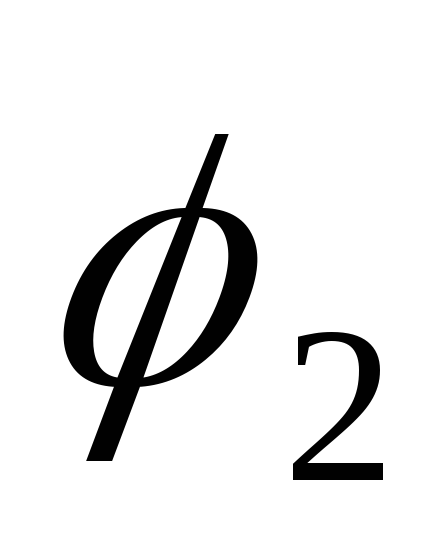 ,
т. е.
,
т. е.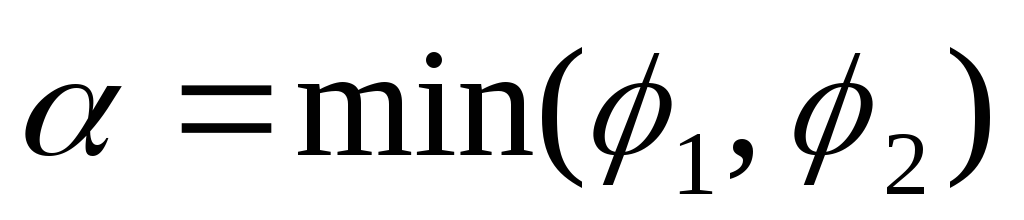 .
.
Если
скалярное произведение двух ненулевых
неколлинеарных векторов  и
и 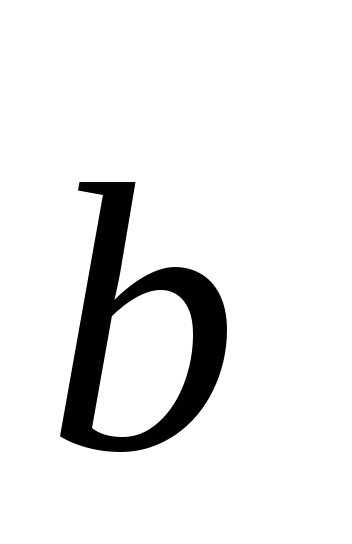 положительно (отрицательно), то эти два
вектора составляют острый (тупой) угол.
положительно (отрицательно), то эти два
вектора составляют острый (тупой) угол.
Свойства скалярного произведения:
 .
.
Доказательство. Это свойство непосредственно вытекает
из определения скалярного произведения: 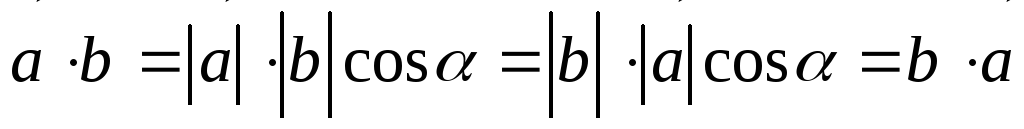 .
Свойство доказано.
.
Свойство доказано.
 .
.
Доказательство. Для доказательства этого свойства
воспользуемся формулой (2.18) для определения
скалярного произведения и свойствами
проекций векторов на ось: 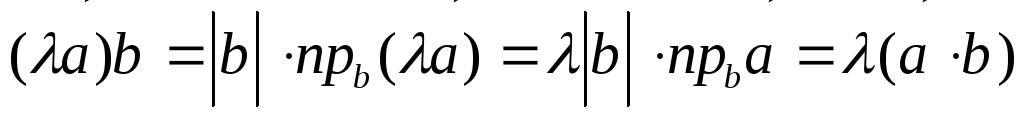 .
Свойство доказано.
.
Свойство доказано.
 .
.
Доказательство. Воспользуемся
формулой (2.18) для определения скалярного
произведения и свойствами проекций
векторов на ось. Получим: 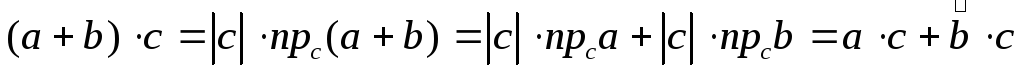 .
Свойство доказано.
.
Свойство доказано.
 ,
если
,
если  ,
и
,
и ,
если
,
если .
.
Доказательство. Из определения скалярного произведения
с использованием соотношения (2.16)
следует, что 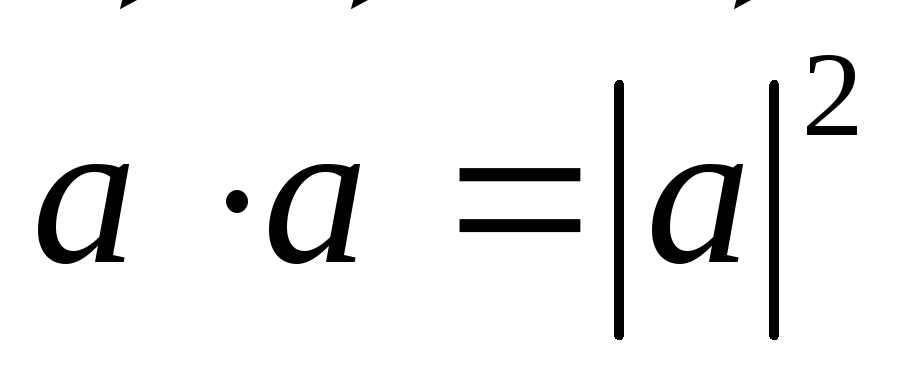 .
Если
.
Если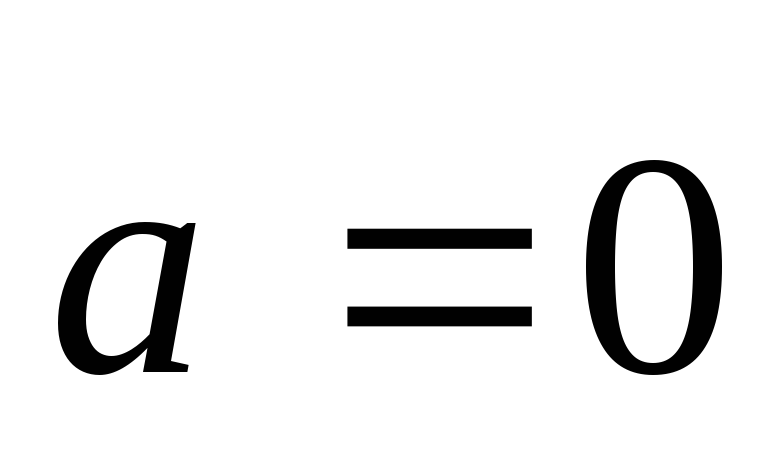 ,
то
,
то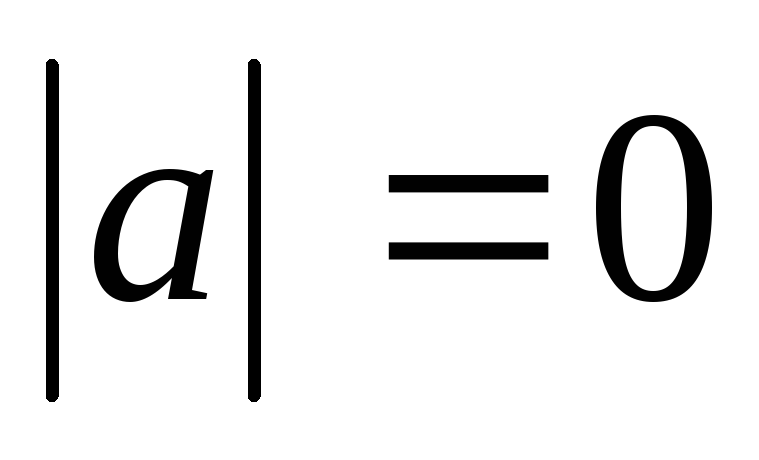 и
и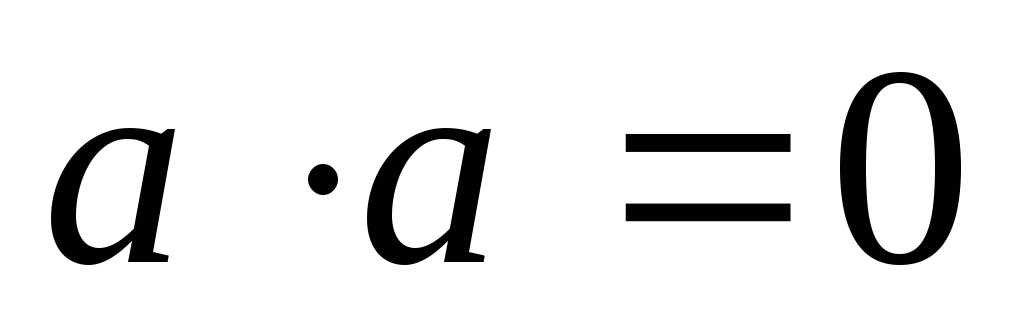 .
Если же
.
Если же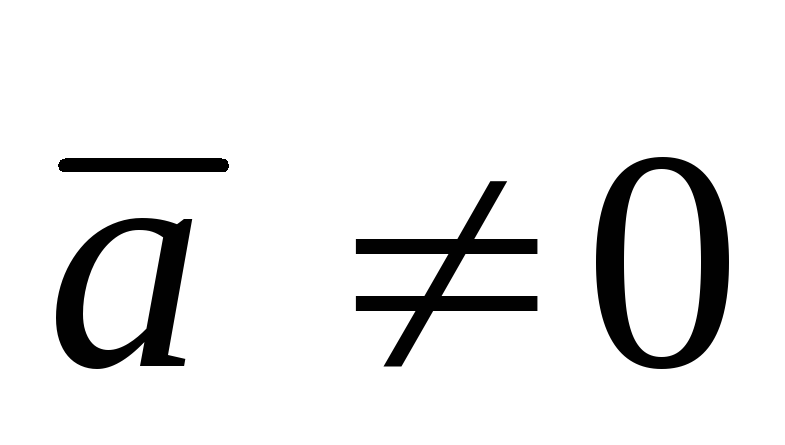 ,
то
,
то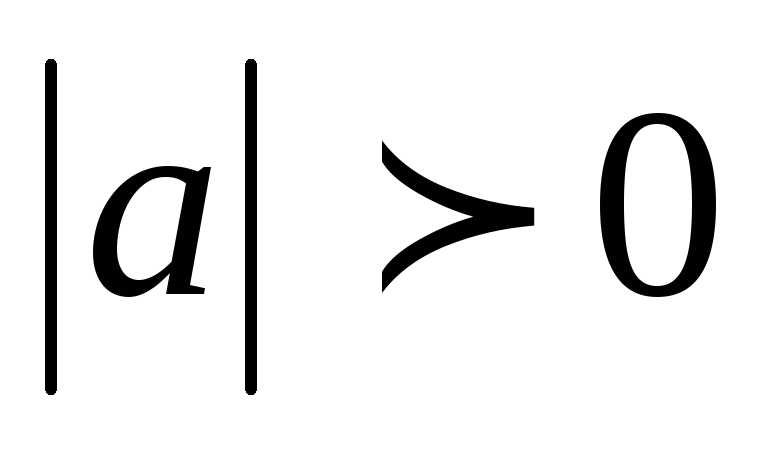 ,
поэтому
,
поэтому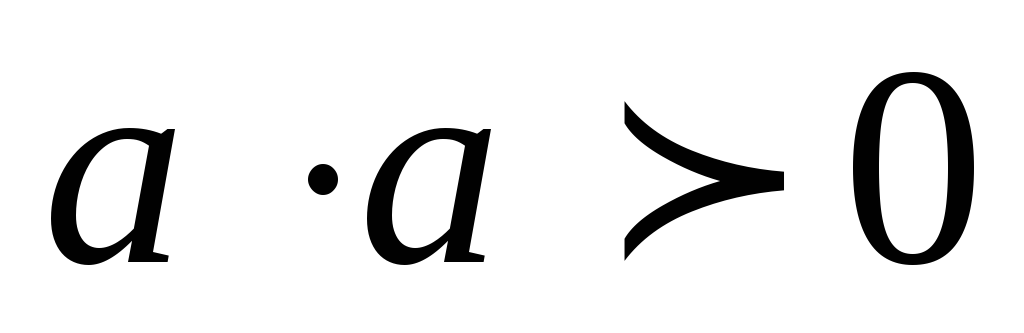 .
Свойство доказано.
.
Свойство доказано.
Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, не учитывая порядок векторных сомножителей и сочетая числовые множители.
Из
определения и свойств скалярного
произведения векторов следует, что для
базисных векторов 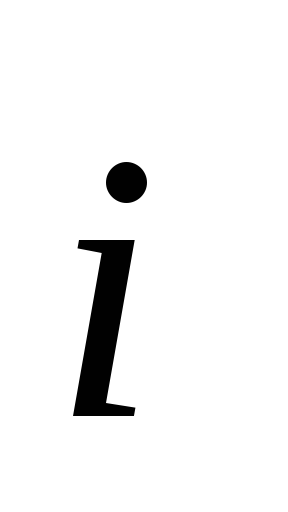 ,
,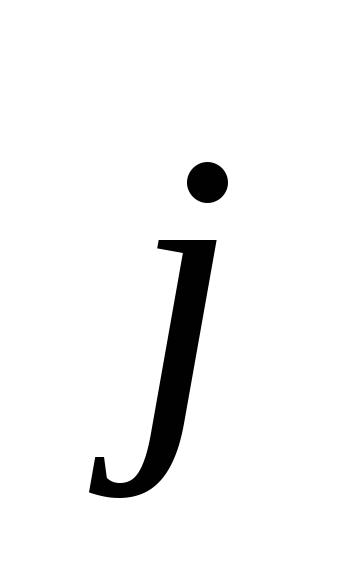 ,
, выполняются соотношения
выполняются соотношения
 ;
(2.19)
;
(2.19) .
(2.20)
.
(2.20)
Теорема 9. Если векторы  и
и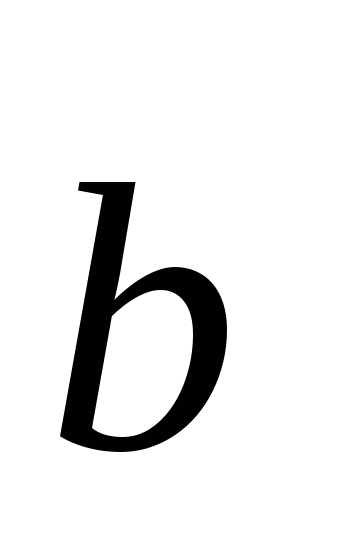 заданы своими координатами, т. е.
заданы своими координатами, т. е.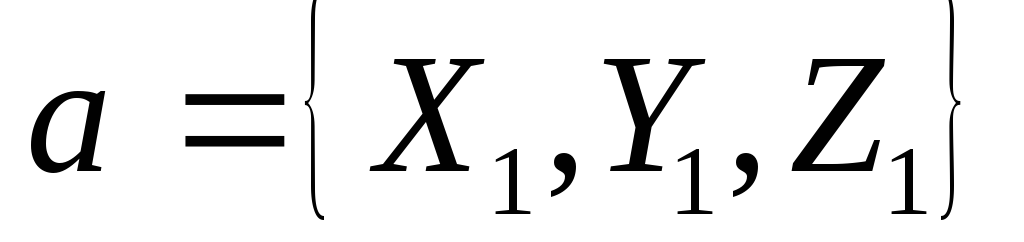 ,
,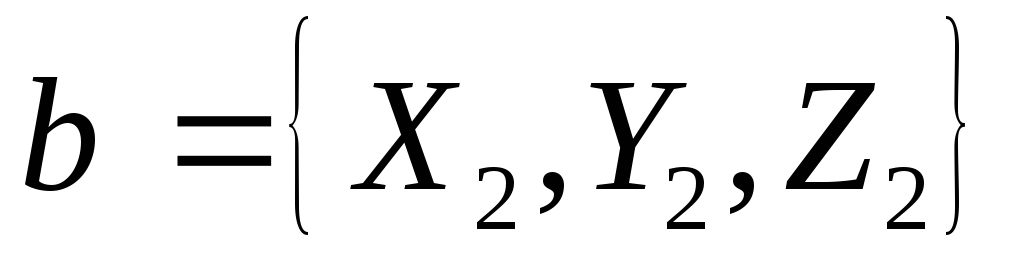 ,
то скалярное произведение векторов
,
то скалярное произведение векторов и
и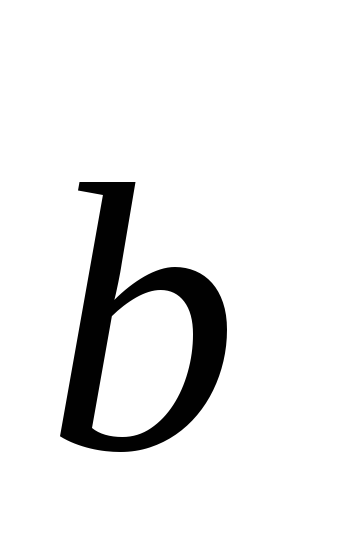 вычисляется по формуле
вычисляется по формуле
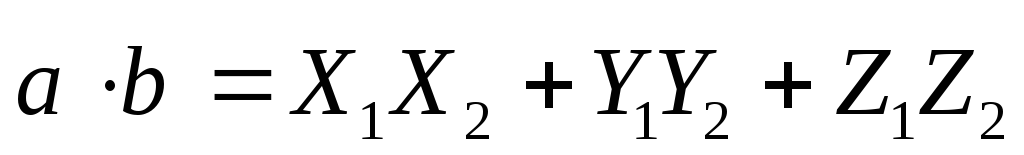 .
(2.21)
.
(2.21)
Доказательство. Разложим векторы  и
и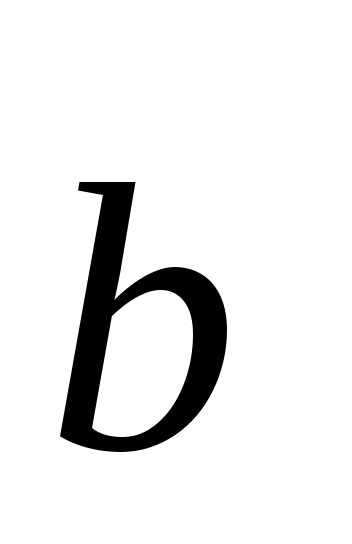 по базису
по базису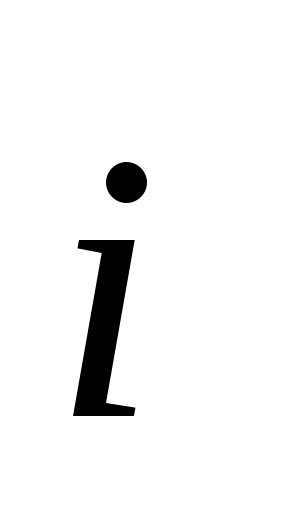 ,
,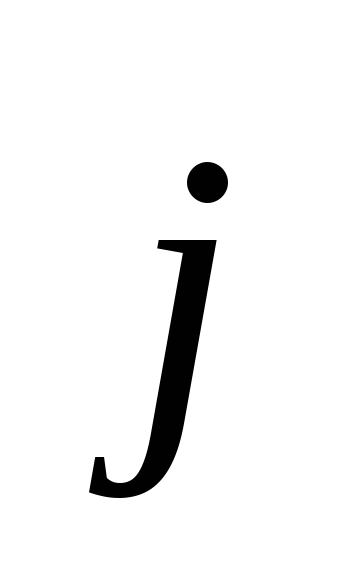 ,
, ,
получим
,
получим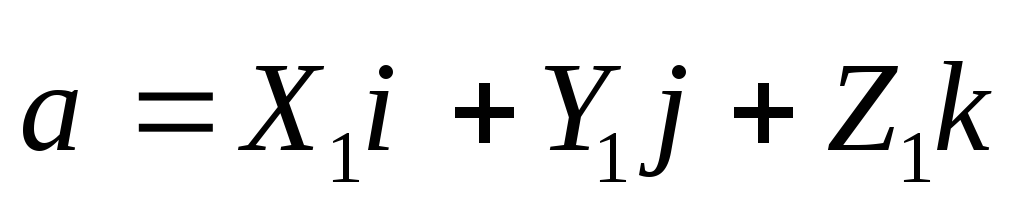 ,
,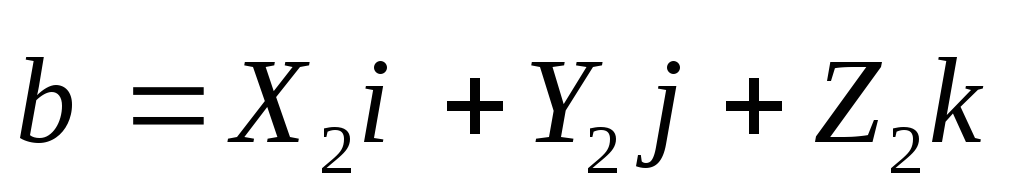 .
Тогда по свойствам скалярного произведения
векторов, используя формулы (2.19), (2.20),
имеем
.
Тогда по свойствам скалярного произведения
векторов, используя формулы (2.19), (2.20),
имеем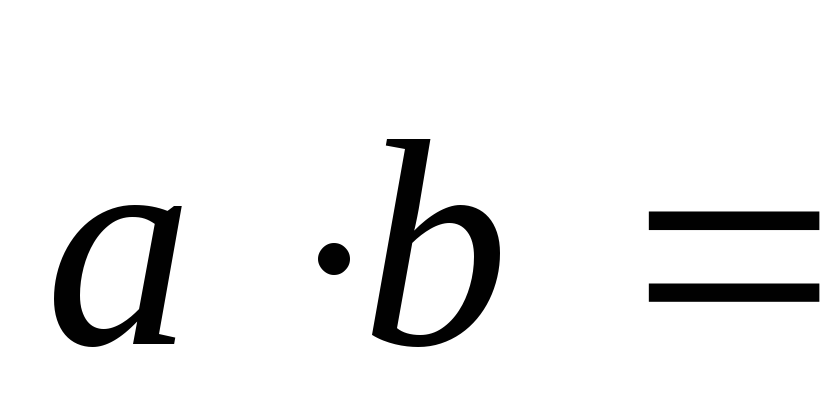
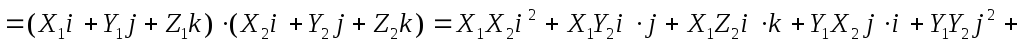
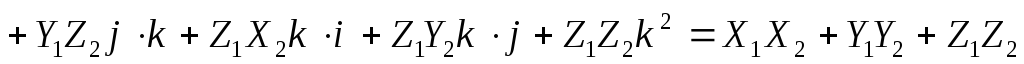 .
Теорема доказана.
.
Теорема доказана.
Следствие. Угол  между ненулевыми векторами
между ненулевыми векторами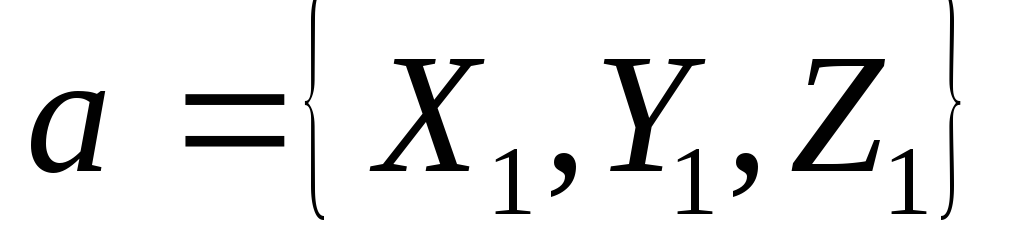 и
и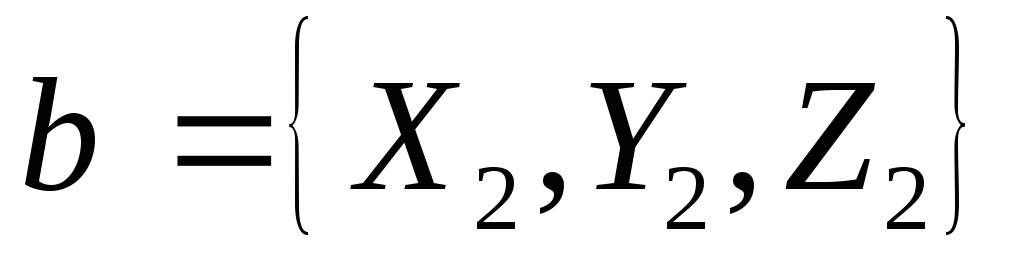 определяется по формуле
определяется по формуле
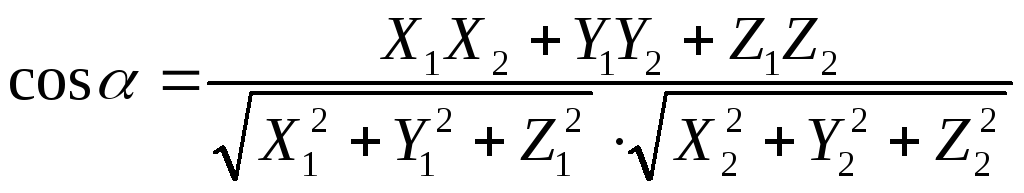 .
(2.22)
.
(2.22)
Доказательство. По определению
скалярного произведения двух ненулевых
векторов 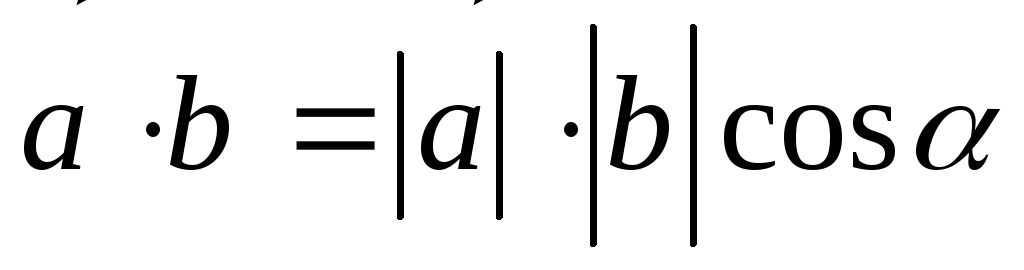 ,
поэтому
,
поэтому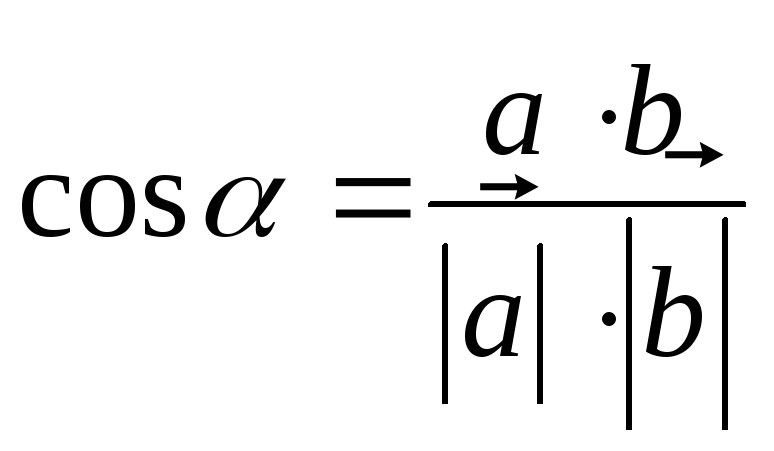 .
Воспользовавшись формулами (2.21) и (2.9)
для скалярного произведения и длин
векторов, заданных своими координатами,
получим формулу (2.22).
.
Воспользовавшись формулами (2.21) и (2.9)
для скалярного произведения и длин
векторов, заданных своими координатами,
получим формулу (2.22).
Замечание. Если один из векторов  или
или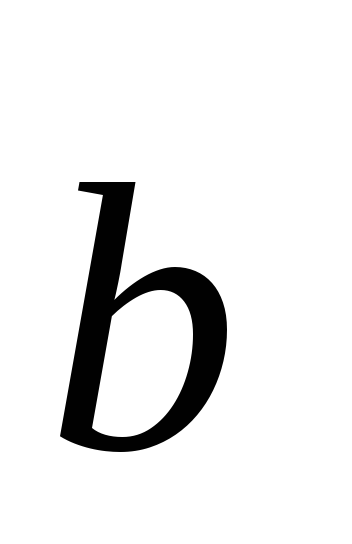 является нулевым, то угол между векторами
определяется неоднозначно и может быть
выбран произвольным.
является нулевым, то угол между векторами
определяется неоднозначно и может быть
выбран произвольным.
П р и м е р 24. Дано, что 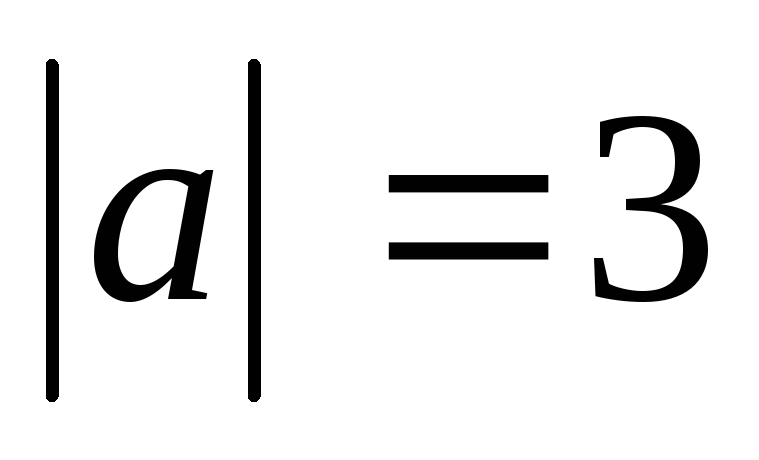 ,
,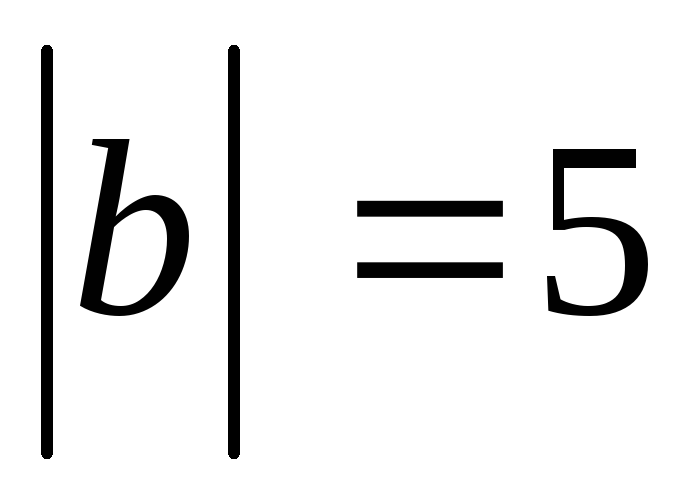 .
Определить, при каком значении
.
Определить, при каком значении векторы
векторы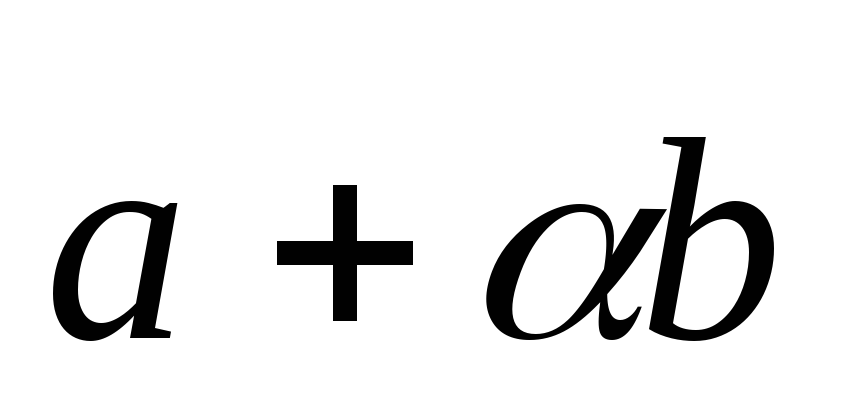 и
и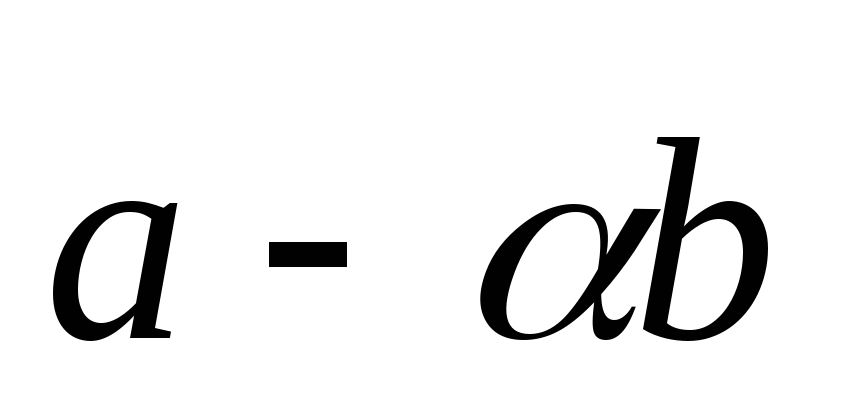 будут взаимно перпендикулярны.
будут взаимно перпендикулярны.
Решение. Условием перпендикулярности векторов
является равенство нулю их скалярного
произведения, т. е. 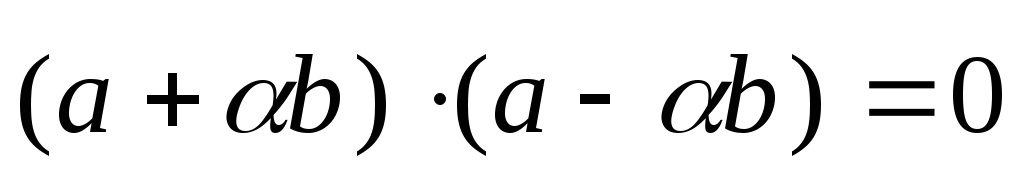 .
По свойствам скалярного произведения
.
По свойствам скалярного произведения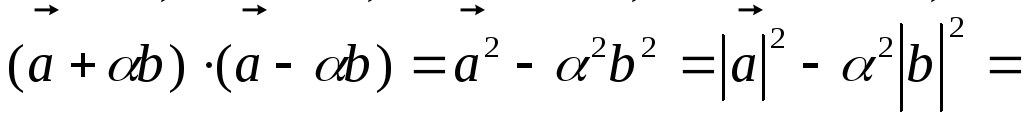
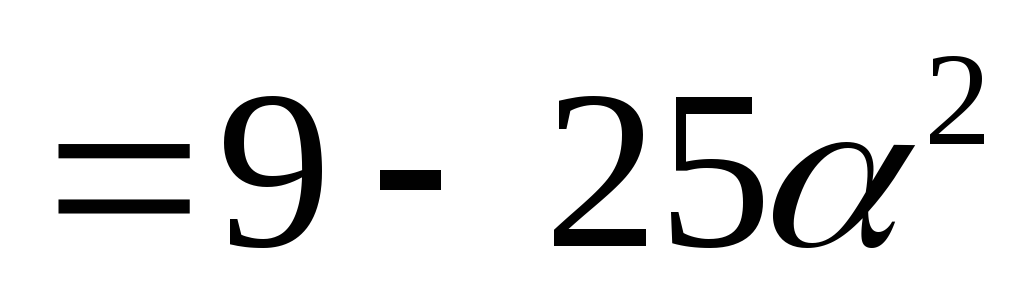 .
Таким образом,
.
Таким образом,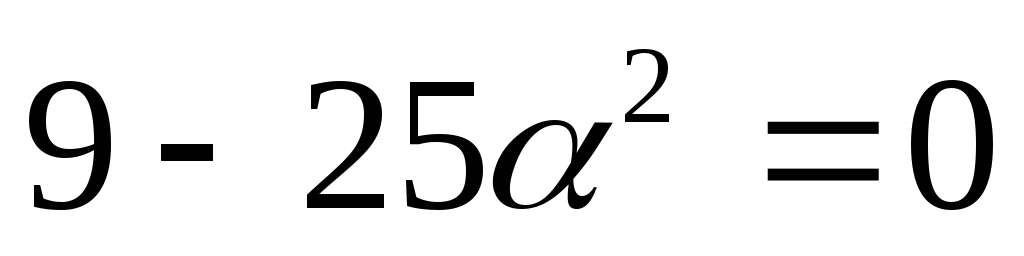 ,
или
,
или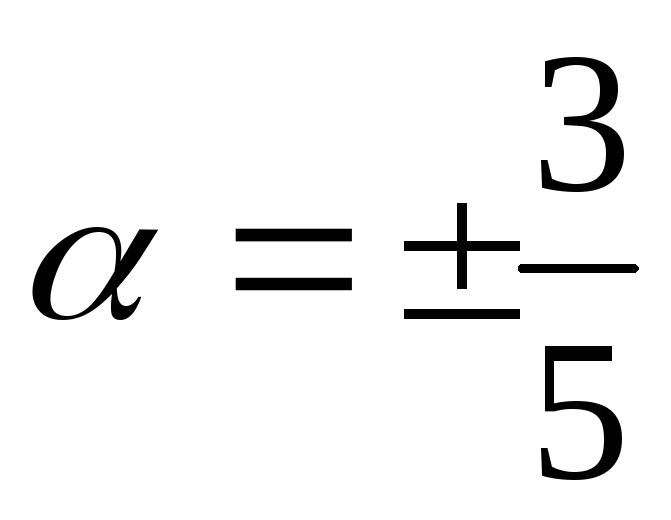 .
.
П р и м е р 25. Векторы  и
и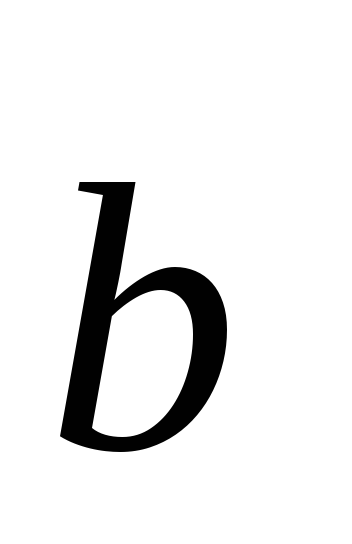 образуют угол
образуют угол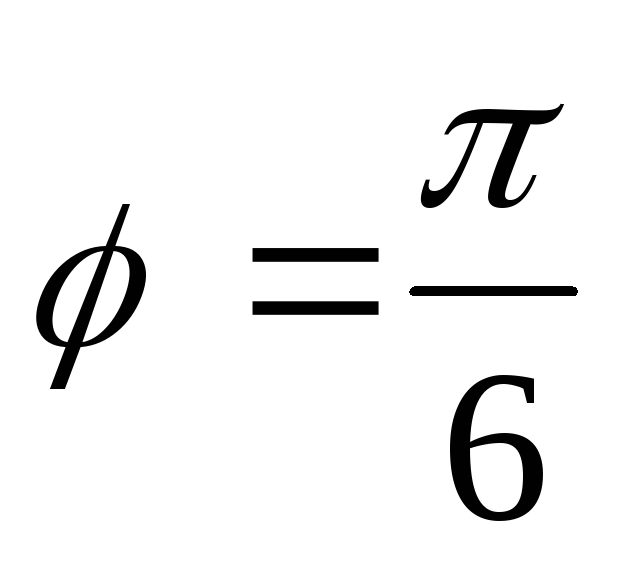 .
Зная, что
.
Зная, что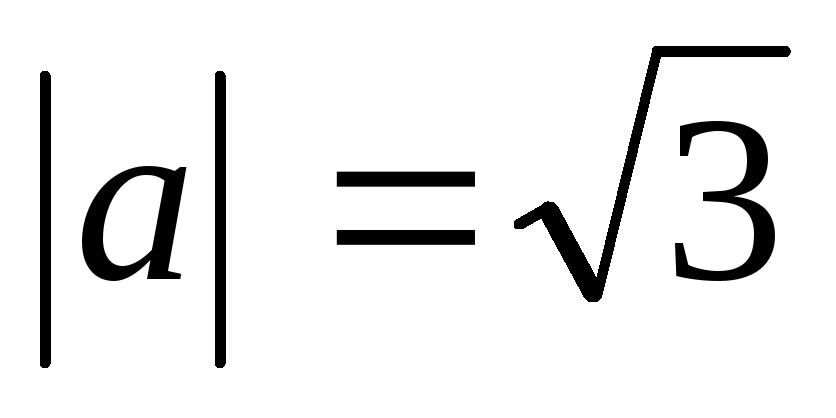 ,
,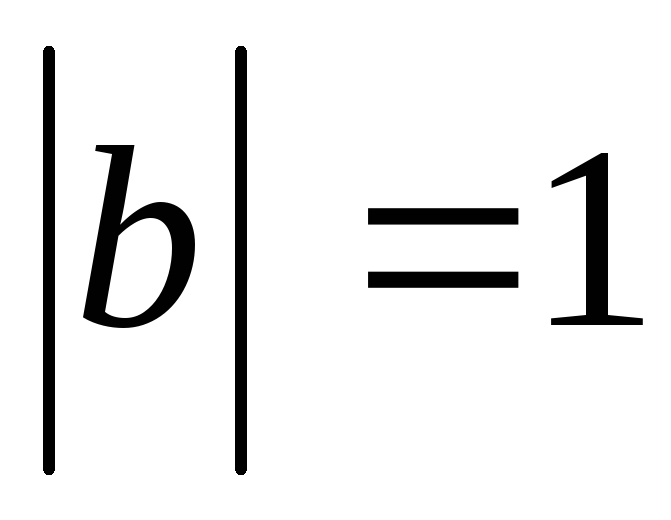 ,
вычислить угол
,
вычислить угол между векторами
между векторами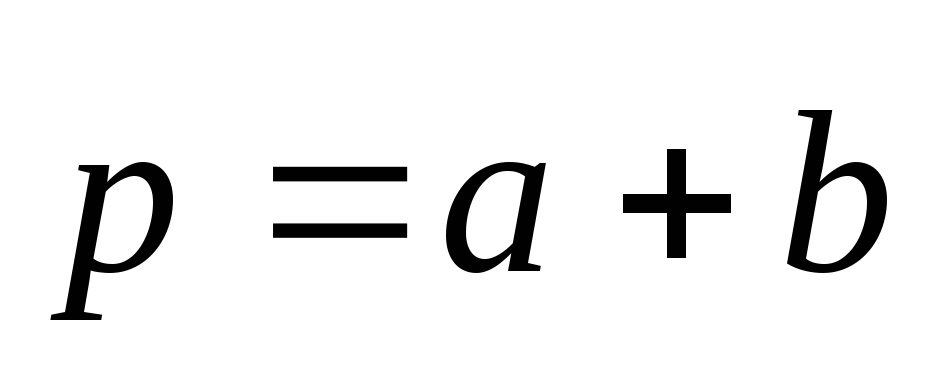 и
и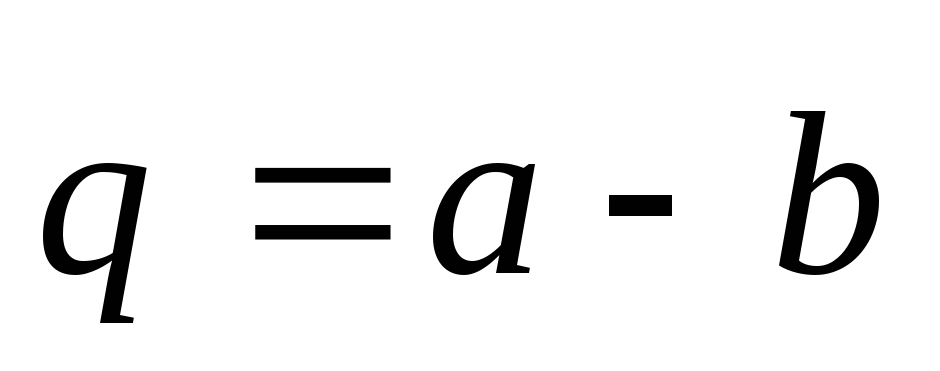 .
.
Решение. Для нахождения косинуса угла  между векторами
между векторами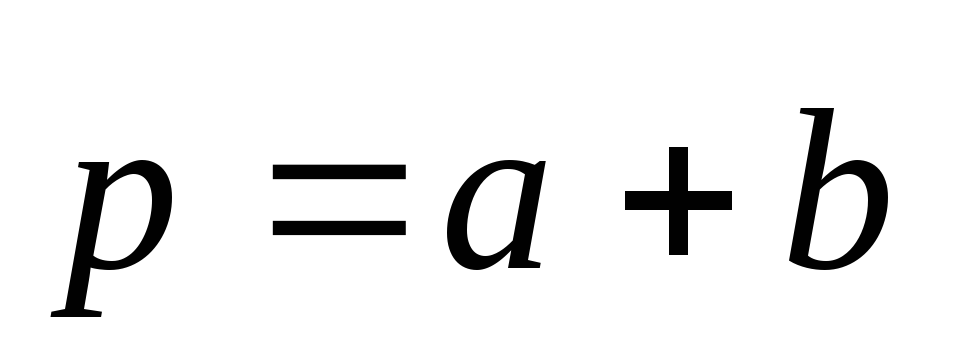 и
и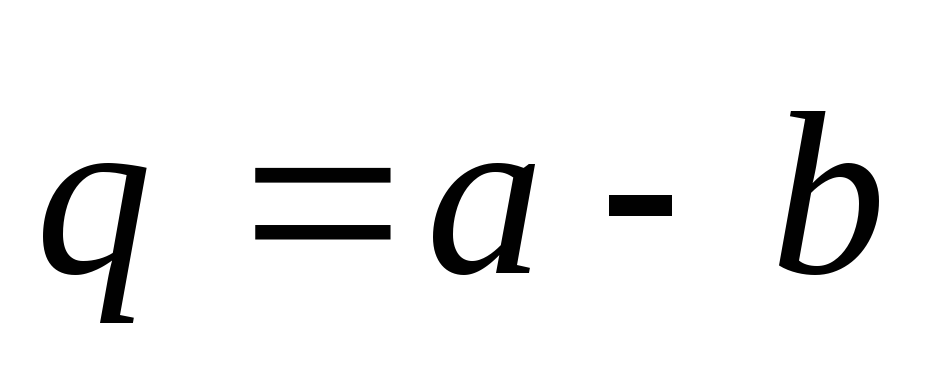 воспользуемся соотношением (2.22). По
формуле (2.21):
воспользуемся соотношением (2.22). По
формуле (2.21):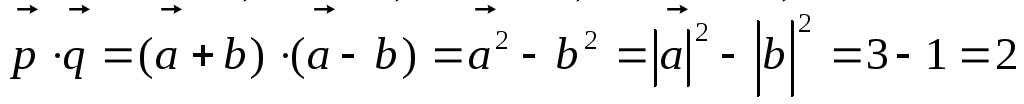 .
Найдем длины векторов
.
Найдем длины векторов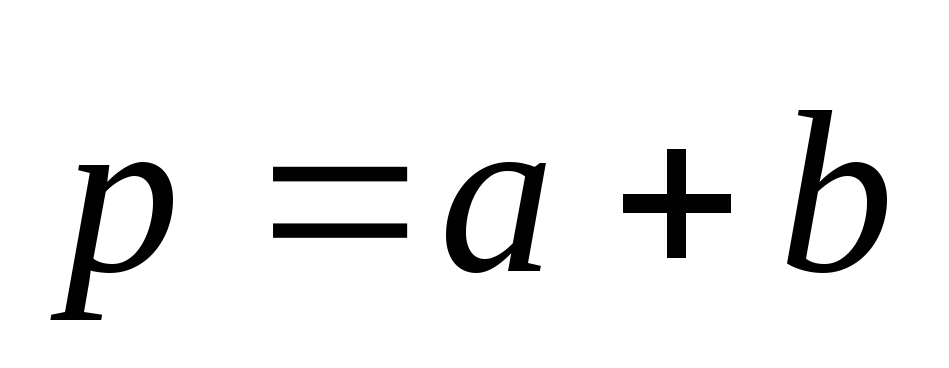 и
и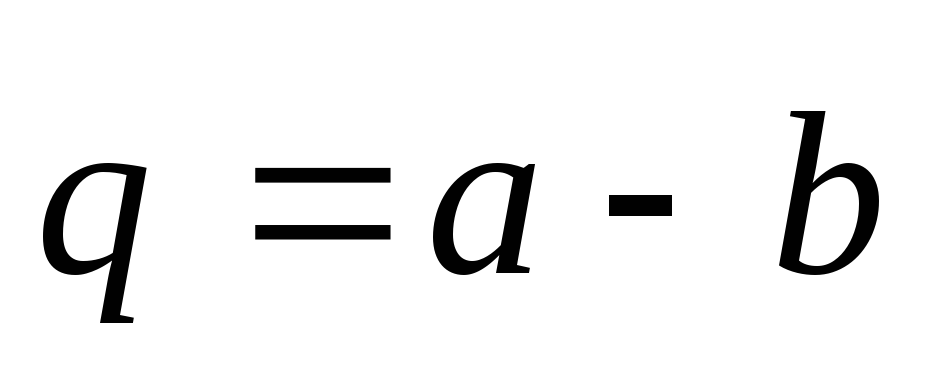 ,
используя свойства скалярного
произведения:
,
используя свойства скалярного
произведения: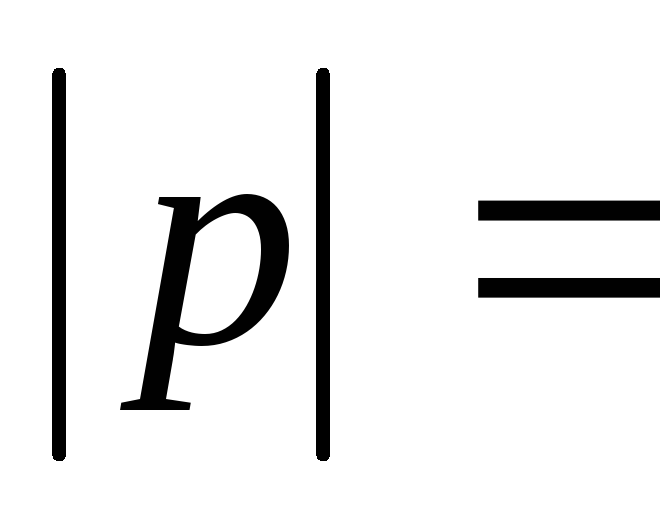
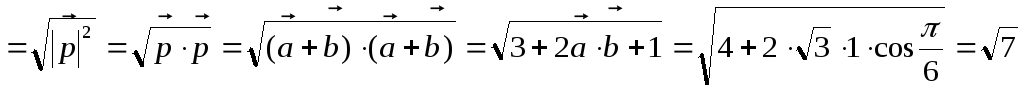 .
Аналогично находим, что
.
Аналогично находим, что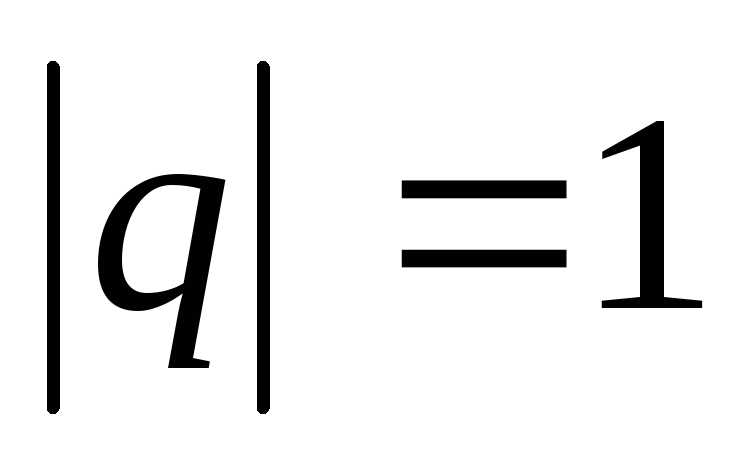 .
Тогда
.
Тогда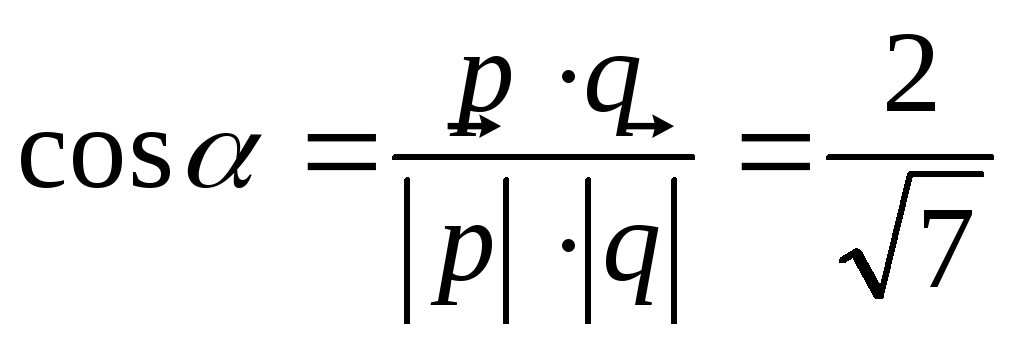 и
и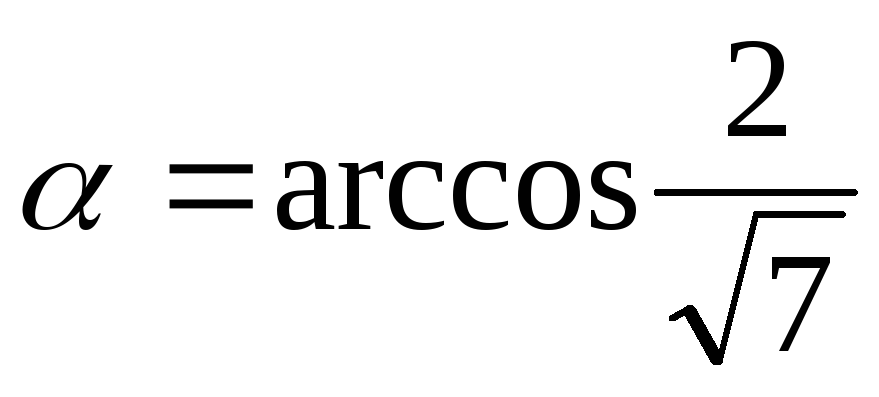 .
.
12. Скалярное произведение. Координатная форма скалярного произведения.
Скалярным
произведением двух векторов  и
и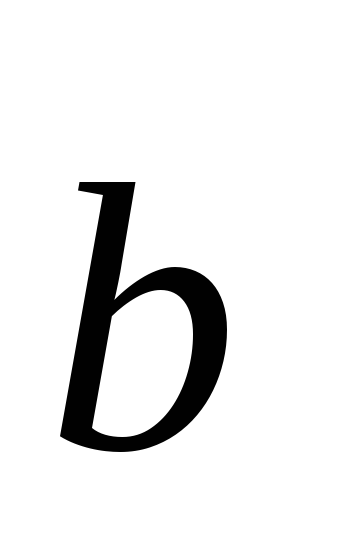 называется
число S =|
называется
число S =| |
|
|
|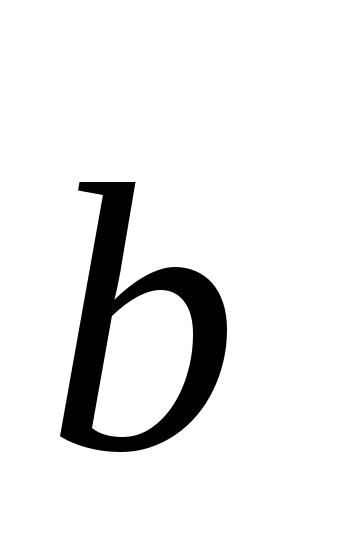 |
сos ().
Эта операция обозначается
|
сos ().
Эта операция обозначается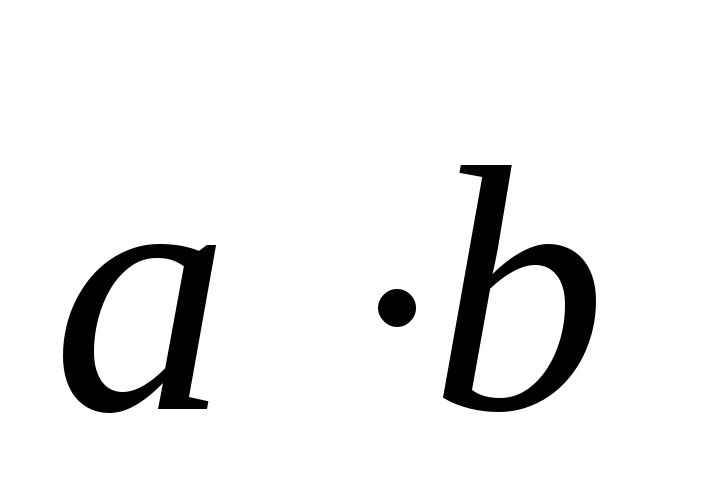 .В
частности, скалярный квадрат вектора
равен квадрату его длины, т.е.
.В
частности, скалярный квадрат вектора
равен квадрату его длины, т.е.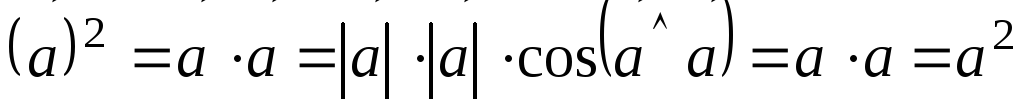 .
Если один из перемножаемых векторов
единичный, то:
.
Если один из перемножаемых векторов
единичный, то:
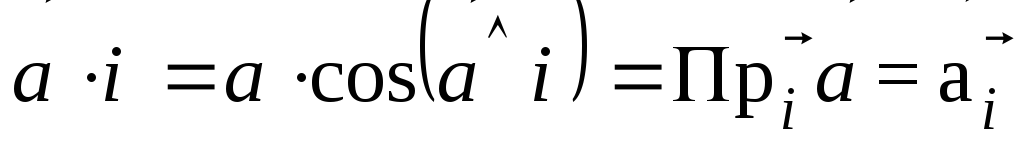 .
.
В этом случае
результат представляет собой проекцию
вектора  на направление единичного вектора
на направление единичного вектора 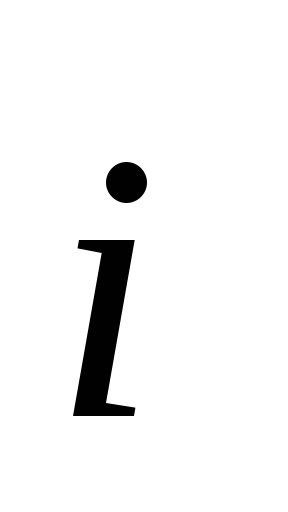 .
Следовательно, любой вектор можно
представить как
.
Следовательно, любой вектор можно
представить как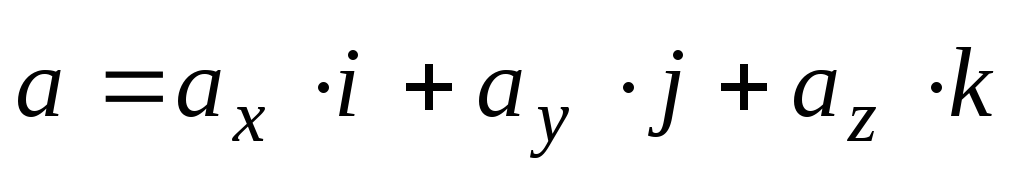 ,
где
,
где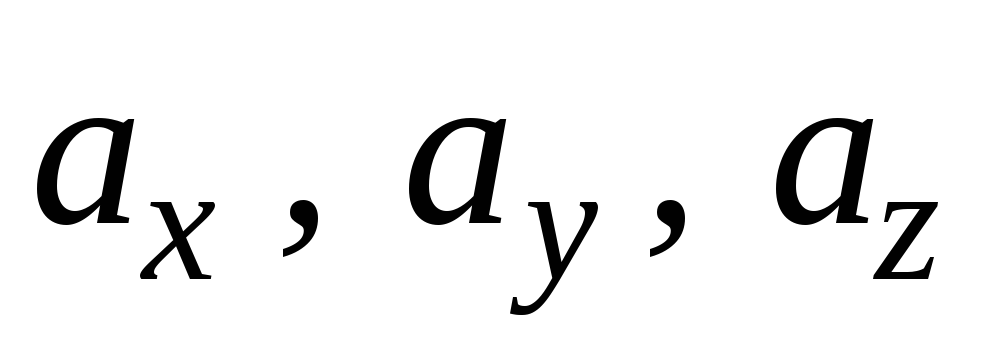 — проекции вектора
— проекции вектора  соответственно на оси 0х, 0у и 0z.
соответственно на оси 0х, 0у и 0z.
Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда
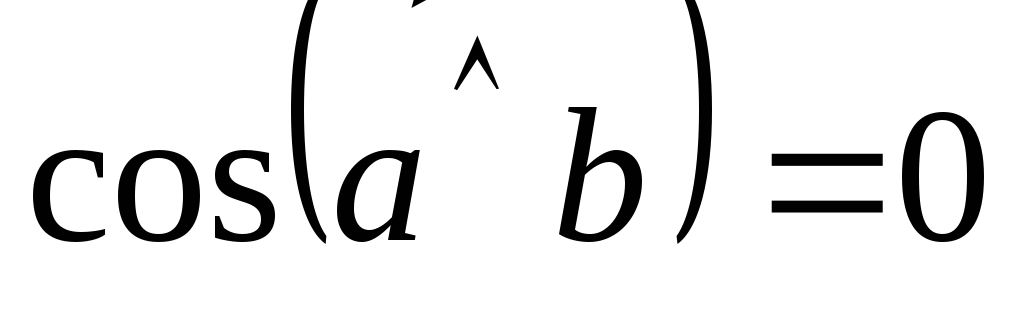 ,
т.е.
,
т.е. 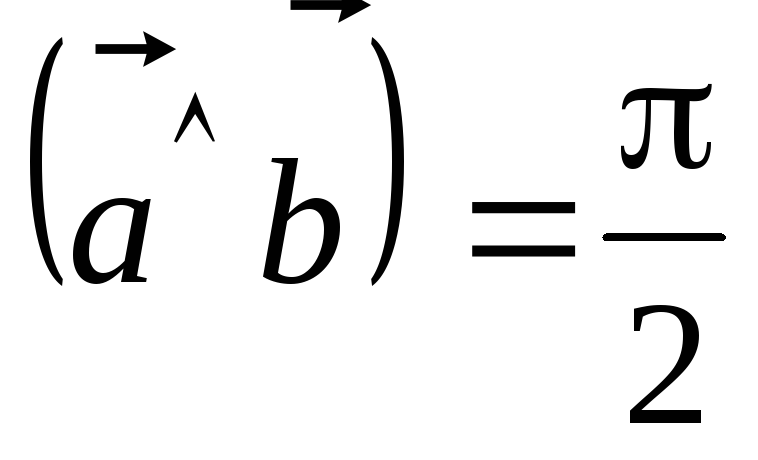 .
.
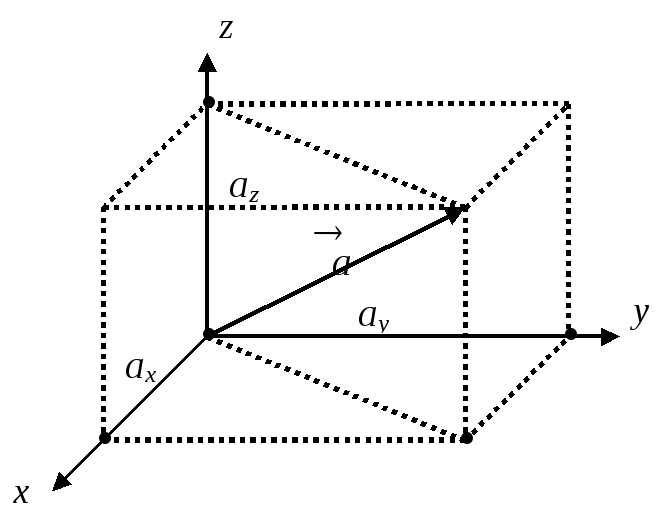
Если вектор
представлен через проекции на базисные
векторы, то говорят о разложении
вектора  по ортогональному базису. Из рисунка
видно, что в этом случае вектор
по ортогональному базису. Из рисунка
видно, что в этом случае вектор  является главной диагональю прямоугольного
параллелепипеда, ребра которого
параллельны осям координат и равны
длинам проекций вектора
является главной диагональю прямоугольного
параллелепипеда, ребра которого
параллельны осям координат и равны
длинам проекций вектора  на эти оси. Из этого же рисунка следует,
что модуль вектора
на эти оси. Из этого же рисунка следует,
что модуль вектора  численно будет равен
численно будет равен
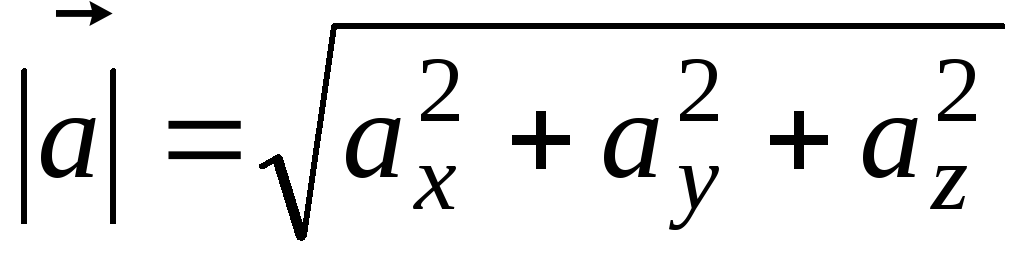 .
.
Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:
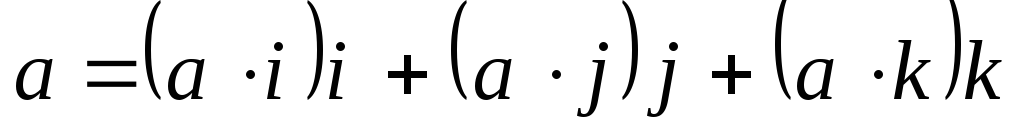 ,
,
где 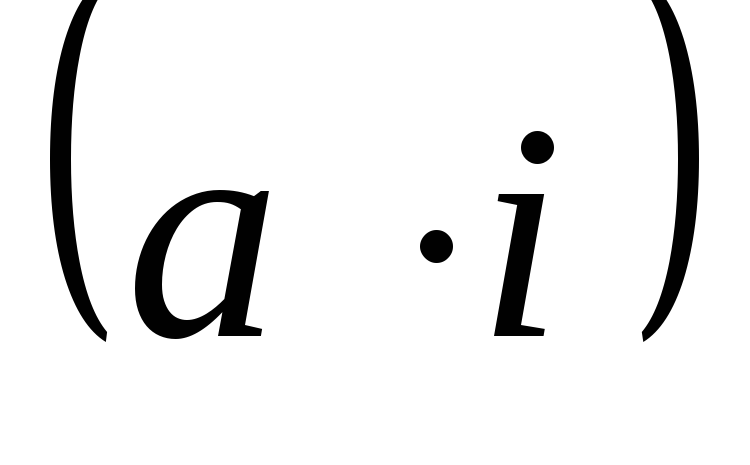 ,
,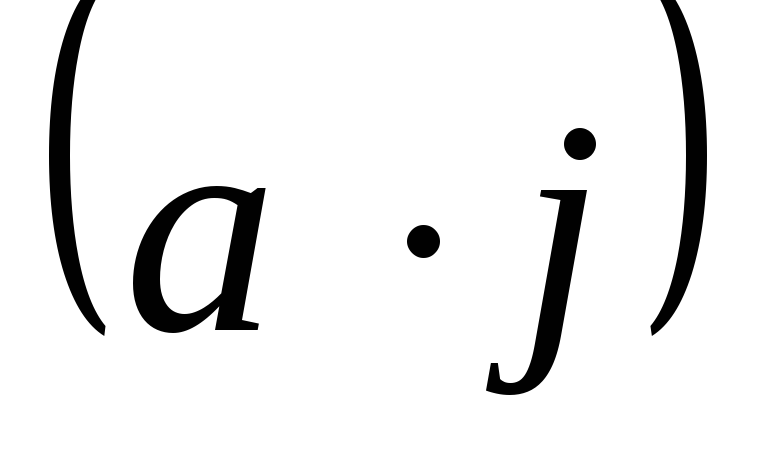 и
и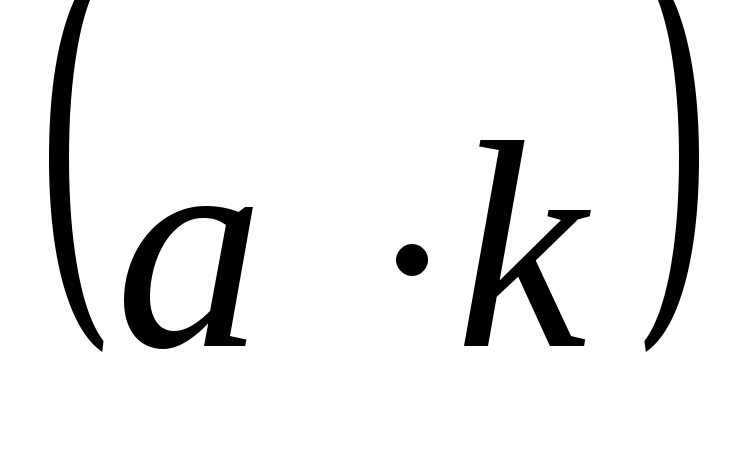 есть
скалярное произведение вектора
есть
скалярное произведение вектора  с ортами осей координат. Тогда из
последнего равенства имеем
с ортами осей координат. Тогда из
последнего равенства имеем
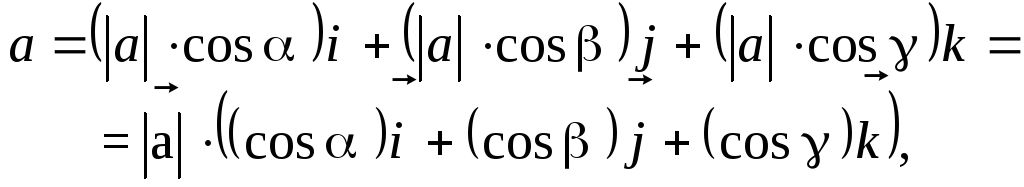
где ,
и
— углы, которые составляет вектор  соответственно
с осями 0х, 0у и 0z.
соответственно
с осями 0х, 0у и 0z.
СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Если скалярное
произведение двух векторов равно нулю,
то эти векторы ортогональны. Действительно,
если ни один из векторов не нулевой, то,
по определению скалярного произведения,
последнее может быть равно нулю только
тогда, когда 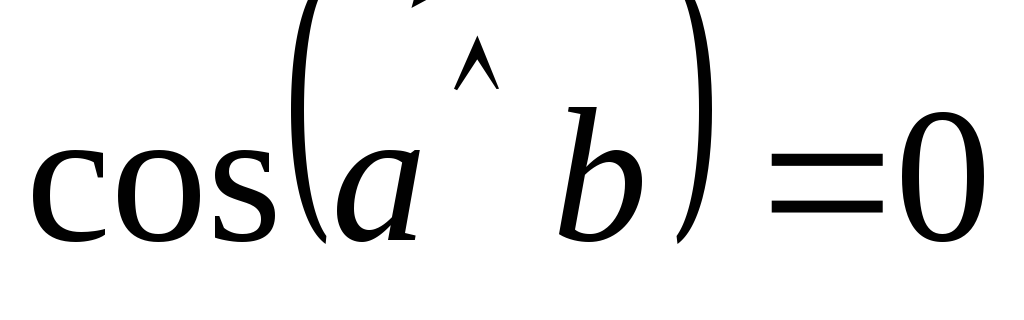 ,
т.е.
,
т.е.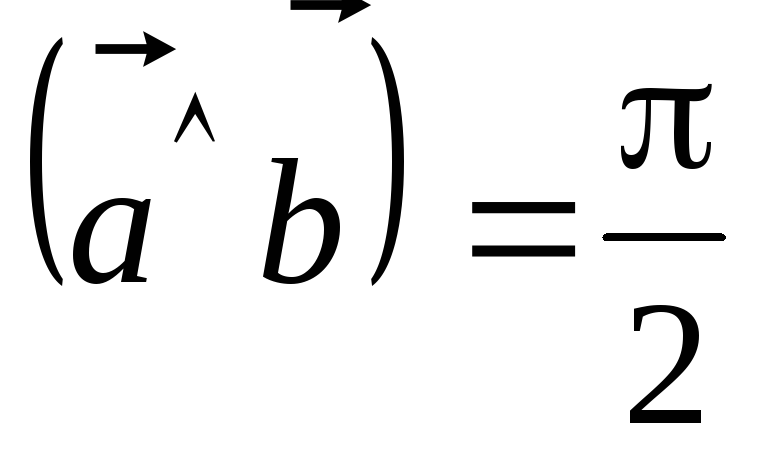 .
.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТНОЙ ФОРМЕ
Скалярное произведение векторов в координатной форме
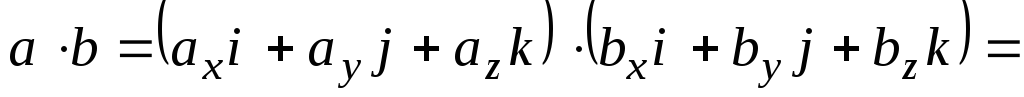
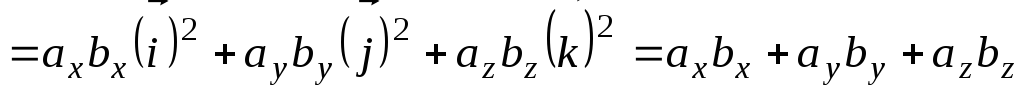 .
.
13.Векторное произведение. Координатная форма векторного произведения.
Под векторным
произведением векторов  и
и 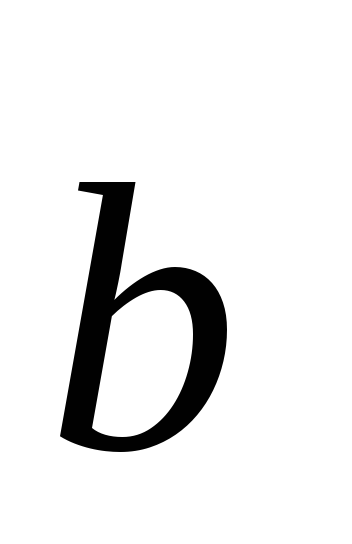 понимают
вектор
понимают
вектор ,
имеющий длину и направленный перпендикулярно
к плоскости
,
имеющий длину и направленный перпендикулярно
к плоскости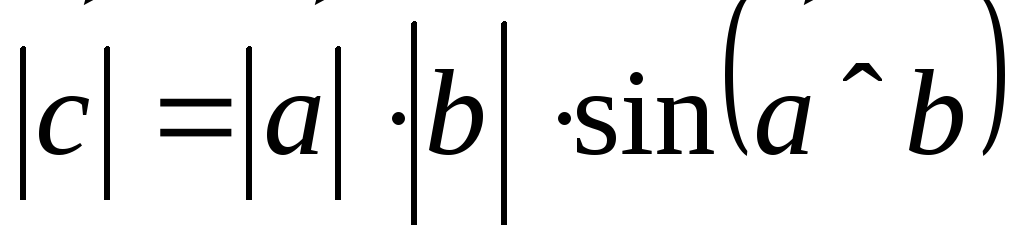 ,определяемой
векторами
,определяемой
векторами  и
и 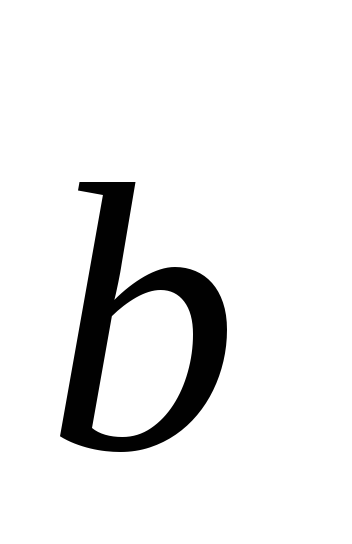 ,
причем так, что векторы
,
причем так, что векторы  ,
,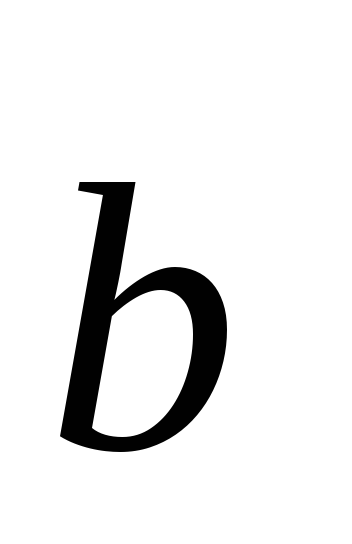 и
и образуютправую тройку
векторов (длина вектора
образуютправую тройку
векторов (длина вектора  численно равна площади параллелограмма,
построенного на векторах и
численно равна площади параллелограмма,
построенного на векторах и 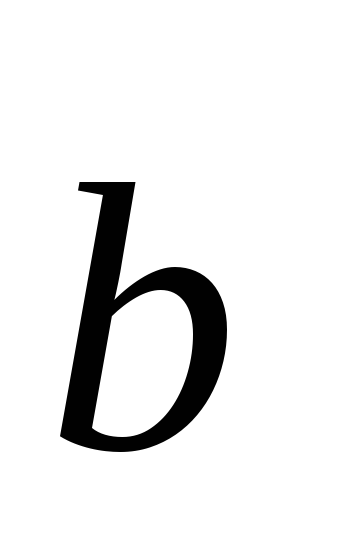 как
на сторонах (это геометрический смысл
векторного произведения).
как
на сторонах (это геометрический смысл
векторного произведения).
Векторное
произведение обозначают: 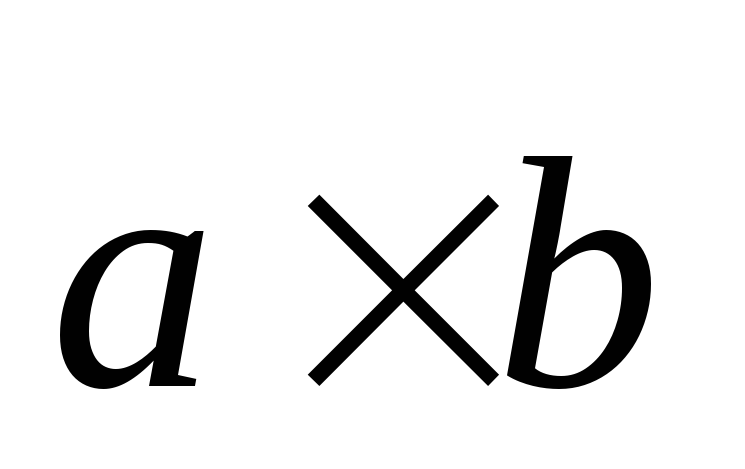 или
или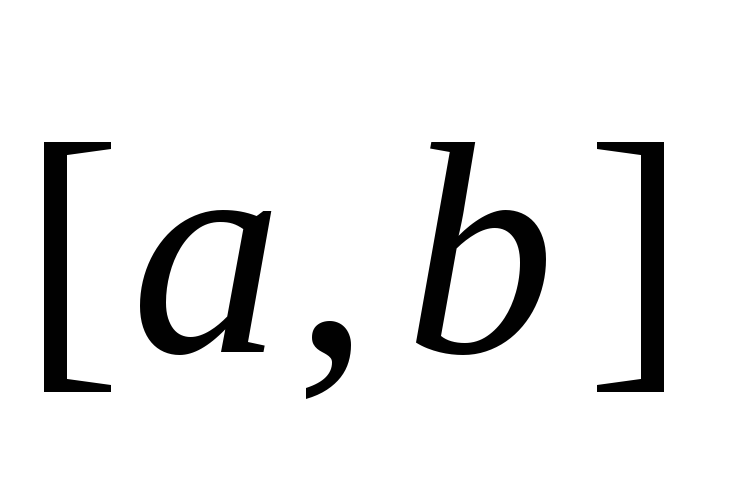 .
Очевидно, что
.
Очевидно, что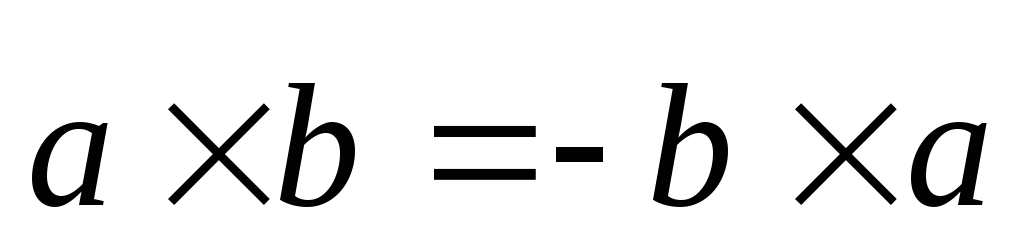 (из определения векторного произведения).
(из определения векторного произведения).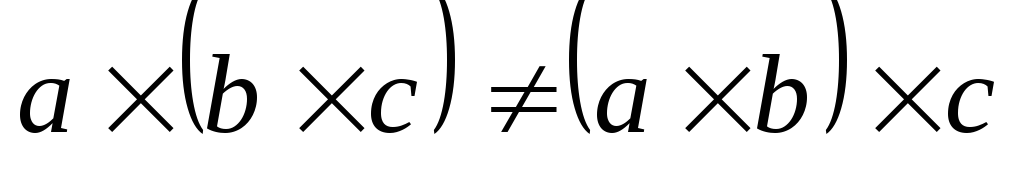 .
Векторное произведение подчиняется
только распределительному закону:
.
Векторное произведение подчиняется
только распределительному закону:
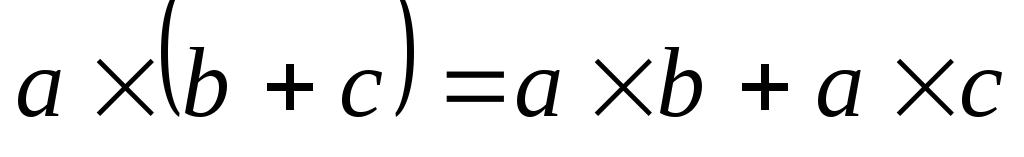 .
.
Теорема.
Пусть 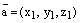 ,
,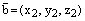 ,
,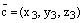 .
Тогда:
.
Тогда:
1) 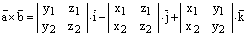 ;
;
2) 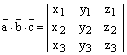 .
.
Доказательство. 1) Используем свойстволинейностивекторногопроизведения:
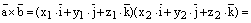
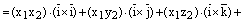
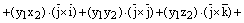
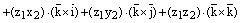 .
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
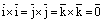 .
.
Рассмотрим другие векторныепроизведения базисных векторов:
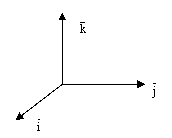
рис.4.
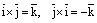 ,
, 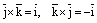 ,
,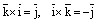 .
.
Эти равенства легко устанавливаются с помощьюрис.4.
Отсюда следует: 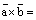
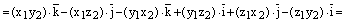
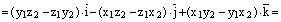
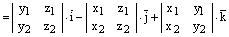 ,
ч.т.д.
,
ч.т.д.
2) Воспользуемся только что доказанной формулой:
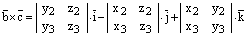 .
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
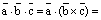
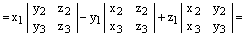
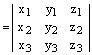 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Замечание. Векторное произведениечасто записывают в форме определителя:
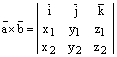 .
.
Разумеется это не определитель, а лишь форма записи векторногопроизведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двухстрок (столбцов) определитель меняет знак.
Доказательство. С одной стороны,
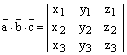 .
.
С другой стороны,
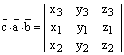 .
.
Но, 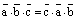 ,
откуда и следует утверждение. Далее,
т.к.
,
откуда и следует утверждение. Далее,
т.к.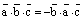 ,
то
,
то
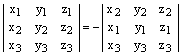 .
.
Так как определитель не изменяется при транспонировании, то доказанное свойствосправедливо и для столбцов определителя.
Скалярное произведение векторов [wiki.eduVdom.com]
Скалярным произведением векторов $\overrightarrow{a}\{x_1; y_1\} \,и\, \overrightarrow{b}\{х_2; у_2\}$ (обозначается $ \overrightarrow{a}\overrightarrow{b} $ ) называется число $x_1x_2 + y_1y_2$ . Скалярное произведение $\overrightarrow{a}\overrightarrow{a}$ обозначается $\overrightarrow{a}^2$. Очевидно, $\overrightarrow{a}^2 = |\overrightarrow{a}|^2$ .
Из определения скалярного произведения векторов следует, что для любых векторов $\overrightarrow{a}\{х_1; y_1\}\,, \overrightarrow{b}\{х_2; у_2\}\,, \overrightarrow{c}\{х_3; у_3\}$ $$ (\overrightarrow{a} + \overrightarrow{b})\overrightarrow{c} = \overrightarrow{a}\overrightarrow{c} + \overrightarrow{b}\overrightarrow{c} $$ Действительно, левая часть равенства есть $(х_1 + х_2)х_3 + (у_1 + у_2)у_3$ , а правая $х_1х_3 + у_1у_3 + х_2х_3 + у_2у_3$ . Очевидно, они равны.
Углом между ненулевыми векторами $\overrightarrow{АВ} \,и\, \overrightarrow{АС}$ называется угол BAC (рис.1).
Рис.1
Углом между любыми двумя ненулевыми векторами $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.
Теорема 1. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Из этой теоремы получаем следствия.
Следствие 1. Если векторы перпендикулярны, то их скалярное произведение равно нулю.Следствие 2. Если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.
Пример 1. Даны векторы $\overrightarrow{a}\{1; 0\} \,и\, \overrightarrow{b}\{1; 1\}$ . Найти такое число $\lambda$ , чтобы вектор $\overrightarrow{a} + \lambda\overrightarrow{b}$ был перпендикулярен вектору $\overrightarrow{a}$ .
Решение. Имеем: $ \overrightarrow{a}(\overrightarrow{a} + \lambda\overrightarrow{b}) = 0\,; \overrightarrow{a}^2 + \lambda(\overrightarrow{a}\overrightarrow{b}) = 0$ . Отсюда $ \lambda = — \frac{\overrightarrow{a}^2}{\overrightarrow{a}\overrightarrow{b}} = — \frac{1}{1} = -1 $


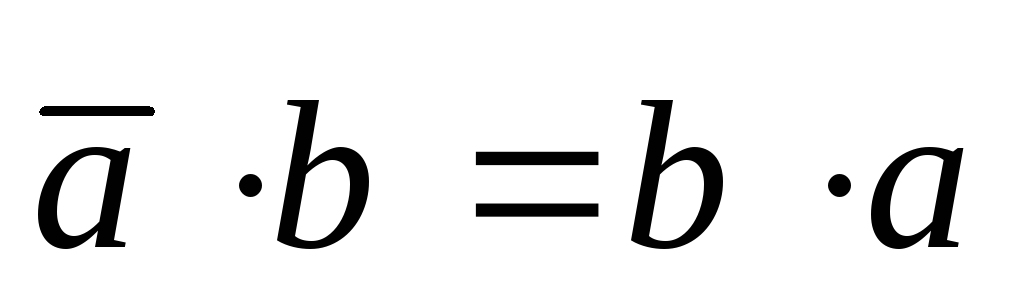 .
.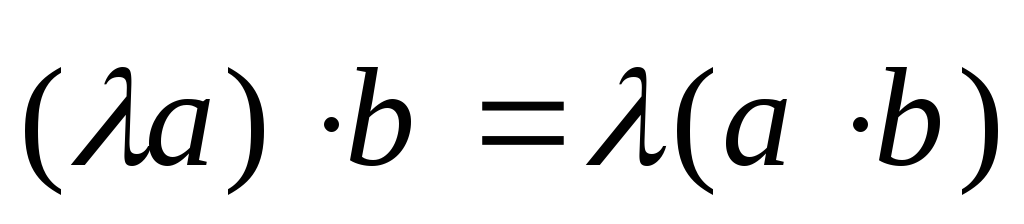 .
.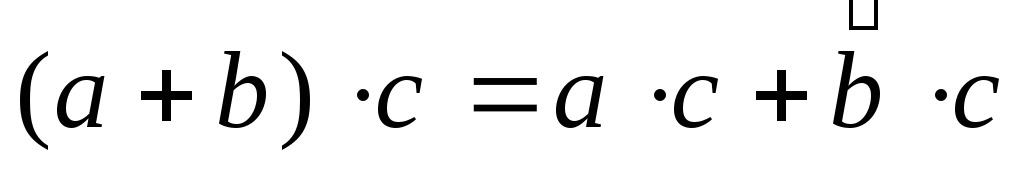 .
.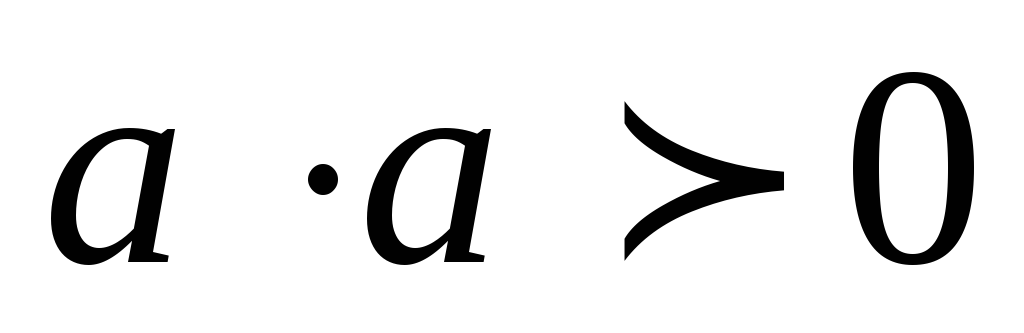 ,
если
,
если 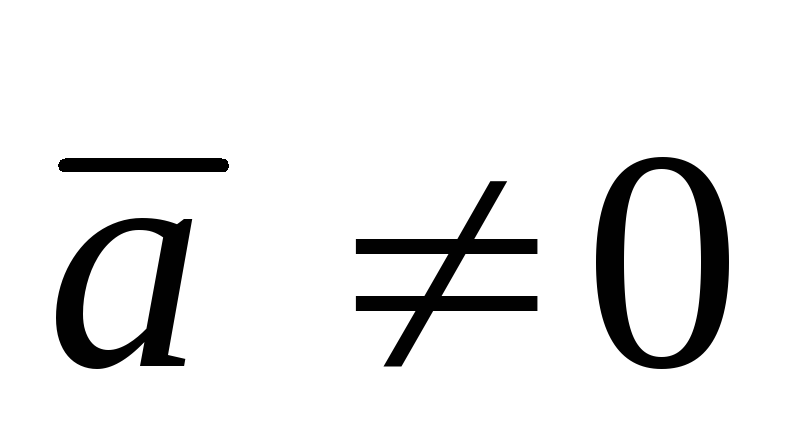 ,
и
,
и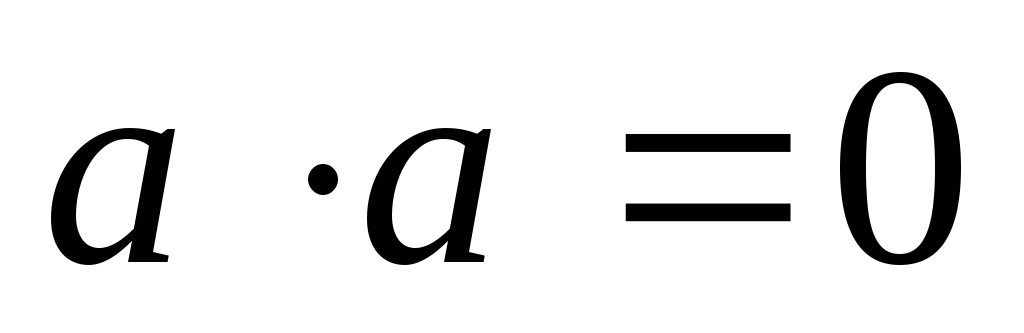 ,
если
,
если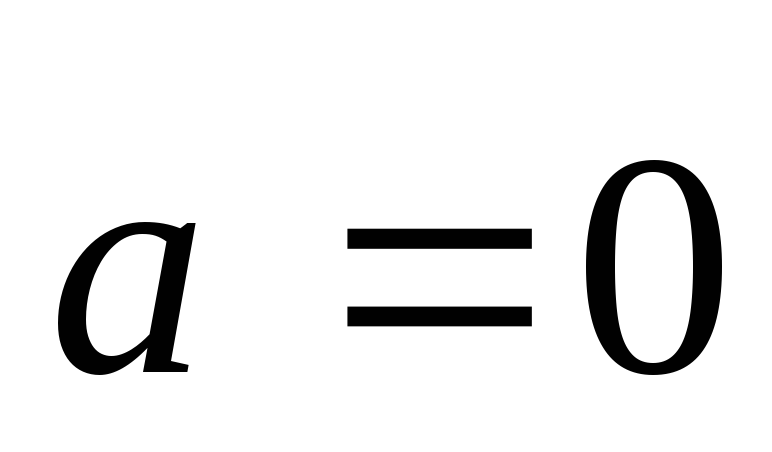 .
.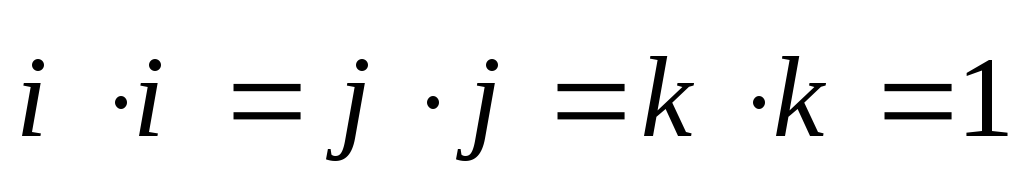 ;
(2.19)
;
(2.19)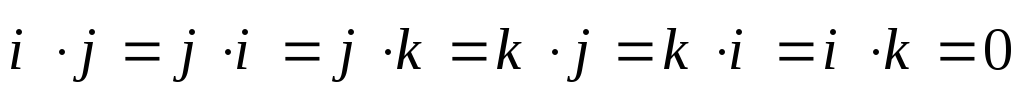 .
(2.20)
.
(2.20)