правила соединения модулей между собой и анализ простых логических схем / Хабр
appplemacВремя на прочтение 2 мин
Количество просмотров30K
Электроника для начинающих
Приветствую всех.
Продолжаю написание статей про простейшие логические цепи.
В этом посте – правила соединения логических элементов и цепей между собой, а также два простых метода анализа логических схем.
По многочисленным просьбам хабралюдей, а также для упрощения восприятия написанного, буду кроме западного названия определённого элемента приводить и русское.
Правила соединения цепей и их компонентов
В прошлой статье мы познакомились с такими логическими модулями, как Not-1 (логическое отрицание, !A), Or-2 (логическая сумма, AvB) и And-2 (логическое умножение, A^B), но ни слова не было сказано о том, как соединять между собой эти простейшие комбинационные логические цепи (КЛЦ, они же – комбинационные схемы).
Вот несколько правил, которые помогут избежать ошибок при соединении проводников и логических модулей:
1. Не соединяйте два выхода напрямую. Это может привести к конфликту сигналов.
2. Если у логического модудя два входа, они оба должны иметь значение. Если неизвестен сигнал на одном из входов, то скорее всего не получится узнать значение исходящего сигнала.
3. Не должно быть циклов. Эффект может быть любым – от нестабильности работы цепи до её неспособности функционировать.
Анализ логических схем
Для упрощения анализа цепей мы будем использовать некоторые условные обозначения. Например:
Как видите, определённый набор элементов изображается с помощью одного-единственного модуля.
Анализ цепи из 6-8 элементов
Возьмём любую сделанную по правилам комбинационную схему. Например вот эту:
Если вам по каким-то причинам не нравится моя схема, нарисуйте свою 🙂
Суть анализа цепи заключается в выявлении исходящих сигналов в зависимости от значений входов.
Существует два метода этого самого анализа – горизонтальный (по строкам) и вертикальный (по столбцам).
Анализ по строкам
Этот тип исследования цепей заключается в следующем: мы поочерёдно выставляем разные значения на входах цепи, и смотрим, как изменяется сигнал во время его прохождения дальше по цепи. Вот наглядный пример:
Таким способом удобно анализировать небольшие схемы с одним-двумя входами, потому что не обязательно строить таблицу истинности.
Для таких цепей, как выбранная нами ранее, лучше всё-таки нарисовать эту самую таблицу и вписывать туда найденные значения. Вот так, например:
Анализ по столбцам
Суть этого метода – поочерёдно, с помощью логических выражений, найти значения для всех частей цепи, и только потом вычислить результат для выходов цепи.
Как видно на картинке, мы вычисляем значения сигнала для каждого элемента цепи, постепенно приближаясь к выходу.
Для нашей цепи это будет выглядеть так:
Теперь можно сравнить результаты, полученные с помощью двух методов. Если они совпадают, то это значит, что либо всё сделано правильно, либо мы допустили больше одной ошибки ( 😀 ).
На данный момент всё.
В следующей статье мы начнём создавать свои логические схемы по заданным параметрам.
Спасибо за внимание, и хороших всем выходных!
Теги:
- логические цепи
- логические модули
- простейший
- схемотехника
- анализ
- правила
Хабы:
- Электроника для начинающих
Реализация логической функции на простых логических элементах
В данной статье описывется изучение и построение логических схем на простых логических элементах.
Электронными приборами называются активные вакуумные, газоразрядные и полупроводниковые элементы электрических цепей.
Логические схемы — физические устройства, реализующие функции математической логики. Логические схемы подразделяются на комбинационные схемы (схемы без памяти) и последовательные схемы (схемы с памятью).
Логические схемы являются основой любых систем обработки дискретной информации.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию («И», «ИЛИ», «НЕ» и «исключающее ИЛИ»).
В полупроводниковых приборах в качестве уровня используются соответствующие значения напряжения.
Например, в ТТЛ схемах при Uпит = 5В низкий уровень составляет 0…1,8В (16% Uпит), высокий – 2…5В.
1. Синтез комбинационной логической схемы
1.1 Составление таблицы истинности
Исходя из задания, было дано следующее условие для построения комбинационной логической схемы:
Y = (1, 2, 3, 5, 7, 12)
Таблица истинности будет выглядеть следующим образом:
Таблица 3.1 — Таблица истинности
Состояние входов | Варианты выходных состояний | ||||
a | b | c | d | y | |
0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 1 | 1 |
2 | 0 | 0 | 1 | 0 | 1 |
3 | 0 | 0 | 1 | 1 | 1 |
4 | 0 | 1 | 0 | 0 | 0 |
5 | 0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | |
7 | 0 | 1 | 1 | 1 | 1 |
8 | 1 | 0 | 0 | 0 | 0 |
9 | 1 | 0 | 0 | 1 | 0 |
10 | 1 | 0 | 1 | 0 | 0 |
11 | 1 | 0 | 1 | 1 | 0 |
12 | 1 | 1 | 0 | 0 | 1 |
13 | 1 | 1 | 0 | 1 | 0 |
14 | 1 | 1 | 1 | 0 | 0 |
15 | 1 | 1 | 1 | 1 | 0 |
Алгебраическое выражение ДНФ записывается в виде:
1.
2 Минимизация логической функции
Для минимизации логической схемы следует применить метод карт Карно.
Карта Карно — графический способ представления переключательных булевых функций с целью наглядной и удобной их минимизации, обеспечивающий упрощение сложных логических функций многих переменных. Основным методом минимизации логических функций, представленных в виде ДНФ или КНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
Применив данный метод к условию, получаем следующую схему:
| ||||
|
|
|
| |
ab |
|
|
| 1 |
1 | 1 |
| ||
1 | 1 | 1 |
|
Парные элементы объединены в группы.
Исключив члены, дополняющие друг друга внутри контура, получим минимизированную функцию:
y =
Минимизацию схем целесообразно применять, для уменьшения стоимость конечных устройств, а также их уменьшения. Так как для реализации одной и той же функции требуется, очевидно, гораздо меньше элементов.
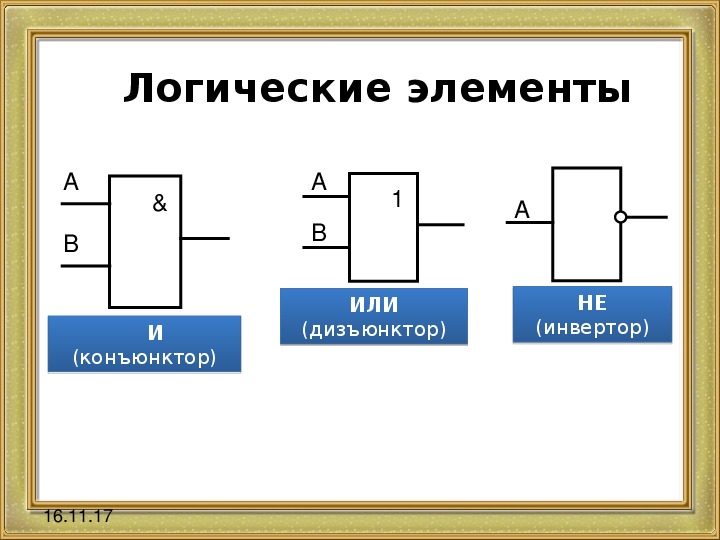
1.3 Построение комбинационной логической схемы с использованием элементов «И», «ИЛИ», «НЕ»
«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Рисунок 1.1 – графическое обозначение элемента «И»
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. Далее логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.
Вход Х1 | Вход Х1 | Выход Y |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Таблица 1.
1 — таблица истинности для элемента «И»
Таблица истинности для элемента «И» показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе «И» на втором входе. В остальных трех возможных случаях на выходе будет ноль.
Обозначается элемент «И» как прямоугольник с закруглением на выходе или как прямоугольник с символом «1».
«ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же, как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом.
Вход Х1 | Вход Х1 | Выход Y |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Таблица 1.
2 — таблица истинности для элемента «ИЛИ»
Таблица истинности для элемента «ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
Обозначается элемент «ИЛИ» как закругление на входе и закругление с заострением на выходе или как прямоугольник с символом «1».
«НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал.
Вход Х | Выход Y |
0 | 1 |
1 | 0 |
Таблица 1.3 — таблица истинности для элемента «НЕ»
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
Обозначается элемент «НЕ» в форме треугольника с кружочком на выходе или как прямоугольник с символом «1», с кружком на выходе.
Согласно условию, была получена следующая схема, с использованием логических элементов «И», «ИЛИ», «НЕ», на основе минимизированной функции:
Рисунок 1.2 — Комбинационная логическая схема
с использованием элементов «И», «ИЛИ», «НЕ»
2. Синтез комбинационной логической схемы с использованием логических элементов «И-НЕ», «ИЛИ-НЕ»
2.1 Построение комбинационной логической схемы с использованием элементов «И-НЕ»
«И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это элемент «И», дополненный элементом «НЕ».
Вход Х1 | Вход Х1 | Выход Y |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Таблица 2.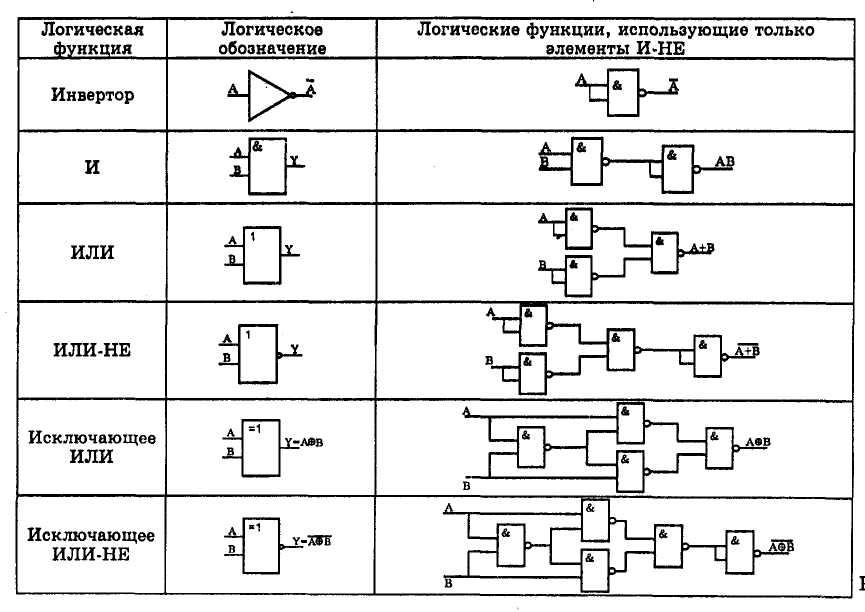
1 — таблица истинности для элемента «И-НЕ»
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
Согласно условию, была получена следующая схема, на основе минимизированной функции:
Рисунок 2.1 — Комбинационная логическая схема
с использованием элементов «И-НЕ»
2.2 Построение комбинационной логической схемы с использованием элементов «ИЛИ-НЕ»
«ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».
Вход Х1 | Вход Х1 | Выход Y |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Таблица 2.
2 — таблица истинности для элемента «ИЛИ-НЕ»
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы.
Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Согласно условию, была получена следующая схема, на основе минимизированной функции:
Рисунок 2.2 — Комбинационная логическая схема
с использованием элементов «ИЛИ-НЕ»
3. Синтез комбинационной логической схемы с использованием логических элементов «И-НЕ», «ИЛИ-НЕ» с использованием мультиплексора
Мультиплексором — называют комбинационное устройство, обеспечивающее передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на один выход. Мультиплексоры обозначают через MUX (от англ. multiplexor), а также через MS (от англ. multiplex or selector).
Схематически мультиплексор можно изобразить в виде коммутатора, обеспечивающего подключение одного из нескольких входов (их называют информационными) к одному выходу устройства.
Рисунок 3.1 — Схема и графическое обозначение мультиплексора
Основой данной схемы являются две схемы совпадения на элементах «И», которые при логическом уровне «1» на одном из своих входов повторяют на выходе то, что есть на другом входе.
Переключение работы функций осуществляется подачей логического сигнала на шину SW. В зависимости от сигнала «0» или «1» будет включена в работу соответствующая функция. Переключение работы функций осуществляется как по входным сигналам, так и по выходным.
Рисунок 3.2 — Логическая схема мультиплексора
4. Исследование электронных схем методом моделирования в симуляторе
Моделирование всех схем производилось в симуляторе Electronics Workbench.
Electronics Workbench – один из самых известных пакетов схематического моделирования цифровых, аналоговых и аналогово-цифровых электронных схем различной степени сложности.
Данная система схемотехнического моделирования показала достаточно высокую гибкость и точность вычислений, найдя широкое применение, как на предприятиях, так и в высших учебных заведениях.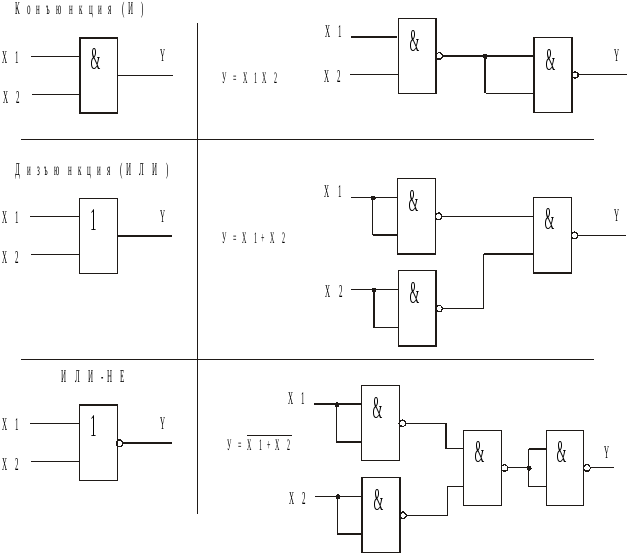
Он включает инструменты для моделирования, редактирования, анализа и тестирования электрических схем. Программа имеет простой интерфейс и идеально подходит для начального обучения электронике. Библиотеки предлагают огромный набор моделей радиоэлектронных устройств от самых известных иностранных производителей с широким диапазоном значений параметров. Кроме этого, есть возможность создания собственных компонентов. Активные элементы могут быть показаны как идеальными, так и реальными моделями. Всевозможные приборы (мультиметры, осциллографы, вольтметры, амперметры, частотные графопостроители, динамики, светодиоды, лампы накаливания, логические анализаторы, сегментные индикаторы) позволяют делать измерения любых величин, строить графики.
Моделирование комбинационной логической схемы с использованием элементов «И», «ИЛИ», «НЕ»:
Рисунок 4.1 — Схема электрическая принципиальная
с использованием элементов «И», «ИЛИ», «НЕ»
Моделирование комбинационной логической схемы с использованием элементов «И-НЕ»:
Рисунок 4.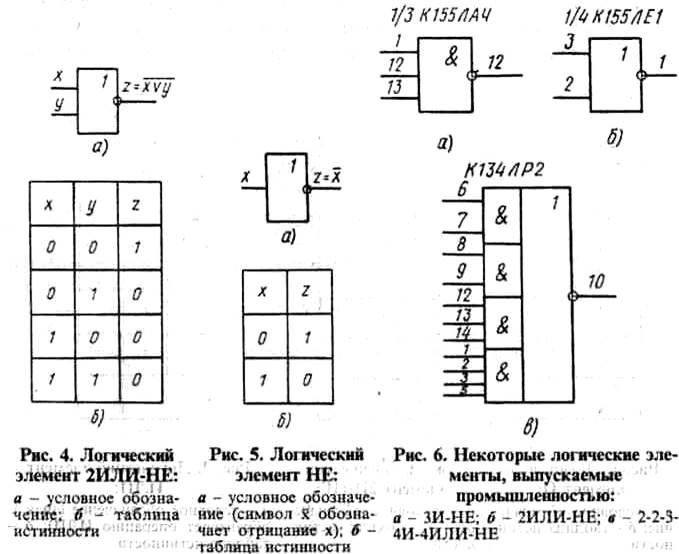
2 — Схема электрическая принципиальная
с использованием элементов «И-НЕ»
Моделирование комбинационной логической схемы с использованием элементов «ИЛИ-НЕ»:
Рисунок 4.3 — Схема электрическая принципиальная
с использованием элементов «ИЛИ-НЕ»
Моделирование комбинационной логической схемы с использованием мультиплексора для переключения схем «И-НЕ» и «ИЛИ-НЕ»:
Рисунок 4.4 — Схема электрическая принципиальная
с использованием мультиплексора
В процессе симулирования, на вход испытуемых схем были поданы все комбинации сигналов из приведенной таблице истинности. На выходе схемы были получены верные сигналы, соответствующие условию задания.
Подача сигналов осуществляется переключением переключателей A, B, C, D, которые позволяют вставить логические сигналы «0» и «1». Контроль за состоянием сигналов можно осуществлять по индикаторным лампам.
На схеме с мультиплексором, для переключения состояния используется клавиша «пробел».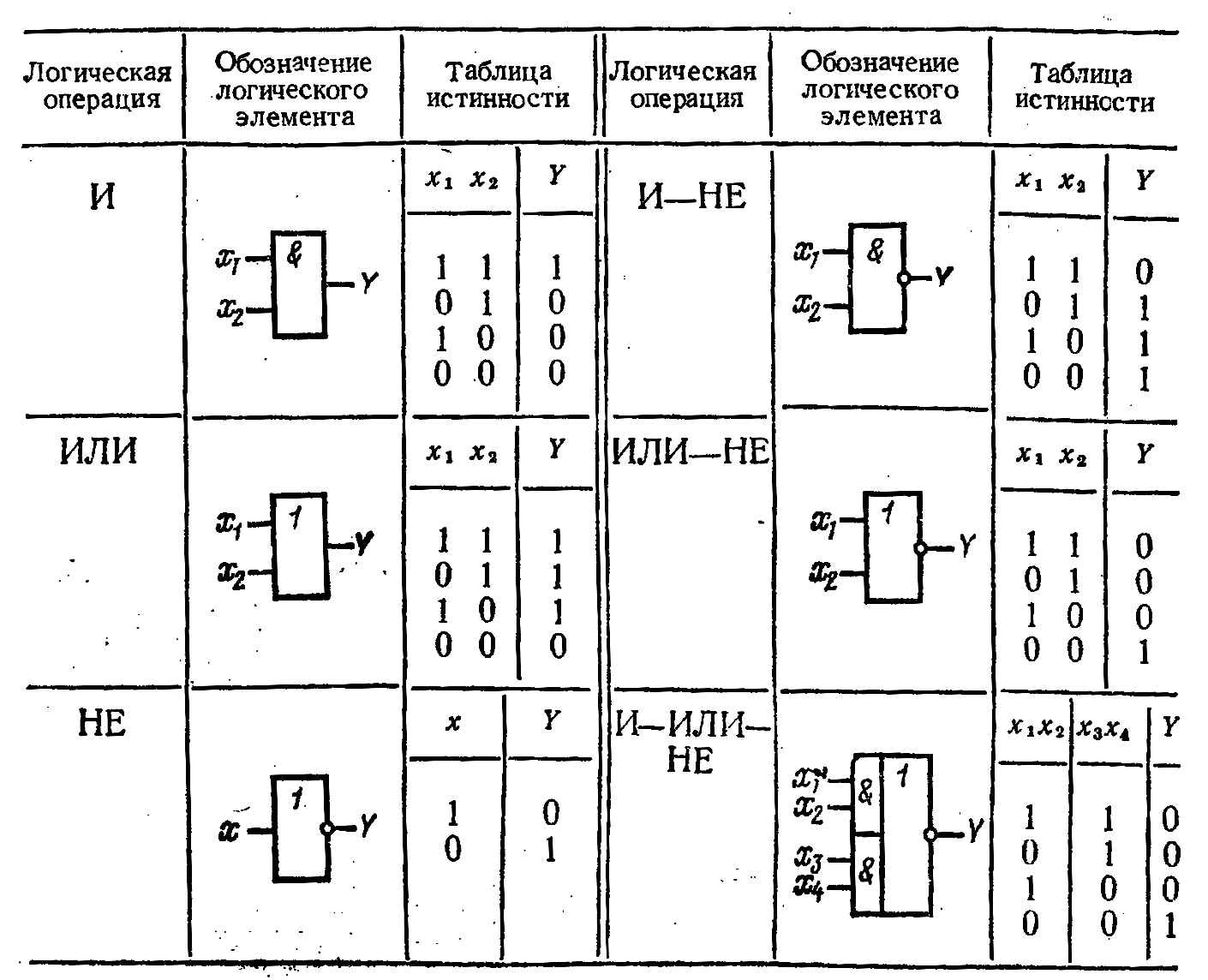
Так как обе схемы описывают одну и ту же логику – вне зависимости от переключения мультиплексора, выходной результат будет одинаковый.
Дополнительно для проверки работоспособности разработанной схемы была построена реальная модель устройства на основе имеющихся в наличии микросхем логики «НЕ», «И-НЕ» серии CD4000B с буферизированным выходом. Схема построена на базе схемы с элементами «И-НЕ».
Полная принципиальная схема устройства приведена ниже. Она состоит из: источника питания напряжением от 8 до 24 вольт; переключателей и индикаторных светодиодов для отображения состояния логических сигналов; микросхем логики; транзистора в качестве ключа включения индикаторного светодиода на выходе логической функции; ограничительных резисторов.
Устройство выполнено на макетной плате. Все элементы соединены дорожками и перемычками в соответствии со схемой.
| |
5 – лицевая и обратная сторона модели устройства
Рисунок 4.6 — принципиальная схема устройства
Для реализации логической функции потребовались 3 комбинированных микросхем.
В качестве инвертора сигналов DD1 применилась микросхема CD4069 (6НЕ), так как была в наличии. Она состоит из 6 независимых логических элемента «НЕ». В этом случае понадобится задействовать только 4 её элемента. В качестве аналога, можно было применить для инвертора микросхему CD4011B (4И-НЕ) с соединенными парами входов у каждого элемента.
Для реализации логики применялись две микросхемы: CD4012B (2И-НЕ) и CD4023B (3И-НЕ). CD4012B представляет собой два элемента И-НЕ с 4 входами, а CD4023B – три элемента «И-НЕ» с 3 входами. Элементы DD1, DD2, DD3 соединены между собой в соответствии с полученной функцией по заданию. Так как микросхемы в своем составе содержат несколько элементов, некоторые из них остались не задействованы.
Параметры у данной серии микросхем следующие: напряжение питания 3-8В; низкий логический уровень 1.
5-4В; высокий логический уровень 3.5-11В.
Для индикации логических сигналов применены светодиоды LED1-6 с ограничивающими ток резисторами. По результатам замеров тока светодиодов было выяснено, что для индикаторов (3мм) LED1-5 – A, B, C, D и питания, достаточно тока около 5мА, а для выходного индикатора (5мм) LED6 – 12мА. При напряжении 5В были применены резисторы в 1 кОм и 240 Ом соответственно.
Для управления включением выходного светодиода, в качестве ключа, был применен маломощный биполярный транзистор npn-структуры T1, типа KSP2222A.
Питание построено на базе линейного стабилизатора напряжения VR1 типа LM7805 с фиксированным выходным напряжением 5 вольт. Его характеристики: максимальное входное напряжение 35В; выходное напряжение 5В; максимальный ток нагрузки 1.5А. Для фильтрации возможных импульсов по питанию были применены конденсаторы до и после стабилизатора. Применение стабилизированного напряжения 5В дает возможность напрямую использовать это напряжение для логического «1».
Так как устройство не имеет собственного источника питания, для защиты от переполюсовки применяется последовательно включенный диод D1. Падением напряжения на нем в данном случае можно пренебречь.
Питание схемы осуществляется от батареи типа «КРОНА» напряжением 9В или любого другого источника питания с напряжением от 8 до 24В. Потребляемый ток во время работы составляет около 35мА.
Работает устройство следующим образом. Для включения, необходимо перевести переключатель S5 в положение «ON». Светодиод LED5 зеленого цвета будет говорить о включении устройства. Комбинация входных логических сигналов осуществляется переключателями S1-4, а контроль их положений индицируют красные светодиоды LED1-4. Светодиод желтого цвета LED6 отображает состояние выходного сигнала с данной функции, в зависимости от поданных на нее входных сигналов. Свечение светодиодов означают присутствие логического сигнала «1», а отсутствие свечения – «0».
Для проверки корректности работы был осуществлен тест, в котором на вход схемы были поданы все сигналы из приведенной таблицы истинности, а на выходе схемы были получены те же сигналы, в соответствии с заданием.
Рисунок 4.7 – общий вид устройства
Литература
1. Ширин, И.Я. Схемотехника аналоговых и цифровых устройств: Учебное пособие для ву- зов.- Минск: БНТУ, 2005. — 309 с.
2. Основы электронной техники: Элементы, схемы, системы: [Краткая энциклопедия по электронике] 2-е изд./ К.Ф. Ибрагим; Пер. В.М. Матвеев, Г.Ф. Хохлов и Ф.Г. Хохлов / Под ред. Н.И. Аникушина М.: Мир, 2001. — 397 с.
3. Гусев, В. Г. Электроника / В. Г. Гусев, В. М. Гусев. — М: Высш. шк.,2000.-621 с.
4. Хоровиц, П. Искусство схемотехники. / П. Хоровиц, У. Хилл; пер. с англ. Б. Н. Бронин [и др.]; — М., Мир, 2001. — 704 с.
Таблица истинности, принципиальная схема, работа и ее приложения
В области цифровой электроники логические вентили — это устройства, выполняющие логические операции с двумя входами и одним выходом.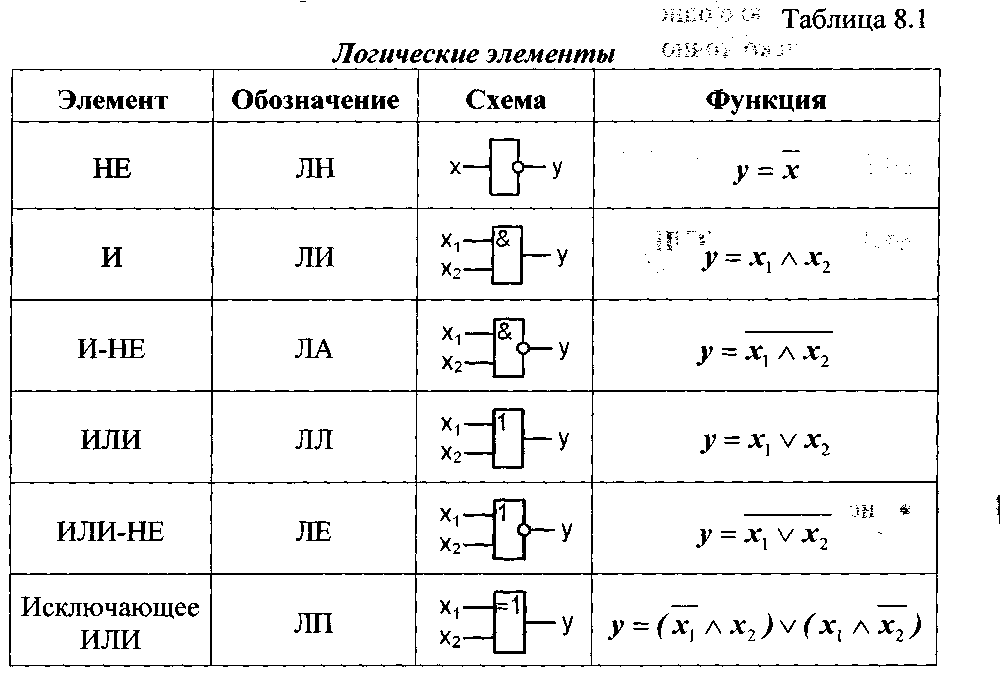
В зависимости от логического элемента меняется логическая функциональность, и выходные данные также меняются. В 1886 году в письме Чарльз Пирс заявил, что логические функции могут выполняться путем переключения схем. Наконец, электронные лампы были заменены логическими операциями. И единственный логический вентиль, который мы собираемся обсудить сегодня, — вентиль И. Первые и современные ворота И были изобретены Вальтером Боте в 19 году.54. В этой статье объясняется, как определить логический элемент И , его схема, его разработка с использованием транзистора, мультиплексора и приложений.
Этот логический элемент является логическим элементом, который принимает два или более входных данных и отображает результат как один выходной сигнал. Когда оба входа находятся в состоянии логического «0», на выходе также присутствует логический «0» (НИЗКИЙ), а когда на обоих входах находится логическая «1», на выходе также логическая «1» (ВЫСОКИЙ). Функциональность такая же, даже у ворот есть 2 входа, 3 входа и т.
д. 9Правила шлюза 0003 И основаны на операции логического умножения.
И Теория ворот
Чтобы иметь четкое представление, дайте нам знать, как он работает в соответствии со своими входами.
Предположим, что есть два двоичных входа: «0» и «1». Поскольку операция основана на двоичном умножении. Таким образом, когда «0» умножается на «1» или «1» умножается на «0», на выходе получается «0». Выход равен «1» только тогда, когда «1» умножается на «1». То есть
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Символ показан ниже:
Основной вентиль И
Здесь X и Y рассматриваются как входы, а Z — выход. Входы X и Y могут быть либо «0», либо «1».
У него может быть несколько входов, но только один выход. При этом логическая формула задается как
XY = Z
Все комбинации X и Y представлены в табличном формате, который представляет собой таблицу истинности И вентиля 9.
0004 и показано ниже. Таблица истинности показывает результат соответствующей цифровой логики для всех возможных входных комбинаций. Здесь
| Х | Д | З |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Приведенная выше таблица истинности предназначена для логического элемента И с двумя входами. Например, на картинке ниже показано число 9.0003 Структура вентиля И , когда он имеет три входа, тогда логическое представление и таблица истинности представлены следующим образом:
XYZ = A
Логическая схема
3 входа И вентиль
Таблица истинности, когда вентиль имеет три входа , и один выход:
| X | Д | З | А |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Логический элемент И с несколькими входами
На рисунке ниже показано, как построен логический элемент с несколькими входными битами.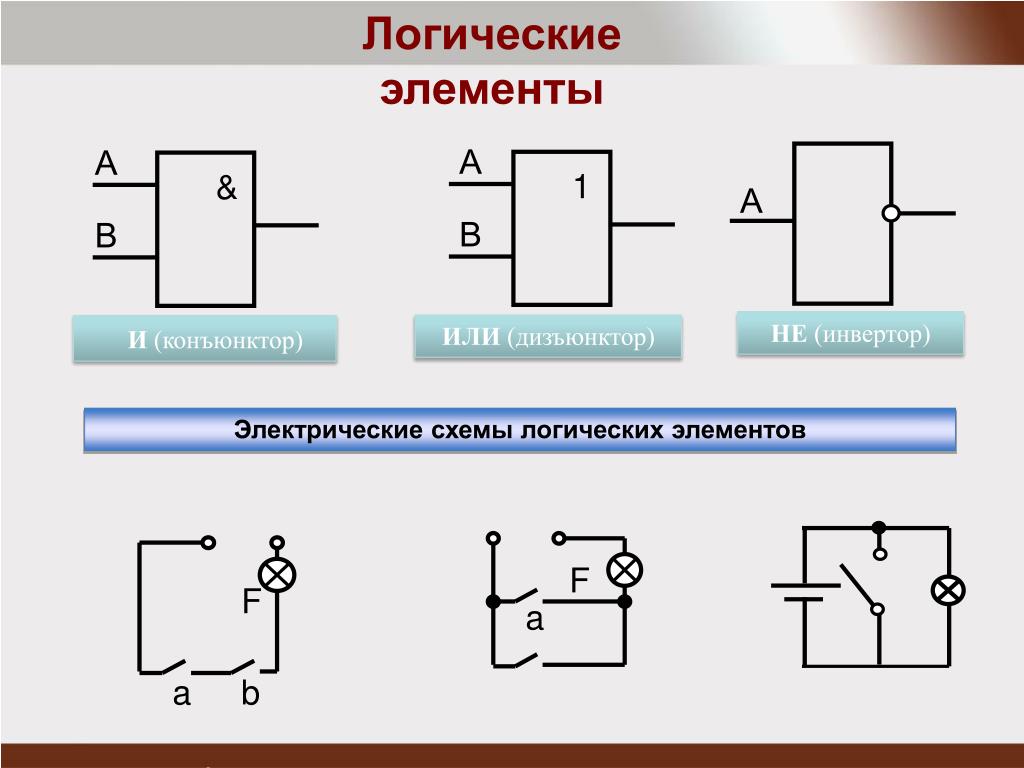
Предположим, что у нас есть 6 входов как U, V, W, X, Y и Z. Тогда выход будет
Multi Input Gate
A = (U.V). (WX). (Y.Z)
Если общее количество входов нечетное и если какой-либо из входов не используется, то они могут быть ВЫСОКИМ, подключив их к источнику питания через подтягивающие резисторы.
Работа с использованием диода
Обычно операция И выполняется либо диодами, либо транзисторами. Когда затвор разработан с использованием диодов, он называется затвором с диодом И. Схема И затвора с использованием диода выглядит так:
И затвора с использованием диода
В соответствии с приведенной выше схемой, сначала в точке A прикладывается уровень напряжения 5 В, затем в точках X и Y подается напряжение +5 В. Теперь оба диода будут в состоянии обратного смещения и перейдут в состояние ВЫКЛ. В этом состоянии схема работает как разомкнутая цепь, где ток не будет течь через резистор, а +5 В течет до выходного контакта «Z».
Поскольку выход имеет определенное напряжение, результат рассматривается как логический «ВЫСОКИЙ».
Принимая во внимание, что когда на любой из входных контактов подается 0 В или когда они заземлены, диоды будут смещены в прямом направлении, и схема перейдет в состояние ВКЛ. Теперь напряжение питания, приложенное к точке А, пройдет через любой из диодов или через оба на землю. Поскольку ток течет от точки A к земле через резистор R, тогда все напряжение питания падает на резисторе, поэтому в точке Z не будет выхода, и результат рассматривается как логический «НИЗКИЙ».
Когда диоды находятся в прямом смещении, тогда будет некоторый уровень падения напряжения, который равен уровню напряжения прямого смещения. Соответствующее падение напряжения появляется на «Z», что означает, что напряжение на выходном контакте составляет 0,6 В или 0,7 В, что почти считается «0». Это операция логического элемента И с использованием диода .
Логический элемент И с использованием транзистора
Работа и построение функции И также могут быть получены с использованием транзистора.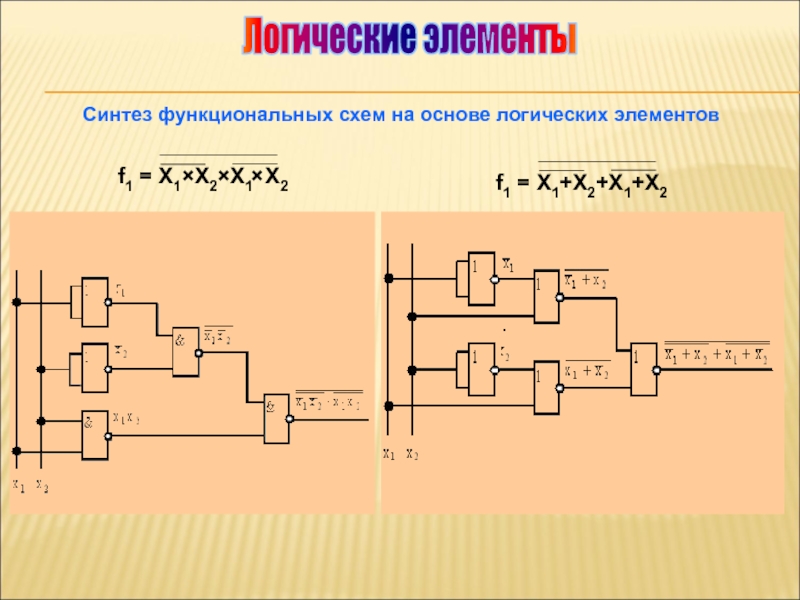
Ниже приведена принципиальная схема с использованием транзистора.
Транзисторная схема AND
Случай 1:
Когда на входные контакты X и Y подается «0» В или когда оба контакта заземлены, транзисторы T A и T B перемещаются в состояние OFF соответственно. Поскольку входные контакты подключены к базовым клеммам обоих транзисторов, транзистор будет находиться в выключенном состоянии при нулевом уровне базового напряжения. Когда путь между T A и T B становится разомкнутым, то T C База транзистора получает необходимый потенциал, чтобы он был в состоянии ON.
В этом состоянии ток начинает течь от источника питания к земле через транзистор T C . Затем все напряжение питания падает на резисторе R1, делая уровень выходного напряжения на клемме Z «0». Это то же самое состояние, когда любой из транзисторов T A и T B находится в выключенном состоянии, поскольку они соединены последовательно.
Случай 2:
Когда на оба входных контакта X и Y подается высокая логика (+5 В), это означает, что на базовые клеммы обоих транзисторов подается напряжение +5 В. Это переводит транзисторы Т А и Т В во включенное состояние. При этом все напряжение питания падает на резисторе R1, а на базе транзистора Tc будет 0 вольт, так что он переходит в состояние ВЫКЛ. В целом, напряжение питания появляется на выводе Z, что означает, что результат — ВЫСОКИЙ логический уровень.
Это рабочий сценарий с использованием транзисторов.
Логический элемент И с использованием мультиплексора
При просмотре таблицы истинности видно, что когда на любом из входов находится логический НИЗКИЙ уровень, то на выходе НИЗКИЙ уровень, а когда на обоих входах логический ВЫСОКИЙ уровень, тогда на выходе ВЫСОКИЙ уровень. Это соответствует тому, что результат основан на обоих входных данных. При этом операция И с использованием мультиплексора может быть представлена четырьмя способами, как показано на рисунке ниже.
MUX Использование AND
Таблица истинности:
| А | Б | С0 | S0 – > В |
| 0 | 0 | 0 | S0 = 0 |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | С0 = В |
| 1 | 1 | 1 |
Таким образом, операция И с использованием MUX может быть получена с помощью строк выбора «n-1».
Реализация шлюза И с использованием шлюза NOR
Для реализации операции И с использованием вентиля ИЛИ-НЕ рекомендуется знать теорему Де Моргана. Эта теорема утверждает, что сумма дополнения входов равна дополнению произведения входов. Это может быть представлено как:
AND Gate с использованием NOR
(X+Y)’ = X’ . Y’
В приведенной выше схеме используются два вентиля ИЛИ-ИЛИ, где входные клеммы обоих вентилей закорочены.
Это дает результат в виде X’ + Y’
Затем этот вывод предоставляется в качестве входа для других вентилей ИЛИ-НЕ, где это дает результат в виде (X’ + Y’)’
- (Х’)’ + (Б’)’
- Д
Итак, результатом является произведение двух входов, которое равно
X.Y
ИС логического элемента И
IC 7408
В логике ТТЛ ИС логического элемента И равен 7408. Это Четырехканальный 2-вход ИС, состоящая из четырех вентилей. Схема выводов микросхемы показана ниже:
IC 7408
Поскольку имеется четыре затвора, выводы 1 и 2 являются входами затвора 1, а соответствующий выход находится на выводе 3. Таким же образом, для затвора 2, входы находятся на контактах 4 и 5, а соответствующий выход — на контакте 6. Для четвертого элемента входы находятся на контактах 12 и 13, а выход — на контакте 11.
14-й контакт -й подает напряжение питания на ИС, а максимальный уровень напряжения, подаваемого на ИС, составляет 5,2 вольта, и напряжение выше этого уровня вызывает потери в ИС.
IC 4081
В КМОП-логике ИС логического элемента И имеет значение 4081. Это четырехканальная ИС с двумя входами, состоящая из четырех логических элементов. Схема выводов микросхемы показана ниже:
IC 4081
Поскольку имеется четыре затвора, выводы 1 и 2 являются входами затвора 1, а соответствующий выход находится на выводе 3. Таким же образом, для затвора 2, входы находятся на контактах 5 и 6, а соответствующий выход — на контакте 4. Для третьего вентиля входы находятся на контактах 8 и 9.и выход находится на контакте 10. Контакт 7 заземлен.
А для четвертого вентиля входы присутствуют на выводах 12 и 13, а выход на выводе 11. 14 -й вывод обеспечивает напряжение питания ИС с максимальным уровнем 5,2 вольта. Здесь может быть обеспечен постоянный ток, который активирует ИС. Здесь также обеспечение высокого уровня напряжения приводит к повреждению ИС.
Другие микросхемы:
74LS11 – 3 входа TTL AND Gate
Эта ИС состоит из трех независимых вентилей, где каждый вентиль выполняет операцию AND.
74LS11
Функциональные условия 74LS11:
- Напряжение питания – минимум 4,75 В и максимум 5,25 В
- Входные напряжения НИЗКОГО и ВЫСОКОГО уровней составляют 0,8 В и 2 В
- Выходные токи ВЫСОКОГО и НИЗКОГО уровня составляют 8 А и -0,4 А
- Функциональная температура наружного воздуха находится в диапазоне от 0 до 70 0 C
- Характеристики переключения 74LS 11:
- Задержка распространения по времени от НИЗКОГО до ВЫСОКОГО уровня лежит в диапазоне 4 – 13 нс для C L 15 пФ и 6 – 18 нс для C L 50 пФ
- Задержка распространения по времени от ВЫСОКОГО до НИЗКОГО уровня лежит в диапазоне 3–11 нс для C L 15 пФ и 5–18 нс для C L 50 пФ
CD4073 – CMOS с 3 входами
Этот затвор разработан по технологии CMOS, которая сочетается с N- и P-типами MOSFET-устройств. Используя эту ИС, производители систем используют работу вентиля И и дополняют преобладающую группу вентилей CMOS.
CD4073
Преимущество этой ИС заключается в том, что она работает в широком диапазоне напряжений, что позволяет использовать ее в различных конструкциях DLD. Выход CD4073 представлен в логике TTL, что позволяет устройству легко взаимодействовать со схемами NMOS, CMOS и TTL. Это 14-контактная микросхема, структура выводов которой объясняется следующим образом:
- A0, A1 и A2 — входные контакты Gate 1 .
- B0, B1 и B2 — входные контакты Gate 2 .
- C0, C1 и C2 — входные контакты Gate 3
- Vss и Vdd являются истоком и стоком IC .
- Q0, Q1 и Q2 — выходные контакты затвора 1, затвора 2 и затвора 3
Основные характеристики ИМС CD4073:
- Быстродействие 60 нс при напряжении питания 10В
- Максимальный уровень входного тока составляет 1 мкА при уровне напряжения 18 В и температурном диапазоне 100 нА
Приложения
- Основное приложение И ворота в цифровой электронике и в передаче данных.
Где логический элемент И помогает разрешить или запретить передачу данных по каналу. - Используется в цифровых измерительных устройствах
- Используется в цепях сигнализации
- Другим приложением является Inhibit gate. Это обратный подход включения ворот .
- Цепи автоматического регулирования температуры
- Устройства звукового оповещения морозильной камеры
Где логический элемент И помогает разрешить или запретить передачу данных по каналу.Перейдите по этой ссылке, чтобы узнать больше об Open Drain и Freewheeling Diode.
Это все о концепции логических вентилей И. В этой статье представлено подробное объяснение того, как работает вентиль И, его принципиальная схема, таблица истинности, микросхемы вентиля И, примеры и приложения. Кроме того, знаете, как вентиль выполняет И умножение вентиля и А ND деление вентиля ?
Основные логические элементы — типы, функции, таблица истинности и логические выражения
Логические элементы — важная концепция, если вы изучаете электронику.
Это важные цифровые устройства, которые в основном основаны на булевой функции. Логические элементы используются для выполнения логических операций с одним или несколькими двоичными входами и получения одного двоичного выхода. Проще говоря, логические вентили — это электронные схемы в цифровой системе.
В этом уроке мы дополнительно рассмотрим различные типы основных логических элементов с их таблицей истинности и поймем, для чего каждый из них предназначен.
Содержание
- Типы базовых логических элементов
- Применение логических вентилей
- Теорема де Моргана
- Важные преобразования
Типы базовых логических элементов
Существует несколько основных логических вентилей, используемых при выполнении операций в цифровых системах. Обычных
- Ворота ИЛИ
- И Ворота
- НЕ Ворота
- Ворота исключающего ИЛИ
Кроме того, эти ворота также можно найти в комбинации из одного или двух.
Поэтому мы получаем другие ворота, такие как NAND Gate, NOR Gate, EXOR Gate и EXNOR Gate.
Читайте также: Транзистор
ИЛИ Ворота
В элементе ИЛИ выход элемента ИЛИ достигает состояния 1, если один или несколько входов достигают состояния 1.
Логическое выражение вентиля ИЛИ: Y = A + B, читаемое как Y равно A ‘OR’ B.
Таблица истинности базового вентиля ИЛИ с двумя входами задается как
.| А | Б | Д |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
И Ворота
В вентиле И выход вентиля И достигает состояния 1 тогда и только тогда, когда все входы находятся в состоянии 1.
Логическое выражение вентиля И: Y = A.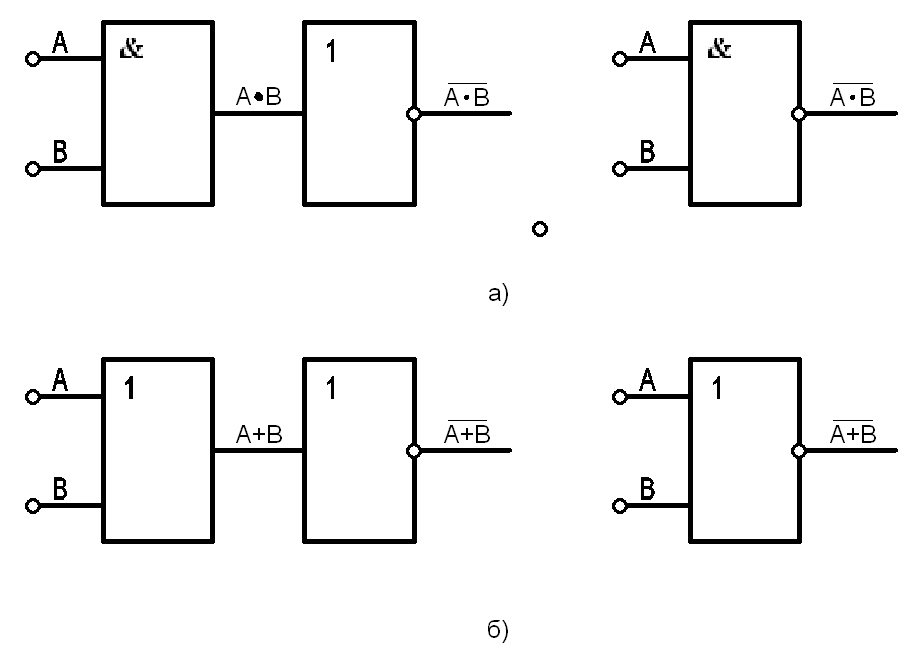
B
Таблица истинности двухвходового элемента И задается как
| А | Б | Д |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
НЕ Ворота
В элементе НЕ выход элемента НЕ достигает состояния 1 тогда и только тогда, когда вход не достигает состояния 1.
Логическое выражение:
\(\begin{array}{l}Y=\bar{A}\end{array} \)
Читается как Y равно НЕ A.
Таблица истинности вентиля НЕ выглядит следующим образом
| А | Д |
| 0 | 1 |
| 1 | 0 |
При соединении в различных комбинациях три вентиля (ИЛИ, И и НЕ) дают нам базовые логические вентили, такие как вентили НЕ-И и НЕ-ИЛИ, которые являются универсальными строительными блоками цифровых схем.
Ворота И-НЕ
Этот базовый логический вентиль представляет собой комбинацию вентилей И и НЕ.
Логическое выражение вентиля И-НЕ равно 9.0005
\(\begin{array}{l}Y=\overline{AB}\end{array} \)
Таблица истинности вентиля И-НЕ имеет вид
.| А | Б | Д |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR Gate
Этот вентиль представляет собой комбинацию вентилей ИЛИ и НЕ.
Логическое выражение вентиля НЕ-ИЛИ:
\(\begin{array}{l}Y =\overline{A+B}\end{array} \)
Таблица истинности вентиля НЕ-ИЛИ выглядит следующим образом
| А | Б | Д |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Схема исключающего ИЛИ (XOR Gate)
В вентиле XOR выход двухвходового вентиля XOR достигает состояния 1, если добавляется только вход и достигается состояние 1.
Логическое выражение вентиля XOR:
\(\begin{array}{l}A.\bar{B}+\bar{A}.B\end{array} \)
или\(\begin{array}{l}Y = A \bigoplus B\end{array} \)
Таблица истинности вентиля XOR равна
.| А | Б | Д |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Эксклюзив-NOR Gate (XNOR Gate)
В вентиле XNOR выход находится в состоянии 1, когда оба входа одинаковы, то есть оба 0 или оба 1.
Логическое выражение вентиля XNOR
Таблица истинности вентиля XNOR приведена ниже
| А | Б | Д |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Применение логических вентилей
Логические вентили имеют множество применений, но в основном они основаны на их режиме работы или их таблице истинности.
Базовые логические вентили часто встречаются в таких схемах, как предохранительные термостаты, кнопочные замки, автоматические системы полива, световые охранные сигнализации и многие другие электронные устройства.
Одним из основных преимуществ является то, что базовые логические вентили можно использовать в различных комбинациях, если операции расширены. Кроме того, нет ограничений на количество вентилей, которые можно использовать в одном устройстве. Однако это может быть ограничено из-за данного физического пространства в устройстве. В цифровых интегральных схемах (ИС) мы найдем массив из единиц площади логических элементов.
Теорема де Моргана
Первая теорема – В ней говорится, что вентиль НЕ-И эквивалентен вентилю ИЛИ с пузырьком.
\(\begin{array}{l}\bar{AB} = \bar{A}+ \bar{B}\end{array} \)
Вторая теорема – В ней утверждается, что вентиль ИЛИ-НЕ эквивалентен вентилю И с пузырьком.
\(\begin{array}{l}\overline{A+B} = \bar{A}.
\bar{B}\end{array} \)
Важные преобразования
1) Вентиль «И-НЕ»: Из вентилей «И» и «НЕ».
Булево выражение и таблица истинности
\(\begin{array}{l}Y=\overline{A.B}\end{array} \)
| А | Б | Y’=А⋅В | \(\begin{array}{l}Y=\overline{AB}\end{array} \) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
(2) Ворота «ИЛИ»: Из ворот «ИЛИ» и «НЕ».
Булево выражение и таблица истинности
\(\begin{array}{l}Y=\overline{A+B}\end{array} \)
| А | Б | Y’=А+В | \(\begin{array}{l}Y=\overline{A+B}\end{array} \) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
(3) Элемент «исключающее ИЛИ»: Из элементов «НЕ», «И» и «ИЛИ».
Логический вентиль, который дает высокий выходной сигнал (т. е. 1), если либо вход A, либо вход B, но не оба имеют высокий уровень (т. е. 1), называется вентилем исключающее ИЛИ или вентилем исключающее ИЛИ. Можно отметить, что если на обоих входах логического элемента XOR высокий уровень, то на выходе низкий уровень (т. е. 0).
Логическое выражение и таблица истинности
\(\begin{array}{l}A.\bar{B}+\bar{A}.B\end{array} \)
или\(\begin{array}{l}Y = A \bigoplus B\end{array} \)
| А | Б | Д |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
(4) Вентиль Исключающее-ни (ИСКЛЮЧАЮЩЕЕ ИЛИ) Исключающее ИЛИ + НЕ
Логическое выражение
\(\begin{array}{l}Y= \bar{(A\bigoplus B)}\end{array} \)
| А | Б | Выход |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Часто задаваемые вопросы о базовых логических вентилях
Q1
Для чего используются базовые логические вентили?
Основные логические функции выполняются с помощью базовых логических вентилей.
