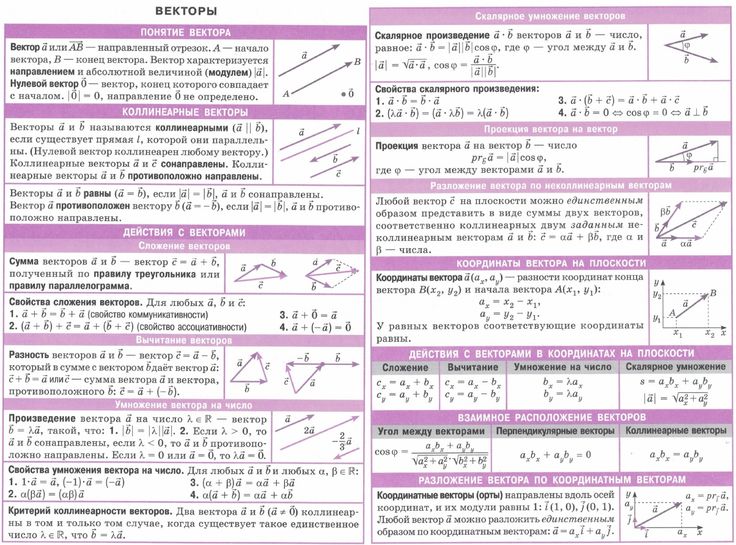
Векторы — что это, определение и ответ

ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ

Вектор – отрезок, у которого есть начало и конец, то есть указано его направление.

Вектор обозначается через точки начала и конца вектора, например \(\overrightarrow{АВ}\) (первая буква – начало вектора, вторая – конец) или, если мы хотим обозначить вектор без указания точек, пишем просто \(\overrightarrow{a}\).

Точка тоже может быть вектором, в таком случае вектор называют нулевым, т.к. его началом и концом является одна и та же точка. Обозначаем нулевой вектор как, например, \(\overrightarrow{\text{MM}}\) или \(\overrightarrow{0}\).

Длина или модуль вектора – это длина отрезка (как если бы у него не было направления).

Длина вектора \(\overrightarrow{АВ}\) обозначается как \(\left| \overrightarrow{АВ} \right|\), длина вектора \(\overrightarrow{a}\ \)как \(\left| \overrightarrow{a} \right|\), а длина нулевого вектора всегда равна нулю:

\(\left| \overrightarrow{АВ} \right| = 7\)

\(\left| \overrightarrow{a} \right| = 3\)

\(\left| \overrightarrow{\text{MM}} \right| = \left| \overrightarrow{0} \right| = 0\)

РАСПОЛОЖЕНИЕ ВЕКТОРОВ

Коллинеарные векторы – это векторы, которые лежат на параллельных прямых или на одной прямой. Нулевой вектор коллинеарен любому вектору.

Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону.

Обозначается как \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) сонаправлен вектору \(\overrightarrow{b}\))

Противоположно направленные векторы – это коллинеарные векторы, которые направлены в противоположные стороны.

Обозначаются как \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) противоположно напрвлен вектору \(\overrightarrow{b}\))

Равные векторы – это сонаправленные векторы, у которых равны длины, т.е. у них одинаковые и направление, и длина.

Например:

1. \(\overrightarrow{АВ}\) и \(\overrightarrow{a}\) – коллинеарны, при этом противоположно направлены, т.к. лежат параллельных прямых и направлены в разные стороны:

\(\overrightarrow{АВ} \uparrow \downarrow \overrightarrow{a}\)

2. \(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – коллинеарны, при этом сонаправлены, т. к. лежат параллельных прямых и направлены в одну сторону:

\(\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}\)

3. \(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – равны, т.к. сонаправлены (из п.2) и равны по модулю:

\(\left. \ \frac{\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}}{\overrightarrow{\left| \text{CD} \right|} = 5 = \left| \overrightarrow{b} \right|} \right\} \Longrightarrow \overrightarrow{\text{CD}} = \overrightarrow{b}\)

4. \(\overrightarrow{М}\) коллинеарен всем векторам, и может являться им как сонаправленным, так и противоположно направленным, т.к. \(\overrightarrow{М} = \overrightarrow{0}\).

СВОЙСТВА НЕНУЛЕВЫХ КОЛЛИНЕАРНЫХ ВЕКТОРОВ:

\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{b} \upuparrows c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)

Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{b} \upuparrows c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)

\(\left. \ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)

Если \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) и \(\overrightarrow{b} \uparrow \downarrow c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)

\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}} \right\} \Longrightarrow \overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)

Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}\), то \(\overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)

ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ТОЧКИ:

Говорят, что вектор отложен от точки, если она является его началом. Например, \(\overrightarrow{АВ}\) отложен от точки А, \(\left| \text{CD} \right|\) отложен от точки С и так далее.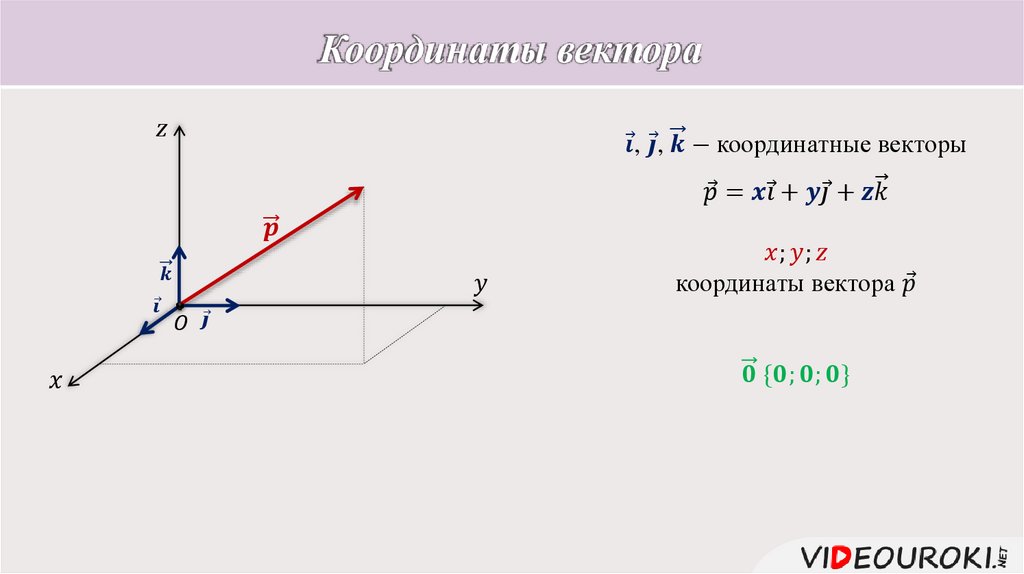 Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:

От любой точки можно отложить вектор, равный данному и при том только один.

Например, возьмем точку М и два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Мы можем отложить от точки М вектора, равные \(\overrightarrow{a}\) и \(\overrightarrow{b}\) всего один раз. Делается это параллельным переносом:

Таким образом \(\overrightarrow{a} = \overrightarrow{a’}\), и \(\overrightarrow{b} = \overrightarrow{b’}\), при этом \(\overrightarrow{a’}\ и\ \overrightarrow{b’}\) отложены от точки М.

СЛОЖЕНИЕ ВЕКТОРОВ:

При сложении векторов нужно учитывать их направления, поэтому проще всего складывать вектора визуально. Существуют два самых простых способа сложить два вектора – это правило треугольника и правило параллелограмма.

ПРАВИЛО ТРЕУГОЛЬНИКА

Если нужно найти сумму двух векторов, по правилу треугольника нужно:

1. Параллельным переносом перенести начало одного вектора в конец другого.

2. Пусть эти векторы будут сторонами треугольника, тогда третья его сторона – их сумма.

3. Обозначить направление получившегося вектора суммы – от начала первого вектора в конец второго (стрелка к стрелке).

Пример №1:

Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:

1. Перенесем вектор \(\overrightarrow{b}\) так, чтобы он начинался там, где заканчивается вектор \(\overrightarrow{a}\).

2. Соединим эти векторы в треугольник, третьей стороной которой будет вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).

3. Направление вектора \(\overrightarrow{c}\) будет идти от начала \(\overrightarrow{a}\) до конца \(\overrightarrow{b}\) (стрелка к стрелке)

ПРАВИЛО ПАРАЛЛЕЛОГРАММА:

Если нужно найти сумму двух векторов, по правилу параллелограмма нужно:

1. Параллельным переносом перенести начала этих векторов в одну точку.

2. Пусть эти векторы будут сторонами параллелограмма, тогда диагональ этого параллелограмма – их сумма.

3. Обозначить направление получившегося вектора суммы – от начала векторов в противоположный конец параллелограмма (по диагонали).

Пример №2:

Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:

1. Перенесем оба вектора параллельным переносом так, чтобы они начинались из одной точки.

2. Представим, что они являются сторонами параллелограмма.

3. Диагональ этого параллелограмма, которая начинается в точке начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – это вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).

СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ:

1. Переместительное свойство:

\(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)

2. Сочетательное свойство:

\((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)

СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ:

Чтобы сложить несколько векторов, нужно ставить их друг за другом, сохраняя их направление (используя параллельный перенос), тогда их суммой будет являться вектор, начала которого – это начало первого вектора, а конец – конец последнего вектора (как в правиле треугольника).

Пример №3:

Найдите сумму векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\):

1. Поставим эти векторы как бы по порядку сохраняя их длину и направление. По переместительному свойству неважно, в каком порядке мы будем располагать вектора. Соединим их, например, в таком порядке — \(\overrightarrow{d}\), \(\overrightarrow{e}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{a}\).

2. Проведем вектор их суммы от начала первого вектора в конец второго:

ВЫЧИТАНИЕ ВЕКТОРОВ:

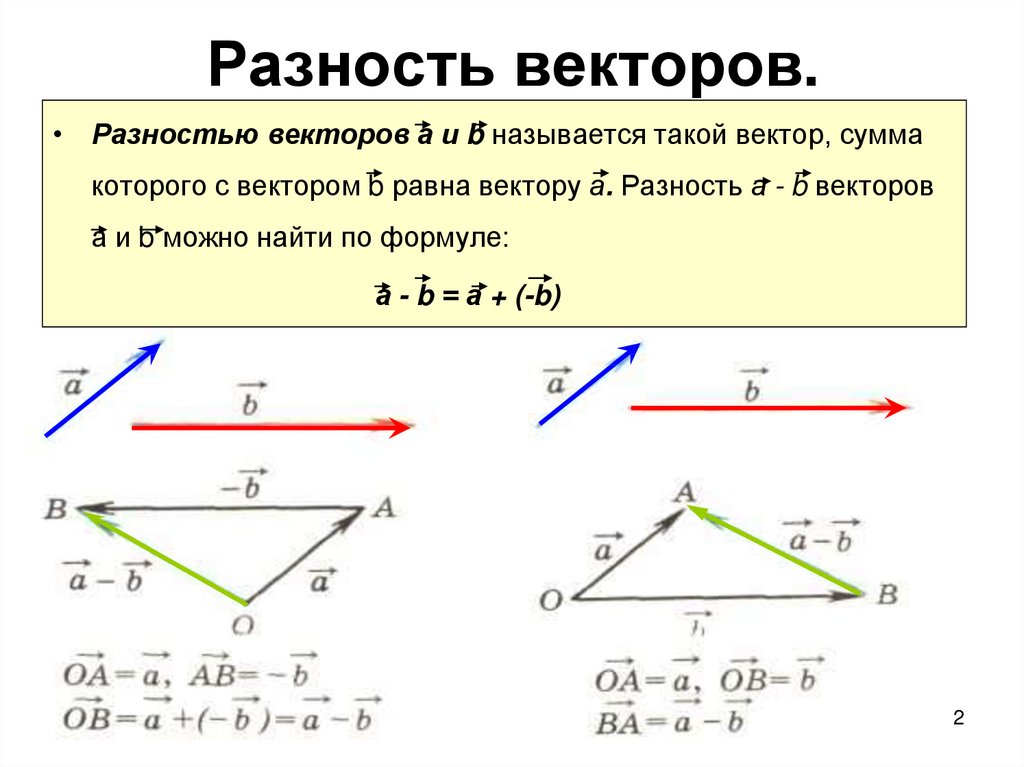
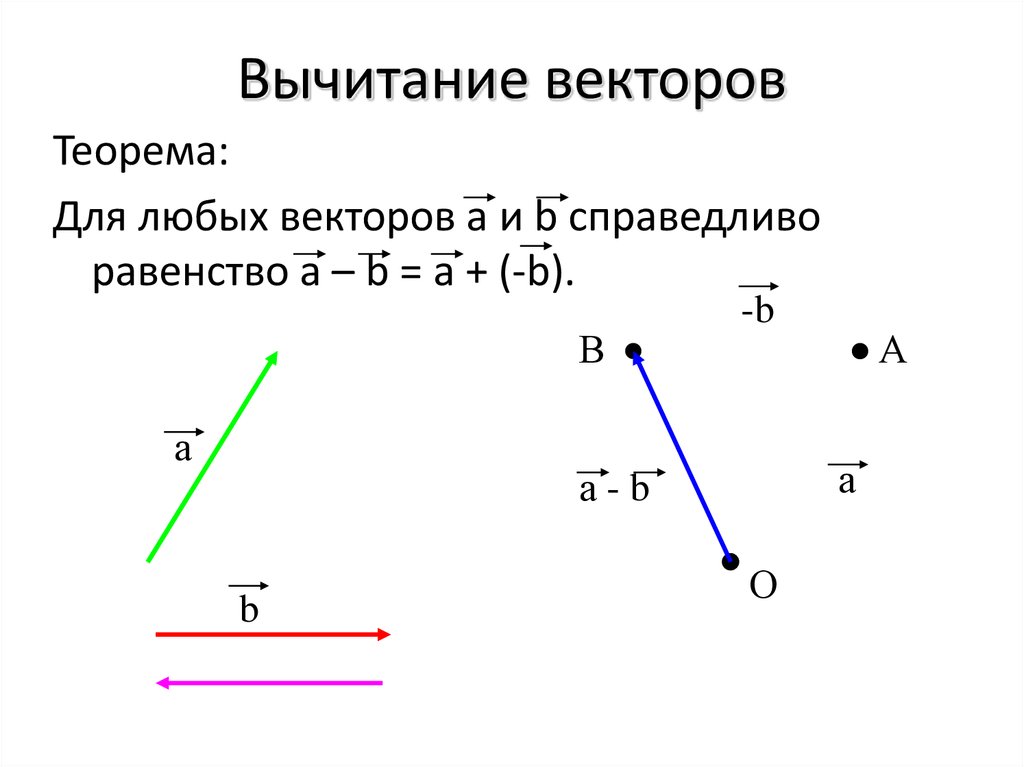
Вычесть вектор – это то же самое, что прибавить отрицательный вектор:

\(\overrightarrow{a}\ –\ \overrightarrow{b} = \overrightarrow{a} + (–\overrightarrow{b})\)

То есть и при вычитании можно использовать правила сложения.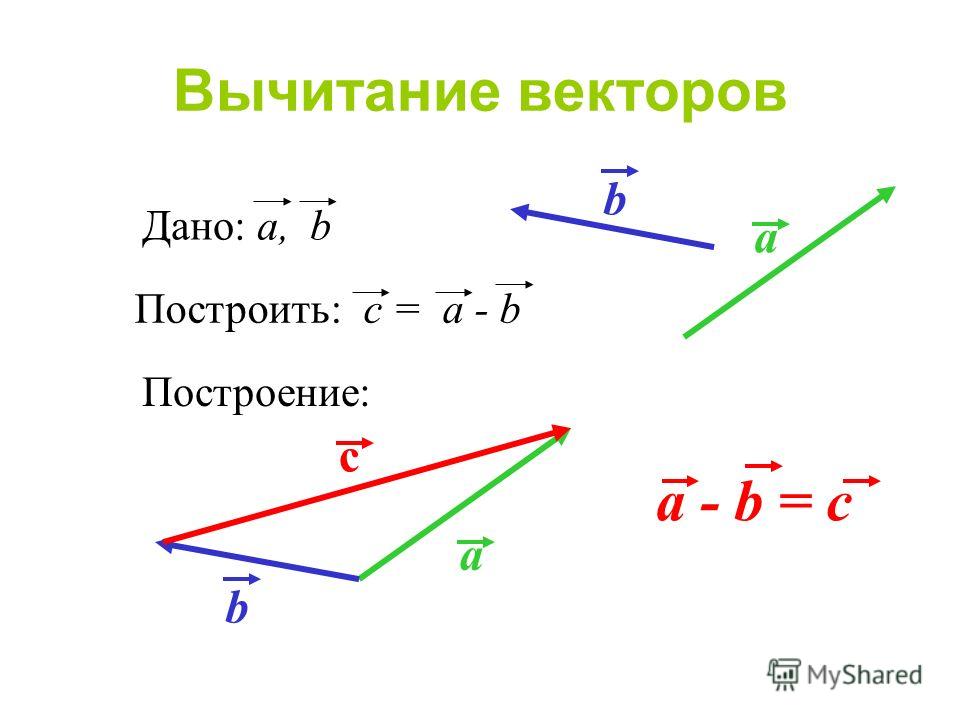 Главное – найти противоположный вектор.

Само словосочетание «противоположный вектор» говорит о том, что такие вектора направлены в разные стороны.

Значит вычесть вектор – значит прибавить вектор с противоположным ему направлением.

Мы можем проверить это свойство алгебраически. Мы знаем, что противоположные числа в сумме дают 0:

\(a + (–a) = a\ –\ a = 0\)

Тогда и сумма противоположных векторов дадут 0 (т.е. если мы «пойдем» от начала до конца \(\overrightarrow{a}\) и обратно по –\(\overrightarrow{a}\), то мы вернемся снова в начало \(\overrightarrow{a}\)):

Значит и для векторов справедливо это свойство:

\(\overrightarrow{a}\ + (–\ \overrightarrow{a}) = 0\)

Пример №4:

Найдите \(\overrightarrow{f} = \overrightarrow{a}\ –\ \overrightarrow{b} + \overrightarrow{c}\ –\ \overrightarrow{d}\ –\ \overrightarrow{e}\), если

1. Можем использовать сложение векторов, если мы найдем отрицательные векторы. В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:

2. Теперь сложим все векторы, учитывая отрицательные:

ПРОИЗВЕДЕНИЕ ВЕКТОРА И ЧИСЛА:

Произведением ненулевого вектора и числа является вектор, коллинеарный данному, длина которого равна произведению длины данного вектора и числа:

\(k \bullet \overrightarrow{a} = \overrightarrow{\text{ka}}\)

где k – это число, при этом:

\(\overrightarrow{a} \upuparrows \overrightarrow{\text{ka}}\) при \(k > 0\)

\(\overrightarrow{a} \uparrow \downarrow \overrightarrow{\text{ka}}\) при \(k < 0\)

Произведением любого вектора на ноль является нулевой вектор.

Пример №5:

Найдите 5\(\overrightarrow{a}\) и –2\(\overrightarrow{a}\) , если:

1. Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:

\(5\overrightarrow{a} = \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a}\):

\(5\overrightarrow{a} \upuparrows \overrightarrow{a}\), т.к 5 > 0

2. Аналогично поступим и с отрицательным числом, только теперь уже складываем противоположные векторы:

\(–2\overrightarrow{a} \uparrow \downarrow \overrightarrow{a}\), т.к –2 < 0

СВОЙСТВА ПРОИЗВЕДЕНИЯ ВЕКТОРА И ЧИСЛА:

1. Сочетательное свойство:

\(kl \bullet \overrightarrow{a} = k(l\overrightarrow{a}) \)

2. Распределительный закон:

\(\overrightarrow{a}(k + l) = k\overrightarrow{a} + l\overrightarrow{a}\)

и

\(k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}\)

ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ:

Используя векторы и связанные с ними свойства можно решать различные геометрические задачи.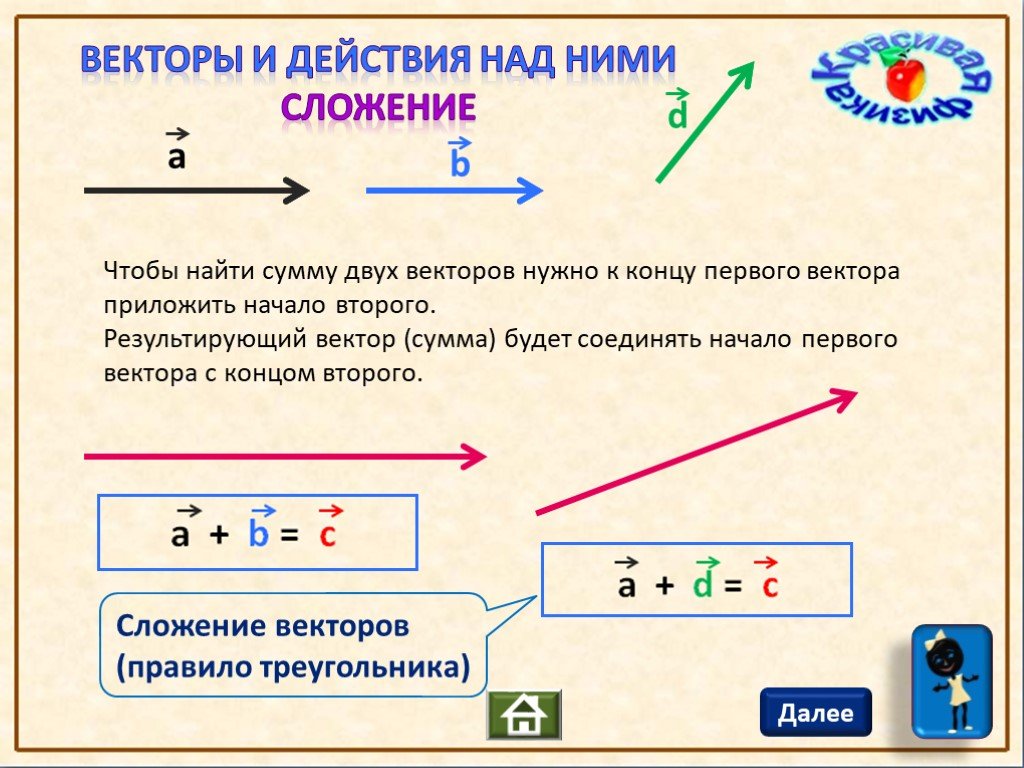

Пример №6:

Точка С – середина отрезка АВ, О – произвольная точка на плоскости. Докажите, что

\(ОС = \frac{1}{2}(АО + ОВ)\)

1. По правилу треугольника:

\(\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{АС}\)

\(\overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС}\)

2. Сложим два этих выражения, получим:

\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)

3. При этом \(\overrightarrow{АС}\) и \(\overrightarrow{ВС}\) – противоположные векторы, т.к. равны по модулю (точка С середина АВ), и имеют противоположное направление, значит:

\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)

\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + 0\)

\(ОС = \frac{1}{2}(АО + ОВ)\)

Что и требовалось доказать.

Пример №7:

ABCD – трапеция. Точки M и N середины оснований BC и AD соответственно. Точка О – точка пересечения прямых AB и CD. Докажите, что О, M и N лежат на одной прямой.

1. Треугольники OAD и OBC подобны по двум углам:

\(\left. \ \frac{\angle\text{OBC} = \angle OAD\ как\ соответствующие\ углы}{\angle O\ — \ общий} \right\}\Delta\text{OAD}\sim\text{ΔOBC}\)

\(\frac{\text{OA}}{\text{OB}} = \frac{\text{OD}}{\text{OC}} = k\)

2. При этом соответствующие стороны коллинеарны, значит можем выразить их как произведение числа и вектора:

\(\overrightarrow{\text{OA}} \upuparrows \overrightarrow{\text{OB}} \Longrightarrow \overrightarrow{\text{OA}} = k\overrightarrow{\text{OB}}\)

\(\overrightarrow{\text{OD}} \upuparrows \overrightarrow{\text{OC}} \Longrightarrow \overrightarrow{\text{OD}} = k\overrightarrow{\text{OC}}\)

3. В данной задаче можем выразить \(\overrightarrow{\text{OM}}\) и \(\overrightarrow{ON}\) как

\(\overrightarrow{\text{OM}} = \frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)

\(\overrightarrow{\text{ON}} = \frac{1}{2}(\overrightarrow{\text{OA}} + \overrightarrow{\text{OD}})\)

т.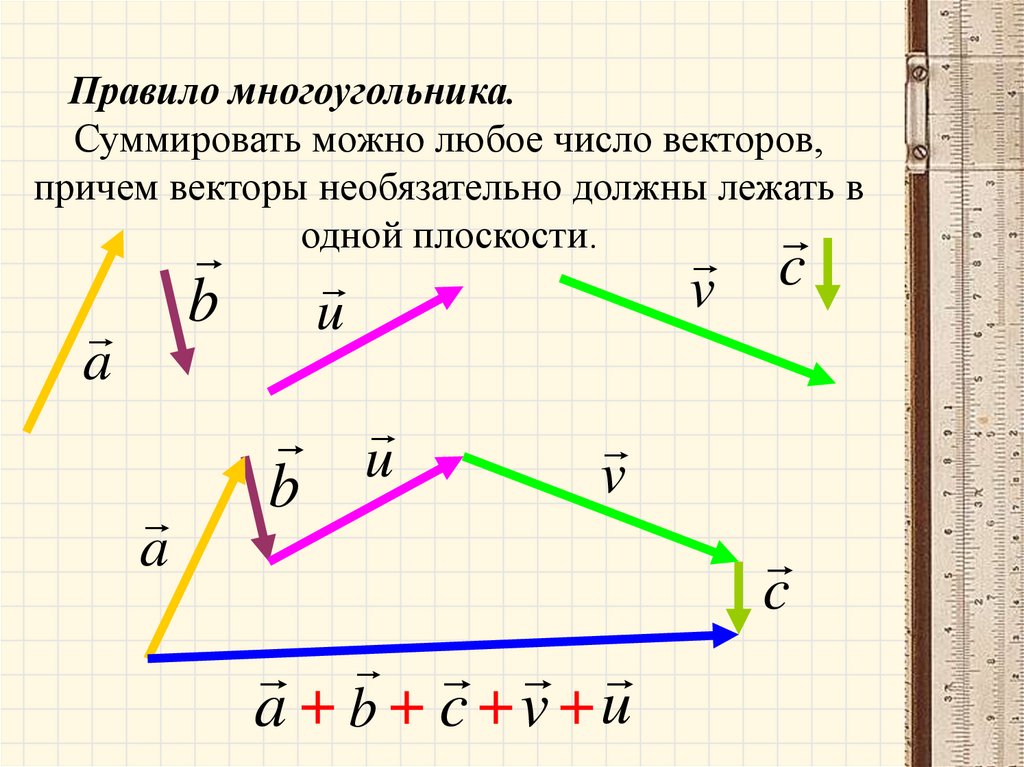 к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).

4. Соединим выразим вектор \(\overrightarrow{\text{ON}}\) через \(\overrightarrow{\text{OA}}\) и \(\overrightarrow{\text{OD}}\) из пункта 3:

\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OD}} \right)\)

\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( k\overrightarrow{\text{OB}} + k\overrightarrow{\text{OC}} \right)\)

\(\overrightarrow{\text{ON}} = \frac{1}{2}k\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)

\(\overrightarrow{\text{ON}} = k(\frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)) = k\overrightarrow{\text{OM}}\)

5. Если вектор \(\overrightarrow{\text{ON}}\) можно представить как произведение числа k с вектором \(\overrightarrow{\text{OM}}\), значит \(\overrightarrow{\text{ON}}\) и \(\overrightarrow{\text{OM}}\) коллинеарны, а значит лежат на одной прямой (они не могут быть параллельны, т. к. уже пересекаются в точке О).

Что и требовалось доказать.

Векторы в пространстве. (11 класс)

B1
A1
Векторы в
пространстве.
D1
B
Геометрия,
11 класс.
C1
A
C
D
AC1 AB AD AA1
Воробьев Леонид Альбертович, г.Минск
I. Определение вектора. Основные понятия, связанные с векторами.
Как и в плоскости, в пространстве вектор определяется как направленный
отрезок:
B
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого
начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A
Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
m n
Обозначение коллинеарных векторов:
a b, a c, c b.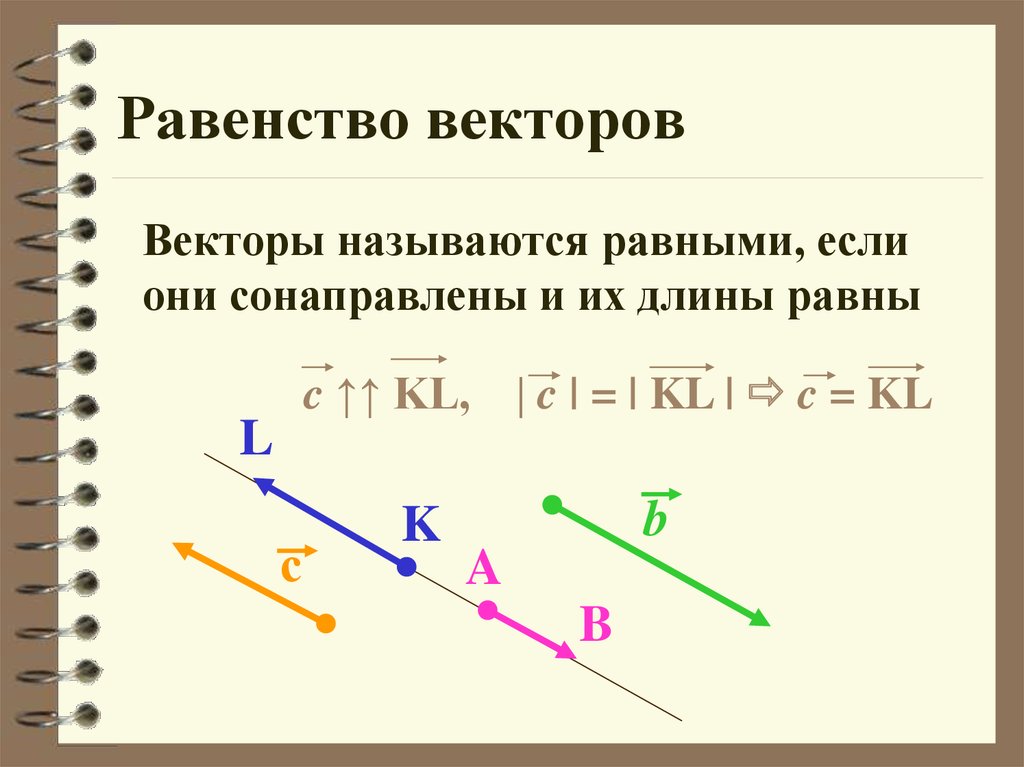
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b
От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.
II. Действия с векторами.
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются правила треугольника или параллелограмма:
1) При применении правила треугольника один из векторов откладывают от конца
другого, т. е. MK KF MF :
a b
a
b
2) При применении правила параллелограмма оба вектора откладывают из общей
начальной точки, т.е. MK MN MF , где F – вершина параллелограмма,
противоположная общей начальной точке векторов.
a b
a
b
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a
Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т.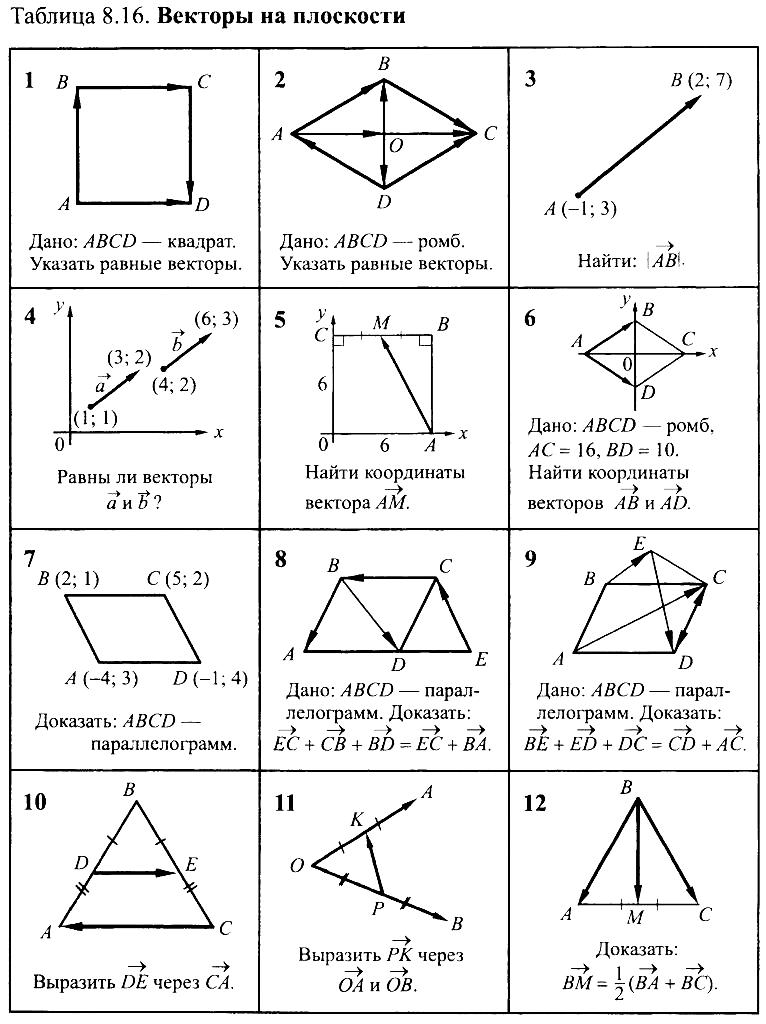 к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b
Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3
И еще одно действие с векторами – умножение двух векторов. В школьном курсе
геометрии изучается скалярное произведение векторов. В результате этого
действия (в отличии от предыдущих действий с векторами) получается число,
равное произведению модулей двух данных векторов на косинус угла между этими
векторами, т. е.
a·b a · b ·cos a,b.
Геометрически скалярное произведение векторов можно понимать как площадь
параллелограмма (или противоположная ей величина), стороны которого
образуются одним из данных векторов и вектором, перпендикулярным второму с
таким же модулем:
S a ·b’ ·sin 900 a ·b ·cos a·b;
S a ·b’ ·sin 900 a ·b ·cos a·b.
ò .å. a·b S
a
900
b’
b b’
b’
– острый угол
a
b
900
– тупой угол
b
III. Координаты вектора. Действия в координатах.
Теперь рассмотрим все эти понятия и действия с точки зрения координатного
пространства. Вспомним, что любая точка пространства задается тремя
координатами А(x;y;z).
A(x1;y1;z1)
Естественно, что
Если принять вектор за параллельный
B(x2;y2;z2) перенос начальной точки A(x1;y1;z1)
в
конечную точку B(x2;y2;z2), то координаты
вектора показывают: на сколько изменяются
соответствующие координаты начальной
точки при параллельном переносе в
конечную, т. е.
AB x2 x1; y2 y1; z2 z1
AA 0;0;0 и BA x1 x2 ; y1 y2 ; z1 z2 .
Т.к. модуль вектора равен длине изображающего его отрезка, то:
AB
m2 n2 k 2
, где
AB m; n; k
– координаты вектора.
Два вектора, заданные координатами a m1 ; n1 ; k1 è b m2 ; n2 ; k2 будут равны,
если (подумайте) …
…равны их соответствующие координаты, т.е. m1 m2 ,n1 n2 ,k1 k2 .
Для сложения двух векторов, заданных координатами, нужно просто сложить их
соответствующие координаты, т.е.
m1; n1; k1 m2 ; n2 ; k2 m1 m2 ;n1 n2 ;k1 k2 .
При вычитании векторов, заданных координатами, нужно найти разности
соответствующих координат, т.е.
их
m1; n1; k1 m2 ; n2 ; k2 m1 m2 ; n1 n2 ; k1 k2 .
Умножение вектора, заданного координатами, на число выполняется так:
a· m; n; k am; an; ak , ăäĺ a R/.
Скалярное произведение двух векторов, заданных координатами, равно сумме
произведений соответствующих координат, т.е.
m1; n1; k1 · m2 ; n2 ; k2 m1m2 n1n2 k1k2 .
Условием коллинеарности двух векторов, заданных
пропорциональность их соответствующих координат:
a
b
m1
n
k
1 1
m2
n2
k2
Самостоятельно разберитесь, когда
a ↑↑ b
координатами,
čëč a xb.
и
a ↑↓ b .
будет
Для выяснения компланарности трех векторов необходимо, чтобы любой из этих
векторов можно было разложить по двум оставшимся, т.е.
a,b,c c x·a y·b, x, y R..
Напомним как это выглядит геометрически:
a
c
B
b
C
A
D
AC AB AD . Но AC c , AB a, AD b.
Значит, AB x·a , AD y·b c x·a y·b, x, y R..
По правилу параллелограмма:
В данном конкретном случае:
c 2a 3b
, если аппликаты всех точек равны.
Аналитически выяснить компланарность трех векторов, заданных координатами,
можно решая систему:
a m1 ; n1 ; k1
m3 xm1 ym2 ,
n3 xn1 yn2 , ãäå b m2 ; n2 ; k 2 .
k xk yk ,
c m3 ; n3 ; k3
1
2
3
Если система имеет единственное решение, то векторы
a ,b,c компланарны.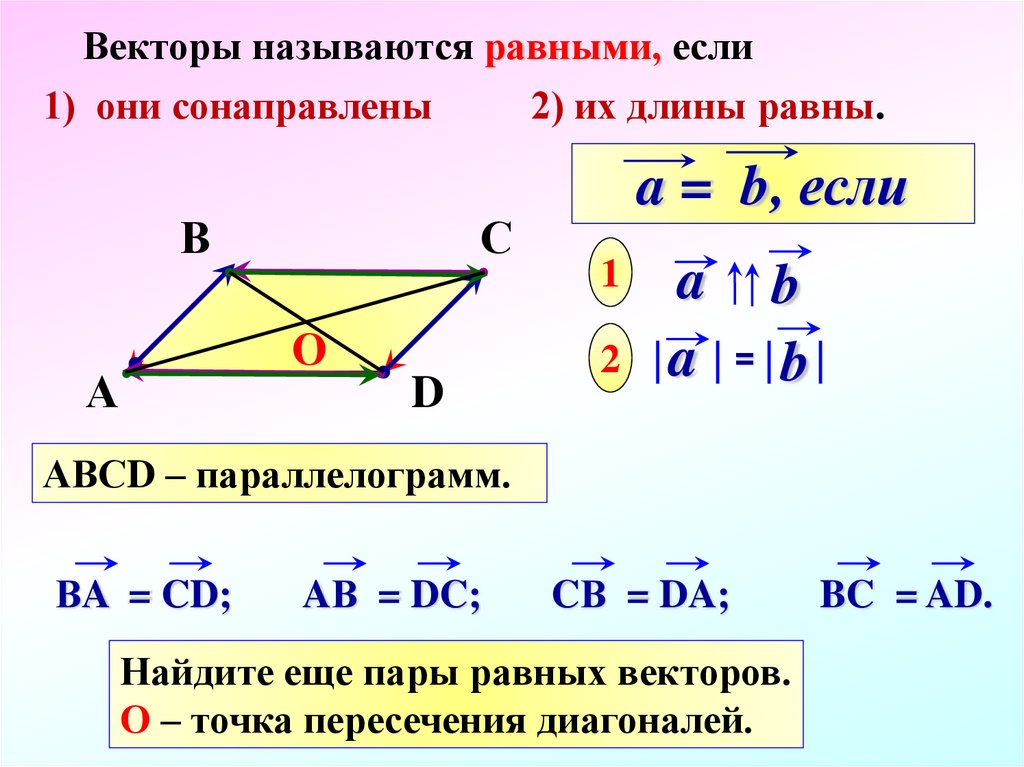
Любой вектор пространства можно разложить по трем некомпланарным векторам,
т.е.
d x·a y·b z·c, ãäå a,b,c ; x, y,z R..
Аналитически разложение любого вектора d m4 ; n4 ; k4 по трем некомпланарным
векторам
a m1; n1; k1 , b m2 ; n2 ; k2 è
c m3 ; n3 ; k3 сводится к решению
системы:
m4 xm1 ym2 zm3 ,
n4 xn1 yn2 zn3 ,
k xk yk zk ,
1
2
3
4
А решение этой системы – числа x, y и z являются коэффициентами разложения
вектора d по трем векторам a,b è c.
Геометрически это означает возможность построения параллелепипеда, в котором
диагональ задается вектором
, а все три измерения – векторами,
d
коллинеарными векторам a,b è c .
a
c
b
D1
d
C1
A1
B1
D
AC1 AA1 AB AD
d x·a y·b z·c
C
A
B
В прямоугольной системе координат в пространстве векторы i 1;0;0 , j 0;1;0 и
k 0;0;1 называются единичными координатными векторами (или óртами). Т.к.
эти векторы являются некомпланарными, то любой вектор пространства можно
разложить по ортам. При этом образуется прямоугольный параллелепипед, а
коэффициенты разложения – координаты данного вектора.
D1
z
C1
A1
B1
D
1
1
x
k
0
i A j1
C
B
y
AC1 AD AB AA1 x·i y· j z·k AC1 x; y; z
В данном случае x=–3; y=4; z=6, т.е. координаты вектора AC1 3;4; 6 .
Умение выполнять действия с векторами и понимание вышеизложенного
материала позволяет решать некоторые геометрические задачи с помощью
векторов. Этот способ получил название векторного способа решения задач. Мы
познакомимся с ним на следующих уроках… .
S
C
A
O
M
N
B
Для любого тетраэдра: SO
1
SA SB SC
3

векторов по математике | Введение в векторы

Векторы в математике — это объекты, которые имеют как величину, так и направление. Величина определяет размер вектора. Он представлен линией со стрелкой, где длина линии является величиной вектора, а стрелка указывает направление. Он также известен как Евклидов вектор или Геометрический вектор или Пространственный вектор или просто « вектор ».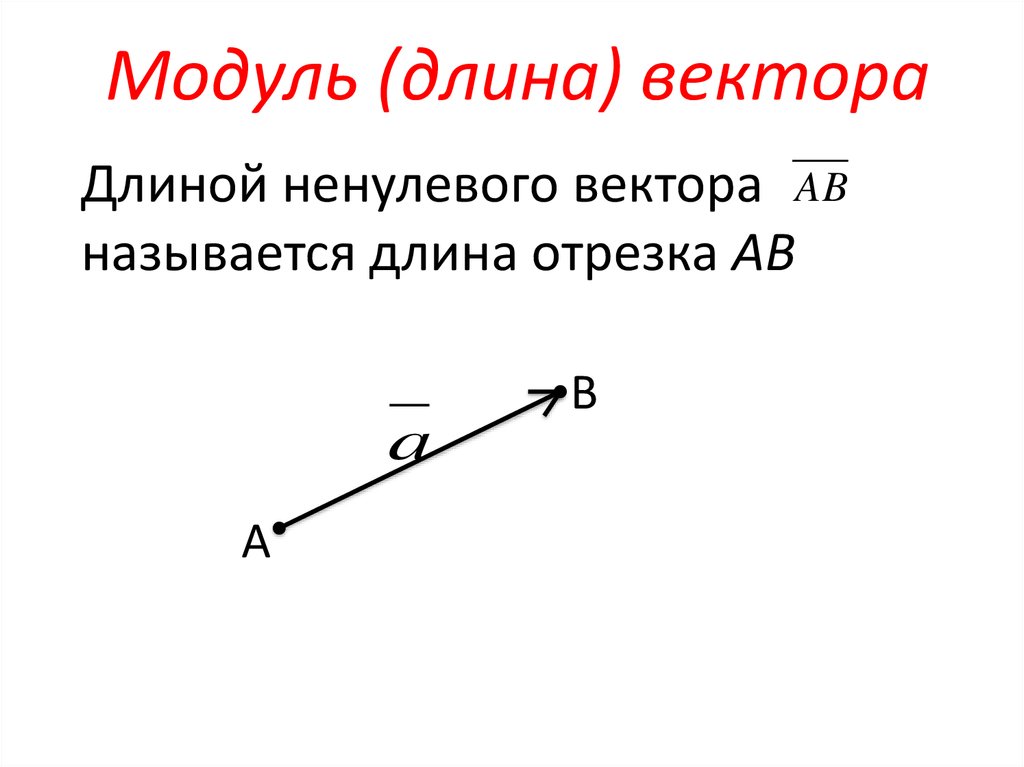

Два вектора называются равными, если их величина и направление одинаковы. Он играет важную роль в математике, физике, а также в технике. Согласно векторной алгебре, вектор может быть добавлен к другому вектору, голова к хвосту. Порядок сложения двух векторов не имеет значения, потому что результат будет одинаковым. Проверьте законы сложения векторов для более подробной информации.

Содержание: Определение Пример Представительство Величина векторов Единичный вектор Нулевой вектор Операции Компоненты вектора Приложения Проблемы Часто задаваемые вопросы

Определение векторов

Векторы определены как объект, содержащий как величину, так и направление. Вектор описывает движение объекта из одной точки в другую. Векторная математика может быть геометрически представлена ​​направленным отрезком прямой.

Длина отрезка направленной линии называется величиной вектора, а угол, под которым наклонен вектор, показывает направление вектора. Начальная точка вектора называется «Хвост», а конечная точка (со стрелкой) называется «Голова».

Вектор определяется как математическая структура. Он имеет множество приложений в области физики и геометрии. Мы знаем, что расположение точек на координатной плоскости можно представить с помощью упорядоченной пары, такой как (x, y). Использование вектора очень полезно в процессе упрощения трехмерной геометрии.

Наряду с термином вектор мы слышали термин скаляр. Скаляр фактически представляет «действительные числа». Проще говоря, вектор «n» измерений представляет собой упорядоченный набор из n элементов, называемых «

компонентов ».

Примеры векторов

Наиболее распространенными примерами вектора являются скорость, ускорение, сила, увеличение/уменьшение температуры и т. д. Все эти величины имеют как направление, так и величину.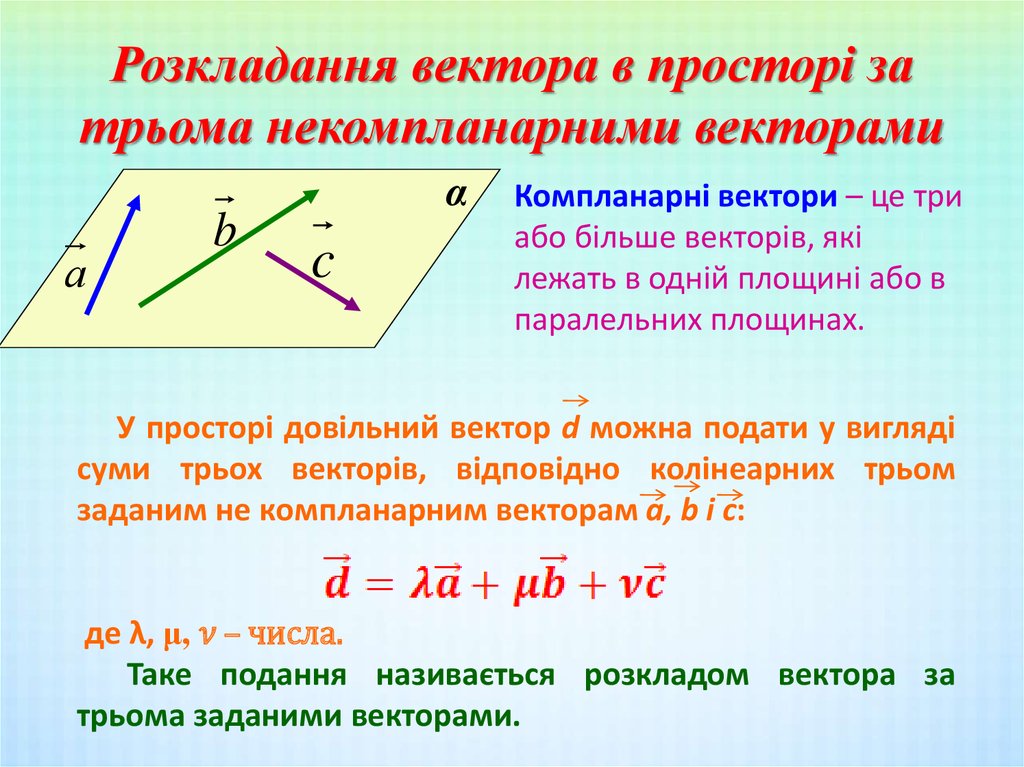 Поэтому необходимо вычислять их в векторной форме.

Кроме того, скорость — это величина, которая имеет величину, но не имеет направления. Это основное различие между скоростью и скоростью.

Векторное обозначение

Как мы уже знаем, вектор имеет как величину, так и направление. На приведенном выше рисунке длина линии AB равна величине, а острие стрелки указывает направление.

\(\begin{array}{l}\text{Поэтому векторы между двумя точками A и B задаются как } \overrightarrow{AB},\ \text{или вектор a.} \\ \text{Стрелка над начало вектора показывает направление вектора.}\end{array} \)

Величина вектора

Величина вектора показана вертикальными линиями по обе стороны от данного вектора «|a|». Он представляет собой длину вектора. Математически величина вектора вычисляется с помощью «Теоремы Пифагора», т.е.

|a|= √(x ² +y ² )

Единичный вектор

Единичный вектор имеет длину (или величину), равную единице, которая в основном используется для указания направления любого вектора.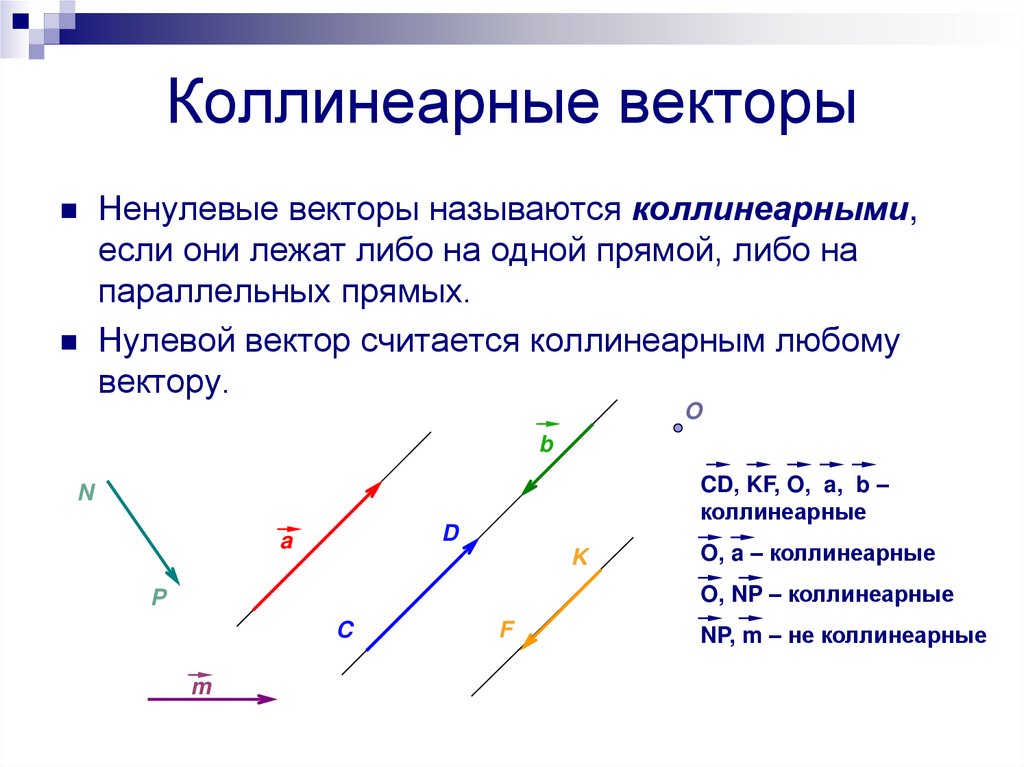

).

Если a является вектором произвольной длины и его величина равна ||a||, то единичный вектор определяется как:

\(\begin{array}{l}\hat{\mathbf{a}}=\frac{\mathbf{a}}{\|\mathbf{a}\|}\end{array} \)

Это также известно как нормализация вектора.

Нулевой вектор

Вектор с нулевыми величинами называется нулевым вектором. Координаты нулевого вектора задаются как (0,0,0) и обычно представляются 0 со стрелкой (→) вверху или просто 0. 

Сумма любого вектора с нулевым вектором равна самому вектору, т. е. если «а» — любой вектор, то;

0+а = а

Примечание. Для нулевого вектора нет единичного вектора, и его нельзя нормализовать.

Операции над векторами

Изучая математику, мы узнали о различных операциях, которые мы выполняем над числами. Давайте изучим здесь векторную операцию, такую ​​​​как сложение, вычитание, умножение на векторах.

Добавление векторов

Можно сложить два вектора a и b, получив сумму a + b.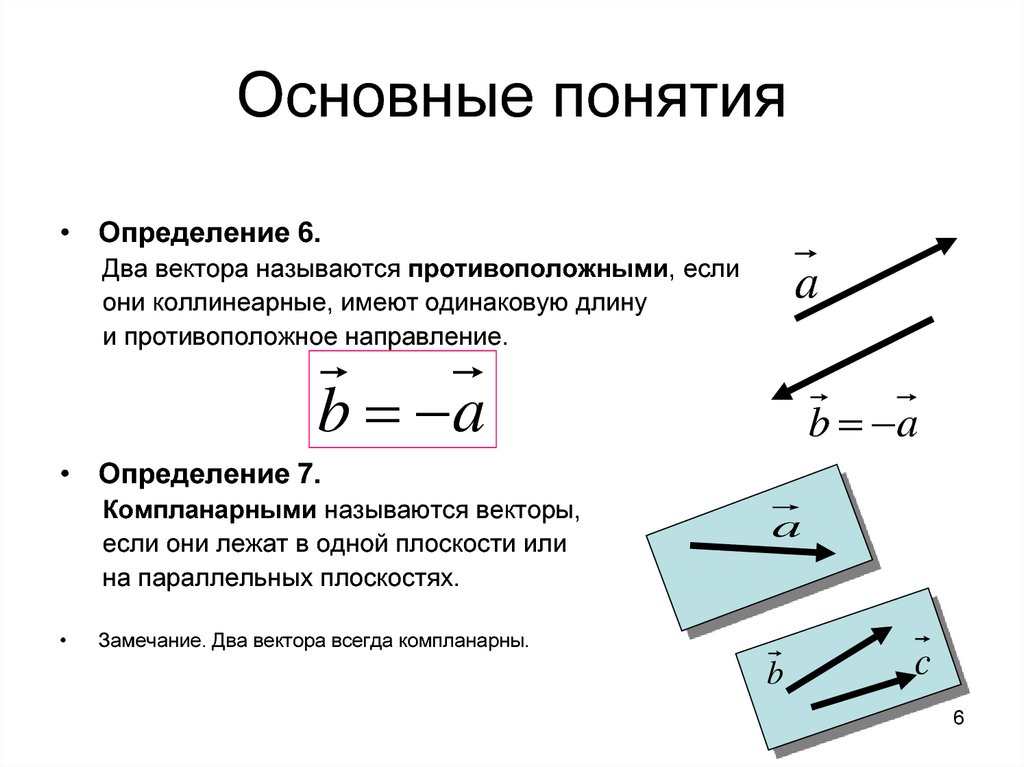 Это требует соединения их головы к хвосту.

Мы можем перемещать вектор b до тех пор, пока его хвост не встретится с вершиной вектора a. Отрезок линии, направленный от хвоста вектора a к началу вектора b, называется вектором «a + b».

Характеристики векторного математического сложения

• Коммутативный закон — порядок сложения не имеет значения, т. е. a + b = b + a
• Ассоциативный закон — сумма трех векторов не зависит от того, какая пара векторов добавлена ​​в начале.

т. е. (а + b) + с = а + (b + с)

Вычитание векторов

Перед операцией необходимо знать об обратном векторе(-а).

Обратный вектор (-а), который противоположен «а», имеет ту же величину, что и «а», но направлен в противоположном направлении.

Сначала находим обратный вектор.

Затем добавьте их как обычно.

Например, если мы хотим найти вектор b – a

Тогда b – a = b + (-a)

Скалярное умножение векторов

Умножение вектора на скалярную величину называется «масштабированием». В этом типе умножения изменяется только величина вектора, а не направление.

• S(a+b) = Sa + Sb
• (С+Т)а = Са + Та
• а.1 = а
• а.0 = 0
• а.(-1) = -а

Скалярное тройное произведение

Скалярное тройное произведение, также называемое коробочным произведением или смешанным тройным произведением, трех векторов, скажем, a, b и c равно

(а×б)⋅с . Поскольку он включает скалярное произведение и оценивает одно значение, поэтому указывается как скалярное произведение. Он также обозначается ( a b c ).

( a b c ) = (a×b)⋅c

\(\begin{array}{l}\begin{aligned} (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c} &=\left|\begin{array}{ ll} a_{2} & a_{3} \\ b_{2} & b_{3} \end{массив}\right| c_{1}-\left|\begin{массив}{ll} a_{1} & a_{3} \\ b_{1} & b_{3} \end{массив}\right| c_{2}+\left|\begin{массив}{ll} a_{1} & a_{2} \ \ b_{1} & b_{2} \end{массив}\right| c_{3} \\ &=\left|\begin{массив}{lll} c_{1} & c_{2} & c_{3 } \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{массив}\right| \end{выровненный}\end{массив } \)

Основное применение скалярного тройного произведения можно увидеть при определении объема параллелепипеда, который равен абсолютной величине |(a×b)⋅c|, где a, b и c — векторы, обозначающие стороны параллелепипеда соответственно. Следовательно,

Объем параллелепипеда = ∥a×b∥ ∥c∥ |cosϕ|=|(a×b)⋅c|

Векторное умножение

В основном существует два типа векторного умножения:

• Перекрестное произведение
• Скалярный продукт

Перекрестное произведение векторов

В результате перекрестного произведения двух векторов получается векторная величина. Он представлен знаком креста между двумя векторами.

т. е. a × b

Математическое значение перекрестного произведения-

где,

| а | есть величина вектора а.

| б | является величиной вектора b.

θ — угол между двумя векторами a и b.

\(\begin{array}{l}\hat{n} \text{ — единичный вектор, показывающий направление умножения двух векторов.}\end{array} \)

Скалярное произведение векторов

Скалярное произведение двух векторов всегда приводит к скалярной величине, т. е. имеет только величину и не имеет направления. Он представлен точкой (.) между двумя векторами.

точка б = а. b

Математическое значение скалярного произведения задается как

а . б = | а | | б | cos θ

Компоненты векторов (горизонтальные и вертикальные)

Два компонента вектора в плоскости x-y.

1. Горизонтальный компонент
2. Вертикальный компонент

Разбиение вектора на его компоненты x и y в векторном пространстве является наиболее распространенным способом решения векторов.

Вектор «а» наклонен к горизонтали под углом, равным θ.

Этот заданный вектор «а» можно разбить на две составляющие, т.е. _x и _y .

Компонент a

x называется «горизонтальным компонентом», значение которого равно cos θ.

Компонент a _y называется «вертикальным компонентом», значение которого равно sin θ.

Применение векторов

Некоторые из важных применений векторов в реальной жизни перечислены ниже:

• Направление приложения силы для перемещения объекта можно найти с помощью векторов.
• Чтобы понять, как гравитация использует силу притяжения объекта для работы.
• Движение тела, ограниченного плоскостью, можно получить с помощью векторов.
• Векторы помогают определить силу, приложенную к телу одновременно в трех измерениях.
• Векторы используются в области машиностроения, где сила намного больше, чем выдержит конструкция, иначе она рухнет.
• В различных осцилляторах используются векторы.
• Векторы также находят применение в «квантовой механике».
• Скорость в трубе можно определить с помощью векторного поля, например, гидромеханики.
• Мы также можем наблюдать их повсюду в общей теории относительности.
• Векторы используются при распространении различных волн, таких как распространение вибрации, распространение звука, распространение волны переменного тока и т.д.

Проблемы и решения

Пример 1. Дан вектор V, имеющий величину 10 единиц и наклоненный под углом 60°. Разбейте заданный вектор на две его составляющие.

Решение:

Дан вектор V, имеющий величину |V| = 10 единиц и θ = 60°

Горизонтальная составляющая (V _x ) = V cos θ

В _x = 10 cos 60°

В _х = 10 х 0,5

В _x = 5 шт.

Теперь вертикальная составляющая (V _y ) = V sin θ

В _y = 10 sin 60°

В _y = 10 × √3/2

В _y = 10√3 единиц

Пример 2:

Найдите модуль вектора a (3,4).

Решение-

Данный вектор a = (3,4)

|a|= √(x ² +y ² )

|а|= √(3 ² +4 ² )

|а|= √(9+16) = √25

Следовательно, | а |= 5

Пример 3:

Найдите скалярное и векторное произведение двух векторов «a» и «b», заданных как 3i – 1j + 2k и 1i + -2j + 3k соответственно.

Решение-

Дан вектор a (3,-1,2) и вектор b (1,-2,3)

Где θ – угол между векторами. Но мы не знаем угол между векторами, поэтому можно использовать другой метод умножения.

а.б = (3i – 1j + 2k) . (1i -2j +3k)

a.b = 3(i.i) + 2(j.j) + 6(k.k)

а.б = 3 + 2 + 6

а.б = 11

Чтобы изучать все концепции математики более увлекательным способом, зарегистрируйтесь на сайте BYJU’S. Кроме того, смотрите интересные видеоролики на различные темы по математике, загрузив BYJU’S — The Learning App.

Часто задаваемые вопросы о векторах – Часто задаваемые вопросы

Что такое вектор в математике?

Вектор – это величина, которая имеет как величину, так и направление. Он определяет перемещение объекта из одной точки в другую.

Какие примеры векторов?

Примерами векторов являются сила, скорость, ускорение и т. д. , поскольку эти величины имеют как величину, так и направление.

Какие бывают типы векторов?

Десять типов векторов в математике:
Нулевой вектор
Единичный вектор
Вектор положения
Ко-начальный вектор
Векторы сходства и отличия
Копланарный вектор
Коллинеарный вектор
Равный вектор
Вектор смещения
Отрицательное значение вектора

Какова величина вектора?

Величина вектора показана вертикальными линиями с обеих сторон данного вектора «|a|». Он представляет собой длину вектора.

В чем разница между скаляром и вектором?

Скалярная величина имеет только величину (размер или измерение), тогда как векторная величина имеет и величину, и направление. Например, скорость — это скалярная величина, а скорость — векторная величина.

вектор по математике — Определение, умножение и примеры (видео)

Написано

Малкольм МакКинси

12 января 2023

Проверка по факту

9000 3 9000. 9005. 9000. 9005.

. количество в математике, имеющее звездная величина  (расстояние, скорость или размер) и  направление  (как на стрелке компаса, например, запад, вверх, юго-восток, вниз или с севера на северо-запад).

Переплывая бухту на лодке, вы можете думать, что плывете прямо на юг со скоростью 3 узла, но если приливы отступают, вы можете двигаться со скоростью 5 узлов на юго-восток.

Вектор или несколько векторов, работающих вместе, будут учитывать расстояние, которое вы гребете, вашу скорость и фактическое направление.

Символ вектора

Для представления векторов математики, физики и инженеры используют лучи, обозначая их строчными или прописными буквами, например:

Символ вектора

Советы по маркировке векторов Вот почему у нас есть вектор

AB , а не вектор BA .

Если вы маркируете свои векторы, решение использовать прописные или строчные буквы остается за вами; если вам даны векторы, обратите внимание на направление вектора (посмотрите на стрелки).

Векторы могут быть параллельны и указывать в одном и том же или противоположном направлении (посмотрите на стрелки).

Векторы одинаковой величины, но направленные в противоположные стороны, являются противоположными, поэтому вектор b можно также записать как -a , что отрицает величину a.

Репетиторы

Вектор единичной длины называется единичным вектором и обозначается так называемой шляпой: ˆ

Сложение и вычитание векторов

Простая векторная математика не так уж сложна.

Чтобы добавить векторы, мы соединяем хвост одного вектора с головой другого, используя стрелку. Луч прямой линии, соединяющий два вектора, является равнодействующим r , как показано на этом рисунке:

Вот загадка: эта цифра дает те же результаты, что и предыдущая цифра?

Сложение вектора

Здесь мы добавляем вектор EF к вектору CD и еще получаем результирующее r . Векторы подчиняются тем же правилам арифметики, что и целые числа (в данном случае свойство коммутативности).

В реальном мире два путешествия вдоль векторов могут показать совершенно разные пейзажи. В математике, поскольку два вектора не изменили своего направления или величины, результаты идентичны: CD + EF = EF + CD = r .

Vector Fuctraction предпринимает только два шага:

1. Отрицайте вектор, который вы хотите вычесть

2. , затем добавьте два вектора вместе

Вот векторы SA и il , показывают, что на демонстрации маршрута. мы брали парусник:

Вычитание вектора

Мы не знали, что течение было сильным; мы заблудились в тумане; солнце ослепляло. По какой-то причине вместо следования вектору IL , мы пошли в противоположном направлении. Поэтому вместо добавления вектора IL нам нужно его вычесть. Мы делаем это, инвертируя вектор IL и добавляя его к вектору SA :

Умножение векторов на скаляр

Умножение вектора на скаляр (действительное число) называется скалярным умножением .

Векторы состоят из двух частей (величина и направление), но мы не можем умножить направление. Это не имеет смысла: два «юга» не обращены к югу больше, чем один «юг». Но мы может умножить величину вектора:

• Умножение вектора на положительный целочисленный скаляр > 1 дает больший вектор.

• Умножение вектора на отрицательный целочисленный скаляр < −1 дает больший вектор в направлении , противоположном .

• Умножение векторов на 1 возвращает тот же вектор ( 0 смещение).

• Умножение вектора на положительный дробный скаляр < 1 дает меньший вектор.

• Умножение вектора на отрицательный дробный скаляр > −1 дает меньший вектор в направлении , противоположном .

Два вектора также можно умножить друг на друга с помощью перекрестного произведения или скалярного произведения.

Умножение двух векторов методом перекрестного произведения дает новый вектор, а скалярное произведение дает число, иногда называемое скалярным произведением.

Величина вектора

Величина вектора отображается как абсолютное значение,  |a| или двумя строками, чтобы не спутать его с абсолютным значением, | |а|| .

Если вы знаете значения оси x и оси y вектора (как если бы он был на карте или в декартовой системе координат), вы можете легко вычислить его величину, применив теорему Пифагора к изменению положения от хвоста к наконечнику :

Рассчитать звездную величину вектора

Итак, здесь с хвостом на (1, 4) и стрелка на (7, 8) , мы имеем изменение значения x на 6 и изменение значения y на 4 , поэтому:

Величина вектор 7,2111 единиц .

Единица измерения определяется тем, что вы измеряете; дюймы, километры, мили в час (миль/час) и т. д. Итак, если бы мы просто измерили расстояние в милях, то 7,2111 миль  было бы длиной вектора.

Скаляр против векторов

Для ясности, скаляр  величины — это только величины: масса, температура, скорость, объем, расстояние, энергия, работа и т. д. Думайте о них как о чистых числах.

Внимательно прослушайте или прочитайте: Услышать или прочитать две величины, например скорость  и  направление? Тогда вы имеете дело с вектором. Не читаешь и не слышишь две величины? Вероятно, вы имеете дело со скаляром.

Векторы смещения

Летающие супергерои редко выбирают кратчайший путь от Дэйли Бьюгл или Дэйли Плэнет до катастрофы того дня. Они налетают, петляют, прыгают и перекатываются, прежде чем, наконец, прибывают в самый последний момент.

Если бы мы использовали векторы для определения курса летающего супергероя, нам могло бы понадобиться пять или шесть векторов, чтобы учесть все эти обходные пути. Вектор смещения пересекает прямую линию от начала до конца:

Определение вектора смещения и пример

Смещение в этом значении исходит из физики, означая изменение положения по сравнению с начальным положением.

Вы засовываете правую руку; вы убираете правую руку: нулевое смещение. Ты ча-ча три шага влево и два шага вправо: Вектор смещения на один шаг влево.

На этом рисунке мы видим, что вектор смещения также является результирующим.

Расчет смещения по-прежнему вектор n + вектор v = r , потому что векторы a и y отрицают друг друга!

Вы можете подумать, что мы потратили много усилий, чтобы преодолеть такое небольшое расстояние, но что, если бы мы находились на корабле ВМФ и должны были перемещаться вокруг пристани или охраняемого заповедника? Тогда мы увидим, что это действительно был кратчайший маршрут

Примеры векторов

All of these measurements are examples of vectors because they all involve distance or size of a force and a direction:

• Velocity

• Force

• Acceleration

• Momentum

• Displacement

Коммерческие авиалайнеры, истребители, лодки, автомобили, велосипедисты, бегуны, падающие объекты, ракеты, воздушные шары, бумажные самолетики и подводные лодки — все это примеры движущихся объектов, которые используют векторы в повседневной жизни.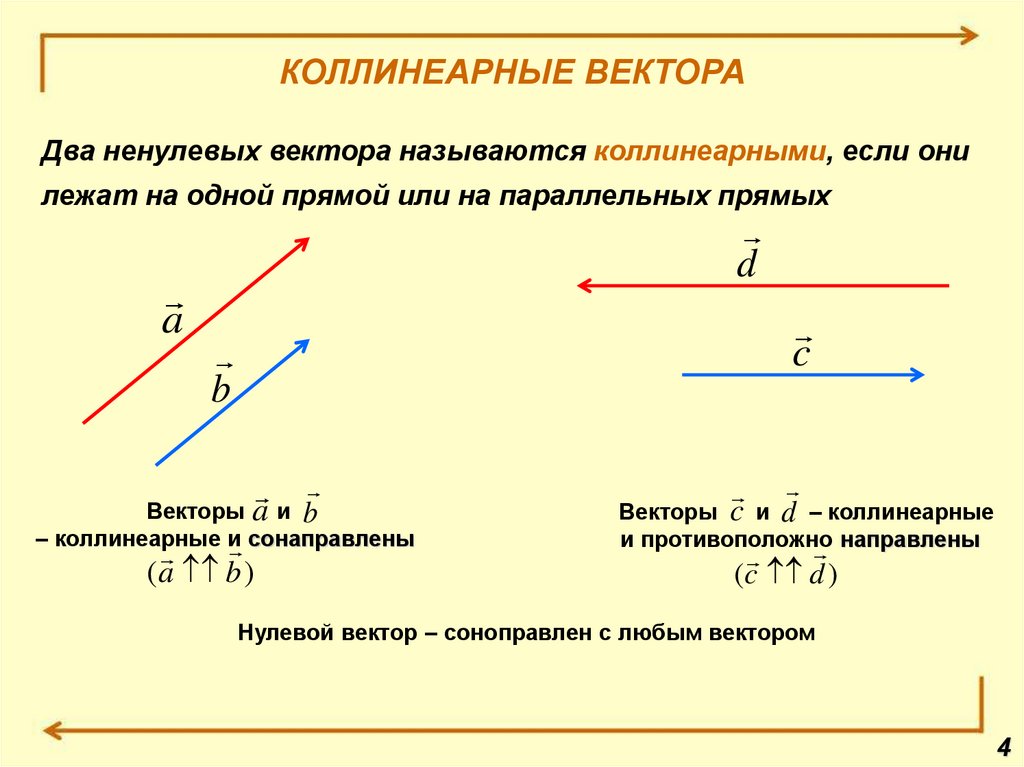

Пилоты и навигаторы должны использовать векторы, чтобы добраться до места назначения. Ученые-ракетчики и аэрокосмические инженеры используют векторы для управления ракетами.

Существует одно исключение для векторов, имеющих длину и направление, и это нулевой вектор. Нулевой вектор не имеет длины, поэтому он не указывает ни в каком конкретном направлении. Это означает, что нулевой вектор имеет неопределенное направление.

Основные векторные задачи

1. Что произойдет, если мы умножим вектор на 4 ? Надеемся, вы сказали, что он будет указывать в том же направлении, но будет в четыре раза длиннее!

2. Является ли «25 узлов к югу на юго-запад» скаляром или вектором? Это вектор, так как он дает величину и направление.

3. Что произойдет с вектором, если мы умножим его на −12-\frac{1}{2}−21​? Мы надеемся, вы сказали, что он будет вдвое короче и пойдет в противоположном направлении!

4. Два вектора параллельны, но направлены в противоположные стороны.