Умножение и деление чисел в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше
Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.
Умножение чисел
Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.
Умножение чисел в ячейке
Для выполнения этой задачи используйте арифметический оператор

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.
Умножение столбца чисел на константу
Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.
-
Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.
Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.
 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения. Перетащите формулу вниз в другие ячейки столбца.
Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.
Перемножение чисел в разных ячейках с использованием формулы
Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.
Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).
Деление чисел
Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.
Деление чисел в ячейке
Для этого воспользуйтесь арифметическим оператором / (косая черта).
Например, если ввести =10/5 в ячейке, в ячейке отобразится
Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01. 12.1936 и отобразит в ячейке значение «1-дек».
12.1936 и отобразит в ячейке значение «1-дек».
Примечание: В Excel нет функции DIVIDE.
Деление чисел с помощью ссылок на ячейки
Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.
Пример:
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Копирование примера
-
Создайте пустую книгу или лист.
-
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

Выделите пример в разделе справки.
Примечание: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Описание (результат) |
|
2 |
15000 |
=A2/A3 |

|
|
3 |
12 |
Деление столбца чисел на константу
Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.
|
A |
B |
C |
|
|
|
Данные |
Формула |
Константа |
|
2 |
15000 |
=A2/$C$2 |
3 |
|
3 |
12 |
=A3/$C$2 |
|
|
4 |
48 |
=A4/$C$2 |
|
|
5 |
729 |
=A5/$C$2 |
|
|
6 |
1534 |
=A6/$C$2 |
|
|
7 |
288 |
=A7/$C$2 |
|
|
8 |
4306 |
=A8/$C$2 |
В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.
Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.
Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Умножение столбца чисел на одно и то же число
Умножение на процентное значение
Создание таблицы умножения
Операторы вычислений и порядок операций
2.2. Арифметические операции над числами, представленными в различных системах счисления. Информатика: аппаратные средства персонального компьютера
2.2. Арифметические операции над числами, представленными в различных системах счисления. Информатика: аппаратные средства персонального компьютераВикиЧтение
Информатика: аппаратные средства персонального компьютера
Яшин Владимир Николаевич
Содержание
2. 2. Арифметические операции над числами, представленными в различных системах счисления
2. Арифметические операции над числами, представленными в различных системах счисления
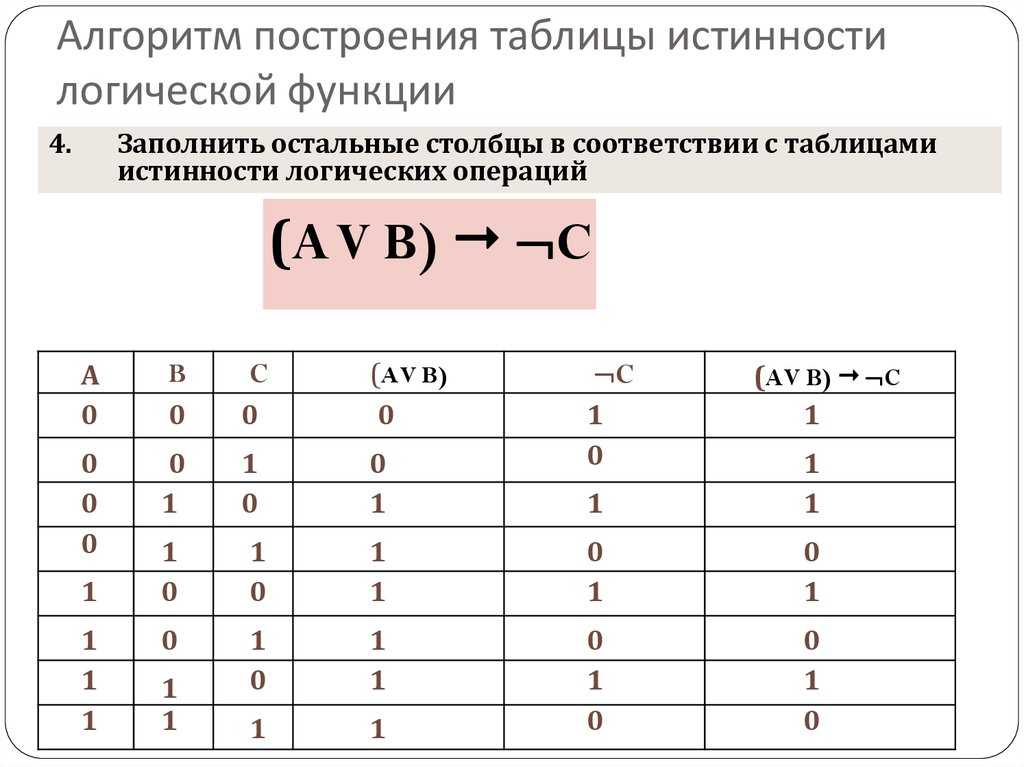
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления.
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.
Ниже приведены примеры выполнения арифметических операций над числами, представленными в различных системах счисления:
Арифметические операции над целыми числами, представленными в различных системах счисления, достаточно просто реализуются с помощью программ Калькулятор и MS Excel.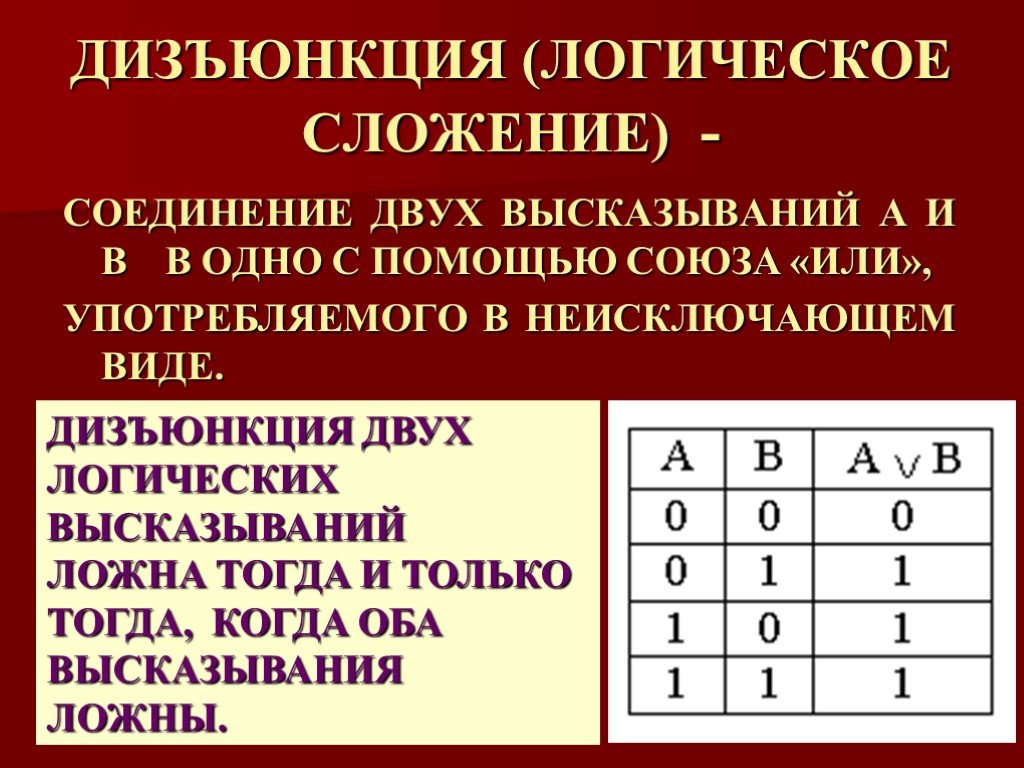
Данный текст является ознакомительным фрагментом.
Арифметические операции
Арифметические операции Для работы с числами используют арифметические операции.• Сложение – знак плюс (+). Например, 5 + 7 = 12.• Вычитание – знак минус (-). Например, 67 – 43 = 24.• Умножение – звездочка (*). Например, 2 * 2 = 4.• Деление – косая черта (/). Например, 45 / 5 = 9.• Остаток от
Арифметические операции
Арифметические операции + – сложение— – вычитание* – умножение/ – делениеDIV – деление нацелоMOD – остаток от деления
Арифметические операции
Арифметические операции
Унарные операции – применяются к одной переменной. ++ – увеличение на единицу (x++ выдаёт старое значение, ++x – новое значение).– – – уменьшение на единицу, аналогично операции ++.Бинарные операции – стоят между двумя переменными или
++ – увеличение на единицу (x++ выдаёт старое значение, ++x – новое значение).– – – уменьшение на единицу, аналогично операции ++.Бинарные операции – стоят между двумя переменными или
5.2. Основные операции над числами
5.2. Основные операции над числами Обычные операции сложения, вычитания, умножения и деления в Ruby, как и во всех распространенных языках программирования, обозначаются операторами +, -, *, /. Операторы в большинстве своем реализованы в виде методов (и потому могут быть
5.17. Поразрядные операции над числами
5.17. Поразрядные операции над числами Иногда требуется работать с двоичным представлением объекта Fixnum. На прикладном уровне такая необходимость возникает нечасто, но все-таки возникает.Ruby обладает всеми средствами для таких операций. Для удобства числовые константы
I.
 Арифметические операции
Арифметические операцииI. Арифметические операции + Прибавляет величину, находящуюся справа, к величине, стоящей слева — Вычитает величину, стоящую справа, из величины, указанной слева — Будучи унарной операцией, изменяет знак величины, стоящей справа * Умножает величину справа на величину,
Арифметические операции (Arithmetic operations)
Арифметические операции (Arithmetic operations) Библиотека обеспечивает базовые классы функциональных объектов для всех арифметических операторов языка.template ‹class T›struct plus: binary_function‹T, T, T› { Т operator()(const T& x, const T& y) const {return x + y;}};template ‹class T›struct minus: binary_function‹T, T, T› { Т operator()(const T&
Глава 2. Обработка сканированных изображений для использования в различных системах САПР и ГИС
Глава 2. Обработка сканированных изображений для использования в различных системах САПР и ГИС
Векторизация есть процесс, требующий обязательного участия человека, поскольку только человек, глядя на черные и белые точки на экране (а результат сканирования — это черные и
Обработка сканированных изображений для использования в различных системах САПР и ГИС
Векторизация есть процесс, требующий обязательного участия человека, поскольку только человек, глядя на черные и белые точки на экране (а результат сканирования — это черные и
4.2. Арифметические операции
4.2. Арифметические операции Таблица 4.1. Арифметические операции Символ операции Значение Использование * Умножение expr*expr / Деление expr / expr % Остаток от деления expr % expr + Сложение expr + expr — Вычитание expr – expr Деление целых чисел дает в результате целое
4.6. Операции с комплексными числами
4.6. Операции с комплексными числами Класс комплексных чисел стандартной библиотеки С++ представляет собой хороший пример использования объектной модели. Благодаря перегруженным арифметическим операциям объекты этого класса используются так, как будто они
Арифметические операции
Арифметические операции
Арифметические выражения вычисляются слева направо за исключением случаев, когда возникает двусмысленность. В этих случаях арифметические операции вычисляются в соответствии с приоритетами, описанными в табл. 21.3. Например, умножение
В этих случаях арифметические операции вычисляются в соответствии с приоритетами, описанными в табл. 21.3. Например, умножение
Пример 8-2. Арифметические операции
Пример 8-2. Арифметические операции #!/bin/bash# От 1 до 6 пятью различными способами.n=1; echo -n «$n «let «n = $n + 1» # let «n = n + 1» тоже допустимоecho -n «$n «: $((n = $n + 1))# оператор «:» обязателен, поскольку в противном случае, Bash будет#+ интерпретировать выражение «$((n = $n + 1))» как команду.echo -n «$n «n=$(($n + 1))echo
Операции с числами
Операции с числами Перечень арифметических операций в XPath довольно ограничен. К ним относится сложение, вычитание, умножение, деление и унарная операция отрицания, которая меняет значение операнда на противоположное. Кроме того, числа можно сравнивать при помощи
Арифметические операции
Арифметические операции
К арифметическим относятся бинарные операции +, -, *, / для вещественных и целых чисел, бинарные операции div и mod для целых чисел и унарные операции + и — для вещественных и целых чисел.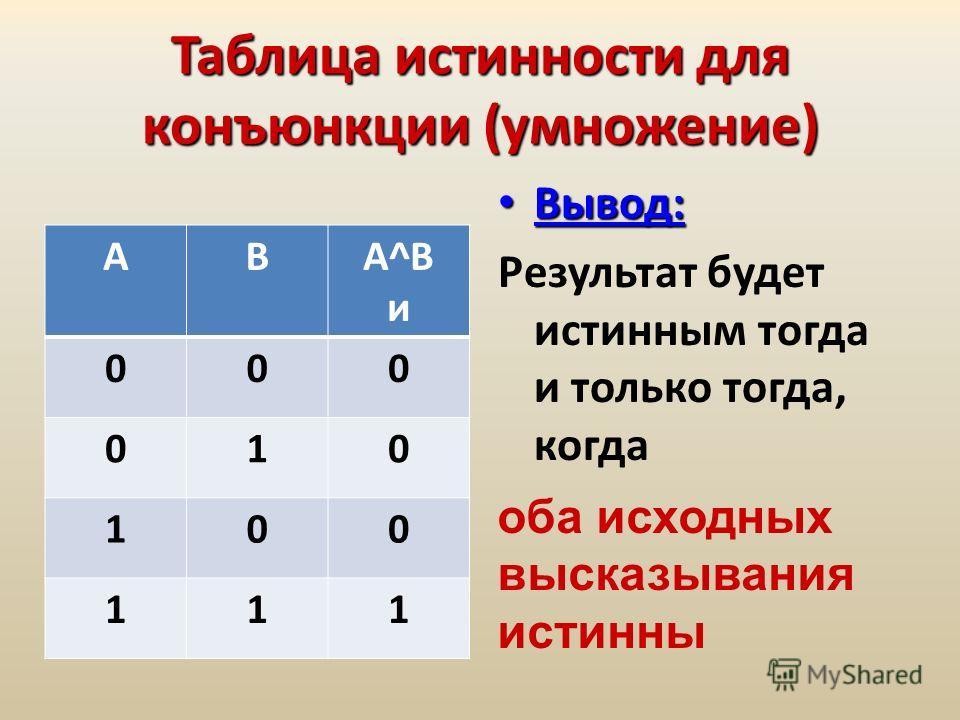 Тип выражения x op y, где op — знак бинарной операции +, — или *,
Тип выражения x op y, где op — знак бинарной операции +, — или *,
Алгоритм умножения в представлении величины со знаком
Улучшить статью
Сохранить статью
- Уровень сложности: Средний
- Последнее обновление: 21 авг, 2019
Улучшить статью
Сохранить статью
Умножение двух двоичных чисел с фиксированной запятой в представлении величины со знаком выполняется с помощью процесса последовательного сдвига и операции сложения .
В процессе умножения мы рассматриваем последовательные биты множителя, начиная с самого младшего бита.
Если бит множителя равен 1, множимое копируется вниз, в противном случае копируются нули.
Числа, скопированные в последующих строках, сдвигаются на одну позицию влево от предыдущего числа.
Наконец числа складываются, и их сумма образует произведение.
Знак произведения определяется по знаку множимого и множителя. Если они одинаковы, знак произведения положительный, иначе отрицательный.
Аппаратная реализация:
Следующие компоненты необходимы для Аппаратной реализации алгоритма умножения:
- Регистры:
Два регистра B и Q используются для хранения соответственно множителя и множителя.
Регистр A используется для хранения частичного произведения во время умножения.
Регистр счетчика последовательности (SC) используется для хранения количества битов в множителе. - Флип-флоп:
Для хранения знакового бита регистров нам потребуется три триггера (знак A, знак B и знак Q).
Триггер E используется для хранения бита переноса, сгенерированного при частичном добавлении продукта. - Дополнительный и параллельный сумматор:
Этот аппаратный блок используется для расчета частичного произведения, т. е. для выполнения требуемого сложения.
е. для выполнения требуемого сложения.
Блок-схема умножения:
- Первоначально множимое сохраняется в регистре B, а множитель хранится в регистре Q.
- Знак регистров B (Bs) и Q (Qs) сравнивается с использованием функции XOR (т. е., если оба знака одинаковы, вывод операции XOR равен 0, если не 1) и выход сохраняется в As (знак регистра A ).
Примечание: Первоначально 0 назначается триггерам регистров A и E. Счетчик последовательности инициализируется значением n, n — количество битов в множителе.
- Теперь проверяется младший бит множителя. Если он равен 1, добавьте содержимое регистра A к множителю (регистр B), и результат присваивается в регистре A с битом переноса в триггере E. Содержимое E A Q сдвигается вправо на одну позицию, т. Е. Содержимое E сдвигается на старший бит (MSB) A и младший бит A сдвигаются к старшему биту Q.
- Если Qn = 0, аналогичным образом выполняется только операция сдвига вправо над содержимым E A Q.

- Содержимое счетчика последовательности уменьшается на 1.
- Проверить содержимое счетчика последовательности (SC), если он равен 0, завершить процесс и конечный продукт присутствует в регистрах A и Q, в противном случае повторить процесс.
Пример:
Множимое = 10111 Множитель = 10011
Арифметика с фиксированной точкой: сложение и вычитание
В компьютере основными арифметическими операциями являются сложение и вычитание. Умножением и делением всегда можно управлять с последовательным сложением или вычитанием соответственно. Однако для умножения и деления реализованы аппаратные алгоритмы.
Следует помнить, что компьютеры имеют дело с двоичными числами, если не используется специальное оборудование для работы с другими системами счисления. Хотя могут быть доступны инструкции для обработки операций со знаком и без знака, программист должен иметь дело с числами и обработкой результата. Аппаратное обеспечение помогает программисту с помощью соответствующих инструкций и флагов.
Добавление двух чисел является сложением. Мы можем добавлять числа со знаком или без знака. Когда мы складываем два числа, скажем, 8 и 5, получается 13, т.е. при сложении двух однозначных чисел мы можем получить в результате двузначное число. Аналогичная возможность существует и в двоичной системе. Правило большого пальца двоичного сложения:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10
Примеры (a–e) беззнакового двоичного сложения приведены на рис. 8.1.
Рисунок 8.1 Примеры двоичного сложения Сумматор Аппаратная схема, которая выполняет это сложение, называется Сумматор . Существует два типа сумматоров, а именно Полусумматор и Полный сумматор . Базовая схема сумматора выполняет 1-битное сложение и расширяется для n-битного сложения. Характеристики схемы сумматора детализированы схемой, таблицей истинности, формулой и блочным символом. Схемы сумматора построены из логических элементов, которые удовлетворяют формуле согласно таблице истинности. Их также называют комбинационной логикой. Выход комбинационной логики отражает вход без тактирования.
Схемы сумматора построены из логических элементов, которые удовлетворяют формуле согласно таблице истинности. Их также называют комбинационной логикой. Выход комбинационной логики отражает вход без тактирования.
Полусумматор (HA) имеет два входа (A, B) и два выхода (Sum и Carry). Сумма — это XOR ввода, а Carry — это AND ввода. Полусумматор подробно показан на рис. 8.2.
Полный сумматор (FA) также выполняет 1-битное сложение, но принимает 3 входа (A, B и C i ) и производит два выхода (Sum и Carry). Как и HA, FA генерирует результат, состоящий из суммы (S) и выполнения (C из ). C из используется как C i+1 при каскадировании для нескольких битов слова. Полный сумматор подробно показан на рис. 8.3. Полный сумматор также может быть построен с использованием половинных блоков сумматора, как показано на рис. 8.4.
Рис. 8.3 Полный сумматор Основа двоичного вычитания:0 - 0 = 0 0 - 1 = -1 1 - 0 = 1 1 - 1 = 0
Конечно, как и в случае с десятичными числами, применяется обычная логика заимствования из соседней цифры. Примеры двоичного вычитания со знаком приведены ниже:
Примеры двоичного вычитания со знаком приведены ниже:
Обратите внимание, что приведенные выше примеры представлены в представлении со знаком. В форме знака-величины MSB зарезервирован для представления знака. Это только для базового понимания. Компьютеры внутренне используют представление дополнения до 2.
Напомним: в представлении дополнения до 2 MSB является знаковым битом, (n-1) битов представляют величину числа. Пример преобразования 8-битного слова показан на рис. 8.5.
Рисунок 8.5 Представление дополнения до единиц и двоек Дополнение до двоек для вычитания«Дополнение до единицы + 1 = дополнение до 2» Схема XOR будет генерировать дополнение до 1. Управляющий сигнал, называемый SUBTRACT, используется как значение сложения 1. Таким образом, сумматор выполняет вычитание. См. приведенный ниже пример, где случай (b), случай (c) и случай (e) обработаны как представление дополнения до 2; и AB становится A + (дополнение 2 (B)).
Интерпретация дополнительных чисел до 2Результат получается в виде дополнения до 2 без переноса. Обратите внимание, что этот метод работает для всех типов данных.
- Учитывать бит знака (MSB)
- Если ‘0’, число положительное; биты (n-1) означают абсолютное значение числа в двоичном формате
- Если ‘1’, число отрицательное; (n-1) биты означают дополнительное значение числа до 2 в двоичном формате; Инвертируйте (n-1) бит и добавьте 1, чтобы получить абсолютное значение этого отрицательного числа.
Никто не делает математику идеально, но компьютеры могут, если ваши данные верны! Существует вероятность того, что ваши данные могут быть неправильно определены или могут быть вне допустимого диапазона. По этой причине ЦП обнаруживает определенные ошибки, такие как ПЕРЕПОЛНЕНИЕ(O), НЕДОСТАТОК(U) и CARRY(C). Он также определяет статус SIGN(S) и ZERO(Z). Акроним ZSOC (ноль, знак, переполнение и перенос), так как многие процессоры могут рассматривать переполнение и потерю значимости одновременно как выход за пределы допустимого диапазона.
Обнаружение осуществляется арифметико-логическим блоком (АЛУ) ЦП. При обнаружении соответствующий флаг устанавливается в состояние ON. Эти флаги имеют битовые позиции, выделенные в регистре состояния процессора и наиболее известные как слово состояния процессора (PSW). Флаги ZSOC вместе известны как коды состояния. Назначение этих флагов состояния кодов состояний — помочь программисту выявлять ошибки, зависящие от данных, и действовать соответствующим образом.
Переполнение : Проще говоря, когда полученный результат превышает максимально возможное число для представления, говорят, что происходит переполнение. Другими словами, сложение двух чисел со знаковым битом «0», приводящее к значению со знаковым битом «1», называется ПЕРЕПОЛНЕНИЕМ.
Например: 8-битное слово может максимально представлять +127 в десятичном виде, 01111111 в двоичном. Если мы добавим, 120 + 10 -> 130;
120 -> 0111 1000 10 -> 0000 1010 --------- 1000 0010 -> в форме величины знака, MSB (значащий бит Mos) '1' означает отрицательное число, в то время как мы ожидаем +130Максимум +127, следовательно, это сценарий переполнения.
В сценарии переполнения результат неверен, и об этом необходимо сообщить программисту/пользователю, что произошла ошибка. Эта ситуация обнаруживается аппаратным обеспечением ЦП и устанавливает бит состояния, называемый «ПЕРЕПОЛНЕНИЕ». Пользователь, если он заинтересован, может поймать эту ошибку, прочитав этот бит состояния ПЕРЕПОЛНЕНИЕ, и предпринять необходимые действия по обработке данных.
Недополнение : В то время как переполнение связано с положительной величиной, недозаполнение связано с отрицательной величиной по тем же причинам. Например, при сложении двух отрицательных чисел, таких как -120 и -10, ожидаемый результат равен -130, что выходит за пределы представляемого диапазона в определении 8-битного слова со знаком. Это сценарий UNDERFLOW. Другими словами, сложение двух чисел со знаковыми битами «1», приводящее к числу со знаковым битом «0», называется ПОНИЖЕНИЕМ. Аппаратное обеспечение ЦП обнаруживает и устанавливает для этого бит состояния, называемый UNDERFLOW.
Опять же, этот бит состояния доступен программисту/пользователю для выполнения необходимых действий по обработке данных.
Перенос : ПЕРЕНОС — это еще один статус, определяемый и устанавливаемый ЦП при выполнении арифметических инструкций. Флаг CARRY относится к арифметическим операциям без знака, тогда как OVERFLOW и UNDERFLOW относятся к операциям со знаком.
Флаг CARRY устанавливается ЦП в конце арифметических операций, если есть перенос (C out ) из старшего бита слова. Перенос устанавливается в конце цикла выполнения инструкций сложения или вычитания. Многие ЦП не различают операции со знаком и без знака, и в этом случае CARRY и ПЕРЕПОЛНЕНИЕ могут быть установлены ЦП. Однако существуют ЦП, которые имеют разные коды инструкций и инструкции для целочисленных операций со знаком и без знака, и в этом случае ЦП соответствующим образом устанавливает флаг CARRY или OVERFLOW.
Никогда не забывайте, что именно программист решает, оперировать ли он числами со знаком или без знака .
Таким образом, программист должен решить, должен ли он перехватывать флаг ПЕРЕПОЛНЕНИЯ, НЕПОЛУЧЕНИЯ или ПЕРЕНОСА для обнаружения ошибок и корректирующих действий.
НОЛЬ : В конце цикла выполнения инструкции, если значение аккумулятора равно нулю, этот бит состояния устанавливается ЦП. Это может быть возможность в конце арифметических или логических инструкций или инструкций загрузки.
ЗНАК : Знаковый бит отражает старший разряд аккумулятора. Это также устанавливается в конце цикла выполнения инструкции.
Формирование n-битного сумматора4-битовый полный сумматор интегрируется путем каскадирования четырех однобитовых сумматоров, как показано на рис. 8.6. При каскадировании C из i-й позиции становится C в i+1-й позиции, и, следовательно, считается, что перенос распространяется. S — сумма битов, C , out — окончательный перенос сумматора. A и B — входные числа. С i при наличии.
Рис. 8.6 4-битный полный сумматор с неравномерным переносомТакое каскадирование может быть расширено до любого количества битов с использованием 1-битных блоков FA или n-битных блоков FA.
Этот метод расширения сумматора известен как пространственное расширение, поскольку вывод всех n-битов доступен одновременно с 1-битной операцией, вероятно, за один тактовый цикл. Пространственное расширение также известно как параллельный сумматор. Другое название этого метода — сумматор Ripple Carry, поскольку перенос распространяется внутри. Однако при большом значении n задержка распространения переноса для чистого и установленного вывода пропорционально увеличивается. Это недостаток Ripple Carry Adder, который решается с помощью метода Carry-Look-Ahead Adder.
Сумматор переноса с опережениемЭто также тип пространственного расширения и пульсирующего переноса. Сумматор переноса с опережением (CLA) использует специализированную логику, называемую логикой переноса с опережением, для параллельного вычисления переносов и, следовательно, работает быстрее, чем сумматор переноса с пульсацией.


 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.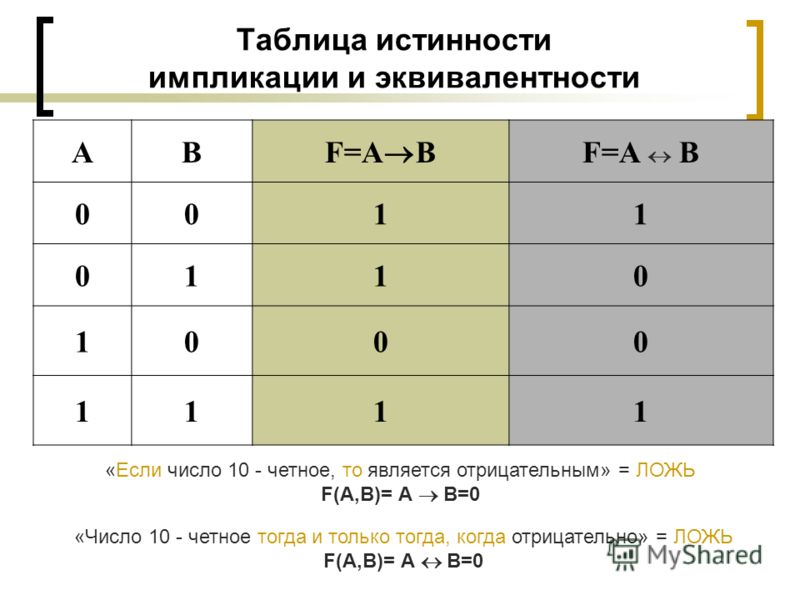
 е. для выполнения требуемого сложения.
е. для выполнения требуемого сложения.
 Результат получается в виде дополнения до 2 без переноса. Обратите внимание, что этот метод работает для всех типов данных.
Результат получается в виде дополнения до 2 без переноса. Обратите внимание, что этот метод работает для всех типов данных. Обнаружение осуществляется арифметико-логическим блоком (АЛУ) ЦП. При обнаружении соответствующий флаг устанавливается в состояние ON. Эти флаги имеют битовые позиции, выделенные в регистре состояния процессора и наиболее известные как слово состояния процессора (PSW). Флаги ZSOC вместе известны как коды состояния. Назначение этих флагов состояния кодов состояний — помочь программисту выявлять ошибки, зависящие от данных, и действовать соответствующим образом.
Обнаружение осуществляется арифметико-логическим блоком (АЛУ) ЦП. При обнаружении соответствующий флаг устанавливается в состояние ON. Эти флаги имеют битовые позиции, выделенные в регистре состояния процессора и наиболее известные как слово состояния процессора (PSW). Флаги ZSOC вместе известны как коды состояния. Назначение этих флагов состояния кодов состояний — помочь программисту выявлять ошибки, зависящие от данных, и действовать соответствующим образом.
 Опять же, этот бит состояния доступен программисту/пользователю для выполнения необходимых действий по обработке данных.
Опять же, этот бит состояния доступен программисту/пользователю для выполнения необходимых действий по обработке данных. Таким образом, программист должен решить, должен ли он перехватывать флаг ПЕРЕПОЛНЕНИЯ, НЕПОЛУЧЕНИЯ или ПЕРЕНОСА для обнаружения ошибок и корректирующих действий.
Таким образом, программист должен решить, должен ли он перехватывать флаг ПЕРЕПОЛНЕНИЯ, НЕПОЛУЧЕНИЯ или ПЕРЕНОСА для обнаружения ошибок и корректирующих действий. Такое каскадирование может быть расширено до любого количества битов с использованием 1-битных блоков FA или n-битных блоков FA.
Такое каскадирование может быть расширено до любого количества битов с использованием 1-битных блоков FA или n-битных блоков FA.