Оптические логические элементы

Оптические логические элементы

Для создания цифровой машины принципиально уметь строить основные логические элементы И, ИЛИ, НЕ. Ниже рассматрены основные принципы, предлагаемые сегодня для построения таких элементов, управляемых светом.

Волноводные логические элементы

Волноводный модулятор представляет собой интерференционный прибор, осуществляющий амплитудную модуляцию входного оптического сигнала, представляющего собой линейно поляризованное световое излучение лазера. Входной волновод модулятора разветвляется на два параллельных канала, которые затем снова сливаются, образуя выходной волновод. Волновод изготавливается из материала, обладающего электрооптическим эффектом. Обе ветви волновода симметричны, поэтому входной световой сигнал на разветвлении делится на две равные по амплитуде волны, которые далее распространяются по параллельным каналам с относительным сдвигом фаз.

Разность фаз этих волн определяется электрическим напряжением, приложенным к управляющим электродам. Логическая «1» отождествляется со значением напряжения U0, а двоичный «0»- с нулевым потенциалом. Таким образом, если напряжение U0 приложено к четному числу управляющих электродов, то волны, сходящиеся в выходном разветвлении усиливают друг друга, образуя выходной оптический сигнал с амплитудой, практически равной амплитуде входного сигнала, который принимается за единичный сигнал. В противном случае волны практически полностью гасят друг друга, образуя нулевой выходной сигнал.

Условные обозначения волноводных логических устройств:

Оптический транзистор (трансфазор)

Трансфазор редставляет собой оптический аналог электронного транзистора и является оптически бистабильным прибором, способным переключаться в одно из двух четко различимых состояний за время, измеряемое пикосекундами.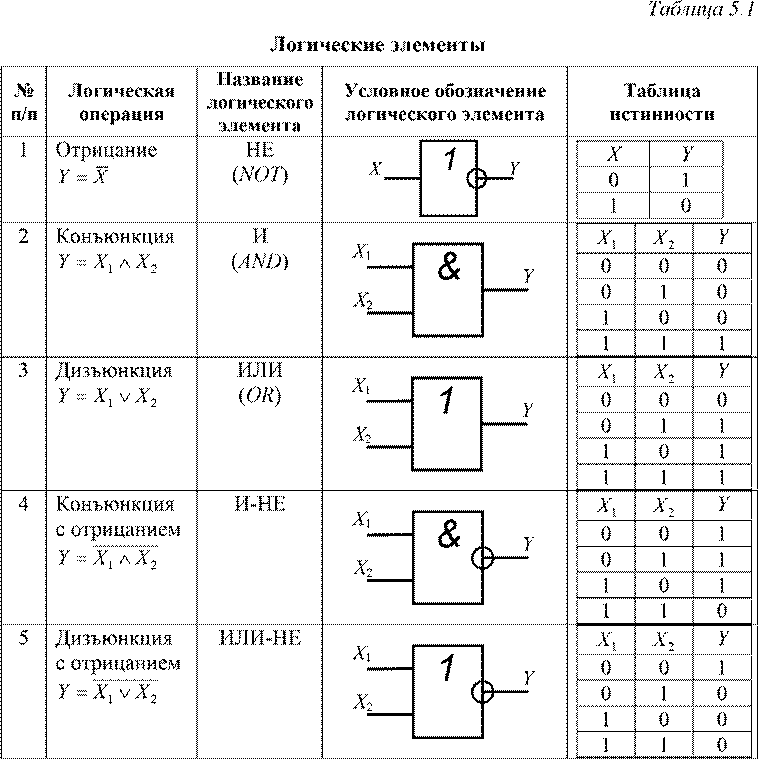 Он может иметь такие же малые раэмеры, как и электронный транзистор. Для поддержания бистабильного состояния в трансфазоре требуется мощность порядка 10 мВт и энергия переключения порядка 10 фемто Дж. На основе трансфазора реализуется функционально полная система логических элементов, из которых можно строить любые логические схемы и функциональные узлы вычислительных машин.

Для образования основных логических элементов И, ИЛИ и НЕ в оптических компьютерах можно использовать бистабильные оптические устройства. Такое устройство представляет собой резонатор Фабри-Перо, заполненный нелинейным веществом (например антимонид индия — InSb). Показатель преломления данного вещества зависит от интенсивности падающего пучка, поэтому на выходе можно получить два стабильных состояния, одно из которых условно принимается за «0», а другое за «1».

Один и тот же трансфазор (оптический транзистор) может служить как элементом И, так и элементом ИЛИ, в зависимости от подведённых к нему пучков. Если два падающих пучка подобраны так, что ни один из них сам по себе не способен переключить трансфазор, а оба вместе обладают достаточной интенсивностью для его переключения, то образуется оптический элемент И. Если же падающие пучки подобраны так, что любой из них способен переключить трансфазор, образуется оптический элемент ИЛИ. Элемент НЕ можно создать, используя в качестве выходного сигнала отражённый пучок. Так как он является инверсией прошедшего пучка, то повышение интенсивности падающего пучка приводит к снижению интенсивности на выходе и наоборот (смотри рисунки).

Резонатор Фабри-Перо

В качестве бистабильного оптического элемента применяется резонатор Фабри-Перо, заполненный нелинейной средой, показатель преломления которой n зависит от интенсивности I по закону: . Прозрачность резонатора T зависит от фазового набега между зеркалами :

В резонаторе, заполненном нелинейной средой, полный фазовый набег зависит от интенсивности:

где — констата, . Cхема совместного решения уравнений (1) и (2) представлена на рисунке (a).

Пересечение прямой с наклоном с кривой пропускания резонатора дает положение рабочей точки — результат совместного решения (1) и (2). Прослеживая за изменением положения рабочей точки при изменении входной мощности Iвх, можно построить зависимость , приведённую на рисунке (б):

Среда, заполняющая резонатор, и имеющая кубическую нелинейность, характери- зуется двумя важными параметрами: величиной нелинейного коэффициента n2 и временем релаксации нелинейного отклика Tнл (инерционностью).

На рисунке (в) систематизированы экспериментальные данные по различным нелинейным материалам:

Из рисунка видно, что вещества обладающие сильной нелинейностью, имеют достаточно большое время переключения, поэтому выбирают вещества с наиболее оптимальными значениями n2 и Tнл (обведены кружками).

Схематически интерферометр Фари-Перо изображён на рисунке:

---

Оптические процессоры

Логические элементы и их релейные эквиваленты

Дата 22.06.201605.04.2020 Автор ElectricianКомментироватьПросмотров: 18 625

С помощью логических элементов довольно легко реализуются функции алгебры логики, которая является костяком устройств автоматики и вычислительных машин. Логические элементы могут реализовываться огромным количеством способов в зависимости от надобности и состоять из полупроводниковых, релейных, интегральных, пневматических и других элементов и схем.

Между величинами, входящими и выходящими из логического элемента, существует определенная зависимость, которая называется функциональной и обозначается как y = f(x) для устройств с одной переменной и как y = f(x₁, x₂) для устройств с двумя переменными величинами.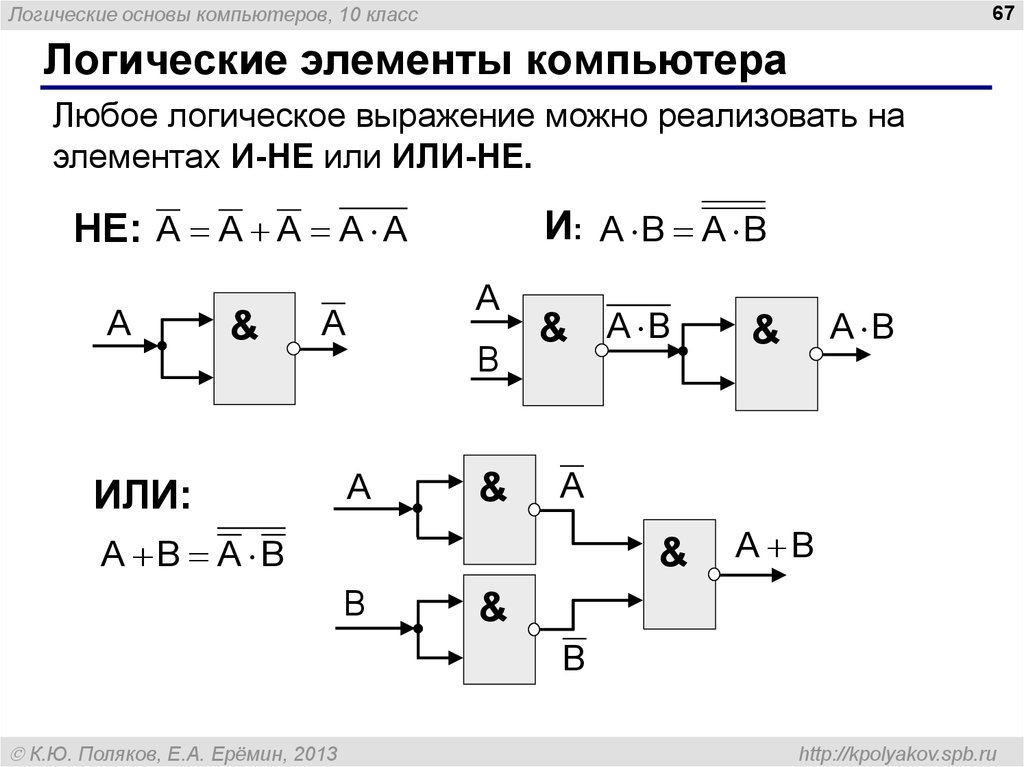 В этой записи Х называют независимую переменную или аргумент, а Y – зависимая переменная, так как ее значение напрямую зависит от значения аргумента Х.

Ниже показана таблица логических элементов и эквивалентных им положений контактов реле:

Функция повторения

Реализуется логическим элементом повторителем (пункт 1 в таблице). Повторитель можно сравнить с нормально открытым контактом реле. При открытом контакте Х=0 и, соответственно Y=0, то есть цепь находится в непроводящем состоянии, а при закрытом наоборот Х=1 и Y=1, то есть цепь находится в проводящем состоянии.

Функция отрицания

Реализует данную функцию логический элемент НЕ или как его часто называют – инвертор (пункт 2 в таблице). Его сравнивают с нормально закрытым контактом реле, когда при отсутствии напряжения на катушке управления (Х=0) его контакт находится в проводящем состоянии (Y=1). При подаче напряжения на катушку (Х=1) контакт размыкается и разрывает цепь (Y=0).

Функция логического сложения

В схемотехнике носит название дизъюнкция или функция ИЛИ (пункт 3 в таблице).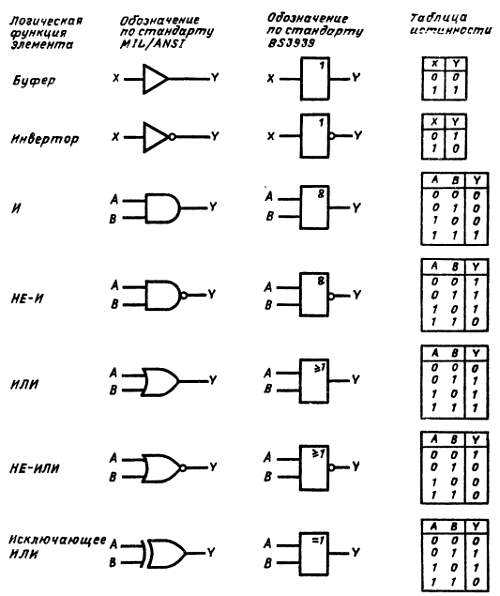 Реализуема эта функция логическим элементом дизъюнктором. Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X₁ + X₂ = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.

Функция логического умножения

В схемотехнике носит название конъюнкция или функция И (пункт 4 в таблице). Реализует ее специальный логический элемент – конъюктор. Данная функция – логическое перемножение сигналов:

Если сравнить с реле – то это два последовательно включенные нормально открытые контакты. А при таком подключении контактов реле проводимость можно получить только в случае, когда оба контакта замкнуты.

Функция равнозначности

Имеет следующий вид — X₁≡X₂ = Y или в виде логических символов: 0≡0 =1; 1≡0 = 0; 0≡1 = 0; 1≡1 = 1.

Значения 1 будет только при условии, что X₁ = X₂. Эквивалентом в релейной схеме будет два последовательно включенных переключающихся контакта (пункт 5 в таблице).

Функция неравнозначности

Противоположная функции равнозначности (пункт 6 в таблице) и часто носит название функции сложности по модулю m2:

Posted in Станки с ЧПУ, Схемотехника

Загрузка музыки Logical Elements — Beatport

Сортировать по: От новых к старымОт старых к новымЗаголовок A-ZЗаголовок Z-ALЯрлык A-ZЯрлык Z-AGЖанр A-ZЖанр Z-A

Дата выпуска

Сброс

Сегодня Вчера Последние 7 дней Последние 30 дней

к

ПРИМЕНИТЬ

ударов в минуту

Сброс

к ПРИМЕНИТЬ

Жанр

Сбросить

• Электроника 46

Ключ

Сброс

• майор 1
• ля минор 2
• Аб мажор 1
• Ab минор 1
• Си мажор 3
• до мажор 6
• до минор 3
• Ре мажор 1
• ре минор 1
• Ре-мажор 1
• Ре-бемоль мажор 5
• Ре-бемоль минор 2
• Ми-бемоль мажор 3
• Ми-бемоль минор 3
• Фа мажор 2
• Фа минор 3
• Фа-диез мажор 1
• соль мажор 1
• соль минор 4
• Гб мажор 1
• ГБ Минор 1

Исполнители

Сброс

• Логические элементы 46
• Альфа Гипнотика 2
• Древнее ядро ​​1

Этикетки

Сброс

• Мелюзин Рекордс 15
• ДАРК Рекордс 9
• Рекорды Mind Tweakers 9
• Голубые мелодии, отдых 7
• Фейр 2
• Овнимун Рекордс 2
• Блю Мелодии Рекордс 1
• LW записи 1

Сбросить все

Уменьшить логические массивы до одного значения — MATLAB & Simulink

Main Content

Open Live Script

В этом примере показано, как использовать функции any и all , чтобы свести весь массив к одному логическому значению.

Функции any и all являются естественными расширениями логических функций | 9Операторы 0120 (ИЛИ) и и (И) соответственно. Однако вместо сравнения только двух элементов функции any и all сравнивают все элементы в определенном измерении массива. Как будто все эти элементы соединены и или | Операторы и функции any или all оценивают результирующие длинные логические выражения. Поэтому, в отличие от основных логических операторов, any и все функции уменьшают размер измерения массива, с которым они работают, до размера 1. Это позволяет свести множество логических значений к одному логическому условию.

Сначала создайте матрицу A , содержащую случайные целые числа от 1 до 25. Сбросьте генератор случайных чисел в состояние по умолчанию для воспроизводимости.

 звонок по умолчанию
А = ранди(25,5) 

 А =  5×5 
    21 3 4 4 17
    23 7 25 11 1
     4 14 24 23 22
    23 24 13 20 24
    16 25 21 24 17
 

Затем используйте функцию mod вместе с логическим оператором НЕ, ~ , чтобы определить, какие элементы в A являются четными.

 A = ~mod(A,2) 

 A =  Логический массив 5x5 
   0 0 1 1 0
   0 0 0 0 0
   1 1 1 0 1
   0 1 0 1 1
   1 0 0 1 0
 

Результирующие матрицы имеют значения логического 1 ( true ), где элемент четный, и логического 0 ( false ), где элемент нечетный.

Поскольку функции any и all уменьшают размерность, над которой они работают, до размера 1, обычно требуется два применения одной из функций, чтобы свести двумерную матрицу к одному логическому условию, например any (любой(А)) . Однако, если вы используете нотацию A(:) , чтобы рассматривать все элементы A как один вектор-столбец, вы можете использовать any(A(:)) , чтобы получить ту же логическую информацию без вложения вызовы функций.

Определите, являются ли какие-либо элементы в A четными.

 любой(A(:)) 

 ответ =  логический 
   1
 

Вы можете выполнять логические и реляционные сравнения внутри вызова функции любой или все .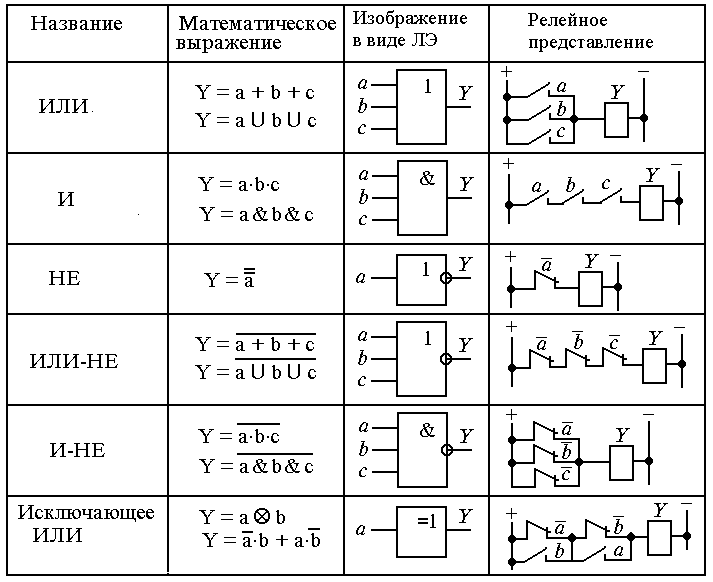 Это упрощает быструю проверку массива на различные свойства.

Определите, все ли элементы в A являются нечетными.

 все(~A(:)) 

 ответ =  логический 
   0
 

Определить, есть ли главные или супердиагональные элементы в A четные. Поскольку векторы, возвращаемые diag(A) и diag(A,1) , имеют разный размер, вам сначала нужно свести каждую диагональ к одному скалярному логическому условию перед их сравнением. Вы можете использовать оператор короткого замыкания ИЛИ || для выполнения сравнения, так как если какие-либо элементы на первой диагонали четные, то все выражение оценивается как истинное независимо от того, что появляется в правой части оператора.

 любой(диаг(А)) || любой(диаг(А,1)) 

 ответ =  логический 
   1
 

любой | все | и | или | или | Короткое замыкание И | Короткое замыкание ИЛИ

У вас есть модифицированная версия этого примера.