Вопросы, знание которых необходимо для допуска к выполнению работы
5
Работа № 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ
МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА
Цель работы: определение момента инерции некоторых тел относительно оси вращения, проходящей через центр масс, исследование влияния на момент инерции переноса осей вращения (проверка теоремы Штейнера методом крутильных колебаний).
Принадлежности: трифилярный подвес, секундомер, штангенциркуль, тела для измерения момента инерции.
1. Угловая скорость. Связь между угловой скоростью тела и линейной скоростью его точек. Единицы измерения.
2. Угловое ускорение. Связь между угловым ускорением тела и линейным ускорением его точек. Единицы измерения.
3. Что называется плечом силы?
4.
Что называется моментом силы? Чем
обусловлены его величина и направление?
Единицы измерения.
5. Что называется моментом инерции твердого тела? Единицы измерения. От чего зависит величина момента инерции?
6. Напишите и поясните основное уравнение динамики вращательного движения. Какова роль момента инерции в этом уравнении?
7. Сформулируйте теорему Штейнера.
8. В чем отличие крутильных колебаний от колебаний физического маятника?
9. Почему натяжение нитей трифилярного подвеса должно быть одинаково?
10. Под действием какой силы трифилярный подвес совершает крутильные колебания?
11. Расскажите порядок выполнения работы.
П
65
ри рассмотрении вращения твердого
тела с динамической точки зрения понятие
о силах заменяется понятием о моментах
сил, понятие о массе —
понятием о моменте инерции. Если разделить
мысленно вращающееся твердое тело на
n элементарных масс Dmi,
находящихся на расстоянии ri от оси вращения, то все они будут иметь
в данный момент одинаковые угловые
скорости и
угловые ускорения .
Момент
инерции материальной точки численно
равен произведению массы точки Dmiна
квадрат расстояния r
. (1)
Величина момента инерции тела зависит от характера распределения масс относительно оси вращения и поэтому одно и то же тело может иметь разные моменты инерции относительно разных осей.
Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на него момента силы. Моментом силы относительно неподвижной оси называется величина, численно равная произведению силы F на ее плечо h. Плечо силы – есть кратчайшее расстояние от центра вращения до линии действия силы.
M = Fh. (2)
Вращательное движение тела характеризуется угловой скоростью и угловым ускорением :
= ; = , (3)
где
— угловое перемещение тела.
Основной закон динамики вращательного движения, выражающий зависимость углового ускорения от момента силы, записывается в виде:
. (4)
Так
как момент инерции зависит от расстояния
массы относительно оси вращения, то при
смещении оси момент инерции изменяется.
Момент инерции тела относительно оси,
проходящей через центр масс (J
Для случая параллельных осей применима теорема Штейнера: момент инерции относительно любой оси вращения равен сумме момента инерции относительно оси вращения, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями (d):
J
= J (5)
(5)
Н
Рис. 1
апример. Подсчитаем момент инерции cплошного стержня длины l относительно оси О’О’1, проходящей через конец стержня (рис.1). По теореме Штейнера J = J0 + md2. Момент инерции относительно оси oo1, проходящей через центр масс, J0 равен
Следовательно:
На практике момент инерции тела можно определить методом трифилярного подвеса.
68
латформа может совершать крутильные
колебания вокруг вертикальной оси,
перпендикулярной к ее плоскости и
проходящей через ее центр. Центр тяжести
платформы при этом перемещается по оси
вращения. Период колебания определяется
величиной момента инерции платформы,
он будет другим, если платформу нагрузить
каким-либо другим телом. Этим и пользуются
в настоящей р аботе.
Если платформа массы m,
вращаясь в одном направлении, поднялась
на высоту h, то приращение потенциальной
энергии будет равно E
Центр тяжести
платформы при этом перемещается по оси
вращения. Период колебания определяется
величиной момента инерции платформы,
он будет другим, если платформу нагрузить
каким-либо другим телом. Этим и пользуются
в настоящей р аботе.
Если платформа массы m,
вращаясь в одном направлении, поднялась
на высоту h, то приращение потенциальной
энергии будет равно E
. (6)
Считая, что платформа совершает гармонические колебания, можем написать зависимость углового смещения
Рис. 2 Рис. 3
платформы от времени в виде:
, (7)
где
a0 — амплитуда колебаний, Т — период колебаний,
t
—
текущее время. Угловая скорость,
являющаяся первой производной j
по времени, выражается как:
Угловая скорость,
являющаяся первой производной j
по времени, выражается как:
. (8)
В момент прохождения через положение равновесия (t = 0; (1/2)T; (3/2)Т и т.д.) абсолютное значение этой величины будет
. (9)
Из (6) и (9) имеем:
. (10)
.
Так как (ВС)2 = (АВ)2 — (AC)2 = l2 — (R — r)2,
(ВС1)2 = (ВА1)2 — (А1С1)2 = l2 — (R2 + r2 — 2Rrcosa0),
то .
При
малых углах отклонения a0 значение синуса этого угла можно
заменить просто значением a Тогда
Тогда
h = и mg = ,
откуда
J = . (11)
По формуле (11) может быть определен не только момент инерции платформы, но также и тела, помещенного на нее, поскольку все величины в правой части формулы могут быть непосредственно измерены.
Вращательный
импульс, необходимый для начала крутильных
колебаний, сообщается платформе путем
поворота
Для удобства отсчета колебаний на платформе имеется метка, против которой при покоящейся платформе устанавливается указатель — стержень на подставке.
|
Момент инерции твердого тела относительно некоторой оси вращения определяется выражением (15): . Суммирование распространяется на элементы всего твердого тела. Если разбиение тела проводить на все более и более мелкие элементы, то тогда сумма в пределе трансформируется в интеграл, и в результате чего получим: (16) (интегрирование ведется по всему объему твердого тела). Можно получить еще одну формулу полезную для расчета момента инерции. Для этого воспользуемся выражением для плотности вещества: . После подстановки dm = rdV в (16) получим: . (17) В качестве примера применения формулы (16) найдем момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину (рис.11). Длина стержня l, масса стержня т. Разобьем весь стержень на отрезки малой длины . Масса такого отрезка равна , а расстояние до оси вращения r = x. Момент инерции всего стержня найдем, воспользовавшись формулой (16):
.
Приведем, для справок, формулы для моментов инерции тел простейшей геометрической формы. Момент инерции однородного диска (рис.12) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр равен: , где радиус диска R, масса т.
Эта же формула справедлива и для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра. Момент инерции тонкого обруча относительно оси, перпендикулярной к плоскости обруча и проходящей через его центр будет (рис.13): . где радиус обруча – R, масса обруча – т. Эта же формула справедлива для тонкостенного цилиндра. Момент инерции шара относительно оси проходящей через его центр. . Момент инерции тонкого диска массы m и радиуса R, (толщина диска b << R), относительно оси совпадающей с диаметром диска: : ,
Все приведенные формулы справедливы для моментов инерции относительно оси проходящей через центр масс (центр инерции) твердого тела. Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера: Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела (центр масс тела) и произведения массы тела на квадрат расстояния между осями. .
В качестве примера получим с помощью этой теоремы выражение для момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через один из его концов (рис. Поэтому по теореме Штейнера получим: .
Главные оси инерции Момент инерции твердого тела произвольной формы и распределения масс зависит от ориентации оси вращения. Допустим, что ось проходит через центр масс тела (центр инерции). Найдем такую ориентацию оси, для которой момент инерции максимален. Далее, как доказывается в теоретической механике, существует также ось перпендикулярная найденной, и проходящая через центр масс, для которой момент импульса твердого тела будет минимален. Для третьей оси, ортоганальной к первым двум, момент импульса в общем случае имеет величину промежуточную между максимальным и минимальным значениями. Введенные таким образом оси вращения называются главными осями инерции. Моменты инерции относительно этих осей не обязательно отличаются друг от друга по величине. Действительно, если однородное по плотности твердое тело обладает той или иной симметрией, то некоторые главные моменты инерции могут равняться друг другу. Однородный куб с массой М и длиной ребра имеет также три равных момента инерции относительно главных осей инерции . Главные оси инерции перпендикулярны граням куба и проходят через центр куба.. Тонкий однородный по плотности диск имеет максимальный по величине момент инерции относительно оси, проходящей через центр диска перпендикулярно его плоскости, а также два других главных момента инерции равных друг другу. Приведем также пример тела, когда все три момента инерции относительно главных осей инерции различны — однородный по плотности параллелепипед с отличающимися по длине ребрами.
Предыдущая12345678910111213141516Следующая Читайте также: |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
Теоретические основы лабораторной работы Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Момент инерции сплошного твёрдого тела определяется по формуле , где — расстояние от элемента объема с массой dm до оси вращения, r — плотность вещества.
Рис. 5.1. Общий вид экспериментальной установки
Таким образом, момент инерции тел различной формы можно найти как результат интегрирования по соответствующему объёму тела. Частные случаи. 1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения (5.1) 2. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к плоскости основания цилиндра и проходящей через его центр масс (ось цилиндра) (5.2) здесь R, m — радиус и масса цилиндра. Так как момент инерции не зависит от высоты цилиндра, эта же формула справедлива для момента инерции однородного диска относительно оси перпендикулярной к плоскости диска. 3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси, совпадающей с осью цилиндра. (5.3) 4. Момент инерции шара массой m и радиуса R относительно оси проходящей через его центр масс (5.4) 5. Момент инерции тонкого стержня массой m и длиной l относительно оси проходящей через его середину перпендикулярно стержню. (5.5) Эти формулы справедливы для момента инерции относительно оси симметрии. Момент инерции относительно произвольной оси параллельной оси симметрии можно найти с помощью теоремы Штейнера. Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр масс тела и произведения массы тела на квадрат расстояния d между осями. (5.6) Например, с помощью теоремы Штейнера, зная момент инерции стержня относительно оси перпендикулярной к стержню и проходящей через его центр масс, можно получить формулу для вычисления момента инерции стержня относительно оси проходящей через его конец. (5.7) В общем случае расчет момента инерции представляет собой достаточно сложную задачу. В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний. Исследуемые тела насаживаются на ось спиральной пружины. M=Dj (5.8) В этой формуле коэффициентом пропорциональности D является модуль кручения пружины. С другой стороны из определения момента силы следует, что это вектор, модуль которого определяется по формуле М=Fl (5.9) Крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания. В соответствии с теорией период крутильных колебаний определяется по формуле (5.10) Отсюда момент инерции тела (5.11) Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины. Методика лабораторной работы позволяет измерять моменты инерции стержня без грузов, стержня с грузами, сплошного цилиндра, полого цилиндра, диска и шара.
Порядок выполнения работы I. Определение модуля кручения пружины. 1. Возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру. 2. Поверните стержень на 90о (p/2 радиан).
3. Прикрепите к стержню (у края грузов) динамометр и измерьте величину силы F, необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню и оси вращения). 4. Проделайте эти измерения для углов j, равных 180о, 270о, 360о. 5. Полученные данные занесите в таблицу 5.1. ⇐ Предыдущая1234Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 856; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Вращательная инерция – College Physics
Глава 10 Вращательное движение и угловой момент
Резюме
- Понять взаимосвязь между силой, массой и ускорением.
- Изучите вращающее действие силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу [латекс]{F}[/латекс] к точечной массе [латекс]{м}[/латекс], которая находится на расстоянии [латекс]{r}[/латекс] от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна [латекс]{r},[/латекс] ускорение [латекс]{а= \frac{F}{m}}[/latex] получается в направлении [latex]{F}.[/latex] Мы можем изменить это уравнение так, что [latex]{F=ma}[/latex] и затем ищите способы связать это выражение с выражениями для вращательных величин.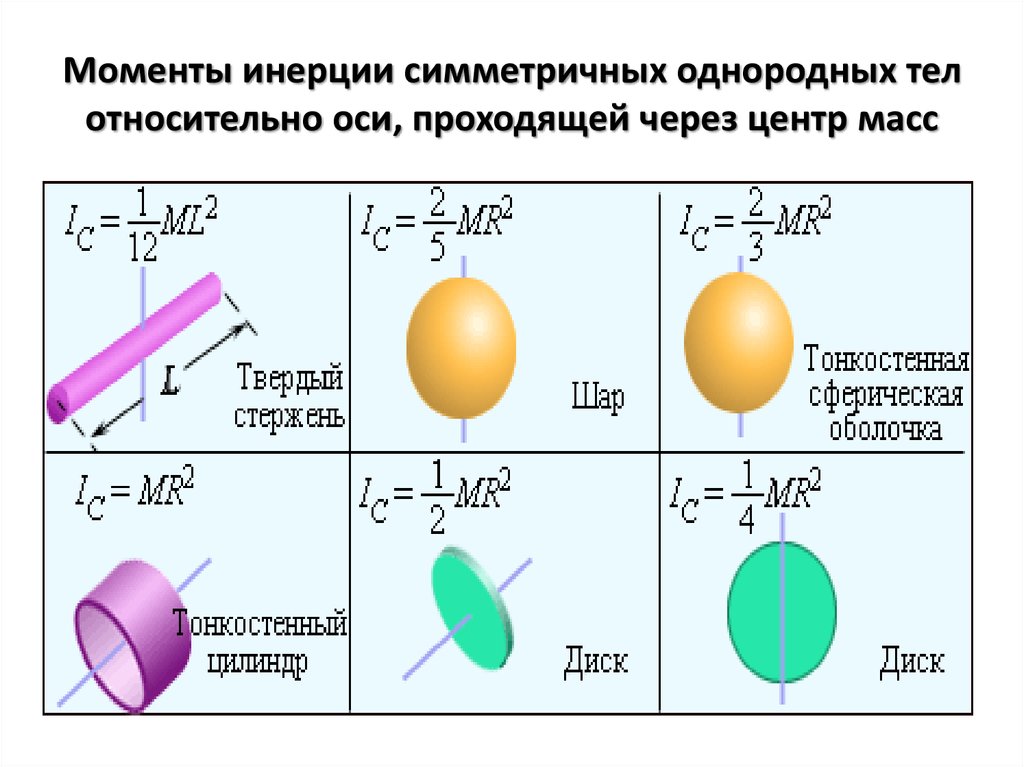 Заметим, что [latex]{a=r\omega},[/latex] и подставим это выражение в [latex]{F=ma},[/latex], получив 92}[/latex] называется вращательной инерцией или моментом инерции точки массы [латекс]{m}[/латекс] на расстоянии [латекс]{r}[/латекс] от центра вращения .
Заметим, что [latex]{a=r\omega},[/latex] и подставим это выражение в [latex]{F=ma},[/latex], получив 92}[/latex] называется вращательной инерцией или моментом инерции точки массы [латекс]{m}[/латекс] на расстоянии [латекс]{r}[/латекс] от центра вращения .
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта. 2}[/latex] ), как и следовало ожидать. из его определения.
2}[/latex] ), как и следовало ожидать. из его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет
.[латекс] {\ текст {нетто} \ тау = I \ альфа} [/ латекс]
или
[латекс] {\ альфа \: =} [/латекс] [латекс] {\ гидроразрыва {\ текст {сеть} \ тау} {I}}, [/латекс]
, где net [латекс] {\ тау} [/латекс] — это общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [latex]{\ tau = I \ alpha}, \: {\ alpha = \ frac {\ text {net} \ tau} {I}} [/latex] является вращательным аналогом второго закона Ньютона и представляет собой весьма общеприменимо. Это уравнение действительно справедливо для любой крутящий момент, примененный к любому объекту относительно любой оси .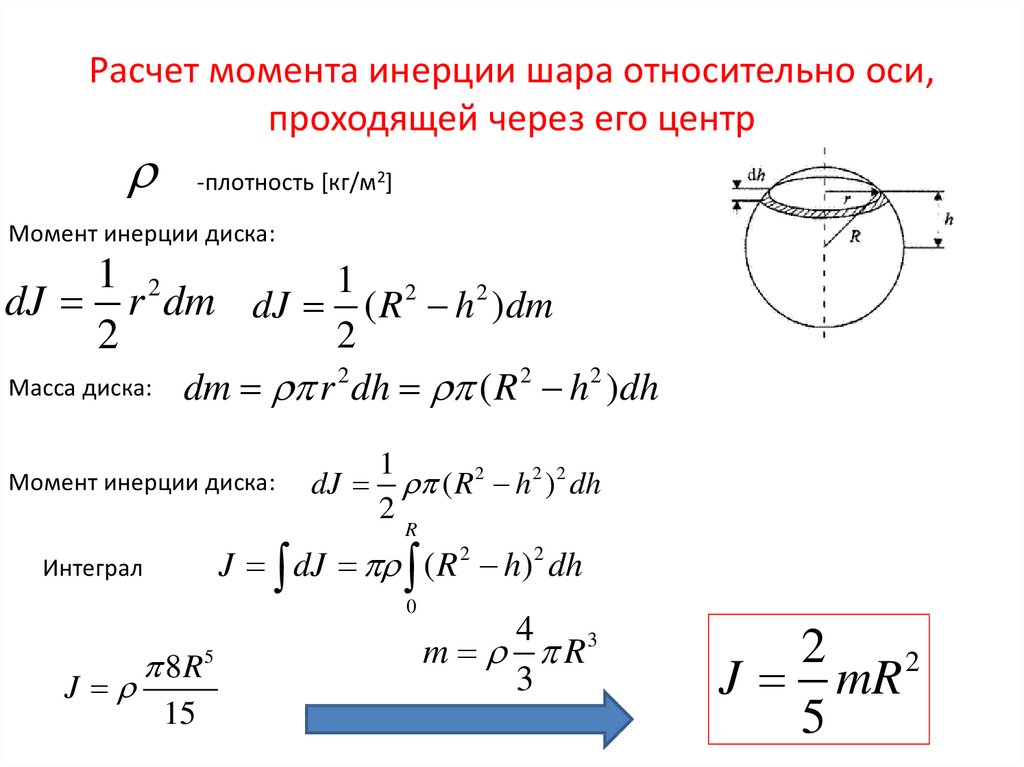
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
ЭКСПЕРИМЕНТ ДЛЯ ДОМА
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .
- Нарисуйте свободную диаграмму тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить [латекс] {\ текст {сеть} \ тау = I \ альфа}, \: {\ альфа = \ гидроразрыва {\ текст {сетка} \ тау {I}}, [/латекс] вращательный эквивалент второго закона Ньютона для решения задачи .
 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения. - Как всегда, проверьте решение, чтобы убедиться, что оно разумно .
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 3. Некоторые инерции вращения.Пример 1. Расчет влияния распределения масс на карусель
Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Strategy
Угловое ускорение определяется непосредственно выражением :=}[/latex] [latex]{\frac{\tau}{I}}.[/latex]
Чтобы найти [латекс]{\alpha},[/latex], мы должны сначала вычислить крутящий момент [ латекс]{\тау}[/латекс] (одинаковый в обоих случаях) и момент инерции [латекс]{I}[/латекс] (больше во втором случае). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что 92}}.[/latex]
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели -круглый. Чтобы найти общий момент инерции [latex]{I},[/latex], мы сначала находим момент инерции ребенка [latex]{I_{\textbf{c}}}[/latex], считая ребенка эквивалентным к точечной массе на расстоянии 1,25 м от оси. 2}.[/латекс] 92}}.[/latex]
2}.[/латекс] 92}}.[/latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
- Чем дальше приложена сила от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы приложим силу [латекс]{F}[/латекс] к точечной массе [латекс]{м}[/латекс], которая находится на расстоянии [латекс]{r}[/латекс] от точки вращения и поскольку сила перпендикулярна [латексу]{r},[/латекс] ускорение [латекс]{а = F/m}[/латекс] получается в направлении [латекса]{F}.
 [/латекс] Мы можем изменить это уравнение так, что
[/латекс] Мы можем изменить это уравнение так, что[латекс]{F = ма},[/латекс]
, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]{a = r\alpha},[/latex] и подставим это выражение в [latex]{F=ma},[/latex], что даст
[латекс]{F=г-н\альфа}[/латекс]
- Крутящий момент — это вращающая способность силы. В этом случае, поскольку [латекс]{F}[/латекс] перпендикулярен [латексу]{r},[/латекс] крутящий момент будет просто [латекс]{\тау=rF}.[/латекс] Если мы умножим оба части уравнения выше на [латекс]{r},[/латекс] мы получаем крутящий момент в левой части. То есть, 92}.[/латекс]
- Общая взаимосвязь между крутящим моментом, моментом инерции и угловым ускорением такова:
[латекс] {\ тау = I \ альфа} [/ латекс]
или
[латекс] {\ альфа =} [/ латекс] [латекс] {\ гидроразрыва {\ текст {сеть} \ тау} {I}} [/ латекс]
- крутящий момент
- поворотная эффективность силы
- инерция вращения
- сопротивление изменению вращения.
 Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex] и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex] и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
В предыдущих главах мы рассмотрели последствия приложения силы к свободно перемещаемому объекту. В этой главе мы изучаем объекты, которые закреплены на некоторой оси, так что объект не может быть смещен целиком при приложении силы, но может вращаться вокруг этой оси. Существует несколько способов измерения скорости вращения объекта. Возможно, самым простым является подсчет количества полных оборотов объекта вокруг оси вращения. Точно так же, как нас интересовала скорость изменения линейного положения со временем в случае линейного движения, нас интересует скорость изменения углового положения, когда мы исследуем вращательное движение. Мы можем описать это числом оборотов в секунду, но этот метод измерения не очень удобен для последующего анализа. Мы знаем, что длина окружности C или расстояние вокруг окружности выражается через радиус r, как C = 2 pi r, где pi — фундаментальная математическая константа, равная 3,1416. Если мы определим меру угла как длину вдоль дуги, деленную на радиус дуги, как показано на рис. 8.2 на стр. 136 в тексте, у нас будет метод измерения углов, который хорошо работает в нашем последующем анализе. . Для полного круга длина вокруг дуги называется окружностью. Это означает, что угол будет 2 пи r / r = 2 пи. Мы называем единицу измерения угла, определяемую как длина вдоль дуги, деленная на радиус, как радиан. Полный круг равен 2 пи (или 6,2832) радианам. Существует простая зависимость между скоростью объекта, движущегося по круговой траектории, и угловой скоростью w , с которой объект вращается вокруг оси вращения. Линейная скорость по касательной к окружности определяется как произведение радиуса окружности и угловой скорости или v = r w . Это уравнение верно только , если угловая скорость w измеряется в радианах в секунду. Мы определяем величины для описания вращательного движения, которые аналогичны величинам, которые мы использовали для описания линейного движения. Это означает, что нам не нужно запоминать весь новый набор уравнений, если мы можем определить, какую роль играют соответствующие угловые величины в уравнениях формы, используемой для описания линейного движения. Вместо использования x для линейного положения мы используем q для углового положения. Вместо использования v для линейной скорости мы используем w для угловой скорости. Вместо использования и для линейного ускорения мы используем и для углового ускорения. С этими заменами уравнения для углового движения, перечисленные в таблице 8.1 на странице 145 в тексте, теперь принимают ту же самую форму, что и те, которые мы имели для линейного движения для положения, скорости и ускорения. Единицы измерения будут выражены в радианах, радианах в секунду и радианах в секунду 2 соответственно. Крутящий момент вокруг точки поворота создается силой, действующей на плечо рычага. Крутящий момент, t , определяется как произведение приложенной силы F и плеча рычага l . Крутящий момент — это векторная величина, для которой полный векторный анализ выходит за рамки текста. Мы можем отметить векторный эффект крутящего момента, определив, производит ли он вращение по часовой стрелке или против часовой стрелки. Обычный выбор положительного направления состоит в том, чтобы считать крутящие моменты против часовой стрелки положительными, хотя такой выбор не требуется. Крутящий момент выражается в силе, умноженной на длину, или в ньютонах, умноженных на метры. Крутящий момент имеет тенденцию вызывать изменение вращательного движения объекта. Понятия крутящего момента и плеч рычага используются для определения местоположения центра тяжести объекта. Мы знаем, что распределение массы на качелях важно для поддержания равновесия. Если два человека на качелях не имеют одинаковой массы и если оба человека находятся на одинаковом расстоянии от точки вращения, качели не будут работать. Аналогия между поступательным движением и вращательным движением может быть продолжена, если мы рассмотрим второй закон Ньютона. В случае линейного движения мы записали F net = m a , где масса была константой пропорциональности, связывающей линейное ускорение с результирующей силой. Для углового движения мы можем написать аналогичное уравнение, связывающее чистый крутящий момент t net с угловым ускорением, определив соответствующую константу пропорциональности. Таким образом, мы пишем t net = I a , где I определяется как момент инерции. Момент инерции учитывает количество массы и то, как эта масса распределяется относительно оси вращения. Момент инерции зависит от квадрата расстояния массы от оси вращения. К счастью, значение момента инерции для объектов правильной формы, таких как диски, кольца и сферы, было рассчитано и доступно в таблицах в учебниках и справочниках. Некоторые репрезентативные формулы приведены на рис. Поскольку константа пропорциональности между чистым крутящим моментом и угловым ускорением во втором законе Ньютона для вращения является моментом инерции, важно распределение массы относительно оси вращения. Действительно, момент инерции зависит от квадрата расстояния от оси до массы, так что это большой эффект; чем больше расстояние от оси, тем больше момент инерции. Вот почему запустить набитую людьми карусель труднее, чем пустую карусель. На нагруженной карусели на большом расстоянии от точки поворота находится большое количество массы. В главе 7 мы определили линейный импульс как произведение массы и скорости или p = m v . По аналогии мы определяем угловой момент как произведение момента инерции на угловую скорость или L = I w . Точно так же, как сила вызывает изменение линейного количества движения, крутящий момент вызывает изменение углового момента. Когда чистая сила была равна нулю, линейный момент сохранялся, поэтому мы не должны удивляться, узнав, что когда чистый момент равен нулю, угловой момент сохраняется. Сохранение углового момента отвечает за второй закон Кеплера, который рассматривался в главе 5. Равные площади сметаются за равные промежутки времени радиус-вектором между Солнцем и планетой из-за сохранения углового момента. Планеты движутся быстрее, когда они ближе к Солнцу, чтобы иметь тот же угловой момент, который они будут иметь, когда они будут дальше от Солнца. |
Инерция зависит от массы; Вращательная инерция зависит от массы и чего-то еще. Какая?
Действительно, инерция вращения объекта зависит от его массы . Это также зависит от распределения этой массы относительно оси вращения. Когда масса удаляется дальше от оси вращения, становится все труднее изменить скорость вращения системы.
Момент инерции зависит как от массы, так и от распределения массы . Дальше от оси вращения единица массы вызывает больший момент инерции.
Какая связь между центром тяжести и основанием опоры для объекта, находящегося в устойчивом равновесии? Вертикальная линия, проходящая через центр тяжести, должна проходить через опорное основание.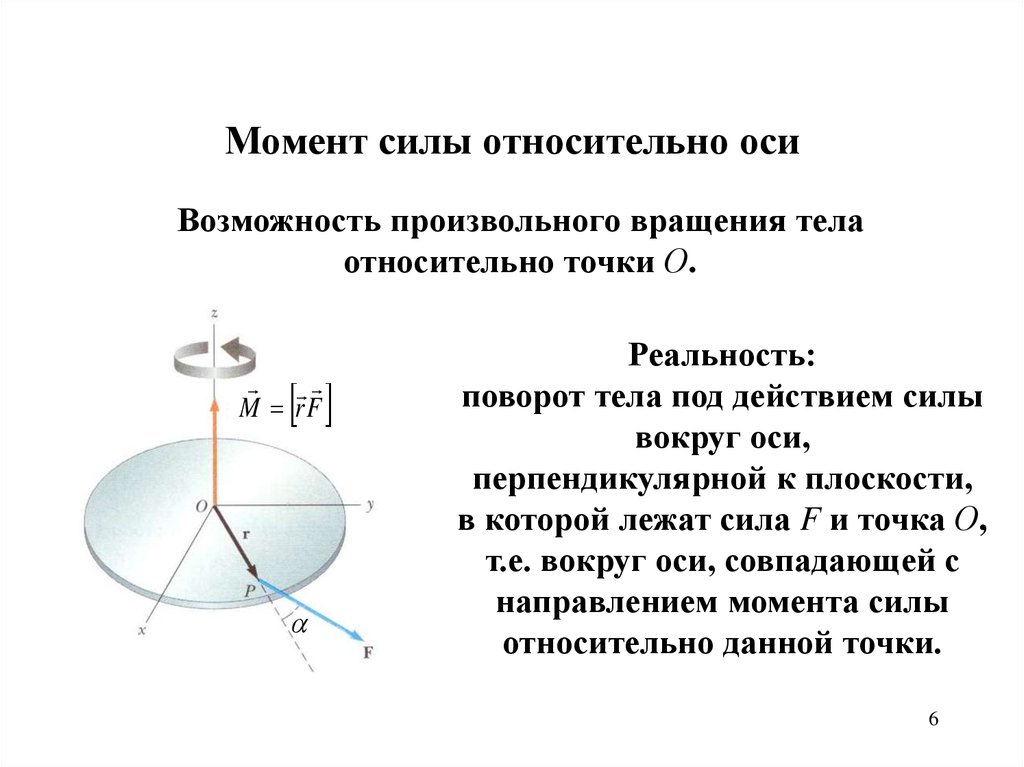
Масса как мера величины инерции
Все объекты сопротивляются изменению своего состояния движения . … Чем больше инерция у объекта, тем больше у него массы. Более массивный объект имеет большую тенденцию сопротивляться изменениям в своем состоянии движения. 92 . … Итак, формула, которую мы собираемся использовать для инерции вращения, такова: i это символ инерции вращения, равный массе, умноженной на квадрат радиуса.
Какие факторы влияют на момент инерции?
Момент инерции тела прямо пропорционален его массе и расстоянию частиц тела от оси вращения . Следовательно, момент инерции зависит от массы и расстояния от оси вращения, а сила и плотность не влияют на момент инерции тела.
Инерция вращения равна моменту инерции?
Момент инерции — это название, данное вращательной инерции вращательному аналогу массы для линейного движения. Он появляется в соотношениях для динамики вращательного движения.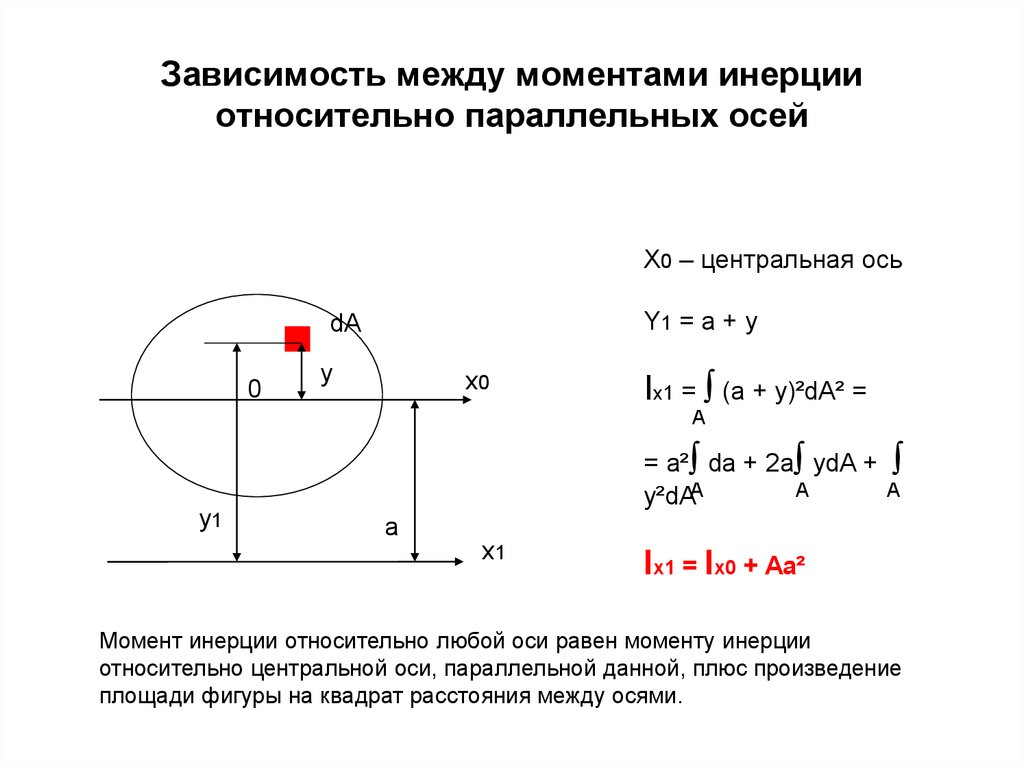 Момент инерции должен быть указан относительно выбранной оси вращения.
Момент инерции должен быть указан относительно выбранной оси вращения.
Какие два фактора определяют момент инерции объекта?
Момент инерции зависит от следующих факторов
- Плотность материала.
- Форма и размер корпуса.
- Ось вращения (распределение массы относительно оси)
Как инерция зависит от массы примера?
Тело большей массы, которое будет иметь меньшее ускорение, чем другое тело . Именно так масса обеспечивает природе сопротивление изменению ее состояния, т. е. инерции тела. Например, очень трудно сдвинуть тяжелый валун (большой массы), потому что его масса очень велика, и поэтому инерция больше.
Что зависит от массы объекта?
Поскольку мы знаем, что вес объекта является произведением массы и гравитации, то отсюда мы можем сказать, что вес зависит от массы объекта и ускорения, обусловленного действием силы тяжести.
Зависит ли момент инерции от центра масс?
Момент инерции зависит не только от массы объекта , но и от распределения его массы относительно оси, вокруг которой он вращается.
Как можно смоделировать гравитацию на орбитальной космической станции?
Как можно смоделировать гравитацию на орбитальной космической станции? Гравитацию можно смоделировать на космической станции , вращая ее . … Луна «падает», потому что ее притягивает земное притяжение, пока она движется вперед.
Что такое закон инерции для вращающихся систем?
Крутящий момент стремится увеличить инерцию вращения объекта. B. Крутящий момент имеет тенденцию увеличивать линейную скорость объекта. C. Крутящий момент стремится скрутить или изменить состояние вращения объекта.
Как соотносится скорость вращения меньшего колеса со скоростью вращения большего колеса?
Чем отличается скорость вращения меньшего колеса от скорости вращения большего колеса? … Меньшие колеса вращаются в два раза быстрее, чем большее , чтобы не отставать от него. Тангенциальные скорости одинаковы.
Почему масса влияет на инерцию вращения?
Требуется больше усилий, чтобы во вращение вошла большая масса . Таким образом, момент инерции зависит от массы. Не одинаково легко вращать их обоих вокруг одной и той же оси вращения. Требуется больше усилий, чтобы объект на большем расстоянии разогнался до той же угловой скорости.
Таким образом, момент инерции зависит от массы. Не одинаково легко вращать их обоих вокруг одной и той же оси вращения. Требуется больше усилий, чтобы объект на большем расстоянии разогнался до той же угловой скорости.
Что вызывает инерцию?
Инерция прямо пропорциональна массе объекта/тела , то есть чем больше масса тела/объекта, тем большей будет инерция, которой обладает этот объект/тело. … Причиной инерции является сопротивление тела/объекта изменению его состояния покоя или движения.
Что такое инерция Что дает измерение инерции?
Чем больше инерция объекта, тем больше его масса. Таким образом, объект с большей массой имеет большую тенденцию сопротивляться изменениям в состоянии своего движения. Масса дает меру инерции.
Как зависит инерция вращения диска от его радиуса?
При увеличении радиуса от оси вращения момент инерции увеличивается, что замедляет скорость вращения.
Зависит ли инерция от радиуса?
Момент инерции прямо пропорционален квадрату радиуса .



 12
12 Радиус шара R, масса т:
Радиус шара R, масса т: 14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен:
14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен: Так, например, однородный по плотности шар имеет три равных момента инерции относительно главных осей, каждый из которых равен: , где M, R — масса и радиус шара.
Так, например, однородный по плотности шар имеет три равных момента инерции относительно главных осей, каждый из которых равен: , где M, R — масса и радиус шара. МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА
МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА Все правила по сольфеджио
Все правила по сольфеджио


 В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы) . Модуль момента пропорционален углу закручивания пружины
В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы) . Модуль момента пропорционален углу закручивания пружины

 Обратная связь — 161.97.168.212 (0.006 с.)
Обратная связь — 161.97.168.212 (0.006 с.) [/латекс] Мы можем изменить это уравнение так, что
[/латекс] Мы можем изменить это уравнение так, что Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex] и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex] и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции Существует еще один способ измерения эффектов вращения, при котором окружность делится на 360 равных частей, называемых «градусами». Таким образом, имеется 360 градусов (или 360 o ) до полного круга. Мы могли бы измерить скорость вращения с помощью числа градусов в секунду, но и это оказывается неудовлетворительной единицей для последующего анализа.
Существует еще один способ измерения эффектов вращения, при котором окружность делится на 360 равных частей, называемых «градусами». Таким образом, имеется 360 градусов (или 360 o ) до полного круга. Мы могли бы измерить скорость вращения с помощью числа градусов в секунду, но и это оказывается неудовлетворительной единицей для последующего анализа. Выше мы утверждали, что полный круг имеет 360 90 234 o 90 235 . Это дает нам преобразование между двумя методами измерения углов, потому что 360 o = 2 пи радиана. Если мы разделим обе части уравнения на 2, мы получим 180 o = пи в радианах в качестве удобной формулы преобразования градусов в радианы. Поскольку радиан определяется как длина вдоль дуги, деленная на радиус дуги, единицы длины сокращаются, и радиан, строго говоря, является безразмерной величиной. Тем не менее мы используем термин радианы, чтобы подчеркнуть наличие вращательного движения. Скорость изменения углового положения измеряется в радианах в секунду.
Выше мы утверждали, что полный круг имеет 360 90 234 o 90 235 . Это дает нам преобразование между двумя методами измерения углов, потому что 360 o = 2 пи радиана. Если мы разделим обе части уравнения на 2, мы получим 180 o = пи в радианах в качестве удобной формулы преобразования градусов в радианы. Поскольку радиан определяется как длина вдоль дуги, деленная на радиус дуги, единицы длины сокращаются, и радиан, строго говоря, является безразмерной величиной. Тем не менее мы используем термин радианы, чтобы подчеркнуть наличие вращательного движения. Скорость изменения углового положения измеряется в радианах в секунду. Это неверно, если угол измеряется в градусах.
Это неверно, если угол измеряется в градусах.
 Произведение массы и расстояния от точки вращения является релевантной величиной в этом случае. Единственная сила в точке поворота способна поддерживать качели для достижения баланса, когда массы расположены правильно. Так и с другими предметами, даже с людьми. Мы можем найти единственную точку, в которой мы можем вообразить, что действует вся сила тяжести, и мы можем уравновесить объект, прилагая равную и противоположную направленную вверх силу через эту точку, называемую центром тяжести, потому что вес самого объекта действует нет чистого крутящего момента относительно центра тяжести. Распределение массы важно в этом определении, потому что масса, которая находится на большем расстоянии от точки вращения, будет иметь большее влияние на вращение объекта. Если мы сможем определить местонахождение центра тяжести, то во многих случаях мы сможем рассматривать объект, независимо от его формы и распределения массы, как точечный объект, вся масса которого считается сосредоточенной в центре тяжести для целей расчета эффекта.
Произведение массы и расстояния от точки вращения является релевантной величиной в этом случае. Единственная сила в точке поворота способна поддерживать качели для достижения баланса, когда массы расположены правильно. Так и с другими предметами, даже с людьми. Мы можем найти единственную точку, в которой мы можем вообразить, что действует вся сила тяжести, и мы можем уравновесить объект, прилагая равную и противоположную направленную вверх силу через эту точку, называемую центром тяжести, потому что вес самого объекта действует нет чистого крутящего момента относительно центра тяжести. Распределение массы важно в этом определении, потому что масса, которая находится на большем расстоянии от точки вращения, будет иметь большее влияние на вращение объекта. Если мы сможем определить местонахождение центра тяжести, то во многих случаях мы сможем рассматривать объект, независимо от его формы и распределения массы, как точечный объект, вся масса которого считается сосредоточенной в центре тяжести для целей расчета эффекта. внешних сил.
внешних сил. 8.15 на стр. 151 в тексте.
8.15 на стр. 151 в тексте.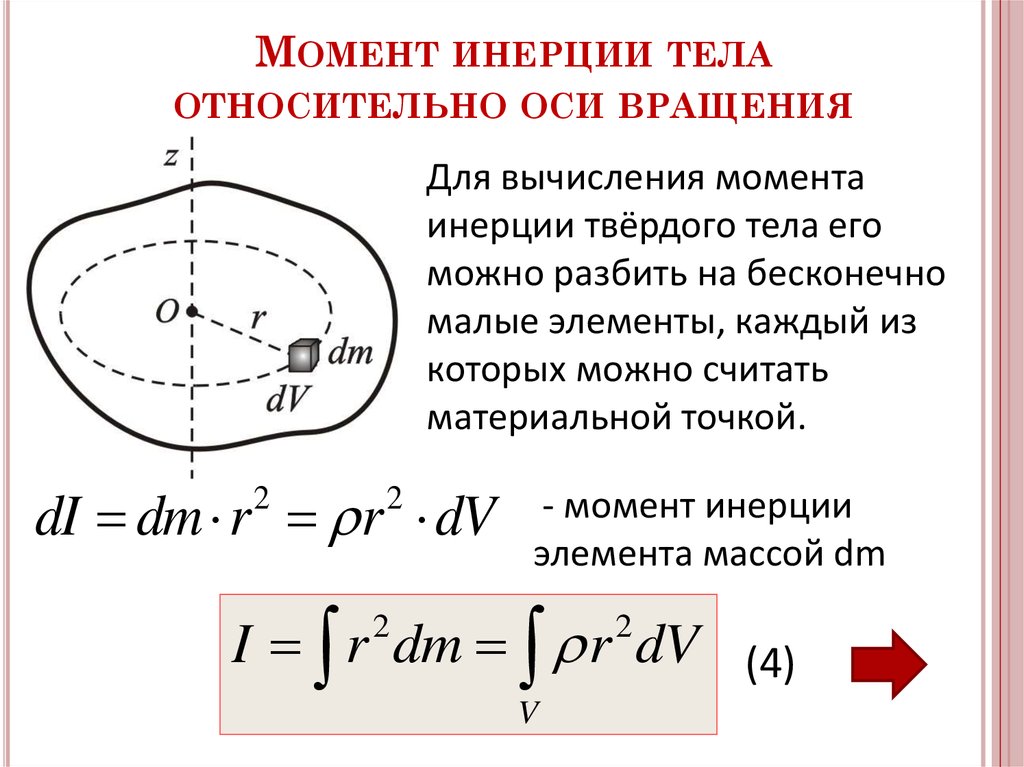 В предыдущей главе мы узнали, что линейный импульс сохраняется, когда нет чистой внешней силы. Точно так же для вращательного движения, когда нет чистого внешнего крутящего момента, угловой момент сохраняется. Угловой момент зависит от момента инерции и угловой скорости, поэтому, если нет чистого внешнего крутящего момента и момент инерции уменьшен, угловая скорость должна увеличиться. Мы видим это в случаях с крутящимися балеринами или фигуристами, когда они начинают вращение с вытянутыми руками, а затем подтягивают руки ближе к туловищу. При вытянутых руках момент инерции достаточно велик, так как масса рук расположена на большом расстоянии от оси вращения. Когда руки собраны, момент инерции уменьшается. Произведения момента инерции и угловой скорости должны быть постоянными, если нет чистого внешнего крутящего момента, поэтому меньший момент инерции должен приводить к большей угловой скорости. Следовательно, балерина и фигуристка начинают вращаться быстрее всякий раз, когда сжимают руки.
В предыдущей главе мы узнали, что линейный импульс сохраняется, когда нет чистой внешней силы. Точно так же для вращательного движения, когда нет чистого внешнего крутящего момента, угловой момент сохраняется. Угловой момент зависит от момента инерции и угловой скорости, поэтому, если нет чистого внешнего крутящего момента и момент инерции уменьшен, угловая скорость должна увеличиться. Мы видим это в случаях с крутящимися балеринами или фигуристами, когда они начинают вращение с вытянутыми руками, а затем подтягивают руки ближе к туловищу. При вытянутых руках момент инерции достаточно велик, так как масса рук расположена на большом расстоянии от оси вращения. Когда руки собраны, момент инерции уменьшается. Произведения момента инерции и угловой скорости должны быть постоянными, если нет чистого внешнего крутящего момента, поэтому меньший момент инерции должен приводить к большей угловой скорости. Следовательно, балерина и фигуристка начинают вращаться быстрее всякий раз, когда сжимают руки.