4.1. Логические переменные и логические операции. Информатика: аппаратные средства персонального компьютера
4.1. Логические переменные и логические операции
Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, может принимать значения 1 (высокий уровень электрического напряжения) и 0 (низкий уровень электрического напряжения) и рассматривается как импульсный сигнал, который математически может быть описан в виде двоичной переменной, принимающей также значения 0 или 1. Для решения различных логических задач, например, связанных с анализом и синтезом цифровых схем и электронных блоков компьютера, широко используются логические функции и логические операции с двоичными переменными, которые называются также логическими переменными.
Логические переменные изучаются в специальном разделе математики, который носит название алгебры логики (высказываний), или булевой алгебры.
Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. В алгебре логики используются следующие логические операции.
В алгебре логики используются следующие логические операции.
1. Логическая операция ИНВЕРСИЯ (отрицание). В естественных языках соответствует словам неверно, ложь
Инверсия каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Математическая запись данной операции для логической переменной А будет иметь вид:
2. Логическая операция КОНЪЮНКЦИЯ (логическое умножение). В естественных языках соответствует союзу и, в языках программирования обозначается And, в алгебре логики обозначается & .
Конъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие составное высказывание.
Математическая запись данной операции для логических переменных Д В, С, … будет иметь вид:
F = A & B & C & …
3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.
Дизъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.
Математическая запись данной операции для логических переменных A, В, С, … будет иметь вид:
F = AvBvC…
4. Логическая операция ИМПЛИКАЦИЯ (логическое следование). В естественных языках соответствует обороту речи, если…, то …, в языках программирования обозначается If, в алгебре логики обозначается ?.
Импликация каждым простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно.
Математическая запись данной операции для двух логических переменных А и В будет иметь вид:
F = A?B.
5. Логическая операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). В естественных языках соответствует обороту речи тогда и только тогда, в алгебре логики обозначается ?.
Эквиваленция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие составное высказывание, одновременно истинны или одновременно ложны.
Математическая запись данной операции для логических переменных A, В, С… будет иметь вид:
F = A?B?C?…
Данный текст является ознакомительным фрагментом.
Логические операции
Логические операции
Логические операции позволяют комбинировать выражения, возвращающие логические величины. Язык JavaScript поддерживает три логические операции.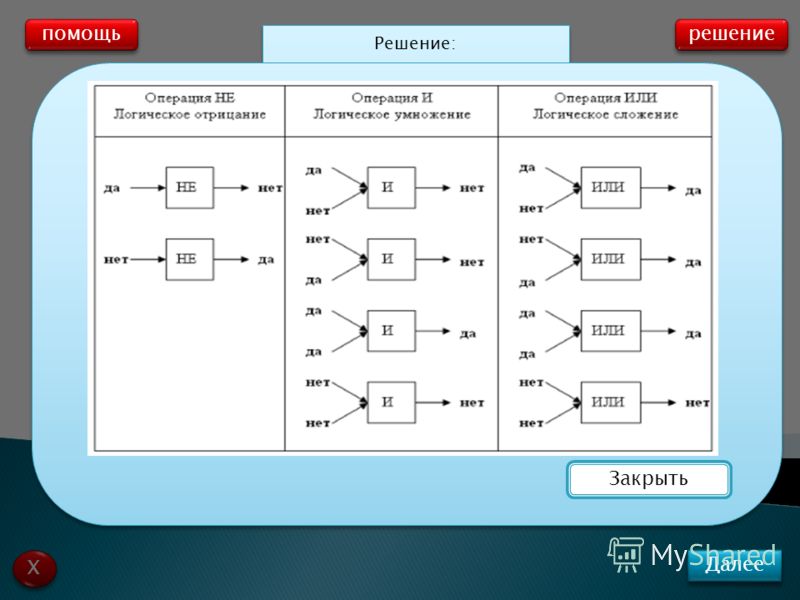 Операция логического И (&&) возвращает true, если только оба операнда истинны. Например, (1<7)&&(3>2). При
Операция логического И (&&) возвращает true, если только оба операнда истинны. Например, (1<7)&&(3>2). При
Логические схемы
Логические схемы Рабочая версия PSpice содержит более сотни логических устройств, доступных в коммерческой версии программного обеспечения. Имеется большинство логических схем серии 7400, триггеры, счетчики и т.п. Полная распечатка логических устройств демонстрационной
Логические операции
Логические операции Для создания объектов более сложных, чем изначальные звезды, прямоугольники и эллипсы, мы можем использовать логические операции. Это гораздо проще, чем полноценная векторная графика, где мы будем создавать фигуры с нуля.Для выполнения логических
Логические И и ИЛИ
 Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:выражение_1&&выражение_2Сначала
Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:выражение_1&&выражение_2СначалаКогда использовать логические переменные
Когда использовать логические переменные Переменные типа Boolean могут хранить только два значения: True (в числовом представлении это 1) или False (0). Используйте переменные типа Boolean, когда нужно выяснить, какое из двух альтернативных условий имеет место в данный момент.
Глава 16 Логические операции
Глава 16 Логические операции • Понятие логических операций• Использование логических операцийРаботая с выделением, с которым мы познакомились в прошлой главе, можно использовать логические операции – это позволит в некоторых случаях упростить создание выделения или
Резюме: логические операции и выражения
Резюме: логические операции и выражения
1. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Операндами логических операций обычно являются условные выражения. У операции != имеется только один операнд. Остальные имеют по два — один слева от знака и другой справа от него. && И|| ИЛИ! НЕII.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ Операндами логических операций обычно являются условные выражения. У операции != имеется только один операнд. Остальные имеют по два — один слева от знака и другой справа от него. && И|| ИЛИ! НЕII.
IV. Логические операции
IV. Логические операции Обычно логические операции «считают» условные выражения операндами. Операция ! имеет один операнд, расположенный справа. Остальные операции имеют два операнда: один слева и один справа. && Логическое И: результат операции имеет значение «истина»,
Поразрядные логические операции
Поразрядные логические операции
Четыре операции производят действия над данными, относящимися к классу целых, включая char. Они называются «поразрядными», потому что выполняются отдельно над каждым разрядом независимо от разряда, находящегося слепа или справа.
4. Null-значения и логические операции
4. Null-значения и логические операции Обычно в системах управления базами данных непосредственно поддерживаются только три логические операции: отрицание ¬, конъюнкция & и дизъюнкция ?. Операции следования ? и равносильности ? выражаются через них с помощью
Логические операции (Logical operations)
Логические операции
Логические операции
Логические операции выполняют над своими операндами логические функции И (&&) и ИЛИ (||). Операнды логических операций могут иметь целый, плавающий тип, либо быть указателями. Типы первого и второго операндов могут различаться. Сначала всегда
Операнды логических операций могут иметь целый, плавающий тип, либо быть указателями. Типы первого и второго операндов могут различаться. Сначала всегда
4.3. Операции сравнения и логические операции
4.3. Операции сравнения и логические операции Символ операции Значение Использование ! Логическое НЕ !expr меньше exprexpr = Меньше либо равно expr=expr больше exprexpr = больше либо равно expr=expr == равно expr==expr != не равно expr!=expr логическое
Логические операции
Логические операции В XSLT имеются две логические операции — or и and. Эти операции бинарны, то есть каждая из них определена для двух операндов. Если операнды не являются булевыми значениями, они неявным образом приводятся к булевому типу.Семантика or и and очевидна — они
3.
 ~ »» ««применяются к целым, то есть к объектам типа char, short, int, long и их unsigned аналогам, результаты тоже цлые.Одно из стандартных применений побитовых логических опраций – реализация маленького множества
~ »» ««применяются к целым, то есть к объектам типа char, short, int, long и их unsigned аналогам, результаты тоже цлые.Одно из стандартных применений побитовых логических опраций – реализация маленького множестваЛогические операции
Логические операции К логическим относятся бинарные операции and, or и xor, а также унарная операция not, имеющие операнды типа boolean и возвращающие значение типа boolean. Эти операции подчиняются стандартным правилам логики: a and b истинно только тогда, когда истинны a и b, a or b истинно
Высказывания. Логические значения | Кабинет информатики
В меню кабинета | Высказывания. Логические значения
Понятие высказывания
Высказывание — это повествовательное предложение, о котором можно (по крайней мере в пределах определенного контекста) говорить, что оно истинно или ложно (Х. Фрейденталь) 2.
Фрейденталь) 2.
Высказывания являются одним из основополагающих видов носителей информации 3. Примерами высказываний на русском языке являются предложения: “Вчера было полнолуние”, “Москва — столица Российской Федерации”. Для определенного объекта, как, например, луна, город, страна, высказывания характеризуют определенные свойства или состояния, с помощью высказываний мы устанавливаем взаимосвязи между объектами.
Высказывание будет истинным, если оно адекватно отображает эту связь, в противном случае оно ложно. Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание “Число 1 + 225 = 4 294 967 297 — простое”, принадлежащее Ферма (1601–1665), долгое время считалось истинным, пока в 1732 году Эйлер не доказал, что оно ложно.
Изучением высказываний как математических объектов занимается алгебра логики. Однако обоснование истинности или ложности простых высказываний решается вне алгебры логики.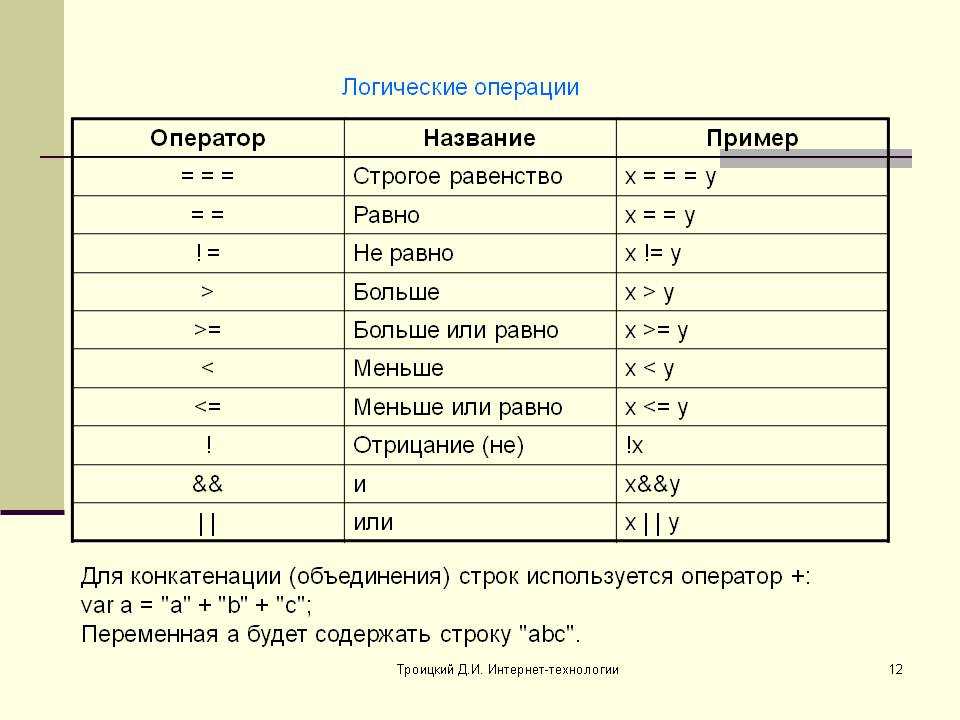 Например, истинность или ложность высказывания “Сумма углов треугольника равна 180о” устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
Например, истинность или ложность высказывания “Сумма углов треугольника равна 180о” устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
Приведенное выше определение высказывания не является математически точным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению “Это предложение является ложным” невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его собственному утверждению. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно. Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием.
Причина этого парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя и, следовательно, устранены возникающие отсюда парадоксы.
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например, из двух чисел можно составить высказывания, соединив их знаками равенства или неравенства: “5 < 7” (истинное высказывание), “5 = 7” (ложное высказывание).
Понятие высказывательной формы
Однако не всякое повествовательное предложение является высказыванием. Например, в предложении “х < 12” не содержится никакого утверждения, следовательно, нельзя ставить вопрос о его истинности или ложности. Но это предложение становится высказыванием при замене переменной х каким-либо конкретным значением.
Буква х, входящая в это предложение, играет роль переменной. Переменная — это языковое выражение, служащее для обозначения произвольного объекта из некоторого конкретного множества, называемого областью допустимых значений этой переменной. Если переменная употребляется таким образом, что вместо нее допускается подстановка любого значения из области допустимых значений, то эта переменная называется свободной. Так, переменная х в предложении “х < 12” является свободной. Переменные a, b, с и y в предложении ay2 + by + c = 0 также являются свободными.
Переменная — это языковое выражение, служащее для обозначения произвольного объекта из некоторого конкретного множества, называемого областью допустимых значений этой переменной. Если переменная употребляется таким образом, что вместо нее допускается подстановка любого значения из области допустимых значений, то эта переменная называется свободной. Так, переменная х в предложении “х < 12” является свободной. Переменные a, b, с и y в предложении ay2 + by + c = 0 также являются свободными.
Однако встречается такое употребление переменных, например, в математике, которое не предполагает и не допускает возможность подстановки вместо переменных конкретных имен объектов (значений). Так, предложение “Не существует действительной переменной z, квадратный корень которой равен –1” содержит переменную z, однако подстановка конкретных значений вместо переменной z лишена какого-либо смысла.
В случае, когда по смыслу выражения, содержащего переменную, подстановка вместо нее конкретных значений невозможна, эта переменная называется связанной.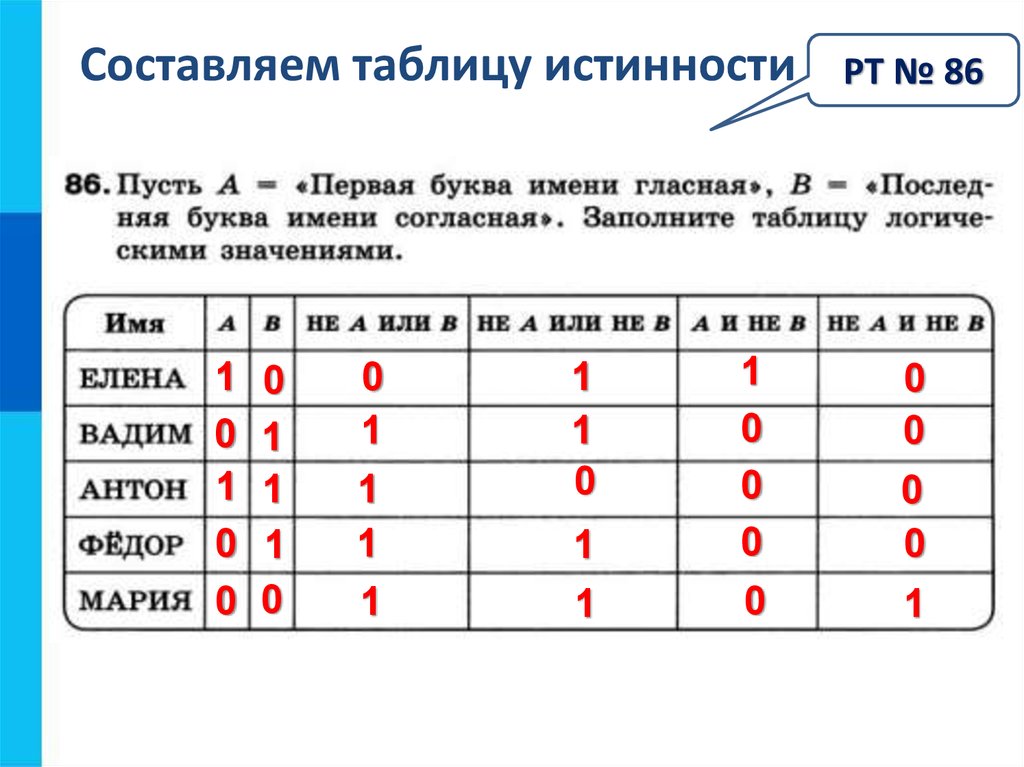 Повествовательное предложение, содержащее свободные переменные, называется высказывательной формой. Например, предложения типа “х < 12” есть высказывательная форма.
Повествовательное предложение, содержащее свободные переменные, называется высказывательной формой. Например, предложения типа “х < 12” есть высказывательная форма.
Логические переменные и логические значения
Высказывание называется простым или элементарным, если никакая его часть сама не является высказыванием. Если высказывание является истинным, то говорят, что его истинностное значение есть И (истина), если высказывание является ложным, то его истинностное значение есть Л (ложь). Как уже было сказано ранее, обоснование истинности или ложности простых высказываний решается вне логики.
Из элементарных высказываний можно получать новые, более сложные высказывания. Способ построения сложного высказывания из элементарных высказываний, при котором истинностное значение сложного высказывания полностью определяется истинностными значениями исходных высказываний, называется логической операцией (см. “Логические операции.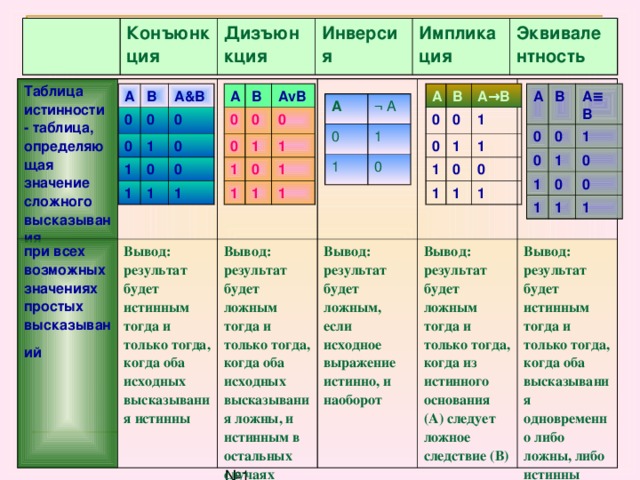 Кванторы”). В русском языке сложные высказывания из элементарных высказываний строятся при помощи логических связок типа: и, или, а, но, либо, если … то, неверно, что… и т.д.
Кванторы”). В русском языке сложные высказывания из элементарных высказываний строятся при помощи логических связок типа: и, или, а, но, либо, если … то, неверно, что… и т.д.
Логической переменной называется переменная, значением которой может быть любое, наперед заданное высказывание. Логические переменные обозначаются латинскими буквами, быть может, снабженными индексами, как обычные алгебраические переменные: x, y, x1, y1, xk, yn и т.п. Очевидно, что логические переменные могут принимать только значения “истина” или “ложь”. Эти значения называют логическими. В алгебре логики, в языках программирования для обозначения значений логических переменных используют также 1 или true (истина), 0 или false (ложь).
Методические рекомендации
Как уже было сказано в статье, высказывания являются одной из основных форм представления информации. Действительно, с помощью высказываний мы можем описывать свойства объектов (“Число 5 — нечетное”, “15 апреля 2007 года в Хабаровске был ураганный ветер”), взаимоотношения объектов (“Если в ромбе все углы прямые, то это — квадрат”, “Дробь является правильной только тогда, когда ее числитель меньше знаменателя”). При помощи высказываний мы записываем алгоритмы в текстовой форме, строим информационные системы и т.д.
Действительно, с помощью высказываний мы можем описывать свойства объектов (“Число 5 — нечетное”, “15 апреля 2007 года в Хабаровске был ураганный ветер”), взаимоотношения объектов (“Если в ромбе все углы прямые, то это — квадрат”, “Дробь является правильной только тогда, когда ее числитель меньше знаменателя”). При помощи высказываний мы записываем алгоритмы в текстовой форме, строим информационные системы и т.д.
Каждое элементарное высказывание в определенной системе контекста несет значение истина или ложь. Одну из первых попыток постичь понятие высказывания предпринял древнегреческий ученый и философ, основоположник формальной логики Аристотель (384–322 до н.э.). Он писал: “Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности”. Для точного определения понятия высказывания и формальной работы с высказываниями в информатике строятся специальные формальные системы. В рамках таких систем мы можем представлять информацию в формальном виде, например, в виде логических формул, — так называемая внешняя форма представления информации, вычислять значение информации (в смысле описания свойств объекта, взаимоотношений объектов и т. д.) — так называемая собственно “абстрактная” информация.
д.) — так называемая собственно “абстрактная” информация.
Манфред Брой (немецкий ученый, лауреат премии Лейбница в области информатики) дает следующее определение информации: “Информацией называют абстрактное содержание (“содержательное значение”, “семантика”) какого-либо высказывания, описания, указания, сообщения или известия. Внешнюю форму изображения информации называют представлением информации”. Выявление подходящих систем представления (“языков”) для определенных классов информации является одной из задач информатики.
Понятие высказывания вводится в средней школе, как правило, в 8–9-м классе. Однако с этим понятием учащиеся начинают работать с младших классов. Авторы некоторых учебников называют высказывания суждениями. Однако дело не в терминологии. Важно, чтобы школьник научился понимать, является ли конкретное предложение высказыванием или нет, чтобы он умел обосновать свой ответ. Если в рамках изучаемой темы (например, “Человек и информация” или “Основы алгоритмизации и программирования”) школьникам приходится строить сложные высказывания и определять их истинность, то последовательность изложения материала может быть следующая:
· понятие простого и сложного высказывания;
· понятие истинности высказывания;
· знакомство с основными логическими связками;
· отработка навыков построения сложных высказываний, устанавливающих взаимосвязь между объектами;
· отработка навыков построения высказываний, описывающих заданные объекты.
2Фрейденталь Х. Язык логики. М.: Наука, 1969.
3Брой М. Информатика. Основополагающее введение: часть I. М.: Диалог–МИФИ, 1996.
Алгебра логики
Алгебра логики
Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.
|
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними. |
Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
|
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. |
Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.
Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?
Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.
|
Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). |
Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, B, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем B, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и B». Здесь А, В — логические переменные, «и» — логическая связка.
|
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». |
Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
|
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний. |
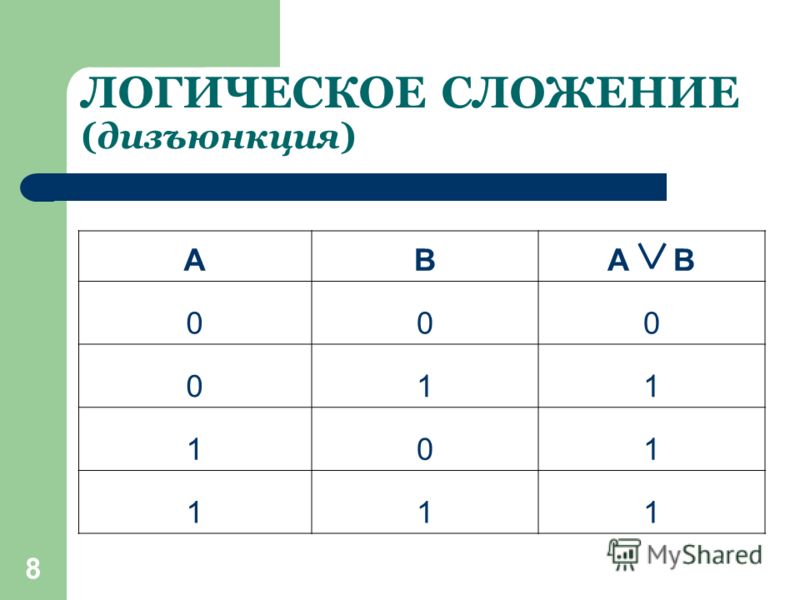
Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением. Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением. Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией. При построении отрицания простого высказывания:
|
Рассмотрим несколько новых логических операций.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием. |
Операция импликации обозначается символом -» и задаётся следующей таблицей истинности:
В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией. |
Строгая дизъюнкция обозначается символом ⊕ и задаётся следующей таблицей истинности:
В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.
В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.
Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью. |
В логике эквиваленция обозначается символом ↔ и задаётся следующей таблицей истинности:
В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».
Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».
Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.
А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот. Можно сделать выводы:
- операция эквиваленции есть отрицание операции строгой дизъюнкции
- операция строгой дизъюнкции есть отрицание операции эквиваленции
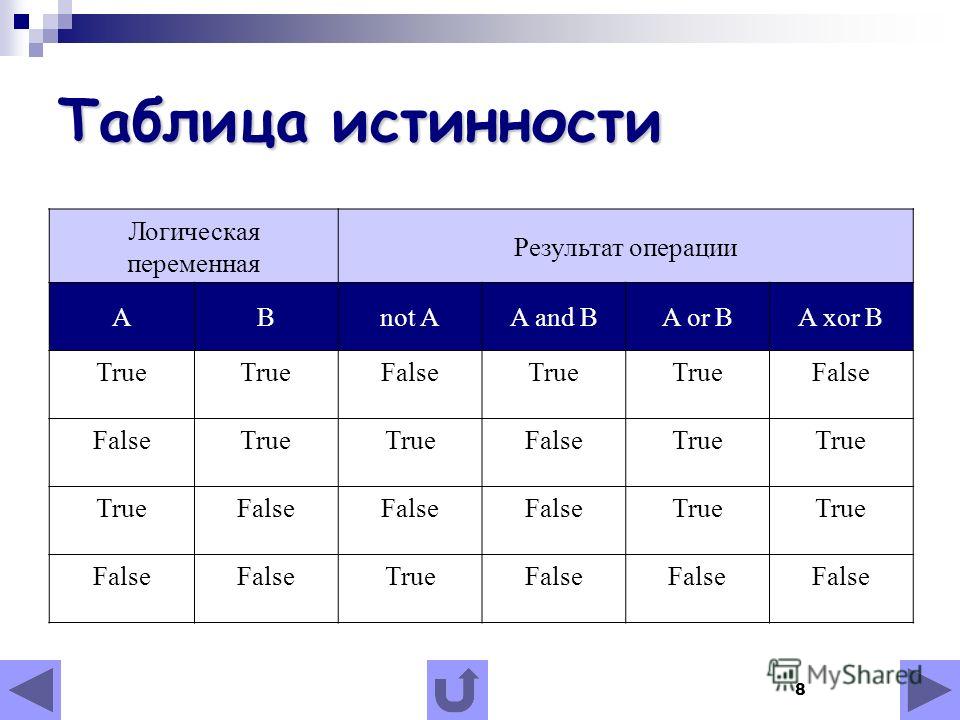
На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций.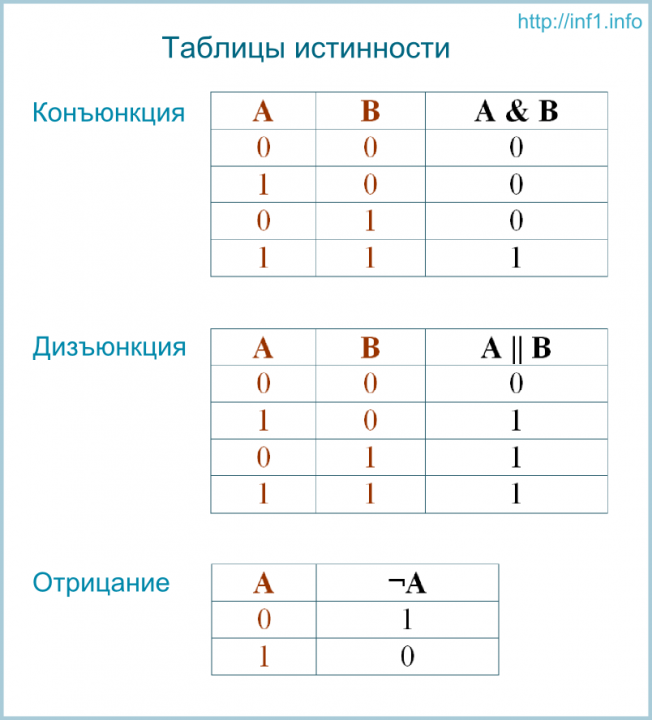 В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.
В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.
Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.
|
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок. |
Для логического выражения справедливо:
1) всякая логическая переменная, а также логические константы (0, 1) есть логическое выражение;
2) если А — логическое выражение, то и А — логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.
Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная → вторая буква согласная) & (последняя буква гласная → предпоследняя буква гласная):
1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.
Вычислим значение логического выражения для каждого из данных слов:
1) (0 → 1) & (0 → 1) = 1 & 1 = 1;
2) (0 → 1) & (1 → 0) = 1 & 0 = 0;
3) (1 → 0) & (1 → 1) — 0 & 1 = 0;
4) (1 → 1) & (0 → 1) = 1 & 1 = 1.
Итак, заданному условию удовлетворяют первое и четвёртое слова.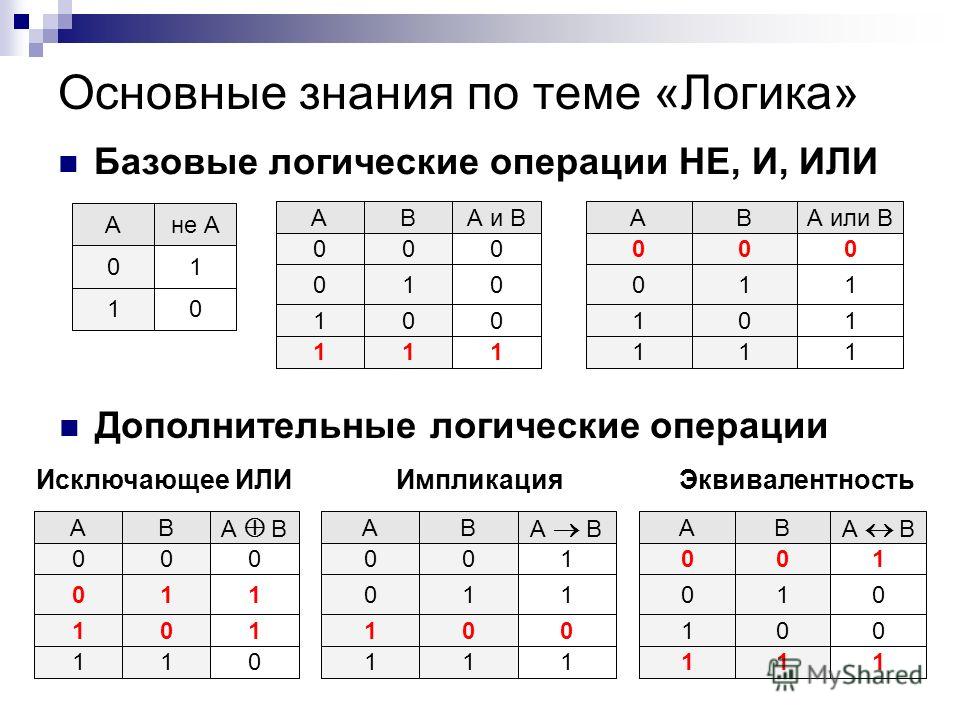
Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.
Пример 2. Решим логическое уравнение
Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:
Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.
Подставим найденные значения переменных в уравнение Получим: или т. е. В = 1.
Ответ: А = 1, В = 1, С = 0, D = 0.
Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.
Пример 3. Выясним, сколько различных решений имеет логическое уравнение
Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:
Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:
Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.
Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).
Сколько решений имеет исходное уравнение?
Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х1 & х2 → х3 & х4 = 1.
Введём замену переменных. Пусть t1 = х1 & х2, t2 = х3 & х4. Тогда исходное уравнение примет вид: t1 ↔ t2 = 1.
На t1 никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2y при которых t1 ↔ t2 = 1.
Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2y при которых t1 ↔ t2 = 1.
Получаем для t1 и t2 три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х1 & х2, вторая — х3 & х4. Рассмотрим первый набор: существует три набора х1 и х2 таких, что х1 & х2 = 0, другими словами, первый 0 мы можем получить тремя способами. Второй 0 в этом наборе мы также можем получить тремя способами.
Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.
Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.
Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (x3 & х4 = 1 при x3 = 1 и x4 = 1). Следовательно, есть ещё три набора переменных х1, х2, х3, х4, являющихся решением исходного уравнения.
Самостоятельно доведите решение этой задачи до конца.
Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х < 12 становится истинным высказыванием при x = 5 (5 < 12 — истина) и ложным при x = 15 (15 < 12 — ложь). Предложения такого рода называют высказывательными формами или предикатами.
|
Предикет — это утверждение, содержащее одну или несколько переменных. |
Выделим некоторый предикат Р(x) и рассмотрим множество всевозможных объектов I, к которым он относится, — область определения предиката. Можно выделить такое подмножество Р множества I, что на всех его элементах предикат Р(х) будет превращаться в истинное высказывание. Определённое таким образом Р называется множеством истинности предиката Р(х).
Рассмотрим множество учеников некоторого класса. Известно, что в этом классе два отличника — Иван и Саша. Предикат «Он отличник» будет истинным высказыванием только по отношению к этим двум ученикам и ложным по отношению ко всем остальным.
Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката Р(х) = (х < 0) — множество отрицательных чисел; множество истинности предиката Р(х, у) = (х2 + у2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение х2 — 3х + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (х2 — 3х + 2 = 0).
Например, стандартное задание «Решить квадратное уравнение х2 — 3х + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (х2 — 3х + 2 = 0).
Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката
Пример 5.
Найдём все целые числа 2, превращающие предикат
P(z) = (2 > 5) & (z — 2 < 15)
в истинное высказывание. Другими словами, требуется найти множество истинности предиката P(z), заданного на множестве целых чисел
Предикат P(z) состоит из двух предикатов, соединённых операцией конъюнкции: P(z) = A(z) & B(z). Рассмотрим каждый из них в отдельности.
Множеством истинности предиката A(z) = (z > 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката B(z) = (z — 2 < 15) являются все целые числа, меньшие 17.
д. Множеством истинности предиката B(z) = (z — 2 < 15) являются все целые числа, меньшие 17.
Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:
|P| = A ∩ B = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,}
Его мощность P = 11.
Пример 6. Рассмотрим предикат (50 < х2) → (50 > (х + 1)2), определённый на множестве целых чисел. Найдём множество истинности этого предиката.
|
Зачастую задания такого рода формулируют несколько иначе. Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 < х2) → (50 > (х + 1)2)». |
Проанализируем отдельно каждый из элементарных предикатов (50 < х2) → (50 > (х + 1)2), решив соответствующие неравенства:
50 < х2 истинно для всех целых х ⊂ ]-∞; -8] ∪ [8; +∞[;
50 > (m + 1)2 истинно для всех целых х ⊂ [8; 6].
Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):
Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.
Самое главное
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.
Логические операции имеют следующий приоритет:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Boolean тип данных в Python
Python boolean Тип — это один из встроенных типов данных, предоставляемых Python, который представляет одно из двух значений, т. е. True или False. Как правило, он используется для представления значений истинности выражений. Например, 1==1 — это Истина, а 2<1 — Ложь.
Python Boolean Type
Логическое значение может быть только двух типов, т. е. True или False. Выход <класс 'bool'> указывает, что переменная имеет логический тип данных.
Example: Boolean type
Python3
|
Вывод:
<класс 'bool'> <класс 'bool'>
Оценка переменных и выражений
Мы можем оценивать значения и переменные, используя функцию Python bool() . Этот метод используется для возврата или преобразования значения в логическое значение, т. е. True или False, с использованием стандартной процедуры проверки истинности.
е. True или False, с использованием стандартной процедуры проверки истинности.
Синтаксис:
BOOL ([x])
Пример: Python Bool () Метод
Python3
|
Выход
Ложь ЛОЖЬ ЛОЖЬ ЛОЖЬ ЛОЖЬ True
Мы также можем вычислить выражение без использования функции bool(). Булевы значения будут возвращены в результате некоторого сравнения. В приведенном ниже примере переменная res будет хранить логическое значение False после выполнения сравнения на равенство.
Пример: логическое значение из выражения
Python3
|
Output:
FalseЦелые числа и числа с плавающей запятой как логические значения
Числа могут использоваться как логические значения с помощью встроенного в Python метода bool() . Любое целое число, число с плавающей запятой или комплексное число, имеющее ноль в качестве значения, считается ложным, а если они имеют значение как любое положительное или отрицательное число, оно считается истинным.
Python3
|
Вывод:
Ложь Истинный TrueЛогические операторы
Логические операции представляют собой простую арифметику значений True и False. Этими значениями можно управлять с помощью логических операторов, в том числе И, ИЛИ и НЕ . Общие логические операции —
Этими значениями можно управлять с помощью логических операторов, в том числе И, ИЛИ и НЕ . Общие логические операции —
- или
- и
- , а не
- == (эквивалентно)
- != (не эквивалентно)
Логический оператор ИЛИ
Логический оператор или возвращает значение Истина, если любой из входных параметров имеет значение Истина, в противном случае возвращает значение Ложь.
| A | B | A or B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| Ложь | Ложь | Ложь |
Example: Python Boolean OR Operator
Python3
|
9007
По крайней мере одно число имеет логическое значение True 9. В приведенном выше примере мы использовали логическое значение Python с оператором if и оператором OR, который проверяет, больше ли a, чем b, или b меньше, чем c, и возвращает True, если какое-либо из условий истинно (b Логический оператор и возвращает значение False, если любой из входных параметров имеет значение False, в противном случае возвращает значение True. Вывод Логический оператор Not требует только одного аргумента и возвращает отрицание аргумента, т. е. Оба оператора используются для сравнения двух результатов. == (эквивалентный оператор возвращает True, если два результата равны, и != (неэквивалентный оператор возвращает True, если два результата не совпадают. 9003 9003 Ключевое слово is используется для проверки того, принадлежат ли две переменные одному и тому же объекту. Вывод в операторе проверяет членство, т. Вывод Исторические заметки о логических значениях Как вы видели в видео, есть куча терминов, которые, как правило, говорят об одном и том же. Логические значения, логические значения, логические выражения: Условия, условные операторы, условные операторы : Обычный тип условия для проверки — это сравнение двух значений. Мы используем Распространенная ошибка: писать что-то вроде Мы используем Ниже приведено несколько примеров того, как можно увидеть сравнения в коде. Просмотрите их, если вам нравится, или продолжите и вернитесь, если вам нужна ссылка. Сравнивает два значения — числа, строки или другие логические значения — и возвращает true , если они равны, иначе false . 1. Несмотря на то, что Сравнивает два значения — числа, строки или другие логические значения — и возвращает Сравнивает два значения, чтобы определить, больше ли число слева на , чем число справа на . Сравнивает два значения, чтобы определить, меньше ли число слева на 91 180, чем число справа на 91 181. Сравнивает два значения, чтобы определить, является ли число слева на меньше или равно числу справа. Сравнивает два значения, чтобы определить, является ли число слева на больше или равно числу справа. Булева логика лежит в основе
Python и большинство языков программирования. Это позволяет программистам проводить сравнения, выполнять условные операторы и реализовывать общие алгоритмы. Символы «больше чем» ( Булев тип данных может иметь одно из двух логических значений , «истина» или «ложь». Эти значения иногда представляются двоичными цифрами «1» и «0». «Истина» эквивалентна «1» или «включено», а «Ложь» соответствует «0» и «отключено». Булевы значения названы в честь математика Джорджа Буля, создавшего систему логической алгебры. Поскольку оно названо в честь человека, слово «логическое» всегда пишется с большой буквы. Везде, где оно появляется как прилагательное, логическое значение указывает на двоичный атрибут true/false. Обсуждаемый пункт либо включен, либо выключен, а не то и другое, и не какое-то другое значение. Таким образом, логическая схема имеет бинарные логические вентили, а в булевой алгебре переменные ограничены двумя значениями истинности. С точки зрения программирования наиболее полезной булевой концепцией является Логическое выражение . Python использует встроенный тип данных с именем Если вы еще этого не сделали, создайте учетную запись Linode и вычислительный экземпляр. Смотрите наши
Начало работы с Linode и
Инструкции по созданию вычислительного инстанса. Следите за нашими
Руководство по настройке и защите вычислительного экземпляра для обновления вашей системы. Вы также можете установить часовой пояс, настроить имя хоста, создать ограниченную учетную запись пользователя и усилить доступ по SSH. Убедитесь, что Python правильно установлен на Linode, и вы можете запускать и использовать среду программирования Python. Чтобы запустить Python в Ubuntu, используйте команду Действия в этом руководстве написаны для пользователей без полномочий root. Команды, требующие повышенных привилегий, имеют префикс Python предоставляет полный набор логических операторов для использования в логических выражениях. Эти операторы позволяют вычислить выражение либо как В дополнение к операциям сравнения и логическим операторам Python имеет тип Если «True» заключено в кавычки, то это строка, содержащая последовательность символов «True». Переменные могут быть преобразованы в другой тип, когда им присвоено новое значение. Это известно как неявное преобразование типов . Функция Python Целое число, отличное от нуля, всегда равно Целое число со значением Операторы сравнения Python сравнивают два элемента, но их можно использовать только для сопоставимых элементов. Например, два целых числа можно сравнить на равенство, как и две строки. Но нельзя сравнивать два элемента разных типов, например целое число и строку. При попытке такого сравнения возвращается ошибка типа Существует несколько различных операторов сравнения, которые обычно возвращают логические значения. Не все операторы имеют смысл для всех типов. К наиболее распространенным из этих операторов относятся: Некоторые из этих операторов являются зеркальными отображениями друг друга, а некоторые являются удобным сокращением для операции, которая иначе потребовала бы двух сравнений. Оператор 9Оператор 0025 != используется для определения того, являются ли два элемента неравными. Для получения дополнительной информации см.
Документация Python по сравнению значений. Пример ниже демонстрирует, как можно использовать оператор В этих примерах не путайте оператор присваивания Если те же две переменные проверяются на неравенство, Python возвращает логическое значение Два сравниваемых элемента не обязательно должны быть переменными. Переменную можно сравнить с жестко запрограммированной константой. В этом случае Строки должны быть идентичными по регистру и длине, чтобы считаться равными в Python. Строка Эти операторы также могут проверять коллекции на эквивалентность. В этом случае Оператор Когда эти операторы используются в строках, строки оцениваются на основе значений символов ASCII. Это соответствует алфавитному порядку в верхнем или нижнем регистре. Однако заглавные буквы имеют меньшие значения ASCII, чем их аналоги в нижнем регистре. Таким образом, строка, начинающаяся с заглавной буквы, всегда «меньше» строчной. Не все типы и объекты можно сравнивать с помощью этих операторов. В некоторых других случаях сравнения могут быть неинтуитивными. Например, когда эти операторы используются для сравнения списков, они принимают решение на основе первых неравных элементов списка. Чтобы проверить, больше ли Используйте Те же сравнения можно выполнить для строк. Строка Операторы В следующем примере показано, как сравнение Логические операторы Python используются для вычисления логических выражений. Они выполняют простую логическую арифметику на одном или двух входах и возвращают либо Логику каждого оператора можно продемонстрировать с помощью таблицы истинности . В таблице истинности для данной операции перечислены выходные данные для каждой возможной комбинации входных данных. Он используется для анализа булевых функций в простом для понимания формате. Булевы выражения могут быть созданы в Python из трех основных логических операторов. Оператор Простая таблица истинности может показать, как вычисляются Операторы Чтобы результатом оператора Следующая таблица истинности показывает, как результат операции Python does not have оператор «исключающее или», также известный как «исключающее ИЛИ». Чтобы выполнить тест «исключающее ИЛИ», один, но не оба аргумента, должны иметь значение Оператор The following examples demonstrate how to use the Иногда логические операторы Python могут возвращать результат без оценки обоих входных данных. Это известно как короткое замыкание . Например, при оценке Не путайте логические операторы Python с побитовыми операторами. Эти операторы выполняют логические операции над отдельными битами двух чисел или двухбитных полей. Оператор «побитовое и» равен 9 : Есть несколько других логических операторов, полезных в определенных обстоятельствах. Оператор Наиболее важная роль логических операторов заключается в их использовании в условных операторах . Когда логическое выражение оценивается как Условный оператор обычно предшествует предложению , которое представляет собой блок из одной или нескольких строк кода. Логическое значение условного оператора определяет предложение, которое должно быть выполнено, если таковое имеется. Дополнительные сведения о различных условных операторах см.
Документация Python для составных операторов. Операторы В приведенном ниже примере показано, как оператор Более сложная последовательность условных операторов показана в файле В следующем примере показано, как работает программа, используя список из Хотя в этих примерах используется оператор Логические выражения и операторы незаменимы при написании программы на Python. Два логических значения в Python — это Python предоставляет полный набор операций сравнения и логических операторов. Операторы сравнения Python сравнивают два значения. К ним относится равенство  0063
0063 Логический оператор И
A B A и B True True True True False False False True False False False False Example: Python Boolean And Operator
Python3
A = 0 B = 2 C 2 C 2 C 2 C 2 C 2 0026 = 4 Если A> B и B .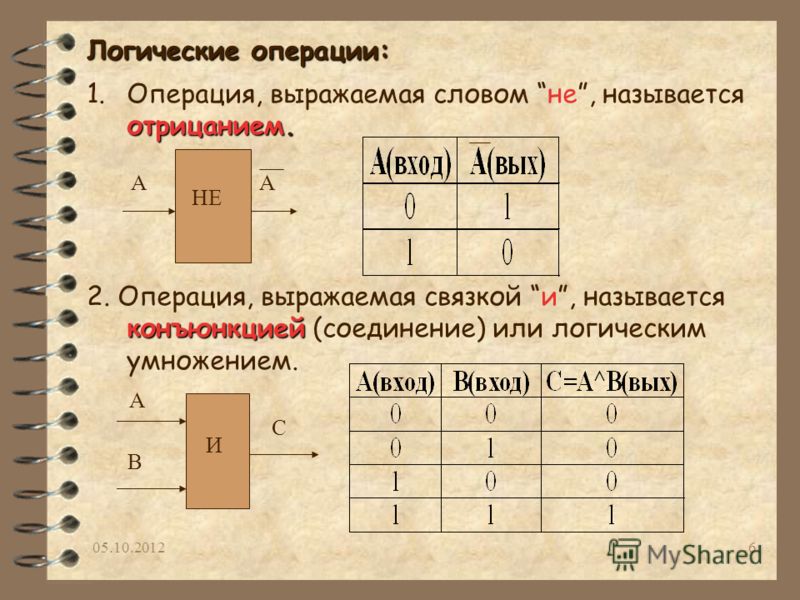 :
: print ( False ) if a and b и C: Печать ( "Все цифры имеют логическое значение, как и True" ) ELS "По крайней мере одно число имеет логическое значение как Ложь" ) Ложь
По крайней мере одно число имеет логическое значение False
Boolean Not Operator
 возвращает True для False и False для True.
возвращает True для False и False для True. A Not A True False False True Example: Python Boolean Not Operator
Python3
а = 0 IF Не A: Печать ( "Значение лобового. Логическое значение a равно False
Логическое значение == (эквивалентно) и != (не эквивалентно) Оператор
 9)0007
9)0007 Example: Python Boolean == (equivalent) and != (not equivalent) Operator
Python3
a = 0 b = 1 if a = = 0 : print ( True ) if a = = b: print ( True ) if a ! = B: Печать ( True ) is Operator
 Тест вернет True, если два объекта одинаковы, в противном случае он вернет False, даже если два объекта равны на 100%.
Тест вернет True, если два объекта одинаковы, в противном случае он вернет False, даже если два объекта равны на 100%. Example: Python is Operator
Python3
x = 10 y = 10 if x is y: print ( True ) else : print ( False ) x = [ "a" , "b" , "c" , "d" ] y = [ "a" , "b" , "c" , "d" ] печать (x равно y) True
Ложь
в операторе
 е. проверяет, присутствует ли значение в списке, кортеже, диапазоне, строке и т. д.
е. проверяет, присутствует ли значение в списке, кортеже, диапазоне, строке и т. д. Пример: в операторе
Python3
Животные = [ " , " LION "" . if "lion" in animals: print ( True ) Истинный
Открытия CS | Булевы значения и операторы сравнения

if ) Операторы сравнения
 Вот 6 распространенных операторов сравнения . Каждый сравнивает значение слева со значением справа и возвращает логическое значение -- истина или ложь . Большинство из них делают то, что вы ожидаете.
Вот 6 распространенных операторов сравнения . Каждый сравнивает значение слева со значением справа и возвращает логическое значение -- истина или ложь . Большинство из них делают то, что вы ожидаете. Почему эти символы:
== , != , <= и >= ? == , потому что единственный знак равенства = является оператором присваивания. Нам нужно что-то другое, чтобы указать, что мы хотим сравнить два значения, а не присваивать одно другому. если (возраст = 18) вместо , если (возраст == 18) . Мы позаботимся об этом позже. != , <= и >= , потому что они требуют только символов ASCII. Исторически сложилось так, что математические символы ≠ , ≤ и ≥ было трудно или невозможно воспроизвести в некоторых системах.
! повсеместно читается как «нет». Ссылка: Примеры
"Hello" == "hello" возвращает false -- потому что строки пишутся с заглавной буквы по-разному. "3" == 3 возвращает true -- потому что == пытается быть прощающим. Если он может «преобразовать» строку в число, он сделает это для сравнения. 1 (2+1) == 3 возвращает true -- потому что арифметическое выражение оценивается как 3. x == 7 возвращает true -- когда переменная x имеет значение 7.
== преобразует строку в число, это полезная функция, считается ТРЮКОЙ , потому что строка «3» не совпадает с целым числом 3. Бывают случаи, когда вы бы поверили, что они не равны. Есть оператор "строгого" равенства - "тройное равенство" === , что гарантирует, что и тип данных, и значение равны. Итак, "3" === 3 ложно. true , если они не равны , иначе false . "Hello" != "hello" возвращает true -- потому что строки немного отличаются. "3" != 3 возвращает ложь -- потому что строка 3 может быть преобразована в число перед сравнением с 3. (см. примечания выше о прощающем ==). (2+1) != 3 возвращает false -- потому что арифметическое выражение оценивается как 3.
x != 7 возвращает true -- когда переменная x имеет любое значение, отличное от 7. 4 > 3 возвращает верно 3 > 7 возвращает ложь age > 17 возвращает true -- когда значение переменной age строго больше 17, в противном случае false. 4 < 3 возвращает ложь 3 < 7 возвращает верно age < 17 возвращает true -- когда значение переменной age строго меньше 17, иначе false.
3 <= 4 возвращает верно 4 <= 3 возвращает ложь age <= 18 возвращает true -- когда значение переменной age равно 18 или меньше. 3 >= 4 возвращает ложь 4 >= 3 возвращает верно age >= 18 возвращает true -- когда значение переменной age равно 18 или больше. Использование логических переменных, операторов и условных выражений в Python |
Linode
> ) и «равно» ( == ) являются примерами операторов сравнения Python, а и и или являются некоторыми из логических операторов Python. В этом руководстве объясняется логическая логика и выражения, а также обсуждается, как использовать логические операторы Python.
В этом руководстве объясняется логическая логика и выражения, а также обсуждается, как использовать логические операторы Python. Введение в логическую логику и логические значения
 Логическое выражение приводит к логическому значению при его оценке. Он может состоять из логических значений, операторов или функций. Большинство людей понимают это интуитивно.
Логическое выражение приводит к логическому значению при его оценке. Он может состоять из логических значений, операторов или функций. Большинство людей понимают это интуитивно. 2 + 2 = 4 верно, а 2 + 2 = 5 ложно. Булева логика и логические выражения являются более строгими расширениями этой концепции. bool для представления логических значений. Тип bool наследует свои свойства от типа int . Из-за странной причуды дизайна языка bool не является встроенным значением и может быть переопределено, хотя это очень плохая идея. Бул 9 Python Переменная 0026 имеет два возможных значения: . True и False . В Python 3 эти значения на самом деле являются ключевыми словами Python и пишутся с заглавной буквы. Поэтому их нельзя использовать в качестве переменных и им нельзя присваивать разные значения. True и False можно присвоить любой переменной, которая затем станет bool . Python расширяет эту концепцию до числовых значений и других типов данных. Ненулевое целое число равно
Python расширяет эту концепцию до числовых значений и других типов данных. Ненулевое целое число равно True , тогда как 0 оценивается как 9.0025 Ложь Перед началом работы
питон3 . Для получения информации о том, как использовать Python, см. наше руководство по
Как установить Python 3 на Ubuntu 20. 04.
04. Примечание
sudo . Если вы не знакомы с командой sudo , см.
Руководство по пользователям и группам Linux. Логические операторы Python
True или False , что позволяет использовать результат в условных операторах и других управляющих структурах. В Python есть два основных типа логических операторов. True или False . Верно или Ложно .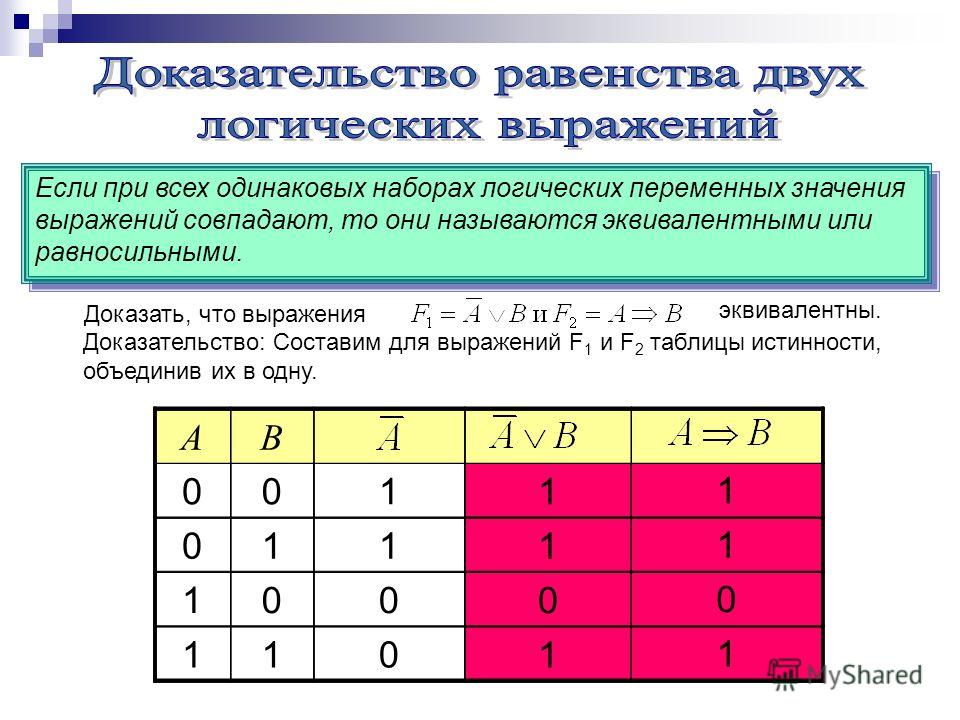
bool . Любая переменная, которой присвоено значение True или False , имеет тип bool . Подтвердить тип переменной можно с помощью встроенной функции типа . а = правда
наберите "А)
а = "Верно"
наберите "А)
а = "Верно"
наберите "А)
<класс 'str'>
a = Истина
наберите "А)
bool позволяет программистам оценивать любую переменную, выражение или объект как логическое значение. Эта функция всегда возвращает Верно или Ложно . Python использует собственный набор правил для определения истинности переменной. Некоторые из менее очевидных правил, определяющих, является ли что-то
Python использует собственный набор правил для определения истинности переменной. Некоторые из менее очевидных правил, определяющих, является ли что-то True или False , включены в список ниже. Проконсультируйтесь с
Документация Python для функции bool для получения дополнительной информации. True . Значения 0 и 0.0 равны False . True . False . Непустые строки или структуры данных имеют значение True .
Нет равно Ложь . inf , -inf и NaN (для неопределенных или непредставимых значений) равны True . True . True . а = 1
печать (логический (а))
True
0 равно False . б = 0
печать (логический (б))
False
Операторы сравнения в Python
TypeError: '<' не поддерживается между экземплярами 'int' и 'str' . Сравниваемые элементы могут быть как константами, так и переменными.
Сравниваемые элементы могут быть как константами, так и переменными. == : Оператор «равно». != : Оператор «не равно». < : Оператор «меньше чем». > : Оператор «больше чем». <= : Оператор «меньше или равно». >= : Оператор «больше или равно». Операторы «равно» и «не равно» в Python
== проверяет равенство.
x == y возвращает True , если значения x и y равны или относятся к одному и тому же объекту. Оператор равенства можно использовать для большинства типов. Две строки равны, если они содержат одну и ту же последовательность символов в одном и том же порядке. Две встроенные коллекции, такие как списки, равны, если они имеют одинаковый тип, одинаковую длину и все соответствующие элементы равны. Ограничение по типу означает, что список никогда не может быть равен набору, даже если обе коллекции содержат одни и те же элементы. x != y возвращает True , если x и y имеют разные значения или ссылаются на разные объекты. Списки и наборы различаются, если они имеют разные типы или длину или если соответствующие элементы в любой позиции различны. Все операторы равенства симметричны. Если
Если x == y равно True , то y == x также равно True . То же соотношение справедливо и для х != у . == для проверки a и b на равенство. Поскольку эти два элемента действительно равны, Python возвращает True . Примечание
= с оператором равенства == . Замена 9Оператор 0025 = вместо == приводит к странным и вводящим в заблуждение ошибкам. а = 4
б = 4
печать (а == б)
True
False .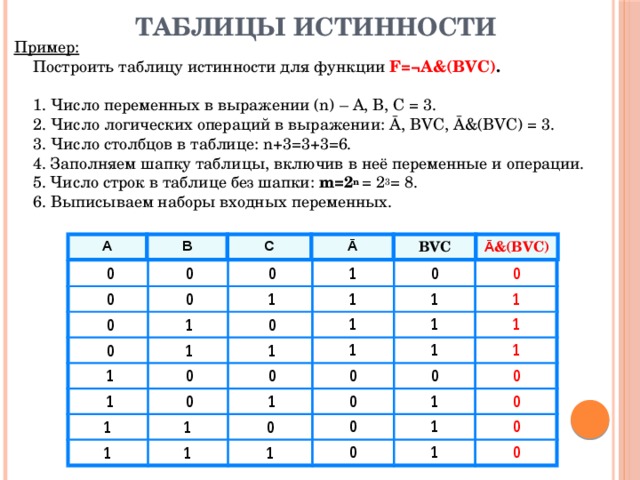
печать (а != б)
Ложь
a равно 4 , поэтому сравнение False . печать (а == 5)
False
Linode не совпадает с linode . а = «линод»
б = "линод"
с = "линод"
печать (а == б)
Ложь
print(b == c)
True
list1 имеет те же значения, что и list3 , но отличается от list2 , который имеет другую длину. Таким образом, list1 == list3 возвращает True , но list1 == list2 равно False . список1 = [1, 2, 3]
список2 = [1, 2, 3, 4]
список3 = [1, 2, 3]
печать (список1 == список3)
True
печать (список1 == список2)
False
Операторы меньше и больше в Python
< означает «меньше чем». Сравнение
Сравнение a < b возвращает True только в том случае, если a меньше b . Аналогично, сравнение «больше чем» символизируется оператором > . a > b возвращает True , если первый элемент имеет большее значение. Эти два оператора сравнения симметричны. Другими словами, a < b подразумевает b > a . Это может быть не то поведение, которое вам нужно.
Это может быть не то поведение, которое вам нужно. a , чем b , используйте оператор > . а = 5
б = 3
напечатать (а > б)
Правда
< сравнение, чтобы определить, меньше ли a , чем b . а = 5
б = 3
напечатать (а < б)
False
linode считается меньшей, чем по системе , поскольку в алфавите буква «l» предшествует букве «s». Linode также меньше, чем System , но linode не меньше, чем System , потому что заглавные буквы имеют меньшее значение. а = "линод"
б = "система"
с = "линод"
д = "Система"
напечатать (а < б)
True
print(c < d)
True
print(a < d)
False
Операторы «меньше или равно» и «больше или равно» в Python
<= и >= добавляют проверку на равенство к операторам < и > .
a <= b равно True , если a < b или a == b равно True . Между тем, если a > b или a == b равно True , то a >= b также равно True . Те же самые правила, которые используются для измерения равенства или сравнения с различными типами, применимы и здесь. <= работает на практике. Аналогично работает оператор >= . а = 5
б = 3
печать (а <= б)
Ложь
а = 3
печать (а <= б)
True
Логические операторы в Python
True , либо False . Логические операторы можно объединять в цепочки для формирования еще более длинных выражений.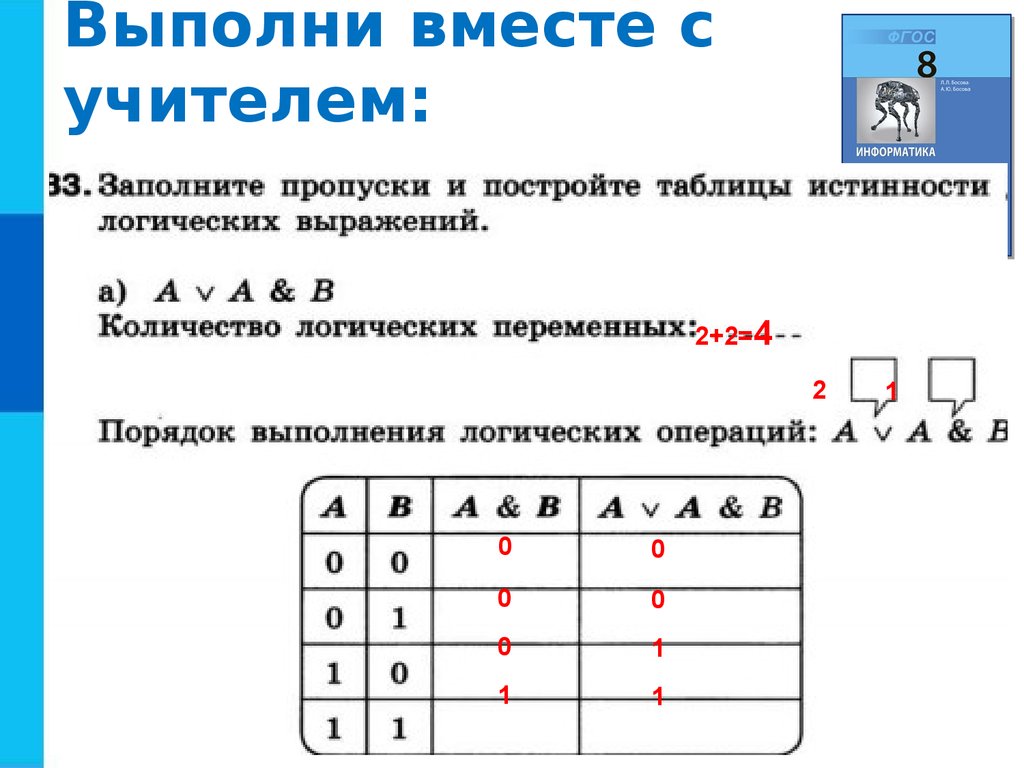
и : это оператор Python «логическое и». Он возвращает True , если оба выражения равны True и False в противном случае. или : оператор Python «логическое или» возвращает True , если любое из выражений равно True и False в противном случае. not : оператор Python «логическое не» возвращает True , только если вычисляемое им выражение равно Ложь . Оператор and в Python
и проверяет, являются ли оба выражения True . Выражение
Выражение a и b оценивается как True только в том случае, когда a равно True и b также равно True и False в противном случае. a и b обычно также являются выражениями. Их иногда называют внутренними выражениями 9.1181 . Внутренние выражения оцениваются первыми и становятся входными данными для основного логического выражения. a и b при различных значениях a и b . В таблице ниже показан результат a и b для каждой из четырех возможных комбинаций. a и b a и b True and True True True and False False False and True False False and False False и часто используются между двумя операторами сравнения, но a и b могут принимать форму любого выражения, результатом которого является логическое значение. Вот пример, иллюстрирующий, как 9Используется оператор 0025 и . Поскольку
Вот пример, иллюстрирующий, как 9Используется оператор 0025 и . Поскольку a равно b , а c равно d , результатом операции и будет True . После изменения значения b оно больше не равно a . a == b теперь равно False , поэтому результатом всей операции и является False . а = 3
б = 3
с = 4
д = 4
print((a == b) и (c == d))
Правда
б = 4
print((a == b) и (c == d))
False
Оператор Or в Python
или было True , одно или оба выражения должны быть True . Оператор или использует логику «включающее или». Следовательно, a или b равно True , если a равно True , b равно True , или если оба a и b равны Верно . Если
Если a и b определены как False , то a или b также являются False . или изменяется при различных входных данных. a or b a or b True or True True True or False True False or True True False or False False Note
True .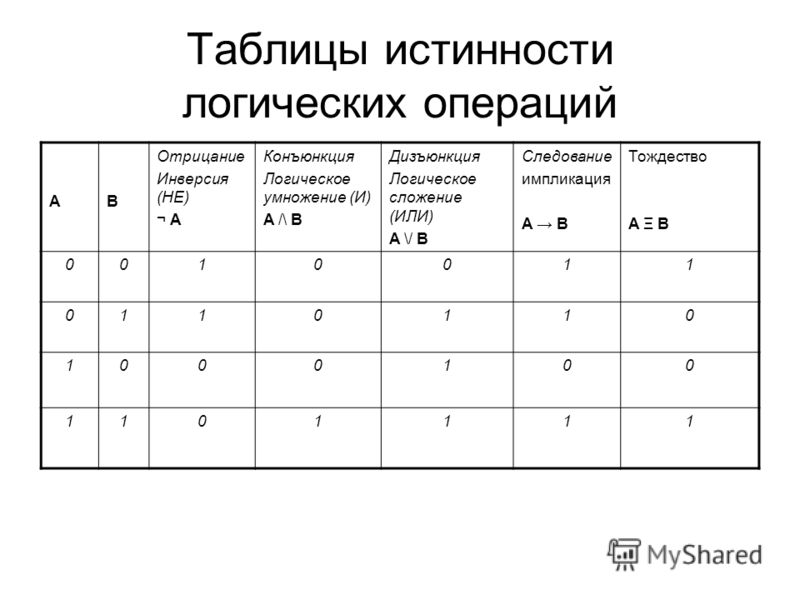 Некоторые библиотеки Python предоставляют эту функцию. Функция «исключающее ИЛИ» также может быть получена из других операторов.
Некоторые библиотеки Python предоставляют эту функцию. Функция «исключающее ИЛИ» также может быть получена из других операторов. а = 3
б = 3
с = 4
д = 5
print((a == b) или (c == d))
Правда
б = 4
print((a == b) или (c == d))
False
Оператор not в Python
not — самый простой для понимания оператор. Он принимает одно логическое выражение и возвращает противоположное логическое значение. Выражение не равно True , если a равно False и False , если a равно Верно . Таблица истинности для , а не чрезвычайно проста. not a not a not True False not False True , а не оператор. Они используют тот факт, что ненулевое целое число оценивается как
Они используют тот факт, что ненулевое целое число оценивается как True , а ноль равен 9.0025 Ложь . Когда a равно 3 , не равно False . Но когда a устанавливается в 0 , не становится True . а = 3
печатать (не (а))
Ложь
а = 0
печатать (не (а))
True
Примечание
или , Python может вернуть True , как только любое выражение оценивается как True . Это гарантирует, что выражение или равно True независимо от второго аргумента. Эта оптимизация ускоряет выполнение. К сожалению, это также может привести к тонким ошибкам, таким как сбои, которые происходят только при оценке второго предложения.
True , если ровно один из двух битов равен True . ~ : Побитовое нет. Этот оператор используется для инвертирования каждого бита с целью «переворачивания битов». is используется для подтверждения того, что два объекта ссылаются на один и тот же объект. x равно y равно True если x и y — это один и тот же объект. Оператор в проверяет членство и обычно используется с такими коллекциями, как списки и наборы. Если x в y равно True , это означает, что x является одной из записей в списке y .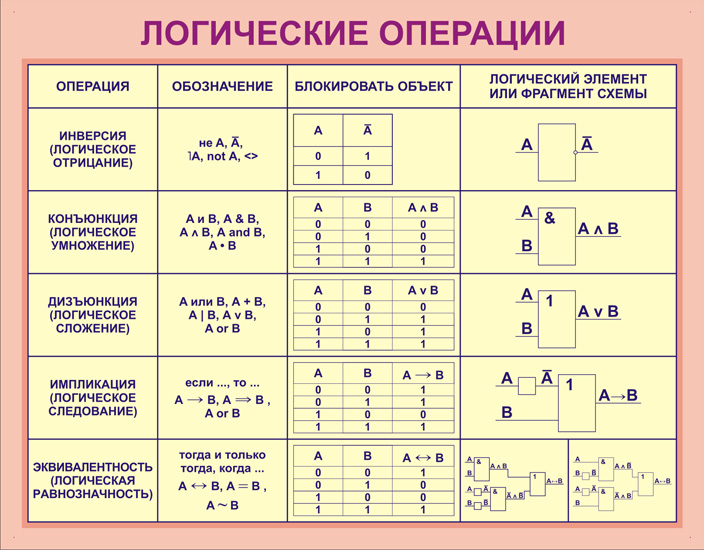
True или False , его можно использовать для управления потоком программы. Логические выражения используются в , если и , иначе операторов, а также в циклах. If or Else в Python
if и else являются общим местом в любой программе. Если результат условного оператора после , если ключевое слово равно True , соответствующий блок кода вводится и выполняется. За условным оператором
За условным оператором if может следовать один или несколько операторов elif , что означает «else if». Каждое условное выражение elif проверяется по очереди, пока не будет получено значение True . Затем выполняется соответствующий кодовый блок elif . Как только Python достигает оператора else , он автоматически выполняет блок кода else . Если все , если операторы и elif равны False и нет оператора else , ничего не выполняется. Программное управление переходит к следующей строке кода. if работает с условным оператором. Оператор if оценивает условный оператор влажность > 80 . В этом случае влажность больше, чем 80 , поэтому условие равно True . Управление переходит к кодовому блоку с отступом и печатается строка Это влажный день .
влажность = 85
если влажность > 80:
... print("Сегодня влажный день")
Влажный день
py_temp.py ниже. Цикл для обрабатывает список из трех показаний влажности. Условный оператор if последовательно обрабатывает каждое значение. Если показания больше 80 , он удовлетворяет оператору if , и Python печатает Эта влажность слишком высока . Если нет, оператор elif проверяет, находится ли влажность ниже 60 . Если это так, Python печатает Влажность слишком низкая . Во всех остальных случаях управление переходит к оператору else , и Python печатает строку . Эта влажность в самый раз . [50, 70, 90] . Первое значение удовлетворяет условию elif , а последнее значение соответствует условию if . Второе значение —
Второе значение — False для обоих тестов, поэтому управление переходит к предложению else . 1
2
3
4
5
6
7
8
9
влажность = [50, 70, 90]
для влажности во влажностях:
если влажность > 80:
print(влажность, ": Эта влажность слишком высока")
Элиф влажность < 60:
print(влажность, ": Эта влажность слишком низкая")
еще:
print(humidity, ": Эта влажность в самый раз") 50 : Слишком низкая влажность
70 : Эта влажность в самый раз
90 : Слишком высокая влажность
if , другие управляющие структуры также могут использовать условные операторы. Например, оператор while (условие) продолжает циклически выполнять следующий блок кода до тех пор, пока условие продолжает оцениваться как True .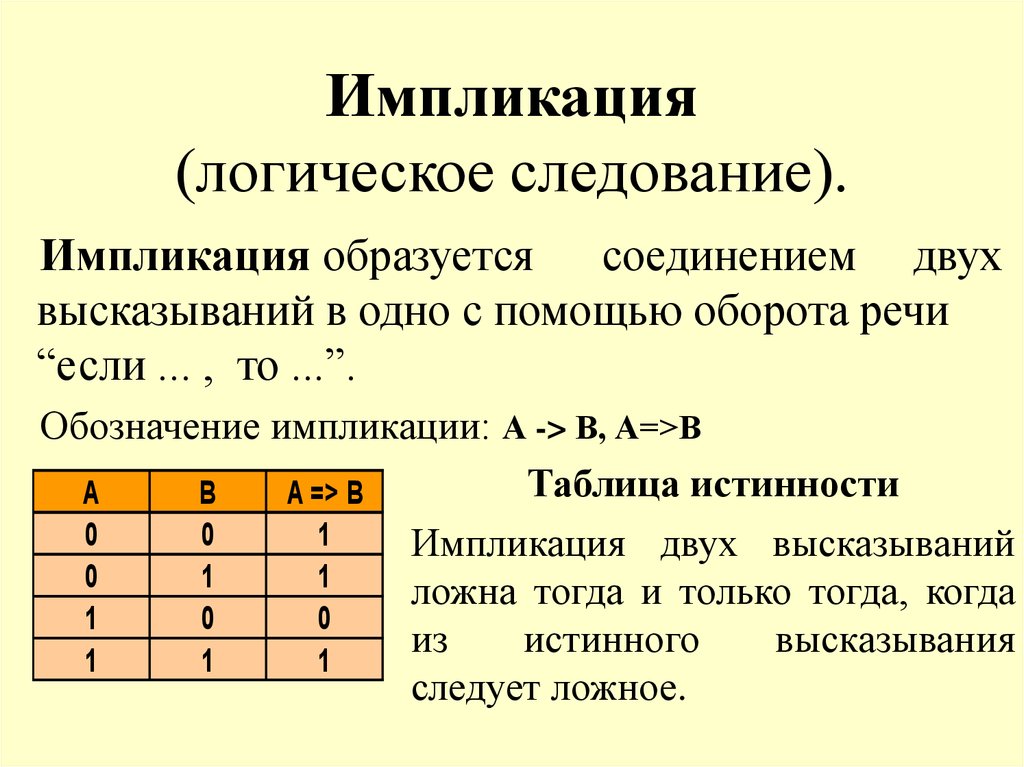
Краткий обзор логических операторов и условий Python
True и False , и логическое выражение Python всегда оценивает одно из этих двух значений. Оператор Python bool можно использовать для определения логического значения выражения. Python поддерживает определенные правила для определения истинности выражения. Например, ненулевое целое число всегда равно True . == , неравенство != , больше > , больше или равно >= , меньше < и меньше или равно <= операторов. Логические операторы Python выполняют логическую логику над логическими значениями. Оператор и возвращает True только в том случае, если оба выражения также равны True .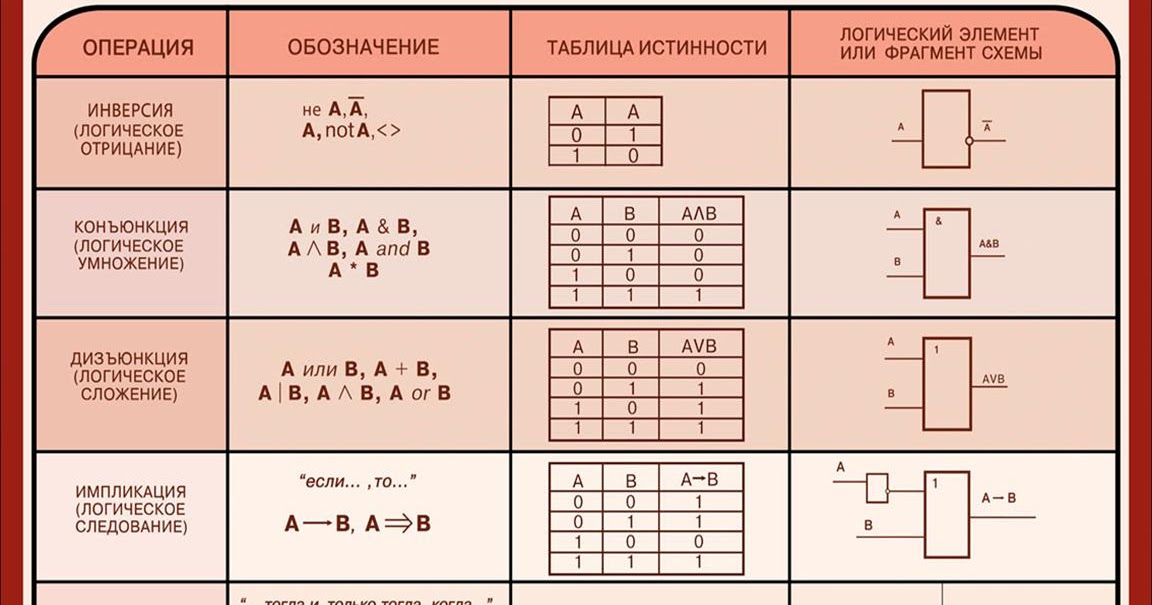





 0007
0007