формула, взаимное влияние, нормы, характеристики
Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Нормируемые требования к показателям
В РФ требования к качеству работы энергосистемы стандартизированы.
В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.
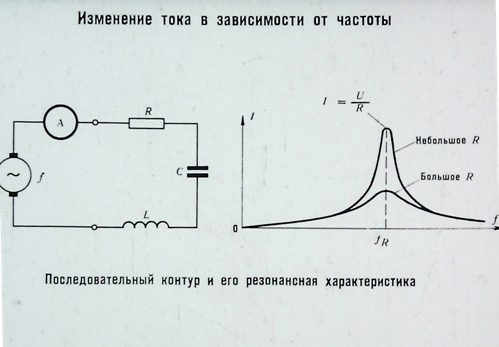
Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.
То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
Математическое выражение зависимости будет иметь следующий вид: I = UCω;
Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).
Сопротивления в цепях переменного тока
Цепь переменного тока с активным сопротивлением. Сопротивления в цепях переменного тока бывают активными и реактивными. Активные сопротивления расходуют энергию, реактивные — не расходуют.
Реактивными сопротивлениями, включенными в цепь переменного тока, являются сопротивления катушки индуктивности L и конденсатора С. Сопротивление катушки называется индуктивным сопротивлением (Xj), сопротивление конденсатора — емкостным (Хс).
На рис. 1.5 показана цепь переменного тока с активным сопротивлением и векторная диаграмма, из которой видно, что ток и напряжение совпадают по фазе. Они изменяются по одному и тому же закону, следовательно, можно записать:
i = IMsin t, (1.12)
u = U m sin t. (1.13)
Действующее значение силы тока в цепи с активным сопротивлением равно:
I= (1.14)
где U— действующее значение напряжения на сопротивлении; R — значение активного сопротивления.
Это выражение является выражением закона Ома для цепи с активным сопротивлением. Мощность, расходуемая в цепи на активном сопротивлении, равна:
P = IU cosy, (1.15)
где ф — угол сдвига фаз между током и напряжением.
Так как ток и напряжение совпадают по фазе, то угол сдвига Ф = 0°, a cos ф = 1.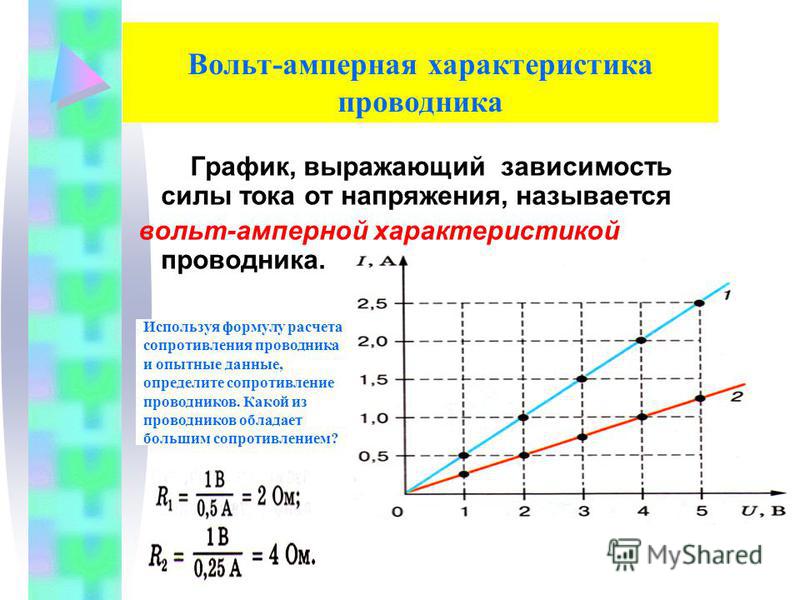 Мощность же в цепи равна произведению действующих значений тока и напряжения:
Мощность же в цепи равна произведению действующих значений тока и напряжения:
Р = IU, Р = I2R. (1,16)
Переменный ток в цепи с индуктивным сопротивлением. Если катушку индуктивности, активное сопротивление которой равно нулю, i подключить к источнику переменного тока (рис. 1.6), то и катушке потечет синусоидально изменяющийся переменный ток.
Согласно правилу Ленца, индуцированная, в катушке ЭДС противодействует изменениям силы тока. Это значит, что при увеличении силы тока в катушке ЭДС самоиндукции стремится создать ток, направленный навстречу вызывавшему ее току, а при уменьшении силы тока она, наоборот, стремится создать ток, совпадающий по направлению с ним.
Из векторной диаграммы видно, что ЭДС самоиндукции отстает по фазе от тока на 90°.
Напряжение на катушке ил на источнике тока равно:
UL = U = 2п fLI = LI. (1.17)
Произведение угловой скорости на индуктивность катушки называется индуктивным сопротивлением Х.
XL= L. (1.18)
Энергия в катушке индуктивности не расходуется. В первую четверть периода она запасается в ее магнитном поле, а во вторую — отдается источнику тока. Произведение напряжения UL на величину силы тока в цепи называется реактивной мощностью.
В первую четверть периода она запасается в ее магнитном поле, а во вторую — отдается источнику тока. Произведение напряжения UL на величину силы тока в цепи называется реактивной мощностью.
В рассмотренной цепи активная мощность равна нулю, так как энергия в ней не расходуется, сдвиг по фазе между векторами тока /и напряжением U равен 90° и cosy = 0.
Переменный ток в цепи с последовательными активным и индуктивным сопротивлениями. Теперь рассмотрим цепь с реальной катушкой, которую можно представить как цепь с последовательно включенными индуктивностью L и активным сопротивлением R (рис. 1.7). Если в цепи с последовательными активным и индуктивным сопротивлениями протекает переменный синусоидальный ток, то напряжение на индуктивности, как было установлено ранее, опережает ток на 90°, а напряжение на активном сопротивлении
Рис. 1.7. Схема цепи с последовательными активным и индуктивным сопротивлениями (а) и векторная диаграмма напряжений (б) совпадает с ним по фазе. Так как напряжения UL, UR по фазе не совпадают, то напряжение, приложенное ко всей цепи, равно их геометрической сумме. Сложив векторы ULn UR, находим величину вектора U, который сдвинут по фазе относительно вектора тока / на угол φ < 90°,
Так как напряжения UL, UR по фазе не совпадают, то напряжение, приложенное ко всей цепи, равно их геометрической сумме. Сложив векторы ULn UR, находим величину вектора U, который сдвинут по фазе относительно вектора тока / на угол φ < 90°,
опережая его. Таким образом, в цепи переменного тока с последовательно соединенным активным сопротивлением и катушкой индуктивности ток отстает по фазе от напряжения.
Построив векторную диаграмму, рассмотрим треугольник со сторонами UL, UR, U. Этот треугольник называется треугольником напряжений. Так как он прямоугольный, то
U = √U2R+U2. (1.19)
Из треугольника напряжений можно получить подобный ему треугольник сопротивлений со сторонами R, XL и Z. Из этого треугольника полное сопротивление цепи равно:
Z = √R2+Xl (1.20)
Так как сдвиг по фазе между током и напряжением меньше 90°, то энергия в такой цепи расходуется лишь на активном сопротивлении R.
Активная мощность при этом равна:
P = IU coscp. (1.21)
(1.21)
Цепь переменного тока с емкостью. Если к источнику переменного тока подключить конденсатор, то в цепи появится ток. Способность конденсатора пропускать переменный ток объясняется тем, что под действием переменного синусоидального напряжения конденсатор периодически заряжается и разряжается, вследствие чего происходит перемещение электрических зарядов в проводниках, соединяющих конденсатор с источником тока. Соотношение фаз тока и напряжения представлено на рис. 1.8. В цепи с емкостью ток опережает по фазе напряжение на 90°. Закон Ома для цепи переменного тока с емкостью определяет действующее значение силы тока:
(1.22)
Величина Хс= называется емкостным сопротивлением. Она
обратно пропорциональна частоте тока в цепи и емкости конденсатора. Измеряется в омах (Ом).
Мощность переменного тока
Для цепей переменного тока различают активную, полную и реактивную мощности.
Активная мощность представляет собой действительную мощность переменного тока, аналогичную мощности, развиваемой постоянным током. Она производит полезную работу; может быть преобразована с помощью электродвигателей в механическую мощность, механическую энергию; измеряется в ваттах (Вт) и определяется по формуле
Она производит полезную работу; может быть преобразована с помощью электродвигателей в механическую мощность, механическую энергию; измеряется в ваттах (Вт) и определяется по формуле
Р = IU cos ф. (1.23)
Полной мощностью называют максимально возможную величину активной мощности, развиваемую переменным током при заданных значениях напряжения и силы тока и при наиболее благоприятных условиях, а именно, когда coscp = 1. Полная мощность обозначается латинской буквой 51 и измеряется в вольт-амперах (В-А). Из определения полной мощности следует выражение
S = UI. (1-24)
Сравнивая между собой формулы (1.23) и (1.24), находим соотношение между активной и полной мощностями:
Р = S coscp, (1.25)
(1.26)
Полной мощностью (кВА) принято измерять мощность генераторов переменного тока, машин, производящих электроэнергию, и трансформаторов, аппаратов, предназначенных для преобразования электрической энергии одного напряжения в электрическую энергию другого напряжения.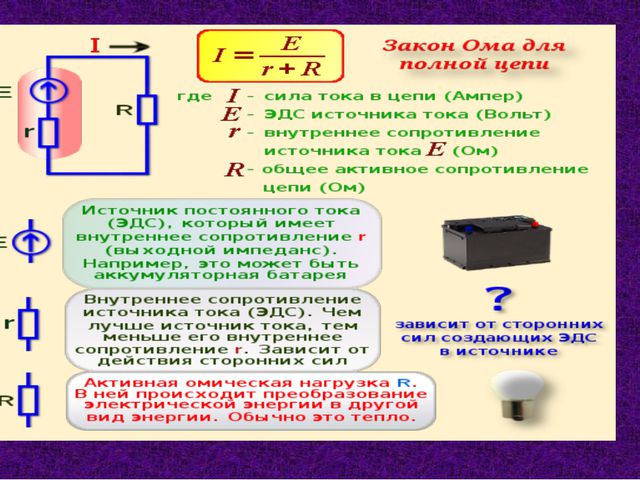 Полная мощность этих машин определяется произведением номинальных (нормальных) величин их напряжения и силы тока (т.е. величин этих параметров, на которые рассчитаны машины). А активная их мощность зависит от коэффициента мощности, при котором они работают (Р.= Scoscp). В свою очередь этот коэффициент мощности зависит от соотношения величин активного и реактивного сопротивления, включенных в цепь, иными словами, от характера электроприемников, питаемых данным генератором или трансформатором.
Полная мощность этих машин определяется произведением номинальных (нормальных) величин их напряжения и силы тока (т.е. величин этих параметров, на которые рассчитаны машины). А активная их мощность зависит от коэффициента мощности, при котором они работают (Р.= Scoscp). В свою очередь этот коэффициент мощности зависит от соотношения величин активного и реактивного сопротивления, включенных в цепь, иными словами, от характера электроприемников, питаемых данным генератором или трансформатором.
Реактивная мощность. Для рассмотрения реактивной мощности необходимо иметь представление об активной и реактивной составляющих переменного тока. Сравнивая между собой формулы для определения мощности переменного и постоянного тока, можно видеть, что на месте полной величины силы тока I в формуле мощности стоит выражение Icosφ, где cosφ — величина, меньше единицы (и только в отдельных случаях равная ей). Отсюда следует, что в цепях переменного тока не весь ток создает полезную, активную мощность, а только некоторая его часть, которая называется активной составляющей тока.
Проекция вектора тока на горизонтальное направление, перпендикулярное вектору напряжения, равная Isincp, называется реактивной составляющей переменного тока. Реактивная составляющая тока не участвует в создании активной мощности.
Произведение действующего в цепи напряжения на реактивную составляющую тока носит название реактивной мощности и обозначается латинской буквой Q. Реактивная мощность измеряется в единицах, называемых «вар». Из приведенного определения реактивной мощности вытекает соотношение
Q = UI sin φ,
где Q — реактивная мощность, вар; U— напряжение, В; /— сила тока, A; sinφ — числовой коэффициент, зависящий от угла сдвига фаз в данной цепи.
Реактивная мощность, так же как и реактивная составляющая тока, характеризует собой ту энергию, которая идет на создание магнитного поля индуктивности или электрического поля конденсатора (если последний включен в данную цепь). Эта энергия в процессе протекания переменного тока в цепях со сдвигом фаз совершает непрерывные колебания между источником энергии и ее потребителем.
Активная, реактивная и полная мощности переменного тока связаны между собой соотношением
S2=P2+Q2. (1.28)
Это соотношение можно представить как векторную диаграмму, получаемую на основании диаграммы напряжений или токов, носящую название «треугольника мощностей» (рис. 1.9). Два катета этого треугольника представляют собой в том или ином масштабе активную и реактивную мощности (соответственно в кВт и квар), а гипотенуза — полную мощность (кВ А). Угол φ численно равен углу сдвига фаз тока и напряжения в цепи. Значение косинуса этого угла называют коэффициентом мощности.
Влияние частоты тока на электроприборы
Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.
Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу.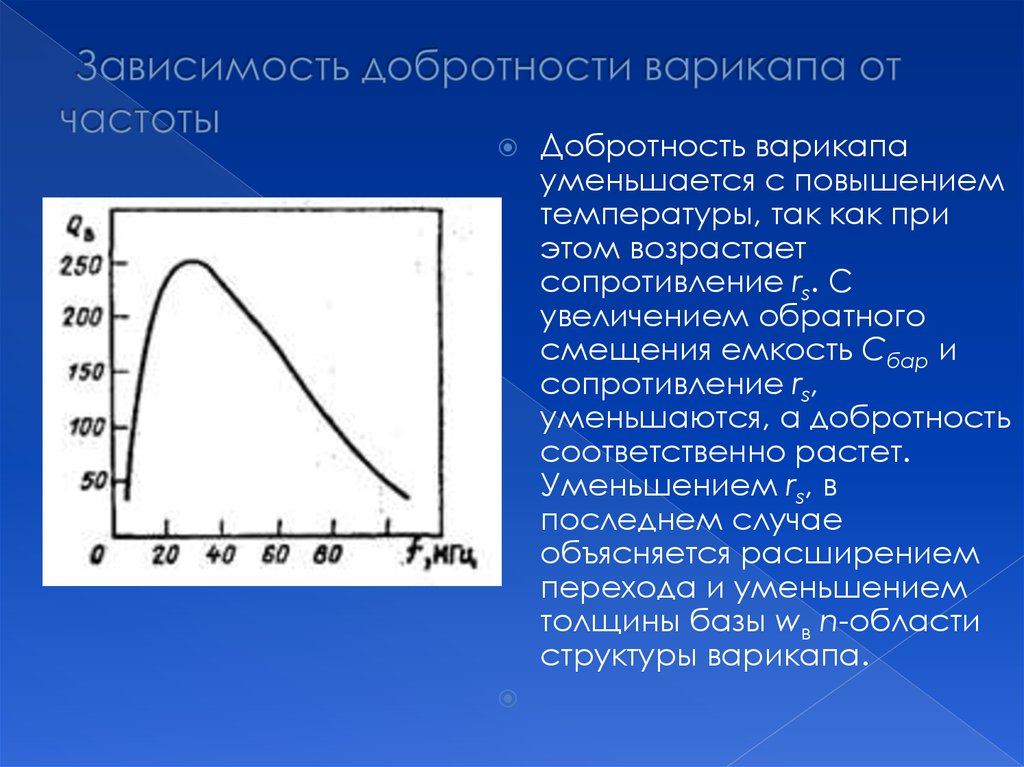 При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.
Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.
Электрическая цепь: понятие и основные элементы
Электрическая цепь – это совокупность различных объектов и устройств, которые образуют путь для нормального протекания электрического тока. Электромагнитные процессы в цепях могут описываться при помощи понятий об электродвижущей силе, электрическом токе и электрическом напряжении.
Для того чтобы проводить расчеты и анализ, электрическую цепь можно представить в виде электрической схемы, которая состоит из условных обозначений ее элементов и способов их соединения.
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Все устройства и элементы, которые входят в состав электрической цепи, условно можно классифицировать на несколько групп:
- Источники электрического питания (энергии). Общее свойство всех источников питания – это преобразование любых видов энергии в электрическую. Источники, в которых осуществляется трансформация неэлектрической энергии в электрическую, называются первичными. Вторичными источниками являются те, в которых и на выходе, и на входе электрическая энергия. В качестве примера можно привести выпрямительные устройства.
- Потребители электроэнергии. Общее свойство всех потребителей электрической энергии – это трансформация электроэнергии в другие виды энергии. Пример – нагревательный прибор. Иногда потребители электроэнергии называют нагрузкой.
- Вспомогательные элементы электрической цепи. Сюда можно отнести коммуникативные устройства, соединительные провода, защитную аппаратуру, а также измерительные приборы, без которых электрическая цепь не функционирует.

Все элементы электрической цепи охватываются одним электромагнитным процессом.
Готовые работы на аналогичную тему
Курсовая работа Постоянная и переменная электрическая цепь 440 ₽ Реферат Постоянная и переменная электрическая цепь 260 ₽ Контрольная работа Постоянная и переменная электрическая цепь 220 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора.
 Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких. - Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Закон Ома для переменного тока Благодаря своим свойствам конденсаторы используются в тех случаях, когда необходимо передать и постоянный, и переменный ток по одним и тем же проводам. Источник постоянного напряжения подключается к общему проводу и второму выводу ёмкости, через которую присоединяется источник переменного напряжения.
 На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.
На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.Распространённый пример подобного использования — это телевизионная наружная антенна с усилителем. Сам телевизор или подключаемое к кабелю устройство, называемое «инжектором», подаёт напряжение питания. В антенном усилителе происходит разделение и фильтрация сигналов. Таким образом, ёмкостное сопротивление конденсатора находит широкое применение. Фильтры обеспечивают задержку одних сигналов и прохождение — других.
Емкостное сопротивление
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин – проводимостей y =
1
/Z
,
G =
1
/R
,
b =
1
/X
.
y = 1/Z = √(G 2 + b 2 )
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Либо в показательной форме:
Здесь: Y
– комплексная проводимость.
G
– активная проводимость.
b
– реактивная проводимость.
y
– общая проводимость цепи, равная модулю комплексной проводимости.
e
– константа, основание натурального логарифма.
j
– мнимая единица.
φ
– угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице. При переключении множителей автоматически происходит пересчёт результата.
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Для расчетов напряжений и токов через элементы электрической цепи нужно знать их общее сопротивление. Источники энергии делятся на два типа:
- постоянного тока (батарейки, выпрямители, аккумуляторы), электродвижущая сила (ЭДС) которых не изменяется во времени;
- переменного тока (бытовые и промышленные сети), ЭДС которых изменяется по синусоидальному закону с определенной частотой.

Как рассчитать сложные схемы соединения резисторов
Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.
Исходные данные:
- источник постоянного тока 12V;
- сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.
Расчет:
- основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
- подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
- эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
- ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.
Сложные схемы
По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.
Расчет 1 (последовательное и параллельное соединение):
- для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
- эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
- второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
- общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
- Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.

Расчет 2 (сложное параллельное соединение):
- в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
- Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
- суммарное значение для цепи: R1 + R2 = 20 Ом;
- по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
- после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
- делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.
В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).
В этом случае разница потенциалов на шестом резисторе составит:
U6 = I *R6 = 1,2 * 7,5 = 9 В.
Соответственно, изменится напряжение между контрольными точками:
Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.
Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип – U6).
Зависимость мощности от частоты формула
Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Нормируемые требования к показателям
В РФ требования к качеству работы энергосистемы стандартизированы.
В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.
Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.
То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
Математическое выражение зависимости будет иметь следующий вид: I = UCω;
Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0—2015 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1. 2—2015 «Межгосударственная система стандартизации. Стандарты межгосударственные. правила, рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
2—2015 «Межгосударственная система стандартизации. Стандарты межгосударственные. правила, рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
Сведения о стандарте
1 РАЗРАБОТАН Акционерным обществом «Системный оператор Единой энергетической системы» (АО «СО ЕЭС»)
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 30 июня 2021 г. Ne 100-П)
За принятие проголосовали:
| Краткое наименование страны по МК | Код страны по МК (ИСО 3166) 004-97 | Сокращенное наименование национальное органа по стандартизации |
| Армения | AM | Минэкономики Республики Армения |
| Беларусь | BY | Госстандарт Республики Беларусь |
| Казахстан | KZ | Госстандарт Республики Казахстан |
| Киргизия | KG | Кыргыэствндарт |
| Россия | RU | Росстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 3 августа 2021 г. № 801 -ст межгосударственный стандарт ГОСТ 34184—2017 введен в действие в качестве национального стандарта с 1 марта 2021 г.
№ 801 -ст межгосударственный стандарт ГОСТ 34184—2017 введен в действие в качестве национального стандарта с 1 марта 2021 г.
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а текст изменении и поправок — в ежемесячном информационном указателе кНациональные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
Стандартинформ. 2017
В Российской Федерации настоящий стандарт не может быть полностью или частично воспроизведен. тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
ГОСТ 34184—2017
Что такое частота тока
Частота тока может относиться только к переменному показателю, который периодически изменяет своё направление и (или) силу в соответствии с синусоидальной функцией. Для того, чтобы вычислить период переменного тока, необходимо определить минимальный промежуток времени, через который повторяются изменение напряжения и силы. Частотой называется количество периодов, которое совершает ток за указанный промежуток или за единицу времени. Стандартное измерение выполняется в герцах (Гц), один период в 1 секунду равен одному Герцу.
Для того, чтобы вычислить период переменного тока, необходимо определить минимальный промежуток времени, через который повторяются изменение напряжения и силы. Частотой называется количество периодов, которое совершает ток за указанный промежуток или за единицу времени. Стандартное измерение выполняется в герцах (Гц), один период в 1 секунду равен одному Герцу.
Работа тока
Вторичное регулирование частоты
Вторичное регулирование частоты — процесс восстановления планового баланса мощности путём использования вторичной регулирующей мощности для компенсации возникшего небаланса, ликвидации перегрузки транзитных связей, восстановления частоты и использованных при первичном регулировании резервов первичной регулирующей мощности. Вторичное регулирование может осуществляться автоматически или по командам диспетчера.
Вторичное регулирование начинается после действия первичного и предназначено для восстановления номинальной частоты и плановых перетоков мощности между энергосистемами в энергообъединении.
Общее понятие о переменном токе
В отличие от постоянного движения электронов в одном направлении, переменный ток меняет как направление, так и значение несколько раз за единицу времени. Изменения происходят по гармоническому закону. Если наблюдать подобный сигнал с помощью осциллографа, можно увидеть картинку в виде синусоиды.
Относительно оси ординат OY ток меняет своё направление с положительного на отрицательное и делает это периодически. Поэтому его мгновенное значение в первой позиции считается положительным, во второй – отрицательным.
Важно! Так как переменный ток – это алгебраическая величина, то говорить о его знаке заряда можно только для конкретного мгновенного значения, смотря, в каком направлении он протекает в этот момент.
Сигнал на экране осциллографа
Напряжение или разность потенциалов?
Надо заметить, что напряжение и разность потенциалов – это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.
Не имеет значения, куда будет направлено это движение.
Разность потенциалов – просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.
В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.
Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.
И все-таки она существует!
Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.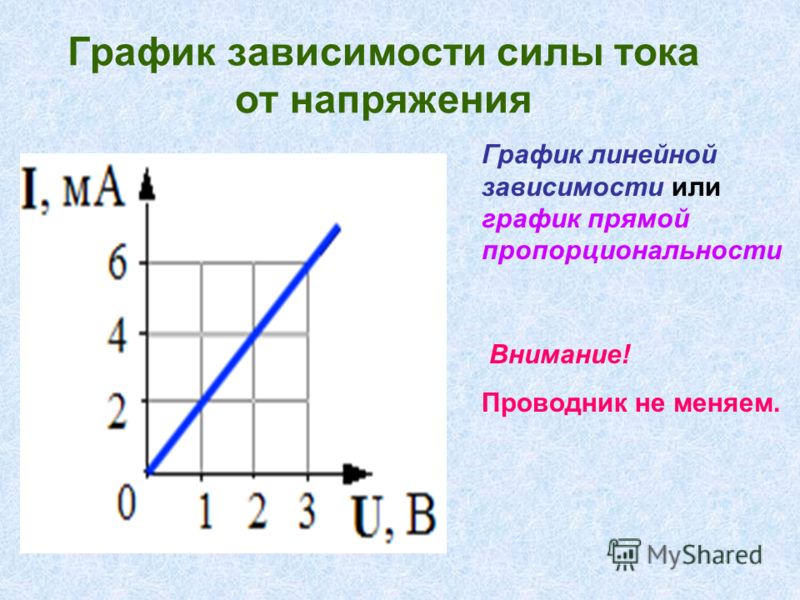
Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.
Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.
Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = Ur + Uxc+ Uxl.
Источник
Какие токи бывают
Для питания электрических устройств и электротехники необходима энергия. Постоянный и переменный токи являются способом передачи энергии из одной точки в другую с использованием проводников.
Важно! Основное различие между ними заключается в характере движения заряженных частиц. Постоянный ток течет равномерно в одном направлении, в то время, как переменный постоянно изменяет направление с заданной скоростью или частотой. Основным следствием этого является полярность напряжения.
Постоянный
Постоянный ток характеризуется неизменным показателем полярности заряженных частиц. Поскольку постоянный ток сохраняет постоянную полярность, важно обращать внимание на то, как подключается устройством – неверное подключение устройства к сети с большой долей вероятности выедет его из строя. Хорошим примером являются устройства с автономным питанием от аккумуляторов – на них всегда наносятся обозначения для их корректного подключения. В противном случае, техника просто не заработает, так как не получит электропитания.
Важно! При использовании постоянного тока, показатель напряжения может сильно разниться, в зависимости от используемого устройства. Типовые значения номинального напряжения автономных источников питания составляют 1.5V, 3.7V, 6V, 9V,12V, 24V и т.д.
Изменение направления тока
Переменный
С переменным током полярность постоянно переключается между положительным и отрицательным значениями. При подобной характеристике силового поля напряжение будет постоянно меняться, а полярность в таком случае не оказывает никакого влияния на работоспособность сети. Именно поэтому, любое бытовое электрическое устройство можно включать в сеть, не задумываясь о положении вилки в розетке, то есть, о соблюдении корректной полярности.
Именно поэтому, любое бытовое электрическое устройство можно включать в сеть, не задумываясь о положении вилки в розетке, то есть, о соблюдении корректной полярности.
Основной причиной широкого распространения переменного тока является относительная легкость и эффективность в увеличении, либо уменьшении напряжения. Это достигается с помощью трансформаторов, а количество изменений количественных показателей определяется числом обмоток.
Важно! Такая же трансформация допускается и для постоянной величины, но это явление не является эффективным для его применения на практике. Также, это является еще одной, дополнительной причиной, по которой в бытовой сети используется именно переменный ток.
Фазы в батарейке
Несмотря на то, что более низкие напряжения легче генерировать, высокие показатели несут меньшие потери при их передаче на расстояния. Поэтому перед подачей потребителям переменное напряжение повышается до нескольких сотен киловольт. Но, как только электричество достигает своего пункта назначения, оно снижается до 110 или 220 вольт. Дело в том, что переменный показатель имеет два установленных стандартных напряжения, которые используются во всем мире: 220В и 110В. Частота в электротехнике играет определяющее значение, и устройства, рассчитанные под напряжение в 110В, не станут работать от сети в 220В.
Дело в том, что переменный показатель имеет два установленных стандартных напряжения, которые используются во всем мире: 220В и 110В. Частота в электротехнике играет определяющее значение, и устройства, рассчитанные под напряжение в 110В, не станут работать от сети в 220В.
Участие электростанций различного типа в покрытии суммарной нагрузки энергосистем
Суммарные графики нагрузки энергосистем неравномерны. Коэффициент заполнения графиков довольно низок – kзап= 0,5…0,7 – и имеет тенденцию к дальнейшему снижению ввиду появления в энергосистемах новых типов потребителей и изменения структуры энергопотребления.
Распределение нагрузки между отдельными электростанциями с целью покрытия суммарного графика нагрузки энергосистемы производят, исходя из особенностей технологического режима электростанций различного типа, с тем, чтобы получить в целом по системе положительный хозяйственный эффект. При этом в базовую часть графика нагрузки в непаводковый период помещают АЭС, ТЭЦ, частично КЭС, ГЭС без водохранилищ, а также частично ГЭС с водохранилищами. В полупиковую часть графика помещают КЭС, а в пиковую часть – ГЭС. Во время паводка мощность ГЭС в базовой части графика нагрузки увеличивается, с тем, чтобы после заполнения водохранилищ не сбрасывать бесполезно избыток воды через водосливные плотины. При этом большая доля мощности КЭС и частично мощности ТЭЦ вытесняется в полупиковую часть графика нагрузки.
В полупиковую часть графика помещают КЭС, а в пиковую часть – ГЭС. Во время паводка мощность ГЭС в базовой части графика нагрузки увеличивается, с тем, чтобы после заполнения водохранилищ не сбрасывать бесполезно избыток воды через водосливные плотины. При этом большая доля мощности КЭС и частично мощности ТЭЦ вытесняется в полупиковую часть графика нагрузки.
Зная графики нагрузки электростанций, можно планировать ремонт оборудования. Агрегаты ГЭС, как правило, ремонтируют зимой, а ТЭС и АЭС – весной и летом. Изменения нагрузки и установленной мощности электростанции в системе в течение года взаимосвязаны.
В энергосистеме должны быть предусмотрены резервы: эксплуатационный (ремонтный, режимный, аварийный), составляющий примерно 10…12 % установленной мощности энергосистемы, и хозяйственный, составляющий около 3 %. Считается, что для нормального функционирования энергосистемы ее общий резерв должен составлять 13…15 % установленной мощности. На практике разность между установленной мощностью электростанций и их фактической нагрузкой в каждый данный момент не есть резервная мощность энергосистемы в обычном понимании.
С учетом устойчивости и надежности работы энергосистемы мощность наиболее крупного агрегата, как показывает опыт эксплуатации, нормально не должна превышать 1,5…3 % установленной мощности энергосистемы. Следовательно, крупные агрегаты мощностью 500, 800 и 1200 МВт могут устанавливаться только в относительно мощных энергосистемах.
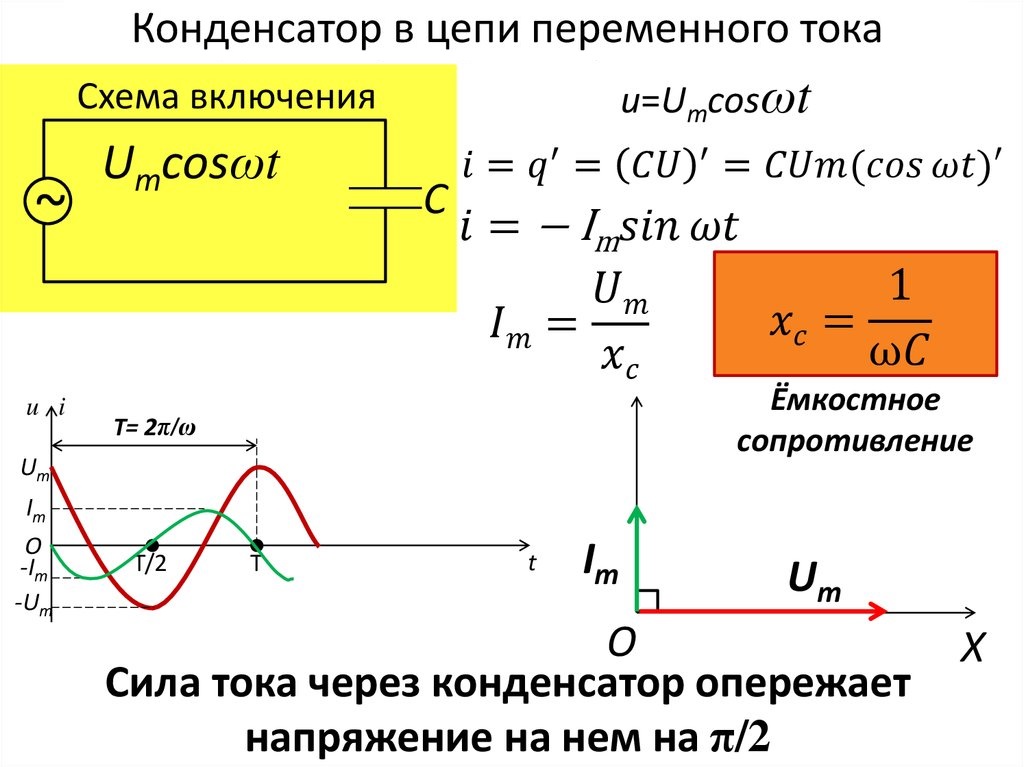
Емкость в цепи переменного тока
XC =
1/ ωc
При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.
Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.
Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.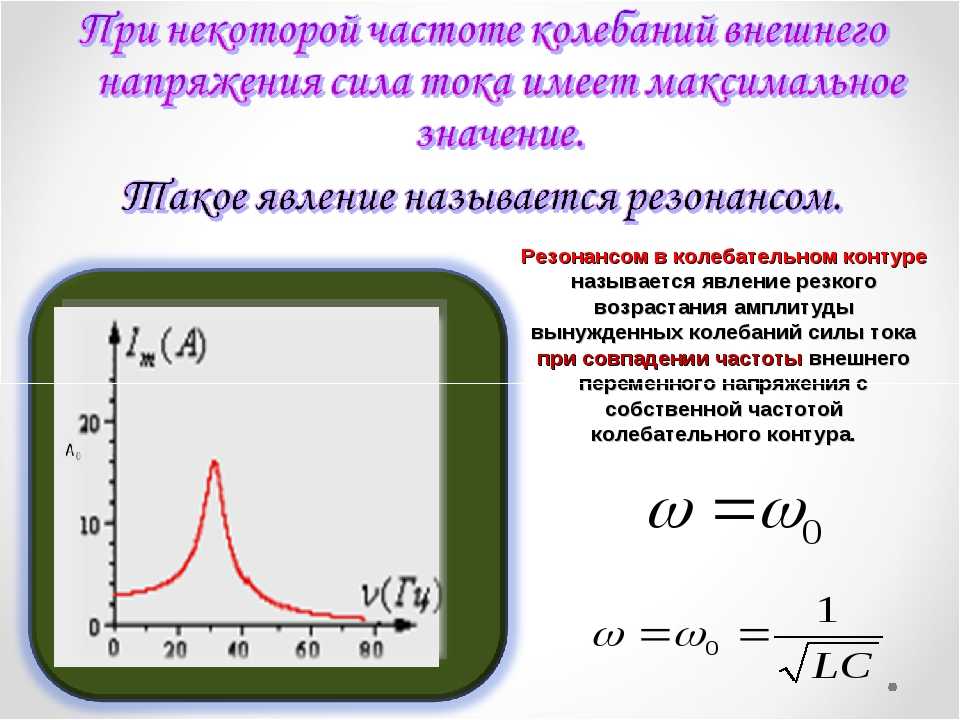
То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2
Какие есть фазы в токе
Многофазным может быть только переменный ток. Всего существует 3 разных фазы, и все они смещены на 120 градусов относительно друг друга. Каждая электростанция выдает по 4 провода: 3 фазовых и один для заземления, который является общим для всех трех. Электростанция вырабатывает три разные фазы переменного тока одновременно, и эти три фазы смещены строго под определённым углом.
Устройство фаз
Почему три фазы? Почему не одна, две или четыре? В 1-фазных и 2-фазных источниках питания имеет место явление, когда синусоида пересекает нулевую отметку 120 раз в секунду. При трехфазном питании в любой текущий момент одна из трех фаз приближается к пику. Таким образом, мощные 3-фазные двигатели (используемые в промышленности) и другие устройства, такие, как 3-фазное сварочное оборудование, имеют равномерную выходную мощность.
Важно! Четыре фазы существенно не улучшат ситуацию, но зато добавят четвертый провод, что повысит сложность многих работ и обслуживания, поэтому 3 фазы – это общепринятое и оптимальное значение.
Трехфазный
Трехфазная электроэнергия является распространенным методом генерации, передачи и распределения электроэнергии переменного показателя. Это тип многофазной системы и наиболее распространенный метод, используемый электрическими сетями во всем мире для передачи энергии. Он также используется для питания больших двигателей и при возникновении тяжелых нагрузок.
Трехфазная цепь, как правило, более экономична, чем эквивалентная двухпроводная однофазная при том же напряжённости линии и заземлении, поскольку для передачи заданного количества электрической энергии используется меньше материала проводника.
Интересный факт: Многофазные энергосистемы были изобретены Галилео Феррари, Михаилом Доливо-Добровольским, Йонасом Венстремом, Джоном Хопкинсоном и Николой Теслой ещё в конце 1880-х годов, и основные принципы работы применяются вплоть до сегодняшнего дня.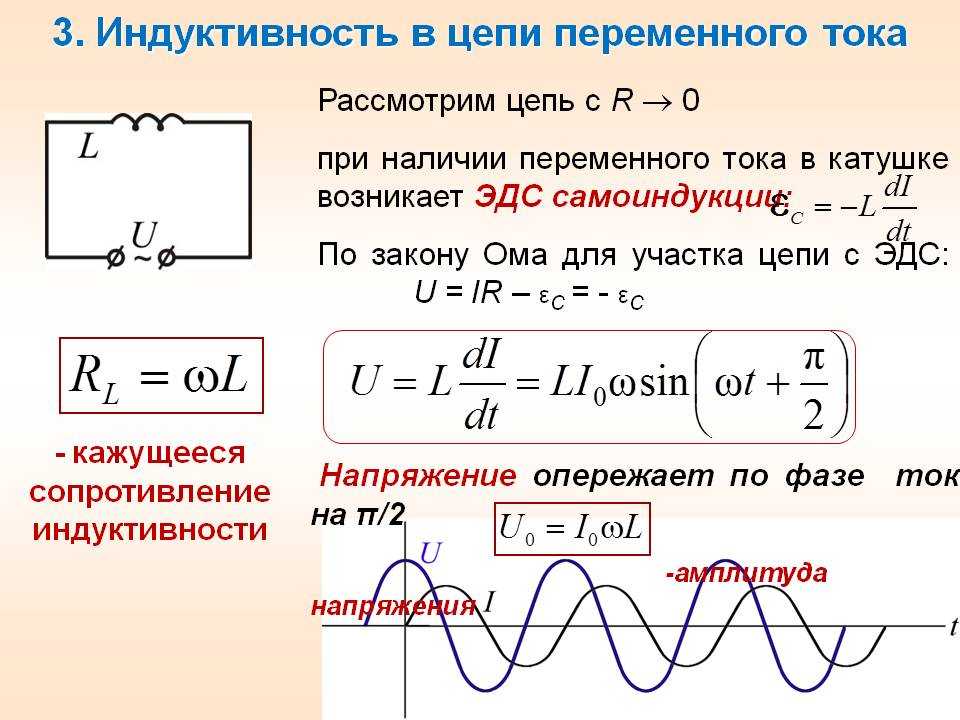
Движение частиц
Двухфазный
Двухфазная электрическая мощность была единственной доступной системой распределения электроэнергии переменного тока в начале 20-го века. В то время использовались две цепи, причем фазы напряжения отличались на четверть цикла, то есть, на 90°. Обычно в схемах применялись четыре провода, по два на каждую фазу. Реже применялись три провода с общим сердечником, но большего диаметра. Некоторые двухфазные генераторы прошлых лет имели две полные роторные сборки с физически смещенными обмотками для обеспечения двухфазной мощности.
На сегодняшний день двухфазный тое приобрёл широкое распространение в быту, так как каждый потребитель – житель квартиры или частного дома имеет определённое количество точек подключения бытовых приборов малой мощности.
Важно! При стандартной работе наиболее распространённых домашних приборов двухфазная электрическая цепь в полном объёме удовлетворяет потребности владельцев жилой недвижимости.
Турбогенераторные установки на Ниагарском водопаде, построенные в 1895 году, были крупнейшими в мире на то время и представляли собой именно двухфазные машины. Однако, в конечном итоге, трёхфазные системы заменили безнадёжно устаревшие и малоэффективные оригинальные агрегаты для генерации и передачи энергии. В настоящее время в мире осталось мало промышленных двухфазных распределительных систем, например, в Филадельфии, штат Пенсильвания.
Двухфазный ток
Общие сведения об энергосистеме
Энергосистема – совокупность электростанций, электрических и тепловых сетей, а также потребителей электроэнергии и тепла, связанных общностью режима в непрерывности процессов производства, преобразования, передачи, распределения и потребления электрической и тепловой энергии при общем управлении этими режимами. Электрическая часть энергосистемы называется электроэнергетической системой.
Объединение электроэнергетических систем на параллельную работу дает следующие преимущества:
- более высокую надежность электроснабжения;
- использование несовмещения максимумов нагрузки;
- меньшие резервы мощности из-за возможности передачи электроэнергии из одной энергосистемы в другую;
- более рациональное использование первичных источников энергии;
- возможность использования более крупных агрегатов, имеющих более высокий коэффициент полезного действия.

Единая энергетическая система России (ЕЭС России) – совокупность производственных и иных имущественных объектов электроэнергетики, связанных единым процессом производства (в том числе производства в режиме комбинированной выработки электрической и тепловой энергии) и передачи электрической энергии в условиях централизованного оперативно-диспетчерского управления в электроэнергетике. Основная цель создания и развития Единой энергетической системы России состоит в обеспечении надежного и экономичного электроснабжения потребителей на территории России с максимально возможной реализацией преимуществ параллельной работы энергосистем.
ЕЭС России охватывает практически всю обжитую территорию страны и является крупнейшим в мире централизованно управляемым энергообъединением. В настоящее время ЕЭС России включает в себя 69 энергосистем на территории 79 субъектов российской Федерации, работающих в составе шести работающих параллельно ОЭС – ОЭС Центра, Юга, Северо-Запада, Средней Волги, Урала и Сибири и ОЭС Востока, работающей изолированно от ЕЭС России. Кроме того, ЕЭС России осуществляет параллельную работу с ОЭС Украины, ОЭС Казахстана, ОЭС Белоруссии, энергосистемами Эстонии, Латвии, Литвы, Грузии и Азербайджана, а также с NORDEL (связь с Финляндией через вставку постоянного тока в Выборге). Энергосистемы Белоруссии, России, Эстонии, Латвии и Литвы образуют так называемое «Электрическое кольцо БРЭЛЛ», работа которого координируется в рамках подписанного в 2001 г. Соглашения о параллельной работе энергосистем БРЭЛЛ.
Кроме того, ЕЭС России осуществляет параллельную работу с ОЭС Украины, ОЭС Казахстана, ОЭС Белоруссии, энергосистемами Эстонии, Латвии, Литвы, Грузии и Азербайджана, а также с NORDEL (связь с Финляндией через вставку постоянного тока в Выборге). Энергосистемы Белоруссии, России, Эстонии, Латвии и Литвы образуют так называемое «Электрическое кольцо БРЭЛЛ», работа которого координируется в рамках подписанного в 2001 г. Соглашения о параллельной работе энергосистем БРЭЛЛ.
Системный оператор выделяет три крупных независимых энергообъединения в Европе – Северную (NORDEL), Западную (UCTE) и Восточную (ЕЭС/ОЭС) синхронные зоны (NORDEL и UCTE в июле 2009 г. вошли в состав нового европейского объединения – ENTSO-E). Под ЕЭС/ОЭС понимается ЕЭС России в совокупности с энергосистемами стран СНГ, Балтии и Монголии.
Влияние частоты тока на электроприборы
Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.
Для измерения частоты в системе используют частотомеры.
Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.
Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.
Вторичное регулирование частоты (АВРЧМ)
Вторичное регулирование частоты — процесс восстановления планового баланса мощности путём использования вторичной регулирующей мощности для компенсации возникшего небаланса, ликвидации перегрузки транзитных связей, восстановления частоты и использованных при первичном регулировании резервов первичной регулирующей мощности. Вторичное регулирование осуществляется автоматически под воздействием центрального регулятора.
Вторичное регулирование осуществляется автоматически под воздействием центрального регулятора.
Вторичное регулирование начинается после действия первичного и предназначено для восстановления номинальной частоты и плановых перетоков мощности между энергосистемами в энергообъединении.
В основном во вторичном регулировании участвуют гидроэлектростанции (ГЭС) в связи с их маневренностью. Все крупные ГЭС России подключены к системе АВРЧМ для участия во вторичном регулировании и получают в режиме реального времени (характерный цикл информационного обмена — 1 сек) задание вторичной мощности, которое через групповой регулятор активной мощности (ГРАМ) поступает непосредственно на исполнение системами управления гидроагрегатами.
В период паводка для наиболее экономичного срабатывания паводковой воды в гидротурбинах к АВРЧМ привлекаются и электростанции других типов (ТЭС, ПГУ). Участие ТЭС, ПГУ в АВРЧМ осуществляется в рамках работы рынка системных услуг.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.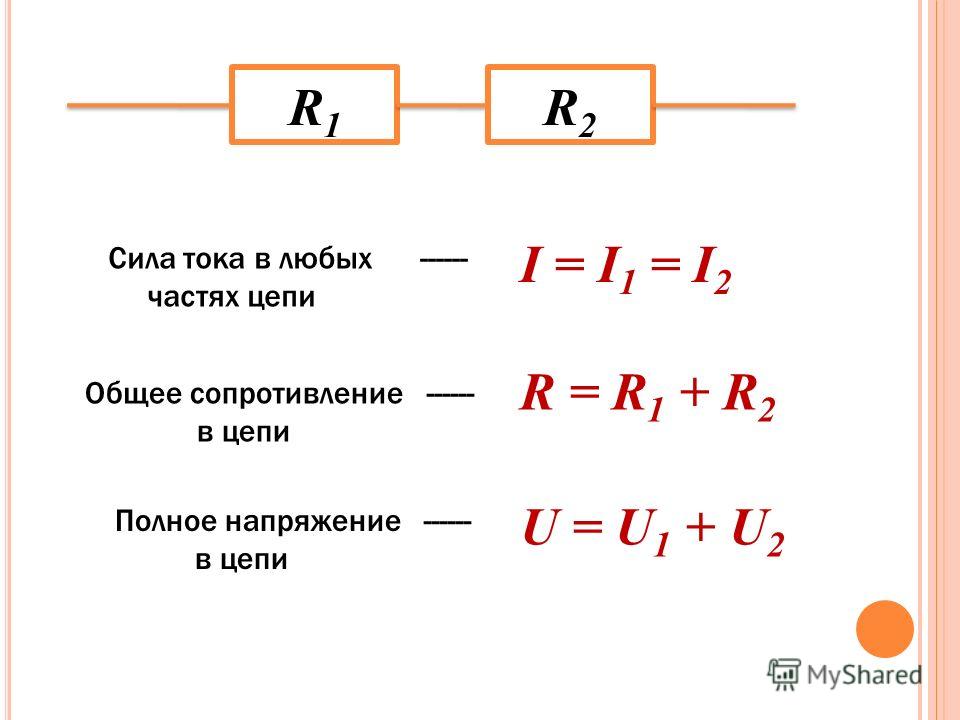
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса
, Z (
полного
или
комплексного сопротивления
для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.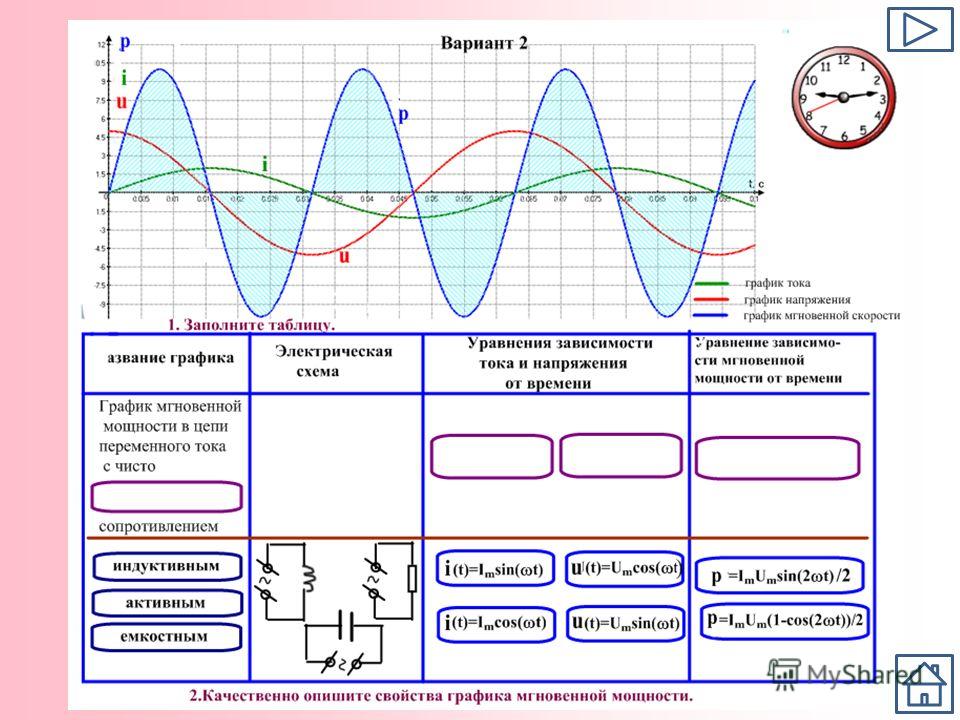 Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице. Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице. Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z
и
коэффициента мощности Cos(φ)
, характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
Производные формулы:
Есть такие резисторы
Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:
- индуктивное;
- емкостное.
Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.
Они представлены на фото выше. И конденсаторами (ниже).
Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.
Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.
Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.
Действующее значение синусоидального тока
Под действующим значением понимают его эффективность. Она равна такому значению постоянного тока, который выполнит ту же работу, что и переменный, за один период времени. Под работой здесь подразумевают его тепловую или электродинамическую направленность. Удобнее всего использовать среднеквадратичное значение переменного электричества.
Тогда действующее значение для синусоидального тока определяют по формуле:
I = * Im ≈ 0,707* Im,
где Im – величина амплитуды тока.
Действующее значение тока
Токи высокой частоты
ТВЧ – такова их аббревиатура, используются для плавки металлов, закалки поверхности металлических изделий. ТВЧ – это токи, имеющие частоту более 10 кГц. В индукционных печах используют ТВЧ, помещая проводник внутрь обмотки, через которую пропускают ТВЧ. Под их воздействием возникающие в проводнике вихревые токи разогревают его. Регулируя силу ТВЧ, контролируют температуру и скорость нагрева.
ТВЧ – это токи, имеющие частоту более 10 кГц. В индукционных печах используют ТВЧ, помещая проводник внутрь обмотки, через которую пропускают ТВЧ. Под их воздействием возникающие в проводнике вихревые токи разогревают его. Регулируя силу ТВЧ, контролируют температуру и скорость нагрева.
Интересно. Расплавляемый металл может быть подвешен в вакууме с помощью магнитного поля. Для него не нужен тигель (специальный ковш для нагрева). Так получают очень чистые вещества.
Плюсы использования ТВЧ в разных случаях:
- быстрый нагрев при ковке и прокате металла;
- оптимальный температурный режим для пайки или сварки деталей;
- расплав даже очень тугоплавких сплавов;
- приготовление пищи в микроволновых печах;
- дарсонвализация в медицине.
Получают ТВЧ с помощью установок, включающих в свой состав колебательный контур, или электромашинных генераторов. У статора и ротора генераторов на сторонах, обращённых друг другу, нанесены зубцы. Их взаимное движение порождает пульсацию магнитного поля. Частота на выходе тем больше, чем больше произведение числа зубцов ротора на частоту его вращения.
Их взаимное движение порождает пульсацию магнитного поля. Частота на выходе тем больше, чем больше произведение числа зубцов ротора на частоту его вращения.
Зависимость напряжения от частоты
Канал ЭлектроХобби на YouTube. Выражение «напряжение тока» не верно по своему смыслу. Напряжение и ток, это две различные электрические характеристики. Если хотеть понять, какова частота у электрического тока, то стоит сначала разобраться с самим понятием этого тока. Потом уже стане ясно, что есть сила тока, его частота, напряжение. Итак, давайте сравним электричество с обычной водой.
Поиск данных по Вашему запросу:
Зависимость напряжения от частоты
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Емкостное и индуктивное сопротивление в цепи переменного тока.
- Частота электрического тока — определение, физический смысл
- Резонанс в цепи переменного тока
- Преимущества и перспективные области применения частотных преобразователей ERMAN
- Вы точно человек?
- Зависимость частоты и напряжений от баланса мощности
- Зависимость тока и частоты: требования, формула, влияние
- Какова частота напряжения тока, а точнее частота электрического тока.
- Переменный ток
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 42 Зависимость силы тока от напряжения
Емкостное и индуктивное сопротивление в цепи переменного тока.
Фотоэффект — вырывание электронов из вещества под действием света. В металле электрон движется свободно, но при вылете его с поверхности сам металл из-за этого заряжается положительным зарядом и препятствует вылету. Поэтому для того, чтобы покинуть металл, электрон должен обладать дополнительной энергией, зависящей от вещества.
Эта энергия называется работой выхода. Для исследования фотоэффекта можно собрать установку, изображенную на рис. Она состоит из стеклянного баллона, из которого выкачан воздух. Окно, через которое падает свет, сделано из кварцевого стекла, пропускающего видимые и ультрафиолетовые лучи.
Внутри баллона впаяны два электрода: один из которых — катод — освещается через окно. Между электродами источник создает электрическое поле, которое заставляет двигаться фотоэлектроны от катода к аноду. При изменении напряжения меняется сила тока. График зависимости I от U — вольтамперная характеристика — приведен на рис. При малых напряжениях не все вырванные из катода электроны достигают анода, при увеличении напряжения их число возрастает.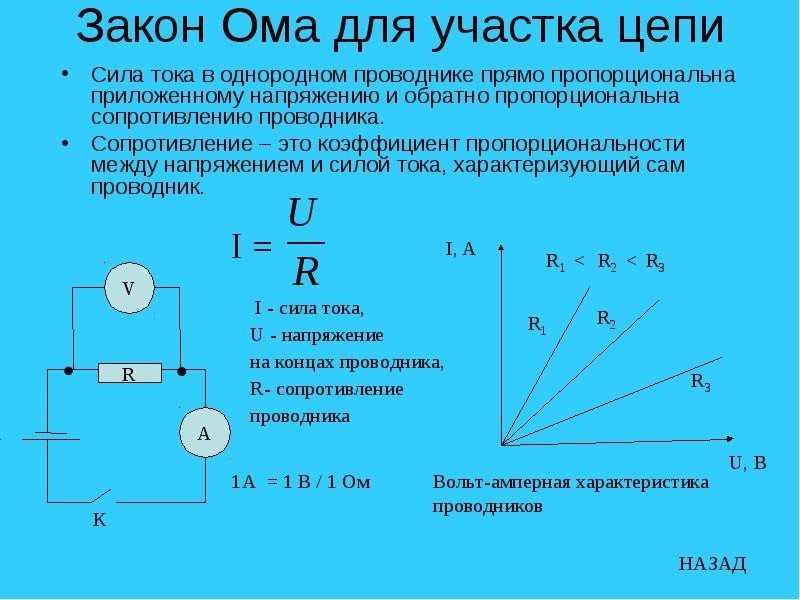 При некотором напряжении все вырванные светом электроны достигают анода, тогда устанавливается ток насыщения I н , при дальнейшем увеличении напряжения ток не изменяется.
При некотором напряжении все вырванные светом электроны достигают анода, тогда устанавливается ток насыщения I н , при дальнейшем увеличении напряжения ток не изменяется.
При увеличении интенсивности падающего излучения наблюдается возрастание тока насыщения, пропорционального числу вырванных электронов. Для измерения кинетической энергии электронов нужно поменять полярность источника тока. На графике этому случаю соответствует участок при U , на котором фототок падает до нуля. Теперь поле не разгоняет, а тормозит фотоэлектроны. При некотором напряжении, названном задерживающим U 3 , фототок исчезает. При этом все электроны будут остановлены полем, затем поле вернет их в бывший катод, подобно тому, как брошенный вверх камень будет остановлен полем тяготения Земли и возвращен снова на Землю.
Оказалось, что максимальная кинетическая энергия электронов зависит не от интенсивности света, а только от частоты. Это утверждение называют 2-м законом фотоэффекта. При некоторой граничной частоте света, которая зависит от конкретного вещества, и при более низких частотах фотоэффект не наблюдается.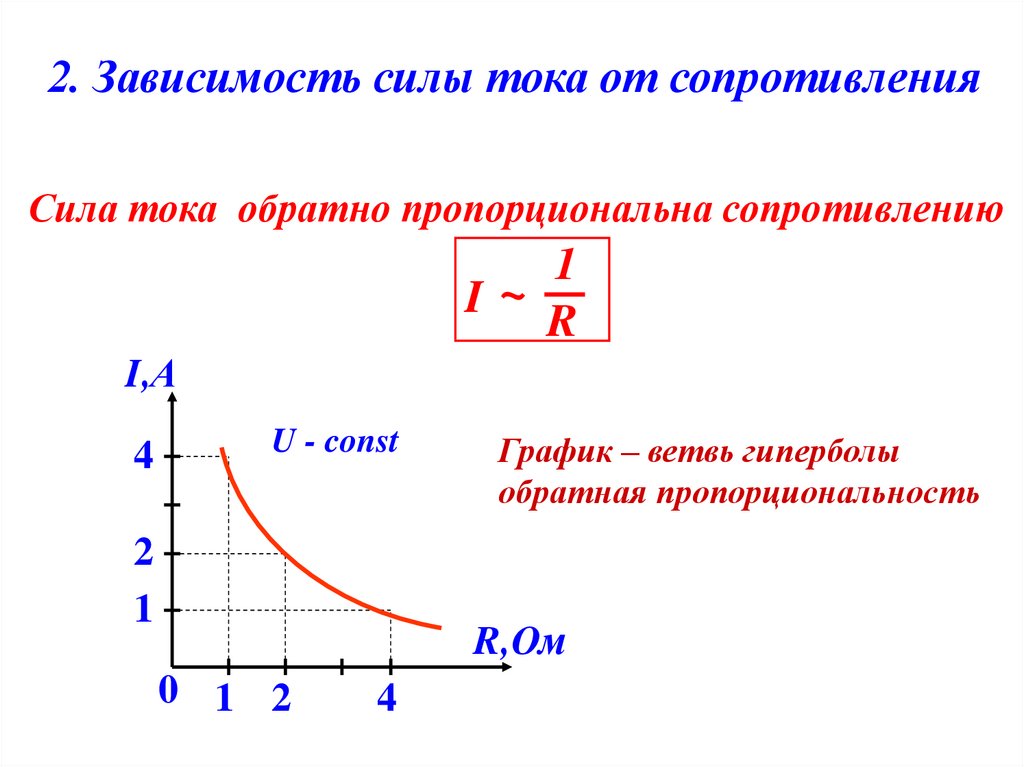 Эта граничная частота носит название «красной» границы фотоэффекта.
Эта граничная частота носит название «красной» границы фотоэффекта.
Объяснил законы фотоэффекта А. Эйнштейн в г. Он воспользовался идеей Планка о квантовой природе света. То есть. Объясним с позиций идеи Эйнштейна 1-й закон фотоэффекта. Если один квант энергии вырывает один электрон, то чем больше квантов поглощает вещество чем больше интенсивность света , тем больше электронов вылетит из вещества. Объясним второй закон фотоэффекта. Работа выхода А зависит от рода вещества и не зависит от частоты света.
Интенсивность света не влияет на кинетическую энергию электрона, потому что уравнение Эйнштейна описывает энергетику одного электрона.
Не важно, сколько вылетит электронов, скорость каждого из них зависит от частоты. Формула Эйнштейна объясняет и тот факт, что свет данной частоты из одного вещества может вырвать электрон, а из другого — не может. Это частота, при которой совершается вырывание электронов без сообщения им кинетической энергии, — частота «красной границы» фотоэффекта.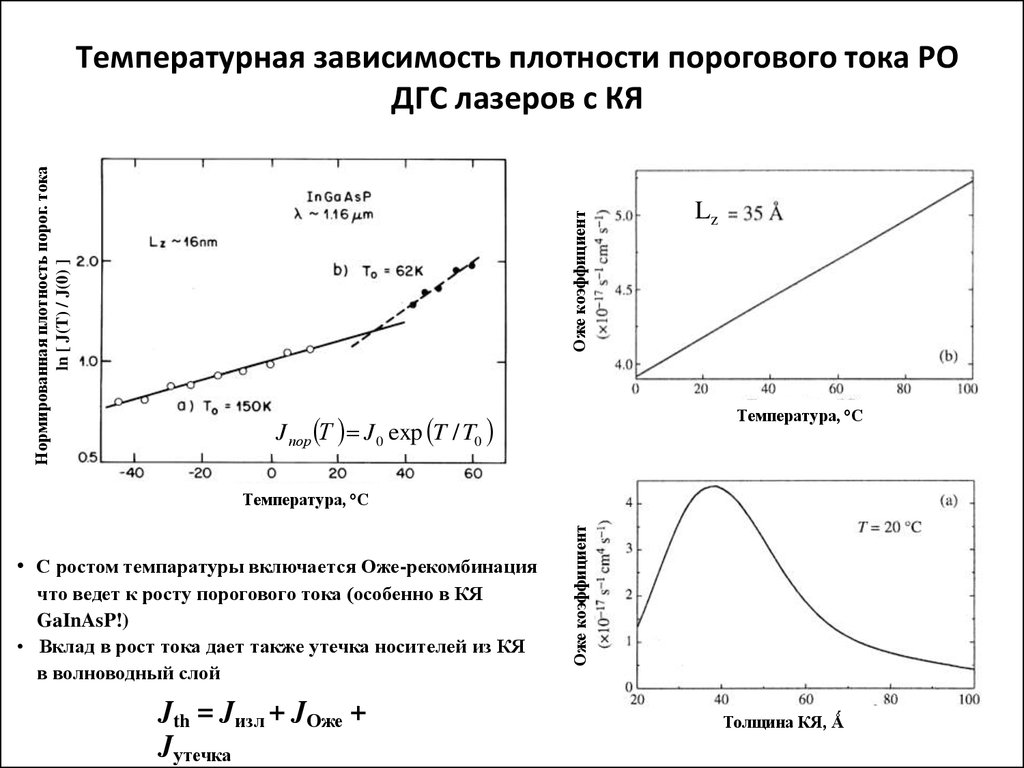
Уравнение Эйнштейна запишем для случая, когда кинетическая энергия электрона равна по величине работе сил электрического поля, то есть при задерживающем напряжении:. Построим график зависимости задерживающего напряжения от частоты рис. Тангенс угла наклона графика:. Теория Фотоэффект — вырывание электронов из вещества под действием света.
Частота электрического тока — определение, физический смысл
Закон Ома для полной цепи переменного тока. Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных амплитудных и действующих значений тока и напряжения. В этом случае:. Учитывая, что отношение напряжения к силе тока — это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим:. Мощность в цепи переменного тока. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. Резонанс в электрической цепи.
C и катушку индуктивности L. На каком из графиков представлена зависимость силы тока I от частоты (при постоянной амплитуде напряжения U)?.
На каком из графиков представлена зависимость силы тока I от частоты (при постоянной амплитуде напряжения U)?.
Резонанс в цепи переменного тока
Хотя переменный ток часто переводят на английский как alternating current , эти термины не эквивалентны. Термин alternating current AC в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток то есть периодический двунаправленный ток. Так как переменный ток в общем случае меняется в электрической цепи не только по величине , но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока. На рисунке приведена развёрнутая диаграмма переменного тока , изменяющегося с течением времени по величине и направлению. Периодическим переменным током называется такой электрический ток , который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине. За единицу измерения частоты переменного тока принят 1 герц 1 гц, 1 Гц, 1 Hz. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ. Частота переменного тока равна одному герцу, если период тока равен одной секунде один полный цикл за одну секунду. В некоторых странах, например, в Японии , используются оба стандарта см.
За единицу измерения частоты переменного тока принят 1 герц 1 гц, 1 Гц, 1 Hz. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ. Частота переменного тока равна одному герцу, если период тока равен одной секунде один полный цикл за одну секунду. В некоторых странах, например, в Японии , используются оба стандарта см.
Преимущества и перспективные области применения частотных преобразователей ERMAN
При протекании токов по электрической цепи, элементы которой соединены последовательно, параллельно или имеют смешанное соединение, могут получаться различные режимы работы этой цепи. Рассмотрим следующие режимы работы электрических цепей: резонанс в цепи с последовательным соединением элементов резонанс напряжений , резонанс в цепи с параллельным соединением элементов резонанс токов. Резонанс напряжений. Резонанс напряжений наблюдается в цепи, в которой последовательно включены все элементы.
Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок.
Вы точно человек?
Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы. Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер к примеру, резистор , то в широком диапазоне сила тока от частоты иметь зависимость не будет.
Зависимость частоты и напряжений от баланса мощности
Остановимся прежде всего на основном и общем для рассматриваемых задач вопросе: выясним, от чего зависят величины частоты и напряжений, устанавливающиеся в электроэнергетической системе. Каждый из приемников энергии, присоединенных к электрической сети, потребляет активную и реактивную мощности, величины которых, как уже отмечалось ранее, определяются величиной напряжения на его зажимах и частотой. Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке. Следовательно, нагрузка любой узловой точки однозначно в области нормальных значений частоты и напряжения определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте.
Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке. Следовательно, нагрузка любой узловой точки однозначно в области нормальных значений частоты и напряжения определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте.
Исследовано влияние частоты переменного синусоидального тока на выход по току и подавать на электроды переменное напряжение с частотой 10 Гц при Зависимость выхода по току от частоты в диапазоне Гц.
Зависимость тока и частоты: требования, формула, влияние
Зависимость напряжения от частоты
Такой преобразователь изменяет пульсации частотой до 9 килогерц в напряжение тока постоянной величины до 9 вольт.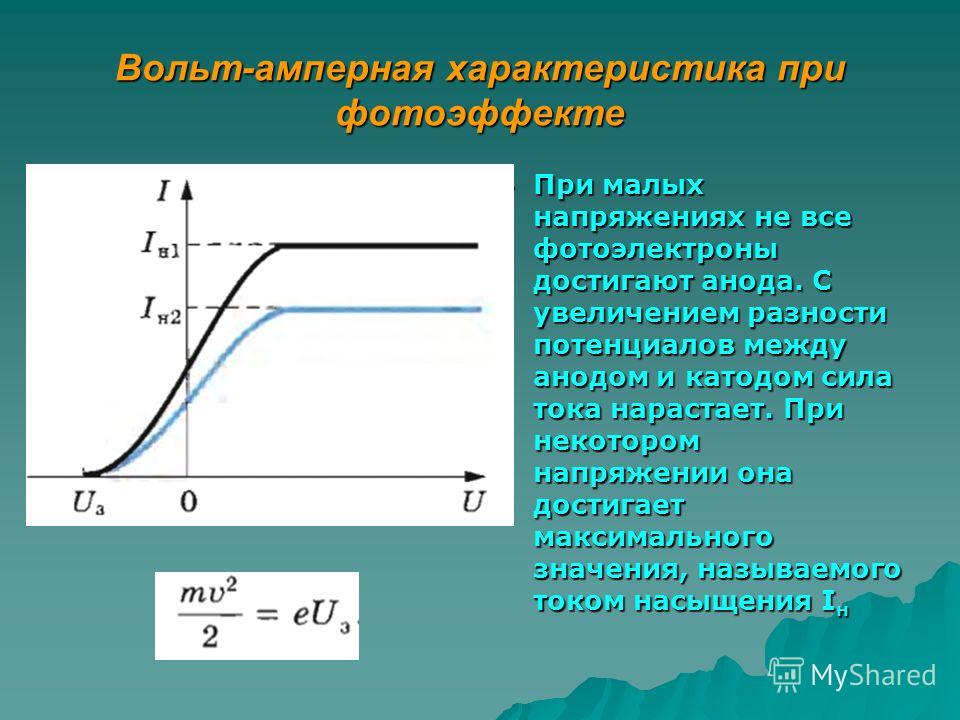 Основная составляющая часть устройства составляет микросхема ТС Сигнал должен иметь амплитуду не больше питающего напряжения, выходит на разъем CON1. Питающее напряжение идет на разъем CON3.
Основная составляющая часть устройства составляет микросхема ТС Сигнал должен иметь амплитуду не больше питающего напряжения, выходит на разъем CON1. Питающее напряжение идет на разъем CON3.
Какова частота напряжения тока, а точнее частота электрического тока.
ВИДЕО ПО ТЕМЕ: Зависимость боли от частоты — ElectroBOOM
Регистрация Вход. Ответы Mail. Вопросы — лидеры Задача по физике 1 ставка. Провод КСПВ, вопрос к электрикам 1 ставка. Мощность рассеивания транзистора? Зачем электродрели нужен редуктор, точнее большая шестеренка?
Широкое распространение асинхронных электродвигателей во второй половине го века было обусловлено простотой, надёжностью и относительно небольшой стоимостью этих машин.
Переменный ток
Московский энергетический институт ТУ. Кафедра инженерной экологии и охраны труда. Учебно-методический комплекс.
Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две.
Глубина проникновения тока в металл
6 ноября 2018
Явление поверхностного эффекта
Постоянный ток в проводнике распределяется равномерно по сечению, переменный ток распределяется по сечению неравномерно в зависимости от частоты тока (рис. 10.6.).
Рис. 10.6. Глубина проникновения тока в металл в зависимости от его частоты: а — постоянный, б, в, г — переменный 50, 10 000, 125 000 Гц соответственно
При пропускании переменного тока наибольшая противоэлектродвижущая сила индуктируется в центре проводника, который охватывается полным магнитным потоком. Чем ближе к поверхности проводника, тем слабее магнитное поле, а, следовательно, меньше противо электродвижущая сила. Существование этой силы равноценно появлению в проводнике некоторого добавочного сопротивления, носящего название индуктивного сопротивления цепи. Встречая в центре проводника наибольшее индуктивное сопротивление, ток будет стремиться пройти в направлении наименьшего сопротивления и вытисниться к поверхности проводника.
Чем ближе к поверхности проводника, тем слабее магнитное поле, а, следовательно, меньше противо электродвижущая сила. Существование этой силы равноценно появлению в проводнике некоторого добавочного сопротивления, носящего название индуктивного сопротивления цепи. Встречая в центре проводника наибольшее индуктивное сопротивление, ток будет стремиться пройти в направлении наименьшего сопротивления и вытисниться к поверхности проводника.
Свойство тока высокой частоты протекать только по поверхностному слою проводника принято называть поверхностным эффектом, или скин-эффектом.
Плотность тока для различных точек сечения проводника будет неодинаковой. Чем выше частота тока, тем больше в центре проводника индуктивное сопротивление и меньше плотность тока. Неравномерное распределение индукционных токов приводит к неравномерному нагреву деталей: поверхностные слои очень быстро нагреваются до высоких температур, а сердцевина или совсем не нагревается или нагревается незначительно, благодаря теплопроводности стали.
Для количественной оценки явления поверхностного эффекта введено понятие глубины проникновения тока 8 (дельта). При этом считают, что переменный ток протекает только в поверхностном слое, толщина которого равна глубине проникновения тока, и имеет на этой глубине равномерную плотность.
Глубина проникновения тока или толщина слоя определяется по формуле:
где р — удельное электрическое сопротивление, Ом-мм2/м; р — магнитная проницаемость, Гс/Э; f- частота тока, Гц.
Следовательно, с увеличением частоты глубина проникновения индукционных токов уменьшается (рис. .103, таблица 10.4.). Если менять частоту тока, то можно в широких пределах изменять глубину проникновения 8, а, следовательно, и толщину слоя, по которому идет ток, вызывающий нагрев поверхности закаливаемой детали.
Из приведенных в табл., данных следует, что с повышением температуры нагрева металла глубина проникновения тока растет и достигает наибольшего значения при температуре потери магнитных свойств — точки Кюри.
50
0,5
7.0
1,0
2500
0,067
1.0
0,13
10000
0.034
0,5
0,07
100000
0,011
0.16
0,022
1 000 000
0,0034
0,05
0,007
С ростом температуры нагрева (рис. 10.7.) стальных деталей удельное сопротивление р возрастает и выше 1000°С достигает своего максимального значения.
10.7.) стальных деталей удельное сопротивление р возрастает и выше 1000°С достигает своего максимального значения.
Рис. 10.7. Кривые изменения магнитной проницаемости и удельного электрического сопротивления стали 45 в зависимости от температуры нагрева
Магнитная проницаемость в интервале 600…700°С почти не зависит от температуры, но при дальнейшем ее повышении резко падает и достигает минимального значения, равного магнитной проницаемости вакуума ( jli =1).
Для практических расчетов глубину проникновения 8 тока в металл вычисляют по упрощенным формулам: для стальных деталей при температуре 15° С:
мм и при температуре 760° С , мм
Где: S- глубина проникновения тока, мм; f- частота тока, Гц.
Для большинства сталей магнитные превращения протекают в интервале критических температур 765-780° С, при которых магнитная проницаемость резко падает и становится равной единице.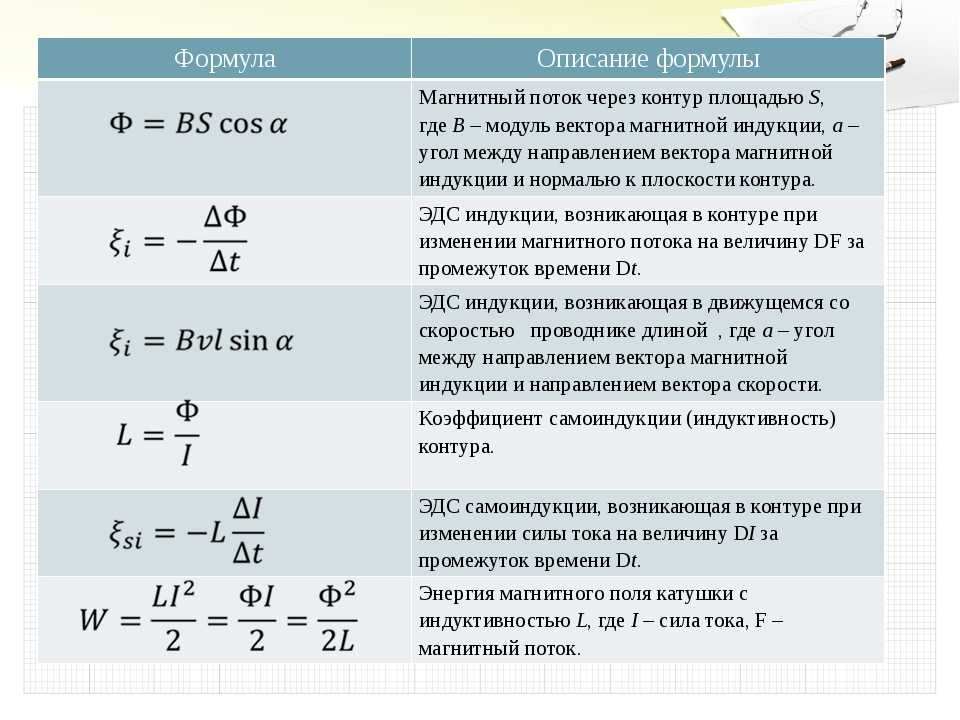 После потери сталью магнитных свойств с образованием аустенита глубина проникновения тока резко возрастает.
После потери сталью магнитных свойств с образованием аустенита глубина проникновения тока резко возрастает.
Наибольшее значение глубины проникновения тока называют горячей глубиной проникновения и обозначают ГОр- Приближенно она может быть определена по упрощенной формуле:
Зная зависимость глубины проникновения тока от температуры, процесс индукционного нагрева стали можно представить по следующей схеме.
В первый момент начинается, нагрев стали в тонком поверхностном слое, равном глубине проникновения тока в холодный металл. После потери этим слоем магнитных свойств, глубина проникновения тока возрастает и нагревается слой, расположенный глубже. Повышение температуры в первом нагретом слое замедляется.
После потери магнитных свойств вторым слоем начинает быстро нагреваться третий слой и т.д. Пределом роста глубины проникновения тока является горячая глубина проникновения.
Повышение температуры в слое с горячей глубиной проникновения происходит за счет индуктированных токов, а в более глубоких слоях — в основном за счет теплопроводности.
Этот процесс нагрева объясняет причину быстрого распространения тепла при нагреве ТВЧ, в связи с изменениями магнитных свойств. На рис. 10.5 изображен график индукционного нагрева, из которого видно, что более быстрый нагрев происходит при температурах ниже точки Кюри (769°С). Выше этой критической точки нагрев замедляется в связи с потерей сталью магнитных свойств и фазовыми превращениями.
Существует три основных способа поверхностной индукционной закалки в зависимости от размера, формы детали и некоторых специальных требований нагрева: одновременный, непрерывно последовательный и последовательный (поочередный).
Рис. 10.8. График индукционного нагрева
График зависимости тока от частоты
Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.
Нормируемые требования к показателям
В РФ требования к качеству работы энергосистемы стандартизированы.
В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.
Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.
То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
Математическое выражение зависимости будет иметь следующий вид: I = UCω;
Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).
Влияние частоты тока на электроприборы
Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.
Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.
Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.
Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.
класс 11 «Б», ОПШМТ № 11, г. Павлодар
Гордова Наталья Владимировна
научный руководитель, преподаватель физики, ОПШМТ № 11, г. Павлодар
1.0cm;line-height:150%;text-autospace:none»>
Интерес, проявляемый в настоящее время к колебательным процессам, весьма широк и далеко выходит за пределы изучения качаний маятника, как это было в начале XVII века, когда ученые только начали интересоваться колебаниями.
1.0cm;line-height:150%;text-autospace:none»>
По современным представлениям науки звуковые, тепловые, световые, электромагнитные явления, т. е. важнейшие физические процессы окружающего нас мира, являются различными видами колебаний. Они играют исключительную роль в таких ведущих отраслях техники, как электричество и радио.
е. важнейшие физические процессы окружающего нас мира, являются различными видами колебаний. Они играют исключительную роль в таких ведущих отраслях техники, как электричество и радио.
1.0cm;line-height:150%;text-autospace:none»>
Выработка, передача и потребление электрической энергии, телефония, телеграфия, радиовещание, радиолокация — все эти важные и сложные отрасли техники основаны на использовании электрических и электромагнитных колебаний.
1.0cm;line-height:150%;text-autospace:none»>
Среди различных колебательных систем особое место занимают электромагнитные системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.
1.0cm;line-height:150%;text-autospace:none»>
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур. Колебательный контур — это электрическая цепь, состоящая из последовательно включенных резистора, катушки индуктивности и конденсатора. Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.
Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.
1.0cm;line-height:150%;text-autospace:none»>
Цель данной работы — исследовать механизм электромагнитных колебаний в RLC контуре на примере его компьютерной модели и подтвердить теоретические выводы, используя реальный RLC-контур, на практике.
1.0cm;line-height:150%;text-autospace:none»>
Для этого необходимо решить следующие задачи:
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· исследовать компьютерную модель RLC-контура в программе «Открытая физика», найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления, построить графики.
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· исследовать реальный RLC-контур с использованием компьютерной программы «Audiotester», а в качестве генератора частоты — звуковую плату компьютера. Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.
Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· сделать выводы о совпадении теоретических и практических результатов.
1.0cm;line-height:150%;text-autospace:none»>
Новизна данной работы заключается в том, что в практической части используется компьютер, звуковая плата которого заменяет генератор переменной частоты и вольтметр переменного напряжения. Для управления звуковой платой и обработки информации применяется специальная программа «Audiotester».
0cm;margin-left:0cm;margin-bottom:.0001pt;text-align:justify;text-indent:1.0cm;
line-height:150%;text-autospace:none»>
1. Основные положения
line-height:150%»>
Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
line-height:150%»>
Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой W, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте W.
line-height:150%»>
Если частота W свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте W внешнего источника.
line-height:150%»>
Явление возрастания амплитуды колебаний тока при совпадении частоты W внешнего источника с собственной частотой W электрической цепи называется электрическим резонансом. При последовательном резонансе (W = W) амплитуды UCи UL напряжений на конденсаторе и катушке резко возрастают.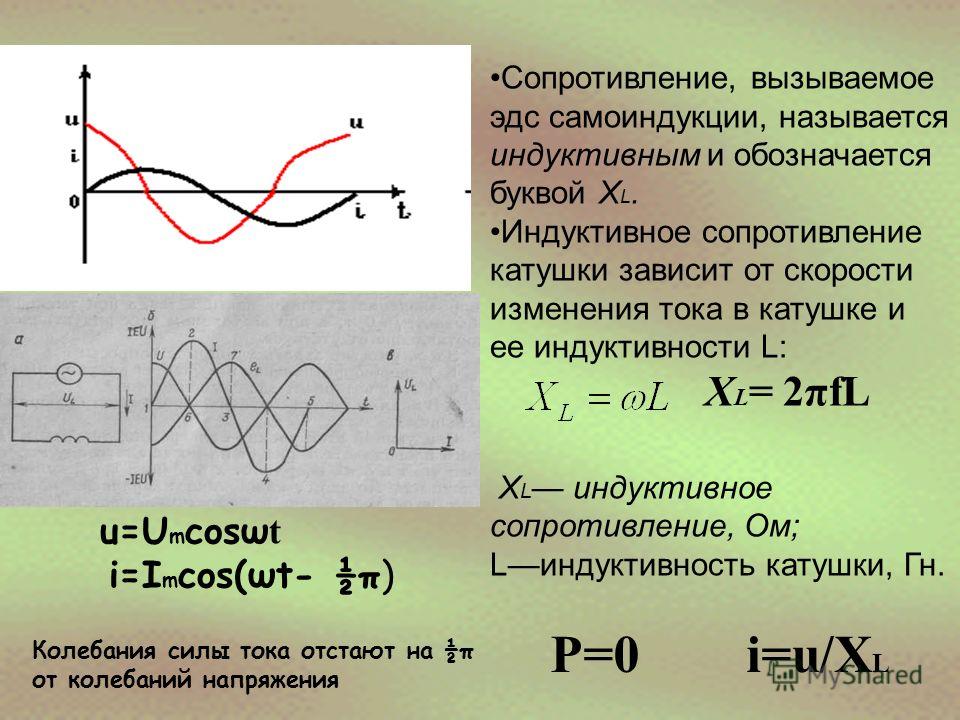
line-height:150%»>
Существует понятие добротности RLC-контура. Она равна отношению амплитуды напряжения на конденсаторе Uc к амплитуде напряжения генератора U: Q = Uc/U.
line-height:150%»>
На рисунке изображен последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рисунок 1):
line-height:150%»>
e(t) = cos ωt,
где: — амплитуда,
line-height:150%»>
ω — круговая частота.
line-height:150%»>
Рисунок 1. Вынужденные колебания в контуре.
line-height:150%»>
2. Исследование компьютерной модели RLC-контура.
Изучим механизм возникновения вынужденных электрических колебаний и вхождения системы в резонанс; определим зависимость тока в контуре от частоты генератора. Для этого будем использовать программу «Открытая физика 1.1» [1, c. 135] .
150%»>
Запустим на компьютере модель RLC-контура.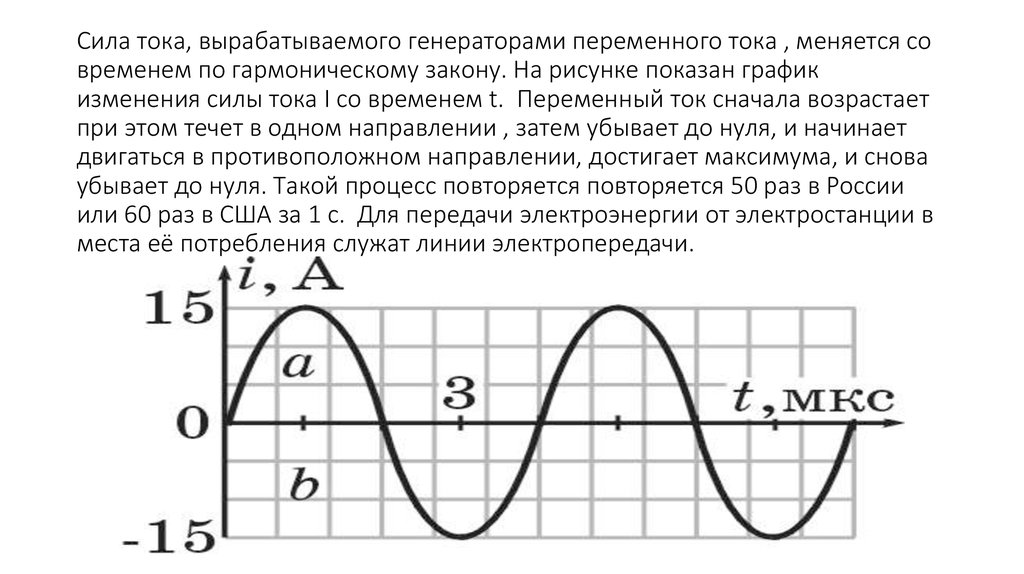 Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.
Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.
line-height:150%»>
В компьютерной модели можно изменять параметры RLC-контура, а также частоту W внешнего источника. При изменении параметров на дисплее высвечивается новая резонансная кривая, на которой точкой отмечается результат компьютерного эксперимента. Одновременно высвечивается векторная диаграмма, на которой с помощью векторов изображаются колебания тока и напряжений на элементах цепи.
150%»>
Выбираем значения параметров RLC-контура: С=50 мкФ, R=1 Ом, L=2 мГн.
150%»>
Рассчитаем собственную циклическую частоту Wo , собственную частоту fo контура и добротность Q.
Wo = 1/, fo = Wo/(2*П), Q = Uc/U.
150%»>
Получаем: Wo = 3162 с-¹, fo= 503,5 Гц , Q = 1,24
150%»>
В состоянии резонанса будем увеличивать сопротивление R и отслежи-вать значение добротности контура Q на экране. Данные заносим в таблицу 1.
класс 11 «Б», ОПШМТ № 11, г. Павлодар
Гордова Наталья Владимировна
научный руководитель, преподаватель физики, ОПШМТ № 11, г. Павлодар
1.0cm;line-height:150%;text-autospace:none»>
Интерес, проявляемый в настоящее время к колебательным процессам, весьма широк и далеко выходит за пределы изучения качаний маятника, как это было в начале XVII века, когда ученые только начали интересоваться колебаниями.
1.0cm;line-height:150%;text-autospace:none»>
По современным представлениям науки звуковые, тепловые, световые, электромагнитные явления, т. е. важнейшие физические процессы окружающего нас мира, являются различными видами колебаний. Они играют исключительную роль в таких ведущих отраслях техники, как электричество и радио.
е. важнейшие физические процессы окружающего нас мира, являются различными видами колебаний. Они играют исключительную роль в таких ведущих отраслях техники, как электричество и радио.
1.0cm;line-height:150%;text-autospace:none»>
Выработка, передача и потребление электрической энергии, телефония, телеграфия, радиовещание, радиолокация — все эти важные и сложные отрасли техники основаны на использовании электрических и электромагнитных колебаний.
1.0cm;line-height:150%;text-autospace:none»>
Среди различных колебательных систем особое место занимают электромагнитные системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.
1.0cm;line-height:150%;text-autospace:none»>
Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур. Колебательный контур — это электрическая цепь, состоящая из последовательно включенных резистора, катушки индуктивности и конденсатора.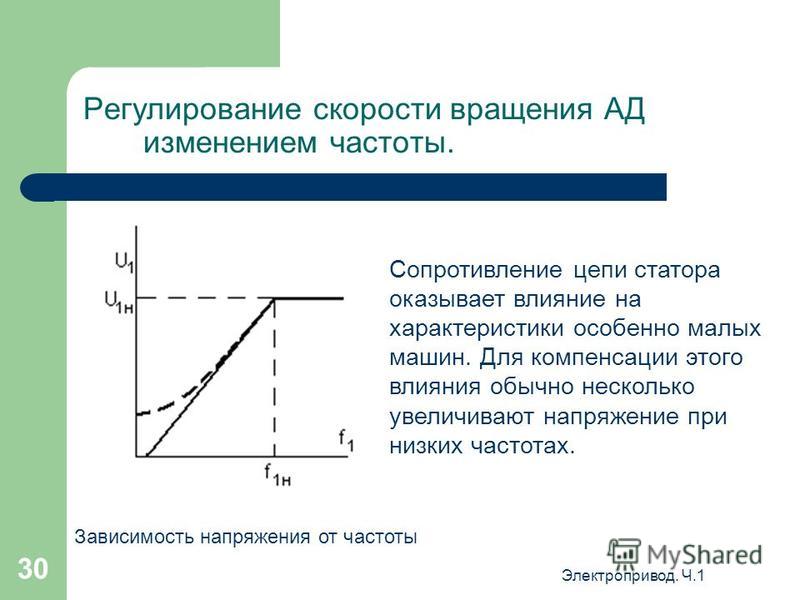 Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.
Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.
1.0cm;line-height:150%;text-autospace:none»>
Цель данной работы — исследовать механизм электромагнитных колебаний в RLC контуре на примере его компьютерной модели и подтвердить теоретические выводы, используя реальный RLC-контур, на практике.
1.0cm;line-height:150%;text-autospace:none»>
Для этого необходимо решить следующие задачи:
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· исследовать компьютерную модель RLC-контура в программе «Открытая физика», найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления, построить графики.
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· исследовать реальный RLC-контур с использованием компьютерной программы «Audiotester», а в качестве генератора частоты — звуковую плату компьютера. Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.
Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.
0cm;margin-left:7.1pt;margin-bottom:.0001pt;text-align:justify;text-indent:
21.25pt;line-height:150%;text-autospace:none»>
· сделать выводы о совпадении теоретических и практических результатов.
1.0cm;line-height:150%;text-autospace:none»>
Новизна данной работы заключается в том, что в практической части используется компьютер, звуковая плата которого заменяет генератор переменной частоты и вольтметр переменного напряжения. Для управления звуковой платой и обработки информации применяется специальная программа «Audiotester».
0cm;margin-left:0cm;margin-bottom:.0001pt;text-align:justify;text-indent:1.0cm;
line-height:150%;text-autospace:none»>
1. Основные положения
line-height:150%»>
Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
line-height:150%»>
Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой W, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте W.
line-height:150%»>
Если частота W свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте W внешнего источника.
line-height:150%»>
Явление возрастания амплитуды колебаний тока при совпадении частоты W внешнего источника с собственной частотой W электрической цепи называется электрическим резонансом. При последовательном резонансе (W = W) амплитуды UCи UL напряжений на конденсаторе и катушке резко возрастают.
line-height:150%»>
Существует понятие добротности RLC-контура. Она равна отношению амплитуды напряжения на конденсаторе Uc к амплитуде напряжения генератора U: Q = Uc/U.
line-height:150%»>
На рисунке изображен последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рисунок 1):
line-height:150%»>
e(t) = cos ωt,
где: — амплитуда,
line-height:150%»>
ω — круговая частота.
line-height:150%»>
Рисунок 1. Вынужденные колебания в контуре.
line-height:150%»>
2. Исследование компьютерной модели RLC-контура.
Изучим механизм возникновения вынужденных электрических колебаний и вхождения системы в резонанс; определим зависимость тока в контуре от частоты генератора. Для этого будем использовать программу «Открытая физика 1.1» [1, c. 135] .
150%»>
Запустим на компьютере модель RLC-контура. Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.
Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.
line-height:150%»>
В компьютерной модели можно изменять параметры RLC-контура, а также частоту W внешнего источника. При изменении параметров на дисплее высвечивается новая резонансная кривая, на которой точкой отмечается результат компьютерного эксперимента. Одновременно высвечивается векторная диаграмма, на которой с помощью векторов изображаются колебания тока и напряжений на элементах цепи.
150%»>
Выбираем значения параметров RLC-контура: С=50 мкФ, R=1 Ом, L=2 мГн.
150%»>
Рассчитаем собственную циклическую частоту Wo , собственную частоту fo контура и добротность Q.
Wo = 1/, fo = Wo/(2*П), Q = Uc/U.
150%»>
Получаем: Wo = 3162 с-¹, fo= 503,5 Гц , Q = 1,24
150%»>
В состоянии резонанса будем увеличивать сопротивление R и отслежи-вать значение добротности контура Q на экране. Данные заносим в таблицу 1.
Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)
Регистрация на конференцию «Проблемы безопасности на транспорте»
Как поступить в БелГУТ:
дневное, заочное полное,
заочное сокращенное
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 | 2 | |||||
3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 | 11 | 12 | 13 | 14 Дата : 2022-10-14 | 15 | 16 |
17 | 18 | 19 | 20 | 21 | 22 | 23 |
24 | 25 | 26 Дата : 2022-10-26 | 27 Дата : 2022-10-27 | 28 | 29 | 30 |
31 | ||||||
Все анонсы
- График проведения открытых занятий на 1 семестр 20.
 ..
.. - С Днем учителя!
- Курсы по 1C, AutoCAD, CorelDRAW, VISIO, Autodesk I…
- Запись на донорство
- Акция «ЭТАЛОН.Студент.by»
- Экспозиции, посвященные Грунтову П.С. и Белому В.А…
- Угадай мелодию
- Открытая лекция Велюгиной Н.Е. «НАДСТРОЙКА, ПРИСТР…
- Конкурс кандидатов в перспективный кадровый резерв…
- Логистика. Обучение для студентов выпускных курсов…
Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
График проведения открытых занятий на 1 семестр 20…
С Днем учителя!
Курсы по 1C, AutoCAD, CorelDRAW, VISIO, Autodesk I…
Запись на донорство
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
- Университет
Новый номер газеты «Вести БелГУТа»
03 октября 2022
- Воспитательная работа
Гомель встретил участников международного детско-молодежного марафона . ..
..
03 октября 2022
- Университет
Заседание комиссии по противодействию коррупции 30 сентября 2022 года…
30 сентября 2022
- Воспитательная работа
Встреча с ветераном спецчастей подразделений оперативной разведки Гене…
30 сентября 2022
- Университет
За верность традициям в образовании
30 сентября 2022
- Студенческая жизнь
ВОЛОНТЁРЫ БЕЛГУТА | КОРОТКО О ВАЖНОМ
30 сентября 2022
- Университет
Делегация российского Военного института железнодорожных войск и военн.. .
.
30 сентября 2022
- Университет
День учителя во Дворце Республики
30 сентября 2022
- Студенческая жизнь
Меломаны БелГУТа сыграли в «Угадай мелодию»…
29 сентября 2022
Другие новости
- Наркотики. Ответственность. Последствия…
- Победа в соревнованиях по гребле на байдарках…
- Команда РОО «Белая Русь» заняла 3 командное место…
- Участие в V Международном образовательном форуме «Алтай – Азия 2022: Е…
- Волонтеры студсовета в приюте для бездомных животных…
- Встреча в общежитии «Я выбираю жизнь!»
- Повышение квалификации по теме «Учет труда и заработной платы в органи…
- Тыдзень роднай мовы «Як ты дорага мне, мая родная мова»…
- Турнир по игре на джойстиках в «Mortal Combat» состоялся.
 ..
.. - Против COVID-19 в БелГУТе
- Единый День информирования: «История белорусской государственности – о…
КУДА ПОСТУПАТЬ
Все факультеты
БелГУТ на Доске почета
Достижения университета
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
Зависимость от напряжения и частоты
R 1.11 ЗАВИСИМОСТЬ НАПРЯЖЕНИЯ Если мы приложим напряжение к резистору, его сопротивление упадет немного в некоторых типах. Следовательно, изменение сопротивления отрицательно. Изменение приложенного напряжения на вольт называется коэффициентом напряжения , VC, и выражается в %/В или лучше, мкВ/В. Коэффициент определяется не только резистивным материалом, но и размерами, т. е. напряженностью электрического поля, и временем приложенного напряжения. Таким образом, MIL-STD-202, метод 309предписывает измерения при прерывистой подаче напряжения менее 0,5 секунды.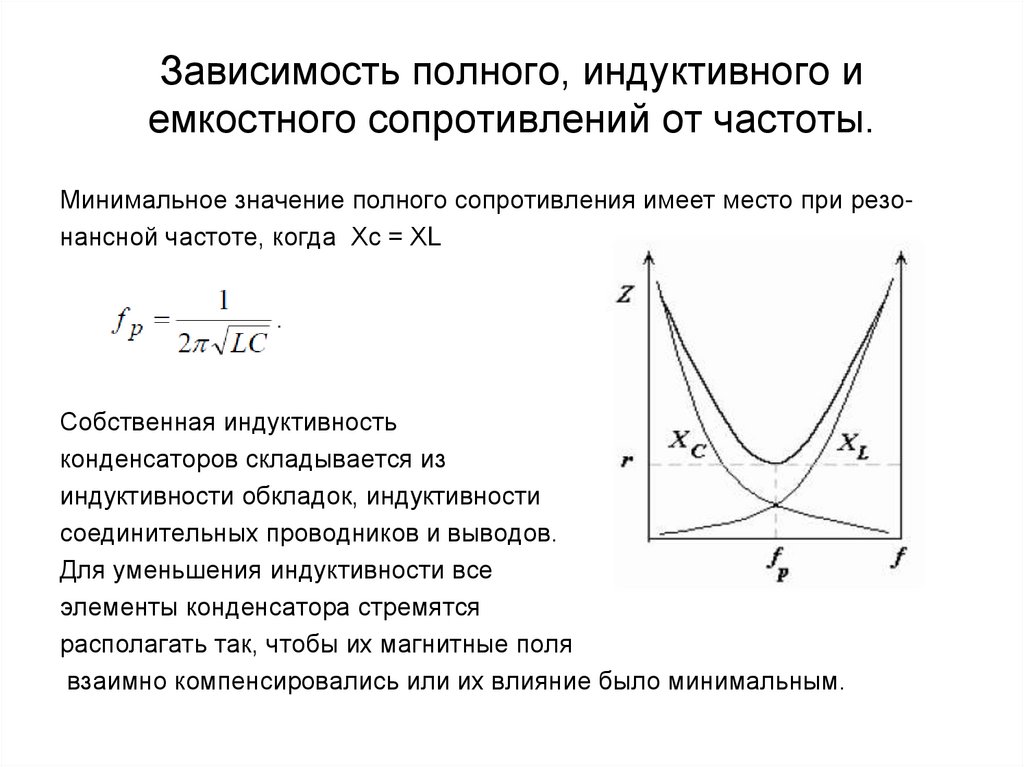 Выполняются два измерения: сопротивление (r) при 0,1 х номинального напряжения (В R ) и сопротивление (R) при 1,0 х В R . Коэффициент напряжения VC рассчитывается как:
Выполняются два измерения: сопротивление (r) при 0,1 х номинального напряжения (В R ) и сопротивление (R) при 1,0 х В R . Коэффициент напряжения VC рассчитывается как:
………………[R1-13]
Если не принимать во внимание чистые металлические резистивные элементы, общие значения коэффициента напряжения составляют от –10 до –100 мкВ/ В. Зависимость от напряжения незначительна для значений сопротивления ниже 1000 Ом .
Явная зависимость от напряжения в сочетании с напряжением переменного тока вызовет искажения и затухание третьей гармоники.
R 1.12 ЧАСТОТНАЯ ЗАВИСИМОСТЬ Резистор имеет определенную паразитную степень как емкости, так и индуктивности. Между витками имеется некая емкостная связь. Индуктивность появляется уже в прямом выводе, длиной примерно 1 нГн/мм, но усиливается действием катушки из обмоток и спиралевидных узоров. В резисторах из углеродного состава проявляется только емкость, возникающая из множества параллельных путей тока.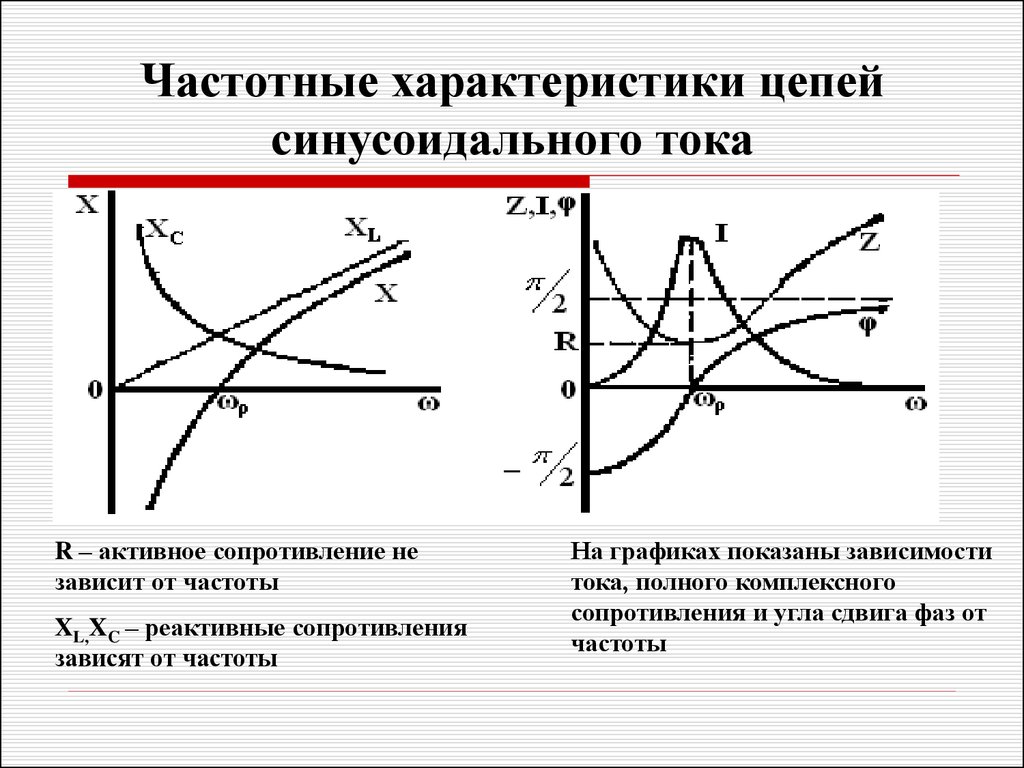
На рис. R1-17 показана эквивалентная схема, упрощенная до моделей для высоких и низких значений сопротивления.
Рисунок R1-17. Примеры схем замещения резисторов в разной степени упрощения.
Зависимость сопротивления от частоты уменьшается , если резисторы:
- имеют малые габариты.
- имеют низкое значение сопротивления.
- имеют тонкопленочную конструкцию. Даже толстопленочный дизайн благоприятен.
- имеют как можно более короткий вывод, как SMD.
- геометрически ровные, т. е. без резких геометрических изменений вдоль корпуса резистора.
Влияние частотной зависимости на импеданс показано на рис. R1-18.
Рисунок R1-18. Примеры частотной зависимости как отношения импеданса переменного тока к сопротивлению постоянному току для некоторых различных типов резисторов:
- Состав углерода, ¼ W, 1 MW.
- Состав углерода, ¼ Вт, 100 кВт.

- Чип, толстопленочный, размер EIA 0603, 100 кВт; в » 0,05 пФ; L » 0,4 нГн.
- Металлическая глазурь или металлическая пленка, размер DIN 0207, 100 кВт; в » 0,4 пФ.
- MELF, размер DIN 0204, 10 кВт.
- Чип, толстопленочный, размер EIA 0603, 10 кВт; в » 0,05 пФ; L » 0,4 нГн.; Чип, металлическая фольга, размер EIA 1210, 10 кВт.
- Чип, толстопленочный, размер EIA 0603, 1 кВт; в » 0,05 пФ; L » 0,4 нГн.
- MELF, размер DIN 0102, высокочастотное исполнение, 10 Вт; в » 0,035 пФ; L » 0,8 нГн.
- MELF, размер DIN 0204, 10 Вт.
- Чип, толстопленочный, размер EIA 0603, 10 Вт; в » 0,05 пФ; L » 0,4 нГн.
- Чип, тонкопленочный, размер EIA 0603, 100 Вт; в » 0,035 пФ; L » 1,2 нГн.
- Чип, толстопленочный, размер EIA 0603, 100 Вт; в » 0,05 пФ; L » 0,4 нГн.
Примеры на рис. R1-18 приведены только в качестве примера. Они взяты из технических паспортов основных производителей.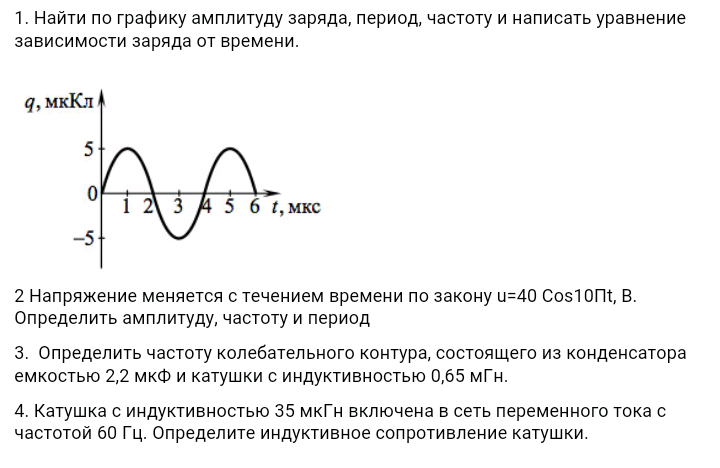 Обратите внимание, как значение сопротивления эквивалентного в остальном компонента влияет на параметры: № 3, 6, 7, 10 и 12. Другой пример № 8 показывает компонент MELF, который с помощью специальной техники спиралеобразования получает превосходное качество. высокочастотные характеристики. Как правило, частотную зависимость различных материалов резисторов можно разделить на три группы:
Обратите внимание, как значение сопротивления эквивалентного в остальном компонента влияет на параметры: № 3, 6, 7, 10 и 12. Другой пример № 8 показывает компонент MELF, который с помощью специальной техники спиралеобразования получает превосходное качество. высокочастотные характеристики. Как правило, частотную зависимость различных материалов резисторов можно разделить на три группы:
| Технология | Зависимость от частоты |
| Состав углерода | высокий |
| Металлическая глазурь, металлокерамика, толстая пленка | от умеренного до низкого |
| Металлическая пленка, оксид металла и углеродная пленка | низкий |
Пленочные резисторы можно приблизительно классифицировать следующим образом:
- значения < 100 Ом являются индуктивными. Значения
- от 100 до 470 Ом практически соответствуют истинному сопротивлению.

- значений выше 470 Ом являются емкостными.
Азбука CLR: Глава R Резисторы
Зависимость от напряжения и частоты
Лицензия EPCI.0151 [2] CLR Passive Components Handbook by P-O.Fagerholt*
*используется в соответствии с авторскими правами EPCI от CTI Corporation, USA
Содержимое этой страницы находится под лицензией Creative Commons Attribution-Share Alike 4.0 International License.
см. предыдущую страницу:
Шум и коррозия
< Страница 4 >
см. следующую страницу:
Резисторы с проволочной обмоткой – конструкция, импульсная нагрузка и типы
Зависимость тока фотоэффекта от частоты на основе моделирования PhET
Задавать вопрос
Спросил
Изменено 4 года, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Итак, я понимаю, что интенсивность должна быть единственным фактором, увеличивающим ток, поскольку ответ на аналогичный вопрос (Фотоэффект — Зависимость тока от частоты) мудро объяснен, предполагая, что Катод, из которого уходят электроны, поддерживается на уровне любовника или того же потенциала, что и анод. Если бы было наоборот, то, однако, насколько я знаю и показывает симулятор, ток зависел бы от напряжения, потому что не каждый высвобождающийся электрон достигал бы анода из-за тормозящего электрического поля. 915 Гц, что является УФ.
Если бы было наоборот, то, однако, насколько я знаю и показывает симулятор, ток зависел бы от напряжения, потому что не каждый высвобождающийся электрон достигал бы анода из-за тормозящего электрического поля. 915 Гц, что является УФ.
Я даже сделал несколько грубых измерений количества электронов, покидающих катод за 20-секундный интервал. Мой результат был таким: на длине волны 196 нм был выпущен 21 электрон. На длине волны 345 нм высвобождается только 13 электронов.
Итак, я хочу сказать, что нам говорят, что ток не зависит от частоты, более того, количество электронов, высвобождаемых с катода, не зависит от частоты. Что-то не так в моих измерениях или симулятор учитывает что-то, о чем не рассказывается в школьном учебнике?
- электрический ток
- моделирование
- частота
- программное обеспечение
- фотоэлектрический эффект
$\endgroup$
$\begingroup$
Хотя интенсивность может быть одинаковой, фотоны с более низкой длиной волны обладают большей энергией и поэтому могут передать больше энергии электрону.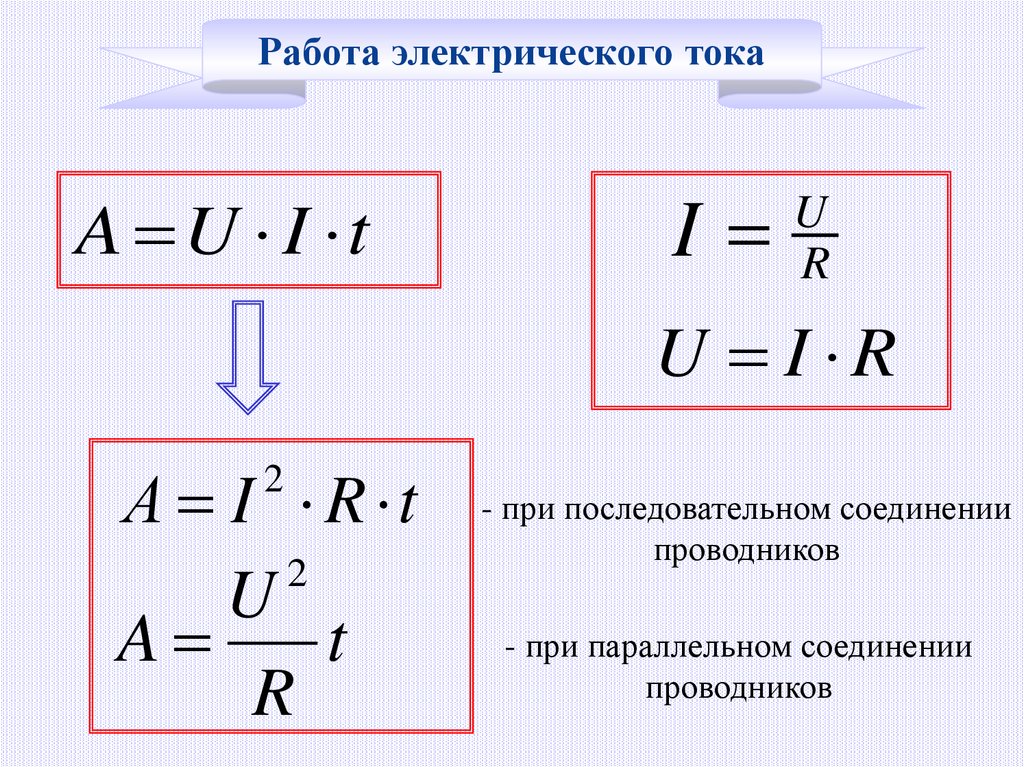
Электрон с большей энергией имеет больше шансов вырваться из металла.
Таким образом, хотя большее количество электронов в секунду может получить энергию от фотонов с более высокой длиной волны, их шансы на спасение меньше, чем меньшее количество электронов в секунду, отдаваемое фотонами с более низкой длиной волны.
В целом улетучивается больше электронов в секунду, которые приобрели большее количество энергии.
Таким образом, ток насыщения зависит от длины волны падающего излучения, но нелинейным образом.
Обновление
Есть несколько советов для учителей, но если вы не можете зарегистрироваться, вот три соответствующих параграфа:
- Электроны излучаются с разным
выбрасывают электроны с разным диапазоном энергий связи. Если больше
энергия фотона используется для высвобождения электрона, испущенный электрон
будет иметь меньшую кинетическую энергию. Обратите внимание, что это поведение отличается
из упрощенной модели, используемой в некоторых учебниках, в которой все
электроны испускаются с одинаковой кинетической энергией.
 Если ты хочешь
использовать эту упрощенную модель, вы можете проверить «показывать только самые высокие
энергия электронов». Эта опция не меняет графики
потому что ток по-прежнему рассчитывается на основе всех электронов.
Если ты хочешь
использовать эту упрощенную модель, вы можете проверить «показывать только самые высокие
энергия электронов». Эта опция не меняет графики
потому что ток по-прежнему рассчитывается на основе всех электронов. Не каждый фотон испускает электрон, даже если у фотонов достаточно энергии для испускания электронов. Если фотон поглощается электроном с энергией связи большей, чем энергия фотона, электрон будет не быть выпущенным. Фотоны с более высокими энергиями с большей вероятностью высвобождают электроны, потому что большая часть электронов в металл имеет энергию связи меньше, чем энергия фотона. Поэтому при увеличении частоты количество излучаемых электронов (и, следовательно, ток) будет увеличиваться до тех пор, пока все фотоны испускают электроны. Обратите внимание, что это поведение отличается от упрощенная модель, используемая во многих учебниках, в которой каждый фотон с частотой выше пороговой частоты выдает электрон, поэтому ток постоянен выше пороговой частоты.

По умолчанию, поскольку интенсивность света пропорциональна к количеству фотонов, умноженному на частоту, если увеличить частота при неизменной интенсивности количество фотонов уменьшится. Поэтому, если вы увеличиваете частоту выше точка, в которой все фотоны испускают электроны (см. предыдущую пуля), количество испущенных электронов (и, следовательно, ток) начнет уменьшаться. Обратите внимание, что это отличается от упрощенная модель, используемая многими учебниками, в которых актуальна постоянной выше пороговой частоты. Если вы хотите иметь возможность изменить частоту без изменения количества фотонов, выберите «Контролировать количество фотонов вместо интенсивности» в «Опциях». меню.
Последний пункт дает вам способ узнать для моделирования Phet среднее число электронов, испускаемых фотоном, как функцию длины волны фотона.
$\endgroup$
$\begingroup$
Чем больше частота света, тем больше количество энергии на фотон.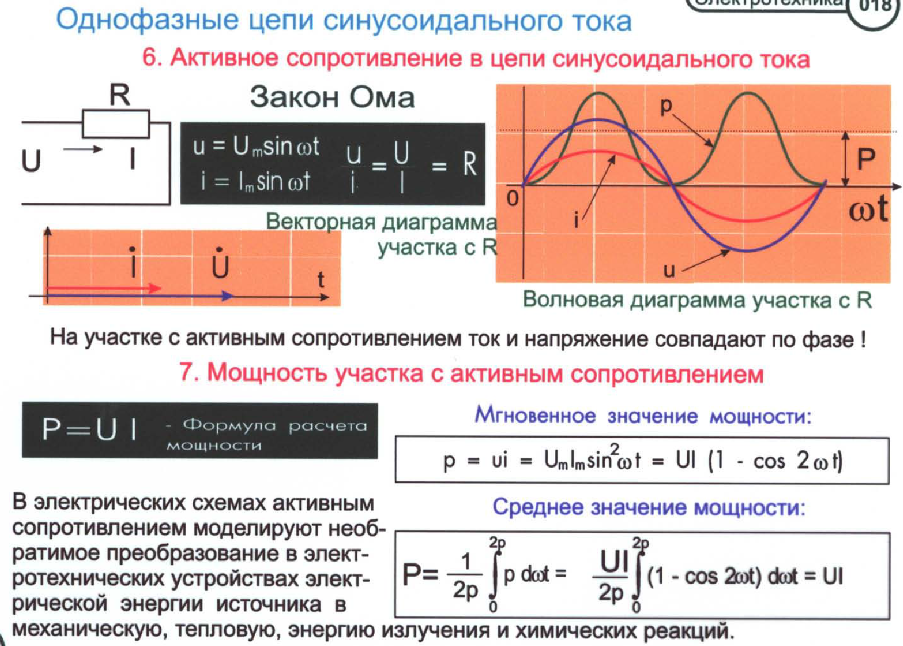 Пороговая частота имеет едва ли достаточную энергию на фотон для выбрасывания электронов и может выбрасывать только те электроны в металле, которые имеют наибольшее количество энергии. (Представьте себе электроны в валентной оболочке или на вершине валентной зоны, хотя это слишком упрощенно, поскольку электроны получают энергию от столкновений атомов и немного «возбуждаются».) Главное, что фотоны с более высоким имеют большую энергию и, следовательно, могут выбрасывать электроны с меньшей энергией. Таким образом, эти фотоны имеют более высокую вероятность выброса электронов. Это как спустить веревку из окна, чтобы вытащить людей. Есть минимальная длина, которая будет работать, но более длинная веревка может дотянуться не только до самых высоких людей, но и до некоторых из более низких людей. Таким образом, вероятность того, что каждый фотон (веревка) может «подтянуть» электрон, возрастает по мере увеличения частоты и, следовательно, увеличения энергии на фотон.
Пороговая частота имеет едва ли достаточную энергию на фотон для выбрасывания электронов и может выбрасывать только те электроны в металле, которые имеют наибольшее количество энергии. (Представьте себе электроны в валентной оболочке или на вершине валентной зоны, хотя это слишком упрощенно, поскольку электроны получают энергию от столкновений атомов и немного «возбуждаются».) Главное, что фотоны с более высоким имеют большую энергию и, следовательно, могут выбрасывать электроны с меньшей энергией. Таким образом, эти фотоны имеют более высокую вероятность выброса электронов. Это как спустить веревку из окна, чтобы вытащить людей. Есть минимальная длина, которая будет работать, но более длинная веревка может дотянуться не только до самых высоких людей, но и до некоторых из более низких людей. Таким образом, вероятность того, что каждый фотон (веревка) может «подтянуть» электрон, возрастает по мере увеличения частоты и, следовательно, увеличения энергии на фотон.
В моделировании с интенсивностью 100% количество фотонов, испускаемых каждую секунду, уменьшается по мере увеличения частоты. Интенсивность, остающаяся постоянной, означает, что энергия, излучаемая в секунду, одинакова. Таким образом, поскольку фотоны более высокой частоты обладают большей энергией, количество фотонов, испускаемых каждую секунду, должно быть меньше. Если вы перейдете в «Параметры» и выберите «Управление количеством фотонов вместо интенсивности», то ток не будет падать, когда частота превысит ~ 196 нм. (Однако кажется, что он достигает максимума, и более высокая частота не влияет на ток. Я могу только предположить, что «веревка» теперь настолько длинная, что касается земли, и поэтому более длинная веревка никому не помогает. )
Интенсивность, остающаяся постоянной, означает, что энергия, излучаемая в секунду, одинакова. Таким образом, поскольку фотоны более высокой частоты обладают большей энергией, количество фотонов, испускаемых каждую секунду, должно быть меньше. Если вы перейдете в «Параметры» и выберите «Управление количеством фотонов вместо интенсивности», то ток не будет падать, когда частота превысит ~ 196 нм. (Однако кажется, что он достигает максимума, и более высокая частота не влияет на ток. Я могу только предположить, что «веревка» теперь настолько длинная, что касается земли, и поэтому более длинная веревка никому не помогает. )
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.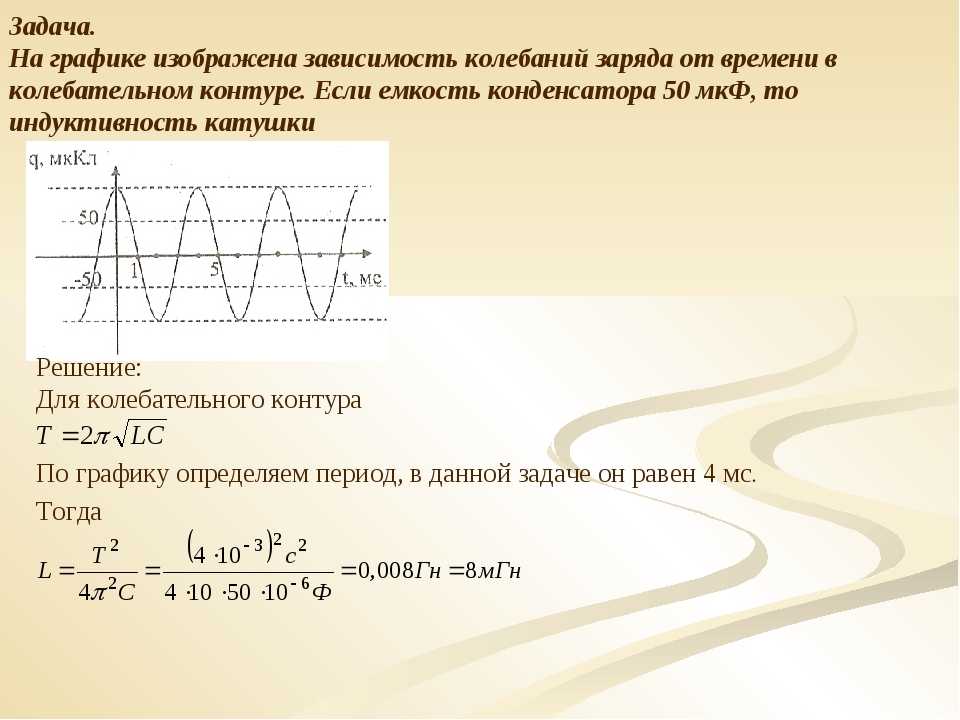
Фотоэлектрический эффект — Зависимость тока от частоты
Спросил
Изменено 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
Все мы знаем, что количество тока, протекающего через пластины, не зависит от частоты. Если бы я спросил, почему это не зависит, вы, вероятно, сказали бы, что это зависит от количества электронов, а не от частоты, или вы могли бы показать мне график зависимости тока от частоты.
Но вот мой теоретический аргумент. Электрический ток определяется как количество заряда, протекающего через точку/пространство/провод в единицу времени. Пусть I ток из-за фотоэлектронов, выбрасываемых фотонами некоторой частоты. Теперь, если я увеличу частоту, кинетическая энергия выброшенного электрона увеличится, поэтому он будет двигаться быстрее и, следовательно, будет давать больший ток (заряд будет проходить через одну и ту же точку много раз в единицу времени). Таким образом, давая чистый ток больше, чем I.
Таким образом, давая чистый ток больше, чем I.
Что не так с моим аргументом?
После долгих размышлений я придумал возможную причину. Как бы быстро ни двигались электроны, при ударе о металлическую пластину они теряют свою скорость и начинают двигаться с дрейфовой скоростью. Теперь есть проблема с этим аргументом. Если бы это было правдой, то я должен был бы ожидать, что большой кусок дополнительных электронов застрянет на аноде.
Если мои рассуждения были верны, то почему я не вижу большого накопления заряда на аноде.
- фотоэффект
$\endgroup$
1
$\begingroup$
Один из способов взглянуть на ток — это «общее количество электронов, проходящих определенную плоскость в единицу времени, умноженное на их заряд».
Неважно, насколько быстро они движутся. Чем быстрее они движутся, тем дальше друг от друга они кажутся.
Заданное количество света (выше критической частоты) выбьет заданное количество фотоэлектронов в космос. Это количество электронов, которые текут, и независимо от их скорости они будут вызывать один и тот же ток.
Если бы у вас была постоянная объемная плотность заряда, то ускорение движения облака электронов увеличило бы ток. Но это не то, что у вас здесь — у вас фиксированное число, а не фиксированная плотность.
Представьте, что машины стоят в пробке. Возможно, четырехполосное шоссе превратилось в однополосное. А давайте представим, что через заданную точку проезжает одна машина в секунду. Может машина едет 10 км/ч. Теперь смотрим пять километров «вниз по течению». Дорога снова 4-полосная, а машины едут со скоростью 120 км/ч. Сколько автомобилей в секунду вы видите проезжающих мимо вас? Конечно, это одна машина в секунду — именно столько машин проезжало через узкое место. Таким образом, хотя автомобили теперь едут намного быстрее, дорога по-прежнему перевозит то же количество автомобилей.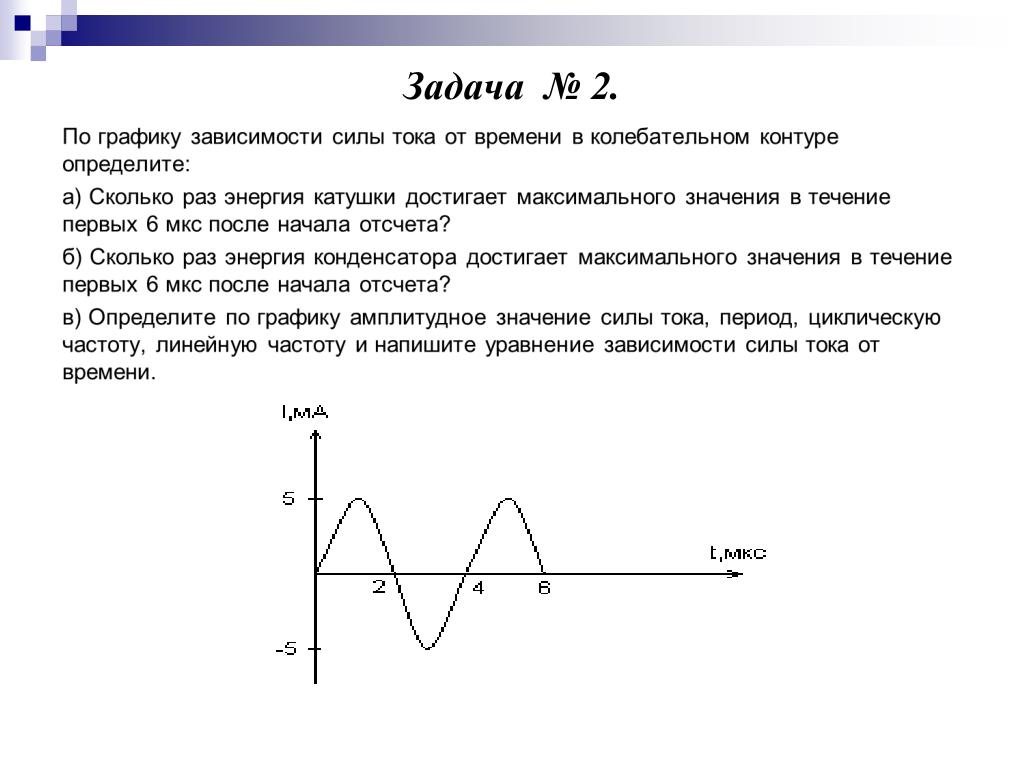 Машины далеко друг от друга. Если бы каким-то образом все в пробке (автомобили стояли бампер к бамперу) поняли, как ехать очень быстро одновременно, количество автомобилей в секунду («текущее») было бы намного больше.
Машины далеко друг от друга. Если бы каким-то образом все в пробке (автомобили стояли бампер к бамперу) поняли, как ехать очень быстро одновременно, количество автомобилей в секунду («текущее») было бы намного больше.
$\endgroup$
6
$\begingroup$
Я думаю, что это зависит от ситуации.
Смотрите, если вы говорите о фототоке насыщения, то НЕТ, фототок не будет зависеть от частоты, потому что все испускаемые фотоэлектроны достигают другой пластины и вносят свой вклад в фототок, любое увеличение частоты не изменит количество фотоэлектронов достигнув другой пластины (поскольку все возможные фотоэлектроны с такой интенсивностью уже испущены), поэтому фототок не изменится.
Но если речь не идет о фототоке насыщения, когда фотон ударяет и испускает фотоэлектрон, фотоэлектрон может потерять свою кинетическую энергию из-за столкновений, и даже если он был удален, он может не достичь другой пластины и не будет способствуют фототоку. В этом случае увеличение частоты может увеличить шансы фотоэлектрона выйти из столкновений и достичь другой пластины.
В этом случае увеличение частоты может увеличить шансы фотоэлектрона выйти из столкновений и достичь другой пластины.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.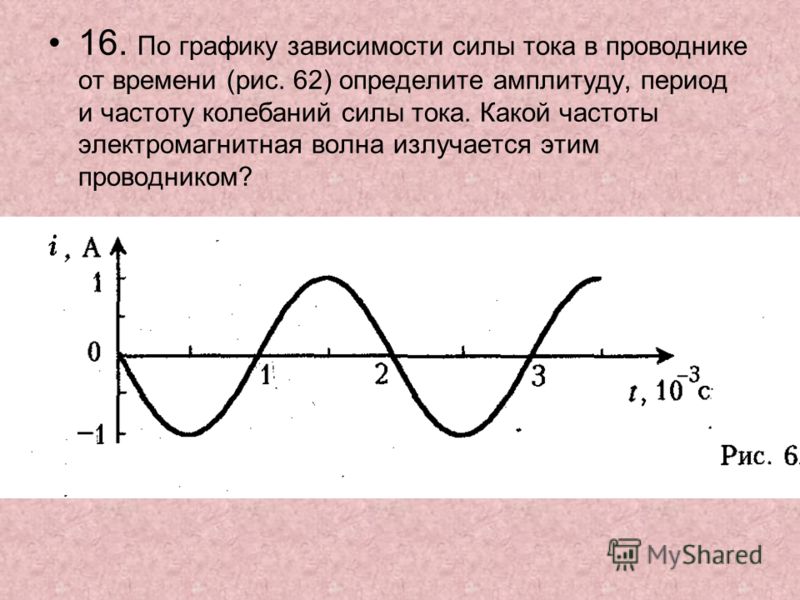
физика элементарных частиц — Зависимость фототока от частоты
Задавать вопрос
Спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 981 раз
$\begingroup$
Звучит как вопрос новичка, но может кто-нибудь объяснить мне, почему фототок не увеличивается, когда мы увеличиваем частоту падающего излучения? Я имею в виду, что увеличение частоты будет означать, что фотоны будут иметь более высокую энергию (E=hf), и эта увеличенная энергия должна соответствовать испускаемому фотоэлектрону. Теперь, поскольку фотоэлектроны имеют более высокую кинетическую энергию, они, очевидно, будут иметь более высокую скорость, а поскольку они будут иметь более высокую скорость, то соотв.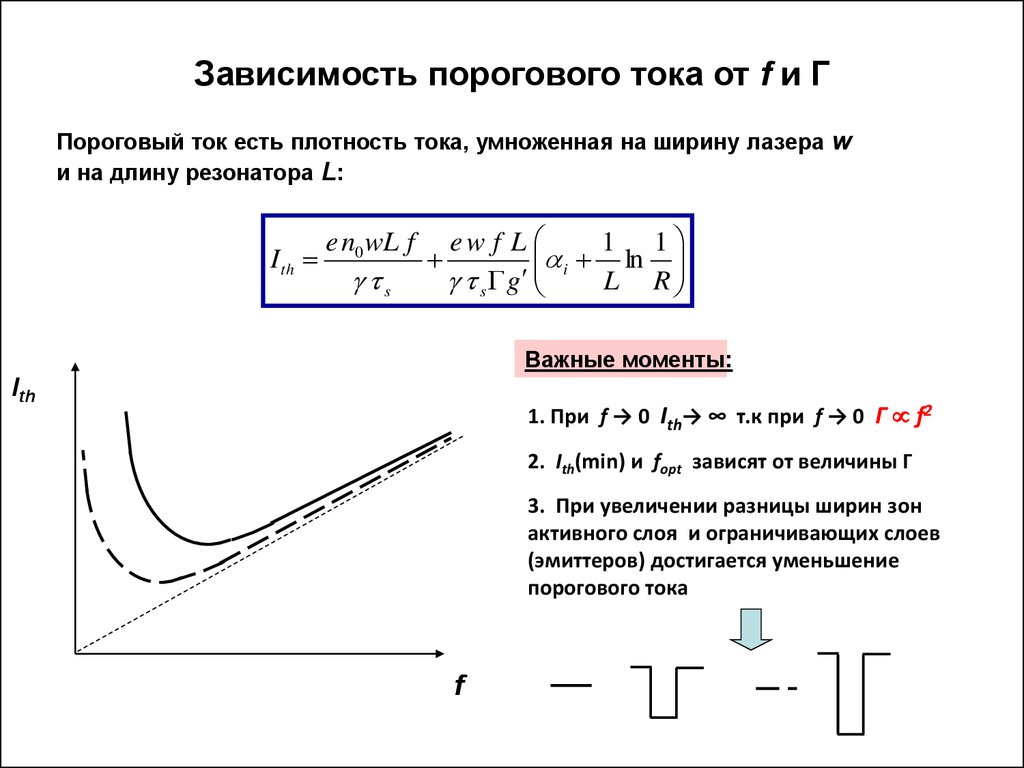 по этой формуле I=nea(vd) ток должен увеличиваться, но не увеличивается (по крайней мере, так написано в моем школьном учебнике). Было бы здорово, если бы кто-нибудь мог объяснить мне это!
по этой формуле I=nea(vd) ток должен увеличиваться, но не увеличивается (по крайней мере, так написано в моем школьном учебнике). Было бы здорово, если бы кто-нибудь мог объяснить мне это!
Редактировать: я не предполагал, что более высокая частота выбьет несколько электронов. То, о чем я спрашиваю, можно объяснить так. Скажем для простоты, что фотодетектор находится в километре от фотоэлектронов, и он показывает ток как количество электронов, достигающих его каждую секунду. Теперь давайте возьмем случай, в котором, скажем, излучаемый свет испускает в общей сложности 10 электронов из данного фоточувствительного материала с заданной частотой и интенсивностью, 5 со скоростью 1 км/с и другие 5 со скоростью 500 РС. Очевидно, через секунду только 5 электронов достигли бы фотодетектора, и он показал бы ток как 5 электронов в секунду. Теперь, в другом случае с тем же прибором, давайте увеличим частоту света, не изменяя его интенсивности, так что скорости испускаемых электронов примерно удвоятся. Несмотря на то, что испускаемые электроны все те же, скорости электронов теперь будут 2 км/с для 5 электронов и 1 км/с для остальных 5 электронов. Теперь, очевидно, через секунду все 10 электронов достигли бы фотодетектора по сравнению только с 5, когда частота была низкой, и фотодетектор показал бы ток как 10 электронов в секунду. Это, безусловно, противоречит тому факту, что фототок не зависит от частоты (учитывая, что частота выше работы выхода светочувствительного материала), поэтому я просто спрашиваю, как объяснить это противоречие.
Несмотря на то, что испускаемые электроны все те же, скорости электронов теперь будут 2 км/с для 5 электронов и 1 км/с для остальных 5 электронов. Теперь, очевидно, через секунду все 10 электронов достигли бы фотодетектора по сравнению только с 5, когда частота была низкой, и фотодетектор показал бы ток как 10 электронов в секунду. Это, безусловно, противоречит тому факту, что фототок не зависит от частоты (учитывая, что частота выше работы выхода светочувствительного материала), поэтому я просто спрашиваю, как объяснить это противоречие.
Спасибо!
- физика элементарных частиц
- электричество
- фотоны
- электрический ток
- фотоэлектрический эффект
$\endgroup$
7
$\begingroup$
Фототок — это постоянный ток.
Давайте возьмем ваш пример и предположим, что ваш источник света излучает 10 фотоэлектронов в секунду.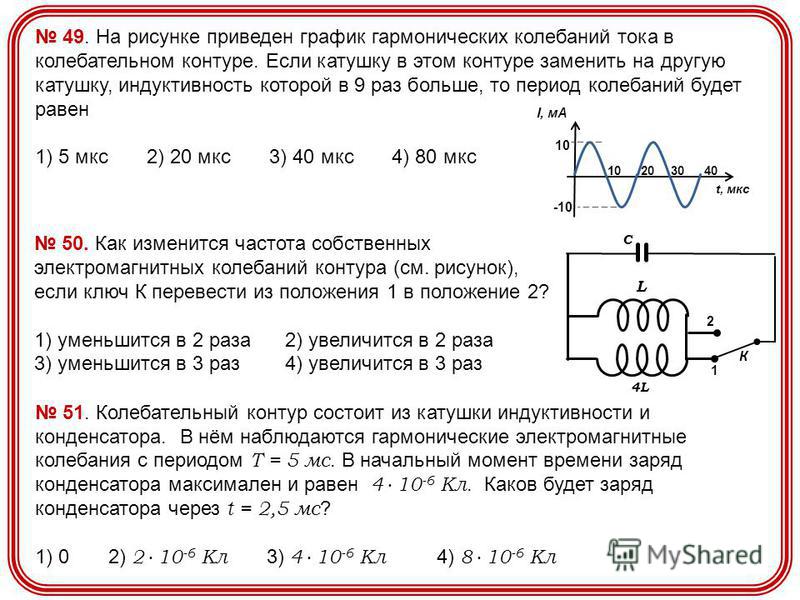 Вы можете использовать две частоты: на более низкой частоте электроны движутся со скоростью 1 км/с, а на более высокой частоте электроны движутся со скоростью 2 км/с.
Вы можете использовать две частоты: на более низкой частоте электроны движутся со скоростью 1 км/с, а на более высокой частоте электроны движутся со скоростью 2 км/с.
Когда вы впервые включаете свет, происходит задержка перед тем, как первые фотоэлектроны достигнут детектора. Для более низкой частоты эта задержка составляет одну секунду, а для более высокой частоты — 0,5 секунды. Таким образом, существует разница между частотами при первом включении света.
Однако, как только ток достигает установившегося состояния, из металла испускается 10 фотоэлектронов в секунду, а детектор принимает 10 электронов в секунду. Неважно, как быстро движутся электроны, потому что это влияет только на начальную задержку, а не на стационарное состояние. Вот почему нет разницы между частотами.
Единственный способ, которым частота будет иметь значение, это если изменится количество электронов, испускаемых в секунду, то есть изменится квантовая эффективность. Это то, что Whit3rd имеет в виду в своем ответе.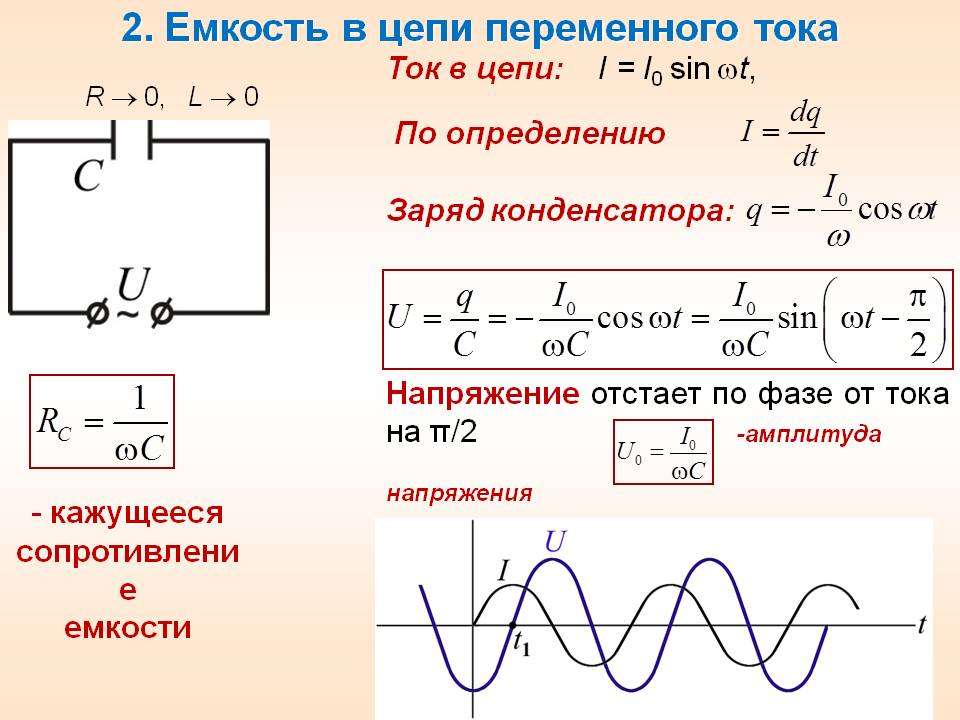 В целом квантовая эффективность меняется с частотой, но для металлов на частотах, близких к работе выхода (и превышающих ее), изменения квантовой эффективности незначительны.
В целом квантовая эффективность меняется с частотой, но для металлов на частотах, близких к работе выхода (и превышающих ее), изменения квантовой эффективности незначительны.
$\endgroup$
$\begingroup$
В некоторых случаях она ДЕЙСТВИТЕЛЬНО увеличивается: примерно один ион на 36 эВ – это эмпирическое правило для рентгеновских лучей, генерирующих свободные заряды, как, например, в детекторе с ионизационной камерой. Это происходит только тогда, когда количество энергии в фотоне настолько велико, что он генерирует каскад ионов при поглощении, а простой фотоэлектрический эффект «один фотон производит один электрон» генерирует электроны с более высокой кинетической энергией, но не МНОЖЕСТВО электронов. (позже достаточно быстрый электрон может врезаться в атомы и освободить больше электронов, но они вторичны по отношению к начальному поглощению фотонов).
Это эмпирическое правило подразумевает, что фотон видимого света (около 2 эВ) не производит несколько свободных электрических зарядов при фотоэлектрическом взаимодействии, потому что вторичные столкновения не будут достаточно энергичными.
$\endgroup$
$\begingroup$
Ну, это зависит. Фотоэлектрон может иметь кинетическую энергию от нуля до
Макс. Кинетическая энергия = hv - (работа выхода металла)
Зависит от электронов. Никогда не знаешь, сколько столкновений он претерпел, прежде чем покинуть металл. Итак, если вы строго говорите, что все электроны будут иметь максимальную кинетическую энергию, то теоретически фототок обязательно увеличится. Но нельзя комментировать строго в практической ситуации.
$\endgroup$
Зависимость резистора от напряжения и частоты
В этой статье мы обсудим, что такое зависимость резистора от напряжения и частоты в основных соотношениях, а также специфичных для резисторных технологий.
Зависимость от напряжения Если мы приложим напряжение к резистору, его сопротивление немного упадет в некоторых типах. Следовательно, изменение сопротивления отрицательно. Изменение приложенного напряжения на вольт называется коэффициент напряжения, VC, и выражается в %/В или лучше, мкВ/В. Коэффициент определяется не только резистивным материалом, но и размерами, т. е. напряженностью электрического поля, и временем приложенного напряжения. Таким образом, MIL-STD-202, метод 309 предписывает измерения, когда напряжение подается прерывисто менее чем на 0,5 секунды. Выполняются два измерения: сопротивление (r) при 0,1 х номинального напряжения (В R ) и сопротивление (R) при 1,0 х В R . Коэффициент напряжения, VC, затем вычисляется как:
Следовательно, изменение сопротивления отрицательно. Изменение приложенного напряжения на вольт называется коэффициент напряжения, VC, и выражается в %/В или лучше, мкВ/В. Коэффициент определяется не только резистивным материалом, но и размерами, т. е. напряженностью электрического поля, и временем приложенного напряжения. Таким образом, MIL-STD-202, метод 309 предписывает измерения, когда напряжение подается прерывисто менее чем на 0,5 секунды. Выполняются два измерения: сопротивление (r) при 0,1 х номинального напряжения (В R ) и сопротивление (R) при 1,0 х В R . Коэффициент напряжения, VC, затем вычисляется как:
Если не принимать во внимание чисто металлические резистивные элементы, то общие значения коэффициента напряжения составляют от –10 до –100 мкВ/В. Зависимость от напряжения незначительна для значений сопротивления ниже 1000 Ом .
Явная зависимость от напряжения в сочетании с напряжением переменного тока вызовет искажения и затухание третьей гармоники.
Резистор имеет определенную паразитную степень как емкости, так и индуктивности. Между витками имеется некая емкостная связь. Индуктивность появляется уже в прямом выводе, длиной примерно 1 нГн/мм, но усиливается действием катушки из обмоток и спиралевидных узоров. В резисторах из углеродного состава проявляется только емкость, возникающая из множества параллельных путей тока.
На рис. 1 показана эквивалентная схема, упрощенная до моделей для высоких и низких значений сопротивления.
Рис. 1. Примеры эквивалентных схем для резисторов с разной степенью упрощения- а) Малые размеры
- б) Низкое значение R
- в) Конструкция микросхемы
- г) Малые выводы или отсутствие выводов (SMD)
- д) Даже корпус
Частотная зависимость сопротивления уменьшается если резисторы:
- имеют небольшие размеры.
- имеют низкое значение сопротивления.

- имеют тонкопленочную конструкцию. Даже толстопленочный дизайн благоприятен.
- имеют как можно более короткий вывод, как SMD.
- геометрически ровные, т. е. без резких геометрических изменений вдоль корпуса резистора.
Как частотная зависимость может влиять на импеданс, показано на рис. 2.
Рис. 2. Примеры частотной зависимости резистора как отношения импеданса переменного тока к сопротивлению постоянному току для некоторых различных типов резисторов- Состав углерода, ¼ W, 1 MW.
- Состав углерода, ¼ Вт, 100 кВт.
- Чип, толстопленочный, размер EIA 0603, 100 кВт; в » 0,05 пФ; L » 0,4 нГн.
- Металлическая глазурь или металлическая пленка, размер DIN 0207, 100 кВт; в » 0,4 пФ.
- MELF, размер DIN 0204, 10 кВт.
- Чип, толстопленочный, размер EIA 0603, 10 кВт; в » 0,05 пФ; L » 0,4 нГн.; Чип, металлическая фольга, размер EIA 1210, 10 кВт.

- Чип толстопленочный, размер EIA 0603, 1 кВт; в » 0,05 пФ; L » 0,4 нГн.
- MELF, размер DIN 0102, высокочастотное исполнение, 10 Вт; в » 0,035 пФ; L » 0,8 нГн.
- MELF, размер DIN 0204, 10 Вт.
- Чип, толстая пленка, размер EIA 0603, 10 Вт; в » 0,05 пФ; L » 0,4 нГн.
- Чип, тонкопленочный, размер EIA 0603, 100 Вт; в » 0,035 пФ; L » 1,2 нГн.
- Чип, толстопленочный, размер EIA 0603, 100 Вт; в » 0,05 пФ; L » 0,4 нГн.
Примеры на рис. 2 приведены только для справки. Они взяты из технических паспортов основных производителей. Обратите внимание, как значение сопротивления эквивалентного в остальном компонента влияет на параметры: № 3, 6, 7, 10 и 12. Другой пример № 8 показывает компонент MELF, который с помощью специальной техники спиралеобразования получает превосходное качество. высокочастотные характеристики. Как правило, частотную зависимость различных материалов резисторов можно разделить на три группы:
| Технология | Частотная зависимость |
| Композиция углерода | High |
| MELLACE, CERMET, толстая пленка | |
| MEALL MALLAZE, CERMET, толстая пленка | |
| MEAL пленочные | низкие |
Пленочные резисторы можно приблизительно классифицировать следующим образом:
- значения < 100 Ом являются индуктивными.
 Значения
Значения - от 100 до 470 Ом являются практически настоящим сопротивлением.
- значения выше 470 Ом являются емкостными.
По мере того, как промышленность расширяет диапазон продуктов выше диапазона ГГц (5G), необходимо учитывать и улучшать характеристики резисторов, особенно в тонкопленочных продуктах.
Характеристики тонкопленочных резисторов на высоких частотах зависят от размера корпуса, метода подгонки, номинала детали и типа подключения. Уменьшение паразитного импеданса для корпусов меньшего размера согласуется с меньшими посадочными площадками и размерами устройства.
Тип окончания:
Рисунок 3. Примеры стиля завершения; источник: Vishay Таблица 1. пример параметров чип-резисторов и их паразитных коэффициентов; источник: Vishay Большое различие между 0201 и 0402 и 0603 может быть связано со значительным уменьшением максимальной площади резистора.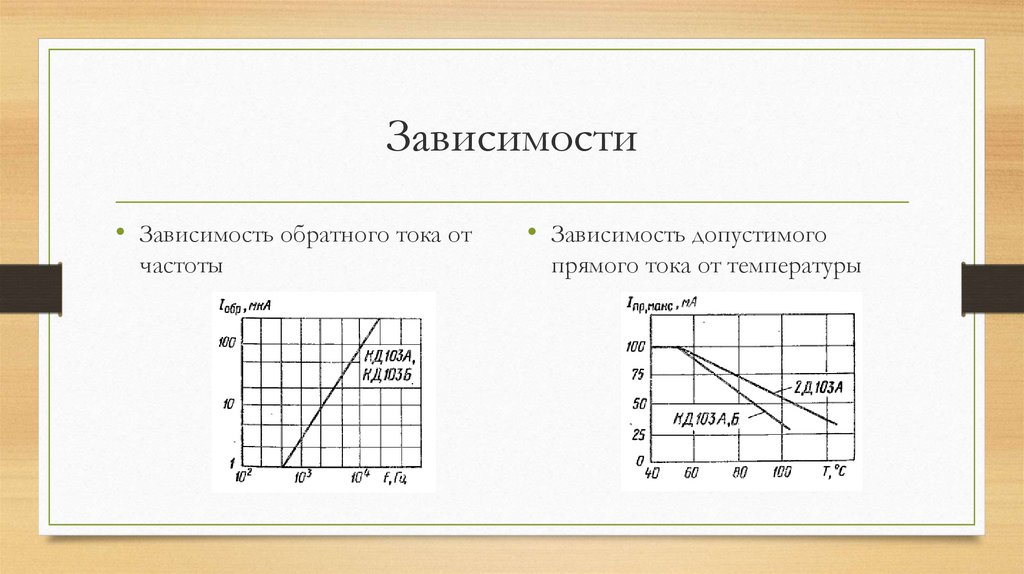 Отношения максимальных площадей резисторов по размеру корпуса (0603 : 0402 : 0201) составляют 1 : 2,32 : 20,4. Небольшое изменение площади устройства для размеров корпуса 0402 и 0603, скорее всего, связано с небольшими различиями и случайным изменением характеристик устройства.
Отношения максимальных площадей резисторов по размеру корпуса (0603 : 0402 : 0201) составляют 1 : 2,32 : 20,4. Небольшое изменение площади устройства для размеров корпуса 0402 и 0603, скорее всего, связано с небольшими различиями и случайным изменением характеристик устройства.
Метод подстройки:
Рис. 4. Методы подстройки резистора: (a) сбалансированное измерение фронта, (b) L-образный вырез и (c) S-cu; источник: Vishay Рисунок 5. Сравнение методов обрезки для корпусов размеров (a) 0402 и (b) 0603. Трим Edge Sense имеет наилучшие характеристики импеданса; источник: Vishay2.3: Photoelectric Effect — Chemistry LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4474
- Дэвид М.
 2с\)) должна переходить в кинетическую энергию испущенных электронов. Кроме того, количество электронов, отрывающихся от металла, должно меняться в зависимости от частоты световой волны. Эта зависимость от частоты была ожидаемой, потому что колеблющееся электрическое поле световой волны заставляет электроны в металле колебаться вперед и назад, и электроны в металле реагируют на разных частотах. Другими словами, ожидалось, что число испускаемых электронов должно зависеть от частоты, а их кинетическая энергия должна зависеть от интенсивности световой волны (при фиксированной длине волны).
2с\)) должна переходить в кинетическую энергию испущенных электронов. Кроме того, количество электронов, отрывающихся от металла, должно меняться в зависимости от частоты световой волны. Эта зависимость от частоты была ожидаемой, потому что колеблющееся электрическое поле световой волны заставляет электроны в металле колебаться вперед и назад, и электроны в металле реагируют на разных частотах. Другими словами, ожидалось, что число испускаемых электронов должно зависеть от частоты, а их кинетическая энергия должна зависеть от интенсивности световой волны (при фиксированной длине волны).Классическое ожидание фотоэффекта заключалось в том, что число испускаемых электронов будет зависеть от частоты, а их кинетическая энергия должна зависеть от интенсивности световой волны.
Как показано на рисунке \(\PageIndex{1}\), в фотоэлектрическом эффекте наблюдается прямо противоположное поведение. Интенсивность влияет на количество электронов, а частота влияет на кинетическую энергию испускаемых электронов.
 Из этих зарисовок мы видим, что:
Из этих зарисовок мы видим, что:- кинетическая энергия электронов линейно пропорциональна частоте падающего излучения выше порогового значения \(ν_0\) (ниже \(ν_0\) ток не наблюдается), а кинетическая энергия не зависит от интенсивности излучения.
- число электронов (т. е. электрический ток) пропорционально интенсивности света (при фиксированной длине волны) и не зависит от частоты падающего излучения выше порогового значения \(ν_0\) (ниже \( ток не наблюдается). ν_0\)).
В 1905 году Альберт Эйнштейн объяснил наблюдения, показанные на рисунке \(\PageIndex{1}\), смелой гипотезой о том, что энергия, переносимая светом, существует в виде пакетов величиной \(h\nu\).
 2\) испущенного электрона. 9{14}\) Гц? Какова скорость этого фотоэлектрона? Из какой области электромагнитного спектра этот фотон?
2\) испущенного электрона. 9{14}\) Гц? Какова скорость этого фотоэлектрона? Из какой области электромагнитного спектра этот фотон?При таком анализе Эйнштейн получил значение \(h\), согласующееся со значением, полученным Планком из спектрального распределения излучения черного тела. Тот факт, что одна и та же константа квантования могла быть получена из двух очень разных экспериментальных наблюдений, был очень впечатляющим и сделал концепцию квантования энергии как для материи, так и для света убедительной. В следующих разделах мы увидим, что длина волны и импульс являются свойствами, которые также связаны как для материи, так и для света.
Эта страница под названием 2.3: Фотоэлектрический эффект распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Дэвидом М. Хэнсоном, Эрикой Харви, Робертом Суини, Терезой Джулией Зелински через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.




 Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.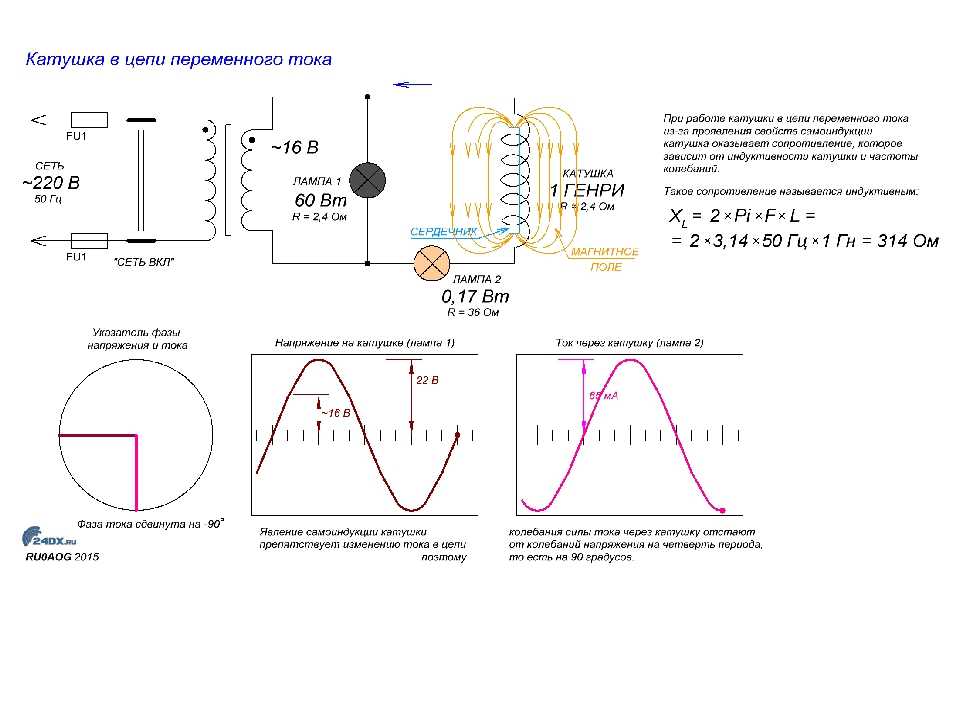

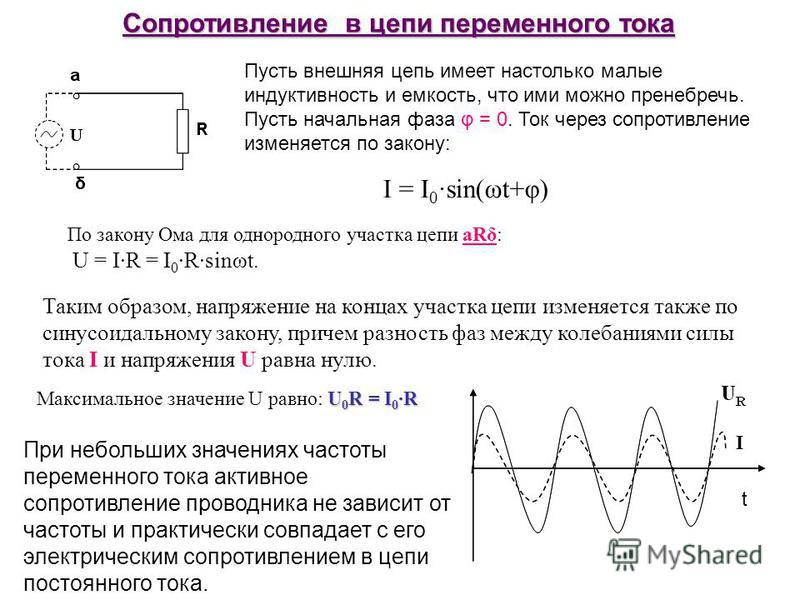
 ..
..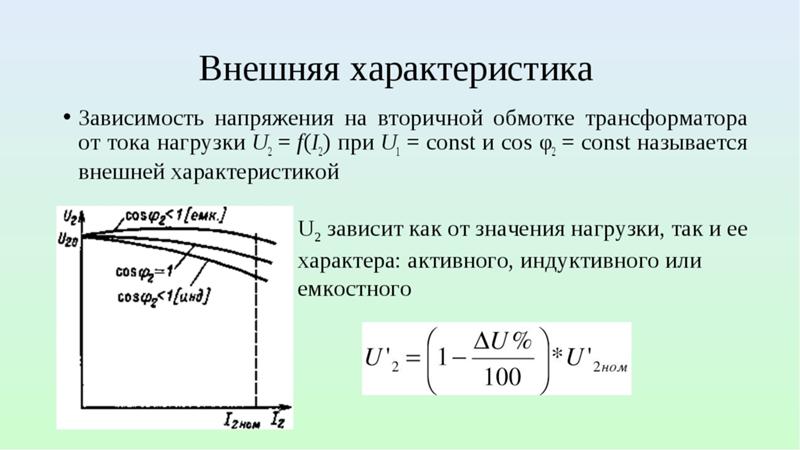 ..
..

 Если ты хочешь
использовать эту упрощенную модель, вы можете проверить «показывать только самые высокие
энергия электронов». Эта опция не меняет графики
потому что ток по-прежнему рассчитывается на основе всех электронов.
Если ты хочешь
использовать эту упрощенную модель, вы можете проверить «показывать только самые высокие
энергия электронов». Эта опция не меняет графики
потому что ток по-прежнему рассчитывается на основе всех электронов.


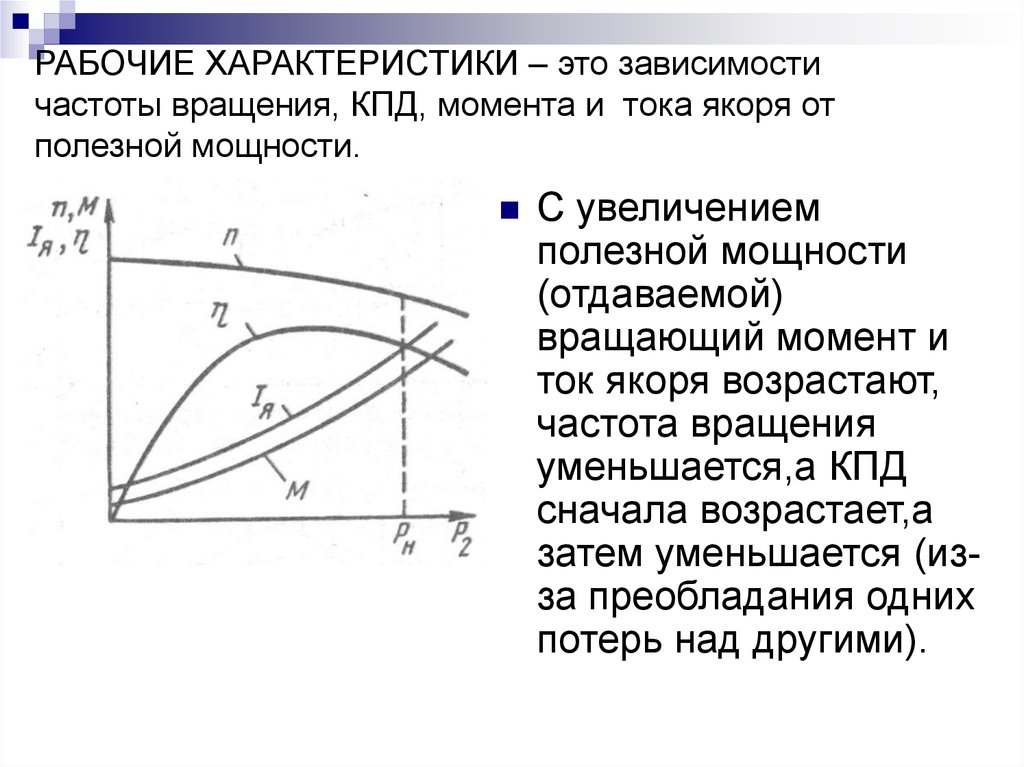
 2с\)) должна переходить в кинетическую энергию испущенных электронов. Кроме того, количество электронов, отрывающихся от металла, должно меняться в зависимости от частоты световой волны. Эта зависимость от частоты была ожидаемой, потому что колеблющееся электрическое поле световой волны заставляет электроны в металле колебаться вперед и назад, и электроны в металле реагируют на разных частотах. Другими словами, ожидалось, что число испускаемых электронов должно зависеть от частоты, а их кинетическая энергия должна зависеть от интенсивности световой волны (при фиксированной длине волны).
2с\)) должна переходить в кинетическую энергию испущенных электронов. Кроме того, количество электронов, отрывающихся от металла, должно меняться в зависимости от частоты световой волны. Эта зависимость от частоты была ожидаемой, потому что колеблющееся электрическое поле световой волны заставляет электроны в металле колебаться вперед и назад, и электроны в металле реагируют на разных частотах. Другими словами, ожидалось, что число испускаемых электронов должно зависеть от частоты, а их кинетическая энергия должна зависеть от интенсивности световой волны (при фиксированной длине волны).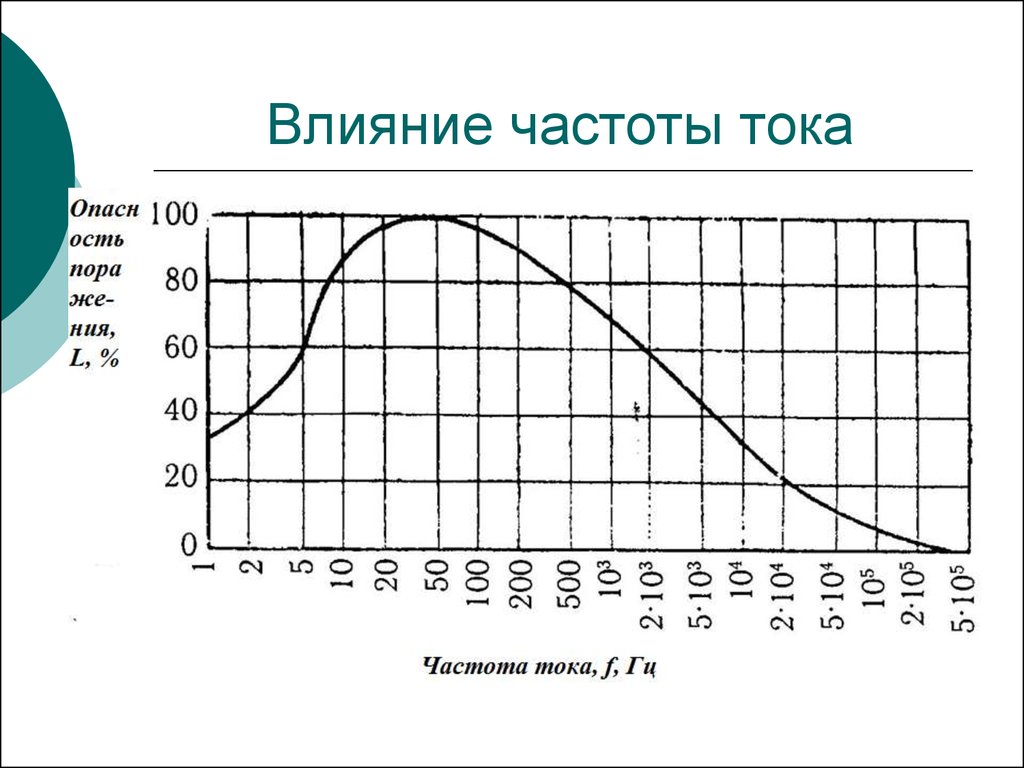 Из этих зарисовок мы видим, что:
Из этих зарисовок мы видим, что: 2\) испущенного электрона. 9{14}\) Гц? Какова скорость этого фотоэлектрона? Из какой области электромагнитного спектра этот фотон?
2\) испущенного электрона. 9{14}\) Гц? Какова скорость этого фотоэлектрона? Из какой области электромагнитного спектра этот фотон?