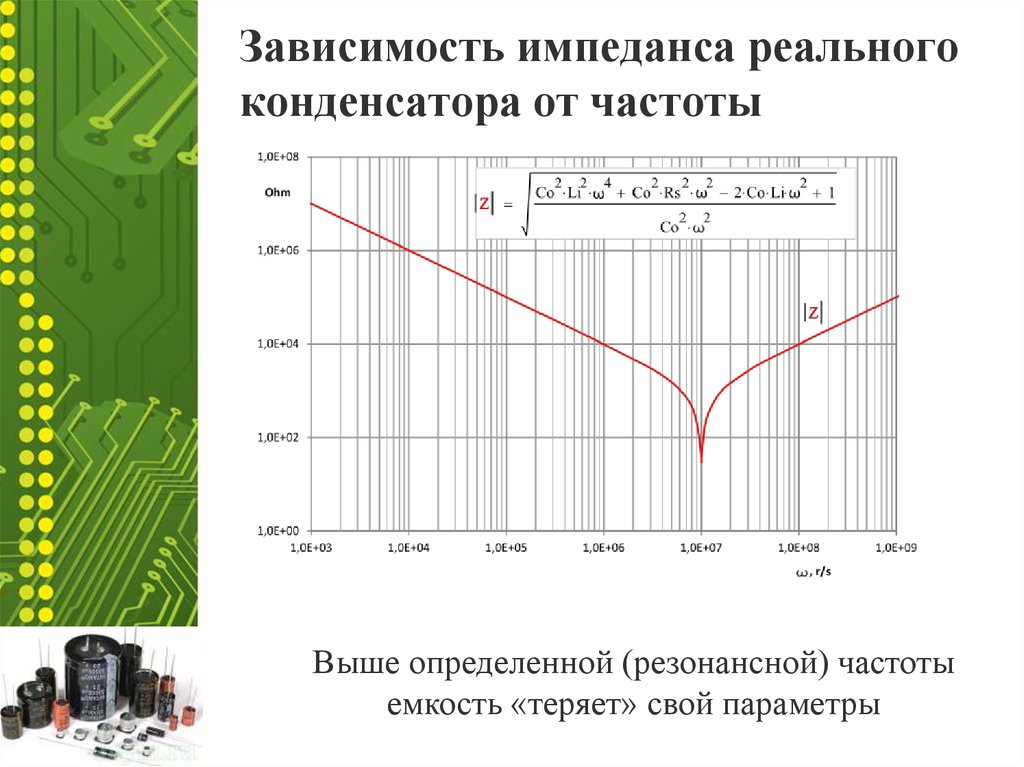
Зависимость частоты от сопротивления
Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Емкостное сопротивление
- Резонанс в цепи переменного тока
- Индуктивное сопротивление катушки
- Зависимость индуктивного и емкостного сопротивления от частоты тока
- Активное и реактивное сопротивление
- Сопротивления
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Зависимость тока от частоты и индуктивности
youtube.com/embed/9r38-SfTbms» frameborder=»0″ allowfullscreen=»»/>Емкостное сопротивление
Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.
Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным. На практике все это надо обязательно учитывать, потому что возможны ситуации обычно связанные с ростом частоты сигнала , когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности.
При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель.
Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про емкостное сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления. Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все рисунок 1.
Рисунок 1 — Конденсатор в цепи переменного тока. К его обкладкам приложено некоторое переменное напряжение U t , и через него течет некоторый ток I t. Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока , там мы про все это довольно подробно говорили.
Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так. В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом.
Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья?
В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа.
Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида. Почему это так, откуда взялось, что здесь какая буковка значит — обо всем уже подробно говорили.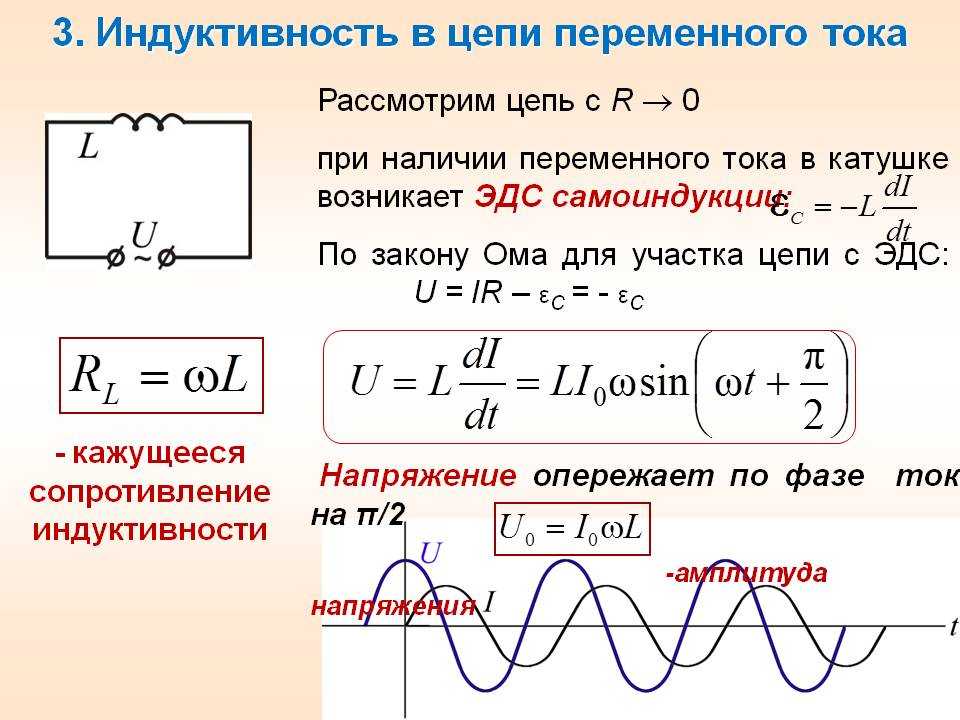 Для повторения можно перейти по ссылке и еще раз со всем ознакомиться. Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого. Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике.
Для повторения можно перейти по ссылке и еще раз со всем ознакомиться. Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого. Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике.
Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала.
Сейчас как раз такой момент. Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями. Итак, у нас имеется три множителя.
Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике , не зря ж я ее писал.
Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид. Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Как мы помним из статьи про закон Ома , у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение — переменные и представлены через комплексные амплитуды.
Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение — переменные и представлены через комплексные амплитуды.
Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току :.
Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное. Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность?
На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье.
Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент. Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло. Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода?
Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло. Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода?
Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно. Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения.
Соответственно, если сдвиг фаз нас не интересует , то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:. Согласитесь, жить стало чуточку легче.
Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала.
Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения.
Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току. По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным.
И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ.
График представлен на рисунке 2. Рисунок 2 кликабельно — Зависимость сопротивления конденсатора от частоты. На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.
Резонанс в цепи переменного тока
В статье расскажем что такое колебательный контур. Последовательный и параллельный колебательный контур. Разделяется на два типа в зависимости от соединения элементов: последовательный и параллельный. Основная радиоэлементная база колебательного контура : Конденсатор, источник питания и катушка индуктивности.
При f=0 сопротивление имеет наибольшее значение, с ростом частоты zh RВ. Зависимость сопротивления тела человека от частоты приложенного.
Индуктивное сопротивление катушки
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление. Еще иногда его называют омическим. Активист готов всегда рвать и метать даже ночью. То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания. Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:. На схеме мы видим генератор частоты и резистор. Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты.
Еще иногда его называют омическим. Активист готов всегда рвать и метать даже ночью. То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания. Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:. На схеме мы видим генератор частоты и резистор. Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты.
Зависимость индуктивного и емкостного сопротивления от частоты тока
Предложить термин Сообщить об ошибке Отправить страницу Добавить в избранное. Емкостное сопротивление зависит от емкости конденсатора и частоты, причем с увеличением частоты емкостное сопротивление в отличие от индуктивного уменьшается. Емкостное сопротивление обратно пропорционально частоте. Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь.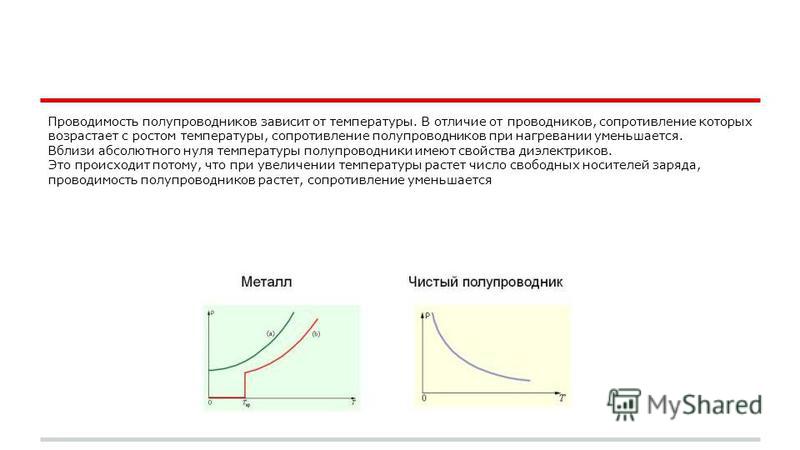 Емкостное сопротивление обратно пропорционально частоте приложенного напряжения.
Емкостное сопротивление обратно пропорционально частоте приложенного напряжения.
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Активное и реактивное сопротивление
В цепи постоянного тока конденсатор представляет собой бесконечно большее сопротивление: постоянный ток не проходит через диэлектрик, разделяющий обкладки конденсатора. Цепи переменного тока конденсатор не разрывает: попеременно заряжаясь и разряжаясь, он обеспечивает движение электрических зарядов, т. Исходя из электромагнитной теории Максвелла см. Таким образом, для переменного тока конденсатор представляет собой конечное сопротивление, называемое емкостным сопротивлением. Сила тока будет, наибольшей в случае прямого провода. Если же провод свернут в виде катушки с большим числом витков, то сила тока в нем значительно уменьшится: особенно резкое снижение тока происходит при введении в эту катушку ферромагнитного сердечника.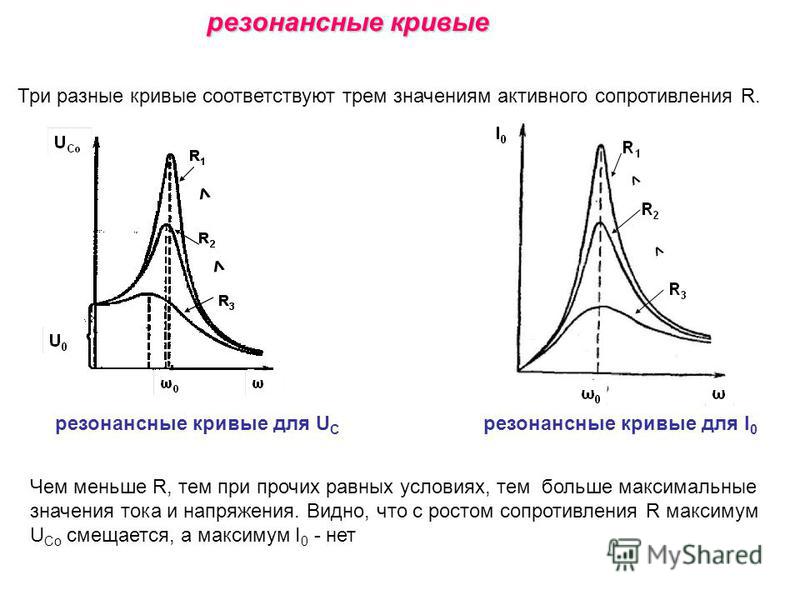
Сопротивления
Активное и реактивное сопротивления. Сопротивление, оказываемое проходами и потребителями в цепях постоянного тока, называется о мическим сопротивлением. Если какой-либо проводник включить в цепь переменного тока, то окажется, что его сопротивление будет несколько больше, чем в цепи постоянного тока. Это объясняется явлением, получившим название скин-эффекта поверхностный эффект. Сущность его заключается в следующем. При прохождении переменного тока по проводнику внутри него существует переменное магнитное поле, пересекающее проводник. Магнитные силовые линии этого поля индуктируют в проводнике ЭДС , однако она будет не одинаковой в различных точках сечения проводника: к центру сечения на больше, а к периферии — меньше. Это объясняется тем, что точки, лежащие ближе к центру, пересекаются большим числом силовых линий.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к .
Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивном элементе пропорционально скорости изменения тока:.
Из формул для расчета емкостного и индуктивного сопротивлений видно, что емкостное сопротивление изменяется обратно пропорционально круговой частоте, а индуктивное сопротивление — прямо пропорционально, что отражено на графике зависимости индуктивного и емкостного сопротивлений от частоты переменного тока рис. Рассмотрим последовательную цепь переменного тока, содержащую резистор, конденсатор и катушку индуктивности рис. Дата добавления: ; просмотров: ; Опубликованный материал нарушает авторские права? Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. Политическая мысль в США в период борьбы за независимость Автоматизация измерения частоты и периода.
Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока.
Изменение частоты переменного тока По замкнутому контуру течет переменный ток частотой 50 гц. Что надо сделать, чтобы на каком-либо Рассчитать магнитный поток в рабочем воздушном зазоре электромагнита переменного тока промышленной частоты Рассчитать магнитный поток в рабочем воздушном зазоре электромагнита переменного тока промышленной Определить амплитудное значение силы тока и частоты. Какие показания амперметра, включенного в этот круг? Определить силу тока в контуре через 0,01 с после отключения от источника тока Здравствуйте уважаемые форумчане. Нужна помощь в задании по физике.
Если подключить катушку индуктивности в цепь электротока переменного типа, то этот ток будет изменяться под влиянием непрерывного изменения электронапряжения. Такие изменения являются генераторами магнитного поля, которое убывает и возрастает периодами. Магнитное поле влияет на катушку, которая создает встречное электронапряжение, что препятствует изменению тока. Соответственно, ток протекает по цепи с постоянным противодействием, которое называется индуктивным сопротивлением.
Соответственно, ток протекает по цепи с постоянным противодействием, которое называется индуктивным сопротивлением.
| U, B | UR, B | UC, B | I, мА | φ, град. | R, Ом | ХΔ, Ом | Z, Ом | Примечание |
· Вычислите:
Фазовый угол
Полное сопротивление цепи
Активное сопротивление цепи
Емкостное реактивное сопротивление цепи
·Выберите масштабы и постройте векторную диаграмму напряжений (рис. 5) и треугольник сопротивлений (рис. 6).
Рис. 3.5 Рис. 3.6
Контрольные вопросы:
- Что называется периодом?
- Что называется частотой?
- Для переменного напряжения и тока записать выражения мгновенных напряжений и токов, дать определение амплитуды и начальной фазы.

- Дать определение действующего напряжения (тока), указать его связь с амплитудой напряжения (тока).
- Дать определения мгновенной и активной мощности.
- Объяснить назначение приборов в измерительной цепи.
- Какие элементы обладают активным сопротивлением.
- Какой вид имеет временная диаграмма напряжений и тока при последовательном соединении R и C-цепей?
- Изобразите треугольники напряжений, сопротивлений и мощностей для цепи с активно-ёмкостной нагрузкой. Чем они отличаются от треугольников для активно-индуктивной нагрузки?
Лабораторная работа 4
Дата добавления: 2016-12-04; просмотров: 1927 | Нарушение авторских прав
Начальная фаза. Сдвиг фаз
 При вращении в них буду находится ЭДС одинаковой частоты и амплитуды.
При вращении в них буду находится ЭДС одинаковой частоты и амплитуды.Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени ЭДС витка будет:
В этих выражениях углы и называются фазными, или фазой. Углы и называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
Любая синусоидальная величина характеризуется:
1. Амплитудой;
2. Угловой частотой;
Угловой частотой;
3. Начальной фазой.
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью . Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.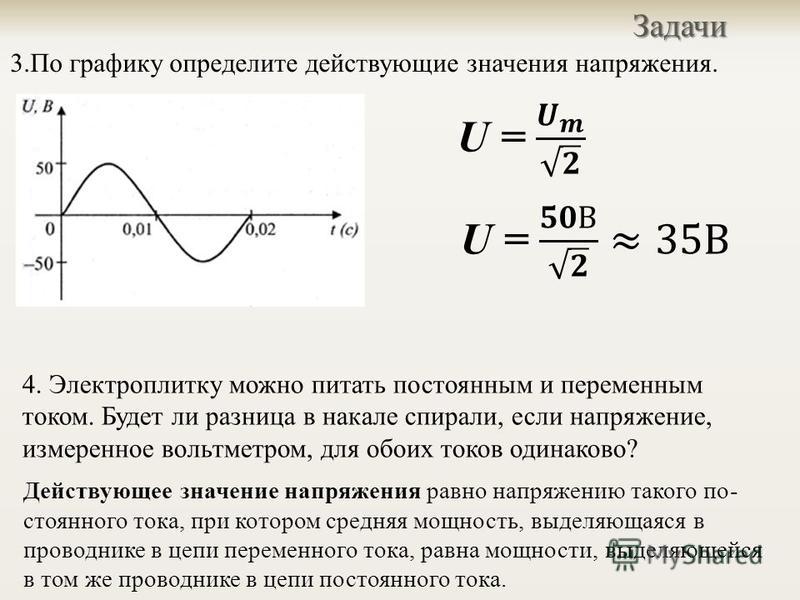
Цепи переменного тока с активным сопротивлением
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом. Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.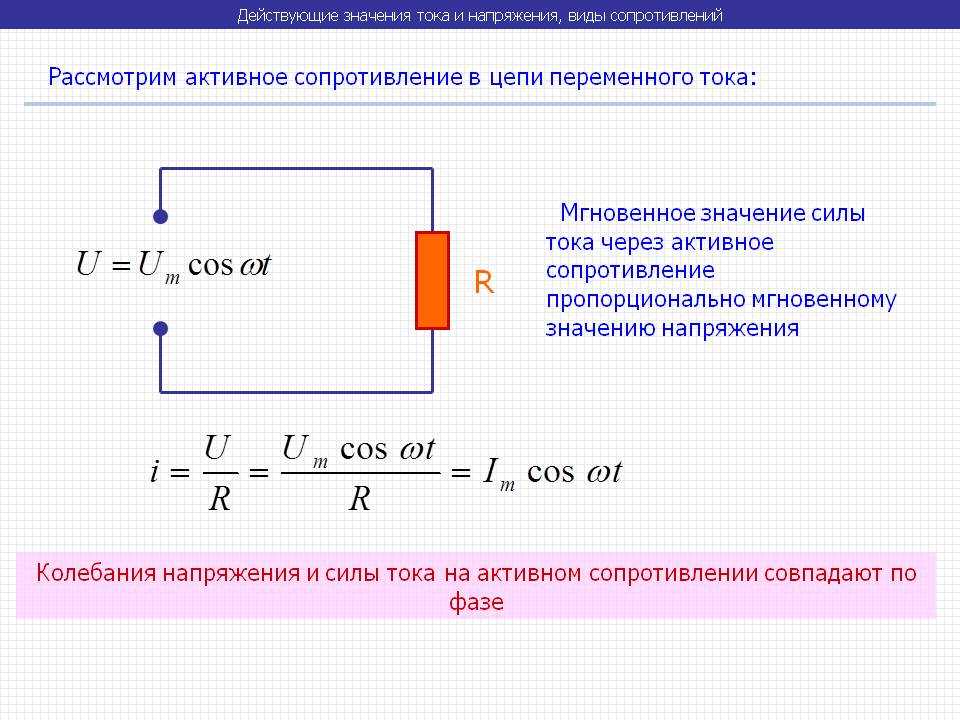
Разделив обе части равенства на , получим действующие значения .
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
Таким образом, мощность состоит из постоянной составляющей и переменной составляющей , среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности выражает среднее за период значение мощности и называется активной мощностью:
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением r только потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
Цепи переменного тока с индуктивностью
ЭДС самоиндукции в любой момент времени уравновешивается напряжением:
Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
— индуктивное (реактивное) сопротивление.
— закон Ома для цепи с индуктивностью.
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
— цепь работает потребителем
— цепь работает генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
Энергия, запасенная в магнитном поле катушки, равна
Цепь переменного тока с емкостью
— закон Ома для цепи с емкостью.
— реактивное емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
Мощность цепи:
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т.е.
— цепь работает потребителем;
— цепь работает источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
Т.о. напряжение опережает ток в этой цепи на угол , причем .
Мощность цепи:
Т.о. мгновенная мощность состоит из двух составляющих: постоянной и переменной , среднее значение за период которой равно нулю.
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
Треугольники напряжений, сопротивлений, мощностей

Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.
— реактивная мощность
— активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью
Допустим:
Общий случай неразветвленной цепи
Резонанс напряжений
Результирующий ток резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
Если параметры цепи подобрать так, что , то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в раз. Отношение называется добротностью цепи (контура).
Т.о. напряжение на емкости и индуктивности будут превышать напряжение сети в раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
Возникновение напряжений на L и С, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.
Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных колебаний можно определить при условии, что .
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.
Для определения тока неразветвленной части цепи необходимо разложить токи и на активные и реактивные составляющие.
Характеристики синусоидальных величин: мгновенное, амплитудное, действующее, среднее значение, период, частота (угловая и циклическая), фаза − мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u.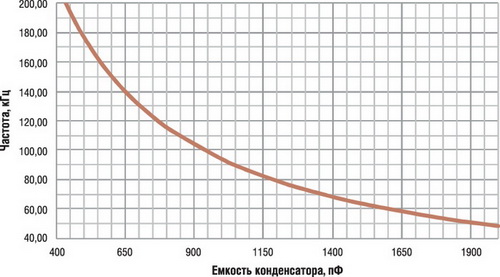 Они являются функциями времени.
Они являются функциями времени.
Зависимость их от времени выражается соотношениями:
− фаза — аргумент синусоидальной функции (wt + j) — показывает, какое значение имеет синусоидальная функция в данный момент времени;
− начальная фаза j — показывает, какое значение имеет синусоидальная функция в момент на чала отсчета, т.е. при t = 0;
− угловая (циклическая) частота изменения тока:
, рад/c.
Для нашей сети w = 314 рад/c.
− Действующее значение переменного тока.
Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220 В, можно определить амплитудное значение фазного напряжения Um = UÖ2 = 307 В. Связь между действующим и амплитудным значениями напряжений важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Цепи переменного тока с резистором: напряжение, ток, мощность, векторная диаграмма
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение.
Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).
Среднее ее значение, которое называют активной мощностью,
P = UI cos
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют реактивной мощностью:
Q = UI sin
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,
рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,
Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла t
Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).
рис. 200, а).
Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,
Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,
S = UI
Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
S = (P2 + Q2)
Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии.
То же самое относится и к электрическим сетям. Ток I = (Ia2 + Ip2), который можно безопасно пропускать по данной электрической сети, определяется, главным образом, поперечным сечением ее проводов. Поэтому если часть Iр проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток Iа, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток Iр и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электрической энергии. При этом увеличиваются и потери мощности Р = I2Rпp в активном сопротивлении Rпp этих проводов.
При этом увеличиваются и потери мощности Р = I2Rпp в активном сопротивлении Rпp этих проводов.
Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos, называемой коэффициентом мощности:
cos = P/(UI) = P/S = P/(P2 + Q2)
По значению cos можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos). При этом уменьшаются потери мощности P = I2Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования.
е. лучшего их использования.
Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ведет к возрастанию активной мощности Р, используемой приемником. При cos = 1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos = 0,25-0,3).
Повышение коэффициента мощности. Cos повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).
Способ повышения cos с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i < i1 и угол сдвига фаз его относительно напряжения также будет меньше.
Для полной компенсации угла сдвига фаз, т. е. для получения cos = 1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin1 тока I1.
е. для получения cos = 1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4.
Рис. 202. Схема, иллюстрирующая способ повышения cos с помощью компенсатора (а), и векторная диаграмма (б)
Компенсатор в этом случае выполняет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos будет равен единице.
При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos будет равен единице.
В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos = 0,95.
Последовательное соединение активного и реактивного элементов
В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов.
Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
Воздушные линии электропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.
Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного XL и емкостного Хс сопротивлений (рис. 192, а) к ним приложены напряжения: активное ua = iR, индуктивное uL = iXL и емкостное uc = iXc. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:
u = ua + uL + uc
Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по времени).
Рис. 193. Треугольник со противлении
Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока и напряжений. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление XL больше емкостного Xc, а рис. 192, в — для цепи, в которой XL меньше Хс. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:
U = (U2a + (UL – Uc)2)
Таким образом, из-за наличия угла сдвига фаз напряжение U всегда меньше алгебраической суммы Ua + UL + UC. Разность UL – UC = Up называется реактивной составляющей напряжения.
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г).
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения Ua = IR; UL = lL и UC=I/(C), то будем иметь: U = ((IR)2+ 2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / ( (R2+ 2) ) = U / Z (72)
где Z = (R2+ 2) = (R2+ (XL – Xc)2)
Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность L — l/(C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Разность L — l/(C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z = (R2+ X2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin ? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол.
Идеальная катушка индуктивности, реальная катушка и конденсатор в цепи переменного тока.
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
>Емкостное сопротивление конденсатора определяется по формуле. Сопротивление конденсатора
Сопротивление конденсатора.

Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.
Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.
Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.
Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.
А теперь замкнем цепь переменного тока.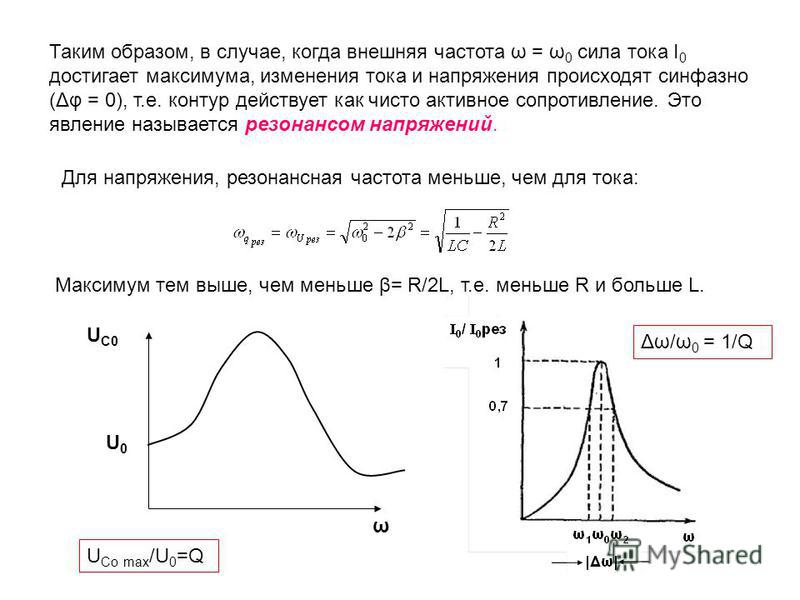 В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
Одновременная поляризация огромного количества атомов образует ток, называемый током смещения. Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.
Емкостное сопротивление конденсатора определяется по формуле
Рассматривая график делаем вывод: ток в цепи с чисто емкостным сопротивлением опережает напряжение на 90 0 .
Возникает вопрос каким образом ток в цепи может опережать напряжение на генераторе? В цепи идет ток от двух источников тока поочередно, от генератора и от конденсатора. Когда напряжение на генераторе равно нулю ток в цепи максимален. Это ток разряда конденсатора.
Когда напряжение на генераторе равно нулю ток в цепи максимален. Это ток разряда конденсатора.
Активное сопротивление, индуктивность и емкость в цепи переменного тока.
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальная фаза напряжения будет иметь некоторое значение φ. При таком условии мгновенные значения силы тока и напряжения и будут выражаться следующими формулами:
i = I m sinωt
u = U m sin(ωt + φ)
a) Активное сопротивление в цепи переменного тока. Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным . Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току.
В цепи переменного тока, имеющей только активное сопротивление, например, в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: и = U т cos ωt.
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:
по фазе с колебаниями напряжения.
b) Катушка индуктивности в цепи переменного тока. Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X L , которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω: X L = ωL.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь. Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней. Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля Е к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства E i = -Е к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции e i) равна по модулю и противоположна по знаку удельной работе кулоновского поля . Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: e i = -и.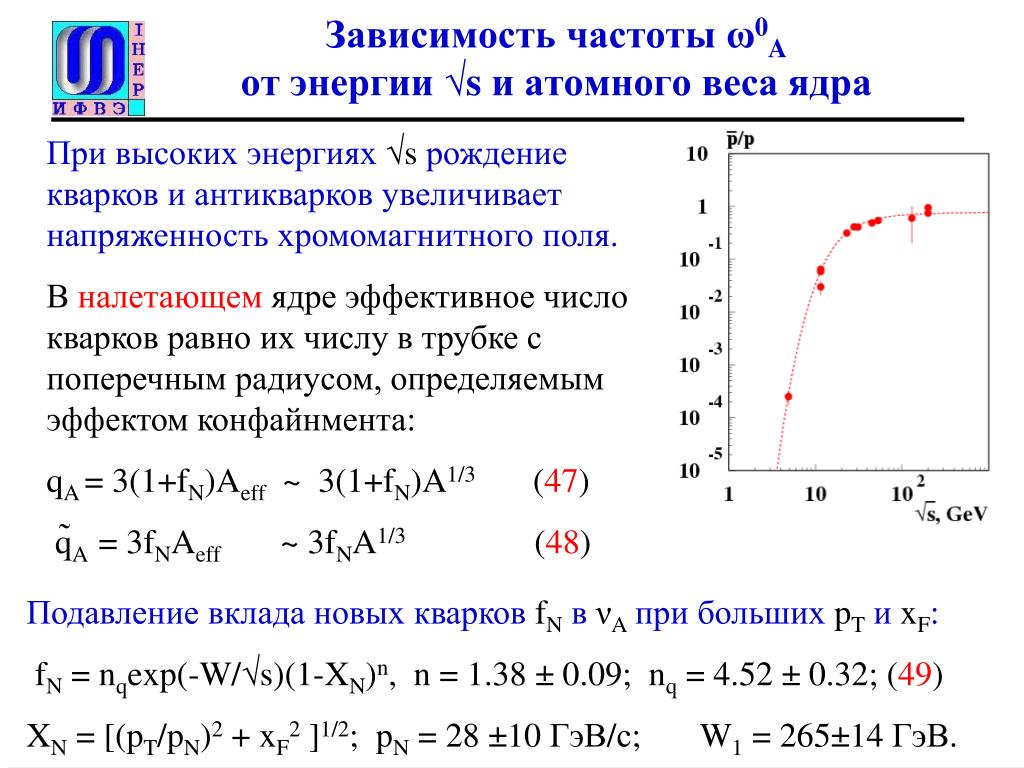
При изменении силы тока по гармоническому закону i = I m sin соsωt, ЭДС самоиндукции равна: е i = -Li» = -LωI m cos ωt. Так как e i = -и, то напряжение на концах катушки оказывается равным
и = LωI m cos ωt = LωI m sin (ωt + π/2) = U m sin (ωt + π/2)
гдеU m = LωI m — амплитуда напряжения.
Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.
Если ввести обозначение X L = ωL, то получим . Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Согласно формуле , значение силы тока связано с значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю. Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .
Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .
c) Конденсатор в цепи переменного тока. Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Х с . Оно обратно пропорционально емкости С и круговой частоте ω: Х с =1/ωС.
Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь.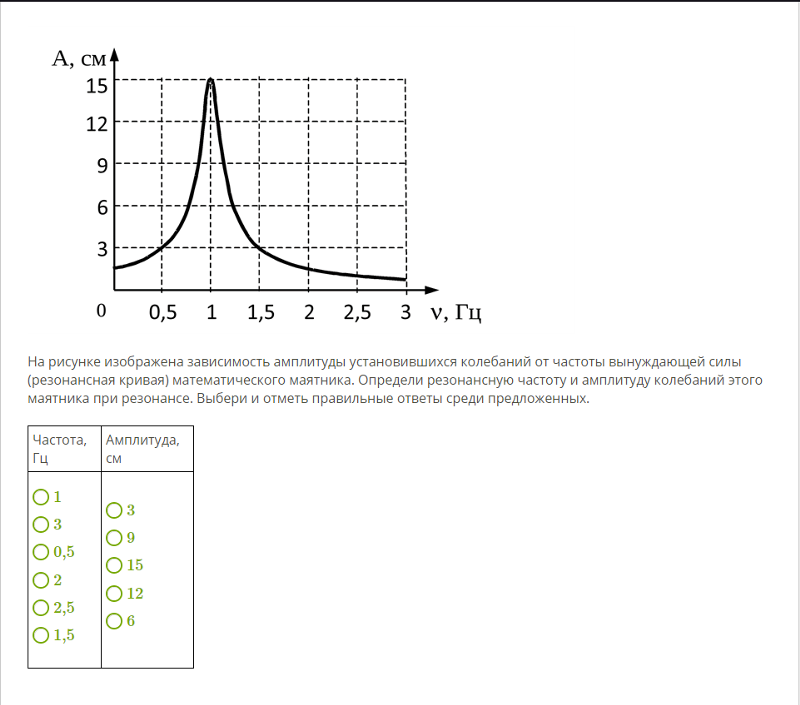
Напряжение на конденсаторе u = q/C равно напряжению на концах цепи u = U m cosωt.
Следовательно, q/C = U m cosωt. Заряд конденсатора меняется по гармоническому закону:
q = CU m cosωt.
Сила тока, представляющая собой производную заряда по времени, равна:
i = q» = -U m Cω sin ωt =U m ωC cos(ωt + π/2).
Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2.
Величину Х с , обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. Значение силы тока связано с значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Х с как сопротивление конденсатора переменному току (емкостное сопротивление).
Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.
В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Из сравнения формул X L = ωL и Х с =1/ωС видно, что катушки индуктивности. представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Индуктивное Х L и емкостное Х C сопротивления называют реактивными.
d) Закон ома для электрической цепи переменного тока.
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С
Мы видели, что при включении по отдельности в цепь активного сопротивления R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами:
; ; I m = U m ωC .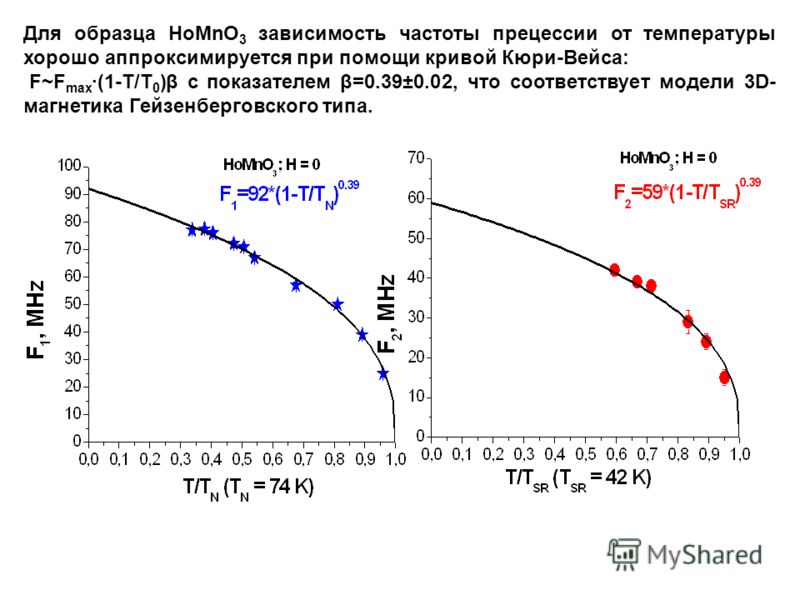
Амплитуды же напряжений на активном сопротивлении, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так: U m = I m R; U m = I m ωL;
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах. Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлениями. Однако только на активном сопротивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний тока на π/2, а на катушке индуктивности колебания напряжения опережают колебания тока на π/2. Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что
Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что
Для получения этого равенства нужно уметь складывать колебания напряжений, сдвинутые по фазе друг относительно друга. Проще всего выполнить сложение нескольких гармонических колебаний с помощью векторных диаграмм. Идея метода основана на двух довольно простых положениях.
Во-первых, проекция вектора с модулем х m вращающегося с постоянной угловой скоростью совершает гармонические колебания: х = х m cosωt
Во-вторых, при сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.
Векторная диаграмма электрических колебаний в цепи, изображенной на рисунке, позволит нам получить соотношение между амплитудой силы тока в этой цепи и амплитудой напряжения. Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока I m . Этот вектор изобразим в виде горизонтальной стрелки. Напряжение на активном сопротивлении совпадает по фазе с силой тока.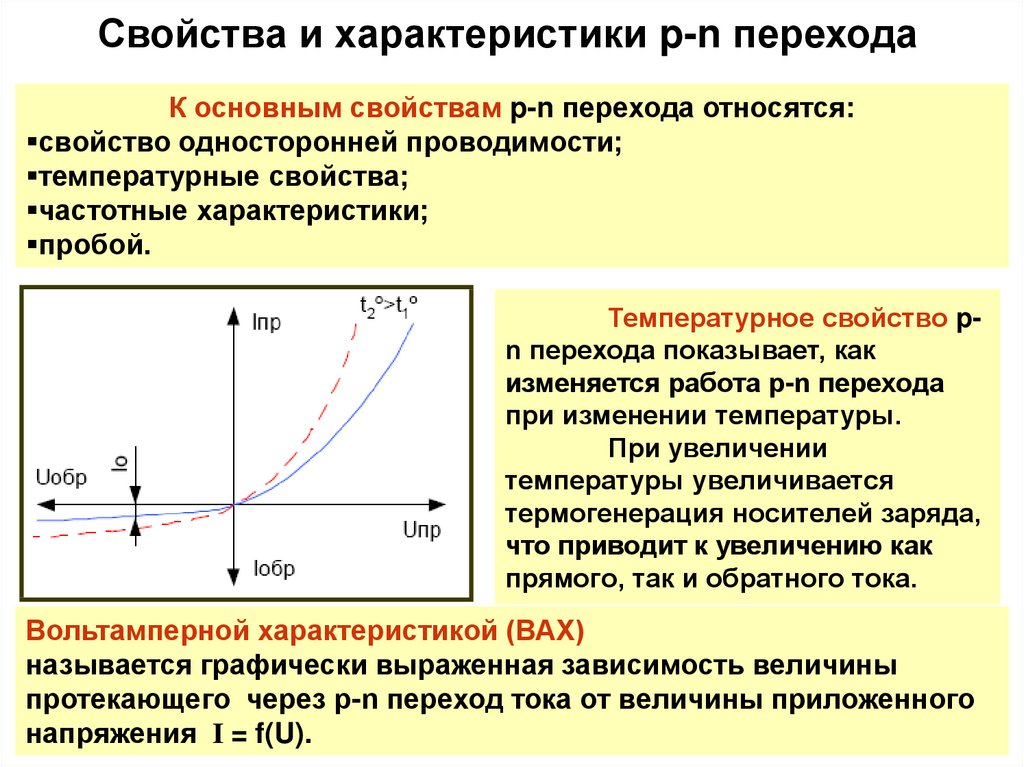 Поэтому вектор U mR , должен совпадать по направлению с вектором I m . Его модуль равен U mR = I m R
Поэтому вектор U mR , должен совпадать по направлению с вектором I m . Его модуль равен U mR = I m R
Колебания напряжения на индуктивном сопротивлении опережают колебания силы тока на π/2, и соответствующий вектор U m L должен быть повернут относительно вектора I m на π/2. Его модуль равен U m L = I m ωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор U m L следует повернуть налево. (Можно было бы, конечно, поступить и наоборот.)
Его модуль равен U mC =I m /ωC . Для нахождения вектора суммарного напряжения U m нужно сложить три вектора: 1) U mR 2) U m L 3) U mC
Вначале удобнее сложить два вектора: U m L и U mC
Модуль этой суммы равен , если ωL > 1/ωС. Именно такой случай изображен на рисунке. После этого, сложив вектор (U m L + U mC) с вектором U mR получим вектор U m , изображающий колебания напряжения в сети. По теореме Пифагора:
Из последнего равенства можно легко найти амплитуду силы тока в цепи:
Таким образом, благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи, изображенной на рисунке, выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин:
Это и есть закон Ома для переменного тока в цепи, изображенной на рисунке 43. Мгновенное значение силы тока меняется со временем гармонически:
Мгновенное значение силы тока меняется со временем гармонически:
i = I m cos (ωt+ φ), где φ — разность фаз между силой тока и напряжением в сети. Она зависит от частоты ω и параметров цепи R, L, С.
e) Резонанс в электрической цепи. При изучении вынужденных механических колебаний мы познакомились с важным явлением — резонансом. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вынужденных колебаний. Совпадение законов механических и электромагнитных колебаний сразу же позволяет сделать заключение о возможности резонанса в электрической цепи, если эта цепь представляет, собой колебательный контур, обладающий определенной собственной частотой колебаний.
Амплитуда тока при вынужденных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой:
При фиксированном напряжении и заданных значениях R, L и С, сила тока достигает максимума при частоте ω, удовлетворяющей соотношению
Эта амплитуда особенно велика при малом R.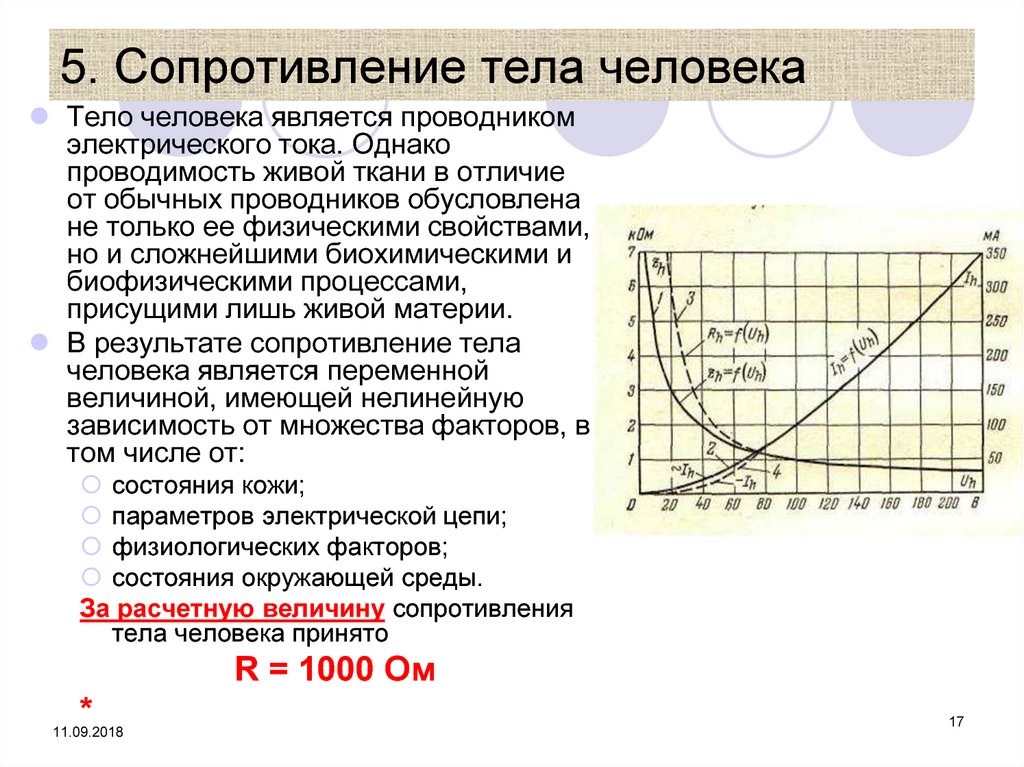 Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:
Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:
Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением.
Резкое возрастание амплитуды вынужденных колебаний тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. В этом состоит явление резонанса в электрическом колебательном контуре.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз превосходят внешнее напряжение.
Действительно,
U м, С,рез =
U м, L ,рез =
Внешнее напряжение связано с резонансным током так:
U м = . Если тоU m , C ,рез = U m , L ,рез >> U m
При резонансе сдвиг фаз между током и напряжением становится равным нулю.
Действительно, колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе.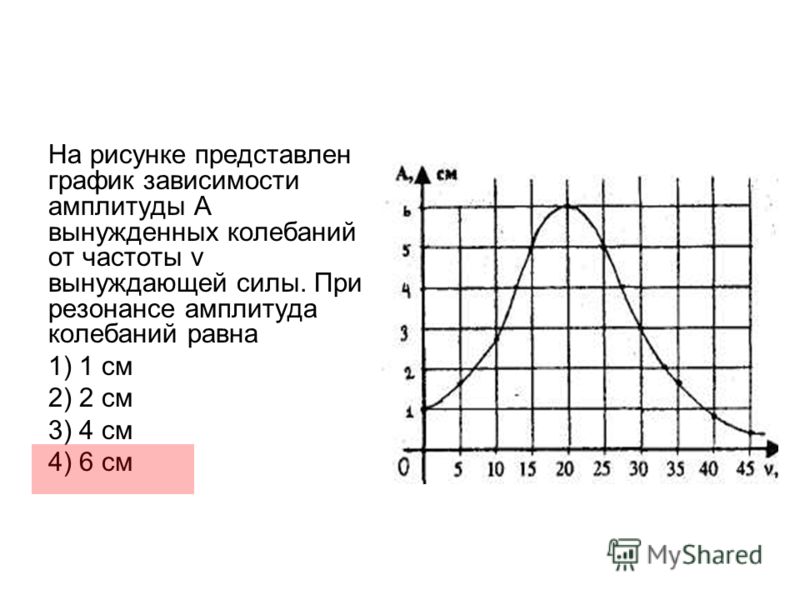 Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга, и падение напряжения происходит только на активном сопротивлении.
Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга, и падение напряжения происходит только на активном сопротивлении.
Равенство нулю сдвига фаз между напряжением и током при резонансе обеспечивает оптимальные условия для поступления энергии от источника переменного напряжения в цепь. Здесь полная аналогия с механическими колебаниями: при резонансе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
Конденсаторы, как и резисторы, относятся к наиболее многочисленным элементам радиотехнических устройств. Основное свойство конденсаторов, это способность накапливать электрический заряд . Основной параметр конденсатора это его емкость .
Емкость конденсатора будет тем значительнее, чем больше площадь его обкладок и чем тоньше слой диэлектрика между ними. Основной единицей электрической емкости является фарада (сокращенно Ф), названная так в честь английского физика М. Фарадея. Однако 1 Ф — это очень большая емкость. Земной шар, например, обладает емкостью меньше 1 Ф. В электро- и радиотехнике пользуются единицей емкости, равной миллионной доле фарады, которую называют микрофарадой (сокращенно мкФ) .
Фарадея. Однако 1 Ф — это очень большая емкость. Земной шар, например, обладает емкостью меньше 1 Ф. В электро- и радиотехнике пользуются единицей емкости, равной миллионной доле фарады, которую называют микрофарадой (сокращенно мкФ) .
Емкостное сопротивление конденсатора переменному току зависит от его емкости и частоты тока: чем больше емкость конденсатора и частота тока, тем меньше его емкостное сопротивление.
Керамические конденсаторы обладают сравнительно небольшими емкостями — до нескольких тысяч пикофарад. Их ставят в те цепи, в которых течет ток высокой частоты (цепь антенны, колебательный контур), для связи между ними.
Простейший конденсатор представляет собой два проводника электрического тока, например: — две металлические пластины, называемые обкладками конденсатора, разделенные диэлектриком, например: — воздухом или бумагой. Чем больше площадь обкладок конденсатора и чем ближе они расположены друг к другу, тем больше электрическая емкость этого прибора. Если к обкладкам конденсатора подключить источник постоянного тока, то в образовавшейся цепи возникнет кратковременный ток и конденсатор зарядится до напряжения, равного напряжению источника тока. Вы можете спросить: почему в цепи, где есть диэлектрик, возникает ток? Когда мы присоединяем к конденсатору источник тока, электроны в проводниках образовавшейся цепи начинают двигаться в сторону положительного полюса источника тока, образуя кратковременный поток электронов во всей цепи. В результате обкладка конденсатора, которая соединена с положительным полюсом источника тока, обедняется свободными электронами и заряжается положительно, а другая обкладка обогащается свободными электронами и, следовательно, заряжается отрицательно. Как только конденсатор зарядится, кратковременный ток в цепи, называемый током зарядки конденсатора, прекратится.
Если к обкладкам конденсатора подключить источник постоянного тока, то в образовавшейся цепи возникнет кратковременный ток и конденсатор зарядится до напряжения, равного напряжению источника тока. Вы можете спросить: почему в цепи, где есть диэлектрик, возникает ток? Когда мы присоединяем к конденсатору источник тока, электроны в проводниках образовавшейся цепи начинают двигаться в сторону положительного полюса источника тока, образуя кратковременный поток электронов во всей цепи. В результате обкладка конденсатора, которая соединена с положительным полюсом источника тока, обедняется свободными электронами и заряжается положительно, а другая обкладка обогащается свободными электронами и, следовательно, заряжается отрицательно. Как только конденсатор зарядится, кратковременный ток в цепи, называемый током зарядки конденсатора, прекратится.
Если источник тока отключить от конденсатора, то конденсатор окажется заряженным. Переходу избыточных электронов с одной обкладки на другую препятствует диэлектрик.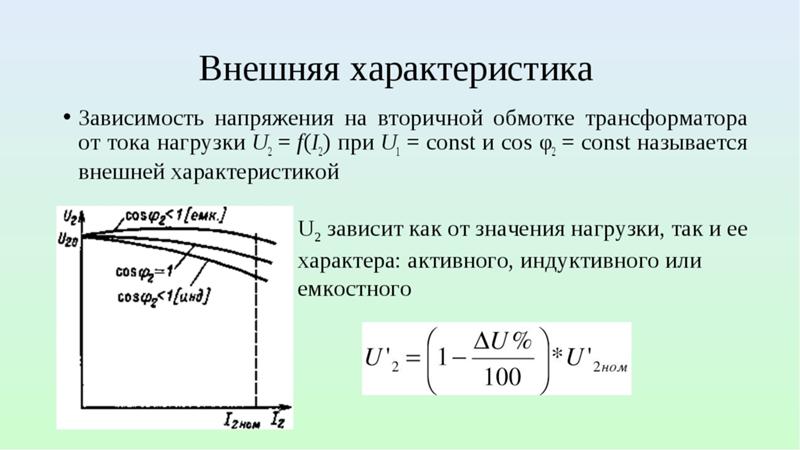 Между обкладками конденсатора тока не будет, а накопленная им электрическая энергия будет сосредоточена в электрическом поле диэлектрика. Но стоит обкладки заряженного конденсатора соединить каким-либо проводником «лишние» электроны отрицательно заряженной обкладки перейдут по этому проводнику на другую обкладку, где их недостает, и конденсатор разрядится. В этом случае в образовавшейся цепи также возникает кратковременный ток, называемый током разрядки конденсатора. Если емкость конденсатора большая, и он заряжен до значительного напряжения, момент его разрядки сопровождается появлением значительной искры и треска. Свойство конденсатора накапливать электрические заряды и разряжаться через подключенные к нему проводники используется в колебательном контуре радиоприемника.
Между обкладками конденсатора тока не будет, а накопленная им электрическая энергия будет сосредоточена в электрическом поле диэлектрика. Но стоит обкладки заряженного конденсатора соединить каким-либо проводником «лишние» электроны отрицательно заряженной обкладки перейдут по этому проводнику на другую обкладку, где их недостает, и конденсатор разрядится. В этом случае в образовавшейся цепи также возникает кратковременный ток, называемый током разрядки конденсатора. Если емкость конденсатора большая, и он заряжен до значительного напряжения, момент его разрядки сопровождается появлением значительной искры и треска. Свойство конденсатора накапливать электрические заряды и разряжаться через подключенные к нему проводники используется в колебательном контуре радиоприемника.
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки). Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки). Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
,
Где j — мнимая единица, ω — циклическая частота (рад/с ) протекающего синусоидального тока, f — частота в Гц , C — ёмкость конденсатора (фарад ). Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
Резонансная частота конденсатора равна
При f > f p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f p , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2-3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где U — напряжение (разность потенциалов), до которого заряжен конденсатор.
Ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т.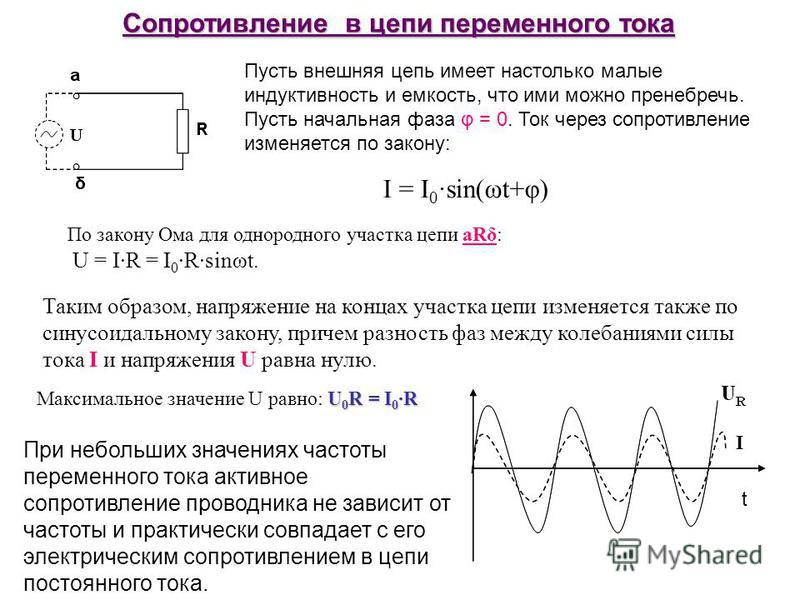 е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Общее описание
Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
За единицу измерения ёмкости принят фарад (F).
На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.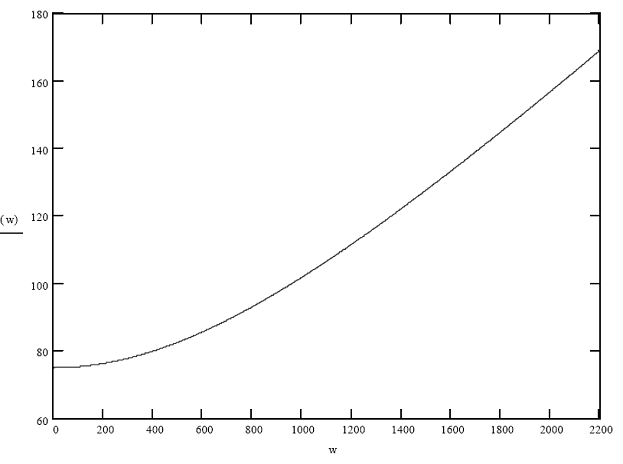
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.
Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции.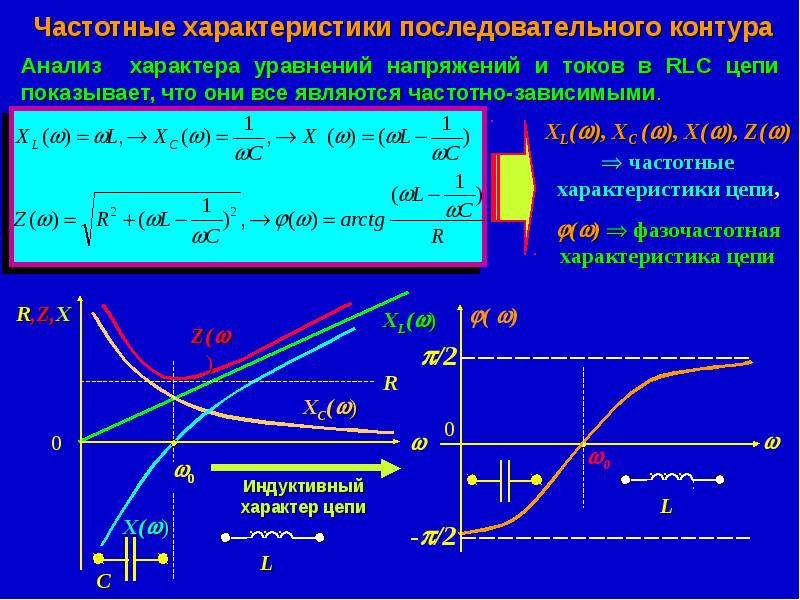 Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное — с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.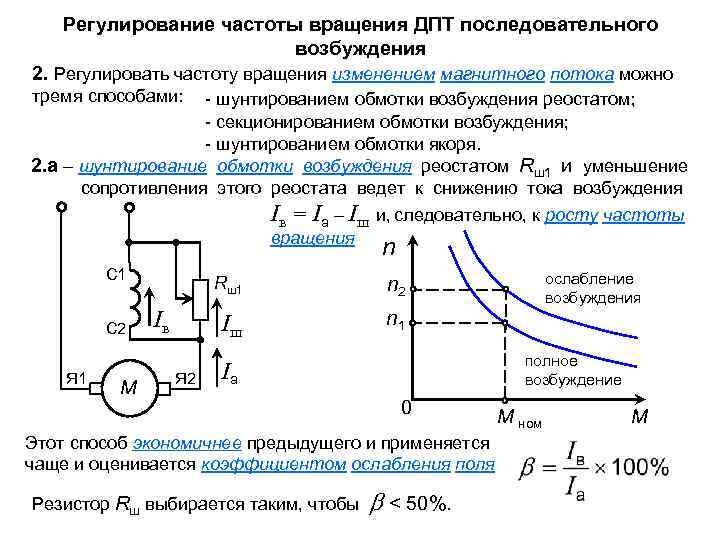
Ёмкостное сопротивление
Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.
Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.
Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:
- Xc = 1/w*C = ½*p*f*C.
 Единица измерения — ом.
Единица измерения — ом.
Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.
Индуктивная составляющая
При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности.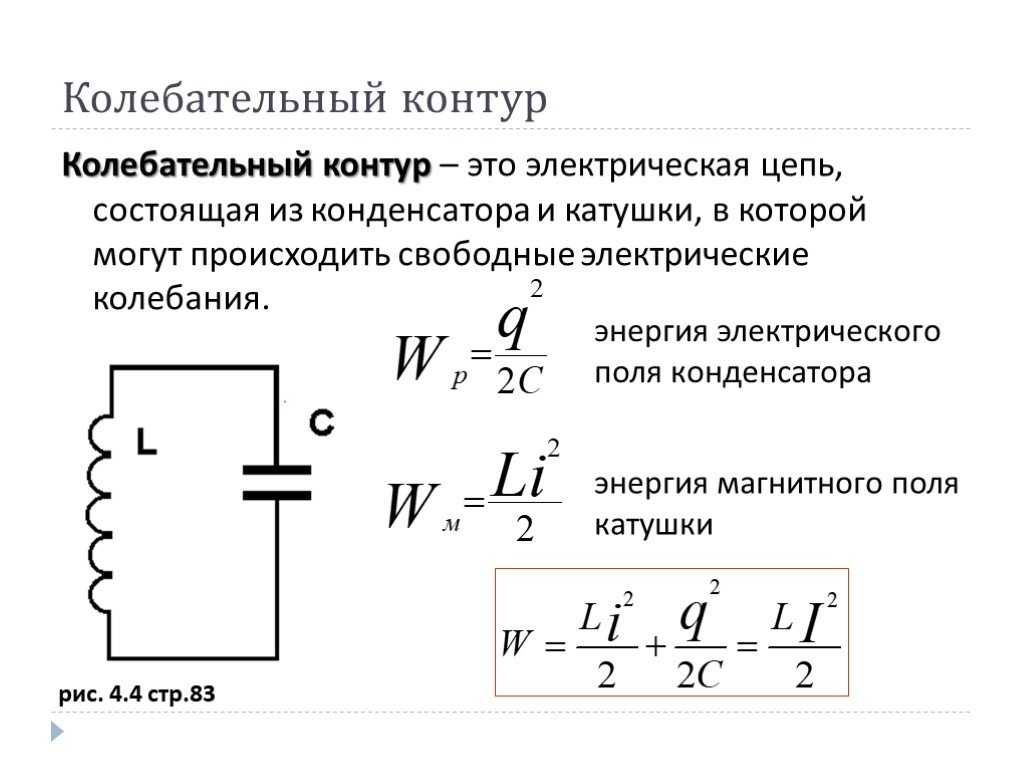 Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .
Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .
Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.
Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.
Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности.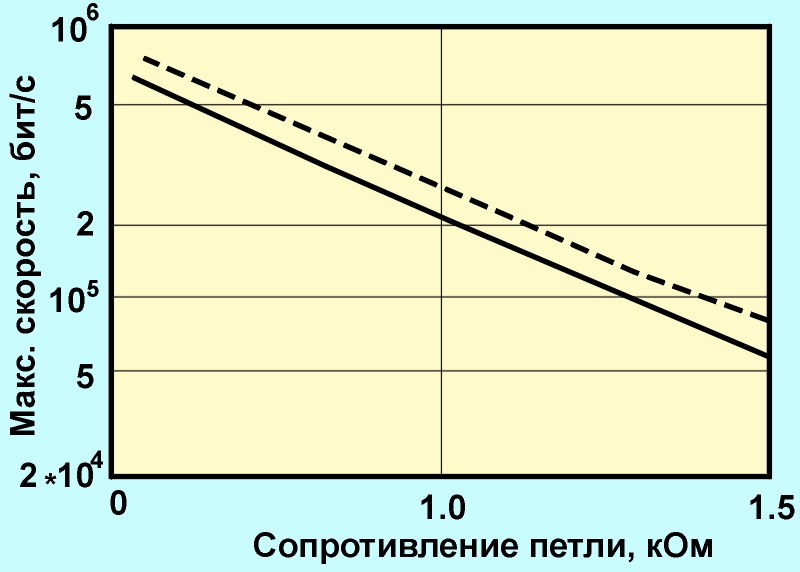 Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.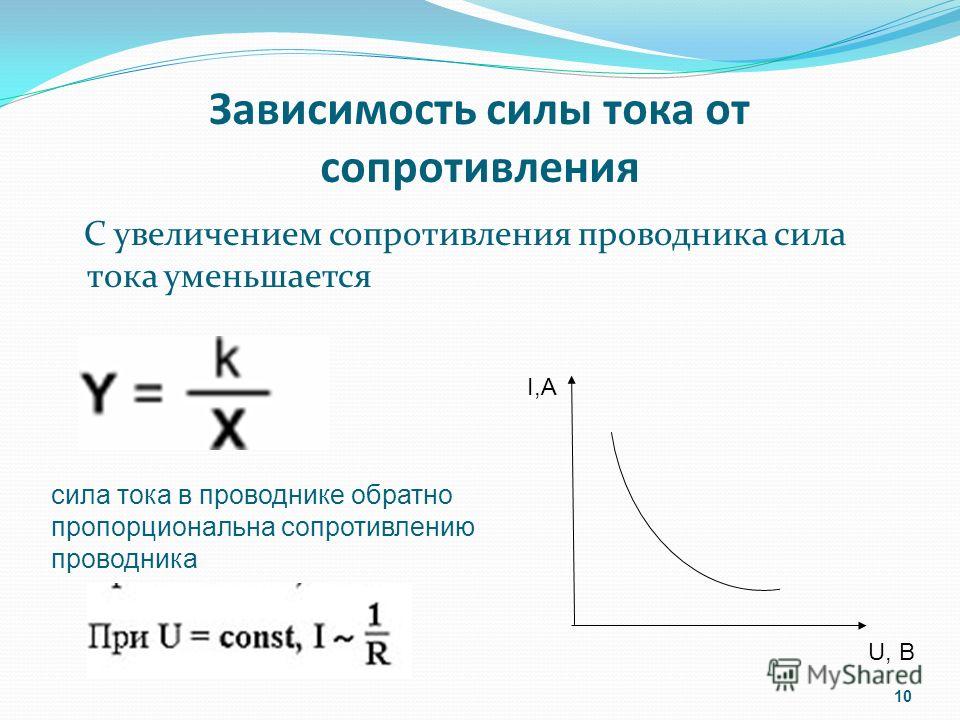
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.
This entry was posted in Ремонт. Bookmark the <a href=»https://kabel-house.ru/remont/kondensator-i-peremennyj-tok/» title=»Permalink to Конденсатор и переменный ток» rel=»bookmark»>permalink</a>.
Лабораторная работа «Элементы цепей переменного тока.
 Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров»
Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров»Лабораторная работа № 2
Элементы цепей переменного тока. Емкостное и индуктивное
сопротивления, их зависимость от частоты переменного тока и
параметров элементов.
Цель: изучить зависимость емкостного и индуктивного сопротивлений от
частоты переменного тока и параметров элементов.
1. Краткое теоретическое описание
В цепи переменного тока кроме резисторов могут использоваться катушки
индуктивности и конденсаторы. Для постоянного тока катушка
индуктивности имеет только активное сопротивление, которое обычно
невелико (если катушка не содержит большое количество витков).
Конденсатор же в цепи постоянного тока представляет «разрыв» (очень
большое активное сопротивление). Для переменного тока эти элементы
обладают специфическим реактивным сопротивлением, которое зависит как
от номиналов деталей, так и от частоты переменного тока, протекающего
через катушку и конденсатор.
1.1. Катушка в цепи переменного тока.
Рассмотрим, что происходит в цепи, содержащей резистор и катушку
индуктивности. Колебания силы тока, протекающего через катушку:
)cos( tIi
m
вызывают падение напряжения на концах катушки в соответствии с законом
самоиндукции и правилом Ленца:
)2/cos()sin( tLItIL
dt
di
Lu
mmL
т.е. колебания напряжения опережают по фазе колебания силы тока на /2.
Произведение LIm является амплитудой колебания напряжения:
mL
LIU
Произведение циклической частоты на индуктивность называют
индуктивным сопротивлением катушки:
(1)
поэтому связь между амплитудами напряжения и тока на катушке совпадает
по форме с законом Ома для участка цепи постоянного тока:
mLL
IXU
(2)
Как видно из выражения (1), индуктивное сопротивление не является
постоянной величиной для данной катушки, а пропорционально частоте
переменного тока через катушку.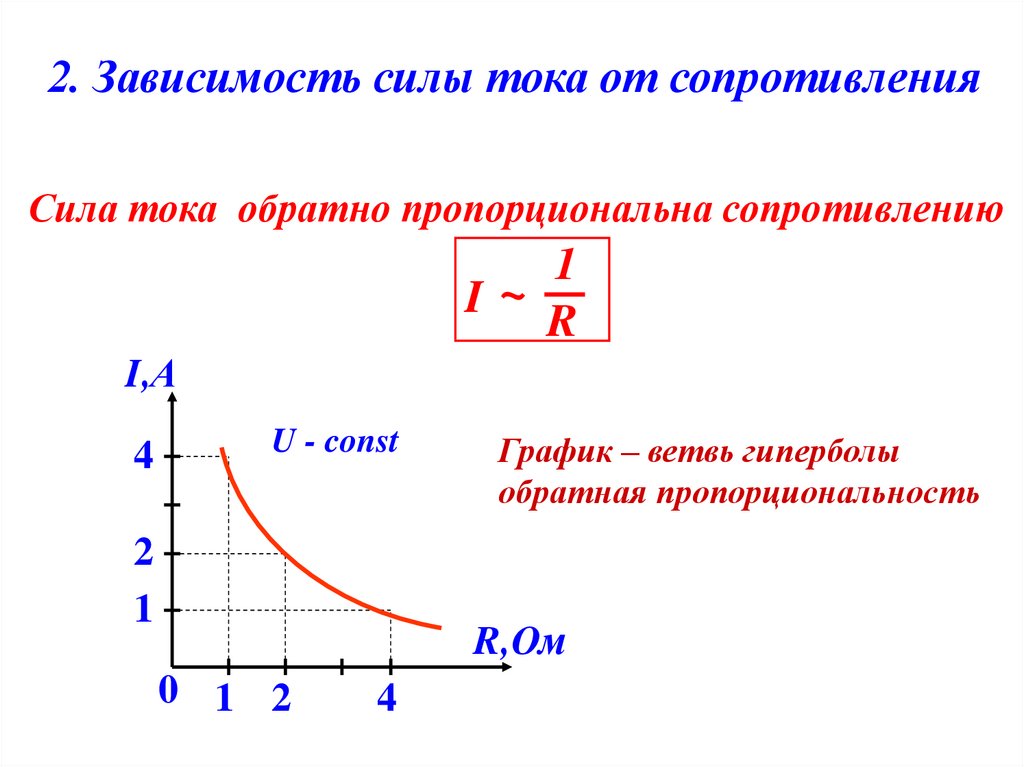 Поэтому амплитуда колебаний силы тока I
Поэтому амплитуда колебаний силы тока I
m
в проводнике с индуктивностью L при постоянной амплитуде U
L
напряжения
убывает обратно пропорционально частоте переменного тока:
L
U
I
m
m
.
1.2. Конденсатор в цепи переменного тока.
При изменении напряжения на обкладках конденсатора по
гармоническому закону:
)cos( tUu
mC
заряд q на его обкладках изменяется
также по гармоническому закону:
)cos( tCUCuq
mC
.
Электрический ток в цепи возникает в результате изменения заряда
конденсатора, поэтому колебания силы тока в цепи будут происходить по
закону:
)2/cos()sin( tCUtCU
dt
dq
i
mm
Видно, что колебания напряжения на конденсаторе отстают по фазе от
колебаний силы тока на /2. Произведение
CU
m
является амплитудой
колебаний силы тока:
mm
CUI
Аналогично тому, как было сделано с индуктивностью, введем понятие
емкостного сопротивления конденсатора:
C
X
C
1
(3)
Для конденсатора получаем соотношение, аналогичное закону Ома:
mCC
IXU
(4)
Формулы (2) и (4) справедливы и для эффективных значений тока и
напряжения.
2. Порядок выполнения работы
2.1.Соберите цепь показанную на рисунке 1.
2.2.Установите следующие значения параметров:
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.
2.3.Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ),
запишите показания вольтметров (напряжение на конденсаторе и на
резисторе).
С,
емкость,мкФ
2.4.Рассчитайте эффективное значение токов, текущих в цепи, в
зависимости от значения емкости конденсатора (для этого надо
напряжение на резисторе разделить на его сопротивление).
2.5.Определите значения емкостных сопротивлений конденсатора для
соответствующих значений его емкости и сравните их с
рассчитанными по формуле (3).
2.6.Установите емкость конденсатора 10 мкФ. Изменяя частоту
генератора от 20 до 100 Гц через 10 Гц, повторите измерения и
расчеты емкостного сопротивления в зависимости от частоты
переменного тока.
ω,частота,Гц
2.7.Соберите цепь показанную на рисунке 2.
Рис.1. Рис.2.
2.8.Установите следующие значения параметров:
Генератор – напряжение (эффективное) 100 В, частота 100 Гц;
Катушка — индуктивность 50 мГн;
Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.
2.9.Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн),
запишите показания вольтметров (напряжение на катушке и на
резисторе).
L,индукт,мГн
U
катушки
2.10. Рассчитайте эффективное значение токов, текущих в цепи, в
зависимости от значения индуктивности катушки (для этого надо
напряжение на резисторе разделить на его сопротивление).
2.11. Определите индуктивные сопротивления катушки для
соответствующих значений ее индуктивности и сравните их с
рассчитанными по формуле (1).
2.12. Установите индуктивность катушки 100 мГн. Изменяя частоту
генератора от 20 до 100 Гц через 10 Гц, повторите измерения и
расчеты индуктивного сопротивления в зависимости от частоты
переменного тока.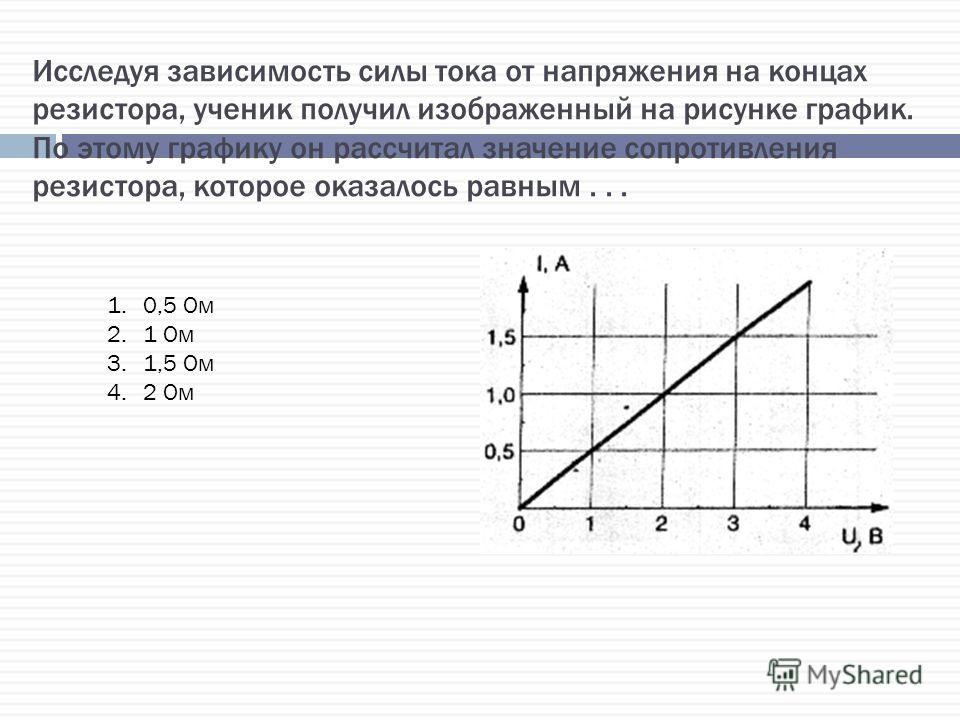
ω,частота,Гц
2.13. Постройте графики зависимостей индуктивного и емкостного
сопротивлений от частоты переменного тока.
3. Контрольные вопросы.
3.1. Почему емкостное сопротивление уменьшается с увеличением
частоты переменного ток а, индуктивное сопротивление – увеличивается?
3.2. Каковы разницы фаз между током и напряжением для катушки и
конденсатора?
3.3. В каких единицах измеряются емкостное и индуктивное
сопротивления?
3.4. Как записывается аналог закона Ома для максимальных
(эффективных) значений тока и напряжения для реактивных элементов –
конденсатора и катушки индуктивности?
Рабочая частота генератора индукционной литейной установки. – Спарк-Дон, ЛТД
Н.А.Швыргун. Главный конструктор проекта ООО «СПАРК-ДОН, ЛТД»
WhatsApp: +7(909)385-68-73

Физическая сущность индукционного нагрева состоит в том, что в электропроводящем теле, помещаемом в переменное электромагнитное поле, индуктируются вихревые токи, нагревающие это тело.
В индукционных литейных установках вокруг индуктора, вследствие пропускании через него переменного тока, возникает переменное магнитное поле. Переменный магнитный поток, пронизывающий находящиеся внутри индуктора заготовки металла, вызывает появление в них индуктированного тока. Плотность этого тока зависит от геометрических размеров, удельного сопротивления, магнитной проницаемости нагреваемого материала, а также от частоты магнитного потока. Эти токи разогревают заготовку в соответствии с законом Джоуля — Ленца, который гласит, что «Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка».
На высокой частоте вихревые токи вытесняются в тонкие поверхностные слои заготовок (скин-эффект), в результате чего их плотность резко возрастает, а по мере приближения к центру заготовки — экспоненциально уменьшается.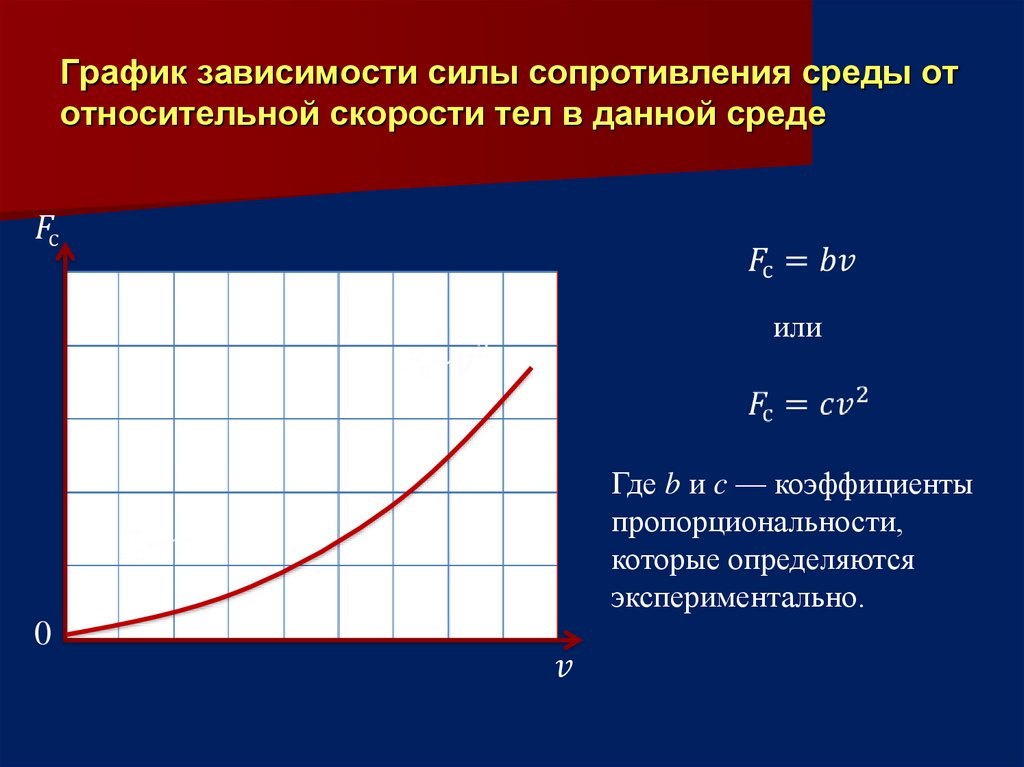 Именно в поверхностном слое, определяемом как «глубина проникновения тока», выделяется более 85% тепла.
Основными электрофизическими свойствами материалов для расчёта установок индукционного нагрева являются удельное электрическое сопротивление и магнитная проницаемость. Они определяют глубину проникновения тока и мощность, выделяемую в нагреваемом образце. При нагреве ферромагнитных металлов их удельное электрическое сопротивление и магнитная проницаемость изменяются.
Так, электрическое сопротивление металлов и сплавов, в зависимости от их химического состава может увеличиться в 10 раз.
Магнитная проницаемость ферромагнитных тел при достижении телом температуры точки Кюри (точка магнитных превращений) резко уменьшается и становится равной единице.
С увеличением значения удельного электрического сопротивления нагреваемого тела и уменьшением его магнитной проницаемости глубина проникновения тока увеличивается.
Максимальное значение глубины проникновения тока называется горячей глубиной проникновения.
Именно в поверхностном слое, определяемом как «глубина проникновения тока», выделяется более 85% тепла.
Основными электрофизическими свойствами материалов для расчёта установок индукционного нагрева являются удельное электрическое сопротивление и магнитная проницаемость. Они определяют глубину проникновения тока и мощность, выделяемую в нагреваемом образце. При нагреве ферромагнитных металлов их удельное электрическое сопротивление и магнитная проницаемость изменяются.
Так, электрическое сопротивление металлов и сплавов, в зависимости от их химического состава может увеличиться в 10 раз.
Магнитная проницаемость ферромагнитных тел при достижении телом температуры точки Кюри (точка магнитных превращений) резко уменьшается и становится равной единице.
С увеличением значения удельного электрического сопротивления нагреваемого тела и уменьшением его магнитной проницаемости глубина проникновения тока увеличивается.
Максимальное значение глубины проникновения тока называется горячей глубиной проникновения. В общих чертах процесс индукционного нагрева ферромагнитной заготовки можно представить по следующей схеме.
В первый момент начинается нагрев образца в тонком поверхностном слое, равном глубине проникновения тока в холодный металл. После потери этим слоем магнитных свойств, глубина проникновения тока возрастает и нагревается слой, расположенный глубже, повышение температуры в первом нагретом слое замедляется. После потери магнитных свойств вторым слоем начинается быстро нагреваться третий слой и так далее.
Пределом роста глубины проникновения тока является горячая глубина проникновения.
Повышение температуры в слое равной горячей глубине проникновения происходит за счет индукционных токов, а в более глубоких слоях — в основном, за счет теплопроводности.
Высокие значения КПД обеспечиваются, прежде всего, расчетом параметров индукционного нагрева под определенные размеры нагреваемого тела. Соотношение размеров индуктора и нагреваемого тела, частота тока и магнитная проницаемость, удельное сопротивление металла — все это определяет эффективность нагрева, т.
В общих чертах процесс индукционного нагрева ферромагнитной заготовки можно представить по следующей схеме.
В первый момент начинается нагрев образца в тонком поверхностном слое, равном глубине проникновения тока в холодный металл. После потери этим слоем магнитных свойств, глубина проникновения тока возрастает и нагревается слой, расположенный глубже, повышение температуры в первом нагретом слое замедляется. После потери магнитных свойств вторым слоем начинается быстро нагреваться третий слой и так далее.
Пределом роста глубины проникновения тока является горячая глубина проникновения.
Повышение температуры в слое равной горячей глубине проникновения происходит за счет индукционных токов, а в более глубоких слоях — в основном, за счет теплопроводности.
Высокие значения КПД обеспечиваются, прежде всего, расчетом параметров индукционного нагрева под определенные размеры нагреваемого тела. Соотношение размеров индуктора и нагреваемого тела, частота тока и магнитная проницаемость, удельное сопротивление металла — все это определяет эффективность нагрева, т. е. электрический КПД.
Важнейшим параметром, определяющим КПД индукционной установки, а значит и эффективность нагрева, является глубина горячего проникновения тока.
Эффективный индукционный нагрев возможен только при определённых значениях отношения диаметра нагреваемой заготовки к глубине горячего проникновения.
е. электрический КПД.
Важнейшим параметром, определяющим КПД индукционной установки, а значит и эффективность нагрева, является глубина горячего проникновения тока.
Эффективный индукционный нагрев возможен только при определённых значениях отношения диаметра нагреваемой заготовки к глубине горячего проникновения.
Рисунок 1 — Зависимость электрического КПД индукционной установки от отношения диаметра цилиндрического тела к горячей глубине проникновения тока.
График на рисунке 1 показывает, что уже при значении этого отношения менее 4 нагрев нежелателен, а при соотношении менее единицы вообще неприемлем.
Из этого графика следует, что для повышения эффективности индукционной установки, следует при заданном диаметре нагреваемой заготовки уменьшать значение горячей глубины проникновения тока. Это может быть достигнуто только повышением частоты.
Для установок индукционного нагрева в Российской Федерации выделен ряд разрешённых для использования частот.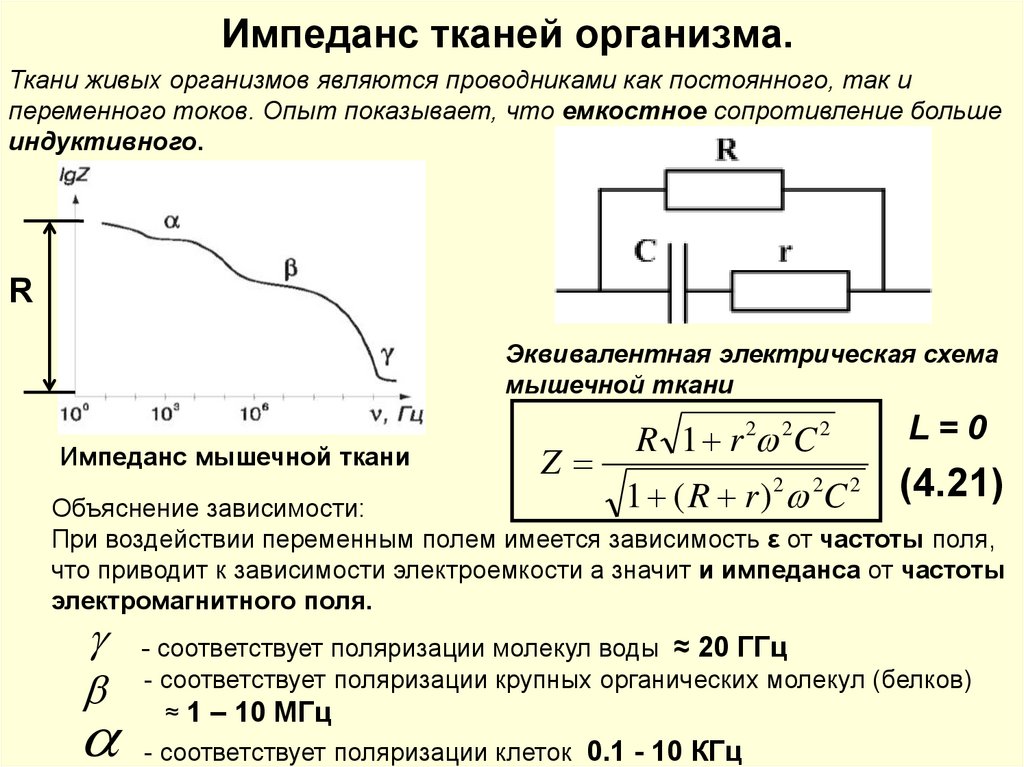 Для индукционных литейных установок, используемых в зуботехнических лабораториях для плавки стоматологических сплавов, определены частоты 66кГц, 440кГц и 1,76МГц.
Обращаем Ваше внимание, что не все импортные литейные установки соответствуют этому требованию.
Принимая решение по оснащению вашей лаборатории литейной установкой, убедитесь в том, что частота её генератора соответствует приведённым выше значениям. В противном случае, в будущем вы рискуете столкнуться с «непониманием» органов государственного надзора.
Индукционные литейные установки, работающие на частоте 1,76МГц, выполнены на основе ламповых генераторов. В настоящее время такие установки потеряли свою актуальность, вследствие их низкого КПД и морального устаревания.
Исходя из изложенных выше ограничений по частоте генератора литейной установки, в дальнейшем мы будем рассматривать только установки с рабочими частотами генератора равными 66кГц и 440кГц.
Индукционные литейные установки, работающие на частоте 66кГц и 440кГц, имеют сходные характеристики.
Для индукционных литейных установок, используемых в зуботехнических лабораториях для плавки стоматологических сплавов, определены частоты 66кГц, 440кГц и 1,76МГц.
Обращаем Ваше внимание, что не все импортные литейные установки соответствуют этому требованию.
Принимая решение по оснащению вашей лаборатории литейной установкой, убедитесь в том, что частота её генератора соответствует приведённым выше значениям. В противном случае, в будущем вы рискуете столкнуться с «непониманием» органов государственного надзора.
Индукционные литейные установки, работающие на частоте 1,76МГц, выполнены на основе ламповых генераторов. В настоящее время такие установки потеряли свою актуальность, вследствие их низкого КПД и морального устаревания.
Исходя из изложенных выше ограничений по частоте генератора литейной установки, в дальнейшем мы будем рассматривать только установки с рабочими частотами генератора равными 66кГц и 440кГц.
Индукционные литейные установки, работающие на частоте 66кГц и 440кГц, имеют сходные характеристики. Их отличает высокий КПД (0,85…0,9), они надёжны, долговечны. Качество литья, получаемое на этих установках, соответствует самым высоким требованиям.
Величина рабочей частоты генератора индукционной литейной установки в значительной степени влияет на её электрические характеристики и эксплуатационные параметры.
Выбор рабочей частоты генератора определяется следующими требованиями:
Их отличает высокий КПД (0,85…0,9), они надёжны, долговечны. Качество литья, получаемое на этих установках, соответствует самым высоким требованиям.
Величина рабочей частоты генератора индукционной литейной установки в значительной степени влияет на её электрические характеристики и эксплуатационные параметры.
Выбор рабочей частоты генератора определяется следующими требованиями:
- электрический КПД установки должен быть максимальным;
- время плавки должно быть минимальным;
- установка должна обеспечивать эффективную работу при плавке стоматологических сплавов, имеющих различные величины диаметра и высоты отдельных заготовок сплава;
- величина электродинамических сил, воздействующих на расплав, должна быть оптимальной, с одной стороны, для обеспечения качественного перемешивания расплава, а с другой стороны — минимального мениска расплава на завершающем этапе плавки.
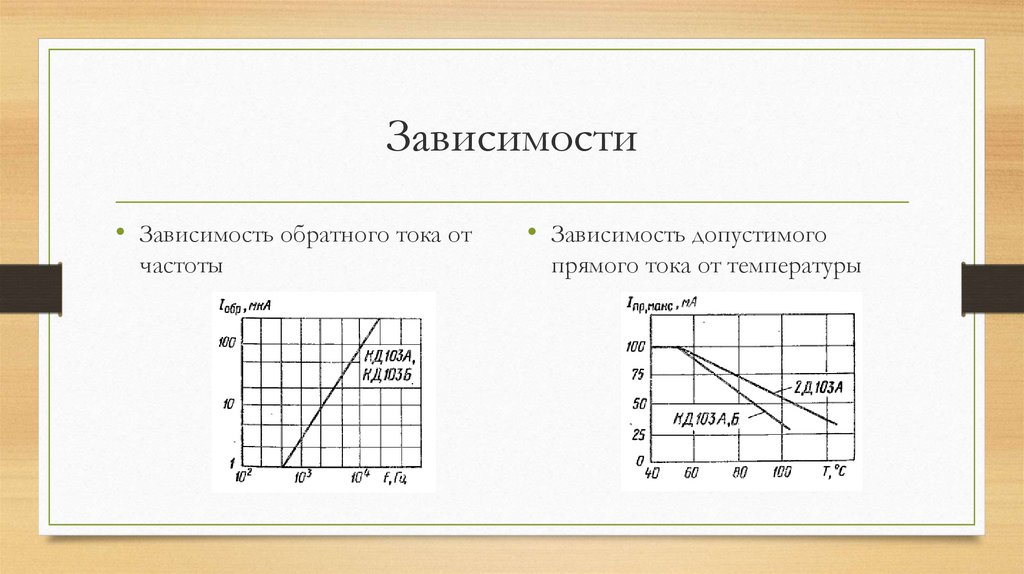
Сравнивая эффективность и качественные показатели литейных индукционных установок, необходимо представлять какая из них лучшим образом подходит для литья стоматологических сплавов, обладающих определёнными физико-химическими свойствами и линейными размерами.
Ввиду большого разнообразия используемых стоматологических сплавов, качественный анализ можно сделать, приняв за основу некий «усреднённый сплав». Для такого сплава, нагретого выше точки магнитных превращений (точки Кюри) горячая глубина проникновения тока при частоте 66кГц равна, примерно, 2мм.
Тогда, как следует из графика на рис.1, производить нагрев заготовки сплава с высокой эффективностью при частоте генератора индукционной установки равной 66кГц возможно, начиная с диаметра заготовки D = 10мм. При диаметре заготовки менее 8мм эффективность нагрева будет уменьшаться, достигая минимального значения при диаметрах заготовки сплава равных 5…6мм.
Для частоты 440кГц горячая глубина проникновения тока, при прочих равных условиях, будет составлять величину порядка 0. 8мм. Т.е. производить нагрев заготовки сплава с высокой эффективностью при частоте генератора индукционной установки равной 440кГц возможно, начиная с диаметра заготовки D = 4мм.
В теории индукционного нагрева существует понятие «минимально допустимой рабочей частоты генератора» для заданного диаметра цилиндрической заготовки, подлежащей нагреву.
График зависимости минимальной частоты генератора индукционной установки от диаметра нагреваемой установки (см.рисунок 2) строится из условия, что отношение диаметра нагреваемого образца цилиндрической формы к величине горячей глубины проникновения тока» (или «скин-слоя») равно 3.
8мм. Т.е. производить нагрев заготовки сплава с высокой эффективностью при частоте генератора индукционной установки равной 440кГц возможно, начиная с диаметра заготовки D = 4мм.
В теории индукционного нагрева существует понятие «минимально допустимой рабочей частоты генератора» для заданного диаметра цилиндрической заготовки, подлежащей нагреву.
График зависимости минимальной частоты генератора индукционной установки от диаметра нагреваемой установки (см.рисунок 2) строится из условия, что отношение диаметра нагреваемого образца цилиндрической формы к величине горячей глубины проникновения тока» (или «скин-слоя») равно 3.
Рисунок 2 — Зависимость величины минимального диаметра нагреваемой заготовки стоматологического сплава от рабочей частоты генератора
Из приведённого графика видно, что:
- минимально допустимый диаметр нагреваемых заготовок сплава при работе на индукционной установке с частотой 440кГц равен 2,5мм.

- минимально допустимый диаметр нагреваемых заготовок сплава при работе на индукционной установке с частотой 66кГц равен 6мм.
Т.е. при работе на литейной установке с частотой 66кГц ограничивается возможность использования в качестве «вторичного металла» элементов литниковой системы, имеющих меньшие размеры.
В случае же их использования они будут нагреваться не под действием индукционных токов, а вследствие передачи им тепловой энергии от более горячих частей загрузки тигля, имеющих больший диаметр. Это будет способствовать увеличению времени плавки, т. е. ухудшению одного из основных параметров.
График на рисунке 2 хорошо объясняет суть проблемы. Из него видно, что для нагрева заготовок сплава, имеющих диаметр порядка 5мм, необходима частота генератора не менее 120кГц. Если же используются заготовки с диаметром 4мм, то минимально допустимая частота генератора возрастает до 180кГц.
Таким образом, выбор рабочей частоты генератора для индукционной литейной установки является важнейшим фактором, определяющим её качественные показатели. Индукционная литейная установка для зуботехнических лабораторий должна обеспечивать эффективный нагрев и плавку за короткий промежуток времени всего спектра стоматологических сплавов, отличающихся как химическим составом, так и линейными размерами заготовок.
Особое внимание необходимо обращать на способность установки обеспечивать высокий электрический КПД при работе с заготовками, имеющими диаметры в диапазоне от 3 до 15мм.
Из рисунка 3 видно, что использование в индукционных литейных установках УЛВК-10М и ЦентроЛит-70М генератора с рабочей частотой 440кГц снимает все ограничения, связанные с минимальными линейными размерами загружаемых в тигель частей металла. Это делает её более универсальной. Кроме того обеспечивается максимально быстрый нагрев металла, что приводит к сокращению длительности процесса плавки и повышению экономической эффективности работы.
Индукционная литейная установка для зуботехнических лабораторий должна обеспечивать эффективный нагрев и плавку за короткий промежуток времени всего спектра стоматологических сплавов, отличающихся как химическим составом, так и линейными размерами заготовок.
Особое внимание необходимо обращать на способность установки обеспечивать высокий электрический КПД при работе с заготовками, имеющими диаметры в диапазоне от 3 до 15мм.
Из рисунка 3 видно, что использование в индукционных литейных установках УЛВК-10М и ЦентроЛит-70М генератора с рабочей частотой 440кГц снимает все ограничения, связанные с минимальными линейными размерами загружаемых в тигель частей металла. Это делает её более универсальной. Кроме того обеспечивается максимально быстрый нагрев металла, что приводит к сокращению длительности процесса плавки и повышению экономической эффективности работы.
Рисунок 3 — Оптимальные размеры заготовок при частотах 66 и 440 кГц
Величина рабочей частоты генератора и циркуляция расплава в тигле.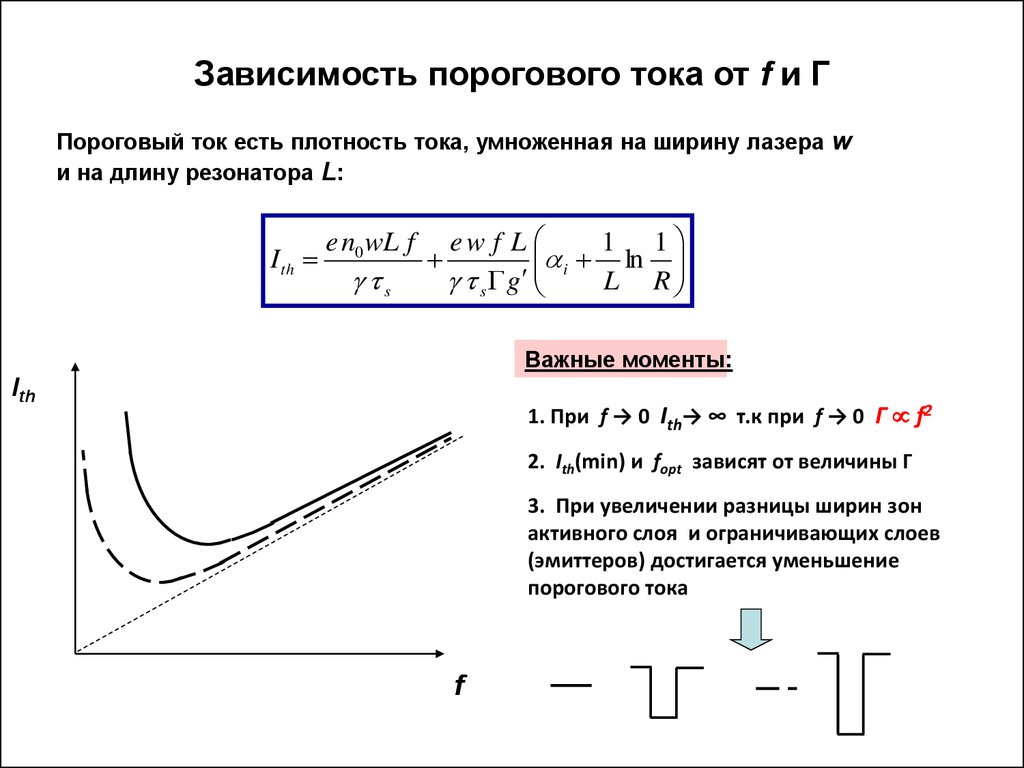
Обращая внимание на частоту генератора при выборе индукционной литейной установки, необходимо учитывать не только энергетические характеристики генератора, но и вопросы магнитогидродинамики, т. е. влияние электромагнитного поля индуктора на расплав в тигле.
Под действием электродинамических сил расплавленный металл в средней части тигля перетекает от периферии к оси, затем по оси тигля выжимается вверх к зеркалу ванны расплава и вниз ко дну тигля. Вверху и внизу он перетекает к стенкам и вдоль стенок возвращается к средней части тигля, совершая так называемую двухконтурную циркуляцию.
Факт электродинамической циркуляции металла является достоинством любой индукционной литейной установки. Циркуляция ускоряет расплавление, выравнивает температуру и химический состав расплава.
Однако циркуляция металла имеет и серьезный недостаток, заключающийся в образовании на поверхности расплава выпуклого мениска. Особенно сильно отрицательное влияние мениска на процесс плавки проявляется при использовании в литейных установках генераторов с относительно низкой рабочей частотой. Это связано с тем, что при неизменной мощности, передаваемой в расплав, силовое воздействие на него усиливается тем больше, чем меньше частота генератора.
Например, при частоте генератора равной 66кГц высота мениска почти в 3 раза больше, чем при частоте 440кГц.
Это связано с тем, что при неизменной мощности, передаваемой в расплав, силовое воздействие на него усиливается тем больше, чем меньше частота генератора.
Например, при частоте генератора равной 66кГц высота мениска почти в 3 раза больше, чем при частоте 440кГц.
Рисунок 4 — Зависимость величины мениска от рабочей частоты генератора.
Рассмотрим подробнее влияние мениска на процесс плавки.
Расплавленный сплав покрывается тонкой оксидной плёнкой, которая благодаря поверхностному натяжению расплава удерживается на его поверхности, предохраняя расплав от окисления. В период расплавления взламывание плёнки происходит, главным образом, вследствие циркуляции металла.
Если электродинамическая циркуляция способствует образованию мениска большой высоты, разрушение оксидной плёнки может произойти слишком рано. Зеркало расплава откроется до момента выравнивания температуры по всему объёму тигля. Расплав будет открыт для его окисления остаточными газами, присутствующими в плавильной камере. Для уменьшения вредного влияния мениска на процесс плавки рекомендуется уменьшать мощность на завершающем этапе плавки. Это необходимо для того, чтобы температура расплава выровнялась по всему объёму тигля. При этом важно, чтобы, для предупреждения окисления расплава остаточными газами, оксидная плёнка не была преждевременно разорвана.
Возникает дилемма: для расплавления высокотемпературных компонентов сплава в течение минимального времени необходима максимальная мощность. Но при этом значительные электродинамические силы, воздействующие на расплав приведут к разрыву оксидной плёнки слишком рано. Расплав подвергнется дополнительному окислению. Идеальным вариантом проведения плавки на завершающем этапе является вариант, при котором плавка ведётся при мощности близкой к максимальной при минимальной высоте мениска.
Именно такой вариант работы реализован в литейных установках УЛВК-10М и ЦентроЛит-70М. Вероятность преждевременного разрыва оксидной плёнки на них значительно ниже, вследствие того, что частота генератора выбрана равной 440кГц и мениск расплава имеет минимальную высоту.
Для уменьшения вредного влияния мениска на процесс плавки рекомендуется уменьшать мощность на завершающем этапе плавки. Это необходимо для того, чтобы температура расплава выровнялась по всему объёму тигля. При этом важно, чтобы, для предупреждения окисления расплава остаточными газами, оксидная плёнка не была преждевременно разорвана.
Возникает дилемма: для расплавления высокотемпературных компонентов сплава в течение минимального времени необходима максимальная мощность. Но при этом значительные электродинамические силы, воздействующие на расплав приведут к разрыву оксидной плёнки слишком рано. Расплав подвергнется дополнительному окислению. Идеальным вариантом проведения плавки на завершающем этапе является вариант, при котором плавка ведётся при мощности близкой к максимальной при минимальной высоте мениска.
Именно такой вариант работы реализован в литейных установках УЛВК-10М и ЦентроЛит-70М. Вероятность преждевременного разрыва оксидной плёнки на них значительно ниже, вследствие того, что частота генератора выбрана равной 440кГц и мениск расплава имеет минимальную высоту.
« Процесс литья на вакуумной индукционной литейной установке УЛВК-10 Плавка и литьё в вакууме. Рекомендации по разработке литниковой системы. »
Укажите правильные высказывания
Возникновение сдвига фаз между силой тока и напряжением при прохождении переменного тока через биологическую ткань доказывает наличие у нее реактивного сопротивления
Диэлектрики, молекулы которых в отсутствии электрического поля обладают дипольным моментом, называются полярными
В области γ-дисперсии (ν~2·1010 Гц) в явлении поляризации ткани участвуют только молекулы воды
При увеличении расстояния от точечного заряда, потенциал создаваемого им электрического поля уменьшается
Единицей СИ индуктивного сопротивления является Ом
Переменный ток — ток, изменяющийся во времени
При уменьшении частоты переменного тока импеданс тканей увеличивается
При пропускании переменного тока через ткани сила тока по фазе опережает приложенное напряжение
Напряженность электрического поля в диэлектриках меньше, чем в вакууме
Носителями тока в электролитах являются положительные и отрицательные ионы
Биологические ткани не обладают индуктивным сопротивлением
Реография – это диагностический метод, основанный на регистрации изменения частотной зависимости импеданса сердца в процессе сердечной деятельности
Активное сопротивление цепи не зависит от частоты переменного тока
На векторной диаграмме напряжений цепи переменного тока вектор амплитуды напряжения на конденсаторе направлен перпендикулярно оси тока
Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них активного сопротивления
Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называется реографией
Металлы обладают электронной проводимостью
Диэлектрическая проницаемость среды является безразмерной величиной
На векторной диаграмме напряжений в цепи переменного тока вектор амплитуды напряжения на резисторе совпадает по направлению с осью тока
Реактивное сопротивление цепи переменного тока обусловлено наличием в ней конденсаторов и катушек индуктивности
Выберете правильный ответ
Дисперсией импеданса называется …зависимость полного сопротивления электрической цепи от частоты тока
Характеристикой диэлектрика является … диэлектрическая проницаемость
Диэлектрическая проницаемость среды равна .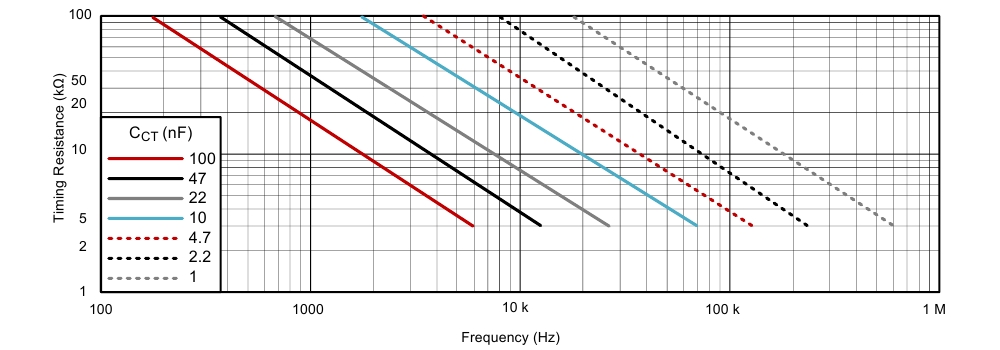 .произведению.. напряженности Е0 электрического поля в вакууме и напряженности Е электрического поля в данной среде
.произведению.. напряженности Е0 электрического поля в вакууме и напряженности Е электрического поля в данной среде
Зависимость импеданса живой ткани от частоты переменного тока обусловлена наличием у нее … емкостного сопротивления
Укажите сопротивление, которым биологические ткани не обладают:индуктивное
Уменьшение импеданса живой ткани при увеличении частоты переменного тока обусловлена свойствами … мембран клеток, как микроконденсаторов
Укажите единицу СИ силы тока: А
Укажите единицу СИ индуктивного сопротивления: Ом
Укажите единицу СИ емкостного сопротивления: Ом
Емкостное сопротивление определяется по формуле:
Напряженность является силовой характеристикой электрического поля
Металлы обладают электронной проводимостью
Диэлектрическая проницаемость среду является безразмерной величиной
Потенциал является энергетической характеристикой электрического поля
Диэлектрики, молекулы которых в отсутствии электрического поля обладают дипольным моментом, называется полярным
Плечом электрического диполя называют величину, равную расстоянию между зарядами диполя
Электрический диполь – система, состоящая из двух равных по величине, но противоположенных по знаку зарядов, расположенных на некотором расстоянии друг от друга
На диполь в однородном электрическом поле действует момент сил, вызывающий ориентацию диполя вдоль линий напряженности поля
Если диполь помещен в центр равностороннего треугольника, то проекции дипольного момента соотносятся как напряжения на соответствующих сторонах треугольника
Токовым диполем называется двухполюсная система, состоящая из истока и стока сил
Электрокардиограмма – временная зависимость разности потенциалов в отделениях
Проводниками являются вещества, которые содержат свободные заряженные частицы
Характеристика электрического диполя: электрический момент
Носителями тока являются положительные и отрицательные частицы
Поляризация полярных диэлектриков под действием, электрического поля
Удельное сопротивление – характеристика электрического поля
Поляризация полярных диэлектролитов под действием электрического поля происходит вследствие поступательного движения дипольных молекул
В диэлектриках находятся связанные заряженные частицы
Напряженность электрического поля точечного заряда обратно пропорционально квадрату расстояния от этого заряда
Дипольный момент электрического поля внутри проводника, помещенного во внешнее электричекое поле, равна нулю
Напряженность электрического поля внутри диэлектрика, помещенного во внешнее электрическое поле, меньше напряженности Е электрического поля в данной среде
Диполь является источником неоднородного электрического поля
Дипольный момент электрического диполя – вектор направленный от отрицательного заряда к положительному
Дипольный момент электрического диполя – вектор, численно равный произведению заряда на плечо диполя
При поляризации диэлектрика на его поверхности создаются связанные электрические заряды
Потенциал поля, создаваемогодиполем в удаленной точке пространства, зависит от дипольного момента, ориентации диполя и расстояния от диполя до данной точки
Если угол сдвига фаз между током и напряжением в цепи переменного тока имеет положительное значение, то цепь обязательно имеет катушку индуктивности
Импеданс – полное сопротивление цепи переменного тока
Емкостное сопротивление уменьшается с увеличением частоты переменного тока
Реактивное сопротивление цепи переменного тока обусловлено наличием в ней конденсаторов и катушек индуктивности
Полное сопротивление – импеданс цепи переменного тока включает активное и реактивное сопротивление
При уменьшении частоты переменного тока активное сопротивление не изменяется
При прохождении переменного тока на активном сопротивлении происходит выделение теплоты
При увеличении частоты переменного тока индуктивное сопротивление увеличивается
Угол сдвига между током и напряжением в цепи переменного тока содержит конденсатор, имеет отрицательное значение
При прохождении переменного тока в цепи с реактивным сопротивлением происходит возникновение разности фаз между током и напряжением
Возникновение сдвига фаз между силой тока и напряжение при прохождении переменного тока биологическая ткань доказывает наличие у нее реактивного сопротивления
При уменьшении частоты переменного тока импеданс тканей увеличивается
При пропускании тока через ткани сила тока по фазе опережает приложенное напряжение
При увеличении частоты переменного тока импеданс тканей уменьшается
Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них активного сопротивления
Укажите правильно выражение для угла сдвига между силой тока и напряжение для биологической ткани
Сдвиг фаз между током и напряжением в цепи переменного тока, содержащей катушку индуктивности, резистор и конденсатор определяется по формуле
При прохождении переменного тока через ткани сила тока по фазе опережает приложенное напряжение
Укажите необходимые и достаточные условия для возникновения трансмембранной разности потенциалов: наличие избирательной проницаемости мембраны и различие концентрации ионов по обе стороны от мембраны
Градиент концентрации – это векторная величина, которая направлена в сторону наибыстрейшего увеличения концентрации диффундирующего вещества
Укажите размерность плотности потока вещества J: моль/м
Укажите правильные высказывания: — потенциал является силовой характеристикой электрического поля — диэлектрическая проницаемость диэлектрика меньше единицы + электролиты обладают ионной проницаемостью + напряженность электрического поля внутри проводника, помещенное во внешнее электрическое поле, равна нулю Укажите правильные высказывания: + напряженность электрического поля в диэлектрике меньше, чем в вакууме — диэлектрическая проницаемость- характеристика электрических свойств проводника — поляризация диэлектриков под действием электрического поля происходит вследствие направленного движения ионов + носителями тока в электролитах являются положительные и отрицательные ионы Укажите правильные высказывания: + напряженность электрического поля точечного заряда обратно пропорциональна квадрату расстояния от этого заряда — диэлектрическая проницаемость среды равна сумме напряженности Ео электрического поля в вакууме и напряженности Е электрического поля в данной среде — удельное сопротивление проводника- безразмерная величина + дипольный момент электрического диполя- векторная величина Диэлектрики, молекулы которых в отсутствие электрического поля обладают дипольным моментом называются ПОЛЯРНЫМИ При поляризации диэлектрика на его поверхности создаются СВЯЗАННЫЕ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ Диэлектрики, молекулы которых в отсутствие электрического поля НЕ обладают дипольным моментом называются НЕПОЛЯРНЫМИ Укажите правильные высказывания: + напряженность является силовой характеристикой электрического поля — потенциал электрического поля- векторная величина + электрический диполь- система, состоящая из двух равных по величине и противоположных по знаку электрических зарядов — удельное сопротивление- характеристика электрических свойств диэлектрика Укажите единицу СИ электрического сопротивления Ом Укажите правильные высказывания: — напряженность является энергетической характеристикой электрического поля + диэлектрики, молекулы которых в отсутствие электрического поля обладают дипольным моментом, называются полярными + при увеличении расстояния от точечного заряда, потенциал создаваемого им электрического поля уменьшается — в диэлектриках находятся свободные заряженные частицы Сопротивление проводника определяется по формуле R=p*l/s, в которой буква p обозначает УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ Укажите единицу СИ силы тока А Укажите правильные высказывания: + источником электрического поля является электрически заряженное тело — направление вектора напряженности электрического поля в каждой точке совпадает с направлением силы, действующей на отрицательный заряд, помещенный в данную точку — заряды электрического диполя находятся в проводящей среде + потенциал является энергетической характеристикой электрического поля При увеличении расстояния от точечного заряда потенциал создаваемого им электрического поля УМЕНЬШАЕТСЯ Укажите правильные высказывания: — электролиты обладают электронной проводимостью — диэлектрики, молекулы которых в отсутствие электрического поля обладают дипольным моментом называются неполярными + дипольный момент электрического диполя- это вектор, численно равный произведению заряда на плечо диполя + при поляризации диэлектрика на его поверхности создаются связанные электрические заряды Укажите правильные высказывания: + металлы обладают электронной проводимостью — напряженность электрического тока в диэлектрике больше, чем в вакууме — при увеличении расстояния от электрического диполя потенциал создаваемого им электрического поля увеличивается + диэлектрическая проницаемость среды является безразмерной величиной Укажите единицу СИ напряженности электрического поля В/м Укажите силовую характеристику электрического поля НАПРЯЖЕННОСТЬ На диполь в однородном электрическом поле действует МОМЕНТ СИЛ, ВЫЗЫВАЮЩИЙ ОРИЕНТАЦИЮ ДИПОЛЯ ВДОЛЬ ЛИНИЙ НАПРЯЖЕННОСТИ ПОЛЯ Электрический диполь — это система . ….. расположенных на фиксированном расстоянии друг от друга ИЗ ДВУХ РАВНЫХ ПО ВЕЛИЧИНЕ И ПРОТИВОПОЛОЖНЫХ ПО ЗНАКУ ЗАРЯДОВ ….. расположенных на фиксированном расстоянии друг от друга ИЗ ДВУХ РАВНЫХ ПО ВЕЛИЧИНЕ И ПРОТИВОПОЛОЖНЫХ ПО ЗНАКУ ЗАРЯДОВ
| |
Полярными называются диэлектрики, молекулы которых ОБЛАДАЮТ ЭЛЕКТРИЧЕСКИМ ДИПОЛЬНЫМ МОМЕНТОМ ДАЖЕ ПРИ ОТСУТСТВИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Неполярными называются диэлектрики, молекулы которых В ОТСУТСТВИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НЕ ИМЕЮТ ДИПОЛЬНЫХ МОМЕНТОВ Поляризация полярных диэлектриков под действием электрического поля происходит вследствие ОРИЕНТАЦИИ ДИПОЛЬНЫХ МОЛЕКУЛ Проводниками являются вещества, которые СОДЕРЖАТ СВОБОДНЫЕ ЗАРЯЖЕННЫЕ ЧАСТИЦЫ Плечом электрического диполя называют величину, равную РАССТОЯНИЮ МЕЖДУ ЗАРЯДАМИ ДИПОЛЯ При возрастании напряженности внешнего электрического поля степень упорядоченности ориентации молекул находящегося в нем полярного диэлектрика УВЕЛИЧИВАЕТСЯ Вода является … диэлектриком ПОЛЯРНЫМ Укажите правильные высказывания: + удельное сопротивление — характеристика электрических свойств проводника — потенциал электрического диполя- векторная величина + направление вектора напряженности электрического поля в каждой точке совпадает с направлением силы, действующей на положительный заряд, помещенный в данную точку — поляризация полярных диэлектриков под действием электрического поля происходит вследствие поступательного движения дипольных молекул Напряженность электрического поля внутри диэлектрика, помещенного во внешнее электрическое поле . .. напряженности внешнего поля МЕНЬШЕ .. напряженности внешнего поля МЕНЬШЕ
|
Укажите формулу для определения напряженности электрического поля, создаваемого точечным зарядом q на расстоянии r от него:
Укажите правильные высказывания:
+ При пропускании переменного тока через ткани сила тока по фазе опережает приложенное напряжение
— Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и катушек индуктивности
+ При уменьшении частоты переменного тока импеданс тканей увеличивается
— Биологические ткани по своим электрическим свойствам проявляют себя только как проводники
Активное сопротивление биологической ткани обусловлено, в частности, наличием в ней ТКАНЕВОЙ ЖИДКОСТИ, ЯВЛЯЮЩЕЙСЯ ЭЛЕКТРОЛИТОМ
Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них….. сопротивления АКТИВНОГО
Биологические ткани по своим электрическим свойствам проявляют себя как ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
Укажите правильные высказывания:
— Биологические ткани по своим электрическим свойствам проявляют себя только как диэлектрики
+ Возникновение сдвига фаз между силой тока и напряжением при прохождении переменного тока через биологическую ткань доказывает наличие у нее реактивного сопротивления
— Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них реактивного сопротивления
+ В области y-дисперсии(v-2*10(10) Гц) в явлении поляризации ткани участвуют только молекулы воды
Укажите правильные высказывания:
+ Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них активного сопротивления
— В области y-дисперсии(v-2*10(10) Гц) в явлении поляризации ткани участвуют все дипольные структуры тканей
— Биологические ткани не обладают емкостным сопротивлением
+ Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называется реографией
Укажите правильные высказывания:
+ Биологические ткани по своим электрическим свойствам проявляют себя как проводники и диэлектрики
+ При увеличении частоты переменного тока импеданс тканей уменьшается
— Биологические ткани обладают индуктивным сопротивлением
— Реография — это диагностический метод, основанный на регистрации изменения биопотенциалов сердца в процессе сердечной деятельности
Укажите элемент, который не должна содержать электрическая схема, эквивалентная живой ткани: КАТУШКА ИНДУКТИВНОСТИ
Укажите правильные высказывания:
— При пропускании через ткани сила тока по фазе отстает от приложенного напряжения
+ Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и конденсаторов
+ В области a-дисперсии( низкие частоты 10(2) < v <10(4) Гц) в явлении поляризации ткани участвует все дипольные структуры тканей
— Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них емкостного сопротивления
Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из…частотная зависимость импеданса которой близка к частотной зависимости импеданса биологической ткани РЕЗИСТОРОВ И КОНДЕНСАТОРОВ
В области а- дисперсии ( низкие частоты 10(2) < v < 10(4) Гц) в явлении поляризации ткани участвуют: ВСЕ ДИПОЛЬНЫЕ СТРУКТУРЫ ТКАНЕЙ
При пропускании переменного тока через ткани сила тока по фазе…ОПЕРЕЖАЕТ ПРИЛОЖЕННОЕ СОПРОТИВЛЕНИЕ
Доказательством наличия у биологической ткани реактивного сопротивления является…ВОЗНИКНОВЕНИЕ СДВИГА ФАЗ МЕЖДУ СИЛОЙ ТОКА И НАПРЯЖЕНИЕМ ПРИ ПРОХОЖДЕНИИ ПЕРЕМЕННОГО ТОКА
Емкостная составляющая импеданса живой биологической ткани…. от частоты переменного тока ОБРАТНО ПРОПОРЦИОНАЛЬНО ЗАВИСИТ
от частоты переменного тока ОБРАТНО ПРОПОРЦИОНАЛЬНО ЗАВИСИТ
Возникновение сдвига фаз между силой тока и напряжением при прохождении переменного тока через биологическую ткань доказывает наличие у нее…РЕАКТИВНОГО СОПРОТИВЛЕНИЯ
Укажите правильные высказывания:
+ Частотная зависимость импеданса тканей позволяет оценить жизнеспособность ткани
+ Биологические ткани не обладают индуктивным сопротивлением
— Реактивное сопротивление биологической ткани обусловлено наличием тканевой жидкости, являющейся электролитом
— Реография — это диагностический метод, основанный на регистрации частотной зависимости импеданса сердца в процессе сердечной деятельности
Укажите сопротивление, которым биологические ткани не обладают: ИНДУКТИВНОЕ
Укажите правильные высказывания:
— Реография – это диагностический метод, основанный на регистрации изменения биопотенциалов сердца в процессе сердечной деятельности
— Биологические ткани обладают индуктивным сопротивлением
+ Биологические ткани по своим электрическим свойствам проявляют себя как проводники и диэлектрики
+ При увеличении частоты переменного тока импеданс тканей уменьшается
При увеличении частоты переменного тока импеданс тканей УМЕНЬШАЕТСЯ
В области B- дисперсии( v= 10(6)-10(7) Гц) в явлении поляризации ткани участвуют: КРУПНЫЕ МОЛЕКУЛЫ – ДИПОЛИ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
Укажите правильное высказывание для угла ф сдвига фаз между силой тока и напряжением для биологической ткани… ф<0
Электрическая схема ,эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и конденсаторов, у которой. . ЧАСТОТНАЯ ЗАВИСИМОСТЬ ИМПЕДАНСА БЛИЗКА К ЧАСТОТНОЙ ЗАВИСИМОСТИ ИМПЕДАНСА БИОЛОГИЧЕСКОЙ ТКАНИ
. ЧАСТОТНАЯ ЗАВИСИМОСТЬ ИМПЕДАНСА БЛИЗКА К ЧАСТОТНОЙ ЗАВИСИМОСТИ ИМПЕДАНСА БИОЛОГИЧЕСКОЙ ТКАНИ
Уменьшение импеданса живой ткани при увеличении частоты переменного тока обусловлена свойствами… МЕМБРАН КЛЕТОК, КАК МИКРОКОНДЕНСАТОРОВ
Реактивное сопротивление биологической ткани обусловлена, в частности, емкостью…БИОЛОГИЧЕСКИХ МЕМБРАН
Дисперсией импеданса называется.. ЗАВИСИМОСТЬ ПОЛНОГО СОПРОТИВЛЕНИЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ОТ ЧАСТОТЫ ТОКА
Зависимость импеданса живой ткани от частоты переменного тока обусловлена наличием у нее…ЕМКОСТНОГО СОПРОТИВЛЕНИЯ
Укажите правильные высказывания:
— В цепи переменного тока всегда происходит сдвиг фаз между силой тока и напряжением
+ Активное сопротивление цепи не зависит от частоты переменного тока
+ На векторной диаграмме напряжений цепи переменного тока вектор амплитуды напряжения на конденсаторе направлен перпендикулярно оси тока
— Величина( модуль) реактивного сопротивления равна сумме сопротивлений конденсатора и резистора
Активное сопротивление…. .от частоты переменного тока НЕ ЗАВИСИТ
.от частоты переменного тока НЕ ЗАВИСИТ
Укажите правильные высказывания:
+ Переменный ток – ток, изменяющийся во времени
+ Единицей СИ индуктивного сопротивления является Ом
— В цепи переменного тока сила тока и напряжение всегда совпадают по фазе
— При увеличении частоты переменного тока емкостное сопротивление увеличивается
Если угол сдвига фаз между током и напряжением в цепи переменного тока имеет положительное значение, то цепь обязательно содержит… КАТУШКУ ИНДУКТИВНОСТИ
Укажите правильные высказывания:
+ Импеданс- полное сопротивление цепи переменного тока
+ Емкостное сопротивление уменьшается с увеличением частоты переменного тока
— Переменный ток – ток, изменяющийся только по гармоническому закону
— Реактивное сопротивление включает емкостное и активное сопротивления
Укажите правильные высказывания:
— Величина( модуль) реактивного сопротивления равна сумме емкостного и индуктивного сопротивлений цепи переменного тока
— Единицей СИ емкостного сопротивления является генри(Гн)
+ На векторной диаграмме напряжений в цепи переменного тока вектор амплитуды напряжения на резисторе совпадает по направлению с осью тока
+ Реактивное сопротивление цепи переменного тока обусловлено наличием в ней конденсаторов и катушек индуктивности
Полное сопротивление- импеданс цепи переменного тока включает…сопротивление АКТИВНОЕ И РЕАКТИВНОЕ
При уменьшении частоты переменного тока активное сопротивление…. НЕ ИЗМЕНЯЕТСЯ
НЕ ИЗМЕНЯЕТСЯ
Вектор амплитуды напряжения на резисторе в векторной диаграмме напряжений цепи переменного тока направлен….к оси тока ПАРАЛЛЕЛЬНО
При уменьшении частоты переменного тока емкостное сопротивление… УВЕЛИЧИВАЕТСЯ
При увеличении частоты переменного тока индуктивное сопротивление…. УВЕЛИЧИВАЕТСЯ
При увеличении частоты переменного тока емкостное сопротивление…. УМЕНЬШАЕТСЯ
При увеличении частоты переменного тока активное сопротивление…. НЕ ИЗМЕНЯЕТСЯ
Индуктивное сопротивление…..от частоты переменного тока ПРЯМО ПРОПОРЦИОНАЛЬНО ЗАВИСИТ
Емкостное сопротивление…..от частоты переменного тока ОБРАТНО ПРОПОРЦИОНАЛЬНО
Активное сопротивление…от частоты переменного тока НЕ ЗАВИСИТ
Укажите правильные высказывания:
— Ток в цепи переменного тока, содержащей катушку индуктивности, по фазе совпадает с напряжением
— При прохождении переменного тока в реактивном сопротивлении происходит выделение тепла
+ Угол сдвига фаз между током и напряжением в цепи переменного тока, содержащий конденсатор, имеет отрицательный заряд
+ При увеличении частоты переменного тока индуктивное сопротивление увеличивается
Укажите единицу СИ индуктивного сопротивления: Ом
Укажите единицу СИ емкостного сопротивления: Ом
Укажите правильные высказывания:
+ Переменный ток в цепи с конденсатором опережает напряжение по фазе на П/2
— Единицей СИ индуктивного сопротивления является фарад (Ф)
-Активное сопротивление цепи зависит от частоты переменного тока
+ При прохождении переменного тока на активном сопротивлении происходит выделение теплоты
При прохождении переменного тока в цепи с реактивным сопротивлением происходит…ВОЗНИКНОВЕНИЕ РАЗНОСТИ ФАЗ МЕЖДУ ТОКОМ И НАПРЯЖЕНИЕМ
Индуктивное сопротивление определяется по формуле: xL = ωL
Емкостное сопротивление определяется по формуле:
| xC = | |
| ωC | |
Укажите формулу для определения импеданса цепи переменного тока, состоящей из последовательно соединенных резистора, катушки индуктивности и конденсатора:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных конденсатора и катушки индуктивности( активное сопротивление катушки индуктивности равно 0):
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора, конденсатора и катушки индуктивности:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора и катушки индуктивности:
Укажите векторную диаграмму цепи переменного тока, состоящей из последовательно соединенных резистора и конденсатора:
Укажите правильные высказывания:
+ При пропускании переменного тока через ткани сила тока по фазе опережает приложенное напряжение
— Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и катушек индуктивности
+ При уменьшении частоты переменного тока импеданс тканей увеличивается
— Биологические ткани по своим электрическим свойствам проявляют себя только как проводники
Укажите правильные высказывания:
+ Активное сопротивление цепи не зависит от частоты переменного тока
+ На векторной диаграмме напряжений цепи переменного тока вектор амплитуды напряжения на конденсаторе…. .
.
Укажите правильное высказывание:
+На векторной диаграмме напряжений в цепи переменного тока вектор амплитуды напряжения на резисторе совпадает….
+Реактивное сопротивление цепи переменного тока обусловлено наличием в ней конденсаторов и катушек индуктивности
Укажите правильные высказывания:
+Переменный ток- ток, изменяющийся во времени
+Единицей СИ индуктивного сопротивления является Ом
Укажите правильное высказывание:
+Импеданс- полное сопротивление цепи переменного тока
+Емкостное сопротивление уменьшается с увеличением частоты переменного тока
Активное сопротивление биологической ткани обусловлено, в частности, наличием в ней ТКАНЕВОЙ ЖИДКОСТИ, ЯВЛЯЮЩЕЙСЯ ЭЛЕКТРОЛИТОМ
При уменьшений частоты переменного тока емкостное сопротивление увеличивается
Активное сопротивление не зависит от частоты переменного тока
При увеличении частоты переменного тока индуктивное сопротивление увеличивается
При увеличении частоты переменного тока активное сопротивление не изменяется
При уменьшении частоты переменного тока активное сопротивление не изменяется
Вектор амплитуды напряжения на резисторе в векторной диаграмме напряжений цепи переменного тока направлен параллельно к оси тока
Если угол сдвига фаз между током и напряжением в цепи переменного тока имеет положительное значение, то цепь обязательно. . катушку индуктивности
. катушку индуктивности
Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них….. сопротивления АКТИВНОГО
Полное сопротивление- импеданс цепи переменного тока включает активное и реактивное сопротивление
Биологические ткани по своим электрическим свойствам проявляют себя как ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
Укажите правильные высказывания:
— Биологические ткани по своим электрическим свойствам проявляют себя только как диэлектрики
+ Возникновение сдвига фаз между силой тока и напряжением при прохождении переменного тока через биологическую ткань доказывает наличие у нее реактивного сопротивления
— Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них реактивного сопротивления
+ В области y-дисперсии(v-2*10(10) Гц) в явлении поляризации ткани участвуют только молекулы воды
Укажите правильные высказывания:
+ Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них активного сопротивления
— В области y-дисперсии(v-2*10(10) Гц) в явлении поляризации ткани участвуют все дипольные структуры тканей
— Биологические ткани не обладают емкостным сопротивлением
+ Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называется реографией
Укажите правильные высказывания:
+ Биологические ткани по своим электрическим свойствам проявляют себя как проводники и диэлектрики
+ При увеличении частоты переменного тока импеданс тканей уменьшается
— Биологические ткани обладают индуктивным сопротивлением
— Реография- это диагностический метод, основанный на регистрации изменения биопотенциалов сердца в процессе сердечной деятельности
Укажите элемент, который не должна содержать электрическая схема, эквивалентная живой ткани: КАТУШКА ИНДУКТИВНОСТИ
Укажите правильные высказывания:
— При пропускании через ткани сила тока по фазе отстает от приложенного напряжения
+ Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и конденсаторов
+ В области a-дисперсии( низкие частоты 10(2)<v<10(4) Гц) в явлении поляризации ткани участвует все дипольные структуры тканей
— Выделение тепла в тканях при прохождении электрического тока обусловлено наличием у них емкостного сопротивления
Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из…частотная зависимость импеданса которой близка к частотной зависимости импеданса биологической ткани РЕЗИСТОРОВ И КОНДЕНСАТОРОВ
В области В- дисперсии (v= 106-107 Гц) в явлении поляризации ткани участвуют: крупные молекулы- диполи органических соединений
Укажите правильное выражение для угла ф сдвига фаз между силой тока и напряжением для биологической ткани- ф<0
Электрическая схема, эквивалентная живой ткани, представляет собой схему, состоящую из резисторов и конденсаторов, у которой частотная зависимость импеданса близка к частотной зависимости импеданса биологической ткани
Уменьшение импеданса живой ткани при увеличении частоты переменного тока обусловлена свойствами- мембран клеток, как микроконденсаторов
В области а- дисперсии ( низкие частоты 10(2)<v< 10(4) Гц) в явлении поляризации ткани участвуют: ВСЕ ДИПОЛЬНЫЕ СТРУКТУРЫ ТКАНЕЙ
При пропускании переменного тока через ткани сила тока по фазе…ОПЕРЕЖАЕТ ПРИЛОЖЕННОЕ СОПРОТИВЛЕНИЕ
Доказательством наличия у биологической ткани реактивного сопротивления является…ВОЗНИКНОВЕНИЕ СДВИГА ФАЗ МЕЖДУ СИЛОЙ ТОКА И НАПРЯЖЕНИЕМ ПРИ ПРОХОЖДЕНИИ ПЕРЕМЕННОГО ТОКА
Емкостная составляющая импеданса живой биологической ткани….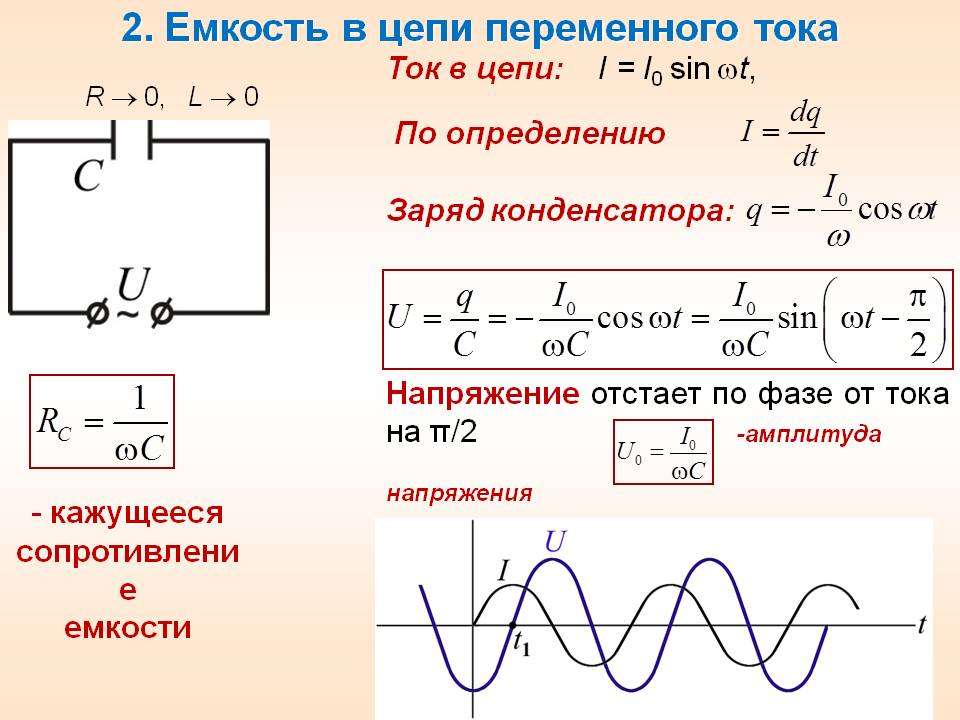 от частоты переменного тока ОБРАТНО ПРОПОРЦИОНАЛЬНО ЗАВИСИТ
от частоты переменного тока ОБРАТНО ПРОПОРЦИОНАЛЬНО ЗАВИСИТ
Возникновение сдвига фаз между силой тока и напряжением при прохождении переменного тока через биологическую ткань доказывает наличие у нее…РЕАКТИВНОГО СОПРОТИВЛЕНИЯ
Укажите правильные высказывания:
+ Частотная зависимость импеданса тканей позволяет оценить жизнеспособность ткани
+ Биологические ткани не обладают индуктивным сопротивлением
— Реактивное сопротивление биологической ткани обусловлено наличием тканевой жидкости, являющейся электролитом
— Реография — это диагностический метод, основанный на регистрации частотной зависимости импеданса сердца в процессе сердечной деятельности
Укажите сопротивление, которым биологические ткани не обладают: ИНДУКТИВНОЕ
Укажите правильные высказывания:
— Реография – это диагностический метод, основанный на регистрации изменения биопотенциалов сердца в процессе сердечной деятельности
— Биологические ткани обладают индуктивным сопротивлением
+ Биологические ткани по своим электрическим свойствам проявляют себя как проводники и диэлектрики
+ При увеличении частоты переменного тока импеданс тканей уменьшается
+Динамическая вязкость зависит от состояния и молекулярных свойств жидкости
-Сила внутреннего трения не зависит от градиента скорости
-При падении шарика в вязкой среде его скорость увеличивается
+В трубе частицы текущей жидкости равноудаленные от оси умеют одинаковую скорость
Гидравлическое сопротивление сосуда ПРЯМО ПРОПОРЦИОНАЛЬНО динамической вязкости жидкости
При турбулентном течении число Рейнольдса БОЛЬШЕ КРИТИЧЕСКОГО
Согласно закону Стокса, при небольшой скорости движения сферического тела в жидкости, сила сопротивления ПРЯМО ПРОПОРИОНАЛЬНА скорости
Кровь является неньютоновской жидкостью так как ОНА СОДЕРЖИТ СКЛОННЫЕ К АГРЕГАЦИИ ЭЛЕМЕНТЫ
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта
Автор: Аронов Леонид Вячеславович
Рубрика: Технические науки
Опубликовано в
Молодой учёный
№12 (116) июнь-2 2016 г.
Дата публикации: 04.06.2016 2016-06-04
Статья просмотрена: 1292 раза
Скачать электронную версию
Скачать Часть 2 (pdf)
Библиографическое описание:Аронов, Л. В. Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта / Л. В. Аронов. — Текст : непосредственный // Молодой ученый. — 2016. — № 12 (116). — С. 202-205. — URL: https://moluch.ru/archive/116/31269/ (дата обращения: 05.10.2022).
В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в диапазоне частот от 50 до 2000 Гц. Выведена расчетная формула для активного сопротивления цилиндрического провода на произвольной частоте. Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и площади поперечного сечения.
Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и площади поперечного сечения.
Ключевые слова: поверхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого провода
This article has shown the problem of high-harmonics influence on cylindrical wire resistance according to the frequency range from 50 to 2000 Hz. Cylindrical wire resistance estimation for any frequency has been deduced.We have also analyzed cylindrical wire resistance dependence of copper and aluminum wires due to the frequency and cross section area.
Keywords: skin effect, high-harmonics, copper wire resistance, aluminum wire resistance
В Российской Федерации системы электроснабжения общего назначения работают на фиксированной частоте 50 Гц. Кроме основной гармоники, в сетях присутствуют также высшие гармоники токов и напряжений [1]. Исследования указывают на то, что при наличии в сети нелинейных нагрузок, наибольшим искажениям подвергается форма кривой тока, в то время как кривая напряжения практически не изменяется [5, 6]. Это объясняется тем, что реальные генераторы по своим свойствам близки к идеальным источникам ЭДС. Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери мощности, с другой происходит ускоренный износ изоляции, изоляторов, растяжение проводов и другие негативные последствия [2]. По мере увеличения частоты, начинает проявляться поверхностный эффект, приводящий к перераспределению плотности тока в сечении проводника, от центра к поверхности, в результате изменяется его сопротивление, что в свою очередь влияет на потери мощности и энергии в линиях электропередачи электрической распределительной сети.
Исследования указывают на то, что при наличии в сети нелинейных нагрузок, наибольшим искажениям подвергается форма кривой тока, в то время как кривая напряжения практически не изменяется [5, 6]. Это объясняется тем, что реальные генераторы по своим свойствам близки к идеальным источникам ЭДС. Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери мощности, с другой происходит ускоренный износ изоляции, изоляторов, растяжение проводов и другие негативные последствия [2]. По мере увеличения частоты, начинает проявляться поверхностный эффект, приводящий к перераспределению плотности тока в сечении проводника, от центра к поверхности, в результате изменяется его сопротивление, что в свою очередь влияет на потери мощности и энергии в линиях электропередачи электрической распределительной сети.
Задача данного исследования: определить степень изменения плотности тока в сечении провода и его сопротивления в зависимости от частоты гармоники тока протекающего по проводнику.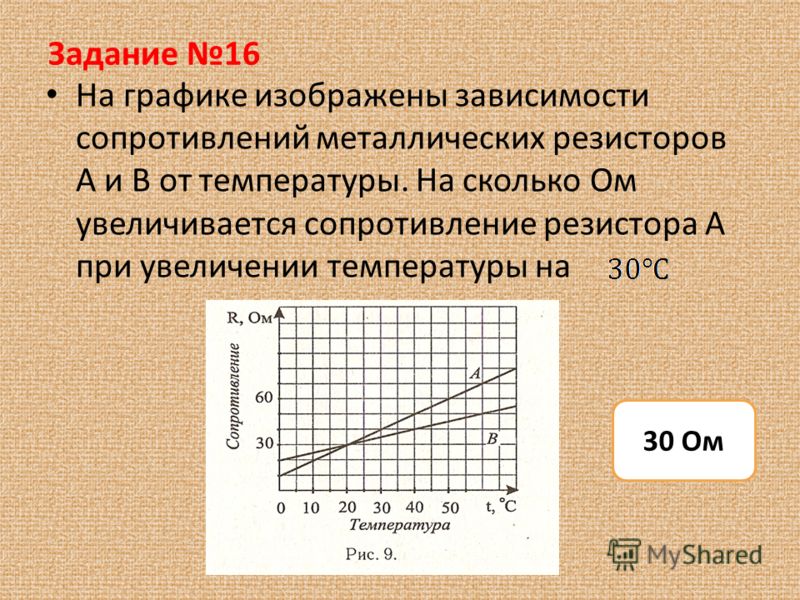 Это позволит более точно рассчитать дополнительные потери мощности на нагрев проводов, обусловленные несинусоидальностью питающего напряжения электрической распределительной сети.
Это позволит более точно рассчитать дополнительные потери мощности на нагрев проводов, обусловленные несинусоидальностью питающего напряжения электрической распределительной сети.
Провод можно приближенно представить в виде цилиндрического проводника, длина которого многократно превышает радиус. Для нахождения плотности тока используют уравнения Максвелла, решение которых производится в цилиндрической системе координат [3]. В результате выражения для плотности тока и напряженности магнитного поля в любой точке сечения цилиндрического проводника:
(1)
(2)
где — комплексная плотность тока, А/м2; — напряженность магнитного поля, А/м; — комплексный ток, А; J0 — функция Бесселя 1-го рода 0-го порядка; J1 — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м; — комплексное волновое число, м-1; — круговая частота, рад/с; f — циклическая частота, Гц; — абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
Формулы (1), (2) не учитывают «эффект близости», т. к. для этого необходимо точно знать пространственное расположение проводников. При расстоянии между проводами многократно превышающем радиус и невысоких значениях тока «эффектом близости» можно пренебречь.
Мощность рассеиваемую цилиндрическим проводом определяют по закону Джоуля-Ленца в комплексной форме:
(3)
С другой стороны рассеиваемую мощность находим, используя теорему Умова-Пойнтинга [3]:
(4)
Приравнивая выражения (3) и (4) получаем:
(5)
В результате комплексное сопротивление выражаем формулой:
(6)
Вектор напряженности электрического поля вычисляем по формуле:
(7)
где σ — удельная проводимость, См/м.
Учитывая, что площадь боковой поверхности цилиндрического проводника равна S=2·π·a·lи радиус поверхности равен радиусу провода r=a получаем:
где l — длина проводника, м.
Таким образом, окончательное выражение для комплексного сопротивления цилиндрического провода приняло вид:
Активное сопротивление при этом определяем, как действительную часть полного комплексного сопротивления:
(8)
Рассчитаем сопротивления медных проводов и алюминиевых проводов марок А, АКП, АН, АНКП, АЖ, АЖКП. Сечения выберем самые распространенные: 16, 25, 35, 50, 70, 95, 120, 150, 185 мм2 [4], хотя каких-либо ограничений по сечению проводов нет. Единственное условие данного метода: длина должна быть много больше радиуса l>>a. Удельная проводимость меди σCu=56·106 См/м, а удельная проводимость алюминия σAl=37·106 См/м. Относительная магнитная проницаемость обоих материалов приблизительно равна µ=1 (медь является диамагнетиком, а алюминий парамагнетиком). Радиус провода выражаем из формулы площади круга:
,
где s — площадь сечения провода, мм2.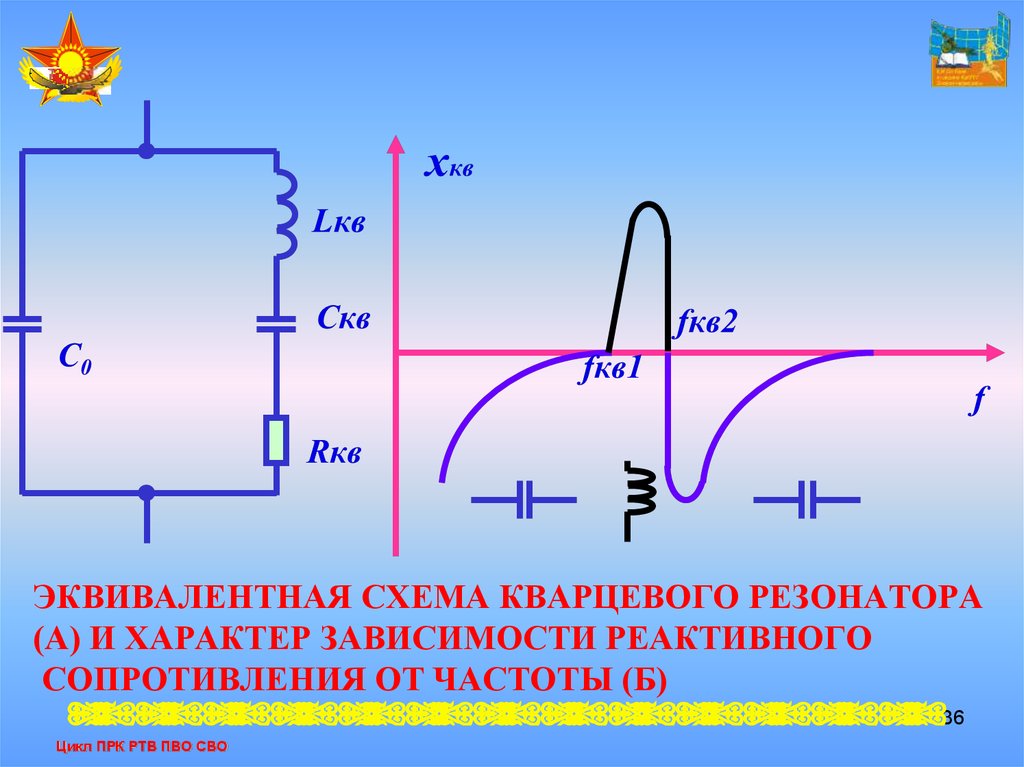
Расчета активного сопротивления медных проводов различных сечений, выполнен в диапазоне частот 0–2 кГц (рисунок 1.). Аналогичный расчет проведен для алюминиевых проводов (рисунок 2.). Выбор диапазона обосновывается тем, что согласно ГОСТ Р54149–2010, гармоники нормируются до 40-й включительно, что соответствует наибольшему значению частоты 2кГц [1].
Рис. 1. Зависимость активного сопротивления медных проводов различных сечений от частоты
Семейства графиков (рисунки 1, 2) показывает зависимость погонного сопротивления проводов как от их сечения, так и от частоты. В полосе частот от 0 до 2000 Гц (рисунок 1.) величина возрастания сопротивления от 10,4 % до 183,9 %, в зависимости от сечения провода. Причем наибольший, в процентном отношении, прирост сопротивления наблюдается на больших сечениях. Например, при сечении 16 мм2 погонное сопротивление увеличивается с 1,08 до 1,19 Ом/км, что составляет 10,4 %, а при наибольшем сечении 185 мм2 погонное сопротивление увеличивается с 0,09 до 0,27 Ом/км, что в пересчете на проценты составляет 183,9 %. Это объясняется большей неравномерностью плотности тока при большем радиусе сечений проводов.
Это объясняется большей неравномерностью плотности тока при большем радиусе сечений проводов.
Рис. 2. Зависимость активного сопротивления алюминиевых проводов различных сечений от частоты
Результаты, полученные для алюминиевых проводов (рисунок 2.), аналогичны результатам для медных проводов. Сопротивление возрастает на величину от 4,4 % до 133,8 %, в зависимости от сечения провода, наименьший прирост погонного сопротивления наблюдается при сечении 16 мм2, в этом случае погонное сопротивление увеличивается с 1,69 до 1,76 Ом/км, что составляет 4,4 %, а при наибольшем приведенном на графике сечении 185 мм2 погонное сопротивление увеличивается с 0,15 до 0, 34 Ом/км, что в пересчете на проценты составляет 133,8 %.
Таким образом для проводников большего сечения поверхностный эффект оказывает более выраженное влияние на сопротивление (для меди сопротивление возросло на 183,9 %, а для алюминия на 133,8 %, в полосе частот от 0 до 2000 Гц), уменьшение же сечения приводит к существенному возрастанию активного сопротивления (рисунки 1,2. ). Проводники с большей удельной проводимостью более подвержены влиянию поверхностного эффекта. При равном сечении, по мере увеличения частоты, активное сопротивление медного провода возрастает быстрее, чем активное сопротивление алюминиевого провода.
). Проводники с большей удельной проводимостью более подвержены влиянию поверхностного эффекта. При равном сечении, по мере увеличения частоты, активное сопротивление медного провода возрастает быстрее, чем активное сопротивление алюминиевого провода.
Литература:
- ГОСТ 32144–2013 Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. [Текст] — М.: Стандартинформ — 2014г. — 38 с.
- Григорьев О. Высшие гармоники в сетях электроснабжения 0,4 кВ/ О. Григорьев, В. Петухов, В. Соколов, И. Красилов [Текст] //«Новости электротехники», № 6(18) 2002–1(19) 2003.
- Бессонов Л. А. Теоретические основы электротехники [Текст] — М.: Высшая школа — 1964г. — 750 с.
- Будзко И. А. Элетроснабжение сельского хозяйства/ И. А. Будзко, Т. Б. Лещинская, В. И. Сукманов [Текст] — М: Колос — 2000 г. — 536 с.
- Бессонов Л. А. Линейные электрические цепи / Л.
 А. Бессонов. — М: Высшая школа, 1983. — 336 с.
А. Бессонов. — М: Высшая школа, 1983. — 336 с. - Лосев А. К. Теория Линейных электрических цепей / А. К. Лосев. — М: Высшая школа, 1987. — 512 с.
Основные термины (генерируются автоматически): активное сопротивление, погонное сопротивление, поверхностный эффект, провод, сечение, цилиндрический провод, радиус провода, сечение провода, цилиндрический проводник, алюминиевый провод.
Ключевые слова
поверхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого проводаповерхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого провода
Похожие статьи
Влияние площади контакта и
сечения провода на величину. ..
..Провода тонкого сечения. Диаметр провода, мм.
ток, аккумуляторная батарея, провода. Похожие статьи. Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Расчет потерь в обмотках электрических машин с учетом…
Активное сопротивление каждого провода обмотки
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Основные термины (генерируются автоматически):
провод…Малое сечение провода обуславливает требования к режиму намотки катушки.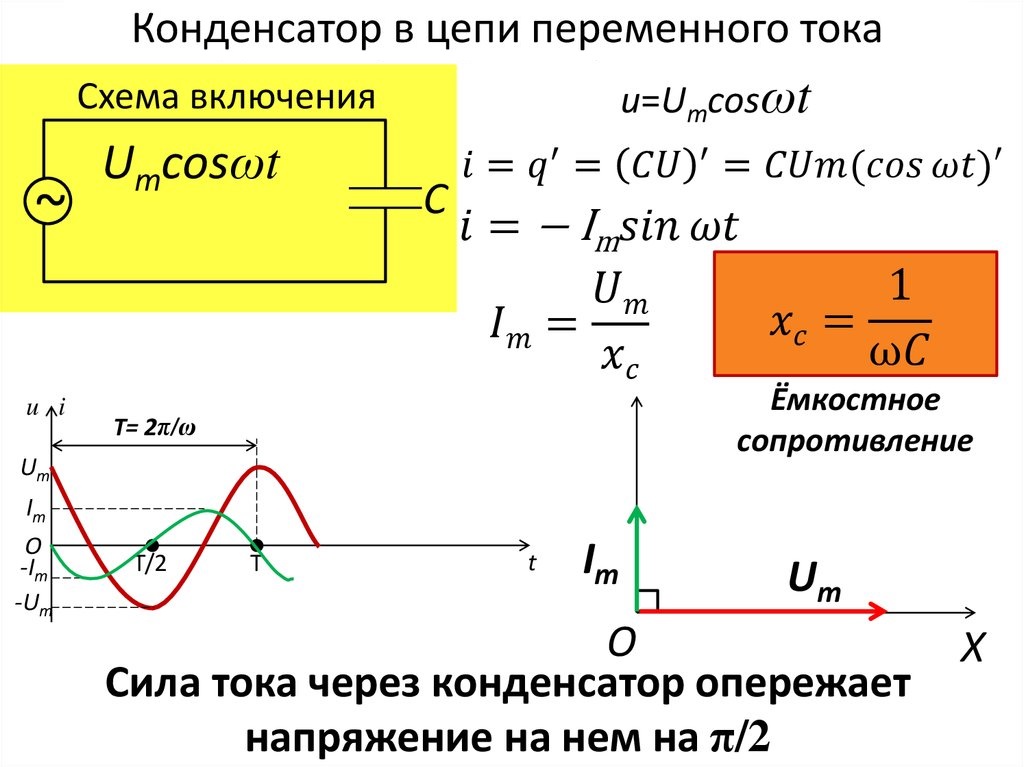 Естественно предполагать, что стремление минимизации размеров, хорошей плотности укладки требует соответствующего натяжения провода при намотке [4,5]…
Естественно предполагать, что стремление минимизации размеров, хорошей плотности укладки требует соответствующего натяжения провода при намотке [4,5]…
Оценивание рабочей ёмкости и эквивалентной диэлектрической…
Кроме того, пренебрегаем потерями в проводах, считая их идеально проводящими (R=0). Так как для идеальных проводников внутренняя индуктивность равна нулю, то в этом случае полная погонная индуктивность линии L сводится к её внешней индуктивности Le.
Напряженно-деформированное состояние пологих и подъемистых…
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта. Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.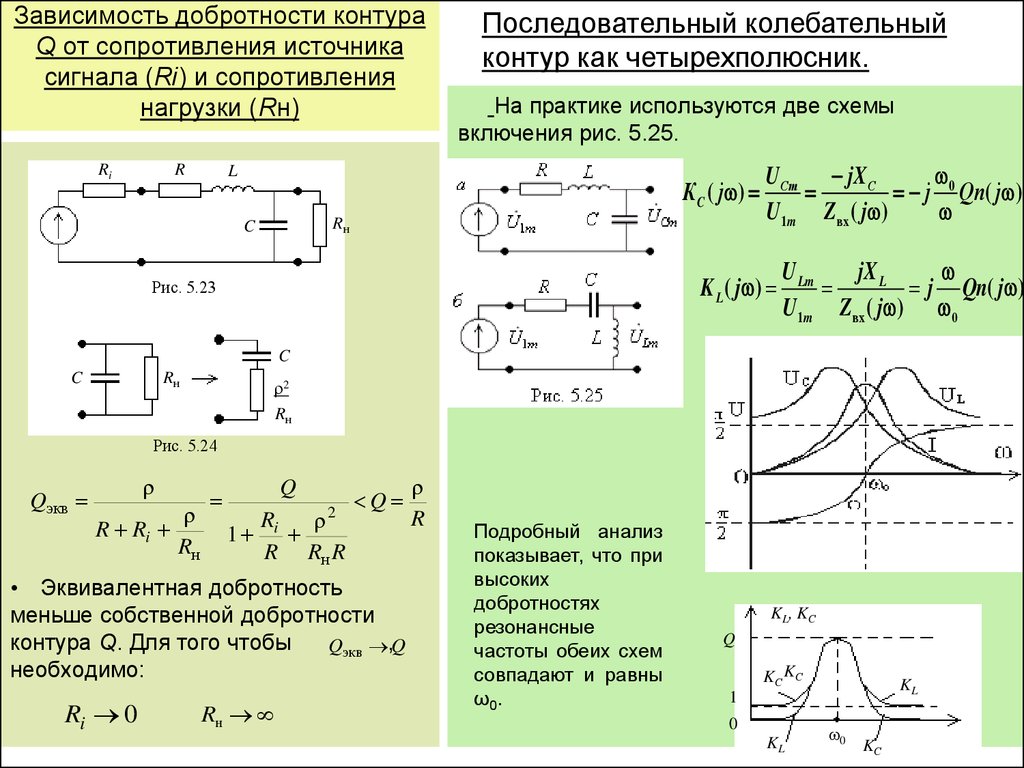
Расчет распределения тока в плоском индукционном нагревателе…
Два проводника одной полярности соединены между собой и между ними размещен третий проводник противоположной полярности (в другом случае не три, а n проводников).
. (6). Активное сопротивление R, Ом определяется по формуле.
Способы сохранения целостности ВЧ-сигнала в печатном…
Печатные проводники при проектировании современных плат
На высоких частотах (ВЧ) проявляются те эффекты, о которых не задумывались раньше и
Они обладают нулевым сопротивлением, имеют одинаковое поперечное сечение по всей длине и бесконечную длину.
Скин-
эффект в асинхронном двигателе с короткозамкнутым…Мысленно разделим сечение каждого стержня на большое число ( ) тонких проводников.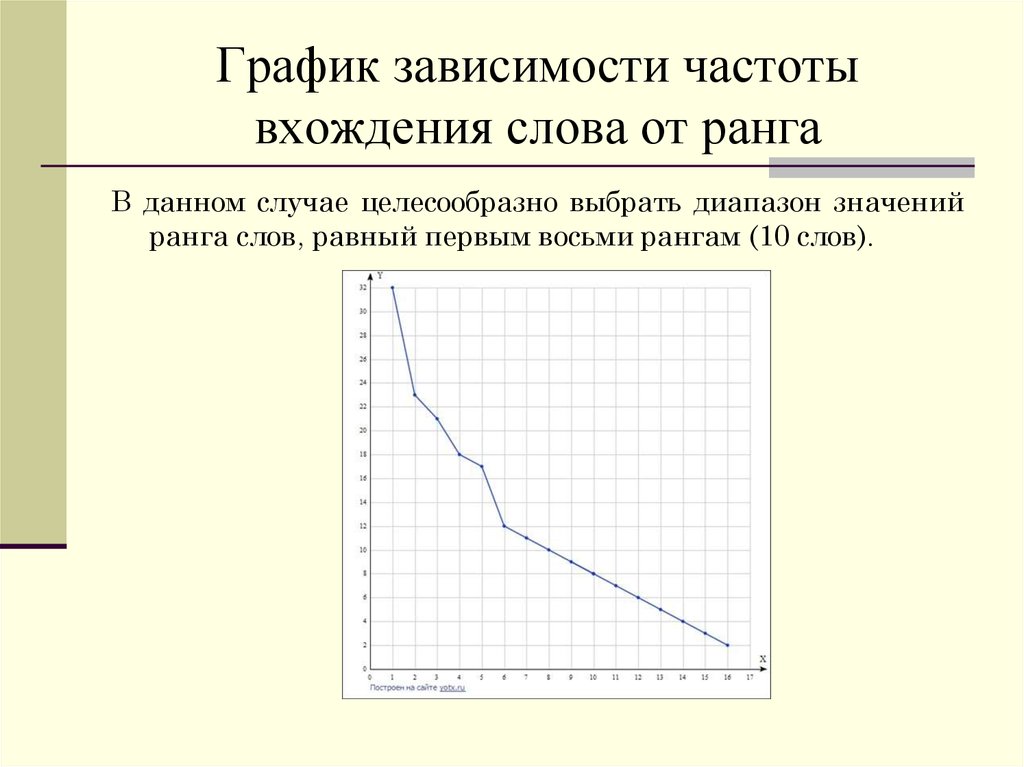 Пусть (для упрощения анализа) активное сопротивление всех тонких проводников будет одинаковым.
Пусть (для упрощения анализа) активное сопротивление всех тонких проводников будет одинаковым.
Влияние площади контакта и
сечения провода на величину…Провода тонкого сечения. Диаметр провода, мм.
ток, аккумуляторная батарея, провода. Похожие статьи. Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Расчет потерь в обмотках электрических машин с учетом…
Активное сопротивление каждого провода обмотки
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Основные термины (генерируются автоматически):
провод…Малое сечение провода обуславливает требования к режиму намотки катушки. Естественно предполагать, что стремление минимизации размеров, хорошей плотности укладки требует соответствующего натяжения провода при намотке [4,5]…
Оценивание рабочей ёмкости и эквивалентной диэлектрической…
Кроме того, пренебрегаем потерями в проводах, считая их идеально проводящими (R=0). Так как для идеальных проводников внутренняя индуктивность равна нулю, то в этом случае полная погонная индуктивность линии L сводится к её внешней индуктивности Le.
Напряженно-деформированное состояние пологих и подъемистых…
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта. Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.
Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.
Расчет распределения тока в плоском индукционном нагревателе…
Два проводника одной полярности соединены между собой и между ними размещен третий проводник противоположной полярности (в другом случае не три, а n проводников).
. (6). Активное сопротивление R, Ом определяется по формуле.
Способы сохранения целостности ВЧ-сигнала в печатном…
Печатные проводники при проектировании современных плат
На высоких частотах (ВЧ) проявляются те эффекты, о которых не задумывались раньше и
Они обладают нулевым сопротивлением, имеют одинаковое поперечное сечение по всей длине и бесконечную длину.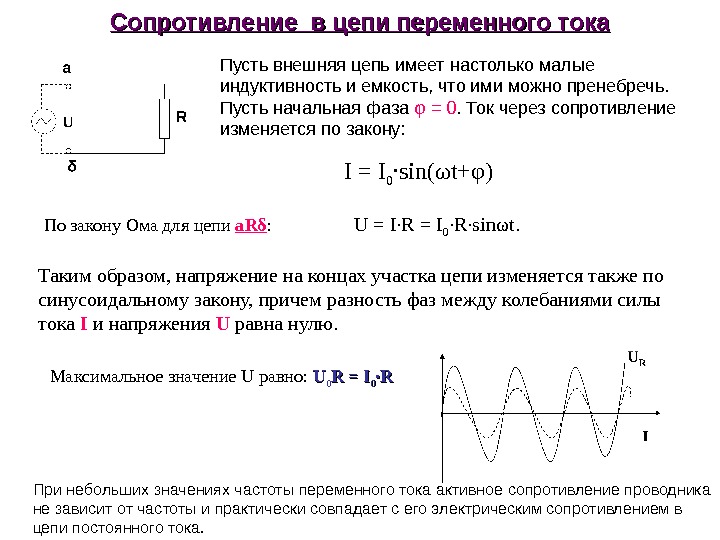
Скин-
эффект в асинхронном двигателе с короткозамкнутым…Мысленно разделим сечение каждого стержня на большое число ( ) тонких проводников. Пусть (для упрощения анализа) активное сопротивление всех тонких проводников будет одинаковым.
Похожие статьи
Влияние площади контакта и
сечения провода на величину…Провода тонкого сечения. Диаметр провода, мм.
ток, аккумуляторная батарея, провода. Похожие статьи. Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Расчет потерь в обмотках электрических машин с учетом.
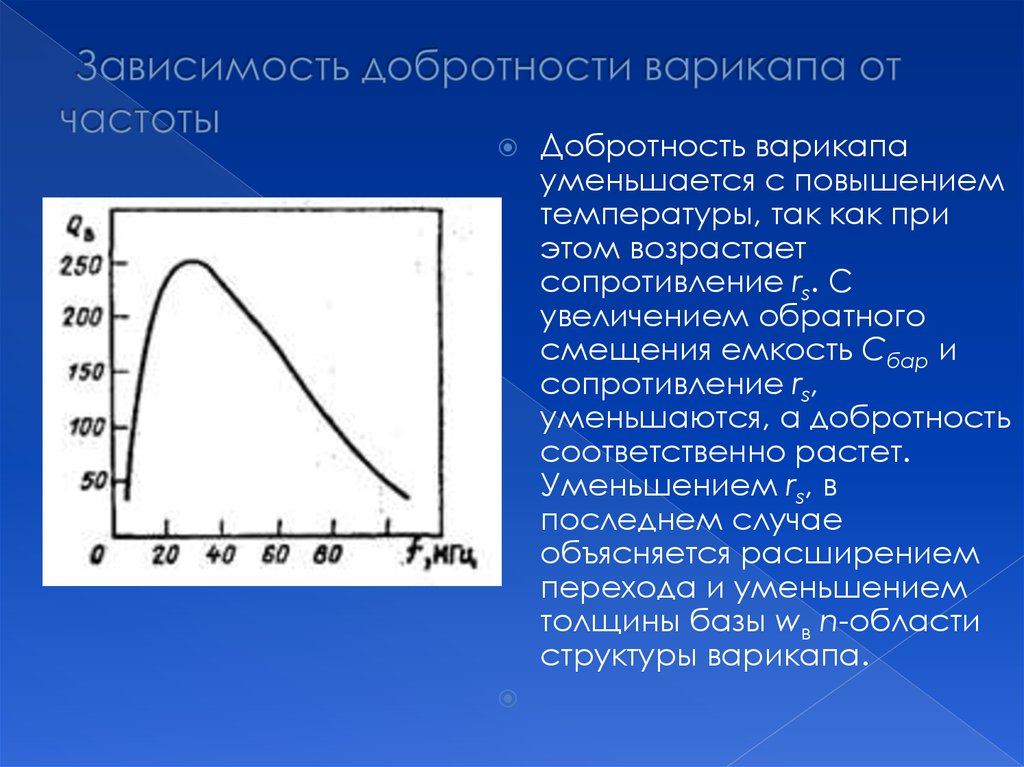 ..
..Активное сопротивление каждого провода обмотки
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Основные термины (генерируются автоматически):
провод…Малое сечение провода обуславливает требования к режиму намотки катушки. Естественно предполагать, что стремление минимизации размеров, хорошей плотности укладки требует соответствующего натяжения провода при намотке [4,5]…
Оценивание рабочей ёмкости и эквивалентной диэлектрической…
Кроме того, пренебрегаем потерями в проводах, считая их идеально проводящими (R=0). Так как для идеальных проводников внутренняя индуктивность равна нулю, то в этом случае полная погонная индуктивность линии L сводится к её внешней индуктивности Le.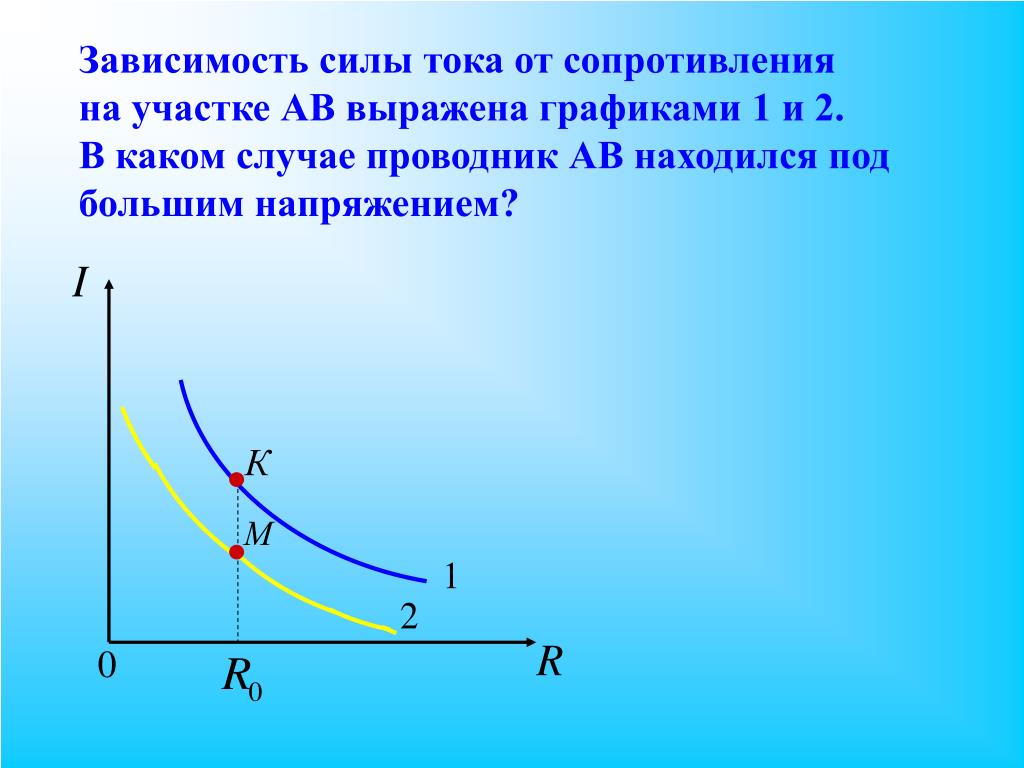
Напряженно-деформированное состояние пологих и подъемистых…
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта. Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.
Расчет распределения тока в плоском индукционном нагревателе…
Два проводника одной полярности соединены между собой и между ними размещен третий проводник противоположной полярности (в другом случае не три, а n проводников).
. (6). Активное сопротивление R, Ом определяется по формуле.
Способы сохранения целостности ВЧ-сигнала в печатном…
Печатные проводники при проектировании современных плат
На высоких частотах (ВЧ) проявляются те эффекты, о которых не задумывались раньше и
Они обладают нулевым сопротивлением, имеют одинаковое поперечное сечение по всей длине и бесконечную длину.
Скин-
эффект в асинхронном двигателе с короткозамкнутым…Мысленно разделим сечение каждого стержня на большое число ( ) тонких проводников. Пусть (для упрощения анализа) активное сопротивление всех тонких проводников будет одинаковым.
Влияние площади контакта и
сечения провода на величину…Провода тонкого сечения. Диаметр провода, мм.
ток, аккумуляторная батарея, провода. Похожие статьи. Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Расчет потерь в обмотках электрических машин с учетом…
Активное сопротивление каждого провода обмотки
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.
Основные термины (генерируются автоматически):
провод…Малое сечение провода обуславливает требования к режиму намотки катушки. Естественно предполагать, что стремление минимизации размеров, хорошей плотности укладки требует соответствующего натяжения провода при намотке [4,5]…
Оценивание рабочей ёмкости и эквивалентной диэлектрической…
Кроме того, пренебрегаем потерями в проводах, считая их идеально проводящими (R=0). Так как для идеальных проводников внутренняя индуктивность равна нулю, то в этом случае полная погонная индуктивность линии L сводится к её внешней индуктивности Le.
Напряженно-деформированное состояние пологих и подъемистых…
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта.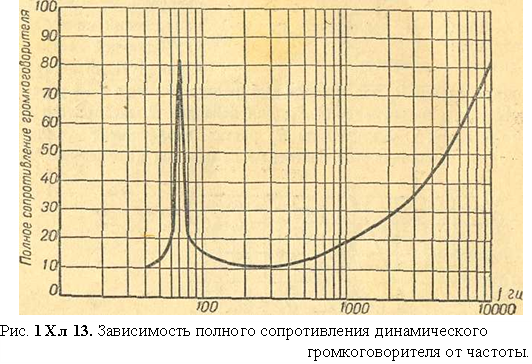 Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.
Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости.
Расчет распределения тока в плоском индукционном нагревателе…
Два проводника одной полярности соединены между собой и между ними размещен третий проводник противоположной полярности (в другом случае не три, а n проводников).
. (6). Активное сопротивление R, Ом определяется по формуле.
Способы сохранения целостности ВЧ-сигнала в печатном…
Печатные проводники при проектировании современных плат
На высоких частотах (ВЧ) проявляются те эффекты, о которых не задумывались раньше и
Они обладают нулевым сопротивлением, имеют одинаковое поперечное сечение по всей длине и бесконечную длину.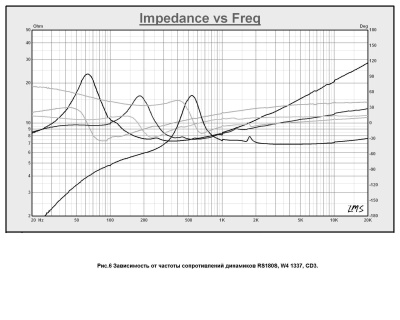
Скин-
эффект в асинхронном двигателе с короткозамкнутым…Мысленно разделим сечение каждого стержня на большое число ( ) тонких проводников. Пусть (для упрощения анализа) активное сопротивление всех тонких проводников будет одинаковым.
[РЕШЕНО] — Связь между сопротивлением и частотой
Добро пожаловать на EDAboard.com
Добро пожаловать на наш сайт! EDAboard.com — это международный дискуссионный форум по электронике, посвященный программному обеспечению EDA, схемам, схемам, книгам, теории, документам, asic, pld, 8051, DSP, сети, радиочастотам, аналоговому дизайну, печатным платам, руководствам по обслуживанию… и многому другому. более! Для участия необходимо зарегистрироваться. Регистрация бесплатна. Нажмите здесь для регистрации.
Регистрация Авторизоваться
JavaScript отключен.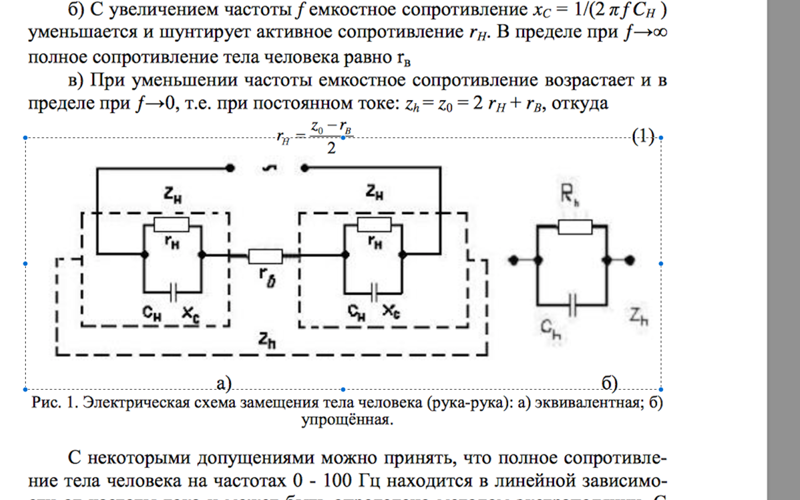 Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы Сиддарт Гасте
- Дата начала
- Статус
- Закрыто для дальнейших ответов.
Сиддарт Гасте
Уровень продвинутого члена 4
HI,
Какая связь между сопротивлением и частотой???
мф1364
Полноправный член уровня 3
Сиддарт Гасте сказал:
HI,
Какая связь между сопротивлением и частотой???Нажмите, чтобы развернуть.
..
полностью нет линейной зависимости между сопротивлением и частотой на низкой частоте, но, возможно, резисторы проявляют особенности индуктивности на высокой частоте
Сиддарт Гасте
Расширенный член уровня 4
Хорошо, спасибо, увеличивается или уменьшается частота высоких частот???
нитишн5
Полноправный член уровня 5
Если вы говорите об Идеальных компонентах, то там нет влияния резистора на частоту.
Если вы делаете какую-то схему типа фильтра RC/RL/RLC, то значение R влияет на отклик схемы на разных частотах. Но этот эффект связан не только с резистором, но в основном с конденсатором и/или катушкой индуктивности, присутствующими вместе с резистором.
Если вы смотрите на настоящие компоненты, резистор будет иметь некоторую паразитную индуктивность из-за того, как он сделан.
Сиддарт Гасте
Расширенный член уровня 4
Хорошо, эффект будет больше или меньше??
нитишн5
Полноправный член уровня 5
Какой эффект?
В реальных компонентах или в цепях RC/RL/RLC?
Что вы подразумеваете под «более или менее»?
Сиддарт Гасте
Расширенный член уровня 4
Извините за неправильный ответ, как это повлияет на резистор….
нитишн5
Полноправный член уровня 5
Я думаю, вы спрашиваете, что происходит с резистором на высоких частотах.
Реальный резистор можно представить как R eff = R +ωL. Это резистор и индуктор последовательно.
R — номинал резистора.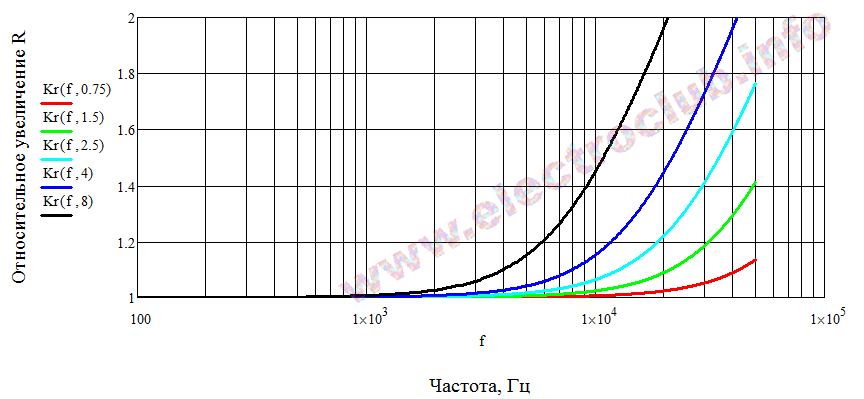
L — паразитная индуктивность.
Значение L будет очень маленьким, порядка nH (10 -9 H)
Следовательно, на низких частотах эффективное сопротивление будет R eff ≈ R
Но на очень высоких частотах скажем ω = R/2πL и выше значение индуктивности будет преобладать, и R eff будет намного выше.
И это будет увеличиваться с частотой.
Сиддарт Гасте
Расширенный член уровня 4
Хорошо, большое спасибо…
Вл@i$
Расширенный член уровня 1
Посмотрите:
https://www.groupdiy.com/index.php?topic=34674.0
- Статус
- Закрыто для дальнейших ответов.
разница между Vgg и Vgs
- Автор mohamis288
- Ответов: 3
Элементарные электронные вопросы
С
Сопротивление ножки резистора ТО220?
- Инициировано cupoftea
- Ответов: 4
Элементарные электронные вопросы
О
Преобразование между mv/g и LSB/g
- Инициировано oswahhad
- Ответов: 18
Элементарные электронные вопросы
Ф
Отрицательное сопротивление — кварцевый осциллятор
- Создано FreshmanNewbie
- Ответов: 3
Элементарные электронные вопросы
разница между «током смещения стока (I-DQ)» и «током стока (I-D)»
- Автор: mohamis288
- Ответов: 4
Элементарные электронные вопросы
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
Верх
Влияние высоко- и низкочастотных силовых тренировок на рост мышечной массы и мышечной силы у нетренированных мужчин
Рандомизированное контролируемое исследование
. 2021 1 августа; 35 (8): 2089-2094.
2021 1 августа; 35 (8): 2089-2094.
doi: 10.1519/JSC.0000000000003145.
Кристиан М.С. Франко 1 , Марсело А. С. Карнейро 1 , Жаиро Ф. Р. де Соуза 1 , Гедерсон К. Гомес 1 , Фабио Л. Орсатти 1 2
Принадлежности
- 1 Исследовательская группа по биологии упражнений (BioEx), Федеральный университет Триангуло Минейро (UFTM), Убераба, Минас-Жерайс, Бразилия; а также.
- 2 Департамент спортивных наук, Институт медицинских наук, Федеральный университет Триангуло Минейро (UFTM), Убераба, Минас-Жерайс, Бразилия.

- PMID: 31009427
- DOI: 10.1519/ОАО.0000000000003145
Рандомизированное контролируемое исследование
Кристиан М. С. Франко и др. J Прочность Конд Рез. .
. 2021 1 августа; 35 (8): 2089-2094.
doi: 10.1519/JSC.0000000000003145.
Авторы
Кристиан М.С. Франко 1 , Марсело А. С. Карнейро 1 , Жаиро Ф. Р. де Соуза 1 , Гедерсон К. Гомес 1 , Фабио Л. Орсатти 1
2
Гомес 1 , Фабио Л. Орсатти 1
2
Принадлежности
- 1 Исследовательская группа по биологии упражнений (BioEx), Федеральный университет Триангуло Минейро (UFTM), Убераба, Минас-Жерайс, Бразилия; а также.
- 2 Департамент спортивных наук, Институт медицинских наук, Федеральный университет Триангуло Минейро (UFTM), Убераба, Минас-Жерайс, Бразилия.
- PMID: 31009427
- DOI: 10.1519/ОАО.0000000000003145
Абстрактный
Франко, CMC, Карнейро, MAS, де Соуза, JFR, Гомес, Г. К., и Орсатти, Флорида. Влияние высокочастотных и низкочастотных тренировок с отягощениями на безжировую массу тела и прирост мышечной силы у нетренированных мужчин. J Прочность Сопротивление 35(8): 2089-2094, 2021-Цель этого исследования состояла в том, чтобы выяснить, дает ли высокочастотная тренировка с отягощениями (HFRT) лучшие результаты в отношении сухой массы тела (LBM) и прироста мышечной силы по сравнению с низкочастотной тренировкой с отягощениями (LFRT). Восемнадцать нетренированных мужчин (рост: 1,76 ± 0,05 м, масса тела: 78,3 ± 13,5 кг, возраст: 22,1 ± 2,2 года) были случайным образом распределены в HFRT (n = 9) и LFRT (n = 9). Мышечная сила {максимум 1 повторения (RM) (жим лежа [BP] и одностороннее разгибание ног [LE])} и LBM (DXA) оценивались до и после 8 недель тренировок. Обе группы выполняли 7 упражнений с сопротивлением всего тела, стандартизированных до 10 подходов в неделю, 8-12 максимальных повторений и 90-120 секунд отдыха в 5-дневной тренировке с отягощениями. LFRT выполнял программу с разделенным телом, тренируя каждую конкретную группу мышц один раз в неделю.
К., и Орсатти, Флорида. Влияние высокочастотных и низкочастотных тренировок с отягощениями на безжировую массу тела и прирост мышечной силы у нетренированных мужчин. J Прочность Сопротивление 35(8): 2089-2094, 2021-Цель этого исследования состояла в том, чтобы выяснить, дает ли высокочастотная тренировка с отягощениями (HFRT) лучшие результаты в отношении сухой массы тела (LBM) и прироста мышечной силы по сравнению с низкочастотной тренировкой с отягощениями (LFRT). Восемнадцать нетренированных мужчин (рост: 1,76 ± 0,05 м, масса тела: 78,3 ± 13,5 кг, возраст: 22,1 ± 2,2 года) были случайным образом распределены в HFRT (n = 9) и LFRT (n = 9). Мышечная сила {максимум 1 повторения (RM) (жим лежа [BP] и одностороннее разгибание ног [LE])} и LBM (DXA) оценивались до и после 8 недель тренировок. Обе группы выполняли 7 упражнений с сопротивлением всего тела, стандартизированных до 10 подходов в неделю, 8-12 максимальных повторений и 90-120 секунд отдыха в 5-дневной тренировке с отягощениями. LFRT выполнял программу с разделенным телом, тренируя каждую конкретную группу мышц один раз в неделю.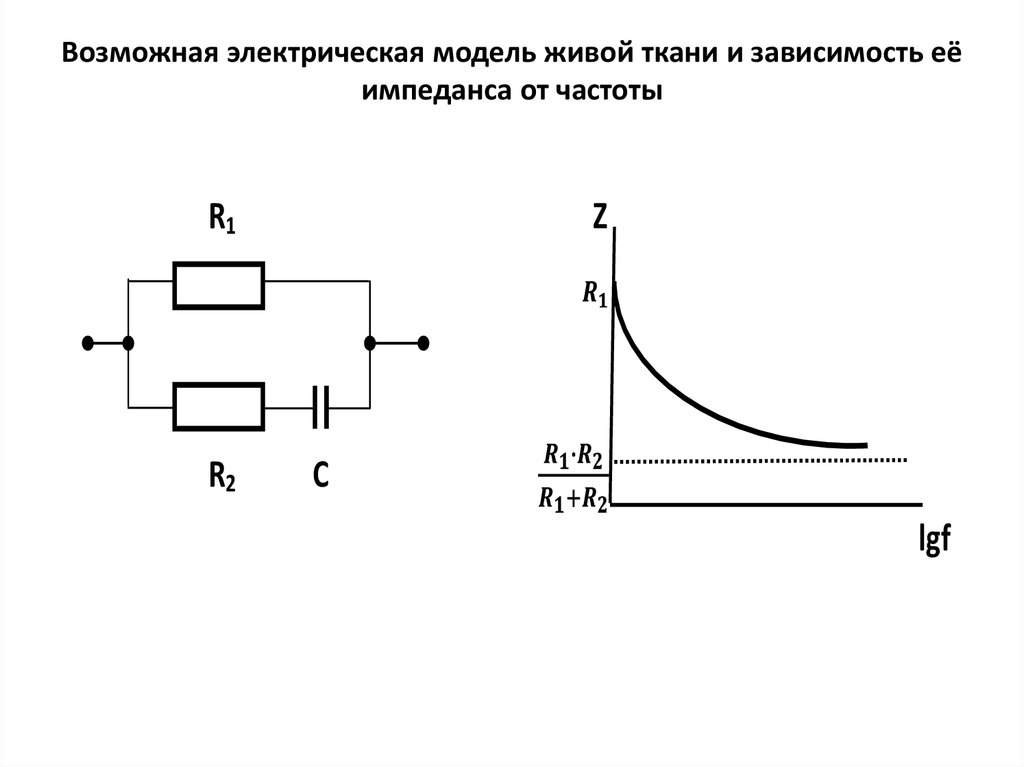 HFRT выполняла комплекс упражнений для всего тела, тренируя все группы мышц каждую сессию, и увеличилась с частоты тренировок один раз в неделю до частоты тренировок 5 раз в неделю. Безжировая масса тела увеличилась без различий между группами (HFRT = 1,0 кг против LFRT = 1,5 кг; p = 0,377). Точно так же 1RM увеличился без различий между группами (справа LE, HFRT = 21,2 кг против LFRT = 19 кг).0,7 кг, р = 0,782; АД, HFRT = 7,1 кг против LFRT = 4,5 кг, p = 0,293). Эти данные свидетельствуют о том, что у молодых нетренированных мужчин переход от частоты тренировок один раз в неделю к частоте тренировок 5 раз в неделю с равным объемом дает такой же прирост LBM и мышечной силы, как и при постоянной частоте тренировок один раз в неделю в течение продолжительного времени. 8-недельный период обучения.
HFRT выполняла комплекс упражнений для всего тела, тренируя все группы мышц каждую сессию, и увеличилась с частоты тренировок один раз в неделю до частоты тренировок 5 раз в неделю. Безжировая масса тела увеличилась без различий между группами (HFRT = 1,0 кг против LFRT = 1,5 кг; p = 0,377). Точно так же 1RM увеличился без различий между группами (справа LE, HFRT = 21,2 кг против LFRT = 19 кг).0,7 кг, р = 0,782; АД, HFRT = 7,1 кг против LFRT = 4,5 кг, p = 0,293). Эти данные свидетельствуют о том, что у молодых нетренированных мужчин переход от частоты тренировок один раз в неделю к частоте тренировок 5 раз в неделю с равным объемом дает такой же прирост LBM и мышечной силы, как и при постоянной частоте тренировок один раз в неделю в течение продолжительного времени. 8-недельный период обучения.
Copyright © 2019 Национальная ассоциация силы и физической подготовки.
Похожие статьи
Высокочастотные тренировки с отягощениями не более эффективны, чем низкочастотные, для увеличения мышечной массы и силы у хорошо тренированных мужчин.

Gomes GK, Franco CM, Nunes PRP, Orsatti FL. Гомеш Г.К. и соавт. J Прочность Конд Рез. 33 июля 2019 г. Дополнение 1:S130-S139. doi: 10.1519/JSC.0000000000002559. J Прочность Конд Рез. 2019. PMID: 29489727
Тренировки с меньшей нагрузкой более эффективны, чем тренировки с отягощениями с большей нагрузкой, для увеличения мышечной массы у молодых женщин.
Franco CMC, Carneiro MADS, Alves LTH, Júnior GNO, de Sousa JFR, Orsatti FL. Франко CMC и др. J Прочность Конд Рез. 33 июля 2019 г. Дополнение 1: S152-S158. doi: 10.1519/JSC.0000000000002970. J Прочность Конд Рез. 2019. PMID: 30640303
Тренировка с отягощениями с низкой и высокой нагрузкой до отказа в одном повторении. Максимальная сила и состав тела у нетренированных женщин.

Дайнер Т.К., Берд М.Т., Гарвер М.Дж., Рикард А.Дж., Миллер В.М., Бернс С., Клэйси Д.Л., Бергстром Х.К. Диньер Т.К. и др. J Прочность Конд Рез. 2019 июль;33(7):1737-1744. doi: 10.1519/JSC.0000000000003194. J Прочность Конд Рез. 2019. PMID: 31136545 Клиническое испытание.
Влияние частоты тренировок с отягощениями на увеличение мышечной силы: систематический обзор и метаанализ.
Grgic J, Schoenfeld BJ, Davies TB, Lazinica B, Krieger JW, Pedisic Z. Гргич Дж. и др. Спорт Мед. 2018 май; 48(5):1207-1220. doi: 10.1007/s40279-018-0872-x. Спорт Мед. 2018. PMID: 29470825 Обзор.
Взаимосвязь доза-реакция при тренировках с отягощениями у здоровых пожилых людей: систематический обзор и метаанализ.

Borde R, Hortobágyi T, Granacher U. Борде Р. и соавт. Спорт Мед. 2015 дек;45(12):1693-720. doi: 10.1007/s40279-015-0385-9. Спорт Мед. 2015. PMID: 26420238 Бесплатная статья ЧВК. Обзор.
Посмотреть все похожие статьи
Цитируется
Влияние горизонтального и наклонного жима лежа на нервно-мышечную адаптацию у нетренированных молодых мужчин.
Chaves SFN, Rocha-Junior VA, EncarnaÇÃo IGA, Martins-Costa HC, Freitas EDS, Coelho DB, Franco FSC, Loenneke JP, Bottaro M, Ferreira-Junior JB. Чавес SFN и др. Int J Exerc Sci. 2020 1 августа; 13 (6): 859-872. Электронная коллекция 2020. Int J Exerc Sci. 2020. PMID: 32922646 Бесплатная статья ЧВК.
использованная литература
- АКСМ.
 Позиционный стенд Американского колледжа спортивной медицины. Модели прогрессии в тренировках с отягощениями для здоровых взрослых. Med Sci Sports Exerc 41: 687–708, 2009.
Позиционный стенд Американского колледжа спортивной медицины. Модели прогрессии в тренировках с отягощениями для здоровых взрослых. Med Sci Sports Exerc 41: 687–708, 2009.
- АКСМ.
- Барселуш С., Дамас Ф., Нобрега С.Р. и др. Высокочастотные тренировки с отягощениями не способствуют большей мышечной адаптации по сравнению с низкочастотными тренировками у молодых нетренированных мужчин. Eur J Sport Sci 18: 1077–1082, 2018.
- Barcelos LC, Nunes PR, de Souza LR, et al. Тренировки с отягощениями с низкой нагрузкой способствуют мышечной адаптации независимо от окклюзии сосудов, нагрузки или объема. Eur J Appl Physiol 115: 1559–1568, 2015.
- Бентон М.Дж., Каспер М.
 Дж., Рааб С.А., Ваггенер Г.Т., Свон П.Д. Кратковременное влияние частоты тренировок с отягощениями на состав тела и силу у женщин среднего возраста. J Прочность Cond Res 25: 3142–3149, 2011.
Дж., Рааб С.А., Ваггенер Г.Т., Свон П.Д. Кратковременное влияние частоты тренировок с отягощениями на состав тела и силу у женщин среднего возраста. J Прочность Cond Res 25: 3142–3149, 2011.
- Бентон М.Дж., Каспер М.
- Бурд Н.А., Холверда А.М., Селби К.С. и соавт. Объем упражнений с отягощениями влияет на синтез миофибриллярных белков и фосфорилирование анаболических сигнальных молекул у молодых мужчин. J Physiol 588: 3119–3130, 2010.
Типы публикаций
термины MeSH
Определение частоты тренировок с отягощениями
Ниже приводится эксклюзивный отрывок из книги NSCA’s Essentials of Personal Training, второе издание, опубликованной Human Kinetics. Весь текст и изображения предоставлены Human Kinetics.
Частота тренировок означает количество тренировок, которые клиент проведет в течение одной недели.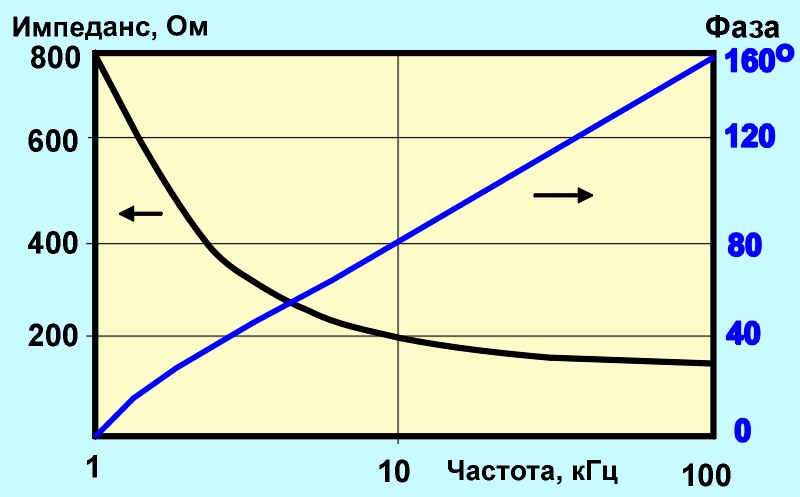 На определение оптимальной частоты для конкретного клиента влияет множество факторов. Такие факторы, как типы используемых упражнений, количество мышечных групп, тренируемых за сеанс, структура программы (объем и интенсивность), а также тренировочный статус клиента и общий уровень физической подготовки определяют частоту тренировок (4). Рабочий график клиента, социальный график и семейные обязанности также сильно влияют на то, как часто клиент может тренироваться.
На определение оптимальной частоты для конкретного клиента влияет множество факторов. Такие факторы, как типы используемых упражнений, количество мышечных групп, тренируемых за сеанс, структура программы (объем и интенсивность), а также тренировочный статус клиента и общий уровень физической подготовки определяют частоту тренировок (4). Рабочий график клиента, социальный график и семейные обязанности также сильно влияют на то, как часто клиент может тренироваться.
Влияющие факторы
Основным фактором, который персональный тренер должен учитывать при определении частоты тренировок, является тренировочный статус клиента и общий уровень физической подготовки. Менее тренированным клиентам обычно требуется больше отдыха между тренировками, что снижает их частоту, а высоко тренированные клиенты могут терпеть большую частоту.
Например, если клиент является строителем, который выполняет повторяющиеся подъемные работы на своей работе, он или она может не захотеть или быть не в состоянии терпеть тренировки с отягощениями более двух или трех дней в неделю.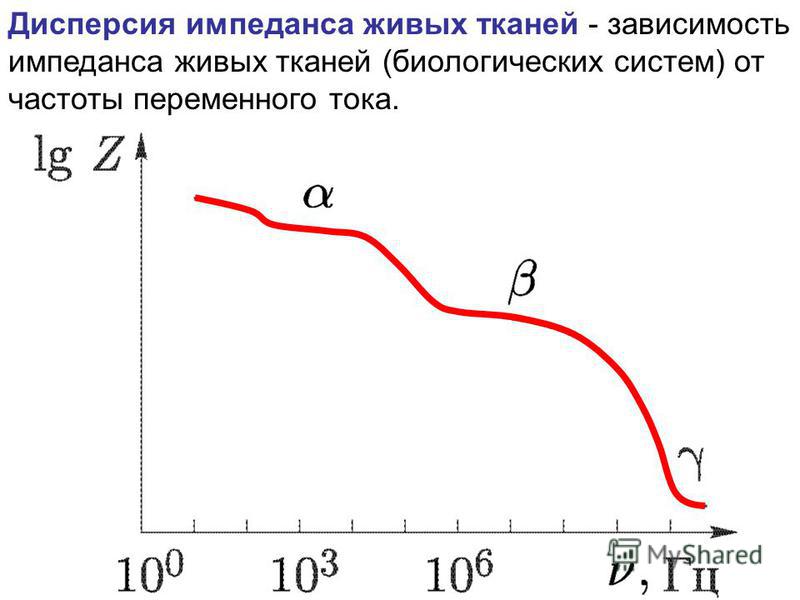
Важным фактором, который упускают из виду многие персональные тренеры, является то, как взаимодействуют различные компоненты тренировочной программы (58, 59, 90). Многие персональные тренеры планируют тренировки с отягощениями, выносливостью, ловкостью и плиометрией, не учитывая, как каждый фактор влияет на общую нагрузку. Важно изучить, как взаимодействуют различные учебные мероприятия, и принять во внимание общую рабочую нагрузку клиента. Например, если клиент занимается бегом по 30 минут в день пять дней в неделю, он или она сможет выдержать силовые тренировки только два дня в неделю.
Руководство по определению частоты тренировок
При определении частоты тренировок важно запланировать достаточное восстановление в программе. Общее правило, которому следуют многие персональные тренеры, заключается в том, что между тренировками, нагружающими одну и ту же группу или группы мышц, должен быть как минимум один день (но не более трех) (5, 14, 54, 85). Более конкретные рекомендации зависят от общего статуса клиента в тренировках с отягощениями (таблица 15. 2). Большинство новичков или начинающих клиентов могут ощутить преимущества тренировок с отягощениями всего за два-три дня в неделю (4,19).,51,86,95). Однако люди, которые уже привыкли к тренировкам с отягощениями, могут только поддерживать прирост силы и не могут повышать уровень силы один или два дня в неделю (4,35). В целом, чем чаще занятия, тем больше прирост силы (4,34).
2). Большинство новичков или начинающих клиентов могут ощутить преимущества тренировок с отягощениями всего за два-три дня в неделю (4,19).,51,86,95). Однако люди, которые уже привыкли к тренировкам с отягощениями, могут только поддерживать прирост силы и не могут повышать уровень силы один или два дня в неделю (4,35). В целом, чем чаще занятия, тем больше прирост силы (4,34).
Статус тренировки с отягощениями для новичков или начинающих
Для новичков или начинающих тренироваться с отягощениями рекомендуется использовать частоту два или три дня в неделю при тренировке всего тела (4,19,22,25,51,95). При такой частоте дни тренировок с отягощениями не должны быть последовательными (например, понедельник и четверг; вторник, четверг и суббота или понедельник, среда и пятница), чтобы обеспечить надлежащее восстановление между тренировками. Как правило, у клиентов-новичков должно быть от 1 до 3 дней между тренировками с отягощениями, но не более 3 дней, чтобы облегчить восстановление.
Если, например, клиент должен тренироваться в понедельник и среду, промежуток времени между тренировкой в среду и следующим понедельником будет больше трех дней, что приведет к менее эффективной программе обучения (35,54). По мере того, как клиент переходит от новичка к среднему уровню, изменение частоты не всегда необходимо (4). Однако увеличение частоты до трех или четырех дней в неделю обеспечивает большую гибкость программы.
Промежуточный статус тренировок с отягощениями
Общая рекомендация для клиентов, достигших промежуточного уровня тренировок, — увеличить частоту тренировок до трех или четырех дней в неделю (4). Однако это увеличение будет означать, что клиент тренируется два и более дня подряд. Распространенной стратегией является использование сплит-программы, которая равномерно распределяет четыре или более тренировок в течение недели. При такой структуре клиент может тренировать только одну часть тела (например, верхнюю часть спины или нижнюю часть тела) (70), определенные области мышц (например, грудь, спину или ноги) (70) или определенные модели движений (т.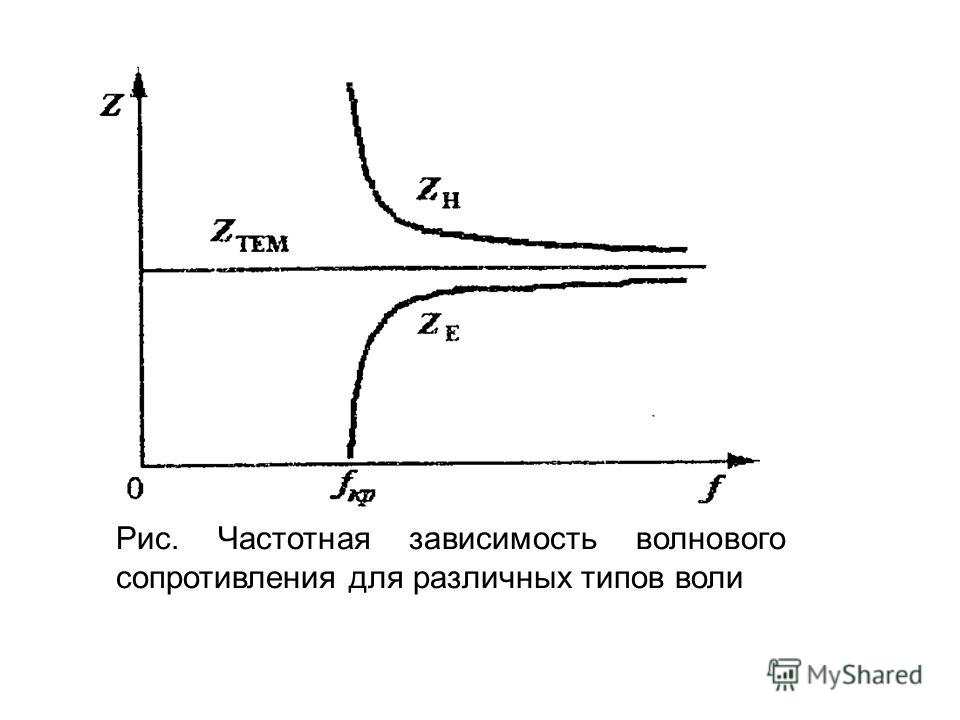 , «толкать» или «тянуть») (117) во время сеанса. Эта структура позволяет увеличить частоту, оставляя при этом достаточно времени для восстановления между сеансами (85,95).
, «толкать» или «тянуть») (117) во время сеанса. Эта структура позволяет увеличить частоту, оставляя при этом достаточно времени для восстановления между сеансами (85,95).
Типичный пример сплит-программы четыре раза в неделю для клиентов среднего уровня включает упражнения для верхней части тела в понедельник и четверг и упражнения для нижней части тела во вторник и пятницу (70). Даже если клиент тренируется два дня подряд, изменение целевых групп мышц обеспечивает адекватное восстановление. Кроме того, между сеансами, нацеленными на одни и те же группы мышц, есть два дня отдыха, что позволяет лучше восстанавливаться между аналогичными сеансами (95). При таком частотном разделении дни тренировок или отдыха без отягощения всегда приходятся на среду, субботу и воскресенье. Что еще более важно, при тренировке определенных групп мышц или частей тела такое разделение позволяет добиться максимальных результатов, поскольку клиент может использовать более высокие объемы (95).
Статус продвинутой тренировки с отягощениями
В зависимости от целей клиентам среднего уровня может потребоваться увеличить частоту тренировок по мере того, как они становятся более опытными и переклассифицируются как продвинутые по статусу.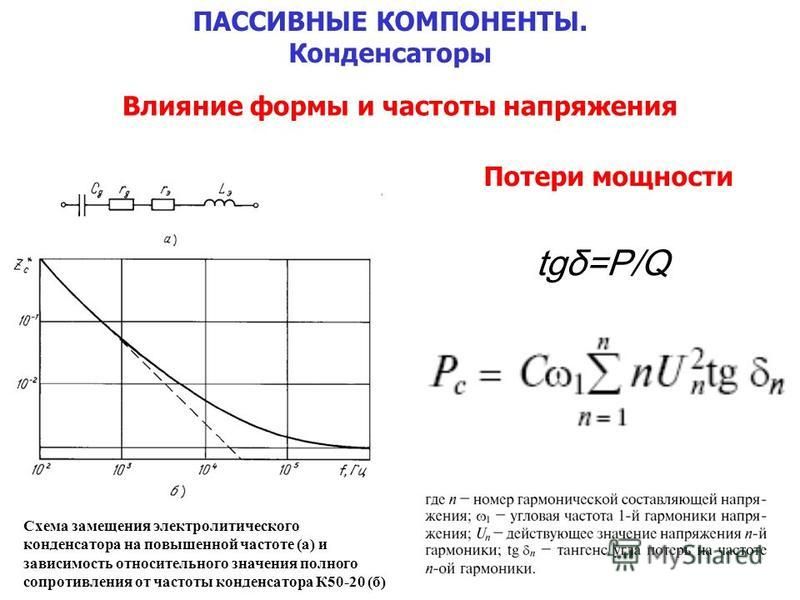 Общая рекомендация для продвинутых людей состоит в том, чтобы тренироваться с отягощениями четыре-шесть дней в неделю, чтобы увеличить тренировочный стимул (4). Эти клиенты обычно используют двойной сплит (44), выполняя два занятия в один и тот же день, что увеличивает количество тренировок с 8 до 12 в неделю (4110). Имеющиеся в научной литературе убедительные доказательства поддерживают концепцию проведения нескольких коротких тренировок в один день (4,44,110).
Общая рекомендация для продвинутых людей состоит в том, чтобы тренироваться с отягощениями четыре-шесть дней в неделю, чтобы увеличить тренировочный стимул (4). Эти клиенты обычно используют двойной сплит (44), выполняя два занятия в один и тот же день, что увеличивает количество тренировок с 8 до 12 в неделю (4110). Имеющиеся в научной литературе убедительные доказательства поддерживают концепцию проведения нескольких коротких тренировок в один день (4,44,110).
Еще один способ увеличить частоту с пяти до шести дней — использовать сплит-программу «три дня перерыва и один выходной». При такой структуре три отдельные тренировки нацелены на определенные группы мышц, и клиент выполняет одну тренировку три дня подряд и отдыхает на четвертый день. Распространенная стратегия состоит в том, чтобы разделить программу на «толкающие» упражнения для верхней части тела (т. е. грудь, плечи, трицепсы), упражнения для нижней части тела и «тянущие» упражнения для верхней части тела (т. В этом типе структуры тренировки проводятся в неуказанные дни; то есть день отдыха не один и тот же каждую неделю.
Основы персонального тренинга NSCA, второе издание, является авторитетным текстом для персональных тренеров, инструкторов по здоровью и фитнесу и других специалистов по фитнесу, а также основным источником подготовки для тех, кто проходит сертификацию NSCA-Certified Personal Trainer® (NSCA-Certified Personal Trainer® (NSCA-Certified Personal Trainer®). экзамен CPT®). Книга доступна в книжных магазинах по всему миру, а также в Интернете в магазине NSCA.
Поставщики беспроводных радиочастот и ресурсы
Веб-сайт RF Wireless World является домом для поставщиков и ресурсов RF и Wireless. На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения, калькуляторы, новости, книги, загрузки и многое другое.
Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee,
LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. д.
Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
д.
Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
Статьи о системах на основе IoT
Система обнаружения падения для пожилых людей на основе IoT : В статье рассматривается архитектура системы обнаружения падения для пожилых людей.
В нем упоминаются преимущества или преимущества системы обнаружения падения IoT.
Подробнее➤
См. также другие статьи о системах на основе IoT:
• Система очистки туалетов AirCraft.
• Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.
Изделия для беспроводных радиочастот
Этот раздел статей охватывает статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE/3GPP и т. д. , стандарты.
Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
д. , стандарты.
Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH была рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP. Подробнее➤
Основные сведения о повторителях и типы повторителей : В нем объясняются функции различных типов повторителей, используемых в беспроводных технологиях. Подробнее➤
Основы и типы замираний : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные замирания, быстрые замирания и т. д., используемые в беспроводной связи. Подробнее➤
Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона.
Подробнее➤
Архитектура сотового телефона.
Подробнее➤
Основные сведения о помехах и типы помех: Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. д. Подробнее➤
5G NR Раздел
В этом разделе рассматриваются функции 5G NR (новое радио), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. д.
5G NR Краткий справочный указатель >>
• Мини-слот 5G NR
• Часть полосы пропускания 5G NR
• БАЗОВЫЙ НАБОР 5G NR
• Форматы 5G NR DCI
• 5G NR UCI
• Форматы слотов 5G NR
• IE 5G NR RRC
• 5G NR SSB, SS, PBCH
• 5G NR PRACH
• 5G NR PDCCH
• 5G NR PUCCH
• Опорные сигналы 5G NR
• 5G NR m-Sequence
• Золотая последовательность 5G NR
• 5G NR Zadoff Chu Sequence
• Физический уровень 5G NR
• MAC-уровень 5G NR
• Уровень 5G NR RLC
• Уровень PDCP 5G NR
Учебные пособия по беспроводным технологиям
В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводным сетям. Он охватывает учебные пособия по таким темам, как
сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS,
GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д.
См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Он охватывает учебные пособия по таким темам, как
сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS,
GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д.
См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы, посвященные технологии 5G:
Учебник по основам 5G
Диапазоны частот
учебник по миллиметровым волнам
Рамка волны 5G мм
Зондирование канала миллиметровых волн 5G
4G против 5G
Испытательное оборудование 5G
Архитектура сети 5G
Сетевые интерфейсы 5G NR
звучание канала
Типы каналов
5G FDD против TDD
Нарезка сети 5G NR
Что такое 5G NR
Режимы развертывания 5G NR
Что такое 5G ТФ
В этом учебнике по GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения,
Типы пакетов GSM, структура кадров GSM или иерархия кадров, логические каналы, физические каналы,
Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM или настройка вызова или процедура включения питания,
Вызов MO, вызов MT, модуляция VAMOS, AMR, MSK, GMSK, физический уровень, стек протоколов, основы мобильного телефона,
Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.
➤Читать дальше.
LTE Tutorial , описывающий архитектуру системы LTE, включая основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он предоставляет ссылку на обзор системы LTE, радиоинтерфейс LTE, терминологию LTE, категории LTE UE, структуру кадра LTE, физический уровень LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, Voice Over LTE, расширенный LTE, Поставщики LTE и LTE vs LTE advanced.➤Подробнее.
RF Technology Материал
На этой странице мира беспроводных радиочастот описывается пошаговое проектирование преобразователя частоты на примере повышающего преобразователя частоты 70 МГц в диапазон C.
для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO,
амортизирующие прокладки. ➤Читать дальше.
➤ Проектирование и разработка РЧ приемопередатчика
➤Дизайн радиочастотного фильтра
➤Система VSAT
➤Типы и основы микрополосковых
➤Основы волновода
Секция испытаний и измерений
В этом разделе рассматриваются ресурсы по контролю и измерению, контрольно-измерительное оборудование для тестирования тестируемых устройств на основе
Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE. ИНДЕКС испытаний и измерений >>
ИНДЕКС испытаний и измерений >>
➤Система PXI для контрольно-измерительных приборов.
➤ Генерация и анализ сигналов
➤ Измерения физического уровня
➤ Тестирование устройства WiMAX на соответствие
➤ Тест на соответствие Zigbee
➤ Тест на соответствие LTE UE
➤ Тест на соответствие TD-SCDMA
Волоконно-оптические технологии
Волоконно-оптический компонент основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель,
фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д. Эти компоненты используются в оптоволоконной связи.
ИНДЕКС оптических компонентов >>
➤Руководство по оптоволоконной связи
➤APS в SDH
➤Основы SONET
➤ Структура кадра SDH
➤ SONET против SDH
Поставщики беспроводных радиочастот, производители
Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений,
см. ИНДЕКС поставщиков >>.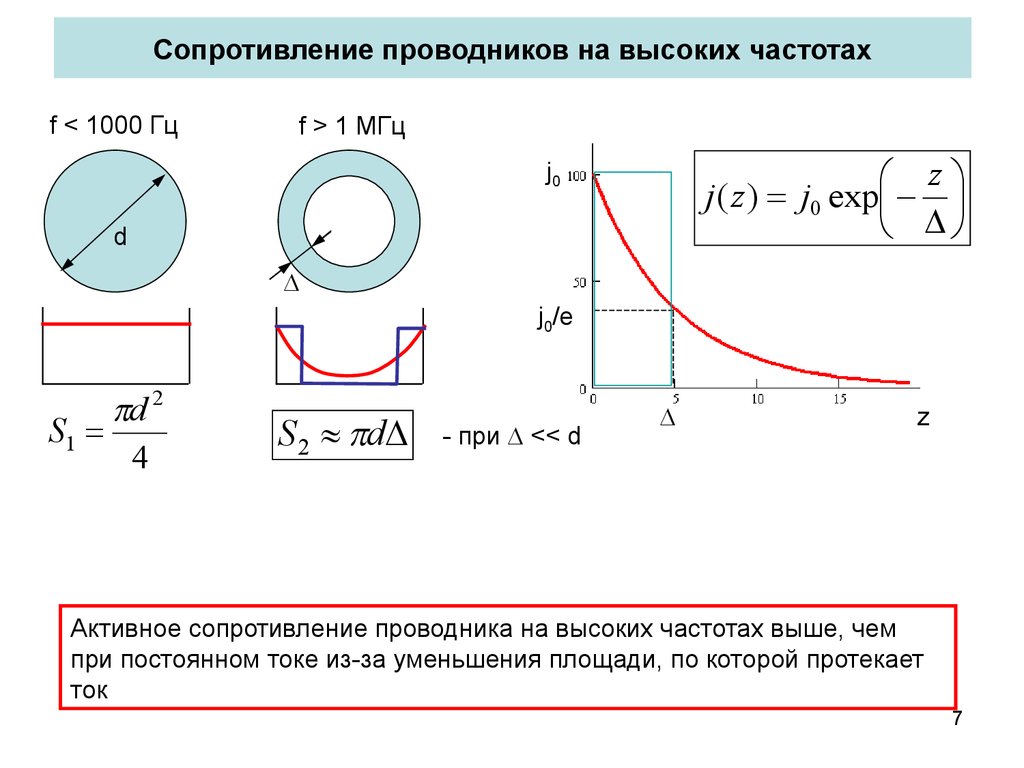
Поставщики ВЧ-компонентов, включая ВЧ-изолятор, ВЧ-циркулятор, ВЧ-смеситель, ВЧ-усилитель, ВЧ-адаптер, ВЧ-разъем, ВЧ-модулятор, ВЧ-трансивер, PLL, VCO, синтезатор, антенну, осциллятор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексер, дуплексер, чип-резистор, чип-конденсатор, чип-индуктор, ответвитель, ЭМС, программное обеспечение RF Design, диэлектрический материал, диод и т. д.
Поставщики радиочастотных компонентов >>
➤Базовая станция LTE
➤ РЧ-циркулятор
➤РЧ-изолятор
➤Кристаллический осциллятор
MATLAB, Labview, Embedded Исходные коды
Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW.
Эти коды полезны для новичков в этих языках.
СМОТРИТЕ ИНДЕКС ИСТОЧНИКОВ >>
➤ 3–8 код VHDL декодера
➤Скремблер-дескремблер Код MATLAB
➤32-битный код ALU Verilog
➤ T, D, JK, SR триггеры коды лаборатории
*Общая медицинская информация*
Сделайте эти пять простых вещей, чтобы помочь остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: Мойте их часто
2. ЛОКОТЬ: Кашляйте в него
3. ЛИЦО: Не прикасайтесь к нему
4. НОГИ: Держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВУЙТЕ: Болен? Оставайтесь дома
Используйте технологию отслеживания контактов >> , следуйте рекомендациям по социальному дистанцированию >> и установить систему наблюдения за данными >> спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таких стран, как США и Китай, чтобы остановить распространение COVID-19так как это заразное заболевание.
Радиочастотные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения.
Они охватывают беспроводные технологии, такие как GSM, UMTS, LTE, 5G NR и т. д.
СМ. КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR
➤ 5G NR ARFCN и преобразование частоты
➤ Калькулятор скорости передачи данных LoRa
➤ LTE EARFCN для преобразования частоты
➤ Калькулятор антенны Yagi
➤ Калькулятор времени выборки 5G NR
IoT-Интернет вещей Беспроводные технологии
В разделе, посвященном IoT, рассматриваются беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet,
6LoWPAN, RF4CE, Bluetooth, Bluetooth с низким энергопотреблением (BLE), NFC, RFID, INSTEON, X10, KNX, ANT+, Wavenis, Dash7, HomePlug и другие. Он также охватывает датчики IoT, компоненты IoT и компании IoT.
Он также охватывает датчики IoT, компоненты IoT и компании IoT.
См. главную страницу IoT>> и следующие ссылки.
➤РЕЗЬБА
➤EnOcean
➤ Учебник LoRa
➤ Учебник по SIGFOX
➤ WHDI
➤6LoWPAN
➤Зигби RF4CE
➤NFC
➤Лонворкс
➤CEBus
➤УПБ
СВЯЗАННЫЕ СООБЩЕНИЯ
Учебники по беспроводным радиочастотам
GSM ТД-СКДМА ваймакс LTE UMTS GPRS CDMA SCADA беспроводная сеть 802.11ac 802.11ad GPS Зигби z-волна Bluetooth СШП Интернет вещей Т&М спутник Антенна РАДАР RFID
Различные типы датчиков
Датчик приближения Датчик присутствия против датчика движения Датчик LVDT и RVDT Датчик положения, смещения и уровня датчик силы и датчик деформации Датчик температуры датчик давления Датчик влажности датчик МЭМС Сенсорный датчик Тактильный датчик Беспроводной датчик Датчик движения Датчик LoRaWAN Световой датчик Ультразвуковой датчик Датчик массового расхода воздуха Инфразвуковой датчик Датчик скорости Датчик дыма Инфракрасный датчик Датчик ЭДС Датчик уровня Активный датчик движения против пассивного датчика движения
Поделиться этой страницей
Перевести эту страницу
СТАТЬИ
Раздел T&M
ТЕРМИНОЛОГИИ
Учебники
Работа и карьера
ПОСТАВЩИКИ
Интернет вещей
Онлайн калькуляторы
исходные коды
ПРИЛОЖЕНИЕ. ЗАМЕТКИ
Всемирный веб-сайт T&M
ЗАМЕТКИ
Всемирный веб-сайт T&M
Частота Температура Сопротивление В мВ мА Калибратор процессов
BRT LB02A Калибратор процессов представляет собой точный надежный многофункциональный генератор сигналов и упрощенный цифровой мультиметр «все в одном». Он выдает 0–24 мА, 0–11 В, 0–110 мВ, 0–10 кГц, 20–400 Ом, тип K, J, N, T, E, S, B и т. д. Сигнал термопары, сигнал CU50 PT100 PT1000, сигнал 24 В, и т. д., и измеряет 0-30 мА, 0-30 В, 0-150 мВ, частотный сигнал 0-10 кГц, 0-999,9 Ом, сигнал термопары, сигнал RTD Cu50 PT1000 PT100 и т. д. Он может выводить номинальный сигнал, когда пользователь вводит значение сигнала с помощью цифровых кнопок. Его цветной ЖК-экран четко и точно отображает значение сигнала и рабочее состояние. Внутри калибратора есть 4 блока PPTC и быстродействующий предохранитель для защиты калибратора от случайных повреждений. Этот калибратор является незаменимым выбором на промышленной площадке и наиболее достойной заменой калибровочного инструмента вместо дорогого калибратора других диапазонов.
Основные характеристики и преимущества
● Карманный переносной чехол: 120x76x30 мм, положите его в карман, экономьте энергию, экономьте деньги, очень удобно носить с собой.
● Высокая точность 0,025%+1/2 разряда; широко используется в качестве калибратора частоты, калибратора контура мА/мВ, калибратора температуры и т. д.
● Имеют полнофункциональный режим работы, пользователь может вводить любое значение с помощью цифровых кнопок, калибратор выводит сигнал напрямую.
● Моделирование и измерение выходного сигнала: частота 0–10 кГц, источник 4–20 мА или пассивный сигнал, 0–11 В, 0–110 мВ, 20–400 Ом, стандартный тип R, E, S, K, J, B, T, N термопара, выходы PT100, CU50, 24В и т.д.
● Аккумулятор емкостью 2200 мАч внутри, имеет строку состояния батареи, очень удобен и удобен для использования в помещении или за пределами промышленной площадки.
● Цветной ЖК-дисплей с высоким разрешением, с подсветкой для различных условий освещения, четкий дисплей с большим экраном.
● Может использоваться в качестве генератора сигналов, калибратора частоты, многофункционального калибратора процессов и простого цифрового мультиметра.
● Описание с помощью клавиш Гц, В, мВ, мА, RTD, TC, Step и Ω, что позволяет пользователю легко управлять им.
● Прецизионные AD, DA, чипы опорного напряжения, схемы OP используются для обеспечения высокой точности, производительности и стабильности.
● Использование 4 блоков PPTC и быстродействующего предохранителя для защиты прибора от повреждений, вызванных высоким напряжением.
Output Parameters (*No Hart, Modbus function)
| FUNC | OUT UNIT | RANGE | SET STEP | ACCURACY (SP: setting point) |
| DC. В | В | 0~11,00 В | 0,01/0,1/1 | ±0,025%SP ±0,004 В |
Постоянный ток. мВ мВ | мВ | 0~110,00 мВ | 0,1/1/10 | ±0,025%SP ±0,02 мВ |
| mA | Sink/Source/Program | 0~24.00mA | 0.01/0.1/1/4 | ±0.025%SP ±0.004mA |
| Ohm | Ω | 0~400Ω | 1/10/100 | ±0.025%SP ±0.3Ω |
| 400~2200Ω | 1/10/100 | ±0.05%SP ±1.5Ω | ||
| Frequency | KHz | 0-10 | 0.01/0.1/1 | ±0.05%SP ±2Hz |
| TC | R | 0~1700℃ | 1/10/100 | ±0,1%SP ±3℃ |
| S | 0~1600℃ | |||
| B | 500 ~ 1800 ℃ | |||
| K | -200 ~ 1370 ℃ | ± 0,05%Sp ± 0,5 ℃ (K) 9909 ± 0,05%Sp ± 0,5 ℃ (K) 9 2909. 9. 0.05%SP ±0.4℃ (J) ±0.05%SP ±0.5℃(T) ±0.05%SP ±0.8℃ (N) | ||
| E | -200~1000℃ | |||
| J | -200~1200℃ | |||
| T | -200~400℃ | |||
| N | 7 -200~1300℃ | |||
| PT1000 | -50 ~ 300 ℃ | 1/10/100 | ± 0,1%PS ± 0,5 ℃ | 77.1 0606060606060606060606060606060606060606060606060600н0тели | 77067777777777777777777777777777777777777777 гг. ℃ |
| CU50 | -50 ~ 150 ℃ | ± 0,1%SP ± 1,5 ℃ | ||
| 24V 77777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777747. | . Измерение тока: 0~24 000 мА | НЕТ |
Параметры измерения
| FUNC | UNIT | RANGE | RESOLUTION | ACCURACY (RD: Read number) |
DC. V V | V | — 30~30,000 В | 0,001 В | ±0,025%RD ±0,004 В |
| Постоянный ток. мВ | мВ | -150~150,00 мВ | 0,01 мВ | ±0,025%RD ±0,02 мВ |
| DC. mA | mA | -30~30.000mA | 0.001mA | ±0.025%RD ±0.004mA |
| Ohm | Ω | 0~999.9Ω | 0.1Ω | ±0.025% RD ±0.2Ω |
| 1000-2500 | 1Ω | ±0.025%RD ±1Ω | ||
| Frequency | KHz | 0-10 | 0.001 | ±0.05%RD ±2Hz |
| TC | R | 0~1700℃ | 0.1℃ | ±0.1%RD ±3℃ (R,S,B) |
| S | 0~1600℃ | |||
| B | 500 ~ 1800 ℃ | |||
| K | -200 ~ 1370 ℃ | ± 0,025%RD ± 0,5 ℃ (K) ± 0,025%RD ± 0,3 ± 0,57777,02,02,02,02,02,02,02,02,02,02,02,02,02,02,02,02,02,025% ,02,025%%%%%%%%,02,025%,1, (J)±0,05%RD ±0,5℃(T) ±0,025%RD ±0,8℃ (N) | ||
| E | -200~1000℃ | |||
| J | -200~1200℃ | |||
| T | -200~400℃ | |||
| N | -200~1300℃ | |||
| RTD | Pt1000 | -50~300 ℃ | 0.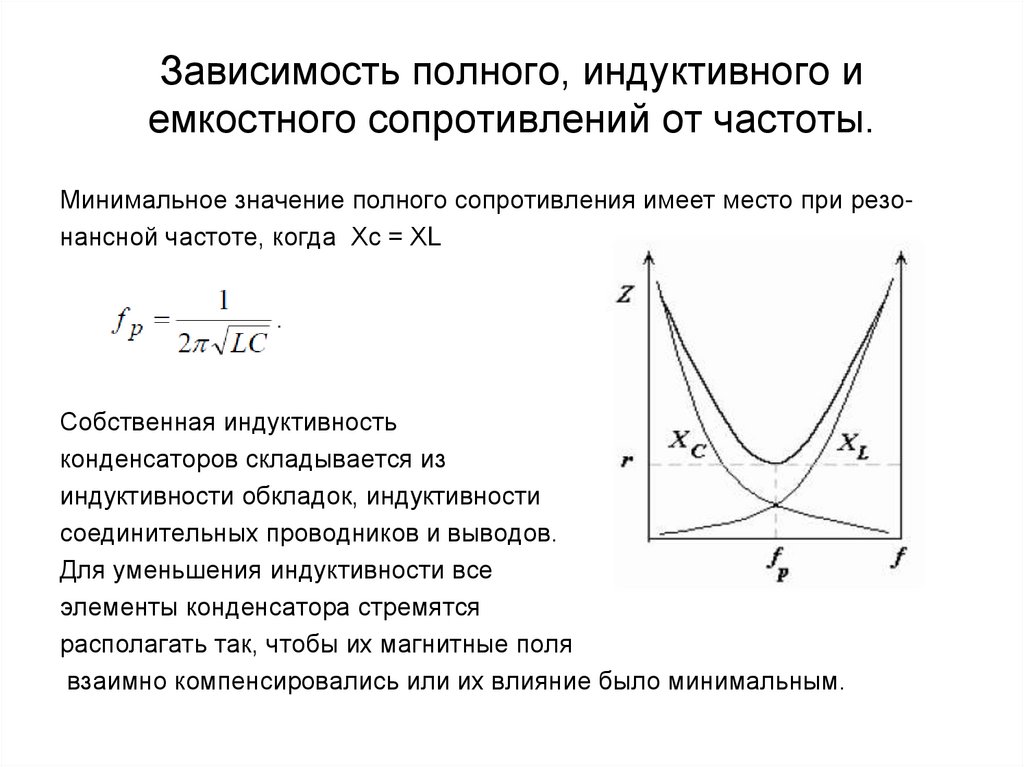 1℃ 1℃ | ±0.1%RD ±0.5℃ |
| Pt100 | -200~850℃ | ±0.1%RD ±0.8℃ | ||
| Cu50 | -50~150℃ | ± 0,1%RD ±1,5℃ | ||
| Переключатель диапазонов | мА | 0~9990 Технические единицы (для измерения тока и измерения тока выхода 24 В) | Макс. 4, мин. 1 (относится к инженерному количеству.) |
* Ом, выход и измерение RTD: Ошибка сопротивления проводов не включена в точность.
* Выход и измерение термопары: Ошибка холодного спая не включена в точность.
* Калибратор процессов LB02A не имеет функций MODBUS, HART (если требуется функция MODBUS, Hart, рекомендуется использовать: Калибратор процессов LB06)
*Этот многофункциональный калибратор процессов LB02A охватывает почти все функции калибратора температуры, калибратора частоты, калибратора контура мВ/мА и т. д.
д.
*Как его заказать?
•А. Оплата Visa, Master, кредитной картой напрямую онлайн, нажав кнопку [Добавить в корзину] выше и оформить заказ соответствующим образом (рекомендуется).
•Б. Безопасная оплата Paypal онлайн, если у вас есть учетная запись Paypal или платеж кредитной картой, обработанный Paypal онлайн напрямую, нажав кнопку [Добавить в корзину] выше.
•С. Заказ розничного продавца или оптовый оптовый заказ или OEM (≥5 единиц), пожалуйста, свяжитесь с нами, чтобы получить последнюю оптовую цену, спасибо.
Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставить отзыв.
Микроволны101 | RF Sheet Resistance
Нажмите здесь, чтобы перейти на нашу страницу по глубине скин-слоя
Нажмите здесь, чтобы перейти на нашу главную страницу по резисторам
Нажмите здесь, чтобы перейти на нашу страницу по математике резисторов
Нажмите здесь, чтобы перейти на нашу страницу по проводимости
Нажмите здесь, чтобы перейти на нашу страницу о потерях в линиях передачи
Нажмите здесь, чтобы узнать о нашей загрузке для расчета поверхностного ВЧ сопротивления в многослойных металлических средах
На этой странице показано, как рассчитать поверхностное сопротивление слоя металла по сравнению с частота. Между прочим, то, что мы называем ВЧ-сопротивлением листа, в учебниках часто называют «поверхностным сопротивлением» или «поверхностным импедансом» или другими названиями.
Между прочим, то, что мы называем ВЧ-сопротивлением листа, в учебниках часто называют «поверхностным сопротивлением» или «поверхностным импедансом» или другими названиями.
Поверхностное сопротивление постоянному току
Термин поверхностное сопротивление должен быть знаком, если вы работаете с электронными тонкими пленками. Это функция объемного удельного сопротивления металлической пленки и ее толщины. Мы обсуждаем это далее на этой странице. Поверхностное сопротивление R ·sh дано в омах на квадрат, где квадраты — безразмерная величина длины, деленная на ширину.
Для более полного обсуждения поверхностного сопротивления постоянному току перейдите на нашу страницу по этой теме. Таким образом, для постоянного тока сопротивление листа рассчитывается по удельному сопротивлению и толщине металла:
Поверхностное сопротивление и послойная проводимость в зависимости от частоты
Не часто принимается во внимание то, что поверхностное сопротивление является функцией частоты.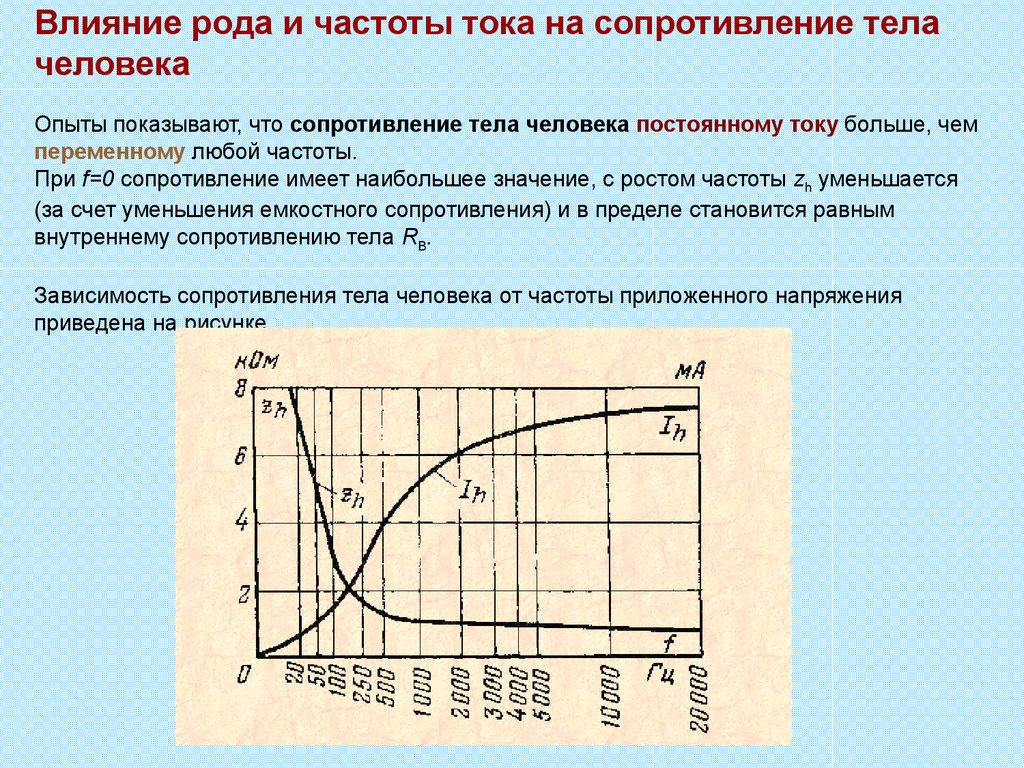 При использовании в радиочастотном мире ошибки могут возникать из-за использования определения постоянного тока.
При использовании в радиочастотном мире ошибки могут возникать из-за использования определения постоянного тока.
Предположение о постоянном поверхностном сопротивлении справедливо только для проводников, тонких по сравнению с толщиной поверхностного слоя (что часто имеет место для тонкопленочных резисторов, но не для линий передачи).
Знание поверхностного ВЧ-сопротивления в зависимости от частоты металлов межсоединений (например, меди или золота) может быть очень полезным для оценки затухания ленточных проводников, таких как микрополосковые.
Мы предлагаем бесплатную загрузку, которую вы должны скачать, если хотите проанализировать ВЧ-сопротивление листов различных металлов (включая металлы, сложенные друг в друга), которые вы укажете. Ищите здесь. Эта опция находится внизу страницы.
Расчет максимальной проводимости листа (минимального сопротивления листа)
Поверхностная электропроводность обратно пропорциональна поверхностному сопротивлению, ее единицами измерения являются сименовские квадраты или мхо-квадраты. Эта величина полезна, когда вы имеете дело с многослойными проводниками, так как их проводимости могут быть добавлены параллельно, затем сумма может быть повторно инвертирована и выражена в составном листовом сопротивлении. Когда задействована радиочастота, может проявиться так называемый скин-эффект, и поэтому расчеты проводимости и удельного сопротивления на постоянном токе недействительны. Скин-эффект учитывается с помощью убывающего экспоненциального коэффициента, показатель степени которого обратно пропорционален параметру, называемому глубиной скин-слоя.
Эта величина полезна, когда вы имеете дело с многослойными проводниками, так как их проводимости могут быть добавлены параллельно, затем сумма может быть повторно инвертирована и выражена в составном листовом сопротивлении. Когда задействована радиочастота, может проявиться так называемый скин-эффект, и поэтому расчеты проводимости и удельного сопротивления на постоянном токе недействительны. Скин-эффект учитывается с помощью убывающего экспоненциального коэффициента, показатель степени которого обратно пропорционален параметру, называемому глубиной скин-слоя.
Максимальная электропроводность листа — это лучшее, что вы можете сделать, и это функция частоты. Добавление большего количества металла сверх пяти значений глубины скин-слоя не помогает!
Процент проводимости в зависимости от глубины проникновения в металл изменяется как отрицательная экспонента глубины, выраженная в толщине скин-слоя. На поверхности имеет место полная проводимость, а удельное сопротивление металла составляет 100 % от его значения при постоянном токе, равном . При одной глубине скин-слоя проводимость металла снижается до 36,8% от , при 2-х глубинах скин-слоя до 13,5% и т. д. К тому времени, когда вы достигаете пяти скин-слоев, проводимость металла снижается всего до 0,7% от его полного значения. Вот откуда берется эмпирическое правило пяти толщин скин-слоя: добавление тонн дополнительного металла сверх пяти толщин скин-слоя может уменьшить ваше радиочастотное сопротивление только на 0,7%, так зачем беспокоиться? Выраженное ниже то, что мы называем инкрементальная радиочастотная проводимость , это проводимость на заданной глубине, уменьшенная с помощью уравнения глубины скин-слоя:
При одной глубине скин-слоя проводимость металла снижается до 36,8% от , при 2-х глубинах скин-слоя до 13,5% и т. д. К тому времени, когда вы достигаете пяти скин-слоев, проводимость металла снижается всего до 0,7% от его полного значения. Вот откуда берется эмпирическое правило пяти толщин скин-слоя: добавление тонн дополнительного металла сверх пяти толщин скин-слоя может уменьшить ваше радиочастотное сопротивление только на 0,7%, так зачем беспокоиться? Выраженное ниже то, что мы называем инкрементальная радиочастотная проводимость , это проводимость на заданной глубине, уменьшенная с помощью уравнения глубины скин-слоя:
Спасибо за исправление, Рон! И благодаря Джованни наше использование греческого алфавита теперь соответствует глубине кожи! Если мы проинтегрируем всю проводимость тонкой пленки от поверхности, включая бесконечные глубины скин-слоя, мы получим максимальную проводимость слоя для данной частоты. Это отличается от проводимости постоянного тока, которая может быть немного выше, поскольку каждый свободный электрон в металле способствует проводимости во время постоянного тока.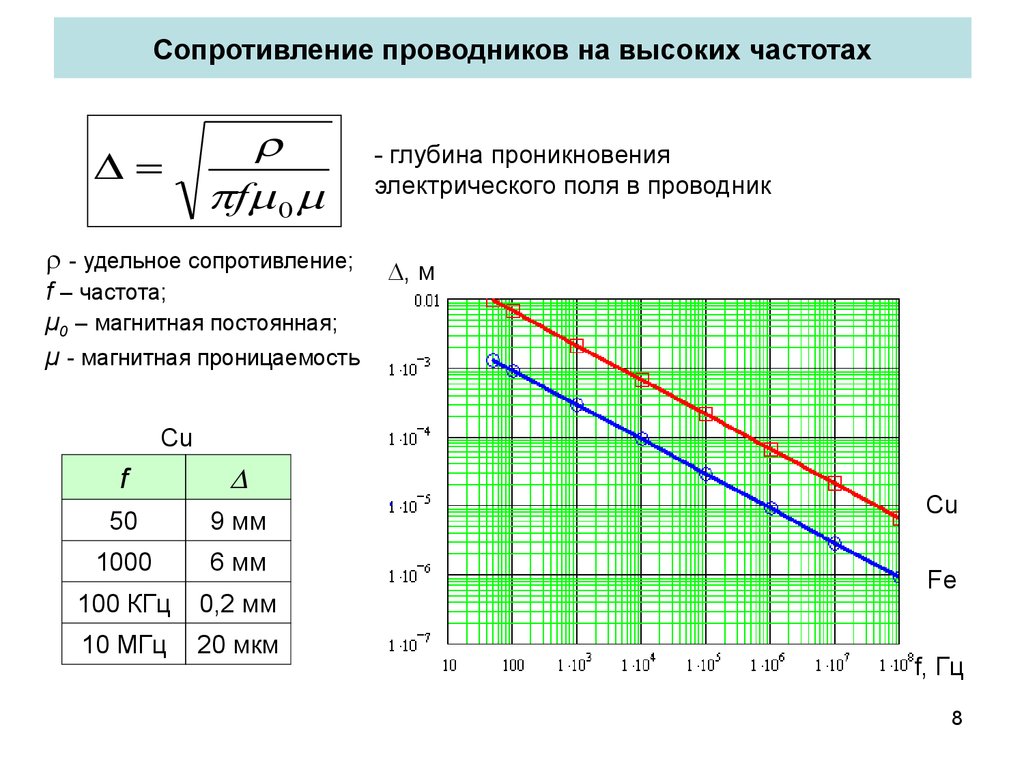 Хотя мы обязались никогда не использовать исчисление на этом веб-сайте, интегрирование экспоненциальной функции настолько просто, что это можем сделать даже мы (но мы не будем показывать вам все промежуточные шаги, которые требуют большого ластика). Максимальная проводимость листа:
Хотя мы обязались никогда не использовать исчисление на этом веб-сайте, интегрирование экспоненциальной функции настолько просто, что это можем сделать даже мы (но мы не будем показывать вам все промежуточные шаги, которые требуют большого ластика). Максимальная проводимость листа:
(Спасибо за исправление, Майкл!) Максимальная проводимость РЧ-листа выражается в единицах сеймен-квадратов (или мхо-квадратов), что является обратной величиной сопротивления листа (единицы Ом/квадрат). Точно так же минимальное поверхностное ВЧ-сопротивление является обратной величиной приведенного выше уравнения:
Вуаля! это уравнение очень похоже на уравнение сопротивления листа постоянному току (вверху страницы), за исключением того, что глубина скин-слоя теперь находится в доминаторе, а не в толщине проводника.
Помните, это лучшее, чего вы можете достичь, независимо от того, сколько металла вы добавите в линию передачи! Теперь давайте посмотрим, что это означает для различных металлов.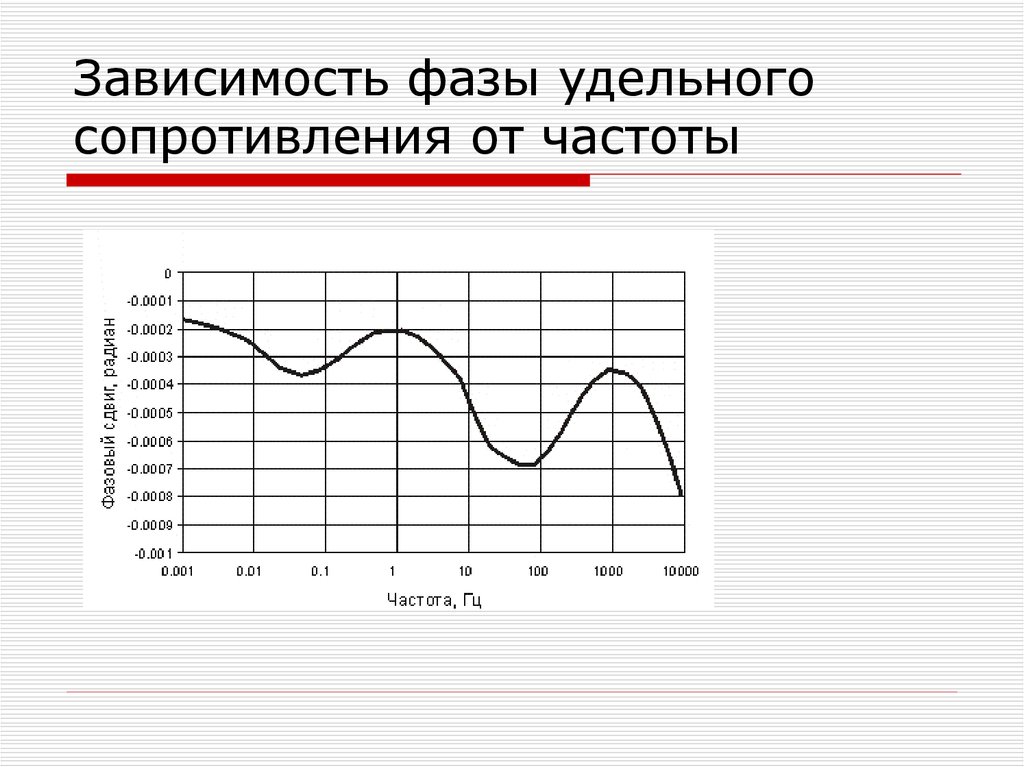 Нажмите здесь, чтобы узнать проводимость различных металлов. На приведенном ниже графике сравниваются алюминий, золото, медь и серебро. Лучше всего серебро, затем медь, затем золото и алюминий. При постоянном токе вы можете добиться почти нулевого поверхностного сопротивления, потому что толщина скин-слоя бесконечна. Но чтобы получить действительно нулевое сопротивление листа, вам понадобится бесконечная толщина металла! Минимальное поверхностное сопротивление влияет на потери в линии передачи, о чем вы можете прочитать на этой странице.
Нажмите здесь, чтобы узнать проводимость различных металлов. На приведенном ниже графике сравниваются алюминий, золото, медь и серебро. Лучше всего серебро, затем медь, затем золото и алюминий. При постоянном токе вы можете добиться почти нулевого поверхностного сопротивления, потому что толщина скин-слоя бесконечна. Но чтобы получить действительно нулевое сопротивление листа, вам понадобится бесконечная толщина металла! Минимальное поверхностное сопротивление влияет на потери в линии передачи, о чем вы можете прочитать на этой странице.
В любом случае, как насчет эмпирического правила?
Минимальное поверхностное ВЧ-сопротивление, которое вы можете получить, составляет порядка 30 мОм/квадрат в X-диапазоне и увеличивается как квадратный корень из частоты до 100 мОм/квадрат в W-диапазоне. Точное значение будет зависеть от проводимости металла.
Примеры
Вот несколько примеров расчетов ВЧ-сопротивления листа.
Вот особый случай металлов с высокой проницаемостью.





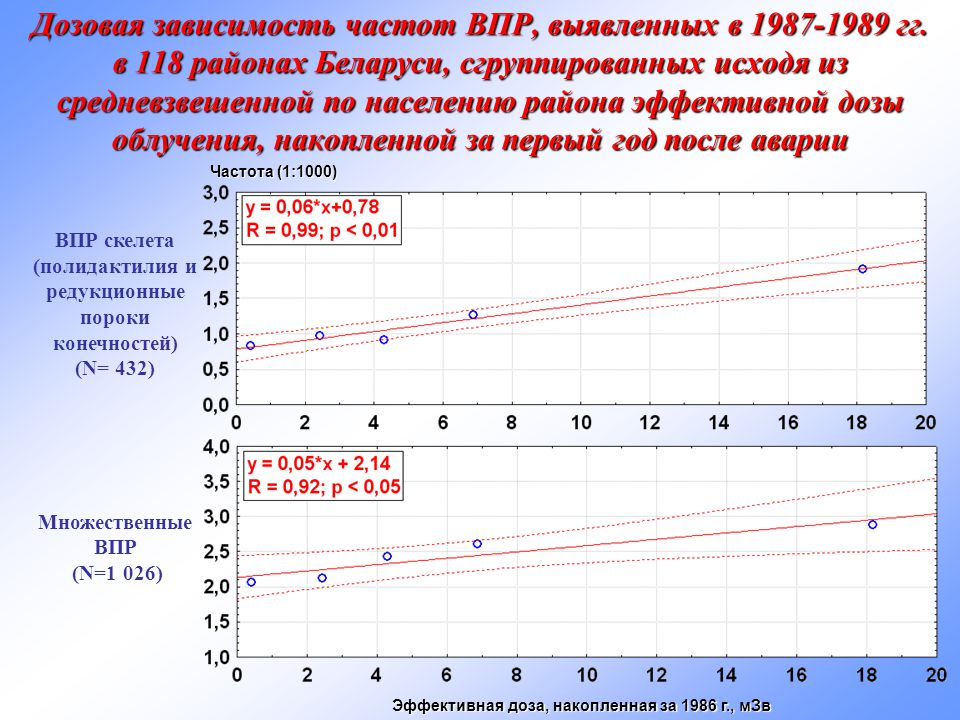
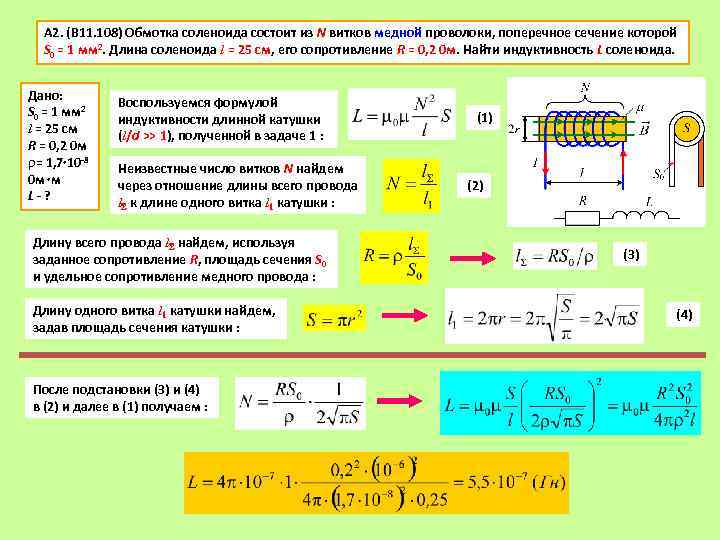 Это показано на рисунке 1. В идеальном конденсаторе нет потерь и эквивалентное последовательное сопротивление (ESR) равно нулю.
Это показано на рисунке 1. В идеальном конденсаторе нет потерь и эквивалентное последовательное сопротивление (ESR) равно нулю. Значение ESR определяется диэлектрическими потерями в конденсаторе.
Значение ESR определяется диэлектрическими потерями в конденсаторе. 


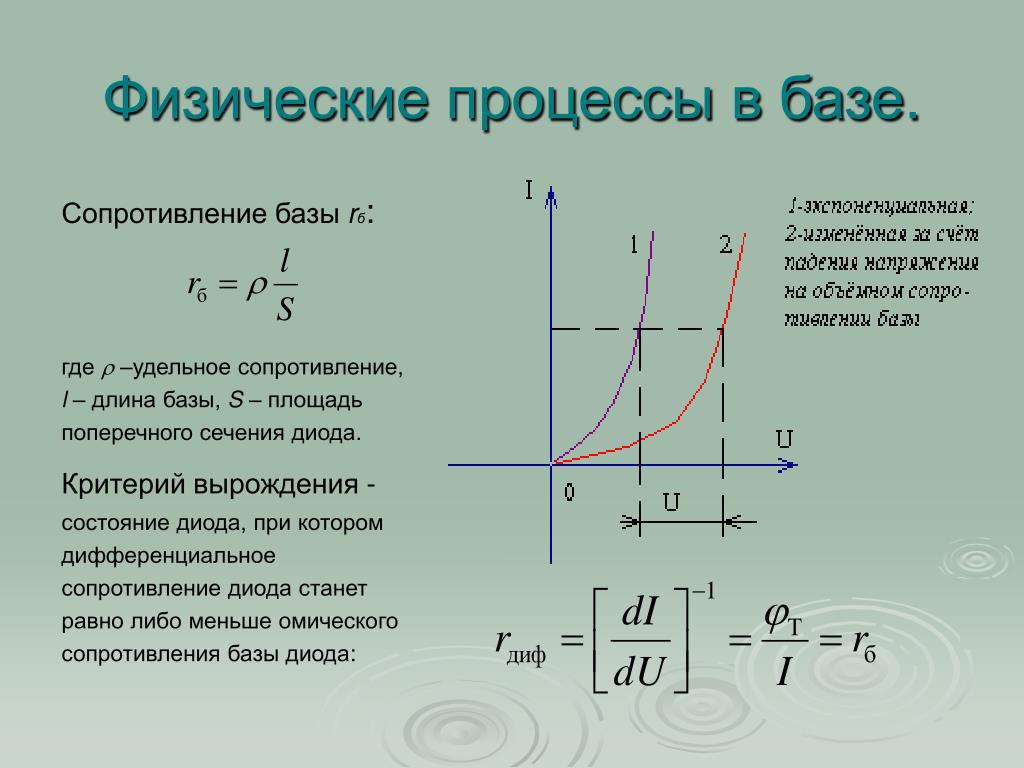
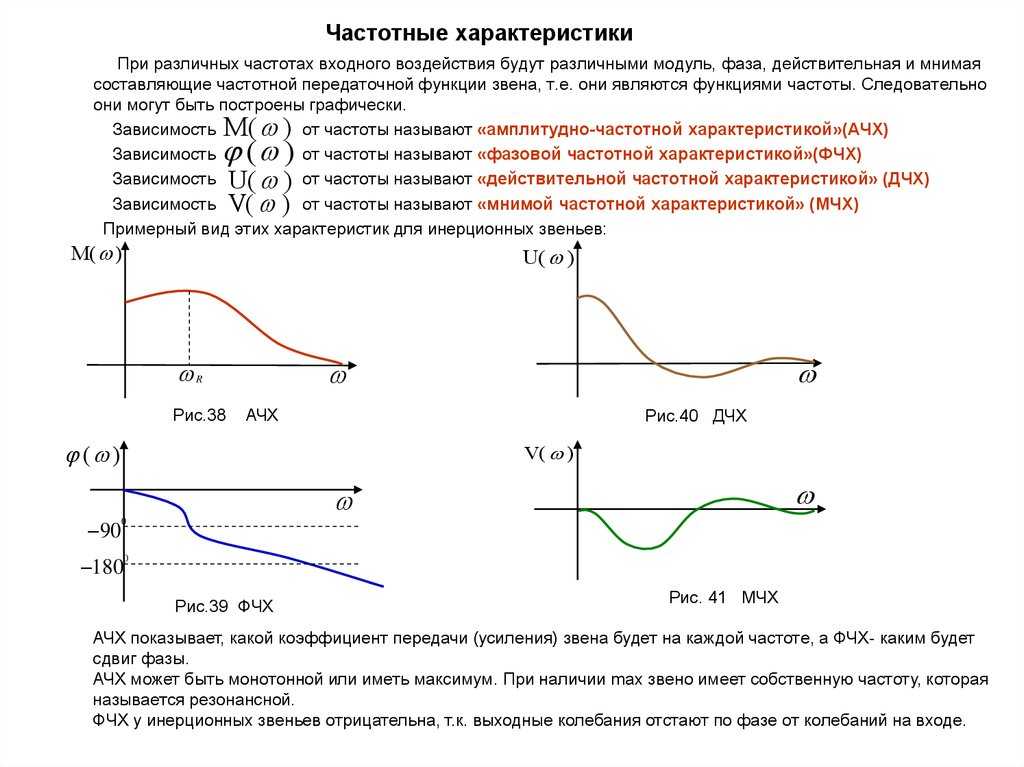
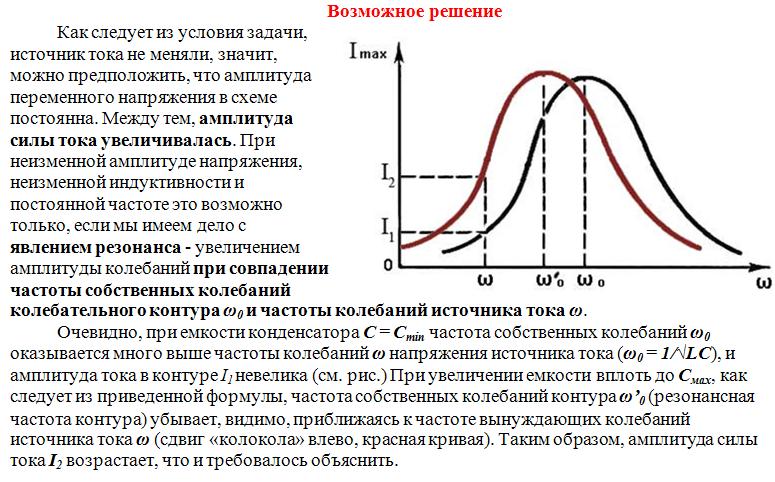 В случае синусоидального напряжения имеем:
В случае синусоидального напряжения имеем: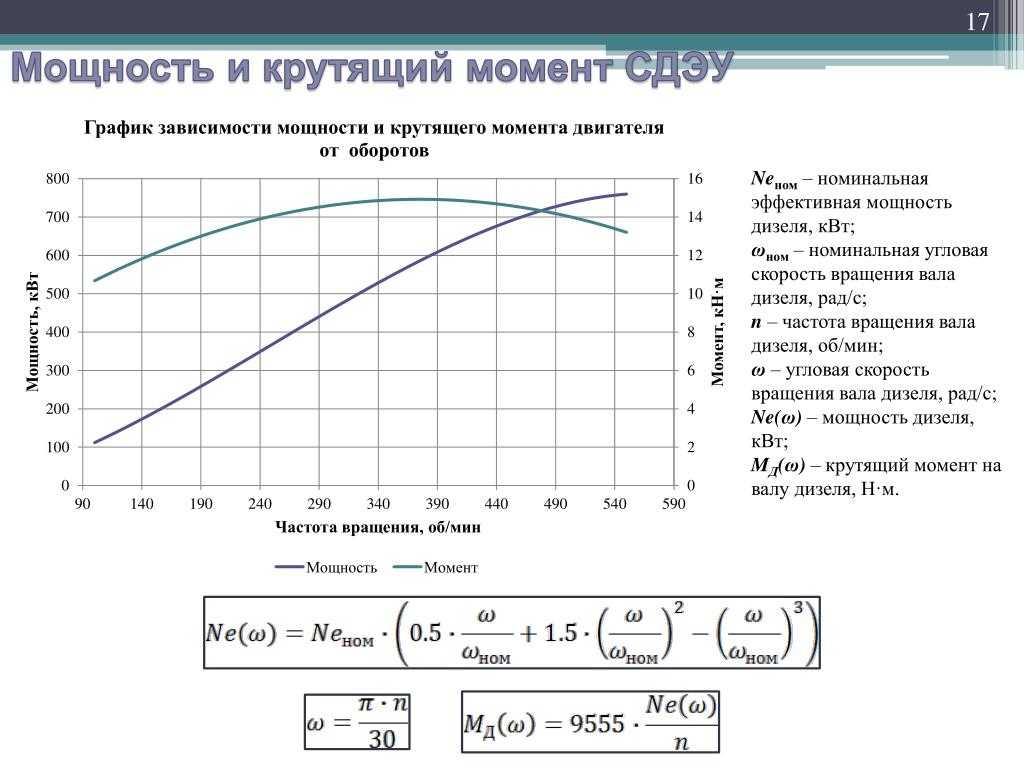 Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 3. 2).
Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 3. 2).

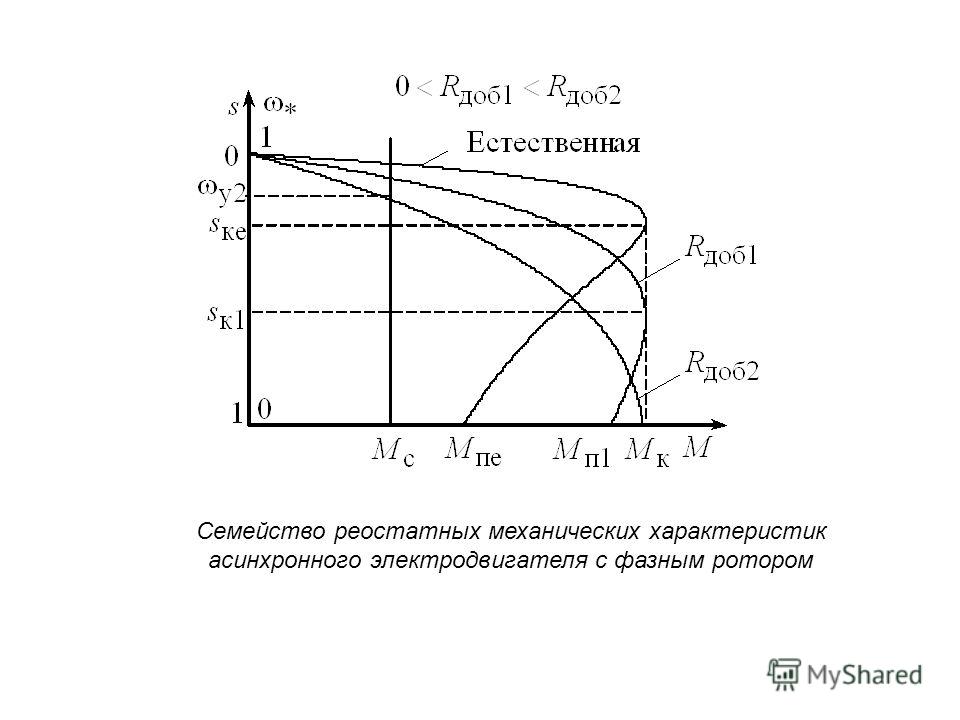
 Единица измерения — ом.
Единица измерения — ом.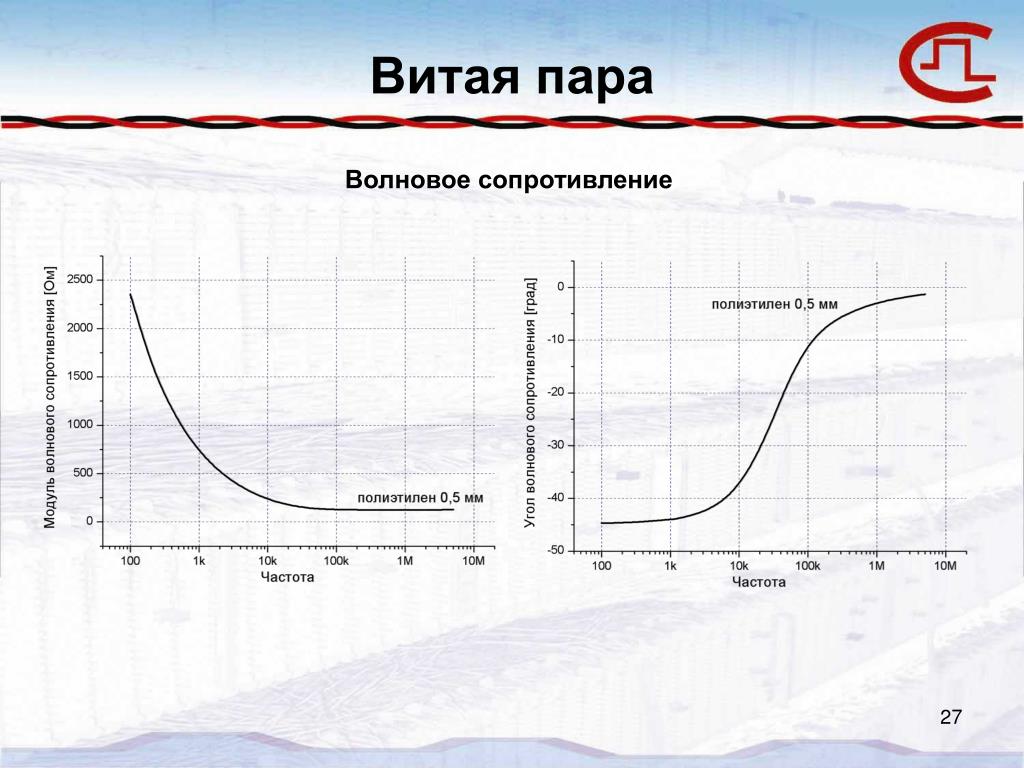
 А. Бессонов. — М: Высшая школа, 1983. — 336 с.
А. Бессонов. — М: Высшая школа, 1983. — 336 с.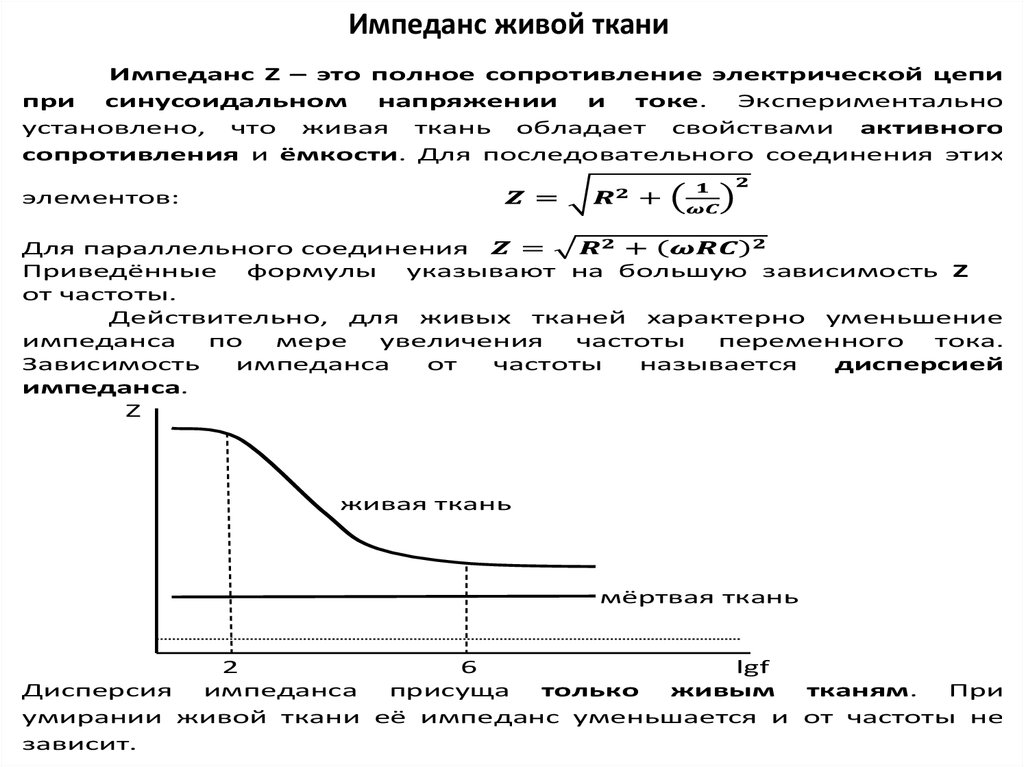 ..
..


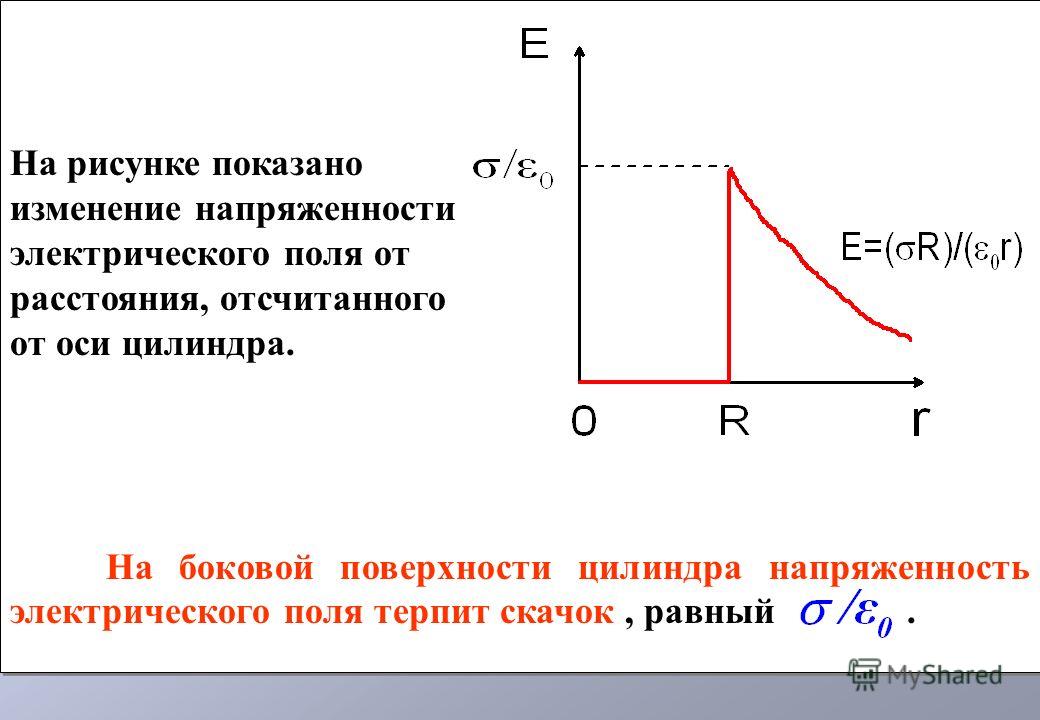
 Позиционный стенд Американского колледжа спортивной медицины. Модели прогрессии в тренировках с отягощениями для здоровых взрослых. Med Sci Sports Exerc 41: 687–708, 2009.
Позиционный стенд Американского колледжа спортивной медицины. Модели прогрессии в тренировках с отягощениями для здоровых взрослых. Med Sci Sports Exerc 41: 687–708, 2009.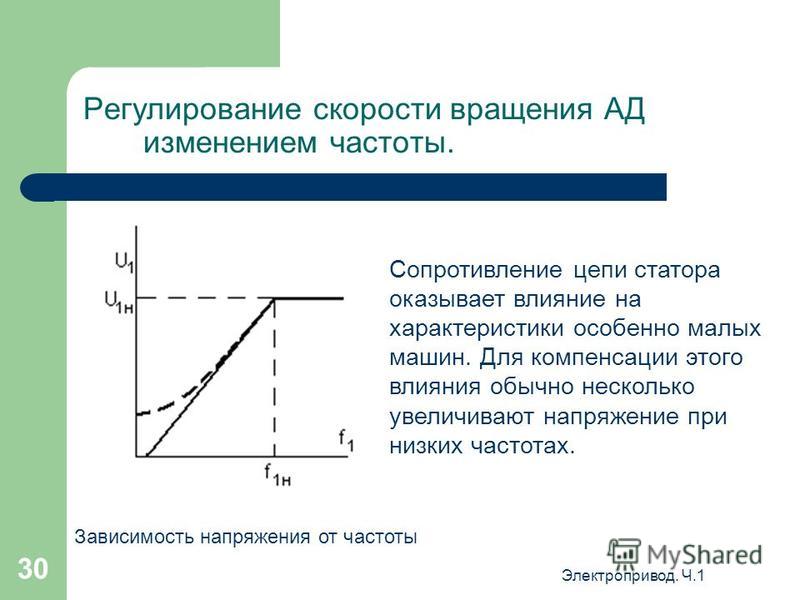 Дж., Рааб С.А., Ваггенер Г.Т., Свон П.Д. Кратковременное влияние частоты тренировок с отягощениями на состав тела и силу у женщин среднего возраста. J Прочность Cond Res 25: 3142–3149, 2011.
Дж., Рааб С.А., Ваггенер Г.Т., Свон П.Д. Кратковременное влияние частоты тренировок с отягощениями на состав тела и силу у женщин среднего возраста. J Прочность Cond Res 25: 3142–3149, 2011. 052%± 0,05%Sp ± 0,5 ℃ (K)
052%± 0,05%Sp ± 0,5 ℃ (K)