Закон Ома для замкнутой цепи постоянного тока – кратко формула с эдс, определение и выводы

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

Обновлено 28 Декабря, 2020

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

Обновлено 28 Декабря, 2020

Соотношение, которое связывает ток в цепи с ее сопротивлением и напряжением, называется законом Ома. Закон Ома имеет несколько форм. Кратко рассмотрим формулу закона Ома для замкнутой цепи постоянного тока.

Причины возникновения тока в замкнутой цепи

Причинами возникновения тока в цепи в общем случае является наличие электрического поля внутри проводника. Поле характеризуется потенциалом, следовательно, если в электрической цепи существует разность потенциалов между какими-то точками, и эти точки соединены элементами, то между ними обязательно потечет электрический ток.

Замкнутая цепь по определению — это такая цепь, которая изолирована от других цепей. А значит, в отличие от участка цепи, источник электрического поля в замкнутой цепи должен находиться внутри нее. Если такого источника не будет, то ток в замкнутой цепи возникать не сможет.

Рис. 1. Схема замкнутой электрической цепи.

Элемент цепи, который является источником электрического поля, называется источником электродвижущей силы (ЭДС).

Суть действия источника ЭДС в том, что внутри этого источника происходит постоянный перенос зарядов между клеммами с помощью сил, природа которых отличается от электрической (сторонних сил). При включении источника ЭДС в замкнутую цепь, сторонние силы создают на его клеммах разность потенциалов, и в замкнутой цепи начинает проходить ток. Рис. 2. Источник ЭДС.

Таким образом, главная характеристика источника ЭДС — это величина сторонних сил. Эта величина и обозначается термином «электродвижущая сила (ЭДС)». Она обозначается символом $\mathscr{E}$ и равна отношению работы сторонних сил к перенесенному заряду:

$$\mathscr{E}={A_{ст}\over q}$$

Из данной формулы видно, что размерность ЭДС та же, что и размерность напряжения, — джоуль на кулон, или вольт.

Вторая характеристика источника ЭДС — внутреннее сопротивление. Вещество источника тока, точно так же, как и любой другой проводник, обладает некоторым электрическим сопротивлением, на котором теряется часть энергии. Физический смысл этого сопротивления такой же, как и у сопротивления проводника или нагрузки, и размерность та же — омы.

Формула закона Ома для замкнутой цепи

Выведем формулу закона Ома для замкнутой цепи.

Сторонние силы, перемещая заряд $Δq$ за время $Δt$, совершают работу:

$$А_{ст}=\mathscr{E}q$$

Ток, по определению, равен отношению заряда, прошедшего по проводнику ко времени прохождения, то есть:

$$I={Δq\over Δt}$$

Подставив значение заряда из этой формулы в предыдущую, получим:

$$А_{ст}=\mathscr{E}IΔt$$

Вся эта работа будет выделена в виде тепла на сопротивлении цепи. Сопротивление цепи состоит из двух компонент: сопротивление самой цепи $R$ и сопротивление источника ЭДС $r$. С учетом закона Джоуля-Ленца:

$$ А_{ст}=I^2RΔt+I^2rΔt$$

Приравнивая левые части формул, получаем:

$$\mathscr{E}IΔt=I^2RΔt+I^2rΔt$$

После сокращений и преобразований имеем:

$$I={\mathscr{E}\over R+r}$$

Сила тока в замкнутой цепи равна отношению ЭДС в замкнутой цепи к сумме сопротивления цепи и внутреннего сопротивления источника ЭДС.

Особенности использования формулы

В формулировку закона Ома для замкнутой цепи входит только одно сопротивление и одно значение ЭДС. Однако в реальных цепях много элементов, и возможны несколько источников ЭДС. В этом случае используется эквивалентное сопротивление цепи, которое находится по специальным формулам преобразования цепей. В качестве значения внутреннего сопротивления используется сумма сопротивлений источников. А в качестве значения ЭДС используется алгебраическая сумма ЭДС источников.

Если цепь очень сложна и составлена из многих узлов, связанных в сложное «кружево», для нахождения тока по такой цепи используются законы Кирхгофа и составление систем уравнений.

Рис. 3. Законы Кирхгофа.

Что мы узнали?

Закон Ома для замкнутой цепи гласит, что сила тока в ней равна отношению ЭДС к сумме сопротивления цепи и внутреннего сопротивления источника ЭДС. Если источников ЭДС несколько, то необходимо использовать сумму их внутренних сопротивлений и алгебраическую сумму ЭДС.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

---

А какая ваша оценка?

19. Закон Ома для замкнутой цепи и участка цепи, содержащего источник эдс.

Закон Ома для замкнутой цепи: ток в цепи, содержащей источник тока, прямо пропорционален э. д. с. источника и обратно пропорционален полному сопротивлению цепи.

Если обозначить э. д. с. источника через ξ, его внутреннее сопротивление через r, сопротивление внешней цепи через R, а ток через I, то закон Ома представится следующей формулой:

Закон Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа — φс)на концах участка цепи и имеющейся на этом участке ЭДС E:

20.

Законы Ома и Джоуля-Ленца.

Закон Ома — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника.

Закон Ома для полной цепи:

где:

— ЭДС источника напряжения (В),

— сила тока в цепи (А),

— сопротивление всех внешних элементов цепи (Ом),

— внутреннее сопротивление источника напряжения (Ом).

Часто выражение:

тоже называют «Законом Ома».

Формулировка: Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Закон Джоуля-Ленца: количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.

Закон Джоуля-Ленца в дифференциальной форме можно представить как:

где w — мощность выделения тепла в единице объёма, σ — проводимость среды, Е — напряжённость электрического поля.

21. Правила Кирхгофа.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю.

Первое правило Кирхгофа является следствием закона сохранения заряда, согласно которому ни в одной точке проводника не должны накапливаться или исчезать заряды.

Первое правило Кирхгофа можно сформулировать и так: количество зарядов, приходящих в данную точку проводника за некоторое время, равно количеству зарядов, уходящих из данной точки за то же время.

Второе правило Кирхгофа является обобщением закона Ома. Второе правило Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:

Правила Кирхгофа позволяют определить силу и направление тока в любой части разветвленной цепи, если известны сопротивления ее участков и включенные в них ЭДС.

22. Природа носителей заряда в металлах. Классическая теория электропроводности.

Зависимость электропроводности от температуры.

Для выяснения природы носителей тока в металлах был поставлен ряд опытов. Опыт Рикке.

Рикке взял три цилиндра два медных и один алюминиевый с тщательно отшлифованными торцами. После взвешивания цилиндры были сложены вместе в последовательности медь — алюминий — медь. Через такой составной проводник непрерывно в течение года пропускался ток одного и того же направления.

За все время через цилиндры прошел заряд, равный . Взвешивание показало, что пропускание тока не оказало на массу цилиндров никакого влияния. При исследовании соприкасавшихся торцов под микроскопом не было обнаружено проникновение одного металла в другой.

Результаты опыта свидетельствовали о том, что перенос заряда в металлах осуществляется не атомами, а какими-то частицами, входящими в состав всех металлов. Чтобы отождествить носители тока в металлах с электронами, нужно было определить знак и числовое значение удельного заряда носителей.

Характер зависимости электропроводности от температуры Т различен у разных веществ.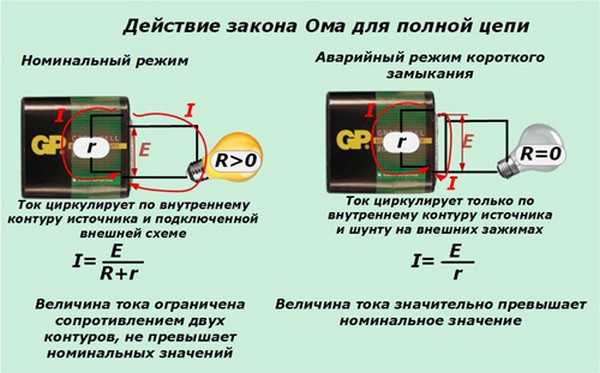

У металлов зависимость σ(Т) определяется в основном уменьшением времени свободного пробега электронов с ростом Т: увеличение температуры приводит к возрастанию тепловых колебаний кристаллической решётки, на которых рассеиваются электроны, и σ уменьшается. При достаточно высоких температурах, превышающих температуру Дебая , электропроводность металлов обратно пропорциональна температуре: σ Электропроводность 1/Т; при Т << σ Электропроводность , однако ограничена остаточным сопротивлением. В полупроводниках σ резко возрастает при повышении температуры за счёт увеличения числа электронов проводимости и положительных носителей заряда — дырок. Диэлектрики имеют заметную электропроводность лишь при очень высоких электрических напряжениях; при некотором значении Е происходит пробой диэлектриков.

Некоторые металлы, сплавы и полупроводники при понижении Т до нескольких градусов К переходят в сверхпроводящее состояние с σ = ∞. При плавлении металлов их электропроводность в жидком состоянии остаётся того же порядка, что и в твёрдом.

Сопротивление и закон Ома – Физические науки

Закон Ома

Закон Ома гласит, что ток пропорционален напряжению; цепи являются омическими, если они подчиняются соотношению V=IR.

Цели обучения

Контрастная форма графиков ток-напряжение для омических и неомических цепей

Основные выводы

Ключевые моменты

• Напряжение вызывает ток, а сопротивление препятствует ему.
• Закон Ома относится к пропорциональному отношению между напряжением и током. Это также относится к конкретному уравнению V = IR, которое справедливо при рассмотрении цепей, содержащих простые резисторы (сопротивление которых не зависит от напряжения и тока).
• Цепи или компоненты, которые подчиняются соотношению V=IR, известны как омические и имеют графики зависимости тока от напряжения, которые являются линейными и проходят через начало координат.
• Имеются неомические компоненты и цепи; их графики ВАХ нелинейны и/или не проходят через начало координат.

Ключевые термины

• простая схема : Цепь с одним источником напряжения и одним резистором.
• омический : То, что подчиняется закону Ома.

Закон Ома

Что вызывает ток? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов V, которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток. Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V. Немецкий физик Георг Симон Ом (1787-1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению: [latex]\text{I} \propto \text{V}[/latex ].

Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место. Напомним, что в то время как напряжение управляет током, сопротивление препятствует ему. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Таким образом, ток обратно пропорционален сопротивлению: [latex]\text{I} \propto \frac{1}{\text{R}}[/latex].

Простая цепь : Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.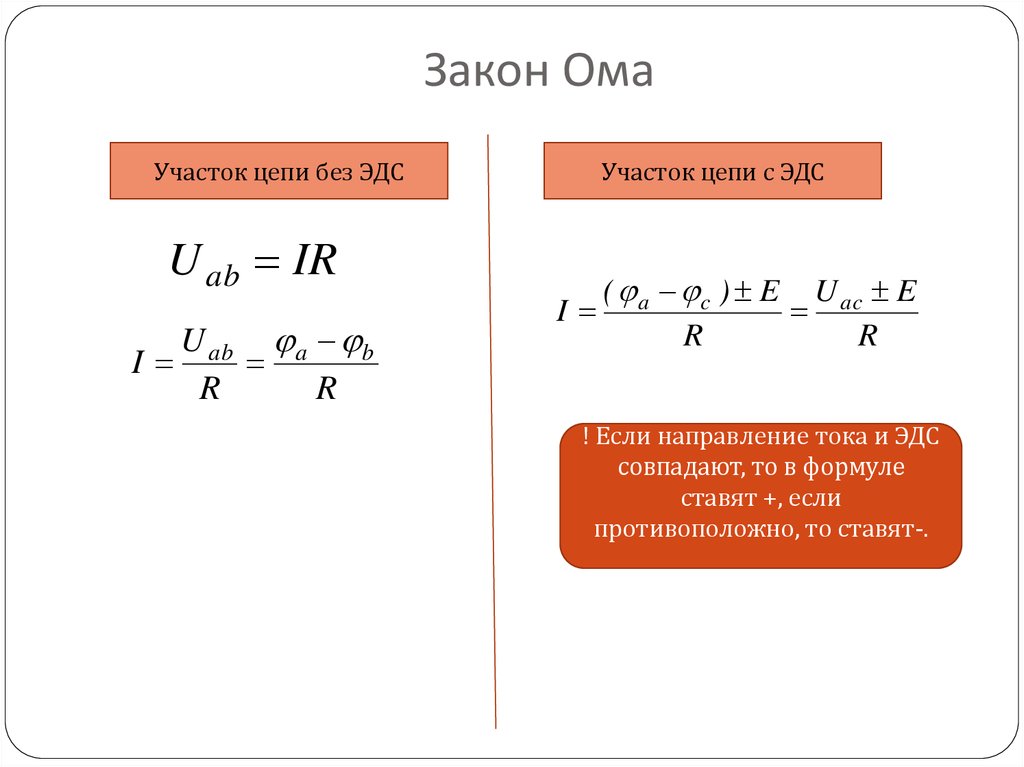

Единицей измерения сопротивления является ом, где 1 Ом = 1 В/А. Мы можем объединить два приведенных выше соотношения, чтобы получить I = V/R. Эту зависимость также называют законом Ома. В этой форме закон Ома действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R, не зависящее от напряжения V и тока I. Предмет, имеющий простое сопротивление, называется резистором, даже если его сопротивление мало.

Падение напряжения

: Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Дополнительную информацию можно получить, решив I=V/R относительно V, что даст V=IR. Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I. Для этого напряжения часто используется фраза IR drop. Если измерять напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку E = qΔV, и через каждый протекает одно и то же q. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.

В истинно омическом устройстве одно и то же значение сопротивления будет рассчитываться из R = V/I независимо от значения приложенного напряжения V. То есть отношение V/I постоянно, и когда ток изображается как функция напряжения кривая линейна (прямая линия). Если напряжение форсируется до некоторого значения V, то это напряжение V, деленное на измеренный ток I, будет равно R. Или, если ток форсируется до некоторого значения I, то измеренное напряжение V, деленное на этот ток I, также равно R. Мы визуализируем график зависимости I от V в виде прямой линии. Однако есть компоненты электрических цепей, которые не подчиняются закону Ома; то есть их связь между током и напряжением (их ВАХ) является нелинейной (или неомической). Примером может служить диод с p-n переходом.

Кривые вольтамперной характеристики : Кривые ВАХ четырех устройств: двух резисторов, диода и батареи. Два резистора подчиняются закону Ома: график представляет собой прямую линию, проходящую через начало координат. Два других устройства не подчиняются закону Ома.

Закон Ома : Краткий обзор закона Ома.

Температура и сверхпроводимость

Сверхпроводимость — это явление нулевого электрического сопротивления и выброса магнитных полей в некоторых материалах ниже критической температуры.

Цели обучения

Описать поведение сверхпроводника при температуре ниже критической и в слабом внешнем магнитном поле

Основные выводы

Ключевые моменты

• Сверхпроводимость является термодинамической фазой и обладает определенными отличительными свойствами, которые в значительной степени независимы микроскопических деталей.
• В сверхпроводящих материалах характеристики сверхпроводимости проявляются при понижении температуры ниже критической. Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств.
• Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже его температуры перехода, магнитное поле выбрасывается.
• Сверхпроводники способны поддерживать ток без приложенного напряжения.

Ключевые термины

• высокотемпературные сверхпроводники : Материалы, которые ведут себя как сверхпроводники при необычно высоких температурах (выше примерно 30 К).
• критическая температура : В сверхпроводящих материалах характеристики сверхпроводимости проявляются при этой температуре (и продолжаются ниже).
• сверхпроводимость : Свойство материала, при котором он не оказывает сопротивления потоку электрического тока.

Сверхпроводимость — это явление абсолютно нулевого электрического сопротивления и выброса магнитных полей, происходящее в некоторых материалах при охлаждении ниже характерной критической температуры. Он был обнаружен Хайке Камерлинг-Оннесом (показан на фото) 8 апреля 1911 года в Лейдене.

Хайке Камерлинг-Оннес : Хайке Камерлинг-Оннес (1853-1819 гг. )26).

Большинство физических свойств сверхпроводников различаются от материала к материалу, например, теплоемкость и критическая температура, критическое поле и критическая плотность тока, при которых сверхпроводимость разрушается. С другой стороны, существует класс свойств, не зависящих от основного материала. Например, все сверхпроводники имеют точно нулевое удельное сопротивление для низких приложенных токов, когда нет магнитного поля или если приложенное поле не превышает критического значения. Существование этих «универсальных» свойств подразумевает, что сверхпроводимость является термодинамической фазой и, таким образом, обладает определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.

В сверхпроводящих материалах характеристики сверхпроводимости проявляются, когда температура T опускается ниже критической температуры T _c . Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств — отличительной чертой фазового перехода. Например, электронная теплоемкость пропорциональна температуре в обычном (несверхпроводящем) режиме. При сверхпроводящем переходе она претерпевает прерывистый скачок и после этого перестает быть линейной, как показано на рис. 9.0005

Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже температуры его перехода, магнитное поле выбрасывается. Эффект Мейснера не приводит к полному выбросу поля. Скорее поле проникает в сверхпроводник на очень небольшое расстояние (характеризуемое параметром λ), называемое лондоновской глубиной проникновения. Он экспоненциально затухает до нуля внутри объема материала. Эффект Мейснера является определяющей характеристикой сверхпроводимости. Для большинства сверхпроводников лондоновская глубина проникновения составляет порядка 100 нм.

Сверхпроводящий фазовый переход : Поведение теплоемкости (cv, синий) и удельного сопротивления (ρ, зеленый) при сверхпроводящем фазовом переходе.

Сверхпроводники также способны поддерживать ток без какого-либо приложенного напряжения — свойство, используемое в сверхпроводящих электромагнитах, например, в аппаратах МРТ.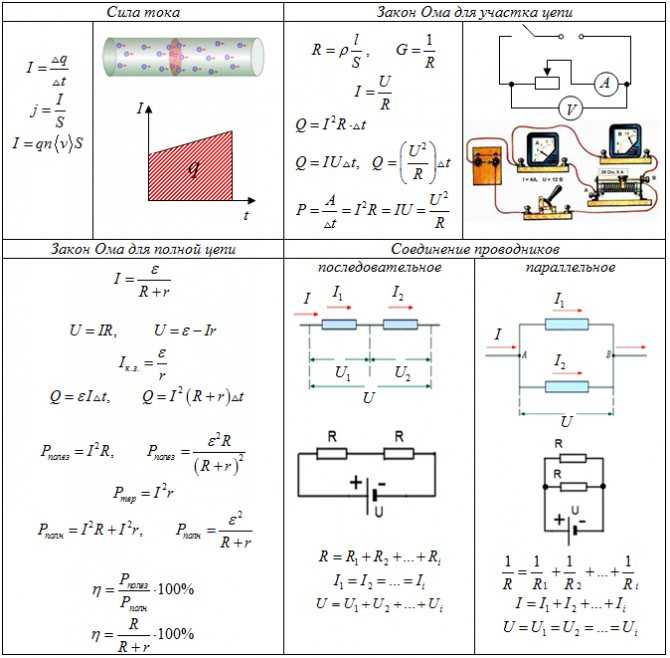 Эксперименты показали, что токи в сверхпроводящих катушках могут сохраняться годами без какого-либо заметного ухудшения. Экспериментальные данные указывают на текущую продолжительность жизни не менее 100 000 лет. Теоретические оценки времени жизни постоянного тока могут превышать расчетное время жизни Вселенной, в зависимости от геометрии проволоки и температуры.

Значение этой критической температуры зависит от материала. Обычно обычные сверхпроводники имеют критические температуры в диапазоне от примерно 20 К до менее 1 К. Например, твердая ртуть имеет критическую температуру 4,2 К. По состоянию на 2009 г. самая высокая критическая температура, обнаруженная для обычного сверхпроводника, составляет 39 К для магния. диборид (MgB ₂ ), хотя экзотические свойства этого материала вызывают сомнения в правильности отнесения его к «обычным» сверхпроводникам. Высокотемпературные сверхпроводники могут иметь гораздо более высокие критические температуры. Например, YBa ₂ Cu ₃ O ₇ , один из первых открытых купратных сверхпроводников, имеет критическую температуру 92 К; были обнаружены купраты на основе ртути с критическими температурами выше 130 К. Следует отметить, что химический состав и кристаллическая структура сверхпроводящих материалов могут быть довольно сложными, как показано на рис. Ячейка сверхпроводника YBaCuO. Атомы обозначены разными цветами.

Сопротивление и удельное сопротивление

Сопротивление и удельное сопротивление описывают степень, в которой объект или материал препятствует прохождению электрического тока.

Цели обучения

Определить свойства материала, описываемые сопротивлением и удельным сопротивлением

Ключевые выводы

Ключевые моменты

• Сопротивление объекта (например, резистора) зависит от его формы и материала, из которого он изготовлен. он составлен.
• Удельное сопротивление ρ является внутренним свойством материала и прямо пропорционально общему сопротивлению R, внешней величине, которая зависит от длины и площади поперечного сечения резистора.
• Удельное сопротивление различных материалов сильно различается. Точно так же резисторы варьируются на много порядков.
• Резисторы расположены последовательно или параллельно. Эквивалентное сопротивление сети резисторов, соединенных последовательно, равно сумме всех сопротивлений. Инверсия эквивалентного сопротивления сети резисторов, соединенных параллельно, представляет собой сумму инверсий сопротивления каждого резистора.

Основные термины

• 9Эквивалентное сопротивление серии 0028 : Сопротивление сети резисторов, расположенных таким образом, что напряжение в сети является суммой напряжений на каждом резисторе. В этом случае эквивалентное сопротивление представляет собой сумму сопротивлений всех резисторов в сети.
• параллельное эквивалентное сопротивление : сопротивление сети, при которой на каждый резистор действует одна и та же разность потенциалов (напряжение), так что токи через них складываются. В этом случае обратное эквивалентное сопротивление равно сумме обратного сопротивления всех резисторов в сети.
• удельное сопротивление : Как правило, сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.

Сопротивление и удельное сопротивление

Сопротивление — это электрическое свойство, препятствующее прохождению тока. Ток, протекающий по проводу (или резистору), подобен воде, протекающей по трубе, а падение напряжения на проводе подобно падению давления, проталкивающему воду по трубе. Сопротивление пропорционально тому, какое давление требуется для достижения данного потока, а проводимость пропорциональна тому, какой поток возникает при данном давлении. Проводимость и сопротивление обратны. Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L, аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же, аналогично потоку жидкости по трубе). На самом деле, R обратно пропорционально площади поперечного сечения цилиндра A.

Цилиндрический резистор : однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, оказываемому трубой потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.

Как уже упоминалось, для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, чтобы сопротивление R объекта было прямо пропорционально ρ. Удельное сопротивление ρ составляет внутреннее свойство материала, не зависящее от его формы или размера. Напротив, сопротивление R является внешним свойством, которое зависит от размера и формы резистора. (Аналогичная внутренняя/внешняя связь существует между теплоемкостью C и удельной теплоемкостью c).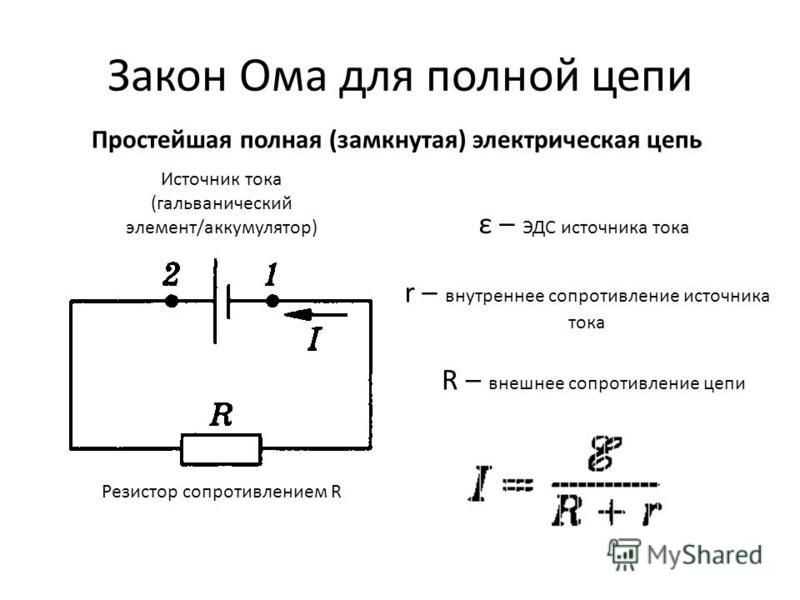 Напомним, что объект, сопротивление которого пропорционально напряжению и току, называется резистором.

Типовой резистор : Типовой резистор с осевым выводом.

Что определяет удельное сопротивление? Удельное сопротивление различных материалов сильно различается. Например, проводимость тефлона примерно в 1030 раз ниже проводимости меди. Почему такая разница? Грубо говоря, металл имеет большое количество «делокализованных» электронов, которые не застревают в одном месте, а свободно перемещаются на большие расстояния, тогда как в изоляторе (например, в тефлоне) каждый электрон прочно связан с одним атомом, и требуется большая сила, чтобы вытащить его. Точно так же резисторы варьируются на много порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹² Ом или больше. У сухого человека сопротивление руки к ноге может составлять 10 ⁵ Ом, тогда как сопротивление человеческого сердца составляет около 10 ³ Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 ⁻⁵ Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Разность потенциалов (напряжение) в сети представляет собой сумму этих напряжений, поэтому общее сопротивление (эквивалентное последовательное сопротивление) можно найти как сумму этих сопротивлений:

[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} + \ text {R} _ {2} + \ cdots + \ text {R} _ {\ текст{N}}[/латекс].

Как частный случай, сопротивление N резисторов, соединенных последовательно, каждый из которых имеет одинаковое сопротивление R, определяется как NR. Резисторы в параллельной конфигурации имеют одинаковую разность потенциалов (напряжение), однако токи через них добавлять. Таким образом, можно рассчитать эквивалентное сопротивление (Req) сети:

[латекс]\frac{1}{\text{R}_{\text{eq}}}=\frac{1}{\text{R }_{1}}+\frac{1}{\text{R}_{2}}+\cdots +\frac{1}{\text{R}_{\text{N}}}[/latex ].

Параллельное эквивалентное сопротивление может быть представлено в уравнениях двумя вертикальными линиями «||» (как в геометрии) в упрощенном виде. Иногда вместо «||» используются две косые черты «//», если в клавиатуре или шрифте отсутствует символ вертикальной линии. Для случая двух параллельных резисторов это можно рассчитать, используя:

[латекс]\текст{R}_{\text{eq}}=\text{R}_{1}\parallel\text{R} _{2}=\frac{\text{R}_{1}\text{R}_{2}}{\text{R}_{1}+\text{R}_{2}}[/ латекс].

Как частный случай, сопротивление N резисторов, соединенных параллельно, каждый из которых имеет одинаковое сопротивление R, выражается как R/N. Сеть резисторов, представляющая собой комбинацию параллельных и последовательных соединений, может быть разбита на более мелкие части, которые являются либо одним, либо другим, как показано на рис. 9.0005

Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный и параллельный компоненты.

Однако некоторые сложные цепи резисторов не могут быть разрешены таким образом. Они требуют более сложного анализа схемы. Одним из практических применений этих взаимосвязей является то, что нестандартное значение сопротивления обычно может быть синтезировано путем последовательного или параллельного соединения ряда стандартных значений.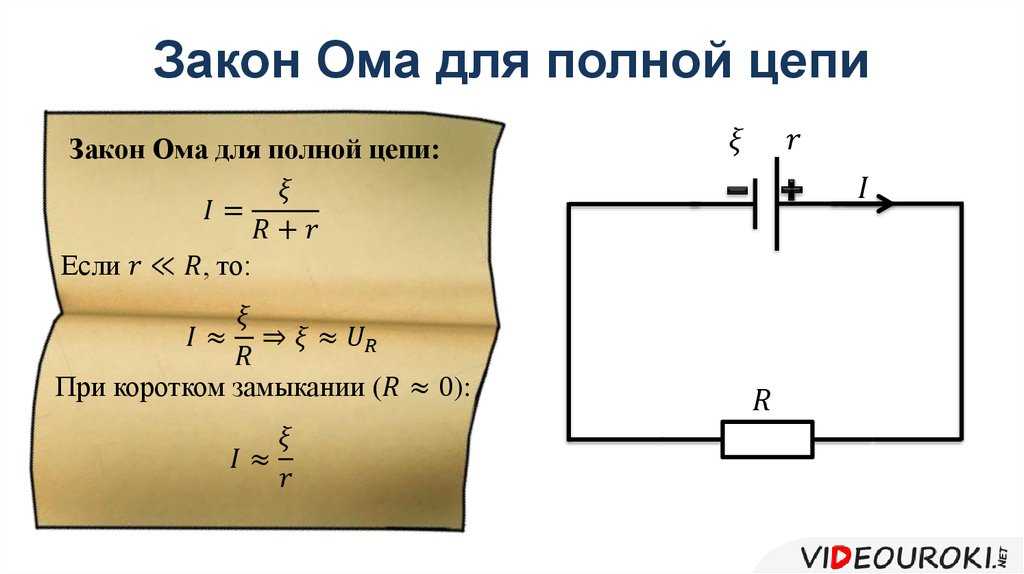 Это также можно использовать для получения сопротивления с более высокой номинальной мощностью, чем у отдельных используемых резисторов. В частном случае N одинаковых резисторов, соединенных последовательно или параллельно, номинальная мощность отдельных резисторов умножается на N.

Сопротивление, резисторы и удельное сопротивление : Краткий обзор сопротивления, резисторов и удельного сопротивления.

Зависимость сопротивления от температуры

Удельное сопротивление и сопротивление зависят от температуры с линейной зависимостью при малых изменениях температуры и нелинейной при больших.

Цели обучения

Сравнение температурной зависимости удельного сопротивления и сопротивления при больших и малых изменениях температуры

Ключевые выводы

Ключевые моменты

• При изменении температуры на 100ºC или менее удельное сопротивление (ρ) зависит от изменения температуры ΔT следующим образом: [латекс]\text{p} = \text{p}_{0}(1 + \alpha \ Delta \text{T})[/latex] где ρ ₀ — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.
• При больших изменениях температуры наблюдается нелинейное изменение удельного сопротивления в зависимости от температуры.
• Сопротивление объекта демонстрирует такую ​​же температурную зависимость, как и удельное сопротивление, поскольку сопротивление прямо пропорционально удельному сопротивлению.

Ключевые термины

• удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
• температурный коэффициент удельного сопротивления : Эмпирическая величина, обозначаемая α, которая описывает изменение сопротивления или удельного сопротивления материала в зависимости от температуры.
• полупроводник : Вещество с электрическими свойствами, промежуточными между хорошим проводником и хорошим изолятором.

Удельное сопротивление всех материалов зависит от температуры. Некоторые материалы могут стать сверхпроводниками (нулевое удельное сопротивление) при очень низких температурах (см.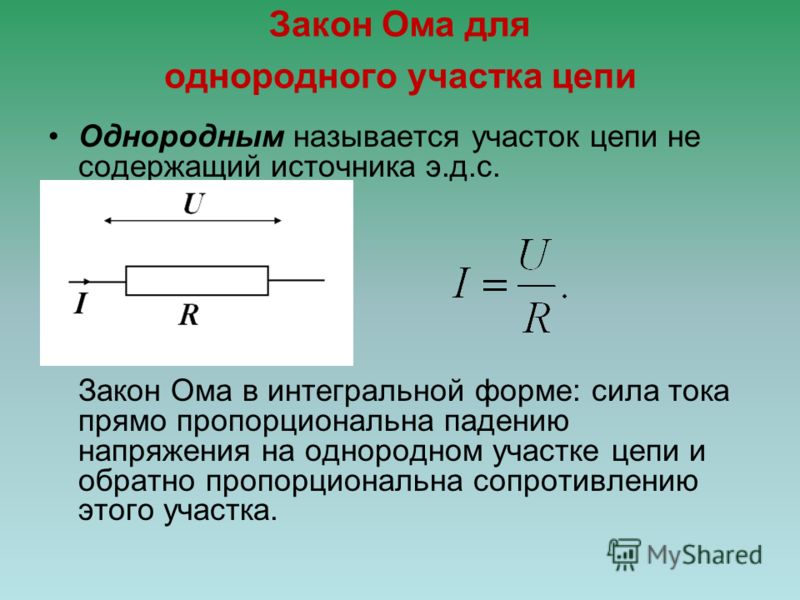 ). И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, например, создают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или менее) удельное сопротивление ρ зависит от изменения температуры ΔT, как это выражается в следующем уравнении:

Сопротивление образца ртути : Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти до линейно с температурой.

[латекс]\текст{р} = \текст{р}_{0}(1 + \альфа \Дельта \текст{Т})[/латекс]

где ρ ₀ — исходное удельное сопротивление и α – температурный коэффициент удельного сопротивления. Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение для нахождения ρ. По этой причине обычно указывается суффикс для температуры, при которой измерялось вещество (например, α ₁₅ ), и соотношение сохраняется только в диапазоне температур, близких к контрольному. Обратите внимание, что α положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Температурный коэффициент обычно составляет от +3×10 ^–3 К ^–1 до +6×10 ^–3 К ^–1 для металлов с температурой, близкой к комнатной. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α, близкую к нулю, поэтому его удельное сопротивление мало зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Обратите внимание, что для полупроводников α отрицательно, а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока.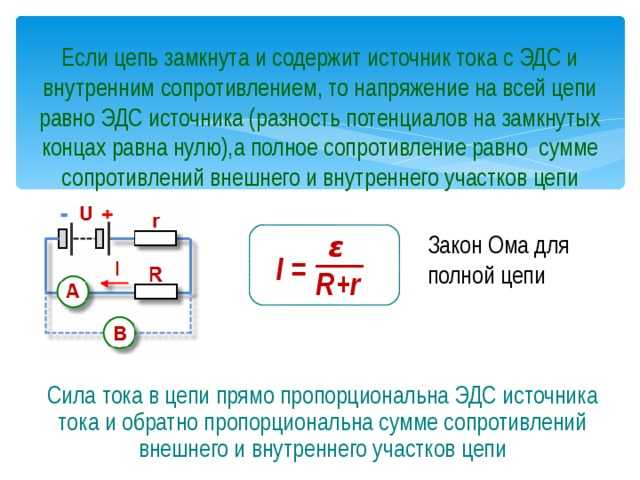 Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, так как R ₀ прямо пропорционально ρ. Для цилиндра мы знаем, что R=ρL/A, поэтому, если L и A не сильно изменяются с температурой, R будет иметь ту же температурную зависимость, что и ρ. (Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ.) Таким образом,

[латекс]\текст{R} = \текст{R}_{0}(1 + \альфа \Дельта \текст{Т})[/латекс]

— зависимость сопротивления объекта от температуры, где R ₀ — исходное сопротивление, а R — сопротивление после изменения температуры T. Многие термометры основаны на влиянии температуры на сопротивление (см. ). Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью тела, к которой прикасается.

Термометры : Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры.

Как применять закон Ома

Как применять закон Ома

Национальный электротехнический кодекс 2017 года

Автор: Wes Gubitz | 07 августа 2019 г.

Электричество работает в предсказуемых пределах. Мы пришли к тому, чтобы определить эти границы как закон Ома. Закон Ома был разработан как средство объяснения того, как электричество работает в замкнутой цепи. Формула закона Ома помогает установить взаимосвязь между различными свойствами в электрической цепи. Мы можем использовать закон Ома, чтобы объяснить, что произошло, а также что произойдет, когда определенные условия накладываются на электрическую цепь.

Основные свойства электрической цепи: Напряжение, Ток и Сопротивление .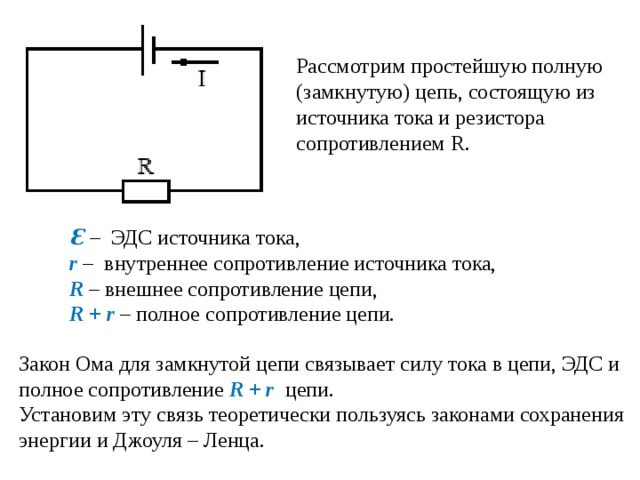 Они специфичны, определены и не меняются — при условии, что все свойства остаются постоянными. Однако если изменить значение только одного из этих свойств, все свойства изменятся соответствующим образом.

Закон Ома — это самая основная электрическая формула, которая была разработана путем простого наблюдения за свойствами электричества в электрической цепи. Электричество ведет себя иначе из-за ограничений, налагаемых формулой закона Ома; формула просто представляет наши наблюдения за поведением, уже происходящим в электрической цепи.

В то время как Закон Ома является лишь вводной ступенью на лестнице науки об электричестве, базовое понимание электрической цепи необходимо для понимания того, как закон Ома, как формула, применяется к простой цепи. Простая цепь состоит из источника питания, нагрузки, проводников, устройства максимального тока и устройства управления. В этой простой цепи будет течь ток, если присутствует достаточное напряжение, чтобы преодолеть любое сопротивление цепи.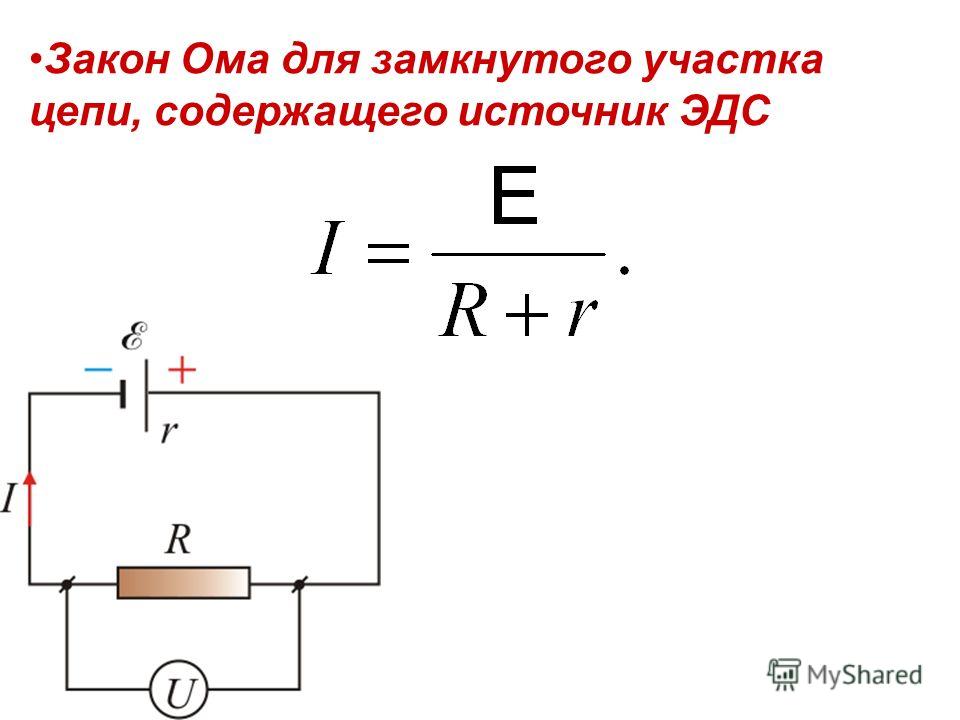
Напряжением считается давление в электрической цепи; это правильно называется Электродвижущей Силой. Это давление или «сила» возникает из-за того, что разнородные электрические полюса стремятся уравновесить себя. Толчок и притяжение, воздействующие на электроны в проводнике, соединенном с этими разными полюсами, заставят электроны двигаться, если для них существует полный путь. Единственное, что может остановить движение электронов, — это сопротивление, приложенное сверх напряжения, заставляющего их двигаться, или разрыв в цепи, который нарушает поток этих электронов. Требуется один вольт (В) этой электродвижущей силы, чтобы протолкнуть один ампер (А) тока через сопротивление в один ом (Ом) — это закон Ома. Напряжение (E или V) равно току (I), умноженному на сопротивление (R). Или, другими словами, E(или V)=IR.

Символы

• Вольты (E или V) = Электродвижущая сила, опять же, это давление, которое заставляет электроны двигаться вдоль проводника (и через нагрузку) в полной цепи.
• Ток(I) = Интенсивность, представляет ток, протекающий в цепи. Помните, что «интенсивность» тока в цепи измеряется в амперах.
• Сопротивление (R) = Ом, сопротивление протеканию тока. Сопротивление может быть преднамеренным или случайным, но в любом случае оно является сопротивлением свободно протекающему току в цепи и отображается в омах на вашем электрическом счетчике. Ноль Ом или близко к нему означает буквально отсутствие сопротивления току. Медь имеет очень низкое значение сопротивления в омах на фут и является превосходным материалом для изготовления эффективных проводников.

Давайте посмотрим на символы закона Ома в треугольнике закона Ома.

Помните, что вольты (E или V) равны току (I), умноженному на сопротивление (R)

Использование треугольника закона Ома в качестве наглядного пособия при запоминании трех уравнений закона Ома — не редкость.

Чтобы найти отсутствующее значение в реальном уравнении закона Ома, просто закройте букву, обозначающую отсутствующее значение, в треугольнике и используйте оставшиеся два значения для расчета этого отсутствующего значения.

Например: если вы знаете, что лампа на 120 вольт (E или V) измеряет ток 0,625 ампер (I) во время использования, сколько омов сопротивления предлагает лампа?

120 вольт (E) разделить на 0,625 ампер (I) равно 192 Ом (R) сопротивления.

Что делать, если вы знаете измеряемый ток (I) протекающего тока и сопротивление (R) нити накала лампы? Можете ли вы тогда рассчитать напряжение, подаваемое на эту лампу? Посмотрите на треугольник закона Ома ниже, чтобы определить свой ответ.

Ток (I), умноженный на сопротивление (R), равен напряжению, приложенному к лампе.

Правило треугольника закона Ома
Помните, глядя на треугольник закона Ома, если числа стоят рядом, вы умножаете, если числа расположены одно над другим, вы делите.

Заключение
Закон Ома и многие другие электрические формулы дают нам средства, с помощью которых мы можем понять самые основные принципы движения электричества и тока. Эти многочисленные формулы дают нам возможность заглянуть в прошлое, а также в будущие электрические приложения.