Закон Ома в дифференциальной форме
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
| (7.6.1) |
Для однородного линейного проводника выразим R через ρ:
| , | (7.6.2) |
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля коллинеарны (рис. 7.6).
Исходя из закона Ома (7.6.1), имеем:
А мы знаем, что или . Отсюда можно записать
| , | (7.6.3) |
это запись закона Ома в дифференциальной форме.
Здесь – удельная электропроводность.
Размерность σ – [].
Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :
.
| (7.6.4) |
Теперь, если удельную электропроводность σ выразить через е, n и b: то вновь получим выражение закона Ома в дифференциальной форме:
.
Закон Ома для неоднородного участка цепи Работа и мощность тока. Закон Джоуля – Ленца
3.2.2. Закон Ома в интегральной и дифференциальной форме
| Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а 1 и 2 – потенциалы на концах проводника. В случае однородного проводника величину 1 — 2 = U можно назвать |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

— закон Ома в интегральной форме
где R – электрическое сопротивление проводника.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника

где — удельное сопротивление проводника.
Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2. Размерность удельного сопротивления в СИ: [
Величина, обратная сопротивлению, называется проводимостью.
Величина, обратная удельному сопротивлению, называется удельной проводимостью:

Единица, обратная Ом, называется Сименсом [См].
Учитывая выше
написанные уравнения, а также  ,
получим:
,
получим:



– закон Ома в дифференциальной форме.
3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс
Для возникновения и существования электрического тока необходимо:
наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно;
наличие электрического поля, энергия которого должна каким-то образом восполняться.
| Соединим проводником два тела с зарядами +q и –q. Кулоновские силы заставляют электроны перемещаться по проводнику. Возникнет ток. Однако тела при этом будут разряжаться, разность потенциалов уменьшится, ток быстро прекратится. |
Т.е. если в цепи действуют только силы электростатического поля, то происходит перемещение носителей таким образом, что потенциалы всех точек цепи выравниваются и электростатическое поле исчезает.
Следовательно, поле кулоновских сил не может являться причиной постоянного электрического тока.
Ток в проводнике нейтрализует заряды на его концах. Для поддержания постоянного тока необходимо поддерживать постоянную разность потенциалов, следовательно, разделять заряды. Электрические силы разделять заряды не могут.
Силы, разделяющие заряды, имеют неэлектрическую природу и называются
Устройство, в котором действуют сторонние силы, называется источником тока.
Сторонние силы заставляют заряды двигаться внутри источника тока против сил поля. Благодаря этому в цепи поддерживается постоянная разность потенциалов.
Перемещая заряды, сторонние силы совершают работу за счет энергии, затраченной в источнике тока. Например, в электрофорной машине разделение зарядов происходит за счет механической работы, в гальваническом элементе – за счет энергии химических реакций и т.д.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется
Обозначим  — вектор напряженности поля сторонних
сил.
— вектор напряженности поля сторонних
сил.
Результирующее поле, действующее на заряды в проводнике, в общем случае
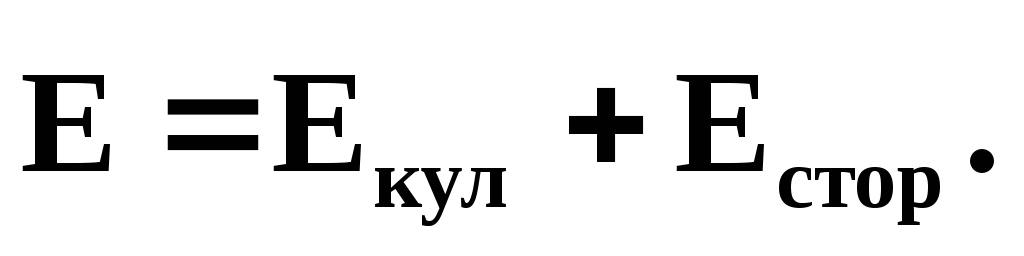
Плотность тока в цепи
 .
.
– закон Ома в дифференциальной форме для цепи, содержащей ЭДС.
| Рассмотрим участок AB замкнутой цепи, содержащей ЭДС (рис.3.18). Выделим мысленно малый элемент dl. |
Плотность тока
на этом участке опишется уравнением  .
Умножим скалярно обе части этого
равенства на
.
Умножим скалярно обе части этого
равенства на

Рассмотрим каждый интеграл в отдельности:
а)

где А — В – разность потенциалов между точками A и B.
Разность потенциалов численно равна работе кулоновских сил по перемещению единичного положительного заряда из т.A в т.B;
б)

где — ЭДС.
ЭДС, действующая на участке цепи, численно равна работе сторонних сил по перемещению единичного положительного заряда из т.A в т.B;
в)

где RAB – сопротивление участка AB.
С учетом выше сказанного можно получить:

— закон Ома для участка цепи с ЭДС.

Частные случаи:
если на данном участке цепи источник тока отсутствует, то получаем закон Ома для однородного участка цепи:

если цепь замкнута (=0), то получим закон Ома для замкнутой цепи:
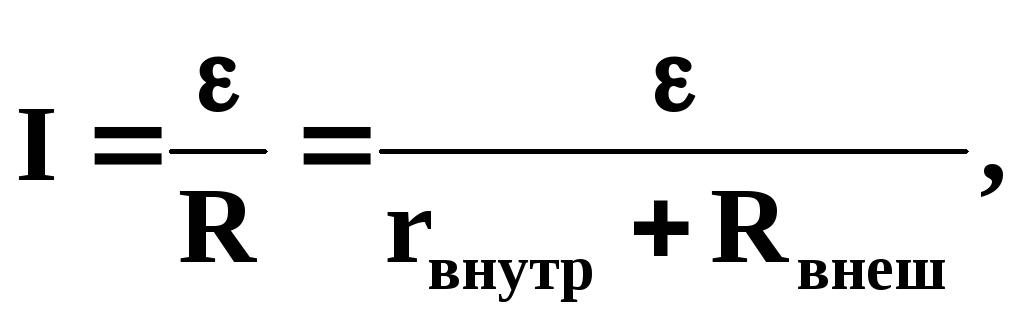
где — ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи, rвнутр – внутреннее сопротивление источника тока, Rвнеш – сопротивление внешней цепи;
если цепь разомкнута, то I = 0 и 12 = 2 — 1, т.е. ЭДС, действующая в разомкнутой цепи равна разности потенциалов на ее концах.
В случае короткого замыкания сопротивление внешней цепи Rвнеш = 0 и сила тока
 в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
Величина IRAB = UAB называется падением напряжения на участке AB.
Падение напряжения на участке AB численно равно работе кулоновских и сторонних сил по перемещению единичного положительного заряда из т.A в т.B.
Если цепь замкнута, то 1 = 2 и

– закон Ома для замкнутой цепи.
Если участок цепи не содержит ЭДС, то

Закон Ома в дифференциальной и интегральной форме
Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
 .
.
Закон Ома можно
представить в дифференциальной форме.
Через поперечное сечение проводника
течет ток силой dI
равной dI
= jdS.
Напря- жение, приложенное на концах
проводника, будет равно Е·dl (т.к.  и dφ
= -Edl).
Для проводника постоянного сечения
длиной l будем иметь
и dφ
= -Edl).
Для проводника постоянного сечения
длиной l будем иметь
 .
.
Отсюда  ,
где
,
где — удельная проводимость проводника.
Таким образом, выражениезакона
Ома в дифференциальной форме в векторном виде будет
— удельная проводимость проводника.
Таким образом, выражениезакона
Ома в дифференциальной форме в векторном виде будет
j = γ E.
Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Рассмотрим замкнутую электрическую цепь, содержащую ЭДС. Источник тока в такой цепи обладает внутренним сопротивлением r. Сопротивление внешней части цепи R называют внешним или сопротивлением нагрузки. Падение напряжения на внутреннем участке цепи равно U1 = Ir, а на внешнем — U =IR. При замкнутой внешней цепи ЭДС источника тока ؏ равна сумме падений напряжения на внутреннем сопротивлении источника тока и во внешней цепи, ؏ = Ir + IR, откуда
I = ؏ / (r + R).
Это есть выражение закона Ома в интегральной форме.
Закон Джоуля-Ленца в дифференциальной и интегральной форме
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ1 – φ2.
Тогда работа по переносу заряда q на этом участке равна
A = q(φ1 – φ2) = qU.
Если
ток постоянный, то  иA
= I
U
t.
иA
= I
U
t.
Эта работа равна количеству теплоты Q и формула Q = I U t выражает закон Джоуля-Ленца в интегральной форме.
Используя
выражение закона Ома  получим
получим
 .
.
Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

 ,
,
где
S
— сечение, l — длина проводника. Подставляя Q
= I2 R
t
и  ,
получим
,
получим  .
.
Здесь 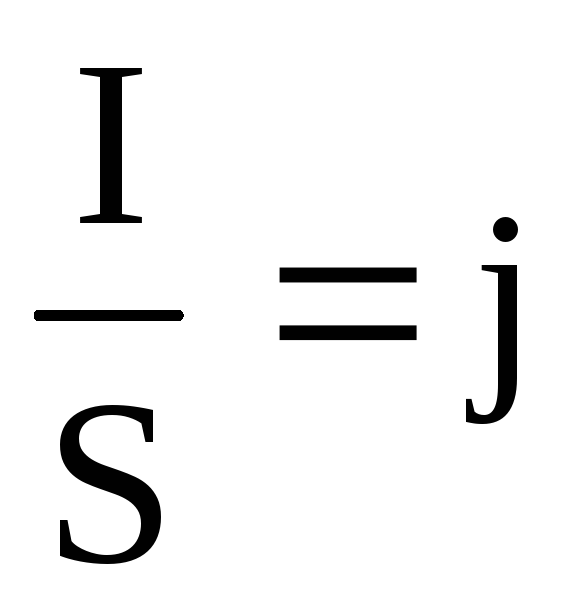 — плотность тока,
— плотность тока, ,
и учитывая, чтоj
= γE,
получим
,
и учитывая, чтоj
= γE,
получим
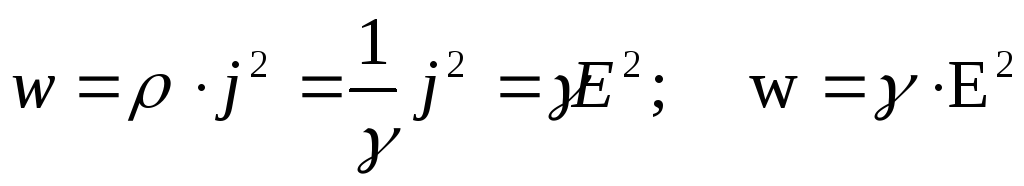 .
.
Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Вывод законов Ома и Джоуля-Ленца из классических электронных представлений
Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·106 Кл. Взвешивание показало неизменный вес цилиндров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.
Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.
Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд.
Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с проводом вокруг ее оси. К концам катушки подключили телефон, в котором был слышен звук, обусловленный импульсами тока. Был получен качественный результат – зарегистрирован импульс тока.
Толмен и Стюарт в 1916 г. получили количественный результат. Катушка с проводом длиной 500 м приводилась во вращение со скоростью v=300 м/с. Катушка резко тормозилась и с помощью баллистического гальванометра измеряли заряд, протекавший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m получалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электропроводности металлов в предположении, что:
— электроны в металле ведут себя подобно молекулам идеального газа;
— движение электронов подчиняется законам классической механики;
— взаимодействие электронов сводится к соударениям с ионами кристалли-ческой решетки;
— силами взаимодействия между электронами можно пренебречь и они между собой не сталкиваются;
— электроны в отсутствие электрического поля движутся хаотически.
Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.
По определению плотность тока j = n e <v> — это заряд, переносимый через единицу площади S = 1м2 за единицу времени t=1 с; n – концентрация электронов, е – заряд электрона, <v> — средняя скорость упорядоченного движения электронов.
На
каждый электрон действует сила F
= eE
= ma,
поэтому электрон приобретает ускорение  и к концу свободного пробега он
достигнет скорости
и к концу свободного пробега он
достигнет скорости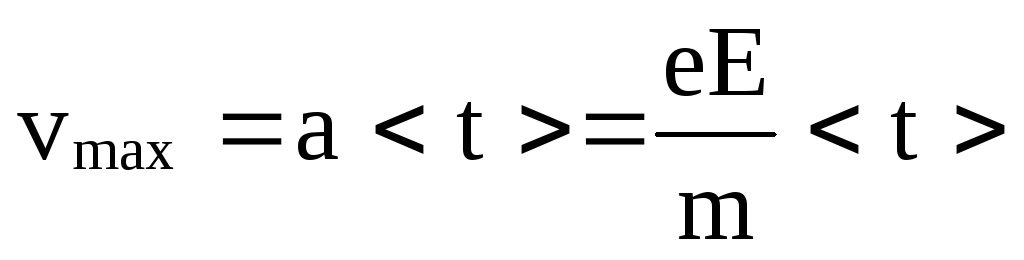 ,
а средняя скорость <v>=vmax/2.
,
а средняя скорость <v>=vmax/2.
Если
<vT>
— средняя скорость теплового хаотичного
движения электронов, а средняя длина
свободного пробега электронов <λ>,
то среднее время между соударениями
<t>
=  .
Подставляя <t>
в формулу для <v>
получим:
.
Подставляя <t>
в формулу для <v>
получим:
 .
.
Подставляя <v> в формулу для j, получим
 ,
,
т.е. плотность тока прямо пропорциональна Е, а это и есть выражение закона Ома в дифференциальной форме. Если положить, что
 то j = γ E.
то j = γ E.
Удельная проводимость
γ ~
n
и < λ>, <vт>
~
T,
поэтому проводимость снижается с
ростом температуры, а удельное
сопротивление  повышается с ростом температуры. К
концу свободного пробега электрон
приобретает кинетическую энергию
повышается с ростом температуры. К
концу свободного пробега электрон
приобретает кинетическую энергию

Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон испытывает <vT>/ < λ > cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в единице объема за единицу времени выделится количество тепла
 .
.
Таким
образом, 
 —
выражение закона Джоуля-Ленца в
дифференциальной форме.
—
выражение закона Джоуля-Ленца в
дифференциальной форме.
Закон Ома в интегральной и дифференциальной форме. — КиберПедия
Закон Ома в интегральной форме:
— для участка цепи: «Сила тока  на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке
на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке  и обратно пропорциональна сопротивлению этого участка
и обратно пропорциональна сопротивлению этого участка  »:
»:
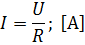
— для всей цепи:

где  – электродвижущая сила, В;
– электродвижущая сила, В;
 – сопротивление всех элементов цепи, Ом;
– сопротивление всех элементов цепи, Ом;
 – внутреннее сопротивление источника питания, Ом;
– внутреннее сопротивление источника питания, Ом;
 – сила тока, А.
– сила тока, А.
Закон Ома в дифференциальной форме:
— для участка цепи: «Плотность тока в каждой точке однородного участка цепи пропорциональна напряженности электрического поля в этой же точке»:

Где  – вектор плотности тока, А/м²;
– вектор плотности тока, А/м²;
 – удельная проводимость, См=
– удельная проводимость, См=  ;
;
 – вектор напряженности электрического поля, В/м.
– вектор напряженности электрического поля, В/м.
Работа и мощность электрического тока. Закон Джоуля-Ленца в интегральной и дифференциальной форме.
За время t по участку электрической цепи будет перенесён заряд и при этом будет совершена работа:

где  – электрический заряд, Кл;
– электрический заряд, Кл;
 – напряжение, В;
– напряжение, В;
 – сила тока, А;
– сила тока, А;
 – время, с.
– время, с.
Работа, совершаемая в единицу времени – мощность электрического тока:
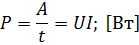
Закон Джоуля-Ленца в дифференциальной форме: «Мощность тепла  , выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока
, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока  на величину напряженности электрического поля
на величину напряженности электрического поля 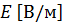 »:
»:

где 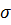 – удельная электрическая проводимость, См=
– удельная электрическая проводимость, См=  .
.
Закон Джоуля-Ленца в интегральной форме:

где  – полное количество теплоты, выделенное за промежуток времени от
– полное количество теплоты, выделенное за промежуток времени от  до
до 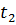 , Дж;
, Дж;
 – сила тока, А;
– сила тока, А;
 – сопротивление. Ом.
– сопротивление. Ом.
Закон Ома для участка цепи и для замкнутой цепи, содержащей э.д.с.
Закон Ома для участка цепи:
«Сила тока  на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке
на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке  и обратно пропорциональна сопротивлению этого участка
и обратно пропорциональна сопротивлению этого участка  »:
»:
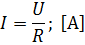
Закон Ома для неоднородного участка цепи (содержащего ЭДС):

где 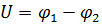 – разность потенциалов (напряжение), В;
– разность потенциалов (напряжение), В;
 – электродвижущая сила, В;
– электродвижущая сила, В;
 – сопротивление участка, Ом.
– сопротивление участка, Ом.
Если направление тока совпадает с направлением обхода, его принято считать положительным; если источник тока повышает потенциал в направлении обхода (источник посылает ток в направлении обхода), то ЭДС такого источника считается положительной.
Закон Ома для замкнутой цепи, содержащей ЭДС:

где  – электродвижущая сила, В;
– электродвижущая сила, В;
 – сопротивление всех элементов цепи, Ом;
– сопротивление всех элементов цепи, Ом;
 – внутреннее сопротивление источника питания, Ом;
– внутреннее сопротивление источника питания, Ом;
 – сила тока, А.
– сила тока, А.
Законы Кирхгофа.
Первое правило Кирхгофа: «Алгебраическая сумма токов, сходящихся в узле, равна нулю:
 ».
».
Второе правило Кирхгофа: «В любом замкнутом контуре алгебраическая сумма напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре:

где  – число источников ЭДС;
– число источников ЭДС;
 – число ветвей в замкнутом контуре;
– число ветвей в замкнутом контуре;
 – ток и сопротивление -той ветви, А, Ом».
– ток и сопротивление -той ветви, А, Ом».
Правило знаков:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
7.5. Закон Ома для неоднородного участка цепи.

Рис. 3 Перемещение заряда на этих участках возможно лишь с помощью сил
неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).
Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися зарядами.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой. Э.Д.С. действующей в цепи.
ε = | A |
| Дж | =[В]; |
| |
| ; |
|
| (7.4.1) | ||
q |
| |||||
|
| Кл |
|
| ||
Ясно, что размерность Э.Д.С. совпадает с размерностью потенциала, т.е. измеряется в вольтах.
Стороннюю силу, действующую на заряд, можно представить в виде:
r | Fст. = Eст.q , | (7.4.2) |
Eст. | – напряженность поля сторонних сил. |
|
| Работа сторонних сил на участке 1 – 2 |
|
| 2 r | r | 2 | r | r |
| ||
A12 | = ∫Fст.dl | = q∫Eст.dl , | (7.4.3) | |||||
| 1 |
| 1 |
|
|
| ||
|
|
|
| A12 |
| 2 r | r |
|
тогда | ε12 | = |
|
| = ∫Eст.dl . | (7.4.4) | ||
| q | |||||||
|
|
|
| 1 |
|
| ||
Для замкнутой цепи: ε = ∑εi | = ∫Eст.dl . | (7.4.5) | ||||||
Циркуляция вектора напряженности сторонних сил равна Э.Д.С., действующей в замкнутой цепи (алгебраической сумме Э.Д.С.).
При этом необходимо помнить, что поле сторонних сил не является потенциальным, и к нему нельзя применять термин – разность потенциалов или напряжение.
Рассмотрим неоднородный участок цепи, участок, содержащий источник Э.Д.С.
(т.е. участок, – где действуют неэлектрические силы). Напряженность E поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
E = Eq +Eст. .
67

Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке U12 (Рис. 4)
| Рис. 4 |
|
| ||
| 2 r r | 2 | r | r |
|
| U12 = ∫Eq dl + | ∫Eст.dl ; | (7.5.1) | ||
| 1 | 1 |
|
|
|
| 2 | r | r |
|
|
т. к. | Eq dl = −dφ и ∫Eq dl | = φ1 −φ2 ; | (7.5.2) | ||
| 1 |
|
|
|
|
тогда | U12 = (φ1 – φ2) + ε12 | (7.5.3) | |||
Напряжение на концах участка цепи совпадает с разностью потенциалов только в | |||||
случае, если на этом участке нет Э.Д.С., т.е. на однородном участке цепи. |
| ||||
| I·R12 = (φ1 – φ2) + ε12 | (7.5.4) | |||
Это обобщенный закон Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих Э.Д.С.), так и для активных.
В электротехнике часто используют термин падения напряжения – изменение напряжения вследствие переноса заряда через сопротивление
U = I R |
| (7.5.5) | |||
В замкнутой цепи: φ1 = φ2 ; |
|
| ε |
| |
I RΣ= ε | или | I = | |||
R∑ | |||||
|
|
| |||
Где R Σ =R + r; r – внутреннее сопротивление активного участка цепи (Рис. 5).
Тогда закон Ома для замкнутого участка цепи, содержащего Э.Д.С. запишется в
виде:
I = | ε | ; | (7.5.6) | |
R + r | ||||
|
|
|
Рис. 5

7.6. Закон Ома в дифференциальной форме.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего Э.Д.С.)
I = U | ; |
| (7.6.1) | ||
R |
|
|
| ||
Для однородного линейного проводника выразим R через ρ |
| ||||
R = ρ | l |
| ; | (7.6.2) | |
S | |||||
|
|
| |||
ρ – удельное объемное сопротивление; [ρ] = [Ом м].
Найдем связь между j и E в бесконечно малом объеме проводника – закон Ома в
дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов (Рис.6) движутся в направлении действия силы, т.е. плотность тока
j ↑↑ E , следовательно, векторы коллинеарны.
|
|
|
|
|
|
| Рис. 6 |
|
| |||||||
|
|
|
| I = | U |
| = |
| Edl |
| = | EdS | ; | |||
|
|
|
| R |
| ρ |
| dl |
| ρ | ||||||
|
|
|
|
| r | dS |
| |||||||||
|
|
|
|
|
|
|
|
|
| |||||||
| dI |
| 1 |
|
|
|
|
| 1 r |
|
| |||||
А мы знаем что: j = |
| = |
| E , т.е. | j = |
|
|
| E j или |
| ||||||
dS | ρ |
| ρ |
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| j = σE |
|
|
|
|
|
|
| (7.6.3) | ||||
это запись закона Ома в дифференциальной форме.
Здесь σ – удельная электропроводность. Размерность j – [ Oм−1 м−1 ]; Плотность тока можно выразить через заряд, n и vrдр. .
j = envrдр.
r
обозначим: b = vEдр. , то vrдр. = bE ;
j = enbE ,
а если σ = enb,
где n – число пар ионов, b – расстояние. j = jE
– закон Ома в дифференциальной форме.

7.7. Работа и мощность тока. Закон Джоуля — Ленца.
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд
dq = I dt | (7.7.1) |
При этом силы электрического поля, действующего на данном участке совершают | |
работу: |
|
dA = U dq = U I dt | (7.7.2) |
Разделив работу на время, получим выражение для мощности: |
|
N = dA =UI | (7.7.3) |
dt |
|
Полезно вспомнить и другие формулы для мощности и работы:
| N = RI2 | (7.7.4) |
| A = RI2t | (7.7.5) |
| В 1841г. Английский физик Джеймс Джоуль и русский физик | |
| Эмилий Ленц установили закон теплового действия электрического | |
| тока. |
|
| ДЖОУЛЬ Джеймс Пресскотт (Рис. 6) |
|
| (24.12.1818 – 11. 10.1889) – английский физик, один |
|
| из первооткрывателей закона сохранения энергии. |
|
| Первые уроки по физике ему давал Дж. Дальтон, под |
|
| влиянием которого Джоуль начал свои эксперименты. |
|
| Работы посвящены электромагнетизму, кинетической |
|
Рис. 6 | теории газов. |
|
ЛЕНЦ Эмилий Христианович (Рис. 7) (24.2.1804 |
| |
|
| |
– 10.2.1865) – русский физик. Основные работы в области |
| |
электромагнетизма. В 1833 установил правило определения | Рис. 7 | |
электродвижущей силы индукции (закон Ленца), а в 1842 (независимо | ||
от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля — Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.
Независимо друг от друга Джоуль и Ленц показали, что при протекании тока в проводнике выделится количество теплоты:
Q = RI2t | (7.7.6) | |
Если ток изменяется со временем, то |
| |
Q = ∫2 | RI 2dt ; | (7.7.7) |
1
(7.7.7) это закон Джоуля – Ленца в интегральной форме.
Следовательно, нагревание происходит за счет работы, совершаемой силами поля над зарядом (мощность выделения тепла N = RI2).
Получим закон Джоуля – Ленца в дифференциальной форме.
dQ = RI 2dt = ρ dSdl (jdS )2 dt = ρj2dldSdt = ρj2dldSdt = ρj2 dVdt,
где dV = dl dS – элементарный объем. |
|
Количество тепла выделяющегося в единицу объема в единицу времени |
|
Q уд = ρj2 | (7.7.8) |
Закон Ома для однородного участка цепи. Сопротивление проводников.
Между
падением потенциала — напряжением U и силой тока в проводнике I существует функциональная зависимость  ,
называемаявольтамперной характеристикой данного проводника (ВАХ). Вид этой
зависимости для разных проводников и
устройств может быть самым разнообразным.
,
называемаявольтамперной характеристикой данного проводника (ВАХ). Вид этой
зависимости для разных проводников и
устройств может быть самым разнообразным.
К ак
показывает опыт, для многих проводящих
материалов выполняется зависимость:
ак
показывает опыт, для многих проводящих
материалов выполняется зависимость:  ,
получившая название закона
Ома (Ohm
G.,
1787-1854) для однородного
участка цепи. (ВАХ приведена на рис. 3.1.).
,
получившая название закона
Ома (Ohm
G.,
1787-1854) для однородного
участка цепи. (ВАХ приведена на рис. 3.1.).
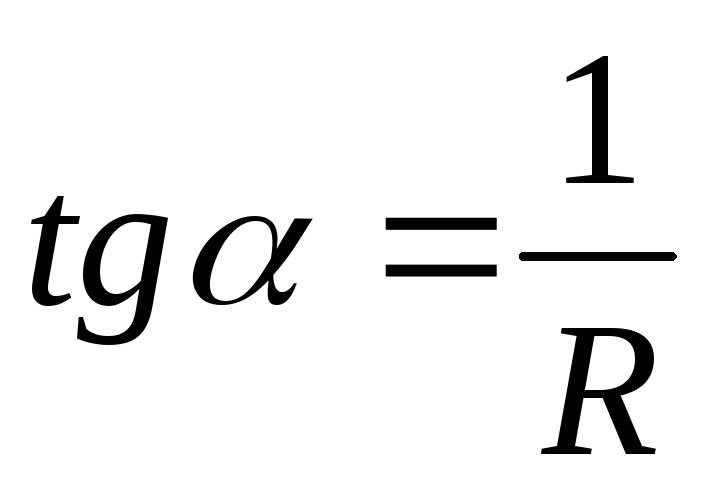
Коэффициент пропорциональности R называется сопротивлением проводника. Сопротивление однородного проводника зависит от материала, из которого он изготовлен, его формы, размеров, а также от температуры.
Рисунок 3.1 Вольтамперная
характеристика.

Размерность
сопротивления: [R]
=  .
.
Кратные единицы измерения: 1кОм = 103Ом ; 1Мом = 106Ом.
ρ – удельное сопротивление. Размерность ρ в СИ: [ρ] = Ом∙м.
Для многих веществ зависимость сопротивления от температуры в широком интервале температур вблизи Т≈300К определяется эмпирической зависимостью от температуры их удельного сопротивления:
 ,
,
где α – температурный коэффициент сопротивления;  —
значение
—
значение при
при  .
.
Для металлов  ,
поэтому сопротивление металлов в
указанной области температур
пропорционально температуре (рис. 3.2.).
,
поэтому сопротивление металлов в
указанной области температур
пропорционально температуре (рис. 3.2.).

Рисунок 3.2. Зависимость сопротивления от температуры (для металлов).
Для электролитов α<0, зависимость их сопротивления от температуры имеет вид, изображенный на рис.. Для разных электролитов α различно.

Рис. 3. Зависимость сопротивления от температуры (для электролитов).
Дифференциальная форма закона Ома.
Если
проводник неоднороден по своему составу
и/или имеет неодинаковое сечение, то
для характеристики тока в различных
частях проводника используют закон
Ома в
дифференциальной форме.
Для его вывода выделим внутри проводника
элементарный цилиндрический объем с
образующими, параллельными вектору
плотности тока  .
Если выделенный объем достаточно мал,
его можно считатьоднородным и
применить к нему закон Ома:
.
Если выделенный объем достаточно мал,
его можно считатьоднородным и
применить к нему закон Ома:
 ,
где
,
где

 ,
откуда
,
откуда
Или в векторном виде:

Величина  называетсякоэффициентом
электропроводности или проводимостью материала. Единицей
измерения σ в
СИ является (Ом∙м)-1=См
(сименс).
называетсякоэффициентом
электропроводности или проводимостью материала. Единицей
измерения σ в
СИ является (Ом∙м)-1=См
(сименс).
Работа и мощность постоянного тока. Закон Джоуля – Ленца.
При протекании по проводнику электрического тока проводник нагревается. Нагревание происходит за счет работы, совершаемой силами поля над носителями заряда:
 ,
,


Джоуль (Joule J., 1818-1889) и независимо от него Э.Х.Ленц (1804-1865) установили экспериментально, что количество теплоты, выделяющейся в проводнике, пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока:

Если
сила тока изменяется со временем, то за
промежуток времени Δt = t2 – t1 выделится теплота:
Написанные соотношения выражают собой закон Джоуля – Ленца.
Если
теплоту измерять в калориях,
то:  .
.
Количество теплоты, выделяющееся в единице объема проводника за единицу времени, называется удельной мощностью:
 ,
где
,
где  —
плотность тока.
—
плотность тока.
Это
соотношение представляет собой закон
Джоуля-Ленца в дифференциальной форме: 
Работа, производимая током за единицу времени, называется мощностью:
 .
.
Размерность
мощности в СИ:  (ватт).
(ватт).
Закон Ома в дифференциальной форме.
Р ассмотрим
небольшой участок однородного проводника
постоянного сечения, находящегося под
напряжением
ассмотрим
небольшой участок однородного проводника
постоянного сечения, находящегося под
напряжением .
Поделив напряжение на сопротивление
участка и, учитывая, что
.
Поделив напряжение на сопротивление
участка и, учитывая, что
 ,
,  ,
,
находим
 ,
,
 .
.
Плотность тока в каждой точке проводника пропорциональна напряжённости электрического поля. Полученное соотношение выражает локальный закон Ома и называется законом Ома в дифференциальной форме.
Отметим, что в случае постоянноготока избыточный заряд внутриоднородногопроводника равен нулю. Действительно, при постоянном токе, заряд, входящий в выделенный объём, равен заряду, выходящему из объема, т.е.
 ,
,
откуда следует
 .
.
Учитывая, что
 ,
, ,
,
 ,
,
т.е. 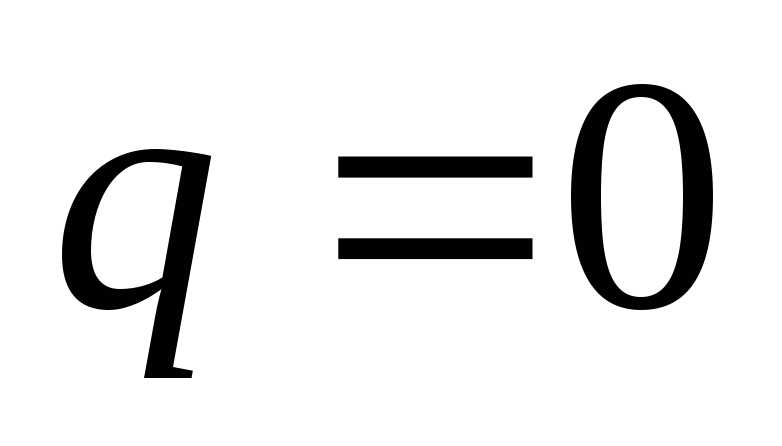 .
.
Избыточный заряд может появиться только на поверхности однородного проводника, где проводник имеет неоднородность.
В проводнике при постоянном токе распределение зарядов не изменяется с течением времени, хотя и происходит движение зарядов, так как в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают электрическое поле аналогичноеполю неподвижных зарядов той же конфигурации, т.е. является потенциальным.
Закон Ома для участка, содержащего сторонние силы.
Сторонниминазывают силы не электростатического происхождения. Они могут быть обусловлены химической и физической неоднородностью проводника, например, таковы силы, возникающие при соприкосновении разнородных проводников (гальванические элементы, аккумуляторы) или проводников различной температуры (термоэлементы) и др.
Постоянный ток возможен только при наличии сторонних сил, так как одни электростатические силы могут вызвать только кратковременный ток.
Сторонние силы должны переносить положительные носители на участках своего действия в сторону возрастания потенциала, компенсируя действие электростатических сил.
Для количественной характеристики сторонних сил вводят понятие поля сторонних сил и его напряженность аналогично полю электрических сил:
 .
.
Очевидно, плотность тока в местах, где существуют электрические и сторонние силы определяется соотношением:
 ,
,
которое называется обобщенным законом Ома в дифференциальной форме.
Закон Ома в интегральной форме для участка, содержащего источник тока.
Д ля
простоты рассмотрим участок проводника
в форме цилиндра (см. рисунок), к торцам
которого приложена разность потенциалов
ля
простоты рассмотрим участок проводника
в форме цилиндра (см. рисунок), к торцам
которого приложена разность потенциалов и в пределах которого действуют сторонние
силы.
и в пределах которого действуют сторонние
силы.
Умножим выражение локального закона Ома:

скалярно на вектор перемещения вдоль линии тока и проинтегрируем от точки 1 до точки 2:
 .
.
После интегрирования получаем:
 ,
,
где  — сопротивление участка цепи между
сечениями 1 и 2,
— сопротивление участка цепи между
сечениями 1 и 2, – сила тока на участке,
– сила тока на участке, — разность потенциалов,
— разность потенциалов, —
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение
—
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение называютпадениемнапряжения на
участке.
называютпадениемнапряжения на
участке.
Э.д.с., как и сила тока  и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то
и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то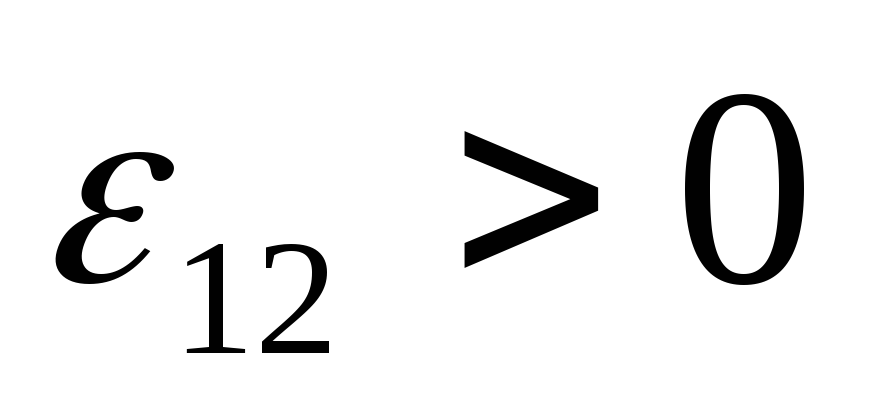 ,
если же препятствует, то
,
если же препятствует, то .
.
Полученное соотношение выражает интегральную форму закона Ома для участка, содержащего сторонние силы.
О бычно
сторонние силы действуют на ограниченном
участке, которые называют источником
постоянного тока. Условно источник
обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.
бычно
сторонние силы действуют на ограниченном
участке, которые называют источником
постоянного тока. Условно источник
обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.
Пример.
Рассмотрим участок, содержащий источник и сопротивление (см. рисунок).
В ыразим
разность потенциалов:
ыразим
разность потенциалов:
 .
.
В нашем примере  .
.
Пусть ток на участке течёт от 1 и 2  .
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно
.
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно ,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если
,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если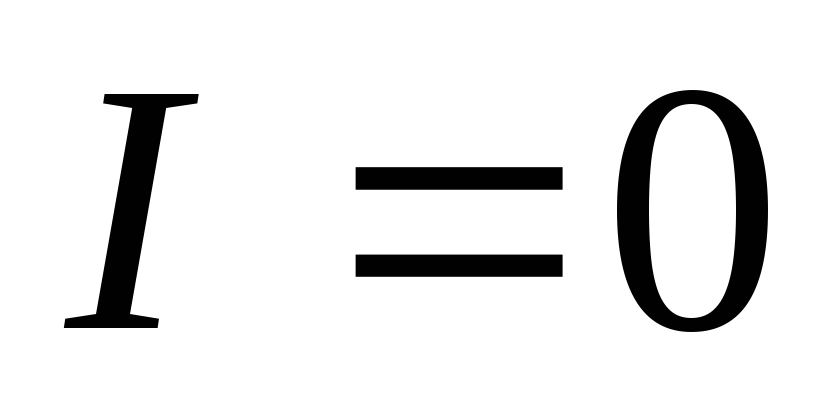 ,
то
,
то ,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.





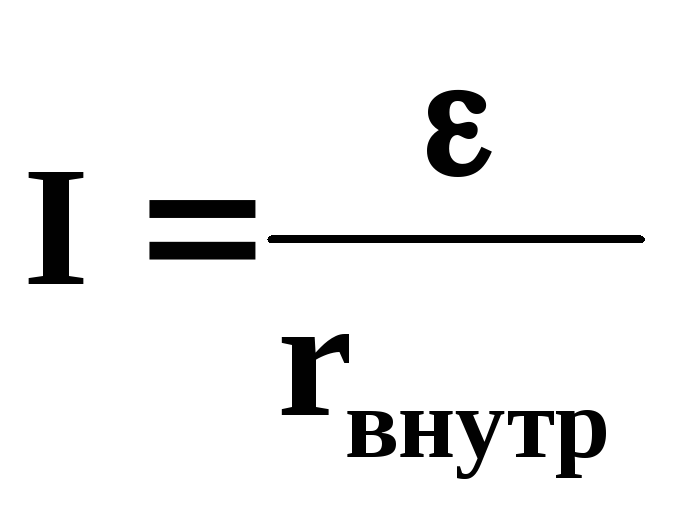 в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.