Закон Лоренца Википедия

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} }, заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца

[3].

Уравнение (единицы СИ)

Заряженная частица

Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.

Частные случаи

Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
mv2r=|q|cvB⇒r=cm|q|⋅vB{\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}	mv2r=|q|vB⇒r=m|q|⋅vB{\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:

СГС	СИ
ω=|q|Bmc{\displaystyle \omega ={|q|B \over mc}}	ω=|q|Bm{\displaystyle \omega ={|q|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:

СГС	СИ
r=mc|q|⋅vsin⁡αB{\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }	r=m|q|⋅vsin⁡αB{\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }

Использование

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

См. также

Примечания

1. ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
2. ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
3. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Преобразования Лоренца — Википедия

Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющие длины или, что эквивалентно, скалярное произведение векторов.

Преобразования Лоренца псевдоевклидова пространства сигнатуры (n−1,1){\displaystyle (n-1,\;1)} находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского).

Преобразования Лоренца в математике[править | править код]

Преобразование Лоренца представляет собой естественное обобщение понятия ортогонального преобразования (то есть преобразования, сохраняющего скалярное произведение векторов) с евклидовых на псевдоевклидовы пространства. Различие между ними состоит в том, что скалярное произведение предполагается не положительно определённым, а знакопеременным и невырожденным (так называемое индефинитное скалярное произведение).

Определение[править | править код]

Преобразование Лоренца (лоренцево преобразование) псевдоевклидова векторного пространства L{\displaystyle L} — это линейное преобразование A:L→L{\displaystyle A\colon L\to L}, сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов x,y∈L{\displaystyle x,\;y\in L} выполняется равенство

⟨A(x),A(y)⟩=⟨x,y⟩,{\displaystyle \langle A(x),\;A(y)\rangle =\langle x,\;y\rangle ,}

где треугольными скобками обозначено индефинитное скалярное произведение ⟨x,y⟩{\displaystyle \langle x,\;y\rangle } в псевдоевклидовом пространстве L{\displaystyle L}.

Аналогично, преобразование Лоренца (лоренцево преобразование) псевдоевклидова аффинного пространства — это аффинное преобразование, сохраняющее расстояние между точками этого пространства (это расстояние определяется как длина вектора, соединяющего данные точки, с помощью индефинитного скалярного произведения).

Общие свойства[править | править код]

• Так как любое аффинное преобразование является композицией параллельного переноса (очевидным образом, сохраняющего расстояние между точками) и преобразования, имеющего неподвижную точку, то группа преобразований Лоренца аффинного пространства (группа Пуанкаре) получается из группы преобразований Лоренца векторного пространства (группа Лоренца) такой же размерности путём добавления к ней всевозможных параллельных переносов.
• Если в псевдоевклидовом векторном пространстве L{\displaystyle L} выбран некоторый базис e1,…,en{\displaystyle e_{1},\;\ldots ,\;e_{n}}, то для индефинитного скалярного произведения ⟨x,y⟩{\displaystyle \langle x,\;y\rangle } определена матрица Грама G{\displaystyle G}. Тогда матрица A{\displaystyle A} преобразования Лоренца удовлетворяет соотношению

ATGA=G,(∗){\displaystyle A^{T}\,G\,A=G,\qquad (*)}

И обратно, любая матрица A{\displaystyle A}, удовлетворяющая соотношению (∗){\displaystyle (*)}, является матрицей преобразования Лоренца. Всегда можно выбрать базис e1,…,en{\displaystyle e_{1},\;\ldots ,\;e_{n}} таким образом, что индефинитное скалярное произведение имеет вид

⟨x,y⟩=x1y1+…+xkyk−xk+1yk+1−…−xnyn,{\displaystyle \langle x,\;y\rangle =x_{1}y_{1}+\ldots +x_{k}y_{k}-x_{k+1}y_{k+1}-\ldots -x_{n}y_{n},}

и в равенстве (∗){\displaystyle (*)} матрица G{\displaystyle G} ― диагональная с элементами 1{\displaystyle 1} (первые k{\displaystyle k}) и −1{\displaystyle -1} (последние n−k{\displaystyle n-k}).

• Из соотношения (∗){\displaystyle (*)} следует, что, как и в случае ортогонального преобразования, определитель |A|=+1{\displaystyle |A|=+1} или |A|=−1{\displaystyle |A|=-1}.
• Если подпространство L1⊂L{\displaystyle L_{1}\subset L} инвариантно относительно лоренцева преобразования A:L→L{\displaystyle A\colon L\to L}, то и его ортогональное (в смысле данного индефинитного скалярного произведения) дополнение L1⊥{\displaystyle L_{1}^{\perp }} тоже инвариантно относительно преобразования A{\displaystyle A}, причем dim⁡L1+dim⁡L1⊥=dim⁡L{\displaystyle \dim L_{1}+\dim L_{1}^{\perp }=\dim L}. Однако, в отличие от ортогональных преобразований евклидовых пространств, равенство L1⊕L1⊥=L{\displaystyle L_{1}\oplus L_{1}^{\perp }=L}, где символ ⊕{\displaystyle \oplus } означает прямую сумму подпространств, вообще говоря, не имеет места (оба подпространства L1{\displaystyle L_{1}} и L1⊥{\displaystyle L_{1}^{\perp }} могут содержать одни и те же ненулевые изотропные векторы, то есть L1∩L1⊥≠0{\displaystyle L_{1}\cap L_{1}^{\perp }\neq 0}, так как любой изотропный вектор ортогонален сам себе).^[1]

Свойства в пространствах сигнатуры (n-1, 1)[править | править код]

• Из равенства ⟨A(x),A(x)⟩=⟨x,x⟩{\displaystyle \langle A(x),\;A(x)\rangle =\langle x,\;x\rangle } следует, что лоренцево преобразование переводит световой конус в себя, а также переводит в себя его внешность (в СТО — область абсолютно удалённого). Однако при этом две компоненты светового конуса, разделенные его вершиной (в СТО они ограничивают конус будущего и конус прошлого), могут либо переходить в себя, либо меняться друг с другом местами.
• Исходя из того, переставляет ли данное лоренцево преобразование A{\displaystyle A} части светового конуса, или оставляет их на месте, а также из знака определителя |A|=±1{\displaystyle |A|=\pm 1}, группу Лоренца можно разделить на 4 части, которые являются её линейно связными компонентами (но подгруппой является лишь одна из них). Этот факт (наличие четырёх компонент связности) часто интерпретируют как наличие четырёх ориентаций псевдоевклидова пространства (в отличие от евклидова пространства, где есть только две ориентации).^[1]

Явный вид преобразований псевдоевклидовой плоскости[править | править код]

Лоренцевы преобразования псевдоевклидовой плоскости можно записать в наиболее простом виде, используя базис e,g{\displaystyle e,\;g}, состоящий из двух изотропных векторов:

⟨e,e⟩=0,⟨g,g⟩=0,⟨e,g⟩=1/2.{\displaystyle \langle e,\;e\rangle =0,\quad \langle g,\;g\rangle =0,\quad \langle e,\;g\rangle =1/2.}

Именно, в зависимости от знака определителя |A|=±1{\displaystyle |A|=\pm 1}, матрица преобразования в данном базисе имеет вид:

A=(a  001/a) ⇔ |A|=+1,A=(0 a1/a0) ⇔ |A|=−1,a≠0.{\displaystyle A={\begin{pmatrix}a&\ \ \,0\\0&\,1/a\end{pmatrix}}\ \Leftrightarrow \ |A|=+1,\qquad A={\begin{pmatrix}0&\ a\\1/a&\,0\end{pmatrix}}\ \Leftrightarrow \ |A|=-1,\qquad a\neq 0.}

Знак числа a{\displaystyle a} определяет то, оставляет ли преобразование A{\displaystyle A} части светового конуса на месте (a>0){\displaystyle (a>0)}, или меняет их местами (a<0){\displaystyle (a<0)}.

Другой часто встречающийся вид матриц лоренцевых преобразований псевдоевклидовой плоскости получается при выборе базиса, состоящего из векторов e′=e+g{\displaystyle e’=e+g} и g′=e−g{\displaystyle g’=e-g}:

⟨e′,e′⟩=+1,⟨g′,g′⟩=−1,⟨e′,g′⟩=0.{\displaystyle \langle e’,\;e’\rangle =+1,\quad \langle g’,\;g’\rangle =-1,\quad \langle e’,\;g’\rangle =0.}

В базисе e′,g′{\displaystyle e’,\;g’} матрица преобразования A{\displaystyle A} имеет одну из четырёх форм:

( ch⁡φ  sh⁡φsh⁡φ ch⁡φ),( −ch⁡φ −sh⁡φ−sh⁡φ−ch⁡φ),(−ch⁡φ−sh⁡φsh⁡φ ch⁡φ),( ch⁡φ sh⁡φ−sh⁡φ−ch⁡φ),(0){\displaystyle {\begin{pmatrix}\ \operatorname {ch} \varphi &\ \ \operatorname {sh} \varphi \\\,\operatorname {sh} \varphi &\ \operatorname {ch} \varphi \end{pmatrix}},\quad {\begin{pmatrix}\ -\operatorname {ch} \varphi &\,\ -\operatorname {sh} \varphi \\\,-\operatorname {sh} \varphi &\,-\operatorname {ch} \varphi \end{pmatrix}},\quad {\begin{pmatrix}-\operatorname {ch} \varphi &\,-\operatorname {sh} \varphi \\\,\operatorname {sh} \varphi &\ \operatorname {ch} \varphi \end{pmatrix}},\quad {\begin{pmatrix}\ \operatorname {ch} \varphi &\ \,\operatorname {sh} \varphi \\\,-\operatorname {sh} \varphi &\,-\operatorname {ch} \varphi \end{pmatrix}},\qquad (0)}

где sh{\displaystyle \operatorname {sh} } и ch{\displaystyle \operatorname {ch} } — гиперболические синус и косинус, а φ{\displaystyle \varphi } — быстрота.

Явный вид преобразований пространства сигнатуры (n-1, 1)[править | править код]

Лоренцевы преобразования n{\displaystyle n}-мерного псевдоевклидова пространства L{\displaystyle L} со скалярным произведением

⟨x,y⟩=x1y1+…+xn−1yn−1−xnyn(1){\displaystyle \langle x,\;y\rangle =x_{1}y_{1}+\ldots +x_{n-1}y_{n-1}-x_{n}y_{n}\quad (1)}

описываются следующей теоремой.

Теорема 1 утверждает, что любое лоренцево преобразование псевдоевклидова пространства L{\displaystyle L} сигнатуры (n−1,1){\displaystyle (n-1,\;1)} задается лоренцевым преобразованием псевдоевклидова пространства L1⊂L{\displaystyle L_{1}\subset L} размерности 1 или 2 или 3 и ортогональным преобразованием евклидова пространства L0⊂L{\displaystyle L_{0}\subset L} дополнительной размерности.

Лемма. Если dim⁡L1=3{\displaystyle \dim L_{1}=3}, то инвариантное псевдоевклидово подпространство L1{\displaystyle L_{1}}, в свою очередь, представимо в виде прямой суммы L1=M1⊕M2⊕M3{\displaystyle L_{1}=M_{1}\oplus M_{2}\oplus M_{3}} или L1=M1⊕M2{\displaystyle L_{1}=M_{1}\oplus M_{2}} подпространств Mi⊂L1{\displaystyle M_{i}\subset L_{1}}, попарно ортогональных и инвариантных относительно преобразования A{\displaystyle A}, за исключением одного единственного случая, когда преобразование A:L1→L1{\displaystyle A\colon L_{1}\to L_{1}} имеет единственное собственное значение λ=±1{\displaystyle \lambda =\pm 1} кратности 3 и единственный собственный вектор e∈L1{\displaystyle e\in L_{1}} является изотропным: ⟨e,e⟩=0{\displaystyle \langle e,\;e\rangle =0}. В этом единственном случае инвариантное подпространство L1{\displaystyle L_{1}} не разлагается в прямую сумму никаких подпространств, инвариантных относительно преобразования A:L1→L1{\displaystyle A\colon L_{1}\to L_{1}}, а является трёхмерным корневым подпространством этого преобразования.[1]

Теорема 1 вместе с леммой позволяют установить следующий результат:

Теорема 2. Для всякого лоренцева преобразования A:L→L{\displaystyle A\colon L\to L} существует такой ортонормированный (относительно индефинитного скалярного произведения (1)) базис e1,…,en{\displaystyle e_{1},\;\ldots ,\;e_{n}}: ⟨e1,e1⟩=…=⟨en−1,en−1⟩=+1,⟨en,en⟩=−1,⟨ei,ej⟩=0(∀i≠j),{\displaystyle \langle e_{1},\;e_{1}\rangle =\ldots =\langle e_{n-1},\;e_{n-1}\rangle =+1,\quad \langle e_{n},\;e_{n}\rangle =-1,\quad \langle e_{i},\;e_{j}\rangle =0\;(\forall i\neq j),} в котором матрица A{\displaystyle A} имеет блочно-диагональный вид с блоками следующих типов: порядка 1 с элементом ±1{\displaystyle \pm 1}, порядка 2 — матрица поворота евклидовой плоскости на угол φ{\displaystyle \varphi }, порядка 2 — матрица лоренцева преобразования псевдоевклидовой плоскости вида (0){\displaystyle (0)}, порядка 3 — матрица лоренцева преобразования трёхмерного псевдоевклидова пространства с трёхкратным собственным значением λ=±1{\displaystyle \lambda =\pm 1} и единственным собственным вектором, являющимся изотропным. При этом матрица A{\displaystyle A} может содержать не более одного блока, относящегося двум последним типам. [1]

Кроме того, имеет место следующее представление лоренцевых преобразований n{\displaystyle n}-мерного псевдоевклидова пространства L{\displaystyle L} со скалярным произведением (1){\displaystyle (1)}.

Теорема 3. Всякое лоренцево преобразование A:L→L{\displaystyle A\colon L\to L} пространства L{\displaystyle L} со скалярным произведением (1){\displaystyle (1)} представимо в виде композиции следующих линейных преобразований: ортогонального преобразования евклидова подпространства, заданного уравнением xn=0{\displaystyle x_{n}=0}, с координатами (x1,…,xn−1){\displaystyle (x_{1},\;\ldots ,\;x_{n-1})}, лоренцева преобразования псевдоевклидовой плоскости с координатами (xi,xn){\displaystyle (x_{i},\;x_{n})} с некоторым i<n{\displaystyle i<n}, отражений вида xi↦±xi{\displaystyle x_{i}\mapsto \pm x_{i}}, i∈{1,…,n}{\displaystyle i\in \{1,\;\ldots ,\;n\}}.[2]

Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (x,y,z,t){\displaystyle (x,\;y,\;z,\;t)} каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.

Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.

Преобразования Лоренца векторного пространства (т.е. без сдвигов начала отсчёта) образуют группу Лоренца, а преобразования Лоренца аффинного пространства (т.е. со сдвигами) — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.

С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами, преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.

Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.

• Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под c{\displaystyle c} следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике).

Вид преобразований при коллинеарных (параллельных) пространственных осях[править | править код]

Если ИСО K′{\displaystyle K’} движется относительно ИСО K{\displaystyle K} с постоянной скоростью v{\displaystyle v} вдоль оси x{\displaystyle x}, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:

x′=x−vt1−v2/c2,{\displaystyle x’={\frac {x-vt}{\sqrt {1-v^{2}/c^{2}}}},}

Закон Видемана — Франца — Википедия

Зако́н Видема́на — Фра́нца — это физический закон, утверждающий, что для металлов отношение коэффициента теплопроводности (либо тензора теплопроводности) K{\displaystyle K} к удельной электрической проводимости (либо тензору проводимости) σ{\displaystyle \sigma } пропорционально температуре^[1]:

Kσ=LT.{\displaystyle {\frac {K}{\sigma }}=LT.}

В 1853 году немецкими учёными Г. Видеманом (1826—1899) и Р. Францем (1827—1902) на основании экспериментальных данных было установлено, что для различных металлов при одинаковой температуре отношение K/σ{\displaystyle K/\sigma } практически не изменяется^[2]. Пропорциональность этого отношения термодинамической температуре была установлена Л. Лоренцем в 1882 году. В его честь коэффициент L{\displaystyle L} носит название числа Лоренца, а сам закон иногда именуют законом Видемана — Франца — Лоренца.

Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов в основном обусловлены движением свободных электронов.

Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии.

Друде, применив классическую кинетическую теорию газов, получил значение коэффициента L{\displaystyle L}:

L=3(ke)2≈2,22×10−8 WΩK−2,{\displaystyle L=3\left({\frac {k}{e}}\right)^{2}\approx 2{,}22\times 10^{-8}~{\text{W}}\Omega {\text{K}}^{-2},}

где k{\displaystyle k} — постоянная Больцмана, e{\displaystyle e} — заряд электрона.

В своём первоначальном расчете Друде ошибся в 2 раза, получив при этом правильный порядок величины. Фактически, классическая статистика даёт результат

L=32(ke)2≈1,11×10−8 WΩK−2.{\displaystyle L={\frac {3}{2}}\left({\frac {k}{e}}\right)^{2}\approx 1{,}11\times 10^{-8}~{\text{W}}\Omega {\text{K}}^{-2}.}

Только с помощью квантовой статистики Зоммерфельдом было получено значение коэффициента L{\displaystyle L}, хорошо согласующееся с экспериментом:

L=π23(ke)2≈2,47×10−8 WΩK−2.{\displaystyle L={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}\approx 2{,}47\times 10^{-8}~{\text{W}}\Omega {\text{K}}^{-2}.}

Закон Видемана — Франца стал триумфом теории свободных электронов.

Классическая теория, приводя к практически правильному конечному результату, давала этому неправильную трактовку. В ней пропорциональность между K{\displaystyle K} и σ{\displaystyle \sigma } объяснялась тем, что средняя кинетическая энергия электронного газа равна 32kT{\displaystyle {\tfrac {3}{2}}kT}, то есть пропорциональна абсолютной температуре. На самом деле закон объясняется тем, что абсолютной температуре пропорциональна не средняя энергия, а теплоёмкость электронного газа. Классическая теория допускала ошибку, завышая в 100 раз теплоёмкость электронного газа, но эта ошибка случайно компенсировалась другой ошибкой. Скорость электронов, участвующих в теплообмене, определяется их кинетической энергией на поверхности Ферми: 2EF/m{\displaystyle {\sqrt {2E_{F}/m}}}, — тогда как в классической теории считалось, что эта скорость порядка классической средней скорости теплового движения 3kT/m{\displaystyle {\sqrt {3kT/m}}}. Тем самым средний квадрат скорости электронов, участвующих в теплообмене, занижался в 100 раз (так же, как и теплоёмкость), а конечный результат получался правильным.

Справедливость закона Видемана — Франца не ограничивается теорией свободных электронов Зоммерфельда. В полуклассической теории проводимости показано, что если пренебречь термоэлектрическим полем, то выражение, аналогичное полученному Зоммерфельдом, будет справедливо, если заменить теплопроводность и проводимость на тензоры соответствующих величин. Тем не менее, следует подчеркнуть, что в полупроводниках нет основания ожидать такой простой связи.

Эксперимент свидетельствует о том, что в действительности закон Видемана — Франца хорошо выполняется при высоких (выше комнатной) и низких (несколько кельвинов) температурах. В промежуточной области он несправедлив.

Его применимость связана с применимостью приближения времени релаксации. При строгом выводе этого закона неявно предполагается, что все столкновения упругие, то есть энергия сохраняется при столкновении. Если имеют место неупругие столкновения, то обязательно будут иметь место процессы рассеяния, которые могут уменьшить поток тепла, не уменьшая электрический ток (поток тепла определяется кроме энергии электрона также химическим потенциалом). Если такие процессы дают потери энергии порядка kT{\displaystyle kT}, как это бывает при промежуточных температурах, то следует ожидать нарушение закона Видемана — Франца.

В 2017 году исследователи из американской Национальной лаборатории в Беркли обнаружили, что диоксид ванадия (VO₂), который в нормальных условиях является прозрачным диэлектриком, при повышении температуры выше 67 градусов Цельсия переходит в металлическую токопроводящую фазу. Пребывая в металлическом состоянии, диоксид ванадия хорошо проводит электрический ток, являясь, одновременно, тепловым изолятором^[3].

• Калашников С. Г. Электричество. — 6-е изд., стереот. — М.: ФИЗМАТЛИТ, 2004. — 624 с — ISBN 5-9221-0312-1.
• Сивухин Д. В. Общий курс физики. В 5 т. Т III. Электричество. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2004. — 654 с — ISBN 5-9221-0227-3.
• Ашкрофт Н., Мермин Н. Физика твердого тела.

Преобразования Лоренца

Ранее мы уже изучили формулы, называемые классическими преобразованиями Галилея, однако они несовместимы с постулатами специальной теории относительности (СТО). Поэтому в данном случае нам нужно использовать другие положения. Благодаря новым преобразованиям мы сможем установить, какая связь существует между некоторым моментом события t, наблюдаемого в системе отсчета K в точке с координатами (x, y, z) и показателями того же события, которое наблюдается в системе отсчета K’.

Определение 1

Преобразования Лоренца представляют собой кинематические формулы, с помощью которых происходит преобразование координат и времени в специальной теории относительности.

Они были впервые сформулированы еще в 1904 году в качестве преобразований, относительно которых были инвариантны уравнения электродинамики.

Обозначим основные системы K и K’, скорость их движения – υ, а ось, вдоль которой они движутся – x. В таком случае преобразования Лоренца примут следующий вид:

K’→Kx=x’+υt’1-β2,y=y’,z=z’,t=t’+υx’/c21-β2.K→K’x’=x-υt1-β2,y’=y,z’=z,t’=t-υx/c21-β2.

β=υc.

Используя эти формулы, мы можем вывести из них множество следствий. Так, именно из системы преобразований Лоренца следует лоренцево сокращение длины и релятивистский эффект замедления времени.

Пример 1

Возьмем случай, когда в системе K’ происходит некий процесс, длительность которого составляет τ0 = t’2 – t’1 (по собственному времени). Здесь t’1 и t’2 – это время на часах в начале данного процесса и в его конце. Чтобы вычислить его общую продолжительность в точке x, необходимо взять для расчета следующую формулу:

τ=t2-t1=t’2+υx’/c21-β2-t’1+υx’/c21-β2=t’2-t’11-β2=τ01-β2.

Формула релятивистского сокращения длины выводится из преобразований Лоренца точно таким же образом.

Принцип относительности одновременности

Еще одно важное следствие, которое необходимо знать, – это положение о том, что любая одновременность относительна.

Преобразования Лоренца

Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x’, y’, z’) и моментом времени t’ этого же события, наблюдаемого в системе отсчета K’.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K’ движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

 

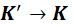
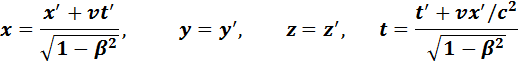
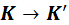
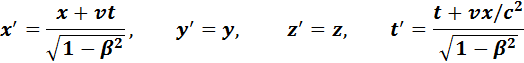
Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x’ системы K’ происходит процесс длительностью τ₀ = t’₂ – t’₁ (собственное время), где t’₁ и t’₂ – показания часов в системе K’ в начале и конце процесса. Длительность τ этого процесса в системе K будет равна

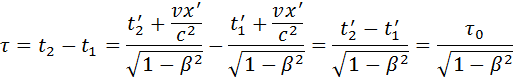
Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K’ (x’₁ ≠ x’₂) одновременно с точки зрения наблюдателя в K’ (t’₁ = t’₂ = t’) происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь

 

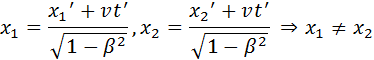
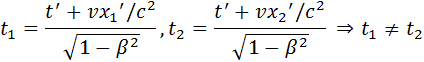
Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t₂ – t₁ определяется знаком выражения υ(x’₂ – x’₁), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

Относительность одновременности пространственно-разобщенных событий можно проиллюстрировать на следующем примере.

Пусть в системе отсчета K’ вдоль оси x’ неподвижно расположен длинный жесткий стержень. В центре стержня находится импульсная лампа B, а на его концах установлены двое синхронизированных часов(рис. 4.4.1(a)), система K’ движется вдоль оси x системы K со скоростью υ. В некоторый момент времени лампа посылает короткие световые импульсы в направлении концов стержня. В силу равноправия обоих направлений свет в системе K’ дойдет до концов стержня одновременно, и часы, закрепленные на концах стержня, покажут одно и то же время t’. Относительно системы K концы стержня движутся со скоростью υ так, что один конец движется навстречу световому импульсу, а другой конец свету приходится догонять. Так как скорости распространения световых импульсов в обоих направлениях одинаковы и равны c, то, с точки зрения наблюдателя в системе K, свет раньше дойдет до левого конца стержня, чем до правого (рис. 4.4.1(b)).

Рисунок 4.4.1. Относительность одновременности. Световой импульс достигает концов твердого стержня одновременно в системе отсчета K’ (a) и не одновременно в системе отсчета K (b)

Преобразования Лоренца выражают относительный характер промежутков времени и расстояний. Однако, в СТО наряду с утверждением относительного характера пространства и времени важную роль играет установление инвариантных физических величин, которые не изменяются при переходе от одной системы отсчета к другой. Одной из таких величин является скорость света в вакууме c, которая в СТО приобретает абсолютный характер. Другой важной инвариантной величиной, отражающей абсолютный характер пространственно-временных связей, является интервал между событиями.

Пространственно-временной интервал определяется в СТО следующим соотношением:

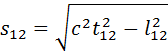
где t₁₂ – промежуток времени между событиями в некоторой системе отсчета, а l₁₂ – расстояние между точками, в которых происходят рассматриваемые события, в той же системе отсчета. В частном случае, когда одно из событий происходит в начале координат (x₁ = y₁ = z₁ = 0) системы отсчета в момент времени t₁ = 0, а второе – в точке с координатами x, y, z в момент времени t, пространственно-временной интервал между этими событиями записывается в виде

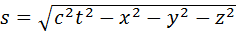
С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета.

Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t (рис. 4.1.3), то

x2 + y2 + z2 = c2t2,

и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s’ окажется равным нулю, так как

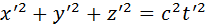
Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.

Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K’ вдоль оси x’ движется частица со скоростью 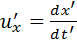 Составляющие скорости частицы u’x и u’z равны нулю. Скорость этой частицы в системе K будет равна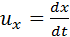

С помощью операции дифференцирования из формул преобразований Лоренца можно найти:

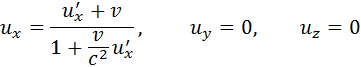
Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости 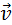 систем отсчета K и K’.

При υ << c релятивистские формулы переходят в формулы классической механики:

ux = u’x + υ,  uy = 0,  uz = 0.

Если в системе K’ вдоль оси x’ со скоростью u’x = c распространяется световой импульс, то для скорости ux импульса в системе K получим

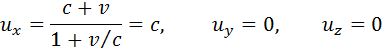
Таким образом, в системе отсчета K световой импульс также распространяется вдоль оси x со скоростью c, что согласуется с постулатом об инвариантности скорости света.

Вывод преобразований Лоренца — Википедия

Вы́вод преобразова́ний Ло́ренца может быть проделан многими способами, исходя из различных предпосылок.

Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым параметром c{\displaystyle c}), как обобщение преобразований Галилея (что было проделано Пуанкаре — см. ниже). Однако впервые они были получены как преобразования, относительно которых уравнения Максвелла ковариантны (которые не меняют вида законов электродинамики и оптики при переходе к другой системе отсчёта). Преобразования можно получить из предположения их линейности и постулата одинаковости скорости света во всех системах отсчёта (являющегося упрощённой формулировкой требования ковариантности электродинамики относительно искомых преобразований, и распространением принципа равноправия инерциальных систем отсчёта — принципа относительности — на электродинамику), как это делается в специальной теории относительности (СТО) (при этом параметр c{\displaystyle c} в преобразованиях Лоренца получается определённым и совпадает со скоростью света).

Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований (однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не сохраняет метрику постоянной).

На основании нескольких естественных предположений (основным из которых является предположение о существовании максимальной скорости распространения взаимодействий) можно показать, что при смене ИСО должна сохраняться величина

ds2=c2dt2−dx2−dy2−dz2{\displaystyle ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}},

называемая интервалом. Из этой теоремы напрямую следует общий вид преобразований Лоренца (см. ниже). Здесь рассмотрим лишь частный случай. Для наглядности при переходе в ИСО K′{\displaystyle K’}, движущуюся со скоростью v{\displaystyle v}, выберем в исходной системе K{\displaystyle K} ось X{\displaystyle X} сонаправленной с v{\displaystyle v}, а оси Y{\displaystyle Y} и Z{\displaystyle Z} расположим перпендикулярно оси X{\displaystyle X}. Пространственные оси ИСО K′{\displaystyle K’} в момент времени t=0{\displaystyle t=0} выберем сонаправленными с осями ИСО K{\displaystyle K}. При таком преобразовании

y′=y,  z′=z,  c2t′2−x′2=c2t2−x2{\displaystyle y’=y,~~z’=z,~~c^{2}t’^{2}-x’^{2}=c^{2}t^{2}-x^{2}}

Мы будем искать линейные преобразования Лоренца, так как при бесконечно малых преобразованиях координат дифференциалы новых координат линейно зависят от дифференциалов старых координат, а в силу однородности пространства и времени коэффициенты не могут зависеть от координат, только от взаимной ориентации и скорости ИСО.

То, что поперечные координаты не могут меняться, ясно из соображений изотропности пространства. Действительно, величина y′{\displaystyle y’} не может изменяться и при этом не зависеть от x{\displaystyle x} (кроме как при вращении вокруг v{\displaystyle v}, которое мы исключаем из рассмотрения), в чём легко убедиться подстановкой таких линейных преобразований в выражение для интервала. Но если она зависит от x{\displaystyle x}, то точка с координатой (0,x,0,0){\displaystyle (0,x,0,0)} будет иметь ненулевую координату y′{\displaystyle y’}, что противоречит наличию симметрии вращения системы относительно v{\displaystyle v} и изотропии пространства. Аналогично для z′{\displaystyle z’}.

Наиболее общий вид таких преобразований:

y′=y,  z′=z,  ct′=ctchα−xshα,  x′=xchα−ctshα{\displaystyle y’=y,~~z’=z,~~ct’=ct\,\operatorname {ch} \,\alpha -x\,\operatorname {sh} \,\alpha ,~~x’=x\,\operatorname {ch} \,\alpha -ct\,\operatorname {sh} \,\alpha }

где α{\displaystyle \alpha } — некоторый параметр, называемый быстротой. Обратные преобразования имеют вид

y=y′,  z=z′,  ct=ct′chα+x′shα,  x=x′chα+ct′shα{\displaystyle y=y’,~~z=z’,~~ct=ct’\,\operatorname {ch} \,\alpha +x’\,\operatorname {sh} \,\alpha ,~~x=x’\,\operatorname {ch} \,\alpha +ct’\,\operatorname {sh} \,\alpha }

Ясно, что точка, покоящаяся в ИСО K{\displaystyle K}, должна будет двигаться в ИСО K′{\displaystyle K’} со скоростью −v{\displaystyle -v}. С другой стороны, если точка покоится, то

dx=dx′chα+cdt′shα=0{\displaystyle dx=dx’\,\operatorname {ch} \,\alpha +c\,dt’\,\operatorname {sh} \,\alpha =0}

dx′cdt′=−vc=−thα ⇒ thα=vc{\displaystyle {\frac {dx’}{c\,dt’}}=-{\frac {v}{c}}=-\operatorname {th} \,\alpha ~\Rightarrow ~\operatorname {th} \,\alpha ={\frac {v}{c}}}

Учитывая, что при смене ИСО не должна меняться ориентация пространства, получим, что

chα⩾0{\displaystyle \operatorname {ch} \,\alpha \geqslant 0}

Следовательно, уравнение для быстроты однозначно разрешимо:

chα=11−v2c2,  shα=vc1−v2c2{\displaystyle \operatorname {ch} \,\alpha ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},~~\operatorname {sh} \,\alpha ={\frac {v}{c{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}}

а преобразования Лоренца имеют вид

 x′=γ(x−vt){\displaystyle \ x’=\gamma (x-vt)}

 t′=γ(t−vc2x){\displaystyle \ t’=\gamma (t-{\frac {v}{c^{2}}}x)}

γ=chα=11−v2c2{\displaystyle \gamma =\operatorname {ch} \,\alpha ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}

Параметр γ{\displaystyle \gamma } называется лоренц-фактором.

Группа симметрий уравнений Максвелла[править | править код]

Наглядный вывод преобразований Лоренца[править | править код]

Примем постулаты СТО, сводящиеся к расширенному принципу относительности, утверждающему, что все физические процессы протекают в точности одинаково во всех инерциальных системах отсчёта (уточняющий его принцип постоянства скорости света в СТО означает расширение принципа относительности на электродинамику вместе с уточняющим утверждением о том, что нет никакой фундаментальной физической среды (эфира), которая выделяла бы одну из систем отсчёта на опыте — то есть, если даже эфир и есть, то его наличие не должно никак нарушать принципа относительности на практике). Кроме того, полезно явно подчеркнуть, что принцип постоянства скорости света означает наличие именно конечной скорости (из эксперимента равной скорости света в вакууме), заложенной в фундаментальные законы (уравнения), одной и той же для всех инерциальных систем отсчёта, причём в каждой системе отсчёта скорость света одинакова для любых направлений его распространения и не зависит от скорости источника. Принцип постоянства скорости света составляет второй постулат СТО, который используется ниже.

Преобразование для поперечных осей (п.1)[править | править код]

Бильярдный шар около угловой лузы. Если бы выполнялось y≠y′{\displaystyle y\neq y’}, шар забивался бы в одних системах отсчёта и не забивался бы в других

Пусть есть две бесконечные плоскости, перпендикулярные оси y. Расстояние между этими плоскостями очевидно не должно зависеть от скорости движения плоскостей вдоль самих себя, а значит — не зависит от системы отсчёта, которая движется относительно другой вдоль оси x{\displaystyle x}. (Действительно, в каждой такой системе время прохождения луча света, движущегося вдоль оси y{\displaystyle y} с одной плоскости на другую, одинаково согласно постулатам СТО).

Также можно представить, как движущееся вдоль оси x{\displaystyle x} тело влетает в неподвижное отверстие такого же размера. Если нет равенства y=y′{\displaystyle y=y’} , то в зависимости от того, в какой системе отсчёта проводится измерение, тело может быть больше или меньше отверстия. Реально же тело может пройти через отверстие или не пройти во всех системах отсчёта.

То же самое, конечно, верно и для оси z{\displaystyle z}. Поэтому, исключив для простоты физически неинтересный случай поворота на постоянный угол второй системы координат относительно первой, получаем:

y=y′,z=z′{\displaystyle y=y’,z=z’}

Замедление времени (п.2)[править | править код]

Покажем, что любой процесс (например ход часов) в движущейся относительно него системе отсчета протекает медленнее, чем в его собственной системе отсчёта (относительно которой он не перемещается).

Рассмотрим «световые часы», состоящие из точечного источника и приемника света на оси y{\displaystyle y}, удаленные друг от друга на расстояние L{\displaystyle L} и отмеряющие интервал времени прохождения импульса (вспышки) света от источника до приемника равный L/c{\displaystyle L/c}.

Если системы отсчета движутся относительно друг друга по оси x{\displaystyle x}, то расстояние L{\displaystyle L} между двумя точками на оси y{\displaystyle y}, измеренное в неподвижной относительно этих точек системе, такое же, как измеренное в движущейся системе отсчета, поскольку по оси y{\displaystyle y} нет относительного движения систем. Тем самым единицы измерения длины будут согласованы между системами. Единицы времени тоже будут согласованы, поскольку согласованы единицы длины, а скорость света не зависит от системы координат.

Таким образом, в каждой системе отсчета можно установить одинаковые световые часы.

Сравним интервал времени прохождения импульса в системе отсчета где световые часы покоятся и интервал времени тех же часов, измеренный идентичными часами в движущейся системе отсчета.

Пусть световые часы покоятся в системе отсчёта K{\displaystyle K} (на рис. слева), а система отсчёта K′{\displaystyle K’} движется вправо вдоль оси x{\displaystyle x} со скоростью V{\displaystyle V}. Источник в момент излучения импульса находится в начале координат A системы отсчета K{\displaystyle K} (красная точка на рис.), а приемник — в точке B (синяя) на оси y{\displaystyle y}. В системе отсчёта K{\displaystyle K} испущенный импульс света достигает приемника B на оси y{\displaystyle y} за время Δt=L/c{\displaystyle \Delta t=L/c}.

В системе же отсчёта K′{\displaystyle K’} импульс света излучается из начала координат в момент его совпадения с началом координат системы K{\displaystyle K} (точкой A), а попадает в приёмник B через время Δt′=L′/c{\displaystyle \Delta t’=L’/c}, которое измеряется часами, движущимися вместе с системой K′{\displaystyle K’}. Координата x′{\displaystyle x’} точки B — смещение, обозначенное на рисунке справа пунктиром, равно −VΔt′{\displaystyle -V\Delta t’}, точка A указывает место откуда был излучен импульс, траектория импульса в K′{\displaystyle K’} изображена зеленой линией.

Поскольку скорость света в любой инерциальной системе отсчета одинакова (не зависит от скорости источника и направления излучения), источник A в момент импульса можно считать неподвижным в системе отсчета K′{\displaystyle K’}.

Путь L′{\displaystyle L’}, пройденный импульсом света от A к B в системе отсчёта K′{\displaystyle K’}, равен гипотенузе прямоугольного треугольника. По теореме Пифагора

L′=L2+(VΔt′)2{\displaystyle {\displaystyle L’}=L^{2}+(V\Delta t’)^{2}},

учитывая, что L′=cΔt′{\displaystyle {\displaystyle L’}=c\Delta t’}и L=cΔt{\displaystyle L=c\Delta t}, найдем выражение для Δt′{\displaystyle \Delta t’}

Δt′=Δt1−V2c2{\displaystyle \Delta t’={\frac {\Delta t}{\sqrt {1-{\frac {V^{2}}{c^{2}}}}}}}.

Отсюда следует, что Δt′>Δt{\displaystyle \Delta t’>\Delta t} при V≠0{\displaystyle V\neq 0}.

Таким образом, интервал времени Δt′{\displaystyle \Delta t’} любого процесса, происходящего в системе отсчёта K{\displaystyle K}, измеренный часами в движущейся системе отсчета K′{\displaystyle K’}, больше, чем интервал времени Δt{\displaystyle \Delta t}, измеренный такими же часами в собственной системе отсчёта K{\displaystyle K}. Коэффициент увеличения интервала постоянен при постоянной скорости.

Поскольку система отсчета K{\displaystyle K} движется относительно системы K′{\displaystyle K’} со скоростью −V{\displaystyle -V}, то говорят, что время в движущейся системе отсчета K{\displaystyle K}с точки зрения системы K′{\displaystyle K’} течет замедленно. Например, земное время жизни Δt′{\displaystyle \Delta t’} короткоживущих частиц, рождающихся при больших скоростях других частиц, больше их времени жизни Δt{\displaystyle \Delta t} в собственной системе отсчета.

Более наглядно замедление времени проявляется в замедлении хода (темпа) часов, движущихся вместе с системой отсчета K{\displaystyle K}. Если источник и приемник снабдить зеркалами, отражающими световой импульс, то интервал любой длительности можно измерять числом периодов между отражениями. Частота колебаний такого маятника характеризует скорость течения времени. Период T{\displaystyle T} повторяющегося процесса связан с его частотой равенством ν=1T{\displaystyle \nu ={\frac {1}{T}}}. Большему периоду соответствует меньшая частота и неравенство Δt′>Δt{\displaystyle \Delta t’>\Delta t} переходит в неравенство для частоты ν′<ν{\displaystyle \nu ‘<\nu }, где ν′{\displaystyle \nu ‘} — частота маятника часов, движущихся вместе с системой K{\displaystyle K}, измеренная часами системы K′{\displaystyle K’}, ν{\displaystyle \nu } — частота маятника в собственной системе отсчета K{\displaystyle K} (относительно которой часы покоятся). Движущиеся часы тикают реже, чем неподвижные.

Поскольку все инерциальные системы отсчета равноправны, то, измеряя длительность прохождения импульса в часах, движущихся вместе с системой отсчёта K′{\displaystyle K’} часами системы отсчёта K{\displaystyle K}, получим обратное неравенство Δt′<Δt{\displaystyle \Delta t'<\Delta t} при V≠0{\displaystyle V\neq 0}, так как в этом случае Δt′{\displaystyle \Delta t’} является собственным временем. С точки зрения системы отсчета K{\displaystyle K} движущиеся часы системы K′{\displaystyle K’} идут медленнее собственных часов системы K{\displaystyle K}.

Относительность одновременности (п.3)[править | править код]

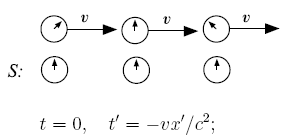
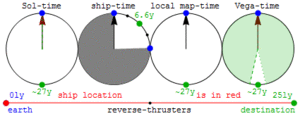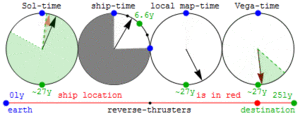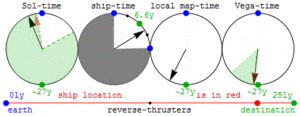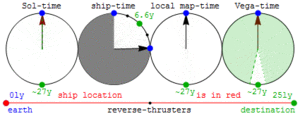Изменение времени на неподвижных звёздах в системе отсчёта движущегося космического корабля. Когда мы около земли, время изменяется на Веге и наоборот. В результате не возникает парадокс близнецов

Кроме замедления времени в движущейся системе отсчёта (замедления хода всех часов в движущейся лаборатории по сравнению с ходом часов в неподвижной лаборатории), оказывается, что начало отсчёта времени в движущейся системе отсчёта также не совпадает с таковым в неподвижной, причем сдвиг этого начала отсчёта — разный в различных точках — зависит от x. Часы в своей собственной системе отсчёта, показывающие одинаковое время, показывают разное опережение/отставание, зависящее от их расположения, если на них смотреть из системы отсчёта, относительно которой их собственная система отсчёта движется.

Чтобы стало понятным само существо проблемы, придется так или иначе обдумать вопрос, а что значит, что часы в разных удаленных друг от друга точках пространства (например, в разных городах) идут одинаково (синхронно), как в этом можно убедиться, или как (с помощью какой процедуры) можно синхронизировать часы в разных местах, если изначально они не были синхронны.

Уже простейший способ синхронизации, заключающийся в том, что все часы синхронизируют в одном месте, а затем их переносят в разные точки, позволяет убедиться в том, что часы, синхронизированные в одной системе отсчёта, будут выглядеть показывающими разное время из другой системы отсчёта. Дело в том, что для часов, которые мы переносим в разные точки по оси x, их скорость относительно другой системы отсчёта будет обязательно различной, поэтому время в разных точках оси x будет сдвинуто по-разному.

Это можно было бы аккуратно рассмотреть количественно, получив так искомый здесь результат. Но более просто этого достичь позволяет рассмотрение синхронизации с помощью световых сигналов (а принцип относительности говорит, что любой корректный способ синхронизации должен дать один и тот же результат, в чём, впрочем, при желании можно убедиться и явно).

Итак, рассмотрим синхронизацию с помощью световых сигналов. Этот процесс может заключаться, например, в обмене световыми сигналами между двумя удаленными хронометрами: если сигналы испущены в одно и то же время, то до получения сигнала по каждым часам пройдет одно и то же время. Но еще проще несколько другой (эквивалентный этому) способ: можно точно в середине отрезка, соединяющего хронометры, произвести вспышку света, и утверждать, что свет придет к обоим хронометрам одновременно.

В собственной системе отсчёта (в которой хронометры неподвижны) картина симметрична. Однако в любой другой системе отсчёта оба хронометра движутся (для определенности будем считать, что вправо), и тогда свету от середины отрезка, соединяющего их в начальный момент, потребуется меньше времени, чтобы дойти до левого хронометра (движущегося навстречу свету), чем до правого (который импульс света должен догонять).

Таким образом, хронометры, синхронно идущие в собственной системе отсчёта, по часам другой системы отсчёта выглядят несинхронными. Одновременность событий относительна: события, одновременные в одной системе отсчёта, неодновременны в другой.

Несложные геометрические выкладки позволяют (изобразив движение световых импульсов и хронометров на плоскости xt), получить выражение для сдвига начала отсчёта времени:

−Vx/c2{\displaystyle -Vx/c^{2}}

• (для упрощения мы здесь рассматривали только часы, разнесенные вдоль оси x, но, конечно, всё может быть рассчитано и для общего случая).

Таким образом, сводя вместе результаты пунктов 2 и 3, получаем для преобразования времени

t′=t−Vx/c21−V2/c2{\displaystyle t’={\frac {t-Vx/c^{2}}{\sqrt {1-V^{2}/c^{2}}}}}.

Данный эффект так же можно доказать от противного: если бы он не существовал, или сдвиг начала отсчёта времени не составлял бы −Vx/c2{\displaystyle -Vx/c^{2}}, то существовал бы так называемый парадокс близнецов.

Лоренцевское сокращение длины (п.4)[править | править код]

Рассмотрев движение светового импульса вдоль оси x (а не вдоль y, как было в п.1), и потребовав (на основании постулата одинаковости скорости света во всех инерциальных системах отсчёта), чтобы расстояние между двумя точками было всегда равно времени, за которое свет идёт от одной точки до другой, умноженному на (константу) скорость света, можно получить фактор сокращения расстояний вдоль оси x, а учитывая, что смещение начала отсчёта равно −Vt{\displaystyle -Vt}, можно получить и преобразование для координаты x:

x′=x−Vt1−V2/c2{\displaystyle x’={\frac {x-Vt}{\sqrt {1-V^{2}/c^{2}}}}}.

Ещё проще теперь понять, что x′{\displaystyle x’} выражается именно таким образом, заметив, что в плоскости x−ct{\displaystyle x-ct} график движения^[1] импульса света должен быть прямой, наклонённой под 45° (из-за того, что скорость света — всегда c), а значит и масштаб по осям x{\displaystyle x}и ct{\displaystyle ct} должен быть одинаковым, а выражения в системе единиц c=1{\displaystyle c=1} — симметричными.

• Таким образом, преобразования Лоренца достаточно наглядно получаются при коллинеарных пространственных осях. Конечно, возможен и обратный порядок рассуждений: можно сначала получить преобразования Лоренца каким-либо более абстрактным способом, например — одним из упомянутых выше, а потом получить все эффекты, разобранные в этапах данного наглядного доказательства, в качестве простого формального следствия преобразований Лоренца.

1. ↑ Минковский назвал такой график движения мировой линией; однако в этом параграфе мы не будем углубляться в связь преобразований Лоренца с понятием пространства Минковского в полном его объёме, прежде всего — чтобы не усложнять и не прерывать элементарный вывод, который удобнее считать независимым от каких-либо дополнительных специальных понятий, ограничившись только элементарными геометрическими и алгебраическими понятиями лишь настолько, насколько они необходимы. По сути, речь идёт именно о преобразовании координат в пространстве Минковского, причём в данном параграфе, исходя из постулата постоянства скорости света, как раз и выясняются определённые свойства этого пространства, как и преобразований Лоренца — в качестве удобных преобразований координат в нём. Но ещё раз для ясности подчеркнем, что для самого вывода не нужно знать ничего кроме того, что явно сказано в основном тексте параграфа.

Преобразования Лоренца

Преобразования Лоренца
_{Lorentz Transformations}

    Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v. Преобразования Лоренца отражают равноправие всех инерциальных систем отсчёта в описании законов природы. Если инерциальная система отсчёта K’ движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид

y = y’, z = z’,

(1)

c — скорость света в вакууме, β = v/c. Формулы, выражающие x’, y’, z’, t’ через x, y, z, t получаются из соотношения (1) заменой v на -v.

Рис. Система координат K’ движется относительно неподвижной системы координат K со скоростью v вдоль оси x.

    При v << c преобразования Лоренца переходят в преобразования Галилея

x = x’ + vt, y = y’, z = z’, t = t’.

Из преобразований Лоренца следует, что промежутки времени Δt и отрезки длины Δl зависят от движения системы отсчёта. Если в системе K’ два события, происходящие в одном и том же месте, разделены интервалом времени Δt’, то в системе K эти же происходящие в разных местах события разделены промежутком времени Δt

Если отрезок, покоящийся в системе K’, имеет длину Δl’, то его длина Δl в системе K, т.е. расстояние между двумя одновременными в K событиями регистрации положения концов отрезка, принимает значение

Поперечные размеры тел при этом не изменяются.
    Формулы преобразования скорости:

Электрическое поле E и магнитное поле H при преобразовании Лоренца преобразуются следующим образом:

Координаты 4-мерного вектора энергии-импульса с компонентами (ε/c, p_x, p_y, p_z) при преобразовании Лоренца преобразуются следующим образом:

Энергия частицы

Импульс частицы

    Преобразования Лоренца, указывающие на относительность промежутков времени и отрезков длины между двумя событиями, оставляют инвариант­ной, т.е. не зависящей от выбора системы отсчёта, их комбинацию, называемую интервалом.

Инвариантом при преобразовании Лоренца является также квадрат 4-вектора энергии-импульса

---

См. также