Эффект Холла
Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в 1879 г. американским физиком Э.Г. Холлом (1855–1938). Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.
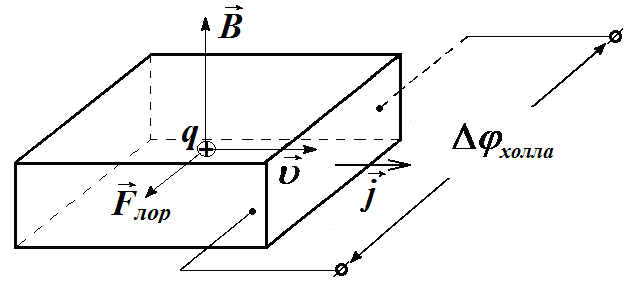
Рассмотрим эффект, обусловленный действием лоренцевой силы на свободные заряды в проводнике. Представим себе проводник с током I в виде плоской ленты, расположенной в магнитном поле с индукцией , направленной от нас (рис. 2.19).
В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.
а б
Рис. 2.19
Это позволяет экспериментально определить знак носителя заряда в проводнике.
При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.
Подсчитаем величину холловской разности потенциалов (Uх).
Обозначим: Ex – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.
| , | (2.10.1) |
Перераспределение зарядов прекратится, когда сила qEx уравновесит лоренцеву силу, т.е.
или
Плотность тока , отсюда . Тогда .
Подставим Ex в (2.10.1) и найдем Ux:
| , | (2.10.2) |
где – коэффициент Холла.
Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р-типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.
Из формулы (2.10.2) можно найти число носителей заряда:
| , | (2.10.3) |
Итак, измерение холловской разности потенциалов позволяет определить:
· знак заряда и тип носителей;
· количество носителей.
Рис 2.20
На рисунке 2.20 показана установка для исследования магнитного поля длинного соленоида с помощью датчика Холла.
Изучение эффекта холла в полупроводниках
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «ВГТУ», ВГТУ)
УЧЕБНО-ЛАБОРАТОРНЫЙ ЦЕНТР КАФЕДРЫ ФИЗИКИ
Методические указания к выполнению лабораторной работы
«Изучение эффекта Холла в полупроводниках»
Для студентов всех направлений (специальностей)
очной формы обучения
Воронеж 2013
Составители: канд. физ.-мат. наук В.С. Железный, канд. физ.-мат. наук Е.А. Косякова.
УДК 531.07
Методические указания к выполнению лабораторной работы «Изучение эффекта Холла в полупроводниках». Для студентов всех направлений (специальностей) / Воронеж. гос. техн. ун-т. Сост. В.С. Железный, Е.А. Косякова. Воронеж, 2005. с.
Методические указания содержат краткий теоретический материал и описание лабораторной работы ”Изучение эффекта холла в полупроводниках” по разделу общего курса физики ”Физика твердого тела”, выполняемых в учебных лабораториях ВГТУ.
Пособие предназначено для студентов технического профиля второго курса всех направлений (специальностей) дневной формы обучения.
Ил. 4. Табл. 1. Библиогр. 4 назв.
Рецензент канд. техн. наук, доцент М. Н. Гаршина
Ответственный за выпуск зав. кафедрой Физики,
канд. физ.-мат. наук, профессор Т.Л. Тураева
Издаётся по решению редакционно-издательского совета Воронежского государственного технического университета
©Воронежский государственный
технический университет, 2013
Цель работы: исследовать зависимость ЭДС Холла от силы тока и величины индукции магнитного поля; определить концентрацию и тип носителей тока в полупроводнике путем измерения ЭДС Холла датчика.
Принадлежности: установка для изучения эффекта Холла ФПК-08.
Теоретическое введение
В 1879 году Эдвин Герберт Холл, будучи молодым студентом, открыл неожиданный эффект. Он обнаружил, что если поместить тонкую золотую пластинку в магнитное поле, направленное перпендикулярно плоскости этой пластинки, и пропустить через нее электрический ток, то в направлении, перпендикулярном направлению и магнитного поля, и тока, возникает разность потенциалов. Это явление получило название эффекта Холла. Оно является одним из так называемых гальваномагнитных явлений, возникающих при одновременном действии на вещество магнитного и электрического полей.
Эффектом Холла
называется возникновение в металле или
полупроводнике электрического поля  ,
перпендикулярного току в образце и
внешнему магнитному полю.
,
перпендикулярного току в образце и
внешнему магнитному полю.
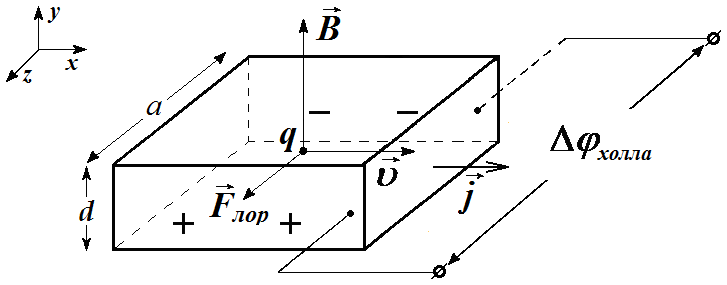
Рис. 1. Датчик Холла дырочного типа проводимости.
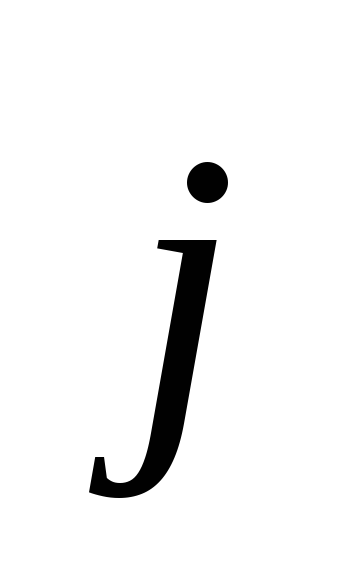 (вдоль оси x),
и одновременно поместить его в магнитное
поле индукцией
(вдоль оси x),
и одновременно поместить его в магнитное
поле индукцией 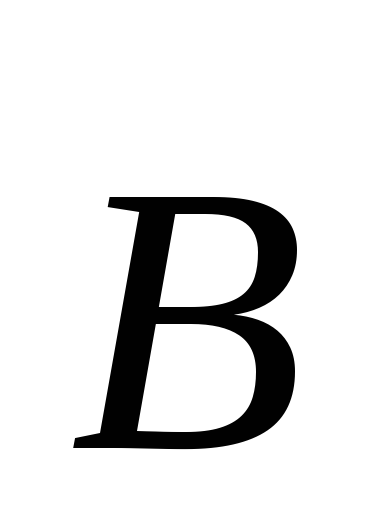 (направленное вдоль оси y),
носители заряда
(направленное вдоль оси y),
носители заряда  ,
будут испытывать действие силы Лоренца
(вдоль оси z):
,
будут испытывать действие силы Лоренца
(вдоль оси z): 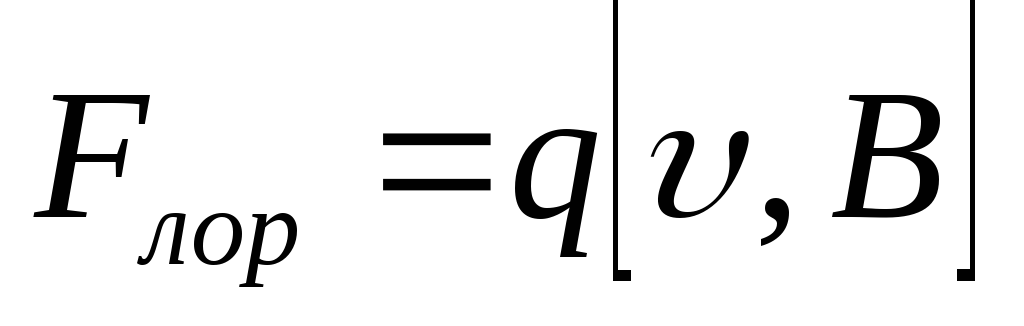
Направление этой силы перпендикулярно и скорости движения зарядов, и направлению магнитного поля. Максимальна она в случае, когда магнитное поле перпендикулярно направлению тока в образце.
Скорость носителей заряда определяется плотностью тока, протекающего через образец:
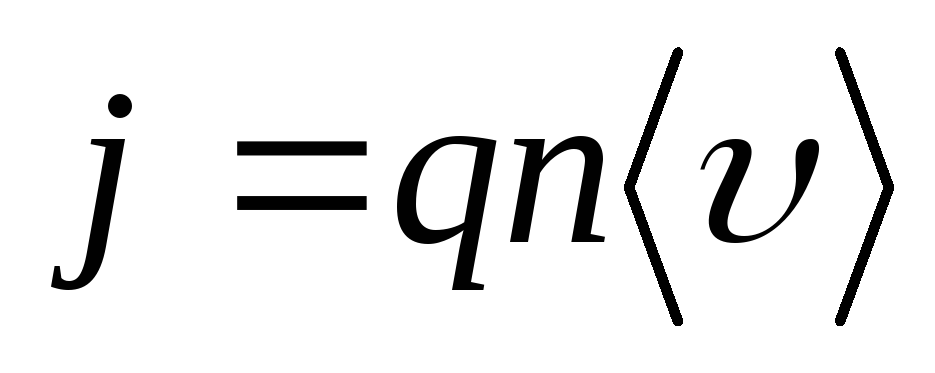 (2)
(2)
где n
— концентрация свободных носителей
заряда в образце, 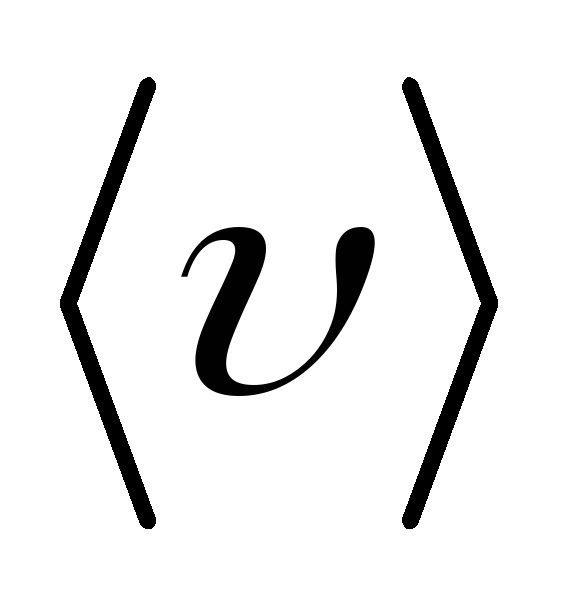 — их дрейфовая скорость. Сила и плотность
тока связаны соотношением:
— их дрейфовая скорость. Сила и плотность
тока связаны соотношением:
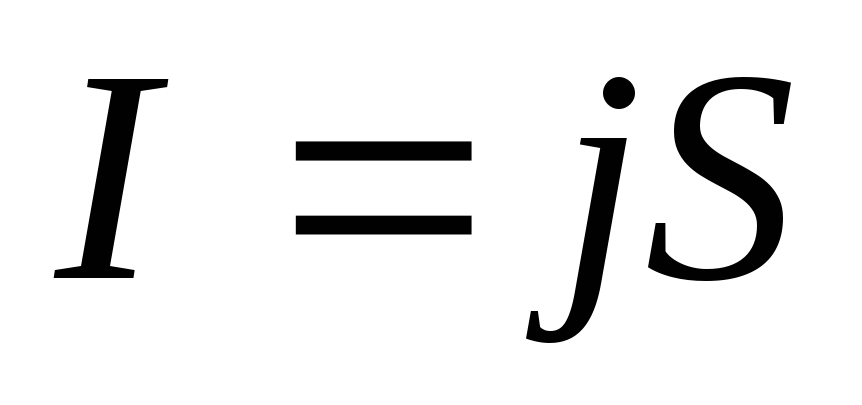 (3)
(3)
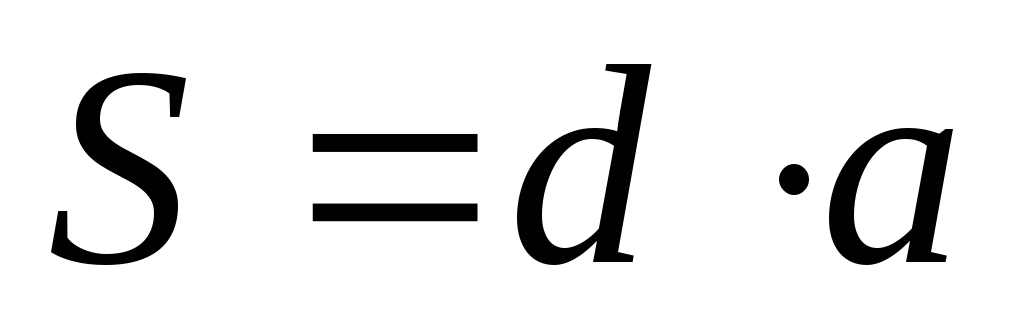 (4)
(4)
где d — толщина, a — ширина исследуемой пластинки.
Под действием силы Лоренца носители заряда противоположных знаков будут сдвигаться к противоположным граням образца. Это движение будет продолжаться до тех пор, пока возникшее при разделении зарядов электрическое поле не скомпенсирует действие силы Лоренца:
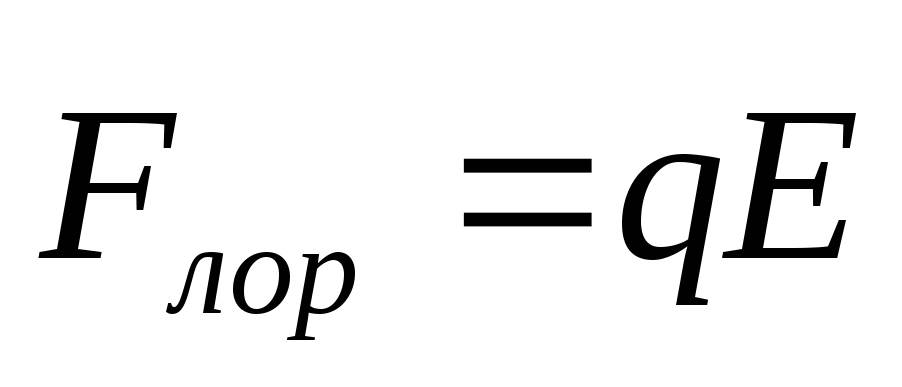 (5)
(5)
Разность потенциалов, возникающая при этом вдоль оси z, называется холловской разностью потенциалов (или ЭДС Холла) и равна:
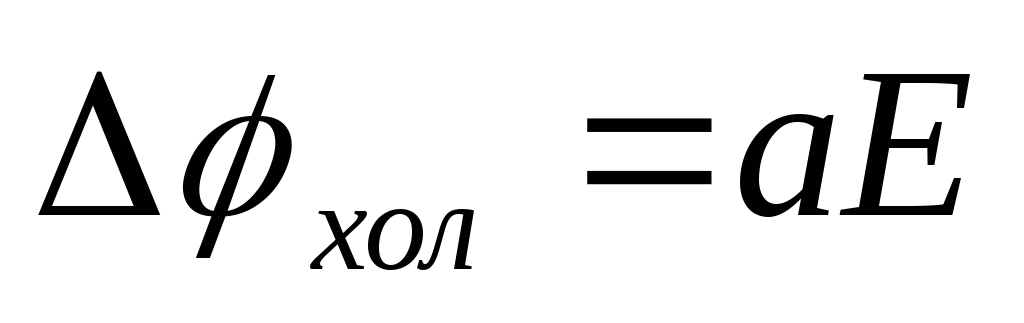 (6)
(6)
В рассмотренном
случае (рис.1)  и
и 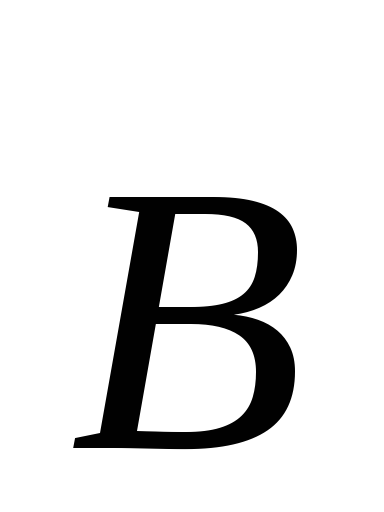
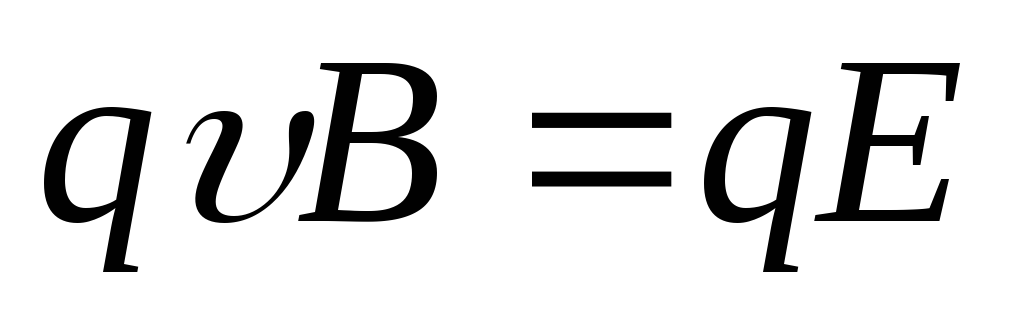 (7)
(7)
С учетом приведенных выше формул получаем:
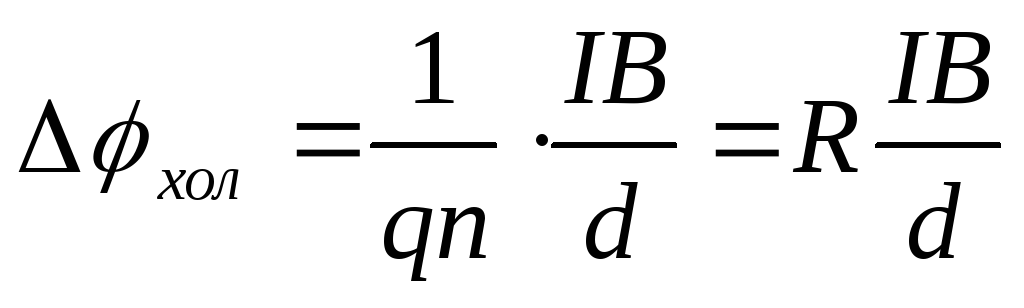 (8)
(8)
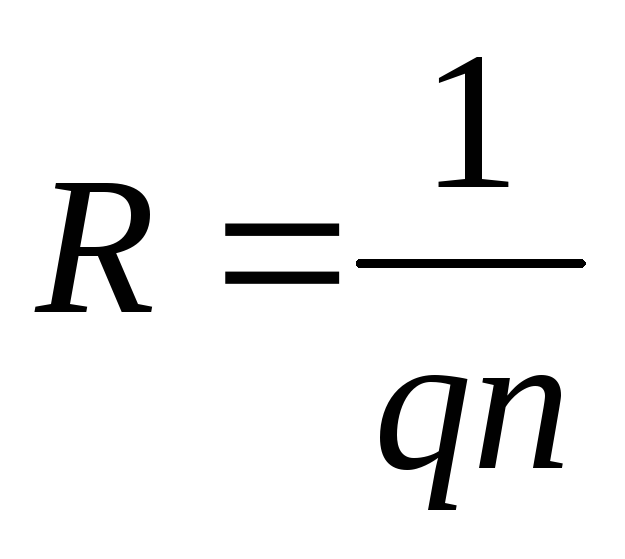 (9)
(9)
Константа 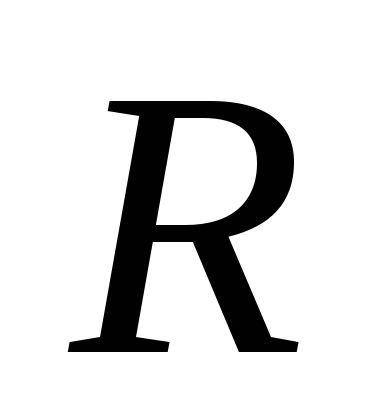 называется постоянной Холла. Знак
постоянной и, следовательно, направление
ЭДС Холла зависят от знака носителей
тока. Для свободных электронов постоянная
Холла отрицательна. Положительная
постоянная Холла означает, что носителями
тока являются положительные заряды.
Т.о., постоянная Холла
называется постоянной Холла. Знак
постоянной и, следовательно, направление
ЭДС Холла зависят от знака носителей
тока. Для свободных электронов постоянная
Холла отрицательна. Положительная
постоянная Холла означает, что носителями
тока являются положительные заряды.
Т.о., постоянная Холла 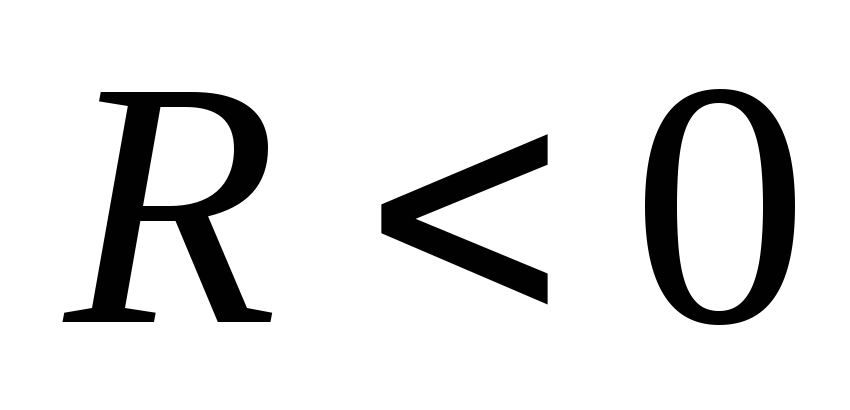 для металлов и полупроводников
электронного типа (n-типа),
для металлов и полупроводников
электронного типа (n-типа), 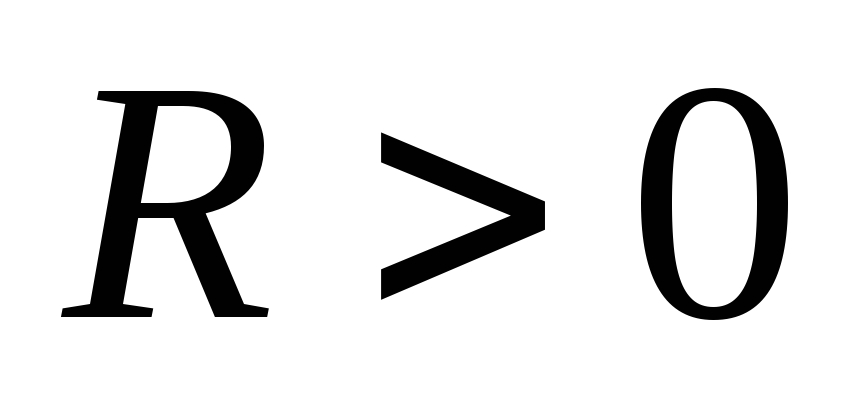 для полупроводников дырочного типа
(р-типа).
для полупроводников дырочного типа
(р-типа).
Определив коэффициент Холла, можно рассчитать концентрацию основных носителей заряда в исследуемом образце.
Выражение (9) для постоянной Холла получено в предположении, что все носители тока имеют одинаковую скорость движения, которая к тому же не изменяется при движении носителей тока в веществе. Такое допущение справедливо для металлов, в которых ток переносится электронами, обладающими одной и той же энергией (энергией Ферми). Мы не учли, следовательно, что при движении в реальном веществе носители тока испытывают столкновения и потому рассеиваются на примесях, на колебаниях решетки. Учет рассеяния носителей тока в веществе приводит к несколько иному выражению для R, вид которого зависит от механизма рассеяния. Например, для чистых полупроводников с собственной проводимостью, когда рассеяние происходит главным образом на тепловых колебаниях решетки, для постоянной Холла получается выражение:
 (10)
(10)
Если основное значение имеет рассеяние на ионизированных атомах примеси (т.е. в примесном полупроводнике), то справедливо выражение:
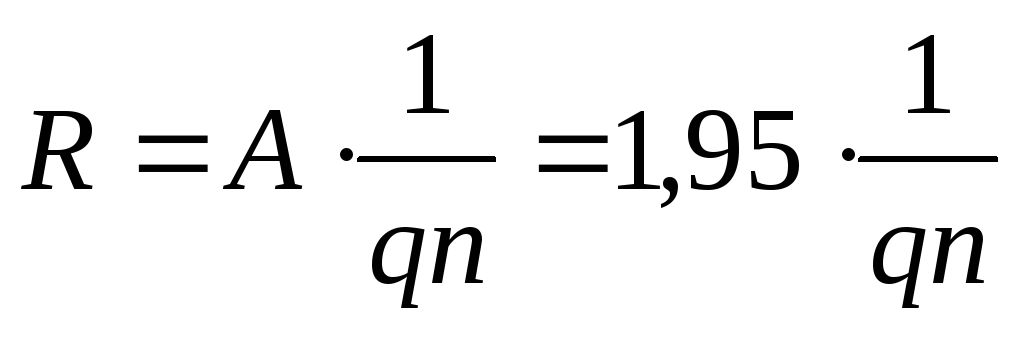 (10′)
(10′)
Для полупроводников со смешанной проводимостью, если концентрации электронов и дырок сравнимы друг с другом, постоянная Холла вычисляется по формуле:
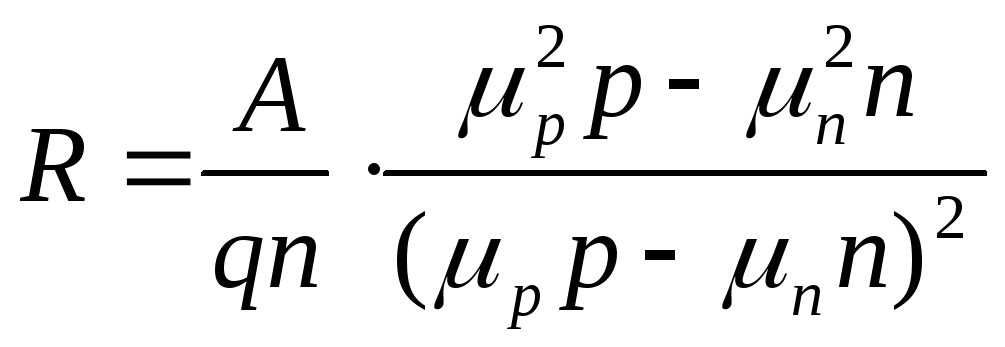 (10′)
(10′)
где 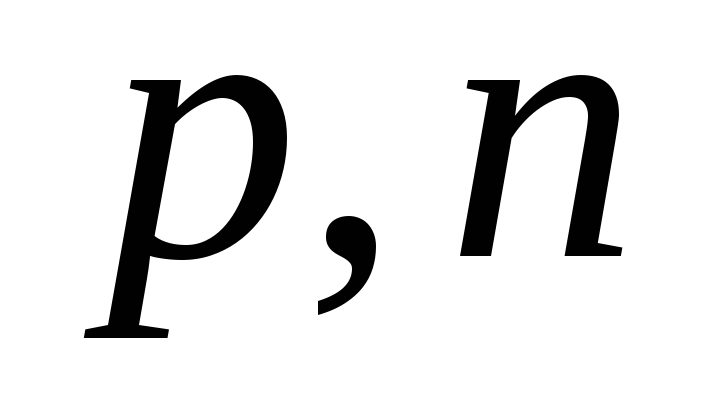 — концентрации дырок и электронов
соответственно,
— концентрации дырок и электронов
соответственно, 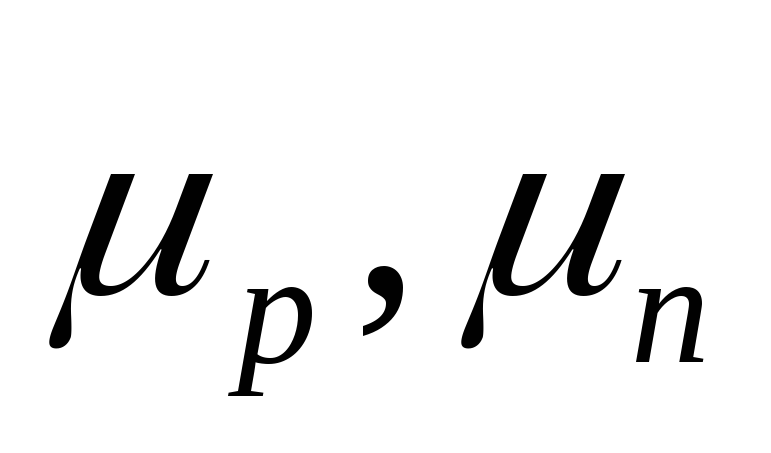 — подвижности дырок и электронов.
— подвижности дырок и электронов.
Подвижностью носителей тока называется величина, численно равная дрейфовой скорости носителей заряда, которую они приобретают в электрическом поле с напряженностью 1 В/м:
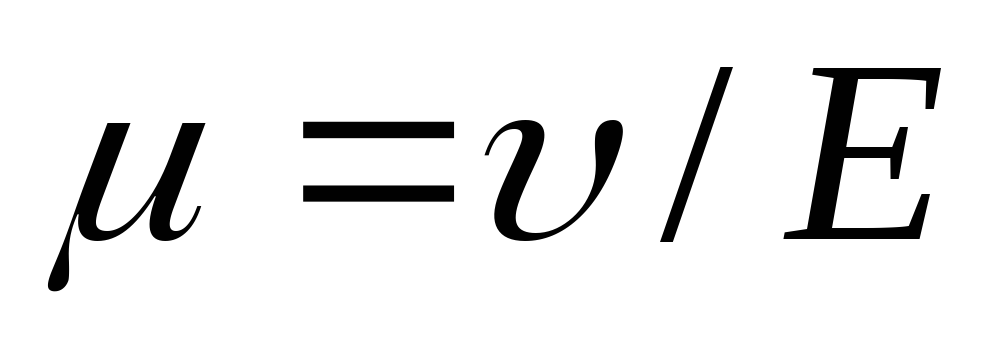 (11)
(11)
Подвижностью
свободных носителей заряда и их
концентрацией определяется
электропроводность материала  .
В частности, тип проводимости чистого
полупроводника принято определять по
соотношению подвижностей электронов
и дырок. Если подвижность, к примеру,
дырок оказывается больше подвижности
электронов, то вещество проявляет
свойства дырочного полупроводника.
.
В частности, тип проводимости чистого
полупроводника принято определять по
соотношению подвижностей электронов
и дырок. Если подвижность, к примеру,
дырок оказывается больше подвижности
электронов, то вещество проявляет
свойства дырочного полупроводника.
Следует заметить, что приведенные выше расчеты справедливы для слабых магнитных полей. В сильных полях наблюдается не просто отклонение носителей зарядов к боковым граням образца, но и их «закручивание» вокруг линий индукции магнитного поля. Критерием применимости формулы (8) является выражение:
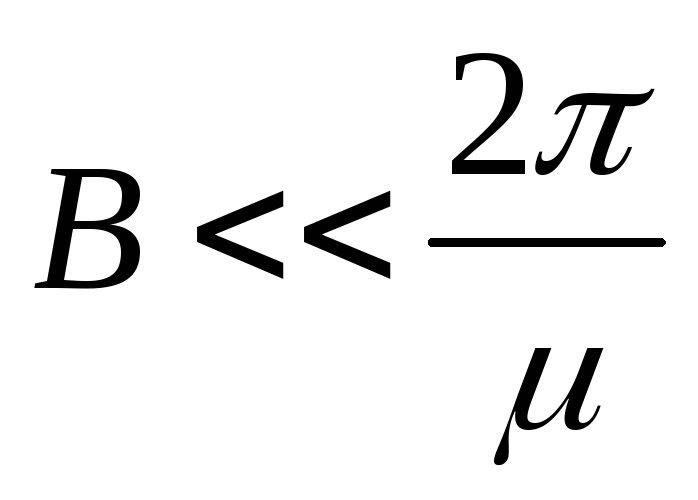 (12)
(12)
Рассмотренный эффект Холла, причиной которого является действие на движущиеся в магнитном поле заряды силы Лоренца, называется классическим эффектом Холла. Как следует из формулы (8), для классического эффекта Холла характерна линейная зависимость ЭДС от величины магнитного поля. Опыт между тем показывает, что в природе есть вещества, для которых эта зависимость нелинейна. Это свидетельствует о существовании другой причины эффекта Холла, которая может быть понята только с позиций квантовой теории твердого тела. В полупроводниках эффект Холла имеет в основном классическую природу, и для его описания справедливо выражение (8).
Эффект Холла сопровождается другим гальваномагнитным явлением — эффектом Эттингсгаузена, который заключается в возникновении в полупроводнике или металле градиента температур, в направлении, перпендикулярном току в образце и внешнему магнитному полю. Кратко его можно объяснить следующим образом: под действием силы Лоренца носители заряда движутся к боковым граням (как это было описано выше). При этом скорость их движения будет неодинаковой вследствие статистического разброса. На заряды, имеющие различную скорость магнитное поле будет действовать по-разному — быстрые носители заряда будут сильнее отклоняться и при это отдавать свою энергию кристаллической решетке, нагревая соответствующую грань. Медленные носители заряда у противоположной грани будут, наоборот, оттягивать энергию у кристаллической решетки, охлаждая ее. Тем самым противоположные грани образца будут иметь различную температуру.
Метод, основанный на использовании эффекта Холла, является наиболее эффективным современным способом определения типа проводимости полупроводников, а также концентрации свободных носителей заряда. Величина константы Холла позволяет сделать заключение о количестве примесей в полупроводнике.
Эффект Холла широко применяют при создании различных приборов и устройств в современной технике. В частности, на основе эффекта Холла работают некоторые виды ионных реактивных двигателей, датчики Холла — приборы, предназначенные для измерения величины магнитного поля, в том числе и для бесконтактного измерения магнитных полей.
Датчики Холла получили большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя, они выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора.
При помощи датчика Холла можно измерять любую физическую величину, которая однозначно связана с магнитным полем, например, силу тока. Амперметры на основе эффекта Холла рассчитаны на измерение токов до 100 кА.
Датчики Холла применяют в аналоговых перемножающих устройствах; при этом токи, пропорциональные перемножаемым величинам, используются один для питания датчика, другой — для создания магнитного поля. ЭДС Холла при этом оказывается пропорциональной произведению этих величин.
Кроме того, датчики Холла применяют в измерителях линейных и угловых перемещений, а также в измерителях градиента магнитного поля, магнитного потока и мощности электрических машин, в бесконтактных преобразователях постоянного тока в переменный. Также датчики Холла входят в конструкцию воспроизводящих головок систем звукозаписи.
23. Эффект Холла.Холловская разность потенциалов.Постоянная Холла
Эффектом Холла называется возникновение поперечного электрического поля в проводнике или полупроводнике с током при помещении его в магнитное поле. Это явление обусловлено влиянием силы Лоренца на движение носителей тока.
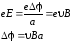 , (13)
, (13)
где а – ширина пластинки, 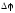 – поперечная (холловская) разность
потенциалов.
– поперечная (холловская) разность
потенциалов.
Учитывая, что сила тока
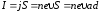
холловской разности потенциалов:
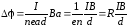 .
.
Холловская
разность потенциалов пропорциональна магнитной индукции 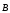 ,
силе токаI и обратно пропорциональна толщине
пластинки d.
,
силе токаI и обратно пропорциональна толщине
пластинки d.
Постоянная Холла зависит от вещества
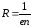 .
.
По измеренному значению постоянной Холла можно: а) определить концентрацию носителей тока в проводнике; б) судить о природе проводимости полупроводников
24. Закон полного тока для магнитного поля в вакууме. Применение теоремы о циркуляции вектора для расчета магнитных полей: магнитное поле прямого тока и соленоида
Циркуляция
вектора 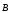 магнитного поля в вакууме.Циркуляцией
магнитной индукции
магнитного поля в вакууме.Циркуляцией
магнитной индукции 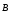 вдоль замкнутого контураL,
проведенного в магнитном поле, называется
линейный интеграл
вдоль замкнутого контураL,
проведенного в магнитном поле, называется
линейный интеграл
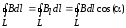 ,
,
Закон
полного тока для магнитного поля в
вакууме (теорема о циркуляции вектора 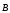 ): циркуляция вектора
): циркуляция вектора 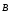 по произвольному замкнутому контуру
равна произведению магнитной постоянной
по произвольному замкнутому контуру
равна произведению магнитной постоянной 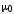 на алгебраическую
сумму токов, охватываемых этим контуром:
на алгебраическую
сумму токов, охватываемых этим контуром:
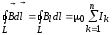 .
.
Сравнение
теорем о циркуляции векторов 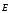 и
и 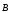 :
:
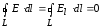 ;
;
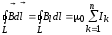 .
.
Между
ними существует принципиальное различие.
Циркуляция вектора 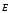 равна нулю,
т.е. электростатическое
поле является
потенциальным. Циркуляция вектора
равна нулю,
т.е. электростатическое
поле является
потенциальным. Циркуляция вектора 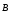 магнитного поля не равна нулю. Такое
поле называетсявихревым.
магнитного поля не равна нулю. Такое
поле называетсявихревым.
Магнитное
поле прямого тока. Применим теорему о циркуляции вектора 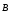 для расчета магнитного поля прямого
тока I, перпендикулярного
плоскости чертежа и направленного к
нам
для расчета магнитного поля прямого
тока I, перпендикулярного
плоскости чертежа и направленного к
нам
Магнитное поле соленоида. Соленоид – свернутый в спираль изолированный проводник, по которому течет электрический ток. Опыт показывает, что магнитное поле сосредоточенное внутри бесконечно длинного соленоида — однородно, а полем вне соленоида можно пренебречь.
25. Поток магнитной индукции. Теорема Гаусса для магнитного поля. Потокосцепление.
Элементарным потоком вектора магнитной индукции (магнитным потоком) сквозь малую площадку dS называется скалярная физическая величина, равная
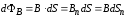 ,
,
Знак
потока магнитной индукции. Поток
вектора 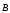 может быть как положительным, так и
отрицательным в зависимости от знака
может быть как положительным, так и
отрицательным в зависимости от знака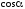 .
Знак определяется выбором положительного
направления нормали
.
Знак определяется выбором положительного
направления нормали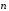 ,
которое связано с током правилом правого
винта.
,
которое связано с током правилом правого
винта.
Поток
вектора 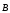 связывают с контуром, по которому течет
ток. Таким образом,магнитный
поток, создаваемый контуром через
поверхность, ограниченную им самим,
всегда положителен.
связывают с контуром, по которому течет
ток. Таким образом,магнитный
поток, создаваемый контуром через
поверхность, ограниченную им самим,
всегда положителен.
Теорема
Гаусса для поля 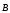 :
поток вектора магнитной индукции сквозь
произвольную замкнутую поверхность
равен нулю.
:
поток вектора магнитной индукции сквозь
произвольную замкнутую поверхность
равен нулю.
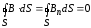 . (9)
. (9)
Этот результат является математическим выражением того, что в природе не существует магнитных зарядов – источников магнитного поля, на которых начинались бы или заканчивались бы линии магнитной индукции, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Такое поле называют соленоидальным или вихревым.
Потокосцепление- полный магнитный поток, пронизывающий электрический контур. Напр., потокосцепление многовитковой катушки индуктивности равно сумме потоков через все ее витки. Единица измерения — Вб.
Постоянная Холла Википедия
У этого термина существуют и другие значения, см. Холл.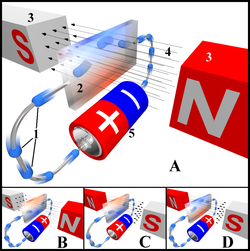 Эффект Холла
Эффект Холла1. Электроны
2. Зонд
3. Магниты
4. Магнитное поле
5. Источник тока
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.
Содержание
- 1 Свойства
- 2 Аномальный эффект Холла
- 3 Квантовый эффект Холла
- 4 Спиновый эффект Холла
- 5 Магнетосопротивление
- 6 Применение
- 7 См. также
- 8 Примечания
- 9 Литература
- 10 Ссылки
Свойства[ | ]
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
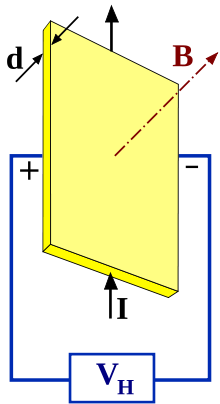
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v}
Определение концентрации и подвижности носителей тока в полупроводнике методом эффекта холла
Содержание
1. Цель работы 4
2. Теоретическая часть 4
2.1. Эффект Холла 4
2.2. Физическая природа эффекта Холла 5
3. Экспериментальная часть 10
3.1. Приборы и принадлежности 10
3.2. Требования по технике безопасности 11
3.3. Порядок выполнения работы 11
4. Требования к отчету 13
5. Контрольные вопросы 13
Список литературы 13
Лабораторная работа № 98
Определение концентрации и подвижности носителей тока в полупроводнике методом эффекта холла
1. Цель работы
Изучение эффекта Холла, измерение концентрации и подвижности носителей тока в полупроводнике с помощью определения постоянной Холла и удельного сопротивления образца.
2. Теоретическая часть
2.1. Эффект Холла
Эффектом
Холла называется появление в металле
(или полупроводнике) с током плотностью 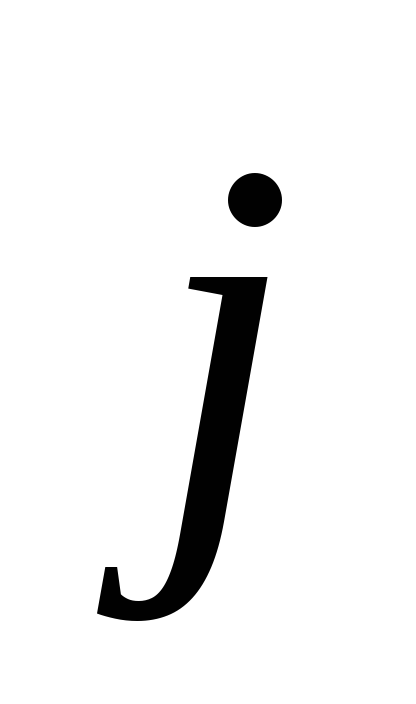 ,
помещённом в магнитное поле
,
помещённом в магнитное поле ,
электрического поля
,
электрического поля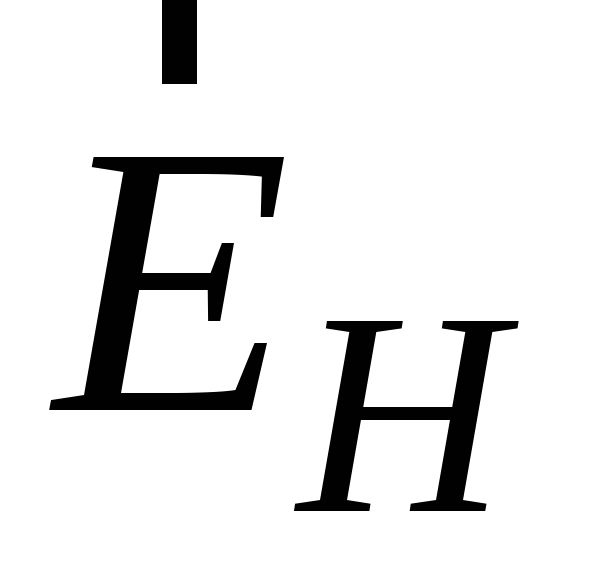 ,
перпендикулярного
,
перпендикулярного и
и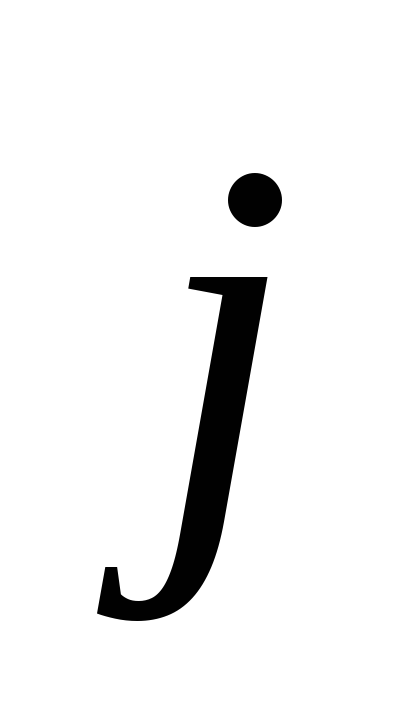 .
При этом напряжённость электрического
поля,называемого
ещё полем Холла, равна
.
При этом напряжённость электрического
поля,называемого
ещё полем Холла, равна
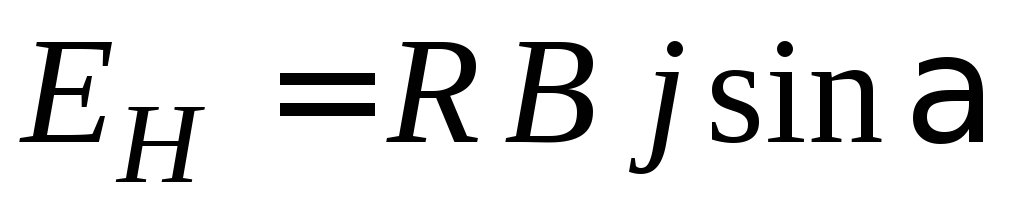 , (2.1)
, (2.1)
где
угол между векторами  и
и 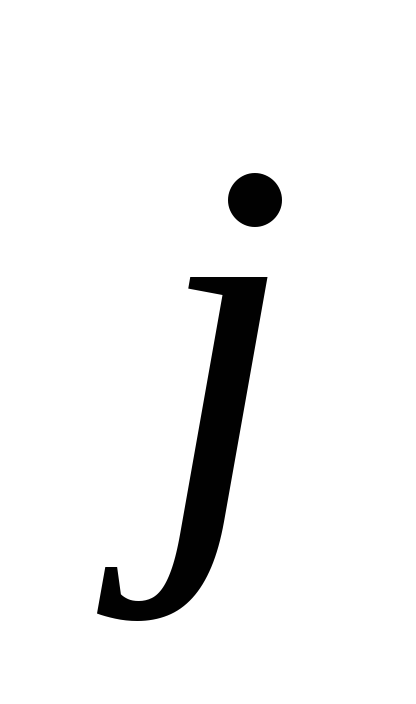 ( < 180°).
Когда
( < 180°).
Когда 
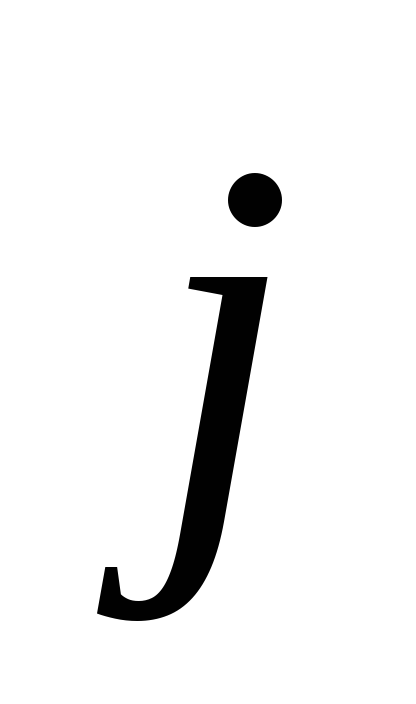 ,
то величина поля Холла
,
то величина поля Холла 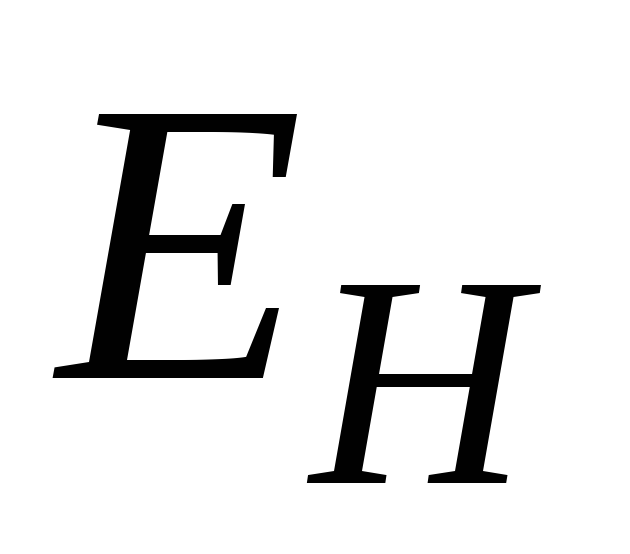 максимальна:
максимальна: 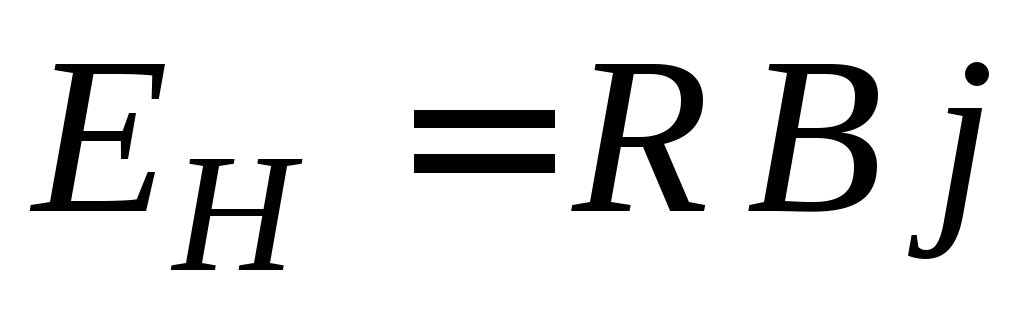 .
Коэффициент пропорциональности R называется постоянной Холла, является
основной характеристикой эффекта Холла.
Эффект был открыт американским физиком
Эдвином Холлом в 1879 в тонких пластинках
золота.
.
Коэффициент пропорциональности R называется постоянной Холла, является
основной характеристикой эффекта Холла.
Эффект был открыт американским физиком
Эдвином Холлом в 1879 в тонких пластинках
золота.
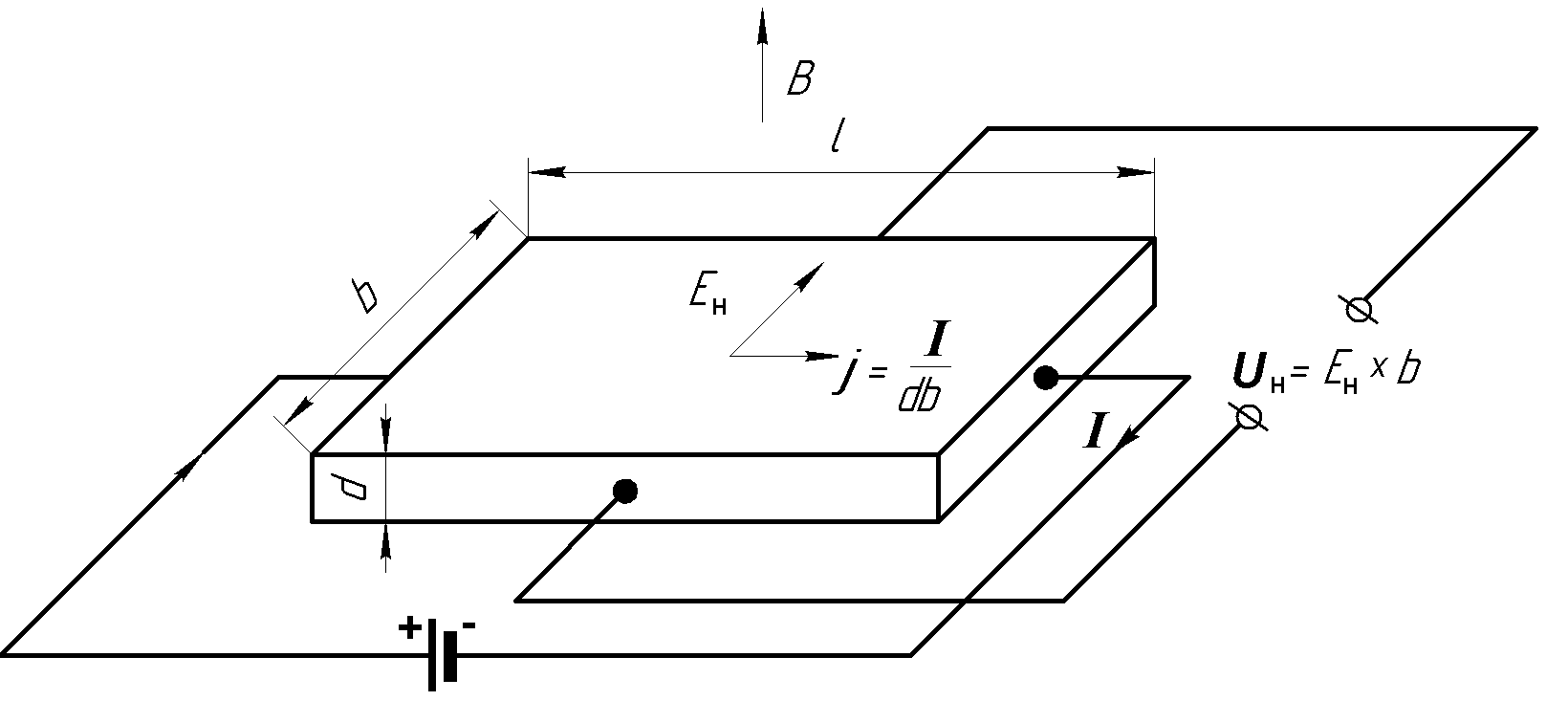
Рис. 2.1
Для наблюдения эффекта Холла вдоль прямоугольной пластины из исследуемого вещества (рис. 2.1), длина которых l значительно больше ширины b и толщины d, пропускается ток
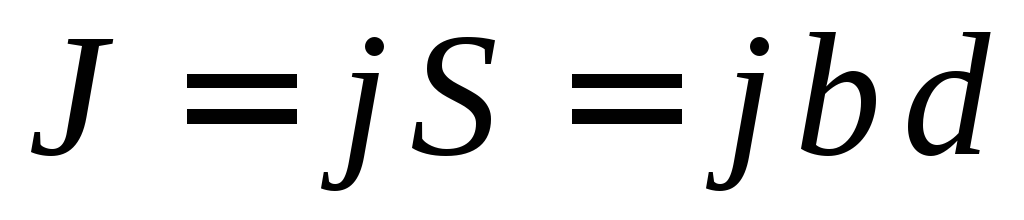 , (2.2)
, (2.2)
на рисунке магнитное поле перпендикулярно плоскости пластинки.
На
середине боковых граней, параллельных
направлению тока, расположены электроды,
между которыми измеряется ЭДС Холла 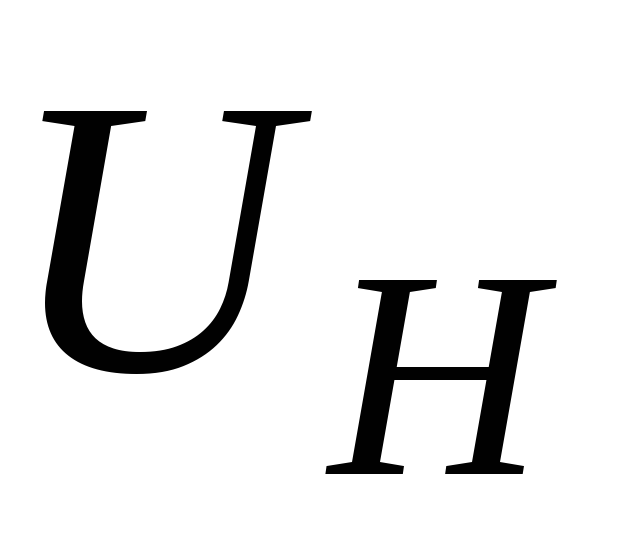
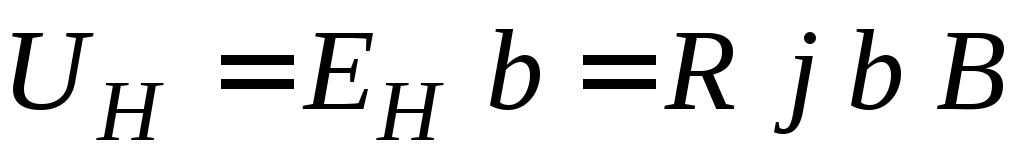 . (2.3)
. (2.3)
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на противоположное направление, то эффект Холла относится к нечётным гальваномагнитным явлениям.
2.2. Физическая природа эффекта Холла
Ток
в пластинке обусловлен упорядоченным
движением частиц – носителей зарядов q.
Под действием электрического поля
носители заряда приобретают направленное
движение (дрейф), средняя скорость
которого (дрейфовая скорость) 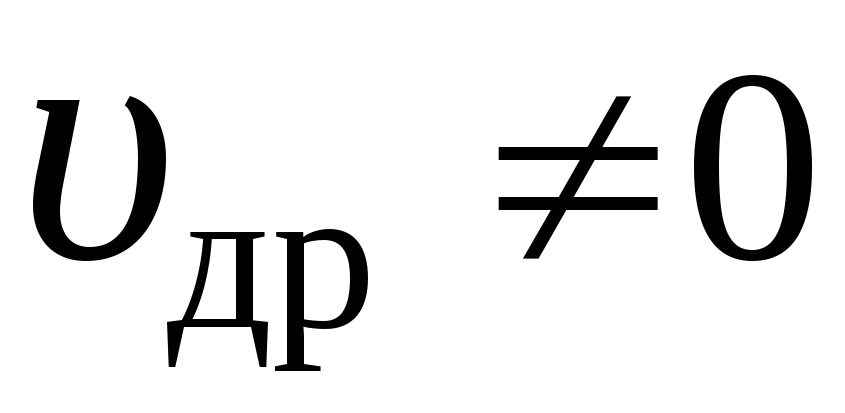 Если
концентрация носителей зарядов – n0,
а средняя скорость их упорядоченного
движения частиц –
Если
концентрация носителей зарядов – n0,
а средняя скорость их упорядоченного
движения частиц –  ,
то плотность тока равна
,
то плотность тока равна
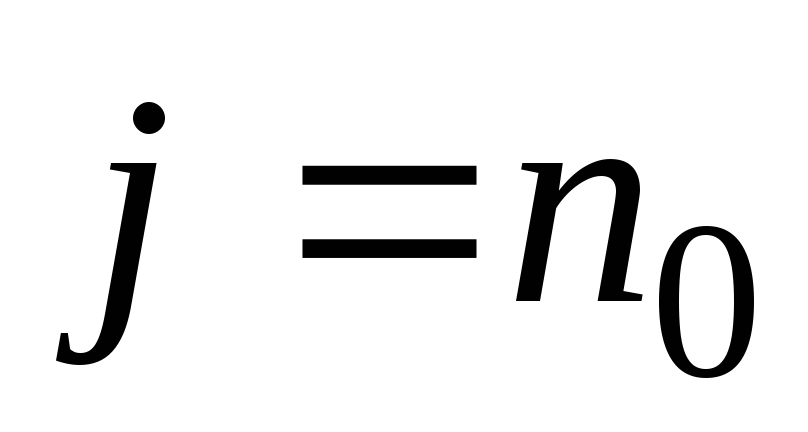
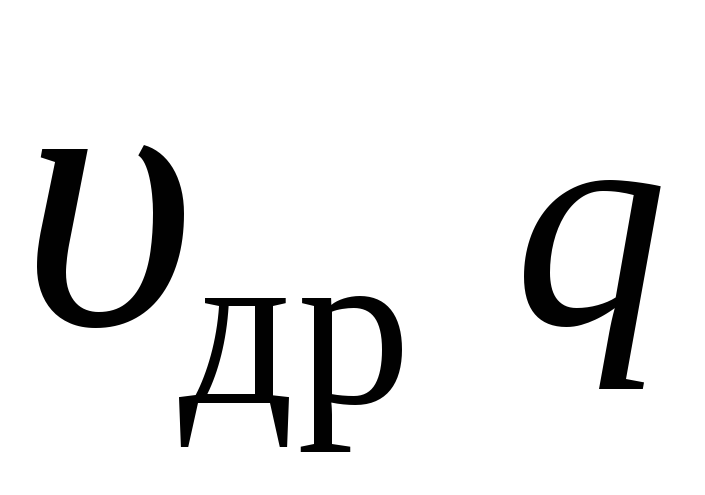 . (2.4)
. (2.4)
Если
заряд частиц, образующих ток q > 0,
то их скорость  совпадает с направлением тока, если же
зарядq < 0,то
скорость частиц
совпадает с направлением тока, если же
зарядq < 0,то
скорость частиц  противоположна по направлению вектору
противоположна по направлению вектору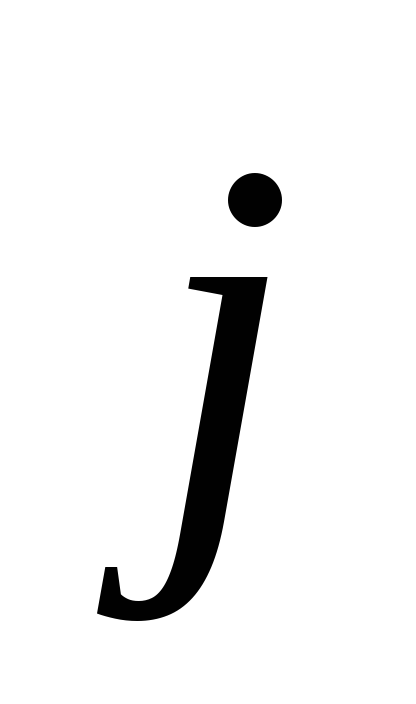 .
.
На
частицу, движущуюся в магнитном поле с
индукцией  ,
действует магнитная составляющая силы
Лоренца
,
действует магнитная составляющая силы
Лоренца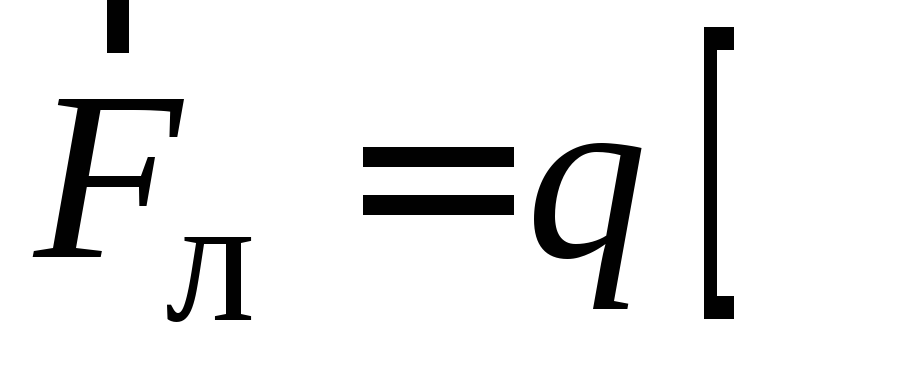
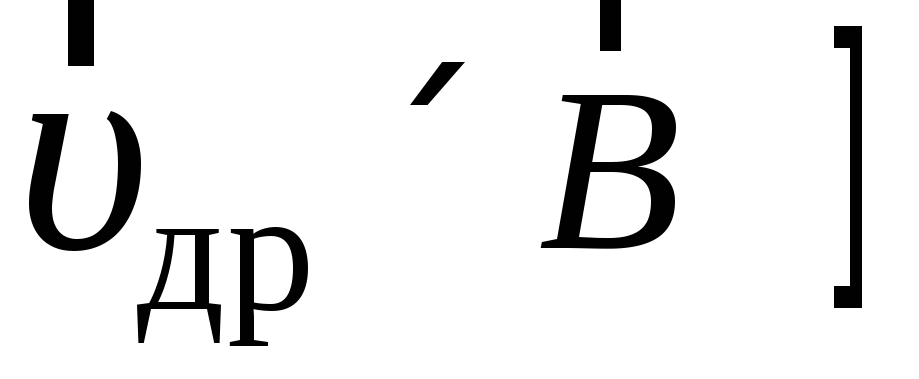 .
При указанных на рис. 2.2 направлениях
тока в пластинке, вектора
.
При указанных на рис. 2.2 направлениях
тока в пластинке, вектора и знака зарядаq сила
и знака зарядаq сила 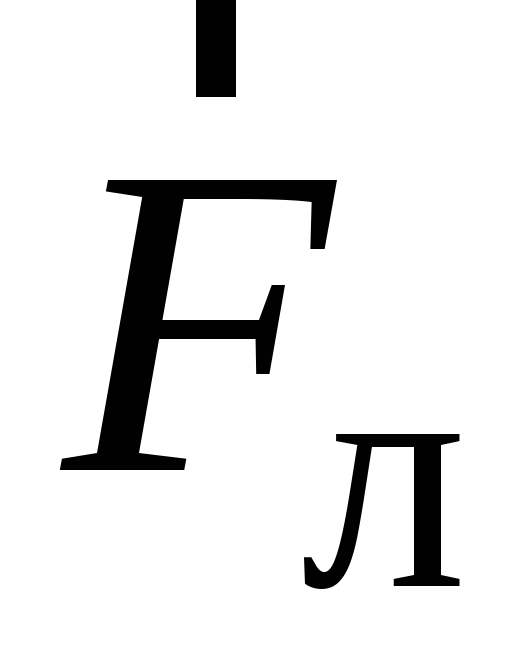 направлена
вверх.
направлена
вверх.
Под
действием силы 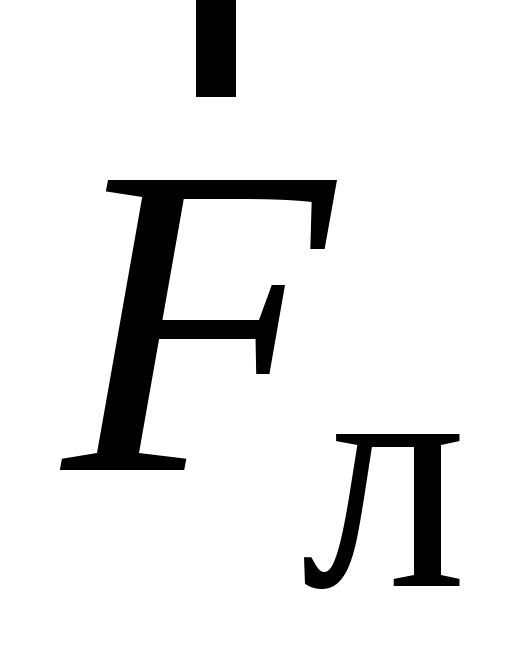 частицы отклоняются к верхней грани
пластинки, так что на верхней грани
возникает избыток отрицательных зарядов,
а на нижней – избыток зарядов
противоположного знака.
частицы отклоняются к верхней грани
пластинки, так что на верхней грани
возникает избыток отрицательных зарядов,
а на нижней – избыток зарядов
противоположного знака.

Следовательно,
возникает дополнительное поперечное
электрическое поле 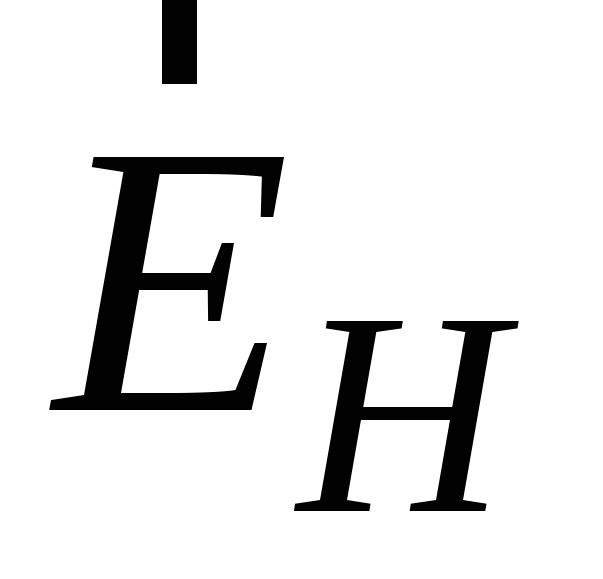 .
Сила
.
Сила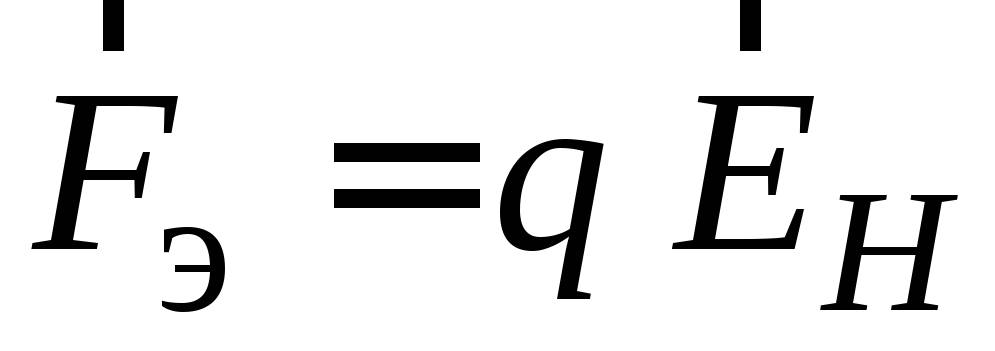 ,
действующая со стороны поперечного
электрического поля на зарядq,
направлена в сторону, противоположную
силе
,
действующая со стороны поперечного
электрического поля на зарядq,
направлена в сторону, противоположную
силе 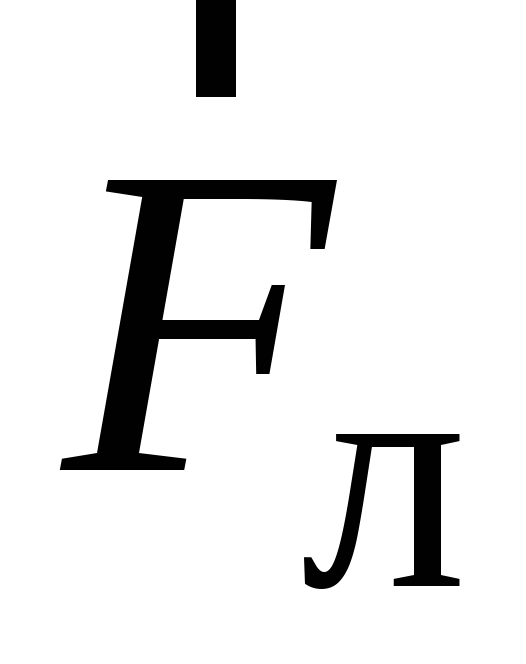 .
В случае установившегося стационарного
распределения зарядов в поперечном
направлении полная сила Лоренца,
действующая на зарядq равна нулю
.
В случае установившегося стационарного
распределения зарядов в поперечном
направлении полная сила Лоренца,
действующая на зарядq равна нулю
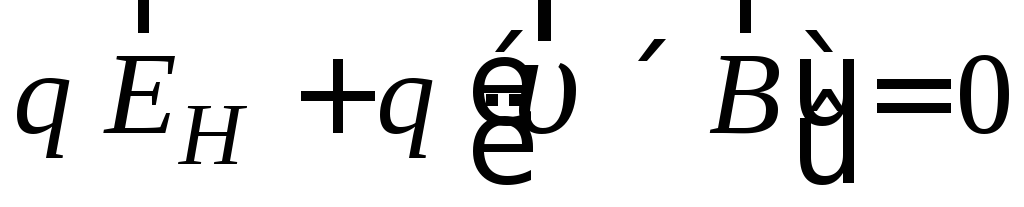 . (2.5)
. (2.5)
В скалярном виде уравнение (2.5) имеет вид
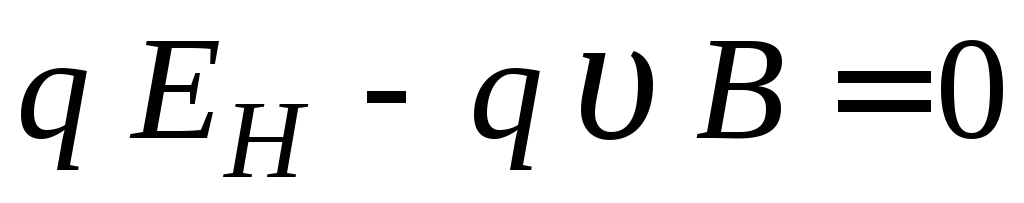 . (2.6)
. (2.6)
Отсюда
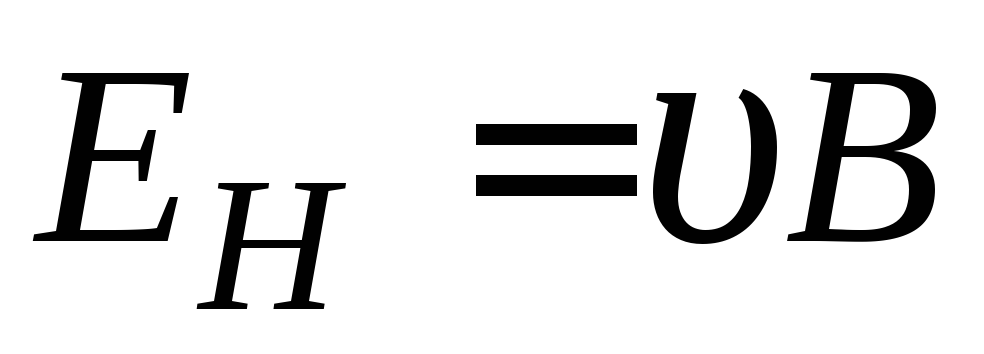 . (2.7)
. (2.7)
Поле 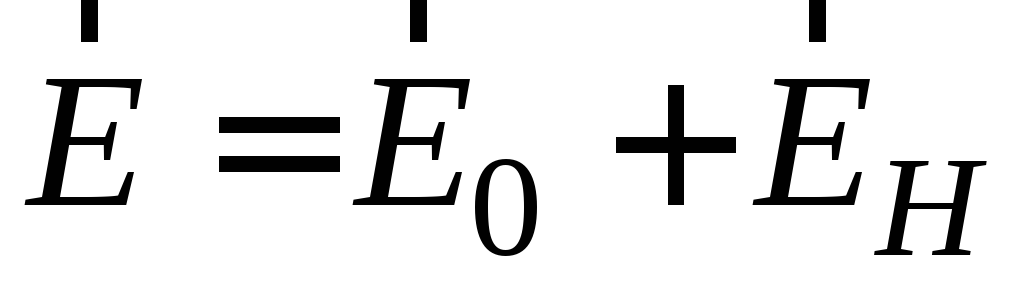 .
Эквипотенциальные поверхности
перпендикулярны к вектору напряжённости
поля
.
Эквипотенциальные поверхности
перпендикулярны к вектору напряжённости
поля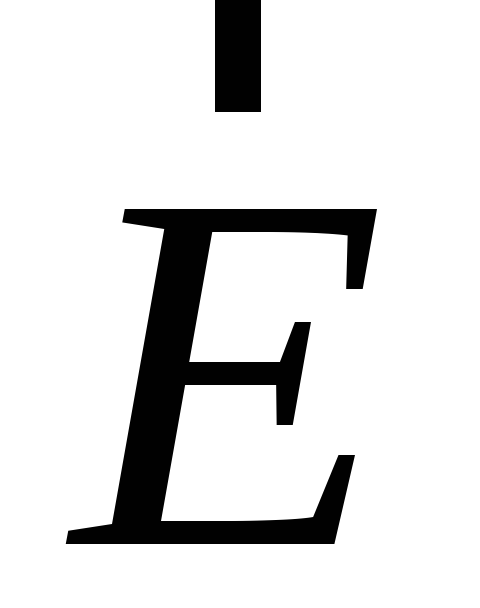 поэтому, они повернутся и займут
положение, изображённое на рис. 2.2
пунктиром. Точки 1 и 2, которые
прежде лежали на одной и той же
эквипотенциальной поверхности, теперь
имеют разные потенциалы. Чтобы найти
напряжение, возникающее между этими
точками, нужно умножить расстояние
между ними на напряженность
поэтому, они повернутся и займут
положение, изображённое на рис. 2.2
пунктиром. Точки 1 и 2, которые
прежде лежали на одной и той же
эквипотенциальной поверхности, теперь
имеют разные потенциалы. Чтобы найти
напряжение, возникающее между этими
точками, нужно умножить расстояние
между ними на напряженность 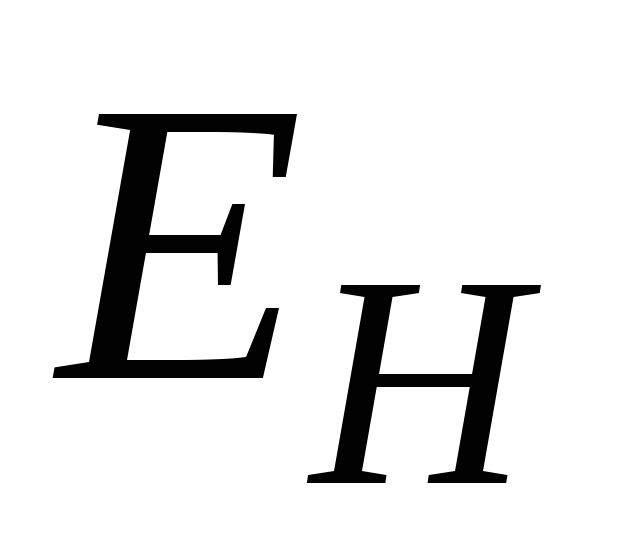
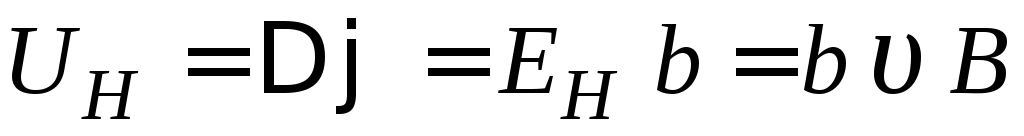 . (2.8)
. (2.8)
Из уравнения (2.4) следует, что
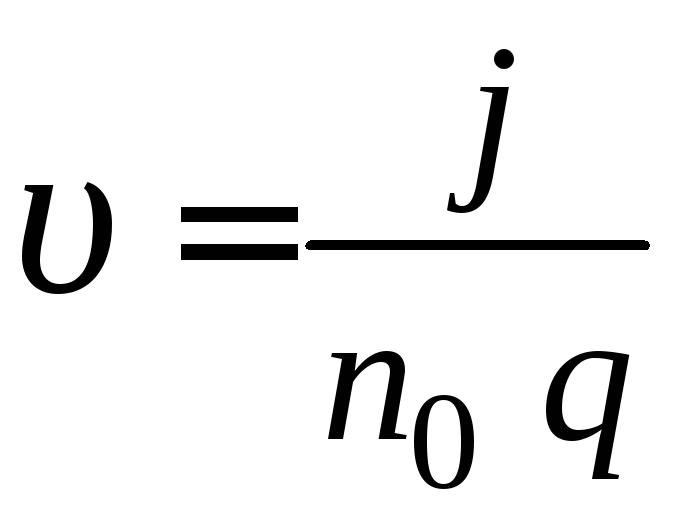 . (2.9)
. (2.9)
Следовательно,
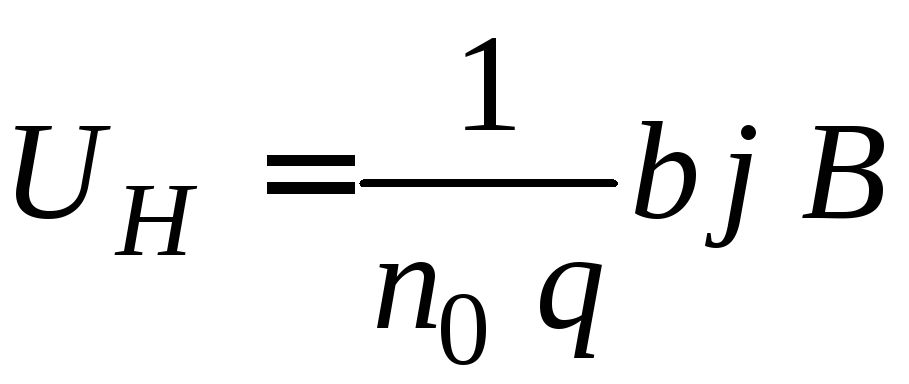 . (2.10)
. (2.10)
Таким образом, полученный результат совпадает с экспериментальной формулой (2.3). Из сравнения (2.3) и (2.10) следует, что постоянная Холла равна
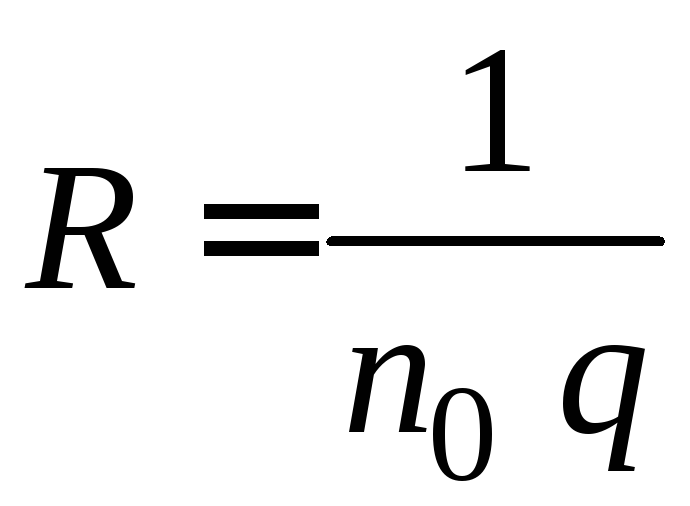 . (2.11)
. (2.11)
Из
формулы (2.11) следует, что знак разности
потенциалов, а следовательно, и постоянной
Холла совпадает со знаком заряда q частиц,
обуславливающих проводимость данного
материала. Для металлов, у которых
концентрация носителей (электронов
проводимости) близка
к плотности атомов  ,R ≈ 10-3 см/Кл,
у полупроводников концентрация носителей
значительно меньше и R ≈ 10-5 см/Кл.
Постоянная Холла может быть выражена
через подвижность носителей заряда
µ = q τ/m* и удельную электропроводность
,R ≈ 10-3 см/Кл,
у полупроводников концентрация носителей
значительно меньше и R ≈ 10-5 см/Кл.
Постоянная Холла может быть выражена
через подвижность носителей заряда
µ = q τ/m* и удельную электропроводность
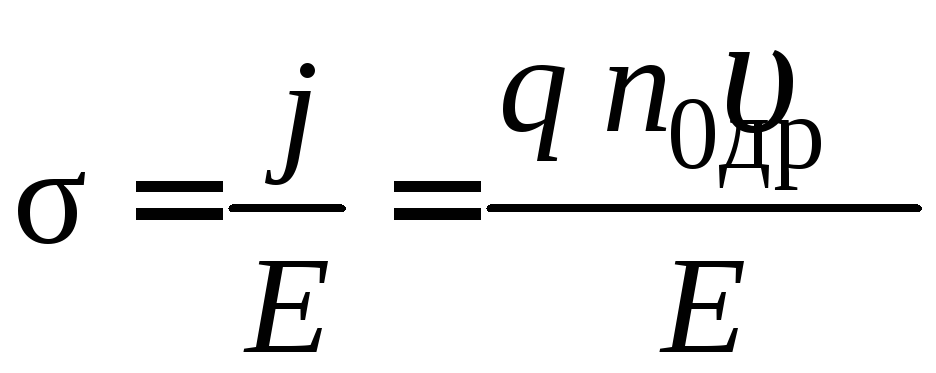 , (2.12)
, (2.12)
где m* – эффективная масса носителей, τ – среднее время между двумя последовательными соударениями с рассеивающими центрами, тогда
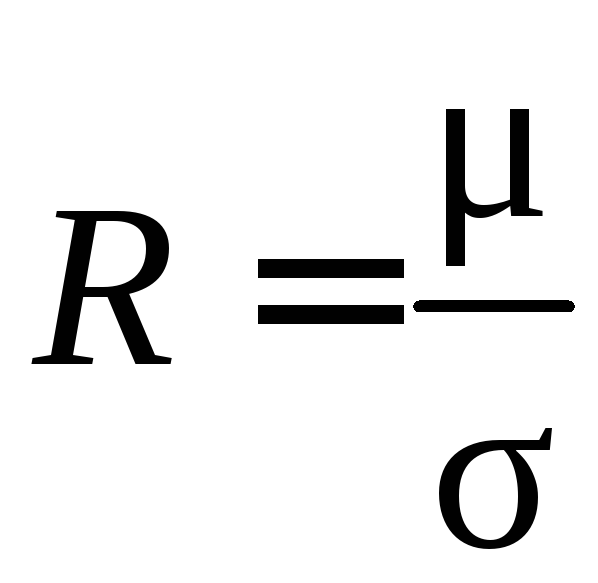 . (2.13)
. (2.13)
Подвижностью
μ носителей тока называется отношение
средней упорядоченной скорости  носителей (электронов и дырок) к
напряженности внешнего электрического
поля Е:
носителей (электронов и дырок) к
напряженности внешнего электрического
поля Е:  ,
тогда удельная проводимость образца
определяется формулой
,
тогда удельная проводимость образца
определяется формулой
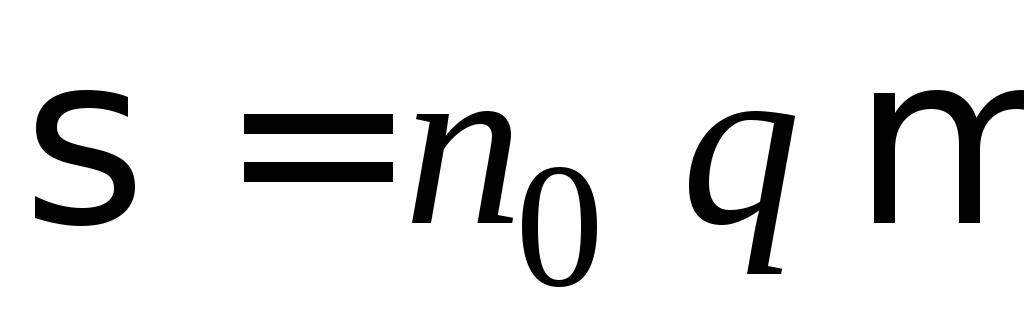 . (2.14)
. (2.14)
На рис. 2.3 сопоставлен эффект Холла для образцов с положительными и отрицательными носителями.
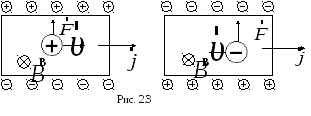
Направление силы Лоренца изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. Следовательно, при одинаковом направлении тока и магнитного поля сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней грани (на рис. 2.3) выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока. Значение постоянной Холла позволяет определить концентрацию носителей заряда, если характер проводимости и их заряд известны.
Все металлы обладают электронной проводимостью, то, казалось бы, что знак эффекта у всех у них должен быть одинаков, так как под действием магнитного поля поток электронов отклоняется вполне определённым образом. Тем не менее, у ряда металлов знак эффекта Холла оказался как раз противоположным. Эту закономерность объясняет зонная теория твёрдого тела. Если зона проводимости металла укомплектована менее чем наполовину, то электроны такой зоны ведут себя нормально, как частицы, обладающие положительной эффективной массой и отрицательным зарядом. Знак постоянной Холла у таких металлов будет отрицательным (к ним относятся металлы 1-й группы таблицы Менделеева). Если зона проводимости металла укомплектована почти полностью. То остающиеся в ней незаполненные уровни – дырки ведут себя как частицы, обладающие положительной эффективной массой и положительным зарядом. Такие металлы имеют дырочную проводимость, вследствие чего знак постоянной Холла у них положительный (аномальный эффект Холла). К таким металлам относятся Be, Cd, Zn и др. Более корректные вычисления, основанные на кинетическом уравнении Больцмана и классической статистике, приводит к результату
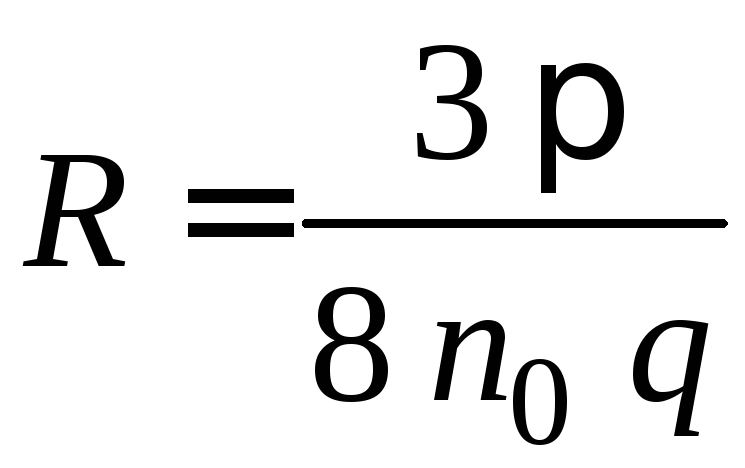 . (2.15)
. (2.15)
Если же применить к электронам в металле статистику Ферми-Дирака, то результаты таких вычислений совпадают с формулой (2.11).
Рассмотренный вывод постоянной Холла является весьма приближенным, так как не учитывает скорость хаотического движения электронов. Более строгий расчет приводит к выражению
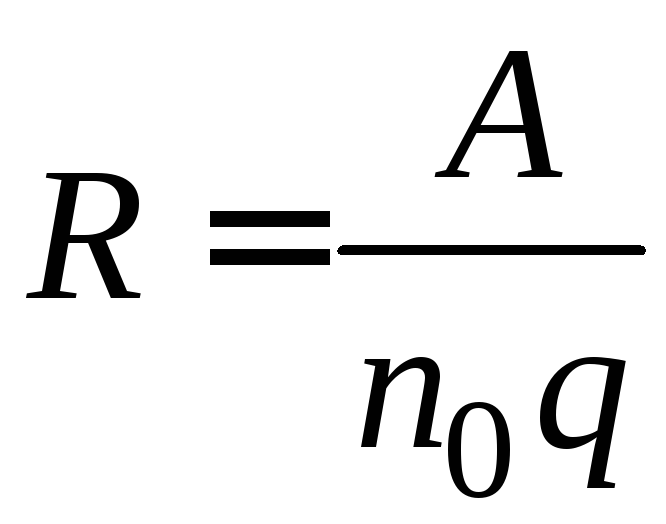 , (2.16)
, (2.16)
где А – постоянная, зависящая от механизма рассеяния носителей заряда. Для полупроводников, обладающих решёткой типа алмаза (германий, кремний, InSb, GaSb, AlAs и др.) и имеющих носителей одного знака
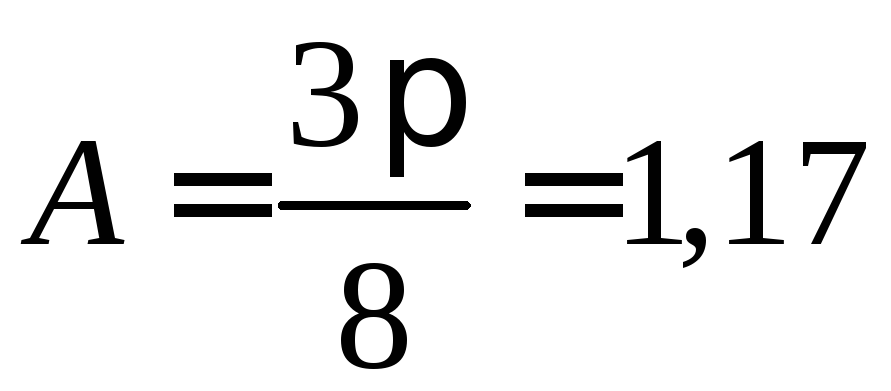 и
и 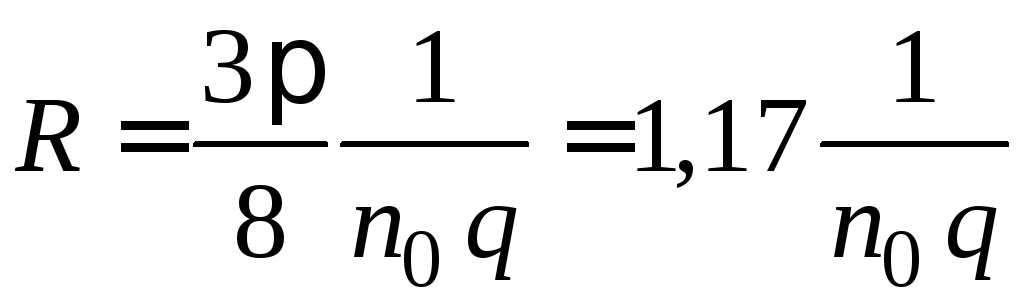 , (2.17)
, (2.17)
если основное значение имеет рассеяние носителей на тепловых колебаниях решётки, и
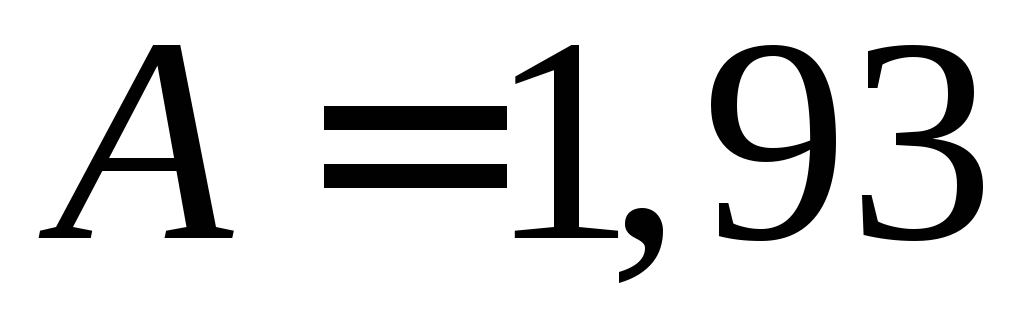 ,
, 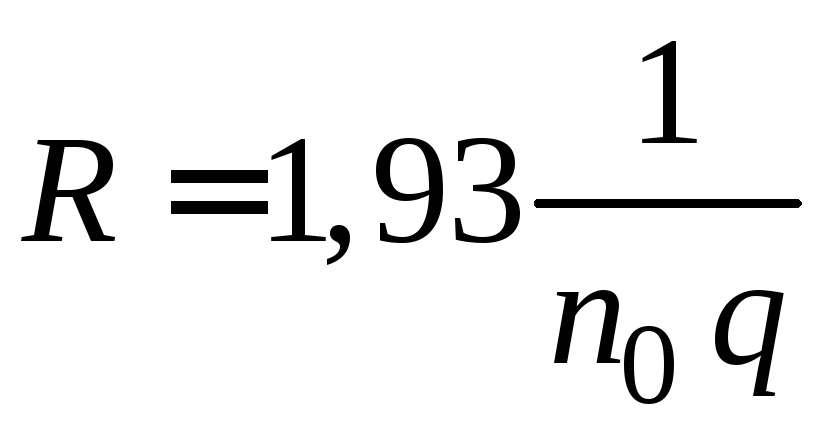 , (2.18)
, (2.18)
если основное значение имеет рассеяние на ионизированных атомах примесей.
Для полупроводников, имеющих два вида носителей – электроны и дырки постоянная Холла равна
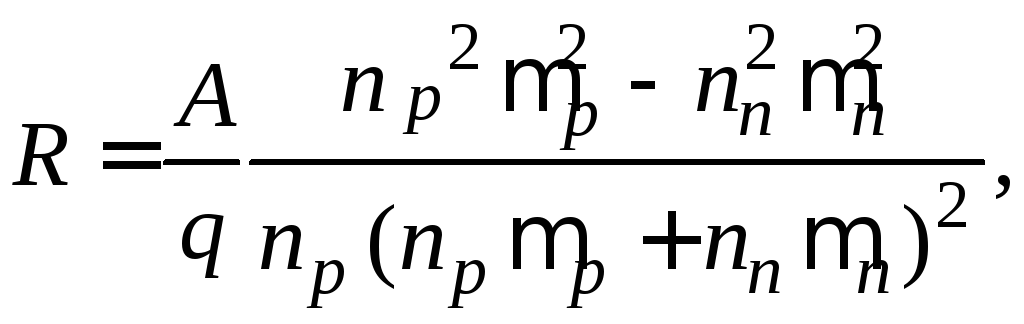 (2.19)
(2.19)
где 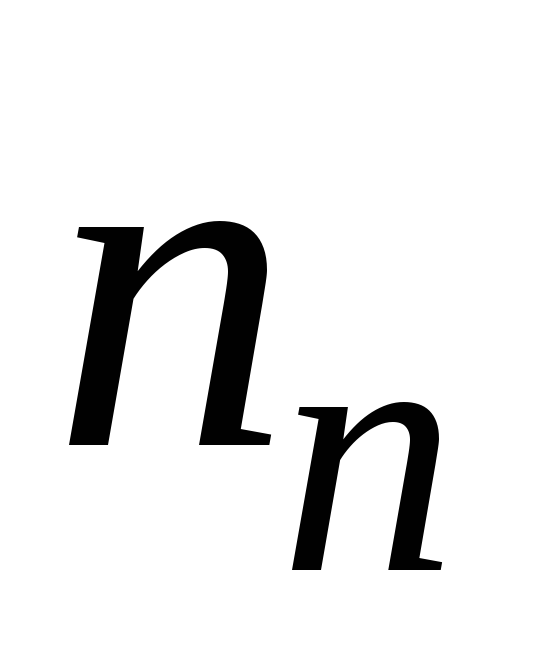 и
и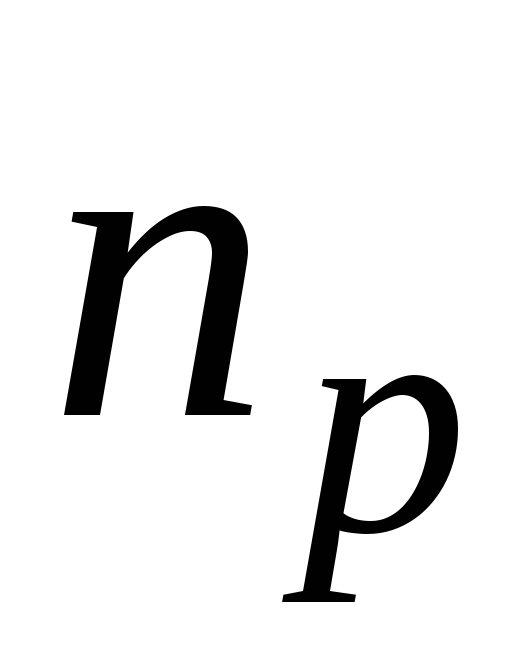 – концентрации
электронов и дырок,
– концентрации
электронов и дырок,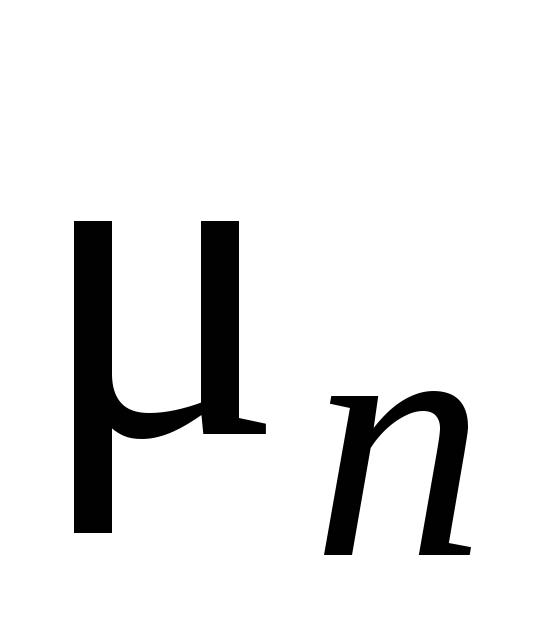 и
и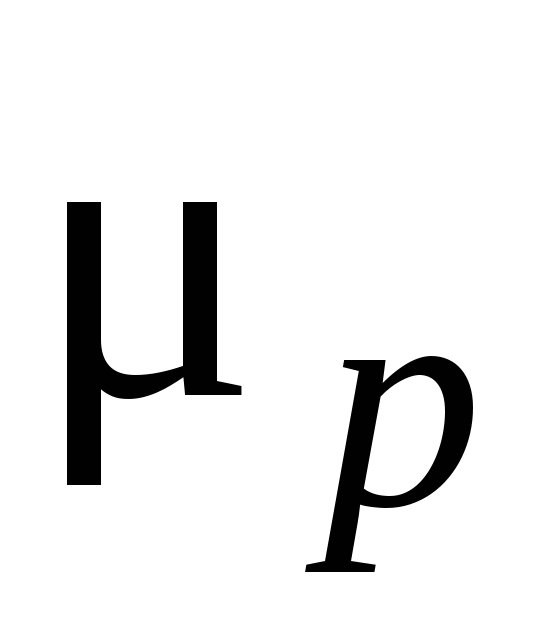 – их
подвижности,A = const,
зависящая от механизма рассеяния.
– их
подвижности,A = const,
зависящая от механизма рассеяния.
В зависимости от типов носителей зарядов знак R может быть как положительный так и отрицательный, что позволяет не спутать в эксперименте эффект Холла с другими возможными эффектами, не зависящими от направления тока.
Эффект Холла получил широкое практическое применение. На его основе оказалось возможным создание ряда устройств и приборов, обладающих исключительно ценными свойствами — приборов для измерения постоянных и переменных магнитных полей, для измерения токов высокой частоты, электронных преобразователей, усилителей и генераторов электрических колебаний и др.
Определение концентрации и подвижности носителей тока в полупроводнике методом эффекта холла
Содержание
1. Цель работы 4
2. Теоретическая часть 4
2.1. Эффект Холла 4
2.2. Физическая природа эффекта Холла 5
3. Экспериментальная часть 10
3.1. Приборы и принадлежности 10
3.2. Требования по технике безопасности 11
3.3. Порядок выполнения работы 11
4. Требования к отчету 13
5. Контрольные вопросы 13
Список литературы 13
Лабораторная работа № 98
Определение концентрации и подвижности носителей тока в полупроводнике методом эффекта холла
1. Цель работы
Изучение эффекта Холла, измерение концентрации и подвижности носителей тока в полупроводнике с помощью определения постоянной Холла и удельного сопротивления образца.
2. Теоретическая часть
2.1. Эффект Холла
Эффектом
Холла называется появление в металле
(или полупроводнике) с током плотностью 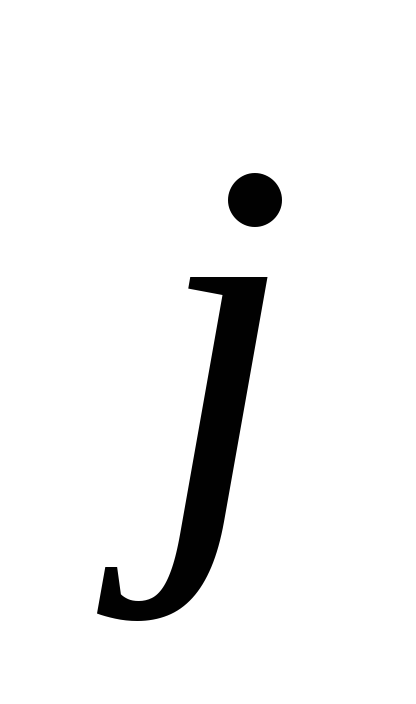 ,
помещённом в магнитное поле
,
помещённом в магнитное поле ,
электрического поля
,
электрического поля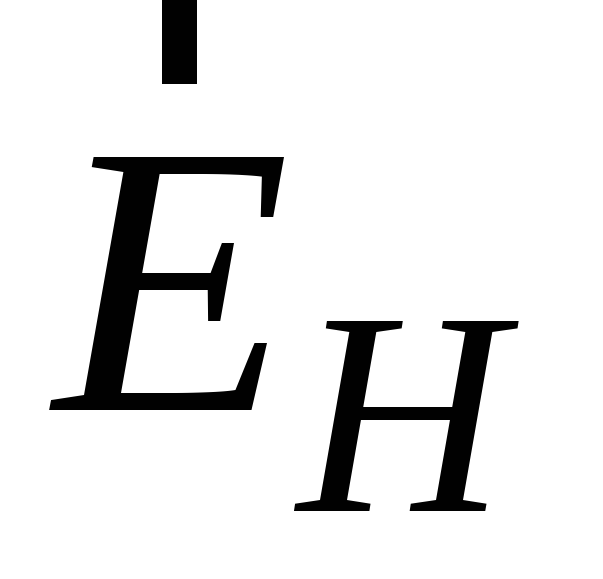 ,
перпендикулярного
,
перпендикулярного и
и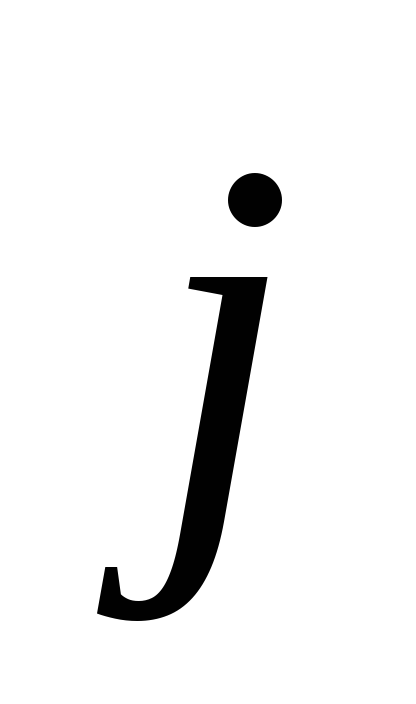 .
При этом напряжённость электрического
поля,называемого
ещё полем Холла, равна
.
При этом напряжённость электрического
поля,называемого
ещё полем Холла, равна
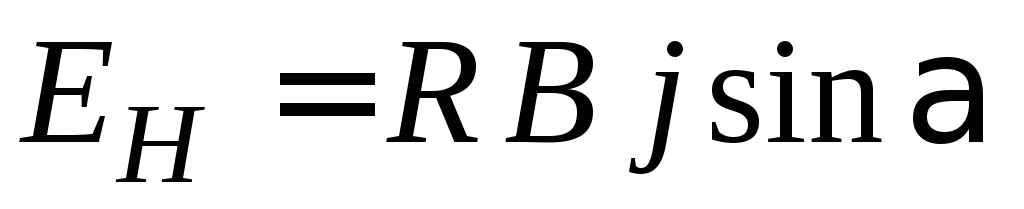 , (2.1)
, (2.1)
где
угол между векторами  и
и 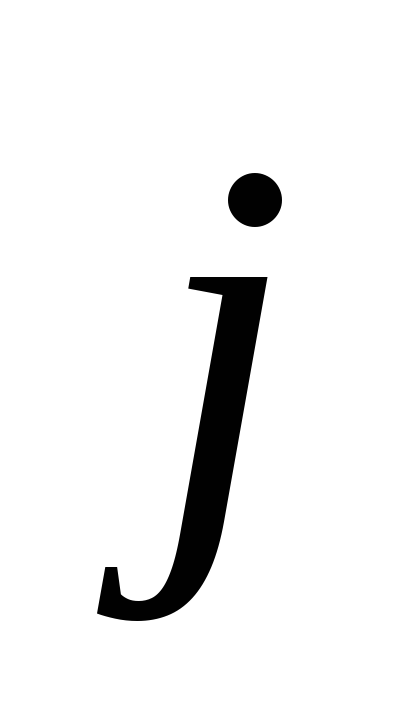 ( < 180°).
Когда
( < 180°).
Когда 
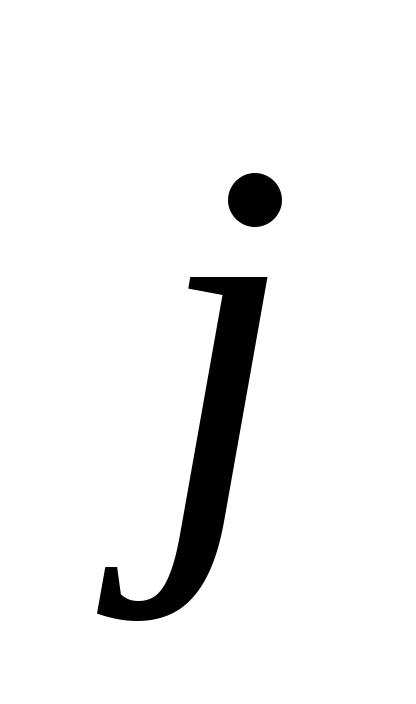 ,
то величина поля Холла
,
то величина поля Холла 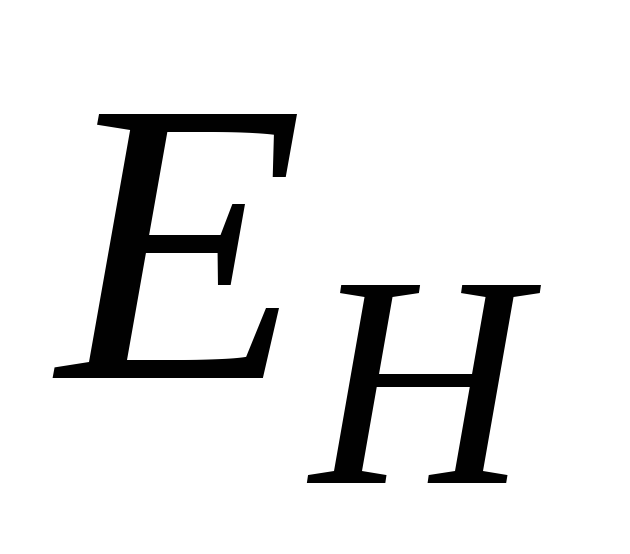 максимальна:
максимальна: 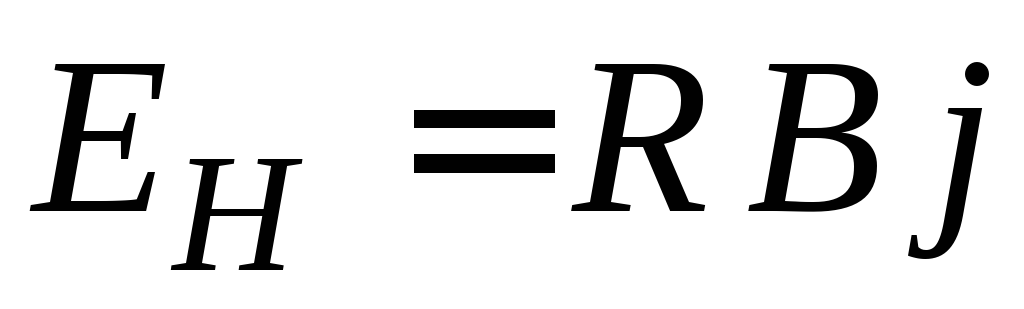 .
Коэффициент пропорциональности R называется постоянной Холла, является
основной характеристикой эффекта Холла.
Эффект был открыт американским физиком
Эдвином Холлом в 1879 в тонких пластинках
золота.
.
Коэффициент пропорциональности R называется постоянной Холла, является
основной характеристикой эффекта Холла.
Эффект был открыт американским физиком
Эдвином Холлом в 1879 в тонких пластинках
золота.
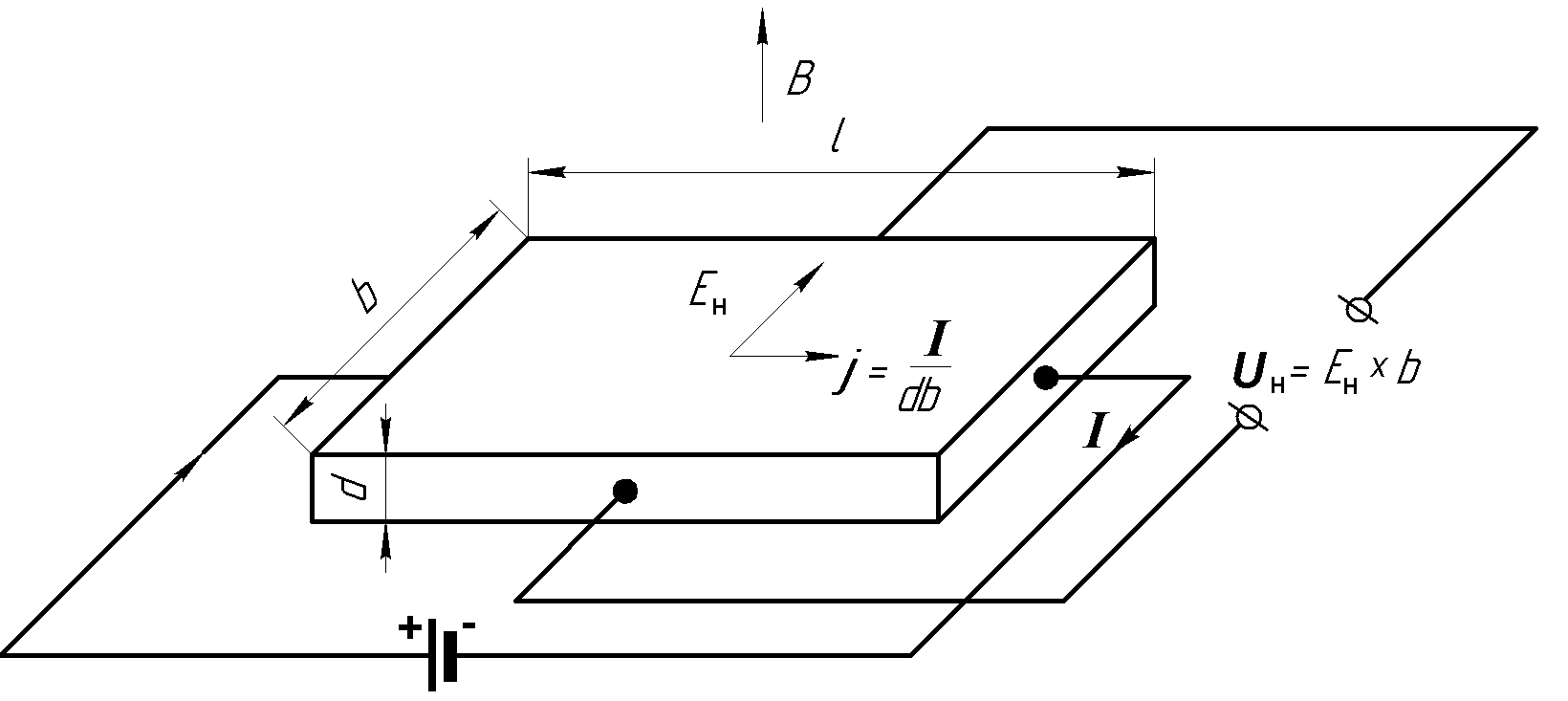
Рис. 2.1
Для наблюдения эффекта Холла вдоль прямоугольной пластины из исследуемого вещества (рис. 2.1), длина которых l значительно больше ширины b и толщины d, пропускается ток
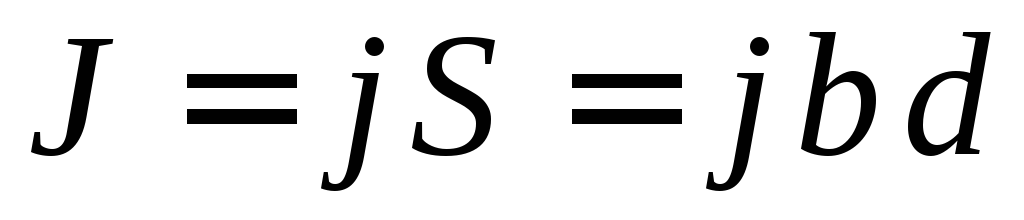 , (2.2)
, (2.2)
на рисунке магнитное поле перпендикулярно плоскости пластинки.
На
середине боковых граней, параллельных
направлению тока, расположены электроды,
между которыми измеряется ЭДС Холла 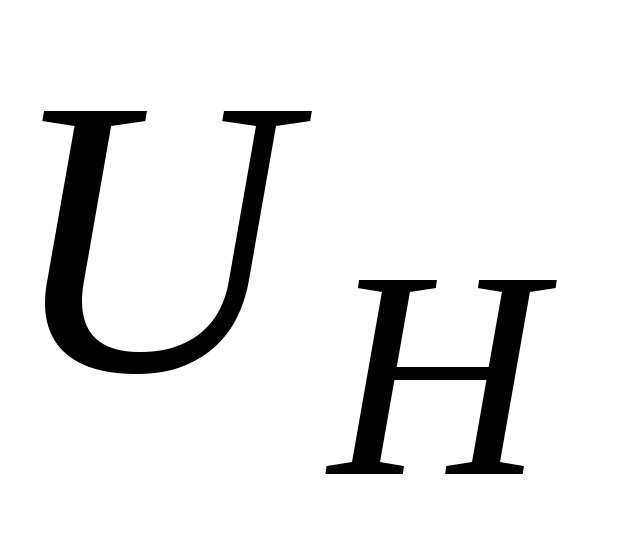
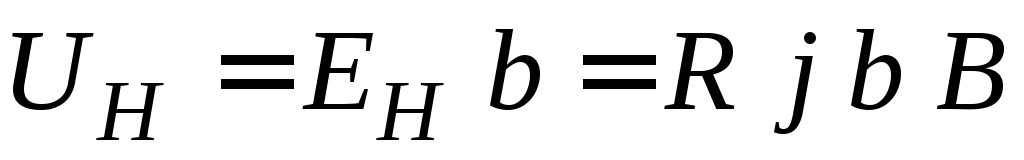 . (2.3)
. (2.3)
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на противоположное направление, то эффект Холла относится к нечётным гальваномагнитным явлениям.
2.2. Физическая природа эффекта Холла
Ток
в пластинке обусловлен упорядоченным
движением частиц – носителей зарядов q.
Под действием электрического поля
носители заряда приобретают направленное
движение (дрейф), средняя скорость
которого (дрейфовая скорость) 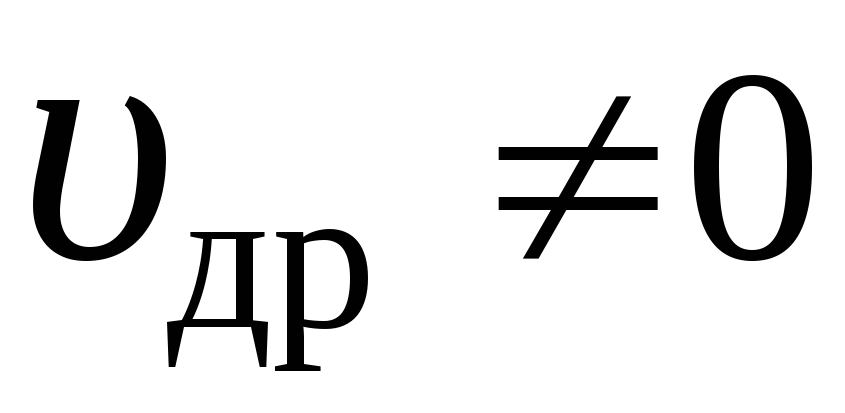 Если
концентрация носителей зарядов – n0,
а средняя скорость их упорядоченного
движения частиц –
Если
концентрация носителей зарядов – n0,
а средняя скорость их упорядоченного
движения частиц –  ,
то плотность тока равна
,
то плотность тока равна
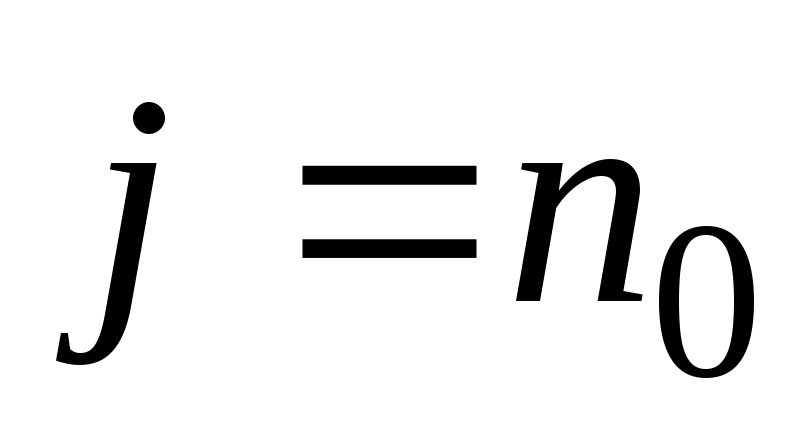
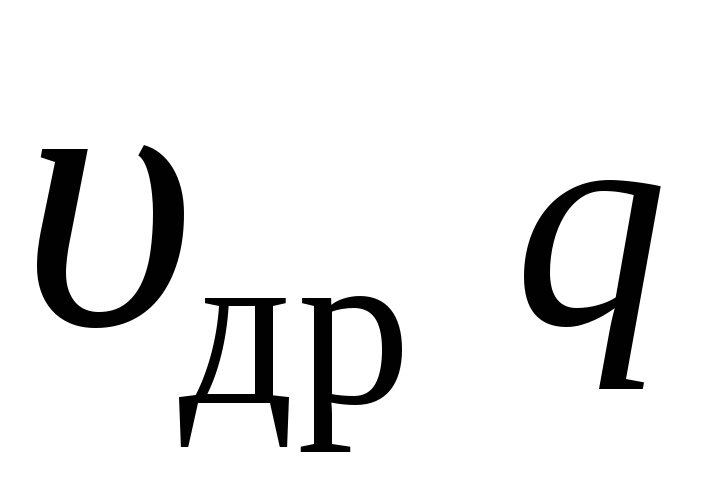 . (2.4)
. (2.4)
Если
заряд частиц, образующих ток q > 0,
то их скорость  совпадает с направлением тока, если же
зарядq < 0,то
скорость частиц
совпадает с направлением тока, если же
зарядq < 0,то
скорость частиц  противоположна по направлению вектору
противоположна по направлению вектору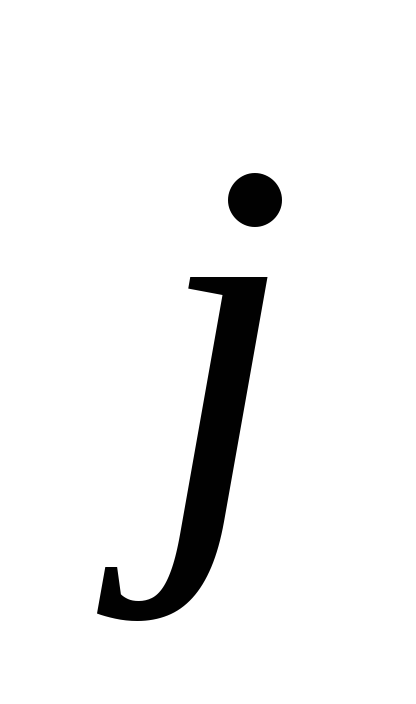 .
.
На
частицу, движущуюся в магнитном поле с
индукцией  ,
действует магнитная составляющая силы
Лоренца
,
действует магнитная составляющая силы
Лоренца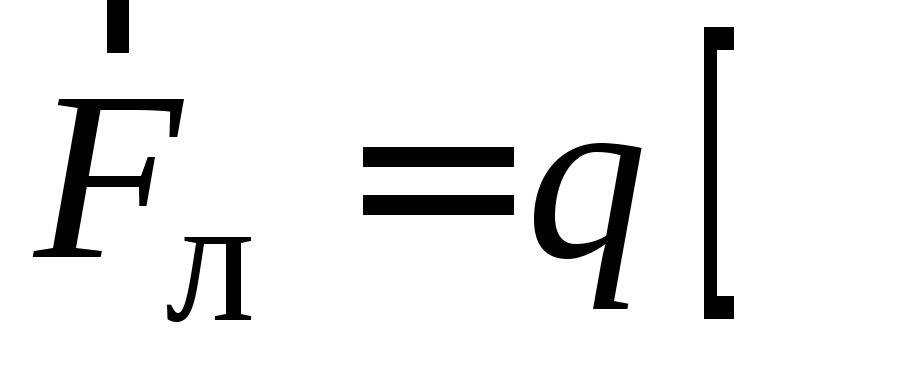
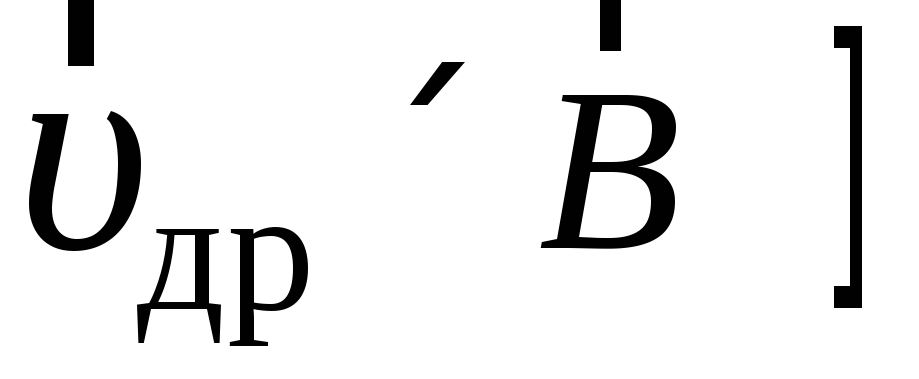 .
При указанных на рис. 2.2 направлениях
тока в пластинке, вектора
.
При указанных на рис. 2.2 направлениях
тока в пластинке, вектора и знака зарядаq сила
и знака зарядаq сила 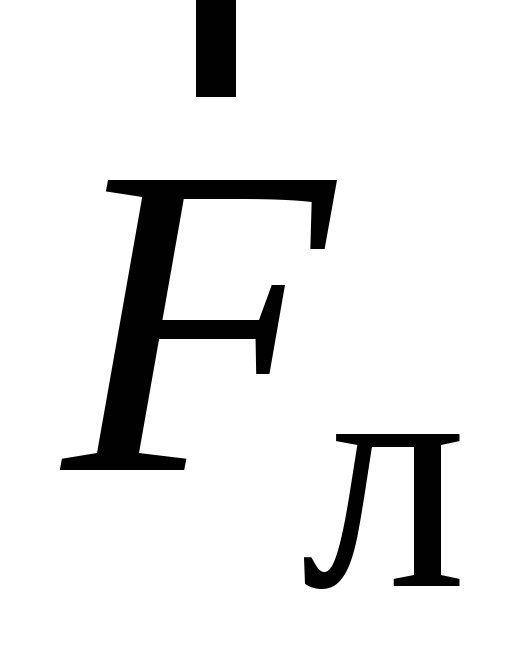 направлена
вверх.
направлена
вверх.
Под
действием силы 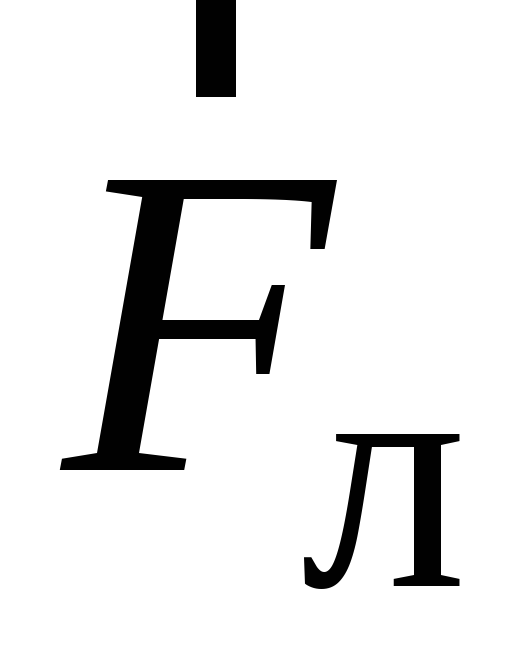 частицы отклоняются к верхней грани
пластинки, так что на верхней грани
возникает избыток отрицательных зарядов,
а на нижней – избыток зарядов
противоположного знака.
частицы отклоняются к верхней грани
пластинки, так что на верхней грани
возникает избыток отрицательных зарядов,
а на нижней – избыток зарядов
противоположного знака.

Следовательно,
возникает дополнительное поперечное
электрическое поле 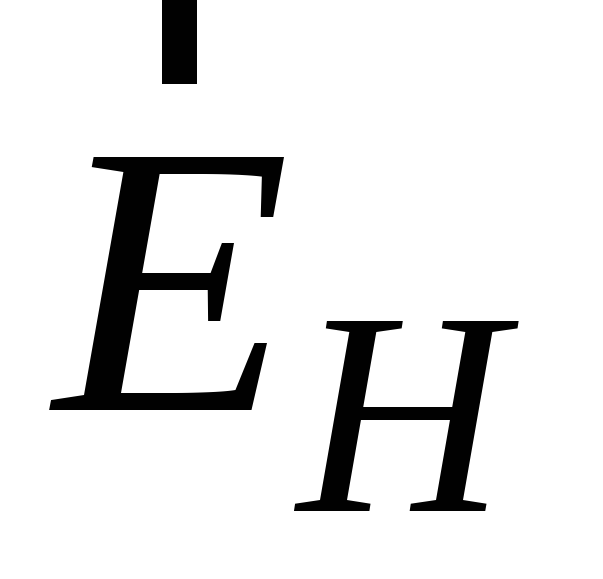 .
Сила
.
Сила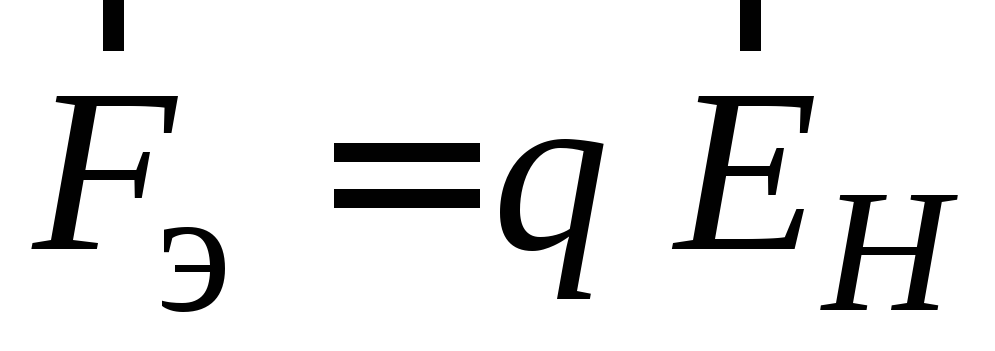 ,
действующая со стороны поперечного
электрического поля на зарядq,
направлена в сторону, противоположную
силе
,
действующая со стороны поперечного
электрического поля на зарядq,
направлена в сторону, противоположную
силе 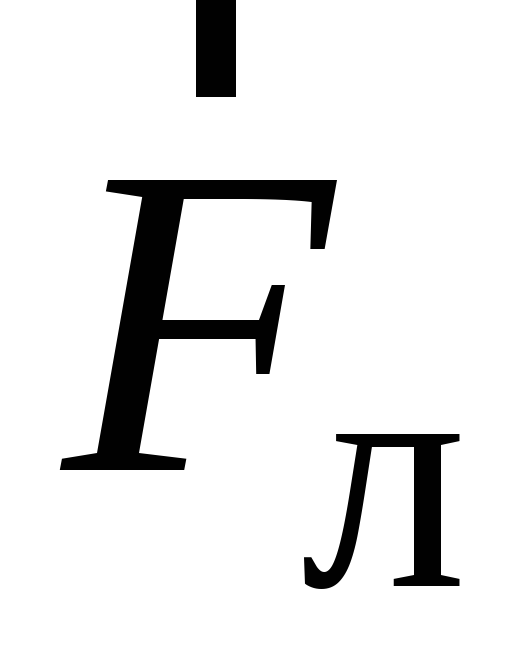 .
В случае установившегося стационарного
распределения зарядов в поперечном
направлении полная сила Лоренца,
действующая на зарядq равна нулю
.
В случае установившегося стационарного
распределения зарядов в поперечном
направлении полная сила Лоренца,
действующая на зарядq равна нулю
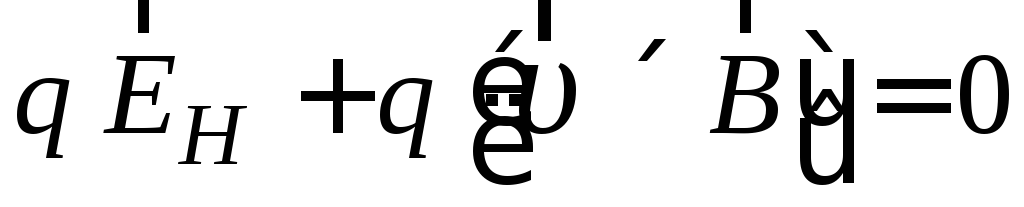 . (2.5)
. (2.5)
В скалярном виде уравнение (2.5) имеет вид
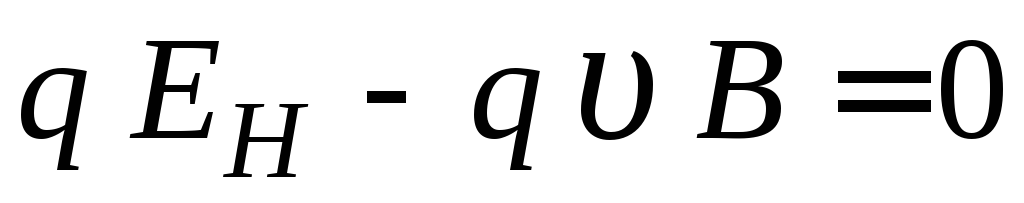 . (2.6)
. (2.6)
Отсюда
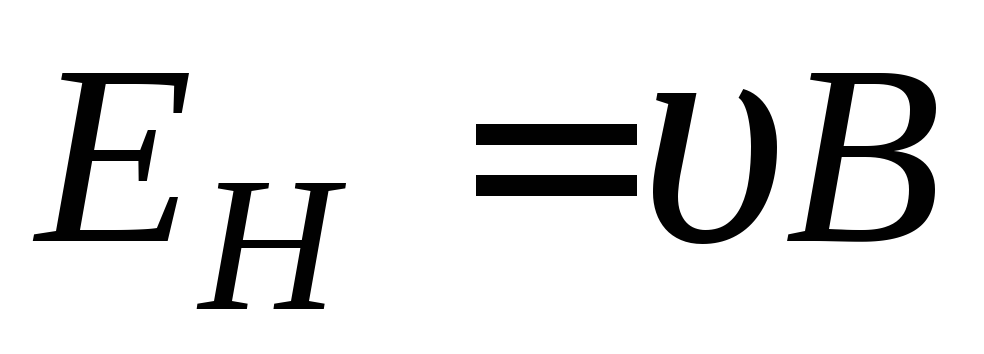 . (2.7)
. (2.7)
Поле 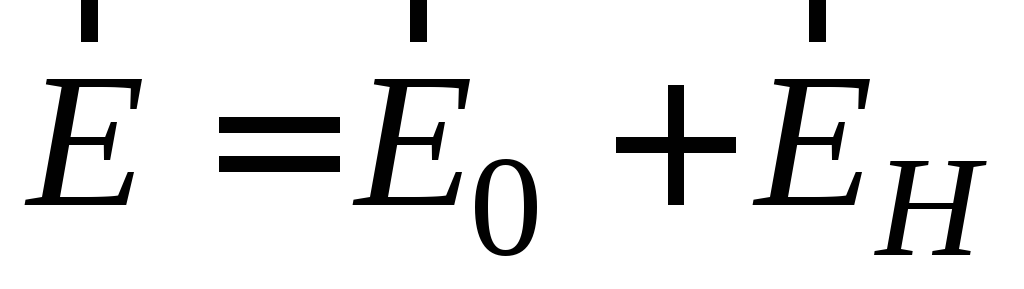 .
Эквипотенциальные поверхности
перпендикулярны к вектору напряжённости
поля
.
Эквипотенциальные поверхности
перпендикулярны к вектору напряжённости
поля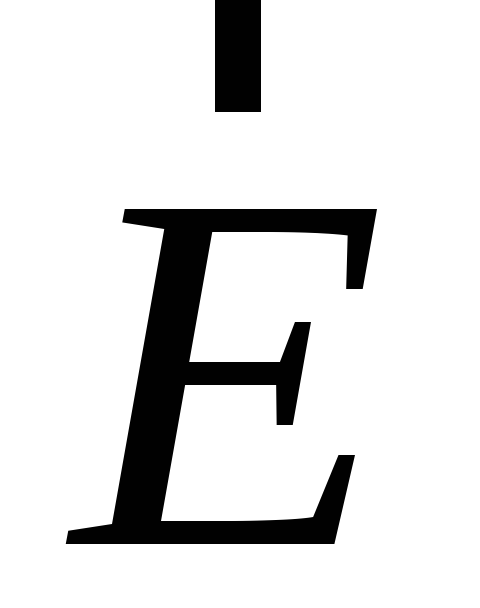 поэтому, они повернутся и займут
положение, изображённое на рис. 2.2
пунктиром. Точки 1 и 2, которые
прежде лежали на одной и той же
эквипотенциальной поверхности, теперь
имеют разные потенциалы. Чтобы найти
напряжение, возникающее между этими
точками, нужно умножить расстояние
между ними на напряженность
поэтому, они повернутся и займут
положение, изображённое на рис. 2.2
пунктиром. Точки 1 и 2, которые
прежде лежали на одной и той же
эквипотенциальной поверхности, теперь
имеют разные потенциалы. Чтобы найти
напряжение, возникающее между этими
точками, нужно умножить расстояние
между ними на напряженность 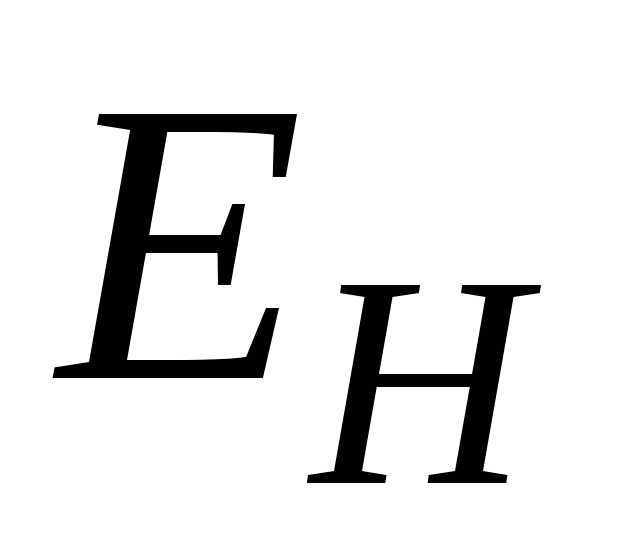
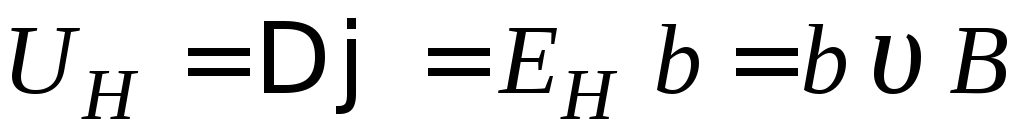 . (2.8)
. (2.8)
Из уравнения (2.4) следует, что
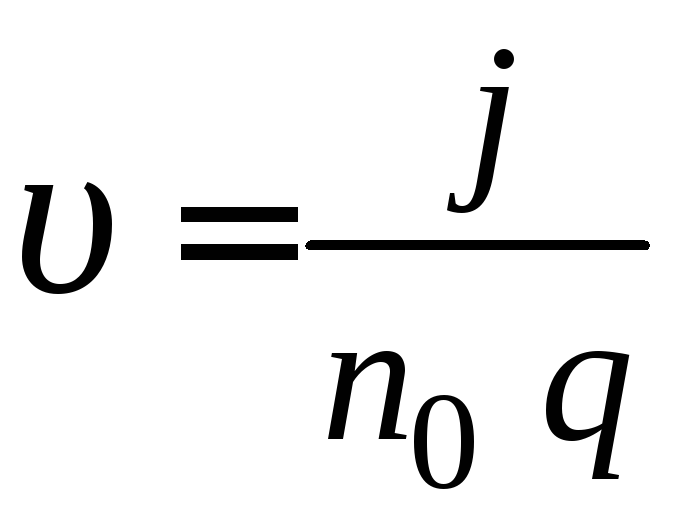 . (2.9)
. (2.9)
Следовательно,
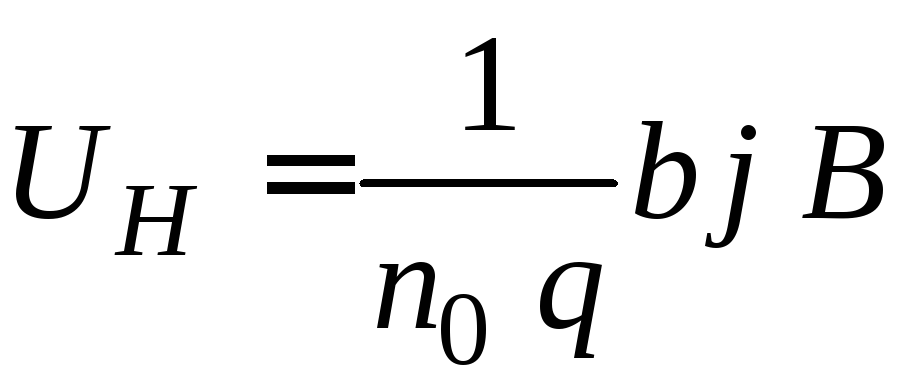 . (2.10)
. (2.10)
Таким образом, полученный результат совпадает с экспериментальной формулой (2.3). Из сравнения (2.3) и (2.10) следует, что постоянная Холла равна
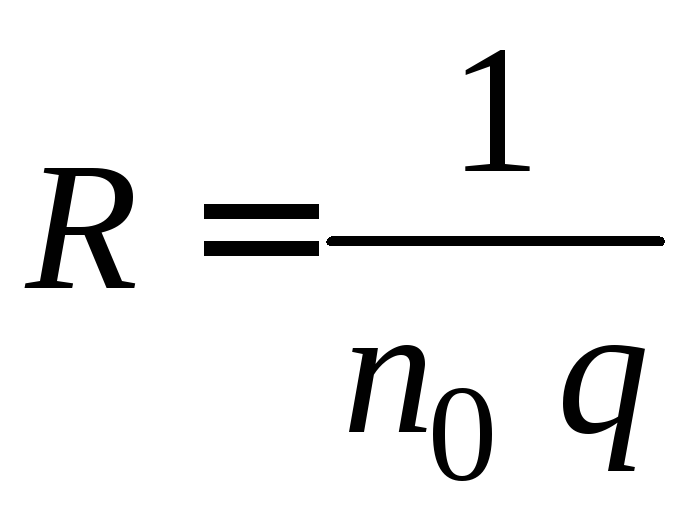 . (2.11)
. (2.11)
Из
формулы (2.11) следует, что знак разности
потенциалов, а следовательно, и постоянной
Холла совпадает со знаком заряда q частиц,
обуславливающих проводимость данного
материала. Для металлов, у которых
концентрация носителей (электронов
проводимости) близка
к плотности атомов  ,R ≈ 10-3 см/Кл,
у полупроводников концентрация носителей
значительно меньше и R ≈ 10-5 см/Кл.
Постоянная Холла может быть выражена
через подвижность носителей заряда
µ = q τ/m* и удельную электропроводность
,R ≈ 10-3 см/Кл,
у полупроводников концентрация носителей
значительно меньше и R ≈ 10-5 см/Кл.
Постоянная Холла может быть выражена
через подвижность носителей заряда
µ = q τ/m* и удельную электропроводность
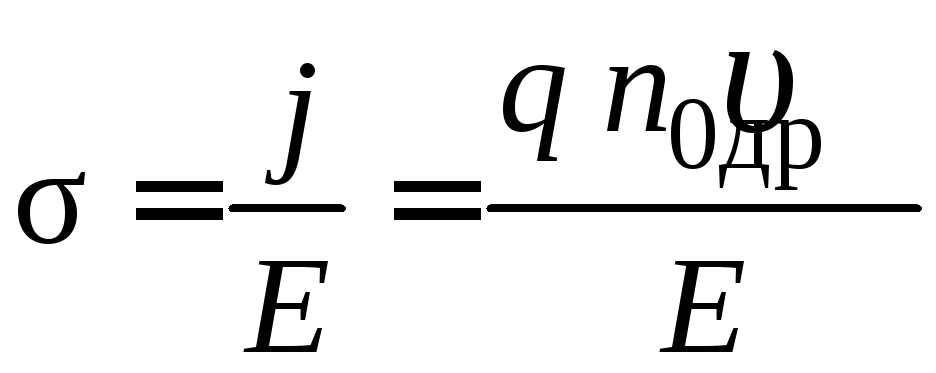 , (2.12)
, (2.12)
где m* – эффективная масса носителей, τ – среднее время между двумя последовательными соударениями с рассеивающими центрами, тогда
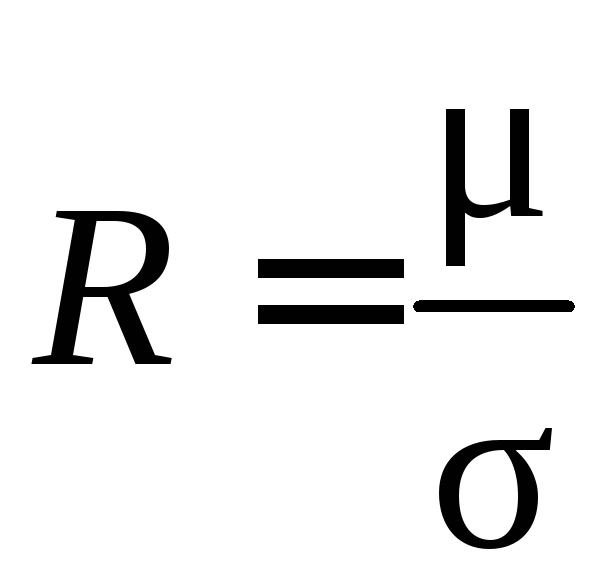 . (2.13)
. (2.13)
Подвижностью
μ носителей тока называется отношение
средней упорядоченной скорости  носителей (электронов и дырок) к
напряженности внешнего электрического
поля Е:
носителей (электронов и дырок) к
напряженности внешнего электрического
поля Е: 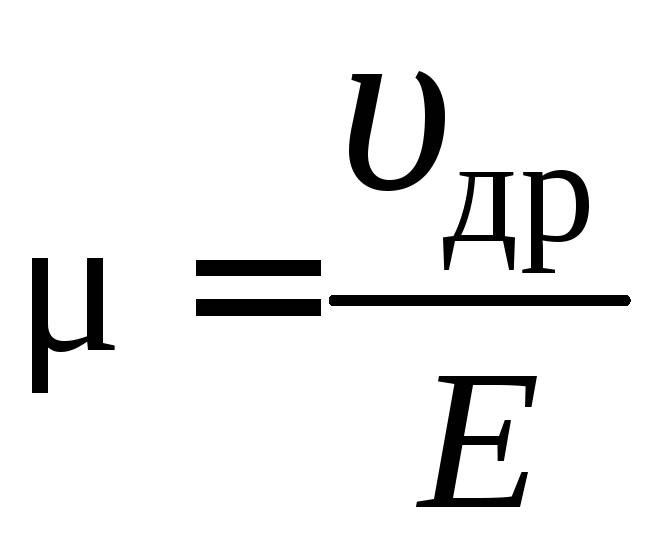 ,
тогда удельная проводимость образца
определяется формулой
,
тогда удельная проводимость образца
определяется формулой
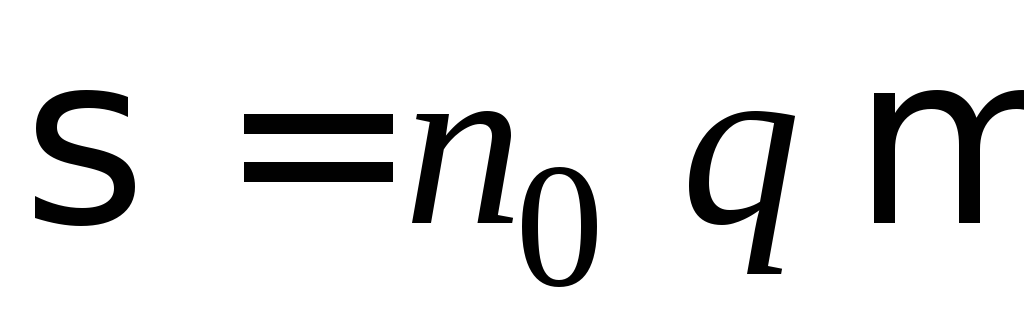 . (2.14)
. (2.14)
На рис. 2.3 сопоставлен эффект Холла для образцов с положительными и отрицательными носителями.
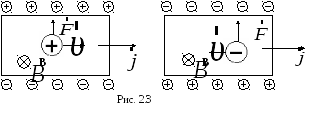
Направление силы Лоренца изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. Следовательно, при одинаковом направлении тока и магнитного поля сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней грани (на рис. 2.3) выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока. Значение постоянной Холла позволяет определить концентрацию носителей заряда, если характер проводимости и их заряд известны.
Все металлы обладают электронной проводимостью, то, казалось бы, что знак эффекта у всех у них должен быть одинаков, так как под действием магнитного поля поток электронов отклоняется вполне определённым образом. Тем не менее, у ряда металлов знак эффекта Холла оказался как раз противоположным. Эту закономерность объясняет зонная теория твёрдого тела. Если зона проводимости металла укомплектована менее чем наполовину, то электроны такой зоны ведут себя нормально, как частицы, обладающие положительной эффективной массой и отрицательным зарядом. Знак постоянной Холла у таких металлов будет отрицательным (к ним относятся металлы 1-й группы таблицы Менделеева). Если зона проводимости металла укомплектована почти полностью. То остающиеся в ней незаполненные уровни – дырки ведут себя как частицы, обладающие положительной эффективной массой и положительным зарядом. Такие металлы имеют дырочную проводимость, вследствие чего знак постоянной Холла у них положительный (аномальный эффект Холла). К таким металлам относятся Be, Cd, Zn и др. Более корректные вычисления, основанные на кинетическом уравнении Больцмана и классической статистике, приводит к результату
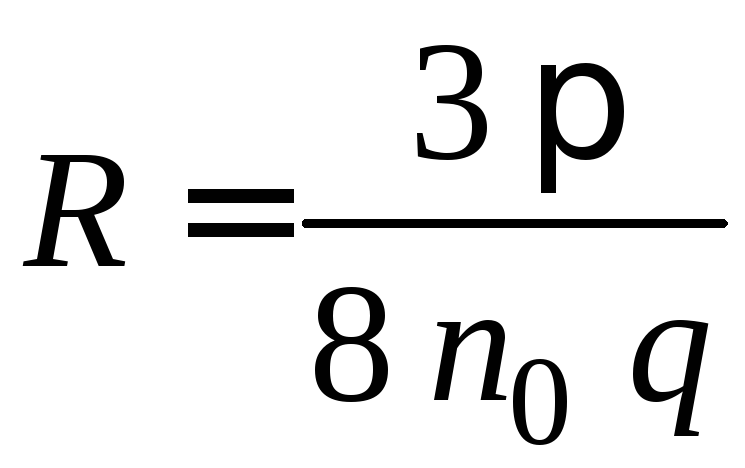 . (2.15)
. (2.15)
Если же применить к электронам в металле статистику Ферми-Дирака, то результаты таких вычислений совпадают с формулой (2.11).
Рассмотренный вывод постоянной Холла является весьма приближенным, так как не учитывает скорость хаотического движения электронов. Более строгий расчет приводит к выражению
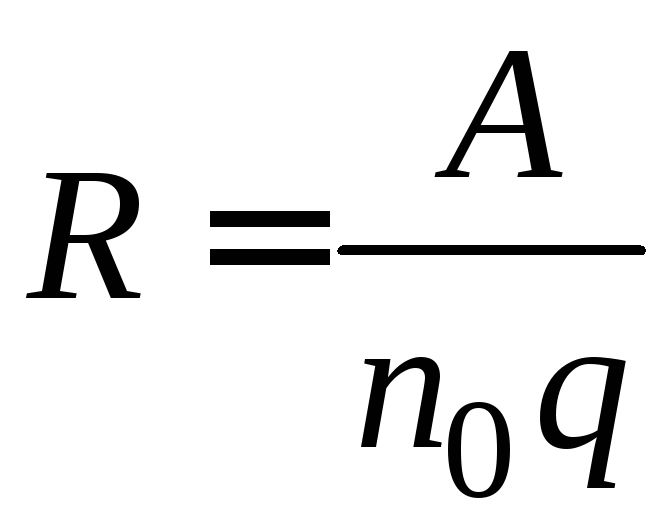 , (2.16)
, (2.16)
где А – постоянная, зависящая от механизма рассеяния носителей заряда. Для полупроводников, обладающих решёткой типа алмаза (германий, кремний, InSb, GaSb, AlAs и др.) и имеющих носителей одного знака
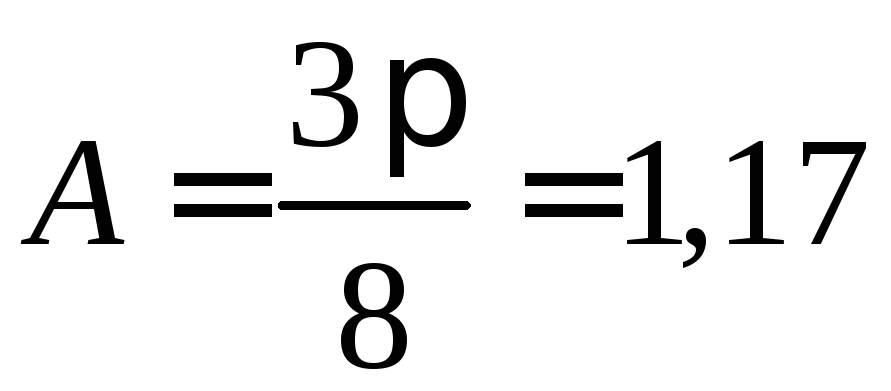 и
и 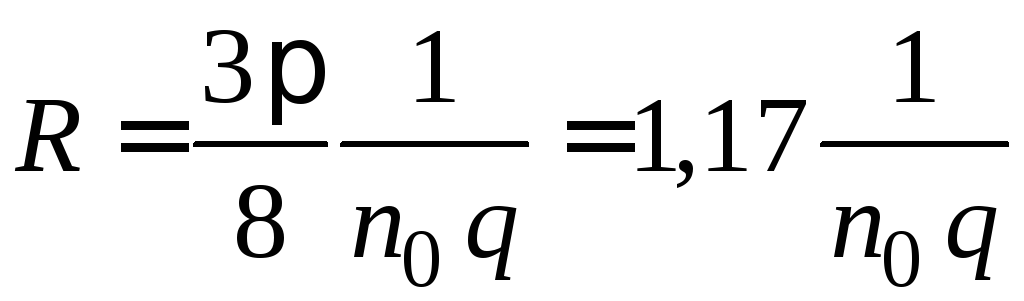 , (2.17)
, (2.17)
если основное значение имеет рассеяние носителей на тепловых колебаниях решётки, и
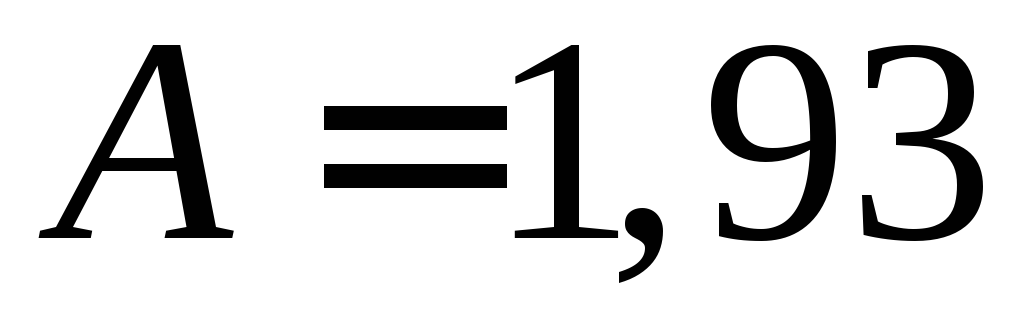 ,
, 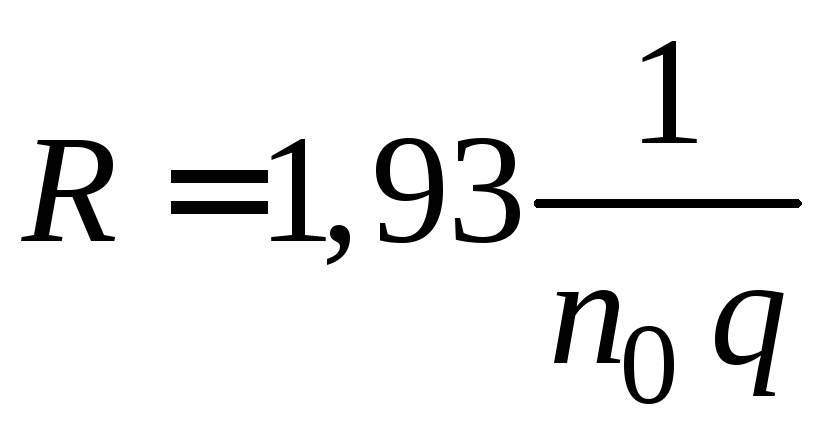 , (2.18)
, (2.18)
если основное значение имеет рассеяние на ионизированных атомах примесей.
Для полупроводников, имеющих два вида носителей – электроны и дырки постоянная Холла равна
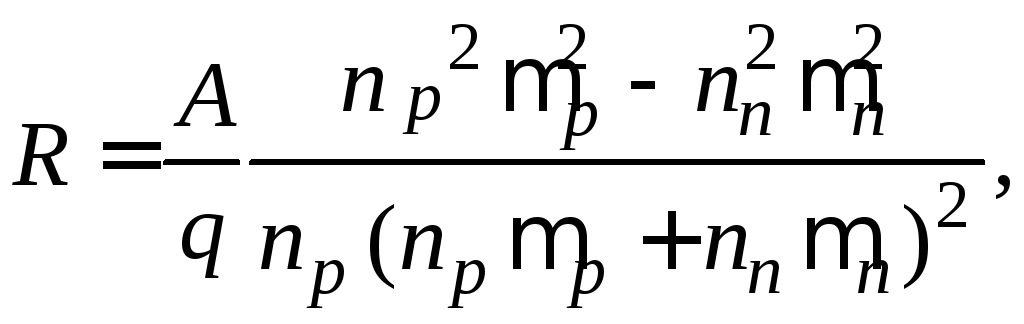 (2.19)
(2.19)
где 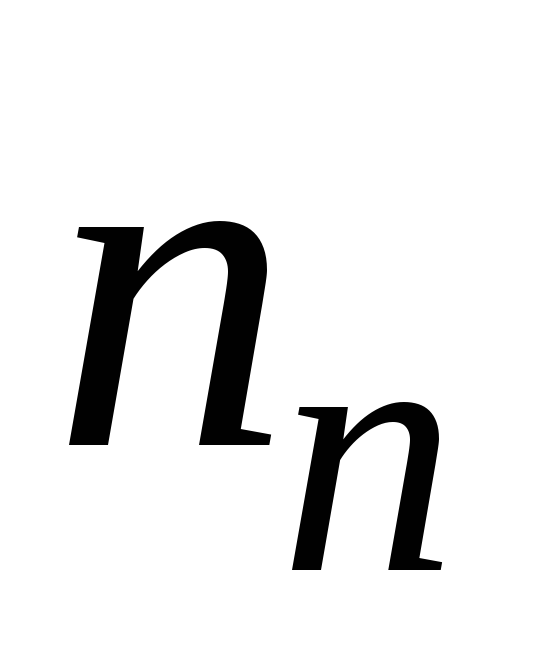 и
и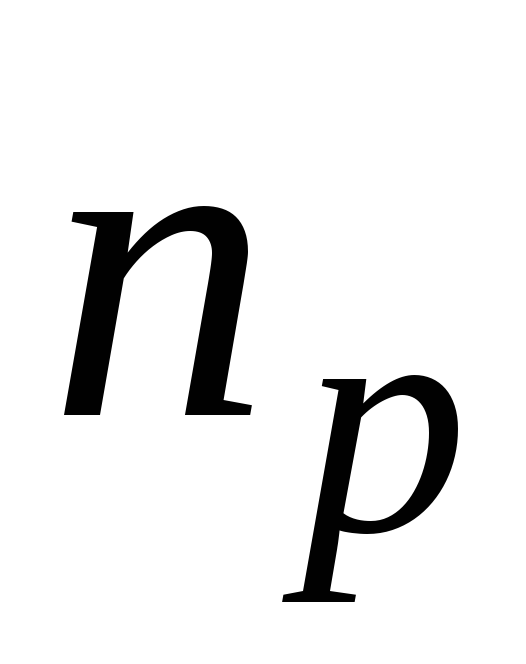 – концентрации
электронов и дырок,
– концентрации
электронов и дырок,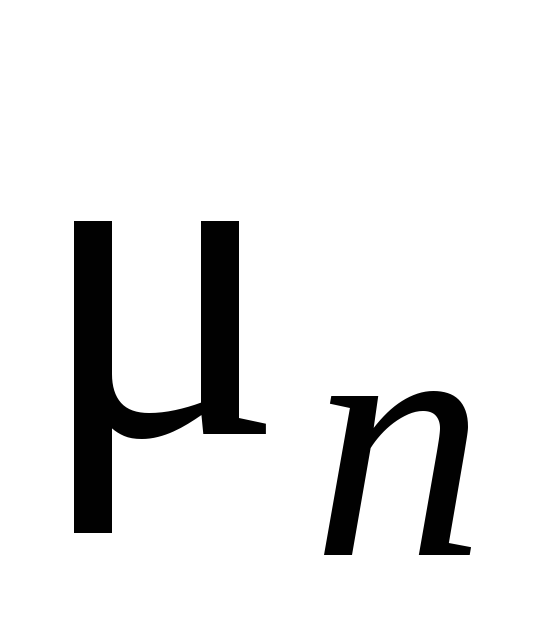 и
и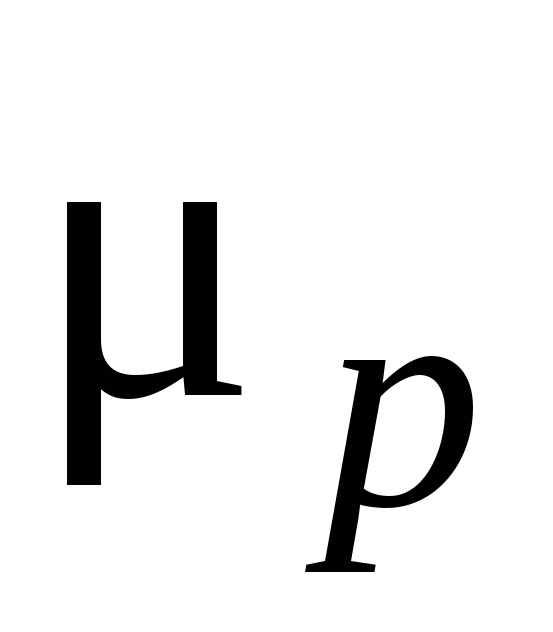 – их
подвижности,A = const,
зависящая от механизма рассеяния.
– их
подвижности,A = const,
зависящая от механизма рассеяния.
В зависимости от типов носителей зарядов знак R может быть как положительный так и отрицательный, что позволяет не спутать в эксперименте эффект Холла с другими возможными эффектами, не зависящими от направления тока.
Эффект Холла получил широкое практическое применение. На его основе оказалось возможным создание ряда устройств и приборов, обладающих исключительно ценными свойствами — приборов для измерения постоянных и переменных магнитных полей, для измерения токов высокой частоты, электронных преобразователей, усилителей и генераторов электрических колебаний и др.
2.3. Эффект Холла в металлах
17
Поскольку σ = q×n×ν и RХ = q1n , то подвижность носителей заряда
µ можно определить, как
Таким образом, одновременное измерение электропроводности и эффекта Холла позволяет определить знак носителей заряда (по знаку RХ), их концентрацию и подвижность µ.
При выводе соотношений для UХ и RХ предполагалось, что все электроны проводимости под действием внешнего электрического поля ε приобретают одинаковую скорость направленного движения vд Это
справедливо только, если скорость хаотического теплового движения всех электронов одинакова, т.е. для всех электронов одинакова длина свободного пробега ln, что имеет место в металлах и вырожденных по- лупроводниках, где проводимость осуществляется ферми-электронами. В общем случае следует учитывать распределение носителей заряда по скоростям и влияние этого распределения на ln.
С учетом такого распределения более строгий расчет приводит к уточненному выражению для RХ:
где А — постоянная, зависящая от механизма рассеяния но- сителей заряда. Для ковалентных кристаллов при рассеянии на тепло-
вых колебаниях решетки A = 38π =1,17 и A =1,93, если основным меха-
низмом рассеяния является рассеяние на ионах примесей. Для метал- лов и вырожденных полупроводников распределение по скоростям учи- тывать не надо, поэтому А = 1.
Под действием магнитного поля Br, перпендикулярного ε, свобод- ные электроны отклоняются к одной из граней кристалла, которая вследствие этого заряжается отрицательно. Другая грань, обедненная электронами, приобретает пояснительныйr заряд, создаваемый ионами
решетки. Возникает холловское полеE X . Физические процессы образо- вания ЭДС Холла в металлах аналогичны рассмотренному выше случаю легированных полупроводников. Следовательно, все полученные соот- ношения остаются справедливыми. Однако так как подвижность элек- тронов в металлах обычно, значительно меньше, чем в легированных полупроводниках, то эффект Холла в них проявляется намного слабее.
Если зона проводимости металла укомплектована менее чем напо-
18
ловину, то электроны такой зоны ведут себя нормально, как частицы, обладающие положительной эффективной массой и отрицательным за- рядом. Знак постоянной Холла в этом случае будет отрицательным. К таким металлам относятся элементы первой группы.
Если зона проводимости металла укомплектована почти полно- стью, то остающиеся в ней незаполненные уровни можно рассматри- вать как дырки — частицы с положительной эффективной массой и положительным зарядом. Такие металлы имеют дырочную проводи- мость, и поэтому знак постоянной Холла у них положительный (ано- мальный эффект Холла). К таким металлам относятся цинк, кадмий, бериллий и некоторые другие.
2.4.Эффект Холла в собственном и полупроводнике
Всобственном полупроводнике концентрации электронов и дырок
равны, т.е. n = р = ni. Поскольку электроны и дырки имеют разные за- ряды и направления скоростей движения, то магнитным полем они от- клоняются в одну сторону (рис. 9).
В | большинстве полупроводников |
|
|
|
|
|
|
|
|
|
|
|
|
|
| r |
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| B |
|
|
|
|
|
|
|
|
| |||
подвижность у электронов выше, чем у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ε |
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
дырок. Следовательно, дрейфовая ско- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
рость движения у электронов vд в поле ε |
|
| r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
будет выше, чем у дырок. Так как сила |
|
| F X ,n |
|
|
|
|
|
| rv |
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
| v д |
|
|
|
|
|
| д |
|
|
|
|
| ||||||||
Лоренца пропорциональна скорости, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
| v p | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
FЛ для | электронов будет по величине v n |
|
| FrЛ,n |
|
|
|
|
|
| F | Л, p | FrX ,p |
| |||||||||||
|
|
|
|
|
|
|
| ||||||||||||||||||
больше, чем для дырок, т.е. FЛ,n > FЛ,р. Со- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
ответственно поперечная скорость дви- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
жения электронов νn будет больше, и они | Рис. 9. Установлениестацио- | ||||||||||||||||||||||||
первыми достигнут грани кристалла. По | нарногосостояния всобствен- | ||||||||||||||||||||||||
мере увеличения на грани отрицательно- |
|
| номполупроводнике, |
|
|
| |||||||||||||||||||
го заряда в кристалле будет создаваться |
|
|
|
|
| когдаµn > µp |
|
|
| ||||||||||||||||
холловское электрическое поле EХ, пре- |
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
пятствующее поперечному движению электронов и способствующее такому движению дырок. Поперечная скорость движения к грани у электронов vn будет уменьшаться, а у дырок vp увеличиваться. Ста-
ционарное состояние установится при выравнивании поперечных ско- ростей движения отклоняющихся к грани электронов и дырок, т.е. при выравнивании величин поперечных дырочного и электронных токов, после чего электроны и дырки будут достигать грани кристалла одно- временно и установившийся отрицательный заряд на ней будет оста- ваться неизменным. Таким образом стационарное состояние обеспечи- вается возникновением поля Холла EХ, величина которого определяется различием в значениях подвижностей электронов µn, и дырок µp. Ко- эффициент Холла для случая собственного полупроводника можно представить в виде
RХ = | µp − µn | . | (34) | |
q ni (µp + µn ) | ||||
|
|
|
19
В большинстве случаев из-за большей подвижности электронов коэффициент Холла отрицателен.
2.5. Эффект Эттингсгаузена
Эффект Эттингсгаузена сопутствует эффекту Холла и заключается
ввозникновении градиента температуры вдоль холловского поля.
Встационарном состоянии при возникновении эффекта Холла в
легированном полупроводнике FЛ = FХ. Однако это равенство выполня- ется только для определенного значения скорости движения зарядов νд,ср, определяемой из соотношения
q vд,ср Β = q ΕX . | (35) |
Вследствие процессов рассеяния дрейфовые скоррсти различных электронов колеблются в широких пределах. Поскольку сила Лоренца пропорциональна скорости, а сила Холла от скорости не зависит, то для частиц, движущихся со скоростью большей, чем средняя, а стационар- ном состоянии сила Лоренца будет превышать силу Холла. Поэтому бы- стрые электроны будут, отклоняться к одной из граней образца, пере- давая излишек своей энергии кристаллической решетке. Соответствен- но более медленные электроны будут под действием силы Холла откло- няться к другой грани, пополняя недостаток своей энергии за счет теп- ловых колебаний кристаллической решетки. Таким образом, одна грань будет нагреваться, а другая охлаждаться, и наряду с поперечной разно- стью потенциалов возникнет поперечная разность температур — эф- фект Эттингсгаузена.
По мере нагревания одной грани и охлаждения другой появится и будет расти поток тепла от нагретой грани к холодной. При некоторой разности температур установится стационарное состояние, при кото- ром отток тепла от нагретой грани за счет теплопроводности сбаланси- рует приток тепла за счет быстрых электронов.
В случае собственного полупроводника стационарное состояние в эффекте Холла обеспечивается равенством потоков электронов и ды- рок, поступающих к боковой поверхности образца. Повышенная кон- центрация электронов и дырок в этой части полупроводника вызовет их усиленную рекомбинацию, тогда как в области пониженной концен- трации вероятность встречи электрона с дыркой, т.е. их рекомбинации, будет меньше обычной. В процессе рекомбинации электрон переходит из зоны проводимости в валентную зону с выделением энергии, разной ширине запрещенной зоны Еg. Так как число пар носителей электрон- дырка, участвующих в рекомбинации, велико, то эффект Эттингсгау- зена в случае собственных полупроводников проявляется значительно сильнее, чем в металлах или легированных полупроводниках.
По мере нагревания одной грани и охлаждения другой Судет усили- ваться и отток тепла от горячей грани за счет теплопроводности. При неко- торой разности температур между гранями, когда потоки тепла сбалансиру- ют друг друга, установится равновесное состояние эффекта Эттингсгаузена.
20
2.6. Магниторезистивный эффект
Эффект заключается в уменьшении подвижности носителей заря- да проводника с током при внесении его в магнитное поле. Так как электропроводность σ пропорциональна подвижности µ, то сопротивле- ние образца при этом возрастает.
В отсутствие магнитного поля носители заряда движутся прямо- линейно и между двумя столкновениями проходят путь, равный длине свободного пробега l за время свободного пробега τ.
При наличии магнитного поля в образце металла или примесного полупроводника с ограниченными размерами возникает холловское по- ле, полностью компенсирующее действие магнитного поля для электро- нов, движущихся с некоторой средней дрейфовой скоростью vд( ср) :
q vд,ср Β = q ΕХ . Такие электроны будут продолжать двигаться вдоль
образца без изменения длины свободного пробега l. Однако из-за про- цессов рассеяния скорости различных электронов (и дырок) будут от- личаться от vд,ср , поэтому на частицы, движущиеся со скоростями,
большими средней скорости, сильнее действует магнитное поле, чем холловское. Наоборот, более медленные частицы отклоняются в проти- воположную сторону под действием холловского поля.
В обоих случаях за время τ частица проходит меньший путь вдоль поля ε, что равносильно уменьшению дрейфовой скорости vд , или под-
вижности µ, т.к. µ пропорциональна пути, проходимому частицей на длине свободного пробега в направлении поля.
Таким образом, в случае легированного полупроводника (или ме- талла) сопротивление образца увеличивается вследствие уменьшения вклада в проводимость быстрых и медленных носителей заряда.
В случае прямоугольного образца полупроводника с собственной проводимостью σi холловское поле проявляется как разностный эффект вследствие различия подвижностей электронов и дырок. В этом случае действие магнитного поля тоже ничем не компенсируется, и носители заряда непрерывно отклоняются на своем пути от направления при- кладываемого электрического поля ε. Соответственно в собственных полупроводниках эффект магнитосопротивления проявляется значи- тельно сильнее, чем в легированных, где холловское поле в значитель- ной степени выправляет траектории движения носителей заряда.
Магниторезистивныи эффект зависит от формы образца. Если взять образец в виде диска, в центре которого расположен один кон- такт, а по окружности нанесен другой (диск Корбино), то такой образец будет моделировать образец с неограниченными размерами. Так как носители заряда движутся по радиусу, то в магнитном поле они откло- няются в направлении, перпендикулярном радиусу, следовательно, разделение зарядов не происходит и холловское поле не образуется.
Кроме того, сопротивление такого образца будет значительно вы- ше, чем прямоугольного, причем величина сопротивления его будетr
прямо пропорциональна величине напряженности магнитного поля B .

