Первый и второй законы Кирхгофа для электрической цепи, метод составления уравнений и анализ цепей

Первый закон Кирхгофа для электрической цепи

Любые электрические цепи всегда подчиняются законам Кирхгофа.

Есть для первого закон Кирхгофа два варианта формулировок:
1. Алгебраическая сумма электрических токов ветвей, сходящихся в одном узле, равна нулю.

2. Сумма электрических токов, которые текут в направлении к узлу, равна сумме электрических токов, которые текут из узла.

Токи, направленные к узлам, обычно считают положительными, а выходящие – отрицательными.

Рис. 1. Направление токов в узле.

Для рисунка 1 можно записать по первой формулировке:

По второй формулировке:

Физический смысл для первого закона заключается в том, что заряды в электрической цепи двигаются таким образом, что не скапливаются ни в каком узле.

Второй закон Кирхгофа для электрической цепи

Для второго закона тоже есть две формулировки:
1. В замкнутом контуре абсолютно любой электрической цепи алгебраическая сумма существующих падений напряжений равна сумме ЭДС контура.

Если слагаемое совпадает с направление, по которому происходит обход контура цепи, то оно входит в уравнение со знаком «+», если же оно не совпадает – то со знаком «–».

2. Алгебраическая сумма напряжений вдоль какого-либо замкнутого контура цепи равна нулю.

Рис. 2. Электрическая схема.

Для контура на рисунке 2 можно записать:

Оба закона Кирхгофа являются справедливыми как для линейных, так и для нелинейных электрических цепей при любых изменениях напряжений и токов во времени.

Метод составления уравнений по законам Кирхгофа

Оба закона Кирхгофа совместно применяют для поиска электрических токов в ветвях. Давайте обозначим число всех ветвей через b, число ветвей, где есть источник тока через b_ит, число узлов через y. По каждой из ветвей схемы протекает свой собственный электрический ток. По причине того, что токи, находящиеся в ветвях с источниками электрического тока, известны, число токов, которые неизвестны, равно b–b_ит.

Перед составление уравнения необходимо выбрать произвольно:
1. Положительное направление электрического тока в каждой из ветви, и затем обозначить их на схеме.
2. Положительные направления для обхода каждого из контуров схемы для записи уравнений по второму закону Кирхгофа.

Для удобства рекомендуется положительные направления для обхода каждого из контуров выбирать одинаковыми, допустим, по часовой стрелке.

С целью получения линейно независимых уравнений, которые были составлены по первому закону Кирхгофа, их количество должно быть равно y–1. Для последнего узла уравнение не составляют, потому что оно совпадало бы с уравнением, которое получено в результате суммирования уравнений для y–1 узлов.

В соответствии со вторым законом Кирхгофа выполняют составление уравнений в количестве, равном количеству ветвей без источника электрического тока (b–b_ит), вычтя те уравнения, которые были составлены по первому закону:

Во время составления уравнения по второму закону Кирхгофа, нужно охватить все ветви, при этом исключив ветви, где есть источник тока, потому что в этом случае в уравнение были бы включены бесконечно большие слагаемые, в связи с чем оно бы не имело смысла.

Есть рекомендуемое, но не обязательное требование, по которому при составлении в соответствии со 2-м законом Кирхгофа линейно независимых уравнений стремятся к тому, чтобы в каждый новый контур, применительно к которому выполняется составление уравнения, входила как минимум одна новая ветвь, которая не вошла в предыдущие контуры, для которых уравнения по 2-му закону уже составлены. Данные контуры называют независимыми контурами.

Анализ электрических цепей с помощью законов Кирхгофа

Произведём анализ электрических цепей для схемы, изображённой на рисунке 3 и составим для неё уравнения.

Рис. 3. Электрическая схема.

Число неизвестных электрических токов для схемы равно числу ветвей. Обозначим число ветвей через m, число узлов через k. Тогда m=6, k=4.

Теперь зададимся произвольным направлением электрических токов отдельных ветвей цепи. Согласно первого закона Кирхгофа составим независимые уравнения в количестве k–1 штук для узлов a, b и c.

a: I₁ + I₅ + I₆ = 0
b: I₂ – I₅ – I₄ = 0
c: I₄ – I₃ – I₆ = 0

Для определения всех токов ветвей недостающие уравнения, количество которых (m–(k–1)), можно составить, если воспользоваться вторым законом для независимых контуров.

Контур I: I₁R₁ – I₂R₂ – I₅R₅ = E₁ – E₂
Контур II: I₂R₂ + I₄R₄ + I₃R₃ = E₂
Контур III: I₅R₅ – I₆R₆ – I₄R₄ = 0

Правила Кирхгофа для электрической цепи, понятным языком

Содержание:

Чтобы сформулировать закон Кирхгофа для электрической цепи, потребовалось ввести новые термины в теорию – узлы, ветви и контур.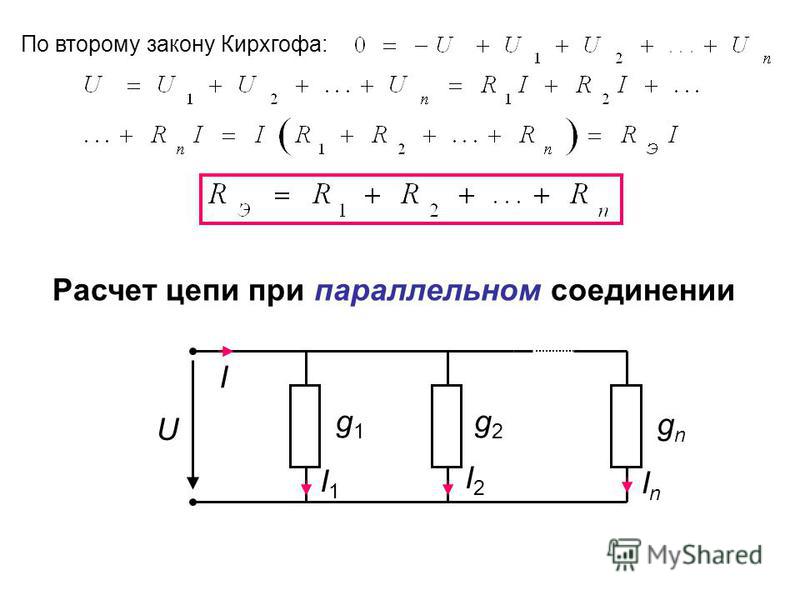 Ветвями называют любой тип двухполюсной цепи. Узлом называют точку, в которой соединяются несколько ветвей. Эти элементы принадлежат одному электрическому контуру. Законы представляют собой различные соотношения между величинами тока на разных участках цепи. С их помощью можно провести расчет величины постоянных или переменных токов при помощи формул, созданный этим ученым.

В данной статье будет рассказано про законы Кирхгофа, как они могут использоваться на практике и как правильно провести расчеты, связанные с ними. В качестве дополнения, статья содержит два видеоролика, одну скачиваемую статью по выбранной теме.

Законы Кирхгофа

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям.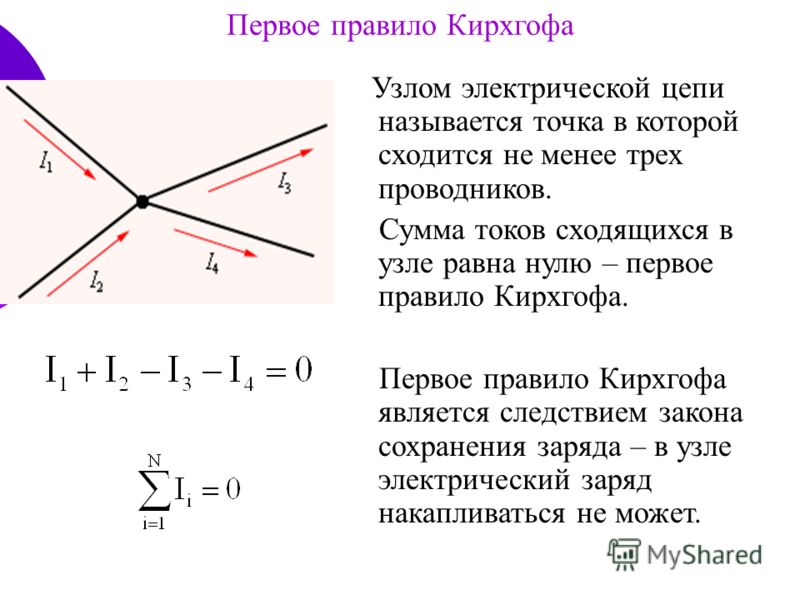 Значе­ния токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

Первый закон

Первый закон Кирхгофа устанавливает зависимость между то­ками для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

?I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А

I1 + I2 + I3 – I4 – I5 = 0 (17)

Это интересно! Все о полупроводниковых диодах.

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа.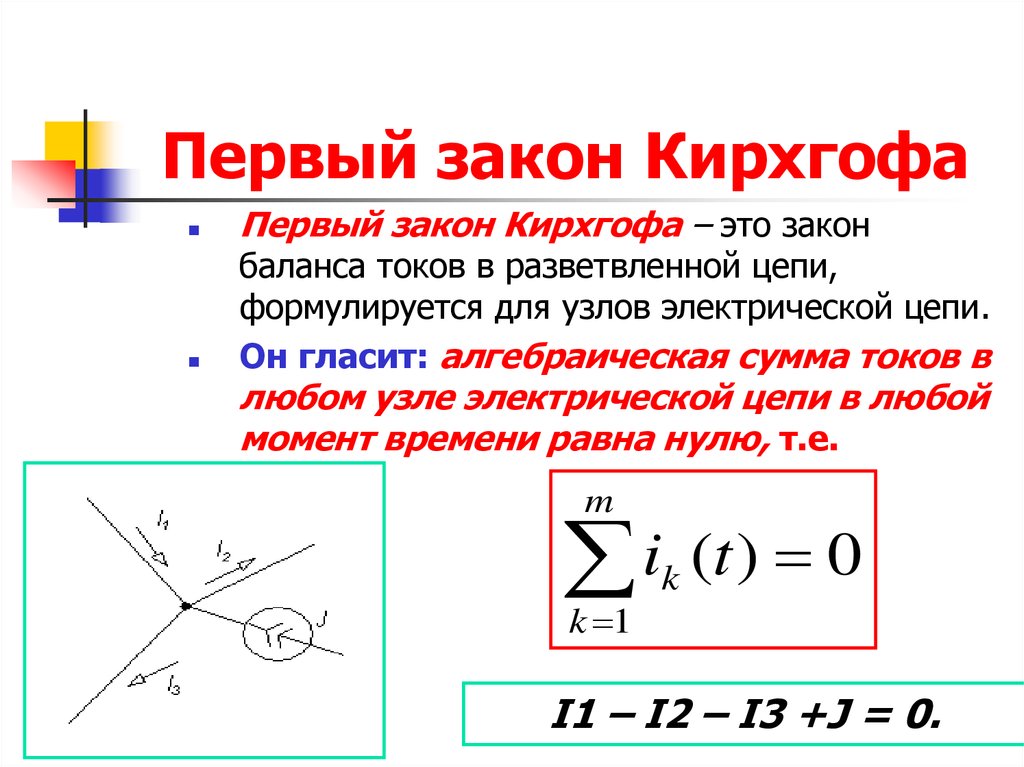 Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах. 

Первый закон Кирхгофа.

 

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

?E = ?IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с.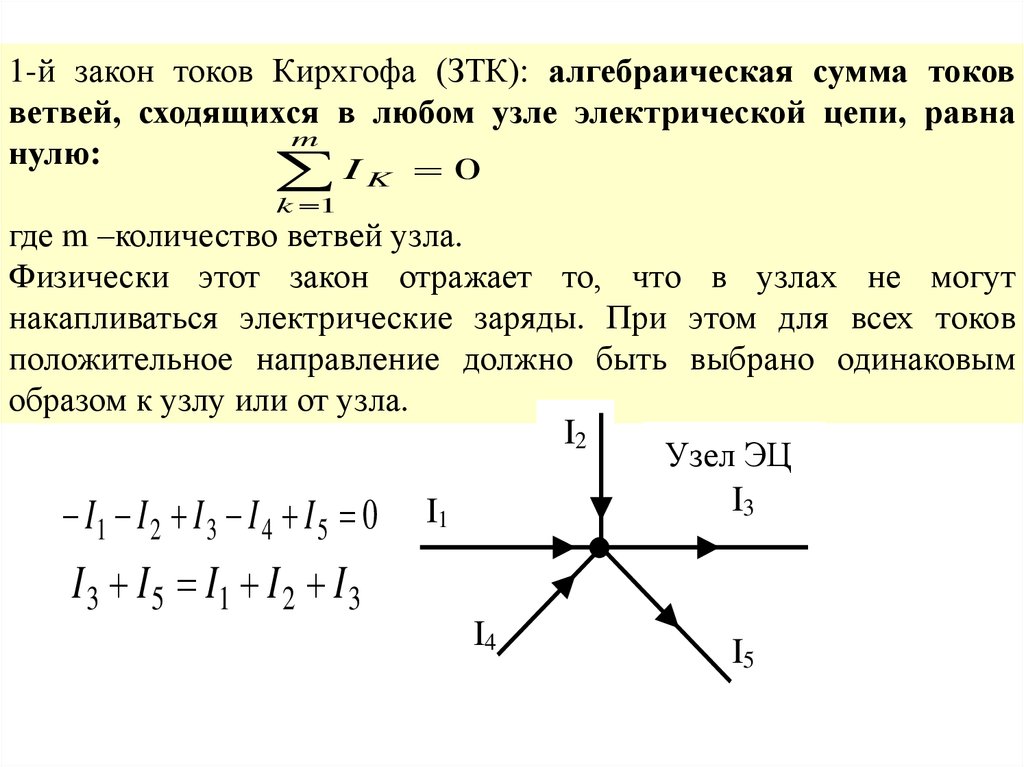 и падения напряжения считают отрицательными.

Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,

получим:

E₁ – E₂ = IR₀₁ + IR₀₂ + IR₁ + IR.

При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).

[stextbox id=’info’] Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.[/stextbox]

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.

При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

 

Алгебраическая сумма разностей потенциалов

Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:

ΣV = 0

Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.

[stextbox id=’info’]Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути. [/stextbox]

Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.

Одиночный контурный элемент — резистор

Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).

Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.

Одиночный контур электрической цепи

Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:

V = I * Rs

где: Rs = R1 + R2.

Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:

I = V / Rs

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.

Интересно по теме: Как проверить стабилитрон.

Требуется рассчитать:

• общее сопротивление,
• ток цепи,
• ток через каждый резистор,
• падение напряжения на каждом резисторе.

Рассчитаем общее сопротивление:

Ro = R1 + R2 + R3  =  10Ω + 20Ω + 30Ω = 60Ω

Ток цепи:

I = V / Ro = 12 / 60 = 0,2A (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2A (200 мА)

Падение потенциала на каждом из резисторов:

VR1 = I * R1 = 0.2 * 10 = 2В

VR2 = I * R2 = 0.2 * 20 = 4В

VR3 = I * R3 = 0.2 * 30 = 6В

Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.

Вывод

Теория второго закона Кирхгофа, также известного как закон сохранения потенциала, особенно полезна для работы с последовательными схемами. Последовательные схемы действуют как делители потенциала, а цепь делителя потенциала — это важный узел многих электрических (электронных) схем.

Второй закон

Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.

E₁ + E₂ + E₃ + . . . = I₁r₁ + I₂r₂ + I₃r₃ + . . .

При этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура.
Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E₁ + E₂. Если же в цепи э. д. с. источников имеют противоположные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.

E = E₁ – E₂.

Второй закон Кирхгофа.

При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Замкнутая цепь обозначена буквами а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I₁, I₂, I₃ и I₄, отличаясь по силе, могут иметь различные направления.
Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:

E₁ – E₂ – E₃ = I₁(r₀₁ + r₁) – I₂(r₀₂ + r₂) – I₃(r₀₃ + r₃) + I₄r₄,

где r₀₁, r₀₂, r₀₃ — внутренние сопротивления источников энергии,
r₁, r₂, r₃, r₄ — сопротивления приемников энергии.
В частном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений.
Если внешняя цепь источника энергии с внутренним сопротивлением r _{состоит, например, из трех последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:}

E = I r _{+ I r1 + I r2 + I r3.}

При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.

Заключение

Рейтинг автора

Написано статей

Более подробную информацию о законах Кирхгофа для электрической цепи Занятие по законом Кирхгофа. Если у вас остались вопросы, можно задать их в комментариях на сайте.

А также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов. Для этого приглашаем читателей подписаться и вступить в группу. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию во время подготовки материала:

www.electrono.ru

www.tehinfor.ru

www.zetsila.ru

www.texnic.ru

www.zamzamstore.ru

Предыдущая

ТеорияЧто такое анод и катод, в чем их практическое применение

Следующая

ТеорияЧто такое электрический ток, виды и условия его существования

правил Кирхгофа | Физика

Цели обучения

К концу этого раздела вы сможете:

• Анализировать сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных членов.

Многие сложные схемы, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы в последовательном и параллельном соединении и Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Рис. 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, эдс.)

Правила Кирхгофа

• Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.

Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.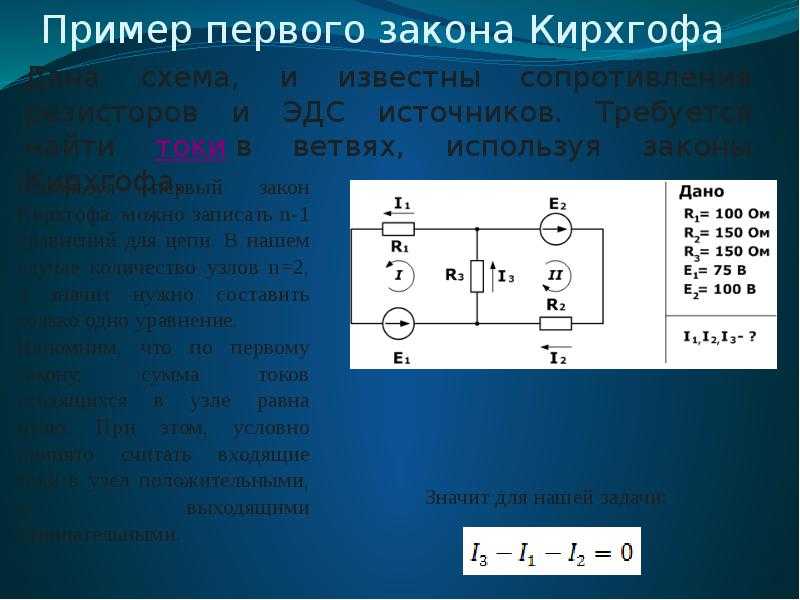

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения ) является применением закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы I ₁ = I ₂ + I ₃ (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.

Установление соединений: законы сохранения

Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.

Рисунок 22.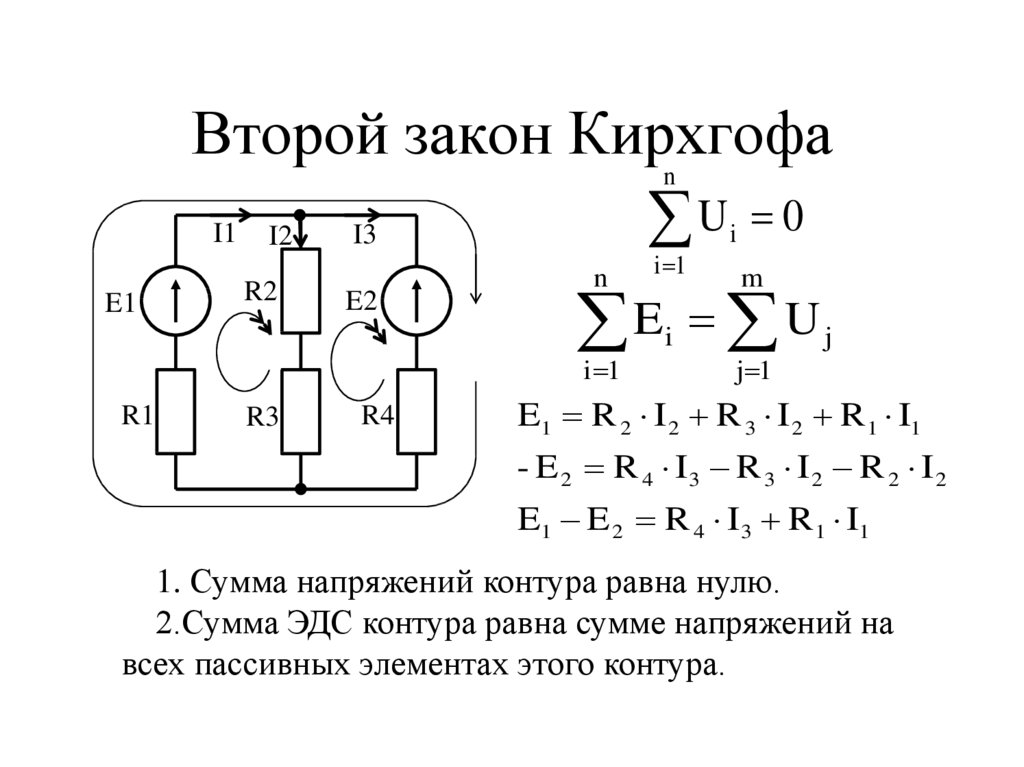 Правило соединения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I ₁ = I ₂ + I ₃ . Здесь I ₁ должно быть 11 А, так как I ₂ равно 7 А, а I ₃ равно 4 A.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило цикла ) является применением закона сохранения энергии. Правило петли сформулировано с точки зрения потенциала, В , а не потенциальной энергии, но они связаны, поскольку PE _elec  = qV . Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке 3 показаны изменения потенциала в простой последовательной цепи. Второе правило Кирхгофа требует ЭДС − IR — IR ₁ — IR ₂ = 0. перестроенный, это EMF = IR + IR ₁ + IR ₂ = 0, что означает EMF EMF MANGE EMF EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MIGE EMF равно сумме IR  (напряжения) падений в контуре.

Рис. 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС. )

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.

1. Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I ₁ , I ₂ , I ₃ и I , а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
2. Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рисунке 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.

Рисунок 4 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 4.)

Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)

• Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет  −IR . (См. рис. 4.)
• Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет + IR . (См. рис. 4.)
• Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
• Когда ЭДС перемещается от + к — (противоположно направлению, в котором движется положительный заряд), изменение потенциала равно — ЭДС. (См. рис. 4.)

Пример 1. Расчет силы тока: использование правил Кирхгофа

Найдите токи, протекающие в цепи на рисунке 5.

Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но сопротивления и ЭДС заданы. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи были обозначены на рисунке I ₁ , I ₂ и I ₃ , и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.

Решение

Начнем с применения первого правила Кирхгофа или правила соединения в точке а. This gives

I ₁  =  I ₂  +  I ₃ ,

since I ₁ flows into the junction, while I ₂ and I ₃ слив. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла. Теперь рассмотрим петлю abcdea. Переходя от a к b, мы проходим R ₂ в том же (предполагаемом) направлении тока I ₂ , поэтому изменение потенциала равно − I ₂ R 8 ₂ . Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала равно +ЭДС ₁ . Пересечение внутреннего сопротивления r ₁ от c к d дает − I ₂ r ₁ . Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала на — I ₁ R ₁ . Правило цикла гласит, что сумма изменений потенциала равна нулю. Thus,

− I ₂ R ₂  + emf ₁  −  I ₂ r ₁  −  I ₁ R ₁  = − I ₂ ( R ₂ + r ₁ ) + ЭДС ₁ − I 1 0011 R ₁  = 0,

Подстановка значений сопротивления и ЭДС из принципиальной схемы и отмена единиц ампер дает 0.

Now applying the loop rule to aefgha (we could have chosen abcdefgha as well) similarly gives

+ I ₁ R ₁  + I ₃ R ₃  + я ₃ r ₂  − emf ₂  = + I ₁ R ₁  + I ₃ ( R ₃  +  r ₂ ) − ЭДС ₂  = 0.

Обратите внимание, что знаки меняются местами по сравнению с другим контуром, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится

+6 I ₁  + 2 I ₃   – 45 = 0,

Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для I ₂ :

I ₂ = 6 − 2 I ₁ .

Теперь решите третье уравнение для I ₃ :

I ₃  = 22,5 − 3 I ₁ .

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I ₁ :

I ₁ = I ₂ + I ₃ = (6–2 I ₁ ) + (2 I ₁ ) + (21111112 ₁ ) + (211111112 ₁ ) + (2 I ₁ ) + (2 I ₁ ) + (6-2 I ₁ ) + (6-2 I ₁ ) + (6-2 I ₁ ). 1 ) = 28,5 − 5 I ₁ .

Комбинирующие условия приведены

6 I ₁ = 28,5 и

I ₁ = 4,75 A.

Заменить это значение для I ₁ назад в четырех.0005

I ₂ = 6 — 2 I ₁ = 6 — 9,50

I ₂ = −3. 50 A.

направление, противоположное предполагаемому на рис. 5. Наконец, подставляя значение I ₁ в пятое уравнение, мы получаем 25

I ₃ = 8,25 A.

Обсуждение

Как будто отметим, что действительно I ₁ = I ₂ + I ₃ . Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.

Стратегии решения задач по правилам Кирхгофа

1. Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
2. Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение является избыточным.
3. Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0008
4. Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
5. Проверить разумность и последовательность ответов. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.

Материал в этом разделе теоретически верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.

Проверьте свое понимание

Можно ли применять правила Кирхгофа к простым последовательным и параллельным цепям, или они ограничены для использования в более сложных цепях, которые не являются комбинацией последовательной и параллельной?

Решение

Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.

Резюме раздела

• Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
• Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
• Два правила основаны соответственно на законах сохранения заряда и энергии.
• При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
• Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.

Концептуальные вопросы

1. Могут ли все токи, входящие в соединение на рисунке 6, быть положительными? Объяснять.

Рисунок 6.

2. Примените правило соединения к соединению b на рис. 7. Получена ли какая-либо новая информация при применении правила соединения в точке e? (На рисунке каждая ЭДС представлена ​​буквой Е.)

Рисунок 7.

3. (a) Какова разность потенциалов при переходе из точки a в точку b на рис. 7? б) Чему равна разность потенциалов при переходе от c к b? в) От е до g? (г) От е до d?

4. Примените правило цикла к циклу afedcba на рисунке 7.

5. Примените правило цикла к циклам abgefa и cbgedc на рисунке 7.

Задачи и упражнения

1. Примените правило цикла к циклу abcdefgha на рисунке 5 (показанном ниже).

Рис. 5. Эта схема аналогична схеме на рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

2. Примените петлевое правило к петле aedcba на рисунке 5.

3. Проверьте второе уравнение в Пример 1 Расчет тока: с использованием правил Кирхгофа  (в тексте выше), путем подстановки найденных значений токов I ₁ и I ₂ .

4. Проверьте третье уравнение в  Пример 1 Расчет тока: с использованием правил Кирхгофа  (в тексте выше), подставив найденные значения токов  I ₁ и I ₃ .

5. Примените правило соединения в точке a на рисунке 8.

Рисунок 8.

6.

Примените правило цикла к кольцу abcdefghija на рисунке 8.

7. Примените правило цикла к кольцу akledcba на рисунке 8.

8. Найдите токи, протекающие в цепи на рисунке 8. В явном виде покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.

9. Решите  Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), но используйте цикл abcdefgha вместо цикла akledcba. Явно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов .

10. Найдите токи, протекающие в цепи на рисунке 7 (показанном ниже).

Рисунок 7.

11. Необоснованные результаты Рассмотрим схему на рисунке 9 и предположим, что ЭДС неизвестны, а токи заданы равными I ₁  = 5,00 А, I ₂  = 3,0 А и I ₃  = –2,00 А. а) Не могли бы вы найти ЭДС? б) Что неверно в предположениях?

Рисунок 9.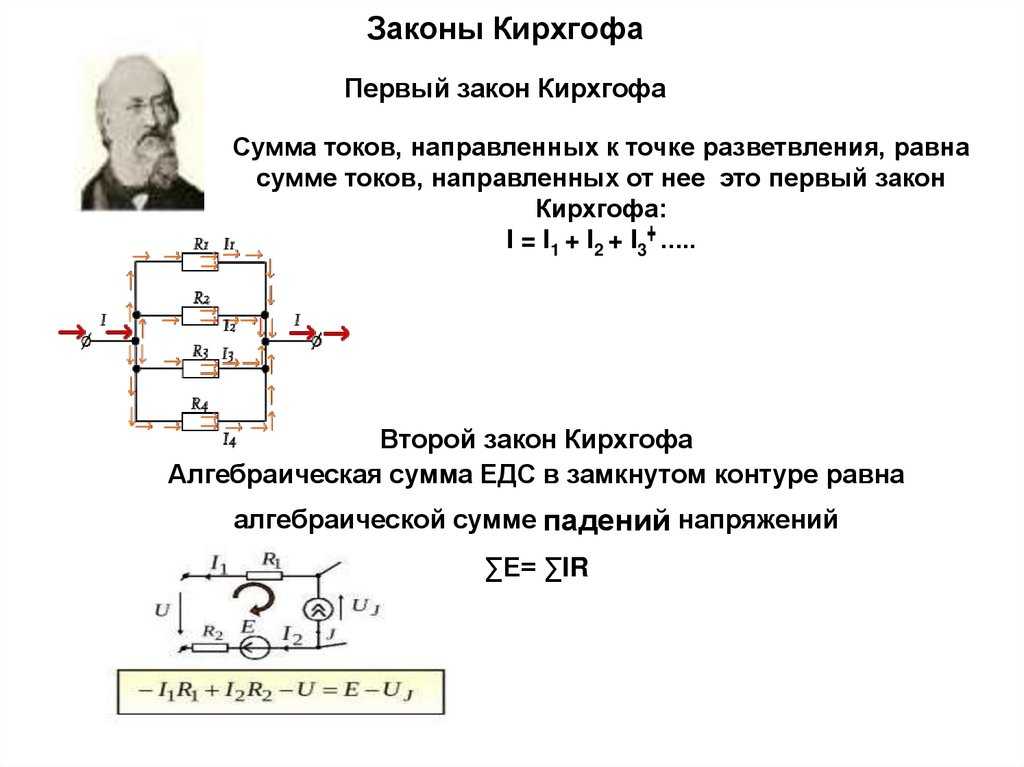

Глоссарий

Правила Кирхгофа:

набор из двух правил, основанных на сохранении заряда и энергии, управляющих током и изменениями потенциала в электрической цепи

правило соединения:

первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; правило может быть указано [latex]{I}_{1}={I}_{2}+{I}_{3}[/latex]

правило цикла:

Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме падений [латекс]\текст{IR}[/латекс] (напряжения) в контуре и может быть сформулирована следующим образом: [латекс]\текст{ЭДС}=\текст{Ir}+{\ text{IR}}_{1}+{\text{IR}}_{2}\\[/латекс]

законов сохранения:

требуют сохранения энергии и заряда в системе

Избранные решения задач и упражнений

1.  [латекс]-{I}_{2}{R}_{2}+{\text{emf}}_{1}-{\text{I}} _{2}{r}_{1}+{\text{I}}_{3}{R}_{3}+{\text{I}}_{3}{r}_{2}- {\text{emf}}_{2}=\text{0}\\[/latex]

5. I ₃ = I ₁ + I ₂

7. [латекс] {\ text {ЭДС}} _ {2} — {\ text {I}} _ {2} {r} _ {2} — {\ text {I}} _ {2} {R} _ {2} + {\ text {I}} _ {1} {R} _ {5} + {I} _ {1} {r} _ {1} — {\ text {ЭДС}} _ {1} + {\ text { I}}_{1}{R}_{1}=0\\[/латекс]

9.(a) I ₁  = 4.75 A (b) I ₂  = −3.5 A (c) I ₃  = 8.25 A

11. (a) No, вы получите противоречивые уравнения для решения. (б) I ₁  ≠ I ₂  + I ₃ . Предполагаемые токи нарушают правило соединения.

Закон напряжения Кирхгофа — справочник Digilent

Понимание контуров в цепи

Закон тока Кирхгофа и закон напряжения Кирхгофа являются основой для анализа схем с сосредоточенными параметрами. Эти законы вместе с вольт-амперными характеристиками элементов цепи в системе дают нам возможность производить систематический анализ любой электрической сети. В этом разделе представлен закон напряжения Кирхгофа.

KVL зависит от концепции петли. Петля — это любой замкнутый путь в цепи, который не встречается ни с одним узлом более одного раза. По сути, чтобы создать петлю, начните с любого узла в цепи и проследите путь по цепи, пока не вернетесь к исходному узлу. Понятие цикла, вероятно, проще всего объяснить с помощью нескольких простых примеров, которые мы привели ниже.

Пример 1:

• Закон напряжения Кирхгофа (обычно сокращенно KVL) гласит:

• Альтернативная формулировка этого закона:

  • Сумма повышений напряжения на замкнутом контуре должна равняться сумме падений напряжения на контуре.

• Или даже:

  • При обходе контура вы должны вернуться к тому же напряжению, с которого начали.

---

Примечание

Полярность напряжения в петле основана на предполагаемой полярности разности напряжений в петле. Пока предполагаемые направления напряжений одинаковы от петли к петле, окончательный результат анализа будет отражать фактическая полярность напряжения в цепи.

---

Пример 2:

На рисунке ниже предполагаемая полярность напряжений V ₁ , V ₂ , V ₃ , V ₄ , V ₅ и V ₆ , как показано. В схеме возможны три петли: a-b-e-d-a, a-b-c-e-d-a и b-c-e-b. Мы применим KVL к каждому из этих циклов.

Наше соглашение о знаках для применения знаков к полярностям напряжения в наших уравнениях КВЛ будет следующим: при обходе контура, если положительный вывод разности напряжений встречается перед отрицательным выводом, разность напряжений будет интерпретироваться как положительный в уравнении КВЛ. Если отрицательная клемма встречается первой, разность напряжений будет интерпретироваться как минус в уравнении KVL. Мы используем это соглашение о знаках для удобства; для правильного применения КВЛ это не требуется, лишь бы знаки разности напряжения трактовались последовательно.

Применение KVL к циклу a-b-e-d-a и использование нашего соглашения о знаках, как указано выше, приводит к следующему результату:

$${V_1} — {V_4} — {V_6} — {V_3} = 0$$

Начальная точка цикла и направление, в котором мы зацикливаемся, произвольны; мы могли бы эквивалентно написать то же уравнение цикла, что и цикл d-e-b-a-d , и в этом случае наше уравнение стало бы таким:

$${V_6} + {V_4} — {V_1} + {V_3} = 0$$

Это уравнение идентично предыдущему уравнению, с той лишь разницей, что знаки всех переменных изменились и переменные стоят в уравнении в другом порядке. Теперь мы применяем KVL к циклу b-c-e-b, что приводит к:

$$- {V_2} + {V_5} + {V_4} = 0$$

Наконец, применение КВЛ к контуру a-b-c-e-d-a обеспечивает:

$${V_1} — {V_2} + {V_5} — {V_6} — {V_3} = 0$$

---

Важный момент

Закон напряжения Кирхгофа гласит, что сумма разностей напряжений вокруг любого замкнутого контура в цепи должна быть равна нулю.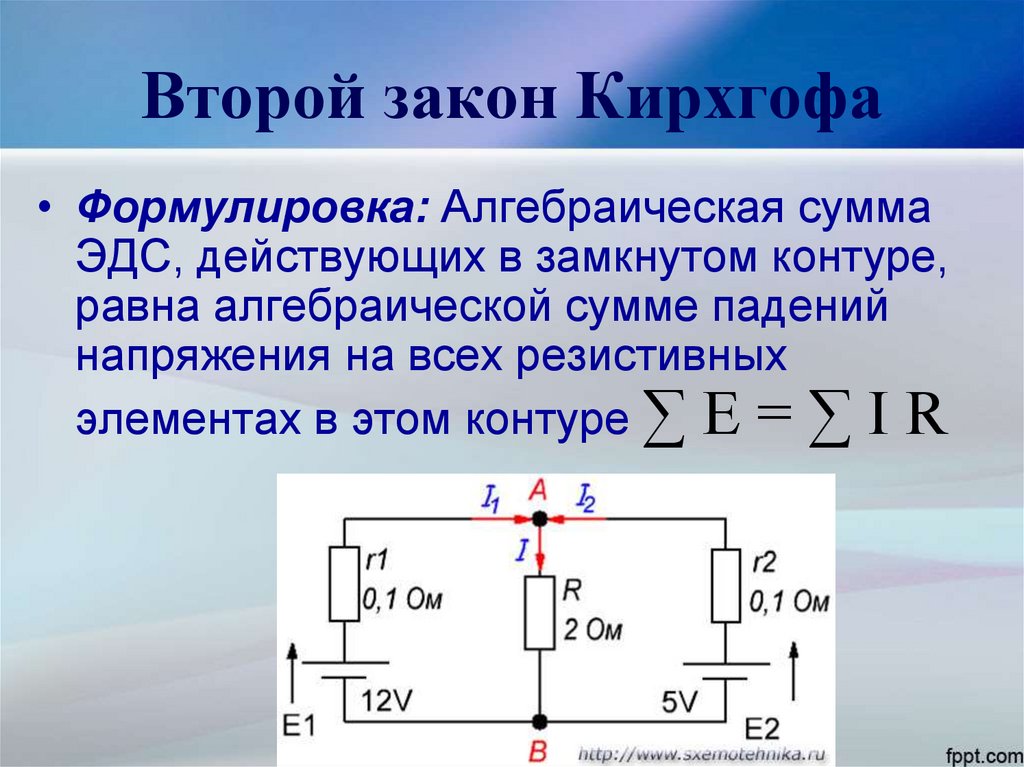 Петля в цепи — это любой путь, который заканчивается в той же точке, в которой он начинается.

---

Проверьте свои знания

1. Какое напряжение V в цепи ниже?
2. Какое напряжение V в цепи ниже?
3. Какое напряжение V в цепи ниже? (Подсказка: это вопрос с подвохом.)
4. Какие напряжения В ₁ , В ₂ и В ₃ в цепи ниже?

Ответы

1. Цикл по часовой стрелке, начиная с левого нижнего угла, дает:

$$- 3В — В + 7В = 0$$

Итак, V = 4 В. (Обратите внимание, что при зацикливании мы принимаем разность напряжений как положительную, если сначала встречаемся с клеммой «+», и как отрицательную, если сначала встречаем клемму «-».

2. Цикл по часовой стрелке, начиная с нижнего левого угла, приводит к:

$$+ 9В — 2В + В = 0$$

Итак, V = -7В. (Обратите внимание, что при зацикливании мы принимаем разность напряжений как положительную, если сначала встречаемся с клеммой «+», и как отрицательную, если сначала встречаем клемму «-».

3. Нет значения напряжения, удовлетворяющего этой схеме. Если вы примените KVL вокруг самого левого цикла, вы получите $3V + 1V — V = 0$, поэтому $V = 4V$. KVL вокруг самого правого цикла приводит к $V + 7V = 0$, поэтому $V = — 7V$. Две петли дают противоречивые результаты!

Корень проблемы в том, что данные напряжения несовместимы с законом напряжения Кирхгофа. Если мы применим KVL вокруг самого внешнего цикла, мы получим:

$$3В + 1В + 7В = 0$$

Что строго неверно.

4. Этот ответ подробно описан в нескольких различных ситуациях в схеме:

• Нахождение V ₁ : КВЛ вокруг петли, показанной ниже, дает: ${V_1} + 1V + 7V — 3V = 0$, поэтому ${V_1} = — 5V$

• Нахождение V ₂ : KVL вокруг петли, показанной ниже, дает: ${V_2} + 7V = 0$, поэтому ${V_2} = — 7V$

• Нахождение V ₃ : KVL вокруг петли, показанной ниже, дает: ${V_3} — V3 = 0$, поэтому ${V_3} = 3V$

---

Важный момент

Вы можете проверить свои результаты, применяя КВЛ вокруг других петель в схеме.