Закон электромагнитной индукции — Класс!ная физика

Закон электромагнитной индукции

Подробности

Просмотров: 314

«Физика — 11 класс»

Опыты Фарадея показали, что сила индукционного тока I_i в проводящем контуре пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром, т.е. скорости изменения магнитного потока.

ЭДС индукции

В цепи появляется электрический ток, когда на свободные заряды проводника действуют сторонние силы.
Величину, численно равную работе этих сил при перемещении единичного положительного заряда вдоль замкнутого контура, называют электродвижущей силой (ЭДС).

При изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризует ЭДС индукции.
Обозначение ЭДС индукции — .

Согласно закону Ома для замкнутой цепи индукционный ток в контуре

Закон электромагнитной индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца?

Пусть положительное направление обхода контура — против часовой стрелки.
Нормаль к контуру образует правый винт с направлением обхода.

Если магнитная индукция В внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем.
Тогда магнитный поток Ф > 0 и скорость измененеия магнитного потока тоже > 0.

По правилу Ленца индукционный ток создает магнитный поток Ф’ меньше 0.
Индукционный ток I_i по правилу буравчика направлен по часовой стрелке (против направления положительного обхода).
ЭДС индукции отрицательна.
Поэтому в формуле для закона электромагнитной индукции должен стоять знак «-»,
указывающий на то, что ЭДС индукции и скорость изменения магнитного потока имеют разные знаки:

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

Закон электромагнитной индукции — Студопедия

Индукцией называется явление возникновения одного поля (например, электрического) при изменении другого поля (например, магнитного).

Электромагнитной индукцией называется

явление возникновения электрического поля при изменении магнитного поля. Впервые это явление было открыто выдающимся английским физиком Майклом Фарадеем в 1831г. Фарадей установил, что индукционный ток возникает в замкнутом контуре при изменении во времени магнитного потока, пронизывающего этот контур.

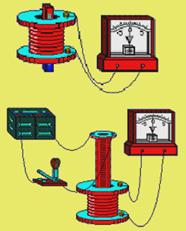
Рис. 15.1

Так, в опытах, показанных на рис. 15.1 при резком введении в катушку постоянного магнита стрелка гальванометра кратковременно отклонялась, что является следствием возникновения индукционного тока в катушке. Направление индукционного тока зависело от того, каким полюсом был обращен к катушке магнит и удалялся он от нее или приближался к ней. При статическом положении катушки и магнита индукционный ток отсутствовал.

Дальнейшие исследования индукционного тока в проводящих контурах различной формы и размеров показали справедливость закона электромагнитной индукции Фарадея:

ЭДС электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока, пронизывающего этот контур:

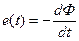. (15.1)

Знак «минус» показывает направление индукционного тока

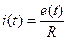, (15.2)

которое определяется правилом Э.Х. Ленца (1833г.) − индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, вызывающего этот ток ( 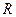— сопротивление контура). Правило Ленца иллюстрирует рис. 15.2.

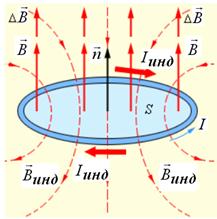
Рис. 15.2

Если ЭДС индукции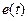

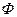появляется вследствие возрастания магнитного потока (внесение магнита в катушку), то индукционный ток создаст магнитное поле, уменьшающее возрастание 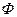, т.е. будет стараться вытолкнуть магнит из катушки и наоборот.

Последователь Фарадея — великий английский физик Джеймс Максвелл (1831-1879), проанализировал все известные к тому времени законы электромагнетизма и в 1861-1864 гг. создал теорию электромагнитного поля, записав ее в виде четырех уравнений (подробно эти уравнения рассмотрены далее, в разделе 16).

Согласно первому уравнению Максвелла, переменное магнитное поле создает вихревое электрическое поле в произвольном замкнутом контуре пространства (не обязательно проводящем контуре). Согласно третьему уравнению Максвелла это вихревое электрическое поле в следующей области пространства порождает переменное магнитное поле и т.д. Таким образом, возникает и распространяется электромагнитная волна.

Экспериментальное подтверждение электромагнитной теории Максвелла было дано примерно через 15 лет в опытах Г. Герца (1888 г.), который впервые получил электромагнитные волны.

На явлении электромагнитной индукции основано действие промышленных генераторов, трансформаторов и т.д., без которых современное развитие электротехники и электроэнергетики было бы невозможно.

Согласно первому уравнению Максвелла,циркуляция вектора напряженности электрического поля вдоль произвольного замкнутого контура 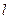равна взятой с обратным знаком скорости изменения магнитного потока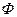

через поверхность , натянутую на контур :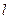

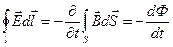, (15.3)

где

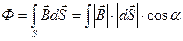, (15.4)

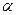— угол между векторам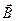и и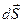

.

Изменяющееся во времени магнитное поле 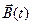порождает вихревое электрическое поле , циркуляция которого для замкнутого контура 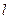равна ЭДС индукции:

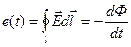. (15.4)

Это и есть закон электромагнитной индукции в интегральной форме.

Если в таком электрическом поле находится

проводящий замкнутый контур, то в нем возникает вихревой электрический ток, величина которого пропорциональна напряженности вихревого электрического поля. Такие токи называются токами Фуко.

Явление электромагнитной индукции. Закон Фарадея — Студопедия

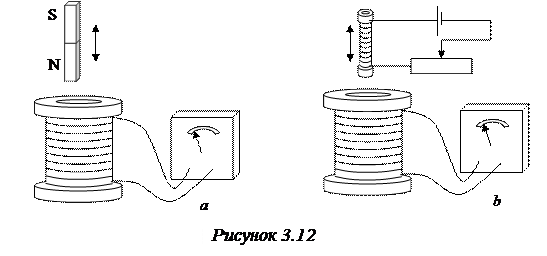После того, как было установлено, что магнитное поле создаётся электрическими токами, учёные пытались решить обратную задачу – при помощи магнитного поля создать электрический ток. Эту задачу в 1831 г. успешно решил М. Фарадей, который открыл явление электромагнитной индукции. Суть этого явления заключается в том, что

в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего этот контур, возникает электрически ток, который называется индукционным. Схема некоторых опытов Фарадея показана на рис. 3.12.

При изменении положения постоянного магнита относительно катушки, замкнутой на гальванометр, в последней возникал электрический ток, причём направление тока оказывалось различным – в зависимости от направления перемещения постоянного магнита. Аналогичный результат достигался и при перемещении другой катушки, по которой шёл электрический ток. Более того, в большой катушке возникал ток даже при неизменном положении меньшей катушки, но при изменении тока в ней.

На основании подобных опытов М. Фарадей пришёл к выводу, что в катушке всегда возникает электрический ток при изменении магнитного потока, сцепленного с этой катушкой. Величина тока зависит от скорости изменения магнитного потока. Сейчас мы формулируем открытия Фарадея в виде закона электромагнитной индукции: при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ЭДС индукции, которая определяется как

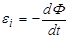. (3.53)

Знак “–” в выражении (3.53) означает, что при увеличении магнитного потока магнитное поле, созданное индукционным током, направлено против внешнего магнитного поля. Если же магнитный поток уменьшается по величине, то магнитное поле индукционного тока совпадает по направлению с внешним магнитным полем. Русский учёный Х. Ленц таким образом определил появление знака минус в выражении (3.53) – индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле имеет такое направление, что препятствует изменению магнитного потока, вызвавшего возникновение индукционного тока.

Дадим ещё одну формулировку закона электромагнитной индукции: ЭДС индукции в замкнутом проводящем контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего этот контур.

Немецкий физик Гельмгольц показал, что закон электромагнитной индукции можно получить из закона сохранения энергии. В самом деле, энергия источника ЭДС по перемещению проводника с током в магнитном поле (см.рис.3.37) будет затрачена как на Джоулев разогрев проводника сопротивлением R, так и на работу по перемещению проводника:

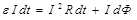. (3.54)

Тогда из уравнения (3.54) сразу же следует, что

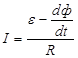. (3.55)

В числителе выражения (3.55) стоит алгебраическая сумма ЭДС, действующих в контуре. Следовательно,

.

Какова же физическая причина возникновения ЭДС? На заряды в проводнике АВ действует сила Лоренца при движении проводника вдоль оси x. Под действием этой силы положительные заряды будут смещаться вверх, в результате чего электрическое поле в проводнике будет ослаблено. Другими словами, в проводнике появится ЭДС индукции. Следовательно, в рассмотренном нами случае физической причиной возникновения ЭДС является сила Лоренца. Однако, как мы уже отмечали, и в неподвижном замкнутом контуре может появиться ЭДС индукции, если будет изменяться магнитное поле, пронизывающее этот контур.

В этом случае заряды можно считать неподвижными, а на неподвижные заряды сила Лоренца не действует. Чтобы объяснить возникновение ЭДС в этом случае, Максвелл предположил, что всякое изменяющееся магнитное поле порождает в проводнике изменяющееся электрическое поле, которое и является причиной возникновения ЭДС индукции. Циркуляция вектора напряжённости, действующей в этом контуре, таким образом, будет равна ЭДС индукции, действующей в контуре:

. (3.56)

Явление электромагнитной индукции используется для превращения механической энергии вращения в электрическую – в генераторах электрического тока. Обратный процесс – превращение электрической энергии в механическую, основанный на вращательном моменте, действующем на рамку с током в магнитном поле, используется в электродвигателях.

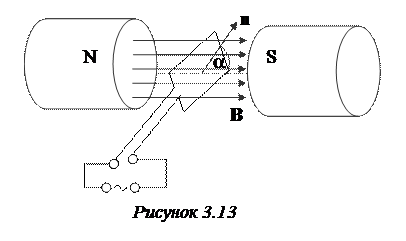
Рассмотрим принцип действия генератора электрического тока (рис. 3.13). Пусть у нас проводящая рамка вращается между полюсами магнита (это может быть и электромагнит) с частотой w. Тогда угол между нормалью к плоскости рамки и направлением магнитного поля изменяется по закону a = wt. В этом случае магнитный поток, сцепленный с рамкой, будет изменяться в соответствии с формулой

, (3.57)

где S – площадь контура. В соответствии с законом электромагнитной индукции в рамке будет индуцироваться ЭДС

, (3.58)

с e_max = BSw. Таким образом, если в магнитном поле вращается с постоянной угловой скоростью проводящая рамка, то в ней будет индуцироваться ЭДС, изменяющаяся по гармоническому закону. В реальных генераторах вращают много витков, соединенных последовательно, а в электромагнитах, для увеличения магнитной индукции, используют сердечники с большой магнитной проницаемостью m..

Индукционные токи могут возникать и в толще проводящих тел, помещённых в переменное магнитное поле. В этом случае эти токи называются токами Фуко. Эти токи вызывают разогрев массивных проводников. Это явление используется в вакуумных индукционных печах, где сильные токи разогревают металл до плавления. Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.

§ 123. Закон Фарадея и его вывод из закона сохранения энергии

Обобщая результаты своих многочислен­ных опытов, Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в кон-

194

туре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции. Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_i определя­ются только скоростью изменения магнит­ного потока, т. е.

Теперь необходимо выяснить знак ξ_i. В § 120 было показано, что знак магнитно­го потока зависит от выбора положитель­ной нормали к контуру. В свою очередь, положительное направление нормали свя­зано с током правилом правого винта (см. § 109). Следовательно, выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

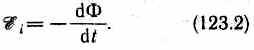
Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно переме­щаться (см. рис. 177). Под действием си­лы Ампера F, направление которой пока­зано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампе­ра производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за вре­мя dt (ξIdt) будет складываться из рабо­ты на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

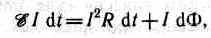
откуда

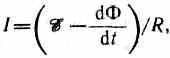
где-dФ/dt=ξ_i есть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея можно сформулиро­вать еще таким образом: э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_i не зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Какова природа э.д.с. электромагнит­ной индукции? Если проводник (подвиж­ная перемычка контура на рис. 177) дви-

195

жется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противо­положного направления (за направление электрического тока принимается движе­ние положительных зарядов). Таким обра­зом, возбуждение э.д.с. индукции при движении контура в постоянном магнит­ном поле объясняется действием силы Ло­ренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникнове­ние э.д.с. электромагнитной индукции возможно и в случае неподвижного кон­тура, находящегося в переменном магнит­ном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить воз­никновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в непод­вижных проводниках предположил, что всякое переменное магнитное поле воз­буждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_В этого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:

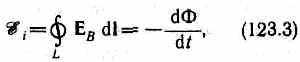
Закон электромагнитной индукции Фарадея | Электромагнетизм

10.3 Закон электромагнитной индукции Фарадея (ESBPY)

Ток, индуцированный изменяющимся магнитным полем (ESBPZ)

В то время как удивительное открытие электромагнетизма Эрстедом проложило путь для более практического применения электричества, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитная индукция .

Фарадей обнаружил, что когда он перемещал магнит около провода, на нем генерировалось напряжение.Если магнит удерживался в неподвижном состоянии, напряжение не генерировалось, оно существовало только во время движения магнита. Мы называем это напряжение индуцированной ЭДС (\ (\ mathcal {E} \)).

Контурная петля, подключенная к чувствительному амперметру, будет регистрировать ток, если он настроен, как показано на этом рисунке, и магнит перемещается вверх и вниз:

Магнитный поток

Прежде чем мы перейдем к определению закона электромагнитной индукции Фарадея и примерам, нам сначала нужно потратить некоторое время на изучение магнитного потока.Для петли площадью \ (A \) в присутствии однородного магнитного поля \ (\ vec {B} \) магнитный поток (\ (φ \)) определяется как: \ [\ phi = BA \ cos \ theta \] Куда: \ begin {align *} \ theta & = \ text {угол между магнитным полем B и нормалью к петле области A} \\ A & = \ text {область петли} \\ B & = \ text {магнитное поле} \ end {align *}

Единицей измерения магнитного потока является Вебер (Вб).

Вы можете спросить себя, почему включен угол \ (\ theta \). Поток зависит от магнитного поля, проходящего через поверхность. Мы знаем, что поле, параллельное поверхности, не может вызвать ток, потому что оно не проходит через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть компонент, который перпендикулярен, и компонент, который параллелен поверхности. Параллельная составляющая не может вносить вклад в поток, только вертикальная составляющая может.

На этой диаграмме мы показываем, что магнитное поле под углом, отличным от перпендикулярного, может быть разбито на составляющие.Компонент, перпендикулярный поверхности, имеет величину \ (B \ cos (\ theta) \), где \ (\ theta \) — угол между нормалью и магнитным полем.

Закон электромагнитной индукции Фарадея

ЭДС \ (\ mathcal {E} \), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь A контура. Математически это можно выразить как:

\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]

где \ (\ phi = B · A \), а B — напряженность магнитного поля.\ (N \) — количество контуров схемы. Магнитное поле измеряется в теслах (Тл). Знак минус указывает направление и что индуцированная ЭДС имеет тенденцию противодействовать изменению магнитного потока. Знак минус можно не учитывать при вычислении звездных величин.

Закон Фарадея связывает наведенную ЭДС со скоростью изменения магнитного потока, который является произведением магнитного поля и площади поперечного сечения, через которую проходят силовые линии.

Это не площадь самого провода, а площадь, которую он охватывает.Это означает, что если вы согнете проволоку в круг, площадь, которую мы будем использовать при вычислении потока, будет площадью поверхности круга, а не проволоки.

На этом рисунке, где магнит находится в той же плоскости, что и контур цепи, не было бы тока, даже если бы магнит перемещался все ближе и дальше. Это связано с тем, что силовые линии магнитного поля не проходят через замкнутое пространство, а параллельны ему. Силовые линии магнитного поля должны проходить через область, ограниченную контуром цепи, чтобы возникла ЭДС.

Направление наведенного тока (ESBQ2)

Самая важная вещь, которую следует помнить, — это то, что индуцированный ток противодействует происходящему изменению.

На первом рисунке (слева) в контуре цепи южный полюс магнита приближается. Величина поля от магнита становится больше. Реакция индуцированной ЭДС будет состоять в том, чтобы попытаться противодействовать усилению поля по направлению к полюсу. Поле является вектором, поэтому ток будет течь в таком направлении, что поля, создаваемые током, имеют тенденцию нейтрализовать поля от магнита, сохраняя результирующее поле неизменным.

Чтобы противостоять переходу от приближающегося южного полюса сверху, ток должен приводить к тому, что силовые линии должны удаляться от приближающегося полюса. Следовательно, индуцированное магнитное поле должно иметь силовые линии, идущие вниз по внутренней стороне петли. Направление тока, указанное стрелками на контуре цепи, будет достигнуто. Проверьте это, используя Правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание, что поле закручивается вниз в область, ограниченную петлей.

На второй диаграмме южный полюс удаляется. Это означает, что поле от магнита станет слабее. Отклик на индуцированный ток будет заключаться в создании магнитного поля, которое добавляется к существующему от магнитного поля, чтобы противостоять его уменьшению в силе.

Другой способ представить ту же функцию — просто использовать полюса. Чтобы противостоять приближающемуся южному полюсу, индуцируемый ток создает поле, которое выглядит как другой южный полюс на стороне приближающегося южного полюса.Подобно отталкиванию полюсов, вы можете представить себе, как течение создает южный полюс, чтобы отразить приближающийся южный полюс. На второй панели ток устанавливает северный полюс, чтобы привлечь южный полюс и остановить его движение.

Мы также можем использовать вариант правила правой руки, помещая пальцы в направлении течения, чтобы большой палец указывал в направлении силовых линий (или северного полюса).

Мы можем проверить все это на случаях, когда северный полюс перемещается ближе или дальше от цепи.В первом случае приближения северного полюса ток будет сопротивляться изменению, создавая поле в направлении, противоположном полю, исходящему от магнита, который становится сильнее. Используйте Правило правой руки, чтобы убедиться, что стрелки создают поле с линиями поля, которые изгибаются вверх в замкнутой области, нейтрализуя те, которые изгибаются вниз от северного полюса магнита.

Подобно отталкиванию полюсов, в качестве альтернативы проверьте, что если поместить пальцы правой руки в направлении течения, большой палец будет указывать вверх, указывая на северный полюс.

Для второй фигуры, когда северный полюс удаляется, ситуация обратная.

Направление индуцированного тока в соленоиде (ESBQ3)

Подход к просмотру направления тока в соленоиде аналогичен подходу, описанному выше. Единственная разница в том, что в соленоиде есть несколько витков провода, поэтому величина наведенной ЭДС будет другой. Поток будет рассчитан с использованием площади поверхности соленоида, умноженной на количество петель.

Помните: направления токов и связанных с ними магнитных полей можно найти, используя только Правило правой руки. Когда пальцы правой руки направлены в направлении магнитного поля, большой палец указывает в направлении тока. Когда большой палец направлен в направлении магнитного поля, пальцы указывают в направлении тока.

Направление тока будет таким, чтобы препятствовать изменению. Мы бы использовали установку, как в этом скетче, для проведения теста:

В случае, когда северный полюс направлен к соленоиду, ток будет течь так, чтобы северный полюс установился на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте, используя Правило правой руки):

В случае, когда северный полюс движется от соленоида, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс движется от соленоида, ток будет течь так, что северный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс направлен к соленоиду, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его:

Простой способ создать магнитное поле изменяющейся интенсивности — переместить постоянный магнит рядом с проволокой или катушкой с проволокой.Магнитное поле должно увеличиваться или уменьшаться по напряженности перпендикулярно проводу (так, чтобы силовые линии магнитного поля «пересекали» проводник), иначе не будет индуцироваться напряжение.

Индуцированный ток создает магнитное поле. Наведенное магнитное поле имеет направление, которое стремится нейтрализовать изменение магнитного поля в петле из проволоки. Итак, вы можете использовать Правило правой руки, чтобы найти направление индуцированного тока, помня, что индуцированное магнитное поле противоположно направлению изменения магнитного поля.

Индукция

Электромагнитная индукция находит практическое применение в конструкции электрических генераторов, которые используют механическую энергию для перемещения магнитного поля мимо катушек с проволокой для генерации напряжения. Однако это далеко не единственное практическое применение этого принципа.

Если мы вспомним, магнитное поле, создаваемое проводом с током, всегда перпендикулярно проводу, и что сила потока этого магнитного поля зависит от величины тока, который проходит через него.Таким образом, мы можем видеть, что провод способен создавать напряжение на своей собственной длине , если ток изменяется. Этот эффект называется самоиндукцией . Самоиндукция — это когда изменяющееся магнитное поле создается изменением тока через провод, вызывая напряжение по длине того же провода.

Если магнитный поток усиливается путем изгибания проволоки в форме катушки и / или наматывания этой катушки на материал с высокой проницаемостью, этот эффект самоиндуцированного напряжения будет более интенсивным.Устройство, предназначенное для использования этого эффекта, называется индуктором .

Помните, что индуцированный ток создает магнитное поле, препятствующее изменению магнитного потока. Это известно как закон Ленца.

Рабочий пример 1: Закон Фарадея

Рассмотрим плоскую квадратную катушку с 5 витками. Катушка расположена \ (\ text {0,50} \) \ (\ text {m} \) с каждой стороны и имеет магнитное поле \ (\ text {0,5} \) \ (\ text {T} \) проходящий через него. Плоскость катушки перпендикулярна магнитному полю: поле направлено за пределы страницы.Используйте закон Фарадея для вычисления наведенной ЭДС, если магнитное поле увеличивается равномерно от \ (\ text {0,5} \) \ (\ text {T} \) до \ (\ text {1} \) \ (\ текст {T} \) в \ (\ text {10} \) \ (\ text {s} \). Определите направление индуцированного тока.

Определите, что требуется

Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле находится под прямым углом к ​​поверхности и поэтому выровнено с нормалью.Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \). Начальное или начальное магнитное поле, \ (B_i \), задается как конечная величина поля, \ (B_f \). Мы хотим определить величину ЭДС, чтобы можно было игнорировать знак минус.

Площадь \ (A \) — это площадь квадратной катушки.

Решить задачу

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ & = N \ frac {\ phi_f- \ phi_i} {\ Delta t} \\ & = N \ frac {B_fA — B_iA} {\ Delta t} \\ & = N \ frac {A (B_f — B_i)} {\ Delta t} \\ & = (5) \ frac {(\ text {0,50}) ^ 2 (\ text {1} — \ text {0,50})} {\ text {10}} \\ & = (5) \ frac {(\ text {0,50}) ^ 2 (\ text {1} — \ text {0,50})} {\ text {10}} \\ & = \ текст {0,0625} \ текст {V} \ end {выровнять *}

Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.

Рабочий пример 2: закон Фарадея

Рассмотрим соленоид из 9 витков с неизвестным радиусом \ (r \). На соленоид действует магнитное поле \ (\ text {0,12} \) \ (\ text {T} \). Ось соленоида параллельна магнитному полю. Когда поле равномерно переключается на \ (\ text {12} \) \ (\ text {T} \) в течение 2 минут, ЭДС с величиной \ (- \ text {0,3} \) \ (\ text {V} \) индуцируется. Определите радиус соленоида.

Определите, что требуется

Требуется определить радиус соленоида.Мы знаем, что связь между наведенной ЭДС и полем регулируется законом Фарадея, который включает геометрию соленоида. Мы можем использовать это соотношение, чтобы найти радиус.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле находится под прямым углом к ​​поверхности и поэтому выровнено с нормалью. Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \).{- \ text {2}} \) \ (\ text {m} \). Соленоид подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \ (\ text {0,4} \) \ (\ text {T} \) до \ (\ text {3,4} \) \ (\ text { T} \) в интервале \ (\ text {27} \) \ (\ text {s} \). Ось соленоида составляет угол \ (\ text {35} \) \ (\ text {°} \) к магнитному полю. Найдите наведенную ЭДС.

Определите, что требуется

Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под углом к ​​нормали к поверхности.{- \ text {3}} \ text {V} \ end {выровнять *}

Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.

Реальные приложения

Следующие устройства используют в своей работе закон Фарадея.

• плиты индукционные

• магнитофонов

• металлоискатели

• трансформаторы

Реальные применения закона Фарадея

Выберите одно из следующих устройств и поищите в Интернете или библиотеке, как работает ваше устройство.В объяснении вам нужно будет сослаться на закон Фарадея.

• плиты индукционные

• магнитофонов

• металлоискатели

• трансформаторы

Высокие оценки в науке — залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.

Зарегистрируйтесь и проверьте себя

Закон Фарадея

Упражнение 10.2

Изложите закон электромагнитной индукции Фарадея словами и запишите математическое соотношение.

ЭДС \ (\ mathcal {E} \), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь A контура. Математически это можно выразить как:

\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]

где \ (\ phi = B · A \), а B — напряженность магнитного поля.\ (N \) — количество контуров схемы. Магнитное поле измеряется в теслах (Тл). Знак минус указывает направление и что индуцированная ЭДС имеет тенденцию противодействовать изменению магнитного потока. Знак минус можно не учитывать при вычислении звездных величин.

Опишите, что происходит, когда стержневой магнит вдавливается в соленоид, подключенный к амперметру, или вытягивается из него. Нарисуйте картинки, подтверждающие ваше описание.

В случае, когда северный полюс направлен к соленоиду, ток будет течь так, чтобы северный полюс установился на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте, используя Правило правой руки):

В случае, когда северный полюс движется от соленоида, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс движется от соленоида, ток будет течь так, что северный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс направлен к соленоиду, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его:

Объясните, как магнитный поток может быть нулевым, когда магнитное поле не равно нулю.

Поток связан с магнитным полем:

\ (\ phi = BA \ cos \ theta \)

Если \ (\ cos \ theta \) равно 0, то магнитный поток будет равен 0, даже если есть магнитное поле. В этом случае магнитное поле параллельно поверхности и не проходит через нее.

Используйте правило правой руки, чтобы определить направление индуцированного тока в соленоиде ниже.

Южный полюс магнита приближается к соленоиду.Закон Ленца говорит нам, что ток будет течь так, чтобы противостоять изменению. Южный полюс на конце соленоида будет противодействовать приближающемуся южному полюсу. Ток будет циркулировать по странице в верхней части катушки, так что большой палец правой руки будет указывать влево.

Рассмотрим круговую катушку из 5 витков с радиусом \ (\ text {1,73} \) \ (\ text {m} \). Катушка подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \ (\ text {2,18} \) \ (\ text {T} \) до \ (\ text {12,7} \) \ (\ text { T} \) в интервале \ (\ text {3} \) \ (\ text {minutes} \).Ось соленоида составляет угол \ (\ text {27} \) \ (\ text {°} \) к магнитному полю. Найдите наведенную ЭДС.

Мы знаем, что магнитное поле расположено под углом к ​​нормали к поверхности. Это означает, что мы должны учитывать угол, который поле образует с нормалью и \ (φ = BA \ cos (θ) \). Начальное или начальное магнитное поле, \ (B_ {i} \), задается как конечная величина поля, \ (B_f \). Мы хотим определить величину ЭДС, чтобы можно было игнорировать знак минус. Площадь A будет равна \ (πr ^ {2} \).{2} \ cos (\ text {13}) (\ text {2,7} — \ text {5,34})} {12} \ right) \\ & = — \ текст {0,14} \ текст {V} \ end {выровнять *}

Если угол изменить на \ (\ text {67,4} \) \ (\ text {°} \), какой радиус должен быть, чтобы ЭДС оставалась прежней?

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ & = N \ frac {\ phi_ {f} — \ phi_ {i}} {\ Delta t} \\ & = N \ frac {B_ {f} A \ cos \ theta — B_ {i} A \ cos \ theta} {\ Delta t} \\ & = N \ frac {A \ cos \ theta (B_ {f} — B_ {i})} {\ Delta t} \\ — \ text {0,14} & = 11 \ left (\ frac {\ pi (r) ^ {2} \ cos (\ text {67,4}) (\ text {2,7} — \ text {5 , 34})} {12} \ right) \\ — \ text {1,68} & = — \ text {35,06} (r) ^ {2} \\ г ^ {2} & = \ текст {0,0479} \\ г & = \ текст {0,22} \ текст {м} \ end {выровнять *}

Найдите изменение потока, если ЭДС равна \ (\ text {12} \) \ (\ text {V} \) за период \ (\ text {12} \) \ (\ text {s} \) .

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ 12 & = 5 \ left (\ frac {\ Delta \ phi} {12} \ right) \\ \ Delta \ phi & = \ text {28,8} \ text {Wb} \ end {выровнять *}

Если угол изменить на \ (\ text {45} \) \ (\ text {°} \), на какой временной интервал нужно изменить, чтобы наведенная ЭДС оставалась прежней?

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ & = N \ frac {\ phi_ {f} — \ phi_ {i}} {\ Delta t} \\ & = N \ frac {B_ {f} A \ cos \ theta — B_ {i} A \ cos \ theta} {\ Delta t} \\ & = \ cos \ theta \ times N \ frac {B_ {f} A — B_ {i} A} {\ Delta t} \ end {выровнять *}

Все значения остаются неизменными в двух описанных ситуациях, за исключением угла и времени.Мы можем приравнять уравнения для двух сценариев:

\ begin {align *} \ mathcal {E} _1 & = \ mathcal {E} _2 \\ \ cos \ theta_1 \ times N \ frac {B_ {f} A — B_ {i} A} {\ Delta t_1} & = \ cos \ theta_2 \ times N \ frac {B_ {f} A — B_ {i} A } {\ Delta t_2} \\ \ cos \ theta_1 \ frac {1} {\ Delta t_1} & = \ cos \ theta_2 \ frac {1} {\ Delta t_2} \\ \ Delta t_2 & = \ frac {\ Delta t_1 \ cos \ theta_2} {\ cos \ theta_1} \\ \ Delta t_2 & = \ frac {(\ text {12} \ cos (\ text {45}} {\ cos (\ text {23})} \\ \ Delta t_2 & = \ text {9,22} \ text {s} \ end {выровнять *} .

Закон электромагнитной индукции Фарадея — Первый закон, Второй закон

Закон электромагнитной индукции Фарадея

В 1831 году Майкл Фарадей сформулировал два закона на основе экспериментов. Эти законы называются законами электромагнитной индукции Фарадея.

ПЕРВЫЙ ЗАКОН

Первый закон электромагнитной индукции Фарадея гласит, что всякий раз, когда проводник помещается в переменное магнитное поле, индуцируются ЭДС, называемые индуцированной ЭДС, если цепь проводника замкнута, индуцируется также ток, который называется индуцированным током.

или

Каждый раз, когда проводник вращается в магнитном поле, индуцируется ЭДС, которая является индуцированной ЭДС.

Закон Фарадея Анимация

ВТОРОЙ ЗАКОН

Второй закон электромагнитной индукции Фарадея гласит, что индуцированная ЭДС равна скорости изменения потоковых связей (потокосцепления — это произведение витков n катушки и связанного с ней потока).

РАЗЪЯСНЕНИЕ ЗАКОНА ФАРАДА

Пусть

Начальные потокосцепления = Nφ1

Конечные потокосцепления = Nφ2

Изменение потокосцепления = Nφ2 — Nφ1

= N ((φ2-φ1)

Если (φ2-φ1) = φ

Тогда изменение потокосцепления = Nφ

Скорость изменения потокосцеплений = Nφ / т wb / sec

Взяв производную от правой части, получаем

Скорость изменения потокосцеплений = Ndφ / dt wb / sec

Rut, согласно законам электромагнитной индукции Фарадея, скорость изменения потоковых связей равна наведенной ЭДС, поэтому мы можем написать

= Ndφ / dt вольт

Обычно законы Фарадея записываются как

e = -Ndφ / dt вольт

Где отрицательный знак представляет направление индуцированного тока в проводнике, будет таким, что создаваемое им магнитное поле будет противодействовать глаголу «причина его создания».

.

Электромагнитная индукция — определение, принципы и законы

• • Классы
    • Класс 1–3
    • Класс 4–5
    • Класс 6–10
    • Класс 11–12
  • КОНКУРЕНТНЫЙ ЭКЗАМЕН
    • BNAT 000 000 NC Книги
      • Книги NCERT для класса 5
      • Книги NCERT для класса 6
      • Книги NCERT для класса 7
      • Книги NCERT для класса 8
      • Книги NCERT для класса 9
      • Книги NCERT для класса 10
      • Книги NCERT для класса 11
      • Книги NCERT для класса 12
    • NCERT Exemplar
      • NCERT Exemplar Class 8
      • NCERT Exemplar Class 9
      • NCERT Exemplar Class 10
      • NCERT Exemplar Class 11
      • NCERT 9000 9000
      • NCERT Exemplar Class
        • Решения RS Aggarwal, класс 12
        • Решения RS Aggarwal, класс 11
        • Решения RS Aggarwal, класс 10
        90 003 Решения RS Aggarwal класса 9
        • Решения RS Aggarwal класса 8
        • Решения RS Aggarwal класса 7
        • Решения RS Aggarwal класса 6
      • Решения RD Sharma
        • RD Sharma Class 6 Решения
        • Решения RD Sharma
        Решения RD Sharma Class 8
        • Решения RD Sharma Class 9
        • Решения RD Sharma Class 10
        • Решения RD Sharma Class 11
        • Решения RD Sharma Class 12
      • PHYSICS
        • Механика
        • Оптика
        • Термодинамика Электромагнетизм
      • ХИМИЯ
        • Органическая химия
        • Неорганическая химия
        • Периодическая таблица
      • MATHS
        • Теорема Пифагора
        0004
        • 000300030004
        9000
        • Простые числа
        • Взаимосвязи и функции
        • Последовательности и серии
        • Таблицы умножения
        • Детерминанты и матрицы
        • Прибыль и убыток
        • Полиномиальные уравнения
        • Деление фракций
      • 000
      • 000
      • 000
      • 000
      • 000
      • 000 Microology
      • 000
      • 000 Microology
      • 000 BIOG3000
        FORMULAS
        • Математические формулы
        • Алгебраические формулы
        • Тригонометрические формулы
        • Геометрические формулы
        • КАЛЬКУЛЯТОРЫ
          • Математические калькуляторы
          • 0003000 PBS4000
          • 000300030002 Примеры калькуляторов химии
          Класс 6
          • Образцы документов CBSE для класса 7
          • Образцы документов CBSE для класса 8
          • Образцы документов CBSE для класса 9
          • Образцы документов CBSE для класса 10
          • Образцы документов CBSE для класса 11
          • Образцы документов CBSE чел для класса 12
        • CBSE Контрольный документ за предыдущий год
          • CBSE Контрольный документ за предыдущий год Класс 10
          • Контрольный документ за предыдущий год CBSE, класс 12
        • HC Verma Solutions
          • HC Verma Solutions Class 11 Physics
          • Решения HC Verma, класс 12, физика
        • Решения Лакмира Сингха
          • Решения Лакмира Сингха, класс 9
          • Решения Лакмира Сингха, класс 10
          • Решения Лакмира Сингха, класс 8
        • Заметки CBSE
        • CBSE Notes
          Примечания CBSE класса 7
          • Примечания CBSE класса 8
          • Примечания CBSE класса 9
          • Примечания CBSE класса 10
          • Примечания CBSE класса 11
          • Примечания CBSE класса 12
          • Примечания к редакции CBSE
            • Примечания к редакции
              • CBSE Class
                • Примечания к редакции класса 10 CBSE
                • Примечания к редакции класса 11 CBSE 9000 4
                • Примечания к редакции класса 12 CBSE
              • Дополнительные вопросы CBSE
                • Дополнительные вопросы по математике класса 8 CBSE
                • Дополнительные вопросы по науке 8 класса CBSE
                • Дополнительные вопросы по математике класса 9 CBSE
                • Дополнительные вопросы по науке класса 9 CBSE
                Дополнительные вопросы по математике для класса 10
                • Дополнительные вопросы по науке, класс 10 по CBSE
              • CBSE, класс
                • , класс 3
                • , класс 4
                • , класс 5
                • , класс 6
                • , класс 7
                • , класс 8
                • , класс 9 Класс 10
                • Класс 11
                • Класс 12
              • Учебные решения
            • Решения NCERT
              • Решения NCERT для класса 11
                • Решения NCERT для класса 11 по физике
                • Решения NCERT для класса 11 Химия
                Решения для биологии класса 11
                • Решения NCERT для математики класса 11
                9 0003 NCERT Solutions Class 11 Accountancy
                • NCERT Solutions Class 11 Business Studies
                • NCERT Solutions Class 11 Economics
                • NCERT Solutions Class 11 Statistics
                • NCERT Solutions Class 11 Commerce
              • NCERT Solutions For Class 12
                • NCERT Solutions For Класс 12 по физике
                • Решения NCERT для химии класса 12
                • Решения NCERT для класса 12 по биологии
                • Решения NCERT для класса 12 по математике
                • Решения NCERT Класс 12 Бухгалтерия
                • Решения NCERT, класс 12, бизнес-исследования
                • Решения NCERT, класс 12 Экономика
                • NCERT Solutions Class 12 Accountancy Part 1
                • NCERT Solutions Class 12 Accountancy Part 2
                • NCERT Solutions Class 12 Micro-Economics
                • NCERT Solutions Class 12 Commerce
                • NCERT Solutions Class 12 Macro-Economics
              • NCERT Solutions For Класс 4
                • Решения NCERT для математики класса 4
                • Решения NCERT для класса 4 EVS
              • Решения NCERT для класса 5
                • Решения NCERT для математики класса 5
                • Решения NCERT для класса 5 EVS
              • Решения NCERT для класса 6
                • Решения NCERT для математики класса 6
                • Решения NCERT для науки класса 6
                • Решения NCERT для социальных наук класса 6
                • Решения NCERT для класса 6 Английский
              • Решения NCERT для класса 7
                • Решения NCERT для класса 7 Математика
                • Решения NCERT для класса 7 Наука
                • Решения NCERT для класса 7 по социальным наукам
                • Решения NCERT для класса 7 Английский
              • Решения NCERT для класса 8
                • Решения NCERT для класса 8 Математика
                • Решения NCERT для класса 8 Science
                • Решения NCERT для социальных наук 8 класса
                • Решение NCERT ns для класса 8 Английский
              • Решения NCERT для класса 9
                • Решения NCERT для социальных наук класса 9
              • Решения NCERT для математики класса 9
                • Решения NCERT для математики класса 9 Глава 1
                • Решения NCERT для Математика класса 9 Глава 2
                • Решения NCERT для математики класса 9 Глава 3
                • Решения NCERT для математики класса 9 Глава 4
                Решения NCERT
                • для математики класса 9 Глава 5
                • Решения NCERT для математики класса 9 Глава 6
                • Решения NCERT для Математика класса 9 Глава 7
                • Решения NCERT для математики класса 9 Глава 8
                Решения NCERT
                • для математики класса 9 Глава 9
                Решения NCERT
                • для математики класса 9 Глава 10
                • Решения NCERT для математики класса 9 Глава 11
                • Решения NCERT для Математика класса 9 Глава 12
                • Решения NCERT для математики класса 9 Глава 13
                Решения
                • NCERT для математики класса 9 Глава 14
                • Решения NCERT для математики класса 9 Глава 15
              • Решения NCERT для науки класса 9
                • Решения NCERT для науки класса 9 Глава 1
                • Решения NCERT для науки класса 9 Глава 2
                • Решения NCERT для класса 9 Наука Глава 3
                • Решения NCERT для Науки Класса 9 Глава 4
                • Решения NCERT для Науки Класса 9 Глава 5
                • Решения NCERT для Науки Класса 9 Глава 6
                • Решения NCERT для Науки Класса 9 Глава 7
                • Решения NCERT для Класса 9 Наука Глава 8
                • Решения NCERT для Науки Класса 9 Глава 9
                • Решения NCERT для Науки Класса 9 Глава 10
                • Решения NCERT для Науки Класса 9 Глава 12
                • Решения NCERT для Науки Класса 9 Глава 11
                • Решения NCERT для Класса 9 Наука Глава 13
                • Решения NCERT для класса 9 Наука Глава 14
                • Решения NCERT для класса 9 по науке Глава 15
              • Решения NCERT для класса 10
                • Решения NCERT для класса 10 по социальным наукам
              • Решения NCERT для математики класса 10
                • Решения NCERT для математики класса 10 Глава 1
                • Решения NCERT для математики класса 10 Глава 2
                • Решения NCERT для математики класса 10 Глава 3
                • Решения NCERT для математики класса 10 Глава 4
                • Решения NCERT для математики класса 10 Глава 5
                • Решения NCERT для математики класса 10 Глава 6
                • Решения NCERT для математики класса 10 Глава 7
                • Решения NCERT для математики класса 10 Глава 8
                • Решения NCERT для математики класса 10 Глава 9
                Решения NCERT
                • для математики класса 10 Глава 10
                Решения
                • NCERT для математики класса 10 Глава 11
                • Решения NCERT для математики класса 10 Глава 12
                • Решения NCERT для математики класса 10 Глава 13
                • NCERT Sol Решения NCERT для математики класса 10 Глава 14
                • Решения NCERT для математики класса 10 Глава 15
              • Решения NCERT для науки класса 10
                • Решения NCERT для науки класса 10 Глава 1
                • Решения NCERT для науки класса 10 Глава 2
                • Решения NCERT для науки класса 10, глава 3
                • Решения NCERT для науки класса 10, глава 4
                • Решения NCERT для науки класса 10, глава 5
                • Решения NCERT для науки класса 10, глава 6
                • Решения NCERT для науки класса 10, глава 7
                • Решения NCERT для науки 10 класса, глава 8
                • Решения NCERT для науки класса 10 Глава 9
                • Решения NCERT для науки класса 10 Глава 10
                • Решения NCERT для науки класса 10 Глава 11
                • Решения NCERT для науки класса 10 Глава 12
                • Решения NCERT для науки 10 класса Глава 13
                • Решения NCERT для науки 10 класса Глава 14
                • Решения NCERT для науки класса 10 Глава 15
                Решения NCERT
                • для науки класса 10 Глава 16
              • Учебный план NCERT
              • NCERT
            • Commerce
              • Class 11 Commerce Syllabus
                ancy Account
                • Программа бизнес-исследований 11 класса
                • Учебная программа по экономике 11 класса
              • Учебная программа по коммерции 12 класса
                • Учебная программа по бухгалтерии 12 класса
                • Учебная программа по бизнесу 12 класса
                • Учебная программа по экономике
                • 9000 9000
                  • Образцы документов по коммерции класса 11
                  • Образцы документов по коммерции класса 12
                  • TS Grewal Solutions
                    • TS Grewal Solutions Class 12 Accountancy
                    • TS Grewal Solutions Class 11 Accountancy
                  • Отчет о движении денежных средств
                  • Что такое Entry eurship
                  • Защита прав потребителей
                  • Что такое основной актив
                  • Что такое баланс
                  • Формат баланса
                  • Что такое акции
                  • Разница между продажей и маркетингом
                • ICSE
                  • Документы ICSE
                  • Вопросы ICSE
                  • ML Aggarwal Solutions
                    • ML Aggarwal Solutions Class 10 Maths
                    • ML Aggarwal Solutions Class 9 Maths
                    • ML Aggarwal Solutions Class 8 Maths
                    • ML Aggarwal Solutions Class 7 Maths
                    • ML 6 Maths
                    • ML Aggarwal Solutions Class 6 Maths
                    • ML Aggarwal Solutions Class
                  • Selina Solutions
                    • Selina Solutions для класса 8
                    • Selina Solutions для Class 10
                    • Selina Solutions для Class 9
                  • Frank Solutions
                    • Frank Solutions для математики класса 10
                    • Frank Solutions для математики класса 9
                  • Класс ICSE 9000 2
                  • ICSE Class 6
                  • ICSE Class 7
                  • ICSE Class 8
                  • ICSE Class 9
                  • ICSE Class 10
                  • ISC Class 11
                  • ISC Class 12
              • IAS
                Exam
                • IAS
                • Civil
                • Сервисный экзамен
                • Программа UPSC
                • Бесплатная подготовка к IAS
                • Текущие события
                • Список статей IAS
                • Пробный тест IAS 2019
                  • Пробный тест IAS 2019 1
                  • Пробный тест IAS 2019 2
              • Экзамен KPSC KAS
              • Экзамен UPPSC PCS
              • Экзамен MPSC
              • Экзамен RPSC RAS ​​
              • TNPSC Group 1
              • APPSC Group 1
              • Экзамен BPSC
              • WBPS3000 Экзамен 9C 9000 MPC4000
              • Вопросник UPSC 2019
                • Ключ ответов UPSC 2019
              • Коучинг IAS
                • IA S Coaching Бангалор
                • IAS Coaching Дели
                • IAS Coaching Ченнаи
                • IAS Coaching Хайдарабад
                • IAS Coaching Мумбаи
            • JEE
              • BYJU’SEE
              • 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
              • Вопросник JEE
              • Биномиальная теорема
              • Статьи JEE
              • Квадратичное уравнение
            • NEET
              • Программа BYJU NEET
              • NEET 2020
              • NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
              • Поддержка
                • Разрешение жалоб
                • Служба поддержки
                • Центр поддержки
            • Государственные советы
              • GSEB
                • GSEB Syllabus
                • GSEB4
                • GSEB3 Образец статьи
                GSEB3 004
                • MSBSHSE
                  • MSBSHSE Syllabus
                  • MSBSHSE Учебники
                  • Образцы статей MSBSHSE
                  • Вопросники MSBSHSE
                • AP Board
                  • APSCERT
                  • APS4
                  • Syll
                  • AP
                  • Syll 9000SC4
                  • Syll
                  • AP 9000S4 9000 Syll
                  • Syll
                • MP Board
                  • MP Board Syllabus
                  • MP Board Образцы документов
                  • Учебники MP Board
                • Assam Board
                  • Assam Board Syllabus
                  • Assam Board Учебники 9000 9000 Board4 BSEB
                    • Bihar Board Syllabus
                    • Bihar Board Учебники
                    • Bihar Board Question Papers
                    • Bihar Board Model Papers
                  • BSE Odisha
                    • Odisha Board Syllabus
                    • Odisha Board Syllabus
                    • Программа PSEB
                    • Учебники PSEB
                    • Вопросы PSEB
                  • RBSE
                    • Rajasthan Board Syllabus
                    • RBSE Учебники
                    • RBSE Question Papers
                  • HPBOSE
                  • HPBOSE
                  • HPBOSE
                  • JKBOSE
                    • Программа JKBOSE
                    • Образцы документов JKBOSE
                    • Шаблон экзамена JKBOSE
                  • TN Board
                    • TN Board Syllabus
                    • TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 Paper 9000 Paper
                    JAC
                    • Учебник JAC
                    • Учебники JAC
                    • Вопросники JAC
                    • Telangana Board
                      • Telangana Board Syllabus
                      • Telangana Board Учебники
                      • Papers
                      • Telangana Board Учебники
                      • Учебный план KSEEB
                      • Типовой вопросник KSEEB
                    • KBPE
                      • Учебный план KBPE
                      • Учебники KBPE
                      • Документы по KBPE
                    • 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
                  • Совет по Западной Бенгалии
                    • Учебный план Совета по Западной Бенгалии
                    • Учебники для Совета по Западной Бенгалии
                    • Вопросы для Совета по Западной Бенгалии
                  • UBSE
                  • TBSE
                  • Гоа Совет
                  • 000
                  • NBSE0003 Board
                  • Manipur Board
                  • Haryana Board
                • Государственные экзамены
                  • Банковские экзамены
                    • Экзамены SBI
                    • Экзамены IBPS
                    • Экзамены RBI
                    • IBPS

                      03

                      Экзамены SSC

                      9SC2

                    • SSC GD
                    • SSC CPO 900 04
                    • SSC CHSL
                    • SSC CGL
                  • Экзамены RRB
                    • RRB JE
                    • RRB NTPC
                    • RRB ALP
                  • O Экзамены на страхование
                  • LIC4
                  • LIC4
                  • UPSC CAPF
                  • Список статей государственных экзаменов
                • Обучение детей
                  • Класс 1
                  • Класс 2
                  • Класс 3
                • Академические вопросы
                  • Вопросы по физике
                  • Вопросы по химии
                  • Вопросы по химии
                  • Вопросы
                  • Вопросы по науке
                  • Вопросы GK
                • Онлайн-обучение
                  • Домашнее обучение
                • Полные формы
            .

            Закон электромагнитной индукции Фарадея

            Название Закон Фарадея Электромагнитной индукции дано в честь известного ученого Майкла Фарадея в 1930-х годах. Он показывает взаимосвязь между электрическим напряжением и изменяющимся магнитным полем. Закон Фарадея об электромагнитной индукции гласит, что «величина напряжения прямо пропорциональна скорости изменения магнитного потока». это означает, что напряжение индуцируется в цепи, когда есть относительное движение между магнитным полем и проводником.

            Электромагнитная индукция

            В замкнутой цепи, когда протекает ток и индуцируется ЭДС, поэтому явление, при котором ЭДС индуцируется в цепи при изменении магнитного потока, связанного с ней, называется Электромагнитная индукция.

            Это можно пояснить на примере

            Рассмотрим катушку с большим количеством витков, к которой подключен гальванометр

            Случай 1: — Катушка неподвижна, а магнит движется

            

            Когда постоянный стержневой магнит приближается к катушке (позиция 2) или от катушки (позиция 1), как показано на рисунке выше, в гальванометре происходит отклонение.В обоих случаях прогибы противоположны.

            Случай 2: — Катушка движется, а магнит неподвижен.

            

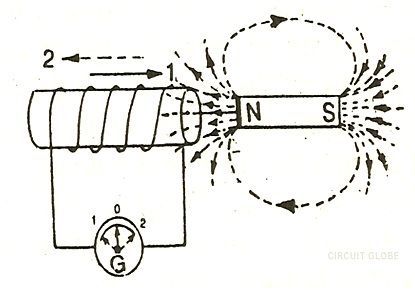
            Если стержневой магнит остается неподвижным, а катушка приближается к магниту (положение 1) или от магнита (положение 2), в гальванометре произойдет отклонение.

            В обоих случаях направление иглы будет противоположным. Это можно объяснить тем, что предположим, что если поднести магнит ближе, чем игла отклонится вправо, а если отодвинуть от магнита, она покажет отклонение с левой стороны.

            Случай 3: — Когда магнит и катушка неподвижны

            Когда и магнит, и катушка остаются неподвижными, в катушке не будет отклонений, независимо от того, какой поток связан с катушкой

            Проанализированы следующие точки

            1. Отклонение стрелки гальванометра указывает на то, что в катушке наведена ЭДС. Отклонение происходит только при изменении магнитного потока, связанного с цепью. то есть либо магнит, либо катушка находятся в движении.
            2. Направление наведенной ЭДС в катушке зависит от направления магнитного поля и направления движения катушки.
            .