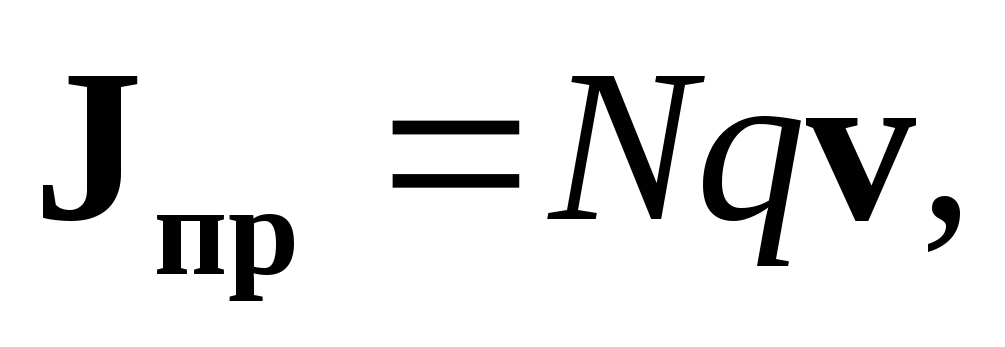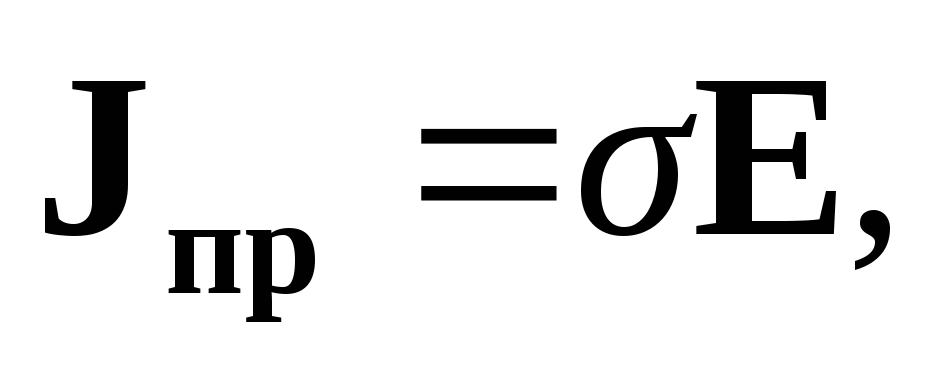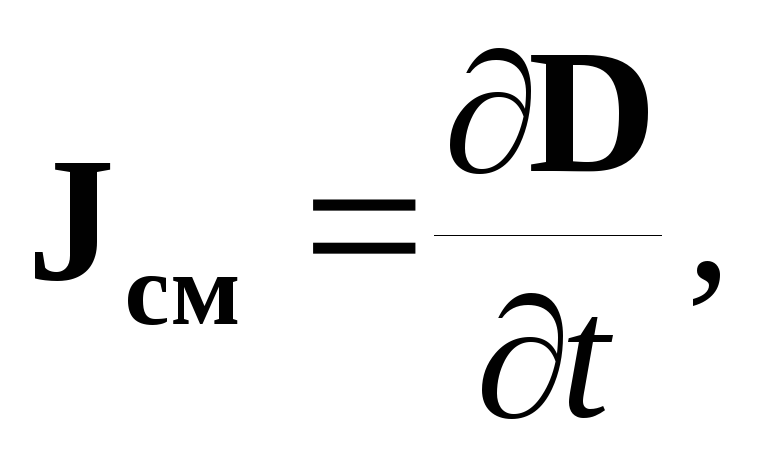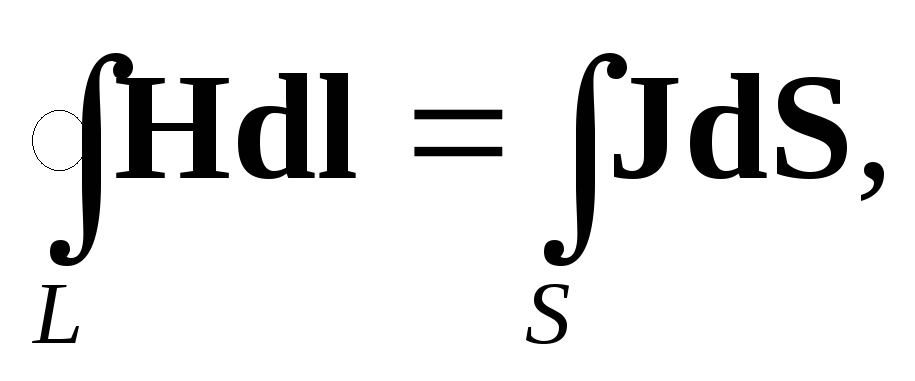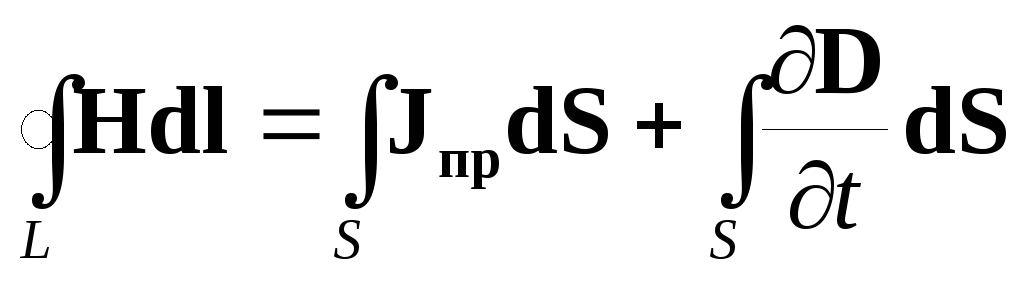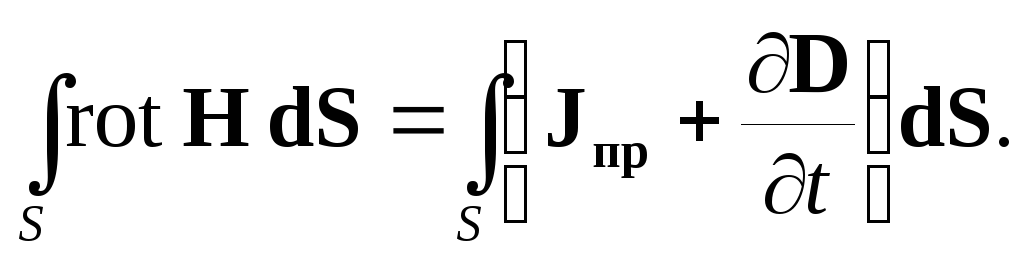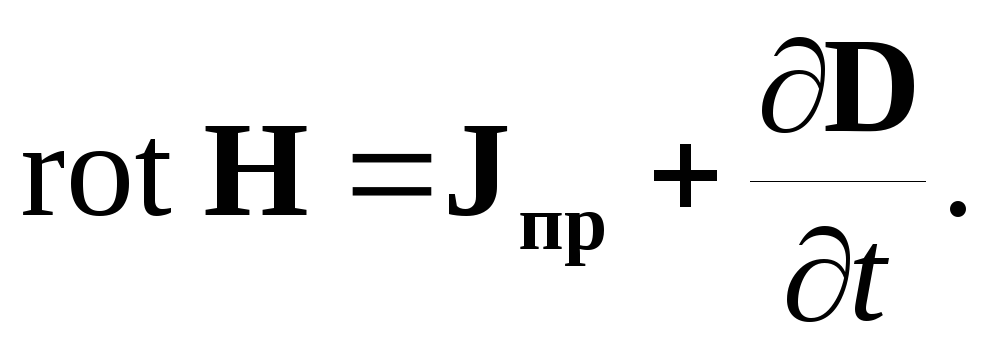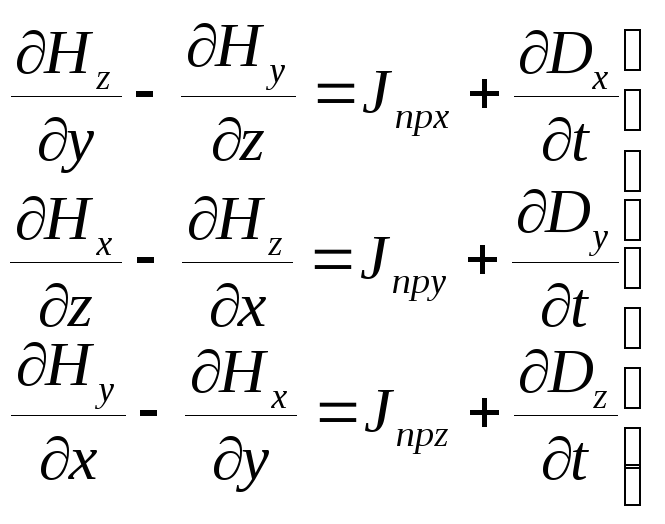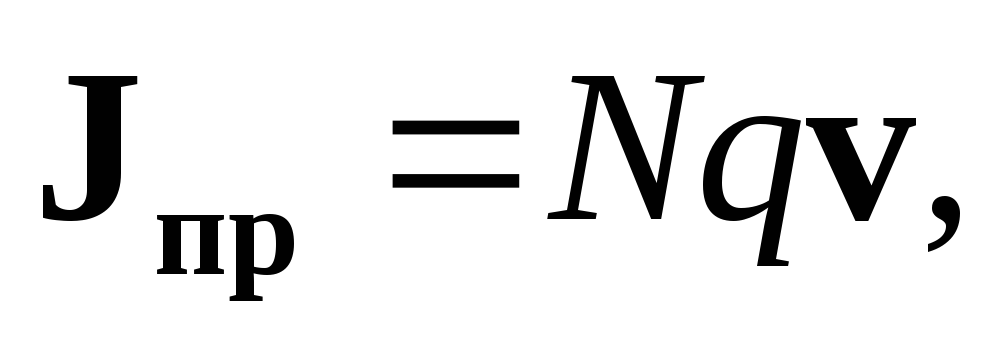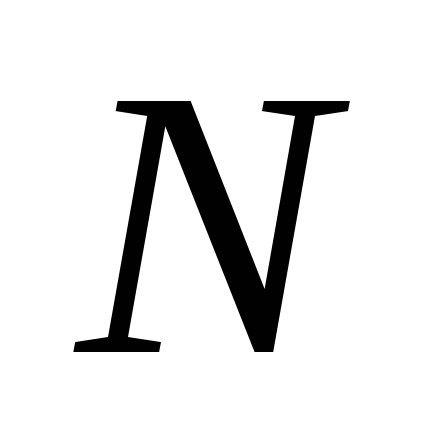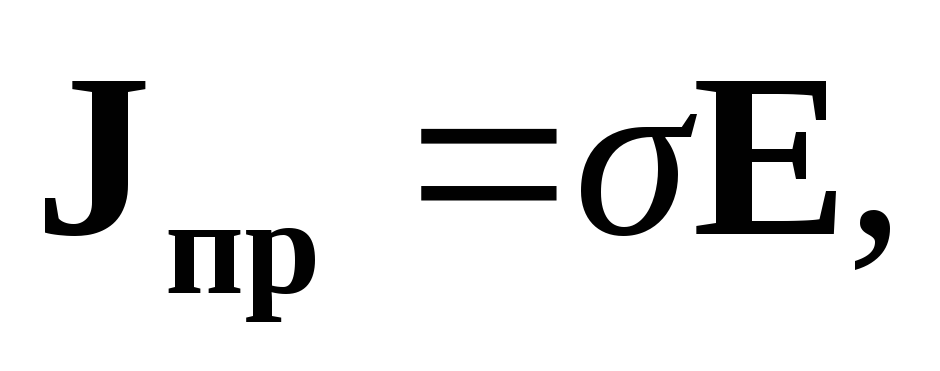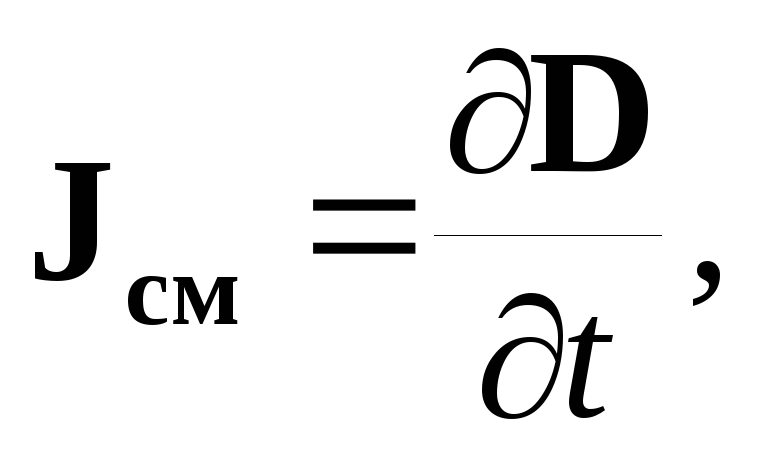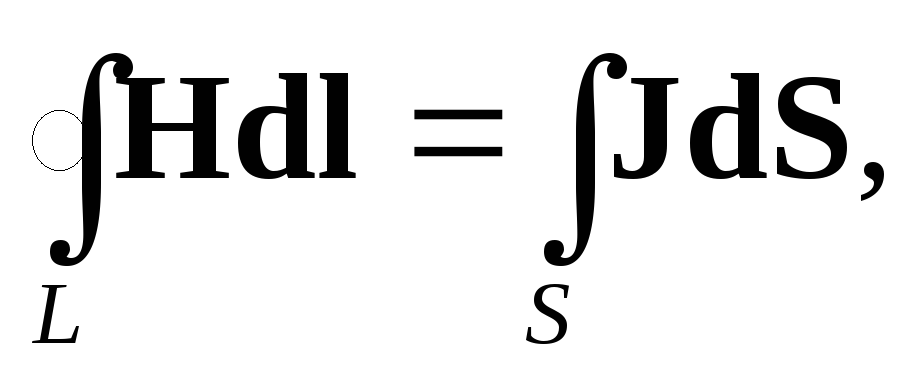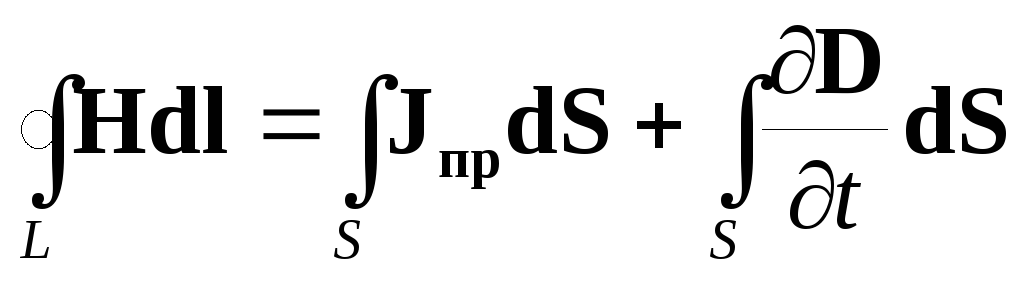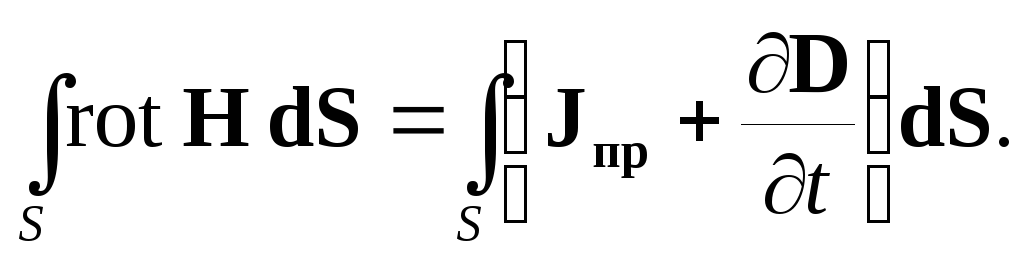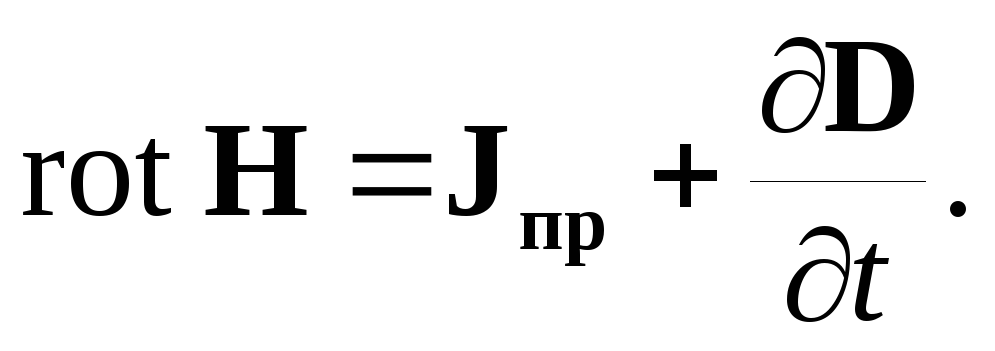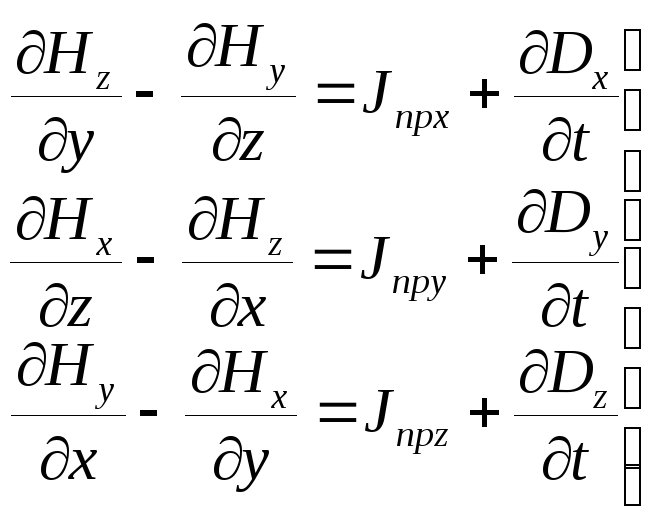Электрический ток
Полным электрическим токомназывают явление направленного движения зарядов и явление изменения электрического поля во времени, сопровождаемые магнитным полем.
Различают три основных вида электрического тока: ток проводимости, ток переноса, ток смещения.
Ток проводимости
Ток
проводимости может возникать в среде,
обладающей электропроводностью и
обусловлен движением свободных заряженных
частиц в проводнике. Количественная
сторона этого явления характеризуется
силой тока i ( [ ] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
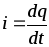
Для
характеристики распределения в проводнике
заряженных частиц используется векторная
величина 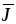 ,
называемаяплотностью
тока. Направление
вектора
,
называемаяплотностью
тока. Направление
вектора 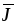 указывает направление движения
положительно заряженных частиц. Величина
указывает направление движения
положительно заряженных частиц. Величина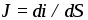 характеризует интенсивность их
прохождения через площадку
характеризует интенсивность их
прохождения через площадку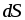 ,
[
,
[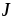
При
известной плотности тока 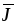 сила тока
сила тока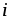 ,
проходящего через некоторую поверхность
,
проходящего через некоторую поверхность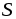 ,
может быть рассчитана по формуле
,
может быть рассчитана по формуле
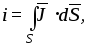
где
вектор 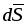
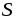 .
. Для
тока проводимости характерна зависимость 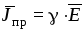 ,
где символом
,
где символом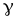 обозначена удельная электрическая
проводимость вещества проводника ([
обозначена удельная электрическая
проводимость вещества проводника ([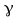 ]
= 1/Ом
]
= 1/Ом м).
м).
Типичным примером тока проводимости является электрический ток в металлах.
Ток переноса
Током
переноса называют явление перемещения
в свободном пространстве электрически
заряженных частиц. Принципиальное
отличие тока переноса от тока проводимости
заключается в том, что плотность тока
переноса 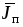 не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью
не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью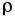 переносимого заряда и скоростью
переносимого заряда и скоростью движения частиц
движения частиц
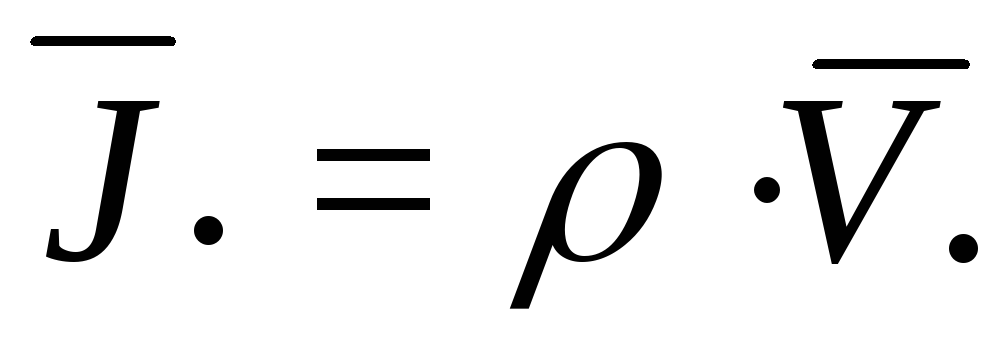
Примером тока переноса может служить поток электронов в электронно-лучевой трубке.
Ток смещения
Ток смещения возникает в случае изменения электрического поля во времени, а под плотностью тока смещения понимают величину
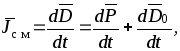
где 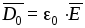 .
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
.
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
Таким образом, в зависимости от характера электрического тока его плотность может быть рассчитана по одному из следующих соотношений:
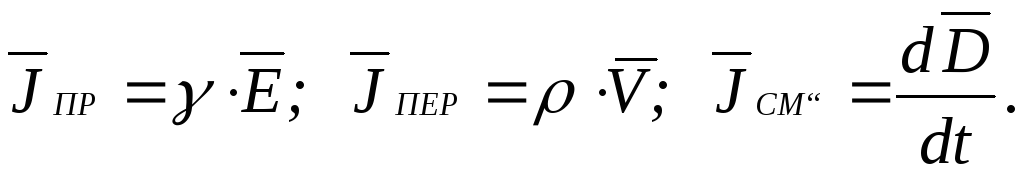
Принцип непрерывности электрического тока
Одним из основных принципов теории электромагнитного поля является принцип непрерывности электрического тока
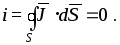
В
этом соотношении символ 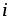 означает полный ток сквозь взятую в
любой среде замкнутую поверхность
означает полный ток сквозь взятую в
любой среде замкнутую поверхность ,
то есть
,
то есть
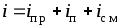 и
и 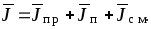 .
.
Из принципа непрерывности электрического тока следует, что линии тока не имеют ни начала, ни конца, то есть являются замкнутыми.
Электрическое напряжение. Разность электрических потенциалов
Электрическое
поле кроме векторов 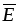 и
и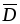 характеризуют скалярной величиной,
которая называется электрическим
напряжением
характеризуют скалярной величиной,
которая называется электрическим
напряжением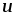 и измеряется в вольтах, [
и измеряется в вольтах, [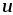 ]
= В .
]
= В .
Для
перемещения заряда 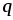
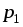 в точку
в точку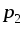 необходимо совершить работу
необходимо совершить работу 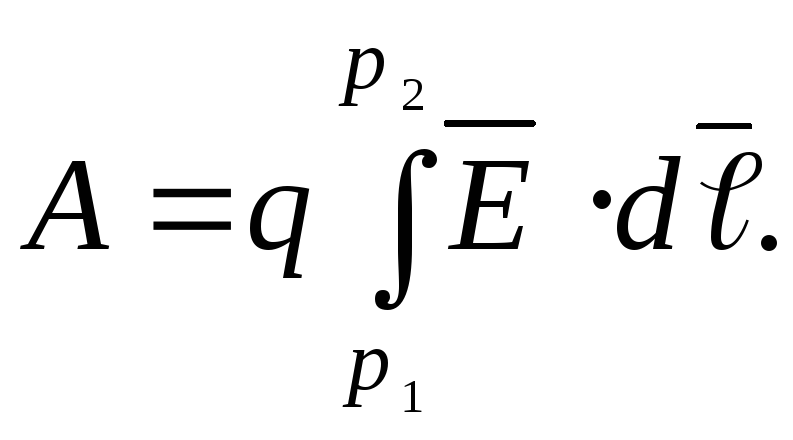
Электрическим
напряжением между точками 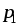 и
и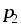 называют величину, равную отношению
этой работы к перемещаемому заряду
называют величину, равную отношению
этой работы к перемещаемому заряду
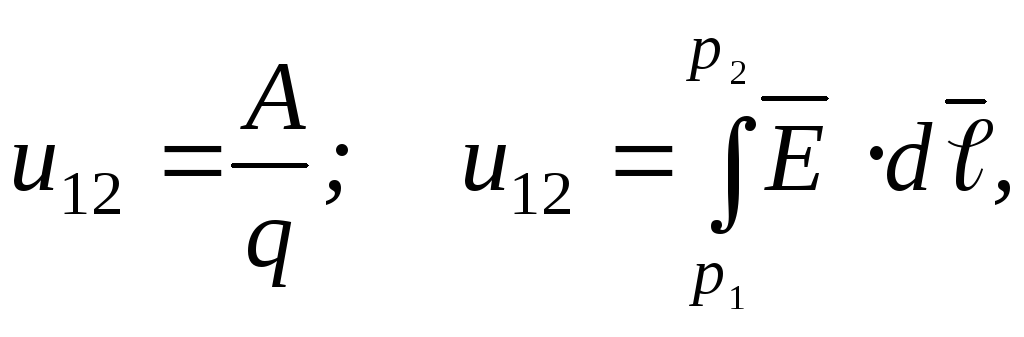
где 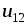 ‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
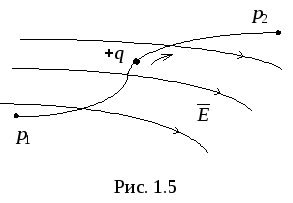
Для электрического поля неподвижных зарядов (электростатического поля) справедливо условие
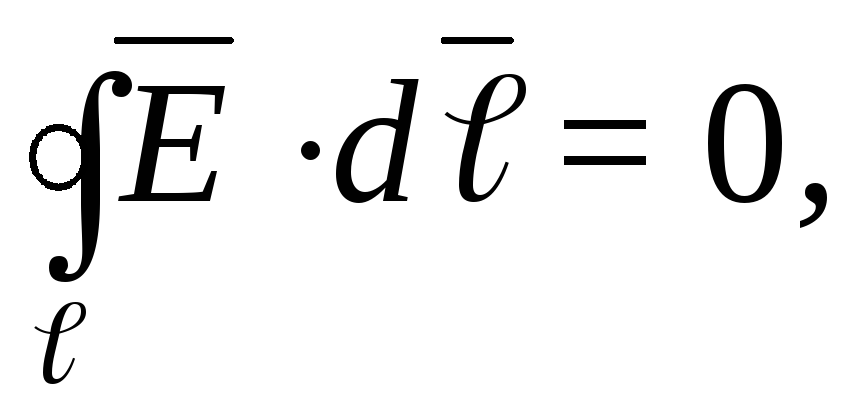
вытекающее из закона сохранения энергии в системе заряженных тел. Следовательно, (рис.1.6),
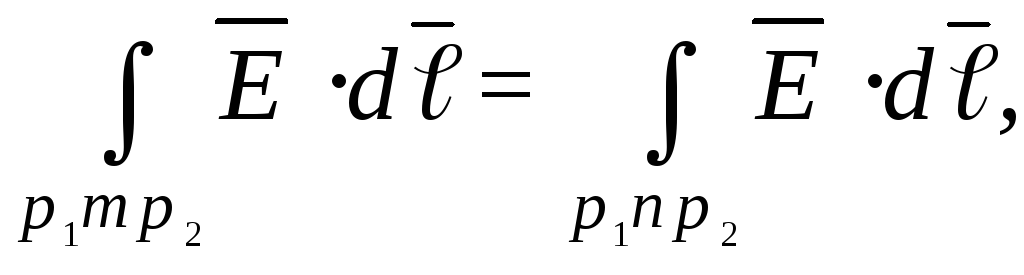
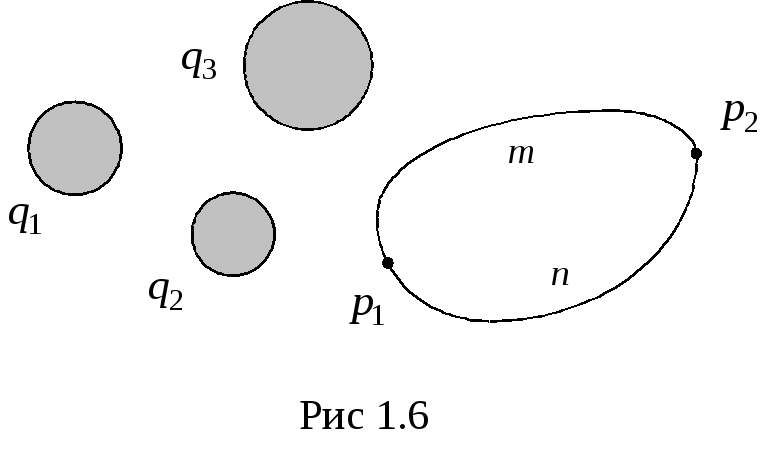
и
интеграл 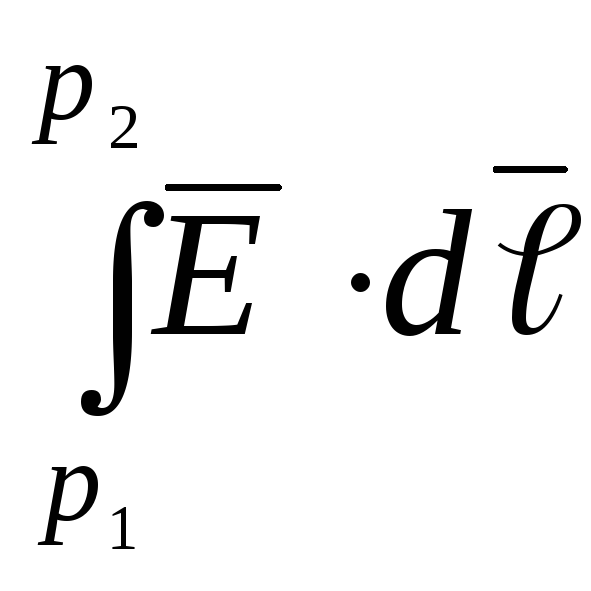 зависит
только от координат точек
зависит
только от координат точек  и
и  .
.
Это
обстоятельство позволяет ввести в
рассмотрение функцию 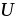
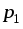 )
в электростатическом поле:
)
в электростатическом поле: 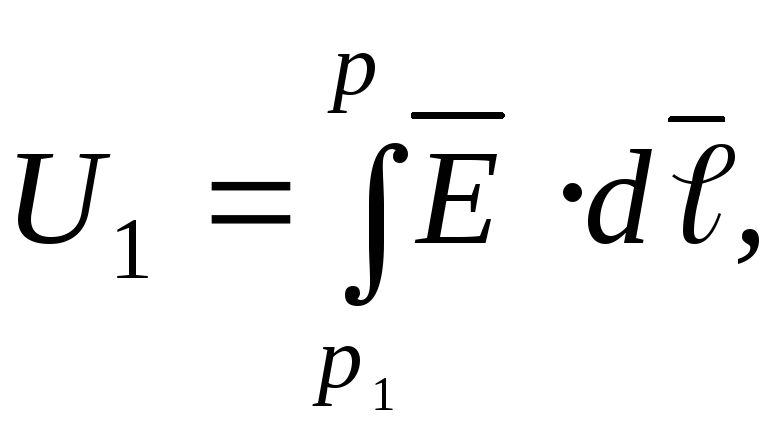
где 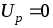 Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка
Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка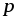 нулевого потенциала.
нулевого потенциала.
В
электростатическом поле напряжение
между точками 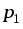
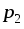 можетбыть вычислено как разность
потенциалов этих точек:
можетбыть вычислено как разность
потенциалов этих точек: 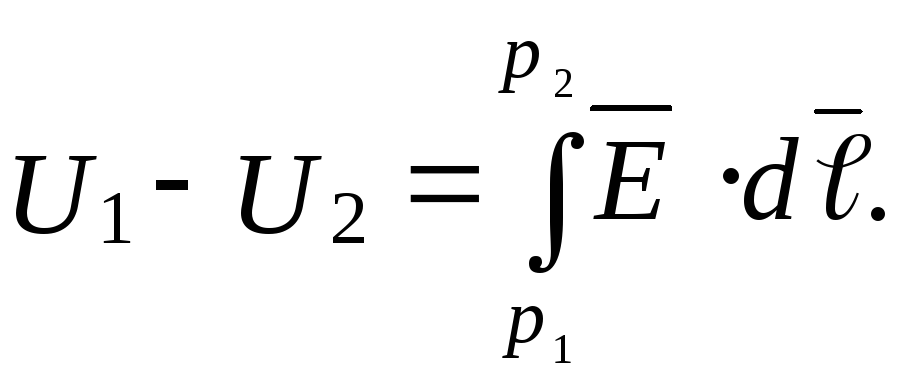
 Электрическое
поле, для которого справедливо условие
Электрическое
поле, для которого справедливо условие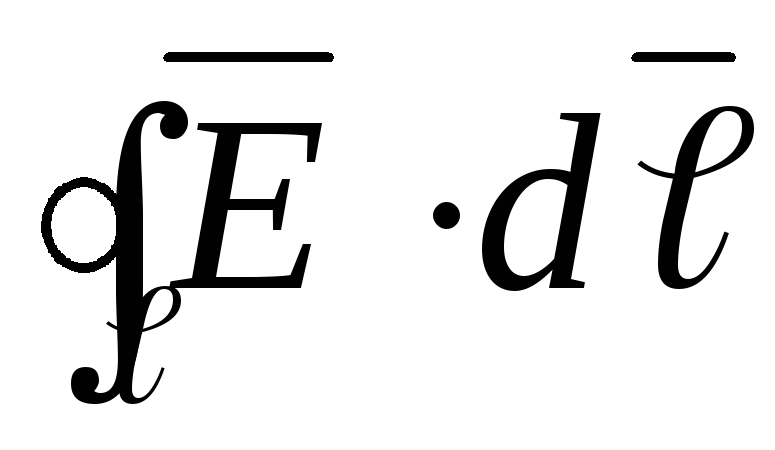 = 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
= 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
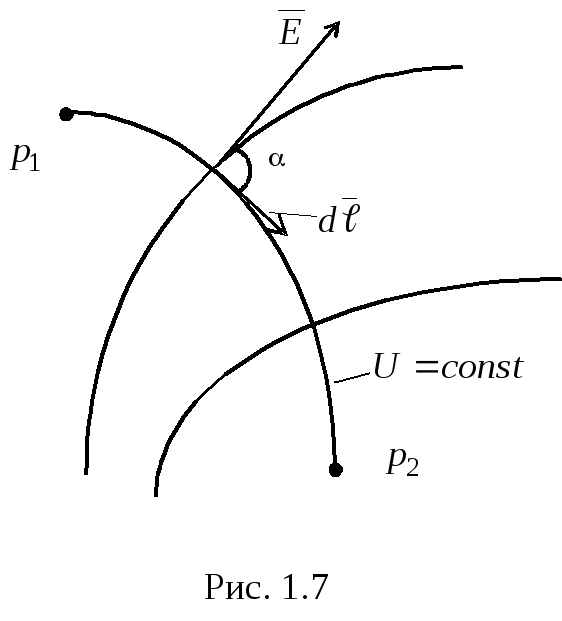
Введем понятие поверхности равного потенциала, как поверхности, во всех точках которой потенциал имеет одно и тоже значение. Силовые линии электрического поля перпендикулярны поверхностям равного потенциала. Действительно:
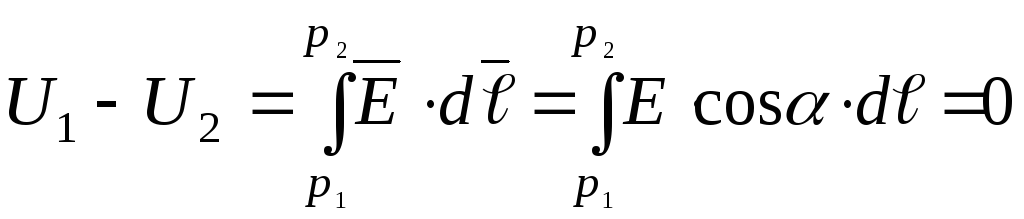
при 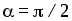 и, следовательно,
и, следовательно,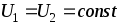 (рис.1.7).
(рис.1.7).
1.3. Ток проводимости и ток смещения
Током проводимости называется движение носителей электрических зарядов под действием электрического поля.
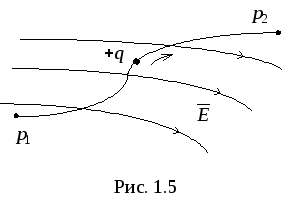
Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.
Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:
| (1.18) |
где | | — количество носителей заряда в единице объема вещества; |
q | — заряд носителя, Кл; | |
v | — вектор скорости движения носителей заряда, м/с. |
Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:
| (1.19) |
где | σ | — электропроводность среды, См/м. |
Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.
Формула (1.19) также относится к материальным уравнениями называется закономОма в дифференциальной форме.
Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро — 6.1*107См/м. У меди она равна 5.7*107См/м, а у алюминия — 3.2*107См/м.
Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.
Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образование тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока смещения. Плотность тока смещения описывается формулой:
| (1.20) |
Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.
Величина тока смещения прямо пропорциональна скорости изменения электрического поля.
2. Основные уравнения электродинамики
2.1. Первое уравнение Максвелла
Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:
| (2.1) |
где | L – замкнутый контур, |
dl – векторный дифференциал длины контура: dl = l0dl, | |
l0 – орт дифференциала длины контура, | |
J – вектор плотности тока, пронизывающего контур, | |
S — произвольная поверхность, опирающаяся на контур L, | |
dS — векторный дифференциал поверхности: dS = n0dS, | |
n0 — орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Форма замкнутого контура L может быть произвольной.
Под током, пронизывающим контур, Ампер понимал только ток проводимости, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:
| (2.2) |
Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.
К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию вектора Н по контуру L интегралом от rot Н по поверхности S, опирающейся на этот контур:
| (2.3) |
Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:
| (2.4) |
Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе координат х, у, z они примут следующий вид:
| (2.5) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
Электрический ток
Полным электрическим токомназывают явление направленного движения зарядов и явление изменения электрического поля во времени, сопровождаемые магнитным полем.
Различают три основных вида электрического тока: ток проводимости, ток переноса, ток смещения.
Ток проводимости
Ток
проводимости может возникать в среде,
обладающей электропроводностью и
обусловлен движением свободных заряженных
частиц в проводнике. Количественная
сторона этого явления характеризуется
силой тока i ( [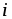 ] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
] =
A).
Величина тока i определяется зарядом q, проходящим
через некоторую поверхность S в единицу времени
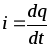 .
.
Для
характеристики распределения в проводнике
заряженных частиц используется векторная
величина 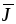 ,
называемаяплотностью
тока. Направление
вектора
,
называемаяплотностью
тока. Направление
вектора 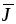 указывает направление движения
положительно заряженных частиц. Величина
указывает направление движения
положительно заряженных частиц. Величина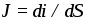 характеризует интенсивность их
прохождения через площадку
характеризует интенсивность их
прохождения через площадку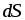 ,
[
,
[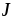 ]
= A/м2.
]
= A/м2.
При
известной плотности тока 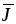 сила тока
сила тока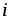 ,
проходящего через некоторую поверхность
,
проходящего через некоторую поверхность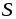 ,
может быть рассчитана по формуле
,
может быть рассчитана по формуле
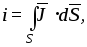
где
вектор 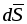 направлен по нормали к поверхности
направлен по нормали к поверхности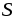 .
.
Для
тока проводимости характерна зависимость 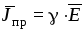 ,
где символом
,
где символом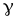 обозначена удельная электрическая
проводимость вещества проводника ([
обозначена удельная электрическая
проводимость вещества проводника ([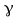 ]
= 1/Ом
]
= 1/Ом м).
м).
Типичным примером тока проводимости является электрический ток в металлах.
Ток переноса
Током
переноса называют явление перемещения
в свободном пространстве электрически
заряженных частиц. Принципиальное
отличие тока переноса от тока проводимости
заключается в том, что плотность тока
переноса 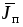 не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью
не пропорциональна напряженности
электрического поля, а определяется
объемной плотностью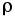 переносимого заряда и скоростью
переносимого заряда и скоростью движения частиц
движения частиц
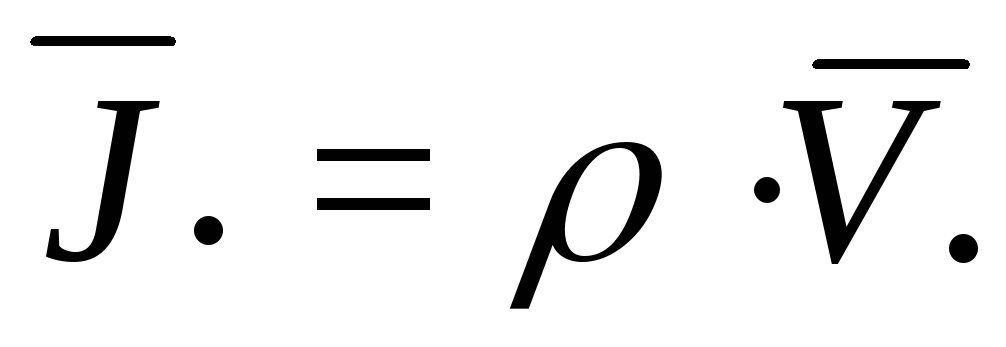
Примером тока переноса может служить поток электронов в электронно-лучевой трубке.
Ток смещения
Ток смещения возникает в случае изменения электрического поля во времени, а под плотностью тока смещения понимают величину
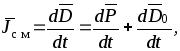
где 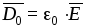 .
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
.
Первое слагаемое характеризует
перемещение связанных зарядов в процессе
поляризации диэлектрика. Второе
слагаемое, называемое током смещения
в пустоте, не имеет столь же наглядной
интерпретации и связано с появлением
магнитного поля, возникающего при
изменении напряженности электрического
поля в пустоте. Характерным примером
тока смещения является ток в конденсаторе.
Таким образом, в зависимости от характера электрического тока его плотность может быть рассчитана по одному из следующих соотношений:
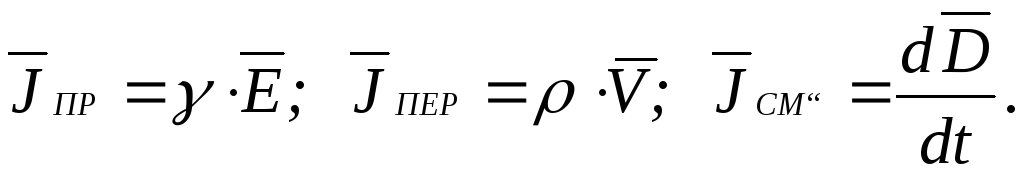
Принцип непрерывности электрического тока
Одним из основных принципов теории электромагнитного поля является принцип непрерывности электрического тока
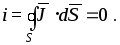
В
этом соотношении символ 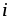 означает полный ток сквозь взятую в
любой среде замкнутую поверхность
означает полный ток сквозь взятую в
любой среде замкнутую поверхность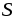 ,
то есть
,
то есть
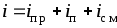 и
.
и
.
Из принципа непрерывности электрического тока следует, что линии тока не имеют ни начала, ни конца, то есть являются замкнутыми.
Электрическое напряжение. Разность электрических потенциалов
Электрическое
поле кроме векторов 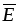 и
и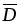 характеризуют скалярной величиной,
которая называется электрическим
напряжением
характеризуют скалярной величиной,
которая называется электрическим
напряжением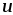 и измеряется в вольтах, [
и измеряется в вольтах, [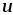 ]
= В .
]
= В .
Для
перемещения заряда 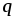 в электрическом поле из точки
в электрическом поле из точки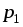 в точку
в точку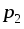 необходимо совершить работу
необходимо совершить работу
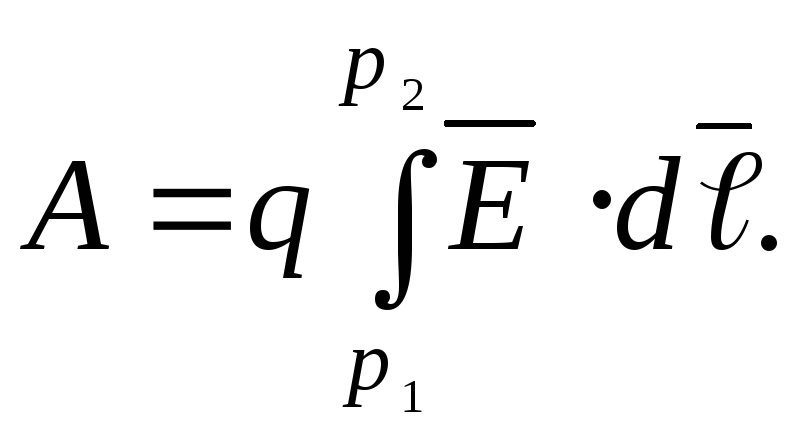
Электрическим
напряжением между точками 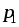 и
и называют величину, равную отношению
этой работы к перемещаемому заряду
называют величину, равную отношению
этой работы к перемещаемому заряду
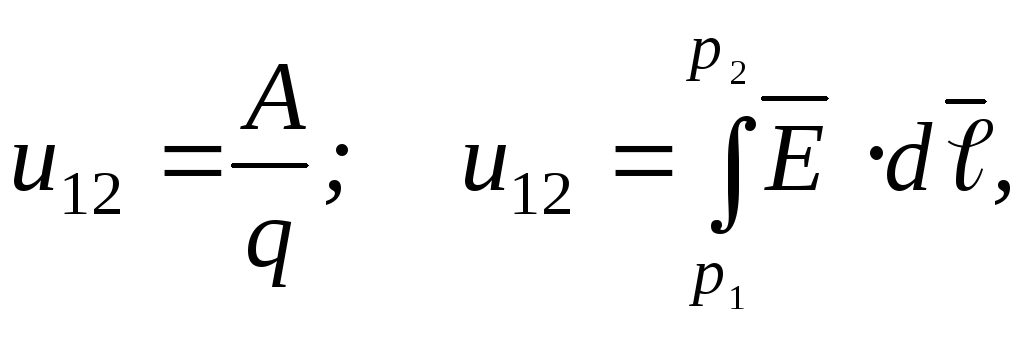
где  ‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
‑ электрическое напряжение (или
падение напряжения) вдоль заданного
пути (рис.1.5).
Для электрического поля неподвижных зарядов (электростатического поля) справедливо условие
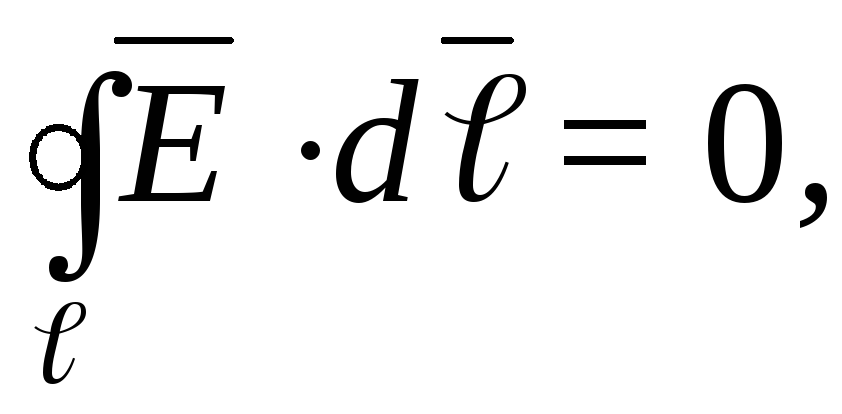
вытекающее из закона сохранения энергии в системе заряженных тел. Следовательно, (рис.1.6),
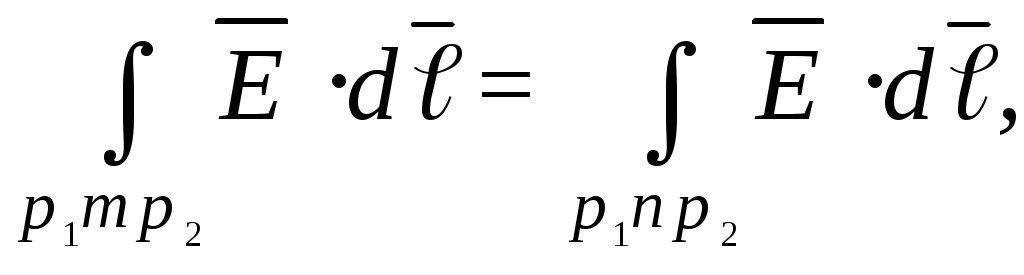
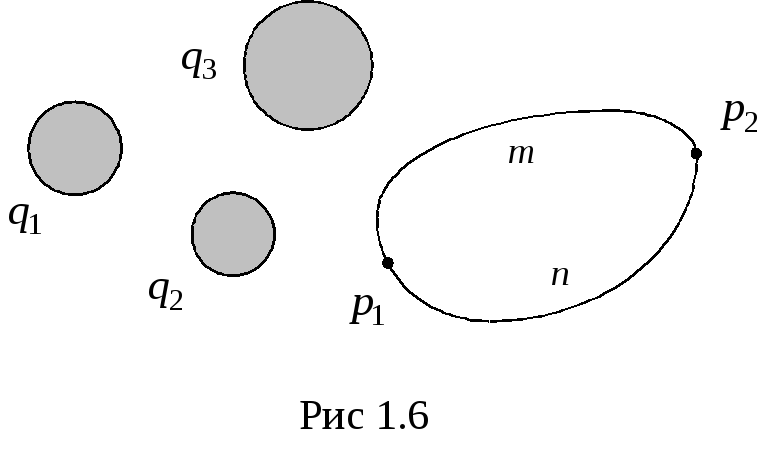
и
интеграл 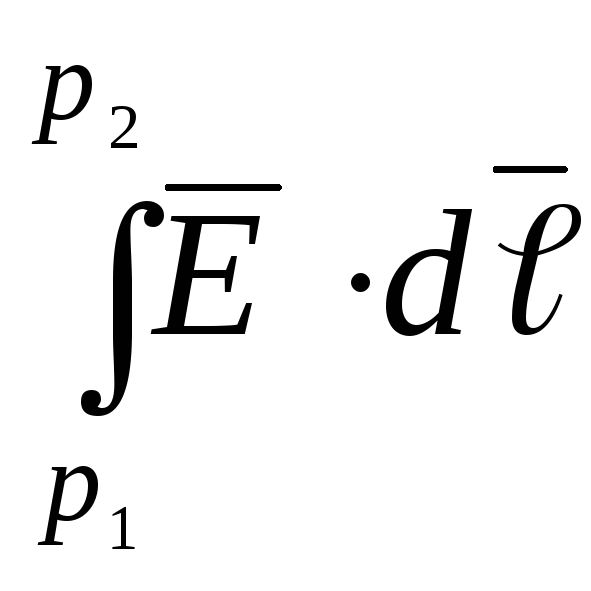 зависит
только от координат точек
зависит
только от координат точек 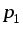 и
и 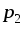 .
.
Это
обстоятельство позволяет ввести в
рассмотрение функцию 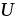 ,
зависящую от положения точки (
,
зависящую от положения точки (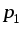 )
в электростатическом поле:
)
в электростатическом поле:
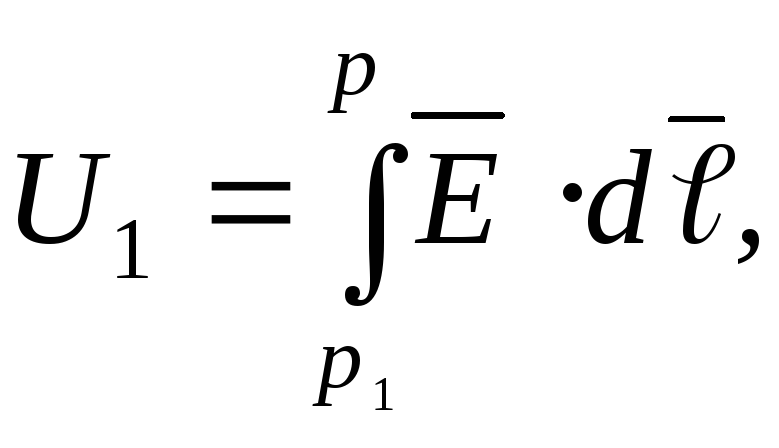
где  Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка
Потенциал точки определяется с точностью
до некоторой постоянной, зависящей от
того, где выбрана точка нулевого потенциала.
нулевого потенциала.
В
электростатическом поле напряжение
между точками  и
и 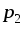 можетбыть вычислено как разность
потенциалов этих точек:
можетбыть вычислено как разность
потенциалов этих точек:
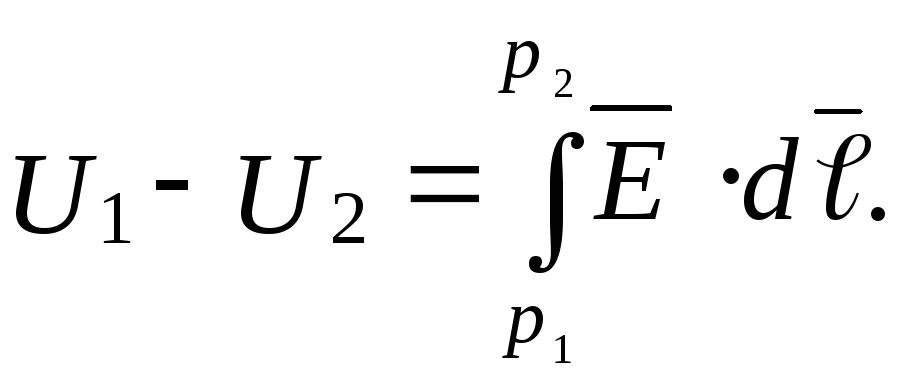
 Электрическое
поле, для которого справедливо условие
Электрическое
поле, для которого справедливо условие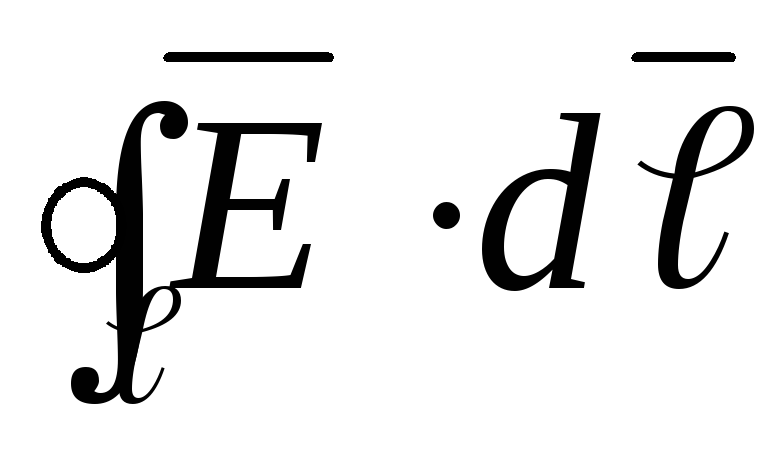 = 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
= 0, называется потенциальным электрическим
полем. При теоретическом исследовании
систем, в которых заряженные тела имеют
конечные размеры, точкаp,
выбирается, как правило, на бесконечности.
На практике часто U = 0 принимают на поверхности одного из
объектов рассматриваемой системы.
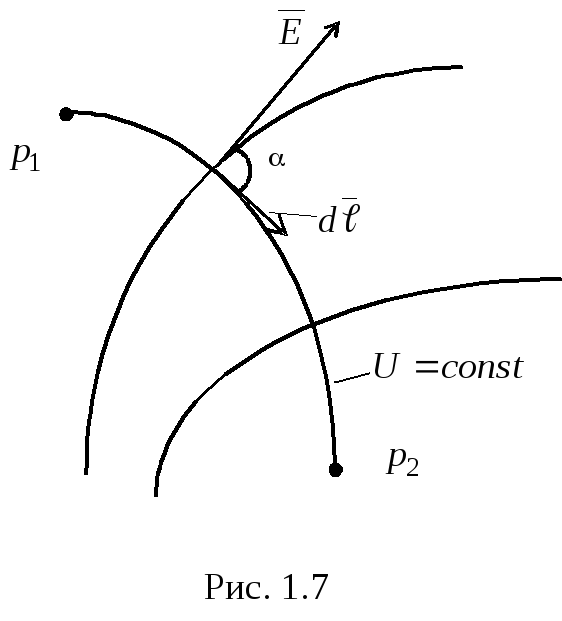
Введем понятие поверхности равного потенциала, как поверхности, во всех точках которой потенциал имеет одно и тоже значение. Силовые линии электрического поля перпендикулярны поверхностям равного потенциала. Действительно:
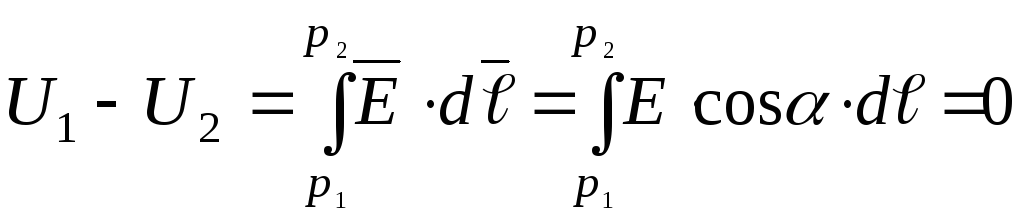
при 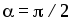 и, следовательно,
и, следовательно,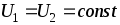 (рис.1.7).
(рис.1.7).
ток проводимости — это… Что такое ток проводимости?
- ток проводимости
- conduction current
Большой англо-русский и русско-английский словарь. 2001.
- ток пробоя
- ток промышленной частоты
Смотреть что такое «ток проводимости» в других словарях:
ток проводимости — то же, что электрический ток. * * * ТОК ПРОВОДИМОСТИ ТОК ПРОВОДИМОСТИ, то же, что электрический ток (см. ЭЛЕКТРИЧЕСКИЙ ТОК) … Энциклопедический словарь
ток проводимости — Явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями… … Справочник технического переводчика
ТОК ПРОВОДИМОСТИ — то же, что (см.), т.е. электрический ток, являющейся результатом упорядоченного движения заряженных частиц относительно среды (т. е. внутри макроскопических тел) в определённом направлении … Большая политехническая энциклопедия
ТОК ПРОВОДИМОСТИ — то же, что электрический ток … Большой Энциклопедический словарь
ТОК ПРОВОДИМОСТИ — электрический ток, связанный с упорядоч. движением заряж. ч ц относительно среды (т. е. внутри макроскопич. тел). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
ток проводимости — laidumo srovė statusas T sritis fizika atitikmenys: angl. conduction current vok. Leitungsstrom, m rus. ток проводимости, m pranc. courant de conduction, m … Fizikos terminų žodynas
ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ — (Electric current) сила Т. Э. количество электричества, проходящее в единицу времени через проводник. Единицей измерения силы Т. Э. в международной системе является один ампер (один кулон в сек.). Сила Т. Э. не имеет ничего общего с механической… … Морской словарь
ток проводимости разрядника, искровые промежутки которого шунтированы сопротивлениями — Ток через разрядник при приложении к нему напряжения постоянного тока заданного значения. У разрядников, не имеющих шунтирующих сопротивлений, этот ток называется током утечки [ГОСТ 16357 83] Тематики высоковольтный аппарат, оборудование … Справочник технического переводчика
Электрический ток проводимости — явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями… … Официальная терминология
электрический ток проводимости — (величина) Скалярная величина, равная пределу отношения заряда, переносимого заряженными частицами сквозь рассматриваемую поверхность в веществе, обладающем электропроводностью, в течение некоторого промежутка времени, к этому промежутку времени … Политехнический терминологический толковый словарь
элементарный ток (проводимости) — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN elementary (conduction) current … Справочник технического переводчика
1.3. Ток проводимости и ток смещения
Током проводимости называется движение носителей электрических зарядов под действием электрического поля.
Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.
Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:
| (1.18) |
где | | — количество носителей заряда в единице объема вещества; |
q | — заряд носителя, Кл; | |
v | — вектор скорости движения носителей заряда, м/с. |
Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:
| (1.19) |
где | σ | — электропроводность среды, См/м. |
Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.
Формула (1.19) также относится к материальным уравнениями называется закономОма в дифференциальной форме.
Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро — 6.1*107См/м. У меди она равна 5.7*107См/м, а у алюминия — 3.2*107См/м.
Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.
Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образование тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока смещения. Плотность тока смещения описывается формулой:
| (1.20) |
Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.
Величина тока смещения прямо пропорциональна скорости изменения электрического поля.
2. Основные уравнения электродинамики
2.1. Первое уравнение Максвелла
Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:
| (2.1) |
где | L – замкнутый контур, |
dl – векторный дифференциал длины контура: dl = l0dl, | |
l0 – орт дифференциала длины контура, | |
J – вектор плотности тока, пронизывающего контур, | |
S — произвольная поверхность, опирающаяся на контур L, | |
dS — векторный дифференциал поверхности: dS = n0dS, | |
n0 — орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Форма замкнутого контура L может быть произвольной.
Под током, пронизывающим контур, Ампер понимал только ток проводимости, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:
| (2.2) |
Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.
К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию вектора Н по контуру L интегралом от rot Н по поверхности S, опирающейся на этот контур:
| (2.3) |
Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:
| (2.4) |
Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе координат х, у, z они примут следующий вид:
| (2.5) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
Ток смещения
Задание: Допустим, что неограниченную однородную проводящую среду поместили в металлический шар, имеющий заряд $Q$. В этой среде возникнут электрические токи, которые потекут в радиальных направлениях. Покажите, что данная ситуация требует введения тока смещения при описании возникающих полей.
Решение:
Электрические токи, которые текут от (или к ) шару, возбуждают магнитное поле. Определим направление вектора магнитной индукции этого магнитного поля.
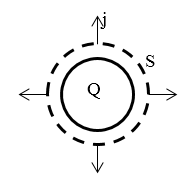
Рисунок 1.
Вектор $\overrightarrow{B}$ не имеет радиальной составляющей. Система обдает сферической симметрией. Если бы радиальная составляющая вектора индукции имелась, то она была бы одинаковой для всех точек сферы $S$ (рис.1), концентрической с поверхностью шара, имела направление от центра шара или к его центру. В обоих случаях поток вектора индукции через сферу $S$ был бы не равен нулю, что противоречит уравнению из системы Максвелла:
\[\oint\limits_S{\overrightarrow{B}d\overrightarrow{S}=0\left(2.1\right).}\]Значит, вектор индукции магнитного поля должен быть перпендикулярен к радиусу, который проведен из центра шара к рассматриваемой точке. Это также невозможно, так как все направления, перпендикулярные к радиусу, равноправны. Единственная возможность, которая не противоречит симметрии шара, заключается в том, что векторы $\overrightarrow{B}\ и\ \overrightarrow{H}$ всюду равны нулю. Следовательно, равна нулю плотность тока проводимости $\overrightarrow{j},\ $ что противоречит уравнению:
\[rot\overrightarrow{H}=\overrightarrow{j}\left(2.2\right).\]Для устранения полученного противоречия следует предположить, что магнитные поля порождаются не только токами проводимости. Добавим к току проводимости ток смещения ($I_{sm}$), который в нашем случае будет уничтожать возбуждаемое магнитное поле. Его величина определяется из условия:
\[I+I_{sm}=0\ \left(2.3\right).\]Ток проводимости, который течет от заряженного шара можно выразить как:
\[I=-\frac{dQ}{dt}\left(2.4\right).\]Из выражения (2.3) следует, что:
\[I_{sm}=\frac{dQ}{dt}\left(2.5\right).\]В соответствии с законом Кулона заряженного проводящего шара, имеем:
\[Q=4\pi r^2D\ \left(2.6\right).\]Найдем производную по времени от заряда, получим:
\[I_{sm}=4\pi r^2\frac{\partial D}{\partial t}\left(2.7\right).\]Плотность тока смещения при этом будет равна:
\[j_{sm}=\frac{I_{sm}}{S_{sf}}=\frac{4\pi r^2\frac{\partial D}{\partial t}}{4\pi r^2}=\frac{\partial D}{\partial t}.\]Полученное выражение совпадает с определением плотности тока смещения.
ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ — это… Что такое ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ?
- ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ
- ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ
-
(Electric current) — сила Т. Э. — количество электричества, проходящее в единицу времени через проводник. Единицей измерения силы Т. Э. в международной системе является один ампер (один кулон в сек.). Сила Т. Э. не имеет ничего общего с механической силой.
Самойлов К. И. Морской словарь. — М.-Л.: Государственное Военно-морское Издательство НКВМФ Союза ССР, 1941
.
- ТОЙ-ТОУ
- ТОК ПЕРЕМЕННЫЙ
Смотреть что такое «ТОК ЭЛЕКТРИЧЕСКИЙ, ТОК ПРОВОДИМОСТИ» в других словарях:
ток проводимости — то же, что электрический ток. * * * ТОК ПРОВОДИМОСТИ ТОК ПРОВОДИМОСТИ, то же, что электрический ток (см. ЭЛЕКТРИЧЕСКИЙ ТОК) … Энциклопедический словарь
ТОК ПРОВОДИМОСТИ — то же, что (см.), т.е. электрический ток, являющейся результатом упорядоченного движения заряженных частиц относительно среды (т. е. внутри макроскопических тел) в определённом направлении … Большая политехническая энциклопедия
ток проводимости — Явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями… … Справочник технического переводчика
Электрический ток проводимости — явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями… … Официальная терминология
электрический ток проводимости — (величина) Скалярная величина, равная пределу отношения заряда, переносимого заряженными частицами сквозь рассматриваемую поверхность в веществе, обладающем электропроводностью, в течение некоторого промежутка времени, к этому промежутку времени … Политехнический терминологический толковый словарь
ТОК ПРОВОДИМОСТИ — то же, что электрический ток … Большой Энциклопедический словарь
ТОК ПРОВОДИМОСТИ — электрический ток, связанный с упорядоч. движением заряж. ч ц относительно среды (т. е. внутри макроскопич. тел). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
(электрический) ток проводимости — 43 (электрический) ток проводимости Явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда,… … Словарь-справочник терминов нормативно-технической документации
(Электрический) ток проводимости — 1. Явление направленного движения свободных носителей электрического заряда в веществе или в пустоте, количественно характеризуемое скалярной величиной, равной производной по времени от электрического заряда, переносимого свободными носителями… … Телекоммуникационный словарь
ток — ((continuous) current carrying capacity ampacity (US)): Максимальное значение электрического тока, который может протекать длительно по проводнику, устройству или аппарату при определенных условиях без превышения определенного значения их… … Словарь-справочник терминов нормативно-технической документации