23. Механика твердого тела. Момент импульса: задачи с ответами

(Все задачи по статике и гидростатике и ответы к ним находятся в zip-архиве (615 кб), который можно скачать и открыть на своем компьютере. Попробуйте решать задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)

23.1.   Легкая металлическая бочка, полностью заполненная водой, скатывается без проскальзывания с наклонной плоскости. Как изменится ускорение бочки, если вода замерзнет?   [смотрите ответ в общем файле темы]

23.2.   Тонкий обруч раскрутили до угловой скорости w и вертикально поставили на горизонтальную поверхность. Какая угловая скорость будет у обруча в установившемся движении?  [смотрите ответ в общем файле темы]

23.3.   Чему равна кинетическая энергия тонкого обруча массой m, катящегося по горизонтальной поверхности со скоростью v?   [смотрите ответ в общем файле темы]

23.4.   Тонкий обруч скатывается без проскальзывания с наклонной плоскости с углом наклона

α. Найти ускорение центра обруча. Каким должен быть коэффициент трения, чтобы не было проскальзывания?   [смотрите ответ в общем файле темы]

23.5.   Тонкий обруч радиусом R раскрутили до угловой скорости w и плашмя положили на стол. Через время t обруч остановился. Определить коэффициент трения между обручем и столом.   [ μ = wR/(gt) ]

23.6.   Два маленьких шарика массами m₁ и m₂ находятся на расстоянии l друг от друга. Определить момент инерции системы относительно ее центра масс.   [смотрите ответ в общем файле темы]

23.7.   Определить момент инерции однородного стержня относительно оси, проходящей через середину стержня и составляющей угол

α со стержнем. Длина стержня равна l, его масса – m.   [смотрите ответ в общем файле темы]

23.8.   Прямоугольник со сторонами a и b сделан из однородной проволоки. Масса единицы длины проволоки равна μ. Определить момент инерции прямоугольника относительно оси, совпадающей со стороной, длина которой равна а.   [смотрите ответ в общем файле темы]

23.9.   Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m₁

и m₂ и длиной l₁ и l₂. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы.   [смотрите ответ в общем файле темы]

23.10.   Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m₁ и m₂ и длиной l₁ и l₂. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы.   [смотрите ответ в общем файле темы]

23.11.   Из однородного диска радиусом R вырезано круглое отверстие радиусом r

. Расстояние между центрами диска и отверстия равно а, а масса фигуры — m. Определить момент инерции фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости.   [указания к решению и ответ смотрите в общем файле темы]

23.12.   Из однородной проволоки сделан правильный треугольник. Масса стороны треугольника равна m, его длина равна l. Определить момент инерции треугольника относительно оси: а) проходящей через центр треугольника и перпендикулярной его плоскости; б) совпадающей с одной из сторон треугольника; в) проходящей через вершину и параллельной противоположной стороне треугольника.   [смотрите ответ в общем файле темы]

23.13.   Однородный шар скатывается с наклонной плоскости с углом наклона а. Найти ускорение центра шара. Каким должен быть коэффициент трения, чтобы шар не скользил?   [смотрите ответ в общем файле темы]

23.14.   В вагоне, движущемся с постоянной скоростью v, к потолку шарнирно подвешен стержень длиной l. На какой максимальный угол от вертикали отклонится стержень, если вагон резко остановить?   [смотрите ответ в общем файле темы]

23.15.   Однородный тонкий стержень длиной l поставили вертикально на горизонтальную гладкую поверхность, слегка вывели из положения равновесия и отпустили.

Какую скорость будет иметь верхний конец стержня в момент удара стержня о поверхность?   [ v = √(3gl) ]

23.16.   Тонкий стержень AB массой m = 1 кг движется поступательно с ускорением a = 1 м/с² под действием двух сил F₁ и F₂. Расстояние между точками приложения сил АС = 20 см. Сила F₂ = 5 Н. Найти длину стержня.   [ 100 см ]

23.17.   Неподвижный блок представляет собой однородный цилиндр массой m, подвешенный на нити к потолку. На цилиндр намотана нить, к которой подвешен груз такой же массы m

. Найти силу натяжения верхней нити при свободном движении системы. Трения нет.   [ T = 4mg/3 ]

23.18.   На однородный диск массой m намотана нить. Свободный конец нити привязали к потолку и диск отпустили. Определить силу натяжения нити в процессе опускания диска. Считать, что нить все время вертикальна.   [ T = mg/3 ]

23.19.   Однородный стержень массой m подвешен горизонтально за концы на двух вертикальных нитях.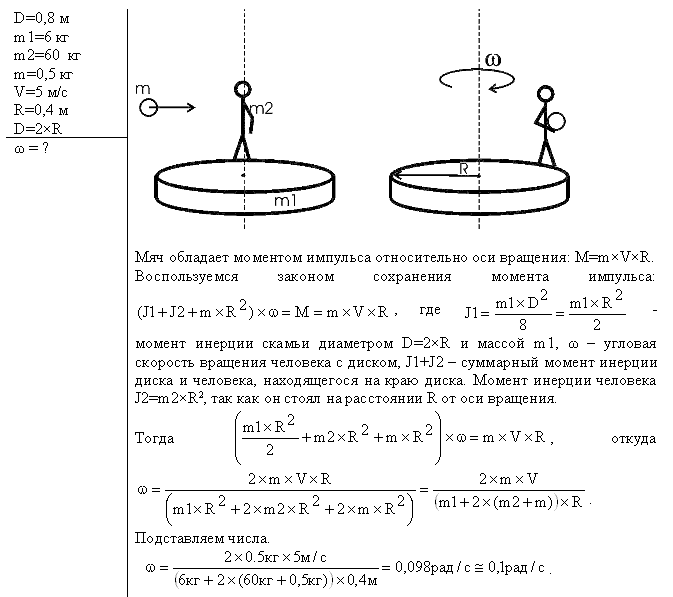 Одна из нитей обрывается. Какова сила натяжения второй нити в момент обрыва?   [ T = mg/4 ]

23.20.   Неподвижный блок представляет собой однородный цилиндр массой m. Через блок перекинута невесомая нить, к концам которой привязаны грузы массами

m₁ и m₂. Определить ускорение грузов и силу натяжения нити слева и справа от блока при свободном движении системы. Проскальзывания нити и трения в блоке нет.   [смотрите ответ в общем файле темы]

23.21.   На однородный цилиндр массой m и радиусом R, лежащий на горизонтальной поверхности, намотана тонкая нить. За нить тянут горизонтальной силой F. При каком значении коэффициента трения цилиндр не будет проскальзывать по поверхности?   [смотрите ответ в общем файле темы]

23.22.   Однородный цилиндр лежит на горизонтальной поверхности. Второй такой же цилиндр катится на первый со скоростью

v. Оси цилиндров параллельны. Между цилиндрами происходит абсолютно упругий удар. Определить конечные установившиеся скорости движения цилиндров.   [указания к решению и ответ смотрите в общем файле темы]

23.23.   Тонкостенную трубу радиусом R раскрутили вокруг оси до угловой скорости w и положили в угол между полом и стеной параллельно ребру угла. Коэффициент трения между трубой и стеной равен μ, а между трубой и полом — 2μ. Сколько оборотов сделает труба до остановки?   [смотрите ответ в общем файле темы]

23.24.   Горизонтально расположенный деревянный стержень массой М и длиной l может вращаться вокруг вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массой m, летящая со скоростью v перпендикулярно стержню и оси его вращения. С какой угловой скоростью начнет вращаться стержень?   [смотрите ответ в общем файле темы]

23.25.   По гладкой горизонтальной поверхности по окружности движется небольшое тело, привязанное к нити. Нить продета в маленькое отверстие в поверхности. Нить начинают медленно втягивать в отверстие, уменьшая радиус окружности движения тела. Как зависит сила натяжения нити от радиуса окружности? Масса тела равна

m. Считать, что при радиусе равном R_o угловая скорость движения тела была равна w_o.   [смотрите ответ в общем файле темы]

23.26.   На массивный неподвижный блок в виде цилиндра радиусом R намотана нить, к свободному концу которой подвешен груз массой m. В момент t = 0 систему отпускают. Написать зависимость момента импульса системы относительно оси блока от времени. Трения нет.   [смотрите ответ в общем файле темы]

23.27.   Стержень, расположенный горизонтально, падает без начальной скорости с высоты h и ударяется одним концом о край стола. Определить скорость центра масс стержня сразу после удара. Удар абсолютно упругий.   [указания к решению и ответ смотрите в общем файле темы]

23.28.   Шарик массой m влетает в спиральный лабиринт, который может свободно двигаться в пространстве, и останавливается в его центре. Начальная скорость шарика равна v, радиус лабиринта R, масса лабиринта М, его момент инерции J. Определить угловую скорость вращения лабиринта после того как шарик остановится. Размерами шарика и внешними силами пренебречь.   [указания к решению и ответ смотрите в общем файле темы]

23.29.   Два диска, имеющие моменты инерции

J₁ и J₂, вращаются на одной оси с угловыми скоростями w₁ и w₂. Диски прижимают друг к другу. Определить установившуюся угловую скорость вращения и количество теплоты, выделившееся при трении дисков.   [смотрите ответ в общем файле темы]

23.30.   Тонкий стержень длиной l и массой M стоит вертикально на гладкой горизонтальной поверхности. В его верхний конец попадает горизонтально летящая пуля массой m (m << М) и застревает в нем. При какой минимальной скорости пули стержень сразу оторвется от поверхности?   [указания к решению и ответ смотрите в общем файле темы]

Далее: 30 задач по механическим колебаниям.   |   Вернуться к списку разделов СТАТИКИ и ГИДРОСТАТИКИ.

Задачи из-за кордона

Контроль знаний

Кинематика и динамика вращательного движения

32. (II) Два тела массами m₁ = 8 кг и m₂ = 10 кг соединены легкой нерастяжимой нитью, перекинутой через блок радиусом 25 см, обладающий моментом инерции I. Тела имеют ускорение a = 1 м/с². Определите силы натяжения T₁ и T₂ участков нити, указанных на рисунке, момент сил, действующих на блок, и величину его момента инерции.

Two blocks are connected by a light string passing over a pulley of radius 0.25 m and moment of inertia I. The blocks move to the right with an acceleration of 1.0 m/s² on inclines with frictionless surfaces (see Figure). (a) Draw a force diagram for the two blocks and the pulley. (b) Determine T₁ and T₂, the tensions in the two parts of the string.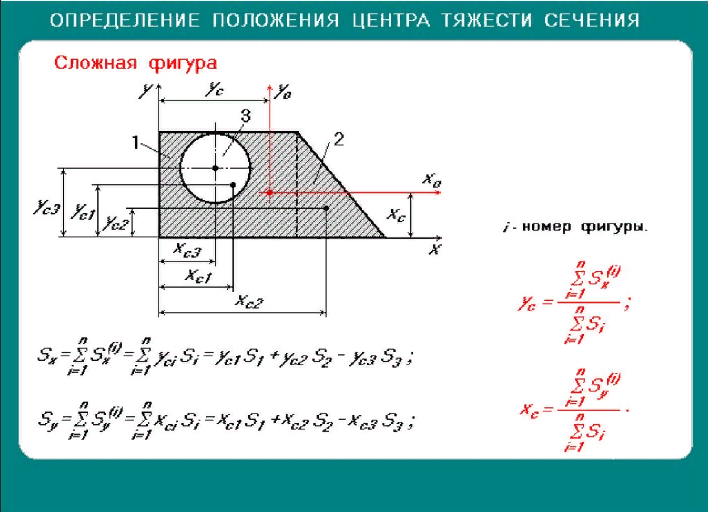 (c) Find the net torque acting on the pulley, and determine its moment of inertia, I.

Решение

Обозначим угловую скорость блока через w, его ускорение через a. Из нерастяжимости нити следует, что wR = v, где R – радиус блока, v – линейная скорость тел. Для ускорений выполняется аналогичное соотношение: aR=a. Запишем уравнения движения тел и блока:

T₁ – m₁g sin30° = m₁a;

m₂g sin60° – T₂ = m₂a;

(T₂ – T₁)R = Ia.

Решая эту систему уравнений, получаем:

33. (II) При броске мяча массой 9 кг с ускорением 8 м/с² работают мышцы предплечья – трицепсы. Оцените необходимый для такого броска момент силы и величину самой силы, используя данные, обозначенные на рисунке. Массой руки пренебречь.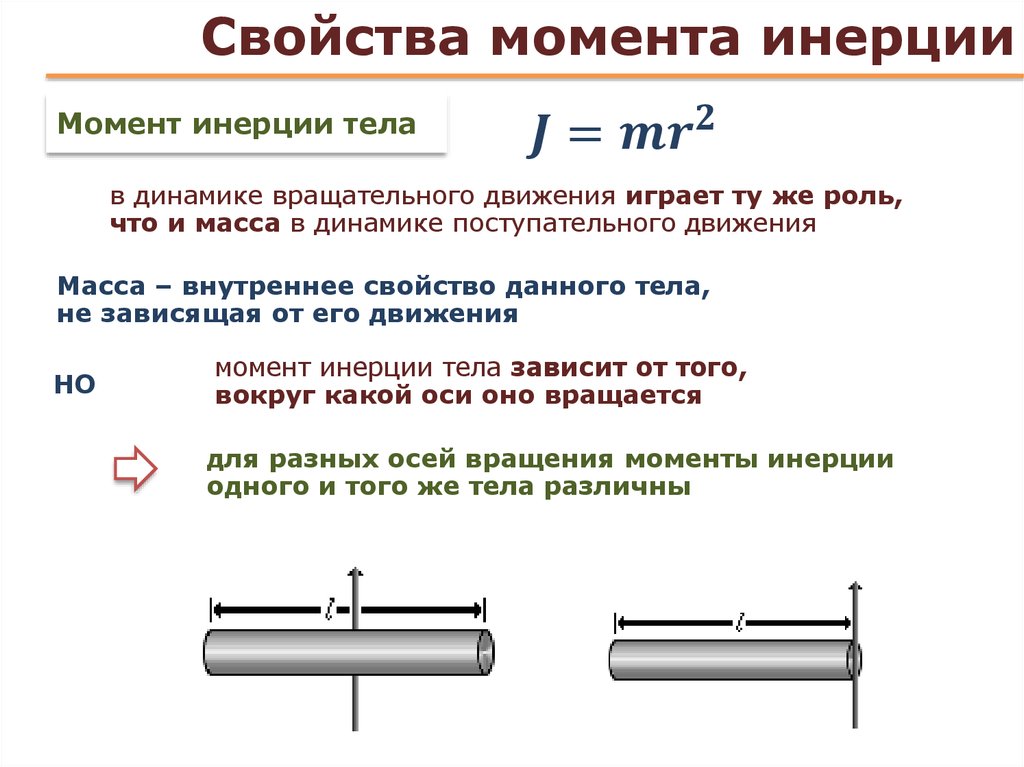

The forearm in Figure accelerates a 9.0-kg ball at 8.0 m/s² by means of the triceps muscle as shown. Calculate (a) the torque needed and (b) the force that must be exerted by the triceps muscle. Ignore the mass of the arm.

Решение

Будем считать, что при броске рука вращается в локтевом суставе, причем плечо силы, создаваемой трицепсом, равно r₁ = 2,5 см, а кисть движется по окружности радиусом r₂ = 30 см. Тогда уравнение вращательного движения запишется в таком виде: M = Fr₁ = mr₂²a = mr₂a = 21,6 НЧм. Отсюда получаем F = 864 Н.

34. (II) Два груза массами m₁ = 3,8 кг и m₂ = 3,4 кг соединены невесомой нерастяжимой нитью, перекинутой через блок. Блок представляет собой однородный цилиндр радиусом R = 3 см и массой m₃ = 0,8 кг. Найдите: а) ускорения грузов, считая, что трением можно полностью пренебречь; б) средний момент силы трения в оси блока, если известно, что при начальном движении груза m₁ вниз со скоростью 20 см/с он останавливается через 6,2 с.

A string passing over a pulley has a 3.8-kg mass hanging from one end and a 3.40-kg mass hanging from the other end. The pulley is a uniform solid cylinder of radius 3.0 cm and mass 0.80 kg. (a) If the bearings of the pulley were frictionless, what would be the acceleration of the two masses? (b) In fact, it is found that if the heavier mass is given a downward speed of 0.20 m/s, it comes to rest in 6.2 s. What is the average frictional torque acting on the pulley?

Решение

Момент инерции блока I = 0,5 m₃ R² = 3,6Ч10^–4 кгЧ м².

Воспользуемся уравнениями, полученными при решении задачи 33, положив в них все углы равными 90°:

m₁g – T₁ = m₁a;

T₂ – m₂g = m₂a;

(T₁ – T₂)R – M_тр = Ia/R.

Если момент силы трения Mтр равен нулю, то для ускорений грузов имеем

Если известно ускорение грузов, то можно найти момент силы трения

В нашем случае a = –v₀/t. Отсюда М_тр = 0,13 НЧм.

35. (III) Тонкий однородный стержень длиной  L, стоявший вертикально на столе, начинает падать так, что его нижний конец не проскальзывает. Определите угловую скорость стержня как функцию угла j его наклона к плоскости стола. Чему равна скорость верхнего конца стержня непосредственно перед ударом о стол?

A thin rod of length L stands vertically on a table. The rod begins to fall, but its lower end does not slide. (a) Determine the angular velocity of the rod as a function of the angle j it makes with the tabletop. (b) What is the speed of the tip of the rod just before it strikes the table?

Решение

(III) Момент инерции стержня относительно нижней точки I = mL²/3 (см. решение задачи 40). Проще всего воспользоваться законом сохранения механической энергии (сила трения работы не совершает):

Отсюда 

Непосредственно перед падением верхний конец стержня имеет скорость

36. (III) Оцените угловое ускорение руки и мышечную силу трицепса при броске шара массой 1 кг (см. рисунок к задаче 33). Известно, что шар ускоряется из состояния покоя до скорости 1 м/с за 0,22 с. Массу предплечья считать равной 3,4 кг и равномерно распределенной по его длине.

Assume that a 1.0-kg ball is thrown solely by the action of the forearm in Figure before rotating about the elbow joint under the action of the triceps muscle. The ball is accelerated from rest to 1.0 m/s in 0.22 s, at which point it is released. Calculate (a) the angular acceleration of the arm and (b) the force required of the triceps muscle. Assume the forearm has a mass of 3.4 kg and rotates like a uniform rod about an axis at its end.

Решение

Примем для предплечья модель однородного стержня, вращающегося вокруг неподвижной оси (локтевой сустав). Обозначим расстояние от локтевого сустава до кисти через r₁ = 30 см, расстояние от локтевого сустава до точки крепления мышцы трицепса через r₂ = 2,5 см, массу шара через m₁, массу предплечья через m₂. Среднее угловое ускорение

Угловое смещение j = at²/2=0,363 рад = 21°. Сила мышцы F совершает работу A = Fjr₂. Эта работа идет на увеличение кинетической энергии руки и шара:

Отсюда F = 117 Н.

37. (II) Метатель молота ускоряет молот массой 7,3 кг в течение четырех полных оборотов руки и бросает его со скоростью 27,2 м/с. Считая угловое ускорение постоянным, а радиус окружности равным 2 м, найдите: а) угловое ускорение молота; б) его тангенциальное ускорение; в) его центростремительное (радиальное) ускорение непосредственно перед броском; г) величину и направление силы (по отношению к радиусу кругового движения), с которой атлет действует на молот непосредственно перед броском. Действием силы тяжести пренебречь.

A hammer thrower accelerates the hammer (mass = 7.3 kg) from rest within four full turns (revolutions) and releases it at a speed of 27.2 m/s.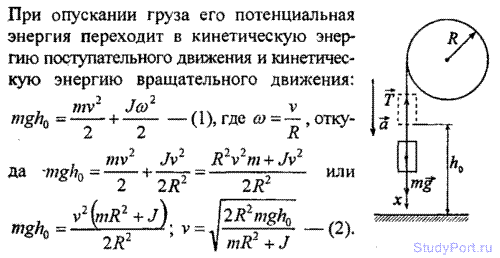 Assuming a uniform rate of increase in angular velocity and a radius of 2.0 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force exerted on the hammer by the athlete just before release, and (e) the angle of this force with respect to the radius of the circular motion. Neglect the effect of gravity.

Решение

Линейное и угловое ускорения соответственно равны: Отсюда находим время ускорения Поэтому a_t =  7,4 м/с²; a = 3,7 рад/с².

Непосредственно перед броском радиальное ускорение

Полная сила, с которой атлет действует на молот:

По отношению к радиусу эта сила направлена под углом

---

Продолжение. См. № 1, 5, 9, 13, 17, 21, 25/01

Преодоление инерции задачи

Перейти к основному содержанию

Джонатан Локк

Джонатан Локк

Менеджер по развитию в Shopify

Опубликовано 13 января 2021 г.

+ Подписаться

Я с гордостью сообщаю, что моя первая книга опубликована и доступна на Amazon как в формате Kindle, так и в мягкой обложке. Добраться до этого момента было не просто сложно, но оно того стоило.

Моя книга называется «Преодоление инерции задачи». Инерция задачи — это теория, которую я придумал, чтобы объяснить умственное сопротивление, которое мы испытываем, пытаясь выполнить работу. Это тот тихий голос в нашей голове, который говорит нам, что эту задачу можно выполнить позже, или она слишком скучна, или что, возможно, вместо этого нам следует проверить социальные сети. В этой книге я называю высокую инерцию к задаче высоким умственным сопротивлением, затрудняющим выполнение работы.

Внутри книги

В книге описано, как борьба во время первого карантина, введенного в Лондоне в 2020 году, привела к снижению моей продуктивности и здравомыслия и заставила меня найти решение. Этим решением стала теория инерции задачи.

В книге подробно описывается теория инерции задачи, в том числе то, как она применима к разным людям, а затем приводится программа лечения, соблюдение которой может привести к значительному снижению инерции задачи и повышению производительности.

Это не означает, что те, кто уже был продуктивным, станут еще более продуктивными, но, возможно, если бы вы боролись, как я, эта книга могла бы просто помочь вам немного лучше справляться с безумием длительных периодов изоляции. В моем случае разница была поразительной — я перешел от абсолютной непродуктивности к написанию и публикации своей первой книги за 6 месяцев.

Серебряная подкладка?

Как и для большинства из нас, прошлый год был для меня невероятно трудным по нескольким причинам. Но это привело меня к открытию теории инерции задач, а затем к написанию и публикации книги о ней.

Если бы не изоляция, какой бы ужасной она ни была, я не уверена, что когда-либо опубликовала бы книгу. Теперь, когда я понимаю, почему я изо всех сил пытался быть продуктивным, я могу предпринять шаги, чтобы исправить и улучшить это. Я не всегда понимаю это правильно, и некоторые дни лучше, чем другие, но все же есть заметная разница.

Я надеюсь, что мои читатели нашли выход из всех страданий, вызванных пандемией.

Получить книгу

Вы можете получить ее на Amazon.com здесь или на Amazon.co.uk здесь. Он также должен быть доступен на других региональных торговых площадках Amazon.

Другие также смотрели

Исследуйте темы

Вращательная динамика — Как найти момент инерции объекта, зная момент инерции его симметричной части?

спросил 2 года 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 74 раза

$\begingroup$

Я немного запутался с расчетом момента инерции симметричных объектов.

Например, если нужно найти $I$ тонкой равносторонней треугольной пластины массой $m$ и стороной $a$ относительно оси, проходящей через ее центр (перпендикулярной плоскости). Если я разделю треугольник на $6$ одинаковых частей и найду момент инерции одной части (относительно оси, проходящей через центр всего треугольника), почему я не могу умножить результат на $6$, чтобы получить общий момент инерции? 92$$

Мой вопрос: не должен ли момент инерции всего треугольника быть в шесть раз больше, чем момент инерции одной шестой?

Другие примеры: Если у меня есть диск и нужно найти момент инерции всего диска относительно оси, проходящей через его центр (перпендикулярной плоскости), то почему я не могу (или не могу) найти момент инерции всего $\frac{ 1}{4}$ диска (относительно оси через центр полного диска) и умножить результат на $4$, чтобы получить момент инерции полного диска?

Последний пример — момент инерции треугольника относительно оси через его высоту.