Вычислить это плюс или минус
Для определителей второго и третьего порядка существуют рациональные способы их вычислений. Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали :. Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:. Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Вычитание отрицательных чисел
- Знак плюс-минус
- Математический калькулятор
- Вычитание чисел
- Умножение и деление рациональных чисел
- Числа от 1 до 10.
Сложение и вычитание +3, -3. Приемы вычислений
- Методы вычисления определителей
- Доверительная зона регрессии в матричном виде
- Арифметические операции
Как найти 10% от числа
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Сложение отрицательных чисел. Сложение чисел с разными знаками.
Вычитание отрицательных чисел
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:. Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно. Избавиться от вредной привычки складывать знаменатели достаточно просто.
Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь внезапно! Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:. Напрямую складывать дроби с разными знаменателями нельзя.
По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Лучше посмотрим на примеры:. Во втором будем искать НОК. Последние множители в этих разложениях равны, а первые взаимно просты. Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло.
Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть. Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:. Если не помните — обязательно повторите. Здесь все просто.
Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время. В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:. Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда: Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Найдите значение выражения: Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем: Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется! Ну и конечно, не забывайте два простых правила: Плюс на минус дает минус; Минус на минус дает плюс.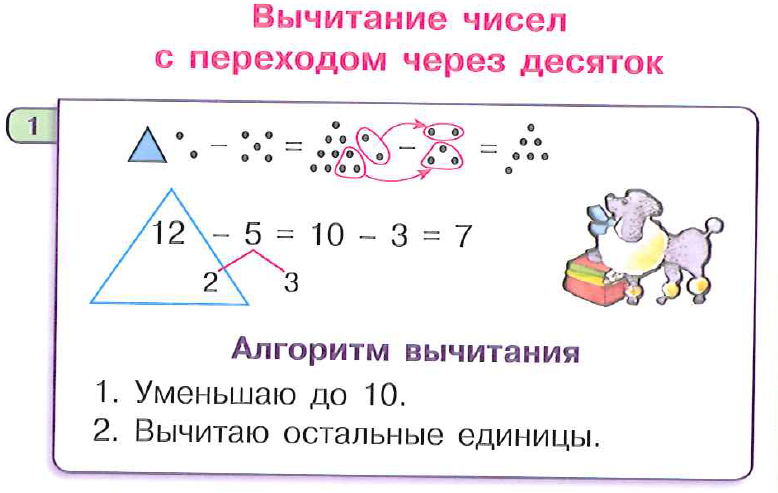
Лучше посмотрим на примеры: Задача. Что делать, если у дроби есть целая часть Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Лучше используйте простую схему, приведенную ниже: Перевести все дроби, содержащие целую часть, в неправильные.
Получим нормальные слагаемые пусть даже с разными знаменателями , которые считаются по правилам, рассмотренным выше; Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ; Если это все, что требовалось в задаче, выполняем обратное преобразование, то есть избавляемся от неправильной дроби, выделяя в ней целую часть. Примеры: Задача. Найдите значение выражения: Здесь все просто. Имеем: Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Резюме: общая схема вычислений В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей: Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные; Приведите все дроби к общему знаменателю любым удобным для вас способом если, конечно, этого не сделали составители задач ; Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями; Если возможно, сократите полученный результат.
Если дробь оказалась неправильной, выделите целую часть. Смотрите также:.
Знак плюс-минус
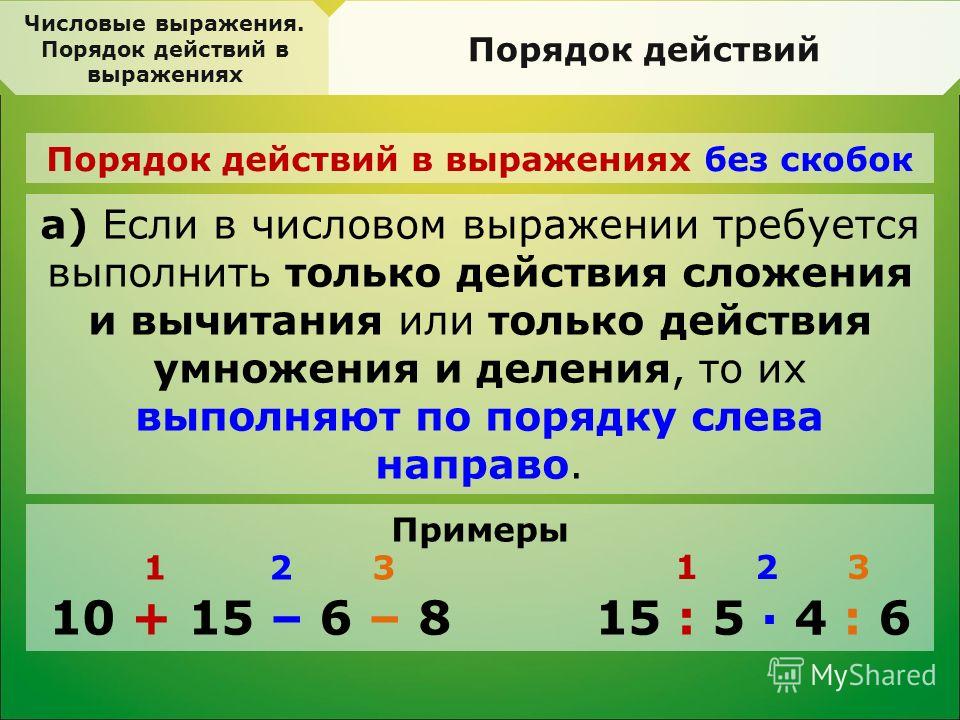
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений. Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
Рассмотрим алгоритм нахождение 15% от числа 1 Число это %, найдем 1% от числа, для этого разделим на 1% от числа равен.
Математический калькулятор
Сколько учеников участвовало в конкурсе? Сколько риса было продано в первый день? Значит, чтобы найти это число, надо 18 умножить на Сколько будет стоить рубашка после скидки? Сколько денег будет на его счету через год? Search for:. Рубрики Быстрый счет Десятичные дроби Дроби с одинаковыми знаменателями Единицы измерения Задачи в 6 классе Задачи на движение в 4 классе Задачи на пропорции КВН по математике Конкурс «Домашнее задание» Математика Математика 4 класса, повторение Математика 5 класса, повторение Обыкновенные дроби Округление чисел Положительные и отрицательные числа Приветствие команды Признаки делимости самостоятельная работа по математике Сокращение дробей Уравнения в 5 классе Уравнения в 6 классе. Свежие записи Как перевести километры в мили Как перевести мили в час в километры в час Как перевести мили в километры Как перевести мили в метры Как перевести метры в минуту в километры в час. Страницы Карта сайта Приветствие.
Страницы Карта сайта Приветствие.
Вычитание чисел
Объявления в Директе показываются по запросам, полностью содержащим вашу ключевую фразу. Например, вы продаете путешествия на Луну. Объявление с ключевой фразой путешествие на луну будет показано не только по запросу купить путешествие на луну , но и по не самым подходящим запросам: книги про путешествия на луну , первое путешествие на луну. Минус-слова и минус-фразы — это слова и словосочетания, по запросам с которыми объявление показываться не будет.
Правила умножения целых чисел справедливы и для рациональных чисел.
Умножение и деление рациональных чисел
Часто используется, например, для указания:. Пример 3, аналогичный второму, тригонометрический :. Пример 4. Здесь истолкование символа плюс-минус иное: надо выбрать знак одночлена в зависимости от его номера в ряду:. Современный вид символу придал Уильям Отред в году [1]. Он используется совместно с одним или несколькими знаками плюс-минус и означает, что знаку плюс в плюс-минусе строго соответствует знак минус в минус-плюсе, и обратно.
Числа от 1 до 10. Сложение и вычитание +3, -3. Приемы вычислений
Вычитание — это арифметическое действие обратное сложению, посредством которого из одного числа вычитают отнимают столько единиц, сколько их содержится в другом числе. Число, из которого вычитают, называется уменьшаемым , число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью или остатком. Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 — вычитаемым, а 4 — остатком разностью :. Для записи вычитания используется знак — минус. Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое — справа.
3 – это 1 и 2 3 – 2 и 1. – Как разложить число 3 на две части? Я диктую примеры, ученики записывают и рассказывают, как вычисляют: 6 плюс 3,; первое слагаемое 4, второе – 3, найдите сумму,; 5 увеличить на 3,; 7 уменьшить на 3,; 6 минус 3,; из 10 вычесть 3.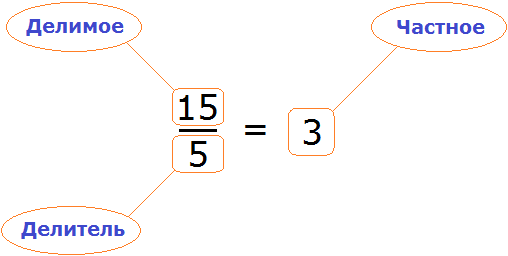 Работа по учебнику. – Что известно в задаче.
Работа по учебнику. – Что известно в задаче.
Методы вычисления определителей
Программа Microsoft Excel это не только большая таблица, но еще и суперсовременный калькулятор с множеством функций и возможностей. В этом уроке мы научимся пользоваться им по назначению. А теперь о знаках, при помощи которых мы будем считать. Также они называются арифметические операторы:.
Доверительная зона регрессии в матричном виде
Процент — это одна сотая доля числа, принимаемого за целое. Проценты используются для обозначения отношения части к целому, а также для сравнения величин. Чтобы найти процент p от числа, нужно умножить это число на дробь p Чтобы отнять от числа p процентов, нужно умножить это число на 1 — p Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на и вычесть Чтобы вычислить, на сколько процентов одно число меньше другого, нужно из вычесть отношение первого числа ко второму, умноженное на
Тема в разделе » Вопросы высшей математики «, создана пользователем Schufter , 26 июл Войти или зарегистрироваться.
Арифметические операции
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений. Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:. Но даже в таких простых действиях люди умудряются допускать ошибки.
Как найти 10% от числа
Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Свойства сложения и вычитания.
 Переместительное и сочетательное
Переместительное и сочетательноеКак в сказке черепаха перехитрила и обогнала зайца, так и мы можем схитрить и решить любое выражение быстрее с помощью упрощения. Для этого разберемся в свойствах сложения и вычитания.
Записывайтесь на онлайн-фестиваль для родителей SmartFest!
Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.
Бесплатный урок по математике
Записаться
Свойства сложения
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения в 1 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Свойства сложения
|
На заметку!
При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.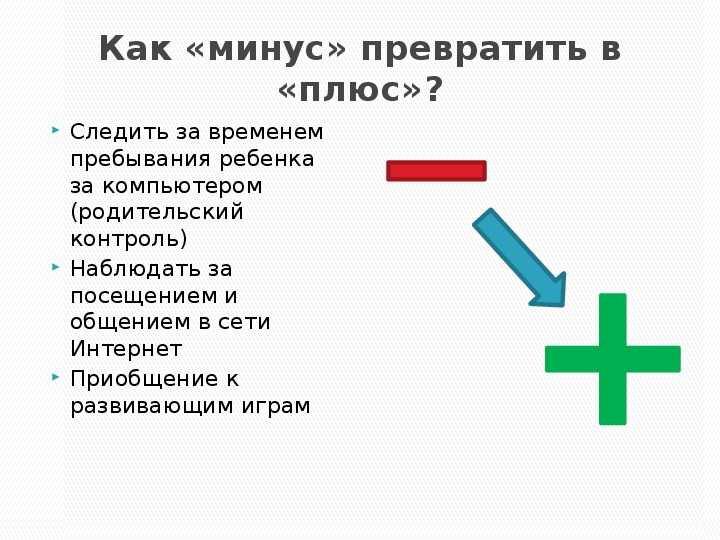
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.
Свойства вычитания
|
На заметку!
Есть случаи, когда скобки не имеют значения при вычитании, и их можно опустить. Например: (a — b) — c = a — b — c.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Скачать
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 6 + 5
б) 9 + 11 + 2
в) 30 + 0 + 13
Как решаем:
а) 4 + 6 + 8 = (4 + 6) + 5 = 10 + 5 = 15
б) 9 + 11 + 2 = (9 + 11) + 2 = 20 + 2 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2
б) 22 — 7 — 5
в) 55 — 55
Как решаем:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 22 — 7 -5 = 22 — (7 + 5) = 22 — 12 = 10
в) 55 — 55 = 0
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9
б) 16 — (6 + 5) + 7
в) 0 + 2 + 4 — 0
Как решаем:
а) 11 + 10 + 3 + 9 = (11 + 9) + (10 + 3) = 20 + 13 = 33
б) 16 — (6 + 5) + 7 = (16 — 6) — 5 + 7 = 10 — 5 + 7 = 5 + 7 = 12
в) 0 + 2 + 4 — 0 = 2 + 4 = 6
Шпаргалки по математике родителей
Все формулы по математике под рукой
Операторы вычислений и их приоритеты в Excel
Операторы указывают тип вычисления, который требуется выполнить с элементами формулы, такими как сложения, вычитания, умножения или деления. В этой статье вы узнаете порядок по умолчанию, в котором операторы работают с элементами в вычислении. Вы также узнаете, как изменить этот порядок с помощью скобок.
В этой статье вы узнаете порядок по умолчанию, в котором операторы работают с элементами в вычислении. Вы также узнаете, как изменить этот порядок с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Для выполнения основных математических операций, таких как сложения, вычитания или умножения или объединения чисел, и получения числовых результатов, используйте арифметические операторы в этой таблице.
|
Арифметический оператор |
Значение |
Пример |
|---|---|---|
|
+ (знак «плюс») |
Сложение |
=3+3 |
|
– (знак «минус») |
Вычитание |
=3–1 |
|
* (звездочка) |
Умножение |
=3*3 |
|
/ (косая черта) |
Деление |
=3/3 |
|
% (знак процента) |
Доля |
=20 % |
|
^ (крышка) |
Возведение в степень |
=2^3 |
С помощью операторов в таблице ниже можно сравнить два значения. При сравнении двух значений с помощью этих операторов результатом является логическое значение TRUE или FALSE.
При сравнении двух значений с помощью этих операторов результатом является логическое значение TRUE или FALSE.
|
Оператор сравнения |
Значение |
Пример |
|---|---|---|
|
= (знак равенства) |
Равно |
=A1=B1 |
|
> (знак «больше») |
Больше |
=A1>B1 |
|
< (знак «меньше») |
Меньше |
=A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
=A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
=A1<=B1 |
|
<> (знак «не равно») |
Не равно |
=A1<>B1 |
Используйте амперсанд (&) для объединения или объединения одной или нескольких текстовых строк для создания одного фрагмента текста.
|
Текстовый оператор |
Значение |
Пример |
|---|---|---|
|
& (амперсанд) |
Соединяет или сцепляет два значения для получения одного непрерывного текстового значения. |
=»North»&»wind» |
Объедините диапазоны ячеек для вычислений с этими операторами.
|
Оператор ссылки |
Значение |
Пример |
|---|---|---|
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
=СУММ(B5:B15) |
|
, (запятая) |
Оператор Union, объединяющий несколько ссылок в одну ссылку. |
=СУММ(B5:B15;D5:D15) |
|
(пробел) |
Оператор пересечения, который создает ссылку на ячейки, общие для двух ссылок. |
=СУММ(B7:D7 C6:C8) |
|
# (решетка) |
Символ #используется в нескольких контекстах:
Используется, чтобы указать недостаточно места для отрисовки. В большинстве случаев столбец можно расширить до тех пор, пока содержимое не отобразится должным образом. |
=СУММ(A2#) |
|
@ (по адресу) |
Оператор ссылки, который используется для определения неявного пересечения в формуле. |
=@A1:A10 =СУММ(Таблица1[@[Январь]:[Декабрь]]) |
Порядок выполнения действий в формулах Excel
В некоторых случаях порядок выполнения вычисления может повлиять на возвращаемое значение формулы, поэтому важно понимать порядок и способ изменения порядка для получения ожидаемых результатов.
Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равенства (=). Знак равенства сообщает Excel, что следующие символы составляют формулу. После этого знака равенства можно вычислить ряд элементов (операндов), разделенных операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Формула в Excel всегда начинается со знака равенства (=). Знак равенства сообщает Excel, что следующие символы составляют формулу. После этого знака равенства можно вычислить ряд элементов (операндов), разделенных операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом — например, операторы деления и умножения, — они выполняются слева направо.
|
Оператор |
Описание |
|---|---|
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, приведенная ниже формула возвращает значение 11, так как Excel вычисляет умножение перед добавлением. Формула сначала умножает 2 на 3, а затем добавляет 5 к результату.
Например, приведенная ниже формула возвращает значение 11, так как Excel вычисляет умножение перед добавлением. Формула сначала умножает 2 на 3, а затем добавляет 5 к результату.
=5+2*3
Напротив, если для изменения синтаксиса используются круглые скобки, Excel 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В приведенном ниже примере скобки, включаемые в первую часть формулы, принудит Excel сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Просмотрите это видео по порядку операторов в Excel, чтобы узнать больше.
Преобразование Excel значений в формулах
При вводе формулы Excel ожидает определенные типы значений для каждого оператора. Если ввести значение, отличное от ожидаемого, Excel может преобразовать это значение.
|
Формула |
Производит |
Описание |
|
= «1»+»2″ |
3 |
При использовании знака «плюс» (+) Excel числа в формуле. Хотя кавычки означают, что «1» и «2» являются текстовыми значениями, Excel автоматически преобразует текстовые значения в числа. |
|
= 1+»$4,00″ |
5 |
Если формула ожидает числа, Excel преобразует текст, если он имеет формат, который обычно принимается для числа. |
|
= «1.06.2001»-«5/1/2001» |
31 |
Excel интерпретирует текст как дату в формате мм/дд/дд/yyyy, преобразует даты в серийные числа, а затем вычисляет разницу между ними. |
|
=SQRT («8+1») |
#ЗНАЧ! |
Excel не удается преобразовать текст в число, так как текст «8+1» не может быть преобразован в число. Для преобразования текста в число и возврата результата 3 можно использовать «9» или «8»+»1″ вместо «8+1». |
|
= «A»&TRUE |
ATRUE |
Если текст ожидается, Excel преобразует числа и логические значения, такие как TRUE и FALSE, в текст. |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
-
Базовые математические Excel
-
Использование Excel в качестве калькулятора
-
Полные сведения о формулах в Excel
org/ListItem»>
-
Поиск ошибок в формулах
-
Сочетания клавиш и горячие клавиши в Excel
-
Функции Excel (по алфавиту)
-
Функции Excel (по категориям)
Рекомендации, позволяющие избежать появления неработающих формул
Математические вычисления в Python 3
30 ноября, 2016 11:48 дп 54 630 views | 1 комментарийPython | Amber | 1 Comment
Программирование невозможно представить без работы с числами. Размеры экрана, выбор цвета путем присвоения числовых кодов, географическое расположение, деньги и очки, продолжительность видео – для всего этого используются числа.
Размеры экрана, выбор цвета путем присвоения числовых кодов, географическое расположение, деньги и очки, продолжительность видео – для всего этого используются числа.
Потому умение выполнять математические операции очень важно для программирования. Конечно, чем выше у вас навык математических вычислений, тем лучше для вас; однако совсем не обязательно уметь выполнять сложнейшие вычисления, чтобы быть хорошим программистом. Если у вас нет опыта работы в области математики, старайтесь представлять математику как инструмент или как способ улучшить ваше логическое мышление.
Данное руководство научит вас работать с двумя наиболее распространёнными числовыми типами данных Python:
- целыми числами (бывают положительными, отрицательными или равными нулю (…, -1, 0, 1, …)).
- и числами с плавающей точкой (числа с десятичными знаками (например, 9.0 или -2.25)).
Читайте также: Типы данных в Python 3
Операторы Python
Оператор – это символ или функция, которая выполняет то или иное действие над данными. К примеру, символ + – это оператор сложения.
К примеру, символ + – это оператор сложения.
В Python присутствуют как общие, так и специальные математические операторы.
Ниже приведена таблица наиболее распространённых математических операторов Python.
| Операция | Результат |
| x + y | Сложение (сумма x и y) |
| x – y | Вычитание (разница между x и y) |
| -x | Смена знака x |
| +x | Тождественность x |
| x * y | Умножение x на y |
| x / y | Деление x на y |
| x // y | Получение целой части от деления x на y |
| x % y | Остаток от деления x / y |
| x ** y | Возведение в степень |
Также руководство охватывает использование операторов присваивания.
Сложение и вычитание
Операции сложения и вычитания в Python выполняются точно так же, как и в обычной математике. Вы даже можете использовать Python вместо калькулятора.
Вы даже можете использовать Python вместо калькулятора.
Например:
print(1 + 5)
6
Также вы можете объявить переменные и указать их в функции print:
a = 88
b = 103
print(a + b)
191
Целые числа бывают положительными и отрицательными. Попробуйте сложить следующие числа:
c = -36
d = 25
print(c + d)
-11
Числа с плавающей точкой складываются аналогичным образом:
e = 5.5
f = 2.5
print(e + f)
8.0
В результате сложения чисел с плавающей точкой также получается число с плавающей точкой, потому Python выводит 8.0, а не 8.
Синтаксис вычитания отличается от сложения только оператором. Попробуйте отнять 32 из 75.67:
g = 75.67
h = 32
print(g - h)
43.67
Примечание: Если в операции присутствует хотя бы одно число с плавающей точкой, в результате Python также выведет число с плавающей точкой.
Унарные арифметические операции
Унарное математическое выражение состоит только из одного компонента или элемента. В Python плюс и минус вместе со значением могут быть использованы в качестве одного элемента, это позволяет показать тождественность значения (+) или изменить его знак (-).
Тождественность используется нечасто. Плюс можно использовать с положительными числами:
i = 3.3
print(+i)
3.3
Если вы используете плюс с отрицательным числом, он также вернёт тождественное (в этом случае – отрицательное) число.
j = -19
print(+j)
-19
Минус позволяет изменить знак. Если вы добавите минус к положительному значению, в результате будет отображено отрицательное значение:
i = 3.3
print(-i)
-3.3
Если добавить минус к отрицательному значению, в результате получится положительное число:
j = -19
print(-j)
19
Умножение и деление
Операции умножения и деления, как сложение и вычитание, выполняются в Python так же, как в обычной математике. Для умножения Python использует *, для деления – /.
Для умножения Python использует *, для деления – /.
Например:
k = 100.1
l = 10.1
print(k * l)
1011.0099999999999
При делении в Python 3 частное всегда возвращается в виде числа с плавающей точкой, даже если вы делите целые числа:
m = 80
n = 5
print(m / n)
16.0
Это одно из главных различий между Python 2 и Python 3. Python 3 возвращает дробный результат, потому при делении 11 на 2 вы получите 5.5. В Python 2 деление привязано к типам данных, потому при делении целого числа невозможно получить число с плавающей точкой; поэтому при делении 11 на 2 Python 2 возвращает 5.
Читайте также: Python 2 vs Python 3
Когда числа по обе стороны символа деления являются целыми, выполняется деление floor, то есть, для фактора х Python 2 возвращает наибольшее целое число меньше или равное х. К примеру, при делении 5 / 2 таким числом будет 2.
Чтобы выполнить деление floor и получить только целую часть числа, Python 3 использует оператор //. К примеру, разделив 100//40, вы получите 2.
К примеру, разделив 100//40, вы получите 2.
Деление по модулю
Оператор % – это модуль, который возвращает остаток от деления. К примеру, это позволяет найти числа, кратные одному и тому же числу.
Например:
o = 85
p = 15
print(o % p)
10
При делении 85 на 15 получается 5 и 10 в остатке.
Попробуйте разделить числа с плавающей точкой:
q = 36.0
r = 6.0
print(o % p)
0.0
Число 36.0 делится на 6.0 без остатка, потому в результате получился 0.0.
Возведение в степень
Оператор ** в Python возводит число в степень. Например, выражение 5 ** 3 значит, что 5 нужно возвести в третью степень. В математике это выглядит так: 5³. В Python можно получить тот же результат (125), умножив 5*5*5.
Например:
s = 52.25
t = 7
print(s ** t)
1063173305051.292
Приоритет операций
Как и в математике, в Python нужно помнить о том, что операции выполняются в порядке их приоритета, а не по порядку справа налево.
К примеру:
u = 10 + 10 * 5
Сначала выполняется умножение (10*5=50), а затем сложение (10+50). Потому результат будет такой:
print(u)
60
Чтобы сначала выполнить операцию сложения, а затем умножить полученный результат на 5, нужно взять сложение в скобки:
u = (10 + 10) * 5
print(u)
100
Математические операции имеют такой приоритет:
- Выражение в скобках;
- Экспоненты;
- Умножение;
- Деление;
- Сложение;
- Вычитание.
Операторы присваивания
Наиболее распространённым оператором присваивания является знак равенства (=). Он присваивает переменной слева значение справа. К примеру, в выражении v = 23 переменной v было присвоено значение 23.
В программировании часто используются составные операторы присваивания, которые выполняют операцию со значением переменной, а затем присваивают этой переменной полученное новое значение. Составные операторы объединяют арифметический оператор с оператором =. Например:
Составные операторы объединяют арифметический оператор с оператором =. Например:
w = 5
w += 1
print(w)
6
Составной оператор += выполнил сложение, а затем присвоил переменной w, значение, полученное в результате сложения.
Составные операторы часто используются в циклах.
for x in range (0, 7):
x *= 2
print(x)
0
2
4
6
8
10
12
Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.
В Python есть составные операторы присваивания для каждой математической операции:
y += 1 # сложение и присваивание
y -= 1 # вычитание и присваивание
y *= 2 # умножение и присваивание
y /= 3 # деление и присваивание
y // = 5 # деление floor и присваивание
y **= 2 # возведение в степень и присваивание
y %= 3 # вывод остатка и присваивание
Операторы присваивания позволяют постепенно увеличить или уменьшить значение, а также автоматизировать некоторые вычисления. 2
2
Минус на минус даёт плюс. А почему?
Репетиторы ❯ Математика ❯ Минус на минус даёт плюс. А почему?
Автор: Владимир Л., онлайн репетитор по математике
●
21.09.2011
●
Раздел: Математика
Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием? С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время.
Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.
Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.
Что мы видим?
Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.
Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Вычитание чисел
Excel
Формулы и функции
Формулы
Формулы
Вычитание чисел
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно. .. Меньше
.. Меньше
Важно: Результаты расчетов формул и некоторых функций рабочего листа Excel могут немного отличаться на ПК с Windows с архитектурой x86 или x86-64 и ПК с Windows RT с архитектурой ARM. Узнайте больше о различиях.
Допустим, вы хотите узнать, сколько товарных единиц убыточных (вычтите из общего запаса прибыльные). Или, может быть, вам нужно знать, сколько сотрудников приближается к пенсионному возрасту (вычтите количество сотрудников моложе 55 лет из общего числа сотрудников).
Что ты хочешь сделать?
Существует несколько способов вычитания чисел, в том числе:
Вычитание чисел в ячейке
Вычитание чисел в диапазоне
Вычитание чисел в ячейке
Чтобы выполнить простое вычитание, используйте арифметический оператор – (знак минус).
Например, если ввести формулу =10-5 в ячейку, ячейка будет отображать 5 в качестве результата.
Вычитание чисел из диапазона
Добавление отрицательного числа идентично вычитанию одного числа из другого. Используйте функцию СУММ , чтобы сложить отрицательные числа в диапазоне.
Примечание. В Excel нет функции ВЫЧИТАТЬ . Используйте SUM и преобразуйте любые числа, которые вы хотите вычесть, в их отрицательные значения. Например, СУММ(100,-32,15,-6) возвращает 77.
Пример
Выполните следующие действия, чтобы вычитать числа разными способами:
Выберите все строки в таблице ниже, затем нажмите CTRL-C на клавиатуре.

Данные
15000
9000
-8000
Формула
=А2-А3
Вычитает 9000 из 15000 (что равно 6000)
-СУММ(А2:А4)
Добавляет все числа в список, включая отрицательные числа (результат 16000)
org/ListItem»>Чтобы переключиться между просмотром результатов и просмотром формул, нажмите CTRL+` (ударение) на клавиатуре. Или нажмите кнопку Показать формулы (на вкладке Формулы ).
На листе выберите ячейку A1 и нажмите CTRL+V.
Использование функции СУММ
Функция СУММ складывает все числа, указанные вами в качестве аргументов. Каждый аргумент может быть диапазоном, ссылкой на ячейку, массивом, константой, формулой или результатом другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек от A1 до A5. Другой пример — SUM(A1, A3, A5) , который складывает числа, содержащиеся в ячейках A1, A3 и A5 (A1, A3 и A5 — это аргумента ).
Складывать и вычитать числа
Складывать и вычитать в Excel легко; вам просто нужно создать простую формулу, чтобы сделать это. Просто помните, что все формулы в Excel начинаются со знака равенства (=), и вы можете использовать панель формул для их создания.
Просто помните, что все формулы в Excel начинаются со знака равенства (=), и вы можете использовать панель формул для их создания.
Добавить два или более числа в одну ячейку
Щелкните любую пустую ячейку и введите знак равенства ( = ), чтобы начать формулу.
После знака равенства введите несколько чисел, разделенных знаком плюс (+).
Например, 50+10+5+3 .
Нажмите ВОЗВРАТ .

Если вы используете номера примеров, результат будет 68.
Примечания:
Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Главная выберите Общие .
Добавить числа, используя ссылки на ячейки
Ссылка на ячейку объединяет букву столбца и номер строки, например A1 или F345. Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
- org/ListItem»>
В ячейке E1 введите знак равенства ( = ), чтобы начать формулу.
После знака равенства введите C1+D1 .
Нажмите ВОЗВРАТ .
Если вы используете номера примеров, результат будет 8.
Примечания:
- org/ListItem»>
Если вы измените значение C1 или D1, а затем нажмете RETURN, значение E1 изменится, даже если формула не изменилась.
Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Главная выберите Общие .
Введите число, например 5 , в ячейку C1. Затем введите другое число, например 9.0015 3 , в D1.
Получить быстрый итог по строке или столбцу
Введите несколько чисел в столбце или в строке, а затем выберите диапазон ячеек, который вы только что заполнили.
org/ListItem»>
В строке состояния посмотрите на значение рядом с Sum . Всего 86.
Вычитание двух или более чисел в ячейке
Щелкните любую пустую ячейку и введите знак равенства ( = ), чтобы начать формулу.
После знака равенства введите несколько чисел, разделенных знаком минус (-).
Например, 50-10-5-3 .
org/ListItem»>
Нажмите ВОЗВРАТ .
Если вы используете номера примеров, результат будет 32.
Вычитание чисел с использованием ссылок на ячейки
Ссылка на ячейку объединяет букву столбца и номер строки, например A1 или F345. Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
Введите число в ячейки C1 и D1.
Например, 5 и 3 .
В ячейке E1 введите знак равенства ( = ), чтобы начать формулу.

После знака равенства введите C1-D1 .
Нажмите ВОЗВРАТ .
Если вы использовали номера примеров, результат будет 2.
Примечания:
Если вы измените значение C1 или D1, а затем нажмете RETURN, значение E1 изменится, даже если формула не изменилась.
Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Главная выберите Общие .

Добавление двух и более чисел в одну ячейку
Щелкните любую пустую ячейку и введите знак равенства ( = ), чтобы начать формулу.
После знака равенства введите несколько чисел, разделенных знаком плюс (+).
Например, 50+10+5+3 .
Нажмите ВОЗВРАТ .
Если вы используете номера примеров, результат будет 68.

Примечание. Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Домашняя в разделе Номер нажмите Общие во всплывающем меню.
Добавить числа, используя ссылки на ячейки
Ссылка на ячейку объединяет букву столбца и номер строки, например A1 или F345. Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
Введите число, например 5 , в ячейку C1. Затем введите другой номер, например 3 , в D1.
org/ListItem»>После знака равенства введите С1+Д1 .
Нажмите ВОЗВРАТ .
Если вы используете номера примеров, результат будет 8.
Примечания:
Если вы измените значение C1 или D1, а затем нажмете RETURN, значение E1 изменится, даже если формула не изменилась.
org/ListItem»>
Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Домашняя в разделе Номер щелкните Общие во всплывающем меню.
В ячейке E1 введите знак равенства ( = ), чтобы начать формулу.
Получить быстрый итог по строке или столбцу
Введите несколько чисел в столбце или в строке, а затем выберите диапазон ячеек, который вы только что заполнили.
В строке состояния посмотрите на значение рядом с Sum= . Всего 86.
Если вы не видите строку состояния, в меню Вид щелкните Строка состояния .

Вычитание двух или более чисел в ячейке
Щелкните любую пустую ячейку и введите знак равенства ( = ), чтобы начать формулу.
После знака равенства введите несколько чисел, разделенных знаком минус (-).
Например, 50-10-5-3 .
Нажмите ВОЗВРАТ .
Если вы используете номера примеров, результат будет 32.

Вычитание чисел с использованием ссылок на ячейки
Ссылка на ячейку объединяет букву столбца и номер строки, например A1 или F345. Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
Введите число в ячейки C1 и D1.
Например, 5 и 3 .
В ячейке E1 введите знак равенства ( = ), чтобы начать формулу.
org/ListItem»>Нажмите ВОЗВРАТ .
Если вы использовали примеры номеров, результат будет -2.
Примечания:
Если вы измените значение C1 или D1, а затем нажмете RETURN, значение E1 изменится, даже если формула не изменилась.
Если вы видите дату вместо ожидаемого результата, выберите ячейку, а затем на вкладке Главная в разделе Номер , нажмите Общие во всплывающем меню.

После знака равенства введите C1-D1 .
См. также
Расчетные операторы и порядок операций
Добавить или вычесть даты
Вычесть раз
Символ Плюс-Минус – Все Математические Символы
- Домашний
- Символ Плюс-Минус
±Мы можем представить, как устроен мир, если в нем нет математических знаков и правил. Жизнь была бы слишком занятой и трудной, если бы в повседневной работе не помогала математика. Существует множество математических символов, каждый из которых имеет определенную цель и способствует удобству вычислений и целей идентификации. Один из этих символов, плюс-минус, также хорошо известен своей помощью в различных математических расчетах и уравнениях, таких как квадратные формулы, которые имеют жизненно важное значение при решении квадратных уравнений.
Никогда нельзя пренебрегать важностью знания знаков плюс-минус, плюс-минус, их применения в разных ситуациях, как набирать его символ в разных программах в этом многогранном мире. В этой статье мы обсудим знак плюс-минус, его использование, значение, как его вводить в различном программном обеспечении, его кодирование и все те вещи, которые нужно иметь при работе со знаком плюс-минус.
Что такое знак плюс-минус в математике и вычислительном процессе?
Роберт Рекорд ввел знак плюс-минус в 1557 году в Великобритании. Он также является тем, кто разработал символ равенства, прежде чем ввести плюс-минус. Хотя плюс-минус имеет широкий спектр значений в зависимости от области, в которой мы его используем, в математике он в основном относится к двойному условию, в котором сначала выполняется сложение, а во второй ситуации выполняется вычитание со значением прикреплен к символу плюс-минус. Делая это, мы получаем два значения: одно добавленное значение и второе значение вычитания. Однако он также широко используется в физике при измерениях, чтобы показать изменение точности и правильности измерения.
Однако он также широко используется в физике при измерениях, чтобы показать изменение точности и правильности измерения.
В математических формулах символ плюс-минус представляет собой символ, который может быть заменен плюсом или минусом. Это означает, что к заданному значению мы можем добавить или вычесть определенную цифру или значение.
Например, при таком значении со знаком плюс-минус x 2 = 25 можно дать возможное решение: x=±5. У уравнения есть два решения: одно получается путем сложения пяти, а другое — путем вычитания 5. Только одно из этих двух замененных уравнений верно для любого действительного уравнения.
В другом примере знак плюс-минус используется для представления точности приближения. Результат «20±0,5» означает, что конечное значение может быть между «20+0,5», что равно 20,5, и «20-0,5», что равно 19,5.
Когда использовать знак плюс-минус?
Знак плюс-минус обычно используется в таких ситуациях, когда нам нужно представить две разные ситуации. Причина в том, что сам этот символ состоит из комбинации двух разных знаков, порождающих новый символ, обладающий качествами обоих знаков.
Причина в том, что сам этот символ состоит из комбинации двух разных знаков, порождающих новый символ, обладающий качествами обоих знаков.
Этот особый знак может добавлять или удалять конкретное значение к конечному значению, создавая два новых возможных значения. Кроме того, знак плюс-минус широко используется в математике и других областях науки. Тем не менее, обычно знак плюс-минус используется в квадратных формулах и уравнениях. Однако использование знака плюс над минусом не ограничивается математикой, нельзя пренебрегать использованием знака плюс над минусом в физике, особенно в измерениях.
Прекрасным примером использования знака плюс-минус является квадратичная формула, показанная ниже.
Как показано выше, знак плюс-минус является первой частью квадратной формулы. Без него сама формула — jack-squad. Наличие знака ± указывает на то, что x имеет два возможных значения, одно со знаком + означает, что получено сложением, а другое со знаком –, что показывает, что вторая возможность будет получена путем вычитания.
Как ввести знак плюс-минус?
Обычный набор текста на английском языке в любом программном обеспечении или устройстве не слишком сложен для понимания. При наборе математических символов и знаков необходимо знать специальные клавиши и короткие клавиши в зависимости от программного обеспечения и устройств. Будучи новичком, вы можете столкнуться с трудностями при наборе знака плюс-минус в этом растущем разнообразии программного обеспечения и устройств. Теперь мы научимся набирать знаки плюс-минус на разных платформах.
Как ввести знак плюс-минус на клавиатуре
Хотя на обычной клавиатуре нет специальной клавиши для знака плюс-минус, вы все равно можете ввести его с помощью метода alt. Чтобы написать знак плюс-минус на клавиатуре, одновременно нажмите и удерживайте клавишу alt и альтернативный код, который равен 0177 . Это 0177 называется альтернативным кодом плюс-минус.
Как набирать знак «плюс-минус» на Mac
Схема набора текста и коды на компьютерах Apple сильно отличаются от других брендов. Если вы являетесь пользователем компьютера Apple и хотите ввести знак плюс-минус в своем задании или документации, нажмите и удерживайте вариант и смещают клавиши и в то же время набирают равные и плюс клавиши в верхнем ряду.
Если вы являетесь пользователем компьютера Apple и хотите ввести знак плюс-минус в своем задании или документации, нажмите и удерживайте вариант и смещают клавиши и в то же время набирают равные и плюс клавиши в верхнем ряду.
Как набирать плюс-минус Вход в Word/Excel
Клавиши и метод, используемые для ввода плюс-минус в документе Word или Excel, такие же, как и на обычной клавиатуре. Чтобы ввести плюс-минус в слове, нажмите и удерживайте клавишу alt , а затем введите 0177 .
Второй способ, щелкните вкладку вставки в верхней части меню документа, затем нажмите « символов ’ в правом верхнем углу, выберите подмножество ‘ Latin-1 Supplement ’ во всплывающем окне, чтобы получить знак плюс-минус.
Коды знака плюс-минус
В информатике и языках существуют разные стандарты кодирования, которые используются для ввода различных символов и уравнений. Вот некоторые коды языков, которые используются для ввода знака плюс-минус.
Вот некоторые коды языков, которые используются для ввода знака плюс-минус.
Часто задаваемые вопросы
Было задано несколько вопросов, связанных со знаком плюс-минус. Люди часто путаются в его использовании и смешивании, давайте обсудим часто задаваемые вопросы ниже:
1. Как использовать знак плюс-минус?
В математике знак ± используется, когда мы должны показать две возможности получения желаемого значения, одно из которых может быть получено сложением, а другое — вычитанием. Означает, что есть два возможных ответа начального значения. В науке он широко используется для отображения стандартного отклонения, экспериментальных ошибок и ошибок измерения
2. В чем разница между плюс-минус (±) и минус-плюс (∓)?
Нет никакой особой разницы, когда мы набираем плюс вместо символа минус или когда мы набираем минус вместо плюса. Функция обоих символов одинакова. Когда в выражении используются знаки, то положительное значение следует записывать с отрицательным, а отрицательное — с положительным.

(x∓ 8) (x±6) означает (x- 8) (x+8) и (x+8) (x-6)
3. Нужны ли коды для разных знаков в информатике и языках? ?
Да. Существуют разные коды для разных знаков в соответствии со стандартами кодирования символов. Они полезны, когда вы имеете дело с компьютерными языками, поскольку эти коды помогают понять компьютер, чтобы лучше и быстрее выполнять работу.
4. Легко ли набирать знак плюс-минус в разных программах?
Его легко ввести в нескольких местах. Вы можете легко напечатать его в MS Word, Excel, PowerPoint и другом программном обеспечении, выполнив шаги, упомянутые в этой статье. Следуйте им и печатайте столько раз, сколько хотите.
Заключение
Учитывая важность знака плюс-минус в квадратной формуле, нельзя пренебрегать его важностью. Если вы хотите ввести этот знак на клавиатуре, MAC или в Word/Excel, вам необходимо следовать определенным методам. Кроме того, коды со знаком плюс-минус необходимы для набора уравнений.
Чтобы понять знак плюс-минус, вам нужно иметь в виду, что что-то будет либо добавлено, либо вычтено, потому что двойные знаки показывают обе возможности. Этот знак имеет большое значение не только в математических задачах, но и в языках информатики.
0 нравится
Вычисление процентного изменения для отрицательных чисел в Excel
Итог: Узнайте, как создавать формулы процентного изменения в Excel с отрицательными числами.
Уровень навыка: Средний
В своем последнем посте я поделился макросом для быстрого создания формул процентного изменения. Я также объяснил две формулы, которые мы можем использовать для расчета процентного изменения.
Формула №1
=(новое значение – старое значение) / старое значение
Формула №2
=(новое значение/старое значение) – 1
Обе эти формулы дадут один и тот же результат, когда числа положительны . Тот, который вы используете, — это просто вопрос личных предпочтений.
Цель формулы процентного изменения состоит в том, чтобы позволить нам проводить сравнения производительности между двумя или более элементами. Это могут быть периоды времени, объекты, категории, предприятия и т. д. Эту формулу также можно использовать для расчета процентов скидок.
Загрузите файл
Загрузите файл, чтобы продолжить.
Формула процентного изменения для отрицательных чисел.zipDownload
Что делать, если числа отрицательные?
После небольшого исследования я не нашел хорошего способа рассчитать процентное изменение, когда либо старое число, либо новое число отрицательно. Определенно есть формулы, которые вы можете использовать, но они, похоже, дают неверные или вводящие в заблуждение результаты.
В Wall Street Journal есть старый справочник по отчетам о прибылях и убытках, в котором говорится следующее:
Процентное изменение чистой прибыли — это изменение по сравнению с тем же периодом прошлого года. Изменение в процентах не предоставляется , если либо последний период, либо период прошлого года содержит чистый убыток [отрицательное число] . На странице дайджеста, если компания сообщает о прибыли за последний период по сравнению с убытком за предыдущий период, процентное изменение представлено как «P». Точно так же, если компания публикует убыток в последнем периоде по сравнению с прибылью в прошлом году, процентное изменение представлено как «L».
Изменение в процентах не предоставляется , если либо последний период, либо период прошлого года содержит чистый убыток [отрицательное число] . На странице дайджеста, если компания сообщает о прибыли за последний период по сравнению с убытком за предыдущий период, процентное изменение представлено как «P». Точно так же, если компания публикует убыток в последнем периоде по сравнению с прибылью в прошлом году, процентное изменение представлено как «L».
Эта статья может быть устаревшей, так как я обнаружил, что последние финансовые страницы WSJ используют метод ABS (подробнее об этом ниже) для расчета процентного изменения, но дело в том, что процентное изменение отрицательных чисел может привести к вводящим в заблуждение результатам.
Как насчет метода ABS (абсолютного)?
Один из распространенных способов расчета процентного изменения с отрицательными числами — сделать знаменатель в формуле положительным. Функция ABS используется в Excel для изменения знака числа на положительный или его 9. 0604 абсолютное значение .
0604 абсолютное значение .
Вот формула, которая обычно используется:
=(новое значение – старое значение) / ABS(старое значение)
Технически эта формула работает для получения числа процентного изменения с правильным знаком (положительным/отрицательным). Однако я считаю, что дает вводящие в заблуждение результаты .
Изображение ниже содержит пример этого. Старое значение отрицательное, а Новое значение положительное.
- Когда значение изменяется от -10 до 50, изменение суммы составляет +60, а процентное изменение составляет 600%.
- Когда значение изменяется от -60 до 50, изменение суммы составляет +110, а процентное изменение составляет 183,3%
Хотя расчет технически верен, поскольку мы изменили знаменатель (старое значение) на положительное число, результаты не совпадают. не имеет смысла для меня.
Если бы вы просто смотрели на цифры процентного изменения, вы бы подумали, что кофе лучше, чем пирожные. В то время как на самом деле торты получили огромную прибыль по сравнению с предыдущим периодом, намного больше, чем кофе.
В то время как на самом деле торты получили огромную прибыль по сравнению с предыдущим периодом, намного больше, чем кофе.
Та же проблема возникает, когда числитель (новое значение) отрицательный. Вот еще один пример, который приводит к вводящим в заблуждение результатам.
В этом примере пирожные имели большее отрицательное изменение значения, но меньшее процентное изменение, чем кофе.
Но я всегда использовал метод ABS!!!
Я знаю, я тоже. Я видел, как этот метод использовался на протяжении всей моей карьеры, и похоже, что Wall Street Journal даже использует его. Я заметил это в некоторых показателях их роста на этой странице финансовой отчетности Bank of America.
Трудно сказать, что использовать формулу ABS совершенно неправильно. Но хорошо знать, что результаты могут вводить в заблуждение. Так что используйте его с осторожностью! 😉
Альтернативные расчеты процентного изменения с отрицательными числами
Вот несколько способов проверить наличие отрицательного числа и предоставить альтернативный результат.
Метод №1: Нет результата для отрицательных значений
Первое, что мы можем сделать, это проверить, является ли какое-либо из чисел отрицательным, а затем отобразить текст, сообщающий читателю, что расчет процентного изменения невозможен.
Следующая формула делает это с функцией ЕСЛИ и функцией МИН.
=ЕСЛИ(МИН(старое значение, новое значение)<=0,"--",(новое значение/старое значение)-1)
Вот как работает формула:
- Логическая проверка функции ЕСЛИ (MIN(старое значение, новое значение)<=0) находит минимальное из двух значений и проверяет, меньше ли значение или равно нулю. Результат будет либо ИСТИНА, либо ЛОЖЬ.
- Если результат ИСТИНА, то существует отрицательное число (или ноль). В этом случае мы можем отобразить некоторый текст, чтобы сообщить читателю. Это может быть что угодно. Я просто использовал два тире «-». Вы также можете заставить его возвращать ошибку N/A с помощью функции NA() или любой другой текст, который позволяет читателю узнать, что процентное изменение не может быть рассчитано.

- Если результат FALSE, то формула процентного изменения используется для возврата процентного изменения двух положительных чисел.
Эта формула также обрабатывает деление на ноль (#ДЕЛ/0!), поэтому нам не нужно заключать ее в функцию ЕСЛИОШИБКА.
Метод № 2: Показать положительное или отрицательное изменение
В справочнике Wall Street Journal говорится, что его отчеты о доходах отображают «P» или «L», если есть отрицательное число, и компания опубликовала прибыль или убыток.
Мы могли бы использовать ту же методологию, чтобы сообщить нашим читателям, было ли изменение положительным (P) или отрицательным (N), когда одно из значений отрицательное.
Следующая формула проверяет это с помощью дополнительной функции ЕСЛИ.
=ЕСЛИ(МИН(старое значение, новое значение)<=0,ЕСЛИ((новое значение - старое значение)>0,"P","N"),(новое значение/старое значение)-1)
Вот как работает формула:
- Мы начинаем с той же логической проверки, чтобы определить, существует ли отрицательное значение, используя функцию MIN.

- Затем используется вторая функция ЕСЛИ, чтобы определить, является ли изменение от старого к новому положительным или отрицательным.
ЕСЛИ((новое значение – старое значение)>0, "P", "N")
Этот оператор IF возвращает «P» для положительного изменения и «N» для отрицательного изменения. - Если оба числа положительные, то для отображения результата используется формула процентного изменения.
Другие методы процентного изменения с отрицательными значениями?
Вычислить процентное изменение при использовании отрицательных чисел непросто. Метод ABS, вероятно, используется чаще всего, но он может давать вводящие в заблуждение результаты.
Конечная цель должна заключаться в том, чтобы все было хорошо, чтобы нам не приходилось беспокоиться о негативе… 😉
Есть ли у вас другие методы расчета? Можем ли мы еще больше упростить любой из вышеперечисленных методов? Мне интересно услышать ваши мысли. Пожалуйста, оставьте комментарий ниже с вопросами или предложениями. Спасибо!
Спасибо!
Преобразование отрицательного числа в положительное
1. Умножение на минус единицу для преобразования положительного числа
2. Преобразование в абсолютное число с помощью функции ABS
3. Множественное использование специальной вставки
4. Удаление отрицательного знака с помощью быстрой заливки
5. Примените пользовательское форматирование для отображения в виде положительных чисел
6. Запустите код VBA для преобразования в положительные числа
7. Используйте Power Query для преобразования Получите положительные числа
Заключение
Дополнительные руководства
поражен тем, что у меня есть 7 различных способов, которые вы можете использовать для работы с отрицательными числами. На прошлой неделе я получил электронное письмо от одного из моих подписчиков с вопросом.
Эй, Пунит, сколько у нас есть способов преобразовать отрицательное число в положительное?
Вы знаете, то, о чем он просил, это обычное задание. Я уверен, это часто происходит с вами, когда вы получаете какие-то отрицательные числовые значения, а после этого конвертируете их в положительные.
Я уверен, это часто происходит с вами, когда вы получаете какие-то отрицательные числовые значения, а после этого конвертируете их в положительные.
В этом нет никакой #ракетной науки. Но вы когда-нибудь проверяли, как мои разные методы у вас есть для этого? Что ж, мне всегда интересно узнать о различных методах выполнения задачи в Excel.
Итак, на этот раз я взял лист бумаги и перечислил все методы, которые я могу использовать для преобразования отрицательного числа в положительное. Итак, сегодня в этом посте я хотел бы поделиться с вами всеми этими методами.
Начнем.
1. Умножьте на минус один, чтобы преобразовать положительное число
В отличие от меня, если вы хорошо разбираетесь в математике, я уверен, что вы знаете, что когда вы перемножаете два знака минус друг с другом, результат всегда положительный. Таким образом, вы можете использовать тот же метод в Excel, чтобы преобразовать отрицательное число в положительное.
Все, что вам нужно сделать, это просто умножить отрицательное значение на -1, и оно вернет положительное число вместо отрицательного.
=отрицательное_значение*-1
Ниже у вас есть диапазон ячеек с отрицательными числами. Поэтому, чтобы преобразовать их в положительные, вам просто нужно ввести формулу в ячейку B2 и перетащить ее до последней ячейки.
Примечание: Если у вас есть смешанные числа (как положительные, так и отрицательные), вы можете использовать вместо этого метод, описанный ниже.
=ЕСЛИ(A1<0,A1*-1,A1)
2. Преобразование в абсолютное число с помощью функции ABS
Превратить отрицательное число в положительное с помощью ABS довольно просто. Эта функция специально для этой задачи.
Краткое введение: Может преобразовать любое число в абсолютное число. Проще говоря, он вернет число после удаления его знака.
Синтаксис: =ABS(число)
Вам просто нужно передать отрицательное число в функцию, и она превратит его в положительное значение.
- В приведенном ниже примере у вас есть отрицательные значения из диапазона A2:A11.

- Введите =ABS(A2) в ячейку B2 и перетащите ее до последней ячейки.
Примечание : Эта функция работает, даже если у вас смешанные числа (как положительные, так и отрицательные).
Давайте подумаем о другой ситуации, когда вместо получения положительных чисел в другом столбце они нужны в том же столбце.
А для этого можно использовать специальную опцию вставки. Интересно, как? Позвольте мне сказать вам. В специальной опции вставки есть опции «операции», которые вы можете использовать для выполнения некоторых простых вычислений. Вы можете использовать эти же параметры, чтобы сделать отрицательные числа положительными без использования какой-либо формулы или добавления дополнительного столбца. Просто выполните следующие действия.
- Прежде всего, в любой ячейке рабочего листа введите -1.
- После этого скопируйте его.
- Теперь выберите диапазон ячеек, в которых у вас есть отрицательные числа.

- Щелкните правой кнопкой мыши ➜ Специальная вставка ➜ Операции ➜ Умножение.
- В конце нажмите OK.
Теперь все отрицательные числа преобразуются в положительные.
Единственное, о чем вам нужно позаботиться, это то, что это не динамический метод. Таким образом, вам нужно делать это снова и снова, если вы часто обновляете свои данные. Но этот метод быстрый и простой в использовании, и вам не нужна никакая формула.
4. Удалите отрицательный знак с помощью Flash Fill
Я уверен, что вы использовали флэш-заполнение хотя бы раз в жизни, а если нет, то вы должны его использовать, это меняет правила игры. Это безумный способ превратить отрицательные числа в положительные, вот шаги.
- Прежде всего, в ячейке B2 введите положительное число для отрицательного числа, которое у вас есть в ячейке A2.
- После этого перейдите в ячейку B3 и нажмите сочетание клавиш Ctrl + E.
- На данный момент в столбце B у вас все числа в положительной форме.

- Теперь нажмите на маленький значок справа от столбца B и выберите «Принять предложения».
Поздравляем, вы преобразовали все отрицательные числа в положительные с помощью быстрой заливки.
Примечание : Этот метод также не является динамическим, но быстрым и простым в использовании.
5. Применить пользовательское форматирование для отображения в виде положительных чисел
Также возможно, что вместо преобразования отрицательного числа вы просто хотите отобразить его как положительное число. И в этой ситуации можно использовать пользовательское форматирование. Вот шаги к этому.
- Прежде всего, выберите диапазон ячеек, которые необходимо преобразовать в положительные числа.
- После этого нажмите сочетание клавиш Ctrl + 1. Откроются пользовательские параметры форматирования.
- Теперь перейдите в «Пользовательский» и в строке ввода введите «#,###;#,###».
- В конце нажмите OK.

Это покажет все отрицательные числа как положительные. Но на самом деле все это по-прежнему отрицательное число, просто изменено форматирование.
Если вы выберете ячейку и посмотрите на строку формул, вы можете убедиться, что это все еще отрицательное число. Таким образом, когда вы используете его в дальнейших вычислениях, оно будет действовать как отрицательное число.
6. Запустите код VBA для преобразования в положительные числа
Если вы любитель VBA, вы можете использовать простой код для мгновенного изменения знака отрицательных чисел.
Суб-номерP2N()
Dim myCell As Range
Для каждой выбранной ячейки myCell
Если myCell.Value <> "" Тогда
Если Числовой(myCell.Value) Тогда
myCell.Value = Abs(myCell.Value)
Конец, если
Конец, если
Следующая моя ячейка
Конец суб Чтобы использовать этот код, вам просто нужно выбрать диапазон отрицательных чисел и запустить этот макрос. Во-первых, он проверит каждую выбранную ячейку, есть ли в ней числовое значение или нет, а затем преобразует его в положительное значение. Как только вы запустите этот код, вы не сможете отменить свое действие.
Как только вы запустите этот код, вы не сможете отменить свое действие.
Связано: Учебник по VBA
7. Используйте Power Query для преобразования Get Положительные числа
Да, вы можете использовать запрос Power для преобразования отрицательного числа в положительное число, и самое приятное то, что это одноразовая настройка . Просто следуйте этим простым шагам.
- Прежде всего, выберите любую из ячеек из диапазона данных, где у вас есть отрицательные числа.
- После этого перейдите на вкладку Данные ➜ Из таблицы.
- Он преобразует диапазон в таблицу и загрузит ее в редактор запросов Power.
- Теперь щелкните правой кнопкой мыши по столбцу и выберите Преобразование ➜ Абсолютное значение.
- В конце концов, в редакторе запросов питания перейдите на вкладку «Главная» ➜ «Закрыть» ➜ «Закрыть и загрузить».
Связано: Учебное пособие по Power Query
Заключение
Как я уже сказал, чтобы превратить отрицательное число в положительное, вам не нужно использовать ракетостроение. Даже одного метода может быть достаточно, но я перечислил все эти методы, чтобы помочь вам справляться с различными ситуациями.
Даже одного метода может быть достаточно, но я перечислил все эти методы, чтобы помочь вам справляться с различными ситуациями.
Я уверен, что вы нашли все эти методы полезными, но теперь вы должны сказать мне одну вещь.
Знаете ли вы какой-либо другой способ для этого? Пожалуйста, поделитесь со мной своим мнением в разделе комментариев. Я хотел бы услышать от вас, и, пожалуйста, не забудьте поделиться им с друзьями, я уверен, что они оценят это.
🔙 Основы Excel
Другие уроки
Добавление знака плюс или минус в формулу, показывающую разницу между числами
MrKowz
Известный член
- #2
Мне удалось сделать это, используя пользовательский формат чисел, используя приведенный ниже пример:
Custom Format: +0;-0;0
| Excel 2013/2016 | |||
|---|---|---|---|
| <br> Alt+click for values & formatting only."/> | F | G | H |
| 9 | 84 | 80 | -4 |
| 10 | 84 | 88 | +4 |
Лист1 | |||
Скотт Т
Известный член
- #3
| A | B | C | |
| 1 | #000[/URL] 000]84[/COLOR] | [COLOR=[URL=https://www.mrexcel.com/forum/usertag.php?do=list&action=hash&hash=000]#000[/ URL] 000]80[/ЦВЕТ] | [ЦВЕТ=[URL=https://www.mrexcel. com/forum/usertag.php?do=list&action=hash&hash=000]#000[/URL] 000]-4.00[/COLOR] com/forum/usertag.php?do=list&action=hash&hash=000]#000[/URL] 000]-4.00[/COLOR] |
| 2 | [COLOR=[URL=https://www.mrexcel.com/forum/usertag.php?do=list&action=hash&hash=000]#000[/URL] 000]84[/COLOR] | [COLOR=[URL=https://www.mrexcel.com/forum/usertag.php?do=list&action=hash&hash=000]#000[/URL] 000]88[/COLOR] | [COLOR= [URL=https://www.mrexcel.com/forum/usertag.php?do=list&action=hash&hash=000]#000[/URL] 000]+4.00[/COLOR] |
<тело>
Использовать форматирование Ячейка C1 и C2
имеет пользовательский формат, измените его, чтобы он соответствовал нужному формату
Код:
+#,##0,00;-#,##0,00
Гримлок
Новый участник
- #4
Извините,
Я новичок в Excel, так что простите мое невежество. Возможно, мое объяснение было недостаточно хорошим, поэтому я попробую еще раз.
Число в ячейке F9 (84 на данный момент), скорее всего, останется прежним, но МОЖЕТ измениться со временем. Число в ячейке G9 будет меняться от месяца к месяцу. Итак, мне нужна формула в ячейке H9, которая способна вычислить разницу между ними, но со знаком плюс или минус впереди. Я не понимаю, как предложения по буксировке, которые у меня были, сделают это?
Очень благодарен за помощь, ребята!
Гримлок
Новый участник
- #5
Извините,
Я новичок в Excel, так что простите мое невежество. Возможно, мое объяснение было недостаточно хорошим, поэтому я попробую еще раз.
Число в ячейке F9 (84 на данный момент), вероятно, останется прежним, но МОЖЕТ измениться со временем. Число в ячейке G9 будет меняться от месяца к месяцу. Итак, мне нужна формула в ячейке H9, которая способна вычислить разницу между ними, но со знаком плюс или минус впереди. Я не понимаю, как предложения по буксировке, которые у меня были, сделают это?
Очень ценю помощь, ребята!
Скотт Т
Известный член
- #6
в H9 используйте
Код:
=G9-F9
Пользовательский числовой формат помещает знак плюс (+) перед положительным числом и отрицательный знак (-) перед отрицательным числом. Поэтому, когда ваша формула возвращает положительное значение 4, вы получаете +4 в ячейке, а если оно возвращает отрицательное значение 4, вы получаете -4. Поскольку формула возвращает отрицательное значение, если G9меньше, чем F9, вы получаете -4, если G9 больше, чем F9, вы получаете +4


 Сложение и вычитание +3, -3. Приемы вычислений
Сложение и вычитание +3, -3. Приемы вычислений