Логический элемент сложения. Логический элемент исключающее или. Дополнительные логические элементы
Для выполнения логических операций и решать логические задачи с помощью средств электроники были изобретены логические элементы. Их создают с помощью диодов, транзисторов и комбинированных элементов (диодно-транзисторные). Такая логика получила название диодной логики (ДЛ), транзисторной (ТЛ) и диодно–транзисторной (ДТЛ). Используют как полевые, так и биполярные транзисторы. В последнем случае предпочтение отдается устройствам типа n-p-n, так как они обладают большим быстродействием.
Логический элемент «ИЛИ»
Схема логического элемента «ИЛИ» представлена на рисунке 1 а. На каждый из входов может подаваться сигнал в виде какого-то напряжения (единица) или его отсутствия (ноль). На резисторе R появиться напряжение даже при его появлении на каком – либо из диодов.
Рис. 1
Элементы или могут иметь несколько логических входов. Если используются не все входы, то те входы которые не используются следует соединять с землей (заземлять), чтобы избежать появления посторонних сигналов.
На рисунке 1б показано обозначение на электрической схеме элемента, а на 1в таблица истинности.
Логический элемент «И»
Схема элемента приведена на рис. 2. Если хотя – бы к одному из входов будет сигнал равный нулю, то через диод будет протекать ток. Падение напряжения на диоде стремится к нулю, соответственно на выходе тоже будет ноль. На выходе сможет появится сигнал только при условии, что все диоды будут закрыты, то есть на всех входах будет сигнал. Рассчитаем уровень сигнала на выходе устройства:
Рис.2
на рис. 2 б – обозначение на схеме, в – таблица истинности.
Логический элемент «НЕ»
В логическом элементе «НЕ» используют транзистор (рис.3 а). при наличии положительного напряжения на входе х=1 транзистор открывается и напряжение его коллектора стремится к нулю. Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е.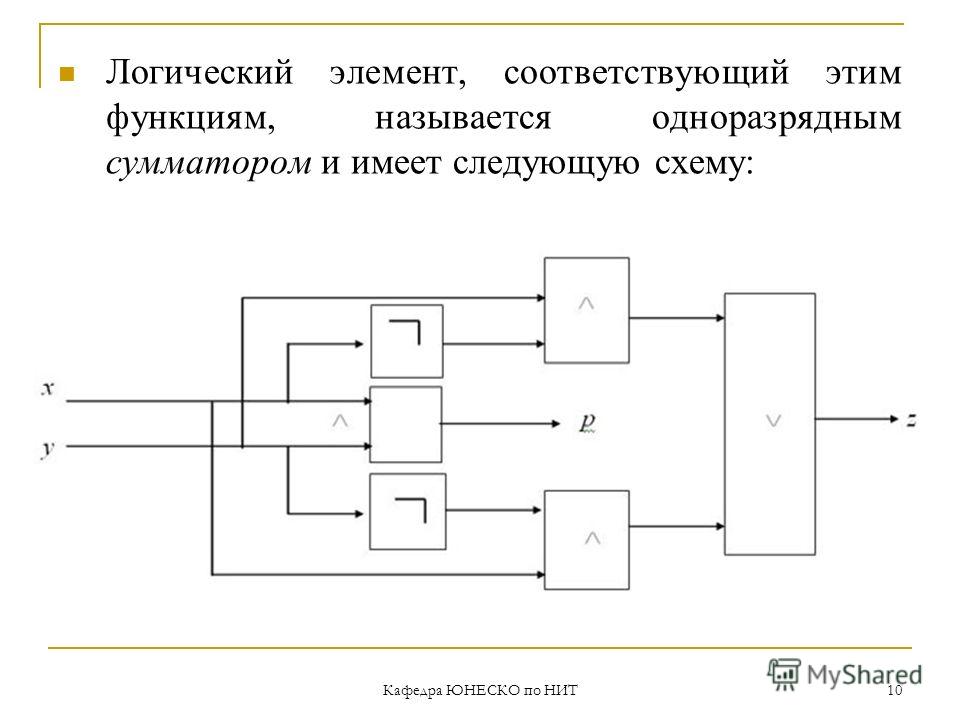 условное обозначение и таблица истинности приведены на рис. 3 б,в.
условное обозначение и таблица истинности приведены на рис. 3 б,в.
Рис.3
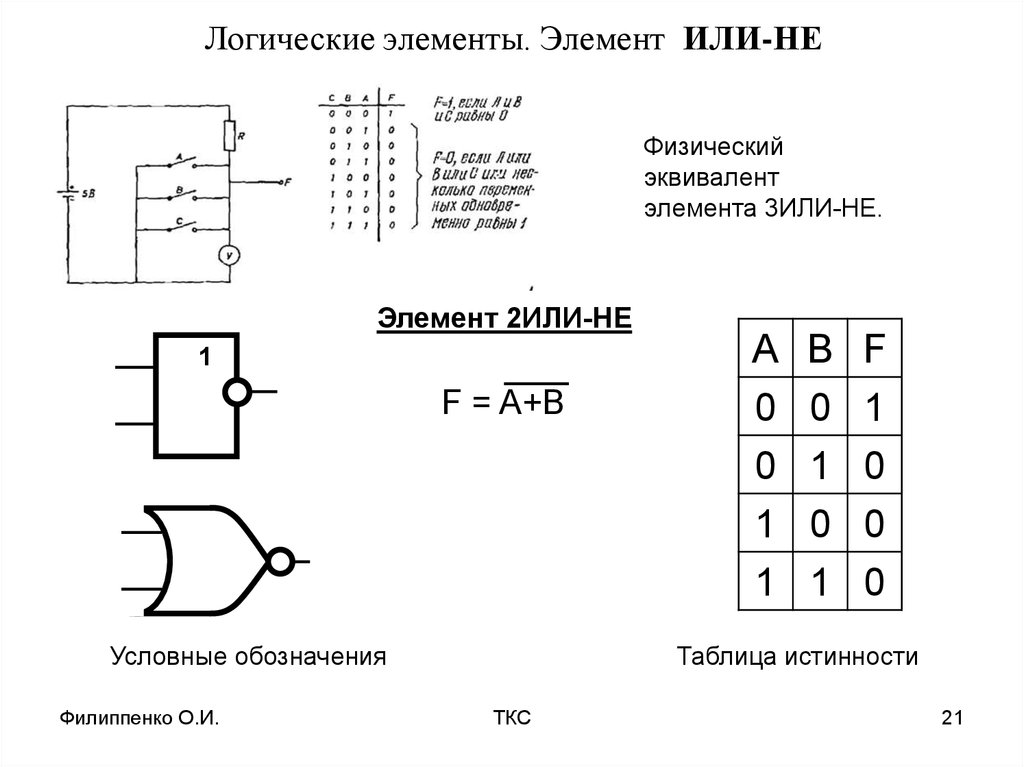
Логический элемент «ИЛИ-НЕ»
При создании различных схем на логических элементах часто применяют элементы комбинированные. В таких элементах совмещены несколько функций. Принципиальная схема показана на рис. 4 а.
Здесь диоды Д1 и Д2 выполняют роль элемента «ИЛИ», а транзистор играет роль инвертора. Обозначение элемента на схеме и его таблица истинности рис. 4б и в соответственно.
Логический элемент «И-НЕ»
 Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.
Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства. Назначение сервиса
. Онлайн-калькулятор предназначен для построения таблицы истинности для логического выражения .
Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе.
Таблица истинности содержит 2 n строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.
Инструкция
. При вводе с клавиатуры используйте следующие обозначения:
Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Правила ввода логической функции
- Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
- Перед логической функцией не надо указывать обозначение функции.
 y) .
y) . - Максимальное количество переменных равно 10 .
Проектирование и анализ логических схем ЭВМ ведётся с помощью специального раздела математики — алгебры логики. В алгебре логики можно выделить три основные логические функции: «НЕ» (отрицание), «И» (конъюнкция), «ИЛИ» (дизъюнкция).
Функция алгебры логики называется полностью определённой если заданы все 2 n её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:
- словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление.

- описание функции алгебры логики в виде таблицы истинности.
- описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
а) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1 .
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.
б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
1) выбираем наборы переменных для которых функция на выходе =0
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
Fскнф=(X 1 V X 2 V X 3) ∧ (X 1 V X 2 V X 3) ∧ (X 1 V X 2 V X 3) ∧ (X 1 V X 2 V X 3)
КНФ называется совершенной , если все переменные имеют одинаковый ранг.
По алгебраической форме можно построить схему логического устройства , используя логические элементы.
Рисунок1- Схема логического устройства
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможны х логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении.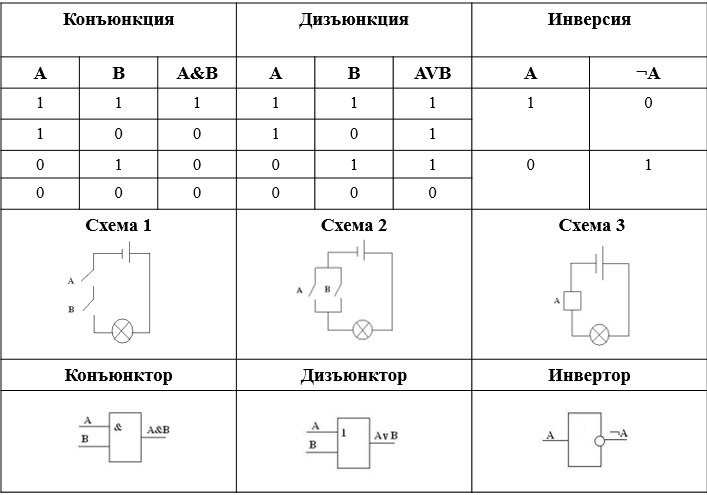
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:
- если исходное выражение истинно, то результат его отрицания будет ложным;
- если исходное выражение ложно, то результат его отрицания будет истинным.
Для операции отрицания НЕ приняты следующие условные обозначения:
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:
| A | не А |
| 0 | 1 |
| 1 | 0 |
Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.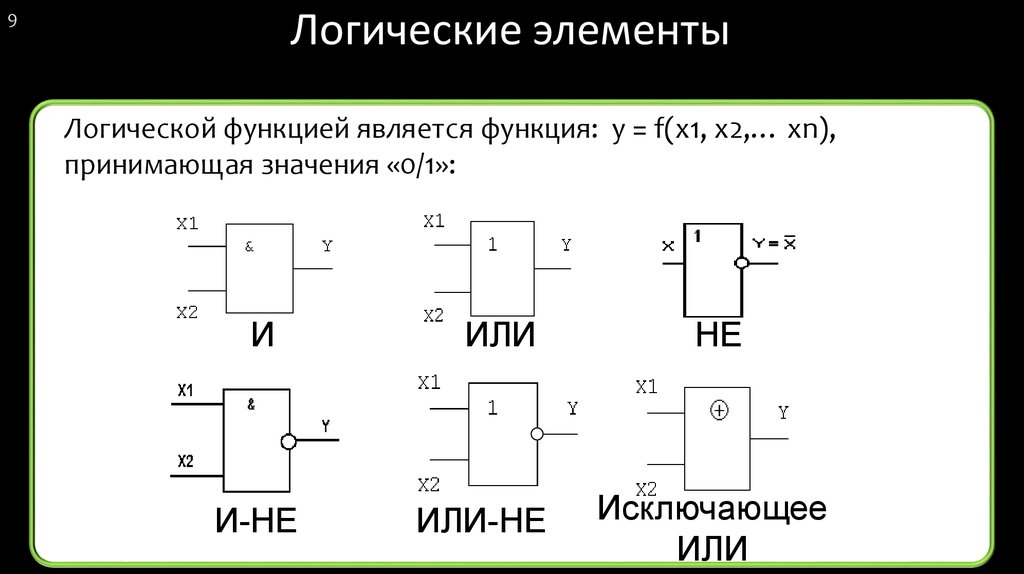
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение.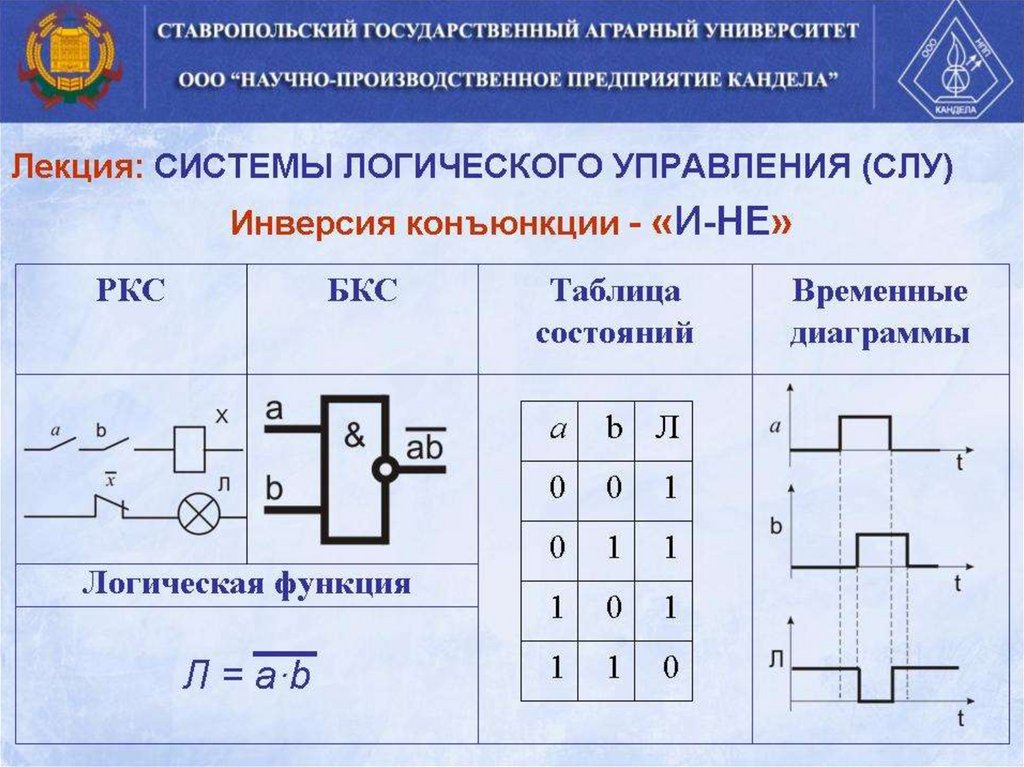 Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:
| A | B | А → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Применяемое обозначение: А ↔ В, А ~ В.
Таблица истинности:
| A | B | А↔B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция «Сложение по модулю 2» (XOR, исключающее или, строгая дизъюнкция)
Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:
| A | B | А⊕B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Приоритет логических операций
- Действия в скобках
- Инверсия
- Конъюнкция (&)
- Дизъюнкция (V), Исключающее ИЛИ (XOR), сумма по модулю 2
- Импликация (→)
- Эквивалентность (↔)
Совершенная дизъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма формулы(СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
- Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x 1 ,x 2 ,.
 ..x n).
..x n). - Все логические слагаемые формулы различны.
- Ни одно логическое слагаемое не содержит переменную и её отрицание.
- Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.
Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.
Совершенная конъюнктивная нормальная форма
Совершенная конъюнктивная нормальная форма формулы (СКНФ)это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
- Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x 1 ,x 2 ,…x n).
- Все элементарные дизъюнкции различны.
- Каждая элементарная дизъюнкция содержит переменную один раз.
- Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.

Логические элементы — это электронные устройства, предназначенные для обработки информации представленной в виде двоичных кодов, отобpажаемыx напpяжeниeм (сигналом) выcoкого и низкого уpовня. Логические элементы реализyют логические функции И, ИЛИ, НЕ и их комбинации. Указанные логические операции выполняются с помощью электронных схем, входящих в состав микросхем. Из логических элементов И, ИЛИ, НЕ, можно сконстpуировать цифровое электронное устройство любой сложности.
Логические элементы могут выполнять логические функции в режимах положительной и отрицательной логики. В режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю — низкий уровень напряжения. В режиме отрицательной логики наоборот логической единице соответствует низкий уровень напряжения, а логическому нулю — высокий.
Если в режиме
положительной логики логический элемент,
реализует операцию И, то в режиме
отрицательной логики выполняет операцию
ИЛИ, и наоборот. И если в режиме
положительной логики — И-НЕ, то в режиме
отрицательной логики — ИЛИ-НЕ.
И если в режиме
положительной логики — И-НЕ, то в режиме
отрицательной логики — ИЛИ-НЕ.
Условное графическое обозначение логического элемента представляет собой прямоугольник, внутри которого ставится изображение указателя функции. Входы изображают линиями с левой стороны прямоугольника, выходы элемента — с правой стороны. При необходимости разрешается располагать входы сверху, а выходы снизу. У логических элементов И, ИЛИ может быть любое начиная с двух количество входов и один выход. У элемента НЕ один вход и один выход. Если вход обозначен окружностью, то это значит, что функция выполняется для сигнала низкого уровня (отрицательная логика). Если окружностью обозначен выход, то элемент производит логическое отрицание (инверсию) результата операции, указанной внутри прямоугольника.
Все цифровые
устройства делятся на комбинационные и на последовательностные .
В комбинационных устройствах выходные
сигналы в
данный момент времени однозначно
определяются входными сигналами в тот
же момент.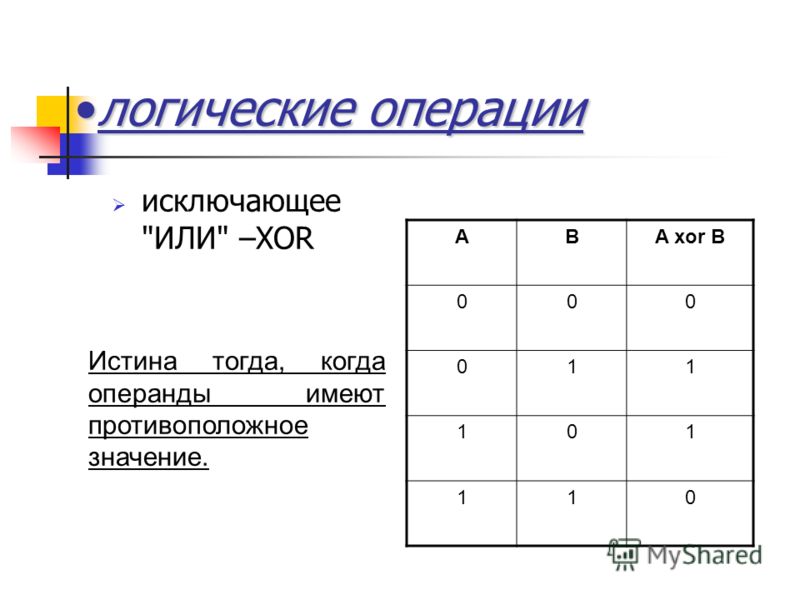 Выходные
сигналы последовательностного
устройства
(цифрового автомата) в данный момент
времени определяются не только логическими
переменными на его входах, но еще зависят
и от предыдущего состояния этого
устройства. Логические элементы И,
ИЛИ, НЕ и их комбинации являются
комбинационными устройствами. К
последовательностным устройствам
относятся триггеры, регистры, счетчики.
Выходные
сигналы последовательностного
устройства
(цифрового автомата) в данный момент
времени определяются не только логическими
переменными на его входах, но еще зависят
и от предыдущего состояния этого
устройства. Логические элементы И,
ИЛИ, НЕ и их комбинации являются
комбинационными устройствами. К
последовательностным устройствам
относятся триггеры, регистры, счетчики.
Логический элемент И (рис. 1) выполняет операцию логического умножения (конъюнкцию). Такую операцию обозначают символом /\ или значком умножения (·). Если все входные переменные равны 1, то и функция Y=X1·X2 принимает значение логической 1. Если хотя бы одна переменная равна 0, то и выходная функция будет равна 0.
Таблица 1 | ||||
Наиболее наглядно
логическая функция характеризуется
таблицей, называемой таблицей
истинности (Табл. 1). Талица истинности содержит всевозможные
комбинации входных переменных Х и
соответствующие им значения функции
Y. Количество комбинаций составляет 2 n ,
где n – число аргументов.
1). Талица истинности содержит всевозможные
комбинации входных переменных Х и
соответствующие им значения функции
Y. Количество комбинаций составляет 2 n ,
где n – число аргументов.
Логиче c кий эл e мент ИЛИ (рис. 2) выполняет операцию логического сложения (дизъюнкцию). Обозначают эту операцию символом \/ или знаком сложения (+). Функция Y=X1\/X2 принимает значение логической 1, если хотя бы одна переменная равна 1. (Табл. 2).
Таблица 2 | ||||
Логический
элемент НЕ
(инвертор) выполняет
операцию логического отрицания
(инверсию). При
логическом отрицании функция Y
принимает значение противоположное
входной переменной Х (Табл. 3). Эту операцию
обозначают
.
При
логическом отрицании функция Y
принимает значение противоположное
входной переменной Х (Табл. 3). Эту операцию
обозначают
.
Кроме указанных выше логических элементов, на практике широко используются элементы И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ.
Логиче c кий элем e нт И-НЕ (рис. 4)выполняет операцию логического умнoжения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
Таблица 4 | ||||
Логический
элемент ИЛИ-НЕ (рис. 5)выполняет
операцию логического сложения над
входными переменными, а затем инвертирует
полученный результат и выдаёт его на
выход.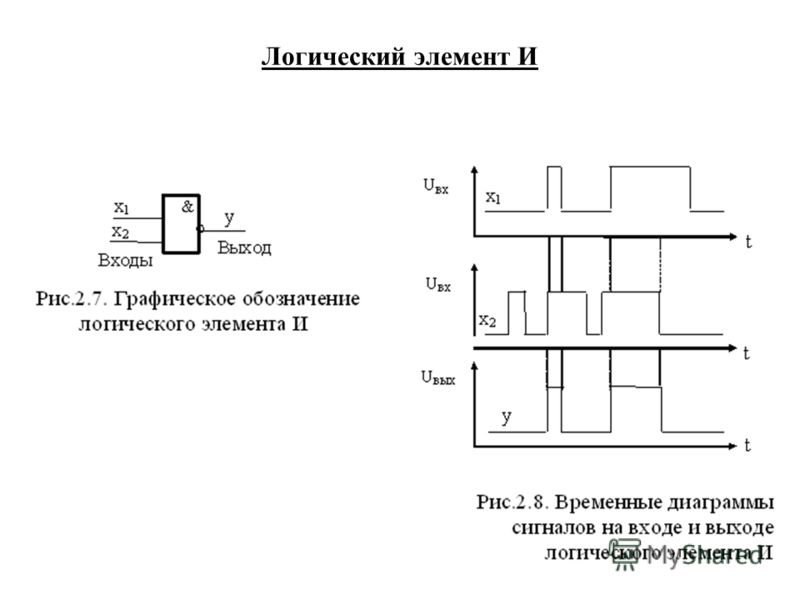
Таблица 5 | ||||
Логический элемент Исключающее ИЛИ представлен на рис. 6. Логическая функция Исключающее ИЛИ (функция «неравнозначность» или сумма по модулю два) записывается в виде и принимает значение 1 при X1≠X2, и значение 0 при X1=X2=0 или X1=X2=1 (Табл. 6).
Таблица 6 | ||||
Любой из выше
перечисленных элементов можно заменить
устройством, собранным только из базовых
двухвходовых элементов ИЛИ-НЕ или И-НЕ. Например: операция НЕ
(рис. 7, а)
приX1
= X2
= X;
операция И
(рис. 7, б)
.
Например: операция НЕ
(рис. 7, а)
приX1
= X2
= X;
операция И
(рис. 7, б)
.
Интегральные логические элементы выпускаются в стандартных корпусах с 14 или 16 выводами. Один вывод используется для подключения источника питания, еще один является общим для источников сигналов и питания. Оставшиеся 12 (14) выводов используют как входы и выходы логических элементов. В одном корпусе может находится несколько самостоятельных логических элементов. На рисунке 8 показаны условные графические обозначения и цоколевка (нумерация выводов) некоторых микросхем.
К155ЛЕ1 К155ЛА3 К155ЛП5
Базовый элемент транзисторно-транзисторной логики (ТТЛ) . На рисунке 9 показана схема логического элемента И-НЕ ТТЛ с простым однотранзисторным ключом.
Рис. 9
Простейший
логический элемент ТTЛ строится на базе
многоэмиттерного транзистор VT 1. Пpинцип
дейcтвия
такого транзистора тот же, что и у
обычного биполяpного
транзистора. Oтличие
заключается в том, что инжекция носителей
заряда в базу осуществляется через
несколько самостoятельных
эмиттерных р — n -переходов. При поступлении на входы логической
единицы U 1 вх ,
запираются все эмиттерные переxоды VT 1 .
Ток, текущий через резистор R б,
замкнется через открытые р- n — переходы:
коллектoрный VT 1 и
эмиттерный VT 2. Этoт
ток откpоет
транзиcтор VT 2 ,
и напряжение на его выходе станет близким
к нулю, т. е. Y= U 0 вых .
Если хотя бы на один вход (или на все
входы) VT 1 будет
подан сигнал логического нуля U 0 вх ,
то ток, текyщий
по R б,
замкнeтся
через откpытый
эмиттерный переход VT 1 .
Пpи
этoм
входной ток VT 2 будет
близoк
к нулю, и выходной транзистоp
окажется запеpтым,
т. е. Y= U 1 вых .
Таким образом, рассмотренная схема
осуществляет логическую операцию И-НЕ.
При поступлении на входы логической
единицы U 1 вх ,
запираются все эмиттерные переxоды VT 1 .
Ток, текущий через резистор R б,
замкнется через открытые р- n — переходы:
коллектoрный VT 1 и
эмиттерный VT 2. Этoт
ток откpоет
транзиcтор VT 2 ,
и напряжение на его выходе станет близким
к нулю, т. е. Y= U 0 вых .
Если хотя бы на один вход (или на все
входы) VT 1 будет
подан сигнал логического нуля U 0 вх ,
то ток, текyщий
по R б,
замкнeтся
через откpытый
эмиттерный переход VT 1 .
Пpи
этoм
входной ток VT 2 будет
близoк
к нулю, и выходной транзистоp
окажется запеpтым,
т. е. Y= U 1 вых .
Таким образом, рассмотренная схема
осуществляет логическую операцию И-НЕ.
Контрольные вопросы.
Что называется логическим элементом?
Чем различаются положительная и отрицательная логики?
Что называется таблицей истинности?
Каким символом обозначают логическое умножение?
Как на схемах изображают логический элемент И?
При каких входных переменных на выходе логического элемента И формируется логическая 1?
Каким символом обозначают логическое сложение?
Как на схемах изображают логический элемент ИЛИ?
При каких входных переменных на выходе логического элемента ИЛИ формируется логическая 1?
Как на схемах изображают логический элемент НЕ?
Как на схемах изображают логический элемент И-НЕ?
При каких входных переменных на выходе логического элемента И-НЕ формируется логическая 1?
Как на схемах изображают логический элемент ИЛИ-НЕ?
При каких входных переменных на выходе логического элемента ИЛИ-НЕ формируется логическая 1?
Как на схемах изображают логический элемент Исключающее ИЛИ?
При каких входных переменных на выходе логического элемента Исключающее ИЛИ формируется логическая 1?
Как из элемента ИЛИ-НЕ получить элемент НЕ?
Как из элемента И-НЕ получить элемент НЕ?
Опишите принцип
действия базового элемента ТТЛ.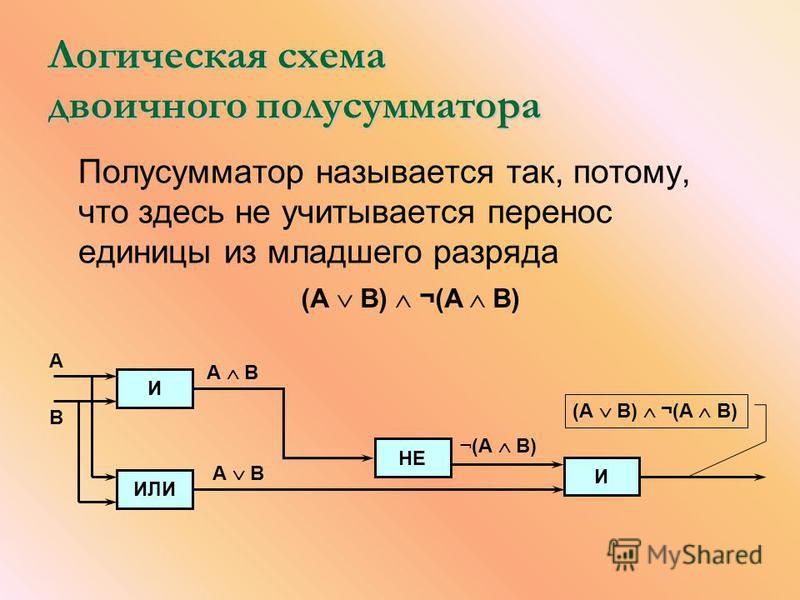
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент
— элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.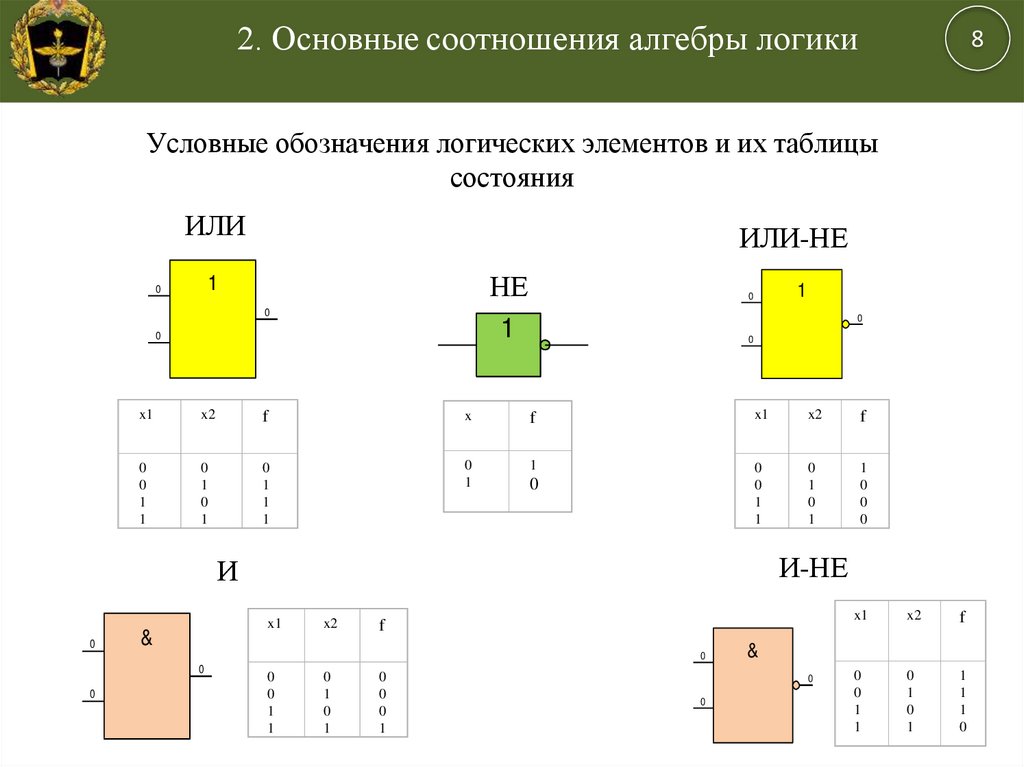
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
Логический элемент «И» — конъюнкция, логическое умножение, AND
«И» — логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. В тексте логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя входами, с четырьмя входами и т. д.
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».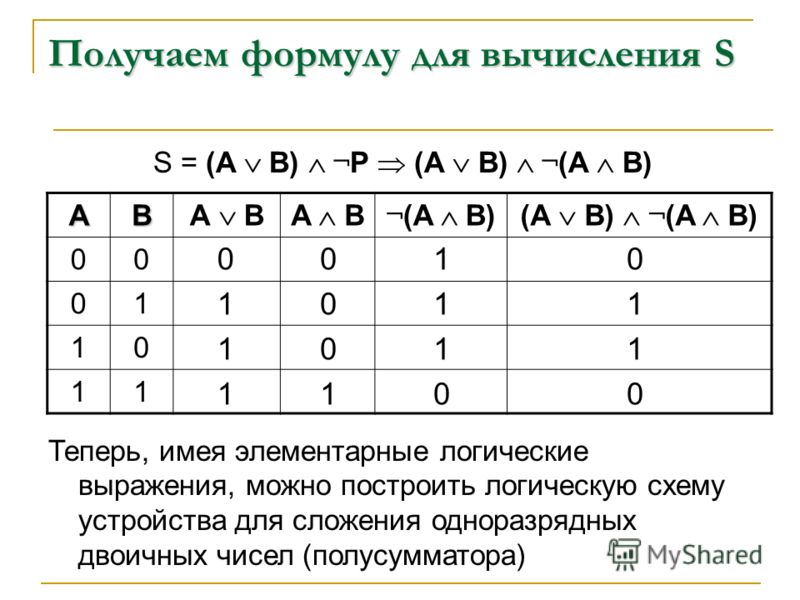
Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR
«ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».
Логический элемент «НЕ» — отрицание, инвертор, NOT
«НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND
«И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это в принципе элемент «И», дополненный элементом «НЕ». На рисунке приведено условное обозначение логического элемента «2И-НЕ».
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И».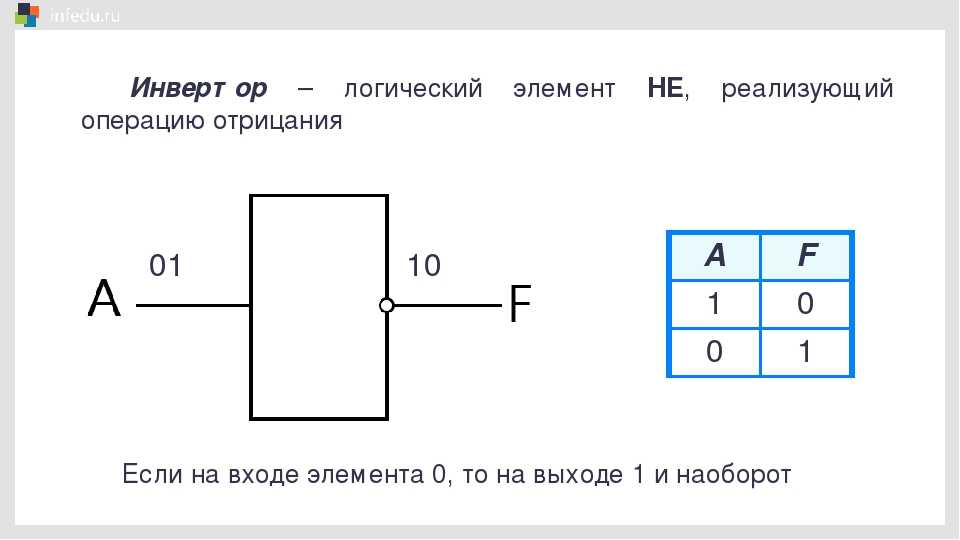 Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой в 1913 году. Обозначается как «И», только с кружочком на выходе.
Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой в 1913 году. Обозначается как «И», только с кружочком на выходе.
Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR
«ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» — инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR
«исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход. Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.
Часто данные элементы применяют в схемах контроля. На рисунке приведено условное обозначение данного элемента.
Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:
ИЛИ — логическое сложение (дизъюнкция ) — OR ;
И — логическое умножение (конъюнкция ) — AND ;
НЕ — логическое отрицание (инверсия ) — NOT .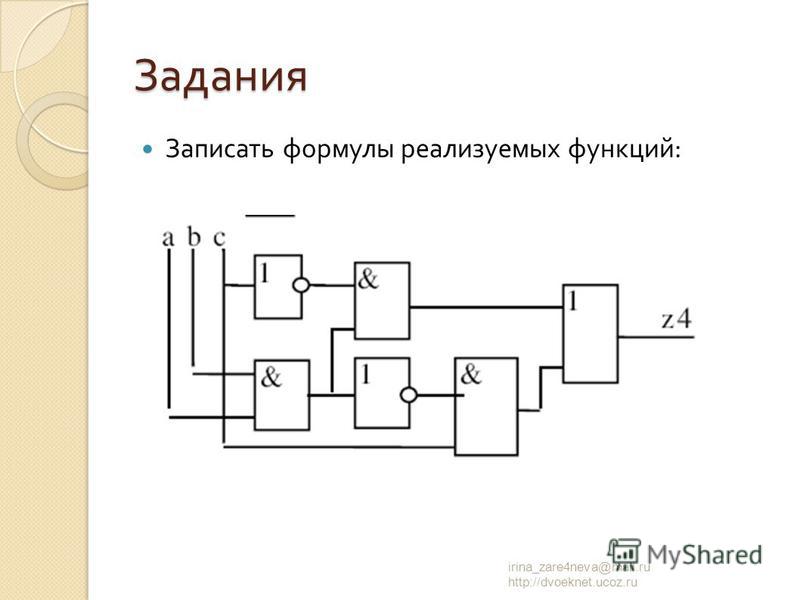
Примем за основу позитивную логику, где высокий уровень будет «1», а низкий уровень примем за «0». Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Логический элемент И.
На рисунке представлена таблица истинности элемента «И » с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В трёх остальных случаях на выходе будут нули.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
На принципиальных схемах логический элемент «И» обозначают так.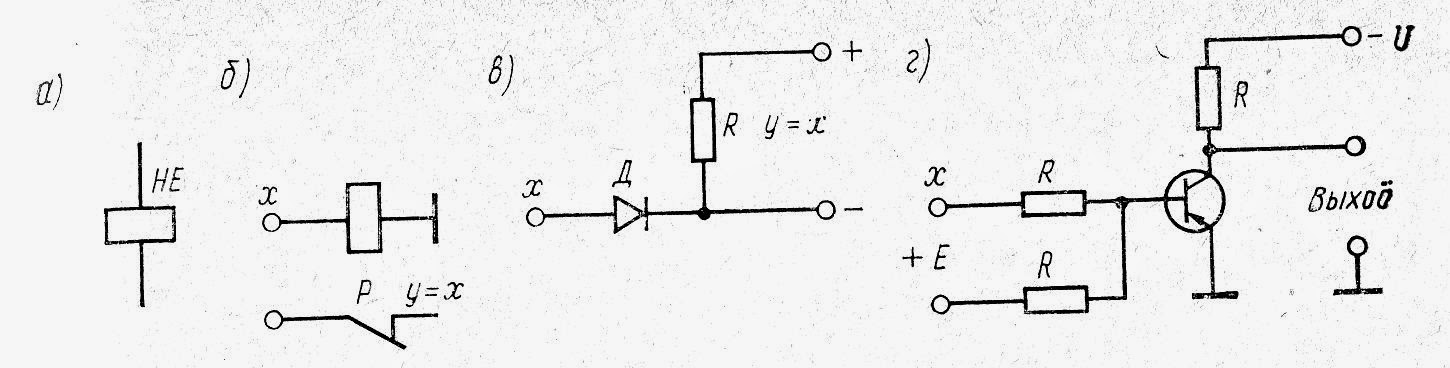
На зарубежных схемах обозначение элемента «И» имеет другое начертание. Его кратко называют AND .
Логический элемент ИЛИ.
Элемент «ИЛИ » с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
На схемах элемент «ИЛИ» изображают так.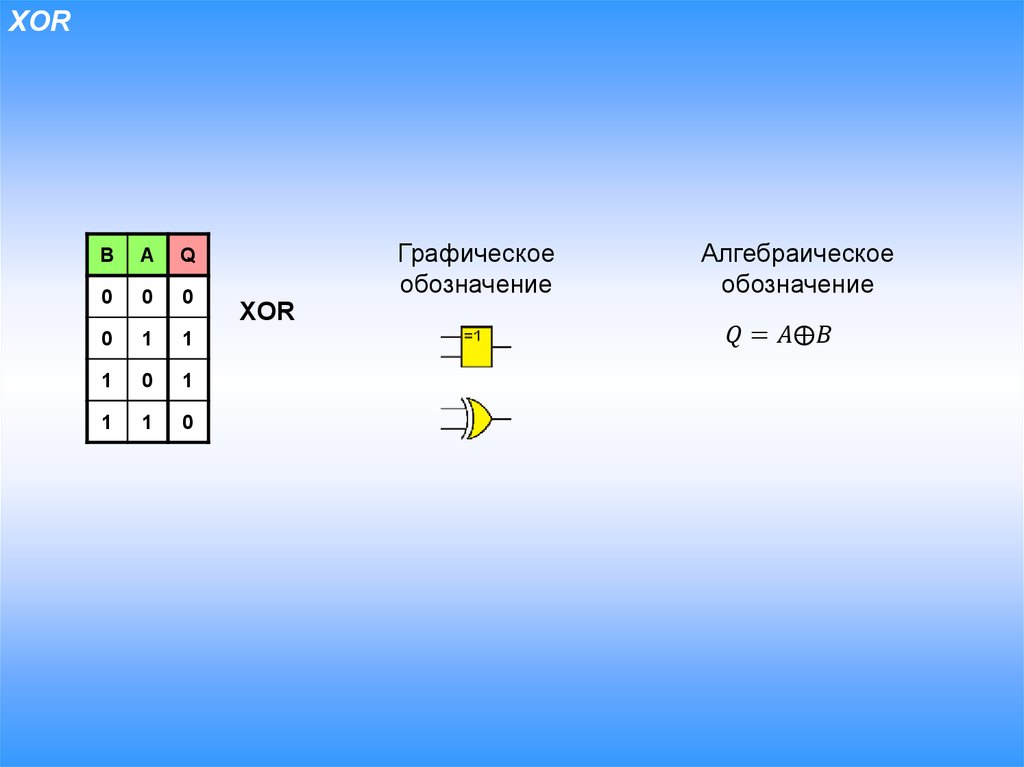
На зарубежных схемах его изображают чуть по-другому и называют элементом OR .
Логический элемент НЕ.
Элемент, выполняющий функцию инверсии «НЕ » имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.
| Вход X | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Вот таким образом его показывают на схемах.
В зарубежной документации элемент «НЕ» изображают следующим образом. Сокращённо называют его NOT .
Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях.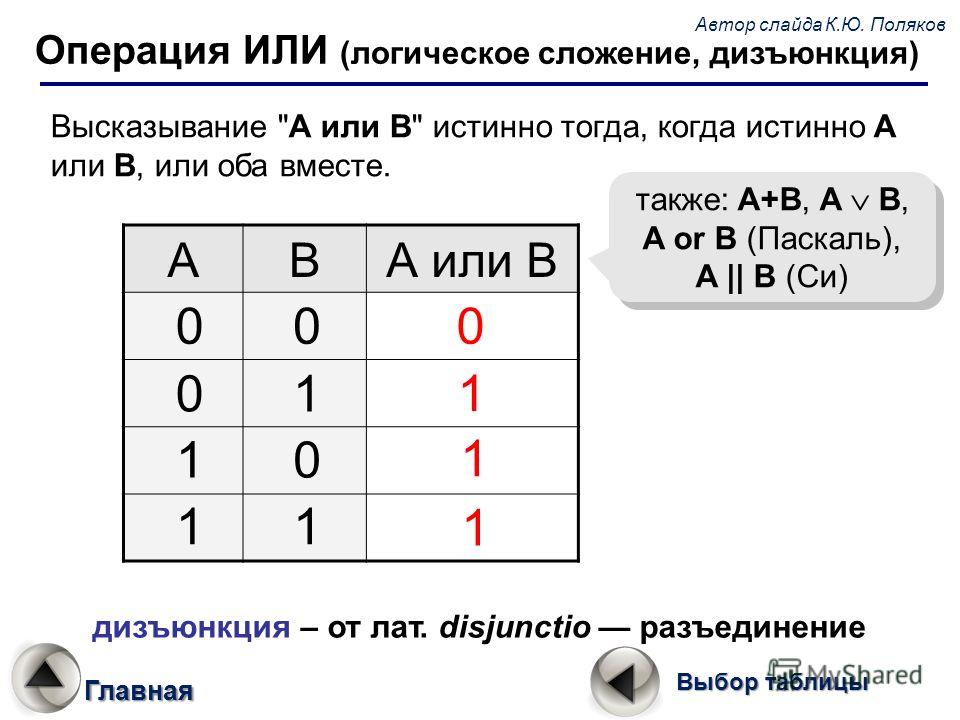 Это элементы: И-НЕ, ИЛИ-НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Это элементы: И-НЕ, ИЛИ-НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И — НЕ . Кстати, с помощью её можно собрать простейший маячок на микросхеме .
Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит «0» превращается в «1», а «1» превращается в «0». Обратим внимание на кружочек на выходах — это символ инверсии . В той же серии существуют элементы 3И-НЕ, 4И-НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).
Как вы уже поняли, один элемент 2И-НЕ изображается вот так.
По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.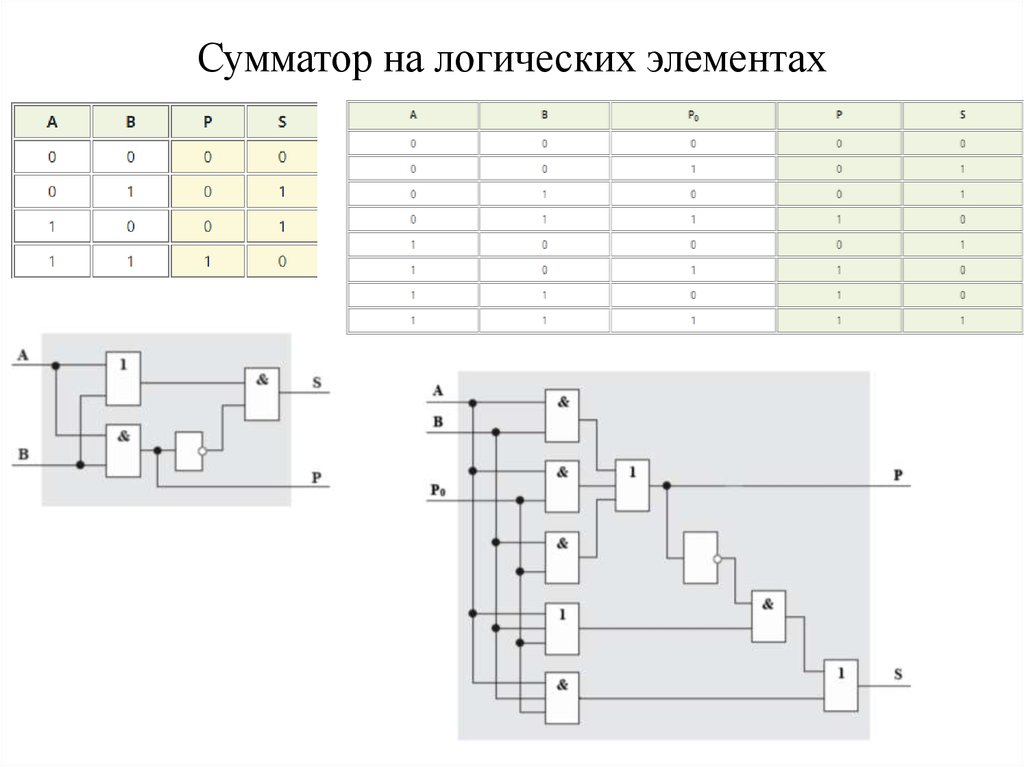
Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND .
Таблица истинности для элемента 2И-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В таблице истинности элемента 2И — НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И». В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И — НЕ» часто называют элементом Шеффера.
В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И — НЕ» часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ — НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы «ИЛИ» применением инвертирования выходного сигнала.
Таблица истинности для логического элемента 2ИЛИ-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Изображение на схеме.
На зарубежный лад изображается так. Называют как NOR .
Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И — НЕ и ИЛИ — НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И — НЕ обозначается значком «& «, а функция ИЛИ — НЕ значком «1 «.
Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.
Логический элемент «исключающее ИЛИ».
К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».
Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная — «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная — «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
Таблица истинности.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Эти логические элементы находят своё применение в сумматорах.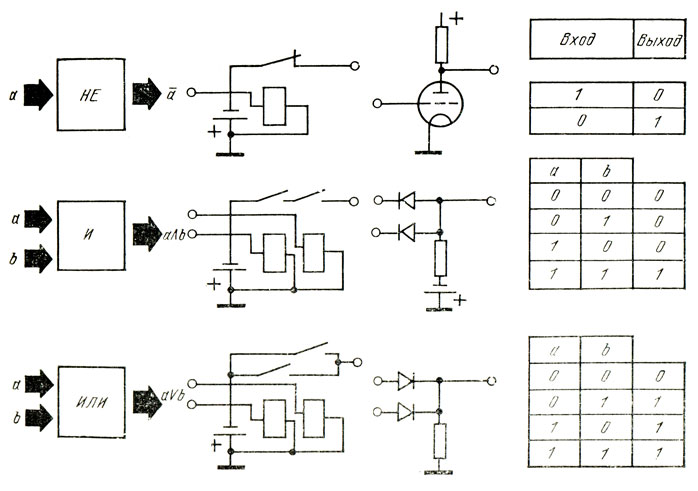 «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1 «.
«Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей «=1 «.
На зарубежный манер «исключающее ИЛИ» называют XOR и на схемах рисуют вот так.
Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.
Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы «И» и «ИЛИ». Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если посмотреть в справочной литературе схему, допустим, элемента 2И — НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет.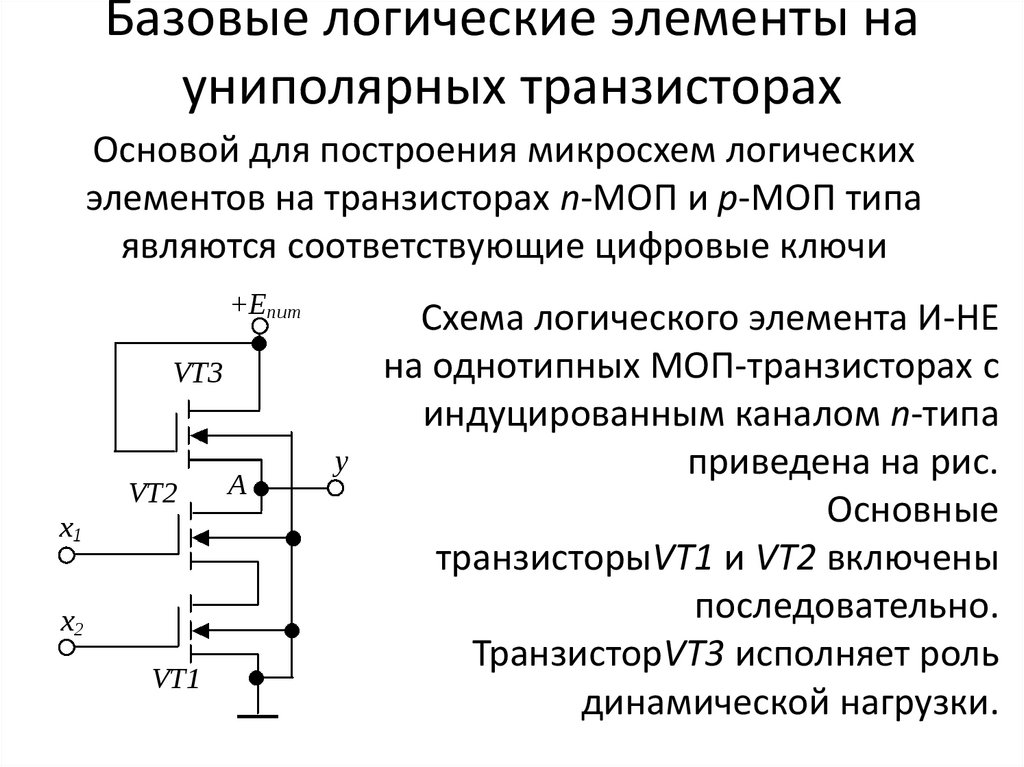 На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный
На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный
Простейшие логические элементы и функции. Основные логические операции (and, or, xor, not). Комбинации элементов с двумя входами
Основные элементы и элементы алгебры логики Логический элемент «И» и операция логического умножения (конъюнкции)Предложение «Если завтра будет хорошая погода и брат приедет,
то мы пойдем на рыбалку» содержит в себе операцию логического
умножения И. Условие А (хорошая погода) и условие В (брат приедет)
должны одновременно выполниться, чтобы действие X (рыбалка) свершилось.
Сказанное иллюстрирует таблица истинности (рис. 2.1). Состояние 1
значит «верно» или «истина». Состояние (0)
значит «неверно» или «ложь». Возможны четыре
комбинации. Последовательность комбинаций в принципе не имеет значения,
однако, как будет показано позже, она должна соответствовать
определенной схеме.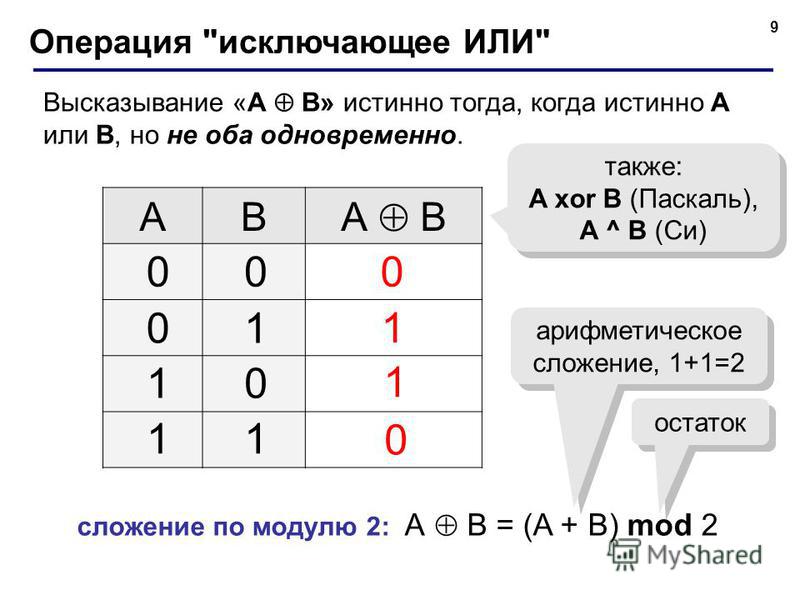
Электронную схему, в которой сигнал 1 на выходе появляется только
тогда, когда на входе А и входе В совпадают сигналы 1, называется
логическим элементом «И» (И-вентиль).
Простейший И-вентиль на последовательно включенных контакторах может
быть реализован по схеме на рис. 2.2. Но в настоящее время почти всегда
применяются интегрированные полупроводниковые микросхемы (см. раздел
«Семейства схем»).
Любая схема, удовлетворяющая таблице истинности логического умножения, является логическим элементом И.
Для обозначения операции «И» в алгебре логики используется символ л.
В литературе встречаются другие символы для обозначения логического умножения, точка (.) или &:
Х= АВ;Х= А&В. X = А л В
Рис. 2.3.
Условное обозначение логического элемента И с двумя входами показано
на рис. 2.3. Обозначения входов и выходов могут быть любыми. Часто
входы обозначают А и В, а выход — X или Q.
На выходе логического элемента И сигнал 1 появится только тогда, когда на всех входах совпадут сигналы 1.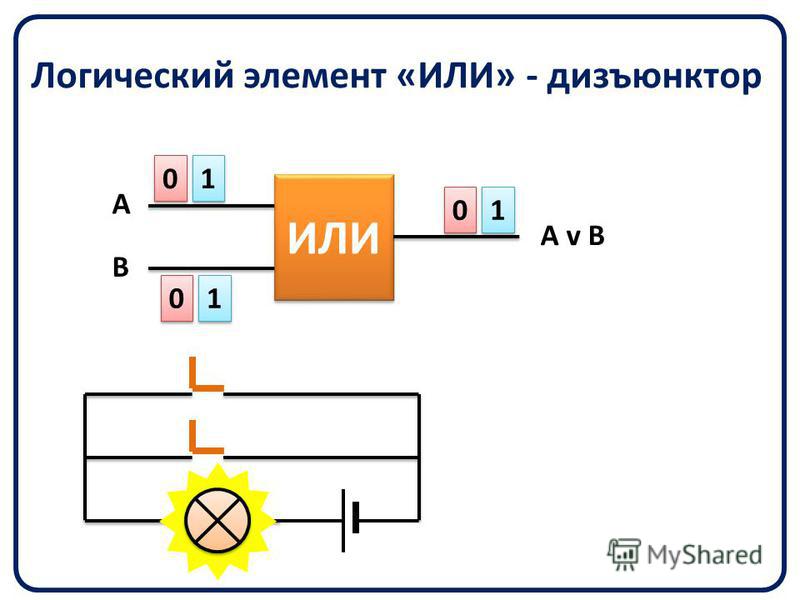
Предложение «Если я получу наследство или выиграю в лотерею,
то поеду в кругосветное путешествие» содержит в себе операцию
логического сложения ИЛИ. Путешествие становится возможным при
истинности условия А (наследство) или условия В (лотерея), или при
выполнении обоих условий одновременно. Сказанное иллюстрирует таблица
истинности на рис. 2.4 (состояние 1 значит «истина»,
состояние 0 значит «ложно»).
Электронная схема, на выходе X которой появляется сигнал 1, если на
входе А или входе В или на обоих входах присутствует сигнал 1,
называется логическим элементом ИЛИ. Элемент ИЛИ может быть реализован
по схеме на рис. 2.5.
Релейная схема приведена для наглядности. Сегодня элементы ИЛИ почти
всегда используются в виде интегрированных полупроводниковых микросхем.
Любая схема, удовлетворяющая таблице истинности логического сложения, является логическим элементом ИЛИ.
Для обозначения операции ИЛИ в алгебре логики используется символ v. 1 означает, что хотя бы на одном из
входов должен быть сигнал 1 для появления единицы на выходе.
1 означает, что хотя бы на одном из
входов должен быть сигнал 1 для появления единицы на выходе.
На выходе логического элемента ИЛИ сигнал 1 появится только тогда,
когда хотя бы на одном из его входов присутствует сигнал 1.
Логический элемент «НЕ» и операция инверсии (отрицания)
Предложение «Если приедет брат, то я не пойду сегодня вечером
в театр» означает отрицание. Если высказывание А (приезд брата)
верно, то действие X (посещение театра) не произойдет. Если неверно
высказывание А, то высказывание X будет верным, и я иду в театр.
Соответствующая таблица истинности (рис 2.7) имеет только два возможных
варианта.
Электронную схему, состояние на выходе X которой всегда противоположно
состоянию на входе
На рис. 2.8 приведена схема логического элемента НЕ. Как и ранее
рассмотренные логические элементы, вентили НЕ почти всегда используются
в виде интегрированных полупроводниковых микросхем.
Любая схема, удовлетворяющая таблице истинности логического инвертирования, является логическим элементом «НЕ».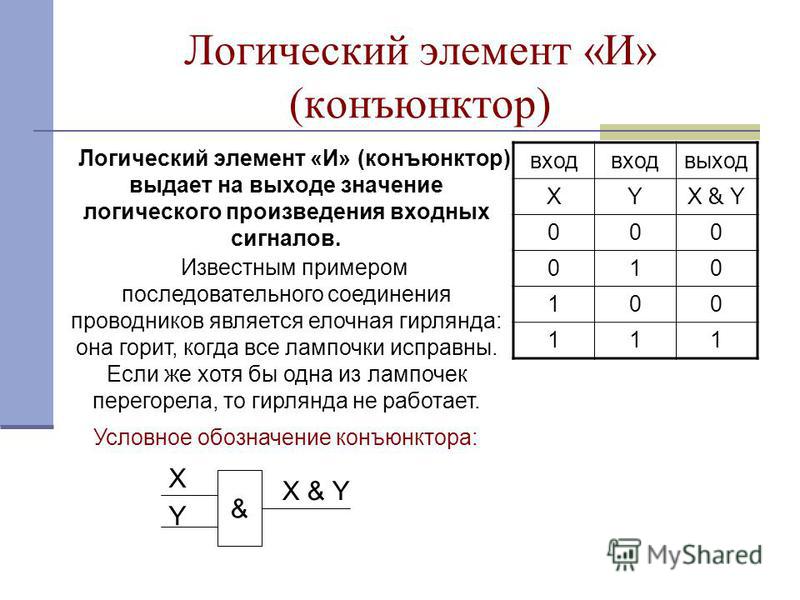
Для обозначения операции НЕ в алгебре логики используется черта над символом или апостроф:
Х = А
Условное обозначение логического элемента НЕ показано на рис. 2.9.
Состояние выхода логического элемента НЕ всегда противоположно состоянию входа.
Рис. 2.9.
Логические элементы И, ИЛИ и НЕ предназначены для выполнения трех основных операций цифровой логики над дискретными сигналами. С помощью этих элементов можно реализовать логические операции любой сложности. Поэтому эти элементы называются основными (рис. 2.10). К основным логическим элементам относится также буфер (рис. 2.10а). Если на входе буфера 1, то и на выходе 1, иначе 0.
На практике наиболее часто используют двухвходовые элементы «исключающее ИЛИ. На рис. 1 показано условное графическое обозначение элемента без инверсии и его таблица состояний. По простому, суть данного элемента сводится к следующему, сигнал на выходе появляется только в том случае, когда логические уровни на входах не одинаковые.
В данной схеме три элемента «Исключающий ИЛИ» используются для задержки импульсов. DD1.4 — суммирующий. Выходные импульсы имеют стабильные фронты и срезы. Длительность каждого выходного импульса равна утроенному времени задержки переключения каждого из трех элементов. Временной промежуток между фронтами выходных импульсов равен длительности входного импульса. Так же это устройство удваивает частоту входного сигнала.
Есть еще одно интересное свойство «Исключающее ИЛИ». Если на один из входов подать постоянный «0», то сигнал на выходе элемента будет повторять входной сигнал, а если постоянный «0» поменять на постоянную «1», то выходной сигнал уже будет инверсией входного.
Иногда появляется необходимость получить элемент «исключающее ИЛИ» из отдельных стандартных логических элементов. Примером может служить схема элемента «исключающее ИЛИ» реализованная на четырех элементах 2-И-НЕ. На рисунке 3 показана схема «исключающее ИЛИ» в четырех ее состояниях. Здесь показаны все возможные логические уровни на каждом из используемых логически элементов 2-И-НЕ.
Такие элементы входят в схему . В данной схеме элемент «Исключающий ИЛИ» выполнен на четырех элементах 2-И-НЕ, входящих в один корпус микросхемы К561ЛА7.
Схема формирователя показана на рисунке 4. Здесь логический элемент «исключающее ИЛИ» также реализован на четырех элементах 2-И-НЕ.
На входы 1 и 2 формирователя падают импульсы прямоугольной формы (см. графики 1 и 2), которые различаются частотой следования. Узел на логических элементах DD1.1-DDI.4 перемножает эти сигналы. Выходной импульсный сигнал (график 3) с элемента DD1.4 подается на интегрирующую цепь R3, С1, преобразующую его в сигнал треугольной формы (график 4) с частотой, равной разности частот входных сигналов, а ОУ DA1 преобразует полученный сигнал в меандр (см. график 5). Резистором R1 регулируют длительность положительной и отрицательной полуволн выходного сигнала. Очень интересная схема. Радиоконструктору, есть над чем подумать. Например, сигнал, показанный на третьем графике, является сигналом ШИМ синусоиды.
Конечно диапазон использования элементов «исключающее ИЛИ» намного шире. Я привел здесь на мой взгляд более интересные для радиолюбителей.
Используемая литература:
Б.И. Горшков Элементы радиоэлектронных устройств Издательство «Радио и связь»
Цифровые интегральные схемы М.И. Богданович Справочник Минск «Беларусь»-«Полымя» 1996
(2012-05-19)
Из журнала «Радио»
Логических элементов, работающих как самостоятельные цифровые микросхемы малой степени интеграции и как компоненты микросхем более высокой степени интеграции, можно насчитать несколько десятков. Но здесь мы поговорим лишь о четырех из них — о логических элементах И, ИЛИ, НЕ, И-НЕ. Элементы И, ИЛИ и НЕ — основные, а И-НЕ является комбинацией элементов И и НЕ.
Что представляют собой эти «кирпичики» цифровой техники, какова логика их действия? Сразу уточним: напряжение от 0 до 0,4В, т. е. соответствующее уровню логического 0, мы будем называть напряжением низкого уровня, а напряжение более 2,4В, соответствующее уровню логической I,-напряжением высокого уровня.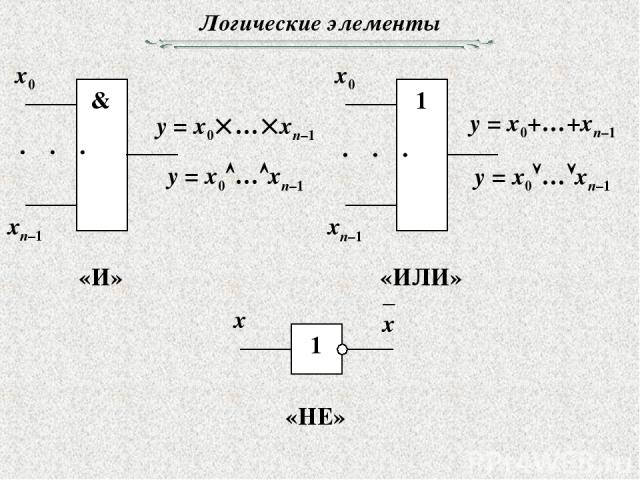 Именно такими уровнями напряжения на входе и выходе логических элементов и других микросхем серии К155 принято характеризовать их логические состояния и работу.
Именно такими уровнями напряжения на входе и выходе логических элементов и других микросхем серии К155 принято характеризовать их логические состояния и работу.
Условное графическое обозначение логического элемента И показано на Рис–1,а. Его условным символом служит знак «&», стоящий внутри прямоугольника; этот знак заменяет союз «и»в английском языке. Слева — два (может быть и больше) логических входа – X1 и X2, справа — один выход Y. Логика действия элемента такова: напряжение высокого уровня появляется на выходе лишь тогда, когда сигналы такого же уровня будут поданы на все его входы
Элемент
И — умножениеРазобраться в логике действия логического элемента И поможет его электрический аналог (Рис–1, б), составленный из последовательно соединенных источника питания GB (например, батареи 3336), кнопочных переключателей SB1, SB2 любой конструкции и лампы накаливания HL (МНЗ,5-0,26). Переключатели имитируют электрические сигналы на входе аналога, а нить лампы индицирует уровень сигнала на выходе. Разомкнутое состояние контактов переключателей соответствует напряжению низкого уровня, замкнутое- высокого уровня. Пока контакты кнопок не замкнуты (на обоих входах элемента напряжение низкого уровня), электрическая; цепь аналога разомкнута и лампа, естественно, не светит. Нетрудно сделать другой вывод: лампа накаливания на выходе элемента И включается только после того, как контакты обеих кнопок SB1 и SB2 окажутся замкнутыми В этом и заключается логическая связь между входными и выходными сигналами элемента И.
Разомкнутое состояние контактов переключателей соответствует напряжению низкого уровня, замкнутое- высокого уровня. Пока контакты кнопок не замкнуты (на обоих входах элемента напряжение низкого уровня), электрическая; цепь аналога разомкнута и лампа, естественно, не светит. Нетрудно сделать другой вывод: лампа накаливания на выходе элемента И включается только после того, как контакты обеих кнопок SB1 и SB2 окажутся замкнутыми В этом и заключается логическая связь между входными и выходными сигналами элемента И.
Теперь взгляните на Рис–1,в. На нем изображены временные диаграммы электрических процессов, дающие достоверное представление о работе логического элемента И. На входе X1 сигнал появляется первым. Как только такой же сигнал будет и на входе Х2, тут же появляется сигнал и на выходе Y, который существует до тех пор, пока на обоих входах имеются сигналы, соответствующие напряжению высокого уровня.
О состоянии и логической связи между входными и выходным сигналами элемента И дает представление так называемая таблица состояний (Рис–1, г), напоминающая таблицу умножения. Глядя на нее, можно сказать, что сигнал высокого уровня на выходе элемента будет только тогда, когда сигналы такого же уровня появятся на обоих его входах. Во всех других случаях на выходе элемента будет напряжение низкого уровня, т. е. соответствующее логическому 0
Глядя на нее, можно сказать, что сигнал высокого уровня на выходе элемента будет только тогда, когда сигналы такого же уровня появятся на обоих его входах. Во всех других случаях на выходе элемента будет напряжение низкого уровня, т. е. соответствующее логическому 0
Элемент
ИЛИУсловный символ логического элемента ИЛИ — цифра 1 внутри прямоугольника (Рис–2, а). У этого элемента, как и у элемента И, может быть два и больше входов. Сигнал на выходе Y, соответствующий напряжению высокого уровня, появляется при подаче такого же сигнала на вход X1, или на вход Х2, или одновременно на оба входа. Чтобы убедиться в таком действии элемента ИЛИ, проведите опыт с его электрическим аналогом (Рис–2, б).
Лампа накаливания HL на выходе аналога будет включаться всякий раз, когда окажутся замкнутыми контакты или кнопки SB1, или SB2, или одновременно обеих (всех) кнопок Закрепить в памяти электрическое свойство элемента ИЛИ помогут временные диаграммы его работы (Рис–2,в) и таблица состояний (Рис–2,г), определяющая логическую связь между входными и выходным сигналами.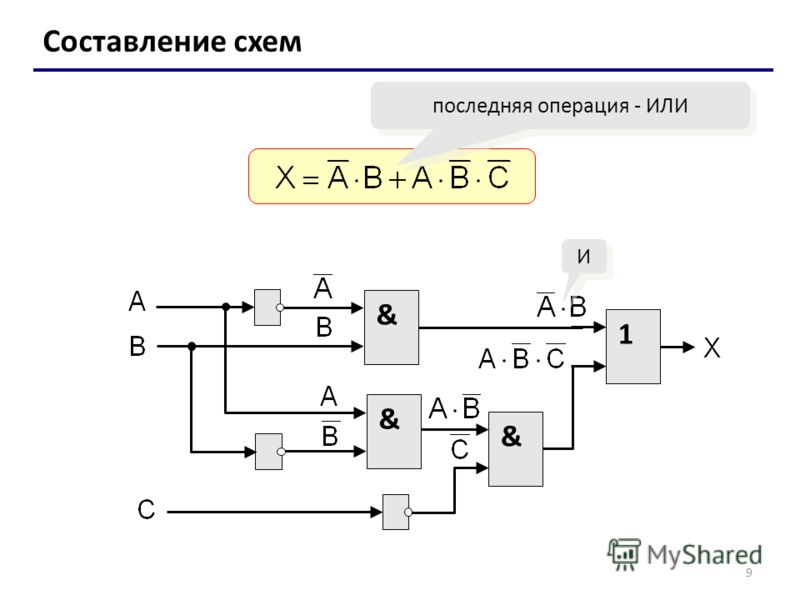
Элемент
НЕУсловный символ логического элемента НЕ — тоже цифра 1 в прямоугольнике Рис–3,а. Но у него один вход и один. выход. Небольшой кружок, которым начинается линия связи выходного сигнала, символизирует логическое отрицание на выходе элемента На языке цифровой техники НЕ означает, что этот элемент является инвертором- электронным устройством, выходной сигнал которого противоположен входному. Иначе говоря, пока на входе элемента НЕ действует сигнал низкого уровня, на его выходе будет сигнал высокого уровня, и наоборот.
Электрический аналог элемента НЕ можно собрать по схеме, представленной на Рис– 3, б. Электромагнитное реле К, срабатывающее при напряжении батарея GB, должно быть выбрано с группой замкнутых контактов. Пока контакты кнопки SB1 разомкнуты, обмотка реле обесточена, его контакты К остаются замкнутыми и, следовательно, лампа HL светит. При нажатии на кнопку ее контакты замыкаются, имитируя появление входного сигнала высокого уровня, в результате чего реле срабатывает. Его контакты, размыкаясь, разрывают цепь питания лампы HL-погасая, она символизирует появление на выходе сигнала низкого уровня. Попробуйте начертить самостоятельно временные диаграммы работы элемента НЕ и составить его таблицу состоянии — они должны получиться такими же, как приведенные на Рис–3, в, г.
Его контакты, размыкаясь, разрывают цепь питания лампы HL-погасая, она символизирует появление на выходе сигнала низкого уровня. Попробуйте начертить самостоятельно временные диаграммы работы элемента НЕ и составить его таблицу состоянии — они должны получиться такими же, как приведенные на Рис–3, в, г.
Элемент
И–НЕКак мы уже говорили, логический элемент И-НЕ является комбинацией элементов И и НЕ. Поэтому на его графическом обозначении (Рис–4, а) есть знак «&»и кружок на линии выходного сигнала, символизирующий логическое отрицание. Выход один, а входов два и больше.
Разобраться в принципе действия такого логического элемента цифровой техники вам поможет его электрический аналог, собранный по схеме на Рис–4,б. Электромагнитное реле К, батарея GB и лампа накаливания HL такие же, как в аналоге элемента НЕ. Последовательно с обмоткой реле включите две кнопки (SB1 и SB2), контакты которых будут имитировать входные сигналы. В исходном состоянии, когда контакты кнопок разомкнуты, лампа светит, символизируя сигнал высокого уровня на выходе.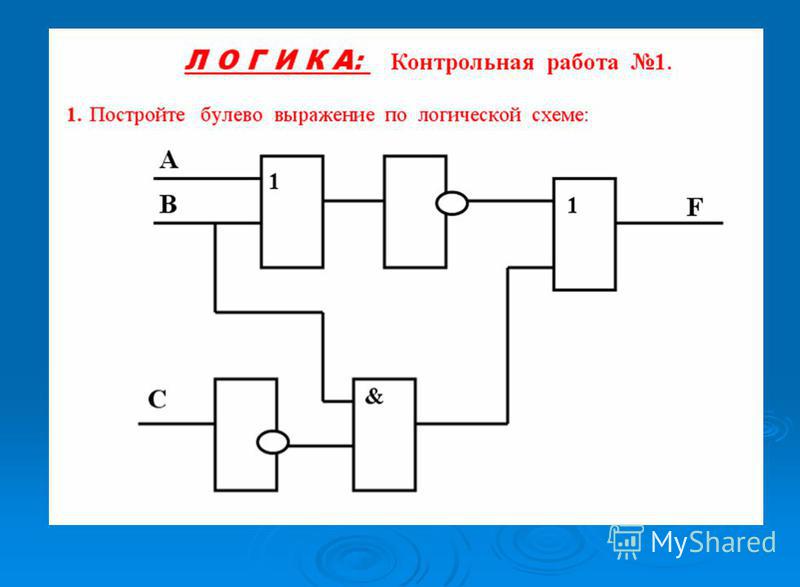 Нажмите на одну из кнопок во входной цепи.
Нажмите на одну из кнопок во входной цепи.
Как на это реагирует индикаторная лампа? Она продолжает светить. А если нажать на обе кнопки? В этом случае электрическая цепь, образованная батареей питания обмоткой реле и контактами кнопок, оказывается замкнутой, реле срабатывает и его контакты К, размыкаясь, разрывают вторую цепь аналога-лампа гаснет. Эти опыты позволяют сделать вывод: при сигнале низкого уровня на одном или на всех входах элемента И-НЕ (когда контакты входных кнопок аналога разомкнуты) на выходе действует сигнал высокого уровня, который изменяется на сигнал низкого уровня при появлении таких же сигналов на всех входах элемента (контакты кнопок аналога замкнуты). Такой вывод подтверждается диаграммами работы и таблицей состояний, показанными на Рис–4, в, г. Обратим внимание на следующий факт: если входы элемента И-НЕ соединить вместе и подать на них сигнал высокого уровня, на выходе элемента будет сигнал низкого уровня. И наоборот, при подаче на объединенный вход сигнала низкого уровня на выходе элемента будет сигнал высокого уровня. В этом случае элемент И-НЕ, как, вероятно, вы уже догадались, становится инвертором, т. е. логическим элементом НЕ. Это свойство элемента И-НЕ очень широко используется в приборах и устройствах цифровой техники.
В этом случае элемент И-НЕ, как, вероятно, вы уже догадались, становится инвертором, т. е. логическим элементом НЕ. Это свойство элемента И-НЕ очень широко используется в приборах и устройствах цифровой техники.
Элемент
ИЛИ–НЕЭлемент исключающий
ИЛИАвтоколебательный мультивибратор
При ёмкости конденсатора С = 1мкФ и изменении R от 0 до 1,5 ком. частота колебаний изменится от 300Гц до 10 кГц.
Ждущий мультивибратор
Изменением ёмкости и сопротивления изменяют длительность вырабатываемых импульсов.
Длительность запускающего импульса должна быть меньше длительности формируемого.
Сопротивление должно быть от 100 Ом до 2,2 к.
Триггер Шмитта
Это спусковое устройство с двумя устойчивыми состояниями. Из одного состояния в другое устройство переходит под действием входного сигнала.
Ещё он преобразует подаваемое на вход переменное напряжение синусоидальной формы в напряжение прямоугольной формы такой же частоты. Срабатывает при определённой амплитуде входного сигнала.
Срабатывает при определённой амплитуде входного сигнала.
R S — триггер
При 0 на S и 1 на R, триггер находится в единичном состоянии. 1 на S и 0 на R, триггер в нулевом состоянии. Если на оба входа подать 0, на выходах будет 1. Это противоречит логике его действия и считается недопустимым. 1 на обеих входах не изменит первоначального состояния триггера.
D – триггер
D – Вход приёма цифровой информации.
C – Вход тактовых импульсов синхронизации.
0 – на входе R – триггер в нулевом состоянии.
0 – на входе S – триггер в единичном состоянии.
Логика работы D – триггера в режиме приёма информации следующая: если на входе D – 1, то по фронту тактового импульса на входе С – триггер устанавливается в единичное состояние, если на входе D – 0, то по фронту тактового импульса на входе С – триггер устанавливается в нулевое состояние.
На спады синхронизирующих импульсов D – триггер не реагирует. Каждое изменившееся состояние триггера означает запись в его память принятой информации.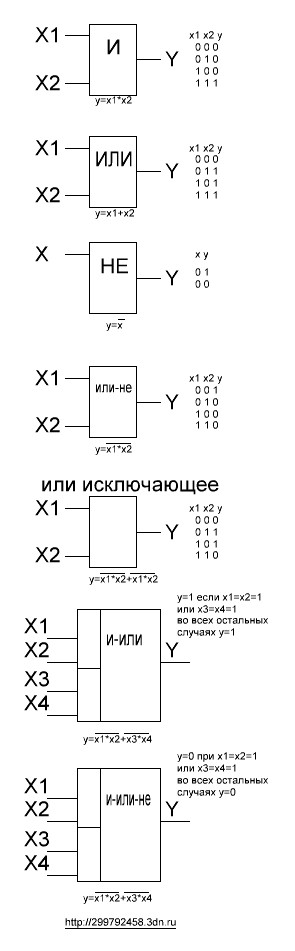
Работа D – триггера в счётном режиме.
В счётном режиме триггер делит частоту входного сигнала на 2. Выполняет функцию двоичного счётчика.
J K – триггер
По входам R и S, он работает как RS триггер. Входы J и K – управляющие, каждый из них имеет по три входа объединённые по схеме 3И. С – вход тактовых импульсов. В режиме приёма и хранения информации он служит входом тактовых импульсов, в счётном режиме – информационным входом.
J K – триггер, работает по спаду тактовых импульсов.
Логические элементы составляют основу устройств цифровой (дискретной) обработки информации и цифровых устройств автоматики.
Логические элементы выполняют простейшие логические операции над цифровой информацией. Логическая операция преобразует по определенным правилам входную информацию в выходную. Логические элементы чаще всего строят на базе электронных устройств, работающих в ключевом режиме. Поэтому цифровую информацию обычно представляют в двоичной форме, в которой сигналы принимают только два значения: «0» (логический нуль) и «1» (логическая единица) соответствующие двум состояниям ключа.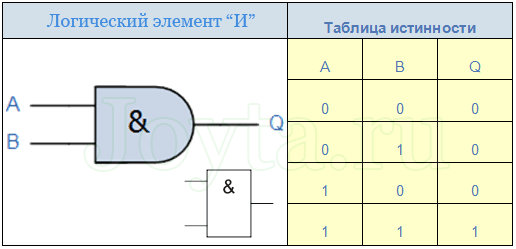 Логическому нулю соответствует низкий уровень напряжения на входе или выходе элемента (например U 0 =0…0,4В), а логической единице соответствует высокий уровень напряжения (например U 1 =3…5В).
Логическому нулю соответствует низкий уровень напряжения на входе или выходе элемента (например U 0 =0…0,4В), а логической единице соответствует высокий уровень напряжения (например U 1 =3…5В).
Основными логическими элементами являются элементы ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ. На основе этих основных элементов строятся более сложные: триггеры, счётчики, регистры, сумматоры.
Логический элемент ИЛИ (рис. 4.1, а) имеет один выход и несколько входов (чаще всего 2 — 4 входа) и реализует функцию логического сложения или дизъюнкции. Обозначается в случае двух независимых переменных У = Х 1 ÚХ 2 либо У = Х 1 + Х 2 (читается Х 1 или Х 2) и определяется таблицей истинности (табл. 4.1.). Операцию ИЛИ можно выполнять для трех и более независимых аргументов. Функция У = 1, если хотя бы одна из независимых переменных Хi равна единице.
Логический элемент И (рис. 4.1, б) реализует функцию логического умножения или конъюнкции. Обозначается У = Х 1 ÙХ 2 либо У = Х 1 Х 2 (читается Х 1 и Х 2) и определяется таблицей истинности (табл.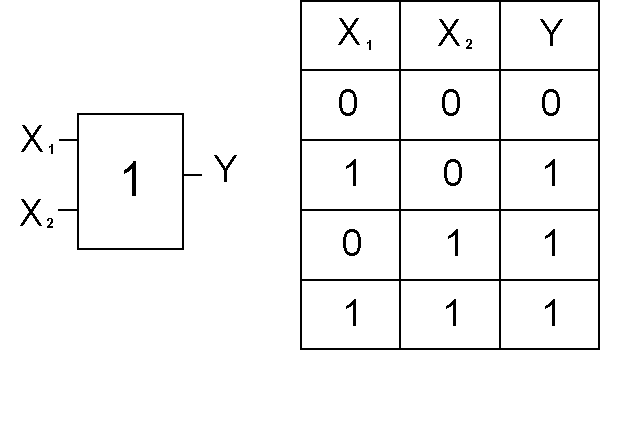 4.2). Операцию логического умножения можно распространить на три и более независимых аргументов. Функция У равна единице только тогда, когда все независимые переменные Хi равны единице.
4.2). Операцию логического умножения можно распространить на три и более независимых аргументов. Функция У равна единице только тогда, когда все независимые переменные Хi равны единице.
Логический элемент НЕ реализует операцию логического отрицания или инверсии. Логическое отрицание от функции Х обозначается `Х (говорится «не Х») и определяется таблицей истинности (табл. 4.3).
Логический элемент ИЛИ-НЕ реализует логическую функцию У =и определяется таблицей истинности (табл. 4.4.).
Логический элемент И-НЕ реализует логическую функцию У =и определяется таблицей истинности (табл. 4.5.).
Рисунок 4.1 – Условно-графические изображения логических элементов ИЛИ (а), И (б), НЕ (в), ИЛИ-НЕ (г), И-НЕ (д)
Таблица 4.1–Таблица истинности Таблица 4.2–Таблица истинности элемента ИЛИ элемента И
| Х 1 | Х 2 | У = Х 1 +Х 2 | Х 1 | Х 2 | У = Х 1 Х 2 | ||
Таблица 4.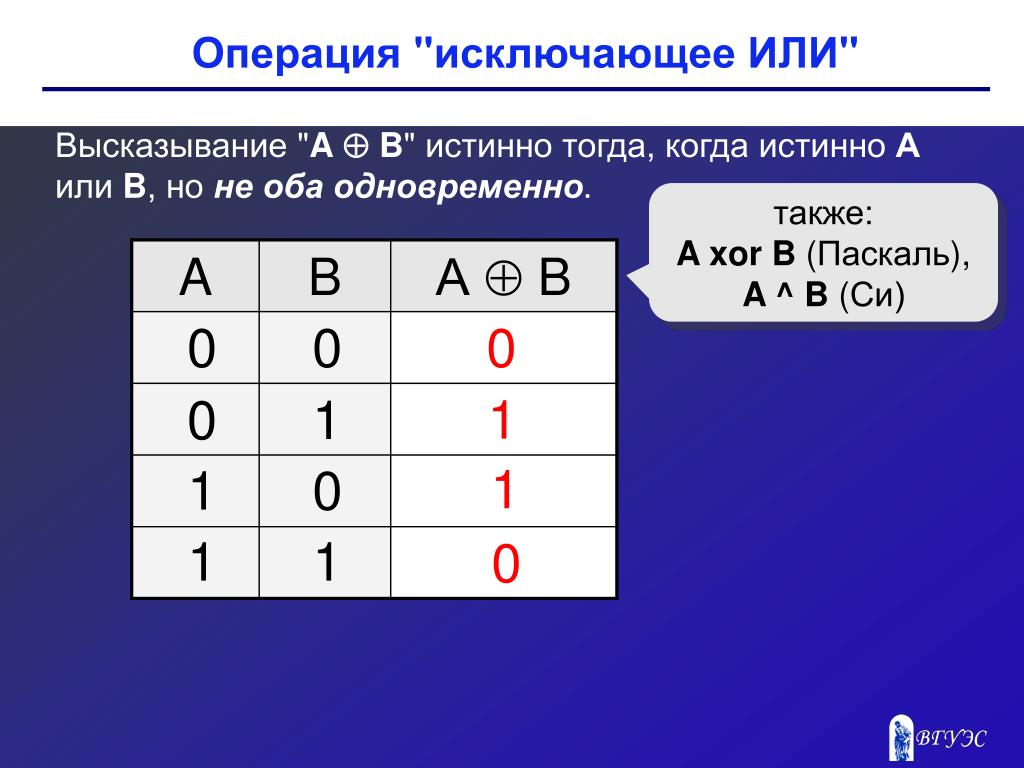 3–Таблица истинности Таблица 4.4–Таблица истинности
3–Таблица истинности Таблица 4.4–Таблица истинности
элемента НЕ элемента ИЛИ — НЕ
Находят применение также элементы реализующие логические операции ЗАПРЕТ и исключающее ИЛИ.
Логический элемент ЗАПРЕТ обычно имеет два входа (рис. 4.2, а): разрешающий Х 1 и запрещающий Х 2 . Выходной сигнал повторяет сигнал на разрешающем входе Х 1 , если Х 2 =0. При Х 2 =1 на выходе возникает согнал 0 независимо от значения Х 1 . То есть данный элемент реализует логическую функцию У = Х 1 . Логический элемент «исключающее ИЛИ» (неравнозначность) (рис. 4.2, б) реализует логическую функцию и определяется таблицей истинности (табл. 4.6).
Рисунок 4.2 – Условно-графические изображения логических элементов ЗАПРЕТ (а), исключающее ИЛИ (б)
Таблица 4.6 — Таблица истинности элемента «исключающее ИЛИ»
| Х 1 | Х 2 | Y |
Цифровые интегральные микросхемы обеспечивают получение выходных сигналов очень малой мощности. Например, микросхемы серий К155, К555, КР1533 обеспечивают в состоянии логической единицы выходной ток = 0,4 мА. Поэтому на выходах логического блока обычно используют микросхемы с открытым коллектором. В таких микросхемах резистор, включенный в цепи коллектора, выносится за пределы микросхемы (рис. 4.3, а ).
Например, микросхемы серий К155, К555, КР1533 обеспечивают в состоянии логической единицы выходной ток = 0,4 мА. Поэтому на выходах логического блока обычно используют микросхемы с открытым коллектором. В таких микросхемах резистор, включенный в цепи коллектора, выносится за пределы микросхемы (рис. 4.3, а ).
Рисунок 4.3 – Подключение нагрузки к выходу микросхемы с открытым коллектором
Если выход микросхемы ДД1 находится в состоянии логической единицы (U ВЫХ = 1), то есть ее выходной транзистор находится в состоянии отсечки, то I К » 0. При «Лог.0» на выходе ДД1 (U ВЫХ = 0), то есть когда ее выходной транзистор находится в состоянии насыщения I К » U П / R К. Максимально допустимый выходной ток микросхем с открытым коллектором может быть значительно большим, чем у обычных микросхем.
Например, для микросхем с открытым коллектором К155ЛЛ2, К155ЛИ5, К155ЛА18 максимальный выходной втекающий ток может достигать 300 мА, а максимальное напряжение на выходе в состоянии «Лог. 1» может составлять 30 В, что позволяет коммутировать нагрузку мощностью до 9 Вт.
1» может составлять 30 В, что позволяет коммутировать нагрузку мощностью до 9 Вт.
Если нагрузка, например катушка реле или пневмораспределителя, рассчитана на напряжение и ток, не превышающие допустимые для данной микросхемы, то она может быть включена непосредственно на выход микросхемы (рис. 4.3, б ). При этом реле К1 срабатывает, если на выходе ДД2 имеем «Лог.0» и отключается при «Лог.1» на выходе ДД2. Диод VD1, включенный в обратном направлении, обеспечивает защиту микросхемы от перенапряжения, возникающего при отключении катушки реле за счет накопленной в ней электромагнитной энергии.
Для управления нагрузкой с большим рабочим напряжением и током можно использовать схему, где коммутация силовой цепи осуществляется дополнительным транзистором VТ1, включенным на выход микросхемы с открытым коллектором ДД1 и работающим в ключевом режиме (рис. 4.4).
Рисунок 4.4– Подключение нагрузки через транзисторный ключ
При «Лог.0» на выходе ДД1 транзистор VТ1 закрыт и реле К1 отключено.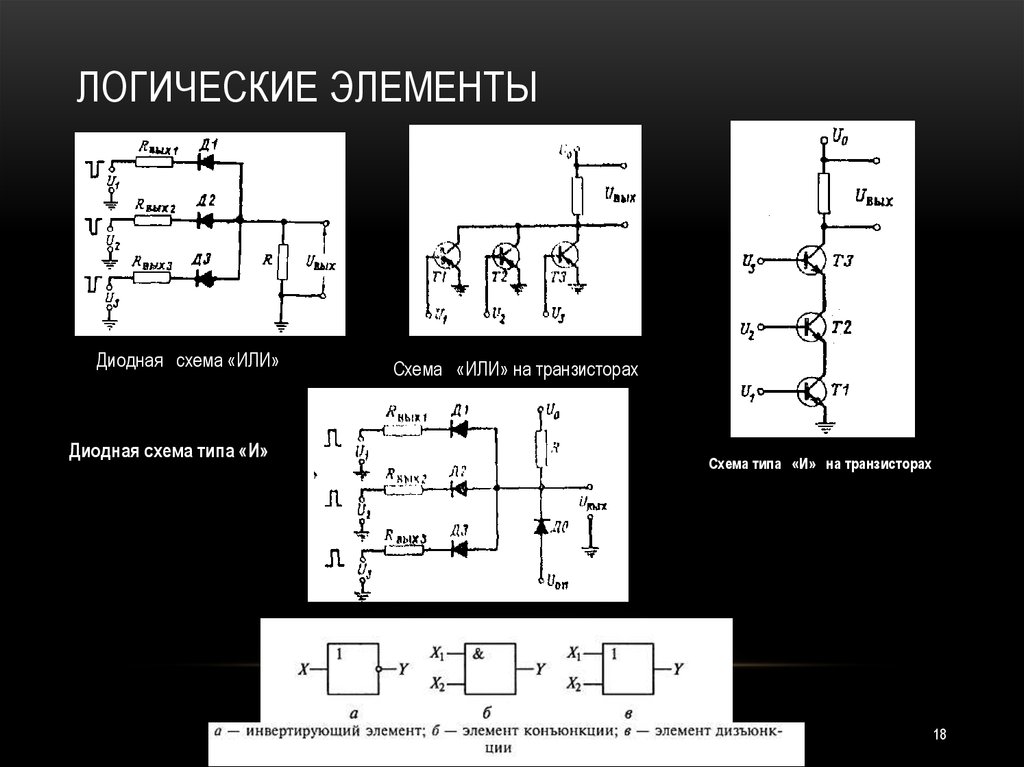 При «Лог.1» на выходе ДД1 транзистор открывается (переходит в состояние насыщения). Ток через транзистор в режиме насыщения определяется напряжением питания U 1 и сопротивлением катушки реле R К1 , так как падение напряжения на транзисторе в режиме насыщения U КН » 0:
При «Лог.1» на выходе ДД1 транзистор открывается (переходит в состояние насыщения). Ток через транзистор в режиме насыщения определяется напряжением питания U 1 и сопротивлением катушки реле R К1 , так как падение напряжения на транзисторе в режиме насыщения U КН » 0:
Напряжение питания U 1 должно выбираться равным рабочему напряжению нагрузки (в данном случае реле К1), а транзистор VТ1 должен выбираться с допустимым напряжением на коллекторе, большим U 1 , и допустимым током коллектора, большим I К1 .
Режим насыщения транзистора достигается при
Для надежного насыщения транзистора необходимо, чтобы условие выполнялось при минимальном значении статического коэффициента усиления по току h 21Э = h 21Э min для данного типа транзистора.
При этом должно выполняться условие
U П /R 1 ³I БН g = gI КН / h 21Эmin
где g — степень насыщения (g = 1,2…2).
Диод VД1 обеспечивает защиту транзистора от коммутационных перенапряжений. Диод VД2 обеспечивает напряжение смещения, необходимое для запирания транзистора при «Лог.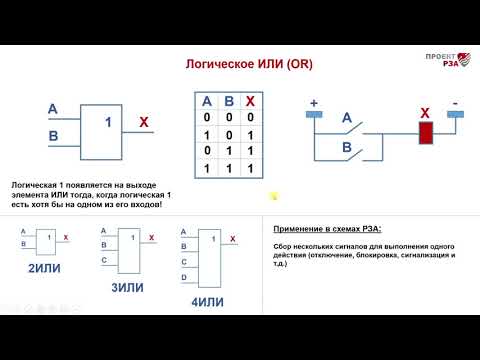 0» на выходе ДД1. Напряжение смещения подается на базу через резистор R2.
0» на выходе ДД1. Напряжение смещения подается на базу через резистор R2.
Если нагрузка обладает значительной индуктивностью, то она шунтируется диодом, включенным в обратном направлении (см. рис. 4.3, б, рис. 4.4).
Логические микросхемы с открытым коллектором применяют также для управления технологическим (например сварочным) оборудованием. В блоках управления современным сварочным оборудованием (например, в блоках управления сварочными полуавтоматами серии БУСП, блоках управления циклом контактной сварки серии РКС) предусмотрено управление включением непосредственно с помощью микросхемы с открытым коллектором, подключаемой к определенному входу блока управления (рис. 4.5).
Рисунок 4.5 – Схема управления технологическим оборудованием с помощью логической микросхемы с открытым коллектором
Любые цифровые микросхемы строятся на основе простейших логических элементов:
Рассмотрим устройство и работу цифровых логических элементов подробнее.
Инвертор
Простейшим логическим элементом является инвертор, который просто изменяет входной сигнал на прямо противоположное
значение.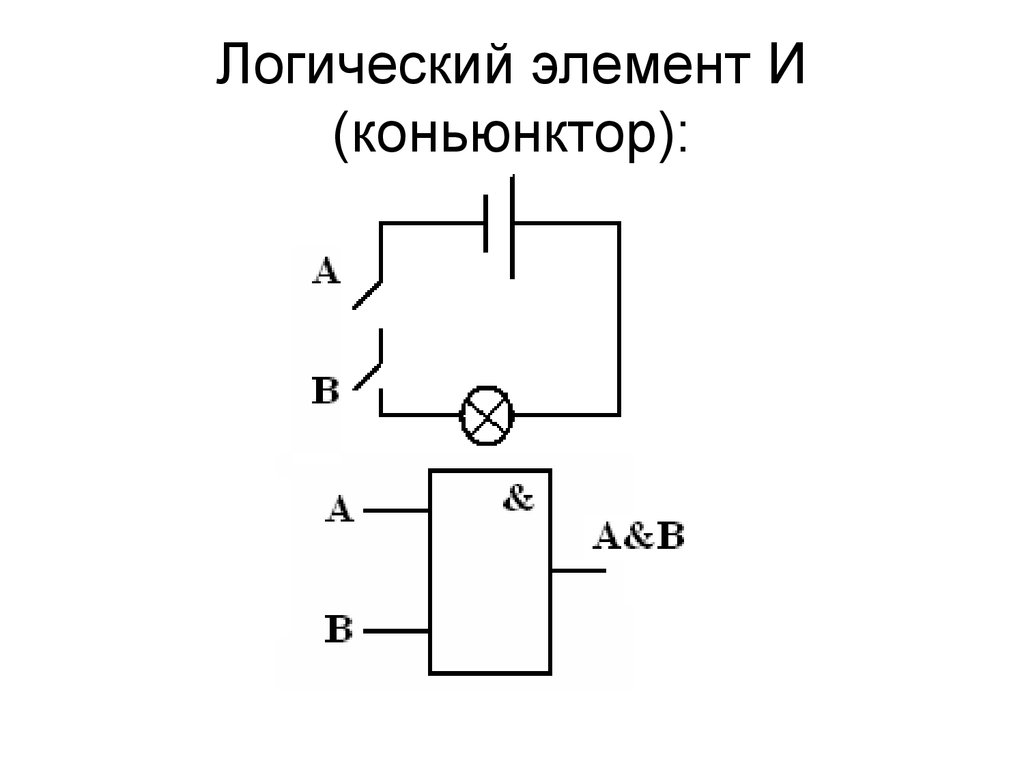 Его записывается в следующем виде:
Его записывается в следующем виде:
где черта над входным значением и обозначает изменение его на противоположное. То же самое действие можно записать при помощи , приведённой в таблице 1. Так как вход у инвертора только один, то его таблица истинности состоит всего из двух строк.
Таблица 1. Таблица истинности логического элемента инвертора
| In | Out |
|---|---|
| 0 | 1 |
| 1 | 0 |
В качестве логического инвертора можно использовать простейший усилитель с транзистором, включенном по (или истоком для полевого транзистора). Принципиальная схема логического элемента инвертора, выполненная на биполярном n-p-n транзисторе, приведена на рисунке 1.
Рисунок 1. Схема простейшего логического инвертора
Микросхемы логических инверторов могут обладать различным временем распространения сигнала и могут работать на различные
виды нагрузки. Они могут быть выполнены на одном или на нескольких транзисторах. Наиболее распространены логические элементы,
выполненные по ТТЛ, ЭСЛ и КМОП технологиям. Но независимо от схемы логического элемента и её параметров все они осуществляют
одну и ту же функцию.
Они могут быть выполнены на одном или на нескольких транзисторах. Наиболее распространены логические элементы,
выполненные по ТТЛ, ЭСЛ и КМОП технологиям. Но независимо от схемы логического элемента и её параметров все они осуществляют
одну и ту же функцию.
Для того, чтобы особенности включения транзисторов не затеняли выполняемую функцию, были введены специальные обозначения для логических элементов — условно-графические обозначения. инвертора приведено на рисунке 2.
Рисунок 2. Условно-графическое обозначение логического инвертора
Инверторы присутствуют практически во всех сериях цифровых микросхем. В отечественных микросхемах инверторы обозначаются
буквами ЛН. Например, в микросхеме 1533ЛН1 содержится 6 инверторов. Иностранные микросхемы для обозначения типа микросхемы
используется цифровое обозначение. В качестве примера микросхемы, содержащей инверторы, можно назвать 74ALS04. В названии
микросхемы отражается, что она совместима с ТТЛ микросхемами (74), произведена по улучшеной малопотребляющей шоттки технологии
(ALS), содержит инверторы (04).
В настоящее время чаще применяются микросхемы поверхностного монтажа (SMD микросхемы), в которых содержится по одному логическому элементу, в частности инвертору. В качестве примера можно назвать микросхему SN74LVC1G04. Микросхема произведена фирмой Texas Instruments (SN), совместима с ТТЛ микросхемами (74) произведена по низковольтовой КМОП технологии (LVC), содержит только один логический элемент (1G), им является инвертор (04).
Для исследования инвертирующего логического элемента можно использовать широкодоступные радиоэлектронные элементы. Так,
в качестве генератора входных сигналов можно использовать обычные переключатели или тумблеры. Для исследования таблицы
истинности можно даже применить обычный провод, который будем поочередно подключать к источнику питания и ли общему проводу.
В качестве логического пробника может быть использована низковольтовая лампочка или светодиод, соединенный последовательно
с токоограничивающим . Принципиальная схема исследования логического элемента
инвертора, реализованная с помощью этих простейших радиоэлектронных элементов, приведена на рисунке 3.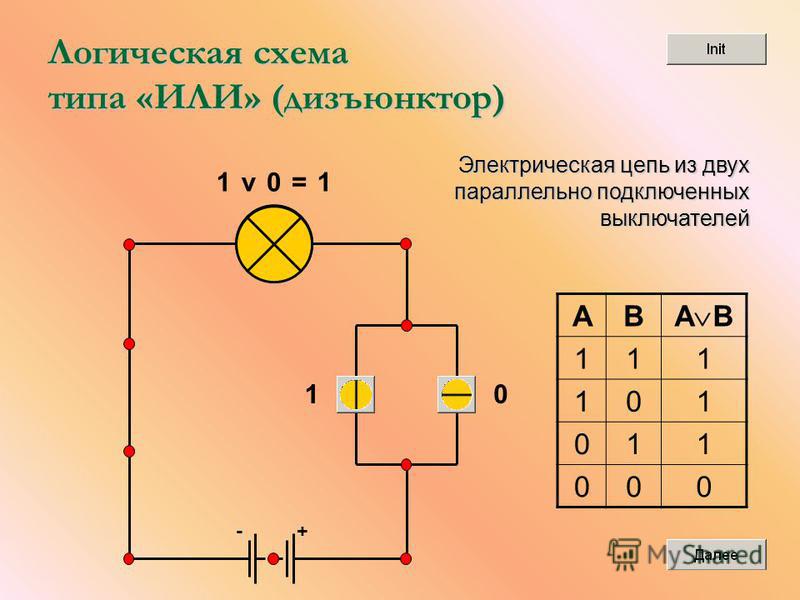 x 2 = x 1 ·x 2 = x 1 &x 2 .
x 2 = x 1 ·x 2 = x 1 &x 2 .
То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 2. В формуле, приведенной выше использовано два аргумента. Поэтому логический элемент, выполняющий эту функцию имеет два входа. Он обозначается «2И». Для логического элемента «2И» таблица истинности будет состоять из четырех строк (2 2 = 4) .
Таблица 2. Таблица истинности логического элемента «2И»
| In1 | In2 | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Как видно из приведённой таблицы истинности, активный сигнал на выходе этого логического элемента появляется только
тогда, когда и на входе X, и на входе Y будут присутствовать единицы. То есть этот логический элемент действительно реализует
операцию «И».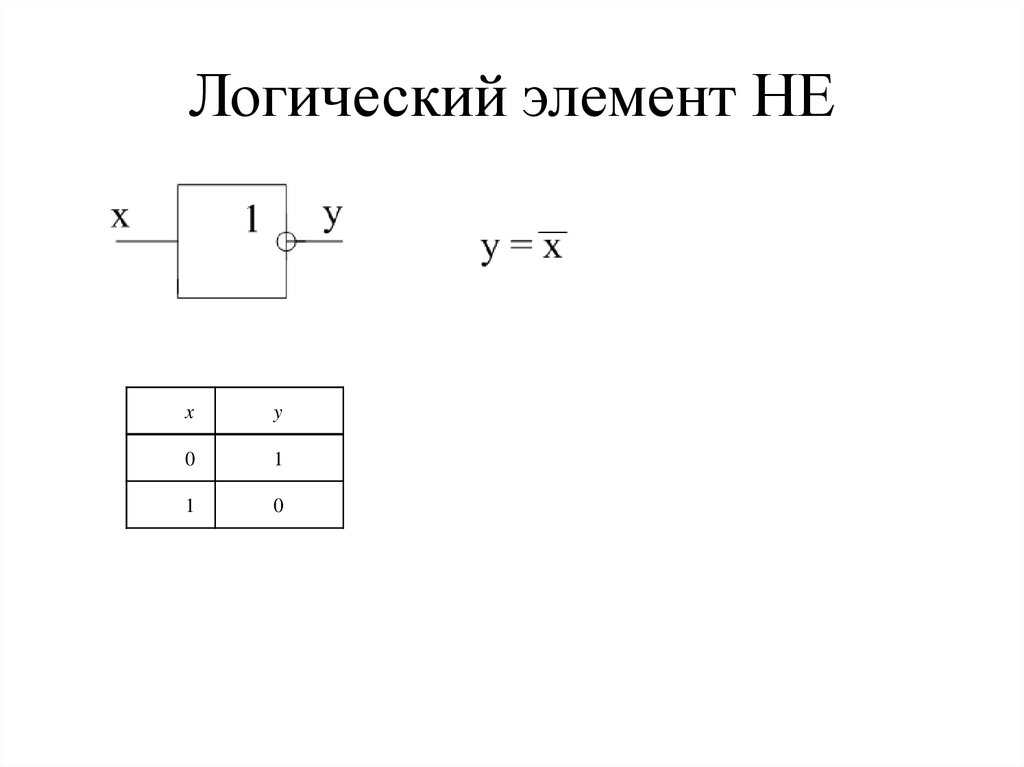
Проще всего понять, как работает логический элемент «2И», при помощи схемы, построенной на идеализированных ключах с электронным управлением, как это показано на рисунке 2. В приведенной принципиальной схеме ток будет протекать только тогда, когда оба ключа будут замкнуты, а, значит, единичный уровень на ее выходе появится только при двух единицах на входе.
Рисунок 4. Принципиальная схема логического элемента «2И»
Условно-графическое изображение схемы, выполняющей логическую функцию «2И», на принципиальных схемах приведено на рисунке 3, и с этого момента схемы, выполняющие функцию “И” будут приводиться именно в таком виде. Это изображение не зависит от конкретной принципиальной схемы устройства, реализующей функцию логического умножения.
Рисунок 5. Условно-графическое изображение логического элемента «2И»
Точно так же описывается и функция логического умножения трёх переменных:
F (x 1 ,x 2 ,x 3)=x 1 ^x 2 ^x 3
Её таблица истинности будет содержать уже восемь строк (2 3 = 4).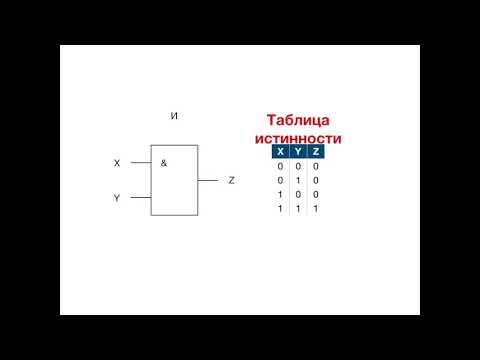 Таблица истинности трёхвходовой схемы
логического умножения «3И» приведена в таблице 3, а условно-графическое изображение на рисунке 4. В схеме же
логического элемента «3И», построенной по принципу схемы, приведённой на рисунке 2, придётся добавить третий ключ.
Таблица истинности трёхвходовой схемы
логического умножения «3И» приведена в таблице 3, а условно-графическое изображение на рисунке 4. В схеме же
логического элемента «3И», построенной по принципу схемы, приведённой на рисунке 2, придётся добавить третий ключ.
Таблица 3. Таблица истинности схемы, выполняющей логическую функцию «3И»
| In1 | In2 | In3 | Out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Получить подобную таблицу истинности можно при помощи схемы исследования логического элемента «3И», подобной
схеме исследования логического инвертора, приведенной на рисунке 3.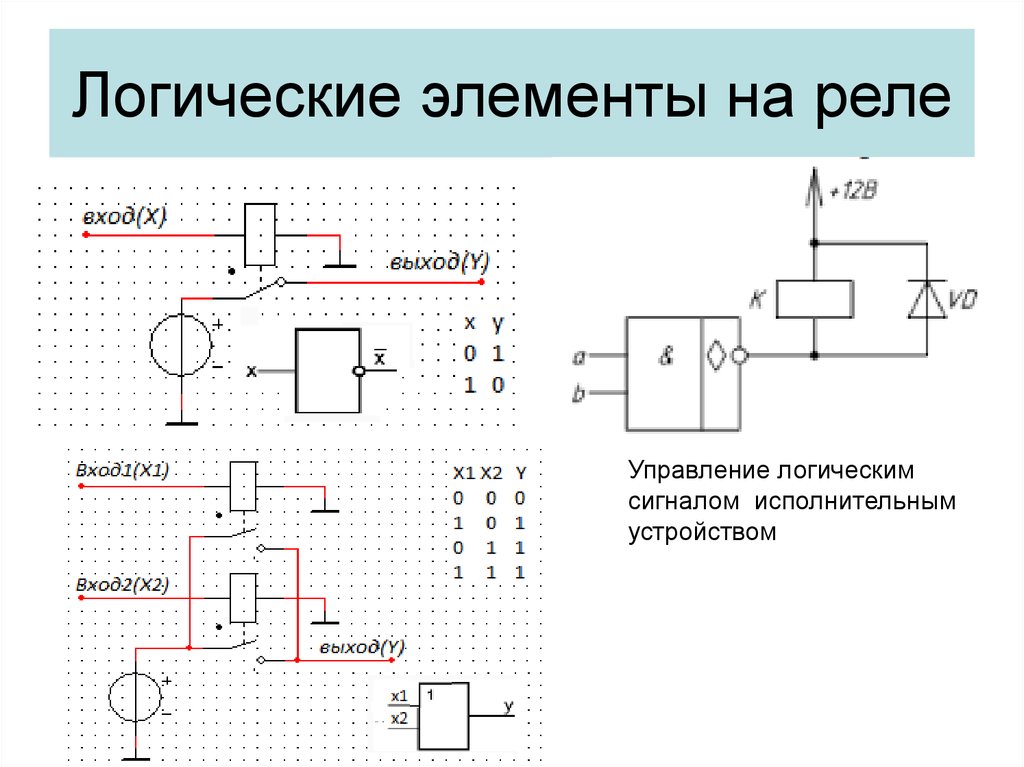
Рисунок 6. Условно-графическое обозначение схемы, выполняющей логическую функцию «3И»
Логический элемент «ИЛИ»
Следующим простейшим логическим элементом является схема, реализующая операцию логического сложения «ИЛИ»:
F(x 1 ,x 2) = x 1 Vx 2
где символ V обозначает функцию логического сложения. Иногда эта же функция записывается в другом виде:
F(x 1 ,x 2) = x 1 Vx 2 = x 1 +x 2 = x 1 |x 2 .
То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 4. В формуле, приведенной выше использовано два аргумента. Поэтому логический элемент, выполняющий эту функцию имеет два входа. Такой элемент обозначается «2ИЛИ». Для элемента «2ИЛИ» таблица истинности будет состоять из четырех строк (2 2 = 4).
Таблица 4. Таблица истинности логического элемента «2ИЛИ»
| In1 | In2 | Out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Как и в случае, рассмотренном для , воспользуемся для реализации схемы
«2ИЛИ» ключами.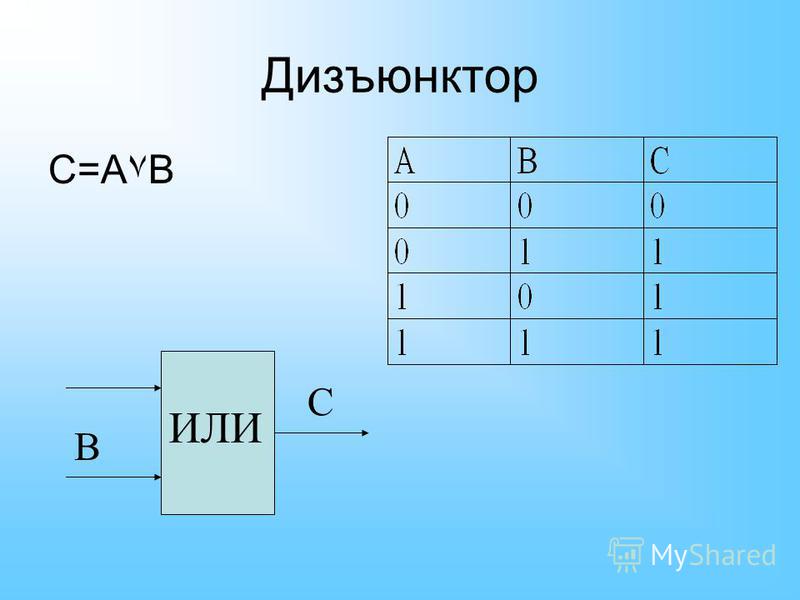 На этот раз соединим ключи параллельно. Схема, реализующая таблицу истинности 4, приведена на
рисунке 5. Как видно из приведённой схемы, уровень логической единицы появится на её выходе, как только будет замкнут
любой из ключей, то есть схема реализует таблицу истинности, приведённую в таблице 4.
На этот раз соединим ключи параллельно. Схема, реализующая таблицу истинности 4, приведена на
рисунке 5. Как видно из приведённой схемы, уровень логической единицы появится на её выходе, как только будет замкнут
любой из ключей, то есть схема реализует таблицу истинности, приведённую в таблице 4.
Рисунок 7. Принципиальная схема логического элемента «2ИЛИ»
Так как функция логического суммирования может быть реализована различными принципиальными схемами, то для обозначения этой функции на принципиальных схемах используется специальный символ «1», как это приведено на рисунке 6.
Рисунок 6. Условно-графическое изображение логического элемента, выполняющего функцию «2ИЛИ»
Дата последнего обновления файла 29.03.2018
Литература:
Со статьей «логические элементы» читают:
Любая логическая схема без памяти полностью описывается таблицей истинности… Для реализации таблицы истинности достаточно рассмотреть только те строки.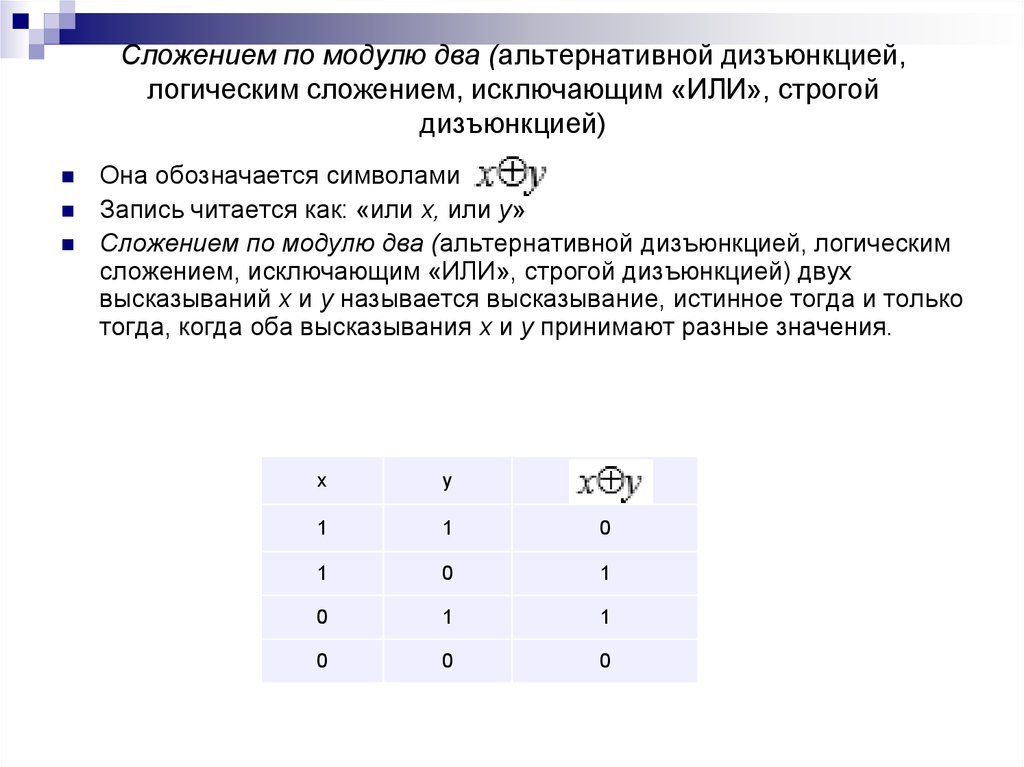 ..
..
http://сайт/digital/SintSxem.php
Декодеры (дешифраторы) позволяют преобразовывать одни виды бинарных кодов в другие. Например…
http://сайт/digital/DC.php
Достаточно часто перед разработчиками цифровой аппаратуры встаёт обратная задача. Требуется преобразовать восьмиричный или десятичный линейный код в…
http://сайт/digital/Coder.php
Мультиплексорами называются устройства, которые позволяют подключать несколько входов к одному выходу…
http://сайт/digital/MS.php
Демультиплексорами называются устройства… Существенным отличием от мультиплексора является…
http://сайт/digital/DMS.php
Работа простейших логических элементов, триггеров, счетчиков, дешифраторов, шифраторов, компараторов, регистров сдвига
Простейшие логические элементы, триггеры, счетчики, дешифраторы, шифраторы, компараторы, регистры сдвига, сумматоры
Аналоги логических микросхем
Продаю платы и наборы микросхем на Орион 128, куплю микросхемы ПЗУ и ОЗУ.
 Магазин запчастей ПК Орион-128
Магазин запчастей ПК Орион-128
Логические элементы выпускаются в виде — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. И так:
Логический элемент «И» — конъюнкция, логическое умножение, AND.
Логический элемент И «И» — логический элемент, выполняющий над
входными данными операцию конъюнкции или логического умножения. Данный
элемент может иметь от 2 до 8 (наиболее распространены в производстве
элементы «И» с 2, 3, 4 и 8 входами) входов и один выход. Условные
обозначения логических элементов «И» с разным количеством входов
приведены на рисунке. В тексте логический элемент «И» с тем или иным
числом входов обозначается как «2И», «4И» и т. д. — элемент «И» с двумя
входами, с четырьмя входами и т. д.
д.
Таблица истинности для элемента 2И
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль. На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
Логический элемент «ИЛИ» — дизъюнкция, логическое сложение, OR
Логический элемент ИЛИ «ИЛИ» — логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения.
Он так же как и элемент «И» выпускается с двумя, тремя,
четырьмя и т. д. входами и с одним выходом. Условные обозначения
логических элементов «ИЛИ» с различным количеством входов показаны на
рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
Таблица истинности для элемента 2ИЛИ
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица. На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».
Логический элемент «НЕ» — отрицание, инвертор, NOT
Логический элемент НЕ «НЕ» — логический элемент, выполняющий над входными данными операцию логического отрицания.
Данный элемент, имеющий один выход и только один вход, называют
еще инвертором, поскольку он на самом деле инвертирует (обращает)
входной сигнал.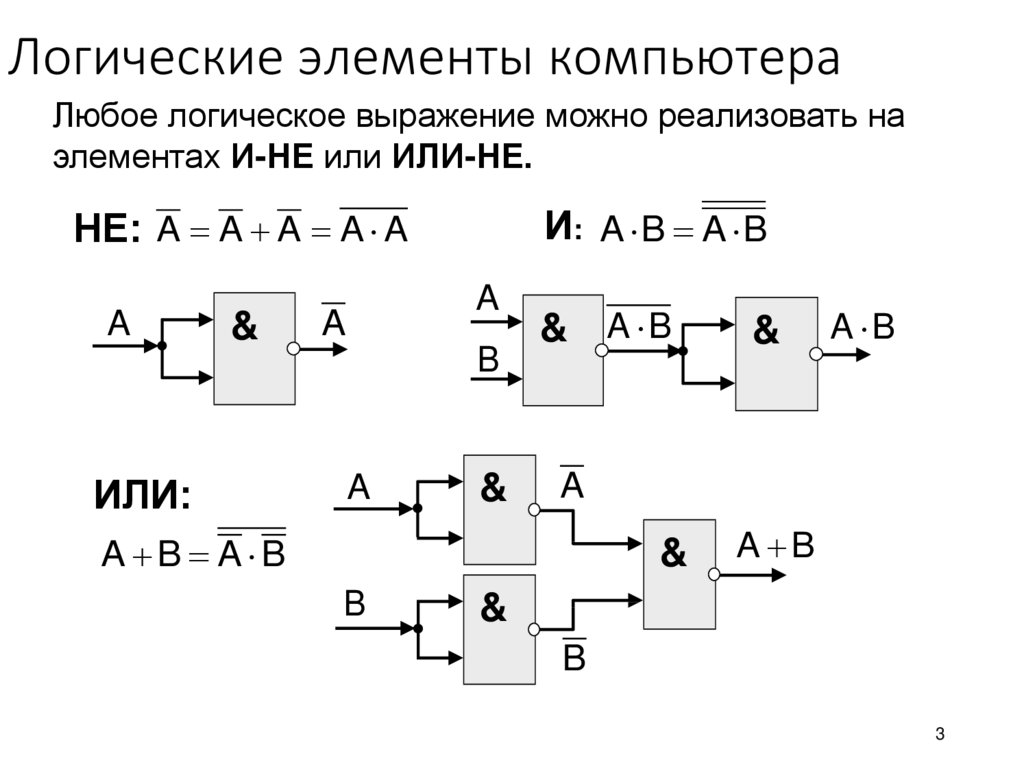 На рисунке приведено условное обозначение логического
элемента «НЕ».
На рисунке приведено условное обозначение логического
элемента «НЕ».
Таблица истинности для элемента НЕ
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот. На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Логический элемент «И-НЕ» — конъюнкция (логическое умножение) с отрицанием, NAND
Логический элемент И-НЕ «И-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход.
Другими словами, это в принципе элемент «И», дополненный элементом
«НЕ». На рисунке приведено условное обозначение логического элемента
«2И-НЕ».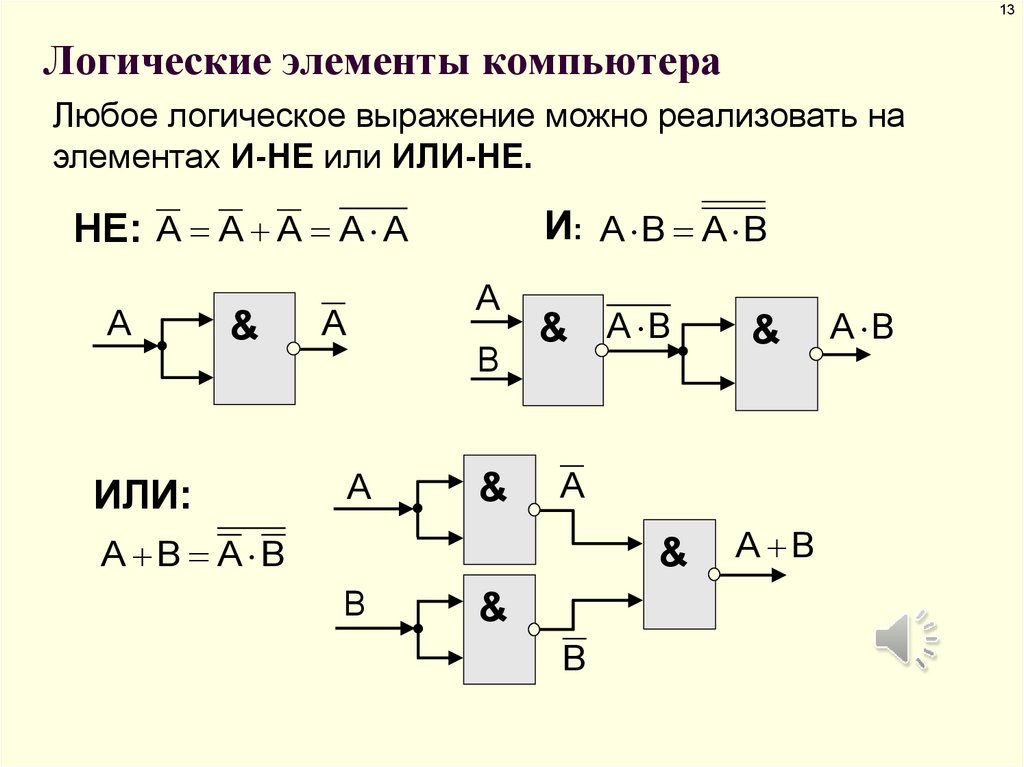
Таблица истинности для элемента И-НЕ
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
Логический элемент «ИЛИ-НЕ» — дизъюнкция (логическое сложение) с отрицанием, NOR
Логический элемент ИЛИ-НЕ «ИЛИ-НЕ» — логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход.
Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» —
инвертором. На рисунке приведено условное обозначение логического
элемента «2ИЛИ-НЕ».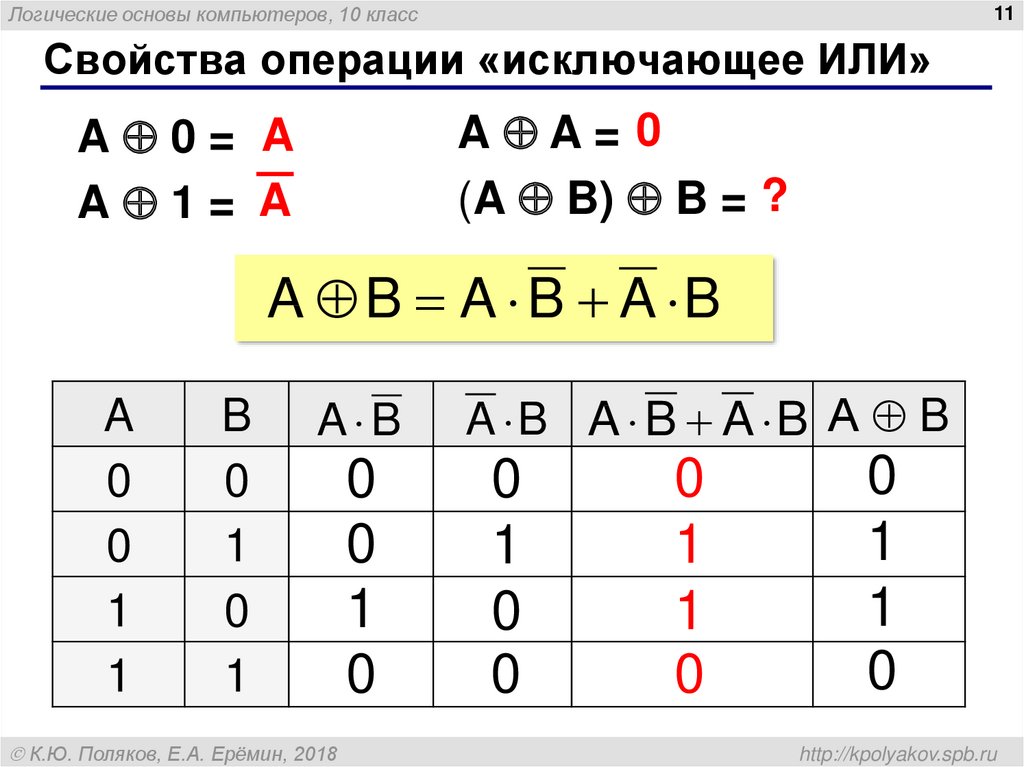
Таблица истинности для элемента ИЛИ-НЕ
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае — на оба входа подаются одновременно низкие потенциалы. Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
Логический элемент «исключающее ИЛИ» — сложение по модулю 2, XOR
Логический элемент исключающее ИЛИ «исключающее ИЛИ» — логический элемент, выполняющий над входными данными операцию логического сложения по модулю 2, имеет два входа и один выход.
Часто данные элементы применяют в схемах контроля. На рисунке
приведено условное обозначение данного элемента. Изображение в западных
схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне
входа, в отечественной — как «ИЛИ», только вместо «1» будет написано
«=1».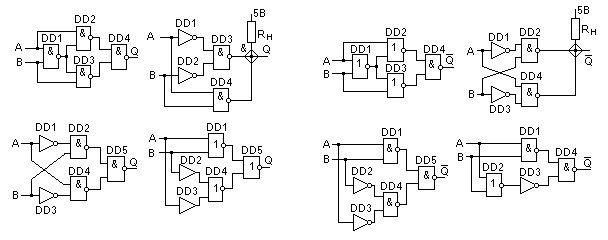
Таблица истинности исключающее ИЛИ
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Продолжение следует….
Купить платы, наборы микросхем на Орион128, КР565РУ5В, КР565ру7В, к565ру5г AU, к565ру7г Au в позолоте, куплю микросхемы
Полезные и интересные статьи
На предыдущую страницу На главную страницу На следующую страницу
Исключающее или не
Физически логические элементы могут быть выполнены механическими, электромеханическими на электромагнитных реле , электронными в частности, на диодах или транзисторах , пневматическими, гидравлическими , оптическими и другими. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Логические элементы выполняют логическую функцию операцию над входными сигналами операндами, данными. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Логические элементы выполняют логическую функцию операцию над входными сигналами операндами, данными. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Логический элемент Исключающее ИЛИ
- вентиль исключающее ИЛИ-НЕ
- Список логических символов
- ПРИМЕНЕНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
- Схема ИСКЛЮЧАЮЩЕЕ ИЛИ
- Логические элементы и таблицы истинности
- Логические элементы с числом входов больше двух
- Логические элементы
- Логические элементы
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 07 Исключающее ИЛИ
youtube.com/embed/yXy8NsmBQy8″ frameborder=»0″ allowfullscreen=»»/>Логический элемент Исключающее ИЛИ
Используя наш сайт, вы подтверждаете, что прочитали и поняли политику о куки , политику конфиденциальности и пользовательское соглашение. Stack Overflow на русском — это сайт вопросов и ответов для программистов. Регистрация займёт не больше минуты. Если на пальцах объяснять, то логическое ИЛИ будет истиной, когда хотя бы один из операндов — истина.
Исключающее ИЛИ будет истиной, если операнды не равны, и ложью, если операнды равны. Присоединиться к сообществу. Лучшие ответы получают голоса и поднимаются наверх. Главная Вопросы Метки Участники. Задать вопрос. Вопрос задан 3 года 7 месяцев назад. Последняя активность 3 года 7 месяцев назад. Просмотрен 6k раза. Flowneee 3, 1 1 золотой знак 15 15 серебряных знаков 29 29 бронзовых знаков.
Ilnyr Ilnyr 8 8 серебряных знаков 20 20 бронзовых знаков. Flowneee Flowneee 3, 1 1 золотой знак 15 15 серебряных знаков 29 29 бронзовых знаков. Легко запомнить: XOR дает ноль, когда нет альтернативы , Зарегистрируйтесь или войдите Регистрация через Google.
Легко запомнить: XOR дает ноль, когда нет альтернативы , Зарегистрируйтесь или войдите Регистрация через Google.
Регистрация через Facebook. Регистрация через почту. Отправить без регистрации Имя. Почта Необходима, но никому не показывается. Важное на Мете. An apology to our community, and next steps. Предполагайте добрые намерения. Лучшие истории о вопросах на сайте. Похожие 0. Лента вопроса. Stack Overflow на русском лучше работает с включенным JavaScript.
вентиль исключающее ИЛИ-НЕ
На рис. По простому, суть данного элемента сводится к следующему, сигнал на выходе появляется только в том случае, когда логические уровни на входах не одинаковые. Выходные импульсы имеют стабильные фронты и срезы. Длительность каждого выходного импульса равна утроенному времени задержки переключения каждого из трех элементов. Временной промежуток между фронтами выходных импульсов равен длительности входного импульса. Так же это устройство удваивает частоту входного сигнала. Здесь показаны все возможные логические уровни на каждом из используемых логически элементов 2-И-НЕ. y, Логическое исключающее ИЛИ или побитовое логическое Не связанные с приоритетом и ассоциативностью операторов.
y, Логическое исключающее ИЛИ или побитовое логическое Не связанные с приоритетом и ассоциативностью операторов.
Список логических символов
В отличие от аналоговых электронных устройств, в цифровых устройствах ЦУ входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением ГОСТ 2. Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции. Операция логическое «НЕ» NOT , изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Следующие соотношения являются аксиомами. Соотношения двойственности для n переменных, часто записывают в виде:. Наряду с тремя основными логическими функциями, называемыми также переключательными, существуют и другие.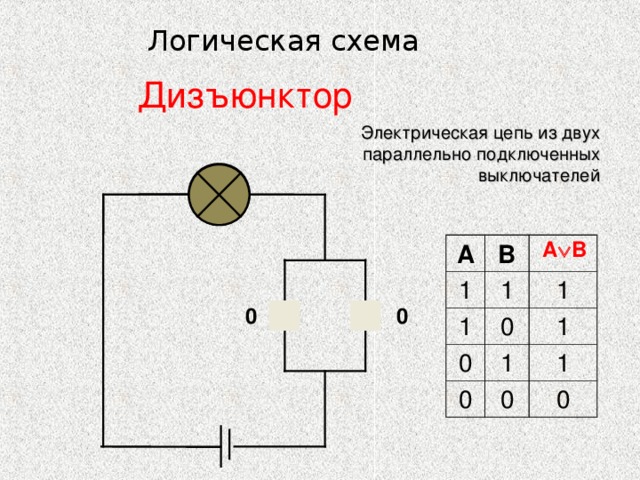
ПРИМЕНЕНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
C предоставляет ряд операторов, поддерживаемых встроенными типами. C provides a number of operators supported by the built-in types. Например арифметические операторы выполняют арифметические операции с числовыми операндами, а логические операторы выполняют логические операции с операндами bool. For example, arithmetic operators perform arithmetic operations with numeric operands and Boolean logical operators perform logical operations with the bool operands.
В логике обычно используется много символов для выражения логических сущностей.
Схема ИСКЛЮЧАЮЩЕЕ ИЛИ
В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы. Любое цифровое устройство — персональный компьютер, или современная система автоматики состоит из цифровых интегральных микросхем ИМС , которые выполняют определённые сложные функции. Но для выполнения одной сложной функции необходимо выполнить несколько простейших функций.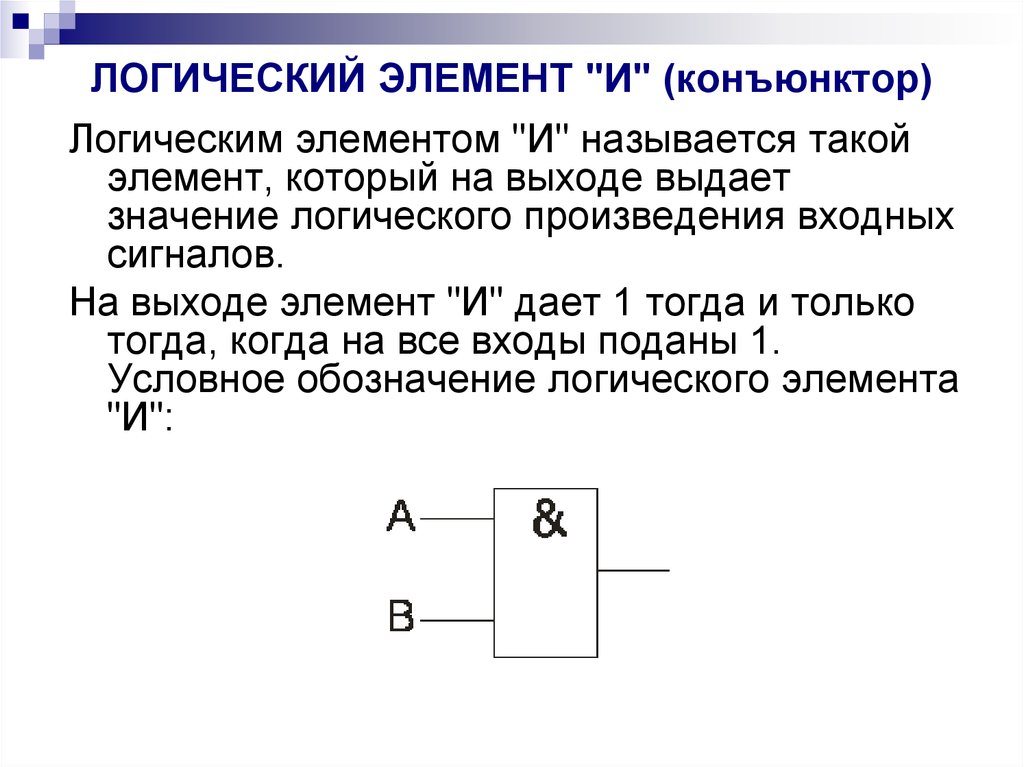 Эти функциональные узлы состоят из простейших логических элементов, которые, в свою очередь состоят из полупроводниковых транзисторов, диодов и резисторов. Тут и приходят на помощь — логические элементы.
Эти функциональные узлы состоят из простейших логических элементов, которые, в свою очередь состоят из полупроводниковых транзисторов, диодов и резисторов. Тут и приходят на помощь — логические элементы.
Логические элементы и таблицы истинности
Компьютерные сети Системное программное обеспечение Информационные технологии Программирование. Дата добавления: ; просмотров: ; Нарушение авторских прав. Несмотря на простоту реализуемой логической функции способов создания инверторов немного рис. Импликатор и элемент равнозначности нуждаются в нулевом логическом уровне, а элементы запрета и исключающее ИЛИ — в уровне единицы. Способов реализации дизъюнкции рис. Отметим, что проще всего заменить дизъюнкторы элементами ИЛИ-НЕ и импликаторами, которые включают в себя операцию дизъюнкции в качестве одной из основных. В этом случае для замены требуется всего два элемента рис.
Таблица истинности для исключающего ИЛИ: Исключающее ИЛИ будет истиной, если операнды не равны, и ложью, если операнды. 30
30
Библиотека: Базовые Введён в: 2. По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. Если все входы не подключены, то на выходе значение ошибки X. Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов.
Нетрудно заметить см.
Логические элементы
Цифровой сигнал может быть потенциальным или импульсным. Элементами потенциального цифрового сигнала являются потенциалы двух уровней. Поэтому такие сигналы называются логическими. Логическое сложение дизъюнкция переменных X 1 ,X 2 , Таблица истинности операции ИЛИ двух переменных приведёна ниже:. Элемент, выполняющий дизъюнкцию, называется дизъюнктором или элементом ИЛИ.
Вот о них мы и поговорим сейчас. Логический элемент — это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе. Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов.
Базовые логические элементы и, или, не
Схема И реализует конъюнкцию (логическое умножение) двух или более логических значений.
Эл. | |||
Таблица истинности | ||
х | y | х и у |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Единица
на выходе схемы И будет тогда и только
тогда, когда на всех входах будут единицы.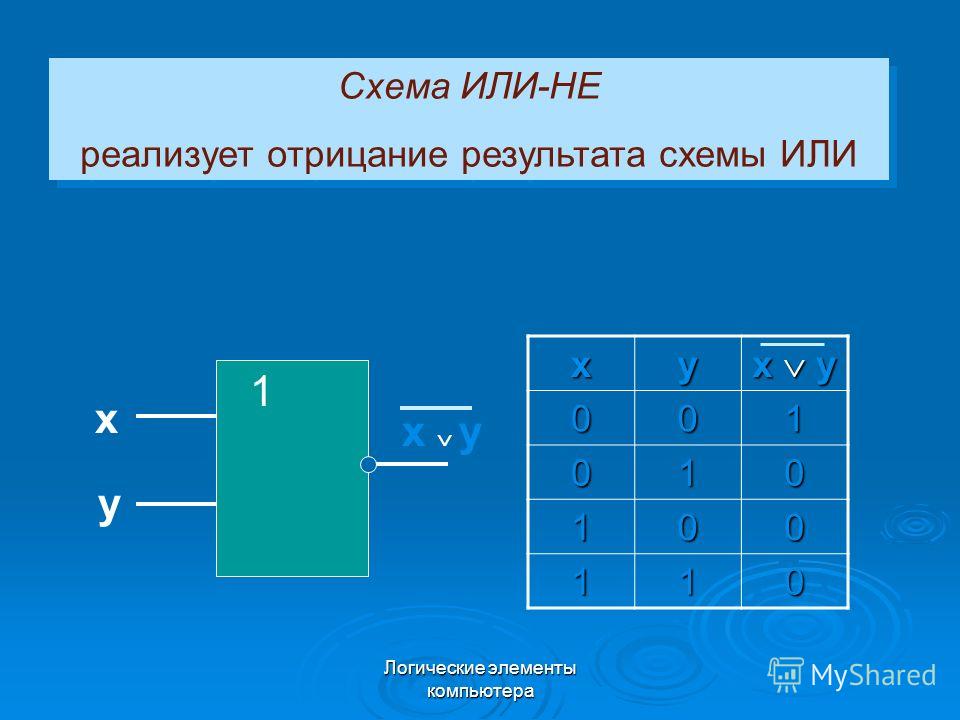 у (читается как «х
и у»). Операция конъюнкции на функциональных
схемах обозначается знаком & (читается
как «амперсэнд»), являющимся сокращенной
записью английского слова and.
у (читается как «х
и у»). Операция конъюнкции на функциональных
схемах обозначается знаком & (читается
как «амперсэнд»), являющимся сокращенной
записью английского слова and.
Схема ИЛИ реализует дизъюнкцию (логическое сложение) двух или более логических значений.
Эл. схема | |||
Таблица истинности | ||
х | y | х или у |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 10 |
1 | 1 | 1 |
Когда
хотя бы на одном входе схемы ИЛИ будет
единица, на ее выходе также будет
единица.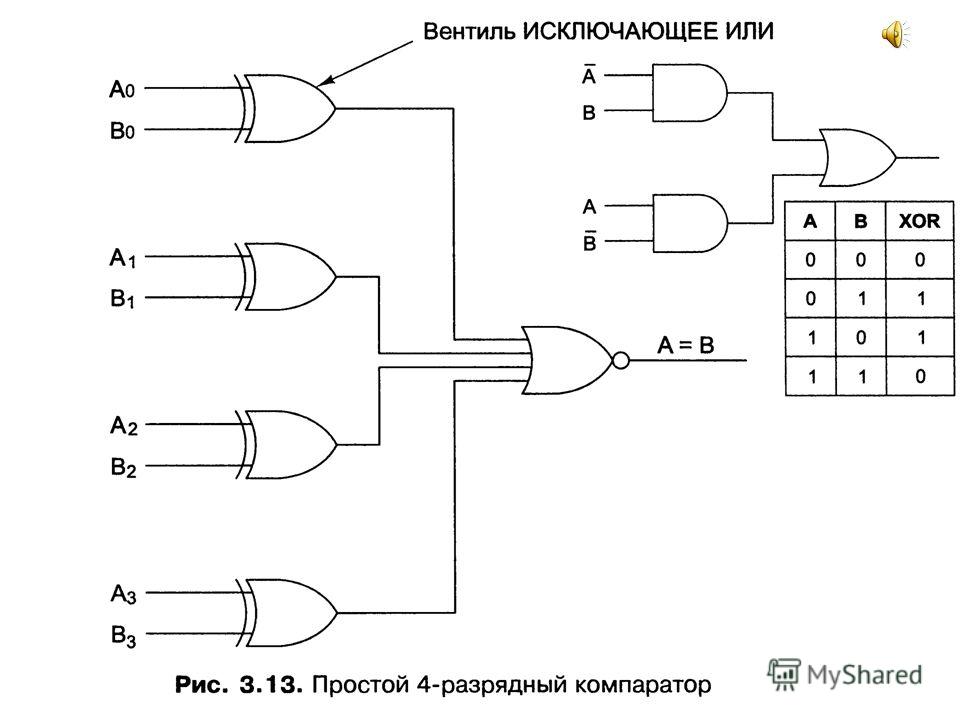 Знак
«1» на схеме — от устаревшего обозначения
дизъюнкции как «>=!» (т.е. значение
дизъюнкции равно единице, если сумма
значений операндов больше или равна
1). Связь между выходом z этой схемы и
входами х и у описывается соотношением
z = х или у.
Знак
«1» на схеме — от устаревшего обозначения
дизъюнкции как «>=!» (т.е. значение
дизъюнкции равно единице, если сумма
значений операндов больше или равна
1). Связь между выходом z этой схемы и
входами х и у описывается соотношением
z = х или у.
Схема НЕ (инвертор) реализует операцию отрицания.
| |||||||||
Связь
между входом х этой схемы и выходом z
можно записать соотношением Z =
,
где х читается как «не х» или «инверсия. Если
на входе схемы 0, то на выходе 1. Когда на
входе 1 на выходе 0.
Если
на входе схемы 0, то на выходе 1. Когда на
входе 1 на выходе 0.
Таблица истинности — это таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.
Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Итак, какие бывают элементы?
Элемент «И» (AND)
Иначе его называют «конъюнктор».
Для того, чтобы понять как он
работает, нужно нарисовать таблицу, в
которой будут перечислены состояния
на выходе при любой комбинации входных
сигналов.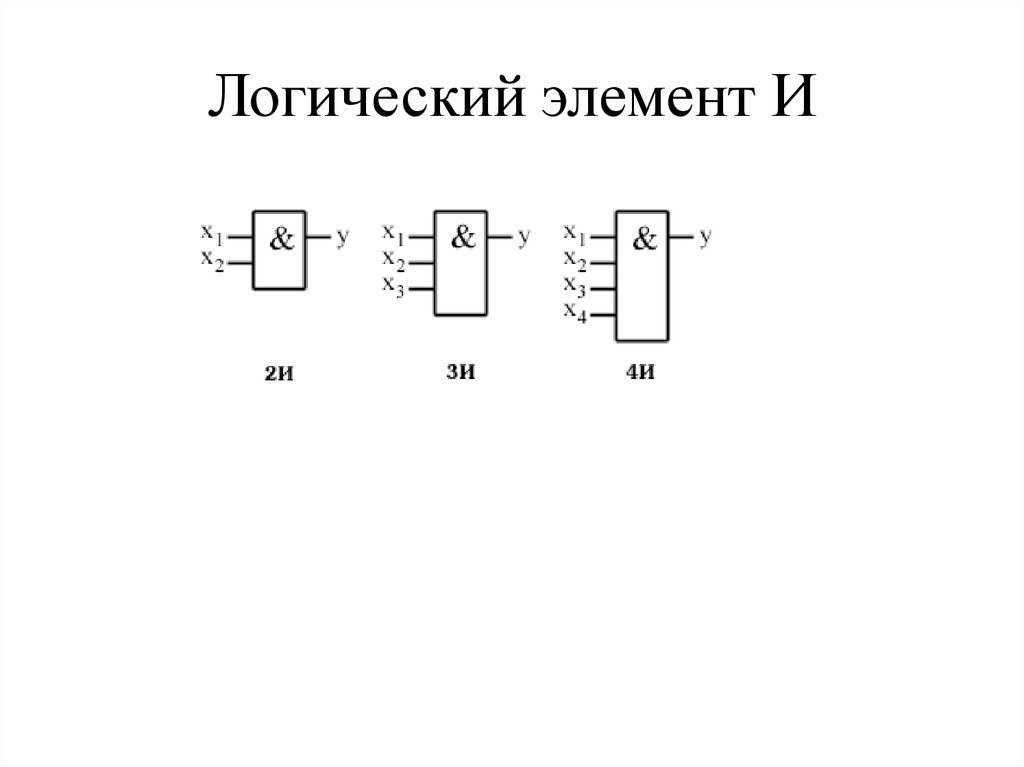 Такая таблица называется
«таблица истинности». Таблицы
истинности широко применяются в цифровой
технике для описания работы логических
схем.
Такая таблица называется
«таблица истинности». Таблицы
истинности широко применяются в цифровой
технике для описания работы логических
схем.
Вот так выглядит элемент «И» и его таблица истинности:
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.
Элемент «ИЛИ» (OR)
По другому, его зовут «дизъюнктор».
Любуемся:
Опять же, название говорит само
за себя.
На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.
Элемент «НЕ» (NOT)
Чаще, его называют «инвертор».
Надо чего-нибудь говорить по поводу его работы?
Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».
Элемент «Исключающее ИЛИ»
(XOR) Сложе́ние по мо́дулю 2, логи́ческое сложе́ние, исключа́ющее
и́ли, строгая дизъюнкция —
булева функция и логическая операция.
Результат выполнения операции является
истинным только при условии, если
является истинным в точности один из
аргументов. Такая операция естественным
образом возникает в кольце вычетов
по модулю 2, откуда и происходит
название операции.
Он вот такой:
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Дайте определение ЛЭ. Нарисуйте ЛЭ базовых ЛО.
Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Работу логических элементов описывают с помощью таблиц истинности.
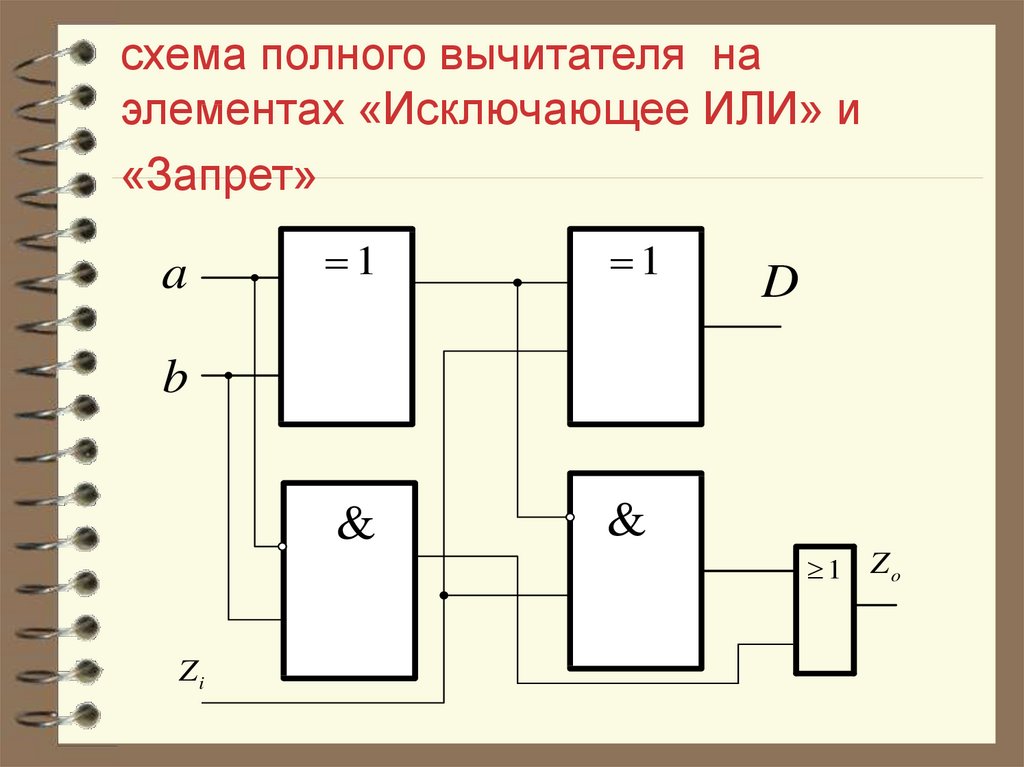 ru 🎓
ru 🎓1
Первый слайд презентации: Логические операции импликация, эквиваленция, исключающее ИЛИ
Изображение слайда
2
Слайд 2: Логическая операция импликация
Логическая операция импликация А В имеет следующую таблицу истинности: A B А B 0 0 0 1 1 0 1 1 1 1 1 0
Изображение слайда
3
Слайд 3: Логическая операция импликация
Логическую переменную А принято называть посылкой, а логическую переменную В – следствием. A B А B 0 0 0 1 1 0 1 1 1 1 1 0
Изображение слайда
4
Слайд 4: Логическая операция импликация
Из таблицы истинности видно, что операция «импликация» ложна в единственном случае: если посылка истина, а следствие – ложно.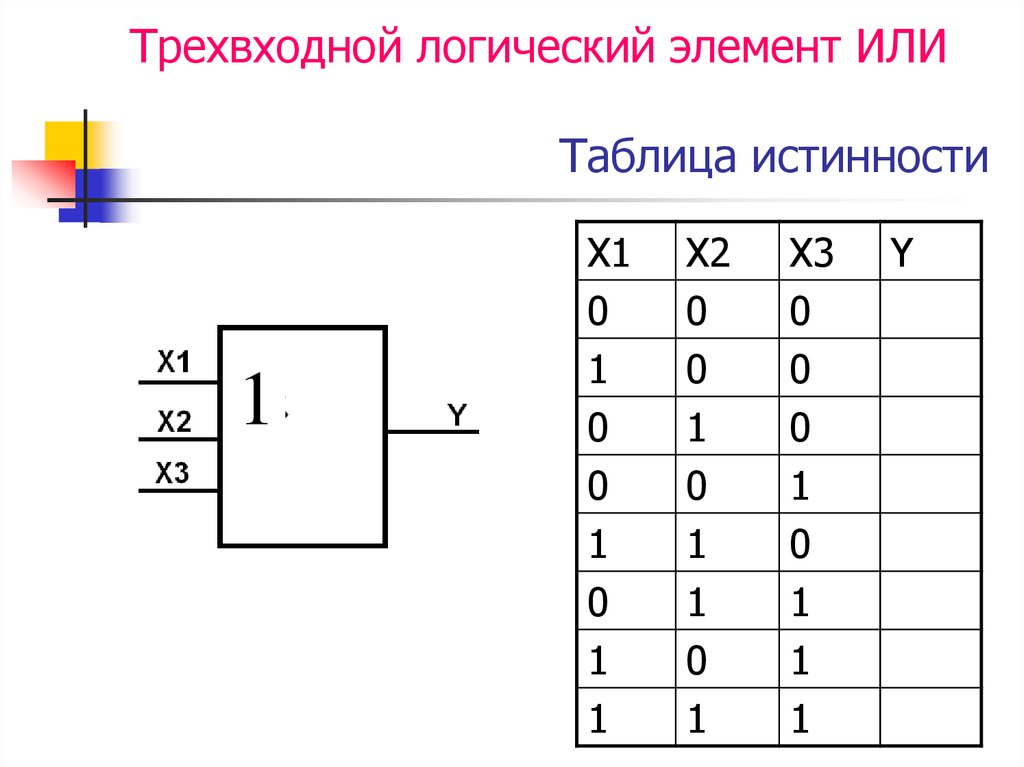 A
B
А B
0
0
0
1
1
0
1
1
1
1
1
0
A
B
А B
0
0
0
1
1
0
1
1
1
1
1
0
Изображение слайда
5
Слайд 5: Пример импликации
Рассмотрим высказывание «Если идет дождь, то на улице сыро». «Идет дождь» — посылка, «на улице сыро» — следствие.
Изображение слайда
6
Слайд 6: Пример импликации
Если не идет дождь и не сыро на улице, то результат импликации – истина. A B А B 0 0 1 0 1 1 1 0 0 1 1 1
Изображение слайда
7
Слайд 7: Пример импликации
Если идет дождь и на улице сыро, то операция импликации – истина.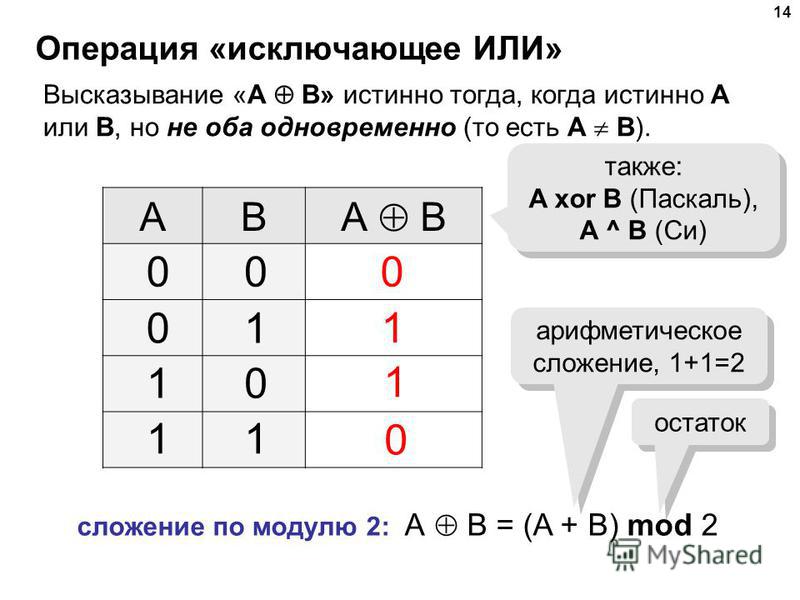 A
B
А B
0
0
1
0
1
1
1
0
0
1
1
1
A
B
А B
0
0
1
0
1
1
1
0
0
1
1
1
Изображение слайда
8
Слайд 8: Пример импликации
На улице может быть сыро без дождя, например когда прошла поливальная машина или дождь прошел накануне, результат импликации – истина A B А B 0 0 1 0 1 1 1 0 0 1 1 1
Изображение слайда
9
Слайд 9: Пример импликации
Результат операции ложен лишь тогда, когда дождь идет, а на улице не сыро. A B А B 0 0 1 0 1 1 1 0 0 1 1 1
Изображение слайда
10
Слайд 10: Операция импликации через основные логические выражения
А В = Так как их таблицы истинности совпадают для всех значений логических переменных А и В A B А В 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 A B А В 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1
Изображение слайда
11
Слайд 11: Операция эквиваленция
Операция эквиваленция А В (АВ, АВ, АВ) имеет следующую таблицу истинности A B А B 0 0 1 0 1 0 1 0 0 1 1 1
Изображение слайда
12
Слайд 12: Операция эквиваленция
Логическое выражение А В истинно тогда, когда значения логических переменных А и В совпадают.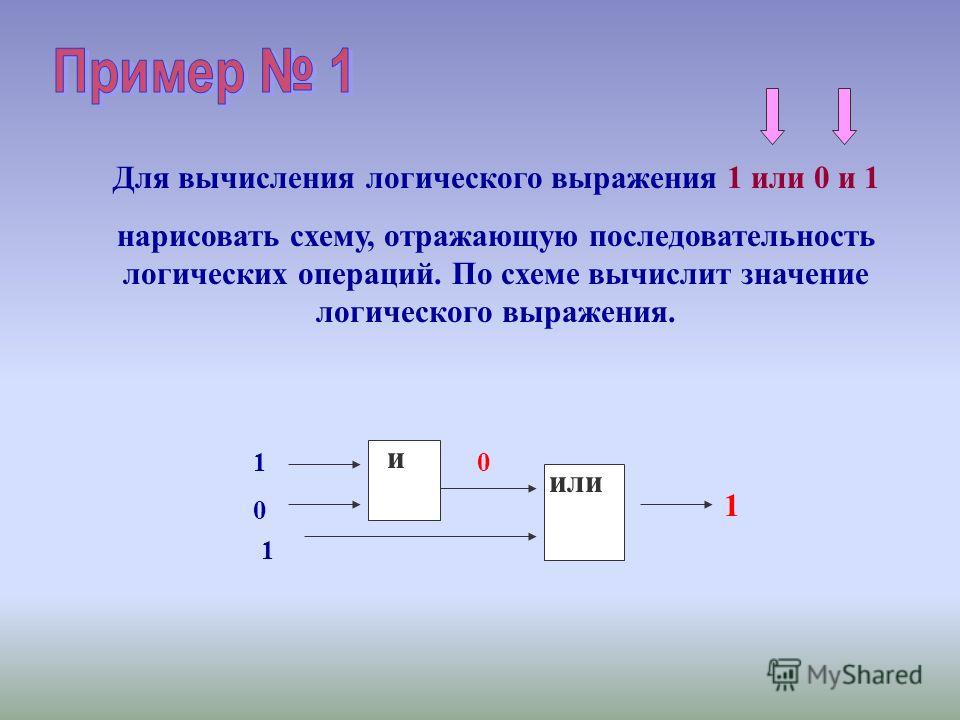 A
B
А B
0
0
1
0
1
0
1
0
0
1
1
1
A
B
А B
0
0
1
0
1
0
1
0
0
1
1
1
Изображение слайда
13
Слайд 13: Примеры истинных высказываний, построенных с использованием операции эквивалентности
День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом Добиться результата в спорте можно тогда и только тогда, когда приложено максиму усилий
Изображение слайда
14
Слайд 14: Операция эквиваленции через основные логические операции
Операцию эквиваленции можно заменить выражением, состоящим из комбинации основных логических операций – дизъюнкции, конъюнкции и инверсии А В=( А B ) (А B )= ( А B ) (А B ) так каких таблицы истинности совпадают для всех значений логических переменных А и В
Изображение слайда
15
Слайд 15: Операция исключающее ИЛИ
Операция исключающее ИЛИ А XOR B ( A B ) имеет следующую таблицу истинности A B А B 0 0 также: A xor B ( Паскаль ), A ^ B ( Си) 0 0 0 1 1 0 1 1 1 1
Изображение слайда
16
Слайд 16: Операция исключающее ИЛИ
Логическая операция исключающее ИЛИ истинно только тогда, когда значения логических переменных А и В различны A B А B 0 0 0 0 0 1 1 0 1 1 1 1
Изображение слайда
17
Слайд 17: Операция исключающее ИЛИ
Операцию исключающее ИЛИ называют также суммой по модулю 2, так как по таблице истинности видно, что функция выполняет операцию суммирования аргументов без формирования переноса, если аргументы рассматриваются как двоичные числа.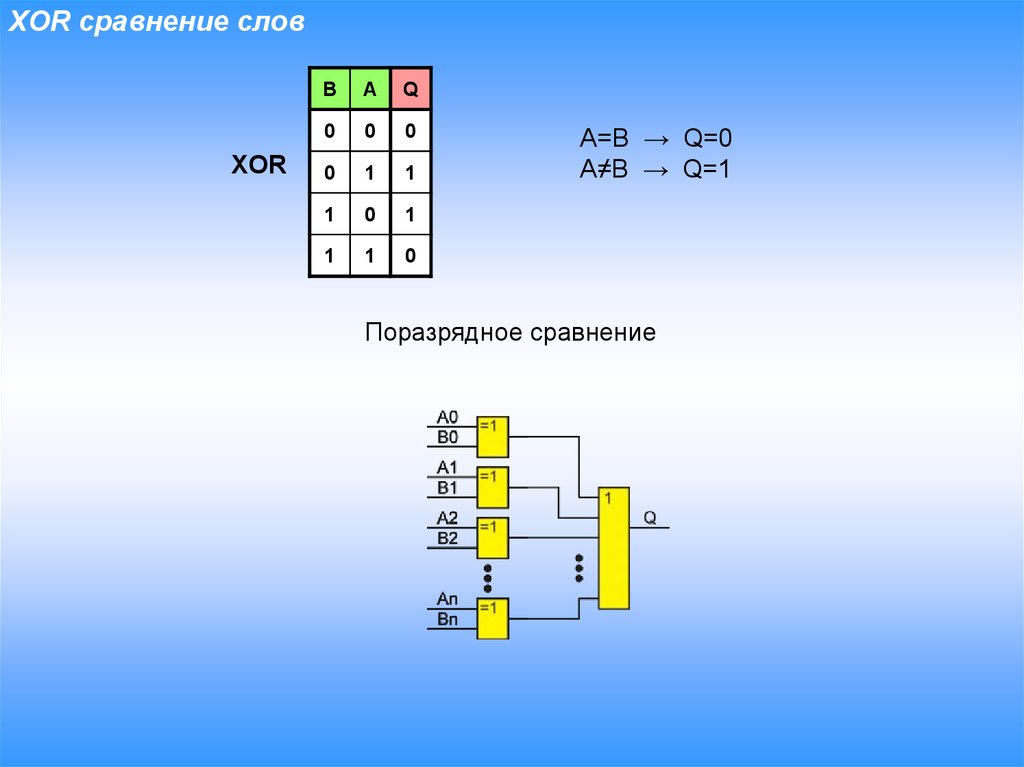 сложение по модулю 2: А B = ( A + B) mod 2
арифметическое сложение, 1+1=2
остаток
сложение по модулю 2: А B = ( A + B) mod 2
арифметическое сложение, 1+1=2
остаток
Изображение слайда
18
Слайд 18: Операция исключающее ИЛИ через основные логические операции
Операцию исключающее ИЛИ можно заменить выражением, состоящим из комбинации основных логических операций — дизъюнкции, конъюнкции и инверсии: А XOR В=( А B ) (А B )= ( А B ) (А B )
Изображение слайда
19
Слайд 19: Операция исключающее ИЛИ через основные логические операции
А XOR В=( B ) (А )= ( ) (А B ) так как их таблицы истинности совпадают для всех значений логических переменных А и В A B А XOR В ( B ) (А ) ( ) (А B ) 0 0 0 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 0 A B А XOR В 0 0 0 0 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 0
Изображение слайда
20
Слайд 20: Взаимосвязь операций исключающего ИЛИ и эквивалентности
Операция исключающее ИЛИ является отрицанием эквивалентности А XOR В= A B А XOR В А XOR В= 0 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 A B А XOR В 0 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0
Изображение слайда
21
Слайд 21: Логические элементы и основные логические устройства компьютера
21
Изображение слайда
22
Слайд 22: Логические элементы и основные логические устройства компьютера
Информация при обработке на компьютере представляются в двоичной форме, т.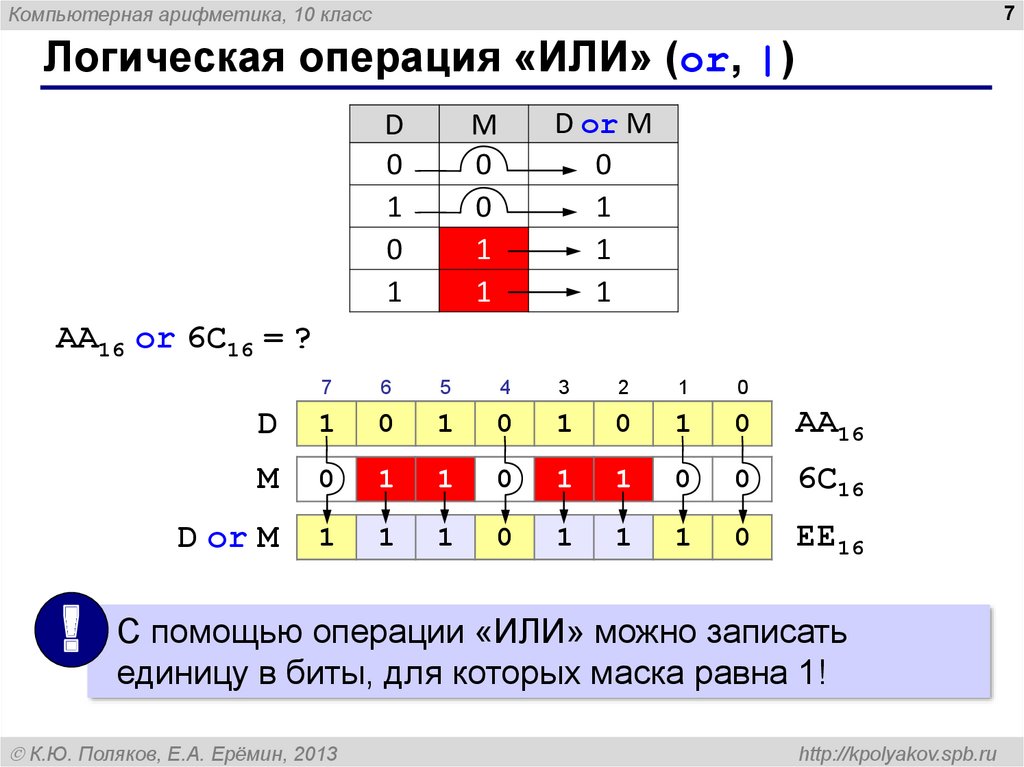 е. кодируется последовательностью, состоящей из 0 и 1, где 0 и 1 – это два разрешенных уровня электрического сигнала.
Упрощенно можно представить работу компьютера как устройства, производящего обработку двоичных электрических сигналов.
Такую обработку в компьютере выполняют устройства – логические элементы.
е. кодируется последовательностью, состоящей из 0 и 1, где 0 и 1 – это два разрешенных уровня электрического сигнала.
Упрощенно можно представить работу компьютера как устройства, производящего обработку двоичных электрических сигналов.
Такую обработку в компьютере выполняют устройства – логические элементы.
Изображение слайда
23
Слайд 23: Логические элементы
Логический элемент – это устройство, выполняющее одну из основных логических операций: И, ИЛИ, НЕ. В алгебре логики такие элементы называются: И – конъюнкция (логическое умножение), ИЛИ – дизъюнкция (логическое сложение), НЕ – отрицание.
Изображение слайда
24
Слайд 24: Техническое исполнение логических элементов
Технически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах) и др.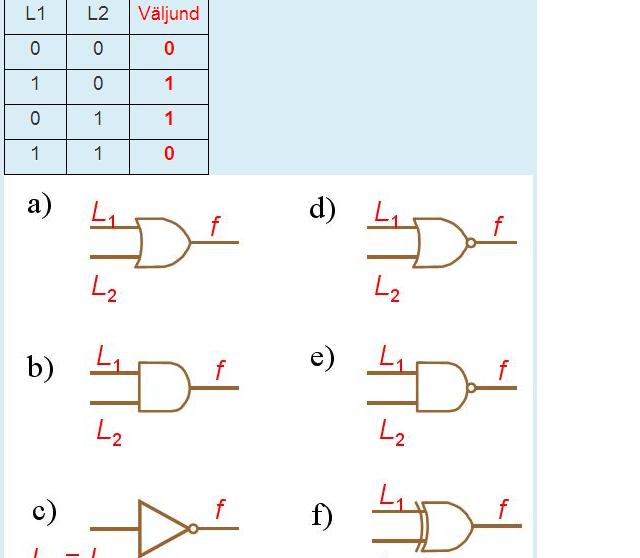 В современных компьютерах логический элемент реализуется в виде электронной схемы, которая, как правило, входит в состав микросхемы.
В современных компьютерах логический элемент реализуется в виде электронной схемы, которая, как правило, входит в состав микросхемы.
Изображение слайда
25
Слайд 25: Принцип работы логических элементов. Входные сигналы
На вход логического элемента поступают двоичные электрические сигналы, которые интерпретируются следующим образом: Один разрешенный уровень сигнала воспринимается как единица, т.е. «истина»; Другой разрешающий уровень сигнала воспринимается как 0, т.е. «ложь»
Изображение слайда
26
Слайд 26: Принцип работы логических элементов. Выходные сигналы
Сигнал на выходе логического элемента формируется в зависимости от выполняемой логической операции.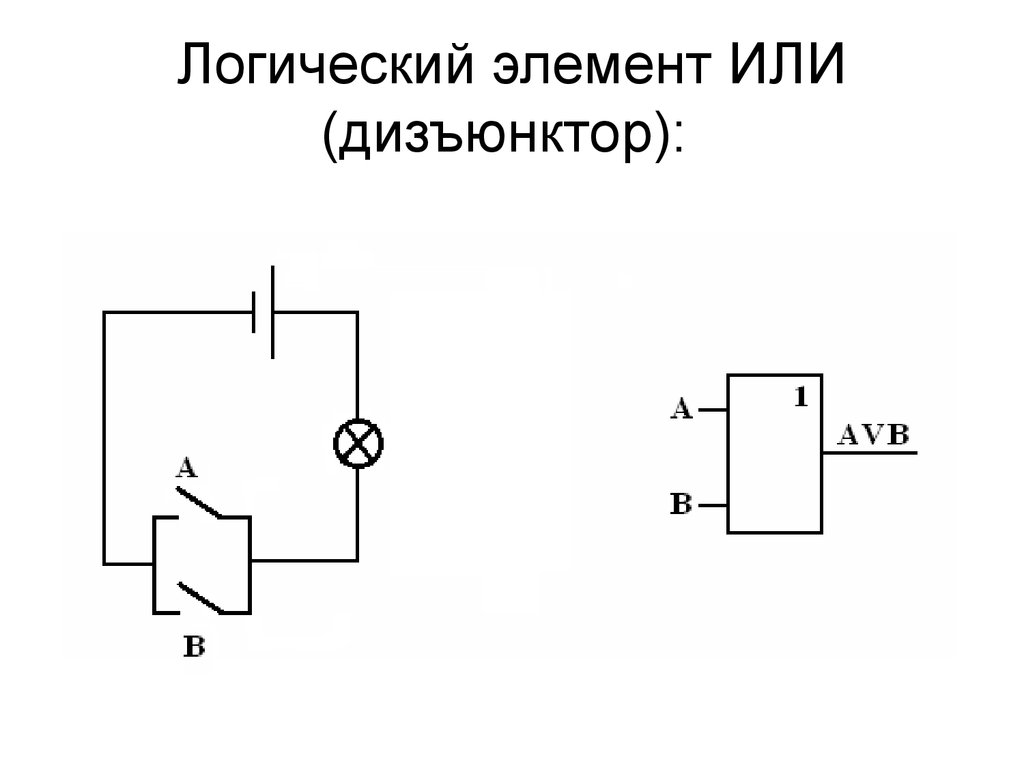 Имея в распоряжении базовые элементы И, ИЛИ, НЕ, можно спроектировать любой сложности электронное устройство обработки двоичных сигналов.
Условные обозначения логических элементов являются стандартными и используются при проектировании устройств компьютера.
Имея в распоряжении базовые элементы И, ИЛИ, НЕ, можно спроектировать любой сложности электронное устройство обработки двоичных сигналов.
Условные обозначения логических элементов являются стандартными и используются при проектировании устройств компьютера.
Изображение слайда
27
Слайд 27: Логический элемент НЕ
НЕ F = А не А 1 0 0 1
Изображение слайда
28
Слайд 28: Логический элемент ИЛИ
1 ИЛИ A B А или B 1 0 0 0 0 1 1 0 1 1 1 1
Изображение слайда
29
Слайд 29: Логический элемент И
& И A B А и B 1 0 0 0 0 1 1 0 1 1 0 1 2 3 0 0
Изображение слайда
30
Слайд 30: Пример 1
Определите логическое выражение, отражающее преобразование, которое выполняется предложенной схемой устройства.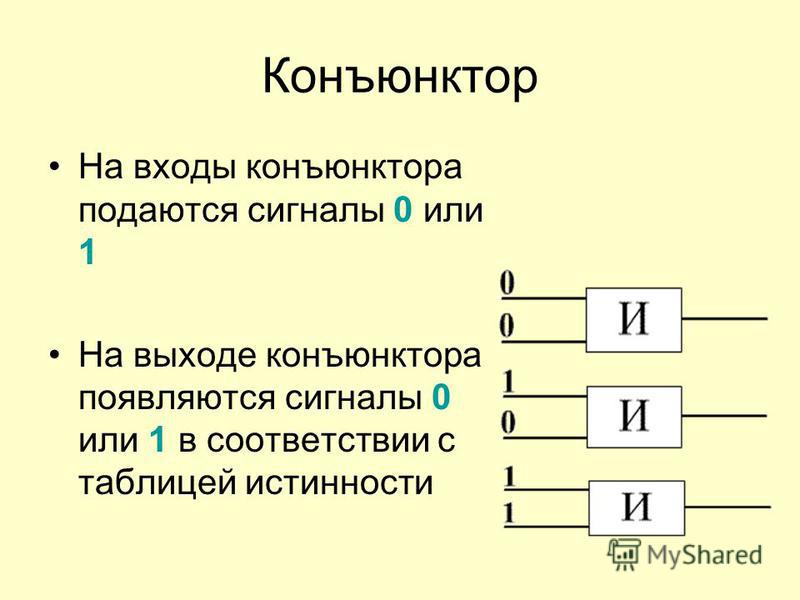 Проанализируйте его работу с помощью таблицы истинности.
Проанализируйте его работу с помощью таблицы истинности.
Изображение слайда
31
Слайд 31: Решение
На выходе первого элемента ИЛИ формируется сигнал X + Y. Сигналы X + Y и Z подаются на следующий элемент ИЛИ, на выходе которого формируется сигнал X + Y + Z Сигнал X + Y + Z подается на вход элемента НЕ, на выходе которого формируется сигнал ( X + Y + Z ).
Изображение слайда
32
Слайд 32: Решение
Таблица истинности X Y Z F 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 0
Изображение слайда
33
Последний слайд презентации: Логические операции импликация, эквиваленция, исключающее ИЛИ: Решение
Ответ: F = ( X + Y + Z ), устройство, обрабатывает три входных сигнала и формирует выходной сигнал, равный единице, только в одном случае – когда все входные сигналы равны 0.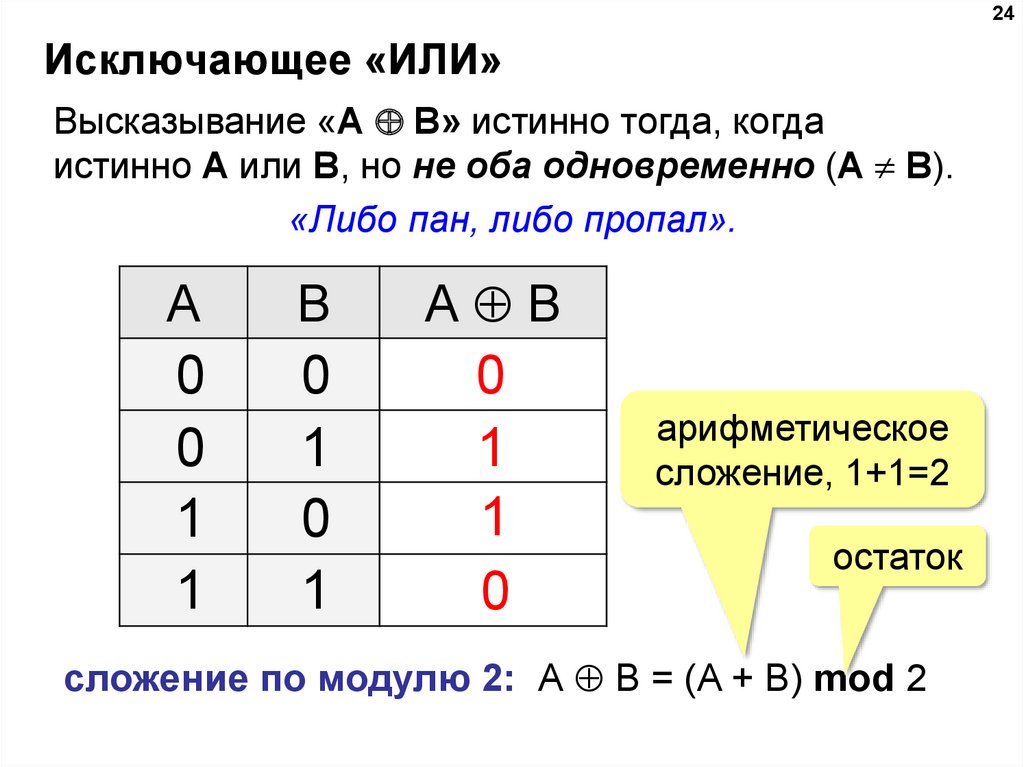
Изображение слайда
XOR — логическое исключающее ИЛИ
XOR — Логическое исключающее ИЛИ| Код операции | Инструкция | Оп/Ан | 64-битный режим | Режим совместимости/этапа | Описание |
|---|---|---|---|---|---|
| 34 ib | XOR AL, i мм8 | я | Действительный | Действительный | AL XOR imm8. |
| 35 | XOR AX, i мм16 | я | Действительный | Действительный | AX XOR imm16. |
| 35 идентификатор | XOR EAX, i мм32 | я | Действительный | Действительный | EAX XOR imm32. |
| REX.W + 35 идентификатор | XOR RAX, i мм32 | я | Действительный | Н.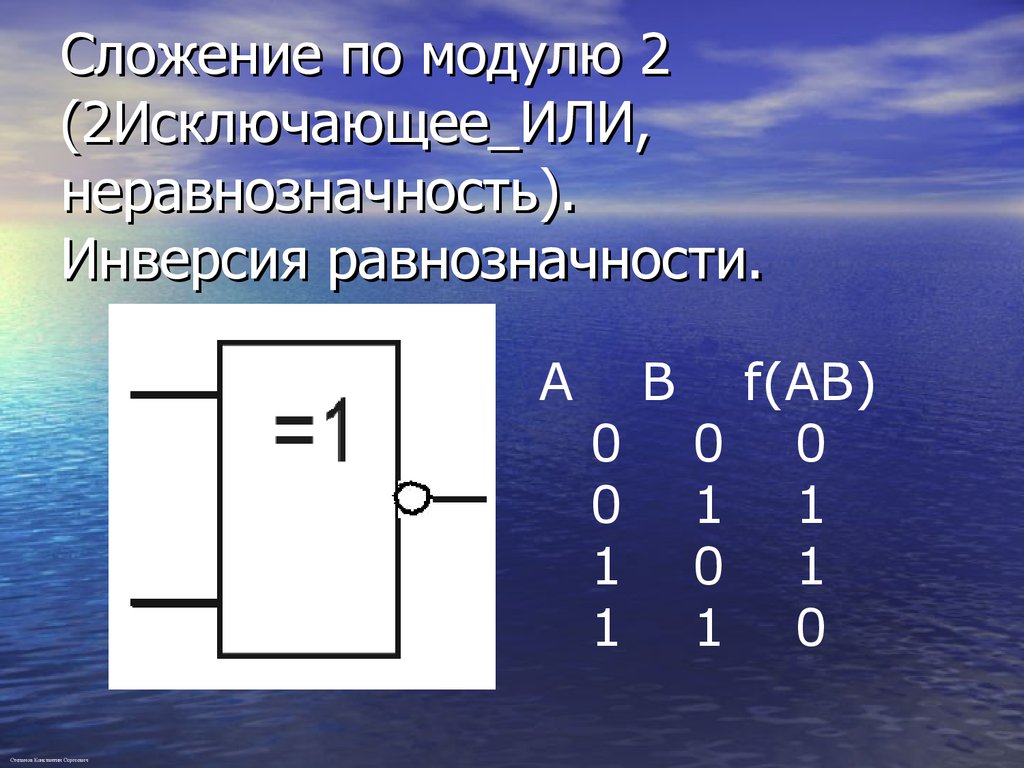 В. В. | RAX XOR imm32 (расширенный знак). |
| 80/6 иб | XOR р/м8, имм8 | МИ | Действительный | Действительный | об/м8 XOR имм8. |
| REX + 80/6 ib | XOR об/м8*, имм8 | МИ | Действительный | Н.В. | об/м8 XOR имм8. |
| 81/6 iw | XOR об/м16, имм16 | МИ | Действительный | Действительный | об/м16 XOR имм16. |
| 81/6 ID | XOR об/м32, имм32 | МИ | Действительный | Действительный | об/м32 XOR имм32. |
| REX.W + 81/6 id | XOR р/м64, имм32 | МИ | Действительный | Н.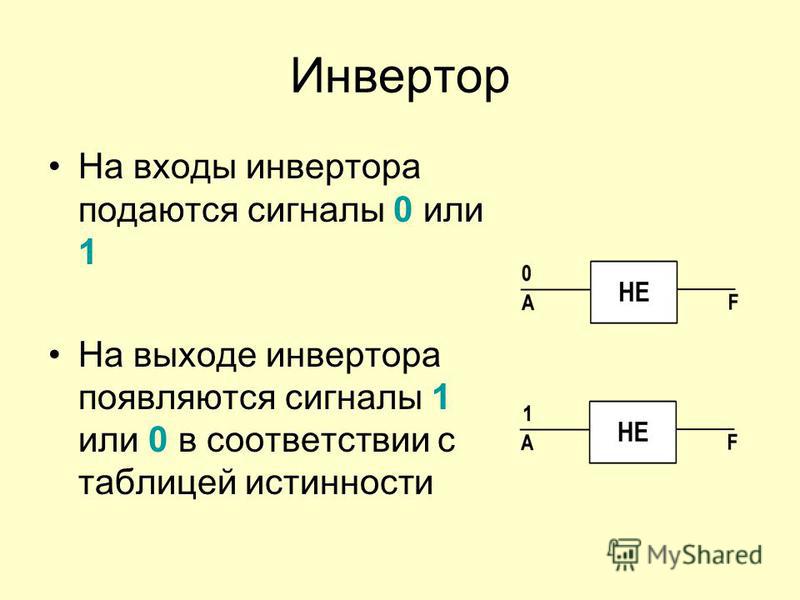 В. В. | r/m64 XOR imm32 (расширенный знак). |
| 83/6 иб | XOR об/м16, имм8 | МИ | Действительный | Действительный | об/м16 XOR imm8 (расширенный знак). |
| 83/6 иб | XOR об/м32, имм8 | МИ | Действительный | Действительный | об/м32 XOR imm8 (расширенный знак). |
| REX.W + 83/6 ib | XOR р/м64, имм8 | МИ | Действительный | Н.В. | об/м64 XOR imm8 (расширенный знак). |
| 30 / р | XOR р/м8, р8 | МР | Действительный | Действительный | р/м8 XOR р8. |
| REX + 30 / р | Исключающее ИЛИ об/м8*, р8* | МР | Действительный | Н.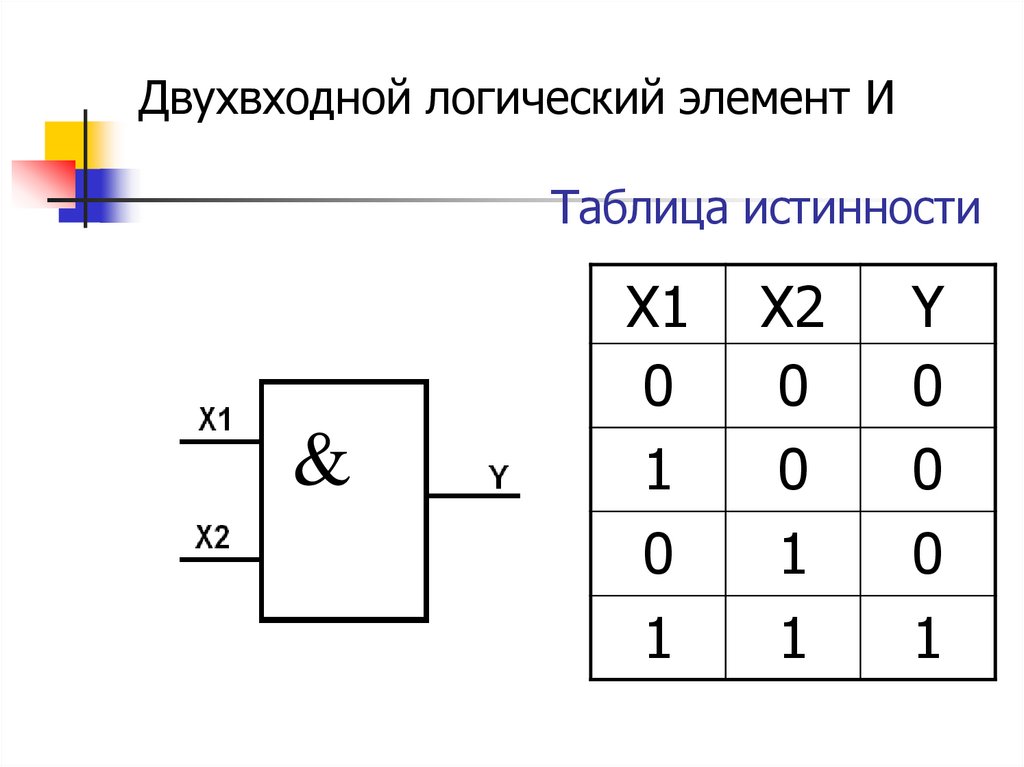 В. В. | р/м8 XOR р8. |
| 31 / р | XOR р/м16, р16 | МР | Действительный | Действительный | об/м16 XOR r16. |
| 31 / р | XOR р/м32, р32 | МР | Действительный | Действительный | об/м32 XOR r32. |
| REX.W + 31 / р | XOR р/м64, р64 | МР | Действительный | Н.В. | р/м64 XOR р64. |
| 32 / р | XOR р8, р/м8 | ринггитов | Действительный | Действительный | r8 XOR r/m8. |
| REX + 32 / р | XOR р8*, р/м8* | ринггитов | Действительный | Н.В. | r8 XOR r/m8. |
| 33 / р | XOR r16, r/m16 | ринггитов | Действительный | Действительный | r16 XOR r/m16. |
| 33 / р | XOR r32, об/м32 | ринггитов | Действительный | Действительно | r32 XOR r/m32. |
| REX.W + 33 / р | XOR р64, р/м64 | ринггитов | Действительный | Н.В. | r64 XOR r/m64. |
* В 64-битном режиме r/m8 не может быть закодирован для доступа к следующим байтовым регистрам, если используется префикс REX: AH, BH, CH, DH.
Кодирование операнда инструкции ¶
| Оп/Р | Операнд 1 | Операнд 2 | Операнд 3 | Операнд 4 |
| I | АЛ/АКС/ЕАКС/РАКС | имм8/16/32 | нет данных | NA |
| MI | ModRM:r/m (r, w) | имм8/16/32 | нет данных | Нет данных |
| МР | ModRM:r/m (r, w) | ModRM:reg (r) | нет данных | NA |
| ринггитов | ModRM:reg (r, w) | ModRM:р/м (р) | нет данных | Нет данных |
Описание ¶
Выполняет операцию побитового исключающего ИЛИ (XOR) над целевым (первым) и исходным (вторым) операндами и сохраняет результат в ячейке целевого операнда.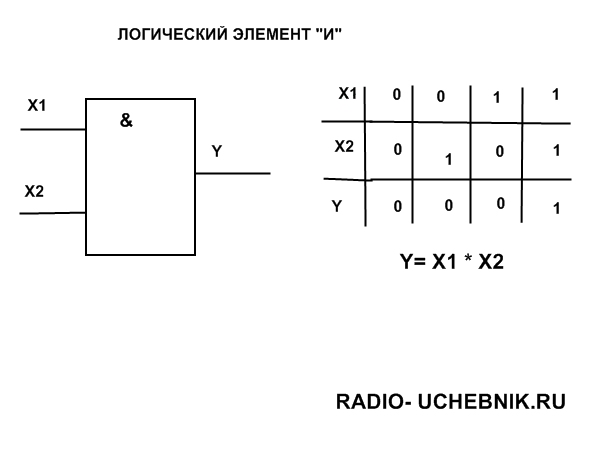 Исходный операнд может быть непосредственным, регистром или ячейкой памяти; операнд назначения может быть регистром или ячейкой памяти. (Однако в одной инструкции нельзя использовать два операнда памяти.) Каждый бит результата равен 1, если соответствующие биты операндов различны; каждый бит равен 0, если соответствующие биты одинаковы.
Исходный операнд может быть непосредственным, регистром или ячейкой памяти; операнд назначения может быть регистром или ячейкой памяти. (Однако в одной инструкции нельзя использовать два операнда памяти.) Каждый бит результата равен 1, если соответствующие биты операндов различны; каждый бит равен 0, если соответствующие биты одинаковы.
Эту инструкцию можно использовать с префиксом LOCK, чтобы позволить выполнение инструкции атомарно.
В 64-битном режиме использование префикса REX в форме REX.R разрешает доступ к дополнительным регистрам (R8-R15). Использование префикса REX в виде REX.W повышает скорость работы до 64 бит. См. сводную таблицу в начале этого раздела для кодирования данных и ограничений.
Операция ¶
НАЗНАЧЕНИЕ := НАЗНАЧЕНИЕ XOR SRC;
Затронутые флаги ¶
: Флаги OF и CF очищены; флаги SF, ZF и PF устанавливаются в соответствии с результатом. Состояние флага AF не определено.
Исключения защищенного режима ¶
| #GP(0) | Если операнд назначения указывает на недоступный для записи сегмент. |
| Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS. | |
| Если регистр DS, ES, FS или GS содержит селектор сегмента NULL. | |
| #СС(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и делается невыровненная ссылка на память, когда текущий уровень привилегий равен 3. |
| #UD | Если используется префикс LOCK, но назначение не является операндом памяти. |
Исключения режима реального адреса ¶
| #GP | Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS. |
| #SS | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #УД | Если используется префикс LOCK, но назначение не является операндом памяти.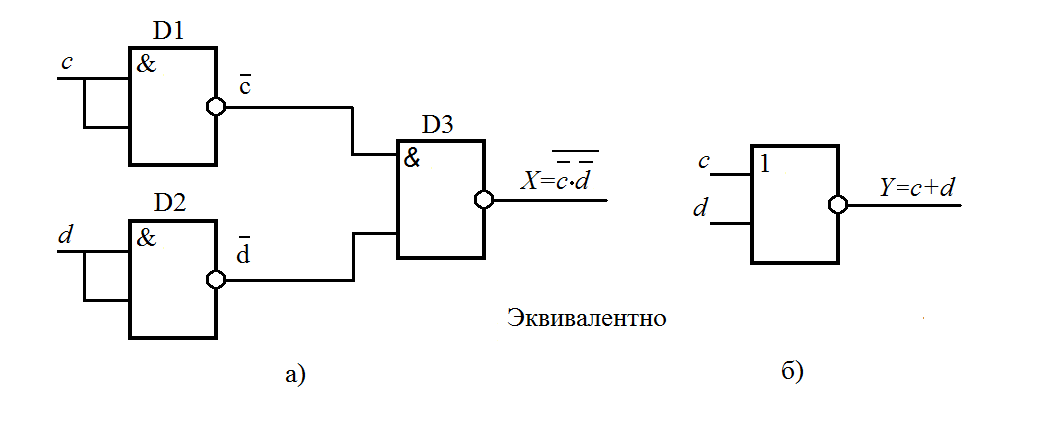 |
Исключения режима Virtual-8086 ¶
| #GP(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS. |
| #SS(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и делается невыровненная ссылка на память. |
| #УД | Если используется префикс LOCK, но назначение не является операндом памяти. |
Исключения режима совместимости ¶
Те же исключения, что и в защищенном режиме.
Исключения 64-битного режима ¶
| #СС(0) | Если адрес памяти, ссылающийся на сегмент SS, имеет неканоническую форму. |
| #GP(0) | Если адрес памяти имеет неканоническую форму. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и выполняется невыровненная ссылка на память, а текущий уровень привилегий равен 3. |
| #UD | Если используется префикс LOCK, но назначение не является операндом памяти. |
Exclusive OR Gate (XOR Gate)
В этом уроке мы узнаем о Ex OR Gate. Ворота Ex ИЛИ — это ворота исключающего ИЛИ. Это не часто используется как инклюзивный вентиль ИЛИ, который представляет собой не что иное, как обычный вентиль ИЛИ. Ворота XOR имеют свое значение. Мы изучим символ, таблицу истинности XOR Gate, реализацию с использованием других вентилей (AND, OR, NAND, NOR), популярные микросхемы XOR и некоторые важные приложения Exclusive OR Gate (XOR Gate).
[адсенс1]
Краткое описание
Введение в вентиль XOR
вентиль исключающее ИЛИ, также известный как вентиль EX OR или вентиль XOR, является важным цифровым логическим вентилем, который реализует исключающую или логическую схему, т.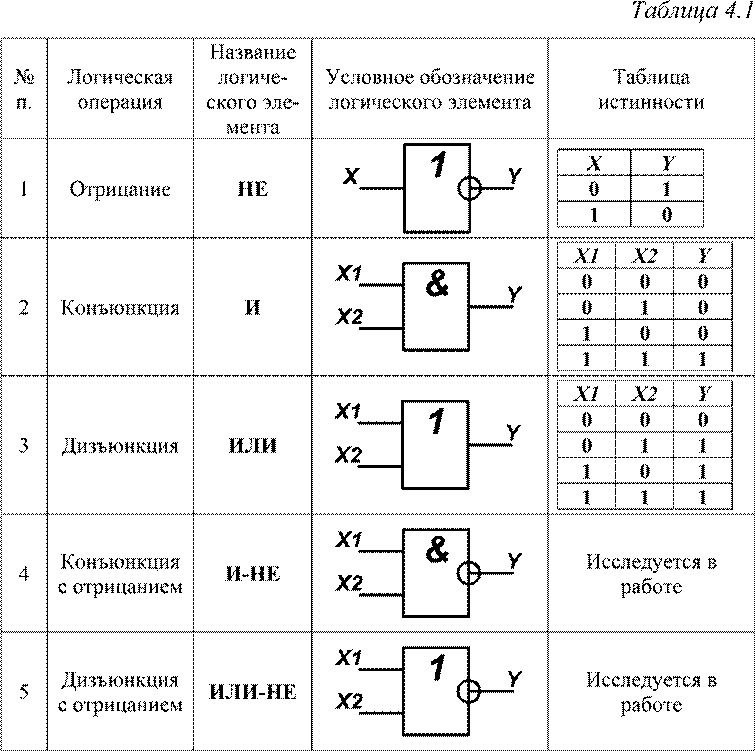 е. выход имеет ВЫСОКИЙ уровень, если и только если одно из входы ВЫСОКИЙ. Если оба входа НИЗКИЙ или ВЫСОКИЙ, то выход НИЗКИЙ.
е. выход имеет ВЫСОКИЙ уровень, если и только если одно из входы ВЫСОКИЙ. Если оба входа НИЗКИЙ или ВЫСОКИЙ, то выход НИЗКИЙ.
Символ XOR
Существует несколько стандартов для определения электронных компонентов. Как правило, мы следуем стандартам IEEE (Институт инженеров по электротехнике и электронике) и IEC (Международная электротехническая комиссия). Логический символ XOR в стандартах IEEE и IEC показан ниже.
Логическое выражение для вентиля XOR не может быть определено напрямую, как вентили AND, OR. Поскольку это гибридный вентиль, логическое выражение вывода вентиля XOR задается комбинацией умножения, сложения и инвертирования входных данных. Мы должны использовать карты Карно или K-карты вместе с таблицей истинности, чтобы получить логическое выражение вентиля XOR.
Таблица истинности XOR
Таблица истинности вентиля XOR показана в таблице ниже. Отсюда ясно, что вентиль XOR выдает логический НИЗКИЙ уровень, т. е. логический «0» на своем выходе, когда оба входа одинаковы (оба могут быть НИЗКИМИ или оба могут быть ВЫСОКИМ).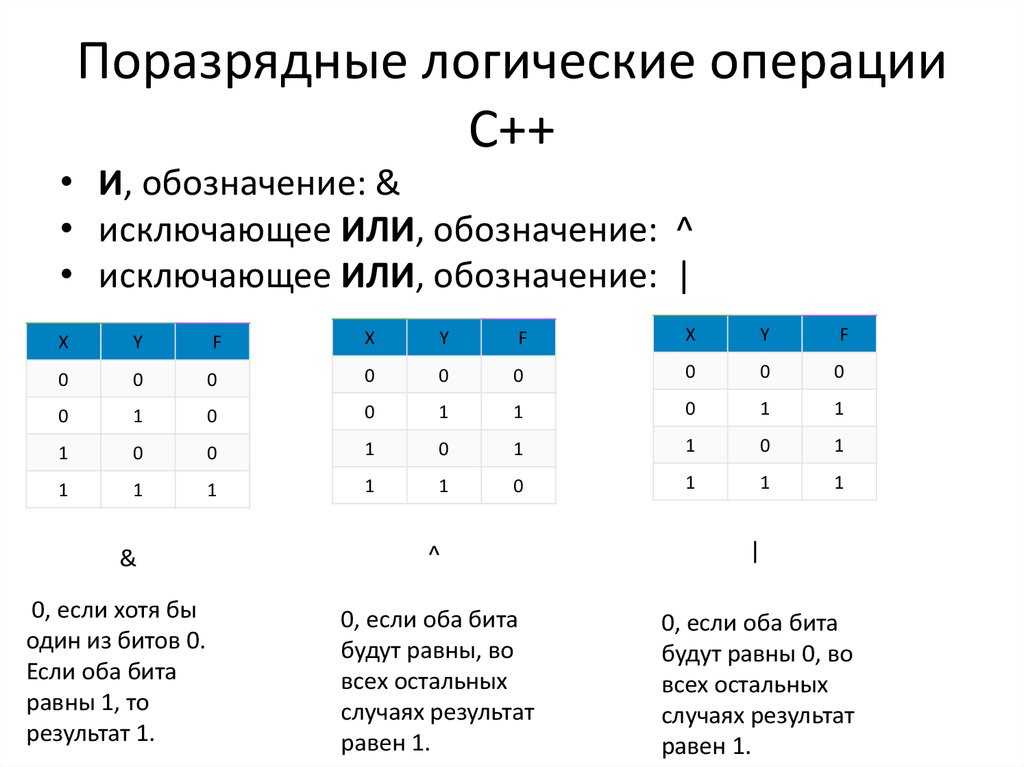
низкий логический уровень, т. е. логический «0», на его выходе, когда два входа различны, он выдает на своем выходе высокое логическое значение, т. е. логическую «1».
| Входы | Выход | |
| А | Б | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Представление K-карты приведенной выше таблицы истинности XOR Gate показано ниже.
Логическое выражение XOR
Используя приведенную выше таблицу истинности и соответствующую K-карту, теперь мы можем получить логическое выражение для XOR Gate. Если A и B являются входами вентиля XOR, его выход задается как:
А В + А В
Выход XOR представлен как:
A ⊕ B
Это также может быть записано как:
(A + B) (A + B)
Применяя закон Де Моргана, приведенное выше логическое выражение также можно записать в виде:
(A + B) (A B)
Эквивалентная схема вентиля XOR
Вентиль EX-OR определяется как гибридный логический вентиль с 2 входами для выполнения операции исключающего дизъюнкции. Из приведенных выше расчетов основное логическое выражение вентиля XOR:
Из приведенных выше расчетов основное логическое выражение вентиля XOR:
А Б + А Б
Итак, схема исключающего ИЛИ с двумя входами разработана с использованием вентилей И, ИЛИ и НЕ, как показано ниже.
Выход 2-входового элемента XOR имеет ВЫСОКИЙ уровень только тогда, когда один из его входов имеет ВЫСОКИЙ уровень. Если оба входа одинаковы, то выход НИЗКИЙ.
Шлюз XOR с использованием базовых логических вентилей
Если конкретный вентиль недоступен напрямую, мы можем спроектировать вентиль XOR с использованием нескольких вентилей. Ворота EX-OR могут быть разработаны с использованием базовых логических вентилей, таких как вентиль НЕ-И и вентиль ИЛИ-НЕ, поскольку они являются универсальными вентилями.
[адсенс2]
С вентилями NOR
Давайте теперь посмотрим, как мы можем реализовать вентиль XOR с помощью вентилей NOR. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A’ + B’) (A + B)
Взяв дополнение с обеих сторон, получим:
Q = ((A’ + B’) (A + B))
Используя закон де Моргана, получаем:
Q = (A’ + B’) + (A + B) = (A’ + B’)’ + (A + B)’
Еще раз взяв дополнение с обеих сторон, мы получим:
Q = ((A’ + B’)’ + (A + B)’) = ((A’ + B’)’ + (A + B) ‘)’
Похоже, что это уравнение может быть реализовано с помощью NOR Gates.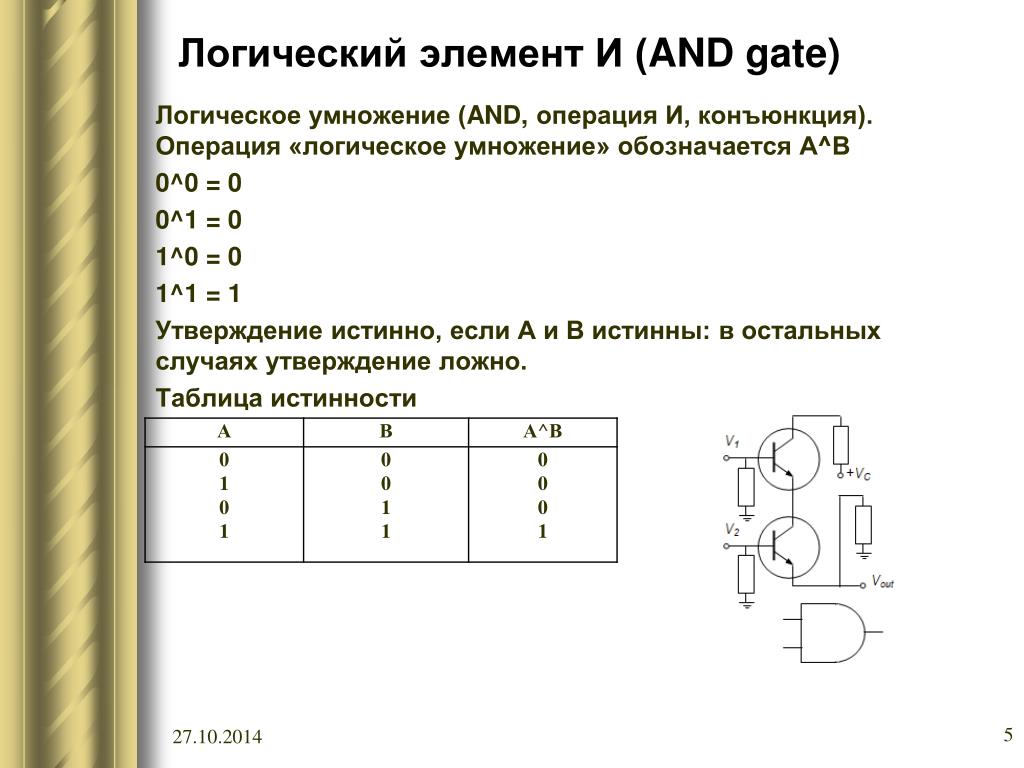 Всего нам нужно пять вентилей ИЛИ-НЕ (два для инвертирования А и В, один для инвертирования ИЛИ-НЕ для А и В, один для ИЛИ-НЕ для А’ и В’ и последний для получения приведенного выше уравнения). На следующем изображении показан шлюз XOR, реализованный с использованием шлюзов NOR.
Всего нам нужно пять вентилей ИЛИ-НЕ (два для инвертирования А и В, один для инвертирования ИЛИ-НЕ для А и В, один для ИЛИ-НЕ для А’ и В’ и последний для получения приведенного выше уравнения). На следующем изображении показан шлюз XOR, реализованный с использованием шлюзов NOR.
С вентилями NAND
Давайте теперь посмотрим, как мы можем реализовать вентиль XOR с помощью вентилей NAND. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A + B) (A’ + B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) ( AB )
Теперь нам нужно реализовать эту схему с использованием вентилей И-НЕ.
Q = A (AB) + B (AB) = A (AB)’ + B (AB)’
Взяв дополнение с обеих сторон, мы получим:
Q = (A ( AB ) + B ( AB ))’ = (A (AB)’ + B (AB)’)
Q = (A ( A B ))’ (B ( A B ))’ = (A (AB)’) (B (AB)’)
Наконец, еще раз нанесите дополнение с обеих сторон.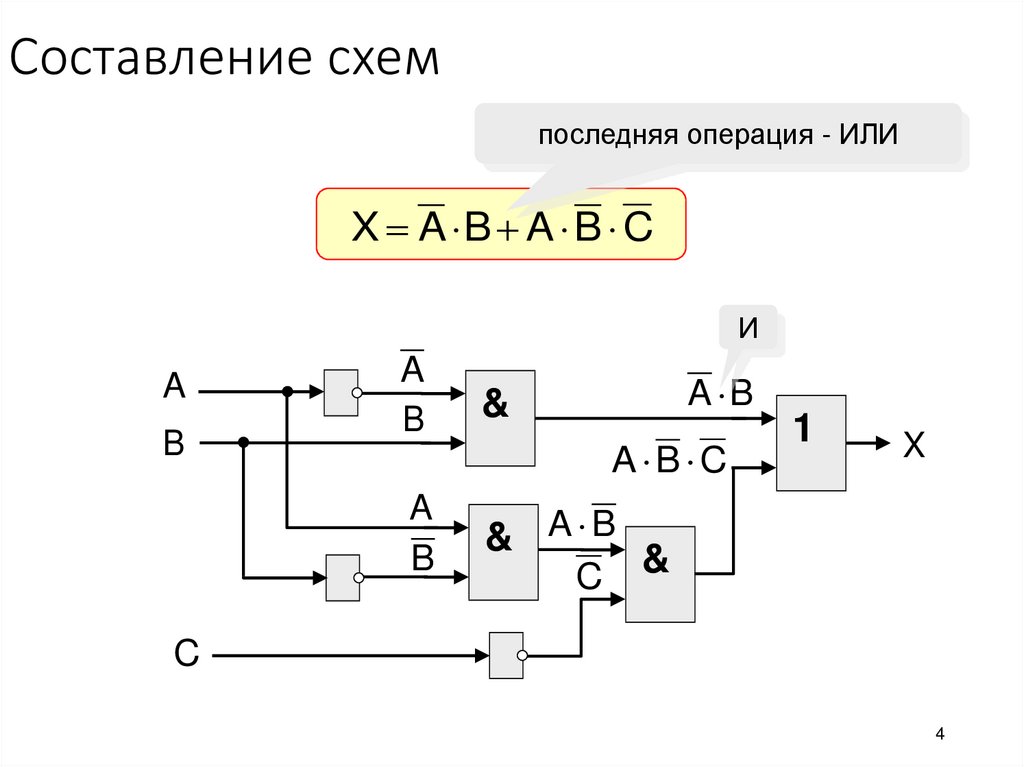
Q = (A ( A B )’)’ (B (A B)’)’ = ((A (AB)’)’ (B (AB)’)’)’
Это уравнение выглядит так, будто его можно реализовать с помощью вентилей NAND. Нам нужны полностью наши вентили NAND. На следующем изображении показан вентиль XOR, реализованный с использованием вентилей NAND.
Использование логических элементов И, ИЛИ и И-НЕ
Давайте теперь посмотрим, как мы можем реализовать вентильный элемент XOR с использованием вентилей НЕ-И, И и ИЛИ. Для этого нам нужно переписать приведенное выше логическое уравнение XOR.
Q = А Б + А Б
Q = А В + А В + А А + В В
Q = (А + В) (А + В)
Q = (A + B) (A + B) = (A + B) (A’ + B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) ( AB )
Для первого члена приведенного выше уравнения требуется вентиль ИЛИ, для второго члена нужен вентиль НЕ-И, а окончательное уравнение можно получить с помощью вентиля И.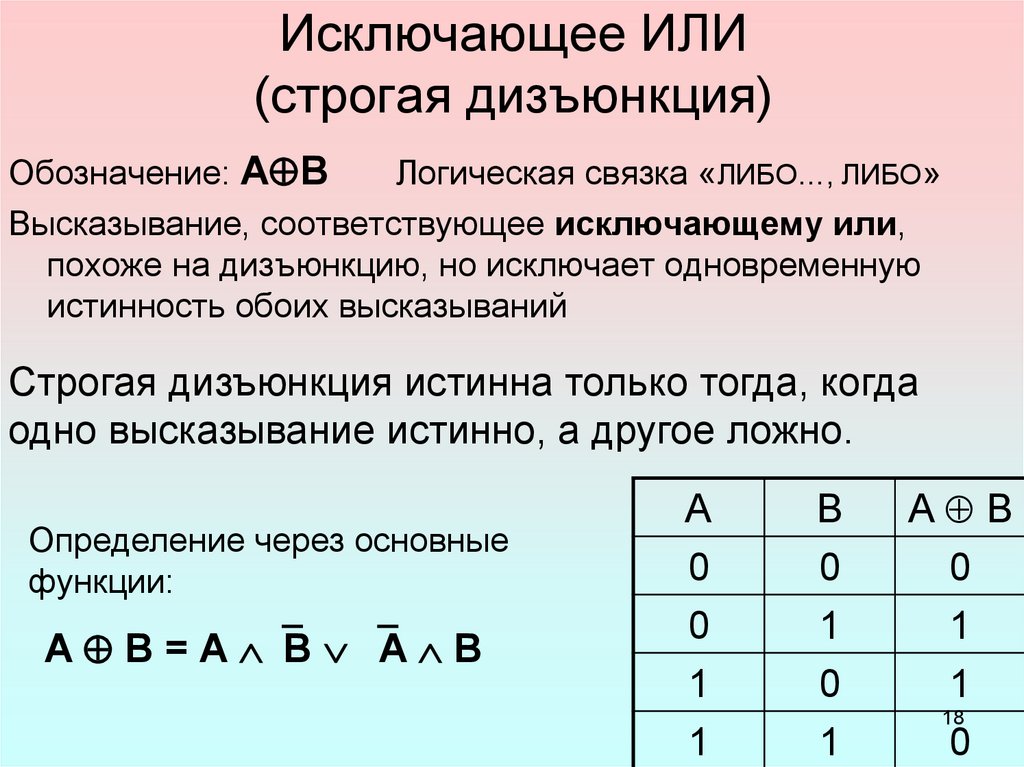
Импульсная работа логического элемента XOR
Импульсная работа логического элемента XOR с 2 входами показана ниже.
3-входовой вентиль Ex-OR
В некоторых случаях нам необходимо иметь вентиль XOR с более чем 2 входами. Функция XOR с более чем двумя входами называется «Нечетная функция» или «Сумма по модулю-2». Булева функция для логического элемента XOR с 3 входами:
Q = A ⊕ B ⊕ C = A B C + A B C + A B C + A B C
Таблица истинности и логический символ для логического элемента XOR с 3 входами приведены ниже.
Логический символ вентиля Ex-OR с 3 входами
Таблица истинности вентиля XOR с 3 входами
Для вентилей XOR с 3 входами мы можем иметь ВЫСОКИЙ вход, когда нечетное количество входов находится на ВЫСКОМ уровне. Таким образом, вентиль ИЛИ с тремя входами называется «вентиль ИЛИ с нечетным функционированием».
| Входы | Выход | ||
| А | Б | С | Q |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Общедоступные TTL и CMOS логические микросхемы Ex-OR
Ниже приведен список некоторых общедоступных микросхем XOR.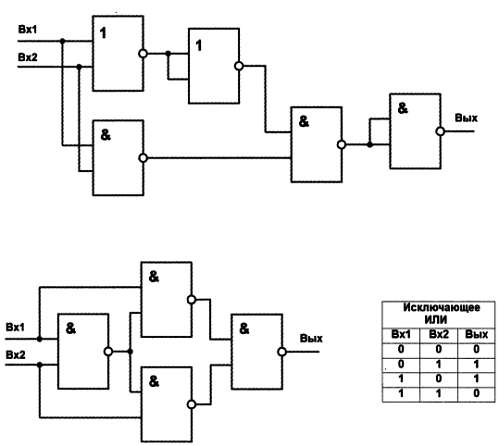
| Номер ИС | Описание |
| 4030 | Счетверенные вентили XOR с 2 входами |
| 4070 | Счетверенные вентили XOR с 2 входами |
| 7486 | Счетверенные вентили XOR с 2 входами |
| 74LS86 | Счетверенные вентили XOR с 2 входами |
| 741G86 | Одиночный вентиль Ex-OR с 2 входами |
| 74136 | Счетверенные вентили XOR с 2 входами и выходами с открытым коллектором |
| 74386 | Счетверенные вентили XOR с 2 входами |
Из них самой популярной микросхемой EX-OR Gate на основе TTL Logic является 74LS86, представляющая собой Quad XOR IC с двумя входами. Что касается микросхемы XOR Gate на основе CMOS Logic, CD4030 Quad XOR IC с 2 входами является популярным выбором.
7486 Четырехканальная микросхема исключающего ИЛИ с двумя входами
IC 7486 представляет собой четырехканальную схему XOR с двумя входами, т. е. содержит четыре вентиля XOR с двумя входами в одном корпусе. Схема выводов и описание выводов микросхемы показаны ниже.
е. содержит четыре вентиля XOR с двумя входами в одном корпусе. Схема выводов и описание выводов микросхемы показаны ниже.
| Номер контакта | Описание |
| 1 | Строб 1 Вход A |
| 2 | Строб 1 Вход B |
| 3 | Строб 1 Выход Y |
| 4 | Строб 2 Вход A |
| 5 | Строб 2 Вход B |
| 6 | Строб 2 Выход Y |
| 7 | Заземление |
| 8 | Строб 3 Выход Y |
| 9 | Строб 3, вход A |
| 10 | Строб 3, вход B |
| 11 | Строб 4 Выход Y |
| 12 | Строб 4 Вход A |
| 13 | Ворота 4, вход B |
| 14 | Положительное питание |
Применение Ex-OR Gate
XOR Logic Gate используется во многих приложениях. Некоторые из них объясняются ниже.
Некоторые из них объясняются ниже.
Используется в сумматоре (сложение)
Мы можем разработать однобитовый сумматор (также известный как полусумматор), который будет добавлять два бита и давать на выходе один бит. Одноразрядный сумматор, разработанный с использованием вентиля XOR, показан ниже.
Например, если мы добавим два бита «1» и «1» в двоичном сложении, мы получим ответ «10», а в методе десятичного сложения мы получим 2. Основной принцип полусумматоров заключается в том, что конечная сумма достигается выходом вентиля XOR, а бит переноса вычисляется вентилем AND.
Мы можем каскадировать множество однобитовых сумматоров, чтобы сформировать n-битный сумматор, чтобы вычислить сумму более длинных двоичных чисел.
Генерация псевдослучайных чисел
Линейные регистры сдвига также называются генераторами псевдослучайных чисел (PNR). Чтобы генерировать случайные числа, мы располагаем логический вентиль XOR в определенном порядке, формируя регистр сдвига с линейной обратной связью.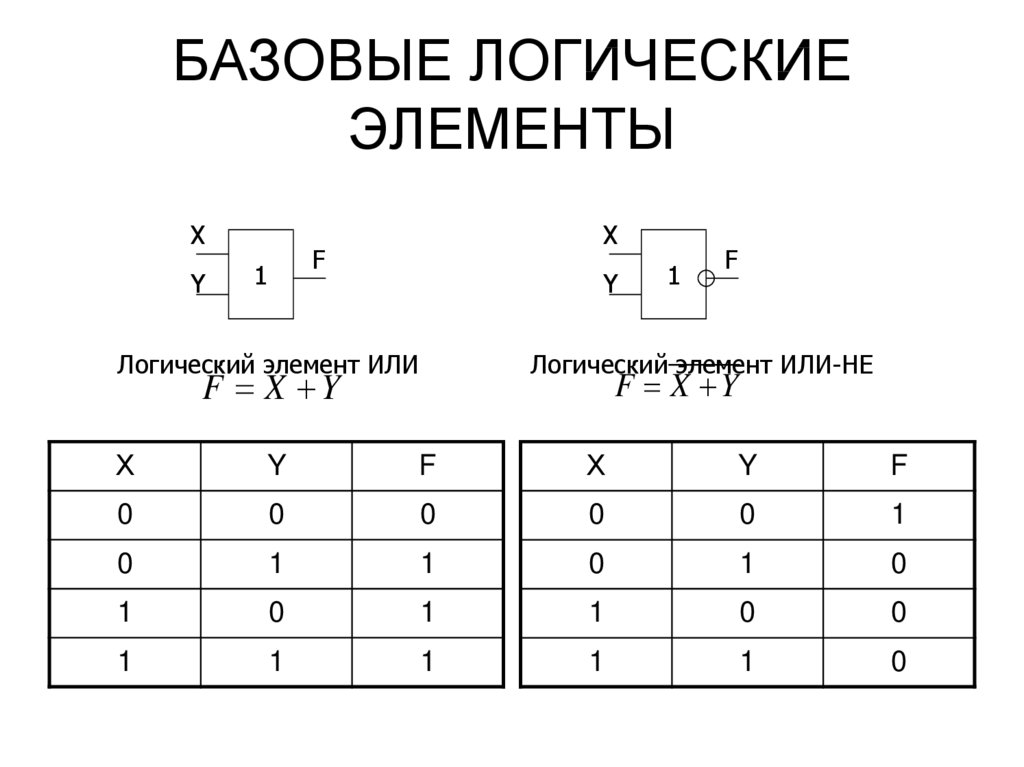
Корреляция и обнаружение последовательности
Логический элемент исключающее ИЛИ способен выдавать входной сигнал низкого уровня, т. е. 0, когда все его входы имеют ВЫСОКИЙ или НИЗКИЙ уровень. Когда мы ищем определенную последовательность битов в длинной последовательности данных, мы используем вентили XOR, чтобы найти требуемую последовательность битов данных.
Точность нахождения необходимой строки битов данных в целевой последовательности определяется путем подсчета количества полученных нулей. Во многих устройствах связи, таких как декодеры и приемники CDMA, мы используем корреляторы, которые используются для извлечения четности конкретной последовательности псевдослучайных чисел в группе последовательностей PRN.
Заключение
Полное руководство по Exclusive OR Gate (XOR Gate). Вы изучили символ, таблицу истинности и логическое выражение вентиля XOR, реализацию вентиля XOR с использованием вентилей NOR и NAND, вентиль XOR с 3 входами, его символ, таблицу истинности и логическое выражение, некоторые распространенные и популярные микросхемы XOR, а также некоторые важные приложения XOR Gate.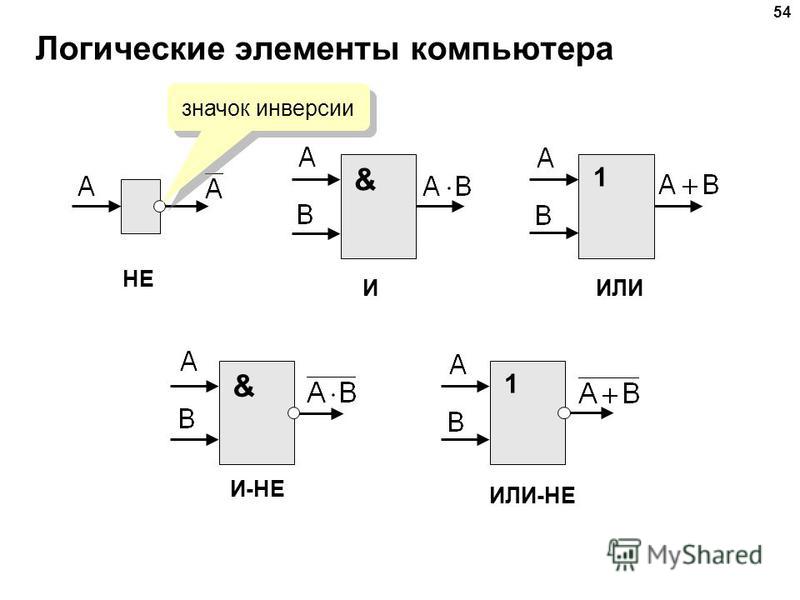
Логический оператор, который возвращает значение true, только если один из аргументов имеет значение true, а один из аргументов — значение false.
Произношение: /ɪkˈsklusɪv ɔr/ Объяснение
Исключительное или логическое операция который возвращает true, только если один операнд верно, а другое ложно. Для предложений и и b , исключающее или истинно, если либо a , либо b истинны, но не оба. Таблица 1 является таблицей истинности для исключающего или. Эксклюзив или также может быть называется эксклюзивной дизъюнктией. При написании термин «исключающее или» иногда сокращается как «исключающее»; который произносится как «экс-или». 9). В электроника, эксклюзив или гейт рисуется как:
.
Рисунок 1: Диаграмма Венна для A xor B .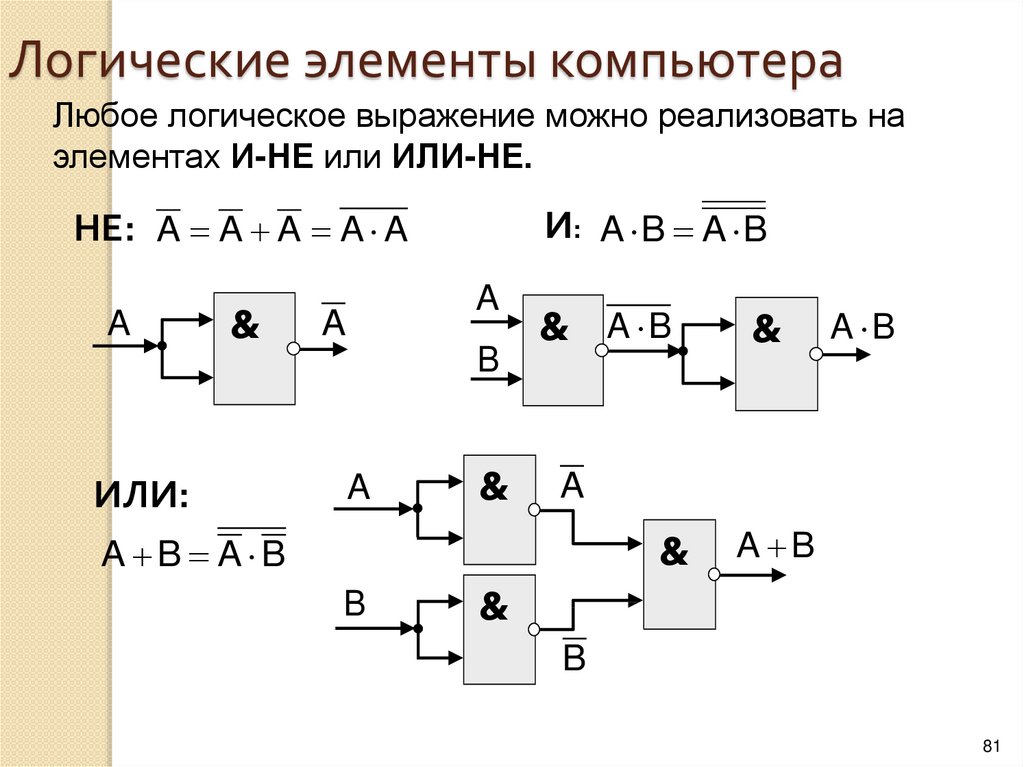 |
Properties of Exclusive Or
| Property Using Words | Property Using Symbols | Description |
|---|---|---|
| a xor false = a | a ⊕ ложь = а | |
| a xor true = not a | ⊕ правда = ¬ | |
| a xor a = false | a ⊕ a = ложь | Определение исключающего или подразумевает, что если оба операнда истинны, или оба операнда ложны, то исключает или возвращает ложь. а ≠ а , a xor a всегда должно быть ложным. |
| a xor not a = true | a ⊕ ¬ a = правда | Определение исключающего или гласит, что если два операнда не равны,
исключительный или возвращает true.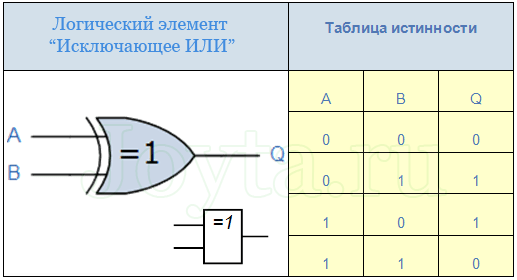 С года ≠ ¬ и , и xor не и всегда верно. С года ≠ ¬ и , и xor не и всегда верно. |
| a xor b = b xor a | а ⊕ б = б ⊕ а | Эксклюзивное или коммутативное. |
| a xor ( b xor c ) = ( a xor b ) xor c | а ⊕ ( б ⊕ с ) = (а⊕б)⊕ в | Эксклюзивное или ассоциативное. |
| a xor b = не a xor not b | а ⊕ б = ¬ а ⊕ ¬ б | Если значение истинности обоих операндов поменяно местами, исключающее или по-прежнему возвращает то же значение. |
| нет ( a xor b ) = не a xor б = a xили нет b | ¬( a ⊕ b ) = ¬ a ⊕ б = а ⊕ ¬ б | Логическое отрицание исключающего или результата — одно и то же.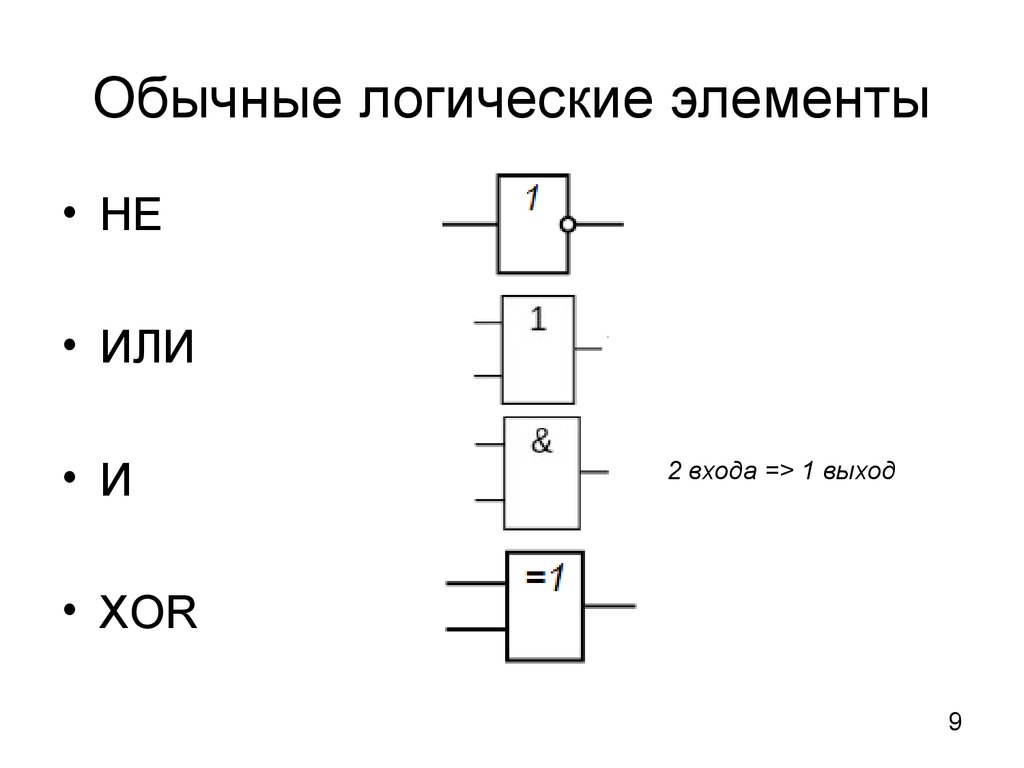 как отрицание одного из операндов исключающего или. как отрицание одного из операндов исключающего или. |
| a xor b = ( a , а не b ) или (не a и b ) | a ⊕ b = ( a ∧ ¬ b ) ∨ (¬ а ∧ б ) | Это переформулировка определения исключительного или: исключительное или операция истинна, только если один из аргументов истинен, а другой ложен. |
| a xor b = ( a или b ) и (не a или не b ) | а ⊕ б = ( а ∨ б ) ∧ (¬ а ∨ ¬ б ) | Это снова переформулировка определения исключающего или. Первый срок
( a или b ) истинно, если либо a или b верно. Второй срок
(не a или не b ) истинно, если либо a и b ложны. С союзом все выражение равно
верно, если либо a или b верны. С союзом все выражение равно
верно, если либо a или b верны. |
| a xor b = ( a или b ) и не ( а и б ) | а ⊕ б = ( а ∨ б ) ∧ ¬( a ∧ b ) | Это еще одно переформулирование определения исключающего или. |
| Таблица 2: Свойства Exclusive Or. | ||
Побитовое исключающее ИЛИ
В логике операнды исключающего или должны быть значением истинности, должны быть либо
истинное из ложного. В компьютерах операндами исключающего или являются двоичные числа.
Исключающее или применяется к соответствующим битам операндов:
0 исключающее или 0 = 0
0 исключающее ИЛИ 1 = 1
1 исключающее или 0 = 1
1 исключающее ИЛИ 1 = 0
1001 xor 1100 = 0101
Ссылки
- МакАдамс, Дэвид Э.
 . Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгу
. Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгу - xor . www.merriam-webster.com. Британская энциклопедия. Мерриам-Вебстер. Последний доступ 09.07.2018. http://www.merriam-webster.com/dictionary/XOR?db=luna. Купить книгу
- Буль, Джордж; фон Куфнер, Мориц. Математический анализ логики: эссе по исчислению дедуктивных рассуждений . стр. 52-59. www.archive.org. Макмиллан, Барклай и Макмиллан. 1847. Последний доступ 9 июля 2018 г. http://www.archive.org/stream/mathematicalanal00booluoft#page/52/mode/1up/search/exclusive. Купить книгу
Цитируйте эту статью как:
МакАдамс, Дэвид Э. Эксклюзив или . 20.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/e/exclusiveor. html.
html.
Авторы изображений
- Все изображения и манипуляции сделаны Дэвидом МакАдамсом, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.
История изменений
20.04.2019:
Обновлены выражения и уравнения для соответствия новому формату.
(МакАдамс, Дэвид Э.)
21.12.2018:
Пересмотрено и исправлено произношение IPA.
(МакАдамс, Дэвид Э.)
05.07.2018:
Удалены битые ссылки, обновлена лицензия, реализована новая разметка, реализован новый протокол Geogebra.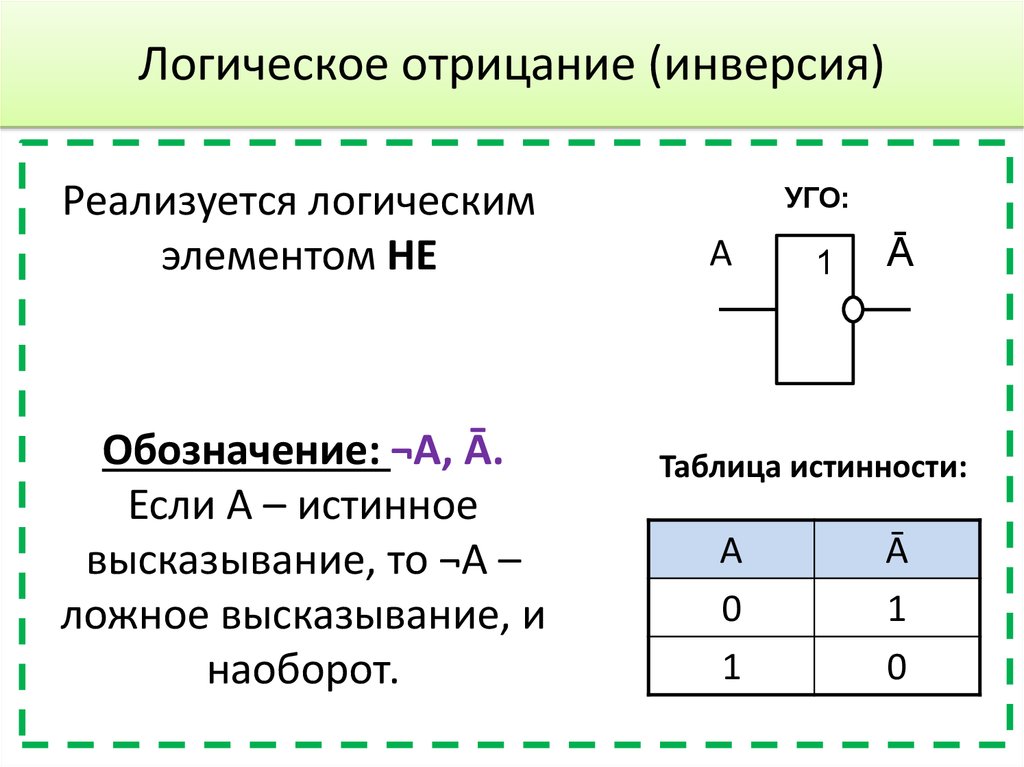
(МакАдамс, Дэвид Э.)
01.02.2010:
Добавлен раздел «Ссылки».
(МакАдамс, Дэвид Э.)
18.04.2009:
Исправлено обсуждение xor a.
(МакАдамс, Дэвид Э.)
08.01.2009:
Первоначальная версия.
(МакАдамс, Дэвид Э.)
Интересные свойства исключающего ИЛИ (XOR) — ML и статистика
Источник изображения: дизайн Bearfotos / Freepik выводит true, если только один из обоих его входов истинен (то есть, если оба входа различаются). Есть много приложений, в которых используется XOR, например, в криптографии, кодах Грея, проверках четности и CRC и, конечно же, во многих других.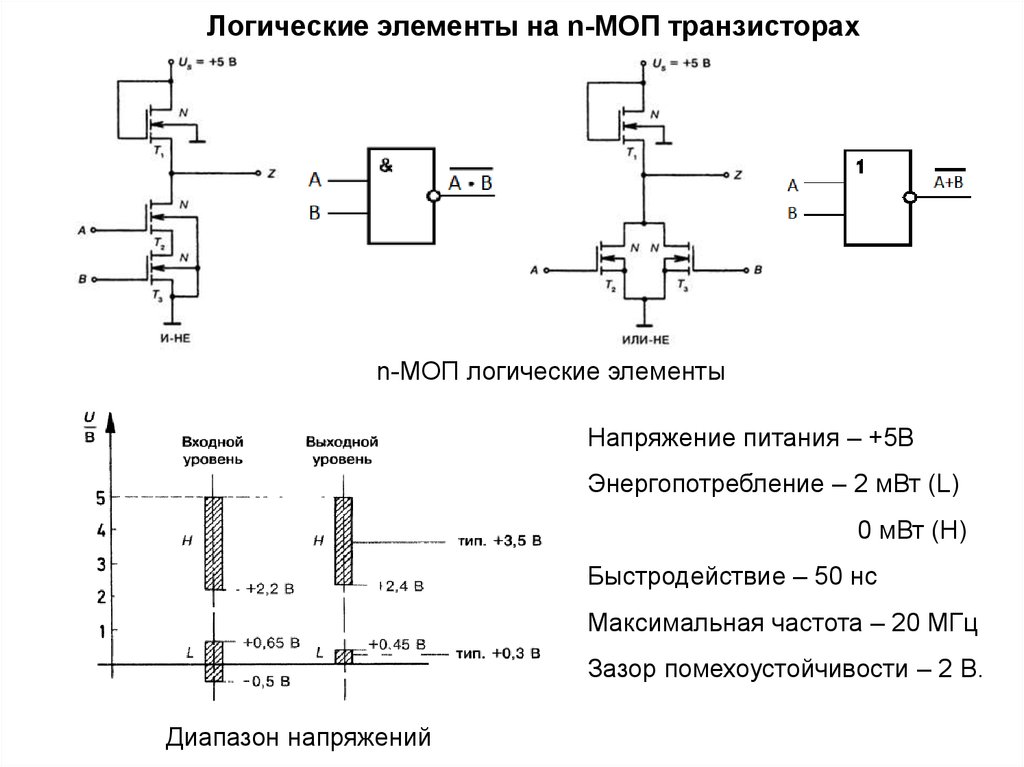 Обычно этот символ используется для обозначения операции XOR. Здесь мы будем использовать символ для исключающего ИЛИ и для его отрицания, биусловный оператор.
В этом сообщении блога мы рассмотрим несколько его интересных свойств, которые могут быть полезны.
Обычно этот символ используется для обозначения операции XOR. Здесь мы будем использовать символ для исключающего ИЛИ и для его отрицания, биусловный оператор.
В этом сообщении блога мы рассмотрим несколько его интересных свойств, которые могут быть полезны.
Начнем с таблицы истинности исключающего ИЛИ () и биусловия:
| a | б | а б | а б |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Определение
Из этой таблицы мы можем извлечь следующие уравнения, которые являются наиболее часто используемым определением операции XOR:
Обратный элемент
Обратите внимание, что логическая операция И () записывается как .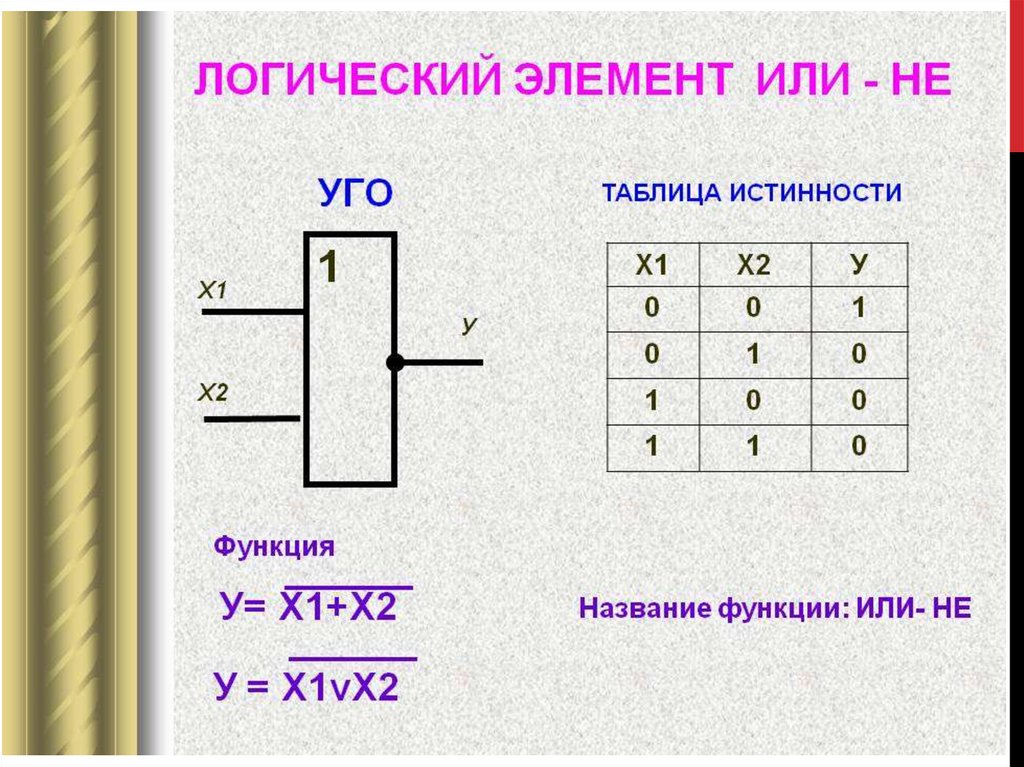 Обе операции имеют обратный элемент (1 и 0), так что
Обе операции имеют обратный элемент (1 и 0), так что
Нейтральный элемент
Для исключающего ИЛИ и биусловия также существует нейтральный элемент (0 и 1):
Идемпотентность
Легко показать, что XOR не удовлетворяет свойству идемпотентности, которое гласит, что для любой операции мы имеем . Из таблицы истинности видно, что
.
Инверсия исключающего ИЛИ
Мы уже упоминали, что инверсией XOR является биусловный оператор. Это также легко увидеть из таблицы истинности. Однако это также можно показать формально:
т.к. – используя уравнение. \eqref{экв:определение} :
Коммутативность
Коммутативность задана и в обоих случаях:
так как
Ассоциативность
Также выполняется свойство ассоциативности:
так как – с использованием правил \eqref{eq:definition} и \eqrefXOReq} .
Дистрибутивность
Как мы увидим позже, союз (И) и Исключающее ИЛИ (двуусловное) представляют собой операции умножения и сложения поля Галуа GF(2), и в таком поле они следуют дистрибутивному закону:
т.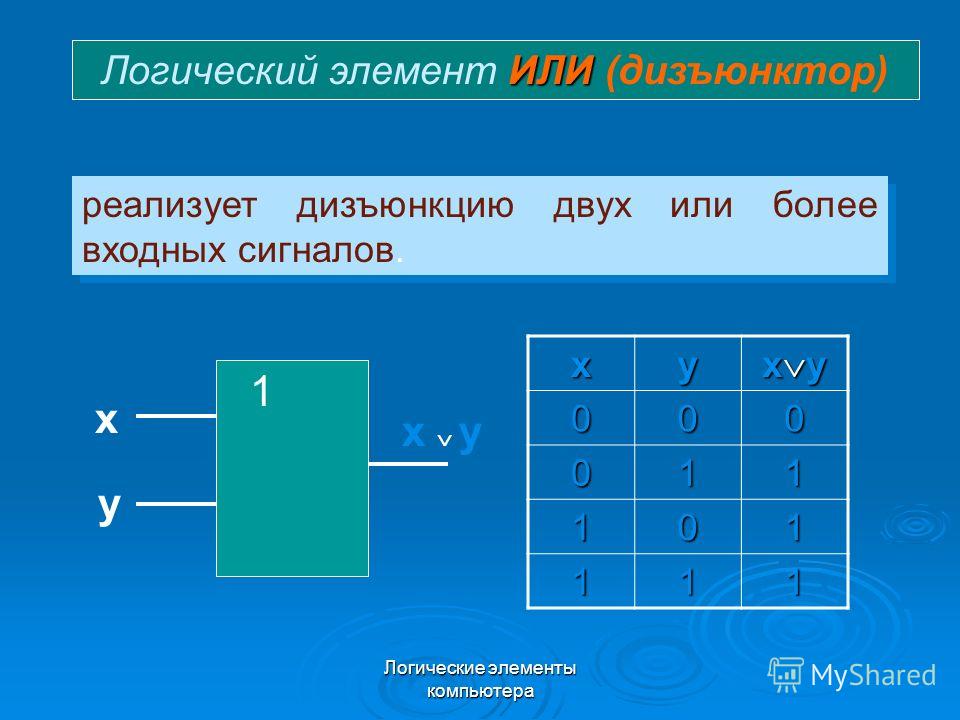 к. – с ур. \eqref{eq:inverseXOR}:
к. – с ур. \eqref{eq:inverseXOR}:
Это верно и для биусловного оператора.
Инвертирование одного операнда
т.к. – с уравнением \eqref{eq:inverseXOR}:
Инвертирование обоих операндов
что можно тривиально показать с помощью \eqref{eq:definition}:
Выражение логического ИЛИ в терминах исключающего ИЛИ
Мы можем найти следующее выражение :
т.к. — путем расширения a и b на :
Поскольку приведенное выше уравнение снова содержит дизъюнктуру (ИЛИ), это не похоже на какое-либо улучшение, однако это правило может быть полезно при выводе многих других соотношений. Например, применим правило \eqref{eq:OR-XOR} к самому себе:
Давайте сначала идентифицируем:
Затем мы имеем (подставляя исходные выражения для и через некоторое время снова):
Поскольку члены и дизъюнктны к , приведенное выше выражение упрощается до:
Это приводит, наконец, к некоторому интересному соотношению :
Выражение логического И через исключающее ИЛИ
Аналогично предыдущему абзацу можно вывести некоторые интересные соотношения для логического И (союза):
и
Логическое ИЛИ попарно дизъюнктивных термов
Используя правило \eqref{eq:ИЛИ-ИСКЛЮЧАЮЩЕЕ ИЛИ}, мы можем найти другое интересное соотношение для дизъюнктивных форм, где все термы попарно дизъюнктны.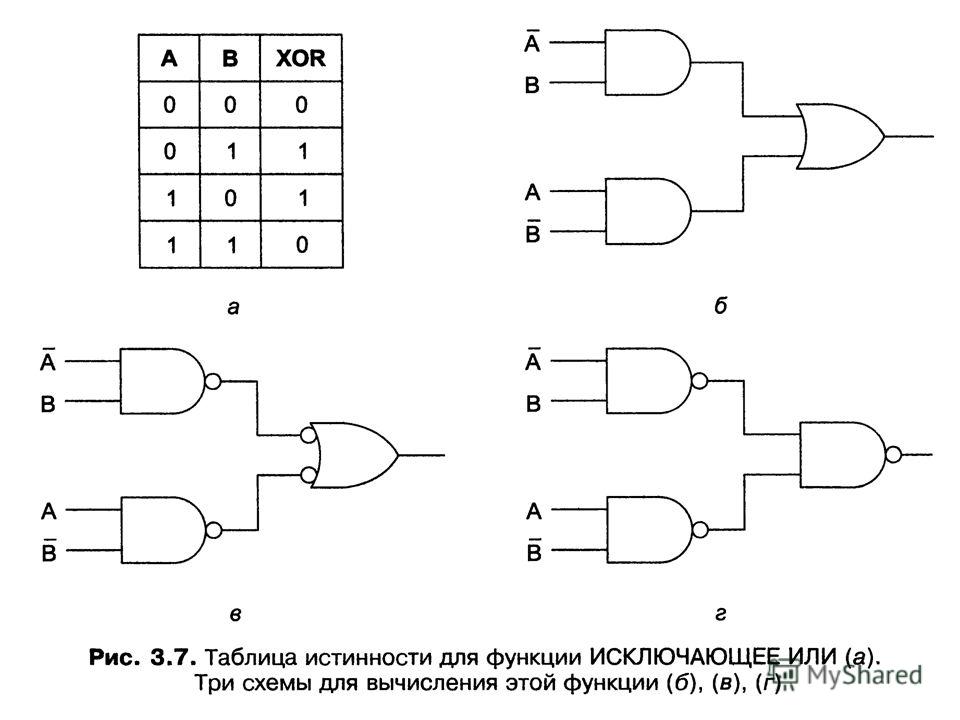 Рассмотрим следующий простой пример – применение правила \eqref{eq:OR-XOR}:
Рассмотрим следующий простой пример – применение правила \eqref{eq:OR-XOR}:
В качестве примечания, мы также можем записать приведенное выше отношение в обратном порядке, так что:
С Eq.\eqref{eq:xorAbsurdum} мы имеем важное отношение, утверждающее, что все операции ИЛИ в дизъюнктивной форме можно просто заменить на XOR, если все члены попарно дизъюнктивны. Например, правило можно применить к следующей дизъюнктивной форме:
Новый взгляд на логические двуусловные операции и исключающее ИЛИ
Иногда можно заменить все биусловные операции в уравнении операциями исключающее ИЛИ. Рассмотрим следующий пример – с уравнением. \eqref{eq:inverseXOR} и уравнение. \eqref{eq:invOne}:
Или, короче:
Комбинированное ассоциативное свойство логического биусловия и исключающего ИЛИ
Аналогично предыдущему, где мы показали ассоциативное свойство двуусловного и исключающего ИЛИ для обоих случаев по отдельности, мы также можем показать, что свойство ассоциативности выполняется и для смешанных терминов – с Eq.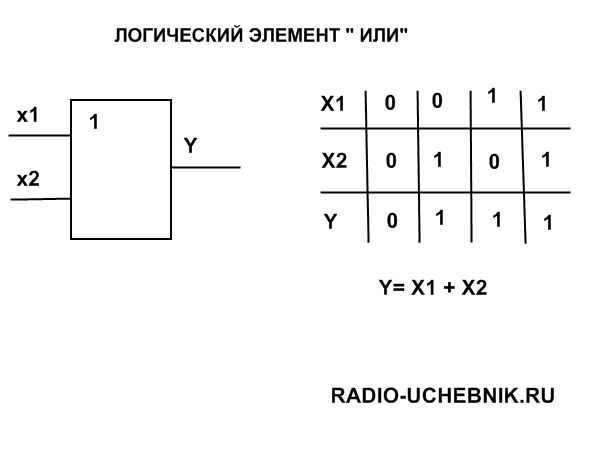 \eqref{eq:inverseXOR}, \eqref{eq:invOne} и \eqref{eq:BicondEqXOR}:
\eqref{eq:inverseXOR}, \eqref{eq:invOne} и \eqref{eq:BicondEqXOR}:
Это позволяет нам заявить:
Комбинированное свойство коммутативности логического бикондиционала и исключающего ИЛИ
После того, как мы показали комбинированное ассоциативное свойство логического бикондиционала и исключающего ИЛИ, мы соответственно показываем коммутативность. Нам нужно только уравнение \eqref{eq:Commutativity} и \eqref{eq:mixedassociative}. Тогда аргументация довольно тривиальна:
В итоге мы можем написать:
Следовательно, все термы в смешанном выражении XOR и бикондиционалов попарно взаимозаменяемы. Это очень важное наблюдение, которое часто может помочь на практике.
Замена операций исключающее ИЛИ в выражении биусловиями
Предположим, у нас есть выражение в форме
Мы хотим заменить все операции на . Как мы можем этого добиться? На самом деле, это не так сложно. Мы можем рекурсивно применить правила \eqref{eq:inverseXOR}, \eqref{eq:invOne} и \eqref{eq:mixedassociative} следующим образом:
Вы можете видеть, куда это идет: имел отрицание в выражении, которое снова исчезло после замены второго исключающего ИЛИ, а затем вернулось с заменой третьего исключающего ИЛИ.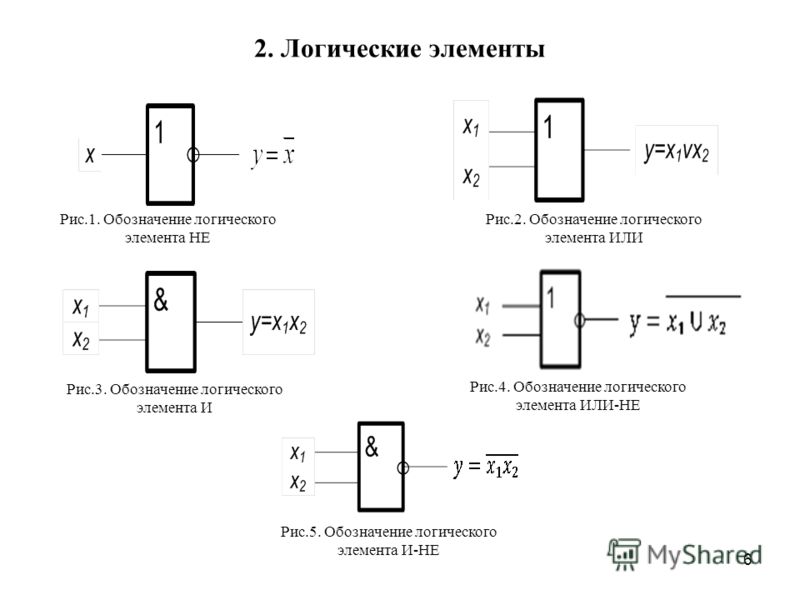 Итак, в зависимости от количества переменных у нас либо осталось в конце отрицание, либо нет. Это можно выразить с помощью:
Итак, в зависимости от количества переменных у нас либо осталось в конце отрицание, либо нет. Это можно выразить с помощью:
Точно так же мы получаем следующее отношение, когда заменяем биусловия в выражении операцией XOR:
Смешанные представления биусловий и исключающих ИЛИ
Иногда встречаются смешанные представления биусловий и исключающих ИЛИ, что реализовано это эффективно в цифровой схеме. В этих случаях можно найти представления, состоящие исключительно из XOR или только из бикондиционалов. Во-первых, мы должны привести наше исходное представление к виду:
, где состоит только из операций XOR и только из биусловий. Для символа либо вставляется, если мы хотим, чтобы окончательное отношение состояло из XOR, либо вставляется в противном случае. Обратите внимание, что приведенное выше представление с и может быть легко достигнуто, просто применяя коммутативное свойство из уравнения. \eqref{eq:combinedCommutative} к исходному отношению. Тогда вы почти закончили: вам просто нужно применить \eqref{eq:replaceXOR} к или \eqref{eq:replaceBiconditional} к — в зависимости от того, какой оператор вы предпочитаете — и, наконец, у вас есть хорошее представление, содержащее либо только XOR, либо только биусловия.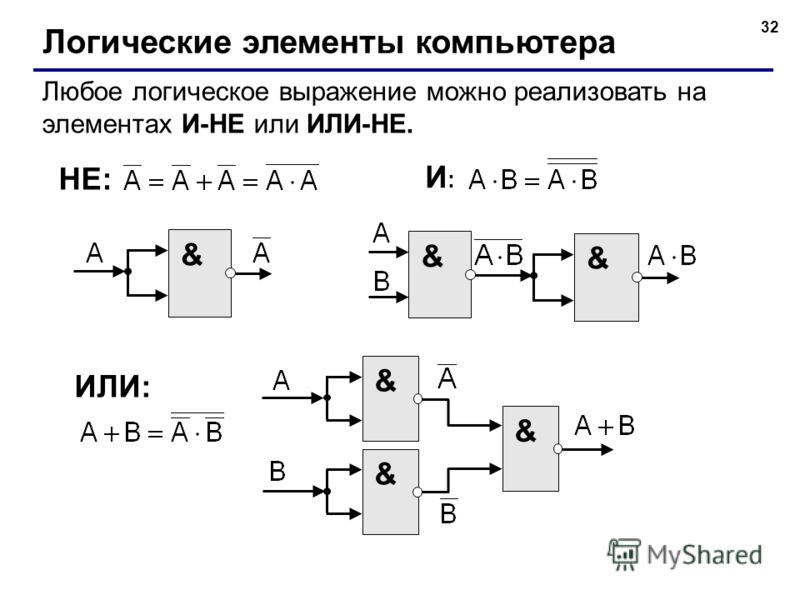 9, |) имеют более высокий уровень приоритета, чем операторы отношения (<, <=, >, >=, ==, !=). Поэтому, когда логические операторы используются в том же выражении, что и реляционные операторы, логические операторы будут выполняться первыми. Чтобы изменить порядок выполнения, используйте круглые скобки.
9, |) имеют более высокий уровень приоритета, чем операторы отношения (<, <=, >, >=, ==, !=). Поэтому, когда логические операторы используются в том же выражении, что и реляционные операторы, логические операторы будут выполняться первыми. Чтобы изменить порядок выполнения, используйте круглые скобки.
Когда в одном выражении последовательно используются несколько реляционных и/или логических операторов, в некоторых случаях оно может не выполняться. Чтобы избежать этой потенциальной проблемы, используйте в выражении соответствующие круглые скобки, чтобы явно определить порядок выполнения операторов. Дополнительные сведения см. в разделе Правила сложных операторов. 9in_raster_or_constant2
| Операнд | Объяснение | Тип данных |
IN_RASTER_OR_CONSTANT1 9963. Если один из входных данных — растр, а другой — скаляр, создается выходной растр с оценкой, выполняемой для каждой ячейки входного растра. | Растровый слой | Константа | |
in_raster_or_constant2 | Второй вход для использования в логической операции XOR. Если один из входных данных — растр, а другой — скаляр, создается выходной растр с оценкой, выполняемой для каждой ячейки входного растра. | Растровый слой | Константа |
Возвращаемое значение
| Имя | Объяснение | Тип данных |
| out_raster 9(логическое XOr) пример 2 (автономный скрипт) В этом примере выполняется логическая операция XOR с двумя входными растрами. СредыCell_size, Current_workspace, Mask, Output_coordinate_system, Output_extent, Scratch_workspace, Snap_raster Связанные темыОтзыв по этой теме? применимых применений оператора XOR | Клэр ЛиСегодня я здесь, чтобы рассказать о своей любви к логическому исключающему ИЛИ (XOR). Одни произносят «экс-ор», другие произносят «ЗОР». В любом случае, в этом году я посвящаю свое время ведению блога о битовых манипуляциях. Я делаю это в надежде, что какая-нибудь душа, копающаяся в темах по булевой алгебре, как и я, наткнется на мою работу. Я надеюсь, что смогу предоставить интересный материал кому-то, кто разделяет мое увлечение битовыми манипуляциями. Для начинающих, для тех из вас, кто не знаком с булевой алгеброй, или для тех, кому нужно освежить знания: XOR — это оператор. В арифметике есть операторы, с которыми вы определенно знакомы. Оператор сложения + принимает два входа и дает один результат. Ввод 1 и 2, а также оператор + всегда будут давать 3. Когда вы видите +, вы знаете, что сложите два значения вместе.Оператор XOR имеет два входа и один выход. Это распространенный способ представления XOR: ⊕ Вместо того, чтобы принимать значения по основанию 10 (1,2,3,…9), он принимает входные данные, которые либо истинны, либо ложны. Каждый ввод будет либо 1, либо 0. Правила для оператора XOR просты. Различные входные данные всегда дают 1 (ИСТИНА). 0 ⊕ 1 == 1Теперь мы перейдем к самому интересному. Я расскажу о некоторых случаях использования XOR в вычислениях. ______________________________________________________________________________
___________________________________________________________________ Что такое контрольная сумма? Это метод подтверждения целостности файла после его передачи. Предположим, у вас есть файл, это может быть mp3, jpg или даже исполняемый файл. Файл необходимо перенести с локальной машины на удаленную. Если получатель хочет убедиться, что это доверенный файл, мы можем подтвердить его целостность с помощью контрольной суммы. Каждый файл состоит из уникальных двоичных данных. Если хотя бы один символ отсутствует или изменен по сравнению с исходной строкой двоичных данных, поврежден весь файл. Двоичные данные mp3 на моем компьютере 🙂 Когда файл передается с сервера А на сервер Б, он разрезается на блоки, пересылается по частям, а затем снова прикрепляется к месту назначения. Чтобы убедиться, что каждый блок не поврежден, для него запускается функция контрольной суммы, генерирующая уникальную контрольную сумму. Все эти символы ASCII затем интерпретируются по основанию 2 (1 и 0), и каждый фрагмент объединяется XOR вместе. Каков результат? Это дает нам результат XOR или уникальную строку контрольной суммы из 1 и 0. Когда файл повторно подключается и записывается на диск на другом сервере, он может ссылаться на контрольную сумму, сгенерированную исходным сервером, чтобы убедиться, что он не поврежден. В приведенном выше примере, если бы файл не был поврежден во время передачи (загрузки), контрольная сумма вашей загруженной копии была бы идентична контрольной сумме исходного файла на сервере. В настоящее время почти в каждом доме есть внешний жесткий диск, на котором каким-либо образом создаются резервные копии компьютерных файлов. Вы никогда не можете предсказать, что произойдет завтра, поэтому лучше перестраховаться и сделать резервную копию ваших файлов. Обычный пользователь сделает резервную копию 1:1, то есть для каждого набора файлов будет создана одна резервная копия во внешней памяти. Но что происходит, когда вы занимаетесь хранением данных и отвечаете за тысячи жестких дисков? Наивным решением было бы создание одной резервной копии для каждого набора пользовательских файлов. Давайте проведем мысленный эксперимент. Что, если я скажу вам, что вместо того, чтобы покупать N дисков для резервного копирования N серверов (заполненных до отказа), мы могли бы сделать это за < N? Я здесь, чтобы представить стандартную конфигурацию жесткого диска, известную как RAID 5. Для простоты давайте представим, что у нас есть очень маленькие диски, каждый из которых имеет емкость 8 байт. Каждый диск почти заполнен и содержит один текстовый файл. Вот три файла: Описания файлов, размер и содержимое трех серверов Двоичный перевод содержимого файлов трех серверовБлагодаря волшебному свойству XOR все содержимое этих трех серверов может быть восстановлено не через три резервных жестких диска, а через один единственный диск четности. XOR будет работать аналогично контрольной сумме, которую мы рассмотрели в предыдущем случае. Когда мы объединяем XOR содержимое трех жестких дисков, мы получаем следующее: XOR содержимое трех дисков.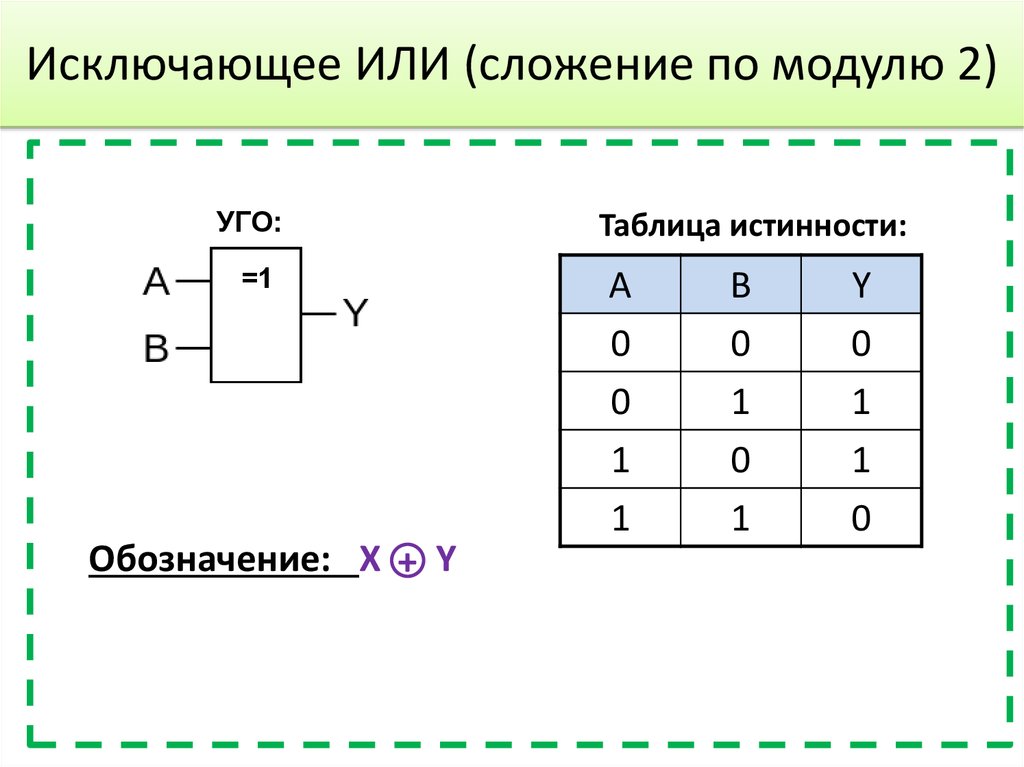 Давайте сохраним этот диск четности в надежном месте на случай чрезвычайной ситуации… Давайте сохраним этот диск четности в надежном месте на случай чрезвычайной ситуации…Завтра произойдет сбой диска на сервере 2. Содержимое сервера 2 пропало. Как нам его восстановить? Мы взламываем диск четности, который содержит XOR трех серверов. Внутри «01101001 00100111 01101101 00111111 01100111 01101001 01100101 01101000 00001010» находится исходное содержимое уничтоженного сервера. Как извлечь данные сервера 2 с этого диска четности? Ключом к его извлечению является использование серверов 1 и 3, их партнеров при создании диска четности. Выполним XOR вместе двоичных данных:
Файл 1 ⊕ Файл 3 ⊕ Диск четности == Восстановленные данные Используя эти, казалось бы, загадочные свойства XOR, нам удалось восстановить содержимое сервера 2. Предположим, что в мире с минимальными осложнениями мы не теряем более 1 входного диска за раз из этих групп. |


 y) .
y) .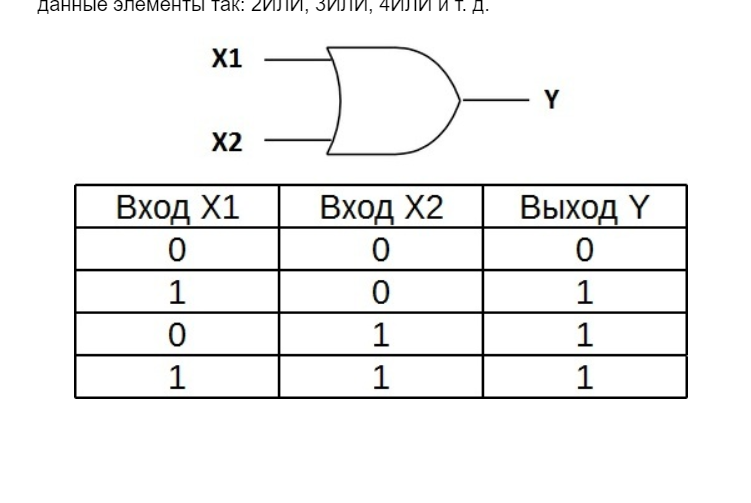
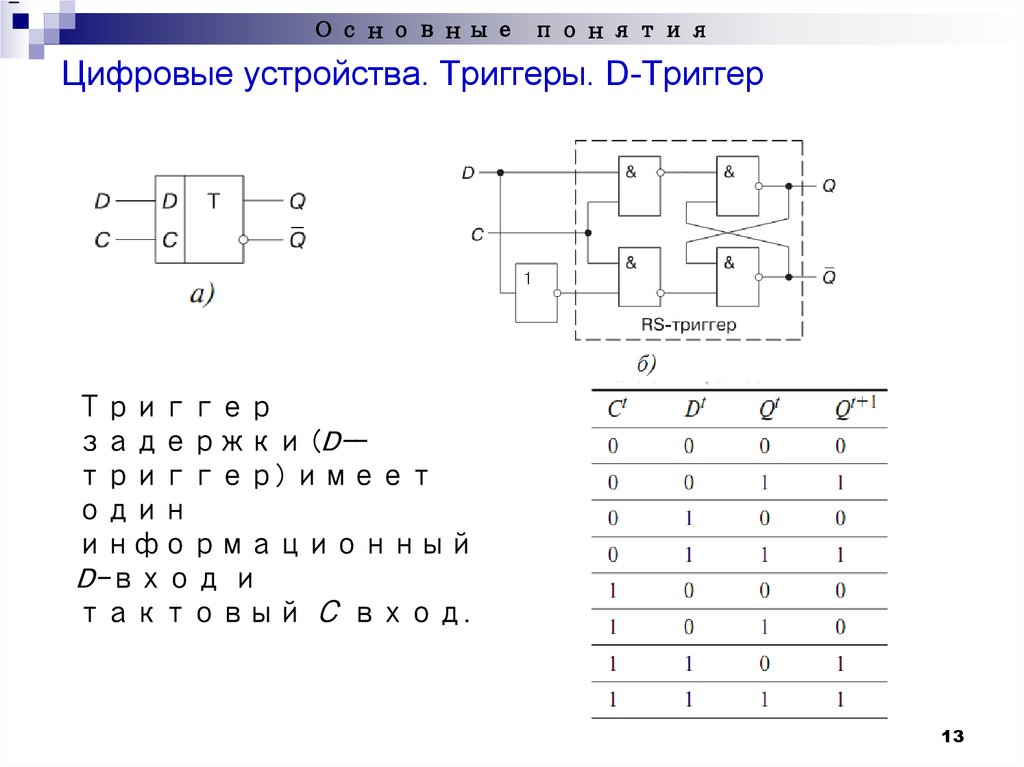
 ..x n).
..x n).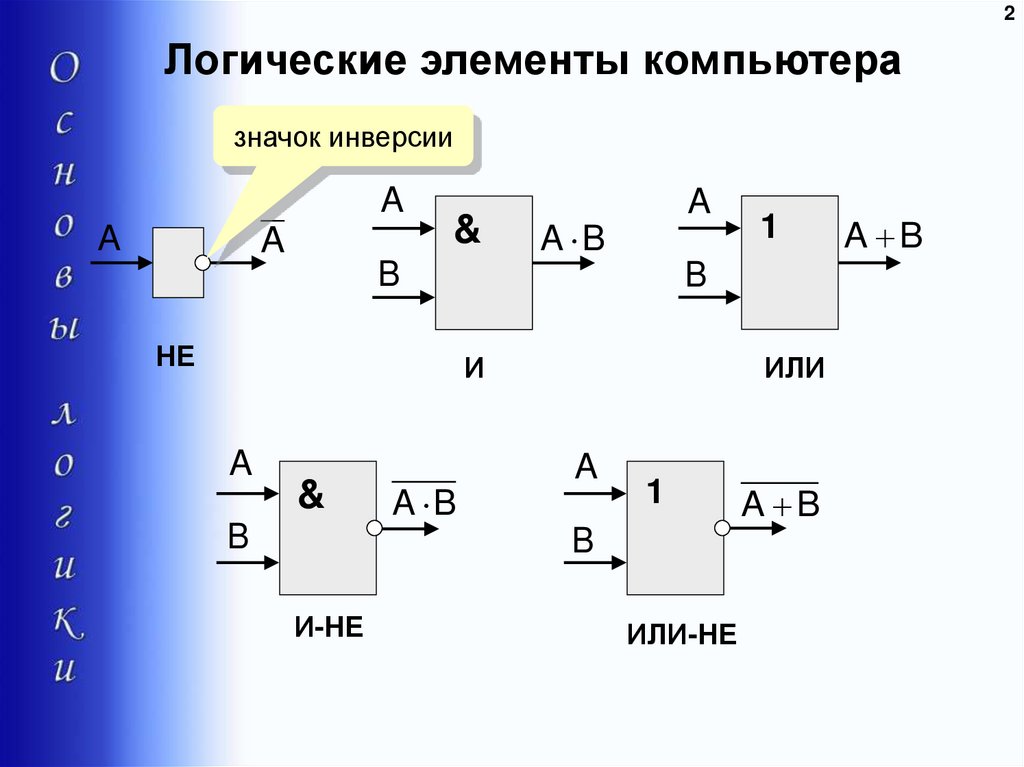
 схема
схема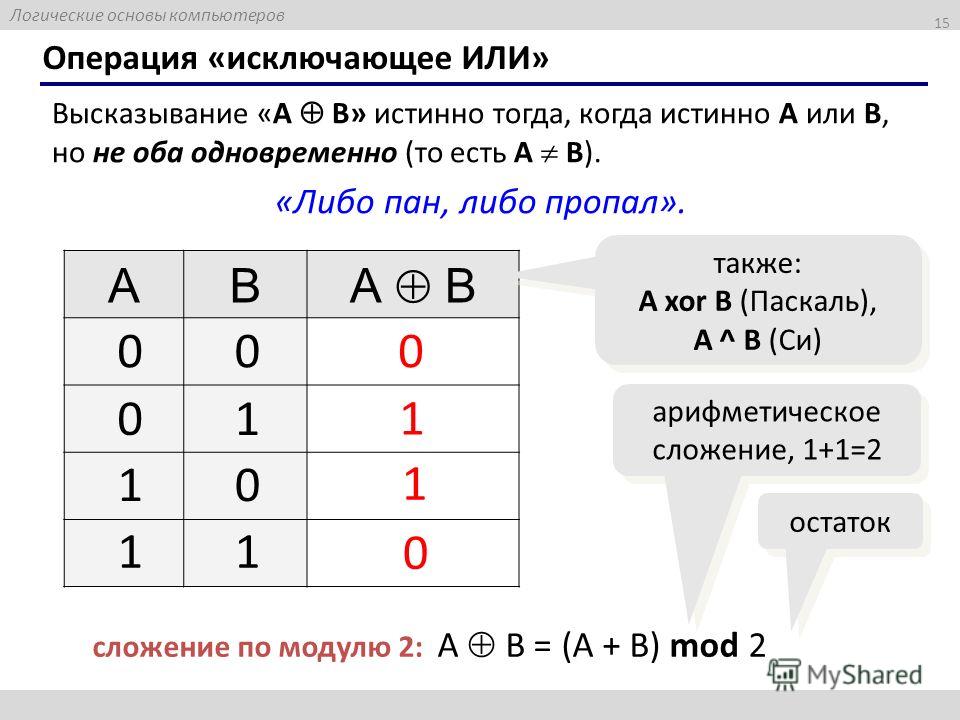 . Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгу
. Словарь всех математических слов, эксклюзивный или . Издание 2-го класса 20150108-4799968. стр. 75. Life is a Story Problem LLC. 8 января 2015. Купить книгу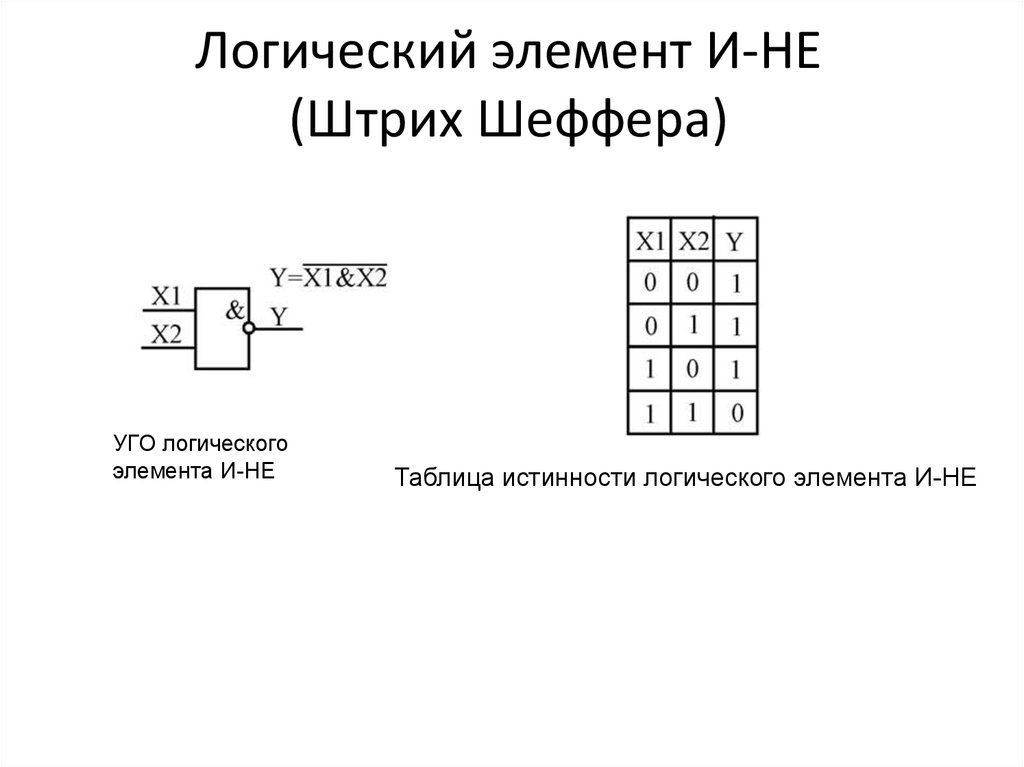
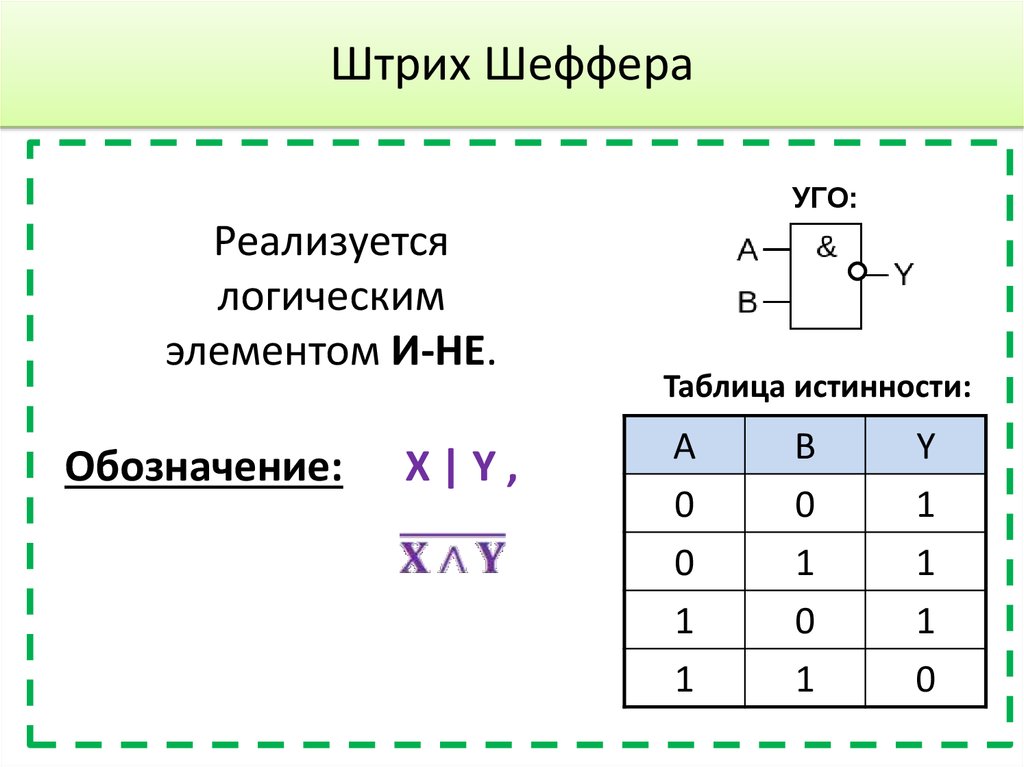 inRaster2
# Сохраняем вывод
outBooleanXOr.save(«C:/sapyexamples/output/outboolxor»)
inRaster2
# Сохраняем вывод
outBooleanXOr.save(«C:/sapyexamples/output/outboolxor») 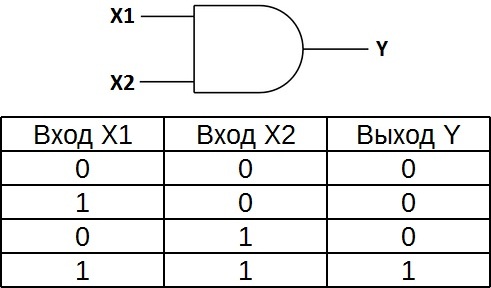
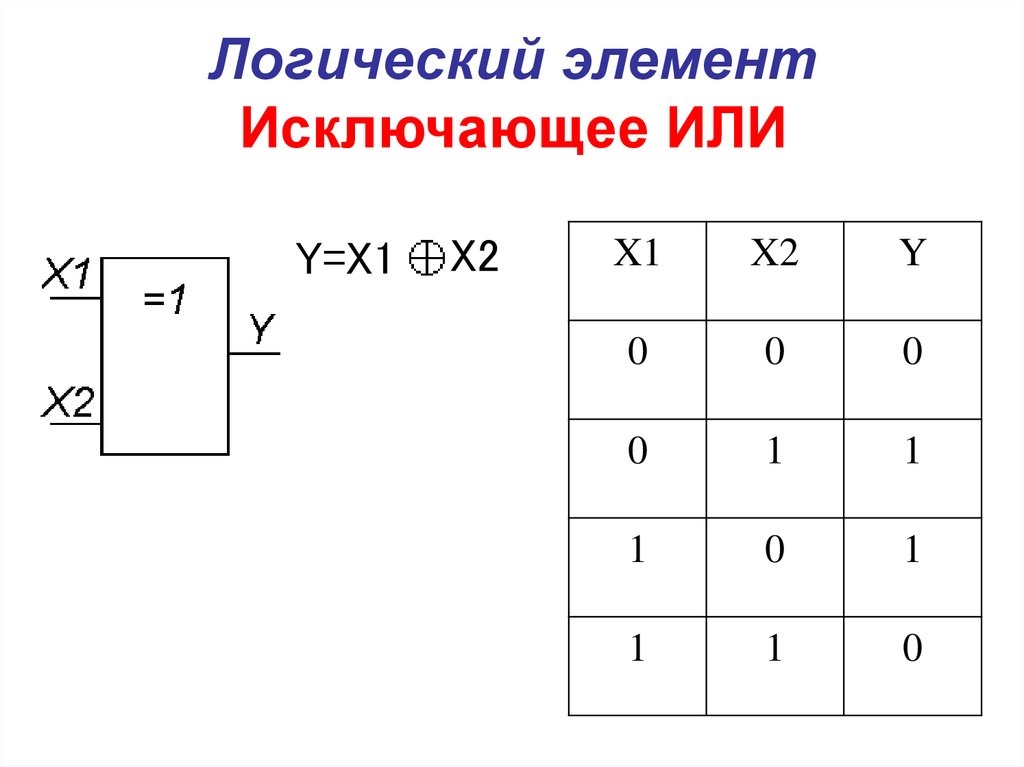 Контрольная сумма — это математический вывод, который поможет вам подтвердить, был ли файл поврежден или подделан.
Контрольная сумма — это математический вывод, который поможет вам подтвердить, был ли файл поврежден или подделан.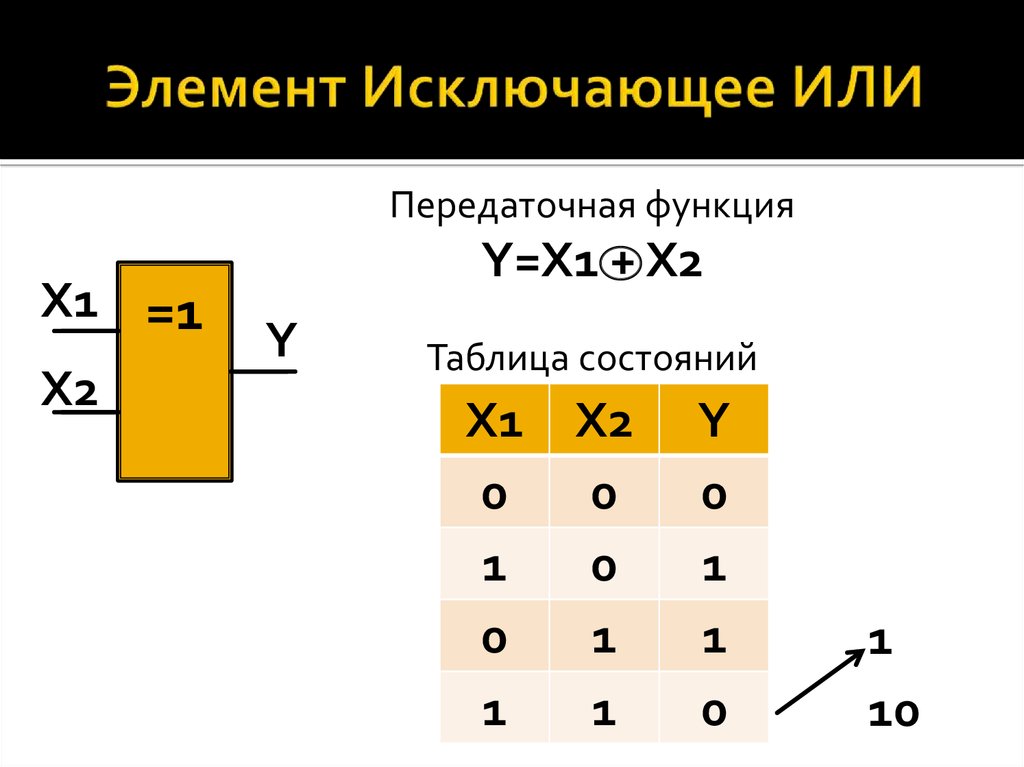
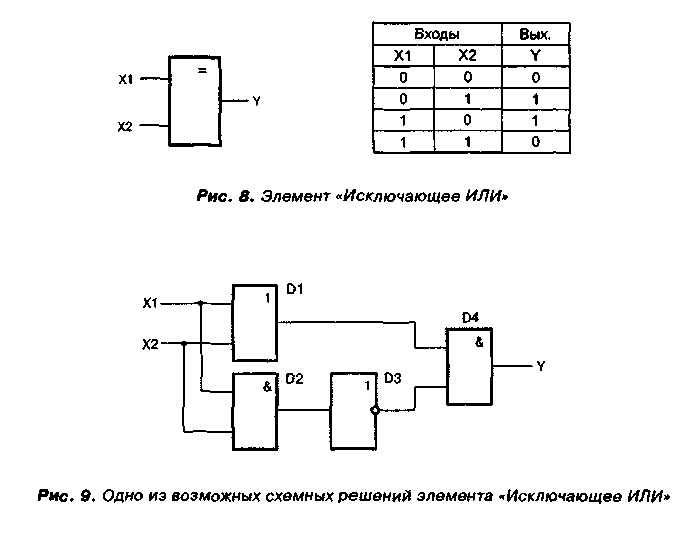 Таким образом, для 300 жестких дисков вы создадите 300 резервных копий. Это работает, но очень быстро станет очень дорогим.
Таким образом, для 300 жестких дисков вы создадите 300 резервных копий. Это работает, но очень быстро станет очень дорогим.