Электричество и магнетизм
Магнитная стрелка — не только прибор, регистрирующий внешнее магнитное поле, она сама является маленьким магнитом, создающим свое собственное поле. Значит, и виток с током должен создавать свое собственное магнитное поле, подобное полю стрелки. Следовательно, любой электрический ток в проводнике создает вокруг него магнитное поле. В частности, такое поле должен создавать движущийся электрический заряд.
Сейчас мы попробуем угадать, какое магнитное поле порождается зарядом q, движущимся со скоростью v (рис. 6.6). Отправной точкой нам послужит аналогия между электрическими и магнитными явлениями. Вспомним то, что мы уже знаем. Чтобы получить силу, действующую на заряд в электростатическом поле, мы умножаем величину заряда на вектор напряженности поля
Рис. 6.6. Магнитное поле движущегося заряда
Чтобы получить силу Лоренца, действующую со стороны магнитного поля на движущийся заряд, мы тоже производим операцию умножения: векторно умножаем на магнитную индукцию
Применим тот же прием для угадывания магнитного поля движущегося заряда.
Электрическое поле покоящегося точечного заряда равно
Заменим q на вектор , электрическое поле — на магнитное, а операцию обычного умножения — на векторное умножение. Получаем
Мы не поставили здесь знака равенства, так как у нас не все в порядке с размерностью в левой и правой частях уравнения. Из выражения для силы Лоренца следует, что размерность магнитной индукции равна
Размерность же правой части уравнения равна
Чтобы размерности обеих частей совпали, правую часть надо разделить на квадрат какой-то скорости. Скорость частицы у нас уже использована, и остается единственная возможность — фундаментальная физическая постоянная, скорость света с
|
(6.2) |
Мы ввели здесь новую константу , связанную с соотношением
|
|
(6. |
Ее называют магнитной постоянной; численное значение ее оказывается равным
|
|
(6.4) |
Конечно, выражение (6.2) получено лишь по аналогии и не может рассматриваться, как строго выведенное. Однако посмотрим, к каким следствиям оно приводит.
Возьмем элемент проводника , по которому течет ток I (рис. 6.7). Направление вектора
Рис. 6.7. Магнитное поле, создаваемое элементом тока
Полный заряд носителей тока в этом элементе равен dq = enSdl, где е — заряд носителей, n — их концентрация, a S — поперечное сечение проводника. Подставим этот заряд в выражение (6.2) и получим (рис. 6.8)
Подставим этот заряд в выражение (6.2) и получим (рис. 6.8)
Сила тока дается выражением
откуда, учитывая, что
получаем
|
(6.5) |
Рис. 6.8. Направление вектора индукции магнитного поля
Вектор проведен от элемента тока к точке наблюдения А. Соответственно, модуль вектора равен
|
(6.6) |
где — угол между направлением данного элемента тока
Рис. 6.9. Ж. Био (1774–1862) — французский физик, геодезист и астроном
6.9. Ж. Био (1774–1862) — французский физик, геодезист и астроном
Рис. 6.10. Ф. Савар (1791–1841) — французский физик
Рис. 6.11. П. Лаплас (1749–1827) — французский математик, физик и астроном
Дополнительная информация
http://dic.academic.ru/dic.nsf/brokgauz_efron/13166/%D0%91%D0%B8%D0%BE — Жан Батист Био;
http://www.hrono.ru/biograf/bio_l/laplas.php — Пьер Симон Лаплас (1749–1827).
Закон Био — Савара — Лапласа определяет магнитную индукцию в любой точке магнитного поля, создаваемого постоянным электрическим током, текущим по проводнику любой формы (см. рис. 6.7). Для этого надо проинтегрировать соотношение (6.5) вдоль всего проводника. При этом магнитные индукции от различных элементов тока векторно складываются, то есть используется принцип суперпозиции для магнитных полей.
Определение по Электродинамике | Объединение учителей Санкт-Петербурга
АКТИВНАЯ МОЩНОСТЬ – физическая величина, равная среднему за период значению мгновенной мощности переменного тока. Позволяет оценить среднюю скорость преобразования электромагнитной энергии в др. виды энергии. В цепи переменного однофазного тока А.м. рассчитывается по формуле: P=IUcosφ. Единица А.м. в СИ – Ватт (Вт).
АКТИВНОЕ СОПРОТИВЛЕНИЕ — физическая величина, равная отношению активной мощности, поглощаемой на участке цепи, к квадрату действующего значения силы переменного тока на этом участке. Позволяет оценить сопротивление электрической цепи или ее участка электрическому току, обусловленное необратимыми превращениями электрической энергии в др. формы (преимущественно во внутреннюю). Единица А.с. в СИ — Ом.
АМПЕРА ЗАКОН — закон взаимодействия двух проводников с токами; параллельные проводники с токами одного направления притягиваются, а с токами противоположного направления — отталкиваются.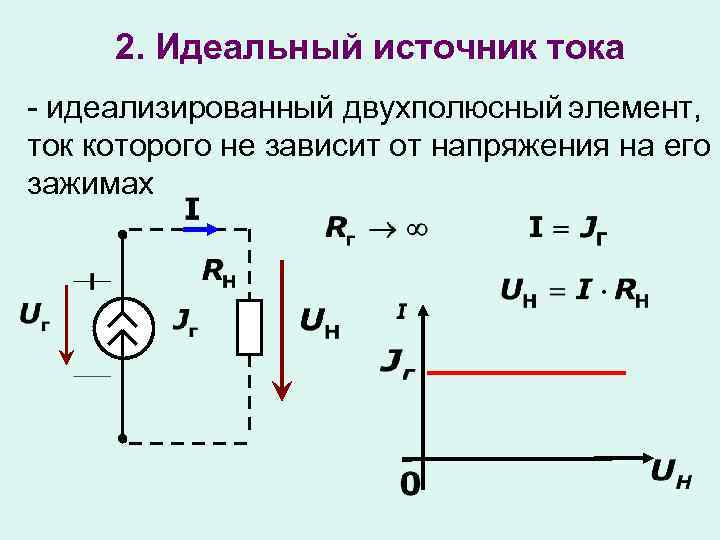 А.з. называют также закон, определяющий силу, действующую в магнитном поле на малый отрезок проводника с током. Открыт в 1820г. А.М. Ампером.
А.з. называют также закон, определяющий силу, действующую в магнитном поле на малый отрезок проводника с током. Открыт в 1820г. А.М. Ампером.
АНИОНЫ — отрицательно заряженные ионы, движущиеся в электрическом поле к аноду.
АНОД — положительный полюс источника электрической энергии или электрод какого-либо прибора, присоединяемый к положительному полюсу источника тока. Потенциал А. при работе источника всегда выше потенциала катода.
БУРАВЧИКА ПРАВИЛО — правило для определения направления вектора магнитной индукции магнитного поля прямолинейного проводника с током: если Б. (правый винт) ввинчивать по направлению тока, то направление вращения рукоятки буравчика показывает направление вектора магнитной индукции. (Ср.правой руки правило)
ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ — источник электрического тока, в котором энергия электрохимической реакции преобразуется в электрическую энергию (элемент Вольта, батарейки, аккумуляторы).
ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ — среднее квадратичное за период значение силы переменного тока и напряжения. Д.з. силы синусоидального тока и напряжения в раз меньше их амплитудных значений. Физический смысл: Д.З. силы переменного тока равно силе такого постоянного тока, при прохождении которого через проводник выделяется то же количество теплоты за то же самое время.
ДЖОУЛЯ-ЛЕНЦА ЗАКОН — закон, описывающий тепловое действие электрического тока. Согласно Д. — Л.з. количество теплоты, выделяющееся в проводнике при прохождении по нему постоянного тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока по проводнику: .
ДИАМАГНЕТИЗМ – явление возникновения в веществе (диамагнетике) намагниченности, направленной навстречу внешнему магнитному полю. Обусловлен индуцированием дополнительного магнитного момента в атомных электронных оболочках под действием внешнего поля и проявляется в том случае, когда атомы, молекулы или ионы не имеют результирующего собственного магнитного момента. Присущ всем веществам, но часто перекрывается более сильными эффектами (см. парамагнетизм и ферромагнетизм).
Присущ всем веществам, но часто перекрывается более сильными эффектами (см. парамагнетизм и ферромагнетизм).
ДИНАМИК – распространенное краткое название электродинамического громкоговорителя.
ДИПОЛЬ ЭЛЕКТИРИЧЕСКИЙ – система двух одинаковых по модулю и противоположных по знаку электрических зарядов, расстояние между которыми (плечо Д.) во много раз меньше, чем расстояние от центра Д. до рассматриваемых точек электрического поля. Во внешнем электрическом поле ориентируется вдоль силовых линий поля. Например, диполем можно считать молекулу воды.
ДИПОЛЬ МАГНИТНЫЙ – электрический ток, протекающий по замкнутому контуру (витку), размеры которого малы по сравнению с расстоянием до рассматриваемых точек магнитного поля. Внешнее магнитное поле оказывает на Д.М. ориентирующее действие.
ДИОД — двух электродный прибор с односторонней электрической проводимостью. Применяется для выпрямления переменного тока, в качестве детектора, для преобразования частоты, ограничения тока и напряжения, переключения электрических цепей.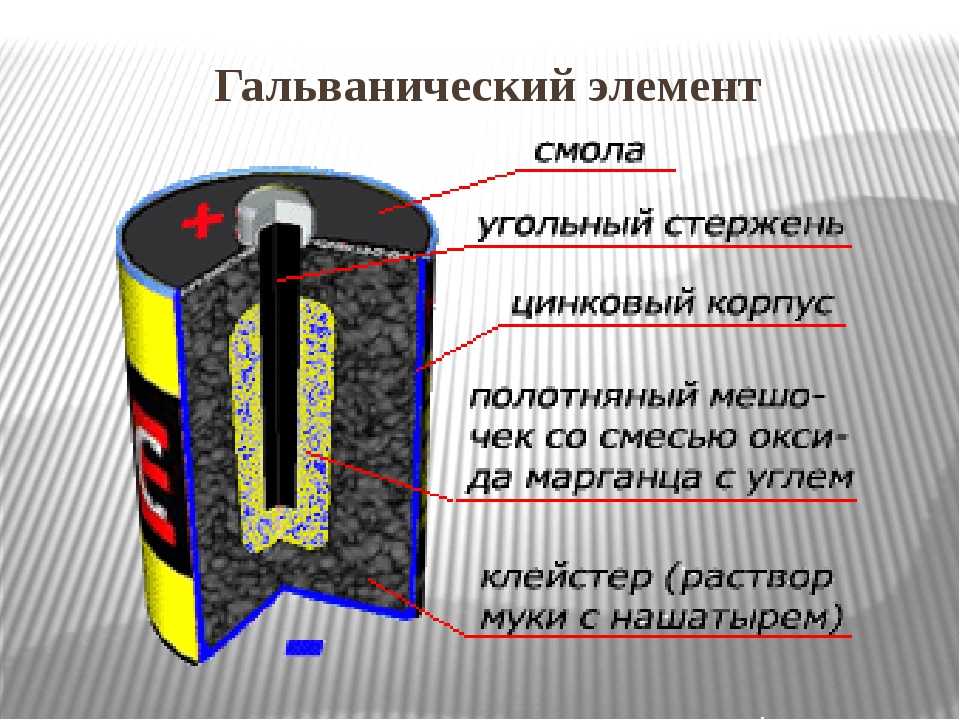 Различают электровакуумные и полупроводниковые Д.
Различают электровакуумные и полупроводниковые Д.
ДИЭЛЕКТРИКИ — вещества, практически не проводящие электрического тока. Обладают большим удельным сопротивлением по сравнению с проводниками. Могут быть твердыми, жидкими и газообразными. Во внешнем электрическом поле Д. поляризуется, что приводит к ослаблению электрического поля в Д. (см.поляризация диэлектриков и диэлектрическая проницаемость.)
ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ – безразмерная физическаявеличина, равная отношению модуля напряженности электрического поля в вакууме Е0 к модулю напряженности электрического поля в однородном диэлектрике: .
ДОМЕНЫ — области в ферромагнитном (сегнетоэлектрическом) кристалле, в которых ниже определенной температуры (точки Кюри) существует самопроизвольная намагниченность (поляризованность).
ДУГА ЭЛЕКТРИЧЕКАЯ, дуговой разряд – один из видов самостоятельного разряда в газе, в котором разрядные явления сосредоточены в ярко светящемся плазменном шнуре. Возможна в любом газе при давлениях, близких к атмосферному и выше. Применяется в электрометаллургии, светотехнике и в электросварке.
Возможна в любом газе при давлениях, близких к атмосферному и выше. Применяется в электрометаллургии, светотехнике и в электросварке.
ДЫРКА – в полупроводнике – не занятая электроном вакансия в валентной зоне, которая ведет себя как избыточный положительный заряд.
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ — физическая величина ХС, которой оценивают сопротивление, оказываемое переменному току проводником вследствие наличия у него электрической емкости. При синусоидальном токе с циклической частотой ω Е.с. равно . Единица в СИ – Ом.
ЕМКОСТЬ ЭЛЕКТРИЧЕСКАЯ — см. электрическая емкость.
ЗАРЯД ЭЛЕКТРИЧЕСКИЙ — см.электрический заряд.
ЗАРЯДА СОХРАНЕНИЯ ЗАКОН — один из фундаментальных законов природы: алгебраическая сумма электрических зарядов любой электрически изолированной системы остается неизменной. В электрически изолированной системе З. с.з. допускает появление новых заряженных частиц (напр., при электролитической диссоциации, ионизации газов, рождении пар частица — античастица и др.), но суммарный электрический заряд появившихся частиц всегда должен быть равен нулю.
с.з. допускает появление новых заряженных частиц (напр., при электролитической диссоциации, ионизации газов, рождении пар частица — античастица и др.), но суммарный электрический заряд появившихся частиц всегда должен быть равен нулю.
ИЗОЛЯТОР ЭЛЕКТРИЧЕСКИЙ – элемент конструкции, выполненный из вещества с очень большим электрическим удельным сопротивлением (диэлектрика). В быту может быть синонимом термина диэлектрик.
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ — физическая величина ХL, которой оценивают сопротивление, оказываемое переменному току проводником вследствие наличия у него индуктивности. При синусоидальном токе с угловой частотой ω: XL=ωL. Единица И.с. в СИ — Ом. Ср.емкостное сопротивление, активное сопротивление.
ИНДУКТИВНОСТЬ — физическая величина, которая характеризует магнитные свойства электрической цепи (проводника) и равна отношению потока магнитной индукции, пересекающего поверхность, ограниченную проводником, к силе тока в этом проводнике. Единица И. в СИ — генри. Ср.электрическая емкость.
Единица И. в СИ — генри. Ср.электрическая емкость.
ИОНИЗАЦИЯ — отрыв от атома или молекулы газа одного или нескольких электронов. Происходит под действием электромагнитного излучения; ударов электронов, ионов или других атомов. Приводит к возникновению ионов.
ИОНЫ — электрически заряженные атомы или группы атомов, образующиеся при потере или присоединении электронов (или других заряженных частиц). Ионы с положительным электрическим зарядом называются катионами, с отрицательным — анионами.
ИСКРОВОЙ РАЗРЯД – вид самостоятельного нестационарного электрического разряд в газе, возникающий в электрическом поле при давлении, близком к атмосферному. Температура в И.р. достигает 10000К. В природе наблюдается в виде молнии.
ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ – устройства, преобразующие различные виды энергии в электрическую. Различают химические (напр. , гальванический элемент) и физические (термоэлемент, фотоэлемент, индукционный генератор и т.д.) И.т.
, гальванический элемент) и физические (термоэлемент, фотоэлемент, индукционный генератор и т.д.) И.т.
КАТИОНЫ — положительно заряженные ионы, в электрическом поле движутся к катоду.
КАТОД — 1) отрицательный полюс источника электрической энергии или электрод прибора, присоединяемый к отрицательному полюсу источника. Потенциал К. работающего источника всегда ниже потенциала анода. 2) Источник электронов в электровакуумных приборах.
КАТУШКА ИНДУКТИВНОСТИ – элемент электрической цепи, конструктивно представляющий катушку из электропроводящего материала с изолированными витками. Обладает значительной индуктивностью при относительно малой емкости и малом активном сопротивлении. Один из основных элементов колебательного контура. Ср. конденсатор электрический.
КИНЕСКОП — приемная телевизионная электронно-лучевая трубка, преобразующая электрические сигналы в видимое изображение.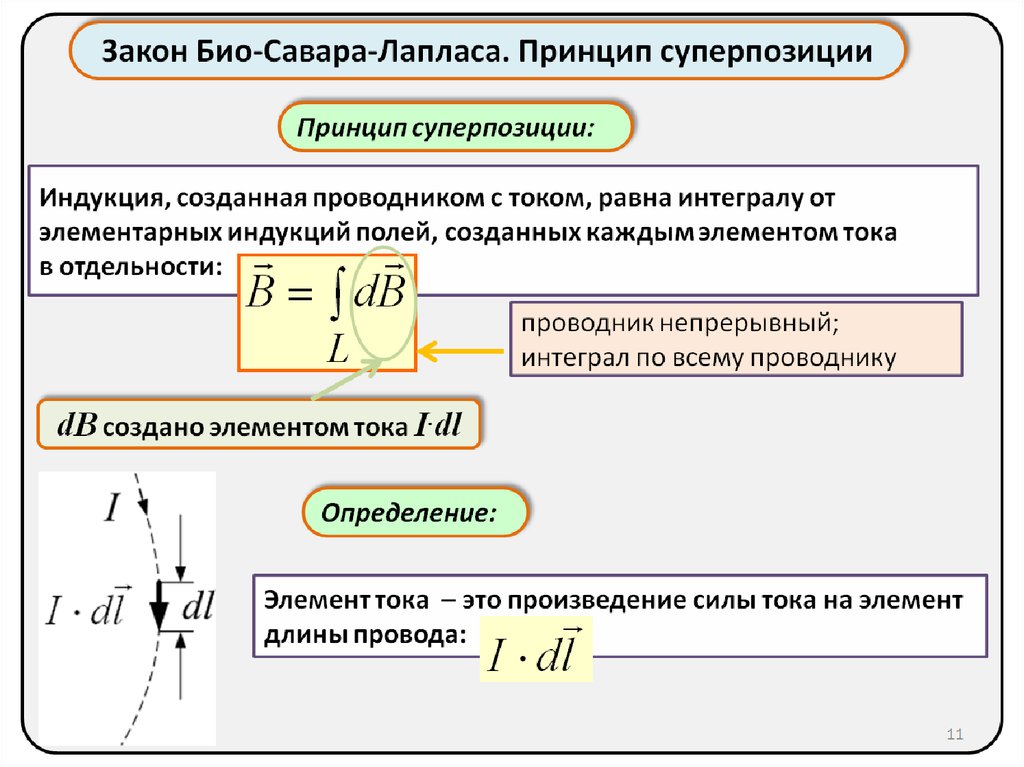
КОЛЕБАТЕЛЬНЫЙ КОНТУР — электрическая цепь из катушки индуктивности и конденсатора, в которой возникает возможность периодического обмена электрической и магнитной энергией при зарядке конденсатора или возбуждении электрического тока в катушке, т.е. возникают электромагнитные колебания. Период равен , где L — индуктивность контура, C — электрическая емкость. Применяется как резонансная система во многих радиотехнических устройствах.
КОНДЕНСАТОР ЭЛЕКТРИЧЕСКИЙ – элемент электрической цепи из двух или более электродов (обкладок), разделенных диэлектриком, толщина которого мала по сравнению с размерами обкладок. Обладает значительной электрической емкостью. Хорошо проводит переменный ток высокой частоты. См. емкостное сопротивление, электрическая емкость.
КОРОТКОЕ ЗАМЫКАНИЕ — не предусмотренное нормальными условиями работы соединение двух точек электрической цепи, имеющих различные потенциалы, через очень малое сопротивление.
КРУТИЛЬНЫЕ ВЕСЫ — чувствительный физический прибор, для измерения малых сил. Изобретен Ш.Кулоном в 1784г. и применялся при установлении Кулона закона.
КУЛОНА ЗАКОН — основной закон электростатики, выражающий зависимость силы взаимодействия двух неподвижных точечных зарядов от расстояния между ними: два неподвижных точечных заряда взаимодействуют с силой прямо пропорциональной произведению значений этих зарядов и обратно пропорциональной квадрату расстояния между ними и диэлектрической проницаемости среды, в которой находятся заряды. В СИ имеет вид: . Величина числено равна силе, действующей между двумя точечными неподвижными зарядами по 1 Кл каждый, находящимися в вакууме на расстоянии 1 м друг от друга. К.з. является одним из экспериментальных обоснований электродинамики.
ЛЕВОЙ РУКИ ПРАВИЛО — правило, определяющее направление силы, которая действует на находящийся в магнитном поле проводник с током (или движущуюся заряженную частицу). Оно гласит: если левую руку расположить так, чтобы вытянутые пальцы показывали направление тока (скорости частицы), а силовые линии магнитного поля (линии магнитной индукции) входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник (положительную частицу; в случае отрицательной частицы направление силы противоположно).
Оно гласит: если левую руку расположить так, чтобы вытянутые пальцы показывали направление тока (скорости частицы), а силовые линии магнитного поля (линии магнитной индукции) входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник (положительную частицу; в случае отрицательной частицы направление силы противоположно).
ЛЕНЦА ПРАВИЛО (ЗАКОН) — правило, определяющее направление индукционных токов, возникающих при электромагнитной индукции. Л.п. — следствие закона сохранения энергии Согласно Л.п. индукционный ток всегда имеет такое направление, что его собственное магнитное поле всегда препятствует тому изменению внешнего магнитного поля, которое является причиной индукционного тока
ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ, силовые линии магнитного поля – воображаемые линии, с помощью которых можно графически изобразить распределение магнитного поля в пространстве. Проводятся так, что вектор магнитной индукции в данной точке пространства направлен по касательной к Л.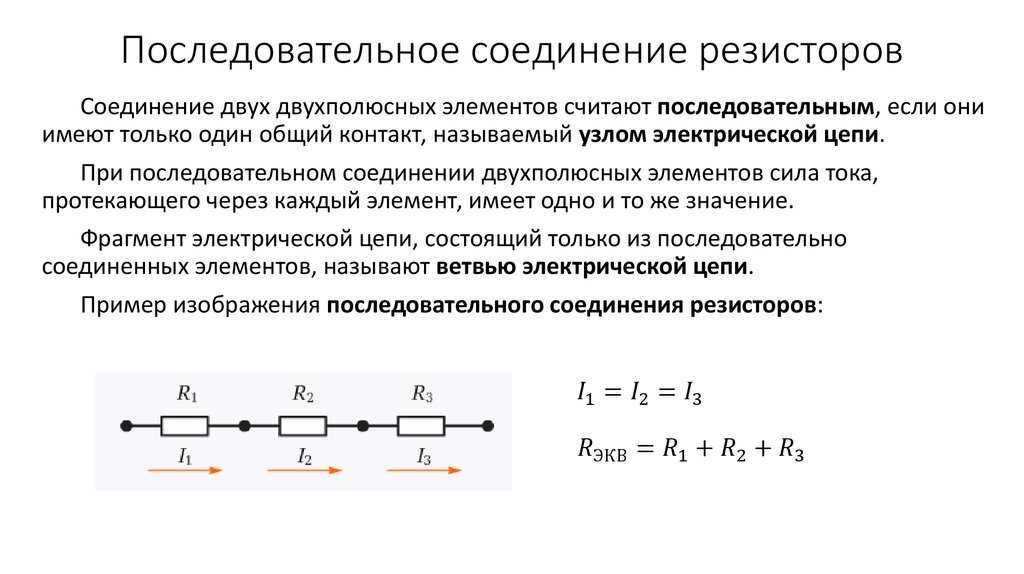 м.и. в этой точке.
м.и. в этой точке.
ЛИНИИ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, силовые линии электрического поля – воображаемые линии, с помощью которых можно графически изобразить распределение электрического поля в пространстве. Проводятся так, что вектор напряженности электрического поля в данной точке пространства направлен по касательной к Л.н. в этой точке.
ЛОРЕНЦА СИЛА– сила, действующая на заряженную частицу с зарядом q, движущуюся в магнитном поле индукции B со скоростью v. Модуль равен F=qvBsinα, где α– угол между векторами индукции магнитного поля и скорости частицы. Направление определяется левой руки правилом.
МАГНЕТИЗМ – совокупность явлений, связанных со взаимодействием между электрическими токами, между электрическими токами и магнитами, между магнитами. Магнитное взаимодействие осуществляется посредством магнитного поля. Проявляется во всех физико-химических процессах, происходящих в веществе. Определяет основные астрофизические и геомагнитные явления (солнечные вспышки, магнитные бури, нарушения радиосвязи и т.д.).
Определяет основные астрофизические и геомагнитные явления (солнечные вспышки, магнитные бури, нарушения радиосвязи и т.д.).
МАГНЕТИКИ — вещества, способные намагничиваться в магнитном поле, т.е. создавать собственное магнитное поле. См. диамагнетизм, парамагнетизм, ферромагнетизм, ферримагнетизм.
МАГНИТ — тело, обладающее намагниченностью, т.е. создающее магнитное поле. Свойства М. присущи некоторым минералам (напр., магнитный железняк), намагниченным магнитным материалам (постоянный магнит) и электромагнитам.
МАГНИТНАЯ ИНДУКЦИЯ (вектор магнитной индукции) — векторная величина, применяющаяся для количественного оценивания действия магнитного поля. Равна отношению максимальной силы, действующей в магнитном поле на элемент проводника с током, к величине силы тока и длине этого элемента проводника . Направление определяется правой руки правилом или буравчика правилом. Единица в СИ — тесла. Ср. напряженность электрического поля.
Ср. напряженность электрического поля.
МАГНИТНАЯ ПОСТОЯННАЯ — величина , входящая в выражения некоторых законов электромагнетизма при записи их в форме, соответствующей Международной системе единиц (СИ). Ср. электрическая постоянная.
МАГНИТНАЯ ПРОНИЦАЕМОСТЬ — физическая величина, характеризующая связь между магнитной индукцией внешнего магнитного поля и магнитным полем в веществе. Обозначается m. У диамагнетиков m<1, у парамагнетиков m>1, у ферромагнетиков m>>1.
МАГНИТНОЕ ПОЛЕ — одна из форм проявления электромагнитного поля. Действует только на движущиеся электрические заряды (заряженные тела), проводники с током и частицы или тела, обладающие магнитным моментом, и создается этими же объектами. Для количественного описания М.п. используются величины магнитная индукция, магнитный поток и др. Ср.электрическое поле.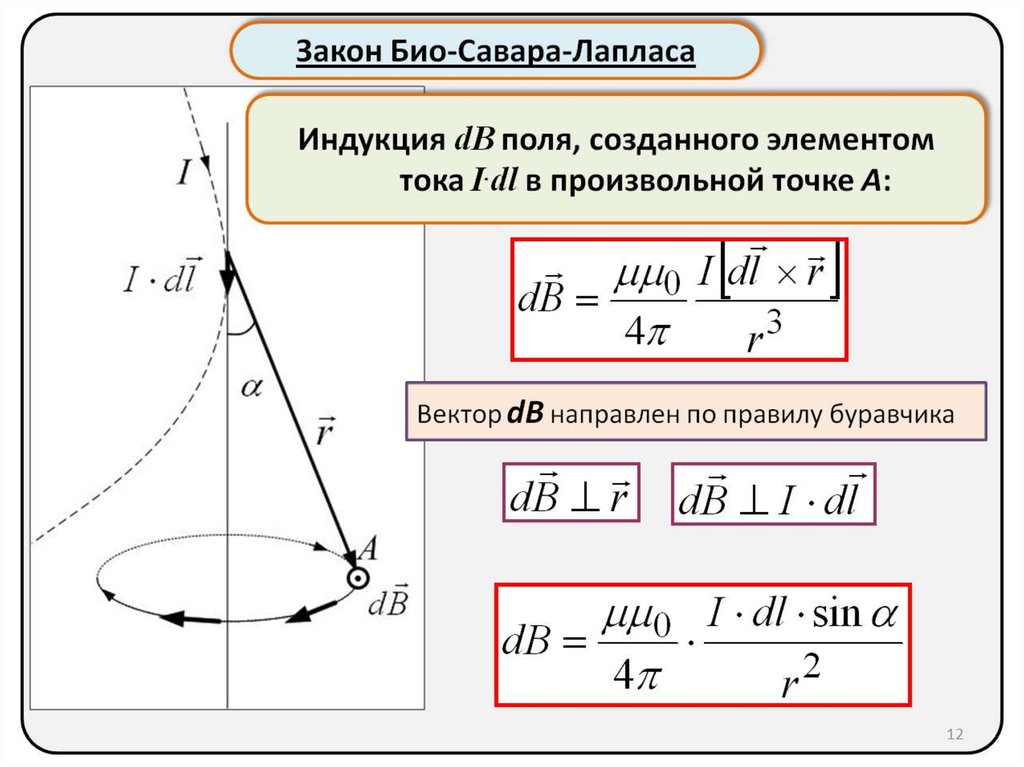
МАГНИТНЫЙ МОМЕНТ — векторная величина, характеризующая магнитные свойства тел и частиц вещества. М.м. тока — вектор, равный произведению силы тока на площадь, ограниченную контуром: p=IS. Направление определяется буравчика правилом. Единица в СИ — ампер-квадратный метр (А.м2). Ср. электрический момент.
МАГНИТНЫЙ ПОЛЮС — участок поверхности намагниченного образца (магнита), на котором нормальная к поверхности составляющая намагниченности отлична от нуля. Договорились считать, что снаружи магнита линии магнитной индукции выходят из северного полюса, а в южный входят. Внутри магнита — наоборот.
МАГНИТНЫЙ ПОТОК — поток вектора магнитной индукции B через какую-либо поверхность. Магнитный поток F через поверхность S выражается формулой F=BScosα, где α— угол между вектором магнитной индукции и нормалью к площадке S. Единица м.п. в СИ — вебер (Вб).
Единица м.п. в СИ — вебер (Вб).
МАКСВЕЛЛА УРАВНЕНИЯ — основные уравнения электродинамики, устанавливающие связь между напряженностями электрического и магнитного полей и распределением в пространстве электрических зарядов и токов. Описывают электромагнитные явления в различных средах и вакууме.
МОЛНИЯ — гигантский искровой разряд атмосферного электричества между облаками или между облаками и землей. Сила тока может достигать 100 кА, длительность — 10-4 c . См. электрический разряд.
НАМАГНИЧЕННОСТЬ — векторная величина, числено равная отношению магнитного момента к объему вещества (магнетика). Единица в СИ — ампер на метр (А/м). Ср. поляризованность.
НАПРЯЖЕНИЕ ЭЛЕКТРИЧЕСКОЕ (падение напряжения) — скалярная величина, равная отношению работы, совершаемой суммарным полем сторонних и кулоновских сил при перемещении заряда на участке электрической цепи, к величине этого заряда: . Единица в СИ — вольт. Ср. электродвижущая сила, разность потенциалов.
Единица в СИ — вольт. Ср. электродвижущая сила, разность потенциалов.
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ — векторная величина E, применяемая для описания силового действие электрического поля на электрически заряженные частицы и тела, равная отношению силы, действующей со стороны поля на точечный электрический заряд, помещенный в данную точку поля: , Единица в СИ — вольт на метр (В/м). Ср. магнитная индукция.
НОСИТЕЛИ ТОКА — электрически заряженные частицы в веществе, обусловливающие его электрическую проводимость. В металлах — это свободные электроны, в электролитах — ионы, в полупроводниках — электроны и дырки.
ОДНОРОДНОЕ ПОЛЕ – физическое поле, напряженность (магнитная индукция) которого одинакова во всех точках.
ОМА ЗАКОН – обобщенное название закона, устанавливающего пропорциональность между силой тока в участке электрической цепи и разностью потенциалов на его концах.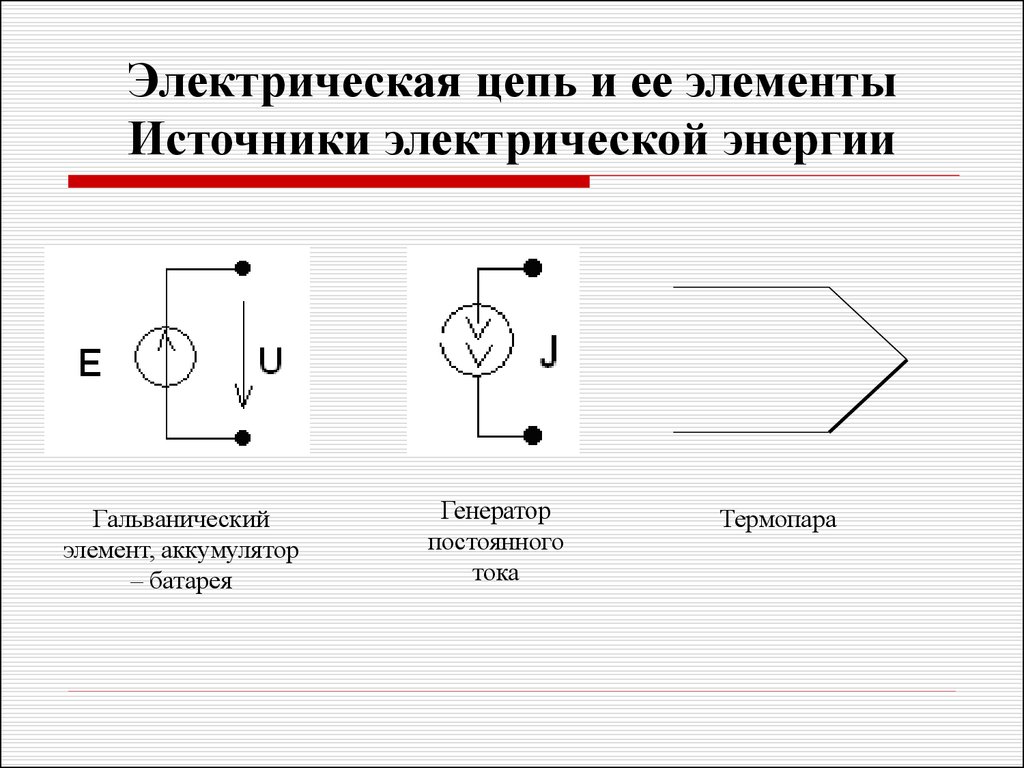 Установлен Г.Омом для металлических проводников. В простейшем случае формулируется следующим образом: сила постоянного тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению (). В этой формулировке справедлив также для электролитов, температура которых поддерживается постоянной. Для переменного тока О.з. может быть сформулирован для действующих или для амплитудных значений силы тока и напряжений. В этом случае под сопротивлением понимается полное сопротивление цепи переменному току . При наличии ЭДС для замкнутой цепи звучит так: сила тока в замкнутой цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи (сумме внешнего сопротивления и сопротивления источника тока).
Установлен Г.Омом для металлических проводников. В простейшем случае формулируется следующим образом: сила постоянного тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению (). В этой формулировке справедлив также для электролитов, температура которых поддерживается постоянной. Для переменного тока О.з. может быть сформулирован для действующих или для амплитудных значений силы тока и напряжений. В этом случае под сопротивлением понимается полное сопротивление цепи переменному току . При наличии ЭДС для замкнутой цепи звучит так: сила тока в замкнутой цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи (сумме внешнего сопротивления и сопротивления источника тока).
ПАРАМАГНЕТИЗМ – явление возникновение в веществе (парамагнетике) намагниченности сонаправленной с внешним магнитным полем. Обусловлено ориентацией под действием внешнего магнитного поля собственных магнитных моментов атомов или молекул парамагнетика.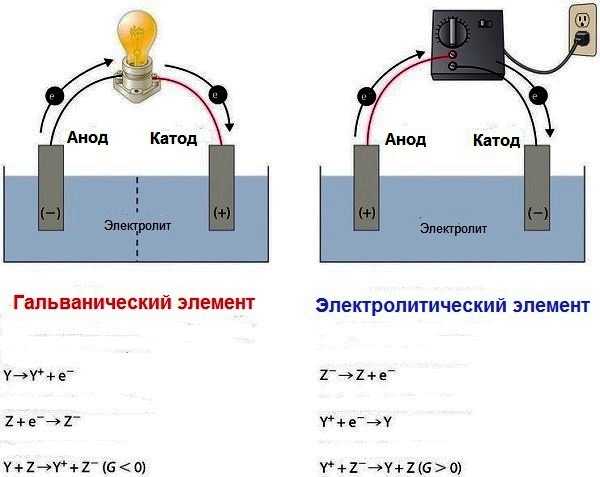 Магнитная проницаемость µ>1. Ср. диамагнетизм, ферромагнетизм.
Магнитная проницаемость µ>1. Ср. диамагнетизм, ферромагнетизм.
ПЕРЕМЕННЫЙ ТОК — электрический ток, изменяющий периодически свое направление в цепи так, что среднее за период значение силы тока равно нулю. Простейший переменный ток — синусоидальный.
ПЛОТНОСТЬ ТОКА – векторная величина, равная по модулю отношению силы тока к площади поперечного сечения проводника: . Направлена в сторону движения положительных зарядов (сонаправлен с вектором напряженности электрического поля). Единица в СИ: А/м2.
ПОЛУПРОВОДНИКИ — вещества, сопротивление (электропроводность) которых при комнатной температуре имеет промежуточное значение между сопротивлением (электропроводностью) металлов и диэлектриков. Сопротивление чистых П. уменьшается с ростом температуры и зависит, кроме того, от облучения, бомбардировки заряженными частицами, наличия примесей и т.д.).
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ — смещение электрических зарядов в диэлектрике под действием внешнего электрического поля. Возникает при сдвиге ионов относительно друг друга, деформации электронных оболочек или ориентации электрических диполей. Происходит, напр., при зарядке конденсатора.
Возникает при сдвиге ионов относительно друг друга, деформации электронных оболочек или ориентации электрических диполей. Происходит, напр., при зарядке конденсатора.
ПОЛЯРИЗОВАННОСТЬ – векторная физическая величина, равная отношению электрического момента малого объема диэлектрика к этому объему. Ср. намагниченность.
ПОСТОЯННЫЙ ТОК — электрический ток, сила и направление которого не меняются с течением времени. Ср.переменный ток.
ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКИЙ — скалярная физическая величина, равная отношению потенциальной энергии заряда, помещенного в данную точку поля, к величине этого заряда. Применяется для энергетического описания электростатического поля. Единица в СИ — вольт (В).
ПРАВОЙ РУКИ ПРАВИЛО — правило, определяющее 1) направление индукционного тока в проводнике, движущемся в магнитном поле: если ладонь правой руки расположить так, чтобы в нее входили линии магнитной индукции, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца покажут направление индукционного тока; 2) направление линий магнитной индукции прямолинейного проводника с током: если большой палец правой руки расположить по направлению тока, то направление обхвата проводника четырьмя пальцами покажет направление линий магнитной индукции. Ср. 1) левой руки правило, 2) буравчика правило.
Ср. 1) левой руки правило, 2) буравчика правило.
ПРОВОДНИКИ ЭЛЕКТРИЧЕСКИЕ — тела (вещества), способные хорошо проводить электрический ток благодаря наличию в них большого числа свободных подвижных заряженных частиц. Делятся на электронные (металлы и полупроводники), ионные (электролиты) и смешанные (плазма).
ПЬЕЗОЭЛЕКТРИЧЕСТВО – явление возникновения электрических зарядов при деформировании кристаллов и деформирование кристаллов под действием электрического поля (прямой и обратный эффекты). Применяется для воспроизведения звука, для получения ультразвука и т.д.
РАБОТА ВЫХОДА электрона — работа, необходимая для выхода электрона из проводника в вакуум. Зависит от рода вещества и состояния поверхности проводника.
РАДИОВОЛНЫ — электромагнитные волны, длина которых более 0,1 мм. Используются в радиосвязи, радиолокации, радиоастрономии и т.д.
РАДИОЛОКАЦИЯ — процесс обнаружения, распознавания, определения местонахождения и скорости движения различных объектов радиотехническими методами.
РАЗНОСТЬ ПОТЕНЦИАЛОВ — скалярная физическая величина, равная отношению работы электрического поля по перемещению положительного заряда из одной точки поля в другую к этому заряду. Единица в СИ — вольт.
РЕЗИСТОР – элемент электрической цепи, основное назначение которого — оказывать активное сопротивление электрическому току. Р. изготовляются сопротивлением 1 Ом — 10 ТОм с указанием рассеиваемой мощности.
РЕКОМБИНАЦИЯ — явление, обратное ионизации, т.е. исчезновение свободных носителей заряда противоположных знаков при их столкновениях. Приводит к образованию нейтральных атомов и молекул.
РЕНТГЕНОВСКИЕ ЛУЧИ — невидимое глазом коротковолновое электромагнитное излучение, возникающее при взаимодействии заряженных частиц с атомами вещества. Длина волны Р.л. 10-7 — 10-12 м. Р.л. обладают большой проникающей способностью. Открыты в 1895 г. немецким физиком В. К.Рентгеном (1845 — 1923).
К.Рентгеном (1845 — 1923).
РЕОСТАТ — устройство для регулирования и ограничения тока или напряжения в электрической цепи, основная часть которого — проводящий элемент с переменным электрическим сопротивлением.
САМОИНДУКЦИЯ – явление возникновения электродвижущей силы в электрической цепи при изменении протекающего в ней электрического тока. Частный случай электромагнитной индукции. Эдс С. пропорциональна скорости изменения силы тока:, где L — индуктивность электрической цепи.
СВЕРХПРОВОДИМОСТЬ — физическое явление, наблюдаемое у некоторых веществ (сверхпроводников) при охлаждении их ниже критической температуры и состоящее в исчезновении сопротивления электрическому току и выталкивании магнитного поля из объема образца.
СВОБОДНЫЕ ЗАРЯДЫ — 1. Избыточные электрические заряды, сообщенные проводящему телу и вызывающие нарушение его электронейтральности. 2. Заряженные частицы, которые под влиянием электрического поля способны перемещаться на макроскопические расстояния (см.носителя тока). Сравните связанные заряды.
2. Заряженные частицы, которые под влиянием электрического поля способны перемещаться на макроскопические расстояния (см.носителя тока). Сравните связанные заряды.
СИЛА ТОКА — скалярная физическая величина, применяемая для описания электрического тока и равная отношению абсолютного значения заряда, который проходит через поперечное сечение проводника за малый промежуток времени, к этому промежутку времени. Единица в СИ — ампер.
СИЛОВЫЕ ЛИНИИ — воображаемые линии, проведенные в каком-либо физическом поле (гравитационном, магнитном, электрическом) так, что в каждой точке пространства направление касательной к этим силовым линиям совпадает с направлением напряженности поля.
СКОРОСТЬ СВЕТА в вакууме (c) — одна из основных физических постоянных, равная скорости распространения электромагнитных волн в вакууме. с=(299 792 458 ± 1,2)м/с. С.с. — предельная скорость распространения любых физических взаимодействий.
СОЛЕНОИД – элемент электрической цепи, предназначенный для создания магнитного поля, обычно в виде намотанного на цилиндрическую поверхность изолированного проводника, по которому течет эл. ток. Если длина С. значительно больше диаметра, то маг. поле направлено параллельно его оси и однородно (внутри С.), а магнитная индукция поля пропорциональна силе тока и числу витков.
СУПЕРПОЗИЦИИ ПРИНЦИП — утверждение, согласно которому эффект от нескольких независимых эффектов представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности (напр., принцип суперпозиции эл. полей: напряженность поля системы зарядов равна геометрической сумме напряженностей полей, созданных каждым зарядом системы). Применим к т.н. линейным моделям.
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ — электромагнитное излучение, испускаемое за счет внутренней энергии веществом, имеющим температуру выше абсолютного нуля. С ростом температуры энергия теплового излучения возрастает.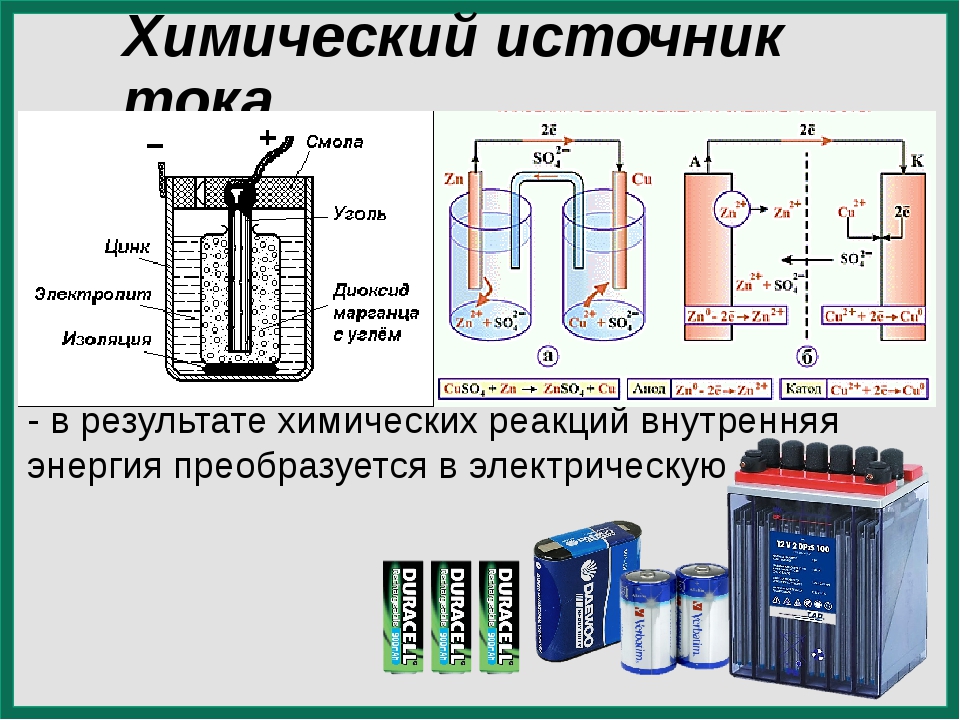
ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ — явление испускания электронов нагретыми твердыми (иногда жидкими) телами (эмиттерами). Интенсивность т.э. зависит от температуры и работы выхода электронов. Используется в электровакуумных приборах.
ТЕРМОЭЛЕМЕНТ (термопара) — устройство, содержащее спай двух разнородных металлов или полупроводников, на свободных неспаянных концах которых возникает термоэдс, зависящая от разности температур спая и свободных концов.
ТОК ПРОВОДИМОСТИ — см. электрический ток.
ТОМСОНА ФОРМУЛА — формула, выражающая зависимость периода незатухающих электромагнитных колебаний в контуре от его параметров — индуктивности катушки L и емкости конденсатораC: . Названа в честь У.Томсона (Кельвина).
ТРАНЗИСТОР — полупроводниковый прибор с тремя или более выводами. Используется для усиления, генерирования и преобразования электрических колебаний.
ФАРАДЕЯ ЗАКОНЫ — основные законы электролиза.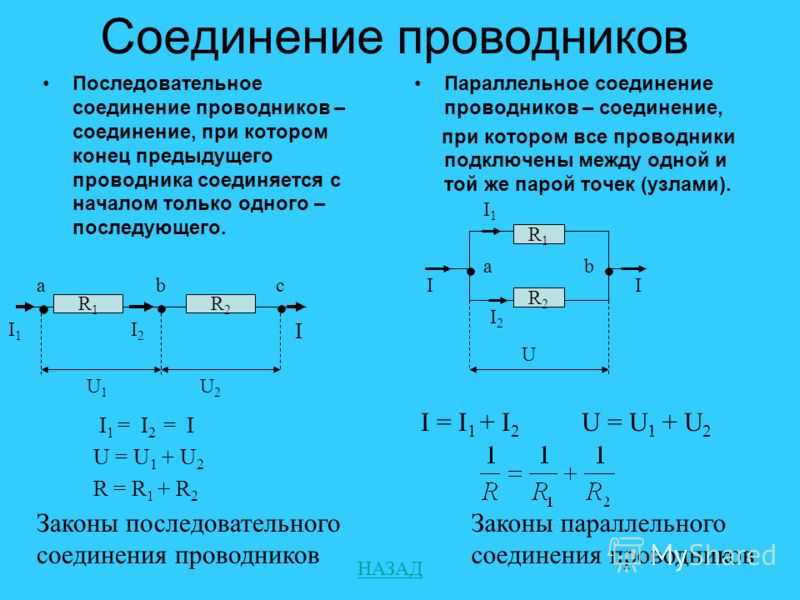 Первый Фарадея закон: масса вещества, выделившегося на электроде при прохождении электрического тока, прямо пропорциональна заряду, прошедшему через электролит. Второй Ф.з.: отношение масс различных веществ, претерпевающих химические превращения на электродах при прохождении одинаковых электрических зарядов через электролит равно отношению химических эквивалентов. Установлены в 1833-34 г. М.Фарадеем.
Первый Фарадея закон: масса вещества, выделившегося на электроде при прохождении электрического тока, прямо пропорциональна заряду, прошедшему через электролит. Второй Ф.з.: отношение масс различных веществ, претерпевающих химические превращения на электродах при прохождении одинаковых электрических зарядов через электролит равно отношению химических эквивалентов. Установлены в 1833-34 г. М.Фарадеем.
ФАРАДЕЯ ПОСТОЯННАЯ, Фарадея число – физическая постоянная, равна произведению элементарного электрического заряда на постоянную Авогадро. F=e.NA. Равна заряду, прохождение которого через электролит приводит к выделению на электроде 1 моля одновалентного вещества. F=(96484,56±0,27) Кл/моль. Названа в честь М.Фарадея.
ФЕРРОМАГНЕТИЗМ – явление наличия самопроизвольной намагниченности в магнитных кристаллических веществах (ферромагнетиках). Обусловлено наличием у электронов устойчивой параллельной ориентацией спиновых магнитных моментов, что и создает самопроизвольную намагниченность. Тепловое движение атомов кристалла разрушает параллельную ориентацию спинов, поэтому при температуре выше некоторой определенной (точка Кюри) Ф. переходит в парамагнетизм.
Тепловое движение атомов кристалла разрушает параллельную ориентацию спинов, поэтому при температуре выше некоторой определенной (точка Кюри) Ф. переходит в парамагнетизм.
ФЕРРОМАГНЕТИКИ — вещества, которым присущ ферромагнетизм. Типичные представители Ф. — железо, кобальт, никель и их сплавы. Широко применяются в электротехнике, радиотехнике, электронике и приборостроении.
ЭКВИПОТЕНЦИАЛЬНАЯ ПОВЕРХНОСТЬ — поверхность, все точки которой имеют одинаковый потенциал. Силовые линии поля перпендикулярны к э. п.
ЭЛЕКТРИЧЕСКАЯ ДУГА, вольтова дуга – электрический самостоятельный разряд в газе в виде ярко светящегося плазменного шнура. Впервые наблюдалась в 1802 г. В.В.Петровым.
ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ — скалярная физическая величина, применяемая для описания способности проводника удерживать эл. заряд. Для конденсатора равна отношению его заряда к разности потенциалов между обкладками. Единица в СИ — фарад (Ф).
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ (e0)- скалярная величина входящая в выражение некоторых законов электрического поля при записи их в СИ. Ср.магнитная постоянная.
ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ — См. электропроводность.
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ – точно или приблизительно повторяющиеся изменения напряжения и тока в эл. цепи. Простейшая система, в которой возникают эл. к. — колебательный контур.
ЭЛЕКТРИЧЕСКИЙ ГЕНЕРАТОР — устройство для преобразования различных видов энергии (механической, химической, тепловой и др.) в электрическую. Ср. электрический двигатель.
ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ — эл. машина, совершающая механическую работу за счет эл. энергии. Ср. электрический генератор.
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД — скалярная физическая величина, служащая для оценивания интенсивности электромагнитного взаимодействия заряженных частиц; источник электромагнитного поля. Различают положительные и отрицательные заряды. Для макроскопического тела э. з. равен алгебраической сумме зарядов всех частиц тела. В эл. изолированной системе выполняется заряда сохранения закон. См. элементарный электрический заряд.
Различают положительные и отрицательные заряды. Для макроскопического тела э. з. равен алгебраической сумме зарядов всех частиц тела. В эл. изолированной системе выполняется заряда сохранения закон. См. элементарный электрический заряд.
ЭЛЕКТРИЧЕСКИЙ РАЗРЯД в газе – явление прохождения эл. тока в газе под действием эл. поля. Для возникновения эл. р. в газе необходимо появление носителей тока — свободных ионов и электронов. Различают несамостоятельный эл. р., когда проводимость обусловлена действием внешнего ионизатора, и самостоятельный эл. р., который продолжается после прекращения действия внешнего ионизатора. Переход несамостоятельного разряда в самостоятельный наз. эл. пробоем газа.
ЭЛЕКТРИЧЕСКИЙ ТОК — направленное упорядоченное движение заряженных частиц (электронов, ионов и др.). Условно за направление эл. тока принимается направление движения положительных зарядов.
ЭЛЕКТРИЧЕСКИЙ ТРАНСФОРМАТОР — электромагнитное устройство, преобразующее переменный эл. ток одного напряжения в переменный эл. ток другого напряжения без изменения частоты и практически без потери мощности. Простейший эл. т. состоит из железного сердечника (магнитопровода) и двух обмоток — первичной и вторичной. Отношение напряжения в обмотках равно отношению числа витков в них. Действие основано на электромагнитной индукции явлении.
ток одного напряжения в переменный эл. ток другого напряжения без изменения частоты и практически без потери мощности. Простейший эл. т. состоит из железного сердечника (магнитопровода) и двух обмоток — первичной и вторичной. Отношение напряжения в обмотках равно отношению числа витков в них. Действие основано на электромагнитной индукции явлении.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — одна из форм проявления электромагнитного поля. В отличие от магнитного поля действует как на неподвижные, так и на движущиеся эл. заряды. Создается эл. зарядами или меняющимся во времени магнитным полем. Описывается напряженностью и потенциалом электрического поля. Ср. магнитное поле.
ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ — см. сопротивление электрическое.
ЭЛЕКТРИЧЕСТВО — совокупность явлений, связанных с существованием, движением и взаимодействием эл. зарядов и полей.
ЭЛЕКТРОВАКУУМНЫЕ ПРИБОРЫ — приборы и устройства, в которых используются закономерности протекания тока в вакууме.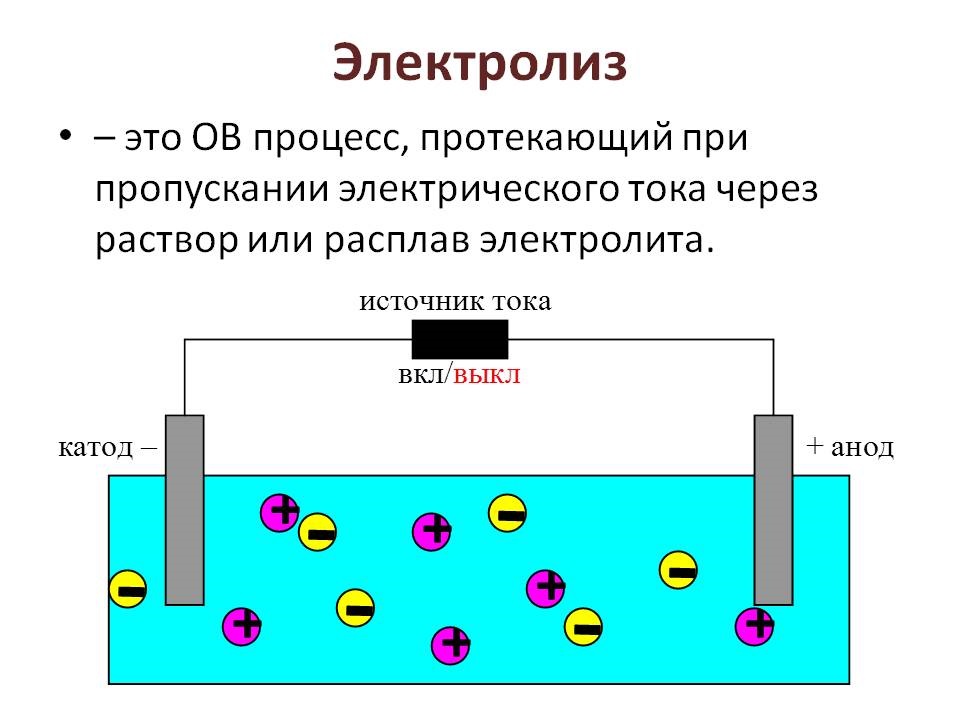 Применяются для генерации и усиления эл. колебаний, выпрямления переменного тока и т.д. Состоят из стеклянного или металлического баллона, в котором создан вакуум, и электродов различной формы, расположенных в баллоне. Примеры: электронные лампы, электронно-лучевые трубки, рентгеновские трубки, газоразрядные приборы и т.д.
Применяются для генерации и усиления эл. колебаний, выпрямления переменного тока и т.д. Состоят из стеклянного или металлического баллона, в котором создан вакуум, и электродов различной формы, расположенных в баллоне. Примеры: электронные лампы, электронно-лучевые трубки, рентгеновские трубки, газоразрядные приборы и т.д.
ЭЛЕКТРОД – конструктивный элемент электрической цепи, соединяющий ее с электролитом, газом или вакуумом. Применяется при электролизе, в гальванических элементах и т.п.
ЭЛЕКТРОДВИЖУЩАЯ СИЛА (ЭДС) – физическая величина, применяемая для источника энергии в электрической цепи, необходимого для поддержания в ней эл. тока. Равна отношению работы сил, разделяющих заряды в источнике, к величине заряда. Единица в СИ — вольт.
ЭЛЕКТРОДИНАМИКА — физическая теория электромагнитных явлений, в которой основную роль играют взаимодействия между заряженными частицами, осуществляемые посредством эл.-маг. поля. Основа э. — Максвелла уравнения.
— Максвелла уравнения.
ЭЛЕКТРОЛИЗ — совокупность электрохимических процессов, происходящих в электролите при прохождении через него постоянного эл. тока. При этом положительно заряженные ионы (катионы) движутся к катоду, а отрицательно заряженные (анионы) — к аноду. Количественно описывается Фарадея законами.
ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ – явление распада молекул на ионы в результате взаимодействия с молекулами растворителя.
ЭЛЕКТРОЛИТЫ — жидкие или твердые растворы или расплавы, эл. ток в которых проходит за счет движения ионов. См. электролиз.
ЭЛЕКТРОМАГНИТ — искусственныймагнит, магнитное поле которого возникает и концентрируется в ферромагнитном сердечнике в результате прохождения эл. тока по охватывающей его обмотке.
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ – явление возникновения электрического поля при изменении магнитного. При этом в замкнутом проводящем контуре возникает индукционный ток. См. самоиндукция, Ленца закон.
См. самоиндукция, Ленца закон.
ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ — один из видов взаимодействия элементарных частиц, осуществляемое посредством эл.-маг. поля. Играет фундаментальную роль в явлениях макромира: строении в-ва, его агрегатное состояние, эл., оптические и др. свойства определяющиеся электромагнитными силами, действующими между атомными ядрами, электронами атомов или молекул. Ср. гравитационное взаимодействие, сильное взаимодействие, слабое взаимодействие.
ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ – то же, что и электромагнитные волны.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ — одно из физических полей посредством которого осуществляется электромагнитное взаимодействие. Описывается с помощью напряженности электрического поля и магнитной индукции. См. Максвелла уравнения.
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ — колебания эл.-маг. поля, распространяющиеся в пространстве с конечной скоростью (см. скорость света). В зависимости от длины волны в вакууме, источника излучения и способа возбуждения различают: низкочастотные колебания, радиоволны, инфракрасное излучение, видимое излучение, ультрафиолетовое излучение, рентгеновское излучение, гамма-лучи.
скорость света). В зависимости от длины волны в вакууме, источника излучения и способа возбуждения различают: низкочастотные колебания, радиоволны, инфракрасное излучение, видимое излучение, ультрафиолетовое излучение, рентгеновское излучение, гамма-лучи.
ЭЛЕКТРОН — стабильная элементарная частица, которой приписывают отрицательный элементарный электрический заряд, обладающая массой покоя me=(9,109558±0,000054).10-31кг и спином, равным 1/2. Входит в состав всех атомов и молекул.
ЭЛЕКТРОННАЯ ЭМИССИЯ — явление испускания электронов твердым телом или жидкостью. См.автоэлектронная эмиссия, термоэлектронная эмиссия, фотоэффект.
ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА – электронно-вакуумный прибор, в котором электронный луч (пучек электронов) используется для преобразования электрических сигналов в световые. Применяется в осциллографах, телевизорах, радиолокации и т. п.
п.
ЭЛЕКТРОННЫЙ ГАЗ — совокупность электронов проводимости в кристалле или плазме, т.е. электронов, способных участвовать в образовании электрического тока.
ЭЛЕКТРОПРОВОДНОСТЬ — способность вещества проводить электрический ток под действием электрического поля. Обусловлена носителями тока, в зависимости от вида которых различают электронную проводимость (металлы, полупроводники). ионную проводимость (электролиты) и смешанную электронно-ионную проводимость (плазма).
ЭЛЕКТРОСКОП — прибор для обнаружения и приближенной оценки степени электризации тел.
ЭЛЕКТРОСТАТИКА — раздел электродинамики, изучающий взаимодействие и условия равновесия неподвижных относительно выбранной инерциальной системы отсчета электрических зарядов. Основной закон э. — Кулона закон.
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ — эл. поле зарядов, покоящихся относительно выбранной инерциальной системы отсчета. В э.п. действуют электростатические силы, которые являются потенциальными силами. Основные применяемые для описания э.п. — напряженность электрического поля и потенциал электрический.
В э.п. действуют электростатические силы, которые являются потенциальными силами. Основные применяемые для описания э.п. — напряженность электрического поля и потенциал электрический.
ЭЛЕКТРОХИМИЧЕСКИЙ ЭКВИВАЛЕНТ – физическая величина, равная отношению массы вещества, выделившейся на электроде при электролизе, к электрическому заряду, прошедшему через электролит. Единица Э=1/273,15 К-1.э. в СИ — кг/Кл.
ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ЗАРЯД (e) — одна из основных физических постоянных, равная наименьшему по модулю из всех возможных положительных и отрицательных эл. зарядов. е=(1,6021917±0,0000070).10-19Кл. Большинство элементарных частиц имеет эл. заряд +е и —е или 0. У некоторых резонансов заряд кратен е. Частицы с дробным зарядом в свободном состоянии не наблюдаются.
Элементарный ток и его магнитный момент
Итак, элементарным током мы будем называть замкнутый ток, который удовлетворяет следующим условиям:
- Размеры контура бесконечно малы в сравнении с расстоянием до точек, в которых необходимо рассмотреть поле.

- Величины, которые характеризуют внешнее поле, постоянны (Точнее постоянны значения магнитной индукции и ее пространственные производные). Для любого замкнутого тока можно создать условия, при которых его считают элементарным.
Векторный потенциал элементарного тока
Выберем контур в виде параллелограмма, стороны которого $l_1,l_2,\ l_3,l_4\ $(рис.1). Начало координат поместим в точку О на поверхности внутри параллелограмма. Так как параллелограмм бесконечно малый, то конкретное место положения точки значения не имеет.
Рис. 1
Векторный потенциал магнитного поля ($\overrightarrow{A}$) в точке B с радиус-вектором $\overrightarrow{r}$ равен:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }I\int\limits_{l_1l_2l_3l_4}{\frac{\overrightarrow{dl}}{r}}\left(1\right).\]
Так как параллелограмм маленький, то значение r можно считать постоянным и равным расстоянию от середины стороны параллелограмма до точки, в которой ищем поле.
Магнитная индукция в вакууме | HomeElectronics
Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Закон Био – Савара – Лапласа
В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:
- магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
- магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
- магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.

Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого
Магнитная индукция dB, создаваемая элементарным участком проводника dl.
Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением
где I – сила тока, протекающая по проводнику,
r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,
dl – минимальный элемент проводника, который создает индукцию dB,
k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ0/(4π)
Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения
где символ l обозначает, что интегрирование происходит по всей длине проводника.
Магнитная индукция прямолинейного проводника
Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.
Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид
где I – ток, протекающий по проводу,
b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.
Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.
Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – ток, протекающий по проводу,
b – расстояние от центра проводника до точки, в которой измеряется индукция.
Магнитная индукция кольца
Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.
В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.
Рассмотрим первый случай.
Магнитная индукция в центре кругового тока.
В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид
Остается только проинтегрировать полученное выражение по всей длине окружности
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник.
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.
Магнитная индукция в точке, лежащей на оси окружности.
В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dBX, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB
Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции
Теперь проинтегрируем данное выражение по всей длине окружности
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник,
х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.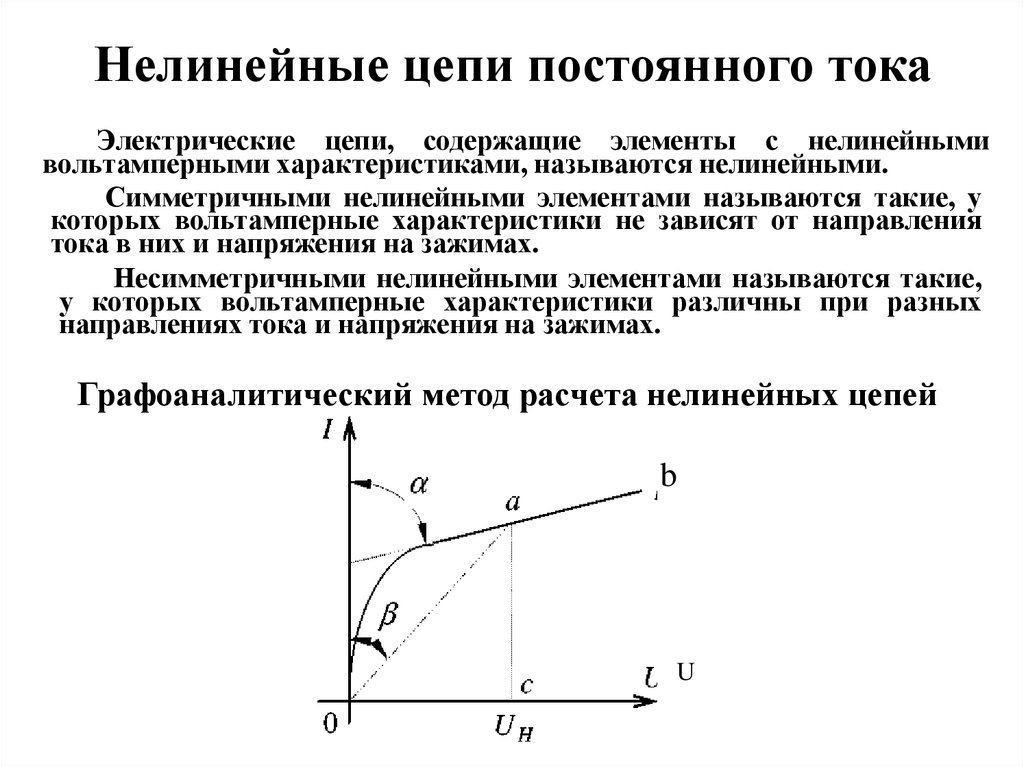
Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.
Циркуляция вектора магнитной индукции
Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.
Циркуляция вектора магнитной индукции по произвольному контуру.
Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением
Так как угол dφ достаточно мал, то векторов dlВ определяется, как длина дуги
Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции
Теперь остаётся проинтегрировать получившееся выражение по всей длине контура
В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:
Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.
Магнитное поле соленоида и тороида
С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.
Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.
Магнитная индукция соленоида.
Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид
Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид
где n – число витков проводника соленоида, которое приходится на единицу длины,
I – ток, протекающий по соленоиду.
Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.
Магнитная индукция тороида.
В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид
где r – радиус контура магнитной индукции.
Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид
где n – число витков проводника, которое приходится на единицу длины,
r – радиус контура магнитной индукции,
R – радиус тороида.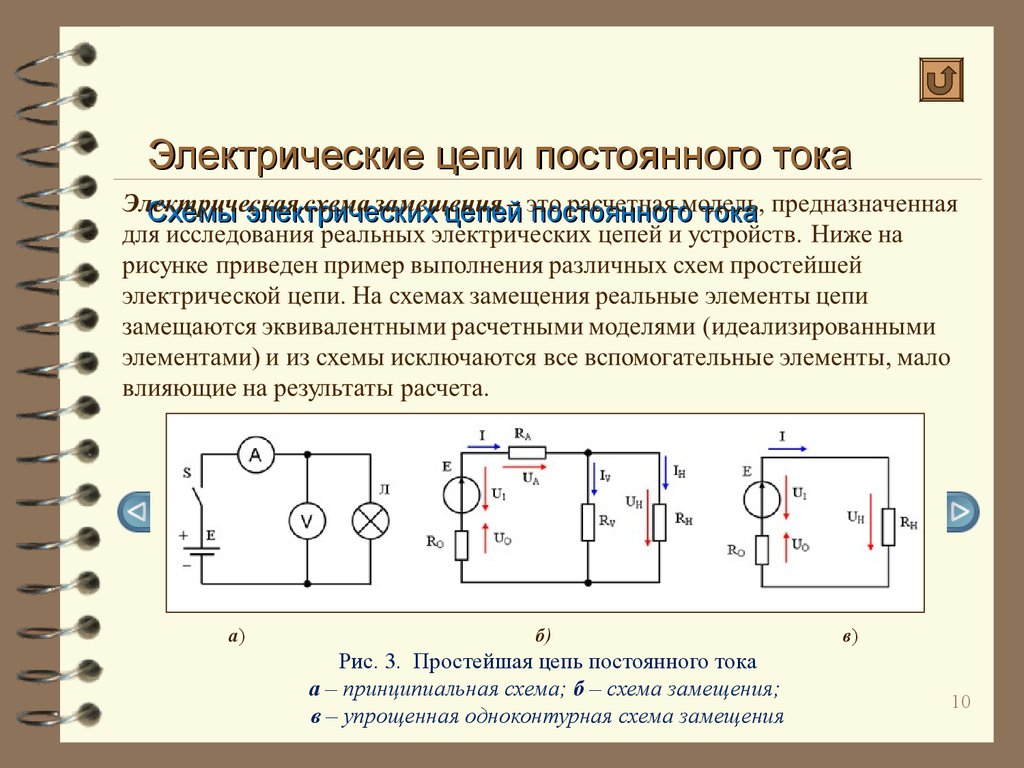
Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБЫВАТЬ МОЖНО ЗДЕСЬ
Закон Био-Савара-Лапласа. Эквивалентность движущегося заряда и элемента тока. Примеры расчета магнитного поля — Мегаобучалка
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде
(110. 1)
1)
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dlпроводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
(110.2)
где a — угол между векторами dl и r.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
(110. 3)
3)
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
· Магнитное поле прямого провода с током.
· Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что
Из рис. 165 следует, что
·
· (радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
· (110.4)
· Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),
·
· Следовательно, магнитная индукция поля прямого тока
· (110.5)
· Магнитное поле на оси кругового тока.
Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.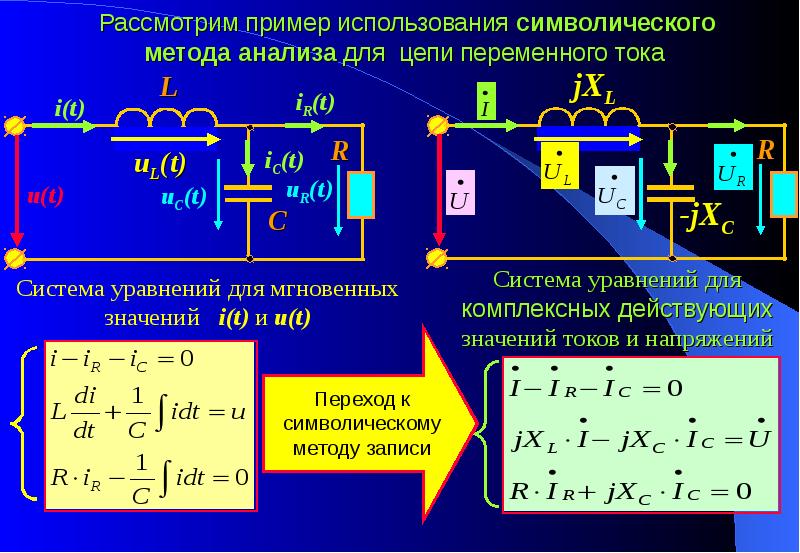 2),
2),
Тогда
Следовательно, магнитная индукция поля в центре кругового проводника с током
· Магнитное поле катушки с током.
· Магнитное поле катушки с током возникает в кольцевой катушке (рис. 1) с W витками, равномерно распределенными вдоль немагнитного сердечника при подключении ее к источнику тока. Увеличение магнитной индукции поля достигается увеличением числа витков катушки и размещением ее на стальном сердечнике, магнитные токи которого, создавая свое поле, увеличивают результирующее поле катушки. Поверхность, ограниченная окружностью радиуса R, совпадающей со средней магнитной линией, пронизывается полным током ΣI = IW. Вследствие симметрии напряженность поля Н во всех точках, лежащих на средней магнитной линии, одинакова, поэтому мдс Fм = Hl = IW = h3πR. По закону полного тока Hl = IW, откуда напряженность магнитного поля на средней магнитной линии, совпадающей с осевой линией кольцевой катушки, H = IW / l , а магнитная индукция B = μaH = μaIW / l = 125μIW / l * 10-8.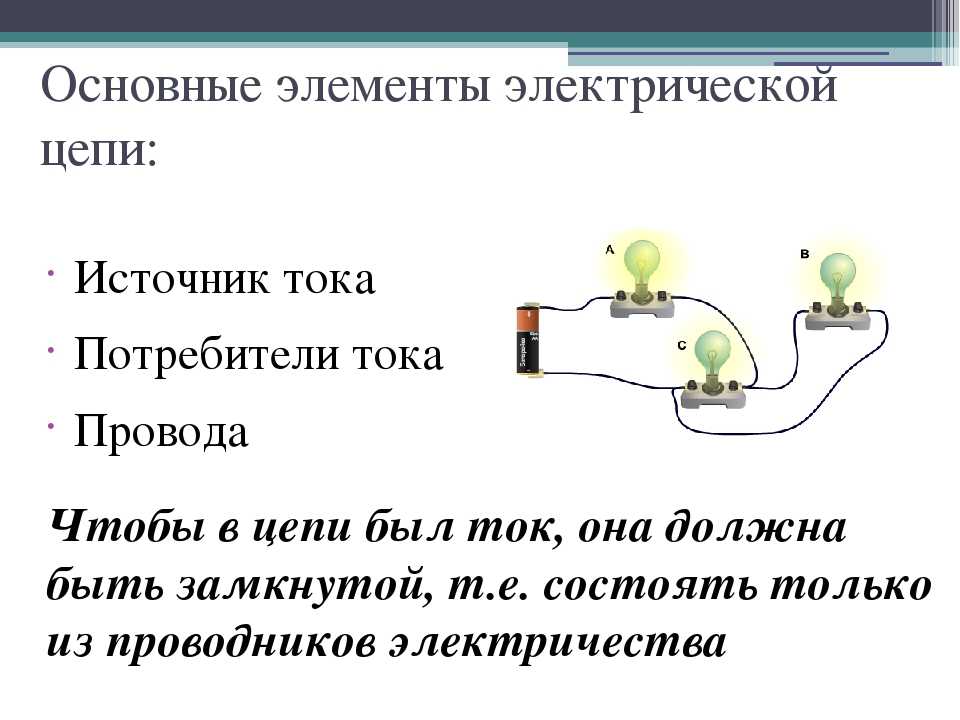
·
· При R1 — R2 << Rl магнитную индукцию на осевой линии с достаточной точностью можно считать равной среднему значению ее, и, следовательно, магнитный поток сквозь поперечное сечение катушки Φ = BS = μaIWS / l . Переписав это уравнение в виде Φ = IW / (μaSl) = Fм / Rм , получим выражение, аналогичное уравнению закона Ома для электрической цепи, т. е. полный магнитный поток равен отношению мдс к магнитному сопротивлению цепи. Цилиндрическую катушку (рис. 1, б) можно рассматривать как часть кольцевой катушки с большим радиусом и с обмоткой, расположенной только на части сердечника, длина которой равна длине катушки. Напряженность поля и магнитной индукции на осевой линии в центре цилиндрической катушки определяется по формулам, которые в этом случае являются приближенными и применимы для катушек.
·
«Взаимодействие токов. Магнитное поле, его характеристики». 11-й класс
Цель урока:
- дать учащимся представление о магнитном поле;
- сформировать представления учащихся о
магнитном поле и его свойствах.

Демонстрации:
1. Опыт Эрстеда, движения проводника с током в
магнитном поле;
2. Силовых линий магнитного поля постоянного
магнита, магнитного поля прямого тока.
Оборудование:
- источник питания;
- ключ;
- переменный резистор;
- амперметр;
- катушка на подставке;
- компас;
- соединительные провода.
ХОД УРОКА
I. Актуализация знаний
- Знакомство с учениками, с классом.
- Знакомство с учебником, правилами и требованиями учителя.
- Запись учениками школьных принадлежностей для урока физики.
а) учебник;
б) тетрадь 48 л.;
в) тетрадь для лабораторных и практических работ – 12-18 л.;
г) тетрадь для контрольных работ – 12-18 л.;
д) микрокалькулятор
е) линейка, карандаш, ластик, треугольник, транспортир, ручка (синяя и чёрная).
II. Правила техники безопасности в кабинете физики и на уроках физики, при выполнении демонстраций, практических и лабораторных работ.
а) ИОТ – 6;
б) ИОТ – 7;
в) ИОТ – 8;
г) журнал по технике безопасности на уроках физики (роспись учащихся об ознакомлении с правилами по ТБ).
III. Изучение нового материала.
Неподвижные электрические заряды создают
вокруг себя электрическое поле. Движущиеся
заряды создают магнитное поле.
Вокруг любого магнита существует магнитное поле.
В 1820 году Эрстед обнаружил, что магнитное поле
порождается электрическим током (демонстрация
опыта Эрстеда).
В 1820 году Ампер предложил, что «магнитные
свойства постоянных магнитов обусловлены
множеством круговых токов, циркулирующих внутри
молекул этих тел».
Свойства магнитного поля.
1. Магнитное поле порождается только движущимися зарядами, в частности электрическим током.
- В отличие от электрического поля магнитное поле обнаруживается по его действию на движущиеся заряды (заряженные тела).
- Магнитное поле материально, т.к. оно действует на тело, следовательно обладает энергией.
- Магнитное поле обнаруживается по действию на магнитную стрелку.
Опыт Ампера
Пропускаем ток по параллельным проводникам. Гибкие проводники укрепляются вертикально, затем присоединяем их к источнику тока. Ничего не наблюдаем. Но если замкнуть концы проводников проволокой, в проводниках возникнут токи противоположного направления. Проводники начнут отталкиваться друг от друга.
В случае токов одного направления проводники
притягиваются. Это взаимодействие между
проводниками с током, т.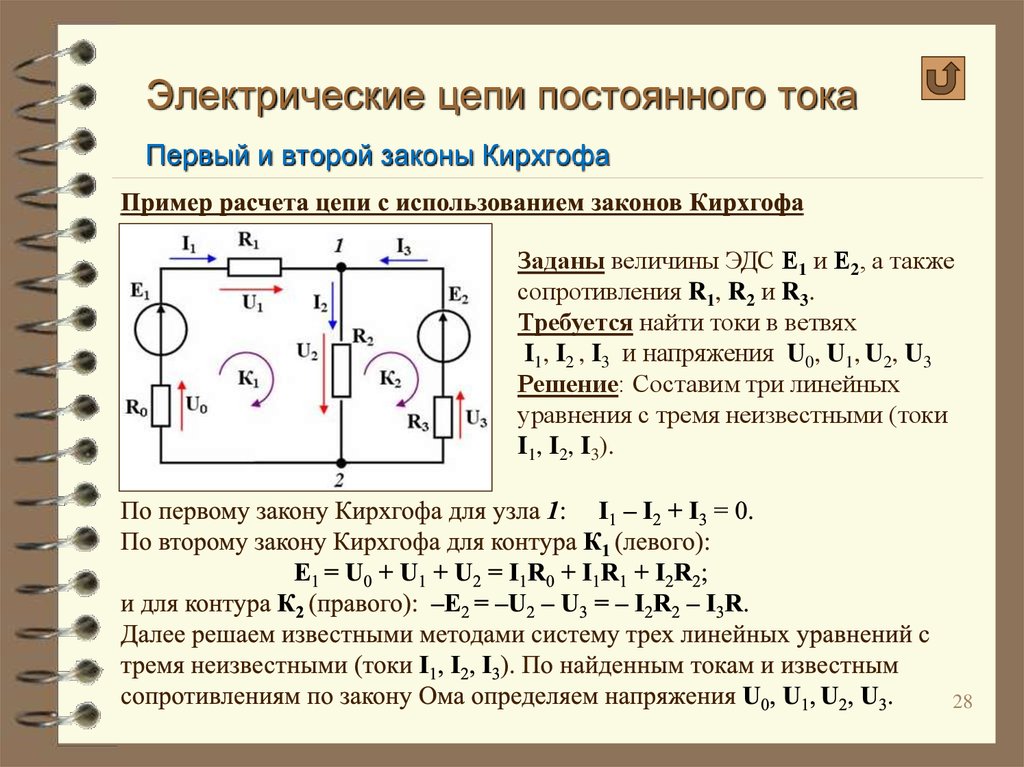 е. взаимодействие между
движущимися электрическими зарядами, называют магнитным.
Силы, с которыми проводники с током действуют
друг на друга, называют магнитными силами.
е. взаимодействие между
движущимися электрическими зарядами, называют магнитным.
Силы, с которыми проводники с током действуют
друг на друга, называют магнитными силами.
Изобретение компаса
В 12 веке в Европе стал известен компас как
прибор, с помощью которого можно определить
направление частей света.
Применение (12 в.) в морских путешествиях для
определения курса корабля в открытом море.
Магнит имеет два полюса: северный и южный,
одноимённые полюсы отталкиваются, разноимённые
– притягиваются.
Эксперимент 1
Расположим перед катушкой компас. Замкнём цепь
и будем наблюдать за поведением компаса.
Вывод: вокруг проводника с током существует
(возникает) магнитное поле.
Эксперимент 2
Расположим перед катушкой компас так, чтобы
расстояние между ними было около 12 см. замкнём
электрическую цепь. В данном случае отклонения
стрелки не наблюдается.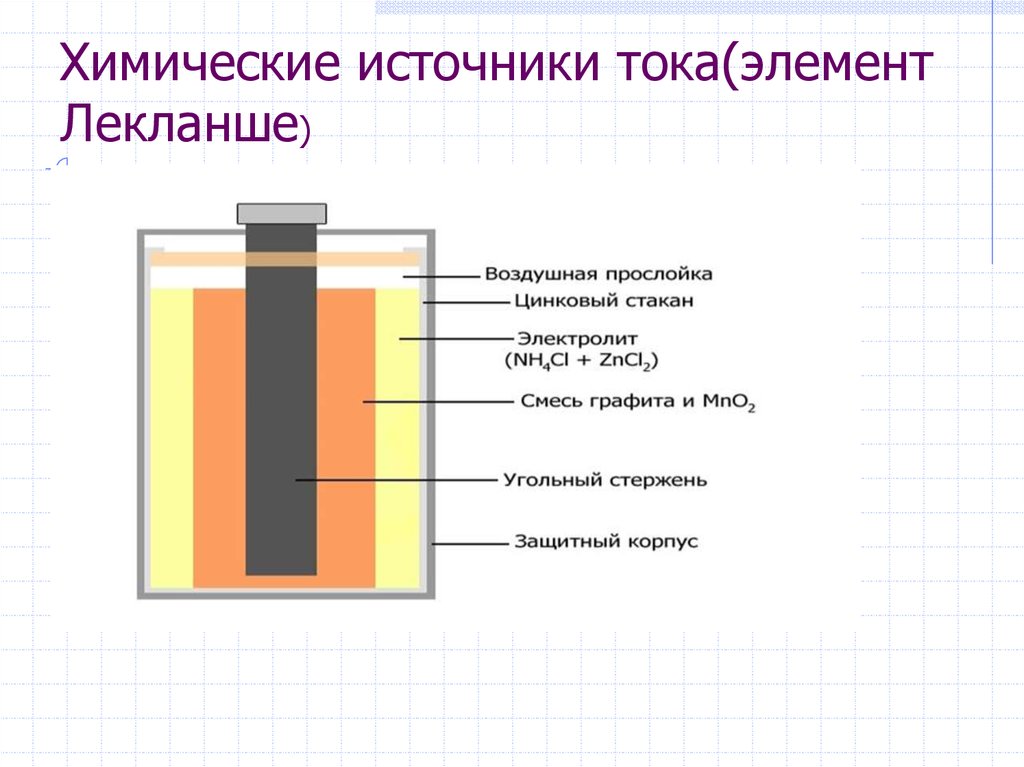 При приближении катушки
к компасу на расстоянии 8 см, наблюдается
отклонение стрелки (300). Уменьшая расстояние,
видим увеличение угла отклонения стрелки. Чем
дальше от проводника с током, тем слабее
магнитное поле.
При приближении катушки
к компасу на расстоянии 8 см, наблюдается
отклонение стрелки (300). Уменьшая расстояние,
видим увеличение угла отклонения стрелки. Чем
дальше от проводника с током, тем слабее
магнитное поле.
Магнитное поле можно изобразить графически при
помощи линий, касательные к которым в каждой
точке совпадают с направление вектора магнитной
индукции.
Линии магнитной индукции не пересекаются. При
изображении магнитного поля с помощью линий
магнитной индукции эти линии наносятся так,
чтобы их густота в любом месте поля была
пропорциональна значению модуля магнитной
индукции.
Характерной особенностью линий магнитной
индукции является их замкнутость. Магнитное
поле вихревое.
Правило правого винта: Если вы
когда-нибудь закручивали винт или шуруп, то вы
наверняка знаете, в какую сторону он
закручивается, а в какую выкручивается. Люди
унифицировали направление закручивая винтов и
шурупов. Это значит, что все шурупы и винты во
всем мире закручиваются в одну сторону. То есть,
если вы купите некий прибор в другой стране, то в
случае его ремонта или сборки вам не потребуются
винты с нарезкой в иную сторону, такие, каких не
купишь в вашей стране. Нарезка всех винтов в мире
совпадает. Это правило нарушают лишь в некоторых
особых случаях, когда от нарезки зависит
вращение некой части устройства. Но для таких
случаев делают специальные детали. Это простое,
но гениальное решение избавило от множества
потенциальных проблем.
Это значит, что все шурупы и винты во
всем мире закручиваются в одну сторону. То есть,
если вы купите некий прибор в другой стране, то в
случае его ремонта или сборки вам не потребуются
винты с нарезкой в иную сторону, такие, каких не
купишь в вашей стране. Нарезка всех винтов в мире
совпадает. Это правило нарушают лишь в некоторых
особых случаях, когда от нарезки зависит
вращение некой части устройства. Но для таких
случаев делают специальные детали. Это простое,
но гениальное решение избавило от множества
потенциальных проблем.
«Правило буравчика», направление тока и линий его магнитного поля
Оказывается, что это правило применимо не
только в механике к закручиванию винтов. Если мы
имеем проводник с током, то это правило помогает
нам определить направление линий
магнитного поля, образованного этим током.
Только это правило в данном случае носит
название «правила буравчика».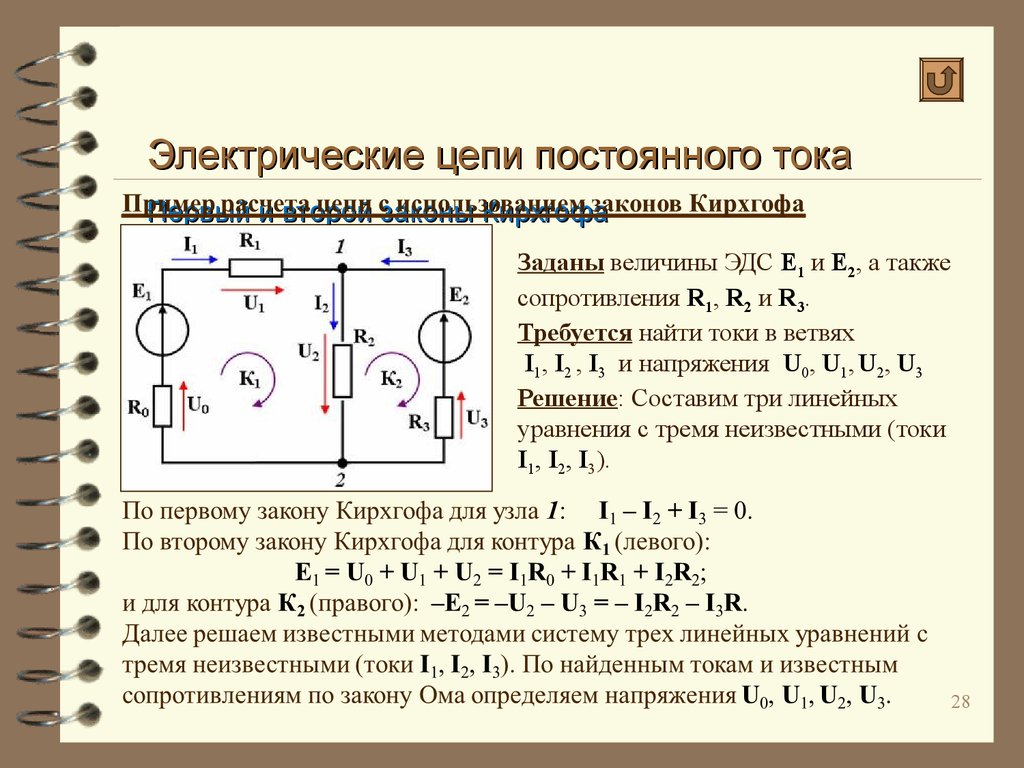 Правило буравчика
звучит следующим образом:
Правило буравчика
звучит следующим образом:
Если направление поступательного движения
буравчика совпадает с направлением тока в
проводнике, то направление вращения ручки
буравчика совпадает с направлением линий
магнитного поля тока.
Буравчик это винт или шуруп, который мы
ввинчиваем. Направление ручки буравчика это
направление вращения нашей руки. Если ток
движется от нас, то и шуруп движется от нас,
то есть мы его ввинчиваем, так как мы условились
считать их направления совпадающими.
Тогда направление вращения нашей руки в процессе
ввинчивания это направление магнитных линий. Они
будут направлены по часовой стрелке.
В случае противоположного направления
электрического тока, линии магнитного поля
будут направлены, соответственно, против часовой
стрелки. Таким же было бы направление руки в
процессе выкручивая винта или направление ручки
буравчика в случае его движения к нам.
А как определить направление тока, если мы знаем
направление магнитных линий? Очень просто. По
тому же правилу. Только изначально бы берем за
известный факт не направление движения
буравчика, а направление вращения его ручки.
Правило правой руки
В случае, когда мы имеем дело с магнитным полем катушки с током или соленоида, картина будет более сложной. Поэтому для простого нахождения направления линий магнитного поля в таком случае существует правило правой руки. Оно гласит:
Если обхватить соленоид ладонью правой руки, направив четыре пальца по направлению тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.
Открытие электромагнетизма:
В XVIII в. электричество и магнетизм считались
хотя и похожими, но все же имеющими различную
природу явлениями. Правда, были известны
некоторые факты, указывающие на существование
как будто бы связи между магнетизмом и
электричеством,
например намагничение железных предметов в
результате ударов молнии. Больше того,
Франклину удалось как будто бы намагнитить
кусок железа с помощью разряда лейденской банки.
Все-таки известные факты не позволяли уверенно
утверждать, что между электрическими и
магнитными явлениями существует связь.
Больше того,
Франклину удалось как будто бы намагнитить
кусок железа с помощью разряда лейденской банки.
Все-таки известные факты не позволяли уверенно
утверждать, что между электрическими и
магнитными явлениями существует связь.
Такую связь впервые обнаружил датский физик Ханс Кристиан Эрстед в 1820 г. Он открыл действие электрического тока на магнитную стрелку.
Интересна история этого открытия. Идею о связи между электрическими и магнитными явлениями Эрстед высказал еще в первом десятилетии XIX в. Он полагал, что в явлениях природы, несмотря на все их многообразие, имеется единство, что все они связаны между собой.
Руководствуясь этой идеей, он поставил перед собой задачу выяснить на опыте, в чем эта связь проявляется.
Эрстед открыл, что если над проводником,
направленным вдоль земного меридиана, поместить
магнитную стрелку, которая показывает на север, и
по проводнику пропустить электрический ток, то
стрелка отклоняется на некоторый угол.
После того как Эрстед опубликовал свое открытие, многие физики занялись исследованием этого нового явления. Французские ученые Био и Савар постарались установить закон действия тока на магнитную стрелку, т. е. определить, как и от чего зависит сила, действующая на магнитную стрелку, когда она помещена около электрического тока. Они установили, что сила, действующая на магнитный полюс (на конец длинного магнита) со стороны прямолинейного проводника с током, направлена перпендикулярно к кратчайшему расстоянию от полюса до проводника и модуль ее обратно пропорционален этому расстоянию.
Познакомившись с работой Био и Савара,
Лаплас заметил, что для расчета «магнитной» силы,
т. е., говоря современным языком, напряженности
магнитного поля, полезно рассматривать действие
очень малых отрезков проводника с током на
магнитный полюс. Из
измерений Био и Савара следовало, что
если ввести понятие элемента проводника ∆l, то
сила ∆F, действующая со стороны этого элемента на
полюс магнита, будет пропорциональна ∆F ~ (∆lr2)sinθ –,
где ∆l – элемент проводника, θ – угол,
образованный этим элементом и прямой,
проведенной из элемента ∆l в точку, в которой
определяется сила, а r – кратчайшее
расстояние от магнитного полюса до линии,
являющейся продолжением элемента проводника.
После того как было введено понятие силы тока и
напряженности магнитного поля, этот закон стали
записывать так:
где ∆H – напряженность магнитного поля, I – сила тока, а k – коэффициент, зависящий от выбора единиц, в которых измеряются эти величины. В международной системе единиц СИ этот коэффициент равен 1/4π.
Новый важнейший шаг в исследовании
электромагнетизма был сделан французским ученым
Андре Мари Ампером в 1820г.
Раздумывая над открытием Эрстеда, Ампер пришел к
совершенно новым идеям. Он предположил, что
магнитные явления вызываются взаимодействием
электрических токов. Каждый магнит представляет
собой систему замкнутых электрических токов,
плоскости которых перпендикулярны оси магнита.
Взаимодействие магнитов, их притяжение и
отталкивание объясняются притяжением и
отталкиванием, существующими между токами.
3емной магнетизм также обусловлен
электрическими токами, которые протекают в
земном шаре.
IV. Закрепление изученного материала.
- Какие взаимодействия называются магнитными.
- Основные свойства магнитного поля.
- Опишите опыт Эрстеда, что доказывает опыт Эрстеда?
- Правило правого винта.
- От чего зависит магнитная индукция поля внутри вытянутой катушки?
V. Домашнее задание.
§ 1,2 учебника Мякишев Г. Я., Буховцев Б. Б. Физика – 11 (базовый и профильный уровни),– М.: Просвещение, 2010 г.
2}.$$ $\mu_o$ — константа, а произведение $Id\vec{s}$ называется текущим элементом, но что такое $d\vec{s}$? Это вектор, величина которого равна длине элемента в направлении тока, протекающего через него. Направление тока определяется как направление движения положительных зарядов. Но факт, что в проводнике заряды сталкиваются друг с другом и атомными решетками. Поэтому нелепо слишком серьезно относиться к определению направления тока хотя бы для проводников . Следовательно, когда мы говорим, что направление тока в проводнике такое-то, мы имеем в виду, что положительные заряды имеют тенденцию двигаться именно таким образом.
Таким образом, направление тока, как определено, слишком расплывчато, по крайней мере, для проводников , чтобы его можно было использовать для определения вектора, подобного $d\vec{s}$. Но ни в одной книге или статье этот вопрос не поднимается и не обсуждается, поэтому я спрашиваю его здесь.
Следовательно, когда мы говорим, что направление тока в проводнике такое-то, мы имеем в виду, что положительные заряды имеют тенденцию двигаться именно таким образом.
Таким образом, направление тока, как определено, слишком расплывчато, по крайней мере, для проводников , чтобы его можно было использовать для определения вектора, подобного $d\vec{s}$. Но ни в одной книге или статье этот вопрос не поднимается и не обсуждается, поэтому я спрашиваю его здесь.- электромагнетизм
- электростатика
- магнитные поля
- электрические поля
- электрический ток
$\endgroup$
3
$\begingroup$
Переменные, такие как магнитное поле $\vec B$, ток $I$ и связанное с ним направление $\vec{ds}$ являются макроскопическими величинами . Это означает, что они усредняются по объему, который намного больше, чем элементы, составляющие систему.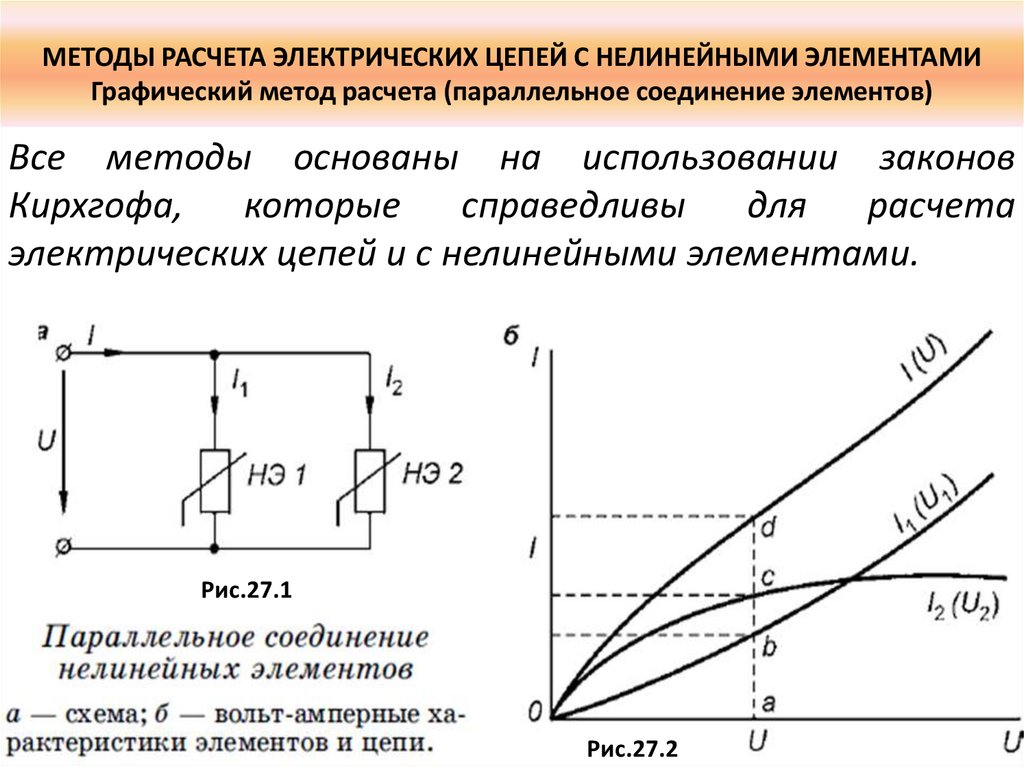 См. понятие термодинамического предела для строгого определения между макроскопическими и микроскопическими величинами.
См. понятие термодинамического предела для строгого определения между макроскопическими и микроскопическими величинами.
В вашем конкретном вопросе поток тока $I$ в законе Био-Савара усредняется как по времени, так и по пространству, что устраняет необходимость учитывать тонкое движение отдельных протонов или электронов. Цитирую Джексона:
До сих пор мы рассматривали электромагнитные поля и источники в вакууме. Уравнения Максвелла (I.1b) для электрического и магнитного полей E и B могут быть рассматривать как уравнения, описывающие поля повсюду в пространстве, при условии, что все указаны источники p и J. Для небольшого числа определенных источников, определяющих нация полей — разрешимая проблема; но для макроскопических агрегатов вещества, решение уравнений практически невозможно. Есть два аспекта здесь. Во-первых, количество отдельных источников, заряженных частиц в каждом атома и ядра непомерно велик. Другой аспект заключается в том, что для макроскопических наблюдения подробное поведение полей, с их резкими изменениями в пространство над атомными расстояниями не имеет значения.
Что имеет значение, так это среднее значение поле или источник над объемом большим по сравнению с объемом, занимаемым отдельного атома или молекулы. Мы называем такие усредненные величины макроскопическими полями и макроскопические источники. В разделе 6.6 подробно показано, что макроскопическая Уравнения Максвелла имеют вид (I.1а), где Е и В — усредненные значения Е и В микроскопический или вакуумный Maxwell
— Классическая электродинамика , JD Jackson 1999, pg 13.
Бывают ситуации, когда вы не можете игнорировать эти микроскопические колебания. Например, в очень чувствительных электрических цепях. См. пример теплового шума в электрических цепях.
$\endgroup$
$\begingroup$
Обычный проводник является (близким к) омическим, т. е. подчиняется закону Ома.
плотность тока направлена и пропорциональна
электрическое поле. Решение для внутреннего поля
фасонный проводник (например, изогнутая проволока или отрезок листового
металл) менее знакомая проблема, чем внешнее поле
в статическом электричестве, но это можно сделать.
Хаотическая природа столкновений электронов проводимости при комнатной температуре вносит большой вклад в закон Ома, и определяет проводимость. Однако при большом количестве полезных носителей тока нет необходимости рассматривать отдельные электроны или столкновения. Средние движения жидкости подвижных электронов равны все, что мы считаем.
$\endgroup$
5
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Почему текущий элемент является векторной величиной? | Помощь с домашним заданием
CBSE, JEE, NEET, NDA
Банк вопросов, пробные тесты, экзаменационные работы
Решения NCERT, образцы документов, заметки, видео
Установить сейчас
Почему текущий элемент является векторной величиной?
Автор: Дипак Панди 1 год, 4 месяца назад
CBSE > Класс 12 > Физика
- 2 ответа
Закон Куламба
Автор: Паял Рават 1 неделя, 6 дней назад
CBSE > Класс 12 > Физика
- 5 ответов
Частица, имеющая заряд +5 UC, изначально находится в состоянии покоя AG в точке x, равной 30 см по оси x. Частица должна двигаться из-за наличия заряда q, фиксированного в начале координат найти кинетическая энергия частицы действует в тот момент, когда она проходит более 15 см от своего начального положения, если вы равна + 5 UC 15 с использованием
Частица должна двигаться из-за наличия заряда q, фиксированного в начале координат найти кинетическая энергия частицы действует в тот момент, когда она проходит более 15 см от своего начального положения, если вы равна + 5 UC 15 с использованием
Автор: Дипенду Гоуп 1 неделя, 1 день назад
CBSE > Класс 12 > Физика
- 0 ответов
जैक्स एक्ससीकिसीएचसी बी fulबी
Автор: Арпит Ядав 4 дня, 13 часов назад
CBSE > Класс 12 > Физика
- 0 ответов
Что такое физика? Какая польза от физики
Автор: Мд Рехман 2 дня, 1 час назад
CBSE > Класс 12 > Физика
- 1 ответ
Кулон
Автор: Пиху Агарвал 1 неделя, 3 дня назад
CBSE > Класс 12 > Физика
- 3 ответа
Что такое собственные полупроводники
Автор: Симму Шариф 5 дней, 23 часа назад
CBSE > Класс 12 > Физика
- 0 ответов
Кусок полиэтилена, натертый шерстью, имеет отрицательный заряд 3×10*- Есть ли перенос массы с шерсти на полиэтилен?
Автор: Дивья Тхакур 1 неделя, 4 дня назад
CBSE > Класс 12 > Физика
- 3 ответа
Связь между градиентом потенциала электрического поля
Автор: Маннат Гангвар 2 недели назад
CBSE > Класс 12 > Физика
- 2 ответа
Что такое суперпозиция основных расходов?
Автор: Бхарат Томар 1 неделя, 3 дня назад
CBSE > Класс 12 > Физика
- 2 ответа
Эксперименты метрового моста
Автор: Акаш Дип 1 неделя, 6 дней назад
CBSE > Класс 12 > Физика
- 1 ответ
myCBSEguide
Доверяют 1 крор+ студентов
Установить сейчас
- Создавайте документы за считанные минуты
- Печать с вашим именем и логотипом
- Скачать в формате PDF
- 5 лакхов+ вопросов
- Включенные решения
- На основе учебного плана CBSE
- Подходит для школ и репетиторов
Создание документов
Тестовый генератор
Создание статей по цене 10 ₹/- за бумагу
Попроб.
Государств | Webflow University
Вы можете добавить интерактивности своим элементам, изменив их внешний вид и поведение в различных состояниях.
В этом уроке:
- Стиль элемента в различных состояниях
- Вернуться к стилю состояния по умолчанию
- Удалить стиль элемента в состоянии
- Стиль текущего состояния элементов ссылки
- Понять, где находятся стили унаследовано от
Стиль элемента в различных состояниях
Чтобы применить различные стили к элементу в разных состояниях, например, в состоянии наведения, откройте раскрывающееся меню «Состояния» в селекторе панели «Стиль» и выберите состояние, для которого требуется стиль.
Когда вы выбираете состояние из раскрывающегося меню «Состояния» в селекторе, в конце поля селектора появляется зеленый класс состояния, также называемый псевдоклассом. Это указывает на то, что вы сейчас стилизуете это состояние для своего элемента.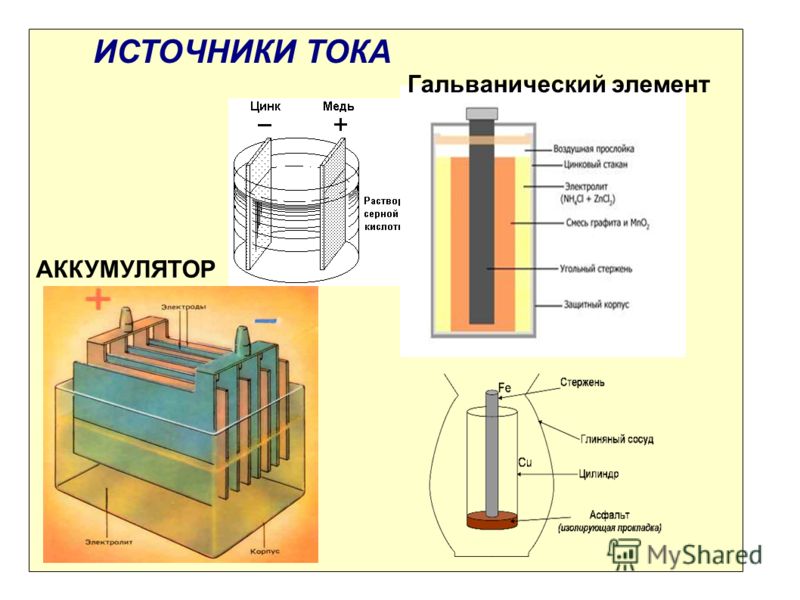
Вы можете выбрать любое количество стилей. Вносимые здесь изменения стиля — это то, что пользователи увидят, взаимодействуя с этим элементом.
В каком бы состоянии вы ни находились, внесенные вами изменения будут видны на холсте до тех пор, пока вы не отмените выбор или не покинете это состояние иным образом.
Меню состояний (раскрывающееся меню)
Выберите состояние, для которого хотите создать стиль, из раскрывающегося меню. Теперь любые изменения, сделанные вами на панели «Стиль», будут сохранены для выбранного состояния.
Состояние NoneСостояние None является состоянием элементов по умолчанию. Так элемент выглядит по умолчанию.
После выбора и стиля другого состояния можно вернуться к стилю состояния по умолчанию, выбрав «нет» в раскрывающемся меню «Состояния».
Состояние наведения Состояние наведения отображается, когда вы наводите указатель мыши на элемент. На большинстве сенсорных устройств наведение курсора невозможно, поэтому помните об этом при проектировании небольших точек останова.
Нажатое или активное состояние — это состояние, которое отображается, когда вы щелкаете или нажимаете на элемент. Это состояние наследует стили от состояния наведения, поскольку нажатие на самом деле является состоянием состояния наведения.
Состояние фокусировкиВы можете сосредоточиться на определенных интерактивных элементах, таких как кнопки и ссылки, не активируя их, используя клавиатуру для перехода к ним. Щелчок по интерактивным элементам с помощью мыши или указателя фокусирует и активирует их. Это состояние эмулируется, когда интерактивный элемент находится в фокусе с помощью клавиатуры, мыши или касания пальцем.
Состояние фокуса (клавиатура) Как и состояние фокуса, это состояние эмулируется, когда интерактивный элемент находится в фокусе, но не обязательно активирован (например, при нажатии на элемент с помощью клавиатуры). Обратите внимание, что это всегда применяется к полям ввода текста, когда они сфокусированы, независимо от того, каким образом они были сфокусированы (например, с помощью мыши, клавиатуры и т. д.).
д.).
Чтобы сделать ваш сайт более доступным для посетителей, использующих клавиатуру для навигации, важно оформить это состояние так, чтобы расположение интерактивных элементов было очевидным на странице. Мы предлагаем установить контур для интерактивных элементов, потому что это не повлияет на макет элемента.
Посещенное состояние — это состояние посещенной ссылки. Это состояние наследует стили от состояния none.
Для состояния «посещено» можно изменить только цвет текста, цвет фона и цвет границы. Цвет фона появится только в том случае, если он уже установлен в другом состоянии.
ЗаполнительЭто состояние будет доступно в раскрывающемся меню «Состояния» для полей формы. Это позволяет вам стилизовать текст-заполнитель отдельно от печатного текста, который наследует типографский стиль состояния по умолчанию.
Для текста-заполнителя можно стилизовать типографику, фон и тени.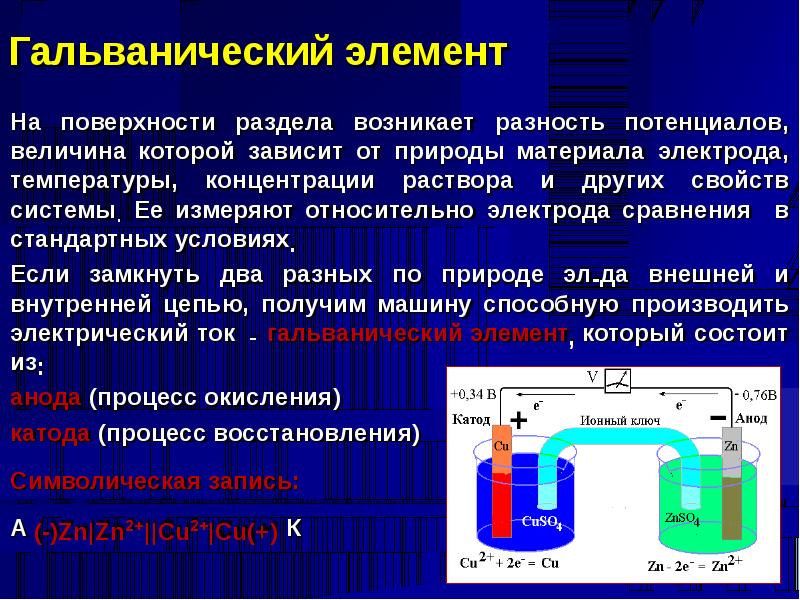
Это состояние будет доступно в раскрывающемся меню «Состояния» для флажков и переключателей форм, для которых в настройках элемента включен пользовательский стиль. Это позволяет вам стилизовать проверенное состояние флажка или переключателя.
Возврат к стилизации состояния по умолчанию
Когда вы закончите стилизацию своих состояний, вы можете вернуться к состоянию по умолчанию «Нет», выполнив любое из следующих действий:
- Выберите «Нет» в раскрывающемся меню «Состояния»
- Нажмите ESC на клавиатуре (это также отменяет выбор текущего элемента)
- Выберите другой элемент
Удалить стиль элемента в состоянии
Чтобы удалить пользовательский стиль или все стили из состояния:
- Выберите element
- Выберите состояние в раскрывающемся меню «Состояния»
- Удалить любые стили (выделены синим цветом)
Стиль текущего состояния элементов ссылок и вкладок
Элементы ссылок также имеют текущее состояние. Когда вы добавляете собственный стиль в текущее состояние, он будет отражать, как выглядит ваш элемент ссылки, когда пользователь находится в этом состоянии.
Когда вы добавляете собственный стиль в текущее состояние, он будет отражать, как выглядит ваш элемент ссылки, когда пользователь находится в этом состоянии.
Текущее состояние автоматически добавляется к тегу Все ссылки или классу выбранного элемента ссылки, когда этот элемент связан с текущей страницей, разделом или вкладкой.
Текущее состояние наследует все стили из состояния по умолчанию «Нет».
Выбор текущего состояния ссылки
Чтобы получить доступ к текущему состоянию любого блока ссылок, текстовой ссылки, кнопки, навигационной ссылки:
- Выберите элемент ссылки и нажмите D, чтобы открыть настройки ссылки
- Выберите параметр страницы и выберите текущую страницу из раскрывающегося списка (если ваша ссылка находится на главной странице, выберите домашнюю страницу)
- Нажмите S, чтобы перейти на панель стилей. Вы увидите, что текущее состояние зеленого цвета активировано в поле селектора, если вы применили класс к своей ссылке.
 Если нет, щелкните в селекторе и выберите тег «Все ссылки» в раскрывающемся списке. Текущее состояние также будет применено к тегу.
Если нет, щелкните в селекторе и выберите тег «Все ссылки» в раскрывающемся списке. Текущее состояние также будет применено к тегу.
Вы также можете выбрать вариант раздела страницы в настройках ссылки. Текущее состояние появится в поле выбора для этого элемента при прокрутке до этого раздела страницы. Это полезно для стилизации кнопок или ссылок, которые фиксируются при прокрутке.
После того, как вы настроите текущее состояние, вы можете обновить настройки ссылок и связать свою кнопку и элементы ссылок с любыми другими страницами или разделами страниц.
Выбор текущего состояния вкладки
Вы можете выбрать стиль текущей вкладки, отличный от стиля обычной вкладки, чтобы различать активные и неактивные вкладки. Например, вы можете отредактировать цвет шрифта и цвет фона, чтобы они отличались от обычной вкладки.
Для оформления текущей вкладки:
- Выберите активную вкладку Ссылка
- Назначить класс.
 Текущее состояние появится автоматически.
Текущее состояние появится автоматически. - Удаление стиля
Стилизация состояния ссылки по умолчанию, когда индикатор текущего состояния отображается в селекторе
Существует несколько способов удалить текущее состояние, если вы хотите изменить состояние по умолчанию. Самый быстрый способ сделать это — выбрать базовый класс по умолчанию в меню «Наследование».
Кроме того, вы можете временно удалить настройку ссылки на панели настроек элемента, изменить класс ссылки, а затем повторно настроить настройку ссылки. Если вы не хотите удалять параметр ссылки, продублируйте элемент ссылки, удалите параметр ссылки на дублирующемся элементе, отредактируйте класс, а затем удалите повторяющийся элемент, когда закончите.
Понять, где стили наследуются от
Все состояния наследуют стили от состояния «нет». «Нажато» также наследует стили от состояния «зависания». Вы можете увидеть, откуда наследуются стили, щелкнув индикатор наследования прямо над полем выбора.
После добавления стилей в состояние значок раскрывающегося меню состояний станет синим. И когда вы откроете раскрывающееся меню «Состояния», вы увидите синие круги, указывающие на то, что в этом состоянии есть локальные стили.
Был ли этот урок полезен? Дайте нам знать!Спасибо за отзыв! Это поможет нам улучшить наш контент.
Свяжитесь с нашим сообществом
Свяжитесь со службой поддержки
Что-то пошло не так при отправке формы.
Связаться со службой поддержки
Есть предложения по уроку? Дайте нам знать
Спасибо! Ваша заявка принята!
Ой! Что-то пошло не так при отправке формы.
Периодическая таблица элементов — IUPAC
Последний выпуск Периодической таблицы (от 4 мая 2022 г.) включает самые последние сокращенные стандартные значения атомного веса, опубликованные Комиссией ИЮПАК по изотопному содержанию и атомному весу (CIAAW), составленные как часть Таблицы 2021 г. Стандартные атомные массы на 2021 год.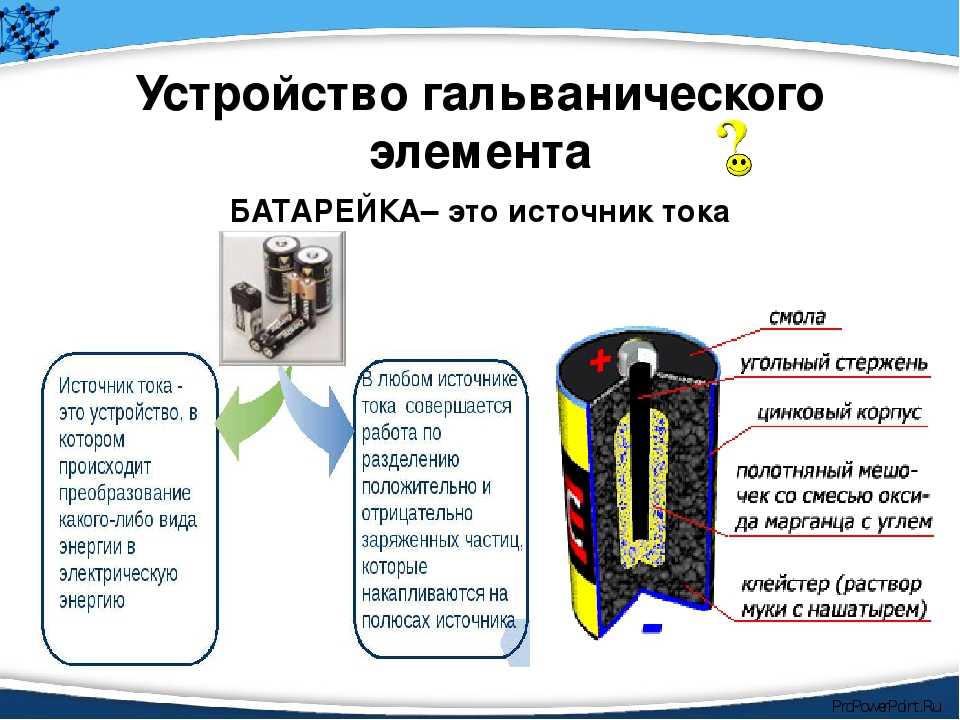 Для элементов, у которых отсутствуют изотопы с характерным изотопным содержанием в природных земных образцах, в квадратных скобках указано массовое число нуклида с самым длительным подтвержденным периодом полураспада. См. PAC (AOP, 4 мая 2022 г.; https://doi.org/10.1515/pac-2019).-0603) для получения полной информации или посетите сайт Commission II.1 @ciaaw.org
Для элементов, у которых отсутствуют изотопы с характерным изотопным содержанием в природных земных образцах, в квадратных скобках указано массовое число нуклида с самым длительным подтвержденным периодом полураспада. См. PAC (AOP, 4 мая 2022 г.; https://doi.org/10.1515/pac-2019).-0603) для получения полной информации или посетите сайт Commission II.1 @ciaaw.org
Загрузите версию в формате PDF (размер Letter или A4) или A3 (PDF) или см. более ранние версии
Ознакомьтесь со SPECIAL Chem Int Январь 2019 г. — Международный год Периодической таблицы (МГПТ) — при участии Яна Ридейка, Натальи Тарасовой, Г.Дж. Ли, Сигурд Хофманн, Эрик Шерри, Юрис Мейя, Норман Э. Холден, Тайлер Б. Коплен, Питер Махаффи, Ян Миллс, Роберто Марквардт и другие.
Периодическая таблица элементов и изотопов IUPAC (IPTEI) для образовательного сообщества
— следуйте проекту IUPAC 2007-038-3-200 и последующему проекту 2014-024-1-200
— читайте «Атомные массы: нет Longer Constants of Nature», Chem Int 33(2), 10–15 (2011), https://doi.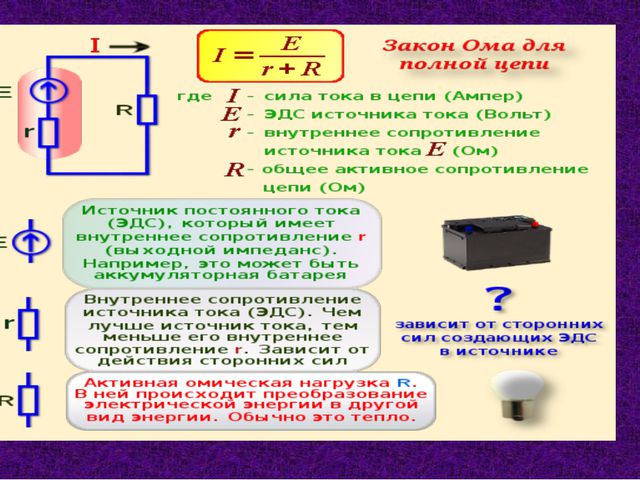 org/10.1515/ci.2011.33.2.10
org/10.1515/ci.2011.33.2.10
— ознакомьтесь с интерактивной версией на iupac.org/isotopes- материя (или см. выпуск)
– Узнайте больше, почему изотопы имеют значение! https://iupac.org/100/stories/why-isotopes-matter/
— Ознакомьтесь с последним поэлементным обзором IPTEI, включая таблицу всех известных стабильных и радиоактивных изотопов для каждого элемента и примеры практического применения изотопных измерений и технологий https://iupac.org/iptei/
— Доступ по адресу http: //ciaaw.org/periodic-table-isotopes.htm полное разрешение этой таблицы в формате PDF (предоставлено Королевским центром визуализации в науке).
Благодаря своей работе, связанной с химическими элементами, IUPAC может выпускать периодическую таблицу, которая соответствует современным требованиям. Участие IUPAC охватывает различные аспекты таблицы и данных, которые она раскрывает, и несколько отчетов и рекомендаций, некоторые из которых совсем недавно, свидетельствуют об этом вкладе.
В частности, ИЮПАК непосредственно участвует в следующем:
- установление критериев для открытия нового элемента
- определение структуры временного имени и символа
- оценка требований, приводящих к проверке и присвоению открытия элемента
- координирует присвоение имени новому элементу, включает исследовательскую лабораторию и допускает общественное обсуждение
- создание точных правил для как назвать новый элемент
- определение групп 1-18 и собирательных имен
- определение того, какие элементы относятся к группе 3
- регулярный пересмотр стандартных атомных весов
Таблица принадлежит вам, чтобы использовать . Подробная информация о последнем выпуске представлена выше . Подробная информация ниже содержит несколько ссылок на журнал IUPAC в Pure and Applied Chemistry 9.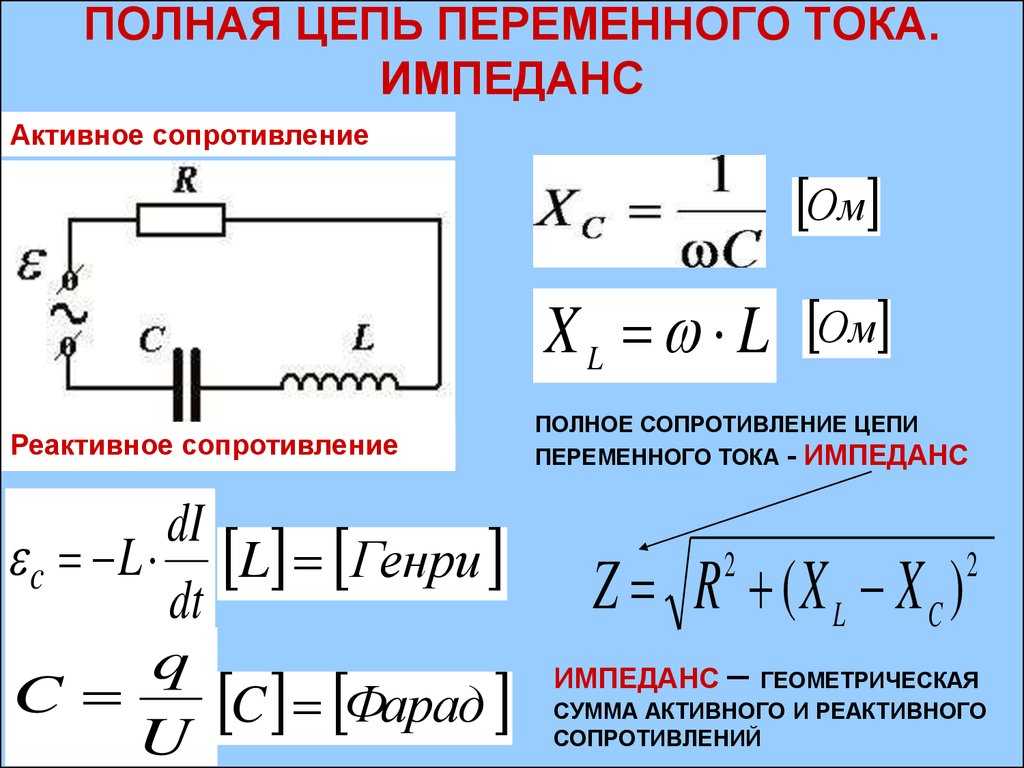 0006 ( PAC ) и журнал Chemistry International ( CI ).
0006 ( PAC ) и журнал Chemistry International ( CI ).
- Критерии открытия нового элемента
Оценка того, был ли элемент «обнаружен», — непростая задача. Изучая профили открытия трансфермиевых элементов в начале 90-х годов, IUPAC и IUPAP установили ряд критериев, которые должны быть выполнены для признания открытия элемента. Подробности в PAC 1991, Vol. 63, № 6, стр. 879-886 (https://doi.org/10.1351/pac199163060879) и PAC 1993, Vol. 65, № 8, стр. 1757-1814 (https://doi.org/10.1351/pac199365081757)
В ноябре 2018 г. IUPAC/IUPAP выпустил предварительный отчет ОБ ОТКРЫТИИ НОВЫХ ЭЛЕМЕНТОВ. Представлены критерии и рекомендации по установлению приоритета открытия потенциальных новых элементов. — узнать больше
- Временное название и условное обозначение
Несмотря на то, что элемент может быть заявлен, до того, как заявление будет подтверждено и до того, как элемент будет официально назван, элемент имеет временное имя и символ. Соответствующие рекомендации, устанавливающие эту систематическую номенклатуру, были опубликованы в 1978 г.; см. PAC 1979, Vol. 51, № 2, стр. 381-384; https://doi.org/10.1351/pac197951020381
Соответствующие рекомендации, устанавливающие эту систематическую номенклатуру, были опубликованы в 1978 г.; см. PAC 1979, Vol. 51, № 2, стр. 381-384; https://doi.org/10.1351/pac197951020381
В результате, именно так в марте 2016 года элемент 113 был назван унунтрием или с символом Uut.
История трехбуквенных символов изложена в статье, подготовленной Ларсом Эрстрёмом и Норманом Холденом и опубликованной в Chem Int 2016, Vol. 38, № 2, с. 4-8; https://doi.org/10.1515/ci-2016-0204
- Проверка и назначение обнаружения элемента
Заявления об открытии новых элементов время от времени появляются в научной литературе. IUPAC вместе с IUPAP участвует в оценке этих заявлений. В результате выпускаются технические отчеты IUPAC, в которых анализируются все соответствующие ссылки и признаются лаборатории(и), заявления которых соответствуют согласованным критериям.
В 2016 году было выпущено два таких отчета, которые охватывают элементы 113, 115, 117 и элемент 118; См. PAC 2016, Vol. 88, № 1-2, стр. 139-153; https://doi.org/10.1515/pac-2015-0502 и PAC 2016, Vol. 88, № 1-2, стр. 155-160; https://doi.org/10.1515/pac-2015-0501
PAC 2016, Vol. 88, № 1-2, стр. 139-153; https://doi.org/10.1515/pac-2015-0502 и PAC 2016, Vol. 88, № 1-2, стр. 155-160; https://doi.org/10.1515/pac-2015-0501
- Именование нового элемента
После проверки обнаружения нового элемента и присвоения приоритета его обнаружения можно начинать процесс именования. Лаборатории, которой поручено открытие, предлагается предложить название и условное обозначение. Затем IUPAC рассмотрит предложение и, если оно будет согласовано, после дополнительного 5-месячного публичного рассмотрения, формализует название. Самый последний пример таких рекомендаций был опубликован в 2012 году и касался названий и символов элементов 114 и 116; См. PAC 2012, Том. 84, № 7, стр. 1669-1672; https://doi.org/10.1351/PAC-REC-11-12-03
Краткий обзор текущих процедур опубликован в недавней статье Джона Кориша; См. CI 2016, Vol. 38, № 2, стр. 9-11; https://doi. org/10.1515/ci-2016-0205
org/10.1515/ci-2016-0205
8 июня 2016 г. IUPAC опубликовал предварительные названия для последних 4 элементов 113, 115, 117 и 118 — см. объявил утвержденные названия и символы — см. релиз.
Для размышлений об опыте именования элементов в 2016 г. см. Chem Int Apr 2017, стр. 30–21, автор Jan Reedijk; https://doi.org/10.1515/CI-2017-0222
См. Архивы с более ранним компиляцией и ссылками
- 13
- 13
Опять же, у IUPAC есть набор рекомендаций, определяющих, какое имя может носить элемент. И корень, и окончание должны соответствовать согласованным рекомендациям. Подробные рекомендации были опубликованы в 2002 г.
 , а пересмотренная версия опубликована в 2016 г. для лучшего учета элементов в группах 17 и 18. См. 9.0005 PAC 2002, Том. 74, № 5, стр. 787-791; https://doi.org/10.1351/pac200274050787 и PAC 2016, Vol. 88, № 4, стр. 401-405 https://doi.org/10.1515/pac-2015-0802 (или https://iupac.org/project/2015-031-1-200)
, а пересмотренная версия опубликована в 2016 г. для лучшего учета элементов в группах 17 и 18. См. 9.0005 PAC 2002, Том. 74, № 5, стр. 787-791; https://doi.org/10.1351/pac200274050787 и PAC 2016, Vol. 88, № 4, стр. 401-405 https://doi.org/10.1515/pac-2015-0802 (или https://iupac.org/project/2015-031-1-200)- Группы 1-18 и собирательные имена
С 1988 г. IUPAC рекомендовал просто нумеровать группы (, т.е. столбцов) от 1 до 18. орг/10.1351/pac198860030431)
Лантаноиды и актиноиды являются собирательными названиями, также рекомендованными IUPAC. Лантаноиды (от La до Lu) предпочтительнее лантанидов, и хотя лантаноид означает «подобный лантану» и поэтому не должен включать лантан, однако лантан стал широко использоваться. Актиноиды включают от Ac до Lr.
- Группа 3
Время от времени обсуждался вопрос о том, какие именно элементы должны быть помещены в группу 3.
 Недавно был инициирован проект IUPAC для решения этого вопроса. Будет ли группа 3 состоять из Sc, Y, Lu и Lr или она будет состоять из Sc, Y, La и Ac?
Недавно был инициирован проект IUPAC для решения этого вопроса. Будет ли группа 3 состоять из Sc, Y, Lu и Lr или она будет состоять из Sc, Y, La и Ac?Оставайтесь с нами и смотрите https://iupac.org/project/2015-039-2-200 и CI 2016, Vol. 38, № 2, стр. 22-23; https://doi.org/10.1515/ci-2016-0213
- Стандартные атомные веса
Одной из задач Комиссии по изотопному содержанию и атомному весу (CIAAW) является периодический пересмотр результатов определения атомного веса. Самый последний отчет «Стандартные атомные веса элементов 2021» был опубликован в PAC в мае 2022 г. (AOP от 4 мая 2022 г.; https://doi.org/10.1515/pac-2019-0603)
Комиссия была создана в 1899 г. (да, в 1899 г.) Отделение неорганической химии ИЮПАК. (см. www.ciaaw.org) Он также регулярно рассматривает изотопные составы элементов; последний сборник также опубликован в PAC в марте 2016 г. ( PAC 2016, том 88, № 3, стр.
 293–306; https://doi.org/10.1515/pac-2015-0503)
293–306; https://doi.org/10.1515/pac-2015-0503) Ваш для использования
Хотя ИЮПАК не рекомендует конкретную форму периодической таблицы, т.е. . 18-колоночный или 32-колоночный формат, представленная здесь версия имеет обычную длинную форму и может использоваться вами.
Ознакомьтесь с предыдущими версиями.
Для сбора может потребоваться способ пропустить текущий элемент в операторе case — Question
shea-hawkins
#1
Рассмотрим следующее:
view
.collect {
case o if f(o) => bigFn(o)
}
.collect {
case p if p.value > 10 => g§
}
https: //pastebin.com/skckN5DF (с форматированием)В этом случае из соображений производительности чем меньше сгенерированных классов, тем лучше.
 bigFn достаточно требователен к производительности, поэтому мы не хотим вызывать его дважды. Если бы мы могли вернуть значение из оператора collect, указывающее, что мы хотим «пропустить» текущий элемент, мы смогли бы избежать потери производительности при вызове collect дважды подряд. Например:
bigFn достаточно требователен к производительности, поэтому мы не хотим вызывать его дважды. Если бы мы могли вернуть значение из оператора collect, указывающее, что мы хотим «пропустить» текущий элемент, мы смогли бы избежать потери производительности при вызове collect дважды подряд. Например:
view
.collect {
case o if f(o) => {
val oVal = bigFn(o)
if oVal.value > 10 oVal else Nothing
}
}
https://pastebin.com/ka8m3eJaЧто вы думаете об этом?
нафг
#2
Вы можете использовать flatMap:
view.flatMap { o =>
if (!f(o)) None
else Some(bigFn(o)).filter(_ > 10)
}
ши-хокинс
#3
Моя главная оговорка по поводу этого — снижение производительности, связанное с плоской картой.
Режим эталонного теста Cnt Score Единицы измерения ошибки FilterBenchmark.withCollect thrpt 10 1359035,689 ± 2749,815 операций/с FilterBenchmark.withCollectTypeMatch порог 10 1361227,743 ± 2337,850 операций/с FilterBenchmark.withFlatMap thrpt 10 113074,826 ± 288,107 операций/с FilterBenchmark.withFlatMapTypeMatch порог 10 113188.419± 262,826 операций/с
FlatMap создает параметры для каждого элемента в последовательности, тогда как collect фильтрует элементы перед операцией с ними. Это приводит к 13-кратному дефициту производительности в обстоятельствах, в которых этот дефицит имеет значение.
Ихоран
#4
Для высокопроизводительного кода, такого как этот, вы получите значительно больший выигрыш от написания пользовательского кода, чем от надежды на то, что библиотека попадет именно в ваш вариант использования.

В вашем конкретном случае вы можете написать более быструю версию с компоновщиком и итератором.
значение b = Array.newBuilder[Foo] значение я = xs.iterator в то время как (i.hasNext) { val o = i.next если (f (о)) { знач.темп = bigFn(o) если (temp.value > 10) b += temp } } б.результат()Это вручную объединяет версию на основе итератора или представления
xs.iterator.filter(f).map(bigFn).filter(_.value > 10).toArray
который, если вы заботитесь о накладных расходах бокса в
Опция, может иметь значение.(Примечание: фильтр/карта/фильтр может работать быстрее, чем
Вариантбокса.)tarsa
#5
Scala 2.13 имеет перегрузки в
scala.PartialFunction, как иdef andThen[C](k: PartialFunction[B, C]): PartialFunction[A, C], которые обеспечивают краткую композицию частичных функций, поэтому вы можете объединить несколько собирается в один. Пример: https://scastie.scala-lang.org/n8QriIZTT1K4qQvA97ljyw
Пример: https://scastie.scala-lang.org/n8QriIZTT1K4qQvA97ljywимпортировать scala.{PartialFunction => PF} val ints = List.tabulate(10)(i => i) val skipOddNumsAndHalveEven: PF[Int, Int] = { case x if x % 2 == 0 => x / 2 } def skipLowerThanAndSubtract (порог: Int): PF[Int, Int] = { case x if x >= порог => x - порог } // частичные функции без объединения, два прохода 'сбора' println(ints.collect(skipOddNumsAndHalveEven).collect(skipLowerThanAndSubtract(3))) // объединенные частичные функции, один проход 'сбора' println(ints.collect(skipOddNumsAndHalveEven.andThen(skipLowerThanAndSubtract(3))))В Scala 2.12 это вызовет MatchError из-за отсутствия поддержки частичных функций в
andThen,составляюти т.д. комбинаторы. На Scala 2.13 это будет работать правильно.ши-хокинс
#6
@Ichoran Вы правы; Я проведу рефакторинг в этом случае.

@tarsa Спасибо за информацию. Это достаточно чисто, я обязательно воспользуюсь этим, когда столкнусь с этим в следующий раз в небольших коллекциях.
Надстройка Visible Elements Operations — Документация TestProject
Надстройка Visible Elements Operations — Документация TestProjectДокументация TestProject
PlatformAddonsBlogForum
Поиск…
Добро пожаловать в TestProject!
Начало работы
Регистрация и совместная работа
Установка и настройка
Создайте свой первый тест
Почему TestProject
Почему вы должны использовать TestProject
Что делает TestProject уникальным
Использование ИИ для улучшения тестирования
Агенты TestProject
Что такое агент TestProject?
Как агент вписывается в экосистему?
Hybrid Cloud and Offline Mode
TestProject Agent in Docker
TestProject Agent on Kubernetes
TestProject Agent CLI
Silent Deployment
Unregistered/Offline Agent
Smart Test Recorder
Web Testing
Mobile Testing
Create Тестовый шаг
Обнаружение и использование элементов
Доступные действия
Доступные валидации
Шаг выходных подтверждений
Использование испытаний и заданий, управляемых данными, в TestProject
Расписание и выполнение тестов
Управление агентами TestProject
Отчеты
Введение в отчеты в TestProject
Типы графиков в отчетах TestProject
Отчеты об отдельных прогонах
Получение отчетов о тестировании через API
Удаление старых отчетов
Надстройки TestProject
Что такое надстройка?
Installing Community Addons from the store
Using Addons in the TestProject Recorder
Creating an Addon
Available Addons
Yaml Validator
Tap and Get Toast Message
XLSX Operations
Base64 Encoder/Decoder Addon
Shell Команды Addon
Android Monkey Addon
Android Lercissions Manager Addon
Расширение элементов Addon
Generic Extensions Addon
Geolocation Utils Addon
GET ATTRIBUT Дополнение Comparison
Дополнение JS Actions
Дополнение Live Currency Converter
Дополнение Mobile Extensions
Дополнение Parameters Operations
Дополнение Reporting Utilities
RESTFUL API CLIENT
Прокрутка в элементе Addon
Действия Slack Addon
Свисание и нахождение элемента Addon
Web Extensions Addon
Веб -сенсорные жесты Addon
Глубокопа Link Toolkit Addon
Google Authenticator OTP Automation Addon
Visible Elements Operations Addon
Angular Element Actions Addon
Clicks Multiplier Addon
Двигатель обработки естественного языка Addon
ADB обертка Addon
Номеры телефонных номеров Addon
Операции Date-Time Addon
Генератор случайных данных ADDON
IOS Network Operation Модуль Key Events
Модуль ориентации экрана iOS
Модуль Math Calculations
Модуль String Utils
Модуль базы данных MSSQL
MySQL Database Addon
PostreSQL Database Addon
Oracle Database Addon
Web List Operations Addon
File Uploader Addon
JSON Operations Addon
jQuery — Slider Addon
jQuery — Spinner Addon
jQuery — Progressbar Addon
jQuery — надстройка Checkboxradio
надстройка jQuery Tabs
jQuery — надстройка Dialog
jQueryUI — надстройка Accordion
Foundation — надстройка Accordion
Робот -операции Addon
Foundation — Pagination Addon
Фонд — Orbit Addon
Фонд — вкладки Addon
Kendoui — Preduler
Kendoui — Grid Addon
BountStrap4 -Buttonta Group Addon 9000 3
Bootstrap4 -00003
BountStrap4 -Buttonta.
 Надстройка базы данных
Надстройка базы данныхПолучить цвет элемента
Действия Google
Open Source SDK
Обзор
OpenSDK (v2)
Использование OpenSDK в рамках CI/CD
Использование OpenSDK с BDD
Legacy SDK (V1)
Интеграции
QTEST Integration
Integration
Teamcity Integration
SALEGSICTION
000 9000 4000 4000 4000 4000 4000 4000 4000 4000 4000 4000 4000 4000 4000 4000 40004 SALEGSIN Slack Integration
CircleCI Integration
GitHub Integration
TestProject API
RESTful API v2
Начало работы с использованием TestProject API
Статьи
Справочные статьи
Советы и хитрости
Поддерживаемые среды
Выпуски
v3.5.0
v3.4.0
Старшие версии
70003
V3.4.0
Старшие версии
4.
База знаний
Powered By GitBook
Дополнение операций с видимыми элементами
Это дополнение предоставляет действия, которые будут выполняться, только если элемент виден.
 Действия не приведут к сбою шага, если элемент не виден. Вы можете увидеть пример того, как вы можете использовать это действие здесь
Действия не приведут к сбою шага, если элемент не виден. Вы можете увидеть пример того, как вы можете использовать это действие здесьОчистить содержимое (если оно видимо)— Очистить содержимое текущего элемента, если он виденЩелкнуть, если он виден— Щелкнуть текущий элемент, если он виден long действие будет ждать, пока элемент станет видимым. По умолчанию, если оставить поле пустым, 3 секундыСодержит текст? (если виден)— Проверить, содержит ли текущий элемент указанный текст?Это действие имеет следующие входные данные:
Текст— Текст, который вы хотите проверить, находится в элементеВремя ожидания— как долго действие будет ждать, пока элемент станет видимым. Значение по умолчанию, если вы оставите это поле пустым, составляет 3 секунды.
Значение по умолчанию, если вы оставите это поле пустым, составляет 3 секунды.
Получить текст (если виден)— Получить текст из элемента, если он виден.Это действие имеет один вход,
Timeout, который указывает, как долго действие будет ждать, пока элемент станет видимым. Значение по умолчанию, если вы оставите это поле пустым, равно 3 секундамКликабельно? (если виден)— Проверить, доступен ли текущий элемент.Это действие имеет один вход,
Timeout, который указывает, как долго действие будет ждать, пока элемент станет видимым. Значение по умолчанию, если оставить поле пустым, составляет 3 секунды.
Значение по умолчанию, если оставить поле пустым, составляет 3 секунды.Жест длительного нажатия (если он виден)— Жест длительного нажатия на текущий элемент, если он виден (только для Android и iOS).Это действие имеет следующие входы:
Duration— Количество времени (в миллисекундах) удержания нажатия наTimeout— сколько времени действие будет ждать, пока элемент станет видимым. Значение по умолчанию, если вы оставите это поле пустым, составляет 3 секунды.
Коснитесь (если он виден)— коснитесь текущего элемента, если он виден (только для Android и iOS)Это действие имеет один вход,
long действие будет ждать, пока элемент станет видимым. Значение по умолчанию, если вы оставите это поле пустым, равно 3 секундамВведите текст (если виден)— Введите указанный текст в текущий элемент, если элемент видимТаймаут- сколько времени действие будет ждать, пока элемент станет видимым.
- 13
- 13






 ;
; Что имеет значение, так это среднее значение
поле или источник над объемом большим по сравнению с объемом, занимаемым
отдельного атома или молекулы. Мы называем такие усредненные величины макроскопическими полями
и макроскопические источники. В разделе 6.6 подробно показано, что макроскопическая
Уравнения Максвелла имеют вид (I.1а), где Е и В — усредненные значения Е и В
микроскопический или вакуумный Maxwell
Что имеет значение, так это среднее значение
поле или источник над объемом большим по сравнению с объемом, занимаемым
отдельного атома или молекулы. Мы называем такие усредненные величины макроскопическими полями
и макроскопические источники. В разделе 6.6 подробно показано, что макроскопическая
Уравнения Максвелла имеют вид (I.1а), где Е и В — усредненные значения Е и В
микроскопический или вакуумный Maxwell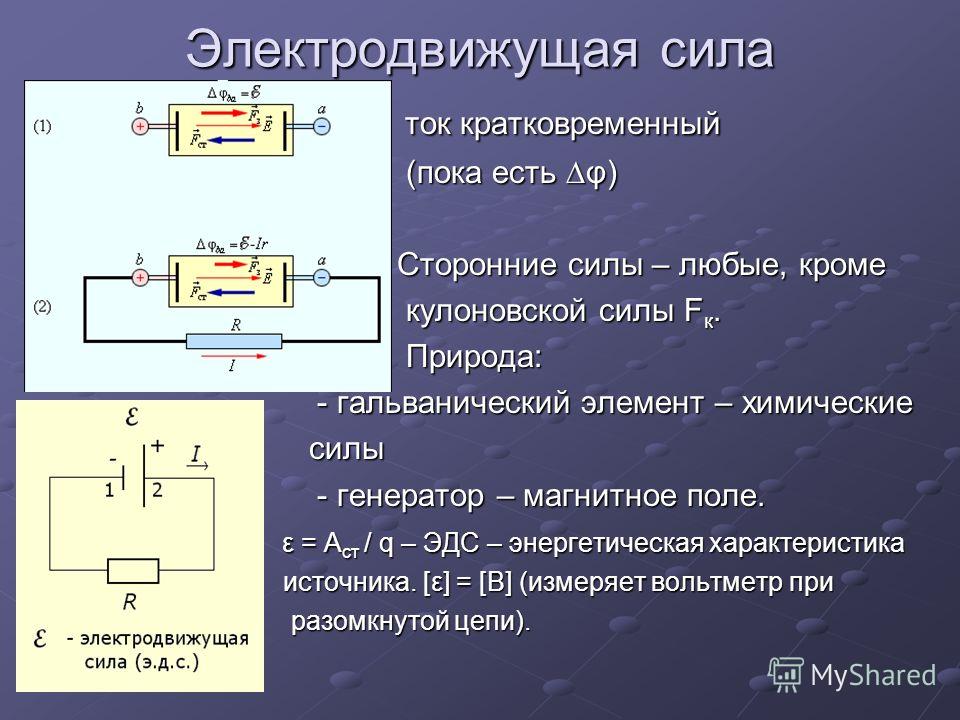 Если нет, щелкните в селекторе и выберите тег «Все ссылки» в раскрывающемся списке. Текущее состояние также будет применено к тегу.
Если нет, щелкните в селекторе и выберите тег «Все ссылки» в раскрывающемся списке. Текущее состояние также будет применено к тегу.  Текущее состояние появится автоматически.
Текущее состояние появится автоматически. , а пересмотренная версия опубликована в 2016 г. для лучшего учета элементов в группах 17 и 18. См. 9.0005 PAC 2002, Том. 74, № 5, стр. 787-791; https://doi.org/10.1351/pac200274050787 и PAC 2016, Vol. 88, № 4, стр. 401-405 https://doi.org/10.1515/pac-2015-0802 (или https://iupac.org/project/2015-031-1-200)
, а пересмотренная версия опубликована в 2016 г. для лучшего учета элементов в группах 17 и 18. См. 9.0005 PAC 2002, Том. 74, № 5, стр. 787-791; https://doi.org/10.1351/pac200274050787 и PAC 2016, Vol. 88, № 4, стр. 401-405 https://doi.org/10.1515/pac-2015-0802 (или https://iupac.org/project/2015-031-1-200)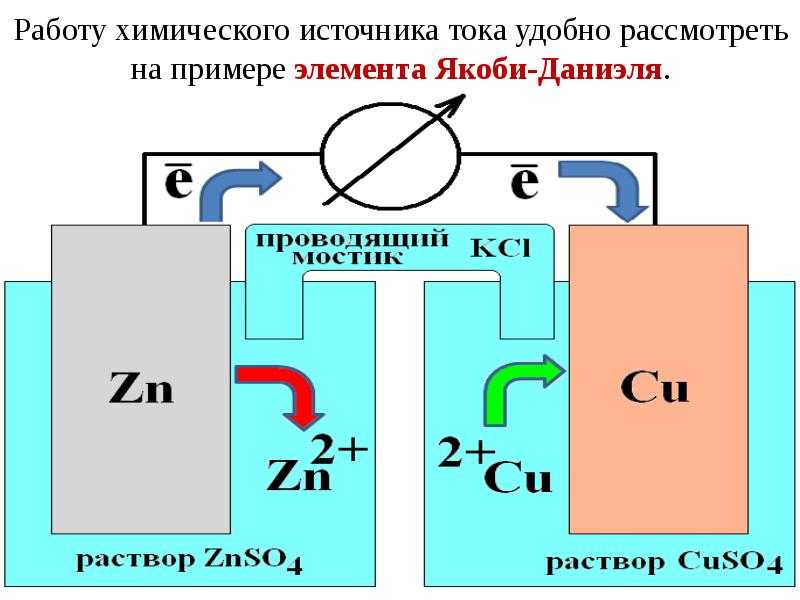 Недавно был инициирован проект IUPAC для решения этого вопроса. Будет ли группа 3 состоять из Sc, Y, Lu и Lr или она будет состоять из Sc, Y, La и Ac?
Недавно был инициирован проект IUPAC для решения этого вопроса. Будет ли группа 3 состоять из Sc, Y, Lu и Lr или она будет состоять из Sc, Y, La и Ac?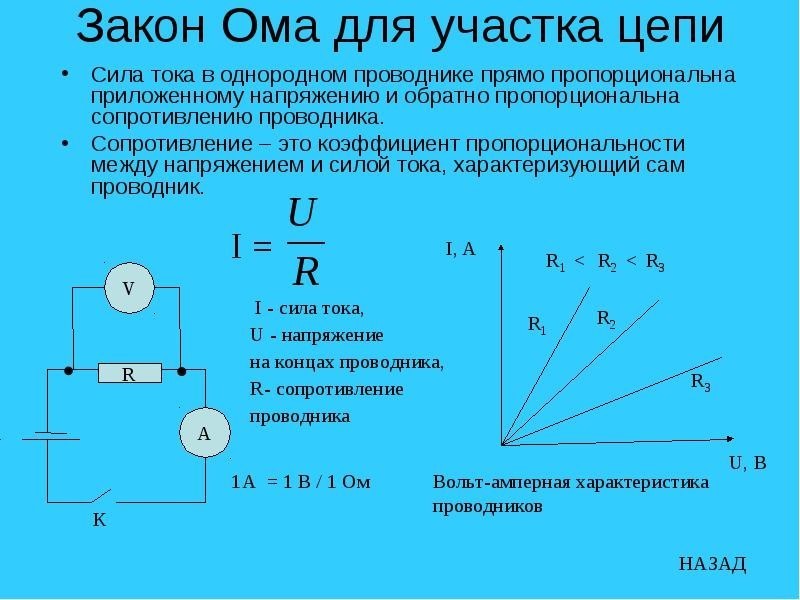 293–306; https://doi.org/10.1515/pac-2015-0503)
293–306; https://doi.org/10.1515/pac-2015-0503) 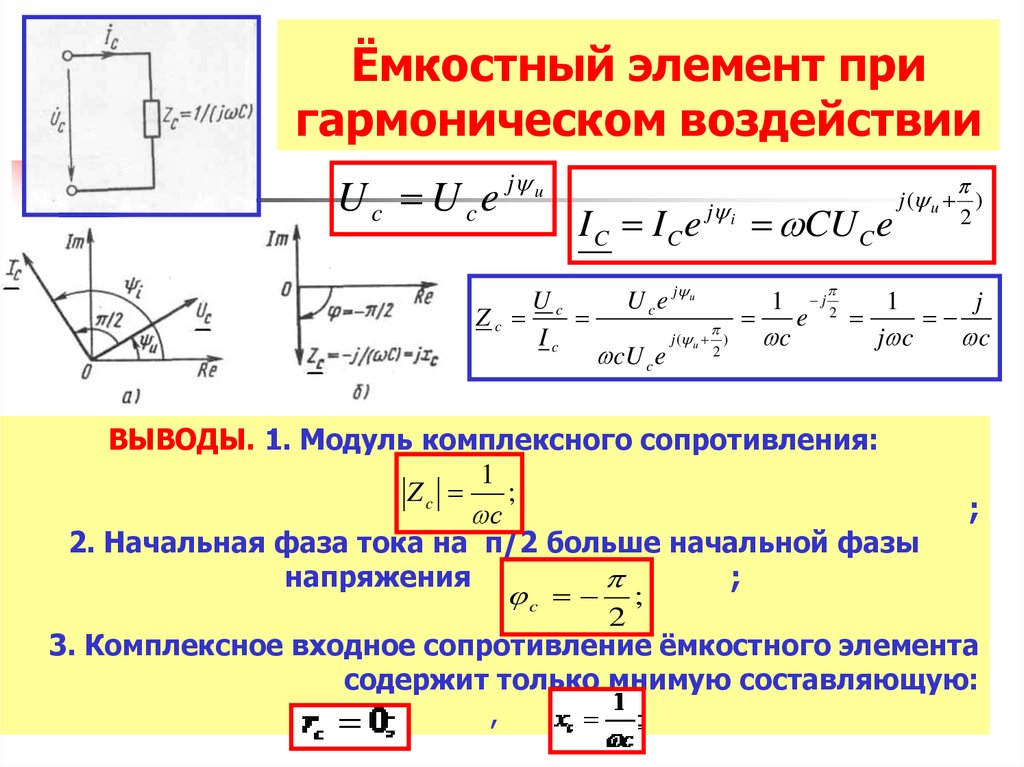 bigFn достаточно требователен к производительности, поэтому мы не хотим вызывать его дважды. Если бы мы могли вернуть значение из оператора collect, указывающее, что мы хотим «пропустить» текущий элемент, мы смогли бы избежать потери производительности при вызове collect дважды подряд. Например:
bigFn достаточно требователен к производительности, поэтому мы не хотим вызывать его дважды. Если бы мы могли вернуть значение из оператора collect, указывающее, что мы хотим «пропустить» текущий элемент, мы смогли бы избежать потери производительности при вызове collect дважды подряд. Например: 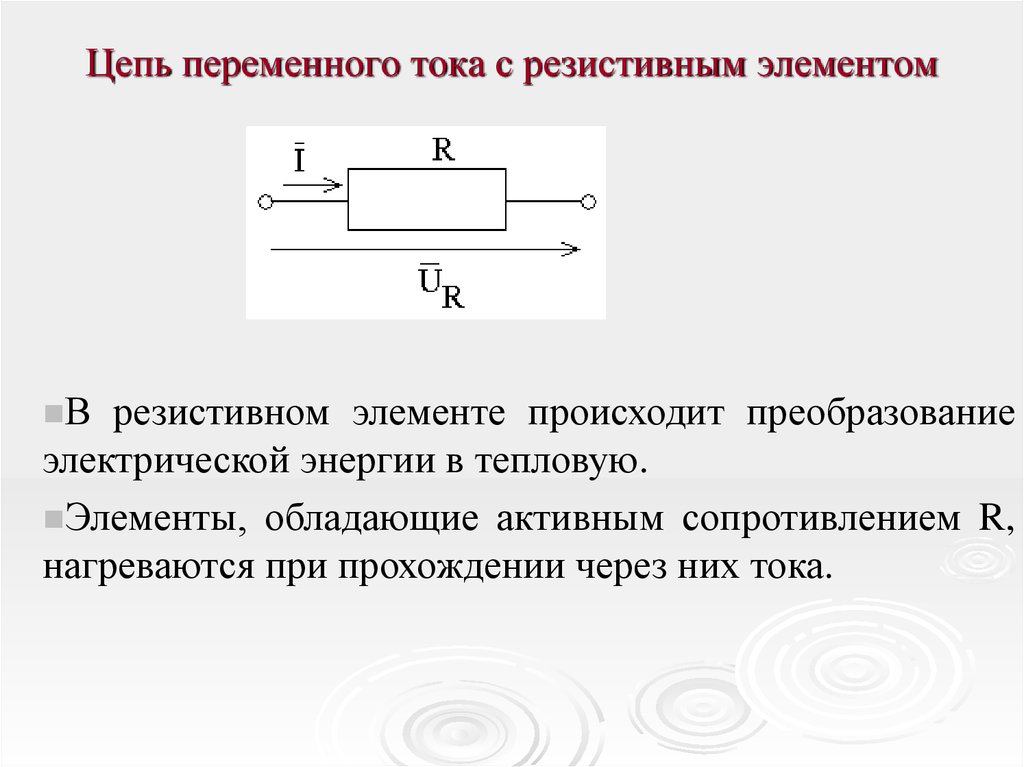
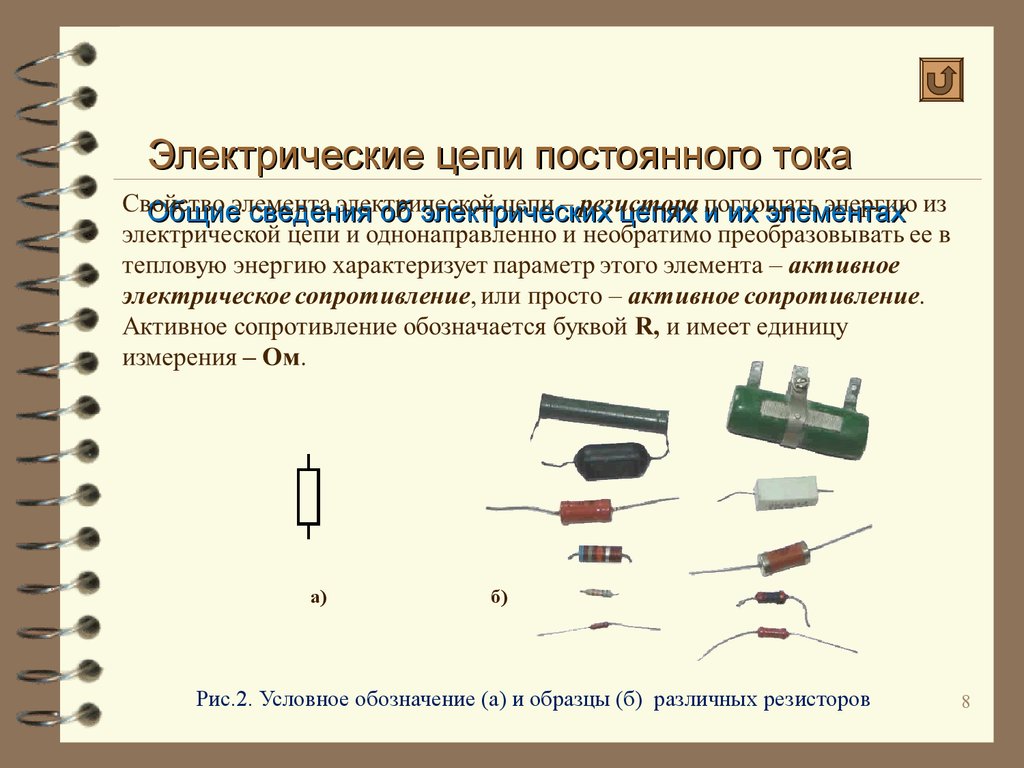 Пример: https://scastie.scala-lang.org/n8QriIZTT1K4qQvA97ljyw
Пример: https://scastie.scala-lang.org/n8QriIZTT1K4qQvA97ljyw
 Надстройка базы данных
Надстройка базы данных Действия не приведут к сбою шага, если элемент не виден. Вы можете увидеть пример того, как вы можете использовать это действие здесь
Действия не приведут к сбою шага, если элемент не виден. Вы можете увидеть пример того, как вы можете использовать это действие здесь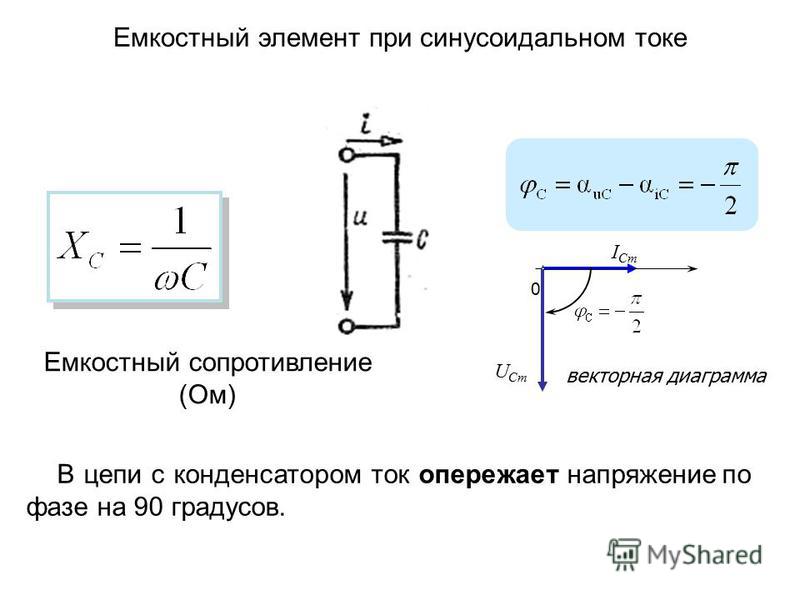 Значение по умолчанию, если вы оставите это поле пустым, составляет 3 секунды.
Значение по умолчанию, если вы оставите это поле пустым, составляет 3 секунды. Значение по умолчанию, если оставить поле пустым, составляет 3 секунды.
Значение по умолчанию, если оставить поле пустым, составляет 3 секунды.
