Кафедра математики Физического факультета МГУ им. М.В.Ломоносова
Аналитическая геометрия является одним из базовых курсов высшей математики, лежащих в основе физико-математического образования.
Общая трудоемкость курса — 108 часов. Курс включает 36 часов лекций, 18 часов семинарских занятий, требует 54 часов самостоятельной работы студентов.
В курсе рассматриваются следующие вопросы: комплексные числа, матрицы и операции над ними, теория определителей, теория систем линейных алгебраических уравнений, элементы теории линейных пространств, системы координат, векторы и операции над ними, скалярное, векторное и смешанное произведения векторов, теория прямых и плоскостей, элементы теории кривых и поверхностей второго порядка. На примерах геометрических объектов малой размерности курс знакомит студентов с основными идеями метода координат и даёт общие навыки работы с простейшими алгебраическими системами.
Лекторы
- Голубцов Петр Викторович
- Корпусов Максим Олегович
- Овчинников Алексей Витальевич
Отчётность
зачет и экзамен
Материалы к экзамену
Вопросы и задачи к экзамену для студентов всех потоков
Содержание курса
- Комплексные числа и операции над ними.
 Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.
Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел. - Алгебра матриц. Матрицы и операции над ними. Умножение матриц. Линейная зависимость и независимость. Теория определителей. Ранг матрицы. Теорема о базисном миноре. Системы линейных уравнений.
- Алгебра векторов. Линейные операции над векторами. Базис и координаты. Скалярное, векторное и смешанное произведение векторов. Двойное векторное произведение.
- Линейные многообразия. Прямые на плоскости. Прямые и плоскости в пространстве.
- Кривые и поверхности второго порядка.
- Элементы теории линейных пространств. Понятие линейного пространства. Основные примеры. Базис и размерность линейного пространства. Основные свойства линейных пространств. Изоморфизмы линейных пространств.
Основная литература
- Овчинников А.В. Конспект лекций по аналитической геометрии. На сайте (см.
 ниже)
ниже) - Овчинников А.В. Алгебра и геометрия в вопросах и задачах. Кн.1. Основы алгебры и аналитической геометрии. — М.: ЛЕНАНД, 2016.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия. — М.: Наука, Физматлит, 1999.
- Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, Физматлит, 1999.
- Клетеник Д.В. Сборник задач по аналитической геометрии. — М.: Наука, Физматлит, 1998.
Дополнительная литература
- Александров П.С. Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979.
- Александров П.С. Лекции по аналитической геометрии. — Наука, 1968.
- Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Физматлит, 2005.
- Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. — М.: Физматлит, 2003.
- Овчинников А.В. Алгебра и геометрия для студентов-физиков. Лекционный курс. — М.: Физический факультет МГУ, 2016.
- Овчинников А.
 В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009.
В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009. - Федорчук В.В. Курс аналитической геометрии и лин. алгебры. — М.: МГУ, 1990.
- Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. — Спб, 2003.
Материалы по курсу
- А.В. Овчинников. Алгебра и геометрия для студентов-физиков. Лекционный курс. Семестр 1
- А.В. Овчинников. Алгебра и геометрия в вопросах и задачах. Файл доступен для скачивания до 15 сентября
- А.В. Овчинников. Конспект лекций по аналитической геометрии
- Наиболее трудные задачи второй части экзамена
- Контрольные задания по аналитической геометрии для студентов 1 курса (2016)
- Г.Н. Медведев 35 задач по аналитической геометрии. Практическое пособие
1 поток. Лектор: проф. П. В. Голубцов
- Лекция 1. Формулы Крамера. Определители 1-го, 2-го и 3-го порядка
- Лекция 2. Простейшие операции с векторами
- Лекция 3.

- Лекция 4. Скалярное, векторное, смешанное произведения. Преобразование прямоугольных координат на плоскости
- Лекция 5. Комплексные числа
- Лекция 6. Прямая на плоскости
http://sites.google.com/site/vkolybasova
2 поток. Лектор: доц. А.В. Овчинников
- А.В. Овчинников. Алгебра и геометрия для студентов-физиков. Лекционный курс. Семестр 1
- А.В. Овчинников. Алгебра и геометрия в вопросах и задачах. Файл доступен для скачивания до 15 сентября
- А.В. Овчинников. Конспект лекций по аналитической геометрии
- Контрольные задания по аналитической геометрии для студентов 1 курса (2016)
3 поток. Лектор: проф. М. О. Корпусов
КОНСУЛЬТАЦИЯ 2-го потока состоится 19 января 2019 c 12-00 в аудитории ЮФА
ВОПРОСЫ СТУДЕНТОВ К КОНСУЛЬТАЦИЯМ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОШУ ПРЕДВАРИТЕЛЬНО ПРИСЫЛАТЬ НА МОЙ АДРЕС korpusov@physics. msu.ru
msu.ru
- Примеры решения задач по курсу «Векторная алгебра»
- Рисунки поверхностей второго порядка
Консультации
- Векторы. Линейные операции
- Векторы. Базис и коорлдинаты
- Системы координат и преобразование базиса
- Скалярное произведение
- Векторное и смешанное произведения
- Прямая на плоскости
- Прямая и плоскость в пространстве
- Векторные уравнения прямой и плоскости
- Эллипс, гипербола, парабола
- Приложения теоремы Кронекера-Капелли
Конспекты лекций.
- Определители 2-го и 3-го порядков
- Свойства определителей 3-го порядка
- Векторы. Линейные операции
- Векторы. Базис
- Системы координат
- Скалярное, векторное, смешанное произведения.
- Прямая на плоскости
- Прямая и плоскость в пространстве
- Эллипс, гипербола и парабола
- Кривые и поверхности второго порядка
- Матрицы
- Линейное пространство столбцов
- Системы линейных уравнений
- Определители n-го порядка
- Теорема о базисном миноре
- Приведение кривой второго порядка к каноническому виду
8 класс.
 Геометрия. Векторы. Применение векторов к решению задач. — Векторы. Повторение теории. Решение задач с применением векторов.Комментарии преподавателя
Геометрия. Векторы. Применение векторов к решению задач. — Векторы. Повторение теории. Решение задач с применением векторов.Комментарии преподавателяПовторение теории. Задачи
Напомним, что существуют такие физические величины, для которых важна не только величина, но и направление. Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.
Мы рассматриваем вектор, который можно отложить от любой точки, заданный вектор от произвольно выбранной точки можно отложить единственным образом.
Было введено понятие равных векторов – это такие сонаправленные векторы, длины которых равны. Сонаправленными называются коллинеарные векторы, направленные в одну сторону.
Были введены правила треугольника и параллелограмма – правила сложения векторов.
Заданы два вектора – векторы и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . – направленный отрезок, точка А – его начало, а точка В – конец. Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: – правило треугольника (см. Рис. 1).
Рис. 1
Задано два вектора – векторы и . Найдем сумму этих двух векторов по правилу параллелограмма.
Откладываем из точки А вектор и вектор (см. Рис. 2). На отложенных векторах можно построить параллелограмм. Из точки В откладываем вектор , векторы и равны, стороны ВС и
Рис. 2
АВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
Для сложения нескольких векторов применяют правило многоугольника (см.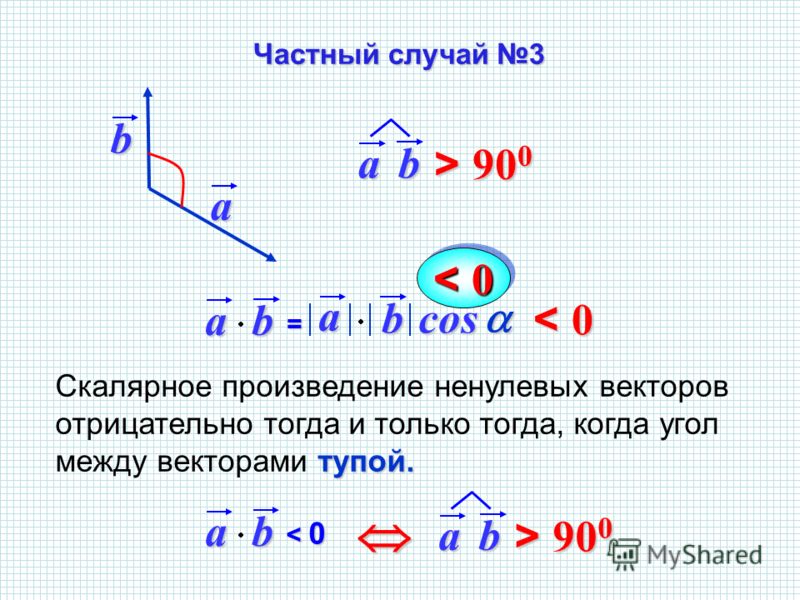 Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.
Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.
Рис. 3
Кроме того, мы рассмотрели понятие обратного вектора – вектора, имеющего такую же длину, как заданный, но ему противонаправленного.
Пример 1 – задача 747: выпишите пары коллинеарных сонаправленных векторов, которые определяются сторонами параллелограмма; укажите противоположно направленные векторы;
Задан параллелограмм MNPQ (см. Рис. 4). Выпишем пары коллинеарных векторов. В первую очередь это векторы и . Они не только коллинеарные, но и равные, т.к. они сонаправлены, и длины их равны по свойству параллелограмма (в параллелограмме противоположные стороны равны). Следующая пара . Аналогично
Следующая пара . Аналогично
Рис. 4
выпишем коллинеарные векторы второй пары сторон: ; .
Противоположно направленные векторы: , , , .
Пример 2 – задача 756: начертите попарно неколлинеарные векторы , и . Постройте векторы ;; ;.
Для выполнения данного задания можем пользоваться правилом треугольника или параллелограмма.
Способ 1 – с помощью правила треугольника (см. Рис. 5):
Рис. 5
Способ 2 – с помощью правила параллелограмма (см. Рис. 6):
Рис. 6
Комментарий: мы применяли в первом способе правило треугольника – откладывали из произвольно выбранной точки А первый вектор, из его конца – вектор, противоположный второму, соединяли начало первого с концом второго, и таким образом получали результат вычитания векторов. Во втором способе мы применили правило параллелограмма – построили на нужных векторах параллелограмм и его диагональ – искомую разность, помня тот факт, что одна из диагоналей – это сумма векторов, а вторая – разность.
Пример 3 – задача 750: докажите, что если векторы и равны, то середины отрезков AD и BC совпадают. Докажите обратное утверждение: если середины отрезков AD и BC совпадают, то векторы и равны (см. Рис. 7).
Из равенства векторов и следует, что прямые АВ и CD параллельны, и что отрезки АВ и CD равны. Вспомним признак параллелограмма: если у четырехугольника пара противоположных сторон лежит на параллельных прямых, и их длины равны, то данный четырехугольник – параллелограмм.
Рис. 7
Таким образом, четырехугольник ABCD, построенный на заданных векторах, – параллелограмм. Отрезки AD и BC являются диагоналями параллелограмма, одно из свойств которого: диагонали параллелограмма пересекаются и в точке пересечения делятся пополам. Таким образом, доказано, что середины отрезков AD и BC совпадают.
Докажем обратное утверждение. Для этого воспользуемся другим признаком параллелограмма: если в некотором четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Отсюда четырехугольник ABCD – параллелограмм, и его противоположные стороны параллельны и равны, таким образом, векторы и коллинеарны, очевидно, что они сонаправлены, и модули их равны, отсюда векторы и равны, что и требовалось доказать.
Для этого воспользуемся другим признаком параллелограмма: если в некотором четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Отсюда четырехугольник ABCD – параллелограмм, и его противоположные стороны параллельны и равны, таким образом, векторы и коллинеарны, очевидно, что они сонаправлены, и модули их равны, отсюда векторы и равны, что и требовалось доказать.
Пример 4 – задача 760: докажите, что для любых неколлинеарных векторов и справедливо неравенство (см. Рис. 8)
Отложим из произвольной точки А вектор , получим точку В, из нее отложим неколлинеарный ему вектор . По правилу параллелограмма или треугольника получим сумму векторов – вектор . Имеем треугольник .
Длина суммы векторов соответствует длине стороны АС треугольника. По неравенству треугольника длина стороны АС меньше, чем сумма длин двух других сторон АВ и ВС, что и требовалось доказать.
Рис. 8
Применение векторов к решению задач
Напомним, что мы уже изучили некоторые факты о векторах, и теперь умеем определять равные векторы, коллинеарные векторы, сонаправленные и противоположно направленные. Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Пример 1 – задача 769: отрезок ВВ1 – медиана треугольника . Выразите через векторы и векторы , , и .
Отметим, что векторы и неколлинеарны, то есть прямые АВ и АС не параллельны.
В дальнейшем мы узнаем, что любой вектор может быть выражен через два неколлинеарных вектора.
Выразим первый вектор (см. Рис. 1): , т. к. по условию ВВ1 – медиана треугольника, значит, векторы и имеют равные модули, кроме того, очевидно, что они коллинеарны и при этом сонаправлены, значит, данные вектора равны.
Рис. 1
Для выражения следующего вектора воспользуемся правилом параллелограмма для вычитания. Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Вектор является противоположным к заданному вектору , отсюда .
Вектор аналогично вектору можно представить в виде разности векторов . При выражении следует учесть тот факт, что точка В1 является серединой отрезка АС, значит, векторы и равны, значит, вектор можно представить как удвоенное произведение вектора .
Перед решением задачи мы сказали, что через заданные два неколлинеарных вектора можно выразить любой вектор.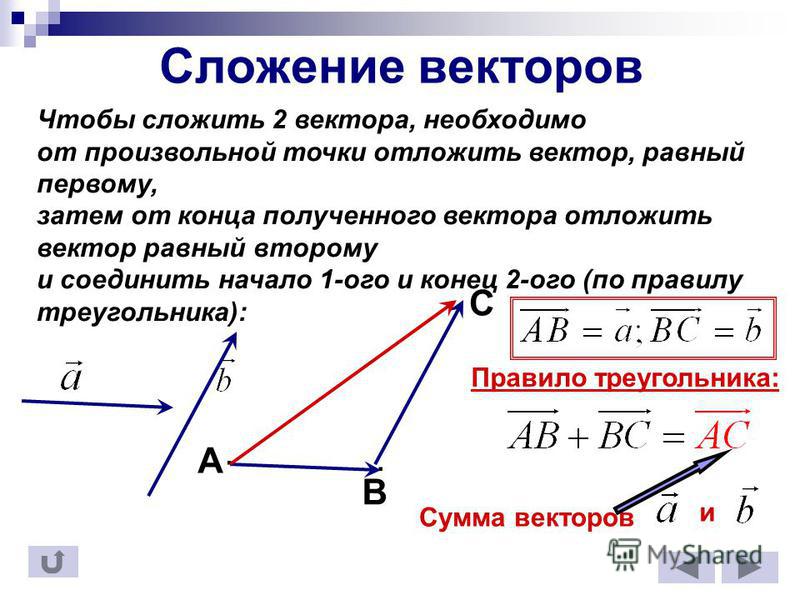 Выразим, например, медиану АА1 (см. Рис. 2).
Выразим, например, медиану АА1 (см. Рис. 2).
Получили систему уравнений, выполним их сложение:
Векторы в сумме составляют нулевой вектор, так как они коллинеарны и противонаправлены, а модули их равны, таким образом получаем:
Рис. 2
Поделим обе части уравнения на два, получим:
Из данной задачи можно сделать вывод, что если заданы два неколлинеарных вектора, то любой третий вектор на плоскости можно однозначно выразить через эти два вектора. Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Пример 2: доказать с помощью векторов свойство средней линии треугольника (см. Рис. 3).
Задан произвольный треугольник , точки M и N – середины сторон АВ и АС соответственно, MN – средняя линия треугольника. Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Доказательство данного свойства аналогично для треугольника и трапеции.
Рис. 3
Выразим вектор двумя способами:
Получили систему уравнений:
Выполним сложение уравнений системы:
Сумма векторов – это нулевой вектор, длины этих векторов равны по условию, кроме того, они очевидно коллинеарны и противонаправлены. Аналогично суммой векторов будет нулевой вектор. Получаем:
Поделим обе части уравнения на два:
Таким образом, мы получили, что средняя линия треугольника равна половине его основания. Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Таким образом, мы доказали свойство средней линии трапеции при помощи векторов.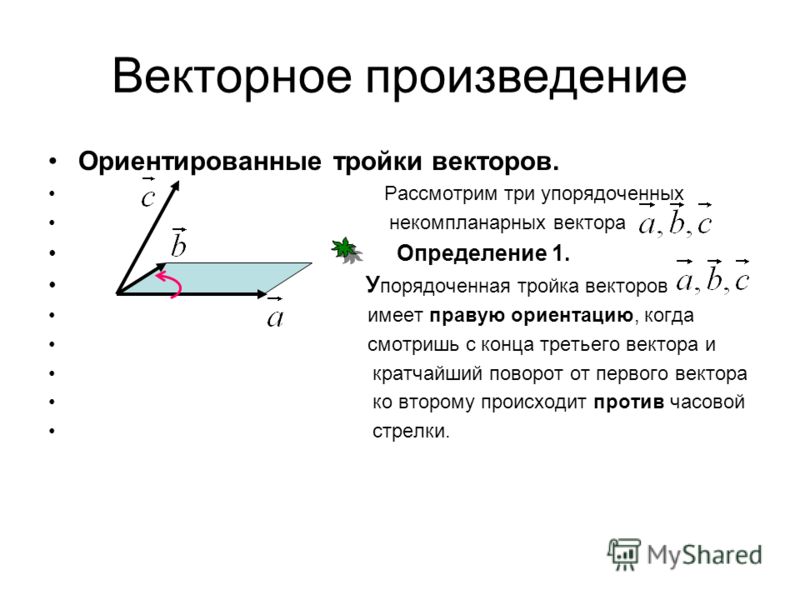
Пример 3: задан произвольный треугольник (см. Рис. 4). В нем проведены медианы АА1, ВВ1, СС1. Точка пересечения медиан – М. Вектор соответствует силе , – силе , – силе . Доказать, что .
Напомним, что медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины.
Иногда точку пересечения медиан называют центром тяжести треугольника.
Выполним сложение векторов , воспользуемся для этого правилом параллелограмма (см. Рис. 5).
Рис. 4
Получаем:
С другой стороны, , так как BMCD – параллелограмм, диагонали параллелограмма точкой пересечения делятся пополам, А1 – точка пересечения диагоналей параллелограмма, значит, отрезки МА1 и А1D равны, отсюда, по свойству точки пересечения медиан, длины векторов и равны, но данные векторы противонаправлены, а значит, их сумма
Рис. 5
5
равна нулевому вектору. Мы помним, что вектор , а вектор , таким образом, , что и требовалось доказать.
Пример 4 – задача 773: докажите, что для любых векторов и справедливо следующее неравенство:
Решение: представим разность векторов в виде суммы: . Также обратим внимание на тот факт, что длины противонаправленных векторов и равны: . Таким образом, можно переписать исходное выражение:
Для удобства введем новую переменную: и перепишем выражение:
. А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке. Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Итак, мы вспомнили все основные определения и свойства векторов, вспомнили основные операции над векторами, рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.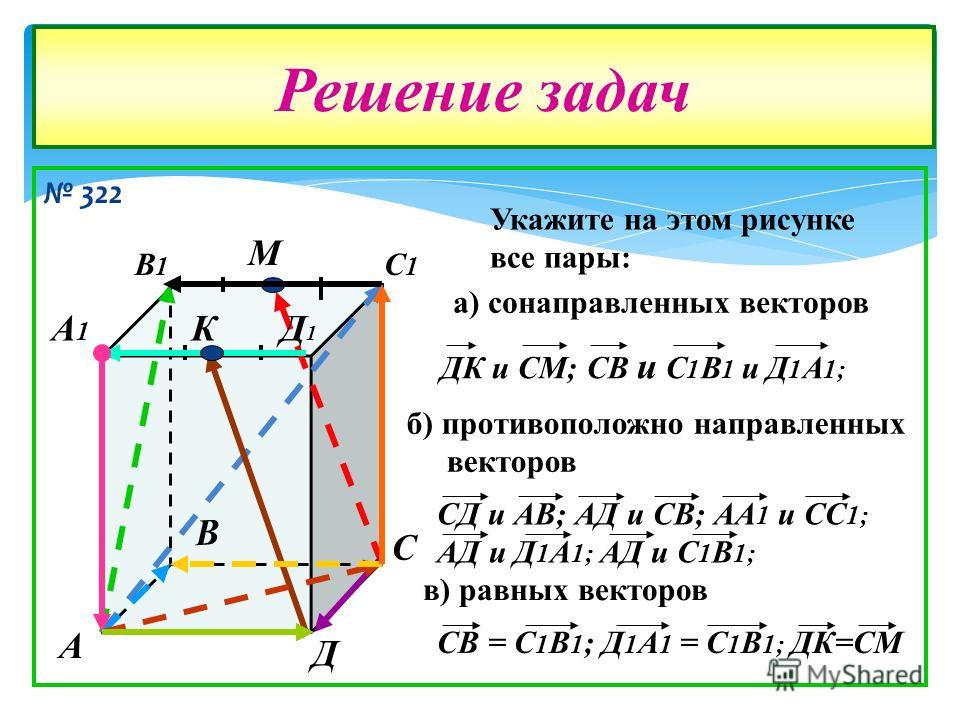
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/vektory/vektory-povtorenie-teorii-zadachi
http://interneturok.ru/ru/school/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/8-itogovyj-test-po-teme-vektory-variant-1.html
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/9-itogovyj-test-po-teme-vektory-variant-2.html
http://uslide.ru/images/22/28455/960/img5.jpg
http://www.studfiles.ru/html/2706/538/html_OqWQ3sDQeV.5bGa/htmlconvd-WBhq8w_html_73af1ab4.png
http://uchkollektor39.ru/uploads/images/items/29cc1d8d90989d9f0e3df70c3d95a9ee.jpg
http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg
http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJh2OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw
http://matssir. ucoz.ru/_ld/0/33_G8p84-85.pptx
ucoz.ru/_ld/0/33_G8p84-85.pptx
http://nsportal.ru/sites/default/files/2014/05/11/vektory._dokazatelstvo.pptx
http://v.5klass.net/zip/b66d124d0243f848a0bf454b75404034.zip
Аналитическая геометрия | Открытые видеолекции учебных курсов МГУ
Курс «Аналитическая геометрия» читается студентам первого курса физического факультета МГУ имени М. В. Ломоносова в 1 семестре.
Аналитическая геометрия является одним из базовых курсов высшей математики, лежащих в основе физико-математического образования.
В курсе рассматриваются следующие вопросы: комплексные числа, матрицы и операции над ними, теория определителей, теория систем линейных алгебраических уравнений, элементы теории линейных пространств, системы координат, векторы и операции над ними, скалярное, векторное и смешанное произведения векторов, теория прямых и плоскостей, элементы теории кривых и поверхностей второго порядка. На примерах геометрических объектов малой размерности курс знакомит студентов с основными идеями метода координат и даёт общие навыки работы с простейшими алгебраическими системами.
Список всех тем лекций
Лекция 1. Понятие аналитической геометрии.
Понятие аналитической геометрии
Понятие системы координат
Криволинейные системы координат
Системы координат в пространстве
Отношение эквивалентности
Декартово произведение
Свойства отношений
Лекция 2. Операции над векторами.
Повторение
Отношения эквивалентности
Операции над векторами
Аксиомы
Определение линейной комбинации
Приемы, полезные для доказательств
Лекция 3. Линейно зависимые и линейно независимые векторы.
Линейно зависимые и линейно независимые векторы.
Повторение
Линейно зависимые и линейно независимые векторы
Разложение векторов по базису
Определитель
Лекция 4. Свойства определителя.
Определитель
Свойства определителя
Необходимое и достаточное условие равенства нулю определителя
Три вектора в пространстве
Основные свойства определителя третьего порядка
Лекция 5. Теорема о свойствах скалярного произведения.
Теорема об инвариантности определителя под действием операции транспонирования
Основные свойства определителя
Фальшивое разложение определителя
Скалярное произведение
Теорема о свойствах скалярного произведения
Векторное произведение
Теорема о свойствах векторного произведения
Смешанное произведение
Лекция 6. Геометрические объекты на плоскости и в пространстве.
Геометрические объекты на плоскости и в пространстве.
Прямые
Взаимное расположение прямых
Плоскость в пространстве
Взаимное расположение прямой и плоскости
Лекция 7. Линии второго порядка.
Прямая в пространстве
Линии второго порядка
Лекция 8. Эллипс. Гипербола. Парабола.
Эллипс
Гипербола
Парабола
Лекция 9. Уравнения линий второго порядка в полярных координатах.
Уравнения линий второго порядка в полярных координатах
Матрицы
Свойства матриц
Умножение строки на столбец
Перемножение матриц
Диагональная матрица
Лекция 10. Свойства матричного умножения.
Свойства матричного умножения.
Свойства матричного умножения
Однородные системы линейных уравнений
Неоднородные системы линейных уравнений
Решение систем уравнений
Лекция 11. Приведение системы к упрощенному виду.
Приведение системы к упрощенному виду
Системы с двумя неизвестными и одним уравнением
Уравнения с тремя неизвестными
Система двух уравнений с тремя неизвестными
Метод преобразования матриц
Однородные системы линейных уравнений
Связь элементарных преобразований с элементами матрицы
Лекция 12. Теория определителей.
Теория определителей
Формула Крамера
Перестановки
Умножение перестановок
Инверсия
Лекция 13. Методы вычисления определителя.
Методы вычисления определителя.
Повторение
Функция, обладающая полилинейностью и кососимметричностью
Определитель при малых значениях матрицы
Теорема о транспонировании определителя
Определитель треугольной матрицы
Теорема об определителе блочной матрицы
Теорема о произведении определителей
Формула разложения определителя по строкам и столбцам
Теорема о фальшивом разложении
Теорема о существовании обратной матрицы
6.1. Векторы управления. Универсум. Общая теория управления
6.1. Векторы управления
Горизонтальное разбиение страт на фреймы – не единственно возможный вариант универсумной дискретизации. Определённый интерес представляет и «вертикальное» представление наборов фреймов как «сборки» элементов векторов управления. Так, например, для универсума СУФУ-3 (Рис. 6.1а) можно этапы описания 1 «Распознавание и анализ фактора среды» и 3 «Реализация принятых решений» представить в виде двух векторов – вектора анализа текущего состояния и вектора синтеза процессов управления (Рис. 6.1б), содержащих по три-четыре элемента.
Так, например, для универсума СУФУ-3 (Рис. 6.1а) можно этапы описания 1 «Распознавание и анализ фактора среды» и 3 «Реализация принятых решений» представить в виде двух векторов – вектора анализа текущего состояния и вектора синтеза процессов управления (Рис. 6.1б), содержащих по три-четыре элемента.
Рис. 6.1. Векторы управления
Элементы векторов «Состояние 4» и «Управление 4» соответствуют этапу 2 СУФУ-3 «Концептуальное решение R по отработке фактора S».
Конечно же, выработка концептуального решения подразумевает наличие элемента «Цель 4» вектора целей, являющегося необходимым атрибутом любого универсума. В сжатом описании СУФУ просто не акцентируется внимание ни на количестве стратификационных элементов векторов, ни на обязательно присутствующем по умолчанию в любом универсуме векторе целей. Все цели нижних иерархических уровней можно именовать «задачами» и «подзадачами», поскольку они вытекают из главной цели – основной целевой функции, размещённой в высшей универсумной страте.
Процесс управления в векторном описании можно представить также в виде универсума класса 4U3, содержащего поле из 12-ти фреймов, конструктов – элементов векторов (Рис. 6.2а), соответствующих трём наборам ранжированной информации – векторам состояния, цели и собственно управления (Рис. 6.2б).
Вектор состояния описывает реальное поведение объекта как соответствующие стратификационным уровням значения элементов универсумного каскада S.
Вектор целей управления (целеполагания, самоуправления) представляет описание желаемого (планируемого, идеального) поведения объекта, соответствующего универсумному каскаду интеллектуальной обработки информации I.
Вектор управления (ошибки управления) описывает величину отклонения реального процесса (состояния универсумного каскада R) от предписанного вектором целей поведения, т. е. величину требуемых управляющих воздействий, необходимых для приведения в соответствие элементов вектора состояния элементам вектора целей. В различных изложениях теории название «векторы управления» часто используется для общего обозначения всех трёх векторов, поэтому следует обращать внимание именно на функциональное назначение конкретных конструктов.
Рис. 6.2. Определение концепции (целевой функции) управления
Минимизация величин вектора ошибки управления, определяемой разностью целей и текущего состояния системы «У=Ц-С» или «R=S-I» и определяет концепцию управления. Можно сказать, что вектор управления (ответ на вопрос «что надо делать») определяется как разница между вектором целей («хочу достичь того-то») и вектором состояния («что есть на самом деле»). Значение всех элементов вектора управления (ошибки) равное нулю означает, что требуемая цель достигнута в полной мере.
Размерность векторов управления – вектора состояний, вектора целей и вектора ошибки одинакова. Важно подчеркнуть, что наибольшее влияние на процесс управления оказывают высокоприоритетные (т. е. преимущественно информационные) элементы векторов. Согласно общепринятым и также универсумным критериям самая важная цель должна находиться в верхней позиции элементов вектора, а наименее приоритетная на последнем. Универсумная логика уточняет этот критерий: верхние строки векторов управления должны занимать максимально информационные задачи, нижние – максимально материальные.
Другими словами, достижение информационных целей (задач) является более приоритетным процессом, чем достижение материальных задач (целей). Чем выше соответствующий универсумной страте уровень задачи, включённой в вектор управления, тем ближе она к решению стратегических вопросов управления процессом, и наоборот, чем ниже уровень задачи, тем более точно её можно определить как задачу тактического или оперативного характера.
Если критерием качества выбран элемент высшего информационного приоритета, то управление можно назвать оптимальным, поскольку определяющее значение для качества управления имеют информационные уровни управления.
Ранжирование векторов управления в соответствии с универсумной логикой позволяет снизить влияние случайных и субъективных факторов на оценку качества управления: чем точнее выстроена иерархия векторов по мере изменения соотношения «Материя-Информация», тем с более высокой степенью прогностики будет определён критерий качества управления. Этот факт соответствия иерархии элементов векторов с U-логикой отражен в следующем U-законе:
10: Закон РАНЖИРОВАНИЯ: Векторы систем управления ранжируются по Мере изменения соотношения между их Материальной и Информационной составляющей.
Следует подчеркнуть, что в данном законе речь ведётся о достижении уровня максимально глубокой прогностики, которую способна осуществить универсумная структура. В случае преднамеренного ограничения горизонта прогностики иерархия элементов в векторах может измениться. Верно и обратное: нарушение U-закона Ранжирования векторов ограничивает горизонт прогностики.
U-закон Ранжирования векторов полностью соответствует этапам ПФУ. Так, распознавание факторов среды, воздействующих на систему (этап 1 ПФУ или конструкт 1 «оценка оперативного состояния»), приводит к пониманию складывающихся стереотипных ситуаций (конструкт 2 «оценка тактического состояния»), из которого, в свою очередь, формируется представление об обстановке (конструкт 3 «оценка стратегического состояния») и понимание общего состояния системы. Все эти конструкты в совокупности с конструктом 4 представляют Вектор состояния, описывающий этапы U-потока или анализа взаимодействия универсума с внешней средой.
Очевидно, что элементы (конструкты 12, 11, 10 и 5), входящие в Вектор целеполагания, также выстроенные в соответствии с U-законом ранжирования, представляют обычный универсумный I-каскад, вырабатывающий наиболее приоритетную, общую цель управления.
Содержанием Вектора управления (конструкты 6, 7, 8 и 9) является концепция решения проблемы (6), порождающая долгосрочную, прогнозного характера стратегию (7), затем среднесрочную тактику воплощения этих задач (8), которые, в свою очередь, приводят в выработке комплексов оперативных решений (9).
Очевидно, что оценка качества управления также должна производиться в соответствии с порядком ранжирования векторов управления – высший приоритет в определении качества должны иметь максимально информационно насыщенные элементы векторов. Вслед за ними размещаются элементы менее важных подцелей и задач вплоть до «самых нижних», материального характера составляющих, от которых при необходимости можно отказаться в первую очередь.
Изменение оценок качества управления должно подчиняться определённым зависимостям. Так, если значение параметра вектора высшего приоритета улучшилось, а большинство всех остальных значений (2-го, 3-го нижних уровней и т. д.) ухудшились, то в целом можно считать, что оценка качества управления улучшилось. Повышение качества управления на более высоком приоритете неизбежно окажет отсроченное влияние на улучшение качества управления во всех нижележащих векторах – управленческих стратах. А если наоборот, все значения нижних элементов векторов управления улучшились, но значение параметра высшего приоритета ухудшилось, то говорить о повышении качества управления не приходится, поскольку рано или поздно в данной иерархии неизбежна ошибка управления высшей страты, которая приведёт к общему снижению качества управления на всех нижележащих уровнях управления.
Повышение качества управления на более высоком приоритете неизбежно окажет отсроченное влияние на улучшение качества управления во всех нижележащих векторах – управленческих стратах. А если наоборот, все значения нижних элементов векторов управления улучшились, но значение параметра высшего приоритета ухудшилось, то говорить о повышении качества управления не приходится, поскольку рано или поздно в данной иерархии неизбежна ошибка управления высшей страты, которая приведёт к общему снижению качества управления на всех нижележащих уровнях управления.
Конечно же, при всех манипуляциях с векторами следует учитывать объективные ограничения на значения векторов. Они не могут выходить за допустимые пределы, обычно принимающие какое-то максимальное и/или минимальное значение[165].
Для практических расчётов в качестве векторов целей и состояний удобно использовать нормированные процентные значения, т. е. такие, сумма которых составляет 100 процентов. При этом сумма значений всех элементов вектора управления будет равна нулю, а эта же сумма по модулю[166] будет являться удобным интегральным показателем степени отклонения системы от целевых параметров (рис. 6.3).
6.3).
Рис. 6.3. Расчёт значений элементов вектора управления
Так, например, первая по приоритетности вектора целей задача прорыва вражеской обороны для командующего фронтом является концептуальной (цель 1) и определяет следующие по приоритетности задачи закрепления на оборонительном рубеже (цель 2), налаживание снабжения армии (цель 3) и другие задачи (цели 4,5,6).
Конечно же, реальные процессы управления должны учитывать различные ошибки, влияние непредусмотренных ранее воздействий, оказываемые внешней средой и корректироваться (для командующего в первую очередь необходимо учитывать возможные действия противника). В этой связи можно говорить не об одном векторе ошибок управления, а об их совокупности или матрице, как допустимом множестве векторов, описывающих некоторую область возможных вариантов осуществления процесса управления.
При работе системы в балансировочных режимах порядок их определения будет одним, при манёврах – другим. При работе в балансировочных режимах (программном или адаптивном класса 4U) следствием влияния различных факторов на систему будет то, что реальный процесс управления не пойдёт как идеальная прямая, а будет в той или иной мере колебаться вокруг неё. При этом все векторы системы управления в заданных границах могут изменять свои числовые значения.
При этом все векторы системы управления в заданных границах могут изменять свои числовые значения.
Пересмотра порядка ранжирования и изменения значений элементов вектора целей при работе системы в балансировочном режиме не происходит. Производится только «перепроцентовка» числовых значений вектора состояний (рис. 6.4а), вызывающая затем соответствующий пересчёт значений вектора управления, возвращающего систему на заданную целевой функцией траекторию (рис. 6.4б).
Рис. 6.4. Значения элементов векторов управления в балансировочном режиме
В момент времени t1вектор состояния может быть описан «процентовкой состояния № 1», в следующий момент времени t2«процентовкой № 2» и т. д., в соответствии с которым и будет осуществляться возврат системы на заданную траекторию изменения параметров.
При работе системы в маневровом режиме ситуация меняется.
Режим «слабого манёвра», рассчитанный на отработку ситуаций, выходящих за рамки балансировочной алгоритмике работы, соответствует пересмотру иерархии целевых функций (рис. 6.5а). Величина этого манёвра определяется уровнем иерархии реорганизуемых элементов вектора целей. Наибольшее влияние на поведение системы оказывает «переранжирование» верхних, информационных страт (например, перенесение цели третьего уровня на второй, а цели второго уровня на пятый).
6.5а). Величина этого манёвра определяется уровнем иерархии реорганизуемых элементов вектора целей. Наибольшее влияние на поведение системы оказывает «переранжирование» верхних, информационных страт (например, перенесение цели третьего уровня на второй, а цели второго уровня на пятый).
В процессе проведения слабых манёвров, т. е. вариабельного подбора необходимой реакции системы R на внешнее воздействие S вектор целей в момент времени t1может быть описан как «переранжирование этап № 1», в момент времени t2как «переранжирование этап № 2» и т. д. В соответствии с новым вариантом ранжирования будет осуществляться переход в новую, расширенную матрицу возможных состояний. В случае подбора успешно работающего ранжирования система может возвратиться в балансировочный режим работы.
Рис. 6.5. Ранжирование элементов вектора целей в режиме слабого и сильного манёвров
В случае невозможности подбора удовлетворяющего систему варианта траектории движения в режиме «слабого манёвра», система может перейти в режим «сильного манёвра» (рис. 6.5б). При этом осуществляется отказ от некоторых целей и задач с заменой их на другие (например, отказ от цели № 1 с заменой её на новую цель № 7 и/или полный отказ от цели № 3 с внесением на первый уровень новой цели № 8). Естественно, что работа в режиме сильного манёвра, подразумевающая переопределение целевой функции и/или вытекающих их них задач и подзадач ещё больше расширяет матрицу возможных состояний универсума, описывающего систему.
6.5б). При этом осуществляется отказ от некоторых целей и задач с заменой их на другие (например, отказ от цели № 1 с заменой её на новую цель № 7 и/или полный отказ от цели № 3 с внесением на первый уровень новой цели № 8). Естественно, что работа в режиме сильного манёвра, подразумевающая переопределение целевой функции и/или вытекающих их них задач и подзадач ещё больше расширяет матрицу возможных состояний универсума, описывающего систему.
Рассмотренный процесс позволяют согласиться с теми философскими воззрениями, которые утверждают, что достижения в адаптивного характера в материальной сфере большей частью «преходящи», неустойчивы – они легко могут быть потеряны, если надёжно не сбалансированы с информационным сопровождением рассматриваемого процесса. И наоборот, решение информационных задач обеспечивает не только достижения материальных целей, но и определённую степень устойчивости управления любыми процессами. Именно поэтому анахронизмы «горячих войн» в современной цивилизации неуклонно сменяются на «войны холодные», затем переходящие в ещё более жестокие, но уже «информационные войны».
Можно также заметить, что в случае, если вектор целей какого-то объекта управления в своей информационной части содержит элементы чуждой ему концепции, то достижение целей материального порядка для этого объекта чаще всего остаётся перманентно недостижимой задачей.
Данный текст является ознакомительным фрагментом.
Функции управления Матрица функций управления
Функции управления Матрица функций управления Классические функции менеджмента мы оформили вот в такую матрицу-схему (табл. 1).По нашему мнению, она наглядно демонстрирует все основные направления деятельности руководителя фирмы.Согласно теории менеджмента в
4. Элементы процесса управления. Функции управления
4. Элементы процесса управления. Функции управления
Управление – это единый процесс, который представлен разными управленческими работниками или органами. Целью их взаимодействия является выработка единого управляющего воздействия на объект управления. К
Элементы процесса управления. Функции управления
Управление – это единый процесс, который представлен разными управленческими работниками или органами. Целью их взаимодействия является выработка единого управляющего воздействия на объект управления. К
4. Этапы управления ЧР
4. Этапы управления ЧР Отметим этапы управления ЧР.1. Планирование ЧР – разработка плана удовлетворения будущих потребностей в человеческих ресурсах.2. Набор персонала – создание резерва потенциальных кандидатов по всем должностям.3. Отбор – оценка кандидатов на
Резервы управления
Резервы управления Эти резервные фонды необходимы для покрытия крупных непредвиденных и потенциальных рисков и поэтому применяются к проекту в целом.Резервы управления организуют после того, как организованы сметные резервы и выделены фонды.Они не зависят от сметных
3.
 Элементы процесса управления. Функции управления
Элементы процесса управления. Функции управления3. Элементы процесса управления. Функции управления Управление – это единый процесс, который представлен разными управленческими работниками или органами. Целью их взаимодействия является выработка единого управляющего воздействия на объект управления. К
8. Американская, европейская и японская модели управления. «Новая философия управления»
8. Американская, европейская и японская модели управления. «Новая философия управления» Все рассмотренные концепции в большей или меньшей степени реализуются в конкретных моделях управления. Основными из них после 1970-х гг. являются американская и японская модели. В
31. Развитие концепции мотивации разными школами управления. Основные принципы управления
31. Развитие концепции мотивации разными школами управления. Основные принципы управления
Разработка современной концепции мотивации началась с открытий школы человеческих отношений, хотя модели мотивации они не создали, но их вывод о важности социального
Основные принципы управления
Разработка современной концепции мотивации началась с открытий школы человеческих отношений, хотя модели мотивации они не создали, но их вывод о важности социального
52. Цели и функции управления. Стратегическая и оперативная роли управления
52. Цели и функции управления. Стратегическая и оперативная роли управления Управление человеческими ресурсами – это проектирование формальных систем организации, которые обеспечивают эффективное использование человеческих знаний, навыков и талантов для достижения
1.2. Место и роль управления персоналом в системе управления организацией
1.2. Место и роль управления персоналом в системе управления организацией Труд – процесс сознательной целесообразной деятельности человека, воздействия его на предметы труда с целью создания материальных и духовных благ для удовлетворения личных и общественных
1.
 3. Персонал как объект управления, понятие и особенности управления персоналом, методы управления
3. Персонал как объект управления, понятие и особенности управления персоналом, методы управления1.3. Персонал как объект управления, понятие и особенности управления персоналом, методы управления Управлять поведением и настроением человека можно, формируя среду и / или непосредственно влияя на личность, «играя на струнах человеческой души». Влияя на поведение, очень
3.7. Финансовое обеспечение управления персоналом: бюджетирование деятельности службы управления персоналом
3.7. Финансовое обеспечение управления персоналом: бюджетирование деятельности службы управления персоналом Бюджетирование – это способ управления финансами организации, заключающийся в построении и исполнении бюджета организации на основе бюджетов отдельных
Методы управления
Методы управления
Методы управления – способы воздействия управляющего субъекта на управляемый объект, руководителя на возглавляемый им коллектив. Следует различать методы управления и методы процесса управления. Методы управления характеризуют законченный акт
Следует различать методы управления и методы процесса управления. Методы управления характеризуют законченный акт
12. Цели системы управления персоналом, этапы организационного проектирования системы управления персоналом
12. Цели системы управления персоналом, этапы организационного проектирования системы управления персоналом Субъектами управления персоналом выступают лица и подразделения аппарата управления организации, осуществляющие функции управления работниками. Ими являются
3. Вражда управления
3. Вражда управления Когда перед компанией ставится задача и идет ее согласование, то часто разгораются жаркие дискуссии о том, а надо ли нам ЭТО?! Разные бизнес-школы по-своему описывают происходящее. Наиболее действенные причины противостояния внутри бизнеса
Случайный вектор — Теория вероятностей
Распределение случайного вектора
Во многих реальных задачах мы имеем не одну, а несколько случайных величин в одном и том же эксперименте. Иногда их удобно рассматривать как единый объект. Это приводит нас к следующему определению.
Иногда их удобно рассматривать как единый объект. Это приводит нас к следующему определению.
Определение 1. -мерным случайным вектором называется набор случайных величин, заданных на одном и том же вероятностном пространстве
Фактически случайный векторесть отображение Нетрудно показать (задача 1), что это отображение является борелевским, т.е. для любого борелевского подмножества (-алгебру всех борелевских подмножеств в мы будем обозначать ) мы имеем . Как и для случайных величин, можно дать следующее
Определение 2 . Распределением случайного вектора называется функция , заданная на -алгебре по правилу
Распределение является объективной характеристикой случайного вектора, которую можно однозначно восстановить из эксперимента. Но распределение, будучи удобной характеристикой в теоретических исследованиях, является довольно сложным для реальных задач. Как и в одномерном случае, используют понятие функции распределения.
Определение 3. Функцией распределения случайного вектора называется функция , такая, что
Основные свойства функции распределения случайного вектора собраны в следующем предложении.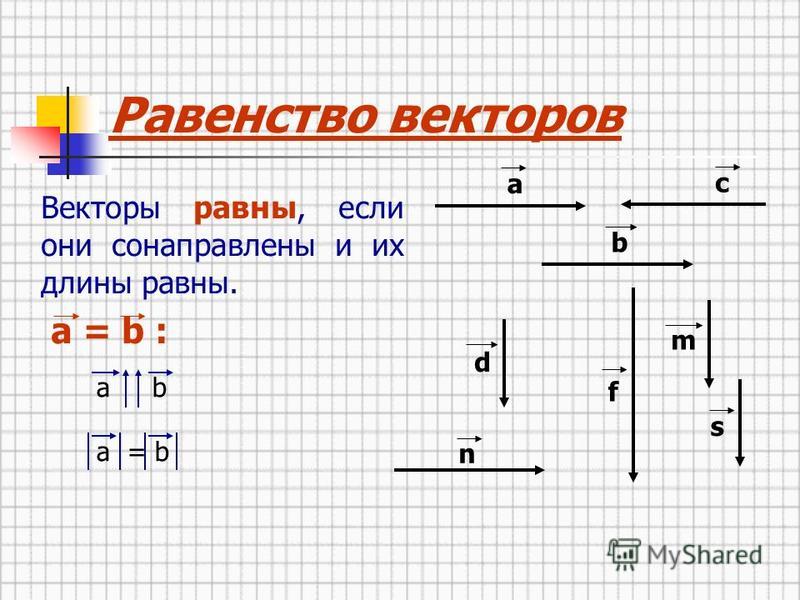
Предложение 1 . Функция распределения случайного вектора обладает следующими свойствами:
1..
2. не убывает по каждому аргументу ,.
3. — непрерывна слева по каждому аргументу х,-И i = 1,п.
4. , если некоторое . , если все .
5-
Где
6. есть функция распределения случайного вектора
Задача 1 . Доказать предложение 1.
Замечание. В силу свойства 5 по функции распределения можно найти вероятности попадания в множества . Далее, так же как и в одномерном случае, можно восстановить распределение для любых борелевских множеств В, аппроксимируя их параллелограммами.
Классификация распределений
Как и в одномерном случае, мы выделим два важных частных случая распределений, которые наиболее часто используются на практике. Конечно, бывают и более общие примеры, но мы не будем их подробно рассматривать в нашем курсе.
Определение 4 . Случайный вектор имеет дискретное распределение, если существует конечное или счетное множество , такое, что
Если — одно из возможных значений случайного вектора , то называется вероятностью
появления значения .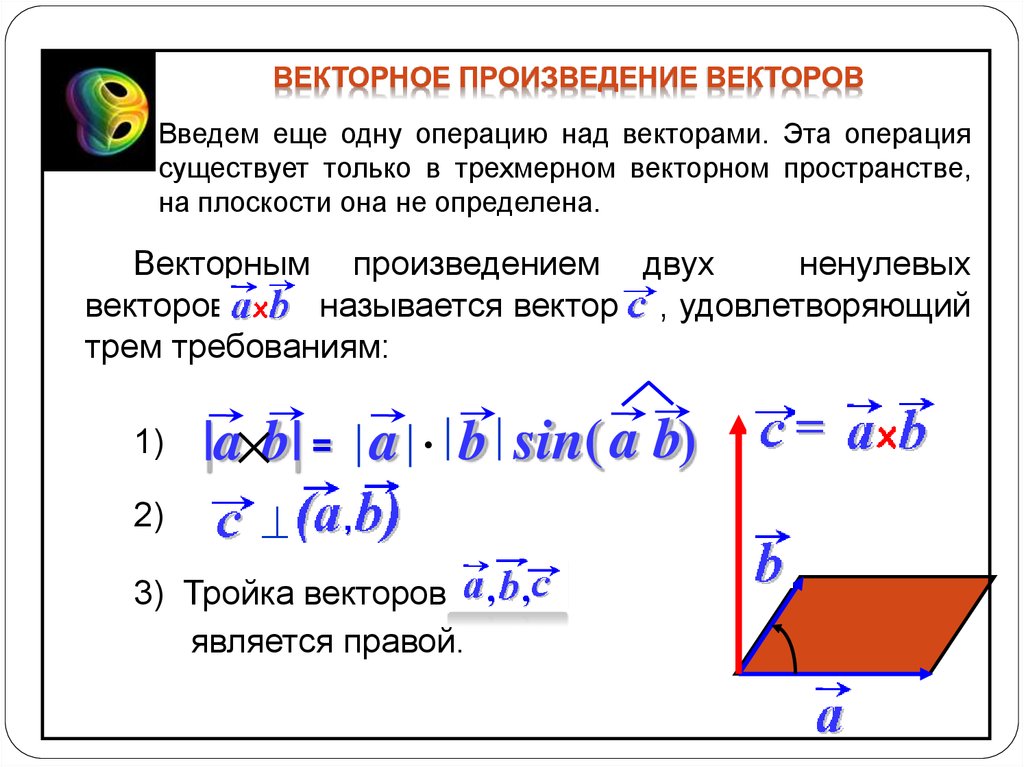
Обычно используют следующую стандартную форму описания распределения дискретного случайного вектора. Ясно, что каждая координата случайного вектора имеет дискретное распределение. Пусть есть множество значений случайной величины . Образуем множество В
Задача. Доказать, что , т.е. можно взять в качестве множества значений случайного вектора .
Для произвольного вектора , где , обозначим через
вероятность появления значения случайного вектора . При таком выборе множества некоторые его элементы будут появляться с вероятностью 0.
Пример. Случайный вектор имеет два значения (1,1) и (2, 2), которые появляются с вероятностями . Точка = (1, 2) входит в построенное выше множество, но
Пару будем называть распределением дискретного случайного вектора , хотя, строго говоря, это не совсем точно. Для распределение дискретного случайного вектора
обычно задают в виде следующей таблицы, называемой таблицей распределения:
Здесь — множество значений для — множество значений для , а
Предложение 2.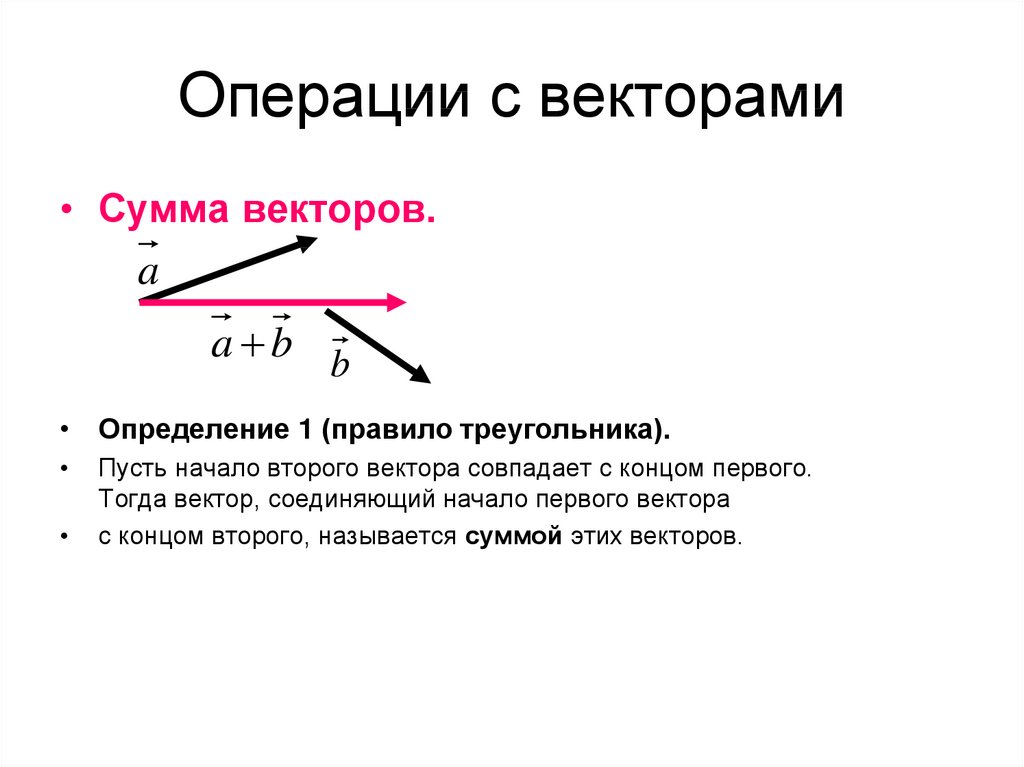 Распределение дискретного случайного вектора обладает следующими свойствами:
Распределение дискретного случайного вектора обладает следующими свойствами:
1)
2)
3)
,
4)
Все эти свойства легко следуют из приведенных выше определений и свойств вероятностей. Поэтому доказательство этого предложения предлагается в виде задачи.
Пример. Пусть мы приводим независимых испытаний, каждое из которых может закончиться одним из исходов и вероятности появления этих исходов одни и те же в каждом испытании и равны . Пусть есть число появлений -го исхода в этих -испытаниях. Тогда есть дискретный случайный вектор. Его значениями являются векторы, такие, что — целые неотрицательные числа и Как было показано выше, при изучении последовательностей независимых испытаний
Такое распределение называется полиномиальным распределением с параметрами
Определение 5 . Случайный вектор имеет абсолютно непрерывное распределение, если существует вещественная функция ,, такая, что
Функция называется плотностью распределения случайного вектора ..jpg)
Нетрудно доказать следующее утверждение, доказательство которого предлагается в качестве задачи.
Предложение 3 . Случайный вектор имеет абсолютно непрерывное распределение с плотностью ,
Тогда справедливы следующие свойства:
1)
2)
3)
4)
,
5)Если — точка непрерывности плотности ,
То ,
6) плотность случайного вектора можно вычислить по формуле
Замечание. Если мы имеем некоторый случайный вектор , то, выбирая некоторые из его координат, например первые , мы получаем новый случайный вектор, который называютподвектором вектора . Выше было показано, как найти распределение подвектора, когда убирают одну из координат. Применяя эту процедуру несколько раз, мы сможем найти распределение произвольногоподвектора. Распределение отдельно взятой координаты вектора называется одномерным или маргинальным распределением.
Как и в одномерном случае, можно ввести понятие смеси распределений, но мы не будем его рассматривать подробно так как здесь не возникает ничего нового.
Примеры. 1. Случайный вектор имеет равномерное распределение в области D, если он обладает плотностью распределения следующего вида:
где — мера Лебега области D. Фактически мы имеем дело с геометрическим определением вероятности.
2. Случайный вектор имеет двумерное нормальное распределение, если он обладает плотностью распределения следующего вида:
Числа называются параметрами двумерного нормального распределения. Их вероятностный смысл будет выяснен позднее.
Независимые случайные величины
При изучении свойств вероятностей случайных событий мы видели, что понятие независимости событий играет важную роль при вычислении вероятностей сложных событий. Аналогично понятие независимости является центральным понятием в теории случайных величин, их функциональных преобразований и других вопросах.
Определение 6 . Случайные величины называются не зависимыми, если для любых борелевских
Дадим эквивалентные формулировки понятия независимости случайных величин в терминах функций распределения, а также для случаев дискретных и непрерывных распределений.
Предложение 4 . Пусть мы имеем случайный вектор . Его компоненты независимы тогда и только тогда, когда
В случае дискретных распределений условие независимости эквивалентно условию
,
а в случае непрерывных – условию
Доказательство. Рассмотрим множества
Для них из (3) следует (4). Обратно, из (4) легко получить (3) для параллелепипедов, а затем аппроксимировать произвольные 1ѕ с помощью сумм отрезков. Свойство (6) получается из (4) дифференцированием. Свойство(5) следует непосредственно из определения независимости.
Пример 1. Пусть мы имеем схему Бернулли с параметрами и . Пусть = 1, если в-м испытании был ’’успех”, и равно 0 в противном случае. Тогда случайные величины -независимы.
Кстати, число успехов в этих испытаниях представимо в виде
Пример 2. Пусть имеет двумерное нормальное распределение. будут независимы тогда и только тогда, когда (задача!).
Нетрудно доказать следующий полезный результат (задача!).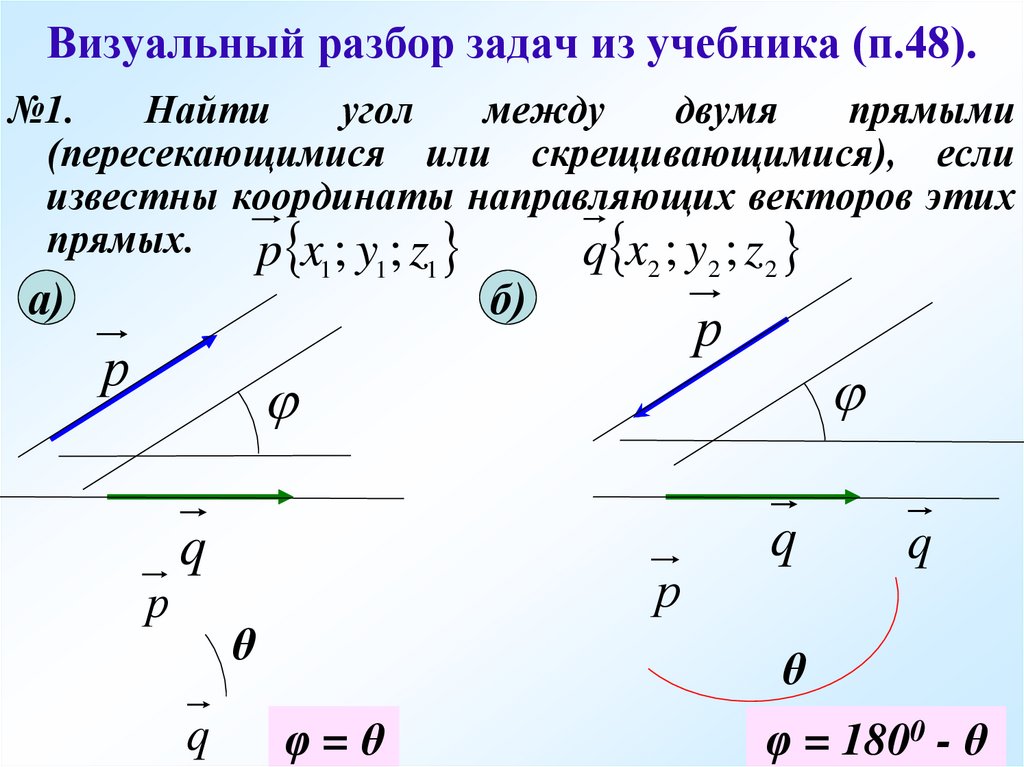
Предложение 5 . Пусть случайные величины , — независимы, а и — борелевские функции. Тогда случайные величины и также являются независимыми.
Пример 3. Пусть мы имеем схему Бернулли с испытаниями. Тогда число успехов в первых испытаниях и число успехов в последующих испытаниях — независимые случайные величины.
Функциональные преобразования случайных векторов
Как и в одномерном случае, важной с практической точки зрения является задача о вычислении распределения функционального преобразования случайного вектора.
Определение 7 . Отображение: называется борелевским, если мы имеем
Если — борелевское отображение, — случайный вектор, то вновь является случайным вектором. Действительно, если , то , а . Отсюда нетрудно получить выражение для распределения вектора, если мы знаем распределение вектора
Рассмотрим теперь отдельно случаи дискретного и непрерывного распределений.
Если имеет дискретное распределение с множеством значений и вероятностями появления этим значений, то ясно, что случайный вектор также имеет дискретное распределение с множеством значений , где каждое для некоторого , а вероятности появления значения можно вычислить по формуле
Пример. Пусть — двумерный случайный вектор с дискретным распределением, — вероятность появления некоторого значения . Рассмотрим функцию
Пусть — двумерный случайный вектор с дискретным распределением, — вероятность появления некоторого значения . Рассмотрим функцию
. Тогда есть дискретная случайная величина и вероятность того, что , где — одно из возможных значений суммы , можно рассчитать по формуле
Если и независимы, то
В этом случае мы получаем
Это формула свертки для дискретных распределений.
Пусть теперь — случайный вектор, который имеет плотность распределения . Как и в одномерном случае, распределение случайного вектора может не иметь плотности и даже быть дискретным. Необходимы некоторые дополнительные ограничения на функцию . Рассмотрим один частный, но практически важный случай.
Предложение 6 . Пусть — случайный вектор, который имеет плотность распределения — взаимно однозначное и непрерывно дифференцируемое отображение. Тогда распределение случайного вектора является абсолютно непрерывным и его плотность можно вычислить по формуле
где — якобиан отображения
Доказательство этого предложения дословно повторяет доказательство в одномерном случае, но теперь мы должны сделать замену переменных в
Пример. Пусть , где — невырожденная квадратная матрица размера , т.е. мы имеем линейное отображение в . В этом случае и
Пусть , где — невырожденная квадратная матрица размера , т.е. мы имеем линейное отображение в . В этом случае и
В тех случаях, когда , последнее предложение не применимо. Но часто можно дополнить отображение еще одним отображениемтак, чтобы отображение уже обладало нужными свойствами.
Пример. Пусть случайный вектор имеет плотность распределения . Найдем плотность распределения случайной величины . Здесь . Рассмотрим еще одну случайную величину . Тогда в целом мы имеем следующее линейное отображение . Матрица этого отображения имеет вид , а обратная матрица равна
В предыдущем примере мы получили, что
Чтобы найти плотность распределения для , достаточно проинтегрировать по координате, т.е.
Если и — независимы, то . Заменяя на, получаем
Это формула свертки для непрерывных распределений.
В более сложных ситуациях, когда не удается свести задачу к предложению б, необходимо провести прямые расчеты, вычисляя распределение (например, функцию распределения), а затем находя плотность. Технически это сводится к нахождению множества и вычислению интеграла от по этому множеству.
Технически это сводится к нахождению множества и вычислению интеграла от по этому множеству.
Чтобы продемонстрировать, как работает этот метод, рассмотрим тот же самый пример: . Вычислим для функцию распределения:
Фактически нам нужно найти вероятность попадания случайного вектора в множество
Тогда мы имеем
Таким образом, мы имеем тот же результат, что и ранее.
Дифференцируя по , окончательно получаем
Далее, расписывая двойной интеграл в виде повторного, получаем
Теория и методика изучения линии векторов и координат
Теория и методика изучения
линии векторов и координат
В помощь студентам ДПП «Образование и педагогика», профиль
«Математика»
История развития векторного исчисления в
математической науке и образовании
Направление
Область изучения
Каспар Вессель
Геометрическое
Отрезки и их
исчисления
Рене Декарт
Физическое
Векторные величины
Огюстен Коши
Алгебраическое
Расширение понятия
операции
Уильям Гамильтон
Лазар Карно
Цель изучения векторного метода
1. продемонстрировать еще один, не похожий на другие, метод решения
продемонстрировать еще один, не похожий на другие, метод решения
различных геометрических задач и доказательства большого числа
теорем;
2. показать, что вектора используются и в других науках, таких как
физика, география, химия, это сможет сделать кругозор учащихся
значительно шире и будет способствовать развитию их взглядов на жизнь;
3. решать задачи векторным методом для того, чтобы развивать у
обучающихся такие мыслительные операции, как обобщение и
конкретизация;
4. способствовать развитию такого рода качеств мышления, как гибкость
(не шаблонность), целенаправленность, рациональность, критичность и
др. у обучающихся;
5. показать, насколько тесно связаны между собой такие предметы, как
алгебра и геометрия.
Требования к уровням освоения
С учетом типа общеобразовательного учреждения, учащиеся вправе изучать
математику на нескольких уровнях – базовом, расширенном и углубленном.
Необходимо подчеркнуть, что тот объем знаний по теме «Векторы и
координаты на плоскости» при изучении математики на базовом уровне можно
считать слишком малым для того, чтобы обучающиеся в полной мере
овладели векторным методом решения планиметрических задач. В условиях
В условиях
расширенного уровня изучения предполагается обучение детей некоторым
составляющим векторного метода, поскольку он включает в себя довольно
большой
перечень
результатов.
Углубленный
уровень
изучения
предусматривает полное освоение обучающимися векторного метода и
использование его при решении многих задач и доказательства некоторых
теорем.
Базовый уровень
Оперировать на базовом уровне понятиями вектор, сумма векторов,
произведение вектора на число, координаты на плоскости;
определять приближенно координаты точки по ее изображению на
координатной плоскости.
В повседневной жизни и при изучении других предметов:
использовать векторы для решения простейших задач на определение
скорости относительного движения.
Расширенный уровень
Оперировать понятиями вектор, сумма, разность векторов, произведение
вектора на число, угол между векторами, скалярное произведение
векторов, координаты на плоскости, координаты вектора;
выполнять действия над векторами (сложение, вычитание, умножение на
число), вычислять скалярное произведение, определять в простейших
случаях угол между векторами, выполнять разложение вектора на
составляющие, применять полученные знания в физике, пользоваться
формулой вычисления расстояния между точками по известным
координатам, использовать уравнения фигур для решения задач;
применять векторы и координаты для решения геометрических задач на
вычисление длин, углов.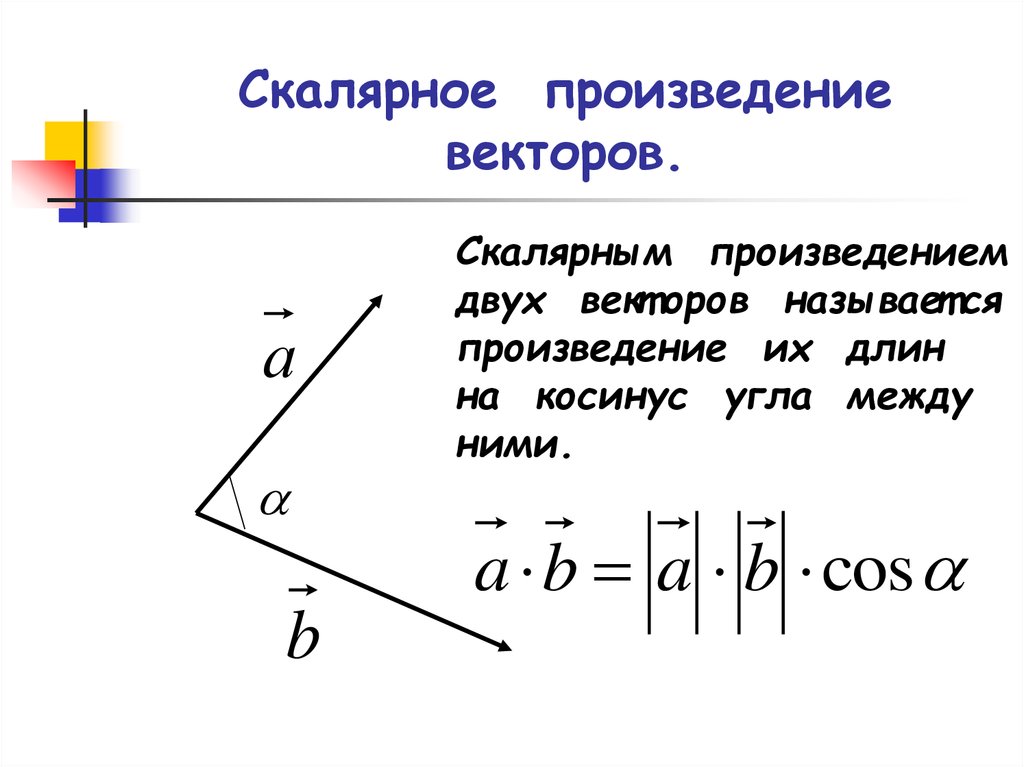
В повседневной жизни и при изучении других предметов:
использовать понятия векторов и координат для решения задач по
физике, географии и другим учебным предметам.
Углубленный уровень
Свободно оперировать понятиями вектор, сумма, разность векторов,
произведение вектора на число, скалярное произведение векторов,
координаты на плоскости, координаты вектора;
владеть векторным и координатным методом на плоскости для решения
задач на вычисление и доказательства;
выполнять с помощью векторов и координат доказательство известных
ему геометрических фактов (свойства средних линий, теорем о
замечательных точках и т.п.) и получать новые свойства известных фигур;
использовать уравнения фигур для решения задач и самостоятельно
составлять уравнения отдельных плоских фигур.
В повседневной жизни и при изучении других предметов:
использовать понятия векторов и координат для решения задач по
физике, географии и другим учебным предметам.
Различные подходы к понятию вектора в школе.
В учебнике Погорелова А.В. дается следующее определение:
«Вектором
мы
будем
называть
направленный
отрезок.
Направление вектора определяется указанием его начала и конца. На
чертеже направление вектора отмечается стрелкой».
В учебнике Атанасяна Л.С. можно увидеть другой подход во введении
этого понятия: «Отрезок, для которого указано, какая из его граничных
точек считается началом, а какая – концом, называется направленным
отрезком или вектором».
Две схемы введения векторов и координат.
Учебник Атанасяна
Глава 9 Векторы
Глава 10 Метод координат
Понятие вектора, нулевой вектор,
длина или модуль вектора, равные
векторы, откладывание вектора от
точки,
сложение
и
вычитание
векторов, умножение вектора на
число,
скалярное
произведение
векторов.
Учебник Погорелова
Параграф 8 Декартовы
координаты на плоскости
Параграф 10 Векторы
Понятие
вектора,
абсолютная
величина (модуль) вектора, равные
векторы,
нулевой
вектор,
откладывание вектора от точки,
координаты
вектора,
сложение
векторов. умножение вектора на
умножение вектора на
число,
коллинеарные
вектора,
скалярное произведение векторов.
Сложение и вычитание векторов
Учебник Атанасяна
Сумма векторов определяется в этом учебнике
следующим образом:
Пусть а и
b — два вектора. Отметим
произвольную точку А и отложим от этой точки
вектор АВ, равный а. Затем от точки В отложим
вектор ВС , равный b. Вектор АС называется
суммой векторов а и Ь .
Такое определение суммы векторов обладает
хорошей наглядностью, легко может быть
мотивировано
рассмотрением
примера
на
перемещение материальной точки. Однако при
этом громоздким является обоснование свойств
сложения векторов и независимости векторов от
выбранной точки.
Вычитание векторов авторы определяют как
действие, обратное сложению. Важное место
здесь занимает теорема о том, что для любых
векторов а и b справедливо соотношение а — b
= а + (- b). Эта теорема дает способ построения
разности
векторов:
чтобы
вычесть
из
вектора а вектор b, надо сложить вектор а с
вектором, противоположным вектору b .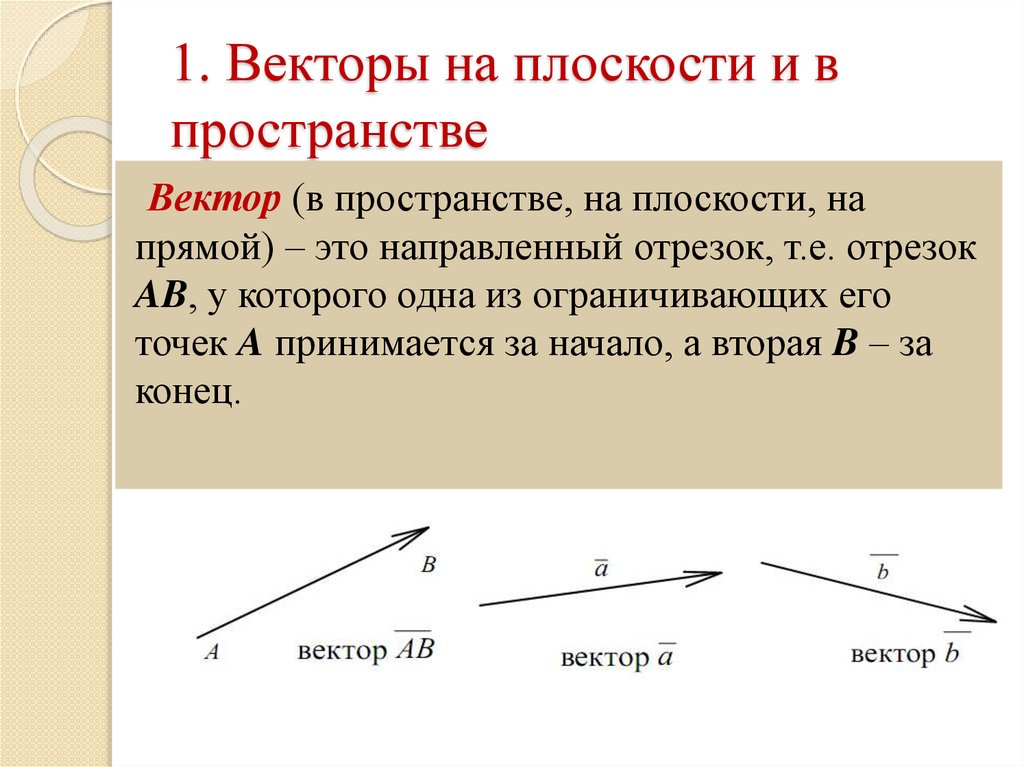
Учебник Погорелова
Суммой векторов а и b с координатами (а1, а2) и
(b1, b2) называется вектор с с координатами (a1
+b1, a2 + b2).
Из определения суммы векторов, признака
равенства
векторов
и
свойств
сложения
действительных чисел следуют все свойства
сложения векторов. Такое определение суммы
векторов позволяет легко обосновать свойства
сложения векторов, но оно не указывает способа
построения суммы двух данных векторов. Один из
таких способов дает теорема: Каковы бы ни были
точки А, В. С имеет место равенство АВ + ВС = АС.
Разностью векторов а (а1, а2) и b (b1,
b2)
называется вектор с (с1, с2) такой,
что с+b=а. Обозначается с=а—b, тогда с1 =а1 –
b1, с2 = а1 — b2.
Способ построения разности двух векторов
рассмотрен здесь в задаче: Даны векторы с общим
началом: АВ и АС. Докажите, что АС- АВ = ВС.
Умножение вектора на число
Учебник Атанасяна
Учебник Погорелова
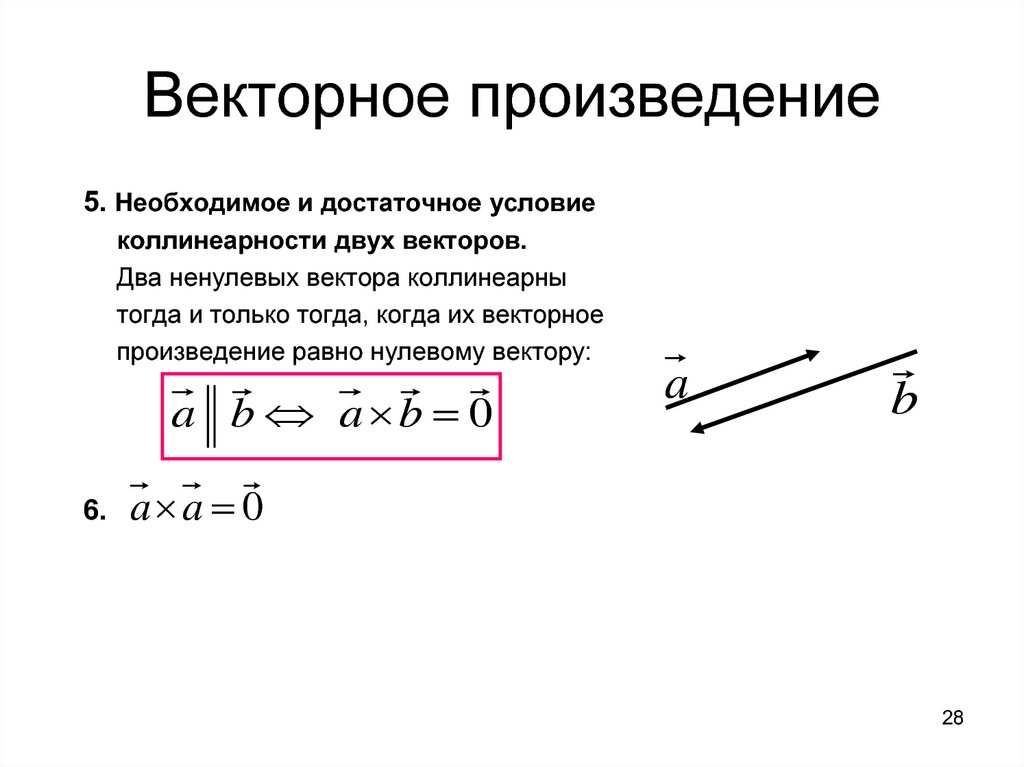
Произведением
ненулевого
вектора а на число к называют
такой вектор b, длина которого
равна | к ∙ а | , причем
векторы а и b сонаправлены
при к >0 и противоположно
направлены
при
к
<
0.
Произведением нулевого вектора
на
любое
число
считается
нулевой вектор.
Свойства умножения вектора
число
в
этом
учебнике
доказываются.
на
не
Произведением вектора а (а1; а2)
на число λ называется вектор (λа1;
λа2)
Координатное
определение
произведения
вектора
на
число
позволяет легко обосновать все
свойства умножения вектора на число.
Однако
оно
не
дает
способа
построения произведения данного
вектора на заданное число. Возникает
проблема отыскания такого способа.
Для
этого
рассматривается
упражнение
на
построение
произведения вектора на число:
Постройте
произведение
вектора ОА (4; 5) на число а) 2; б) -3;
в) 0; г) 5; д) -1,5.
Скалярное произведение векторов
Учебник Атанасяна
Это
понятие
вводится
как
произведение
длины
этих
векторов на косинус угла между
ними. При таком (традиционном)
подходе значительную трудность
представляет
доказательство
распределительного
свойства
скалярного умножения векторов.
Оно очень громоздко.
Учебник Погорелова
Скалярное
произведение
векторов изучается в 8 классе и
определяется
как
сумма
произведений
их
соответствующих координат (т. е.
число):
При этом в учебнике доказывается
теорема: Скалярное произведение
векторов равно произведению их
абсолютных величин на косинус
угла между ними.
Типы задач, обучающие «Векторному методу» в
курсе геометрии 7-9
Перевод геометрического языка на векторный и обратно.
Выполнение операций над векторами.
Представление вектора в виде суммы, разности векторов, произведения
вектора на число.
Переход от соотношения между векторами к соотношению между их
длинами и наоборот.
Нахождение длины вектора и величины угла между векторами
Применение векторного метода в конкретных ситуациях
(Файл с примерами задач будет отправлен на почту)
Координатный метод решения задач
Основные понятия:
1. Абсцисса (от лат. abscissus — отрезанный, отсеченный) — отрезок, отсекаемый на
оси ОХ.
2. Ордината (от лат. ordinatus — упорядоченный) — одна из декартовых координат точки,
обычно вторая, обозначаемая буквой у. Первоначально была только одна ось и
ординатами были отрезки, параллельные друг другу и перпендикулярные оси, то есть в
каждой абсциссе строился свой перпендикуляр.
3. Координаты (точки) — числа, взятые в определенном порядке и характеризующие
положение точки на линии, на плоскости, на поверхности или в пространстве.
4. Координатная прямая прямая, на которой указан способ изображения
действительных чисел.
5. Координатная плоскость — плоскость с введенной на ней системой координат; х = 0, у
= 0 — оси координат; х = const, у = const — координатные линии.
6. Координатный метод — способ определения положения точки (на прямой, плоскости,
в пространстве) с помощью чисел. Используя координатный метод, алгебраические
уравнения можно истолковать в виде геометрических образов (графиков) и, наоборот,
искать решение геометрических задач с помощью аналитических формул (уравнений и
их систем).
Компоненты координатного метода
построение точки по се координатам;
— нахождение координат заданных точек;
— вычисление
координатами;
— оптимальный выбор прямоугольной системы координат;
— составление уравнения фигуры по её характеристическому свойству;
— видение за уравнением конкретного геометрического образа;
— преобразование алгебраических равенств
расстояния
между
точками,
заданными
своими
Этапы решения геометрической задачи
координатным методом
I этап. Оптимальный выбор прямоугольной системы координат.
II этап. Перевод задачи на координатный язык.
III этап. Выполнение преобразований полученного в координатной форме
выражения (решение задачи на координатном языке).
IV этап. Перевод (и осмысление) полученного результата с координатного
языка на тот язык, на котором была сформулирована задача.
Задача: В треугольнике АВС АВ = 4, АС =
6, < А = 60 . Найти медиану,
проведенную из вершины А
/ этап. Выберем прямоугольную систему координат так, как показано на
Выберем прямоугольную систему координат так, как показано на
рис.
II этап. ∆АОВ — прямоугольный, < ABO = 30°, поэтому АО = 2, тогда ОС
= 4,
Значит, А (-2; 0), С (4; 0), В (0; 2√3). Так
как М середина стороны ВС, то М(2; √3).
III этап. По формуле расстояния между двумя точками находим:
/V этап. В нашем случае этот этап осуществляется автоматически:
расстояние между точками А и М (где М — середина ВС) — это и есть длина
медианы, проведенной из вершины А.
Ответ: Медиана АМ= √19
Практическое занятие:
1.Сформулируйте определение вектора, изложите правила сложения векторов,
умножение вектора на число. Как определяются координаты вектора? Дайте
определение скалярного произведения векторов
2. Дайте определение аффинной и декартовой систем координат на плоскости и в
пространстве.
3. Методика введения понятия вектора в школьном курсе
4.Методика введения системы координат в школьном курсе
5.Характеристика системы задач (можно использовать задачи из файла)
6. Решите задачу векторным методом: Докажите, что средняя линия трапеции
Решите задачу векторным методом: Докажите, что средняя линия трапеции
параллельна основаниям и равна их полусумме. Раскройте методику решения данной
задачи.
7. Составить таблицу эвристик «Что требуется доказать (на геометрическом языке)»,
«Что достаточно доказать (на векторном языке)». Предложить методику её
использования на уроке (можно использовать задачи из файла из раздела 6).
8. Методика изучения операций над векторами (одно на выбор):
1.
Разработать фрагменты уроков по введению понятий вектора, длины вектора,
коллинеарных и равных векторов.
2.
Разработать фрагмент урока «Операции над векторами в графической форме» с
использованием интерактивного планшета
3.
Подготовиться к проведению деловой игры «Сложение и вычитание векторов».
4.
Разработать методику изучения умножения вектора на число (скалярного произведения
векторов) в форме урока-лекции.
17.946 Теория Стоковые иллюстрации, клипарты и векторные изображения Теория
Колеса смешивания цветов значения свойства тона комбинации с пояснениями и схемами круга набор инфографики плакат векторные иллюстрации
Теория большого взрыва векторные иллюстрации инфографики. диаграмма масштаба времени и размера вселенной с этапами развития от первых частиц до звезд и галактик, гравитации и света. плакат научной астрономии. карта истории космоса.
диаграмма масштаба времени и размера вселенной с этапами развития от первых частиц до звезд и галактик, гравитации и света. плакат научной астрономии. карта истории космоса.
Хаос и беспорядок превращается в сформировавшийся ровный клубок с одной линией. теории хаоса и порядка. плоская векторная иллюстрация изолирована
Эволюция человека. эволюция человека. исторические иллюстрации. векторная иллюстрация эволюции человека. прогресс рост развитие. обезьяна, неандерталец, хомо сапиенс. примат с оружием.
Расширение и эволюция Вселенной. физическая космология и теория большого взрыва. космическая временная шкала и эволюция звезд, галактик и вселенной после большого взрыва
Стандартные номиналы. целое, половина, четверть и с восьмого по шестьдесят четвертое. в нотной записи значение ноты указывает на относительную продолжительность ноты с использованием нотной головки, штока или флажка. иллюстрация. вектор.
Эволюция Вселенной. космическая хронология и эволюция звезд, галактики и вселенной после большого взрыва
Космическая инфографика на фиолетовом фоне. векторная иллюстрация классификации галактик, черная дыра, млечный путь, теория большого взрыва, солнечная система, пояс астероидов, гравитация луны, диапазон температур.
векторная иллюстрация классификации галактик, черная дыра, млечный путь, теория большого взрыва, солнечная система, пояс астероидов, гравитация луны, диапазон температур.
Плакат по теории цвета. цветовые модели, гармонии, свойства и значения дизайн памятного плаката
Нарисованная теория эволюции человека. векторный силуэт хомо сапиенс. символ от обезьяны до бизнесмена.
Гамма до мажор, полные ноты. ключ c. мажорная шкала на основе c. одна из самых распространенных тональностей в западной музыке. белые клавиши на пианино. у него нет квартир и нет острых предметов. иллюстрация. вектор.
Химический и физический набор элементов на синем фоне. формулы и схемы радиоактивного распада и выделения элементов. модель атома
Скрипичный и басовый ключ на пятистрочном нотоносце. ключ соль помещается на вторую строку, а ключ фа на четвертую строку нотоносца. два музыкальных символа, используемые для обозначения высоты написанных нот. иллюстрация. вектор
Концепция векторной карикатуры эволюции женщины процесс женского развития от обезьяны, примата прямоходящего, охотника и собирателя каменного века, фермера до современной женщины моды против джунглей, поля или города
Научные формулы. математические и физические вычисления на классной доске. алгебра и физика рукописные векторные концепции образования. математический расчет на доске. Физическая научная теорема
математические и физические вычисления на классной доске. алгебра и физика рукописные векторные концепции образования. математический расчет на доске. Физическая научная теорема
Инфографическая диаграмма теории большого взрыва, показывающая, как наша Вселенная расширяется с момента создания до настоящего времени для хронологии и физического образования
Вымирание человеческого вида, временная шкала эволюции, превращение обезьяны в прямоходящего человека разумного, мужской характер эволюционирует от обезьяны до современного человека, идущего в могилу с черепами и мультяшной векторной иллюстрацией знака разрыва как изучение морали и этики концепции крошечного человека
Масштаб до мажор, одна октава на нотном стане и клавишах клавиатуры. Октава показана на клавишах клавиатуры и на пятистрочном нотоносце со скрипичным ключом и целыми нотами. самая распространенная ключевая подпись в музыке. иллюстрация. вектор.
Теория цвета. Цветовые тона колеса дополнительных и вторичных комбинаций.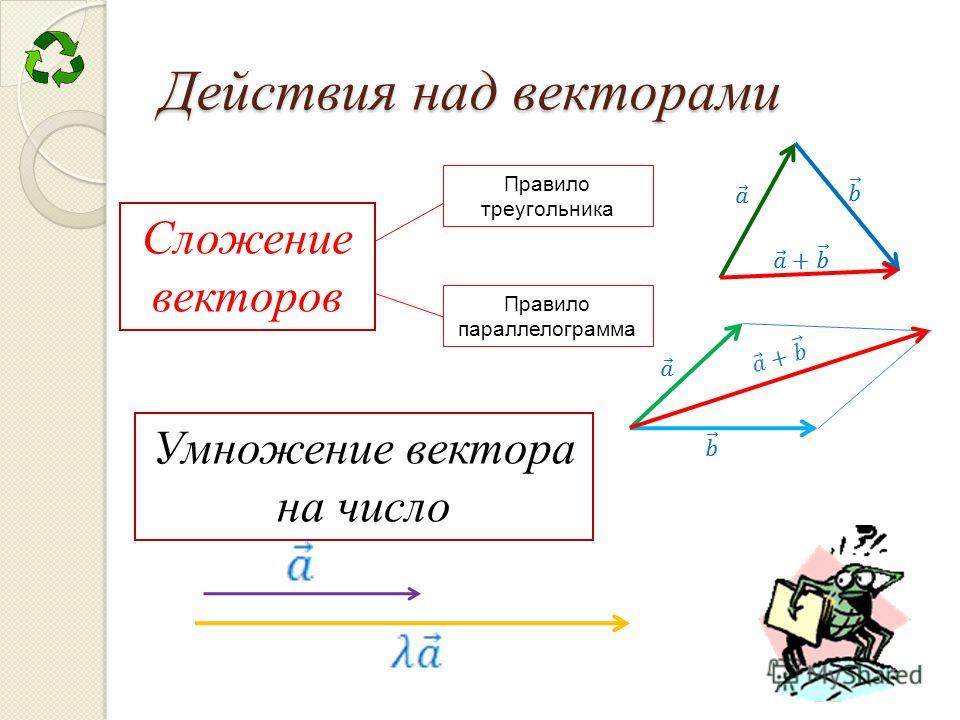 цветовые тона комбинации схема векторные иллюстрации набор
цветовые тона комбинации схема векторные иллюстрации набор
Теория струн. от материи, молекулы и атома к электронам, протонам, нейтронам и кваркам. квантовая физика. атомные модели. Теоретическая основа. векторная диаграмма
Теория социального научения бандура четыре стадии процесса посредничества в теории социального научения мотивация удержания моторной репродукции внимания в плоском стиле диаграммы.
Астрономия и астрофизика, формулы для физики, математики и астрономии на темно-зеленой доске. инфляция Вселенной и теория большого взрыва
Математический школьный предмет. изучение математики, идея образования и знаний. наука, технология, инженерия, математическое образование. изолированная плоская векторная иллюстрация
Концепция теории относительности, показывающая эскиз черной дыры или червоточины с фоном космического поля, заполненным звездами, и связь между временем, энергией, массой, скоростью света для физического образования
Концепция теории заговора. поток дезинформации и ложных представлений о вирусе и тайных планах инопланетян. обеспокоенный мужчина за ноутбуком. цветная плоская векторная иллюстрация на белом фоне
поток дезинформации и ложных представлений о вирусе и тайных планах инопланетян. обеспокоенный мужчина за ноутбуком. цветная плоская векторная иллюстрация на белом фоне
Эволюция человека от обезьяны до женщины-фрилансера, временная шкала, женский персонаж эволюционирует по шагам от обезьяны до стоячего гомо сапиенса до девушки за компьютером, изолированной на белом фоне. Cartoon vector illustration
Древний человек прямоходящий или пещерный человек, предок человека, мультяшный векторная иллюстрация. Неандерталец с деревянной палкой и камнем в руках, один из этапов эволюционной теории Дарвина, изолированный на белом фоне
Значок ноты векторного скрипичного ключа
Эволюция человека
Мультипликационный персонаж бизнесмена, взбирающийся на стрелу, мотивированный тренером или наставником, плоская векторная иллюстрация. бизнес-коучинг или обучение, стратегия достижения успеха.
Векторная иллюстрация естественного отбора. объяснил схему с эволюцией жизни.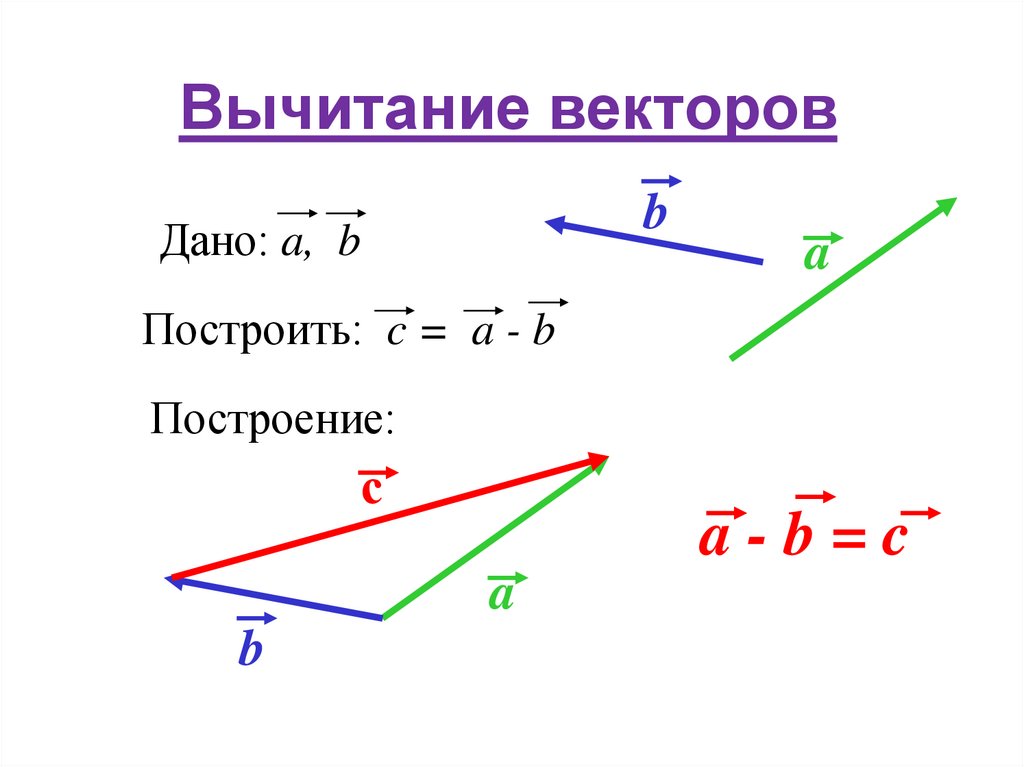 селективный процесс органической среды со всеми видами и людьми. Образовательный пример теории Дарвина и преимущество мутации
селективный процесс органической среды со всеми видами и людьми. Образовательный пример теории Дарвина и преимущество мутации
Теория схематических карт иллюстрации плоской Земли.
Изучение права. стопка книг в очках, открытая книга и судейский молоток на белом фоне. векторная иллюстрация.
Ноты. символы и длины. американская и британская английская маркировка. интервал тишины в музыкальном произведении, отмеченный символом, обозначающим продолжительность паузы. иллюстрация над белой. вектор
Концепция рисования непрерывной линии сердца и мозга, эмоции с векторной иллюстрацией рациональности в стиле одной линии, простая метафора двойственности человеческой личности
Спектр. видимый свет, инфракрасное и ультрафиолетовое излучение. электромагнитное излучение. цвет солнечного света. различные типы электромагнитного излучения по длине волны. в порядке увеличения частоты и уменьшения длины волны
Инфографическая диаграмма кинетической теории материи, показывающая движение твердого жидкого газа, плазмы и частиц в четырех состояниях и соотношение энергии и скорости расстояния для образования в области химии и физики
Набор мультфильмов о биологической иерархии
Дизайн векторной иллюстрации теории эволюции. эволюция видов. ДНК — молекула жизни
эволюция видов. ДНК — молекула жизни
Музыкальные паузы, их символы и длины. пауза – это интервал тишины в музыкальном произведении, отмеченный символом, указывающим продолжительность паузы. черная иллюстрация на белом фоне. вектор.
Теория эволюции человека. силуэт с отражением.
Стандартные длительности нот и пауз в западной нотной записи. относительная продолжительность ноты и интервал тишины в музыкальном произведении, отмеченные определенными символами. иллюстрация над белой. вектор.
Атомные модели. научная теория о частицах. физика. векторная диаграмма
Мозг с запутанным узлом
Векторная иллюстрация атомных моделей. ученые и годы
Теории заговора, фальшивые новости и концепция дезинформации. информационный поток из интернет-СМИ. мифы, факты, ложный поток через интернет. плоская векторная иллюстрация на белом фоне
Абстрактная векторная композиция из геометрических фигур и искривленного пространства в виде сетки
Достаточная экономия. круговая диаграмма новой теории сельского хозяйства. инфографика — векторная иллюстрация
круговая диаграмма новой теории сельского хозяйства. инфографика — векторная иллюстрация
Концепция эволюции векторной карикатуры женщины Процесс женского развития от обезьяны, примата прямоходящего, охотника и собирателя каменного века, фермера до современной модной женщины против джунглей, поля или города
Теория заговора. текстовый заголовок размещается внутри углов. синий векторный резиновый отпечаток теории заговора с грязной текстурой.
Человеческие руки открываются вокруг масонского символа, всевидящее око над священным сердцем и пирамидой. новый мировой порядок. алхимия, религия, духовность, оккультизм. цветная векторная иллюстрация в винтажном стиле изолирована.
Векторная концепция промывания мозгов. символ манипуляции, дезинформации и фейковых новостей, кампании лжи, пропаганды. распространение теорий заговора и альтернативных СМИ
Иконка концепции линии теории хаоса. Теория хаоса плоский векторный знак веб-сайта, символ контура, иллюстрация .
Средняя c на клавиатуре пианино, учебное пособие и шпаргалка. схема двух октавных секций, для скрипичного и басового ключа, на клавиатуре и большом нотоносце, средняя c выделена красным цветом. иллюстрация. вектор.
До мажор и минор. ключ c. мажорная шкала на основе c. одна из самых распространенных тональностей в западной музыке. белые клавиши на пианино. без квартир и без острых предметов. относительный ключ минор. иллюстрация. вектор.
Множественный интеллект — это психологическая теория о людях и их различных типах интеллекта
Примеры физики векторных иллюстраций квантовой механики. отрицательно заряженный электрон, нейтрон и положительно заряженный протон в модели Бора как электронные орбиты, а кванты моделируются как электронные облака.
Значок диаграммы Венна, векторная иллюстрация
Теория пяти элементов. восточная медицина. Теория пяти элементов используется в традиционной китайской медицине как способ диагностики и лечения болезней.
Открытая книга красочных музыкальных нот в стиле вырезки из бумаги. дизайн музыкальных навыков, трехмерная иллюстрация papercut для образования или творческой концепции.
Эволюция человека от обезьяны до современного человека-программиста, пользователя компьютера, изолированного на белом фоне. мужской характер эволюционирует от обезьяны до прямоходящего гомо сапиенса, теория Дарвина. Cartoon vector illustration
Зигмунд Фрейд жонглирует понятиями эго, суперэго, ид на фоне подсознания. Иллюстрация теории личности Фрейда. векторная изолированная иллюстрация на белом фоне.
Набор иконок для гитарных аккордов. векторная иллюстрация урока гитары изолирована на белом. базовая коллекция аккордов. табулирование.
Знания инфографики 10 строк иконки template.subject, образование, информация, опыт простые иконки
Экзамен инструктора для водителя автомобиля, люди учащиеся правила векторные иллюстрации набор, мультфильм плоский женщина мужчина студент обучение изолированы на белом
Вероятность слово облако концепции. коллаж из слов о вероятности. векторная иллюстрация
коллаж из слов о вероятности. векторная иллюстрация
Теория струн. от молекул и атомов до электронов, протонов, нейтронов, кварков и глюонов. квантовая физика. атомные модели. Теоретическая основа. векторная диаграмма
Ключевой показатель эффективности. фон kpi с иконками и ключевыми словами. метрики интеллекта для измерения достижения по сравнению с запланированной целью. kpi инфографики веб-страницы векторный баннер
Векторная карикатура или черно-белый рисунок плоской земли в космосе, концепция или заговор или теория плоской земли, наука и образование.
Теория ограничений или toc как диаграмма контура парадигмы эффективного управления
Современная цветная тонкая линия концепции математики на черном фоне. векторные иллюстрации с различными элементами по теме математики. концепции логотипа для модного дизайна.
Стилизованный клубок нитей теории хаоса и порядка. значок в плоский стиль, изолированные на белом фоне в линейном стиле
Утилитаризм нормативная этическая теория принцип концепции крошечного человека.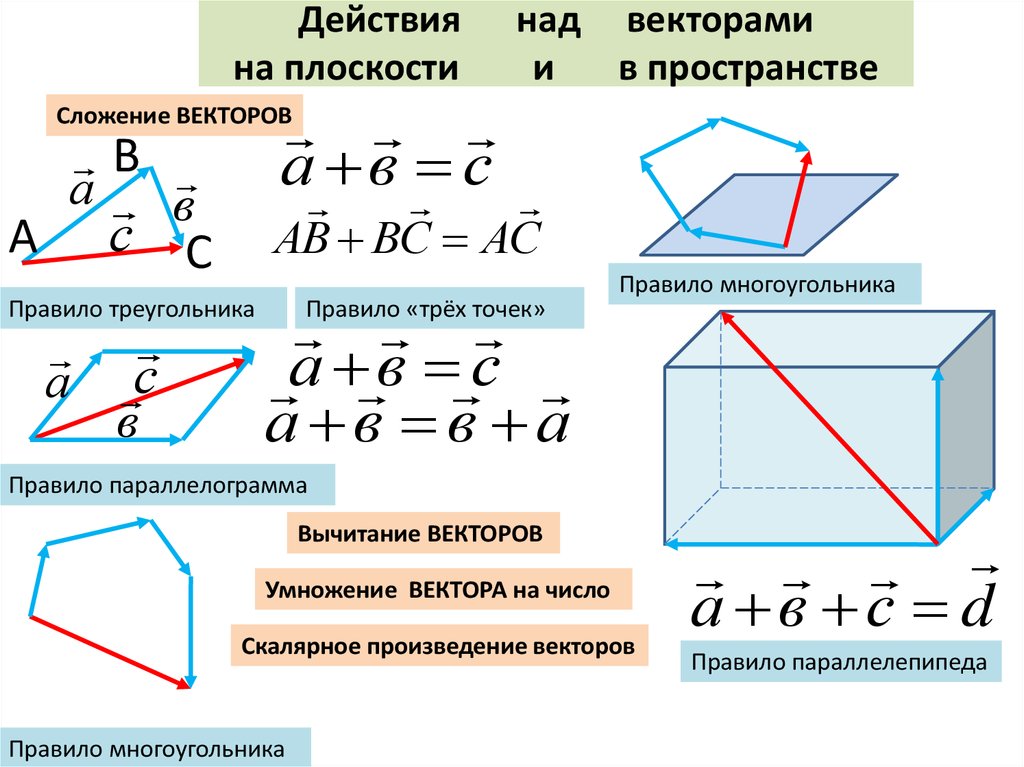 моральное мышление с идеей о личной или общественной выгоде сравнения векторной иллюстрации. полезные преимущества на весах
моральное мышление с идеей о личной или общественной выгоде сравнения векторной иллюстрации. полезные преимущества на весах
Знание модной веб-концепции с иконками. содержит такие значки, как предмет, образование, информация
Набор палитр схем кругов принципов идеального соответствия
Теория цвета с оттенками цветовых оттенков для первичных вторичных и дополнительных комбинаций схем постер векторной иллюстрации
Иллюстрация цветового круга и цветовой палитры.
Музыкальные ноты на фортепианной клавиатуре 88 клавиш, изолированные на белом фоне. сольфеджио. векторная иллюстрация.
Иллюстрация печати цветового круга с разными цветами в градациях
Распутать хаотический беспорядок, головоломку, лабиринт, запутать узел, решить беспорядок, теорию, способ работы. черное мужское лицо рациональное четкое объяснение организовать путь работа идея знак значок абстрактное искусство каракули нарисованный векторный графический стиль
Двое ученых обсуждают научные теории. физика, атом, речевой пузырь, плоская векторная иллюстрация. концепция знаний и науки для баннера, дизайна веб-сайта или целевой веб-страницы
физика, атом, речевой пузырь, плоская векторная иллюстрация. концепция знаний и науки для баннера, дизайна веб-сайта или целевой веб-страницы
Око провидения. мистический рисунок. векторная иллюстрация
Квантовая обработка. глубокое обучение искусственного интеллекта. будущие новые технологии для презентации бизнеса или науки. векторный фон
Концепция теории эволюции Дарвина, проиллюстрированная трансформацией человеческой фигуры от первобытного человека к современному человеку.
Эволюция треугольника Серпинского. шаги построения математической геометрической бесконечной фрактальной прокладки Серпинского. пирамида с бесконечным рисунком, изолированным на белом
Пустой шаблон листа заметок для начинающих. пятистрочный нотоносец со скрипичным ключом для изучения западной нотной грамоты и тренировки музыкального слуха. иллюстрация на белом фоне. вектор.
Изометрические профессора лекционного класса студенты набор изолированных иконок человеческие персонажи и столы с сидящими студентами векторная иллюстрация
Нарисованный вручную бесшовный узор с детской иллюстрацией космоса. векторный рисунок планеты, звезды и спутника в космосе. Мультяшный объект солнечной системы
векторный рисунок планеты, звезды и спутника в космосе. Мультяшный объект солнечной системы
Наиболее распространенные ключи, регулирующие использование в современной музыке. наиболее распространены скрипичный и басовый ключи, за ними следуют альтовый и теноровый ключи. музыкальные символы для обозначения высоты написанных нот. иллюстрация. вектор.
Теория эволюции человека. векторный силуэт хомо сапиенс. символ от обезьяны до сноубордиста.
Теория цвета с оттенками оттенков оттенков для первичных, вторичных и дополнительных схем комбинаций, плакат, векторная иллюстрация
Забавная мультяшная иллюстрация Чарльза Дарвина
Базовые операции теории множеств, диаграмма вектора иконок Венна
Математические и научные формулы с числами на доске.
Теория эволюции женщины. векторный силуэт хомо сапиенс. символ от обезьяны до футболиста.
Пустой шаблон листа заметок. пятистрочный нотоносец со скрипичным ключом. западная нотная запись. иллюстрация на белом фоне. вектор.
иллюстрация на белом фоне. вектор.
Квантовая обработка. глубокое обучение искусственного интеллекта. будущие новые технологии для презентации бизнеса или науки. векторный фон
Теория векторной суммы лидерства
Чтобы быть эффективным лидером в технической области, вы должны уметь мыслить векторными суммами.
Векторы, правда? Что это означает?
Великий поэт А. Янкович однажды написал: «Векторное исчисление просто для развлечения». Итак, на самом деле мы не собираемся обсуждать исчисление, просто тригонометрию. Давайте посмотрим, сможем ли мы избежать воспоминаний о школьной математике, когда будем работать над этой идеей и ее последствиями. Думайте о векторе как о величине, которая имеет как величину, так и направление, например, ветер, дующий на северо-запад со скоростью 10 миль в час.
Каждый член команды вносит свой вклад в достижение или отклонение от целей вашего проекта. Величина вектора — это то, сколько вещей человек может сделать, а направление — это то, что он считает конечной целью своей работы. В отличие от отчета о ветре, направление может состоять из множества различных измерений, но основные принципы остаются в силе. Командой из одного человека управлять просто. Вы решаете, что делать, затем идите и делайте это. То, как быстро вы туда доберетесь, зависит только от того, насколько быстро вы сможете ехать.
В отличие от отчета о ветре, направление может состоять из множества различных измерений, но основные принципы остаются в силе. Командой из одного человека управлять просто. Вы решаете, что делать, затем идите и делайте это. То, как быстро вы туда доберетесь, зависит только от того, насколько быстро вы сможете ехать.
Что происходит, когда вы представляете нового члена команды?
Векторы суммируются. Геометрически вы можете представить вектор как стрелку с определенной длиной и направлением. Сложение — это сложение двух (или более) стрелок хвост к голове. Таким образом, два вектора равной величины, противоположные на 180 градусов, будут эффективно компенсировать друг друга. Два вектора одинаковой величины, направленные в одном и том же направлении, делают стрелку в два раза длиннее.
Если один член команды более продуктивный, возможно, более опытный инженер, его стрелка будет длиннее. Они окажут пропорционально большее влияние на то, чего может достичь вся команда и как. Но если два разных члена команды имеют разное представление о том, в каком направлении движется проект, в какой-то степени они будут работать в противоречии друг с другом.
Но если два разных члена команды имеют разное представление о том, в каком направлении движется проект, в какой-то степени они будут работать в противоречии друг с другом.
Вот что интересно: два вектора, которые в основном указывают в одном направлении, дают почти столько же преимуществ, как если бы они были точно выровнены.
Пример: член команды А тянет на северо-запад со скоростью 10 миль в час. Член команды B тянет на северо-восток со скоростью 10 миль в час. Если рассматривать это как прямоугольный треугольник и применить теорему Пифагора, вы получите приблизительно:
Вклад члена команды А: 7 миль в час по С, 7 миль в час по З
Вклад члена команды В: 7 миль в час по С, 7 миль в час по В
Вклад и компоненты W борются друг с другом, уравновешивая друг друга, и в итоге вы получаете 14 миль в час на север. Несмотря на то, что усилия членов команды направлены в совершенно разные направления, их общая эффективность составляет около 70%. В зависимости от вашего конкретного проекта, может быть, 70% — это очень хорошо, а может быть, это ужасно. Вот тут-то и появляется лидерство. Эффективный лидер помогает установить и сообщить об общей цели, чтобы лучше согласовать членов команды и предотвратить переделки. Это признак сильной команды.
Вот тут-то и появляется лидерство. Эффективный лидер помогает установить и сообщить об общей цели, чтобы лучше согласовать членов команды и предотвратить переделки. Это признак сильной команды.
Например, если мои математические расчеты верны, в случае, когда член команды A тянет NNW, а B тянет NNE, эффективность подскакивает с 70% до 92% (предполагая, как и раньше, что конечной целью было выполнить к северу). Небольшие корректировки курса могут хорошо окупиться.
В технических областях ожидается, что пожилые люди присоединятся не только для того, чтобы что-то делать, но и для того, чтобы помочь понять, что они и другие должны делать. В этом случае в системе есть элемент самокоррекции, поскольку люди склонны следовать общему направлению. Но когда это происходит, для лидера еще более важно тщательно и точно направлять команду к фактическому желаемому конечному состоянию, общаясь со всеми членами команды. Плохо спланированная, команда может триумфально прибыть к месту назначения, только чтобы обнаружить, что они не там, где им действительно нужно быть.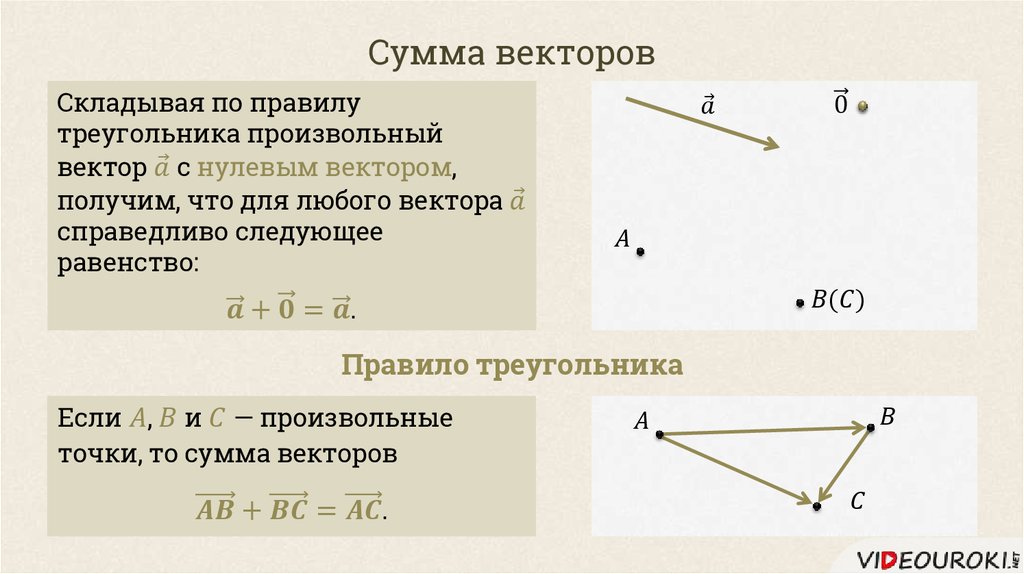
Что делать, если член команды движется не в том направлении?
В частности, менеджеры могут попасть в ловушку микроуправления, которое является грехом упущения сути. Как показал первый пример выше, даже довольно значительное расхождение не является немедленно катастрофическим для общего вектора команды. Как сказал поэт Д. Адамс, «Не паникуйте». Часть того, за что умным людям платят, — это выяснение того, что и как делать. Если один конкретный член команды постоянно указывает в неправильном направлении, наиболее распространенной причиной, по моему опыту, является неспособность руководства. Вполне возможно, что они не осознают, куда должны быть направлены их усилия. Если они не могут или не хотят корректировать курс, это другая (и более серьезная) проблема.
Великие менеджеры нанимают умных людей, следят за тем, чтобы они двигались в правильном направлении, а затем позволяют им продвигаться вперед как можно быстрее. Великие лидеры (которые могут совпадать со званием менеджера, а могут и не совпадать) опережают их ровно настолько, чтобы устранять препятствия до того, как они столкнутся с ними.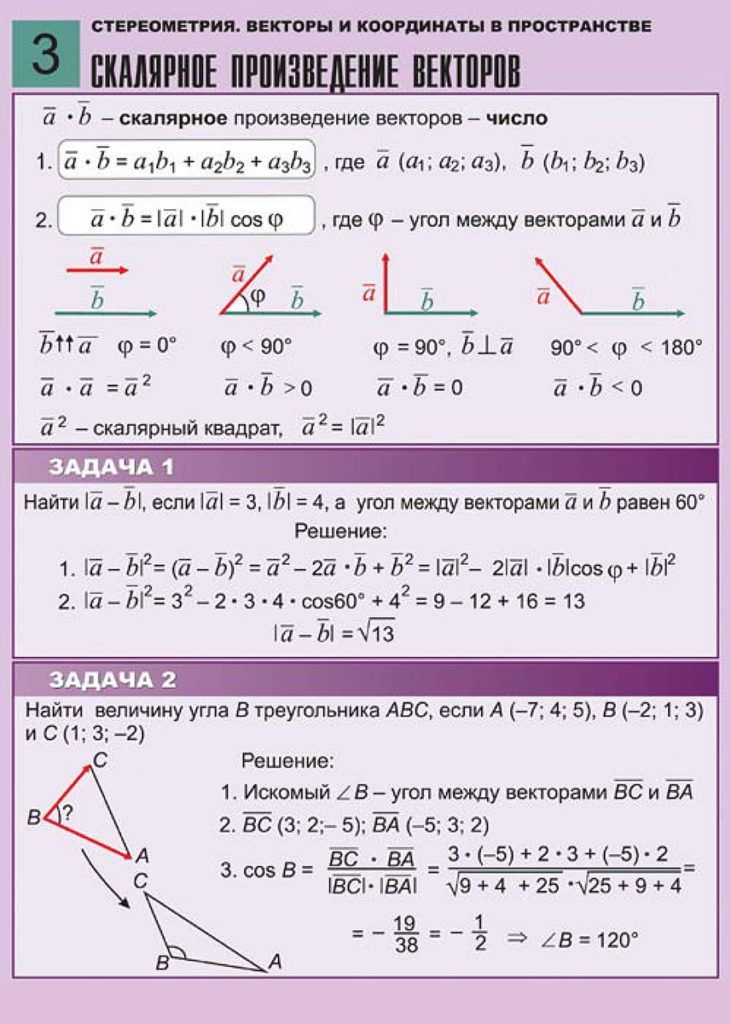 Именно в такой команде я хотел бы работать.
Именно в такой команде я хотел бы работать.
Личное заявление
Недавно я понял, что принцип суммы векторов применим и к многочисленным мыслям, крутящимся в моей голове. Нет, я не говорю об особой ситуации множественной личности после школы. Но каждый день в уме проносятся тысячи мыслей, и каждая имеет величину и направление. Для исполнительной функции очень важно, чтобы все они указывали в одном направлении, более или менее, чтобы быть эффективным человеком.
Это переформулировка популярной концепции, которая известна под разными названиями, например, «Персональный брендинг». Все ли, о чем вы думаете (и впоследствии действуете), помогает вам стать тем, кем вы хотите быть? У вас есть четкое представление, в каком направлении вам нужно двигаться? Что вы можете сделать, чтобы настроить свое мышление в этом направлении?
Я заметил недавнюю перемену в людях; чувство повышенной тревожности, отчужденности и дезориентации. Откровенно говоря, все больше и больше людей говорят мне, что в последнее время они чувствуют себя паршиво. Я готовлю более длительный проект, чтобы записать несколько выстраданных советов о том, как продолжать — продуктивно — несмотря на эти чувства. Люди постоянно читают книги и журналы о незначительных корректировках диеты и физических упражнений. Добавим к этому списку психическое здоровье.
Я готовлю более длительный проект, чтобы записать несколько выстраданных советов о том, как продолжать — продуктивно — несмотря на эти чувства. Люди постоянно читают книги и журналы о незначительных корректировках диеты и физических упражнений. Добавим к этому списку психическое здоровье.
Я работаю над книгой об этом. Присоединяйтесь к моему небольшому списку рассылки, чтобы получать обновления, доступ к ранним материалам, бесплатную инфографику со списком 13 незамедлительных действий, которые вы можете сделать для улучшения своего психического здоровья, и бесплатный мини-курс, который я могу написать так быстро, как только смогу.
Векторное картирование потоков: обзор от теории к практике
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл.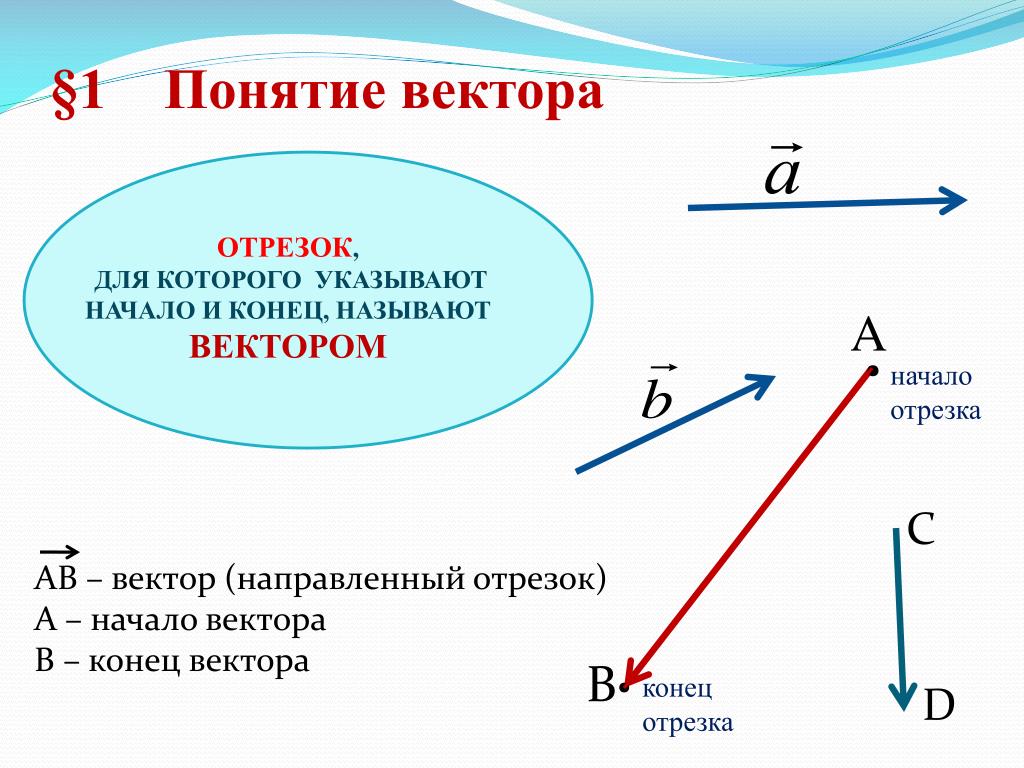 адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Полнотекстовые ссылки
Уайли
Полнотекстовые ссылки
Обзор
. 2021 авг; 38(8):1405-1413.
2021 авг; 38(8):1405-1413.
дои: 10.1111/эхо.15154. Epub 2021 14 июля.
Мартина Авесани 1 2 , Бастьен Дегрелль 1 , Джованни Ди Сальво 2 , Жан-Бенуа Тамбо 1 3 4 , Ксавьер Ириарт 1 3 4
Принадлежности
- 1 Отделение детской и взрослой врожденной кардиологии, Университетская клиника Бордо (CHU), Пессак, Франция.
- 2 Департамент женского и детского здоровья, Падуанский университет, Падуя, Италия.

- 3 Институт электрофизиологии и моделирования сердца, IHU Liryc, Fondation Bordeaux Université, Бордо, Франция.
- 4 Центр кардио-торакальных исследований Бордо, INSERM, Бордо, Франция.
- PMID: 34259359
- DOI: 10.1111/эхо.15154
Обзор
Martina Avesani et al. Эхокардиография. 2021 авг.
. 2021 авг; 38(8):1405-1413.
дои: 10.1111/эхо.15154.
Epub 2021 14 июля.
Авторы
Мартина Авесани 1 2 , Бастьен Дегрелль 1 , Джованни Ди Сальво 2 , Жан-Бенуа Тамбо 1 3 4 , Ксавьер Ириарт 1 3 4
Принадлежности
- 1 Отделение детской и взрослой врожденной кардиологии, Университетская клиника Бордо (CHU), Пессак, Франция.
- 2 Департамент женского и детского здоровья, Падуанский университет, Падуя, Италия.
- 3 Институт электрофизиологии и моделирования сердца, IHU Liryc, Fondation Bordeaux Université, Бордо, Франция.

- 4 Центр кардио-торакальных исследований Бордо, INSERM, Бордо, Франция.
- PMID: 34259359
- DOI: 10.1111/эхо.15154
Абстрактный
Фон: Интерес к анализу внутрисердечного кровотока быстро растет, что стимулирует разработку различных неинвазивных методов визуализации. Среди них векторное картирование потока (VFM), объединяющее данные цветного доплеровского картирования и данные отслеживания спеклов, кажется многообещающим подходом, применимым для взрослых и детей.
Цель обзора: Цель этого обзора — дать историческую перспективу развития метода VFM и краткое изложение текущих алгоритмов и параметров, потенциально поддающихся оценке. Затем мы представим современное состояние VFM с обзором клинических исследований и применений этой техники.
Затем мы представим современное состояние VFM с обзором клинических исследований и применений этой техники.
Ключевые слова: анализ потока; векторное картирование потоков; вихрь.
© 2021 ООО «Вайлей Периодикалс».
Похожие статьи
Точность и ограничения векторного картирования потока: проверка фантома левого желудочка с использованием велосиметрии изображения стереочастиц.
Асами Р., Танака Т., Кавабата К.И., Хашиба К., Окада Т., Нишияма Т. Асами Р. и др. J Эхокардиогр. 2017 июнь;15(2):57-66. doi: 10.1007/s12574-016-0321-5. Epub 2016 15 ноября. J Эхокардиогр. 2017. PMID: 27848215 Бесплатная статья ЧВК.
Ультразвуковое векторное картирование сосудистого потока для двумерной оценки кровотока.

Р. Асами, Т. Танака, М. Симидзу, Ю. Секи, Т. Нишияма, Х. Сакашита, Т. Окада. Асами Р. и др. Ультразвук Медицина Биол. 2019 июль;45(7):1663-1674. doi: 10.1016/j.ultrasmedbio.2019.02.014. Epub 2019 16 апр. Ультразвук Медицина Биол. 2019. PMID: 31003710
Оценка гемодинамики и функции левого желудочка у больных с уремией по вихреобразованию с использованием векторного картирования потока.
Чен Р., Чжао Б.В., Ван Б., Тан Х.Л., Ли П., Пан М., Сюй Л.Л. Чен Р. и др. Эхокардиография. 2012 Октябрь; 29 (9): 1081-90. doi: 10.1111/j.1540-8175.2012.01737.x. Epub 2012 14 июня. Эхокардиография. 2012. PMID: 22694735
Лазерный допплер, спекл и родственные методы картирования и визуализации перфузии крови.
Брайерс Д.
 Д.
Брайерс Дж. Д.
Физиол Изм. 2001 ноябрь; 22(4):R35-66. дои: 10.1088/0967-3334/22/4/201.
Физиол Изм. 2001.
PMID: 11761081
Обзор.
Д.
Брайерс Дж. Д.
Физиол Изм. 2001 ноябрь; 22(4):R35-66. дои: 10.1088/0967-3334/22/4/201.
Физиол Изм. 2001.
PMID: 11761081
Обзор.Визуализация внутрисердечного кровотока: текущее состояние и будущие направления.
Родригес Муньос Д., Маркл М., Мойя Мур Х.Л., Баркер А., Фернандес-Гольфин С., Ланселлотти П., Саморано Гомес Х.Л. Родригес Муньос Д. и др. Eur Heart J Cardiovasc Imaging. 2013 ноябрь;14(11):1029-38. doi: 10.1093/ehjci/jet086. Epub 2013 1 августа. Eur Heart J Cardiovasc Imaging. 2013. PMID: 23
2
Бесплатная статья ЧВК.
Обзор.
Посмотреть все похожие статьи
использованная литература
ССЫЛКИ
- Гариб М., Кремерс Д., Кучесфахани М. и др. Видение Леонардо визуализации потока.
 Опытные жидкости; 33:219-223.
Опытные жидкости; 33:219-223.
- Гариб М., Кремерс Д., Кучесфахани М. и др. Видение Леонардо визуализации потока.
- Херадвар А., Рикерс С., Морисава Д. и соавт. Диагностическое и прогностическое значение образования сердечно-сосудистых вихрей. Дж Кардиол. 2019;74(5):403-411.
- Dyverfeldt P, Bissell M, Barker AJ, et al. Согласованное заявление магнитно-резонансной томографии сердечно-сосудистой системы 4D потока. J Cardiovasc Magn Reson. 2015;17(1):72. 10.
- Фон Кнобельсдорф-Бренкенхофф Ф., Шульц-Менгер Дж. Роль сердечно-сосудистого магнитного резонанса в рекомендациях Европейского общества кардиологов. J Cardiovasc Magn Reason. 2016;18:6. 22.
- Меле Д.
 , Смарраццо В., Педриццетти Г. и др. Анализ внутрисердечного кровотока: методы и потенциальные клинические применения. J Am Soc Эхокардиогр. 2019;32(3):319-332.
, Смарраццо В., Педриццетти Г. и др. Анализ внутрисердечного кровотока: методы и потенциальные клинические применения. J Am Soc Эхокардиогр. 2019;32(3):319-332.
- Меле Д.
Типы публикаций
термины MeSH
Полнотекстовые ссылки
Уайли
Укажите
Формат: ААД АПА МДА НЛМ
Отправка в
[PDF] Спорные векторные машины: Теория и приложения
- DOI: 10.1007/3-540-44673-7_12
- Corpus ID: 31510638 9028
8.
 ppurespROVER.
title={Машины опорных векторов: теория и приложения},
автор={Теодорос Евгений и Массимилиано Понтил},
booktitle={Машинное обучение и его приложения},
год = {2001}
}
ppurespROVER.
title={Машины опорных векторов: теория и приложения},
автор={Теодорос Евгений и Массимилиано Понтил},
booktitle={Машинное обучение и его приложения},
год = {2001}
} В этой главе представлен краткий обзор вопросов, обсуждавшихся в ходе однодневного семинара «Теория и приложения методов опорных векторов (SVM)», организованного в рамках Продвинутого курса по искусственному интеллекту (ACAI ’99) в Ханье, Греция [19]. Цель главы двоякая: представить обзор базовой теории и современного понимания SVM, а также обсудить представленные документы, а также вопросы, возникшие во время семинара.
Просмотр через Publisher
svms.orgМетоды опорных векторов для регрессии: краткий обзор формул крупномасштабного и линейного программирования Кесада Карреон, Х. Росилес
Информатика
- 2013
Вводятся наиболее распространенные методы обучения для SVR и объясняются формулировки SVR на основе линейного программирования, подчеркивая их пригодность для крупномасштабного обучения.
Эмфатические ограничения Машина опорных векторов
- Мостафа Сабзекар, Х. Язди, Махмуд Нагибзаде, С. Эффати , называемая нечеткой ESVM (FESVM), которая сможет одновременно учитывать степень важности выборок как в функции стоимости, так и в ограничениях.
Аппроксимация ступенчатой функции для сокращения опорного вектора
- А. Аллахьяр, Х. Язди
Информатика
- 2013
стандартная SVM с дополнительными ограничениями для уменьшения количества опорных векторов, которые могут быть определены пользователем.
НОВЫЙ ПОДХОД Обертки ДЛЯ ВЫБОРА ПЕРЕМЕННЫХ В МАШИНЕ ОПОРНЫХ ВЕКТОРОВ
- Satoru Koda, R. Nishii, Yuta Fukasawa
Информатика
- 2016
В этой статье предлагаются два критерия выбора переменных для SVM, которые используют методы-оболочки, которые измеряют вклад каждой переменной в целевую функцию.

Схемы классификации с учителем и без учителя на основе SVM
- Л. Стэйт, Юлиана Параскив-Мунтяну
Информатика
- 2010
Алгоритм обучения тестированию производительности в ядре и машине для вспомогательного вектора случай нелинейно разделимых данных с использованием последовательной минимальной оптимизации, введенной Дж. К. Платтом в 1999 предлагается.
Использование машин опорных векторов для прогнозирования производительности нейронных сетей MLP
Использование машин опорных векторов (SVM) для прогнозирования производительности алгоритмов обучения на основе особенностей задач обучения в своего рода метаобучении показало, что SVM получили лучшие результаты в прогнозировании производительности MLP по сравнению с эталонными алгоритмами, примененными в предыдущей работе.
Классификация с использованием метода опорных векторов с градуированным разрешением
По сравнению с традиционным SVM алгоритм SVM-GR требует меньшего количества обучающих выборок и опорных векторов, поэтому требования к вычислительному времени и памяти намного меньше, чем у обычного SVM, использующего весь набор данных.

Использование низкоранговой аппроксимации для повышения эффективности метода опорных векторов и приложений
- М. Эсмаилбейги, О. Чатрабгун
Медицина
- 2020
- А. Чевик, А. Куртоглу, М. Бильгехан, М. Э. Гюльшан, Хасан М. Албегмпрли
Инженерия, информатика
2015 9 2015 Результаты показали 60 90 9 9 что SVM превосходит различные другие методы обучения, учитывая возможности обобщения созданной модели.- Т. Вайзе, Стефан Ахлер, Мартин Гёб, Кристиан Фойгтманн, М. Цапф
Информатика
- 2007
- Э. Осуна, Р. Фройнд, Ф. Джироси
Информатика
- 1997
- B.
 Schölkopf, Alex Smola, R. C. Williamson, P. Bartlett
Schölkopf, Alex Smola, R. C. Williamson, P. Bartlett Commortion Science
Neural Computation
- 2000 .
- К. Краммер, Ю. Сингер
Информатика, математика
Дж. Мах. Учиться. Рез.
- 2001
- T. Evgeniou, M. Pontil, T. Poggio
Информатика
- 1999
- John C. Platt
Информатика
- 1999
Progress of Theoretical Physics Vol. 18 № 6 (1957) стр. 573–590
Описание материи Паули как непрерывной совокупности малых вращающихся тел Такехико Такабаяси и Жан-Пьер Вижье
Progress of Theoretical Physics Vol. 36 No. 1 (1966) pp. 72–85
Новый вывод классических моделей вращающегося электрона из ВКБ-решений уравнений Паули и Дирака Хисаити Ямасаки
Progress of Theoretical Physics Vol. 43 № 4 (1970) 861–869
Формулировка принципа неопределенности в соответствии с гидродинамической моделью квантовой механики HE Wilhelm
Progress of Theoretical Physics Vol. 1983. Т. 69, № 5. С. 1323–1344. 70 № 1 (1983) стр. 1–17
Вихрь, спин и триада для квантовой механики вращающихся частиц.
 0003
0003Copyright (c) 1955 Успехи теоретической физики
Раздел выпуска:
Статьи
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Метод точного стационарного решения уравнения Вадати-Конно-Ичикавы-Симидзу (WKIS)
Гравитационные волны от частицы на круговых орбитах вокруг черной дыры Шварцшильда до 22-го постньютоновского порядка
Применение подхода фиксированного масштаба к статическим энергиям без кварков в закаленной и 2 + 1 ароматической решетке КХД с улучшенным действием кварка Вильсона
Кварк-антикварковые потенциалы из амплитуд Намбу-Бете-Солпитера на решетке
Разделение кирального и деконфайнментного фазовых переходов в искривленном пространстве-времени
Реклама
Семь векторов развития идентичности Чикеринга
На этой странице будут рассмотрены следующие теории:
- Семь векторов развития идентичности Чикеринга и Рейссера
- Влияние окружающей среды на развитие идентичности
Чикеринг и Рейссер (1993)
- Семь векторов:
- Развитие компетенции —
- Человек развивается в рамках интеллектуальных, физических и ручных навыков, а также навыков межличностного общения.

- Интеллектуальная компетентность характеризуется способностью рассуждать и навыками критического мышления
- Физическая и мануальная компетентность характеризуется вовлеченностью и вниманием к оздоровительным, артистическим и спортивным занятиям
- Межличностная компетентность характеризуется способностью хорошо общаться и работать с другими
- Человек развивается в рамках интеллектуальных, физических и ручных навыков, а также навыков межличностного общения.
- Развитие компетенции —
- Управление эмоциями —
- Человек становится компетентным в своей способности распознавать эмоции и управлять ими
- Объединение всех эмоций и способность человека разумно управлять своими реакциями на события
- Движение через автономию к взаимозависимости —
- Человек развивает способность иметь независимый взгляд на жизнь, но понимает, что успешные отношения основаны на взаимозависимости
- Развитие зрелых межличностных отношений
- Человек развивает межкультурные отношения, уважение к другим и терпимость к окружающим
- Рейссер (1995) указывает, что этот вектор указывает на способность принимать других, уважать различия и ценить общность
- Установление личности
- Индивидуум проходит через свою идентичность, чтобы выйти со здоровой самооценкой во всех аспектах идентичности
- Разработка Цель
- Человек имеет твердые взгляды на профессиональную жизнь, находит смысл в своих собственных интересах и устанавливает позитивные отношения с другими
- Развитие честности
- Индивидуум способен сформулировать и подражать своим собственным ценностям, утвержденным как личность, через три этапа: гуманизация ценностей, персонализация ценностей и развитие конгруэнтности
Влияние окружающей среды
- Учреждение может влиять на векторы человека через множество влияний
- Институциональные цели – Последовательность в политике, программах и объектах может привести к тому, что люди оспорят или примут
- Размер учебного заведения — Степень, в которой учащийся имеет возможность участвовать в жизни более крупного сообщества
- Отношения между студентами и преподавателями – Позитивные отношения способствуют более глубокому интеллектуальному и семейному самосознанию людей
- Учебная программа — Люди, которые лучше понимают свою учебную программу, имеют более высокую способность сталкиваться с ситуациями и критически рассуждать в них
- Преподавание – Активное участие в обучении помогает учащимся развивать лучшие межличностные отношения и позитивную межкультурную идентичность
- Дружба и студенческие сообщества – Люди лучше всего учатся друг у друга и в зависимости от ситуации
- Программы и услуги по развитию учащихся .
 Среда совместной работы необходима для реализации программ, бросающих вызов учащимся и поддерживающих их
Среда совместной работы необходима для реализации программ, бросающих вызов учащимся и поддерживающих их
Увещевания
- Три основных элемента учебной среды для позитивного развития
- Интеграция работы и обучения – Преднамеренная интеграция возможностей трудоустройства в кампусе и создание способов для студентов найти стажировку и, в конечном итоге, работу
- Признание и уважение индивидуальных различий – Педагоги должны активно осознавать различия и создавать условия для обучения друг друга и каждого учащегося
- Признание циклического характера обучения и развития – Предоставление возможности бросить вызов и расширить мыслительные процессы человека, получить более глубокое понимание себя и других
Эта страница была написана и создана Мишель Робинсон . Пожалуйста, используйте раздел комментариев ниже, чтобы задать вопросы, поделиться мыслями, обсудить и/или оставить отзыв.

1 Низкие результаты экспериментов показывают, что ранговая ядерная аппроксимация машины опорных векторов, сохраняя при этом производительность классификации в приемлемом диапазоне, время вычислений было значительно сокращено.
Машины опорных векторов в проектировании конструкций: обзор
Развивающиеся классификаторы — эволюционные алгоритмы интеллектуального анализа данных
Подход к использованию эволюционных алгоритмов для выведения систем нечетких классификаторов представлен как часть структурированной процедуры, выполненной студентами Ахлером, Гобом и Фойгтманном в качестве вклада в Data-Mining-2006.
 Кубок конкурса, дающий обнадеживающе положительные результаты.
Кубок конкурса, дающий обнадеживающе положительные результаты.ПОКАЗАНЫ 1-10 ИЗ 72 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантностьНаиболее влиятельные статьиНедавность
Исследование машин с редуцированными опорными векторами
Показано, что формулировка RSVM уже находится в форме линейного SVM, и обсуждаются четыре реализации RSVM, что указывает на то, что в целом точность теста RSVM немного ниже, чем у стандартного SVM.
Методы опорных векторов: обучение и применение
Представлены предварительные результаты по распознаванию лица человека, полученные с применением SVM в реальных изображениях, а основной идеей декомпозиции является итеративное решение подзадач и оценка, а также установление критериев остановки алгоритма.
Новые алгоритмы векторного вектора поддержки
666.s. Neval Ergissivation
.s. Neval Argissivation
. исключает один из других свободных параметров алгоритма: параметр точности в случае регрессии и константу регуляризации C в случае классификации.
Сравнение методов мультиклассовых машин опорных векторов
Приведены реализации декомпозиции для двух мультиклассовых SVM-методов «все вместе» и показано, что для больших задач методы, рассматривающие все данные сразу, в целом требуют меньшего количества опорных векторов.
Об алгоритмической реализации мультиклассовых векторных машин на основе ядра
В этой статье описывается алгоритмическая реализация многоклассовых векторных машин на основе ядра с использованием обобщенного понятия маржи для многоклассовых задач, а также описывается эффективный алгоритм с фиксированной точкой для решения упрощенных задач оптимизации и доказывается его сходимость.

Унифицированная структура для сетей регуляризации и машин опорных векторов
Эта работа представляет Support Machine в унифицированных сетях регуляризации и рамки в контексте теории статистического обучения Вапника, которая обеспечивает общую основу для проблемы обучения, сочетая функциональный анализ и статистику.
Быстрое обучение метода опорных векторов с использованием последовательной минимальной оптимизации, достижения в методах ядра
SMO разбивает эту большую задачу квадратичного программирования на ряд наименьших возможных задач QP, что позволяет избежать использования трудоемкой численной оптимизации QP в качестве внутреннего цикла и следовательно, SMO является самым быстрым для линейных SVM и разреженных наборов данных.

Машины опорных векторов для категоризации спама
Использование машин опорных векторов для классификации электронной почты как спама или неспама изучается путем сравнения его с тремя другими алгоритмами классификации: Ripper, Rocchio и повышающими деревьями решений, которые показали, что SVM работает лучше всего при использовании двоичных функций.
Статистическая теория обучения. эти оценки реальных проблем и многое другое.
Машины опорных векторов для классификации изображений на основе гистограмм
Замечено, что простое переназначение входных данных x(i) -> x(i)(a) улучшает производительность линейных SVM до такой степени, что их, для этой проблемы, действующую альтернативу ядрам RBF.
Векторное представление вращающейся частицы в квантовой теории, I* | Успехи теоретической физики
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Такехико Такабаяси
Такехико Такабаяси
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Progress of Theoretical Physics , Volume 14, Issue 4, October 1955, Pages 283–302, https://doi.
 org/10.1143/PTP.14.283
org/10.1143/PTP.14.283Опубликовано:
01 октября 1955 г.
История статьи
Получено:
22 июля 1955 г.
Опубликовано:
01 октября 1955 г.
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Квантово-механическая нерелятивистская вращающаяся частица представлена эквивалентно нелинейному векторному полю, которое определяет новый вид гидродинамики вращающейся жидкости.
 В этой гидродинамике квантовые эффекты выделяются как нелинейные термины, означающие возникновение «внутреннего потенциала» и «внутреннего магнитного поля».
В этой гидродинамике квантовые эффекты выделяются как нелинейные термины, означающие возникновение «внутреннего потенциала» и «внутреннего магнитного поля».Математически метод основан на замене исходного исчисления в терминах спинора ψ исчислением в терминах тензоров, сформированных как билинейные выражения в ψ * . Эта статья (далее именуемая I ), а также большая часть последующей (далее именуемой II ), которые будут появляться последовательно, являются переводом статьи, опубликованной в Soryusiron-Kenkyu 7 , стр. 600. –640, (19 января55) на японском языке, а краткий отчет об этих работах содержится в Prog. Теор. физ. 12 (1954), 810. Совсем недавно появились статьи Бома, Шиллера и Темно (Nuovo Cimento 1 , Suppl. (1955), 48, 67), в которых они независимо от нас исследовали подобные гидродинамические метод с целью «каузальной интерпретации» квантовой теории в случае нерелятивистской вращающейся частицы.
 Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения и ψ. Эта замена обеспечивается установлением тождеств, которые должны выполняться среди этих тензорных величин.
Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения и ψ. Эта замена обеспечивается установлением тождеств, которые должны выполняться среди этих тензорных величин.*
Эта статья (далее именуемая I ), а также большая часть последующей (далее именуемой II ), которые будут появляться последовательно, являются переводом статьи, появившейся в Soryusiron-Kenkyu 7 , стр. 600–640, (19 января55) на японском языке, а краткий отчет об этих работах содержится в Prog. Теор. физ. 12 (1954), 810.
Совсем недавно появились статьи Бома, Шиллера и Темно (Nuovo Cimento 1 , Suppl. (1955), 48, 67), в которых они независимо от нас исследовали аналогичный гидродинамический метод с целью «каузальной интерпретации» квантовой теории в случае нерелятивистской вращающейся частицы.
 Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения.
Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения.Ссылки
1)
Такабаяси
Т.
. ,
Прог. Теор. физ.
,
1952
, том.
8
10.1143/ptp.8.143
10.1143/ptp.9.187
2)
BOHM
D.
,
Vigier
9000.. P.,
.. P.
. ,
Физ. Ред.
,
1954
, том.
96
10.
 1103/PhysRev.96.208
1103/PhysRev.96.2083)
Pauli
W.
. ,
Хелв. физ. Acta
,
1939
, том.
12
стр.
147
4)
Proca
А.
. ,
J. Phys. Рад.
,
1954
, том.
15
стр.
65
5)
Дарвин
К. Г.
. ,
Проц. Р. Соц. А
,
1927
, том.
A116
стр.

227
6)
Паули
В.
. ,
ЗС. ф. физ.
,
1927
, том.
43
стр.
601
7)
Крамерс
Х. А.
. Акад. Verlagsgsell.
стр.
259
8)
Маделунг
E.
. ,
ЗС. ф. физ.
,
1926
, том.
40
стр.
332
9)
Бом
Д.

. ,
Физ. Ред.
,
1952
, том.
84
10.1103/PhysRev.84.166
10.1103/PhysRev.84.180
10)
Herring
C.
,
Kittel
C.,
Kittel
C.
.. ,
Физ.
,
1951
, том.
81
10.1103/Physrev.81.869
11)
Hönl
H.
,
Papapetrou
Z.
. ,
ЗС. ф. физ.
,
1939
, том.

112
стр.
512
Ссылка на статью(и):


 Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.
Алгебраическая и тригонометрическая форма комплексного числа. Формула Эйлера, формула Муавра. Извлечение корней из комплексных чисел.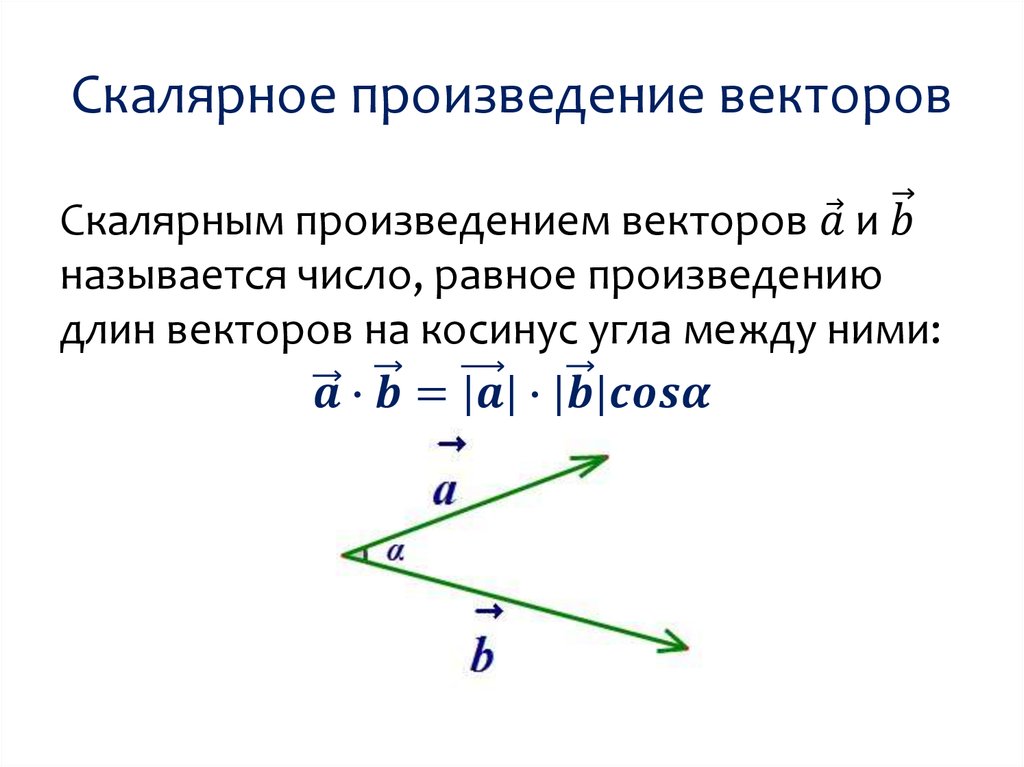 ниже)
ниже)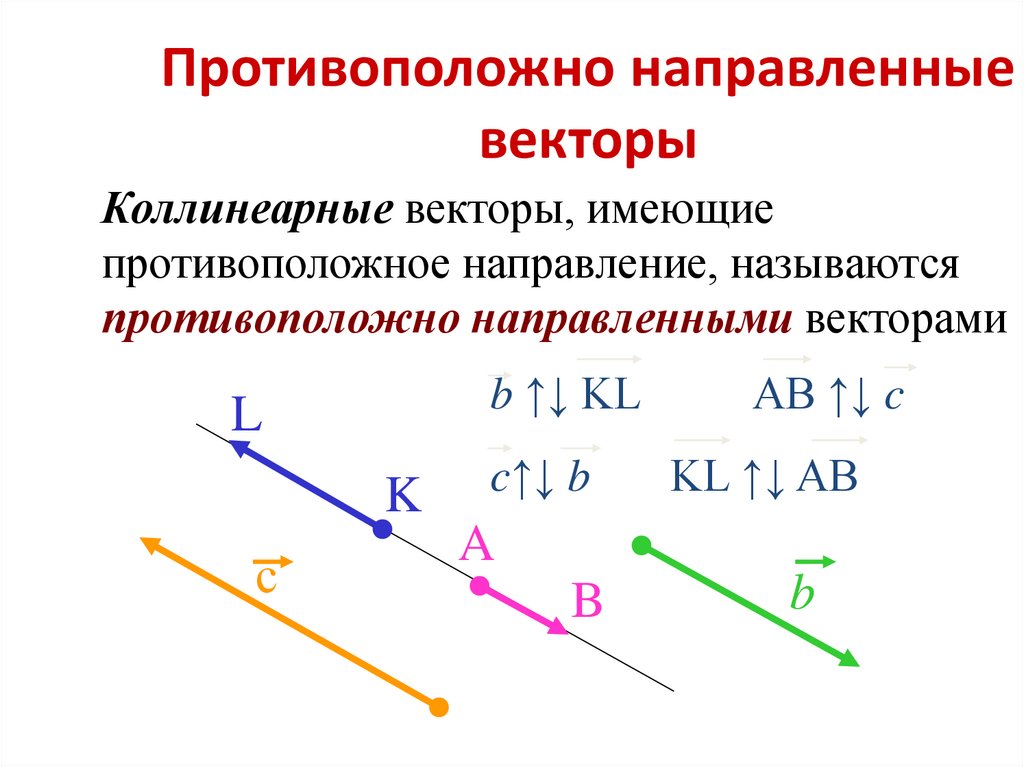 В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009.
В. Контрольные задания по аналитической геометрии для студентов 1 курса. — М., 2009.



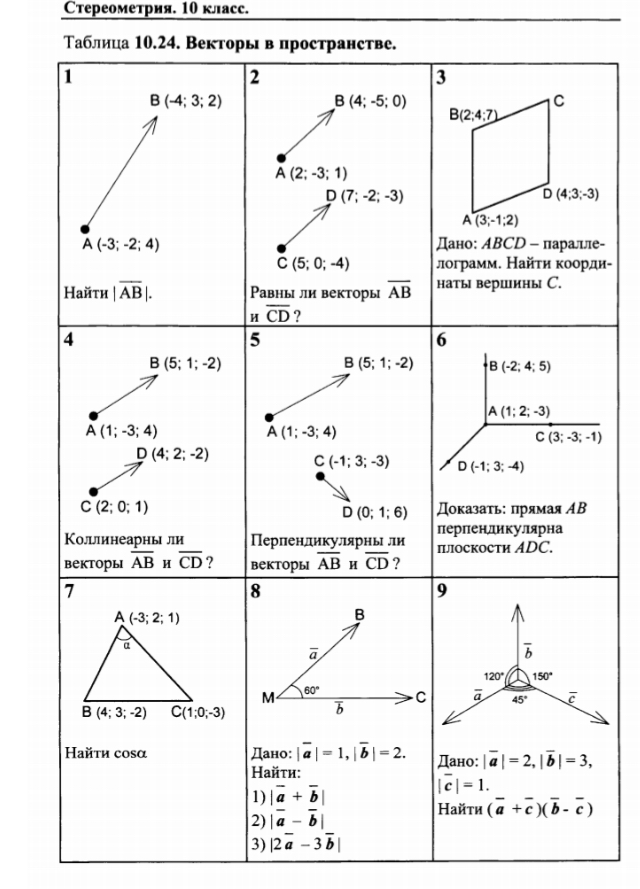 Д.
Брайерс Дж. Д.
Физиол Изм. 2001 ноябрь; 22(4):R35-66. дои: 10.1088/0967-3334/22/4/201.
Физиол Изм. 2001.
PMID: 11761081
Обзор.
Д.
Брайерс Дж. Д.
Физиол Изм. 2001 ноябрь; 22(4):R35-66. дои: 10.1088/0967-3334/22/4/201.
Физиол Изм. 2001.
PMID: 11761081
Обзор.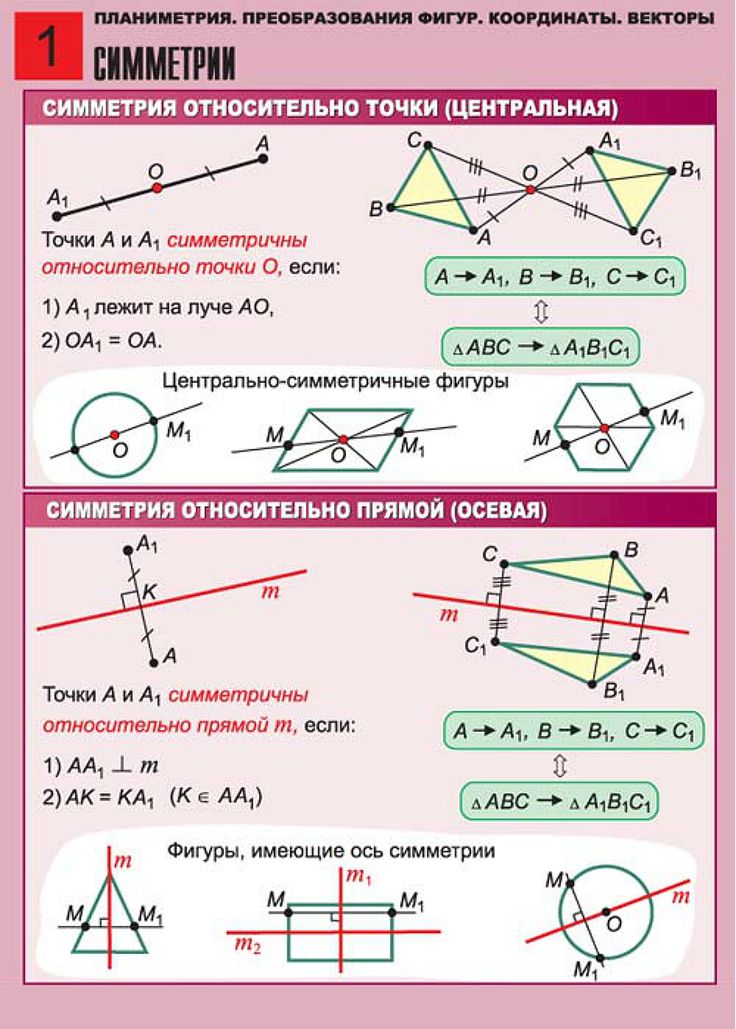 Опытные жидкости; 33:219-223.
Опытные жидкости; 33:219-223. , Смарраццо В., Педриццетти Г. и др. Анализ внутрисердечного кровотока: методы и потенциальные клинические применения. J Am Soc Эхокардиогр. 2019;32(3):319-332.
, Смарраццо В., Педриццетти Г. и др. Анализ внутрисердечного кровотока: методы и потенциальные клинические применения. J Am Soc Эхокардиогр. 2019;32(3):319-332. ppurespROVER.
title={Машины опорных векторов: теория и приложения},
автор={Теодорос Евгений и Массимилиано Понтил},
booktitle={Машинное обучение и его приложения},
год = {2001}
}
ppurespROVER.
title={Машины опорных векторов: теория и приложения},
автор={Теодорос Евгений и Массимилиано Понтил},
booktitle={Машинное обучение и его приложения},
год = {2001}
} 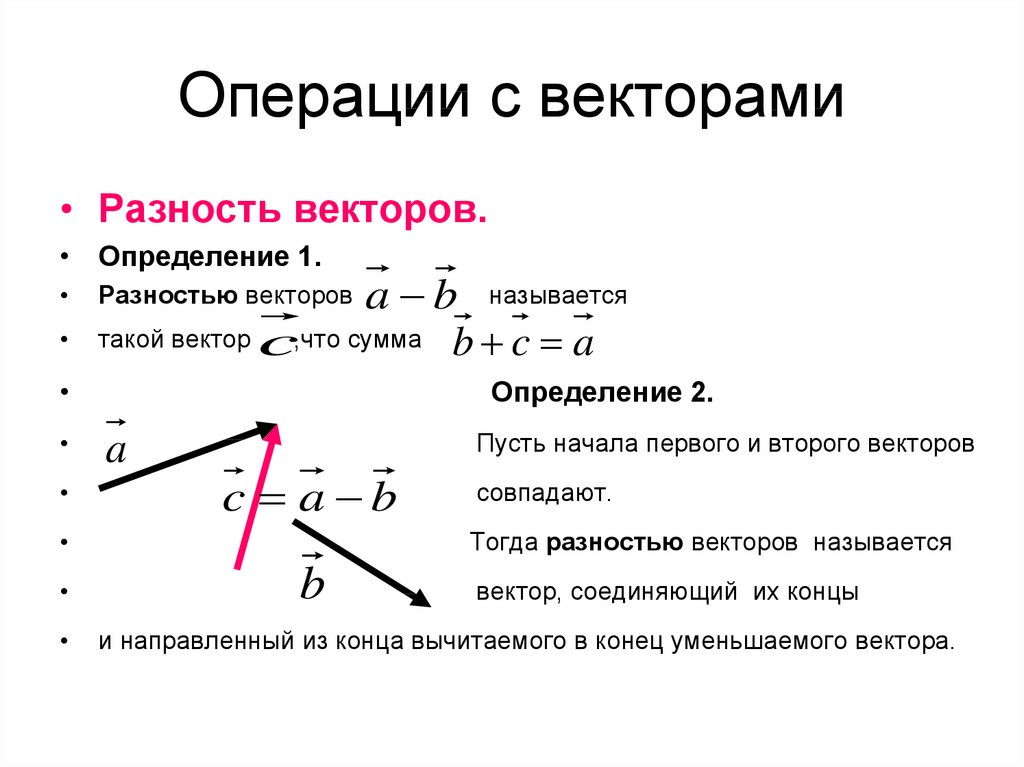
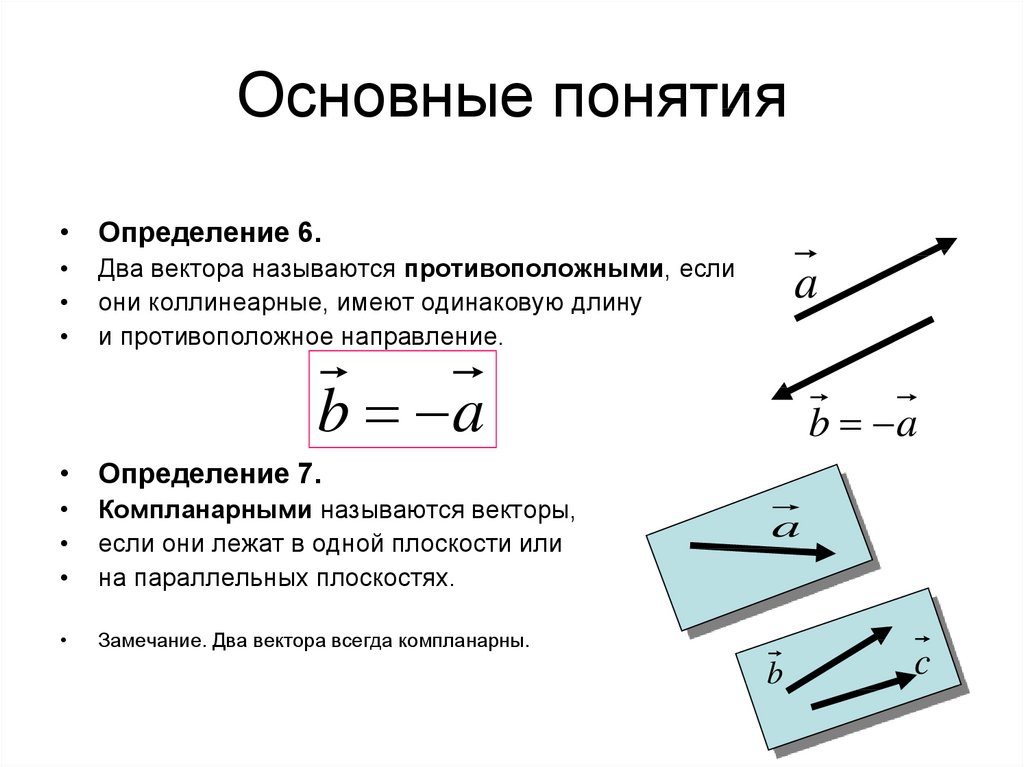
 Кубок конкурса, дающий обнадеживающе положительные результаты.
Кубок конкурса, дающий обнадеживающе положительные результаты.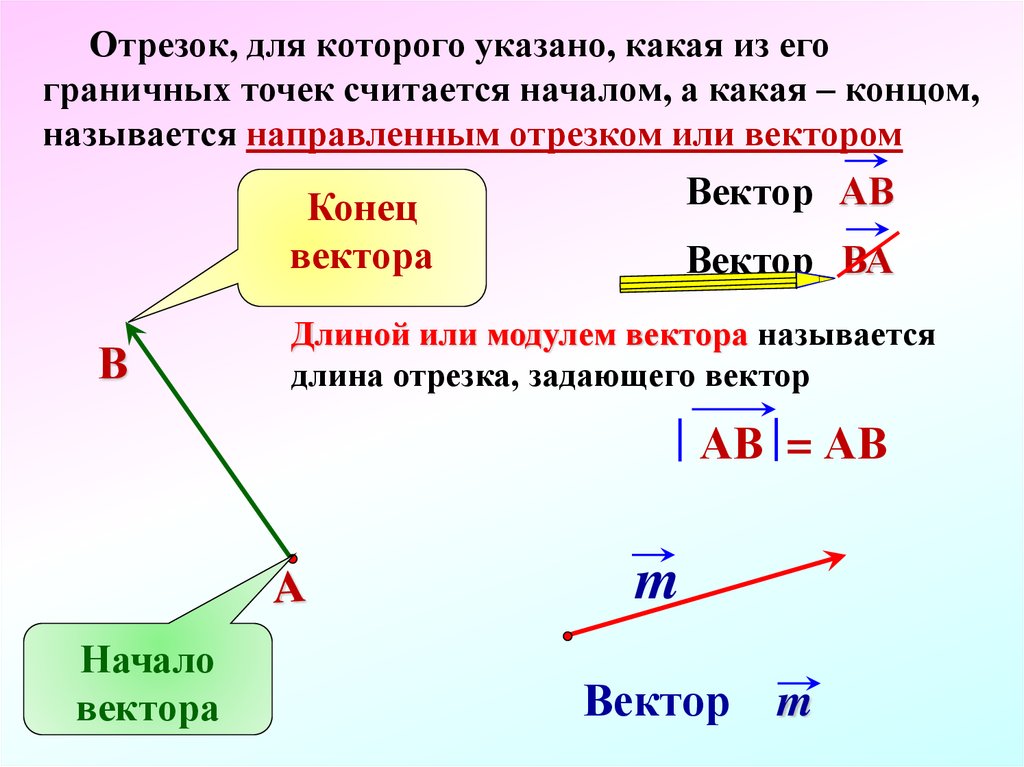 Schölkopf, Alex Smola, R. C. Williamson, P. Bartlett
Schölkopf, Alex Smola, R. C. Williamson, P. Bartlett
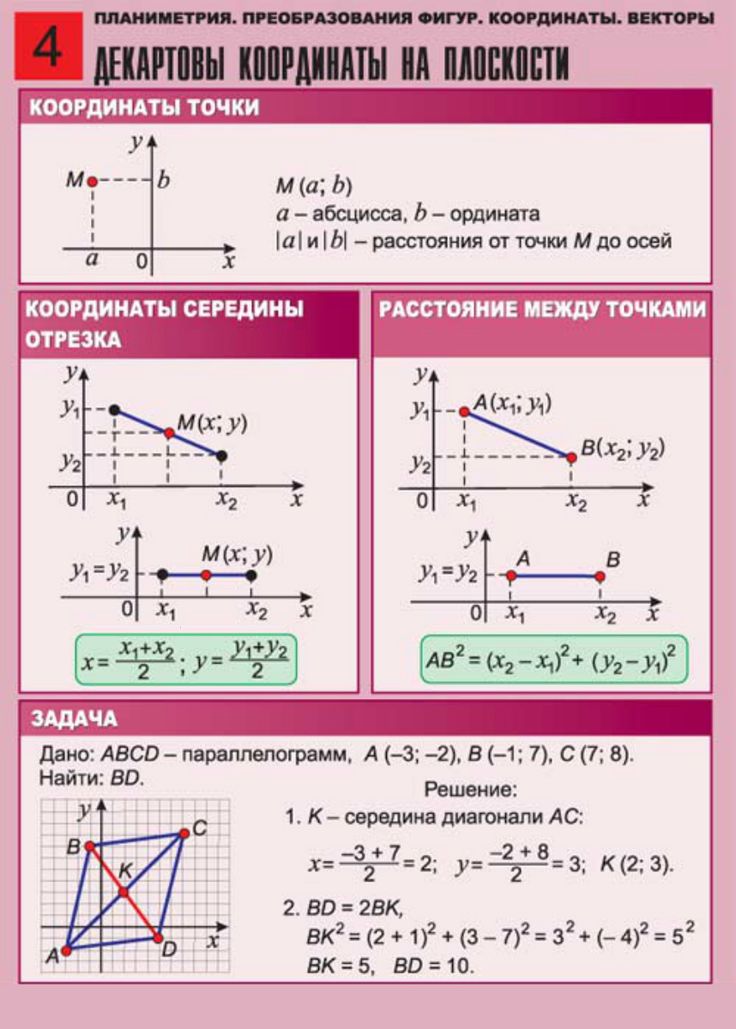
 org/10.1143/PTP.14.283
org/10.1143/PTP.14.283 org/ 10.1143/ПТП.14.283
org/ 10.1143/ПТП.14.283 В этой гидродинамике квантовые эффекты выделяются как нелинейные термины, означающие возникновение «внутреннего потенциала» и «внутреннего магнитного поля».
В этой гидродинамике квантовые эффекты выделяются как нелинейные термины, означающие возникновение «внутреннего потенциала» и «внутреннего магнитного поля». Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения и ψ. Эта замена обеспечивается установлением тождеств, которые должны выполняться среди этих тензорных величин.
Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения и ψ. Эта замена обеспечивается установлением тождеств, которые должны выполняться среди этих тензорных величин. Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения.
Однако их метод основан на представлении спинора под углом Эйлера (ср. II ), не связанный непосредственно с автономной тензорной формулировкой спинорного уравнения. 1103/PhysRev.96.208
1103/PhysRev.96.208
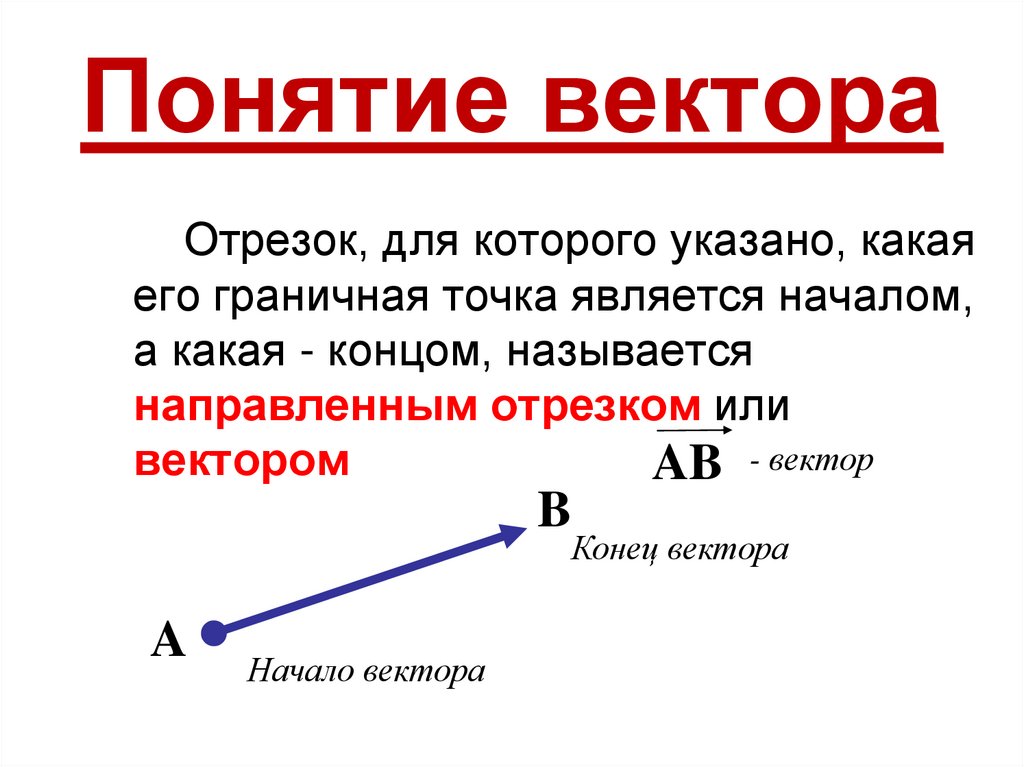

 0003
0003
 Среда совместной работы необходима для реализации программ, бросающих вызов учащимся и поддерживающих их
Среда совместной работы необходима для реализации программ, бросающих вызов учащимся и поддерживающих их