Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
В теории электромагнитного поля применяется некоторый традиционный математический аппарат, без которого невозможно построить ясное и обозримое изложение. К числу математических средств, которые нам потребуются, относятся разделы векторной алгебры и векторного анализа. Эти разделы в общем знакомы из курса высшей математики, однако в нашем курсе они тоже будут кратко описаны.
Первым необходимым понятием являются скалярные и векторные величины.
В математике и технике приходится иметь дело с величинами двух родов: одни из величин связаны с понятием о направлении в пространстве, другие имеют чисто числовой характер и не связаны с направлением. Рассмотрим например, температуру, массу, плотность, энергию, перемещение точки, скорость, ускорение, силу. Четыре последние величины резко отличаются от первых тем, что с ними обязательно должно быть связано понятие о направлении: например, точка может перемещаться вверх или вниз, вперед или назад.
Наоборот, температура, например, не имеет направления. и чтобы охарактеризовать ее, мы должны измерить ее например, в градусах Цельсия, полученное число и даст величину температуры. Точно так же можно измерить в соответствующих единицах массу, плотность и т.п. Эти величины принадлежат к классу величин, называемых скалярами.
Скаляром называется величина, характеризующаяся при выбранной единице меры одним числом.
Рассмотрим теперь один из векторов – скорость точки. Указания величины скорости, измеренной, например в м\с недостаточно для характеристики скорости. Нужно еще знать направление движения точки. Точно так же имеют определенное направление и ускорение точки, и сила, действующая на точку. Дадим поэтому следующее определение:
Вектором называется величина, характеризующаяся, помимо измеряющего ее числа, еще своим направлением в пространстве.
Простейшим вектором является прямолинейный
отрезок 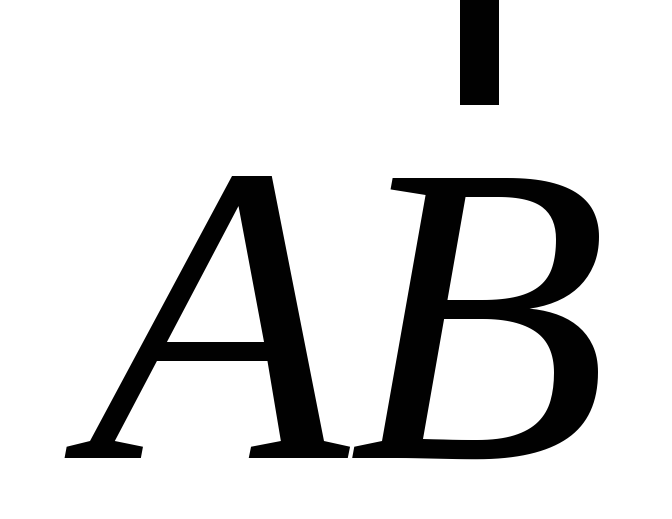 ,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
На чертежах векторы изображаются
стрелками (рисунок Error: Reference source not found).
Направление стрелки указывает на
направление вектора, длина стрелки дает
длину вектора. Обычно векторы обозначаются
жирными латинскими буквами: 
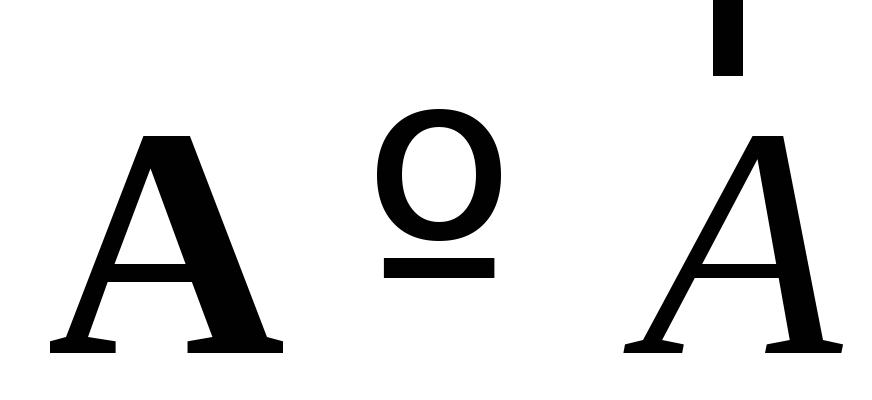 .
. 
− Вектор AB
Иногда приходится рассматривать величины тоже направленного характера, но более сложного, чем векторы, строения. Эти величины называются тензорами. Мы рассмотрим их позднее.
Операции над векторами. Скалярное, векторное, смешанное произведение
Векторное исчисление должно ввести ряд операций с векторами и тензорами, как например сложение, умножение, дифференцирование, и изучить эти операции. Эти операции определяются таким образом, чтобы при их помощи легко было интерпретировать те комбинации векторов, которые приходится изучать. В результате как основные элементы векторного исчисления – вектор и тензор, так и операции над ними оказываются хорошо приспособленными для изучения тех физических явлений, в которых большую роль играет направление величин. С одной стороны, это упрощает исследование, с другой, ведет его более естественным и наглядным образом, не требуя введения посторонних элементов.
Рассмотрим, как определяется величина и направление вектора.
Векторы  ,
, 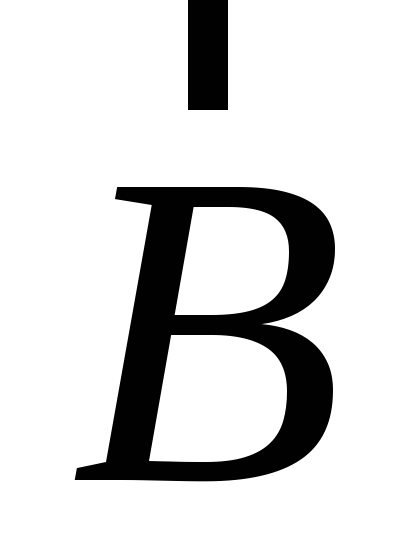 можно представить как
можно представить как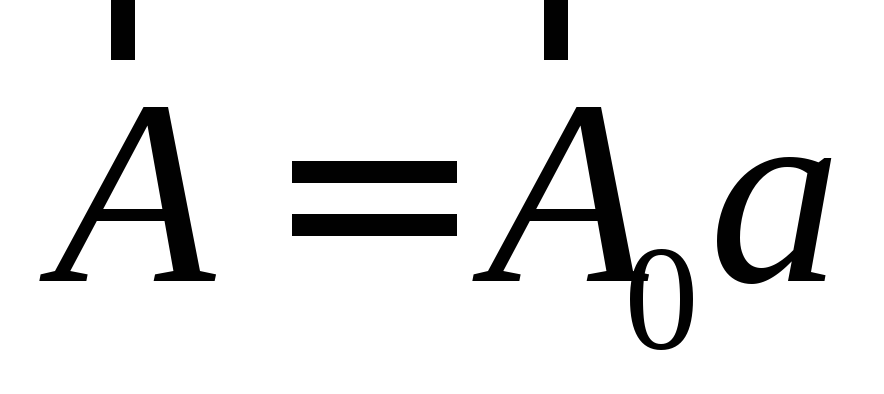 ,
и
,
и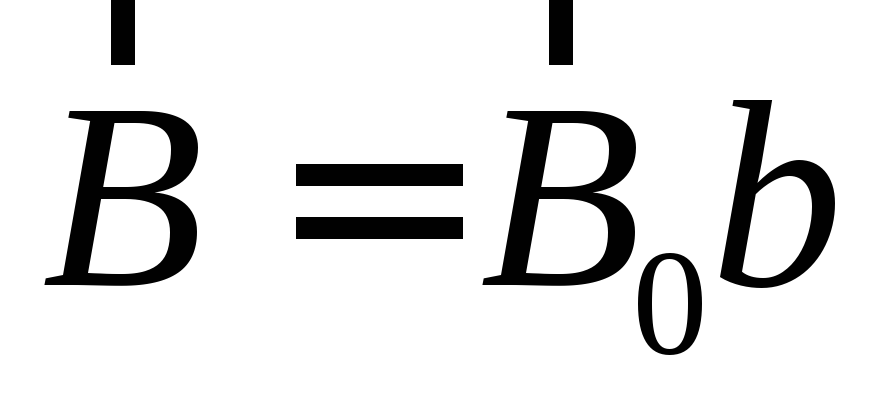 ,
где
,
где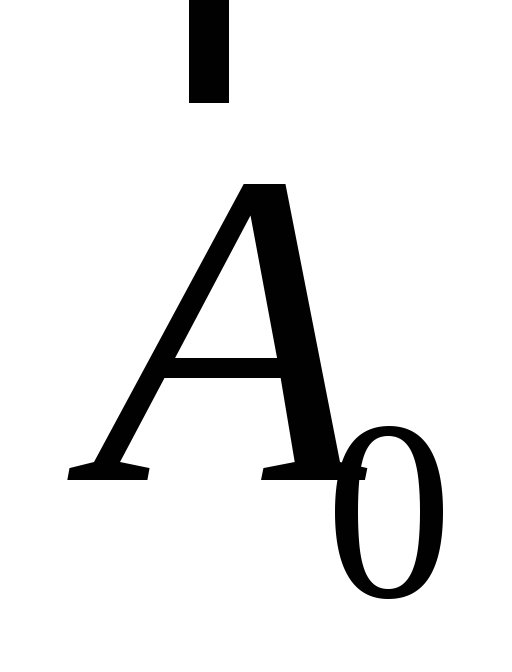 ,
,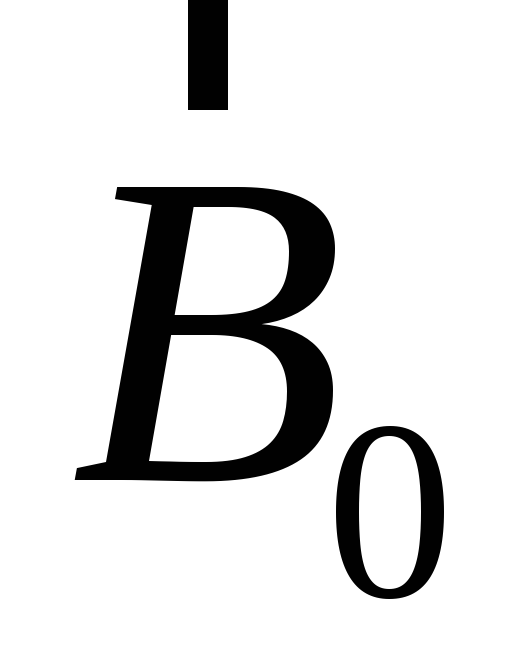 −
единичные векторы, называемые также
ортами, а числа
−
единичные векторы, называемые также
ортами, а числа
 ,
, 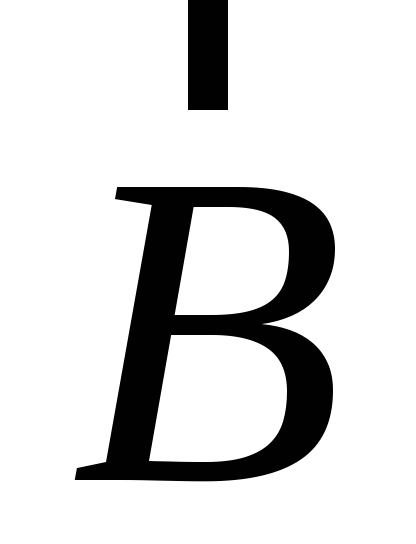 .
. Орты, соответствующие направлениям
осей x,y,zдекартовой координат,
будут обозначаться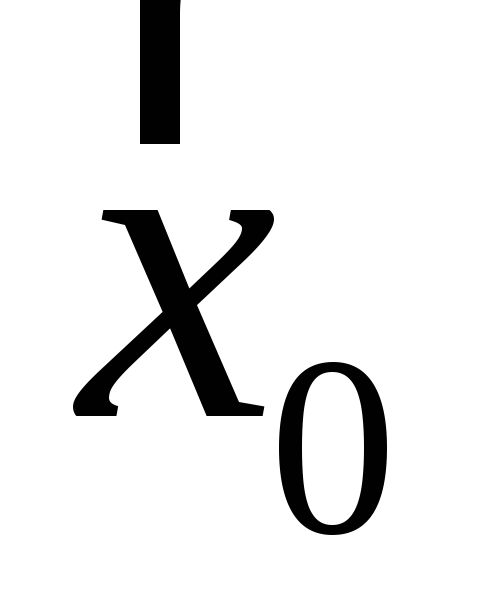 ,
,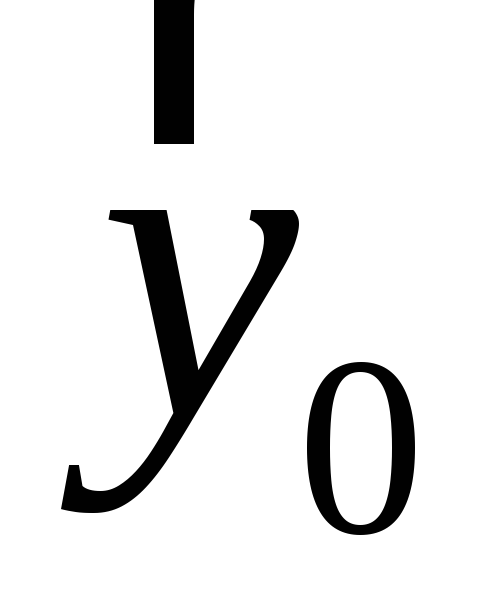 ,
,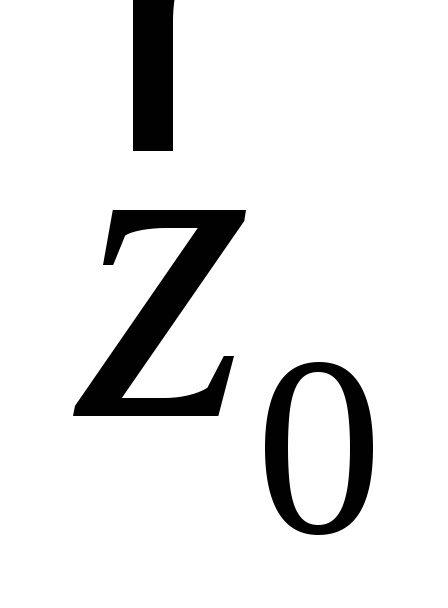 (рисунок Рисунок 2 ). Любой вектор
(рисунок Рисунок 2 ). Любой вектор
 ,
где
,
где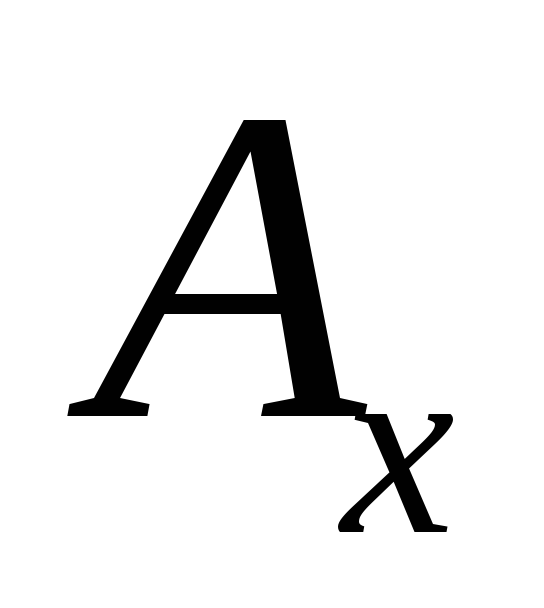 ,
,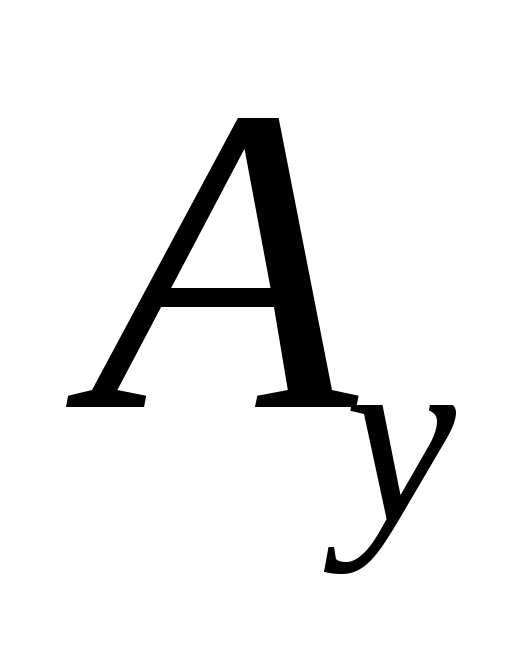 ,
, являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора
являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора .
.Положение какой-либо точки пространства P
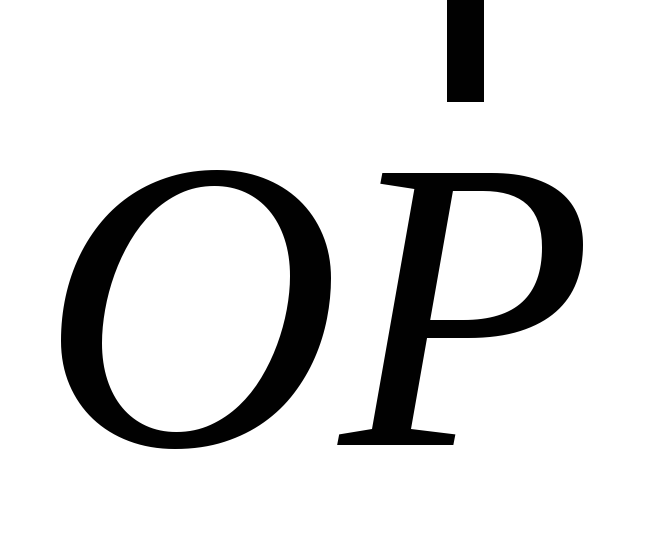 ,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор
,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор 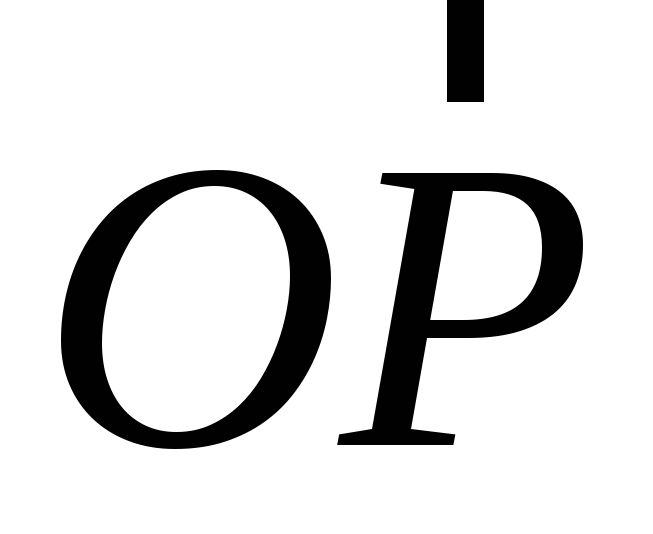 мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как
мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как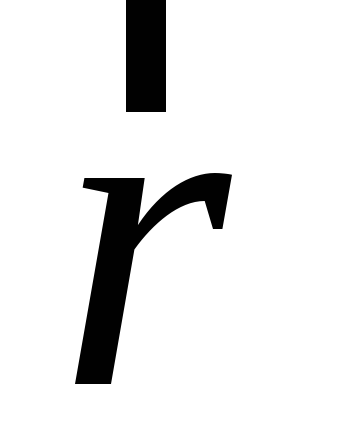 .
Про точкуP, заданную
радиусом-вектором
.
Про точкуP, заданную
радиусом-вектором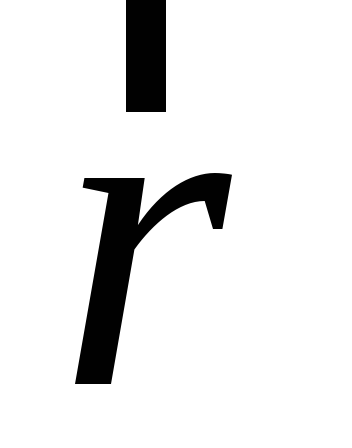 ,
мы будем говорить, для краткости, что
дана точка
,
мы будем говорить, для краткости, что
дана точка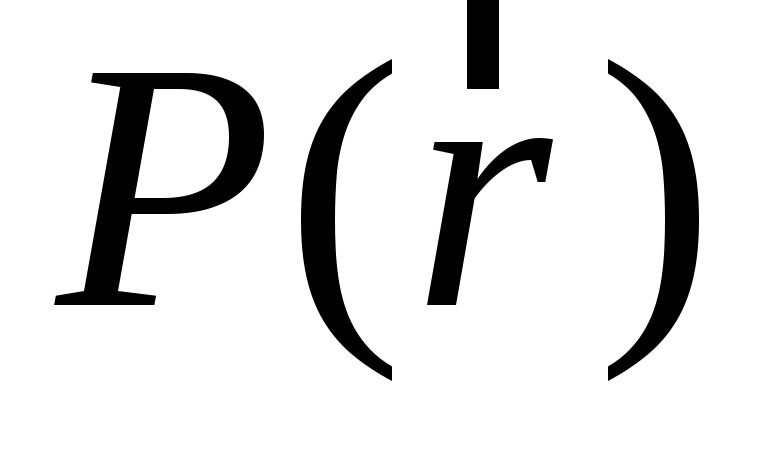
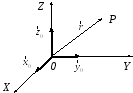
−Орты декартовой системы координат и радиус-вектор
Сложение векторов векторов сводится к сложению их компонент:
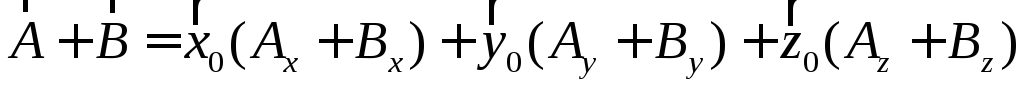 ,
,
эта операция обозначается с помощью
обыкновенного знака алгебраического
сложения: 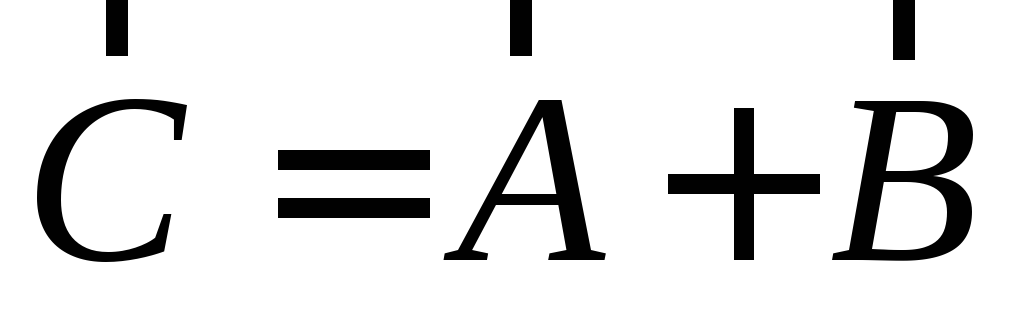 .
Сложение обладает свойством коммутативности:
сумма не меняется от перестановки
слагаемых:
.
Сложение обладает свойством коммутативности:
сумма не меняется от перестановки
слагаемых: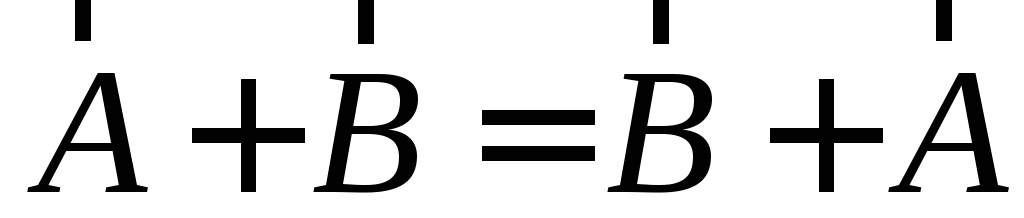
Геометрически это выглядит, как показано на рисунке Рисунок 3 .
— Сложение векторов
Скалярное произведение необходимо,
например, в механике при вычислении
работы, производимой постоянной силой
при прямолинейном перемещении и при
условии, что сила действует под углом
α к перемещению. Работа в этом случае
вычисляется как скалярное произведение
вектора силы и вектора перемещения.
Скалярное произведение двух произвольных
векторов определяется как 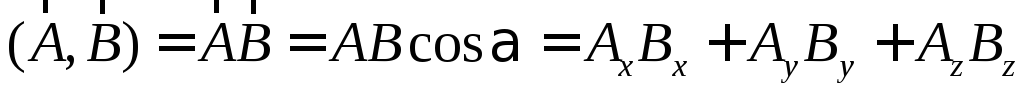

— Скалярное произведение
Векторное произведение. К необходимости рассматривать такую операцию приводят требования геометрического и физического характера.
Векторным произведением векторов  и
и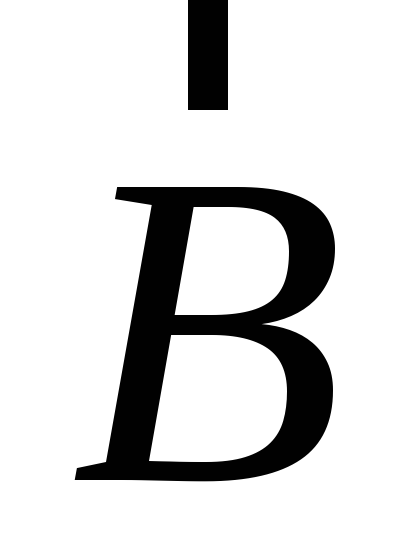
 и
и ,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от
,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от к
к на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).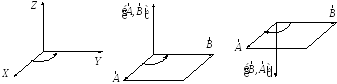
−Векторное произведение
Векторное произведение вычисляется как
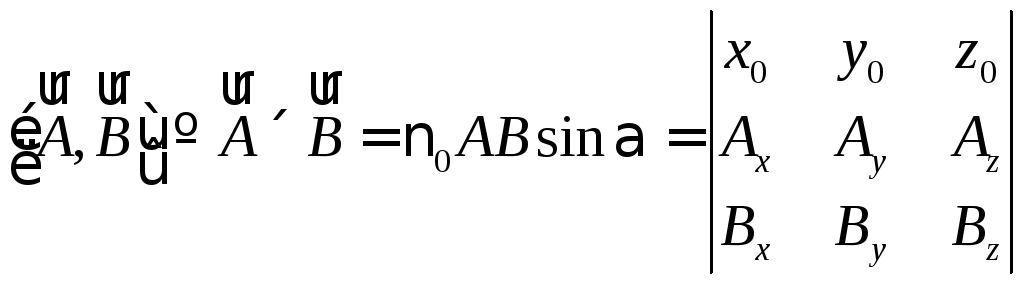 ,
,
тогда компоненты векторного произведения получаются из раскрытия определителя:
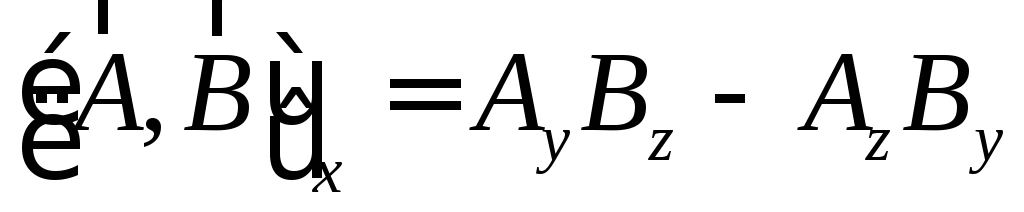

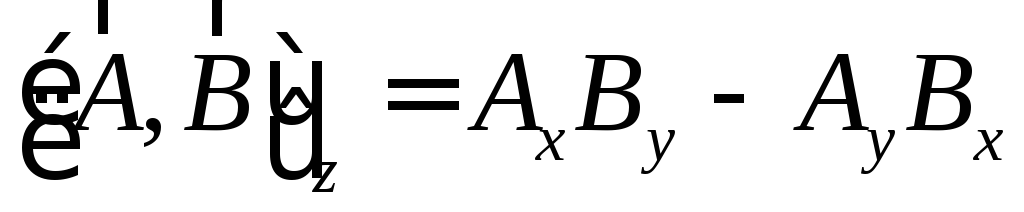
Изменение порядка сомножителей приводит
к изменению знака векторного произведения: 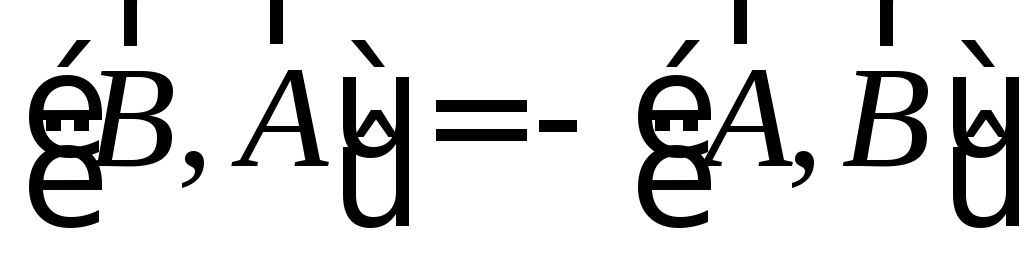 .
.
Размерность векторного произведения – единицы измерения площади, т.е. квадратные метры.
Кроме описанных операций сложения, скалярного и векторного произведений, мы будем использовать векторные дифференциальные операторы. Их определение дается позже, непосредственно перед использованием.
Вопрос 10. Скалярные и векторные величины. Линейные операции с векторами.
Скалярные величины — величины, которые определяются только числовыми значениями. Например: масса, площадь, длина отрезка, температура.
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. Например: сила, скорость, ускорение. Следовательно, вектор полностью определяется числом и направлением. Геометрически вектор изображают отрезком, длина которого соответствует его числовому значению, а для указания направления используют стрелку.
В


А
Обозначают
вектор 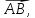 гдеА –
начало вектора, В –
конец вектора, или просто
гдеА –
начало вектора, В –
конец вектора, или просто  .
Заметим, что т. к. длина отрезка
соответствует числовому значению
вектора, то это числовое значение
наз-ютдлиной
или модулем вектора
и обозначают
.
Заметим, что т. к. длина отрезка
соответствует числовому значению
вектора, то это числовое значение
наз-ютдлиной
или модулем вектора
и обозначают 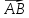 или
или  .
.
Два
вектора будем называть равными,
если они имеют одно и то же направление
и одинаковую длину. Вектор  называется противоположным вектору
называется противоположным вектору 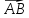 .
.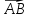 =
= 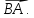 В
этом случае пишут
В
этом случае пишут 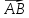 =
–
=
– 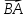 .
.
Нулевым
вектором наз-ся
век-р,
начало
и конец кот-го совпадают.
Его
обозначают 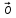 .
Заметим,
что
модуль нулевого вектора равен 0,
а
направление не определено.
.
Заметим,
что
модуль нулевого вектора равен 0,
а
направление не определено.
Единичный вектор — вектор, длина кот-го = единице.
2
Век-ра
наз-ют коллинеарными , если онт лежат на одной и той же прямой
, или 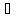 -х
прямых
-х
прямых
Векторы ‖-ые одной и той же плоскости, наз. компланарными.
Одним из самых важных св-в вектора явл-ся то, что его можно перемещать‖-но самому себе в любую точку плоскости или пространства. (Поэтому коллинеарные векторы всегда можно перенести на одну прямую, а компланарные на одну плоскость).
Углом 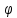 = (
= ( 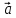 ,
, 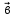 ) между векторами
) между векторами 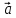 и
и 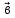 называется
угол при вершине
называется
угол при вершине 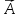 в Δ
в Δ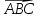 ,
где
,
где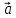 =
= 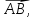
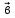 =
= 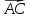 .
.
В

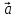
Следовательно,
0 ≤  ≤
≤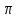
А С
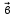 ^
^
Два
вектора 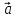 и
и  считаются ортогональными
(перпендикулярными),
если .
считаются ортогональными
(перпендикулярными),
если . 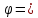 (
(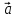 ,
,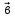 )
=
)
=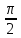 .Обозначают
.Обозначают 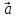

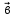 .В
частности
.В
частности 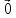
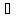
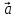 , где
, где 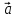 –
любой
вектор.
–
любой
вектор.
Линейными операциями над векторами называют сложение, вычитание, умножение вектора на число.
Суммой векторов
 и
и называют
третий вектор
называют
третий вектор  ,
начало
которого совпадает с началом вектора
,
начало
которого совпадает с началом вектора  ,
а
конец –
с
концом вектора
,
а
конец –
с
концом вектора при
условии,
что
вектор
при
условии,
что
вектор  отложен
из конца вектора
отложен
из конца вектора  .
Вектор
.
Вектор  получается
по
правилу
треугольника или параллелограмма.
получается
по
правилу
треугольника или параллелограмма.
Свойства суммы
1) а + в = в + а,
2) (а + в)+ с = а + (в + с),
3) а + о = а, а + (- а)= о.
Если складываются более двух векторов, то сумма определяется по правилу замыкающей.
с = а1 + а2 +…+ аn .
2) Разностью двух векторов а и в наз-ся такой вектор d , который в сумме с векторами в дает вектор а .
а — в = d, если в + d = а.
Чтобы получить разность а — в двух векторов а и в , необходимо отложить их из одной точки и соединить конец второго вектора с концом первого.
1. Векторные и скалярные величины. Действия над векторами.
Скалярная величина — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только своим значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, масса, плотность, температура и т. д.( длина и площадь, а также время — являются скалярами только в классической (ньютоновской) физике). Примеры векторных физических величин: скорость, сила, поток тепла.
2. Проекция вектора на координатные оси. Действия над проекциями.
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора.
3. Основная задача механики. Поступательное движение. Материальная точка. Положение тела в пространстве. Тело отсчета, система отсчета.
Механика — область физики, изучающая движение материальных объектов и взаимодействие между ними. Поступательное движение — это механическое движение тела, при котором прямая, связаннфя с движущимся телом остается параллельной самой себе.
Материальная точка — тело размерами которого мы можем пренебречь.
Тело отсчета — это тело, относительно которого определяется положение других (движущихся) тел.
Система отсчёта — это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени.
4. Траектория, путь, перемещение. Средняя скорость. Относительность движения. Закон сложения скоростей.
Траекторией — называют линию, вдоль которой двигалось тело.
Пройденный путь — длина траектории движущегося тела.
Путь — это скалярная величина, имеет модуль, но не имеет направления ;
путь не определяет конечное положение тела.
Перемещение — это вектор, соединяющий начальное и конечное положения тела.
Перемещение — это векторная величина, имеет модуль и направление;
перемещение определяет конечное положение тела.
Средняя
скорость – это величина,
равная отношению перемещения тела ко
времени движения: 
Относительность Движения. Движение одного и того же тела в разных системах отсчета будет различным.
Скорость
движения тела относительно
неподвижной системы отсчёта равна
векторной сумме скорости этого тела
относительно подвижной системы отсчета
и скорости самой подвижной системы
отсчета относительно неподвижной
системы 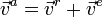 .
.
5. Прямолинейное равномерное движение, уравнения движения и графики: х(t), VX(t), s(t).
Прямолинейное равномерное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени проходит одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:
 .
.
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной:
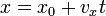 ,
,
где  — начальная координата точки,
— начальная координата точки, 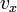 — проекция вектора скорости на
координатную ось.
— проекция вектора скорости на
координатную ось.
6. Скорость при неравномерном движении. Средняя путевая скорость, средняя скорость движения. Мгновенная скорость.
Движение, при котором за равные промежутки времени тело совершает неравные перемещения называют неравномерным или переменным.
Средней
скоростью vср называется величина, равная отношению
перемещения тела ∆r за некоторый
промежуток времени ∆t к этому промежутку: 
Если S— путь, то говорят о путевой скорости движения: vср=S/∆t
Мгновенная
скорость — скорость в
определенный момент времени или в
определенной точке траектории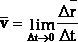 .
.
Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
В теории электромагнитного поля применяется некоторый традиционный математический аппарат, без которого невозможно построить ясное и обозримое изложение. К числу математических средств, которые нам потребуются, относятся разделы векторной алгебры и векторного анализа. Эти разделы в общем знакомы из курса высшей математики, однако в нашем курсе они тоже будут кратко описаны.
Первым необходимым понятием являются скалярные и векторные величины.
В математике и технике приходится иметь дело с величинами двух родов: одни из величин связаны с понятием о направлении в пространстве, другие имеют чисто числовой характер и не связаны с направлением. Рассмотрим например, температуру, массу, плотность, энергию, перемещение точки, скорость, ускорение, силу. Четыре последние величины резко отличаются от первых тем, что с ними обязательно должно быть связано понятие о направлении: например, точка может перемещаться вверх или вниз, вперед или назад.
Наоборот, температура, например, не имеет направления. и чтобы охарактеризовать ее, мы должны измерить ее например, в градусах Цельсия, полученное число и даст величину температуры. Точно так же можно измерить в соответствующих единицах массу, плотность и т.п. Эти величины принадлежат к классу величин, называемых скалярами.
Скаляром называется величина, характеризующаяся при выбранной единице меры одним числом.
Рассмотрим теперь один из векторов – скорость точки. Указания величины скорости, измеренной, например в м\с недостаточно для характеристики скорости. Нужно еще знать направление движения точки. Точно так же имеют определенное направление и ускорение точки, и сила, действующая на точку. Дадим поэтому следующее определение:
Вектором называется величина, характеризующаяся, помимо измеряющего ее числа, еще своим направлением в пространстве.
Простейшим вектором является прямолинейный
отрезок 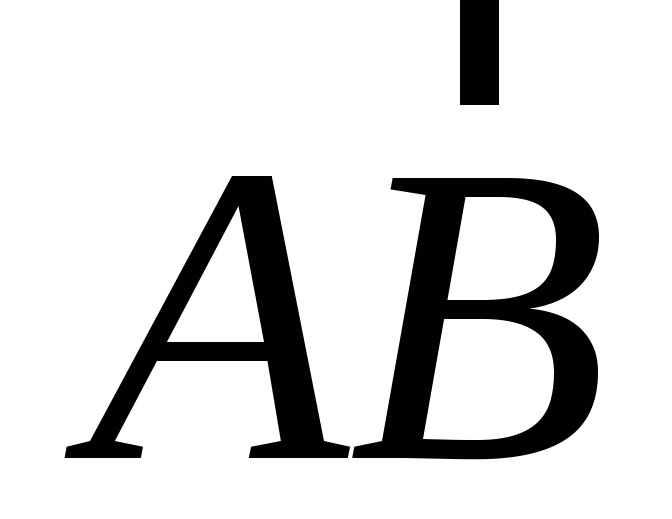 ,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
,
имеющий определенну величину – длинуАВи
определенное направление – от начальной
точкиАк конечной точкеВ.
На чертежах векторы изображаются
стрелками (рисунок Error: Reference source not found).
Направление стрелки указывает на
направление вектора, длина стрелки дает
длину вектора. Обычно векторы обозначаются
жирными латинскими буквами:  ,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой:
,
но при письме от руки это неудобно,
поэтому мы будем пользоваться буквами
со стрелкой: 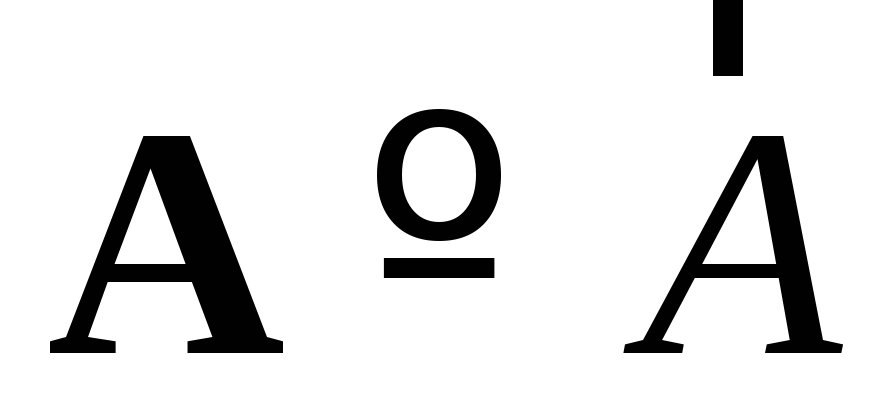 .
.

− Вектор AB
Иногда приходится рассматривать величины тоже направленного характера, но более сложного, чем векторы, строения. Эти величины называются тензорами. Мы рассмотрим их позднее.
Операции над векторами. Скалярное, векторное, смешанное произведение
Векторное исчисление должно ввести ряд операций с векторами и тензорами, как например сложение, умножение, дифференцирование, и изучить эти операции. Эти операции определяются таким образом, чтобы при их помощи легко было интерпретировать те комбинации векторов, которые приходится изучать. В результате как основные элементы векторного исчисления – вектор и тензор, так и операции над ними оказываются хорошо приспособленными для изучения тех физических явлений, в которых большую роль играет направление величин. С одной стороны, это упрощает исследование, с другой, ведет его более естественным и наглядным образом, не требуя введения посторонних элементов.
Рассмотрим, как определяется величина и направление вектора.
Векторы  ,
, 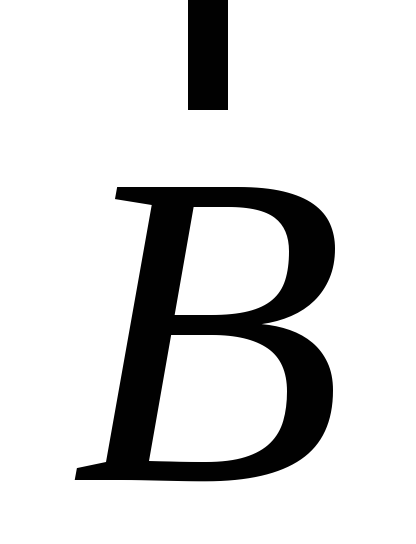 можно представить как
можно представить как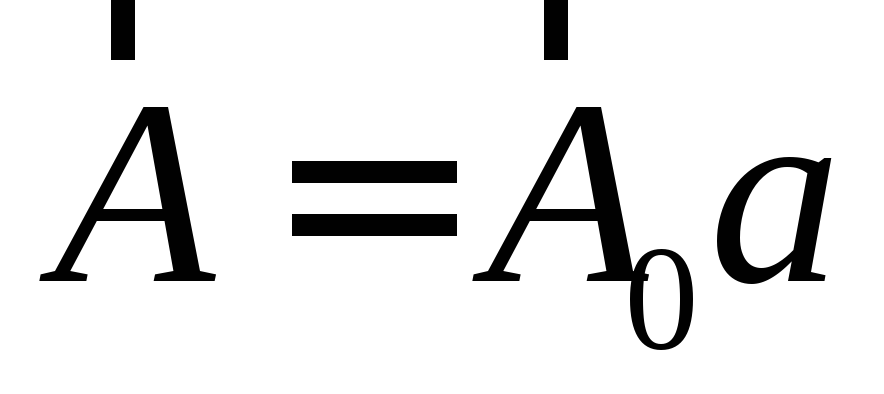 ,
и
,
и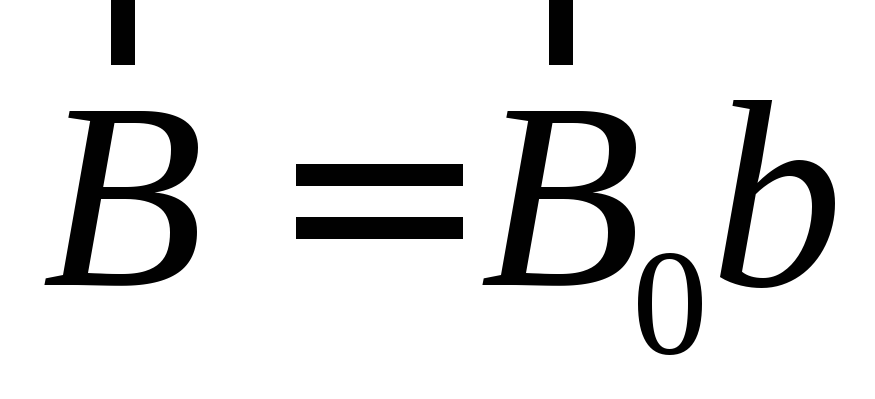 ,
где
,
где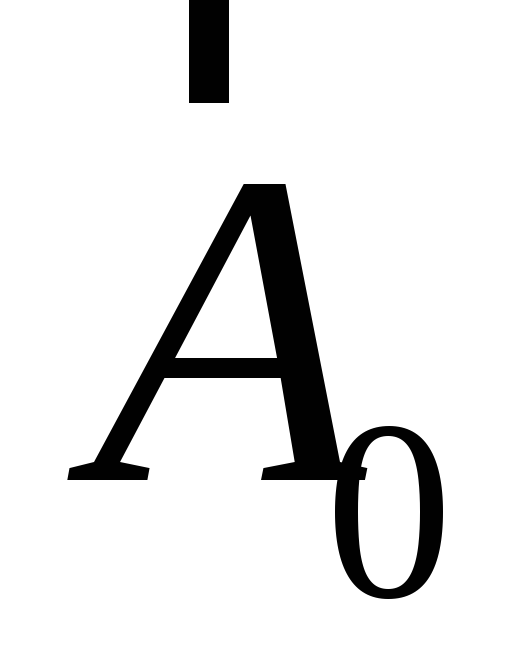 ,
,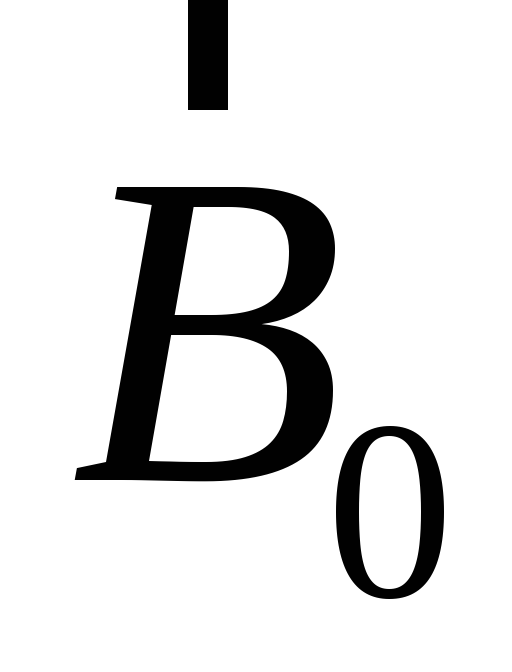 −
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов
−
единичные векторы, называемые также
ортами, а числаа,b− абсолютные значения
векторов ,
, 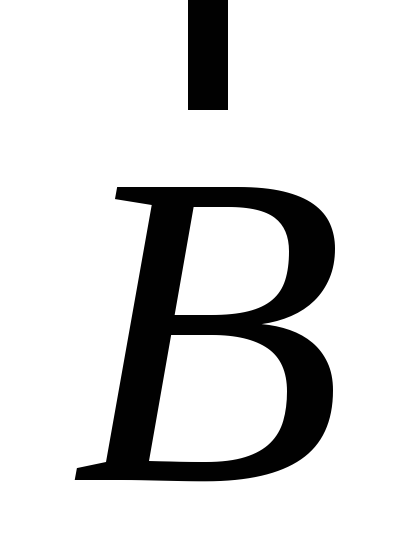 .
.
Орты, соответствующие направлениям
осей x,y,zдекартовой координат,
будут обозначаться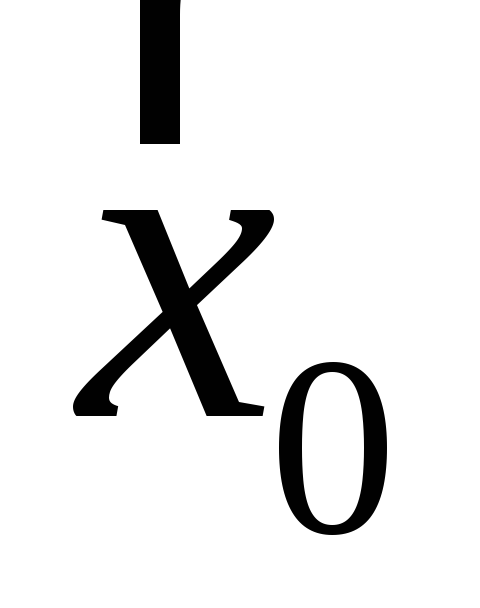 ,
,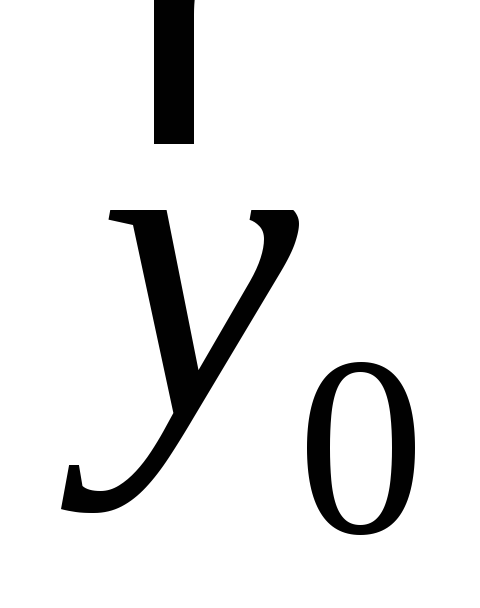 ,
,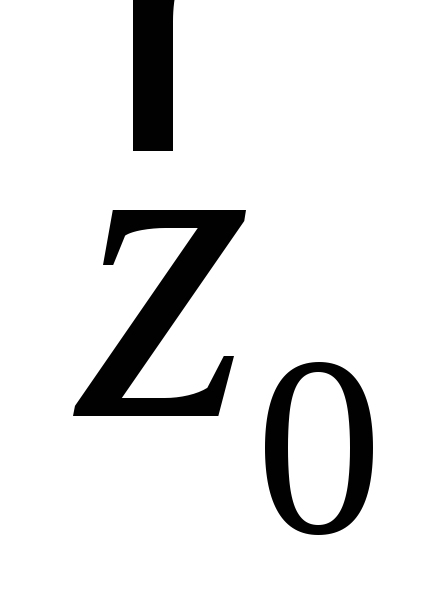 (рисунок Рисунок 2 ). Любой вектор
(рисунок Рисунок 2 ). Любой вектор тогда можно представить в виде разложения
тогда можно представить в виде разложения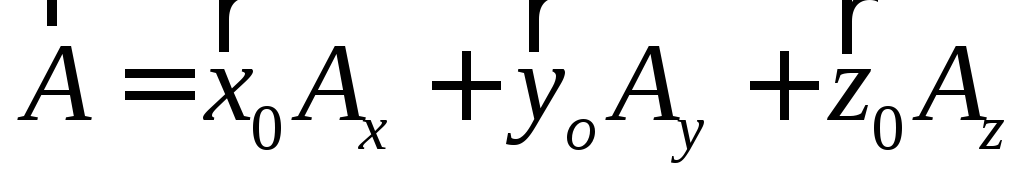 ,
где
,
где ,
,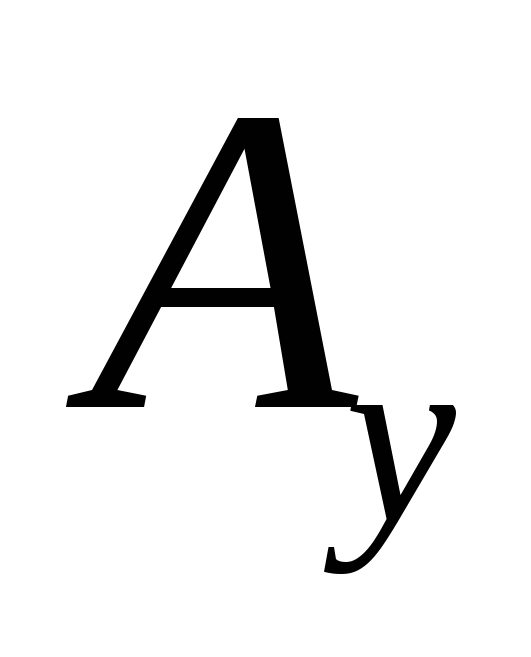 ,
, являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора
являются его проекциями на оси декартовой
системы координат. Они также называются
компонентами (составляющими) вектора .
.
Положение какой-либо точки пространства P может быть определено вектором 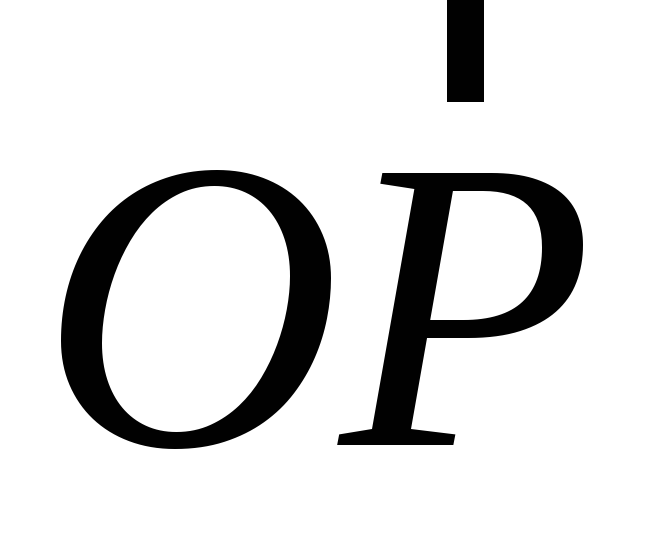 ,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор
,
начальной точкой которого служит
некоторая, определенным образом выбранная
точкаO, а концом –
точкаP. Вектор 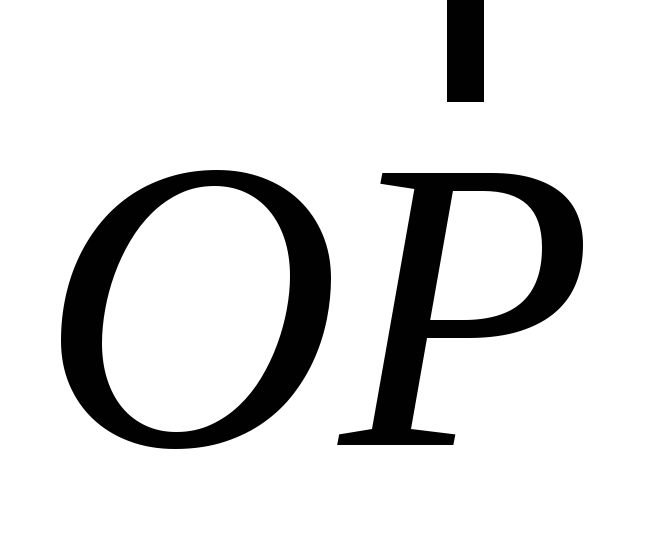 мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как
мы будем называть радиусом-вектором
точкиP относительно точкиОи будем обозначать обычно как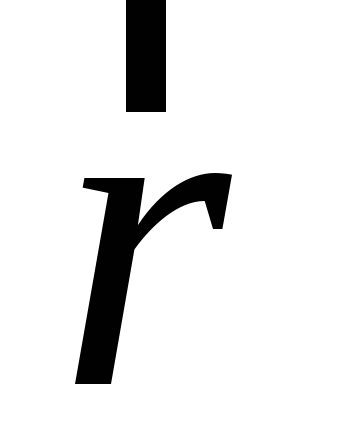 .
Про точкуP, заданную
радиусом-вектором
.
Про точкуP, заданную
радиусом-вектором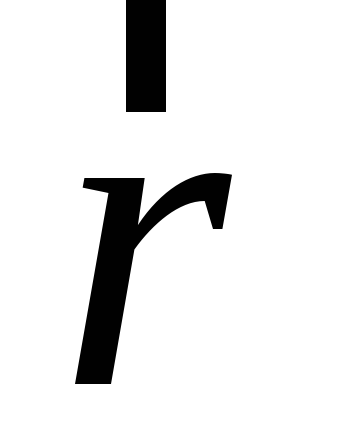 ,
мы будем говорить, для краткости, что
дана точка
,
мы будем говорить, для краткости, что
дана точка .
.
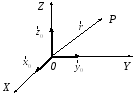
−Орты декартовой системы координат и радиус-вектор
Сложение векторов векторов сводится к сложению их компонент:
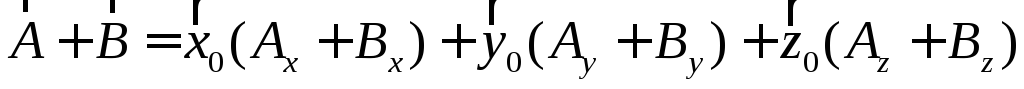 ,
,
эта операция обозначается с помощью
обыкновенного знака алгебраического
сложения: 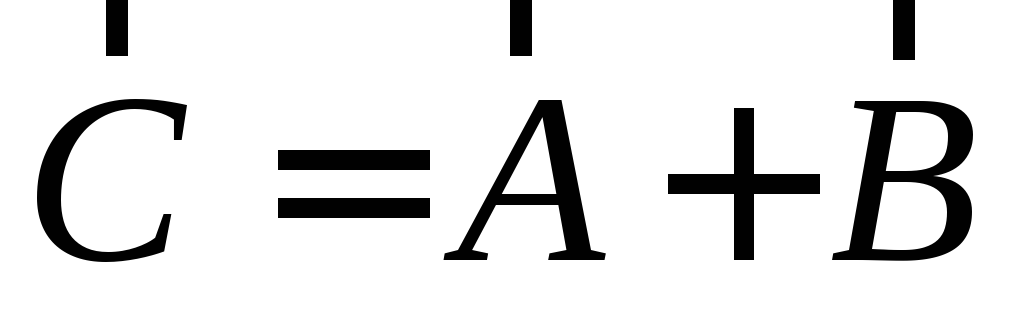 .
Сложение обладает свойством коммутативности:
сумма не меняется от перестановки
слагаемых:
.
Сложение обладает свойством коммутативности:
сумма не меняется от перестановки
слагаемых: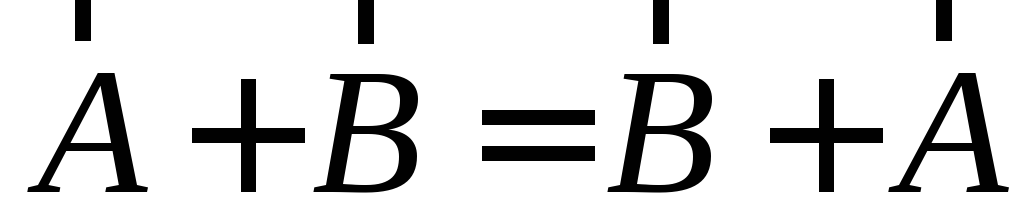 .
.
Геометрически это выглядит, как показано на рисунке Рисунок 3 .
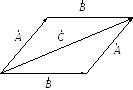
— Сложение векторов
Скалярное произведение необходимо,
например, в механике при вычислении
работы, производимой постоянной силой
при прямолинейном перемещении и при
условии, что сила действует под углом
α к перемещению. Работа в этом случае
вычисляется как скалярное произведение
вектора силы и вектора перемещения.
Скалярное произведение двух произвольных
векторов определяется как 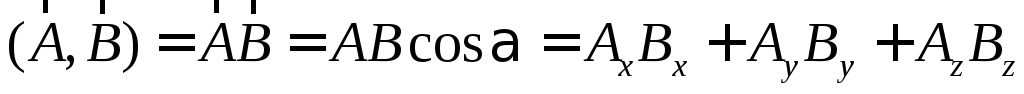 ,
то есть произведение их длин, умноженное
на угол между ними (рисунок Рисунок 4 ).
Результатом скалярного произведения
является скаляр.
,
то есть произведение их длин, умноженное
на угол между ними (рисунок Рисунок 4 ).
Результатом скалярного произведения
является скаляр.

— Скалярное произведение
Векторное произведение. К необходимости рассматривать такую операцию приводят требования геометрического и физического характера.
Векторным произведением векторов  и
и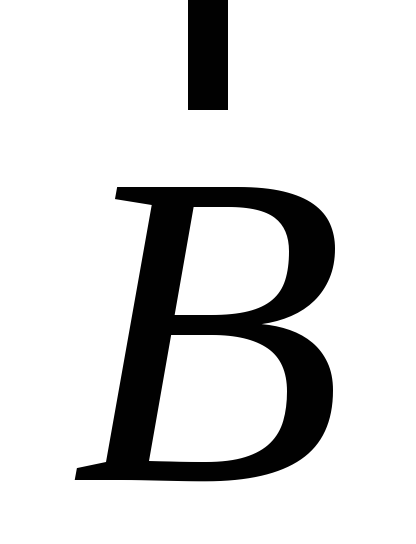 называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах
называется
вектор, по величине равный площади
параллелограмма, построенного на
векторах и
и ,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от
,
перпендикулярный плоскости этих векторов
и направленный в такую сторону, чтобы
вращение от к
к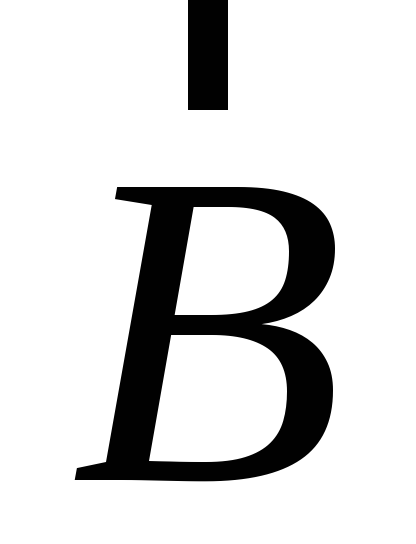 на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
на кратчайшем пути вокруг полученного
вектора происходило в ту же сторону,
как вращение осиxк
осиyвокруг осиz(рисунок Рисунок 5 ).
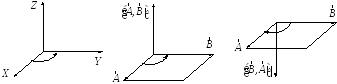
−Векторное произведение
Векторное произведение вычисляется как
 ,
,
тогда компоненты векторного произведения получаются из раскрытия определителя:
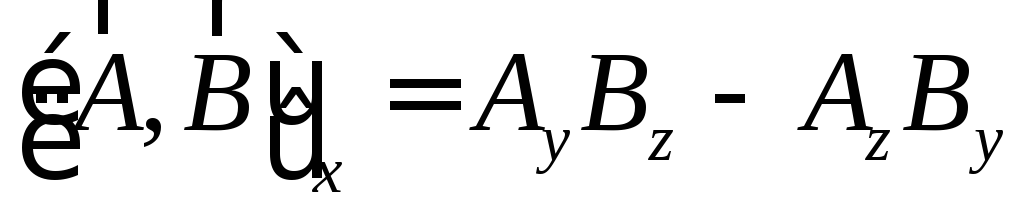
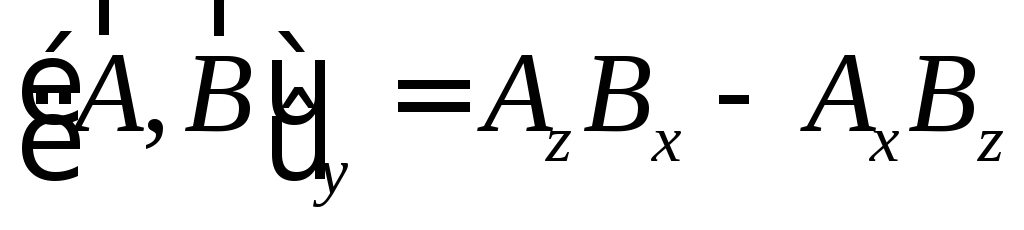

Изменение порядка сомножителей приводит
к изменению знака векторного произведения:  .
.
Размерность векторного произведения – единицы измерения площади, т.е. квадратные метры.
Кроме описанных операций сложения, скалярного и векторного произведений, мы будем использовать векторные дифференциальные операторы. Их определение дается позже, непосредственно перед использованием.
Физические величины, обозначение, векторные и скалярные
Тестирование онлайн
Тест по теме: «Физические величины»
Что такое физическая величина?
Нас окружает много различных материальных предметов. Материальных, потому что их возможно потрогать, понюхать, увидеть, услышать и еще много чего можно сделать. То, какие эти предметы, что с ними происходит, или будет происходить, если что-нибудь сделать: кинуть, разогнуть, засунуть в печь. То, почему с ними происходит что-либо и как именно происходит? Все это изучает физика. Поиграйте в игру: загадайте предмет в комнате, опишите его несколькими словами, друг должен угадать что это. Указываю характеристики задуманного предмета. Прилагательные: белый, большой, тяжелый, холодный. Догадались? Это холодильник. Названные характеристики — это не научные измерения вашего холодильника. Измерять у холодильника можно разное. Если длину, то он большой. Если цвет, то он белый. Если температуру, то холодный. А если его массу, то выйдет, что он тяжелый. Представляем, что один холодильник можно исследовать с разных сторон. Масса, длина, температура — это и есть физическая величина.
Но это лишь та небольшая характеристика холодильника, которая приходит на ум мгновенно. Перед покупкой нового холодильника можно ознакомиться еще с рядом физических величин, которые позволяют судить о том, какой он, лучше или хуже, и почему он стоит дороже. Представь масштабы того, на сколько все окружающее нас разнообразно. И на сколько разнообразны характеристики.
Обозначение физической величины
Все физические величины принято обозначать буквами, чаще греческого алфавита. НО! Одна и та же физическая величина может иметь несколько буквенных обозначений (в разной литературе).
И, наоборот, одной и той же буквой могут обозначаться разные физические величины.
Несмотря на то, что с такой буквой вы могли не сталкиваться, смысл физической величины, участие ее в формулах остается прежним.
Векторные и скалярные величины
В физике существует два вида физических величин: векторные и скалярные. Основное их отличие в том, что векторные физические величины имеют направление. Что значит физическая величина имеет направление? Например, число картофелин в мешке, мы будем называть обыкновенными числами, или скалярами. Еще одним примером такой величины может служить температура. Другие очень важные в физике величины имеют направление, это, например, скорость; мы должны задать не только быстроту перемещения тела, но и путь, по которому оно движется. Импульс и сила тоже имеют направление, как и смещение: когда кто-нибудь делает шаг, можно сказать не только, как далеко он шагнул, но и куда он шагает, то есть определить направление его движения. Векторные величины лучше запомнить.
Почему над буквами рисуют стрелку?
Рисуют стрелку только над буквами векторных физических величин. Согласно тому, как в математике обозначают вектор! Действия сложения и вычитания над этими физическими величинами выполняются согласно математическим правилам действий с векторами. Выражение «модуль скорости» или «абсолютное значение» означает именно «модуль вектора скорости», то есть численное значение скорости без учета направления — знака «плюс» или «минус».
Обозначение векторных величин
Главное запомнить
1) Что такое векторная величина;
2) Чем скалярная величина отличается от векторной;
3) Векторные физические величины;
4) Обозначение векторной величины
Скалярные и векторные величины
Н екоторые
величины в физике, механике и других
науках полностью определяются заданием
одного числа. Например, объем, масса,
температура и др. Такие величины
называютсяскалярными,
а числа иногда называют скалярами. Но
есть величины, для определения которых
надо задать не только число, но и
направление. Например, при изучении
движения тела мы должны указать не
только величину скорости, с которой
движется тело, но и направление движения.
При определении действия силы необходимо
указать не только величину этой силы,
но и направление её действия.
екоторые
величины в физике, механике и других
науках полностью определяются заданием
одного числа. Например, объем, масса,
температура и др. Такие величины
называютсяскалярными,
а числа иногда называют скалярами. Но
есть величины, для определения которых
надо задать не только число, но и
направление. Например, при изучении
движения тела мы должны указать не
только величину скорости, с которой
движется тело, но и направление движения.
При определении действия силы необходимо
указать не только величину этой силы,
но и направление её действия.
Такие величины называются векторными. Для работы с ними было введено понятие вектора, имеющее и самостоятельное значение в математике.
Любая упорядоченная пара точек А и B в пространстве определяет направленный отрезок, т.е. отрезок вместе с заданным на нём направлением. Если точка А – первая, то её называют началом отрезка, а точку B – его концом. Направлением отрезка считается направление от начала к концу отрезка.
Определение. Вектором называется направленный отрезок, или (что то же самое) упорядоченная пара точек.
Вектор
обозначается 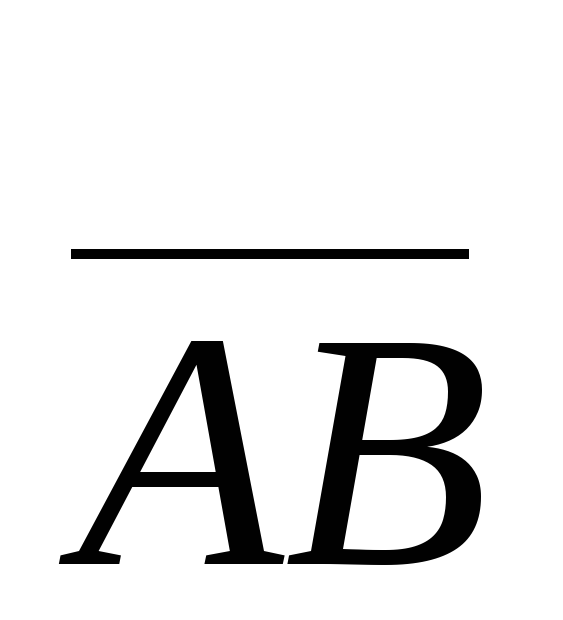 —
двумя буквами, при этом первая буква-
начало вектора, а вторая — его конец.
—
двумя буквами, при этом первая буква-
начало вектора, а вторая — его конец.
В
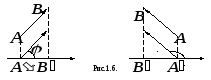
Рис. 1.2.
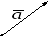 ектор
можно обозначать одной буквой с черточкой
наверху —
ектор
можно обозначать одной буквой с черточкой
наверху — .
Направление вектора на рисунке указывается
стрелкой.
.
Направление вектора на рисунке указывается
стрелкой. Вектор,
у которого начало и конец совпадают,
называется нулевым и обозначается 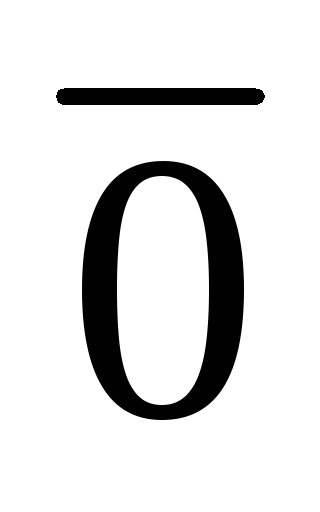 .
.
Расстояние
между началом и концом вектора называется
его длиной (или модулем)и обозначается 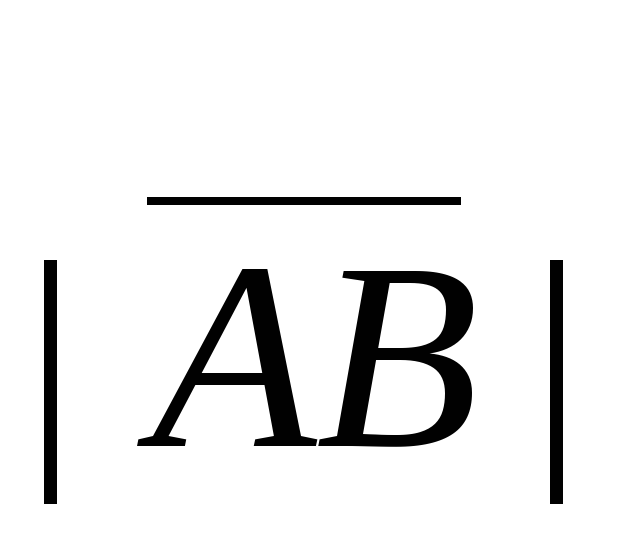 или
или .
.
Векторы  и
и называютсяколлинеарными,
если они лежат на одной прямой или на
параллельных прямых.
называютсяколлинеарными,
если они лежат на одной прямой или на
параллельных прямых.
Нулевой
вектор считается коллинеарным любому
вектору, так как он не имеет определенного
направления, длина его, очевидно, равна
нулю, т.е. 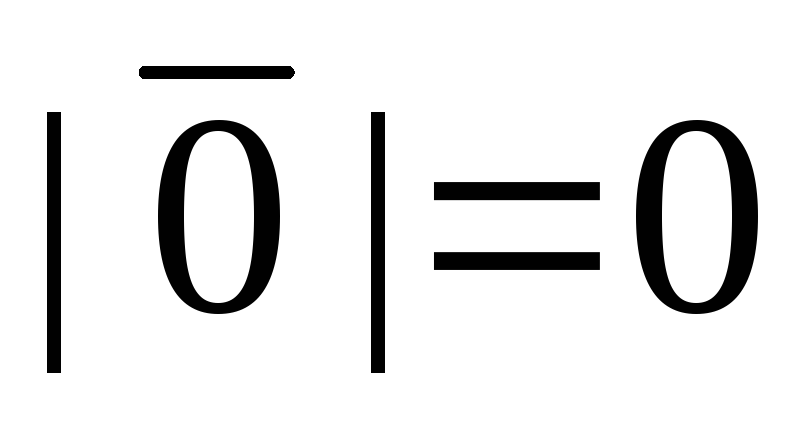 .
.
Определение. Векторы  и
и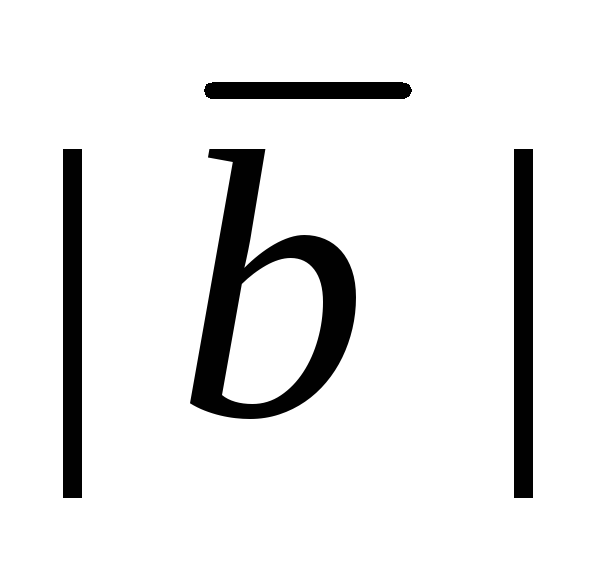 называютсяравными
называютсяравными 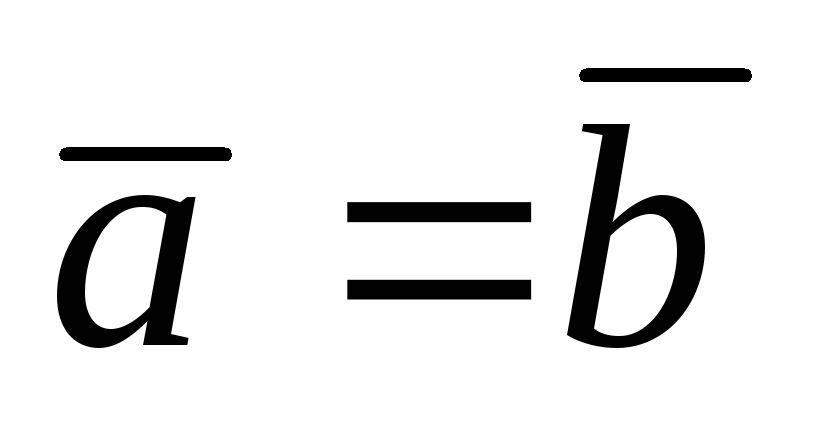 ,
если они:
,
если они:
а) коллинеарны;
б) одинаково направлены;
в) равны по длине.
Рис.1.3.



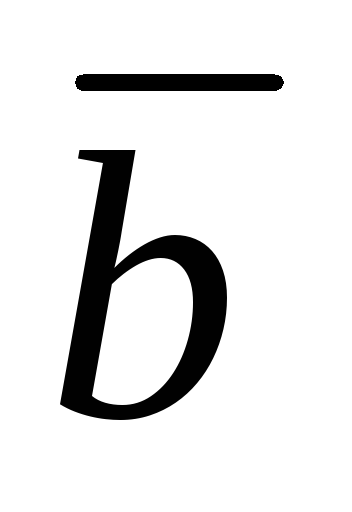
Рис.1.4.




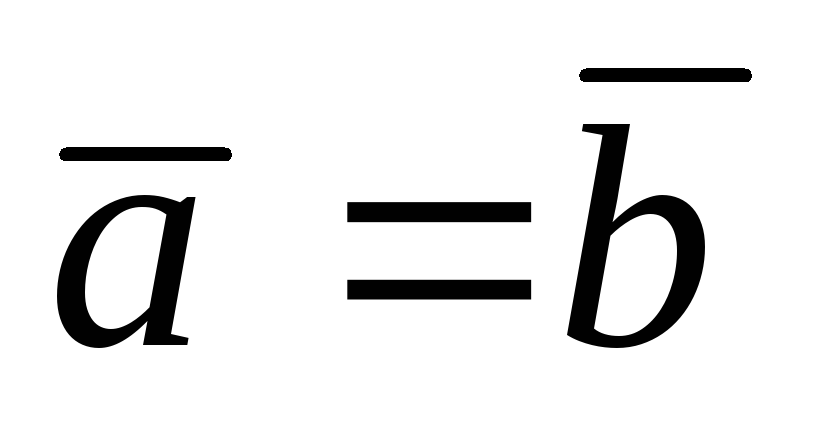
И
Рис.1.5.
 з
определения равенства векторов следует,
что вектор можно переносить параллельно
самому себе, т.е. начало вектора может
быть в любой точке пространства, но
длина и направление фиксированы. Такие
векторы называютсясвободными.
В дальнейшем будем изучать только
свободные векторы, называя их просто
векторами.
з
определения равенства векторов следует,
что вектор можно переносить параллельно
самому себе, т.е. начало вектора может
быть в любой точке пространства, но
длина и направление фиксированы. Такие
векторы называютсясвободными.
В дальнейшем будем изучать только
свободные векторы, называя их просто
векторами.Проекция вектора на ось
Рассмотрим
некоторый вектор 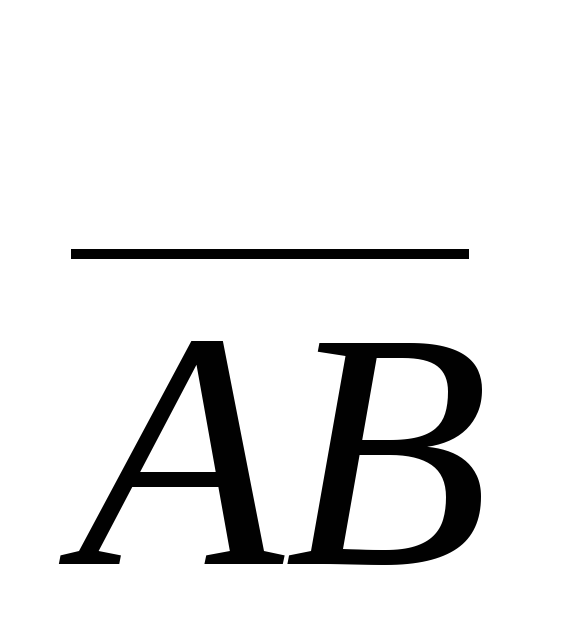 и
числовую осьOu.
Проведём через точки A и B плоскости, перпендикулярные к оси Ou.
Обозначим через
и
числовую осьOu.
Проведём через точки A и B плоскости, перпендикулярные к оси Ou.
Обозначим через  и
и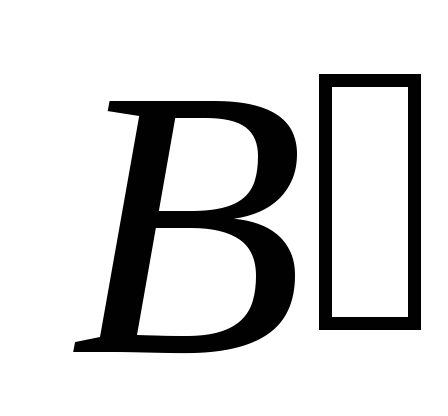 точки
пересечения этих плоскостей с осью.
точки
пересечения этих плоскостей с осью.
П


 роекция
вектораAB на ось Ou обозначается прuAB.
роекция
вектораAB на ось Ou обозначается прuAB.
Определение. Проекцией вектора AB на ось Ou называется число, равное  ,
если направление
,
если направление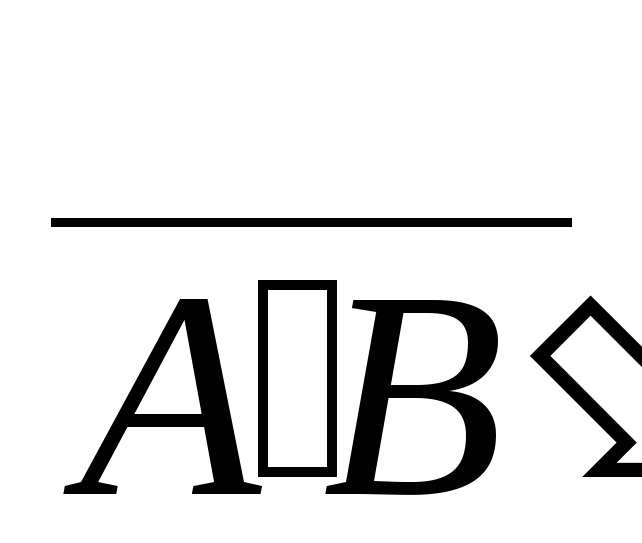 совпадает с направлениемOu и
совпадает с направлениемOu и  ,
если направление
,
если направление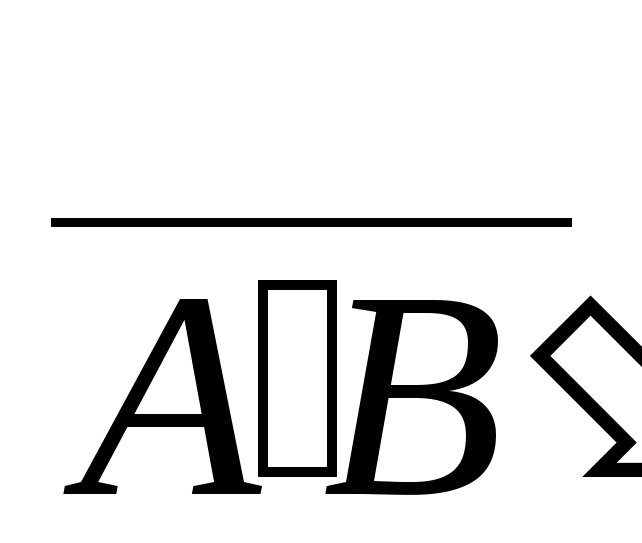 противоположноOu.
противоположноOu.
Нетрудно показать, что
прuAB=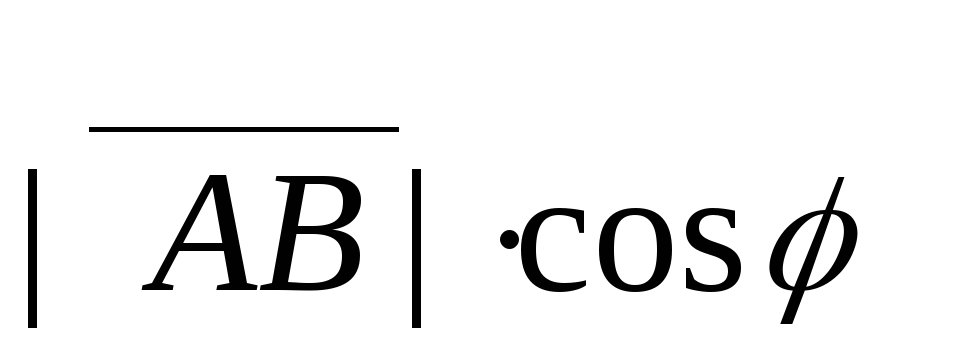 ,
,
где — угол, образованный вектором AB с осью Ou .
Координаты
вектора.
Пусть в пространстве задана прямоугольная
система координат и произвольный вектор 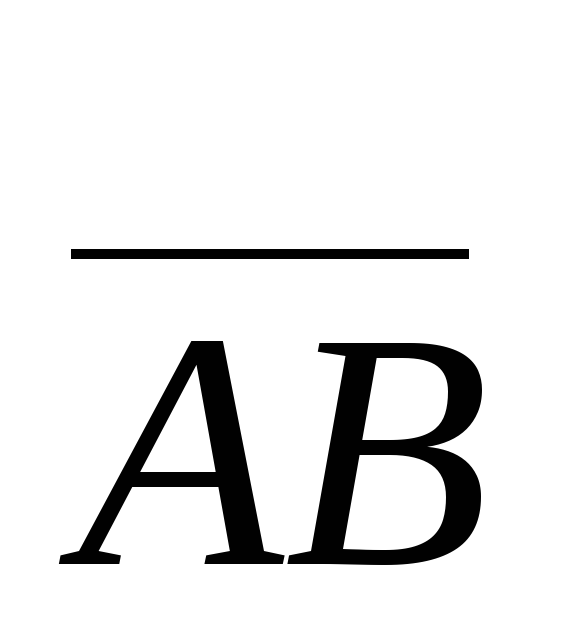 .
Пусть далее
.
Пусть далее
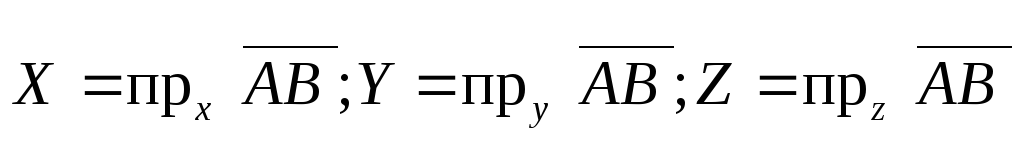 .
.
Проекции X, Y, Z вектора  называют
его координатами и записывают так:
называют
его координатами и записывают так: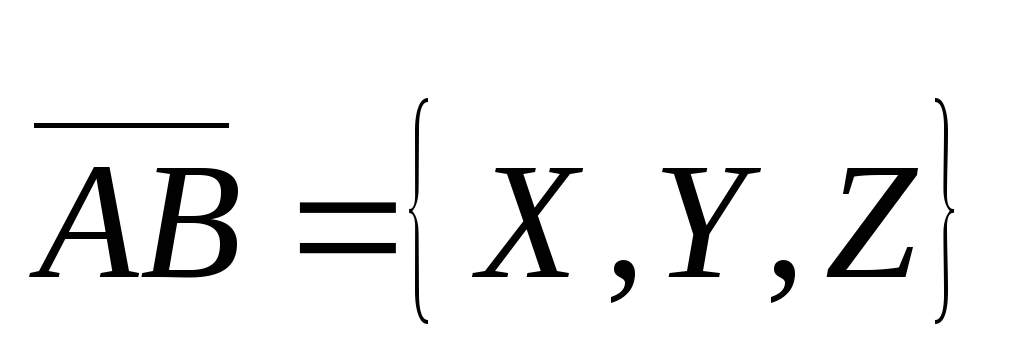 .
.
Для
любых точек  и
и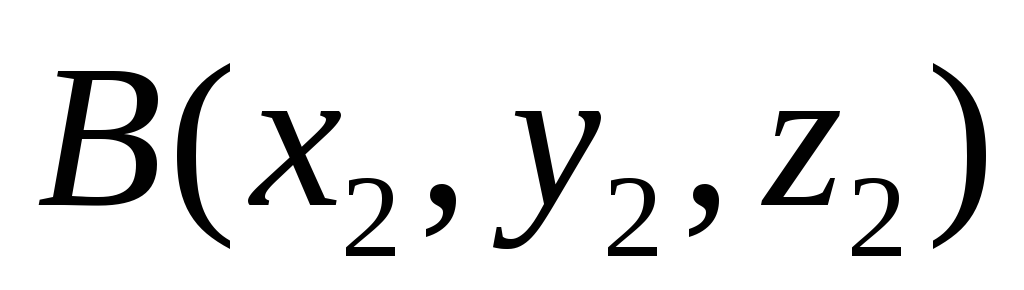 координаты вектора
координаты вектора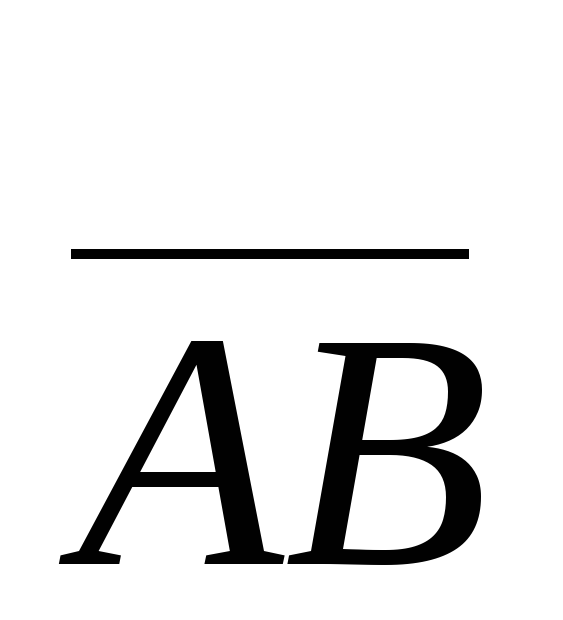 определяются
формулами
определяются
формулами

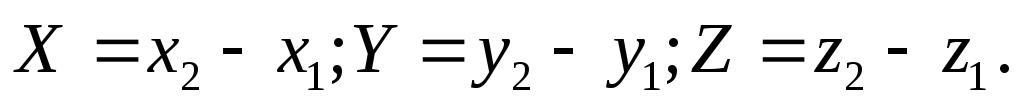
В этом случае модуль вектора находится по формуле
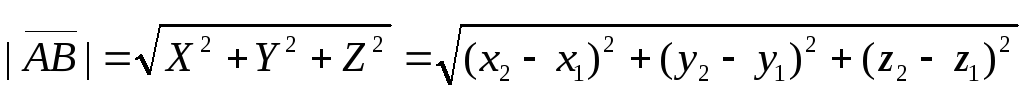 .
.
Если
через 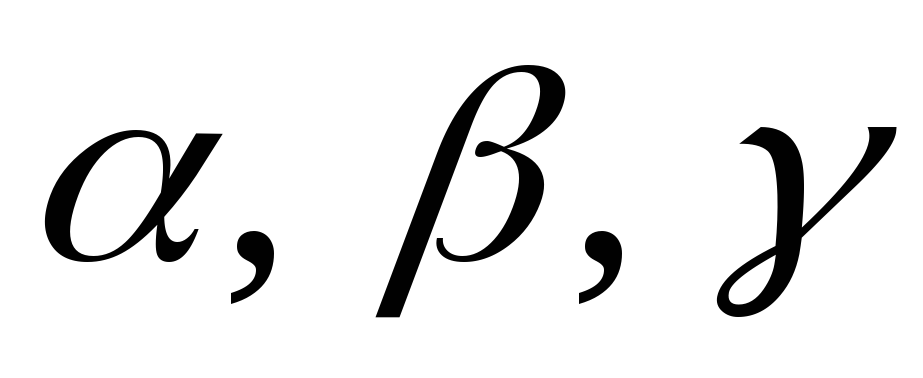 обозначить
углы наклона вектора к осям координат,
то
обозначить
углы наклона вектора к осям координат,
то
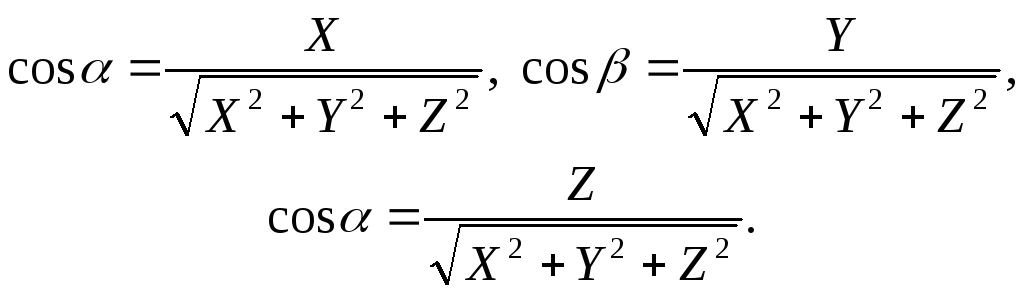
 называют
направляющими
косинусами
вектора
называют
направляющими
косинусами
вектора 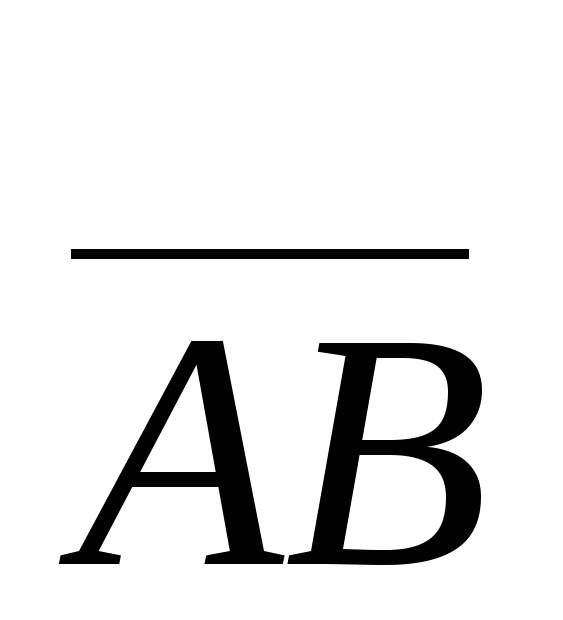 .
.
Очевидно,
что 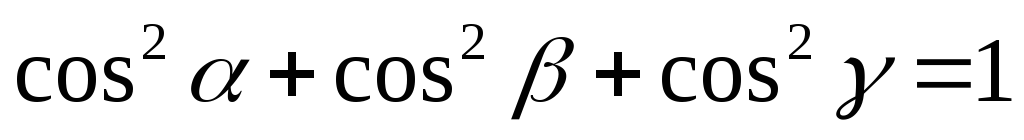 .
.
В чём отличие векторной величины от скалярной?
Скалярная не имеет направления. Масса, к примеру. В отличие от веса.
Вектор — направленный отрезок Скаляр — Его длина, выраженная численно. Cкалярное произведение 2-х векторов — произведение их длин ( длины выражены в абсолютных значениях (модулях)
Векторными величинами, называют величины, имеющие и численное значение, и направление. Скалярными называют величины, имеющие численное значение, но не имеющие направления.
Скалярная — просто сколько, а векторная — сколько и куда…
вектор имеет числовое значение и направление скаляр-только числовое значение


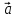 и
и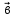 называют
третий вектор
называют
третий вектор 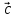 ,
начало
которого совпадает с началом вектора
,
начало
которого совпадает с началом вектора 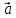 ,
а
конец –
с
концом вектора
,
а
конец –
с
концом вектора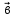 при
условии,
что
вектор
при
условии,
что
вектор 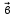 отложен
из конца вектора
отложен
из конца вектора 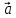 .
Вектор
.
Вектор  получается
по
правилу
треугольника или параллелограмма.
получается
по
правилу
треугольника или параллелограмма.