Урок физики 9 класс. Движение и свойства материи. Векторы и действия над ними.

Урок физики

в 9 классе

ТЕМА: Движение и свойства материи. Векторы и действия над ними.

Цели и задачи урока

Образовательные:

Научить производить действия над векторами, применять правила сложения и вычитания векторов

Воспитательные:

развивать познавательную самостоятельность учащихся;

способствовать их нравственному и эстетическому воспитанию.

Развивающие:

развивать умения выделять главное, существенное, сравнивать изучаемые факты, логически излагать мысли;

Тип урока: объяснение нового материала и решения задач.

Ход урока:

I. Орг. момент.

II. Повторение пройденного материала

Письменная работа. Формулы 8 класс (Обозначения и единицы)

1. Как обозначается и в чем измеряется сила тока?

1. 2. 3.

2. Как обозначается и в чем измеряется сопротивление?

1. 2. 3.

3. Как обозначается и в чем измеряется напряжение?

1. 2. 3.

4. Как обозначается и в чем измеряется работа тока?

1. 2. 3.

5. Как обозначается и в чем измеряется количество теплоты?

1. 2. 3.

6. Как обозначается и в чем измеряется время?

1. 2. 3.

7. Как обозначается и в чем измеряется мощность тока?

1. 2. 3.

8. Как обозначается и в чем измеряется площадь?

1. 2. 3.

9. Как обозначается и в чем измеряется температура?

1. 2. 3.

10. Как обозначается и в чем измеряется масса?

1. 2. 3.

III. Новая тема:

Г л а в а 1. ОСНОВЫ КИНЕМAТИКИ

Движение тел изучается в разделе физики — механике.

Механика делится на кинематику и динамику.

Кинематика — это раздел механики, изучающий связь между величинами, характеризующими движение. В кинематике не рассматриваются причины, обусловливающие движение тела, они рассматриваются в динамике.

§ 1. ДВИЖЕНИЕ — НЕОТЪЕМЛЕМAЯ ЧАСТЬ МАТЕРИИ

1 Механическое движение

В самом широком смысле движение означает любое изменение в природе. В кинематике мы рассматриваем самый простой и широко распространенный вид таких изменений — Механическое движение, которое возникает в связи с перемещением тел.

2 Относительность движения и покоя

Если тело находится в покое относительно какого-либо тела, то оно находится в движении относительно другого тела, так как покой является тоже относительным.

Следовательно, в природе не существуют абсолютно неподвижные тела.

3 Материя

В мире все, что объективно существует вокруг нас, на научном языке называется материей.

Одно из основных свойств материи – движение.

Движение — свойство материального мира. Все то, что мы называем природой или миром, является материей в движении.

Физминутка по видеоролику.

§ 2. ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ

1 Векторы

Величины, которые кроме своего числового значения (модуля) характеризуются еще и направлением в пространстве, называются векторными величинами, или векторами.

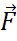
2 Скаляры

Величины, не имеющие направления в пространстве, характеризующиeся только числовым значением, называются скалярными величинами, или скалярами.

F

3 Действия над векторами

Сложение векторов 2-мя способами — презентация

7 Вычитание векторов 2-мя способами

8 Параллельные вектора

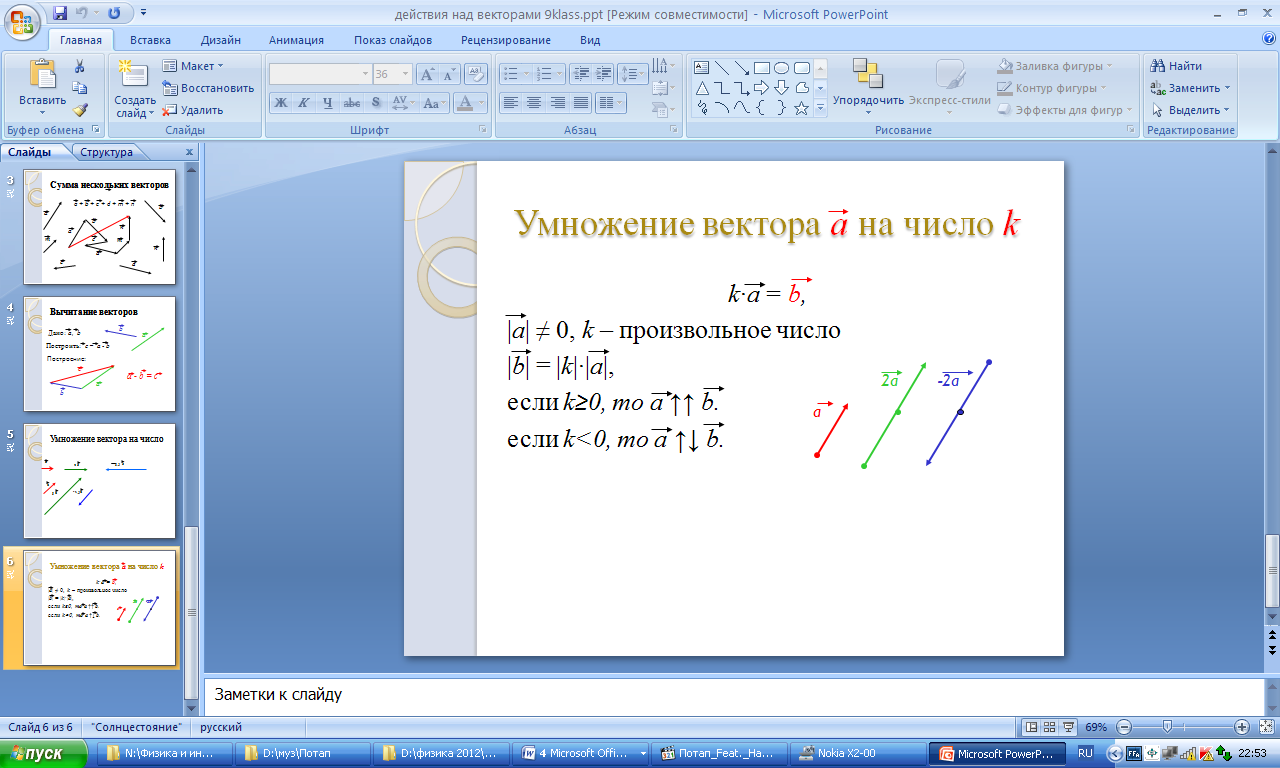
9 Умножение вектора на число

IV. Закрепление решение простейшей задачи

V. Рефлексия. Разноцветные листочки

VI. Д/З 7 и 8 класс формулы, §1,2, Упр.1 №2

Презентация к уроку по геометрии на тему: Векторы. Все действия с векторами

Слайд 1

Векторы Понятие вектора Равенство векторов Откладывание вектора от данной точки Сумма двух векторов Законы сложения. Правило параллелограмма Сумма нескольких векторов Вычитание векторов Умножение вектора на число Глущенко Т.В. ЦО № 43

Слайд 2

Понятие вектора Пусть на тело действует сила в 8Н. Стрелка указывает направление силы, а длина отрезка соответствует числовому значению силы. 8Н

Слайд 3

Понятие вектора Рассмотрим произвольный отрезок. На нем можно указать два направления. Чтобы выбрать одно из направлений, один конец отрезка назовем НАЧАЛОМ , а другой – КОНЦОМ и будем считать, что отрезок направлен от начала к концу. Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется направленным отрезком или вектором.

Слайд 4

Понятие вектора На рисунках вектор изображается отрезком со стрелкой Вектор АВ, А – начало вектора, В – конец. CD EF LK А В АВ C D E F K L

Слайд 5

Понятие вектора Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: Любая точка плоскости также является вектором, который называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: ММ = 0. a b c М

Слайд 6

Понятие вектора Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ: АВ = а = АВ = 5 с = 17 Длина нулевого вектора считается равной нулю: ММ = 0. a М В А с

Слайд 7

Коллинеарные векторы Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарные векторы могут быть сонаправленными или противоположно направленными . Нулевой вектор считается коллинеарным любому вектору. а b c d m n s L

Слайд 8

Равенство векторов Определение. Векторы называются равными , если они сонаправлены и их длины равны. а = b , если а b а = b а c b d m n s f

Слайд 9

Откладывание вектора от данной точки Если точка А – начало вектора а , то говорят, что вектор а отложен от точки А . Утверждение: От любой точки М можно отложить вектор, равный данному вектору а , и притом только один. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой А а М а

Слайд 10

Сумма двух векторов Рассмотрим пример: Петя из дома( D ) зашел к Васе( B ), а потом поехал в кинотеатр( К ). В результате этих двух перемещений, которые можно представить векторами DB и BK , Петя переместился из точки D в К, т.е. на вектор D К: DK=DB+BK . Вектор DK называется суммой векторов DB и BK . D B K

Слайд 11

Сумма двух векторов Правило треугольника Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b . АС = а + b a b A a b B C

Слайд 12

Законы сложения векторов 1) а+ b=b+a (переместительный закон) Правило параллелограмма Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем вектор А D = b . На этих векторах построим параллелограмм АВС D . АС = АВ + B С = а+ b АС = А D + D С = b+a 2) ( а+ b)+c=a+(b+c) (сочетательный закон) a a b b A D C B a b

Слайд 13

Сумма нескольких векторов Правило многоугольника s=a+b+c+d+e+f k+n+m+r+p= 0 a b c d e f s k m n r p O

Слайд 14

Противоположные векторы Пусть а – произвольный ненулевой вектор. Определение. Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены. a = АВ, b = BA Вектор, противоположный вектору c , обозначается так: — c . Очевидно, с+(-с)=0 или АВ+ВА=0 А B a b c -c

Слайд 15

Вычитание векторов Определение. Разностью двух векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а. Теорема. Для любых векторов а и b справедливо равенство а — b = а + (- b ). Задача. Даны векторы а и b . Построить вектор а – b . а а b -b -b a — b

Слайд 16

Умножение вектора на число Определение. Произведением ненулевого вектора а на число k называется такой вектор b , длина которого равна вектору k а , причем векторы а и b сонаправлены при k ≥ 0 и противоположно направлены при k

Слайд 17

Умножение вектора на число Для любых чисел k , n и любых векторов а, b справедливы равенства: ( kn ) а = k (na) ( сочетательный закон) ( k + n ) а = k а + na ( первый распределительный закон) K ( а+ b ) = k а + kb ( второй распределительный закон) Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, p = 2( a – b) + ( c + a ) – 3( b – c + a ) = = 2a – 2b + c + a – 3b + 3c – 3a = — 5b + 4c

Действия над векторами в пространстве

ТЕМА: «Действия над векторами в пространстве »

Плоскость Охуz –координатная плоскость Прямые Ох, Оy, Оz называются координатными осями (или осями координат)  

Оси координат обозначаются так:

Oх- ось абсцисс

Oy- ось ординат

Oz- ось аппликат
точка их пересечения O – начало координат, 
плоскости Оху,  Охz и  Оуz – координатные плоскости . 

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. М(x; y; z).

Прямоугольная система координат в пространстве

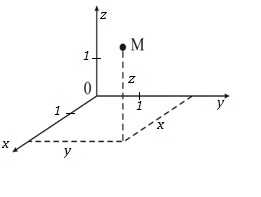
Формула разложения любого вектора по координатным векторам + у∙+z∙ ,

где х,у,z-коэффициенты разложения и они являются координатами вектора

Запишите координаты вектора, если

+ 3∙— 2∙ ,

Координаты вектора

Действия над векторами:

Примеры:

Сложение векторов

Вычитание векторов

Умножение вектора на число k.

Самостоятельная работа

Дано: , Дано: ,

Найти координаты векторов: а)
Найти координаты векторов: а) б)

б) в) в)

Простейшие задачи в координатах:

Задачи:

Координаты середины отрезка AB:

А(x₁;y₁;z₁), B(x₂;y₂;z₂).

Точка М середина отрезка AB.

А(1;-1;0), B(6;-3;-4). Точка N Середина отрезка AB. Найти координаты точки N.

Ответ:

Вычисление длины вектора по его координатам:

Вычисление длины вектора .

Ответ: 5

Расстояние между двумя точками.

А(x₁;y₁;z₁) и B(x₂;y₂;z₂).

Вычислить расстояние между двумя точками

С(2;-3;7) и D(-2;3;7).

Ответ:

Вычисление координат вектора . Если

А(x₁;y₁;z₁), B(x₂;y₂;z₂).

В пространстве расположены три точки, заданные своими координатами: A(1; 6; 3), B (3; − 1; 7) и C(− 4; 3; − 2). Найти координаты векторов ,  и 

Ответ: ;

Скалярное произведение векторов и выражается формулой:

Вычислить скалярное произведение векторов и

Ответ:12

Перпендикулярность векторов: ;

Перпендикулярны ли векторы и

Ответ: да

Коллинеарность векторов: ;

, если координаты векторов не равны нулю.

Задача. Коллинеарны ли векторы:

a) {-5;3;-1} и {-10; 6;-2};

b) {-6;3;-1} и {2; -9;3};

Решение.

a)

Да, векторы коллинеарны

b)

Нет, векторы не коллинеарны

Ответ: a) да b) нет

Косинус угла между ненулевыми векторами векторов и вычисляется по формуле:

Найти косинус угла между векторами  = {4; 3; 0} и  = {0; 12; 5}.

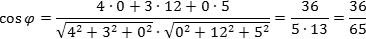
Ответ:36/65

Презентация к уроку по геометрии (9 класс) на тему: 9 класс. Вектора. Действия над векторами

Слайд 2

Вектор — направленный отрезок прямой.(у которого указан начало и конец) В А А – начало вектора В – конец вектора ͢ а ͢ а или обозначение вектора

Слайд 3

Сложение векторов Коллинеарные вектора: ͢ а ͢ b ͢ c ͢ b ͢ а ͢ ͢ ͢ а + b = с а)

Слайд 4

б) В А D C А В C D ― ― ― AB + CD = AD

Слайд 5

Неколлинеарные вектора: а) Правило треугольника ͢ а ͢ а ͢ b ͢ b ͢ c ― ― ― AB + BC = AC A B C Для любых трёх точек верно равенство:

Слайд 6

б)Правило параллелограмма: (применяется в физике при сложении двух сил) ͢ а ͢ b ͢ а ͢ b ͢ с ― ― ― AB + АС = AD D А B С

Слайд 7

в ) Сложение нескольких векторов ͢ а ͢ а1 ͢ а2 ͢ а3 ͢ а4 ͢ а ͢ а1 ͢ а2 ͢ а3 ͢ а4 ͢ х ͢ а ͢ а1 ͢ а2 ͢ а3 ͢ а4 + + + + = ͢ х

Слайд 8

͢ а ͢ а1 ͢ а2 ͢ а3 ͢ а4 ͢ а5 ͢ а ͢ а1 ͢ а2 ͢ а3 ͢ а4 + + + + = ͢ 0 ͢ а5 +

Слайд 9

Законы сложения векторов. Для любых векторов а, b, c справедливы равенства: ͢ ͢ ͢ ͢ а + b= b + a – переместительный закон ͢ ͢ ͢ ͢ ͢ ͢ ( а + b)+c=a+(b+c) – сочетательный закон ͢ ͢ ͢ 3) а +0 = а – поглощение нулевого вектора

Слайд 10

Вычитание векторов. Разностью двух векторов а и b называется вектор с , сумма которого с вектором b равняется вектору а . ͢ ͢ ͢ а — b = с  ͢ ͢ ͢ c + b = a

Слайд 11

I случай ͢ а ͢ b ͢ а ͢ b ͢ c O A B ― ― ― OA — OB = BA

Слайд 12

II случай Теорема : для любых векторов а и b справедливо равенство : ͢ ͢ ͢ ͢ ͢ а — b = а +(- b) = c ͢ а ͢ b ͢ c ͢ а ͢ -b

Слайд 13

Произведение не нулевого вектора любое число k равняется вектору ͢ а на ͢ b → → b = a * k → → 1)│ b│ = │ a │* │k│ → → 2) если k > 0 => b ↑↑ a → → если k b ↑↓ a → → если k = 0 => b = 0

Слайд 14

Свойства умножения вектора на число. → → 1)( m * n) * a = m * (a * n) – сочетательный → → → 2)( m+n) * a = m*a + n*a – I распределительный → → → → 3)( a+b) * m=m*a + m*b – II распределительный → → → 4)0 * a = m*0 = 0 – поглощение нуля и нулевого вектора

Слайд 15

Пример : ͢ а ͢ b Построить: ͢ → → х = 3 a + ½ b ͢ 3 а ͢ ½ b ͢ х