Алгебра свободных и скользящих векторов

Алгебра свободных и скользящих векторов

Меркин Д.Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с. В книге дается подробное изложение алгебры свободных и скользящих векторов. Содержание первой главы соответствует в основном программе по векторной алгебре курса высшей математики втузов. Во второй главе рассматривается теория преобразования системы скользящих векторов и приведения их к простейшему виду. Эта теория имеет важное значение в различных вопросах физики и техники; она может рассматриваться также, как вводная глава винтового исчисления. В книге большое внимание уделено примерам и разъяснению некоторых деталей и особенностей векторного исчисления, весьма важных в приложениях. Книга может служить учебным пособием для студентов и преподавателей втузов и университетов. Она рассчитана также на инженеров, желающих повысить свою теоретическую подготовку. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов.

Идентификаторы векторов

На этой странице перечислены некоторые часто используемые идентификаторы векторов.

2 \] 92. \]

\[\begin{выровнено} \vec{a} \cdot (\vec{b} + \vec{c}) &= \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \\ (\vec{a} + \vec{b}) \cdot \vec{c} &= \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \\ \vec{a} \cdot (\beta \vec{b}) &= \beta (\vec{a} \cdot \vec{b}) = (\beta \vec{a}) \cdot \vec{b}\end{выровнено}\]

Использование выражения координат #rvv-es дает: \[\ начало {выровнено} \vec{a} \cdot (\vec{b} + \vec{c}) &= a_1 (b_1 + c_1) + a_2 (b_2 + c_2) + a_3 (b_3 + c_3) \\ &= (a_1 b_1 + a_2 b_2 + a_3 b_3) + (a_1 c_1 + a_2 c_2 + a_3 c_3) \\ &= \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \\ (\vec{a} + \vec{b}) \cdot \vec{c} &= (a_1 + b_1) c_1 + (a_2 + b_2) c_2 + (a_3 + b_3) c_3 \\ &= (a_1 c_1 + a_2 c_2 + a_3 c_3) + (b_1 c_1 + a_2 c_2 + a_3 c_3) \\ &= \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \\ \vec{a} \cdot (\beta \vec{b}) &= a_1 (\beta b_1) + a_2 (\beta b_2) + a_3 (\beta b_3) \\ &= \бета (a_1 b_1 + a_2 b_2 + a_3 b_3) \\ &= \бета (\vec{a} \cdot \vec{b}) \\ &= (\beta a_1) b_1 + (\beta a_2) b_2 + (\beta a_3) b_3 \\ &= (\beta \vec{a}) \cdot \vec{b}.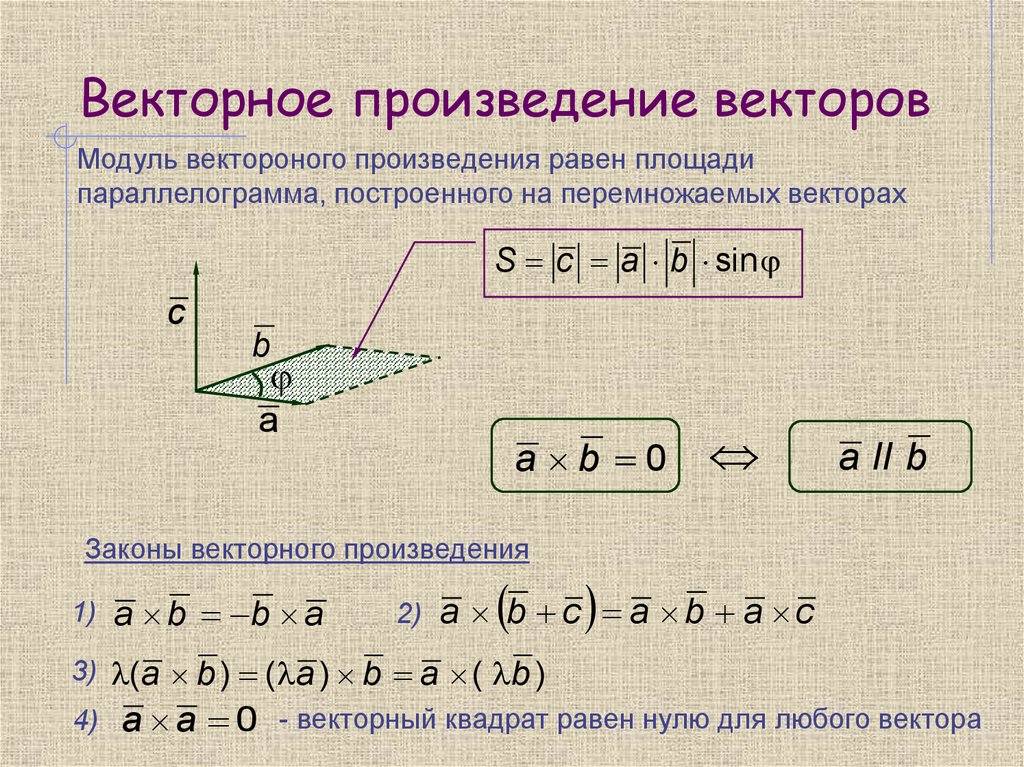

\конец{выровнено}\]

\[\begin{выровнено} \vec{a} \times \vec{b} = — \vec{b} \times \vec{a}\end{выровнено}\]

Запись выражения компонента #rvv-ex дает: \[\ начало {выровнено} \vec{a} \times \vec{b} &= (a_2 b_3 — a_3 b_2) \,\шляпа{\imath} + (a_3 b_1 — a_1 b_3) \,\шляпа{\jmath} + (a_1 b_2 — a_2 b_1) \,\шляпа{k} \\ &= -(a_3 b_2 — a_2 b_3) \,\шляпа{\imath} — (a_1 b_3 — a_3 b_1) \,\шляпа{\jmath} — (а_2 б_1 — а_1 б_2) \,\шляпа{к} \\ &= -\vec{b} \times \vec{a}. \конец{выровнено}\]

\[\ начало {выровнено} \vec{a} \times \vec{a} = 0 \конец{выровнено}\]

Из антисимметрии #rvi-ea мы иметь: \[\ начало {выровнено} \vec{a} \times \vec{a} &= — \vec{a} \times \vec{a} \\ 2 \vec{a} \times \vec{a} &= 0 \\ \vec{a} \times \vec{a} &= 0.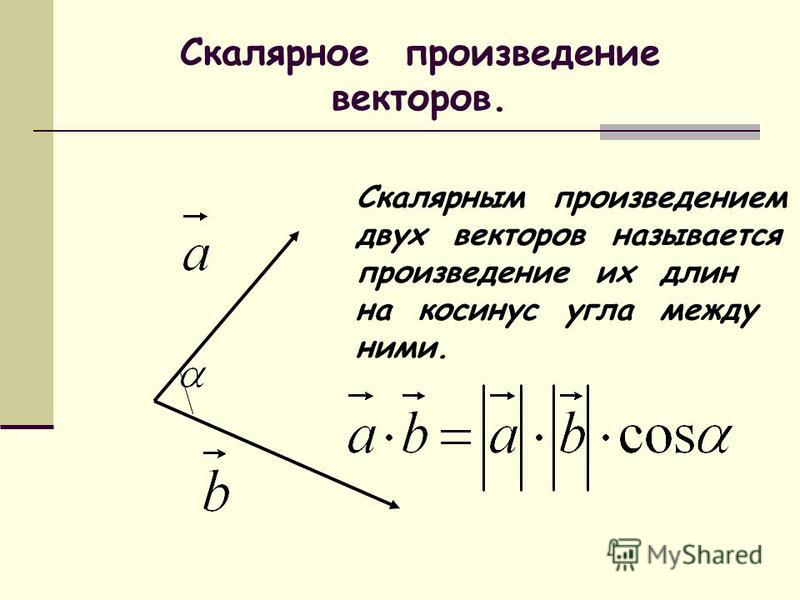

\конец{выровнено}\]

\[\ начало {выровнено} \vec{a} \times (\vec{b} + \vec{c}) &= \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \\ (\vec{a} + \vec{b}) \times \vec{c} &= \vec{a} \times \vec{c} + \vec{b} \times \vec{c} \\ \vec{a} \times (\beta \vec{b}) &= \бета (\vec{a} \times \vec{b}) = (\ бета \ vec {а}) \ раз \ vec {b} \конец{выровнено}\]

Написание выражения компонента #rvv-ex для первого уравнение дает: \[\ начало {выровнено} \vec{a} \times (\vec{b} + \vec{c}) &= (a_2 (b_3 + c_3) — a_3 (b_2 + c_2)) \,\hat{\imath} \\ &\quad + (a_3 (b_1 + c_1) — a_1 (b_3 + c_3)) \,\hat{\jmath} \\ &\quad + (a_1 (b_2 + c_2) — a_2 (b_1 + c_1)) \,\шляпа{k} \\ &= \Big((a_2 b_3 — a_3 b_2) \,\шляпа{\imath} + (a_3 b_1 — a_1 b_3) \,\шляпа{\jmath} + (a_1 b_2 — a_2 b_1) \,\шляпа{k} \Большой) \\ &\quad + \Big((a_2 c_3 — a_3 c_2) \,\шляпа{\imath} + (a_3 c_1 — a_1 c_3) \,\шляпа{\jmath} + (a_1 c_2 — a_2 c_1) \,\шляпа{k} \Большой) \\ &= \vec{a} \times \vec{b} + \vec{a} \times \vec{c}. \\ \конец{выровнено}\] Второе уравнение следует аналогично, а для третьего уравнение имеем: \[\ начало {выровнено} \vec{a} \times (\beta \vec{b}) &= (a_2 (\beta b_3) — a_3 (\beta b_2)) \,\hat{\imath} + (a_3 (\beta b_1) — a_1 (\beta b_3)) \,\hat{\jmath} + (a_1 (\beta b_2) — a_2 (\beta b_1)) \,\шляпа{k} \\ &= \beta \Big( (a_2 b_3 — a_3 b_2) \,\hat{\imath} + (a_3 b_1 — a_1 b_3) \,\шляпа{\jmath} + (a_1 b_2 — a_2 b_1) \,\шляпа{k} \Большой) \\ &= \бета (\vec{a} \times \vec{b}). \конец{выровнено}\] Последнюю часть третьего уравнения можно увидеть с помощью аналогичный вывод.

Скалярное тройное произведение равно \(\vec{a} \cdot (\vec{b} \times \vec{c})\), что дает объем параллелепипеда, определяемый \(\vec{a}, \vec{b}, \vec{c}\).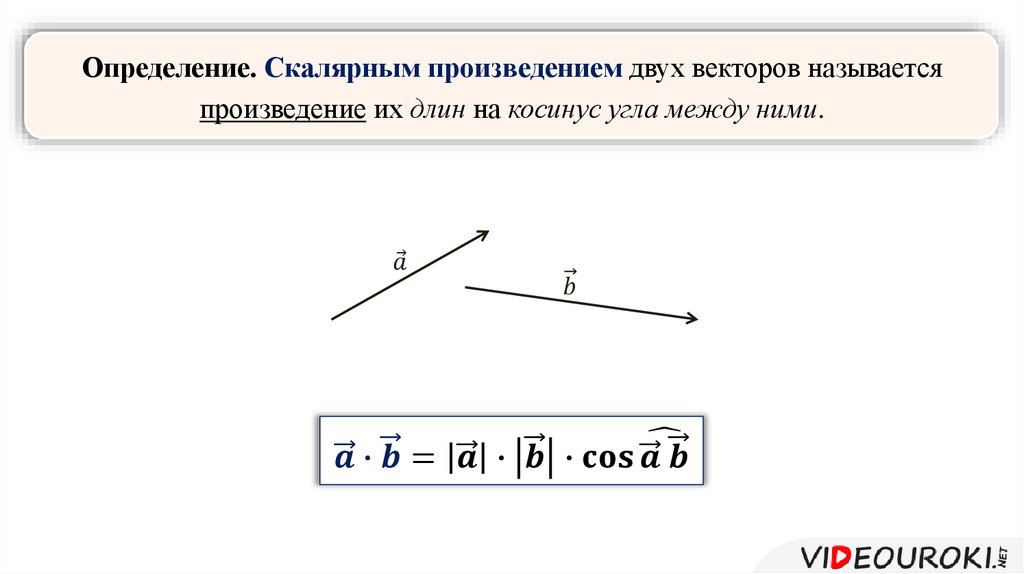 Он удовлетворяет:

\[\begin{выровнено} \vec{a} \cdot (\vec{b} \times \vec{c}) = \vec{b} \cdot (\vec{c} \times \vec{a}) = \vec{c} \cdot (\vec{a} \times \vec{b})\end{выровнено}\]

Записав первые два выражения в компонентах, мы можно проверить, что они дают тот же результат:

\[\begin{выровнено} \vec{a} \cdot (\vec{b} \times \vec{c}) &= (a_1 \,\шляпа{\imath} + a_2 \,\шляпа{\jmath} + a_3 \,\шляпа{k}) \\ &\qquad \cdot \big( (b_1 \,\hat{\imath} + b_2 \,\hat{\jmath} + b_3 \,\шляпа{k}) \times (c_1 \,\шляпа{\imath} + c_2 \,\шляпа{\jmath} + c_3 \,\шляпа{к}) \большая) \\ &= (a_1 \,\шляпа{\imath} + a_2 \,\шляпа{\jmath} + a_3 \,\шляпа{k}) \\ &\qquad \cdot \big( (b_2 c_3 — b_3 c_2) \,\hat{\imath} + (b_3 c_1 — b_1 c_3) \,\hat{\jmath} + (b_1 c_2 — b_2 c_1) \,\шляпа{к} \большой) \\ &= a_1 b_2 c_3 — a_1 b_3 c_2 + a_2 b_3 c_1 — a_2 b_1 c_3 + a_3 b_1 c_2 — a_3 b_2 c_1 \\ \vec{b} \cdot (\vec{c} \times \vec{a}) &= (b_1 \,\hat{\imath} + b_2 \,\шляпа{\jmath} + b_3 \,\шляпа{к}) \\ &\qquad\cdot\big( (c_1 \,\шляпа{\imath} + c_2 \,\шляпа{\jmath} + c_3 \,\шляпа{k}) \times (a_1 \,\hat{\imath} + a_2 \,\hat{\jmath} + a_3 \,\шляпа{к}) \большой) \\ &= (b_1 \,\шляпа{\imath} + b_2 \,\шляпа{\jmath} + b_3 \,\шляпа{к}) \\ &\qquad\cdot\big( (c_2 a_3 — c_3 a_2) \,\hat{\imath} + (c_3 a_1 — c_1 a_3) \,\шляпа{\jmath} + (c_1 a_2 — c_2 a_1) \,\шляпа{k} \big) \\ &= b_1 c_2 a_3 — b_1 c_3 a_2 + b_2 c_3 a_1 — b_2 c_1 a_3 + b_3 c_1 a_2 — b_3 c_2 a_1. \end{выровнено}\]

Третье выражение тоже самое.

Векторное тройное произведение равно \(\vec{a} \times (\vec{b} \times \vec{c})\). Он удовлетворяет:

\[\begin{выровнено} \vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c}) \vec{b} — (\vec{a} \cdot \vec{b}) \vec{c}\end{выровнено}\]

В компонентах имеем:

\[\begin{выровнено} \vec{a} \times (\vec{b} \times \vec{c}) &= (a_1 \,\шляпа{\imath} + a_2 \,\шляпа{\jmath} + a_3 \,\шляпа{k}) \\ &\qquad \times \Big( (b_1 \,\hat{\imath} + b_2 \,\hat{\jmath} + b_3 \,\шляпа{k}) \times (c_1 \,\шляпа{\imath} + c_2 \,\шляпа{\jmath} + c_3 \,\шляпа{k}) \Большой) \\ &= (a_1 \,\шляпа{\imath} + a_2 \,\шляпа{\jmath} + a_3 \,\шляпа{k}) \\ &\qquad \times \Big( (b_2 c_3 — b_3 c_2) \,\hat{\imath} + (b_3 c_1 — b_1 c_3) \,\hat{\jmath} + (b_1 c_2 — b_2 c_1) \,\шляпа{k} \Большой) \\ &= \Большой(a_2 (b_1 c_2 — b_2 c_1) — a_3 (b_3 c_1 — b_1 c_3)\Большой) \,\hat{\imath} \\ &\quad+ \Big(a_3 (b_2 c_3 — b_3 c_2) — a_1 (b_1 c_2 — b_2 c_1)\Big) \,\hat{\jmath} \\ &\quad+ \Big(a_1 (b_3 c_1 — b_1 c_3) — a_2 (b_2 c_3 — b_3 c_2)\Big) \,\hat{k} \\ &= (a_2 b_1 c_2 — а_2 б_2 с_1 — а_3 б_3 с_1 + а_3 б_1 в_3) \,\hat{\imath} \\ &\quad+ (a_3 b_2 c_3 — a_3 b_3 c_2 — a_1 b_1 c_2 + a_1 b_2 c_1) \,\шляпа{\jmath} \\ &\quad+ (a_1 b_3 c_1 — a_1 b_1 c_3 — a_2 b_2 c_3 + a_2 b_3 c_2) \,\hat{k} \\ &= (a_1 b_1 c_1 + a_2 b_1 c_2 + a_3 b_1 c_3 — a_1 b_1 c_1 — a_2 b_2 c_1 — a_3 b_3 c_1) \,\hat{\imath} \\ &\quad+ (a_1 b_2 c_1 + a_2 b_2 c_2 + a_3 b_2 c_3 — a_1 b_1 c_2 — a_2 b_2 c_2 — a_3 b_3 c_2) \,\hat{\jmath} \\ &\quad+ (а_1 б_3 с_1 + а_2 б_3 с_2 + а_3 б_3 с_3 — а_1 б_1 c_3 — a_2 b_2 c_3 — a_3 b_3 c_3) \,\шляпа{k} \\ &= (a_1 b_1 + a_2 c_2 + a_3 c_3) b_1 \,\hat{\imath} + (a_1 c_1 + a_2 c_2 + a_3 c_3) b_2 \,\hat{\jmath} \\ &\qquad + (a_1 c_1 + a_2 c_2 + a_3 c_3) b_3 \,\шляпа{k} \\ &\quad- (a_1 b_1 + a_2 b_2 + a_3 b_3) c_1 \,\шляпа{\imath} — (a_1 b_1 + a_2 b_2 + a_3 b_3) c_2 \,\шляпа{\jmath} \\ &\qquad — (a_1 b_1 + a_2 b_2 + a_3 b_3) c_3 \,\шляпа{к} \\ &= (\vec{a} \cdot \vec{c}) \vec{b} — (\vec{a} \cdot \vec{b}) \vec{c}. \end{выровнено}\]

\[\begin{выровнено} \vec{a} \times \vec{b} \text{ ортогонален обоим } \vec{a} \text{ и } \vec{b}\end{выровнено}\]

Это немедленно следует из скалярного тройного произведения формула #rvi-es:

\[\begin{выровнено} \vec{a} \cdot (\vec{a} \times \vec{b}) = \vec{b} \cdot (\vec{a} \times \vec{a}) = 0,\end{выровнено}\]

и аналогично для \(\vec{b}\).

\[\begin{выровнено} (\vec{a} \times \vec{b}) \cdot (\vec{c} \times \vec{d}) = (\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d}) — (\vec{a} \cdot \vec{d})(\vec{b} \cdot \vec{c})\end{выровнено}\]

Из формулы скалярного тройного произведения #rvi-es и векторного тройного произведения расширение #rvi-ev:

\[\begin{выровнено} (\vec{a} \times \vec{b}) \cdot (\vec{c} \times \vec{d}) &= \vec{c} \cdot \big( \vec{d} \times (\vec{a} \times \vec{b}) \big) \\ &= \vec{c} \cdot \big( (\vec{d} \cdot \vec{b}) \vec{a} — (\vec{d} \cdot \vec{a}) \vec{b} \big) \\ &= (\vec{d} \cdot \vec{b}) (\vec{c} \cdot \vec{a}) — (\vec{d} \cdot \vec{a}) (\vec{c} \cdot \vec{b}). \end{выровнено}\] 92\тета.\конец{выровнено}\]

\[\begin{выровнено} \vec{a} \times (\vec{b} \times \vec{c}) + \vec{b} \times (\vec{c} \times \vec{a}) + \vec{c} \times (\vec{a} \times \vec{b}) = 0\конец{выровнено}\]

Используя расширение векторного тройного произведения #rvi-ev:

\[\begin{выровнено} &\vec{a} \times (\vec{b} \times \vec{c}) + \vec{b} \times (\vec{c} \times \vec{a}) + \vec{c} \times (\vec{a} \times \vec{b}) \\ &\qquad= (\vec{a} \cdot \vec{c}) \vec{b} — (\vec{a} \cdot \vec{b}) \vec{c} + (\vec{b} \cdot \vec{a}) \vec{c} — (\vec{b} \cdot \vec{c}) \vec{a} + (\vec{c} \cdot \vec{b}) \vec{a} — (\vec{c} \cdot \vec{a}) \vec{b} \\ &\qquad= 0. \конец{выровнено}\]

\[\begin{выровнено} (\vec{a} \times \vec{b}) \times (\vec{a} \times \vec{c}) = \big( \vec{a} \cdot (\vec{b} \times \vec{c}) \big) \vec{a}\end{выровнено}\]

Возьмем \(\vec{d} = (\vec{a} \times \vec{b}) \times (\vec{a} \times \vec{c})\). Тогда \(\vec{d}\) находится в \(\vec{a},\vec{b}\) и в плоскости \(\vec{a},\vec{c}\) плоскость, поэтому она кратна \(\vec{a}\). Мы используем скалярная формула тройного произведения #rvi-es и векторное тройное произведение расширение #rvi-ev для вычисления:

\[\begin{выровнено} \vec{d} \cdot \vec{a} &= \vec{a} \cdot \big( (\vec{a} \times \vec{b}) \times (\vec{a} \times \vec{c}) \big) \\ &= (\vec{a} \times \vec{c}) \cdot \big( \vec{a} \times (\vec{a} \times \vec{b}) \big) \\ &= (\vec{a} \times \vec{c}) \cdot \big( (\vec{a} \cdot \vec{b}) \vec{a} — (\vec{a} \cdot \vec{a}) \vec{b} \big) \\ &= — (\vec{a} \cdot \vec{a}) \vec{b} \cdot (\vec{a} \times \vec{c}) \\ &= (\vec{a} \cdot \vec{a}) \big( \vec{a} \cdot (\vec{b} \times \vec{c}) \big). \end{выровнено}\]

Затем

\[\begin{выровнено} \vec{d} = \operatorname{Proj}(\vec{d}, \vec{a}) = \ влево (\ гидроразрыва {\ vec {d} \ cdot \vec{a}}{\vec{a} \cdot \vec{a}}\right) \vec{a} = \big( \vec{a} \cdot (\vec{b} \times \vec{c}) \big) \vec{a}.\end{выровнено}\]

Кокранматематика / Векторные приложения векторного произведения и скалярного произведения

Векторные приложения: векторное произведение и скалярное произведение

---

 

Векторы

Вектор — это величина с заданной величиной и направлением, которая соединяет начальную точку A с конечной точкой B, создавая AB.

(Ссылки на страницы: Приложения касательного и нормального вектора)

 

 

Векторы могут быть записаны одним из двух способов:

Для вектора AB и B () is (c, d), AB можно записать как:

AB = <(C-A), (D-B)>

AB = (C-A) I + (D-B) J

ОСНОВНЫ = < U ₁ , U ₂ > и V = < V ₁ , V ₁ .

1. Векторная сумма U и v — вектор U + V = 1 + V ₁ , U ₂ + V ₂ >

2. Скарал Scalar Suplet of C и 2 2 >

2. u — это вектор c u = 1 , cu ₂ >

3. Отрицательное значение v — это вектор –v = (-1) <-v 900 ₁ , -v ₂ >

4. Разница между и и V — U — V = 1 — V ₁ , U ₂ — V ₂ >

единиц. То же направление, что и заданный вектор, но длина 1.

, если V — это ненулевой вектор в плоскости, то единый вектор A —

Единичный вектор — это вектор, деленный на собственную величину.

 

Скалярное произведение

Скалярное произведение — это тип векторной операции, которая дает скаляр, а не вектор.

Продукт DOT U = 1 , U ₂ > и V = 1 , V ₂ > IS

U 90975 2 > IS

U ·

7 ·

7 ·

7 ·

7 ·

7 · 7 ·

· ₂ >. и ₁ в ₁ + и ₂ в ₂

Для трехмерных векторов, точечный продукт U = 1 , U ₂ , U ₃ > и V = 1 > и V = 1 , и V = 1 , и V = 1 > и V = 1 > и V = 1 > и V = 1 > и V = 1 > и В . , v ₃ > is

u · v = u ₁ v ₁ + u ₂ v ₂ + u ₃ v ₃

 

For more информацию об определении векторов и некоторых свойствах и функциях векторов, щелкните http://mathworld.wolfram.com/Vector.html, чтобы перейти на официальную страницу пояснений WolframAlpha.

 

 

Применение скалярных произведений:

1.  Угол между двумя векторами:

Угол A [0, π] между любыми двумя ненулевыми векторами u и является стандартным7 в их положении и . Приведен Формулой

Доказательство этой формулы: (как видно в этом видео)

Рассмотрим треугольник, определяемый векторами, U , V и U-V , как показано ниже.

 

По закону косинусов, который гласит, что c ² = a ² + b ² — 2(a)(b)(cosC),

, можно сказать, что

 

Используя свойства скалярных произведений, левая часть может быть переписана как:

 

Подставляя это обратно в закон косинусов, получаем:

Пошаговая процедура применения эту формулу можно найти на http://www. wikihow.com/Find-the-Angle-Between-Two-Vectors

2. Определение ортогональных векторов

векторы U и V являются ортогональными (нормальные, перпендикулярные).

Дополнительные сведения об ортогональных векторах см. на http://www.youtube.com/watch?v=tGYvaabMbYA.

Здесь можно найти видео с объяснением проекций.

Проекции позволяют нам анализировать влияние неортогональных векторных сил на желаемый вектор.

Например, это позволяет нам увидеть воздействие силы тяжести F _g на лодку, движущуюся по наклонной рампе, как показано ниже.

 

Проекция одного вектора на другой, как показано ниже в проекции вектора u на v , равна w.

     W определяется как составляющая одного вектора ( u ), действующего с силой желаемого вектора ( v ).

     Другими словами, это «сумма» ( w ) u , которая «помогает» v .

 

Формула проекции u на v дается по формуле:

Доказательство этой формулы можно увидеть в этом видео

0003

Example Problem:

Project vector u onto v given :    u = 5 i + 9 j      and           v = 10 i + 3 j

 

Решение:

1) Нарисуйте картинку. Изображение даст вам лучшее представление о том, как должна выглядеть проекция.

 

2) Подставьте данные векторы в формулу для проекций.

**Обязательно запомните, какой вектор на какой проецируется. Использование неправильного вектора в качестве u, например , может дать вам совершенно неверный ответ.

3) Убедитесь, что ваши цифры имеют смысл, сравнив их с картинкой, которую вы нарисовали.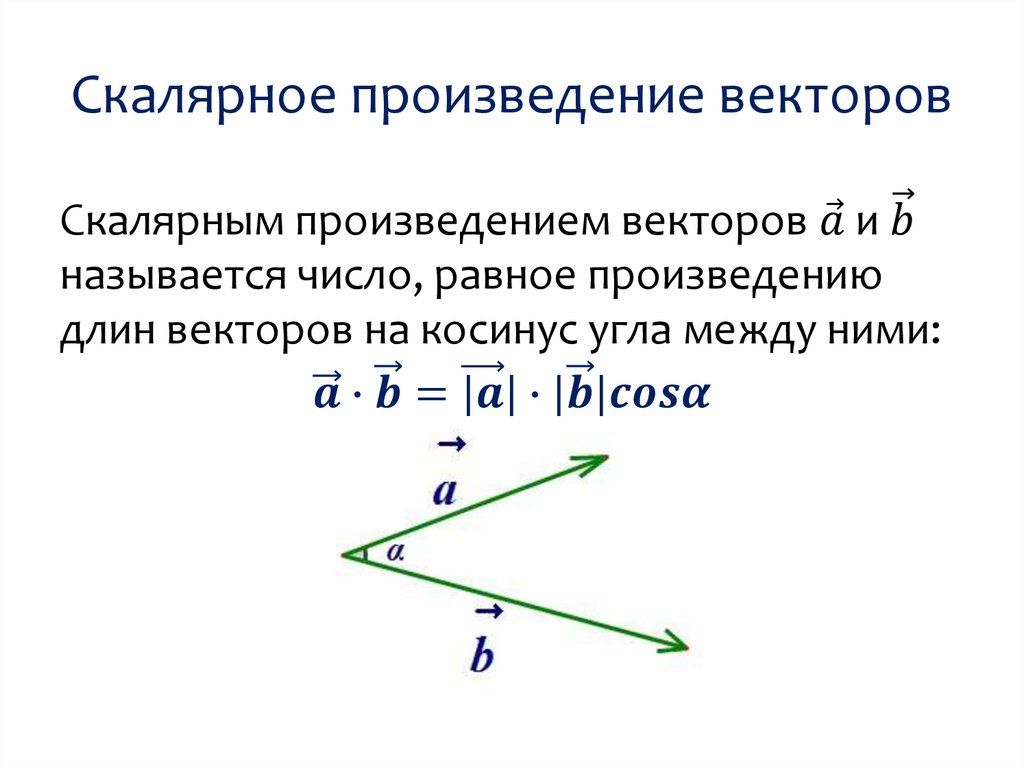 В этом случае они делают. Если нет, вернитесь и проверьте на наличие ошибок.

 

 

 

Для получения дополнительной информации о векторных проекциях и некоторых дополнительных примерах задач посетите http://www.vitutor.com/geometry/vec/vector_projection.html

 

 

 

Перекрестное произведение

С помощью перекрестного произведения можно найти вектор в пространстве, ортогональный (перпендикулярный) двум данным векторам. Перекрестное произведение обычно вычисляется в стандартной форме единичного вектора, и его также можно назвать векторным произведением.

 

Определение перекрестного произведения:

Пусть u= u ₁ i + u ₂ j + u ₃ 6 k

3

Пусть v= v ₁ i + v ₂ j + v ₃ k

Это векторы в пространстве.

Перекрестное произведение u и v представляет собой вектор:

u×v = (u ₂ v ₃ – u ₃ v ₂ ) i 3 3 – (u 19013 – и ₃ в ₁ ) й + (и ₁ в ₂ – и ₂ в ₁ ) к

 

Вычисление векторного произведения с матрицами:

Самый простой способ найти u×v — использовать определители и, таким образом, сначала создать матрицу.

Строка 1 всегда указывается как i, j, k.

Строка 2 в этом примере: u ₁ , u ₂ , u ₃ .

Строка 3 в этом примере: v ₁ , v ₂ , v ₃ .

 

 

 *Определители рассчитываются по следующей методике:

 

 

Example :

Let u= i + 3 j + 2 k

Let v= 2 i + 4 j + k

 

Нажмите здесь, чтобы просмотреть видео с объяснением того, как вычислить векторное произведение.

 

Алгебраические свойства векторного произведения:

   Где u, v и w — векторы в пространстве; и c является скаляром,

 

1. u×v = -(v×u)
2. и × (v + ш) = (и × v) + (и × ш)
3. c(u×v) = (cu)×v = u×(cv)
4. u×0 = 0×u= 0
5. u×u= 0
6. u(v×w) = w(u×v)

Геометрические свойства поперечного продукта:

Свойство 1 Доказательство:

Собственность 1 утверждает, что U X V является ортогональным как U, так и V

(доказательство также можно увидеть здесь.)

и= (-3, 1, 2)

v= (6, -2, 4)

 

 

u*(u×v): (-3, 1, 2) * (8, 24, 0) = -24+24+ 0 = 0

v*(u×v): (6, -2, 4) * (8, 24, 0) = 48 – 48+0 = 0

 

Свойство 2 Доказательство:

Свойство 2 утверждает, что величина u x v равна произведению величин u и v и синуса угла между u и v

Доказательство второго геометрического свойства можно найти на http://www. math.hmc. .edu/calculus/tutorials/vectoranalysis/crossproduct.html.

 

Свойство 3 Доказательство:

Свойство 3 говорит, что u x v равно 0, если u и v являются скалярными кратными друг другу , 8)

Следовательно: 2U = V

= (24-24) I-(16-16) J + (12-12) K

= 0

Свойство 4 Доказательство:

Свойство 4 говорит, что площадь параллелограмма с прилегающими сторонами, заданными векторами u и v, равна величине u x v

  Эта ссылка иллюстрирует четвертое геометрическое свойство векторного произведения.

 

Чтобы просмотреть дополнительные видеоролики о кросс-произведениях, посетите сайт http://www.khanacademy.org/math/linear-алгебра/vectors_and_spaces/dot_cross_products/v/linear-алгебра—cross-product-introduction.

 

 

Приложения с плоскостями:

 

В двумерной плоскости удобно писать уравнения прямых на основе наклонов. В трехмерном пространстве удобно писать уравнения прямых и плоскостей на основе векторов.

 

Стандартное уравнение плоскости в пространстве:

Плоскость, содержащая точку (x1, y1, z1) и имеющую вектор нормали n = , может быть представлена ​​стандартной формой уравнения плоскость

      a(x-x ₁ ) + b(y-y ₁ ) + c(z-z ₁ ) = 0

 

«Нормальный» означает перпендикуляр. Таким образом, вектор нормали ( n ) является вектором, перпендикулярным заданной линии или плоскости.

 

                              

 

После того, как n определено, обычно с помощью перекрестных произведений, легко составить декартово уравнение плоскости, которое нормально к n 90. Если есть две пересекающиеся декартовы плоскости, эти уравнения, в свою очередь, также могут позволить нам найти угол между двумя плоскостями.

    

Однако не всегда задан вектор нормали. Поэтому иногда необходимо вычислить n  с использованием двух заданных векторов, представляющих плоскость. Это делается с помощью перекрестного произведения ( cp ).

Нормальный вектор через поперечный продукт:

U X V = (U ₂ V ₃ — U ₃ V ₂ ) I -(U V ₁ 1 1 1 1 1 1 . — u ₃ v ₁ ) j + (u ₁ v ₂ — u ₂ v ₁ ) k

 

     

  

Наконец, векторы нормалей двух плоскостей можно использовать для нахождения угла между ними. В трехмерном пространстве плоскости либо пересекаются, либо параллельны друг другу. Если они пересекаются, угол между ними равен углу между двумя их векторами нормали (для 0 < тета < 2π).