Определение вектора. Виды векторов — МегаЛекции
Математические или физические величины, которые характеризуются только числом, измеряющим их в определенных единицах меры, называют скалярными или скалярами. Скалярами являются, например масса, объем и т.п.
Кроме скалярных величин существуют величины векторные (скорость, ускорение, сила и т.п.)
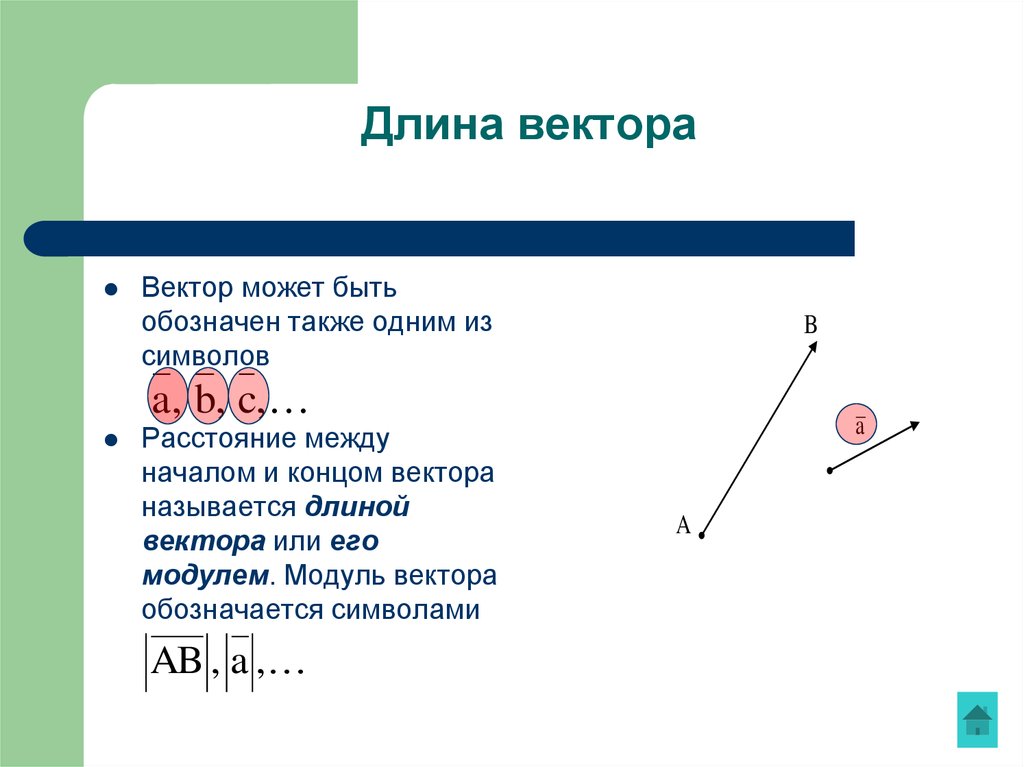
Вектором называется величина, которая характеризуется числом, измеряющим ее в определенных единицах меры, и направлением в пространстве. Обозначается вектор или буквой со стрелкой , или жирной буквой a.
Число , измеряющее вектор в определенных единицах меры, называется модулем или длиной вектора. Зачастую обозначают простой буквой а.
Геометрически вектор изображают отрезком со стрелкой. Направление стрелки указывает направление вектора в пространстве, а длина отрезка изображает модуль вектора (см. рис. 1а).
Рис. 1
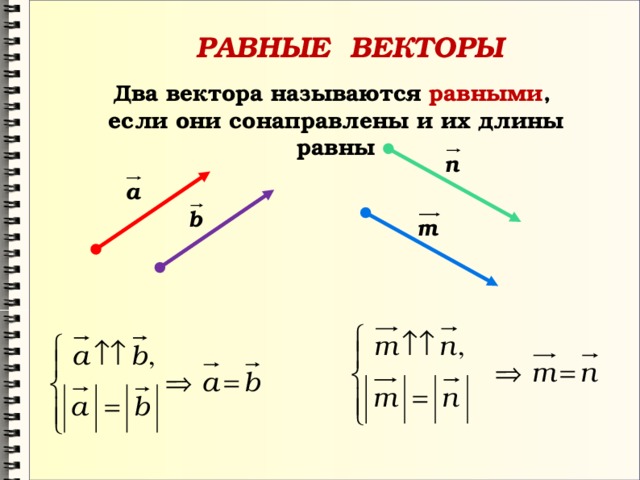
Два вектора называются равными, если равны их длины и совпадают направления.
Вектор, длина которого равна нулю, называется нулевым. Его направление не определено.
Вектор, длина которого равна единице, называется единичным.
Вектор называется противоположным вектору , так как его длина равна длине вектора и он имеет обратное направление.
Единичный вектор расположенный параллельно вектору , может быть определен соотношением . Соответственно, любой вектор может быть представлен в виде .
Проекцией вектора на направление единичного вектора называется вектор , направление которого совпадает с направлением единичного вектора , а длина равна произведению длины вектора на косинус угла между векторами и (см. рис. 2):
, где
Рис.2
В зависимости от видов допускаемых инвариантных[†] преобразований векторы как математическое понятие могут быть разделены на три типа.
1. Простые векторы, которые обычно мы называем одним словом вектор. Инвариантным преобразованием для векторов является параллельный перенос в произвольном направлении (см. рис.1.а).
рис.1.а).
2. Аксиальные векторы. Эти векторы могут располагаться только вдоль определенного направления (см. рис. 1.б). Инвариантным преобразованием для аксиального вектора является его перенос вдоль этого направления.
3. Радиус – вектор соединяет начало координат с точкой, имеющей определенные координаты x, y, z. Для радиус – вектора ни параллельный перенос, ни вращение инвариантными преобразованиями не являются.
Сложение и вычитание векторов
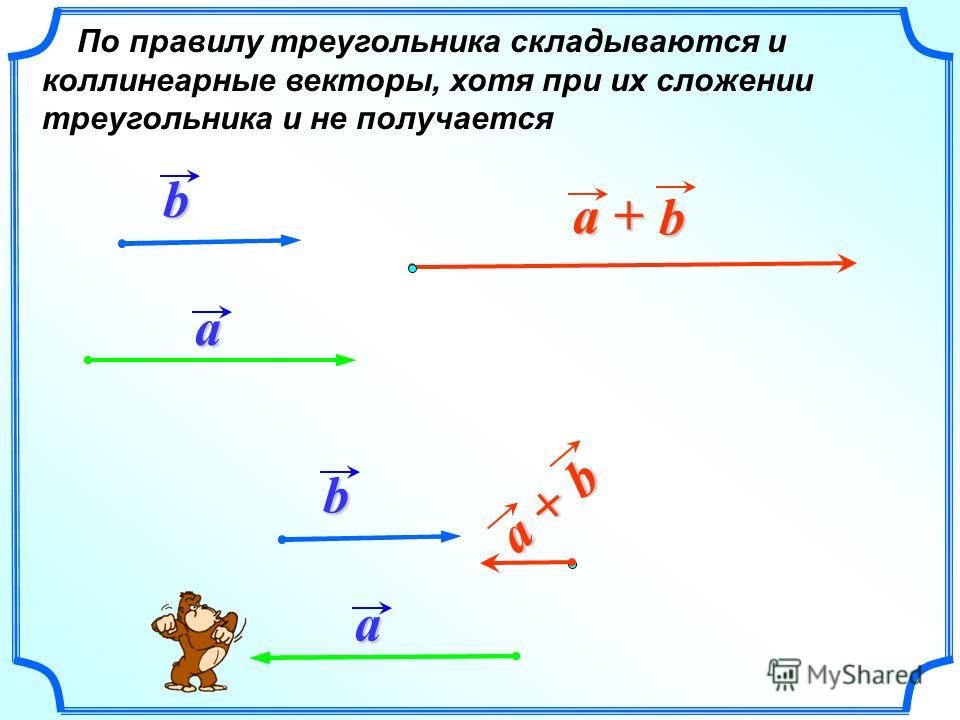
Суммой двух векторов и называется вектор, совпадающий с замыкающей стороной треугольника, построенного на данных двух векторах (см. рис. 1.а).
Рис.4
Правило сложения векторов:
1. ,
2. .
Эти законы позволяют находить сумму любого числа векторов. На рис. 3.б приведено сложение четырех векторов.
 И обратно, если сумма некоторых векторов равна нулю, то построенный на этих векторах многоугольник будет замкнутым.
И обратно, если сумма некоторых векторов равна нулю, то построенный на этих векторах многоугольник будет замкнутым.Разностью двух векторов называется сумма вектора с вектором , противоположным вектору (см. рис. 4):
.
Рис.4
Умножение вектора на число
Произведением скаляра на вектор называется вектор, длина которого равна , а направление его совпадает с направлением , если , и противоположно , если . Произведение вектора на скаляр подчиняется законам умножения чисел:
.
Произведение векторов
Из двух векторов можно образовать два существенно различных произведения: скалярное и векторное.
Скалярное произведение
Скалярным произведением двух векторов и называется произведение модулей этих векторов на косинус угла между этими векторами: . Эквивалентной формой записи скалярного произведения является выражение .
Пусть — единичный вектор, , тогда , т. е. скалярное произведение любого вектора на единичный вектор определяет величину проекции вектора на направление этого единичного вектора.
е. скалярное произведение любого вектора на единичный вектор определяет величину проекции вектора на направление этого единичного вектора.
Скалярное произведение векторов обладает следующими свойствами:
1. ;
2. .
Если векторы и взаимно перпендикулярны, то их скалярное произведение . И обратно, если скалярное произведение двух отличных от нуля векторов равно нулю, то эти векторы взаимно перпендикулярны.
Векторное произведение
Векторным произведением двух векторов и называется
вектор или в эквивалентной форме , который
а) направлен перпендикулярно плоскости, в которой лежат вектора и , в сторону поступательного перемещения правого винта, если его вращать от первого сомножителя ко второму в направлении наименьшего угла между векторами;
б) имеет длину, равную произведению длин векторов и на синус угла между ними (см. рис. 1): .
Векторное произведение обладает следующими свойствами:
;
;
.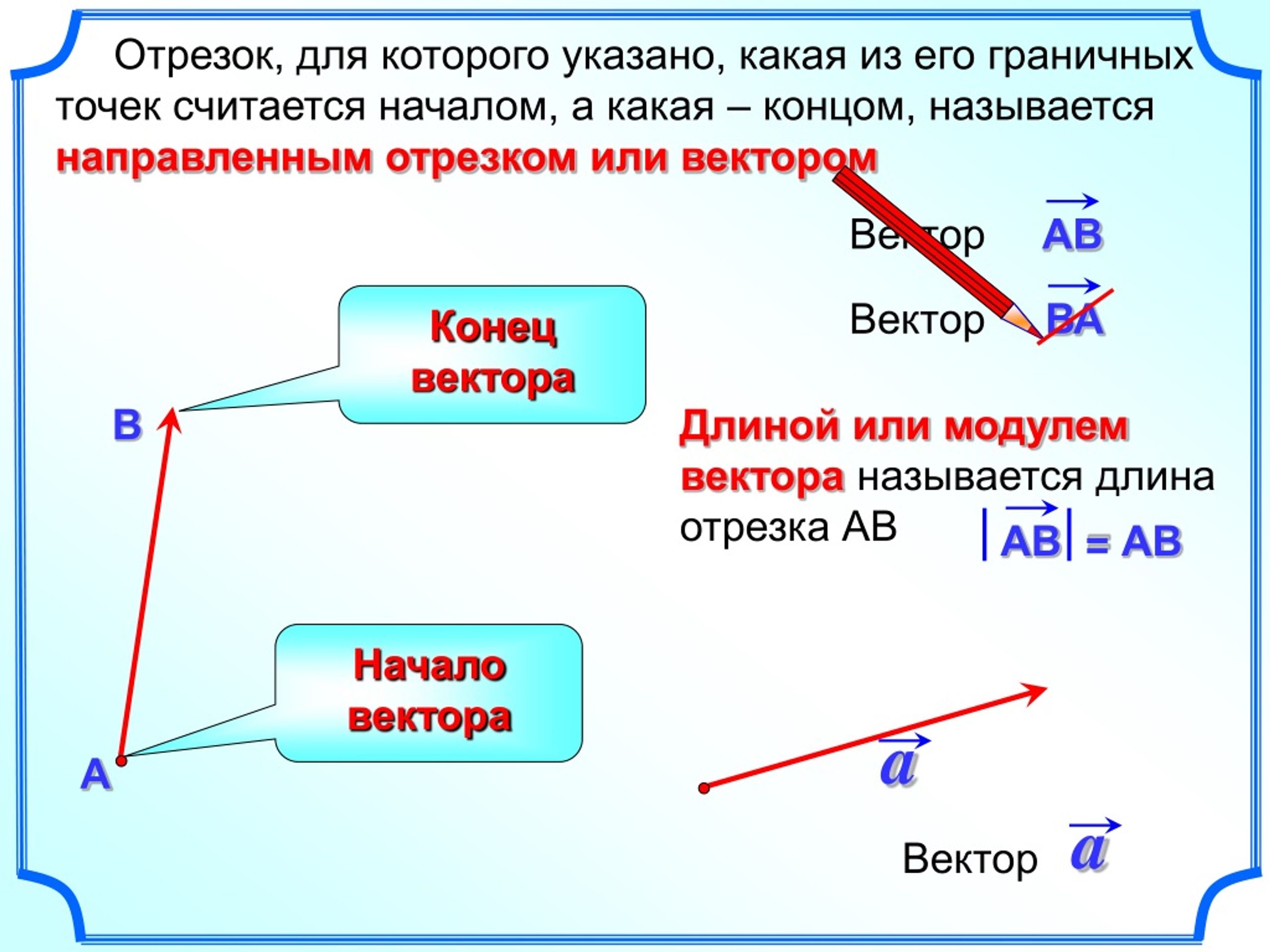
Рис.5
Произведение трех векторов
Из трех произвольных векторов и и можно образовать два существенно различных произведения: смешанное и двойное векторное произведение.
Смешанное произведение трех векторов
Смешанным произведением трех векторов , и называется скалярное произведение одного из них на векторное произведение двух других:
.
Абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих трех векторах.
С помощью смешанного произведения трех векторов решается вопрос об их компланарности.
Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях. Очевидно, любые два вектора являются компланарными.
Три вектора не всегда компланарны. Для того, чтобы три вектора были компланарными необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Двойное векторное произведение
Двойным векторным произведением трех векторов называется векторное произведение одного из них на векторное произведение двух других.
.
Координатная форма представления векторов
В системе координат XYZопределим единичные векторы в направлении OX, OYи OZкак . Тогда произвольный вектор может быть представлен в виде суммы трех взаимно перпендикулярных векторов, направленных по осям координат: ,
где скаляры — проекции вектора на координатные оси OX, OYи OZсоответственно.
Векторы и взаимно перпендикулярны друг другу, поэтому для них выполняются соотношения:
;
.
Радиус – вектор, проведенный из начала координат в некоторую точку М с координатами (x;y;z), также может быть определен в координатной форме (рис.6): .
Рис.6
Правила действия над векторами, заданными в координатной форме:
,
,
.
1. Сложение и вычитание.
2. Скалярное произведение.
3. Векторное произведение.
Из формул для скалярного произведения двух векторов можно получить формулу для вычисления модуля произвольного вектора :
.
С другой стороны,
.
Поэтому .
Если — единичный вектор. Тогда его проекциями на оси координат будут косинусы углов , образованных единичным вектором с осями координат OX, OY, OZсоответственно. Из предыдущей формулы, записанной для случая единичного вектора, получим условие .
Отметим, что направляющие косинусы можно определить и для любого произвольного вектора :
.
Из формулы для скалярного произведения двух векторов можно получить также выражение, определяющее косинус угла между этими векторами:
.
Формулы дифференциального исчисления
Формулы интегрального исчисления
Соотношение между внесистемными единицами и единицами СИ
| Длина | 1 ангстрем ( ) = |
| Время | 1 сут = 86400 с, 1 год = 365,25 сут = |
| Плоский угол | |
| Объем, вместимость | |
| Масса | , |
| Сила | |
| Работа, энергия | , , |
| Мощность | |
| Давление | , , , |
| Напряжение (механическое) | |
| Частота вращения | , |
| Концентрация частиц | |
| Теплота (количество теплоты) | , |
Эффективный диаметр молекул, динамическая вязкость и теплопроводность газов при нормальных условиях
| Вещество | Эффективный диаметр , | Динамическая вязкость , | Теплопроводность , |
| Азот Аргон Водород Воздух Гелий Кислород Пары воды | 0,38 0,35 0,28 – 0,22 0,36 – | 16,6 21,5 8,66 17,2 – 19,8 8,32 | 24,3 16,2 24,1 – 24,4 15,8 |
Динамическая вязкость жидкостей при
Вода …………………. .……………….…… 1,00
.……………….…… 1,00
Глицерин ………………………………….. 1480
Масло касторовое ………………….……… 987
Масло машинное ………………………….. 100
Ртуть ……………………….…………….… 1,58
Основные физические постоянные
(округленные с точностью до трех значащих цифр)
Нормальное ускорение свободного падения ………..
Гравитационная постоянная ……………
Постоянная Авогадро ………………..………
Молярная газовая постоянная …………….
Стандартный объем *……………………….
Постоянная Больцмана ……………………….
Атомная единица массы ………………………
* Молярный объем идеального газа при нормальных условиях
[*] Бесконечно малый угол поворота , может быть представлен в виде вектора, направленного вдоль оси вращения. Это возможно, когда радиус-вектор можно считать неизменным. Определение векторного произведения двух векторов см. в приложении (стр. 103).
[†] Инвариантностью в математике называется свойство неизменности по отношению какому либо преобразованию (условию) или совокупности преобразований.
Воспользуйтесь поиском по сайту:
N-МЕРНЫЕ ВЕКТОРЫ
N-МЕРНЫЕ ВЕКТОРЫНа предыдущую страницу На главную На следующую страницу
N-МЕРНЫЕ ВЕКТОРЫ
2.1 Линейные операции над n-мерными векторами
2.2 Скалярное произведение и длина n-мерных векторов
2.3 Угол между n-мерными векторами
2.4 Коллинеарные векторы
2.5 Разложение вектора по системе векторов
2.6 Векторная форма записи системы линейных уравнений
2.7 Задания
2.1 Линейные операции над n-мерными векторами
В геометрии вектором в пространстве называется направленный отрезок. В фиксированной системе координат каждый вектор а однозначно определяется своими координатами:
(1)
где называются координатами вектора a.
Если – какой-либо другой вектор, то
(2)
(3)
где к – число.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Обобщим понятие вектора следующим образом: назовем последовательность n чисел n-мерным вектором. Число a1 называется первой координатой вектора a; a2– второй координатой и т.д., а число n (количество координат) называется размерностью вектора а.
Если , , то ,
Два n-мерных вектора:
,
считаются равными только тогда, когда равны их соответствующие координаты , , .
Очевидно, что для любого вектора а: , где
Вектор O называется нулевым.
Вектор (-1)a называется противоположным вектору a и обозначается
-a, т. е. Ясно, что
и
.
е. Ясно, что
и
.
Так как операции над n-мерными векторами определяются через операции над их координатами, то свойства арифметических операций справедливы и для операций над векторами.
- (сложение коммутативно).
- (сложение ассоциативно).
- , (сложение дистрибутивно, где к, к1, к2– некоторые вещественные числа).
2.2 Скалярное произведение и длина n-мерных векторов
Как известно из геометрии, если векторы а и в заданы своими координатами и , то их скалярное произведение ав определяется по формуле:
По аналогии скалярным произведением n-мерных векторов , , называется число
Некоторые свойства произведения чисел справедливы и для скалярного произведения векторов:
- причем аа=0 тогда и только тогда, когда а=0 (нулевой вектор).

Длиной n-мерного вектора a называется число . Длина вектора a обозначается .
Из 4-го свойства скалярного произведения векторов вытекает, что каждый n-мерный вектор a обладает длиной, причем нулевой вектор O, является единственным вектором, длина которого равна нулю.
Если а и в n-мерные векторы, то справедливы следующие числовые соотношения:
- , к — число
- (неравенство Коши-Буняковского)
- (неравенство треугольника)
Вектор называется нормированным, если его длина равна 1. Каждый вектор а можно нормировать, т.е. умножить на число к, чтобы вектор ка был нормированным.
В самом деле:
2.3 Угол между n-мерными векторами
Из неравенства Коши-Буняковского
следует
,
Углом между n-мерными векторами а и в называется значение, которое получается из решения уравнения:
(4)
и принадлежит отрезку
Причем решение единственно при любых
и
Следовательно, и угол между векторами а и в определен однозначно.
Перепишем соотношение (4) в виде
отсюда следует, что скалярное произведение векторов а и в равно произведению длин этих векторов на косинус угла между ними.
Геометрическая характеристика векторов – длина вектора и угол между векторами – позволяет сформулировать критерий равенства n-мерных векторов.
Теорема. Ненулевые n-мерные вектора а и в равны тогда и только тогда, когда угол между ними равен нулю и длины этих векторов равны.
2.4 Коллинеарные векторы
Два ненулевых n — мерных вектора называются коллинеарными, если угол между ними равен 0 или π.
Если =0 то коллинеарные векторы считаются одинаково направленными, если же =π, то коллинеарные векторы противоположно направлены.
Символическая запись означает, что векторы а и в одинаково (противоположно) направлены.
Ненулевые векторы а и в коллинеарны, тогда и только тогда, когда можно подобрать такое к (число), что в=ка.
2.5 Разложение вектора по системе векторов
Пусть дана система n -мерных векторов , выбираем n – произвольных чисел .
Вектор называется линейной комбинацией векторов с коэффициентами .
Пусть теперь наряду с векторами дан еще n-мерный вектор в. Будем говорить, что вектор в линейно выражается через векторы , если он равен некоторой линейной комбинации векторов , т.е. найдется такой набор чисел , что
(5)
В этом случае будем говорить также, что вектор в разлагается по векторам . Числа называются коэффициентами разложения вектора в по системе .
Разложение считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один ).
Справедливы следующие утверждения:
1. Нулевой вектор O разлагается по каждой системе векторов
Нулевой вектор O разлагается по каждой системе векторов
2.Если вектор в разлагается по части системы векторов , где , то он разлагается и по всей системе векторов.
Предположим, что
тогда
3. Каждый n-мерный вектор разлагается по диагональной системе n-мерных векторов
с коэффициентами, которые равны координатам вектора в.
В самом деле
4. Если вектор а разлагается по системе векторов , а каждый вектор этой системы разлагается по системе векторов , то вектор а разлагается по системе векторов .
Из условия следует, что
После подстановки получаем:
Т.е. вектор а разлагается по векторам .
2.6 Векторная форма записи системы линейных уравнений
Используя введенные операции над векторами, запишем систему линейных уравнений:
(1)
в векторной форме. Обозначим
столбцы коэффициентов при неизвестных
Обозначим
столбцы коэффициентов при неизвестных
Тогда систему (1) можно представить в виде:
Уравнение (2) называется векторной формой системы линейных уравнений (1).
Последовательность чисел называют решением системы (2), если – верное векторное равенство.
Пусть n-мерный вектор () является решением системы (1). Тогда ясно, что для разложения вектора в по системе достаточно найти решение системы линейных уравнений (2).
Пример. Дана система векторов и вектор в
Пример. Выяснить разлагается ли вектор в по системе векторов . Для этого необходимо решить систему уравнений Имеем:
Получили систему уравнений:
которая эквивалентна исходной (т.е. имеет то же множество решений). Выразим главные неизвестные
x1и x2 через свободные x3и x4. Получим общее решение:
Получим общее решение:
Достаточно положить свободным неизвестным x3и x4 произвольные значения и получить разложение вектора в по системе векторов .
Пример. , тогда и .
Следовательно:
Если же , тогда , и
2.7 Задания
1. Найти разложение вектора В по диагональной системе (упражнение 1).
2. Найти разложение вектора В по системе А1, А2, А3 (упражнение 2).
3. Найти разложение вектора В по векторам А1, А2, А3 (упражнение 3).
4. Разложить каждый вектор системы А1, А2, …, Аn по векторам этой системы.
5. Доказать, что если векторы В1 и В2 разлагаются по системе векторов А1, А2, …, Аn, то векторы В1+В2, k×B1, t1×B1+t2×B2 также разлагаются по системе векторов А1, А2, …, Аn (k, t1, t2 – константы).
6. Вектор В разлагается по системе векторов А1, А2, …, Аm. Доказать, что каждый вектор системы В+А1, В+А2,…, В+Аm разлагается по системе А1, А2, …, Аm.
Упражнения 1, 2, 3 выполняются по вариантам, остальные – без вариантов.
Таблица 1
Наверх
На предыдущую страницу На главную На следующую страницу
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 7Следующая ⇒ Вектор – направленный отрезок, заданной длины. Модуль вектора – длина вектора. , где – координаты вектора Единичный вектор – вектор, длина которого равна 1. Нулевой вектор – вектор, начало которого совпадает с его концом. · Вектора называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. Вектора также равны, если их координаты равны. · Два вектора ортогональны (перпендикулярны), если их скалярное произведение равно нулю. · Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами. Условия коллинеарности векторов: 1. Два вектора и коллинеарны, если существует число n такое, что . 2. Два вектора коллинеарны, если отношения их координат равны (не применимо если одна из координат равна 0). 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. · Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. Условия компланарности векторов: 1. Два отдельно взятых вектора всегда компланарны 2. Три вектора компланарны если их смешанное произведение равно нулю. 3. Три вектора компланарны если они линейно зависимы. 4. Вектора компланарны если среди них не более двух линейно независимых векторов. · · Свойства вектора, умноженного на число. Если , то: 1. 2. , при , и , при 3.
Нелинейная операция скалярного произведения двух векторов = | | · | | · cos α Проекция вектора на ось. Проекция вектора на ось – это длина отрезка этой оси , который расположен между основаниями проекций начала и конца вектора на ось . Она берется со знаком плюс, если направление отрезка совпадает с направлением оси проекций, и со знаком минус, если эти направления противоположны. Угол между вектором и осью – это угол, на который необходимо кратчайшим образом повернуть ось, чтобы она совпадала с направлением вектора. Свойства проекций: · равные векторы имеют равные проекции; · при умножении вектора на число m его проекция на ось также умножается на то же число; · проекция суммы двух векторов на ось равна сумме проекций этих векторов; Направляющие косинусы вектора. Свойства направляющих косинусов Направляющие косинусы вектора – это косинусы углов, которые вектор образует с положительными полуосями координат. Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна 1. (для плоскости: ) ⇐ Предыдущая1234567Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 29; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Единичный вектор — формула, определение, расчет, обозначение
Векторы — это геометрические объекты, имеющие величину и направление. Векторы имеют начальную точку и конечную точку, которая представляет конечное положение точки. К векторам можно применять различные арифметические операции, такие как сложение, вычитание и умножение. Вектор, величина которого равна 1, называется единичным вектором. Например, вектор v = (1, 3) не является единичным, поскольку его модуль не равен 1, т. е. |v| = √(1 2 +3 2 ) ≠ 1.
Любой вектор может стать единичным вектором, если мы разделим его на величину того же заданного вектора. Единичный вектор также иногда называют вектором направления. Давайте узнаем больше об единичном векторе, его формуле вместе с несколькими решенными примерами.
| 1. | Что такое единичный вектор? |
2. | Обозначение единичного вектора |
| 3. | Формула единичного вектора |
| 4. | Как рассчитать единичный вектор? |
| 5. | Применение единичного вектора |
| 6. | Свойства векторов |
| 7. | Решенные примеры |
| 8. | Практические вопросы по единичному вектору |




 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 Свойства проекции вектора на ось
Свойства проекции вектора на ось
 Обратная связь — 161.97.168.212 (0.008 с.)
Обратная связь — 161.97.168.212 (0.008 с.) Вектор имеет как направление, так и величину. Величина векторной формулы суммирует отдельные измерения вектора по осям x, y и z. Величина вектора A равна | А |. Для данного вектора с направлением вдоль оси x, оси y и оси z величина вектора может быть получена путем вычисления квадратного корня из суммы квадратов его соотношений направлений. Давайте ясно поймем это из приведенной ниже величины векторной формулы.
Вектор имеет как направление, так и величину. Величина векторной формулы суммирует отдельные измерения вектора по осям x, y и z. Величина вектора A равна | А |. Для данного вектора с направлением вдоль оси x, оси y и оси z величина вектора может быть получена путем вычисления квадратного корня из суммы квадратов его соотношений направлений. Давайте ясно поймем это из приведенной ниже величины векторной формулы. Это определяется как \(\шляпа{а}\) = и /| и | Где | и | для нормы или величины вектора a . Его можно рассчитать с помощью формулы единичного вектора или с помощью калькулятора.
Это определяется как \(\шляпа{а}\) = и /| и | Где | и | для нормы или величины вектора a . Его можно рассчитать с помощью формулы единичного вектора или с помощью калькулятора. Единичный вектор, полученный после нормализации вектора нормали, является единичным вектором нормали, также известным как «единичная нормаль». Для этого разделим ненулевой вектор нормали на его векторную норму.
Единичный вектор, полученный после нормализации вектора нормали, является единичным вектором нормали, также известным как «единичная нормаль». Для этого разделим ненулевой вектор нормали на его векторную норму.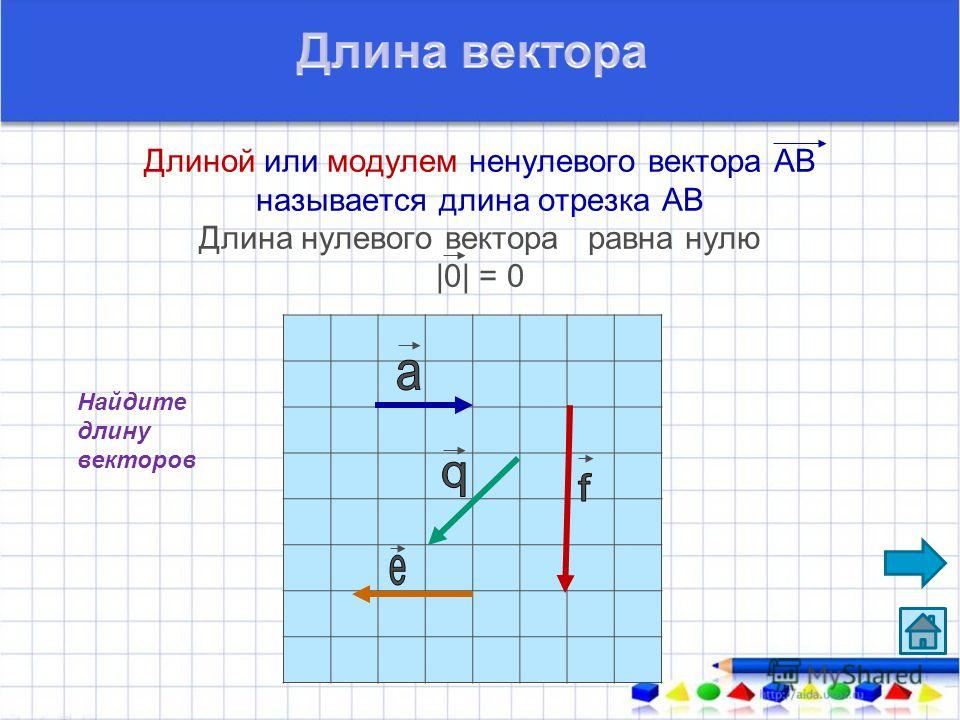 Например, рассмотрим вектор v = (3, 4), величина которого равна | против |. Если мы разделим каждый компонент вектора v на | против | чтобы получить единичный вектор \(\hat{v}\), который имеет то же направление, что и v.
Например, рассмотрим вектор v = (3, 4), величина которого равна | против |. Если мы разделим каждый компонент вектора v на | против | чтобы получить единичный вектор \(\hat{v}\), который имеет то же направление, что и v. В математических обозначениях единичный вектор вдоль оси x представлен как i . Единичный вектор вдоль оси Y представлен как j , а единичный вектор вдоль оси Z представлен как k .
В математических обозначениях единичный вектор вдоль оси x представлен как i . Единичный вектор вдоль оси Y представлен как j , а единичный вектор вдоль оси Z представлен как k . А
А 

 С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
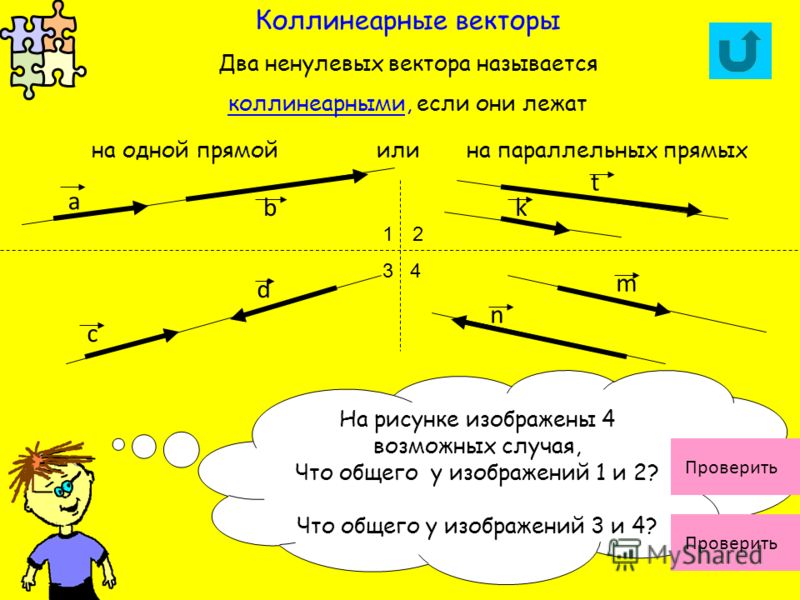 Итак, для заданных двух векторов x и y мы знаем, что x × y будет вектором, перпендикулярным как x , так и y . Далее, чтобы найти единичный вектор этого результирующего вектора, мы делим его на его величину. т. е. ( x × г ) / | x × y |, это дало бы единичный вектор, который перпендикулярен заданным двум векторам.
Итак, для заданных двух векторов x и y мы знаем, что x × y будет вектором, перпендикулярным как x , так и y . Далее, чтобы найти единичный вектор этого результирующего вектора, мы делим его на его величину. т. е. ( x × г ) / | x × y |, это дало бы единичный вектор, который перпендикулярен заданным двум векторам. Это называется N — пространство (обозначено R N ), а векторы в R N — N . Стандартные базисные векторы в R n есть
Это называется N — пространство (обозначено R N ), а векторы в R N — N . Стандартные базисные векторы в R n есть Определить вектор 2 a − b + c .
Определить вектор 2 a − b + c . рисунок ), применяя теорему Пифагора:
рисунок ), применяя теорему Пифагора: Если c является скаляром, как норма c x соотносится с нормой x ?
Если c является скаляром, как норма c x соотносится с нормой x ? Любой вектор, длина которого равна 1, называется единичным вектором . Пусть x будет заданным ненулевым вектором и рассмотрим скалярное кратное x /‖ x ‖. (Нулевой вектор здесь следует исключить из рассмотрения, так как если x было бы 0 , тогда ‖ x ‖ было бы 0, и выражение x /‖ x ‖ было бы неопределенным.) Применяя результат примера 4 (с c = 1/‖ х ‖), норма вектора х /‖ х ‖ равна
Любой вектор, длина которого равна 1, называется единичным вектором . Пусть x будет заданным ненулевым вектором и рассмотрим скалярное кратное x /‖ x ‖. (Нулевой вектор здесь следует исключить из рассмотрения, так как если x было бы 0 , тогда ‖ x ‖ было бы 0, и выражение x /‖ x ‖ было бы неопределенным.) Применяя результат примера 4 (с c = 1/‖ х ‖), норма вектора х /‖ х ‖ равна
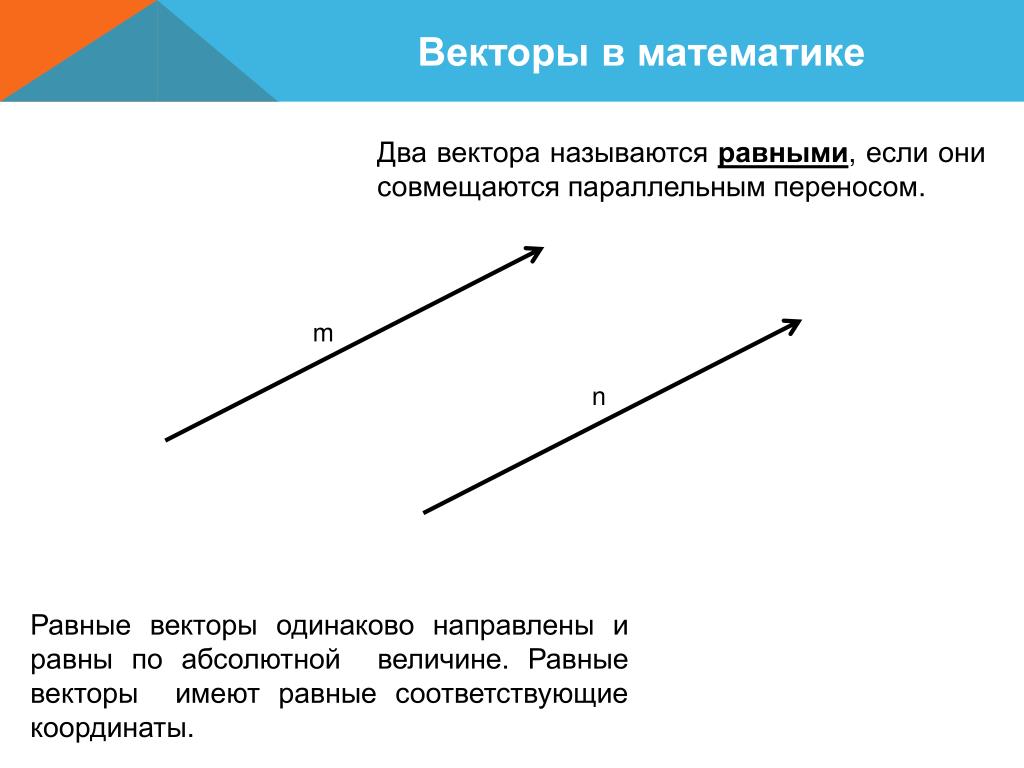 ) Обратите внимание, что, в отличие от перекрестного произведения, скалярное произведение двух векторов равно скаляр . По этой причине скалярное произведение также называют скалярным произведением . Можно легко показать, что скалярное произведение на R n удовлетворяет следующим полезным тождествам:
) Обратите внимание, что, в отличие от перекрестного произведения, скалярное произведение двух векторов равно скаляр . По этой причине скалярное произведение также называют скалярным произведением . Можно легко показать, что скалярное произведение на R n удовлетворяет следующим полезным тождествам: Since ‖ a ‖ 2 = a·a , the distributive and commutative properties of the dot product imply that for any vectors x and y in R n ,
Since ‖ a ‖ 2 = a·a , the distributive and commutative properties of the dot product imply that for any vectors x and y in R n ,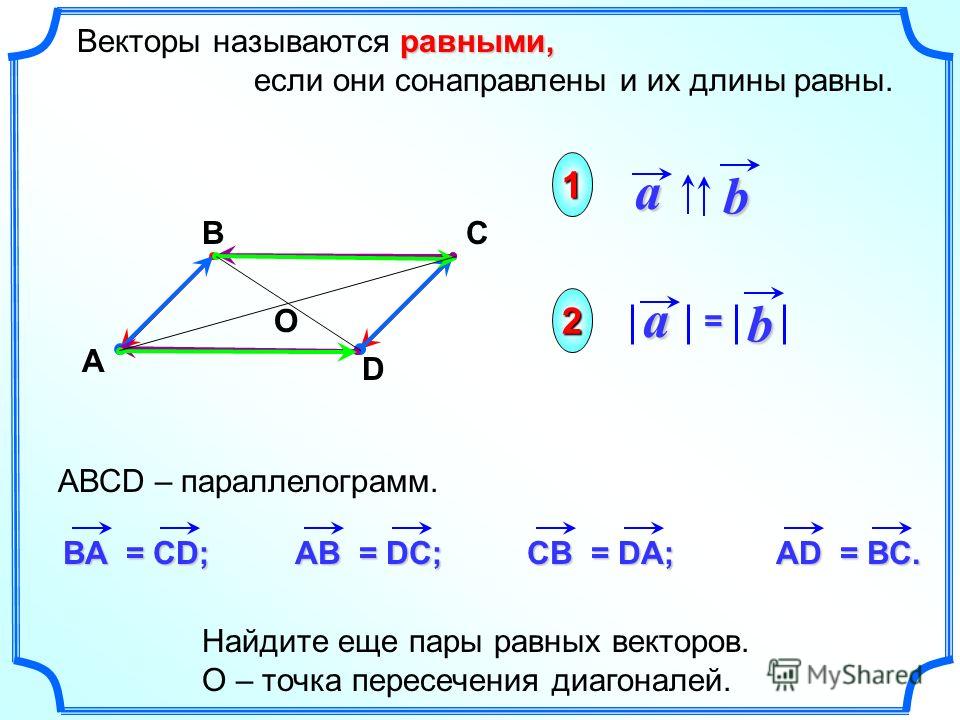
 Из элементарной геометрии вы знаете, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. То есть, если A, B и C являются вершинами треугольника, то
Из элементарной геометрии вы знаете, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. То есть, если A, B и C являются вершинами треугольника, то Обобщенное неравенство треугольника должно учитывать эти вырожденные случаи (отсюда слабое неравенство, ≤), тогда как неравенство треугольника из элементарной геометрии этого не делает (и, следовательно, сильное (или строгое ) неравенство, <).]
Обобщенное неравенство треугольника должно учитывать эти вырожденные случаи (отсюда слабое неравенство, ≤), тогда как неравенство треугольника из элементарной геометрии этого не делает (и, следовательно, сильное (или строгое ) неравенство, <).] Для R n с внутренним произведением это неравенство утверждает
Для R n с внутренним произведением это неравенство утверждает

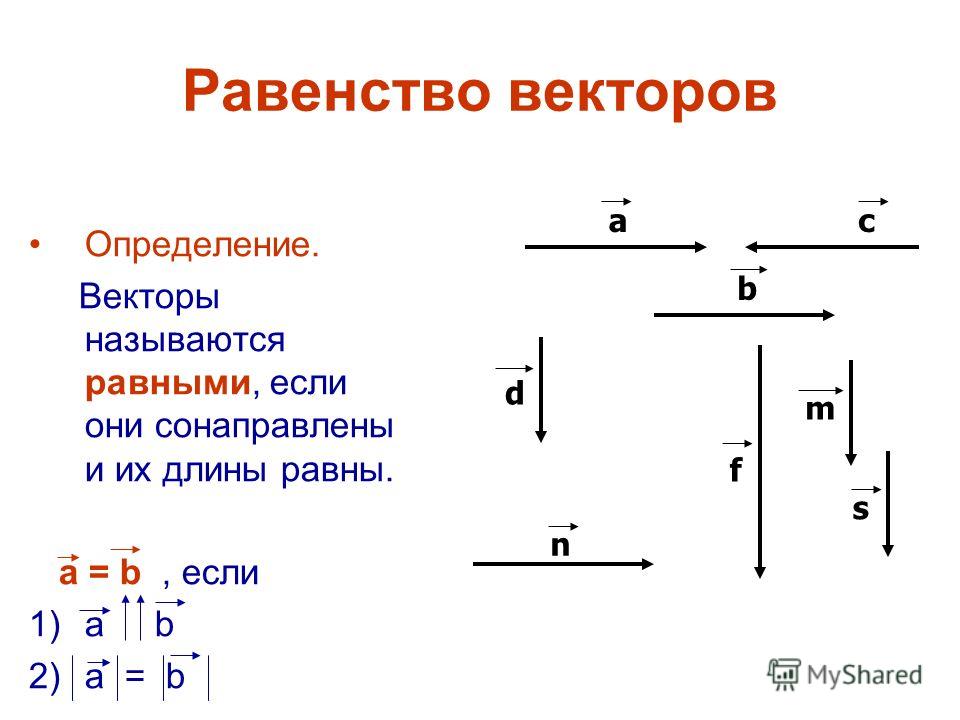 Однако функция косинуса положительна для острых углов и отрицательна для тупых углов, поэтому она может — сразу — различать острый угол и его дополнение.]
Однако функция косинуса положительна для острых углов и отрицательна для тупых углов, поэтому она может — сразу — различать острый угол и его дополнение.] (А если θ = π/2, то comp y x = 0, поскольку ортогональная проекция x на y является нулевым вектором.) В любом случае выполняется следующее уравнение:
(А если θ = π/2, то comp y x = 0, поскольку ортогональная проекция x на y является нулевым вектором.) В любом случае выполняется следующее уравнение:
 Скаляр t является параметром , и каждая точка на линии задается определенным выбором t .
Скаляр t является параметром , и каждая точка на линии задается определенным выбором t . См. рис.
См. рис. Этот вектор v определяет ориентацию плоскости в пространстве; см. рисунок .
Этот вектор v определяет ориентацию плоскости в пространстве; см. рисунок . Поскольку для любой точки x = ( x, y, z ), вектор 3
Поскольку для любой точки x = ( x, y, z ), вектор 3  См. рис.
См. рис. На прошлой неделе мы рассмотрели, как они определяются в этом контексте (как величины с величиной и направлением) и как они складываются (что на самом деле является частью определения). Наша коллекция ответов от Ask Dr. Math на этот раз посвящена идеям единичных векторов, компонентов и «направленных косинусов», которые являются способами описания направления вектора.
На прошлой неделе мы рассмотрели, как они определяются в этом контексте (как величины с величиной и направлением) и как они складываются (что на самом деле является частью определения). Наша коллекция ответов от Ask Dr. Math на этот раз посвящена идеям единичных векторов, компонентов и «направленных косинусов», которые являются способами описания направления вектора. Большое спасибо. 92}$$
Большое спасибо. 92}$$  Единичный вектор .
Мои книги (например, «Векторный и тензорный анализ» Борисенко) неясны и предполагают, что я уже это понимаю. Кроме того, какая польза от единичного вектора?
2. Базисный вектор . Опять же, мои другие источники не ясны.
P.S. Я изучаю теорию относительности самостоятельно, и поэтому я хотел бы понять основы, такие как тензорная алгебра.
Единичный вектор .
Мои книги (например, «Векторный и тензорный анализ» Борисенко) неясны и предполагают, что я уже это понимаю. Кроме того, какая польза от единичного вектора?
2. Базисный вектор . Опять же, мои другие источники не ясны.
P.S. Я изучаю теорию относительности самостоятельно, и поэтому я хотел бы понять основы, такие как тензорная алгебра.  Если мы позволим u представлять вектор в определенном направлении и единичной величины, то 3u, 7u и -8u сразу же можно понять как векторы величин 3, 7 и -8, все в направлении вектора u (кроме -8u, поскольку отрицательный знак означает «в направлении, противоположном +u»).
Если мы позволим u представлять вектор в определенном направлении и единичной величины, то 3u, 7u и -8u сразу же можно понять как векторы величин 3, 7 и -8, все в направлении вектора u (кроме -8u, поскольку отрицательный знак означает «в направлении, противоположном +u»).  Это означает, что КАЖДЫЙ вектор в пространстве может быть задан через его «компоненты», параллельные этим трем осям. Так, например, 5i + 2j - 6k — это вектор в пространстве, и его величина будет представлена длиной линии, соединяющей начало координат (0,0,0) с точкой (5,2,-6).
Кстати, это отвечает на ваш второй вопрос: i, j, k называются «базовыми» векторами, потому что они используются в качестве основы для выражения всех других векторов. Любой другой вектор в трехмерном пространстве может быть задан через i, j и k.
Это означает, что КАЖДЫЙ вектор в пространстве может быть задан через его «компоненты», параллельные этим трем осям. Так, например, 5i + 2j - 6k — это вектор в пространстве, и его величина будет представлена длиной линии, соединяющей начало координат (0,0,0) с точкой (5,2,-6).
Кстати, это отвечает на ваш второй вопрос: i, j, k называются «базовыми» векторами, потому что они используются в качестве основы для выражения всех других векторов. Любой другой вектор в трехмерном пространстве может быть задан через i, j и k.  Точно так же любые три некомпланарных вектора могут использоваться в качестве базовых векторов, «охватывающих» трехмерное пространство. Опять же, наиболее распространенными базовыми векторами являются i, j, k, но бывают случаи, когда используется совершенно другой набор базовых векторов.
Наконец, векторы не ограничиваются 1, 2 или 3 измерениями. Вы можете
имеют многомерные векторы, выраженные через 4, 5, 6 и
высшие базовые векторы. Количество базовых векторов будет равно
размер рассматриваемого пространства.
Точно так же любые три некомпланарных вектора могут использоваться в качестве базовых векторов, «охватывающих» трехмерное пространство. Опять же, наиболее распространенными базовыми векторами являются i, j, k, но бывают случаи, когда используется совершенно другой набор базовых векторов.
Наконец, векторы не ограничиваются 1, 2 или 3 измерениями. Вы можете
имеют многомерные векторы, выраженные через 4, 5, 6 и
высшие базовые векторы. Количество базовых векторов будет равно
размер рассматриваемого пространства.  Это добавлено к вектору N , а результирующее представляет собой вектор величиной 4,75 м, расположенный под углом 39 градусов против часовой стрелки от положительной оси x. Найдите: (а) компоненты N и (б) величину и направление N.
Я нарисовал графическую иллюстрацию проблемы. Но я действительно не могу решить это, потому что я не знаю, как это сделать.
Это добавлено к вектору N , а результирующее представляет собой вектор величиной 4,75 м, расположенный под углом 39 градусов против часовой стрелки от положительной оси x. Найдите: (а) компоненты N и (б) величину и направление N.
Я нарисовал графическую иллюстрацию проблемы. Но я действительно не могу решить это, потому что я не знаю, как это сделать.  Прежде чем вы сможете добавить их, вы должны найти их компоненты . Запомните эту схему:
Мой+-------------* M
| /|
| / |
| / |
| / |
| / |
| л/ |
| / |
sin(a)|-----+ |
| /| |
| 1/ | |
| / | |
| /)а | |
|/____|_______|__________
O cos(a) Mx
Вектор длины 1 имеет компоненты (cos(a), sin(a)). По подобным треугольникам вектор M длины L имеет компоненты Mx = L*cos(a), My = L*sin(a). Сделайте это с обоими векторами M и P, чтобы получить их компоненты (Mx, My) и (Px, Py).
Прежде чем вы сможете добавить их, вы должны найти их компоненты . Запомните эту схему:
Мой+-------------* M
| /|
| / |
| / |
| / |
| / |
| л/ |
| / |
sin(a)|-----+ |
| /| |
| 1/ | |
| / | |
| /)а | |
|/____|_______|__________
O cos(a) Mx
Вектор длины 1 имеет компоненты (cos(a), sin(a)). По подобным треугольникам вектор M длины L имеет компоненты Mx = L*cos(a), My = L*sin(a). Сделайте это с обоими векторами M и P, чтобы получить их компоненты (Mx, My) и (Px, Py).  028)$$
028)$$ Теперь мы хотели бы знать формулу, чтобы найти наклон трехмерной линии . Мы просмотрели учебники и попытались адаптировать формулу, но безуспешно.
Теперь мы хотели бы знать формулу, чтобы найти наклон трехмерной линии . Мы просмотрели учебники и попытались адаптировать формулу, но безуспешно.  Один из способов определения «наклона» плоскости состоит в том, чтобы записать единичный вектор, который перпендикулярен к ней, называемый 9.2), где I, J и K — единичные векторы в направлениях x, y и z. Коэффициенты I, J и K в этом выражении называются направляющими косинусами вектора, потому что они представляют собой косинусы углов между вектором и осями x, y и z соответственно.
Один из способов определения «наклона» плоскости состоит в том, чтобы записать единичный вектор, который перпендикулярен к ней, называемый 9.2), где I, J и K — единичные векторы в направлениях x, y и z. Коэффициенты I, J и K в этом выражении называются направляющими косинусами вектора, потому что они представляют собой косинусы углов между вектором и осями x, y и z соответственно.  Это означает, что вам нужно два линейных уравнения относительно x, y и z, чтобы определить линию. Существует несколько стандартных форм уравнений прямой, но наиболее часто используемой является
х - х0 у - у0 z - z0
------ = ------ = ------
а б в
Здесь (x0, y0, z0) — точка на прямой, а числа a, b и c определяют направление вдоль прямой: вектор a*I = b*J + c*K параллелен прямой. (Примечание: эта форма работает только тогда, когда линия не параллельна ни одной из плоскостей xy, xz или yz, т. е. когда ни a, ни b, ни c не равны нулю).
Это означает, что вам нужно два линейных уравнения относительно x, y и z, чтобы определить линию. Существует несколько стандартных форм уравнений прямой, но наиболее часто используемой является
х - х0 у - у0 z - z0
------ = ------ = ------
а б в
Здесь (x0, y0, z0) — точка на прямой, а числа a, b и c определяют направление вдоль прямой: вектор a*I = b*J + c*K параллелен прямой. (Примечание: эта форма работает только тогда, когда линия не параллельна ни одной из плоскостей xy, xz или yz, т. е. когда ни a, ни b, ни c не равны нулю).  В двух измерениях это просто косинус наклона, который представляет собой угол с осью x, и косинус его дополнения, который является синусом наклона. Наклон - это отношение этих двух, тангенс наклона. Точного аналога нет, потому что не существует «отношения» трех направляющих косинусов или любых трех чисел.
В двух измерениях это просто косинус наклона, который представляет собой угол с осью x, и косинус его дополнения, который является синусом наклона. Наклон - это отношение этих двух, тангенс наклона. Точного аналога нет, потому что не существует «отношения» трех направляющих косинусов или любых трех чисел.