Силы трения

| на главную | доп. материалы | физика как наука и предмет | физические основы механики |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в меха­нике мы будем рассматривать различные силы: трения, упругости, тяготения.

Из опыта известно, что всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедля­ет свое движение и в конце концов останавливается. Это можно объяснить существова­нием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.

Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости (смазки), то трение происходит в слое смазки. В таком случае говорят о

гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазоч­ной прослойки »0,1 мкм и меньше).

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверх­ностей трение обусловлено силами межмолекулярного притяжения.

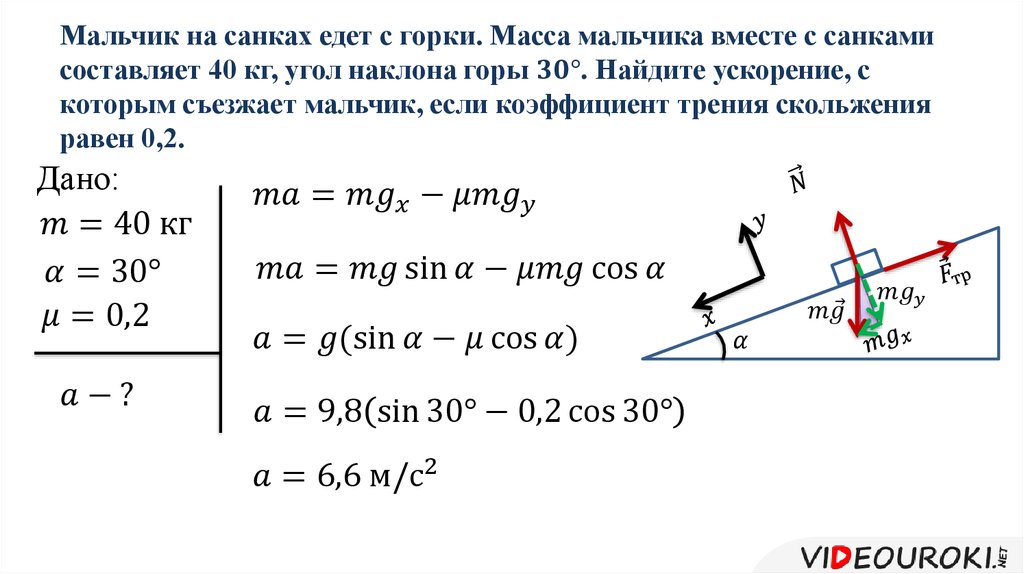
Рассмотрим лежащее на плоскости тело (рис. 11), к которому приложена горизон­тальная сила F. Тело придет в движение лишь тогда, когда приложенная сила F будет больше силы трения F_тр. Французские физики Г. Амонтон (1663—1705) и Ш. Кулон (1736—1806) опытным путем установили следующий закон: сила трения скольжения F_тр пропорциональна силе N нормального давления, с которой одно тело действует на другое:

F_тр =  f N ,

где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Найдем значение коэффициента трения. Если тело находится на наклонной плоско­сти с углом наклона a (рис.12), то оно приходит в движение, только когда тангенциаль­ная составляющая F силы тяжести Р больше силы трения F

тр. Следовательно, в пре­дельном случае (начало скольжения тела)  F=F_тр. или Psin a₀ = f N = f P cos a₀, откуда

f = tga₀.

Таким образом, коэффициент трения равен тангенсу угла a₀, при котором начинается скольжение тела по наклонной плоскости.

Для гладких поверхностей определенную роль начинает играть межмолекулярное притяжение. Для них применяется закон трения скольжения

F_тр = f _ист (N + Sp₀),

где р₀ — добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S — пло­щадь контакта между телами;   f_ист — истинный коэффициент трения скольжения.

Трение играет большую роль в природе и технике. Благодаря трению движется транспорт, удерживается забитый в стену гвоздь и т.

д.

В некоторых случаях силы трения оказывают вредное действие и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьша­ется примерно в 10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно меньшим внут­ренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольже­ния трением качения (шариковые и роликовые подшипники и т. д.). Сила трения качения определяется по закону, установленному Кулоном:

F_тр=f_кN/r,                                                               (8.1)

где r — радиус катящегося тела; f_к — коэффициент трения качения, имеющий размер­ность dim f_к =L. Из (8.1) следует, что сила трения качения обратно пропорциональна радиусу катящегося тела.

---

Практикум «способы определения коэффициента трения скольжения». Как найти силу трения скольжения Коэффициент трения ускорение

Скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G — вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной . Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.

Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. Так как поверхность горизонтальная, сила реакции опоры и сила тяжести направлены вдоль одной прямой и уравновешивают друг друга.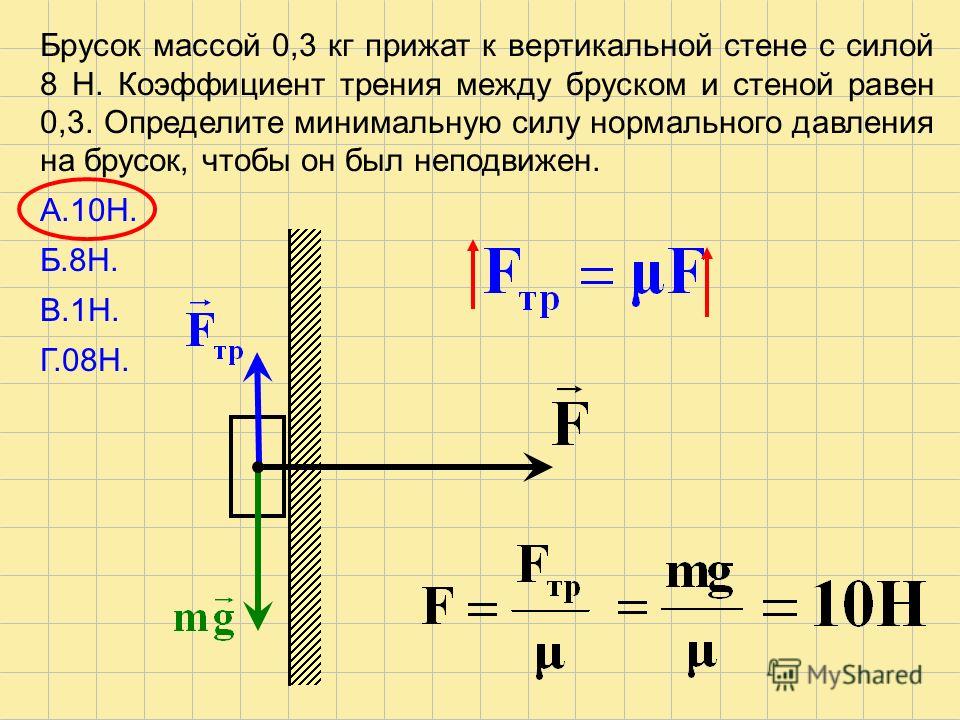

2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.

Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.

Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.

Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.

Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.

Если брусок тянут с помощью динамометра с постоянной скоростью, то динамометр показывает модуль силы трения скольжения (F тр). Здесь сила упругости пружины динамометра уравновешивает силу трения скольжения.

С другой стороны, сила трения скольжения зависит от силы нормальной реакции опоры (N), которая возникает в следствие действия веса тела. Чем вес больше, тем больше сила нормальной реакции. И чем больше сила нормальной реакции, тем больше сила трения . Между этими силами существует прямая пропорциональная зависимость, которую можно выразить формулой:

Здесь μ – это коэффициент трения . Он показывает, как именно сила трения скольжения зависит от силы нормальной реакции (или, можно сказать, от веса тела), какую долю от нее составляет. Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.

Так, например, деревянные предметы трутся друг о друга с коэффициентом от 0,2 до 0,5 (в зависимости от вида деревянных поверхностей).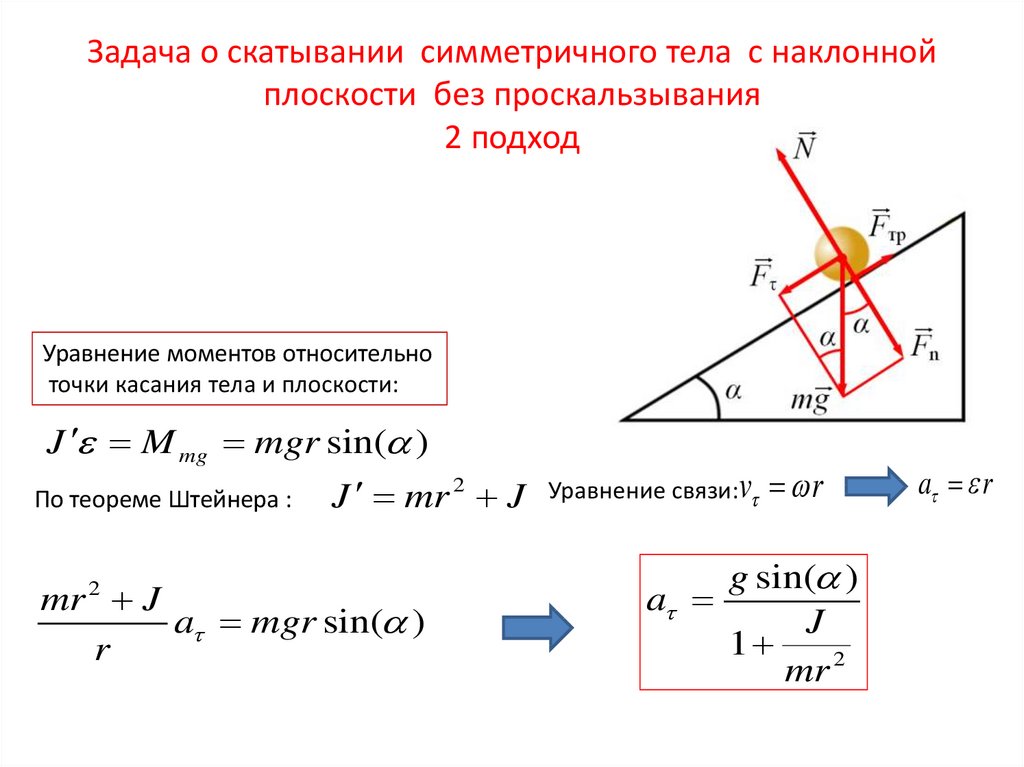 Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.

Из формулы F тр = μN следует, что зная силы трения и нормальной реакции, можно определить коэффициент трения для любых поверхностей:

Сила нормальной реакции опоры зависит от веса тела. Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:

μ = F тр / (mg)

Например, если известно, что сила трения тела массой 5 кг, движущегося по поверхности, равна 12 Н, то можно найти коэффициент трения: μ = 12 Н / (5 кг ∙ 9,8 Н/кг) = 12 Н / 49 Н ≈ 0,245.

Научно-практическая конференция

Коэффициент трения и м етоды его расчета

Пенза 2010 г.

I глава. Теоретическая часть

1. Виды трения, коэффициент трения

II глава. Практическая часть

Расчет трения покоя, скольжения, и качения

Расчет коэффициента трения покоя

Список литературы

I глава. Теоретическая часть

1. Виды трения, коэффициент трения

С трением мы сталкиваемся на каждом шагу. Вернее было бы сказать, что без трения мы и шагу ступить не можем. Но несмотря на ту большую роль, которую играет трение в нашей жизни, до сих пор не создана достаточно полная картина возникновения трения. Это связано даже не с тем, что трение имеет сложную природу, а скорее с тем, что опыты с трением очень чувствительны к обработке поверхности и поэтому трудно воспроизводимы.

Существует внешнее и внутреннее трение (иначе называемое вязкостью ). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.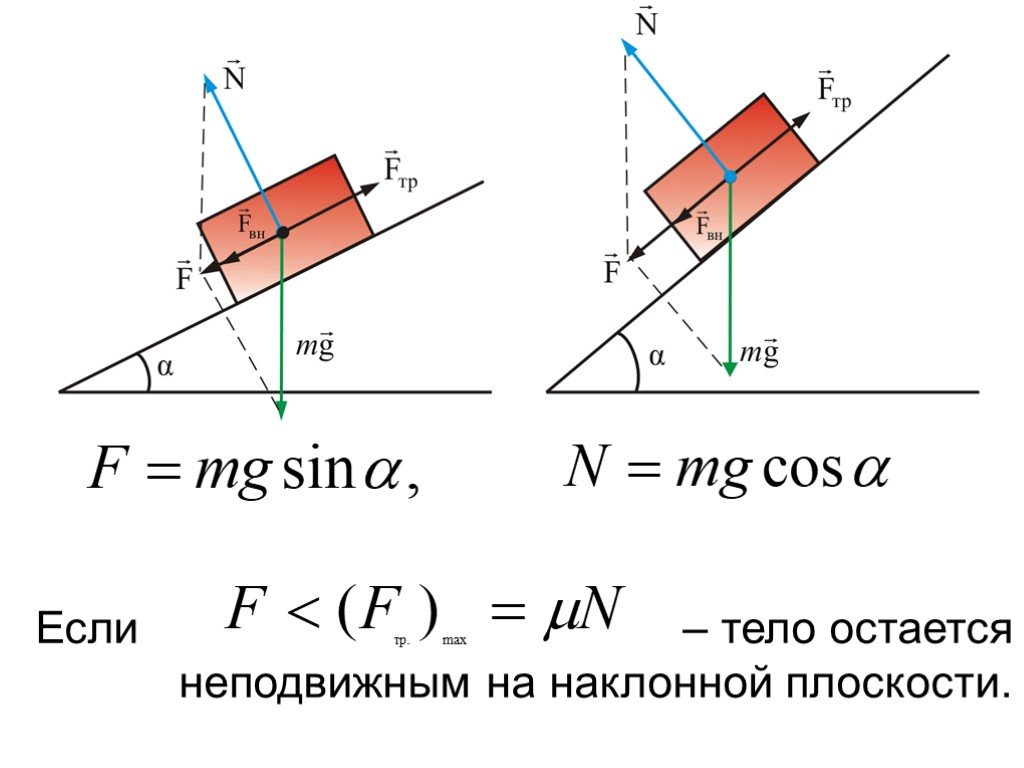

Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.

Внешнее трение подразделяют на трение покоя (статическое трение ) и кинематическое трение . Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения .

В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.

Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.

Где N — сила реакции опоры, a μ — коэффициент трения скольжения.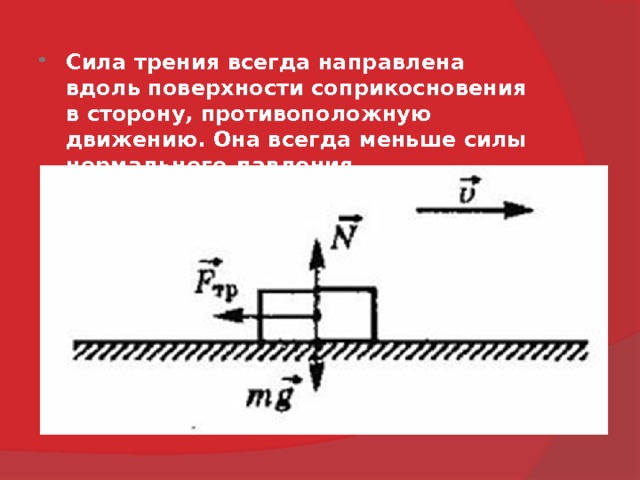 Коэффициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем.

Сила трения скольжения всегда направлена противоположно движению тела. При изменении направления скорости изменяется и направление силы трения.

Сила трения начинает действовать на тело, когда его пытаются сдвинуть с места. Если внешняя сила F меньше произведения μN, то тело не будет сдвигаться — началу движения, как принято говорить, мешает сила трения покоя . Тело начнет движение только тогда, когда внешняя сила F превысит максимальное значение, которое может иметь сила трения покоя

Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого.

II глава. Практическая часть

1. Расчет трения покоя, скольжения и качения

Основываясь на вышесказанное, я, опытном путем, находил силу трения покоя, скольжения и качения. Для этого я использовал несколько пар тел, в результате взаимодействия которых будет возникать сила трения, и прибор для измерения силы – динамометр.

Вот следующие пары тел:

деревянный брусок в виде прямоугольного параллепипеда определенной массы и лакированный деревянный стол.

деревянный брусок в виде прямоугольного параллепипеда с меньшей чем первый массой и лакированный деревянный стол.

деревянный брусок в виде цилиндра определенной массы и лакированный деревянный стол.

деревянный брусок в виде цилиндра с меньшей чем первый массой и лакированный деревянный стол.

После того как были проведены опыты – можно было сделать следующий вывод –

Сила трения покоя, скольжения и качения определяется опытном путем.

Трение покоя:

Для 1) Fп=0.6 Н, 2) Fп=0.4 Н, 3) Fп=0.2 Н, 4) Fп=0.15 Н

Трение скольжение:

Для 1) Fс=0.52 Н, 2) Fс=0.33 Н, 3) Fс=0.15 Н, 4) Fс=0.11 Н

Трение качение:

Для 3) Fк=0. 14 Н, 4) Fк=0.08 Н

Тем самым я определил опытным путем все три вида внешнего трения и получил что

Fп> Fс > Fк для одного и того же тела.

2. Расчет коэффициента трения покоя

Но в большей степени интересна не сила трения, а коэффициент трения. Как его вычислить и определить? И я нашел только два способа определения силы трения.

Первый способ: очень простой. Зная формулу и определив опытным путем и N, можно определить коэффициент трения покоя, скольжения и качения.

1) N  0,81 Н, 2) N  0,56 Н, 3) N  2,3 Н, 4) N  1,75

Коэффициент трения покоя:

= 0,74; 2)  = 0,71; 3)  = 0,087; 4)  = 0,084;

Коэффициент трения скольжения:

= 0,64; 2)  = 0,59; 3)  = 0,063; 4)  = 0,063

Коэффициент трения качения:

3)  = 0,06; 4)  = 0,055;

Сверяясь с табличными данными я подтвердил верность своих значений.

Но также очень интересен второй способ нахождения коэффициента трения.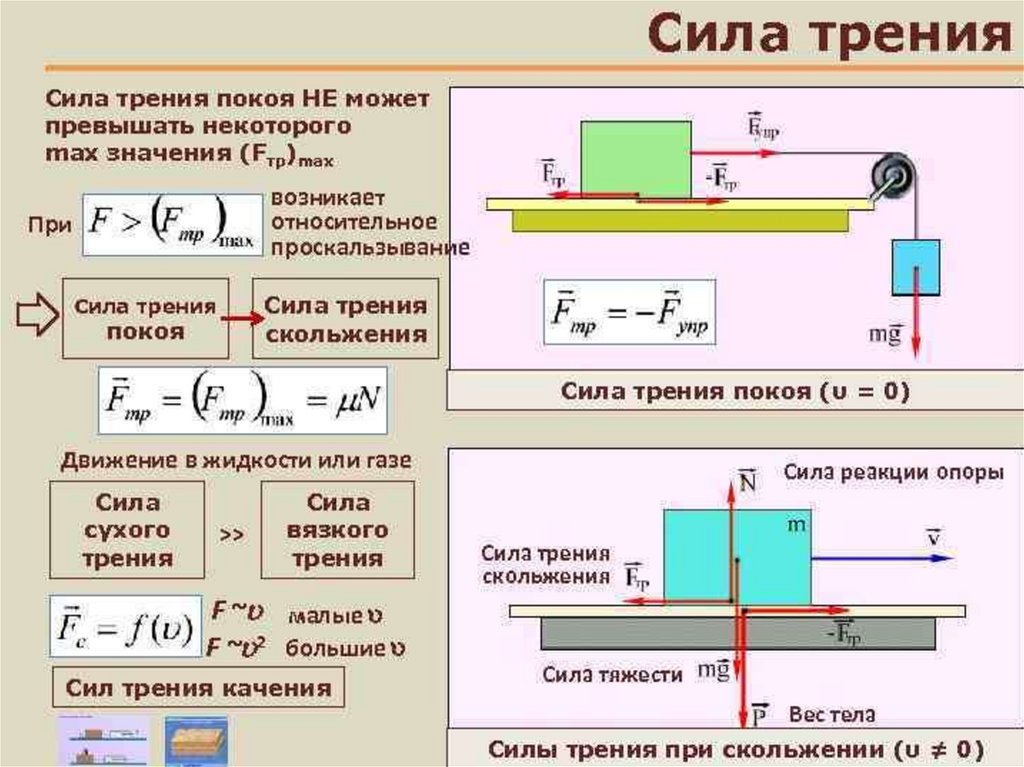

Но этот способ хорошо определяет коэффициент трения покоя, а для вычисления коэффициента трения скольжения и качения возникают ряд затруднений.

Описание: Тело находится с другим телом в покое. Затем конец второго тела на котором лежит первое тело начинают поднимать до тех пор пока первое тело не сдвинется с места.

 = sin  /cos  =tg  =BC/AC

На основе второго способа мной были вычислены некоторое число коэффициентов трения покоя.

Дерево по дереву:

АВ = 23,5 см; ВС = 13,5 см.

П = BC/AC = 13,5/23,5 = 0,57

2. Пенопласт по дереву:

АВ = 18,5 см; ВС = 21 см.

П = BC/AC = 21/18,5 = 1,1

3. Стекло по дереву:

АВ = 24,3 см; ВС = 11 см.

П = BC/AC = 11/24,3 = 0,45

4. Алюминий по дереву:

АВ = 25,3 см; ВС = 10,5 см.

П = BC/AC = 10,5/25,3 = 0,41

5. Сталь по дереву:

АВ = 24,6 см; ВС = 11,3 см.

П = BC/AC = 11,3/24,6 = 0,46

6. Орг. Стекло по дереву:

АВ = 25,1 см; ВС = 10,5 см.

П = BC/AC = 10,5/25,1 = 0,42

7. Графит по дереву:

АВ = 23 см; ВС = 14,4 см.

П = BC/AC = 14,4/23 = 0,63

8. Алюминий по картону:

АВ = 36,6 см; ВС = 17,5 см.

П = BC/AC = 17,5/36,6 = 0,48

9. Железо по пластмассе:

АВ = 27,1 см; ВС = 11,5 см.

П = BC/AC = 11,5/27,1 = 0,43

10. Орг. Стекло по пластику:

АВ = 26,4 см; ВС = 18,5 см.

П = BC/AC = 18,5/26,4 = 0,7

На основе своих расчетов и проведенных экспериментах я сделал вывод что  П >  C >  К , что неоспоримо соответствовало теоретической базе взятой из литературы. Результаты моих вычислений не вышли за рамки табличных данных, а даже дополнили их, в результате чего я расширил табличные значения коэффициентов трений различных материалов.

Литература

1. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. М.: Машиностроение, 1977.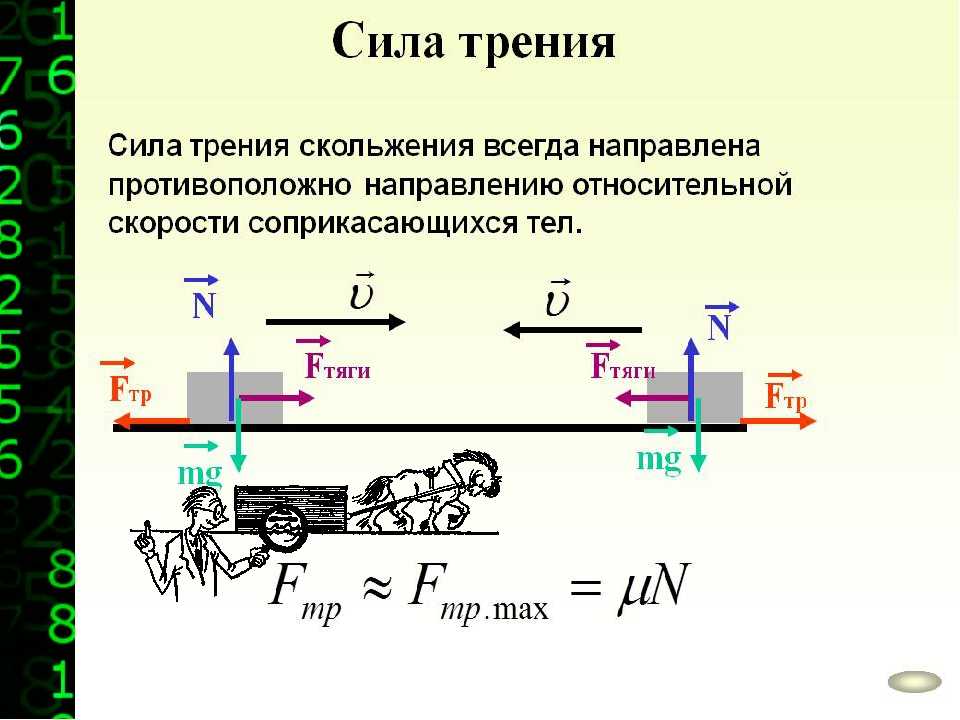 526 с.

Фролов, К. В. (ред.): Современная трибология: Итоги и перспективы . Изд-во ЛКИ, 2008 г.

Елькин В.И.“Необычные учебные материалы по физике”. “Физика в школе” библиотека журнала, №16, 2000.

Мудрость тысячелетий. Энциклопедия. Москва, Олма – пресс, 2006.

Определение

Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и является результатом сопротивления движению окружающей среды или других тел.

Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.

Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев).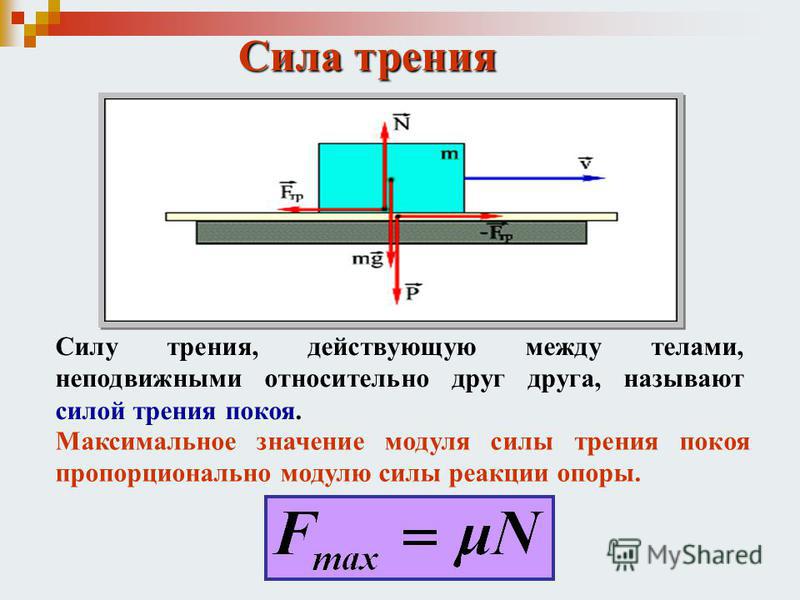 Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.

Виды трения

Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.

Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению. Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:

где – безразмерный коэффициент трения (покоя или скольжения).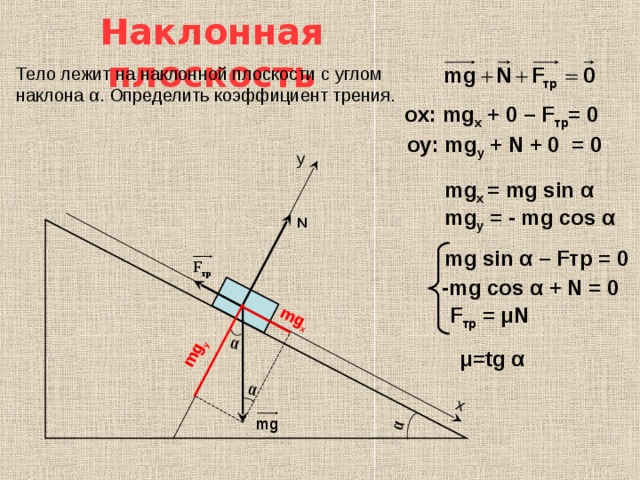 Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей. Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости. Довольно часто вместо коэффициента трения применяют угол трения, который равен:

Угол равен минимальному углу наклона плоскости к горизонту, при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.

Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:

где S – общая площадь контакта тел, p 0 – добавочное давление, которое вызывается силами молекулярного притяжения, – истинный коэффициент трения.

Трение между твердым телом и жидкостью (или газом) называют вязким (жидким). Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.

При движении тела в жидкости или газе появляются силы сопротивления среды, которые могут стать существенно больше, чем силы трения. Величина силы трения скольжения зависит от формы, размеров и состояния поверхности тела, скорости движения тела относительно среды, вязкости среды. При не очень больших скоростях сила трения вычисляется при помощи формулы:

где знак минус означает, что сила трения имеет направление в сторону противоположную направлению вектора скорости. При увеличении скоростей движения тел в вязкой среде линейный закон (4) переходит в квадратичный:

Коэффициенты и существенно зависимы от формы, размеров, состояния поверхностей тел, вязкости среды.

Помимо этого выделяют трение качения.В первом приближении трение качения рассчитывают, применяя формулу:

где k – коэффициент трения качения, который имеет размерность длины и зависит от материала тел, подверженных контакту и качеств поверхностей и т.д. N – сила нормального давления, r – радиус катящегося тела.

Единицы измерения силы трения

Основной единицей измерения силы трения (как и любой другой силы) в системе СИ является: [P]=H

В СГС: [P]=дин.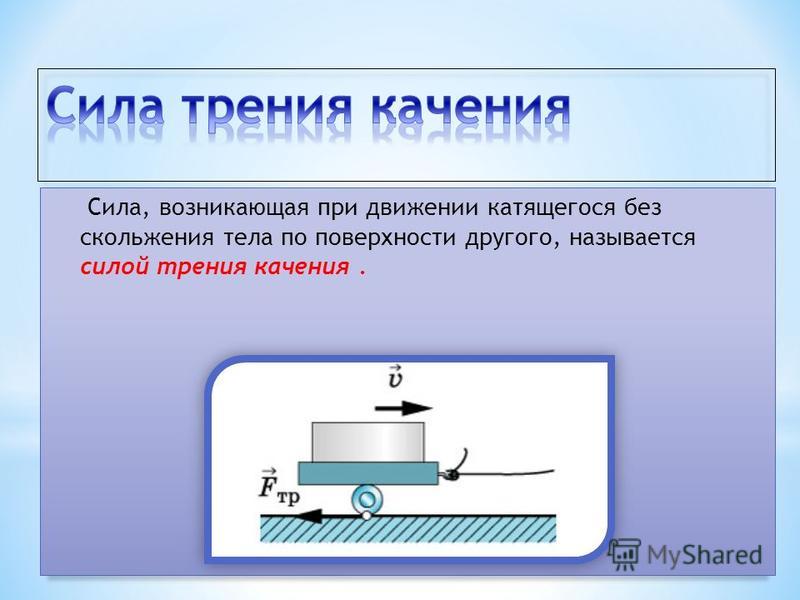

Примеры решения задач

Пример

Задание. На горизонтальном диске лежит маленькое тело. Диск вращается вокруг оси, которая проходит через его центр, перпендикулярно плоскости с угловой скоростью . На каком расстоянии от центра диска может находиться в состоянии равновесия тело, если коэффициент трения между диском и телом равен ?

Решение. Изобразим на рис.1 силы, которые будут действовать на тело, положенное на вращающийся диск.

В соответствии со вторым законом Ньютона имеем:

В проекции на ось Yиз уравнения (1.1) получим:

В проекции на ось X имеем:

где ускорение движения маленького тела равно по модуль нормальной составляющей полного ускорения. Силутрения покоя найдем как:

примем во внимание выражение (1.2), тогда имеем:

приравняем правые части выражений (1.3) и (1.5):

где маленькое тело (так как оно находится в состоянии покоя на диске) движется со скоростью, равной.

Коэффициент трения — это основная характеристика трения как явления.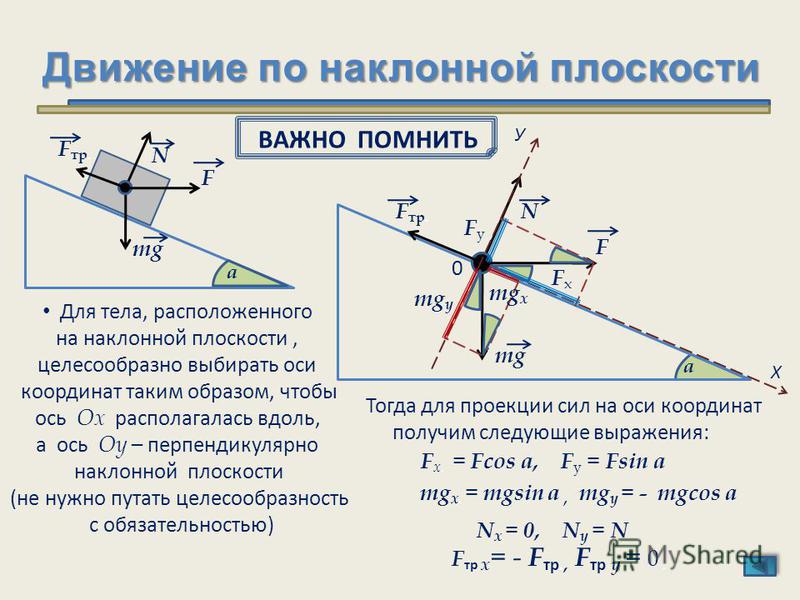 Он определяется видом и состоянием поверхностей трущихся тел.

ОПРЕДЕЛЕНИЕ

Коэффициентом трения называют коэффициент пропорциональности, связывающий силу трения () и силу нормального давления (N) тела на опору. Чаще всего коэффициент трения обозначают буквой . И так, коэффициент трения входит в закон Кулона — Амонтона:

Данный коэффициент трения не зависит от площадей, соприкасающихся поверхностей.

В данном случае речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).

Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения движения.

Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах

Угол трения

Иногда вместо коэффициента трения применяют угол трения (), который связан с коэффициентом соотношением:

Так, угол трения соответствует минимальному углу наклона плоскости по отношению к горизонту, при котором тело, лежащее на этой плоскости, начнет скользить вниз под воздействием силы тяжести.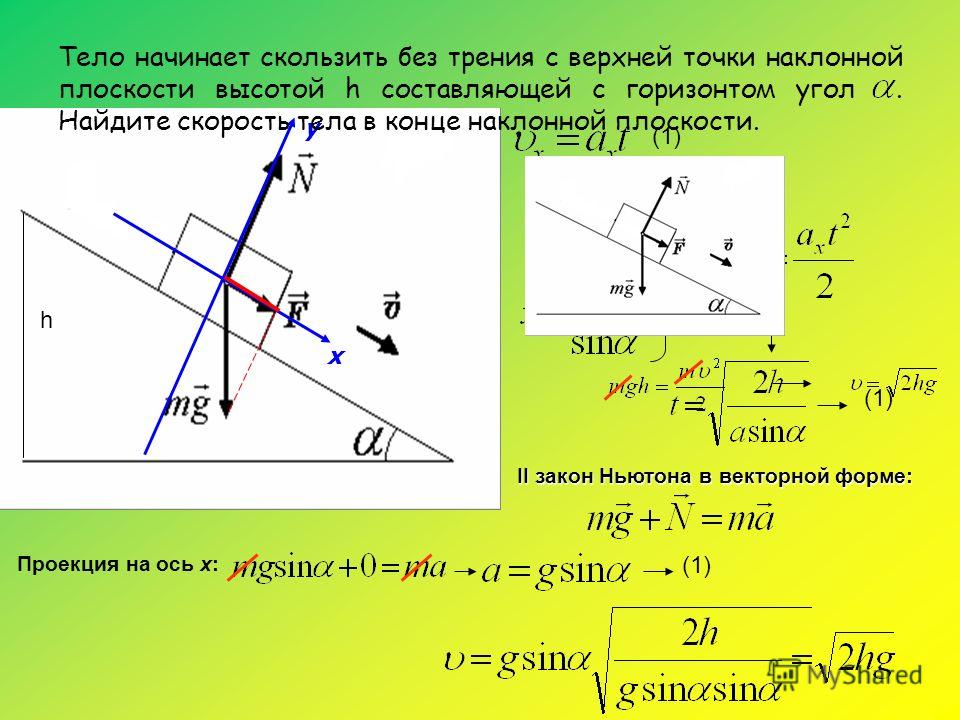 При этом выполняется равенство:

Истинный коэффициент трения

Закон трения, который учитывает влияние сил притяжения между молекулами, трущихся поверхностей записываю следующим образом:

где — называют истинным коэффициентом трения, — добавочное давление, которое вызывается силами межмолекулярного притяжения, S — общая площадь непосредственного контакта трущихся тел.

Коэффициент трения качения

Коэффициент трения качения (k) можно определить как отношение момента силы трения качения () к силе с которой тело прижимается к опоре (N):

Отметим, что коэффициент трения качения обозначают чаще буквой . Этот коэффициент, в отличие от выше перечисленных коэффициентов трения, имеет размерность длины. То есть в системе СИ он измеряется в метрах.

Коэффициент трения качения много меньше, чем коэффициент трения скольжения.

Примеры решения задач

ПРИМЕР 1

Задание	Веревка лежит частично на столе, часть ее свешивается со стола.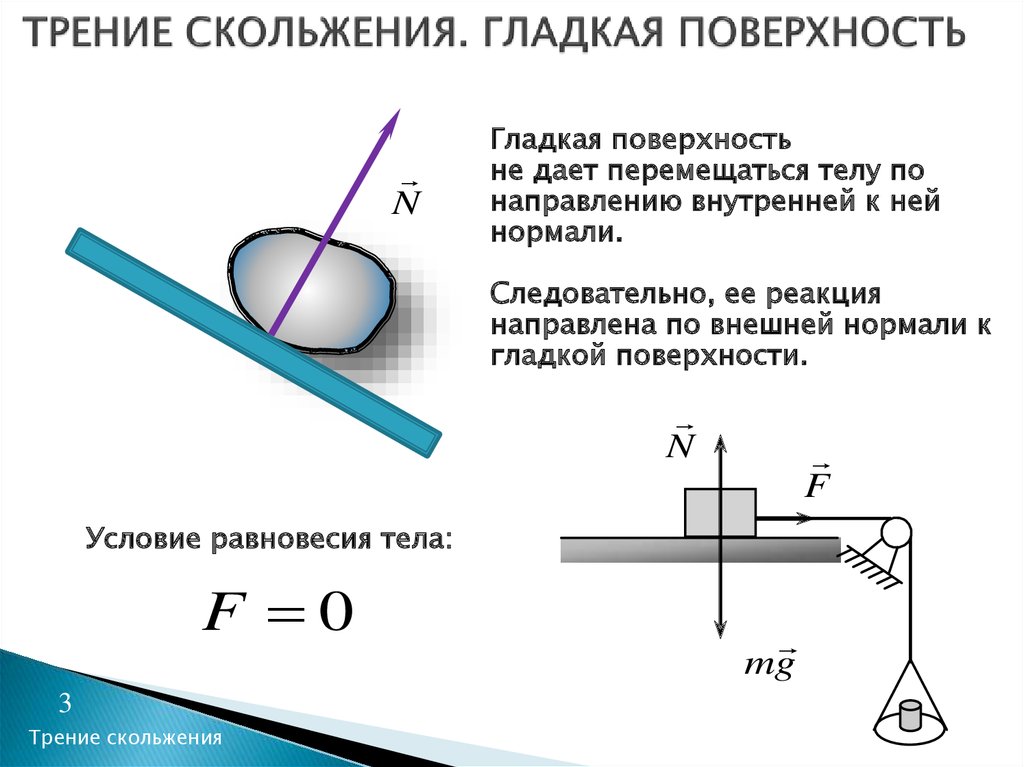 Если треть длины веревки свесится со стола, то она начинает скользить. Каков коэффициент трения веревки о стол?
Решение	Веревка скользит со стола под действием силы тяжести. Обозначим силу тяжести, которая действует на единицу длины веревки как . В таком случае в момент начала скольжения сила тяжести, которая действует на свешивающуюся часть веревки, равна: До начала скольжения эта сила уравновешивается силой трения, которая действует на часть веревки, которая лежит на столе: Так как силы уравновешиваются, то можно записать ():
Ответ

ПРИМЕР 2

Задание	Каков коэффициент трения тела о плоскость (), если зависимость пути, которое оно проходит задано уравнением: где Плоскость составляет угол с горизонтом.
Решение	Запишем второй закон Ньютона для сил, приложенных к движущемуся телу:

3. Сила трения

Рис. 3.1

Свойства силы трения устанавливаются по результатам следующего эксперимента. На горизонтальной поверхности находится тело, к которому приложены две активные силы: нормальная к поверхности сила, модуль которой в ходе эксперимента не изменяется (например, сила тяжести), и силанаправленная параллельно поверхности, модуль которой в ходе эксперимента постепенно увеличивается (Рис. 3.1). Со стороны поверхности возникают в ответ нормальная реакцияи сила трения.

Установленные в результате обработки описанного эксперимента закономерности сводятся к следующим положениям (законы Амантона-Кулона).

1. Сила трения действует в общей касательной плоскости к поверхностям соприкасающихся тел и противоположна тому направлению, в котором активно действующие силы стремятся сдвинуть тело.

2. Модуль силы трения при покое принимает всякий раз значение, необходимое для предотвращения проскальзывания тела по поверхности, но не может превзойти некоторого предельного значения, которое достигается на грани перехода тела от состояния покоя к состоянию скольжения:

3. Максимальное значение силы трения при покое пропорционально нормальному давлению тела на поверхность: , где– коэффициент трения при покое, который определяется экспериментально. Коэффициентзависит от материала тел, шероховатости, влажности, температуры трущихся поверхностей, но на его значение в широких пределах не влияют размеры площадки контакта тел.

4. При скольжении тела по шероховатой поверхности сила трения пропорциональна силе нормальной реакции поверхности: и направлена в сторону, противоположную скольжению. Динамический коэффициент трения(коэффициент трения скольжения), помимо прочего, может зависеть от относительной скорости скольжения.

Пример 3.1.

Установить, будет ли находиться в покое тело, изображённое на Рис. 3.1, если Н;Н;

Предположим, что тело находится в покое; тогда уравнения равновесия имеют вид:

Отсюда: Н;Н.

Вычислим максимально возможную силу трения: Н.

В рассматриваемом случае вычисленная из уравнений равновесия сила трения оказалась меньше максимально возможной, следовательно, условие равновесия выполнено и тело находится в покое иН.

Пример 3.2.

Сохраняя условия предыдущего примера, положим Н.

Аналогично примеру 3.1, вычисляем Н;Н. Очевидно, что покой нарушится, так как необходимая для предотвращения скольжения сила оказалась больше максимально возможной силы трения. Таким образом, нарушено условие равновесия , тело придёт в движение, а сила трения примет максимальное значение:Н.

Пример 3.3

Однородный стержень опирается на гладкую стену и негладкий пол, образуя с полом угол(Рис. 3.2). Вес стержня. В точкепривязан трос, протянутый по полу, который растягивается гирей весом. Коэффициент трения . Определить, при каких значенияхвозможно равновесие. Трением на блокепренебречь.

Рис. 3.2		Рис. 3.3

При потере равновесия возможно скольжение точки по полу как влево, так и вправо. Найдём сначала минимальное значение, при котором ещё возможно равновесие. Если разгружать тело(уменьшать), то при потере равновесия точкабудет скользить влево. Силовая схема представлена на Рис. 3.3. Составим условия равновесия:

При потере равновесия Разрешим полученную систему уравнений относительно. Учитывая, что, находим:.

При определении заметим, что при потере равновесия точкабудет скользить вправо и, следовательно, направление силы трения следует изменить на противоположное, что соответствует изменению знака перед силой трения в полученном выше решении:

Таким образом, равновесие стержня возможно, если его вес заключён в пределах

Пример 3. 4

На верхней грани прямоугольного бруса , вес которого, находится прямоугольный брусвеса. Брусопирается своей нижней гранью на горизонтальную поверхность, причём коэффициент трения между ними(Рис. 3.4). Коэффициент трения между теламииравен. На брусдействует сила, образующая с горизонтом угол. Будет ли брусдвигаться относительно? Будет ли брусдвигаться относительно плоскости?

Рис. 3.4

Предположим, что верхний бруснаходится в покое относительно бруса. Уравнения равновесия имеют вид (Рис. 3.5):

Отсюда:

Вычислим максимальную силу трения:

Как видно, сила трения, найденная из уравнений равновесия, т. е. необходимая для обеспечения равновесия тела, меньше максимально возможной силы трения. Следовательно, условие равновесия выполнено, телобудет покоиться относительно тела, а сила трения оказывается равной

Рис. 3.5		Рис. 3.6

Предположим теперь, что брус покоится относительно опорной плоскости. Уравнения равновесия имеют вид (Рис. 3.6):

Отсюда, учитывая, что и, получаем:

Максимально возможная сила трения равна:

Как видно, сила трения, найденная из уравнений равновесия, т.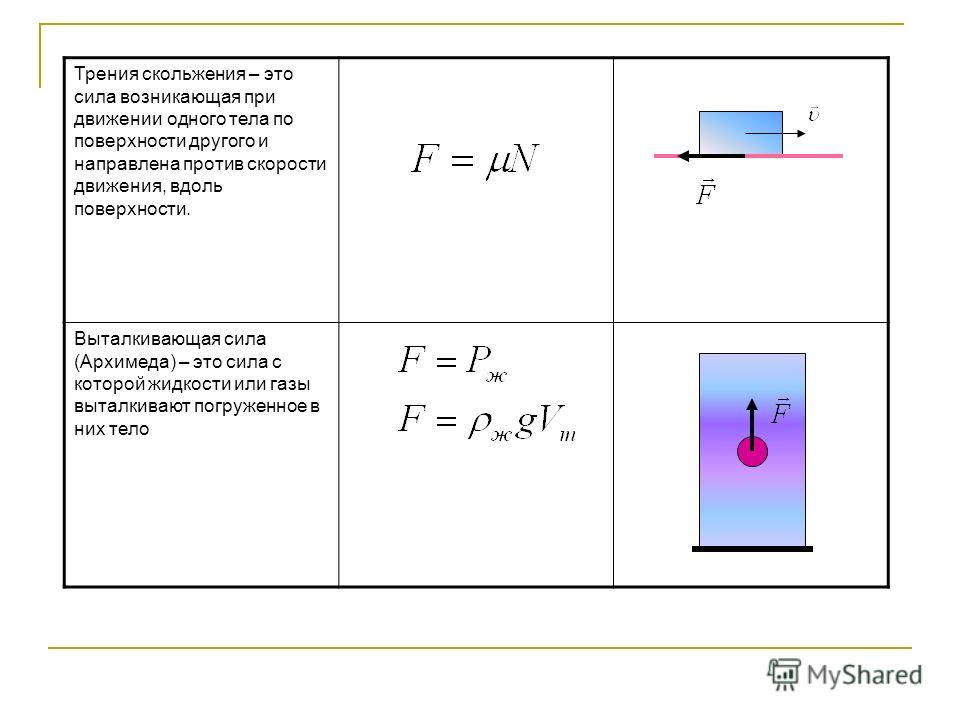 е. необходимая для обеспечения равновесия тела, меньше максимально возможной силы трения. Следовательно, условие равновесия выполнено, телобудет покоиться относительно плоскости, а сила трения оказывается равной

Пример 3.5

На верхней грани прямоугольного бруса , вес которого, находится прямоугольный брусвеса. Брусопирается своей нижней гранью на горизонтальную поверхность, причём коэффициент трения между ними(Рис. 3.5). Коэффициент трения между теламииравен. На брусдействует сила, образующая с горизонтом угол. Будет ли брусдвигаться относительно? Будет ли брусдвигаться относительно плоскости?

Как видно, по сравнению с предыдущим примером изменился коэффициент трения между телами и. Ход решения задачи остаётся прежним, но изменяются числовые результаты.

Теперь сила трения, необходимая для обеспечения покоя тела относительно тела, осталась прежней –а максимально возможная сила трения оказывается равной

Следовательно, условие равновесия не выполнено, телобудет скользить по верхней грани бруса, а сила трения при этом будет максимальной

Для бруса получаем:Условие равновесиявыполнено, телобудет покоиться относительно плоскости.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:

1. Как вычисляется сила трения при относительном покое тел?

2. Как вычисляется сила трения при относительном скольжении тел?

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 5.2; 5.6; 5.7; 5.9; 5.28; 5.29.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-12;

СР-13.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8

Объяснение урока: Равновесие тела на шероховатой горизонтальной плоскости

В этом объяснении мы научимся решать задачи, связанные с равновесие тела на шероховатой горизонтальной плоскости.

Тело, находящееся в равновесии на горизонтальной поверхности, имеет нулевую результирующую силу, действующую на него. На тело действуют две силы: его вес, 𝑊, и нормальная сила реакции от поверхности, 𝑁, как показано на следующем рисунке.

Согласно второму закону движения Ньютона, Величина чистой силы, действующей на тело, является произведением массы и ускорения тела. Тело покоится, поэтому сила, действующая на него, равна нулю. Даже когда тело находится в состоянии покоя, на него действует сила тяжести. Сила тяжести, действующая на тело, 𝑊, действует вертикально вниз и имеет величину, заданную выражением 𝑊=𝑚𝑔, где 𝑚 — масса тела и 𝑔 — ускорение свободного падения.

Сила реакции на тело с поверхности является следствием Третий закон Ньютона. Сила 𝑁 действует нормально к поверхности. Для тела на горизонтальной поверхности 𝑁 действует вертикально вверх. Для неподвешенного тела, находящегося в равновесии на горизонтальной поверхности, 𝑊=𝑁.

Для тела на гладкой поверхности любая результирующая сила, приложенная горизонтально к телу, ускоряется тело горизонтально. Тело на шероховатой поверхности ускоряется только за счет горизонтальной силы применяется к нему, если величина сила больше, чем сила трения между телом и поверхностью. Сила трения действует в направлении, противоположном приложенной силе.

Определим максимальную силу трения, которая может действовать на тело на шероховатой горизонтальной поверхности. поверхности, также называемой предельным трением.

Определение: Предельное трение тела о шероховатую горизонтальную поверхность

Предельное трение, величина максимальной силы трения, 𝐹, между телом, находящимся в покое, и поверхностью, на которую оно опирается, определяется выражением 𝐹=𝜇𝑁, где 𝜇 — коэффициент статического трения между телом и поверхность.

Для горизонтальной поверхности 𝑁=𝑚𝑔, и поэтому 𝐹=𝑚𝑔𝜇.

Рассмотрим пример, где определяется максимальная сила, приложенная к телу, которое остается в равновесии.

Пример 1. Определение величины силы, действующей на тело, находящееся в равновесии на шероховатой горизонтальной плоскости

Тело массой 25,5 Н лежит на шероховатой горизонтальной плоскости. На тело действует горизонтальная сила, заставляющая его двигаться. Учитывая, что коэффициент трения между телом и плоскостью равен 317, определите величину силы.

Ответ

Максимальная сила трения, действующая на тело, определяется выражением 𝐹=𝑚𝑔𝜇.

Это тот случай, когда 𝑊=𝑚𝑔; следовательно, 𝑚𝑔=25,5.N

Значение 𝜇 равно 317. Таким образом, мы имеем, что 𝐹=25,5317=4,5.N

Чтобы тело оставалось в равновесии, приложенная сила должна иметь той же величины, что и сила трения, 4,5 Н.

Теперь давайте рассмотрим пример, в котором определяется равнодействующая сила, предельная сила которой трение является составной частью.

Пример 2. Нахождение равнодействующей нормальной силы и силы трения

Тело покоится на шероховатой горизонтальной плоскости. Коэффициент трения между телом и плоскостью равен 0,2. предельная сила трения, действующая на тело, равна 80 Н. Учитывая, что 𝑅 есть равнодействующая силы трения и нормальной силы реакции, найдите величину 𝑅.

Ответ

Силы, действующие на тело, показаны на следующем рисунке.

Вес и приложенная сила не указаны, а для тела, покоящегося на поверхности, нормальная сила реакции на тело существует за счет веса тела, и фрикционный сила, действующая на такое тело, существует благодаря приложенной к телу силе, поэтому неупомянутые силы должны существовать.

Предельное трение – это максимальная сила трения, поверхность воздействует на тело до того, как тело начнет двигаться из-за приложенная сила. Предельное трение определяется выражением ограничение трения = 𝜇𝑁, где 𝑁 — нормальная сила реакции на тело, а 𝜇 — коэффициент трения покоя между поверхностью и телом.

В вопросе указано, что предельное трение равно 80 Н, а 𝜇 равно 0,2. Отсюда мы видим, что сила реакции равна 80=0,2𝑁𝑁=800,2=400,Н

Утверждается, что сила 𝑅 является равнодействующей силы реакции и ограничивающего трения, как показано на следующем рисунке.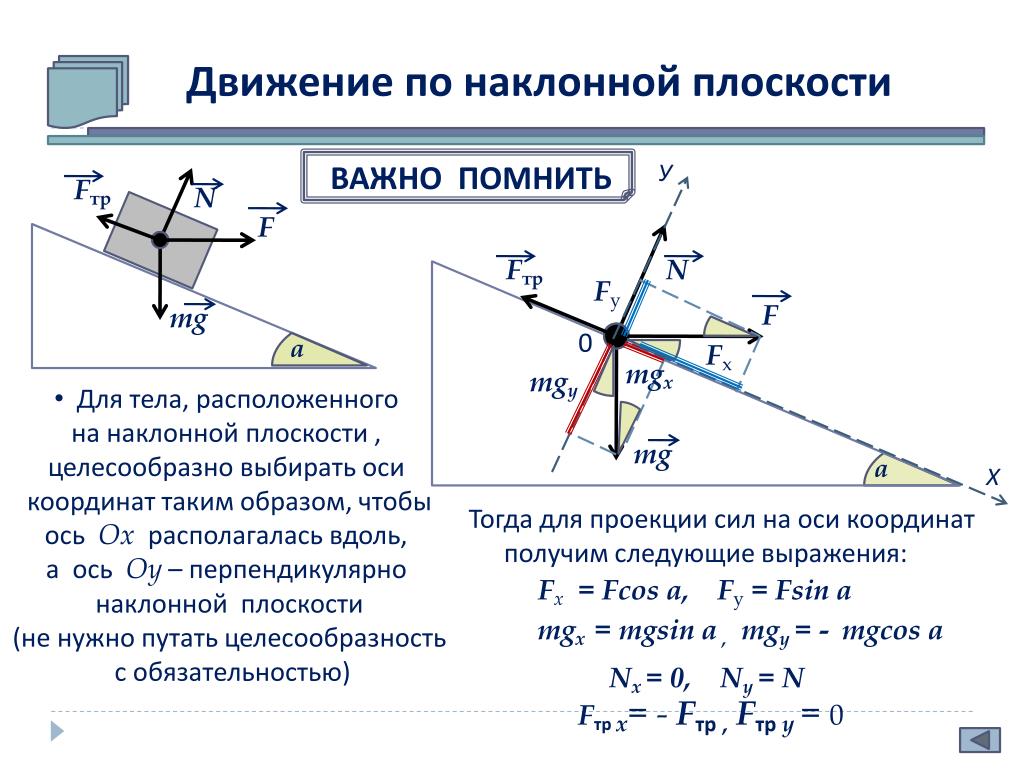

Величину 𝑅 можно определить с помощью теоремы Пифагора: 𝑅=400+80𝑅=166400𝑅=26(6400)𝑅=80√26.N

Тело на шероховатой поверхности имеет угол трения. Угол трения — это угол между нормальной силой реакции на тело и равнодействующей нормальной силы реакции и предельной силы трения на теле.

Рассмотрим следующий рисунок, на котором показаны силы, действующие на тело на шероховатой горизонтальной поверхности. Сила 𝑅 является равнодействующей нормальной силы реакции и силы трения, а не дополнительной силы.

Сила 𝐹 действует горизонтально на тело. Для значений 𝐹 где 𝐹≤𝐹,макс. сила трения о тело имеет величину, равную 𝐹. Когда 𝐹=𝐹,макс. величина силы трения равна предельному трению; следовательно, 𝐹=𝜇𝑁.friction

Нормальная сила реакции и предельное трение действуют перпендикулярно, как показано на следующем рисунке.

Из рисунка видно, что угол 𝜃 между направлением силы нормальной реакции и равнодействующей силы нормальной реакции и силы трения имеет тангенс, который можно определить следующим образом.

Определение: угол трения

Угол трения тела о шероховатую горизонтальную поверхность можно определить по формуле загар𝜃=𝜇𝑁𝑁=𝜇, где 𝜇 — коэффициент трения покоя между телом и поверхностью, а 𝑁 — нормальная сила реакции на тело со стороны поверхности.

Рассмотрим пример определения угла трения.

Пример 3. Нахождение угла трения

Учитывая, что коэффициент статического трения между телом и плоскостью равен √34, чему равен угол трения? При необходимости округлите ответ до ближайшей минуты.

Ответ

Угол трения можно определить по формуле загар𝜃=𝜇.

Значение 𝜃 определяется выражением 𝜃=𝜇=√34.тантан

Округление до ближайшей минуты дает 𝜃=2325′.∘

Сила трения между телом и поверхностью существует только в том случае, если на тело действует нормальная сила реакции. Сила реакции не обязательно должна быть связана с весом тела. Рассмотрим пример, когда вес тела не влияет на силу реакции, действующую на тело.

Пример 4. Нахождение минимальной горизонтальной силы, при которой тело будет находиться в равновесии, если его толкнуть к шероховатой вертикальной стене

На рисунке изображено тело массой 30 кг. толкается горизонтальной силой ⃑𝐹 к шероховатой вертикальной стене. Учитывая, что коэффициент трения покоя между телом и стенкой равен 56, определить минимальную горизонтальную силу ⃑𝐹 что приведет тело в равновесие.

Ответ

Хотя этот вопрос касается тела на вертикальной поверхности, он эквивалентен моделирование тела на горизонтальной поверхности, как показано на следующем рисунке.

Сила реакции на тело с поверхности действует нормально к поверхности, поэтому он действует в направлении, противоположном ⃑𝐹 с величина равна величине ⃑𝐹. Предельное трение о тело 𝐿 определяется выражением 𝐿=𝜇𝑁=56𝐹.

Масса тела определяется по формуле 𝑊=𝑚𝑔=30𝑔.

Чтобы тело находилось в равновесии, величины веса и предельного трения должны быть равны, так что у нас есть это 56𝐹=30𝑔𝐹=1805𝑔𝐹=36𝑔.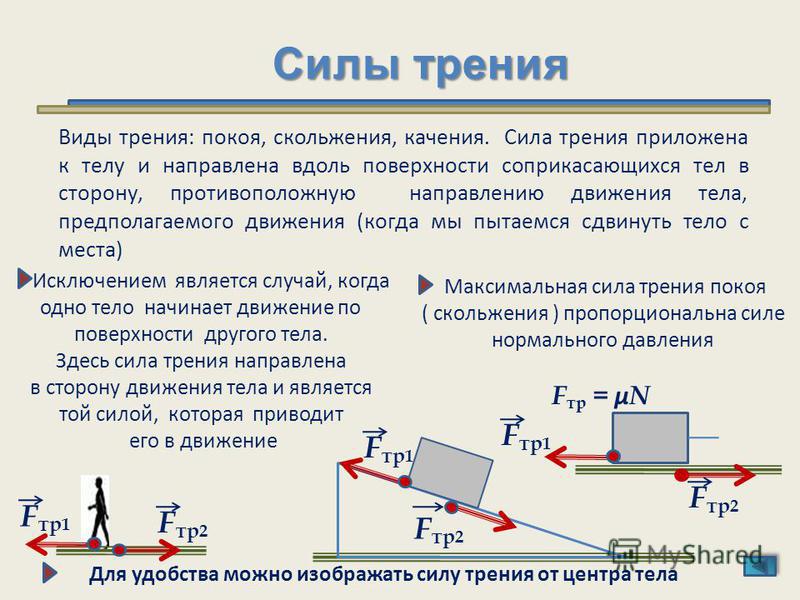 N

В вопросе не указано значение для 𝑔. Таким образом, результат может быть выражен в единицах килограмм-вес как 36 кг-вес.

Теперь рассмотрим пример, показывающий, что сила трения между телом и шероховатой поверхностью может действовать в любом направлении, параллельном этой поверхности.

Пример 5: Определение веса, при котором система окажется в точке движения

Тело массой 79 Н покоится на грубом горизонтальном столе. Он прикреплен легкой нерастяжимой нитью, проходящей через гладкий шкив, закрепленный в край стола к весу 41 Н висит свободно вертикально под шкивом. В этих условиях система находится в состоянии движения. Затем тело прикрепляют второй нерастяжимой нитью, проходящей через вторую шкив, закрепленный на противоположном конце стола вторым свободно висящим грузом 𝑊 N вертикально под шкивом. Определите вес 𝑊, при котором тело будет двигаться.

Ответ

Когда тело массой 79 ньютонов прикреплено к телу массой 41 ньютон, на следующем рисунке показаны некоторые силы, действующие на тела.

Сила трения о тело должна быть равна натяжению нити, чтобы тело находилось в равновесии, а натяжение нити равно весу тела, подвешенного на нити. Сила трения 41 Н — это максимальная сила трения, которая может существовать между телом и поверхностью, поскольку система находится в состоянии движения.

Когда тело массой 79 ньютонов прикрепляется к телу неизвестного веса, результирующая сила, действующая на тело, направлена ​​в сторону тела неизвестного веса, так как тело массой 79 ньютонов теперь находится в точке движется в направлении натяжения струны под действием неизвестного веса. Сила трения на теле весом 79 ньютонов снова имеет величину 41 Н, но действует в направлении, противоположном натяжению струны, прикрепленной к телу неизвестного веса, как показано на следующем рисунке.

Вес тела неизвестного веса равен натяжению нити, прикрепленной к телу. Натяжение этой нити равно сумме натяжения нити, прикрепленной к телу массой 41 Н, и силы трения о тело массой 79 Н. Неизвестный вес 𝑊 определяется выражением 𝑊=41+41=82.N

Подведем итог тому, что мы узнали из этих примеров.

Ключевые моменты

• Нормальная сила реакции тела на горизонтальной поверхности имеет величину, равную весу тела.
• Сила трения между телом и шероховатой поверхностью действует в направлении, противоположном суммарной силе, действующей на тело, и параллельно плоскости.
• Максимальная сила трения между телом и шероховатой поверхностью определяется выражением 𝐹=𝜇𝑁, где 𝑁 — нормальная сила реакции на тело, а 𝜇 — коэффициент трения покоя между телом и поверхностью.
• Угол трения тела о шероховатую горизонтальную поверхность определяется выражением 𝜃=𝜇,загар где 𝜇 — коэффициент трения покоя между телом и поверхностью.

Трение

Трение
Далее: Системы отсчета Вверху: Законы движения Ньютона Предыдущий: Струны, блоки и наклоны Когда тело скользит по шероховатой поверхности, обычно возникает сила трения, которая действует, препятствуя движению. Трение, когда рассматриваемое на микроскопическом уровне, на самом деле представляет собой очень сложное явление. Тем не менее, физикам и инженерам удалось разработать относительно простой эмпирический закон силы, который допускает эффекты трения, которые должны быть включены в их расчеты. Этот закон силы был впервые предложен Леонардо да Винчи (1452-1519 гг.)), а позже расширенный Шарлем Огюстеном де Кулоном (1736-1806) (который более известен открытием закон электростатического притяжения). фрикционный сила, действующая на тело, скользящее по шероховатой поверхности, пропорциональна нормальная реакция на этой поверхности, константа пропорциональности в зависимости от характера поверхности. Другими словами,

(112)

где называется коэффициентом (динамического) трения . Для обычных поверхности, обычно имеет порядок единицы.

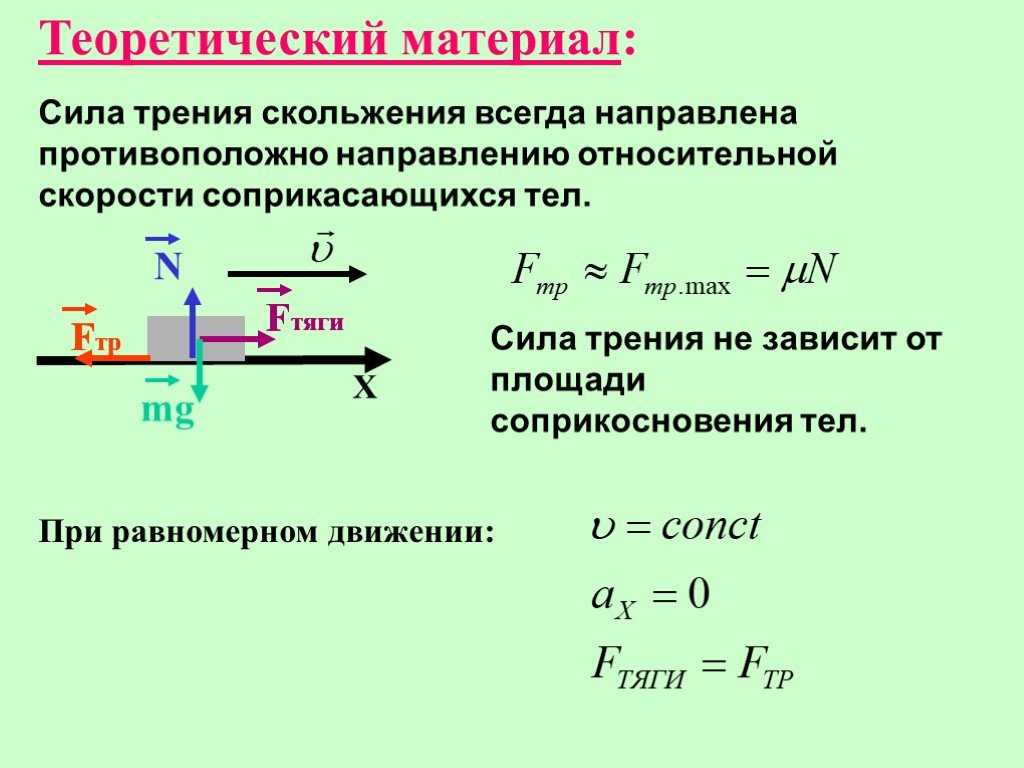
Рассмотрим блок массы, который перетаскивают по горизонтали. поверхность, коэффициент трения которой , горизонтальной сила . См. рис. 32. Вес блока действует вертикально вниз, вызывая реакцию, действующую вертикально вверх. Величина силы трения, которая препятствует движению блока, просто умножает нормальная реакция. Следовательно, . Ускорение блок, следовательно,

(113)

при условии, что . Что произойдет, если: т.е. , если применено сила меньше силы трения? В этом случае общие смысл подсказывает, что блок просто остается в покое (это, конечно, не ускориться назад!). Следовательно, на самом деле максимум сила, которую может создать трение, чтобы препятствовать движению блокировать. Если приложенная сила меньше этого максимального значения, то приложенная сила уравновешивается равной и противоположной силой трения, и блок остается неподвижным. Только если приложенная сила превышает Максимальная сила трения приводит к тому, что блок начинает двигаться.

Рисунок 32: Трение

Рассмотрим блок массы, скользящий по неровному склону (коэффициент трение) которая образует угол с горизонталью, как показано на рис. 33. Вес блока можно разложить на составляющие , действующий перпендикулярно наклону и , действует параллельно наклону. Реакция наклона к весу блока действует нормально наружу от наклона, и величины . Параллельно склону, блок подлежит направленной вниз гравитационной силе , и восходящая сила трения (которая препятствует скольжению блока вниз по наклон). Чтобы блок сдвинулся, величина прежней силы должна превышают максимальное значение последнего, то есть время, когда величина нормальной реакции или . Следовательно, условие чтобы вес блока преодолел трение и, таким образом, заставил блок скользить вниз по склону, это

(114)

или же

(115)

Другими словами, если наклон склона превышает определенное критическое значение, которое зависит от , то блок начнет скользить. Кстати, приведенная выше формула предлагает довольно простой способ определения коэффициента трения для данный объект скользит по определенной поверхности. Просто постепенно наклоняйте поверхность пока объект не начнет двигаться: коэффициент трения — это просто тангенс критический угол наклона (измеряемый относительно горизонтали).

Рис. 33: Блок сползает по неровному склону

До сих пор мы неявно предполагали, что коэффициент трения между объект и поверхность одинаковы независимо от того, остается ли объект неподвижным или скользит по поверхности. На самом деле, это, как правило, не так. Обычно коэффициент трения когда объект неподвижен, немного больше , чем коэффициент, когда объект скользит. Назовем первый коэффициент коэффициент трения покоя , , тогда как последний коэффициент обычно называют коэффициентом кинетического (или динамического) трения , . Тот факт, что это просто означает, что объекты имеют склонность «прилипать» к шероховатым поверхностям, когда на них кладут. Сила, необходимая для отклеить данный предмет и, тем самым, привести его в движение, в разы нормальная реакция на поверхности. После того, как объект был приведен в движение, сила трения, препятствующая этому движению, падает несколько раз нормальная реакция.

---

Далее: Системы отсчета Вверху: Законы движения Ньютона Предыдущий: Струны, блоки и наклоны

Ричард Фицпатрик 2006-02-02

домашнее задание и упражнения — Влияние трения на движущееся тело под действием переменной силы

Вопрос задан 6 лет, 7 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 1к раз

$\begingroup$

Учитывая систему на рисунке:

Блок скользит по горизонтальной поверхности и на него действует сила $P$, которая изменяется по величине, как показано на рисунке.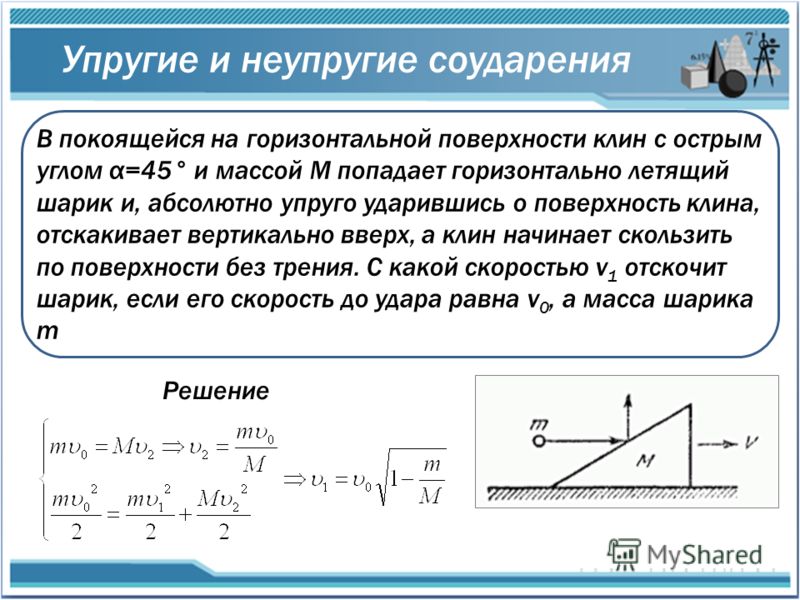 Зная, что коэффициенты трения между блоком и поверхностью равны $\mu_s = 0,6$ и $\mu_k = 0,25$ и что блок изначально покоится, я должен определить скорость блока в момент $t = 5 с. $.

Я использую принцип линейного импульса и импульса для решения проблемы. $$mv_1 + \sum \int fdt= mv_2$$ Я хочу знать, как разделить силу трения. Должен ли я использовать $f_r=\mu_sN$, когда $P$ падает ниже $\mu_sN$ или когда он падает ниже $\mu_kN$. Кроме того, что произойдет, когда $P$ окажется между $\mu_sN$ и $\mu_kN$, останется ли объект в движении или остановится?

То, что я имею в виду, резюмируется в следующем уравнении: $$mv_1 + \int P dt -\mu_kN \times t_1 -\mu_sN \times (5-t_1) = mv_2$$, где $t_1$ — время, когда $P$ падает ниже $\mu_kN$.

• домашние задания и упражнения
• ньютоновская механика
• силы
• трение

$\endgroup$

2

$\begingroup$

Во-первых, необходимо изучить поведение сил трения. Простейшая модель статического трения: $$\влево|\mathcal{F}_s\вправо| \le \mu_s F_N$$, если объект равен не скользящий. Если другая сила толкает с величиной, превышающей $\mu_s F_N$, объект будет скользить, и статического трения больше не будет. Он не появится «повторно», пока объект не перестанет скользить.

Для кинетического трения $$\left|\mathcal{F}_k\right| = \mu_k F_N$$, когда объект скользит (и все время, пока он скользит). Направление этой силы противоположно направлению скольжения. Если нормальная величина силы постоянна, эта величина постоянна до тех пор, пока объект не остановится. Она не зависит от каких-либо других сил, параллельных поверхности.

Итог: 1) Достаточно ли велика начальная сила для скольжения? Если да, то статическое трение никогда не появляется, пока объект не остановится. 2) Если толкающая сила больше кинетического трения, тело будет набирать скорость. 3) Если толкающая сила меньше кинетического трения, объект потеряет скорость. 4) Кинетическое трение в этой задаче постоянно.

Мое предложение состоит в том, чтобы выяснить, возвращается ли общий импульс (от трения P и ) к нулю до прекращения действия силы P.

$\endgroup$

$\begingroup$

Я хочу знать, как разделить силу трения. Должен ли я использовать fr=µsN, когда P(t) падает ниже µsN или когда оно падает ниже µkN. Кроме того, что произойдет, когда P окажется между µsN и µkN, останется ли объект в движении или остановится?

Когда тело начинает двигаться с ускорением, необходимо учитывать кинетический коэффициент трения.

Коэффициент статического трения может указать вам ограничивающее усилие, необходимое для начала движения. Статический коэффициент можно использовать только тогда, когда он препятствует движению.

Подсказка: При t=0 вынуждающая сила равна 100 Н, и в этот момент величина силы трения будет меньше вынуждающей силы.