аналогия с линейным движением, примеры
Любая физическая величина, которая предлагается в математических уравнениях при изучении того или иного явления природы, несет некоторый смысл. Не является исключением из этого правила и момент инерции. Физический смысл этой величины подробно рассмотрен в данной статье.
Момент инерции: математическая формулировка
В первую очередь следует сказать, что рассматриваемая физическая величина используется для описания систем вращения, то есть таких движений объекта, которые характеризуются круговыми траекториями вокруг некоторой оси или точки.
Приведем математическую формулу момента инерции для материальной точки:
I = m*r2.
Здесь m и r — масса и радиус вращения частицы (расстояние до оси) соответственно. Любое твердое тело, каким бы сложным оно ни было, мысленно можно разбить на материальные точки. Тогда формула момента инерции в общем виде будет иметь вид:
I = ∫mr2dm.
Это выражение справедливо всегда, причем не только для трехмерных, но и для двумерных (одномерных) тел, то есть для плоскостей и стержней.
Из этих формул трудно понять смысл физический момента инерции, однако можно сделать важный вывод: он зависит от распределения массы в теле, которое вращается, а также от расстояния до оси вращения. Причем зависимость от r является более резкой, чем от m (см. знак квадрата в формулах).
Движение по окружности
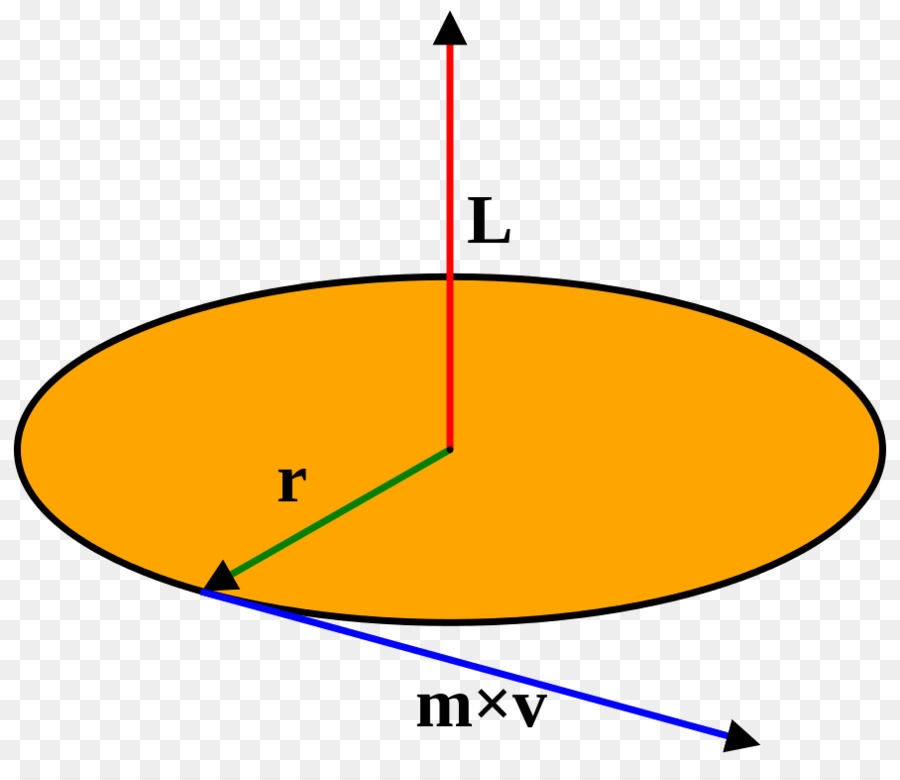
Понять, каков физический смысл момента инерции, невозможно, если не рассмотреть круговое движение тел. Не вдаваясь в подробности, приведем сразу два математических выражения, описывающих вращение:
I1*ω1 = I2*ω2;
M = I *dω/dt.
Верхнее уравнение носит название закона сохранения величины L (момента импульса). Оно означает, что какие бы изменения ни происходили внутри системы (сначала был момент инерции I1, а затем он стал равным I2), произведение I на угловую скорость ω, то есть момент импульса, будет оставаться неизменным.
Нижнее выражение демонстрирует изменение скорости вращения системы (dω/dt) при воздействии на нее некоторого момента силы M, который имеет внешний характер, то есть порождается силами, не связанными с внутренними процессами в рассматриваемой системе.
И в верхнем, и в нижнем равенствах присутствует I, причем чем больше ее значение, тем меньше будет угловая скорость ω или угловое ускорение dω/dt. В этом и заключается физический смысл момента инерции тела: он отражает способность системы сохранять свою угловую скорость. Чем больше I, тем сильнее проявляется эта способность.
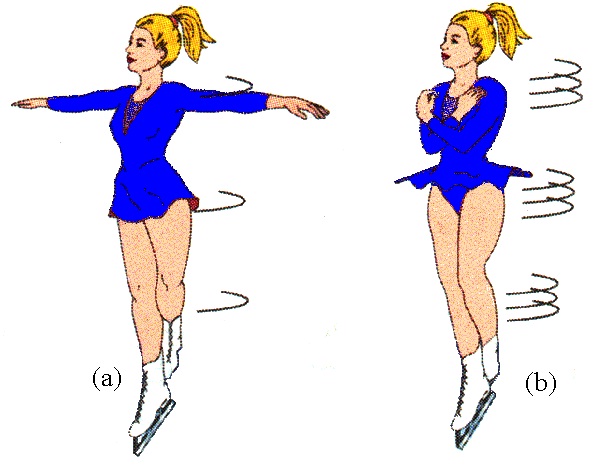
Аналогия с линейным импульсом
Теперь перейдем к тому же выводу, что был озвучен в конце предыдущего пункта, проведя аналогию между вращательным и поступательным движениями в физике. Как известно, последнее описывается следующей формулой:
p = m*v.
Это простое выражение определяет импульс системы. Сравним его форму с таковой для момента импульса (см. верхнее выражение в предыдущем пункте). Мы видим, что величины v и ω имеют одинаковый смысл: первая характеризует скорость изменения линейных координат объекта, вторая — угловых координат. Поскольку обе формулы описывают процесс равномерного (равноуглового) движения, то величины m и I также должны иметь одинаковый смысл.
Теперь рассмотрим 2-й закон Ньютона, который выражается формулой:
F = m*a.
Обращая внимание на форму записи нижнего равенства в предыдущем пункте, имеем подобную рассмотренной ситуацию. Момент силы M в его линейной представлении — это сила F, а линейное ускорение a полностью аналогично угловому dω/dt. И снова мы приходим к эквивалентности массы и момента инерции.
Какой смысл несет масса в классической механике? Она является мерой инерции: чем больше m, тем труднее сдвинуть предмет с места, а тем более придать ему ускорение. То же самое можно сказать и о моменте инерции применительно к движению вращения.
Физический смысл момента инерции на бытовом примере
Зададимся простым вопросом о том, как легче крутить металлический стержень, например, арматуру — когда ось вращение направлена вдоль его длины или когда поперек? Конечно же, легче раскрутить стержень в первом случае, потому что его момент инерции для такого положения оси будет очень маленьким (для тонкого стержня он равен нулю). Поэтому достаточно зажать между ладошек предмет и легким движением привести его во вращение.
Кстати, описанный факт экспериментально проверили наши предки еще в стародавние времена, когда научились добывать огонь. Они раскручивали палочку с огромными угловыми ускорениями, что приводило к созданию больших сил трения и, как следствие, к выделению значительного количества теплоты.
Маховик авто — яркий пример использования большого значения момента инерции
В завершение хотелось бы привести, пожалуй, самый важный для современной техники пример использования физического смысла момента инерции. Маховик авто представляет собой сплошной стальной диск, имеющий относительно большие радиус и массу. Эти две величины обуславливают существование значительной величины I, характеризующей его. Маховик призван «смягчать» любые силовые воздействия на коленвал автомобиля. Импульсивный характер действующих моментов сил от цилиндров двигателя на коленвал сглаживается и делается плавным благодаря тяжелому маховику.
Кстати, чем больше момент импульса, тем больше энергии находится во вращающейся системе (аналогия с массой). Этот факт хотят использовать инженеры, запасая энергию торможения авто в маховике, чтобы впоследствии направить ее на разгон транспортного средства.
Физический смысл момента инерции
Определение и смысл момента инерции
Пусть материальная точка вращается по окружности вокруг неподвижной оси, которая проходит через центр траектории данной точки. Момент ее импульса (L) относительно этой оси будет равен:
где m – масса этой точки; v – скорость движения точки; r – радиус окружности, по которой точка движется. Если угловую скорость точки обозначить как и принять равной:
тогда величину момента импульса можно определить как:
Если представить, что вокруг рассматриваемой оси вращается несколько материальных точек с одинаковой угловой скоростью, то L будет равен:
В выражении (4) суммирование происходит по всем материальным точка, входящим в систему. Так как – величина постоянная, то ее можно вынести за знак суммы, тогда имеем:
Где – величина, равная сумме произведений масс материальных точек на расстояния в квадрате от каждой из них до оси вращения, называют моментом инерции рассматриваемой системы по отношению к оси.
Уравнение (5) отражает тот факт, что момент импульса системы при ее вращении относительно оси равен произведению момента инерции на угловую скорость. Если кроме вращения материальных точек имеется их движения по радиусам, то выражение (5) останется справедливым. Это следствие линейной зависимости момента импульса точки (L) от скорости ее движения (v). Если вектор скорости направлен по радиусу или параллельно оси вращения, то момент импульса относительно этой оси равен нулю. Вследствие чего данные виды движения не оказывают непосредственного влияния на вид связи между моментом импульса системы относительно оси вращения и угловой скоростью. Такое влияние проявляется косвенно. Момент инерции перестает быть постоянной величиной и изменяется во времени, в зависимости от конфигурации системы. Уравнение движения для такой системы имеет вид:
где – момент внешних сил, приложенных к телу относительно оси вращения. Уравнение (6) называют основным уравнением динамики вращательного движения тела вокруг неподвижной оси. Проведем аналогию между ним и уравнением Ньютона для поступательного движения материальной точки:
Роль массы в уравнении (6) играет момент инерции J, роль скорости угловая скорость, роль силы – момент силы.
Получается, что момент инерции тела относительно оси вращения выступает мерой инертности тела по отношению к вращению, так же как масса является мерой инертности в поступательном движении.
Аналогию между поступательным движением материальной точки и вращением твердого тела можно продолжить, при рассмотрении кинетической энергии твердого тела.
Где – кинетическая энергия твердого тела, вращающегося около неподвижной оси. Данное выражение напоминает формулу для расчета кинетической энергии при поступательном движении материальной точки.
Примеры решения задач
Момент инерции и его физический смысл. Теорема Штейнера.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Момент инерции представляет собой меру инерции тела во вращательном движении.
Теорема Штейнера. Момент инерции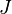 
тела относительно произвольной оси равен сумме момента инерции этого тела 
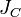относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 
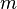на квадрат расстояния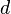 
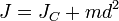, где
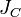— известный момент инерции относительно оси, проходящей через центр масс тела,
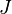— искомый момент инерции относительно параллельной оси,
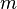— масса тела,
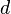— расстояние между указанными осями.
Закон сохранения импульса.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
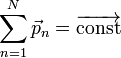
Закон сохранения момента импульса.
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):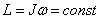 
Закон сохранения энергии.
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
,
,
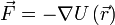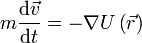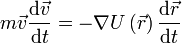
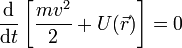
РаботойA, совершаемой постоянной силой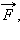 
называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы 
и перемещения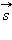 
: A = F*s* cosα
Мощность — это работа за единицу времени (1 с):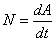 
Кинетическая и потенциальная энергия.
Потенциальной энергией называется энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.
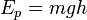
Потенциальная энергия упругих тел: 
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.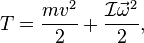 
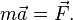
Скалярно умножим уравнение на перемещение частицы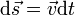 
. Учитывая, что 
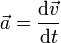, получим: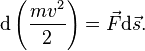 
Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то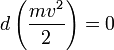 
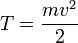остаётся постоянной. Эта величина называется кинетической энергией частицы.
Уравнение Бернулли.
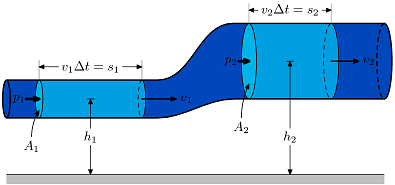
Уравнение Бернулли — для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.
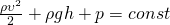
Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.
Характеристики колебаний.
Для описания колебательного движения существуют следующие характеристики:
Модуль максимально возможного смещения относительно положения равновесия называется амплитудой колебания А.
Промежуток времени, в течение которого происходит одно полное колебание, называется периодом колебания Т. Измеряется в секундах.
Число колебаний за одну секунду называетсячастотой 
. Измеряется в герцах (Гц). Если частота равна 1 Гц, то это значит, что за одну секунду тело совершает одно колебание.
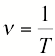
Циклическая частота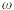 
—это величина на 
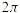больше частоты. Она показывает сколько колебаний совершается за 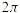секунд. Измеряется в с-1
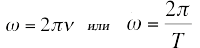
Гармонические колебания.
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
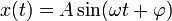
или
,
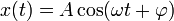где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;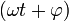 
— полная фаза колебаний, 
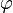— начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
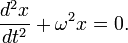
Физический смысл момента инерции твердого тела? — Мегаобучалка
Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело
| (5.4) |
В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом
| (5.5) |
о где — расстояние от элемента до оси вращения.
Распределение массы в пределах тела можно охарактеризовать с помощью
плотности
| (5.5) |
где m — масса однородного тела, V — его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.
Плотность в данной точке в этом случае определяется следующим образом
и тогда
| (5.6) |
Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Момент инерции полого цилиндра с тонкими стенками, радиуса R.
Для полого цилиндра с тонкими стенками
Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки и массой . Для него
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:
Момент инерции шара относительно оси, проходящей через центр тяжести.
Момент инерции стержня длиной L и массой m относительно оси, проходящей:
а) через центр стержня —
б) через начало стержня —
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
Получить расчетные формулы (31) и (44) для определения момента инерции?
Записать второй закон Ньютона для движения центра масс и основной закон динамики вращательного движения, дать определение всех величин, входящие в данные законы?
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
8. Динамика твердого тела
В механике под твердым телом понимают систему материальных точек, расстояние между любыми двумя точками которого в процессе движения остается неизменным. Поэтому все результаты, полученные в предыдущих темах (“Динамика материальной точки”, “Закон сохранения импульса”, “Закон сохранения энергии” и “Закон сохранения момента импульса”) для системы материальных точек, применимы и к твердому телу.
Момент инерции твердого тела
Момент инерции – это величина, зависящая от распределения масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением
,
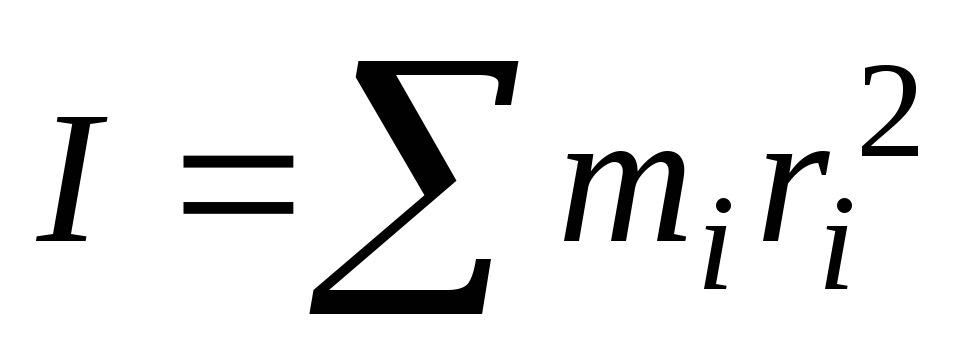где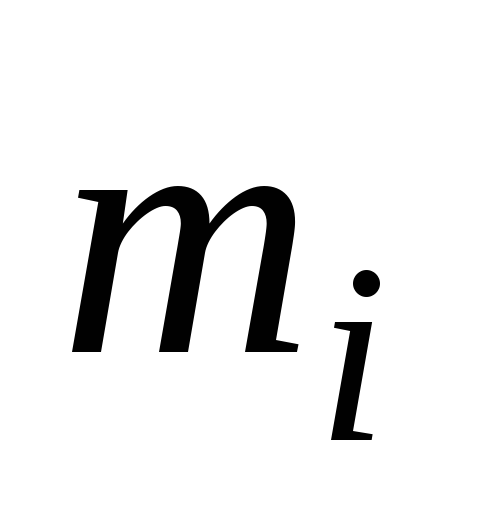
—
элементарные массы тела;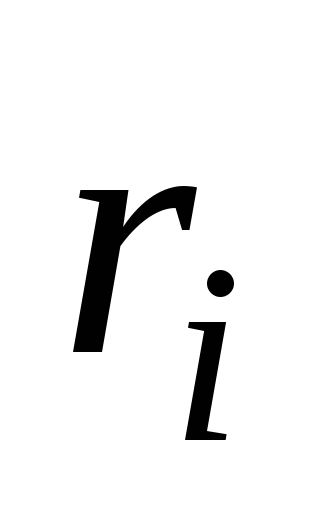
—
их расстояния от оси вращения.
Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла
,
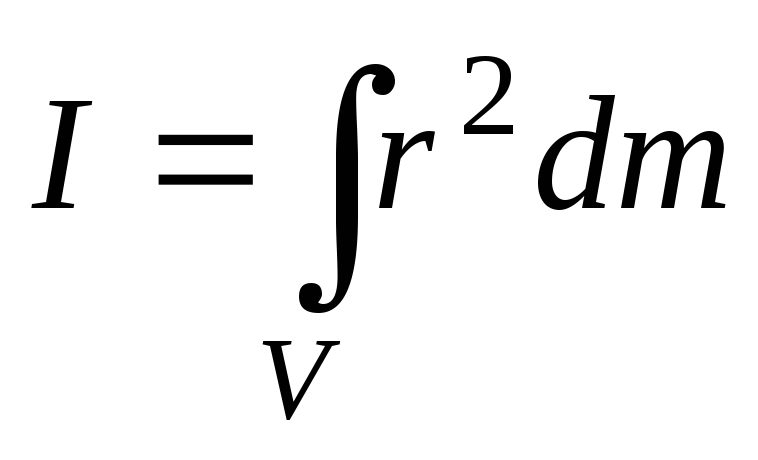(1)
где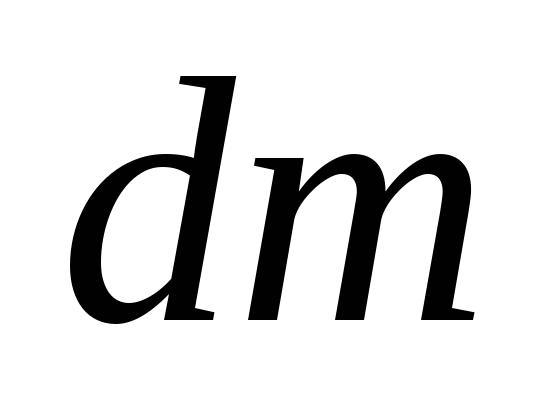 
–
масса элемента тела, находящегося на
расстоянии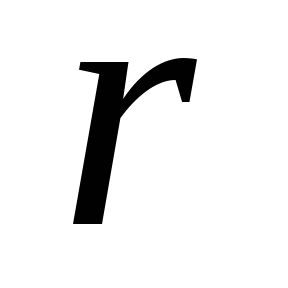
от интересующей нас оси. Интегрирование
должно производиться по всему объему
тела.
Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы.
Если
известен момент инерции тела относительно
какой-либо оси, можно найти момент
инерции относительно любой другой оси,
параллельной данной. Используя теорему
Штейнера, согласно которой момент
инерции 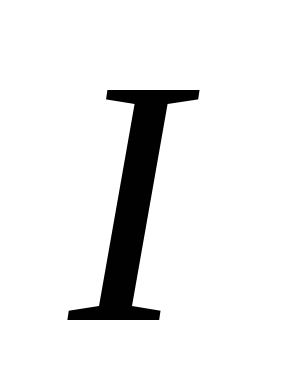тела 
относительно произвольной оси равен
сумме момента инерции тела относительно
оси, проходящей через центр масс тела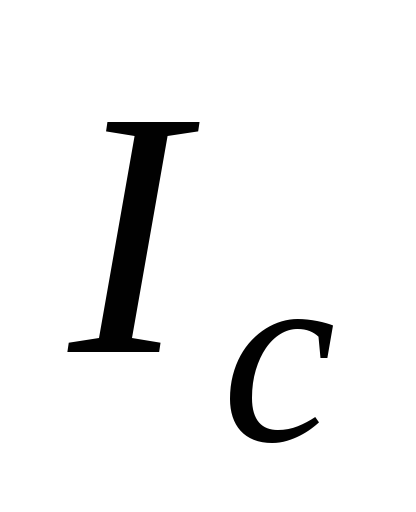
и параллельной данной оси, и произведения
массы телат на квадрат расстояния между осями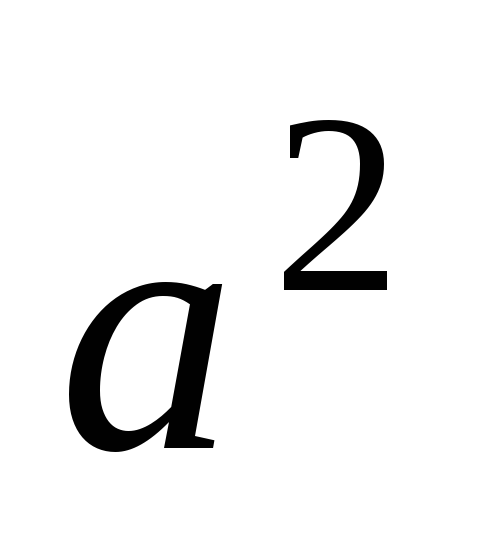 
:
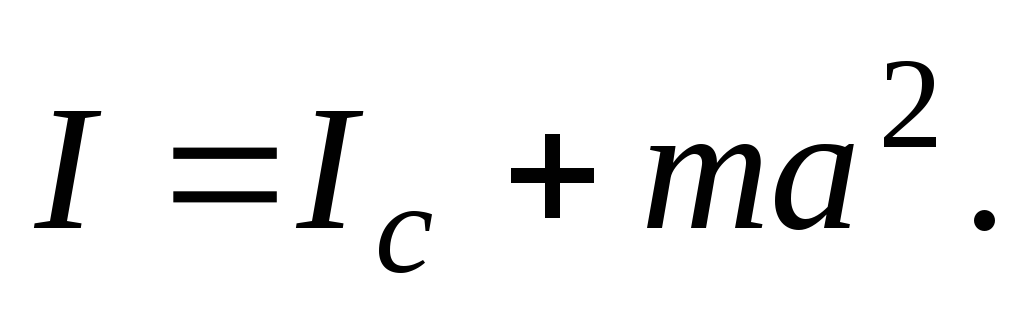(2)
Вычисление
момента инерции тела относительно оси
часто можно упростить, вычислив
предварительномомент
инерции относительно точки.
Сам по себе момент инерции тела
относительно точки не играет никакой
роли в динамике. Он является чисто
вспомогательным понятием, служащим для
упрощения вычислений.
Рассмотрим
некоторую точку твердого тела массой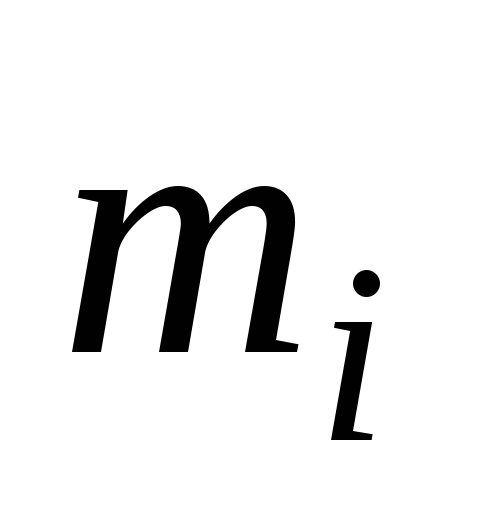 
и с координатами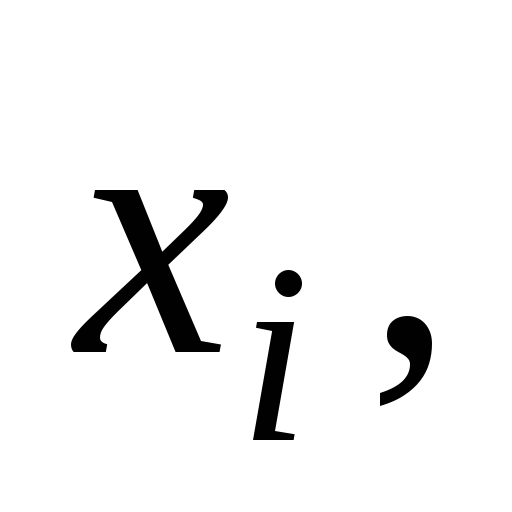
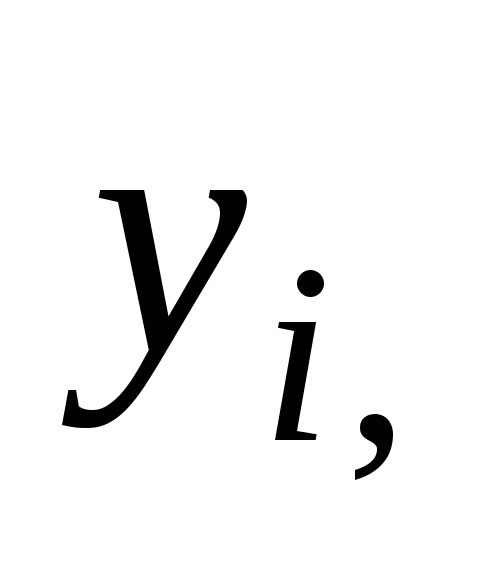
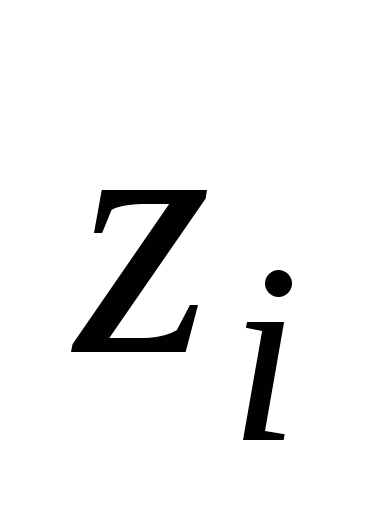относительно прямоугольной системы
координат (рис. 1). Квадраты расстояний
ее до координатных осей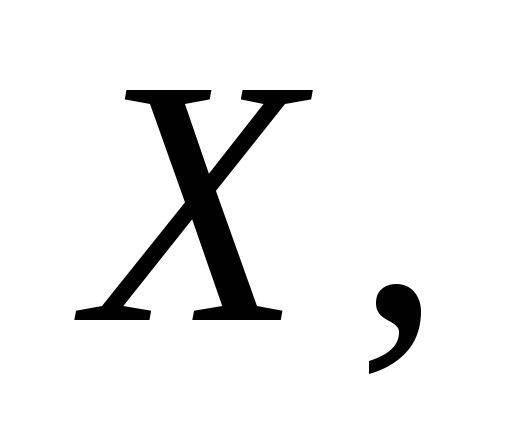
равны соответственно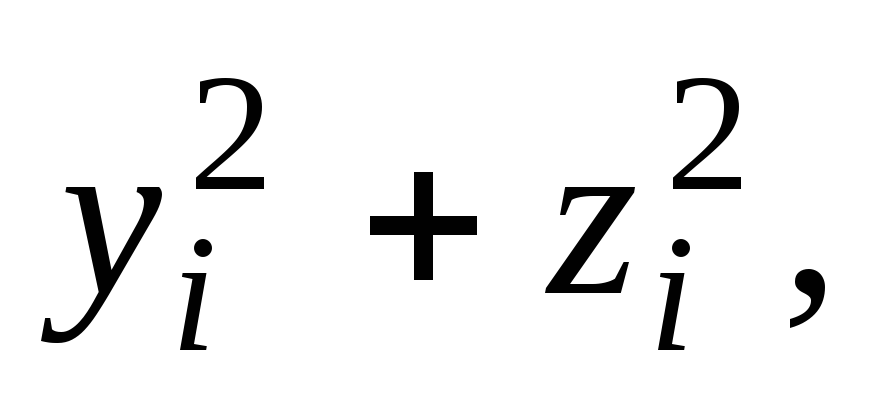
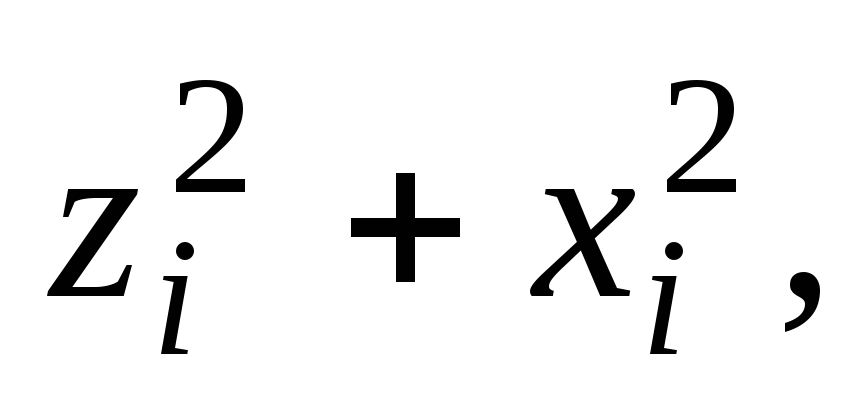
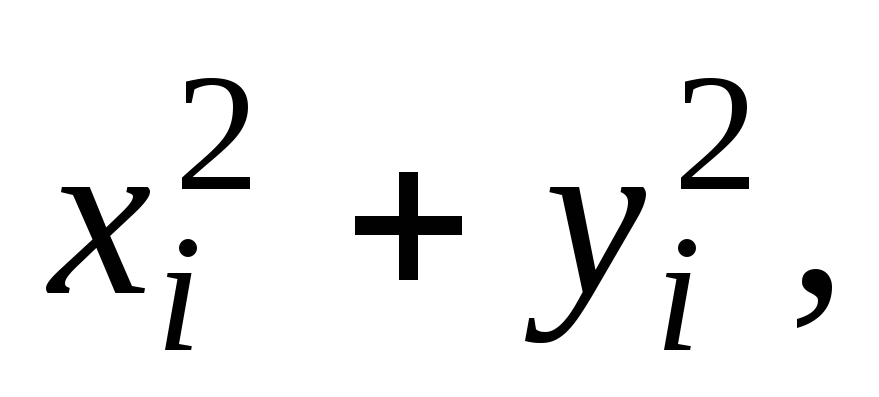а
моменты инерции относительно тех же
осей
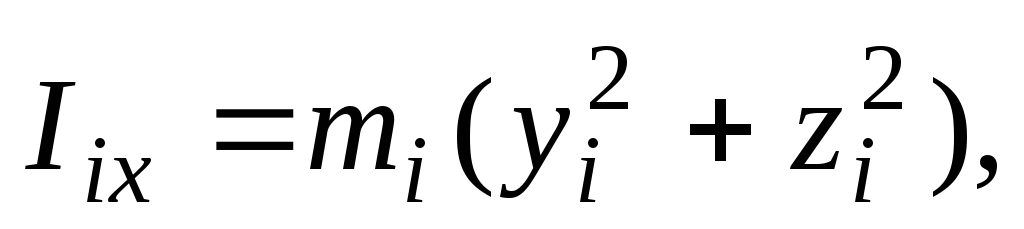
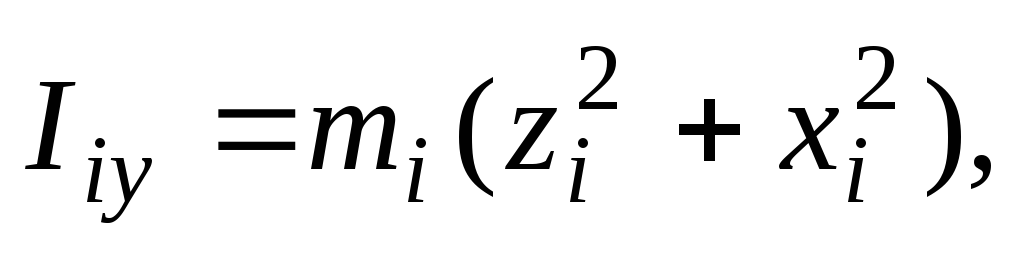
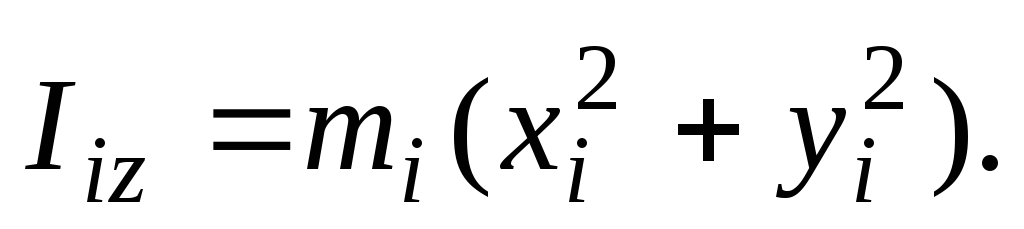(3)
Сложив эти равенства и просуммировав по всему объему тела
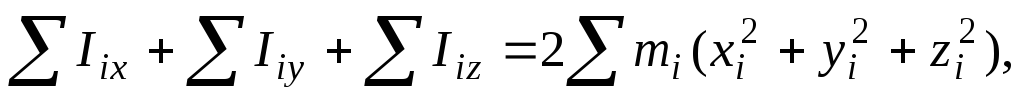(4)
получим
(5)
где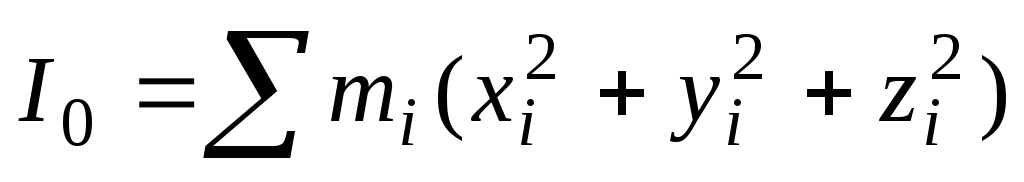 
– момент инерции телаотносительно
точки.
Из
этого выражения можно получить связь
между моментами инерции плоского тела,
относительно осей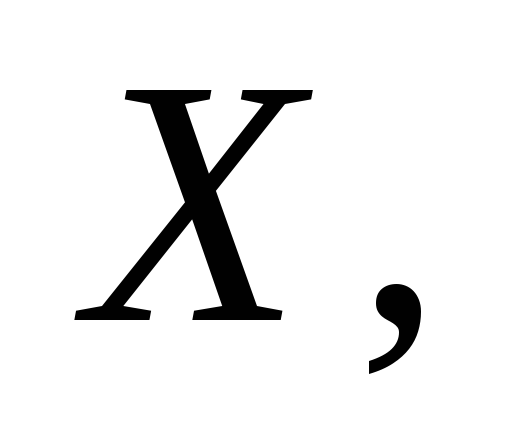 
.
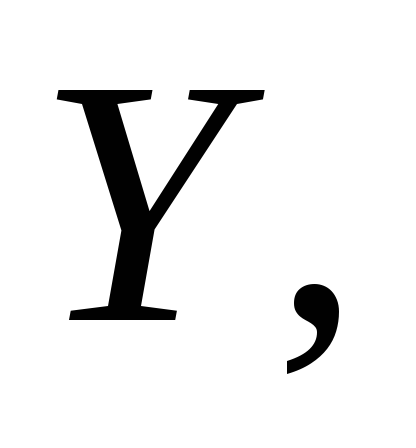
Пусть масса плоского тела сосредоточена
в плоскости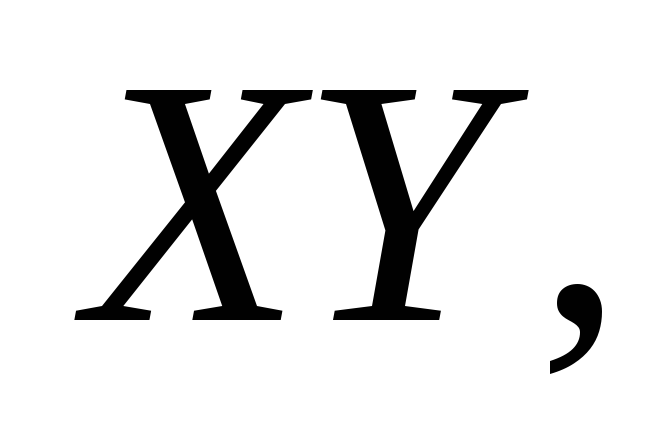
т.е. координата
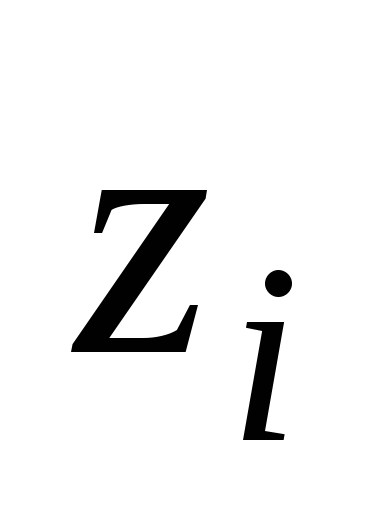любой точки такого тел равна нулю,
тогда из
уравнений (3) и (4) следует, что
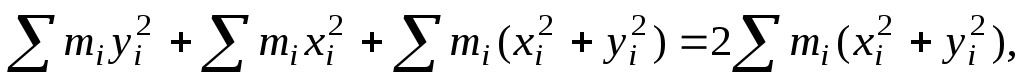
или
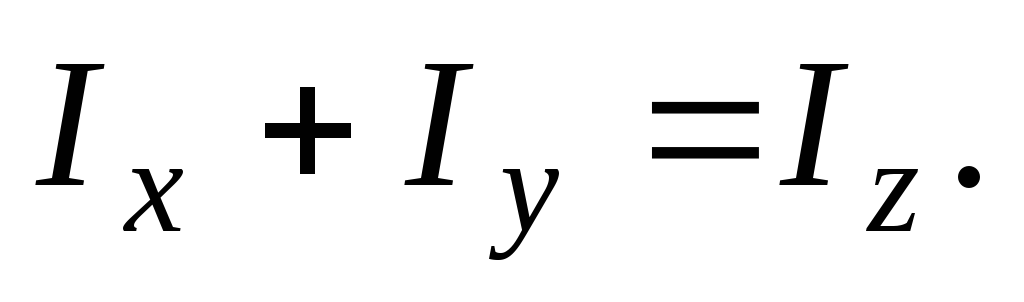(6)
Вращение твердого тела вокруг неподвижной оси
Рассмотрим
твердое тело массой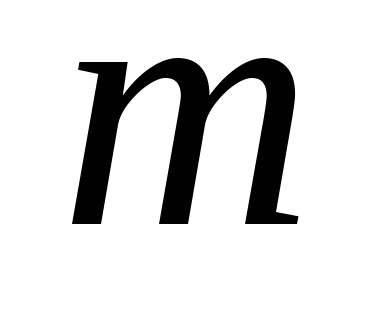 
,
вращающееся вокруг неподвижной оси с
угловой скоростью
.
Для того чтобы получить уравнение,
описывающее это движение, применим
уравнение моментов относительно оси,
полученное в разделе “ Закон сохранения
момента импульса”
,
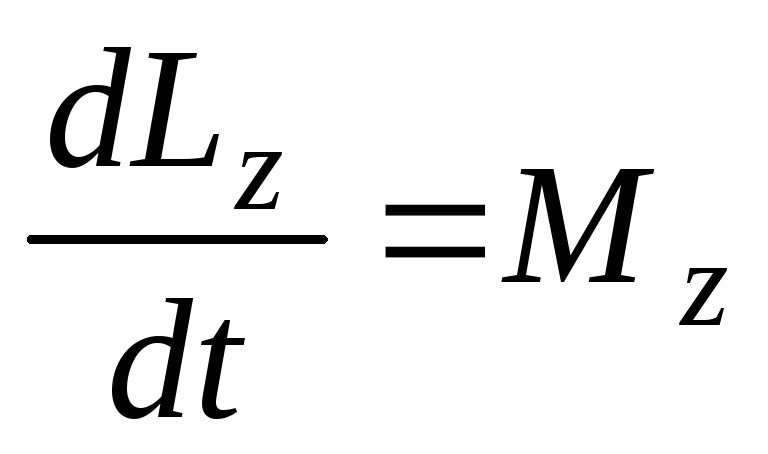(7)
напомним,
что в этом уравнени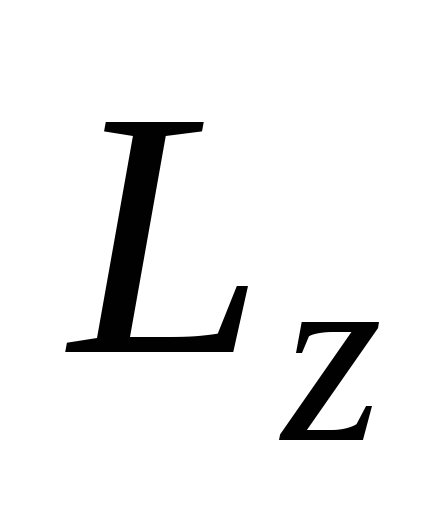и 
и
– момент импульса и момент силы
относительно оси, вокруг которой
вращается твердое тело.
Момент
импульса некоторой точки тела массой 
вращающейся
по окружности радиуса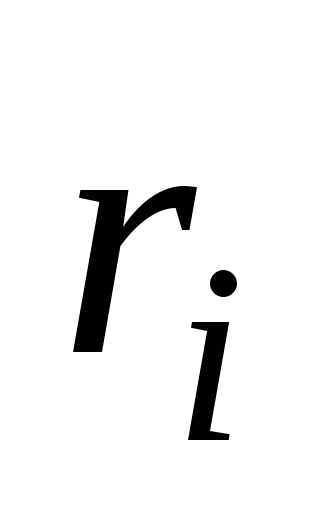
со скоростью
,
равен
Просуммировав
по всему объему тела, учитывая, что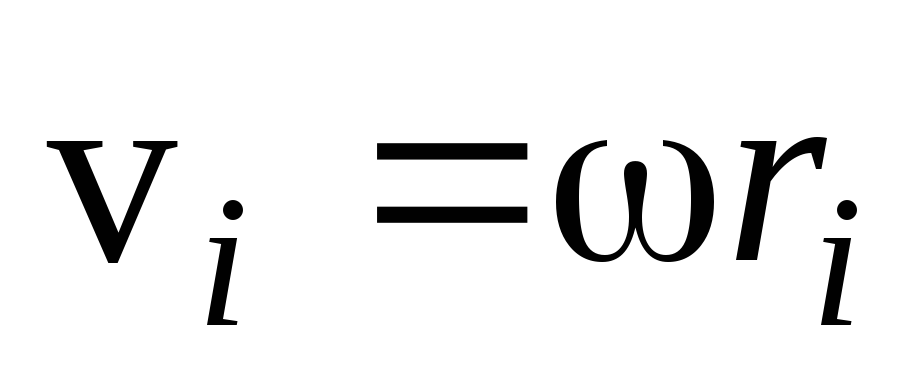 
получим
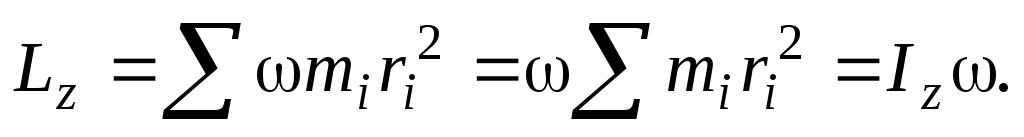
Таким образом, момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции тела относительно этой оси на его угловую скорость.
Подставляя полученное выражение в (7), получим уравнение динамики твердого тела, вращающегося вокруг неподвижной оси,
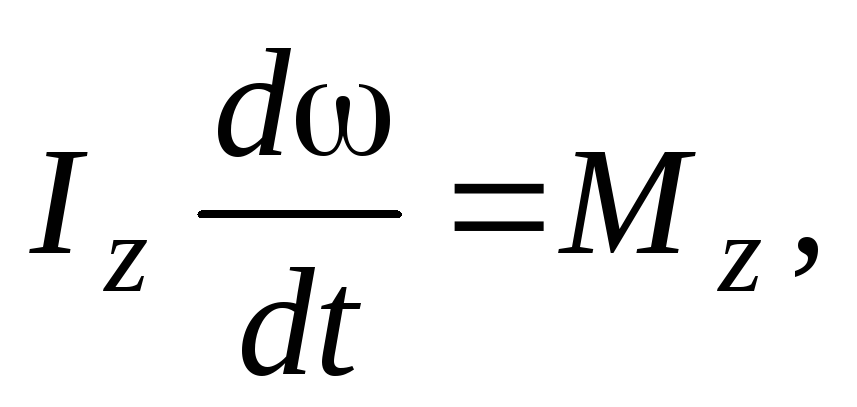или 
(8)
где 
– угловое ускорение тела.
Найдем кинетическую энергию вращающегося тела. Для этого просуммируем по всему объему тела кинетические энергии отдельных его частей
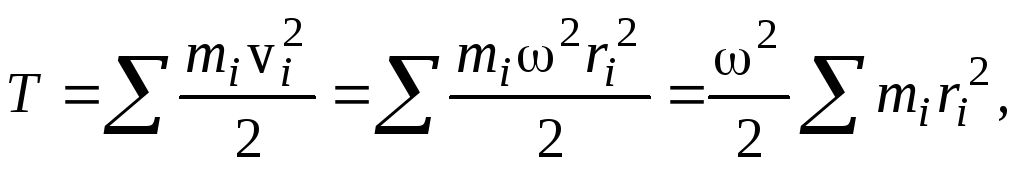
или
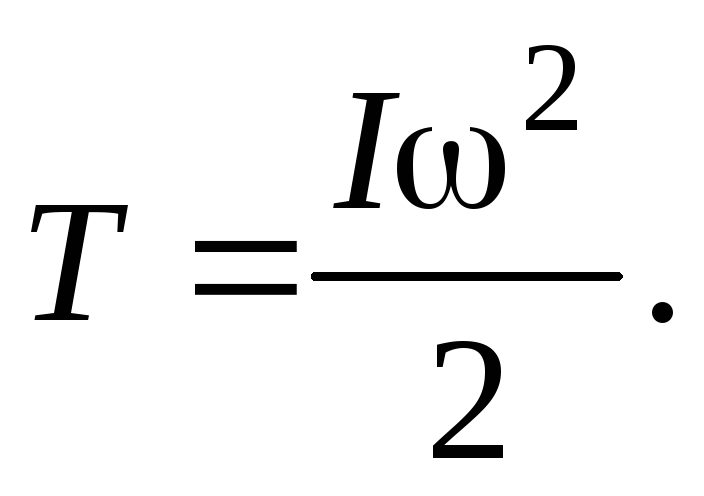(9)
Зная
зависимость момента сил, действующих
на тело, от угла поворота, можно найти
работу этих сил при повороте тела на
конечный угол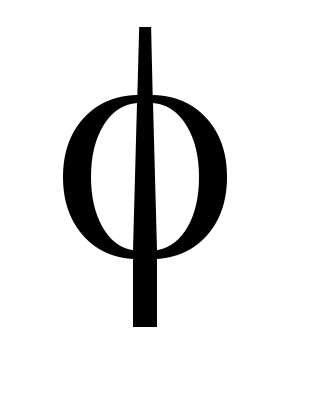 
.
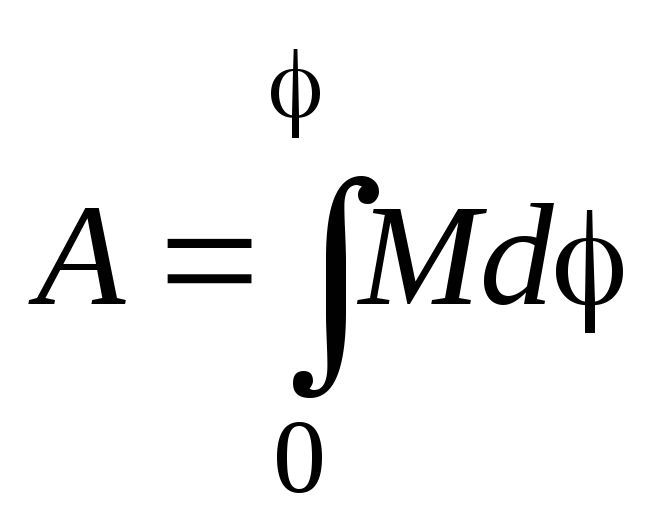Момент инерции тела относительно оси вращения. Его физический смысл.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Геометрический момент инерции — геометрическая характеристика сечения вида
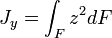
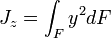
где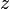 
— расстояние от центральной 
оси до любой элементарной площадки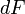 
относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки.
Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела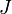 
относительно произвольной оси равен сумме момента инерции этого тела 
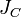относительно параллельной ей оси, проходящей через центр масс 
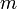тела, и произведения массы тела 
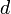на квадрат расстояния между осями:
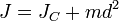
где
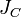— известный момент инерции относительно оси, проходящей через центр масс тела,
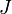— искомый момент инерции относительно параллельной оси,
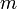— масса тела,
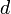— расстояние между указанными осями.
Момент силы относительно точки и оси вращения
Момент силы относительно оси
Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментов силы относительно оси. Момент силы относительно оси вычисляется как момент проекции силы F⃗ на плоскость Π,
перпендикулярную оси, относительно точки пересечения оси с плоскостью Π:
Момент силы относительно точки О — это вектор, модуль которого равен произведению модуля силы на плечо — кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.
Основной закон динамики для вращательного движения
Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение». Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
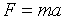где F – сила, приложенная к телу массой m; а – линейное ускорение тела
