Равенство векторов / Векторы / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Векторы
5. Равенство векторов

Определение

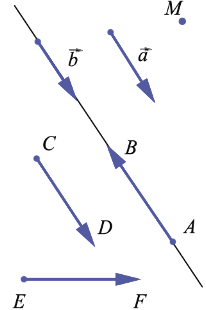
На данном рисунке векторы , , 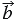, , коллинеарны, а векторы и , а также

и не коллинеарны.

Два коллинеарных ненулевых вектора и 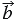могут быть направлены либо одинаково, либо противоположно. В первом случае векторы и 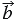 называются сонаправленными (обозначается 

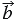), а во втором — противоположно направленными (обозначается 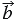). Любое направление можно считать направлением нулевого вектора, так как его начало совпадает с его концом. Поэтому нулевой вектор сонаправлен с любым вектором.

На рисунке

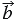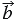
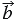
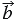, , , , , и , и т.д.

Ненулевые коллинеарные векторы обладают следующими свойствами:

1. Если , , то ().
2. Если
   , , то .
3. Если , , то .

Определение

Векторы называются равными, если они сонаправлены и их длины равны

Таким образом, векторы

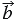и равны, есл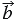и и =. Равенство векторов и обозначается так: =.

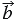
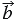Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Понятие вектора

Откладывание вектора от данной точки

Сумма двух векторов

Законы сложения векторов. Правило параллелограмма

Сумма нескольких векторов

Вычитание векторов

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции

Векторы

Правило встречается в следующих упражнениях:

7 класс

Задание 740, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 772, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 790, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 903, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 916, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 928, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1069, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1163, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Ортогональность векторов.

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = {a_x; a_y} и b = {b_x; b_y}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y = 0

Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y + a_z · b_z = 0

Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 4
2n — 4 = 0
2n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

равные векторы — это… Что такое равные векторы?



• равны
• равные возможности

Смотреть что такое «равные векторы» в других словарях:

• Координаты вектора — ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору. где   координаты вектора. Свойства Равные векторы в единой системе координат имеют равные координаты Координаты …   Википедия

• Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор …   Википедия

• Вектор (геометрия) — Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых  точка A  называется его началом, а вторая  B  его концом. Содержание 1 Определение …   Википедия

• Вектор (Геометрические представления) — Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых  точка A  называется его началом, а вторая  B  его концом. Содержание 1 Определение …   Википедия

• Направленный отрезок — Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых  точка A  называется его началом, а вторая  B  его концом. Содержание 1 Определение …   Википедия

• ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… …   Энциклопедия Кольера

• Векторное произведение — в трёхмерном пространстве. Векторное произведение  это псевдовектор, перпендикулярный плоскости, построенной по двум …   Википедия

• СИММЕТРИЯ КРИСТАЛЛОВ — свойство кристаллов совмещаться с собой при поворотах, отражениях, параллельных переносах либо части или комбинации этих операций. Симметрия означает возможность преобразования объекта, совмещающего его с собой. Симметрия внеш. формы (огранки)… …   Физическая энциклопедия

• Истинное ортогональное разложение — Метод Главных Компонент (англ. Principal components analysis, PCA)  один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… …   Википедия

• Метод Главных Компонент — (англ. Principal components analysis, PCA)  один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих областях, таких как… …   Википедия

• Преобразование Карунена-Лоэва — Метод Главных Компонент (англ. Principal components analysis, PCA)  один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) в 1901 г. Применяется во многих… …   Википедия

Равные векторы – это _ длины которых равны сонаправленные векторы, противоположно направленные векторы,

Верны ли утверждения?
А) Длина нулевого вектора равна нулю
В) Координаты нулевого вектора равны нулю
Подберите правильный ответ
 (*ответ*) А — да, В — да
 А — да, В — нет
 А — нет, В — да
 А — нет, В — нет
Подберите правильный ответ
 (*ответ*) А — да, В — да
 А — да, В — нет
 А — нет, В — да
 А — нет, В — нет
Два ненулевых коллинеарных вектора могут лежать на:   _
 (*ответ*) одной прямой
 (*ответ*) двух параллельных прямых
 двух перпендикулярных прямых
 любых двух прямых
Длина нулевого вектора считается равной   _(число)
 (*ответ*) 0
Длиной вектора  называется   _отрезка АВ
 (*ответ*) длина
На рисунках вектор изображается отрезком   _ на конце
 (*ответ*) со стрелкой
 с косым крестом
 с кружочком
 с дугой
Ненулевые векторы называются равными, если они   _
 (*ответ*) сонаправлены и их длины равны
 коллинеарны и их длины равны
 лежат на одной прямой
 лежат на параллельных прямых и их длины равны
Ненулевые векторы, лежащие либо на одной прямой, либо на параллельных прямых, называются   _
 (*ответ*) коллинеарными
 компланарными
 сонаправленными
 сопряженными
Ненулевые коллинеарные векторы, концы которых лежат по одну сторону от прямой, проходящей через их начала. называются   _
 (*ответ*) сонаправленными
Ненулевые коллинеарные векторы, концы которых лежат по разные стороны от прямой, проходящей через их начала, называются   _ направленными
 (*ответ*) противоположно
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется   _:
 (*ответ*) направленным отрезком
 (*ответ*) вектором
 стрелкой
 лучом
 полупрямой
Примерами векторных величин являются:
 (*ответ*) сила
 (*ответ*) скорость
 (*ответ*) перемещение материальной точки
 масса
 температура
 плотность
Равные векторы – это   _ длины которых равны
 (*ответ*) сонаправленные векторы,
 противоположно направленные векторы,
 векторы, начала которых совпадают и
 векторы, концы которых совпадают и
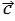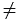