Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы.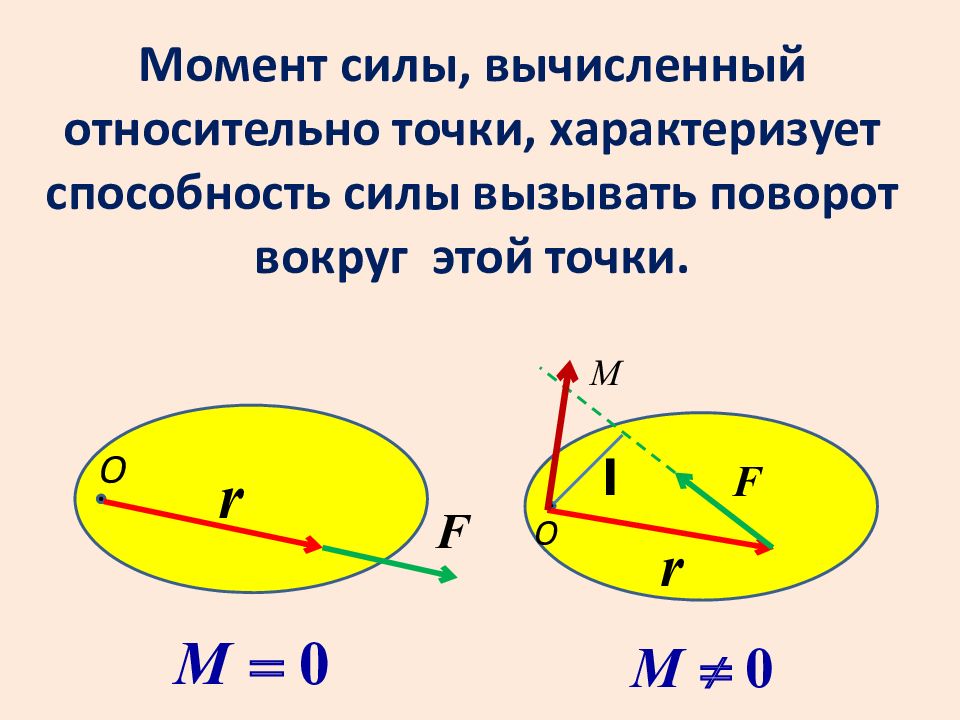
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.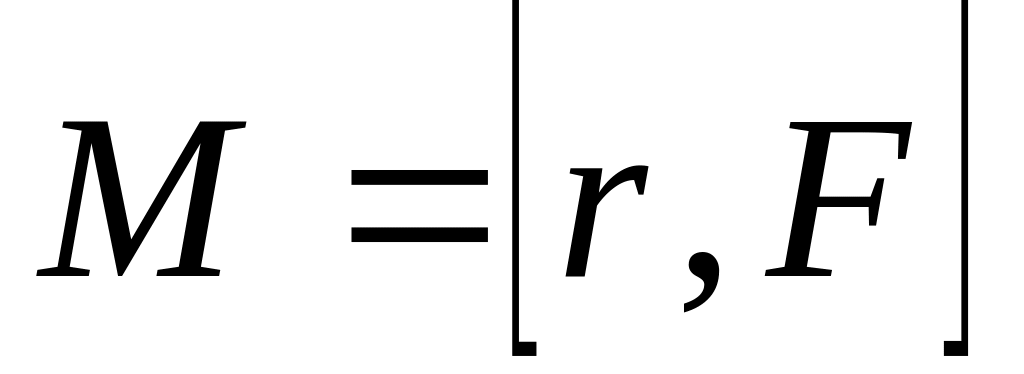
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в. м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Конвертер вращающего момента • Механика • Определения единиц • Онлайн-конвертеры единиц измерения
Определения единиц конвертера «Конвертер вращающего момента»
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Определения единиц конвертера «Конвертер вращающего момента» на русском и английском языках
ньютон-метрНьютон-метр (Н·м) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в Международной системе единиц (СИ). Один ньютон-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один ньютон в направлении, перпендикулярном рычагу.
ньютон-сантиметрНьютон-сантиметр (Н·см) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в Международной системе единиц (СИ), дольная по отношению к единице ньютон-метр. Один ньютон-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один ньютон в направлении, перпендикулярном рычагу.
ньютон-миллиметрНьютон-миллиметр (Н·мм) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в Международной системе единиц (СИ), дольная по отношению к единице ньютон-метр. Один ньютон-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один ньютон в направлении, перпендикулярном рычагу.
килоньютон-метрКилоньютон-метр (кН·см) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в Международной системе единиц (СИ), кратная единице ньютон-метр. Один ньютон-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один ньютон в направлении, перпендикулярном рычагу.
дина-метрДина-метр (дин·м) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в системе СГС, кратная единице дина-сантиметр. Одна дина-сантиметр равна моменту, возникающему при действии на рычаг с плечом в один сантиметр силы в одну дину в направлении, перпендикулярном рычагу.
дина-сантиметрДина-сантиметр (дин·см) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в системе СГС. Одна дина-сантиметр равна моменту, возникающему при действии на рычаг с плечом в один сантиметр силы в одну дину в направлении, перпендикулярном рычагу.
дина-миллиметрДина-миллиметр (дин·мм) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в системе СГС, дольная по отношению к единице дина-сантиметр. Одна дина-сантиметр равна моменту, возникающему при действии на рычаг с плечом в один сантиметр силы в одну дину в направлении, перпендикулярном рычагу.
килограмм-сила-метрКилограмм-сила-метр (кгс·м) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один килограмм-сила-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один килограмм-сила в направлении, перпендикулярном рычагу.
килограмм-сила-сантиметрКилограмм-сила-сантиметр (кгс·см) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один килограмм-сила-сантиметр равен моменту, возникающему при действии на рычаг с плечом в один сантиметр силы в один килограмм-сила в направлении, перпендикулярном рычагу.
килограмм-сила-миллиметрКилограмм-сила-миллиметр (кгс·мм) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один килограмм-сила-миллиметр равен моменту, возникающему при действии на рычаг с плечом в один миллиметр силы в один килограмм-сила в направлении, перпендикулярном рычагу.
грамм-сила-метрГрамм-сила-метр (гс·м) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один грамм-сила-метр равен моменту, возникающему при действии на рычаг с плечом в один метр силы в один грамм-сила в направлении, перпендикулярном рычагу.
грамм-сила-сантиметрГрамм-сила-сантиметр (гс·см) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один грамм-сила-сантиметр равен моменту, возникающему при действии на рычаг с плечом в один сантиметр силы в один грамм-сила в направлении, перпендикулярном рычагу.
грамм-сила-миллиметрГрамм-сила-миллиметр (гс·мм) — внесистемная метрическая единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент). Один грамм-сила-миллиметр равен моменту, возникающему при действии на рычаг с плечом в один миллиметр силы в один грамм-сила в направлении, перпендикулярном рычагу.
унция-сила-футУнция-сила-фут (унция-сила·фут) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в американской и английской традиционных системах мер. Одна унция-сила-фут равна моменту, возникающему при действии на рычаг с плечом в один фут силы в одну унцию-сила в направлении, перпендикулярном рычагу.
унция-сила-дюймУнция-сила-дюйм (унция-сила·дюйм) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в американской и английской традиционных системах мер. Одна унция-сила-дюйм равна моменту, возникающему при действии на рычаг с плечом в один дюйм силы в одну унцию-сила в направлении, перпендикулярном рычагу.
фунт-сила футФунт-сила-фут (фунт-сила·фут) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в американской и английской традиционных системах мер. Один фунт-сила-фут равен моменту, возникающему при действии на рычаг с плечом в один фут силы в один фунт-сила в направлении, перпендикулярном рычагу.
фунт-сила дюймФунт-сила-дюйм (фунт-сила·дюйм) — единица измерения момента силы (тж. крутящий момент, вращательный момент, вращающий момент) в американской и английской традиционных системах мер. Один фунт-сила-дюйм равен моменту, возникающему при действии на рычаг с плечом в один дюйм силы в один фунт-сила в направлении, перпендикулярном рычагу.
Преобразовать единицы с помощью конвертера «Конвертер вращающего момента»
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Формула момента силы в физике
Содержание:
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы, $l=r \sin \alpha$– плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор $\bar{M}$ (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:
$$\bar{M}=\sum_{i=1}^{k} \bar{M}_{i}=\sum_{i=1}^{k} \bar{r}_{i} \times \bar{F}_{i}(3)$$При этом точку О называют центром приведения системы сил.{\prime}}$ — радиус-вектор, который проведен из точки О к точке О’, $\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’. Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
Слишком сложно?
Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Формула вращающий момент
Момент силы, формулы 📙 — Физика
1. Основные понятия
2. Формулы для нахождения момента силы
3. Момент нескольких сил
Момент силы – это характеристика вращательного воздействия силы на объект. Момент силы рассчитывают, как векторное произведение вектора силы и радиус-вектора, опущенного от центра вращения до точки, к которой приложена сила.
Определение 1
Момент силы есть вращательным или крутящим моментом, представляющим собой векторную величину.
При этом понятия «крутящий» и «вращающий» нельзя отождествлять, потому что технически вращающим моментом принято считать внешнее усилие, которое прикладывается к телу, а крутящий момент обозначает внутреннее усилие, появляющееся в теле при нагрузке. Данное понятие применимо при расчете сопротивления материалов.
Не нашли что искали?
Просто напиши и мы поможем
Момент силы – это вращающая сила. По международной системе СИ единицей измерения момента вращающей силы есть ньютон-метр. Архимед при работе с рычагами отмечал, что моментом силы также считается момент пары сил.
Замечание 1
При перпендикулярном прикладывании силы к рычагу, момент данной силы прямо пропорционален ее величине и расстоянию до оси вращения этого рычага.
Таким образом, сила в \(3 Н\), что действует на рычаг в точке, отдаленной на 2 м от оси вращения, формирует момент, что равняется силе в \(1 Н\), что действует в точке, отдаленной на 6 м. Наиболее точным определением момента силы есть следующее выражение:
\(\vec {M}=\vec{r}\vec{F}\),
где \(\vec {F}\)– сила, что действует на объект;
\(\vec {r}\)– радиус-вектор объекта.
С точки зрения физики момент силы есть псевдо векторной величиной, в отличие от энергии, которая есть величиной скалярной. Но совпадение их размерности не случайно. Момент силы величиной \(1 Н∙м\), что приложена через целый оборот при совершении механической работы, передает энергию в \(2π\) Джоуля:
\(E=Mθ\),
где \(E\) – энергия;
\(θ\) – угол;
\(M\) – вращающий момент.
На сегодняшний день момент силы измеряют при помощи оптических, индуктивных и тензометрических приборов нагрузки.
Момент силы рассчитывают таким образом:
\(\vec{M} = \vec{M_1}\vec{F}\),
где \(\vec{M_1}\) – момент рычага;
\(\vec{F}\)– сила действия.
Данная формула позволяет определить только значение момента силы, но не его направление. Когда сила перпендикулярна вектору \(r ⃗,\) то момент рычага равняется расстоянию от центра вращения до точки действия силы, а момент силы имеет наибольшее значение:
\(\vec{T}=\vec{r}\vec{F}\)
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Если сила воздействует на определённом расстоянии, это значит, что она делает механическую работу. Момент силы тоже делает работу, выполняя действие через угловое расстояние.
\(P = \vec {M}\omega\)
где \(P\) – мощность, Ватт;
\(\vec{M}\)– момент силы, ньютон-метр;
\(ω\) – угловая скорость, радиан/секунда.
Замечание 2
Если на тело воздействуют две равных силы, что направлены противоположно и не лежат на одной прямой, тело пребывает в неравновесном состоянии. Это происходит по причине того, что результирующий момент данных сил по отношению к любой оси не равен нулю, поскольку они представлены моментами с одинаковым направлением. То есть, это пара сил.
Если тело закрепить на оси, то под воздействием пары сил оно будет вращаться вокруг этой оси. Если же пару сил приложить к свободному телу, то его вращение будет вокруг оси, проходящей через его центр тяжести.
Момент пары сил одинаков по отношению к любой оси, перпендикулярной плоскости пары. Суммарный момент M пары равняется произведению одной силы \(F\) на отдаленность этих сил \(L\), то есть плечо пары, в независимости от длины отрезков, на которые плечо делит ось.
\(M=FL_1+FL_2=F(L_1+L_2 )=FL\)
Если равнодействующая момента нескольких сил равняется нулю, то он будет одинаковым по отношению ко всем параллельным между собой осям. Поэтому действие на объект данных сил можно заменить воздействием одной пары сил с таким же моментом.
Момент силы. Формула, определение и примеры расчета
Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта (оси, точки).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
Момент определяется как произведение силы F на плечо h:
M(F)=F∙h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент M=7×0,35=2,45 кНм.
Пример момента силы
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h4>h3).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
Рассмотрим порядок определения плеча h момента:
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МA=F×AB=F×3м
Сила расположена под углом к оси стержня
Момент силы относительно точки B:
MB=F×cos300×AB=F×cos300×3м
Известно расстояние от точки до линии действия силы
Момент силы относительно точки B:
MB=F×3м
См. также:
Формула момента силы в физике
Определение и формула момента силы
ОпределениеВекторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы, $l=r \sin \alpha$– плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось.{\prime}}$ — радиус-вектор, который проведен из точки О к точке О’, $\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
ПримерЗадание. На рис.1 показано тело, которое имеет ось вращения OO’. Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
ПримерЗадание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Вы поняли, как решать? Нет?
Помощь с решением
Мощность и вращающий момент электродвигателя. Что это такое?
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Вращающий момент (T) — это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы — или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила — любая сила — вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент — момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Как видно из названия — «постоянный вращающий момент» — подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
Переменный вращающий момент и мощность
«Переменный вращающий момент» — эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения — мал, а потребный вращающий момент при высокой частоте вращения — велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность — кубу скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
P1 (кВт) Входная электрическая мощность насосов — это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя — это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
что такое, формула и в чем измеряется
Мощность двигателя – важнейший его показатель. Как в плане эксплуатации, так и в плане начисления налогов на авто. Крутящий момент нередко путают с мощностью или упускают его из виду в процессе оценки ходовых качеств авто. Многие упрощают автомобиль, считая, что большое количество лошадиных сил – главное преимущество любого мотора. Однако, вращающий момент – более важный показатель. Особенно, если автомобиль не предполагается использовать в качестве спортивного.
Что такое крутящий момент
Крутящим моментом называют единицу силы, которая необходима для поворота коленчатого вала ДВС. Эта не «лошадиная сила», которой должна обозначаться мощность.
ДВС вырабатывает кинетическую энергию, вращая таким образом коленвал. Показатель мощности двигателя (сила давления) зависит от скорости сгорания топлива. Крутящий момент – результат от действия силы на рычаг. Эта сила в физике считается в ньютонах. Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.
Технически, крутящий момент – это усилие, которое должно осуществляться двигателем для разгона и движения машины. При этом сила, оказывающая действие на поршень, пропорциональна объему двигателя.
Маховик – одна из важнейших деталей, которая должна через редуктор передавать вращательный момент от мотора к коробке передач, от стартера на коленвал, от коленвала на нажимной диск. Собственно, крутящий момент – итог давления на шатун.
Формула расчета крутящего момента
Показатель КМ рассчитывается так: мощность (в л. с.) равно крутящий момент (в Нм) умножить на обороты в минуту и разделить на 5,252. При меньших чем 5,252 значениях крутящий момент будет выше мощности, при больших – ниже.
В пересчете на принятую в России систему (кгм – килограмм на метр) – 1кг = 10Н, 1 см = 0,01м. Таким образом 1 кг х см = 0,1 Н х м. Посчитать вращательный момент в разных системах измерений ньютоны/килограммы и т.д. поможет конвертер – в практически неизменном виде он доступен на множестве сайтов, с его помощью можно определять данные по практически любому мотору.
График:
На графике изображена зависимость крутящего момента двигателя от его оборотов
От чего зависит крутящий момент
На КМ будут влиять:
- Объем двигателя.
- Давление в цилиндрах.
- Площадь поршней.
- Радиус кривошипа коленвала.
Основная механика образования КМ заключается в том, что чем больше двигатель по объему, тем сильней он будет нагружать поршень. То есть – будет выше значение КМ. Аналогична взаимосвязь с радиусом кривошипа коленвала, но это вторично: в современных двигателях этот радиус сильно изменить нельзя.
Давление в камере сгорания – не менее важный фактор. От него напрямую зависит сила, давящая на поршень.
Для снижения потерь крутящего момента при тряске машины во время резкого газа можно использовать компенсатор. Это специальный (собранный вручную) демпфер, компенсация которого позволит сохранить вращающий момент и повысить срок эксплуатации деталей.
На что влияет крутящий момент
Главная цель КМ – набор мощности. Часто мощные моторы обладают низким показателем КМ, поэтому не способны разогнать машину достаточно быстро. Особенно это касается бензиновых двигателей.
ВАЖНО! При выборе авто стоит рассчитать оптимальное соотношение вращательного момента с количеством оборотов, на которых чаще всего мотор будет работать. Если держать вращательный момент на соответствующем уровне, это позволит оптимально реализовать потенциал двигателя.
Высокий КМ также может влиять на управляемость машины, поэтому при резком увеличении скорости не лишним будет использование системы TSC. Она позволяет точнее направлять авто при резком разгоне.
Широко распространенный 8-клапанный двигатель ВАЗ выдает вращательный момент 120 (при 2500-2700 оборотах). Ручная коробка или АКПП стоит на машине – не принципиально. При использовании КПП немаловажен опыт водителя, на автоматической коробке плавный старт обеспечивает преобразователь.
Как увеличить крутящий момент
Увеличение рабочего объема. Чтобы повышать КМ используются разные методы: замена установленного коленвала на вал с увеличенным эксцентриситетом (редко встречающаяся запчасть, которую трудно находить) или расточка цилиндров под больший диаметр поршней. Оба способа имеют свои плюсы и минусы. Первый требует много времени на подбор деталей и снижает долговечность двигателя. Второй, увеличение диаметра цилиндров с помощью расточки, более популярен. Это может сделать практически любой автосервис. Там же можно настроить карбюратор для повышения КМ.
Изменение величины наддува. Турбированные двигатели позволяют достичь более высокого показателя КМ благодаря особенностям конструкции – возможности отключить ограничения в блоке управления компрессором, который отвечает за наддув. Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.
Изменение газодинамики. Редко используемый вариант, поскольку двигатель – сложная конструкция, созданием которого занимаются профессионалы. Теоретически можно придумать, как убрать ограничения, заложенные конструкторами для увеличения срока эксплуатации двигателя и его деталей. Но на практике, если убрать ограничитель, результат не гарантирован, поскольку поменяются все характеристики: например, динамика вырастет, но шина не будет цепляться за дорогу. Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.
ВАЖНО! Простой способ повысить КМ – использовать масляный фильтр. Он снизит засорение двигателя и продлит срок эксплуатации всех деталей.
Определение крутящего момента на валу
Для измерения крутящего момента на валу автомобильного двигателя применяется множество методик. Это может быть показатель подачи топлива, температуры выхлопных газов и т.д. Такие методы не гарантируют высокой точности.
Распространенный метод повышенной точности – применение тензометрического моста. На вал крепятся тензометры, электрически соединенные по мостовой схеме. Сигнал передается на считывающее устройство.
Измеритель крутящего момента
Главная сложность в измерителе крутящего момента, использующего тензометры, является точность передачи данных. Применявшиеся ранее контактные, индукционные и светотехнические устройства не гарантировали необходимой эффективности. Сейчас данные передаются по цифровым радиоканалам. Измеритель представляет собой компактный радиопередатчик, который крепится на вал и передает данные на приемник.
Сейчас такие устройства доступны по стоимости и просты в эксплуатации. Применяются в основном в СТО.
Датчик крутящего момента
Аналогичные устройства, измеряющие КМ, в автомобиле могут быть установлены не только на коленвал, но и на рулевое колесо. Он ставится на модели машин с электроусилителем руля и позволяет отслеживать работу системы управление автомобилей. При выходе датчика из строя, усилитель, как правило, отключается.
Максимальный крутящий момент
Максимальным называется крутящий момент, представляющий пик, после которого момент не растет, несмотря на количество оборотов. На малых оборотах в цилиндре скапливается большой объем остаточных газов, в результате чего показатель КМ значительно ниже пикового. На средних оборотах в цилиндры поступает больше воздуха, процент газов снижается, крутящий момент продолжает расти.
При высоких оборотах растут потери эффективности: от трения поршней, инерционных потерь в ГРМ, разогрева масла и т.д. будет зависеть работа мотора. Поэтому рост качества работы двигателя прекращается или само качество начинает снижаться. Максимальный крутящий момент достигнут и начинает снижаться.
В электродвигателях максимальный вращательный момент называется «критический».
Таблица марок автомобилей с указанием крутящего момента:
| Модели автомобиля ВАЗ | Крутящий момент (Нм, разные марки двигателей) | |
| 2107 | 93 – 176 | |
| 2108 | 79-186 | |
| 2109 | 78-118 | |
| 2110 | 104-196 | |
| 2112 | 104-162 | |
| 2114 | 115-145 | |
| 2121 (Нива) | 116-129 | |
| 2115 | 103-132 | |
| 2106 | 92-116 | |
| 2101 | 85-92 | |
| 2105 | 85-186 | |
| Двигатели ЗМЗ | ||
| 406 | 181,5-230 | |
| 409 | 230 | |
| Других популярные в России марки автомобилей | ||
| Ауди А6 | 500-750 | |
| БМВ 5 | 290-760 | |
| Бугатти Вейрон | 1250-1500 | |
| Дэу Нексия | 123-150 | |
| КАМАЗ | ~650-2000+ | |
| Киа Рио | 132-151 | |
| Лада Калина | 127-148 | |
| Мазда 6 | 165-420 | |
| Мицубиси Лансер | 143-343 | |
| УАЗ Патриот | 217-235 | |
| Рено Логан | 112-152 | |
| Рено Дастер | 156-240 | |
| Тойота Королла | 128-173 | |
| Хендай Акцент | 106-235 | |
| Хендай Солярис | 132-151 | |
| Шевроле Каптив | 220-400 | |
| Шевроле Круз | 118-200 | |
Какому двигателю отдать предпочтение
Сегодня множество моделей производители оснащают разными типами моторов: бензиновым или дизельным. Эти модели идентичны только по цене и другим характеристикам.
Из-за разных типов мотора одна и та же модель может отличаться по показателям мощности мотора и крутящему моменту, при этом разница может быть значительной.
Бензиновый двигатель
Бензиновый двигатель формирует воздушно-топливную смесь, заполняющую цилиндр. Температура внутри него поднимается до примерно 500 градусов. У таких моторов номинальный коэффициент сжатия составляет порядка 9-10, реже 11 единиц. Поэтому, когда происходит впрыск необходимо использование свечей зажигания.
Дизельный двигатель
В цилиндрах работающего на дизеле движка коэффициент сжатия смеси может достигать показателя в 25 единиц, температура – 900 градусов. Поэтому смесь зажигается без использования свечи.
Электродвигатель
Автомобильный трехфазный асинхронный электродвигатель работает по совершенно другим законам, поэтому его мощность и КМ отличаются от традиционных кардинально. Электромотор состоит из ротора и статора, кратность которых позволяет выдавать пиковый КМ (600 Нм) на любой скорости. При этом мощность электродвигателя, например, у Теслы, составляет 416 л. с.
Чтобы ответить на вопрос – дизельный, бензиновый или электродвигатель лучше, надо сначала исключить третий вариант, поскольку электродвигатели пока не так распространены, как первые два типа.
ВАЖНО! Что касается выбора между бензиновым и дизельным двигателями, они в первую очередь отличаются мощностью и крутящим моментом. На практике это означает, что при одинаковом объеме двигателя дизельный быстрее разгоняется, а бензиновый позволяет давать более высокую скорость.
Кроме того, благодаря большему крутящему момент автомобиль, использующийся как грузовой, обладает большей грузоподъемностью за счет двигателя. Особенно если двигатель дизель-генераторный.
Улучшение разгона авто за счет изменения момента вращения
Чем выше показатель крутящего момента – тем быстрее двигатель набирает мощность. Таким образом, вырастет скорость движения. На практике это означает, что, например, во время разгона крутящий момент позволит быстрее обогнать едущий впереди автомобиль.
Чтобы улучшить разгон автомобиля за счет изменения момента вращения, достаточно повысить показатели последнего. Как это сделать – описано выше.
Зависимость мощности от крутящего момента
Крутящий момент, как говорилось выше, это показатель того, с какой скоростью двигатель может набирать обороты. По сути, мощность мотора – прямая производная от КМ на коленвале. Чем больше оборотов – тем выше показатель мощности.
Зависимость мощности от вращательного момента выражается формулой: Р = М*n (Р – мощность, М – крутящий момент, n – количество оборотов коленвала/мин).
7.2: Классическая механика
Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.
ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью — ускорение отсутствует.
СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.
Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.
В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.
Сила = Крутящий момент/Радиус колеса
В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.
Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.
Пример 7.2
Пример 7.3
Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.
Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.
Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.
Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.
Пример 7.4
Пример 7.5
Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.
Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.
Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.
Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).
Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.
Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]
1 Ватт = 1 (Ньютон х Метр) / Секунда
Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.
Формула крутящего момента (момент инерции и угловое ускорение)
При вращательном движении крутящий момент требуется для создания углового ускорения объекта. Величина крутящего момента, необходимого для создания углового ускорения, зависит от распределения массы объекта. Момент инерции — это величина, описывающая распределение. Его можно найти путем интегрирования по массе всех частей объекта и их расстояниям до центра вращения, но также можно найти моменты инерции для общих форм.Крутящий момент на данной оси является произведением момента инерции и углового ускорения. Единицы крутящего момента — ньютон-метры (Н ∙ м).
крутящий момент = (момент инерции) (угловое ускорение)
τ = Iα
τ = крутящий момент вокруг определенной оси (Н ∙ м)
I = момент инерции (кг ∙ м 2 )
α = угловое ускорение (радиан / с 2 )
Формула крутящего момента Вопросы:
1) Момент инерции твердого диска равен, где M — масса диска, а R — радиус.Каждое колесо игрушечной машинки имеет массу 0,100 кг и радиус 20,0 см. Если угловое ускорение колеса составляет 1,00 радиан / с 2 , каков крутящий момент?
Ответ: Крутящий момент можно найти с помощью формулы крутящего момента и момента инерции твердого диска. Крутящий момент:
τ = Iα
τ = 0,0020 Н ∙ м
Крутящий момент, прилагаемый к одному колесу, составляет 0,0020 Н ∙ м.
2) Момент инерции тонкого стержня, вращающегося на оси, проходящей через его центр, равен, где M — масса, а L — длина стержня.Предположим, что лопасть вертолета представляет собой тонкий стержень массой 150,0 кг и длиной 8,00 м. Какой крутящий момент требуется для достижения углового ускорения 18,00 радиан / с 2 ?
Ответ: Крутящий момент можно найти с помощью формулы крутящего момента и момента инерции тонкого стержня. Крутящий момент:
τ = Iα
τ = 14 400 Н ∙ м
Требуемый крутящий момент составляет 14 400 Н ∙ м.
.Формула крутящего момента (сила на расстоянии)
Формула крутящего момента (сила на расстоянии)Вопросы по формуле крутящего момента:
1) Автомеханик прикладывает усилие 800 Н к гаечному ключу, чтобы ослабить болт. Она прикладывает силу перпендикулярно рычагу гаечного ключа. Расстояние от болта до руки — 0,40 м. Какова величина прилагаемого крутящего момента?
Ответ: Угол между моментным плечом (рычагом гаечного ключа) и силой равен 90 °, а sin 90 ° = 1.Крутящий момент:
Величина крутящего момента 320 Н ∙ м.
2) Анемометр — это прибор для измерения скорости ветра. Он имеет несколько металлических чашек, установленных на горизонтальных стержнях, которые вращают центральный стержень. Ветер ловит одну из чашек перпендикулярно ее турнику. Ветер оказывает на чашу силу 70,0 Н на расстоянии 0,30 м от центральной оси. Какова величина крутящего момента, создаваемого ветром?
Ответ: Угол между рычагом момента (горизонтальной штангой) и силой равен 90 °, а sin 90 ° = 1.Крутящий момент:
Величина крутящего момента 21,0 Н ∙ м.
Формула крутящего момента (сила на расстоянии)
.Соотношение крутящего момента и мощности
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11 9plar
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Книги NCERT
Какова размерная формула крутящего момента и его вывод?
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11 9plar
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- RD Sharma
- RD Sharma Class 6 Решения
- RD Sharma Class 7 Решения
- Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- PHYSICS
- Механика
- Оптика
- Термодинамика
- Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Статистика
- Числа
- Числа Пифагора Тр Игонометрические функции
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Разделение фракций
- Microology
- Книги NCERT
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 000E
- 000
- 000
- 000 Калькуляторы
- 000 Образцы документов для класса 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 1 1
- Образцы документов CBSE для класса 12
- Вопросники предыдущего года CBSE
- Вопросники предыдущего года CBSE, класс 10
- Вопросники предыдущего года CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- HC Verma Solutions Класс 12 Физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха класса 9
- Решения Лахмира Сингха класса 10
- Решения Лакмира Сингха класса 8
9000 Класс
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке
- CBSE Вопросы
- CBSE Class 10 Дополнительные вопросы по математике
- CBSE Class 10 Science Extra questions
- Class 3
- Class 4
- Class 5
- Class 6
- Class 7
- Class 8 Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия
- Решения NCERT для биологии класса 11
- Решение NCERT s Для класса 11 по математике
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions for Class 12
- Решения NCERT для физики класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- Решения NCERT, класс 12, бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- NCERT Solutions Class 12 Economics
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solut Ионы Для класса 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для класса 6 по социальным наукам
- Решения NCERT для класса 6 Английский язык
- Решения NCERT для класса 7
- Решения NCERT для математики класса 7
- Решения NCERT для науки класса 7
- Решения NCERT для социальных наук класса 7
- Решения NCERT для класса 7 Английский язык
- Решения NCERT для класса 8
- Решения NCERT для математики класса 8
- Решения NCERT для науки 8 класса
- Решения NCERT для социальных наук 8 класса ce
- Решения NCERT для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для класса 9 по социальным наукам
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для математики класса 9, глава 2 Решения NCERT
- для математики класса 9, глава 3
- Решения NCERT для математики класса 9, глава 4
- Решения NCERT для математики класса 9, глава 5 Решения NCERT
- для математики класса 9, глава 6
- Решения NCERT для математики класса 9 Глава 7 Решения NCERT
- для математики класса 9 Глава 8
- Решения NCERT для математики класса 9 Глава 9
- Решения NCERT для математики класса 9 Глава 10 Решения NCERT
- для математики класса 9 Глава 11 Решения
- NCERT для математики класса 9 Глава 12 Решения NCERT
- для математики класса 9 Глава 13
- NCER Решения T для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для науки класса 9 Глава 3
- Решения NCERT для науки класса 9 Глава 4
- Решения NCERT для науки класса 9 Глава 5
- Решения NCERT для науки класса 9 Глава 6
- Решения NCERT для науки класса 9 Глава 7
- Решения NCERT для науки класса 9 Глава 8
- Решения NCERT для науки класса 9 Глава 9
- Решения NCERT для науки класса 9 Глава 10
- Решения NCERT для науки класса 9 Глава 12
- Решения NCERT для науки класса 9 Глава 11
- Решения NCERT для науки класса 9 Глава 13 Решения NCERT
- для науки класса 9 Глава 14
Простая английская Википедия, бесплатная энциклопедия
Взаимосвязь между векторами силы, крутящего момента и импульса во вращающейся системеВ физике крутящий момент — это тенденция силы к повороту или скручиванию. Если сила используется, чтобы начать вращать объект или остановить вращение объекта, создается крутящий момент.
Сила, приложенная к рычагу, умноженная на расстояние от точки опоры рычага, снова умноженная на синус созданного угла, описывается как крутящий момент.Это также известно как «r cross f» или «сила, умноженная на расстояние опоры, умноженное на синус тета».
Точка опоры — это ось вращения или точка опоры, на которой рычаг поворачивается при подъеме или перемещении чего-либо.
Уравнение крутящего момента:
- τ = r × F {\ displaystyle {\ boldsymbol {\ tau}} = \ mathbf {r} \ times \ mathbf {F} \, \!}
, где F — вектор чистой силы, а r — вектор от оси вращения до точки, в которой действует сила.Греческая буква Тау используется для обозначения крутящего момента.
Единицы измерения крутящего момента — это сила, умноженная на расстояние. [1] В системе СИ единицей измерения крутящего момента является ньютон-метр. Самая распространенная английская единица — фут-фунт.
- ↑ Хольцнер, Стивен (2010). Основы физики для чайников . Wiley Publishing. п. 122. ISBN 978-0-470-61841-7 .
Угловое движение — мощность и крутящий момент
Мощность и момент тела при угловом движении
Сила вращающегося тела может быть выражена как
P = T ω
= T 2 π n об / с
= T π n об / мин /30 (1)
где
P = мощность (Вт)
T = крутящий момент или момент (Нм)
= угловая скорость (рад / с)
π = 3.14 …
n об / с = оборотов в секунду (об / с, 1 / с)
n об / мин = оборотов в минуту (об / мин, 1 / мин)
- 1 рад = 360 o /2 π = ~ 57,29578 .. o
Примечание! — объект, такой как электродвигатель, может иметь активный момент без вращения, но без вращения ( ω = 0 ) не вырабатывается энергия.
В имперских единицах
P = T n об / мин /5252 (1b)
где
P = мощность (л.с.)
T = крутящий момент (фут-фунт f )
Пример — момент, создаваемый вращающимся двигателем
Электродвигатель работает со скоростью 3600 об / мин с измеренной потребляемой мощностью 2000 Вт .Момент, создаваемый двигателем (без потерь), можно рассчитать, переставив (1) на
T = 30 P / (π n об / мин )
= 30 (2000 Вт) / (π ( 3600 об / мин))
= 5,3 Нм
Калькулятор моментов
P — мощность (Вт)
n м — обороты (об / мин)
Крутящий момент тела в угловом движении
.T = I α (2)
где
I = момент инерции (кг · м 2 , фунт f фут · с 2 )
α = угловое ускорение (рад / с 2 )
Измерение крутящего момента | Как измерить крутящий момент?
Как разные типы датчиков крутящего момента используются для измерения крутящего момента и в чем разница между ними? В этом всеобъемлющем введении к датчикам крутящего момента для измерения крутящего момента мы выделяем наиболее важные факты.
Датчики измерения крутящего момента , произведенные в США компанией FUTEK Advanced Sensor Technology (FUTEK), ведущим производителем, производящим огромный выбор датчиков крутящего момента, использующим одну из самых передовых технологий в сенсорной индустрии: технологию тензодатчика с металлической фольгой .Он определяется как датчик, используемый для измерения крутящего момента (измерения крутящего момента), который преобразует входной механический крутящий момент в электрический выходной сигнал. Датчики кручения также широко известны как датчик крутящего момента , датчик крутящего момента , тестер крутящего момента, датчик крутящего момента или датчик момента . Существует два основных типа датчиков крутящего момента: Reaction Датчики крутящего момента или датчики крутящего момента.
Посетите наш магазин датчиков крутящего момента с более чем 100 типами датчиков крутящего момента!
Что такое датчик измерения крутящего момента?
По определению, датчик измерения крутящего момента — это тип преобразователя, в частности преобразователь крутящего момента , который преобразует измерение крутящего момента (реактивного, динамического или вращательного) в другую физическую переменную, в данном случае в электрический сигнал, который можно измерить, преобразовать и стандартизированы.По мере увеличения крутящего момента, приложенного к датчику, электрический выходной сигнал изменяется пропорционально (датчик крутящего момента). Датчики крутящего момента являются одним из устройств измерения силы и инструмента для измерения крутящего момента, на котором специализируется компания FUTEK.
Рис. 1: Датчик крутящего момента на основе тензодатчика.Посетите наш магазин датчиков крутящего момента с более чем 100 типами датчиков крутящего момента!
Какие бывают типы датчиков измерения крутящего момента?
Существует две основные категории датчиков крутящего момента: вращающийся датчик крутящего момента и датчики реактивного крутящего момента. Таким образом, датчик реакции измеряет стационарный крутящий момент (статический или невращающийся) , а поворотный измеряет крутящий момент (датчик динамического крутящего момента) .
Понимание области применения и определение требований — важная часть выбора правильного датчика крутящего момента.
Датчики крутящего момента (динамический или крутящий момент)
Датчики вращения (или тестер динамического крутящего момента) используются в приложениях, где измерение крутящего момента должно производиться на вращающемся валу, двигателе или неподвижном двигателе.В этом случае преобразователь должен вращаться в линию, прикрепленную к валу. Вращающийся датчик крутящего момента оснащен контактным кольцом или беспроводной электроникой для передачи сигнала крутящего момента во время вращения (бесконтактный датчик).
Датчики крутящего момента часто используются в качестве инструментов тестирования / аудита для двигателей, инструментов для измерения крутящего момента, турбин и генераторов для измерения крутящего момента . Датчик крутящего момента между валом может также использоваться для управления с обратной связью, контроля крутящего момента и анализа эффективности испытательных стендов, а также для измерения крутящего момента вращающегося вала с помощью тензодатчика (т.е. анализатор крутящего момента).
Как измерить крутящий момент двигателя? Измерение крутящего момента (также известное как измерение крутящего момента) связано между двигателем и нагрузкой. Когда вал вращается, датчик кручения измеряет крутящий момент, создаваемый двигателем в ответ на нагрузку, приложенную к вращающемуся валу. Некоторые поворотные датчики оснащены встроенными энкодерами. Эти энкодеры измеряют угол / скорость, полученные во время испытания. Измерения кручения можно успешно контролировать на локальном цифровом дисплее (также известном как индикатор датчика крутящего момента), например, на панельном дисплее, портативном дисплее, подключенном к ПЛК или передаваемым на ПК с помощью цифрового USB-инструмента (т.е.е. цифровой датчик крутящего момента).
Рис. 2: Датчик крутящего момента.Датчик крутящего момента также является важной частью динамометров (или для краткости динамометра), поскольку он обеспечивает измерение крутящего момента и угловую скорость ( об / мин ) для простого расчета выходной мощности , что позволяет точно рассчитать мощности двигателя или двигателя в кВт или л.с., а также его электромеханический КПД .
Хотите узнать больше? Посетите наш магазин датчиков крутящего момента
Датчики крутящего момента (статические)
В некоторых приложениях измерение крутящего момента, выполняемое встроенным датчиком вращения, может быть измерено в точке, где крутящий момент передается на землю, с помощью датчика реактивного крутящего момента ( Измерение статического крутящего момента ).
Реакционный датчик кручения (кроме датчиков перемещения LVDT) имеет два монтажных фланца (датчик «фланец-фланец»). Одна поверхность прикреплена к земле или жесткому конструктивному элементу, а другая — к вращающемуся валу или вращающемуся элементу. Вращение создает поперечные силы между фланцами, которые улавливаются тензодатчиками из фольги, прикрепленными к балкам датчика, и преобразуются в электрический ток мостом Уитстона.
Для конкретного применения датчик реакции (он же датчик момента) часто менее сложен и, следовательно, менее дорогой, чем датчик вращения.Датчики реактивного крутящего момента часто используются в качестве инструмента для калибровки крутящего момента или инструмента для калибровки динамометрического ключа. Датчики реактивного крутящего момента также могут использоваться в качестве миниатюрных электрических динамометрических отверток, что позволяет инженерам получать обратную связь по крутящему моменту и / или изучать крутящий момент, прилагаемый во время сборки. FUTEK также настраивает легкие низкопрофильные встроенные высокоточные датчики крутящего момента с гармонической зубчатой передачей с волновой деформацией для обратной связи с обратной связью с высокой гибкостью в геометрии и конструкции.
Инжир.3: Датчик реактивного момента.Как работает датчик крутящего момента?
Как измерить крутящий момент? Во-первых, нам необходимо понять физику и материалы, лежащие в основе принципа работы датчика крутящего момента , который представляет собой тензодатчик (он же тензодатчик ). Тензодатчик из металлической фольги — это датчик силы, электрическое сопротивление которого зависит от приложенной силы. Другими словами, он преобразует деформацию, полученную из силы, давления (так называемые промышленные датчики давления для измерения давления), растяжения, сжатия, крутящего момента, веса (также известные как датчики веса) и т. Д., В изменение электрического сопротивления, которое затем может быть стандартизировано для измерение крутящего момента.
Рис. 4: Тензорезистор из металлической фольги. Источник: ScienceDirectКонструктивно датчик кручения выполнен из металлического корпуса (также называемого изгибом), к которому прикреплены фольговые датчики деформации . Корпус датчика обычно изготавливается из алюминия или нержавеющей стали, что придает датчику две важные характеристики: (1) обеспечивает прочность, чтобы выдерживать высокие крутящие моменты; и (2) обладает эластичностью, позволяющей минимально деформироваться и возвращаться к своей исходной форме при снятии крутящего момента.
При приложении крутящего момента ( по часовой стрелке или против часовой стрелки ) металлический корпус действует как «пружина» и слегка деформируется, и, если он не перегружен, он возвращается к своей исходной форме. По мере деформации изгиба тензодатчик также изменяет свою форму и, следовательно, свое электрическое сопротивление, что создает изменение дифференциального напряжения через цепь моста Уитстона . Таким образом, изменение напряжения пропорционально крутящему моменту, приложенному к преобразователю, который может быть рассчитан с помощью выходного напряжения цепи датчика крутящего момента.
В датчике крутящего момента Rotary тензодатчик прикреплен к вращающемуся валу , который слегка деформируется при приложении крутящего момента. Прогиб вала вызывает напряжение в тензодатчике, которое изменяет его сопротивление. Комбинация тензодатчиков (обычно 4) размещена в электрической цепи, усилителе на мосту Уитстона, который преобразует изменения сопротивления в выходное напряжение, которое можно калибровать и измерять.
Инжир.5: Тензодатчик, прикрепленный к вращающемуся валу. Источник: веб-семинар FUTEK на Youtube.Посетите наш магазин датчиков крутящего момента, где доступно более 100 типов датчиков крутящего момента!
Датчики крутящего момента предназначены для измерения крутящего момента вращающегося вала . Таким образом, необходимо передавать мощность на мост тензодатчика, а также средства для приема сигнала от измерителя крутящего момента или вала. Это может быть выполнено с помощью контактных колец, беспроводной телеметрии или вращающихся трансформаторов.Дополнительно в датчики могут быть встроены энкодер для измерения угла или скорости .
Рис. 6: Датчик крутящего момента и его внутренние компоненты. Источник: веб-семинар FUTEK на YouTube.Датчики должны быть тщательно спроектированы, чтобы исключить внеосевую нагрузку (также называемую боковыми нагрузками или посторонними моментами), и должны быть чувствительны только к нагрузке против часовой стрелки и против часовой стрелки. Выходной сигнал датчика является функцией силы и расстояния (T = F x d) и обычно выражается в дюймах-фунтах (дюймах-фунтах)., фут-фунт (фут-фунт) или ньютон-метр (Н-м).
Для получения дополнительной информации посмотрите наш веб-семинар о том, как работают датчики крутящего момента.
Как выбрать датчик крутящего момента для вашего приложения?
Мы часто слышим вопрос: «Какой датчик лучше всего подходит для моего применения?» Причина, по которой его так часто спрашивают, заключается в том, что может быть сложно ориентироваться в различных предложениях датчиков на рынке. Таким образом, будь то небольшой датчик крутящего момента или датчики крутящего момента с высокой пропускной способностью (не струнный потенциометр), обязательно выполните следующие шаги для выбора подходящего размера датчика крутящего момента.
Чтобы помочь вам выбрать датчик крутящего момента, компания FUTEK разработала простое руководство из 4 шагов. Вот краткая информация, которая поможет вам сузить круг выбора. Ознакомьтесь с нашим полным руководством «Как выбрать датчик крутящего момента» для получения дополнительной информации.
- Шаг 1: Изучите свое приложение и то, что вы хотите измерять или контролировать . Во-первых, разобраться в вашем приложении и определить тип крутящего момента, который вы хотите измерить — крутящий момент реакции или крутящий момент? Также, какова окружающая среда (температура, давление, влажность).Для этого приложения могут потребоваться подводные датчики крутящего момента в комплекте с датчиком давления.
- Шаг 2 : Определите монтажные характеристики датчика и его сборку. Как вы будете устанавливать датчик? (Фланец к фланцу, квадратный привод, вал к валу, шестигранник и т. Д.) Вы будете использовать его по часовой стрелке, против часовой стрелки или и то, и другое?
- Шаг 3 : Определите минимальную и максимальную емкость и ключевые требования. Обязательно выберите мощность выше максимального рабочего крутящего момента и определите все посторонние нагрузки (боковые нагрузки или нецентральные нагрузки) и моменты до выбора мощности.Кроме того, каковы ваши максимальные обороты в минуту? Вам нужно измерить скорость и угловое положение?
- Шаг 4: Определите тип вывода, который требуется вашему приложению. Некоторые датчики выдают сигнал мВ / В, который может быть соединен с усилителем до ± 10 В постоянного тока, в то время как другие бесконтактные датчики вращения обеспечивают выходное напряжение ± 5 В постоянного тока. Итак, если вашему ПЛК или DAQ требуется аналоговый выход, цифровой выход или последовательная связь, вам понадобится усилитель датчика крутящего момента или формирователь сигнала.Убедитесь, что вы выбрали правильный усилитель тензодатчика, а также откалибруйте всю систему измерения (датчик + формирователь сигнала). Это готовое решение обеспечивает большую совместимость и точность всей системы измерения крутящего момента.
ПРИМЕЧАНИЕ: В некоторых специальных приложениях измерение крутящего момента может выполняться с помощью датчика веса.
Что такое датчик крутящего момента вращения? Как это работает?
Датчик крутящего момента TRH605 с универсальным усилителем USB520
FUTEK имеет специальные типы универсальных модулей формирования сигналов, которые поддерживают широкий диапазон входов датчиков, таких как ± 10 В постоянного тока, 0-20 мА, ± 400 мВ / В и входы импульсного типа TTL.Универсальный модуль формирования сигнала USB520 USB может работать в паре с датчиками различных типов и устраняет необходимость во внешнем источнике питания для датчика и оборудования отображения. Модуль питается от ПК через USB-кабель, обеспечивая напряжение возбуждения 5-24 В постоянного тока на датчик и одновременно 5 В постоянного тока для энкодеров.
Для получения более подробной информации о нашем Руководстве по 4 шагам, пожалуйста, посетите полное руководство «Как выбрать датчик крутящего момента».
Как измерить крутящий момент (крутящий момент) вашего автомобиля
Независимо от того, покупаете ли вы новый автомобиль или собираете хотрод в своем гараже, при определении характеристик двигателя играют роль два фактора: мощность и крутящий момент.Если вы похожи на большинство механиков DIY или автомобильных энтузиастов, вы, вероятно, хорошо понимаете взаимосвязь между мощностью и крутящим моментом, но можете с трудом понять, как достигаются эти «фут-фунты». Вы не поверите, но на самом деле это не так уж и сложно.
Прежде чем перейти к техническим аспектам, давайте разберем несколько простых фактов и определений, которые помогут понять, почему мощность и крутящий момент являются важными факторами, которые необходимо учитывать. Мы должны начать с определения трех элементов измерения производительности двигателя внутреннего сгорания: скорости, крутящего момента и мощности.
Часть 1 из 4. Понимание того, как частота вращения, крутящий момент и мощность двигателя влияют на общую производительность
В недавней статье журнала Hot Rod одна из величайших загадок характеристик двигателя была наконец разгадана, вернувшись к основам фактического учета мощности. Большинство людей полагают, что динометры (динометры двигателя) предназначены для измерения мощности двигателя.
На самом деле динометры измеряют не мощность, а крутящий момент. Это значение крутящего момента умножается на число оборотов в минуту, при котором он измеряется, а затем делится на 5 252 для получения значения мощности в лошадиных силах.
Вот уже более 50 лет динометры, используемые для измерения крутящего момента и оборотов двигателя, просто не могут справиться с большой мощностью, производимой этими двигателями. Фактически, один цилиндр на этих 500 кубических дюймах, сжигающий нитрометан Hemis, производит примерно 800 фунтов тяги через одну выхлопную трубу.
Все двигатели внутреннего сгорания или с электрическим приводом работают с разной скоростью. По большей части, чем быстрее двигатель завершает свой рабочий такт или цикл, тем больше мощности он производит.Что касается двигателя внутреннего сгорания, три элемента, которые влияют на общую производительность этого двигателя, — это скорость, крутящий момент и мощность.
Скорость определяется как скорость двигателя, выполняющего свою работу. Когда мы применяем скорость двигателя к числу или единице измерения, мы измеряем скорость двигателя в оборотах в минуту или об / мин. «Работа», которую выполняет двигатель, — это сила, приложенная к измеренному расстоянию. Крутящий момент определяется как особый вид работы, вызывающей вращение.Это происходит, когда сила действует на радиус (или, в случае двигателя внутреннего сгорания, на маховик), и обычно измеряется в фут-фунтах.
лошадиных сил — это скорость, с которой выполняется работа. В прежние времена, если предметы нужно было переместить, люди обычно использовали лошадь, чтобы переместить их. Было подсчитано, что одна лошадь могла двигаться приблизительно 33 000 футов фунтов в минуту. Отсюда и возник термин «лошадиные силы». В отличие от скорости и крутящего момента, мощность в лошадиных силах может быть измерена в нескольких единицах, включая: 1 л.с. = 746 Вт, 1 л.с. = 2545 БТЕ и 1 л.с. = 1055 джоулей.
Эти три элемента работают вместе, чтобы произвести мощность двигателя. Поскольку крутящий момент остается постоянным, скорость и мощность остаются пропорциональными. Однако по мере увеличения частоты вращения двигателя увеличивается и мощность, чтобы поддерживать постоянный крутящий момент. Однако многие люди не понимают, как крутящий момент и мощность влияют на скорость двигателя. Проще говоря, с увеличением крутящего момента и мощности увеличивается и частота вращения двигателя. Верно и обратное: когда уменьшаются крутящий момент и мощность, уменьшается и частота вращения двигателя.
Часть 2 из 4: Как устроены двигатели для достижения максимального крутящего момента
Современный двигатель внутреннего сгорания можно модифицировать для увеличения мощности или крутящего момента, изменяя размер или длину шатуна и увеличивая отверстие или диаметр цилиндра. Это часто называют соотношением диаметр цилиндра / ход поршня.
Крутящий момент измеряется в Ньютон-метрах. Проще говоря, это означает, что крутящий момент измеряется при круговом движении на 360 градусов. В нашем примере используются два идентичных двигателя с одинаковым диаметром отверстия (или диаметром цилиндра сгорания).Однако один из двух двигателей имеет более длинный «ход» (или глубину цилиндра, создаваемую более длинным шатуном). Двигатель с более длинным ходом имеет более прямолинейное движение при вращении через камеру сгорания и имеет больше рычагов для выполнения той же задачи.
Крутящий момент измеряется в фунт-футах или величине «крутящей силы», прилагаемой для выполнения задачи. Например, представьте, что вы пытаетесь ослабить ржавый болт. Предположим, у вас есть два разных трубных ключа: один длиной 2 фута, другой — длиной 1 фут.Предполагая, что вы прикладываете такое же усилие (в данном случае 50 фунтов давления), вы фактически прикладываете 100-футовый крутящий момент для двухфутового ключа (50 x 2) и всего 50 фунтов. крутящего момента (1 x 50) с помощью гаечного ключа на одну ногу. Какой ключ поможет вам легче ослабить болт? Ответ прост — тот, у которого больше крутящего момента.
Инженеры разрабатывают двигатель, обеспечивающий более высокое соотношение крутящего момента и мощности для транспортных средств, которым требуется дополнительная «мощность» для ускорения или подъема. Как правило, вы видите более высокие значения крутящего момента для грузовиков большой грузоподъемности, используемых для буксировки, или двигателей с высокими рабочими характеристиками, где ускорение имеет решающее значение (например, приведенный выше пример NHRA Top Fuel Engine).
Вот почему производители автомобилей часто подчеркивают потенциал двигателей с высоким крутящим моментом в рекламе грузовиков. Крутящий момент двигателя также может быть увеличен путем изменения угла опережения зажигания, регулирования подачи воздуха к топливным смесям и даже манипулирования для увеличения выходного крутящего момента в определенных сценариях.
Часть 3 из 4: Понимание других переменных, влияющих на общий номинальный крутящий момент двигателя
Когда дело доходит до измерения крутящего момента, в двигателе внутреннего сгорания есть три уникальные переменные, которые вы должны учитывать:
Сила, создаваемая при определенных оборотах: это максимальная мощность двигателя, развиваемая при желаемых оборотах.Когда двигатель ускоряется, отображается кривая оборотов или мощности. По мере увеличения оборотов двигателя увеличивается и мощность, пока не достигнет максимального уровня.
Расстояние: это длина хода шатуна: чем длиннее ход, тем больший крутящий момент создается, как мы объясняли выше.
Константа крутящего момента: это математическое число, которое присваивается всем двигателям, 5252 или постоянная частота вращения, при которой мощность и крутящий момент уравновешены. Число 5252 было получено из наблюдения, что одна лошадиная сила эквивалентна 150 фунтам, которые преодолевают 220 футов за одну минуту.Чтобы выразить это в фут-фунтах крутящего момента, Джеймс Ватт ввел математическую формулу, которая изобрела первый паровой двигатель.
Формула выглядит следующим образом:
Предполагая, что сила в 150 фунтов приложена к одному футу радиуса (или круга, который находится, например, внутри цилиндра двигателя внутреннего сгорания), вам придется преобразовать это в фут-фунты крутящего момента.
220 футов в минуту необходимо экстраполировать в число оборотов в минуту. Для этого вам нужно дважды увеличить число Пи (или 3.141593), что равно 6,283186 футов. Возьмите 220 футов и разделите на 6,28, и мы получим 35,014 оборотов в минуту на каждый оборот.
Возьмите 150 футов и умножьте на 35,014, и вы получите 5252,1 — это наша константа, учитываемая при измерении крутящего момента в фут-фунтах.
Часть 4 из 4: Как рассчитать крутящий момент автомобиля
Формула для вычисления крутящего момента: крутящий момент = мощность двигателя x 5252, который затем делится на число оборотов в минуту.
Проблема с крутящим моментом, однако, заключается в том, что он измеряется в двух разных местах: непосредственно от двигателя и до ведущих колес.Другие механические компоненты, которые могут увеличивать или уменьшать номинальный крутящий момент колес, включают: размер маховика, передаточные числа трансмиссии, передаточные числа ведущей оси и окружность шины / колеса.
Чтобы вычислить крутящий момент на колесе, все эти элементы должны быть учтены в уравнении, которое лучше всего оставить компьютеризированной программе, включенной в динамометрический стенд. На этом типе оборудования автомобиль размещается на стойке, а ведущие колеса размещаются рядом с рядом роликов.Двигатель подключен к компьютеру, который отслеживает обороты двигателя, кривую расхода топлива и передаточные числа. Эти числа учитываются со скоростью вращения колес, ускорением и оборотами переключения, поскольку транспортное средство движется на динамометрическом стенде в течение желаемого промежутка времени.
Расчет крутящего момента двигателя определить намного проще. Следуя приведенной выше формуле, становится ясно, как крутящий момент двигателя пропорционален мощности и частоте вращения двигателей, как описано в первом разделе. Используя эту формулу, вы можете вычислить номинальные крутящий момент и мощность в каждой точке кривой частоты вращения.Для расчета крутящего момента вам необходимо иметь данные о мощности двигателя, указанные производителем двигателя.
Калькулятор крутящего моментаНекоторые люди используют онлайн-калькулятор, предлагаемый MeasureSpeed.com, который требует, чтобы вы вводили максимальные значения мощности двигателя (предоставленные производителем или полученные во время профессионального динамического тестирования двигателя) и желаемое число оборотов в минуту.
Если вы заметили, что ваш двигатель с трудом ускоряется и не обладает необходимой мощностью, попросите одного из сертифицированных механиков YourMechanic провести осмотр, чтобы определить источник проблемы.
лошадиных сил против крутящего момента: в чем разница?
Эндрю Трэхан Автомобиль и водитель
Что лучше? Вот как можно прекратить споры о ночном баре.
Йоги Берра, который никогда не останавливался на деталях двигателя, пришел бы к выводу, что крутящий момент и мощность — это одно и то же, только разные. Собственно, это упрощение отчасти верно.
Крутящий момент и мощность — это то, что двигатели производят, когда вы поворачиваете ключ и нажимаете педаль акселератора.Воздух и топливо, воспламеняющиеся в камерах сгорания, вызывают скручивание коленчатого вала, трансмиссии и ведущих мостов. Это чудо преобразования энергии: потенциальная энергия, содержащаяся в галлоне переработанного динозавра, эффективно изменилась на кинетическую энергию, необходимую для вождения.
Копая глубже, рассмотрим эти определения из учебников:
Энергия — это способность выполнять работу. В этом случае двигатели выполняют ту тяжелую работу (работу), которую раньше выполняли лошади.
Работа является результатом силы, действующей на некотором расстоянии.Единица измерения работы (а также энергии) в США — фут-фунт. В Международной системе (СИ) работа измеряется в джоулях и, в редких случаях, в ньютон-метрах.
Крутящий момент — это сила вращения, создаваемая коленчатым валом двигателя. Чем выше крутящий момент двигатель, тем выше его способность выполнять работу. Измерение такое же, как у работы, но немного отличается. Поскольку крутящий момент является вектором (действующим в определенном направлении), он измеряется в единицах фунт-фут и ньютон-метр.
Конечно, всегда есть исключения. В этом случае различие составляет статический крутящий момент , который вы прикладываете с помощью гаечного ключа для затягивания болтов головки. Во избежание путаницы единицами измерения статического крутящего момента традиционно являются фунты-футы. Напротив, SI придерживается ньютон-метров как для статических, так и для динамических измерений крутящего момента.
Power — это скорость выполнения работы. Шотландский изобретатель восемнадцатого века Джеймс Ватт дал нам эту удобную эквивалентность: одна лошадиная сила — это мощность, необходимая для подъема 33000 фунтов ровно один фут за одну минуту.В соответствии с этим вкладом единицей измерения мощности в системе СИ является киловатт.
Возвращаясь к теореме Берра, крутящий момент — это способность выполнять работу, а мощность — это скорость, с которой можно выполнить некоторую трудоемкую задачу. Другими словами, мощность — это скорость выполнения работы (или приложения крутящего момента) за заданный промежуток времени. Математически мощность в лошадиных силах равна крутящему моменту, умноженному на число оборотов в минуту. H = T x об / мин / 5252, где H — мощность в лошадиных силах, T — фунт-фут, об / мин — это скорость вращения двигателя, а 5252 — постоянная, заставляющая единицы двигаться.Таким образом, для получения большей мощности двигателю необходимо генерировать больший крутящий момент, работать на более высоких оборотах или и то, и другое.
Хотя определения эскизов отлично подходят для учебников, применение их к реальным движкам — другое дело. Одна проблема заключается в том, что у каждого автомобильного двигателя есть рабочий диапазон от холостого хода до красной черты. Например, 6,2-литровый двигатель Hellcat V-8 Dodge Challenger выдает 707 лошадиных сил ТОЛЬКО при 6000 об / мин. Он выдает существенно меньшую мощность на холостом ходу (достаточную только для вращения аксессуаров с приводом от двигателя) и чуть меньше 700 лошадиных сил на красной границе 6200 об / мин.И он обеспечивает максимальный крутящий момент 650 фунт-фут ТОЛЬКО при 4000 об / мин.
Другая проблема — точное определение мощности и крутящего момента вращающегося коленчатого вала. Инструмент для этой задачи — динамометр двигателя. Хотя это слово означает «устройство измерения мощности», на практике крутящий момент и частота вращения двигателя измеряются, а его мощность рассчитывается с использованием приведенной выше формулы.
Вихретоковые динамометры используют магнитное поле для передачи крутящего момента от вращающегося коленчатого вала на опору плеча рычага против статического датчика силы (известного как датчик нагрузки), расположенного на точном расстоянии от центра кривошипа.Другой широко используемый тип динамометра — это водяной тормоз; он использует один вращающийся и один статический набор лопаток насоса для передачи крутящего момента коленчатого вала через плечо рычага на датчик нагрузки.
Совершенный двигатель развивает достаточный крутящий момент на низких оборотах и выдерживает его до минимального уровня. Величина создаваемого крутящего момента прямо пропорциональна потоку воздуха, проходящего через двигатель. Большие двигатели перекачивают больше воздуха и, следовательно, создают больший крутящий момент. Бустеры — нагнетатели, турбокомпрессоры — доставляют дополнительный воздух, помогая маленьким двигателям работать крупными.Конечно, в камеры сгорания должно подаваться соответствующее количество топлива, но это простая часть, особенно с электронным управлением впрыском.
Чтобы восполнить легкость впрыска нужного количества топлива, конструкторы двигателей сталкиваются с несколькими сложными задачами. Один из них — сделать все компоненты достаточно прочными, чтобы выдерживать нагрузки, которым они подвергаются из-за давления сгорания и, в случае движущихся частей, их собственной инерции.Потребности в охлаждении и смазке примерно пропорциональны производимой мощности. А закачка воздуха в любой двигатель на сверхвысоких оборотах и из него — это то место, где инженерное дело становится видом искусства. Включите топливную экономичность и чистоту выхлопных газов в уравнение разработки, и станет ясно, почему мастера двигателей редко тусуются у водоохладителя.
На этом этапе обсуждения должно быть ясно, что крутящий момент и лошадиные силы подобны разлученным братьям и сестрам; они тесно связаны, но не имеют много общего.Но как насчет более серьезной моральной проблемы, стоящей перед человечеством в целом и автолюбителями в частности: что лучше?
Мы ответим, что Йоги Берра был бы признателен. В бейсболе, если крутящий момент аналогичен кетчеру, то питчер — это лошадиные силы. И то, и другое необходимо для игры в мяч, но ответственность питчера — определение скорости и траектории каждого брошенного мяча — определяет ход игры. Крутящий момент жизненно важен для работы каждого двигателя, но мощность — это то, что отличает отличный двигатель от хорошего.
Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.
Как измерить крутящий момент на существующем валу
Как измерить крутящий момент на существующем валу
Вот три наиболее распространенных метода измерения крутящего момента на существующем валу без модификации или разборки.
1) Счетчик электроэнергии
Относительно простой метод оценки крутящего момента на выходном валу электродвигателя — это измерение потребляемой им электрической мощности с помощью измерителя электрической мощности. Измеритель рассчитывает потребляемую мощность, измеряя ток и напряжение в линии, приводящей двигатель. Потребляемая электрическая мощность преобразуется в расчетный крутящий момент, зная скорость вала (обычно измеряемую тахометром) и КПД двигателя (обычно указывается производителем двигателя).Это считается косвенным измерением крутящего момента, поскольку это не истинный механический крутящий момент, а скорее отношение измерений электрической мощности к теоретическому значению крутящего момента.
Несмотря на то, что этот метод довольно недорогой и простой в установке, точность этого метода невысока, поскольку эффективность двигателя может существенно варьироваться в зависимости от ряда факторов, включая скорость, входное напряжение, выходную нагрузку и температуру. Этот метод действителен только для трансмиссий с электродвигателем и неточно реагирует на быстро меняющиеся условия крутящего момента, что делает его идеальным только в ситуациях, когда требуется «полное» измерение крутящего момента.
2) Ячейка крутящего момента с зажимом
Фиксирующая ячейка крутящего момента физически закреплена на валу. Эти системы включают предварительно установленный датчик (обычно тензодатчик или оптический). Датчик измеряет деформацию (или «скручивание») вала и преобразует это значение в значение измерения крутящего момента с помощью ряда вычислений, которые зависят от геометрии и свойств вала.
Основным преимуществом этих систем является то, что установка не требует применения датчика (например, тензодатчика).Одна из основных проблем, связанных с системами измерения крутящего момента с фиксацией, заключается в том, что датчик находится на значительном удалении от поверхности вала, что может привести к высокой степени погрешности измерения. Сложение механических компонентов между валом и датчиком добавляет неопределенности измерениям и усугубляет влияние изменений окружающей среды (например, температуры) на систему. Системы зажимов также довольно громоздки. Для правильной установки им требуется значительная доступная площадь вала, что может быть проблематичным, если вы работаете в ограниченном пространстве.
3) Телеметрия крутящего момента для поверхностного монтажа
Рис. 1. Телеметрическая система крутящего момента Binsfeld TorqueTrak 10K.
Система измерения вращающего момента для поверхностного монтажа основана на тензометрическом датчике , установленном непосредственно на поверхности вала. Датчик работает так же, как датчик крутящего момента с зажимом (измеряя «скручивание» вала), и передает данные с вала с помощью телеметрии, которая представляет собой беспроводной бесконтактный метод передачи данных.(Более подробное объяснение рабочих концепций системы телеметрии см. В Как работает телеметрия крутящего момента )
Почему бы не использовать контактное кольцо?
Контактные кольца — распространенный метод передачи данных, но у них есть несколько недостатков по сравнению с телеметрией. Поскольку контактное кольцо требует контакта между валом и статором, узел может создавать шум в сигнале. Контактные поверхности со временем изнашиваются, что со временем требует замены компонентов.По этим причинам передача данных телеметрии является более эффективным и долгосрочным вариантом.
Поскольку тензодатчик монтируется непосредственно на валу и как можно ближе к нагрузке, телеметрия крутящего момента для поверхностного монтажа обеспечивает одно из самых прямых, точных и экономичных решений для измерения крутящего момента. Уменьшенный профиль систем позволяет использовать их во многих приложениях с ограниченным пространством, где фиксация крутящего момента невозможна.
Потенциальная проблема с системами телеметрии крутящего момента для поверхностного монтажа заключается в том, что они требуют установки тензодатчиков в полевых условиях.Тем не менее, этого можно легко достичь при надлежащей тренировке. Типичное время установки полной системы телеметрии Бинсфельда составляет 4 часа на каждую шахту.
Сравнение методов измерения крутящего момента вращения
Приведенная ниже таблица предлагает четкое сравнение всех четырех методов измерения крутящего момента, обсуждаемых в этой статье:
Таблица 1. Сравнение распространенных систем измерения крутящего момента.
Какая система измерения крутящего момента мне подходит?
Если вы ищете лучший способ измерения крутящего момента на существующем валу, выбор между упомянутыми выше вариантами сводится к тому, что для вас наиболее важно.Если ваше приложение выиграет от получения наиболее точных результатов при небольшом профиле и по разумной цене, система телеметрии крутящего момента для поверхностного монтажа, вероятно, станет лучшим вариантом. Конечно, необходимо учитывать множество других факторов.
Если вам нужна помощь в определении наиболее подходящего метода измерения крутящего момента для вашего приложения, не стесняйтесь обращаться к экспертам Binsfeld Engineering Inc. Мы будем рады ответить на любые ваши вопросы об измерении крутящего момента на существующем вращающемся валу.Позвоните нам по телефону 231-334-4383 или свяжитесь с нами через Интернет сегодня.
Измерение крутящего момента — SENSY
Определения
Измерение крутящего момента основано на фундаментальном понятии момента силы, определяемом следующим образом (см. Рис. 1):
Момент силы, где M — точка приложения по отношению к точке O определяется как:
Это псевдовектор, образованный векторным произведением вектора на векторную силу. Он приложен к O перпендикулярно плоскости, содержащей вектор силы и точку O, и его интенсивность равна произведению интенсивности силы F на длину OH опущенного перпендикуляра точки O в направлении силы.
Система двух параллельных нелинейных сил равной интенсивности и противоположного направления составляет «крутящий момент» сил. Момент такого крутящего момента равен сумме моментов каждой из сил. Его интенсивность, следовательно, равна произведению интенсивности F, общей для обеих сил, на расстояние D обеих сил, измеренное перпендикулярно их линии действия.
Необходимо всегда определять, находимся ли мы в присутствии момента силы или крутящего момента, потому что условия их хорошего измерения очень разные.
Измеритель крутящего момента: рассчитан на кручение
Измеритель крутящего момента — это измерительный прибор, аналог динамометра, предназначенный для работы на кручение. Его испытательный корпус имеет цилиндрическую форму, подверженную деформациям сдвига, измеряемым тензодатчиками. Этот тип деформации обеспечивает измерения, которые точно пропорциональны крутящему моменту, приложенному к преобразователю.
Что касается динамометра, измеритель крутящего момента связан с измерительным мостом, позволяющим ему питать датчик и обрабатывать передаваемый сигнал.
Измерение крутящего момента с помощью измерителя крутящего момента
- Два применения измерителя крутящего момента:
Измеритель крутящего момента может использоваться для двух операций:
- Чистое измерение крутящего момента
- калибровка или проверка динамометрического ключа
- На измеритель крутящего момента действуют два основных момента
Условия работы, требуемые для измерителя крутящего момента, труднее достичь, чем для динамометра.Фактически, на измеритель крутящего момента действуют два основных момента: первый возникает из-за измеряемого крутящего момента, а второй — из-за крутящего момента, препятствующего вращению измерителя крутящего момента вокруг своей оси. Эти два момента соединяются мешающими моментами и усилиями, возникающими из-за отказов в устройствах приложения двух основных моментов.
Качество измерения крутящего момента
Качество измерения в основном зависит от совмещения трех осей:
- ось измеряемого псевдовектора крутящего момента
- ось реактивного момента псевдовектор
- измеритель крутящего момента ось
Для этого все три оси должны быть материализованы с помощью механических элементов, которые центрированы и выровнены относительно друг друга.
Предотвращение ошибок измерения крутящего момента
Ошибки центровки
Неисправности центровки вызывают мешающие моменты, перпендикулярные оси измерителя крутящего момента, которые вызывают погрешности измерения, изменяющиеся на несколько процентных пунктов по сравнению с выполненным измерением крутящего момента.
Моменты помех могут быть значительно уменьшены с помощью специальных соединительных механических устройств, которые ограничивают влияние нарушений центровки. Это карданные шарниры, упругие лопатки или диски. Сцепные устройства Rexnord особенно эффективны.
ПРИМЕЧАНИЕ: Испанская версия / en / tecnologia / esfuerzo-de-torsion / medicion-del-par
Измерение крутящего момента и мощности: краткий обзор
На протяжении всей истории человечество полагалось на вращающиеся валы и крутящий момент вала для обеспечения своего общества. От древнеримской мукомольной мельницы в Барбегале, Франция, до современного атомного авианосца, общим знаменателем является вращение вала, генерирующего крутящий момент и мощность. Естественно, измерение крутящего момента и мощности, производимой системой привода вала, имеет решающее значение для понимания и оптимизации всей машины или процесса.В этой статье представлен обзор различных инструментов для измерения крутящего момента и мощности, включая преимущества и ограничения каждой системы.
ОПРЕДЕЛЕНИЕ МОМЕНТА И МОЩНОСТИ
Крутящий момент определяется как крутящая сила, которая имеет тенденцию вызывать вращение. Слово произошло от латинского слова Torquere, означающего скручивание. Крутящий момент также можно количественно определить с помощью уравнения (где плечо рычага — это перпендикулярное расстояние от оси вращения до линии действия силы):
Крутящий момент = приложенная сила x плечо рычага
Крутящий момент измеряется в футах-фунтах или Ньютон-метры.Архимед, знаменитый греческий математик и изобретатель, был так взволнован силой и рычагами, что ему приписали заявление: «Дайте мне достаточно длинный рычаг и место, где я смогу стоять, и я переверну мир». Одно из самых узнаваемых уравнений, обычно используемых инженерами-механиками:
- P = Мощность, л.с.
- T = крутящий момент, фут-фунт сила
- N = оборотов в минуту
- 5252 = Константа
Количественное определение крутящего момента и мощности помогло инженерам разрабатывать и улучшать различные конструкции, но для правильного и точного измерения по-прежнему требовались соответствующие инструменты.Прорывная концепция была разработана Сэмюэлем Кристи, а позже, усовершенствованная и популяризированная Чарльзом Уитстоном, стала известна как мост Уитстона.
Схема моста Уитстона
Значение моста Уитстона нельзя недооценивать. Эта концепция легла в основу изобретения тензодатчика, изобретенного в 1938 году Эдвардом Симмонсом и Артуром Руге. Руге и Симмонс, работая независимо друг от друга, оба обнаружили, что провода небольшого диаметра, сделанные из сплавов с электрическим сопротивлением, могут быть прикреплены к конструкции для измерения поверхностной деформации.Преимущество этого типа манометра заключается в том, что он хорошо реагирует на статические деформации. Именно из-за требований этой быстрорастущей отрасли был сделан важный шаг вперед в разработке тензодатчиков из фольги.
Объединив концепции моста Уитстона и тензодатчика, инженеры и изобретатели смогли разработать различные типы оборудования для точного измерения крутящего момента и мощности. У каждого из них есть свои преимущества и недостатки, но все они основаны на установленных концепциях и общих целях мониторинга механических сил и способствуют совершенствованию системы.
Универсальный тензодатчик Vishay с полным мостом — диаграмма сдвига / крутящего момента
ДИНАМОМЕТР
Динамометр — это наиболее распространенный инструмент, используемый для оценки крутящего момента и мощности. Преимущество динамометров в том, что они очень точны, что позволяет проводить много типов испытаний. Для каждого требования доступно множество подходящих динамометров — от единой системы до полного тестирования транспортного средства.
При всех своих преимуществах динамометры, однако, ограничены своей стоимостью, размером и возможностями.Их размер ограничивает их возможности для испытаний на борту морских судов и в ограниченном пространстве. Кроме того, некоторые системы слишком велики для любого типа динамометрических испытаний.
НАГРУЗОЧНАЯ ЯЧЕЙКА И МОМЕНТНЫЙ РЫЧАГ
Простое, но экономичное устройство для испытания крутящего момента включает в себя тензодатчик с устройством крутящего момента, установленным на определенную нагрузку. При приложении силы к нагрузке якорь сжимает тензодатчик. Информация о крутящем моменте может быть рассчитана на основе данных датчика нагрузки и длины плеча момента.
Недостатки такой системы связаны с ограничениями тензодатчика, точностью и сбором данных. Система измеряет не фактический крутящий момент на валу, а, скорее, силы на плече момента. Система также ограничена пространством, гибкостью и редко используется на современных морских судах или крупном оборудовании.
ДАТЧИК МОМЕНТА ВРАЩЕНИЯ
Более современный подход к сбору данных о крутящем моменте и мощности — это линейный датчик крутящего момента. Датчики крутящего момента вращения предлагают диапазон диапазонов крутящего момента, высокую степень точности, возможность цифрового вывода и различные типы функций сбора данных, т.е.е. Число оборотов, направление вала, а также крутящий момент и мощность. Некоторые модели с вращающимся моментом также обладают преимуществом выдерживания очень высоких оборотов (до 50 000 об / мин) и уровня G-Force. Однако встроенные датчики дороги, не обладают универсальностью и имеют ограничения по крутящему моменту. Они также требуют модификации вала перед установкой. Это может быть очень дорогостоящим при использовании валов большого диаметра.
Показанное изображение: Динамометр для тяжелого двигателя (фото предоставлено UC Riverside
Вверху: Якорь и датчик нагрузки для измерения крутящего момента (фото предоставлено: Dr.Скотт К. Томас, Государственный университет Райта)
РАДИОТЕЛЕМЕТРИЧЕСКАЯ СИСТЕМА МОМЕНТА
Очень эффективным и более универсальным вариантом измерения крутящего момента и мощности является система радиотелеметрии крутящего момента. Типичные агрегаты не ограничены каким-либо уровнем крутящего момента и могут использоваться или определяться для почти любого диаметра вала. Они также обладают такими преимуществами, как разумная цена, простая калибровка, портативность и удобная установка (не требуется модификации вала).
При использовании систем радиотелеметрии крутящего момента существуют ограничения, которые необходимо учитывать.Скорость вращения вала является важной информацией из-за механических ограничений вращающихся компонентов, например, аккумулятора, клейкой ленты и т. Д. Иногда радиопомехи от соседних устройств могут создавать проблемы в работе системы крутящего момента. Правильное применение тензодатчика, необходимое для успешной работы системы, может быть утомительным. Неправильно установленные тензодатчики могут привести к ошибкам в точности и данных.
Binsfeld Engineering Inc. производит широкий выбор систем бесконтактного измерения крутящего момента и мощности как для временного, так и для постоянного применения.Радиотелеметрические системы Binsfeld TorqueTrak обладают всеми описанными здесь преимуществами, включая удобство, универсальность и разумную цену, а также удобство эксплуатации. BEI также обеспечивает дружелюбную и немедленную техническую поддержку по любым системным проблемам.
Система радиотелеметрии крутящего момента TorqueTrak 10K
РЕЗЮМЕ
Понимание теорий крутящего момента, мощности и испытательного оборудования может оказаться полезным при поиске системы телеметрии крутящего момента. Поскольку идеального решения не существует, понимание ограничений каждой системы дает представление о выборе наилучшего и наиболее экономичного варианта.◆
Брайан Карр — менеджер по продажам систем измерения крутящего момента в Binsfeld Engineering Inc. в США. Брайан получил степень бакалавра медицинских наук в Мичиганском технологическом университете и степень магистра экономических наук в Бостонском университете и более трех лет занимается продажей систем измерения крутящего момента. С ним можно связаться по адресу [email protected]. Для получения дополнительной информации посетите www.binsfeld.com.
____________________________________________
MODERN PUMPING TODAY, August 2015
Вам понравилась эта статья?
Подпишитесь на БЕСПЛАТНОЕ цифровое издание журнала Modern Pumping Today Magazine!
Как измерить крутящий момент (крутящий момент) вашего автомобиля
Независимо от того, покупаете ли вы новый автомобиль или собираете хотрод в своем гараже, при определении характеристик двигателя играют роль два фактора: мощность и крутящий момент.Если вы похожи на большинство механиков DIY или автомобильных энтузиастов, вы, вероятно, хорошо понимаете взаимосвязь между мощностью и крутящим моментом, но можете с трудом понять, как достигаются эти «фут-фунты». Вы не поверите, но на самом деле это не так уж и сложно.
Прежде чем перейти к техническим аспектам, давайте разберем несколько простых фактов и определений, которые помогут понять, почему мощность и крутящий момент являются важными факторами, которые необходимо учитывать. Мы должны начать с определения трех элементов измерения производительности двигателя внутреннего сгорания: скорости, крутящего момента и мощности.
Часть 1 из 4: Понимание того, как частота вращения, крутящий момент и мощность двигателя влияют на общую производительность
В недавней статье журнала Hot Rod одна из величайших загадок характеристик двигателя была наконец разгадана, вернувшись к основам фактического учета мощности. Большинство людей полагают, что динометры (динометры двигателя) предназначены для измерения мощности двигателя.
На самом деле динометры измеряют не мощность, а крутящий момент. Это значение крутящего момента умножается на число оборотов в минуту, при котором он измеряется, а затем делится на 5 252 для получения значения мощности в лошадиных силах.
Вот уже более 50 лет динометры, используемые для измерения крутящего момента и оборотов двигателя, просто не могут справиться с большой мощностью, производимой этими двигателями. Фактически, один цилиндр на этих 500 кубических дюймах, сжигающий нитрометан Hemis, производит примерно 800 фунтов тяги через одну выхлопную трубу.
Все двигатели внутреннего сгорания или с электрическим приводом работают с разной скоростью. По большей части, чем быстрее двигатель завершает свой рабочий такт или цикл, тем больше мощности он производит.Что касается двигателя внутреннего сгорания, три элемента, которые влияют на общую производительность этого двигателя, — это скорость, крутящий момент и мощность.
Скорость определяется как скорость двигателя, выполняющего свою работу. Когда мы применяем скорость двигателя к числу или единице измерения, мы измеряем скорость двигателя в оборотах в минуту или об / мин. «Работа», которую выполняет двигатель, — это сила, приложенная к измеренному расстоянию. Крутящий момент определяется как особый вид работы, вызывающей вращение. Это происходит, когда сила действует на радиус (или, в случае двигателя внутреннего сгорания, на маховик), и обычно измеряется в фут-фунтах.
лошадиных сил — это скорость, с которой выполняется работа. В прежние времена, если предметы нужно было переместить, люди обычно использовали лошадь, чтобы переместить их. Было подсчитано, что одна лошадь могла двигаться приблизительно 33 000 футов фунтов в минуту. Отсюда и возник термин «лошадиные силы». В отличие от скорости и крутящего момента, мощность в лошадиных силах может быть измерена в нескольких единицах, включая: 1 л.с. = 746 Вт, 1 л.с. = 2545 БТЕ и 1 л.с. = 1055 джоулей.
Эти три элемента работают вместе, чтобы произвести мощность двигателя.Поскольку крутящий момент остается постоянным, скорость и мощность остаются пропорциональными. Однако по мере увеличения частоты вращения двигателя увеличивается и мощность, чтобы поддерживать постоянный крутящий момент. Однако многие люди не понимают, как крутящий момент и мощность влияют на скорость двигателя. Проще говоря, с увеличением крутящего момента и мощности увеличивается и частота вращения двигателя. Верно и обратное: когда уменьшаются крутящий момент и мощность, уменьшается и частота вращения двигателя.
Часть 2 из 4: Как устроены двигатели для достижения максимального крутящего момента
Современный двигатель внутреннего сгорания можно модифицировать для увеличения мощности или крутящего момента, изменяя размер или длину шатуна и увеличивая отверстие или диаметр цилиндра.Это часто называют соотношением диаметр цилиндра / ход поршня.
Крутящий момент измеряется в Ньютон-метрах. Проще говоря, это означает, что крутящий момент измеряется при круговом движении на 360 градусов. В нашем примере используются два идентичных двигателя с одинаковым диаметром отверстия (или диаметром цилиндра сгорания). Однако один из двух двигателей имеет более длинный «ход» (или глубину цилиндра, создаваемую более длинным шатуном). Двигатель с более длинным ходом имеет более прямолинейное движение при вращении через камеру сгорания и имеет больше рычагов для выполнения той же задачи.
Крутящий момент измеряется в фунт-футах или величине «крутящей силы», прилагаемой для выполнения задачи. Например, представьте, что вы пытаетесь ослабить ржавый болт. Предположим, у вас есть два разных трубных ключа: один длиной 2 фута, другой — длиной 1 фут. Предполагая, что вы прикладываете такое же усилие (в данном случае 50 фунтов давления), вы фактически прикладываете 100-футовый крутящий момент для двухфутового ключа (50 x 2) и всего 50 фунтов. крутящего момента (1 x 50) с помощью гаечного ключа на одну ногу. Какой ключ поможет вам легче ослабить болт? Ответ прост — тот, у которого больше крутящего момента.
Инженеры разрабатывают двигатель, обеспечивающий более высокое соотношение крутящего момента и мощности для транспортных средств, которым требуется дополнительная «мощность» для ускорения или подъема. Как правило, вы видите более высокие значения крутящего момента для грузовиков большой грузоподъемности, используемых для буксировки, или двигателей с высокими рабочими характеристиками, где ускорение имеет решающее значение (например, приведенный выше пример NHRA Top Fuel Engine).
Вот почему производители автомобилей часто подчеркивают потенциал двигателей с высоким крутящим моментом в рекламе грузовиков. Крутящий момент двигателя также может быть увеличен путем изменения угла опережения зажигания, регулирования подачи воздуха к топливным смесям и даже манипулирования для увеличения выходного крутящего момента в определенных сценариях.
Часть 3 из 4: Понимание других переменных, влияющих на общий номинальный крутящий момент двигателя
Когда дело доходит до измерения крутящего момента, в двигателе внутреннего сгорания есть три уникальные переменные, которые вы должны учитывать:
Сила, создаваемая при определенных оборотах: это максимальная мощность двигателя, развиваемая при желаемых оборотах. Когда двигатель ускоряется, отображается кривая оборотов или мощности. По мере увеличения оборотов двигателя увеличивается и мощность, пока не достигнет максимального уровня.
Расстояние: это длина хода шатуна: чем длиннее ход, тем больший крутящий момент создается, как мы объясняли выше.
Константа крутящего момента: это математическое число, которое присваивается всем двигателям, 5252 или постоянная частота вращения, при которой мощность и крутящий момент уравновешены. Число 5252 было получено из наблюдения, что одна лошадиная сила эквивалентна 150 фунтам, которые преодолевают 220 футов за одну минуту. Чтобы выразить это в фут-фунтах крутящего момента, Джеймс Ватт ввел математическую формулу, которая изобрела первый паровой двигатель.
Формула выглядит следующим образом:
Предполагая, что сила в 150 фунтов приложена к одному футу радиуса (или круга, который находится, например, внутри цилиндра двигателя внутреннего сгорания), вам придется преобразовать это в фут-фунты крутящего момента.
220 футов в минуту необходимо экстраполировать в число оборотов в минуту. Для этого вам нужно дважды умножить число Пи (или 3,141593), что равно 6,283186 фута. Возьмите 220 футов и разделите на 6,28, и мы получим 35,014 оборотов в минуту на каждый оборот.
Возьмите 150 футов и умножьте на 35,014, и вы получите 5252,1 — это наша константа, учитываемая при измерении крутящего момента в фут-фунтах.
Часть 4 из 4: Как рассчитать крутящий момент автомобиля
Формула для вычисления крутящего момента: крутящий момент = мощность двигателя x 5252, который затем делится на число оборотов в минуту.
Проблема с крутящим моментом, однако, заключается в том, что он измеряется в двух разных местах: непосредственно от двигателя и до ведущих колес.Другие механические компоненты, которые могут увеличивать или уменьшать номинальный крутящий момент колес, включают: размер маховика, передаточные числа трансмиссии, передаточные числа ведущей оси и окружность шины / колеса.
Чтобы вычислить крутящий момент на колесе, все эти элементы должны быть учтены в уравнении, которое лучше всего оставить компьютеризированной программе, включенной в динамометрический стенд. На этом типе оборудования автомобиль размещается на стойке, а ведущие колеса размещаются рядом с рядом роликов.Двигатель подключен к компьютеру, который отслеживает обороты двигателя, кривую расхода топлива и передаточные числа. Эти числа учитываются со скоростью вращения колес, ускорением и оборотами переключения, поскольку транспортное средство движется на динамометрическом стенде в течение желаемого промежутка времени.
Расчет крутящего момента двигателя определить намного проще. Следуя приведенной выше формуле, становится ясно, как крутящий момент двигателя пропорционален мощности и частоте вращения двигателей, как описано в первом разделе. Используя эту формулу, вы можете вычислить номинальные крутящий момент и мощность в каждой точке кривой частоты вращения.Для расчета крутящего момента вам необходимо иметь данные о мощности двигателя, указанные производителем двигателя.

