Применение законов Кирхгофа для анализа цепей постоянного тока.

Для цепи постоянного тока можно записать законы Кирхгофа:

1. Алгебраическая сумма токов, сходящихся в узле, равна 0. — число ветвей, сходящихся в узле.

2.

Алгебраическая сумма напряжения на пассивных участках контура равна алгебраической сумме ЭДС, действующих в электрическом контуре.

Порядок расчета:

Пусть электрическая цепь постоянного тока содержит x ветвей. Для ее расчета по законам Кирхгофа необходимо составить x линейно независимых уравнений по законам Кирхгофа.

1. Выбираем «+» направление токов в ветвях, записываем N-1-е уравнение по первому закону Кирхгофа, где N – число узлов в цепи.

2. Остальные уравнения запишем по второму закону Кирхгофа. Их число C=x-(N-1) и равно числу неизвестных контуров цепи.

3. Решаем систему алгебраических уравнений, находим токи во всех ветвях.

   Если какой- либо ток в результате расчета оказался «-», то его действительное значение противоположно выбранному за условно «+».

Электрическая цепь содержит 3 ветви, должны составить 3 линейных, но независимых уравнений. 2 узла.

I₁+I₃-I₅=0

(R₁+R₂)I₁+R₅I₅=E₁+E₅

-R₅I₅-(R₃+R₄)I₃=-E₄-E₅

Метод контурных токов следует из законов Кирхгофа и принципа наложения. Этот метод позволяет сократить число решаемых уравнений. Уравнения составляются относительно контурных токов. Число уравнений равно числу уравнений, которые необходимо было бы составить по 2 закону Кирхгофа. Предполагается, что в каждом независимом контуре протекает свой контурный ток, составляется система уравнений относительно контурных токов.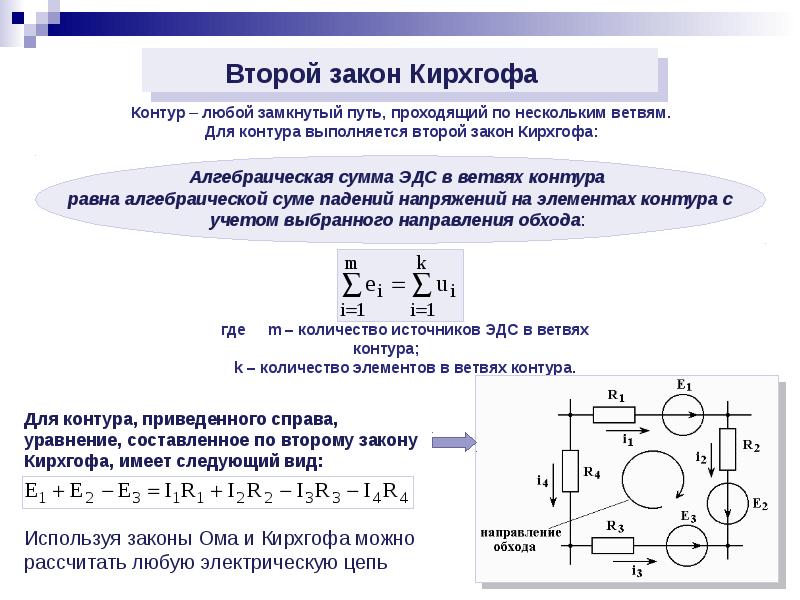

После написания контурных токов рассчитываются токи в ветвях.

Для получения основных расчетных соотношений рассмотрим схему:

Схема содержит 2 независимых контура.

Предполагается, что в каждом протекает свой контурный ток I₁₁ и I₂₂.

Токи в ветвях могут быть выражены через контурные токи следующим образом:

I₁=I₁₁; I₃=-I₂₂; I₅=I₁₁-I₂₂.

В несмежных ветвях токи в ветвях равны противоположным по знаку контурным токам. В смежной ветви ток ветви равен разности контурных токов.

Обозначим:

<обрезалось> 1-го контура.

<обрезалось> = сумме сопротивлений всех ветвей.

R₂₂=R₃+R₄+R₅ – полное (контурное) сопротивление 2-го контура = сумме сопротивлений всех ветвей контура.

R₁₂=R₂₁=-R₅ – сопротивление смежной ветви со знаком «-».

E₁₁=E₁+E₅ – контурная ЭДС – алгебраическая сумма ЭДС контура.

E22=-E4-E5 – контурная ЭДС 2-го контура.

В общем случае, если электрическая цепь содержит N независимых контуров, составляется система уравнений для N контурных токов.

Правило: составляется сумма произведений контурных токов на сопротивления и сопротивления смежных ветвей с соответствующими знаками, и эта сумма приравнивается контурной ЭДС. В результате решения системы уравнений находятся контурные токи. Токи в ветвях выражаются через контурные токи.

3 независимых контура, контурных уравнений будет 3. Для единообразия желательно, чтобы все контурные токи были направлены в одну сторону.

(*)

Систему (*) можно представить в матричном виде:

В общем случае, если электрическая цепь содержит N независимых контуров, то контурный ток в K-м контуре может быть найден по формуле:

, где

Δk – определитель матрицы, получаемый из матрицы [R] заменой k-го столбца на матрицу-столбец контурных ЭДС.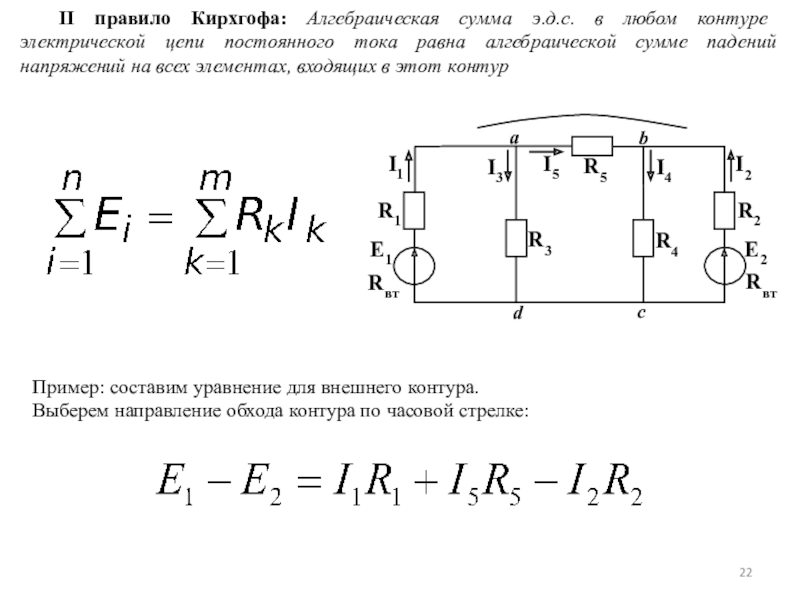

Последовательное и параллельное соединение сопротивлений в цепи постоянного тока (метод эквивалентных преобразований).

Если электрическая цепь содержит 1 источник ЭДС, можно применить МЭП и рассчитать электрическую цепь, используя закон Ома. Существуют 4 основных вида соединения элементов:

• Последовательное

• Параллельное

• Треугольник

• Звезда

(2) (**)

(1)

При последовательном соединении элементов через все элементы протекает один и тот же ток:

Для цепи (1) можно записать 2-й закон Кирхгофа:

IR₁+IR₂+…+IR_N=E

(R₁+R₂+…+R_N)I=E (*)

Эквивалентность понимается в смысле равенства токов в схеме (1) и (2).

Сравнивая (*) и (**): Rэк=R₁+R₂+…+R_N.

При последовательном соединении сопротивлений их эквивалентное сопротивление равно сумме отдельных сопротивлений.

Параллельное соединение – все элементы (сопротивления) подключаются к одной паре узлов.

I=I₁+I₂+…I_N.

.

Сравнивая(*) и (**), получаем:

;

Так как суммарная (эквивалентная) проводимость не может быть меньше проводимости ветви с наименьшим сопротивлением при параллельном соединении сопротивлений, эквивалентное сопротивление всегда меньше сопротивления ветви с наименьшим сопротивлением.

Рассчитать токи I₁, I₂, I₃.

Расчет сложных цепей постоянного тока по I и II законам Кирхгофа

Технология урока: интерактивная.

Тип урока: урок усвоения новых знаний.

Цели урока:

образовательные:

• помочь учащимся получить представление об основах расчета сложных цепей постоянного тока по I и II законам Кирхгофа;
• разобраться в выборе направлений протекания токов и обходов контуров;

воспитательные:

• воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности, организованности;

развивающие:

• развитие познавательных интересов;
• самоконтроля;
• умения конспектировать;
• памяти.

Оборудование: доска, компьютер, мультимедиа проектор, программа презентаций Microsoft Office PowerPoint 2003.

Методическое обеспечение урока: компьютерная презентация, электронные тесты, карточки самоконтроля учащихся, карточка контроля учащихся

План проведения урока.

Организационный момент – 2 мин.

Проверка и актуализация опорных знаний – 5 мин.

Объяснение нового материала – 20 мин.

Проверка усвоения новых знаний и умений – 12 мин.

Подведение итогов – 4 мин.

Домашнее задание – 2 мин.

План урока

Этапы урока	Время	Организация работы
1. Организационный момент	1 мин.	учащиеся рассаживаются достают тетради, ручки
2. Формулировка темы урока. Постановка цели урока	2 мин.	сообщение учителем плана работы
3. Проверка опорных знаний	4 мин.	учащиеся устно отвечают на вопросы учителя
4. Объяснение нового материала	20 мин.	объяснение нового материала ответы на вопросы учащихся
5. Проверка усвоения новых знаний и умений	12 мин.	объяснение правил выполнения теста заполнение карточек самоконтроля учащимися
6. Подведение итогов	4 мин.	учащиеся подсчитывают баллы за выполненные упражнения и выставляют себе оценки в карточках самоконтроля (соответствие оценок набранным баллам приведено на доске) рефлексия
7. Домашнее задание	2 мин.	получение учащимися индивидуальных заданий

Ход урока

Организационный момент

Учащиеся заходят в класс, приветствуют преподавателя, рассаживаются, достают тетради и ручки

Формулировка темы урока. Постановка цели урока

Учитель сообщает тему урока “Расчет сложных цепей постоянного тока по I и II законам Кирхгофа” и его план.

Сегодня мы проверим, как вы усвоили материал прошлого урока и научимся рассчитывать сложные цепи постоянного тока по законам Кирхгофа. Затем мы проверим, как вы усвоили новый материал.

У вас на столах лежат карточки самоконтроля. В них вы будете заносить полученные баллы за ответы на уроке, а также за тест. За каждый правильный устный ответ вы будете ставить себе один балл. За каждый правильный ответ на вопрос из теста оценивается также в один балл. На доске находится таблица соответствия набранных баллов оценке. При подведении итогов урока вы выставите эти оценки в карточки самоконтроля и сдадите их. Эти оценки будут выставлены в журнал.

В конце урока вы получите домашнее задание.

Проверка опорных знаний

Дайте определение сложной электрической цепи.

Сложными называются разветвленные электрические цепи со многими источниками энергии.

Дайте формулировку I закону Кирхгофа.

Алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным. Алгебраическая сумма токов, направленных к узлу равна сумме токов, направленных от узла.

где I_i – ток в узле,

n – число проводников, сходящихся в узле

Иными словами, сколько тока втекает в узел, столько из него и вытекает.

Дайте формулировку II закону Кирхгофа

Алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.

Объяснение нового материала

На рисунке представлена схема электрической цепи.

Для ее расчета, т.е. для определения токов во всех ее ветвях, необходимо составить систему уравнений по законам Кирхгофа. Общее число уравнений в системе должно соответствовать числу неизвестных токов, т.е. числу ветвей.

Давайте посчитаем количество ветвей в нашей электрической цепи.

Получилось пять ветвей, а значит и пять неизвестных токов I₁, I₂, I₃, I₄ и I₅ (токам пока не задано направление).

По первому закону Кирхгофа составляется число уравнений, на единицу меньшее числа узлов цепи, поскольку уравнение для последнего узла есть следствие всех предыдущих уравнений и не дает ничего нового для расчета.

Посчитаем количество узлов электрической цепи.

В цепи три узла, значит по 1-му закону Кирхгофа надо составить (3 – 1 = 2) два уравнения.

По второму закону Кирхгофа составляются все недостающие уравнения для любых произвольно выбранных контуров цепи.

Посчитаем количество недостающих уравнений: 5 – 2 = 3.

В нашем примере по II закону Кирхгофа надо составить три уравнения.

Предварительно следует задаться (произвольно) направлением токов во всех ветвях цепи и направлением обхода выбранных контуров.

Заметим, что произвольность выбора направлений токов в ветвях цепи и направлений обхода контуров не влияет на конечный результат расчета. Если в результате расчетов некоторые из найденных токов будут иметь знак (–), то это будет означать, что их истинное направление противоположно предварительно принятому.

Зададим направление токов во всех ветвях цепи.

При составлении уравнений по первому закону Кирхгофа токи, подходящие к узлу, будем считать положительными и брать со знаком (+), а токи, отходящие от узла – отрицательными и брать со знаком (–).

По I закону Кирхгофа надо составить два уравнения. Для этого выберем любые два узла цепи. Например, первый и второй.

Узел 1: –I₁ – I₃ – I₄ = 0

Узел 2: I₁ – I₂ + I₄ + I₅ = 0

Зададим направление обхода выбранных контуров.

При составлении уравнений по II закону Кирхгофа ЭДС и токи, совпадающие с выбранным направлением обхода контура будем брать со знаком (+), а несовпадающие – со знаком (–).

Контур I: I₁R₁ – I₄R₄ = E₁

Контур II: I₄R₄ – I₅R₅ – I₃R₃ = E₃

Контур III: I₂R₂ + I₄R₄ = –E₂

Запишем систему уравнений.

–I₁ – I₃ – I₄ = 0

I₁ – I₂ + I₄ + I₅ = 0

I₁R₁ – I₄R₄ = E₁

I₄R₄ – I₅R₅ – I₃R₃ = E₃

I₂R₂ + I₄R₄ = –E₂

Решим полученную систему уравнений и определим токи во всех пяти ветвях этой цепи.

Выводы.

Количество уравнений по законам Кирхгофа = количество неизвестных токов цепи, т.е. количеству ветвей цепи.

1. Количество уравнений по I закону Кирхгофа = количество узлов цепи – 1.
2. Количество уравнений по II закону Кирхгофа = общее количество уравнений – количество уравнений по I закону Кирхгофа.
3. Для уравнений по I закону Кирхгофа: токи входящие в узел записываются со знаком (+), а выходящие – со знаком (–).
4. Для уравнений по II закону Кирхгофа: ЭДС и токи, совпадающие с выбранным направлением обхода контура записываются со знаком (+), а несовпадающие – со знаком (–).

Проверка усвоения новых знаний и умений.

Учащиеся выполняют тест (приложение 1). Проверяют его сами (приложение 2). Заполняют карточки самоконтроля (приложение 3). Выставляют себе отметки. Таблица соответствия отметок и баллов определяется учителем и выводится на доске.

Рефлексия.

Домашнее задание.

Учащиеся получают домашнее задание.

Презентация

одновременных уравнений | Теоремы о цепях

Одновременные уравнения | Цепные теоремы | Теория постоянного тока

Рассмотрим схему, которая была решена с помощью теоремы суперпозиции в предыдущем разделе. Используя этот альтернативный метод, направления токи и падения напряжения угадываются для начала. Если эти догадки окажутся неверными, значения, полученные из расчеты окажутся отрицательными и их можно будет потом скорректировать.

Закон напряжения Кирхгофа можно применить к любому контуру цепи.
(Закон Кирхгофа о напряжении утверждает, что вокруг любого контура в цепи сумма ЭДС s равна сумме напряжений капли.)

• Применение закона Кирхгофа для напряжения к контуру 1 дает E ₁ = V ₁ + V ₂ .
• Применение закона напряжения Кирхгофа к контуру 2 дает E ₂ = V ₃ + В ₂ .

с использованием закона Ома, V = IR, для замены V ₁ , V ₂ и V ₃ в приведенных выше выражениях дает.

• Е ₁ = И ₁ Р ₁ + И ₂ Р ₂ .
• E ₂ = I ₃ R ₃ + I ₂ R ₂ .

Ввод значений резисторов и ЭДС дает;

• 10 = 4I ₁ + 6I ₂      (1) .
• 15 = 10I ₃ + 6I ₂     (2) .

Применение действующего закона Кирхгофа к перекрестку:

• I ₂ = I ₁ + I ₃ .
• Следовательно, I ₃ = I ₂ — I ₁     (3) .

замена I ₃ в уравнении (2) дает;

• 15 = 10(I ₂ — И ₁ ) + 6И ₂ .
• 15 = 10I ₂ — 10I ₁ + 6I ₂ .
• 15 = — 10I ₁ + 16I ₂    (4) .

умножение уравнения (1) на 10
& умножение уравнения (4) на 4 дает:

• 100 = 40I ₁ + 60I ₂    (5) .
• 60 = -40I ₁ + 64I ₂    (6) .

добавление уравнения (5) к уравнению (6) .

• 160 = 124I ₂ .
• I ₂ = 160/124 = 1,29 А .

подставив это значение I ₂ в уравнение (1) .

• 10 = 4I ₁ + 6 х 1,29.
• 10 = 4I ₁ + 7,74 .
• 10 — 7,74 = 4I ₁ .
• 2,26 = 4I ₁ .
• я ₁ =2,26/4 = 0,565 А .

, помещая значения для I ₁ и I ₂ в уравнение (3).

• I ₃ = I ₂ — I ₁ .
• Следовательно, I ₃ = 1,29 — 0,565 = 0,725 А .

Это дает те же ответы (с точностью до 0,001 А из-за ошибок округления), что и теорема суперпозиции.
В этом случае все текущие значения были положительными, что указывает на то, что первоначальные предполагаемые направления тока были правильными.
Падение напряжения теперь можно было найти, используя закон Ома, как показано в примере с теоремой суперпозиции.

Закон Кирхгофа о напряжении — цепи постоянного тока

Цепи постоянного тока

В 1847 г. Г. Р. Кирхгоф расширил использование закона Ома, разработав простой понятие о напряжениях, содержащихся в контуре последовательной цепи. Закон напряжения Кирхгофа гласит:

Алгебраическая сумма напряжений на любом замкнутом пути в цепи равна до нуля.

Закон напряжения Кирхгофа можно записать в виде уравнения, как показано ниже:

где В ₁ , В ₂ и т.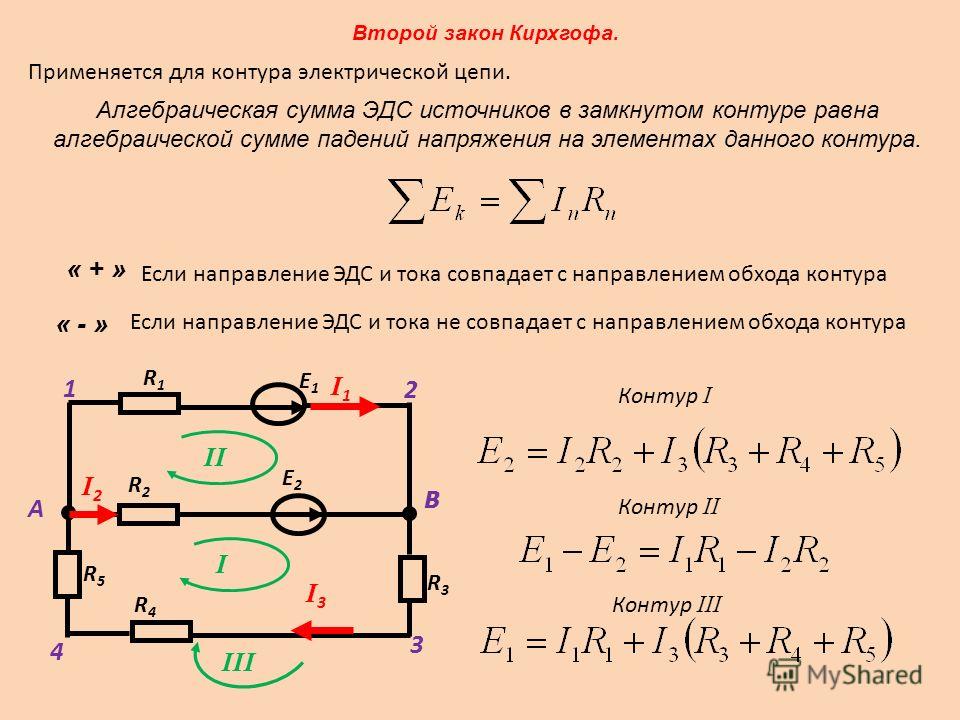 д. – напряжения вокруг любой замкнутой цепи.

Используя закон Кирхгофа, можно решить схемные задачи, которые быть трудным, а часто и невозможным, зная только закон Ома. Когда При правильном применении закона Кирхгофа можно составить уравнение для замкнутой петля и неизвестные значения цепи могут быть рассчитаны.

Полярность напряжения

Чтобы применить закон напряжения Кирхгофа, значение полярности напряжения должны быть поняты.

В цепи, показанной на рисунке ниже, показано, что ток течет в направление против часовой стрелки. Обратите внимание, что конец резистора R ₁ , в который течет ток, маркируется положительным (+). Конец R ₁ , на котором отмечен текущий лист отрицательный (-). Эти обозначения полярности используются, чтобы показать, что конец из R ₁ , в который течет ток, находится на более высоком положительном потенциала, чем конец резистора, с которого уходит ток. Точка А более положительна, чем точка Б.

Полярность напряжения.

Точка С, имеющая тот же потенциал, что и точка В, считается положительной. Этот означает указать, что точка C более положительна, чем точка D. Сказать, что точка положительный (или отрицательный) без указания полярности на основе не имеет смысла. В работе с законом Кирхгофа положительные и отрицательная полярность назначается в направлении протекания тока.

Полярность напряжения также может быть обозначена стрелкой, указывающей от положительной (+) точки в отрицательную (-) точку (красная стрелка на рисунке выше). В случае резисторов стрелка напряжения имеет того же направления, что и ток. Часто это более практичное указание полярностей.

Применение закона Кирхгофа о напряжении

Закон напряжения Кирхгофа применяется к цепи следующим образом:

Предположим направление тока в цепи. (Правильное направление желательно, но не обязательно.)

Используя предполагаемое направление тока, назначьте полярность напряжения для всех резисторы, через которые протекает ток.

Соблюдайте полярность всех источников, включенных в цепь.

Начиная с любой точки цепи, обведите цепь (петлю) в выбранном направлении (по часовой стрелке или против часовой стрелки), записывая сумму и полярность напряжения последовательно на каждом компоненте. Полярность используется знак перед предполагаемый ток прошел через компонент. Остановиться, когда будет достигнута точка, в которой была начата трассировка.
Когда стрелки используются для указания полярности напряжения, полярность (знак) напряжения можно получить с помощью следующего Правило: Если стрелка имеет то же направление, что и кривая, знак напряжения в уравнение положительное (+). Напротив, если стрелка имеет противоположное направлении знак отрицательный (-).

Поместите эти напряжения с их полярностями в уравнение и решить для нужного количества.

Пример :
Три резистора подключены к источнику 50 В (см. рисунок ниже). Каково будет напряжение на третьем резисторе, если напряжение упадет на первые два резистора на 25 вольт и на 15 вольт?

Определение неизвестного напряжения в последовательной цепи.

Решение :
Сначала предполагается направление тока (как показано). Используя этот ток, маркировка полярности («+» и «-» знаки и/или стрелки) размещены на каждом конце каждого резистора, а также на клеммах источника. Начиная с точки А, обведите цепь в направлении протекания тока, записывая напряжение и полярность каждого компонента. Начиная с точки А и используя компоненты из схемы:

Подставляем значения из схемы:

Неизвестное напряжение ( В _x ) равно 10 В.

Используя ту же идею, что и выше, вы можете решить задачу, в которой ток является неизвестной величиной.

Пример :
Цепь с источником напряжения 60 вольт содержит три резистора 5 Ом, 10 Ом и 15 Ом. Найдите ток в цепи.

Правильное направление предполагаемого тока.

Решение: Нарисуйте и обозначьте схему (рисунок выше). Установить направление тока и назначить полярность. Далее, начиная с любой точки — точки В этом примере будет использоваться A — запишите уравнение контура.

Основное уравнение:

Поскольку V = I × R , заменой:

Объединение подобных терминов:

Вычисление I :

Поскольку ток, полученный в приведенных выше расчетах, составляет положительные 2 ампера, предполагаемое направление тока было правильным. Чтобы показать, что произойдет, если предполагается неправильное направление тока, проблема будет решаться, как и раньше, но с противоположным направлением тока. схема перерисована, показывая новое направление тока и новые полярности на рисунке ниже. Начиная с точки A уравнение контура:

Основное уравнение:

Поскольку V = I × R , заменой:

Объединение подобных терминов:

Вычисление I :

Неправильное направление предполагаемого тока.

Обратите внимание, что сумма тока такая же, как и раньше. полярность, однако отрицательный .