Удельное сопротивление меди, алюминия, нихрома, стали и других проводников
Приведенная ниже таблица удельного электрического сопротивления содержит значения удельного сопротивления для многих веществ, широко используемых в электрике и электронике. В частности, она включает в себя удельное сопротивление меди, алюминия, нихрома, стали, никеля и так далее.
Удельное электрическое сопротивление особенно важно, поскольку оно определяет электрические характеристики и, следовательно, пригодность материала для использования во многих электрических компонентах. Например, можно увидеть, что удельное сопротивление меди, удельное сопротивление алюминия, а также нихрома, никеля, серебра, золота и т.д. определяет, где эти металлы используются.
Для того чтобы сравнить способность различных материалов проводить электрический ток, используются показатели удельного сопротивления.
Что означают показатели удельного сопротивления?
Для того чтобы иметь возможность сравнивать удельное сопротивление различных материалов, от таких изделий, как медь и алюминий, до других металлов и веществ, включая висмут, латунь и даже полупроводники, необходимо использовать стандартное измерение.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м.
Единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м2, изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2
[1]
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких “популярных” материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
| Материал | Удельное сопротивление, ρ, при 20 °C (Ом·м) | Источник |
|---|---|---|
| Латунь | ~0.6 – 0.9 x 10-7 | |
| Серебро | 1.59×10−8 | [3][4] |
| Медь | 1.68×10−8 | [5][6] |
| Обожжённая медь | 1.72×10−8 | [7] |
| Золото | 2.44×10−8 | [3] |
| Алюминий | 2.65×10−8 | [3] |
| Кальций | 3.36×10−8 | |
| Вольфрам | 5.60×10−8 | [3] |
| Цинк | 5.90×10−8 | |
| Кобальт | 6.24×10−8 | |
| Никель | 6.99×10−8 | |
| Рутений | 7.10×10−8 | |
| Литий | 9.28×10−8 | |
| Железо | 9.70×10−8 | [3] |
| Платина | 1. 06×10−7 06×10−7 | [3] |
| Олово | 1.09×10−7 | |
| Тантал | 1.3×10−7 | |
| Галлий | 1.40×10−7 | |
| Ниобий | 1.40×10−7 | [8] |
| Углеродистая сталь (1010) | 1.43×10−7 | [9] |
| Свинец | 2.20×10−7 | [2][3] |
| Галинстан | 2.89×10−7 | [10] |
| Титан | 4.20×10−7 | |
| Электротехническая сталь | 4.60×10−7 | [11] |
| Манганин (сплав) | 4.82×10−7 | [2] |
| Константан (сплав) | 4.90×10−7 | [2] |
| Нержавеющая сталь | 6.90×10−7 | |
| Ртуть | 9.80×10−7 | [2] |
| Марганец | 1.44×10−6 | |
| Нихром (сплав) | 1. 10×10−6 10×10−6 | [2][3] |
| Углерод (аморфный) | 5×10−4 – 8×10−4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 – 5.0×10−6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 | |
| Арсенид галлия | 10−3 to 108 | |
| Германий | 4.6×10−1 | [3][4] |
| Морская вода | 2.1×10−1 | |
| Вода в плавательном бассейне | 3.3×10−1 – 4.0×10−1 | |
| Питьевая вода | 2×101 – 2×103 | |
| Кремний | 2.3×103 | [2][3] |
| Древесина (влажная) | 103 – 104 | |
| Деионизированная вода | 1.8×105 | |
| Стекло | 1011 – 1015 | [3][4] |
| Углерод (алмаз) | 1012 | |
| Твердая резина | 1013 | [3] |
| Воздух | 109 – 1015 | |
| Древесина (сухая) | 1014 – 1016 | |
| Сера | 1015 | [3] |
| Плавленый кварц | 7. 5×1017 5×1017 | [3] |
| ПЭТ | 1021 | |
| Тефлон | 1023 – 1025 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах – никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.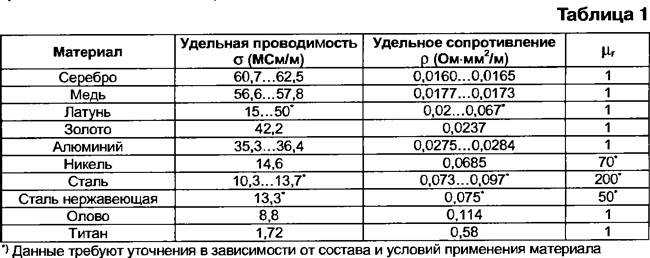
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Список использованной литературы
- Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с.
- Giancoli, Douglas C., Physics, 4th Ed, Prentice Hall, (1995).
- Raymond A. Serway (1998). Principles of Physics (2nd ed.). Fort Worth, Texas; London: Saunders College.
- David Griffiths (1999) [1981]. “7 Electrodynamics”. In Alison Reeves (ed.). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, New Jersey.

- Matula, R.A. (1979). “Electrical resistivity of copper, gold, palladium, and silver”. Journal of Physical and Chemical Reference Data.
- Douglas Giancoli (2009) [1984]. “25 Electric Currents and Resistance”. In Jocelyn Phillips (ed.). Physics for Scientists and Engineers with Modern Physics (4th ed.). Upper Saddle River, New Jersey.
- “Copper wire tables”. United States National Bureau of Standards. Retrieved 3 February 2014.
- https://www.plansee.com/en/materials/niobium.html
- AISI 1010 Steel, cold drawn. Matweb
- Karcher, Ch.; Kocourek, V. (December 2007). “Free-surface instabilities during electromagnetic shaping of liquid metals”.
- “JFE steel” (PDF). Retrieved 2012-10-20.
Удельное электрическое сопротивление – формула, таблица
4.1
Средняя оценка: 4.1
Всего получено оценок: 235.
4.1
Средняя оценка: 4.1
Всего получено оценок: 235.
Величина электрического тока, возникающего в образце вещества под воздействием электрического поля, зависит от геометрических размеров образца и от величины удельного электрического сопротивления вещества.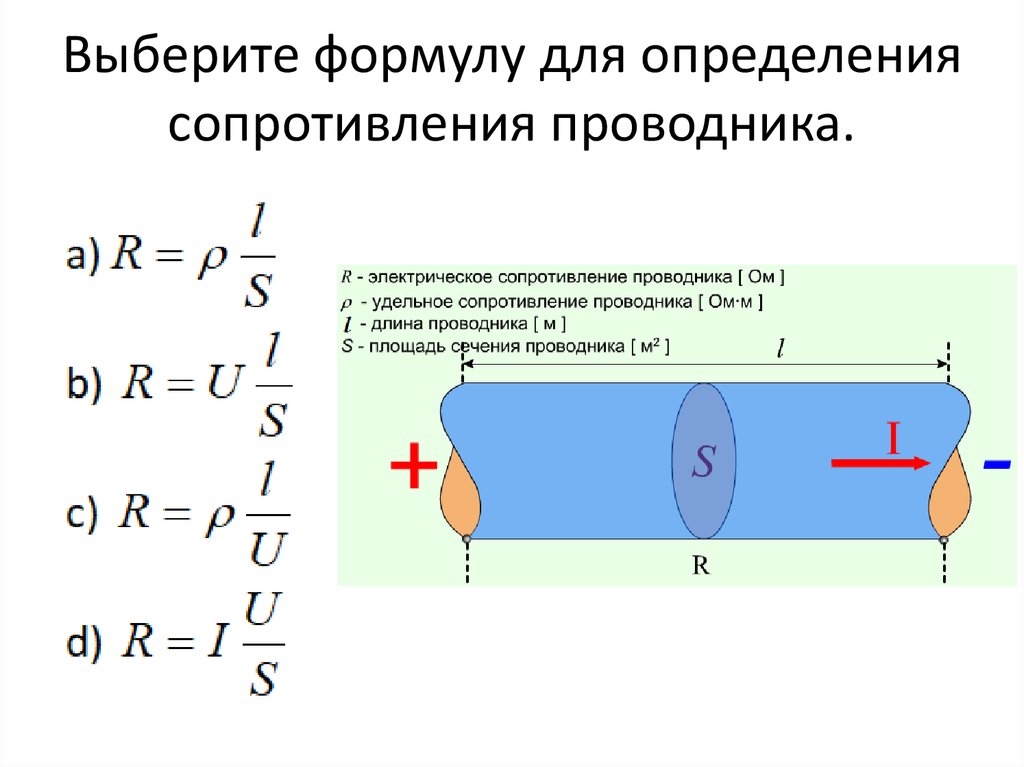 Удельное сопротивление характеризует способность различных веществ по разному проводить электрический ток. Чем больше величина удельного сопротивления вещества, тем меньше будет значение электрического тока, протекающего через образец (провод) при одинаковых величинах электрического поля и размерах образца.
Удельное сопротивление характеризует способность различных веществ по разному проводить электрический ток. Чем больше величина удельного сопротивления вещества, тем меньше будет значение электрического тока, протекающего через образец (провод) при одинаковых величинах электрического поля и размерах образца.
Напряжение, сила тока, сопротивление
Сила тока I, протекающего через участок цепи, к которому приложено электрическое напряжение U, определяется по формуле закона Ома:
$ I = {U\over R} $ (1),
Измеряя на образцах из различных материалов вольт-амперные характеристики I(U), немецкий физик Георг Ом обнаружил, что величина сопротивления R разная у одинаковых по размерам образцов из различных материалов. Количественная характеристика вещества, указывающая на это свойство, называется удельным электрическим сопротивлением.
Рис. 1. Вольт-амперные характеристики проводников.
Как рассчитать сопротивление
Экспериментальные данные на большом количестве образцов показали, что:
- Сопротивление R , обратно пропорционально поперечной площади образца
- Сопротивление R прямо пропорциональна длине образца, то есть чем больше длина образца L, тем больше его сопротивление, то есть $ R∼ L$;
- Так как значения R у образцов из разных материалов с одинаковыми размерами S и L отличались, то была введена новая физическая величина, названная удельным электрическим сопротивлением ρ.
Полученные данные хорошо описывались формулой:
$ R = ρ * {L\over S} $ (2).
Из уравнения (2) следует формула удельного электрического сопротивления:
$ ρ = R * { S \over L } $ (3).
Значения ρ для большинства веществ можно найти, воспользовавшись справочниками в печатном или электронном виде.

Единицы измерения удельного сопротивления
Из уравнения (3) следует, что в Международной системе СИ единицей измерения ρ будет (Ом*м), так как сопротивление измеряется в омах, а длина и площадь — в метрах и метрах квадратных соответственно. То есть единица удельного сопротивления равна сопротивлению образца площадью 1 м2 и длиной 1 м. Но на практике эта единица оказалась не очень удобной из-за слишком больших числовых значений. Поэтому для электротехнических расчетов чаще используют внесистемную единицу (Ом*мм
Алюминиевые провода устойчивы к коррозии, имеют низкое удельное сопротивление 0,026 (Ом*мм2/м) и небольшой вес на метр длины, что делает этот материал очень востребованным при изготовлении проводов и кабелей, работающих за пределами помещений.
Проводники, полупроводники, диэлектрики
По величине удельного сопротивления все вещества разделяют на три основные вида: проводники, полупроводники, диэлектрики. Кроме значительной разницы в величине ρ, вещества, относящиеся к разным видам, имеют разные температурные зависимости
Проводники (металлы) | Полупроводники | Диэлектрики (изоляторы) |
Имеют низкие значения ρ (хорошо проводят электрический ток) ρ < 10-6 Ом*м | Занимают промежуточное положение по величине ρ между проводниками и диэлектриками 10-6 Ом*м < ρ <108 Ом*м | Имеют высокие значения ρ (практически не проводят ток) ρ > 108 Ом*м |
Металлы: алюминий, серебро, Медь, железо, сплавы металлов (латунь, бронза и т. | Кремний, германий, селен, индий, мышьяк и др. | Пластмассы, стекло, фарфор, Бумага, дерево (сухое) и др. |
С ростом температуры у проводников наблюдается возрастание величины удельного сопротивления, а у полупроводников и диэлектриков — падение. Облучение полупроводников и диэлектриков электромагнитным излучением приводит к уменьшению ρ, а у проводников удельное сопротивление при облучении не меняется.
Что мы узнали?
Итак, мы узнали, что удельное электрическое сопротивление характеризует способность веществ и материалов пропускать электрический ток. Приведена формула для вычисления удельного сопротивления. Проводники, полупроводники и диэлектрики отличаются друг от друга значениями удельных сопротивлений и поведением этой величины от воздействия внешних факторов (температуры, облучения).
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 235.
А какая ваша оценка?
Удельное электрическое сопротивление
Удельное электрическое сопротивление является физической величиной, которая показывает, в какой степени материал может сопротивляться прохождению через него электрического тока. Некоторые люди могут перепутать данную характеристику с обыкновенным электрическим сопротивлением. Несмотря на схожесть понятий, разница между ними заключается в том, что удельное касается веществ, а второй термин относится исключительно к проводникам и зависит от материала их изготовления.
Обратной величиной данного материала является удельная электрическая проводимость. Чем выше этот параметр, тем лучше проходит ток по веществу.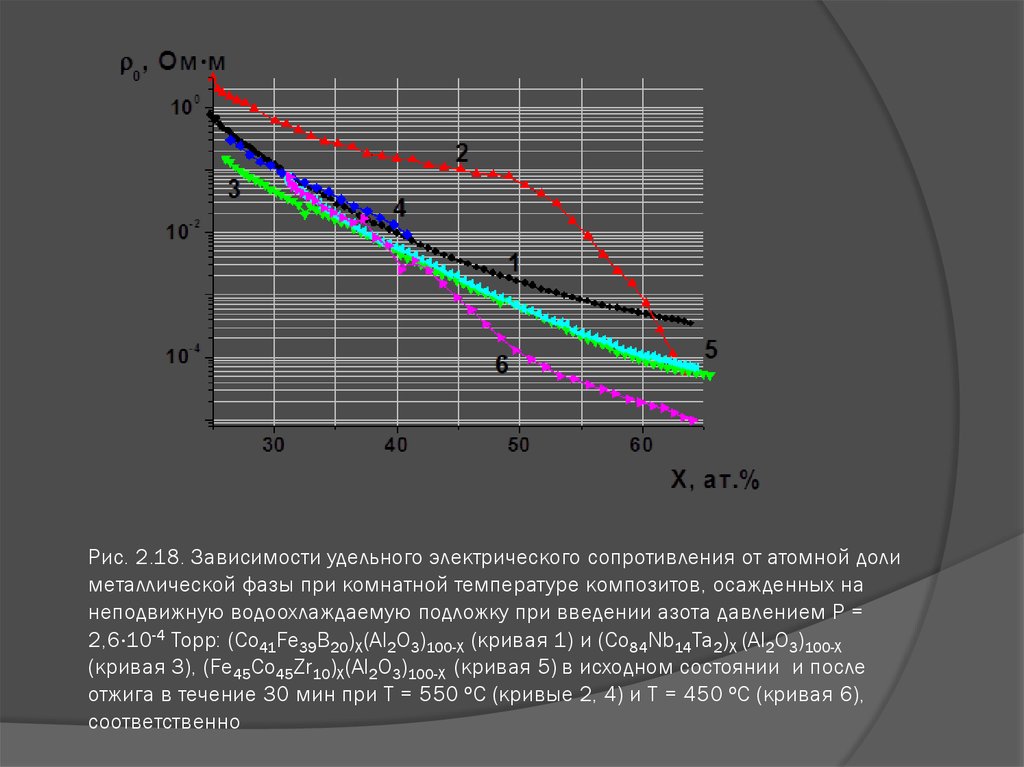 Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — ·[1]. Из соотношения ρ = R ⋅ S l {\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке.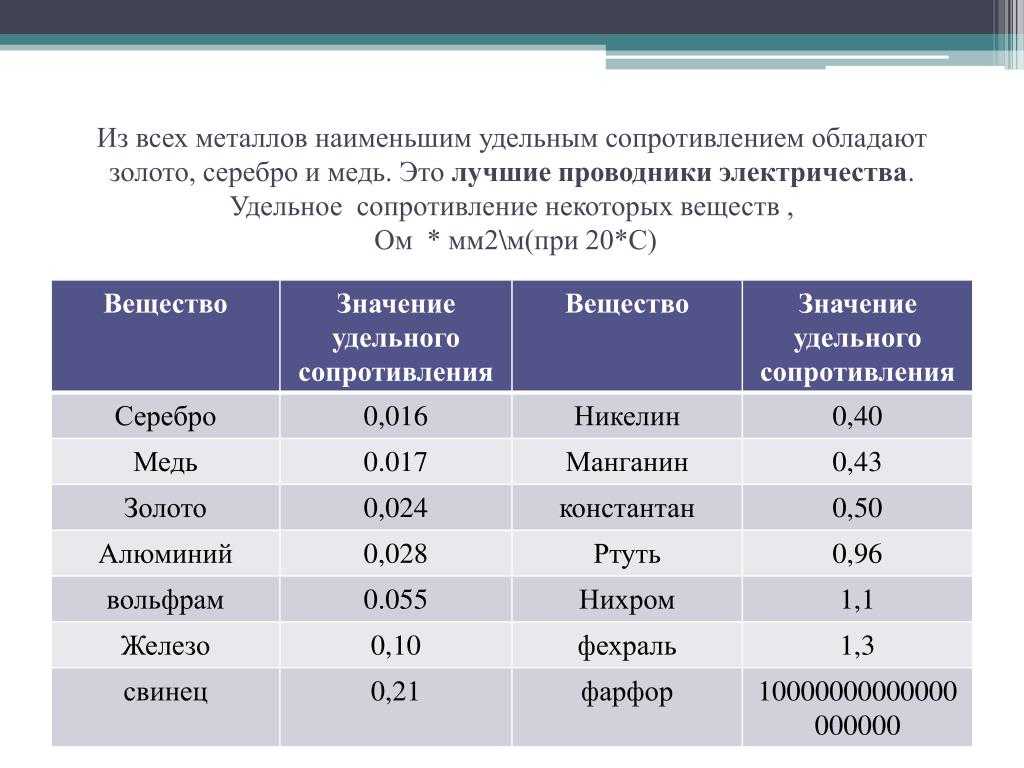 В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → ( r → ) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → ( r → ) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} . Указанная связь выражается законом Ома в дифференциальной форме:
В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → ( r → ) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → ( r → ) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} . Указанная связь выражается законом Ома в дифференциальной форме:
E → ( r → ) = ρ ( r → ) J → ( r → ) . {\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρ i j {\displaystyle \rho _{ij}} . В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
E i ( r → ) = ∑ j = 1 3 ρ i j ( r → ) J j ( r → ) . {3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρ i j {\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρ i j {\displaystyle \rho _{ij}} симметричен
, то есть для любых i {\displaystyle i} и j {\displaystyle j} выполняется ρ i j = ρ j i {\displaystyle \rho _{ij}=\rho _{ji}} .
Как и для всякого симметричного тензора, для ρ i j {\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρ i j {\displaystyle \rho _{ij}} становится диагональной
, то есть приобретает вид, при котором из девяти компонент ρ i j {\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ 11 {\displaystyle \rho _{11}} , ρ 22 {\displaystyle \rho _{22}} и ρ 33 {\displaystyle \rho _{33}} . В этом случае, обозначив ρ i i {\displaystyle \rho _{ii}} как ρ i {\displaystyle \rho _{i}} , вместо предыдущей формулы получаем более простую
E i = ρ i J i . {\displaystyle E_{i}=\rho _{i}J_{i}. }
}
Величины ρ i {\displaystyle \rho _{i}} называют главными значениями
тензора удельного сопротивления.
Использование в электротехнике
Изменение параметра при разных температурах широко применяется в электротехнике. Наиболее простым примером является лампа накаливания, где используется нихромовая нить. При нагревании она начинает светиться. При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
Широкое применение коснулось и благородных металлов, которые обладают подходящими характеристиками для электротехники. Для ответственных схем, которым требуется быстродействие, подбираются серебряные контакты. Они обладают высокой стоимостью, но с учетом относительно небольшого количества материалов их применение вполне оправданно. Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
В условиях, где можно использовать предельно низкие температуры, применяются сверхпроводники. Для комнатной температуры и уличной эксплуатации они не всегда уместны, так как при повышении температуры их проводимость начнет падать, поэтому для таких условий лидерами остаются алюминий, медь и серебро.
На практике учитывается много параметров и этот является одним из наиболее важных. Все расчеты проводятся еще на стадии проектирования, для чего и используются справочные материалы.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ {\displaystyle \rho } и удельной проводимостью σ {\displaystyle \sigma } выражается равенством
ρ = 1 σ . {\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {\displaystyle \rho _{ij}} и тензора удельной проводимости σ i j {\displaystyle \sigma _{ij}} имеет более сложный характер. {3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],} ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}
где det ( σ ) {\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1
,
2
и
3
[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
| 0,015…0,0162 | |
| Медь | 0,01724…0,018 |
| Золото | 0,023 |
| Алюминий | 0,0262…0,0295 |
| Иридий | 0,0474 |
| Молибден | 0,054 |
| Вольфрам | 0,053…0,055 |
| Цинк | 0,059 |
| Никель | 0,087 |
| Железо | 0,098 |
| Платина | 0,107 |
| Олово | 0,12 |
| Свинец | 0,217…0,227 |
| Титан | 0,5562…0,7837 |
| Висмут | 1,2 |
| Никелин | 0,42 |
| Константан | 0,5 |
| Манганин | 0,43…0,51 |
| Нихром | 1,05…1,4 |
| Фехраль | 1,15…1,35 |
| Хромаль | 1,3…1,5 |
| Латунь | 0,025…0,108 |
| Бронза | 0,095…0,1 |
Значения даны при температуре t
= 20 °C.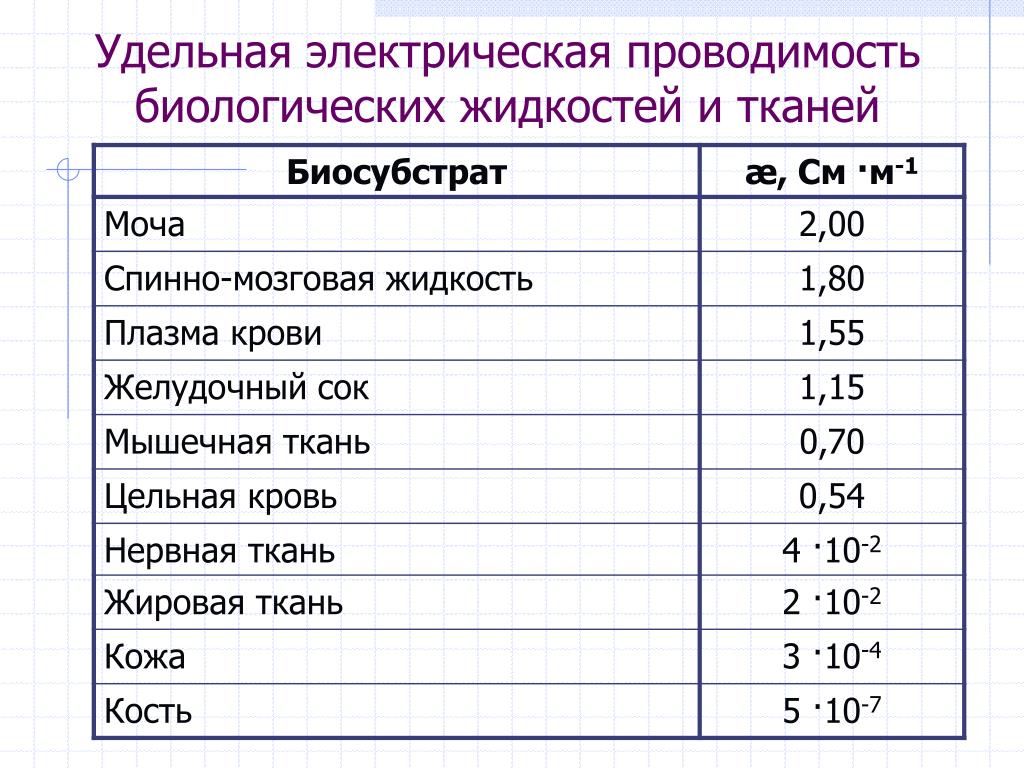 Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
| Вещество | ρ, Ом·мм²/м |
| Сжиженные углеводородные газы | 0,84·1010 |
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1.2·10-7 |
| Платина | 1.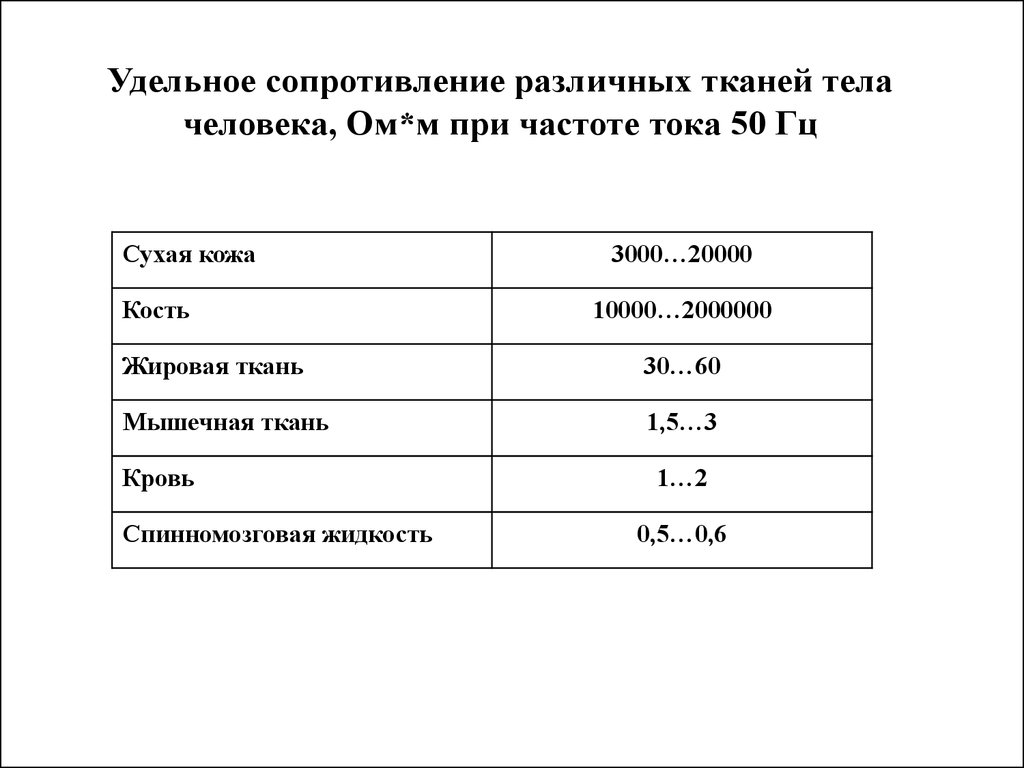 07·10-7 07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», R S q . {\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W
: R S q = R W / L , {\displaystyle R_{\mathrm {Sq} }=RW/L,} где
R
— измеренное сопротивление.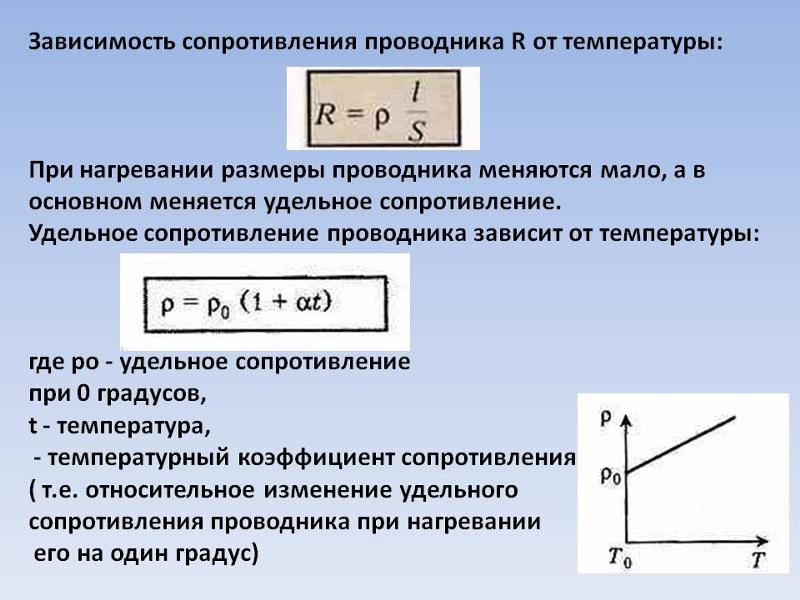 В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Ток, проходящий через электрическую изоляцию в установившемся режиме (после достаточно продолжительного промежутка времени после приложения напряжения), является постоянным и называется сквозным током утечки. Величина сопротивления изоляции Rиз равна отношению приложенного напряжения U, В к сквозному току утечки Iиз, А:
Rиз = U/ Iиз
Величина проводимости изоляции Gиз является обратной к Rиз:
Gиз = 1 / Rиз.
Различают объемное сопротивление электрической изоляции, равное сопротивлению через толщу материала, и поверхностное сопротивление, которое определяется наличием загрязнений (влага, растворы солей, кислот), нарушениями структуры поверхности, поскольку поверхность диэлектрика в большей степени подвержена воздействию внешних факторов. Соответственно, различают и токи утечки – на объемный и поверхностный (рис. 1).
Рис. 1. Объемный Iv и поверхностный Is токи утечки через образец изоляции.
Порядок величины токов составляет очень малые величины до10-15 и даже до 10-17 А. Поэтому особое внимание при проведении измерений уделяют устранению паразитных токов утечки, которые могут существенно повлиять на точность получаемых результатов.
Для исключения поверхностного тока утечки при измерении объемного электрического сопротивления диэлектриков применяют специальное охранное кольцо, окружающее измерительный электрод. При этом потенциал охранного кольца равен потенциалу измерительного электрода, именно в этом случае ток утечки между ними будет отсутствовать (рис. 2).
Рис. 2. Расположение концентрических электродов при измерении объемного сопротивления диэлектрика.
1 — охранное кольцо; 2- центральный электрод; 3- нижний электрод.
Для измерений применяют напыленные или фольговые электроды, которые вырезают из оловянной или отожженной алюминиевой фольги толщиной 5–20 мкм. Контакт фольгового электрода с образцом создается путем притирания с помощью тонкого слоя вазелина, трансформаторного, конденсаторного или вазелинового масла, кремнийорганической жидкости или другого аналогичного вещества. Толщина смазки не должна превышать 1 мкм.
Толщина смазки не должна превышать 1 мкм.
Тогда удельное объемное сопротивление материала может быть рассчитано по формуле:
ρV = RV × S / h = U × S/( IV × h),
где IV – измеряемый объемный ток; U – напряжение на электродах; S – площадь центрального измерительного электрода; h – толщина диэлектрика; RV– объемное сопротивление образца.
При измерении поверхностного электрического сопротивления диэлектрика при данной системе электродов напряжение прикладывается между охранным кольцом и центральным электродом.
В такой системе удельное поверхностное сопротивление может быть рассчитано по формуле:
где RS– поверхностное электрическое сопротивление образца диэлектрика, заключенного между электродами; d1 – внутренний диаметр охранного кольца; d2 – диаметр центрального электрода.
Удельное объемное сопротивление имеет размерность [Ом×м], а удельное поверхностное – [Ом]. Это разные физические величины, которые нельзя сравнивать друг с другом.
При измерении сопротивления электрической изоляции следует учесть, что в первый момент времени выдержки под напряжением через нее протекает не только сквозной электрический ток, но и сопровождающий его ток абсорбции (смещения), связанный с установлением замедленных видов поляризации (рис. 3).
3).
Электропроводность диэлектрика определяется при постоянном напряжении по величине сквозного тока, значение сопротивления образца вычисляется по формуле: Rиз = U / Iиз = U / ( IΣ – Iабс), где Iиз – сквозной ток утечки, IΣ – суммарное значение тока, Iабс – ток абсорбции.
Следовательно, если измерить сопротивление изоляции в первый же момент приложения напряжения, то можно получить его завышенное значение.
В связи с тем, что величины токов абсорбции очень малы, измерять их крайне сложно. Поэтому сопротивление изоляции принято измерять после 1 минуты выдержки образца под постоянным напряжением. Считается, что за это время поляризационные процессы, вносящие основной вклад в ток абсорбции диэлектрика, закончатся.
Рис. 3. Зависимость тока через диэлектрик от времени
Iиз – сквозной ток утечки;
IΣ – суммарное значение тока;
Iабс – ток абсорбции.
Вас также может заинтересовать:
- Общие сведения о диэлектриках
- Электрическое старение изоляции
- Частичные разряды
- Анализ процесса отверждения
- Кинетика отверждения
Примечания
- ↑ 1 2Деньгуб В.
 М., Смирнов В. Г.
М., Смирнов В. Г.
Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5. - ↑ 12Чертов А. Г.
Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с. - Давыдов А. С.
Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с. - Шувалов Л. А. и др.
Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Удельное электрическое сопротивление — формула, обозначение и физический смысл
При проектировании электронных устройств применяются различные соотношения, позволяющие рассчитать некоторые параметры электрической цепи. Один из них зависит от температуры и называется удельным электрическим сопротивлением, формула которого включает все компоненты, влияющие на искомую величину. Их необходимо разобрать подробно, поскольку это влияет на работоспособность радиокомпонентов, входящих в состав аппаратуры.
Содержание
- Общие сведения
- Удельное сопротивление
- Проведение опыта
- Температурный коэффициент
Общие сведения
Электрическое сопротивление проводника зависит не только от его геометрических параметров и вещества, а также от температуры. Чтобы выяснить и доказать это, нужно изучить теорию. Электропроводимость — способность проводника пропускать электрический ток.
Следует отметить, что каждое вещество состоит из атомов, образующий узлы кристаллической решетки. Под действием электромагнитного поля происходит упорядоченное движение заряженных частиц (электротока). Последние ударяются об узлы этой решетки, т. е. взаимодействуют с ними. В результате происходит выделение тепловой энергии. После этого они снова «разгоняются» электромагнитным полем до следующего взаимодействия.
Этот процесс и получил название электрического сопротивления. Последнее зависит от нескольких факторов:
Последнее зависит от нескольких факторов:
Если рассмотреть формулу для определения электросопротивления «R=pL/S», то она состоит из трех параметров.
Первый из них — удельное сопротивление (обозначается буквой «р»). Он является параметром, который зависит от типа вещества, а также и от температуры. Для его расчета применяется специальное соотношение, имеющее такой вид: p=p0+aT, где р0 — табличное значение удельного сопротивления, а — константа (для металла равна единице, раствора — «0,5» и других компонентов — «0,25») и T — температура проводника в Цельсиях.
Вторая величина «L» — длина проводника, а третья «S» — величина площади поперечного сечения. Параметр зависит от геометрической формы проводника. Например, если жила имеет форму цилиндра, то значит, необходимо рассчитывать величину по следующей формуле: S= Pi*R 2 , где Pi — постоянная, равная 3,1415, а R — радиус. Кроме того, соотношение возможно записать в другом формате: S= Pi (d 2 /4), где D — диаметр проводника. Последний рекомендуется измерять при помощи штангенциркуля.
Кроме того, соотношение возможно записать в другом формате: S= Pi (d 2 /4), где D — диаметр проводника. Последний рекомендуется измерять при помощи штангенциркуля.
Если проводник имеет форму прямоугольника или квадрата, то площадь сечения находится по формуле «S=mn», где m и n — стороны фигуры.
Кроме того, одним из факторов проводимости является наличие свободных электронов, которое определяется по электронной конфигурации элемента в периодической системе Д. И. Менделеева.
Удельное сопротивление
Физический смысл удельного сопротивления в таблице имеет такую формулировку: величина «р» эквивалентна отношению сопротивления проводника из заданного материала в 1 Ом площадью поперечного сечения 1 мм 2 к длине 1 м. Математическая форма записи: p=[1 Ом * 1 мм 2 ]/1м.
На основании общего соотношения можно вывести формулу удельного сопротивления: p=(RS)/L. Однако к этому физики пришли не сразу. После открытия закона Ома для полной цепи и ее участка применялись только три составляющих, а именно: сила тока, напряжение и сопротивление.
Однако к этому физики пришли не сразу. После открытия закона Ома для полной цепи и ее участка применялись только три составляющих, а именно: сила тока, напряжение и сопротивление.
На протяжении определенного времени физики не могли понять различные измерения параметров (отклонения) в электрических схемах при постоянном напряжении и токе, которые фиксировались приборами. Оказалось, что причиной стала температура окружающей среды. Для обыкновенных металлов (золота, стали и никелина) величина сопротивления при высоком температурном коэффициенте увеличивалась, а при низком — уменьшалась.
Опытным путем был открыт новый параметр, зависящий не только от типа материала, но и от температуры. Его назвали удельным сопротивлением.
Проведение опыта
Опыт позволяет определить зависимость сопротивления от температуры. Для этого подойдет проволока из любого проводника (рекомендуется использовать никелин).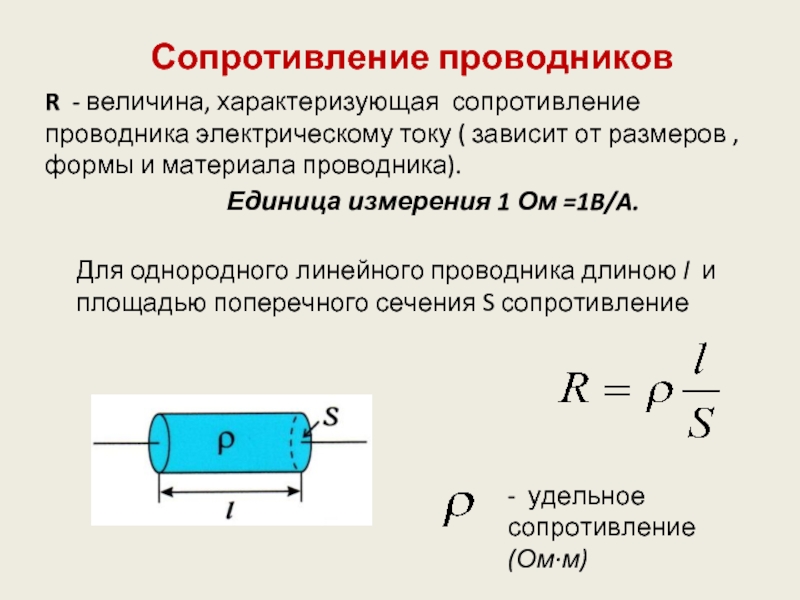 Кроме того, понадобится источник питания, напряжение которого составляет примерно от 12 до 24 В постоянного тока. Далее необходимо собрать схему, дополнив ее лампой накаливания и выключателем. Элементы необходимо соединить последовательно.
Кроме того, понадобится источник питания, напряжение которого составляет примерно от 12 до 24 В постоянного тока. Далее необходимо собрать схему, дополнив ее лампой накаливания и выключателем. Элементы необходимо соединить последовательно.
После сборки схемы выключатель должен быть в положении «отключено». Если его включить, то лампочка будет гореть сначала ярко. Однако это будет длиться недолго — до нагрева спирали. Специалисты рекомендуют следить за техникой безопасности. Схему необходимо собирать, используя негорючие монтажные элементы.
Изменение свечения лампы доказывает, что при нагревании никелиновой проволоки происходит увеличение величины сопротивления. При этом уменьшается сила тока, поскольку она обратно пропорционально зависит от этой величины.
Температурный коэффициент
Формула, связывающая сопротивление и температурный коэффициент выглядит таким образом: (R-R0)/R=at. Она состоит из следующий параметров:
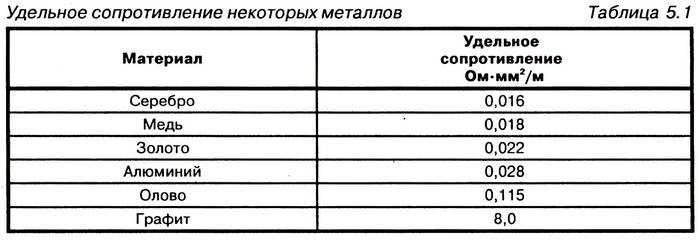
Чтобы рассчитать температурный коэффициент, нужно найти опытным путем величину электросопротивления при нулевом значении температуры. Она измеряется при помощи прибора, который называется омметром. Далее требуется посчитать p через формулу «p=p0+aT».
Нахождение неизвестной величины р0 осуществляется по специальным таблицам, в которых ученые уже позаботились и измерили опытным путем параметр при температуре 20 градусов по Цельсию.
Таким образом, расчет сопротивления проводника производится не только по его геометрическим параметрам и веществу, из какого он состоит, а также по величине температуры.
Предыдущая
ФизикаСтроение вещества — первоначальные сведения для учащихся 7 класса
Следующая
ФизикаОбщее сопротивление цепи — правила, формулы и примеры вычисления
Online Electric | Удельное сопротивление грунта
ОНЛАЙН ЭЛЕКТРИК > БАЗА ДАННЫХ > Удельное сопротивление грунта
Начинаете свою деятельность в сфере проектирования электроснабжения? Возникли сложности с расчетами по электроэнергетике и электротехнике? Свяжитесь с репетитором по электроэнергетике!
Страница: 1 | 2
| Материал грунта | Минимальное удельное сопротивление грунта, Ом*м | Максимальное удельное сопротивление грунта, Ом*м | Опции |
|---|---|---|---|
| Материал грунта | Минимальное удельное сопротивление грунта, Ом*м | Максимальное удельное сопротивление грунта, Ом*м | Опции |
Источники информации: [62]
Описание справочника:
В базе данных представлено удельное сопротивление грунта в зависимости от материала грунта.
Ключевые слова:
Удельное сопротивление грунта ,
удельное электрическое сопротивление грунта,
удельное сопротивление грунта таблица,
измерение удельного сопротивления грунта ,
удельное сопротивление грунта ом,
удельное сопротивление грунта пуэ,
удельное сопротивление грунта ом м ,
удельное сопротивление грунта таблица пуэ,
определение удельного сопротивления грунта,
расчетное удельное сопротивление грунта,
значения удельного сопротивления грунта,
коэффициент удельного сопротивления грунта,
удельное сопротивление грунта формула,
удельное сопротивление грунта суглинок,
величина удельного сопротивления грунта
| Библиографическая ссылка на ресурс «Онлайн Электрик»: |
| Алюнов, А.Н. Онлайн Электрик: Интерактивные расчеты систем электроснабжения / А.Н. Алюнов. — Режим доступа: http://online-electric.ru |
Journal of the RAS
Asia and Africa Today
asaf-today. ru
ru
Публикует научные статьи о политических, экономических и социальных процессах, происходящих в азиатских и африканских государствах, об их культуре, искусстве и литературе.
Show more
Chelovek
chelovek-journal.ru
Журнал «Человек» – научное издание, публикующее результаты изучения человека в социально-гуманитарных и естественных науках в тесной связи с осмыслением человека в философии, изначально стремящейся ответить на вопрос «Что есть человек?». Журнал открыт различным интеллектуальным традициям и теоретическим платформам. Особенно приветствуются работы, развивающие комплексные исследования человека на стыке наук. Статьи журнала адресованы междисциплинарному читательскому сообществу. Наряду с исследовательскими статьями журнал публикует аналитические обзоры дискуссий и научных конференций, полемические эссе, рецензии на книги.
Show more
Ekonomika i matematicheskie metody
emm.jes.su
Журнал «Экономика и математические методы» позиционирует себя как открытая площадка межнационального общения и обмена научной информацией, результатами фундаментальных и прикладных исследований специалистов академического и экспертно-аналитического профиля. Журнал стремится поддерживать высокий научный уровень дискуссии о проблемах, методах изучения и развития экономики, вовлекая в этот процесс наиболее квалифицированных экспертов – исследователей и практиков.
Журнал стремится поддерживать высокий научный уровень дискуссии о проблемах, методах изучения и развития экономики, вовлекая в этот процесс наиболее квалифицированных экспертов – исследователей и практиков.
Show more
Energy law forum
mlcjournal.ru
Цель журнала — повышение качества освещения основных результатов диссертационных работ и создание базовых условий выполнения требований Высшей аттестационной комиссии Министерства образования и науки России, предъявляемых к научным публикациям соискателей ученых степеней кандидатов и докторов юридических наук (5.1.2, 5.1.3, 5.1.5)
Show more
Etnograficheskoe obozrenie
«Этнографическое обозрение» — один из старейших российских академических журналов, посвященных исследованиям в области наук о народах. Основан в 1889 г. Журнал специализируется в первую очередь на публикации статей по вопросам этнографии, этнологии и социальной/культурной антропологии, а также обзоров и рецензий научной литературы в данных областях.
Show more
Gosudarstvo i pravo
gospravo-journal.ru
В журнале освещаются: теоретические вопросы государства и права; проблемы становления правового государства; права и свободы человека и гражданина; анализ нового законодательства; хроника научной жизни.
Show more
Izvestiia Rossiiskoi akademii nauk. Seriia literatury i iazyka
izv-oifn.ru
Журнал охватывает проблемы лингвистики и литературоведения, фольклористику, искусствознание, теорию литературы и историю русской и зарубежной литературы.
Show more
Latin America
latamerica-journal.ru
Журнал «Латинская Америка» — уникальное для России и СНГ полноценное мультидисциплинарное профессиональное издание на русском языке, анализирующее актуальные теоретические и научно-практические проблемы Иберо-Америки; — дает читателям широкую панораму иберо-американского мира, печатает эксклюзивные интервью глав государств, министров, политиков, дипломатов, парламентариев и общественных деятелей, видных представителей науки, бизнеса, культуры и искусства, произведения всемирно известных писателей Латинской Америки, Испании и Португалии.
Show more
Mirovaia ekonomika i mezhdunarodnye otnosheniia
Ежемесячный журнал “Мировая экономика и международные отношения” создан в 1956 г. и выходит в свет с января 1957 г. Является ведущим мультидисциплинарным изданием в России и СНГ по актуальным теоретическим и научно-практическим проблемам международной политики, мирохозяйственных связей, развития отдельных стран и регионов.
Show more
Novaia i noveishaia istoriia
nni.jes.su
В журнале публикуются статьи ведущих российских и зарубежных историков о политических, экономических и социальных процессах, происходящих в странах Западной и Восточной Европы, в США, Канаде и в Латиноамериканских странах. Большое внимание уделяется истории, внешней политике ведущих стран Азии и Африки.
Show more
Obshchestvennye nauki i sovremennost
ons-journal.ru
На страницах журнала обсуждаются следующие проблемы: экономика, социум, политика, культура России; построение общенаучной картины мира; особенности и перспективы трансформационных процессов; синергетика и методология обществознания; перспективы человека и мировой цивилизации; регионалистика и модернизационные процессы; межнациональные отношения.
Show more
Obshchestvo i ekonomika
oie.jes.su
«Общество и экономика» международный научный и общественно-политический журнал, посвященный экономическим, политическим и социальным процессам, происходящим в постсоциалистических странах.
Show more
Problemy Dalnego Vostoka
pdv.jes.su
Журнал предоставляет возможность своим читателям знакомиться с историей, культурой, политикой и экономикой стран АТР, следить за развитием международного сотрудничества в этом динамичном и стратегически важном районе мира, к которому, помимо лидеров современной мировой экономики — Китая и Японии – а также быстро растущих Индии, Вьетнама и других стран АСЕАН, относятся Сибирь и Дальний Восток России с их колоссальным потенциалом.
Show more
Psikhologicheskii zhurnal
psy.jes.su
В журнале публикуются статьи по фундаментальным проблемам психологии, ее методологическим, теоретическим и экспериментальным основаниям, а также результаты исследований, связанных с прикладными вопросами общественной и научной жизни. Дискуссии на страницах журнала способствуют выявлению общих тенденций в развитии психологии и ее сближению с практикой.
Дискуссии на страницах журнала способствуют выявлению общих тенденций в развитии психологии и ее сближению с практикой.
Show more
Rossiiskaia arkheologiia
Журнал насчитывает более 50 лет существования.Журнал ориентирован на профессиональных ученых – археологов, историков материальной культуры, искусства и архитектуры.Как фундаментальное научное издание, журнал принимает к печати только оригинальные авторские произведения (статьи, небольшие заметки, рецензии на книги, хронику проходящих научных форумов.
Show more
Rossiiskaia istoriia
russian-history.ru
Научный журнал, публикующий материалы по истории, историографии и методам исторических исследований. Журнал охватывает все области изучения российского исторического процесса с древности до современности, поощряет междисциплинарный и компаративный подходы. Приоритетом журнала является публикация оригинальных материалов, основанных на вводе в научный оборот новых источников и написанных с учётом новейшей отечественной и зарубежной историографии. Также журнал уделяет большое внимание профессиональному обсуждению новых научных изданий (монографий, сборников статей и академических публикаций источников), которое осуществляется как в формате рецензий (отдел критики и библиографии — самый большой из всех аналогичных отделов отечественной исторической периодики), так и в рубрике «Диалог о книге».
Также журнал уделяет большое внимание профессиональному обсуждению новых научных изданий (монографий, сборников статей и академических публикаций источников), которое осуществляется как в формате рецензий (отдел критики и библиографии — самый большой из всех аналогичных отделов отечественной исторической периодики), так и в рубрике «Диалог о книге».
Show more
Russkaia literatura
На страницах журнала читатель знакомится с работами, посвященными народному творчеству, литературам древнерусской и XVIII века, классическому наследию, литературе Новейшего периода (XX век). Теоретические и историко-литературные исследования соседствуют в нем с разысканиями биографическими и текстологическими, тематическими рубриками, связанными с юбилейными датами писателей-классиков, критическими обзорами, полемикой, атрибуциями, обширной информацией о текущей научной жизни по материалам многочисленных международных конференций.
Show more
Russkaya Rech’
Научно-популярный академический журнал о русском языке (о его истории и современном состоянии), о русской культуре и литературе
Show more
Slavianovedenie
slav. jes.su
jes.su
Публикуются проблемно-тематические статьи, материалы дискуссий, круглых столов, документы, критические обзоры, библиография, хроника научной жизни, информация о книгах, выпущенных Институтом славяноведения, и др.
Show more
Sotsiologicheskie issledovaniya
Журнал публикует статьи по всему спектру социологической науки: теория, методология и история социологии, методы и результаты социологических исследований в сфере экономической, социальной, политической и духовной жизни общества как в России, так и за рубежом. Среди ведущих рубрик — этносоциология, социология культуры, семьи, образования, науки, религии, управления, права, молодежи, демография и миграция. Новые рубрики — «Историческая социология», “Социология здоровья и медицины”, “Социология международных отношений”, “Социология профессий”.
Show more
USA & Canada: ekonomika, politika, kultura
usacanada.jes.su
Журнал «США & Канада: экономика, политика, культура» был основан в 1970 году как “США: экономика, политика, идеология” (с 1998 года была добавлена Канада). Его главная цель была и остается — информировать читателей о всех аспектах внутренней и внешней политики США и Канады, а также актуальным теоретическим и практическим проблемам международной политики, мирохозяйственных связей, развития в разных странах мира. Журнал публикует материалы, представляющие результаты исследований российских специалистов и иностранных аналитиков на российско – американские и российско – канадские отношения.
Его главная цель была и остается — информировать читателей о всех аспектах внутренней и внешней политики США и Канады, а также актуальным теоретическим и практическим проблемам международной политики, мирохозяйственных связей, развития в разных странах мира. Журнал публикует материалы, представляющие результаты исследований российских специалистов и иностранных аналитиков на российско – американские и российско – канадские отношения.
Show more
Vestnik drevnei istorii
Журнал публикует оригинальные научные статьи по всем областям древней истории, классической и древневосточной филологии и археологии античной и древневосточных цивилизаций, на русском, английском, французском и немецком языках.
Show more
Voprosy istorii estestvoznaniia i tekhniki
vietmag.org
Основной блок материалов журнала образуют оригинальные статьи, в которых квалифицированные специалисты по истории и философии науки и техники публикуют результаты своих исследований. Журнал издается под руководством Президиума РАН.
Журнал издается под руководством Президиума РАН.
Show more
Voprosy Jazykoznanija
Тематика журнала: теория языка, ареальное, типологическое и сравнительно-историческое изучение языков мира, а также социолингвистика, корпусная и компьютерная лингвистика, психолингвистика и смежные дисциплины.
Show more
Vostok. Afro-Aziatskie obshchestva: istoriia i sovremennost
vostokoriens.jes.su
Журнал издается под руководством Отделения историко-филологических наук РАН. В журнале публикуются статьи по актуальным вопросам истории, экономики, политики, культуры, экономики, социологии, литературы и языка стран зарубежного и российского Востока.
Show more
Удельное электрическое сопротивление | Определение, формула, символ, единицы измерения
Что такое удельное электрическое сопротивление? Удельное электрическое сопротивление – это электрическое сопротивление конкретного образца материала единичной длины и единичной площади поперечного сечения. Удельное электрическое сопротивление показывает сопротивление тока проводника.
Удельное электрическое сопротивление показывает сопротивление тока проводника.
Если сопротивление образца материала длиной 1 метр и площадью поперечного сечения 1 квадратный метр составляет 1 Ом. Это означает, что удельное сопротивление материала равно 1 Омметр.
Чем сильнее сопротивление, тем выше удельное сопротивление и меньше ток, проходящий через него. Поэтому удельное сопротивление материала имеет первостепенное значение в электротехнике.
Легко сравнить использование различных материалов на основе их удельного сопротивления.
Удельное сопротивление различных материалов указано в таблице ниже.
| Материал | Удельное сопротивление (Ом-м) при 20°C |
| Silver | 1.59×10 −8 |
| Copper | 1.68×10 −8 |
| Gold | 2.44×10 −8 |
| Aluminum | 2.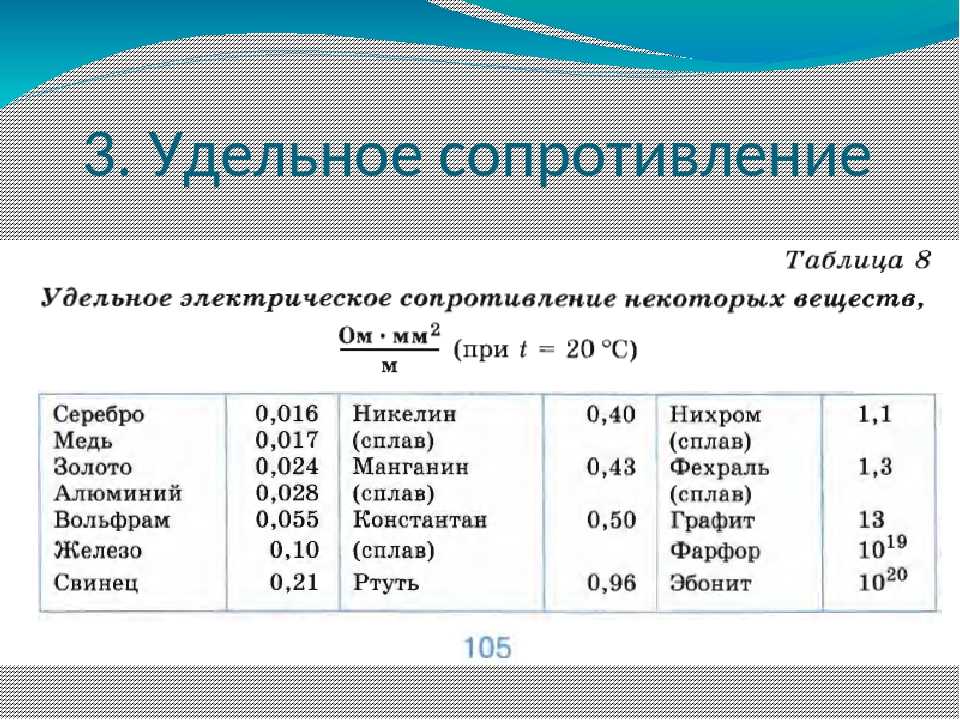 82×10 −8 82×10 −8 |
| Tungsten | 5.60×10 −8 |
| Zinc | 5.90×10 −8 |
| Nickle | 6.99×10 −8 |
Серебро имеет наименьшее удельное сопротивление среди всех металлов. Медь имеет меньшее удельное сопротивление по сравнению с алюминием. Поэтому медь является лучшим проводником электричества.
Удельное сопротивление изоляторов находится в диапазоне от 1012 до 1020 Ом·метров. Таким образом, изоляторы обладают отличным свойством блокирования тока.
Удельное сопротивление проводящих материалов увеличивается с повышением температуры. Электроны сталкиваются и препятствуют прохождению электрического тока при более высоких температурах. В результате удельное сопротивление проводника увеличивается с повышением температуры.
В противоположность этому удельное сопротивление изоляторов и полупроводников уменьшается с повышением температуры. В результате эти материалы начинают легко пропускать через себя электрический ток. Если повышение температуры превышает максимально допустимый температурный предел, изолятор выходит из строя.
В результате эти материалы начинают легко пропускать через себя электрический ток. Если повышение температуры превышает максимально допустимый температурный предел, изолятор выходит из строя.
Точно так же удельное сопротивление полупроводников уменьшается с повышением температуры. Следовательно, изоляторы и полупроводники надежно функционируют, если температура остается значительно ниже максимально допустимого диапазона температур,
Символ удельного электрического сопротивленияСимвол удельного электрического сопротивления , обозначаемый греческой буквой ρ (rho) , численно равен сопротивлению R образца материала, такого как шина, умноженному на площадь поперечного сечения A и на длину L; ( ρ =RA/L).
Формула удельного электрического сопротивленияСопротивление проводника зависит от следующих параметров.
- Resistivity of the material
- Cross-sectional area
- Length
Derivation of electrical resistivity equation/ Formula
R ∝ ρ ——-(1) R ∝ L -—- (2) R ∝ 1 / A ——- (3)
Таким образом,
R = ρ 110 L / A— —- (4)
ρ = RA/L ——-(5)
Здесь R — сопротивление в Ом ( Ом )
A = Площадь поперечного сечения в см 2 или м 2
проводник в сантиметрах (см) или метрах (м)
ρ = Удельное сопротивление материала ( Ом -см) или ( Ом -м)
Удельное электрическое сопротивление материала прямо пропорциональна площади поперечного сечения и обратно пропорциональна длине.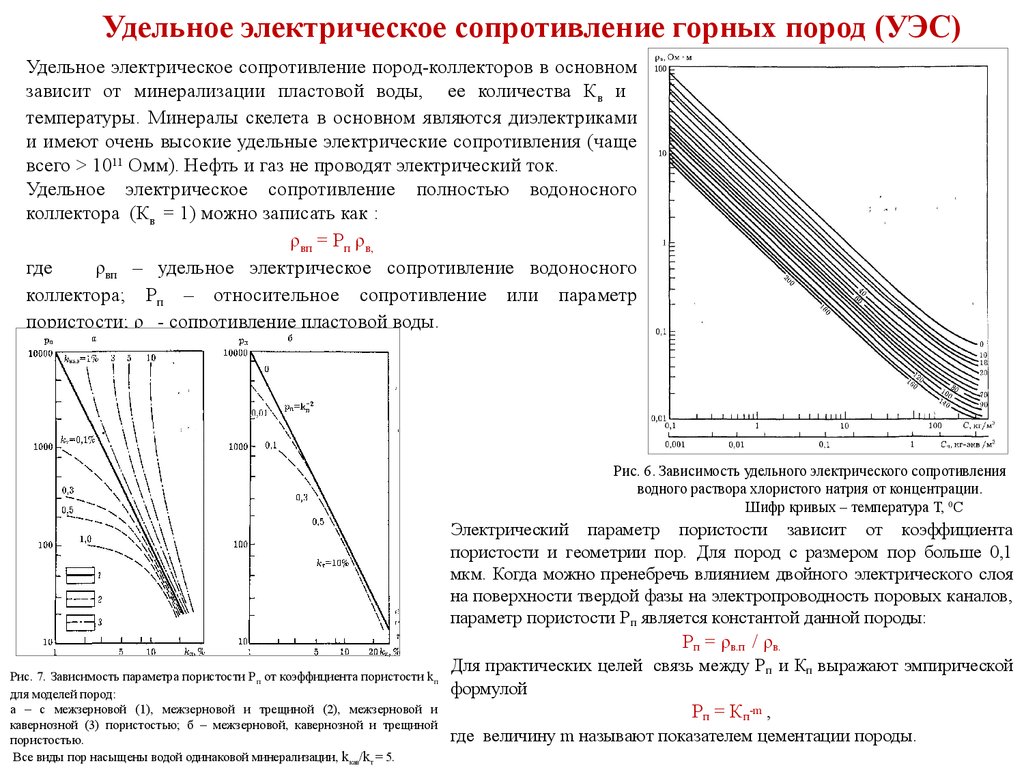
ρ ∝ RA, также ρ ∝ L
Следовательно,
ρ ∝ R (a/l)
Выше надлежащим образом. Сопротивление
ρ 111111111111111111111111111111111111111111111111111111111111111111111111110
. R(A/L)
ρ ∝ Ом(см 2 /см) ∝ Ом-сантиметры
Единицей сопротивления является Ом. В системе мкс (метр-килограмм-секунда) соотношение площади и длины упрощается до нескольких метров. Так, в системе МКС единицей удельного сопротивления является ом-метр. Если длина и площадь поперечного сечения выражены в сантиметрах и квадратных сантиметрах соответственно, то единица удельного сопротивления равна 9.0003 Ом-сантиметр.
Обратной величиной удельного сопротивления является проводимость. Электропроводность показывает способность материала пропускать через себя электрический ток.
Решенные задачи по удельному электрическому сопротивлениюЗадача 1:
Рассчитайте удельное сопротивление данного материала, сопротивление, площадь поперечного сечения и длина которого равны 4 Ом , 50 см 260 ?
Приведены данные,
R = 4 Ом
L = 30 см = 0,3 м
A = 50 см 2 = 0,25 м 2
Формула устойчиво
=( 4 x 0,25)/0,3
= 3,33 Ом·м
Задача 2:
Проводник имеет длину, площадь и сопротивление 0,4 м, 1,5 м 2 и 2 0,4 м соответственно.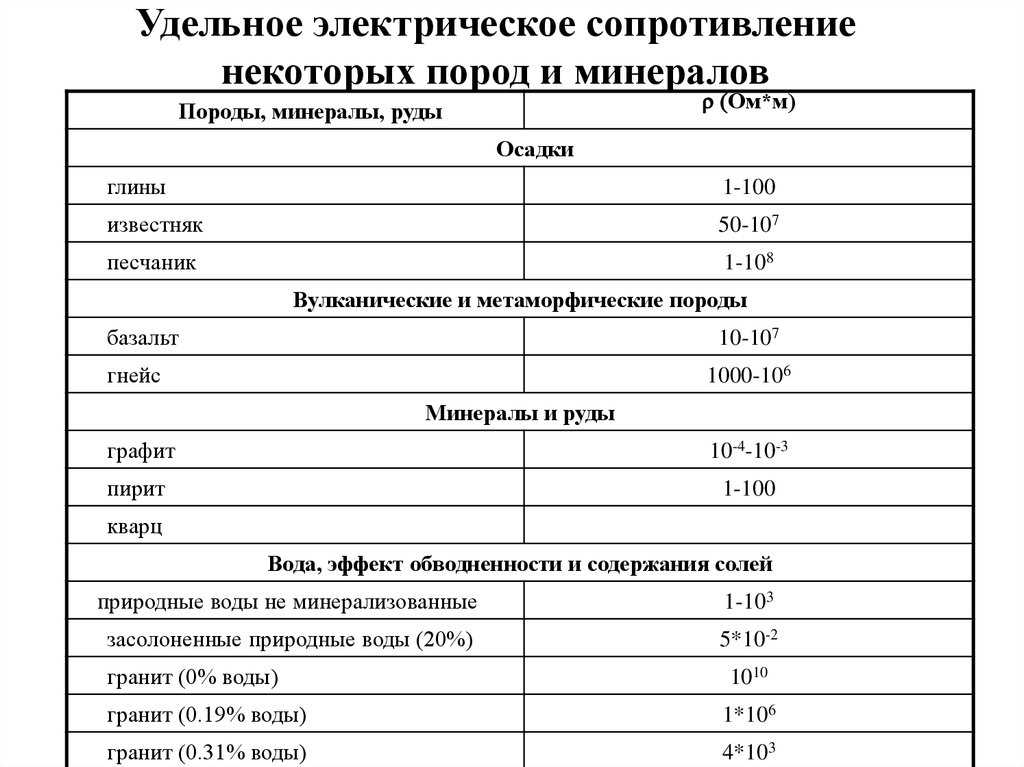 Вычислить удельное сопротивление?
Вычислить удельное сопротивление?
Дано
R = 2 Ом
L = 0,4 м и
A = 1,5 м 2
Формула удельного сопротивления
ρ = RA/L
= (2 x 1,5) /0.4
= 7,5 ωm
Задача 3: 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444 4.
Рассчитайте сопротивление 100-метрового провода с однородной площадью поперечного сечения 0,2 мм 2 , если провод изготовлен из манганина с удельным сопротивлением 50 × 10 -8 Ом-м. ℓ = 100 метров
A = 0,2 мм 2 = 0,2 X 10 -6 м 2
ρ = 50 × 10 -8 Ом-м.
Задача 4
Сопротивление проводника сечением 1 мм2 и длиной 40 м равно 0,692 Ом. Определить удельное сопротивление проводящего материала.
ℓ = 10 м
A = 1 мм 2 = 1 X 10 -6 м
R = 0,692 Ом
ρ = ?
Читать далее:
Похожие сообщения:
Подпишитесь на нас и поставьте лайк:
ВведениеПонимание того, как удельное электрическое сопротивление (или проводимость) связано с реальными геологическими свойствами земли, имеет важное значение. На следующие вопросы он может помочь ответить:
В этой главе электрические свойства геологических материалов обсуждаются отдельно для металлических минералов, горных пород, почв и электролитов (подземных флюидов). Что такоеудельное сопротивление ?Электропроводность (или удельное сопротивление) — это объемное свойство материала, описывающее, насколько хорошо этот материал пропускает через себя электрический ток.
Электропроводность земных материалов варьируется на много порядков. Это зависит от многих факторов, в том числе: типа породы, пористости, связности пор, природы жидкости и содержания металлов в твердой матрице. Очень приблизительное указание диапазона проводимости горных пород и минералов показано на следующем рисунке. Напоминание об этом разделе описывает факторы, влияющие на электропроводность минералов, горных пород, жидкостей в земле, почв Электропроводность металлических минералов Металлические рудные минералы встречаются относительно редко по сравнению с другими материалами земной коры. Тем не менее, они часто являются целью разведки полезных ископаемых. Даже в небольших количествах они могут существенно влиять на объемное удельное сопротивление геологических материалов.
Хотя металлические минералы (особенно сульфиды) могут быть проводящими, существуют как минимум две причины, по которым месторождения этих минералов с содержанием руды могут быть не такими проводящими, как ожидалось.
Электрические свойства горных пород Из всех геофизических свойств горных пород удельное электрическое сопротивление является наиболее изменчивым. Могут встречаться значения в диапазоне до 10 порядков, и даже отдельные типы горных пород могут различаться на несколько порядков. Следующий рисунок представляет собой репрезентативную диаграмму (адаптированную из Palacky , 1987), иллюстрирующую в очень общем виде, как удельные сопротивления важных групп горных пород сравниваются друг с другом.
Большая часть наших знаний об удельном сопротивлении пористых пород пришла из индустрии каротажа нефтяных и газовых скважин. Влияние жидкостей, отличных от воды, закон Арчи, коэффициент формирования и т. Д. Подробно описаны в следующих нескольких разделах. Электролиты в землеЭлектропроводность жидкостей зависит от количества и подвижности (скорости) носителей заряда. Подвижность зависит от вязкости жидкости (следовательно, температуры) и диаметра носителей заряда. Температурная зависимость существенна. Для растворов хлорида натрия изменение проводимости составляет примерно 2,2% на градус Цельсия. Таким образом, изменение на 40 o °С удваивает проводимость. На иллюстрации, показывающей проводимость воды в Великих озерах (ниже), сравните проводимость в изверженных (западных) и осадочных (восточных) регионах и обратите внимание на зависимость проводимости от температуры вод этих озер.
, где R — удельное сопротивление, t — температура, а a — приблизительно 0,025, где R 18C — удельное сопротивление при комнатной температуре (18 градусов С). Напомним, что удельное сопротивление = 1/проводимость. Влияние пористостиНасыщенные чистые (без глины) почвы или горные породы: Эмпирическая формула Арчи связывает пористость и проводимость воды с объемной проводимостью для различных консолидированных горных пород, а также для рыхлых материалов. Другой способ выражения соотношения Арчи, чаще используемый в каротажных работах для нефтегазовых скважин, выглядит следующим образом: F=1/ м , где F , «коэффициент формации », равен F = Ro/ Rw , Ro – объемное удельное сопротивление, если поровое пространство на 100% заполнено рассолом (связанной водой), Rw – удельное сопротивление самой связанной воды, и – пористость. Как всегда, не путайтесь с использованием проводимости или удельного сопротивления — они просто обратны друг другу.
В фуникулярной зоне грунтов (рисунок справа) влага не полностью заполняет поровые пространства, но пути проводимости все же имеются. Можно использовать закон, аналогичный закону Арчи, где n теперь представляет собой долю объема пор, заполненную электролитом, а не пористость, а m = 2 . Используя это, проводимость оказывается очень малой при низком содержании влаги. Однако «смачивание» материала имеет решающее значение для воздействия на проводимость, а слегка влажные материалы обладают гораздо большей проводимостью, чем сухие материалы. Следовательно, водонасыщенность можно оценить, если
Это похоже на определение водонасыщенности, Sw , когда часть порового пространства заполнена нефтью или газом, как это часто делается по данным ГИС в углеводородных коллекторах. Удельное сопротивление грунтов Электропроводность грунтов довольно сложная, на объемные свойства влияет множество факторов. Пористость колеблется от 20% до 70% для большинства рыхлых материалов (т.е. для грунтов). Тем не менее, не является обычным иметь большой диапазон пористости в одной ситуации. Как отмечалось выше, пористость является основным свойством, связанным с удельным сопротивлением, поэтому трудно отличить песок от гравия с одинаковой пористостью. Влияние замерзания на проводимость почв Снижение температуры снижает электролитическую активность и, следовательно, проводимость. На рисунке справа показан этот эффект с точки зрения удельного сопротивления. При замерзании проводимость воды становится проводимостью льда, что очень мало. Конечным эффектом является небольшое и устойчивое снижение проводимости по мере приближения температуры к температуре замерзания, затем выравнивание до 0 градусов и дальнейшее снижение ниже точки замерзания. Коллоидная проводимость(проводимость глины) Сложность и разнообразие типов почв показаны на тройной диаграмме внизу слева. Не нужно много глины, чтобы изменить электрические свойства почвы. Любой мелкозернистый минерал обладает определенной емкостью катионного обмена (ЕЕС). То есть заряды (катионы) могут быть d сорбируются (прикрепляются к поверхности) на слегка отрицательно заряженной поверхности, и их впоследствии можно заменить или растворить.
Поскольку глина имеет огромное отношение площади поверхности к объему, она обладает гораздо более высокой обменной способностью. Анизотропный грунт
Вертикально анизотропный грунт: Горизонтально анизотропный грунт: Противоречащий здравому смыслу эффект: Почему возникает анизотропия:
где Дж — векторная плотность тока, Дж i — i th компонента плотности тока, E — вектор электрического поля, В — 90 3 напряжение и8 ik th компонента тензора проводимости. Аспекты почвообразования, влияющие на электрические свойства почв Стоит обсудить формирование грунтов, чтобы лучше понять, что происходит при прогнозировании электрических свойств приповерхностных материалов и при интерпретации неглубоких геофизических исследований. Это обсуждение не заменяет курс по почвоведению, но некоторые вопросы, влияющие на удельное электрическое сопротивление, должны стать более понятными. Выветривание включает механические, химические и биологические процессы, которые превращают поверхностные материалы в гумус (вещество органического происхождения), глину и мелкозернистые отложения. В присутствии воды и СО 2 породы расщепляются на ионы (часто растворяются и удаляются дренажем), образуются глинистые минералы, вода расходуется (входит в состав глинистых соединений), растворы становятся более щелочными (т.е. менее кислый). Этот процесс является самовоспроизводящимся, поскольку тонкий слой почвы вызывает более быстрое протекание соответствующих процессов на поверхности породы. Это потому, что слой удерживает воду и CO 2 , который производит слабую угольную кислоту, которая соединяется с компонентами горных пород с образованием глин.
На влажность почвы влияют несколько факторов. См. рис. 7 выше:
ПРИМЕЧАНИЕ: обсуждаемые здесь процессы являются естественными. При наличии конструкционного материала поверхностная слоистость может быть совершенно иной. Ссылки
| |||||||||||||||||||||||||||||||||||||
Обзор измерений удельного электрического сопротивления и расчетов Fe и Fe-сплавов, относящихся к планетарным ядрам планетарные ядра. Для планетарных тел земного типа, которые содержат преимущественно ядра Fe, приложениями являются тепловая эволюция ядра, которая включает замораживание внутреннего ядра и поддержание динамо.
 Для моделирования тепловой эволюции активной зоны необходим адиабатический тепловой поток, который обычно рассчитывается через коэффициент теплопроводности ( к ). Хотя ρ и k металлов напрямую связаны с переносом заряда и энергии электронами, соответственно, следующая цитата указывает на допустимость изменения каждого из этих свойств в связи с нашим пониманием основных процессов. Фактор неопределенности ρ, равный двум или около того, не кажется критическим для теории динамо, но оказывает сильное влияние на расчеты теплового режима активной зоны. » (Стейси и Андерсон, 2001). Литература по ρ чистого железа богата, и значения разбросаны, в то время как сообщаемые данные по сплавам Fe более скудны, но менее разбросаны. Несоответствия в измерениях и моделировании могут быть результатом различных методов в дополнение к диапазону давлений и температур, приписываемых планетарным ядрам. Большая часть общей работы была выполнена за последнее десятилетие, и на рисунке 1 показано совокупное количество статей, опубликованных по ρ чистого Fe и Fe-сплавов за последние полвека.
Для моделирования тепловой эволюции активной зоны необходим адиабатический тепловой поток, который обычно рассчитывается через коэффициент теплопроводности ( к ). Хотя ρ и k металлов напрямую связаны с переносом заряда и энергии электронами, соответственно, следующая цитата указывает на допустимость изменения каждого из этих свойств в связи с нашим пониманием основных процессов. Фактор неопределенности ρ, равный двум или около того, не кажется критическим для теории динамо, но оказывает сильное влияние на расчеты теплового режима активной зоны. » (Стейси и Андерсон, 2001). Литература по ρ чистого железа богата, и значения разбросаны, в то время как сообщаемые данные по сплавам Fe более скудны, но менее разбросаны. Несоответствия в измерениях и моделировании могут быть результатом различных методов в дополнение к диапазону давлений и температур, приписываемых планетарным ядрам. Большая часть общей работы была выполнена за последнее десятилетие, и на рисунке 1 показано совокупное количество статей, опубликованных по ρ чистого Fe и Fe-сплавов за последние полвека. На момент написания этой статьи четыре исследования, отмеченные на Рисунке 1, в сумме насчитывали более 1000 цитирований и считаются ответственными за повышенный уровень активности после их публикации. В этом обзоре делается попытка обобщить как более ранние, так и недавние результаты, чтобы определить диапазон надежных и репрезентативных значений ρ ядер планетарных тел земного типа, состоящих из чистого Fe или Fe-сплавов.
На момент написания этой статьи четыре исследования, отмеченные на Рисунке 1, в сумме насчитывали более 1000 цитирований и считаются ответственными за повышенный уровень активности после их публикации. В этом обзоре делается попытка обобщить как более ранние, так и недавние результаты, чтобы определить диапазон надежных и репрезентативных значений ρ ядер планетарных тел земного типа, состоящих из чистого Fe или Fe-сплавов.РИСУНОК 1 . Совокупное количество публикаций по теоретическим и экспериментальным методам оценки ρ сплавов Fe, Fe-Ni, Fe-O и Fe-Si и S в условиях ядра Земли, Луны, Меркурия, Марса и Ганимеда.
Общая формула адиабатического теплового потока ядра описывается следующим образом: ускорение свободного падения, T – температура в верхней части активной зоны, а Cp – теплоемкость при постоянном давлении ( P ). Прямые измерения k трудно выполнить на соответствующих ядрам P и T . Напротив, прямые измерения электропроводности (σ), которая обратно пропорциональна ρ, достижимы с относительно высокой точностью. Эти две переменные могут быть связаны через электронный компонент k ( k e ) с законом Видемана-Франца (WFL), где L число Лоренца:
Эти две переменные могут быть связаны через электронный компонент k ( k e ) с законом Видемана-Франца (WFL), где L число Лоренца:
ke=LTσ=LT/ρ(2)
Теплопроводность контролируется электронами и фононами, но фононный вклад пренебрежимо мал в металлах и металлических сплавах (Klemens and Williams, 1986). Соответствующие значения числа Лоренца для конкретных композиций при соответствующих T ограничены недостаточно. Теоретическое значение, значение Зоммерфельда (L0 = 2,44·10 −8 Вт·Ом·K −2 ), как было показано, составляет более 99% от k e для Fe, что позволяет предположить, что его использование при высоких T и P < 6 ГПа является разумным (Secco, 2017). В то время как L > L 0 для сплавов Fe-Si при высоких T и низких P (Secco, 2017), расчеты в условиях ядра Земли P , T 901 L 101111 < L 0 (de Koker et al. , 2012; Xu et al., 2018). Следующее соотношение было получено на основе измерений коэффициента Зеебека Fe до 6 ГПа и 2 100 K (Secco, 2017):
, 2012; Xu et al., 2018). Следующее соотношение было получено на основе измерений коэффициента Зеебека Fe до 6 ГПа и 2 100 K (Secco, 2017):
[dLdP]граница расплава, <5 ГПа=ρkeKTT{13−KTT(dTdP)граница расплава, <5 ГПа} = -3,98⋅10−10WΩK2ГПа(3)
где K объемный модуль. Для металлов в целом ρ определяется скоростью рассеяния электронов проводимости. Точно так же было показано, что число Лоренца может быть как ниже, так и выше L 0 в зависимости от состояния и состава системы (Pozzo et al., 2012; Pozzo et al., 2013; Pozzo et al., 2014; Поццо и Альфе, 2016а; Поццо и Альфе, 2016б; Пуровский и др., 2020). На скорость рассеяния электронов проводимости влияют электрон-фононные, электрон-магнонные и электрон-электронные взаимодействия. Удельное электрическое сопротивление обратно пропорционально длине свободного пробега электрона ( d ), которая пропорциональна амплитудам колебаний атомов ( A ) и, таким образом, пропорциональна T :
ρ∝ 1d∝A2∝ T(4)
Электрон-фононные взаимодействия – это рассеяние электронов, вызванное колебания решетки и относительно незначительны при низких T . При высоких T заполнение фононной плотности состояний смещается в сторону более высоких энергетических состояний, что увеличивает частоту столкновений с электронами проводимости. Электронно-магнонные взаимодействия или рассеяние спинового беспорядка имеют значение только для ферромагнитных металлов, таких как Fe и их ферромагнитных сплавов. Это взаимодействие увеличивает рассеяние в зависимости от T 2 до Кюри T ( T c ) и доминирует в ρ примерно до 300 K. скорость рассеяния электронов проводимости. Увеличенные дефекты решетки вызывают возмущения электронной структуры и более короткую длину свободного пробега электронов, что приводит к большему ρ. Взаимодействия между электронами и дефектами решетки преобладают над электрон-фононными, электрон-магнонными и электрон-электронными взаимодействиями при низких Т . В целом, чистый эффект T заключается в увеличении ρ, в то время как ρ уменьшается с P , поскольку уменьшенная амплитуда колебаний решетки увеличивает длину свободного пробега электрона.
При высоких T заполнение фононной плотности состояний смещается в сторону более высоких энергетических состояний, что увеличивает частоту столкновений с электронами проводимости. Электронно-магнонные взаимодействия или рассеяние спинового беспорядка имеют значение только для ферромагнитных металлов, таких как Fe и их ферромагнитных сплавов. Это взаимодействие увеличивает рассеяние в зависимости от T 2 до Кюри T ( T c ) и доминирует в ρ примерно до 300 K. скорость рассеяния электронов проводимости. Увеличенные дефекты решетки вызывают возмущения электронной структуры и более короткую длину свободного пробега электронов, что приводит к большему ρ. Взаимодействия между электронами и дефектами решетки преобладают над электрон-фононными, электрон-магнонными и электрон-электронными взаимодействиями при низких Т . В целом, чистый эффект T заключается в увеличении ρ, в то время как ρ уменьшается с P , поскольку уменьшенная амплитуда колебаний решетки увеличивает длину свободного пробега электрона. Критерий Иоффе-Регеля утверждает, что рост удельного сопротивления снижается с увеличением T, т. е. достигает насыщения, когда длина свободного пробега электронов приближается к межатомному расстоянию (Mooij, 1973; Wiesmann et al., 1977; Gurvitch, 1981). Боненкамп и др. (2002) оценили значение насыщения 1,68 мкОм·м для Fe при 1 атм и температуре до 1663 К, в то время как значение насыщения сплавов Fe-Si варьируется при высоких температурах P (Kiarasi, Secco, 2015; Gomi et al., 2016). Гоми и др. (2013) были первыми, кто предложил идею насыщения удельного сопротивления Fe в условиях ядра Земли, однако недавняя работа (Zhang et al., 2020) дает противоречивые результаты и предполагает, что поведение насыщения удельным сопротивлением было экспериментальным артефактом.
Критерий Иоффе-Регеля утверждает, что рост удельного сопротивления снижается с увеличением T, т. е. достигает насыщения, когда длина свободного пробега электронов приближается к межатомному расстоянию (Mooij, 1973; Wiesmann et al., 1977; Gurvitch, 1981). Боненкамп и др. (2002) оценили значение насыщения 1,68 мкОм·м для Fe при 1 атм и температуре до 1663 К, в то время как значение насыщения сплавов Fe-Si варьируется при высоких температурах P (Kiarasi, Secco, 2015; Gomi et al., 2016). Гоми и др. (2013) были первыми, кто предложил идею насыщения удельного сопротивления Fe в условиях ядра Земли, однако недавняя работа (Zhang et al., 2020) дает противоречивые результаты и предполагает, что поведение насыщения удельным сопротивлением было экспериментальным артефактом.
Методы определения удельного электрического сопротивления
Теория: расчеты из первых принципов
Первоначально предназначенная для описания диффузии газов в атмосфере, Больцман (1894) разработал следующее уравнение, которое учитывает электронную зонную структуру, фононную дисперсию и электрон-фононное взаимодействие:
ρ=πΩkBTN(εF)VF2 λtr(5)
спин на уровне энергии Ферми (ε F ), kB — постоянная Больцмана, Ω — объем элементарной ячейки, VF — скорость Ферми, λtr — коэффициент переноса. За этой работой последовало введение модели свободных электронов Зоммерфельдом (1928), основанный на классической модели электропроводности Друде (Друде, 1900а; Друде, 1900б) и статистике Ферми-Дирака, описывающей распределение частиц по энергетическим состояниям. Модель предсказывает σ по плотности электронов, среднему времени свободного пробега (время между столкновениями) и заряду электрона. Модель включает множество соотношений, в том числе закон Видемана-Франца, коэффициент Зеебека термоэлектрического эффекта и форму функции электронной плотности состояний. В своем анализе вариаций магнитного поля Земли Эльзассер (1946) оценил ρ ядра из чистого Fe из теории электронной проводимости, которая утверждает, что σ обратно пропорционально абсолютному T и прямо пропорционально квадрату температуры Дебая (Θ D ).
За этой работой последовало введение модели свободных электронов Зоммерфельдом (1928), основанный на классической модели электропроводности Друде (Друде, 1900а; Друде, 1900б) и статистике Ферми-Дирака, описывающей распределение частиц по энергетическим состояниям. Модель предсказывает σ по плотности электронов, среднему времени свободного пробега (время между столкновениями) и заряду электрона. Модель включает множество соотношений, в том числе закон Видемана-Франца, коэффициент Зеебека термоэлектрического эффекта и форму функции электронной плотности состояний. В своем анализе вариаций магнитного поля Земли Эльзассер (1946) оценил ρ ядра из чистого Fe из теории электронной проводимости, которая утверждает, что σ обратно пропорционально абсолютному T и прямо пропорционально квадрату температуры Дебая (Θ D ).
ρ∝ ΘD−2 (6)
Температура Дебая пропорциональна скорости звука и частоте отсечки акустических фононов и обратно пропорциональна объему (Kittel, 2005). Ziman (1960) позже описал модель почти свободных электронов, которая основана на поведении электронов, ионов и дырок. В модели свободного электрона разрешены все энергетические состояния от 0 до ∞, тогда как модель почти свободного электрона допускает слабые возмущения электронов периодическими потенциальными ионами. Следуя этой идее, Зиман (1961) разработал теорию поведения жидких металлов. Эта модель была модифицирована Evans et al. (1971), чтобы включить матричный член перехода, вводя более сложный метод расчета ρ металлической жидкости для металлов, которые имеют пустые состояния d-зоны, в которые могут перескакивать электроны s-проводимости (переходы s-d):
Ziman (1960) позже описал модель почти свободных электронов, которая основана на поведении электронов, ионов и дырок. В модели свободного электрона разрешены все энергетические состояния от 0 до ∞, тогда как модель почти свободного электрона допускает слабые возмущения электронов периодическими потенциальными ионами. Следуя этой идее, Зиман (1961) разработал теорию поведения жидких металлов. Эта модель была модифицирована Evans et al. (1971), чтобы включить матричный член перехода, вводя более сложный метод расчета ρ металлической жидкости для металлов, которые имеют пустые состояния d-зоны, в которые могут перескакивать электроны s-проводимости (переходы s-d):
ρ=3πΩ0e2ℏVF2 ∫01d(q2KF)*4(q2KF)*a(q)*|t(q2KF)|2(7)
где e — заряд электрона, KF — радиус поверхности Ферми, q=K− K’ относится к углу рассеяния поверхности Ферми, Ω0 – атомный объем жидкости, a(q) – структурный фактор, ℏ – модифицированная постоянная Планка, t(K, K’) – матрица перехода, которая описывает сечение рассеяния, связанное с рассеянием s-электронов в d-диапазоне (s-d). Хотя эта формулировка фокусируется на жидком состоянии металла, Мотт (1972) и Мотт (1980) вывели соотношение для твердого состояния металла. Теория Мотта учитывает тепловой и примесный вклады, а также магнитный вклад в ферромагнитных металлах. Теория описывает связь между ρ и площадью поверхности Ферми ( S F ). Соотношение можно записать следующим образом:
Хотя эта формулировка фокусируется на жидком состоянии металла, Мотт (1972) и Мотт (1980) вывели соотношение для твердого состояния металла. Теория Мотта учитывает тепловой и примесный вклады, а также магнитный вклад в ферромагнитных металлах. Теория описывает связь между ρ и площадью поверхности Ферми ( S F ). Соотношение можно записать следующим образом:
ρ=12π3ℏSFe2d(8)
Более сложная и часто используемая формула Кубо-Гринвуда (Kubo, 1957; Greenwood, 1958) описывает частотно-зависимую электронную проводимость и дает линейный вклад к текущему ответу. T зависимость ρ, связанная с электрон-фононным взаимодействием, описывается уравнением Блоха–Грюнайзена. В сочетании с уравнением Блоха–Грюнайзена для ρ как функции объема ( V ) и T уравнение Кубо–Гринвуда можно записать следующим образом:
ρ(V,T) = ρ0R[VVR]a+ ρ1R[VVR]bTTR(9)
где a и b – константы, относящиеся к объемной зависимости частот колебаний, индекс R относится к эталонному состоянию, а ρ0R и ρ1R — параметры модели, зависящие от состава (de Koker et al. , 2012). Электронная структура системы может быть исследована с помощью теории функционала плотности (DFT), которая в основном описывает потенциальные энергии системы. Подход DFT исследует приближенное решение уравнения Шрёдингера в 3D на основе плотности электронов, что приводит к решениям для потенциальных энергий ион-электрон, ион-ион и электрон-электрон (Аргаман и Маков, 2000). Теория динамического среднего поля (DMFT), часто используемая в сочетании с DFT, представляет собой мощную численную аппроксимацию потенциала системы многих частиц, такой как электроны в твердых телах. Сложная многочастичная система изучается путем сведения ее к более простой одночастичной системе с внешним средним полем. Внешнее поле по существу объясняет другие частицы в дополнение к взаимодействиям и локальным квантовым флуктуациям, которые могут иметь место в системе многих частиц (Vollhardt et al., 2012). Дрчал и др. (2019) и Корелл и др. (2019) исследовали влияние магнетизма на электронные свойства металлов с помощью уравнения Кубо-Гринвуда наряду с DFT и методом Tight-Binding Linear Muffin-Tin Orbital (метод расчета короткодействующих переходов между электронами в s-, d — и f- орбитали) соответственно.
, 2012). Электронная структура системы может быть исследована с помощью теории функционала плотности (DFT), которая в основном описывает потенциальные энергии системы. Подход DFT исследует приближенное решение уравнения Шрёдингера в 3D на основе плотности электронов, что приводит к решениям для потенциальных энергий ион-электрон, ион-ион и электрон-электрон (Аргаман и Маков, 2000). Теория динамического среднего поля (DMFT), часто используемая в сочетании с DFT, представляет собой мощную численную аппроксимацию потенциала системы многих частиц, такой как электроны в твердых телах. Сложная многочастичная система изучается путем сведения ее к более простой одночастичной системе с внешним средним полем. Внешнее поле по существу объясняет другие частицы в дополнение к взаимодействиям и локальным квантовым флуктуациям, которые могут иметь место в системе многих частиц (Vollhardt et al., 2012). Дрчал и др. (2019) и Корелл и др. (2019) исследовали влияние магнетизма на электронные свойства металлов с помощью уравнения Кубо-Гринвуда наряду с DFT и методом Tight-Binding Linear Muffin-Tin Orbital (метод расчета короткодействующих переходов между электронами в s-, d — и f- орбитали) соответственно. Корелл и др. (2019) предположили, что необходимо учитывать спиновую поляризацию, чтобы согласовать расчеты ρ из первых принципов с измерениями. Помимо аналогичного вывода, Drchal et al. (2019) предположил, что вклады различных механизмов рассеяния (вызванных электрон-фононными взаимодействиями, электрон-магнонными взаимодействиями, электрон-электронными взаимодействиями и дефектами электрон-решетки) сравнимы, но не аддитивны. Благодаря этим расчетам из первых принципов, для которых требуются значения тепловых свойств при эталоне P и T , теоретические исследования могут оценить ρ любого металла или металлических сплавов.
Корелл и др. (2019) предположили, что необходимо учитывать спиновую поляризацию, чтобы согласовать расчеты ρ из первых принципов с измерениями. Помимо аналогичного вывода, Drchal et al. (2019) предположил, что вклады различных механизмов рассеяния (вызванных электрон-фононными взаимодействиями, электрон-магнонными взаимодействиями, электрон-электронными взаимодействиями и дефектами электрон-решетки) сравнимы, но не аддитивны. Благодаря этим расчетам из первых принципов, для которых требуются значения тепловых свойств при эталоне P и T , теоретические исследования могут оценить ρ любого металла или металлических сплавов.
Эксперименты
Статика: Пресс с несколькими наковальнями
Статические эксперименты обычно проводятся в прессе с несколькими упорами. Типичный пресс с несколькими упорами использует гидравлические насосы для одноосного привода гидравлического плунжера для сжатия ячейки давления, расположенной в центре набора упоров из карбида вольфрама (WC). Например, в 3000-тонном прессе в Университете Западного Онтарио есть три стальных клина в нижней и три клина в верхней части модуля давления. Клинья обеспечивают гнездо для восьми усеченных кубов туалета, которые вмещают и сходятся на восьмигранной сборке камеры давления. Октаэдрическая ячейка может различаться по размеру в зависимости от длины ребра усечения (TEL) кубов WC. TEL может варьироваться от 3 до 25 мм, а наименьшие размеры используются для достижения более высоких P , хотя и на меньших объемах выборки. Октаэдрические ячейки давления обычно состоят из оксида магния (MgO), который обеспечивает баланс между обрабатываемостью, низкой k и твердостью, что позволяет эффективно преобразовывать приложенную силу к образцу внутри. При сжатии октаэдрическая ячейка выдавливается между кубами туалета, создавая прокладки. Точно так же другие конструкции устройств с несколькими наковальнями, такие как пресс с кубическими наковальнями, который состоит из шести наковален WC, которые сжимают сборку кубических ячеек давления, обычно изготовленную из минерального пирофиллита, создают прокладки, когда ячейка выдавливается между наковальнями.
Например, в 3000-тонном прессе в Университете Западного Онтарио есть три стальных клина в нижней и три клина в верхней части модуля давления. Клинья обеспечивают гнездо для восьми усеченных кубов туалета, которые вмещают и сходятся на восьмигранной сборке камеры давления. Октаэдрическая ячейка может различаться по размеру в зависимости от длины ребра усечения (TEL) кубов WC. TEL может варьироваться от 3 до 25 мм, а наименьшие размеры используются для достижения более высоких P , хотя и на меньших объемах выборки. Октаэдрические ячейки давления обычно состоят из оксида магния (MgO), который обеспечивает баланс между обрабатываемостью, низкой k и твердостью, что позволяет эффективно преобразовывать приложенную силу к образцу внутри. При сжатии октаэдрическая ячейка выдавливается между кубами туалета, создавая прокладки. Точно так же другие конструкции устройств с несколькими наковальнями, такие как пресс с кубическими наковальнями, который состоит из шести наковален WC, которые сжимают сборку кубических ячеек давления, обычно изготовленную из минерального пирофиллита, создают прокладки, когда ячейка выдавливается между наковальнями. Изоляционный материал, печь, образец и электроды помещаются внутрь ячейки и располагаются коаксиально в отверстии, соединяющем две противоположные стороны. Повышенные температуры создаются джоулевым нагревом электростойкой печи, обычно сделанной из графита, хромита лантана или рениевой фольги, окружающей образец. Электрическое сопротивление ( R ) образца измеряют четырехпроводным методом, при котором пара проводов термопары размещается на каждом конце образца. Каждая пара действует как датчик температуры, а противоположные пары назначаются как потенциальные и токовые выводы в переключаемой конфигурации схемы. Затем рассчитывается удельное электрическое сопротивление с использованием следующего уравнения, которое объединяет закон Ома и закон Пуйе:
Изоляционный материал, печь, образец и электроды помещаются внутрь ячейки и располагаются коаксиально в отверстии, соединяющем две противоположные стороны. Повышенные температуры создаются джоулевым нагревом электростойкой печи, обычно сделанной из графита, хромита лантана или рениевой фольги, окружающей образец. Электрическое сопротивление ( R ) образца измеряют четырехпроводным методом, при котором пара проводов термопары размещается на каждом конце образца. Каждая пара действует как датчик температуры, а противоположные пары назначаются как потенциальные и токовые выводы в переключаемой конфигурации схемы. Затем рассчитывается удельное электрическое сопротивление с использованием следующего уравнения, которое объединяет закон Ома и закон Пуйе:
ρ=ΔEI⋅Al(10)
, где Δ E — падение напряжения на образце, I — входной ток, A — площадь поперечного сечения проволочного образца и l — длина образца. Общие экспериментальные методы для аппаратов с несколькими наковальнями более подробно описаны Либерманном (2011) и Ито (2015).
Статика: эксперименты с ячейкой с алмазной наковальней
Ячейка с алмазной наковальней (DAC) состоит из двух противоположных алмазов ювелирного качества, которые позволяют сжимать небольшие (∼10 −4 мм в масштабе 3 ) образцы, помещенные между две алмазные калеты. Приложение умеренной силы создает высокое давление из-за небольшого диаметра, обычно 50–250 мкм, стеклобой. Учитывая, что P применяется одноосно, металлическая прокладка с отверстием, просверленным для формирования камеры для образца, обеспечивает боковую поддержку. Среда, передающая давление, такая как газ (Ne, Ar, He, N 2 ) в камеру для образца, должна быть добавлена для получения гидростатического давления, но для высоких T экспериментов твердая среда (SiO 2 , KCl, Al 2 O 3 , KBr, NaCl). Таким образом, система является полупрозрачной и позволяет использовать XRD для определения кристаллографической структуры образца. Двумя основными шкалами давления являются уравнение состояния эталонного вещества и сдвиг линий флуоресценции рубина, хотя последний менее надежен при высоких Т . Уравнение состояния описывает соотношение между P , T и V . Измерения изменений V сравнивают с известной зависимостью V-P для определения экспериментального P . Вторая шкала давления основана на P -зависимом смещении длины волны флуоресценции облученного рубина, находящегося в камере для образцов. Образец изолируют от прокладки, добавляя слой изоляционного материала, такого как Al 9.0438 2 О 3 . Высоких температур можно достичь с помощью одностороннего или двустороннего лазерного нагрева или внутреннего резистивного нагрева металлического элемента, которым может быть сам образец. Резистивное нагревание позволяет точно измерять Тл с помощью термопар, но оно ограничено окислением алмаза в воздухе при температуре приблизительно 973 К.
Двумя основными шкалами давления являются уравнение состояния эталонного вещества и сдвиг линий флуоресценции рубина, хотя последний менее надежен при высоких Т . Уравнение состояния описывает соотношение между P , T и V . Измерения изменений V сравнивают с известной зависимостью V-P для определения экспериментального P . Вторая шкала давления основана на P -зависимом смещении длины волны флуоресценции облученного рубина, находящегося в камере для образцов. Образец изолируют от прокладки, добавляя слой изоляционного материала, такого как Al 9.0438 2 О 3 . Высоких температур можно достичь с помощью одностороннего или двустороннего лазерного нагрева или внутреннего резистивного нагрева металлического элемента, которым может быть сам образец. Резистивное нагревание позволяет точно измерять Тл с помощью термопар, но оно ограничено окислением алмаза в воздухе при температуре приблизительно 973 К. Лазерный нагрев может достигать гораздо более высоких значений Тл (до 7000 К), хотя большие градиенты Тл могут существовать, и необходимо позаботиться о расположении измерений образца в относительно однородном Т-поле. Распространенным методом измерения сопротивления образца в экспериментах с DAC является метод Ван дер Пау. Этот метод используется для образцов произвольной формы, если образец является приблизительно двумерным, таким как лист или фольга. Четыре электрода присоединены к периметру образца. Два противоположных электрода служат потенциальными выводами, которые могут быть изготовлены из той же фольги, что и образец, или аккуратно соединены вручную и зафиксированы путем приложения давления. ρ образца в конкретном P можно рассчитать следующим образом:
Лазерный нагрев может достигать гораздо более высоких значений Тл (до 7000 К), хотя большие градиенты Тл могут существовать, и необходимо позаботиться о расположении измерений образца в относительно однородном Т-поле. Распространенным методом измерения сопротивления образца в экспериментах с DAC является метод Ван дер Пау. Этот метод используется для образцов произвольной формы, если образец является приблизительно двумерным, таким как лист или фольга. Четыре электрода присоединены к периметру образца. Два противоположных электрода служат потенциальными выводами, которые могут быть изготовлены из той же фольги, что и образец, или аккуратно соединены вручную и зафиксированы путем приложения давления. ρ образца в конкретном P можно рассчитать следующим образом:
ρ=ρ0(VV0)13RR0(11)
, где нулевой индекс относится к условиям окружающей среды. Экспериментальные методы DAC более подробно описаны Mao and Mao (2007) и Anzellini and Boccato (2020).
Динамика: эксперименты по ударному сжатию
Ударное сжатие — это динамический метод создания высоких давлений, который можно использовать в сочетании с экспериментальной конфигурацией, позволяющей определить физические свойства образца, обычно проводимой в вакууме. Этот аппарат состоит из использования сжатого газа и/или пороха для запуска металлического снаряда в неподвижный образец. Столкновение создает сильную ударную волну, которая приводит к одновременному высокому уровню P и высокий T по всей выборке. Снаряд, обычно называемый летательной пластиной и сделанный из W или Fe, разгоняется до желаемой скорости порядка нескольких км/с (Bi et al., 2002). Зона высокой проводимости P , T распространяется по образцу при ударном сжатии. σ образца можно измерить контактным или бесконтактным методами. Бесконтактный метод требует дистанционного зондирования образца источниками оптического и электромагнитного полей, в результате чего получаются значения скорости удара летательного аппарата и скорости удара. Приход ударных волн создает две электродвижущие силы, которые связаны с произведением σ и толщины образца (Гилев, 2011). Контактный метод обычно требует четырех электродов, помещенных в контакт с образцом. Два электрода обеспечивают измерение напряжения, а два других используются для ввода постоянного тока. Температуры интерфейсов обычно измеряются оптическим пирометром (Гилев, 2011). Наиболее фундаментальной ударно-волновой характеристикой образца является его главная кривая Гюгонио, образованная геометрической формой ударных состояний вдоль пути сжатия от начальных P , T и плотность. P , T и свойства плотности в конечном состоянии получены с использованием стандартного метода согласования импеданса (Bi et al., 2002). В обоих методах σ можно рассчитать по формуле:
Приход ударных волн создает две электродвижущие силы, которые связаны с произведением σ и толщины образца (Гилев, 2011). Контактный метод обычно требует четырех электродов, помещенных в контакт с образцом. Два электрода обеспечивают измерение напряжения, а два других используются для ввода постоянного тока. Температуры интерфейсов обычно измеряются оптическим пирометром (Гилев, 2011). Наиболее фундаментальной ударно-волновой характеристикой образца является его главная кривая Гюгонио, образованная геометрической формой ударных состояний вдоль пути сжатия от начальных P , T и плотность. P , T и свойства плотности в конечном состоянии получены с использованием стандартного метода согласования импеданса (Bi et al., 2002). В обоих методах σ можно рассчитать по формуле:
σF= (ΔE0/ΔEF)(V0/ΔEF)σ0(12)
, где индексы 0 и F относятся к начальному и конечному состояниям соответственно. V – удельный объем. Экспериментальные методы для экспериментов по ударному сжатию более подробно описаны Аренсом (2007) и Асимовым (2015).
Экспериментальные методы для экспериментов по ударному сжатию более подробно описаны Аренсом (2007) и Асимовым (2015).
Удельное электрическое сопротивление ядер тел земного типа
Земля
Общепризнано, что состав ядра Земли должен состоять из Fe, Ni и некоторых легких элементов, чтобы удовлетворить плотность ядра (Birch, 1961; Birch , 1964; Жанло, 1979; Мао и др., 1990). Во внешнем ядре ожидается около 10 % масс. легких элементов (Пуарье, 1994; Литасов, Шацкий, 2016). Предполагается, что во внутреннем ядре содержится примерно 3–8 % масс. легких элементов (Alfe et al., 2007; Badro et al., 2007; Mao et al., 2012). В дополнение к примерно 5–10 % масс. Ni в ядре легкие элементы включают C, H, Si, O и S (Пуарье, 1994; Стиксруд и др., 1997; Ли и Фей, 2003 г.; Альфе и др., 2007). Соответственно, необходимо исследовать ρ множественных бинарных, тройных и даже четверных сплавов Fe.
Гардинер и Стейси (1971) использовали имеющиеся в литературе измерения ρ жидкого Fe для исследования влияния T , P и состава. Они сообщили о ρ 0,25 мкОм·м при 2500 К и 3000 км, что соответствует границе ядра и мантии (CMB). Точно так же они сообщили о 0,69 мкОм·м при 5 500 К и 5 000 км, что соответствует границе внутреннего ядра (ICB). Эти экстраполяции были достигнуты путем применения P — зависимость ρ твердого Fe (Bridgeman, 1957) от измерений жидкого Fe при 1 атм (Baum et al., 1967), как показано ниже:
Они сообщили о ρ 0,25 мкОм·м при 2500 К и 3000 км, что соответствует границе ядра и мантии (CMB). Точно так же они сообщили о 0,69 мкОм·м при 5 500 К и 5 000 км, что соответствует границе внутреннего ядра (ICB). Эти экстраполяции были достигнуты путем применения P — зависимость ρ твердого Fe (Bridgeman, 1957) от измерений жидкого Fe при 1 атм (Baum et al., 1967), как показано ниже:
ρP(T)= ρ0(T)(ΘD0ΘDP) 2DPD0(13)
, где нижний индекс P относится к конечному давлению, нижний индекс 0 относится к нулевому давлению, а D — к плотности. Эксперименты с ударной волной, проведенные Киллером и Ройсом (1971), показали аналогичное значение 0,67 мкОм·м при 140 ГПа, что соответствует условиям реликтового излучения. Однако это было предложено Bi et al. (2002), что предыдущие эксперименты по ударному сжатию выше 50 ГПа занижали ρ из-за шунтирующего эффекта эпоксидной смолы, которая используется для заполнения зазоров между образцом и изолятором. Би и др. (2002) провели измерения ударного сжатия σ Fe до 208 ГПа, с поправкой на шунтирующий эффект и предложили значение ρ, равное 0,69.мкОм·м в условиях, близких к CMB (2010 К, 101 ГПа), и 1,31 мкОм·м для условий, близких к ICB (5 220 K, 208 ГПа). Хотя эти значения представляют собой поправку к ранее заниженным значениям, они остаются ниже значений, указанных Джейном и Эвансом (1972). Джейн и Эванс (1972) выполнили расчеты из первых принципов с использованием модели почти свободных электронов и сообщили, что ρ ядра из чистого железа составляет от 1,00 до 2,00 мкОм·м. Эти более высокие значения согласуются с прямыми измерениями Секко и Шлессина (1989), который с помощью пресса большого объема измерил ρ Fe до 7 ГПа и выше плавления T . Сходство их измерений с расчетами плотности функций состояния при низком и высоком P позволяет предположить, что ρ растворителя Fe, вероятно, находится между 1,2 и 1,5 мкОм·м во внешнем ядре.
Би и др. (2002) провели измерения ударного сжатия σ Fe до 208 ГПа, с поправкой на шунтирующий эффект и предложили значение ρ, равное 0,69.мкОм·м в условиях, близких к CMB (2010 К, 101 ГПа), и 1,31 мкОм·м для условий, близких к ICB (5 220 K, 208 ГПа). Хотя эти значения представляют собой поправку к ранее заниженным значениям, они остаются ниже значений, указанных Джейном и Эвансом (1972). Джейн и Эванс (1972) выполнили расчеты из первых принципов с использованием модели почти свободных электронов и сообщили, что ρ ядра из чистого железа составляет от 1,00 до 2,00 мкОм·м. Эти более высокие значения согласуются с прямыми измерениями Секко и Шлессина (1989), который с помощью пресса большого объема измерил ρ Fe до 7 ГПа и выше плавления T . Сходство их измерений с расчетами плотности функций состояния при низком и высоком P позволяет предположить, что ρ растворителя Fe, вероятно, находится между 1,2 и 1,5 мкОм·м во внешнем ядре.
Стейси и Андерсон (2001) разработали теорию, предполагающую постоянную величину ρ вдоль границы плавления чистых металлов, таких как Fe, на основе устранения уменьшающих эффектов P на ρ возрастающим влиянием T на ρ. Описание их анализа, основанного главным образом на термоупругих соображениях, начинается с теории электронной проводимости, как упоминалось ранее Эльзассером (1946), при этом также рассматривается энергия электронов. Согласно модели свободных электронов и аппроксимации энергии электрона на поверхности Ферми, полная энергия зависит от объема как В -2/3 . Этот член умножается на обратный квадрат числа Дебая T в уравнении 6 для расчета ρ. Стейси и Андерсон (2001) затем экстраполировали ρ Fe при 140 ГПа (Матасов, 1977) и 2180 К (Андерсон, 1998) на температуру ядра и сообщили о значениях 1,22 мкОм·м в CMB и 1,12 мкОм·м в ICB, что согласуется с более ранними оценками ( Джейн и Эванс, 1972 г.; Секко и Шлоссин, 1989 г.; Стейси и Андерсон, 2001 г.). Стейси и Лопер (2007) пересмотрели теорию постоянного ρ вдоль границы плавления и предположили, что постоянное поведение применимо только к электронно простым металлам с заполненными d-зонами, таким как Cu, но не к Fe.
Описание их анализа, основанного главным образом на термоупругих соображениях, начинается с теории электронной проводимости, как упоминалось ранее Эльзассером (1946), при этом также рассматривается энергия электронов. Согласно модели свободных электронов и аппроксимации энергии электрона на поверхности Ферми, полная энергия зависит от объема как В -2/3 . Этот член умножается на обратный квадрат числа Дебая T в уравнении 6 для расчета ρ. Стейси и Андерсон (2001) затем экстраполировали ρ Fe при 140 ГПа (Матасов, 1977) и 2180 К (Андерсон, 1998) на температуру ядра и сообщили о значениях 1,22 мкОм·м в CMB и 1,12 мкОм·м в ICB, что согласуется с более ранними оценками ( Джейн и Эванс, 1972 г.; Секко и Шлоссин, 1989 г.; Стейси и Андерсон, 2001 г.). Стейси и Лопер (2007) пересмотрели теорию постоянного ρ вдоль границы плавления и предположили, что постоянное поведение применимо только к электронно простым металлам с заполненными d-зонами, таким как Cu, но не к Fe. Они сообщили о пересмотренном значении ρ Fe, равном 3,62 мкОм·м в CMB и 4,65 мкОм·м в ICB, что выше, чем значения, о которых сообщалось до сих пор. Эксперименты с несколькими простыми металлами показали, что предсказание Stacey and Loper (2007) инвариантности ρ чрезмерно упрощено, поскольку ρ Cu (Ezenwa et al., 2017), Ag (Littleton et al., 2018), Au (Berrada et al. ., 2018), все они уменьшаются на границах плавления, зависящих от давления, тогда как Zn (Ezenwa and Secco, 2017a), Co (Ezenwa and Secco, 2017b), Ni (Silber et al., 2017) и Fe (Silber et al., 2018 г., Йонг и др., 2019 г.) все показывают инвариант ρ вдоль границы плавления. Точно так же Davies (2007) пересмотрел результаты Stacey and Anderson (2001) и Bi et al. (2002) путем поправки на T в верхней части ядра (∼4023 K, 135 ГПа), что предполагает ρ 1,25–1,9 мкОм·м для Fe в условиях реликтового излучения.
Они сообщили о пересмотренном значении ρ Fe, равном 3,62 мкОм·м в CMB и 4,65 мкОм·м в ICB, что выше, чем значения, о которых сообщалось до сих пор. Эксперименты с несколькими простыми металлами показали, что предсказание Stacey and Loper (2007) инвариантности ρ чрезмерно упрощено, поскольку ρ Cu (Ezenwa et al., 2017), Ag (Littleton et al., 2018), Au (Berrada et al. ., 2018), все они уменьшаются на границах плавления, зависящих от давления, тогда как Zn (Ezenwa and Secco, 2017a), Co (Ezenwa and Secco, 2017b), Ni (Silber et al., 2017) и Fe (Silber et al., 2018 г., Йонг и др., 2019 г.) все показывают инвариант ρ вдоль границы плавления. Точно так же Davies (2007) пересмотрел результаты Stacey and Anderson (2001) и Bi et al. (2002) путем поправки на T в верхней части ядра (∼4023 K, 135 ГПа), что предполагает ρ 1,25–1,9 мкОм·м для Fe в условиях реликтового излучения.
Расчеты из первых принципов с использованием уравнения Больцмана показали, что ρ составляет 0,75 мкОм·м для твердого ε-Fe в условиях ICB (Sha and Cohen, 2011), а использование уравнения Кубо–Гринвуда через уравнение Блоха–Грюнайзена для жидкого Fe предполагает ρ ~0,61–0,69мкОм·м в основных условиях (de Koker et al. , 2012). Эти результаты сопоставимы с первопринципными расчетами транспортных свойств на основе DFT для жидких смесей сплавов Fe Pozzo et al. (2012), которые сообщили о значении 0,64 мкОм·м на ICB и 0,73–0,74 мкОм·м на CMB. Вскоре после этой работы Pozzo et al. (2013) использовали моделирование из первых принципов из расчетов DFT с соотношением Кубо-Гринвуда, чтобы получить k , в то время как ρ был рассчитан независимо от σ. Соответствующее число Лоренца для жидкого Fe (2,47–2,51·10 −8 WΩ K −2 ) затем рассчитывали с использованием закона Видемана-Франца. Их результаты также показали 0,64 мкОм·м для Fe в ICB и 0,747 мкОм·м в CMB. Расчеты из первых принципов в сочетании с молекулярно-динамическим моделированием твердого Fe Pozzo et al. (2014) предложили более низкие значения 0,50–0,53 мкОм·м в условиях ICB. Поццо и Альфе (2016a) расширили набор расчетов ядра ρ ε-Fe, проведенный Pozzo et al. (2014) к более низким температурам, чтобы исследовать зависимость T от ρ.
, 2012). Эти результаты сопоставимы с первопринципными расчетами транспортных свойств на основе DFT для жидких смесей сплавов Fe Pozzo et al. (2012), которые сообщили о значении 0,64 мкОм·м на ICB и 0,73–0,74 мкОм·м на CMB. Вскоре после этой работы Pozzo et al. (2013) использовали моделирование из первых принципов из расчетов DFT с соотношением Кубо-Гринвуда, чтобы получить k , в то время как ρ был рассчитан независимо от σ. Соответствующее число Лоренца для жидкого Fe (2,47–2,51·10 −8 WΩ K −2 ) затем рассчитывали с использованием закона Видемана-Франца. Их результаты также показали 0,64 мкОм·м для Fe в ICB и 0,747 мкОм·м в CMB. Расчеты из первых принципов в сочетании с молекулярно-динамическим моделированием твердого Fe Pozzo et al. (2014) предложили более низкие значения 0,50–0,53 мкОм·м в условиях ICB. Поццо и Альфе (2016a) расширили набор расчетов ядра ρ ε-Fe, проведенный Pozzo et al. (2014) к более низким температурам, чтобы исследовать зависимость T от ρ. Их результаты показали, что ρ линейно увеличивается с T и, в конечном итоге, достигает насыщения при высоких значениях T , что означает ρ Fe примерно 0,72 мкОм·м недалеко от условий реликтового излучения (4350 K, 97 ГПа) и ∼0,54 мкОм·м в центре Земли (6 350 K, 365 ГПа), что сравнимо с предыдущим упомянутые выше результаты. Это исследование также согласуется с экспериментами ЦАП до 70 ГПа и 300 К, проведенными Гоми и Хиросе (2015), которые предложили значения 0,537 (+0,049/–0,077) мкОм·м и 0,431 (+0,058/–0,095) мкОм·м при реликтовом излучении ( 3750 К, 135 ГПа) и ICB (4971 К, 330 ГПа) соответственно. Напротив, экстраполяция измерений DAC от 26 до 51 ГПа до 2 880 K, предполагая насыщение удельным сопротивлением, показала, что ρ Fe составляет 0,404 (+0,065/-0,09).7) мкОм·м в условиях реликтового излучения (Охта и др., 2016). Однако в первом исследовании по измерению тыс. Fe в условиях реликтового излучения Konopkova et al. (2016) измерили распространение тепловых импульсов по фольге Fe в ЦАП до 130 ГПа и 3000 К, а затем смоделировали зависимости ρ T и P .
Их результаты показали, что ρ линейно увеличивается с T и, в конечном итоге, достигает насыщения при высоких значениях T , что означает ρ Fe примерно 0,72 мкОм·м недалеко от условий реликтового излучения (4350 K, 97 ГПа) и ∼0,54 мкОм·м в центре Земли (6 350 K, 365 ГПа), что сравнимо с предыдущим упомянутые выше результаты. Это исследование также согласуется с экспериментами ЦАП до 70 ГПа и 300 К, проведенными Гоми и Хиросе (2015), которые предложили значения 0,537 (+0,049/–0,077) мкОм·м и 0,431 (+0,058/–0,095) мкОм·м при реликтовом излучении ( 3750 К, 135 ГПа) и ICB (4971 К, 330 ГПа) соответственно. Напротив, экстраполяция измерений DAC от 26 до 51 ГПа до 2 880 K, предполагая насыщение удельным сопротивлением, показала, что ρ Fe составляет 0,404 (+0,065/-0,09).7) мкОм·м в условиях реликтового излучения (Охта и др., 2016). Однако в первом исследовании по измерению тыс. Fe в условиях реликтового излучения Konopkova et al. (2016) измерили распространение тепловых импульсов по фольге Fe в ЦАП до 130 ГПа и 3000 К, а затем смоделировали зависимости ρ T и P . Они получают ρ Fe 3,7 ± 1,5 мкОм·м во внешнем ядре. Хотя это согласуется с высокими значениями, указанными Стейси и Лопер (2007), это значение выше, чем удельное сопротивление насыщения 1,43 мкОм·м, предложенное Xu et al. (2018). Сюй и др. (2018) рассчитали электрон-фононный и электрон-электронный вклады в ρ твердого ε-Fe на основе расчетов из первых принципов и молекулярной динамики. Они предложили значения 0,998 мкОм·м и 1,008 мкОм·м при ICB (6000 K, 330 ГПа) и CMB (4 000 K, 136 ГПа) соответственно. Их результаты также показали, что предыдущие данные DAC (Ohta et al., 2016) могли переоценивать эффект насыщения. Чжан и др. (2020) предположили, что эффект насыщения, наблюдаемый при высоких значениях T Ohta et al. (2016) следует считать экспериментальным артефактом из-за неправильного позиционирования лазера над образцом при нагреве и неточной геометрии четырехзондового метода. Во-первых, смещение лазера при нагреве приводит к большому T градиент по образцу. Затем в измерениях ρ при высоких значениях T преобладают более холодные регионы, что приводит к более низким значениям ρ.
Они получают ρ Fe 3,7 ± 1,5 мкОм·м во внешнем ядре. Хотя это согласуется с высокими значениями, указанными Стейси и Лопер (2007), это значение выше, чем удельное сопротивление насыщения 1,43 мкОм·м, предложенное Xu et al. (2018). Сюй и др. (2018) рассчитали электрон-фононный и электрон-электронный вклады в ρ твердого ε-Fe на основе расчетов из первых принципов и молекулярной динамики. Они предложили значения 0,998 мкОм·м и 1,008 мкОм·м при ICB (6000 K, 330 ГПа) и CMB (4 000 K, 136 ГПа) соответственно. Их результаты также показали, что предыдущие данные DAC (Ohta et al., 2016) могли переоценивать эффект насыщения. Чжан и др. (2020) предположили, что эффект насыщения, наблюдаемый при высоких значениях T Ohta et al. (2016) следует считать экспериментальным артефактом из-за неправильного позиционирования лазера над образцом при нагреве и неточной геометрии четырехзондового метода. Во-первых, смещение лазера при нагреве приводит к большому T градиент по образцу. Затем в измерениях ρ при высоких значениях T преобладают более холодные регионы, что приводит к более низким значениям ρ. Во-вторых, ожидается, что погрешности измерения будут значительно больше, чем сообщаемые значения, учитывая небольшой размер образца по сравнению с расположением электродов. Геометрия сборки по существу приводит к методу с двумя зондами. При рассмотрении этих ключевых факторов Zhang et al. (2020) использовали расчеты из первых принципов для сравнения с их измерениями ρ ε-Fe до ~ 170 ГПа и ~ 3000 К в ЦАП с лазерным нагревом с использованием метода Ван дер Пау. Их анализ показал, что ρ составляет 0,80 ± 0,05 мкОм·м в условиях реликтового излучения (4000 К, 136 ГПа). Таким образом, ожидается, что значения, полученные из измерений DAC, экстраполированных на основе модели насыщения удельного сопротивления (Gomi and Hirose, 2015; Ohta et al., 2016), почти удвоятся в соответствии с результатами Zhang et al. (2020). Тем не менее, эти результаты остаются ниже результатов, экстраполированных из измерений пресса с несколькими упорами (Secco and Schloessin, 19).89; Йонг и др., 2019). Например, сообщаемое значение Yong et al.
Во-вторых, ожидается, что погрешности измерения будут значительно больше, чем сообщаемые значения, учитывая небольшой размер образца по сравнению с расположением электродов. Геометрия сборки по существу приводит к методу с двумя зондами. При рассмотрении этих ключевых факторов Zhang et al. (2020) использовали расчеты из первых принципов для сравнения с их измерениями ρ ε-Fe до ~ 170 ГПа и ~ 3000 К в ЦАП с лазерным нагревом с использованием метода Ван дер Пау. Их анализ показал, что ρ составляет 0,80 ± 0,05 мкОм·м в условиях реликтового излучения (4000 К, 136 ГПа). Таким образом, ожидается, что значения, полученные из измерений DAC, экстраполированных на основе модели насыщения удельного сопротивления (Gomi and Hirose, 2015; Ohta et al., 2016), почти удвоятся в соответствии с результатами Zhang et al. (2020). Тем не менее, эти результаты остаются ниже результатов, экстраполированных из измерений пресса с несколькими упорами (Secco and Schloessin, 19).89; Йонг и др., 2019). Например, сообщаемое значение Yong et al. (2019) в 1,6 раза выше, чем у Zhang et al. (2020). В то время как Йонг и др. (2019) сообщили об измеренных значениях ρ Fe на жидкой стороне границы плавления, их сообщенное значение ρ на CMB было линейно экстраполировано до 200 ГПа на основе зависимости P , наблюдаемой между 14–24 ГПа. Чжан и др. (2020) предположили, что удельное сопротивление при плавлении увеличится на 10%, но экстраполировали только от 133 до 136 ГПа. В целом, различия в значениях ρ в реликтовом излучении, зарегистрированные в экспериментальных исследованиях с несколькими наковальнями и DAC, могут возникать из-за неопределенностей из-за больших экстраполяций, из-за предрасположенностей, характерных для каждого метода, таких как ошибки в геометрии образца, температурная однородность нагретой области образца, отсутствие симметрии образца, возможных термоэлектрических эффектов и других паразитных напряжений и др.
(2019) в 1,6 раза выше, чем у Zhang et al. (2020). В то время как Йонг и др. (2019) сообщили об измеренных значениях ρ Fe на жидкой стороне границы плавления, их сообщенное значение ρ на CMB было линейно экстраполировано до 200 ГПа на основе зависимости P , наблюдаемой между 14–24 ГПа. Чжан и др. (2020) предположили, что удельное сопротивление при плавлении увеличится на 10%, но экстраполировали только от 133 до 136 ГПа. В целом, различия в значениях ρ в реликтовом излучении, зарегистрированные в экспериментальных исследованиях с несколькими наковальнями и DAC, могут возникать из-за неопределенностей из-за больших экстраполяций, из-за предрасположенностей, характерных для каждого метода, таких как ошибки в геометрии образца, температурная однородность нагретой области образца, отсутствие симметрии образца, возможных термоэлектрических эффектов и других паразитных напряжений и др.
Силбер и др. (2018) сообщили об инвариантном поведении Fe ρ при ~1,2 мкОм·м по результатам прямых измерений в прессе с несколькими упорами до 12 ГПа и при температуре жидкости T . Аналогичный метод использовали Yong et al. (2019), которые проводили статические эксперименты на 3000-тонном прессе с несколькими упорами при давлении 14–24 ГПа в жидкость. Их результаты показали, что инвариант ρ жидкого Fe составляет 1,20 ± 0,02 мкОм·м вдоль границы плавления. Однако статистическая линейная регрессия их измерений для учета эффекта P , предполагал небольшое отклонение от инвариантного поведения до 1,28 ± 0,09 мкОм вдоль границы плавления Fe при 200 ГПа. Wagle и Steinle-Neumann (2018) сосредоточились на поведении жидкого Fe на основе расчетов из первых принципов, основанных на теории Зимана о жидких металлах. Сочетая их значение ICB 0,58 мкОм·м для ε-Fe с литературными значениями жидких сплавов Fe-Si/S (de Koker et al., 2012; Pozzo et al., 2014), ожидается, что ρ внешнего ядра будет до на 36% больше, чем у внутреннего ядра. Напротив, оценки чистого Fe с помощью DFT и молекулярной динамики не показали почти никакого увеличения между условиями ICB и CMB, с 0,60 ± 0,27 мкОм·м до 0,67 ± 0,27 соответственно (Wagle et al.
Аналогичный метод использовали Yong et al. (2019), которые проводили статические эксперименты на 3000-тонном прессе с несколькими упорами при давлении 14–24 ГПа в жидкость. Их результаты показали, что инвариант ρ жидкого Fe составляет 1,20 ± 0,02 мкОм·м вдоль границы плавления. Однако статистическая линейная регрессия их измерений для учета эффекта P , предполагал небольшое отклонение от инвариантного поведения до 1,28 ± 0,09 мкОм вдоль границы плавления Fe при 200 ГПа. Wagle и Steinle-Neumann (2018) сосредоточились на поведении жидкого Fe на основе расчетов из первых принципов, основанных на теории Зимана о жидких металлах. Сочетая их значение ICB 0,58 мкОм·м для ε-Fe с литературными значениями жидких сплавов Fe-Si/S (de Koker et al., 2012; Pozzo et al., 2014), ожидается, что ρ внешнего ядра будет до на 36% больше, чем у внутреннего ядра. Напротив, оценки чистого Fe с помощью DFT и молекулярной динамики не показали почти никакого увеличения между условиями ICB и CMB, с 0,60 ± 0,27 мкОм·м до 0,67 ± 0,27 соответственно (Wagle et al. , 2019).). Недавнее моделирование DFT, проведенное Pourovskiy et al. (2020) объяснили электрон-электронные взаимодействия при высоких температурах Тл и предложили внутреннее ядро ρ 0,637 мкОм·м для чистого Fe, что в целом согласуется с более низкими значениями, упомянутыми выше. Пуровский и др. (2020) применили DFT и DMFT к Fe и пришли к выводу, что тепловой беспорядок подавляет нефермижидкостное поведение ОЦК Fe, что снижает электрон-электронное рассеяние при высоких T . Вариации среди результатов чистого Fe, по-видимому, находятся в диапазоне от 0,25 мкОм·м (Гардинер и Стейси, 1971) и 3,7 ± 1,5 мкОм·м (Конопкова и др., 2016), и это может быть связано не только с используемым методом.
, 2019).). Недавнее моделирование DFT, проведенное Pourovskiy et al. (2020) объяснили электрон-электронные взаимодействия при высоких температурах Тл и предложили внутреннее ядро ρ 0,637 мкОм·м для чистого Fe, что в целом согласуется с более низкими значениями, упомянутыми выше. Пуровский и др. (2020) применили DFT и DMFT к Fe и пришли к выводу, что тепловой беспорядок подавляет нефермижидкостное поведение ОЦК Fe, что снижает электрон-электронное рассеяние при высоких T . Вариации среди результатов чистого Fe, по-видимому, находятся в диапазоне от 0,25 мкОм·м (Гардинер и Стейси, 1971) и 3,7 ± 1,5 мкОм·м (Конопкова и др., 2016), и это может быть связано не только с используемым методом.
Тепловые свойства сплавов Fe-Ni демонстрируют аналогичные изменения. Гардинер и Стейси (1971) также оценили ρ Fe с содержанием до 25% легкого элемента (Ni, S, Si, MgO). Их результаты указывают на верхнюю границу 2,77 мкОм·м в условиях CMB и 6,03 мкОм·м в условиях ICB. Прямые измерения при 1 атм до ~1373 К, проведенные Джонстоном и Стренсом (1973), показывают сопоставимые результаты. Предполагая, что ρ при давлении в керне меньше, чем при 1 атм, Джонстон и Стренс (1973) предположил, что ρ не должно превышать 2,0 мкОм·м для Fe-10% масс. Ni-2,6% масс. C-15% масс. S (далее Fe10Ni2,6C15S) при начальном давлении. Стейси и Андерсон (2001) предсказали, что добавление 23 % масс. и 15 % масс. Si (или Fe23Ni15Si) увеличит ρ до 2,12 мкОм·м при CMB и 2,02 мкОм·м при ICB, в согласии с Johnston and Strens (1973). Дэвис (2007) также сообщил о ρ в диапазоне 2,15–2,8 мкОм·м для Fe23Ni15Si в условиях реликтового излучения. Напротив, эксперименты DAC в сочетании с уравнением Блоха-Грюнайзена предложили значения 0,675 мкОм·м для ε-Fe10Ni, 1,26 (+0,05/-0,17) мкОм·м для ε-Fe5Ni4Si и 1,77 (+0,05/-0,25) мкОм·м для ε-Fe5Ni8Si при Условия CMB (4000 K, 140 ГПа) (Zhang et al., 2021). Гоми и Хиросе (2015) предложили аналогичные значения ρ для Fe-Ni с содержанием легких элементов (O, Si, S, C) до 13,4 мас.%: 0,53–1,19.мкОм·м при CMB и 0,39–0,96 мкОм·м при ICB. Точно так же Охта и соавт. (2016) объединили свои измерения DAC с правилом Маттиссена и моделью насыщения удельного сопротивления, чтобы получить ρ Fe11,9Ni13,4Si, равное 0,869 (+0,154/-0,216) мкОм·м при 140 ГПа и 3750 К.
Предполагая, что ρ при давлении в керне меньше, чем при 1 атм, Джонстон и Стренс (1973) предположил, что ρ не должно превышать 2,0 мкОм·м для Fe-10% масс. Ni-2,6% масс. C-15% масс. S (далее Fe10Ni2,6C15S) при начальном давлении. Стейси и Андерсон (2001) предсказали, что добавление 23 % масс. и 15 % масс. Si (или Fe23Ni15Si) увеличит ρ до 2,12 мкОм·м при CMB и 2,02 мкОм·м при ICB, в согласии с Johnston and Strens (1973). Дэвис (2007) также сообщил о ρ в диапазоне 2,15–2,8 мкОм·м для Fe23Ni15Si в условиях реликтового излучения. Напротив, эксперименты DAC в сочетании с уравнением Блоха-Грюнайзена предложили значения 0,675 мкОм·м для ε-Fe10Ni, 1,26 (+0,05/-0,17) мкОм·м для ε-Fe5Ni4Si и 1,77 (+0,05/-0,25) мкОм·м для ε-Fe5Ni8Si при Условия CMB (4000 K, 140 ГПа) (Zhang et al., 2021). Гоми и Хиросе (2015) предложили аналогичные значения ρ для Fe-Ni с содержанием легких элементов (O, Si, S, C) до 13,4 мас.%: 0,53–1,19.мкОм·м при CMB и 0,39–0,96 мкОм·м при ICB. Точно так же Охта и соавт. (2016) объединили свои измерения DAC с правилом Маттиссена и моделью насыщения удельного сопротивления, чтобы получить ρ Fe11,9Ni13,4Si, равное 0,869 (+0,154/-0,216) мкОм·м при 140 ГПа и 3750 К. Gomi et al. (2016) оценили ρ Fe12Ni15Si (или Fe 65 Ni 10 Si 25 ) между 1,12 и 1,16 мкОм·м при 4000–5500 K и 156–175 ГПа по формуле Кубо–Гринвуда. Как и ожидалось от дополнительного рассеяния примесей, предыдущие значения Fe-сплавов (Gomi and Hirose, 2015; Gomi et al., 2016) выше, чем у чистого Fe (Ohta et al., 2016) с использованием аналогичных методов. Первопринципные расчеты электронной зонной структуры сплавов Fe с учетом теории насыщения предложили значения в диапазоне от 0,58–0,74 мкОм·м для Fe-(от 5,4 до 31,6 мас.%) Ni в условиях реликтового излучения (Gomi and Yoshino, 2018). В соответствии с этими исследованиями Zidane et al. (2020) также использовали расчеты из первых принципов, основанные на соотношении Кубо-Гринвуда, и сообщили значения 0,62–1,22 мкОм·м для Fe-Ni с 2,7–37,7% масс. легких элементов (O, Si, S) в условиях ICB (5500 K, 360 ГПа).
Gomi et al. (2016) оценили ρ Fe12Ni15Si (или Fe 65 Ni 10 Si 25 ) между 1,12 и 1,16 мкОм·м при 4000–5500 K и 156–175 ГПа по формуле Кубо–Гринвуда. Как и ожидалось от дополнительного рассеяния примесей, предыдущие значения Fe-сплавов (Gomi and Hirose, 2015; Gomi et al., 2016) выше, чем у чистого Fe (Ohta et al., 2016) с использованием аналогичных методов. Первопринципные расчеты электронной зонной структуры сплавов Fe с учетом теории насыщения предложили значения в диапазоне от 0,58–0,74 мкОм·м для Fe-(от 5,4 до 31,6 мас.%) Ni в условиях реликтового излучения (Gomi and Yoshino, 2018). В соответствии с этими исследованиями Zidane et al. (2020) также использовали расчеты из первых принципов, основанные на соотношении Кубо-Гринвуда, и сообщили значения 0,62–1,22 мкОм·м для Fe-Ni с 2,7–37,7% масс. легких элементов (O, Si, S) в условиях ICB (5500 K, 360 ГПа).
Результаты Gomi and Yoshino (2018) также предполагают значения в диапазоне от 0,71–0,88 мкОм·м для Fe-(от 1,6 до 11,7 масс. %)O в условиях реликтового излучения. Точно так же де Кокер и соавт. (2012) сообщили о диапазоне 0,67–0,82 мкОм·м для сплавов Fe-O в основных условиях, в то время как Pozzo et al. (2012) также сообщили о значении ~0,80 мкОм·м для Fe-O-S/Si (2,7–3,5% масс. O и масс.% S/Si от 9,1 до 11,4) в ICB и 0,90 мкОм·м в CMB. Уэгл и др. (2019) сообщили о значениях ρ, которые очень хорошо согласуются с de Koker et al. (2012) для тех же сплавов. Их результаты показали, что в условиях ICB ρ составляет 0,65 ± 0,24 мкОм·м и 0,71 ± 0,27 мкОм·м, а в условиях реликтового излучения ρ составляет 0,74 ± 0,24 мкОм·м и 0,81 ± 0,27 мкОм·м для Fe3.9.O (или Fe 7 O) и Fe8.7O (или Fe 3 O) соответственно (Wagle et al., 2019). Точно так же Pozzo et al. (2013) reported a calculated ρ of ∼0.79 µΩm for Fe2.7O6Si (or Fe 0.82 O 0.08 Si 0.10 ) and ∼0.80 µΩm for Fe4.6O4.9Si (or Fe 0.79 O 0.13 Si 0,08 ) в ICB, что мало чем отличается от прямых расчетов удельного сопротивления для Fe-O-S/Si Pozzo et al.
%)O в условиях реликтового излучения. Точно так же де Кокер и соавт. (2012) сообщили о диапазоне 0,67–0,82 мкОм·м для сплавов Fe-O в основных условиях, в то время как Pozzo et al. (2012) также сообщили о значении ~0,80 мкОм·м для Fe-O-S/Si (2,7–3,5% масс. O и масс.% S/Si от 9,1 до 11,4) в ICB и 0,90 мкОм·м в CMB. Уэгл и др. (2019) сообщили о значениях ρ, которые очень хорошо согласуются с de Koker et al. (2012) для тех же сплавов. Их результаты показали, что в условиях ICB ρ составляет 0,65 ± 0,24 мкОм·м и 0,71 ± 0,27 мкОм·м, а в условиях реликтового излучения ρ составляет 0,74 ± 0,24 мкОм·м и 0,81 ± 0,27 мкОм·м для Fe3.9.O (или Fe 7 O) и Fe8.7O (или Fe 3 O) соответственно (Wagle et al., 2019). Точно так же Pozzo et al. (2013) reported a calculated ρ of ∼0.79 µΩm for Fe2.7O6Si (or Fe 0.82 O 0.08 Si 0.10 ) and ∼0.80 µΩm for Fe4.6O4.9Si (or Fe 0.79 O 0.13 Si 0,08 ) в ICB, что мало чем отличается от прямых расчетов удельного сопротивления для Fe-O-S/Si Pozzo et al. (2012). Они также сообщают о числе Лоренца для жидких сплавов Fe в диапазоне от 2,17 до 2,24·10 9 .0036 −8 WΩK −2 из закона Видемана-Франца (Pozzo et al., 2013).
(2012). Они также сообщают о числе Лоренца для жидких сплавов Fe в диапазоне от 2,17 до 2,24·10 9 .0036 −8 WΩK −2 из закона Видемана-Франца (Pozzo et al., 2013).
Недавние эксперименты с DAC, проведенные Zhang et al. (2021) предложил значение 1,00 мкОм·м для ε-Fe1,8Si в условиях реликтового излучения. Гоми и Йошино (2018) рассмотрели более высокое содержание Si и сообщили значения в диапазоне от 0,71–1,13 мкОм·м для Fe-(от 2,8 до 18,8% масс.%)Si и 0,72–0,94 мкОм·м для Fe-(от 3,1 до 20,9% масс.%)S в условиях реликтового излучения. . Первопринципные расчеты и моделирование молекулярной динамики на Fe4,5Si (или Fe 0,92 Si 0,08 ) и Fe3,9Si (или Fe 0,93 Si 0,07 ) предполагали ρ 0,65–0,66 мкОм·м в ICB (Pozzo et al., 2014). Согласие с указанными значениями Fe3.9O (de Koker et al., 2012) и Fe (Keeler and Royce, 1971) позволяет предположить, что вклад Si и O в общее ρ во внутренних условиях ядра может быть незначительным. ТАБЛИЦА 1 . Значения удельного электрического сопротивления Fe в условиях реликтового излучения Земли (4000 К, 136 ГПа) и ICB (5000 К, 330 ГПа), определенных разными методами. ТАБЛИЦА 2 . Значения удельного электрического сопротивления сплавов Fe-Ni в условиях земного реликтового излучения (4000 К, 136 ГПа) и ICB (5000 К, 330 ГПа), определенных разными методами. ТАБЛИЦА 3 . Значения удельного электрического сопротивления сплавов Fe-O в условиях земного реликтового излучения (4000 К, 136 ГПа) и ICB (5000 К, 330 ГПа), определенных разными методами. ТАБЛИЦА 4 . Значения удельного электрического сопротивления сплавов Fe-Si/S в условиях земного реликтового излучения (4000 К, 136 ГПа) и ICB (5000 К, 330 ГПа), определенных разными методами. РИСУНОК 2 . Комбинированные значения ρ из литературы, примененные к ядру Земли, представлены в порядке дат. Синяя пунктирная линия представляет средние значения (без значений > 3 мкОм·м) в CMB, а красная пунктирная линия представляет средние значения в ICB. Среднее значение всех зарегистрированных значений в условиях CMB (4000 K, 136 ГПа) составляет 1,07 мкОм·м, а при ICB (5 000 K, 330 ГПа) — 0,9. Рассмотрено большое количество теоретических и экспериментальных оценок ρ земного ядра из чистого Fe. В целом, значения ρ для Fe составляют около 1,05 и 1,08 мкОм·м в CMB и ICB, соответственно, без учета высоких значений (>3 мкОм·м) из Stacey and Loper (2007) и Konopkova et al. (2016). Высокие значения, указанные в теоретической работе Стейси и Лопер (2007), и очень сложная экспериментальная работа Конопковой и др. (2016) вряд ли можно объяснить выбором P и T , поскольку они аналогичны тем, о которых сообщается в исследованиях, сообщающих о более низких значениях ρ. Однако значения, указанные Конопковой и соавт. (2016) являются прямыми измерениями k , которые включают фононный вклад. Таким образом, ожидается, что их значения будут выше, чем измерения или расчеты k e , хотя такое большое расхождение (в 3,5 раза выше среднего) не может быть объяснено понятой в настоящее время физикой относительных вкладов электронов и фононов. Комбинация лунных сейсмических профилей (Weber et al., 2011) и измерений скорости звуковых волн в сплавах Fe (Antonangeli et al., 2015) указывает на то, что Луна в настоящее время состоит из жидкого внешнего ядра и твердое внутреннее ядро. Точное количество и природа легких элементов в активной зоне не ограничены, но ожидается S, C и Ni (Wieczorek et al. Рассчитанное Андерсоном (1998) и Стейси и Андерсоном (2001) значение k Fe (25–50 Вт·м −1 K −1 ) широко использовалось в моделях тепловой эволюции лунного динамо ( Stegman et al., 2003; Zhang et al., 2013; Evans et al., 2014; Laneuville et al., 2014; Scheinberg et al., 2015; Laneuville et al., 2018). Однако соответствующее ρ по закону Видемана-Франца варьируется от исследования к исследованию из-за больших вариаций T , приписываемых лунному реликтовому излучению. Прямые измерения удельного сопротивления Fe в прессе с несколькими наковальнями от 3–12 ГПа и в жидком состоянии показали, что ρ составляет 1,23–1,31 мкОм·м на центральной стороне реликтового излучения (1687–1800 К, 4,9ГПа) (Silber et al. ТАБЛИЦА 5 . Значения удельного электрического сопротивления Fe и Fe-сплавов по разным методикам на лунном реликтовом излучении. РИСУНОК 3 . Комбинированные значения ρ из литературы, примененные к ядру Луны, представлены в порядке дат. Синяя пунктирная линия представляет средние значения CMB. Среднее значение всех зарегистрированных значений в условиях реликтового излучения (1687–1800 К, 4,5 ГПа) составляет 1,40 мкОм·м. Повторяющиеся ссылки указывают на разные композиции. Хотя точная идентичность и количество легких элементов в лунном ядре не ограничены, насколько нам известно, только в нескольких исследованиях сообщалось о значениях ρ для соответствующих P и T условия лунного ядра. Наше понимание содержания легких элементов в Меркурии в основном основано на химическом содержании Солнечной системы, моделях, основанных на составе Земли и Луны, и данных, полученных с рентгеновского спектрометра MESSENGER (Harder and Schubert, 2001; McCubbin и др., 2012). Ранние оценки состава ядра Меркурия предполагают, что примерно 99 % по массе составляют металлы (Fe, Ni, Co) и примерно 1 % по массе составляют Fe36,5S (или FeS) (Морган и Андерс, 1980). Ниттлер и др. (2017) утверждал, что ядро, содержащее Si, может содержать небольшое количество S и C, в то время как Rivoldini et al. Ранние модели формирования ядра Меркурия обычно рассматривают k при 40–43 Вт·м −1 K −1 , что соответствует 1,06–1,15 мкОм·м, при 1880 K для ядра, состоящего в основном из Fe с 1–5 % масс. S (Stevenson et al., 1983). ; Christensen, 2006; Tosi et al., 2013). В моделях тепловой эволюции Knibbe and van Westrenen (2018) рассматривался диапазон k от 30 до 60 Вт·м −1 K −1 для ядра Fe-Si с T между 1800–2200 K, что соответствует 0,73–1,79 мкОм·м по закону Видемана-Франца . ТАБЛИЦА 6 . Значения удельного электросопротивления Fe и Fe-сплавов по разным методикам в условиях ртутного реликтового излучения и ICB. РИСУНОК 4 . Комбинированные значения ρ из литературы, примененные к ядру Меркурия, представлены в порядке дат. Синяя пунктирная линия представляет средние значения в CMB, а красная пунктирная линия представляет средние значения в ICB. Среднее значение всех сообщаемых значений в CMB (1,900 К, 5 ГПа) составляет 0,88 мкОм·м, а при ICB (2 200–2 500 К, 36 ГПа) составляет 1,12 мкОм·м. Сообщаемые теоретические и экспериментальные значения ρ Fe применительно к условиям реликтового излучения и ICB Меркурия показывают важное расхождение. Денг и др. (2013) сообщили о более низких значениях (примерно на 35% меньше), чем те, о которых сообщил Konôpkova et al. (2016), Secco (2017), Silber et al. (2018 г.) и Эзенва и Секко (2019 г.). Таким расхождением нельзя пренебречь при расчете q и в верхней части внешнего ядра. На основании анализа марсианских метеоритов предполагается, что химический состав марсианского ядра представляет собой Fe14.2S (Wänke et al., 1988). Эксперименты DAC с лазерным нагревом и рентгеновская дифракция in situ подтверждают фазовую стабильность Fe36.5S в керновых условиях (Kavner et al., 2001). В моделях термической эволюции также рассматривается ядро, состоящее в основном из Fe с содержанием 6–8 % масс. Ni и 10–17 % масс. S, а также содержащего меньшее количество O, C, H и P (Rivoldini et al., 2011). Стивенсон и др. (1983) исследовали модели эволюции ядра Марса, объединив теории геомагнетизма и гидродинамики. ТАБЛИЦА 7 . Значения удельного электрического сопротивления Fe и Fe-сплавов по разным методикам в условиях марсианского CMB (1770 К, 23 ГПа) и ICB (2 000 K, 40 ГПа). РИСУНОК 5 . Комбинированные значения ρ из литературы, примененные к ядру Марса, представлены в порядке дат. Синяя пунктирная линия представляет средние значения в CMB, а красная пунктирная линия представляет средние значения в ICB. Литературы по значениям ρ в условиях марсианского ядра недостаточно, чтобы определить разумное значение в условиях CMB и ICB. В то время как Дэн и соавт. (2013) и Silber et al. (2018) сообщили значения для твердого Fe, значение, указанное Deng et al. (2013) лучше всего согласуется с опубликованными значениями жидкого Fe (Wagle et al., 2019; Ezenwa and Yoshino, 2021). Однако Зильбер и соавт. (2018) считается ниже T на CMB, чем Ezenwa and Yoshino (2021). Поэтому ожидается, что их измеренный ρ будет ниже, чем у Ezenwa and Yoshino (2021), хотя наблюдается обратное. Согласно результатам Wagle et al. (2019), влияние O на увеличение ρ, по-видимому, меньше, чем влияние Si и S, хотя все сплавы, по-видимому, согласуются в пределах неопределенности. Присутствие Fe36.5S в метеоритах указывает на то, что S, вероятно, является основным легким элементом в ядре Ганимеда (Крот, 2005). Водород также является кандидатом на роль легкого элемента, учитывая, что был предложен слой H 2 O в недрах Ганимеда (Anderson et al., 1996). Хотя точный состав не ограничен, содержание легких элементов сильно зависит от размера ядра и степени окисления внутренней части во время дифференциации. Ожидается, что условия реликтового излучения будут около 2000 К и 7 ГПа в случае низкого содержания серы (1 % масс.), а в случае почти эвтектического содержания серы (36,5 % масс. Силбер и др. (2018) измерили ρ Fe на уровне 1,20 мкОм·м при 1500 К (Shibazaki et al., 2011) и 5,9 ГПа (Hussmann et al., 2007), в то время как Pommier (2018) предложил значительно более низкое значение 0,59 мкОм·м при 1400 К. К и 4,5 ГПа. Аналогично измерениям Silber et al. (2018), Ezenwa и Secco (2019) оценили значения 1,17 мкОм·м и 1,38 мкОм·м на твердой и жидкой сторонах ICB (2200 K, 9 ГПа) соответственно. Независимо от различий в этих результатах Fe, ожидается, что добавление S увеличит ρ, что согласуется с прямыми измерениями Pommier (2018). Pommier (2018) сообщил о значениях 2,23 мкОм·м для Fe5S при 1880 К и 4,5 ГПа и 4,32 мкОм·м для Fe20S при 1 400 К и 4,5 ГПа. Насколько нам известно, только в двух исследованиях сообщалось об измерениях Fe36,5S при соответствующих P и T условия. Во-первых, результаты Manthilake et al. (2019), примененные к условиям Ганимеда, предполагают 8,01 мкОм·м вблизи реликтового излучения. ТАБЛИЦА 8 . Значения удельного электрического сопротивления Fe и Fe-сплавов по разным методикам на реликтовом излучении Ганимеда. РИСУНОК 6 . Комбинированные значения ρ из литературы, примененные к ядру Ганимеда, представлены в порядке дат. Синяя пунктирная линия представляет средние значения в CMB, а красная пунктирная линия представляет средние значения в ICB. Среднее значение всех зарегистрированных значений при условиях CMB (1400–2000 K, 5–7 ГПа) составляет 1,90 мкОм·м, а при ICB (2200 K, 9 ГПа) — 1,28 мкОм·м. Повторяющиеся ссылки указывают на разные композиции. Как и в случае с другими рассмотренными малыми планетными телами, доступная литература скудна и недостаточна, чтобы определить разумное значение ρ в условиях ядра. На рисунке 7 показаны контурные карты, созданные на основе доступной литературы по ρ для Fe, сплавов Fe-Ni, сплавов Fe-O и сплавов Fe-Si/S, не исключая высоких значений (>3 мкОм·м). Контурные карты предполагают, что ρ( P , T ) уникален для каждого состава и вряд ли может быть определен линейной функцией P и T . РИСУНОК 7 . 3D-визуализация сообщаемого ρ с P и T из сплавов (A) Fe, (B) сплавов Fe-Ni, (C) сплавов Fe-O и (D) сплавов Fe-Si/S. Исследования, в которых не указаны точные условия P , T для реликтового излучения Земли и ICB, относятся к 4000 K и 136 ГПа и 5000 K и 330 ГПа соответственно. Интерес к определению q и вызван именно моделированием тепловой эволюции. Прямые измерения тепловых свойств, и в частности k , металлов и металлических сплавов в условиях планетарного ядра сложны, а экстраполяции относительно низких P и T условий не всегда согласуются. Дальнейшие экспериментальные исследования ρ должны быть сосредоточены на различных составах легких элементов, особенно в Fe со сплавами из нескольких легких элементов, чтобы надежно ограничить ρ для вероятных составов ядра в условиях планетарного ядра. Потребуется больший набор данных по измерениям k для проверки как теоретически определенных значений числа Лоренца при экстремальных условиях Р и Т для чистого Fe и его многочисленных сплавов, так и для обоснования использования данных ρ для расчета0110 к . Очевидно, что предстоит еще многое сделать в области определения свойств ρ и k для применения в тепловом моделировании планетарных тел земного типа в нашей Солнечной системе. Однако еще большая проблема, появляющаяся на горизонте, заключается в том, чтобы аналогичные исследования проводились в еще более высоких P, T условиях экзопланет земного типа, где внутреннее давление на порядок выше, чем на Земле. Исследования этих систем, которые в настоящее время находятся на начальной стадии описания уравнения состояния и других структурных характеристик железа (Smith et al., 2018) и сплавов Fe (Wicks et al., 2018), затем обратятся к изучению внутренних моделирование теплового потока и динамики ядра для понимания динамо-машин в суперземлях, для чего потребуются знания ρ и k поведение в гораздо большем пространстве P, T. МБ отвечает за формальный анализ, написание и редактирование. RS отвечает за надзор, рецензирование, редактирование и финансирование. Эта работа была поддержана средствами RS от Совета по естественным наукам и инженерным исследованиям Канады (номер гранта 2018-05021). Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Все претензии, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем. Мы очень благодарны доктору Герду Штайнле-Нойманну и доктору Монике Поццо за их проницательные комментарии к рукописи и двум рецензентам за их конструктивные комментарии. Ahrens, TJ (2007). «Эксперименты с ударными волнами», в Энциклопедии геомагнетизма и палеомагнетизма . Редакторы Д. Габбинс и Э. Эрреро-Бервера (Дордрехт: Springer Netherlands), 912–920. Google Scholar Альфе, Д., Гиллан, М. Дж., и Прайс, Г. Д. (2007). Температура и состав ядра Земли. Контемп. физ. 48 (2), 63–80. doi:10.1080/00107510701529653 CrossRef Full Text | Академия Google Андерсон, Дж. Д., Лау, Э. Л., Шегрен, В. Л., Шуберт, Г., и Мур, В. Б. (1996). Гравитационные ограничения на внутреннюю структуру Ганимеда. Природа 384 (6609), 541–543. doi:10.1038/384541a0 CrossRef Полный текст | Google Scholar Андерсон, О.Л. (1998). Параметр Грюнайзена для железа во внешнем сердечнике и результирующие кондуктивные тепло и мощность в сердечнике. Физ. Планета Земля. Интерьеры 109 (3), 179–197. дои: 10.1016/s0031-9201(98)00123-x CrossRef Полный текст | Google Scholar Антонангели Д. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Анцеллини С. и Боккато С. (2020). Практический обзор ячейки с алмазной наковальней с лазерным нагревом для университетских лабораторий и синхротронных применений. Crystals 10 (6), 459. doi:10.3390/cryst10060459 CrossRef Полный текст | Google Scholar Аргаман Н. и Маков Г. (2000). Теория функционала плотности: введение. 90 110 утра. Дж. Физ. 68 (1), 69–79. doi:10.1119/1.19375 CrossRef Полный текст | Google Scholar Armytage, RMG, Georg, RB, Williams, HM, and Halliday, AN (2012). Изотопы кремния в лунных породах: значение для формирования Луны и ранней истории Земли. Geochimica et Cosmochimica Acta 77, 504–514. doi:10.1016/j.gca. Полный текст CrossRef | Google Scholar Asimow, PD (2015). «Динамическое сжатие», в Трактате по геофизике . Редактор Г. Шуберт, второе издание (Оксфорд: Elsevier), 393–416. doi:10.1016/b978-0-444-53802-4.00050-6 Полный текст CrossRef | Google Scholar Бадро Дж., Фике Г., Гайо Ф., Грегорьянц Э., Окчелли Ф., Антонанджели Д. и др. (2007). Влияние легких элементов на скорость звука в твердом железе: влияние на состав ядра Земли. Планета Земля. науч. лат. 254 (1), 233–238. doi:10.1016/j.epsl.2006.11.025 Полный текст CrossRef | Google Scholar Баум Б., Гельд П., Тягунов Г. (1967). Удельное сопротивление сплавов ферросилиция в интервале температур 800–1700 С. 90–110 Физ. Встретились. Металлография 24 (181), 52–57. doi:10.1016/0016-2361(73)-4 Полный текст CrossRef | Google Scholar Беррада М., Секко Р. А. и Йонг В. (2021). Адиабатический тепловой поток в ядре Меркурия по данным измерения удельного электрического сопротивления жидкого Fe-8,5 мас. CrossRef Полный текст | Google Scholar Беррада М., Секко Р. А. и Йонг В. (2018). Снижение удельного электрического сопротивления золота по границе плавления до 5 ГПа. Высокий пресс. Рез. 38 (4), 367–376. doi:10.1080/08957959.2018.1493476 CrossRef Full Text | Google Scholar Беррада М., Секко Р. А. и Йонг В. (2020). Измерения удельного электрического сопротивления Fe-Si с учетом раннего лунного динамо. Ж. Геофиз. Рез. Планеты 125 (7), e2020JE006380. doi:10.1029/2020je006380 Полный текст CrossRef | Google Scholar Bi, Y., Tan, H., and Jing, F. (2002). Электропроводность железа при ударном сжатии до 200 ГПа. J. Phys. Конденсированные вещества 14 (44), 10849–10854. doi:10.1088/0953-8984/14/44/389 CrossRef Full Text | Google Scholar Берч, Ф. (1961). Состав мантии Земли. Геофиз. Дж. Междунар. Полный текст CrossRef | Google Scholar Берч, Ф. (1964). Плотность и состав мантии и ядра. Ж. Геофиз. Рез. 69 (20), 4377–4388. 1896-1977 гг. doi:10.1029/jz069i020p04377 CrossRef Full Text | Google Scholar Бланд, М. Т., Шоумен, А. П., и Тоби, Г. (2008). Создание магнитного поля Ганимеда. Икар 198 (2), 384–399. doi:10.1016/j.icarus.2008.07.011 CrossRef Полный текст | Академия Google Боненкамп, У., Сандстрем, Р., и Гримвалл, Г. (2002). Удельное электрическое сопротивление сталей и гранецентрированного кубического железа. Дж. Заявл. физ. 92 (8), 4402–4407. doi:10.1063/1.1502182 CrossRef Полный текст | Google Scholar Больцман, Л. (1894 г.). Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Энн. физ. 289 (13), 959–964. doi:10.1002/andp.189428 CrossRef Full Text | Google Scholar Бриджмен, П. Google Scholar Шабо, Н. Л., Воллак, Э. А., Клима, Р. Л., и Минитти, М. Э. (2014). Экспериментальные ограничения на состав ядра Меркурия. Планета Земля. науч. лат. 390, 199–208. doi:10.1016/j.epsl.2014.01.004 Полный текст CrossRef | Google Scholar Christensen, UR (2006). Глубокое динамо, генерирующее магнитное поле Меркурия. Природа 444 (7122), 1056–1058. doi:10.1038/nature05342 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Дэвис, Г. Ф. (2007). Мантийное регулирование охлаждения ядра: геодинамо без радиоактивности ядра? Физ. Планета Земля. Интерьеры 160 (3), 215–229. doi:10.1016/j.pepi.2006.11.001 Полный текст CrossRef | Google Scholar де Кокер Н., Штайнле-Нойманн Г. и Влчек В. (2012). PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar де Мейер, Р. Дж., Анисичкин, В. Ф., и ван Вестренен, В. (2013). Формирование Луны из земного материала, богатого силикатами. Хим. Геология. 345, 40–49. doi:10.1016/j.chemgeo.2012.12.015 CrossRef Full Text | Google Scholar Дэн Л., Сигл К., Фей Ю. и Шахар А. (2013). Удельное электрическое сопротивление железа при высоких давлениях и температурах и последствия для планетарных ядер. Геофиз. Рез. лат. 40 (1), 33–37. doi:10.1029/2012gl054347 Полный текст перекрестной ссылки | Google Scholar Дрчал В., Кудрновский Дж., Вагенкнехт Д. и Турек И. (2019). Сплавный беспорядок и флуктуирующие магнитные моменты в ядре Земли. Дж. Магнетизм Magn. Матер. CrossRef Full Text | Google Scholar Друде, П. (1900a). Zur Elektronentheorie der Metalle. Энн. физ. 306 (3), 566–613. doi:10.1002/andp.160312 Полнотекстовая перекрестная ссылка | Google Scholar Друде, П. (1900b). Zur Elektronentheorie der Metalle; II. Тейл. Гальваномагнитные и термомагнитные эффекты. Энн. физ. 308 (11), 369–402. doi:10.1002/andp.181102 CrossRef Full Text | Google Scholar Эльзассер, В. М. (1946). Индукционные эффекты в земном магнетизме. Часть II. Светская вариация. Физ. Ред. 70 (3–4), 202–212. doi:10.1103/physrev.70.202 Полный текст CrossRef | Академия Google Эванс, А. Дж., Зубер, М. Т., Вайс, Б. П., и Тикоо, С. М. (2014). Влажный, гетерогенный лунный интерьер: нижняя мантия и эволюция основного динамо. Ж. Геофиз. Рез. Планеты 119 (5), 1061–1077. doi:10.1002/2013je004494 Полный текст CrossRef | Google Scholar Эванс Р. Полнотекстовая перекрестная ссылка | Google Scholar Эзенва, И. К., и Секко, Р. А. (2017a). Постоянное удельное электрическое сопротивление Zn по границе плавления до 5 ГПа. Высокий пресс. Рез. 37 (3), 319–333. doi:10.1080/08957959.2017.1340473 CrossRef Full Text | Google Scholar Эзенва, И. К., и Секко, Р. А. (2019). Переход плавления Fe: удельное электрическое сопротивление, теплопроводность и тепловой поток на внутренних границах ядра Меркурия и Ганимеда. Кристаллы 9 (7). doi:10.3390/cryst59 Полный текст CrossRef | Google Scholar Эзенва, И. К., и Секко, Р. А. (2017b). Инвариантное удельное электрическое сопротивление Co вдоль границы плавления. Планета Земля. науч. лат. 474, 120–127. doi:10.1016/j.epsl.2017.06.032 Полный текст CrossRef | Google Scholar Эзенва И. CrossRef Full Text | Google Scholar Эзенва, И. К., и Йошино, Т. (2021). Тепловой поток марсианского ядра: удельное электрическое сопротивление и теплопроводность жидкого Fe в марсианском ядре P-T условиях. Icarus 360, 114367. doi:10.1016/j.icarus.2021.114367 CrossRef Полный текст | Google Scholar Гардинер Р. Б. и Стейси Ф. Д. (1971). Удельное электрическое сопротивление активной зоны. Физ. Планета Земля. Интерьеры 4 (5), 406–410. doi:10.1016/0031-9201(71) CrossRef Full Text | Google Scholar Гилев С. Д. (2011). Измерение электропроводности конденсированных веществ в ударных волнах (обзор). Воспламенение Взрывы Ударные волны 47 (4), 375–393. doi:10.1134/s0010508211040010 Полный текст CrossRef | Google Scholar Гоми Х. CrossRef Full Text | Google Scholar Гоми, Х., и Хиросе, К. (2015). Удельное электрическое сопротивление и теплопроводность сплавов Fe-Ni с ГПУ под высоким давлением: влияние на тепловую конвекцию в ядре Земли. Физ. Планета Земля. Интерьеры 247, 2–10. doi:10.1016/j.pepi.2015.04.003 Полный текст CrossRef | Google Scholar Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J., et al. (2013). Высокая проводимость железа и тепловая эволюция ядра Земли. Физ. Планета Земля. Интерьеры 224, 88–103. Статья. doi:10.1016/j.pepi.2013.07.010 CrossRef Full Text | Google Scholar Гоми Х. и Йошино Т. (2018). Удельное сопротивление примесей ГЦК и ГПУ сплавов на основе Fe: тепловое расслоение в верхней части ядра суперземли. CrossRef Полный текст | Google Scholar Гринвуд, Д. А. (1958). Уравнение Больцмана в теории электропроводности металлов. Проц. физ. соц. 71 (4), 585–596. doi:10.1088/0370-1328/71/4/306 CrossRef Full Text | Google Scholar Гурвич, М. (1981). Критерий Иоффе-Регеля и удельное сопротивление металлов. Физ. Ред. B 24 (12), 7404–7407. doi:10.1103/physrevb.24.7404 Полный текст CrossRef | Google Scholar Хардер, Х., и Шуберт, Г. (2001). Сера в ядре Меркурия? Икар 151 (1), 118–122. doi:10.1006/icar.2001.6586 CrossRef Full Text | Академия Google Хаук, С.А., Орну, Дж.М., и Домбард, А.Дж. (2006). Влияние серы на эволюцию ядра и генерацию магнитного поля на Ганимеде. Ж. Геофиз. Рез. Планеты 111 (E9). doi:10.1029/2005je002557 Полный текст CrossRef | Google Scholar Се В.-П., Гончаров А. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Хуссманн Х., Сотин К. и Лунин Дж. И. (2007). «Внутренности и эволюция ледяных спутников», в Трактате по геофизике . Редактор Г. Шуберт (Амстердам: Elsevier), 509–539. doi:10.1016/b978-044452748-6.00168-1 CrossRef Full Text | Google Scholar Иноуэ Х., Суэхиро С., Охта К., Хиросе К. и Охиши Ю. (2020). Насыщение удельного сопротивления сплавов Hcp Fe-Si в ячейке с алмазной наковальней с внутренним подогревом: ключ к оценке проводимости ядра Земли. Планета Земля. науч. лат. 543, 116357. doi:10.1016/j.epsl.2020.116357 CrossRef Полный текст | Google Scholar Ито, Э. (2015). «Ячейки с несколькими наковальнями и экспериментальные методы высокого давления», в «Трактате по геофизике и физике минералов» . Полный текст CrossRef | Google Scholar Джейн А. и Эванс Р. (1972). Расчет удельного электрического сопротивления жидкого железа в ядре Земли. Нац. физ. науч. 235 (61), 165–167. doi:10.1038/physci235165a0 Полный текст CrossRef | Google Scholar Жанло Р. (1979). Свойства железа при высоких давлениях и состояние активной зоны. Ж. Геофиз. Рез. 84 (В11), 6059–6069. doi:10.1029/jb084ib11p06059 CrossRef Full Text | Google Scholar Johnston, MJS, and Strens, RGJ (1973). Электропроводность расплавленной керновой смеси FeNiSC. Физ. Планета Земля. Интерьеры 7 (2), 219–222. doi:10.1016/0031-9201(73) Полный текст CrossRef | Google Scholar Кавнер А., Даффи Т.С. и Шен Г. (2001). Фазовая стабильность и плотность FeS при высоких давлениях и температурах: последствия для внутренней структуры Марса. Полнотекстовая перекрестная ссылка | Google Scholar Киллер Р. Н. и Ройс Э. Б. (1971). Ударные волны в конденсированных средах. Физ. Высокая энергия. Плотность , 51–150. Google Scholar Киараси, С. (2013). . Лондон, Онтарио: Школа аспирантуры и докторантуры Университета Западного Онтарио. Киараси, С., и Секко, Р. А. (2015). Насыщение удельного электрического сопротивления Fe17Si под давлением. Физ. Статус Solidi B 252 (9), 2034–2042. дои: 10.1002/pssb.201552029 Полнотекстовая перекрестная ссылка | Google Scholar Кимура Дж., Накагава Т. и Курита К. (2009). Размер и композиционные ограничения металлического ядра Ганимеда для приведения в действие динамо-машины. Икар 202 (1), 216–224. doi:10.1016/j.icarus.2009.02.026 Полный текст CrossRef | Google Scholar Киттель, К. (2005). Введение в физику твердого тела . Клеменс, П.Г., и Уильямс, Р.К. (1986). Теплопроводность металлов и сплавов. Междунар. Встретились. 31 (1), 197–215. doi:10.1179/imtr.1986.31.1.197 CrossRef Full Text | Google Scholar Книббе, Дж. С., и ван Вестренен, В. (2017). Тепловая эволюция Меркурия и генерация магнитного поля с помощью базового материала Fe-Si, представленного на 48-й Лунной и планетарной научной конференции . Вудлендс, Техас. Вклад ФИАН № 1964, ид. 1094. Книббе, Дж. С., и ван Вестренен, В. (2018). Термическая эволюция ядра Fe-Si Меркурия. Планета Земля. науч. лат. 482, 147–159. doi:10.1016/j.epsl.2017.11.006 Полный текст CrossRef | Google Scholar Конопкова З., Маквильямс Р. С., Гомес-Перес Н. и Гончаров А. Ф. (2016). Прямое измерение теплопроводности в твердом железе в условиях планетарного ядра. Природа 534 (7605), 99–101. doi:10.1038/nature18009 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Корелл, Дж. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Крот А. Н. (2005). Классификация метеоритов. Метеориты, кометы и планеты , 83–142. doi:10.1007/978-3-642-65863-1_2 CrossRef Full Text | Google Scholar Кубо, Р. (1957). Статистико-механическая теория необратимых процессов. I. Общая теория и простые приложения к задачам магнитного поля и проводимости. J. Phys. соц. Япония. 12 (6), 570–586. doi:10.1143/jpsj.12.570 Полный текст CrossRef | Google Scholar Ланевиль, М., Тейлор, Дж., и Вечорек, Массачусетс (2018). Распределение радиоактивных источников тепла и тепловая история Луны. Ж. Геофиз. Рез. Планеты 123 (12), 3144–3166. doi:10.1029/2018je005742 CrossRef Полный текст | Google Scholar Ланевиль М. Полный текст CrossRef | Google Scholar Ли, Дж., и Фей, Ю. (2003). «2.14 — Экспериментальные ограничения на состав керна», в «Трактат по геохимии ». Редакторы Х. Д. Холланд и К. К. Турекян (Оксфорд: Пергамон), 1–31. Полнотекстовая перекрестная ссылка | Google Scholar Liebermann, RC (2011). Аппарат высокого давления с несколькими наковальнями: полвека развития и прогресса. Высокое давление. Рез. 31 (4), 493–532. doi:10.1080/08957959.2011.618698 CrossRef Full Text | Google Scholar Литасов К.Д., Шацкий А.Ф. (2016). Состав ядра Земли: обзор. рус. Геология. Геофиз. 57 (1), 22–46. doi:10.1016/j.rgg.2016.01.003 Полный текст CrossRef | Google Scholar Литтлтон, Дж. А. Х., Секко, Р. CrossRef Полный текст | Google Scholar Литтлтон, Дж. А. Х., Секко, Р. А., и Йонг, В. (2021). Удельное электрическое сопротивление FeS при высоких давлениях и температурах: последствия теплового переноса в ядре Ганимеда. Ж. Геофиз. Рез. Планеты 126 (5), e2020JE006793. doi:10.1029/2020je006793 Полный текст CrossRef | Google Scholar Малаверн В., Топлис М. Дж., Бертет С. и Джонс Дж. (2010). Сильно восстановительные условия во время формирования ядра на Меркурии: последствия для внутренней структуры и происхождения магнитного поля. Икар 206 (1), 199–209. doi:10.1016/j.icarus.2009.09.001 CrossRef Полный текст | Google Scholar Manthilake, G., Chantel, J., Monteux, J., Andrault, D., Bouhifd, M.A., Bolfan Casanova, N., et al. (2019). Полный текст CrossRef | Google Scholar Мао, Х.-К., и Мао, В.Л. (2007). «Теория и практика: ячейки с алмазными наковальнями и зонды для изучения физики минералов с высоким P-T», в Трактат по геофизике . Редактор Г. Шуберт, второе издание (Оксфорд: Elsevier), 263–291. doi:10.1016/b978-0-444-53802-4.00036-1 Полный текст CrossRef | Google Scholar Мао Х.К., Ву Ю., Чен Л.К., Шу Дж.Ф. и Джефкоут А.П. (1990). Статическое сжатие железа до 300 ГПа и сплава Fe0,8Ni0,2 до 260 ГПа: влияние на состав активной зоны. Ж. Геофиз. Рез. 95 (B13), 21737–21742. doi:10.1029/jb095ib13p21737 Полный текст перекрестной ссылки | Академия Google Мао, З., Линь, Дж.-Ф., Лю, Дж., Алатас, А., Гао, Л., Чжао, Дж., и другие. (2012). Скорости звука Fe и сплава Fe-Si в ядре Земли. Проц. Натл. акад. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Матасов Г. (1977). Электропроводность железокремниевых сплавов при высоких давлениях и ядро Земли . Калифорнийский университет. МакКаббин, Ф. М., Ринер, М. А., Вандер Кааден, К. Э., и Буркемпер, Л. К. (2012). Является ли Меркурий богатой летучими планетами? Геофиз. Рез. лат. 39 (9), L09202. doi:10.1029/2012gl051711 Полный текст перекрестной ссылки | Google Scholar Mooij, JH (1973). Электропроводность в концентрированных неупорядоченных сплавах переходных металлов. Физ. Стат. Сол. (А) 17 (2), 521–530. doi:10.1002/pssa.2210170217 CrossRef Полный текст | Google Scholar Морган, Дж. В., и Андерс, Э. (1980). Химический состав Земли, Венеры и Меркурия. Проц. Натл. акад. науч. 77 (12), 6973–6977. doi:10.1073/pnas.77.12.6973 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Мотт, Н. CrossRef Full Text | Google Scholar Мотт, Н. Ф. (1972). Удельное электрическое сопротивление жидких переходных металлов. Фил. Маг. 26 (6), 1249–1261. doi:10.1080/14786437208220339 CrossRef Full Text | Академия Google Назаров М.А., Демидова С.И., Аносова М.О., Костицын Ю.А., Нтафлос Т. и Брандштеттер Ф. (2012). Самородные силициды кремния и железа в лунном метеорите Dhofar 280. Петрология 20 (6), 506–519. doi:10.1134/s08695060021 CrossRef Full Text | Google Scholar Ниммо Ф. и Стивенсон Д. Дж. (2000). Влияние ранней тектоники плит на тепловую эволюцию и магнитное поле Марса. Ж. Геофиз. Рез. 105 (Е5), 11969–11979. doi:10.1029/1999je001216 CrossRef Full Text | Google Scholar Ниттлер Л. Р., Шабо Н. Л., Гроув Т. Л. и Пепловски П. Н. (2017). «Химический состав ртути», в Mercury: The View after MESSENGER (Cambridge University Press). Google Scholar Охта К., Куваяма Ю., Хиросе К., Симидзу К. и Охиши Ю. (2016). Экспериментальное определение удельного электрического сопротивления железа в условиях ядра Земли. Природа 534 (7605), 95–98. doi:10.1038/nature17957 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Пуарье Ж.-П. (1994). Легкие элементы во внешнем ядре Земли: критический обзор. Физ. Планета Земля. Интерьеры 85 (3), 319–337. doi:10.1016/0031-9201(94)-1 Полный текст CrossRef | Google Scholar Поммье, А. (2018). Влияние серы на удельное электрическое сопротивление кристаллизующегося ядра в малых земных телах. Планета Земля. науч. лат. 496, 37–46. doi:10.1016/j.epsl.2018.05.032 Полный текст CrossRef | Google Scholar Поммье А., Лейненвебер К. и Тран Т. (2019). Термическая эволюция Меркурия контролируется изолирующей жидкостью в самом внешнем ядре? Планета Земля. науч. лат. 517, 125–134. CrossRef Full Text | Google Scholar Пуровский Л.В., Мравлье Дж., Поццо М. и Альфе Д. (2020). Электронные корреляции и транспорт в железе в условиях ядра Земли. Нац. коммун. 11 (1), 4105. doi:10.1038/s41467-020-18003-9 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Поццо М. и Альфе Д. (2016b). «Удельное электрическое сопротивление насыщения твердого железа в условиях ядра Земли на основе теории функционала плотности», в AGU Abstract DI13A-2356 (Сан-Франциско, Калифорния): Осеннее совещание AGU). Google Scholar Поццо М. и Альфе Д. (2016a). Насыщение удельного электрического сопротивления твердого железа в условиях ядра Земли. SpringerPlus 5 (1), 256. doi:10.1186/s40064-016-1829-x CrossRef Полный текст | Google Scholar Поццо М., Дэвис К., Габбинс Д. и Альфе Д. (2012). Тепло- и электропроводность железа в условиях ядра Земли. Природа 485 (7398), 355–358. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Поццо М., Дэвис К., Габбинс Д. и Альфе Д. (2014). Тепло- и электропроводность твердого железа и железо-кремниевых смесей в условиях ядра Земли. Планета Земля. науч. лат. 393, 159–164. doi:10.1016/j.epsl.2014.02.047 CrossRef Full Text | Google Scholar Поццо, М., Дэвис, К., Губбинс, Д., и Алфе, Д. (2013). Транспортные свойства жидких кремний-кислород-железных смесей в условиях ядра Земли. Физ. Rev. B 87 (1), 014110. doi:10.1103/physrevb.87.014110 CrossRef Полный текст | Google Scholar Риволдини А., Ван Хулст Т., Верховен О., Мокке А. и Дехант В. (2011). Геодезические ограничения внутренней структуры и состава Марса. Икар 213 (2), 451–472. doi:10.1016/j.icarus.2011.03.024 Полный текст CrossRef | Google Scholar Риволдини А., Ван Хулст Т. и Верховен О. (2009). Внутренняя структура Меркурия и содержание серы в его ядре. Полный текст CrossRef | Google Scholar Шейнберг А., Содерлунд К. М. и Шуберт Г. (2015). Генерация магнитного поля в ядре Луны: роль роста внутреннего ядра. Икар 254, 62–71. doi:10.1016/j.icarus.2015.03.013 CrossRef Полный текст | Google Scholar Сигл, К. Т., Коттрелл, Э., Фей, Ю., Хаммер, Д. Р., и Пракапенка, В. Б. (2013). Электрические и тепловые транспортные свойства железа и сплава железо-кремний при высоком давлении. Геофиз. Рез. лат. 40 (20), 5377–5381. doi:10.1002/2013gl057930 Полный текст перекрестной ссылки | Google Scholar Секко, Р. А., и Шлессин, Х. Х. (1989). Удельное электрическое сопротивление твердого и жидкого Fe при давлениях до 7 ГПа. Ж. Геофиз. Рез. 94 (В5), 5887–5894. doi:10.1029/jb094ib05p05887 Полный текст CrossRef | Google Scholar Секко, Р. А. (2017). Теплопроводность и коэффициент Зеебека сплавов Fe и Fe-Si: последствия для переменного числа Лоренца. Полный текст CrossRef | Google Scholar Ша, X., и Коэн, Р. Э. (2011). Первые принципы исследования удельного электрического сопротивления железа под давлением. J. Phys. Конденс. Matter 23 (7), 075401. doi:10.1088/0953-8984/23/7/075401 CrossRef Полный текст | Google Scholar Шибазаки Ю., Отани Э., Терасаки Х., Татеяма Р., Сакамаки Т., Цучия Т. и др. (2011). Влияние водорода на температуру плавления FeS при высоком давлении: значение для ядра Ганимеда. Планета Земля. науч. лат. 301 (1), 153–158. doi:10.1016/j.epsl.2010.10.033 CrossRef Full Text | Академия Google Зильбер, Р. Э., Секко, Р. А., и Йонг, В. (2017). Постоянное удельное электрическое сопротивление никеля по границе плавления до 9 ГПа. Ж. Геофиз. Рез. Твердая Земля 122 (7), 5064–5081. doi:10.1002/2017jb014259 Полный текст перекрестной ссылки | Google Scholar Зильбер, Р. Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar Зильбер, Р. Э., Секко, Р. А., Йонг, В., и Литтлтон, Дж. А. Х. (2019). Тепловой поток в ядре Земли от инвариантного удельного электрического сопротивления Fe-Si на границе плавления до 9 ГПа: имеют ли значение легкие элементы? Ж. Геофиз. Рез. Solid Earth 124 (6), 5521–5543. doi:10.1029/2019jb017375 CrossRef Полный текст | Google Scholar Smith, R. F., Fratanduono, D. E., Braun, D. G., Duffy, T. S., Wicks, J. K., Celliers, P. M., et al. (2018). Уравнение состояния железа в условиях ядра крупных каменистых экзопланет. Нац. Астрон. 2 (6), 452–458. doi:10.1038/s41550-018-0437-9 CrossRef Full Text | Google Scholar Зоммерфельд, А. Полный текст CrossRef | Google Scholar Стейси Ф.Д. и Андерсон О.Л. (2001). Электрическая и теплопроводность сплава Fe–Ni–Si в основных условиях. Физ. Планета Земля. Интерьеры 124 (3), 153–162. doi:10.1016/s0031-9201(01)00186-8 CrossRef Full Text | Google Scholar Стейси, Ф. Д., и Лопер, Д. Э. (2007). Пересмотренная оценка проводимости сплава железа при высоком давлении и последствия для энергетического баланса активной зоны. Физ. Планета Земля. Интерьеры 161 (1), 13–18. doi:10.1016/j.pepi.2006.12.001 Полный текст CrossRef | Google Scholar Стинстра, Э. С., и ван Вестренен, В. (2017). «Сульфиды на Луне», в Энциклопедия лунной науки . Редактор Б. Кудник (Cham: Springer International Publishing), 1–6. doi:10.1007/978-3-319-05546-6_119-1 CrossRef Полный текст | Google Scholar Стегман Д. PubMed Abstract | Полный текст перекрестной ссылки | Академия Google Steinbrügge, G., Dumberry, M., Rivoldini, A., Schubert, G., Cao, H., Schroeder, D.M., et al. (2021). Проблемы внутренней структуры Меркурия, связанные с новыми измерениями его наклона и приливов. Геофиз. Рез. лат. 48 (3), e2020GL089895. doi:10.1029/2020gl089895 CrossRef Полный текст | Google Scholar Стивенсон Д. Дж., Спон Т. и Шуберт Г. (1983). Магнетизм и тепловая эволюция планет земной группы. Икар 54 (3), 466–489. doi:10.1016/0019-1035(83)-5 CrossRef Full Text | Google Scholar Стюарт, А. Дж., и Шмидт, М. В. (2007). Сера и фосфор в ядре Земли: система Fe-PS при 23 ГПа. Геофиз. Рез. лат. 34 (13), L13201. doi:10.1029/2007gl030138 Полный текст перекрестной ссылки | Google Scholar Стиксруд Л. Полный текст перекрестной ссылки | Google Scholar Суэхиро С., Охта К., Хиросе К., Морар Г. и Охиши Ю. (2017). Влияние серы на удельное электрическое сопротивление железа с ГПУ: последствия для проводимости ядра Марса и Земли. Геофиз. Рез. лат. 44 (16), 8254–8259. doi:10.1002/2017gl074021 CrossRef Полный текст | Google Scholar Шургот, М. (2017). Несжатая плотность Луны, лунной мантии и ядра . Будапешт, Венгрия: применение аналитических методов к Земле. Документ, представленный на семинаре по модерну. Терасаки Х., Ривольдини А., Симояма Ю., Нисида К., Уракава С., Маки М. и др. (2019). Влияние давления и состава на скорость звука и плотность образующих ядро жидкостей: влияние на состав ядер земных планет. Ж. Геофиз. Рез. Планеты 124 (8), 2272–2293. doi:10.1029/2019je005936 Полный текст CrossRef | Google Scholar Този Н. Полный текст CrossRef | Google Scholar Фоллхардт Д., Бычук К. и Коллар М. (2012). «Динамическая теория среднего поля», в сильно коррелированных системах . Редакторы М. Ф. Авелла, (Берлин, Гейдельберг: Springer), 171. doi:10.1007/978-3-642-21831-6_7 CrossRef Полный текст | Google Scholar Вагле Ф., Штайнле-Нойманн Г. и де Кокер Н. (2019). Насыщение удельного сопротивления в жидких сплавах железа с легкими элементами в условиях планетарных ядер из расчетов из первых принципов. Comptes Rendus Geosci. 351 (2), 154–162. doi:10.1016/j.crte.2018.05.002 Полный текст CrossRef | Google Scholar Вагле Ф., Штайнле-Нойманн Г. и де Кокер Н. (2018). Насыщение и отрицательный температурный коэффициент удельного электрического сопротивления в жидких сплавах железо-сера при высоких плотностях из расчетов из первых принципов. CrossRef Полный текст | Google Scholar Вагл Ф. и Штайнле-Нойманн Г. (2018). Неоднородность удельного электрического сопротивления железа вдоль кривой плавления. Геофиз. Дж. Междунар. 213 (1), 237–243. doi:10.1093/gji/ggx526 Полный текст CrossRef | Google Scholar Wänke, H., Dreibus, G., Runcorn, S.K., Turner, G., and Woolfson, M.M. (1988). Химический состав и история аккреции планет земной группы. Фил. Транс. Р. Соц. Лонд. А. 325 (1587), 545–557. doi:10.1098/rsta.1988.0067 Полный текст CrossRef | Google Scholar Weber, R.C., Lin, P.-Y., Garnero, E.J., Williams, Q., and Lognonné, P. (2011). Сейсмическое обнаружение лунного ядра. Наука 331 (6015), 309–312. doi:10.1126/science.1199375 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Уикс Дж. К., Смит Р. Ф., Фратандуоно Д. Э., Коппари Ф., Краус Р. Г., Ньюман М. Резюме PubMed | Полный текст перекрестной ссылки | Google Scholar Wieczorek, M.A., Jolliff, B.L., Khan, A., Pritchard, M.E., Weiss, B.P., Williams, J.G., et al. (2006). Конституция и структура лунного интерьера. Ред. Минералогия Геохим. 60 (1), 221–364. doi:10.2138/rmg.2006.60.3 Полный текст CrossRef | Google Scholar Wiesmann, H., Gurvitch, M., Lutz, H., Ghosh, A., Schwarz, B., Strongin, M., et al. (1977). Простая модель для характеристики удельного электрического сопротивления в сверхпроводниках A-15. Физ. Преподобный Летт. 38 (14), 782–785. doi:10.1103/physrevlett.38.782 Полный текст CrossRef | Google Scholar Сюй Дж., Чжан П., Хауле К., Минар Дж., Виммер С., Эберт Х. и др. (2018). Теплопроводность и удельное электрическое сопротивление твердого железа в условиях ядра Земли из первых принципов. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Инь Ю., Чжай К., Чжан Б. и Чжай С. (2019). Удельное электрическое сопротивление фосфидов железа в условиях высокого давления и высокой температуры с учетом теплопроводности лунного ядра. Ж. Геофиз. Рез. Solid Earth 124 (6), 5544–5556. doi:10.1029/2018jb017157 CrossRef Полный текст | Академия Google Йонг, В., Секко, Р. А., Литтлтон, Дж. А. Х., и Силбер, Р. Э. (2019). Инвариантность железа: последствия для тепловой конвекции в ядре Земли. Геофиз. Рез. лат. 46 (20), 11065–11070. doi:10.1029/2019gl084485 CrossRef Полный текст | Google Scholar Зайцев А.И., Доброхотова З.В., Литвина А.Д., Могутнов Б.М. (1995). Термодинамические свойства и фазовые равновесия в системе Fe-P. J. Chem. соц. Фарадей Транс. 91 (4), 703–712. Дои: 10.1039/FT995 Полнотекстовая перекрестная ссылка | Google Scholar Zambardi, T. Полный текст CrossRef | Google Scholar Чжан С., Лин Дж. Ф., Лю Ю., Фэн С., Джин С., Хоу М. и др. (2018). Удельное электрическое сопротивление сплава Fe-C при высоком давлении: влияние углерода как легкого элемента на теплопроводность ядра Земли. Ж. Геофиз. Рез. Solid Earth 123 (5), 3564–3577. doi:10.1029/2017jb015260 Полный текст перекрестной ссылки | Google Scholar Чжан Н., Парментье Э. М. и Лян Ю. (2013). Трехмерное численное исследование тепловой эволюции Луны после кумулятивного переворота мантии: важность реологии и затвердевания ядра. Ж. Геофиз. Рез. Планеты 118 (9), 1789–1804 гг. doi:10.1002/jgre.20121 Полный текст CrossRef | Google Scholar Zhang, Y. PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Zhang, Y., Hou, M., Driscoll, P., Salke, N.P., Liu, J., Greenberg, E., et al. (2021). Транспортные свойства сплавов Fe-Ni-Si в условиях ядра Земли: понимание жизнеспособности тепловой и композиционной конвекции. Планета Земля. науч. лат. 553, 116614. doi:10.1016/j.epsl.2020.116614 CrossRef Полный текст | Академия Google Зидан М., Салмани Э. М., Маджумдар А., Эз-Захрауи Х., Беньюссеф А. и Ахуджа Р. (2020). Электрические и тепловые транспортные свойства тройных сплавов на основе Fe-Ni во внутреннем ядре Земли: исследование Ab Initio. Физ. Планета Земля. Interiors 301, 106465. doi:10.1016/j.pepi.2020.106465 CrossRef Полный текст | Google Scholar Зиман, Дж. CrossRef Full Text | Google Scholar Зиман, Дж. М. (1960). Электроны и фононы; Теория явлений переноса в твердых телах . Оксфорд: Кларендон Пресс. . 2021 сен 22;14(19):5476. дои: 10.3390/ma14195476. Инносент С Эзенва 1
2 , Такаси Ёсино 1 Бесплатная статья ЧВК Innocent C Ezenwa et al.
Материалы (Базель). . Бесплатная статья ЧВК . 2021 сен 22;14(19):5476. дои: 10.3390/ma14195476. Иннокентий К. Эзенва 1
2 , Такаси Ёсино 1 Удельное электросопротивление твердых и жидких Cu и Au измеряли при высоких давлениях от 6 до 12 ГПа и температурах на ~150 К выше плавления. Также измеряли удельное сопротивление металлов в зависимости от давления при комнатной температуре. Их удельное сопротивление уменьшалось и увеличивалось с увеличением давления и температуры соответственно. С повышением давления при комнатной температуре мы наблюдали резкое уменьшение величины удельного сопротивления на ~4 ГПа в обоих металлах. По сравнению с данными 1 атм и данными относительно более низкого давления из предыдущих исследований, наши измеренные сопротивления в зависимости от температуры в твердом и жидком состояниях показывают аналогичную тенденцию. Наблюдаемые температуры плавления при различных фиксированных давлениях находятся в разумном согласии с предыдущими экспериментальными и теоретическими исследованиями. Ключевые слова: постоянное удельное сопротивление; электрическое сопротивление; взаимодействия электронов и фононов; высокое давление и температура; кривая плавления; теплопроводность. Рисунок 1 3D-эскиз SolidWork… Рисунок 1 3D-эскиз узла датчика давления в SolidWork и 2D-эскиз… 3D-эскиз узла датчика давления в SolidWork и 2D-эскиз внутренних частей узла вместе с установкой для измерения сопротивления. Изменено из Ezenwa and Yoshino 2020a [19]. Рисунок 2 Изображение в обратно рассеянных электронах (BSE)… Рисунок 2 Изображение в обратно рассеянных электронах (BSE) восстановленного образца меди ex-situ при 8 ГПа и… Изображение в обратно рассеянных электронах (BSE) извлеченного ex-situ образца меди при 8 ГПа и ~1800 K вместе с графиком линейного профиля результатов электронного микрозонда (EPMA). Рисунок 3 Изображение в обратно рассеянных электронах (BSE)… Рисунок 3 Изображение в обратно рассеянных электронах (BSE) извлеченного ex-situ образца золота при 10 ГПа и… Изображение в обратно рассеянных электронах (BSE) извлеченного ex-situ образца золота при 10 ГПа и ∼1800 K вместе с графиком линейного профиля результатов электронного микрозонда (EPMA). Линия от точки 1 до 69 была разделена на единицы, каждая из которых имела размеры около ~10–14 мкм. Рисунок 4 Удельное электрическое сопротивление, зависящее от температуры… Рисунок 4 Зависящее от температуры удельное электрическое сопротивление меди, измеренное при фиксированном давлении в сравнении с… Зависимое от температуры удельное электрическое сопротивление меди, измеренное при фиксированном давлении, по сравнению с предыдущими исследованиями [10,19]. Рисунок 5 Удельное электрическое сопротивление, зависящее от температуры… Рисунок 5 Зависимое от температуры удельное электрическое сопротивление золота при фиксированном давлении по сравнению с… Зависимое от температуры удельное электрическое сопротивление золота при фиксированном давлении по сравнению с предыдущими исследованиями [12,19]. Рисунок 6 ( a ) это… Рисунок 6 ( a ) — удельное сопротивление Cu, зависящее от давления, измеренное до… ( a ) — удельное сопротивление Cu, зависящее от давления, измеренное до 17 ГПа, а ( b ) — сопротивление Au, измеренное до 16 ГПа при комнатной температуре по сравнению с экспериментальными [10,12] и теоретическими [20]. Рисунок 7 Натуральный логарифм… Рисунок 7 Натуральный логарифм удельного электрического сопротивления Cu ( a ) и… Натуральный логарифм электрического сопротивления Cu ( a ) и Au ( b ) по границе плавления, зависящей от давления. Линия соответствия имеет наклон (-1,77782 × 10 -4 ± 0,00344) ГПа-1 для Cu и (7,05413 × 10 -4 ± 0,00141) ГПа-1 для Au. Данные по более низкому давлению на вставке взяты из [10,12] для Cu и Au соответственно. Рисунок 8 Температура плавления Cu (… Рисунок 8 Температура плавления Cu ( a ) и Au ( b ) как… Температура плавления Cu ( a ) и Au ( b ) в зависимости от давления по сравнению с предыдущими исследованиями. Рисунок 9 Термозависимый электронный компонент… Рисунок 9 Зависящая от температуры электронная составляющая теплопроводности Cu ( a )… Температурно-зависимая электронная составляющая теплопроводности Cu ( a ) и Au ( b ) в диапазоне давлений от 6 до 5 ГПа, рассчитанная по данным электросопротивления по закону Видемана–Франца со значением Зоммерфельда числа Лоренца. Данные сравниваются с данными, рассчитанными по удельному электрическому сопротивлению, зарегистрированному при 1 атм, и данными, измеренными при относительно более низком давлении по сравнению с измеренной общей теплопроводностью. См. это изображение и информацию об авторских правах в PMC Плавление лития под высоким давлением. Шеффер А.М., Талмадж В.Б., Темпл С.Р., Димиад С.
Шеффер А.М. и соавт.
Phys Rev Lett. 2012 2 ноября; 109(18):185702. doi: 10.1103/PhysRevLett.109.185702. Epub 2012 2 ноября.
Phys Rev Lett. 2012.
PMID: 23215297 Электрические свойства и поведение кубов закиси меди под высоким давлением. Лю CL, Sui YM, Ren WB, Ma BH, Li Y, Su NN, Wang QL, Li YQ, Zhang JK, Han YH, Ma YZ, Gao CX.
Лю С.Л. и соавт.
Неорг хим. 2 июля 2012 г .; 51 (13): 7001-3. дои: 10.1021/ic3007662. Epub 2012 21 июня.
Неорг хим. 2012.
PMID: 22721445 Методика, сборка ячейки и измерение Т-зависимого удельного электрического сопротивления жидкого Fe, не содержащего примесей, в условиях P, T. Эзенва И.С., Йошино Т.
Эзенва И.С. и соавт.
Преподобный Научный Инструм. 2020 1 февраля; 91 (2): 023903. дои: 10.1063/1.5112045.
Преподобный Научный Инструм. 2020.
PMID: 32113395 Удельное электрическое сопротивление жидкого Fe до 12 ГПа: последствия для теплового потока в ядрах земных тел. Зильбер Р.Э., Секко Р.А., Йонг В., Литтлтон Дж.А.Х.
Зильбер Р.Э. и соавт.
Научный представитель 2018 г. 17 июля; 8 (1): 10758. дои: 10.1038/s41598-018-28921-ж.
Научный представитель 2018.
PMID: 30018313
Бесплатная статья ЧВК. Разработка одновременного измерения Гюгонио и температуры для ударных экспериментов с предварительно нагретым металлом: температуры плавления Та при давлении 100 ГПа. Ли Дж. Посмотреть все похожие статьи Методы удельного электрического сопротивления направляют электрический ток в землю, а затем сопоставляют сопротивление с этим потоком тока. Методы индуцированной поляризации (IP) измеряют заряжаемость земли, которая, как и удельное электрическое сопротивление, будет различаться в зависимости от текущего состояния почвы. Система удельного электрического сопротивления может быть эффективным инструментом для картографирования подземных условий, таких как коренная порода или уровень грунтовых вод, когда вам нужен неразрушающий метод исследования и/или требуется улучшенный охват данных по сравнению с традиционным точечным, интрузивные методы (например, бурение или копание). Методы удельного электрического сопротивления чаще всего применяются для исследования водоносных горизонтов подземных вод и для картирования отходов (свалок) и загрязнителей подземных вод (включая проникновение соленой воды). Геологические исследования для картирования типов почвы и коренных пород или изменений почвы и коренных пород также являются обычными приложениями. Метод удельного электрического сопротивления также эффективно работает для обнаружения и картирования полостей, а также для исследования руд и месторождений полезных ископаемых. Подробнее об использовании удельного сопротивления в горных работах читайте здесь: Разведка полезных ископаемых Добыча полезных ископаемых Операции после добычи Поскольку измерение удельного сопротивления является «гальваническим» методом, для него требуется физическое электрическое соединение с землей. Обычно это означает, что стальные электроды должны быть вставлены в исследуемый материал, хотя на некоторых твердых поверхностях можно использовать пластинчатые электроды. Два электрода используются для подачи тока («токовые электроды»), и как минимум два электрода используются для считывания напряжения («потенциальные электроды»). Затем значение сопротивления пересчитывается в кажущееся сопротивление. Кажущееся удельное сопротивление является результатом тока, протекающего через всю землю под электродами, а не просто информацией от отдельной точки или слоя. Эти значения сами по себе не подходят для интерпретации, поэтому требуется дополнительный этап обработки, называемый инверсией. В этом процессе программное обеспечение используется для поиска модели распределения удельного сопротивления, которая дала бы тот же результат, что и данные, записанные в полевых условиях. Значения удельного сопротивления в возвращенной модели станут основой для интерпретации. В гидрогеофизических исследованиях, таких как картирование подземных вод, глину (низкое сопротивление) можно отличить от песка (высокое сопротивление), соленую воду (низкое сопротивление) от пресной воды (высокое сопротивление) или влажный песок (низкое сопротивление) от сухого песка. Однако удельное сопротивление перемещению материала не является уникальным, и диапазоны удельного сопротивления различных геологических компонентов перекрываются, поэтому, возможно, придется иметь дело с определенным уровнем неоднозначности. Кроме того, совершенно разные геологические слои в совершенно разных геологических сценариях могут иметь одинаковое удельное сопротивление, поэтому некоторые предварительные знания о геологических условиях из местных знаний, геологических карт и/или скважин всегда должны способствовать геологической интерпретации геофизических исследований. Использование исследований IP (индуцированной поляризации) может облегчить различение некоторых из этих материалов из-за различий в их способности заряжаться. Узнайте больше о расследованиях в области интеллектуальной собственности В зависимости от положения электродов тока и потенциала данные будут собираться на разных глубинах (координата z) и под разными поверхностями (координаты X и Y) в виде отдельных точек. Вертикальное электрическое зондирование (ВЭЗ) представляет собой сбор данных с разных глубин под фиксированной точкой на поверхности. Это означает, что все точки данных будут иметь одинаковое положение на поверхности (координаты X и Y), но будут измерены на разных глубинах (координата Z). Размещение электродов основано на средней точке. Чем дальше от средней точки расположены электроды, тем глубже будет измерение. Для каждой точки данных электроды необходимо перемещать вручную. Данные обычно представлены в виде графика с глубиной на одной оси и кажущимся удельным сопротивлением на другой. Эти необработанные данные затем выдвигаются для инверсии. ABEM Terrameter LS 2 Компоновка VES с двумя электродами для измерения потенциала и двумя электродами для измерения тока, сдвинутая дальше для каждой глубины измерения. Исследование удельного сопротивления также можно проводить на постоянной глубине, но при различных положениях на поверхности, что обычно называется профилированием. Путем объединения измерений как на разных глубинах, так и в латеральных положениях завершается исследование ERT (электросопротивление томографии), также иногда называемое визуализацией. Поскольку ERT является многомерным методом, точки данных можно измерять в 2D-профиле или в 3D-сетке. Для 2D-профиля несколько электродов располагаются в линию на заданном расстоянии. Система автоматически выбирает, какие электроды использовать для подачи тока и считывания напряжения, и за короткое время может измерить большое количество точек данных. Точки данных будут иметь различные координаты X и Z, но фиксированную координату Y. Для крупномасштабной 3D-съемки данные нескольких (в идеале параллельных) 2D-профилей могут быть объединены в программном обеспечении для одновременного моделирования вариаций удельного сопротивления по осям X, Y и Z; этот процесс формирования набора 3D-данных конкретно относится к съемке 2. Схема ABEM Terrameter LS 2 ERT. В зависимости от расстояния между потенциальным и токовым электродами измеряются разные объемы 2D-профиля. Удельное сопротивление — отличный метод для использования в качестве инструмента мониторинга для регистрации изменений состояния грунта. Типичные области применения включают мониторинг грунтовых вод вокруг полигонов, чтобы увидеть распространение фильтрата или мониторинг просачивания воды через земляные дамбы. Измерения можно проводить, несколько раз возвращаясь в одно и то же место для повторения измерений, или оборудование можно оставлять на месте в рамках проекта автоматизированного мониторинга. Варианты метода определения удельного электрического сопротивления: IP (индуцированная поляризация) и SP (самопотенциал). IP (Индуцированная поляризация) — активная модель (т. е. модель, требующая подачи тока), в которой мы записываем, как напряжение в земле реагирует на подачу и снятие тока; эта реакция называется поляризуемостью материала. Данные о заряжаемости могут быть собраны в течение того же цикла измерения, что и данные об удельном сопротивлении, и наличие этого дополнительного набора данных может помочь нам в интерпретации материалов. Например, минеральные руды и месторождения глины обладают высокой способностью к заряду, связанной с ними. Эти электрические методы (исследования удельного сопротивления и ВП) не ограничиваются измерениями на поверхности земли, они также могут применяться в водоемах для исследования отложений и лежащей под ними геологии, а также в скважинах, что позволяет улучшить разрешение на глубине. Существуют и другие наборы данных, которые можно собирать с помощью того же оборудования. SP (самопроизвольный или собственный потенциал) — это средство регистрации естественных напряжений в земле без подачи тока от прибора. Узнать больше о SP УЗНАТЬ БОЛЬШЕ О ABEM TERRAMETER LS 2 Измерения удельного сопротивления работают в огромном диапазоне различных грунтовых условий, но метод имеет некоторые ограничения: забить электроды, и их нужно будет просверлить, что является трудоемким процессом. Иногда можно заказать изготовленные на заказ пластинчатые электроды. Existing client?YesNo CountryAfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAntigua and BarbudaArgentinaArmeniaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBosnia and HerzegovinaBotswanaBrazilBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral African RepublicChadChileChinaColombiaComorosCongo, Democratic Republic of theCongo, Republic of theCosta RicaCôte d ‘IvoireCroatiaCubaCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEast TimorEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFaroe IslandsFijiFinlandFranceFrench PolynesiaGabonGambiaGeorgiaGermanyGhanaGreeceGreenlandGrenadaGuamGuatemalaGuineaGuinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsraelItalyJamaicaJapanJordanKazakhstanKenyaKiribatiNorth Ko reaSouth KoreaKosovoKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMauritaniaMauritiusMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew ZealandNicaraguaNigerNigeriaNorthern Mariana IslandsNorwayOmanPakistanPalauPalestine, State ofPanamaPapua New GuineaParaguayPeruPhilippinesPolandPortugalPuerto RicoQatarRomaniaRussiaRwandaSaint Kitts and NevisSaint LuciaSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint MaartenSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSpainSri LankaSudanSudan, SouthSurinameSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTogoTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited StatesUruguayUzbekistanVanuatuVatican CityVenezuelaVietnamVirgin Islands, BritishVirgin Острова, СШАЙеменЗамбияЗимбабве Введите Emailconfirm Email РекламаGoogleLinkedInFair/ExpoRecommendationДругое Это поле предназначено для проверки и должно быть оставлено без изменений. Skip Nav Destination 01 декабря 1942 г. Г.Е. Арчи Транс. 146 (01): 54–62. Номер бумаги:
СПЭ-942054-G https://doi.org/10.2118/942054-G Получить разрешения Цитирование Арчи, Г. Скачать файл цитирования: Расширенный поиск Полезность каротажа удельного электрического сопротивления при определении характеристик резервуара в значительной степени определяется: точностью, с которой может быть определено истинное удельное сопротивление пласта; объем подробных данных, касающихся связи измерений удельного сопротивления с характеристиками пласта; имеющаяся информация о электропроводности сопутствующих или пластовых вод; объем геологических знаний о возможных изменениях фаций в пределах заданных горизонтов, как по вертикали, так и по латерали, особенно в отношении результирующего воздействия на электрические свойства коллектора. На следующих страницах приведены простые примеры, иллюстрирующие использование каротажа удельного сопротивления при решении некоторых задач, связанных с нефтяными и газовыми коллекторами. Из имеющейся информации становится очевидным, что следует проявлять большую осторожность при применении предложенных методов к более сложным случаям. Следует помнить, что приведенные уравнения не являются точными и представляют собой лишь приблизительные соотношения. Однако считается, что при благоприятных условиях их применение находится в допустимых пределах точности. Введение Электрический каротаж широко использовался для качественной корреляции пластов, вскрытых буром при разработке нефтяных и газовых месторождений, и для получения некоторых указаний на содержание коллектора. Однако его использование в количественном отношении было ограничено из-за различных факторов, которые, как правило, затемняют значимость полученных электрических показаний. Некоторыми из этих факторов являются размер ствола скважины, удельное сопротивление бурового раствора в стволе скважины, эффект проникновения фильтрата бурового раствора в пласт, отношение зарегистрированной мощности пластов к расстоянию между электродами, неоднородность геологических формаций, соленость или проводимость реликтовых пород. На побережье Мексиканского залива было обнаружено, что влияние размера скважины и удельного сопротивления бурового раствора, как правило, не имеет большого значения, за исключением случаев, когда речь идет о высоком удельном сопротивлении пласта или чрезвычайно низком удельном сопротивлении бурового раствора. зафиксированы значения более высоких удельных сопротивлений. Низкое удельное сопротивление бурового раствора встречается нечасто, но когда это происходит, его можно исправить, заменив столб бурового раствора. Имея передовые знания о борьбе с буровым раствором, проникновение фильтрата бурового раствора в пески можно свести к минимуму, тем самым повысив надежность электрического каротажа. Влияние расстояния между электродами на зарегистрированную толщину пласта часто подлежит компенсации или может быть учтено в достаточной степени, чтобы обеспечить приемлемое приближение к истинному удельному сопротивлению пласта. Хотя было показано, что при более низких давлениях увеличение содержания Si с 2 до 17 мас.% увеличивает ρ (Berrada et al., 2020), однако Wagle et al. (2019) сообщили о более низких значениях, чем Zhang et al. (2021) для более высокого содержания Si. В условиях CMB и ICB расчетное значение ρ для Fe6,7Si (или Fe 7 Si) составляет 0,81 ± 0,5 мкОм·м и 0,73 ± 0,5 мкОм·м, а для Fe14,4Si (или Fe 3 Si) составляет 1,02 ± 0,5 мкОм·м и 0,92 ± 0,5 мкОм·м (Wagle et al., 2019). Уэгл и др. (2019) также пересмотрели предыдущие оценки Wagle et al. (2018) для Fe7.6S (или Fe 7 S) и Fe16.1S (или Fe 3 S) и зарегистрированных значений 0,82 ± 0,22 мкОм·м и 1,01 ± 0,42 мкОм·м в условиях реликтового излучения и 0,75 ± 0,22 мкОм·м и 0,95 ± 0,42 мкОм·м в условиях ICB соответственно. Гоми и др. (2013) оценили, что ρ ε-Fe13.2Si (или Fe 78 Si 22 ) составляет 1,02 (+0,04/-0,11) мкОм·м в реликтовом излучении и 0,820 (+0,054/-0,131) мкОм·м в ICB.
Хотя было показано, что при более низких давлениях увеличение содержания Si с 2 до 17 мас.% увеличивает ρ (Berrada et al., 2020), однако Wagle et al. (2019) сообщили о более низких значениях, чем Zhang et al. (2021) для более высокого содержания Si. В условиях CMB и ICB расчетное значение ρ для Fe6,7Si (или Fe 7 Si) составляет 0,81 ± 0,5 мкОм·м и 0,73 ± 0,5 мкОм·м, а для Fe14,4Si (или Fe 3 Si) составляет 1,02 ± 0,5 мкОм·м и 0,92 ± 0,5 мкОм·м (Wagle et al., 2019). Уэгл и др. (2019) также пересмотрели предыдущие оценки Wagle et al. (2018) для Fe7.6S (или Fe 7 S) и Fe16.1S (или Fe 3 S) и зарегистрированных значений 0,82 ± 0,22 мкОм·м и 1,01 ± 0,42 мкОм·м в условиях реликтового излучения и 0,75 ± 0,22 мкОм·м и 0,95 ± 0,42 мкОм·м в условиях ICB соответственно. Гоми и др. (2013) оценили, что ρ ε-Fe13.2Si (или Fe 78 Si 22 ) составляет 1,02 (+0,04/-0,11) мкОм·м в реликтовом излучении и 0,820 (+0,054/-0,131) мкОм·м в ICB. Их результаты очень хорошо согласуются с Wagle et al. (2019) и были экстраполированы на основе комбинации измерений DAC до 100 ГПа и расчетов из первых принципов с учетом влияния насыщения ρ. Силбер и др. (2019) провели прямые измерения ρ Fe4.5Si от 3 до 9ГПа и до жидкого T и постулировал, что ρ жидкого Fe, легированного легкими элементами, остается неизменным по сравнению с Fe в условиях внутреннего ядра, но изменение T в реликтовом излучении предполагает, что ρ может увеличиться до ∼1,50 мкОм. Только во втором исследовании по экспериментальному измерению 90 110 k 90 111 состава в системе Fe в условиях ядра Земли Hsieh et al. (2020) использовали импульсный лазерный метод с ЦАП для измерения k сплавов Fe-Si с давлением до 144 ГПа и 3300 К. Расчеты ρ с использованием закона Видемана-Франца, со значением Зоммерфельда числа Лоренца и экстраполяциями до высокого T предполагает приблизительно 4,6 мкОм·м (или 20 Вт·м −1 K −1 ) при ~136 ГПа и 3750 K для ε-Fe8,7Si (или Fe 0,85 Si 4,39 90 , 2020).
Их результаты очень хорошо согласуются с Wagle et al. (2019) и были экстраполированы на основе комбинации измерений DAC до 100 ГПа и расчетов из первых принципов с учетом влияния насыщения ρ. Силбер и др. (2019) провели прямые измерения ρ Fe4.5Si от 3 до 9ГПа и до жидкого T и постулировал, что ρ жидкого Fe, легированного легкими элементами, остается неизменным по сравнению с Fe в условиях внутреннего ядра, но изменение T в реликтовом излучении предполагает, что ρ может увеличиться до ∼1,50 мкОм. Только во втором исследовании по экспериментальному измерению 90 110 k 90 111 состава в системе Fe в условиях ядра Земли Hsieh et al. (2020) использовали импульсный лазерный метод с ЦАП для измерения k сплавов Fe-Si с давлением до 144 ГПа и 3300 К. Расчеты ρ с использованием закона Видемана-Франца, со значением Зоммерфельда числа Лоренца и экстраполяциями до высокого T предполагает приблизительно 4,6 мкОм·м (или 20 Вт·м −1 K −1 ) при ~136 ГПа и 3750 K для ε-Fe8,7Si (или Fe 0,85 Si 4,39 90 , 2020). Хси и др. (2020) отмечают, что расхождение с ранее упомянутыми результатами может быть вызвано предположениями, сделанными в исследованиях, которые не измеряли напрямую k . Как смоделированная T-зависимость ρ, так и использование значения Зоммерфельда числа Лоренца при высоких P и T приводят к недооценке k в условиях ядра Земли. Эксперименты Матасова (1977) по ударному сжатию сплавов Fe-Si при давлении до 140 ГПа и 2700 К показали, что ρ составляет 1,12 мкОм·м для ядра Fe33,5Si, что находится в пределах ранее опубликованных значений по измерениям ударной волны. Как упоминалось ранее, это значение может быть занижено из-за шунтирующего эффекта эпоксидной смолы при давлении выше 50 ГПа (Bi et al., 2002). Результаты de Koker et al. (2012) также предложили более низкий диапазон 0,74–1,03 мкОм·м для сплавов Fe-Si в условиях сердцевины. Подобно результатам de Koker et al. (2012), измерения DAC до 60 ГПа и 300 К указывают значения ρ для Fe9.Si 0,6–1,3 мкОм·м в реликтовом излучении (Seagle et al.
Хси и др. (2020) отмечают, что расхождение с ранее упомянутыми результатами может быть вызвано предположениями, сделанными в исследованиях, которые не измеряли напрямую k . Как смоделированная T-зависимость ρ, так и использование значения Зоммерфельда числа Лоренца при высоких P и T приводят к недооценке k в условиях ядра Земли. Эксперименты Матасова (1977) по ударному сжатию сплавов Fe-Si при давлении до 140 ГПа и 2700 К показали, что ρ составляет 1,12 мкОм·м для ядра Fe33,5Si, что находится в пределах ранее опубликованных значений по измерениям ударной волны. Как упоминалось ранее, это значение может быть занижено из-за шунтирующего эффекта эпоксидной смолы при давлении выше 50 ГПа (Bi et al., 2002). Результаты de Koker et al. (2012) также предложили более низкий диапазон 0,74–1,03 мкОм·м для сплавов Fe-Si в условиях сердцевины. Подобно результатам de Koker et al. (2012), измерения DAC до 60 ГПа и 300 К указывают значения ρ для Fe9.Si 0,6–1,3 мкОм·м в реликтовом излучении (Seagle et al. , 2013). Их измерения были экстраполированы на условия реликтового излучения с использованием модели зависимости ρ от T , V и температуры Дебая. Эти результаты согласуются с измерениями в прессе с кубическими наковальнями при давлении до 5 ГПа и 2200 К, показывая, что ρ Fe17Si находится в диапазоне 0,90–0,94 мкОм·м в условиях внешнего ядра (Kiarasi, 2013). Для сравнения, Suehiro et al. (2017) сообщили о значениях реликтового излучения примерно 0,699 мкОм·м для Fe12,8S (или Fe 80,8 S 19,2 ), 0,741 мкм для Fe6,1SI6,7S (или FE 79,7 SI 10,3 S 10 ) и 0,784 µωmm для Fe13.5SI (OR FE 888.88.88.88. Суэхиро и др. (2017) провели измерения в ЦАП с лазерным нагревом до 110 ГПа и 300 К и использовали правило Маттиссена и значение удельного сопротивления насыщения 1,68 мкОм·м, чтобы получить ρ сплавов Fe-Si-S в условиях активной зоны. Таким образом, вклад S в ρ сплавов Fe оказывается более слабым, чем вклад Si. Гоми и Хиросе (2015) предложили более высокие значения ρ для Fe13,5Si, равные 1,02 (+0,04/-0,13) мкОм·м и 0,820 (+0,055/-0,130) мкОм·м в CMB и ICB соответственно.
, 2013). Их измерения были экстраполированы на условия реликтового излучения с использованием модели зависимости ρ от T , V и температуры Дебая. Эти результаты согласуются с измерениями в прессе с кубическими наковальнями при давлении до 5 ГПа и 2200 К, показывая, что ρ Fe17Si находится в диапазоне 0,90–0,94 мкОм·м в условиях внешнего ядра (Kiarasi, 2013). Для сравнения, Suehiro et al. (2017) сообщили о значениях реликтового излучения примерно 0,699 мкОм·м для Fe12,8S (или Fe 80,8 S 19,2 ), 0,741 мкм для Fe6,1SI6,7S (или FE 79,7 SI 10,3 S 10 ) и 0,784 µωmm для Fe13.5SI (OR FE 888.88.88.88. Суэхиро и др. (2017) провели измерения в ЦАП с лазерным нагревом до 110 ГПа и 300 К и использовали правило Маттиссена и значение удельного сопротивления насыщения 1,68 мкОм·м, чтобы получить ρ сплавов Fe-Si-S в условиях активной зоны. Таким образом, вклад S в ρ сплавов Fe оказывается более слабым, чем вклад Si. Гоми и Хиросе (2015) предложили более высокие значения ρ для Fe13,5Si, равные 1,02 (+0,04/-0,13) мкОм·м и 0,820 (+0,055/-0,130) мкОм·м в CMB и ICB соответственно. Эти более высокие значения согласуются с Zhang et al. (2018), которые применили свою модель k до Fe13,5Si и сообщил значения ρ 0,92 мкОм·м в условиях реликтового излучения (4050 K, 136 ГПа). Недавно удельное сопротивление насыщения сплавов ε-Fe-Si было дополнительно исследовано в DAC с внутренним нагревом до 117 ГПа и 3120 К (Inoue et al., 2020). Результаты показывают, что удельное сопротивление насыщения сплавов ε-Fe-Si сравнимо с сопротивлением чистого Fe при ~100 ГПа (Inoue et al., 2020). Они получили значения ρ для ε-Fe12,7Si, равные 1,040 (+0,126/-0,212) мкОм·м и 0,775 (+0,150/-0,231) мкОм·м при ICB (3760 K, 135 ГПа) и CMB (5 120 K, 330 GPa) соответственно. Все рассмотренные выше значения приведены в таблицах 1–4. Изменения ρ, организованные по составу, представлены на рис. 2.9.0009
Эти более высокие значения согласуются с Zhang et al. (2018), которые применили свою модель k до Fe13,5Si и сообщил значения ρ 0,92 мкОм·м в условиях реликтового излучения (4050 K, 136 ГПа). Недавно удельное сопротивление насыщения сплавов ε-Fe-Si было дополнительно исследовано в DAC с внутренним нагревом до 117 ГПа и 3120 К (Inoue et al., 2020). Результаты показывают, что удельное сопротивление насыщения сплавов ε-Fe-Si сравнимо с сопротивлением чистого Fe при ~100 ГПа (Inoue et al., 2020). Они получили значения ρ для ε-Fe12,7Si, равные 1,040 (+0,126/-0,212) мкОм·м и 0,775 (+0,150/-0,231) мкОм·м при ICB (3760 K, 135 ГПа) и CMB (5 120 K, 330 GPa) соответственно. Все рассмотренные выше значения приведены в таблицах 1–4. Изменения ρ, организованные по составу, представлены на рис. 2.9.0009
 7 мкОм·м. * обозначает теоретические исследования. Повторяющиеся ссылки указывают на разные композиции.
7 мкОм·м. * обозначает теоретические исследования. Повторяющиеся ссылки указывают на разные композиции. компоненты к в металлах. Среднее значение ρ сплавов Fe-Ni составляет 1,35 и 1,22 мкОм·м в условиях CMB и ICB соответственно, без учета высокого значения, полученного Гардинером и Стейси (1971) в условиях ICB. В теоретической работе Гардинера и Стейси (1971) сообщалось о самых высоких значениях, соответствующих расчетным значениям ρ для Fe-25Ni,S,Si,MgO. Сообщаемые данные о сплавах Fe-Ni разрознены, и нельзя сразу увидеть четкую связь между содержанием легких элементов и ρ или даже между теоретическими и экспериментальными методами. Среднее значение ρ сплавов Fe-O составляет 0,80 и 0,74 мкОм·м при CMB и ICB соответственно. Теоретические и экспериментальные значения ρ для сплавов Fe-Si/S составляют примерно 1,08 и 0,83 мкОм·м в CMB и ICB соответственно, без учета высокого значения из Hsieh et al. (2020) в условиях ICB. Действительно, ожидается, что значение ρ для Fe8,7Si (Hsieh et al., 2020) будет выше, чем для Fe7,6Si (Wagle et al., 2019).), но ниже, чем у Fe9Si (Seagle et al.
компоненты к в металлах. Среднее значение ρ сплавов Fe-Ni составляет 1,35 и 1,22 мкОм·м в условиях CMB и ICB соответственно, без учета высокого значения, полученного Гардинером и Стейси (1971) в условиях ICB. В теоретической работе Гардинера и Стейси (1971) сообщалось о самых высоких значениях, соответствующих расчетным значениям ρ для Fe-25Ni,S,Si,MgO. Сообщаемые данные о сплавах Fe-Ni разрознены, и нельзя сразу увидеть четкую связь между содержанием легких элементов и ρ или даже между теоретическими и экспериментальными методами. Среднее значение ρ сплавов Fe-O составляет 0,80 и 0,74 мкОм·м при CMB и ICB соответственно. Теоретические и экспериментальные значения ρ для сплавов Fe-Si/S составляют примерно 1,08 и 0,83 мкОм·м в CMB и ICB соответственно, без учета высокого значения из Hsieh et al. (2020) в условиях ICB. Действительно, ожидается, что значение ρ для Fe8,7Si (Hsieh et al., 2020) будет выше, чем для Fe7,6Si (Wagle et al., 2019).), но ниже, чем у Fe9Si (Seagle et al. , 2013) и сплавов с более высоким содержанием Si. Средние значения всех исследований, в которых сообщаются значения для Земли, составляют 1,07 и 0,97 мкОм·м в условиях CMB и ICB соответственно. Более высокое содержание P и более низкое содержание легких элементов обычно приводит к более низкому ρ для данного состава ядра, в то время как высокое T приводит к увеличению ρ. Тем не менее, постоянно более высокие средние значения в условиях CMB, которые учитывают более высокое содержание легких элементов и более низкое P , предполагают, что эффекты содержания легких элементов и P преобладают над эффектами T .
, 2013) и сплавов с более высоким содержанием Si. Средние значения всех исследований, в которых сообщаются значения для Земли, составляют 1,07 и 0,97 мкОм·м в условиях CMB и ICB соответственно. Более высокое содержание P и более низкое содержание легких элементов обычно приводит к более низкому ρ для данного состава ядра, в то время как высокое T приводит к увеличению ρ. Тем не менее, постоянно более высокие средние значения в условиях CMB, которые учитывают более высокое содержание легких элементов и более низкое P , предполагают, что эффекты содержания легких элементов и P преобладают над эффектами T . Луна
 , 2006; Steenstra and van Westrenen, 2017). Присутствие Si в лунном ядре также считается возможным, поскольку лунный изотопный состав Si предполагает состав мантии, аналогичный земному (Armytage et al., 2012; Nazarov et al., 2012; de Meijer et al., 2013; Zambardi et al. др., 2013). Szurgot (2017) сообщил о не менее 2,7 мас.% Si в лунном ядре, учитывая несжатую плотность Луны.
, 2006; Steenstra and van Westrenen, 2017). Присутствие Si в лунном ядре также считается возможным, поскольку лунный изотопный состав Si предполагает состав мантии, аналогичный земному (Armytage et al., 2012; Nazarov et al., 2012; de Meijer et al., 2013; Zambardi et al. др., 2013). Szurgot (2017) сообщил о не менее 2,7 мас.% Si в лунном ядре, учитывая несжатую плотность Луны. , 2018). Используя аналогичный метод, Pommier (2018) измерил ρ в аппарате с несколькими наковальнями до 10 ГПа и в широком диапазоне T . Их результаты предполагают значение 0,66 мкОм·м, или чуть больше половины значения, измеренного Силбером и соавт. (2018). Кроме того, Pommier (2018) сообщил о значении ρ, равном 2,15 мкОм·м, для Fe5S при 4,5 ГПа и 1700 К. Согласно их результатам, влияние серы даже при таком малом весовом % нельзя пренебрегать. Недавно Инь и др. (2019) сообщили об измерениях ρ Fe35.7P (или FeP), Fe21.7P (или Fe 2 P) и Fe15.6P (или Fe 3 P) в прессе с несколькими упорами при 3,2 ГПа. Эти авторы относят P к возможному легкому элементу в ядре Луны, учитывая его большую растворимость в жидком Fe и сплавах Fe-S (Зайцев и др., 1995; Stewart, Schmidt, 2007). Их результаты показывают, что ρ Fe35.7P примерно в четыре раза выше, чем у Fe. Инь и др. (2019) заключают, что ожидается, что ρ будет ниже 1,65 мкОм·м для лунного ядра с Fe15,6P. Кроме того, прямые измерения Berrada et al.
, 2018). Используя аналогичный метод, Pommier (2018) измерил ρ в аппарате с несколькими наковальнями до 10 ГПа и в широком диапазоне T . Их результаты предполагают значение 0,66 мкОм·м, или чуть больше половины значения, измеренного Силбером и соавт. (2018). Кроме того, Pommier (2018) сообщил о значении ρ, равном 2,15 мкОм·м, для Fe5S при 4,5 ГПа и 1700 К. Согласно их результатам, влияние серы даже при таком малом весовом % нельзя пренебрегать. Недавно Инь и др. (2019) сообщили об измерениях ρ Fe35.7P (или FeP), Fe21.7P (или Fe 2 P) и Fe15.6P (или Fe 3 P) в прессе с несколькими упорами при 3,2 ГПа. Эти авторы относят P к возможному легкому элементу в ядре Луны, учитывая его большую растворимость в жидком Fe и сплавах Fe-S (Зайцев и др., 1995; Stewart, Schmidt, 2007). Их результаты показывают, что ρ Fe35.7P примерно в четыре раза выше, чем у Fe. Инь и др. (2019) заключают, что ожидается, что ρ будет ниже 1,65 мкОм·м для лунного ядра с Fe15,6P. Кроме того, прямые измерения Berrada et al. (2020) ограничили ρ сплавов Fe-Si (2, 8,5, 17 мас.% Si) между 1,17–1,66 мкОм·м в верхней части лунного внешнего ядра (1600 K, 5–7 ГПа). Во всех этих исследованиях для измерения ρ использовался прибор с несколькими наковальнями и четырехпроводным методом измерения. Значения, обсуждаемые в этом разделе, сведены в Таблицу 5, а изменения ρ показаны на Рисунке 3.
(2020) ограничили ρ сплавов Fe-Si (2, 8,5, 17 мас.% Si) между 1,17–1,66 мкОм·м в верхней части лунного внешнего ядра (1600 K, 5–7 ГПа). Во всех этих исследованиях для измерения ρ использовался прибор с несколькими наковальнями и четырехпроводным методом измерения. Значения, обсуждаемые в этом разделе, сведены в Таблицу 5, а изменения ρ показаны на Рисунке 3. В условиях реликтового излучения измеренное значение ρ Fe15.6P ниже, чем указанное для сплавов Fe-Si (до 17 мас.% Si) и Fe5S, что позволяет предположить, что влияние P на ρ ядра относительно незначительно. Сообщаемые сплавы Fe показывают большее значение ρ, чем у Fe, как и ожидалось, учитывая дополнительный механизм рассеяния, вызванный взаимодействием электронов с примесями. Среднее значение всех исследований, сообщающих о значениях в условиях CMB, составляет 1,40 мкОм·м.
В условиях реликтового излучения измеренное значение ρ Fe15.6P ниже, чем указанное для сплавов Fe-Si (до 17 мас.% Si) и Fe5S, что позволяет предположить, что влияние P на ρ ядра относительно незначительно. Сообщаемые сплавы Fe показывают большее значение ρ, чем у Fe, как и ожидалось, учитывая дополнительный механизм рассеяния, вызванный взаимодействием электронов с примесями. Среднее значение всех исследований, сообщающих о значениях в условиях CMB, составляет 1,40 мкОм·м. Меркурий
 (2009 г.) предполагают минимум 5 % масс. S. Различные модели термической эволюции рассматривают ядро Fe-Si с неопределенностью относительно точного состава Si (Knibbe and van Westrenen, 2017; Knibbe and van Westrenen, 2018). Оценки содержания Si колеблются от 5 до 25 мас.% Si (Malavergne et al., 2010; Chabot et al., 2014), хотя недавние исследования показывают, что 10,5 мас.% Si обеспечивает наилучшие результаты моделирования упругих свойств керна и данных геодезии. (Terasaki et al., 2019; Steinbrügge et al., 2021).
(2009 г.) предполагают минимум 5 % масс. S. Различные модели термической эволюции рассматривают ядро Fe-Si с неопределенностью относительно точного состава Si (Knibbe and van Westrenen, 2017; Knibbe and van Westrenen, 2018). Оценки содержания Si колеблются от 5 до 25 мас.% Si (Malavergne et al., 2010; Chabot et al., 2014), хотя недавние исследования показывают, что 10,5 мас.% Si обеспечивает наилучшие результаты моделирования упругих свойств керна и данных геодезии. (Terasaki et al., 2019; Steinbrügge et al., 2021). Напротив, прямые измерения ρ γ-Fe при 5, 7 и 15 ГПа в жидком состоянии в прессе с несколькими упорами показали значения ~ 0,36 мкОм·м и ~ 0,44 мкОм·м при ICB (2200–2500 К, 36 ГПа) и Условия CMB (1800–2000 K, 5–7 ГПа) соответственно (Deng et al., 2013). Прямые измерения ρ для γ-Fe при температуре ядра Меркурия в ЦАП с лазерным нагревом показали значения 1,08–2,44 мкОм·м (или 35 ± 10 Вт·м −1 K −1 ) при 2200–2500 K и ~40 ГПа (Конопкова и др., 2016). Учитывая изменения числа Лоренца с T , Secco (2017) сообщил, что ρ для Fe составляет 1,044 мкОм · м при 1823 K и 5,5 ГПа. Силбер и др. (2018) использовали прямые измерения ρ Fe от 3–12 ГПа и до жидкости T и предложили значение 0,87 ± 0,10 мкОм·м для Fe в условиях реликтового излучения (1900 K, 5 ГПа). Эзенва и Секко (2019) пересмотрели предыдущие измерения ρ Fe в условиях реликтового излучения Меркурия (1880 К, 5 ГПа) до 1,18 мкОм·м на твердой стороне непосредственно перед плавлением и 1,24 мкОм·м на жидкой стороне.
Напротив, прямые измерения ρ γ-Fe при 5, 7 и 15 ГПа в жидком состоянии в прессе с несколькими упорами показали значения ~ 0,36 мкОм·м и ~ 0,44 мкОм·м при ICB (2200–2500 К, 36 ГПа) и Условия CMB (1800–2000 K, 5–7 ГПа) соответственно (Deng et al., 2013). Прямые измерения ρ для γ-Fe при температуре ядра Меркурия в ЦАП с лазерным нагревом показали значения 1,08–2,44 мкОм·м (или 35 ± 10 Вт·м −1 K −1 ) при 2200–2500 K и ~40 ГПа (Конопкова и др., 2016). Учитывая изменения числа Лоренца с T , Secco (2017) сообщил, что ρ для Fe составляет 1,044 мкОм · м при 1823 K и 5,5 ГПа. Силбер и др. (2018) использовали прямые измерения ρ Fe от 3–12 ГПа и до жидкости T и предложили значение 0,87 ± 0,10 мкОм·м для Fe в условиях реликтового излучения (1900 K, 5 ГПа). Эзенва и Секко (2019) пересмотрели предыдущие измерения ρ Fe в условиях реликтового излучения Меркурия (1880 К, 5 ГПа) до 1,18 мкОм·м на твердой стороне непосредственно перед плавлением и 1,24 мкОм·м на жидкой стороне. Беррада и др. (2021) сообщили о более высоких значениях ρ Fe8,5Si в диапазоне 1,40–1,44 мкОм·м в условиях реликтового излучения (1600–2100 К, 5–7 ГПа) по результатам измерений в прессе с несколькими наковальнями до 24 ГПа и выше жидкости Т . Точно так же Pommier et al. (2019) провели прямые измерения в аппарате с несколькими наковальнями до 10 ГПа и в широком диапазоне T . Их результаты показали приблизительно 0,35 мкОм·м для Fe10Si, 0,49 мкОм·м для Fe33,5Si и 0,33 мкОм·м для Fe8Si3S в условиях реликтового излучения (2000 К, 6 ГПа). Напротив, Manthilake et al. (2019) представили данные σ из измерений сопротивления Fe36,5S, которые преобразуются в 8,01 мкОм·м вблизи условий реликтового излучения (1300 K, 8 ГПа). Этот результат значительно больше, чем для любой композиции, о которой сообщалось в литературе до сих пор при аналогичных P и T условия. Значения, обсуждаемые в этом разделе, суммированы в таблице 6, а изменения ρ показаны на рисунке 4.
Беррада и др. (2021) сообщили о более высоких значениях ρ Fe8,5Si в диапазоне 1,40–1,44 мкОм·м в условиях реликтового излучения (1600–2100 К, 5–7 ГПа) по результатам измерений в прессе с несколькими наковальнями до 24 ГПа и выше жидкости Т . Точно так же Pommier et al. (2019) провели прямые измерения в аппарате с несколькими наковальнями до 10 ГПа и в широком диапазоне T . Их результаты показали приблизительно 0,35 мкОм·м для Fe10Si, 0,49 мкОм·м для Fe33,5Si и 0,33 мкОм·м для Fe8Si3S в условиях реликтового излучения (2000 К, 6 ГПа). Напротив, Manthilake et al. (2019) представили данные σ из измерений сопротивления Fe36,5S, которые преобразуются в 8,01 мкОм·м вблизи условий реликтового излучения (1300 K, 8 ГПа). Этот результат значительно больше, чем для любой композиции, о которой сообщалось в литературе до сих пор при аналогичных P и T условия. Значения, обсуждаемые в этом разделе, суммированы в таблице 6, а изменения ρ показаны на рисунке 4.
 прямой k измерений Konopkova et al. (2016) преобразуют значения ρ в значения, аналогичные прямым измерениям ρ, проведенным Secco (2017), Silber et al. (2018) и Эзенва и Секко (2019). Значения, указанные для сплавов Fe-Si/S, также демонстрируют две отчетливые тенденции. Беррада и др. (2021) сообщили о более высоких значениях, чем Pommier et al. (2019), хотя Pommier (2018) считал более высокое содержание легких элементов (до 33,5 мас.% Si). Действительно, ожидается, что содержание легких элементов увеличит вклад рассеяния и, следовательно, измеренное значение ρ. Значения, указанные Pommier (2018), согласуются с более низкими значениями ρ для Fe, указанными Deng et al. (2013) и Konopková et al. (2016). Точно так же значения, указанные Berrada et al. (2021) согласуются с высокими значениями ρ Fe, о которых сообщают Secco (2017), Silber et al. (2018 г.) и Эзенва и Секко (2019 г.). Средние значения всех исследований, сообщающих о значениях для Меркурия, составляют 0,88 и 1,12 мкОм·м в условиях CMB и ICB соответственно, без учета высоких значений (>3 мкОм·м) из Manthilake et al.
прямой k измерений Konopkova et al. (2016) преобразуют значения ρ в значения, аналогичные прямым измерениям ρ, проведенным Secco (2017), Silber et al. (2018) и Эзенва и Секко (2019). Значения, указанные для сплавов Fe-Si/S, также демонстрируют две отчетливые тенденции. Беррада и др. (2021) сообщили о более высоких значениях, чем Pommier et al. (2019), хотя Pommier (2018) считал более высокое содержание легких элементов (до 33,5 мас.% Si). Действительно, ожидается, что содержание легких элементов увеличит вклад рассеяния и, следовательно, измеренное значение ρ. Значения, указанные Pommier (2018), согласуются с более низкими значениями ρ для Fe, указанными Deng et al. (2013) и Konopková et al. (2016). Точно так же значения, указанные Berrada et al. (2021) согласуются с высокими значениями ρ Fe, о которых сообщают Secco (2017), Silber et al. (2018 г.) и Эзенва и Секко (2019 г.). Средние значения всех исследований, сообщающих о значениях для Меркурия, составляют 0,88 и 1,12 мкОм·м в условиях CMB и ICB соответственно, без учета высоких значений (>3 мкОм·м) из Manthilake et al. (2019). Хотя все представленные данные в ICB состоят только из измерений чистого Fe, среднее значение ρ в условиях ICB больше, чем в условиях CMB, в которых учитываются сплавы Fe. Этот контраст с наблюдениями в условиях ядра Земли можно объяснить сильным влиянием T на эффекты легких элементов и P в основных условиях Меркурия, хотя необходимы дальнейшие исследования, чтобы сделать надежные выводы.
(2019). Хотя все представленные данные в ICB состоят только из измерений чистого Fe, среднее значение ρ в условиях ICB больше, чем в условиях CMB, в которых учитываются сплавы Fe. Этот контраст с наблюдениями в условиях ядра Земли можно объяснить сильным влиянием T на эффекты легких элементов и P в основных условиях Меркурия, хотя необходимы дальнейшие исследования, чтобы сделать надежные выводы. Марс
 В их модели значение k Fe, используемое для Земли, Меркурия, Марса и Венеры, составляет 40 Вт·м −1 K −1 , что соответствует 1,15 мкОм·м при 1880 K (Stevenson et al., 1983). ). Модели тепловой эволюции, основанные на измерениях Андерсона (1998), предложили диапазон 43–88 Вт·м –1 K –1 при марсианских условиях реликтового излучения (25 ГПа, 1 800 К) (Ниммо и Стивенсон, 2000). Используя закон Видемана-Франца, это предложило значения ρ для Fe в диапазоне 0,50–1,02 мкОм·м, что ниже, чем упоминалось ранее. На самом деле Дэн и др. (2013) оценили ρ γ-Fe не более 0,40 мкОм·м в самой внешней части марсианского ядра (2000 K, 24 ГПа) на основе их измерений при 7 ГПа. Недавние измерения Silber et al. (2018) сообщил, что ρ Fe составляет 1,7 мкОм·м в условиях реликтового излучения (1770 K, 23 ГПа), что выше, чем сообщалось ранее. Аналогичные эксперименты Эзенвы и Йошино (2021 г.) в аппарате с несколькими наковальнями от 14 до 22,5 ГПа и выше жидкости T , расчетное значение ρ составляет 0,68 ± 0,03 мкОм·м в условиях реликтового излучения (2106 K, 23 ГПа).
В их модели значение k Fe, используемое для Земли, Меркурия, Марса и Венеры, составляет 40 Вт·м −1 K −1 , что соответствует 1,15 мкОм·м при 1880 K (Stevenson et al., 1983). ). Модели тепловой эволюции, основанные на измерениях Андерсона (1998), предложили диапазон 43–88 Вт·м –1 K –1 при марсианских условиях реликтового излучения (25 ГПа, 1 800 К) (Ниммо и Стивенсон, 2000). Используя закон Видемана-Франца, это предложило значения ρ для Fe в диапазоне 0,50–1,02 мкОм·м, что ниже, чем упоминалось ранее. На самом деле Дэн и др. (2013) оценили ρ γ-Fe не более 0,40 мкОм·м в самой внешней части марсианского ядра (2000 K, 24 ГПа) на основе их измерений при 7 ГПа. Недавние измерения Silber et al. (2018) сообщил, что ρ Fe составляет 1,7 мкОм·м в условиях реликтового излучения (1770 K, 23 ГПа), что выше, чем сообщалось ранее. Аналогичные эксперименты Эзенвы и Йошино (2021 г.) в аппарате с несколькими наковальнями от 14 до 22,5 ГПа и выше жидкости T , расчетное значение ρ составляет 0,68 ± 0,03 мкОм·м в условиях реликтового излучения (2106 K, 23 ГПа). Измерения, проведенные Эзенва и Йошино (2021 г.), согласуются с первопринципными расчетами чистого железа, сообщающими о значениях от 0,74 ± 0,29 мкОм·м до 0,75 ± 0,29 в ICB и CMB соответственно (Wagle et al., 2019). Уэгл и др. (2019) также рассчитали ρ Fe3.9O, Fe8.7O, Fe7.6S, Fe16.1S, Fe6.7Si и Fe14.4Si в марсианских условиях ICB и CMB, как указано в таблице 7. Прямые измерения ρ до 110 ГПа при 300 К. Предлагаемые значения от 1,064 мкОм·м в CMB до 0,952 мкОм·м в центре ядра Fe15S (или Fe 77,7 S 22,3 ) (Suehiro et al., 2017). Значения, обсуждаемые в этом разделе, суммированы в таблице 7, а изменения ρ показаны на рисунке 5.
Измерения, проведенные Эзенва и Йошино (2021 г.), согласуются с первопринципными расчетами чистого железа, сообщающими о значениях от 0,74 ± 0,29 мкОм·м до 0,75 ± 0,29 в ICB и CMB соответственно (Wagle et al., 2019). Уэгл и др. (2019) также рассчитали ρ Fe3.9O, Fe8.7O, Fe7.6S, Fe16.1S, Fe6.7Si и Fe14.4Si в марсианских условиях ICB и CMB, как указано в таблице 7. Прямые измерения ρ до 110 ГПа при 300 К. Предлагаемые значения от 1,064 мкОм·м в CMB до 0,952 мкОм·м в центре ядра Fe15S (или Fe 77,7 S 22,3 ) (Suehiro et al., 2017). Значения, обсуждаемые в этом разделе, суммированы в таблице 7, а изменения ρ показаны на рисунке 5. Среднее значение всех зарегистрированных значений в условиях реликтового излучения (1770 K, 23 ГПа) составляет 0,9.5 мкОм·м, а при ICB (2000 К, 40 ГПа) — 0,93 мкОм·м. * обозначает теоретические исследования. Повторяющиеся ссылки указывают на разные композиции.
Среднее значение всех зарегистрированных значений в условиях реликтового излучения (1770 K, 23 ГПа) составляет 0,9.5 мкОм·м, а при ICB (2000 К, 40 ГПа) — 0,93 мкОм·м. * обозначает теоретические исследования. Повторяющиеся ссылки указывают на разные композиции. Значения для Fe15S (Suehiro et al., 2017) согласуются со значениями для Fe16.1S (Wagle et al., 2019). Среднее значение всех исследований, сообщающих о значениях в условиях CMB, составляет 0,9.5 мкОм·м, а в условиях ICB – 0,93 мкОм·м. Большее среднее значение в условиях CMB по сравнению с условиями ICB сравнимо со средним значением, наблюдаемым в условиях ядра Земли.
Значения для Fe15S (Suehiro et al., 2017) согласуются со значениями для Fe16.1S (Wagle et al., 2019). Среднее значение всех исследований, сообщающих о значениях в условиях CMB, составляет 0,9.5 мкОм·м, а в условиях ICB – 0,93 мкОм·м. Большее среднее значение в условиях CMB по сравнению с условиями ICB сравнимо со средним значением, наблюдаемым в условиях ядра Земли. Ганимед
 ) – около 1400 К и 5 ГПа (Hauck и др., 2006 г., Бланд и др., 2008 г., Кимура и др., 2009 г.).
) – около 1400 К и 5 ГПа (Hauck и др., 2006 г., Бланд и др., 2008 г., Кимура и др., 2009 г.). Напротив, прямые измерения ρ Fe36.5S от 2 до 5 ГПа и до 1785 К в прессе с несколькими наковальнями показали значение 4,13 ± 0,07 мкОм·м в условиях реликтового излучения (1411 К, 5 ГПа) (Littleton et al. ., 2021). Значения, обсуждаемые в этом разделе, суммированы в таблице 8, а изменения ρ показаны на рисунке 6.
Напротив, прямые измерения ρ Fe36.5S от 2 до 5 ГПа и до 1785 К в прессе с несколькими наковальнями показали значение 4,13 ± 0,07 мкОм·м в условиях реликтового излучения (1411 К, 5 ГПа) (Littleton et al. ., 2021). Значения, обсуждаемые в этом разделе, суммированы в таблице 8, а изменения ρ показаны на рисунке 6. В целом, добавление рассеяния примеси S увеличивает ρ, как и ожидалось. Однако ρ Fe36.5S, измеренный Littleton et al. (2021) больше, чем у Fe20S (Pommier, 2018). Ожидается, что давление уменьшит ρ, но ρ Fe36.5S из Manthilake et al. (2019) при 8 ГПа почти вдвое больше, чем у Littleton et al. (2021) при 5 ГПа. Хотя общее количество измерений 90 110 k 90 111 включает фононный вклад в проводимость, это, вероятно, не объясняет степень расхождения между этими двумя исследованиями. Среднее значение всех исследований, сообщающих о значениях в условиях реликтового излучения, составляет 1,90 мкОм·м, что больше, чем у других рассмотренных планетарных тел, в то время как среднее значение в условиях ICB составляет 1,28 мкОм·м.
В целом, добавление рассеяния примеси S увеличивает ρ, как и ожидалось. Однако ρ Fe36.5S, измеренный Littleton et al. (2021) больше, чем у Fe20S (Pommier, 2018). Ожидается, что давление уменьшит ρ, но ρ Fe36.5S из Manthilake et al. (2019) при 8 ГПа почти вдвое больше, чем у Littleton et al. (2021) при 5 ГПа. Хотя общее количество измерений 90 110 k 90 111 включает фононный вклад в проводимость, это, вероятно, не объясняет степень расхождения между этими двумя исследованиями. Среднее значение всех исследований, сообщающих о значениях в условиях реликтового излучения, составляет 1,90 мкОм·м, что больше, чем у других рассмотренных планетарных тел, в то время как среднее значение в условиях ICB составляет 1,28 мкОм·м. Контурные карты ρ(
P , T ) Обширная литература по Fe в условиях реликтового излучения Земли и Меркурия и ICB дает точную контурную карту в соответствующих P и Т . Точно так же результаты контурной карты ρ Fe в лунном и марсианском реликтовом излучении состоят из среднего значения нескольких зарегистрированных значений. Однако о сплавах Fe-Ni сообщалось только в условиях P и T , относящихся к ядру Земли. Таким образом, результаты контурной карты для сплавов Fe-Ni для ядер Луны, Меркурия, Марса и Ганимеда являются ненадежными экстраполяциями. Контурная карта сплавов Fe-Ni показывает, что ρ при низких P и T значительно выше, чем значения, указанные при высоких Р и Т . Это означало бы, что эффект уменьшения P , который действует на увеличение ρ, доминирует над эффектом уменьшения T , который действует на уменьшение ρ. В той же идее ρ сплавов Fe-O сообщалось только в условиях ядра Земли и Марса, что означает, что наиболее надежные области контурной карты находятся в пределах этих границ P и T .
Обширная литература по Fe в условиях реликтового излучения Земли и Меркурия и ICB дает точную контурную карту в соответствующих P и Т . Точно так же результаты контурной карты ρ Fe в лунном и марсианском реликтовом излучении состоят из среднего значения нескольких зарегистрированных значений. Однако о сплавах Fe-Ni сообщалось только в условиях P и T , относящихся к ядру Земли. Таким образом, результаты контурной карты для сплавов Fe-Ni для ядер Луны, Меркурия, Марса и Ганимеда являются ненадежными экстраполяциями. Контурная карта сплавов Fe-Ni показывает, что ρ при низких P и T значительно выше, чем значения, указанные при высоких Р и Т . Это означало бы, что эффект уменьшения P , который действует на увеличение ρ, доминирует над эффектом уменьшения T , который действует на уменьшение ρ. В той же идее ρ сплавов Fe-O сообщалось только в условиях ядра Земли и Марса, что означает, что наиболее надежные области контурной карты находятся в пределах этих границ P и T . Контурная карта сплавов Fe-Si/S согласуется с представленными данными в условиях планетарного ядра Земли, Луны, Меркурия, Марса и Ганимеда. Преимущество контурных карт в том, что они учитывают различные 9Значения 0110 P и T , используемые для условий ядра планеты, позволяют получить общую оценку для конкретной комбинации P и T . Например, контурная карта Fe-Si/S показывает ρ около 1,70 мкОм·м в лунном реликтовом излучении (при 1750 К, что соответствует среднему диапазону 90 110 T 90 111, и 4,5 ГПа), в то время как среднее значение из зарегистрированных значений составляет 1,66 мкОм·м. без учета различий условий P и T .
Контурная карта сплавов Fe-Si/S согласуется с представленными данными в условиях планетарного ядра Земли, Луны, Меркурия, Марса и Ганимеда. Преимущество контурных карт в том, что они учитывают различные 9Значения 0110 P и T , используемые для условий ядра планеты, позволяют получить общую оценку для конкретной комбинации P и T . Например, контурная карта Fe-Si/S показывает ρ около 1,70 мкОм·м в лунном реликтовом излучении (при 1750 К, что соответствует среднему диапазону 90 110 T 90 111, и 4,5 ГПа), в то время как среднее значение из зарегистрированных значений составляет 1,66 мкОм·м. без учета различий условий P и T . Точно так же лунное реликтовое излучение находится при температуре 1750 К (что соответствует среднему диапазону 1687–1800 К) и 4,5 ГПа. CMB и ICB Меркурия находятся на уровне 1900 K и 5 ГПа, а также 2 350 K (что соответствует середине T в диапазоне 2200–2500 К) и 36 ГПа соответственно. Марсианские реликтовое излучение и ICB находятся при 1770 К и 23 ГПа и 2000 К и 40 ГПа соответственно. Реликтовое излучение Ганимеда находится при 1700 К (что соответствует среднему диапазону T 1 400–2 000 К) и 6 ГПа (что соответствует среднему диапазону P 5–7 ГПа), в то время как ICB находится при 2 200 К. и 9 ГПа. Области, охватывающие отчетные данные, выделены полным цветом, а бледные цвета — это области экстраполяции.
Точно так же лунное реликтовое излучение находится при температуре 1750 К (что соответствует среднему диапазону 1687–1800 К) и 4,5 ГПа. CMB и ICB Меркурия находятся на уровне 1900 K и 5 ГПа, а также 2 350 K (что соответствует середине T в диапазоне 2200–2500 К) и 36 ГПа соответственно. Марсианские реликтовое излучение и ICB находятся при 1770 К и 23 ГПа и 2000 К и 40 ГПа соответственно. Реликтовое излучение Ганимеда находится при 1700 К (что соответствует среднему диапазону T 1 400–2 000 К) и 6 ГПа (что соответствует среднему диапазону P 5–7 ГПа), в то время как ICB находится при 2 200 К. и 9 ГПа. Области, охватывающие отчетные данные, выделены полным цветом, а бледные цвета — это области экстраполяции. Обсуждение
 Экспериментальный прогресс, достигнутый к настоящему времени в измерении k в условиях ядра, является очень многообещающим, и необходимы будущие исследования, чтобы окончательно установить это важное свойство ядра. Доступная литература по ρ в условиях ядра Земли сосредоточена на чистом Fe, в то время как в нескольких исследованиях рассматривались различные легкие элементы и диапазон концентраций. Результаты показывают, что ρ Fe-сплавов в реликтовом излучении Земли и ICB существенно не отличается от чистого Fe. Скудная литература по ρ в лунном ядре предполагает, что влияние фосфора незначительно по сравнению с влиянием кремния и серы при аналогичном весовом %. Напротив, влияние Si и S на условия ядра Меркурия остается неясным, поскольку литература, кажется, разделена на две отдельные группы ρ с разницей примерно 35%. В ядре Марса ρ сплавов Fe находится в пределах вариаций ρ чистого Fe. Напротив, сообщаемое ρ сплавов Fe-S в условиях реликтового излучения Ганимеда показывает большое отклонение от измерений чистого Fe.
Экспериментальный прогресс, достигнутый к настоящему времени в измерении k в условиях ядра, является очень многообещающим, и необходимы будущие исследования, чтобы окончательно установить это важное свойство ядра. Доступная литература по ρ в условиях ядра Земли сосредоточена на чистом Fe, в то время как в нескольких исследованиях рассматривались различные легкие элементы и диапазон концентраций. Результаты показывают, что ρ Fe-сплавов в реликтовом излучении Земли и ICB существенно не отличается от чистого Fe. Скудная литература по ρ в лунном ядре предполагает, что влияние фосфора незначительно по сравнению с влиянием кремния и серы при аналогичном весовом %. Напротив, влияние Si и S на условия ядра Меркурия остается неясным, поскольку литература, кажется, разделена на две отдельные группы ρ с разницей примерно 35%. В ядре Марса ρ сплавов Fe находится в пределах вариаций ρ чистого Fe. Напротив, сообщаемое ρ сплавов Fe-S в условиях реликтового излучения Ганимеда показывает большое отклонение от измерений чистого Fe. В целом, рассчитанный ρ из сообщенных 9Значения 0110 k по закону Видемана-Франца со значением Зоммерфельда для L существенно не отличаются от прямых измерений ρ. Результаты расчетов из первых принципов находятся в пределах отклонений от результатов прямых измерений пресса с несколькими упорами, DAC и экспериментов по ударному сжатию. Хотя значения ρ зависят от P и T , различия в выборе P и T в условиях планетарного ядра в литературе, по-видимому, оказывают незначительное влияние на средние значения ρ. Контурные карты обеспечивают интерполяцию ρ как функции P и T в границах сообщаемых значений.
В целом, рассчитанный ρ из сообщенных 9Значения 0110 k по закону Видемана-Франца со значением Зоммерфельда для L существенно не отличаются от прямых измерений ρ. Результаты расчетов из первых принципов находятся в пределах отклонений от результатов прямых измерений пресса с несколькими упорами, DAC и экспериментов по ударному сжатию. Хотя значения ρ зависят от P и T , различия в выборе P и T в условиях планетарного ядра в литературе, по-видимому, оказывают незначительное влияние на средние значения ρ. Контурные карты обеспечивают интерполяцию ρ как функции P и T в границах сообщаемых значений. Недавно были разработаны расчеты, учитывающие спиновую поляризацию и влияние магнетизма на рассеяние электронов, и вероятен дальнейший прогресс в этой области для количественной оценки этого важного вклада в электрические и тепловые свойства в условиях планетарного ядра.
Недавно были разработаны расчеты, учитывающие спиновую поляризацию и влияние магнетизма на рассеяние электронов, и вероятен дальнейший прогресс в этой области для количественной оценки этого важного вклада в электрические и тепловые свойства в условиях планетарного ядра.
Вклад авторов
Финансирование
Конфликт интересов
Примечание издателя
Благодарности

Ссылки
 , Морар Г., Шмерр Н. К., Комабаяши Т., Криш М., Фике Г. и др. (2015). На пути к эталонной модели по физике минералов для ядра Луны. Проц. Натл. акад. науч. 112 (13), 3916–3919. doi:10.1073/pnas.14174
, Морар Г., Шмерр Н. К., Комабаяши Т., Криш М., Фике Г. и др. (2015). На пути к эталонной модели по физике минералов для ядра Луны. Проц. Натл. акад. науч. 112 (13), 3916–3919. doi:10.1073/pnas.14174 2011.10.032
2011.10.032 % Si до 24 ГПа. Планета Земля. науч. лат. 568, 117053. doi:10.1016/j.epsl.2021.117053
% Si до 24 ГПа. Планета Земля. науч. лат. 568, 117053. doi:10.1016/j.epsl.2021.117053 4 (Прил._1), 295–311. doi:10.1111/j.1365-246x.1961.tb06821.x
4 (Прил._1), 295–311. doi:10.1111/j.1365-246x.1961.tb06821.x В. (1957). Влияние давления на бинарные сплавы. VI. Системы большей частью из разбавленных сплавов тугоплавких металлов. Проц. Являюсь. акад. Искусство. науч. 84, 179–216.
В. (1957). Влияние давления на бинарные сплавы. VI. Системы большей частью из разбавленных сплавов тугоплавких металлов. Проц. Являюсь. акад. Искусство. науч. 84, 179–216. Удельное электрическое сопротивление и теплопроводность жидких сплавов Fe при высоких P и T и тепловой поток в ядре Земли. Проц. Натл. акад. науч. 109 (11), 4070–4073. doi:10.1073/pnas.1111841109
Удельное электрическое сопротивление и теплопроводность жидких сплавов Fe при высоких P и T и тепловой поток в ядре Земли. Проц. Натл. акад. науч. 109 (11), 4070–4073. doi:10.1073/pnas.1111841109 475, 767–771. doi:10.1016/j.jmmm.2018.11.112
475, 767–771. doi:10.1016/j.jmmm.2018.11.112 , Гринвуд Д. А. и Ллойд П. (1971). Расчеты транспортных свойств жидких переходных металлов. Физ. лат. А 35 (2), 57–58. дои: 10.1016/0375-9601(71)-3
, Гринвуд Д. А. и Ллойд П. (1971). Расчеты транспортных свойств жидких переходных металлов. Физ. лат. А 35 (2), 57–58. дои: 10.1016/0375-9601(71)-3 К., Секко Р. А., Йонг В., Поццо М. и Альфе Д. (2017). Удельное электрическое сопротивление твердой и жидкой меди до 5 ГПа: уменьшение вдоль границы плавления. J. Phys. хим. Сол. 110, 386–393. doi:10.1016/j.jpcs.2017.06.030
К., Секко Р. А., Йонг В., Поццо М. и Альфе Д. (2017). Удельное электрическое сопротивление твердой и жидкой меди до 5 ГПа: уменьшение вдоль границы плавления. J. Phys. хим. Сол. 110, 386–393. doi:10.1016/j.jpcs.2017.06.030-7  , Хиросе К., Акаи Х. и Фей Ю. (2016). Удельное электрическое сопротивление неупорядоченных по замещению ГПУ сплавов Fe-Si и Fe-Ni: химически индуцированное насыщение удельного сопротивления в ядре Земли. Планета Земля. науч. лат. 451, 51–61. doi:10.1016/j.epsl.2016.07.011
, Хиросе К., Акаи Х. и Фей Ю. (2016). Удельное электрическое сопротивление неупорядоченных по замещению ГПУ сплавов Fe-Si и Fe-Ni: химически индуцированное насыщение удельного сопротивления в ядре Земли. Планета Земля. науч. лат. 451, 51–61. doi:10.1016/j.epsl.2016.07.011 Фронт. наук о Земле. 6 (217). Оригинальное исследование. doi:10.3389/feart.2018.00217
Фронт. наук о Земле. 6 (217). Оригинальное исследование. doi:10.3389/feart.2018.00217 Ф., Лаброс С., Хольтгрю Н., Лобанов С.С., Чувашова И. и др. (2020). Низкая теплопроводность железо-кремниевых сплавов в условиях ядра Земли с последствиями для геодинамо. Нац. коммун. 11 (1), 3332. doi:10.1038/s41467-020-17106-7
Ф., Лаброс С., Хольтгрю Н., Лобанов С.С., Чувашова И. и др. (2020). Низкая теплопроводность железо-кремниевых сплавов в условиях ядра Земли с последствиями для геодинамо. Нац. коммун. 11 (1), 3332. doi:10.1038/s41467-020-17106-7 Редакторы Р.Б.Г. Шуберт и А. Дзиевонски Второе издание (Elsevier), 233–261. doi:10.1016/b978-0-444-53802-4.00035-x
Редакторы Р.Б.Г. Шуберт и А. Дзиевонски Второе издание (Elsevier), 233–261. doi:10.1016/b978-0-444-53802-4.00035-x Планета Земля. науч. лат. 185 (1), 25–33. doi:10.1016/s0012-821x(00)00356-3
Планета Земля. науч. лат. 185 (1), 25–33. doi:10.1016/s0012-821x(00)00356-3 8-е изд. Нью-Йорк: Дж. Уайли.
8-е изд. Нью-Йорк: Дж. Уайли. А., Френч, М., Стейнле-Нойманн, Г. и Редмер, Р. (2019). Парамагнитный переход в диамагнитный в плотном жидком железе и его влияние на электронные транспортные свойства. Физ. Преподобный Летт. 122 (8), 086601. doi:10.1103/PhysRevLett.122.086601
А., Френч, М., Стейнле-Нойманн, Г. и Редмер, Р. (2019). Парамагнитный переход в диамагнитный в плотном жидком железе и его влияние на электронные транспортные свойства. Физ. Преподобный Летт. 122 (8), 086601. doi:10.1103/PhysRevLett.122.086601 , Вечорек М. А., Брейер Д., Обер Дж., Морар Г. и Рюкримен Т. (2014). Долгоживущее лунное динамо, работающее за счет кристаллизации ядра. Планета Земля. науч. лат. 401, 251–260. doi:10.1016/j.epsl.2014.05.057
, Вечорек М. А., Брейер Д., Обер Дж., Морар Г. и Рюкримен Т. (2014). Долгоживущее лунное динамо, работающее за счет кристаллизации ядра. Планета Земля. науч. лат. 401, 251–260. doi:10.1016/j.epsl.2014.05.057 А., и Йонг, В. (2018). Снижение удельного электрического сопротивления серебра по границе плавления до 5 ГПа. Высокое давление. Рез. 38 (2), 99–106. doi:10.1080/08957959.2018.1435786
А., и Йонг, В. (2018). Снижение удельного электрического сопротивления серебра по границе плавления до 5 ГПа. Высокое давление. Рез. 38 (2), 99–106. doi:10.1080/08957959.2018.1435786 Теплопроводность FeS и ее влияние на длительное магнитное поле Меркурия. Ж. Геофиз. Рез. Планеты 124 (9), 2359–2368. doi:10.1029/2019je005979
Теплопроводность FeS и ее влияние на длительное магнитное поле Меркурия. Ж. Геофиз. Рез. Планеты 124 (9), 2359–2368. doi:10.1029/2019je005979 науч. 109 (26), 10239–10244. doi:10.1073/pnas.1207086109
науч. 109 (26), 10239–10244. doi:10.1073/pnas.1207086109 Ф. (1980). ЖИДКИЕ И АМОРФНЫЕ МЕТАЛЛЫ. J. Phys. Коллоки 41 (C8), C1–7. doi:10.1051/jphyscol:1980801
Ф. (1980). ЖИДКИЕ И АМОРФНЫЕ МЕТАЛЛЫ. J. Phys. Коллоки 41 (C8), C1–7. doi:10.1051/jphyscol:1980801
 doi:10.1016/j.epsl.2019.04.022
doi:10.1016/j.epsl.2019.04.022 doi:10.1038/nature11031
doi:10.1038/nature11031 Икар 201 (1), 12–30. doi:10.1016/j.icarus.2008.12.020
Икар 201 (1), 12–30. doi:10.1016/j.icarus.2008.12.020 Продлить. Энерг. 113, 23–34. doi:10.1016/j.pepi.2017.01.005
Продлить. Энерг. 113, 23–34. doi:10.1016/j.pepi.2017.01.005 Э., Секко, Р. А., Йонг, В., и Литтлтон, Дж. А. Х. (2018). Удельное электрическое сопротивление жидкого железа до 12 ГПа: значение для теплового потока в ядрах земных тел. науч. 8 (1), 10758. doi:10.1038/s41598-018-28921-w
Э., Секко, Р. А., Йонг, В., и Литтлтон, Дж. А. Х. (2018). Удельное электрическое сопротивление жидкого железа до 12 ГПа: значение для теплового потока в ядрах земных тел. науч. 8 (1), 10758. doi:10.1038/s41598-018-28921-w (1928). Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. für Physik 47 (1), 1–32. doi:10.1007/bf013
(1928). Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. für Physik 47 (1), 1–32. doi:10.1007/bf013 Р., Еллинек А. М., Затман С. А., Баумгарднер Дж. Р. и Ричардс М. А. (2003). Раннее динамо-ядро Луны, движимое термохимической мантийной конвекцией. Природа 421 (6919), 143–146. doi:10.1038/nature01267
Р., Еллинек А. М., Затман С. А., Баумгарднер Дж. Р. и Ричардс М. А. (2003). Раннее динамо-ядро Луны, движимое термохимической мантийной конвекцией. Природа 421 (6919), 143–146. doi:10.1038/nature01267 , Вассерман Э. и Коэн Р. Э. (1997). Состав и температура внутреннего ядра Земли. Ж. Геофиз. Рез. 102 (В11), 24729–24739. doi:10.1029/97jb02125
, Вассерман Э. и Коэн Р. Э. (1997). Состав и температура внутреннего ядра Земли. Ж. Геофиз. Рез. 102 (В11), 24729–24739. doi:10.1029/97jb02125 , Гротт М., Плеса А.-К. и Брейер Д. (2013). Термохимическая эволюция недр Меркурия. Ж. Геофиз. Рез. Планеты 118 (12), 2474–2487. doi:10.1002/jgre.20168
, Гротт М., Плеса А.-К. и Брейер Д. (2013). Термохимическая эволюция недр Меркурия. Ж. Геофиз. Рез. Планеты 118 (12), 2474–2487. doi:10.1002/jgre.20168 Физ. Rev. B 97 (9), 094307. doi:10.1103/physrevb.97.094307
Физ. Rev. B 97 (9), 094307. doi:10.1103/physrevb.97.094307 Г. и др. (2018). Кристаллическая структура и уравнение состояния сплавов Fe-Si в условиях сверхземного ядра. науч. Доп. 4 (4), eaao5864. doi:10.1126/sciadv.aao5864
Г. и др. (2018). Кристаллическая структура и уравнение состояния сплавов Fe-Si в условиях сверхземного ядра. науч. Доп. 4 (4), eaao5864. doi:10.1126/sciadv.aao5864 Физ. Преподобный Летт. 121 (9), 096601. doi:10.1103/PhysRevLett.121.096601
Физ. Преподобный Летт. 121 (9), 096601. doi:10.1103/PhysRevLett.121.096601 , Poitrasson, F., Corgne, A., Meheut, M., Quitte, G., and Anand, M. (2013). Вариации изотопов кремния во внутренней Солнечной системе: значение для формирования, дифференциации и состава планет. Geochimica et Cosmochimica Acta 121, 67–83. doi:10.1016/j.gca.2013.06.040
, Poitrasson, F., Corgne, A., Meheut, M., Quitte, G., and Anand, M. (2013). Вариации изотопов кремния во внутренней Солнечной системе: значение для формирования, дифференциации и состава планет. Geochimica et Cosmochimica Acta 121, 67–83. doi:10.1016/j.gca.2013.06.040 , Hou, M., Liu, G., Zhang, C., Prakapenka, B.B., Greenberg, E., et al. (2020). Согласование экспериментов и теории транспортных свойств железа и геодинамо. Физ. Преподобный Летт. 125 (7), 078501. doi:10.1103/PhysRevLett.125.078501
, Hou, M., Liu, G., Zhang, C., Prakapenka, B.B., Greenberg, E., et al. (2020). Согласование экспериментов и теории транспортных свойств железа и геодинамо. Физ. Преподобный Летт. 125 (7), 078501. doi:10.1103/PhysRevLett.125.078501 М. (1961). Теория электрических свойств жидких металлов. I: Одновалентные металлы. Фил. Маг. 6 (68), 1013–1034. doi:10.1080/14786436108243361
М. (1961). Теория электрических свойств жидких металлов. I: Одновалентные металлы. Фил. Маг. 6 (68), 1013–1034. doi:10.1080/14786436108243361 Удельное электрическое сопротивление Cu и Au при высоком давлении выше 5 ГПа: последствия для теории постоянного электрического сопротивления вдоль кривой плавления простых металлов
Принадлежности


Авторы
Принадлежности
 3390/ma14195476
3390/ma14195476 Абстрактный
 Настоящее исследование показало, что вдоль кривой плавления удельное сопротивление остается постоянным в диапазоне исследованных нами давлений (6-12 ГПа) в соответствии с теоретическим предсказанием. Наши результаты показывают, что теория инвариантного удельного сопротивления может применяться к простым металлам, но при более высоком давлении выше 5 ГПа. Эти результаты обсуждались с точки зрения насыщения доминирующего эффекта ядерного экранирования, вызванного возрастающей разницей в уровне энергии между уровнем Ферми и д -лента с повышением давления.
Настоящее исследование показало, что вдоль кривой плавления удельное сопротивление остается постоянным в диапазоне исследованных нами давлений (6-12 ГПа) в соответствии с теоретическим предсказанием. Наши результаты показывают, что теория инвариантного удельного сопротивления может применяться к простым металлам, но при более высоком давлении выше 5 ГПа. Эти результаты обсуждались с точки зрения насыщения доминирующего эффекта ядерного экранирования, вызванного возрастающей разницей в уровне энергии между уровнем Ферми и д -лента с повышением давления. Заявление о конфликте интересов
gov/pub-one»> Авторы заявляют об отсутствии конфликта интересов. Цифры
 Линия от точки 1 до 90 был разделен на единицы, каждая из которых имела размеры около 10–14 мкм. Четвертый электрод был потерян во время разрезания, чтобы обнажить центральную часть образца.
Линия от точки 1 до 90 был разделен на единицы, каждая из которых имела размеры около 10–14 мкм. Четвертый электрод был потерян во время разрезания, чтобы обнажить центральную часть образца.
 данные.
данные. Температуру плавления при фиксированном давлении принимали за зарегистрированную температуру в начале плавления.
Температуру плавления при фиксированном давлении принимали за зарегистрированную температуру в начале плавления.
Похожие статьи

 , Чжоу С., Ли Дж., Ву К., Кай Л., Дай С.
Ли Дж. и др.
Преподобный Научный Инструм. 2012 май;83(5):053902. дои: 10.1063/1.4716459.
Преподобный Научный Инструм. 2012.
PMID: 22667628
, Чжоу С., Ли Дж., Ву К., Кай Л., Дай С.
Ли Дж. и др.
Преподобный Научный Инструм. 2012 май;83(5):053902. дои: 10.1063/1.4716459.
Преподобный Научный Инструм. 2012.
PMID: 22667628 использованная литература
 doi: 10.1103/PhysRev.135.A1691.
—
DOI
doi: 10.1103/PhysRev.135.A1691.
—
DOI Грантовая поддержка
Удельное электрическое сопротивление и вызванная поляризация
ЧТО ТАКОЕ ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ И ВЫНУЖДЕННАЯ ПОЛЯРИЗАЦИЯ?
 Сопротивление может быть преобразовано в удельное сопротивление, свойство, используемое для прогнозирования состава, структуры и/или прочности нижележащих материалов. Например, разные геологические материалы имеют разное удельное сопротивление, присутствие воды или минеральных руд обычно снижает удельное сопротивление материала, а загрязняющие вещества также влияют на регистрируемые значения. Как правило, более прочные и твердые отложения будут иметь более высокое удельное сопротивление, связанное с ними, по сравнению с породой со слабой структурой.
Сопротивление может быть преобразовано в удельное сопротивление, свойство, используемое для прогнозирования состава, структуры и/или прочности нижележащих материалов. Например, разные геологические материалы имеют разное удельное сопротивление, присутствие воды или минеральных руд обычно снижает удельное сопротивление материала, а загрязняющие вещества также влияют на регистрируемые значения. Как правило, более прочные и твердые отложения будут иметь более высокое удельное сопротивление, связанное с ними, по сравнению с породой со слабой структурой. ОБЛАСТИ ПРИМЕНЕНИЯ МЕТОДОВ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ
ЗАЧЕМ МНЕ НУЖНА СИСТЕМА ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ?
 Ассортимент моделей и аксессуаров в линейке продуктов ABEM Terrameter LS 2 делает его подходящим для многих приложений и бюджетов. ABEM Terrameter LS 2 также можно использовать для измерения эффекта IP (индуцированной поляризации), а также SP (собственного потенциала). Измерения могут быть простыми зондированиями (просто измерение удельного сопротивления по глубине), 2D-профилями (так называемая ERT, электротомография) или даже 3D-объемами. Данные могут быть собраны на суше, в воде или в скважинах и могут быть однократными измерениями «на момент времени» или повторными показаниями для удовлетворения потребности в мониторинге изменений в недрах.
Ассортимент моделей и аксессуаров в линейке продуктов ABEM Terrameter LS 2 делает его подходящим для многих приложений и бюджетов. ABEM Terrameter LS 2 также можно использовать для измерения эффекта IP (индуцированной поляризации), а также SP (собственного потенциала). Измерения могут быть простыми зондированиями (просто измерение удельного сопротивления по глубине), 2D-профилями (так называемая ERT, электротомография) или даже 3D-объемами. Данные могут быть собраны на суше, в воде или в скважинах и могут быть однократными измерениями «на момент времени» или повторными показаниями для удовлетворения потребности в мониторинге изменений в недрах. Измерения удельного электрического сопротивления широко используются для исследования глубины коренных пород, топографии коренных пород и идентификации зон трещин и разломов.
Измерения удельного электрического сопротивления широко используются для исследования глубины коренных пород, топографии коренных пород и идентификации зон трещин и разломов. Картирование изменения удельного сопротивления в недрах
 Зная введенный ток и измеренное напряжение, можно рассчитать сопротивление земли.
Зная введенный ток и измеренное напряжение, можно рассчитать сопротивление земли. (высокое сопротивление).
(высокое сопротивление). точки, данные 1D, 2D или 3D?
 Затем их можно комбинировать для создания 1D-звучания или профиля, 2D-профиля или 3D-объема.
Затем их можно комбинировать для создания 1D-звучания или профиля, 2D-профиля или 3D-объема. Одномерное зондирование (ВЭЗ) и профилирование
 Эти данные обычно не подвергаются инверсии, и конечным результатом является график зависимости сопротивления или кажущегося удельного сопротивления от расстояния по профилю.
Эти данные обычно не подвергаются инверсии, и конечным результатом является график зависимости сопротивления или кажущегося удельного сопротивления от расстояния по профилю. 2D и 3D измерения (ERT)
 5D. Для меньших площадей съемки электроды могут располагаться в виде сетки, а набор 3D-данных формируется непосредственно на приборе; это «настоящая» 3D съемка.
5D. Для меньших площадей съемки электроды могут располагаться в виде сетки, а набор 3D-данных формируется непосредственно на приборе; это «настоящая» 3D съемка. Запись изменений состояния грунта с течением времени (мониторинг)
ВАРИАНТЫ МЕТОДА СОПРОТИВЛЕНИЯ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ

 Это чаще всего используется в качестве средства идентификации крупных сульфидных рудных тел, но также имеет применение для выявления просачивания воды и выявления шлейфов загрязнения.
Это чаще всего используется в качестве средства идентификации крупных сульфидных рудных тел, но также имеет применение для выявления просачивания воды и выявления шлейфов загрязнения.
Справочные статьи по удельному сопротивлению
Связаться с нами
Связаться с отделом продаж
Чтобы связаться с отделом продаж, пожалуйста, заполните форму ниже. Поскольку все наши продукты являются модульными, включите любую имеющуюся у вас информацию о предполагаемом применении, геологии/рельефе, конструкционных/грунтовых условиях, требованиях к глубине и предыдущем опыте использования нашего оборудования – и мы свяжемся с вами с рекомендацией. узнать о нас?
узнать о нас? Каротаж удельного электрического сопротивления как помощь в определении некоторых характеристик коллектора | Транзакции AIME
 Э.. «Карта удельного электрического сопротивления как помощь в определении некоторых характеристик коллектора». Транс. 146 (1942): 54–62. doi: https://doi.org/10.2118/942054-G
Э.. «Карта удельного электрического сопротивления как помощь в определении некоторых характеристик коллектора». Транс. 146 (1942): 54–62. doi: https://doi.org/10.2118/942054-G
панель инструментов поиска
 вода, и, что, пожалуй, самое важное, отсутствие данных, свидетельствующих о зависимости удельного сопротивления пласта in situ от его характера и содержания флюидов.
вода, и, что, пожалуй, самое важное, отсутствие данных, свидетельствующих о зависимости удельного сопротивления пласта in situ от его характера и содержания флюидов.


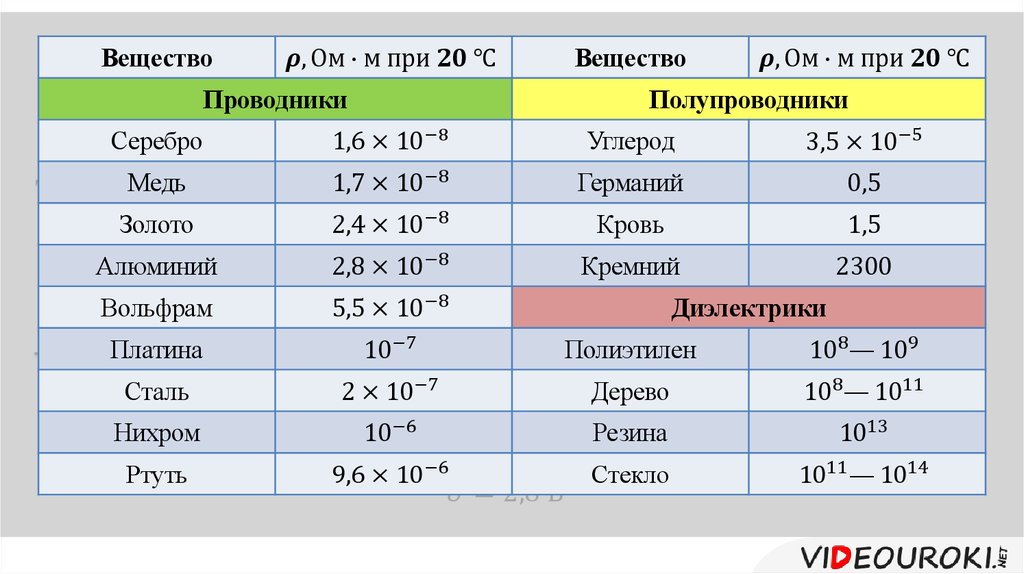
 п.) и др.
п.) и др. М., Смирнов В. Г.
М., Смирнов В. Г. Соответствуют ли эти результаты и указывают ли они на наличие промышленного рудного тела?
Соответствуют ли эти результаты и указывают ли они на наличие промышленного рудного тела? Сопротивление изменится, если изменится геометрия измерения или объем материала. Следовательно, это НЕ физическое свойство.
Сопротивление изменится, если изменится геометрия измерения или объем материала. Следовательно, это НЕ физическое свойство. Таким образом, 1 мСм/м = 1000 Ом-м, поскольку удельное сопротивление и проводимость обратно пропорциональны.
Таким образом, 1 мСм/м = 1000 Ом-м, поскольку удельное сопротивление и проводимость обратно пропорциональны. Большинство металлических рудных минералов являются электронными полупроводниками. Их удельное сопротивление ниже, чем у металлов, и сильно варьируется, поскольку включение примесных ионов в тот или иной металлический минерал оказывает большое влияние на удельное сопротивление. Например, чистый пирит имеет удельное сопротивление около 3×10 -5 Ом-м, но смешивание с небольшими количествами меди может увеличить удельное сопротивление на шесть порядков до 10 Ом-м. Свойства электропроводности некоторых важных минералов можно обобщить следующим образом:
Большинство металлических рудных минералов являются электронными полупроводниками. Их удельное сопротивление ниже, чем у металлов, и сильно варьируется, поскольку включение примесных ионов в тот или иной металлический минерал оказывает большое влияние на удельное сопротивление. Например, чистый пирит имеет удельное сопротивление около 3×10 -5 Ом-м, но смешивание с небольшими количествами меди может увеличить удельное сопротивление на шесть порядков до 10 Ом-м. Свойства электропроводности некоторых важных минералов можно обобщить следующим образом:

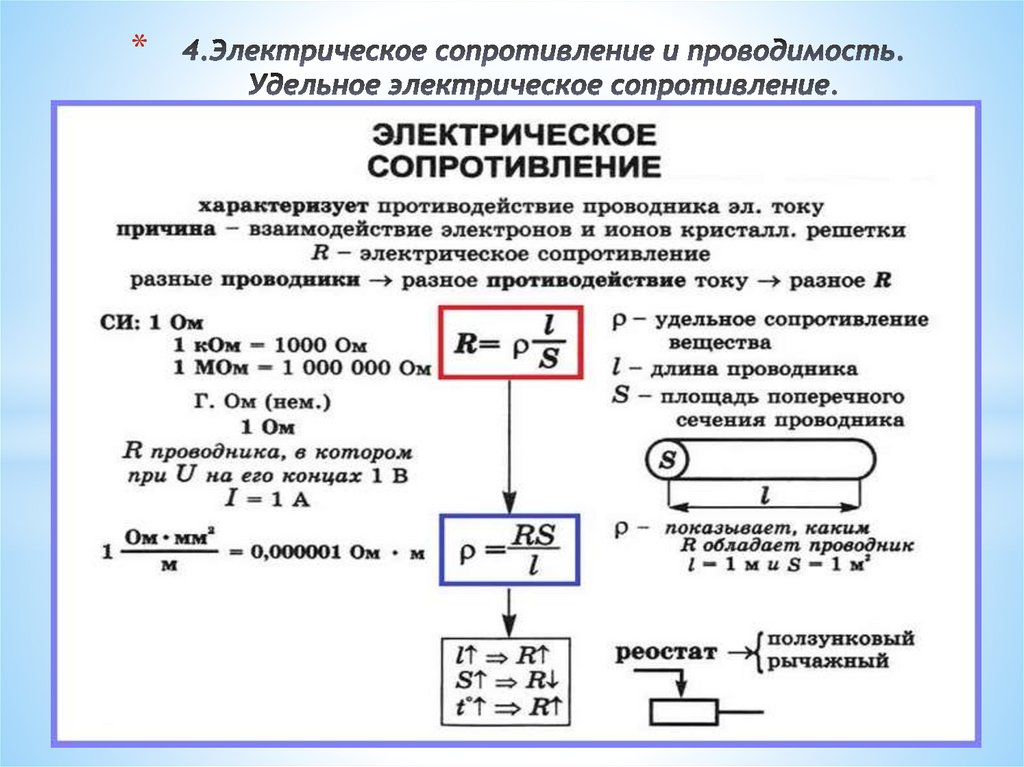 Этот тип рисунка приводится в большинстве текстов по прикладной геофизике.
Этот тип рисунка приводится в большинстве текстов по прикладной геофизике.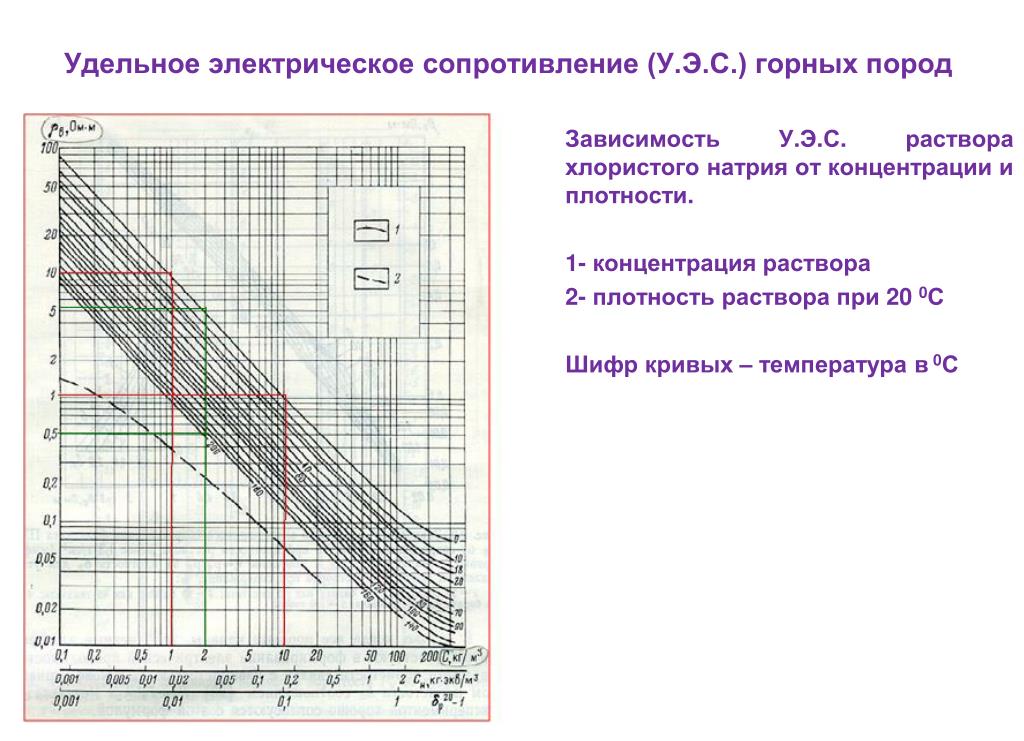
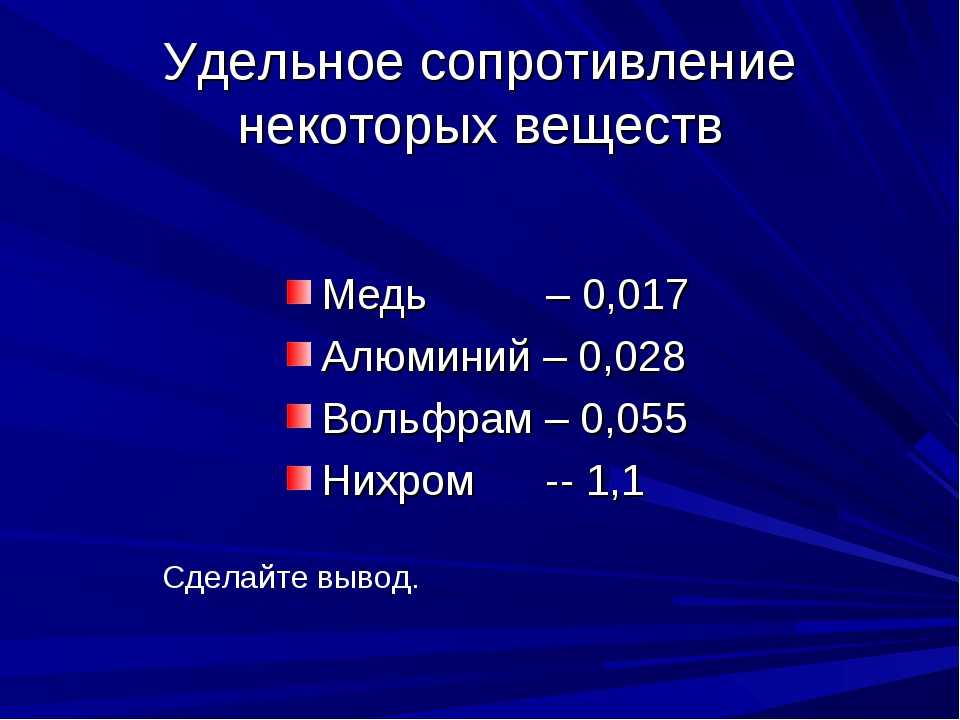 Однако удельное сопротивление, измеренное индуктивно (с использованием методов электромагнитной индукции), может быть выше, потому что токи, индуцированные колеблющимися электромагнитными полями, не должны течь на большие расстояния. См. «Фундаменты => Методы съемки» и «Фундаменты => Геофизические исследования» для получения подробной информации об этих методах съемки.
Однако удельное сопротивление, измеренное индуктивно (с использованием методов электромагнитной индукции), может быть выше, потому что токи, индуцированные колеблющимися электромагнитными полями, не должны течь на большие расстояния. См. «Фундаменты => Методы съемки» и «Фундаменты => Геофизические исследования» для получения подробной информации об этих методах съемки.