Расчет добротности контура

⇐ ПредыдущаяСтр 8 из 10Следующая ⇒

 

8. По резонансным кривым, снятым экспериментально, определите частоты f₁ и f₂, соответствующие границам полосы пропускания контура и их разность Df = f₂ — f₁. Результаты измерений занесите в табл. 2.

 

Таблица 2

Сопротивление контура, Ом	R1	R2
U0 РЕЗ, В
0,7U0 РЕЗ, В
fРЕЗ,МГц
f1, МГц
f2, МГц
Df, МГц
Q1 =
E0, В
Q2 =
QСР = (Q1 + Q2)/2
QТЕОР = Q =

 

9. Вычислите значения добротности Q₁ и Q₂ по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.

 

10. Определите среднее арифметическое значение добротности при различных фиксированных значениях сопротивлений контура:

 

Q_СР = (Q₁ + Q₂)/2.

11. Оцените относительную погрешность определения добротности по косвенным измерениям:

 

dQ₁ = = + + ,

dQ₂ = = + ,

 

где Df_РЕЗ, Df₁, Df₂,DU_{0 РЕЗ}, DE₀ – ошибки в определении соответствующих значений

f_РЕЗ, f₁, f₂, U_{0 РЕЗ}, E₀.

 

Вычислите теоретическое значение добротности контура по формуле (9) и сравните его с результатами расчета по формулам (10) и (12). Объясните возможные причины расхождения результатов измерений и расчета.

 

 

Контрольные вопросы

1. Какие колебания называются вынужденными?

2. В чем заключается явление резонанса?

3. От чего зависит добротность контура?

4. Перечислите методы определения добротности контура.

5. Дайте определение полосы пропускания контура.

6. Чему равна частота вынуждающей э. д. с. в момент резонанса?

7. Каким образом снимается резонансная кривая в данной работе?

 

 

Список литературы

 

3. Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

4. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

 

 

Работа 129

 

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

 

Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.

 

 

Введение

 

На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор емкостью C, катушку индуктивностью L и активное сопротивление R.

Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления

R = 0 при сообщении конденсатору заряда q₀.

Вначале энергия электрического поля конденсатора емкостью C равна:

W_C = q₀²/2C = CU₀²/2,

 

где U₀ = q₀/С – максимальнаяразность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:

I(t) = — dq(t)/dt, (1)

 

где dq(t) – изменение заряда на обкладках конденсатора.

Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).

Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции E(t), препятствующей изменению тока (E < 0):

 

E(t) = –

L(dI/dt).

 

При полном разряде конденсатора его электрическое поле исчезает, а ток в контуре, наоборот, достигает максимального значения I₀. Максимального значения достигает и энергия магнитного поля в катушке:

 

W_L = LI₀²/2.

 

С этого момента начинается перезарядка конденсатора под действием э.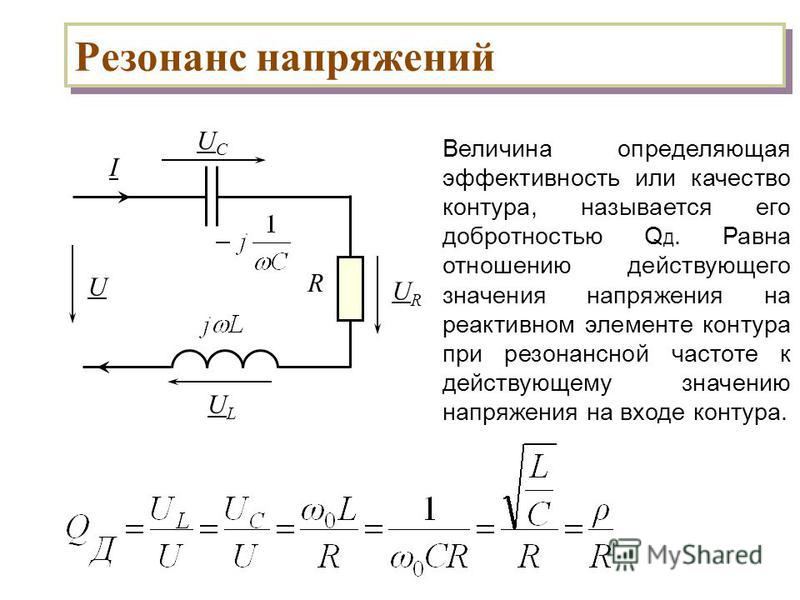 д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.

Интервал времени между двумя последовательными максимальными значениями колеблющейся величины называется периодом колебаний T.

Заметим, что описанные выше колебания происходили бы бесконечно долго лишь при отсутствии испускания таким контуром электромагнитного излучения.

Если колебательный контур содержит активное сопротивление

R, то при протекании по нему тока часть общей энергии контура W выделяется в виде тепла:

 

Q = W_R = I²Rt.

При этом уменьшаются с течением времени амплитудные значения тока в контуре и разности потенциалов на обкладках конденсатора. Колебания затухают.

Временная зависимость разности потенциалов на обкладках конденсатора U(t) = j₁ — j₂ наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э. д. с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:

 

IR =j₁ – j₂ + E = U – L(dI/dt). (2)

 

Преобразуем это уравнение, используя формулу (1) и соотношение q = CU. Тогда уравнение (2) примет вид:

 

LC(d²U/dt²) + RC(dU/dt) + U = 0. (3)

 

Разделив обе части уравнения (3) на LC и введя обозначения

 

R/2L = b, 1/LC = w

0²,

 

где w₀ называется собственной циклической (круговой) частотой контура, а b – коэффициентом затухания, получим дифференциальное уравнение:

 

d²U/dt² + 2b(dU/dt) + w₀²U = 0, (4)

 

решение которого дает искомую зависимость U(t).

Следует отметить, что аналогичные дифференциальные уравнения могут быть получены для различного рода механических, электромеханических и других колебательных систем, в которых отсутствуют внешние вынуждающие воздействия, а силы сопротивления при малых скоростях движения (скоростях изменения параметра системы, совершающей колебания) линейно зависят от скорости.

При этом энергия, внесенная в сиcтему извне, непрерывно уменьшается в процессе колебаний, переходя, в конечном счете, в тепловую энергию. Уравнение (4) есть линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для частного случая, когда b < w₀, его решение имеет вид:

U(t) = U₀e^—βtcos(wt + j₀), (5)

 

где j₀ – начальная фаза колебаний; w – циклическая частота затухающих колебаний:

w = = (6)

На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.

Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний

T = = . (7)

 

Амплитудой затухающих колебаний называют величину

 

A(t) = U₀e^—bt, (8)

 

где U₀ – максимально возможное значение амплитуды напряжения:

 

U₀= A(t = 0).

 

Вообще говоря, при b¹ 0 разность потенциалов U(t) не является строго периодической функцией времени: U(t) ¹ U(t + T). Периодом колебаний в этом случае принято считать минимальные промежутки времени между наибольшими значениями напряжения одного знака.

Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания b. Согласно (8) коэффициент затухания есть физическая величина, обратная времени t, в течение которого амплитуда колебаний уменьшается в е раз:

 

U₀/A(t) = e при t = t= 1/b.

 

Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при b = 0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а):

U(t) = U₀cos(w₀t + j₀)

 

с периодом T₀ = 2p/w₀ = 2p (формула У.Томсона).

При критическом сопротивлении (см. формулы (6) и (7))

 

R = R_КР = 2

b = w₀, и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).

При R < R_КР (т. е. при b < w₀) в контуре реализуется затухающий колебательный процесс (рис. 2б).

При R > R_КР (b > w₀) циклическая частота wи период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).

Для характеристики затухающих колебаний наряду с коэффициентом затухания b используются и другие параметры: логарифмический декремент d и добротность контура Q.

Логарифмический декремент вводится как натуральный логарифм отношения амплитуд колебаний, разделенных во времени на период Т (рис. 2):

 

d = ln = ln = bT = T/t = 1/N, (9)

 

т.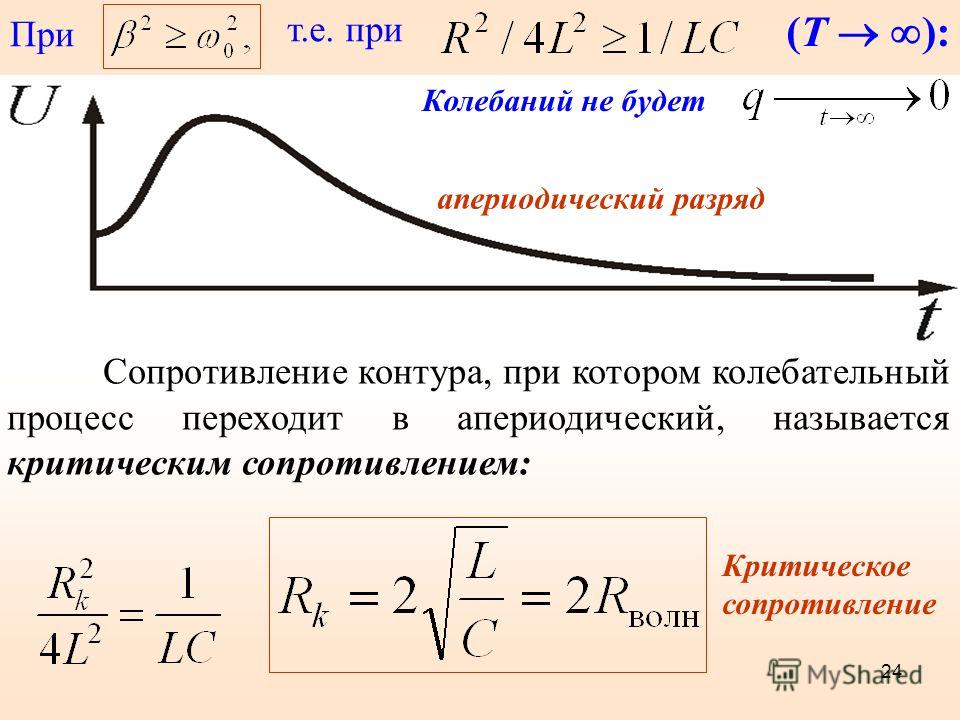 е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N = t/T).

Из соотношения между d и b

 

d = bT = RT/(2L) (10)

 

при малых затуханиях (b << w₀): T » T₀ = 2p можно, зная d, определить коэффициент затухания b:

 

b = d/T₀ = d/(2p ). (11)

 

Добротность контура Q – важный параметр, характеризующий быстроту потери энергии, запасенной в контуре. Добротность контура показывает, во сколько раз амплитуда вынужденных колебаний напряжения на конденсаторе при резонансе превышает амплитуду внешней прикладываемой электродвижущей силы, и определяется формулой:

Q = w₀/2b.

 

Для колебаний при малых b частота затухающих колебаний ω приблизительно равна собственной частоте колебаний w₀ (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:

 

Q = w₀/2b ≈ w/2b = 2p/2βT = p/d. (12)

 

Для колебательного контура:

 

b = R/2L, и w₀ = 1/ .

 

Добротность в этом случае:

 

Q = w₀/2b = = r/R. (13)

Физическую величину r = называют волновым или характеристическим сопротивлением колебательного контура.

Из соотношения (13) следует, что контур, имеющий большое активное сопротивление, обладает малой добротностью и интенсивно теряет электромагнитную энергию, колебания быстро затухают.

Все рассмотренные процессы относятся к колебательному контуру с сосредоточенными параметрами R, L и C. В реальных колебательных контурах нельзя выделить ни одного участка цепи, не обладающего активным сопротивлением, индуктивностью и емкостью, т.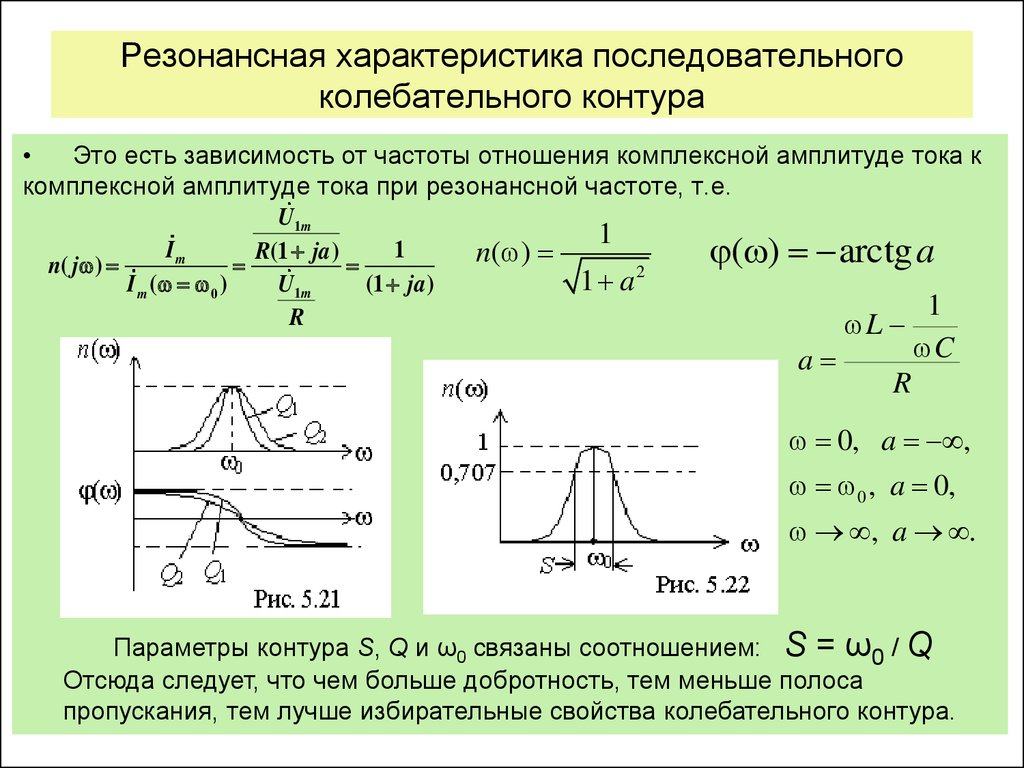 е. параметры R, L и С не являются сосредоточенными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При этом также необходимо учитывать входные электрические параметры измерительных приборов.

 

 

⇐ Предыдущая12345678910Следующая ⇒

 

Поиск по сайту:

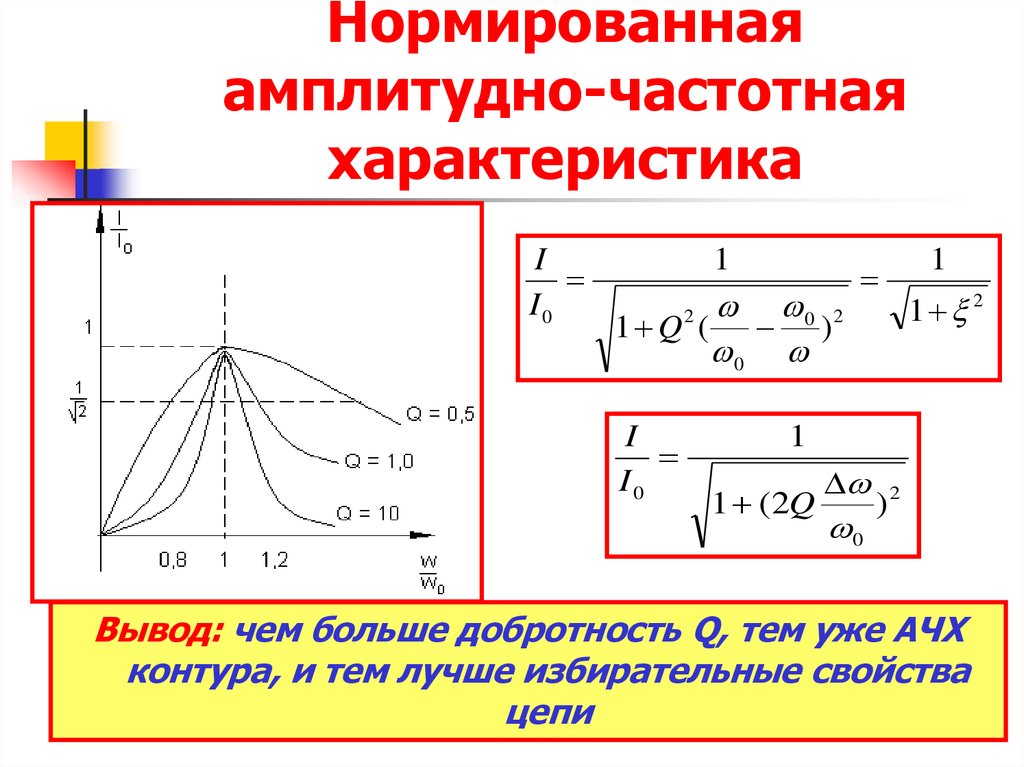
7.5. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с

Любой резонансный контур, в том числе и последовательный принято характеризовать добротностью Q и характеристическим сопротивлением .

Напомним, что в данном случае будем рассматривать определение добротности контура при изменении частоты источника питания.

При резонансе .

Добротность контура определяет кратность превышения напряжения на зажимах индуктивного или емкостного элемента сопротивления при резонансе над напряжением всей цепи U = U_R.

В электротехнических и радиотехнических установках добротности могут быть любого порядка, вплоть до десятков тысяч. При больших добротностях (50–500) U_L0 >> U_R, U_R = U_ВХ = U, т. е. напряжение на индуктивности (или на емкости) во много раз больше приложенного напряжения.

Выясним влияние добротности на резонансные кривые при последовательном соединении

R, L, С. Ток в цепи равен

Относительное значение тока: , т.е..

Пои выводе этой формулы учитывалось, что .

Иногда вводят понятие относительной частоты .

Тогда предыдущая формула запишется так

Построим резонансные кривые в относительных (по току) единицах (рис. 7.8) для трех добротностей. Рассматривая три резонансные кривые, видим, что чем больше добротность, тем острее получается резонансная кривая. Полоса пропускания контура определяется разностью частот, которые получатся при пересечении резонансной кривой горизонтальной линией на уровне .

Из рис. 7.8 видно, что чем меньше добротность, тем шире полоса пропускания. В радиоприемниках колебательные контуры имеют большие добротности (500–1000), поэтому эти контуры обладают достаточно узкими полосами пропускания, что способствует избирательному радиоприему только одной станции.

На практике резонансные частотные характеристики реальных контуров можно получать, изменяя частоту генератора в определенных пределах и снимая показания вольтаметра, подключенного параллельно резистору (см. рис. 7.9 а). Строят экспериментальную резонансную кривую и по этой кривой определяют полосу пропускания. Выведем соответствующую формулу для расчета добротности по резонансной кривой, снятой экспериментально.

Из рис. 7.9 б следует:

.

В этом равенстве знаменатели равны, поэтому

Отсюда .

Запишем дважды: при итакие выражения;.

После сложения последних выражений получим

или

Отсюда

И далее .

Очень важно: добротность обратно пропорциональна .

Для последовательного контура R, L, С построена резонансная кривая тока при изменении

емкости С (рис. 7.10).

Пользуясь этой кривой, определим добротность контура. Выражение для тока

Выполним ряд преобразований последней формулы

;

.

Проведем горизонтальную прямую на уровне .

Отметим значения емкости C₁ и С₂.

Далее сделаем ряд очевидных выкладок. Выразим добротность Q через значения

емкости С₁ и С₂. Запишем

Найдем сумму и разность емкостей

Запишем отношение .

Напомним, что добротность контура определяется превышением напряжения на индуктивном (или емкостном) сопротивлении при резонансе над напряжением всей цепи (или напряжением на активном сопротивлении), т. е.

Таким образом,

Кроме этого результата, представляется возможным получить значения параметров катушки индуктивности (L и R)

.

Откуда ;.

Откуда .

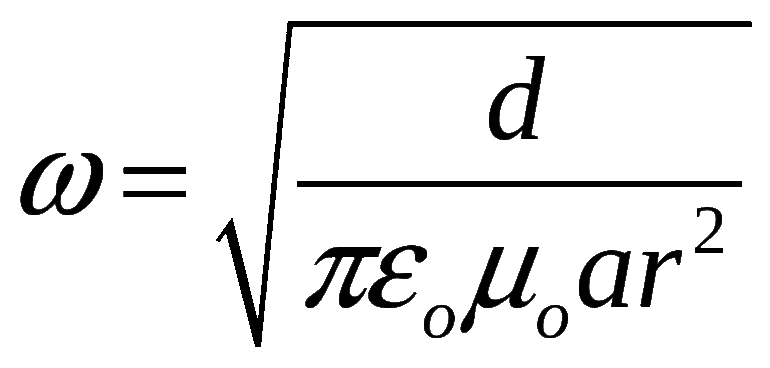
Величина емкости С₀, при которой наступает резонанс, определится так:

; ;;.

Откуда .

Резонанс напряжений может наблюдаться в схеме, показанной на рис. 7.11.

Входное сопротивление такой схемы

При резонансе реактивная составляющая входного сопротивления должна быть равна нулю, т. е.

3.5. Резонансные цепи – В помощь студентам БНТУ – курсовые, рефераты, лабораторные !

Последовательный колебательный контур. Последовательный колебательный контур образуется при последовательном соединении катушки индуктивности и конденсатора. Эквивалентная схема рис.3.7 для анализа цепи включает и омическое сопротивление R, при помощи которого учитываются потери в реальной индуктивности и емкости.

Рис. 3.7 Эквивалентная схема последовательного контура.

Пусть на входе контура действует гармоническое колебание U. Из рис.3.7 видно, что комплексное сопротивление равно:

Z=R+j(ωL-1/ωС)                                                                               (3.41)

зная приложенное напряжение U и сопротивление контура определяем ток в контуре:

I=(U/Z)=U/[R+j(ωL-1/ωС)]                                                              (3.42)

 

Сдвиг фаз между током и напряжением равен:

;                                                                 (3.43)

 

Падения напряжений на резисторе, индуктивности и емкости определяются выражениями:

                                             (3.44)

Из полученных соотношений видно, что Z, UL и UC зависят от частоты.

Когда частота входного сигнала равна собственной частоте колебательного контура, то хL=хC и в контуре возникает резонанс.

Рассмотрим процессы в цепи при наступлении резонанса исходя из условия, что xL=ωL=xC=l/(ωC).

Откуда собственная частота контура:

Определим Z, UL и UC при резонансе. Учитывая, что при резонансе xL=xC выражения (3.41-3.44) примут вид:

 

                                                                                                   (3.45)

Важной    характеристикой    колебательного    контура    является    его добротность (качество), которое по определению равно: Q=UL(p) /U=UC(p) /U.

Подставляя в эту формулу значения напряжений из (3.45) будем иметь:

 

где                                                       (3.46)

Q показывает во сколько раз сопротивление контура на резонансной частоте больше сопротивления омических потерь. В среднем Q=10.. 100 раз.

ρ – волновое сопротивление, которое равно индуктивному и емкостному сопротивлениям на резонансной частоте.

 

Учитывая (3.46) соотношения (3.45) примут вид:

                                                     (3. 47)

Из (3.47) видно, что при возникновении в контуре резонанса напряжение на реактивных элементах L и С в Q раз (10.. 100 раз) больше приложенного к контуру напряжения. Поэтому говорят, что в последовательном колебательном контуре имеет месторезонанс напряжений.

 

Частотные характеристики и полоса пропускания последовательного колебательного контура. Зависимости сопротивлений и сдвига фазы между током и напряжением от частоты называются частотными и фазовыми характеристиками контура и определяются формулами:

                                                                    (3.48)

                         

Графики зависимости xL(ω), хC(ω), х(ω) и Z(ω) изображены на рис.3.8.а, а зависимости φ(ω) –на рис.З.8.б.

Рис. 3.8. Частотные (а) и фазовая (б) характеристики последовательного колебательного контура.

Из выражений (3.48) и графиков рис.3.8 видно, что при ω<ω0 цепь носит емкостной характер (х<0, φ<0) и ток в контуре опережает по фазе приложенное к нему напряжение.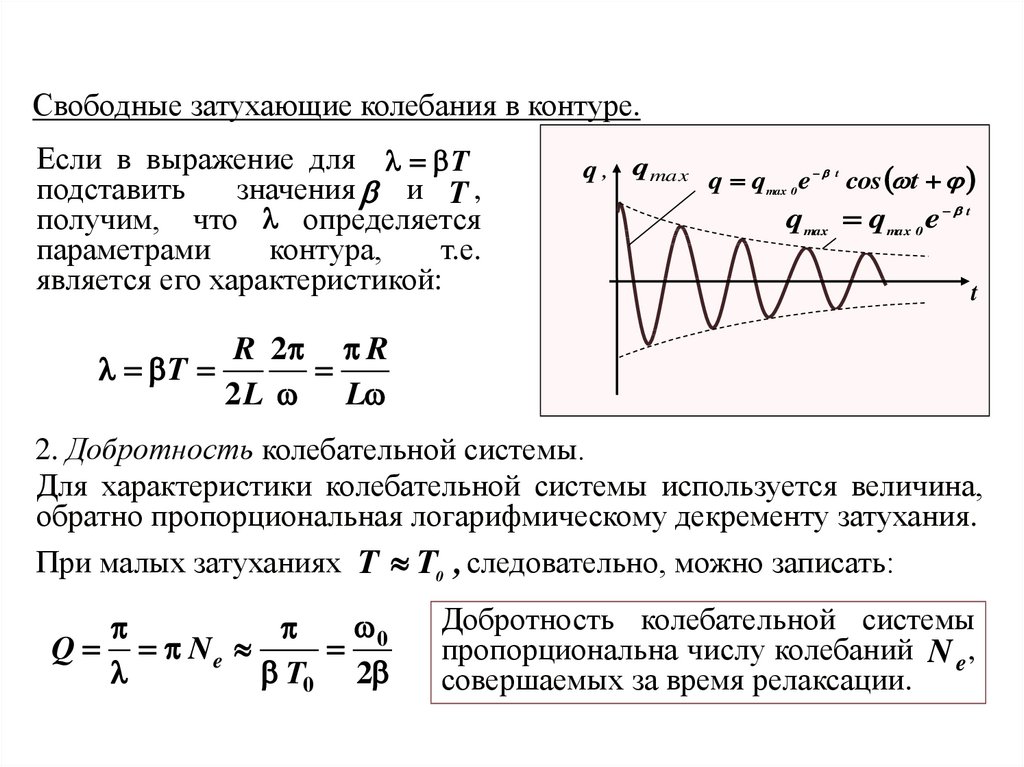 При ω>ω0 цепь имеет индуктивный характер (х>0,φ>0) и ток отстает по фазе от приложенным напряжения. При ω=ω0 в контуре наступает резонанс напряжений (х=0, φ=0) и ток совпадает по фазе с приложенным напряжением. На резонансной частоте контур имеет минимальное значение сопротивления, которое равно сопротивлению потерь в катушке индуктивности и в конденсаторе, т.е. Z=R.

Зависимости тока и напряжений от частоты называют амплитудно-частотными характеристиками (АЧХ) или резонансными характеристиками контура. Эти зависимости определяются следующими выражениями:

 

                   (3.49)

Зависимости, определяемые выражениями (3.49) изображены на рис 3.9.

Рис. 3.9. Амплитудно-частотные характеристики последовательного колебательного контура.

Из (3.49) и графиков рис 3.9 видно, что ток в контуре при резонансе (ω=ω0) достигает максимального значения и равен I0=U/R. Значения напряжений на индуктивности UL(ω) и емкости UC(ω) на резонансной частоте (ω=ω0) равны:

UL(ω0)=UL0=UC(ω0)= UC0=I0ρ=UQ                                                 (3. 50)

Максимальные значения Ui(co) и Uc(co) можно определить из условия:

;                                                            (3.51)

Решив уравнения (3.51) с учетом (3.49), получим, что UL(ω) и UC(ω) принимают максимальные значения на частотах:

 

                                                                      (3.52)                                       

Максимальные значения UL(ω) и UC(ω) на частотах ωL и ωC определяются выражениями:

                                               (3.53)

Таким образом на резонансной частоте (ω=ω0) принимает максимальное значение только ток в контуре, а напряжение UL, и UC становятся максимальными на частотах ωL и ωC, которые не совпадают с резонансной частотой ω0 (см.рис.3.9,а). Однако, как видно из (3.52), с увеличением добротности контура Q , частоты ωL и ωC сближаются с резонансной частотой ω0, поэтому на практике рассматривают одну резонансную характеристику, которая показана на рис.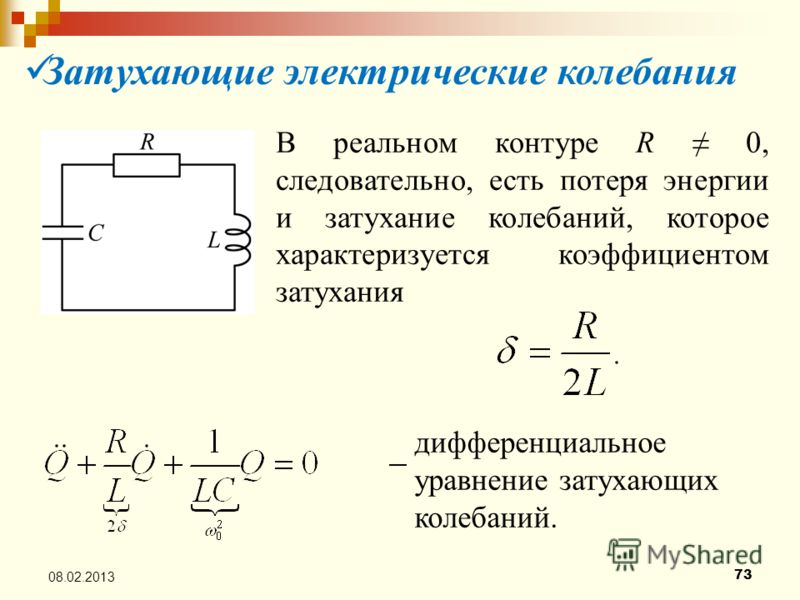 3.9,б.

В результате изменения частоты воздействующего на контур сигнала или изменения параметров контура режим резонанса может быть нарушен. Степень отклонения режима колебательного контура от резонанса оценивают абсолютной (Δω,Δƒ), относительной (δ) и обобщенной (ξ) расстройками, которые определяются выражениями:   

 

  или 

                                                                                            (3.54)

АЧХ (3.49) и ФЧХ (3.48) последовательного колебательного контура можно записать через обобщенную расстройку ξ в следующей форме:

 

                                                                                                      (3.55)                                           

Из рис.3.9,б видно, что контур пропускает сигналы без существенного ослабления в некотором диапазоне частот от ƒ1 до ƒ2. Диапазон частот вблизи резонанса, на границе которого ток уменьшается в относительно I0 называют полосой пропускания контура.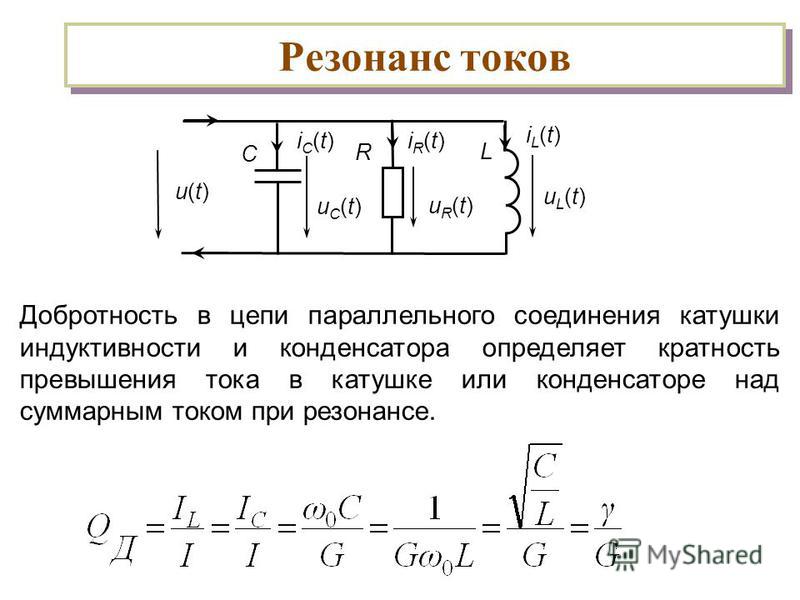 Граничные частоты полосы пропускания ƒ1 и ƒ2 определим из уравнения:

Учитывая значения ξ (3.54) получим ξ1,2=Q(ω/ω0 – ω0/ω) = ± 1, откуда

                                          (3.56)

Учитывая   (3.56)   ширина   полосы   пропускания   последовательного колебательного контура будет равна:

                                                                     (3.57)

Из (3.57) следует, что ширина полосы пропускания контура зависит от его качества Q. И чем больше Q , тем уже полоса пропускания.

Параллельный колебательный контур. Параллельный колебательный контур образуется при параллельном соединении катушки индуктивности и конденсатора с генератором тока (рис.3.10). Действительные сопротивления R1 и R2 введены в схему для отображения соответственно потерь энергии в катушке индуктивности и конденсаторе.

Рис. 3.10. Эквивалентная схема параллельного колебательного контура.

 

Определим сопротивление контура и токи в ветвях до резонанса и в момент резонанса. Из схемы видно, что:

                                                                            (3.58)

На частотах близких к резонансным всегда выполняется условие R1<<ω0L и R2<<1/(ω0C) поэтому в выражении для Z (3.58) в числителе R1 и R2 можно пренебречь:

     (3.59)

Из   полученных   выражений   видно,   что   на   частотах   меньших резонансной частоты (ω<ω0) xL<xC, поэтому IL>IC и контур носит индуктивный характер. На частотах больших резонансной частоты (ω>ω0) xL>xC, поэтому IC>IL и контур носит емкостной характер.

При частоте входного сигнала равного собственной частоте контура |xL|=|xC| и в контуре наступает резонанс на частоте равной  .

Из выражения (3.59) видно, что при |xL|=|xC| с учетом, что Q= ρ/R сопротивление контура равно:

Zρ=ρ2/R=Qρ                                                                                       (3.60)

При резонансе ток в контуре определяется выражением Ik=U/ρ. Учитывая, что U=Iг ZP и учитывая выражение (3.60) будем иметь:

Ik=Iг ZP/ρ=Iг Q                                                                                  (3.61)

Из (3.61) видно, что при ω=ω0 ток в контуре превышает ток входного генератора в Q раз. Такое явление называют резонансом тока.

Частотные характеристики параллельного контура без потерь определяются зависимостью параметров его элементов от частоты и имеют вид:

 

;

;                                       (3.62)

Графики частотных зависимостей (3.62) изображены на рис.3.11

Рис. 3.11. Частотные характеристики параллельного колебательного контура.

Из рисунка видно, что при ω<ω0 входное сопротивление контура носит индуктивный характер, а при ω>ω0 – емкостной характер. На резонансной частоте ω=ω0 вследствие отсутствия потерь входное реактивное сопротивление контура претерпевает разрыв (|Х|= ∞).

 

Согласно Закону Ома токи в ветвях контура определяются формулами:

                                                          (3. 63)

Анализ (3.63) показывает, что с увеличением частоты ω ток I1(ω) уменьшается, а I2 растет. При ω=∞ токи становятся равными I1(∞)=0; I2(∞)=U/R.

Если контур подключен к источнику с напряжением Uг и внутренним сопротивлением Rг, то комплексное напряжение на контуре определяется уравнением:

.                                                         (3.64)

где Z определятся (3.59). На резонансной частоте ξ=0, поэтому (3.64) с учетом (3.59) примет вид:

                                                           (3.65)

Определим частотную зависимость Uk/Uk(p) . Учитывая (3.64-3.65) и (3.59) будем иметь:

                         (3.66)

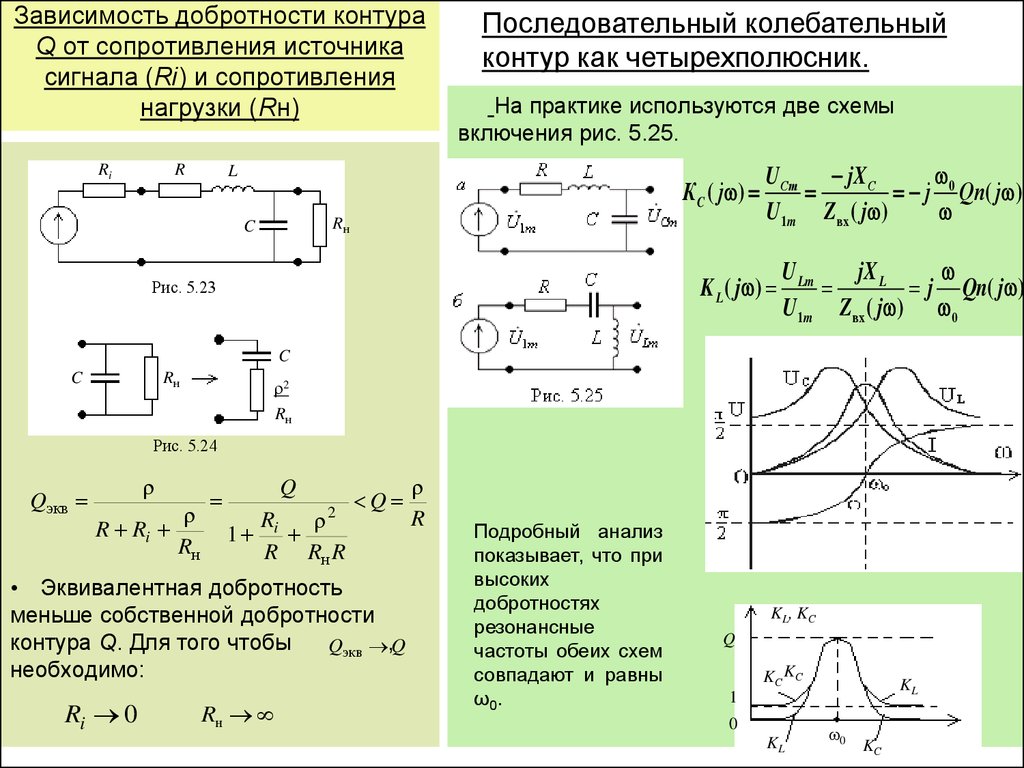
Введем понятие эквивалентной добротности контура:

QЭ=Q/(1+RОЭ/Rг)                                                                             (3.67)

Учитывая (3.67) и значение £ (3.54) выражение (3.66) можно преобразовать к виду:

                                  (3.68)

На основании частотной зависимости (3. 68) определяем АЧХ и ФЧХ параллельного колебательного контура:

 

                                                  (3.69)

Из (3.67) и (3.69) видно, что АЧХ контура зависит от внутреннего сопротивления генератора Rг. Вид АЧХ (3.69) для двух значений Rг приведена на рис.3.12:

Рис. 3.12. АЧХ параллельного колебательного контура.

Ширину полосы пропускания контура определим как диапазон частот, на границе которого напряжение на контуре уменьшается в раз относительно Uk(p).

Из этого уравнения получаем граничные частоты полосы пропускания:

Отсюда ширина полосы пропускания параллельного колебательного контура равна:

                           (3.70)

Анализ выражения (3.70) показывает, что Δƒ зависит от величины внутреннего сопротивления генератора Rг и что только при Rг→ ∞ можно получить узкую полосу(см.рис.3.12). Отсюда следует, что для улучшения избирательных свойств параллельного контура (для уменьшения Δƒ) его необходимо возбуждать источником тока.

3.4. КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ | Политех в Сети

Другой разновидностью линейных цепей являются колебательные контуры. С их помощью решается одна из важнейших задач радиотехники – осуществление частотной селекции (избирательности). Из множества несущих частот различных радиостанций, поступающих в антенну радиоприемника, необходимо выбрать узкую полосу частот интересующей нас радиостанции. Для решения этой задачи нужны частотно–избирательные цепи в виде колебательных контуров. Колебательный контур – это линейная электрическая цепь, составленная из конденсатора и катушки индуктивности

3.4.1.Свободные колебания в идеальном контуре

Рассмотрим вначале колебательный контур, в котором отсутствуют потери электрической энергии, то есть контур из идеальной катушки индуктивности и идеального конденсатора. Зарядим однократно конденсатор от внешней батареи до напряжения . При этом электрическая энергия, запасенная конденсатором, будет равна

(3.45)

За счет разряда конденсатора через катушку индуктивности происходит преобразование электрической энергии в магнитную энергию. При этом магнитная энергия, запасенная катушкой индуктивности, становится равной

. (3.46)

Затем происходит обратное преобразование магнитной энергии в электрическую энергию. В результате в контуре происходит колебательный процесс на некоторой частоте , Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:

. (3.47)

Учитывая, что , подставим значение В предыдущее выражение:

(3.48)

Отсюда резонансная частота колебаний

, (3.49)

А период колебаний

. (3.50)

Из равенства энергий найдем волновое (характеристическое) сопротивление контура :

. (3.51)

На резонансной частоте модуль реактивного сопротивления катушки индуктивности равен модулю реактивного сопротивления конденсатора:

(3.52)

Подставляя значение резонансной частоты в выражения для модулей реактивных сопротивлений, получим:

, (3. 53)

=(3.54)

Таким образом, на резонансной частоте сопротивления реактивных элементов контура равны волновому сопротивлению. В идеальном контуре колебания будут незатухающими.

3.4.2.Свободные колебания в реальном контуре

Рассмотрим физические процессы в реальном контуре, состоящем из последовательно соединенных катушки индуктивности, конденсатора и некоторого активного сопротивления потерь . Сопротивление эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.

Рис. 3.11. Последовательный колебательный контур

Если зарядить однократно от внешней батареи конденсатор, то в контуре возникнет колебательный процесс. На основе второго закона Кирхгофа можно записать:

. (3.55)

Или:

(3.56)

Продифференцируем все слагаемые уравнения (2.55) по времени и разделим на :

(3.57)

Обозначим , Где — коэффициент затухания.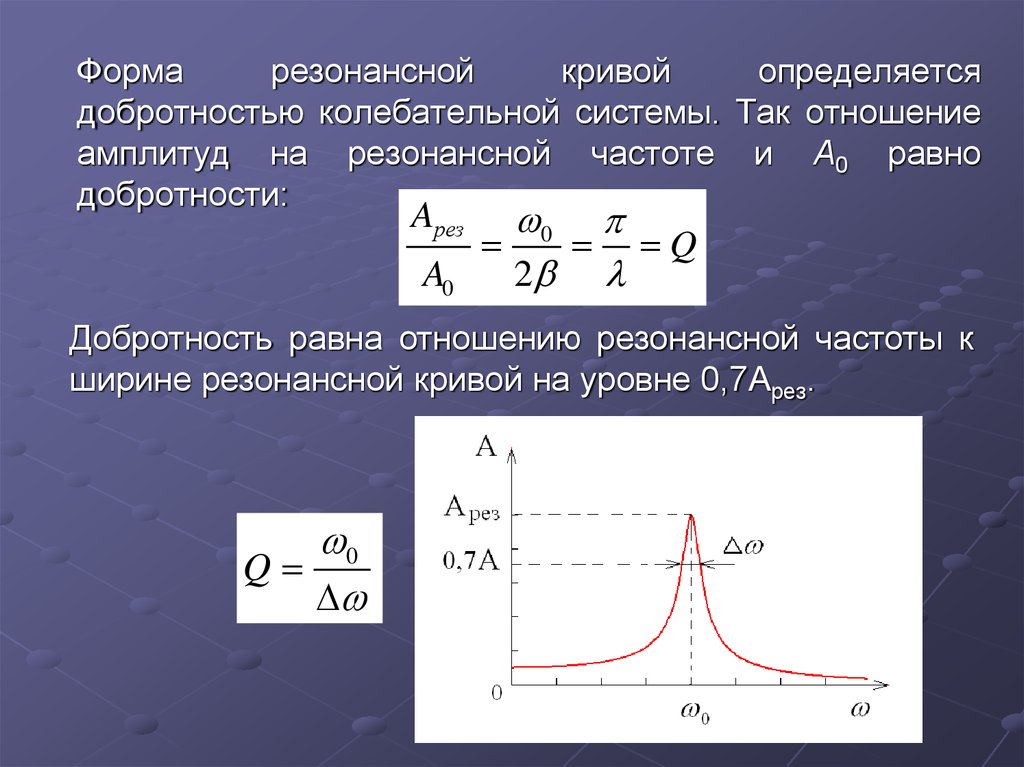

Учитывая, что , перепишем уравнение в следующем виде:

(3.58)

Ищем решение этого уравнения в виде: .

Подставим это решение в уравнение:

(3.59)

Или:

, (3.60)

Где: .

— резонансная частота реального контура.

Решение последнего уравнения имеет вид:

(3.61)

Отсюда ток в контуре равен:

. (3.62)

Полагая начальную фазу j=0, ток в контуре будет равен:

(3.63)

Если a=0, то колебания не затухают. При этом:

(3.64)

(3.65)

В реальном контуре , поэтому колебания на частоте Будут затухающими.

Рис. 3.12. Затухающие колебания в контуре с потерями

Период колебаний реального контура:

(3.66)

Если , то период колебаний . При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.

Колебательный процесс возможен только, когда или .

Отсюда: или .

У радиотехнических контуров волновое сопротивление .

Поэтому с большой степенью точности можно считать, что период колебаний и резонансная частота в реальном контуре определяются следующими выражениями:

(3.67)

(3.68)

По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается добротностью:

(3.69)

Для радиотехнических контуров добротность

Добротность контура равна отношению напряжения на индуктивности или на емкости к напряжению на активном сопротивлении при резонансе:

(3.70)

В этом выражении — Ток в контуре на резонансной частоте.

Умножим числитель и знаменатель на :

. (3.71)

Добротность равна умноженному на 2 отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.

Величина обратная добротности называется затуханием контура:

. (3.72)

3.4.3.Последовательный контур. Вынужденные колебания.

На рис. 3.13 представлен последовательный колебательный контур, к которому подключен генератор гармонических сигналов , внутреннее сопротивление которого равно нулю.

Рис3.13. Последовательный контур с внешним генератором

На основании второго закона Кирхгофа запишем:

. (3.73)

Ток в контуре будет равен:

(3.74)

Входное сопротивление

. (3.75)

Реактивная составляющая входного сопротивления

. (3.76)

В зависимости от расстройки контура относительно резонансной частоты возможны три случая:

— При этом реактивная составляющая входного сопротивления носит индуктивный характер;

При этом реактивная составляющая входного сопротивления носит емкостный характер;

при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.

На резонансной частоте входное сопротивление контура равно активному сопротивлению и ток в контуре равен значению .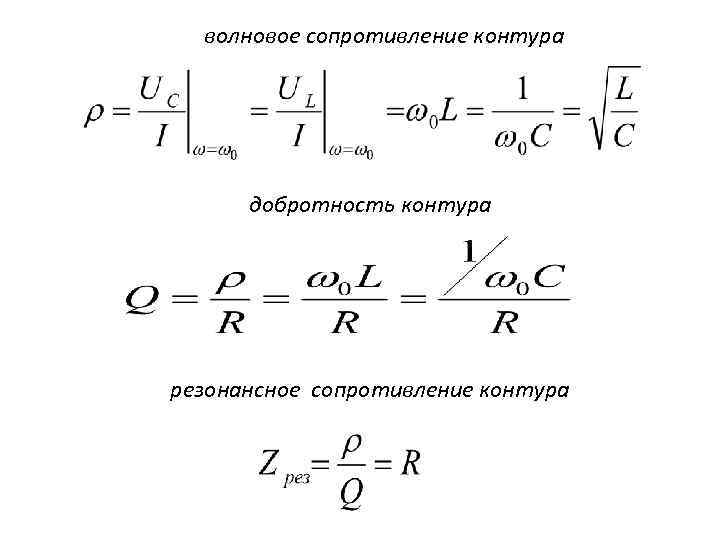

Эквивалентная схема контура при резонансе приведена на рисунке.

Рис. 3.14. Эквивалентная схема последовательного контура на

Резонансной частоте.

Амплитуды напряжений на реактивных элементах на резонансной частоте равны по величине и противоположны по фазе.

. (3.77)

Из этого выражения найдем резонансную частоту:

. (3.78)

Оценим величину отношения напряжений на реактивных элементах на резонансной частоте к напряжению внешнего генератора:

, (3.79)

. (3.80)

Таким образом, на резонансной частоте в последовательном контуре напряжения на реактивных элементах равны по абсолютной величине и в Q раз превышают напряжение внешнего генератора. Такой резонанс называется резонансом напряжений.

3.4.4.Амплитудно-частотная характеристика последовательного контура.

Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.

Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, представленного на рис. 2.14, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:

=. (3.81)

Реактивная составляющая входного сопротивления контура равна:

(3.82)

Здесь

(3.83)

— относительная расстройка контура.

Для небольших абсолютных расстроек контура (в пределах полосы пропускания)

(3.84)

С учетом этого амплитудно-частотная характеристика контура

, (3.85)

Где: — обобщенная расстройка контура.

Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:

. (3.86)

Фазовая характеристика контура

(3.87)

При настройке контура в резонанс , обобщенная расстройка , реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно . Характер зависимости свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности , который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров . АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.

Рис.2.15 АЧХ последовательного контура

Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:

. (3.88)

Отсюда полоса пропускания контура на уровне Будет равна:

(3.89)

Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:

(3. 90)

Фазовая характеристика последовательного контура, построенная по выражению (2.98), приведена на рис. 3.16.

(3.91)

Рис.3.16. Фазовая характеристика последовательного контура

3.4.5. Параллельный колебательный контур.

Параллельный колебательный контур состоит из параллельно включенных катушки индуктивности и конденсатора, как показано на рис. 3.17. Активное сопротивление катушки индуктивности равно , а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению . Контур питается идеальным генератором тока.

Рис. 3.17. Параллельный колебательный контур.

Входное сопротивление контура равно:

. (3.92)

Для высокодобротных контуров в области резонансной частоты и . Учитывая это, можно записать:

(3.93)

Где: ; .

Таким образом, входное сопротивление зависит от частоты. Токи в ветвях контура также зависят от частоты. На резонансной частоте сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток

. (3.94)

Входное сопротивление контура при резонансе становится активным и равно:

(3.95)

Следовательно, ток в контуре на резонансной частоте равен:

(3.96)

Таким образом, токи в ветвях контура при резонансе в раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.

Зависимость отношения амплитуды напряжения на контуре на текущей частоте к амплитуде напряжения на контуре на резонансной частоте от частоты называют амплитудно-частотной характеристикой параллельного контура.

Запишем выражение для амплитудно-частотной характеристики параллельного контура:

(3.97)

Входное сопротивление контура равно:

(3.98) Умножим числитель и знаменатель этого выражения на ():

. (3.99)

Найдем модуль входного сопротивления:

. (3.100)

Подставив модуль входного сопротивления в выражение (3. 97), окончательно получим:

. (3.101)

Таким образом, АЧХ параллельного и последовательного контуров описываются одним и тем же выражением.

Фазовая характеристика параллельного контура (рис. 2.18) построена на основании выражения

(3.102)

Рис. 3.18. Фазовая характеристика параллельного контура

3.4.6. Методы измерения добротности колебательных контуров

Существует несколько методов измерения добротности колебательных контуров.

Если подключить к контуру генератор гармонических сигналов и, изменяя частоту генератора, снять резонансную кривую контура, то добротность можно рассчитать по формуле:

, (3.103)

Где: — резонансная частота;

— полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.

Добротность контура можно также измерить по затухающим колебаниям в контуре, если подключить к контуру генератор прямоугольных импульсов. При этом прямоугольные импульсы должны быть достаточно короткими и с большим периодом, чтобы к моменту прихода следующего импульса колебания в контуре уже успели закончится (рис. 3.19).

Рис. 3.19. Определение добротности по затухающим колебаниям

Если обозначить начальную амплитуду затухающих колебаний , то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в раз, можно рассчитать добротность, исходя из следующих выражений:

, (3.104)

, (3.105)

. (3.106)

Таким образом, добротность равна умноженному на числу периодов, в течение которых начальная амплитуда колебаний уменьшается в Раз.

Кроме названных методов измерения добротности существуют специальные приборы — измерители добротности колебательных контуров.

3.4.7. Связанные контуры.

Недостатком одиночных колебательных контуров является их плохая избирательность. Количественно избирательность оценивается коэффициентом прямоугольности, который равен отношению ширины полосы пропускания на уровне 0,7 к ширине полосы пропускания на уровне 0,1 (иногда на уровне 0,01):

. (3.107)

Чем ближе значение коэффициента прямоугольности к 1, тем лучше избирательность контура.

Коэффициент прямоугольности одиночного контура = 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.

Ценным свойством связанных контуров является возможность осуществить АЧХ по форме, близкую к прямоугольной. Связанные контуры взаимно влияют друг на друга. Степень влияния зависит от сопротивления связи. В качестве элементов связи используют конденсаторы и индуктивности. Чаще всего используют индуктивную (трансформаторную) связь. В этом случае степень связи определяется коэффициентом взаимной индукции . В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где — коэффициент взаимной индукции, – сопротивление связи.

Рис. 3.20. Связанные контуры и их эквивалентная схема

Коэффициент взаимной индукции равен:

, (3.108)

Где: — магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;

— магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.

Для неферромагнитной среды .

Эдс, индуцируемая во втором контуре, равна:

(3.109)

Сопротивление связи равно

. (3.110)

Степень связи между контурами оценивается коэффициентом связи , который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.

Коэффициент передачи напряжения из первого контура во второй равен:

(3. 111)

Если включить генератор во второй контур, то получим коэффициент передачи напряжения из второго контура в первый:

. (3.112)

Коэффициент связи между контурами равен среднему геометрическому из коэффициентов передачи:

(3.113)

Коэффициент связи выражает отношение общего магнитного потока, пронизывающего обе катушки индуктивности, к полному магнитному потоку. Величина () характеризует поток рассеяния.

Выясним характер и форму амплитудно-частотной характеристики системы из двух индуктивно связанных контуров, представленных на рис.2.20. Для упрощения предположим, что контуры состоят из одинаковых элементов и поэтому имеют одинаковую резонансную частоту . АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис. 2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте . Две другие соответствуют максимуму коэффициента передачи и будут на частотах

, (3.114)

. (3.115) .

Частоты зависят от коэффициента связи и величины затухания контуров и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи. — быстрая частота связи, а — медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.

Рис. 3.21. Зависимость частот связи от коэффициента связи

При критической связи и на резонансной кривой будет один максимум на частоте .

При связи меньше критической формулы для частот связи и не имеют смысла и на АЧХ будет только один максимум на частоте .

При связи больше критической () на АЧХ появляются два максимума на частотах и .

Рис. 3.22. АЧХ одиночного и двух связанных контуров ().

Полоса пропускания связанных контуров определяется, как ширина АЧХ на уровне 0,7 от максимальной ординаты при этом минимум АЧХ также должен быть на уровне 0,7. Можно показать, что при одинаковом затухании и Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности = 0,6 , а для трёх – 0,65.

В серийно выпускаемой радиоаппаратуре в качестве элементов, обеспечивающих высокую избирательность используют пъезофильтры, созданные на основе пьезоэлектриков. Пьезоэлектрики – кристаллические вещества, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация (прямой пьезоэффект). Следствием прямого пьезоэффекта является обратный пьезоэффект – появление механической деформации под действием электрического поля. Пьезофильтр состоит из отдельных, объединенных в группы пьезоэлементов (стержней, пластинок) с нанесенными на определенные поверхности электродами, к которым подводится электрическое напряжение, для создания деформации в результате обратного пьезоэффекта. Пьезофильтр обеспечивает хорошую прямоугольность АЧХ. Добротность керамических пьезофильтров составляет несколько тысяч, а затухание вне полосы составляет -60дБ.

Резонансные усилители с умножителем добротности. — Студопедия.Нет

 

Как известно, полоса частот пропускания резонансного усилителя связана с добротностью простым соотношением:

 

	f		1	,
	f		2Q
где f – резонансная частота усилителя,				f – полоса пропускания, Q –

 

добротность колебательного контура. В случае необходимости получения очень узкой полосы пропускания требуется применять частотно-избирательную систему с высоким значением добротности. Обычно применяемые колебательные контура чаще всего имеют добротность не превышающую 100 единиц. Катушки колебательных контуров с большей добротностью становятся громоздкими, так как их приходится мотать более толстым или многожильным проводом типа литцендрат. Получить добротность обычного колебательного контура порядка 1000 единиц вообще нереально. В этом случае вместо колебательных контуров применяют электромеханические частотно-избирательные системы: кварцевые фильтры, пьезоэлектрические фильтры, электромеханические фильтры. Однако такие фильтры промышленность изготавливает на фиксированные частоты с вполне определенным значением полосы пропускания. Такие фильтры не всегда можно применить. В ряде случаев поставленную задачу можно решить применением усилителя с умножением добротности. Такие усилители известны давно. Например, умножение добротности применяется в узкополосных усилителях с мостом Вина или двойным Т-образным мостом. На заре развития радиотехники умножение добротности широко применялось в радиоприемной аппаратуре. Однако в настоящее время эффект умножения добротности мало известен.

 

69

В усилителях с умножением добротности одновременно применяют два вида обратной связи: частотно-независимую отрицательную и частотно-зависимую положительную. При этом суммарная обратная связь должна оставаться отрицательной, что обеспечивает стабильность работы усилителя. На рисунке 9,7 показана схема такого усилителя. На схеме резисторы R1 и R2 образуют цепь частотно-независимой отрицательной обратной связи, а резистор Ro — цепь положительной обратной связи. Частотная характеристика усилителя определяется свойствами используемого LC колебательного контура. Второй операционный усилитель является буферным каскадом и необходим для согласования нагрузки с выходом усилителя.

 

Рисунок 9.7

 

Анализ этой схемы показал, что результирующая добротность определяется выражением

 

Q		Qo
		Qo
1
		RoC

 

где Qo – добротность используемого колебательного контура, ω – резонансная частота колебательного контура. Таким образом, данная схема

 

позволяет получить добротность большую в			1		раз большую по
	1		Qo
			RoC

 

70

сравнению с добротностью LC колебательного контура. В зависимости от величины сопротивления резистора Ro добротность может изменяться от значения Qo до бесконечности, когда усилитель самовозбуждается, причем всегда отрицательная обратная связь больше положительной и только при возбуждении они сравниваются. Экспериментально на частоте 600 кГц легко получить значение добротности порядка 1000. На резонансной частоте выходной сигнал превышает входной в такое же число раз, во

 

сколько раз увеличивается добротность. Следует иметь ввиду, что добротность Qo с ростом температуры уменьшается. Она уменьшается прежде всего за счет увеличения с ростом температуры омического сопротивления катушки индуктивности. Результирующая добротность в связи с этим также будет изменяться. Причем она будет изменяться быстрее изменения добротности используемого колебательного контура во столько раз, во сколько увеличится добротность, и может стать весьма заметной. Для борьбы с этим явлением последовательно с резистором Ro можно включить полупроводниковое термосопротивление RT . Его сопротивление с ростом температуры растет и компенсирует уменьшение сопротивления Ro. Для хорошей компенсации сопротивление RT должна быть, примерно, в десять раз меньше сопротивления

 

Ro.

 

Схема транзисторного усилителя с умножением добротности изображена на рисунке 9,8. Усилитель построен по обычной каскодной схеме типа общий эмиттер — общая база. Выбор схемы обусловлен большим внутренним сопро-тивлением каскодного усилителя, в результате чего колебательный контур слабо шунтируется и сохраняет высокую добротность. Вторая причина выбора

 

— большое усиление, даваемое схемой, что позволяет меньше шунтировать колебательный контур цепью обратной связи.

 

71

 

 

Рисунок 9.8

 

Резкое уменьшение полосы пропускания, которое можно приписать возрастанию добротности колебательного контура, обусловлено подачей в цепь эмиттера нижнего транзистора сигналов положительной и отрицательной обратной связи.

 

Отрицательная обратная связь по току широкополосна и возникает при прохождении тока эмиттера через сопротивление в цепи эмиттера, а так как ток коллектора второго транзистора и ток эмиттера первого в данной схеме отличаются очень мало, то напряжение отрицательной обратной связи оказывается пропорциональным току через колебательный контур.

 

Напряжение положительной обратной связи, которая возникает в результате передачи части выходного напряжения в цепь эмиттера первого транзистора, пропорционально выходному напряжению и зависит от частоты. Совместное действие этих двух цепей обратной связи эквивалентно действию частотно-зависимой мостовой схемы. Диагональ моста подключена к эмиттеру нижнего транзистора. Стабильность усиления, не худшая, чем у исходного усилителя с выключенными цепями обратной связи, будет наблюдаться во всех случаях, когда совместное действие двух упомянутых цепей не приведет ни на каких частотах к появлению результирующей положительной обратной связи.

 

 

Рассмотрим случай оптимальной обратной связи, когда на резонансной частоте колебательного контура положительная к отрицательная обратная

 

72

связь взаимно компенсируются («мост» сбалансирован). Практически оптимальную обратную связь можно установить следующим образом. Сначала сопротивление в цепи эмиттера нижнего транзистора шунтируют конденсатором большой емкости. Обе цени обратной связи оказываются выключенными. На вход усилителя подают переменное напряжение и замечают величину выходного напряжения на резонансной частоте. Затем шунтирующий конденсатор отключают и переменным резистором R₆, регулирующим величину положительной обратной связи, устанавливают то же значение выходного напряжения. При этом необходимо производить некоторую подстройку частоты до получения максимального усиления, так как ширина полосы пропускания резко уменьшается н малейшая расстройка по частоте становится очень заметна.

 

Итак, при оптимальной обратной связи на частоте резонанса положительная и отрицательная обратная связь взаимно компенсируются и усилитель имеет тот же коэффициент усиления напряжения, что и без обратной связи. При отходе от резонансной частоты глубина положительной обратной связи быстро падает, а глубина отрицательной полностью сохраняется. Результирующая обратная связь оказывается отрицательной, и усиление падает в большей степени, чем без обратных связей. В результате достигается уменьшение поло-сы пропускания, которое можно приписать возрастанию добротности колебательного контура. В первом приближении, при оптимальной обратной связи добротность можно подсчитать по формуле Q=Q₀n_k/n_0.Здесь Qo — добротность колебательного контура с учетом шунтирующего действия нагрузки и выходного сопротивления усилителя; n_к — коэффициент включения контура к усилителю; n₀ — коэффициент включения к контуру цепи обратной связи. Первый коэффициент равен отношению напряжения на коллекторе верхнего транзистора к напряжению на всем контуре, второй — отношению напряжения на входе цепи положительной обратной связи к напряжению на

 

 

73

всем контуре. Из приведенного выражения видно, что добротность колебательного контура умножается на некоторое число.

С точки зрения получения более высокой добротности было бы желательно колебательный контур подключать к усилителю целиком, что соответствует значению n_к=1. Однако в этом случае увеличивается нестабильность резонансной частоты из-за непостоянства емкости коллекторного перехода второго транзистора. Применение частичного включения колебательного контура заметно улучшает стабильность. Так, например, при n_н = 0,5 нестабильность резонансной частоты снижается в 4 раза.

 

Рассматриваемая формула дает значение добротности при оптимальной обратной связи. Изменяя сопротивление цепи положительной обратной связи, можно получить как большие, так и меньшие значения добротности. Но такой путь получения больших значений добротности нежелателен, так как приводит к резкому уменьшению стабильности усиления.

 

В процессе наладки усилителя могут встретиться трудности, связанные с измерением очень больших значений добротности. Измерять добротность по полосе пропускания становится затруднительно вследствие недостаточной точности отсчета частоты по шкале генератора. Лучше определять добротность по времени затухания собственных колебаний, возбуждаемых прямоугольным низкочастотным напряжением, подаваемым на вход усилителя. Как известно, интервал времени τ, в течение которого амплитуда собственных колебаний упадет в 2,72 раза, связан с добротностью Q и резонансной частотой соотношением Q=πf₀τ. Интервал τ можно определить непосредственно по измерительной сетке электронно-лучевой трубки осциллографа. Непосредственные измерения показали, что рассмотренная схема на частоте 465 кГц дает возможность получать добротность достигающую 10000.

 

 

На низких частотах катушки индуктивности получаются слишком громоздкими. Использовать пьезоэлектрические и электромеханические

 

74

фильтры затруднительно по тем же причинам. Поэтому на низких частотах получили большое распространение узкополосные усилители, у которых частотная характеристика формируется за счет применения усилителей с частотно зависимыми обратными связями, полученными с помощью различных RC цепей. В качестве классического примера можно рассмотреть усилитель с мостом Вина. Схема моста Вина показана на рисунке 9.8.

 

 

Рисунок 9.8 Мост Вина обладает частотно-избирательными свойствами. На частоте

 

fo=1/2πRC, называемой квазирезонансной частотой, мост балансируется и выходное напряжение становится равным нулю. Поэтому мост Вина часто используется для подавления сигнала определенной частоты. Частотная характеристика моста Вина показана на рисунке 9.9.

 

75

Рисунок 9.9

 

Если поместить мост Вина в цепь отрицательной обратной связи усилителя, то на квазирезонансной частоте отрицательная обратная связь отсутствует и усилитель имеет высокий коэффициент усиления. При отличии частоты сигнала от квазирезонансной частоты мост Вина несбалансирован, на его выходе появляется сигнал отрицательной обратной связи и усиление усилителя уменьшается. Таким образом, усилитель с мостом Вина может работать в качестве узкополосного усилителя. На рисунке 9.10 показана схема такого усилителя.

 

Анализ схемы показывает, что частотная характеристика такой схемы получается точно такой же , как и при применении одиночного колебательного контура с резонансной частотой fo=1/2πRC и добротностью порядка Ко/3, где Ко коэффициент усиления операционного усилителя без цепи обратной связи. Однако добротность у такого усилителя получается слишком большой.

 

Рисунок 9.10 Кроме того, схема усилителя с мостом Вина очень чувствительна к

 

малейшему разбалансу моста, вызванного, например, изменением температуры. Поэтому рассмотренную схему можно рекомендовать лишь для усилителя с

 

76

низкой добротностью. Это можно легко получить в рассмотренной схеме путем разбаланса моста с помощью подстроечного резистора таким образом, чтобы на квазирезонансной частоте на выходе моста

Вина имелось небольшое напряжение, обеспечивающее отрицательную обратную связь. При этом уменьшается добротность и коэффициент усиления усилителя. Более или менее стабильную работу усилителя можно получить лишь при добротности не превышающей 10 единиц.

 

Для большей добротности можно рекомендовать схему с низкочастотным гиратором. На рисунке 9.11 показана схема низкочастотного гиратора. Основная функция гиратора, в данном случае, создавать искусственную индуктивность. Анализ схемы показывает, что если бы характеристики операционных усилителей были бы идеальными, то входное сопротивление схемы было бы чисто индуктивным с индуктивностью L=R²C. Если к этой индуктивности присоединить еще один конденсатор С, то получился бы колебательный контур с резонансной частотой f_o=1/2πRC и бесконечной добротностью, поскольку идеальный гиратор создает индуктивность без потерь.

 

Рисунок 9.11

 

На самом деле с повышением частоты в операционных усилителях появляются фазовые сдвиги и добротность уменьшается. Однако при использовании достаточно высокочастотных операционных усилителей

 

77

возможно получение добротности в диапазоне звуковых частот не менее 1000. Получить большую добротность затруднительно еще и по той причине, что трудно найти конденсаторы с низкими потерями.

 

Рассмотрим две схемы резонансных усилителей с гираторами. На рисунке 9.12 показана схема усилителя с параллельным колебательным контуром.

 

 

Рисунок 9.12

 

Добротность продуцируемого колебательного контура в этой схеме равна Q=R₁/R. На резонансной частоте выходные сигналы U₂ и U₃ равны по величине и в корень из двух раз больше входного сигнала. Они сдвинуты по фазе один относительно другого на 90 градусов и на 45 градусов относительно входного сигнала. Если производить перестройку резонансной частоты сдвоенным переменным сопротивлением R, то при этом на резонансной частоте не будут изменяться величина сигнала и ширина полосы пропускания. Такие свойства данной схемы идеальны для измерительных усилителей.

 

На рисунке 9.13 показана схема резонансного усилителя с использованием последовательного колебательного контура.

 

 

78

 

Рисунок 9.13

 

Добротность контура, как и предыдущей схеме, равна Q = R₁/R. Но на резонансной частоте выходной сигнал получается в Q раз больше, чем в предыдущей схеме: U2 U3 Q 2U1.

Таким образом, данная схема имеет большой коэффициент усиления и в этом ее достоинство. Но при перестройке резонансной частоты сдвоенным переменным сопротивлением R величина выходного сигнала будет изменяться, хотя полоса пропускания останется неизменной.

 

Схема резонансного усилителя с гиратором допускает возможность перестройки резонансной частоты одним переменным сопротивлением или конденсатором. Если использовать резисторы с разными сопротивлениями и конденсаторы различной емкости, определяющие резонансную частоту, то для резонансной частоты получим формулу:

 

fo	1	.
	2 R1R2C1C2

 

Любой элемент в подкоренном выражении можно сделать переменным и в соответствии с этой формулой будет меняться частота.

 

79

Если необходимо получить на резонансной частоте отсутствие фазового сдвига для выходного сигнала относительно входного, то можно использовать другую схему гиратора, показанную на рисунке 9. 14.

 

 

Рисунок 9.14

 

 

Характеристики этой схемы с повышением частоты становятся несколько хуже, по сравнению с предыдущей, но на самых низких частотах разницы нет.

 

 

Синхронные фильтры

 

 

Синхронное выделение сигнала получило довольно широкое распространение. Это наиболее простой способ получения предельно узкой полосы пропускания на низких частотах, если только есть источник так называемого опорного сигнала. В самом простом случае опорный сигнал формируется из сигнала генератора, который служит источником сигнала подлежащего выделению. В этом случае можно говорить, что опорный сигнал когерентен выделяемому. В когерентном случае нестабильность частоты сходного генератора не имеет никакого значения даже при предельно узкой полосе пропускания. Например, частота может меняться на 100 Гц при полосе

 

80

пропускания I Гц и это никак не отразится на величине выходного сигнала. Такой результат получается вследствие того, что синхронная система выделения как бы всегда настроена на частоту опорного сигнала. Сигналы когерентные проходят через синхронную систему без ослабления, а сигналы некогерентные

 

Рисунок 14.15

 

 

ослабляются в зависимости от расстройки по частоте и полосы пропускания. Наиболее просто устроен синхронный фильтр. На рисунке 14.15 показана схема иллюстрирующая принцип действия простейшего синхронного фильтра. Фильтр состоит из резистора и двух конденсаторов, мгновенно переключаемых в моменты прохождения входного сигнала через нуль, так что один из этих конденсаторов будет заряжаться от положительных полуволн входного напряжения, а второй от отрицательных.

 

Как правило, постоянная времени RC цепочки берётся очень большой, так что за время одного полупериода напряжение на конденсаторах существенно измениться не может и форма выходного напряжения становиться прямоугольной. Конденсатор C_о, показанный на схеме, является суммой всех действующих в схеме паразитных емкостей и ухудшает работу синхронного фильтра на высоких частотах. Среднее значение входного напряжения за

 

81

полупериод равно ² Uo . Среднее значение выходного напряжения равно Vo.

При переброске ключа конденсатор Co					перезаряжается за счёт заряда,
протекающего черeз резистор R. Поэтому можно написать равенство
2			Uo Vo T
					2VoCo	(1)
			R	2

 

Откуда			2		Uo		(2)
	Vo
		1 4fRCo
Где f частота сигнала.
По мере роста частоты сигнала выходное напряжение падает. Синхронный
фильтр работает частотно независимо, пока							4fRCo <<1. На частоте
	fв				2 1		(3)
				4RCo
величина выходного сигнала падает в					2 раз, по сравнению со значением на

низких частотах. Эта частота определяет верхнюю частотную границу применения данного синхронного фильтра.

 

Полоса пропускания синхронного фильтра, как известно, определяется значением его добротности, а добротность равна

 

Q fRC

(4)

 

 

Поэтому ширина полосы пропускания равна

 

f	1	(5)
	RC

 

Выбирая соответствующее значение произведения RC можно легко получить любое необходимоe, значение полосы пропускания. Например при R

 

82

=1MOм и 0=0,33 мкФ получаем f=1 Гц. На частоте 100кГц этой полосе пропускание, будет соответствовать добротность равная 100000. Впрочем, идя по такому пути нельзя получить как угодно большое значение добротности, так как всё более сильно будет сказываться действие паразитной ёмкости C_o. Подставив в выражение (4) значение частоты из (3) находим максимально возможное значение добротности

 

				C		(6)
Q max	4		2 1 Co
Если взять разумные значения С=10мкФ и Со=10пФ, то						Qmax =300000.

Важной особенностью синхронного фильтра является зависимость амплитуды выходного сигнала от сдвига фаз между выделяемым и опорным сигналом. Эта зависимость учитывается добавлением соответствующего множителя . Вместо формулы (2) имеем

 

	2			Uo		(7)
Vo					cos
		1 4fRCo

 

Для устранения фазовой зависимости в цепи опорного сигнала ставят фазовращатель.

 

В реальной схеме синхронного фильтра переключение конденсаторов осуществляется обычно электронными ключами на биполярных или полевых транзисторах с изолированными или неизолированным затвором. Лучший результат получается при использование ключей в интегральном исполнении.

 

Для нормальной работы синхронного фильтра чрезвычайно важно обеспечить переключение так, чтобы не было даже кратковременного одновременного состояния проводимости обеих колючей, когда конденсаторы на это время оказываются соединенные параллельно и сбрасывают заметную долю своего заряда. Этот эффект, наряду с действием паразитной емкости, ведет к ухудшению работы синхронного фильтра на повышенных частотах.

 

83

Обычно не удается обеспечить работу синхронного фильтра на частотах не превышающих 100 КГц.

 

На рисунке 14.16 показана схема синхронного фильтра с использованием интегрального ключа и формирователя опорного сигнала на операционных усилителях. Поскольку коммутирующие сигналы имеют амплитуду до нескольких вольт и между затвором и каналом ключевого транзистора имеется ёмкость и некоторый ток утечки, работа синхронного фильтра сопровождается появлением так называемых коммутационных помех, ограничивающих возможность пропускания слабых сигналов . В чистом виде коммутационные помехи обнаруживается на выходе при отсутствии входного сигнала, получаемом замыканием входа. В момент переброса напряжения на затворах ключей ёмкость между затворами и каналом совместно с сопротивлением канала дифференцирует коммутационный сигнал и на выходе появляются кратковременные импульсы. Амплитуда их имеет величину порядка 10 мВ, длительность менее I мкс. Несмотря на довольно значительную амплитуду помехи, из за незначительной длительности ее, среднее значение помехи получается небольшим, так как данная схема чаще всего используется для выделения сигналов на низких частотах. Одновременно с дифференцированием на нелинейности сопротивления канала происходит детектирование сигнала, что приводит к появлению сигнал помехи, имеющего прямоугольную форму. Эту помеху можно скомпенсировать, введя компенсирующий

 

84

 

Рисунок 14.16

 

 

сигнал из цепи управления работы ключами подстроечным резистором R6. Опорные сигналы формируются компараторами на операционных усилителях из гармонического сигнала величиной в 2,5 В. Для устранения сквозного тока пороги срабатывания компараторов несколько смещены делителями напряжения на резисторах R2-R6. В результате напряжения отпирающие ключи не совпадают во времени. Оптимальный результат получается при вполне определенном соотношении между величиной напряжения подаваемого на вход компараторов и величиной напряжения смещения.

 

Схема пропускает сигналы до 5В по амплитуде. При указанных величинах R и С усредняющей цепочки уже на частоте 12 кГц наблюдается падение коэффициента передачи напряжения на 30 %, обусловленное паразитной ёмкостью.

 

Рассматриваемая схема синхронного фильтра пропускает сигналы не только совпадающие по частоте и фазе с опорным сигналом, но и сигналы частота которых в нечётное число раз больше частоты опорного сигнала,

 

85

причём частота выходного сигнала по-прежнему совпадает с частотой опорного сигнала а амплитуда уменьшается пропорционально номеру гармоники. Эта особенность может ухудшить качество выделения полезного сигнала, например в полосах пропускания нечётных гармоник будут проходить добавочные шумовые сигналы. Для создания однополосной частотно избирательной системы перед синхронным фильтром можно поставить обычный пассивный или активный фильтр нижних частот или узкополосный фильтр, пропускающий сигнал на частоте опорного сигнала и подавляющий на частотах более высоких. Добротность такого фильтра может быть невысокой, так как важно хорошо подавить сигналы в три и более раз более высокие, чем частота опорного сигнала.

 

Как определить собственную частоту колебательного контура

Содержание

• Последовательный колебательный контур
• Резюме
• Подпишись на RSS!
• Формула индуктивности
• Последовательный колебательный контур
• Формула Томсона (резонанса) для последовательного колебательного контура
• Резонансная частота
• Применение колебательных контуров
• Добротность последовательного колебательного контура
• Амплитуда резонанса
• Эффект резонанса
• Эффект резонанса
• Резонансный усилитель мощности тока промышленной частоты
• Резонансная частота. Расстройка

Последовательный колебательный контур

Если соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Этот эффект называется резонансом колебательного контура, сама схема из конденсатора и индуктивности — последовательным колебательным контуром, а частота, на которой проявляется этот эффект — частотой резонанса.

Хотя и катушка индуктивности, и конденсатор имеют некоторое реактивное сопротивление, вместе они реактивного сопротивления не проявляют. Причина проста. Конденсатор и катушка накапливают и отдают энергию, но делают это по-разному. В тот момент, когда катушка накапливает энергию, конденсатор ее отдает, и наоборот. Конечно, этот эффект проявляется только для синусоидального сигнала, на определенной частоте, в установившемся режиме. Если частота сильно отличается от резонансной, то схема теряет свои чудесные качества и проявляет себя, как катушка и конденсатор. Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы.

Если пропускать через последовательный колебательный контур синусоидальный электрический ток резонансной частоты, то падение напряжения на контуре будет равно нулю. Но падение напряжения на конденсаторе отдельно, индуктивности отдельно будет иметь место. Просто эти напряжения компенсируют друг друга в каждый момент времени. Напряжения на конденсаторе и катушке могут быть очень значительными. Одной из популярных ошибок при проектировании последовательного колебательного контура является неправильная оценка напряжения на конденсаторе. Напряжение может в разы, десятки, сотни раз превышать напряжение источника питания. На основе этого эффекта даже разработаны схемы повышающих преобразователей напряжения.

[Амплитудное значение напряжения на конденсаторе, В] = [Амплитудное значение силы тока через контур, А] * [ZC], где [ZC] = 1 / (2 * ПИ * [Частота сигнала, Гц] * [Емкость конденсатора, Ф])

Необходимо также обратить внимание, чтобы ток через последовательный контур не приводил к насыщению сердечника катушки индуктивности. В схемотехнике последовательный колебательный контур применяется, если необходимо пропустить сигнал определенной частоты и отфильтровать все другие

Колебательные контуры бывают небольшие, рассчитанные на работу с небольшими токами и напряжениями, например, во входных и внутренних цепях радиоприемника. Но бывают и силовые, рассчитанные на большие токи и напряжения, например, в радиопередатчиках, силовых резонансных фильтрах и т. д

В схемотехнике последовательный колебательный контур применяется, если необходимо пропустить сигнал определенной частоты и отфильтровать все другие. Колебательные контуры бывают небольшие, рассчитанные на работу с небольшими токами и напряжениями, например, во входных и внутренних цепях радиоприемника. Но бывают и силовые, рассчитанные на большие токи и напряжения, например, в радиопередатчиках, силовых резонансных фильтрах и т. д.

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса – индуктивную составляющую тока.

Подпишись на RSS!

Подпишись на RSS и получай обновления блога!

Получать обновления по электронной почте:

• • Измеритель тока напряжения и мощности на INA226
    11 сентября 2020
  • Программа взаимодействия INA226 с микроконтроллером PIC
    29 июля 2020
  • Миллиомметр цифровой на базе модулей ADS1115 и TM1637
    22 июля 2020
  • Транзисторный ключ с ограничением тока
    3 июня 2020
  • Зарядное для аккумуляторов шуруповерта на базе XL4015
    5 апреля 2020

• • Зарядное устройство для автомобильных аккумуляторов — 237 498 просмотров
  • Стабилизатор тока на LM317 — 173 704 просмотров
  • Стабилизатор напряжения на КР142ЕН12А — 125 019 просмотров
  • Реверсирование электродвигателей — 101 848 просмотров
  • Зарядное для аккумуляторов шуруповерта — 98 528 просмотров
  • Карта сайта — 96 170 просмотров
  • Зарядное для шуруповерта — 88 495 просмотров
  • Самодельный сварочный аппарат — 87 896 просмотров
  • Схема транзистора КТ827 — 82 543 просмотров
  • Регулируемый стабилизатор тока — 81 588 просмотров

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.

Вам это будет интересно Формулы электрического тока

Приборы индуктивности различных типов

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках

Последовательный колебательный контур

Если соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Этот эффект называется резонансом колебательного контура

, сама схема из конденсатора и индуктивности –последовательным колебательным контуром , а частота, на которой проявляется этот эффект –частотой резонанса .

Хотя и катушка индуктивности, и конденсатор имеют некоторое реактивное сопротивление, вместе они реактивного сопротивления не проявляют. Причина проста. Конденсатор и катушка накапливают и отдают энергию, но делают это по-разному. В тот момент, когда катушка накапливает энергию, конденсатор ее отдает, и наоборот. Конечно, этот эффект проявляется только для синусоидального сигнала, на определенной частоте, в установившемся режиме. Если частота сильно отличается от резонансной, то схема теряет свои чудесные качества и проявляет себя, как катушка и конденсатор. Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы.

Если пропускать через последовательный колебательный контур синусоидальный электрический ток резонансной частоты, то падение напряжения на контуре будет равно нулю. Но падение напряжения на конденсаторе отдельно, индуктивности отдельно будет иметь место. Просто эти напряжения компенсируют друг друга в каждый момент времени. Напряжения на конденсаторе и катушке могут быть очень значительными. Одной из популярных ошибок при проектировании последовательного колебательного контура является неправильная оценка напряжения на конденсаторе. Напряжение может в разы, десятки, сотни раз превышать напряжение источника питания. На основе этого эффекта даже разработаны схемы повышающих преобразователей напряжения.

[Амплитудное значение напряжения на конденсаторе, В

] = [Амплитудное значение силы тока через контур, А ] * [ZC ], где [ZC ] = 1 / (2 * ПИ * [Частота сигнала, Гц ] * [Емкость конденсатора, Ф ])

Формула Томсона (резонанса) для последовательного колебательного контура

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонансная частота

При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:

• с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
• с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.

Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.

Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным. Резонансная частота формула, которой имеет вид:

Резонансная частота формула, которой имеет вид:

где:

• L – индуктивность, Гн;
• C – ёмкость, Ф.

Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.

Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.

Применение колебательных контуров

Хорошим примером применения силовых последовательного и параллельного колебательных контуров является силовой резонансный фильтр для получения синусоидального напряжения

Еще интересные схемы:

(А), (Б), (В) — фильтры сигнала заданной частоты, (Г) — фильтр-пробка, (Д) — входная цепь радиоприемника, (Е) — стабилизатор переменного напряжения. Катушка L2 специально сделана насыщающейся при некотором нужном переменном напряжении на ней, что обеспечивает поддержание этого выходного напряжения по форме близкого к синусоиде.

(читать дальше…) :: (в начало статьи)

:: ПоискТехника безопасности :: Помощь

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.

Позвольте не согласиться с вашим выражением (Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы). Что означает ‘постепенно’? Читать ответ…

Насколько я помню в контуре (и последовательном, и в параллельном) на резонансной частоте сопротивление носит активный характер, вы же при рассмотрении параллельного контура допустили выражение реактивное сопротивление контура на резонансной частоте. На частотах ниже резонансной (в параллельном контуре) сопротивление носит индуктивный характер, на частотах выше резонансной соп Читать ответ…

Еще статьи

Расчет дросселя, катушки индуктивности. Рассчитать, посчитать онлайн, …
Форма для онлайн расчета дросселя, катушки индуктивности. Для изготовления индук…

Практика проектирования электронных схем. Самоучитель электроники….
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы….

Резонансный инвертор, преобразователь напряжения повышающий. Схема, ко…
Инвертор 12/24 в 300. Резонансная схема….

Генератор синусоидального напряжения, сигнала, синуса, синусоиды. Гир…
Расчет гиратора и генератора синусоидального сигнала на нем….

Силовой резонансный фильтр для получения синусоиды от инвертора…
Для получения синусоиды от инвертора нами был применен самодельный силовой резон…

Металлоискатель самодельный. Сделать, собрать самому, своими руками. С…
Схема металлоискателя с высокой разрешающей способностью. Описание сборки и нала…

Блокинг генератор. Схема, устройство….
Схема и устройство блокинг генератора…

Индуктивность. Генри. Henry. Гн. Единицы измерения. Доли, миллигенри, …
Понятие индуктивности. Единицы измерения. Катушки индуктивности….

Добротность последовательного колебательного контура

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R – сопротивление потерь в контуре, Ом

L – индуктивность, Генри

С – емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура – это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Амплитуда резонанса

В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.

Амплитуда тока

Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.

В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:

Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.

Амплитуда напряжения

Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.

Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е – I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е

Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.

Эффект резонанса

Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В

Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка

Она состоит из следующих компонентов:

• электродвигатель;
• механизм, превращающий вращение в возвратно-поступательное движение;
• ЛАТР – лабораторный автотрансформатор;
• медная пружина из проволоки с набором грузиков;
• направляющая для пружины.

Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.

Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (~30 см).

Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден

Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.

Пружинный маятник

Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.

Эффект резонанса

Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В

Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка

Она состоит из следующих компонентов:

• электродвигатель;
• механизм, превращающий вращение в возвратно-поступательное движение;
• ЛАТР – лабораторный автотрансформатор;
• медная пружина из проволоки с набором грузиков;
• направляющая для пружины.

Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.

Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (

Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден

Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.

Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.

Резонансный усилитель мощности тока промышленной частоты

Резонансный усилитель мощности тока промышленной частоты – это статический электромагнитный аппарат, предназначенный для усиления мощности тока промышленной частоты 50 Гц.

Резонанс (франц. resonance, от лат. resono – звучу в ответ, откликаюсь), относительно большой (селективный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте ее собств. колебаний. При Р. происходит резкое возрастание амплитуды вынужденных колебаний осциллятора.

• Физический энциклопедический словарь/ Гл. ред. А.М. Прохоров. Ред. кол. Д.М. Алексеев, А.М. Бонч- Бруевич, А.С. Боровик-Романов и др. – М.: Сов. энциклопедия, 1983. – 928 с., ил., 2 л. цв. ил.

Резонанс играет очень большую роль в самых разнообразных явлениях, причем в одних полезную, в других вредную.

В 1906 г. в Петербурге обрушился Египетский мост через реку Фонтанку.

Причина – резонансные явления, вызванные переходом через мост кавалерийского эскадрона. Шаг лошадей, обученных церемониальному маршу, попал в резонанс с периодом моста. Таких примеров из истории техники можно привести много. Резонанс в этих случаях вредное явление и для устранения его принимаются специальные меры (расстройка периодов, увеличение затухания – демпфирование и др.).

В радиотехнике резонанс используется, в основном, как полезное явление.

Явление электрического резонанса позволяет настраивать передатчики и приемники на заданные частоты и обеспечить их работу без взаимных помех. Вообще применения резонансных явлений в электро-радиотехнике неисчислимы. Однако законы сохранения накладывают запреты на применение резонанса для получения Свободной энергии, а у сторонников получения ее сложились устойчивые стереотипы относительно параметрического резонансного усиления. Поэтому не все еще применения явления резонанса реализованы на практике.

В настоящее время очень много копий сломано при рассмотрении темы «Резонанс Мельниченко». Есть даже категория людей, которые объявляют его шарлатаном.

Мельниченко скрывает секрет своих изобретений, несмотря на полученные патенты. Но секрет Мельниченко – это «Секрет Полишинеля».

Попробуем доказать это. Возьмем всем известную книгу «Элементарный учебник физики под ред. акад. Г.С. Лансберга Том III Колебания, волны. Оптика. Строение атома. – М.: 1975г., 640 с. с илл.» откроем ее на страницах 81 и 82 где приведено описание экспериментальной установки для получения резонанса на частоту городского тока

В приведенном примере ясно показывается, как можно на индуктивности и емкости получить напряжения в десятки раз большие, чем напряжение источника питания. Если не принимать специальных мер, то мощность, развиваемая резонансом, разрушит элементы установки.

Резонансная частота. Расстройка

Знаете ли Вы,

что такое мысленный эксперимент, gedanken experiment? Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки. Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей. Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.

Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).

Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.

Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.

Понятие «мысленный эксперимент» придумано специально спекулянтами — релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим «честным словом». Подробнее читайте в FAQ по эфирной физике.

Tags: амплитуда, бра, вид, вред, генератор, двигатель, дом, е, емкость, зажим, знак, как, категория, колебательный, конденсатор, контур, кт, лс, магнит, магнитный, мощность, напряжение, осциллограф, правило, принцип, проверка, провод, проект, пуск, р, работа, расчет, резонанс, резонансный, ряд, сад, самодельный, сопротивление, стабилизатор, схема, тен, тип, ток, транзистор, трансформатор, ук, установка, фильтр, щит, электродвигатель, эффект

Коэффициент добротности в электротехнике и электронике

Добротность в Электротехника и электроника

В настроенной цепи отношение между реактивным сопротивлением и сопротивлением называется добротностью или добротностью … Или …

Противоположность коэффициента мощности называется добротностью -Фактор или добротность катушки или ее добротность.

Коэффициент добротности = 1/ Коэффициент мощности=1/Cosθ= Z/R    …    (где коэффициент мощности Cosθ = R/Z)

Если R слишком мало по отношению к реактивному сопротивлению

Тогда добротность = Z/R = ωL/R = 2πfL / R    …    (ωL/R = 2πf)

Кроме того, добротность может быть определена как отношение между сохраненными энергия и Энергия, рассеиваемая за цикл в цепи

Q = 2π x (Запасенная энергия/Потеря мощности)

В резонаторе Q представляет собой отношение между накопленной в резонаторе энергией и энергией, подаваемой генератором, для поддержания постоянной амплитуды сигнала

Q = 2π (Максимальная накопленная энергия/рассеиваемая энергия за цикл) в катушке.

Полезно знать * ¹ :

В электрических системах и цепях накопленная энергия представляет собой сумму накопленных энергий в катушках индуктивности и конденсаторах без потерь. И потерянная энергия представляет собой сумму энергий, рассеиваемых в резисторах (тепло, свет и т. д.) за цикл

Принимая во внимание;

 Конденсатор поглощает реактивную мощность и сохраняет энергию в виде электрического поля

Катушка индуктивности поглощает реактивную мощность и сохраняет энергию в форме магнитного поля

И

Резистор поглощает реальную мощность и рассеивает в виде тепла и света

Коэффициент добротности в чисто емкостных (C) и чисто индуктивных (L) цепях Индуктивные цепи равны нулю. Таким образом, коэффициент мощности цепи также равен нулю. Но коэффициент добротности цепи является обратным коэффициенту мощности, поэтому коэффициент добротности как в чисто емкостных, так и в индуктивных цепях бесконечен (∞).

Коэффициент добротности в последовательной цепи RL

Последовательная цепь RL, полное сопротивление (Z) = индуктивное реактивное сопротивление = X _L = 2πfL, поэтому добротность «Q»

= Z/ R → = X _L /R → = 2πf _r L/R

Коэффициент добротности в последовательной RC-цепи

В последовательной RC-цепи полное сопротивление (Z) = емкостное реактивное сопротивление = X _{C =} 1/2πfC, поэтому добротность «Q»

= Z / R → = X _C /R → = (1/2πf _r C) /R → = 1 / 2πf _r КР.

, где

z = наносимость = сопротивление в цепях переменного тока (z = x _L ² -x _C ² ω)

r = Сопротивление в ω

c = емкость на фардадах

L

L = Индуктивность в Хеннери

X _L = Индуктивное сопротивление в Ом

X _C = Реактивное сопротивление емкости в Ом

f _r = Резонансная частота в Гц

Q

Q = F _R / B

Q = F _R / (F ₂ — F ₁ )

, где

F _R = частота резонанса в Hertz

B = BandWIDTID = = BandWIDTID = = randIDTID = = randWIDTID = = BandWIDTID = = BandWIDTID = = randIDTID = = randWIDTID = = BandWIDTID = = BandWIDTID = = BandWIDTID = = BandWIDTID = = randIDTID = = BandWIDTID = = BandWIDTID = r )

. разность между верхней и нижней частотами в непрерывном наборе частот = B = (f ₂ – f ₁ )

Коэффициент добротности в последовательной цепи RLC (резонансная цепь входа напряжения)

В идеале последовательная цепь RLC (Также в настроенном радиочастотном приемнике (TRF)) Коэффициент добротности равен

Q = (1/R) x (√ (L/C) = ω ₀ L/R

Из приведенного выше уравнения ясно, что чем больше последовательное сопротивление, тем меньше добротность Контур, т. е. чем больше теряется энергии и тем шире полоса пропускания

Полезно знать* ² : Высокая добротность резонансного контура имеет узкую полосу пропускания по сравнению с низкой добротностью

Добротность в Параллельная цепь RLC (резонансная цепь тока на входе)

Добротность в параллельной цепи RLC является обратной величиной добротности в последовательной цепи RLC

Q = R x (√ (C /L) = R /ω ₀ L

Где

R = сопротивление в Ом

C = емкость в фарадах

L = индуктивность в Генри

3

2 Из приведенного выше уравнения следует, что чем ниже сопротивление, тем больше добротность цепи, т. е. меньше потерь энергии и более узкая полоса пропускания, и было бы полезно определить полосу пропускания в схемах проектирования фильтров. Цепь со сложным импедансом

Как мы обсуждали выше, «в настроенной цепи соотношение между реактивным сопротивлением и сопротивлением называется добротностью или добротностью… Или

Противоположность коэффициенту мощности называется добротностью или добротностью катушки.

Коэффициент добротности = 1/Коэффициент мощности=1/Cosθ= Z/R    …    (Где коэффициент мощности Cosθ = R/Z)”

Для; мы также можем определить «добротность» цепи со сложным импедансом, если мы знаем коэффициент мощности цепи, где

коэффициент мощности = Cosθ = R/Z   … или…

Тангенс фазового угла (θ) между током и напряжением.

Полезно знать * ³ :

Высокая добротность резонансного контура имеет узкую полосу пропускания по сравнению с низкой добротностью

Низкая добротность дает широкую полосу пропускания (широкая полоса пропускания)
A высокая добротность дает узкую полосу (маленькая полоса пропускания )

Показать полную статью

Связанные статьи

Q

Q

---

Такие слова, как «качество», подразумевают «хорошесть» и может ввести в заблуждение при использовании в технических контекстах. Коэффициент качества, Q, Резонансная система считается высокой, если система теряет мало энергии за времени по сравнению с энергией системы. Качели, которые качают сотни раз после одиночного толчка будет «высокая Q» по сравнению с замахом комплект, который останавливается после нескольких качаний из-за чрезмерного трения в подшипниках. Катушки индуктивности и конденсаторы с малыми потерями создают схемы с высокой добротностью. как и пружинно-массовые механические системы с низким коэффициентом трения, и такие компоненты в целом качественно. Но не всегда хорошо иметь высокий Q. Далее когда ваш автомобиль попадает в выбоину, поблагодарите свои амортизаторы за то, что они дали вашему автомобилю подвеска ужасно низкая добротность. Настроенные цепи в вашем радио должны иметь только нужное количество Q, не слишком много и не слишком мало. Слишком много Q и некоторые пропущен спектр модуляции; слишком мало и другие сигналы или чрезмерно шум получает через. Хотя высокая добротность не всегда желательна, обычно это действительно так. лучше всего иметь компоненты с высокой добротностью, такие как катушки индуктивности и конденсаторы или пружины, и подшипники, которые преднамеренно демпфируются резисторами, приборными панелями или другими устройствами с потерями, чтобы дизайнер сохраняет хороший контроль над значением Q.

Простым определением Q может быть отношение полной энергии в системе к энергии, теряемой за цикл. Теперь это разумное и легко запоминающееся определение, но это произвольное определение, которое мы можем «возиться с», и есть изменение, которое упрощает математику. Давайте дать определение отношения полной энергии в системе к потерянной энергии на радиан. Какая? Зачем использовать часть цикла? Ну, есть 2 пи радиана за цикл и при использовании радианов из множества полезных значений Q выпадает несколько 2 пи. уравнения. Это делает Q примерно в 6 раз выше, чем это было бы с наше первоначальное более простое определение. Есть два эквивалентных способа сказать это:

Q = (2 pi) (общая накопленная энергия) / (потеря энергии за цикл)

Q = (общая накопленная энергия) / (потеря энергии на радиан)

Если вы чувствуете, что скоро забудете о 2 пи лет, просто постарайтесь запомнить, что «циклы в секунду» или «Гц» обычно не используются в эти типы вычислений, потому что радианы более удобны с математической точки зрения. Всякий раз, когда в формулах, включающих импедансы, появляются «частота» или «циклы», старайтесь мыслить последовательно. «радианы».

Представьте себе «параллельную» настроенную схему, в которой катушка индуктивности, конденсатор и резистор соединены параллельно. Сначала рассмотрим числитель, полная накопленная энергия. Можно написать уравнение для мгновенная энергия в конденсаторе как функция синусоидального напряжения и в индукторе как функция синусоидального тока; квадрат каждого и добавить чтобы получить итог. Или можно сократить путь! В какой-то момент вся энергия будет в конденсаторе (когда напряжение находится на пике). Энергия в конденсатор «половина C V в квадрате»:

ш = (С х В ² ) / 2

, где V — пиковое напряжение.

В уравнении Q знаменатель представляет собой энергию, потерянную в резисторе в течение одного радиан, который представляет собой ватты (джоули в секунду), деленные на частоту в радианах. (Если вы теряете мощность X в секунду, вы теряете частоту X/радиан за одну секунду. время в радианах.) Мощность, теряемая в резисторе, равна квадрату среднеквадратичного напряжения. деленное на сопротивление («v-квадрат на R»). Ну и среднеквадратичное напряжение в 0,707 раз больше пикового напряжения для синусоиды, и когда вы возведете 0,707 в квадрат, вы получите 0,5, что дает «0,5 В в квадрате на R», где V — пиковое напряжение. К получаем мощность, потерянную на радиан, мы делим на w (радиан частота).

Уравнение Q принимает вид:

(CV ² ) / 2 (0,5) V ² / wR _p = wR _p C

Q = wR _p C

Посмотрите, как аккуратно стало!

Используя формулу резонанса, w = 1 / (LC) ^1/2 , легко показать, что:

Q = R _p (C/L) ^1/2 = R _p / X _c = Р _p / X _l
Q = R _p / wL  

, где X — реактивное сопротивление катушки индуктивности или конденсатора (они равны по величине при резонанс). Небольшой нижний индекс «p» напоминает нам, что это параллельное сопротивление.

Аналогичное упражнение можно выполнить для случая последовательно настроенной схемы. но не должно быть большим сюрпризом увидеть эти результаты:

Q = wL / R _с

Q = 1/R _s (L/C) ^1/2 = X _c / R _s = X _l / R _с
Q = X / R _с

_{Для конденсатора с последовательным сопротивлением:}

Q = 1/ wCR _с

В параллельном баке большой шунтирующий резистор дает высокую добротность, а в последовательный бак низкий последовательный резистор дает высокую добротность (обратите внимание на R в числителе в в одном и знаменателе в другом). В параллельном баке с низким реактивным сопротивлением «замыкает». вне» резистор, делающий добротность высокой, а в последовательном баке высокое реактивное сопротивление делает небольшой последовательный резистор несущественным (обратите внимание на C/L в одном и L/C в Другой).

Q = wR p C

Q = 1/ wCR с

Q = wL / R с

Q = R p / Вт

Математика оказывается простой, если учесть влияние на пропускная способность настроенного контура тоже:

Q = частота/полоса пропускания

, где частота — это резонансная частота бака, а ширина полосы разница частот между точками на 3 дБ.

---

Какова формула добротности?

RLC-цепи

Для параллельной RLC-цепи коэффициент добротности равен , что является обратным последовательному случаю . Рассмотрим схему, в которой R, L и C соединены параллельно. Чем меньше параллельное сопротивление, тем сильнее оно влияет на демпфирование цепи и, следовательно, тем ниже добротность. Это полезно при разработке фильтров для определения полосы пропускания.

Чем больше последовательное сопротивление, тем ниже Q цепи. Для параллельной RLC-цепи коэффициент добротности является обратным последовательному случаю: frac {R} {omega _ {0}L}} = omega _ {0}RC}. Рассмотрим схему, в которой R, L и C соединены параллельно.

Что такое добротность цепи?

Определение добротности

В системе переменного тока добротность представляет собой отношение энергии, накопленной в конденсаторе, к энергии, рассеиваемой в виде тепловых потерь на эквивалентном последовательном сопротивлении . Например, конденсатор, способный накапливать 2000 джоулей энергии при потере только 1 джоуля, имеет добротность 2000.

Что такое добротность RC-цепи?

Добротность или добротность конденсатора на рабочей частоте ω определяется как отношение реактивного сопротивления конденсатора к его сопротивлению .

Какова формула цепи RLC?

Для последовательной цепи RLC треугольник импеданса можно нарисовать, разделив каждую сторону треугольника напряжения на его ток I. Падение напряжения на резистивном элементе равно I*R, напряжение на двух реактивных элементах равно I*X = I*X _L – I*X _C , при этом напряжение источника равно I*Z.

Что такое добротность цепи?

Значение Q является параметром , который указывает качество катушки индуктивности . «Q» означает «фактор качества». Катушки легко пропускают постоянный ток, но действуют как резистор для переменного тока. Такое поведение называется индуктивным реактивным сопротивлением. Чем выше частота переменного тока, тем выше индуктивное сопротивление.

Родственный

Как рассчитывается добротность параллельного резонансного контура RLC?

Как рассчитывается добротность параллельного резонансного контура RLC? Следовательно, \(Q\) параллельной RLC-цепи рассчитывается как отношение сопротивления, деленное на реактивное сопротивление либо емкости, либо индуктивности .

Связанные

Что такое добротность последовательного резонансного контура?

Коэффициент качества связывает максимальную или пиковую энергию, накопленную в цепи (реактивное сопротивление), с энергией, рассеиваемой (сопротивление) во время каждого цикла колебаний, что означает, что это отношение резонансной частоты к ширине полосы частот и чем выше добротность цепи. , тем меньше полоса пропускания, Q = ƒ _r /BW.

Связанные

Что такое добротность класса 12?

Определение: В физике добротность, также называемая добротностью, представляет собой безразмерный параметр, описывающий резонансное поведение гармонического генератора с недостаточным демпфированием . Вы можете задаться вопросом, что такое осциллятор с недостаточным демпфированием. Итак, в осцилляторе трение или демпфирование замедляют движение системы.

Связанные

Что такое добротность и резонансная частота?

Добротность резонанса определяется как отношение центральной частоты резонанса к его ширине полосы половинной мощности . Он говорит нам, насколько острым или крутым является резонанс. Два графика на рис. 4.2 служат наглядной иллюстрацией. 29 марта 2018 г.

Что такое добротность мостов?

Коэффициент добротности катушки можно измерить путем точного измерения индуктивности и эффективного сопротивления катушки для определенного сигнала . Индуктивность катушки индуктивности обычно измеряется обычной индуктивной схемой, такой как мост Максвелла-Вейна, мост Хэя и т. д.

Родственный

Что такое добротность и резонансная частота в цепи LCR?

Добротность: В цепи LCR отношение резонансной частоты к разности соседних частот, так что их соответствующий ток составляет 1/2 пикового значения, называется добротностью цепи.

Родственный

Что такое последовательная цепь RLC?

Цепь RLC представляет собой электрическую цепь, состоящую из резистора (R), катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно. Название схемы происходит от букв, которые используются для обозначения составляющих компонентов этой схемы, где последовательность компонентов может отличаться от RLC.

Связанные

Что такое добротность цепи RLC?

• Сопротивление параллельной цепи RLC: Коэффициент мощности: Резонансная частота: Когда индуктивное сопротивление XL и емкостное сопротивление Xc цепи равны. Коэффициент качества: это отношение накопленной энергии к энергии, рассеиваемой в цепи. Полоса пропускания: резонансный ток цепи: общий ток в цепи, когда цепь находится в резонансе. Текущее увеличение. … Еще элементы…

Родственный

Как рассчитать добротность?

• Для расчета добротности Q катушки индуктивности можно использовать приведенную ниже формулу или уравнение: Q = X L R Поскольку сопротивление равно 2 π f L, его можно подставить в формулу чтобы дать: Q = 2 π f L R

Родственные

Что такое добротность?

• В физике и технике добротность или добротность — это безразмерный параметр , который описывает степень недостаточного демпфирования генератора или резонатора и характеризует полосу пропускания резонатора относительно его центральной частоты.

Связанные

Какова добротность цепи?

• Что такое добротность. Добротность или добротность резонансного контура равна отношение накопленной мощности к рассеиваемой мощности в реактивном сопротивлении и сопротивлении цепи. Вообще говоря, более высокая добротность соответствует более узкой полосе пропускания.

Связанные

Какова добротность идеальной цепи RLC? Какова добротность идеальной цепи RLC?

Коэффициент добротности идеальной последовательной цепи RLC и настроенного радиочастотного приемника (TRF) приведен ниже. где сопротивление, индуктивность и емкость настроенной цепи равны R, L и C. Чем больше сопротивление последовательности, тем ниже будет значение Q в цепи.

Родственный

Что такое добротность ВЧ резонансного контура? Что такое добротность ВЧ резонансного контура?

Добротность или добротность — это безразмерный параметр, который используется для описания недостаточно демпфированного резонатора и характеризует полосу пропускания и центральную частоту резонатора. Математическое представление таково: Q = E сохраняется / E теряется за цикл. Коэффициент добротности ВЧ-резонансного контура определяется как:

Родственный

Как сопротивление влияет на добротность фильтра? Как сопротивление влияет на добротность фильтра?

Введение любого сопротивления в цепь приведет к потерям и уменьшит добротность фильтра. Схема с последовательной настройкой: схема с последовательной настройкой во многом обратна схеме с параллельной настройкой в ​​том, что вместо пика импеданса в резонансе есть минимум.

Родственный

Как найти добротность LC-цепи? Как найти добротность LC-цепи?

Уравнения коэффициента добротности LC При определении добротности LC-настроенного контура необходимо определить, является ли контур настроенным последовательно или параллельно. Коэффициент добротности LC для последовательно настроенной схемы: Q = 1 R L C

Родственный

Что такое добротность?

Коэффициент добротности равен общей ширине установленной системы шатунов , измеренной параллельно корпусу каретки от внешней стороны одной точки вставки педали до другой. Вы можете думать об этом так: чем больше добротность, тем дальше будут ваши ноги.

Связанные

Что такое Q-фактор, запишите его значение?

Добротность: в цепи LCR отношение резонансной частоты к разности соседних частот, при котором соответствующий ток в 1/2 раза превышает пиковое значение, называется добротностью цепи. Формула: Q=R1CL .

Связанные

Почему важна добротность?

При работе с радиочастотными цепями фактор добротности важен по многим причинам. … Полоса пропускания: С увеличением добротности или добротности, поэтому полоса пропускания настроенного контурного фильтра уменьшается . По мере уменьшения потерь настроенная цепь становится более четкой, поскольку энергия лучше сохраняется в цепи.

Родственный

Какова единица добротности?

Добротность является безразмерной величиной и, следовательно, не будет иметь безразмерных единиц . 8 января 2016 г.

Как увеличить добротность резонансного контура?

Высокая добротность обусловлена ​​низким сопротивлением последовательно с катушкой индуктивности. Это дает более высокий пик на более узкой кривой отклика. Высокая добротность достигается за счет намотка индуктора большего диаметра (меньшего сечения) , провод меньшего сопротивления. Параллельный резонансный отклик зависит от Q.

Связанные

Что такое Q в полосовом фильтре?

Калькулятор добротности (добротность) вычисляет добротность схемы полосового фильтра или схемы режекторного фильтра. Для полосового фильтра добротность представляет собой отношение центральной частоты полосы пропускания по всей области полосы пропускания от нижней к верхней частоте среза.

Родственный

Что такое Q-фактор последовательной и параллельной цепи RLC?

В серии RLC, Добротность. В параллельном RLC он определяется как сопротивление реактивному сопротивлению реактивного элемента. Добротность Q также определяется как отношение резонансной частоты к ширине полосы. Q = f r B W .

общий Информация СМИ Нажмите галерея иллюстрация

Поделиться этой записью:

[PDF] пропускная способность fig — Скачать PDF бесплатно

БЛОК 5 РЕЗОНАНСНЫЕ ЦЕПИ Q.1) Определить добротность и полосу пропускания. Также установите связь между ними в последовательном резонансном контуре.

ИЮНЬ 2014, ИЮНЬ 2013, ИЮНЬ 2015

Ответ: Добротность: Добротность последовательного резонансного контура есть не что иное, как добротность катушки индуктивности или конденсатора в последовательном резонансном контуре на резонансной частоте. При резонансе реактивное сопротивление индуктора такое же, как и у конденсатора по величине. Следовательно, энергия, запасенная обоими элементами, будет одинаковой. Добротность последовательного резонансного контура обозначается Q0. В резонансе Q0 определяется выражением

Таким образом, вышеприведенное выражение дает добротность последовательного резонансного контура в пересчете на элементы резонансного контура. Ширина полосы: Ширина полосы последовательной цепи RLC определяется как ширина резонансной кривой до частоты, при которой мощность в цепи составляет половину ее максимального значения. На резонансной частоте максимальный ток I0 определяется выражением

. Этот ток максимален, так как импеданс при резонансе минимален. Следовательно, при резонансной частоте мощность в цепи максимальна и определяется выражением P0 = Pmax = (I0)2 .R Теперь половина максимальной мощности определяется выражением

Таким образом, на частотах, где мощность в цепи составляет половину от ее максимального значения, ток становится 1/√ 2 раза или 0,707 раза от своего максимального значения. Частоты, при которых мощность в цепи составляет половину своего максимального значения, называются частотами половинной мощности. Ширина полосы последовательного резонансного контура показана на рис. P’ = ½ (I0)2. R и Аналогично, на частоте f2 мощность в цепи уменьшается вдвое и определяется выражением P’ = ½ (I0)2 . R Таким образом, f1 называется нижней частотой половины мощности, а f2 называется верхней частотой половины мощности. В соответствии с определением полосы пропускания, полоса пропускания последовательной цепи RLC определяется следующим образом: Полоса пропускания = (f2-f1) Гц. Частоты половинной мощности также называются частотами 3 дБ или точками 3 дБ, поскольку мощность на этих частотах на 3 дБ меньше, чем что в резонансе. Давайте теперь определим эти частоты 3 дБ и оценим полосу пропускания и выборочно для последовательного резонансного контура. Взаимосвязь между добротностью и полосой пропускания Ток в последовательной RLC-цепи определяется уравнением 9.0003

Таким образом, из приведенного выше уравнения видно, что на частотах половинной мощности f1 и f2 реактивная часть импеданса последовательной RLC-цепи равна резистивной части импеданса. Мы можем написать,

Избирательность резонансного контура определяется как способность контура различать или различать желаемые и нежелательные частоты. Селективность также определяется как отношение резонансной частоты к ширине полосы резонансного контура.

Таким образом, селективность последовательного резонансного контура прямо пропорциональна добротности контура на резонансной частоте. Таким образом, избирательность резонансного контура зависит от Q0. Если Q0 очень велико, кривая амплитудной характеристики становится более резкой, что приводит к уменьшению полосы пропускания. Если Q0 очень мало, полоса пропускания увеличивается, что делает кривую амплитудной характеристики более плоской.

Таким образом, полоса пропускания последовательного резонансного контура обратно пропорциональна добротности Q0 контура на резонансной частоте. Q.2) Последовательный резонансный контур с R = 17 Ом. L = 0,1H и C = 50 мкФ имеет приложенное напряжение V = 50ﮮ0° с переменной частотой. Найдите резонансную частоту, значение частоты

при

, при которой максимальное напряжение возникает на катушке индуктивности, и значение частоты, при которой максимальное напряжение возникает на конденсаторе.

ИЮНЬ 2015, ЯНВАРЬ 2014

Q.3) Покажите, что резонансная частота последовательного резонансного контура равна среднему геометрическому двух частот половинной мощности.

ЯНВ.2015

Таким образом, f1 называется нижней частотой половины мощности, а f2 называется верхней частотой половины мощности. В соответствии с определением полосы пропускания, полоса пропускания последовательной цепи RCL определяется следующим образом: Полоса пропускания = (f2-f1) Гц. Частоты половинной мощности также называются частотами 3 дБ или точками 3 дБ, поскольку мощность на этих частотах на 3 дБ меньше. чем в резонансе. Давайте теперь определим эти частоты 3 дБ и оценим полосу пропускания и выборочно для последовательного резонансного контура.

Таким образом, из приведенного выше уравнения видно, что на частотах половинной мощности f1 и f2 реактивная часть импеданса последовательной цепи RCL равна резистивной части импеданса. Приведенное выше уравнение квадратично по ω, что дает два значения ω как ω1 и ω2, частоты половинной мощности которых (т. е. f1 и f2) такие, как показано на рис. 20. Мы можем написать,

ниже на рис. индуктивность 0,1 Гн с добротностью 5 подключена параллельно конденсатору. Определить величину емкости и сопротивления катушки при резонансной частоте 500 рад/сек. 9 января 2015 г.0003

Ответ: Данная схема является практической параллельной резонансной схемой. Антирезонансная частота с точки зрения добротности определяется как

Q.5) Определите параметры параллельной цепи R-L-C, кривая отклика которой показана на рис. Каковы будут новые значения ωr и ширины полосы, если c увеличить в 4 раза? JAN.2013

Q.6) В случае последовательного резонансного контура с изменением частоты получить выражения для i) ωC, при котором на C возникает максимальное напряжение ii) ωL, при котором на L возникает максимальное напряжение, и показать, что ω1>ωC

JAN.2014

Q.7) Выведите выражение для резонансной частоты контура, показанного на рис. Также покажите, что контур будет резонировать на всех частотах, если RL = RC = √ L/C

JAN.2014, ИЮНЬ 2015

Две параллельно соединенные ветви будут создавать резонанс, когда результирующий ток через комбинацию, т. е. I, находится в фазе с напряжением V, как показано на рис. 10(b). Условие параллельного резонанса состоит в том, что импеданс параллельной комбинации является чисто резистивным. Условие резонанса может быть получено следующим образом: Полная проводимость ветви, содержащей L и RL, равна

где далеко частота резонанса. Значения RL и RC в целом варьируются незначительно. RL — омическое сопротивление катушки или индуктора, RC — сопротивление утечки и диэлектрических потерь конденсатора. Оба они неизбежны, но на самом деле оба очень малы. Если два сопротивления выбраны так, что тогда мнимый член в уравнении (1) становится равным нулю. Таким образом, реактивное сопротивление равно нулю. Для всех частот схема находится в условиях единичного коэффициента мощности. При указанном выше условии антирезонанс возможен на всех частотах в цепи.

Q-фактор для калькулятора параллельной RLC-цепи

✖Сопротивление — это мера противодействия протеканию тока в электрической цепи. Сопротивление измеряется в омах, что обозначается греческой буквой омега (Ω).0003	+10% -10%
✖Capacitance is defined as capacitance measured in micro farad units.ⓘ Capacitance [C]		AbfaradAttofaradCentifaradCoulomb per VoltDecafaradDecifaradEMU of CapacitanceESU of CapacitanceExafaradFaradFemtofaradGigafaradHectofaradKilofaradMegafaradMicrofaradMillifaradNanofaradPetafaradPicofaradStatfaradTerafarad	+10% -10%
✖Индуктивность – это способность электрического проводника сопротивляться изменению электрического тока, протекающего через него. The flow of electric current creates a magnetic field around the conductor. ⓘ Inductance [L]		AbhenryAttohenryCentihenryDecahenryDecihenryEMU of InductanceESU of inductanceExahenryFemtohenryGigahenryHectohenryHenryKilohenryMegahenryMicrohenryMillihenryNanohenryPetahenryPicohenryStathenryTerahenryWeber per Ampere	+10% -10%

✖Коэффициент качества определяется как отношение начальной энергии, запасенной в резонаторе, к энергии, теряемой в одном радиане цикла колебаний.ⓘ Добротность для параллельного RLC-контура [q]

⎘ Копировать

👎

Формула

Перезагрузить

👍

Q-фактор для решения с параллельной схемой RLC

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовую единицу

Сопротивление: 59 Ом —> 59 Ом Преобразование не требуется
Емкость: 5,7 мкФ —> 5,7E-06 Фарад ( Проверьте преобразование здесь)
Индуктивность: 5,7 Миллигенри —> 0,0057 Генри (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу измерения выхода < 3 калькулятора частоты и добротности

Q-фактор для формулы параллельной цепи RLC

Коэффициент качества = сопротивление * (sqrt (емкость / индуктивность))
q = R * (квадрат (C / L))

Что такое добротность?

Добротность есть не что иное, как соотношение между накопленной энергией и скоростью энергии в электрических компонентах, устройствах. Отношение реактивного сопротивления в омах к сопротивлению в омах определяется как добротность.

Как рассчитать добротность для параллельной цепи RLC?

Калькулятор Q-фактора для параллельной RLC-цепи использует Коэффициент добротности = Сопротивление*(sqrt(Емкость/индуктивность)) для расчета добротности. Формула добротности для параллельной RLC-цепи определяется как безразмерный параметр, описывающий степень недостаточного осциллятор или резонатор. Она приблизительно определяется как отношение начальной энергии, запасенной в резонаторе, к энергии, теряемой за один радиан цикла колебаний. Коэффициент качества обозначается цифрой q символ.

Как рассчитать добротность для параллельной RLC-цепи с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для Q-фактора для параллельной цепи RLC, введите сопротивление (R) , емкость (C) и индуктивность (L) и нажмите кнопку расчета. Вот как можно объяснить Q-фактор для расчета параллельной цепи RLC с заданными входными значениями -> 1,865744 = 59*(sqrt(5.7E-06/0,0057)) .

Часто задаваемые вопросы

Что такое добротность для параллельной цепи RLC?

Формула добротности для параллельной RLC-цепи определяется как безразмерный параметр, описывающий степень недостаточного демпфирования генератора или резонатора. Он приблизительно определяется как отношение начальной энергии, запасенной в резонаторе, к энергии, теряемой за один радиан цикла колебаний, и представляется как q = R*(sqrt(C/L)) или Добротность = Сопротивление*(sqrt(емкость/индуктивность)) 908:20 . Сопротивление является мерой сопротивления току, протекающему в электрической цепи. Сопротивление измеряется в омах, что обозначается греческой буквой омега (Ом), емкость определяется как емкость, измеряемая в микрофарадах, а индуктивность — это тенденция электрического проводника сопротивляться изменению электрического тока, протекающего через него. Поток электрического тока создает вокруг проводника магнитное поле.

Как рассчитать добротность для параллельной цепи RLC?

Формула добротности для параллельной цепи RLC определяется как безразмерный параметр, описывающий степень недостаточного демпфирования генератора или резонатора. Он приблизительно определяется как отношение начальной энергии, запасенной в резонаторе, к энергии, теряемой за один радиан цикла колебаний, рассчитывается с использованием Коэффициент качества = Сопротивление*(sqrt(Емкость/Индуктивность)) . Чтобы рассчитать добротность для параллельной RLC-цепи, вам нужно сопротивление (R) , емкость (C) и индуктивность (л) . С помощью нашего инструмента вам нужно ввести соответствующие значения сопротивления, емкости и индуктивности и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Сколько существует способов расчета добротности?

В этой формуле коэффициент качества использует сопротивление, емкость и индуктивность. Мы можем использовать 1 другой способ (способы) для расчета того же самого, который выглядит следующим образом:

• Коэффициент качества = sqrt (индуктивность) / (сопротивление * sqrt (емкость))

Поделиться

Скопировано!

Резонанс: фактор качества — Infinity Learn

Введение

Идея Q, фактора качества, впервые была предложена инженером по имени К. С. Джонсон из инженерного отдела Western Electric Company в США. Он оценивал производительность и качество различных катушек. Во время своих исследований он разработал концепцию Q. Удивительно, но в итоге он выбрал букву Q, потому что все остальные буквы алфавита были взяты, а не из-за термина «фактор качества», хотя, оглядываясь назад, алфавит Q для коэффициента качества не могло быть лучше. Понятие добротности применимо во многих областях физики и техники. Q описывается в электронных схемах как отношение энергии, запасенной в резонаторе, к энергии, подводимой к нему за цикл, чтобы поддерживать постоянную амплитуду сигнала на частоте, при которой запасенная энергия постоянна во времени. Хотя добротность элемента связана с потерями, она напрямую связана с шириной полосы резонатора по отношению к его центральной частоте.

Обзор

Коэффициент добротности, или добротность, на самом деле является безразмерным параметром в физике и технике, который описывает степень недостаточного демпфирования генератора или резонатора. На самом деле она определяется как отношение начальной энергии резонатора к энергии, теряемой в одном радиане цикла колебаний. При воздействии осциллирующей движущей силы добротность определяется как отношение центральной частоты резонатора к его ширине полосы. Численные результаты этих двух определений похожи, но не идентичны. Большее Q означает меньшую скорость потери энергии и более медленное затухание колебаний. Маятник, подвешенный на одном высококачественном подшипнике и колеблющийся в воздухе, имеет высокую добротность, а погруженный в масло — низкую. Резонаторы с высокими коэффициентами качества имеют ограниченное демпфирование, что позволяет им звенеть или вибрировать в течение более длительного периода времени.

Бесплатный материал IIT-JEE/NEET/NCERT/CBSE

Загрузите БЕСПЛАТНО PDF-файлы, решенные вопросы, работы за предыдущий год, викторины и головоломки!

+91

Проверьте код OTP (обязательно)

класс
— Класс 6CLASS 7CLASS 9CLASS 9CLASS 10CLASS 11CLASS 12

КУРС
— CBSEIIT-JEENEET

ШКОЛА/Колледж название

SRI CHAITANEA?
НетДа

Я согласен с условиями и политикой конфиденциальности.

Резонанс: добротность

Добротность — это всего лишь параметр, который описывает резонансное поведение гармонического генератора с недостаточным демпфированием (резонатора). Синусоидальные резонаторы с более высокой добротностью резонируют с большей амплитудой (на резонансной частоте), но имеют меньший диапазон частот вокруг той частоты, на которой они резонируют; полоса пропускания будет диапазоном частот, для которых резонирует осциллятор. Таким образом, настроенную схему с высокой добротностью в радиоприемнике было бы труднее настроить, но она была бы более избирательной; он будет лучше фильтровать сигналы от других станций в той же полосе частот. Высокодобротные генераторы имеют более узкий частотный диапазон и более стабильны.

Добротность генераторов различается в зависимости от их конструкции от системы к системе. Q близок к 1/2 в системах, где важно демпфирование (например, демпферы, удерживающие дверь от захлопывания). Высококачественные факторы необходимы для часов, лазеров и других резонирующих систем, требующих либо сильного резонанса, либо стабильности на высоких частотах. Камеры имеют добротность исчисляемую тысячами. Атомные часы, сверхпроводящие ВЧ-резонаторы, используемые в ускорителях, и некоторые высокодобротные лазеры имеют добротность 1011 и выше.

Физики и инженеры используют множество различных величин для описания степени демпфирования генератора. Важными примерами являются коэффициент демпфирования, относительная пропускная способность, ширина линии и пропускная способность, измеренная в октавах.

В электронных схемах Q описывается как отношение энергии, запасенной в резонаторе, к энергии, подводимой к нему за цикл для поддержания постоянной амплитуды сигнала на частоте, при которой накопленная энергия остается постоянной во времени. Это также является мерой эффективности катушки индуктивности и может быть определено как отношение ее индуктивного реактивного сопротивления к ее сопротивлению на определенной частоте.

Влияние добротности

Существует множество причин, по которым добротность важна при работе с ВЧ-схемами. Обычно предпочтителен высокий уровень добротности, но в некоторых приложениях может потребоваться определенный уровень добротности.

Ниже приведены некоторые аспекты, связанные с добротностью настроенных радиочастотных цепей:

• Ширина полосы: По мере увеличения добротности или добротности увеличивается и полоса пропускания настроенного схемного фильтра. Всякий раз, когда потери уменьшаются, настроенная цепь обостряется, поскольку энергия лучше хранится в цепи. Кажется, что с увеличением добротности увеличивается полоса пропускания по уровню 3 дБ и общий отклик настроенной схемы. Во многих случаях для достижения желаемого уровня селективности требуется высокая добротность.
• Широкая полоса пропускания: Во многих радиочастотных приложениях требуется процедура широкой полосы пропускания. Для некоторых схем модуляции требуется широкая полоса пропускания, тогда как для других приложений требуются фиксированные фильтры для обеспечения широкополосного покрытия. Хотя может потребоваться сильное подавление нежелательных сигналов, также требуется широкая полоса пропускания. В результате во многих приложениях необходимо определить уровень добротности, необходимый для обеспечения общей производительности, необходимой для удовлетворения требований к широкой полосе пропускания и адекватному подавлению нежелательных сигналов.
• Фазовый шум генератора: Фазовый шум генерируется генератором. Это состоит из случайных фазовых сдвигов в сигнале. Один из них выражается в виде шума, исходящего от основной несущей. Как и следовало ожидать, такой шум нежелателен и должен быть уменьшен. Компоновка генератора может быть адаптирована для уменьшения этого различными способами, наиболее важным из которых является увеличение добротности или добротности настроенной схемы генератора.
• Общие ложные сигналы: Для удаления паразитных сигналов часто используются настроенные цепи и фильтры. Чем выше уровень добротности и острее фильтр, тем лучше схема сможет удалять паразитные сигналы.
• Звон: При этом добротность резонансного контура возрастает, а значит и потери. Таким образом, это означает, что любые колебания, создаваемые внутри цепи, будут длиться дольше. То есть схема будет «звонить» чаще. Поскольку в настроенной схеме теряется меньше энергии, это идеально подходит для использования в схеме генератора, поскольку его легче настроить и поддерживать колебание.

Формулы добротности

Основная формула добротности основана на потерях энергии в катушке индуктивности, цепи или другом типе компонента.

Коэффициент добротности может быть математически выражен с помощью приведенной ниже формулы добротности, основанной на приведенном выше определении добротности:

При рассмотрении полосы пропускания ВЧ-резонансного контура получается формула коэффициента добротности:

Каждый отдельный компонент в любой радиочастотной или другой цепи может вносить вклад в добротность или добротность цепи в целом. Такие компоненты, как катушки индуктивности и конденсаторы, часто называют имеющими определенную добротность или добротность.

Коэффициент добротности и демпфирование

Демпфирование является важным аспектом добротности во многих схемах. Коэффициент добротности, Q, определяет качественное поведение простых демпфированных генераторов и влияет на другие схемы, такие как отклик фильтра и т. д.

Когда речь идет о демпфировании и добротности, необходимо учитывать три основных режима: демпфированный (Q > 1/2): Нижняя система имеет коэффициент добротности больше половины. Когда ступенчатый импульс применяется к системе с добротностью менее половины, колебание может произойти один или два раза, прежде чем оно исчезнет. С увеличением добротности затухание уменьшается и колебания длятся дольше. В какой-то теоретической системе с бесконечной добротностью колебание будет поддерживаться бесконечно без необходимости в каком-либо дополнительном стимуле. Некоторый сигнал возвращается обратно в генераторы для обеспечения дополнительного стимула, но высокая добротность дает гораздо более чистый результат. Сигнал содержит более низкие уровни фазового шума.

С избыточным демпфированием (Q <1/2): Коэффициент добротности системы с избыточным демпфированием меньше 1/2. Потери в системе такого типа высоки, и система не имеет перерегулирования. Вместо этого после подачи ступенчатого импульса система будет экспоненциально затухать, асимптотически приближаясь к установившемуся значению. По мере уменьшения добротности (или добротности) система реагирует медленнее.

Критическое демпфирование (Q = 1/2): Похоже, что система с критическим демпфированием имеет коэффициент добротности 0,5, а выходной сигнал, подобно системе с чрезмерным демпфированием, не колеблется и не выходит за пределы установившегося выходного сигнала. Эта же система будет приближаться к стационарной асимптоте как можно быстрее, без перерегулирования.