26. Проводники в электростатическом поле

1. Опред.Проводники – материалы, в которых есть свободные носители тока, т.е. заряды, которые способны перемещаться под действием сколь угодно малой силы.

Условия равновесия заряда в проводнике:

1) т.е. потенциал внутри проводникавнутри нет электрических сил, действующих на заряд.

2) вдоль поверхности=0, т.е. поверхность проводника эквипотенциальна.

Из 1) плотность заряда в любой внутренней точке проводника, т.к..

Из 2) — поверхность проводника является эквипотенциальной.

2.Выясним, чему равна нормальная составляющая вектора напряженностина поверхности проводника.

Здесь — диэлектрическая проницаемость среды, окружающей металл.

2а. Обсудим электрическое поле Земли

Если это так, то напряженность электрического поля в околоземном пространстве

Вопр. Почему мы не ощущаем напряжения между пятками и макушкой или кончиком носа?

Отв. Человек – хороший проводник, следовательно, человек представляет собой эквипотенциальную поверхность и сам вносит искажения в электростатическое поле.

Между «небом» и Землей в ясный день разность потенциалов U=, и течет постоянный ток, обусловленный потоком отрицательных ионов от Земли к небу, с плотностью. Интеграл по всей поверхности Земли дает ток 1800 А от Земли к небу. Чтобы заряд сохранялся, нужен механизм обратного тока отрицательного заряда к Земле. Эту функцию выполняют грозы.

Напряжение поля Земли в течение суток меняется следующим образом

Т.о. 22 часа по московскому времени – наиболее вероятное время гроз на Земле, т.е. над Тихим океаном наиболее вероятны грозы утром, а над Атлантическим – вечером.

Разность потенциалов Земля-небо во время грозы много больше, чем в ясную погоду.

Каждый удар молнии приносит (20 – 30) Кл на Землю.

Время восстановления дипольного момента тучи ~5 с. В «грозовой машине» течет ток ~4 А. Т.о. атмосфера является непрерывно действующей электрической машиной.

Если природа обычной молнии описана в многочисленных научных работах и даже учебниках (например, Сивухин «Электричество»), то природа шаровой молнии не известна. Существует ряд гипотез. Например, гипотеза Родионова основана на существовании магнитных монополей, которые представляют собой кончики вихрей кварков. Кварковый вихрь, как шланг пылесоса, подсасывает своим магнитным полем атомы, которые , приближаясь к монополю, распадаются сначала на элементарные частицы, а потом на кварки, которые достраивают монополь.

Т.о. получается следующая цепочка:

При этом возникает ионизация воздуха с появлением светящегося плазменного шара диаметром ~10 см. С помощью этой гипотезы автор сделал попытку объяснить загадку тунгусского метеорита, полагая, что тунгусское сияние было вызвано ядерным взрывом, спровоцированным шаровой молнией. Эта гипотеза, разумеется, оставляет ряд вопросов:

1. Она противоречит уравнению Максвелла

– магнитных зарядов не обнаружено,

т.к. монополи, лежащие в основе гипотезы, и есть пока не обнаруженные магнитные заряды.

2. Если тунгусский метеорит являлся ядерным взрывом, почему никто не пострадал от излучения.

Впрочем, Максвеллу в свое время тоже мало, кто поверил. Этот пример продемонстрирует, что и наше время богато головокружительными гипотезами и нерешенными физическими проблемами.

Вернемся к изучению свойств проводников в электростатическом поле.

3. Как распределен заряд по поверхности металла?

На больших расстояниях от заряженной поверхности проводника эквипотенциальные поверхности – сферы, на малых расстояниях – у острия линии сгущаются, т.е. у острия больше напряженность поляна острие заряды сгущаются.

Вопр. Почему так?

Отв.Заряды на поверхности проводника стремятся как

можно дальше расположиться друг от друга, а т. к. острие

отстоит дальше от остальной поверхности, то туда и убегают заряды. В результате:

Эквивалентная схема вытянутого тела:

вывод:

На поверхности заряженного проводника плотность заряда велика на выступающих частях и мала во впадинах.

Если надо зарядить тело до высокого потенциала, то надо убедиться, что поверхность его гладкая и на ней нет мест, где Eбудет очень велико, т.к. с этих мест может происходить истечение зарядов.

Если поместить вблизи тела с острием, находящимся под высоким напряжением, другой изолированный от первого проводник, то последний будет заряжаться зарядом того же знака, что и острие, вследсвие ионизации воздуха вблизи острия. При этом одноименные заряды с таким же знаком заряда, как у острия, движутся от него, а разноименные к нему. Возникает ионный ветер, увлекающий за собой и нейтральные молекулы.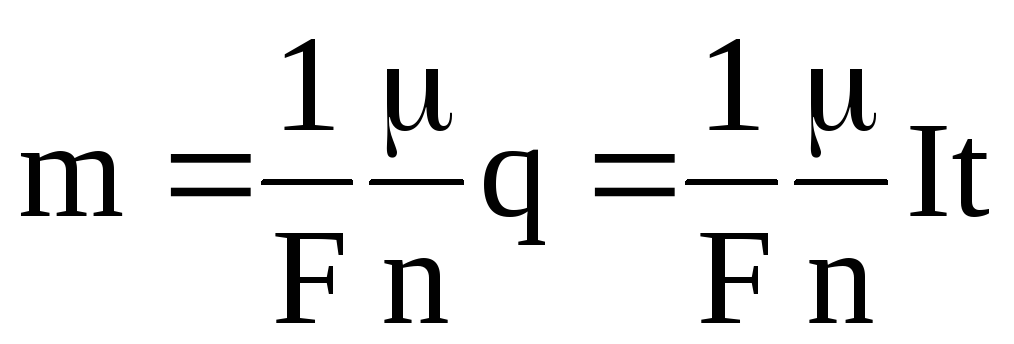

4. Свойства замкнутой проводящей оболочки:

(1) Внешние заряды, в частности заряды на наружной поверхности

проводника не создают в полости внутри проводника никакого электрического поля

электростатическая защита.

5. Заряды внутри проводящего слоя.

Что происходит?

—суммарный заряд, индуцированный на внутренней поверхности замкнутой проводящей оболочки, равен и противоположен по знаку суммарному заряду, окруженному этой оболочкой.

(2) Кулоновское поле зарядов, окруженных проводящей оболочкой, и зарядов, индуцированных на ее поверхности, равно 0 во всем внешнем пространстве.

(1)+(2) Теорема Фарадея:

замкнутая проводящая оболочка разделяет все пространство на внутреннюю и внешнюю части, в электрическом отношении независимые друг от друга.

Например, перемещение малого шарика не влияет на поле внутри большого шара или сферического слоя.

6. Примеры:

1) Заряд внутри электронейтрального проводящего сферического слоя.

Если — не в центре сферы, то это отразится на неравномерности распределения заряда только на внутренней поверхности, снаружи все будет также.

2) Если проводящий слой заземлен, то распределение поля и потенциала во внешнем пространстве будет другим.

В этом случае Земля является источником недостающего отрицательного заряда, проводник заряжается отрицательно зарядом -и полностью экранирует поле центрального заряда, поэтому напряженность поля и потенциал равны 0 во всем пространстве при

Электричество и магнетизм

Если к проводнику добавить (отнять) часть электронов, то он заряжается отрицательно (положительно). Рассмотрим условия равновесия за­рядов на проводнике. При равновесии зарядов их направленное движение внутри проводника отсутствует. Это означает, что поле внутри проводника равно нулю:

. В противном случае  заряды должны были бы двигаться. Поскольку внутри проводника , то по теореме Остроградского-Гаусса в каждой точке объема образца , поэтому объемная плотность зарядов внутри проводника также равна нулю , а избыточные заряды могут быть расположены только на поверхности проводника. Это происходит потому, что одноименные заряды отталкиваются и стремятся расположиться как можно дальше друг от друга.

Видео 2.2. Поле заряженного проводника. Сетка Кольбе.

Ответим на вопрос: что будет, если в толще заряженного проводника имеется замкнутая внутренняя полость? Будут ли располагаться за­ряды также и на ее стенках? Исходя из качественных соображений, мы должны ответить отрицательно: заряды, отталкиваясь друг от друга, расположатся только на внешней поверхности проводника.

К такому же выводу приводит теорема Остроградского — Гаусса. Если взять такую воображаемую поверхность, чтобы она целиком лежала в толще провод­ника и была бесконечно близка к стенкам полости, то во всех точках этой поверхности поле равно нулю, и, следовательно, равен нулю поток век­тора электрической напряженности. Следовательно, на стенках полости зарядов нет.

Видео 2.3. Поле заряженного проводника. Клетка Фарадея.

Отсутствие поля внутри заряженного проводника означает постоянство потенциала внутри него: поскольку , то . Таким образом, потенциал на поверхности проводника также постоянен и равен по величине потенциалу в объеме проводника. Следовательно, поверхность проводника эквипотенциальная (рис. 2.2).

Рис. 2.2. Потенциалы двух проводников: левый проводник имеет заряд +1 (в условных единицах), правый проводник не заряжен. Потенциалы постоянны по объему каждого проводника

Видео 2.4. Эквипотенциальность проводника в условиях равновесия.

Электрические заряды, располагающиеся на поверхности проводника с некоторой плотностью , создают вне проводника электрическое поле. Вблизи поверхности проводника напряженность поля направлена по нормали  в каждой точке поверхности, т. е.  так как эквипотенциальная поверхность перпендикулярна силовым линиям. Для вычисления поля вблизи проводника снова используем теорему Остроградского — Гаусса. В качестве воображаемой поверхности возьмем поверхность бесконечно малого цилиндра, расположенного перпендикулярно проводнику так, что одно из его оснований находится вне проводника, а другое — внутри (рис. 2.3).

Рис. 2.3. Электрическое поле вблизи поверхности изолированного заряженного проводника

В этом случае поток через основание внутри проводника равен нулю, так как внутри проводника нет поля. Далее, поток через боковые стенки также равен нулю, поскольку они параллельны вектору напряженности поля. Остается поток через основание площадью  вне проводника.

Тогда полный поток вектора электрической напряженности  через поверхность цилиндра будет равен:

(2.1)

Согласно теореме Остроградского — Гаусса,                                                             

откуда

(2.2)

 

Таким образом, напряженность электрического поля вблизи поверхно­сти заряженного проводника (с его внешней стороны) пропорциональна поверхностной плотности зарядов. Внутри проводника, напомним, поле равно нулю.

Видео 2.5. Распределение зарядов по поверхности проводника в условиях равновесия.

Видео 2.6. Электрический ветер.

Видео 2. 7. «Плазменный двигатель» Франклина.

Задача. Исследования атмосферного электричества показали, что у земной поверхности существует стационарное электрическое поле со средней напряженностью . Поле это направлено вниз. Отметим, что во время грозы распределение атмосферного электричества имеет более сложный характер (рис. 2.4). 

Рис. 2.4. Распределение атмосферного электричества в созревшей грозовой ячейке: 1 — центр положительных зарядов, 2 — центр отрицательных зарядов, 3 — дождь с отрицательным зарядом, 4 — центр положительного заряда в области сильного дождя

Пользуясь этими данными и предполагая, что Земля — проводник, оценить полный электрический заряд нашей планеты.

Решение. Сначала определим знак этого заряда. Т. к. поле направлено вниз, к Земле, а силовые линии начинаются на положительных зарядах и кончаются на отрицательных, мы заключаем, что заряд Земли отри­цателен. Далее, из уравнения (2. 2) находим:

 

Зная радиус Земли  км, определяем площадь земной поверхности  м² . Наконец, находим электрический заряд Земли  кКл!

 

электромагнетизм — Теорема Гаусса и Закон Фарадея

спросил 6 лет, 9 месяцев назад

Изменено 3 года, 1 месяц назад

Просмотрено 2к раз

$\begingroup$

Я изучаю магнитные поля и у меня есть большая проблема. Теорема Гаусса утверждает, что магнитный поток через замкнутую поверхность равен нулю, поскольку линии потока входят и выходят из нее в одинаковой степени. Однако закон Фарадея говорит о потокосцеплении с поверхностью, которая может быть не нулевой, если, например, магнитное поле непостоянно во времени.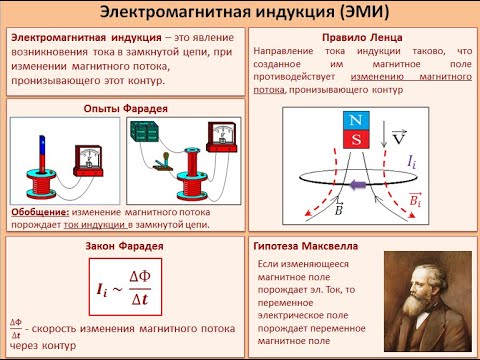 Почему также не равен нулю, если это поток через поверхность?

• электромагнетизм
• закон Гаусса

$\endgroup$

$\begingroup$

Закон Фарадея говорит о потоке, пронизывающем открытых поверхностей, в то время как закон Гаусса для магнитных полей действует для закрытых поверхностей.

$\endgroup$

7

$\begingroup$

Два рассматриваемых уравнения

\begin{align}\mathbf \nabla \times \mathbf E &= -\frac{\partial{\mathbf B}}{\partial t}\tag 1 \\ \mathbf \nabla \cdot \mathbf B & = 0\tag 2\end{align}

передают совершенно разные значения.

В то время как первый $(1)$ связывает циркуляцию индуцированного электрического поля с отрицательной скоростью изменения связанного с ним магнитного поля во времени; более поздний, т. е. $(2)$ говорит о том, что дивергенция магнитного поля практически равна нулю.

Давайте перейдем к настоящему контексту, где OP, похоже, путается с интегральной формой уравнения: Интегральные формы соответственно:

\begin{align} \int_\textrm C \mathbf E \cdot \mathrm d\mathbf s &= -\frac{\mathrm d}{\mathrm dt}\, \underbrace{\color{red}{\ int _\mathrm S\mathbf B\cdot\mathrm d\mathbf a}}_{\Phi\equiv\, \textrm{магнитный поток}}\tag 1 \\ \underbrace{\int_\mathrm S\mathbf B\ cdot \mathrm d\mathbf a}_{\textrm{поток через}\,\color{red}{\textrm{замкнутая поверхность}}} &= 0\tag 2\end{align}

OP может видеть отчетливое красный отмечен член в первом уравнении; последний так не говорит. Возможное неправильное толкование можно было бы предотвратить, если бы OP преобразовывал дифференциальную форму в интегральную с учетом Гаусса или теорема о расходимости и теорема Стокса.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

10.

1 Закон Фарадея. Введение в электричество, магнетизм и электрические цепи

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Определить магнитный поток через поверхность, зная напряженность магнитного поля, площадь поверхности и угол между нормалью к поверхности и магнитным полем
• Используйте закон Фарадея для определения величины ЭДС индукции в замкнутом контуре из-за изменения магнитного потока через контур

Первые плодотворные эксперименты по влиянию изменяющихся во времени магнитных полей были проведены Майклом Фарадеем в 1831 году. Один из его ранних экспериментов представлен на Рисунке 10.1.1. ЭДС индуцируется, когда магнитное поле в катушке изменяется путем вталкивания стержневого магнита в катушку или из нее. ЭДС противоположных знаков создаются движением в противоположных направлениях, а направления ЭДС также меняются на противоположные при смене полюсов. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.

(рис. 10.1.1)  

Рисунок 10.1.1  Движение магнита относительно катушки создает ЭДС, как показано (a–d). Такие же ЭДС возникают, если катушку перемещать относительно магнита. Эта кратковременная ЭДС присутствует только во время движения. Чем больше скорость, тем больше величина ЭДС, а ЭДС равна нулю, когда нет движения, как показано на (е).

Фарадей также обнаружил, что аналогичный эффект можно получить, используя две цепи: изменение тока в одной цепи индуцирует ток во второй, соседней цепи. Например, когда переключатель замыкается в цепи 1 на рисунке 10.1.2 (а), стрелка амперметра в цепи 2 на мгновение отклоняется, указывая на то, что в этой цепи был индуцирован кратковременный скачок тока. Стрелка амперметра быстро возвращается в исходное положение, где и остается. Однако если теперь внезапно разомкнуть выключатель цепи 1, то в цепи 2 наблюдается еще один кратковременный выброс тока в направлении, противоположном предыдущему. 0005

(рис. 10.1.2)  

Рисунок 10.1.2  (a) Замыкание переключателя цепи 1 вызывает кратковременный скачок тока в цепи 2. (b) Если переключатель остается замкнутым, ток в цепи 2 отсутствует. (c) Повторное размыкание переключателя производит кратковременный ток в цепи 2, но в направлении, противоположном предыдущему.

Фарадей понял, что в обоих экспериментах ток протекал по цепи, содержащей амперметр, только тогда, когда магнитное поле в области, занятой этой цепью, составляло изменение . При перемещении магнита фигуры сила ее магнитного поля в петле менялась; а при включении или выключении тока в цепи 1 изменялась напряженность его магнитного поля в цепи 2. В конце концов Фарадей смог интерпретировать эти и все другие эксперименты с магнитными полями, меняющимися во времени, в соответствии со следующим законом:

ЗАКОН ФАРАДЕЯ

---

Индуцированная ЭДС представляет собой отрицательное изменение магнитного потока в единицу времени. Любое изменение магнитного поля или изменение ориентации области катушки по отношению к магнитному полю индуцирует напряжение (ЭДС).

Магнитный поток  – это измерение количества силовых линий магнитного поля, проходящих через заданную площадь поверхности, как показано на Рисунке 10.1.3. Это определение аналогично рассмотренному ранее электрическому потоку. Это означает, что если у нас есть

(10.1.1)  

, то ЭДС индукции или напряжение, создаваемое проводником или катушкой, движущейся в магнитном поле, равно

(10.1.2)  

Знак минус описывает направление, в котором ЭДС индукции вызывает ток в цепи. Однако это направление легче всего определить с помощью правила, известного как закон Ленца, который мы вскоре обсудим.

(рис. 10.1.3)  

Рисунок 10.1.3  Магнитный поток – это количество линий магнитного поля, пересекающих площадь поверхности A , определяемую единичным вектором площади . Если угол между единицей площади и вектором магнитного поля параллелен или антипараллелен, как показано на диаграмме, магнитный поток является максимально возможным значением при заданных значениях площади и магнитного поля.

Часть (а) рисунка 10.1.4 изображает контур и произвольную поверхность, которую он ограничивает. Обратите внимание, что  это  открытая поверхность . Можно показать, что любая открытая поверхность, ограниченная рассматриваемой схемой, может быть использована для оценки . Например, одинакова для различных поверхностей части (b) рисунка.

(рис. 10.1.4)  

Рисунок 10.1.4  (a) Схема, ограничивающая произвольную открытую поверхность. Плоская область, ограниченная контуром, не является частью . (b) Три произвольные открытые поверхности, ограниченные одним и тем же контуром. Значение   одинаково для всех этих поверхностей.

Единицей измерения магнитного потока в системе СИ является  вебер  (),

   

Иногда единица измерения магнитного поля выражается в веберах на квадратный метр () вместо тесла, исходя из этого определения. Во многих практических приложениях представляющая интерес схема состоит из ряда плотно намотанных витков (см. рис. 10.1.5). На каждый виток действует один и тот же магнитный поток. Следовательно, чистый магнитный поток через цепи умножен на поток через один виток, и закон Фарадея записывается как

(10.1.3)  

ПРИМЕР 10.1.1

---

Квадратная катушка в изменяющемся магнитном поле

Квадратная катушка на рисунке 10.1.5 имеет длинные стороны и плотно намотана витками проволоки. Сопротивление катушки равно . Катушка помещена в пространственно однородное магнитное поле, которое направлено перпендикулярно лицевой стороне катушки и величина которого уменьшается со скоростью . а) Чему равна ЭДС индукции в катушке? б) Какова величина тока, циркулирующего по катушке?

(рис. 10.1.5)  

Рисунок 10.1.5  Квадратная катушка с витками провода с однородным магнитным полем, направленным вниз, перпендикулярно катушке.

Стратегия

Вектор площади или направление перпендикулярно площади, покрывающей контур. Мы выберем это так, чтобы оно было направлено вниз, чтобы  параллельно  и чтобы поток превратился в произведение магнитного поля на площадь. Площадь петли не меняется во времени, поэтому ее можно вычесть из производной по времени, оставив магнитное поле единственной величиной, изменяющейся во времени. Наконец, мы можем применить закон Ома, если мы знаем ЭДС индукции, чтобы найти ток в петле.

Решение

1. Поток через один виток

      

   , поэтому мы можем вычислить величину ЭДС по закону Фарадея. Знак ЭДС будет обсуждаться в следующем разделе о законе Ленца:

      

2. Величина тока, индуцируемого в катушке, равна

      

Значение

Если бы площадь петли изменялась во времени, мы бы не смогли вытащить ее из производной по времени. Поскольку петля представляет собой замкнутый путь, результатом этого тока будет небольшой нагрев проводов до тех пор, пока магнитное поле не перестанет изменяться. Это может немного увеличить площадь петли по мере нагрева проводов.