Основы логики — что это, определение и ответ

Математическая логика (она же булева алгебра) является неотъемлемым блоком знаний как в школьном курсе информатики, так и в ЕГЭ. В чистом виде логика в экзамене представлена в двух заданиях: №2 и №15, которые идут по увеличению сложности. Кроме этого, логика в том или ином виде встречается и в других разделах экзамена – от кодирования информации до программирования.

Цель логики как науки – определить, истинно или ложно некоторое высказывание, а также прослеживать связь между высказываниями относительно друг друга. Высказывания обозначаются логическими переменными, которые могут принимать лишь два значения:

Истина = 1, Ложь = 0

Логические выражения (которые состоят из более чем одного высказывания) на естественном языке образуются с помощью связок «И», «ИЛИ», «НЕ». В математической логике аналогом этих связок являются базовые логические операции – конъюнкция, дизъюнкция и инверсия. Чтобы определить значение составного логического выражения, надо знать значения входящих в него логических переменных (высказываний). Чтобы рассмотреть все возможные случаи, в булевой алгебре есть специальный аппарат – таблица истинности. Таблица истинности строится следующим образом: в столбцах записываются логические переменные и само выражение, а в строках – всевозможные комбинации переменных и соответствующий для них результат выражения. Для выражения, содержащего n переменных, количество комбинаций для них будет равно 2ⁿ. Подробнее про таблицы истинности написано ниже.

Логическое умножение. Конъюнкция

Конъюнкция (логическое умножение, логическое «И») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда и только тогда, когда истинны все входящие в него высказывания. Пусть есть два высказывания:

Эти высказывания истинны. Значит, их объединение с помощью конъюнкции («В ЕГЭ по информатике есть программирование И логика») – истинно.

Операцию конъюнкции в булевой алгебре принято обозначать знаком « /\ » или, реже, « & » (амперсанд). Операция логического умножения, аргументами которой являются логические переменные А и В, записываются следующей формулой: A /\ B. Таблица истинности для конъюнкции:

A	B	A /\ B
0	0	0
0	1	0
1	0	0
1	1	1

Логическое сложение. Дизъюнкция

Дизъюнкция (логическое сложение, логическое «ИЛИ») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда, когда истинно хотя бы одно входящее в него высказывание.

Операцию дизъюнкции в булевой алгебре принято обозначать знаком « \/ ». Операция логического сложения, аргументами которой являются логические переменные А и В, записывается следующей формулой: A \/ B. Таблица истинности для дизъюнкции:

A	B	A \/ B
0	0	0
0	1	1
1	0	1
1	1	1

Логическое отрицание. Инверсия

Инверсия (логическое отрицание, логическое «НЕ») получает из истинного высказывания ложное и, наоборот, из ложного – истинное. Например, высказывание «Москва – столица России» истинно, а данное высказывание, образованное с помощью логического отрицания («Москва – не столица России») – ложно. Ложное высказывание можно сделать истинным с помощью инверсии:

Операцию инверсии в булевой алгебре принято обозначать знаком « ¬ ». Операция логического отрицания, аргументом которой является логическая переменная А, записывается следующей формулой: ¬A. Результатом операции логического отрицания является Истина, когда аргумент Ложь, и значение Ложь, когда аргумент Истина. Таблица истинности для инверсии:

A	¬A
0	1
1	0

Построение таблиц истинности логических выражений

Для каждого логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений логических переменных. Алгоритм построения таблиц истинности:

1. Определить количество строк, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (если переменных n штук, то количество строк будет равно 2ⁿ). Еще одну строку стоит добавить для указания самих переменных, итого строк в таблице будет 2ⁿ + 1.

2. Определить количество столбцов, которое равно количеству логических переменных плюс количество логических операций. Это нужно для того, чтобы вычислять значение логического выражения поэтапно, последовательно выполняя все логические операции над исходными переменными.

3. Построить таблицу с указанным количеством столбцов и строк и внести всевозможные наборы логических переменных. Наборы входных переменных рекомендуется заполнять следующим образом:

• разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю – единицами;

• разделить столбец значений второй переменной на четыре части и заполнить четверти чередующимися группами нулей и единиц;

• продолжать деление столбцов значений последующих переменных на 8, 16, 32 и т.д. частей.

4. Заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с таблицей истинности.

Порядок выполнения логических операций, содержащих конъюнкцию, дизъюнкцию и инверсию

При определении значения сложных логических выражений стоит соблюдать строгий порядок выполнения входящих в выражение операций:

1. Инверсия

2. Конъюнкция

3. Дизъюнкция

4. Более сложные логические операции, о которых поговорим чуть позже.

Аналогично тому, как это делается в арифметике, приоритет выполнения логических операций можно менять с помощью скобок.

Например, у выражения A \/ B /\ (С \/¬D) будет следующий порядок действий:

1. ¬D

2. (С \/¬D)

3. B /\ (С \/¬D)

4. A \/ B /\ (С \/¬D)

Кабинет информатики — Построение таблиц истинности для сложных выражений

Кабинет информатики К уроку информатики Планирование Олимпиады и конкурсы ЕГЭ и ГИА по информатике Открытые мероприятия по информатике Форма входа Построение таблиц истинности для сложных выражений: Количество строк = 2n + две строки для заголовка  (n — количество простых высказываний) Количество  столбцов = количество переменных + количество логических операций При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 исходных выражений. Затем – определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций. ПРИМЕР:  составить таблицу истинности сложного логического выражения D = неA & ( B+C ) А,В, С — три простых высказывания, поэтому : количество строк  = 23 +2 = 10 (n=3, т.к. на входе три элеманта А, В, С) количество столбцов :  1) А 2) В 3) С 4) не A  это инверсия А  (обозначим Е) 5) B + C это операция дизъюнкции (обозначим F) 6) D = неA & ( B+C ), т.е. D = E &  F это операция конъюнкции 1 2 3 4  5  6   А  В  С E = не А  (не 1) F = В+С (2+3)  D = E&F (4*5)  1   1  1 0 1  0  1  1  0 0 1 0 1  o  1 0 1 0 1  o  0 0 0 0 0  1  1 1 1 1 0  1  0 1 1 1 0  0  1 1 1 1 0  0  0 1 0 0 ГБОУ СОШ № 11 Учителя информатики Цитатник Обратная связь Календарь «  Июнь 2023  » Пн Вт Ср Чт Пт Сб Вс       1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Архив записей 2011 Ноябрь 2012 Октябрь Informatika11 © 2023 Бесплатный хостинг uCoz

2.

6: Проверка достоверности таблицы истинности

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

26812

• Мэтью Ван Клив
• Lansing Community College

До сих пор мы научились переводить некоторые английские предложения на наш язык символов, который состоит из набора констант (т. Но какова отдача от этого? В этом разделе мы узнаем, что такое выплата. Короче говоря, выигрыш будет заключаться в том, что у нас будет чисто формальный метод определения достоверности определенного класса аргументов, а именно тех аргументов, достоверность которых зависит от функционирования функциональных связок истинности. Это то, что логики называют «логикой высказываний» или «логикой высказываний».

В первой главе мы изучили неформальный критерий достоверности, который требовал от нас попытаться представить сценарий, в котором посылки аргумента были бы верны, а вывод — ложен. Мы увидели, что если мы можем представить себе такой сценарий, то аргумент недействителен. С другой стороны, если невозможно представить сценарий, в котором посылки верны, а вывод ложен, то аргумент действителен. Рассмотрим этот аргумент:

1. Осужденный сбежал либо проползая по канализационным трубам, либо спрятавшись в кузове грузовика доставки.
2. Но осужденный не сбежал, проползая по канализационным трубам.
3. Таким образом, осужденный сбежал, спрятавшись в кузове грузовика доставки.

Используя неформальный критерий достоверности, мы можем видеть, что если мы представим, что первая посылка и вторая посылка верны, то вывод должен следовать. Однако мы также можем доказать, что этот аргумент верен, не придумывая сценариев и не задаваясь вопросом, будет ли вывод верным в этих сценариях. Мы можем сделать это, а) переведя это предложение на наш язык символов, а затем б) используя таблицу истинности, чтобы определить, верен ли аргумент. Начнем с перевода. Первая посылка содержит два атомарных предложения. Вот предложения и константы, которые я буду использовать для их обозначения:

S = Осужденный сбежал через канализационные трубы

D = Осужденный сбежал, спрятавшись в кузове фургона

Как мы видим, первая посылка является дизъюнкцией, поэтому, используя указанные выше константы, мы можем перевести эту первую посылку следующим образом:

С против Д

Вторая посылка — это просто отрицание S:

~S

Наконец, заключение представляет собой просто атомарное предложение D. Соединяя все это вместе в стандартной форме, мы имеем:

1. С в Д
2. ~С
3. ∴ Д

Мы будем использовать символ «∴» для обозначения заключения и будем читать его «поэтому».

Следующее, что нам нужно сделать, это построить таблицу истинности.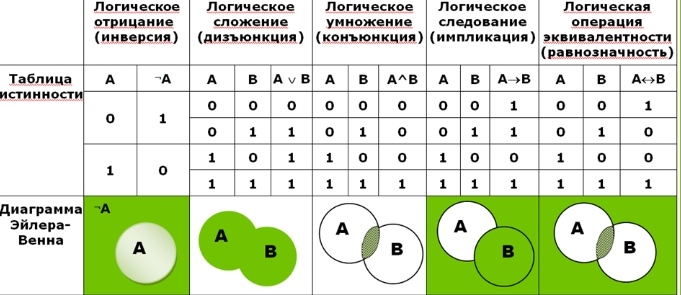 Мы уже видели несколько примеров таблиц истинности, когда я определял функциональные связки истинности, которые я ввел до сих пор (конъюнкция, дизъюнкция и отрицание). Таблица истинности (как мы видели в разделе 2.2) — это просто устройство, которое мы используем для представления того, как значение истинности сложного предложения зависит от истинности предложений, составляющих его, во всех возможных сценариях. При построении таблицы истинности первое, что нужно задать, — сколько атомарных предложений должно быть представлено в таблице истинности. В этом случае ответ «два», так как в этом аргументе содержится только два атомарных предложения (а именно, S и D). Учитывая, что существует только два атомарных утверждения, наша таблица истинности будет содержать только четыре строки — по одной строке для каждого возможного сценария. Будет одна строка, в которой и S, и D верны, одна строка, в которой и S, и D ложны, одна строка, в которой S истинна, а D ложна, и одна строка, в которой S ложна, а D истинна.

Д	С	С против Д	~С	Д
Т	Ф
Т	Ф
Ф	Т
Ф	Ф

Два крайних левых столбца — это то, что мы называем опорными столбцами таблицы истинности.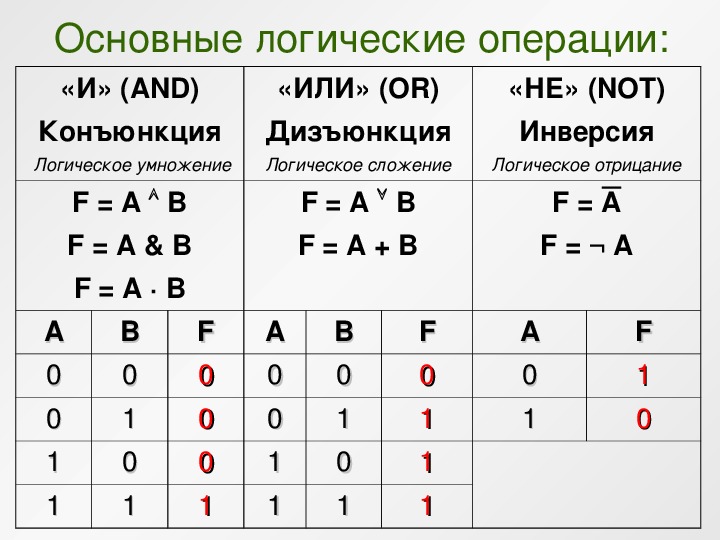 Справочные столбцы присваивают все возможные сочетания значений истинности атомарным предложениям аргумента (в данном случае только D и S). Справочные столбцы охватывают каждый логически возможный сценарий. Поступая таким образом, мы можем заменить использование вашего воображения для воображения различных сценариев (как в неформальном тесте на достоверность) механической процедурой, которая не требует от нас воображения или даже размышлений. Таким образом, вы можете думать о каждой строке таблицы истинности как об указании одного из возможных сценариев. То есть каждая строка является одним из возможных присвоений значений истинности атомарным предложениям. Например, строка 1 таблицы истинности (первая строка после строки заголовка) представляет собой сценарий, в котором верно, что осужденный сбежал, спрятавшись в задней части автофургона, а также верно, что осужденный сбежал, ползать по канализационным трубам. Напротив, ряд 4 представляет собой сценарий, в котором осужденный не сделал ни того, ни другого.

Следующее, что нам нужно сделать, это выяснить, каковы значения истинности предпосылок и заключения для каждой строки таблицы истинности. Мы можем определить, каковы эти истинностные значения, потому что понимаем, как истинностное значение составного предложения зависит от истинностного значения атомарных предложений. Учитывая значения функциональных связок истинности (обсуждавшихся в предыдущих разделах), мы можем заполнить нашу таблицу истинности следующим образом:

Д	С	С против Д	~С	Д
Т	Ф	Т	Ф	Т
Т	Ф	Т	Т	Т
Ф	Т	Т	Ф	Ф
Ф	Ф	Ф	Т	Ф

Чтобы определить значения истинности для первой посылки аргумента («S v D»), нам просто нужно знать значения истинности S и D и значение функциональной связки истинности, дизъюнкции. Таблица истинности дизъюнкции говорит, что дизъюнкция истинна, пока истинна хотя бы одна из ее дизъюнкций. Таким образом, каждая строка в столбце «S v D» должна быть истинной, за исключением последней строки, поскольку в последней строке и D, и S ложны (тогда как в первых трех строках хотя бы одно из них истинно). Значения истинности для второй посылки (~S) легко определить: мы просто смотрим на то, что мы присвоили «S» в нашей справочной колонке, а затем отрицаем эти значения истинности — T становится F, а F становится T. Именно это я и сделал в четвертом столбце таблицы истинности выше. Наконец, вывод в последнем столбце таблицы истинности будет просто повторять то, что мы присвоили «D» в нашем опорном столбце, поскольку последний вывод просто повторяет атомарное предложение «D».

Приведенная выше таблица истинности завершена. Теперь возникает вопрос: как мы используем эту заполненную таблицу истинности, чтобы определить, является ли аргумент действительным? Чтобы сделать это, мы должны применить то, что я назову «проверкой достоверности таблицы истинности». Согласно тесту на достоверность таблицы истинности , аргумент действителен тогда и только тогда, когда для каждого присвоения значений истинности атомарным предложениям, если посылки истинны, то и вывод верен. Аргумент недействителен , если существует присвоение значений истинности атомарным предложениям, посылки которых истинны, а заключение ложно. Крайне важно, чтобы вы понимали (а не просто запоминали), что означают эти определения. Вы должны заметить, что эти определения действительности и недействительности имеют структуру, аналогичную неофициальным определениям действительности и недействительности (обсуждаемым в главе 1). Сходство в том, что мы ищем возможность того, что посылки верны, а заключение ложно. Если это возможно, то аргумент недействителен; если это невозможно, то аргумент действителен. Разница, как я уже отмечал выше, заключается в том, что при проверке достоверности с помощью таблицы истинности мы заменяем использование вашего воображения механической процедурой присвоения истинностных значений атомарным предложениям, а затем определения истинностных значений предпосылок и выводов для них. каждое из этих заданий.

Применяя эти определения к приведенной выше таблице истинности, мы можем видеть, что аргумент действителен, поскольку нет присвоения значений истинности атомарным предложениям (т. вывод ложный. Посмотрите на первый ряд. Разве это ряд, в котором все посылки верны, а заключение ложно? Нет, это не так, потому что не все посылки в этом ряду верны. В частности, «~S» в этой строке ложно. Посмотрите на второй ряд. Разве это ряд, в котором все посылки верны, а заключение ложно? Нет, это не так; хотя обе посылки верны в этом ряду, вывод также верен в этом ряду. Теперь рассмотрим третий ряд. Разве это ряд, в котором все посылки верны, а заключение ложно? Нет, потому что это не тот ряд, в котором обе посылки верны. Наконец, рассмотрим последнюю строку. Разве это ряд, в котором все посылки верны, а заключение ложно? Опять же, ответ «нет», потому что в этой строке не обе посылки верны. Таким образом, мы можем видеть, что нет строки таблицы истинности, в которой все посылки верны, а заключение ложно. А это значит, что аргумент в силе.

Поскольку проверка достоверности таблицы истинности является формальным методом оценки достоверности аргумента, мы можем определить, является ли аргумент достоверным только в силу его формы, даже не зная, о чем этот аргумент! Вот пример:

1. (А в В) в С
2. ~А
3. ∴ С

Вот аргумент, написанный на нашем символическом языке. Я не знаю, что означают A, B и C (т. е. какие атомарные предложения они обозначают), но это не имеет значения, потому что мы можем определить, верен ли аргумент, не зная, что такое A, B и C. иметь в виду. A, B и C могут быть любыми атомарными предложениями. Если эта форма аргумента недействительна, то какое бы значение мы ни придавали A, B и C, аргумент всегда будет недействительным. С другой стороны, если эта форма аргумента верна, то какое бы значение мы ни придавали А, В и С, аргумент всегда будет действительным.

Первое, что нужно понять об этом аргументе, это то, что есть три атомарных предложения, A, B и C. А это означает, что наша таблица истинности будет иметь 8 строк, а не только 4 строки, как в нашей предыдущей таблице истинности. Причина, по которой нам нужно 8 строк, заключается в том, что требуется вдвое больше строк для представления каждого логически возможного сценария, когда мы работаем с тремя разными предложениями. Вот простая формула, которую вы можете использовать, чтобы определить, сколько строк нужно вашей таблице истинности:

2n (где n — количество атомарных предложений)

Вы прочитали эту формулу «два в n-й степени». Итак, если у вас есть одно атомарное утверждение (как в таблице истинности для отрицания), ваша таблица истинности будет иметь только две строки. Если у вас есть два атомарных предложения, у них будет четыре строки. Если у вас есть три атомарных предложения, в нем будет 8 строк. Количество необходимых строк растет экспоненциально по мере того, как количество атомарных предложений растет линейно. В приведенной ниже таблице представлены те же отношения, что и в приведенной выше формуле:

.

Количество атомарных предложений	Количество строк в таблице истинности
1	2
1	4
3	8
4	16
5	32

Итак, наша таблица истинности для приведенного выше аргумента должна иметь 8 строк.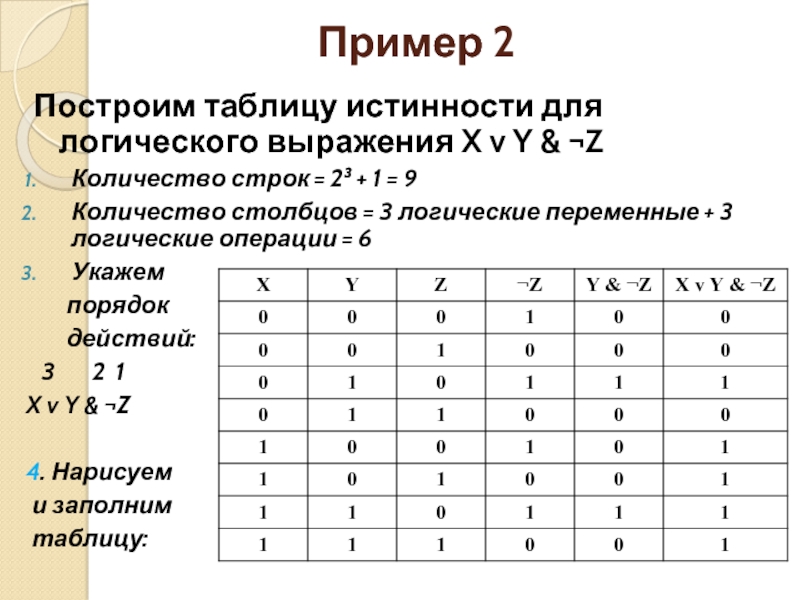 Вот как выглядит эта таблица истинности:

А	Б	С	(А в В) в С	~А	С
Т	Т	Т
Т	Т	Ф
Т	Ф	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Т	Ф
Ф	Ф	Т
Ф	Ф	Ф

Вот важный момент, на который следует обратить внимание при настройке таблицы истинности. Вы должны убедиться, что ваши ссылочные столбцы охватывают каждое отдельное возможное назначение значений истинности. Один из способов убедиться, что вы делаете это, — следовать одному и тому же шаблону каждый раз, когда вы строите таблицу истинности. Не существует единственно правильного способа сделать это, но вот как это делаю я (и рекомендую сделать это и вам). Постройте опорные столбцы так, чтобы атомарные предложения располагались в алфавитном порядке слева направо. Затем в самом правом справочном столбце (столбец C выше) чередуйте true и false в каждой строке, вплоть до самого низа. В справочном столбце слева от него (столбец B выше) чередуйте две строки true, две строки false, вплоть до самого низа. В следующем столбце слева (столбец А выше) чередуйте 4 верных, 4 ложных, вплоть до самого низа.

Следующим шагом является определение истинностных значений посылок и заключения. Обратите внимание, что наша первая посылка представляет собой более сложное предложение, состоящее из двух дизъюнкций. Основным оператором является вторая дизъюнкция, поскольку две основные группы, обозначенные скобками, — это «A v B» и «C». Заметьте, однако, что мы не можем вычислить истинностные значения основного оператора предложения, пока не вычислим истинностные значения левого дизъюнкта «A v B». Вот с чего нам нужно начать. Таким образом, в приведенной ниже таблице истинности я заполнил значения истинности непосредственно под частью «A v B» предложения, используя значения истинности, которые я присвоил A и B в справочных столбцах. Как вы можете видеть в приведенной ниже таблице истинности, каждая строка верна, за исключением двух последних строк, которые ложны, поскольку дизъюнкция ложна только тогда, когда обе дизъюнкции ложны. (Если вам нужно просмотреть таблицу истинности для дизъюнкции, см. раздел 2.3.)

А	Б	С	(А в В) в С	~А	С
Т	Т	Т	Т
Т	Т	Ф	Т
Т	Ф	Т	Т
Т	Ф	Ф	Т
Ф	Т	Т	Ф
Ф	Т	Ф	Ф
Ф	Ф	Т	Ф
Ф	Ф	Ф	Ф

Теперь, поскольку мы вычислили значения истинности левого дизъюнкта, мы можем вычислить значения истинности основного оператора (который я выделил жирным шрифтом в таблице истинности ниже). Два столбца, на которые вы смотрите, чтобы определить значения истинности основного оператора, — это столбец «A v B», который мы только что выяснили выше, и опорный столбец «C» слева. Крайне важно понимать, что значения истинности под «A v B» не имеют значения, как только мы выяснили значения истинности под основным оператором предложения. Этот столбец был только средством для достижения цели (конца определения основного оператора), поэтому я выделил их серым цветом, чтобы подчеркнуть, что мы больше не обращаем на них внимания. (Когда вы составляете свои собственные таблицы истинности, вы можете даже стереть эти вспомогательные столбцы после того, как определили значения истинности основного оператора предложения. Или вы можете просто обвести значения истинности под основным оператором, чтобы отличать их от остальных.)

А	Б	С	(А в В) в С	~А	С
Т	Т	Т	Т Т
Т	Т	Ф	Т Т
Т	Ф	Т	Т Т
Т	Ф	Ф	Т Т
Ф	Т	Т	Т Т
Ф	Т	Ф	Т Т
Ф	Ф	Т	Ф Т
Ф	Ф	Ф	Ф Ф

Наконец, мы заполним оставшиеся две колонки, что очень просто. Все, что нам нужно сделать для «~A», — это отменить значения истинности, которые мы присвоили нашему справочному столбцу «A». И все, что нам нужно сделать для последнего столбца «C», — это просто дословно повторить значения истинности, которые мы присвоили нашему эталонному столбцу «C».

А	Б	С	(А в В) в С	~А	С
Т	Т	Т	Т Т	Ф	Т
Т	Т	Ф	Т Т	Ф	Ф
Т	Ф	Т	Т Т	Ф	Т
Т	Ф	Ф	Т Т	Ф	Ф
Ф	Т	Т	Т Т	Т	Т
Ф	Т	Ф	Т Т	Т	Ф
Ф	Ф	Т	Ф Т	Т	Т
Ф	Ф	Ф	Ф Ф	Т	Ф

Приведенная выше таблица истинности завершена. Следующим шагом является применение проверки достоверности таблицы истинности, чтобы определить, является ли аргумент действительным или недействительным. Помните, что мы ищем строку, в которой посылки верны, а заключение ложно. Если мы находим такую ​​строку, аргумент недействителен. Если мы не находим такой строки, то аргумент действителен. Применяя это определение к приведенной выше таблице истинности, мы видим, что аргумент недействителен из-за 6-й строки таблицы (которую я выделил). Таким образом, объяснение того, почему этот аргумент недействителен, заключается в том, что шестая строка таблицы показывает сценарий, в котором посылки верны, а заключение ложно.

Используйте проверку достоверности таблицы истинности, чтобы определить, являются ли следующие аргументы допустимыми или недействительными.

1.
1. A v B
2. B
3. ∴ ~A

2.
1. A ⋅ B
2. ∴ A v B

3.
1. ~C
2. ∴ ~(C v A)

4.
1. (A v B) ⋅ (A v C)
2. ~A
3. ∴ B v C

5 900 76 .
1. R ⋅ (T v S)
2. T
3. ∴ ~S

6 .
1. A v B
2. ∴ A ⋅ B

7.
1. ~(A ⋅ B)
2. ∴ ~A v ~B

8.
1. ~(A v Б)
2. ∴ ~A v ~B

9.
1. (R v S) ⋅ ~D
2. ~R
3. ∴ S ⋅ ~D

---

Эта страница под названием 2.6: Проверка достоверности таблицы правды распространяется под лицензией CC BY 4.0, ее автором, ремиксом и/или куратором является Мэтью Ван Клив.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Мэтью Ван Клив

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   На этой странице нет тегов.

[SL07] Срок действия

---

§1. Метод полной таблицы истинности

В этом руководстве мы изучаем, как использовать метод полной таблицы истинности для проверки правильности последовательности в SL. Рассмотрим эту допустимую последовательность:

P, (P→Q) &модели; Вопрос

Чтобы доказать его правильность, мы рисуем таблицу, в которой верхняя строка содержит все различные буквы предложений в аргументе, за которыми следуют посылки, а затем заключение. Затем, используя тот же метод, что и при составлении сложных таблиц истинности, мы перечисляем все возможные присвоения значений истинности буквам предложения слева. В нашем конкретном примере, поскольку есть только две буквы предложения, должно быть 4 присвоения:

9 1062 )

P	Q			P			(	P	→	Q			Q
T	T							9109 2
T	F
Ф	Т
Ж	Ж	910 92

Следующим шагом будет составление таблицы истинности для всех посылок, а также заключение:

В заполненной таблице истинности первые две ячейки в каждой строке дают нам присвоение значений истинности, а следующие три ячейки сообщают нам значения истинности посылок и заключение по каждому заданию. Если аргумент верен, то каждое присваивание, в котором все посылки верны, также является присваиванием, в котором верен вывод. Так получилось, что есть только одно задание (первая строка), где обе посылки верны. Из последней клетки строки видно, что и при таком присваивании вывод верен. Таким образом, этот аргумент оказался верным.

В общем, чтобы определить достоверность, просмотрите каждую строку таблицы истинности, чтобы найти строку, в которой ВСЕ посылки верны, а заключение ложно. Сможете ли вы найти такой ряд? Если нет, то аргумент действителен. Если имеется одна или несколько строк, аргумент недействителен.

Обратите внимание, что в таблице выше вывод неверен во второй и четвертой строке. Почему они не показывают, что аргумент недействителен?

§2. Еще примеры

Помните, что (P→Q), ~P, поэтому ~Q недействительно. Посмотрите на таблицу истинности и определите, какая строка должна это показывать?

Чтобы показать, что секвенция недействительна, мы находим одно или несколько присвоений, в которых все посылки верны, а заключение ложно. Такое присвоение известно как , аннулирующее присвоение (контрпример) для секвенции.

Давайте рассмотрим несколько более сложную секвенцию и нарисуем таблицу истинности:

(~P∨Q), ~(Q→P) &модели; (Q↔~P)

Снова рисуем таблицу истинности для предпосылок и заключения:

Чтобы помочь нам рассчитать истинностные значения WFF для каждого задания, мы используем метод полной таблицы истинности, чтобы сначала записать истинностные значения букв предложения, а затем шаг за шагом вычислить истинностные значения всех WFF. шаг. Значения истинности полных WFF для каждого назначения записываются под основным оператором WFF. Как видите, критически важным для проверки является третье задание. Поскольку не существует присваивания, в котором посылки верны, а заключение ложно, секвенция верна.

Изучите эту таблицу и ответьте на вопросы:

1. Какая последовательность проверяется на достоверность в этой таблице?
2. Является ли секвенция действительной в соответствии с этой таблицей?

Правда или ложь?

1. Для любых трех формул φ, ψ и γ, если φ ⊧ ψ и ψ &модели; γ, то φ ⊧ γ.