ФИЗИКА ДП Сила Лоренца Кшинин Иван

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»

Инженерная школа

неразрушающего контроля и безопасности

12.03.01 «Приборостроение»

Эксперемент Сила ЛОРЕНЦА

по дисциплине:

ФИЗИКА

Исполнитель:	ФИО
студент группы	1Б92		Кшинин Иван Бахтиёрович
Руководитель:	ФИО
преподаватель	Кандидат технических наук		Грязнова Елена Николаевна

Томск – 2020

ЭКСПЕРЕМЕНТ СИЛА ЛОРЕНЦА

Эксперимент с ТВ программы Галилео

ВИДЕО, Клик и все

ССЫЛКА

Теория о силе Лоренца

Сила Лоренца это сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу.  

Модуль силы Лоренца   равен произведению модуля индукции магнитного поля  , в котором находится заряженная частица, модуля   заряда q этой частицы, величины ее скорости   и синуса угла α между направлениями скорости   и вектора индукции магнитного поля 

Сила Лоренца, действующая в магнитном поле на движущиеся в одном направлении положительные и отрицательные заряды, имеет противоположное направление.

Силу Лоренца находят по правилу левой руки:

1. Вытянутую ладонь разворачивают так чтобы вектор заряженных частиц входил в нее

2. Если имеем положительный заряд, то вытянутые пальцы указывают движение частицы

3. Вытянутый большой палец показывает направление силы Лоренца

Если ориентация известна, то определить вектора можно по правилу правой руки

Обоснование эксперимента

При проведении эксперимента использовалась электронная пушка для наглядного представления воздействия силы Лоренца на луч с заряженными частицами.

Такая вот штука, своего названия не носит, но обозвали его прибором для демонстрации силы Лоренца

Рисунок 1 «Прибор для демонстрации силы Лоренца»

Видно, что при прямой подаче напряжения на пушку, луч направлен прямо по своему вектору. Характеризуется это тем, что на луч не воздействует какое-либо внешнее магнитное поле.

При подаче напряжения на магнитную катушку возбуждения, вокруг луча создается равномерное магнитное поле.

Направление воздействия силы Лоренца в магнит поле на луч мы находим по правилу левой руки, большой палец направлен вверх, как и видно и ясно в эксперименте луч направляется под воздействием силы Лоренца вверх в кольцеобразную форму, под n-м углом, при увеличении напряжения в магнитной катушке.

В середине эксперимента “КРЕНДЕЛЯ” можно обосновать тем, что когда скорость частицы имеет составляющую вдоль направления магнитного поля, в этом случае луч заряженных частиц совершает спиралевидно движение, потому что был поднесен другой магнит с другим магнитным полем который оттолкнул луч и послал его под углом его первоначального направления.

То есть в однородном магнитном поле, луч будет закручиваться в круг, а при направлении луча под углом к линии магнитной индукции она двигается спиралеобразно.

В эксперименте показана лишь пара витков луча.

Рисунок 2 Спиральное движение луча

P.S Силу Лоренца также можно исследовать и продемонстрировать на старых лучевых телевизорах и мониторах, так как принцип их работы основан на основе кинескопов и спектрографов

как устроены виртуальные лаборатории для школьников / Новости города / Сайт Москвы

Образование

29 сентября 2021 в 12:07

Что можно изучать с помощью виртуальных лабораторий библиотеки «Московской электронной школы» и чем они удобны для учащихся и учителей — в материале mos.ru.

Создать собственную головоломку, провести эксперименты по термодинамике, изучить Python или Pascal — это и многое другое позволяют сделать виртуальные лаборатории «Московской электронной школы» («МЭШ»). Онлайн-симуляторы опытов и экспериментов помогают школьникам изучать свойства различных вещей и явлений, создавать собственные объекты. А еще с их помощью школьники могут провести такие эксперименты, которые в реальной лаборатории выполнить невозможно. Рассказываем, как устроены виртуальные лаборатории «МЭШ», и выясняем, чем они полезны ученикам и преподавателям.

Что такое виртуальная лаборатория

По сути, виртуальная лаборатория — это среда, которая на экране планшета, смартфона, компьютера или классной интерактивной панели имитирует инструменты учебной лаборатории. Здесь можно собирать электрические цепи, строить чертежи или графики, проводить измерения и так далее. Сейчас в библиотеке «МЭШ» 23 виртуальные лаборатории по пяти предметам: физике, биологии, математике, информатике и технологии.

Лабораториями могут пользоваться как учителя, так и школьники. Педагоги применяют их на уроках и создают с их помощью собственные интерактивные задания. А дети могут ставить онлайн-эксперименты не только в школе, но и дома.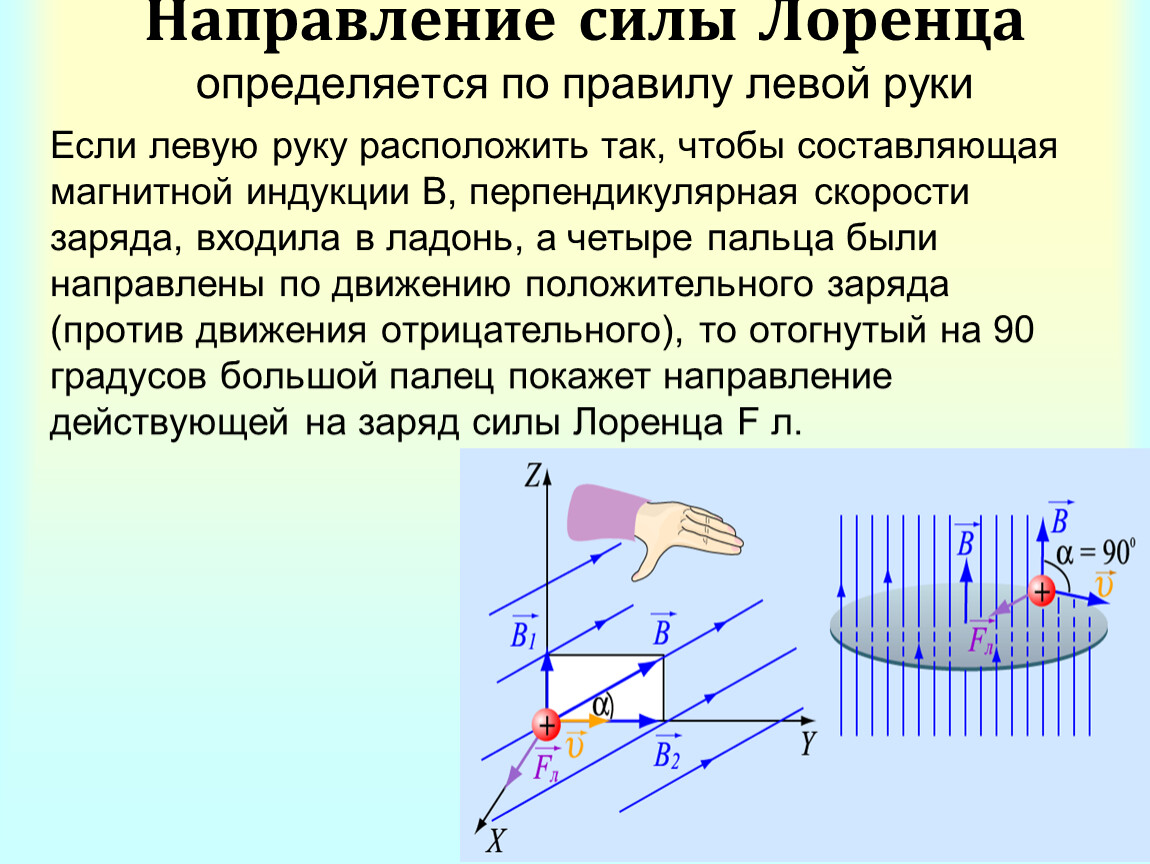 Таким образом, школьникам проще усваивать материал и повторять его.

Закон Ома и магнитные поля

В виртуальных лабораториях по физике можно проводить опыты по электродинамике, оптике, механике и другим разделам. Так, с помощью виртуального инструментария лаборатории «Оптика», включающего коллекцию источников света, препятствий, оптических элементов и измерителей, можно проводить классические эксперименты по измерению длины волны света, изучению законов геометрической оптики, определению оптических свойств линз и зеркал. Лаборатория «Механика» открывает возможности для экспериментов по статике и гидростатике, кинематике, динамике и законам сохранения.

В лаборатории «Электродинамика» пользователи получили в свое распоряжение «черный ящик». С его помощью можно создавать увлекательные задачи-загадки на определение участвующих в эксперименте приборов, их элементов и характеристик любого уровня сложности, включая олимпиадный («черный ящик» скрывает их от пользователей). А еще есть возможность превратить лабораторию в место виртуальных поединков и целых турниров.

«Например, дети изучают закон Ома — как зависит сила тока от напряжения. У них на панели сбоку есть все необходимые инструменты. Они мышкой переносят на рабочее поле резистор, амперметр, вольтметр, источник тока, все это соединяют по схеме с проводами, ставят батарейку и проводят измерения. Можно заменить резистор — взять с большим или меньшим сопротивлением. Дети могут посмотреть зависимость силы тока от напряжения для разных резисторов и сравнить их», — объясняет Юлия Казакова, учитель физики Бауманской инженерной школы № 1580.

Совсем недавно в блоке физики появилась виртуальная лаборатория «Электромагнитное поле. Фарадей». Здесь можно изучать электрические и магнитные поля, а также электромагнитные явления. Есть возможность выбрать нужные параметры и свойства объектов, сохранить свой опыт или эксперимент на любом этапе, а потом его продолжить.

Плюс виртуальных лабораторий в том, что они не ограничивают возможности учителей и учеников для проведения экспериментов. Например, во время реальных лабораторных дети работают с источником напряжения около 4,5 вольта — больше нельзя. В виртуальной среде таких ограничений нет, там можно смоделировать любые параметры.

«Было бы интересно развивать эти вещи в сторону исследовательской работы для детей, которые углубленно изучают физику. То есть создавать эксперименты, которые нельзя провести в реальных условиях или которые не входят в школьную программу. Это огромные возможности! Например, детям было бы интересно повторить опыт Галилео Галилея — как он бросал шары с Пизанской башни, изучал равноускоренное движение тел с помощью наклонной плоскости. Или воссоздать опыт Ампера — посмотреть на взаимодействие проводников с током и измерить силу Ампера. В реальной жизни это трудновоспроизводимый опыт», — говорит Юлия Казакова.

В то же время, отмечает учитель, виртуальные лаборатории хороши как дополнение реальных, а не их замена. Виртуальная работа, какой бы хорошей она ни была, не заменит работу с настоящими приборами, явлениями и объектами.

«Какие-то вещи, которые в реальной жизни воссоздать невозможно или очень трудно, можно и нужно создавать в виртуальной среде. Там ведь можно сделать все что угодно — вплоть до моделирования адронного коллайдера, создать экстремальные температуры, магнитные и электрические поля. Дети могут изучать действие силы Лоренца на движущиеся заряженные частицы в электронно-лучевой трубке», — рассказывает учитель.

Головоломки и роботы

Ринат Закиров, учитель физики школы № 1466, работает с виртуальными лабораториями не только по физике, но и по технологии. В частности, с разделом «Логитариум», который посвящен изучению сложных механизмов и принципов взаимодействия между объектами. А еще «Логитариум» может служить отличной площадкой для интеллектуальных соревнований.

«Я работал с виртуальной лабораторией “Логитариум”, когда наши ученики принимали участие в турнире “Технобой”. Мы с детьми изучали эту виртуальную лабораторию, в которой требовалось составлять головоломки на основе машин Голдберга. “Логитариум” позволяет развить техническое мышление у детей, показать работу таких механизмов, как зубчатые колеса, реечные передачи и многие другие. В лабораторию периодически добавляют новые механизмы», — рассказывает учитель.

Лаборатория помогает детям развивать смекалку, воплощать оригинальные идеи при создании машин Голдберга — механизма, где каждое действие является толчком к следующему действию, — и технических головоломок на их основе. А учителям технологии, физики и информатики лаборатория позволяет создавать интерактивные модели для демонстрации устройств из мира техники и механики.

«Детям очень нравится эта история, они с удовольствием составляют механизмы, придумывают собственные головоломки. Там есть такая опция — сохранить головоломку и дать ее решить одноклассникам, — говорит Ринат Закиров. — Я пробовал показывать “Логитариум” ученикам начальных классов — им интересно, но все-таки сложно. А вот начиная с седьмого класса дети уже вполне могут самостоятельно создавать сложные модели. Проявляют интерес к механизму и старшеклассники (в рамках предмета “Индивидуальный проект”). Мы с ребятами работаем над созданием интерактивных моделей».

Помимо «Логитариума», в блоке «Технология» есть виртуальные лаборатории, посвященные построению логических схем (для школьников, изучающих современную электронную технику и схемотехнику) и использованию микроконтроллеров. Также есть лаборатория «Моделирование роботов», которая позволяет освоить основы робототехники, сконструировать и запрограммировать собственного мобильного, промышленного или сервисного робота.

Пять языков программирования и почти 300 тестов

С этого учебного года для учеников 7–11-х классов открыта виртуальная лаборатория по информатике. Это огромная база для углубления знаний и подготовки к экзаменам и олимпиадам: лаборатория включает 290 готовых тестов, более девяти тысяч заданий и свыше 250 курсов по программированию.

Лаборатория охватывает такие разделы, как информационные технологии, математические основы информатики, основы программирования, базовые и продвинутые алгоритмы.

«Там есть задания самого разного уровня — от базового до продвинутого. Все начинается с основ. Есть пять языков программирования: C#, С++, Python, Pascal, Java. Соответственно, ребенок выбирает один из них, и ему дают задания, начиная с самых простых. Есть небольшие обучающие видеоролики, описания к заданиям, и ребенок их выполняет: пишет какой-то код самостоятельно или меняет уже готовый код и отправляет на проверку. Программа делает тесты кода и выдает результат, насколько правильно он выполнил задание», — объясняет Игорь Линьков, учитель информатики школы № 1539.

Ученики выполняют задания виртуальной лаборатории как в классе, вместе с учителем, так и самостоятельно дома. Важно, что, если ребенок пропустил занятие, он может благодаря лаборатории освоить пропущенный материал.

В ближайшее время у учителей появится возможность прикреплять материалы лаборатории к цифровому домашнему заданию в электронном журнале. Учащиеся видят их в разделе «Домашние задания» электронного дневника и, переходя по ссылке, выполняют.

Еще одна полезная опция для детей — возможность посмотреть статистику своих результатов: время, затраченное на прохождение задания, верные и неверные ответы, процент правильно выполненных заданий.

«В целом виртуальные лаборатории — очень хорошая вещь, нам не хватало такого ресурса. Важно, что они продолжают развиваться. Что касается моего предмета, информатики, то хотелось бы в будущем увидеть лабораторию по моделированию. Это создание 3D-моделей в специализированных программах и возможность напечатать эти модели на 3D-принтере», — добавляет Игорь Линьков.

Теги

школы образование школьники МЭШ виртуальные лаборатории

Сферы

Образование,  Технологии,  «Московская электронная школа»

Департаменты

Департамент информационных технологий города Москвы, Департамент образования и науки города Москвы

Все новости

Световой постулат Эйнштейна спас Галилея

Добрый вечер (время местное)! Я хотел бы поделиться с вами ответом, который я дал сегодня одному из моих студентов. Он спросил, как постулат Эйнштейна о постоянной скорости света (независимой от собственного состояния движения наблюдателя) может спасти галилеевскую теорию относительности.

В теории относительности Галилея законы физики одинаковы для всех наблюдателей, имеющих постоянную скорость относительно друг друга (прочитайте этот пост, чтобы напомнить, как это работает). Ключ здесь постоянное движение ; как только наблюдатели начинают ускоряться, начинают играть роль силы инерции — и относительность Галилея больше не действует.

Все хорошо, Максвелл*?

Однако в девятнадцатом веке был открыт новый тип силы: электромагнитная, или сила Лоренца. Эта сила отличается от ньютоновской гравитации тем, что зависит от скорости частицы (а не только от ускорения): величина силы Лоренца, действующей на заряженную частицу, движущуюся в магнитном поле, зависит от скорости частицы относительно поле (см. рисунок выше).

В теории электромагнетизма Максвелла магнитное поле покоится относительно абсолютного пространства. Таким образом, нам нужно абсолютное пространство, чтобы определить, насколько сильна электромагнитная сила, но теория Эйнштейна известна тем, что отвергает понятие абсолютного пространства. В результате нет понятия абсолютного движения и, следовательно, нет способа определить силу силы Лоренца. Эйнштейн решил эту проблему, введя свой постулат о свете. Постулат света решает проблему? Почему постоянная скорость света — скорость, одинаковая для всех наблюдателей, независимо от их собственного состояния движения — спасает галилеевскую относительность?

Теория относительности Лоренца

Чтобы ответить на этот вопрос, мы должны сначала понять, что значит «спасти» теорию относительности Галилея. Что такое относительность Галилея? Ладно, законы физики должны быть одинаковыми для всех наблюдателей, но что это значит? Это означает, что все наблюдатели могут договориться о величине силы, действующей на какой-либо объект , если они знают скорости, которые имеют они сами относительно друг друга и объекта . Но в этом и есть подвох! Потому что без понятия абсолютного пространства нет понятия абсолютного движения, и поэтому бессмысленно говорить о двух движущихся объектах, что один движется быстрее другого (единственное, что мы измеряем, это относительная скорость , поэтому мы можем только сказать, что они движутся относительно друг друга). А если мы не знаем скорости какой-то заряженной частицы, мы не можем сказать, насколько велика сила Лоренца, действующая на нее.

Скорость света как спасательный круг

Как решает эту проблему постоянная скорость света? Давайте рассмотрим простой пример: предположим, мы хотим измерить скорость заряженной частицы, регистрируя фотоны, которые она отражает, в два момента времени (t_1 и t_2; см. изображение ниже). Скорость частицы — это длина пройденного ею пути, деленная на интервал времени между двумя обнаружениями фотонов. Но как узнать длину этого пути? Мы можем вычислить его, сравнив положение частицы в момент времени t_1 и ее положение в момент времени t_2. Но только если мы знаем скорость фотонов (которую в классической физике мы бы не знали, потому что в абсолютном пространстве мы не можем быть уверены, что сами находимся в покое).

Ниже вы найдете подробный расчет. Мы видим, что мы можем определить дельту x, если мы знаем значение c, поскольку t-значения — в уравнении внизу — могут быть измерены.

Constant-lightspeedDownload

*) Если вы не поняли каламбур, нажмите здесь.

Нравится:

Нравится Загрузка…

Эта запись была опубликована в Философия физики с пометками абсолютное пространство, Эйнштейн, электромагнетизм, теория относительности Галилея, специальная теория относительности. Добавьте постоянную ссылку в закладки.

ЭПИЛОГ | Принципы и теории относительности от Галилея до Эйнштейна

Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиOxford Scholarship OnlineBooksJournals Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиOxford Scholarship OnlineBooksJournals Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер

Укажите

Дарригол, Оливье, «ЭПИЛОГ», Принципы и теории относительности от Галилея до Эйнштейна (

Oxford

, 2021; онлайн-издание, Oxford Academic, 18 августа 2022 г. ), https://doi.org/10.1093/oso/9780192849533.003 .0011, по состоянию на 17 мая 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиOxford Scholarship OnlineBooksJournals Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиOxford Scholarship OnlineBooksJournals Введите поисковый запрос

Advanced Search

Abstract

В этой последней главе кратко обсуждаются исторические условия (роль эксперимента, математики, философии, теоретических взглядов и т. д.) событий, описанных в этой книге. Затем он обращается к тому, как вопрос об референции движения возник в предыдущих главах, с целью показать концептуальную непрерывность и разрывы на протяжении трех столетий размышлений о пространстве, времени и инерции. Наконец, критическое внимание уделяется утверждению Эйнштейна о том, что общая теория относительности вытекает из обобщенного принципа относительности.

Ключевые слова: пространство, время, пространство-время, системы отсчета, принцип относительности, независимость от фона, принцип Маха

Предмет

Вычислительная физикаИстория физики

Коллекция: Оксфордская стипендия онлайн

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.