ЕГЭ информатика 2 задание разбор, теория, как решать
ЕГЭ информатика 2 задание разбор, теория, как решать
Таблица истинности логической функции, (Б) — 1 балл
26.10.2022ЕГЭ Задание 2АдминистраторКомментарии: 0Миша заполнял таблицу истинности логической функции F ¬(y → x) \/ (z → w) \/ ¬z, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите …
Читать далее
21.02.2022ЕГЭ Задание 2АдминистраторКомментарии: 0Ученик заполнял таблицу истинности логической функции F = (w ≡ z) ∨ (x ∧ ¬y) ∨ w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, х, у, z в том порядке, в котором идут …
Читать далее
14.
Логическая функция F задаётся выражением: (¬y → (z ≡ w)) ∧ ((z → x) ≡ w) Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие …
Читать далее
25.01.2022ЕГЭ Задание 2АдминистраторКомментарии: 0Логическая функция F задаётся выражением (x ˄ (y ˅ ¬z) ˄ w) ≡ (x → ¬y ˄ z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции Есоответствует каждая из переменных х, у, z, w. В ответе напишите буквы х, у, z, w в том порядке, …
Читать далее
08.12.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Логическая функция F задаётся выражением: (y → z) /\ ¬((y \/ w) → (z /\ x)). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие …
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие …
Читать далее
10.11.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Читать далее
14.09.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Миша заполнял таблицу истинности логической функции F ¬(y → (x ≡ w)) /\ (z → x), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Читать далее
16.06.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Миша заполнял таблицу истинности функции (x \/ ¬y) /\ ¬(x≡z) /\ w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, …
Читать далее
11.06.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Читать далее
04. 02.2021ЕГЭ Задание 2АдминистраторКомментарии: 0
02.2021ЕГЭ Задание 2АдминистраторКомментарии: 0Логическая функция F задаётся выражением (x → y /\ ¬ z) \/ w. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие …
Читать далее
ЕГЭ по информатике 2022 — Задание 2 (Ай да Питон!)
Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2022. Сегодня разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь).
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый мощнейший метод, но автоматизированный с помощью питона.
Нам нужно будет запрограммировать логическую функцию на языке Питон. Вот таблица, которая поможет это сделать.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
Перейдём к практике решения задач задания 2 с помощью языка программирования Python.
Задача (Классическая)
Миша заполнял таблицу истинности логической функции F
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция F задана выражением ¬x \/ y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.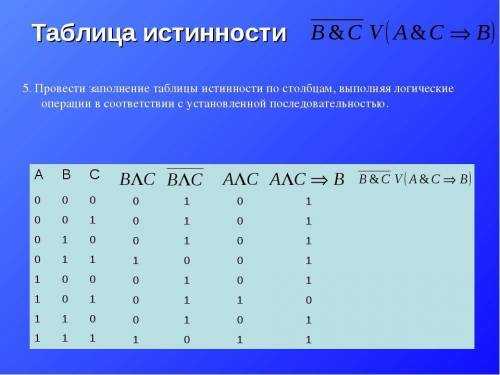
Решение:
Решать задачу будем с помощью шаблона на языке Python (Питон).
print('x y z w')
for x in range(0, 2):
for y in range(0, 2):
for w in range(0, 2):
for z in range(0, 2):
if (not(w) or z) and ((not(y) or x) == (not(z) or y)):
print(x, y, z, w)
В задаче у нас 4 переменные, значит, формируем 4 вложенных цикла. В каждом цикле перебираем все возможные значения для конкретной переменной. Мы перебираем значения 0 и 1.
Функция должна выдавать всегда 1 (единицу, истину). Внутри всех циклов прописываем условие, которое срабатывает как раз на истину. В этом условии прописываем нашу функцию. Если наша функция будет выдавать истину, то мы распечатаем значения переменных, при которых это произошло. Если функция будет выдавать ложь, значит, ничего распечатано не будет.
Четыре вложенных цикла проверяют все возможные варианты (24 = 16 вариантов), и мы получим таблицу истинности, почти такую же, как нам и дали в условии задачи.
Так же вверху печатаем названия переменных, чтобы знать, какие значения каким переменным принадлежат.
Запустим программу, и на экране распечатается табличка:
В получившийся табличке может быть больше строчек, чем в условии. Так же при поиске переменных нельзя опираться на порядок, в котором идут нули и единицы в нашей табличке. А можно опираться лишь на количество нулей и единиц в строчках или столбцах.
Можно вычеркнуть первую строчку и последнюю, потому что в таблице, которую дали в условии, в каждой строчке есть хотя бы один ноль и хотя бы одна единица.
Сразу видно, что первый столбец принадлежит переменной x, только там могут быть все единицы.
Второй столбец принадлежит переменной w, только там могут быть все нули.
У нас остались две пустые клеточки в самой таблице. Нам нужно где-то поставить единицу, а где-то ноль, потому что у нас остались столбцы с двумя единицами и одним нулём, а так же с двумя нулями и одной единицей. Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
А в условии сказано, что строки не должны повторяться. Поэтому нужно ноль и единицу расставить наоборот.
Получается, что в третий столбец идёт z, а в четвёртый y
Ответ: xwzy
Посмотрим, как решать задачи второго задания из ЕГЭ по информатике, когда функция выдаёт нули в таблице истинности.
Задача (Классическая, закрепление)
Миша заполнял таблицу истинности функции (x ≡ ¬y) → ((x ∧ w) ≡ z), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.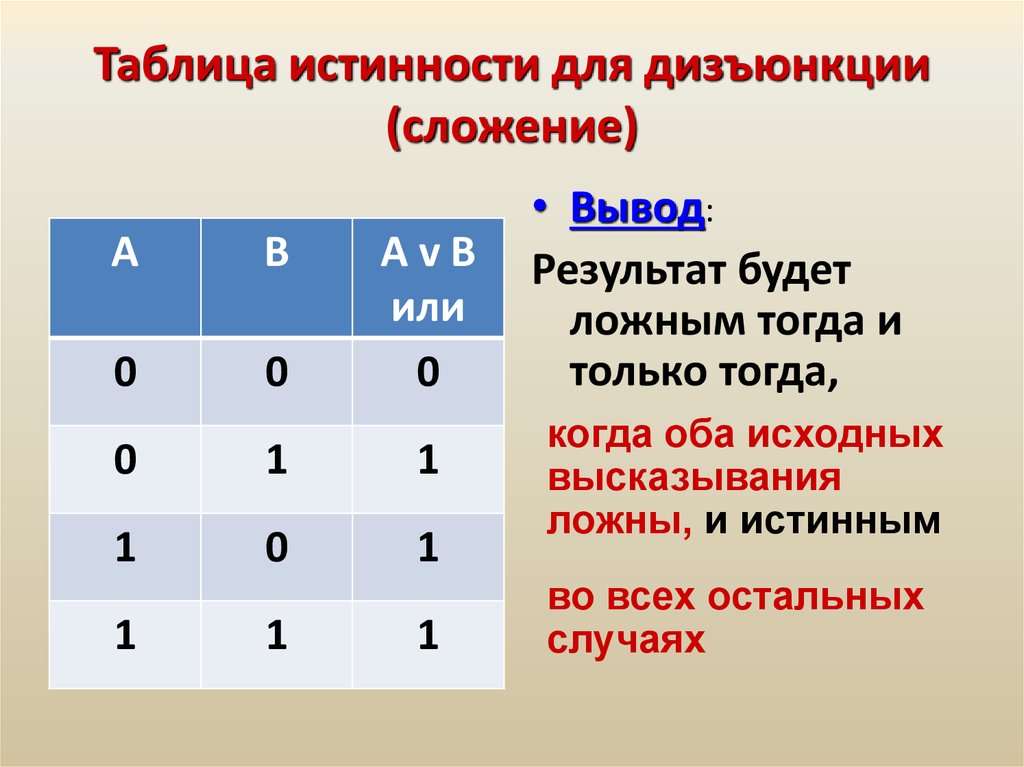 д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Функция F задана выражением ¬x \/ y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать: yx.
Решение:
Воспользуемся программой на языке Python.
print('x y z w')
for x in range(0, 2):
for y in range(0, 2):
for w in range(0, 2):
for z in range(0, 2):
if not( not(( x == (not(y)) )) or ((x and w) == z) ):
print(x, y, z, w)
От прошлой программы эта программа отличается только функцией!
В таблице видим, что функция должна выдавать ноль. Поэтому в условии мы функцию «оборачиваем» в not().
После == операцию not() мы заключили в скобки, чтобы не было синтаксической ошибки.
Получаем следующую таблицу истинности:
Разгадаем, где какая переменная находится.
Последнюю строку из нашей таблицы можно вычеркнуть, потому что, если мы вычеркнем другую строку, то не получится столбца, где все три единицы, а он должен быть.
Получается, что второй столбец достаётся переменной z.
В первом столбце должно быть две единицы. На эту роль подходит переменная y.
В нашей таблице нет строчки, где все единицы, значит, во второй строчке в пустом окошке выставляем ноль. И в этой строчке нулём обладает переменная x. Следовательно, в третьем столбце будет находится x.
А в последний столбец идёт переменная w по остаточному принципу.
Ответ: yzxw
А как Питон справится с более сложной функцией из примерного варианта ЕГЭ по информатике?
Задача (Сложная функция)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).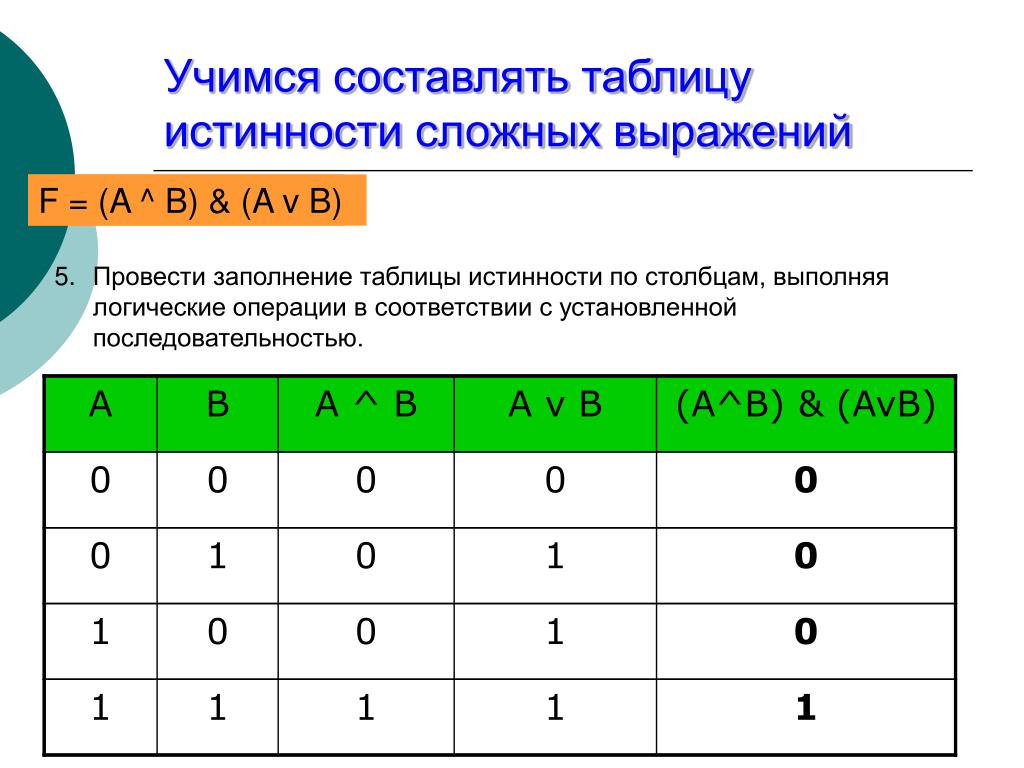
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Источник задачи сайт решу ЕГЭ: https://inf-ege.sdamgia.ru/
Решение:
Запрограммируем функцию на языке Python.
print('x y z w')
for x in range(0, 2):
for y in range(0, 2):
for w in range(0, 2):
for z in range(0, 2):
if not( ((not(x) or y) and (not(y) or w)) or (z == (x or y)) ):
print(x, y, z, w)
Запустим программу и расставим переменные по своим местам.
Переменная z может быть только в третьем столбце.
Во второй столбец идёт переменная w, только этот столбец может иметь одну единицу.
Посмотрим на строчку, где у w стоит единица. В этой же строчке и у x единица. Значит, x идёт в последний столбец, а y в первый столбец.
Ответ: ywzx
Тот же шаблон работает, когда у нас во втором задании три переменные.
Задача (Три переменные)
(№ 1608) Логическая функция F задаётся выражением (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z)
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.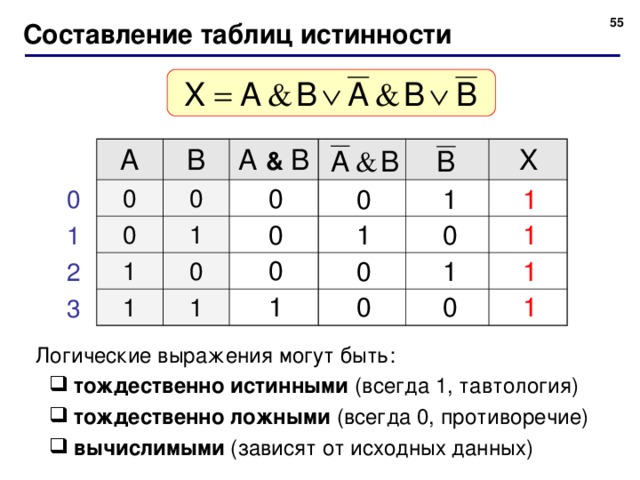 Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Для трёх переменных шаблон на Питоне отлично работает.
print('x y z')
for x in range(0, 2):
for y in range(0, 2):
for z in range(0, 2):
if (not(x) and z) or (not(x) and not(y) and not(z)):
print(x, y, z)
Здесь и так понятно, куда какая переменная идёт.
Ответ: yxz
Посмотрим, как решать задачи из второго задания ЕГЭ по информатике, когда в таблице истинности разные значения у функции F.
Задача (Разные значения функции)
Логическая функция F задаётся выражением (¬a ∨ b ∨ ¬c) ∧ (b ∨ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.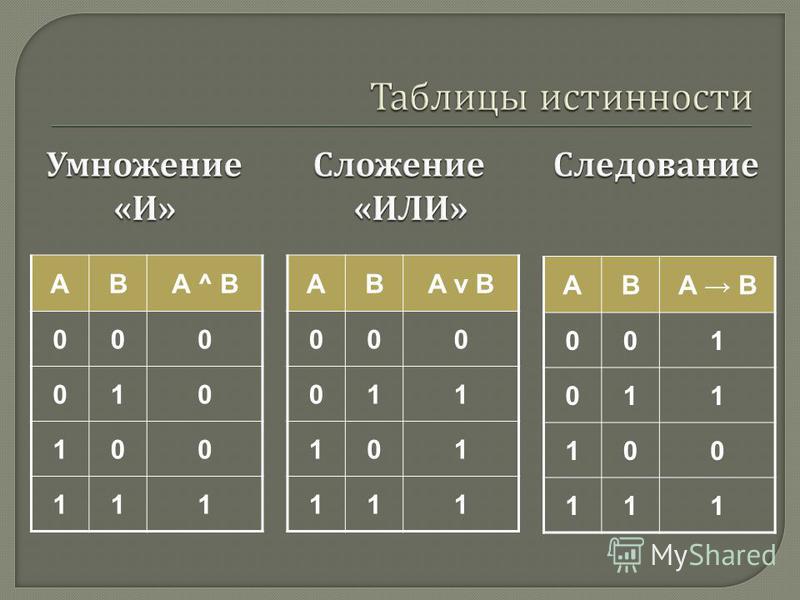
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Когда такая ситуация, что функция имеет различные значения в таблице, мы можем проверить, какие значения переменных дают единицу у всей функции. А потом проверить, какие значения выдают ноль у всей функции, если это потребуется.
print('a b c')
for a in range(0, 2):
for b in range(0, 2):
for c in range(0, 2):
if (not(a) or b or not(c)) and (b or not(c)):
print(a, b, c)
В таблице 6 строчек, в которых главная функция превращается в единицу. Далее эти строчки и будем рассматривать. У нас тоже получилось 6 строчек.
Переменная a имеет три единицы. Это второй столбец, потому что там три единицы.
Переменная b имеет четыре единицы, значит, она расположена в первом столбце.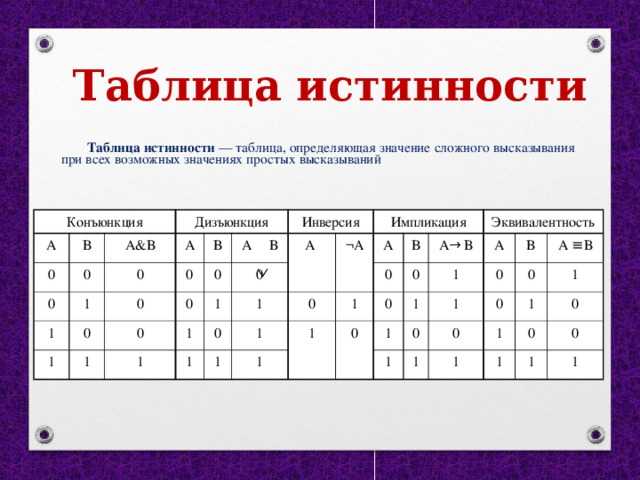
Переменной c достаётся последний столбец.
Ответ: bac
Ещё одна интересная задача для подготовки к ЕГЭ по информатике 2022.
Задача(С подвохом)
Логическая функция F задаётся выражением a ≡ b ∨ b → c.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
Источник задачи группа Евгения Джобса: https://vk.com/inform_web
Решение:
Подвох заключается в том, что если мы переведём бездумно функцию на язык Питон, то получится a==b or not(b) or c. Но у нас существуют приоритеты для логических операций, которые описаны в прошлогодней статье по подготовке к ЕГЭ по информатике.
В начале должно обрабатываться или, которое было изначально.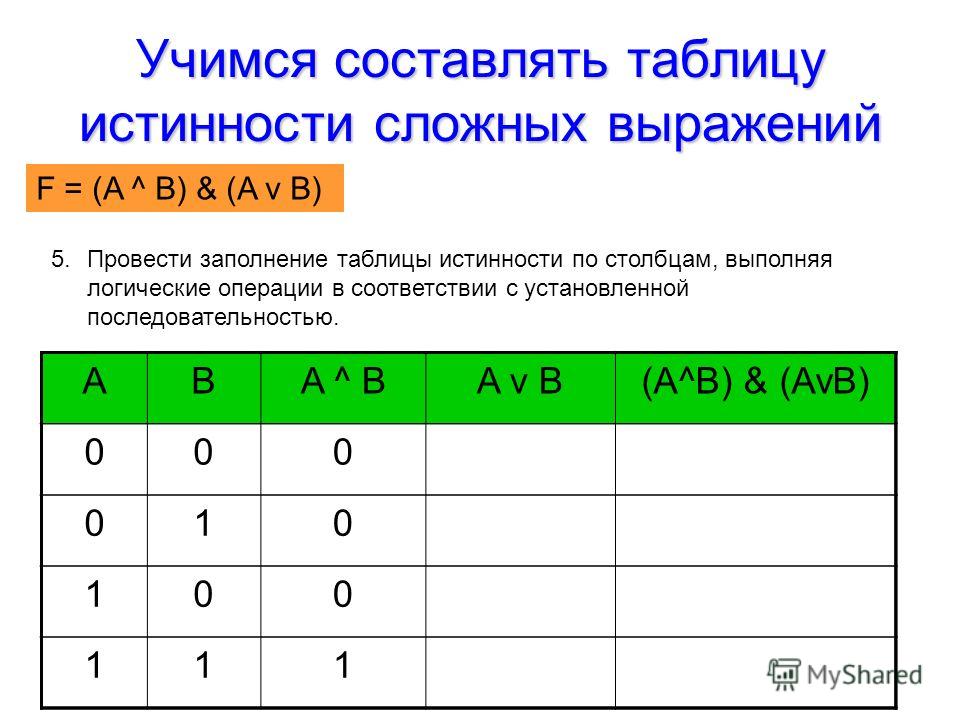 Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Операцию b ∨ b можно представить, как просто b. Ведь, если b принимает значение 0, тогда будет 0 ∨ 0 = 0. Если значение будет 1, то 1 ∨ 1 = 1. Поэтому формулу можно переписать следующим образом:
В предыдущих задачах нам не приходилось думать над приоритетами, потому что везде были расставлены скобки. И в основном они уже расставлены в задачах второго задания из ЕГЭ по информатике.
Дальше решаем как обычно.
print('a b c')
for a in range(0, 2):
for b in range(0, 2):
for c in range(0, 2):
if a == (not(b) or c):
print(a, b, c)
Последнюю строчку можно вычеркнуть из нашей таблицы, т.к. у нас в каждой строчке есть хотя бы один ноль.
Последний столбец занимает переменная a, т. к. только в последний столбец может влезть две единицы.
к. только в последний столбец может влезть две единицы.
В строчке, где у a ноль, так же ноль и у переменной c. Значит, во второй столбец идёт переменная c. Если мы ноль поставим в первой строчке в первом столбце, то получится первый столбец из всех нулей. А такого у нас в таблице истинности нет.
Тогда переменная b в первом столбце.
Ответ: bca
Как решать задачи с таблицами истинности
Таблица истинности представляет собой список всех возможных комбинаций входных значений и результатов, к которым они приводят. Название происходит от того факта, что это математическая таблица, которая показывает все возможные результаты всех возможных фактов. В логических задачах, например в булевой алгебре и электронных схемах, обычно используются таблицы истинности.
Таблица истинности — это математическая таблица, которая помогает определить, является ли сложное утверждение истинным или ложным. В таблице истинности каждое утверждение обычно представляется буквой или переменной, например p, q или r. Каждое утверждение также имеет свой собственный столбец в таблице, в которой перечислены все возможные значения истинности. В этом уроке мы рассмотрим несколько примеров таблиц истинности и изучим основные правила их составления.
Возможно, в повседневной жизни мы не рисуем таблицы истинности, но мы по-прежнему используем ту же логику, которая используется для составления таблиц истинности, чтобы выяснить, правда это или ложь. Скажем, кто-то говорит нам: «Если на улице идет дождь, футбольный матч не состоится». Мы можем использовать правила логического рассуждения, чтобы выяснить, является ли утверждение истинным или ложным, и, возможно, составить план Б. таблица — это способ увидеть все способы решения проблемы.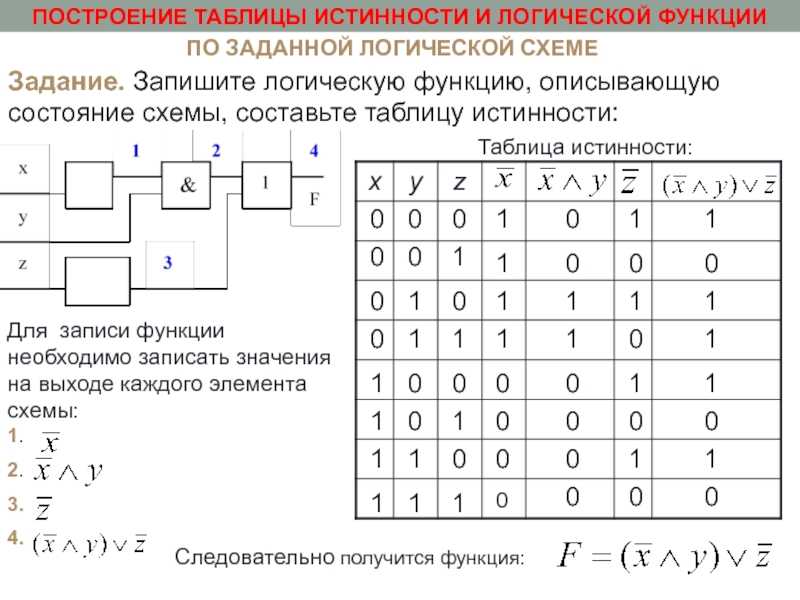 Для дискретной математики вы должны знать, как использовать таблицы истинности. Здесь мы рассмотрим все ответы на простое уравнение p q.
Для дискретной математики вы должны знать, как использовать таблицы истинности. Здесь мы рассмотрим все ответы на простое уравнение p q.
Шаг 2: Изучите знаки
Первый шаг к получению таблицы истинности — выяснить, что означают знаки. В этой конкретной задаче «» означает «не». «p» и «q» могут меняться. «» — это то же самое, что и слово «и». Это уравнение можно записать как «не p и q», что означает, что оно истинно, если p ложно, а q истинно.
Шаг 3: Форматирование таблицы
Теперь давайте сделаем таблицу. Важно рассматривать каждую часть проблемы отдельно. Для этой задачи мы разобьем ее на p, p, q и p q. Изображение дает вам хорошее представление о том, как должен выглядеть ваш стол.
Шаг 4: Присвоение значений True и False
Поскольку переменных всего две, для каждой переменной есть только четыре возможных ответа. Для p мы помещаем T (истинно) в половину пробелов и F в другую половину (ложно).
Шаг 5: Отрицание
Поскольку p противоположно p, вы записываете знак, которого у p нет.
Шаг 6: Переменная «q»
Чтобы получить все возможные комбинации для q, вы переключаетесь между T и F. Поскольку уравнение касается только p, мы можем игнорировать столбец p при выяснении, верно ли оно . «» означает, что и p, и q должны быть истинными, чтобы уравнение было верным.
Шаг 7: Нахождение False в последнем столбце
Для первой строки p равно F, q равно T, поэтому, если p равно F, а q равно T, то p q равно F. Только если оба p и q T делает уравнение равным T.
Шаг 8: Найдите правильный ответ в последнем столбце
Это означает, что третья строка единственная с буквой T.
Шаг 9: Завершение таблицы
Проверьте еще раз, чтобы убедиться, что ваша таблица верна. Для этого вам нужно убедиться, что ваши знаки верны и что последний столбец сделан правильно. В последнем столбце вы можете увидеть результат всех различных способов объединения переменных.
Шаг 10: Готово
Теперь, когда вы знаете, как составить простую таблицу истинности, продолжайте делать это.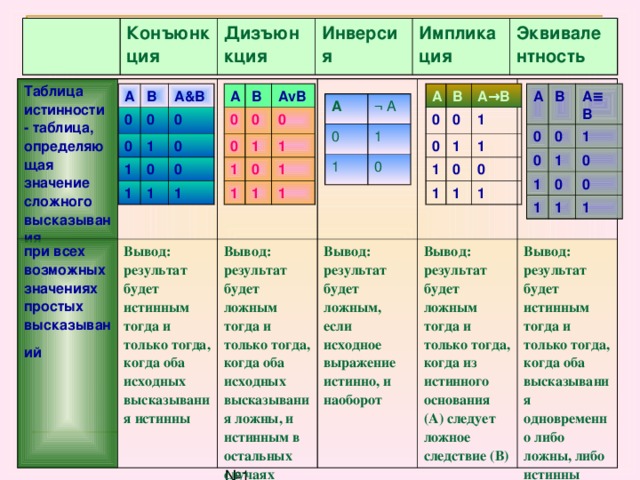 Больше практики сделает вас лучше в их выполнении.
Больше практики сделает вас лучше в их выполнении.
Пример 1: Используйте конъюнкцию, чтобы найти логическую таблицу истинности для набора значений.
Если P равно F F T F T и Q равно F T T T F,
Решение:
P | Q | 210003|
F | F | F |
F | T | F |
T | T | T |
F | T | F |
T | F | F |
Пример 2: Составьте таблицу истинности для выражений ~P∨∼Q и ∼(P∧Q).
Solution:
P | Q | ~P | ~Q | ~P∨∼Q | (P∧Q) | ~(P∧Q) | ||||||||||||
T | T | F | F | F | T | F | ||||||||||||
T | F | F | T | T | F | T | ||||||||||||
F | T | T | F | T | 191919191919191919191919191919191319191913 | 29009 2 | 99191919132 | 2 | T9003 | 994 | T | 0094 | T | |||||
F | F | T | T | T | F | T |
Example 3 : Пусть S будет непустой частью R.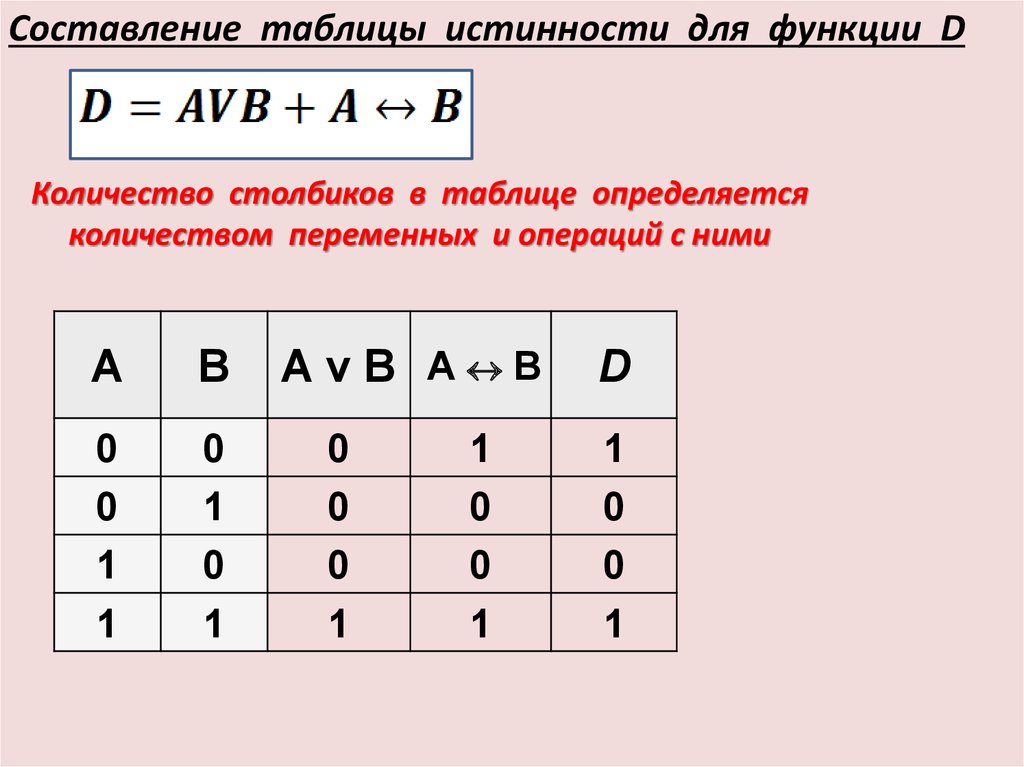 Подумайте о следующем предложении: P: В S есть рациональное число x, большее 0. Какое из приведенных ниже утверждений противоположно утверждению p?
Подумайте о следующем предложении: P: В S есть рациональное число x, большее 0. Какое из приведенных ниже утверждений противоположно утверждению p?
- A) x > S и x > 0 > x не является рациональным утверждением.
- B) Существует рациональное число x такое, что x 0.
- C) Не существует рационального числа x S, для которого x 0.
- D) Каждое рациональное число x S удовлетворяет условию x 0.
Решение:
P: Существует рациональное число x S, где x > 0.
P: Каждое рациональное число x S удовлетворяет условию x 0.
Заключениекоторый показывает логическое выражение функции логического вентиля. В таблице истинности логического вентиля перечислены все возможные входы вентиля или схемы и выходы, которые являются результатом этих входов (ов).
Использование таблиц истинности для решения логических задач | Использование таблиц истинности для решения логических задач
Создано 30 апреля 2021 г. пользователем
Администратор userSTEMToolkit
пользователем
Администратор userSTEMToolkitРезюме
Учащиеся будут использовать таблицы истинности с двумя, тремя или четырьмя входными данными для решения логических задач. Этот урок предполагает, что учащиеся знают, как реализовать логические решения для цифровых логических элементов (инженерное дело) или программного обеспечения (информатика).
Предварительные требования
Учащиеся будут знать, как реализовать логические решения для цифровых логических элементов (инженерное дело) или программного обеспечения (информатика). Возможные решения включают следующее:
Цифровые логические элементы
Учащиеся получат базовое представление о цифровых логических элементах (И, ИЛИ и инверторы). Решения простых проблем можно реализовать с помощью littleBits (littlebits.com) или комплектов Snap Circuit Kit (www.elenco.com/brand/snap-circuits/). Более сложные решения могут быть реализованы с использованием полупроводников, макетов и проводов.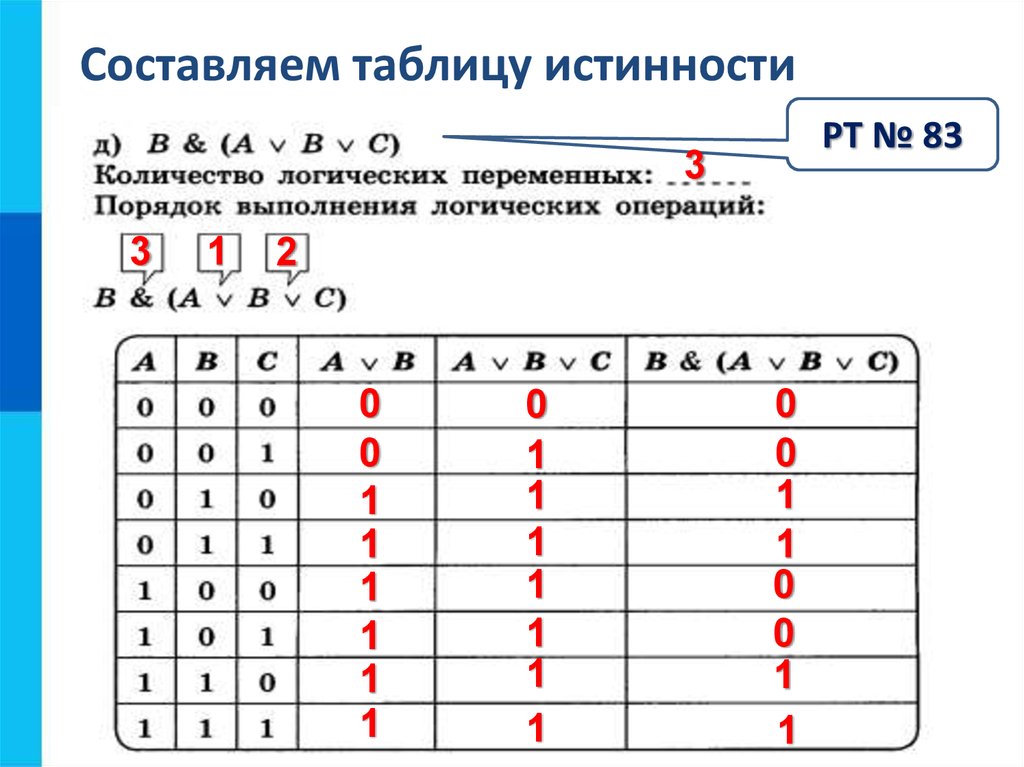
Программное обеспечение
Учащиеся будут иметь базовое представление о компьютерном программном обеспечении. Решения простых задач могут быть реализованы с использованием блочных языков, таких как Scratch (scratch.mit.edu/) или AppInventor (ai2.appinventor.mit.edu). Решения также можно реализовать с помощью набора LittleBits Code Kit (littlebits.com/pages/code-kit-download), который будет использоваться с littleBits. Более сложные решения могут быть реализованы с использованием текстовых языков, таких как Python или Java. Текстовые решения должны быть реализованы в интегрированной среде разработки, такой как jGRASP (www.jgrasp.org/) для Python, Java или других языков и BlueJ (www.bluej.org/) для Java.
Процедура
1) Представить прилагаемый урок по таблицам истинности
Рассмотрите возможность увеличения размера шрифта в презентации для облегчения доступа.
Практикуйте студентов на протяжении всей презентации.
Встраивайте вопросы и отзывы в презентацию.
Скачать: Solving_Logic_Problems_using_Truth_Tables_1_WwZ3MG0.pptxPPT имеет более крупный шрифт для более удобного просмотра.
Слайд | Пояснение |
1 | Титульный слайд для презентации |
2 | Индекс презентация |
3 | Определение логики проблема |
4 | Определение 0/1
зависит от конкретного входного датчика. Определение 0/1 зависит от конкретного устройства вывода, хотя большинство устройств равно 1, когда они включены и 0, когда они выключены. |
5 | Пользователю необходимо подсчитайте количество входных данных и используйте таблицу истинности для этого количества входы. В примере на слайде 4 используется три входа, поэтому вы должны использовать таблицу истинности с тремя входами. |
6 | Входы
таблица истинности уже введена. Выходы
вводится на основе ожидаемого результата для данного ввода
комбинация. В этом случае, если грабитель
будильник выключен, выход был бы выключен, поэтому первые четыре комбинации
имеют выход 0. Для пятого
комбинация, охранная сигнализация включена, а окно равно 0 или открыто, поэтому
прозвучит сигнал тревоги. Для шестого
комбинация, охранная сигнализация включена, окно открыто, движение
обнаружен, поэтому сработает сигнал тревоги. |
7 | Задокументировать решение
отметив, где выход равен 1. Вы
запишите каждый минимальный термин, отметив, в каком состоянии находится каждый вход. Если вход равен 0, вы записываете имя
ввода (X, Y или Z в данном случае) и поместите линию над отдельными
письмо. Это указывает на то, что вывод
будет 1, когда этот вход равен 0 (а другие входы являются
соответствующие состояния). Итак, первый
min-term (обратите внимание, что над
Y и Z. Это связано с порядком
операций, что выходит за рамки данного урока). Каждый из мини-термов объединяется по ИЛИ вместе с
знаки плюс (три минимальных члена объединяются, чтобы сформировать решение). |
8 | Можно упростить решение (некоторые учащиеся могут признать, что упрощенное решение )). Есть два способа упростить логику выражения, булева алгебра и карты Карно. И то, и другое выходит за рамки этого урока, поэтому мы будем продолжать использовать неупрощенное выражение. |
Есть два способа
протестировать решение; с помощью оборудования или с помощью программного обеспечения. Существует несколько методов проверки
аппаратное обеспечение, но есть два довольно простых способа: использовать littleBits или Snap Circuit.
Комплекты. На этом слайде показано, как
реализовать инверторы. Входы
те, над которыми есть линия (обратитесь к слайду 7), должны быть инвертированы в первую очередь. Возьмите выход датчика и подключите
его на вход инвертора. | |
10 | Следующее, что нужно сделать
заключается в объединении входных данных для формирования минимального термина. В этом примере есть три входа, поэтому
для каждого минимального термина потребуются два логических элемента И.
Подключите выход двух датчиков (или инвертор датчика, если
они были перевернуты на слайде 9) и соедините их с одним из логических элементов И
входы. Один датчик подключается к одному
вход, а другой датчик подключается к другому входу. Подключите выход первого элемента И к
один из входов второго вентиля И и подключить третий датчик к
оставшийся вход второго вентиля И.
Обратите внимание, что если у вас есть только два датчика/входа, вам нужен только один И
ворота; подключите один датчик к одному входу, а другой датчик к другому
вход. Если у вас четыре
датчики/входы, тогда вам понадобятся три логических элемента И. |
11 | Окончательно соединить все минимальных терминов с использованием вентилей ИЛИ. В В этом примере есть три минимальных термина, поэтому два минимальных термина (выходные данные их соответствующие вентили И) соединены с одним вентилем ИЛИ, а третий min-term и выход первого вентиля ИЛИ подключен ко второму ИЛИ ворота. Решение является выходом второй вентиль ИЛИ и подключен к выходному устройству (тревога в этом пример). |
12 | Второй способ
проверить решение заключается в использовании программного обеспечения.
Существует несколько методов тестирования программного обеспечения, но два довольно простых
Методы — использовать LittleBits Code Kit или Scratch. |
13 | Так же, как в оборудования (слайд 9), некоторые входы датчиков должны быть предварительно инвертированы. Это можно сделать с помощью команды НЕ. |
14 | Для формирования min-terms, используя команду AND. первая команда И объединяет первые два входа и вторую команду И объединяет вывод первой команды И и оставшийся ввод. |
15 | Для формирования финала
решения, используйте команду ИЛИ, чтобы объединить минимальные термины. |
2) Продемонстрируйте решение логической задачи, используя этот процесс, и протестируйте решение с помощью аппаратного или программного обеспечения, в зависимости от того, что доступно в вашем классе. Пустые таблицы истинности с двумя, тремя и четырьмя входами прилагаются.
Загрузить: Truth_Tables.pdfРассмотрите возможность увеличения размера таблиц для облегчения доступа. Позвольте учащимся работать со сверстниками, когда они начинают решать проблемы.
3) Решите задачу в качестве практического руководства, затем назначьте одну или несколько задач ниже или другие, которые вы создаете для самостоятельной практики, с обратной связью.
а. Детектор огня/дыма – подает звуковой сигнал, когда датчик обнаруживает огонь или дым. Используйте датчик температуры для обнаружения тепла и датчик света и света для обнаружения дыма.


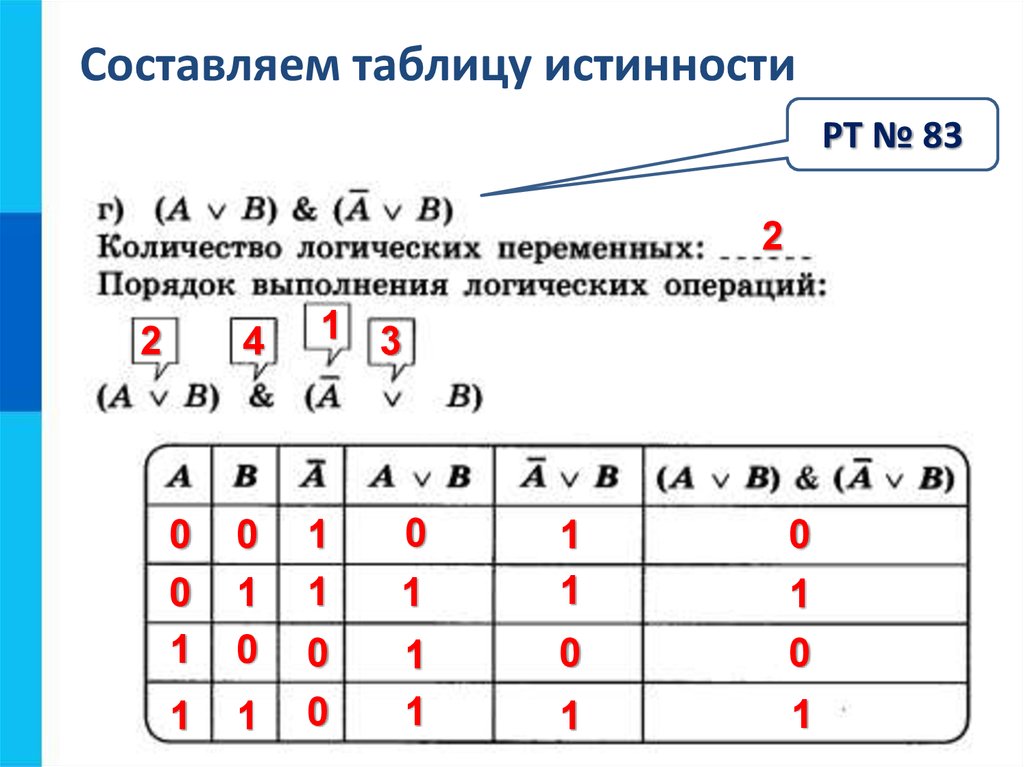 Охранная сигнализация равна 0, когда она выключена или отключена, и 1, когда
он включен или занят. Окно или
Дверные датчики — это электронные выключатели, которые находятся в состоянии 1, когда окно или дверь открыты.
закрыты и 0, когда они открыты. А
Детектор движения равен 1, если движение обнаружено, и 0, если оно не обнаружено.
Охранная сигнализация равна 0, когда она выключена или отключена, и 1, когда
он включен или занят. Окно или
Дверные датчики — это электронные выключатели, которые находятся в состоянии 1, когда окно или дверь открыты.
закрыты и 0, когда они открыты. А
Детектор движения равен 1, если движение обнаружено, и 0, если оно не обнаружено. По соглашению числа «считаются» в двоичном формате от всех нулей до всех
те. Самый простой способ визуализации
это то, что последний бит (в данном случае Z) является младшим битом и
он меняется с 0 на 1, а затем повторяется.
Следующий бит (в данном случае Y) считает каждое число дважды перед изменением
к следующему числу (0, 0, 1, 1).
последний бит (в данном случае X) является старшим битом, и он подсчитывает каждый
число четыре раза, прежде чем перейти к следующему числу (0, 0, 0, 0, 1, 1, 1,
1). Если есть четвертый бит
слева от X, то каждое число будет пересчитываться восемь раз перед изменением.
По соглашению числа «считаются» в двоичном формате от всех нулей до всех
те. Самый простой способ визуализации
это то, что последний бит (в данном случае Z) является младшим битом и
он меняется с 0 на 1, а затем повторяется.
Следующий бит (в данном случае Y) считает каждое число дважды перед изменением
к следующему числу (0, 0, 1, 1).
последний бит (в данном случае X) является старшим битом, и он подсчитывает каждый
число четыре раза, прежде чем перейти к следующему числу (0, 0, 0, 0, 1, 1, 1,
1). Если есть четвертый бит
слева от X, то каждое число будет пересчитываться восемь раз перед изменением.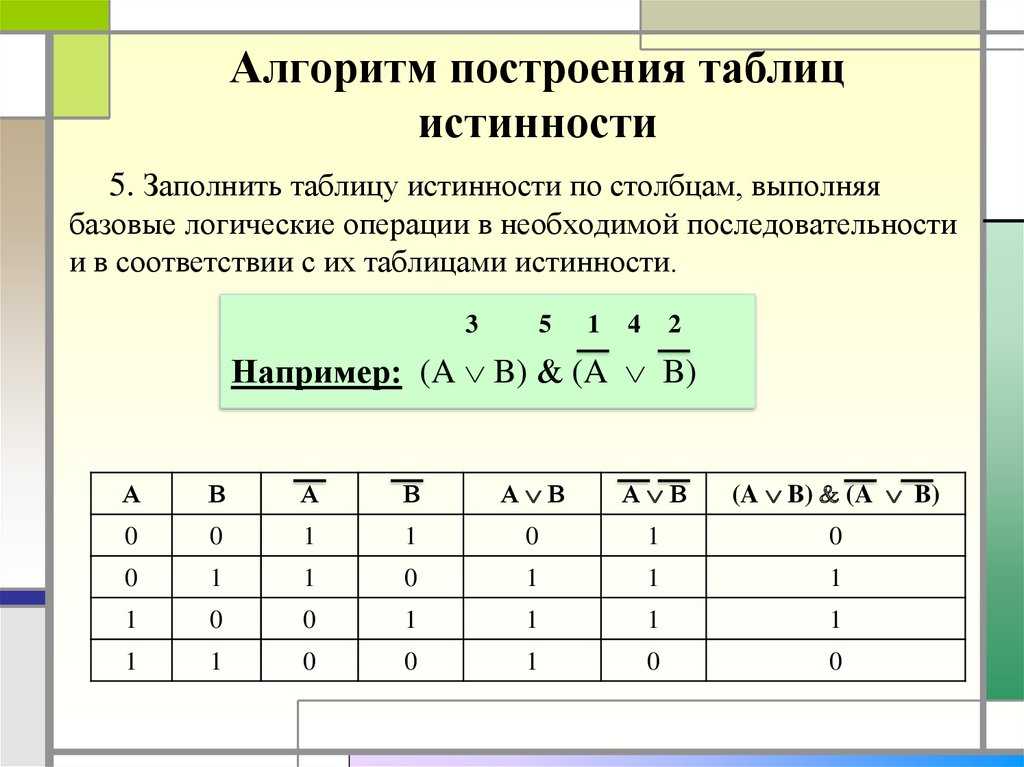 Для седьмой комбинации включается охранная сигнализация, но
окно закрыто и движение не обнаружено, поэтому сигнализация не сработает. Для восьмой и последней комбинации
охранная сигнализация включена и обнаружено движение, поэтому сработает сигнал тревоги.
Для седьмой комбинации включается охранная сигнализация, но
окно закрыто и движение не обнаружено, поэтому сигнализация не сработает. Для восьмой и последней комбинации
охранная сигнализация включена и обнаружено движение, поэтому сработает сигнал тревоги.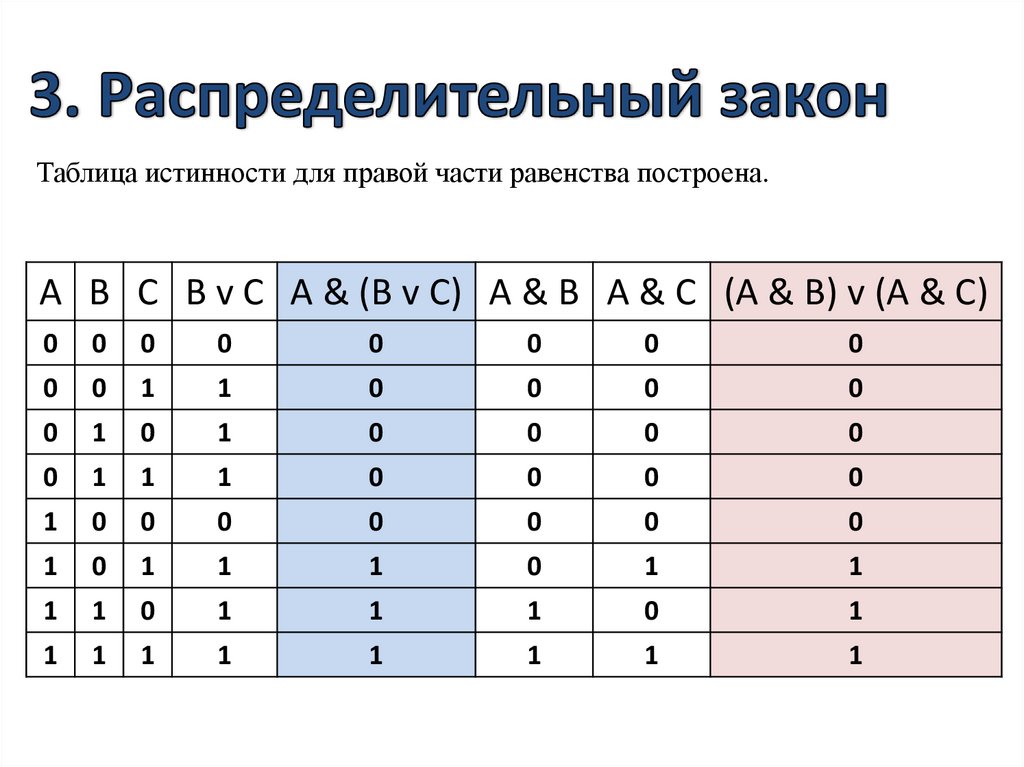
 выход инвертора будет инвертированным сигналом.
выход инвертора будет инвертированным сигналом.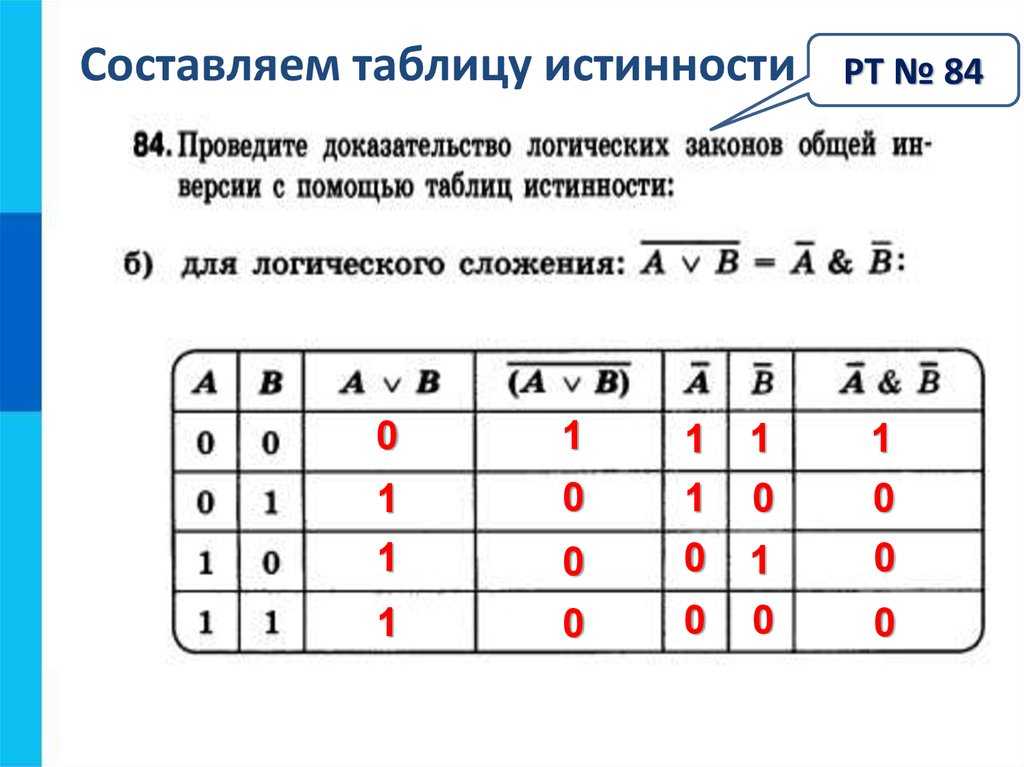 Подключите два датчика к первому вентилю И,
два датчика ко второму вентилю И, а затем соедините выходы двух
Логические элементы И на входы третьего вентиля И.
Подключите два датчика к первому вентилю И,
два датчика ко второму вентилю И, а затем соедините выходы двух
Логические элементы И на входы третьего вентиля И.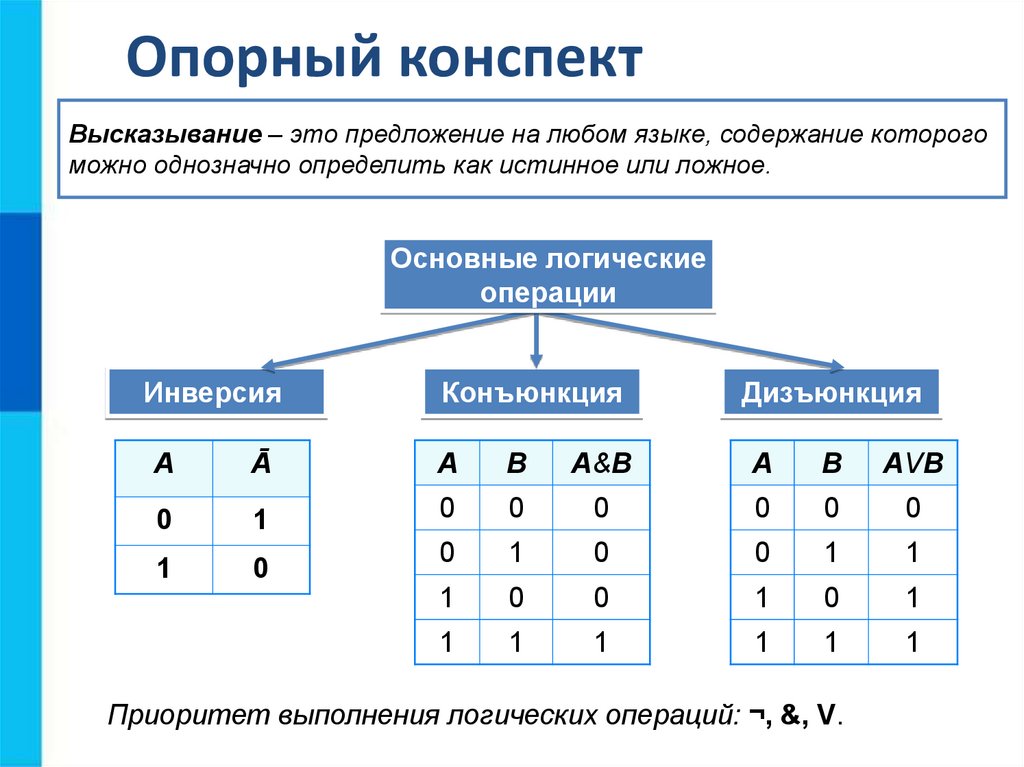 В обоих случаях вам нужно создать переменные
для представления входных сигналов датчика. С
комплект кода littleBits, вы можете использовать эту переменную для чтения вывода
датчик. С помощью Scratch пользователь
необходимо ввести значение датчика.
В обоих случаях вам нужно создать переменные
для представления входных сигналов датчика. С
комплект кода littleBits, вы можете использовать эту переменную для чтения вывода
датчик. С помощью Scratch пользователь
необходимо ввести значение датчика.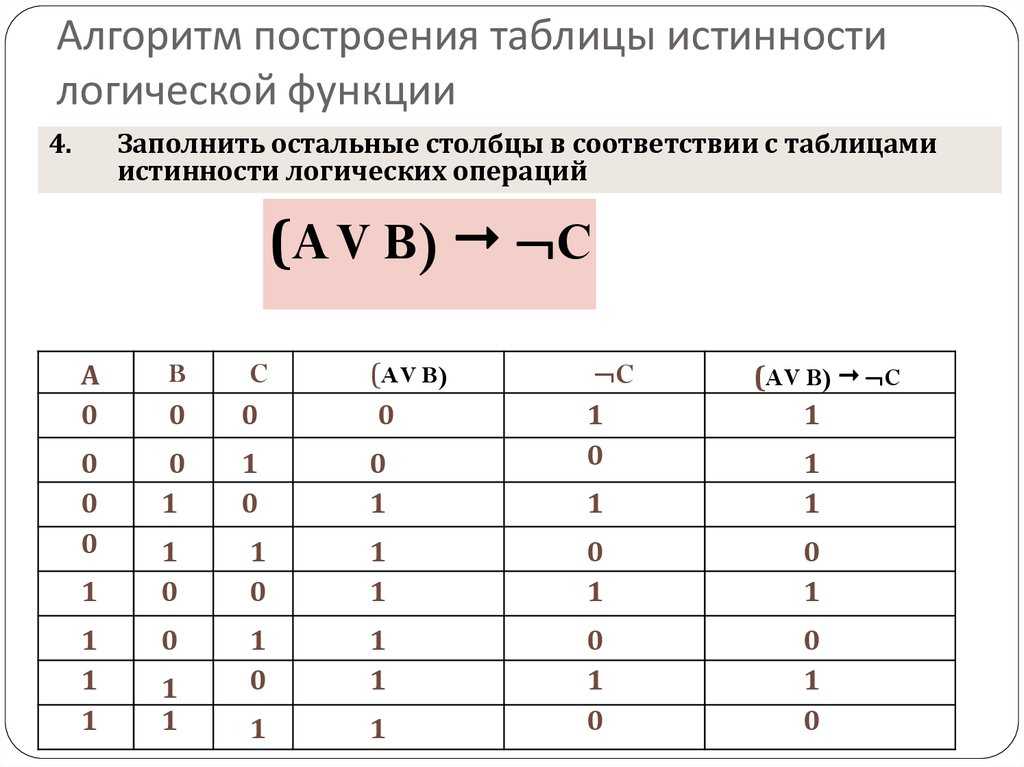 В этом случае первая команда ИЛИ объединяет
первые два минимальных условия и вторая команда ИЛИ объединяют вывод
первая команда ИЛИ и оставшийся минимальный срок.
В этом случае первая команда ИЛИ объединяет
первые два минимальных условия и вторая команда ИЛИ объединяют вывод
первая команда ИЛИ и оставшийся минимальный срок.