Равновесие тела. Момент силы | Физика

Вы уже знаете, что если сумма всех действующих на точечное тело сил равна нулю, то это тело в инерциальной системе отсчета (ИСО) покоится или движется равномерно и прямолинейно. Следовательно, всегда можно выбрать такую инерциальную систему отсчета, в которой это тело покоится. В этом случае говорят, что тело находится в равновесии. Таким образом, условием равновесия точечного тела в ОСО является равенство нулю суммы всех действующих на него сил.

А как быть, если интересующее нас тело не является точечным? В этом случае действующие силы могут быть приложены к разным точкам тела. Тогда, даже если сумма сил равна нулю, реальное тело может деформироваться, т. е. различные его части могут двигаться относительно друг друга. Однако при изучении статики нас будут интересовать только такие тела, деформации которых пренебрежимо малы. Такие тела называют твердыми. Как правило, твердыми телами считают детали машин и механизмов, строительные конструкции из бетона, стали и т.

п.

Если можно выбрать ИСО, в которой все точки твердого тела покоится, то о таком теле говорят, что оно находится в состоянии равновесия.

В отличие от точечного тела, не имеющего размеров, для твердого тела условия равенства нулю суммы всех действующих на него сил недостаточно для того, чтобы оно находилось в состоянии равновесия. Эксперименты показывают, что если сумма всех действующих на твердое тело сил равна нулю, то у тела можно найти точку, которая будет неподвижной в ИСО. При этом тело может оставаться неподвижным, а может начать раскручиваться вокруг этой точки. Понятно, что во втором случае не все точки тела будут покоиться и, следовательно, тело не будет находиться в равновесии.

Если сумма всех действующих на твердое тело сил равна нулю, то у тела можно найти точку, которая будет неподвижной в ИСО.

Поясним сказанное на примере. Лежащая на столе тетрадь покоится. Если же вы потяните эту тетрадь за противоположные углы с одинаковыми по модулю, но противоположными по направлению силами (рис. 135), то увидите, что тетрадь начнет раскручиваться. При этом центр – точка C пересечения диагоналей останется неподвижной.

Таким образом, одного условия (равенства нулю суммы всех действующих на твердое тело сил) недостаточно для того, чтобы все точки этого тела оставались в покое.

Найдем дополнительное условие равновесия, при котором изначально покоившееся твердое тело не начинает раскручиваться под действием прикладываемых к нему сил. Рассмотрим твердое тело, закрепленное на оси, вокруг которой оно может вращаться. Пусть это будет, например, велосипедное колесо, которое закреплено на оси, обозначенной точкой O (рис. 136). Исследуем, как будет изменяться вращение колеса под действием одной и той же силы F. Для этого приложим силу F к точке A обода колеса и будем изменять направление этой силы.

Вначале подействуем на колесо силой F в направлении, перпендикулярном радиусу OA (рис. 136, а). Эксперимент показывает, что в этом случае колесо начнет раскручиваться по ходу стрелки часов (по часовой стрелке).

Если же направление силы F будет таким, как на рис. 136, б, то неподвижное колесо также начнет раскручиваться по часовой стрелке, но уже медленнее, чем в первом случае. Дальнейшие эксперименты показывают, что с увеличением угла α между направлением действия силы и радиусом OA раскручивающее действие силы будет уменьшаться. Наконец, если сила F будет направлена точно вдоль радиуса колеса (рис. 136, в), то колесо вообще не начнет раскручиваться.

Если продолжать увеличивать угол α между направлением силы F и радиусом OA (рис. 136, г), то неподвижное колесо начнет раскручиваться в противоположную сторону.

Понятно, что в случаях а, б и г увеличение модуля силы приведет к увеличению раскручивающего действия силы. Таким образом, раскручивающее действие силы на колесо зависит как от направления силы, так и от ее модуля. Как же описать это действие? Для того чтобы ответить на этот вопрос, введем новые понятия.

На каждом из рис. 136 пунктиром изображена линия, вдоль которой действует сила F. Эту линию называют линией действия силы F. Расстояние от оси вращения до линии действия силы F называют

плечом силы. (На рис. 136 плечи силы F перпендикулярны линиям действия силы и обозначены буквой l.)

Линию, вдоль которой действует сила, называют линией действия этой силы. Расстояние от оси вращения до линии действия силы называют плечом этой силы.

Из рисунка видно, что чем больше плечо силы – длина отрезка l, тем большее раскручивающее действие оказывает сила. В случае, когда плечо силы равно нулю (см. рис. 136, в). раскручивающее действие силы также равно нулю. Когда плечо силы F максимально (см. рис. 136, а), максимально и ее раскручивающее действие.

Раскручивающее действие силы описывают физической величиной – моментом силы. Его принято обозначать буквой M.

Моментом M силы F относительно данной оси называют физическую величину, равную произведению модуля силы на ее плечо.

M = F · l.

Если сила стремится раскручивать тело против часовой стрелки (см. рис. 136, г), то ее момент считают положительным (M > 0). Напротив, если сила стремится раскручивать тело по часовой стрелке (см. рис. 136, а и б), то ее момент считают отрицательным (M

Из определения понятно, почему единицу момента силы в СИ называют ньютон-метр (Н · м).

Эксперименты показывают, что если на твердое тело действуют несколько сил, то суммарное раскручивающее действие этих сил равно сумме моментов этих сил. Например, если на тело действуют две силы, моменты которых равны по модулю, но противоположны по знаку, то сумма моментов этих сил будет равна нулю и данное тело не будет раскручиваться.

Таким образом,
твердое тело в ИСО остается в равновесии, если выполнены два условия:
1) сумма всех действующих на твердое тело сил равна нулю;
2) сумма моментов всех действующих на твердое тело сил равна нулю.

Итоги

Если можно выбрать ИСО, в котором точечное тело покоится, то говорят, что это тело находится в равновесии.

Условием равновесия точечного тела в ИСО является равенство нулю суммы всех действующих на него сил.

Если можно выбрать ИСО, в которой все точки твердого тела покоятся, то о таком теле говорят, что оно находится в положении равновесия.

Линию, вдоль которой действует сила, называют линией действия силы.

Расстояние от оси вращения до линии действия силы называют плечом силы.

Моментом M силы F относительно данной оси называют физическую величину, равную произведению модуля силы на ее плечо.
M = F · l

Если сила стремится раскручивать тело в направлении против часовой стрелки, то ее момент считают положительным (M > 0). Если сила стремится раскручивать тело в направлении по часовой стрелке, то ее момент считают отрицательным (M

Вопросы

1. В каком случае говорят, что точечное тело находится в равновесии?
2. Сформулируйте условие равновесия точечного тела в ИСО.
3. Какое тело называют твердым?
4. В каком случае говорят, что твердое тело находится в равновесии?
5. Что такое линия действия силы? Что называют плечом силы?
6. Какая физическая величина характеризует раскручивающее действие силы?
7. Сформулируйте определение момента силы относительно оси.
8. Как называют единицу момента силы в СИ?
9. Когда момент силы считают положительным (отрицательным)?
10. Сформулируйте условия равновесия твердого тела.
11. Почему дверную ручку прикрепляют на противоположной от петель стороне двери?

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

4.3 Уравнения равновесия твердого тела.

Инженерная механика: статика

Глава 4. Твердые тела

Мы используем уравнения равновесия для расчета любых неизвестных сил и моментов, используя известные силы и значения, и следующие уравнения:

Уравнения равновесия частиц были рассмотрены в разделе 2.3. Это:

$$
\Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma F_{z}=0
$$

Теперь для твердого тела, где анализируются силы в разных точках тела, мы можем учитывать моменты. Есть 3 уравнения для 2d и 4 уравнения для 3d: 9{\prime}}=0
\end{собрано}
$$

Поскольку это статические тела, правая часть уравнений равна 0. В динамике они будут равны массе, умноженной на ускорение поступательного движения и вращения.

 

Для твердого тела , находящегося в статическом равновесии, то есть недеформируемого тела, в котором силы не действуют одновременно, сумма сил и моментов , действующих на тело, должна быть равна нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.

Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси z). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма компонентов силы в направлениях x и y и моментов относительно оси z. Сумма каждого из них будет равна нулю.

Для двумерной задачи мы разобьем наше уравнение одной векторной силы на два уравнения скалярных компонент.

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0$$

Одномоментное векторное уравнение становится одномоментным скалярным уравнением.

$$\sum\vec M=0\\\sum M_z=0$$

Если мы рассмотрим трехмерную задачу, то увеличим число возможных уравнений равновесия до шести. Есть три уравнения равновесия для силы, где сумма компонентов в направлениях x, y и z должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма компонентов момента относительно осей x, y и z также должна быть равна нулю.

Разобьем силы на три уравнения составляющих

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0\:\sum F_z=0$$

Разобьем моменты в трехкомпонентные уравнения

$$\sum\vec M=0\\\sum M_x=0\:\sum M_y=0\:\sum M_z=0$$

Как и в случае с частицами, первый шаг в нахождении уравнения равновесия состоит в том, чтобы нарисовать диаграмму свободного тела анализируемого тела. На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На диаграмме свободного тела задайте значения для любых известных величин, направлений и точек приложения векторов силы и задайте имена переменных для любых неизвестных (величин, направлений или расстояний).

Далее вам нужно будет выбрать оси x, y, z. Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.

После того, как вы выбрали оси, вам необходимо разбить все векторы сил на составляющие по направлениям x, y и z (см. страницу векторов в Приложении 1 для более подробной информации об этом процессе). Ваше первое уравнение будет суммой величин компонентов в направлении x, равных нулю, второе уравнение будет суммой величин компонентов в направлении y, равных нулю, а третье (если вы имеют трехмерную задачу) будет равна сумме величин в направлении z, равной нулю.

Далее вам нужно будет составить уравнения моментов. Для этого вам нужно будет выбрать точку, о которой будут сниматься моменты. Подойдет любая точка, но обычно выгоднее выбрать точку, которая уменьшит количество неизвестных в уравнении. Помните, что любой вектор силы, проходящий через данную точку, не будет иметь никакого момента относительно этой точки. Чтобы записать уравнения моментов, просто суммируйте моменты, создаваемые каждой силой (добавляя чистые моменты, показанные на диаграмме) относительно данной точки и данной оси (x, y или z), и установите эту сумму равной нулю. Все моменты будут относиться к оси z для двухмерных задач, хотя моменты могут быть связаны с осями x, y и z для трехмерных задач.

Когда у вас есть уравнения равновесия, вы можете решить эти формулы для неизвестных. Количество неизвестных, которые вы сможете решить, снова будет числом или уравнениями, которые у вас есть.

 

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/3_equations_rigid_body/3-6_equations_rigid_body/equations_rigid_body.html

 

Вот наглядный пример использования уравнений равновесия:

Источник: Инженерная механика, Джейкоб Мур и др. http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-1_statically_equivalent_systems/images/equivalentexample. png

Если рассматривать только направление Y (вертикальное), 200 фунтов, давящих на балку, должны быть уравновешены силами реакции толкая вверх. Две силы реакции эквивалентны, потому что силы сверху равномерно уравновешены между силами реакции. Если они находятся в разных местах, мы используем сумму уравнения моментов и расстояний людей, чтобы определить размер сил реакции.

Пример 1:

Автомобиль ниже имеет массу 1500 фунтов с центром масс в 4 футах позади передних колес автомобиля. Каковы нормальные силы, действующие на переднее и заднее колеса автомобиля?

 

Пример 2:

Сидя на стуле, человек прикладывает силы, показанные на схеме ниже. Определите все силы, действующие на стул в точках A и B. (Предположим, что A не имеет трения, а B — шероховатая поверхность).

Источник: Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/3_equations_rigid_body/3-6_equations_rigid_body/pdf/EquilibriumEquationsExtended_WorkedProblem5. pdf

 

 

 

В основном: Уравнения равновесия для твердых тел — это способ определения неизвестных сил и моментов с использованием известных сил и моментов, разделяя движение на 2 (или 3) направления для поступательного движения и вращения. Моменты можно рассчитать, потому что твердые тела также учитывают форму и длину.

Применение:  Расчет сил реакции на основе совокупного веса объекта.

Заглядывая вперед: Этот метод будет широко использоваться в главах 5 и 6.

 

Моменты и равновесие: принцип и примеры

Вы когда-нибудь видели двух детей на качелях и наблюдали за их движением? Качели вращаются вокруг фиксированной точки, известной как точка опоры, одна сторона поднимается, а другая опускается, но задумывались ли вы когда-нибудь, какова физика движения качелей? Качели воздействуют на важное понятие в физике, известное как момент.

Рис. 1: Качели — это балка, закрепленная на рычаге.

Теперь предположим, что по какой-то причине качели идеально балансируют в центре. Такое может случиться, конечно, с какой-то физикой, и это понятие в физике называется равновесием моментов, о котором и пойдет речь в этой статье. Чтобы понять принцип равновесия, нам нужно получить представление о том, что такое момент. Позже мы рассмотрим принцип момента, изображая моменты и равновесие.

Соотношение момента и равновесия

Если вы возьмете мизинец и попытаетесь закрыть им открытую дверь, поднеся палец к дверной ручке, дверь легко закроется. Теперь попытайтесь снова закрыть дверь мизинцем, но на этот раз попробуйте толкнуть дверь, поместив палец рядом с петлей. Закрывается ли дверь так же легко, как если бы вы приложили мизинец к ручке?

Было бы гораздо труднее закрыть дверь, поместив палец рядом с петлей. Почему это? Расстояние или, в частности, перпендикулярное расстояние от петли до дверной ручки больше, поэтому сила, создаваемая для создания эффекта поворота, также больше.

Рис. 2: Расстояние \(d_2\) создает большую вращающую силу по сравнению с \(d_1\).

Мы часто используем силы, чтобы заставить объект вращаться, другими словами, нам нужны силы, чтобы создать момент. Момент также может объяснить, почему легче использовать более длинный гаечный ключ, чем более короткий.

Сила в точке A вызовет меньший вращательный эффект по сравнению с силой в точке B. Wikimedia

Момент силы

Вращательный или вращательный эффект силы называется момент силы.

Момент силы можно рассчитать по уравнению:

\[M=Fd\]

Где момент в Нм, сила в ньютонах, а расстояние по нормали к сила в м. Одна вещь, которую важно иметь в виду в приведенном выше уравнении, заключается в том, что расстояние — это перпендикулярное расстояние от линии действия силы до оси вращения. Таким образом, большая сила должна быть приложена далеко от точки поворота для большего момента.

Перпендикулярное расстояние означает расстояние под прямым углом. На рисунке ниже расстояние по перпендикуляру от точки, в которой действует приложенная сила A, до оси B (центра гайки), поскольку сила и расстояние до оси составляют прямые углы друг к другу.

Приложенная сила образует прямой угол с расстоянием от оси вращения. Адаптировано из Викимедиа.

Если приложенная сила оказывается не под прямым углом, как показано на рисунке ниже, момент, возникающий при повороте, также будет меньше. Расстояние от точки поворота B до приложенной силы A не перпендикулярно на рисунке ниже; но вам не о чем беспокоиться, так как перпендикулярное расстояние будет указано в любой задаче, которую вам попросят решить.

Сила, приложенная под углом к ​​расстоянию от оси вращения, не считается перпендикулярным расстоянием. Адаптировано из Викимедиа.

Рассчитайте момент, создаваемый гаечным ключом, если приложенная сила равна и перпендикулярное расстояние от силы до центра гайки равно .

Решение:

Расстояние по перпендикуляру от оси вращения до приложенной силы равно , а приложенная сила равна .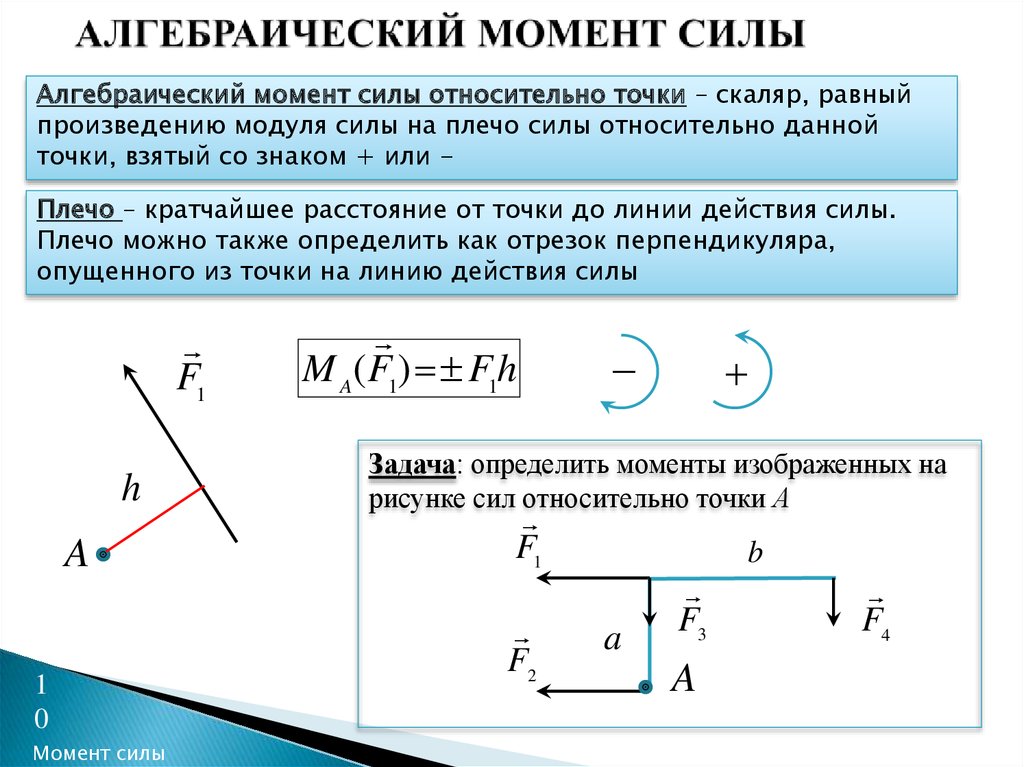 Используя формулу момента, которую мы получаем,

Обратите внимание, что момент может быть направлен против часовой стрелки (положительное направление) или по часовой стрелке (отрицательное направление), поскольку это, по сути, вращение, которое может быть в любом направлении в зависимости от расстояния и направление приложенной силы. Теперь, конечно, на объект может действовать и более одного момента, например, два человека на качелях. Но направления по часовой стрелке и против часовой стрелки и множественные моменты приводят к важной концепции в физике, известной как принцип равновесия момента или просто принцип момента.

Принцип момента и равновесия

Принцип момента и равновесия гласит, что когда система находится в равновесии, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.

Механическая измерительная шкала, подобная показанной на рисунке ниже, демонстрирует принцип момента и равновесия. Мы используем весы, чтобы сравнить вес двух тел.

Весы используются для сравнения разницы в массе двух объектов. Викимедиа.

Когда гири разбалансированы, инструмент наклоняется так, что шкала с более тяжелым объектом опускается, а шкала с более легким объектом поднимается. Этот «наклон» представляет собой момент против часовой стрелки или по часовой стрелке, возникающий из-за дисбаланса направленных вниз сил с обеих сторон. Поскольку длина каждого рычага, к которому подвешены весы, одинакова, если мы хотим сбалансировать инструмент, вес объектов с обеих сторон должен быть одинаковым. Это приведет к тому, что момент по часовой стрелке и момент против часовой стрелки станут равными, и, следовательно, тело будет в равновесии.

Весы находятся в равновесии, если момент по часовой стрелке и момент против часовой стрелки становятся равными. Адаптировано из Викимедиа.

Моменты и примеры равновесия

Допустим, Джон сидит на правой стороне качелей относительно нас. Сила из-за его веса есть, и он сидит на расстоянии от оси вращения. Как упоминалось ранее, моменты могут быть по часовой стрелке или против часовой стрелки, и в случае Джона создаваемый момент будет по часовой стрелке. Момент по часовой стрелке для случая Джона будет:

На этой диаграмме общий момент, действующий на качели, направлен по часовой стрелке (отрицательный), потому что один момент действует по часовой стрелке из-за веса человека, сидящего на качелях.

Вскоре после этого Питер присоединяется к Джону на качелях, которые создают момент против часовой стрелки. Если мы хотим вычислить общий момент качелей, нам нужно будет принять во внимание как момент по часовой стрелке, так и момент против часовой стрелки, а затем посмотреть, какой момент больше, чем другой.

Момент по часовой стрелке и против часовой стрелки создается качелями в результате действия двух сил, действующих в одном направлении на противоположных концах. Адаптировано из Викимедиа.

Если каким-то образом два момента станут равными, то есть момент, направленный против часовой стрелки, будет равен моменту, направленному по часовой стрелке, то качели не будут вращаться.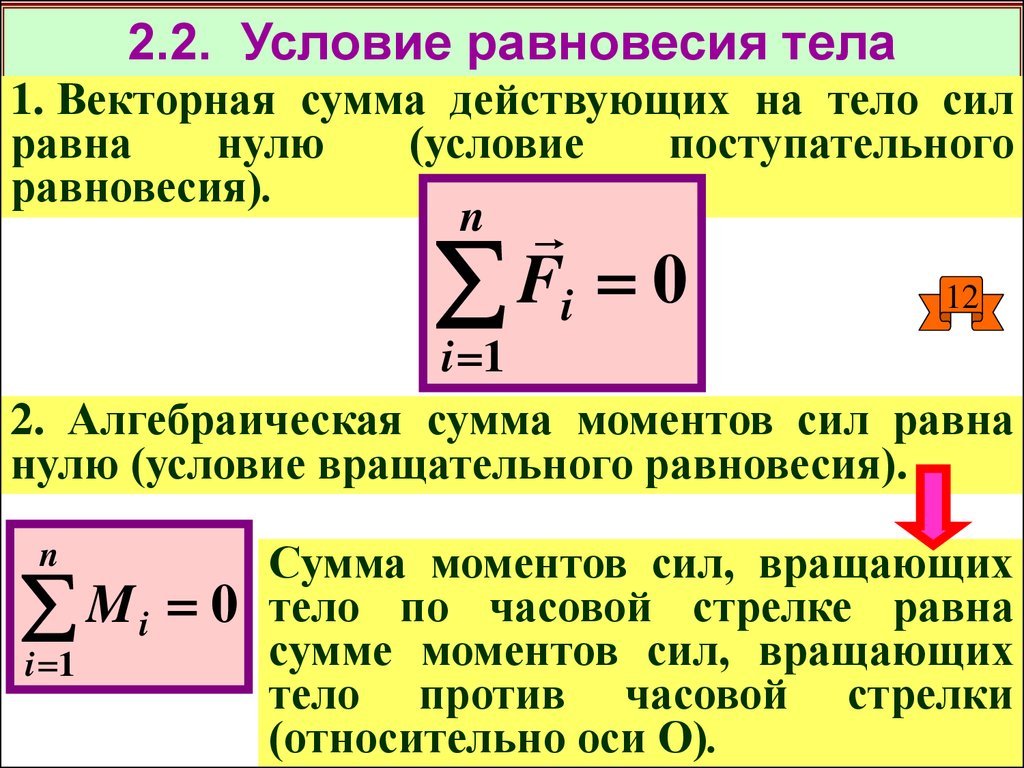 Другими словами, если моменты станут равными, то качели будут в равновесии, что и утверждает принцип момента.

Моменты и уравнение равновесия

В сценарии Петра и Иоанна, на каком расстоянии от равновесия должен сидеть Питер, чтобы качели достигли равновесия? Мы рассчитали момент, создаваемый силой Джона, поэтому момент Питера должен быть таким же, как момент Джона. Мы знаем, что сила со стороны Питера равна, поэтому мы можем написать:

Итак, Питер должен сидеть на расстоянии от оси вращения, чтобы качели были сбалансированы.

Применение моментов и равновесия

Существует ряд применений моментов и равновесий, которые мы используем в повседневной жизни. Здесь мы перечислим и обсудим несколько примеров, чтобы завершить эту статью.

Классический пример, который мы уже рассмотрели, — качели. Это простое, но забавное игровое оборудование не могло бы работать без принципов моментов. Момент на каждом конце качелей обеспечивается толчком людей, сидящих на любом из рычагов качелей, или их откидыванием назад, чтобы изменить свой центр масс так, чтобы он находился дальше от оси вращения.

Другое приложение, которое мы изучили, это весы. Весы работают по принципу, согласно которому уравновешивание моментов по часовой стрелке и против часовой стрелки приводит к тому, что рассматриваемая система находится в состоянии равновесия, т. е. чистого движения нет, поскольку чистый момент равен нулю. Мы можем сбалансировать объект на одной чаше весов и постепенно добавлять гири известной массы на другую чашу весов, пока весы не будут уравновешены. Суммируя массу гирь, необходимых для уравновешивания весов, получим общую массу взвешиваемого объекта.

Моменты и равновесие – основные выводы

• Вращательное или вращательное действие силы называется моментом силы.
• Мы можем рассчитать момент силы, используя уравнение:

• Расстояние , в формуле момента представляет собой перпендикулярное расстояние от линии действия силы до оси вращения.
• Для более важного момента необходимо приложить большую силу вдали от точки поворота.