как посчитать мощность зная линейный ток и фазное напряжение (Страница 1) — Студенческий Раздел — Советы бывалого релейщика
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
1 Тема от
RT-40/10 2016-09-23 13:03:54- RT-40/10
- Пользователь
- Неактивен
Тема: как посчитать мощность зная линейный ток и фазное напряжение
как посчитать мощность зная линейный ток и фазное напряжение
2 Ответ от
doro 2016-09-23 13:20:08- doro
- свободный художник
- Неактивен
Re: как посчитать мощность зная линейный ток и фазное напряжение
Нагрузки симметричная? В таком случае, как правило, используется формула S=1,73*Uл*Iф. 1,73 — это квадратный корень из трех. Выводится формула довольно просто. Скорее всего, у Вас — модификация этой формулы. Измерение линейных токов — довольно сложная (хотя и выполнимая) задача. При несимметричной нагрузке задача усложняется, нужны значения токов и напряжений во всех сочетаниях. Там уж — свои извращения.
Измерение линейных токов — довольно сложная (хотя и выполнимая) задача. При несимметричной нагрузке задача усложняется, нужны значения токов и напряжений во всех сочетаниях. Там уж — свои извращения.
Сайт doro
3 Ответ от
SVG 2016-09-23 13:57:07- SVG
- guest
- Неактивен
Re: как посчитать мощность зная линейный ток и фазное напряжение
doro пишет:
как правило, используется формула S=1,73*Uл*Iф. 1,73 — это квадратный корень из трех.
Если есть фазные напряжения и фазные токи, то S=3*Uф*Iф . Если токи линейные, то Iл=1.73Iф. Отсюда
S=3*Uф*Iл/1,73=1,73*Uф*Iл
Чему бы грабли не учили, а сердце верит в чудеса
4 Ответ от
matu 2016-09-23 16:28:02- matu
- Пользователь
- Неактивен
Re: как посчитать мощность зная линейный ток и фазное напряжение
SVG пишет:
Если токи линейные, то Iл=1.
73Iф
Это если нагрузка треугольником соединена.
doro, поясните, в чем сложность измерения линейных токов?
Для случая симметричного источника/приемника и соединения приемника звездой имеем 3*Iлин*Uф.
5 Ответ от
doro 2016-09-23 16:38:42- doro
- свободный художник
- Неактивен
Re: как посчитать мощность зная линейный ток и фазное напряжение
Да, в принципе, эта проблема давно решена в части дистанционных защит от междуфазных КЗ. На трансркеакторе суммируются (точнее, вычитаются) токи двух фаз. Но исхожу из возможностей посетителя Студенческого раздела. Ему ведь междкфазные токи в случае чего доведется измерять самостоятельно! Впрочем, и эта проблема решаема.
matu пишет:
3*Iлин*Uф.
В данном вопросе есть некоторые сомнения.
Сайт doro
Присоединяйтесь!!! Мы в социальных сетях и на Ютуб. |
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
-
2.
 1 Кинематика
1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
2.
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
-
4.

- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
4.
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
-
5.
 5 Излучение и спектры
5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- ссылки на другие сайты
и многое другое.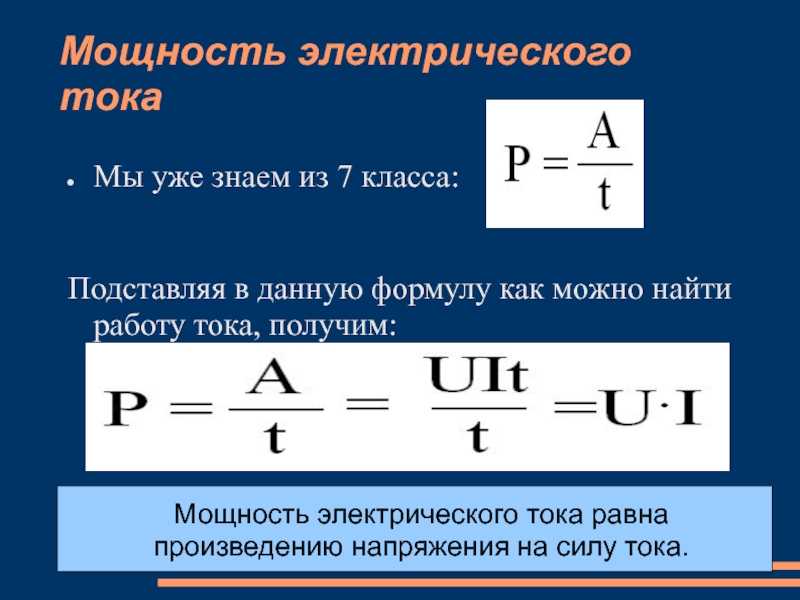
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
15.4 Мощность в цепи переменного тока – University Physics Volume 2
Глава 15. Цепи переменного тока
Цели обучения
К концу раздела вы сможете:
- Описывать, как можно представить среднюю мощность от цепи переменного тока в виде пикового тока и напряжения и среднеквадратичного значения тока и напряжения
- Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с [латекс]P=IV,[/латекс], где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность [латекс]p\left(t\right)=i\left(t\right)v\left(t\right)[/latex] также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.
Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность [латекс]p\left(t\right)=i\left(t\right)v\left(t\right)[/latex] также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.
 [/латекс] (г) для источника [латекс] {P} _ {\ text { ave}}={I}_{0}{V}_{0}\left(\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi \right)\text{/}2 ,[/latex], который может быть положительным, отрицательным или нулевым, в зависимости от [latex]\varphi .[/latex]
[/латекс] (г) для источника [латекс] {P} _ {\ text { ave}}={I}_{0}{V}_{0}\left(\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi \right)\text{/}2 ,[/latex], который может быть положительным, отрицательным или нулевым, в зависимости от [latex]\varphi .[/latex]Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем 9.{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\omega t-\varphi\right)\phantom{\ правило {0.2em} {0ex}} \ text {sin} \ phantom {\ правило {0.2em} {0ex}} \ omega t \ phantom {\ правило {0.2em} {0ex}} дт. [/латекс]
Используя тригонометрическое соотношение [латекс]\фантом{\правило{0.2em}{0ex}}\текст{sin}\фантом{\правило{0.2em}{0ex}}\left(AB\right)=\phantom{ \rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}A\text{cos}\phantom{\rule{0.2em}{0ex}}B-\ фантом {\ правило {0. 2em} {0ex}} \ текст {sin} \ фантом {\ правило {0.2em} {0ex}} B \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ phantom{\rule{0.2em}{0ex}}A,[/latex] получаем 9{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\text{cos}\phantom{\rule{0.2em }{0ex}}\omega tdt=0.[/latex]
2em} {0ex}} \ текст {sin} \ фантом {\ правило {0.2em} {0ex}} B \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ phantom{\rule{0.2em}{0ex}}A,[/latex] получаем 9{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\text{cos}\phantom{\rule{0.2em }{0ex}}\omega tdt=0.[/latex]
Следовательно, средняя мощность, связанная с элементом схемы, равна
[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \ phantom {\ rule {0.2em} {0ex} }\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]
В инженерных приложениях [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi[/латекс] известен как коэффициент мощности , равный 9.0047, что является величиной, на которую мощность, подаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе. Для резистора [латекс]\варфи =0,[/латекс], поэтому средняя рассеиваемая мощность равна
. [латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0}. [/latex]
[/latex]
Сравнение p ( t ) и [латекс]{P}_{\text{ave}}[/latex] показано на рис. 15.16(d). Чтобы [латекс]{P}_{\text{ave}}=\left(1\text{/}2\right){I}_{0}{V}_{0}[/latex] выглядел как его аналог на постоянном токе, мы используем среднеквадратичные значения {0ex}}{V}_{\text{rms}}[/latex] тока и напряжения. По определению это 9{2}\влево(т\вправо)дт.[/латекс]
С [латекс] я \ влево (т \ вправо) = {I} _ {0} \ фантом {\ правило {0.2em} {0ex}} \ текст {грех} \ фантом {\ правило {0.2em} {0ex }}\left(\omega t-\varphi\right)\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}v\left(t \right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t,[/latex] получаем
[латекс] {I} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} {I} _ {0} \ phantom {\ rule {0.2em} {0ex}} \ text {и}\phantom{\rule{0.2em}{0ex}}{V}_{\text{rms}}=\frac{1}{\sqrt{2}}{V}_{0}.[/ латекс] 9{2}Р.[/латекс]
Это уравнение еще раз подчеркивает, почему для обсуждения выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет [латекс]110\sqrt{2}\phantom{\rule{0.2em}{0ex}}\text{V}=\text{156 В}\text{.}[/latex] Потому что большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.
Для конденсатора и катушки индуктивности [латекс]\varphi =\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{ 0ex}}-\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad,}[/latex] соответственно. Поскольку [latex]\text{cos}\pi \text{/}2=\text{cos}\left(\text{−}\pi \text{/}2\right)=0,[/latex] мы найдите из уравнения 15.12, что средняя мощность, рассеиваемая любым из этих элементов, равна [латекс] {P} _ {\ text {аве}} = 0. [/латекс] Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода и затем разрядите его обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.
[/латекс] Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода и затем разрядите его обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение. Если [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi > 0,[/latex] генератор вырабатывает энергию; если [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ phantom {\ rule {0.2em} {0ex }}\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]
Для генератора в цепи RLC ,
9{2}R,[/латекс], что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс. {4} \ текст {рад} \ текст{/} \ текст {s} \ справа) t \ справа][/латекс] 9{-6}\phantom{\rule{0.2em}{0ex}}\text{F}[/latex] и [латекс]R=5.00\phantom{\rule{0.2em}{0ex}}\text{ Ω}[/латекс]. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?
{4} \ текст {рад} \ текст{/} \ текст {s} \ справа) t \ справа][/латекс] 9{-6}\phantom{\rule{0.2em}{0ex}}\text{F}[/latex] и [латекс]R=5.00\phantom{\rule{0.2em}{0ex}}\text{ Ω}[/латекс]. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?
Стратегия
Среднеквадратичное значение напряжения равно амплитуде напряжения, умноженной на [latex]1\text{/}\sqrt{2}[/latex]. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное значение напряжения [латекс] {V} _ {\ text {среднеквадратичное значение}} [/латекс] и сопротивление R .
Решение
Показать ответ- Поскольку [латекс]{V}_{0}=4.00\phantom{\rule{0.2em}{0ex}}\text{V,}[/latex] среднеквадратичное значение напряжения на генератор
[латекс] {V} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} \ left (4.
 {1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где В заменяет среднеквадратичное значение напряжения.
{1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где В заменяет среднеквадратичное значение напряжения.Проверьте свои знания
Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Показать решение[латекс]v\left(t\right)=\left(10.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)\phantom{\rule{0.2 em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}90\pi t[/latex]
Проверьте свои знания
Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока со среднеквадратичным значением тока равно [латекс]{I}_{\text{среднеквадратичное значение}}[/латекс] по [латексу] {I} _ {\ text {rms}} R, {I} _ {\ text {rms}} {X} _ {C}, \ phantom {\ rule {0.2em} {0ex}} \ text{and}\phantom{\rule{0.2em}{0ex}}{I}_{\text{rms}}{X}_{L},[/latex] соответственно.
Show Solution Определить эти значения для компонентов Цепь RLC по уравнению 15.12.
Определить эти значения для компонентов Цепь RLC по уравнению 15.12.2,00 В; 10,01 В; 8,01 В
Сводка
- Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
- Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
- В цепи переменного тока существует угол сдвига фаз между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
- Средняя мощность, подаваемая на Цепь RLC зависит от фазового угла.
- Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла [latex]\varphi[/latex] между выходным напряжением источника переменного тока и током средняя выходная мощность источника максимальна?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Показать решение
Мгновенная мощность — это мощность в данный момент времени. Средняя мощность — это мощность, усредненная по циклу или числу циклов.
Средний переменный ток, подаваемый в цепь, равен нулю. Несмотря на это, мощность рассеивается в цепи. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Показать решениеМгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Задачи
ЭДС источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0.
 2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.
2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.Расчет среднеквадратичного значения тока для источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0.2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex] при соединении через (a) [латекс] 20\text{-}\mu \text{F}[/latex] конденсатор, (b) катушка индуктивности 20 мГн и (c) [латекс]50\text{-}\text{Ом}[/latex ] резистор.
Показать решениеа. 0,89 А; б. 5,6 А; в. 1,4 А
Катушка индуктивности 40 мГн подключена к источнику переменного тока частотой 60 Гц, амплитуда напряжения которого составляет 50 В.
 Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?
Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?Для цепи РЛК серии амплитуда напряжения и частота источника 100 В и 500 Гц соответственно; [латекс] R = 500 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]; и [латекс] L = 0,20 \ фантом {\ правило {0,2em} {0ex}} \ текст {H} [/латекс]. Найдите среднюю мощность, рассеиваемую на резисторе, при следующих значениях емкости: (а) [латекс]С=2,0 мкМ \текст{F}[/латекс] и (б) [латекс]С=0,20\фантом{\ правило{0.2em}{0ex}}\mu \text{F}\text{.}[/latex]
Показать раствора. 7,3 Вт; б. 6,3 Вт
Источник переменного тока с амплитудой напряжения 10 В отдает электрическую энергию мощностью 0,80 Вт при выходном токе 2,5 А. Каков фазовый угол [латекс]\varphi[/латекс] между ЭДС и током?
Цепь серии RLC имеет импеданс [латекс]60\фантом{\правило{0.2em}{0ex}}\текст{Ом}[/латекс] и коэффициент мощности 0,50, при этом напряжение отстает от текущий. а) Следует ли последовательно с элементами включить конденсатор или катушку индуктивности, чтобы повысить коэффициент мощности цепи? б) При каком реактивном сопротивлении катушки индуктивности коэффициент мощности увеличится до единицы?
Показать раствора.
 индуктор; б. [латекс] {X} _ {L} = 52 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]
индуктор; б. [латекс] {X} _ {L} = 52 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]Глоссарий
- средняя мощность
- среднее значение мгновенной мощности за один цикл
- коэффициент мощности
- величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
Питание в цепи переменного тока. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/15-4-power-in-an-ac-circuit. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Понимание коэффициента мощности — Laurens Electric Cooperative
Коэффициент мощности — это показатель того, насколько эффективно вы используете электроэнергию.
 Различные виды энергии работают, чтобы обеспечить нас электрической энергией. Вот что делает каждый.
Различные виды энергии работают, чтобы обеспечить нас электрической энергией. Вот что делает каждый.Рабочая мощность
Индуктивной нагрузке, такой как двигатель, компрессор или балласт, также требуется реактивная мощность для создания и поддержания магнитного поля для работы. Мы называем эту нерабочую мощность кВАр или киловольт-ампер-реактивная.
В каждом доме и офисе есть резистивные и индуктивные нагрузки. Соотношение между этими двумя типами нагрузок становится важным по мере добавления индуктивного оборудования. Рабочая мощность и реактивная мощность составляют полную мощность, которая называется кВА, или киловольт-ампер. Полную мощность определяем по формуле:
Формула полной мощности
кВА2 = кВ*А
Еще один шаг вперед: коэффициент мощности (PF) представляет собой отношение рабочей мощности к полной мощности, или формула PF = кВт / кВА . Высокий PF приносит пользу как потребителю, так и коммунальному предприятию, в то время как низкий PF указывает на плохое использование электроэнергии.

Формула коэффициента мощности
PF = кВт/кВА
Вот пример:
Операция штамповки стали выполняется при 100 кВт (рабочая мощность), а измеритель полной мощности показывает 125 кВА. Чтобы найти коэффициент мощности, разделите 100 кВт на 125 кВА, чтобы получить коэффициент мощности 80 %. Это означает, что только 80 % поступающего тока совершает полезную работу, а 20 % тратится на нагрев проводников. Поскольку Laurens Electric должна обеспечивать потребности всех клиентов как в кВт, так и в кВА, чем выше коэффициент мощности, тем эффективнее становится наша распределительная система.
Улучшение коэффициента мощности может максимизировать пропускную способность по току, улучшить напряжение на оборудовании, снизить потери мощности и снизить счета за электроэнергию.
Самый простой способ улучшить коэффициент мощности — добавить в электрическую систему корректирующие конденсаторы коэффициента мощности. Конденсаторы коррекции коэффициента мощности действуют как генераторы реактивного тока.
 Они помогают компенсировать нерабочую мощность, используемую индуктивными нагрузками, тем самым улучшая коэффициент мощности. Взаимодействие между конденсаторами PF и специализированным оборудованием, таким как приводы с регулируемой скоростью, требует хорошо спроектированной системы.
Они помогают компенсировать нерабочую мощность, используемую индуктивными нагрузками, тем самым улучшая коэффициент мощности. Взаимодействие между конденсаторами PF и специализированным оборудованием, таким как приводы с регулируемой скоростью, требует хорошо спроектированной системы.Конденсаторы коррекции коэффициента мощности могут включаться каждый день при запуске индуктивного оборудования. Включение конденсатора может вызвать кратковременное состояние «перенапряжения». Если у заказчика возникают проблемы с самопроизвольным отключением преобразователей частоты из-за «перенапряжения» каждый день примерно в одно и то же время, проверьте последовательность управления переключением. Если клиент жалуется на перегорание предохранителей на некоторых, но не на всех конденсаторах, проверьте гармонические токи.
Коррекция коэффициента мощности с помощью конденсаторов
Описание
Улучшение коэффициента мощности может максимизировать пропускную способность по току, улучшить напряжение на оборудовании, снизить потери мощности и снизить счета за электроэнергию.

Самый простой способ улучшить коэффициент мощности — добавить в электрическую систему корректирующие конденсаторы коэффициента мощности. Конденсаторы коррекции коэффициента мощности действуют как генераторы реактивного тока. Они помогают компенсировать нерабочую мощность, используемую индуктивными нагрузками, тем самым улучшая коэффициент мощности. Взаимодействие между конденсаторами PF и специализированным оборудованием, таким как приводы с регулируемой скоростью, требует хорошо спроектированной системы.
Конденсаторы коррекции коэффициента мощности могут включаться каждый день при запуске индуктивного оборудования. Включение конденсатора может вызвать кратковременное состояние «перенапряжения». Если у заказчика возникают проблемы с самопроизвольным отключением преобразователей частоты из-за «перенапряжения» каждый день примерно в одно и то же время, проверьте последовательность управления переключением. Если клиент жалуется на перегорание предохранителей на некоторых, но не на всех конденсаторах, проверьте гармонические токи.

Эффекты
Система распределения электроэнергии в здании или между зданиями может быть перегружена избыточным (бесполезным) током.
Мощность систем производства и распределения электроэнергии, принадлежащих Laurens Electric, измеряется в кВА (килоамперах).
кВА = ВОЛЬТ X АМПЕР X 1,73 (трехфазная система) / 1000
При единичном коэффициенте мощности (100%) потребуется 2000 кВА мощности генерирующей и распределительной сети для обеспечения 2000 кВт. Однако, если бы коэффициент мощности упал до 85%, потребовалась бы мощность 2353 кВА. Таким образом, мы видим, что более низкий коэффициент мощности оказывает негативное влияние на генерирующие и распределительные мощности.
Низкий коэффициент мощности вызывает перегрузку генерирующих, распределительных и сетей с избытком кВА.
Если вы владеете большим зданием, вам следует рассмотреть возможность коррекции низкого коэффициента мощности по одной или обеим из следующих причин:
- Чтобы уменьшить вероятность дополнительных сборов за коэффициент мощности в случае, если Laurens Electric начнет выставлять счета за корректировку коэффициента мощности.

- Для восстановления мощности (кВА) перегруженных фидеров в здании или комплексе зданий.
Существует несколько методов коррекции низкого коэффициента мощности. Обычно используются: емкость.
Блоки конденсаторов
Наиболее практичным и экономичным устройством коррекции коэффициента мощности является конденсатор. Это улучшает коэффициент мощности, потому что влияние емкости прямо противоположно влиянию индуктивности.
Значение var номинальной мощности конденсатора показывает, сколько реактивной мощности будет отдавать конденсатор. Поскольку этот вид реактивной мощности компенсирует реактивную мощность, вызванную индуктивностью, каждый киловар емкости уменьшает чистую потребность в реактивной мощности на ту же величину. Например, конденсатор на 15 кВАр компенсирует 15 кВА индуктивной реактивной мощности.
Конденсаторы могут быть установлены в любой точке электрической системы и улучшат коэффициент мощности между точкой приложения и источником питания.



 73Iф
73Iф

 1 Кинематика
1 Кинематика

 5 Излучение и спектры
5 Излучение и спектры
 {1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где В заменяет среднеквадратичное значение напряжения.
{1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где В заменяет среднеквадратичное значение напряжения. Определить эти значения для компонентов Цепь RLC по уравнению 15.12.
Определить эти значения для компонентов Цепь RLC по уравнению 15.12.
 2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.
2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор. Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?
Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет? индуктор; б. [латекс] {X} _ {L} = 52 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]
индуктор; б. [латекс] {X} _ {L} = 52 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс] Различные виды энергии работают, чтобы обеспечить нас электрической энергией. Вот что делает каждый.
Различные виды энергии работают, чтобы обеспечить нас электрической энергией. Вот что делает каждый.
 Они помогают компенсировать нерабочую мощность, используемую индуктивными нагрузками, тем самым улучшая коэффициент мощности. Взаимодействие между конденсаторами PF и специализированным оборудованием, таким как приводы с регулируемой скоростью, требует хорошо спроектированной системы.
Они помогают компенсировать нерабочую мощность, используемую индуктивными нагрузками, тем самым улучшая коэффициент мощности. Взаимодействие между конденсаторами PF и специализированным оборудованием, таким как приводы с регулируемой скоростью, требует хорошо спроектированной системы.


