Комплексное сопротивление — цепь — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Разветвленная цепь переменного тока.  [16]

Полученная в результате этого комплексная величина Z X — — jY и будет представлять собой полное комплексное сопротивление цепи.  [17]

Отношения приложенных комплексных фазных напряжений прямой, обратной и нулевой последовательностей к соответствующим комплексным фазным токам называют соответственно комплексными сопротивлениями цепи прямой ( Zi), обратной ( Z2) и нулевой ( Z0) последовательностей.  [18]

Зависимость погрешности бр от углов Р и 9.  [19]

Анализ функций W и векторных диаграмм ( см. раздел 3.1.2) показывает, что тангенс угла Э зависит от добротности или тангенса угла диэлектрических потерь преобразуемого или полного комплексного сопротивления цепи.

 [20]

Так как обе линии не совпадают по направлению с линией отвода, результирующее сопротивление цепи ( изображаемое для данных случаев отрезками АРг и АР3) не будет совпадать по направлению с отрезком АР, изображающим исходное комплексное сопротивление цепи.  [21]

Здесь U и / — комплексные действующие значения напряжения и тока, г — вещественная часть комплексного сопротивления Z, равная активному сопротивлению цепи, х — числовая величина мнимой части Z, равная реактивному сопротивлению цепи, z — модуль комплексного сопротивления цепи, равный полному сопротивлению цепи, ср — аргумент Z, равный углу сдвига фаз между током и напряжением.  [22]

Полученная в результате этого комплексная величина Z X jY и будет представлять собой полное комплексное сопротивление цепи.  [23]

Схема замещения параллельного РП.  [24]

При резонансе, когда сок ю № параллельное соединение L, Си R представляет собой активное сопротивление для основной гармоники. Более высокие гармоники тока / встречают комплексные сопротивления, соответствующие данной гармонике: чем выше частота гармоники входного тока, тем меньше модуль комплексного сопротивления цепи

.  [25]

Схема операционного усилителя.  [26]

Операционный усилитель представляет собой усилитель постоянного тока с большим коэффициентом усиления ( до тысячи и более), охваченный отрицательной обратной связью. Схема ОУ приведена на рис. 2.10, где через Zmb… Z обозначены комплексные в общем случае активно-емкостные входные сопротивления ОУ, a Zoc — комплексное сопротивление цепи обратной связи.  [27]

Страницы:      1    2

Символический (комплексный) метод расчета цепей переменного тока

Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета.

Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):

Рис.1. Вращающийся вектор

С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина

а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ

имеет положительное максимальное значение при угле ωt₃, когда при времени t₃ сумма ωt₃ + φ = 90° и соответственно,

имеет отрицательное максимальное значение при угле ωt₇, когда при времени t₇ сумма углов ωt₇ + φ = 270° 

и, соответственно,

и имеет два нулевых значения при ωt_n + φ = 0, когда ωt_n = —φ (на рис. 1 эта область не показана и находится слева от начала координат)

и тогда

и имеет нулевое значение при угле ωt₁₁, когда при времени t₁₁ сумма ωt₁₁ + φ = 360° и соответственно,

Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от  значения  0 В до максимальных 311 В и обратно.

2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)

Рис.2. Комплексное число на комплексной плоскости

Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины.

С учетом начальной фазы φ такое число записывают как .

На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна

На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли

При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.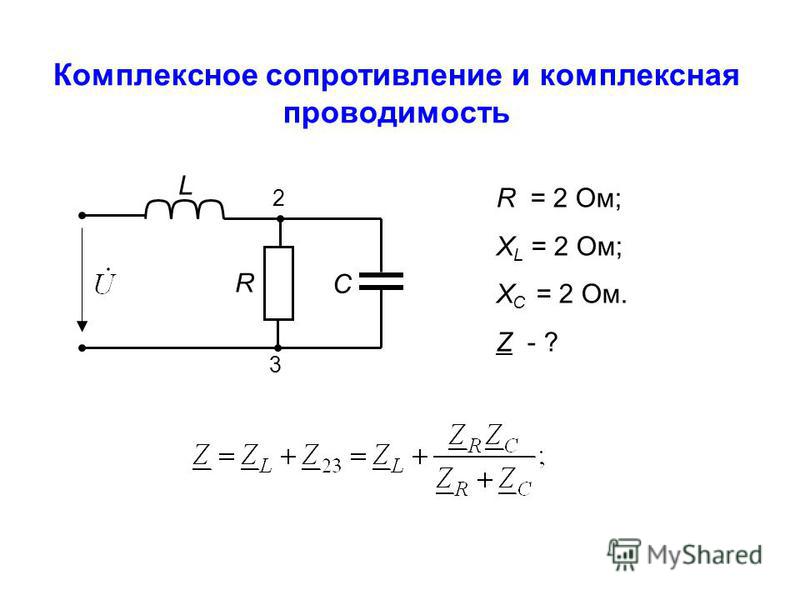
Итак, три формы записи комплексного числа:

1) показательная форма в виде

2) тригонометрическая форма в виде

3) алгебраическая форма

где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.

Например, имеем комплексное число в показательной форме вида

в тригонометрической форме записи это запишется как

при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что

В итоге получим

где

При переходе от алгебраической формы к показательной комплексное число вида

переходит к показательному виду  по следующим преобразованиям

а угол

Таким образом, и получим

Перейдем к рассмотрению несложных примеров использования  символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:

1. 1. • Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
      • В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
      • При необходимости составляют комплексные уравнения по выбранному методу решения.
      • Решают уравнения относительно комплексного значения искомой величины.
      • Если требуется, записывают мгновенные значения найденных комплексных величин.

Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.

Рис.3. Схема с последовательным соединением элементов

Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.

4):

Рис.4. Схема с комплексными обозначениями

По закону Ома ток в цепи равен

где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как

Пояснение: здесь начальная фаза  φ = 0°, так как  общее выражение для мгновенного значения напряжение вида при  φ = 0° равно

Соответственно, комплекс входного напряжения в показательной форме запишется как

Полное комплексное сопротивление цепи в общем виде

Находим комплексное сопротивление индуктивности

Находим комплексное сопротивление емкости

Соответственно, общее комплексное сопротивление цепи

Ток в цепи

Комплексные напряжения на элементах

Проверяем второй закон Кирхгофа для замкнутого контура, т. е. должно выполняться равенство

Проверяем

С небольшим расхождением из-за округлений промежуточных вычислений всё верно.

Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1)  полное сопротивление электрической цепи и его характер;
2)  действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;

1. Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.

Рис.5.Цепь однофвзного синусоидального тока

Решение:
1.  Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что

Комплексное сопротивление первой ветви:

Комплексное сопротивление второй ветви:

Комплексное сопротивление третьей ветви:

Общее сопротивление цепи

Откуда

— нагрузка носит активно-индуктивный характер

2. Находим действующие значения токов в ветвях:

 

Рис.6. Схема с обозначенными комплексными токами

Действующие значения, соответственно,

3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом,  активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:

Комплексная схема — Физика StickMan

Сложные схемы состоят из компонентов, которые находятся в ряду , а некоторые из них находятся в ряду , параллельном . Давайте начнем с рассмотрения последовательных и параллельных цепей, а затем посмотрим, как сложная схема работает как комбинация.

Последовательные схемы и правила (Нажмите здесь, чтобы перейти к уроку)

Последовательная схема у вас нет ответвлений , ток имеет только один путь. Один и тот же ток проходит через все компоненты от положительной клеммы и обратно к отрицательной клемме аккумулятора.

Закон Ома   (V=IR):

Вы можете использовать это в одном месте (T, 1, 2, 3 и любом другом), как показано ниже

• (V _T ) = (I _T )(R _T )
• (V ₁ ) = (I ₁ )(R ₁ )
• (V ₂ ) = (I ₂ )(R ₂ )
• (V ₃ ) = (I ₃ )(R ₃ )

Общие правила цепей серии

• V _T = V ₁ + V ₂ + V ₃ + … 4 4
• I _T = I ₁ = I ₂ = I ₃ = …
• Р _Т = Р ₁ + Р ₂ + Р ₃ + …

Правила параллельной цепи (Нажмите здесь, чтобы перейти к этому уроку)

В параллельной цепи есть ответвления , несколько путей для следования. Таким образом, ток разделяется, но затем снова собирается вместе, возвращаясь к батарее.

Вы можете использовать Закон Ома (V=IR) в одном месте, как указано выше, в последовательных цепях.

Правила общей параллельной цепи

• В _Т = В ₁ = В ₂ = В ₃ = … 4 4
• I _T = I ₁ + I ₂ + I ₃ + …
• 1/R _T = 1/R ₁ + 1/R ₂ + 1/R ₃ + …

Сложная цепь

Следите за током от положительной клеммы аккумулятора в анимации. Некоторые части цепи соединены последовательно, а некоторые параллельно.

1. Батарея и резистор 1   входят в серию : Ток 2 А начинается с батареи и протекает через них обоих.
2. Ветка с резистором 2, ветвь с резистором 3   и 4, а ветвь с резистором 5   параллельны : Ток разделяется между этими ветвями.
3. Резистор 3   и резистор 4 входят в серию : Как только ток идет вниз по ветви, тот же самый ток должен течь от обоих резисторов.

Решение сложной цепи для сопротивления

При вычислении сопротивления в последовательной цепи цель состоит в том, чтобы разрушить все различные части, чтобы они работали как одна единая последовательная цепь. Следуйте инструкциям или нашему примеру, как мы это делаем.

Примеры задач

1. Найдите полное сопротивление приведенной ниже сложной цепи.

Сначала добавьте резистор 3 и резистор 4, последовательно расположенные в ответвлении

R _T = R ₁ + R ₂

R _T = 10 Ом + 5 Ом = 15 Ом 9 00027 Теперь возьмите резистор 2, эквивалент резисторов 3 и 4 и резистор 5, которые все находятся на ответвлениях, и соедините их вместе по параллельным правилам. В этом случае R _T будет эквивалентом этих трех ветвей.

R _T = ((1/R ₁ ) + (1/R ₂ ) + (1/R ₃ )) ^-1

R 90(0025/T _{10 Ом) + (1/15 Ом) + (1/20 Ом)) ^-1 = 4,615 Ом}

Ток должен протекать через резистор 5 Ом и эквивалент резистора 4,615 Ом, чтобы они действовали так, как будто они соединены последовательно. Используйте правила серии, чтобы собрать их вместе.

Р _Т = Р ₁ + Р ₂

R _T = 5 Ом + 4,615 Ом = 9,615 Ом

Это сопротивление батареи, эквивалентное сопротивлению всей цепи.

2. Найдите неизвестные компоненты следующей сложной схемы.

Объединить резистор 2 и резистор 3 параллельно

R _T = ((1/R ₁ ) + (1/R ₂ )) ^-1

R _{T 9002 = ((1/R 2 )) 30 Ом) + (1/30 Ом)) ^-1 = 15 Ом}

Объедините 15 Ом эквивалент из резистора 2 и 3 с резистором 1, который в серии

R _T = R ₁ + R ₂

R _T = 15 Ха. + 5 Ом = 20 Ом

Это сопротивление цепи, подключенной к батарее. Мы использовали и больше не нуждаемся в эквиваленте или резисторе 2 и резисторе 3, поэтому вы увидите, что на следующем шаге эквивалент уменьшился.

Теперь определите ток в батарее, используя закон Ома 9.0007

I _T =V _T /R _T

I _T = 40 В/20 Ом = 2 А

1. Эта ветвь тока не течет перед резистором и не проходит через резистор 2 А от батареи. 1 Имеет тот же ток

Серия Правило

I _T = I ₁

I ₁ = 2A

Теперь решайте напряжение на резисторе 1, используя Закон OHM

V ₁ = (RESTSOR 1 OHM’ Я _Т )(Р _Т )

В ₁ = (2A)(5 Ом) = 10 В

10 В падает на первый резистор, оставляя 30 В для остальной части цепи. Параллельно оставшееся напряжение будет падать на всех и одинаково на обеих ветвях, которые имеют резистор 2 и резистор 3

Правило параллельности, которому мы следовали, было следующим:

Теперь мы можем использовать закон Ома, чтобы решить эту проблему.

На обоих резисторах 2 и 3 вы должны сделать следующее.

I = V/R

I= 30 В/30 Ом = 1 А

Для нашей окончательной проверки мы видим, что 2 А тока от резистора разделяются математически правильно, и знаем, что мы правы.

I _T = I ₁ + I ₂

2A = 1A + 1A

3. Найдите неизвестные компоненты следующей сложной схемы.

Используйте закон Ома для определения тока на резисторе 4

В ₁ = (I _T ) (R _T )

V ₁ = (2A) (5ω) = 10 В

V ₄ = (I ₄ ) (R ₄ )

I ₄ = (R ₄ )

I ₄ = (R ₄ ) V ₄ )/(R ₄ )

I ₄ =(16 В)/(16 Ом)= 1 А

Резистор 2 и резистор 3 включены последовательно. Последовательный ток равен

Правило последовательной схемы

I _T = I ₁ = I ₂ = I ₃ = …

Таким образом, ток 4 А на резисторе 2 также проходит через резистор 2. . С тех пор как я ₃  = 4А, I ₂ = 4А.

Теперь используйте закон OHM’s для решения для падения напряжения резистора 3.

V ₃ = I ₃ R ₃

V ₃ = (4A) (1 Ом) = 4V

5

• Ветвь с резистором 2 и резистором 3 параллельна ветви с резистором 4.
• Таким образом, вся ветвь с резистором 2 и резистором 3 должна быть равна 16 В, падающим на другую ветвь.
• Теперь обратите внимание, что резистор 2 и резистор 3 включены последовательно, и ток должен протекать через оба резистора.
• они должны суммироваться до 16 В в соответствии с правилом серии.

Следовательно, падение напряжения на резисторе 2 должно быть 12 В, так как падение напряжения на V ₂ и V ₃ на дополнительные 4 В должно добавить к 16 В другой ветви.

Теперь вы можете использовать закон Ома для определения сопротивления резистора 2.

В ₂ =I ₂ R ₂

R ₂ = V ₂ /I ₂

R ₂ = 12V /4A = 3 Ом

Теперь посмотрите на ветвь, который находится на противоречие 2 и сопротивление. 3. По этой ветви протекает ток силой 4 ампера. Это те же 4 ампера тока, так как эти два соединены последовательно. (Посмотрите на анимацию параллельной цепи ранее в этом уроке, если вы запутались)

Дополнительный ток 1 ампер течет по отдельной ветви с резистором 4

Таким образом, общий ток, выходящий из резистора 1, составил 5 ампер.

Батарея и резистор 5 с другой стороны также соединены последовательно, так что они тоже будут на 5 ампер.

Теперь Закон о том, чтобы определить снижение напряжения на резисторе 1.

V ₁ = I ₁ R ₁

V ₁ = (5A) (8 Ом) = 40 В

и Ом. для падения напряжения на резисторе 5

В ₅ =I ₅ R ₅

В ₅ = (5 А)(4 Ом) = 20 В 

Наконец, примените закон Ома, чтобы определить сопротивление всей цепи на аккумуляторе.

V _T =I _T R _T

R _T =V _T /I _T

R _T =76V/5A = 15.2Ω

You can потратьте немного времени на окончательную проверку, рассчитав сопротивление всей цепи в качестве последней проверки, и вы получите R _T = 15,2 Ом при правильном расчете общего сопротивления цепи.

Нажмите на картинку ниже, чтобы увидеть анимацию течения тока. Это для понимания окончательных ответов на текущий.

домашнее задание и упражнения — Нахождение эквивалентного сопротивления в сложной цепи

спросил 9 лет, 4 месяца назад

Изменено 7 лет, 3 месяца назад

Просмотрено 39 тысяч раз

$\begingroup$

В моем предыдущем вопросе Phys. SE, расположенном здесь, я спрашивал о нахождении эквивалентного сопротивления следующей цепи:

Я получил очень хорошие ответы и несколько советов. А что, если ту же схему изменить, добавив еще два резистора на свободные соединительные провода, например:

Как мне теперь найти эквивалентное сопротивление?
Вероятно, я не смогу перерисовать схему, как указано в ответах на мой предыдущий вопрос, поскольку на каждом проводе есть резистор.

• домашние задания и упражнения
• электрические цепи
• электрические сопротивления

$\endgroup$

3

$\begingroup$

Если у вас есть такая схема, которую нельзя упростить с помощью закона последовательной или параллельной схемы, вам следует проверить преобразование звезда-треугольник (http://en.wikipedia.org/wiki/Y-%CE% 94_трансформировать).

Общие законы Кирхгофа, конечно же, также будут работать.

$\endgroup$

2

$\begingroup$

То, как вы нарисовали схему, скрывает топологию. Схемы должны прояснять, а не запутывать. Это также помогает рисовать их аккуратно.

Вот схема, нарисованная для большей наглядности:

Надеюсь, теперь вы видите стратегию решения этой проблемы.

$\endgroup$

5

$\begingroup$

Ваша диаграмма точно такая же, как пример моста на странице преобразования Y-Δ в Википедии. После преобразований (показанных в этом примере) это становится тривиальным.

$\endgroup$

2

$\begingroup$

Диаграмма представляет собой сеть мостов Уитстона, но она должна удовлетворять условию, после которого легко вычислить чистое сопротивление между точками

Сопротивление R2 будет в середине и им можно пренебречь, если выполняется условие моста Уитстона, т. е. R1.R4=R5.R3

$\endgroup$

1

$\begingroup$

Эту схему можно перерисовать в более простой вариант. Схема, сформированная таким образом, будет в точности напоминать «мост Уитстона» с резистором вместо гальванометра (который обычно используется для проверки малейшего тока, проходящего через него).

Сначала отметьте точки на стыках как «1», «2», «3», «4» соответственно слева направо. Затем вы можете заметить, что точки с 1 по 2 имеют резистор № 1, поэтому сначала нарисуйте его. Затем мы можем заметить, что точки с 1 по 3 имеют резистор №. 4, поэтому нарисуйте Резистор №. 4 от точки 1 (отмеченной ранее) до точки 3. Теперь мы видим, что точки со 2 по 3 имеют резистор No. 2 между ними, поэтому нарисуйте его между точками 2 и 3 (обе точки отмечены на предыдущих шагах, поэтому просто нарисуйте резистор между ними). Теперь перенесите резистор 3 и резистор 5 из точек 3 и 4 соответственно в точку 5.