PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Измерение мощности современных сигналов — статьи компании «Диполь»

29 мая 2020

подписаться подписаться

Николай Шакуров, технический специалист, отдел продаж Keysight IDR
ShakurovNA@dipaul. ru

Технологии, используемые в процессе разработки и производства ВЧ/СВЧ-систем, достигли уровня, о котором ранее можно было только мечтать. Разработка средств беспроводной связи, как правило, отличается жестким графиком проектирования. Инженеры должны быстро ориентироваться в вопросах выбора приборов для измерения мощности, обеспечивая точность и воспроизводимость результатов измерений для новейших форматов модуляции. Новые беспроводные технологии для широкополосной передачи данных требуют приборов и первичных преобразователей мощности, способных измерять не только среднюю мощность, но и профили пиковой мощности и мощности в заданном временном интервале, а также отношение пиковой мощности к средней. При этом все измерения должны выполняться с высокой скоростью.

Обычно первичные преобразователи мощности рассчитаны на работу с определенными сигналами и видами модуляций. Измерители мощности создаются с учетом пожеланий пользователя к представлению результатов измерений.

Обзор технологий преобразователей

Термисторные преобразователи

Преобразователи на термисторах построены по принципу сбалансированного моста Уитстона. СВЧ-мощность рассеивается на согласованном резисторе, и полученное тепло изменяет сопротивление термистора, установленного в одно из плеч согласованного моста. Это изменение сопротивления приводит к рассогласованию моста и создает дифференциальный входной сигнал для усилителя. Недостаток таких типов преобразователей состоит в их чувствительности к изменениям температуры. Данную проблему решает добавление второго термистора для коррекции результатов измерения в зависимости от температуры окружающей среды. Эта давняя, зарекомендовавшая себя технология в настоящее время используется почти исключительно для стандартизации и обеспечения единства измерений.

Преобразователи на основе термопары

Работа термопары основана на том, что при соединении двух проводников из разнородных металлов и нагреве одного из соединений — «горячего» спая — между ними возникает напряжение. За счет поглощения ВЧ/СВЧ-сигнала нагревается «горячий» спай термопары преобразователя. В результате корректно определяется средняя мощность для сигналов всех типов — от немодулированных синусоидальных до импульсных со сложными видами цифровой модуляции, независимо от наличия гармоник, формы или искажений сигнала. Именно это и сделало преобразователи мощности на основе термопар предпочтительным типом преобразователя для систем со сложными видами модуляции, так как инженеры-испытатели могут быть уверены, что преобразователь реагирует на полную суммарную мощность сигналов во всем динамическом диапазоне. Пиковая импульсная мощность РЛС часто вычисляется на основе средней мощности и учета скважности сигнала. Однако типовой динамический диапазон преобразователей на основе термопары составляет лишь 50 дБ, от –30 дБм (1 мкВт) до +20 дБм (100 мВт). Обычно для беспроводных систем проводится «тихое» тестирование, при котором выход усилителя мощности отключен. Преобразователи на термопаре, пригодные для измерения мощности усилителя, недостаточно чувствительны для измерений при «тихом» тестировании, когда мощность не превышает –55 дБм. Измерение столь низких уровней мощности невозможно преобразователем с ограниченным динамическим диапазоном, поэтому приходится выполнять длительную и сложную процедуру, включающую замену преобразователей на основе термопары на диодные преобразователи и последующую перекалибровку измерительных трактов. Даже измерения у нижней границы динамического диапазона термопарных преобразователей (как правило от –25 до –30 дБм) требуют большого количества усреднений для получения точного и стабильного показания.

Диодные преобразователи

Диоды преобразуют ВЧ-энергию в постоянный ток за счет эффекта выпрямления, обусловленного их нелинейной вольт-амперной характеристикой. Традиционно диодные преобразователи мощности использовались для измерения мощности в диапазоне от –70 до –20 дБм, что делает их более предпочтительным типом преобразователей для приложений, в которых требуются такие высокочувствительные измерения, как проверка входных уровней при тестировании чувствительности приемника. В приложениях, предусматривающих высокую скорость измерений, диодные преобразователи предпочтительнее термопарных из-за их быстрой реакции на изменения входной мощности. При необходимости тестирования в диапазоне от –70 до +20 дБм (это все более частая ситуация), традиционный подход заключается в применении диодных преобразователей для перекрытия нижнего диапазона и преобразователей на основе термопары для верхнего диапазона измерений. В условиях больших объемов производства такой двойной набор преобразователей приводит к серьезному ограничению времени тестирования, особенно если должна быть сохранена оптимальная точность.

Измерение мощности сигналов с аналоговыми модуляциями

Традиционные измерители уровня мощности непрерывных сигналов предназначены для измерения немодулированных сигналов или непрерывных сигналов, однако при определенных условиях они также могут применяться для измерения модулированных сигналов, что значительно расширяет диапазон их применения. С точки зрения измерителя мощности любой сигнал с постоянной огибающей является непрерывным сигналом, то есть всегда могут выполняться точные измерения сигналов с частотной (FM) или фазовой (PM) модуляцией. Но при использовании любого типа амплитудной модуляции возникает ряд проблем.

Измерители мощности с диодными преобразователями, работающие в области квадратичного детектирования, могут использоваться для вывода истинного значения среднего уровня мощности огибающей модулированного сигнала, что достаточно для большинства радиоинженеров. Однако эти датчики характеризуются ограниченным динамическим диапазоном, что препятствует измерению комплексных сигналов. Когда диодный детектор используется для модулированных сигналов с уровнями мощности выше области квадратичного детектирования, измеритель мощности непрерывных сигналов переходит в нелинейный и непредсказуемый режим.

Решением данной проблемы становится применение диодных измерителей мощности с несколькими диодами внутри, работающими в области квадратичного детектирования.

Это выполняется с помощью интегрированного делителя мощности и переменных аттенюаторов для того, чтобы каждый диодный детектор работал в своей «области наилучшего функционирования» общего динамического диапазона датчика. Если диапазоны перекрываются, то измеритель мощности может объединить выходы этих детекторов для вывода точного результата измерения среднего уровня мощности в относительно широком динамическом диапазоне.

Измерение мощности сигналов с импульсной модуляцией

Измерение мощности импульсно-модулированного сигнала измерителем средней мощности

Измеритель средней мощности может использоваться для получения данных о средней мощности и среднем значении мощности импульса, если коэффициент заполнения сигнала известен. У данного метода есть свои преимущества, но необходимо учитывать некоторые моменты.

Среднее или максимальное значение мощности в импульсе, демонстрируемое измерителем средней мощности, рассчитывается на основе значений измерений средней мощности и известного коэффициента заполнения. Результат точен для идеального или близкого к идеальному импульсного сигнала, но он не отражает искажения из-за неквадратичной формы импульса и не обнаруживает максимальный размах, который может возникнуть из-за проявлений так называемого звона или выброса. Главное преимущество измерителей средней мощности состоит в том, что они являются самым недорогим решением для измерений мощности. Стоимость альтернативных измерителей пиковой мощности и преобразователей выше. Измерители средней мощности также способны выполнять измерения в более широком динамическом и частотном диапазоне и полосе пропускания, они определяют сигнал независимо от того, насколько мало время нарастания или длительность импульса. На рис. 1 приведен пример измерений среднего значения мощности импульса и средней мощности с использованием измерителя средней мощности и учетом известного коэффициента заполнения. В примере использован простой импульс длительностью 10 мкс с периодом повторения 40 мкс. Импульсный сигнал установлен с уровнем мощности приблизительно 0 дБм. Средняя мощность в результате составляет –6,79 дБм. Поскольку коэффициент заполнения известен (10 мкс, поделенные на 40 мкс, или 25%), перед измерением его значение может быть введено в интерфейс измерителя мощности для получения действующего значения мощности импульса, которое определяется величиной –0,77 дБм.

Рис 1. Использование измерителя средней мощности для получения действующего значения мощности импульса

В реальной ситуации, как упоминалось ранее, импульс может быть не чисто прямоугольным, поскольку имеются связанные с ним длительности фронта и спада, так же как и возможен выброс на сигнале. Комбинация этих эффектов создает погрешность в вычисленном результате.

Измерение мощности импульсно-модулированного сигнала измерителем пиковой мощности

Преимущество измерителя пиковой мощности с датчиком в том, что он демонстрирует не пересчеты, а непосредственное измерение максимальной мощности и действующего значения мощности. Это особенно важно для сформированных или модулированных импульсов, у которых измеренное действующее значение мощности импульса из средней мощности может быть неточным.

На рис. 2 приведен пример измерения максимальной мощности и действующего значения мощности импульса с помощью измерителя пиковой мощности Keysight P-серии. Его преимущество состоит в том, что он имеет индикатор с разверткой, позволяющий рассмотреть огибающую измеряемого импульсного сигнала. Измеритель пиковой мощности работает путем непрерывных выборок сигнала дискретизатором с частотой 100 млн выборок/с, буферизации данных и вычисления результата. Это обеспечивает гибкость измерений, включая гибкий запуск, временную селекцию многочисленными стробирующими импульсами и способность получать короткие однократные измерения.

Рис. 2. Использование измерителя пиковой мощности Keysight P-серии для измерения максимальной мощности, стробированного действующего значения мощности импульса и отношения максимальной мощности к средней мощности. Благодаря режиму просмотра огибающей импульса видно, что максимальная мощность на 1,39 дБ выше действующего значения мощности импульса

На рис. 3 показан временной селектор, установленный для возможности измерения более одного импульса. Устройство способно одновременно сообщать результаты измерения максимальной мощности, средней мощности и отношения максимальной мощности к средней мощности в пределах времени селекции. В приведенном случае полученный результат средней мощности –0,09 дБм равен действующему значению мощности импульса, так как время селекции установлено, в частности, для измерения одного импульса. Максимальная мощность незначительно выше 0,24 дБм, вероятно, в результате некоторого выброса (сигнала). Отношение максимальной мощности к средней мощности 0,32 дБ является разницей между двумя значениями.

Рис. 3. Благодаря автоматической установке стробирующего сигнала на импульс измеритель мощности Keysight P-серии обладает способностью измерять действующее значение мощности импульса непосредственно (без сопутствующих пересчетов)

Измеритель пиковой мощности P-серии отличается и другими преимуществами, удобными при измерении радиолокационных сигналов. На рис. 4 проиллюстрирована способность прибора автоматически измерять характеристики импульса: длительность импульса, период повторения импульса, длительность фронта и спада. Способность автоматически настраивать время стробирования по длительности импульса, используя бесконечную установку, показана на рис. 3. Данный функционал упрощает процедуру измерения действующего значения мощности импульса, не требуя знания значения длительности импульса. Это особенно удобно при эксплуатации радиолокаторов, имеющих динамическую длительность импульса.

Рис. 4. Измеритель пиковой мощности Р-серии автоматически измеряет характеристики импульса, включая длительность фронта, спада, импульса, а также период повторения импульсов

У измерителей пиковой мощности есть и свои ограничения. Одно из них — перекрытие по частоте. Например, для преобразователей пиковой мощности P-серии максимальный диапазон составляет 40 ГГц (110 ГГц — для преобразователя средней мощности). Измерители пиковой мощности с преобразователями обычно также имеют ограничения на диапазон мощности. Диапазон преобразователей мощности P-серии составляет приблизительно от –35 дБм до +20 дБм, тогда как преобразователи средней мощности E9300 охватывают диапазон от –60 дБм до +20дБм. Измерители пиковой мощности имеют также ограничения на время установления, длительности импульсов и полосы частот модуляции сигнала, который они могут измерить. Этими ограничениями можно частично управлять с помощью установки полосы частот видеосигнала.

Измерения мощности сигналов со сложными видами модуляции для беспроводной связи

Проведение измерений ВЧ-мощности новых сигналов со сложными видами фазовой/амплитудной модуляции вызвано необходимостью тщательного анализа тестовых сигналов. Создание технологии беспроводной связи ускорило переход от аналогового к цифровому типу модуляции. Вскоре появилось множество цифровых форматов модуляции: BPSK, QPSK, 8-PSK, 16QAM, 64 QAM и т. д. Затем были разработаны более сложные виды модуляции, такие как pi/4-DQPSK. Во многих системах для передачи потоков данных использовалась технология TDMA (множественный доступ с временным разделением каналов), например в стандарте GSM. Другие разработчики систем стали конкурировать, применяя формат CDMA с кодовым разделением каналов (например, IS-95A). Конструирование преобразователей как для базовых станций, так и для абонентских терминалов требует от специалистов немалых усилий для того, чтобы уложиться в заданную ширину спектра и снизить потребляемую мощность. Используется ли система TDMA, которая передает несколько несущих через общий выходной усилитель, или система CDMA, кодирующая несколько потоков данных в одну несущую с псевдослучайным кодом, в результате передается спектр мощности, очень похожий на спектр белого шума. Средняя мощность передаваемого сигнала является лишь одним из важных параметров, так же как и в случае белого шума. Из-за статистического характера сигнала в системах с несколькими несущими отношение пиковой мощности сигнала к средней мощности имеет решающее значение, поскольку мгновенная пиковая мощность может превышать среднюю мощность в 10–30 раз в зависимости от видов модуляции и фильтрации.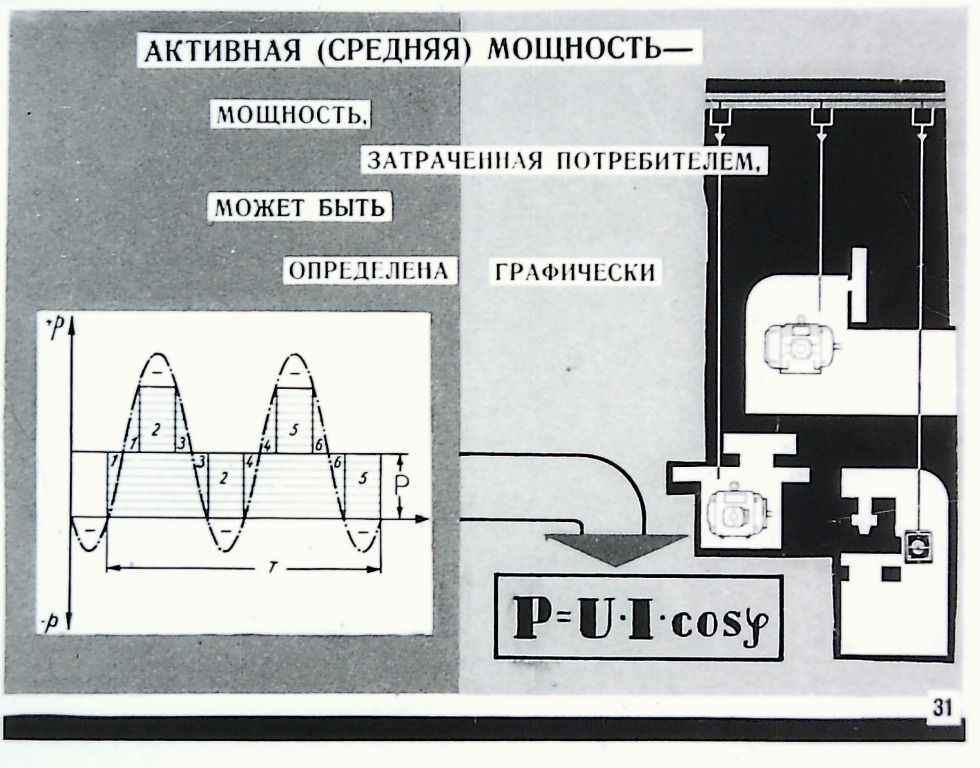

Такие высокие значения отношения пиковой мощности к средней могут ввести усилители мощности в опасный режим насыщения. Когда происходит насыщение, не хватает места для размещения крайних символов, что приводит к появлению битовых ошибок и нестабильному действию системы. Разработчики решают эту проблему с помощью выбора усилителя с запасом по мощности. Это гарантирует, что даже при пиковой мощности сигнала усилитель всегда будет функционировать в линейном режиме. Таким образом, для всех этих технологий требуется точное измерение импульсной выходной мощности усилителей, в том числе значения отношения пиковой мощности к средней, и стробируемая оценка параметров для определения профиля импульсных сигналов с целью обеспечения соответствия установленным предельным значениям.

Статистический анализ сигналов современных систем связи

В самых современных форматах беспроводной связи, подобных DVB, WiMax, WLAN и LTE, используются схемы модуляции OFDM с несколькими несущими для передачи цифровой информации. OFDM (мультиплексирование с ортогональным частотным разделением сигналов) представляет собой схему модуляции с несколькими несущими с высоким коэффициентом амплитуды для передачи больших объемов данных. Введение этой технологии привело к необходимости использования пиков мощности, превышающих среднюю мощность на 20 дБ. Для обработки ожидаемых пиков напряжения и предотвращения возникновения повреждений или дугового разряда ВЧ-компоненты должны быть указаны соответствующим образом. Для корректного указания этих компонентов следует определить коэффициент амплитуды (или пик-фактор), то есть отношение пикового к среднему значению или к среднеквадратичному значению. Пиковая мощность нескольких сопряженных передатчиков может превышать уровень тепловой или средней мощности в 100 и более раз. Выбор ВЧ-компонентов для системы передачи (антенные комбинаторы, коаксиальные линии и антенны) не может выполняться исключительно на основе уровня тепловой или средней мощности.

Редко возникающие кратковременные выбросы напряжения являются критическими при определении требуемого размера и возможности обработки мощности ВЧ-компонентов. Измерения коэффициента амплитуды выше 12 дБ (Ppep/Рavg) трудно выполнять с повторяемыми результатами. Для надлежащего определения столь высоких коэффициентов амплитуды одного измерения пикового значения недостаточно, и необходимо использовать статистический анализ. Сигналы систем связи низкой амплитуды с высоким коэффициентом амплитуды хотя и важны при учете коэффициента битовых ошибок (ВЕR), имеют большее значение с точки зрения их содействия повреждению системы. Высокое напряжение, ассоциированное с большими пиками мощности, может привести к возникновению дугового разряда в системе передатчиков и повредить компоненты оборудования. Статистика служит важным инструментом для анализа этих редких случаев с точки зрения предотвращения травм обслуживающего персонала и повреждения оборудования. Поскольку мгновенные значения уровня мощности сортируются по амплитуде, а не по их времени возникновения, они подсчитываются и не усредняются. Этот процесс может выполняться в течение длительного времени и ограничиваться только размером доступной памяти, либо может работать бесконечно долго при применении прореживания. Такой процесс не имеет никакой ценности для характеризации событий, поскольку максимальная пиковая мощность сигнала OFDM может возникнуть один раз в день. Получение импульсных данных с использованием статистики дает дополнительное понимание редких событий при сборе результатов измерений амплитуды в зависимости от времени.

Рис. 5. CCDF синусоидального сигнала (с частотой несущей), сигнал огибающей OFDM и белый шум

На рис. 5 представлена реальная картина комплементарной интегральной функции распределения (CCDF) сигнала HDTV (телевидение высокой четкости) с модуляцией OFDM (мультиплексирование с ортогональным частотным разделением сигналов). Кривая А показывает синусоидальный сигнал со 100%-ной амплитудной модуляцией, которая характеризуется «прямоугольной» функцией CCDF, указывающей отношение пикового к среднему уровню мощности 3 дБ как с низкой, так и высокой вероятностью. Подобный характер кривой обусловлен периодической формой сигнала с высокой степенью предсказуемости. Сигнал OFDM (кривая В) имеет отношение пикового к среднему уровню мощности около 15 дБ и характеризуется шаблоном рэлеевского распределения. Кривая С для справки указывает белый гауссовский шум, который имеет теоретически бесконечно большое отношение пикового к среднему уровню мощности, составляющее около 17 дБ с уровнем вероятности 1012.

Заключение

Точные измерения мощности очень важны для обеспечения необходимых характеристик и для проверки на соответствие стандартам современных телекоммуникационных и радиолокационных систем. И хотя эти измерения могут выполняться множеством разных способов, каждый из них обладает своими достоинствами и недостатками. Решение, которое выберет инженер, зависит от конкретной измерительной задачи и от того, какие преимущества он рассчитывает получить и на какие компромиссы готов пойти.

Источники

1. Choosing the Right Power Meter and Sensor — Product Note. Keysight Technologies, 2007–2017. Published in USA, December 1, 2017 5968-7150E. www.literature.cdn.keysight.com/litweb/pdf/5968-7150E.pdf
2. Radar Measurements — Application Note. Keysight Technologies, 2014 Published in USA, August 22, 2014. www.literature.cdn.keysight.com/litweb/pdf/5989-7575EN.pdf.
3. Principles of power measurement. Wireless Telecom Group, 2015 B/REFGUIDE/0815/EN. www.boonton.com/resource-library/principles-of-power-measurement-guide.

Средняя мощность за период. Активная, реактивная и полная и мощность переменного тока. Сдвиг фаз

Пусть в заданной схемес последовательным соединением элементов R, L и C (рис. 47) протекает переменный ток

.

По 2-му закону Кирхгофа для мгновенных значений функций получим уравнение в дифференциальной форме:

.

где  комплексное сопротивление,

 реак­тивное (эквивалентное) сопротивление,

 модуль ком­плексного или полное сопротивление,

 аргу­мент комплекс­ного сопротивления или угол сдвига фаз между напряжением и током на входе схемы. При

фазный уголφ >0, при этом цепь в целом носит ак­тивно-индуктивный характер, а при

иφ

Уравнение закона Ома для последовательной схемы будет иметь вид:

в комплексной форме,

в обычной форме для модулей.

Векторная диаграмма тока и напряжений при φ >0 показана на рис. 48.

В рассматриваемой цепи на переменном токе будут происходить одно­временно два физических процесса: преобразование энергии в другие виды в резисторе R (активный про­цесс) и взаимный обмен энергией между магнитным полем катушки, электрическим полем конденсатора и источником энергии (ре­активный процесс).

8. Электрическая цепь с параллельным соединением элементов r, l и с

Пусть на входе схемы рис. 49 действует переменное напряжение:

По 1-му закону Кирхгофа для мгновенных значений функций получаем уравнение в дифференциальной форме:

То же уравнение в комплексной форме получит вид:

где  комплексная проводимость,

 ак­тивная проводимость,

 реактивная индуктивная проводимость,

 реак­тивная емкостная проводимость,

 реактивная (эк­вивалентная) проводи­мость,

 модуль комплексной про­водимости или полная проводи­мость,

 аргумент комплекс­ной проводимости или угол сдвига фаз ме­жду напряжением и током на входе схемы. При

иφ >0 – цепь в целом носит активно-индуктивный ха­рактер, а при

иφ

Уравнение закона Ома для параллельной схемы будет иметь вид:

в комплексной форме;

в обычной форме для модулей.

Векторная диаграмма токов и напряжения при φ >0 показана на рис. 50.

На переменном токе в рассматриваемой цепи будут происходить одно­временно два физических процесса: преобразование электрической энергии в другие виды (активный процесс) и взаимный обмен энергией между магнит­ным полем катушки, электрическим по­лем конденсатора и источником энергии (реактивный процесс).

9. Активные и реактивные составляющие токов и напряжений

При расчете электрических цепей переменного тока реальные элементы цепи (при­емники, источники) заменяются эквивалентными схемами замещения, состоящими из ком­бинации идеальных схемных элементов

R, L и С .

Пусть некоторый приемник энергии носит в целом активно-индуктив­ный характер (например, электродвигатель). Такой приемник может быть пред­ставлен двумя простей­шими схемами замещения, состоящими из 2-х схемных элементов R и L : а) последовательной (рис. 51а) и б) параллельной (рис. 51б):

Обе схемы будут эквивалентны друг другу при условии равенства пара­метров ре­жима на входе:

,

.

Для последовательной схемы (рис. 51а) справедливы соотношения:

Для параллельной схемы (рис. 51б) справедливы соотношения:

Сравнивая правые части уравнений для U и I , получим соотношения между пара­метрами эквивалентных схем:

,

,

,

.

Из анализа полученных уравнений следует сделать вывод, что в общем случае

и

и соответственно

и

, как это имеет место для цепей постоян­ного тока.

Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.

Последовательной схеме замещения соответствует представление век­тора напряже­ния в виде суммы двух составляющих: активной составляющей U а, совпадающей с векто­ром тока I , и реактивной составляющей U р, перпенди­кулярной к вектору тока (рис. 52а):

Из геометрии рис. 52а следуют соотношения:

,

,

. Треугольник, составленный из векто­ров,

,получил назва­ние треугольника напряжений.

Если стороны треугольника напряжений разделить на ток I , то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются полное сопротивление Z , активное сопротивление R и реактивное сопро­тивление X . Треугольник со сторонами Z, R, X называется треугольником со­противлений (рис. 52б). Из треугольника сопротивлений следуют соотношения: R=Z cosφ, X=Z sinφ,

,

.

Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей I а , совпадаю­щей с вектором напряже­ния U , и реактивной составляющей I р , перпендикуляр­ной к вектору U (рис. 53а):

Из геометрии рисунка следуют соотношения:

,

,

.

Треугольник, составленный из векторов

получил название треугольника токов.

Если стороны треугольника токов разделить на напряжение U , то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются проводимости: пол­ная – Y , активная — G , реактивная – B (рис. 53б). Тре­угольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:

,

,

,

.

Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета не­сложных цепей пере­менного тока.

Для этого, скажем так, почти идеального случая, формула мощности будет такой же как и в случае с постоянным током

На рисунке ниже нарисована кривая изменения мгновенных значений мощности для данного случая (т.е направление тока и напряжения одинаковые). Таким образом, фазы тока и напряжения совпадают .

Мощность переменного тока. Сдвиг фаз I и U

Если в цепи переменного тока стоит конденсатор или катушки индуктивности, фазы тока и напряжения совпадать не будут.

Предположим, что в начальный момент радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с постоянной скоростью, то угол между ними будет одинаковым во все время их вращения. На рисунке ниже изображен случай отставания вектора тока I m от вектора напряжения U m на угол в 45° .

Как будут меняться при этом ток и напряжение. Из рисунка видно, что когда напряжение проходит через точку нуля, ток имеет отрицательное значение. когда напряжение достигает своего максимального значения и начинает уже убывать, а ток хоть и становится положительным, но еще не набирает максимального уровня и продолжает увеличиваться. Напряжение меняет свое направление, а ток все еще идет в прежнем и т. д. Фаза тока все время отстает от фазы напряжения, т.е между ними имеется существует постоянный сдвиг, который получил название сдвиг фаз .

Вследствие отставания фазы тока от фазы напряжения их направления в некоторые моменты не будут одинаковыми. В эти моменты мощность тока будет отрицательной. Это означает, что внешняя цепь в эти самые моменты становится источником электрической энергии и даже возвращает обратно некоторое количество энергии.

Чем сильне сдвиг фаз , тем длинее периоды, в течение которых мощность отрицательная, тем ниже будет средняя мощность переменного тока.

При сдвиге фаз в 90° мощность в течение первой четверти периода будет положительной, а в течение второй четверти периода — отрицательной. поэтому, средняя мощность переменного тока будет равна нулю, и ток не будет совершать никакой работы

Мощность переменного тока

Предположим, что мы тянем тележку с грузом, по рельсам. Но мы тянем ее не вдоль рельсов, а под определенным углом к ним. Угол между направлением движения и направлением наших усилий обозначим буквой φ (фи).

Если мы знаем сколько полезной силы, потратили протащив определенный путь, то достаточно легко можно посчитать и работу

Теперь вернемся к нашим ба.., радиусам-векторам тока и напряжения. И применим этот же способ. Мощность переменного тока при разности фаз φ = 0° равняется половине произведения вектора напряжения U m и вектора тока I m .

В случае, если мощность переменного тока, при разности фаз φ≠ 0 , будет равна половине произведения вектора напряжения U m и проекции вектора тока I m , проектируемого на вектор напряжения. Как нетрудно заметить, величина проекции зависит, от длины проектируемого вектора и от угла между ним и направлением, на которое он проектируется.

Если обозначить этот угол буквой φ , то длина проекции определяется длиной проектируемого вектора, умноженного на некоторый коэффициент, характеризующий этот угол, называемый косинусом угла (cos φ ). Значения косинусов различных углов даны в таблице.

Тоесть, проекция радиуса-вектора равна длине радиуса-вектора, умноженной на cos φ .
Тогда мощность переменного тока рассчитывается по следующей формуле:

Мгновенной мощностью p(t) принято считать произведение приложенного к цепи мгновенного значения тока i(t) на мгновенное напряжения u(t) .

p(t)=u(t)×i(t)=U m ×I m ×sin(wt)×sin(wt+φ)

График мгновенной мощности для этого случая показан на рисунке чуть ниже:

График — А

На рисунке мощность изображена заштрихованной областью. Знак мощности зависит толька от сдвига фаз между напряжением и током. Т.к в идеальном случае в цепи имеются только активные сопротивления, сдвиг фаз отсутствует, поэтому мощность со знаком поюс. Рассмотрим другой график, имеющий реактивную состовляющую.

График — В

На этои рисунке хороши видны области p(t) с минусовым знаком. Такой график соответствует схеме, в которой имется конденсатор или индуктивность, причем положительные участки — это мощность, которая ушла в цепь и рассеялась на сопротивлении, либо запаслась емкости или индуктивности, а отрицательные участки — был возврат обратно источнику питания.

Всем доброго времени суток! В сегодняшней статье мы будем разбираться с понятиями работы и мощности электрического тока . Для начала рассмотрим , а затем проведем аналогичные «исследования» и для цепей 🙂 Тема довольно обширная, формул много, так что давайте приступать!

Работа и мощность постоянного тока.

Давайте вспомним первую статью курса «Электроника для начинающих» — . Там мы определили напряжение как работу, которую необходимо затратить для переноса единичного заряда из одной точки в другую. Обозначим эту величину — . Чтобы найти работу, которую совершат несколько зарядов, нам необходимо работу одного заряда умножить на количество зарядов:

По определению мощность — это работа за единицу времени. Таким образом, мы получаем формулу мощности:

Снова возвращаемся мысленно к уже упомянутой первой статье курса, в которой мы обсуждали понятия тока и напряжения и вспоминаем, что количество зарядов, проходящее через проводник в единицу времени () — это и есть ток по определению 😉 И в итоге мы приходим к следующему выражению для мощности электрического тока:

Здесь мы также учли, что работа — численно равна напряжению на данном участке цепи.

Собственно, мы получили одну из основных формул для нахождения мощности постоянного тока. А учитывая закон Ома получаем следующее:

Единицей измерения мощности является Ватт, а 1 Вт — мощность, при которой за 1 секунду совершается работа 1 Джоуль.

Тут необходимо остановиться на одном довольно интересном нюансе. Часто при обсуждении работы электрического тока можно услышать сочетание — киловатт-час. Например, электросчетчики в домах показывают работу именно в этих единицах измерения. Так вот несмотря на схожесть в названиях единиц измерения мощности (ватт) и работы (киловатт-час/ватт-час) не стоит забывать, что эти термины относятся к разным физическим величинам. Чтобы перевести КВт*ч в более привычные с точки зрения системы измерений Си джоули можно воспользоваться следующим математическим соотношением:

1 КВт*ч = 3600000 Дж

Давайте рассмотрим небольшой пример для иллюстрации вышесказанного 🙂 Итак, пусть у нас есть чайник, мощность которого составляет 1200 Вт (1. 2 КВт). Мысленно включим его на 10 минут (1/6 часа). В итоге, работа электрического тока (а вместе с ней и потребленная чайником энергия) составит:

1200 Вт * 1 / 6 ч = 200 Вт*ч = 0.2 КВт*ч

С работой и мощностью постоянного тока все понятно, давайте перейдем к цепям .

Пусть у нас ток и напряжение изменяются по следующим законам:

Мы приняли, что ток и напряжение сдвинуты по фазе на величину .

Мгновенная мощность (мощность переменного тока в любой момент времени) будет равна:

Преобразуем формулу в соответствии с тригонометрической формулой произведения синусов:

Вот так будут выглядеть зависимости тока, напряжения и мощности переменного тока от времени:

На самом деле практический интерес представляет не мгновенное значение мощности (которое постоянно меняется), а среднее. Для среднего значения мощности переменного тока за период запишем следующее выражение:

Не буду особо нагружать математическими выкладками, давайте просто обратим внимание на то, что в формуле мгновенной мощности второе слагаемое () при интегрировании (суммировании) будет равно нулю. Это связано с тем, что если мы рассматриваем конкретный период, то значение косинуса в течение одного полу-периода сигнала будет иметь положительную величину, а в течение другого — отрицательное). Поэтому в финальной формуле средней мощности переменного тока останется только интеграл от первого слагаемого:

Вот мы и получили выражение для вычисления средней за период мощности в цепи переменного тока (ее также называют активной мощностью ) 🙂

Если сдвиг фаз между током и напряжением будет равен нулю, то значение средней мощности будет максимальным (поскольку ). В случае сдвига фаз часть мощности передается в нагрузку (активная мощность), а часть нет (реактивная мощность). Реактивная мощность приводит к потерям на излучение и на нагрев. Из формулы понятно, что чем больше , тем больше мощности попадет непосредственно в нагрузку, поэтому величину называют коэффициентом мощности. Активную мощность мы определили ранее, а вот для реактивной мощности справедлива немного другая формула:

Ну а полная мощность переменного тока равна:

На сегодня на этом все, мы разобрались с понятиями работы и мощности электрического тока, до скорых встреч на нашем сайте!

Формула средней мощности | Instantaneous Power Formula

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

В линейных сетях, входы которых являются периодическими функциями времени, генерируемые установившиеся токи и напряжения являются периодическими, каждый из которых имеет одинаковые периоды.

Рассмотрим мгновенную мощность

$\begin{matrix}   p=vi & \cdots  & (1)  \\\end{matrix}$

Где v и i периодичны с периодом T, то есть

$\begin{align}  & v(t+T)=v(t) \\ & и \\ & i(t+T)=i(t) \\\end{align}$

В этом случае ,

$\begin{align}  & p(t+T)=v(t+T)i(t+T) \\ & =v(t)i(t) \\ & =\begin{matrix} p(t) & \cdots  & (2)  \\\end{matrix} \\\end{align}$

Следовательно, мгновенная мощность также является периодической с периодом T, то есть p повторяется каждые T секунд.

Фундаментальный период T ₁ p (минимальное время, в течение которого p повторяется) не обязательно равен T, однако T должен содержать целое число периодов T 9{2}}$

В этом случае ${{T}_{1}}=T=\frac{2\pi }{\omega }$ и n=1 в (3). Это видно и из графика функции на рис. {{{t}_{1}}+{{T}_{1}}}{p\text{ }dt} & \cdots  & (4)  \\\end{matrix}$ 9{\pi }/{}_{\omega}$ $4.\text{ sin(m}\omega \text{t+}\alpha \text{)cos(n}\omega \text{t+} \alpha \text{)*}$ $0$ $5.\text{ cos(m}\omega \text{t+}\alpha \text{)cos(n}\omega \text{t+} \beta \text{)*}$ $\left\{ \begin{matrix}
\begin{matrix}
0, & m\ne n \\
\end{matrix} \\
\begin{matrix }
\frac{\pi \cos (\alpha -\beta )}{\omega }, & m=n \\
\end{matrix} \\
\end{matrix} \right.$

* m и n — целые числа

Сначала рассмотрим обычное двухполюсное устройство на рис. 3, которое предполагается находящимся в установившемся режиме переменного тока. Если в частотной области

$Z=\left| Z \right|\angle \theta $

Входное сопротивление устройства, тогда для

\[\begin{matrix}   v={{V}_{m}}cos(\omega t+\phi ) & \cdots  & (7)  \\\end{matrix}\]

У нас есть

\[\begin{matrix}   i={{I}_{m}}cos(\omega t+\phi -\theta ) & \cdots  & (8)  \\\end{matrix}\] 9{2\pi}/{}_{\omega}}{\cos (\omega t+\phi)}\cos (\omega t+\phi -\theta)dt$

Ссылаясь на таблицу 1, запись 5, мы найти для m = n = 1, α = ϕ и β = ϕ-θ

$\begin{matrix}   P=\frac{{{V}_{m}}{{\operatorname{I}} _{m}}}{2}\cos \theta  & \cdots  & (9)  \\\end{matrix}$

Таким образом, средняя мощность, поглощаемая двухполюсником, определяется амплитудами V _m и I _m и угол θ, на который напряжение v опережает ток i.

С точки зрения фазоров v и i,

$V={{V}_{m}}\угол \phi =\left| {{V}_{m}} \right|\angle \phi $

Из (9) имеем

\[\begin{matrix}   P=\left| В \право|\лево| I \right|\cos (ang(V)-ang(I)) & \cdots  & (10)  \\\end{matrix}\]

Где

$ang(V)=\phi \text{       } и\text{      }ang(I)=\phi -\theta $

— углы векторов V и I.

=RI _m , так что (9{2}$

В случае индуктора θ=90 ^o , а в случае конденсатора θ=-90 ^o , и, таким образом, для любого из них по (9) P=0 . Следовательно, катушка индуктивности или конденсатор, или, если уж на то пошло, любая цепь, полностью состоящая из идеальных катушек индуктивности и конденсаторов, в любой комбинации рассеивает нулевую среднюю мощность. По этой причине идеальные катушки индуктивности и конденсаторы иногда называют элементами без потерь. Физически элементы без потерь сохраняют энергию в течение части периода и выделяют ее в течение другой части, так что средняя отдаваемая мощность равна нулю. 9{2}\operatorname{Re}(Z) & \cdots  & (11)  \\\end{matrix}\]

Теперь рассмотрим этот результат, если устройство является пассивной нагрузкой, что мы знаем из определения пассивности что чистая энергия, переданная пассивной нагрузке, неотрицательна. Поскольку средняя мощность представляет собой среднюю скорость, с которой энергия доставляется в нагрузку, отсюда следует, что средняя мощность неотрицательна. То есть Р≥0. Для этого согласно (11) требуется, чтобы

               $\operatorname{Re}\text{ Z(j}\omega \text{)}\ge 0$

Или эквивалентно

               $-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}$

Если θ=0, устройство эквивалентно сопротивлению, а если θ=π/2 (или – π/2), устройство эквивалентно катушке индуктивности (или конденсатору). Для

\[-\frac{\pi }{2}<\theta <0\]

устройство эквивалентно RC-комбинации, где для

\[0<\theta <\frac{\pi }{2}\]

устройство эквивалентно комбинации RL.

Наконец, если |θ|>π/2, то P<0, и устройство активно, а не пассивно. В этом случае устройство подает питание от своих клемм и, конечно же, действует как источник. 9{2}}}{2}=25W$

Эта мощность, конечно же, равна мощности, подводимой к Z, поскольку индуктор не потребляет мощности.

Мощность, поглощаемая источником, равна

$Pg=-\frac{{{V}_{m}}{{I}_{m}}}{2}\cos \theta =-25W$

Где используется знак минус, потому что ток течет от положительной клеммы источника. Таким образом, источник отдает на Z мощность 25 Вт. Заметим, что мощность, вытекающая из источника, равна мощности, поглощаемой нагрузкой, что иллюстрирует принцип сохранения мощности.

Вы нашли apk для Android? Вы можете найти новые бесплатные игры и приложения для Android.

15.4 Питание в цепи переменного тока — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Опишите, как средняя мощность от цепи переменного тока может быть выражена через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
• Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности

Элемент схемы рассеивает или производит мощность в соответствии с P=IV,P=IV, где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность p(t)=i(t)v(t)p(t)=i(t)v(t) также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) изменяются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.

Рисунок 15.16 График мгновенной мощности для различных элементов цепи. (a) Для резистора Pave=I0V0/2, Pave=I0V0/2, тогда как для (b) конденсатора и (c) катушки индуктивности Pave=0.Pave=0. (d) Для источника Pave=I0V0(cosϕ)/2, Pave=I0V0(cosϕ)/2, что может быть положительным, отрицательным или нулевым, в зависимости от ϕ.ϕ.

Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем средней мощностью. Он определяется средней по времени мгновенной мощностью за один цикл:

Pave=1T∫0Tp(t)dt,Pave=1T∫0Tp(t)dt,

где T=2π/ωT=2π/ω – период колебаний. С заменами v(t)=V0sinωtv(t)=V0sinωt и i(t)=I0sin(ωt−ϕ),i(t)=I0sin(ωt−ϕ) этот интеграл принимает вид

Pave=I0V0T∫0Tsin( ωt−ϕ)sinωtdt.Pave=I0V0T∫0Tsin(ωt−ϕ)sinωtdt.

с использованием тригонометрической связи sin (a -b) = sinacosb -sinbcosa, sin (a -b) = sinacosb -sinbcosa, мы получаем

pave = i0v0cosϕt∫0tsin2ωtdt -I0V0SinϕT∫0STCOSTDSINTDTDT -I0V0SINϕ0STDCOSTD. TSINTDSIN0VIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SIN0SINSINTDSINTDTDTDTDTDTDTDTDT -I0VIN0SIN0SIN0SIN0SIN0SINSINTDSINTDTDTDTDTDTDTDTDT -I0VIN. 0Tsinωtcosωtдт.

Вычисление этих двух интегралов дает

Следовательно, средняя мощность, связанная с элементом схемы, определяется как

Pave=12I0V0cosϕ.Pave=12I0V0cosϕ.

15.12

В технических приложениях cosϕcosϕ известен как коэффициент мощности, который представляет собой величину, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения фаз напряжения и тока. Для резистора ϕ=0,ϕ=0, поэтому средняя рассеиваемая мощность равна

Задать=12I0V0.Задать=12I0V0.

Сравнение p ( t ) и PavePave показано на рис. 15.16(d). Чтобы сделать Pave=(1/2)I0V0Pave=(1/2)I0V0 похожим на его аналог постоянного тока, мы используем среднеквадратичные значения IrmsandVrmsIrmsandVrms тока и напряжения. По определению это

Irms=iave2andVrms=vave2,Irms=iave2andVrms=vave2,

, где )dt и vave2=1T∫0Tv2(t)dt.

При i(t)=I0sin(ωt−ϕ) и v(t)=V0sinωt, i(t)=I0sin(ωt−ϕ)и v(t)=V0sinωt получаем

Irms=12I0и Vrms=12V0.Irms=12I0andVrms=12V0.

Затем мы можем написать для средней мощности, рассеиваемой резистором,

Pave=12I0V0=IrmsVrms=Irms2R.Pave=12I0V0=IrmsVrms=Irms2R.

15.13

Это уравнение еще раз подчеркивает, почему для обсуждения выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.

Переменные напряжения и токи обычно описываются их среднеквадратичными значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет 1102 В = 156 В. 1102 В = 156 В. Поскольку большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.

Для конденсатора и катушки индуктивности , ϕ=π/2 и −π/2рад, ϕ=π/2 и −π/2рад соответственно. Поскольку cosπ/2=cos(−π/2)=0, cosπ/2=cos(−π/2)=0, из уравнения 15.12 мы находим, что средняя мощность, рассеиваемая любым из этих элементов, равна Pave=0.Pave =0. Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем возвращают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.

Фазовый угол генератора переменного тока может иметь любое значение. Если cosϕ>0,cosϕ>0, генератор вырабатывает мощность; если cosϕ<0,cosϕ<0, он поглощает мощность. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как

Pave=IrmsVrmscosϕ.Pave=IrmsVrmscosϕ.

Для генератора в цепи RLC ,

tanϕ=XL−XCRtanϕ=XL−XCR

и

cosϕ=RR2+(XL−XC)2=RZ. cosϕ=RR2+(XL−XC)2= РЗ.

Следовательно, средняя мощность генератора равна

Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.

15.14

Это также можно записать как

Pave=Irms2R,Pave=Irms2R,

, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.

Пример 15,3

Выходная мощность генератора

Генератор переменного тока, ЭДС которого определяется выражением

v(t)=(4,00 В)sin[(1,00×104 рад/с)t]v(t)=(4,00 В)sin[(1,00×104 рад/с)t]

подключен к RLC , для которой L=2,00×10-3HL=2,00×10-3H, C=4,00×10-6FC=4,00×10-6F и R=5,00ΩR=5,00Ω. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?

Стратегия

Среднеквадратичное напряжение – это амплитуда напряжения, умноженная на 1/21/2. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное напряжение VrmsVrms и сопротивление R .

Решение

1. Поскольку V0=4,00 В, V0=4,00 В, среднеквадратичное значение напряжения на генераторе равно

   Вэфф=12(4,00В)=2,83В. Вэфф=12(4,00В)=2,83В.

2. Полное сопротивление цепи

   Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)−1(1,00×104рад/с)(4,00×10-6F)] 2}1/2=7,07 Ом. Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)−1(1,00×104 рад/с) (4,00×10-6F)]2}1/2=7,07 Ом.

3. Из уравнения 15.14 средняя мощность, передаваемая в цепь, равна

   Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0,801 Вт. Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0,801 Вт.

Значение

Если сопротивление намного больше, чем реактивное сопротивление конденсатора или индуктора, средняя мощность представляет собой уравнение цепи постоянного тока P=V2/R, P=V2/R, где В заменяет среднеквадратичное значение напряжения.

Проверьте свое понимание 15,4

Проверьте свои знания Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.

Проверьте свое понимание 15,5

Проверьте свои знания Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичное значение тока равно IrmsIrms, выражается как IrmsR, IrmsXC и IrmsXL, IrmsR, IrmsXC и IrmsXL соответственно. Определите эти значения для компонентов схемы RLC по уравнению 15. 12.

Что такое нормализованная мощность по сравнению со средней мощностью? – Триатлет

Чтобы получить доступ ко всем нашим тренировкам, экипировке и репортажам о гонках, а также эксклюзивным планам тренировок, фотографиям FinisherPix, скидкам на мероприятия и приложениям GPS, Зарегистрируйтесь на Outside+.

Для тех, кто тренируется с измерителем мощности на велосипеде (а если вы не тренируетесь с мощностью, то должны), анализ данных после тренировки доставляет почти такое же удовольствие, как и сама поездка. Но если вы не знаете, как интерпретировать собираемые данные о мощности, вы не сможете воспользоваться всеми преимуществами этого обучающего инструмента.

Измерители мощности бывают разных форм (например, в педалях или шатунах) и измеряют выходную мощность велосипедиста в ваттах в результате умножения крутящего момента (силы на педали) на частоту вращения педалей (об/мин или число оборотов в минуту) ). В отличие от других показателей тренировки, таких как частота сердечных сокращений и количество километров в час, на которые могут влиять внешние факторы, такие как погода, местность или усталость, мощность является абсолютной. Это данные о фактической выполняемой работе в режиме реального времени.

Мощность используется для определения вашей функциональной пороговой мощности (FTP), которую можно использовать для установки тренировочных зон и определения целей для тренировок и забегов. Но FTP и мощность в реальном времени — не единственные термины, которые вам следует знать. Существует ряд терминов и точек данных, которые следует учитывать при использовании мощности: нормализованная мощность, средняя мощность, индекс изменчивости и коэффициент интенсивности.

СВЯЗАННЫЕ: Начните тренироваться с мощностью

Средняя мощность по сравнению с нормализованной мощностью

При анализе данных после поездки чаще всего встречаются два термина мощности: средняя мощность и нормализованная мощность.

Средняя мощность — это просто среднее количество ватт, произведенных во время тренировки, включая нули. Единственным недостатком этой метрики является то, что все значения мощности имеют одинаковый вес, поэтому периоды более низкой производительности, такие как движение накатом, дрейф или остановка, могут значительно снизить среднее значение. Вот тут-то и появляется нормализованная мощность. Нормализованная мощность — это оценка мощности, которую вы могли бы поддерживать при той же рабочей нагрузке при постоянном усилии. Он снижает акцент на периоды низкой выходной мощности и придает больший вес более тяжелым усилиям.

«Подумайте о постоянном курсе», — сказал Джефф Боуман из Rev Tri Coaching. «Большинство людей будут увеличивать мощность, поднимаясь в гору, взбираться на вершину холма, а затем немного спускаться вниз. Вот почему в конце поездки вы увидите разницу между нормализованной мощностью и средней мощностью. Нормализованная мощность более точно отражает то, что на самом деле чувствует ваше тело».

Вопреки распространенному мнению, нормализованная мощность не просто убирает нули для улучшения среднего. Вместо этого тренировочное программное обеспечение, например, TrainingPeaks, использует довольно сложный, закулисный, четырехэтапный алгоритм для расчета нормализованной мощности.

В качестве примера рассмотрим две разные поездки продолжительностью один час. Первая поездка представляет собой устойчивую тренировку на тренажере, в результате чего мощность составляет в среднем 150 Вт. Теперь представьте себе часовую поездку по холмистой трассе с подъемами, которые вызывают всплески мощности в 250 Вт в течение нескольких минут, за которыми следуют периоды менее 50 Вт при спуске. Средняя мощность для этой поездки может по-прежнему равняться 150 Вт, но вторая поездка с периодами высокой интенсивности, безусловно, будет намного тяжелее, чем стационарная тренировка. Нормализованная мощность будет отражать эти колебания мощности и в некоторых случаях может обеспечить более точное представление вашего выхода.

СВЯЗАННЫЕ: Как получить максимальную отдачу от чтения ваших файлов мощности

Когда использовать нормализованную мощность против средней мощности гонка на время на плоской трассе. Но для поездки с колебаниями интенсивности, например, на холмистой трассе, нормализованная мощность может быть более надежным показателем.

Нормализованная мощность очень полезна для триатлонистов во время гонки, особенно на холмистой трассе. В то время как многие люди настраивают свои велокомпьютеры на отображение 3-секундной или 10-секундной мощности, Боуман предлагает добавить еще одно поле данных: нормализованную мощность.

«Например, если я даю спортсмену диапазон мощности для гонки, я скажу ей настроить свой велокомпьютер на отображение нормализованной мощности», — сказал он. «Я всегда хочу видеть стоимость поездки с точки зрения общей картины, а не только с шагом от 3 до 10 секунд. Вы можете повышать свою мощность в горах, в пределах разумного, но вы хотите, чтобы ваша нормализованная мощность оставалась в пределах определенного диапазона на протяжении всей гонки».

Просматривая несколько полей данных, вы получаете данные в режиме реального времени и лучше понимаете, как у вас дела в целом. Одно из предложений от Боумена — проверить нормализованную мощность примерно через 30 минут после начала гонки, чтобы убедиться, что вы остаетесь в пределах установленного диапазона. Если вы едете немного жарко, а ватты слишком высоки, вам, возможно, придется уделить больше внимания остальной части поездки, чтобы восстановить часть энергии перед пробежкой.

Есть один сценарий, когда нормализованная мощность не так полезна — при любом усилии короче 20 минут.

Влияние нормализованной мощности на другой анализ производительности

Нормализованная мощность также играет роль в определении других функций анализа производительности. «Нормализованная мощность вводится в коэффициент интенсивности и показатель тренировочного стресса [уникальный для платформы TrainingPeaks], которые помогают определить, насколько тяжелой была тренировка или гонка», — сказал Боуман.

TrainingPeaks использует нормализованную мощность для расчета показателя тренировочного стресса (TSS), который является оценкой общей тренировочной нагрузки и физиологического стресса, вызванного тренировкой. (Для справки, езда на полную катушку в течение часа составляет примерно 100 TSS.