SPICE Differentiation. Различия в реализациях симуляторов SPICE

Симулятор SPICE (англ. SPICE — Simulation Program with Integrated Circuit Emphasis, симулятор электронных схем общего назначения с открытым исходным кодом, разработан в Electronics Research Laboratory в Калифорнийском университете в Беркли) применяется для компьютерного моделирования аналоговых схем, потому что он может в самом широком диапазоне просчитывать поведение сигналов в произвольных схемах. Популярность SPICE обусловлена тремя числовыми методами моделирования, которые используются в нем как основа для симуляции аналоговых схем:

• метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции, используется для нахождения решений в схемах с нелинейными элементами;
• метод разреженной матрицы (то есть матрицы с преимущественно нулевыми элементами) предназначен для того, чтобы поместить огромные матрицы в адресное пространство компьютера;
• неявное интегрирование — предназначено для интегрирования дифференциальных уравнений, возникающих в схемах, описывающих реактивные сопротивления.

Возможность симулятора SPICE выдавать надежный результат зависит от того, насколько правильно эти методы реализованы. Данная статья объясняет, почему симулятор LTspice от корпорации Linear Technology показывает лучшие результаты в отличие от других реализаций SPICE.

 

Метод Ньютона

Метод Ньютона включает разложение вольт-амперной характеристики (ВАХ) каждого нелинейного элемента схемы в ряд Тейлора, но с сохранением при этом только первых двух результатов и дальнейшим решением получившейся системы линейных уравнений. Если решение системы линейных уравнений действительно находится в той точке, для которой было применено разложение в ряды Тейлора, тогда (поскольку разложение в ряды Тейлора соответствует этой точке или ее окрестностям) решение этой системы линейных уравнений является правильным для исходной нелинейной схемы (в других случаях решение линейной системы используется в качестве шага итерации. При этом оригинальная нелинейная схема вновь расширяется до нового ряда Тейлора этого решения, опять сохраняя только два первых его члена, а затем снова решается полученная новая система линейных уравнений.

Процесс повторяется до тех пор, пока не будет получено доказательство того, что правильное решение было успешно найдено). Результат сходимости метода Ньютона приводит к нахождению числового доказательства тому, что было найдено корректное решение для нашей схемы.

Корректность метода Ньютона зависит от (1) наличия непрерывных значений крутизны вольт-амперной характеристики каждого элемента схемы и (2) шунтирования всех нелинейных элементов конденсаторами так, что решение для предыдущей точки во времени является подходящей точкой для старта метода Ньютона для текущего временного значения. Условия (1) и (2) встречаются в любой физической схеме, но программы, использующие SPICE, как правило, не умеют правильно их применять, потому что представление ВАХ полупроводниковых устройств в оригинальной реализации SPICE от Университета Беркли является дискретным. Это приводит к погрешностям, и такие ошибки реализации исходных моделей присутствуют изначально и в платных версиях SPICE. В симуляторе LTspice такая дискретность отсутствует.

Для иллюстрации этих отличий на рис. 1 приведены вольт-амперные характеристики диода в PSpice по сравнению с их представлением в симуляторе LTspice. (PSpice является зарегистрированной торговой маркой компании Cadence. В приведенных иллюстрациях используется версия 9.2.). Для каждого случая был использован следующий текстовый файл списка соединений (netlist):

Рис. 1.
а) Неравномерная вольт-амперная характеристика диода в PSpice;
б) равномерная вольт-амперная характеристика в LTspice. Неравномерности негативно влияют на способность симулятора моделировать нелинейные схемы

* I-V discontinuity in PSpice diode
V1 N001 0 0
D1 N001 0 D
.dc V1 -.3 -.2 2u
.probe
.model D D(Is=10n)
.end

Вольт-амперная характеристика диода в PSpice является дискретной и по значению, и по крутизне. Такая дискретность наличествует в большинстве моделей полупроводниковых приборов в PSpice, но отсутствует в моделях полупроводниковых приборов симулятора LTspice.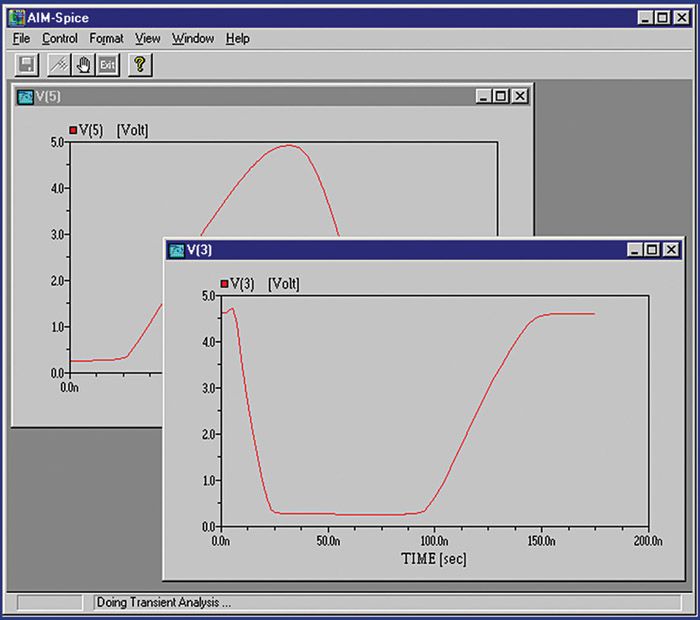

 

Метод разреженной матрицы

Ряды Тейлора являются многомерными — для каждого неизвестного узлового потенциала в схеме предусмотрено одно измерение. Для аналоговых микросхем количество неодинаковых узловых потенциалов может достигать 100 000, что ведет к формированию матрицы проводимости размером 100 000 на 100 000, или 80 млрд байт для двойной точности коэффициентов матрицы. Даже современные 64‑битные процессоры не имеют достаточного количества выводов, чтобы обеспечить требуемое количество адресных линий для доступа к такому объему памяти. К счастью, практически каждый элемент такой матрицы равен нулю, потому они не требуют хранения. Метод разреженной матрицы отслеживает только ненулевые элементы, что позволяет решать большие матрицы в достаточно маленьких адресных пространствах.

Разреженность матрицы проистекает из физической природы схем. Большинство узлов всегда подключено к нескольким другим узлам. Например, даже если вы пишете матрицу проводимости схемы, которая выглядит как сетка из резисторов, она будет практически диагональной, поскольку каждый узел резистивно связан только со смежным узлом. Соединения в реальных схемах не расположены так часто, как узлы в сетке. Разреженность в больших аналоговых схемах составляет один к миллиону и позволяет производить решение матриц на современных компьютерах. Метод Ньютона для аналоговых схем невозможен без метода разреженных матриц.

Используя самомодифицирующийся код на языке ассемблера, симулятор LTspice устраняет переполнение при передаче данных в FPU во время выполнения операций, когда память под матрицу уже выделена и известен адрес, который вернула функция malloc (). Чтобы эффективно загрузить данные, этот код совместно с основным кодом может определять точный адрес элемента матрицы, позволяя FPU работать с полностью загруженным конвейером.

Наибольшим сходством среди всех реализаций SPICE обладает метод разреженных матриц. Все программы SPICE применяют LU-факторизацию матриц (LU-факто-ризация — представление матрицы A в виде произведения двух матриц, A = LU, где L — это нижняя треугольная матрица, а U — верхняя треугольная матрица). Большинство реализаций симулятора SPICE использует библиотеку для работы с разреженными матрицами, которая распространяется вместе с основным кодом SPICE от Университета Беркли. Однако некоторые компании, которые предлагают известные на рынке решения в виде быстрых симуляторов SPICЕ, пытаются улучшать свои продукты с помощью расширенной библиотеки SuperLU (чем разреженнее матрица, тем ближе она может быть переписана в диагональную, то есть решенную матрицу. Поскольку матрицы аналоговых схем очень разрежены, улучшенная LU-факторизация матриц с помощью SuperLU не дает настолько большого преимущества в скорости ее обработки, как этого можно было бы ожидать).

Наилучший подход — разрешить процессору выполнять математические операции на теоретическом пределе быстродействия FLOP (англ. FLOP — Floating Point Operations per Second, число операций с плавающей запятой в секунду) используемого оборудования. Проблема в том, что доставка данных к процессору (в модуль обработки чисел с плавающей запятой FPU — Floating-Point Unit) занимает намного больше времени, чем сами вычисления.

Конвейер FPU часто работает вхолостую. Прежде всего, это результат того, что все операционные системы используют динамическое выделение памяти. В то время когда симулятор пишется и компилируется, участки памяти с данными матрицы еще не известны. В ходе выполнения операций симулятор запрашивает выделение памяти с помощью функции malloc(), возвращающей адрес, по которому симулятор может безопасно сохранить данные матрицы. Поскольку дать имя каждому элементу матрицы невозможно, для хранения применяются массивы. Это значит, что симулятор запрашивает выделение меньших по количеству, но больших по размеру участков памяти, а индивидуальные индексы рассчитываются на основе базового адреса, который вернула функция malloc(). Все, что известно во время компиляции, — это адрес адреса базового адреса, указывающего на местонахождение элемента матрицы. Вычисление адреса во время выполнения и выборка данных по нему в FPU занимает больше времени, чем само вычисление (устранение неизвестных из матрицы включает в основном сложение, вычитание и умножение. Эти инструкции для выполнения требуют всего три такта. (Деление занимает больше, чем три такта, но понадобится всего одно деление на одну неизвестную, которую нужно удалить.) Получение данных, которые известны по адресу адреса базового адреса, от которого можно оттолкнуться, занимает гораздо больше, чем три такта). В идеале, чтобы нужные данные были эффективно получены без простоя FPU, адреса данных, необходимых для вычислений, должны быть известны непосредственно перед вычислениями.

Интегральный метод Гира (Gear integration method) в PSpice часто выдает ошибочные результаты. Интегрирование по методу Гира подавляет не только числовые колебания, но и все колебания, включая физические. В результате схема некорректно функционирует в реальных условиях, так как симулятор показывает идеально стабильную работу модели, поскольку физические колебания демпфированы на этапе вычислений.

Уникальность LTspice заключается в том, что он использует самомодифицирующийся, самоассемблируемый и самолинкующийся код для вычисления разреженных матриц. Этот метод работает значительно лучше, чем другие технологии.

 

Неявное интегрирование

Для того чтобы отслеживать поведение емкостей и индуктивностей, симуляция аналоговых схем требует численного интегрирования дифференциальных уравнений. Здесь благодаря использованию различных методов интегрирования дифференциальных уравнений наблюдается значительная разница между реализациями симуляторов SPICE.

Численное интегрирование допускает ошибки. Симуляция аналоговых схем влечет за собой интегрирование поведения многих временных констант. Особенность интегрирования дифференциальных уравнений заключается в том, что их решения выглядят как e^–t

^t и за исключением случаев, когда численные методы используют неявную интеграцию (в литературе встречается мнение, что численное решение не будет единственным, если гарантированно можно выбрать достаточно малый временной интервал, но на практике подход с явной интеграцией и ограниченным временным интервалом не работает, пока вы не сможете выполнить численное интегрирование с бесконечной точностью. Ошибки не складываются в бесконечности из-за округления и из-за аппроксимации производной при заданных конечных разностях. На данный момент не существует успешных симуляторов общих аналоговых схем, которые использовали бы явное интегрирование), их ошибки фактически суммируются до бесконечности. Без неявного интегрирования анализ переходных процессов в симуляторах SPICE был бы невозможен.

В SPICE предусмотрено интегрирование второго порядка. Большинство реализаций SPICE являются производными от оригинальной версии SPICE Университета Беркли и предоставляют два метода неявного интегрирования второго порядка: метод Гира и метод трапеций (периодически SPICE применяет интегрирование первого порядка. Если происходит событие с известной прерывающейся временной производной первого порядка (такое как переход между двумя прямолинейными сегментами кусочно-линейной или импульсной функции независимого источника тока или напряжения), большинство реализаций SPICE используют уменьшение интегрирования до первого порядка для описания поведения реактансов (реактивных сопротивлений).

Методы Гира и трапеций для первого порядка берут свое начало у метода Эйлера). Метод трапеций более быстрый и точный по сравнению с интегрированием методом Гира, однако может вносить нарастающие числовые искажения, которые при интегрировании дискретного временного шага способны показывать колебания между временными шагами в пределах реального постоянного по времени поведения. Это приводит к тому, что возникают сомнения в корректной работе симулятора, даже если каждая трапеция содержит верную интегрируемую область.

Разработчики аналоговых схем считали, что интегрирование методом трапеций недопустимо для аналоговых схем (некоторые пользователи вынуждены с недоверием относиться к SPICE из-за популярной литературы, которая недооценивает значение симуляции в SPICE), поэтому оно было удалено из коммерческой версии реализации SPICE — PSpice, а как единственно доступный был оставлен более медленный и менее точный метод Гира.

Но интегрирование по методу Гира гасит не только числовые колебания, но и все колебания, включая физические.

Данная особенность чревата тем, что схема некорректно работает в реальных условиях из-за присутствия колебаний, хотя симулятор показывает идеально стабильное функционирование модели. Так происходит потому, что нестабильность схемы демпфирована на этапе вычислений. В результате возникали катастрофические ситуации, в которых интегральная микросхема, промоделированная и рассчитанная в PSpice, а затем изготовленная в промышленных масштабах, оказывалась неработоспособной. Впоследствии потребовались значительные временные и финансовые затраты для устранения этой нестабильности и достижения необходимой функциональности этой микросхемы.

Если разработчик микросхемы установит максимально короткий временной шаг, то в принципе ошибки интегрирования по методу Гира могут быть устранены. Но это не станет полноценным решением, поскольку (1) короткие временные шаги значительно уменьшают скорость симуляции и (2) нет никакого способа убедиться в том, что временной шаг действительно достаточно короткий.

В документации к симулятору PSpice указано, что он использует модифицированный метод Гира, который лучше справляется с задачей выбора действительно коротких временных шагов, чем реализация интегрирования по методу Гира в реализации SPICE от Университета Беркли.

Но метод, примененный в симуляторе PSpice, часто не работает. Очень просто создать обычную схему и увидеть, что численно интегрированный результат PSpice значительно отличается от реального решения, которое можно найти при расчете вручную. На рис. 2 показан параллельный резонансный контур с параллельно включенным источником тока. Источник тока выдает максимальный импульс тока в первые 0,2 мс, а затем падает до нуля. Решение предполагает, что резонансный контур возбуждается этим броском тока, а затем остается в режиме генерации с постоянной амплитудой. Netlist для данной схемы выглядит так:

Рис. 2. Простая схема с известным решением, выбранная для проверки

* Gear (PSpice) integration error
L1 N001 0 50m
I1 0 N001 PWL(0 0 . 1m .1 .2m 0)
C1 N001 0 .1u
.tran 1 1 0 50u
.probe
.end

На рис. 3 показано, что модифицированное интегрирование методом Гира в PSpice искусственно гасит генерацию, в то время как симулятор LTspice выдает правильное решение. Ошибки в PSpice могут быть уменьшены путем выставления максимально низкого значения для временного шага (четвертое число в операторе .tran). Модифицированное интегрирование по методу Гира в PSpice может просчитывать только простые схемы. Однако симулятор PSpice не способен рассчитывать схемы с большим количеством различных временных констант. В этом случае понадобится непосредственное участие разработчика, который уже в ручном режиме будет отслеживать действие схемы после установки еще более низких временных шагов для интегрирования.

Рис. 3. PSpice (слева) использует модифицированное интегрирование по методу Гира, что приводит к некорректному подавлению «звона» для схемы, приведенной на рис. 2

Исходя из опыта автора статьи, модифицированный метод трапеций является лучшим средством для интегрирования дифференциальных уравнений для аналоговых схем, который не используется в других реализациях SPICE. Этот метод является единственным, который автор считает нужным рекомендовать для разработки схем.

На рис. 3 видно, что интегрирование по методу Гира в симуляторе PSpice некорректно объединяет две реактивные нагрузки в обычной схеме с одним узлом. В основе этих ошибок лежит то, что интегрирование по методу Гира пытается сделать схемы более стабильными в симуляции, чем они есть на самом деле. Чтобы показать практические последствия таких ошибок, на рис. 4 показан аудиоусилитель, нестабильно работающий потому, что величина емкости компенсационного конденсатора С2 слишком мала.

Рис. 4. Нестабильный усилитель мощности

PSpice некорректно моделирует данную схему как стабильную, в то время как симулятор LTspice демонстрирует верный результат. В каждом из этих случаев использовался следующий netlist:

* Unstable Power Amplifier
Q5 N001 N006 N007 0 Q3904
Q7 N001 N007 OUT 0 Q2219A
Q8 OUT N013 N014 0 Q2219A
Q6 N013 N012 OUT 0 Q3906
V1 N001 0 10
V2 N014 0 -10
R11 N012 N014 5K
R14 OUT 0 8
R9 N006 N008 2K
R10 N008 N012 1K
Q4 N006 N008 N012 0 Q3904
Q1 N005 N009 N011 0 Q3904
Q2 N002 N010 N011 0 Q3904
R3 N011 N014 1K
Q3 N006 N004 N003 0 Q3906
R6 N010 0 20K
R7 OUT N010 200K
V3 IN 0 pulse(0 . 1 0
+ 5u 5u 50u 100u)
R8 N001 N003 100
R4 N004 N005 10K
C2 N006 N004 10p
R13 N013 N014 1K
R12 N007 OUT 1K
C3 N006 N012 .001u
Q9 N005 N002 N001 0 Q3906
Q10 N002 N002 N001 0 Q3906
R2 IN N009 9.09K
.tran 100u 100u
.model Q3904 NPN(Is=1E-14 Vaf=100
+ Bf=300 Ikf=0.4 Xtb=1.5

+ Br=4 Cjc=4p Cje=8p Rb=20 Rc=0.1
+ Re=0.1 Tr=250n Tf=.35n
+ Itf=1 Vtf=2 Xtf=3)
.model Q3906 PNP(Is=1E-14 Vaf=100
+ Bf=200 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4.5p Cje=10p Rb=20
+ Rc=0.1 Re=0.1 Tr=250n
+ Tf=.35n Itf=1 Vtf=2 Xtf=3)
.model Q2219A NPN(Is=14.34f
+ Xti=3 Eg=1.11 Vaf=74.03
+ Bf=255.9 Ne=1.307 Ise=14.34f
+ Ikf=.2847 Xtb=1.5
+ Br=6.092 Nc=2 Isc=0 Ikr=0
+ Rc=1 Cjc=7.306p Mjc=.3416
+ Vjc=.75 Fc=.5 Cje=22.01p
+ Mje=.377 Vje=.75 Tr=46.91n
+ Tf=411.1p Itf=.6 Vtf=1.7
+ Xtf=3 Rb=10)
.probe
.end

На рис. 5 демонстрируется ошибочный стабильный результат (рис.  5а), а также верный результат с наличием автоколебательного процесса от LTspice (рис. 5б). На рис. 5 показана симуляция реакции на большой скачок напряжения. Если установить достаточно малый временной шаг симуляции в PSpicе, можно принудительно приблизиться к верному результату, допуская, что PSpice правильно интерпретирует уравнения моделей транзисторов и просто неточно интегрирует дифференциальные уравнения.

Рис. 5. Симуляция ответной реакции нестабильного усилителя мощности на большой скачок напряжения:
а) демонстрирует ошибочный стабильный результат;
б) показывает верный результат с наличием автоколебательного процесса от LTspice

Что же необходимо для получения метода, в котором сочетаются скорость обработки и точность метода трапеций, но без присущего ему «звона»? В то время как для решения данной задачи в PSpice убрали метод трапеций и используют интегрирование по методу Гира в сочетании с необходимостью подбирать наилучшие временные шаги, другой подход предполагает применение модифицированной версии интегрирования методом трапеций так, что он будет гасить «звон», но при этом допускать небольшие ошибки в поведении реальной схемы. Вполне возможно, но не рекомендуется использовать модифицированный метод трапеций с помощью недокументированной опции trapdamp, добавляя директиву .options trapdamp=.01 в свою схему.

Вероятно, вы могли бы найти значение trapdamp в процедуре интегрирования в программе HSPICE. Тем не менее автор не рекомендует применять данную опцию, поскольку она уменьшает амплитуду колебаний при моделировании реальной схемы и в этом нет необходимости в программе LTspice, которая предусматривает лучший способ устранения «звона» с помощью метода трапеций.

Используемый для интегрирования в симуляторе LTspice модифицированный метод трапеций имеет такую же точность и скорость, как и оригинальный метод трапеций, однако без искажений в виде паразитного «звона». Модифицированный метод трапеций создан автором несколько лет назад и впервые стал широкодоступным в программе LTspice. Исходя из своего опыта, автор считает модифицированный метод трапеций, который не используется в других реализациях SPICE, лучшим средством для интегрирования дифференциальных уравнений для аналоговых схем. Симулятор LTspice также поддерживает и другие методы, традиционный метод трапеций и метод Гира, однако они присутствуют в программе лишь для того, чтобы пользователь мог повторить ошибочные результаты из других реализаций симулятора SPICE и убедиться, что модели интерпретируются одинаково, но отличаются только методами интегрирования.

Применяемый в программе LTspice модифицированный метод трапеций представлен на рис. 3. Следует обратить внимание, что в амплитуде паразитного «звона» не произошло никаких изменений даже после тысячи циклов интегрирования. Это означает, что LTspice не подавляет искажения принудительно. Представленный на рис. 5 пример работы модифицированного метода трапеций, используемого в LTspice, показывает, что симулятор LTspice корректно отображает нестабильность усилителя.

Для того чтобы продемонстрировать, как в симуляторе LTspice модифицированный метод трапеций устраняет искажения в виде «звона», понадобится схема, которая подвержена проявлению неустойчивости в виде автогенерации. Искажения появляются, когда дискретное время шага интегрирования второго порядка не может представить точное непрерывное во времени поведение схемы. Этот эффект может быть уменьшен или устранен продуманным использованием временных интервалов и разумным выбором порядка интегрирования.

Поскольку LTspice была самой популярной реализацией SPICE в течение последних десяти лет (симулятор LTspice скачивают четыре раза в минуту, и у него самое большое сообщество пользователей по сравнению с любым другим симулятором. Используя данные, полученные при общении с представителями компаний, разрабатывающих и продающих другие реализации SPICE, автор сделал вывод, что симулятор LTspice распространяется и используется в три раза чаще, чем другие реализации SPICE), с ее помощью смоделировано множество схем, а в модуль устранения паразитного «звона» было вложено много знаний, поэтому придется постараться, чтобы найти противоречащий пример. На рис. 6 показана схема, которая создает паразитный «звон» из-за весьма высокой нелинейности  емкости, вызванной нетрадиционно подключенными MOSFET-транзисторами в инверторе. «Звон» виден в источнике тока I(V1). На рис. 7 приведено сравнение традиционного метода трапеций и модифицированного метода трапеций, использованного в LTspice. Верхний график показывает увеличенную область нижнего графика, четко отображая паразитный «звон». Если есть необходимость повторить такой же результат в LTspice, следует перейти на закладку SPICE в Control Panel и выбрать в области Default Integration Method (метод интегрирования, принятый по умолчанию) пункт trapezoidal вместо установленного по умолчанию modified trap. Ниже приведен netlist для данной симуляции:

Рис. 6. Схема, которая подвержена «звону»

Рис. 7. Интегрирование методом трапеций по сравнению с модифицированным методом трапеций в LTspice (применительно к схеме, приведенной на рис. 6):
а) обычный метод интегрирования методом трапеций допускает появление «звона»;
б) интегрирование с использованием модифицированного метода трапеций в симуляторе LTspice полностью устраняет «звон»

* Trap Ringing Example
V2 N001 0 3. 3
V1 N002 0 PULSE(0 3.3 1n 1u)
M1 OUT N002 N001 N001 P
M2 OUT N002 0 0 N
.tran 0 1.2u 0 .1n
.model N NMOS(Tox=20n Vto=.5
+ Gamma=.5 UO=650 Rs=10)
.model P PMOS(Tox=20n
+ Vto=-.5 Gamma=.5 UO=650
+ Rs=10)
.probe
.end

Обратите внимание, что большинство реализаций SPICE не сможет запустить данную симуляцию, так как в них используется емкостная модель Мейера для этого типа MOSFET-транзисторов. Но поскольку емкостная модель Мейера не сохраняет заряд и выдает неточные результаты для коротких каналов, от нее отказались еще в 1990‑х годах.

Как в LTspice, так и в PSpice, емкостная модель Мейера (Meyer) заменена моделью заряда Янга — Чаттерджи (Yang — Chatterjee). В связи с тем что оба симулятора используют одни и те же обновленные уравнения сохранения зарядов, они должны выдавать и одинаковые результаты. Но если мы сравним результаты в программах PSpice и LTspice, как показано на рис. 8, то увидим, что PSpice демонстрирует крайне ошибочные результаты. Колебания, наблюдаемые в PSpice, не дают «звона», потому что они не происходят на каждом временном интервале, а PSpice не использует метод трапеций. Эти искажения практически полностью происходят вследствие ошибки дифференцирования уравнений Янга — Чаттерджи для емкостей, реализованных в модели зарядов в симуляторе PSpice.

Рис. 8.
а) Пример схемы, приведенный на рис. 6 в PSpice, не показывает «звон», но демонстрирует другие искажения, скорее всего из-за ошибки в применении модели заряда Янга — Чаттерджи;
б) симулятор LTspice дает корректный результат

 

Заключение

LTSpice не первая и не единственная бесплатная реализация SPICE, но это самая лучшая и широко используемая реализация данного симулятора.

Метод Ньютона, метод разреженных матриц и метод неявного интегрирования формируют ядро численных методов в SPICE. Надежность симулятора, его скорость работы и комплексность зависят от того, насколько хорошо эти методы реализованы.

Думается, симулятор LTspice вполне способен завоевать доверие разработчиков, наглядно продемонстрировав им свое умение корректно просчитывать поведение схем и выполнять важнейшие численные методы и делая это гораздо лучше других реализаций SPICE.

SPICE-моделирование устойчивости ОУ

15 января 2019

телекоммуникациисистемы безопасностиучёт ресурсовмедицинапотребительская электроникаответственные применениялабораторные приборыинтернет вещейTexas Instrumentsстатьяинтегральные микросхемысредства разработки и материалы

Статья является частью руководства, посвященного практическим аспектам и особенностям проектирования электроники с использованием операционных усилителей (ОУ) – от выбора типа ОУ до тайных приемов опытного разработчика и хитростей отладки. Руководство написано Брюсом Трампом, инженером-разработчиком с почти тридцатилетним стажем, успевшим до Texas Instruments поработать в легендарной компании Burr-Brown. В настоящее время Трамп является ведущим блогером информационного ресурса Texas Instruments “E2E” по аналоговой тематике и готовит к печати книгу об операционных усилителях.

Мы публикуем перевод руководства Трампа на нашем сайте регулярно – дважды в месяц.

Подписаться на получение уведомлений о публикации новых глав

Программы SPICE-моделирования являются полезным инструментом, помогающим обнаруживать потенциальные проблемы с устойчивостью схем усилителей. Рассмотрим один конкретный пример.

На рисунке 35 показан типовой неинвертирующий усилитель на базе OPA211 с несколькими незначительными типовыми особенностями. Звено R₃ – C₁ является входным фильтром. R₄ – выходной резистор для защиты от коротких замыканий на выходе. Конденсатор C_L имитирует пятифутовый кабель.

Рис. 35. Неинвертирующий усилитель с некоторыми типовыми особенностями

Анализ отклика системы на воздействие прямоугольного или ступенчатого сигнала является самым быстрым и простым способом поиска возможных проблем с устойчивостью. На рисунке 36 показана моделируемая схема. Можно заметить, что вход схемы притянут к земле, а тестовый сигнал подключается непосредственно к неинвертирующему входу ОУ. Таким образом, фильтр оказывается исключенным из схемы, так как он мог бы сгладить необходимый для моделирования фронт ступенчатой ​​функции. Как гласит японская пословица, если вы хотите знать, как звонит колокол – ударьте его молотом, а не резиновой колотушкой!

Рис. 36. Моделируемая схема: входной вывод притянут к земле, а тестовый сигнал подключается непосредственно к неинвертирующему входу ОУ

В данном случае анализируется не только сигнал на выходе схемы (V_OUT), но и напряжение на выходе ОУ (V_opamp). Выходные фильтры R₄ и C_L сглаживают напряжение V_OUT, поэтому форма сигнала не показывает истинного перерегулирования ОУ. Чтобы оценить устойчивость схемы, нужно знать, как ведет себя операционный усилитель.

Обратите внимание, что амплитуда тестового импульса равна 1 мВ (что создает на выходе сигнал 4 мВ). Таким образом, выполняется анализ отклика схемы именно на малый сигнал. Импульс с большой амплитудой будет вызывать меньшее перерегулирование и не позволит обнаружить потенциальную неустойчивость.

Моделирование показывает примерно 27-процентное перерегулирование на выходе ОУ. Это слишком много для того чтобы быть уверенным в абсолютной устойчивости данной схемы при любых условиях (рисунок 37).

Рис. 37. Схема усилителя с 27-процентным перерегулированием может быть неустойчивой

Если учесть, что это – схема второго порядка, то запас по фазе составляет примерно 38°. Также обратите внимание, что на частотной характеристике наблюдается значительный пик амплитуды – это еще один признак потенциальной неустойчивости. Пик происходит на частоте 14 МГц – это частота осцилляций во временной области. Общепринятым ориентиром для обеспечения адекватной устойчивости является запас по фазе 45° или выше, что соответствует перерегулированию в 20% или менее (рисунок 38).

Рис. 38. Перерегулирование 20%, соответствующее запасу по фазе примерно 45º, в большинстве схем рассматривается как достаточное условие устойчивости

Есть и другие, более интересные виды анализа, которые вы можете выполнить с помощью SPICE-моделирования, например, анализ Боде для определения фазы и коэффициента усиления в контуре с разорванной ОС. Но для большинства относительно простых схем (один ОУ с контуром обратной связи) приведенный выше подход является хорошим индикатором возможных проблем с устойчивостью.

Стоит отметить, что качество SPICE-симуляции зависит от точности макромоделей ОУ. Даже лучшие модели SPICE превосходны, но не идеальны. Кроме того, моделирование не способно учесть неидеальность пассивных компонентов, паразитные параметры печатной платы, плохую развязку цепей питания, а ведь все это может повлиять на устойчивость схемы. Вот почему необходимо создавать опытные образцы, испытывать их, сравнивать показанные результаты с результатами моделирования и оптимизировать. SPICE – полезный, но все-таки не идеальный инструмент.

Покойный Боб Пиз, истинный гуру аналоговой схемотехники, скептически отзывался об использовании SPICE. Вот пример его мнения на этот счет: «SPICE It Up! … but does Bob Pease say no?».

Оригинал статьи

1. Диапазоны входных и выходных рабочих напряжений ОУ. Устраняем путаницу
2. Что нужно знать о входах rail-to-rail
3. Работа с напряжениями близкими к земле: случай однополярного питания
4. Напряжение смещения и коэффициент усиления с разомкнутым контуром обратной связи — двоюродные братья
5. SPICE-моделирование напряжения смещения: как определить чувствительность схемы к напряжению смещения
6. Где выводы подстройки? Некоторые особенности выводов коррекции напряжения смещения
7. Входной импеданс против входного тока смещения
8. Входной ток смещения КМОП- и JFET-усилителей
9. Температурная зависимость входного тока смещения и случайный вопрос на засыпку
10. Использование входных резисторов для устранения входного тока смещения. Действительно ли они нужны?
11. Использование входных резисторов для устранения входного тока смещения. Действительно ли они нужны?
12. Почему в схемах с ОУ возникают колебания: интуитивный взгляд на две наиболее частые причины
13. Приручаем нестабильный ОУ
14. Приручаем колебания: проблемы с емкостной нагрузкой

Перевел Вячеслав Гавриков по заказу АО КОМПЭЛ

•••

Товары

org/Product» data-pid=»Eagr»> org/Product» data-pid=»C9MN»> org/Product» data-pid=»3sr»>

Наименование
OPA211AIDGKT (TI)
OPA2111KP (TI)
OPA211 PITCH PACKS (TI)
OPA2111BM (TI)
OPA2111SM (TI)
OPA211AIDGK (TI)
OPA211AIDGKTG4 (TI)
OPA140AID (TI)
OPA140AIDGKR (TI)
OPA140ATDD2 (TI)
OPA140AIDBV (TI)
OPA140AIDGKT (TI)
OPA140AIDBVR (TI)
OPA140AIDR (TI)
OPA376AIDBVT (TI)
OPA376AIDBVR (TI)
OPA376 (TI)
OPA376AIDCKR (TI)
OPA376AIDG4 (TI)
OPA376AIBBVT (TI)

Имитационные модели SPICE — NI

Лучше всего искать модели SPICE на веб-сайте поставщика или производителя. Ниже перечислены некоторые из самых популярных поставщиков чипов, которые предлагают модели SPICE на своем веб-сайте.

Поставщик	Описание
Аналоговые устройства	Усилители и компараторы, аналого-цифровые преобразователи, цифро-аналоговые преобразователи, встроенные процессоры и DSP, МЭМС и датчики, ВЧ/ПЧ компоненты, переключатели/мультиплексоры, аналоговые микроконтроллеры, интерфейс, управление питанием и температурой
Микротехнологии Apex	Линейные усилители, ШИМ-усилители
Кристоф Бассо	Импульсные источники питания
Coilcraft, Inc.	Power Magnetics, RF Inductors, EMI / RFI Filters, Broadband Magnetics
Дункан Ампс	Усилители, электронные лампы
Инфинеон Текнолоджиз АГ	Волоконная оптика, микроконтроллеры, силовые полупроводники, дискретные устройства для малых сигналов
Домашняя страница Kemet	Конденсаторы для поверхностного монтажа из алюминия, керамики и тантала и конденсаторы с выводами из керамики и тантала
Максим	Усилители и компараторы, аналоговые переключатели и мультиплексоры, часы, счетчики, линии задержки, осцилляторы, RTC, преобразователи данных, выборка и хранение, цифровые потенциометры, оптоволокно и связь, фильтры (аналоговые), высокочастотные ASIC, горячие Переключение и переключение питания, интерфейс и межсоединение, память: энергозависимая, энергонезависимая, многофункциональная, управление температурным режимом, датчики, формирователи датчиков, источники опорного напряжения, беспроводная связь, радиочастота и кабель
ПО Полупроводник	Управление питанием, усилители, компараторы, аналоговые переключатели, тиристоры, диоды, выпрямители, биполярные транзисторы, полевые транзисторы, стандартная логика, дифференциальная логика,
Полифет	Транзисторы Полифет
STMicroelectronics	Усилители и ИС линейных, аналоговых и смешанных сигналов, диоды, фильтрация и формирование электромагнитных помех, логика, переключатели сигналов, память, микроконтроллеры, управление питанием, защитные устройства, датчики, ИС смарт-карт, тиристоры и переключатели переменного тока, транзисторы
Техас Инструментс	Буферы, драйверы и приемопередатчики, триггеры, защелки и регистры, вентили, счетчики, декодеры/кодировщики/мультиплексоры, цифровые компараторы
Tyco Electronics (ранее Amp)	Электромеханические компоненты, пассивные компоненты, источники питания, радиочастотные и микроволновые изделия
Вишай	Производитель аналоговых переключателей, конденсаторов, диодов, катушек индуктивности, интегральных модулей, силовых интегральных схем, светодиодов, силовых МОП-транзисторов, резисторов и термисторов.

Модели SPICE | Дизайн Центр

AD22050	Усилитель для интерфейса датчика с одним приложением	AD22050 Spice Macro Model0193	AD22057	Single Supply Sensor Interface Amplifier	AD22057 SPICE Macro Models AD22057N SPICE Macro Model Rev. A, 11/95 AD22057T SPICE Macro Model Rev. A, 11/95
AD5144	Четырехканальный, 256-позиционный, I2C/SPI, энергонезависимый цифровой потенциометр	AD5144_10k Макромодель SPICE AD5144_10k Макромодель SPICE
AD536A	— Преобразователь True RMS-DC в интегральную схему0012	AD536A SPICE Macro Model AD536A SPICE Macro Model
AD549	Ultralow Input-Bias Current Operational Amplifier	AD549 SPICE Macro Model AD549 SPICE Macro Model
AD5686R	Quad, 16 -Bit nanoDAC+™ со встроенным эталоном 2 ppm/°C и интерфейсом SPI	Макромодель AD5686R SPICE Макромодель AD5686R SPICE
AD5767	16-Channel, 12-Bit Voltage Output denseDAC	AD5767 SPICE Macro Model AD5767 SPICE Macro Model
AD581	High Precision 10 V IC Reference	AD581 SPICE Macro Models AD581 SPICE Macro Модель, версия A, 11/93 AD581J Макромодель SPICE, версия A, 11/93 AD581K Макромодель SPICE, версия A, 11/93 AD581L Макромодель SPICE, версия A, 11/93 AD581S02 AD581S Макромодель SPICE, ред. A, 11/93 AD581T Spice Macro Model Rev. A, 11/93 AD581U Spice Macro Model Rev. A, 11/93
AD584	PIN -программируем Макромодель AD584J SPICE, ред. B, 1/01 Макромодель AD584K SPICE, ред. B, 1/01 AD584L SPICE, макромодель, ред. Макромодель AD584S SPICE, версия B, 1/01 AD584T Spice Macro Model Rev. B, 1/01
AD587	Высокая точность 10 В. Ссылка	AD587 Spice Macro Model A, 11/93 AD587K Макромодель SPICE, версия A, 11/93 AD587L Макромодель SPICE, версия A, 11/93 AD587S SPICE Макромодель, версия A, 11/93 AD587T SP587T Макромодель, версия A, 11/93 AD587U Макромодель SPICE, версия A, 11/93 Макромодель AD587U SPICE, версия A, 11/93
AD588	Многоканальный выход, высокая точность, двойное отслеживание Эталон	Макромодели AD588 SPICE , AD584/ADro 5 AD588A Макромодель SPICE, версия A, 4/94 AD588B Макромодель SPICE, версия A, 4/94 AD588J Макромодель SPICE, версия A, 4/94 AD588K Макромодель SPICE, версия A, 4 /94 AD588S SPICE Macro Model Rev. A, 4/94 AD588T SPICE Macro Model Rev. A, 4/94
AD600	Двойной малошумящий широкополосный усилитель с регулируемым усилением, от 0 дБ до +40 дБ Модель Rev. A, 2/93 AD600J SPICE Macro Model Rev. A, 2/93
AD602	Двойной малошумящий широкополосный усилитель с регулируемым усилением, усиление от -10 дБ до +30 дБ	AD602 SPICE Макромодели AD602 SPICE Macro Model Rev. A, 2/93 AD602J Spice Macro Model Rev. A, 2/93
AD603	Низкий шум, 90 МГц Усилитель усиления	AD603 SPICE MACRO модели 9202 AD603A SPICE Macro Model Rev. A, 12/94
AD604	Dual, Ultralow Noise Variable Gain Amplifier	AD604 SPICE Macro Model AD604 SPICE Macro Model
AD605	Dual, Low Noise, Усилитель с регулируемым коэффициентом усиления с однополярным питанием	AD605 Spice Macro Model AD605 SPICE MACRO MODEL
AD620	Низкий дрифт, с низкой мощностью усилитель AMP с увеличением набора 1-10000	AD620 MACRO MACRO модели SPICE MACRO. B, 10/95 Макромодель AD620A SPICE, ред. B, 10/95 Макромодель AD620B SPICE, ред. Недорогой инструментальный усилитель Rail-to-Rail с одинарным и двойным питанием	AD623 Spice Macro Model AD623 SPICE MACRO MODEL
AD624	Высокая точность, модели с низким уровнем шума 24247 AD624 SPICE MACRO MODEL Макромодель AD624A SPICE, версия A, 9/91 Макромодель AD624B SPICE, версия A, 9/91 Макромодель AD624C SPICE, версия A, 9/91 AD624S Макромодель SPICE, версия A, 9/91
АД626	Недорогой дифференциальный усилитель с однополярным питанием	Макромодели AD626 SPICE Макромодель AD626 SPICE Версия A, 11/95 AD626A Модель SPICE Macro Версия A, 11/93 Модель AD206B 9022 Rev. A, 11/95
AD627	Microper, одно и двойное снабжение R/R Инструментационное усилитель	AD627A Spice Macro Moder Ред. А, 2/2001
AD628	High Common-Mode Voltage, Programmable Gain Difference Amplifier	AD628 SPICE Macro Model AD628 SPICE Macro Model
AD629	High Common-Mode Voltage, Difference Amplifier	AD629A SPICE Macro Модель Минимальные значения Макромодель AD629A SPICE Минимальные значения
AD629	Высокое синфазное напряжение, дифференциальный усилитель	AD629B SPICE Macro Model Minimum Values ​​ AD629B SPICE Macro Model Minimum Values ​​
AD629	High Common-Mode Voltage, Difference Amplifier	AD629A SPICE Macro Model Typical Values ​​ AD629A SPICE Macro Model Typical Values ​​
AD629	Высокое синфазное напряжение, дифференциальный усилитель	Макромодель AD629B SPICE Типичные значения Макромодель AD629B SPICE Типичные значения
AD630	Balanced Modulator/Demodulator	AD630 SPICE Macro Model AD630 SPICE Macro Model
AD633	Low Cost Analog Multiplier	AD633 SPICE Macro Models AD633 SPICE Macro Model Analog Multiplier Версия A, 12/93 Макромодель AD633J SPICE Аналоговый умножитель Версия A, 12/93
AD636	Низкоуровневый преобразователь истинного среднеквадратичного значения в постоянный ток	AD636P SPICE Macro Model AD636P SPICE Macro Model
AD637	High Precision, Wideband RMS-to-DC Converter	AD637 SPICE Macro Model AD637 SPICE Macro Model
AD645	Low Noise , Операционный усилитель на полевых транзисторах с малым дрейфом	Макромодели AD645 SPICE Макромодель AD645 SPICE, ред. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника