Системы связи с шумоподобными сигналами
Системы связи с шумоподобными сигналами
ОглавлениеПредисловиеРАЗДЕЛ I. ОСНОВНЫЕ СВЕДЕНИЯ О ШУМОПОДОБНЫХ СИГНАЛАХ 1.  1.2. Помехозащищенность 1.3. Помехоустойчивость ШСС 1.4. Скрытность системы связи 1.5. Кодовое разделение абонентов 1.6. Эффективность ААСС 1.7. Борьба с многолучевостью 1.8. Измерение координат подвижных объектов 1.9. Электромагнитная совместимость 1.10. Основные структурные схемы ШСС 2. ШУМОПОДОБНЫЕ СИГНАЛЫ 2.2. Основы оптимальной обработки сигналов 2.3. Корреляционные функции сигналов 2.4. Основные типы ШПС 3. ФАЗОМАНИПУЛИРОВАННЫЕ СИГНАЛЫ 3.2. Сигналы Баркера 3.3. М-последовательности. Основные свойства 3.4. Последовательности Лежандра и Якоби. Минимаксные последовательности 3.6. Дополнительные последовательности 3.7. Последовательности максимальной вероятности 3.8. Многофазные сигналы. Сигналы Фрэнка 3.9. Амплитудно-фазоманипулированные сигналы 3.10. Минимаксные ФМ сигналы 3.11. Оценки апериодических АКФ 4.  СИСТЕМЫ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ4.1. Многоканальные системы связи с кодовым разделением абонентов и системы сигналов 4.2. Полный код 4.3. Системы Уолша 4.4. Коды Велти. Четверичные коды 4.5. Производные системы сигналов 4.6. Сегментные системы 4.8. Системы многофазных сигналов 4.9. Большие производно-циклические системы 4.10. Линейно-производные системы ФМ сигналов 4.11. Объем больших систем ФМ сигналов 4.12. Оценки апериодических ВКФ 5. СИСТЕМЫ ДИСКРЕТНЫХ ЧАСТОТНЫХ СИГНАЛОВ 5.2. Распределение числа совпадений в корреляционных функциях ДЧ сигналов 5.3. Алгоритмы построения оптимальных и квазиоптимальных систем ДЧ сигналов 5.4. Большие квазиоптимальные композиционные системы ДЧ сигналов 5.5. Объем больших систем ДЧ сигналов 5.6. Дискретные составные частотные сигналы РАЗДЕЛ II. ПОМЕХОУСТОЙЧИВОСТЬ ШИРОКОПОЛОСНЫХ СИСТЕМ СВЯЗИ 6.1. Шумоподобные сигналы и широкополосные системы связи  2. Основы передачи сообщений в системах связи6.3. Многоканальные системы связи 6.4. Методы уплотнения и разделения каналов и абонентов 7. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЕМА ДИСКРЕТНЫХ СООБЩЕНИЙ 7.2. Скорость передачи информации 7.3. Помехоустойчивость двоичных систем связи 7.4. Помехоустойчивость m-ичных систем связи 7.5. Сравнение двоичных и m-ичных систем связи 8. СОВМЕСТНОЕ ПРИМЕНЕНИЕ ШПС И КОРРЕКТИРУЮЩИХ КОДОВ 8.2. Вероятность ошибки 8.3. Выбор оптимального кода 8.4. Оптимальные коды Рида — Соломона 9.2. Помехоустойчивость приема ШИМ-ШПС 9.3. Помехоустойчивость приема ЧМ-ШПС 9.4. Сравнение помехоустойчивости ШИМ-ШПС и ЧМ-ШПС 9.5. Помехоустойчивость ИКМ-ШПС 10. ФИЛЬТРАЦИЯ МОЩНЫХ ПОМЕХ 10.2. Оптимальный прием элемента сигнала 10.3. Накопление элементов 10.4. Фильтрация сосредоточенных помех 10.5. Реальная база и помехоустойчивость ШСС 11. АДАПТИВНЫЙ ПРИЕМ ШПС 11.  2. Элементное отношение сигнал-помеха11.3. Согласованный фильтр и линейное накопление 11.4. Адаптивный прием и оптимальное накопление 11.6. Оптимальный адаптивный приемник 11.7. Квазиоптимальный адаптивный приемник 12. ОГРАНИЧИТЕЛЬ В ТРАКТЕ ОБРАБОТКИ ШПС 12.1. Идеальный полосовой ограничитель 12.2. Воздействие на ИПО двух сигналов и шума 12.3. Нелинейное кодовое уплотнение и разделение абонентов в синхронных адресных системах связи 13. ФИЛЬТРАЦИЯ ВЗАИМНЫХ И СТРУКТУРНЫХ ПОМЕХ 13.2. Основы кодового разделения абонентов в ААС 13.3. Фильтрация взаимных помех 13.4. Оптимизация ААС с КР 13.5. Фильтрация мощных ФМ структурных помех 13.6. Фильтрация мощных ДЧ структурных помех 14. ОБНАРУЖЕНИЕ И АНАЛИЗ ШПС В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ 14.2. Энергетический обнаружитель ШПС 14.4. Квазиоптимальный многоканальный обнаружитель ШПС 14.5. Анализ параметров М-последовательностей РАЗДЕЛ III.  ПОИСК И СИНХРОНИЗАЦИЯ ШПС15.1. Прием информации и неопределенность по времени и по частоте в широкополосных системах связи 15.2. Потенциальные точности измерения времени задержки и частоты 15.3. Отношение сигнал-помеха на выходе измерителя в ШСС 15.4. Пространство параметров и многоканальный измеритель 15.5. Одноканальный следящий измеритель 16. КОГЕРЕНТНАЯ ОБРАБОТКА ШПС И НЕКОГЕРЕНТНОЕ НАКОПЛЕНИЕ 17. ПОИСК И СИНХРОНИЗАЦИЯ ШПС ПО ВРЕМЕНИ 17.2. Сравнение непрерывного и дискретного поиска ШПС по времени 17.3. Алгоритмы поиска ШПС по времени задержки 17.4. Поиск ШПС с некогерентным накоплением 18. ПОИСК И СИНХРОНИЗАЦИЯ ШПС ПО ВРЕМЕНИ И ПО ЧАСТОТЕ 18.2. Время поиска ШПС при когерентной обработке 18.3. Время поиска ШПС при некогерентном накоплении 19. СИНХРОНИЗАЦИЯ СТАРТСТОПНЫХ ШИРОКОПОЛОСНЫХ СИСТЕМ СВЯЗИ 19.2. Вероятность ошибки 19.3. Минимизация вероятности ошибки при заданном количестве информации РАЗДЕЛ IV.  20. ОСНОВЫ ФОРМИРОВАНИЯ И ОБРАБОТКИ ШПС 20.2. Пассивные и активные фильтры для оптимального приема ШПС 20.3. Основы формирования ШПС 20.4. Критерии качества формирования и обработки ШПС 20.5. Оценка общих рассогласований 21. ЛИНЕЙНЫЕ СОГЛАСОВАННЫЕ ФИЛЬТРЫ 21.2. Частотно-временной метод обработки дискретных частотных сигналов 21.3. Многоканальные согласованные фильтры при частотном методе обработки многочастотных сигналов 21.4. Согласованные фильтры с многоотводными линиями задержки при временном методе обработки фазоманипулированных сигналов 21.5. Комбинированные методы обработки 21.7. Влияние рассогласований на работу согласованных фильтров с МЛЗ 21.8. Сравнение линейных согласонаванных фильтров 22. ДИСКРЕТНЫЕ И ЦИФРОВЫЕ СОГЛАСОВАННЫЕ ФИЛЬТРЫ 22.2. Дискретно-аналоговый согласованный фильтр 22.3. Приборы с зарядовой связью 22.4. Программируемые согласованные фильтры 22.  5. Цифровые согласованные фильтры23. ПЕРСПЕКТИВЫ СОВЕРШЕНСТВОВАНИЯ ЭЛЕМЕНТНОЙ БАЗЫ УСТРОЙСТВ ОБРАБОТКИ ШПС Список литературы |
Теория систем сигналов
Теория систем сигналов
ОглавлениеПредисловиеРаздел I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИЕМА СИСТЕМ СИГНАЛОВ 1.1. Сигналы и спектры 1.2. Классификация сигналов 1.3. Классификация систем сигналов 1.4. Комплексная огибающая сигнала и ее спектр 1.6. Дискретные частотные сигналы Комплексная огибающая и спектр ДЧ сигнала первого порядка. Корреляционные функции ДЧ сигналов первого порядка. Дискретные частотные сигналы произвольного порядка. 1.7. Частотные и дискретные сигналы Дискретные сигналы. Сигналы со смещением по частоте. Частотно-временная дуальность частотных и дискретных сигналов.  Спектры кодовых последовательностей. Корреляционные функции частотного сигнала. Корреляционные функции дискретных сигналов. Связь между корреляционными функциями и спектрами кодовых последовательностей. Корреляционные функции сигналов со смещением по частоте. Глава 2. СИСТЕМЫ СИГНАЛОВ И ПЕРЕДАЧА ИНФОРМАЦИИ 2.1. Системы передачи информации 2.2. Дискретная система передачи информации Скорость передачи информации. Помехоустойчивость двоичных СПИ. Помехоустойчивость m-ичных СПИ. 2.3. Пороговый эффект в m-ичных системах передачи информации 2.4. Сравнение двоичных и m-ичных систем передачи информации 2.5. Выбор объема алфавита сигналов Глава 3. СИНХРОННЫЕ АДРЕСНЫЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ 3.1. Линейное уплотнение и разделение абонентов Помехоустойчивость при линейном разделении. Использование общей полосы частот. 3.2. Адаптивное частотное уплотнение и разделение абонентов 3.3. Адаптивное кодовое уплотнение и разделение абонентов 3.  4. Нелинейное кодовое уплотнение и разделение абонентовГлава 4. АСИНХРОННЫЕ АДРЕСНЫЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ 4.1. Кодовое уплотнение и разделение абонентов в асинхронных адресных системах Основы кодового разделения абонентов в ААС. Эффективность использования общей полосы частот в ААС. 4.1 Корреляционные и статистические свойства взаимной помехи Плотность вероятности взаимной помехи при приеме противоположных сигналов. Плотность распределения взаимной помехи при приеме ортогональных сигналов. 4.3. Выбор систем сигналов для асинхронных адресных систем Правило выбора систем сигналов при нормализации взаимной помехи. Правило выбора систем сигналов, когда распределение взаимной помехи отличается от нормального. Вероятность ошибки при приеме ортогональных сигналов и правило выбора систем сигналов. О выборе сигналов при действии мощных взаимных помех. Глава 5. ОСНОВЫ ФИЛЬТРАЦИИ МОЩНЫХ ПОМЕХ 5.1. Классификация помех 5.2. Оптимальный прием элемента сигнала 5.  3. Накопление элементов5.4. Фильтрация сосредоточенных помех 5.5. Фильтрация узкополосных и импульсных помех 5.6. Фильтрация структурных помех 5.7. Радиотехнические системы, инвариантные к комплексу помех Глава 6. ОСНОВНЫЕ МЕТОДЫ ОБРАБОТКИ СИСТЕМ СИГНАЛОВ 6.1. Оптимальная и квазиоптимальная линейная обработка сигналов 6.2. Линейные согласованные фильтры Многоканальные согласованные фильтры при частотном методе обработки частотных сигналов. Согласованные фильтры с многоотводными линиями задержки при временном методе обработки дискретных сигналов. Комбинированные методы обработки. 6.3. Дискретный согласованный фильтр 6.4. Дискретно-аналоговый согласованный фильтр 6.5. Активные фильтры Глава 7. РЕАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ РАДИОТЕХНИЧЕСКИХ СИСТЕМ СО СЛОЖНЫМИ СИГНАЛАМИ 7.1. Помехоустойчивость приема сложных сигналов с идеальными корреляционными функциями 7.2. Помехоустойчивость приема сложных сигналов с реальными корреляционными функциями 7.  3. Помехоустойчивость приема сложных сигналов при неидеальной синхронизации по времени и частоте7.4. Помехоустойчивость приема сложных сигналов при рассогласованиях 7.5. Определение числа активных абонентов в ААС с учетом рассогласований Раздел II. ОБЩАЯ ТЕОРИЯ СИСТЕМ СИГНАЛОВ 8.1. Комбинаторика и теория систем сигналов 8.2. Дискретные частотные сигналы произвольного порядка 8.3. Сигналы с двоичной амплитудной манипуляцией 8.4. Сигналы с заданным числом блоков Глава 9. ПОЛНЫЙ ПРОИЗВОЛЬНЫЙ КОД 9.1. Алгебраические свойства полного кода 9.2. Ортогональность полного кода 9.3. Корреляционные функции полного кода 9.4. Распределение весов полного кода 9.5. Распределение корреляционных функций 9.6. Статистические характеристики полного кода Глава 10. ПОЛНЫЙ ДВОИЧНЫЙ КОД 10.2. Статистические характеристики 10.3. Средняя спектральная плотность мощности полного кода 10.4. Произвольная система сигналов Глава 11. ОПТИМАЛЬНОЕ ЧИСЛО БЛОКОВ И СИСТЕМЫ СИГНАЛОВ Эффективная ширина спектра.  Квадратическое отклонение между энергетическими спектрами идеального и оптимального сигналов. Известные системы ФМ сигналов (кодовых последовательностей). Системы Уолша. Производные системы. Случайные ФМ сигналы. 11.2. Вероятность экстремальных пиков и оптимальное число блоков 11.3. Число блоков в кодовой последовательности и ее вес 11.4. Число блоков в производной кодовой последовательности и вероятность экстремальных пиков Раздел III. СИСТЕМЫ СИГНАЛОВ 12.1. Системы Уолша Мультипликативно-двоичное представление кодовых последовательностей Уолша. Групповые свойства. 12.2. Производные системы сигналов 12.3. Сегментные системы 12.4. Циклические системы 12.5. Системы многофазных сигналов Глава 13. СИСТЕМЫ ЧАСТОТНЫХ СИГНАЛОВ 13.1. Системы частотных сигналов 13.2. Системы сигналов со смещением по частоте Глава 14. СИСТЕМЫ ДИСКРЕТНЫХ ЧАСТОТНЫХ СИГНАЛОВ И ДИСКРЕТНЫХ СОСТАВНЫХ СИГНАЛОВ 14.1. Корреляционные функции дискретных частотных сигналов и число совпадений элементов 14. 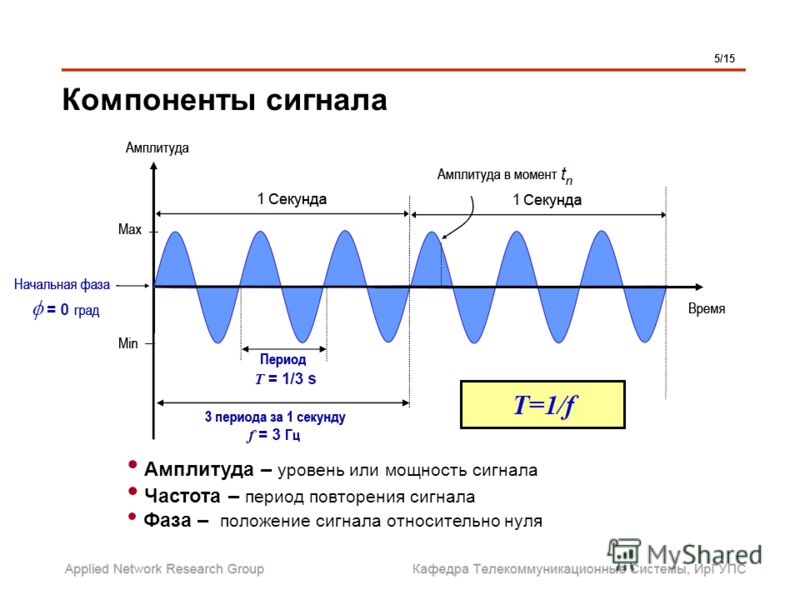 2. Комбинаторный анализ систем дискретных частотных сигналов14.3. Полный код дискретных частотных сигналов первого порядка 14.4. Регулярные методы построения дискретных частотных систем 14.5. Дискретные составные частотные сигналы 14.6. Системы дискретных составных фазоманипулированных сигналов Послесловие |
Составные сигналы
Составные сигналы при передаче данных
Одночастотный синусоидальный сигнал (простой синусоидальный сигнал) бесполезен при передаче данных; нам нужно изменить одну или несколько его характеристик, чтобы сделать его полезным. Когда мы меняем одну или несколько характеристик одного одночастотного сигнала, он становится составным сигналом, состоящим из множества частот.
Составной сигнал может быть периодическим или непериодическим. Периодический составной сигнал можно разложить на ряд простых синусоидальных сигналов с дискретными частотами, причем частоты имеют целые значения (1, 2, 3 и т.
д.). Непериодический составной сигнал можно разложить на комбинацию бесконечного числа простых синусоид с непрерывными частотами, частотами, имеющими реальные значения.
На следующем рисунке показан периодический составной сигнал с частотой f. Этот тип сигнала не типичен для передачи данных. Мы можем рассматривать это как три системы сигнализации, каждая с разной частотой.
Вам также могут понравиться:
Основы данных и сигналов
Цифровые сигналы
Различные методы цифровой передачи сигналов последовательность простых синусоид. На следующем рисунке показан результат разложения вышеуказанного сигнала как во временной, так и в частотной областях.
Амплитуда синусоиды с частотой f почти такая же, как пиковая амплитуда составного сигнала. Амплитуда синусоиды с частотой 3f составляет одну треть от амплитуды первой, а амплитуда синусоиды с частотой 9f составляет одну девятую от первой.
Частота синусоиды с частотой f совпадает с частотой составного сигнала; она называется основной частотой или первой гармоникой.
Синусоида с частотой 3f имеет частоту, в 3 раза превышающую основную частоту; она называется третьей гармоникой. Третья синусоида с частотой 9f имеет частоту, в 9 раз превышающую основную частоту; она называется девятой гармоникой.
Обратите внимание, что частотное разложение сигнала является дискретным; у него есть частоты f, 3f и 9f, потому что f — целое число, 3f и 9f — тоже целые числа. Нет таких частот, как 1.2f или 2.6f. Частотная область периодического составного сигнала всегда состоит из дискретных пиков.
Полоса пропускания
Диапазон частот, содержащихся в составном сигнале, является его пропускной способностью. Пропускная способность обычно представляет собой разницу между двумя числами. Например, если композитный сигнал содержит частоты от 1000 до 5000, его полоса пропускная способность составляет 5000 — 1000, или 4000.
Вам также нравится:
. Разное. Сети
Вернуться к вопросам и ответам DCN
Что такое составной сигнал? » Парень на Simulink
Автор: Сет Попинчалк ,
59 просмотров (последние 30 дней) | 0 лайков | 9 комментариев
Ответ короткий и приятный. Композитный сигнал представляет собой мультиплексор или сигнал шины. Их можно рассматривать как набор других составляющих сигналов. Тонкости использования сигналов шины и сигналов мультиплексора являются распространенным источником вопросов о моделировании, и в 2006 году The MathWorks опубликовала новый раздел документации Simulink, специально посвященный композитным сигналам. В этом посте я начну делиться своей ментальной моделью мультиплексора и шины. Все началось с мультиплексора Основной концепцией блока мультиплексирования является идея объединения сигналов.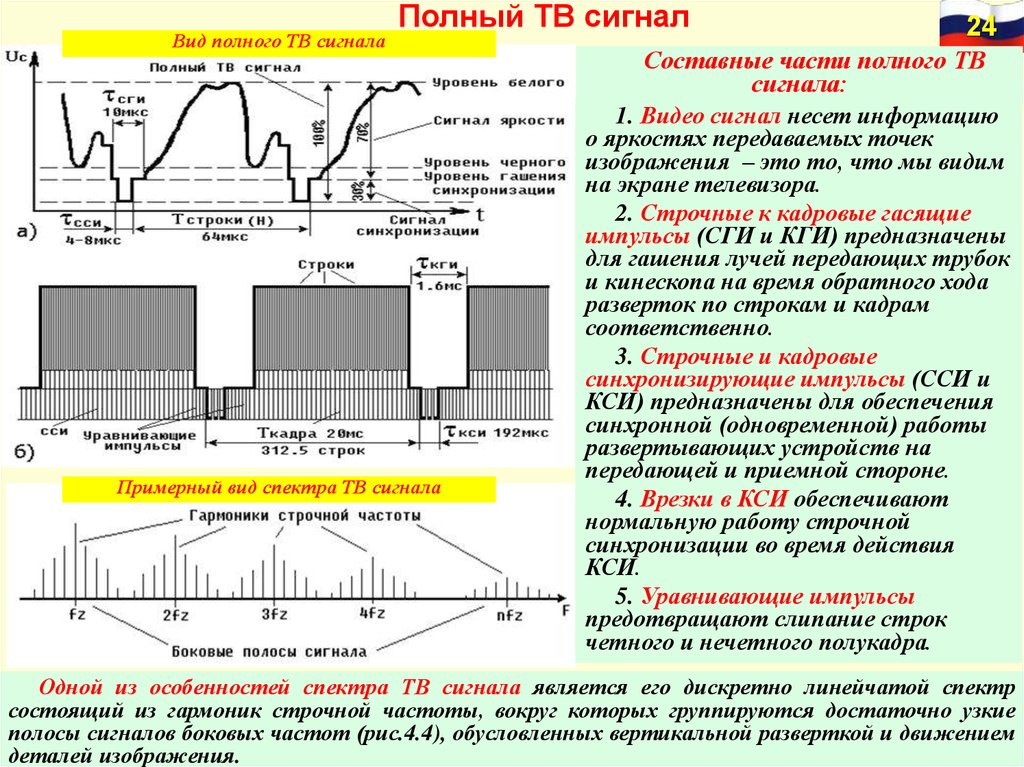
Этот пучок сигналов можно направить через модель, а затем использовать как коллективную единицу. (Мультиплексирование на самом деле означает мультиплексирование.) Наряду с блоком мультиплексирования есть блок демультиплексирования, который разбивает сигналы на отдельные компоненты для индивидуальной обработки. Взгляните на этот пример. Мультиплексор помещает три сигнала (x, y, z) в одну линию шириной 3. Блок демультиплексора используется для разделения сигналов на их основные элементы. Mux и Demux не изменяют сигналы и считаются виртуальными. Когда модель запускается, блоки как будто не существуют, и остаются только соединения от источника к месту назначения, например: Важной ментальной моделью мультиплексора является идея создания вектора. Это означает, что вы можете делать с выходным сигналом то, что вы делаете с вектором. Например, умножьте вектор на 2. Эти типы векторных операций налагают важное требование, чтобы все сигналы, передаваемые в блок мультиплексирования, имели один и тот же тип данных.
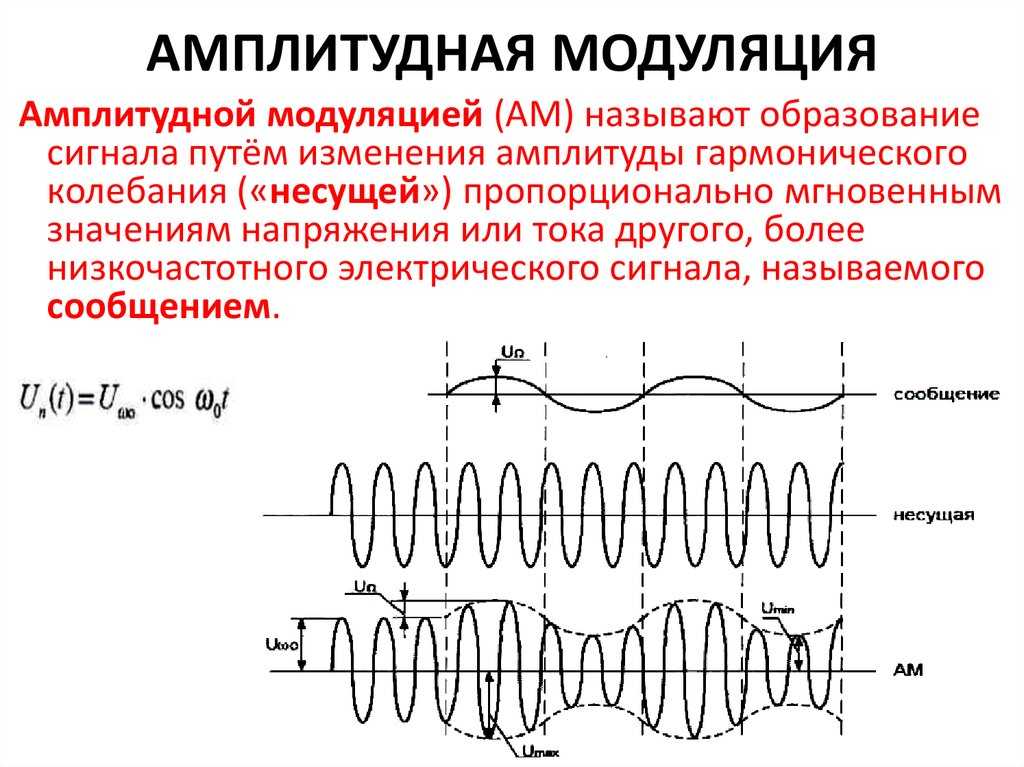В моей ментальной модели мультиплексора имеет смысл объединять сигналы только в том случае, если они имеют смысл как вектор. Обычно элементы имеют одинаковые единицы или они полезны как группа. Единственная спецификация, которая вам нужна для блока мультиплексирования, — это количество входов. Еще одно преимущество использования мысленной модели вектора заключается в том, что вы можете индексировать блок селектора, чтобы отбирать сигналы или переназначать соединения. Позже приехал автобус Когда мне нужно объединить сигналы разных типов или я не могу естественным образом выразить свою диаграмму с помощью вектора, я использую шину. Сигналы шины могут действительно очистить вашу диаграмму. Создатели шин и селекторы шин предоставляют графически удобный способ управления сигналами и организации вашей модели. В моей мысленной модели автобуса я представляю радугу проводов, связанных вместе стяжкой. Без этой скрепляющей ленты я бы быстро потерял способность упорядочивать сигналы.
Чтобы продемонстрировать это, я хочу посмотреть на пример модели DeHaviland Beaver из Aerospace Blockset: На верхнем уровне модели все красиво и упорядоченно, потому что вся информация, вычисляемая каждой подсистемой, собирается в шину. Каждая система упаковывает все соответствующие сигналы в шину с помощью Bus Creator, а затем передает шину системам, которые потребляют эти сигналы. Можете ли вы представить, если бы сигналы не были объединены шиной? Это относительно скромная модель, но это был бы беспорядок! Большинство компонентных систем в этой модели используют сигналы шины для обеспечения упрощенного интерфейса. Я заметил, что некоторые люди помещают сигналы в шину на тот случай, если они могут понадобиться в другой системе. Вот пример системы, интерфейс которой определяется шинными сигналами. Бегло взглянув на эту диаграмму, вы можете определить, что параметры полета (FltParams) могут быть рассчитаны на основе сигналов окружающей среды (EnvirBus) и сигналов самолета (ACBus).
Внутри системы вы можете увидеть селекторы шин, используемые для извлечения определенных элементов из пакета сигналов. Вычисленные параметры полета объединяются с помощью Bus Creator для определения шины FltParams. Сигналы шины могут представлять иерархию Давайте посмотрим на иерархию в Environment Bus. Это простой пример подключения шины к другой шине. Сигналы окружающей среды для гравитации (g), давления (rho) и скорости ветра (Vwind) передаются в Bus Creator. Шина ветра определяется скоростями тела (uvw_wind) и скоростью тела (pqr_wind). Это приводит к организованному набору сигналов в шине, как показано в диалоговом окне Bus Creator. На самом базовом уровне вам нужно только указать количество входов для вашего создателя шины. Имена элементов получены из имен сигналов. Как и Mux Blocks, эти создатели шины вообще не изменили сигналы, поэтому мы можем назвать их виртуальными. Здесь все не заканчивается Мы только начинаем углубляться в эту тему.
