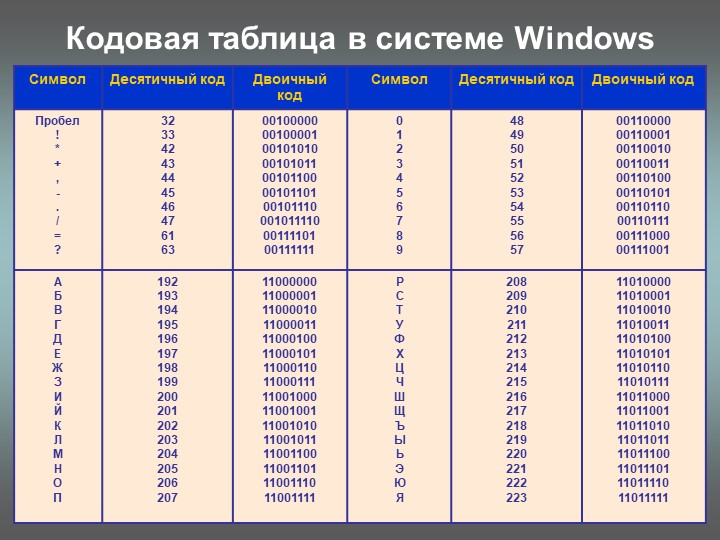
Бинарные коды |
Нашли ошибку? Сообщите нам |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Термин «бинарный» по смыслу — состоящий из двух частей, компонентов. Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска. Существуют различные возможности кодирования информации. Двоичный код В цифровой технике способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы ДК называют битами. Одним из обоснований применения ДК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства магнитного потока в данной ячейке носителя магнитной записи. Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества битов в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный или 3-битовый код:
Отсюда видно, что для числа больше 7 при 3-разрядном коде уже нет кодовых комбинаций из 0 и 1. Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее количество значений m какой-либо величины (температуры, напряжения, тока и др.), которое может быть выражено двоичным кодом, зависит от числа используемых разрядов n как m=2n. Если n=3, как в рассмотренном примере, то получим 8 значений, включая ведущий 0.
Двоичный код является многошаговым кодом. Это означает, что при переходе с одного положения (значения) в другое могут изменятся несколько бит одновременно. Например число 3 в двоичном коде = 011. Число же 4 в двоичном коде = 100. Соответственно при переходе от 3 к 4 меняют свое состояние на противоположное все 3 бита одновременно. Считывание такого кода с кодового диска привело бы к тому, что из-за неизбежных отклонений (толеранцев) при производстве кодового диска изменение информации от каждой из дорожек в отдельности никогда не произойдет одновременно. Это в свою очередь привело бы к тому, что при переходе от одного числа к другому кратковременно будет выдана неверная информация. Код Грея Грей-код является так называемым одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой-то один из всех бит. Погрешность при считывании информации с механического кодового диска при переходе от одного числа к другому приведет лишь к тому, что переход от одного положения к другом будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения при переходе от одного положения к другому полностью исключается.
Преимуществом Грей-кода является также его способность зеркального отображения информации. Так, инвертируя старший бит, можно простым образом менять направление счета и таким образом подбирать к фактическому (физическому) направлению вращения оси. Поскольку информация выраженная в Грей-коде имеет чисто кодированный характер не несущей реальной числовой информации должен он перед дальнейшей обработкой сперва преобразован в стандартный бинарный код. Осуществляется это при помощи преобразователя кода (декодера Грей-Бинар) который к счастью легко реализуется с помощью цепи из логических элементов «исключающее или» ( XOR ) как программным так и аппаратным способом. Соответствие десятичных чисел в диапазоне от 0 до 15 двоичному коду и коду Грея
Код Gray-Excess
Обычный одношаговый Грей-код подходит для разрешений, которые могут быть представлены в виде числа возведенного в степень 2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Двоичный код | Двоичный: 0101 | Десятичный: 5
Двоичный код | Двоичный: 0101 | Десятичный: 5 | Биты: 4« Предыдущая (100)Следующая (110) »
Двоичный калькулятор
Двоичный «=» Десятичный
| Binary | 0101 |
|---|---|
| Decimal | 5 |
| Hexadecimal | 5 |
| Bits | 4 |
| Equation | 4 + 1 |
Двоичный код
| Десятичный | Двоичный | пишется | |
|---|---|---|---|
| + | 4 | 100 | Four |
| + | 1 | 1 | One |
| = | 5 | 0101 | Пять |
8-битные числа: 11111100 01000110 00001000 01001100 10010011 11001110 10111100 11101010 00010011 01111101
16-битные числа: 1101101110000011 1110110101001111 0100110110101111 0010010100011010 1000111101010110 1100101101100101 0110101000000011 0110111001110100 1010111110011110 0101101101011110
Еще номера: 1010101101110101110000001000010111100000011101110000101001101100101011111110010001111100010000100111110011010010001100101101110010000011101101100001101111111011100000110101101111011001010001110100001110001110001000001100011111111100010110110101010000111111110001000011011111000111000110110100111010110011111110100001000101000101110010111110010100100100101111100100000111101010111110000011111011011010111110010101101011101110000010000000111010011111110010100000001010001100101001111011000001011101011011111001111101111111001011100011110101110111011100100000110100111100001001011001011010111110011010100011110110101110101100101000001001101100110010000111110100100111011011001110110010101010101111111001000001110111110011111110011100101111110101000011001110000111001011001101010111010101000000010111111110010011000100001001110010111111011001111001010011000111110100010110101110011010100101110001100110000111011101111110001010111011111100100100001101001101110001111010001101101110111000000000001000110111 0111000000101011101010101101010000101101010100101000111100111100101111110011101110001011000011100011100100010011101011110111010010110111011001111101111011110001011011111011010000111010110110111100001101101101110100011111111100000111011101101011100111110000110011100000110111100100010011111011000000011100001011111000001011101111001011110010011001111000010011111101101111100100101110101000111100010000000101011101111101101001011100101010000111000011100001110110100101111111100010111000001110000000001001100010001100011011101111101011111111011010010011001000111101001101101111111001010100011111111010110001010001001101010100100010001110001011111101001110010100000101100011000001100100000101111101000100111110110101010100000110001001100001111000001110000110001011111000010011111101100011101100000000000001010011110100001100010111101110101101110010100011100111011110010010010010111100111110100111110111100001001
101 в двоичном формате — Как преобразовать 101 из десятичного в двоичный?
101 в двоичной системе равно 1100101. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, равные 0 и 1 (биты). Мы использовали 7 бит для представления 101 в двоичном формате. В этой статье мы покажем, как преобразовать десятичное число 101 в двоичное.
В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, равные 0 и 1 (биты). Мы использовали 7 бит для представления 101 в двоичном формате. В этой статье мы покажем, как преобразовать десятичное число 101 в двоичное.
- 101 в двоичном формате: 101₁₀ = 1100101₂
- 101 в восьмеричном: 101₁₀ = 145₈
- 101 в шестнадцатеричном формате: 101₁₀ = 65₁₆
- 1100101₂ в десятичном формате: 101₁₀
Как преобразовать 101 в двоичный код?
Шаг 1: Разделите 101 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0.
| Дивиденд | Остаток |
|---|---|
| 101/2 = 50 | 1 |
| 50/2 = 25 | 0 |
| 25/2 = 12 | 1 |
| 12/2 = 6 | 0 |
| 6/2 = 3 | 0 |
| 3/2 = 1 | 1 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т.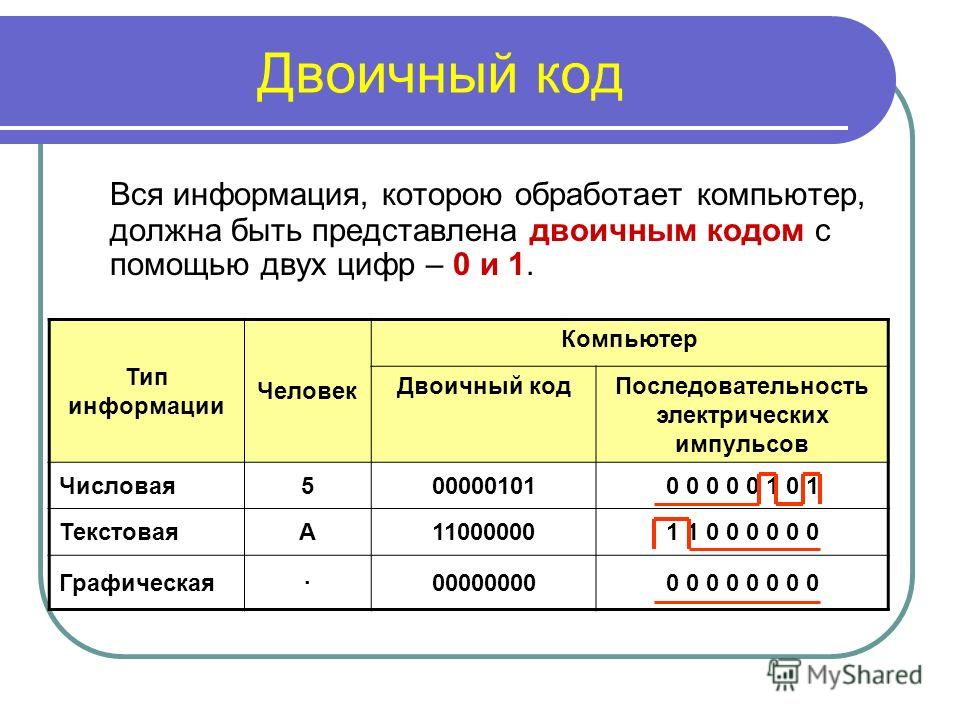 е. в обратном хронологическом порядке. Это даст двоичный эквивалент 101.
е. в обратном хронологическом порядке. Это даст двоичный эквивалент 101.
Следовательно, двоичным эквивалентом десятичного числа 101 является 1100101.
☛ Калькулятор преобразования десятичного числа в двоичное
Постановка задачи:
Часто задаваемые вопросы о числе 101 в двоичном формате
101 в двоичном формате равно 1100101. Чтобы найти десятичный эквивалент в двоичном, последовательно делите 101 на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
☛ Двоичный код в десятичный
Как преобразовать 101 в двоичный эквивалент?
Мы можем разделить 101 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.
- 101 mod 2 = 1 — LSB (младший значащий бит)
- 50 мод 2 = 0
- 25 модуль 2 = 1
- 12 мод 2 = 0
- 6 мод 2 = 0
- 3 мод 2 = 1
- 1 mod 2 = 1 — MSB (самый старший бит)
Записать остатки от MSB до LSB. Следовательно, десятичное число 101 в двоичном виде можно представить как 1100101.
Следовательно, десятичное число 101 в двоичном виде можно представить как 1100101.
Что такое двоичный эквивалент 101 + 99?
101 в двоичной системе счисления равно 1100101, а 99 равно 1100011. Мы можем сложить двоичный эквивалент 101 и 99, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1100101)₂ + (1100011)₂ = (11001000)₂, что есть не что иное, как 200.
☛ Калькулятор двоично-десятичных чисел
Сколько бит имеет 101 в двоичном формате?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 101 в двоичном формате, т. е. 1100101. Таким образом, мы использовали 7 бит для представления 101 в двоичном формате.
Найдите значение 7 × 101 в двоичной форме.
Мы знаем, что 101 в двоичном формате равно 1100101, а 7 равно 111. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0, 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1100101.




 Изменение направления счета таким образом может легко изменяться управляя так называемым входом » Complement «. Выдаваемое значение может таким образом быть возрастающим или спадающим при одном и том же физическом направлении вращения оси.
Изменение направления счета таким образом может легко изменяться управляя так называемым входом » Complement «. Выдаваемое значение может таким образом быть возрастающим или спадающим при одном и том же физическом направлении вращения оси.
 значение
значение
 В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещается на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализуются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещается на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализуются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
 Это позиционная система счисления, которая имеет 10 арабских цифр от 0 до 9 и, следовательно, основание 10. Т. е. число 6235,89 в десятичной системе счисления представляется выражением
Это позиционная система счисления, которая имеет 10 арабских цифр от 0 до 9 и, следовательно, основание 10. Т. е. число 6235,89 в десятичной системе счисления представляется выражением 2)
2) В позиции этих степеней подставляются единицы (голубые столбцы), остальные позиции заполняются нулями (белые столбцы). Старший разряд расположен слева, как и в других позиционных системах счисления. В нашем примере (171,75) = (10101011,11) . Поскольку далее будут использоваться небольшие десятичные целые числа, такой способ перевода их в двоичные эквиваленты является наиболее удобным. Аналогичным образом выполняется обратное преобразование. Т. е. для перевода двоичного числа в десятичное необходимо складывать степени двойки, соответствующие позициям с единичными значениями. В нашем примере
В позиции этих степеней подставляются единицы (голубые столбцы), остальные позиции заполняются нулями (белые столбцы). Старший разряд расположен слева, как и в других позиционных системах счисления. В нашем примере (171,75) = (10101011,11) . Поскольку далее будут использоваться небольшие десятичные целые числа, такой способ перевода их в двоичные эквиваленты является наиболее удобным. Аналогичным образом выполняется обратное преобразование. Т. е. для перевода двоичного числа в десятичное необходимо складывать степени двойки, соответствующие позициям с единичными значениями. В нашем примере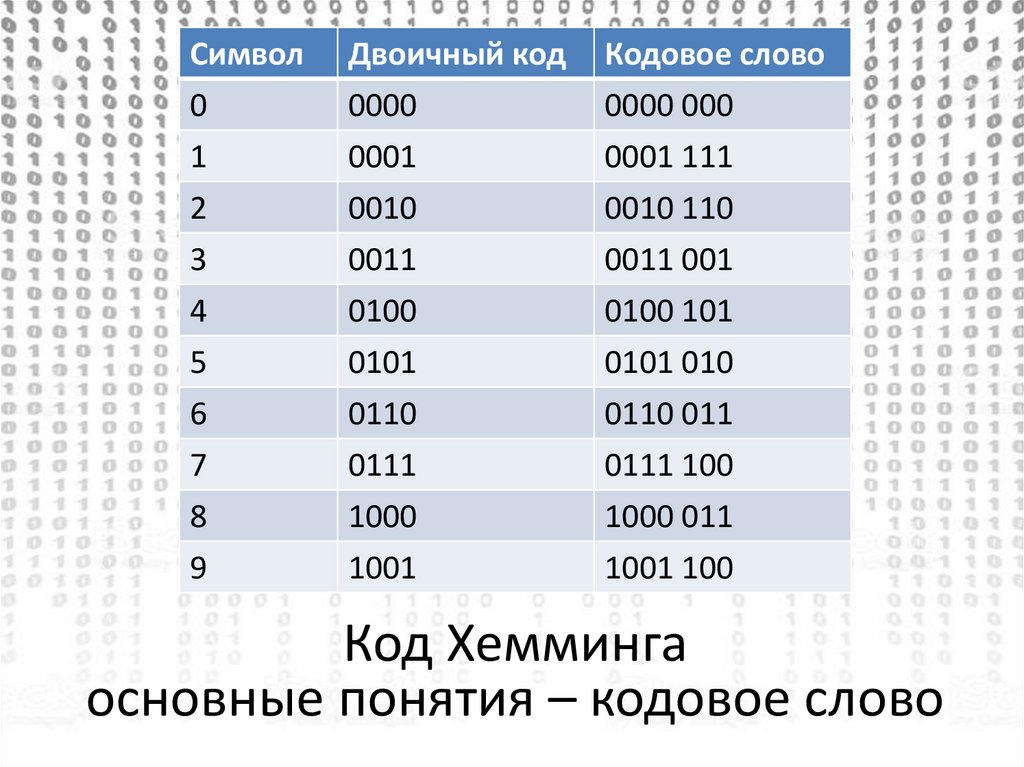 Следующий пример иллюстрирует данное правило.
Следующий пример иллюстрирует данное правило.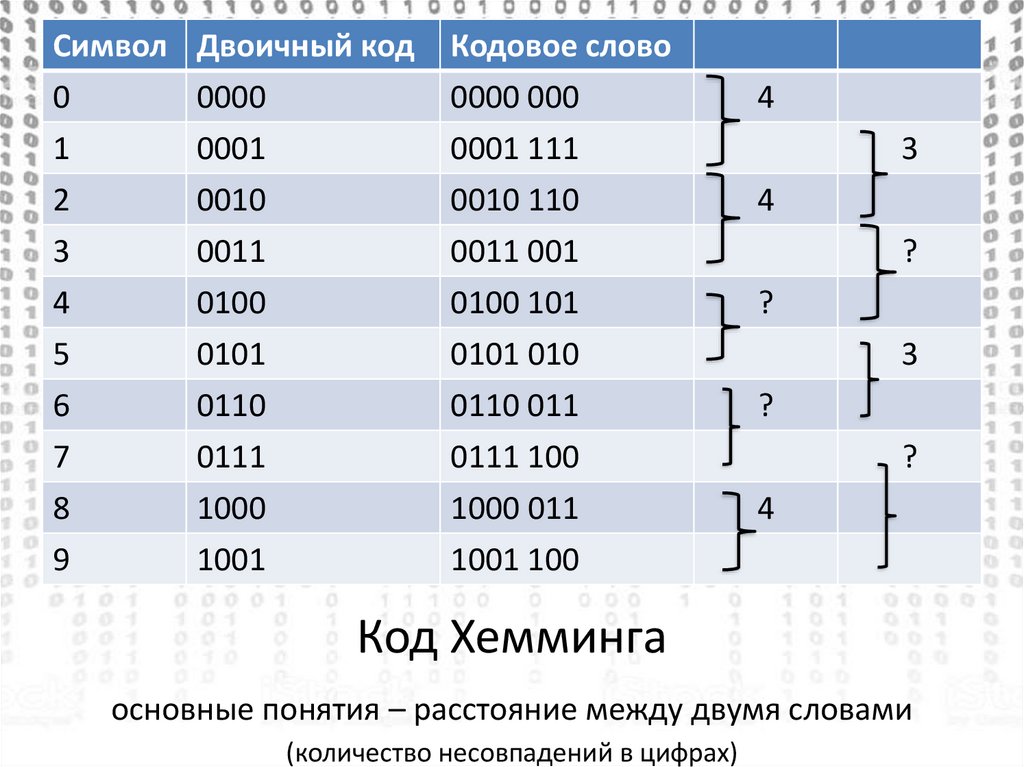 В этом случае с помощью специальных преобразователей человек может получать двоичную информации в восьмиричном или шестнадцатиричном коде. Подразумевается, что в случае необходимости, пользователь сам перейдет к двоичному коду. Это делается весьма просто и к тому же размер восьмиричного (шестнадцатиричного) кода гораздо меньше двоичного — = = — 3, 4 символа воспринимаются человеком комфортнее, чем 12.
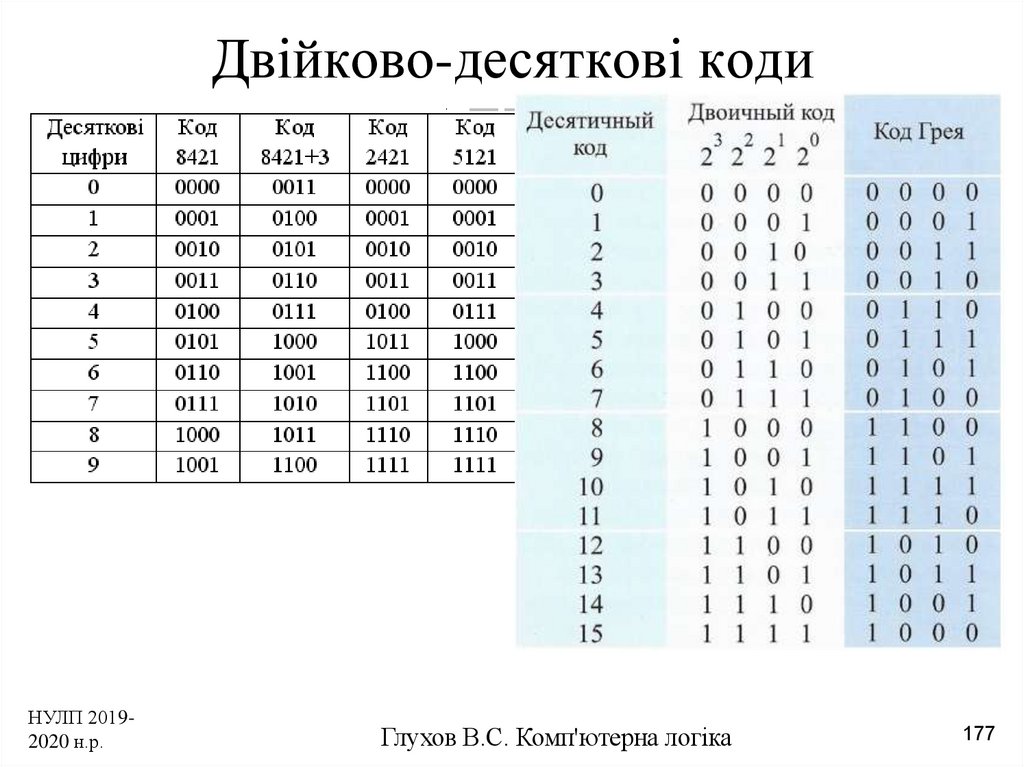
В этом случае с помощью специальных преобразователей человек может получать двоичную информации в восьмиричном или шестнадцатиричном коде. Подразумевается, что в случае необходимости, пользователь сам перейдет к двоичному коду. Это делается весьма просто и к тому же размер восьмиричного (шестнадцатиричного) кода гораздо меньше двоичного — = = — 3, 4 символа воспринимаются человеком комфортнее, чем 12. Для представления цифры в таком коде необходимо 4 двоичных разряда. В таблице 1.3 приведены примеры некоторых двоично-десятичных кодов десятичных цифр.
Для представления цифры в таком коде необходимо 4 двоичных разряда. В таблице 1.3 приведены примеры некоторых двоично-десятичных кодов десятичных цифр.