Физика Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока
Материалы к уроку
12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.doc
55 KBСкачать12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.ppt
2.78 MBСкачать
Конспект урока
Огромное практическое значение имеют незатухающие вынужденные колебания. Свободные электромагнитные колебания в контуре быстро затухают и поэтому практически не используются. Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания. Частота переменного тока показывает число колебаний за 1 секунду. Стандартная частота промышленного тока равна 50 Герц. Значит, на протяжении 1 с ток 50 раз течет в одну сторону и 50 раз в другую. Частота 50 Герц принята для промышленного тока во многих странах мира. Сила тока и напряжение меняются со временем по гармоническому закону. Это вытекает из следующих рассуждений. Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Если время распространения изменений поля в цепи гораздо меньше периода колебаний напряжения, то можно считать, что электрическое поле во всей цепи меняется почти мгновенно при изменении напряжения на концах цепи.
Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания. Частота переменного тока показывает число колебаний за 1 секунду. Стандартная частота промышленного тока равна 50 Герц. Значит, на протяжении 1 с ток 50 раз течет в одну сторону и 50 раз в другую. Частота 50 Герц принята для промышленного тока во многих странах мира. Сила тока и напряжение меняются со временем по гармоническому закону. Это вытекает из следующих рассуждений. Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Если время распространения изменений поля в цепи гораздо меньше периода колебаний напряжения, то можно считать, что электрическое поле во всей цепи меняется почти мгновенно при изменении напряжения на концах цепи.


Здесь изображен график зависимости мгновенной мощности от времени. На протяжении одной четверти периода мощность больше половины амплитудного значения. Но на протяжении следующей четверти периода мощность меньше этой величины. На протяжении одной четверти периода эта функция пробегает ряд положительных значений. Половина квадрата амплитуды силы тока в колебательном электромагнитном контуре есть среднее за период значение квадрата силы тока. Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током, равнялась энергии, выделяемой за то же время переменным током. Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.



Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания. Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.

Колебательный контур обладает замечательным свойством – пропускать колебания только определенной частоты, зависящей от емкости конденсатора и индуктивности катушки, под действием резонанса. Эти свойства контура широко применяются в радио- и телеприёмной и передающей аппаратуре для селекции сигналов.
Задача
Конденсатор включен в цепь переменного тока с частотой 200 Герц. Напряжение в цепи 40 Вольт, сила тока 0,64 Ампера. Какова емкость конденсатора?
Вспомнив закон Ома для цепи с колебательным контуром, выразим емкость конденсатора как отношение силы тока к напряжению и циклической частоте. Чтобы определить циклическую частоту, необходимо частоту переменного тока разделить на два-пи. Получаем результат 0,5 микрофарад есть емкость конденсатора.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Активное сопротивление в цепи переменного тока: описание, формула
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Треугольник сопротивлений
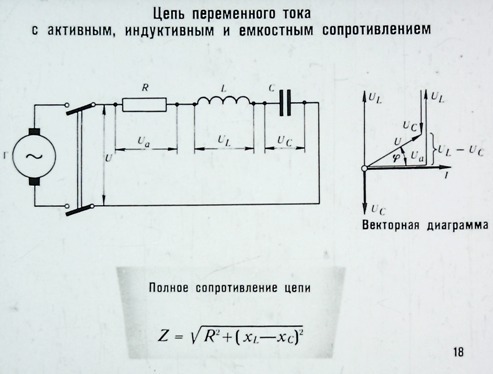
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения. Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока. В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части.Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
https://youtube.com/watch?v=NSxgxMNG2fwrel%3D0%26amp%3Bcontrols%3D0%26amp%3Bshowinfo%3D0
- electrosam.ru
- electrono.ru
- electroandi.ru
- fazaa.ru
Основные понятия
Ёмкостное сопротивление — это величина, которая создаётся конденсатором, включённым в цепь. Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.
Период разбивается на четыре четверти. В течение первой четверти напряжение растёт. В этот момент по цепи проходит зарядный ток, сила которого будет уменьшаться, достигнув нуля, когда электродвижущая сила достигнет положительного максимума. Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.
Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.
К концу полупериода величина напряжения будет равна нулю, а сила тока будет наибольшей. Разрядка завершена. В начале третьей четверти электродвижущая сила будет возрастать, изменив своё направление. Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.
Электродвижущая сила достигнет своего наибольшего отрицательного значения. А на той обкладке, на которой в течение первого полупериода был положительный заряд, теперь будет отрицательный. Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.
Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Емкостное сопротивление
В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.
Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.
В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.
Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.
Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.
В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Индуктивное сопротивление катушки
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь.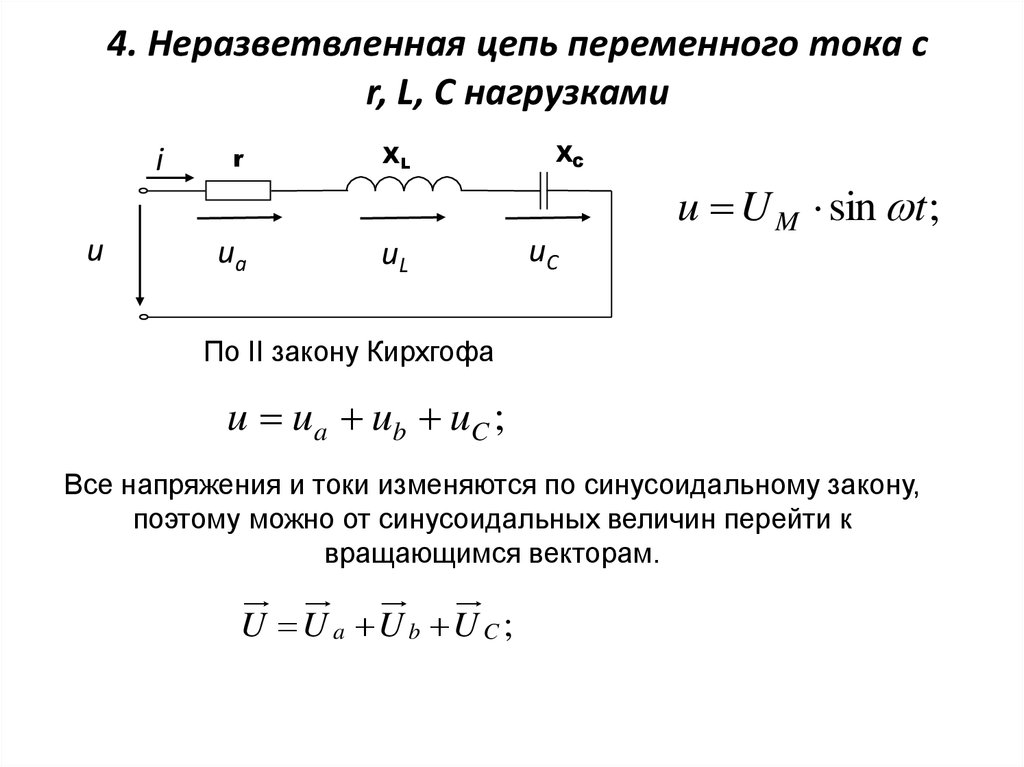 Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега).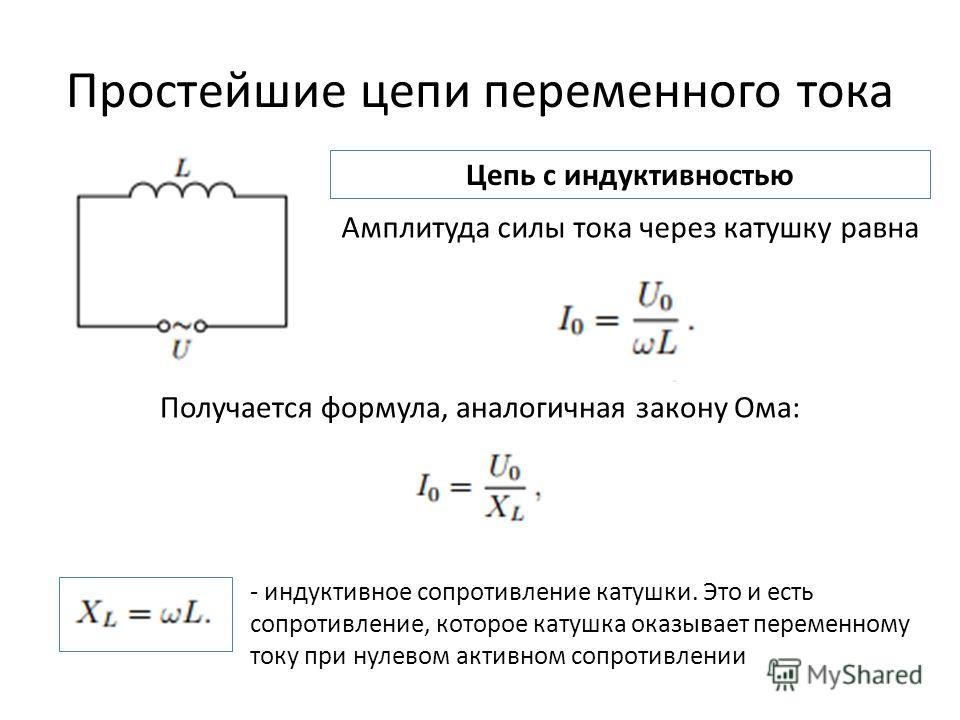 Поэтому приведенная выше формула может быть представлена так:
Поэтому приведенная выше формула может быть представлена так:
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
Источник
Индуктивное сопротивление
Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.
При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.
Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.
В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.
Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь. От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.
От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Измерение сопротивления конденсаторов.
Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи.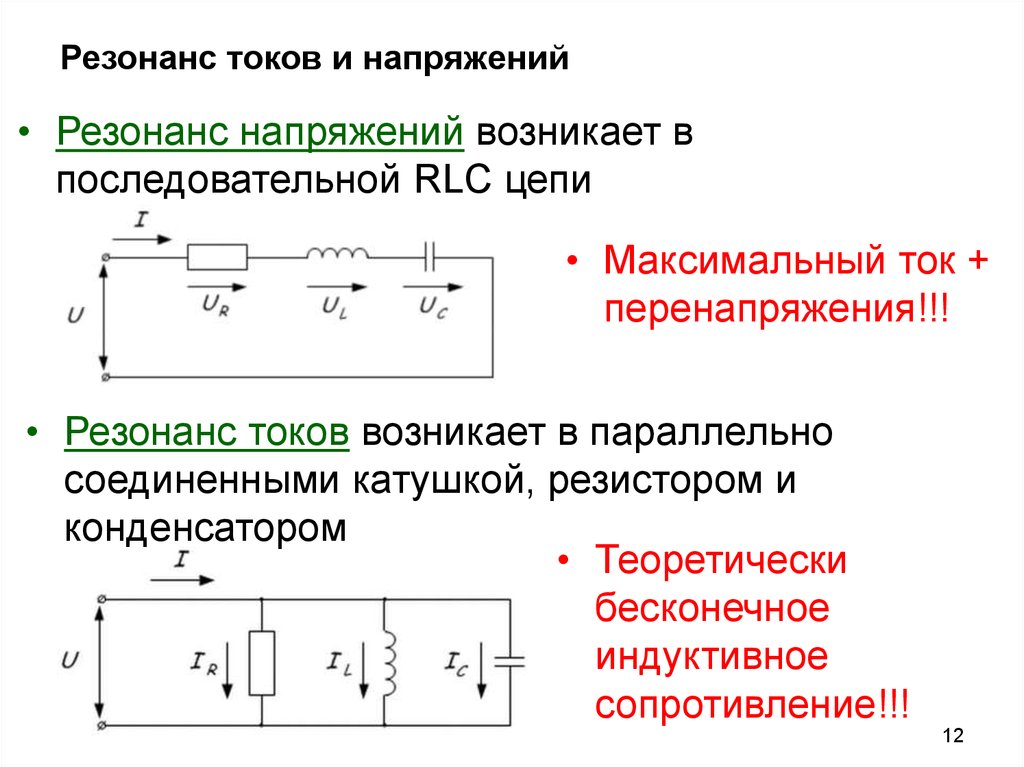 Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.
Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивноесопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости.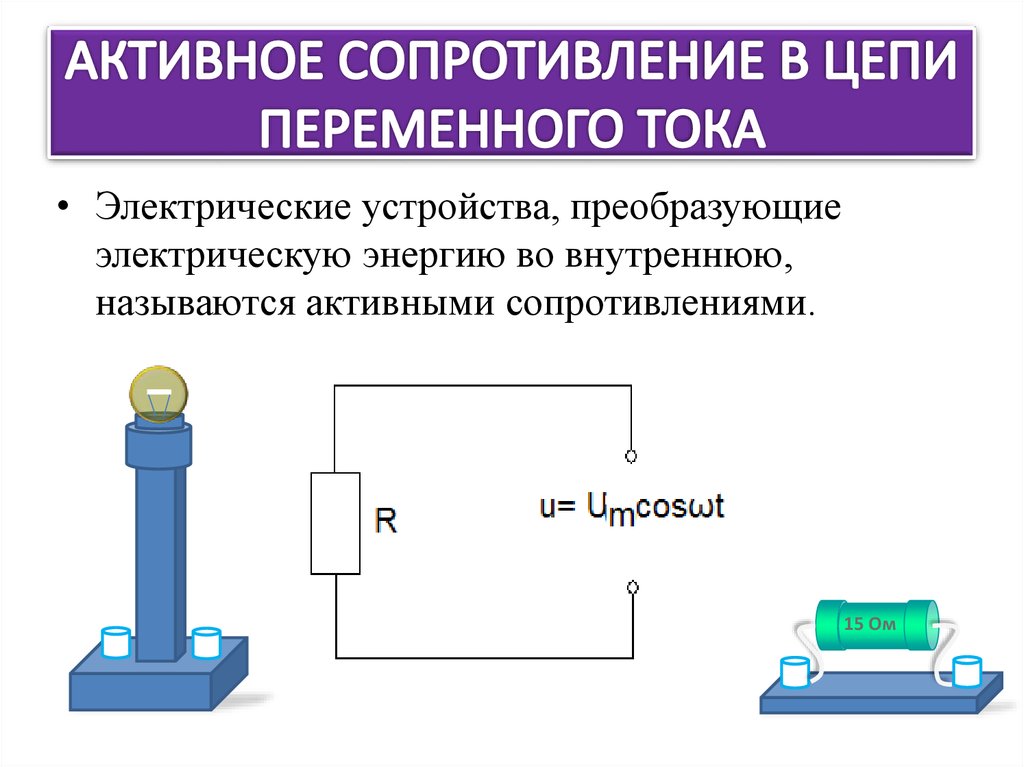 Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C.
RC цепь
Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Здесь U – напряжение источника питания.
Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное.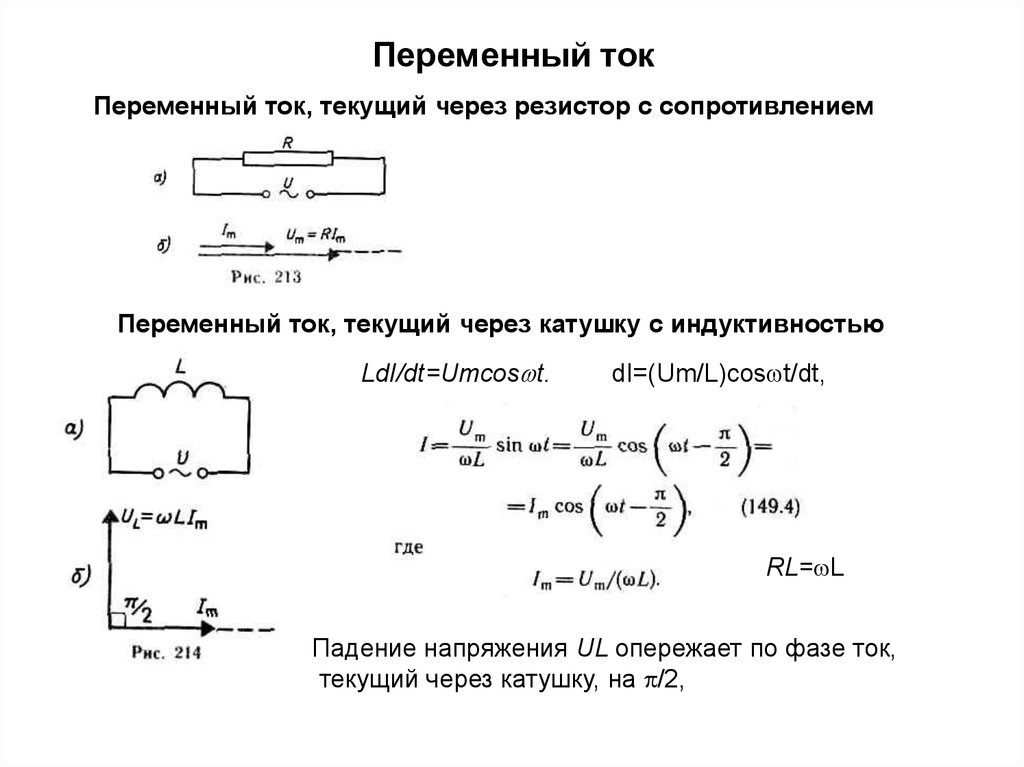 Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься.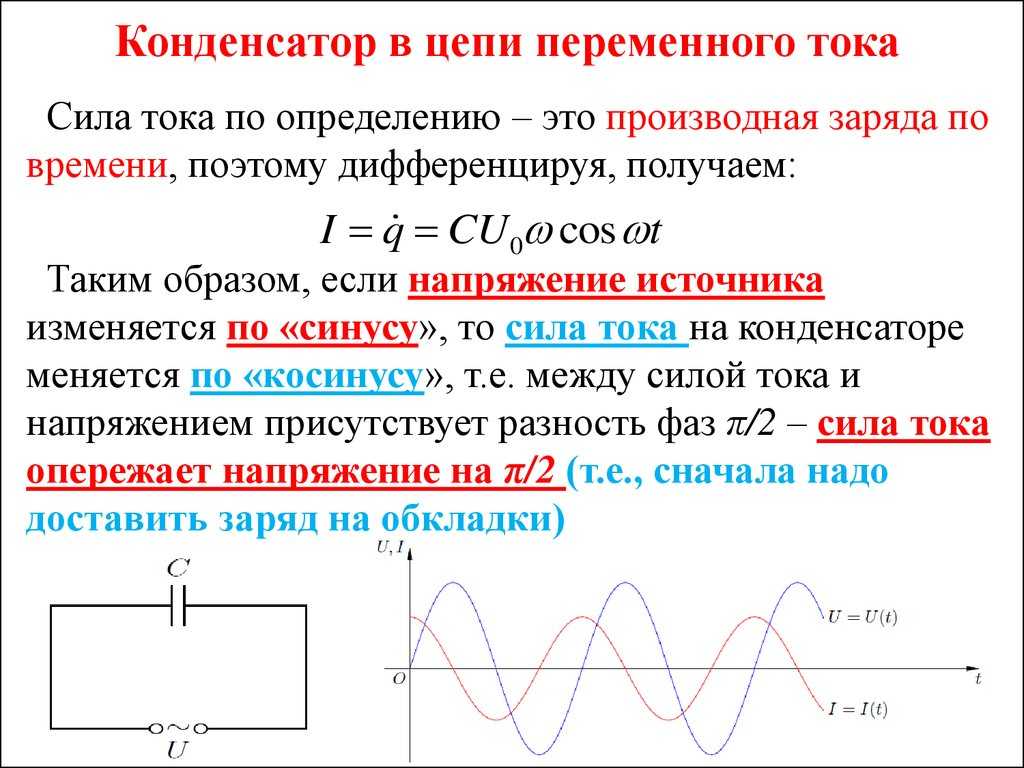 И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L — собственно сама индуктивность катушки
С — межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r — сопротивление диэлектрика и корпуса между обкладками
С — собственно сама емкость конденсатора
ESI (ESL) — эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Что надо знать про электрические процессы
Если говорить простым языком, то под сопротивлением принято понимать свойство среды, по которой протекает электрический ток, снижающее его величину.
Так работают провода и изоляторы высоковольтной линии электропередач, показанные на верхней картинке, да и любое вещество.
Изоляторы обладают очень высокими диэлектрическими свойствами, изолируют высоковольтное напряжение, присутствующее на токоведущих шинах от контура земли. Это их основное назначение.
Провода же должны максимально эффективно передавать транслируемые по ним мощности. Их создают так, чтобы они обладали минимальным электрическим сопротивлением, работали с наименьшими потерями энергии на нагрев.
В этом случае передача электричества от источника напряжения к потребителю на любое расстояние будет проходить эффективно.
Приведу для примера картинку из предыдущей моей статьи.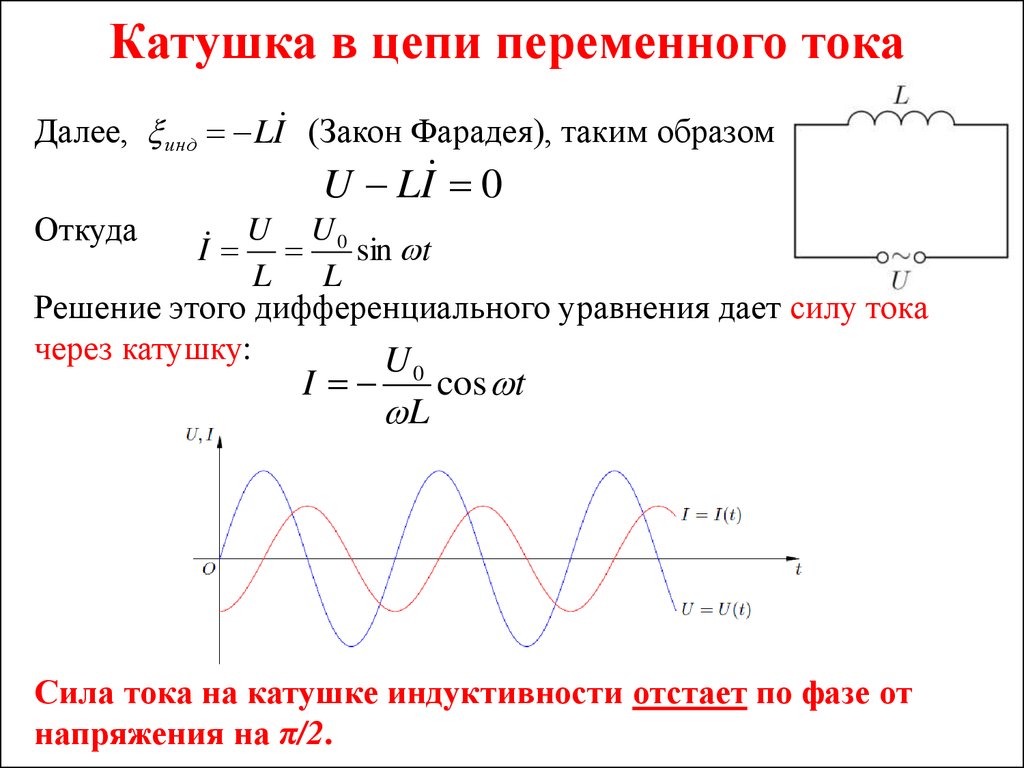
Ее, как и верхнюю, можно представить таким обобщенным видом.
На внешнем участке цепи токоведущие жилы отделены друг от друга воздушной средой и слоем изоляции с высокими диэлектрическими свойствами.
Хорошей проводимостью обладают токоведущие жилы. Подключенный к ним электрический прибор функционирует оптимально.
Как работает резистор
Ток в металлах проходит под действием приложенного напряжения за счет направленного движения электронов. При этом они соударяются, встречаются с положительно и отрицательно заряженными ионами.
Такие столкновения повышают температуру среды, уменьшают силу тока.
За направление электрического тока в электротехнике принято движение заряженных частиц от плюса к минусу. Электроны же движутся от катода к аноду.
Электрическое сопротивление металла зависит от его структуры и геометрических размеров.
Аналогичные процессы протекают в любой другой токопроводящей среде, включая газы или жидкости.
Какие существуют виды сопротивлений
В домашних электрических приборах используется большое разнообразие резисторов с постоянной или регулируемой величиной.
Они ограничивают величину тока всех бытовых устройств, а в наиболее сложных модулях их количество может достигать тысячи или более. Резисторы работают практически во всех схемах.
При использовании в цепях переменного тока они обладают активным сопротивлением, а конденсаторы и дроссели — реактивным.
Причем, на конденсаторах создается емкостное сопротивление, а у дросселей — индуктивное.
Реактивная составляющая на конденсаторах и дросселях сильно зависит от частоты электромагнитного колебания.
2 Шутки электриков о токах через конденсатор и дроссель
Их я привожу потому, что они позволяют запомнить характер прохождения тока через реактивные элементы.
Шутка №1 о емкости
В домашней сети и внутри многих приборов работают переменный и постоянный токи. Они по-разному ведут себя, если встречают на своем пути конденсатор.
Поскольку он состоит из двух токопроводящих пластин, разделенных слоем диэлектрика, то его обозначают на схемах двумя жирными черточками, расположенными параллельно.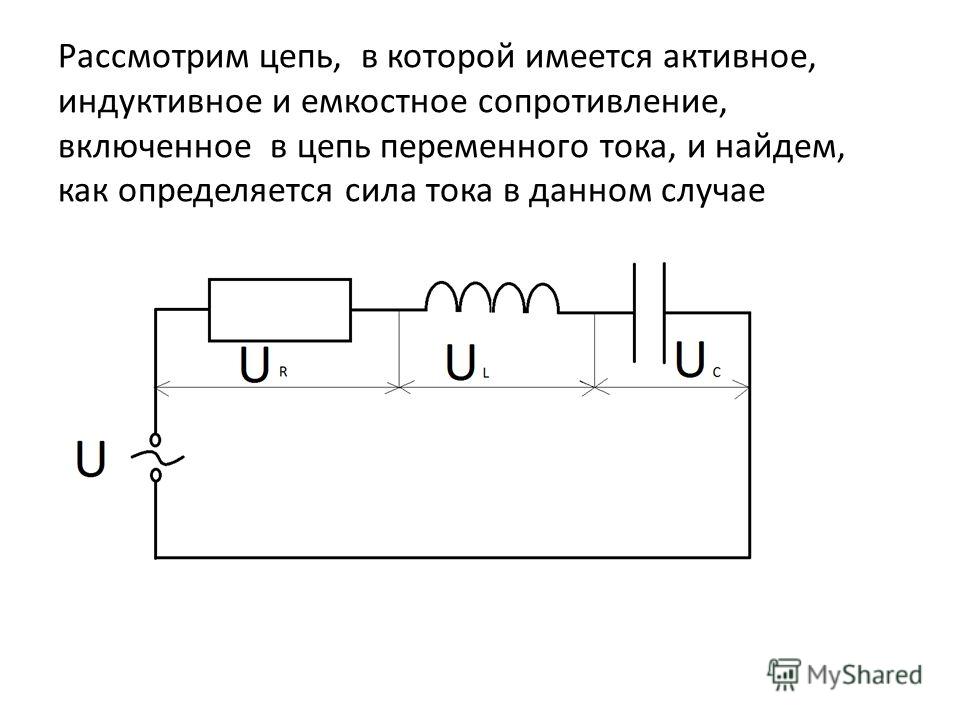 К их серединам подключены провода, нарисованные перпендикулярными линиями.
К их серединам подключены провода, нарисованные перпендикулярными линиями.
Переменный ток имеет форму гармоничной синусоиды, состоящей из двух симметричных половинок.
Такая гармоника движется от начала координат, встречает на своем пути обкладки, переваливается через них и, скатившись, начинает обгонять приложенное напряжение.
Постоянный ток таким свойством не обладает. Его тупой конец просто упирается в обкладку и останавливается. Пройти через конденсатор он не может. Это для него непреодолимое препятствие.
Шутка №2 о дросселе
Индуктивность выполнена витками изолированного провода. Любой ток проходит по нему. Но синусоида своими волнами путается в витках катушки, начинает отставать от напряжения.
Постоянка же спокойно перемещается внутри провода дросселя без ощущения какого-либо значительного противодействия. Поэтому постоянное напряжение может своим током спалить дроссель, созданный для работы на переменке.
Что же это за зверь: сверхпроводимость
Сто лет назад выявлена способность определенных металлов полностью терять свое сопротивление электрическому току при сверхнизких температурах.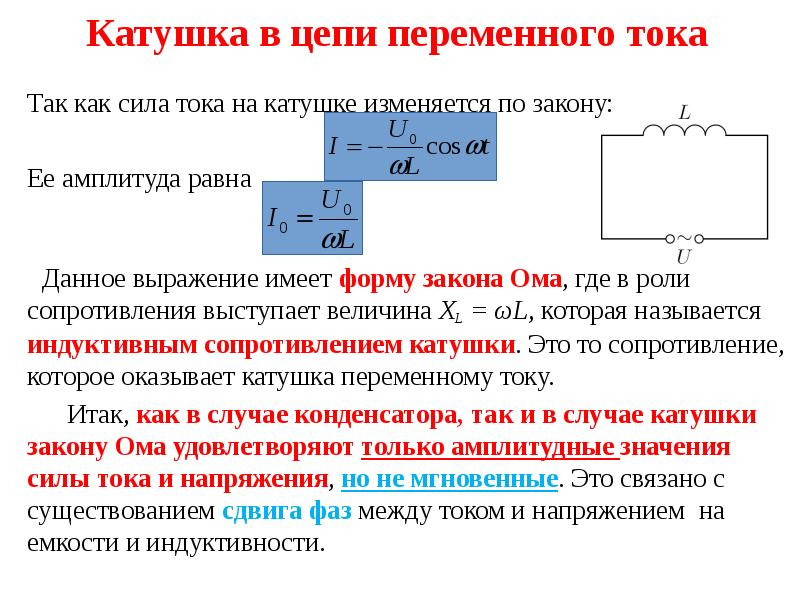 Выглядит этот процесс следующим образом.
Выглядит этот процесс следующим образом.
Со сверхпроводниками домашний мастер не работает
Но на верхнюю часть приведенного графика рекомендую обратить внимание: нагрев металла повышает его электрическое сопротивление
При электротехнических расчетах, требующих получения точного результата, необходимо учитывать температурный коэффициент, взятый из справочников.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Цепи RLC
Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.
Что мы узнали?
Сопротивление, на котором энергия электрического тока выделяется в виде тепла, называется активным. Оно не обладает инерционностью. Ток, протекающий через активное сопротивление, синфазен с напряжением на нем, и его можно найти по закону Ома для действующих значений. Мощность, выделяемая на активном сопротивлении, можно найти по закону Джоуля-Ленца для действующих значений.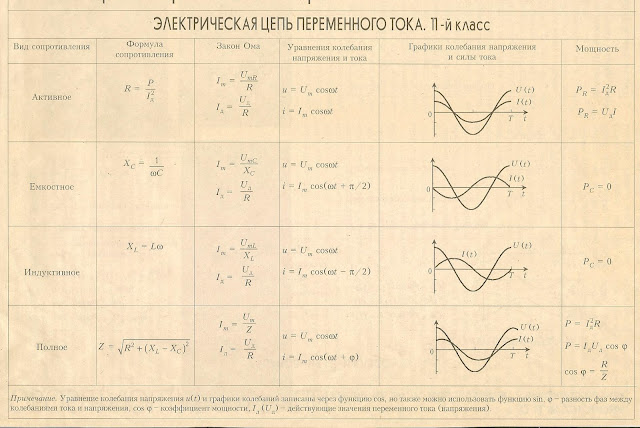
Предыдущая
ФизикаОткрытие электромагнитной индукции кратко и понятно о значении явления магнитного потока и что стало возможным появление (11 класс)
Следующая
ФизикаВиды излучений – кратко таблица характеристики и применения, диапазоны альфа, бета, гамма (11 класс)
Емкостное и индуктивное сопротивление в цепи переменного тока — Студопедия
Поделись
| Емкостное сопротивление в цепи переменного тока | |
| При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. | |
| Мгновенное значение напряжения равно . Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. | |
Т. к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: , где — емкостное сопротивление. к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: , где — емкостное сопротивление.
| |
| Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). | |
| Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). | |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. | |
| Индуктивное сопротивление в цепи переменного тока | |
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки.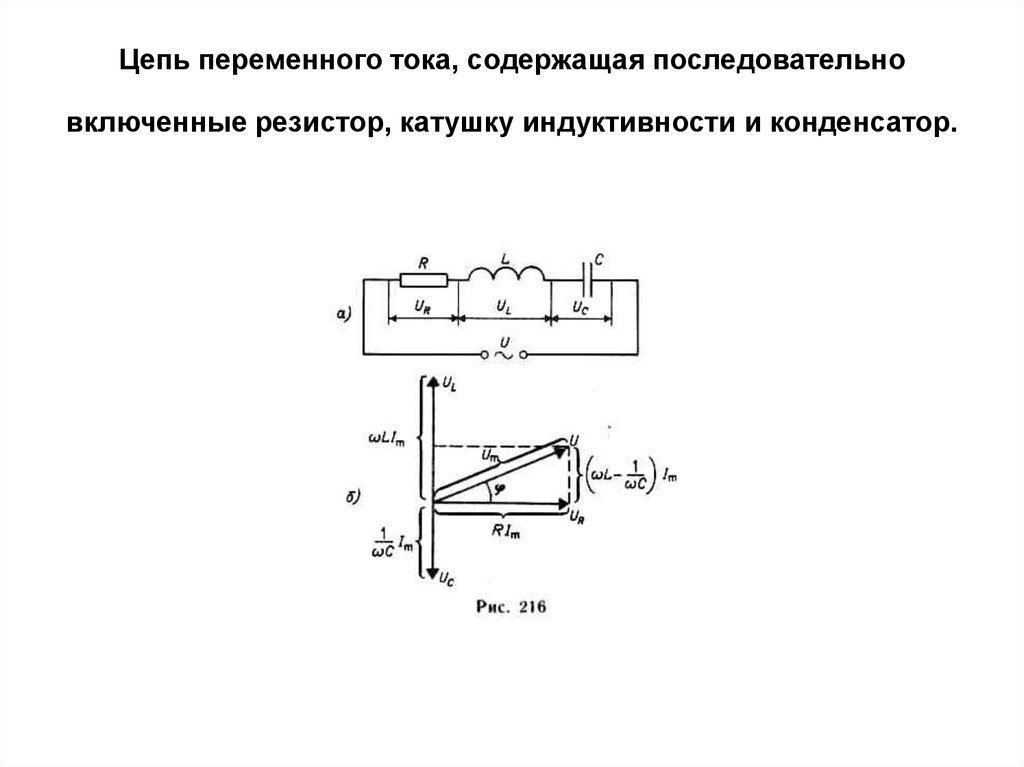 Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
| |
| Мгновенное значение силы тока: | |
| Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. | |
| . Следовательно , где амплитуда напряжения. Напряжение опережает ток по фазе на π/2. | |
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой.
| |
| Величина — индуктивное сопротивление. | |
| Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. | |
| В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. | |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
Колебания > Переменный ток > Полное сопротивление в цепи переменного тока (Z).
| Содержание | Величина | Наименование |
Обычно цепь переменного тока включает в себя и активное сопротивление, и емкость, и индуктивность. Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. — полное сопротивление цепи. Здесь: — активное сопротивление. — емкостное сопротивление. — индуктивное сопротивление. — полное сопротивление определяет силу тока в цепи по закону Ома. Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. — полное сопротивление цепи. Здесь: — активное сопротивление. — емкостное сопротивление. — индуктивное сопротивление. — полное сопротивление определяет силу тока в цепи по закону Ома.
| I — действующее значение силы тока | А |
| U — действующее значение напряжения | В | |
| XL — индуктивное сопротивление | Ом | |
| ω — циклическая частота переменного тока | рад/с | |
| L — индуктивность | Гн | |
| C — емкость | Ф | |
| XC — индуктивное сопротивление | Ом | |
| Z — полное сопротивление | Ом | |
| R — активное сопротивление | Ом | |
| ρ — удельное сопротивление проводника | Ом м | |
| l — длина проводника | м | |
| S — площадь сечения проводника | м2 |
|
⇐ ПредыдущаяСтр 5 из 8Следующая ⇒
Полное сопротивление в цепи переменного тока. Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Резонанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот. Физические основы реографии Реография — метод, который позволяет измерять кровенаполнение конечностей, мозга ,сердца и многих других органов. Билет 24 Датчики как устройство съема биологических сигналов. Генераторные и параметрические датчики, их классификация и характеристики Датчиком называют устройство ,преобразующее измеряемую или контролируемую величину в сигнал, удобный для передачи ,дальнейшего преобразования и регистрации. Некоторые типы датчиков 1) пьезоэлектрические ,пьезоэлектрический эффект. 2)термоэлектрические ,термоэлектричество-явление возникновения ЭДС в электрической цепи, состоящей из последовательно соединенных разнородных проводников ,имеющих различную температуру спаев. 3) индукционные ,электромагнитная индукция. 4)фотоэлектрические ,фотоэффект. 1)емкостные, емкость. 2) реостатные ,омическое сопротивление. 3)индуктивные, индуктивность или взаимная индуктивность. В зависимости от вида энергии , являющейся носителем информации , различают механические, акустические(звуковые) , температурные, электрические, оптические и другие датчики. Билет 25 Требования, предъявляемые к мед. Аппаратуре. Понятие электробезопасности и надежности мед аппаратуры Основные требования -не касайтесь приборов одновреенно двумя обнаженными руками, частями тела; Электробезопасность медицинской аппаратуры Основное и главное требование — сделать недоступным касание частей аппаратуры, находящихся под напряжением. Для этого прежде всего изолируют части приборов и аппаратов, находящиеся под напряжением, друг от друга и от корпуса аппаратуры. Изоляция, выполняющая такую роль, называется основной или рабочей. Отверстия в корпусе должны исключать возможность случайного проникновения и касания внутренних частей аппаратуры пальцами, металлическими цепочками украшений и т. п. Однако даже если части аппаратуры, находящиеся под напряжением, и закрыты от прикосновения, это еще не обеспечивает полной безопасности по крайней мере по двум причинам. Во-первых, какой бы ни была изоляция между внутренними частями аппаратуры и ее корпусом, сопротивление приборов и аппаратов переменному току не бесконечно. Не бесконечно и сопротивление между проводами электросетии землей. Во-вторых, не исключено, что благодаря порче рабочей изоляции (старение, влажность окружающего воздуха) возникает электрическое замыкание внутренних частей аппаратуры с корпусом — «пробой на корпус», и внешняя, доступная для касания часть аппаратуры (корпус) окажется под напряжением. Чтобы избежать неприятных последствий, следует пользоваться общими правилами: не касайтесь приборов одновременно двумя обнаженными руками, частями тела; не работайте на влажном, сыром полу, на земле; не касайтесь труб (газ, вода, отопление), металлических конструкций при работе с электроаппаратурой; не касайтесь одновременно металлических частей двух аппаратов (приборов). ⇐ Предыдущая12345678Следующая ⇒ |
Активное сопротивление, индуктивность и емкость в цепи переменного тока.
 Реактивное сопротивление конденсатора
Реактивное сопротивление конденсатораТок в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
где Xc — реактивное сопротивление конденсатора, f — частота, C — емкость.
Для расчета реактивного сопротивления конденсатора заполните предложенную форму:
Расчет ёмкости для реактивного сопротивления:
- Похожие статьи
- — Бестрансформаторные источники питания с гасящим конденсатором удобны своей простотой, имеют малые габариты и массу, но не всегда применимы из-за гальванической связи выходной цепи с сетью 220 В.
 В бестрансформаторном источнике питания к сети переменного напряжения подключены последовательно…
В бестрансформаторном источнике питания к сети переменного напряжения подключены последовательно… - — Принципиальная электрическая схема цифрового широкодиапазонного измерителя емкости показана на рисунке. Принцип работы прибора – измерение длительности импульса автогенератора, в состав времязадающей цепи которого входит измеряемый конденсатор. Далее, формируется пачка импульсов образцовой частоты…
- — Данная статья посвящена простому блоку со стабилизатором типа КРЕН. КРЕН это 3-х или 4-х выводные микросхемы, для примера взята 3-х выводная микросхема. Для стабилизированного напряжения (положительного) можно взять микросхему КРЕН5А, на +5В. Силовая часть (см. рис.1) примерно одинакова для…
- — Габариты и масса высоковольтных трансформаторов из-за необходимости обеспечения электрической прочности становятся очень большими. Поэтому удобнее использовать в высоковольтных маломощных источниках питания умножители напряжения. Умножители напряжения создаются на базе схем выпрямления с емкостной.
 ..
.. - — Приемник может быть перестроен в диапазоне 70…150 МГц без изменения номиналов подстроечных элементов. Реальная чувствительность приемника около 0,3 мкВ, напряжение питания 9 В. Следует заметить, что напряжение питания МС3362 — 2…7 В, а МС34119 2…12 В, поэтому МС3362 питается через…
Положим теперь, что участок цепи содержит конденсатор емкости C , причем сопротивлением и индуктивностью участка можно пренебречь, и посмотрим, по какому закону будет изменяться напряжение на концах участка в этом случае. Обозначим напряжение между точками а и b через u и будем считать заряд конденсатора q и силу тока i положительными, если они соответствуют рис.4. Тогда
и, следовательно,
Если сила тока в цепи изменяется по закону
то заряд конденсатора равен
.
Постоянная интегрирования q 0 здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим . Следовательно,
Следовательно,
. (2)
Сравнивая (1) и (2), мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону косинуса. Однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2. Изменения тока и напряжения во времени изображены графически на рис.5. Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой-либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому и колебания напряжения запаздывают относительно колебаний тока.
Формула (2) показывает, что амплитуда напряжения на конденсаторе равна
Сравнивая это выражение с законом Ома для участка цепи с постоянным током (), мы видим, что величина
играет роль сопротивления участка цепи, она получила название емкостного сопротивления. Емкостное сопротивление зависит от частоты w, и при высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.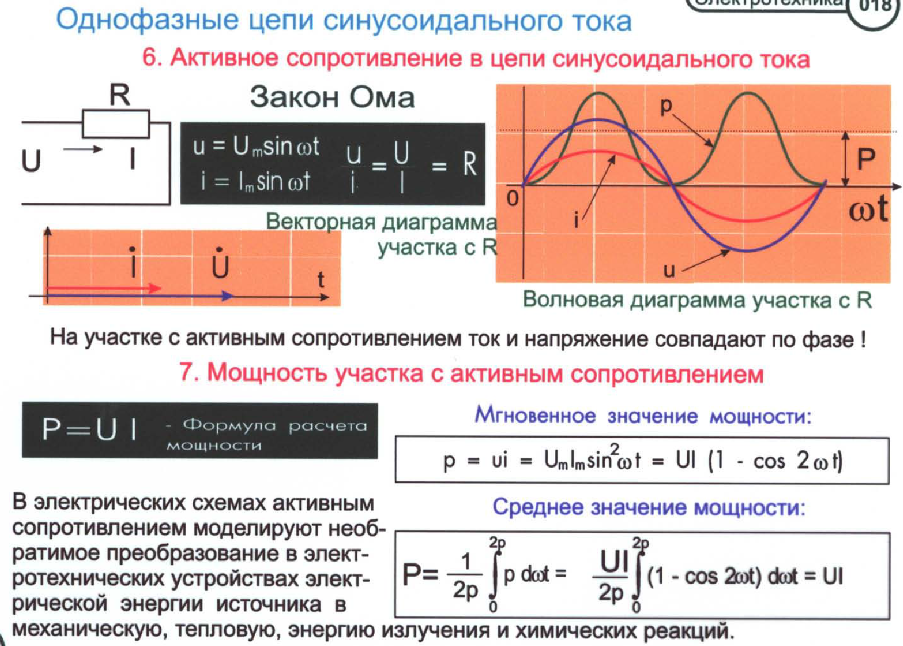 Важно отметить, что емкостное сопротивление определяет связь между амплитудными, а не мгновенными значениями тока и напряжения.
Важно отметить, что емкостное сопротивление определяет связь между амплитудными, а не мгновенными значениями тока и напряжения.
Мгновенная мощность переменного тока
меняется со временем по синусоидальному закону с удвоенной частотой. В течение времени от 0 до T /4 мощность положительна, а в следующую четверть периода ток и напряжение имеют противоположные знаки и мощность становится отрицательной. Поскольку среднее значение за период колебаний величины равно нулю, то средняя мощность переменного тока на конденсаторе .
Конденсаторы, как и резисторы, относятся к наиболее многочисленным элементам радиотехнических устройств. Основное свойство конденсаторов, это способность накапливать электрический заряд . Основной параметр конденсатора это его емкость .
Емкость
конденсатора будет тем значительнее,
чем больше площадь его обкладок и чем
тоньше слой диэлектрика между ними.
Основной единицей электрической емкости
является фарада (сокращенно Ф), названная
так в честь английского физика М. Фарадея. Однако
1 Ф — это очень большая емкость. Земной
шар, например, обладает емкостью меньше
1 Ф. В электро- и радиотехнике пользуются
единицей емкости, равной миллионной
доле фарады, которую называют микрофарадой
(сокращенно мкФ) .
Фарадея. Однако
1 Ф — это очень большая емкость. Земной
шар, например, обладает емкостью меньше
1 Ф. В электро- и радиотехнике пользуются
единицей емкости, равной миллионной
доле фарады, которую называют микрофарадой
(сокращенно мкФ) .
Емкостное сопротивление конденсатора переменному току зависит от его емкости и частоты тока: чем больше емкость конденсатора и частота тока, тем меньше его емкостное сопротивление.
Керамические конденсаторы обладают сравнительно небольшими емкостями — до нескольких тысяч пикофарад. Их ставят в те цепи, в которых течет ток высокой частоты (цепь антенны, колебательный контур), для связи между ними.
Простейший
конденсатор представляет собой два
проводника электрического тока, например:
— две металлические пластины, называемые
обкладками конденсатора, разделенные
диэлектриком, например: — воздухом или
бумагой. Чем больше площадь обкладок
конденсатора и чем ближе они расположены
друг к другу, тем больше электрическая
емкость этого прибора.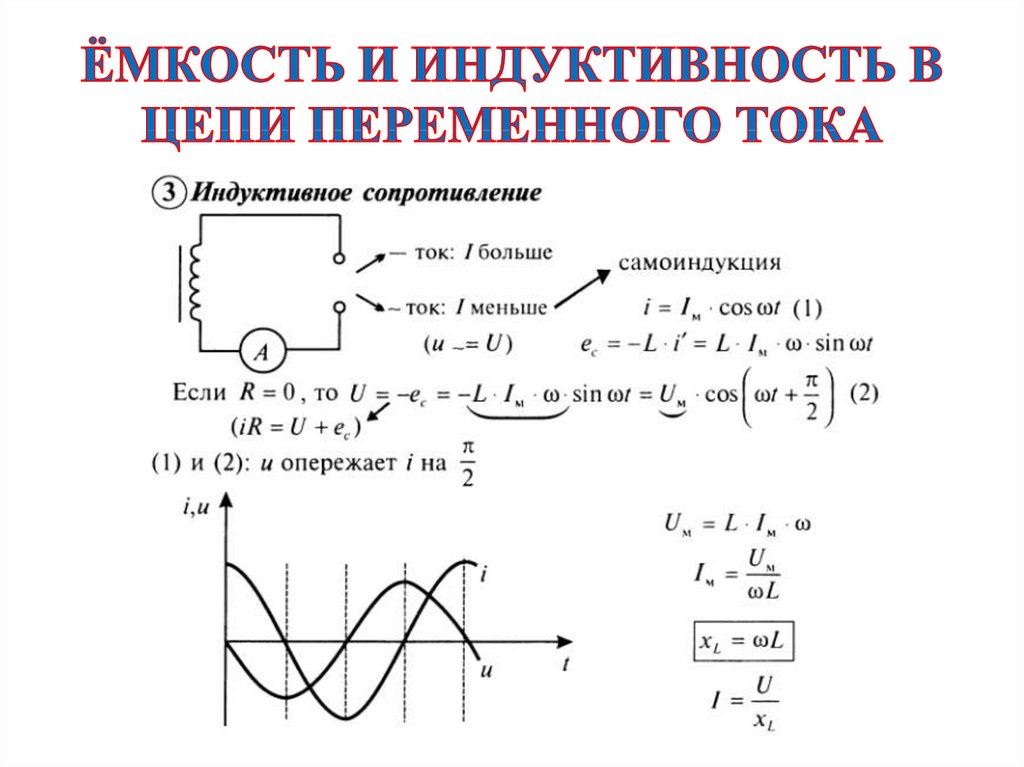 Если к обкладкам
конденсатора подключить источник
постоянного тока, то в образовавшейся
цепи возникнет кратковременный ток и
конденсатор зарядится до напряжения,
равного напряжению источника тока. Вы
можете спросить: почему в цепи, где есть
диэлектрик, возникает ток? Когда мы
присоединяем к конденсатору источник
тока, электроны в проводниках образовавшейся
цепи начинают двигаться в сторону
положительного полюса источника тока,
образуя кратковременный поток электронов
во всей цепи. В результате обкладка
конденсатора, которая соединена с
положительным полюсом источника тока,
обедняется свободными электронами и
заряжается положительно, а другая
обкладка обогащается свободными
электронами и, следовательно, заряжается
отрицательно. Как только конденсатор
зарядится, кратковременный ток в цепи,
называемый током зарядки конденсатора,
прекратится.
Если к обкладкам
конденсатора подключить источник
постоянного тока, то в образовавшейся
цепи возникнет кратковременный ток и
конденсатор зарядится до напряжения,
равного напряжению источника тока. Вы
можете спросить: почему в цепи, где есть
диэлектрик, возникает ток? Когда мы
присоединяем к конденсатору источник
тока, электроны в проводниках образовавшейся
цепи начинают двигаться в сторону
положительного полюса источника тока,
образуя кратковременный поток электронов
во всей цепи. В результате обкладка
конденсатора, которая соединена с
положительным полюсом источника тока,
обедняется свободными электронами и
заряжается положительно, а другая
обкладка обогащается свободными
электронами и, следовательно, заряжается
отрицательно. Как только конденсатор
зарядится, кратковременный ток в цепи,
называемый током зарядки конденсатора,
прекратится.
Если
источник тока отключить от конденсатора,
то конденсатор окажется заряженным.
Переходу избыточных электронов с одной
обкладки на другую препятствует
диэлектрик. Между обкладками конденсатора
тока не будет, а накопленная им
электрическая энергия будет сосредоточена
в электрическом поле диэлектрика. Но
стоит обкладки заряженного конденсатора
соединить каким-либо проводником
«лишние» электроны отрицательно
заряженной обкладки перейдут по этому
проводнику на другую обкладку, где их
недостает, и конденсатор разрядится. В
этом случае в образовавшейся цепи также
возникает кратковременный ток, называемый
током разрядки конденсатора. Если
емкость конденсатора большая, и он
заряжен до значительного напряжения,
момент его разрядки сопровождается
появлением значительной искры и треска.
Свойство конденсатора накапливать
электрические заряды и разряжаться
через подключенные к нему проводники
используется в колебательном контуре
радиоприемника.
Между обкладками конденсатора
тока не будет, а накопленная им
электрическая энергия будет сосредоточена
в электрическом поле диэлектрика. Но
стоит обкладки заряженного конденсатора
соединить каким-либо проводником
«лишние» электроны отрицательно
заряженной обкладки перейдут по этому
проводнику на другую обкладку, где их
недостает, и конденсатор разрядится. В
этом случае в образовавшейся цепи также
возникает кратковременный ток, называемый
током разрядки конденсатора. Если
емкость конденсатора большая, и он
заряжен до значительного напряжения,
момент его разрядки сопровождается
появлением значительной искры и треска.
Свойство конденсатора накапливать
электрические заряды и разряжаться
через подключенные к нему проводники
используется в колебательном контуре
радиоприемника.
Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник
с определённым значением ёмкости
и малой проводимостью;
устройство для накопления заряда
и энергии электрического поля. Конденсатор
является пассивным электронным
компонентом.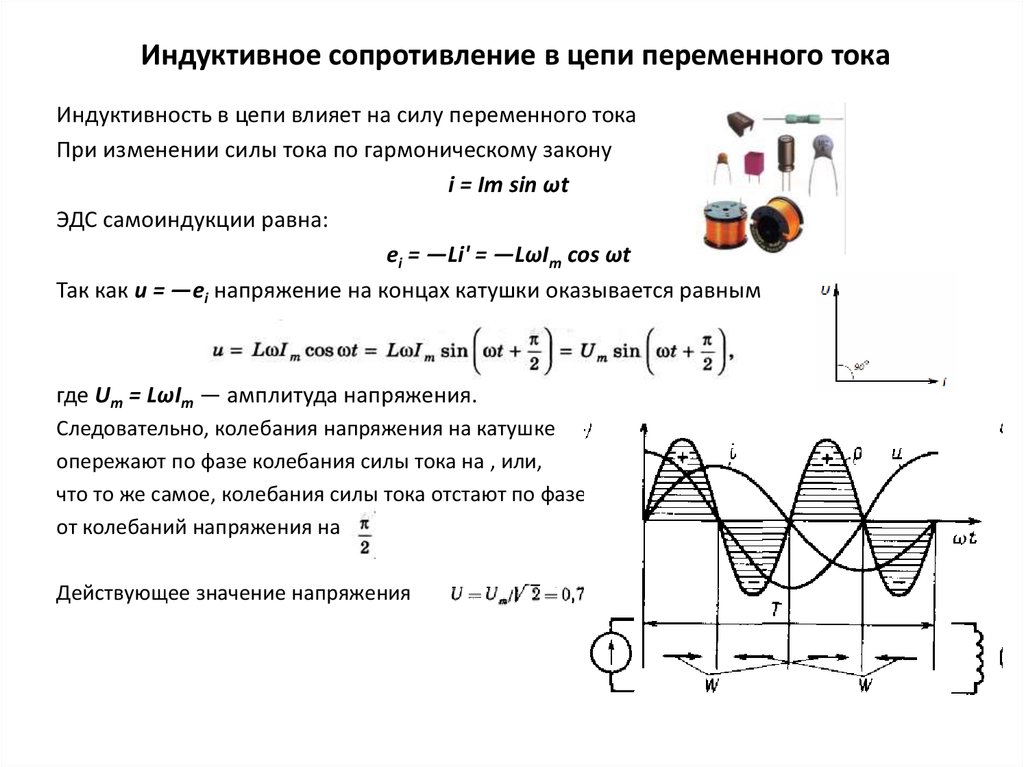 В простейшем варианте
конструкция состоит из двух электродов
в форме пластин (называемых обкладками ),
разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок (см. рис.). Практически
применяемые конденсаторы имеют много
слоёв диэлектрика и многослойные
электроды, или ленты чередующихся
диэлектрика и электродов, свёрнутые в
цилиндр или параллелепипед со скруглёнными
четырьмя рёбрами (из-за намотки).
Конденсатор
в цепи постоянного
тока
может проводить ток в момент включения
его в цепь (происходит заряд или перезаряд
конденсатора), по окончании переходного
процесса
ток через конденсатор не течёт, так как
его обкладки разделены диэлектриком.
В цепи же переменного
тока
он проводит колебания переменного тока
посредством циклической перезарядки
конденсатора, замыкаясь так называемым
током
смещения.
В простейшем варианте
конструкция состоит из двух электродов
в форме пластин (называемых обкладками ),
разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок (см. рис.). Практически
применяемые конденсаторы имеют много
слоёв диэлектрика и многослойные
электроды, или ленты чередующихся
диэлектрика и электродов, свёрнутые в
цилиндр или параллелепипед со скруглёнными
четырьмя рёбрами (из-за намотки).
Конденсатор
в цепи постоянного
тока
может проводить ток в момент включения
его в цепь (происходит заряд или перезаряд
конденсатора), по окончании переходного
процесса
ток через конденсатор не течёт, так как
его обкладки разделены диэлектриком.
В цепи же переменного
тока
он проводит колебания переменного тока
посредством циклической перезарядки
конденсатора, замыкаясь так называемым
током
смещения.
С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
,
Где j —
мнимая
единица, ω —
циклическая
частота
(рад/с )
протекающего синусоидального
тока, f —
частота в Гц , C —
ёмкость конденсатора (фарад ). Отсюда также следует, что реактивное
сопротивление
конденсатора равно:
.
Для постоянного тока частота равна
нулю, следовательно, реактивное
сопротивление конденсатора бесконечно
(в идеальном случае).
Отсюда также следует, что реактивное
сопротивление
конденсатора равно:
.
Для постоянного тока частота равна
нулю, следовательно, реактивное
сопротивление конденсатора бесконечно
(в идеальном случае).
Резонансная частота конденсатора равна
При f > f p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f p , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2-3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где U — напряжение (разность потенциалов), до которого заряжен конденсатор.
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальная фаза напряжения будет иметь некоторое значение φ. При таком условии мгновенные значения силы тока и напряжения и будут выражаться следующими формулами:
При таком условии мгновенные значения силы тока и напряжения и будут выражаться следующими формулами:
i = I m sinωt
u = U m sin(ωt + φ)
a) Активное сопротивление в цепи переменного тока. Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным . Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току.
В цепи переменного тока, имеющей только активное сопротивление, например, в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: и = U т cos ωt.
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:
Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:
по фазе с колебаниями напряжения.
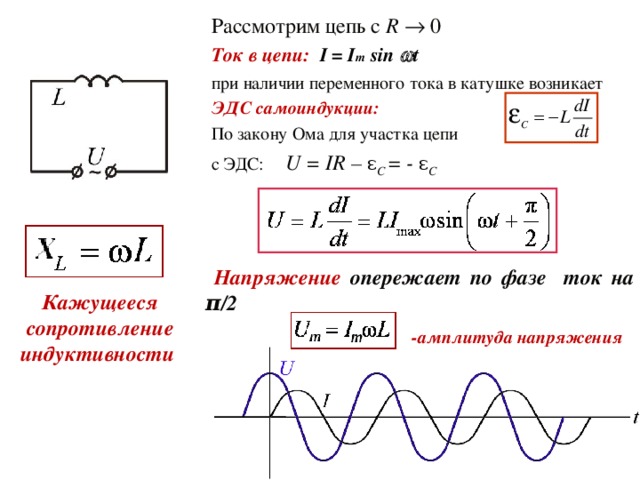
b) Катушка индуктивности в цепи переменного тока. Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X L , которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω: X L = ωL.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь. Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней. Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля Е к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства E i = -Е к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции e i) равна по модулю и противоположна по знаку удельной работе кулоновского поля . Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: e i = -и.
При изменении силы тока по гармоническому закону i = I m sin соsωt, ЭДС самоиндукции равна: е i = -Li» = -LωI m cos ωt. Так как e i = -и, то напряжение на концах катушки оказывается равным
Так как e i = -и, то напряжение на концах катушки оказывается равным
и = LωI m cos ωt = LωI m sin (ωt + π/2) = U m sin (ωt + π/2)
гдеU m = LωI m — амплитуда напряжения.
Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.
Если ввести обозначение X L = ωL, то получим . Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Согласно формуле , значение силы тока связано с значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю. Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .
Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .
c) Конденсатор в цепи переменного тока. Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.
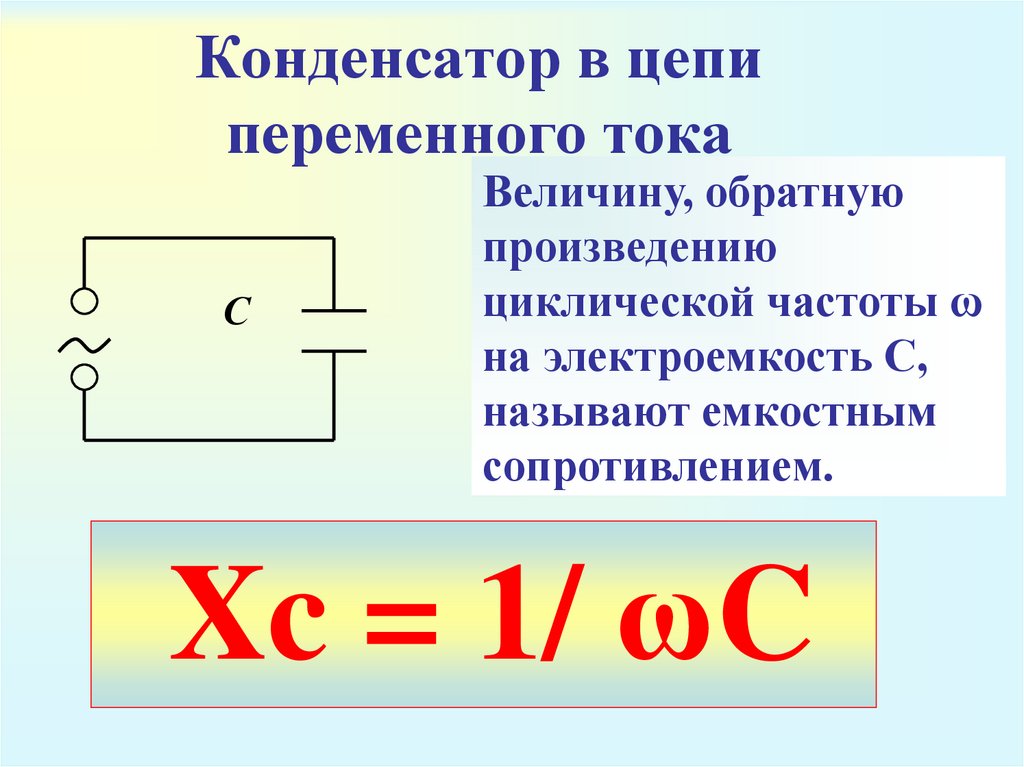
Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Х с . Оно обратно пропорционально емкости С и круговой частоте ω: Х с =1/ωС.
Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь.
Напряжение на конденсаторе u = q/C равно напряжению на концах цепи u = U m cosωt.
Следовательно, q/C = U m cosωt. Заряд конденсатора меняется по гармоническому закону:
q = CU m cosωt.
Сила тока, представляющая собой производную заряда по времени, равна:
i = q» = -U m Cω sin ωt =U m ωC cos(ωt + π/2).
Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2.
Величину Х с , обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. Значение силы тока связано с значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Х с как сопротивление конденсатора переменному току (емкостное сопротивление).
Чем больше емкость конденсатора, тем больше ток перезарядки.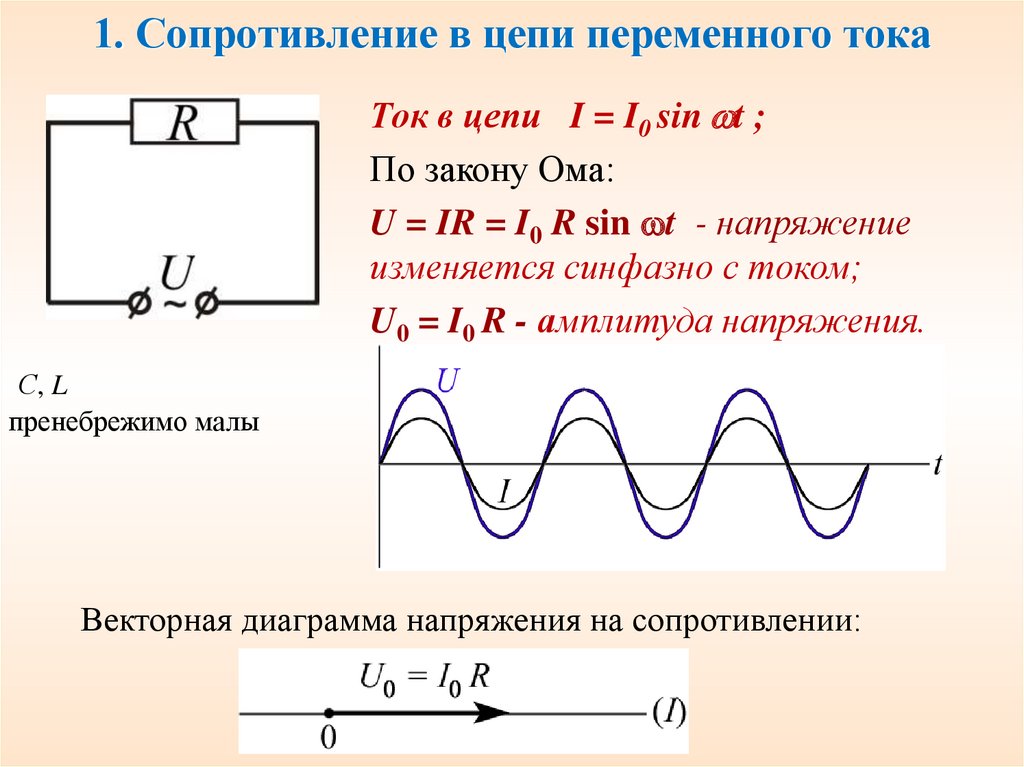 Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.
В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Из сравнения формул X L = ωL и Х с =1/ωС видно, что катушки индуктивности. представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Индуктивное Х L и емкостное Х C сопротивления называют реактивными.
d) Закон ома для электрической цепи переменного тока.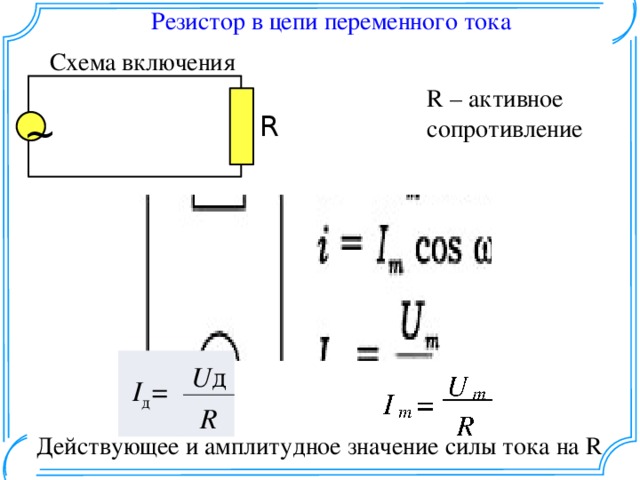
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С
Мы видели, что при включении по отдельности в цепь активного сопротивления R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами:
; ; I m = U m ωC .
Амплитуды же напряжений на активном сопротивлении, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так: U m = I m R; U m = I m ωL;
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах. Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлениями. Однако только на активном сопротивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний тока на π/2, а на катушке индуктивности колебания напряжения опережают колебания тока на π/2. Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что
Для получения этого равенства нужно уметь складывать колебания напряжений, сдвинутые по фазе друг относительно друга. Проще всего выполнить сложение нескольких гармонических колебаний с помощью векторных диаграмм. Идея метода основана на двух довольно простых положениях.
Во-первых, проекция вектора с модулем х m вращающегося с постоянной угловой скоростью совершает гармонические колебания: х = х m cosωt
Во-вторых, при сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.
Векторная диаграмма электрических колебаний в цепи, изображенной на рисунке, позволит нам получить соотношение между амплитудой силы тока в этой цепи и амплитудой напряжения. Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока I m . Этот вектор изобразим в виде горизонтальной стрелки. Напряжение на активном сопротивлении совпадает по фазе с силой тока. Поэтому вектор U mR , должен совпадать по направлению с вектором I m . Его модуль равен U mR = I m R
Колебания напряжения на индуктивном сопротивлении опережают колебания силы тока на π/2, и соответствующий вектор U m L должен быть повернут относительно вектора I m на π/2. Его модуль равен U m L = I m ωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор U m L следует повернуть налево. (Можно было бы, конечно, поступить и наоборот.)
Его модуль равен U mC =I m /ωC .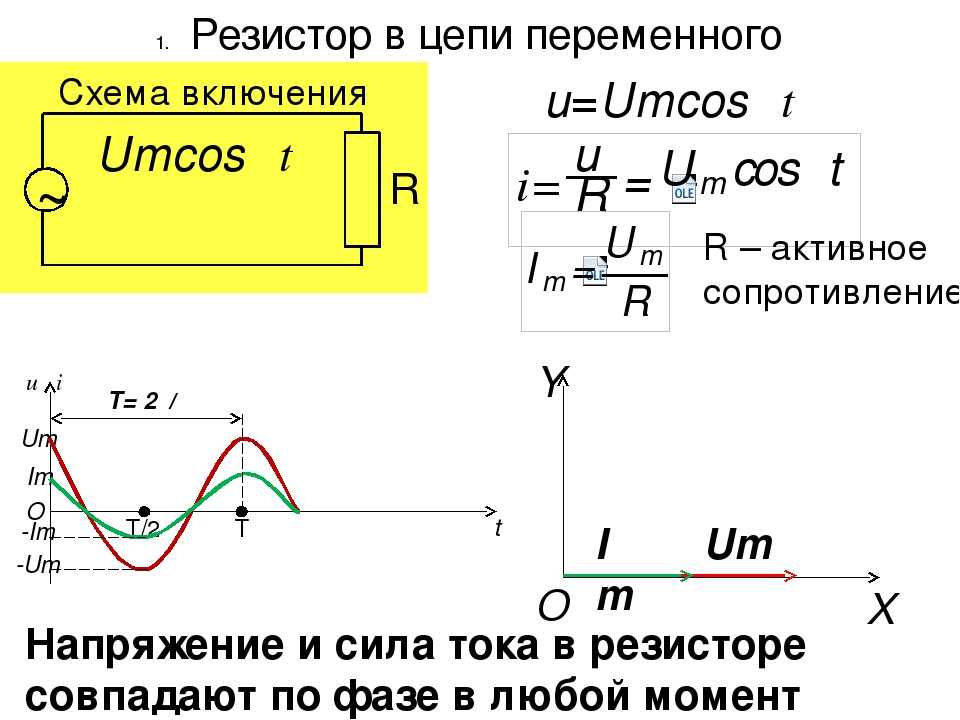 Для нахождения вектора суммарного напряжения U m нужно сложить три вектора: 1) U mR 2) U m L 3) U mC
Для нахождения вектора суммарного напряжения U m нужно сложить три вектора: 1) U mR 2) U m L 3) U mC
Вначале удобнее сложить два вектора: U m L и U mC
Модуль этой суммы равен , если ωL > 1/ωС. Именно такой случай изображен на рисунке. После этого, сложив вектор (U m L + U mC) с вектором U mR получим вектор U m , изображающий колебания напряжения в сети. По теореме Пифагора:
Из последнего равенства можно легко найти амплитуду силы тока в цепи:
Таким образом, благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи, изображенной на рисунке, выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин:
Это и есть закон Ома для переменного тока в цепи, изображенной на рисунке 43. Мгновенное значение силы тока меняется со временем гармонически:
i = I m cos (ωt+ φ), где φ — разность фаз между силой тока и напряжением в сети. Она зависит от частоты ω и параметров цепи R, L, С.
Она зависит от частоты ω и параметров цепи R, L, С.
e) Резонанс в электрической цепи. При изучении вынужденных механических колебаний мы познакомились с важным явлением — резонансом. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вынужденных колебаний. Совпадение законов механических и электромагнитных колебаний сразу же позволяет сделать заключение о возможности резонанса в электрической цепи, если эта цепь представляет, собой колебательный контур, обладающий определенной собственной частотой колебаний.
Амплитуда тока при вынужденных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой:
При фиксированном напряжении и заданных значениях R, L и С, сила тока достигает максимума при частоте ω, удовлетворяющей соотношению
Эта амплитуда особенно велика при малом R.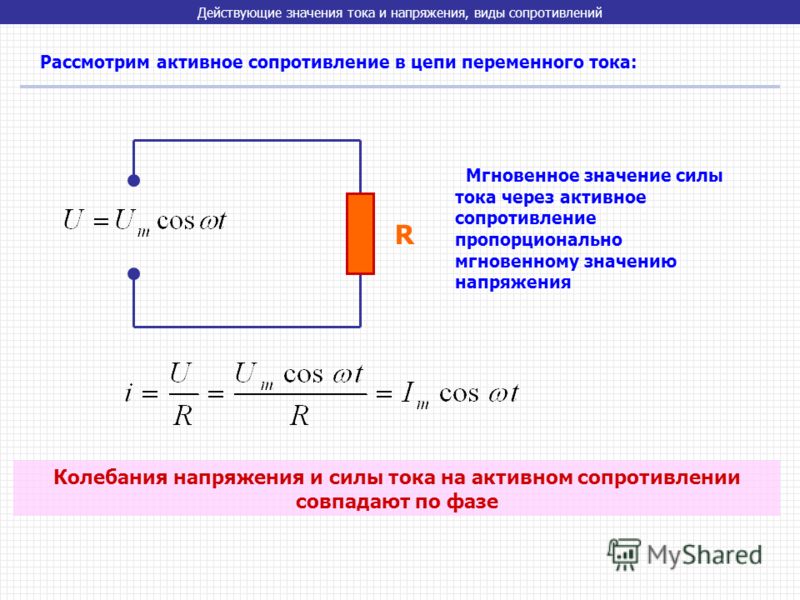 Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:
Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:
Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением.
Резкое возрастание амплитуды вынужденных колебаний тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. В этом состоит явление резонанса в электрическом колебательном контуре.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз превосходят внешнее напряжение.
Действительно,
U м, С,рез =
U м, L ,рез =
Внешнее напряжение связано с резонансным током так:
U м = . Если тоU m , C ,рез = U m , L ,рез >> U m
При резонансе сдвиг фаз между током и напряжением становится равным нулю.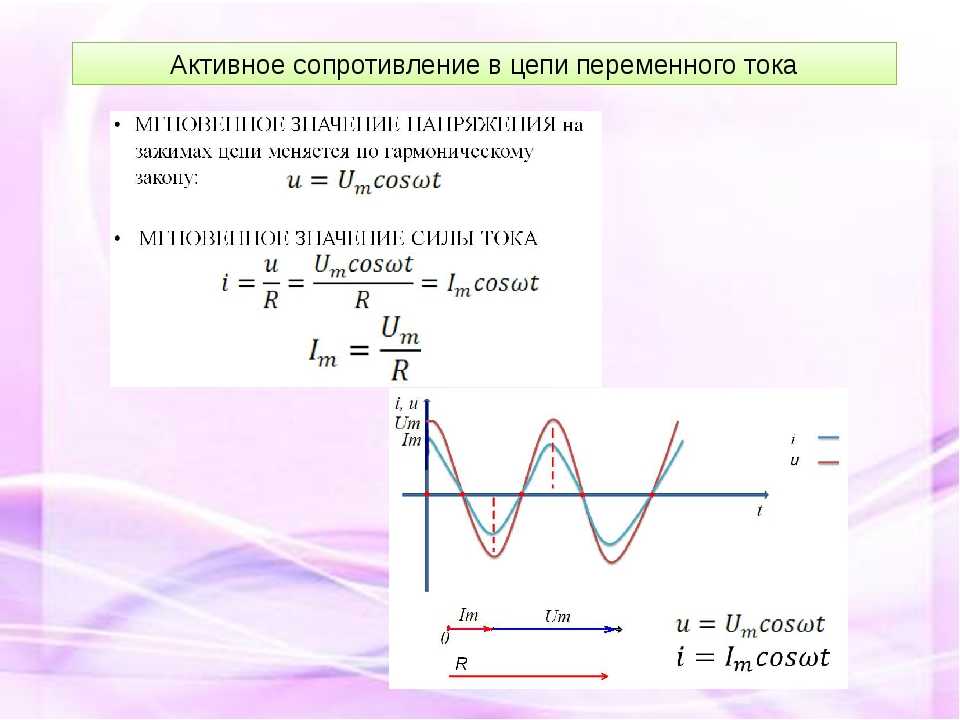
Действительно, колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга, и падение напряжения происходит только на активном сопротивлении.
Равенство нулю сдвига фаз между напряжением и током при резонансе обеспечивает оптимальные условия для поступления энергии от источника переменного напряжения в цепь. Здесь полная аналогия с механическими колебаниями: при резонансе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
Что такое резисторы в цепях переменного и постоянного тока
Закон Ома (V = IR) по-прежнему применяется в цепи с резистором и источником питания переменного тока. Прохождение электрического заряда только в одном направлении известно как постоянный ток (DC). Это устойчивое состояние цепи постоянного напряжения. С другой стороны, большинство известных приложений полагаются на переменный во времени источник напряжения. Поток электрического заряда, который иногда меняет направление, известен как переменный ток (AC). Цепь известна как цепь переменного тока, если источник часто меняется, особенно синусоидально. Коммерческая и жилая электроэнергия, например, отвечает широкому спектру наших требований. предоставляет графики зависимости напряжения и тока от времени для обычных источников питания постоянного и переменного тока. Напряжение и частота переменного тока, которые обычно используются в домах и на предприятиях, различаются в разных странах.
Поток электрического заряда, который иногда меняет направление, известен как переменный ток (AC). Цепь известна как цепь переменного тока, если источник часто меняется, особенно синусоидально. Коммерческая и жилая электроэнергия, например, отвечает широкому спектру наших требований. предоставляет графики зависимости напряжения и тока от времени для обычных источников питания постоянного и переменного тока. Напряжение и частота переменного тока, которые обычно используются в домах и на предприятиях, различаются в разных странах.
В этой статье вы узнаете о резисторах в цепях переменного и постоянного тока, их формуле, расходных материалах, схемах, расчетах и примерах. Вы также узнаете сопротивление между переменным и постоянным током.
Read more: Understanding combination resistors in series and parallel
Contents
- 1 AC and DC circuit resistors
- 1.0.0.1 Diagram of AC and DC resistor circuit:
- 2 Разница между сопротивлением переменного тока и постоянного тока
- 2.
 1 Сопротивление переменного тока
1 Сопротивление переменного тока- 2.1.1 Измерение сопротивления переменного тока
- 2.2 Присоединяйтесь к нашему информационному бюллетене
- 2.3 Сопротивление DC
- 2.3.1. сопротивление, какое из них больше:
- 2.
- 2.4 Формула скин-эффекта:
- 9.1 Пример 4.10018
- 4.2 Пример 2
- 4.2.0.1 Посмотрите видео ниже, чтобы узнать больше о резисторах в цепях переменного и постоянного тока:
Резисторы цепи переменного и постоянного тока
Поток электричества является однонаправленным при постоянном токе (DC). Полярность и направление напряжения и тока в постоянном токе всегда одинаковы. Аккумулятор используется для получения постоянного тока. С другой стороны, в переменном токе (AC) поток электрического заряда иногда меняет направление.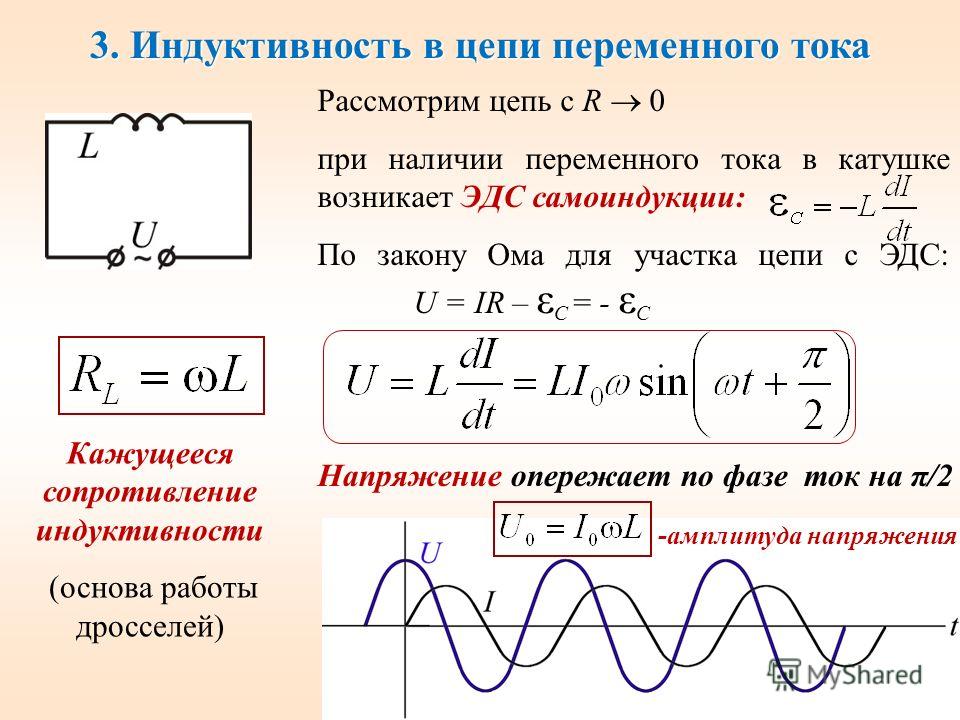 Со временем полярность напряжения переменного тока меняется с положительной на отрицательную. Из-за изменения направления тока сместилась полярность напряжения.
Со временем полярность напряжения переменного тока меняется с положительной на отрицательную. Из-за изменения направления тока сместилась полярность напряжения.
Переменный ток — это тип электричества, который используется для питания домов, предприятий и других учреждений. Хотя синусоидальная волна является наиболее распространенным типом источника переменного тока, в некоторых приложениях также используются другие формы волны, такие как треугольная волна, прямоугольная волна и пилообразная волна.
Сопротивление — это качество вещества или материала, препятствующее прохождению через него электричества. ИЛИ, сопротивление — это способность цепи или элемента (называемого резистором) сопротивляться протеканию через него тока. Дерево, воздух, слюда, стекло, резина, вольфрам и другие материалы являются примерами высокоомных резисторов. Единицей сопротивления является «Ом», который определяется как Ω и обозначается буквой «R».
Подробнее: Что такое резисторы
Схема цепи резисторов переменного и постоянного тока:
Разница между сопротивлением постоянному и постоянному току
Сопротивление переменному току
Импеданс — это термин, используемый для описания сопротивления в цепях переменного тока. Полное сопротивление в цепях переменного тока представляет собой общее сопротивление (сопротивление, индуктивное сопротивление и емкостное сопротивление) (Z). Когда переменный ток протекает через провод (резистор, катушку индуктивности или конденсатор), он создает магнитное поле на этом проводе, которое сопротивляется потоку переменного тока, а также сопротивлению этого провода. Эта противоположная причина называется индуктивностью. Свойство катушки (или провода), препятствующее любому увеличению или уменьшению тока или потока через нее, называется индуктивностью. Мы также знаем, что индуктивность существует только при переменном токе, поскольку величина тока постоянно меняется.
Полное сопротивление в цепях переменного тока представляет собой общее сопротивление (сопротивление, индуктивное сопротивление и емкостное сопротивление) (Z). Когда переменный ток протекает через провод (резистор, катушку индуктивности или конденсатор), он создает магнитное поле на этом проводе, которое сопротивляется потоку переменного тока, а также сопротивлению этого провода. Эта противоположная причина называется индуктивностью. Свойство катушки (или провода), препятствующее любому увеличению или уменьшению тока или потока через нее, называется индуктивностью. Мы также знаем, что индуктивность существует только при переменном токе, поскольку величина тока постоянно меняется.
Свойство катушки провода в цепи переменного тока, которое противодействует изменению тока, известно как индуктивное реактивное сопротивление X L . Индуктивное реактивное сопротивление имеет ту же единицу измерения, что и емкостное реактивное сопротивление, а именно Ом (Ом), хотя соответствующий символ для емкостного реактивного сопротивления — X L .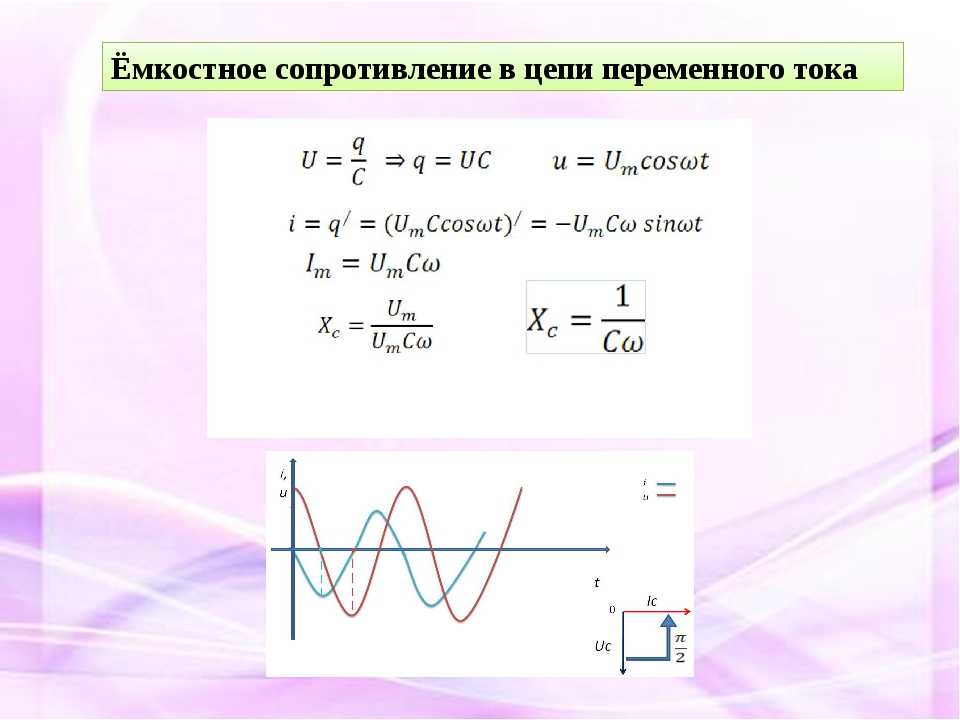
В емкостной цепи емкостное реактивное сопротивление является сопротивлением току, протекающему исключительно в цепях переменного тока. Единица измерения емкостного сопротивления такая же, как у сопротивления и индуктивного сопротивления, а именно Ом (Ом), однако соответствующий символ X С .
Измерение сопротивления переменному токуФормулы электрического сопротивления и импеданса в цепях переменного тока
В цепях переменного тока (емкостная или индуктивная нагрузка), сопротивление = полное сопротивление, т. е. R = Z L 2 ) … В случае индуктивной нагрузки
Z = √ (R 2 + X C 2 ) … В случае емкостной нагрузки
901 + 4 X 4 Л – Х C ) 2 …В случае как индуктивных, так и емкостных нагрузок.Где;
X L = индуктивное сопротивление
X L = 2π f L… Где L = индуктивность в Генри
А;
X C = емкостное реактивное сопротивление
X C = 1/2π f C… Где C = емкость в фарадах.
Присоединяйтесь к нашему информационному бюллетеню
Кроме того, в цепях переменного тока синусоидальная волна является наиболее часто используемым типом питания переменного тока. Типичное напряжение переменного тока описывается математической функцией.
В (t) = VMax sin ωt. Где:
В (t) – напряжение в функции времени. Напряжение меняется со временем.
t — переменное время в секундах.
VMax — это максимальное значение, которое может достигать синусоида как в положительном, так и в отрицательном направлении. Для положительного цикла это VMax, а для отрицательного цикла это -VMax.
ω – угловая частота. ω = 2πf.
f — частота синусоиды.
Подробнее: Понимание термистора
Сопротивление постоянному току
В цепях постоянного тока нет понятия индуктивного и емкостного сопротивления. Поскольку цепи постоянного тока не имеют частоты, а амплитуда постоянного тока постоянна, емкостное и индуктивное сопротивление в цепях постоянного тока равны нулю.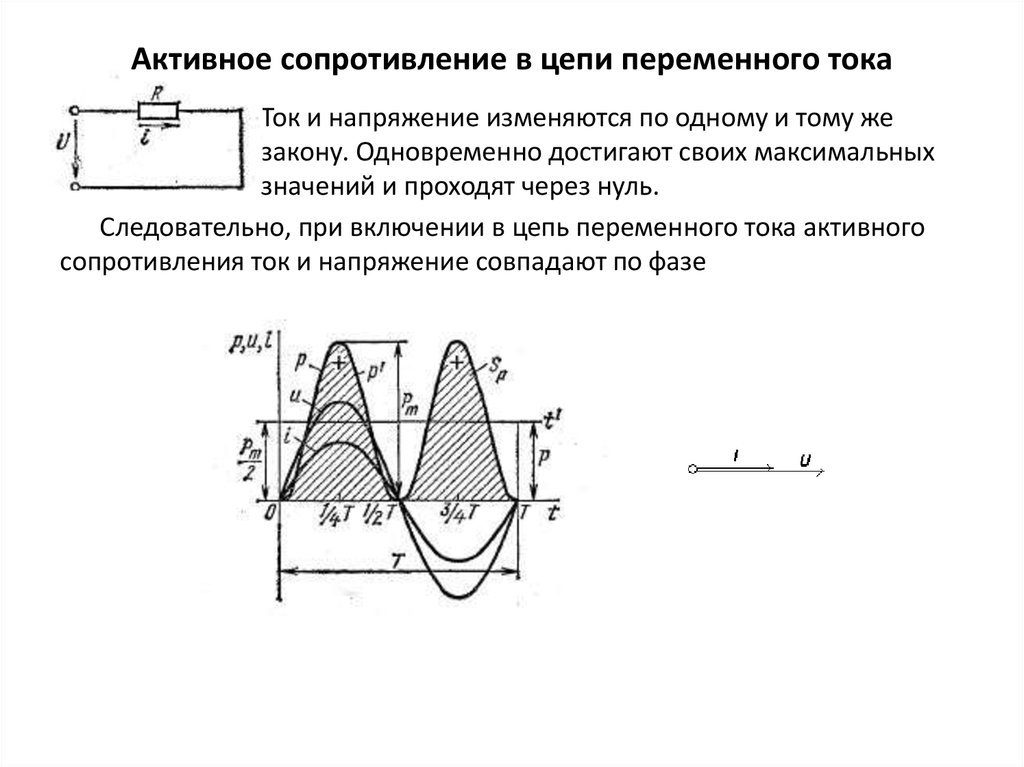 В результате используется только исходное сопротивление провода. В результате сопротивление провода для постоянного тока ниже, чем для переменного, поэтому линии переменного тока требуют большей изоляции, чем линии постоянного тока.
В результате используется только исходное сопротивление провода. В результате сопротивление провода для постоянного тока ниже, чем для переменного, поэтому линии переменного тока требуют большей изоляции, чем линии постоянного тока.
Формулы электрического сопротивления. В цепях постоянного тока мы рассчитываем сопротивление по закону Ома.
Р = В/И.
Если вы пытаетесь выяснить, какое сопротивление использовать в электрической цепи, и не уверены, использовать ли переменный или постоянный ток, выберите переменный, если ток переменный, и постоянный, если ток постоянный.
Для цепей постоянного тока определение тока, напряжения и мощности в цепях постоянного тока выполняется по закону Ома. В этом примере полярность напряжения и тока считается постоянной. Значения индуктивности и емкости в чисто резистивных цепях переменного тока незначительны. В результате ток, напряжение и мощность будут рассчитываться с использованием того же закона Ома и правил схемы Кирхгофа. Различие заключается в использовании среднеквадратичного значения или мгновенного значения размаха.
Различие заключается в использовании среднеквадратичного значения или мгновенного значения размаха.
Подробнее: Значение проволочного резистора
Сопротивление переменному или постоянному току, какое из них больше:
Как уже говорилось ранее, частота источника постоянного тока равна нулю, поэтому нет скин-эффекта (поведение переменного тока при протекании через поверхность, т. е. внешний слой проводника вместо сердечника провода). при использовании в цепях постоянного тока сопротивление переменному току в цепях переменного тока выше, чем подача постоянного тока в цепях постоянного тока из-за скин-эффекта.
Формула эффекта кожи:δ = √(2ρ/ωµ)
Где;
δ = глубина скин-эффекта
ρ = удельное сопротивление
ω = 2π f = угловая частота
µ = проницаемость проводника
Таким образом, частота и скин-эффект напрямую связаны, т. е. если частота увеличивается. , скин-эффект также увеличивается, тогда как в постоянном токе нет ни частоты, ни скин-эффекта.
Как правило; Сопротивление переменному току = 1,6 x сопротивление постоянному току.
Подробнее: Знакомство с металлооксидными пленочными резисторами
Резистор с питанием постоянного и переменного тока
Пассивное устройство представляет собой резистор. Он не использует и не генерирует энергию. Здесь используется электрическая энергия. Однако резистор тратит электрическую энергию в виде тепла. Ниже расположен резистор с источником питания постоянного тока.
Сопротивление, представляющее собой отношение напряжения к току в резистивных цепях постоянного тока, является линейным.
Ниже расположен резистор с источником питания переменного тока.
Отношение напряжения к току в цепях переменного тока в основном определяется частотой питания f и фазовым углом или разностью фаз. В результате термин «импеданс» используется для описания сопротивления в цепях переменного тока, поскольку оно имеет как амплитуду, так и фазу, тогда как сопротивление в цепях постоянного тока имеет только величину. Импеданс обозначается буквой Z.
Импеданс обозначается буквой Z.
Подробнее: Цветовые коды резисторов
Примеры резисторов в цепях переменного тока
Пример 1Используя следующую схему.
Резистивный нагревательный элемент подключен к источнику питания 240 В переменного тока. Нагревательный элемент потребляет 1,2 КВт мощности. Сопротивление нагревательного элемента можно оценить по формуле Ток, протекающий через нагревательный элемент, равен
I = P/V
P = 1,2 КВт = 1200 Вт.
В = 240 В.
Следовательно, I = 1200 / 240 = 5 Ампер.
Значение сопротивления нагревательного элемента можно рассчитать по закону Ома следующим образом:
R = V / I
R = 240 / 5 = 48 Ом.
Пример 2Рассмотрим следующую цепь, в которой резистор сопротивлением 47 Ом подключен к источнику питания 120 В. Закон можно использовать для вычисления тока, протекающего через резистор.
I = V / R
I = 120 / 47 = 2,55 Ампер.
Мощность, потребляемая резистором, равна
P = I2 * R = V2 / R
P = 1202 / 47 = 306 Вт.
Подробнее: Что такое резисторы для поверхностного монтажа (резисторы для поверхностного монтажа)
Посмотрите видео ниже, чтобы узнать больше о резисторах в цепях переменного и постоянного тока:
Подробнее: Что такое параллельные резисторы
Заключение
Поток электричества однонаправленный в постоянном токе (DC). Полярность и направление напряжения и тока в постоянном токе всегда одинаковы. С другой стороны, в переменном токе (AC) поток электрического заряда иногда меняет направление. Со временем полярность напряжения переменного тока меняется с положительной на отрицательную.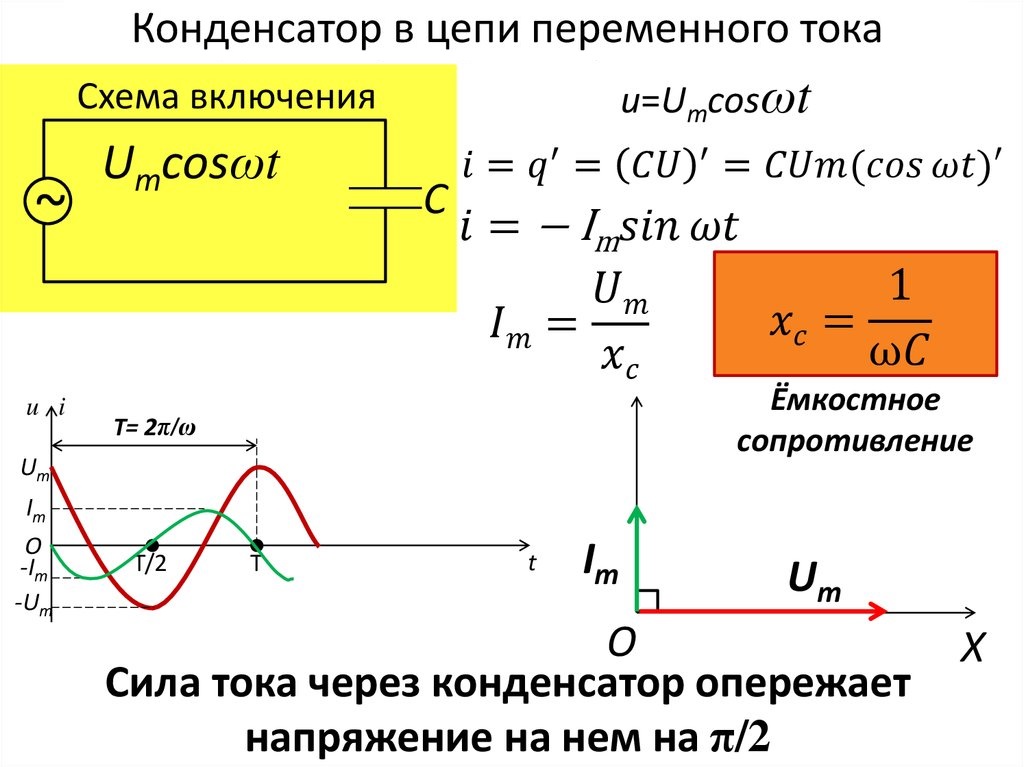 Это все для этой статьи, где обсуждаются схема, сопротивление, формула и примеры резисторов цепи переменного и постоянного тока. Также рассматривается разница между этим резистором переменного и постоянного тока.
Это все для этой статьи, где обсуждаются схема, сопротивление, формула и примеры резисторов цепи переменного и постоянного тока. Также рассматривается разница между этим резистором переменного и постоянного тока.
Надеюсь, вы многому научились, если да, поделитесь с другими учениками. Спасибо за чтение, увидимся!
Калькулятор сопротивления переменному току круглого провода
Калькулятор сопротивления переменному току круглого провода Логотип Chemandy Electronics Логотип Chemandy Electronics CHEMANDY ELECTRONICSПоставщики необычногоРассчитывает сопротивление переменному току круглого прямого провода для обычных проводящих материалов, используя уравнение и данные, указанные ниже, или вводя данные материала вручную.
| ВХОДНЫЕ ДАННЫЕ | |
| Материал проводника: | Введите данныеAluminiumCopperGoldNickelSilver |
| Частота: | МГц |
| Длина: | мм |
| Диаметр: | мм |
| РЕЗУЛЬТАТЫ | |
| Удельное сопротивление (ρ): | x 10 -8 Ом. м м |
Относительная магнитная проницаемость (µ r 1 6): | |
| Глубина скин-эффекта (δ): | мкм |
| переменный ток Сопротивление: | Ом |
Примечание. Чтобы использовать разные значения удельного сопротивления и относительной проницаемости, выберите «Ввести данные» в текстовом поле «Выбор материала проводника», а затем введите соответствующие значения в поля, выделенные желтым цветом.
Этот калькулятор использует JavaScript и будет работать в большинстве современных браузеров. Подробнее см. О наших калькуляторах
.сопротивление для длины круглого прямого провода рассчитывается с использованием удельного сопротивления проводника, длины проводника и эффективной площади поперечного сечения, используемой скин-эффектом.
Где ρ — удельное сопротивление проводника в Ом·м
l — Длина проводника в мм
A eff — эффективная площадь поперечного сечения, используемая в мм
Площадь поперечного сечения, используемая скин-эффектом, определяется путем первоначального расчета номинальной глубины проникновения проводника.
Из «Линий и сетей передачи» Уолтера С. Джонсона, McGraw-Hill, 1963, стр. 58.
Где ρ — удельное сопротивление проводника в Ом·м
f — частота в Герцах
μ — абсолютная магнитная проницаемость проводника
Абсолютная магнитная проницаемость (μ) = μ o x μ r
μ o = 4π x 10 -7 Гн/4 Значения для μ r взяты из Справочник по проектированию линий электропередач Брайана К. Уоделла, Artech House 1991, таблица 9.3.2, стр.
446. Значения ρ взяты из CRC Handbook of Chemistry and Physics 1st Student Edition 1998 стр. F-88 и предназначены для элементов высокой чистоты при 20°C. Фактическая площадь поперечного сечения, используемая из-за скин-эффекта, может быть рассчитана несколькими методами с разной степенью точности. Самый простой способ — умножить глубину скин-слоя на длину окружности проводника. Где d — диаметр проводника Этот метод делает используемую площадь поперечного сечения слишком большой от высоких частот до точки, где глубина поверхностного слоя становится примерно половиной радиуса проводника, после чего увеличиваются погрешности, и в конечном итоге расчетная используемая площадь становится больше фактической площади проводника. Второй простой метод заключается в вычислении общей площади проводника, а затем вычитании площади круга, представляющего центральную область без использования скин-эффекта. Где r — радиус проводника Этот метод является более точным, чем первый метод, когда r >> δ, но становится очень неточным ниже точки, где d/δ = π, и может иметь огромные положительные или отрицательные колебания значения. Гораздо более точный метод описан Дэвидом Найтом в очень подробной статье под названием Zint.pdf, которую можно найти по адресу http://www.g3ynh.info/zdocs/comps/part_1.html. В этом методе используется метод усеченного экспоненциального затухания. для устранения ошибок, возникающих, когда фактическая площадь проводника становится меньше, чем расчетная площадь толщины скин-слоя в простом методе, описанном выше, и модифицированная коррекция Лоренца, которая устраняет ошибку, возникающую, когда вычисленная площадь скин-слоя приближается к фактической площади проводника. Метод расчета предполагает наличие одного изолированного проводника и не учитывает обратный путь. Это затрудняет измерение от начала до конца, поэтому результаты этого калькулятора были сопоставлены с цифрами, приведенными в оригинальной статье, чтобы доказать точность. В. Дж. Хайтон 30 сентября 2011 г. Этот калькулятор бесплатно предоставляется компанией Chemandy Electronics для продвижения
ФЛЕКСИ-БОКС Вернуться к индексу калькулятора Сопротивление переменному току и постоянному току — это противодействие протеканию переменного и постоянного тока соответственно через проводник. Однако в цепи переменного тока сопротивление называется импедансом. Полное сопротивление — это эффективное сопротивление, оказываемое току, протекающему по цепи, содержащей как сопротивление, так и реактивное сопротивление. Как вы знаете, в цепи переменного тока векторы напряжения и тока представляются математически в сложной форме. Синусоидальные формы сигнала во временной области могут быть преобразованы в пространственную или векторную область, чтобы можно было построить векторные диаграммы для нахождения этой векторной зависимости напряжение-ток. Любой идеальный элемент цепи, такой как резистор, катушка индуктивности или конденсатор, может быть описан математически с точки зрения его напряжения и тока. Как правило, напряжение на чисто омическом резисторе линейно пропорционально протекающему через него току в соответствии с законом Ома. Рассмотрим схему, показанную ниже. Он состоит из источника переменного напряжения V, переключателя и нагрузочного резистора R. Когда переключатель замкнут, переменное напряжение подается на резистор. Это напряжение вызовет протекание тока по цепи. Другими словами, при сопротивлении переменному току напряжение и ток достигают своих максимальных значений и падают через ноль одновременно, и поэтому говорят, что они совпадают по фазе друг с другом.. Электрический ток, протекающий через сопротивление переменному току представлено выражением , где I м – пиковая амплитуда тока, а θ – фазовый угол между напряжением и током. По закону Ома максимальное или пиковое напряжение на выводах резистора R будет равно, и мгновенное значение тока, I (t) будет Таким образом, для чисто резистивной цепи переменный ток изменяется пропорционально напряжению, протекающему через резистор. по той же синусоидальной схеме. То есть отсутствует разность фаз между током и напряжением при использовании сопротивления переменного тока. Это связано с тем, что и напряжение, и ток одновременно достигают своего максимального, нулевого и минимального значений. В цепи постоянного тока соотношение между напряжением и током обычно называется сопротивлением, а в цепи переменного тока это отношение называется импедансом. Другими словами, электрическое сопротивление в цепи переменного тока называется « Импеданс ». Можно сказать, что для резистора сопротивление постоянному току = импедансу переменного тока (R = Z). Полное сопротивление обозначается символом ‘ Z ’. Единицей сопротивления переменного тока или импеданса является Ом (Ом), что совпадает с сопротивлением постоянному току. Полное сопротивление (или сопротивление переменному току) может быть определено как Полное сопротивление также может быть представлено комплексным числом, поскольку оно зависит от частоты цепи ω при наличии реактивных компонентов. Но в случае чисто резистивной цепи реактивная составляющая всегда будет равна нулю. Таким образом, общее выражение для импеданса в чисто резистивной цепи в терминах комплексного числа дается как0075 Осциллограммы напряжения и тока сопротивления переменного тока показаны ниже. На векторной диаграмме отчетливо видна «синфазная» зависимость. В комплексной области сопротивление — это просто действительное число, оно не включает мнимую составляющую. Следовательно, векторы напряжения и тока лежат на одной прямой. Это означает, что между ними не будет разности фаз ( θ = 0 ) или они будут находиться в фазе друг с другом. Таким образом, векторы напряжения и тока накладываются друг на друга вдоль оси отсчета. Приведенный выше вектор представляет среднеквадратичное значение напряжения и тока через сопротивление. Среднеквадратичные значения задаются как Соотношение фазного напряжения и тока задается как Это показывает, что чистое сопротивление в цепи переменного тока точно определяет соотношение между ее векторами напряжения и тока. так же, как и в цепи постоянного тока. Закон Ома применим как для цепи переменного, так и для постоянного тока. В обоих случаях зависимость напряжения от тока всегда линейна для чистого сопротивления. Мощность, потребляемая резистором в цепи переменного тока, зависит от фазового угла. Она задается как Но в чисто резистивной цепи фазовый угол θ = 0. Таким образом, мощность становится равной Приведенные выше уравнения такие же, как и для цепей постоянного тока. Можно применить основные законы, такие как закон Ома и закон Кирхгофа, чтобы найти напряжение, ток и импеданс в цепи переменного тока, аналогичной цепи постоянного тока. Примером чистых сопротивлений являются нагревательные элементы и лампы, которые имеют незначительные значения индуктивности или емкости. Электрическая лампа с сопротивлением 40 Ом подключена к однофазной сети переменного тока 230 В. Рассчитайте ток, потребляемый от источника питания, и мощность, потребляемую лампой. Также нарисуйте соответствующую векторную диаграмму . Решение: Дано: Напряжение = 230 В, сопротивление лампы = 40 Ом Ток, потребляемый от источника питания, Мощность, потребляемая лампой, Поскольку это резистивная нагрузка, разность фаз отсутствует, поэтому θ = 0. SIM921 Мост сопротивления переменному току SIM921 Мост сопротивления переменному току Мост сопротивления переменному току SIM921 — это точный прибор с низким уровнем шума, разработанный для криогенной термометрии. При мощности возбуждения ниже 100 аВт термисторы и другие резистивные образцы можно измерять при температурах ниже 50 мК с незначительными ошибками самонагрева. Измерение сопротивления SIM921 измеряет сопротивление по четырехпроводной схеме, исключая прямое влияние сопротивления выводов на результат. Использование источника переменного тока возбуждения позволяет избежать термоЭДС и дрейфа смещения усилителя. Частоту возбуждения можно регулировать в диапазоне от 2 Гц до 60 Гц либо с передней панели, либо через интерфейс компьютера. Эта гибкость позволяет пользователю работать на синхронной субгармонике частоты сети питания (например, 15 Гц/12,5 Гц) или на некоторой несоизмеримой частоте, в зависимости от требований. Несколько SIM921 могут работать на разных частотах в одной и той же экспериментальной установке без риска внутриполосных перекрестных помех. Кроме того, при измерениях очень высокого импеданса переменная частота позволяет исследовать любые емкостные эффекты в результате измерения сопротивления. Возбуждения являются синусоидальными, что устраняет содержание высокочастотных гармоник, связанное с прямоугольными возбуждениями. Фактическое определение сопротивления достигается логометрическим путем, пропуская выбранный ток возбуждения как через внутренний высокостабильный эталонный резистор, так и через измеряемое устройство пользователя. Доступна внутренняя автокалибровка для калибровки двух плеч показаний отношения для большей точности. Возбуждение В SIM921 доступны два режима возбуждения: постоянный ток и постоянное напряжение. В большинстве приложений низкотемпературной термометрии используются резисторы с отрицательным температурным коэффициентом. Преимущество режима постоянного напряжения заключается в уменьшении мощности, рассеиваемой термометром при падении температуры. В этом режиме SIM921 управляет приложенным возбуждением переменного тока для поддержания выбранного напряжения на пользовательском резисторе. Режим постоянного тока подходит для измерения малых сопротивлений, например, для характеристики сверхпроводящих переходов. В режиме постоянного тока внутренний эталонный резистор используется в качестве входа сервопривода, обеспечивая постоянный ток, равный выбранному напряжению, деленному на половину диапазона сопротивления (например, 100 мкВ в диапазоне 20 кОм дает среднеквадратичное значение тока возбуждения 10 нА). ). Блок-схема SIM921 SIM921 Мост сопротивления переменного тока Фазочувствительное обнаружение Пара двухфазных синусоидальных демодуляторов переменного тока в SIM921 обеспечивает превосходное соотношение сигнал/шум в самых сложных условиях испытаний. Автодиапазон Когда выбран автодиапазон, SIM921 динамически регулирует коэффициент усиления мостового усилителя для оптимальной работы со слабыми сигналами и изменяет масштаб дисплея на основе результата измерения. При отключении автодиапазона диапазон отображения остается фиксированным, а мостовые усилители поддерживают полное усиление. Это может быть особенно важно при использовании SIM921 в приложении контура управления. Как в автоматическом, так и в ручном режиме диапазона параметры возбуждения никогда не изменяются прибором, что обеспечивает пользователю полный контроль над условиями измерения в эксперименте. Термометрия SIM921 совместим со всеми резистивными датчиками, включая датчики NTC (германий, углеродное стекло , состав углерода, Cernox , оксид рутения и т. Выход В дополнение к выходу дисплея и компьютерному интерфейсу аналоговый выход обеспечивает напряжение постоянного тока, пропорциональное сопротивлению или температуре. Пользователь имеет полный контроль над масштабом (В/К или В/Ом) и смещением (К или Ом) этого выхода. Контроль температуры Аналоговый выходной сигнал хорошо подходит для подключения к аналоговому ПИД-контроллеру SIM960. Эта комбинация модулей обеспечивает гибкое и экономичное решение для контроля температуры. Дисплей на передней панели Основным считывающим устройством является легко читаемый 5½-разрядный светодиодный дисплей (со статическим управлением для низкого уровня шума). На этом дисплее может отображаться измеренное значение (сопротивление или температура), значение за вычетом смещения, фазовый сдвиг, смещение, частота возбуждения, шкала аналогового выхода и калибровочная кривая. Интерфейсы Всеми параметрами прибора можно управлять и отображать их на передней панели или устанавливать и запрашивать через интерфейс компьютера. Аналоговый выход постоянного тока доступен на разъеме BNC на передней панели. На задней панели имеется стандартный 9-контактный разъем D-sub для датчика. Питание и последовательная связь осуществляются через 15-контактный разъем D-sub, который соединяется с основным блоком SIM900. Автономная работа SIM921 возможна при подаче питания ±15 В и +5 В непосредственно на 15-контактный разъем. Разрешение Разрешение указано в таблице ниже. Верхние значения показывают ток возбуждения, а нижние значения представляют собой типичные среднеквадратичные значения шума сопротивления, измеренные при 50 % полной шкалы на резисторе, работающем при комнатной температуре, с постоянной времени выхода 3 с. Возбуждение Полное сопротивление — это помеха, создаваемая электрической цепью при протекании тока в цепи переменного тока. Теперь у нас должно возникнуть много вопросов. Чем этот импеданс отличается от сопротивления, хотя и имеет ту же единицу измерения? Из чего состоит это сопротивление? И еще много подобных вопросов. Не так ли? Прочтите статью полностью и вы получите ответы на все вопросы. Цепи переменного тока — это те, в которых мы имеем синусоидальное напряжение питания и, следовательно, синусоидальный ток. Они сильно отличаются от цепей постоянного тока. Здесь снова и снова будет приходить один термин, фазоры. Вектор — это способ представления комплексного числа, которое дополнительно представляет синусоидальную функцию, начальная фаза (θ), амплитуда (A) и угловая частота ( ω ) зависят от времени. По закону Ома мы знаем, что в цепи постоянного тока напряжение на резисторе и ток через него имеют линейную зависимость. Теперь давайте рассмотрим случай цепи переменного тока. Напряжение здесь будет переменным напряжением с синусоидальной формой волны. Выражение напряжения можно записать как В = В макс sin(wt + 𝛉), , где В макс — максимальная амплитуда, а «w» — угловая частота. Точно так же ток, создаваемый в цепи, будет синусоидальным и может быть выражен как I = I max sin(wt + 𝛉). Здесь вы должны заметить одну вещь. Спроси «что? Да, вы должны заметить одну вещь, которая здесь есть, у нас нет никакого фазового сдвига, т.е. и напряжение, и ток имеют одинаковую угловую частоту со сдвигом на 𝛉-градус. Поэтому мы говорим, что в случае чисто резистивной цепи переменного тока и напряжение, и ток синфазны. В приведенной выше схеме мы видим, что к источнику приложено синусоидальное напряжение. Это напряжение зависит от времени и создаст ток в резисторе, который будет следовать полярности напряжения с той же или другой амплитудой (в зависимости от значения сопротивления). Применяя КВЛ в цепи, имеем V(t) = I(t) * R = I max sin(wt + 𝛉) Итак, в чисто резистивной цепи переменного тока форма волны тока следующая той же синусоидальной формы, что и напряжение, т. е. ток изменяется пропорционально напряжению. Глядя на форму сигнала, мы можем сказать, что рост напряжения и тока происходит с одинаковой частотой и одинаково для падения обеих величин. Следовательно, по форме сигнала также доказано, что и напряжение, и ток не имеют фазового сдвига и, следовательно, находятся в фазе. Тот же результат получается и для вектора приведенной выше сети переменного тока. Мы должны знать, что вектор представляет среднеквадратичное значение величин. Таким образом, чтобы представить напряжение и ток, нам нужно разделить максимальное значение обеих величин на √2. В действ. = В макс. / √2 I ср.кв. = I макс. цепь постоянного тока, имеющая линейную зависимость, тогда в чем разница? Ну, на самом деле никакой разницы (пока индуктивность или/и емкость не присутствуют), а только то, что в цепи постоянного тока мы называем это сопротивлением, а здесь в цепи переменного тока мы называем это импедансом. Опять же, как обсуждалось ранее, полное сопротивление переменному току, когда в качестве энергопоглощающего (пассивного) элемента подключено только сопротивление, тогда: В = Z * I , где Z = полное сопротивление цепи Z обычно определяется в сложной форме, так как зависит от частоты. пусть Z = R + jX , где R = сопротивление цепи, а X — реактивное сопротивление цепи, j называется йотой и используется для отображения мнимой части числа. Следовательно, Z = (В / I) Ом В случае чисто резистивной цепи Z = R + j0 = R (Ом) В случаях, когда подключены другие пассивные элементы, такие как конденсаторы и катушки индуктивности. Коэффициент мощности представляет собой косинус угла между напряжением и током. Поскольку в омической цепи угол между напряжением и током равен нулю, следовательно, коэффициент мощности cosႴ = cos0 = 1, т. е. единичный коэффициент мощности (УПМ). Еще один фактор, который мы можем рассчитать здесь, это мощность. Тогда мгновенная мощность, потребляемая резистором, определяется как: P = V*I = V max sin(wt) * I max sin(wt) = V max * I max sin 2 (wt) Therefore, P = P max sin 2 (wt) where, P max = V max * I max Средняя мощность представляет собой мощность постоянного тока и поглощается только резистором. P = V*I = I 2 R = V 2 /R В повседневной жизни цепи переменного тока, такие как нагревательные элементы и лампы, имеют только омическое сопротивление и незначительное значение индуктивности и емкости. В таких цепях мы можем использовать закон Кирхгофа, закон Ома или любое другое правило схемы, чтобы получить все параметры цепи. Скорее всего, это цепь постоянного тока только до тех пор, пока в игру не вступят индуктивность и емкость. Обычно мы используем значения RMS с такими правилами. Рассмотрим электрическую лампу с сопротивлением переменному току 100 Ом, подключенную к однофазной сети переменного тока напряжением 300 вольт. Ток от источника питания: I = V/R = 300 / 100 = 3 Ампер Активная мощность, потребляемая лампой P = I 2 R = 3 2 *100 = 900 ватт Также по другим формулам мощности: P = V*I = 3 * 300 = 900 Вт Таким образом, мы видим, что использование любой из формул дает один и тот же результат. Поскольку 𝛉 = 0, в этом случае вектор будет направлен в одном направлении как для напряжения, так и для тока, как: Рассмотрим источник синусоидального напряжения, поскольку V(t) = 100cos (wt + 60 o ) подается на чистое сопротивление 25 Ом. Найдите его пиковое значение тока и полного сопротивления цепи. Также покажите фазовращатель для того же самого. Теперь это синусоидальное напряжение можно записать в виде вектора как V = 10060 O вольт 460 O Ампер Векторная диаграмма, представляющая вышеуказанные условия, будет выглядеть так: Есть определенные моменты, которые вы должны помнить, когда речь идет об импедансе переменного тока с чисто омическим элементом. Надеюсь, вы получили хорошее представление об импедансе в цепях переменного тока. Далее в нашем следующем уроке мы увидим влияние индуктивных и емкостных нагрузок в цепях переменного тока и их фазовую взаимосвязь. По любым другим вопросам, касающимся статьи, вы можете прокомментировать ниже, и я буду рад ответить на них все. Сопротивление — это способность цепи или элемента (называемого резистором) противодействовать прохождению через него тока. Примерами резисторов с высоким сопротивлением являются стекло, воздух, дерево, слюда, пластик, резина, вольфрам и т. д. Единицей сопротивления является «Ом», она обозначается Ω и обозначается буквой «R». . Проще говоря, сопротивление в цепях переменного тока называется импедансом. или Общее сопротивление (сопротивление, индуктивное сопротивление и емкостное сопротивление) в цепях переменного тока называется импедансом (Z). Когда переменный ток проходит через провод (резистор, катушку индуктивности, конденсатор), то ток создает магнитное поле на этом проводе, которое противодействует потоку переменного тока в нем вместе с сопротивлением этого провода. . Эта природа оппозиции в цепи переменного тока называется индуктивностью. Индуктивность — это свойство катушки (или провода), благодаря которому она противостоит любому увеличению или уменьшению тока или потока через нее. Индуктивное реактивное сопротивление X L , это свойство катушки или провода в цепи переменного тока, которое препятствует изменению тока. Единица измерения индуктивного реактивного сопротивления такая же, как сопротивление, емкостное реактивное сопротивление, т. е. Ом (Ом), но репрезентативным символом емкостного реактивного сопротивления является X L . Аналогично, емкостное реактивное сопротивление в емкостной цепи является сопротивлением току, протекающему только в цепях переменного тока. Единица емкостного реактивного сопротивления такая же, как сопротивление, индуктивное реактивное сопротивление, т.е. Ом (Ом), но репрезентативным символом емкостного реактивного сопротивления является X С . Формулы электрического сопротивления и импеданса в цепях переменного тока В цепях переменного тока (емкостная или индуктивная нагрузка), сопротивление = полное сопротивление, т. е. 3 Z = Z  Сделать метод расчета только приблизительным и использовать его только тогда, когда r >> δ.
Сделать метод расчета только приблизительным и использовать его только тогда, когда r >> δ. Автор называет это уравнение Rac — TED — ML и указывает максимальную ошибку 0,09.%.
Автор называет это уравнение Rac — TED — ML и указывает максимальную ошибку 0,09.%. Сопротивление переменному току и импеданс
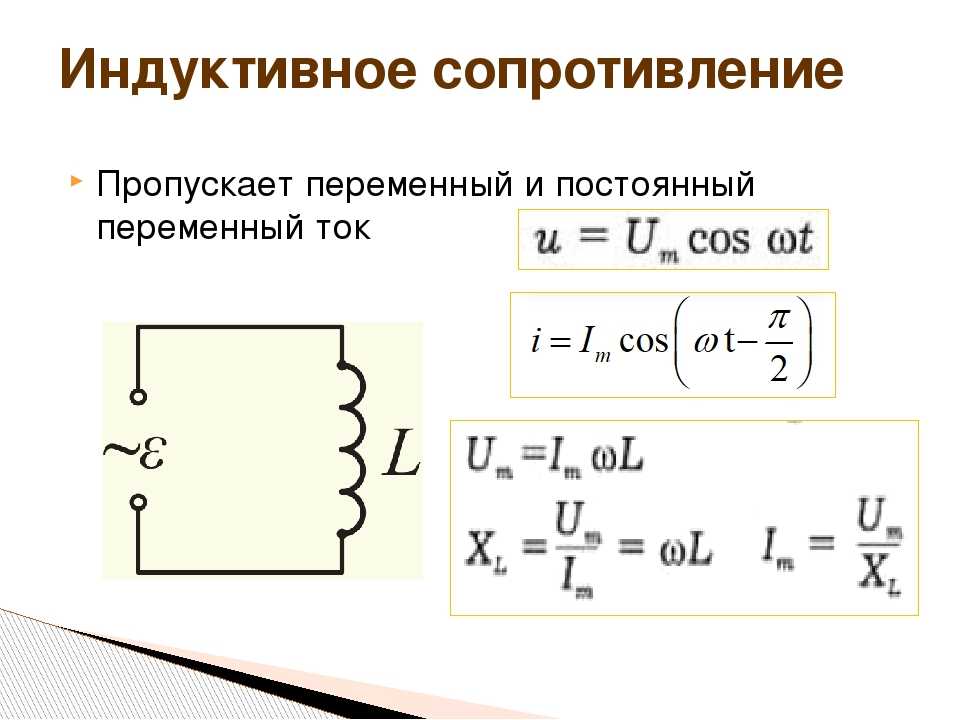 Измеряется в Омах.
Измеряется в Омах. Сопротивление переменному току при синусоидальном питании
 Поскольку приложенное напряжение является переменным, оно возрастает и падает синусоидально. Одновременно ток, протекающий через цепь, также будет увеличиваться и уменьшаться.
Поскольку приложенное напряжение является переменным, оно возрастает и падает синусоидально. Одновременно ток, протекающий через цепь, также будет увеличиваться и уменьшаться.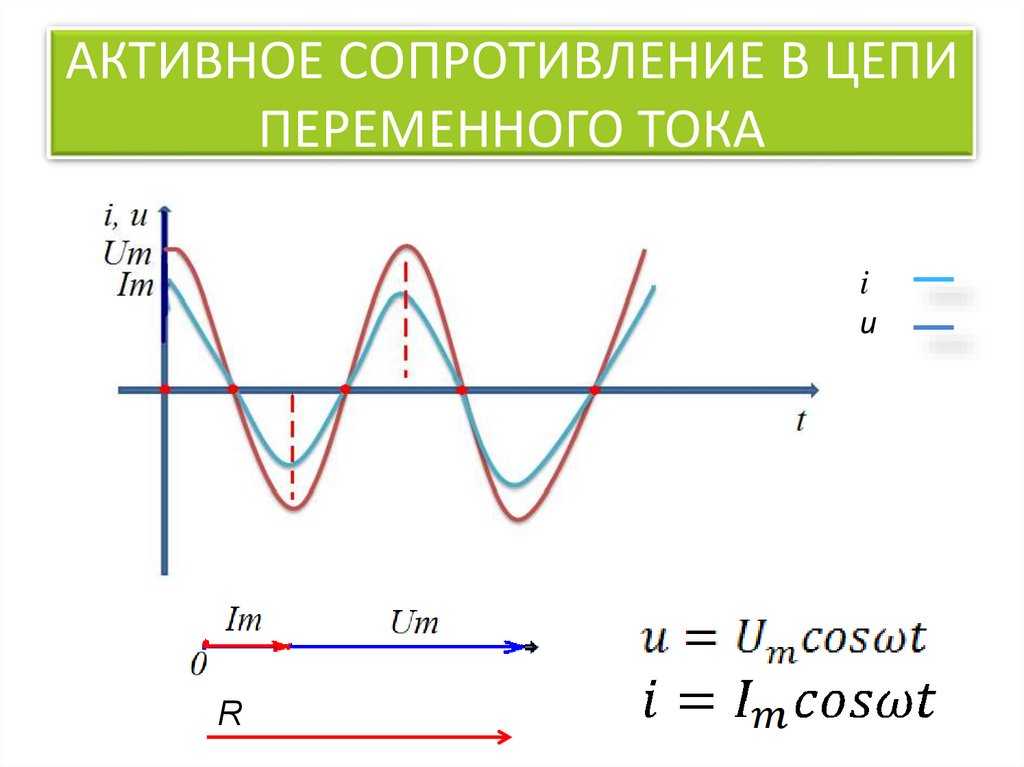 Поскольку частота питания одинакова как для напряжения, так и для тока, их векторы лежат на одной линии, в результате чего ток находится «в фазе» с напряжением.
Поскольку частота питания одинакова как для напряжения, так и для тока, их векторы лежат на одной линии, в результате чего ток находится «в фазе» с напряжением. Полное сопротивление

 Синусоидальная диаграмма во временной области преобразуется в векторную область, как показано ниже.
Синусоидальная диаграмма во временной области преобразуется в векторную область, как показано ниже. Взаимосвязь напряжения и мощности
 Таким образом, можно сказать, что эффективная мощность, потребляемая сопротивлением переменного тока, равна мощности, потребляемой тем же резистором в цепи постоянного тока.
Таким образом, можно сказать, что эффективная мощность, потребляемая сопротивлением переменного тока, равна мощности, потребляемой тем же резистором в цепи постоянного тока. Пример задачи
 Соответствующая векторная диаграмма представлена ниже:
Соответствующая векторная диаграмма представлена ниже: SIM921 — Мост сопротивления переменному току


Икс  Кроме того, двухфазная демодуляция позволяет измерять сопротивление и фазовый сдвиг. Большие фазовые сдвиги могут предупредить пользователя о чрезмерном реактивном сопротивлении свинца. Выбираемые постоянные времени после демодуляции от 300 мс до 300 с дают вам полный контроль над компромиссом между временем отклика измерения и максимальным разрешением.
Кроме того, двухфазная демодуляция позволяет измерять сопротивление и фазовый сдвиг. Большие фазовые сдвиги могут предупредить пользователя о чрезмерном реактивном сопротивлении свинца. Выбираемые постоянные времени после демодуляции от 300 мс до 300 с дают вам полный контроль над компромиссом между временем отклика измерения и максимальным разрешением. д.) и датчики PTC (родий-железо RTD , платиновый RTD и т. д.). Через компьютерный интерфейс в прибор можно загрузить до четырех калибровочных кривых пользователя (от Ом до Кельвина) с 200 точками данных в каждой.
д.) и датчики PTC (родий-железо RTD , платиновый RTD и т. д.). Через компьютерный интерфейс в прибор можно загрузить до четырех калибровочных кривых пользователя (от Ом до Кельвина) с 200 точками данных в каждой. Отдельные дисплеи в виде полос показывают диапазон сопротивления, возбуждение и постоянную времени выходного сигнала, а также режим возбуждения (ток или напряжение) и настройку автоматического диапазона.
Отдельные дисплеи в виде полос показывают диапазон сопротивления, возбуждение и постоянную времени выходного сигнала, а также режим возбуждения (ток или напряжение) и настройку автоматического диапазона.
Диапазон 30 мВ 10 мВ 3 мВ 1 мВ 300 мкВ 100 мкВ 30 мкВ 10 мкВ 3 мкВ 20 мОм н/д н/д н/д н/д н/д 100 мА
44 мкОм 3 мА
130 мкОм 1 мА
510 мкОм 300 мкА
1,5 мОм 200 мОм н/д н/д н/д 10 мА
8,9 мкОм 3 мА
12 мкОм 1 мА
32 мкОм 300 мкА
120 мкОм 100 мкА
590 мкОм 30 мкА
1,4 мОм 2 Ом н/д 10 мА
4,3 мкОм 3 мА
5,5 мкОм 1 мА
7,9 мкОм 300 мкА
23 мкОм 100 мкА
70 мкОм 30 мкА
220 мкОм 10 мкА
730 мкОм 3 мкА
1,8 мОм 20 Ом 3 мА
20 мкОм 3 мА
21 мкОм 300 мкА
33 мкОм 100 мкА
41 мкОм 30 мкА
100 мкОм 10 мкА
390 мкОм 3 мкА
1,7 мОм 1 мкА
4,1 мОм 300 нА
10 мОм 200 Ом 300 мкА
200 мкОм 100 мкА
200 мкОм 30 мкА
370 мкОм 10 мкА
430 мкОм 3 мкА
1,1 мОм 1 мкА
2,8 мОм 300 нА
9,7 мОм 100 нА
25 мОм 30 нА
120 мОм 2 кОм 30 мкА
2,0 мОм 10 мкА
2,0 мОм 3 мкА
2,9 мОм 1 мкА
4,0 мОм 300 нА
12 мОм 100 нА
40 мОм 30 нА
120 мОм 10 нА
300 мОм 3 нА
900 мОм 20 кОм 3 мкА
20 мОм 1 мкА
25 мОм 300 нА
31 мОм 100 нА
56 мОм 30 нА
200 мОм 10 нА
640 мОм 3 нА
2,4 Ом 1 нА
5,3 Ом 300 пА
23 Ом 200 кОм 300 нА
250 мОм 100 нА
350 мОм 30 нА
640 мОм 10 нА
1,4 Ом 3 нА
4,5 Ом 1 нА
16 Ом 300 пА
47 Ом 100 пА
150 Ом 30 пА
710 Ом 2 МОм 30 нА
3,4 Ом 10 нА
5,9 Ом 3 нА
16 Ом 1 нА
46 Ом 300 пА
190 Ом 100 пА
480 Ом 30 пА
1,7 кОм 10 пА
5,4 кОм 3 пА
15 кОм 20 МОм 3 нА
50 Ом 1 нА
190 Ом 300 пА
540 Ом 100 пА
1,1 кОм 30 пА
5,4 кОм 10 пА
12 кОм 3 пА
56 кОм 1 пА
180 кОм 300 фА
750 кОм Сопротивление и полное сопротивление переменному току — EEE PROJECTS
 По сути, это комбинация резистивных и реактивных компонентов (из-за катушек индуктивности и конденсаторов). Он следует принципу закона Ома. Кроме того, мы можем сказать, что импеданс подобен сопротивлению в цепи постоянного тока, поэтому он имеет ту же единицу измерения, что и сопротивление, то есть «Ом».
По сути, это комбинация резистивных и реактивных компонентов (из-за катушек индуктивности и конденсаторов). Он следует принципу закона Ома. Кроме того, мы можем сказать, что импеданс подобен сопротивлению в цепи постоянного тока, поэтому он имеет ту же единицу измерения, что и сопротивление, то есть «Ом». Цепи переменного тока
 Мы изучим его применение по ходу статьи.
Мы изучим его применение по ходу статьи. Сопротивление переменному току при синусоидальном питании

Синусоидальные сигналы для сопротивления переменному току

Векторная диаграмма сопротивления переменному току
Полное сопротивление переменному току
 Например,
Например, Коэффициент мощности
Average Power
 Средняя мощность в реактивной или резистивной цепи зависит от угла между напряжением и током. Поскольку 𝛉 = 0, коэффициент мощности равен единице, поэтому средняя мощность, потребляемая сопротивлением переменного тока, определяется по закону Ома:
Средняя мощность в реактивной или резистивной цепи зависит от угла между напряжением и током. Поскольку 𝛉 = 0, коэффициент мощности равен единице, поэтому средняя мощность, потребляемая сопротивлением переменного тока, определяется по закону Ома: Пример 1: Сопротивление переменному току
 Рассчитайте ток, потребляемый от источника питания, и мощность, потребляемую лампой. Также покажите векторную зависимость между напряжением и током в лампе.
Рассчитайте ток, потребляемый от источника питания, и мощность, потребляемую лампой. Также покажите векторную зависимость между напряжением и током в лампе. Пример 2: Сопротивление переменному току

Резюме импеданса переменного тока

Цепи переменного и постоянного тока — Foretec Electric India
Сопротивление 
 Кроме того, мы знаем, что индуктивность существует только в переменном токе, потому что величина тока постоянно меняется
Кроме того, мы знаем, что индуктивность существует только в переменном токе, потому что величина тока постоянно меняется 
2
+ X L 2 )…
В случае индуктивной нагрузки
Z = √ (R 2 + X C 2 )… In случай емкостной нагрузки
z = √ (r 2 + (x L — x C )
, где
x L = индуктивная реактивная способность
x L = 2π106 L = 2π106 L = 2π106 9095 L = 2π106 9095 L .
And X C = Capacitive reactance X C = 1/2π f C…
Where C = Capacitance in Farads.
Сопротивление постоянному токуМы знаем, что в цепях постоянного тока не существует концепции индуктивных и емкостных реактивных сопротивлений. то есть емкостное и индуктивное реактивное сопротивление в цепях постоянного тока равны нулю, потому что в цепях постоянного тока нет частоты, т.е. величина постоянного тока постоянна. Поэтому в игру вступает только исходное сопротивление провода.
Измерение сопротивления постоянному токуФормулы электрического сопротивления
В цепях постоянного тока сопротивление рассчитывается по закону Ома.
R = V/I
При решении электрических цепей для нахождения сопротивления и вы не уверены, какую из них следует учитывать, сопротивление переменному или постоянному току, тогда, если проходящий ток является переменным, то берите переменный сопротивление, иначе, если проходящий ток является постоянным, возьмите сопротивление постоянному току.
Какое из них больше – сопротивление переменному или постоянному току?Поскольку мы хорошо знаем, что частота в источнике постоянного тока равна нулю, поэтому нет скин-эффекта (поведение переменного тока, протекающего через поверхность, т.е. внешний слой проводника, а не сердцевину провода). в цепях постоянного тока. Из-за скин-эффекта сопротивление переменному току в цепях переменного тока больше, чем подача постоянного тока в цепях постоянного тока.
Это причина в области гармоник качества электроэнергии, скин-эффект более преобладает выше 7 й заказ, все из которых относятся к положительной последовательности.



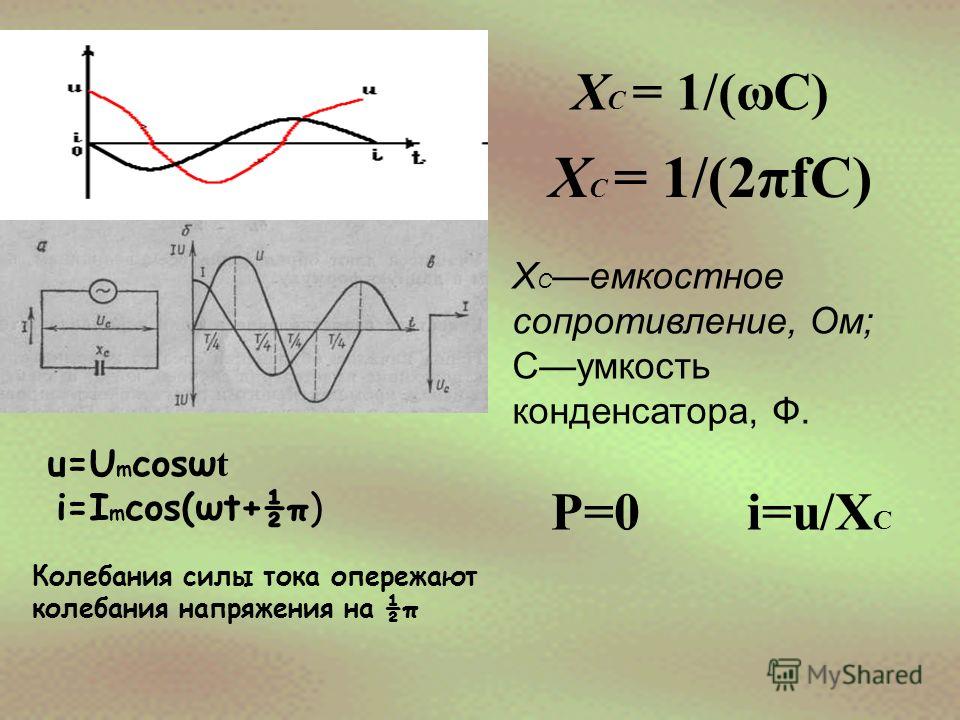 Активное, емкостное сопротивление. Понятие импеданса. Частотная зависимость импеданса. Физические основы реографии.
Активное, емкостное сопротивление. Понятие импеданса. Частотная зависимость импеданса. Физические основы реографии. Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного ток.
Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного ток. 
 Датчик ,в котором подведена измеряемая величина, т.е. первый в измерительной цепи, называется первичным.
Датчик ,в котором подведена измеряемая величина, т.е. первый в измерительной цепи, называется первичным.
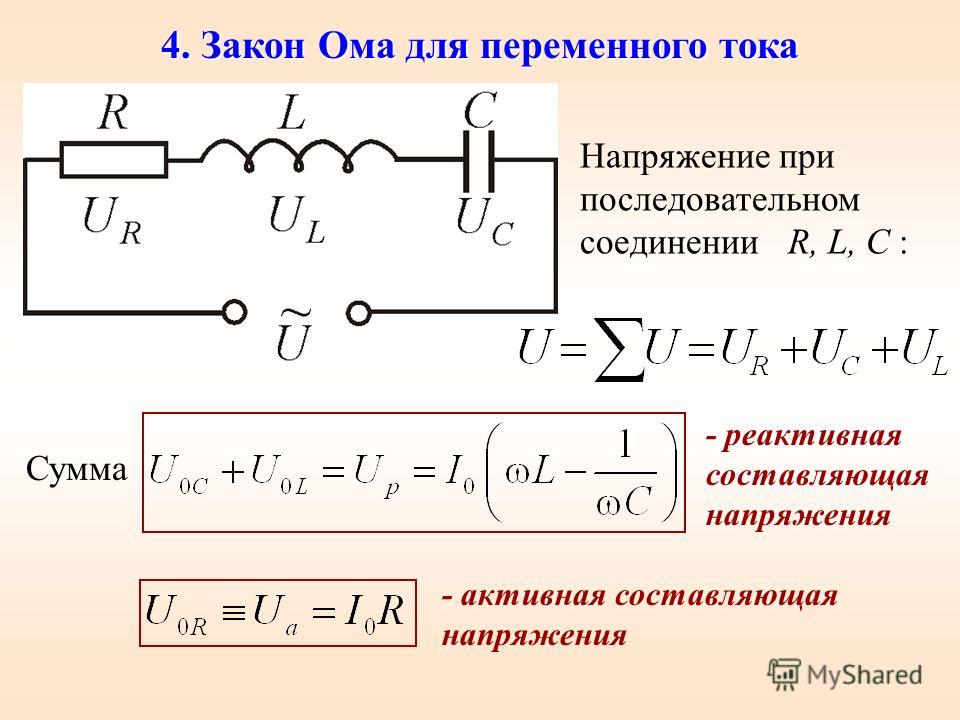
 Поэтому при касании человеком корпуса аппаратуры через тело человека пройдет некоторый ток, называемый током утечки.
Поэтому при касании человеком корпуса аппаратуры через тело человека пройдет некоторый ток, называемый током утечки.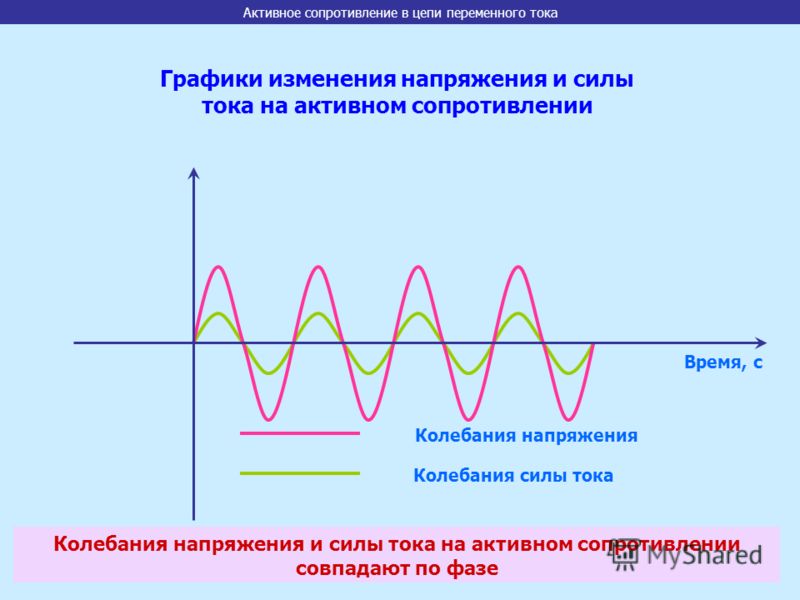 В бестрансформаторном источнике питания к сети переменного напряжения подключены последовательно…
В бестрансформаторном источнике питания к сети переменного напряжения подключены последовательно…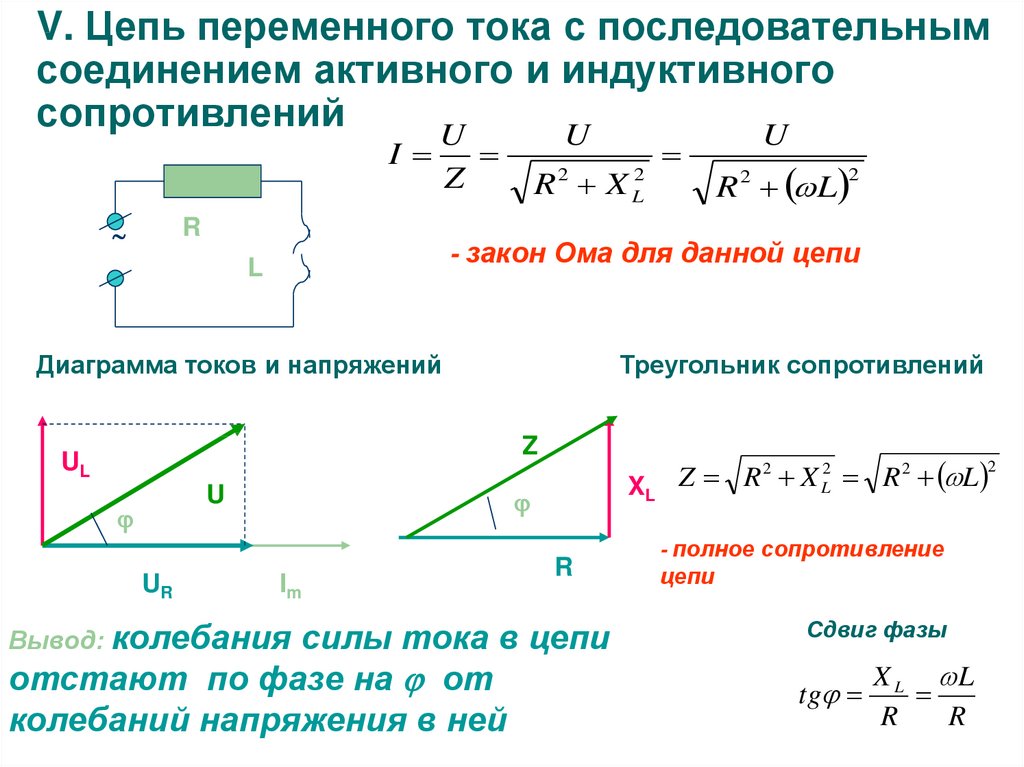 ..
.. 1 Сопротивление переменного тока
1 Сопротивление переменного тока