Физика Длина волны. Скорость волны
Материалы к уроку
Конспект урока
Хорошей моделью образования волны в шнуре может служить цепочка маленьких шариков (точек), массой m каждый, между которыми действует сила упругости. Мы можем вообразить, что между шариками расположены маленькие пружинки. Пусть точка 1 отведена вверх и
отпущена. Пружинка, связывающая ее с точкой 2, при этом растянется, возникнет сила упругости, которая действует не только на точку 1, но и на точку 2. Начнет, следовательно, колебаться и точка 2. Это приведет к деформации следующей пружинки, так что начнет совершать колебания и точка 3 и т.д. Так как у всех шариков одинаковые массы и у всех пружинок одинаковые жесткости, то все шарики будут колебаться (каждый около своего положения равновесия) с одинаковыми периодами и одинаковыми амплитудами. Однако начнутся эти колебания неодновременно. Ведь все шарики обладают инертностью (у них есть масса!) и, значит, на изменение их скорости требуется время. Поэтому вторая точка начнет колебаться позже, чем первая, третья — позже, чем вторая, и т.д. Допустим, что к тому моменту времени, когда точка 1 пройдет путь от положения равновесия до крайнего верхнего положения (на это уйдет четверть периода колебаний), успеют начать колебания точки 2 и 3. Точки, правее третьей, еще покоятся. До них не дошла «очередь». К моменту, когда точка 1 вернется в положение равновесия, начнут свои колебания точки 4—6 и т. д. Через промежуток времени, равный периоду колебаний шариков, шарик 1 завершит свое первое колебание. К этому времени соседняя точка 2 этого сделать не успеет, потому что она начала двигаться позже. Она и закончит свое первое колебание позже точки 1. Еще позже это сделают точки 3, 4 и т. д. На некотором расстоянии от точки 1 находится точка,
Ведь все шарики обладают инертностью (у них есть масса!) и, значит, на изменение их скорости требуется время. Поэтому вторая точка начнет колебаться позже, чем первая, третья — позже, чем вторая, и т.д. Допустим, что к тому моменту времени, когда точка 1 пройдет путь от положения равновесия до крайнего верхнего положения (на это уйдет четверть периода колебаний), успеют начать колебания точки 2 и 3. Точки, правее третьей, еще покоятся. До них не дошла «очередь». К моменту, когда точка 1 вернется в положение равновесия, начнут свои колебания точки 4—6 и т. д. Через промежуток времени, равный периоду колебаний шариков, шарик 1 завершит свое первое колебание. К этому времени соседняя точка 2 этого сделать не успеет, потому что она начала двигаться позже. Она и закончит свое первое колебание позже точки 1. Еще позже это сделают точки 3, 4 и т. д. На некотором расстоянии от точки 1 находится точка,
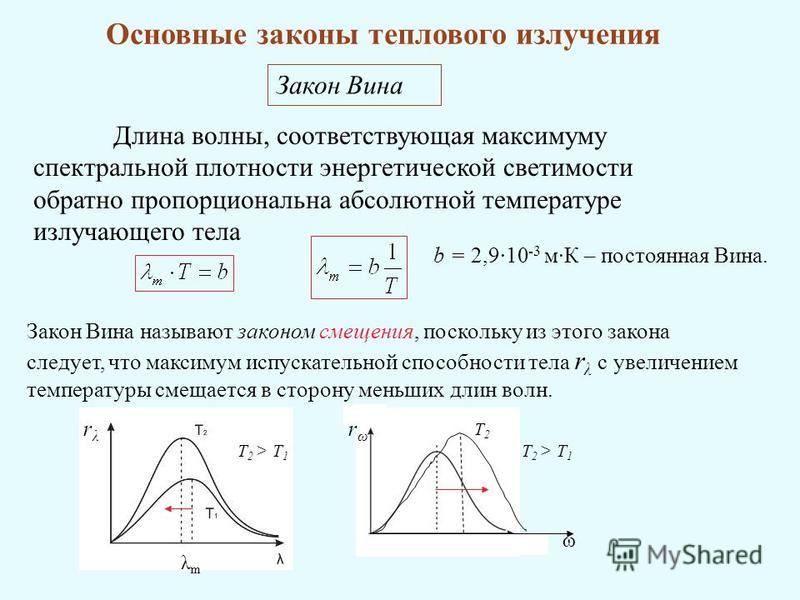 Эта точка начнет свое первое колебание в тот момент, когда точка 1 начнет свое второе колебание. Обозначим расстояние, на которое колебание распространяется за время Т, греческой буквой λ (лямбда). Называется оно длиной волны.
Эта точка начнет свое первое колебание в тот момент, когда точка 1 начнет свое второе колебание. Обозначим расстояние, на которое колебание распространяется за время Т, греческой буквой λ (лямбда). Называется оно длиной волны.Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний. Так как длина волны — это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
где λ — длина волны, v — скорость волны, T — период колебаний.
Учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ (ню), можно вывести связь скорости распространения волны с частотой колебаний:
v=λυ .
Скорость волны равна произведению частоты колебаний в волне на длину волны.
 Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения. Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае. Прежде чем, говорить о решении задач, на применение данных формул, обратимся к стандартным единицам измерения данных физических величин, к Системе Интернациональной.
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения. Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае. Прежде чем, говорить о решении задач, на применение данных формул, обратимся к стандартным единицам измерения данных физических величин, к Системе Интернациональной.Определите, с какой скоростью будет распространяться бегущая волна с частотой 20 Гц и длиной волны 15 м.
Решение. Дана длина волны (лямбда) 15 метров и частота волны (ню) 20 Герц.
 Необходимо определить скорость волны V (вэ). Запишем формулу, для расчета скорости волны. Подставляем числовые значения. 15 метров умножить на 20 Герц, получаем ответ. Скорость волны равна 300 метров в секунду.
Необходимо определить скорость волны V (вэ). Запишем формулу, для расчета скорости волны. Подставляем числовые значения. 15 метров умножить на 20 Герц, получаем ответ. Скорость волны равна 300 метров в секунду.
Задача
На поверхности озера механическая волна движется со скоростью 5,6 м/с. Найдите значение частоты и периода колебаний поплавка удочки, если длина механической волны равна 4 м?
Решение. Скорость волны V (вэ) равна 5,6 метров секунду, длина волны λ (лямбда) равна 4 метрам. Определить период Т (тэ) и частоту волны ν (ню). Запишем формулу для расчета скорости волны. Выразим из данной формулы частоту волны ν (ню). Подставим числовые значения: 5,6 м/с разделить на 4 м. Получим 1,4 Герц. Запишем формулу для расчета периода волны. Период волны (тэ) и частота волны (лямбда) связаны обратно пропорциональной зависимостью. Подставим числовые значения, получим значение периода равное 0,7секунд.
Ответ: частота волны (ню) равна 1,4 Герц, период волны (тэ) равен 0,7 секунды.
Задача
Какая из величин и во сколько раз изменится при переходе звука из воздуха вводу — частота или длина волны? Так как скорость звука в воздухе равна 340 м/с, а в воде 1535 м/с, найдем отношение скоростей в разных средах. Рассчитав, можно сделать вывод о том, что скорость волны больше в воде в 4,5 раза. Между скоростью движения волны V(вэ) и длиной волны λ (лямбда) наблюдается пропорциональная зависимость. Следовательно, длина волны λ в воде больше в 4,5 раза при условии, что частота звуковой волны остается величиной постоянной.
Задача.
На рисунке представлен график механической волны, которая распространяется в воздухе. Используя данные графика, рассчитайте длину данной волны. Период волны Т (тэ) равен 4 секунды; а по условию задачи, волна распространяется в воздухе со скоростью V (вэ), равной 340 м/с. Чтобы определить длину волны λ (лямбда), необходимо скорость волны V (вэ) умножить на период Т (тэ). Подставим числовые значения и получим ответ: длина волны равна 1360 м.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Формула расчета длины волны от частоты
Одна из основных характеристик колебаний. Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты. Получить соотношение, связывающее длину волны с фазовой скоростью и частотой можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний , поэтому. Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p , соответствуют:.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Скорость и длина волны
- Длина волны
- Волны и ветер. Расчет характеристик волны
- Что такое WiFi? Подробно о свойствах WiFi сигнала
- Формула длины волны
- Длина и скорость волны.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Колебания и волны — ещё одна формула для вычисления частоты
Скорость и длина волны
Критическая длина волны для , рассчитывается по формуле. Закон зависимости длины волны в волноводе от длины волны в свободном пространстве носит название дисперсионной характеристики волновода. В явном виде эта характеристика описывается формулой, вытекающей из 8 :. Длина волны в свободном пространстве меньше длины волны в волноводе, обусловленной тем, что волны типа E, и типа H в волноводах с идеально проводящими стенками распространяются с фазовыми скоростями большими, чем скорость света в вакууме.
Закон зависимости длины волны в волноводе от длины волны в свободном пространстве носит название дисперсионной характеристики волновода. В явном виде эта характеристика описывается формулой, вытекающей из 8 :. Длина волны в свободном пространстве меньше длины волны в волноводе, обусловленной тем, что волны типа E, и типа H в волноводах с идеально проводящими стенками распространяются с фазовыми скоростями большими, чем скорость света в вакууме.
Поскольку , и частота связаны очевидным соотношением, то из формулы 8 следует формула для вычисления фазовой скорости :.
При переходе через граничное значение в волноводе имеются уже не бегущие, а экспоненциально затухающие волны. Всю область частот, которой соответствуют , называют областью отсечки. Дата добавления: ; Просмотров: ; Нарушение авторских прав? Нам важно ваше мнение! Был ли полезен опубликованный материал?
Да Нет. Непосредственное вычисление вероятности III. Влияние длины поезда. Продольные и поперечные волны. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение. Звуковые волны. Главная Случайная страница Контакты. Отключите adBlock!
Фазовая скорость. Волновое уравнение. Звуковые волны. Главная Случайная страница Контакты. Отключите adBlock!
Длина волны
Сидящий у реки рыболов заметил, что его поплавок колеблется на волнах так, что за десять секунд совершает десять колебаний. При этом расстояние между гребешками волны оказалось равным 0,5 метра. Какова скорость распространения этой волны? Волна — это распространение колебаний в упругой среде. Надо четко понимать, что распространение волны и перемещение частиц в ней — это совершенно разные вещи: частицы колеблются около положения равновесия, не перемещаясь вместе с волной. Скорость распространения волны — это скорость перемещения гребней и впадин в поперечной волне или сжатий и разрежений в продольной.
Частота свободных колебаний открытого контура зависит от его емкости и получить формулы для расчета собственной длины волны или частоты.
Волны и ветер. Расчет характеристик волны
Здесь вы найдете подходящего репетитора быстро, удобно и бесплатно. Мы всегда рады проконсультировать Вас по вопросам образования. Задайте свои вопросы профессионалам. Совет 1. Чтобы значительно упростить процесс поиска, достаточно лишь позвонить нам, и оператор найдет репетитора, который максимально подходит под ваши требования. Совет 2. Совет 3. Вопреки сложившемуся мнению, студент-репетитор очень хорошо справляется со своей задачей. Он более мобилен, цена ниже, и он с легкостью найдет общий язык с учеником. Абсолютно все в этом мире происходит с какой-либо скоростью.
Мы всегда рады проконсультировать Вас по вопросам образования. Задайте свои вопросы профессионалам. Совет 1. Чтобы значительно упростить процесс поиска, достаточно лишь позвонить нам, и оператор найдет репетитора, который максимально подходит под ваши требования. Совет 2. Совет 3. Вопреки сложившемуся мнению, студент-репетитор очень хорошо справляется со своей задачей. Он более мобилен, цена ниже, и он с легкостью найдет общий язык с учеником. Абсолютно все в этом мире происходит с какой-либо скоростью.
Что такое WiFi? Подробно о свойствах WiFi сигнала
У вас уже есть абонемент? На этом уроке вы сможете познакомиться с особенными характеристиками волн. В первую очередь вы узнаете, что такое длина волны. Мы рассмотрим ее определение, способ ее обозначения и измерения.
Random converter. Этот калькулятор определяет длину волны звуковых колебаний, если известны их частота и скорость распространения звука в среде.
Формула длины волны
В этой статье: Вычисление длины волны по известным скорости и частоте Вычисление длины волны по известной энергии фотона Поиск ошибок 11 Источники. Длина волны — это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие «длина волны» ассоциируется с электромагнитным спектром. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой. В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. Категории: Физика.
Длина волны — это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие «длина волны» ассоциируется с электромагнитным спектром. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой. В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. Категории: Физика.
Длина и скорость волны.
Реклама и пожертвования позволяют нам быть независимыми! Длина волны де Бройля — длина волны , которая проявляется у всех частиц в квантовой механике согласно корпускулярно-волновому дуализму , и определяющая плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства. Длина волны де Бройля обратно пропорциональна импульсу частицы. В году французский физик Луи де Бройль предположил, что для частиц справедливы те же самые соотношения, что и для фотона : [1].
Существует формула, позволяющая определять длину волны по частоте: Высокие частоты (ВЧ-сантиметровый диапазон) v = МГц — 3 ГГц .. В данном случае, для расчётов в физике элементарных частиц.
Что такое WiFi? Связь частоты и длины волны. Свойства WiFi сигнала. Огибание препятствий.
Всего на сайте: тыс. Основываясь на приведенном здесь анализе волн типа Е, найдем связь между продольным волновым числом, двумя геометрическими параметрами волновода — размерами сечения и и длиной волны возбуждающего генератора. Напомним, что входящие в это уравнение постоянная распространения в свободном пространстве и продольное волновое число очень просто связаны с длиной волны генератора и длиной волны в волноводе :. В свою очередь, поперечное волновое число , определяемое формулой , зависит лишь от геометрических размеров сечения и от индексов выбранного типа волны и совершенно не зависит от частоты. Выражение для поперечного волнового числа позволяет вскрыть важнейшую особенность работы любого волновода рассматриваемого типа.
Выражение для поперечного волнового числа позволяет вскрыть важнейшую особенность работы любого волновода рассматриваемого типа.
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой.
Кстати, свет это тоже электромагнитные волны, обладающие схожими с радиоволнами свойствами отражение, преломление, затухание и т. Радиоволны переносят через пространство энергию, излучаемую генератором электромагнитных колебаний. А рождаются они при изменении электрического поля, например, когда через проводник проходит переменный электрический ток или когда через пространство проскакивают искры, то есть ряд быстро следующих друг за другом импульсов тока. Электромагнитное излучение характеризуется частотой, длиной волны и мощностью переносимой энергии. Частота электромагнитных волн показывает, сколько раз в секунду изменяется в излучателе направление электрического тока и, следовательно, сколько раз в секунду изменяется в каждой точке пространства величина электрического и магнитного полей. Измеряется частота в герцах Гц — единицах названных именем великого немецкого ученого Генриха Рудольфа Герца.
Измеряется частота в герцах Гц — единицах названных именем великого немецкого ученого Генриха Рудольфа Герца.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Как правило, длина волны используется применительно к гармоническому или квазигармоническому например, затухающему или узкополосному модулированному волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной наиболее низкочастотной, фундаментальной гармоники спектра.
Определяем, чему равна длина волны — формула расчета. Узнаем как рассчитывается длина звуковой волны
Волна представляет собой возмущение материи, которое, распространяясь в пространстве, переносит энергию без переноса самой материи. Каждая волна имеет определенные характеристики. Одной из важных характеристик процессов возмущения является длина волны, формула для расчета которой приводится в статье.
Каждая волна имеет определенные характеристики. Одной из важных характеристик процессов возмущения является длина волны, формула для расчета которой приводится в статье.
Виды волн
Все волны классифицируют по их физической природе, по типу движения частиц материи, по их периодичности и по способу распространения в пространстве.
Согласно типу движения частиц материи при распространении в ней волны выделяют следующие виды:
- Поперечные волны — это такой тип возмущения, при котором частицы материи колеблются в направлении, которое перпендикулярно направлению распространения волны. Примером поперечной волны является свет.
- Продольные волны — это волны, в которых частицы материи колеблются в направлении распространения волны. Звук является хорошим примером продольной волны.
Согласно физической природе выделяют следующие типы волн:
- Механические. Этому типу волн необходимо вещество, чтобы они возникли, то есть твердая, жидкая или газообразная среда.
 Примером механических волн являются волны на море.
Примером механических волн являются волны на море. - Электромагнитные. Этот тип волн не нуждается в веществе для своего распространения, а может распространяться в вакууме. Ярким примером электромагнитных волн являются радиоволны.
- Гравитационные. Эти волны приводят к возмущению пространства-времени. Порождают такие волны крупные космические объекты, например, двойная звезда, которая вращается вокруг общего центра тяжести.
В соответствии с размерностью волны они могут быть:
- Одномерные, то есть такие, которые распространяются в одном измерении, например, вибрация веревки.
- Двумерные или поверхностные. Эти волны распространяются в двух измерениях, например, волны на поверхности воды.
- Трехмерные или сферические. Эти волны распространяются в трех измерениях, например, свет или звук.
В соответствии с периодичностью волны можно сказать, что существуют:
- Периодические возмущения, которые отличаются строго повторяющимися характеристиками через определенный промежуток времени, например, звуковые волны.

- Не периодические, такие волны не повторяют своих характеристик, через определенные интервалы времени, например, волны электрокардиограммы.
Физические характеристики волны
Волна характеризуется 6 параметрами, из которых только 3 являются независимыми, остальные выводятся из этих трех по соответствующим формулам:
- Длина волны L — расстояние между двумя максимумами волны.
- Высота H — вертикальное расстояние между максимумом и минимумом волны.
- Амплитуда — величина, равная половине высоты.
- Период T — время, за которое два максимума или два минимума волны пройдут через одну и ту же точку пространства.
- Частота — величина обратная периоду волны, то есть она описывает количество максимумов или минимумов, которые проходят через конкретную точку пространства за единицу времени.
- Скорость — величина, характеризующая распространение волны. Она вычисляется по формуле: длина волны делить на период, то есть v = L/T.
Независимыми характеристиками являются, например, длина волны, период и ее амплитуда.
Длина волны
Эта характеристика содержит информацию о волне, которая во многом описывает ее свойства. В физике длина волны определяется как расстояние между двумя ее максимумами (минимумами), или в более общем случае как расстояние между двумя точками, которые колеблются в одной фазе. Под фазой волны понимается мгновенное состояние каждой точки волны. Понятие «фаза» имеет смысл только для периодических волновых процессов. Длина волны обычно обозначается греческой буквой λ (лямбда).
В физике формула для длины волны зависит от начальной информации, которая имеется о данном колебании. Например, в случае электромагнитных колебаний можно знать частоту и скорость распространения волны, а затем для вычисления длины волны применить обычную формулу расчета, либо можно знать энергию отдельного фотона, тогда уже следует применять специфическую формулу именно для энергии.
Синусоидальные волны
Согласно теореме Фурье, любая периодическая волна может быть представлена суммой синусоидальных волн различной длины. Эта теорема позволяет изучать каждую периодическую волну благодаря изучению ее синусоидальных компонентов.
Эта теорема позволяет изучать каждую периодическую волну благодаря изучению ее синусоидальных компонентов.
Для синусоидальной волны с частотой f, периодом T и скоростью распространения v формула длины волны имеет вид: λ = v/f = v*T.
Скорость распространения волны зависит от типа среды, в которой происходит волновой процесс, а также от частоты колебаний. Скорость распространения электромагнитной волны в вакууме является величиной постоянной и приблизительно равна 3*108 м/с.
Звуковые волны
Этот тип механических волн порождается за счет локального изменения давления в веществе, возникающего при колебательных процессах. Например, в воздушной среде речь идет о разряженных и сжатых областях, которые распространяются в виде сферической волны от порождающего их источника. Этот тип волн является периодическим, поэтому формула для длины звуковой волны является такой же, как и для синусоидальной.
Отметим, что в жидкостях и газах могут распространяться только продольные волны, поскольку в этих средах не возникает упругой силы при сдвиге слоев вещества относительно друг друга, в то время как в твердом теле помимо продольных, могут существовать и поперечные волны.
Скорость звуковых волн в различных средах
Скорость распространения таких волн определяется характеристиками колебательной среды: ее давлением, температурой и плотностью вещества. Поскольку элементарные частицы, составляющие твердые тела, находятся ближе друг к другу, чем эти частицы в жидкостях, то такая структура твердого вещества позволяет передавать колебательную энергию через него быстрее, чем через жидкость, поэтому скорость распространения волны в них больше. По этой же причине скорость звука в жидкостях выше, чем в газах.
Данные о скорости звука в некоторых средах:
| среда | воздух, 20 ºC | вода, 22 ºC | дерево | алюминий | стекло | сталь |
| скорость, м/с | 343 | 1505 | 3990 | 5090 | 5190 | 6099 |
В случае воздуха отметим, что Ньютоном была выведена формула для скорости звука в этой среде в зависимости от температуры, которая впоследствии была модифицирована Лапласом. Эта формула имеет вид: v = 331+0,6*t ºC.
Эта формула имеет вид: v = 331+0,6*t ºC.
Таким образом, формула для длины звуковой волны с частотой f в воздухе при 25 ºC приобретет вид: λ = v/f = 346/f.
Электромагнитные волны
В отличие от механических волн, природа которых заключается в возмущении вещества, в котором они распространяются, электромагнитные волны не требуют материи для своего распространения. Они возникают по причине двух эффектов: во-первых, переменное магнитное поле создает электрическое поле, во-вторых, переменное электрическое поле создает магнитное поле. Осциллирующие магнитное и электрическое поля направлены перпендикулярно друг к другу и перпендикулярно к направлению движения волны, поэтому по своей природе электромагнитные волны являются поперечными.
В вакууме эти волны движутся со скоростью 3*108 м/с и могут иметь различные значения частоты, поэтому длина электромагнитной волны выражается в виде: λ = v/f = 3*108/f, где f — частота колебаний.
Спектр электромагнитного излучения
Спектр электромагнитного излучения представляет собой совокупность всех длин электромагнитных волн.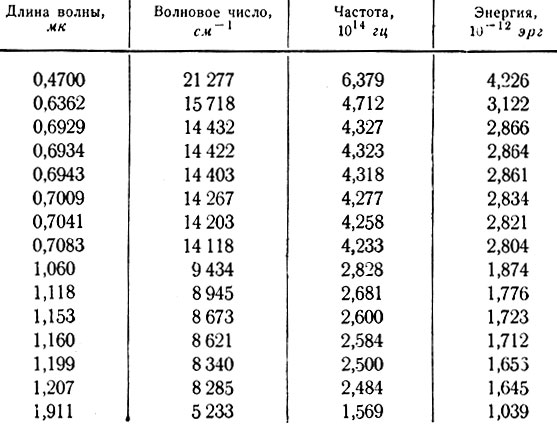 Различают следующие части спектра:
Различают следующие части спектра:
- Радиоэлектрическое излучение. Длина волны спектра для этого излучения составляет от нескольких сантиметров до тысяч километров. Используются эти волны в телевидении и различных типах связи.
- Инфракрасное излучение. Это тепловое излучение имеет длины волн порядка нескольких микрометров.
- Видимый свет. Это та часть спектра, которую человеческий глаз способен различать. Его длина волн находится в пределах от 400 нм (синий) до 700 нм (красный).
- Ультрафиолетовый спектр. Его длины волн лежат в пределах 15-400 нм.
- Рентгеновское излучение. Используется главным образом в медицине. Их длина волны лежит в области 10 нм — 10 пм. Источником их излучения являются колебания электронов в атомах.
- Гамма-лучи. Это самая высокочастотная часть спектра, с длиной волны меньше 10 пк. Гамма-лучи обладают огромной проникающей способностью через любое вещество. Порождаются они в результате процессов, происходящих в ядре атома.

Расчет длины волны через энергию фотона
Очень часто в физике возникают задачи, которые ставят вопрос, чему равна длина волны для фотона, имеющего энергию E. Для решения такого рода задач следует использовать следующую формулу: E=h*c/λ, где c — скорость движения фотона, h — постоянная Планка, которая равна 6,626*10-34 Дж*с.
Из приведенной формулы получим длину волны фотона: λ = h*c/E. Например, пусть энергия фотона E = 2,88*10-19 Дж, а фотон движется в вакууме, то есть c = 3*108 м/с. Тогда получаем: λ = h*c/E = 6,626*10-34*3*108/2,88*10-19 = 6,90*10-7 м = 690 нм. Таким образом, этот фотон имеет длину волны, которая лежит вблизи верхней границы видимого спектра, и будет восприниматься человеком, как красный луч света.
Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)
Регистрация на конференцию «Проблемы безопасности на транспорте»
Как поступить в БелГУТ:
дневное, заочное полное,
заочное сокращенное
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 Дата : 2022-09-01 | 2 | 3 | 4 | |||
5 Дата : 2022-09-05 | 6 Дата : 2022-09-06 | 7 Дата : 2022-09-07 | 8 Дата : 2022-09-08 | 9 Дата : 2022-09-09 | 10 Дата : 2022-09-10 | 11 Дата : 2022-09-11 |
12 | 13 | 14 | 15 Дата : 2022-09-15 | 16 Дата : 2022-09-16 | 17 Дата : 2022-09-17 | 18 |
19 | 20 | 21 Дата : 2022-09-21 | 22 Дата : 2022-09-22 | 23 | 24 | 25 |
26 | 27 | 28 Дата : 2022-09-28 | 29 | 30 Дата : 2022-09-30 | ||
Все анонсы
- С Днем учителя!
- Курсы по 1C, AutoCAD, CorelDRAW, VISIO, Autodesk I.
 ..
.. - Запись на донорство
- Акция «ЭТАЛОН.Студент.by»
- Экспозиции, посвященные Грунтову П.С. и Белому В.А…
- Угадай мелодию
- Открытая лекция Велюгиной Н.Е. «НАДСТРОЙКА, ПРИСТР…
- Конкурс кандидатов в перспективный кадровый резерв…
- Логистика. Обучение для студентов выпускных курсов…
- Турнир на джойстиках по игре в MORTAL COMBAT IX…
Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
С Днем учителя!
Курсы по 1C, AutoCAD, CorelDRAW, VISIO, Autodesk I…
Запись на донорство
Акция «ЭТАЛОН.Студент.by»
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
- Университет
За верность традициям в образовании
30 сентября 2022
- Студенческая жизнь
ВОЛОНТЁРЫ БЕЛГУТА | КОРОТКО О ВАЖНОМ
30 сентября 2022
- Университет
Делегация российского Военного института железнодорожных войск и военн. ..
..
30 сентября 2022
- Университет
День учителя во Дворце Республики
30 сентября 2022
- Студенческая жизнь
Меломаны БелГУТа сыграли в «Угадай мелодию»…
29 сентября 2022
- Воспитательная работа
Наркотики. Ответственность. Последствия…
27 сентября 2022
- Спорт
Победа в соревнованиях по гребле на байдарках…
26 сентября 2022
- Спорт
Команда РОО «Белая Русь» заняла 3 командное место…
26 сентября 2022
- Университет
Участие в V Международном образовательном форуме «Алтай – Азия 2022: Е. ..
..
26 сентября 2022
Другие новости
- Волонтеры студсовета в приюте для бездомных животных…
- Встреча в общежитии «Я выбираю жизнь!»
- Повышение квалификации по теме «Учет труда и заработной платы в органи…
- Тыдзень роднай мовы «Як ты дорага мне, мая родная мова»…
- Турнир по игре на джойстиках в «Mortal Combat» состоялся…
- Против COVID-19 в БелГУТе
- Единый День информирования: «История белорусской государственности – о…
- Сетевое взаимодействие трех университетов…
- Гомельский транспортный прокурор в ИПК и ПК…
- Состязания в рамках всемирного дня студенческого спорта…
- ДИАЛОГ | Выпуск 14 | БелГУТ |ВЛАДИМИР КОЛОТ О ПРОЕКТАХ, ПЛАНАХ И НОЧЁВ…
КУДА ПОСТУПАТЬ
Все факультеты
БелГУТ на Доске почета
Достижения университета
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
Что такое WiFi? Подробно о свойствах WiFi сигнала
на картинке: графическое отображение WiFi волн в городе.
1. Что такое WiFi?
1.1. Связь частоты и длины волны.
2. Свойства WiFi сигнала.
2.1. Поглощение.
2.2. Огибание препятствий.
2.3. Естественное затухание.
2.4. Отражения сигнала.
2.5. Плотность данных.
2.6. Почему сложно дать однозначный ответ: на какое расстояние будет передавать сигнал WiFi оборудование?
3. Диапазоны и частоты WiFi
3.1. Диапазон 2,4 ГГц.
3.2. Диапазон 5 ГГц.
Что такое WiFi?
WiFi — беспроводной способ связи, основанный на всем нам знакомом электромагнитном излучении. Сигнал WiFi относят к радиоволнам, соответственно, он имеет такие же свойства, характеристики и поведение. Радиоволны, в свою очередь, подчиняются практически тем же физическим законам, что и свет: распространяются в пространстве с такой же скоростью (почти 300 000 километров в секунду), подвержены дифракции, поглощению, затуханию, рассеиванию и т. д.
Основные характеристики радиоволны, а значит и сигнала WiFi — это ее длина и частота (частотный диапазон). Последний параметр означает частоту переменного тока, необходимую для получения волны нужной длины и используется для классификации радиоволн. Другое определение частоты — это количество волн, проходящих через определенную точку пространства в секунду.
Последний параметр означает частоту переменного тока, необходимую для получения волны нужной длины и используется для классификации радиоволн. Другое определение частоты — это количество волн, проходящих через определенную точку пространства в секунду.
Существует распределение радиоволн по диапазонам, в зависимости от частоты, утвержденная Международным союзом электросвязи (МСЭ, английская аббревиатура — ITU).
Буквенные обозначения диапазона | Название волн. Название частот. | Диапазон частот | Диапазон длины волны |
| ОНЧ (VLF) | Мириаметровые. Очень низкие | 3—30 кГц | 100–10 км |
| НЧ (LF) | Километровые. Низкие. | 30—300 кГц | 10–1 км |
| СЧ (MF) | Гектометровые. Средние. | 300—3000 кГц | 1–0.1 км |
| ВЧ (HF) | Декаметровые. Высокие. | 3—30 МГц | 100–10 м |
| ОВЧ (VHF) | Метровые. Очень высокие. Очень высокие. | 30—300 МГц | 10–1 м |
| УВЧ (UHF) | Дециметровые. Ультравысокие. | 300—3000 МГц | 1–0.1 м |
| СВЧ (SHF) | Сантиметровые. Сверхвысокие. | 3—30 ГГц | 10–1 см |
| КВЧ (EHF) | Миллиметровые. Крайне высокие. | 30—300 ГГц | 10–1 мм |
| THF | Дециметровые. Гипервысокие. | 300—3000 ГГц | 1–0.1 мм |
Сфера применения радиоволн зависит от частотного диапазона. Это может быть телевидение, радиосвязь, мобильная связь, радиорелейная связь и т. д. Вообще, радиочастотный эфир занят довольно плотно: использование всех диапазонов буквально расписано:
В том числе это и беспроводная связь WiFi. Для нее используются дециметровые и сантиметровые волны ультравысокой и сверхвысокой частоты (УВЧ и СВЧ) в частотных диапазонах 2,4 ГГц, 5 ГГц и и других редкоиспользуемых: 900 МГц, 3,6 ГГц, 10 ГГц, 24 ГГц.
Главное преимущество WiFi-связи отражено во втором ее названии — беспроводная связь. Именно отсутствие проводов вкупе со все возрастающей скоростью передачи данных является ключевым моментом при выборе этого способа соединения.
Именно отсутствие проводов вкупе со все возрастающей скоростью передачи данных является ключевым моментом при выборе этого способа соединения.
Если речь идет о домашних пользователях — беспроводная связь удобна, она позволяет не привязываться к определенному месту в квартире для входа в интернет.
Если мы говорим о корпоративной связи, о провайдерских услугах, то иногда прокладка кабеля для передачи данных — это дорого, нецелесообразно или вообще невозможно. Например, нужно раздать интернет в частном секторе, прокинуть магистральный канал через ущелье, в удаленный населенный пункт и т. д. В этом случае на выручку приходит WiFi. Проблемная территория преодолевается с помощью беспроводного канала.
Связь частоты сигнала WiFi и длины волны
Характеристики длины волны сравнительно редко используются в параметрах оборудования WiFi. Однако иногда, для понимания физических свойств и поведения сигнала беспроводной связи в различных условиях неплохо разбираться в связи частоты и длины радиоволн.
Общее правило: Чем выше частота, тем короче длина волны. И наоборот.
Формула для расчета длины волны:
Длина волны WiFi сигнала (в метрах)= Скорость света (в м/сек) / Частота сигнала (в герцах).
Скорость света в м/сек = 300 000 000.
После упрощения формулы получаем: Длина волны в метрах = 300/ Частота в МГц.
Свойства WiFi сигнала
Поглощение.
Главное условие для создания беспроводного линка на расстояние большее, чем сотня метров — прямая видимость между точками установки оборудования. Проще говоря, если мы стоим рядом с одной точкой доступа WiFi, то наш взгляд, направленный в сторону второй точки, не должен упираться в стену, лес, многоэтажный дом, холм и т. д. (Это еще не все, нужно также учитывать помехи в Зоне Френеля, но об этом в другой статье.)
Такие объекты просто-напросто отражают и поглощают сигнал WiFi, если не весь, то львиную его часть.
То же самое происходит и в помещении, где сигнал от WiFi роутера или точки доступа проходит через стены в другие комнаты/на другие этажи. Каждая стена или перекрытие «отбирает» у сигнала некоторое количество эффективности.
На небольшом расстоянии, например, от комнатного роутера до ноута, у радиосигнала еще есть шансы, преодолев стену, все-таки добраться до цели. А вот на длинной дистанции в несколько километров любое такое ослабление существенно сказывается на качестве и дальности WiFi связи.
Процент ухудшения сигнала вай-фай при прохождении через препятствия зависит от нескольких факторов:
- Длины волны. В теории, чем больше длина волны (и ниже частота вай-фай), тем больше проникающая способность сигнала. Соответственно, WiFi в диапазоне 2,4 ГГц имеет большую проникающую способность, чем в диапазоне 5 ГГц. В реальных условиях выполнение этого правила очень тесно зависит от того, через препятствие какой структуры и состава проходит сигнал.

- Материала препятствия, точнее, его диэлектрических свойств.
Преграда | Дополнительные потери при прохождении (dB) | Процент эффективного расстояния*, % |
Открытое пространство | 0 | 100 |
Нетонированное окно (отсутствует металлизированное покрытие) | 3 | 70 |
Окно с металлизированным покрытием (тонировкой) | 5-8 | 50 |
Деревянная стена | 10 | 30 |
Стена 15,2 см (межкомнатная) | 15-20 | 15 |
Стена 30,5 см (несущая) | 20-25 | 10 |
Бетонный пол или потолок | 15-25 | 10-15 |
Цельное железобетонное перекрытие | 20-25 | 10 |
* Процент эффективного расстояния — эта величина означает, какой процент от первоначально рассчитанной дальности (на открытой местности) сможет пройти сигнал после преодоления препятствия.
Например, если на открытой местности дальность сигнала Wi-Fi — до 200 метров, то после прохождения через нетонированное окно она уменьшится до 140 метров (200 * 70% = 140). Если следующим препятствием для этого же сигнала станет бетонная стена, то после нее дальность составит уже максимум 21 метр (140*15%).
Отметим, что вода и металл — самые эффективные поглотители WiFi, т. к. являются электрическими проводниками и «забирают» на себя большое количество энергии сигнала. Например, если дома на пути вай-фай от роутера до вашего ноута стоит аквариум, то практически наверняка соединения не будет.
Именно поэтому во время дождя и других «влажных» атмосферных осадков наблюдается небольшое снижение качества беспроводного соединения, поскольку капли воды в атмосфере поглощают сигнал.
Частично этот фактор влияет и на затухание WiFi передачи в листве деревьев, т. к. они содержат большой процент воды.
- Угла падения луча на препятствие.
 Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Огибание препятствий.
По-научному это поведение луча WiFi называется дифракцией, хотя на самом деле понятие дифракции гораздо сложнее, чем простое «огибание препятствий».
В общем можно вывести правило — чем короче длина волны (выше частота), тем хуже она огибает препятствия.
Основывается это правило на известном физическом свойстве волны: если размер препятствия меньше, чем длина волны, то она его огибает. В целом отсюда логично проистекает, что чем короче длина волны, тем меньшее остается вариантов препятствий, которые она может в принципе обойти, и поэтому принимается, что ее огибающая способность хуже.
Огибание на практике означает меньшее рассеивание волны как луча энергии вокруг препятствия, меньшее количество потерь сигнала.
Возьмем популярные частоты 2,4 ГГц (длина волны 12,5 см) и 5 ГГц (длина волны 6 см). Мы видим подтверждение правила на примере прохождения лесного массива. Стандартные размеры листьев, стволов, веток деревьев, в среднем будут меньше, чем 12,5 см, но больше, чем 6 см. Поэтому сигнал WiFi 5 ГГц диапазона при прохождении через густую листву “потеряется” практически полностью, в то время как 2,4 ГГц справится лучше.
Поэтому WiFi оборудование, работающее в диапазоне 900 МГц, используется в условиях отсутствия прямой видимости сигнала — его длина волны составляет 33,3 см, что позволяет огибать большее количество преград. Однако надо учитывать размеры предполагаемых препятствий и понимать, что сигнал 900 МГц не сможет “обойти” бетонную стену, расположенную перепендикулярно направлению сигнала. Здесь уже сыграют роль проникающие способности волны, которые, как мы уже говорили у сигналов с низкой частотой довольно неплохие.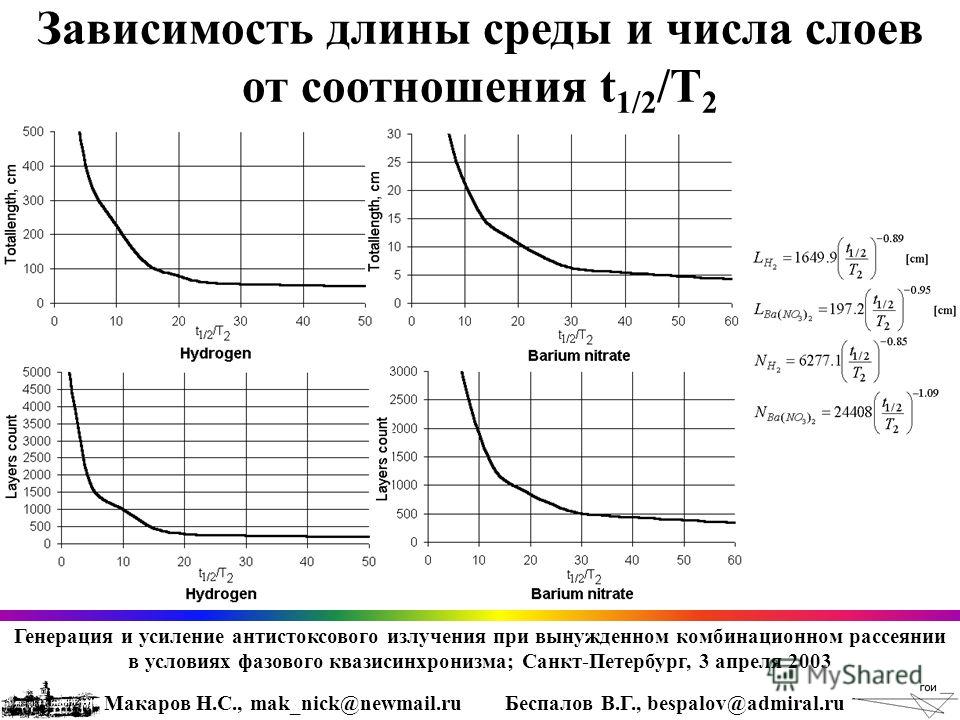
Также именно поэтому для нормальной работы беспроводного оборудования, использующего частоту 24ГГц (длина волны 1,25 см) необходима абсолютно чистая видимость, потому что все препятствия больше сантиметра будут отражать и поглощать сигнал.
Как мы уже упоминали, в отношении прохождении сигнала через лесной массив играет роль также содержание воды в листьях, а также длина волны.
Естественное затухание.
Как далеко мог бы передаваться сигнал WiFi, если создать ему идеальные условия прямой видимости? В любом случае не бесконечно, потому что чем больше дальность беспроводного “пролета”, тем больше сигнал затухает сам по себе. Происходит это по 2 причинам:
Земная поверхность поглощает часть энергии сигнала. Чем выше частота WiFi, тем интенсивнее идет поглощение.
Сигнал WiFi даже из самой узконаправленной антенны распространяется не прямой линией, а лучом.
 Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Отражения сигнала.
Сигнал WiFi, как любая радиоволна, как свет, отражается от поверхностей и ведет себя при этом аналогично. Но тут есть нюансы — какие-то поверхности будут поглощать сигнал (полностью или частично), а какие-то — отражать (полностью или частично). Это зависит от материала поверхности, его структуры, наличия неровностей на поверхности и частоты WiFi.
Неконтролируемые отражения сигнала ухудшают его качество. Частично — из-за потери общей энергии сигнала (до принимающей антенны, упрощенно говоря, “долетает не всё” или долетает после переотражений, с задержками). Частично — из-за интерференции с негативным влиянием, когда волны накладываются в противофазе и ослабляют друг друга.
Интерференция может иметь и положительное влияние, если волны WiFi накладываются друг на друга в одинаковых фазах. Это часто используется для усиления мощности сигнала.
Плотность данных.
Частота WiFi влияет также на еще один важный параметр — объем передаваемых данных. Здесь существует прямая связь — чем выше частота, тем больше данных в единицу времени можно передать. Возможно, именно поэтому первая высокопроизводительная РРЛ от Ubiquiti — AirFiber 24, а также ее более мощная модификация — Airfiber 24HD были выпущены на частоте 24 ГГц.
Почему сложно дать однозначный ответ: на какое расстояние будет передавать сигнал WiFi оборудование?
Физические свойства и поведение радиоволны в окружающем мире довольно сложны. Нельзя взять какой-то один параметр и по нему рассчитать дальность беспроводного сигнала. В каждом конкретном случае на дальность будут оказывать влияние различные факторы окружающей среды:
В каждом конкретном случае на дальность будут оказывать влияние различные факторы окружающей среды:
- Поглощение сигнала препятствиями, земной корой, поверхностью водоемов.
- Дифракция и рассеивание сигнала из-за преград на пути.
- Отражения сигнала от препятствий, земли, воды и возникающие в результате этого интерференции волны.
- На больших расстояниях — радиогоризонт, т. е. искривление земной коры.
- Зона Френеля и, соответственно — высота расположения оборудования над поверхностью земли.
Именно поэтому реальная дальность оборудования, как, впрочем, и пропускная способность, может очень сильно отличаться в различных условиях.
Диапазоны и частоты WiFi
Как мы уже сказали, для WiFi связи выделено несколько разных частотных диапазонов: 900 МГц, 2,4 ГГц, 3,65 ГГц, 5 ГГц, 10 ГГц, 24 ГГц.
В Украине на данный момент чаще всего применяются точки доступа WiFi и антенны WiFi 2,4 ГГц и 5ГГц.
Основные отличия 2,4 ГГц и 5ГГц:
2,4 ГГц. Длина волны 12,5 см. Относится к дециметровым волнам ультравысокой частоты (УВЧ).
- В реальных условиях — меньшая дальность сигнала из-за более широкой зоны Френеля, что чаще всего не компенсируется тем, что сигнал на этой частоте меньше подвержен естественному затуханию.
- Лучшее преодоление небольших преград, например, густых лесных массивов, благодаря хорошей проникающей способности и огибанию препятствий.
- Меньше относительно неперекрывающихся каналов (всего 3), а значит, “ пробки на дорогах” — теснота в эфире, и как результат — плохая связь.
- Дополнительная зашумленность эфира другими устройствами, работающими на этой же частоте, в том числе мобильных телефонов, микроволновок и т. п.
5 ГГц. Длина волны 6 см. Относится к сантиметровым волнам сверхвысокой частоты (СВЧ).
- Большее количество относительно неперекрывающихся каналов (19).

- Большая емкость данных.
- Большая дальность сигнала, в связи с тем, что Зона Френеля меньше.
- Такие препятствия, как листва деревьев, стены волны диапазона 5ГГц преодолевают гораздо хуже, чем 2,4.
Диапазоны 900 МГц, 3,6 ГГц, 10 ГГц, 24 ГГц для нас скорее экзотика, однако могут использоваться:
Для работы в условиях, когда стандартные диапазоны плотно заняты.
Если требуется создать беспроводное соединение между двумя точками при отсутствии прямой видимости (лес и другие препятствия). Это касается такой частоты, как 900 МГц (в нашей стране ее нужно использовать с осторожностью, так как на ней работают сотовые операторы).
Если для использования частоты не требуется получать лицензию в контролирующих органах. Такое преимущество часто встречается в презентациях зарубежных производителей, однако для Украины это не совсем актуально, так как условия лицензирования в нашей стране другие.

В IEEE ведутся разработки по принятию новых стандартов и, соответственно, использованию других частот для WiFi. Не исключено, к примеру, что в ближайшее время диапазон 60 ГГц также станет использоваться для беспроводной передачи. Точно также, как и возможна вероятность “отжатия” в будущем некоторых частот, сейчас принадлежащих WiFi, в пользу, например, сотовых операторов.
Зависимость интенсивности рассеянного света от частоты света
Из экспериментов известно, что сильнее всего рассеивается коротковолновое излучение (фиолетовый и синий свет). Это явление в XIX веке объяснил Рэлей. Основным положением, от которого отталкивался ученый, стало то, что в центрах рассеяния под воздействием электромагнитной волны появляются вынужденные колебания, частота которых равна частоте волны. В таком случае центр рассеивания можно считать микро диполем, совершающим колебания, соответственно, излучающим вторичные волны. Дипольный момент такого диполя равен:
где $E_0{cos \left(\omega t\right)\ }$ — член, определяющий колебания напряженности электрического поля волны коллинеарной оси $Z$ в плоскости $Y=0$, $m$ — масса электрона, $q_e$ — его заряд, ${\omega }_0$ — собственная частота колебаний электрона, которая определяется силой упругости, которая удерживает электрон в положении равновесия. 2},$ который опирается на элемент площади $d\sigma $ равен:
2},$ который опирается на элемент площади $d\sigma $ равен:
Интенсивность рассеяния ($I_1(\theta ,\varphi )$) определена как:
Надо отметить, что выражение (8) задает плотность энергии рассеянного потока от одного элементарного излучателя. Данное выражение чаще представляют в виде:
где $\left\langle P_0\right\rangle $ — среднее значение потока энергии в падающей волне.
В том случае, если размеры рассеивателя много меньше длины волны, то все элементарные диполи излучают когерентно. Под рассеянием Рэлея понимают рассеяние молекулами вещества, следовательно, их размер обычно много меньше длины волны видимого света. Элементарные рассеиватели относят к разным молекулам, они излучают некогерентно. Учитывая вышесказанное, сделаем вывод о том, что интенсивность рассеянной волны от одной молекулы увеличивается пропорционально квадрату количества элементарных рассеивателей ($N_0$) в ней. Если концентрацию молекул обозначить как N. Тогда в единице объема содержится $NN_0$ элементарных диполей. Используя известное соотношение:
Используя известное соотношение:
где $n$ — показатель преломления вещества. Подставим в (9) левую часть формулы (10) вместо соответствующего выражения, получим интенсивность рассеяния от одной молекулы:
Полученная формула справедлива, когда собственная частота ${\omega }_0$ много больше частот видимого света и ближнего ультрафиолета. Если все частоты электронов одинаковы, то полная интенсивность рассеяния одной частицей по всем направления равна:
Для вычисления интенсивности рассеяния в единице объема используют при рассеянии в неплотных газах формулу:
Соответственно это выражение можно преобразовать и получить зависимость $I_V$ от частоты:
Так, Рэлей показал, что при прочих равных условиях интенсивность света, рассеиваемого частицей пропорциональна четвертой степени частоты волны света или обратно пропорциональна четвертой степени длины волны (закон Рэлея).
Из формулы Рэлея следует, что интенсивность света связана с углом рассеяния.
Можно представить интенсивность рассеянного света в зависимости от угла рассеяния:
где $\varphi -\ $угол рассеивания, $N\ $ — концентрация рассеивающих объектов$\ (молекул),\ \ $ Изменение интенсивности симметрично относительно первоначальному распространению пучка света. 4}\left\langle P_0\right\rangle \left(2.1\right).\]
4}\left\langle P_0\right\rangle \left(2.1\right).\]
В числителе мы видим показатель преломления ($n)$ , который сам пропорционален концентрации ($n\sim N$). Показатель преломления возведен в квадрат, получается, что как и следовало ожидать $I_V\sim N.$ Интенсивность рассеянного света тем больше, чем выше концентрация рассеивающих частиц.
17.2 Скорость звука | University Physics Volume 1
Звук, как и все волны, распространяется с определенной скоростью и обладает свойствами частоты и длины волны. Вы можете наблюдать прямое свидетельство скорости звука, наблюдая за фейерверком ((Рисунок)). Вы видите вспышку взрыва задолго до того, как услышите его звук и, возможно, почувствуете волну давления, подразумевая, что звук распространяется с конечной скоростью и что он намного медленнее света.
Разницу между скоростью света и скоростью звука можно ощутить и во время грозы. Вспышку молнии часто можно увидеть перед ударом грома. Возможно, вы слышали, что если посчитать количество секунд между вспышкой и звуком, то можно оценить расстояние до источника. Каждые пять секунд преобразуются примерно в одну милю. Скорость любой волны связана с ее частотой и длиной волны как
Каждые пять секунд преобразуются примерно в одну милю. Скорость любой волны связана с ее частотой и длиной волны как
, где v — скорость волны, f — ее частота, а [латекс] \лямбда [/латекс] — ее длина волны. Вспомним из книги «Волны», что длина волны — это длина волны, измеренная между последовательными идентичными точками. Например, для поверхностной водной волны или синусоидальной волны на струне длина волны может быть измерена между любыми двумя удобными последовательными точками с одинаковой высотой и наклоном, например, между двумя последовательными гребнями или двумя последовательными впадинами. Точно так же длина волны звуковой волны — это расстояние между последовательными идентичными частями волны, например, между последовательными сжатиями ((Рисунок)). Частота такая же, как и у источника, и представляет собой количество волн, проходящих через точку в единицу времени.
Скорость звука в различных средах
(Рисунок) показывает, что скорость звука сильно различается в разных средах. Скорость звука в среде зависит от того, насколько быстро вибрационная энергия может передаваться через среду. По этой причине вывод скорости звука в среде зависит от среды и от состояния среды. В общем, уравнение для скорости механической волны в среде зависит от квадратного корня из восстанавливающей силы или свойства упругости, деленного на свойство инерции, 9{2}}. [/latex]
Скорость звука в среде зависит от того, насколько быстро вибрационная энергия может передаваться через среду. По этой причине вывод скорости звука в среде зависит от среды и от состояния среды. В общем, уравнение для скорости механической волны в среде зависит от квадратного корня из восстанавливающей силы или свойства упругости, деленного на свойство инерции, 9{2}}. [/latex]
Напомним из Waves, что скорость волны на струне равна [latex] v=\sqrt{\frac{{F}_{T}}{\mu }}, [/latex] где восстанавливающая сила — это натяжение струны [латекс] {F}_{T} [/латекс], а линейная плотность [латекс] \mu [/латекс] — инерционное свойство. В жидкости скорость звука зависит от объемного модуля и плотности:
[латекс] v=\sqrt{\frac{\beta}{\rho}}. [/latex]
Скорость звука в твердом теле зависит от модуля Юнга среды и плотности,
[латекс] v=\sqrt{\frac{Y}{\rho}}. [/латекс]
В идеальном газе (см. Кинетическая теория газов во втором томе этого текста) уравнение для скорости звука имеет вид
[латекс] v=\sqrt{\frac{\gamma R {T}_{\text{K}}}{M}}, [/latex]
, где [латекс] \gamma [/латекс] — показатель адиабаты, [латекс] R=8,31\,\текст{J /mol}·\text{K} [/latex] — газовая постоянная, [latex] {T}_{\text{K}} [/latex] — абсолютная температура в кельвинах, M — молекулярная масса. В общем, чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта, измеряемой k , жесткость пружины. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна м , массе колеблющегося тела. Скорость звука в воздухе мала, потому что воздух легко сжимается. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах.
В общем, чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта, измеряемой k , жесткость пружины. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна м , массе колеблющегося тела. Скорость звука в воздухе мала, потому что воздух легко сжимается. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах.
Поскольку скорость звука зависит от плотности материала, а плотность зависит от температуры, существует зависимость между температурой в данной среде и скоростью звука в среде.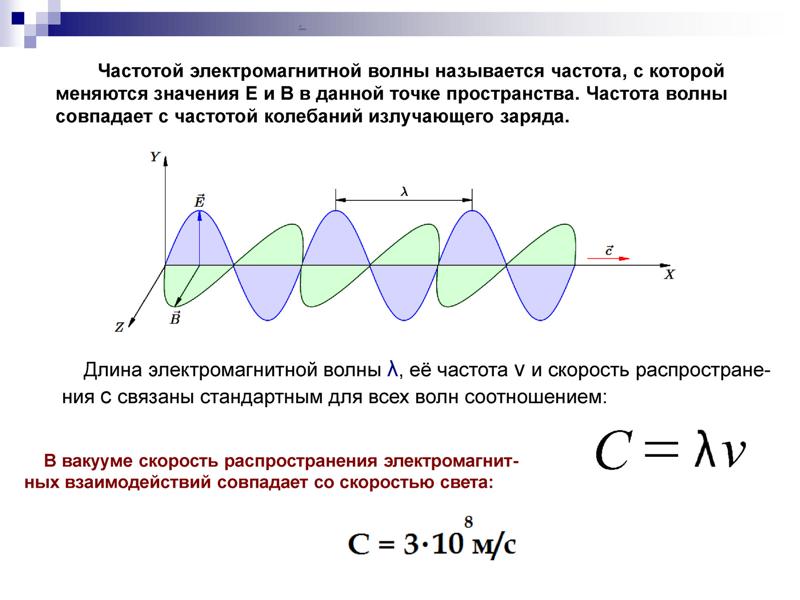 { -23}\,\text{J/K}) [/latex] и m — масса каждой (идентичной) частицы в газе. Обратите внимание, что v относится к скорости когерентного распространения возмущения (волны), тогда как [latex] {v}_{\text{rms}} [/latex] описывает скорости частиц в случайных направлениях. Таким образом, разумно, что скорость звука в воздухе и других газах должна зависеть от квадратного корня из температуры. Хотя это и не пренебрежимо мало, это не сильная зависимость. При [латексе] 0\text{°C} [/latex] скорость звука составляет 331 м/с, а при [латексе] 20,0\text{°C} [/латекс] — 343 м/с, менее чем на [латекс] 4\text{%} [/латекс]. (Рисунок) показывает, как летучая мышь использует скорость звука для определения расстояния.
{ -23}\,\text{J/K}) [/latex] и m — масса каждой (идентичной) частицы в газе. Обратите внимание, что v относится к скорости когерентного распространения возмущения (волны), тогда как [latex] {v}_{\text{rms}} [/latex] описывает скорости частиц в случайных направлениях. Таким образом, разумно, что скорость звука в воздухе и других газах должна зависеть от квадратного корня из температуры. Хотя это и не пренебрежимо мало, это не сильная зависимость. При [латексе] 0\text{°C} [/latex] скорость звука составляет 331 м/с, а при [латексе] 20,0\text{°C} [/латекс] — 343 м/с, менее чем на [латекс] 4\text{%} [/латекс]. (Рисунок) показывает, как летучая мышь использует скорость звука для определения расстояния.
Рисунок 17.6 Летучая мышь использует звуковое эхо, чтобы ориентироваться и ловить добычу. Время возвращения эха прямо пропорционально расстоянию.
Расчет скорости звука в воздухе
Как уже говорилось ранее, скорость звука в среде зависит от среды и состояния среды.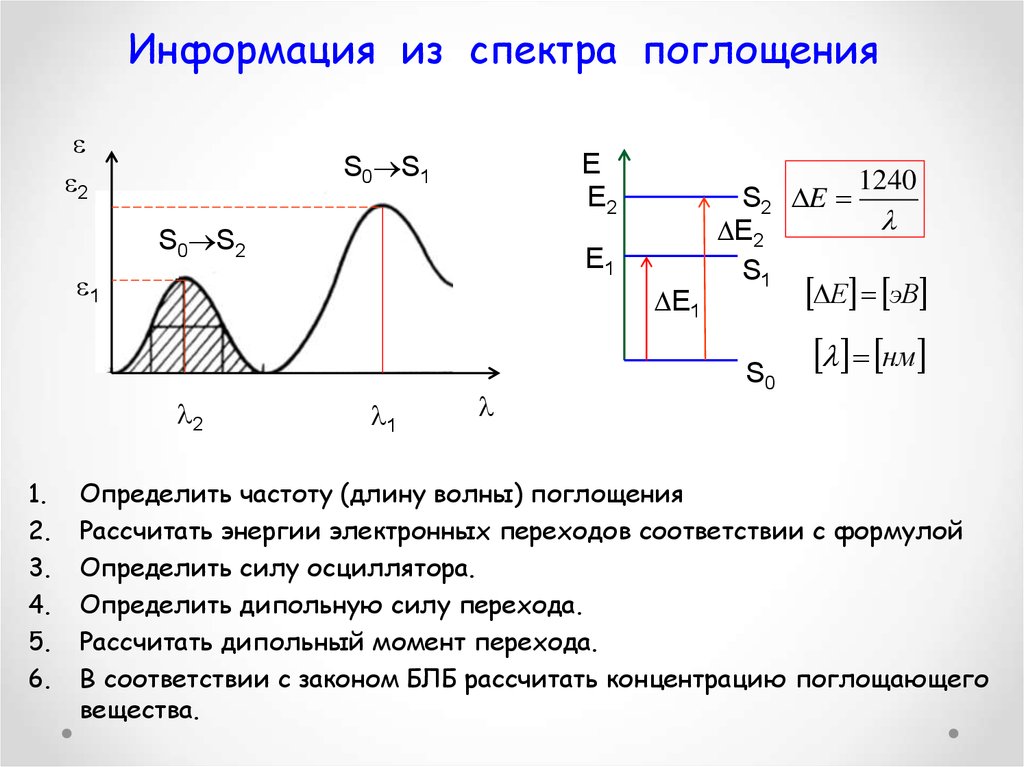 Вывод уравнения для скорости звука в воздухе начинается с массового расхода и уравнения неразрывности, обсуждаемых в механике жидкости.
Вывод уравнения для скорости звука в воздухе начинается с массового расхода и уравнения неразрывности, обсуждаемых в механике жидкости.
Рассмотрим поток жидкости по трубе с площадью поперечного сечения А ((Рисунок)). Масса в небольшом объеме трубы длиной x равна произведению плотности на объем, или [латекс] m=\rho V=\rho Ax. [/latex] Массовый расход
[латекс] \frac{dm}{dt}=\frac{d}{dt}(\rho V)=\frac{d}{dt}(\rho Ax) =\rho A\frac{dx}{dt}=\rho Av. [/latex]
Уравнение неразрывности из механики жидкости утверждает, что массовый расход в объеме должен равняться массовому расходу из объема, [латекс] {\ rho } _ {\ text {in}} {A } _ {\ text {in}} {v} _ {\ text {in}} = {\ rho} _ {\ text {out}} {A} _ {\ text {out}} {v} _ {\ текст{выход}}. [/латекс]
Рисунок 17.7 Масса жидкости в объеме равна произведению плотности на объем, [латекс] m=\rho V=\rho Ax. [/latex] Массовый расход представляет собой производную массы по времени.
Теперь рассмотрим звуковую волну, проходящую через воздушный поток. Воздушная посылка представляет собой небольшой объем воздуха с воображаемыми границами ((Рисунок)). Плотность, температура и скорость на одной стороне объема жидкости задаются как [латекс] \rho ,T,v, [/латекс], а на другой стороне как [латекс] \rho +d\rho ,T +дТ,в+дв. [/латекс]
Воздушная посылка представляет собой небольшой объем воздуха с воображаемыми границами ((Рисунок)). Плотность, температура и скорость на одной стороне объема жидкости задаются как [латекс] \rho ,T,v, [/латекс], а на другой стороне как [латекс] \rho +d\rho ,T +дТ,в+дв. [/латекс]
Рисунок 17.8 Звуковая волна проходит через объем жидкости. Плотность, температура и скорость жидкости изменяются с одной стороны на другую.
Уравнение неразрывности утверждает, что массовый расход, входящий в объем, равен массовому расходу, выходящему из объема, поэтому
[латекс] \rho Av=(\rho +d\rho )A(v+dv). [/latex]
Это уравнение можно упростить, заметив, что площадь сокращается, и учитывая, что умножение двух бесконечно малых приблизительно равно нулю: [latex] d\rho (dv)\приблизительно 0, [/latex]
[латекс] \begin{array}{ccc}\hfill \rho v& =\hfill & (\rho +d\rho )(v+dv)\hfill \\ \hfill \rho v& =\hfill & \rho v+\rho (dv)+(d\rho )v+(d\rho )(dv)\hfill \\ \hfill 0& =\hfill & \rho (dv)+(d\rho )v\hfill \\ \hfill \rho \,dv& =\hfill & \text{−}vd\rho .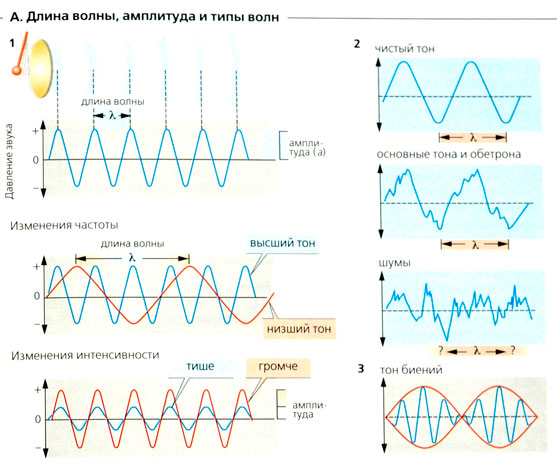 \hfill \end{array} [/latex]
\hfill \end{array} [/latex]
Суммарная сила, действующая на объем жидкости ((Рисунок)) равна сумме сил на левой грани и правой грани:
[латекс] \begin{array}{ccc}\hfill {F}_{\text{net}}& =\hfill & p\,dy\,dz-(p +dp)dy\,dz\hfill \\ & =\hfill & p\,dy\,dz-pdy\,dz-dp\,dy\,dz\hfill \\ & =\hfill & \text{−} dp\,dy\,dz\hfill \\ \hfill ma& =\hfill & \text{−}dp\,dy\,dz.\hfill \end{array} [/latex]
Рисунок 17.9 Звуковая волна проходит через объем жидкости. Сила, действующая на каждую грань, может быть найдена путем умножения давления на площадь.
Ускорение равно силе, деленной на массу, а масса равна произведению плотности на объем, [латекс] m=\rho V=\rho \,dx\,dy\,dz. [/latex] У нас есть
[латекс] \begin{array}{ccc}\hfill ma& =\hfill & \text{−}dp\,dy\,dz\hfill \\ \hfill a& =\hfill & — \frac{dp\,dy\,dz}{m}=-\frac{dp\,dy\,dz}{\rho \,dx\,dy\,dz}=-\frac{dp}{(\ rho \,dx)}\hfill \\ \hfill \frac{dv}{dt}& =\hfill & -\frac{dp}{(\rho \,dx)}\hfill \\ \hfill dv& =\hfill & -\frac{dp}{(\rho \,dx)}dt=-\frac{dp}{\rho }\,\frac{1}{v}\hfill \\ \hfill \rho v\,dv& =\hfill & \text{−}dp. {\gamma}=\text{константа,} [/латекс] где 9{\gamma}=\text{constant}\text{.} [/latex] Беря натуральный логарифм обеих сторон, получаем [latex] \text{ln}\,p-\gamma \,\text{ln}\, \rho =\text{constant}\text{.} [/latex] Дифференцируя по плотности, уравнение принимает вид
{\gamma}=\text{константа,} [/латекс] где 9{\gamma}=\text{constant}\text{.} [/latex] Беря натуральный логарифм обеих сторон, получаем [latex] \text{ln}\,p-\gamma \,\text{ln}\, \rho =\text{constant}\text{.} [/latex] Дифференцируя по плотности, уравнение принимает вид
[latex] \begin{array}{ccc}\hfill \text{ln}\,p -\gamma \,\text{ln}\,\rho & =\hfill & \text{константа}\hfill \\ \hfill \frac{d}{d\rho }(\text{ln}\,p- \gamma \,\text{ln}\,\rho )& =\hfill & \frac{d}{d\rho }(\text{константа})\hfill \\ \hfill \frac{1}{p} \,\frac{dp}{d\rho}-\frac{\gamma}{\rho}& =\hfill & 0\hfill \\ \hfill \frac{dp}{d\rho}& =\hfill & \frac{\gamma p}{\rho}.\hfill \end{массив} [/latex]
Если воздух можно считать идеальным газом, мы можем использовать закон идеального газа:
[латекс] \begin{array}{ccc}\hfill pV& =\hfill & nRT=\frac{m}{M} RT\hfill \\ \hfill p& =\hfill & \frac{m}{V}\,\frac{RT}{M}=\rho \frac{RT}{M}.\hfill \end{array} [ /латекс]
Здесь M — молярная масса воздуха:
[латекс] \frac{dp}{d\rho }=\frac{\gamma p}{\rho }=\frac{\gamma ( \rho \frac{RT}{M})}{\rho}=\frac{\gamma RT}{M}.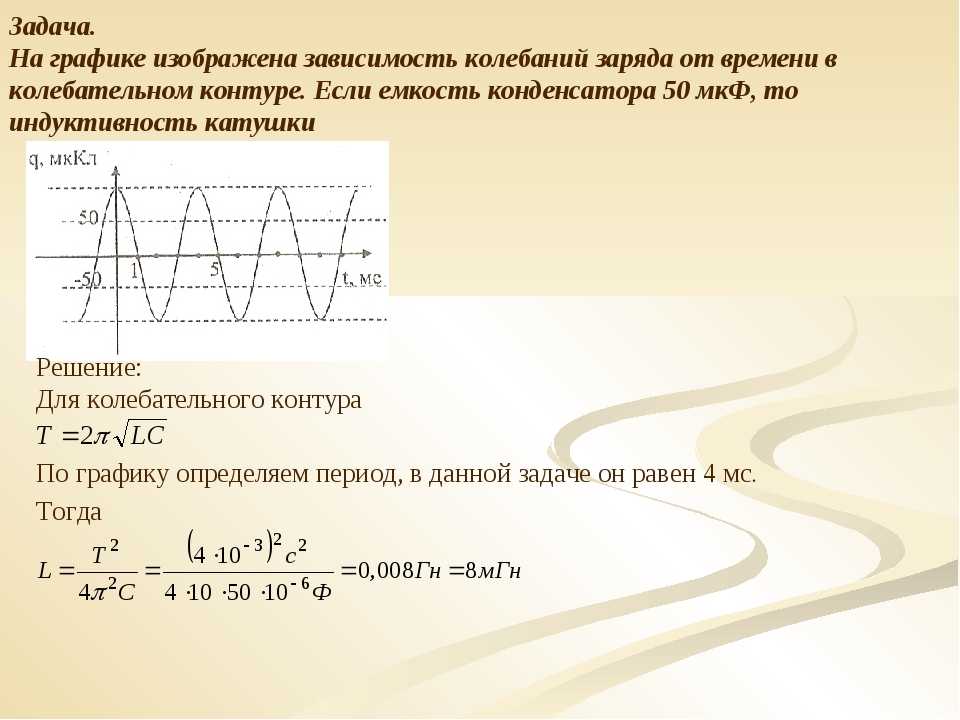 [/latex]
[/latex]
Так как скорость звука равна [latex] v=\sqrt{\frac{dp}{d\rho }} [/latex], скорость равна
[латекс] v=\sqrt{\frac{\gamma \,RT}{M}}. [/latex]
Обратите внимание, что скорость выше при более высоких температурах и ниже при более тяжелых газах. Для воздуха [латекс] \gamma =1,4, [/латекс] [латекс] M=0,02897\frac{\text{кг}}{\text{моль}}, [/латекс] и [латекс] R=8,31\ frac{\text{J}}{\text{mol}·\text{K}}. [/latex] Если температура [латекс] {T}_{\text{C}}=20\text{°}\text{C}(T=293\,\text{K}), [/latex ] скорость звука [латекс] v=343\,\text{м/с}\текст{.} [/латекс]
Уравнение скорости звука в воздухе [латекс] v=\sqrt{\ frac{\gamma RT}{M}} [/latex] можно упростить, чтобы получить уравнение для скорости звука в воздухе как функции абсолютной температуры:
[латекс] \begin{array}{cc}\hfill v& =\sqrt{\frac{\gamma RT}{M}}\hfill \\ & =\sqrt{\frac{\gamma RT}{M} (\ frac {273 \, \ text {K}} {273 \, \ text {K}})} = \ sqrt {\ frac {(273 \, \ text {K}) \ gamma R} {M}} \ sqrt {\ frac {T} {273 \, \ text {K}}} \ hfill \\ & \ приблизительно 331 \ frac {\ text {m}} {\ text {s}} \ sqrt {\ frac {T }{273\,\text{K}}.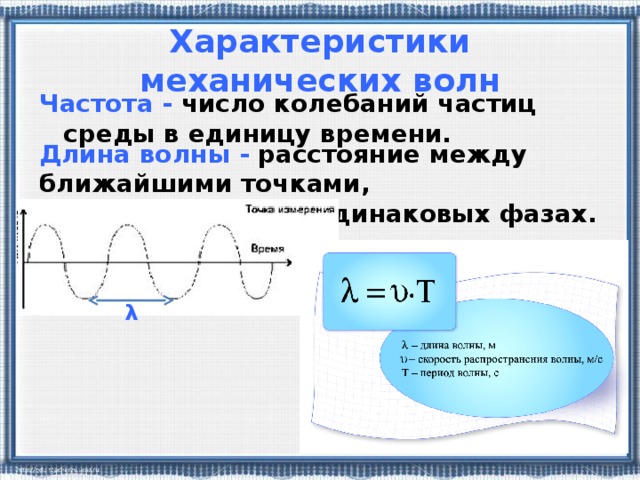 }\hfill \end{array} [/latex]
}\hfill \end{array} [/latex]
Одним из наиболее важных свойств звука является то, что его скорость почти не зависит от частоты. Эта независимость, безусловно, верна для звуков в слышимом диапазоне на открытом воздухе. Если бы эта независимость не была истинной, вы бы наверняка заметили ее в музыке, которую играет марширующий оркестр, например, на футбольном стадионе. Предположим, что высокочастотные звуки распространяются быстрее — тогда чем дальше вы находитесь от группы, тем больше звук низкочастотных инструментов будет отставать от высокочастотных. Но музыка всех инструментов доносится с ритмом, не зависящим от расстояния, поэтому все частоты должны распространяться почти с одинаковой скоростью. Напомним, что
[латекс] v=f\лямбда . [/latex]
В данной среде при фиксированных условиях v постоянно, поэтому существует связь между f и [latex] \lambda ; [/latex] чем выше частота, тем меньше длина волны ((Рисунок)).
Рисунок 17. 10 Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
10 Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Пример
Вычисление длин волн
Вычислите длины волн звуков на крайних значениях слышимого диапазона, 20 и 20 000 Гц, в [латексе] 30,0\text{°C} [/латекс] воздухе. (Предположим, что значения частоты точны до двух значащих цифр.)
Стратегия
Чтобы найти длину волны по частоте, мы можем использовать [латекс] v=f\lambda . [/latex]
Решение
- Определить известные. Значение для v определяется выражением
[латекс] v=(331\,\text{м/с})\sqrt{\frac{T}{273\,\text{K}}}. [/латекс]
- Преобразуйте температуру в кельвины, а затем введите температуру в уравнение
[латекс] v = (331 \, \ text {м / с}) \ sqrt {\ frac {303 \, \ text {K}} {273 \, \ text {K}}} = 348,7 \, \ text {м/с}\текст{.
 } [/латекс]
} [/латекс] - Решите зависимость между скоростью и длиной волны для λ :
[латекс] \lambda =\frac{v}{f}. [/латекс]
- Введите скорость и минимальную частоту, чтобы получить максимальную длину волны:
[латекс] {\ lambda} _ {\ text {max}} = \ text {} \ frac {348,7 \, \ text {м/с}} {20 \, \ text {Гц}} = 17 \, \текст{м}\текст{.} [/латекс]
- Введите скорость и максимальную частоту, чтобы получить минимальную длину волны:
[латекс] {\ lambda} _ {\ text {мин}} = \ frac {348,7 \, \ text {м / с}} {20 000 \, \ text {Гц}} = 0,017 \, \ text {м} =1,7\,\текст{см}\текст{.} [/латекс]
Значение
Поскольку произведение f , умноженное на [латекс] \лямбда [/латекс], равно константе, меньшее f is, тем больше должен быть [латекс] \лямбда [/латекс], и наоборот.
Скорость звука может изменяться при переходе звука из одной среды в другую, но частота обычно остается неизменной. Это подобно частоте волны на струне, равной частоте силы, колеблющей струну. Если v изменится, а f останется прежним, то длина волны [латекс]\лямбда[/латекс] должна измениться. То есть, поскольку [латекс] v=f\лямбда [/латекс], чем выше скорость звука, тем больше его длина волны для данной частоты.
Если v изменится, а f останется прежним, то длина волны [латекс]\лямбда[/латекс] должна измениться. То есть, поскольку [латекс] v=f\лямбда [/латекс], чем выше скорость звука, тем больше его длина волны для данной частоты.
Проверьте свое понимание
Представьте, что вы наблюдаете, как взрываются два фейерверка. Вы слышите взрыв одного из них, как только видите его. Однако вы видите другой снаряд за несколько миллисекунд, прежде чем услышите взрыв. Объясните, почему это так.
Показать решение
Хотя звуковые волны в жидкости являются продольными, звуковые волны в твердом теле распространяются как в виде продольных, так и поперечных волн. Сейсмические волны, которые по сути являются звуковыми волнами в земной коре, создаваемыми землетрясениями, представляют собой интересный пример того, как скорость звука зависит от жесткости среды. Землетрясения производят как продольные, так и поперечные волны, и они распространяются с разной скоростью.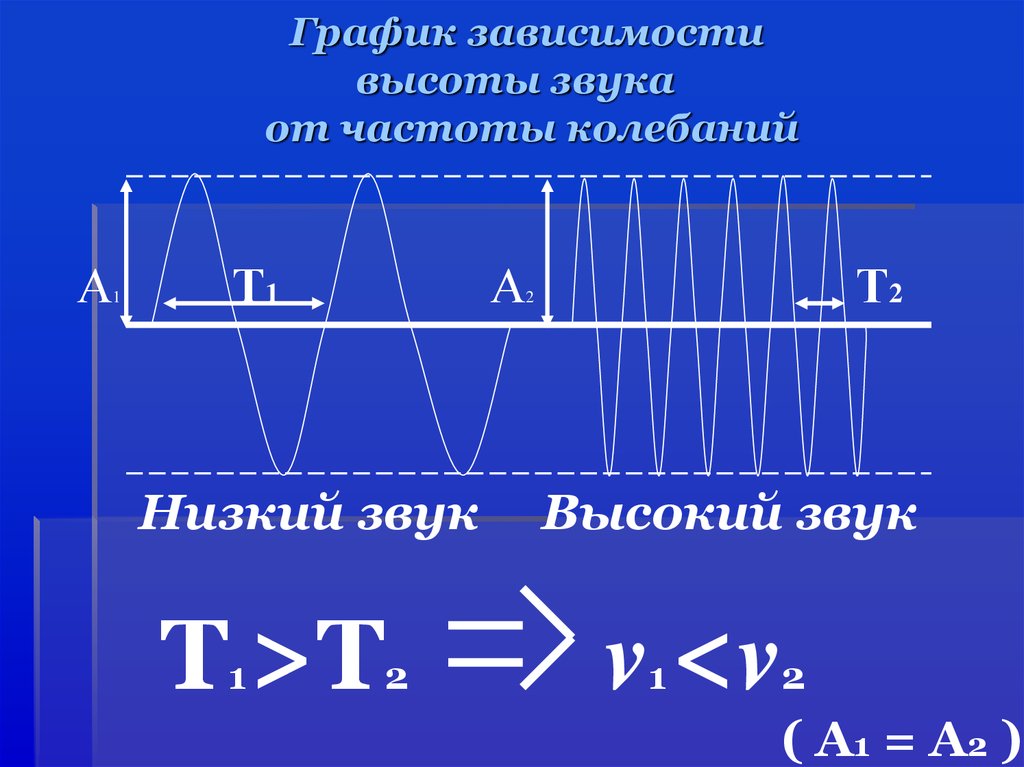 Объемный модуль гранита больше, чем его модуль сдвига. По этой причине скорость продольных волн или волн давления (Р-волн) при землетрясениях в граните значительно выше скорости поперечных или сдвиговых волн (S-волн). Оба типа волн землетрясения распространяются медленнее в менее жестком материале, таком как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны имеют скорость от 2 до 5 км/с, причем обе они быстрее в более жестком материале. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору. Время между P- и S-волнами обычно используется для определения расстояния до их источника, эпицентра землетрясения. Поскольку S-волны не проходят через жидкое ядро, образуются две теневые области ((Рисунок)).
Объемный модуль гранита больше, чем его модуль сдвига. По этой причине скорость продольных волн или волн давления (Р-волн) при землетрясениях в граните значительно выше скорости поперечных или сдвиговых волн (S-волн). Оба типа волн землетрясения распространяются медленнее в менее жестком материале, таком как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны имеют скорость от 2 до 5 км/с, причем обе они быстрее в более жестком материале. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору. Время между P- и S-волнами обычно используется для определения расстояния до их источника, эпицентра землетрясения. Поскольку S-волны не проходят через жидкое ядро, образуются две теневые области ((Рисунок)).
Рисунок 17.11 Землетрясения производят как продольные волны (P-волны), так и поперечные волны (S-волны), и они распространяются с разными скоростями. Обе волны распространяются с разной скоростью в разных регионах Земли, но в целом Р-волны распространяются быстрее, чем S-волны. S-волны не могут поддерживаться жидким ядром, создавая теневые области.
S-волны не могут поддерживаться жидким ядром, создавая теневые области.
По мере удаления звуковых волн от динамика или от эпицентра землетрясения их мощность на единицу площади уменьшается. Вот почему звук очень громкий рядом с динамиком и становится менее громким по мере удаления от него. Это также объясняет, почему в эпицентре землетрясения могут быть огромные повреждения, но в районах, удаленных от эпицентра, ощущаются только толчки. Мощность на единицу площади известна как интенсивность, и в следующем разделе мы обсудим, как интенсивность зависит от расстояния от источника.
17.2 Скорость звука, частота и длина волны – Колледж физики главы 1-17
17 Физика слуха
Резюме
- Определение высоты тона.
- Опишите взаимосвязь между скоростью звука, его частотой и длиной волны.
- Опишите влияние звука на скорость его распространения в различных средах.
- Опишите влияние температуры на скорость звука.

Звук, как и все волны, распространяется с определенной скоростью и обладает свойствами частоты и длины волны. Вы можете наблюдать прямое свидетельство скорости звука, наблюдая за фейерверком. Вспышка взрыва видна задолго до того, как слышен его звук, что подразумевает как то, что звук распространяется с конечной скоростью, так и то, что он намного медленнее света. Вы также можете непосредственно ощущать частоту звука. Восприятие частоты называется шаг . Длина волны звука непосредственно не ощущается, но косвенные свидетельства обнаруживаются в соотношении размеров музыкальных инструментов с их высотой звука. Маленькие инструменты, такие как пикколо, обычно издают высокие звуки, в то время как большие инструменты, такие как туба, обычно издают низкие звуки. Высокий тон означает малую длину волны, а размер музыкального инструмента напрямую связан с длиной волны звука, который он производит. Таким образом, небольшой инструмент создает коротковолновые звуки. Аналогичные аргументы утверждают, что большой инструмент создает длинноволновые звуки.
Таким образом, небольшой инструмент создает коротковолновые звуки. Аналогичные аргументы утверждают, что большой инструмент создает длинноволновые звуки.
Зависимость скорости звука, его частоты и длины волны такая же, как и для всех волн:
[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс]
, где[latex]\boldsymbol{v_{\textbf{w}}}[/latex]– скорость звука,[latex]\boldsymbol{f}[/latex]– его частота, а[latex]\boldsymbol{ \lambda}[/latex] — его длина волны. Длина волны звука — это расстояние между соседними идентичными частями волны, например, между соседними сжатиями, как показано на рис. 2. Частота такая же, как у источника, и представляет собой количество волн, проходящих через точку на единицу. время.
Рис. 2. Звуковая волна исходит от источника, вибрирующего с частотой f , распространяется с частотой v w и имеет длину волны λ0 . Таблица 1 показывает, что скорость звука сильно различается в разных средах. Скорость звука в среде определяется сочетанием жесткости среды (или сжимаемости в газах) и ее плотности. Чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна массе колеблющегося объекта. Скорость звука в воздухе мала, потому что воздух сжимаем. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах.
Скорость звука в среде определяется сочетанием жесткости среды (или сжимаемости в газах) и ее плотности. Чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна массе колеблющегося объекта. Скорость звука в воздухе мала, потому что воздух сжимаем. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах.
| Средний | v w (м/с) |
|---|---|
| Газы при 0ºC | |
| Воздух | 331 |
| Углекислый газ | 259 |
| Кислород | 316 |
| Гелий | 965 |
| Водород | 1290 |
| Жидкости при 20ºC | |
| Этанол | 1160 |
| Меркурий | 1450 |
| Вода пресная | 1480 |
| Морская вода | 1540 |
| Ткань человека | 1540 |
| Твердые вещества (продольные или объемные) | |
| Вулканизированная резина | 54 |
| Полиэтилен | 920 |
| Мрамор | 3810 |
| Стекло, пирекс | 5640 |
| Свинец | 1960 |
| Алюминий | 5120 |
| Сталь | 5960 |
Таблица 1. Скорость звука в различных средах. Скорость звука в различных средах. | |
Землетрясения, по существу звуковые волны в земной коре, являются интересным примером того, как скорость звука зависит от жесткости среды. Землетрясения имеют как продольную, так и поперечную составляющую, и они распространяются с разной скоростью. Объемный модуль гранита больше, чем его модуль сдвига. По этой причине скорость продольных волн или волн давления (Р-волн) при землетрясениях в граните значительно выше скорости поперечных или сдвиговых волн (S-волн). Оба компонента землетрясений распространяются медленнее в менее жестком материале, таком как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны, соответственно, имеют скорость от 2 до 5 км/с, причем обе они быстрее в более жестком материале. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору. Время между P- и S-волнами обычно используется для определения расстояния до их источника, эпицентра землетрясения.
На скорость звука влияет температура в данной среде. Для воздуха на уровне моря скорость звука равна
.[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}},[/латекс]
, где температура (обозначается как[латекс]\жирныйсимвол{Т})[/латекс]выражается в единицах Кельвина. Скорость звука в газах связана со средней скоростью частиц в газе,[латекс]\жирныйсимвол{v_{\textbf{среднеквадратичное значение}}},[/латекс]и что 9{\circ}\textbf{C}}[/latex] это 343 м/с, увеличение менее чем на 4%. На рис. 3 показано, как летучая мышь использует скорость звука для определения расстояния. Эхо также используется в медицинской визуализации.
Рисунок 3. Летучая мышь использует звуковое эхо, чтобы ориентироваться и ловить добычу. Время возвращения эха прямо пропорционально расстоянию. Одним из наиболее важных свойств звука является то, что его скорость почти не зависит от частоты. Эта независимость, безусловно, верна на открытом воздухе для звуков в слышимом диапазоне от 20 до 20 000 Гц. Если бы эта независимость не была истинной, вы бы наверняка заметили ее, например, в музыке, которую играет марширующий оркестр на футбольном стадионе. Предположим, что высокочастотные звуки распространяются быстрее — тогда чем дальше вы находитесь от группы, тем больше звук низкочастотных инструментов будет отставать от высокочастотных. Но музыка всех инструментов доносится с ритмом, не зависящим от расстояния, поэтому все частоты должны распространяться почти с одинаковой скоростью. Напомним, что
Если бы эта независимость не была истинной, вы бы наверняка заметили ее, например, в музыке, которую играет марширующий оркестр на футбольном стадионе. Предположим, что высокочастотные звуки распространяются быстрее — тогда чем дальше вы находитесь от группы, тем больше звук низкочастотных инструментов будет отставать от высокочастотных. Но музыка всех инструментов доносится с ритмом, не зависящим от расстояния, поэтому все частоты должны распространяться почти с одинаковой скоростью. Напомним, что
[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда}.[/латекс]
В данной среде при фиксированных условиях [латекс]\boldsymbol{v _{\textbf{w}}}[/латекс]постоянна, так что существует связь между[латекс]\жирныйсимвол{f}[/латекс] и[латекс]\жирныйсимвол{\лямбда};[/латекс]чем выше частота, тем меньше длина волны. См. рис. 4 и рассмотрим следующий пример.
Рисунок 4. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером. 9{\circ}\textbf{C}}[/latex]воздух. (Предположим, что значения частоты точны до двух значащих цифр.)
Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером. 9{\circ}\textbf{C}}[/latex]воздух. (Предположим, что значения частоты точны до двух значащих цифр.)Стратегия
Чтобы найти длину волны по частоте, мы можем использовать [латекс]\жирныйсимвол{v_{\textbf{w}}=f\lambda}. [/latex]
Решение
- Определить известные. Значение для[латекс]\жирныйсимвол{v_{\textbf{w}}},[/латекс]задается как
[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}}.[/латекс]
- Преобразуйте температуру в кельвины, а затем введите температуру в уравнение
[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{303\textbf{K}} {273\textbf{ K}}}}[/latex][latex]\boldsymbol{=348,7\textbf{ м/с}}.[/latex]
- Решите зависимость между скоростью и длиной волны для [латекс]\жирныйсимвол{\лямбда}:[/латекс]
[латекс]\boldsymbol{\lambda\:=}[/латекс][латекс]\boldsymbol{\frac{v _{\textbf{w}}}{f}}.
 [/latex]
[/latex] - Введите скорость и минимальную частоту, чтобы получить максимальную длину волны:
[латекс]\boldsymbol{\lambda _{\textbf{max}}\:=}[/latex][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20\textbf{Гц}} }[/латекс][латекс]\boldsymbol{=17\textbf{м}}.[/латекс]
- Введите скорость и максимальную частоту, чтобы получить минимальную длину волны:
[латекс]\boldsymbol{\lambda _{\textbf{мин}}=}[/латекс][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20 000\textbf{Гц}}}[ /латекс][латекс]\жирныйсимвол{=0,017\textbf{м}=1,7\текстбф{см}}.[/латекс]
Обсуждение
Поскольку произведение [латекс]\boldsymbol{f}[/latex], умноженное на [латекс]\boldsymbol{\lambda}[/latex], равно константе, чем меньше [латекс]\boldsymbol{ f}[/latex]есть, тем больше должен быть [латекс]\boldsymbol{\lambda}[/latex], и наоборот.
Скорость звука может изменяться при переходе звука из одной среды в другую. Однако частота обычно остается неизменной, потому что она похожа на возбужденное колебание и имеет частоту исходного источника.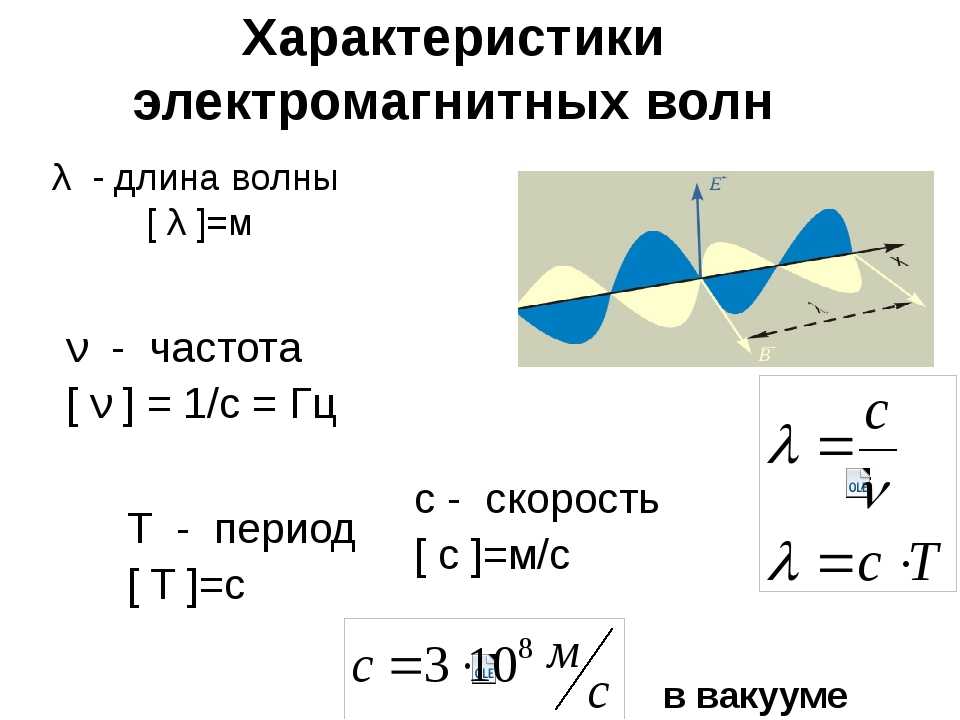 Если [латекс]\boldsymbol{v_{\textbf{w}}}[/latex]изменяется, а [латекс]\boldsymbol{f}[/latex]остается прежним, то длина волны[латекс]\boldsymbol{\lambda} [/latex] должен измениться. То есть, потому что[latex]\boldsymbol{v_{\textbf{w}}=f\lambda}[/latex]чем выше скорость звука, тем больше его длина волны для данной частоты.
Если [латекс]\boldsymbol{v_{\textbf{w}}}[/latex]изменяется, а [латекс]\boldsymbol{f}[/latex]остается прежним, то длина волны[латекс]\boldsymbol{\lambda} [/latex] должен измениться. То есть, потому что[latex]\boldsymbol{v_{\textbf{w}}=f\lambda}[/latex]чем выше скорость звука, тем больше его длина волны для данной частоты.
Установление связей: домашнее исследование — Голос как звуковая волна
Подвесьте лист бумаги так, чтобы верхний край бумаги был зафиксирован, а нижний край мог свободно двигаться. Вы можете приклеить верхний край бумаги к краю стола. Аккуратно подуйте возле края нижней части листа и обратите внимание, как движется лист. Говорите тихо, а затем громче, чтобы звуки касались края нижней части бумаги, и отмечайте, как движется лист. Объясните эффекты.
Зависимость скорости звука[латекс]\boldsymbol{v_{\textbf{w}}},[/latex]его частоты[латекс]\boldsymbol{f},[/latex]и его длины волны[латекс]\ жирныйсимвол{\lambda}[/латекс]равно
[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс]
, что является одним и тем же соотношением для всех волн.
В воздухе скорость звука связана с температурой воздуха[latex]\boldsymbol{T}[/latex]по
[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}}.[/латекс]
[латекс]\boldsymbol{v_{\textbf{w}}}[/латекс]одинаково для всех частот и длин волн.
- шаг
- восприятие частоты звука
Интенсивность – Гиперучебник по физике
[закрыть]
интенсивность в зависимости от амплитуды
Амплитуда звуковой волны может быть количественно определена несколькими способами, каждый из которых является мерой максимального изменения величины, которое происходит, когда волна распространяется через некоторую область среды.
- Амплитуды, связанные с изменением кинематических величин частиц, составляющих среду
- Амплитуда смещения – это максимальное изменение положения.
- Амплитуда скорости — это максимальное изменение скорости.

- Амплитуда ускорения — это максимальное изменение ускорения.
- Амплитуды, связанные с изменением объемных свойств сколь угодно малых участков среды
- Амплитуда давления представляет собой максимальное изменение давления (максимальное манометрическое давление).
- Амплитуда плотности — это максимальное изменение плотности.
Измерение смещения может быть и невозможным. Для типичных звуковых волн максимальное смещение молекул в воздухе всего в сто или тысячу раз больше, чем сами молекулы — да и какие вообще существуют технологии для отслеживания отдельных молекул? Изменения скорости и ускорения, вызванные звуковой волной, одинаково трудно измерить в частицах, составляющих среду.
Колебания плотности ничтожны и недолговечны. Период звуковой волны обычно измеряется в миллисекундах. Есть некоторые оптические методы, которые позволяют изобразить сильные сжатия и разрежения, связанные с ударными волнами в воздухе, но это не те звуки, с которыми мы сталкиваемся в нашей повседневной жизни.
Колебания давления, вызванные звуковыми волнами, гораздо легче измерить. Животные (включая людей) уже несколько сотен миллионов лет делают это с помощью устройств, называемых ушами. Люди уже около сотни лет делают это с помощью электромеханических устройств, называемых микрофонами. Все типы амплитуд в равной степени подходят для математического описания звуковых волн, но амплитуды давления — это то, с чем мы, люди, имеем самую тесную связь.
В любом случае, результаты таких измерений редко публикуются. Вместо этого измерения амплитуды почти всегда используются в качестве исходных данных в некоторых вычислениях. Когда это делается электронной схемой (например, схемой в телефоне, которая подключается к микрофону), результирующее значение называется интенсивностью. Когда это делается нейронной цепью (например, цепью в вашем мозгу, которая связана с вашими ушами), результирующее ощущение называется громкостью.
Интенсивность звуковой волны представляет собой комбинацию ее скорости и плотности передачи энергии. Это объективная величина, связанная с волной. Громкость — это реакция восприятия на физическое свойство интенсивности. Это субъективное качество, связанное с волной, и оно немного сложнее. Как правило, чем больше амплитуда, тем больше интенсивность, тем громче звук. Звуковые волны с большой амплитудой называются «громкими». Звуковые волны с малой амплитудой называются «тихими» или «мягкими». Слово «низкий» иногда также используется для обозначения тихого, но этого следует избегать. Используйте «low» для описания звуков низкой частоты. Громкость будет рассмотрена в конце этого раздела, после определения термина «уровень» и его единицы децибел.
Это объективная величина, связанная с волной. Громкость — это реакция восприятия на физическое свойство интенсивности. Это субъективное качество, связанное с волной, и оно немного сложнее. Как правило, чем больше амплитуда, тем больше интенсивность, тем громче звук. Звуковые волны с большой амплитудой называются «громкими». Звуковые волны с малой амплитудой называются «тихими» или «мягкими». Слово «низкий» иногда также используется для обозначения тихого, но этого следует избегать. Используйте «low» для описания звуков низкой частоты. Громкость будет рассмотрена в конце этого раздела, после определения термина «уровень» и его единицы децибел.
По определению, интенсивность ( I ) любой волны представляет собой усредненную по времени мощность (⟨ P ⟩), которую она передает на единицу площади ( A ) через некоторую область пространства. Традиционный способ указать усредненное по времени значение переменной величины — заключить его в угловые скобки (⟨⟩).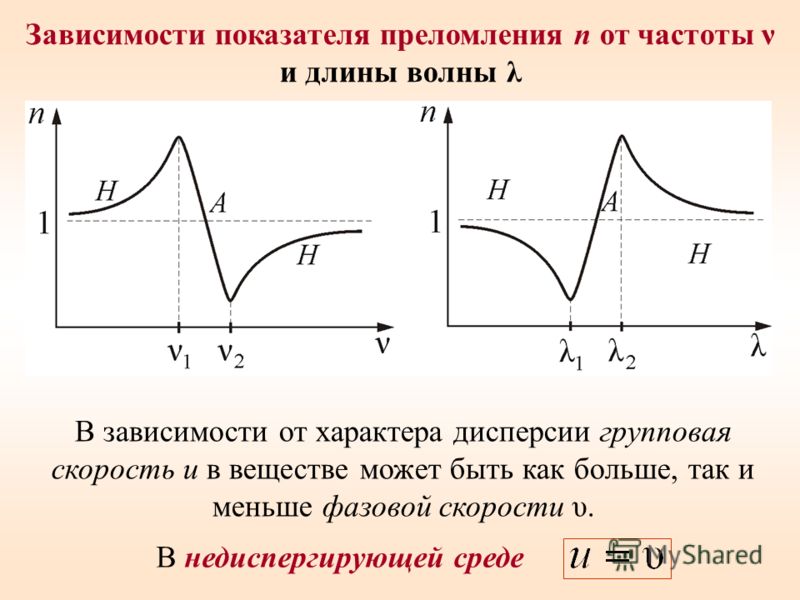 Они похожи на символы «больше» и «меньше», но они выше и менее заострены. Это дает нам уравнение, которое выглядит так…
Они похожи на символы «больше» и «меньше», но они выше и менее заострены. Это дает нам уравнение, которое выглядит так…
| I = | ⟨ P ⟩ |
| A |
ватт на квадратный метр — единица, не имеющая особого названия.
| ⎡ ⎢ ⎣ | Вт | = | Вт | ⎤ ⎥ ⎦ |
| м 2 | м 2 |
интенсивность и смещение
Для простых механических волн, таких как звук, интенсивность связана с плотностью среды и скоростью, частотой и амплитудой волны. Это можно показать длинным ужасным расчетом. Если вам не нравится смотреть, как делают колбасу внизу, переходите к уравнению прямо перед ярким столом.
Начните с определения интенсивности. Замените мощность энергией (как кинетической, так и упругой) с течением времени (один период для удобства).
| |||
| |||
|
Поскольку кинетическая и упругая энергии всегда положительны, мы можем разделить усредненную по времени часть на две части.
| |||||||
| |||||||
| |||||||
Механические волны в сплошной среде можно рассматривать как бесконечный набор бесконечно малых связанных гармонических осцилляторов.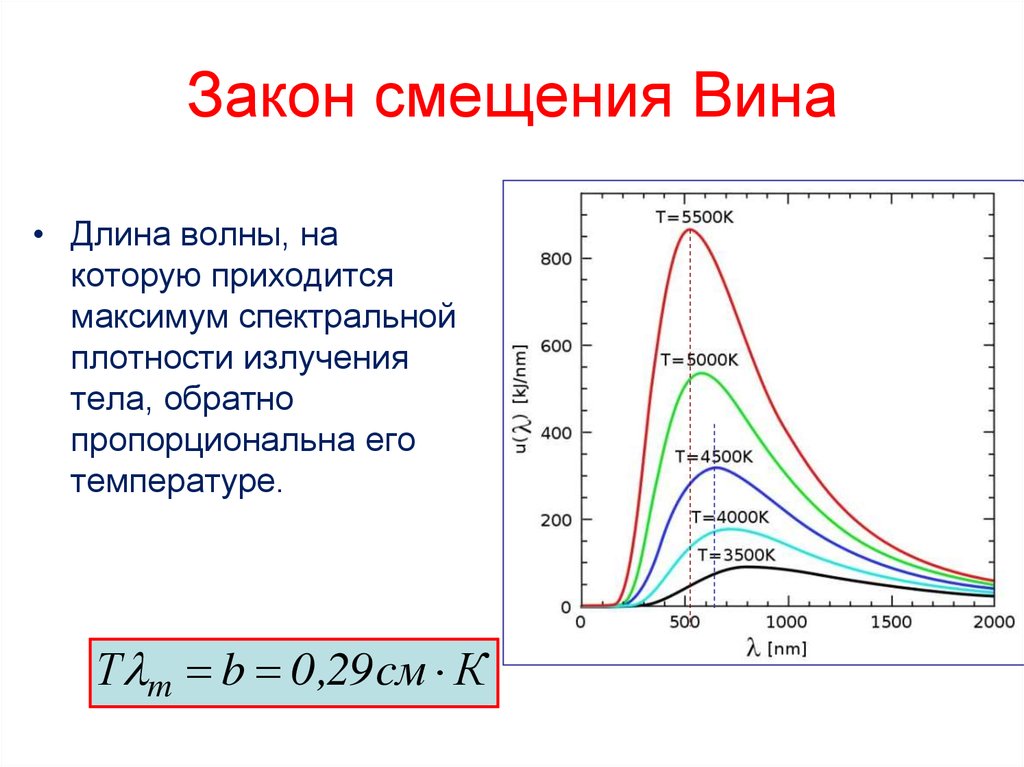 Маленькие массы соединены с другими маленькими массами маленькими пружинками, насколько хватает глаз. В среднем половина энергии простого гармонического осциллятора приходится на кинетическую, а половина на упругую. Тогда усредненная по времени полная энергия либо удваивает среднюю кинетическую энергию, либо удваивает среднюю потенциальную энергию.
Маленькие массы соединены с другими маленькими массами маленькими пружинками, насколько хватает глаз. В среднем половина энергии простого гармонического осциллятора приходится на кинетическую, а половина на упругую. Тогда усредненная по времени полная энергия либо удваивает среднюю кинетическую энергию, либо удваивает среднюю потенциальную энергию.
| ⟨ P ⟩ = | 2⟨ К ⟩ | = | 2⟨ U с ⟩ | |
| Т | Т | |||
Давайте поработаем над кинетической энергией и посмотрим, куда она нас приведет. Он состоит из двух важных частей — массы и скорости.
К = ½ мв 2
Частицы в продольной волне смещаются из своих положений равновесия функцией, которая колеблется во времени и пространстве. Используйте для этого одномерное волновое уравнение.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов − | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
где…
| ∆ с ( x , t ) = | мгновенных смещения в любом положении ( x ) и времени ( т ) |
| ∆ с = | амплитуда смещения |
| ƒ = | частота |
| λ = | длина волны |
| π = | всеми любимая математическая константа |
Возьмите производную по времени, чтобы получить скорость частиц в среде (а не скорость волны в среде).
| ||||||||
|
Затем возведите его в квадрат.
| ∆ v 2 ( x , t ) = | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
На массу. Плотность, умноженная на объем, равна массе. Объем материала, который нас интересует, представляет собой коробку, площадь которой представляет собой поверхность, по которой распространяется волна, а длина — расстояние, которое проходит волна. За один период волна будет двигаться вперед на одну длину волны (λ).
Плотность, умноженная на объем, равна массе. Объем материала, который нас интересует, представляет собой коробку, площадь которой представляет собой поверхность, по которой распространяется волна, а длина — расстояние, которое проходит волна. За один период волна будет двигаться вперед на одну длину волны (λ).
м = ρ В = ρ А λ
В объеме, охватываемом одной длиной волны, все частицы материи движутся с разными скоростями. Исчисление необходимо для объединения множества различных значений в одно интегрированное значение. Здесь мы имеем дело с периодической системой, которая повторяется снова и снова. Мы можем начать наш расчет в любое время, если мы закончим на один цикл позже. Для удобства выберем время равным нулю — началу синусоидальной волны.
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
Очистить константы.
½ (ρ A ) (4π 2 F 2 ∆ S 2 ) = 2π 2 ρ AF ) = 2π 2 ρ AF ) = 2π 2 ρ AF ) = 2π 2 ρ 9075 AF ) = 2π 2 ρ 9075 AF
Затем работайте над интегралом. Это может выглядеть тяжело, но это не так. Просто визуализируйте кривую квадрата косинуса, вычерченную за один цикл. Видите, как он делит ограничивающий его прямоугольник на равные половины?
Высота этого прямоугольника равна единице (как в числе 1 без единиц измерения), а его ширина равна длине волны. Это дает площадь в одну длину волны и половину площади в половину длины волны.
| λ | ||||||
| ⌠ ⎮ ⌡ | потому что 2 | ⎡ ⎢ ⎣ | – 2π | х | ⎤ ⎥ ⎦ | дх = ½λ |
| λ | ||||||
| 0 | ||||||
Сложите константы вместе с интегралом и разделите на один период, чтобы получить усредненную по времени кинетическую энергию. (Помните, что длина волны, деленная на период, равна скорости волны.)
(Помните, что длина волны, деленная на период, равна скорости волны.)
| ||||||||
|
На этом сложная часть завершена. Удвойте приведенное выше уравнение и разделите на площадь…
| ||||||
|
Еще немного алгебры, и все готово.
I = 2π 2 ρ f 2 v ∆ s 2
Теперь у нас есть уравнение, связывающее интенсивность ( I ) с амплитудой смещения (∆ с ).
Имеет ли смысл эта формула? Давайте проверим, как каждый из факторов влияет на интенсивность.
| коэффициент | комментариев |
|---|---|
| I ∝ ρ | Чем плотнее среда, тем интенсивнее волна. Это имеет смысл. Плотная среда упаковывает больше массы в любой объем, чем разреженная среда, и кинетическая энергия идет с массой. |
| I ∝ f 2 | Чем чаще волна сотрясает среду, тем интенсивнее волна. Я вижу это мысленным взором. Тусклая волна, которая просто не приводит в движение среду, не будет нести столько энергии, сколько волна, которая сотрясает среду как сумасшедшая. |
| I ∝ v | Чем быстрее распространяется волна, тем быстрее она передает энергию. Здесь вы должны помнить, что интенсивность измеряет не столько количество переданной энергии, сколько скорость передачи этой энергии. |
| I ∝ ∆ с 2 | Чем больше амплитуда смещения, тем интенсивнее волна. Просто подумайте об океанских волнах на мгновение. Водяная стена, движимая ураганом, дает гораздо больше силы, чем рябь в ванне. Метафора визуально неверна, поскольку звуковые волны продольные, а океанские волны сложны, но интуитивно она верна. |
Движение частиц можно описать в терминах смещения, скорости или ускорения. Интенсивность также может быть связана с этими величинами. Мы только что завершили тяжелую работу по связыванию интенсивности ( I ) с амплитудой смещения (∆ с ). Для полноты (и почему бы и нет) давайте также выведем уравнения для интенсивности через амплитуду скорости (∆ 90 675 v 90 676 ) и амплитуду ускорения (∆ 90 675 a 90 676 ).
интенсивность и скорость
Как интенсивность связана с максимальной скоростью (амплитуда скорости)? Давай выясним. Начните с одномерного волнового уравнения.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов − | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Напомним, что скорость — это производная смещения по времени.
| ||||||||
|
Перед функцией косинуса стоит амплитуда скорости.
∆ v = 2π f ∆ с
Решите это для амплитуды смещения.
| ∆ с = | ∆ v |
| 2π ф |
Совсем недавно мы вывели уравнение для интенсивности через амплитуду смещения.
I = 2π 2 ρ f 2 v ∆ s 2
Объединить эти два уравнения…
| I = 2π 2 ρ f 2 v | ⎛ ⎜ ⎝ | ∆ в | ⎞ 2 ⎟ ⎠ |
| 2π ф |
и упростить.
| I = ρ V | ∆ V 2 |
| 2 |
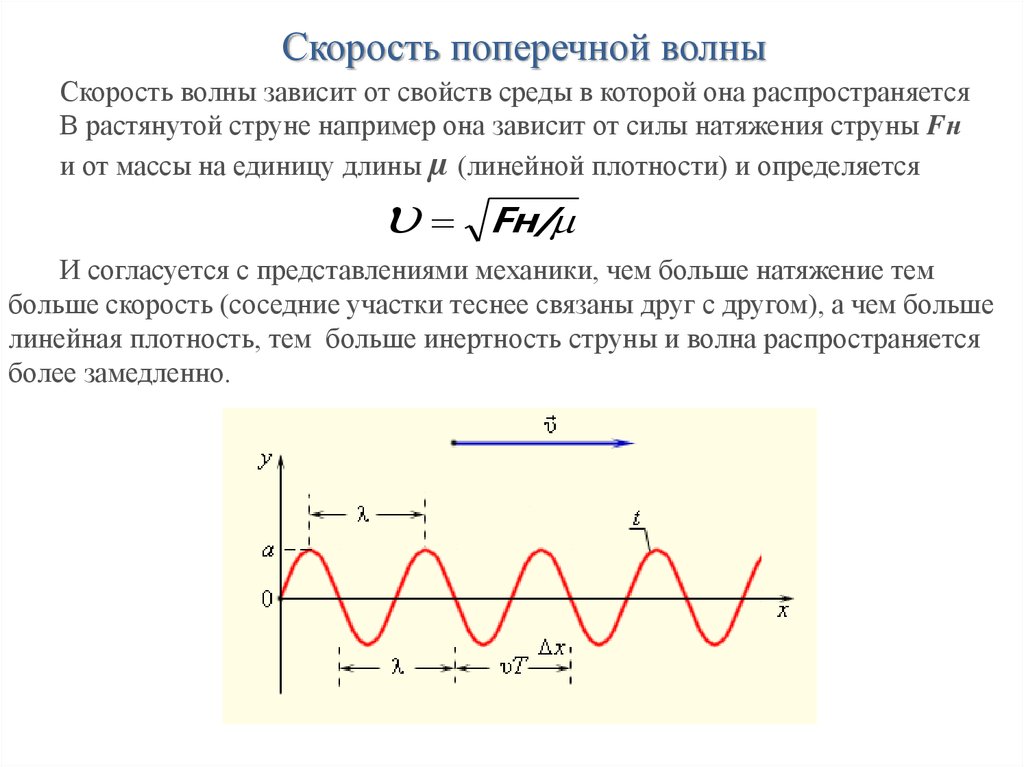
интенсивность и ускорение
Как интенсивность связана с максимальным ускорением (амплитуда ускорения)? Еще раз, давайте узнаем. Опять же, начнем с одномерного волнового уравнения.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов − | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Вспомним, что скорость есть производная смещения по времени…
| ||||||||
|
и что ускорение есть производная скорости по времени.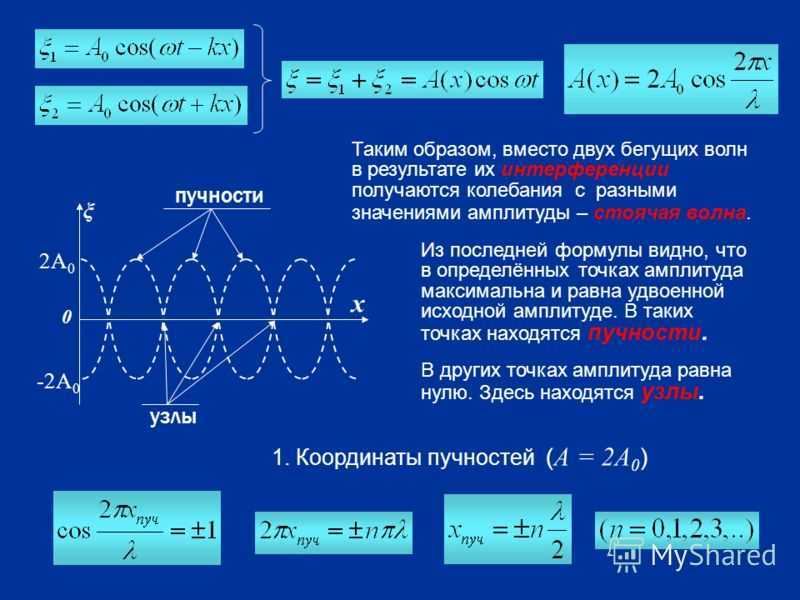
| ||||||||
|
Амплитуда ускорения — это то, что стоит перед функцией синуса (без учета знака минус).
∆ a = 4π 2 f 2 ∆ s
Измените это, чтобы сделать амплитуду смещения предметом.
| ∆ с = | ∆ и |
| 4π 2 f 2 |
Пришло время вернуться к нашему уравнению для интенсивности с точки зрения амплитуды смещения.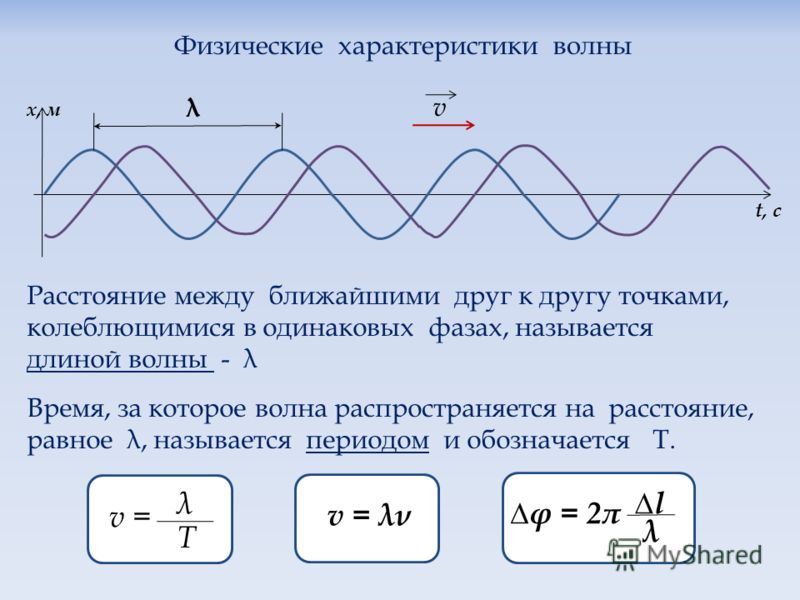
I = 2π 2 ρ f 2 v ∆ s 2
Объединить два предыдущих уравнения…
| I = 2π 2 ρ f 2 v | ⎛ ⎜ ⎝ | ∆ и | ⎞ 2 ⎟ ⎠ |
| 4π 2 f 2 |
и упростить.
| I = ρ V | ∆ A 2 | |||||||
8π 2 F| 8π 2 F | 8π 2 F | 2 | F | 2 | F | 2 | 2 | |
Теперь у нас есть уравнение, связывающее интенсивность ( I ) с амплитудой ускорения (∆ a ).
интенсивность и давление
Амплитуду звуковой волны гораздо легче измерить с помощью давления (объемное свойство материала, подобного воздуху), чем смещение (смещение субмикроскопических молекул, составляющих воздух). Вот быстрый и грязный вывод более полезного уравнения интенсивность-давление из фактически бесполезного уравнения интенсивности-смещения.
Начните с уравнения, связывающего интенсивность с амплитудой смещения.
I = 2π 2 ρ f 2 v ∆ s 2
Теперь давайте поиграем в небольшую игру с символами — в игру под названием алгебра. Обратите внимание, что многие символы в приведенном выше уравнении возведены в квадрат. Возведите их все в квадрат, умножив числитель и знаменатель на 2ρ v .
| I = | 4π 2 ρ 2 f 2 v 2 ∆ s 2 |
| 2р v |
Запишите числитель в виде количества в квадрате.
| I = | (2πρ fv ∆ с ) 2 |
| 2р v |
Посмотрите на стопку символов в скобках.
2πρ fv ∆ с
Посмотрите единицы измерения каждой физической величины.
| ⎡ ⎢ ⎣ | кг | 1 | м | м | ⎤ ⎥ ⎦ | |||
| м 3 | с | с | 1 |
Еще немного магии — на этот раз не алгебра, а анализ измерений.
| ⎡ ⎢ ⎣ | кг | = | кг м | = | Н | 90 686 = Па ⎤ ⎥ ⎦ |
| мс 2 | м 2 с 2 | м 2 |
Единицами этой мешанины являются паскали, поэтому величина в скобках в предыдущем уравнении — это давление, точнее максимальное манометрическое давление. Теперь у нас есть уравнение, связывающее интенсивность с амплитудой давления.
Теперь у нас есть уравнение, связывающее интенсивность с амплитудой давления.
| I = | ∆ P 2 |
| 2ρ V |
… V
.
| I = | интенсивность [Вт/м 2 ] |
| ∆ P = | амплитуда давления [Па] |
| ρ = | плотность [кг/м 3 ] |
| v = | скорость волны [м/с] |
Вот медленный и четкий вывод уравнения интенсивность-давление. Начните с версии закона Гука, в которой используется объемный модуль ( K ).
| F | = K | ∆ V |
| A | V 0 |
The fraction on the left is the compressive stress, also known как давление ( P ). Дробь справа представляет собой деформацию сжатия, также известную как дробное изменение объема (θ). Последний из этих двух интересует нас прямо сейчас. Представьте себе звуковую волну, которая растягивает и сжимает среду только в одном направлении. Если это так, то дробное изменение объема фактически совпадает с дробным изменением длины.
Дробь справа представляет собой деформацию сжатия, также известную как дробное изменение объема (θ). Последний из этих двух интересует нас прямо сейчас. Представьте себе звуковую волну, которая растягивает и сжимает среду только в одном направлении. Если это так, то дробное изменение объема фактически совпадает с дробным изменением длины.
| θ = | ∆ В | = | ∂∆ с ( x , т ) |
| В 0 | ∂ х |
Здесь мы должны использовать исчисление, чтобы получить это дробное изменение, поскольку бесконечно малые кусочки и кусочки среды сжимаются и растягиваются с разной скоростью в разных точках пространства. Изменения длины описываются одномерным волновым уравнением.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов − | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Его пространственная производная такая же, как дробное изменение объема.
| θ = | ∂∆ с ( x , т ) | = — | 2π | ∆ с соз | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов − | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| ∂ х | λ | λ |
Интересно отметить, что изменения объема не совпадают по фазе со смещениями, поскольку взятие производной изменило синус на отрицательный косинус. Изменения громкости 90° позади смещения, поскольку отрицательный косинус отстает от синуса на 90°. Наиболее резкие изменения объема происходят в местах, где частицы возвращаются в свои равновесные положения.
Интересно, но сейчас не очень полезно. Нас больше волнует , где эти экстремальные значения, чем , где они встречаются. Для этого мы заменяем выражение отрицательного косинуса его крайним абсолютным значением +1.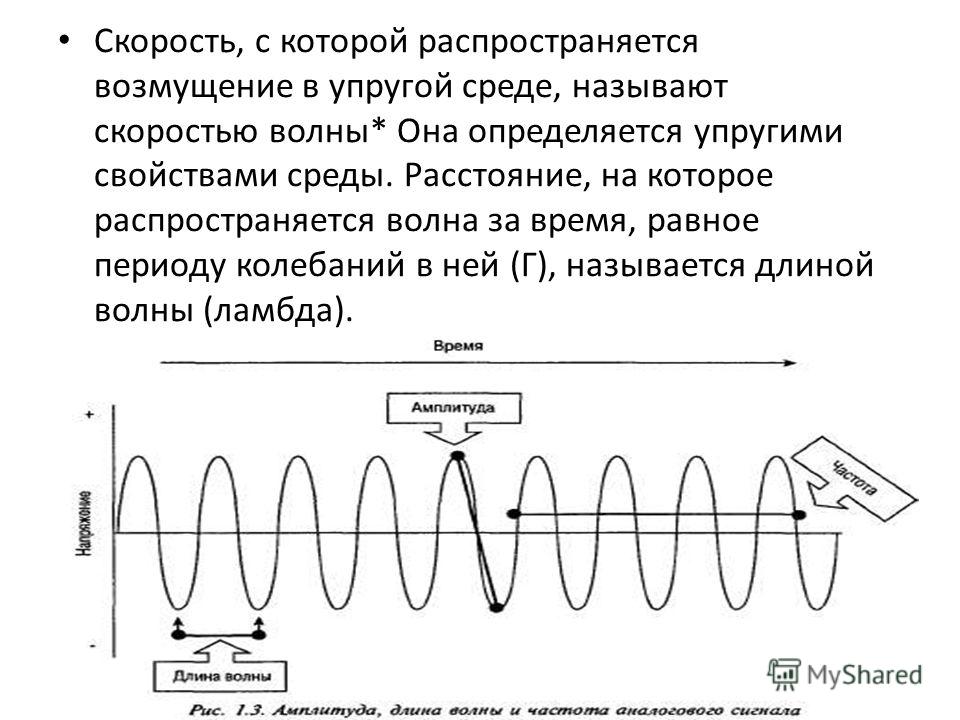 Это оставляет нам это выражение для максимальной деформации (∆θ).
Это оставляет нам это выражение для максимальной деформации (∆θ).
| ∆θ = | 2π | ∆ с |
| λ |
Подставив это обратно в уравнение объемного модуля, мы получим максимальное манометрическое давление.
| ∆ P = K | 2π | ∆ с |
| λ |
А теперь о грязной работе. Вспомним эти два уравнения для скорости звука.
| v = f λ | ⇒ |
|
| ⇒ | К = v 2 ρ |
Подставить в предыдущее уравнение…
| ∆ P = v 2 ρ | 2π ж | ∆ с |
| против |
и упростить.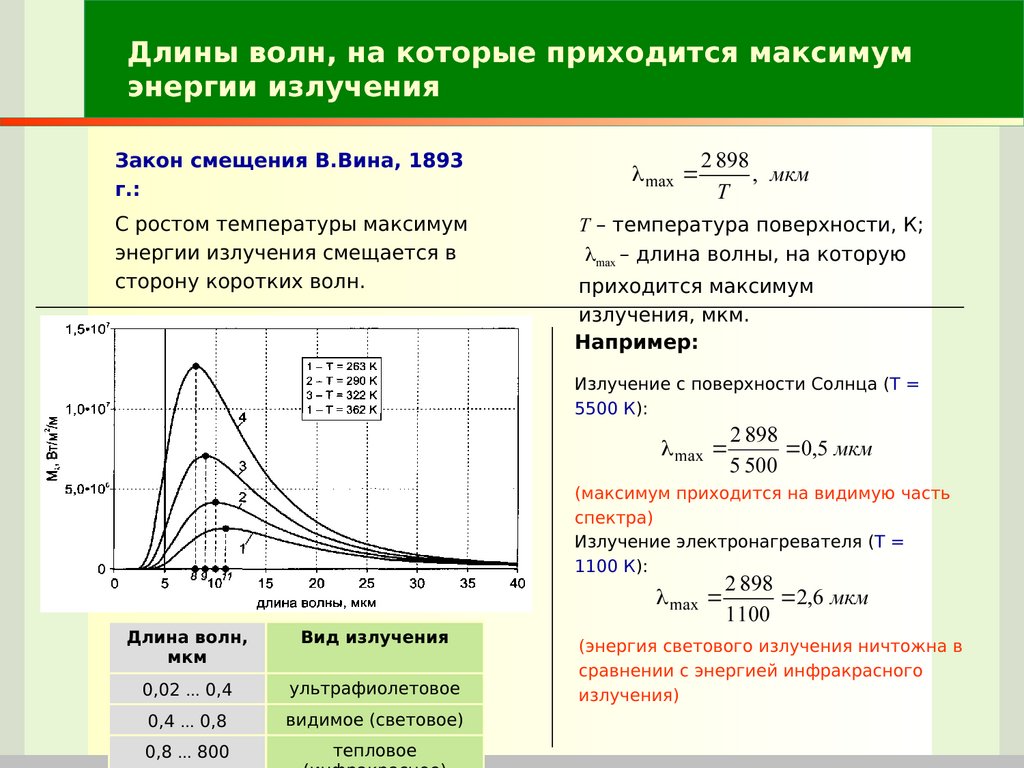
∆ P = 2πρ fv ∆ с
Знакомый? Он находится в числителе выражения, которое появилось ранее.
| I = | (2πρ fv ∆ с ) 2 |
| 2р v |
Замените стопку символов в скобках и вот. Мы снова получаем эту вещь — соотношение интенсивности и амплитуды давления.
| I = | ∆ П 2 |
| 2р v |
где…
| I = | интенсивность [Вт/м 2 ] |
| ∆ Ч = | амплитуда давления [Па] |
| ρ = | плотность [кг/м 3 ] |
| v = | скорость волны [м/с] |
интенсивность и плотность
Изменения плотности среды, связанные со звуковой волной, прямо пропорциональны изменениям давления.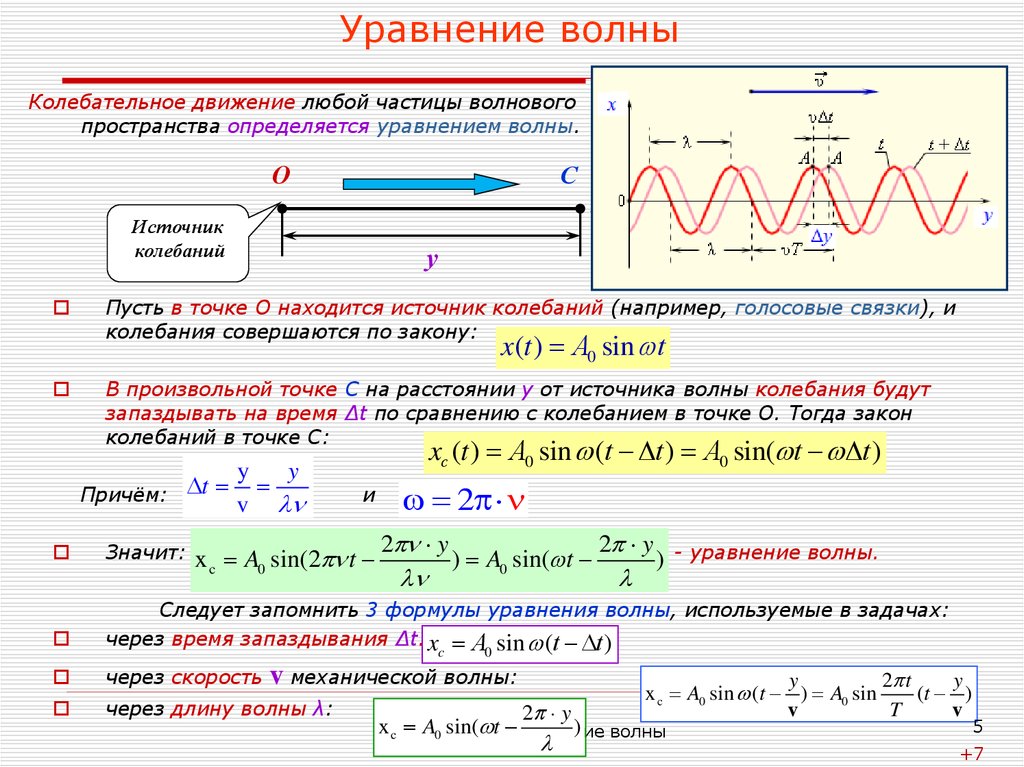 Связь следующая…
Связь следующая…
| v = √ | ∆ П |
| ∆ρ |
Это похоже на уравнение Ньютона-Лапласа для скорости звука в идеальном газе, но в нем отсутствует коэффициент теплоемкости γ (гамма). Почему?
| v = √ | γ Р |
| р |
Предполагая, что первое уравнение правильное, решите его для ∆ρ.
| ∆ρ = | ∆ П |
| v 2 |
Возьмите отношение амплитуды давления к амплитуде смещения…
∆ P = 2πρ fv ∆ с
замена…
| ∆ρ = | 2πρ fv ∆ с |
| v 2 |
и упростим, чтобы получить зависимость амплитуды плотности от смещения.
| ∆ρ = | 2πρ ж ∆ с |
| против |
Слегка забавно.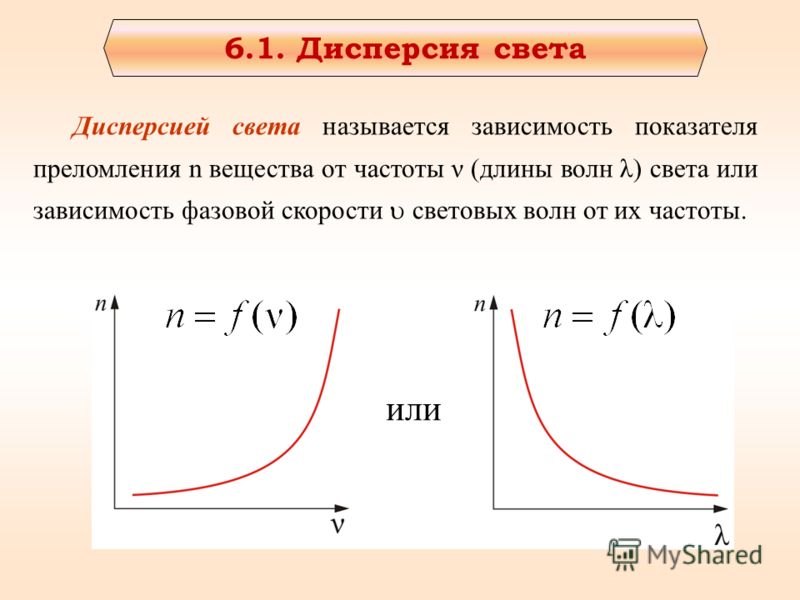 Давайте попробуем что-нибудь еще.
Давайте попробуем что-нибудь еще.
Опять же, предполагая, что первое уравнение правильное, решите его для ∆ P .
∆ P = ∆ρ v 2
Возьмем уравнение, связывающее интенсивность с амплитудой давления…
| I = | ∆ П 2 |
| 2ρ v |
сделать аналогичную замену…
| I = | (∆ρ v 2 ) 2 |
| 2р v |
и упростите, чтобы получить уравнение, связывающее интенсивность с амплитудой плотности.
| I = | ∆ρ 2 V 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2ρ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2ρ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2ρ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
уровеньНАПИСАТЬ ЭТУ ЧАСТЬ Что такое уровень? Типы уровней.
Для любого периодического сигнала уровень его интенсивности ( L I ) в бел [B] определяется как десятичный логарифм отношения его интенсивности к интенсивности [B].0673 опорный сигнал . Так как для большинства целей эта единица великовата, принято делить бел на десятые доли или децибела [дБ]. Бел — безразмерная единица.
When the signal is звуковая волна, эта величина называется уровнем интенсивности звука , часто сокращенно SIL . pressure
sound pressure level, SPL
text
Примечания
В равной степени разумно было бы использовать натуральные логарифмы вместо десятичной системы счисления, но это встречается гораздо реже. Для любого периодического сигнала отношение натурального логарифма его интенсивности к эталонному сигналу является мерой его уровня интенсивности ( L ) в neper [Np]. Как и в случае с белом, непер принято делить на десятые доли или децинепера [dNp].
Непер и децибел настолько редки по сравнению с белами и децибелами, что по существу являются ответом на простой вопрос. Примечания и цитаты.
слух
сейсмические волныРасширенная цитата, которую необходимо перефразировать.
Скорость волны: определение, формула и примерСкорость волны — это скорость прогрессивной волны, которая представляет собой возмущение в форме колебаний, которые перемещаются из одного места в другое и переносят энергию. Скорость волны зависит от ее частоты «f» и длины волны «λ». Скорость волны является важным параметром, так как позволяет рассчитать, насколько быстро волна распространяется в среде, которая является веществом или материалом, несущим волну. В случае океанских волн это вода, а в случае звуковых волн — воздух. Скорость волны также зависит от типа волны и физических характеристик среды, в которой она движется. Рис. Как рассчитать скорость волныЧтобы рассчитать скорость волны, нам нужно знать длину волны, а также частоту волны. См. приведенную ниже формулу, где частота измеряется в герцах, а длина волны измеряется в метрах. Длина волны «λ» — это общая длина от одного гребня до другого, как показано на рисунке 2. Частота «f» — обратное время, которое требуется гребню, чтобы переместиться на позицию следующего. Рисунок 2. Период волны – это время, за которое гребень волны достигает положения следующего гребня. В этом случае первый гребень имеет время Ta и перемещается в положение, в котором до этого находился гребень Xb в момент времени Ta’. Источник: Мануэль Р. Камачо, StudySmarter. Другой способ расчета скорости волны — использование периода волны «Т», который определяется как величина, обратная частоте, и указывается в секундах. Это дает нам другой расчет скорости волны, как показано ниже: Период волны составляет 0,80 секунды. Какова его частота? Скорость волны может варьироваться в зависимости от нескольких факторов, не включая период, частоту или длину волны. Волны по-разному движутся в море, в воздухе (звук) или в вакууме (свет). Измерение скорости звукаСкорость звука — это скорость механических волн в среде. Помните, что звук также распространяется через жидкости и даже твердые тела. Скорость звука уменьшается по мере того, как плотность среды ниже, что позволяет звуку распространяться в металлах и воде быстрее, чем в воздухе. Скорость звука в газах, таких как воздух, зависит от температуры и плотности, и даже влажность может влиять на его скорость. В средних условиях, таких как температура воздуха 20°C и на уровне моря, скорость звука составляет 340,3 м/с. В воздухе скорость можно рассчитать, разделив время, за которое звук проходит между двумя точками. Здесь «d» — пройденное расстояние в метрах, а «Δt» — разница во времени. Скорость звука в воздухе при средних условиях используется в качестве эталона для объектов, движущихся с высокой скоростью, с использованием числа Маха. Число Маха — это скорость объекта «u», деленная на «v», скорость звука в воздухе при средних условиях. Как мы уже говорили, скорость звука зависит еще и от температуры воздуха. Термодинамика говорит нам, что теплота газа — это среднее значение энергии молекул воздуха, в данном случае его кинетической энергии. По мере повышения температуры молекулы, из которых состоит воздух, набирают скорость. Более быстрые движения позволяют молекулам вибрировать быстрее, легче передавая звук, а это означает, что звуку требуется меньше времени для перемещения из одного места в другое. Например, скорость звука при 0°C на уровне моря составляет около 331 м/с, что соответствует уменьшению примерно на 3%. Рис. Измерение скорости волн на водеСкорость волн на воде отличается от скорости звуковых волн. При этом скорость зависит от глубины океана, где распространяется волна. Если глубина воды более чем в два раза превышает длину волны, скорость будет зависеть от силы тяжести «g» и периода волны, как показано ниже. В этом случае g = 9,81 м/с на уровне моря. Это также может быть аппроксимировано следующим образом: Если волны движутся к мелководью и длина волны более чем в два раза превышает глубину h (λ > 2h), то скорость волны рассчитывается следующим образом: Как и для звука , волны на воде с большей длиной волны распространяются быстрее, чем волны меньшего размера. По этой причине большие волны, вызванные ураганами, достигают побережья раньше, чем ураган. Вот пример того, как скорость волн зависит от глубины воды. Волна с периодом 12 с В открытом океане на волну не влияет глубина воды, и ее скорость приблизительно равна v = 1,56 • T. Далее волна движется к более мелким водам с глубина 10 метров. Вычислите, насколько изменилась его скорость. Скорость волны «Vd» в открытом океане равна периоду волны, умноженному на 1,56. Если мы подставим значения в уравнение скорости волны, мы получим: Затем волна распространяется к берегу и входит в пляж, где ее длина волны больше, чем глубина пляжа. В этом случае на его скорость «Vs» влияет глубина пляжа. Разница в скорости равна вычитанию Vs из Vd. Как видите, скорость волны уменьшается, когда она входит в мелководье. Как мы уже говорили, скорость волн зависит от глубины воды и периода волны. Большие периоды соответствуют большей длине волны и более короткой частоте. Очень большие волны с длиной волны, достигающей более ста метров, образуются в результате сильных штормовых систем или непрерывных ветров в открытом океане. Рисунок 4. Волны — это длинные волны с высокой скоростью, которые могут перемещаться по всему океану. Источник: Даниэль Рамирес, Flickr (CC BY 2.0). Скорость электромагнитных волнЭлектромагнитные волны отличаются от звуковых волн и волн на воде тем, что им не требуется среда для распространения, и поэтому они могут двигаться в космическом вакууме. Вот почему солнечный свет может достигать Земли или почему спутники могут передавать сообщения из космоса на земные базовые станции. Электромагнитные волны распространяются в вакууме со скоростью света, т. е. примерно 300 000 км/с. Однако их скорость зависит от плотности материала, через который они проходят. Например, в алмазах свет распространяется со скоростью 124 000 км/с, что составляет всего 41% от скорости света. Зависимость скорости электромагнитных волн от среды, в которой они распространяются, известна как показатель преломления, который рассчитывается следующим образом: Здесь ‘n’ — показатель преломления материала, ‘c’ — скорость света, а «v» — скорость света в среде. Если мы решим это для скорости в материале, мы получим формулу для расчета скорости электромагнитных волн в любом материале, если мы знаем показатель преломления n. 93] | Refractive index | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vacuum of space | 300,000,000 | 1 atom | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Air | 299,702,547 | 1.2041 | 1,00029 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Water | 225,000,000 | 9998.23 | 1,333 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стекло | 200 000 000 | 2,5 | 1,52 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Diamond | 124 000 000 | 3520 060 | 2,418 |
Значения для воздуха и воды даны при стандартном давлении 1 [атм] и температуре 20°C.
Как мы сказали и показано в таблице выше, скорость света зависит от плотности материала. Эффект вызван светом, воздействующим на атомы в материалах.
Рис. 5. Свет поглощается атомами при прохождении через среду. Источник: Мануэль Р. Камачо, StudySmarter.
Рис. 6. После того, как свет был поглощен, он снова будет испущен другими атомами. Источник: Мануэль Р. Камачо, StudySmarter.
По мере увеличения плотности свет встречает на своем пути все больше атомов, поглощая фотоны и снова испуская их. Каждое столкновение создает небольшую временную задержку, и чем больше атомов, тем больше задержка.
Скорость волны — основные выводы
- Скорость волны — это скорость, с которой волна распространяется в среде. Среда может быть космическим вакуумом, жидкостью, газом или даже твердым телом. Скорость волны зависит от частоты волны «f», которая является обратной величиной периода волны «T».
- В море более низкие частоты соответствуют более быстрым волнам.

- Электромагнитные волны обычно распространяются со скоростью света, но их скорость зависит от среды, в которой они распространяются. Более плотные среды заставляют электромагнитные волны двигаться медленнее.
- Скорость океанских волн зависит от их периода, хотя на мелководье она зависит только от глубины воды.
- Скорость звука, распространяющегося по воздуху, зависит от температуры воздуха, так как при более низких температурах звуковые волны замедляются.
Цвет света определяется его частотой или длиной волны?
Цвет света определяется его частотой или длиной волны?Цвет света определяется его частотой или длиной волны?
Электронная почта получена:
Я учусь в *****, участвую в научной олимпиаде, и был бы очень признателен вам, если бы вы ответили на вопрос, касающийся физической оптики. Цвет света определяется его частотой или длиной волны? Кроме того, если бы луч цветного света, скажем, красного, прошел из воздуха в стекло, теоретически изменился бы цвет внутри стекла? Я был бы очень признателен, если бы вы ответили на эти вопросы, потому что никто из учителей в моей школе, кажется, не может этого сделать.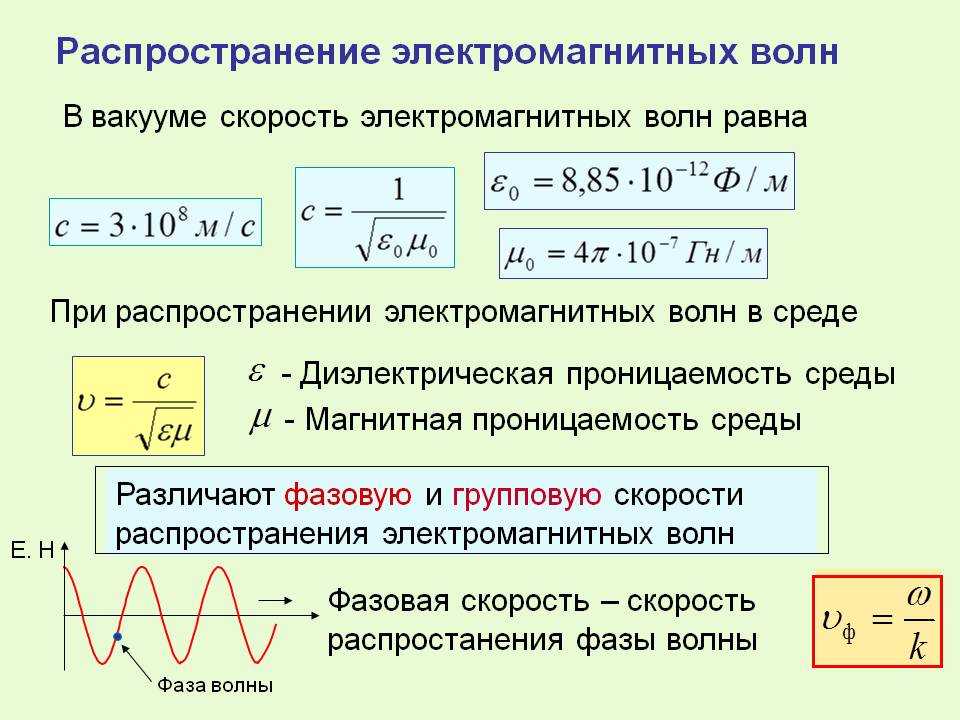
Ответ Теда:
Большинство людей, вероятно, сказали бы, что цвет света всегда в зависимости от его длины волны. Но это верно только , если свет распространяется только через одну среду, например воздух. Действительно, в одной среде разные длины волн света выглядят как разные цвета; и чем больше длина волны, тем ниже частота света.
Если свет попадает в другую среду, например стекло, то длина волны изменится. Однако цвет останется прежним, поскольку частота этого цвета света равна 9.0675 остается одним и тем же от одного носителя к другому. Цвет всегда зависит от частоты света, которая представляет собой количество световых волн, проходящих данную плоскость в пространстве в секунду (то есть количество циклов в секунду). Если бы цвет света всегда зависел от его длины волны, то его цвет изменился бы, когда он входит в среду с другим показателем преломления; но это не так.
Например, если вы наблюдаете за надувным мячом, сидящим у края бассейна, затем прыгаете в бассейн и смотрите на надувной мяч, пока ваша голова погружена под воду, все цвета на надувном мяче будут отображаться так же, как они делали, когда вы стояли в воздухе. Что меняется, когда свет переходит из одной среды в другую, так это скорость света и длина волны света. Но частота серии световых волн не изменяет ; поэтому цвет не меняется.
Что меняется, когда свет переходит из одной среды в другую, так это скорость света и длина волны света. Но частота серии световых волн не изменяет ; поэтому цвет не меняется.
Предположим, что красный лазерный луч направлен на пластину из плотного краун-стекла с показателем преломления 1,60. Свет входит с одной стороны, проходит через стекло и выходит с другой стороны. Луч света будет одного оттенка красного как снаружи, так и внутри стекла. Причина этого в следующей важной формуле:
Когда свет попадает в стекло, он замедляется. В то же время длина волны света также пропорционально сокращается. Так что частота (и, следовательно, цвет) остается той же , потому что фиксированную плоскость в пространстве за секунду (циклов в секунду) проходит одинаковое количество волн, независимо от того, находится ли свет внутри стекла или в воздухе снаружи . Вот графическое представление этого:| Закон Снеллса: |
Как видите, длина волны красного света в стекле сокращается, как и скорость света. Но частота остается прежней, как и цвет. Таким образом, красный свет с длиной волны 700 нм в воздухе будет иметь тот же цвет, что и красный свет с длиной волны 438 нм в этом типе стекла. (Обратите внимание, что свет с длиной волны 438 нм 90 675 в воздухе 90 676 будет казаться индиго, цветом где-то между синим и фиолетовым; но та же самая длина волны в плотном краун-стекле будет красной.)
Но частота остается прежней, как и цвет. Таким образом, красный свет с длиной волны 700 нм в воздухе будет иметь тот же цвет, что и красный свет с длиной волны 438 нм в этом типе стекла. (Обратите внимание, что свет с длиной волны 438 нм 90 675 в воздухе 90 676 будет казаться индиго, цветом где-то между синим и фиолетовым; но та же самая длина волны в плотном краун-стекле будет красной.)
Те же самые обстоятельства были бы верны, если бы это был огромный сосуд с водой, застекленный со всех четырех сторон. Если бы вы были погружены в воду, и красный лазерный луч светил бы в одну сторону, а затем, проходя через стекло и воду и попадая вам в глаза, он бы казался вам таким красным, как если бы вы находились вне контейнера и смотрели на тот же лазерный луч в воздухе. Показатель преломления воды составляет около 1,33, поэтому длина волны красного света, проходящего через воду, будет равна 9.4270 700 нм 1,33 = 526 нм .
Простой способ проверить, выглядит ли красный цвет объекта одинаковым в разных средах, — наполнить стакан водой и взять красную соломинку. Обратите внимание, как красная соломинка выглядит в воздухе. Поместите соломинку с другой стороны стакана с водой и посмотрите на нее сквозь воду и стакан; цвет не изменится. Затем погрузите соломинку в воду и посмотрите на нее сверху, прямо в воду, а затем через боковую часть стакана. Краснота соломинки будет одинаковой, независимо от того, как вы на нее смотрите, даже несмотря на то, что длина волны красного света меняется при переходе из одной среды в другую.
Обратите внимание, как красная соломинка выглядит в воздухе. Поместите соломинку с другой стороны стакана с водой и посмотрите на нее сквозь воду и стакан; цвет не изменится. Затем погрузите соломинку в воду и посмотрите на нее сверху, прямо в воду, а затем через боковую часть стакана. Краснота соломинки будет одинаковой, независимо от того, как вы на нее смотрите, даже несмотря на то, что длина волны красного света меняется при переходе из одной среды в другую.
Теперь предположим, что вы с другом собираетесь плавать. Прежде чем прыгнуть в бассейн с водой, вы можете увидеть, что он одет в красные плавки. Если вы прыгнете первым, погрузитесь в воду и посмотрите на своего друга, все еще стоящего на краю бассейна, красный цвет его плавок будет таким же, как и до того, как вы прыгнули в бассейн. Далее он прыгнет в бассейн. Если стоять головой над водой, то можно посмотреть на его стволы, находящиеся ниже поверхности воды, и они будут такого же красного цвета. Наконец, если вы полностью погрузитесь в воду, вы не заметите изменений в красном цвете стволов.
В двух случаях, когда красный свет переходит из воздуха в воду или из воды в воздух, длина волны изменяется, но частота красного света остается неизменной . Так что цвет останется постоянным, даже если длина волны изменится при переходе от одной среды к другой, так как именно частота света определяет его цвет во всех средах.
Вернуться к электронной почте Вопросы и ответы Teds
Перейти к Библейским комментариям Теда и другим ссылкам
Посмотреть новую международную версию Библии
Перейти на домашнюю страницу Teds
Зависимость уравнения передачи Фрииса от частоты и поляризации
Ключевые выводы
По мере увеличения частоты радиоволн потери на пути распространения в свободном пространстве ❲FSPL❳ увеличиваются, а мощность на приемном конце уменьшается, пар.

Модифицированное уравнение передачи Фрииса учитывает несоответствие поляризации и определяется как:
Рисунок 1: Коэффициент усиления, высота и апертура e антенны влияют на характеристики антенны
Антенны жизненно важны для телекоммуникационных систем, поскольку они обеспечивают передачу и прием сигналов. Мощность сигнала, высота и апертура антенны влияют на характеристики антенны. Уравнение передачи Фрииса количественно определяет мощность, принимаемую на приемном конце антенны, и потери мощности.
Расчет мощности на приемном конце можно рассчитать с помощью уравнения передачи Фрииса при условии, что известны плотность передаваемой мощности и эффективная апертура приемной антенны. Применение уравнения передачи Фрииса оказалось эффективным, особенно в спутниковой связи и системах, где требуются минимальные отражения.
Уравнение передачи Фрииса
Уравнение передачи Фрииса названо в честь Харальда Т. Фрииса, пионера в области радиоприемников и антенн. Его работа в лабораториях Белла была в основном связана с распространением радиоволн, микроволновыми системами и антеннами. Он ввел аналитическое уравнение для расчета потерь при передаче, показанное ниже.
Фрииса, пионера в области радиоприемников и антенн. Его работа в лабораториях Белла была в основном связана с распространением радиоволн, микроволновыми системами и антеннами. Он ввел аналитическое уравнение для расчета потерь при передаче, показанное ниже.
, где P t и P r — мощность сигнала на стороне передачи и на стороне приема соответственно. А t и A r дают эффективную апертуру передающей и приемной антенн. Расстояние между антеннами обозначается d и представляет собой длину волны сигнала.
Исходное уравнение Фрииса модифицировано с учетом коэффициентов усиления антенны и считается основным уравнением в теории антенн. Сегодня уравнение передачи Фрииса широко используется и чаще всего встречается в следующей форме:
, где G t и G r дает коэффициенты усиления передающей и приемной концевых антенн. Это уравнение дает влияние потерь при передаче, усиления антенны и длины волны на передаваемую и принимаемую мощности. В исходном уравнении Фрииса нет числового коэффициента, и это было названо одним из преимуществ исходного уравнения. Однако модифицированное уравнение содержит коэффициенты усиления антенн на обоих концах.
В исходном уравнении Фрииса нет числового коэффициента, и это было названо одним из преимуществ исходного уравнения. Однако модифицированное уравнение содержит коэффициенты усиления антенн на обоих концах.
Уравнение Фрииса и его частотная зависимость
Как известно, все электромагнитные волны подчиняются следующему уравнению:
Где c — скорость электромагнитной волны, равная 3×10 8 м/с, а f — частота волна.
Преобразовывая приведенное выше уравнение для и подставляя в уравнение 2, мы можем получить соотношение между мощностью, доступной на приемной антенне:
Мощность, принимаемая на приемной антенне P r и частота f имеют обратную пропорциональность. На более низких частотах или на более длинных волнах P r более сопоставимы с более высокими частотами. Если вы передаете известное количество мощности P t на частотах f 1 и f 2 , так что f 1 > f 2 и P r1 и P 3 r2 на приемном конце антенны с усилением G на этих частотах соответственно, то P r2 > P r1 .
Потери мощности в телекоммуникационной системе даются как системные потери, L s , выраженные в дБ. Это разница между переданной мощностью P t и принятой мощностью P r .
По мере увеличения частоты принимаемая мощность P r уменьшается. Это означает, что потери в системе тем больше, чем выше частота. На более высокой частоте системные потери увеличиваются и влияют на качество приема.
Высокие системные потери, связанные с высокочастотными сигналами, требуют двухточечной связи, когда передающая и принимающая оконечные антенны размещаются поблизости. Для мобильной связи поставщики услуг придерживаются более низкой частоты, что улучшает их обслуживание и доступность. Однако низкочастотная связь может быть проблемой, поскольку производители мобильных телефонов должны разрабатывать антенны для более длинных волн.
Потери на пути в свободном пространстве ❲FSPL❳ — это еще одна потеря, присутствующая в системе радиочастотной связи, представленная следующим уравнением:
Обратное значение того же FSPL присутствует в уравнении передачи Friis, показанном в уравнении 4. Потери на пути составляют значительную долю передаваемой мощности на более высоких частотах и вызывают снижение мощности на приемном конце. FSPL также увеличивается по мере увеличения расстояния между двумя антеннами.
Потери на пути составляют значительную долю передаваемой мощности на более высоких частотах и вызывают снижение мощности на приемном конце. FSPL также увеличивается по мере увеличения расстояния между двумя антеннами.
Обобщение уравнения передачи Фрииса на основе поляризации антенн
Любое электромагнитное поле состоит из электрического и магнитного полей. Электрическое поле колеблется в каком-то направлении по отношению к электромагнитной волне, и это направление определяет поляризацию волны. Электромагнитные волны классифицируются на основе колебаний электрического поля.
Линейная поляризация — При линейной поляризации электрическое поле и электромагнитная волна колеблются в одной плоскости. Электрическое поле линейно с электромагнитной волной. Если электрическое поле колеблется горизонтально, это называется горизонтальной поляризацией. При вертикальной поляризации электрическое поле колеблется в вертикальном направлении, а наклонную поляризацию можно отличить по углу колебаний +45° или -45°.

Круговая поляризация — При этой поляризации электромагнитная волна вращается, а электрическое поле, если его проследить, образует спиралевидную форму. В зависимости от направления вращения существует два типа круговой поляризации, а именно: правая круговая поляризация ❲RHCP❳ и левая круговая поляризация ❲LHCP❳.
Эллиптическая поляризация — Эллиптическая поляризация также называется смешанной поляризацией. Это смесь линейной и круговой поляризации.
Поляризация антенны — это поляризация передаваемой и принимаемой ею электромагнитной волны, и приведенная выше классификация применима и к антеннам. При связи между антеннами и передающая, и приемная антенны должны иметь одинаковую поляризацию.
Приема не будет, если поляризация антенны принимающей стороны отличается от поляризации передающей стороны. Если существует какая-либо разница в углах поворота двух антенн одной поляризации, то возможен прием с потерей мощности. Этот тип несоответствия поляризации представлен фактором, называемым коэффициентом поляризационных потерь ❲PLF❳. Принимая во внимание рассогласование поляризации в антеннах, уравнение Фрииса, показанное в уравнении 4, можно пересмотреть и обобщить следующим образом:
Если существует какая-либо разница в углах поворота двух антенн одной поляризации, то возможен прием с потерей мощности. Этот тип несоответствия поляризации представлен фактором, называемым коэффициентом поляризационных потерь ❲PLF❳. Принимая во внимание рассогласование поляризации в антеннах, уравнение Фрииса, показанное в уравнении 4, можно пересмотреть и обобщить следующим образом:
Если вы работаете над радиоканалами связи в свободном пространстве и ищете подходящую антенну для приема сигналов, то уравнение передачи Friis может помочь вам в выборе антенны. Применение уравнения Фрииса для определения усиления любой из двух антенн оказалось очень эффективным. В связи между антеннами невозможно спроектировать антенны без использования уравнения передачи Фрииса.
Если вы хотите быть в курсе наших материалов по системному анализу, подпишитесь на нашу рассылку, в которой собраны ресурсы о текущих тенденциях и инновациях. Если вы хотите узнать больше о том, как у Cadence есть решение для вас, поговорите с нами и нашей командой экспертов.


 Примером механических волн являются волны на море.
Примером механических волн являются волны на море.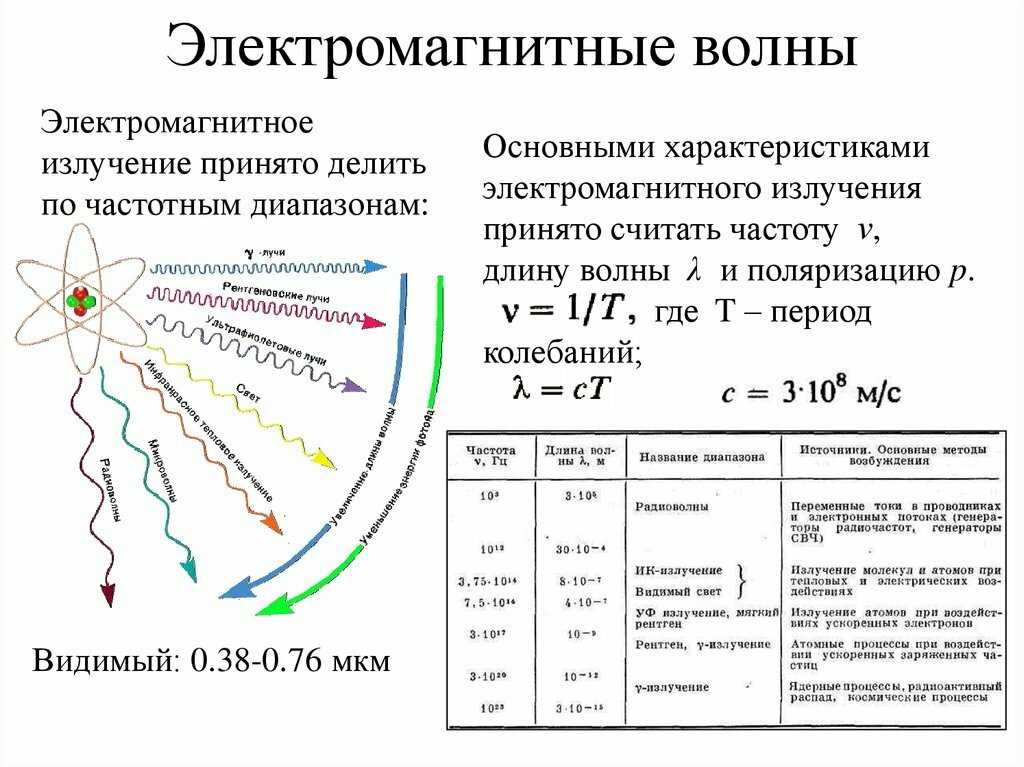

 ..
..
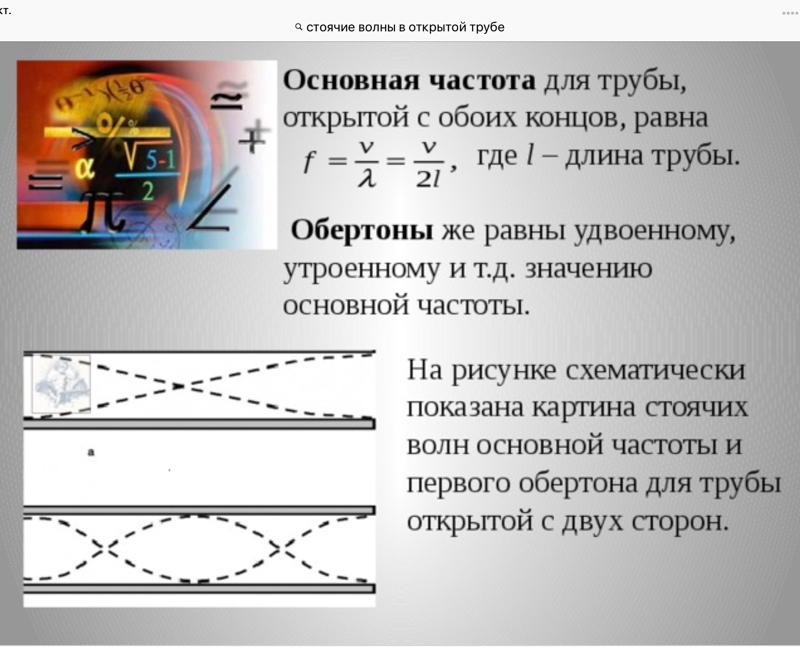 Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине.
Помимо материала преграды, через которую проходит сигнал вай-фай, важен также угол падения луча. Так, если сигнал проходит через препятствие под прямым углом, это обеспечит меньшие потери, чем если бы он падал на него под углом 45 градусов. Еще хуже, если сигнал проходит через преграду под очень острым углом. В этом случае, грубо говоря, можно смело умножать толщину стены на 10 и рассчитывать потери WiFi передачи согласно этой величине. Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
Соответственно, чем дальше расстояние, тем шире становится луч, тем меньшая мощность сигнала приходится на единицу площади, и тем меньше энергии сигнала попадает в принимающую антенну.
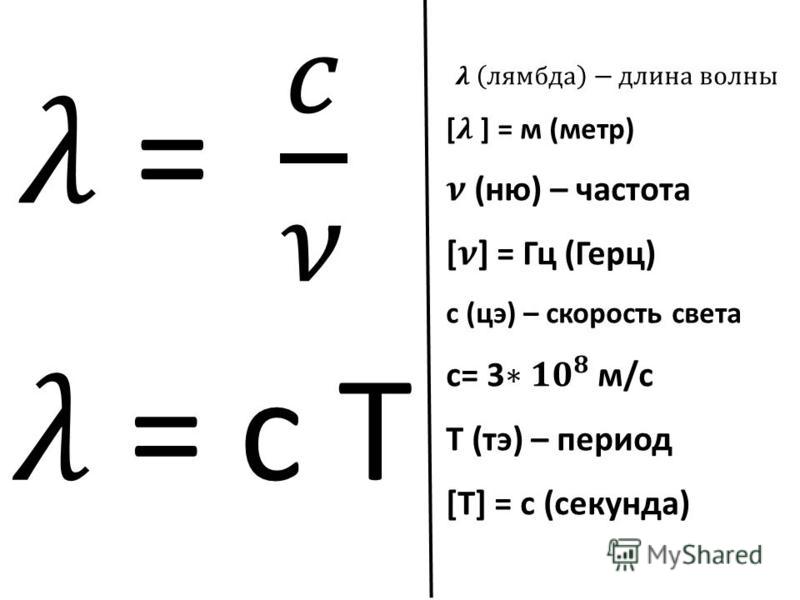
 } [/латекс]
} [/латекс]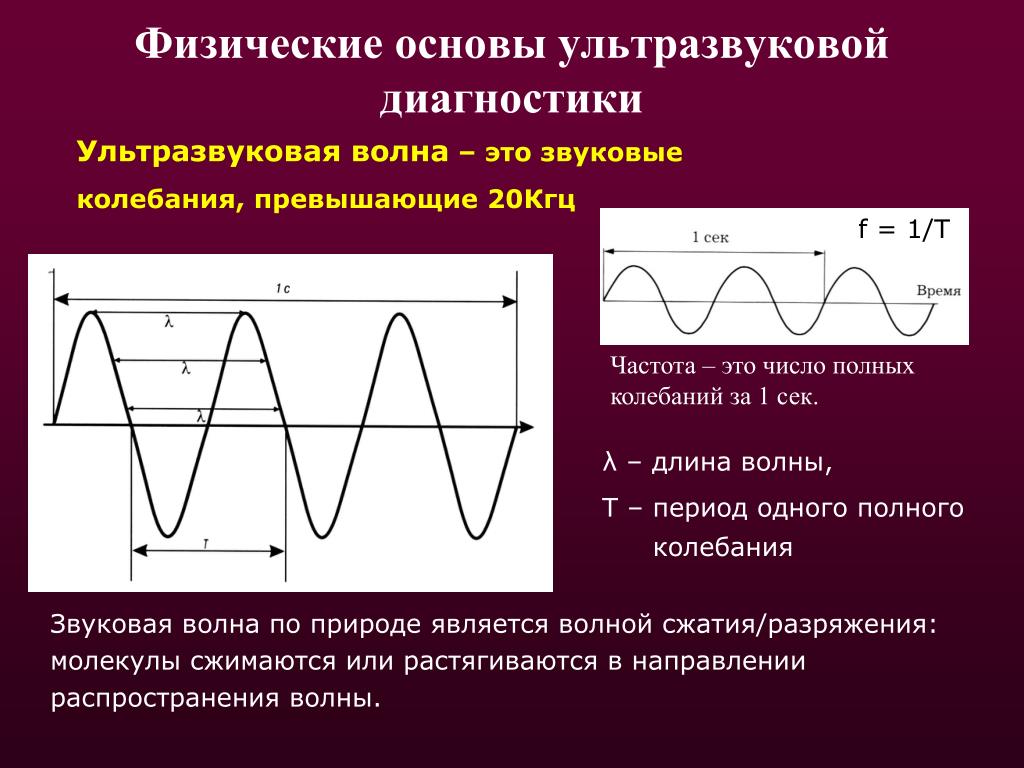
 [/latex]
[/latex]
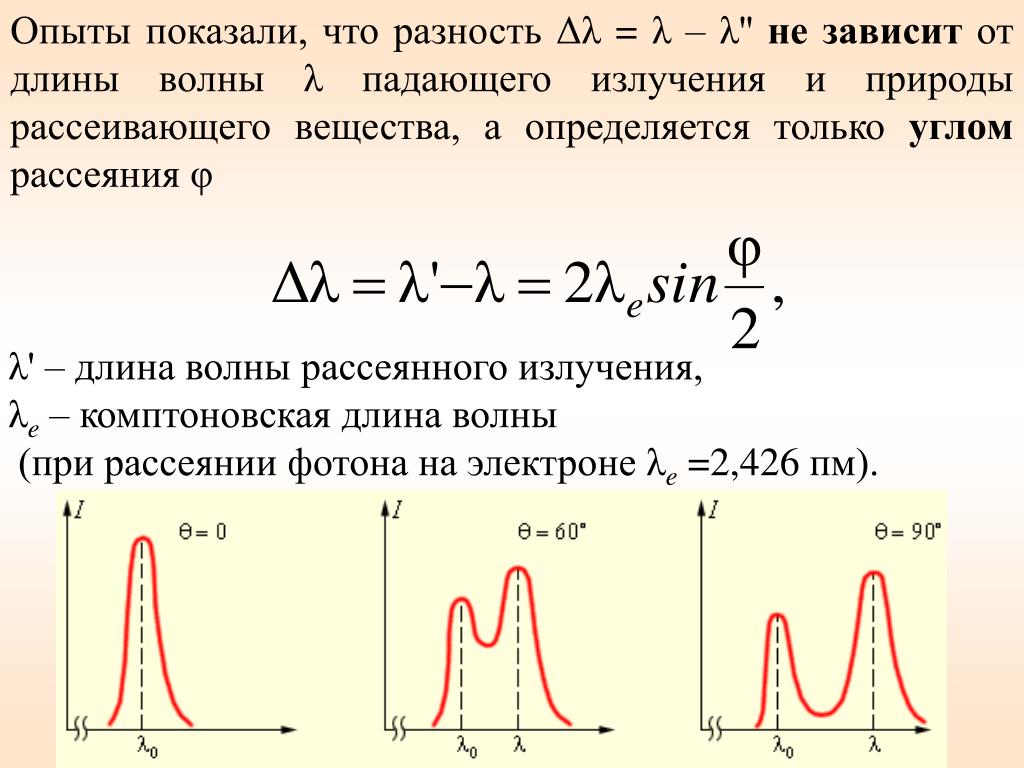 = скорость волны, ∆ v = амплитуда скорости
= скорость волны, ∆ v = амплитуда скорости

 Это общепринятое мнение порог слышимости для человека. Звуки с интенсивностью ниже этого значения неслышны (вполне возможно) каждому человеку.
Это общепринятое мнение порог слышимости для человека. Звуки с интенсивностью ниже этого значения неслышны (вполне возможно) каждому человеку.
 Непер также является безразмерной единицей.
Непер также является безразмерной единицей.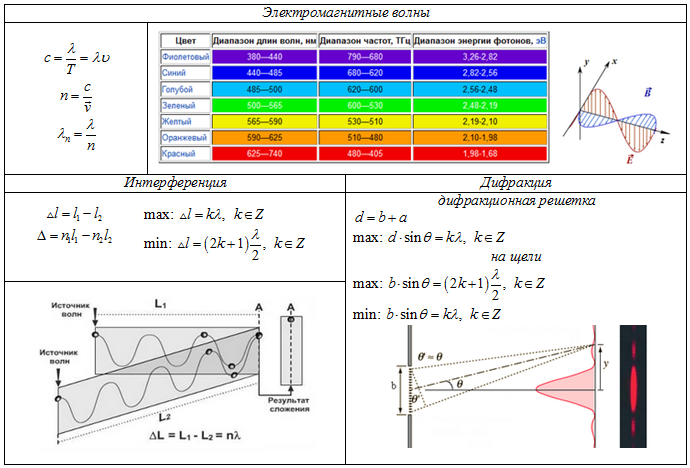 AHD «Шотландский математик, который изобрел логарифмы и ввел использование десятичной точки в записи чисел».
AHD «Шотландский математик, который изобрел логарифмы и ввел использование десятичной точки в записи чисел».
 95(i)(1): Работодатели должны предоставить средства защиты органов слуха всем сотрудникам, подвергающимся воздействию средневзвешенного по времени уровня 85 децибел или выше за 8 часов бесплатно для сотрудников.
95(i)(1): Работодатели должны предоставить средства защиты органов слуха всем сотрудникам, подвергающимся воздействию средневзвешенного по времени уровня 85 децибел или выше за 8 часов бесплатно для сотрудников. извержение вулкана Кракатау, 1908 г. Тунгусский метеор
извержение вулкана Кракатау, 1908 г. Тунгусский метеор Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха). также известная как Межушная разница во времени (ITD)
Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха). также известная как Межушная разница во времени (ITD) С помощью этих шкал измеряется размер землетрясения, выраженный амплитудой сейсмической волны (количество сотрясений в точке, удаленной от землетрясения), а не интенсивностью или степенью разрушительности. Большинство шкал магнитуд имеют логарифмическую основу, так что увеличение на одно целое число соответствует землетрясению в 10 раз сильнее, чем землетрясение, указанное следующим меньшим числом. Это означает примерно 30-кратное увеличение количества высвобождаемой энергии. Таким образом, магнитуда 5 представляет собой движение грунта примерно в 10 раз больше, чем магнитуда 4, и примерно в 30 раз больше высвобождаемой энергии. Землетрясение магнитудой 5 представляет собой 100-кратное движение грунта и 900 раз больше энергии, выделившейся при землетрясении магнитудой 3.
С помощью этих шкал измеряется размер землетрясения, выраженный амплитудой сейсмической волны (количество сотрясений в точке, удаленной от землетрясения), а не интенсивностью или степенью разрушительности. Большинство шкал магнитуд имеют логарифмическую основу, так что увеличение на одно целое число соответствует землетрясению в 10 раз сильнее, чем землетрясение, указанное следующим меньшим числом. Это означает примерно 30-кратное увеличение количества высвобождаемой энергии. Таким образом, магнитуда 5 представляет собой движение грунта примерно в 10 раз больше, чем магнитуда 4, и примерно в 30 раз больше высвобождаемой энергии. Землетрясение магнитудой 5 представляет собой 100-кратное движение грунта и 900 раз больше энергии, выделившейся при землетрясении магнитудой 3. Он собрал записи сейсмических волн от большого количества землетрясений и разработал калиброванную систему измерения их магнитуды. Он откалибровал свою шкалу магнитуд, используя измеренные максимальные амплитуды поперечных волн на сейсмометрах, особенно чувствительных к поперечным волнам с периодами около одной секунды. Записи должны были быть получены с помощью специального прибора, называемого сейсмографом Вуда-Андерсона. Хотя его работа изначально была откалибрована только для этих конкретных сейсмометров и только для землетрясений в южной Калифорнии, сейсмологи разработали масштабные коэффициенты, чтобы распространить шкалу магнитуд Рихтера на многие другие типы измерений на всех типах сейсмометров по всему миру. На самом деле, были сделаны оценки магнитуд тысяч лунотрясений и двух землетрясений на Марсе.
Он собрал записи сейсмических волн от большого количества землетрясений и разработал калиброванную систему измерения их магнитуды. Он откалибровал свою шкалу магнитуд, используя измеренные максимальные амплитуды поперечных волн на сейсмометрах, особенно чувствительных к поперечным волнам с периодами около одной секунды. Записи должны были быть получены с помощью специального прибора, называемого сейсмографом Вуда-Андерсона. Хотя его работа изначально была откалибрована только для этих конкретных сейсмометров и только для землетрясений в южной Калифорнии, сейсмологи разработали масштабные коэффициенты, чтобы распространить шкалу магнитуд Рихтера на многие другие типы измерений на всех типах сейсмометров по всему миру. На самом деле, были сделаны оценки магнитуд тысяч лунотрясений и двух землетрясений на Марсе. Недостатком этого метода является то, что 90 675 M 90 389 с 90 390 90 676 вычисляется из полосы пропускания примерно от 18 до 22 с. В настоящее время известно, что энергия, излучаемая землетрясением, концентрируется в другой полосе пропускания и на более высоких частотах. Обратите внимание, что это не полная «внутренняя» энергия землетрясения, переданная от источников, таких как гравитационная энергия, или к поглотителям, таким как тепловая энергия. Это только количество, излучаемое землетрясением в виде сейсмических волн, которое должно составлять небольшую долю от общей энергии, передаваемой во время процесса землетрясения.
Недостатком этого метода является то, что 90 675 M 90 389 с 90 390 90 676 вычисляется из полосы пропускания примерно от 18 до 22 с. В настоящее время известно, что энергия, излучаемая землетрясением, концентрируется в другой полосе пропускания и на более высоких частотах. Обратите внимание, что это не полная «внутренняя» энергия землетрясения, переданная от источников, таких как гравитационная энергия, или к поглотителям, таким как тепловая энергия. Это только количество, излучаемое землетрясением в виде сейсмических волн, которое должно составлять небольшую долю от общей энергии, передаваемой во время процесса землетрясения.
 1. Синусоида (синусоидальный сигнал) распространяется слева направо (от А до В). Скорость, с которой распространяются синусоидальные колебания, называется скоростью волны. Источник: Мануэль Р. Камачо, StudySmarter.
1. Синусоида (синусоидальный сигнал) распространяется слева направо (от А до В). Скорость, с которой распространяются синусоидальные колебания, называется скоростью волны. Источник: Мануэль Р. Камачо, StudySmarter.

 3. На скорость звука в жидкостях влияет их температура. Большая кинетическая энергия из-за более высоких температур заставляет молекулы и атомы вибрировать быстрее со звуком. Источник: Мануэль Р. Камачо, StudySmarter.
3. На скорость звука в жидкостях влияет их температура. Большая кинетическая энергия из-за более высоких температур заставляет молекулы и атомы вибрировать быстрее со звуком. Источник: Мануэль Р. Камачо, StudySmarter.
 Волны разной длины смешиваются в создающих их штормовых системах. Однако, поскольку более крупные волны движутся быстрее, они первыми покидают штормовые системы, достигая побережья раньше более коротких волн. Когда эти волны достигают побережья, они называются волнами.
Волны разной длины смешиваются в создающих их штормовых системах. Однако, поскольку более крупные волны движутся быстрее, они первыми покидают штормовые системы, достигая побережья раньше более коротких волн. Когда эти волны достигают побережья, они называются волнами.
