Система параллельных сил. Момент силы
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ. МОМЕНТ СИЛЫ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.СТАТИКА
ЛЕКЦИЯ 3
2. НА ПРЕДЫДУЩЕЙ ЛЕКЦИИ
Научитьсязаменять равнодействующей параллельные силы,
определять момент силы относительно точки и
оси
2
Цель лекции
3. СЛОЖЕНИЕ ДВУХ СОНАПРАВЛЕННЫХ СИЛ
Имеет ли такая система сил равнодействующую?(F , F ‘) ~ (F , F ‘, Q, Q’) ~ (R1, R2 ) ~ R
С
D
A
B
Q Q’
R1 F Q,
R2 F ‘ Q’
R R1 R2 F Q F ‘ Q’ F F ‘
R F F’
3
Система параллельных сил
R F F’
4.
 СЛОЖЕНИЕ ДВУХ СОНАПРАВЛЕННЫХ СИЛГде находится точка приложения равнодействующей?
СЛОЖЕНИЕ ДВУХ СОНАПРАВЛЕННЫХ СИЛГде находится точка приложения равнодействующей?tg AD / CD
tg Q / F
С
D
B
A
AD F ‘
BD F
4
Система параллельных сил
tg BD / CD
tg Q’ / F ‘
AD / CD Q / F
BD/ CD Q’ / F ‘
AD F Q CD
BD F ‘ Q’ CD
Две сонаправленные силы имеют
равнодействующую,
направленную …
равную по модулю …
ее точка приложения …
5. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
Имеет ли такая система сил равнодействующую?С
B
A
F1 F2
(F1, F2 ) ~ (F1, F1′, R) ~ R
F2 F1′ R
R F2 F1
5
Система параллельных сил
F1′ F1
R F2 F1
6. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
Где находится точка приложения равнодействующей?C
A
F1
B
F2
AC F2
BC F1
R
F1 A
R F2 F1
C
F1′
F2
6
Система параллельных сил
B
R
AC R
BC F1
AC F2 F1
BC
F1
Две противоположно направленные
и не равные по модулю силы имеют
равнодействующую,
направленную …
равную по модулю …
ее точка приложения …
7.
 СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛF2 F1
СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛF2 F1Имеет ли такая система сил равнодействующую?
F1
C
A
F2
7
Система параллельных сил
R F2 F1
R 0
AC F2 F1
BC
F1
BC
Две противоположно направленные
равные по модулю силы не имеют
равнодействующей
8. СЛОЖЕНИЕ ДВУХ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ СИЛ
F1C
A
F2
Две противоположно направленные, равные по модулю силы,
не лежащие на одной прямой, будем называть парой сил
Пара сил, действующая на свободное тело, будет вызывать его
вращение
Мерой вращательного взаимодействия в
механике является момент
8
Система параллельных сил
9. МОМЕНТ СИЛЫ
Относительно точкив плоскости –
алгебраический
момент (скаляр)
Относительно точки
в пространстве –
вектор момента
Относительно оси
(вектор или скаляр?)
Вращательное действие силы вокруг закрепленной точки тела характеризуют
следующие факторы:
1) Модуль силы.

2) Плечо силы.
3) Плоскость вращения (поворота) – плоскость, содержащая силу и точку,
4) Направление вращения.
9
Момент силы
10. АЛГЕБРАИЧЕСКИЙ МОМЕНТ СИЛЫ
Алгебраический момент силы относительно точки – скаляр, равныйпроизведению модуля силы на плечо силы относительно данной
точки, взятый со знаком + или —
Плечо – кратчайшее расстояние от точки до линии действия силы.
Плечо можно также определить как отрезок перпендикуляра,
опущенного из точки на линию действия силы
F1
h
A
1
0
Момент силы
M A(F1) F1h
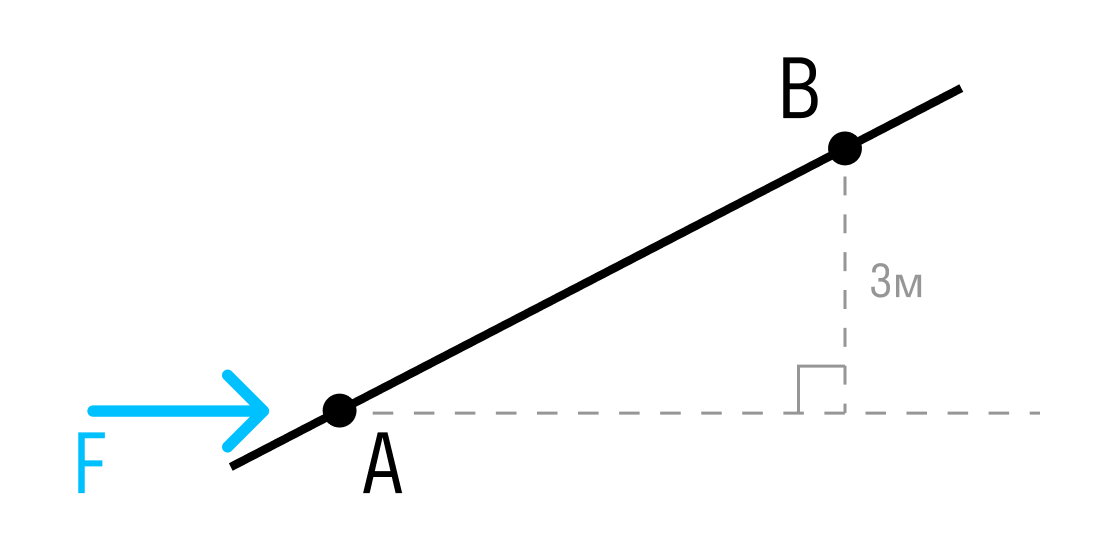
Задача: определить моменты изображенных на
рисунке сил относительно точки А
F1
F2
b
a
F3
A
F4
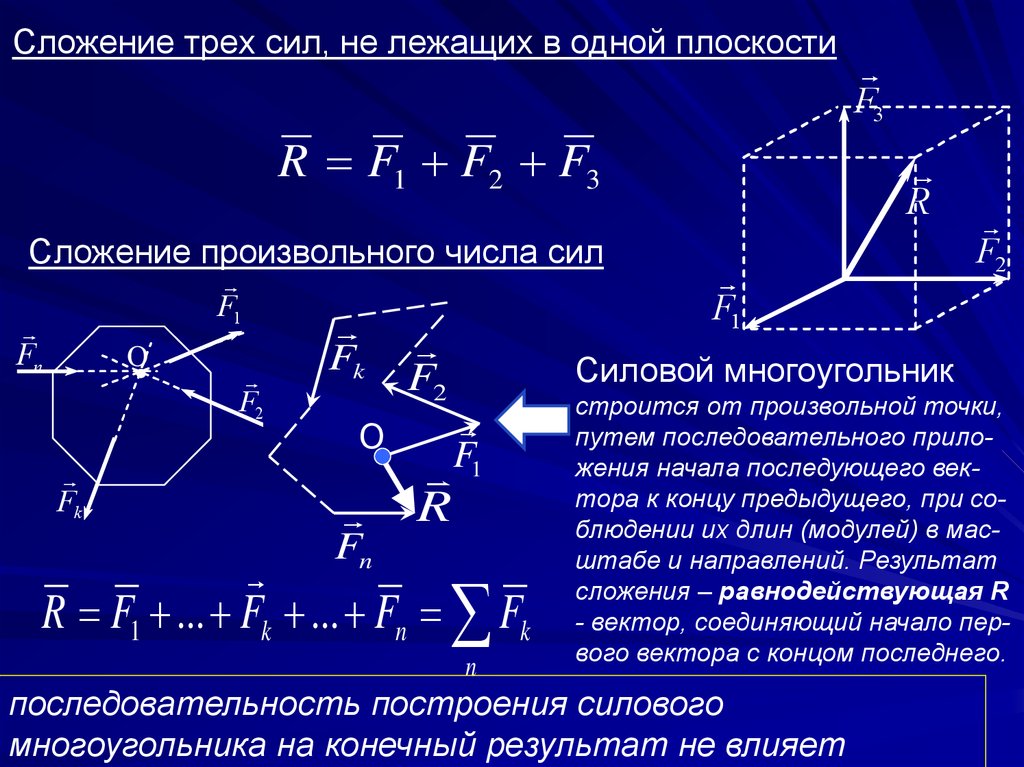
11. ВЕКТОР МОМЕНТА СИЛЫ
Вектор момента силы относительно точки – вектор, равный помодулю произведению модуля силы на плечо относительно данной
точки, и направленный перпендикулярно плоскости, в которой
расположены точка и линия действия силы, в ту сторону, откуда
вращение под действием силы видно происходящим против часовой
стрелки
B
F
z
M O (F )
h
O
x
11
Момент силы
r
A
M O (F ) r F
M O ( F ) r F F r sin F h
y
M O ( F ) F h 2S OAB
12.
 ВЕКТОР МОМЕНТА СИЛЫB
ВЕКТОР МОМЕНТА СИЛЫBF
z
M O (F )
h
O
r
A
M O (F ) r F
y
x
i j k
M O ( F ) x y z ( yFz zFx )i ( zFx xFz ) j ( xFy yFx )k
Fx Fy Fz
12
Момент силы
13. ТЕОРЕМА ВАРИНЬОНА
Векторное произведение удовлетворяет законудистрибутивности:
r ( F1 F2 Fn ) r F1 r F2 r Fn
Теорема Вариньона (для ССС): момент
равнодействующей системы сходящихся сил
относительно произвольной точки (центра)
равен векторной сумме моментов сил
системы относительно того же центра.
1654-1722
M O ( R) rA ( F1 F2 Fn )
13
Момент силы
M O ( Fk )
14. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
M Z (F )M Z (F ) 0
z
СИЛА || ОСИ
F
( xy )
O
14
Момент силы
h Fxy
ЛИНИЯ ДЕЙСТВИЯ
СИЛЫ ПЕРЕСЕКАЕТ ОСЬ
Fz
A
M z ( F ) M O ( Fxy ) Fxy h
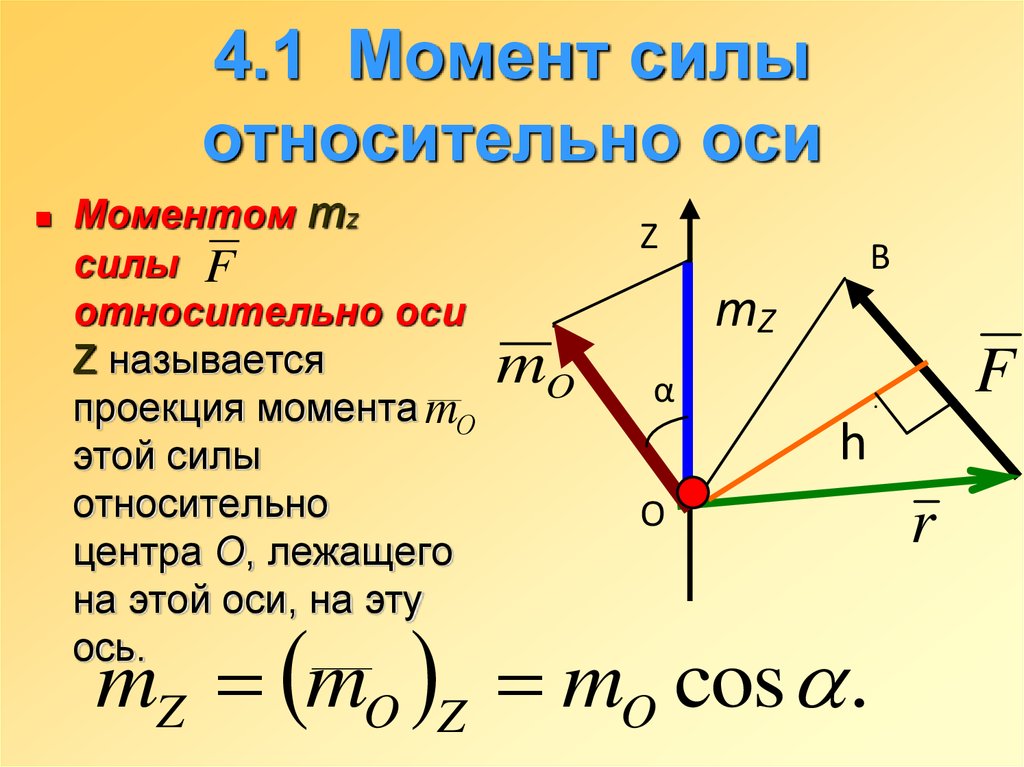
Момент силы относительно оси — скалярная
величина, равная алгебраическому моменту
проекции этой силы на плоскость,
перпендикулярную оси, относительно точки
пересечения оси и плоскости
15.
 ТЕОРЕМА О СВЯЗИ МОМЕНТОВ Моменты сил относительно осей в системе координат Oxyz
ТЕОРЕМА О СВЯЗИ МОМЕНТОВ Моменты сил относительно осей в системе координат Oxyzравны проекциям момента силы относительно начала
координат О
Если воспользоваться теоремой Вариньона и вычислить момент силы,
разложив ее на составляющие, получим
z
F
.
O
x
15
Fx
y
M Z ( F ) ( xFy yFx )
Fy
Fxy
i j k
M O ( F ) x y z ( yFz zFx )i ( zFx xFz ) j ( xFy yFx )
Fx Fy Fz
( xFy yFx )k
Момент силы
English Русский Правила
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
-
2.
 3 Законы сохранения
3 Законы сохранения
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
-
4.
 3 Магнетизм
3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
-
6.
 1 Атомная физика. Квантовая теория
1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
-
6.
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Вопрос Видео: Нахождение суммы моментов пяти сил, действующих на квадрат
Стенограмма видео
Учитывая, что 𝐴𝐵𝐶𝐷 является квадратом
с длиной стороны семь сантиметров и силами, действующими на нее, как показано на рисунке,
вычислить алгебраическую сумму моментов относительно вершины 𝐵.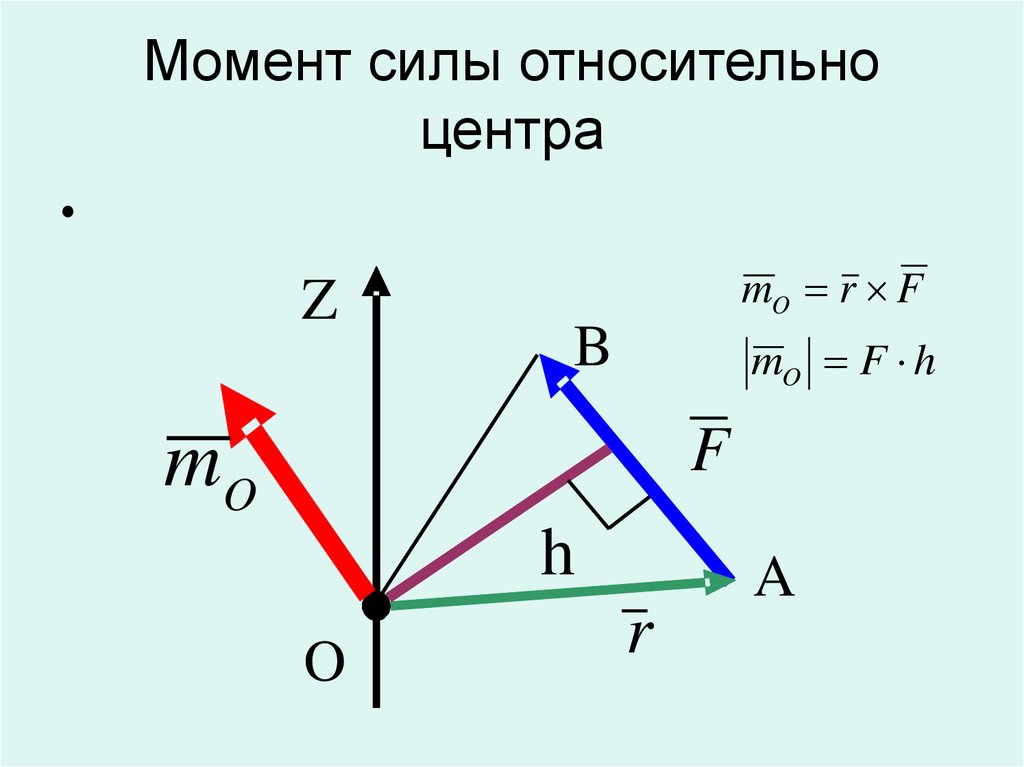
Напомним, что величина момент 𝐌 силы 𝐅, действующей из точки 𝑃 относительно точки вращения 𝑂, определяется выражением величина 𝐅, умноженная на перпендикулярное расстояние 𝑑 между точкой опоры точка и линия действия силы.
Вопрос просит нас найти алгебраическая сумма моментов относительно вершины 𝐵. Итак, это наша точка опоры. Имеем пять сил, действующих на площадь. Два из них имеют линию действия которая проходит непосредственно через точку вращения 𝐵: сила трех ньютонов, действующая по линии 𝐴𝐵 и сила в три ньютона, действующая по линии 𝐵𝐶. Следовательно, перпендикуляр расстояния между линиями действия этих двух сил и точкой вращения 𝐵 равны оба ноль. Поэтому величина их моменты относительно точки 𝐵 также равны нулю, поэтому их можно игнорировать.
Для остальных сил нам нужно
для вычисления перпендикулярного расстояния между их линиями действия и точкой
𝐵. На схеме для силы
два ньютона, действующие вдоль линии 𝐴𝐷, это расстояние 𝑑 единица, так как это
квадрат и прямая 𝐴𝐷 перпендикулярна прямой 𝐴𝐵. Аналогично, для силы четырех
ньютонов, действующих вдоль линии 𝐷𝐶, это расстояние 𝑑 два, так как 𝐷𝐶
также перпендикулярно 𝐶𝐵. И, наконец, для силы четырех
корень из двух ньютонов, действующих по линии 𝐴𝐶, это расстояние 𝑑 три.
На схеме для силы
два ньютона, действующие вдоль линии 𝐴𝐷, это расстояние 𝑑 единица, так как это
квадрат и прямая 𝐴𝐷 перпендикулярна прямой 𝐴𝐵. Аналогично, для силы четырех
ньютонов, действующих вдоль линии 𝐷𝐶, это расстояние 𝑑 два, так как 𝐷𝐶
также перпендикулярно 𝐶𝐵. И, наконец, для силы четырех
корень из двух ньютонов, действующих по линии 𝐴𝐶, это расстояние 𝑑 три.
Нам также необходимо определить направление, положительное или отрицательное, каждого из моментов каждой из сил. Вопрос говорит нам использовать принято считать, что моменты против часовой стрелки положительны. Из схемы мы видим, что все три силы имеют линию действия в направлении против часовой стрелки вокруг точки 𝐵. Так что все они будут положительными моменты.
Таким образом, алгебраическая сумма
моментов 𝐌 равно два раза 𝑑 один плюс четыре раза 𝑑 два плюс четыре корень два
раз 𝑑 три. 𝑑 один и 𝑑 два равны
длина стороны квадрата, значит, они оба равны семи сантиметрам. 𝑑 три равно половине
длина диагонали квадрата. Диагональ любого квадрата является корнем
в два раза больше длины его стороны. Итак, 𝑑 три — это семь корней над двумя.
два. Следовательно, 𝐌 равно удвоенному
семь плюс четыре раза семь плюс четыре корень два раза семь корень два над двумя.
𝑑 один и 𝑑 два равны
длина стороны квадрата, значит, они оба равны семи сантиметрам. 𝑑 три равно половине
длина диагонали квадрата. Диагональ любого квадрата является корнем
в два раза больше длины его стороны. Итак, 𝑑 три — это семь корней над двумя.
два. Следовательно, 𝐌 равно удвоенному
семь плюс четыре раза семь плюс четыре корень два раза семь корень два над двумя.
Корневые двойки здесь умножаются на дайте два, сократив двойку в знаменателе, оставив всего четыре раза Семь. Выполнив этот расчет и упрощение дает нам величину алгебраической суммы моментов относительно вершины 𝐵, 70. И единицей измерения является ньютон сантиметры.
ньютоновская механика — Почему вы можете добавлять векторы моментов?
Базовое понимание
Вектор момента говорит вам, где в пространстве действует сила.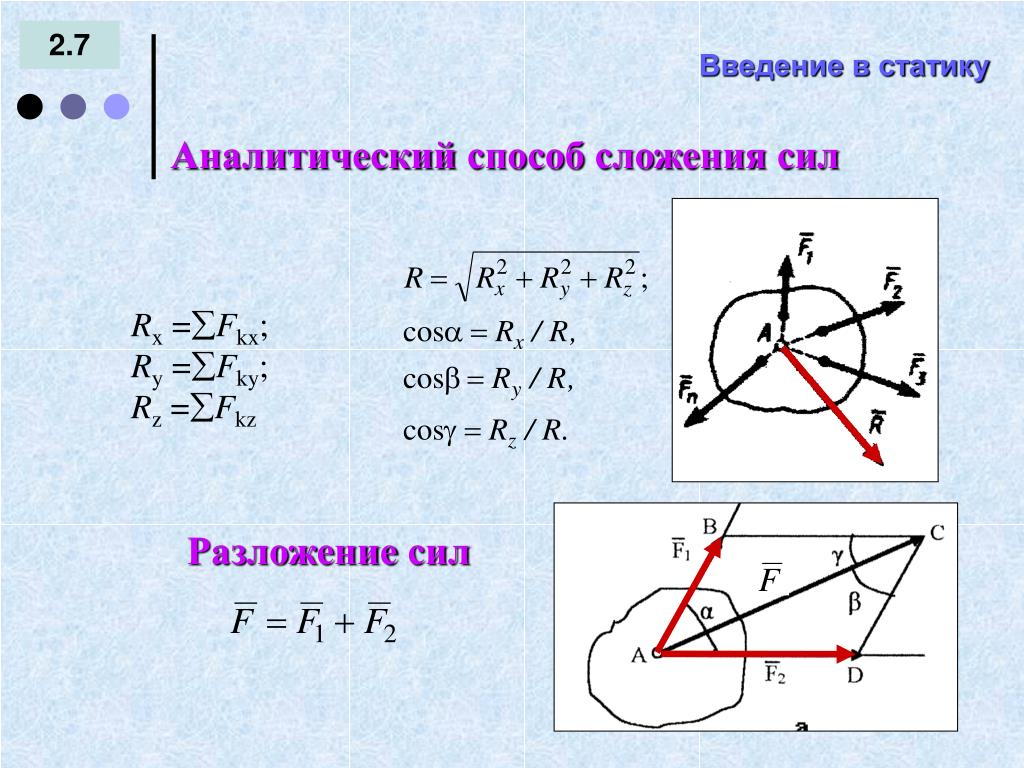 Вы можете думать о величине момента как о минимальном расстоянии до линии действия силы, а об отдельных компонентах момента как о трехмерном местоположении указанной силы в пространстве.
Вы можете думать о величине момента как о минимальном расстоянии до линии действия силы, а об отдельных компонентах момента как о трехмерном местоположении указанной силы в пространстве.
Оказывается, чтобы учесть влияние двух или более сил, действующих в разных местах, достаточно сложить компоненты векторов моментов. $$ \vec{M} = \vec{M}_1 + \vec{M}_2 = \left( \vec{r}_1 \times \vec{F}_1 \right) + \left( \vec{r }_2 \times \vec{F}_2 \right) $$
Если результат может быть нулевым, когда отдельные величины $\| \vec{M}_1 \|$ и $\| \vec{M}_2 \|$ нет. Это будет ситуация, когда либо
- Две равные и противоположные силы действуют через одно и то же место (линию действия). $$ \vec{M} = \vec{r} \times \left( \vec{F} — \vec{F} \right) = 0$$
- Две равные силы действуют по разные стороны от начала координат (точки измерения). $$ \vec{M} = (\vec{r}) \times \vec{F} + (- \vec{r}) \times \vec{F} =0 $$
- Две параллельные, но разные силы уравновешивают друг друга.
 $$ \vec{M} = \vec{r}_1 \times \hat{e} F_1 + \vec{r}_2 \times \hat{e} F_2 = \hat{k} (d_1 F_1-d_2 F_2) =0 $$
$$ \vec{M} = \vec{r}_1 \times \hat{e} F_1 + \vec{r}_2 \times \hat{e} F_2 = \hat{k} (d_1 F_1-d_2 F_2) =0 $$ - Через начало координат действуют две непараллельные и разные силы. $$ \vec{F} = \vec{r}_1 \times \vec{F}_1 + \vec{r}_2 \times \vec{F}_2 = 0 $$
К вашему сведению. Обычно две косые ненулевые силы всегда создают ненулевой результирующий момент.
Глубокий вопрос почему немного сложнее объяснить.
Проще говоря, вы можете объединить силы и моменты в одну вещь с 6 компонентами, называемыми гаечным ключом (тип винта), который представляет собой линию в пространстве, через которую действует сила, а также величину силы, использующей что-либо. называемые координатами линии Плюкера. Точно так же, как векторы передают величину и направление , все винты (например, ключ выше) передают величину , направление , местоположение и шаг .
Таким образом, сила и моменты — это винты, которые представляют линии в пространстве (с помощью направления и местоположения, например, луча) в координатах Плюкера. Кроме того, проективная геометрия говорит нам, что геометрическими объектами, такими как точки, линии и плоскости в пространстве , можно манипулировать с помощью линейной алгебры геометрически значимыми способами.
Кроме того, проективная геометрия говорит нам, что геометрическими объектами, такими как точки, линии и плоскости в пространстве , можно манипулировать с помощью линейной алгебры геометрически значимыми способами.
Одним из таких способов является сложение, когда сложение двух линейных векторов Плюкера (винтов) приводит к третьему линейному вектору, который является линейной комбинацией двух исходных. Другими словами, подумайте обо всех точках, составляющих линию, и если две линии имеют общую точку (пересекаются), то линейная комбинация также будет содержать эту точку. 9\top \boldsymbol{\ell} = 0 $ с линейной алгеброй.
Таким образом, точка, пересекающая две прямые $\boldsymbol{\ell}_1$ и $\boldsymbol{\ell}_2$, также будет пересекать сложение двух прямых посредством дистрибутивных свойств линейной алгебры.
$$ \boldsymbol{p} \cdot \left( \boldsymbol{\ell}_1 + \boldsymbol{\ell}_2 \right) = \boldsymbol{p} \cdot \boldsymbol{\ell}_1 + \boldsymbol {p} \cdot \boldsymbol{\ell}_2 = 0 + 0 $$
Если вы научились складывать векторы сил, то знаете, что результатом будет линейная комбинация двух сил.


 3 Законы сохранения
3 Законы сохранения
 3 Магнетизм
3 Магнетизм
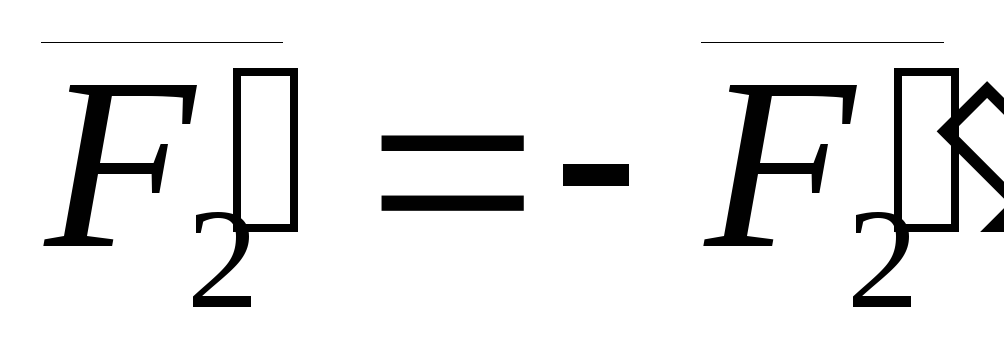 1 Атомная физика. Квантовая теория
1 Атомная физика. Квантовая теория
 $$ \vec{M} = \vec{r}_1 \times \hat{e} F_1 + \vec{r}_2 \times \hat{e} F_2 = \hat{k} (d_1 F_1-d_2 F_2) =0 $$
$$ \vec{M} = \vec{r}_1 \times \hat{e} F_1 + \vec{r}_2 \times \hat{e} F_2 = \hat{k} (d_1 F_1-d_2 F_2) =0 $$