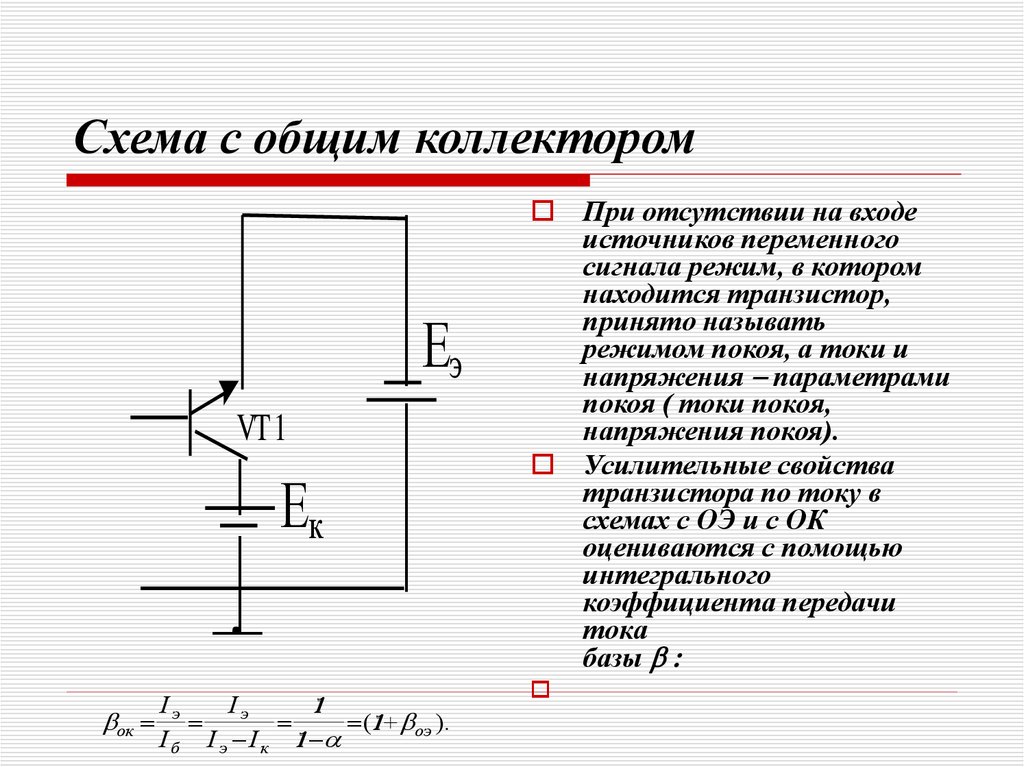
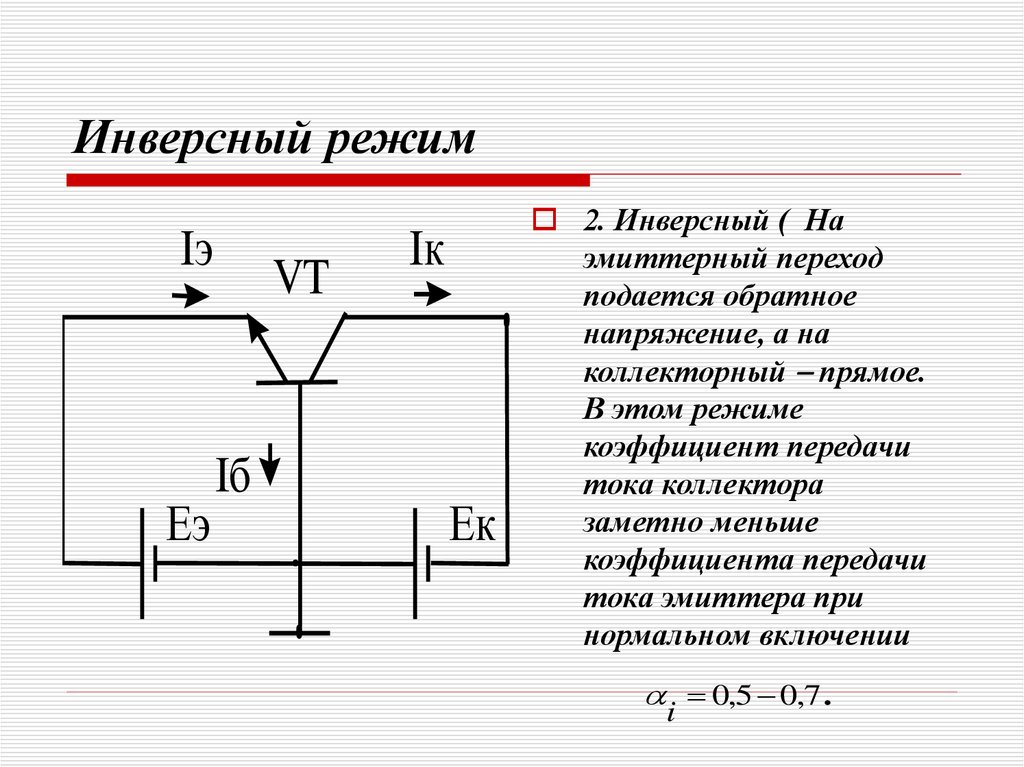
Частотные свойства биполярных транзисторов

Зависимость значения коэффициента передачи тока транзистора от частоты для
каскадов с общей базой (ОБ) и общим эмиттером (ОЭ).
Онлайн калькулятор зависимости коэффициента передачи тока от частоты

Частотные свойства транзистора – это набор характеристик, которые определяют диапазон частот входных сигналов, в пределах которого прибор тем или иным образом выполняет присущие ему функции по усилению или преобразованию этих сигналов.
Для биполярных транзисторов для определения частотных характеристик принято использовать (среди прочих) частотную зависимость коэффициентов передачи входного тока в схемах ОБ и ОЭ.
Обозначаются эти коэффициенты, как правило: h31б (можно встретить α – альфа) и h31э (или β – бета).

Параметр коэффициента передачи транзистора h31б

(включённого по схеме с ОБ), как правило, в перечне справочных характеристик не приводится, но его всегда можно рассчитать, исходя из следующего соотношения: α = β/(1 + β).
Значение этого параметра всегда будет меньше 1, т. к. мы помним, что схема ОБ обладает усилением по напряжению, но не усиливает ток. Но дело в данном случае не в этом, а в том, что если мы поочерёдно подставим в эту формулу два значения β (т. е. h31э), например 100 и 50 (разница в 50%), то легко убедимся, что изменение α (т. е. h31б) составляет всего 1%.
А с учётом того, что для каскада с ОБ, как мы помним:

K_u ≈ R_к x α/R_э, то и зависимость его усиления по напряжению от β транзистора будет значительно снижена. А потому и частотные свойства по отношению к ОЭ у него окажутся более предпочтительными, так как β транзистора существенно зависит от частоты, а Ku каскада ОЭ – от β. Поясним сказанное рисунком.

Рис.1 Зависимость коэффициентов передачи тока транзисторов от частоты

Здесь β₀ (h31э) и α₀ (h31б) – это коэффициенты передачи тока транзисторов в схемах ОЭ и ОБ по постоянному току.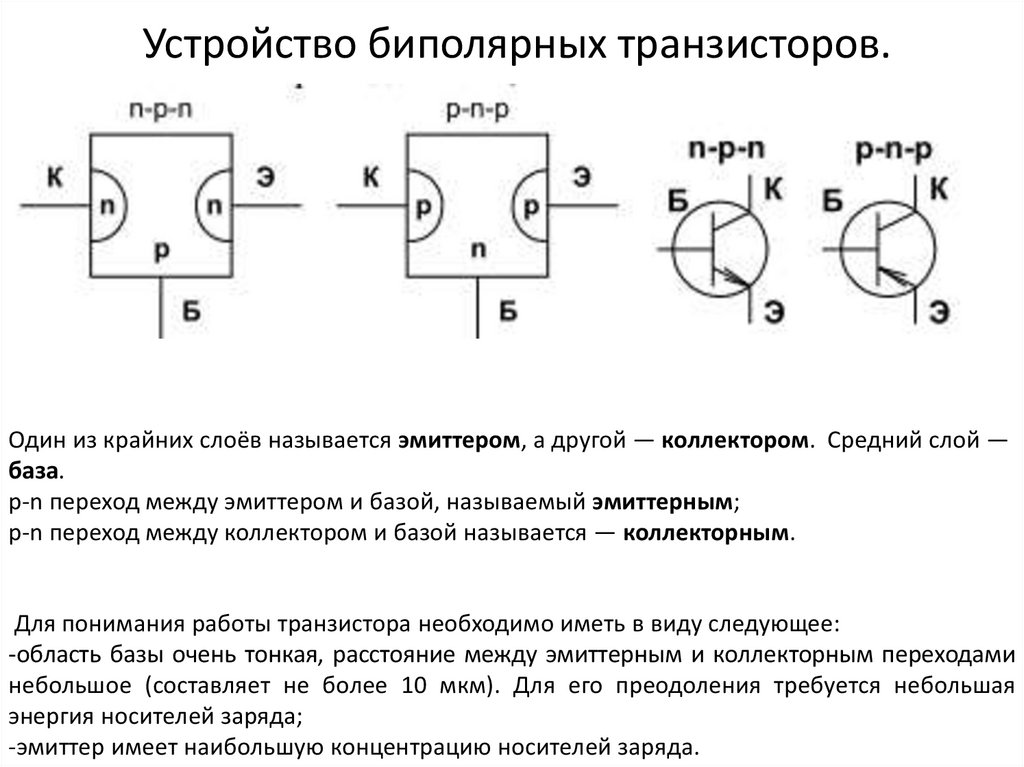

f_h31э и f_h31б – это предельные частоты коэффициентов передачи тока (для схем ОЭ и ОБ). Они представляют собой частоты, на которой коэффициенты передачи снижаются в 1,41 раза (на 3 дБ) от максимального значения.
f_т – это граничная частота коэффициента передачи тока биполярного транзистора, при которой модуль коэффициента передачи тока в схеме с общим эмиттером становится равным единице.

Величину коэффициента передачи тока транзисторов в зависимости от рабочей частоты для схемы ОЭ можно определить по следующей формуле:
, где:
h_21э0 – это статический коэффициент передачи тока транзистора для схемы ОЭ (является паспортной характеристикой),
F – это рабочая частота, на которой определяется β,
f_h31э – это предельная частота коэффициента передачи тока для схемы ОЭ.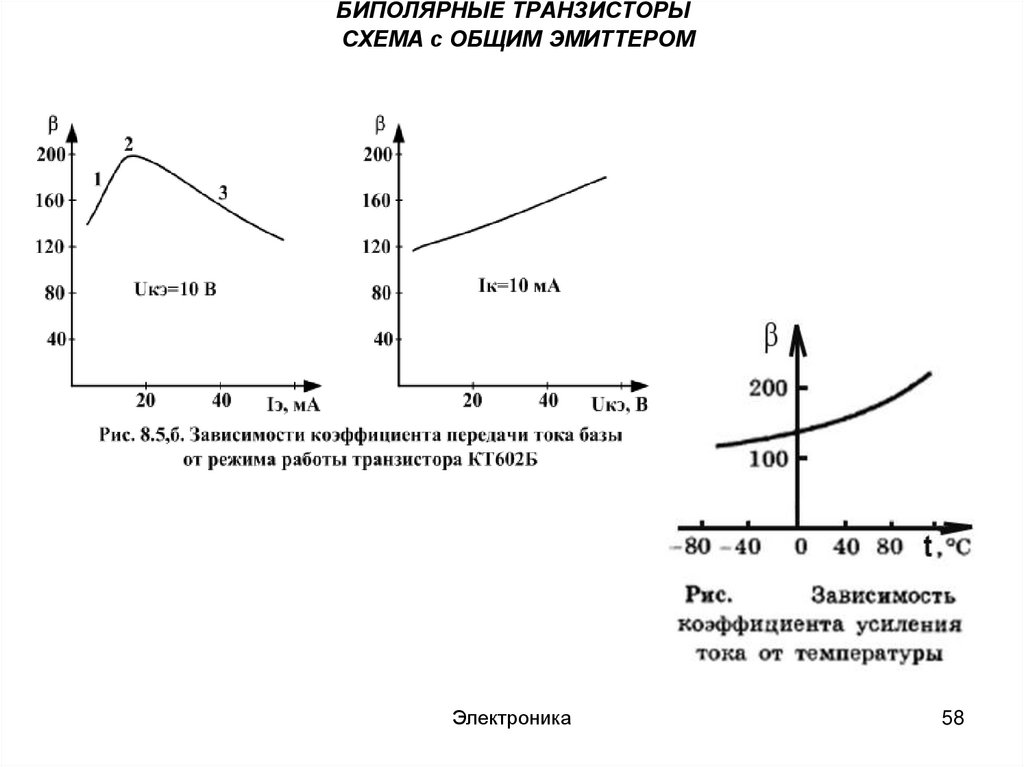

f_h31э связана с граничной частотой f_т

(которая также является паспортной характеристикой) простым соотношением: f_h31э ≈ f_Т/ β₀.

Теперь, после того как мы собрали все данные, можно рассчитать величину коэффициента передачи тока транзистора β на реальной частоте.
А далее, подставив полученное значение в формулу α = β/(1 + β), также получить и значение коэффициента передачи и для схемы ОБ.
Сдобрим пройденный материал онлайн калькулятором.

РАСЧЁТ ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ ТОКА ТРАНЗИСТОРА ОТ ЧАСТОТЫ

h21э0 транзистора
Граничная частота усиления транзистора fт (МГц)
Рабочая частота F (МГц)
β транзистора на рабочей частоте
α транзистора на рабочей частоте

 

Статический коэффициент передачи тока биполярного транзистора

Термин и определение

отношение постоянного тока коллектора к постоянному току базы при заданных постоянном обратном напряжении коллектор-эмиттер и токе эмиттера в схеме с общим эмиттером.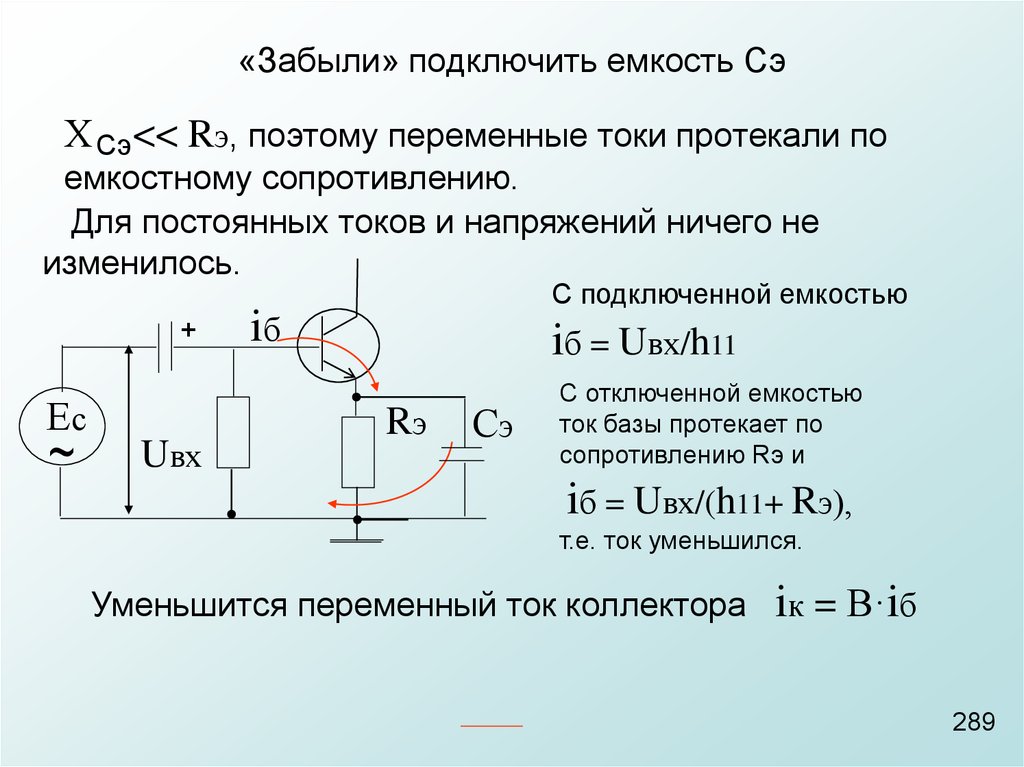

Научные статьи на тему «Статический коэффициент передачи тока биполярного транзистора»

В радиотехнике самыми распространенными транзисторами являются полевые и биполярные….
В полупроводниковой структуре биполярного

транзистора сформировано два р-n-перехода, перенос заряда через…
электрический ток, входная проводимость, коэффициент передачи по току, обратный ток коллектора, время…
Сначала нам необходимо рассчитать максимальную статическую мощность, рассеивающуюся на транзисторе в…
Напряжения в коллекторе в статическом режиме транзистора можно вычислить по следующей формуле: Uко =

Статья от экспертов

Индивидуальное прогнозирование надежности полупроводниковых приборов с учетом постепенных отказов является актуальной задачей, так как позволяет выбрать высоконадежные экземпляры для ответственных электронных устройств длительного функционирования.

Применительно к биполярным транзисторам предлагается подход, позволяющий решать задачу прогнозирования путем использования в качестве имитационного воздействия электрическое напряжение, прикладываемое к переходу коллектор — эмиттер. На примере бипо…

Научный журнал

Creative Commons

Нелинейный управляемый элемент, в качестве которого может выступать полевой или

биполярный транзистор…
Расчет усилительного каскада на биполярном транзисторе Основными параметрами, которые биполярных транзисторов…
являются статический коэффициент передачи электрического тока, показывающий соотношение постоянного…
предельная частота до которой коэффициент усиления передачи электрического тока больше единицы; максимальное…
Схема биполярного транзистора.

Статья от экспертов

В статье рассматриваются особенности проектирования инструментального усилителя (ИУ) для датчиковых систем при его реализации на основе радиационно-стойких микросхем базовых матричных кристаллов АБМК_1_4, АБМК_2_1 (ОАО «МНИПИ», г. Минск). Разработана новая архитектура ИУ, которая может работать без резисторов общей отрицательной обратной связи с классическими мостовыми измерительными схемами и обеспечивает повышенный коэффициент ослабления входного синфазного сигнала. В ИУ допускается цифрово…

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Характеристики передачи

BJT | Проекты самодельных схем

В биполярных транзисторах или биполярных транзисторах передаточные характеристики можно понимать как график зависимости выходного тока от управляющей входом величины, которая, следовательно, демонстрирует прямую «передачу» переменных от входа к выходу на кривой, представленной на графике. .

Мы знаем, что для биполярного переходного транзистора (BJT) выходной ток коллектора IC и управляющий входной ток базы IB связаны параметром бета, который считается постоянным для анализа.

Ссылаясь на приведенное ниже уравнение, мы находим линейную зависимость, существующую между IC и IB. Если мы сделаем уровень IB 2x, то IC также удвоится пропорционально.

Но, к сожалению, эта удобная линейная зависимость может быть недостижима в JFET для их входных и выходных величин. Скорее, связь между током стока ID и напряжением затвора VGS определяется уравнением Шокли :

Здесь квадратичное выражение становится ответственным за нелинейный отклик между ID и VGS, что приводит к возрастанию кривой экспоненциально по мере уменьшения величины VGS.

Хотя математический подход проще реализовать для анализа постоянного тока, графический способ может потребовать построения приведенного выше уравнения.

Это может представить рассматриваемое устройство и график уравнений сети, относящихся к идентичным переменным.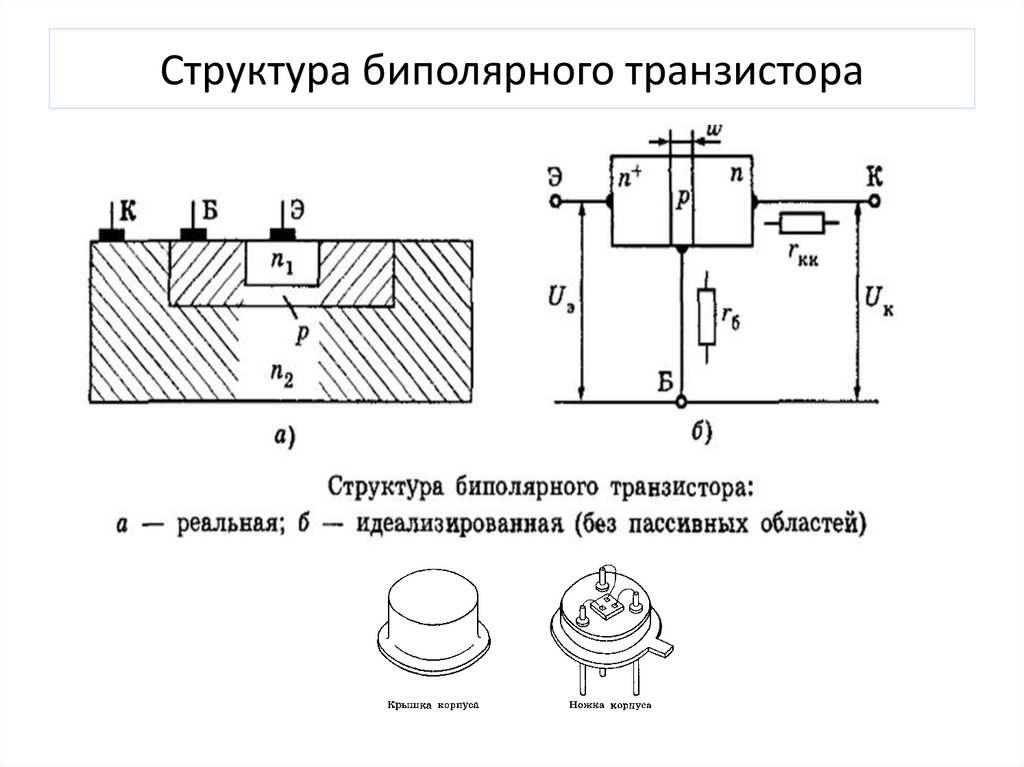

Мы находим решение, глядя на точку пересечения двух кривых.

Помните, что при использовании графического метода характеристики устройства не зависят от сети, в которой оно реализовано.

Изменение точки пересечения двух кривых также меняет сетевое уравнение, но это не влияет на передаточную кривую, определяемую приведенным выше уравнением 5.3.

Таким образом, в целом можно сказать, что:

Передаточная характеристика, определяемая уравнением Шокли, не зависит от сети, в которой реализовано устройство.

Мы можем получить кривую передачи, используя уравнение Шокли, или из выходных характеристик, как показано на рис. 5.10

На рисунке ниже мы видим два графика. Вертикальная линия измеряет миллиампер для двух графиков.

На одном графике показана зависимость тока стока ID от напряжения сток-исток VDS, на втором графике показана зависимость тока стока от напряжения затвор-исток или ID от VGS.

С помощью характеристик стока, показанных справа от оси «y», мы можем провести горизонтальную линию, начинающуюся в области насыщения кривой, показанной как VGS = 0 В, до оси, обозначенной как ID.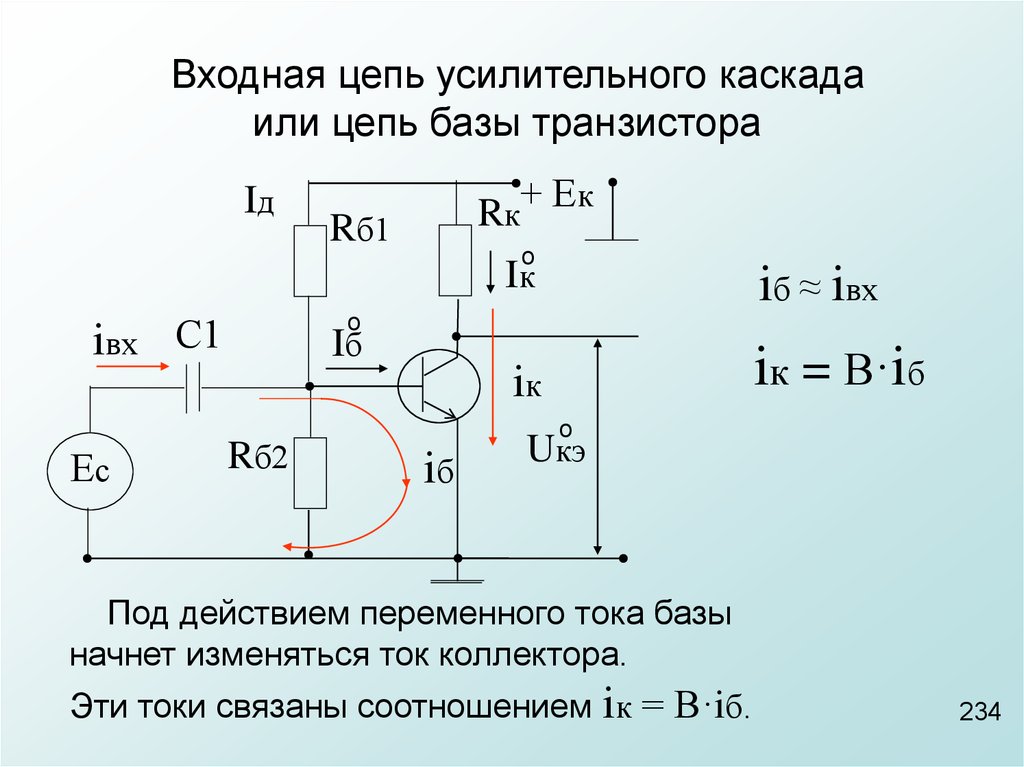

Текущие уровни, достигнутые таким образом для двух графиков, являются IDSS.

Точка пересечения на кривой зависимости ID от VGS будет такой, как указано ниже, поскольку вертикальная ось определена как VGS = 0 В

Обратите внимание, что характеристики стока показывают взаимосвязь между одной величиной выхода стока с другой величиной выхода стока , при этом две оси интерпретируются переменными в одной и той же области характеристик MOSFET.

Таким образом, передаточные характеристики можно определить как график зависимости тока стока полевого МОП-транзистора от величины или сигнала, действующего как входное управление.

Следовательно, это приводит к прямому «переносу» между входными/выходными переменными, когда используется кривая слева на рис. 5.15. Если бы это была линейная зависимость, график зависимости ID от VGS был бы прямой линией между IDSS и VP.

Однако это приводит к параболической кривой из-за вертикального расстояния между VGS, перешагивающими через характеристики стока, которое заметно уменьшается по мере того, как VGS становится все более отрицательным, на рис. 5.15.

Если мы сравним расстояние между VGS = 0 В и VGS = -1 В с пространством между VS = -3 В и отсечкой, мы увидим, что разница будет идентичной, хотя она сильно отличается для значения ID .

Мы можем определить другую точку на кривой переноса, проведя горизонтальную линию от кривой VGS = -1 V до оси ID, а затем продлив ее до другой оси.

Обратите внимание, что VGS = — 1 В на нижней оси кривой передачи, когда ID = 4,5 мА.

Также обратите внимание, что в определении ID при VGS = 0 В и -1 В используются уровни насыщения ID, а омическая область не учитывается.

Двигаясь дальше, с VGS = -2 В и -3 В, мы можем закончить график кривой передачи.

Вы также можете напрямую получить передаточную кривую на рис. 5.15, применив уравнение Шокли (уравнение 5.3), при условии, что заданы значения IDSS и Vp.

Уровни IDSS и VP определяют пределы кривой для двух осей и требуют только нанесения нескольких промежуточных точек.

Подлинность уравнения Шокли (5. 3) как источника передаточной кривой на рис. 5.15 может быть прекрасно выражена путем изучения определенных отличительных уровней конкретной переменной и последующего определения соответствующего уровня другой переменной в следующем способ:

Это соответствует графику, показанному на рис. 5.15.

Обратите внимание на то, как тщательно обрабатываются отрицательные знаки для VGS и VP в приведенных выше расчетах. Пропуск даже одного отрицательного знака может привести к совершенно ошибочному результату.

Из приведенного выше обсуждения довольно ясно, что если у нас есть значения IDSS и VP (которые можно взять из таблицы данных), мы можем быстро определить значение ID для любой величины VGS.

С другой стороны, с помощью стандартной алгебры мы можем вывести уравнение (через уравнение 5.3) для результирующего уровня VGS для заданного уровня ID.

Это можно было бы вывести довольно просто, чтобы получить:

Теперь давайте проверим приведенное выше уравнение, определив уровень VGS, который создает ток стока 4,5 мА для MOSFET с характеристиками, соответствующими рис.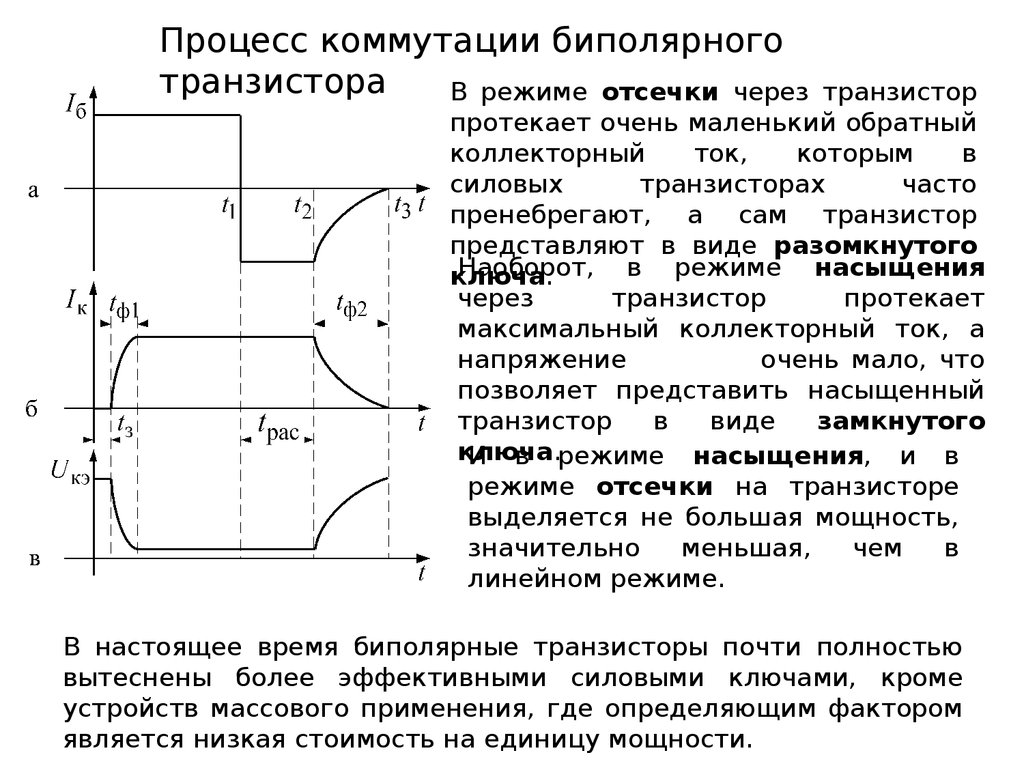 5.15.

Результат подтверждает уравнение, поскольку оно соответствует рис. 5.15.

Использование сокращенного метода

Поскольку нам приходится строить кривую переноса довольно часто, может оказаться удобным использовать сокращенную технику построения кривой. Желательно, чтобы метод позволял пользователю быстро и эффективно строить кривую без ущерба для точности.

Уравнение 5.3, которое мы узнали выше, разработано таким образом, что определенные уровни VGS создают уровни ID, которые можно запомнить для использования в качестве точек графика при построении кривой переноса. Если мы укажем VGS как 1/2 значения отсечения VP, результирующий уровень ID можно определить с помощью уравнения Шокли следующим образом:

Следует отметить, что приведенное выше уравнение не создано для определенного уровня VP. . Уравнение является общей формой для всех уровней VP, пока VGS = VP/2. Результат уравнения предполагает, что ток стока всегда будет составлять 1/4 уровня насыщения IDSS, пока напряжение затвор-исток имеет значение, которое на 50% меньше значения отсечки.

Обратите внимание, что уровень ID для VGS = VP/2 = -4V/2 = -2V согласно рис. 5.15

Выбрав ID = IDSS/2 и подставив его в уравнение 5.6, мы получим следующие результаты:

Хотя можно установить и другие точки, достаточного уровня точности можно достичь, просто нарисовав передаточную кривую, используя только 4 точки графика, как указано выше, а также в таблице 5.1 ниже.

В большинстве случаев мы можем использовать только точку графика, используя VGS = VP/2, в то время как пересечение осей в IDSS и VP даст нам кривую, достаточно надежную для большей части анализа.

Q: Биполярный переходной транзистор

Q: Биполярный переходной транзистор

3.17.1 Синтаксис

Устройство

Q xxxxxxx nc nb ne ns mname { область } { аргументы }
.BJT метка nc nb ne ns mname { область } { аргументов }

Модель (обязательно)

.model mname NPN { args }
.model mname PNP { args }

3.

17.2 Цель биполярный переходной транзистор,

3.17.3 Комментарии

Nc , nb , ne , и ns коллектор, основание, узлы эмиттера и подложки соответственно. Mname это модель название. Узел субстрата является необязательным.

Площадь — безразмерный множитель площади.

Параметры (команда .options) rstray определяет, включены не последовательные сопротивления. rstray используется по умолчанию. Norstray эквивалентен установке всех параметров модели rc, re и rb равными нулю.

Ввод значения параметра 0 не равнозначен не указанию Это. Это поведение несовместимо со SPICE. В SPICE значение 0 часто интерпретируется как не указанное, в результате чего как-то иначе вычислить. Если вы хотите, чтобы он был рассчитан, не указывайте его.

Другое тонкое отличие от SPICE заключается в том, что Gnucap может опускать некоторые ненужные части модели, которые могут повлиять на некоторые сообщаемые значения. Он не должен влиять ни на напряжения, ни на токи.

3.17.4 Параметры элемента

Параметры, совместимые с Basic Spice

М = х

Множитель устройства. (По умолчанию = 1.) Эквивалентное количество устройств, подключенных параллельно.

ПЛОЩАДЬ = x

Зона соединения. (По умолчанию = 1) Это параметр масштабирования с нет соответствующих фактических единиц.

ВЫКЛ

(По умолчанию = не указано) Если это слово указано, начальное предположение будет считать, что устройство выключено.

ТЕМП = x

Температура соединения. (По умолчанию = глобальная температура.)

ICVBE = x

Исходное состояние, Vbe. (По умолчанию = NA) Используйте это в качестве начального условие, когда указана опция UIC. Синтаксис отличается от Spice, но функция такая же.

ICVCE = x

Исходное состояние, Vce. (По умолчанию = NA) Используйте это в качестве начального условие, когда указана опция UIC. Синтаксис отличается от Spice, но функция такая же.

3.17.5 Параметры модели

Основные параметры постоянного тока

БФ = х

Идеальная максимальная форвардная бета. (По умолчанию = 100) Альтернативное имя — BFM.

БР = х

Идеальная максимальная обратная бета. (По умолчанию = 1) Альтернативное имя — BRM.

IBC = x

BC Транспортное насыщение Ток на единицу площади. (По умолчанию = IS) Если опущено, используется ИС. Вы должны указать либо IS, либо IBC, не оба.

МБП = x

BE Ток насыщения транспорта на единицу площади. (По умолчанию = IS) Если опущено, используется ИС. Вы должны указать либо IS, либо IBE, не оба.

ИС = х

Ток насыщения транспорта на единицу площади. (По умолчанию = 1e-16) Если IBE и IBC указаны, они используются вместо них. Не указывать оба.

НФ = x

Коэффициент эмиссии прямого тока. (По умолчанию = 1)

NR = x

Коэффициент эмиссии обратного тока. (По умолчанию = 1)

Модуляция ширины базы

ВАФ = x

Вперед Раннее напряжение. (По умолчанию = Infinite) Альтернативные имена: VA и VBF.

ВАР = x

Обратное раннее напряжение. (По умолчанию = Infinite) Альтернативное имя — VB.

Слаботочная бета-дегенерация

МСК = х

Ток насыщения утечки B-C. (по умолчанию = c4 * is)

C4 = x

Масштабный коэффициент утечки B-C. (По умолчанию = 0) Альтернативное имя — JLC.

НЗ = x

Коэффициент эмиссии утечки B-C. (По умолчанию = 2)

ISE = x

Ток насыщения утечки B-E. (по умолчанию = c2 * is)

C2 = x

Масштабный коэффициент утечки B-E. (По умолчанию = 0) Альтернативное имя — JLE.

СВ = x

Коэффициент эмиссии утечки B-E. (По умолчанию = 1,5)

Сильноточная бета-дегенерация

ИКФ = х

Угловой ток прямого бета-спада. (По умолчанию = Бесконечно) Альтернативный зовут JBF и IK.

ИКР = х

Угловой ток обратного бета-спада. (По умолчанию = Бесконечно) Альтернативный зовут ЖБР.

Паразитическая устойчивость

IRB = x

Ток для базового сопротивления = (rb+rbm)/2″. (По умолчанию = Бесконечно) Ток где базовое сопротивление падает на полпути к своему минимальному значению. Альтернативный имя JRB.

РБ = х

Базовое сопротивление нулевого смещения. (По умолчанию = 0)

RBM = x

Минимальное базовое сопротивление при большом токе. (по умолчанию = rb)

RE = x

Сопротивление эмиттера. (по умолчанию = 0)

КР = х

Сопротивление коллектора. (По умолчанию = 0)

Емкость перехода

КСК = х

Емкость истощения B-C при нулевом смещении. (По умолчанию = 0)

CJE = x

Емкость истощения BE при нулевом смещении. (По умолчанию = 0)

ЧСС = x

Емкость CS с нулевым смещением. (По умолчанию = 0) Альтернативное имя — CCS.

ФК = х

Коэффициент для формулы емкости истощения при прямом смещении. (По умолчанию = .5)

MJC = x

Коэффициент классификации соединения B-C. (По умолчанию = .33) Альтернативные имена МЮ и МС.

MJE = x

Коэффициент градации соединения BE. (По умолчанию = .33) Альтернативное имя МНЕ.

МДС = х

Коэффициент сортировки соединения подложки. (По умолчанию = 0) Альтернативные имена являются MS и MSUB.

ВСК = х

B-C встроенный потенциал. (По умолчанию = 0,75) Альтернативное имя — ПК.

VJE = x

B-E встроенный потенциал. (По умолчанию = .75) Альтернативное имя — PE.

VJS = x

Субстратный переход встроен в потенциал. (По умолчанию = 0,75) Альтернативное имя это ПС.

XCJC = x

Доля емкости B-C, подключенная к внутреннему базовому узлу. (по умолчанию = 1)

Паразитная емкость

CBCP = x

Внешняя постоянная паразитная емкость B-C. (По умолчанию = 0)

CBEP = x

Внешняя Б-Э постоянная паразитная емкость. (По умолчанию = 0)

CBSP = x

Внешняя Б-С постоянная паразитная емкость для боковых транзисторов. (По умолчанию = 0)

CCSP = x

Внешняя постоянная паразитная емкость B-C для вертикальных транзисторов. (по умолчанию = 0)

Время в пути

ИТФ = x

Высокая токовая зависимость TF. (По умолчанию = 0)

PTF = x

Фаза превышения на частоте = 1,0/(TF*2PI) Гц. (По умолчанию = 0)

TF = x

Идеальное время транзита вперед. (По умолчанию = 0)

TR = x

Идеальное время обратного транзита. (По умолчанию = 0)

VTF = x

Напряжение, дающее зависимость VBC от TF. (По умолчанию = Бесконечно)

XTF = x

Коэффициент зависимости TF от смещения. (По умолчанию = 0)

Влияние температуры

XTB = x

Экспонента прямой и обратной бета-температуры. (По умолчанию = 0)

XTI = x

Температурный показатель влияния на IS. (по умолчанию = 3)

ЭГ = х

Энергетическая щель для температурной зависимости ИС. (по умолчанию = 1,11)

TNOM = x

Температура измерения параметра, Цельсия. (По умолчанию = 27)

3.17.6 Датчики

Это не полный список. Все «расчетные параметры» могут быть зондировал. Список см. в исходном файле d_bjt.model.

Все параметры внутренних элементов (Ice, Ipi, Imu, Cbx, Cbc, Ccs, Cbe, Rc, Re, Yb, Cbcp, Cbep, Cbs). Чтобы получить к ним доступ, соединить метки внутреннего элемента с этим устройством, разделены точкой. Cbe.Q6 является емкостью база-эмиттер Q6.

В анализе переменного тока нет датчиков, кроме внутреннего элементы.

VBEINT

Внутреннее напряжение база-эмиттер.

VBCINT

Внутреннее напряжение база-коллектор.

VBXINT

Внешнее базовое напряжение к внутреннему базовому.

VCSINT

Внутреннее напряжение коллектор-подложка.

VBS

Напряжение база-подложка.

VBE

Напряжение база-эмиттер.

VBC

Напряжение база-коллектор.

VCS ​​

Напряжение коллектор-подложка.

VCB

Напряжение коллектор-база.

VCE

Напряжение коллектор-эмиттер.

ВЭЗ

Напряжение эмиттер-подложка.

ВЭБ

Напряжение эмиттер-база.

VEC

Напряжение эмиттер-коллектор.

VB

Напряжение база-земля.

VC

Напряжение коллектор-земля.

VE

Напряжение эмиттер-земля.

VS

Напряжение подложка-земля.

VBI

Внутреннее напряжение база-земля.

VCI

Внутреннее напряжение коллектор-земля.

ВЭИ

Внутреннее напряжение между эмиттером и землей.

ДВС

Ток коллектор-эмиттер.

ICEOffset

Смещенная часть ICE.

GO

Выходная (коллектор-эмиттер) проводимость.

GM

Транскондуктивность.

IPI

Ток база-эмиттер.

IPIOffset

Смещенная часть IPI.

GPI

Проводимость база-эмиттер.

IMU

Ток база-коллектор.

IMUOffset

Смещенная часть IMU.

GMU

База-коллектор проводимости.

IB

Базовый ток.

GX

Проводимость основного сопротивления растеканию.

RX

Базовое сопротивление растеканию.

ИС

Ток коллектора.

IE

Ток эмиттера.

QBX

Внешняя база-коллектор заряда.

CQBX

Внешняя емкость база-коллектор.

CBX

Внешняя емкость база-коллектор (CQBX).

QBC

Внутренняя база-коллектор заряда.

CQBC

Внутренняя емкость база-коллектор.

CBC

Внутренняя емкость база-коллектор (CQBC).

CMU

Внутренняя емкость база-коллектор (CQBC).

QCS

Коллекторно-подложная загрузка.

CQCS

Емкость коллектор-подложка.

CCS

Емкость коллектор-подложка (CQCS).

QBE

Заряд база-эмиттер.

CQBE

Емкость база-эмиттер.

CBE

Емкость база-эмиттер. (CQBE).

CPI

Емкость база-эмиттер. (CQBE).

P

Мощность.

ПД

Сила рассеялась. Энергия рассеивалась в виде тепла. Это всегда положительный и не включает источник питания. Это должно быть так же, как P, потому что транзисторы не могут генерировать энергию.