3. Основные технические показатели усилителей. Основы схемотехники. Курс лекций
3.1. Коэффициент усиления усилителя
3.2. Амплитудная характеристика и динамический диапазон усилителя. Помехи в усилителях
3.3. Амплитудно-частотная и фазо-частотная характеристики
3.4. Нелинейные искажения
3.5. Временные характеристики усилителя
3.1. Коэффициент усиления усилителя
Всякий усилитель имеет две пары входных клемм и его можно представить в виде четырёхполюсника связи рис. 2.2 и рис. 2.6:
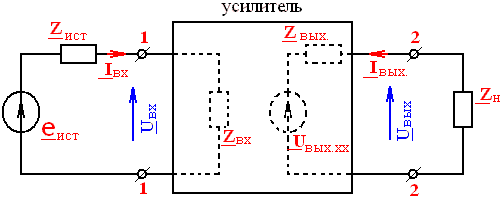
Рис. 2.6. Усилитель как четырёхполюсник связи
Отношение выходного напряжения UВЫХ к входному напряжению принято называть коэффициентом усиления по напряжению:
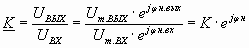
где: 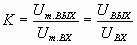
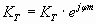 ;
; 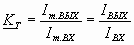
φт = φт.вых – φт.вх — учитывает изменение фазы тока при усилении.
Выходной ток IВЫХ, как видно из рис. 2.6, равен:
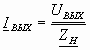
Влияние выходного сопротивления усилителя учитывается с помощью коэффициента усиления по ЭДС (сквозной коэффициент усиления)
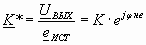
Сквозной коэффициент усиления можно определить и по другому:
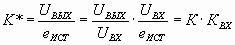 ;
;
где 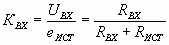
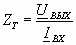 и
и 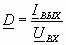
Называется сопротивление передачи (ZT) и крутизны (D) усилителя и имеющие размерность [Ом] и [См]. Усиление усилителя по мощности КМ равно:
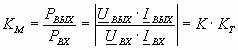
В технике связи коэффициенты усиления обычно выражают в логарифмических единицах (децибелах) обозначая их соответственно:
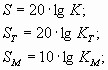
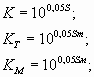
3.2. Амплитудная характеристика и динамический диапазон усилителя. Помехи в усилителях
Амплитудной характеристикой усилителя называется зависимость UВЫХ = f (UВХ). Она имеет вид, показанный на рис. 2.7:
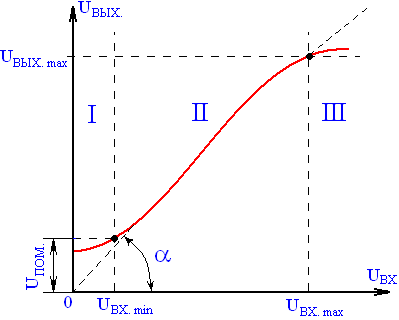
Рис. 2.7. Амплитудная характеристика усилителя
Как видно из рис. 2.7амплитудная характеристика имеет три участка: два нелинейных (I и III) и линейный участок (II). Первый участок обусловлен влиянием собственных помех усилителя, а третий – нелинейностью характеристик усилительных элементов. Рабочим участком является второй. Он позволяет определить минимальное UВХ. min и максимальное значение входного сигнала. Отношение входных напряжений 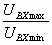
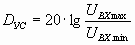 ;
;
По амплитудной характеристике можно найти напряжение собственных помех UПОМ.ВЫХ усилителя при UВХ = 0. Это напряжение представляет сумму напряжений собственных шумов усилительных элементов усилителя, напряжение тепловых шумов резисторов, наводок, пульсаций источника питания (питание от сети). Собственные помехи усилителя характеризуют часто коэффициентом шума:
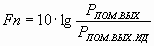
где РПОМ.ВЫХ.ИД. – мощность собственных помех на выходе усилителя, элементы которого обладают помехами теплового происхождения.
Угол наклона характеристики α характеризует усилительные свойства усилителя. При большом коэффициенте усиления амплитудная характеристика идёт круче (угол α больше).
3.3. Амплитудно-частотная и фазо-частотная характеристики
Коэффициент усиления и фаза любого усилителя зависят от частоты. Зависимость коэффициента усиления K(f) называется амплитудно-частотной характеристикой, а аргумента φ(f) фазо-частотной характеристикой. Их часто обозначают сокращенно: АЧХ и ФЧХ соответственно.
Форма сигнала после его усиления может быть сохранена в том случае, если усилитель является идеальным (т.е. не вносит искажений). Искажения будут отсутствовать, если в диапазоне частот, соответствующем спектру этого сигнала (от fН до fВ) АЧХ и ФЧХ будут иметь вид показанный на рис.2.8 и 2.9 соответственно.
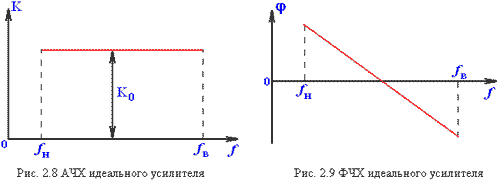
В реальных усилителях эти условия обычно не выполняются. Отличие реальных характеристик от идеальных определяют амплитудно-частотные фазо-частотные искажения усилителя.
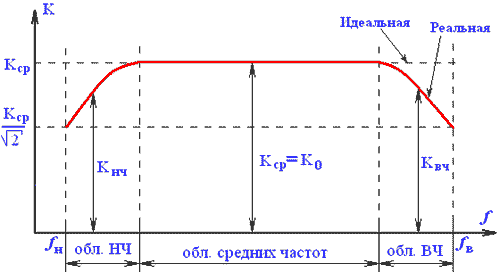
Рис. 2.10. Зависимость коэффициента усиления по напряжению от частоты
Количественно амплитудно-частотные искажения на любой частоте fi определяются коэффициентом амплитудно-частотных искажений Mi (индекс i показывает частоту fi):
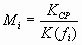 ;
;
Здесь КФ = К0 – коэффициент усиления в области средних частот. Часто коэффициент амплитудно-частотных искажений определяют в логарифмических единицах:
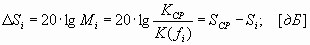
Мi = 100,05·∆Si
В технике МСП часто используют усилители, частотные характеристики усиления которых имеют заданную форму, отличную от идеальной. В данном случае задаются допустимым отклонением коэффициента усиления реального усилителя от номинального значения на различных частотах рабочего диапазона. На рис. 2.11 показана заданная частотная характеристика (пунктирная линия) и характеристика реального усилителя (сплошная линия).
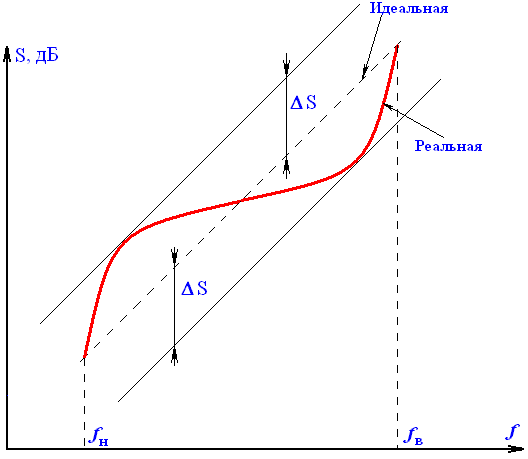
Рис. 2.11. АЧХ группового усилителя МСП ∆S – допустимые отклонения АЧХ
Во многих случаях допустимые фазо-частотными искажениями усилителя вообще не задаются, поскольку они не имеют значения. Чаще используют характеристику неравномерности группового времени распространения ∆tГР(f):
∆tГР. i = tГР. i – tГР. МИН.
Где tГР. i – абсолютное время задержки сигнала усилителем на данной частоте; tГР. МИН. – абсолютное время задержки, определённое на той частоте рабочего диапазона, усилителя, где оно минимально. Величина t
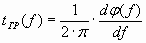
Т.о. tГР(f) соответствует крутизне ФЧХ усилителя на данной частоте.
3.4. Нелинейные искажения
Элементы схемы усилителя в определённой степени зависят от воздействующего на них напряжения (тока) и, следовательно, обладают некоторой нелинейностью. Наиболее значительной нелинейностью обладают усилительные элементы, индуктивности и ферромагнитными сердечниками, трансформаторы. Нелинейность элементов схемы приводит к тому, что зависимость выходного напряжения усилителя от входного также становится нелинейной, рис. 2.12:
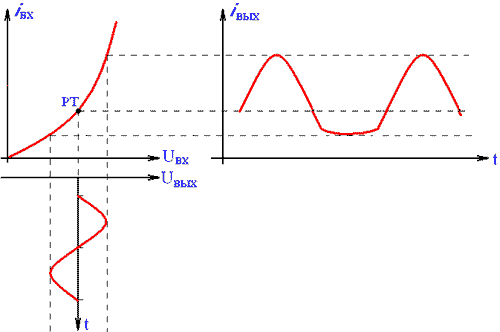
Рис. 2.12. Влияние нелинейности характеристик усилительного элемента на форму выходного сигнала.
В результате на выходе усилителя появляются спектральные составляющие, которые отсутствовали в исходном сигнале.
В многоканальной системе передачи нелинейность характеристик не только искажает передаваемую информацию, но вызывает дополнительные помехи, т.к. сигналы одних каналов могут образовывать спектральные составляющие, попадающие в полосу частот сигналов других каналов. Количественная оценка нелинейных искажений в усилителе производится с помощью коэффициента нелинейных искажений КГ, равно:
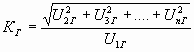 ;
;
где U1Г, U2Г, … , UnГ – амплитуды напряжений 1, 2, … , n-й гармоник, возникающих на выходе усилителя при подаче на его вход синусоидального напряжения.
В технике МСП часто оценивают степень нелинейности по 2-ой и 3-ей гармоникам:
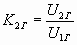 ;
; 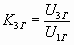 ;
;
или в логарифмических единицах – затуханием нелинейности (в децибелах) по соответствующим гармоникам:
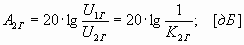
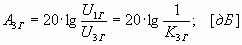
Установлено, что при возрастании уровня сигнала на выходе усилителя на ∆p:
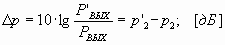
затухание по i-ой гармонике уменьшается на величину (i – 1)·∆p, дБ:
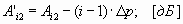
На рис. 2.13 приведены зависимости затухания нелинейности по второй и третьей гармоникам от выходного уровня сигнала.
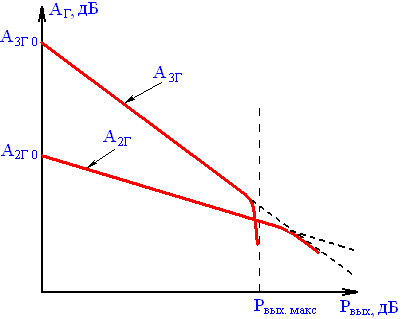
Рис. 2.13. Зависимость затухания нелинейности по второй и третьей гармоникам от выходного уровня сигнала
Отметим, что затухание A’i2 справедливо лишь при малой нелинейности усилителя, т.е. до определённого значения РВЫХ. МАКС. Нужно иметь ввиду, что основная доля нелинейных искажений возникает за счет выходного каскада усилителя, поэтому нелинейными искажениями за счет предварительных каскадов, обычно приобретают. Заметим, что величины А2Г0 и А3Г0 соответствуют выходной мощности РВЫХ = 1 мВт.
3.5. Временные характеристики усилителя
При передачи импульсных сигналов в усилителях возникают искажения, обусловленные нестационарными (переходными) процессами из-за наличия в нём реактивных элементов (емкостей и индуктивностей). Для оценки этих искажений пользуются временными характеристиками: переходной и импульсной.
Переходной характеристикой h(t) усилителя называется зависимость мгновенного значения напряжения на его выходе от времени UВЫХ(t) при подаче на вход напряжения в виде единичной функции 1(t). Различают переходную характеристику для малых и больших времён. На рис. 2.14 приведена h(t) для малых времён.
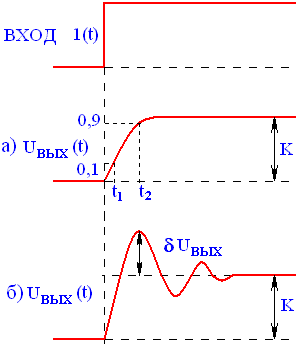
Рис. 2.14. Зависимость выходного напряжения усилителя при подаче на вход единичной функции 1(t) в области малых времен
Характеристика для малых времён определяет вид искажений фронтов импульсного сигнала. Реальная переходная характеристика для малых времён чаще всего изменяется по закону экспоненты, рис. 2.14 а). Реже переходный процесс сопровождается колебательным процессом, рис.2.14 б). Меру искажения импульсного сигнала определяют по времени установления tУСТ. Время в течение которого напряжение на выходе изменяется от 0,1 до 0,9 от установившегося значения:
tУСТ = t2 – t1;
При колебательном процессе tУСТ меньше, но при этом появляются дополнительные искажения в виде выброса δUВЫХ:
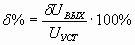 .
.
Отметим, что искажение фронтов заметны при усиление импульсов малой длительности. При усилении импульсов большой длительности важно знать – насколько долго усилитель может сохранять постоянное напряжение на выходе, после подачи на вход усилителя единичной функции 1(t), рис 2.15.
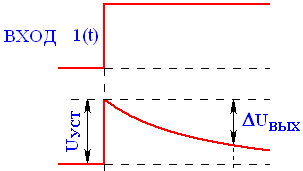
Рис. 2.15. Зависимость выходного напряжения усилителя при подаче на вход единичной функции 1(t) в области больших времен.
Реальная h(t) для больших времён чаще всего спадает плавно. Искажения оцениваются величиной спада:
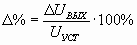
Искажения импульсных и гармонических сигналов взаимосвязаны. Те и другие обусловлены реактивными элементами схем и инерционностью работы усилительных элементов. Поэтому эти искажения называются линейными.
Коэффициенты усиления усилителей — КиберПедия
Среди многих показателей, усилительных устройств важнейшими являются коэффициенты усиления. Различают коэффициенты усиления по мощности KP = РВЫХ/РВХ, по напряжению K = UВЫХ/UВХ и по току KТ = IВЫХ/IВХ. Особенно широко используется коэффициент усиления сигнала по напряжению (поэтому его обычно приводят без индекса), а также сквозной коэффициент усиления по напряжению KСКВ. Все они определяются при гармоническом входном сигнале в режиме усиления.
Коэффициент усиления по напряжению K представляет собой отношение значения комплексной амплитуды напряжения сигнала на выходе к комплексной амплитуде напряжения сигнала на входе усилителя:
где – модуль коэффициента усиления; φK – сдвиг фазы между выходным и входным напряжениями сигнала, возникающий из-за влияния реактивных составляющих сопротивлений в цепях усилителя и в нагрузке, а также из-за влияния инерционности УЭ.
Сквозной коэффициент усиления по напряжению KСКВ представляет собой отношение значения комплексной амплитуды напряжения сигнала на выходе усилителя к амплитуде ЭДС источника сигнала:
,
где – модуль сквозного коэффициента усиления по напряжению;
– напряжение источника сигнала;
– сдвиг фазы между выходным напряжением сигнала усилителя и ЭДС источника сигнала.
Сквозной коэффициент усиления по напряжению позволяет оценить усилительные свойства усилителя в целом с учетом входной цепи, что совершенно необходимо при использовании усилителя с обратной связью. Его можно представить в виде произведения коэффициента передачи напряжения входной цепи усилителя и коэффициента усиления по напряжению :
,
где – комплексный коэффициент передачи напряжения входной цепи усилителя, характеризуемый модулем k1И = Uвх/e1И и углом сдвига фазы φвх между входным напряжением сигнала усилителя и ЭДС источника сигнала.
Коэффициент усиления по току KT представляет собой отношение установившегося значения комплексной амплитуды тока сигнала на выходе к комплексной амплитуде тока сигнала на входе усилителя:
где – модуль коэффициента усиления по току;
φKт – сдвиг фазы между выходным и входным токами усилителя.
Как видно, в общем случае K, KСКВ, k1И и KТ являются комплексными величинами, зависящими от частоты.
Очень часто представляют интерес коэффициенты усиления и коэффициент передачи входной цепи в области средних частот, где влияние реактивных составляющих сопротивлений в цепях усилителя и инерционных свойств УЭ пренебрежимо мало и сдвиги фаз равны нулю φK= 0, φвх = 0, φKт = 0, а модули коэффициентов усиления и коэффициента передачи входной цепи не зависят от частоты, являясь действительными величинами:
; ; .
Здесь индекс ноль обозначает средние частоты.
На практике проще всего измерять коэффициент усиления по напряжению, так как в этом случае не надо разрывать цепь для проведения измерений. Он удобен для сравнительной оценки усилительных свойств на различных УЭ, так как измерительных приборов, таких как вольтметр или осциллограф, в лабораториях значительно больше других.
И наконец, коэффициент усиления по мощности KPпредставляет собой отношение мощности сигнала Рвых, отдаваемой усилителем в нагрузку, к мощности сигнала Рвх, подводимой к входу усилителя от источника сигнала: KP = Рвых/Рвх.
Следует отметить, что иногда применяют так называемый коэффициент усиления номинальной мощности источника сигнала KPном = Рвых/Рвхном, где Рвхном = Е2ист/4Rвх – номинальная мощность, отдаваемая источником сигнала на согласованный с ним вход усилителя, т. е. при Rист = Rвх, когда k1И = 0,5 и Uвх = 0,5e1И.
Коэффициенты усиления выражаются как в относительных значениях (в разах), так и в логарифмических единицах – децибелах:
KP (дБ) = 10 lg KP ; KТ (дБ) = 20 lg KТ;
K (дБ) = 20 lg K; KСКВ (дБ) = 20 lg KСКВ.
Схема усилителя
Для анализа свойств (показателей и характеристик) усилителя источник сигнала, усилитель и нагрузку представляют в виде эквивалентных электрических схем по сигналу (по переменному току).
Источник сигнала представляют в виде независимого активного двухполюсника, т. е. либо в виде независимого источника ЭДС ė1И с внутренним (выходным) сопротивлением Ż1И, как изображено на рис. 5, либо в виде независимого источника тока İ1И = ė1И/Ż1И с параллельно подключенным к нему тем же сопротивлением Ż1И или, иначе говоря, с выходной проводимостью Ỳ1И = 1/ Ż1И, под действием которого (того или другого) на входе усилителя возникают входной ток İВХ и входное напряжение ŮВХ сигнала, и, следовательно, к входу подводится мощность сигнала РВХ. Нагрузку представляют обычно в виде сопротивления Ż2H.
Рис. 5. Режим переменного тока
В общем случае все приводимые в эквивалентных схемах величины (за исключением мощностей) имеют комплексный характер и зависят от частоты сигнала. Это обусловлено нестационарными (переходными) процессами в цепях усилителя, вызываемых влиянием реактивных элементов схемы (индуктивных и емкостных), а также влиянием инерционных свойств УЭ (на высоких частотах). При этом все сопротивления Ż1И, ŻВХ, ŻВЫХ и Ż2Н содержат кроме резистивных составляющих сопротивлений R и реактивные составляющие соответственно ± jX1И, таким образом, для источника сигнала е1И внутреннее сопротивление Ż1И = R1И ± jX1И.
Следует отметить, что для практики особый интерес представляют случаи, когда влиянием реактивных составляющих сопротивлений можно пренебречь ввиду их малости, например в области средних частот. В этих случаях все сопротивления становятся резистивными и не зависящими от частоты, Z2Н = R2Н, а следовательно, и все ЭДС, напряжения и токи становятся действительными и не зависящими от частоты. Рассмотренные ниже примеры с различными активными четырехполюсниками в целях упрощения анализа приводятся как раз для области средних частот.
Простейший усилитель содержит один УЭ с пассивными элементами связи (ЭС), например резисторами, конденсаторами, трансформаторами, соединяющими УЭ с источником сигнала, с нагрузкой и с источником питания, создающими ему наивыгоднейшие условия работы. На структурной схеме УЭ и ЭС объединяют и представляют одним активным четырехполюсником (рис. 5).
3. Основные технические показатели усилителей
3. Основные технические показатели усилителей
3.1. Коэффициент усиления усилителя.
Всякий усилитель имеет две пары входных клемм и его можно представить в виде четырёхполюсника связи рис. 2.2 и рис. 2.6:
Рис. 2.6. Усилитель как четырёхполюсник связи
Отношение выходного напряжения UВЫХ к входному напряжению принято называть коэффициентом усиления по напряжению:
где:
; φн = φн.вых – φн.вх — учитывает изменение фазы сигнала при усилении.
Аналогично, коэффициент усиления по току КТ равен:
;
φт = φт.вых – φт.вх — учитывает изменение фазы тока при усилении.
Выходной ток IВЫХ, как видно из рис. 2.6, равен:
Влияние выходного сопротивления усилителя учитывается с помощью коэффициента усиления по ЭДС (сквозной коэффициент усиления)
Сквозной коэффициент усиления можно определить и по другому:
;
где – коэффициент передачи входной цепи.
Приведённые коэффициенты усиления по напряжению и току являются безразмерными величинами. Иногда используются величины:
и
Называется сопротивление передачи (ZT) и крутизны (D) усилителя и имеющие размерность [Ом] и [См].
Усиление усилителя по мощности КМ равно:
;
В технике связи коэффициенты усиления обычно выражают в логарифмических единицах (децибелах) обозначая их соответственно:
3.2. Амплитудная характеристика и динамический диапазон усилителя. Помехи в усилителях.
Амплитудной характеристикой усилителя называется зависимость
UВЫХ = f (UВХ). Она имеет вид, показанный на рис. 2.7:
Рис. 2.7. Амплитудная характеристика усилителя
Как видно из рис. 2.7амплитудная характеристика имеет три участка: два нелинейных (I и III) и линейный участок (II). Первый участок обусловлен влиянием собственных помех усилителя, а третий – нелинейностью характеристик усилительных элементов. Рабочим участком является второй. Он позволяет определить минимальное UВХ. min и максимальное значение входного сигнала. Отношение входных напряжений определяет динамический диапазон усилителя:
;
По амплитудной характеристике можно найти напряжение собственных помех UПОМ.ВЫХ усилителя при UВХ = 0. Это напряжение представляет сумму напряжений собственных шумов усилительных элементов усилителя, напряжение тепловых шумов резисторов, наводок, пульсаций источника питания (питание от сети). Собственные помехи усилителя характеризуют часто коэффициентом шума:
[дБм]
где РПОМ.ВЫХ.ИД. – мощность собственных помех на выходе усилителя, элементы которого обладают помехами теплового происхождения.
Угол наклона характеристики α характеризует усилительные свойства усилителя. При большом коэффициенте усиления амплитудная характеристика идёт круче (угол α больше).
3.3. Амплитудно-частотная и фазо-частотная характеристики.
Коэффициент усиления и фаза любого усилителя зависят от частоты. Зависимость коэффициента усиления K(f) называется амплитудно-частотной характеристикой, а аргумента φ(f) фазо-частотной характеристикой. Их часто обозначают сокращенно: АЧХ и ФЧХ соответственно.
Форма сигнала после его усиления может быть сохранена в том случае, если усилитель является идеальным (т.е. не вносит искажений). Искажения будут отсутствовать, если в диапазоне частот, соответствующем спектру этого сигнала (от fН до fВ) АЧХ и ФЧХ будут иметь вид показанный на рис.2.8 и 2.9 соответственно.
В реальных усилителях эти условия обычно не выполняются. Отличие реальных характеристик от идеальных определяют амплитудно-частотные фазо-частотные искажения усилителя.
Рис. 2.10. Зависимость коэффициента усиления по напряжению от частоты
Количественно амплитудно-частотные искажения на любой частоте fi определяются коэффициентом амплитудно-частотных искажений Mi (индекс i показывает частоту fi):
;
Здесь КФ = К0 – коэффициент усиления в области средних частот. Часто коэффициент амплитудно-частотных искажений определяют в логарифмических единицах:
Мi = 100,05·∆Si
В технике МСП часто используют усилители, частотные характеристики усиления которых имеют заданную форму, отличную от идеальной. В данном случае задаются допустимым отклонением коэффициента усиления реального усилителя от номинального значения на различных частотах рабочего диапазона. На рис. 2.11 показана заданная частотная характеристика (пунктирная линия) и характеристика реального усилителя (сплошная линия).
Рис. 2.11 АЧХ группового усилителя МСП ∆S – допустимые отклонения АЧХ
Во многих случаях допустимые фазо-частотными искажениями усилителя вообще не задаются, поскольку они не имеют значения. Чаще используют характеристику неравномерности группового времени распространения ∆tГР(f):
∆tГР. i = tГР. i – tГР. МИН.
Где tГР. i – абсолютное время задержки сигнала усилителем на данной частоте; tГР. МИН. – абсолютное время задержки, определённое на той частоте рабочего диапазона, усилителя, где оно минимально.
Величина tГР(f) связана с ФЧХ уравнением:
Т.о. tГР(f) соответствует крутизне ФЧХ усилителя на данной частоте.
3.4. Нелинейные искажения
Элементы схемы усилителя в определённой степени зависят от воздействующего на них напряжения (тока) и, следовательно, обладают некоторой нелинейностью. Наиболее значительной нелинейностью обладают усилительные элементы, индуктивности и ферромагнитными сердечниками, трансформаторы. Нелинейность элементов схемы приводит к тому, что зависимость выходного напряжения усилителя от входного также становится нелинейной, рис. 2.12:
Рис. 2.12. Влияние нелинейности характеристик усилительного элемента на форму выходного сигнала.
В результате на выходе усилителя появляются спектральные составляющие, которые отсутствовали в исходном сигнале.
В многоканальной системе передачи нелинейность характеристик не только искажает передаваемую информацию, но вызывает дополнительные помехи, т.к. сигналы одних каналов могут образовывать спектральные составляющие, попадающие в полосу частот сигналов других каналов. Количественная оценка нелинейных искажений в усилителе производится с помощью коэффициента нелинейных искажений КГ, равно:
;
где U1Г, U2Г, … , UnГ – амплитуды напряжений 1, 2, … , n-й гармоник, возникающих на выходе усилителя при подаче на его вход синусоидального напряжения.
В технике МСП часто оценивают степень нелинейности по 2-ой и 3-ей гармоникам:
; ;
или в логарифмических единицах – затуханием нелинейности (в децибелах) по соответствующим гармоникам:
Установлено, что при возрастании уровня сигнала на выходе усилителя на ∆p:
затухание по i-ой гармонике уменьшается на величину (i – 1)·∆p, дБ:
На рис. 2.13 приведены зависимости затухания нелинейности по второй и третьей гармоникам от выходного уровня сигнала.
Рис. 2.13 Зависимость затухания нелинейности по второй и третьей гармоникам от выходного уровня сигнала
Отметим, что затухание A’i2 справедливо лишь при малой нелинейности усилителя, т.е. до определённого значения РВЫХ. МАКС. Нужно иметь ввиду, что основная доля нелинейных искажений возникает за счет выходного каскада усилителя, поэтому нелинейными искажениями за счет предварительных каскадов, обычно приобретают. Заметим, что величины А2Г0 и А3Г0 соответствуют выходной мощности РВЫХ = 1 мВт.
3.5. Временные характеристики усилителя
При передачи импульсных сигналов в усилителях возникают искажения, обусловленные нестационарными (переходными) процессами из-за наличия в нём реактивных элементов (емкостей и индуктивностей). Для оценки этих искажений пользуются временными характеристиками: переходной и импульсной.
Переходной характеристикой h(t) усилителя называется зависимость мгновенного значения напряжения на его выходе от времени UВЫХ(t) при подаче на вход напряжения в виде единичной функции 1(t). Различают переходную характеристику для малых и больших времён. На рис. 2.14 приведена h(t) для малых времён.
Рис. 2.14. Зависимость выходного напряжения усилителя при подаче на вход единичной функции 1(t) в области малых времен
Характеристика для малых времён определяет вид искажений фронтов импульсного сигнала. Реальная переходная характеристика для малых времён чаще всего изменяется по закону экспоненты, рис. 2.14 а). Реже переходный процесс сопровождается колебательным процессом, рис.2.14 б). Меру искажения импульсного сигнала определяют по времени установления tУСТ. Время в течение которого напряжение на выходе изменяется от 0,1 до 0,9 от установившегося значения:
tУСТ = t2 – t1;
При колебательном процессе tУСТ меньше, но при этом появляются дополнительные искажения в виде выброса δUВЫХ:
.
Отметим, что искажение фронтов заметны при усиление импульсов малой длительности.
При усилении импульсов большой длительности важно знать – насколько долго усилитель может сохранять постоянное напряжение на выходе, после подачи на вход усилителя единичной функции 1(t), рис 2.15.
Рис. 2.15. Зависимость выходного напряжения усилителя при подаче на вход единичной функции 1(t) в области больших времен.
Реальная h(t) для больших времён чаще всего спадает плавно. Искажения оцениваются величиной спада:
Искажения импульсных и гармонических сигналов взаимосвязаны. Те и другие обусловлены реактивными элементами схем и инерционностью работы усилительных элементов. Поэтому эти искажения называются линейными.
1.3.3. Коэффициент усиления
Коэффициент усиления или коэффициент передачи — это отношение выходного сигнала к входному. Используют различные варианты коэффициентов передачи. Это коэффициент передачи по напряжению, который определяется отношением амплитудных или действующих значений выходного и входного напряжений (рис. 1.1, а): Кu=Uвых/Uвх. Он определяется относительно установившегося гармонического входного сигнала.
Достаточно часто используется коэффициентом сквозной передачи или коэффициентом передачи ЭДС. Относительно этого коэффициента из рис. 1.1, а следует, что:
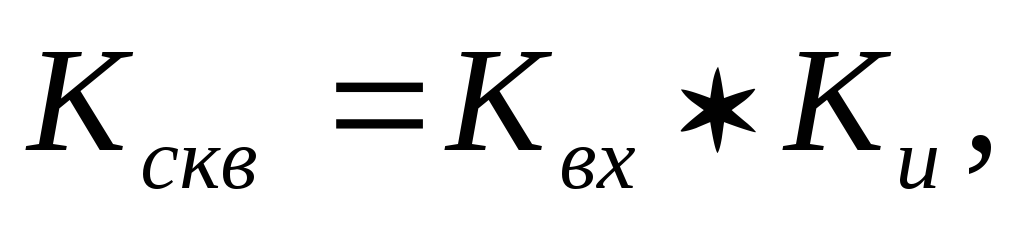 (1.1)
(1.1)
где Квх=Zвх/(Zc+Zвх) — коэффициент передачи (в комплексной форме) входной цепи, состоящей из входного сопротивления Zвх и внутреннего сопротивления эквивалентного генератора входного сигнала Zc. Очевидно, что с повышением входного сопротивления увеличивается Квх, а значит, и Кскв.
Коэффициентом усиления тока определяется соотношением:
Ki = Iвых/Iвх (1.2)
Он используется реже, так как для измерения токов требуется осуществлять разрыв цепей, что трудоемко.
Иногда используют также понятия сопротивления передачи Zп = Uвых/Iвх и проводимость передачи Yп=Iвых/Uвх.
Отношение мощности усиленного колебания в нагрузке к мощности, передаваемой на вход, называется коэффициентом усиления мощности
Кр=Рн/Рвх. Все три основных коэффициента усиления (по току, напряжению и мощности) связаны между собой очевидными соотношениями:
Кр = Ki*KU, Ki=Ku*Zвх/Zн.
Для сравнения мощностей двух колебаний была введена логарифмическая величина БЕЛ. Она названа по имени изобретателя телефона А. Белла. Коэффициент усиления мощности обычно выражают в более мелких единицах — децибелах: Кр, дБ = 10 IgKp.
Если мощность Рн и Рвх выделяются на одинаковых сопротивлениях (Rн=Rвx=R), то их отношение в децибелах можно выразить через отношение напряжений:
 (1.3)
(1.3)
Это соотношение используется для выражения в децибелах коэффициента усиления напряжения даже при RнRвх ,хотя это и не корректно. В данном случае записывают КU, дБ = 20 IgKU. Для тока это будет Кi,дБ = 20lnKi. Логарифмические единицы удобны тем, что позволяют перемножение коэффициентов усиления заменить сложением.
1.3.4. Амплитудно-частотная и фазочастотная характеристики
Коэффициент
усиления по напряжению в комплексной
форме имеет вид 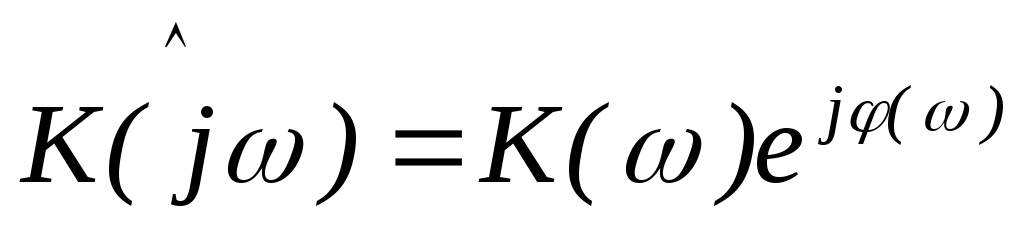 .Его модуль
.Его модуль 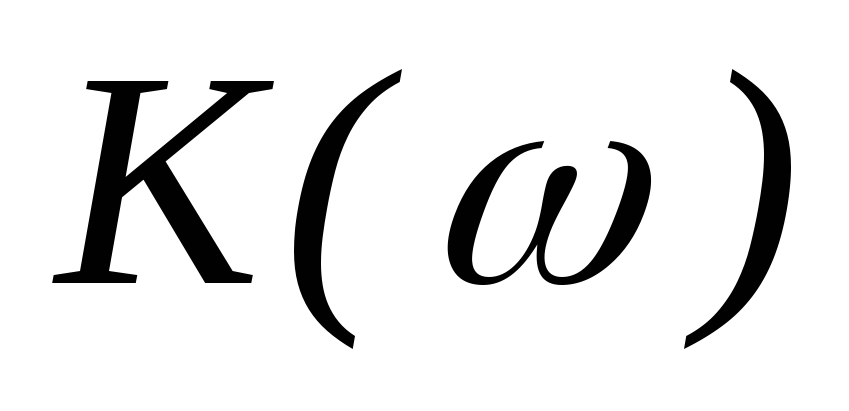 ,
зависящий от частоты, называетсяамплитудно-частотной
характеристикой (АЧХ) усилителя (рис. 1.4., а). На рис. 1.4. по
горизонтали отложена угловая частота
= 2f.
Для АЧХ характерно наличие области
средних частот, в которой К почти не
зависит от частоты и обозначается Ко
(номинальный коэффициент усиления). По
вертикальной оси чаще всего откладывается
относительное (нормированное) усиление
М = К/Ко,
т.е. коэффициент усиления, отнесенный
к коэффициенту усиления на средних
частотах (нормированная АЧХ).
,
зависящий от частоты, называетсяамплитудно-частотной
характеристикой (АЧХ) усилителя (рис. 1.4., а). На рис. 1.4. по
горизонтали отложена угловая частота
= 2f.
Для АЧХ характерно наличие области
средних частот, в которой К почти не
зависит от частоты и обозначается Ко
(номинальный коэффициент усиления). По
вертикальной оси чаще всего откладывается
относительное (нормированное) усиление
М = К/Ко,
т.е. коэффициент усиления, отнесенный
к коэффициенту усиления на средних
частотах (нормированная АЧХ).
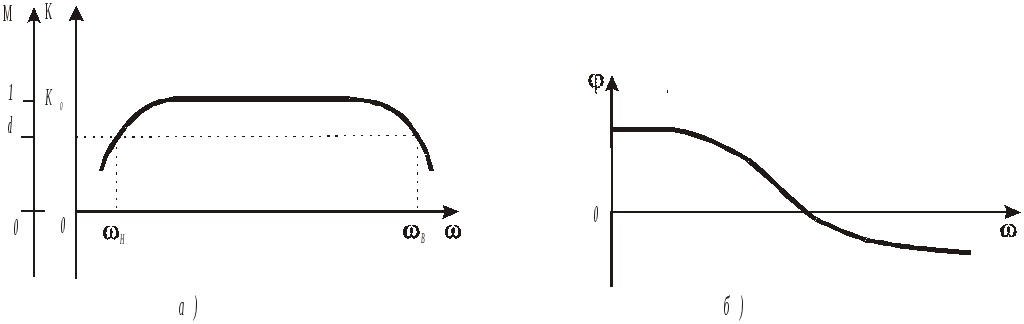
Рис. 1.4.
На
нижних и верхних частотах АЧХ обычно
спадает. Частоты, на которых нормированное
усиление уменьшается до условного
уровня отсчета d,
называются граничными частотами
усиления: fн
и fв.
Типовым (стандартным) уровнем отсчета
считается значение d
= 1/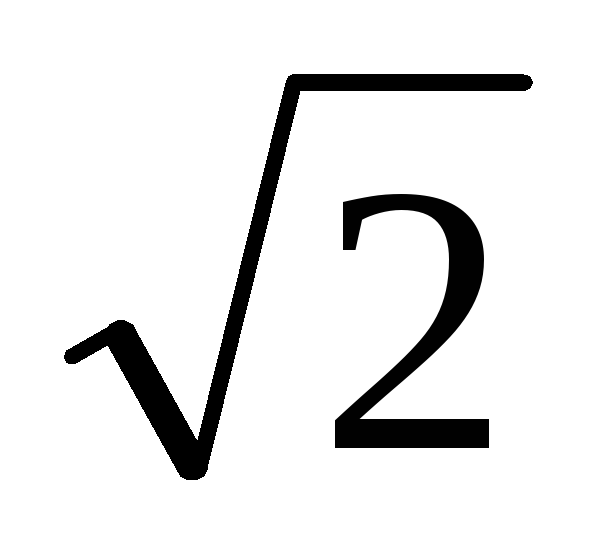 =0,707.
Частоты от fн
до fв,
как отмечено ранее, называют полосой
пропускания усилителя.
=0,707.
Частоты от fн
до fв,
как отмечено ранее, называют полосой
пропускания усилителя.
В усилителе не все спектральные составляющие сложного колебания усиливаются в одинаковое число раз. Это приводит к искажению формы сигнала (амплитудно-частотные или частотные искажения). Искажения характеризуются неравномерностью АЧХ (выражается в децибелах: 20lgM и указывается в ТУ на аппаратуру, М=К/Ко). Неравномерность нормированной АЧХ может характеризуется спадом характеристики (f) = M(f) – 1 при M(f)<l или подъемом при (M(f)>l.
В звуковых сигналах частотные искажения воспринимаются на слух как изменения тембра (высоты тона). В усилителях звуковых частот допускается спад величины М не более чем на 3дБ (в 1,41 раза), а в усилителях измерительной техники не более чем на 0,1дБ.
Зависимость от частоты фазового сдвига, вносимого усилителем, характеризуют фазо-частотной характеристикой (ФЧХ) (рис. 1.4, б). Из теории цепей известно, что если ФЧХ четырехполюсника не является прямой линией, то время прохождения через четырехполюсник различных спектральных составляющих сложного колебания различно. Это приводит к
искажению сигнала, которое характеризуется изменением формы сигнала (фазочастотные искажения). На практике ФЧХ используется реже, чем АЧХ, ввиду меньшей значимости и сравнительной сложности измерения фазовых сдвигов. Однако применительно, например, к волоконно-оптическим линиям связи, подобные сдвиги различных спектральных составляющих сигнала могут привести к размыванию импульса сигнала и соответственно к потере информации. Применительно к проводным протяженным линиям связи можно также отменить существование данной проблемы, поскольку скорость распространения спектральных составляющих различных частот различна (рис. 1.5).
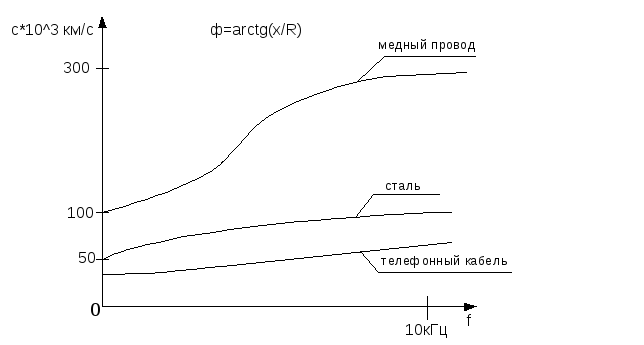
Рис. 1.5.
Частотные и фазовые искажения называются линейными, если создаются емкостями и индуктивностями схемы, являющимися линейными элементами. Они искажают лишь форму сложного колебания, изменяются соотношения амплитуд и фаз между отдельными спектральными составляющими, а форму гармонического (синусоидального) колебания не изменяют. Соответственно это не приводит к появлению новых спектральных составляющих в спектре сигнала.
Масштаб для АЧХ и ФЧХ по оси частот обычно берут логарифмический. Это позволяет растянуть график в области низких частот и сжать в области высоких частот, что обеспечивает большую наглядность.
Основные показатели усилительных устройств, страница 14
где К* — модуль сквозного коэффициента усиления по напряжению, а jk*– угол сдвига фазы между выходным напряжением сигнала усилителя и ЭДС источника сигнала.
Сквозной коэффициент усиления по напряжению позволяет оценить усилительные свойства усилителя в целом, с учетом входной цепи, что совершенно необходимо при использовании в усилителе обратной связи. Его можно представить в виде произведения коэффициента усиления по напряжению К и коэффициента передачи напряжения входной цепи усилителя Квх.ц усилителя :
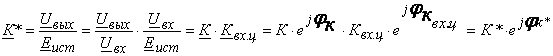 ,
(1.7)
,
(1.7)
где 
 – комплексный коэффициент передачи напряжения
входной цепи усилителя, характеризуемый модулем
– комплексный коэффициент передачи напряжения
входной цепи усилителя, характеризуемый модулем  и
углом сдвига фазы jвх.ц между входным
напряжением сигнала усилителя и ЭДС источника сигнала.
и
углом сдвига фазы jвх.ц между входным
напряжением сигнала усилителя и ЭДС источника сигнала.
Коэффициент усиления по току КТ представляет собой отношение установившегося значения комплексной амплитуды тока сигнала на выходе к комплексной амплитуде тока сигнала на входе усилителя:
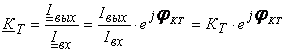 ,
(1.8)
,
(1.8)
где 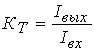 —
модуль коэффициента усиления по току, а
—
модуль коэффициента усиления по току, а 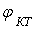 –
угол сдвига фазы между выходным и входным токами усилителя.
–
угол сдвига фазы между выходным и входным токами усилителя.
Как видно, в общем случае К, К* (КЕ), Квх.ци КТ являются комплексными величинами, зависящими от частоты из-за влияния
реактивных составляющих сопротивлений в цепях усилителей и из-за влияния
инерционных свойств УЭ. На практике особый интерес представляют эти
коэффициенты усиления и коэффициент передачи входной цепи в области средних
частот, где влияние реактивных составляющих сопротивлений в цепях усилителя и
инерционных свойств УЭ пренебрежимо мало и углы сдвига фаз равны нулю jк=0, jк*=0, jк.вх.ц=0, 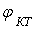 =0, а модули
коэффициентов усиления и коэффициента передачи входной цепи не зависят от
частоты, являясь действительными величинами:
=0, а модули
коэффициентов усиления и коэффициента передачи входной цепи не зависят от
частоты, являясь действительными величинами:
47-58, правка
58
Пример
19.2. Какой глубины ООС нужно
ввести в усилитель, чтобы уменьшить
погрешность коэффициента усиления до
1%, если температурная нестабильность 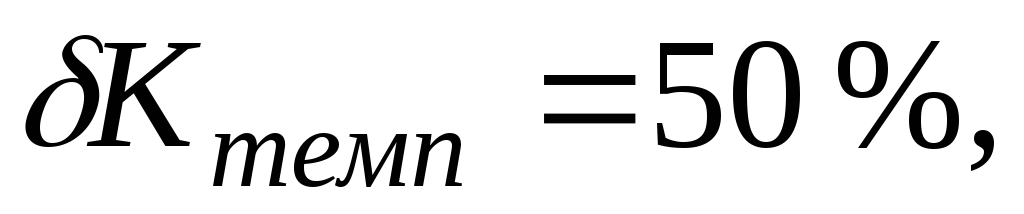 технологический
разброс
технологический
разброс 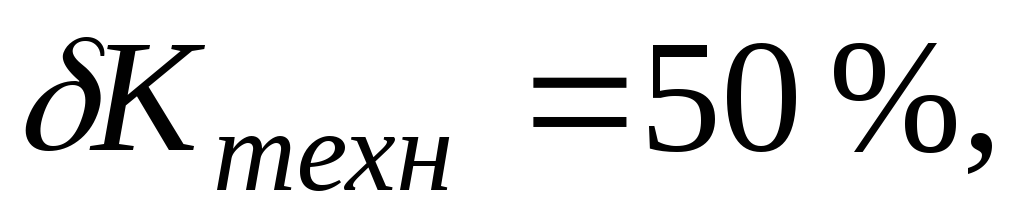 а погрешность коэффициента передачи
цепи обратной связи
а погрешность коэффициента передачи
цепи обратной связи 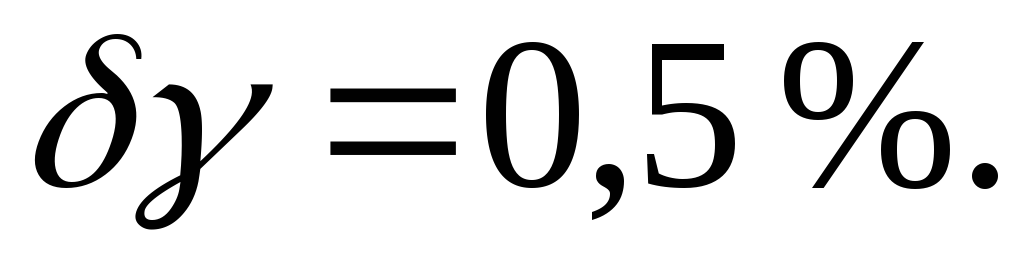
Решение: Результирующая нестабильность коэффициента усиления усилителя до введения обратной связи определяется квадратичным суммированием температурной нестабильности и технологического разброса (составляющие погрешности не коррелированны):
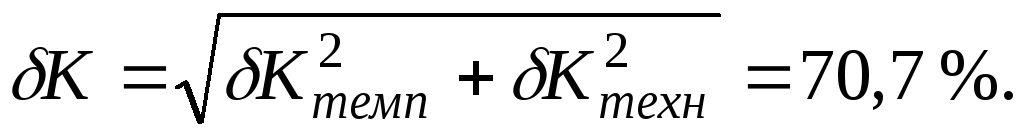
Соотношение
(19.8), полагая 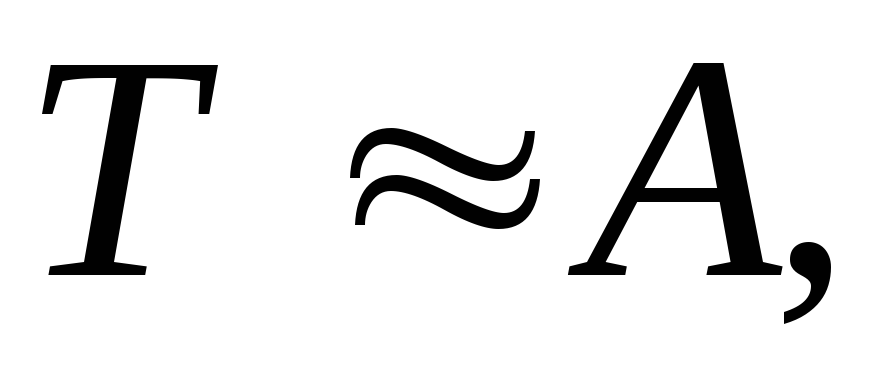 для наихудшего случая можем записать
в виде
для наихудшего случая можем записать
в виде 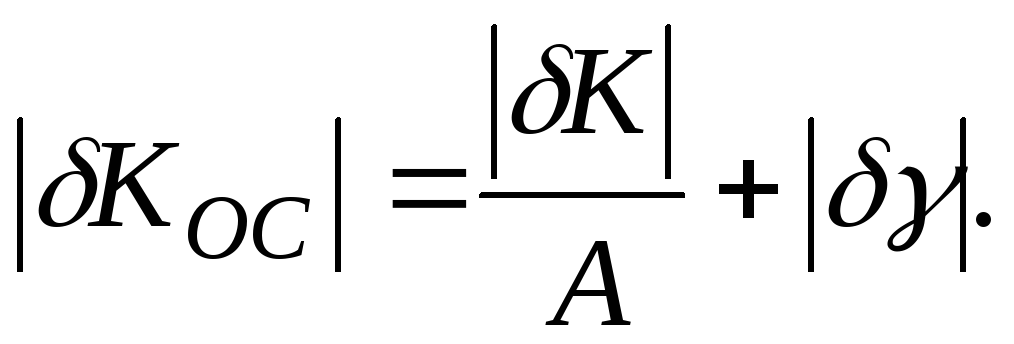
Из этого выражения можно определить требуемую глубину отрицательной обратной связи

19.3. Усилительный каскад с общим эмиттером
П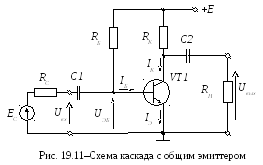 ростейшая
схема УНЧ на биполярном транзисторе
приведена на рис. 19.11. С помощью резистора
в цепи базы эмиттерный переход смещается
в прямом направлении, и на нем
устанавливается напряжение
ростейшая
схема УНЧ на биполярном транзисторе
приведена на рис. 19.11. С помощью резистора
в цепи базы эмиттерный переход смещается
в прямом направлении, и на нем
устанавливается напряжение  ,
примерно равное 0,3 В для германиевого
и 0,7 В для кремниевого транзистора. В
цепи базы протекает ток
,
примерно равное 0,3 В для германиевого
и 0,7 В для кремниевого транзистора. В
цепи базы протекает ток 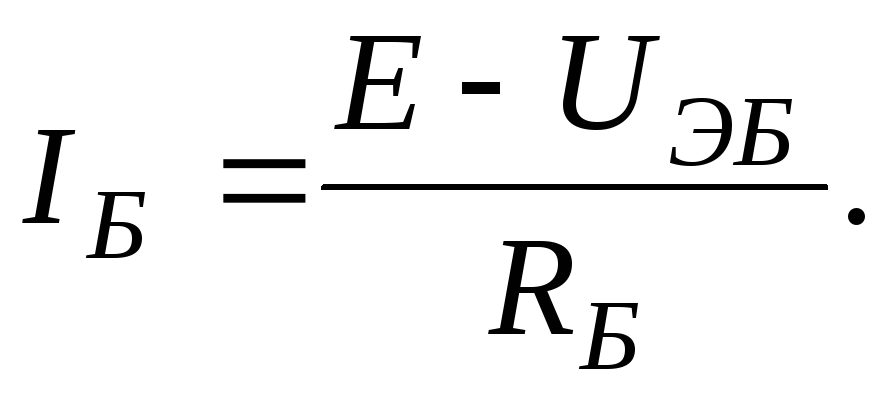 Коллекторный переход смещен в обратном
направлении. В цепи коллектора протекает
значительно больший ток
Коллекторный переход смещен в обратном
направлении. В цепи коллектора протекает
значительно больший ток 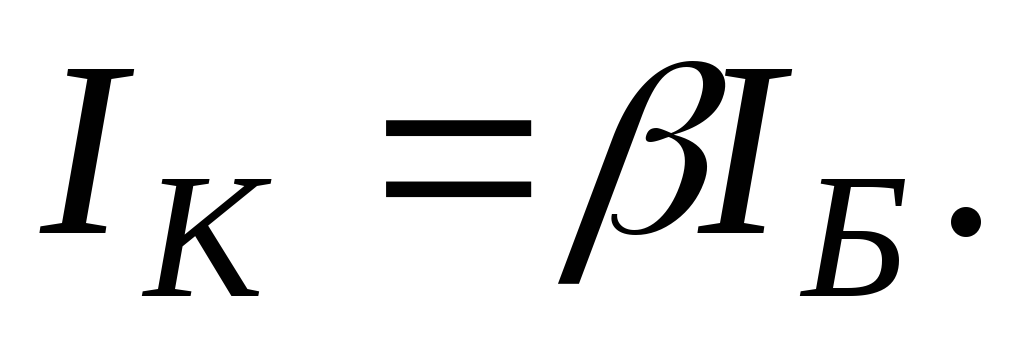 В цепи эмиттера
протекает ток IЭ = IК +IБ , примерно равный току IК.
Эмиттер является
общим электродом для входной и выходной
цепей. Поэтому рассматриваемый каскад
выполнен по схеме с общим
эмиттером (ОЭ).
В цепи эмиттера
протекает ток IЭ = IК +IБ , примерно равный току IК.
Эмиттер является
общим электродом для входной и выходной
цепей. Поэтому рассматриваемый каскад
выполнен по схеме с общим
эмиттером (ОЭ).
П еременная
составляющая входного напряжения uвх(t)подается
через разделительный конденсатор
еременная
составляющая входного напряжения uвх(t)подается
через разделительный конденсатор  и вызывает изменения тока базы транзистора VT1 iБ(t),
которые можно определить по входной
характеристике транзистора (рис. 19.12).
и вызывает изменения тока базы транзистора VT1 iБ(t),
которые можно определить по входной
характеристике транзистора (рис. 19.12).
Изменение тока базы приводит к пропорциональному изменению тока в коллекторной цепи. Для его преобразования в соответствующие изменения выходного напряжения поставлен резистор RК.
 На
выходных характеристиках транзистора
точка покоя А, соответствующая
выбранному значению тока базы, лежит
на нагрузочной прямой постоянного тока
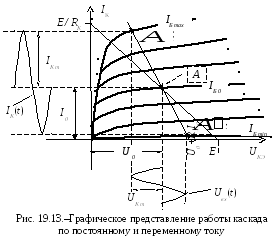
(рис. 19.13). Ее координаты обозначены как I0 и U0. Нагрузочная
прямая постоянного тока проходит через точку Е на оси абсцисс и точку Е
/ RК на оси ординат в соответствии с уравнением
второго закона Кирхгофа для коллекторной
цепи
На
выходных характеристиках транзистора
точка покоя А, соответствующая
выбранному значению тока базы, лежит
на нагрузочной прямой постоянного тока
(рис. 19.13). Ее координаты обозначены как I0 и U0. Нагрузочная
прямая постоянного тока проходит через точку Е на оси абсцисс и точку Е
/ RК на оси ординат в соответствии с уравнением
второго закона Кирхгофа для коллекторной
цепи
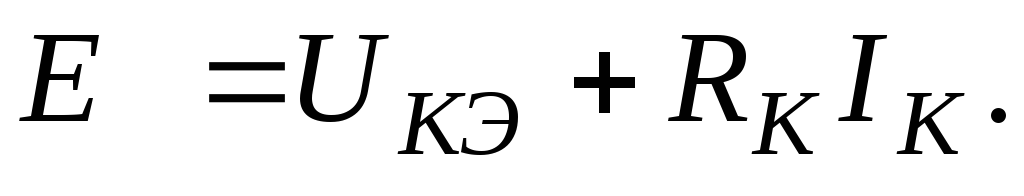 (19.11)
(19.11)
Наклон нагрузочной прямой постоянного
тока определяется сопротивлением
выходной цепи постоянному току  В общем случае оно включает все
сопротивления, последовательно
подключенные в выходной цепи, кроме
транзистора к источнику питания.
В общем случае оно включает все
сопротивления, последовательно
подключенные в выходной цепи, кроме
транзистора к источнику питания.
Через разделительный конденсатор C2 к коллектору подключена нагрузка Rн,
в которую передается часть переменной
составляющей коллекторного тока. Другая
часть ответвляется в резистор RК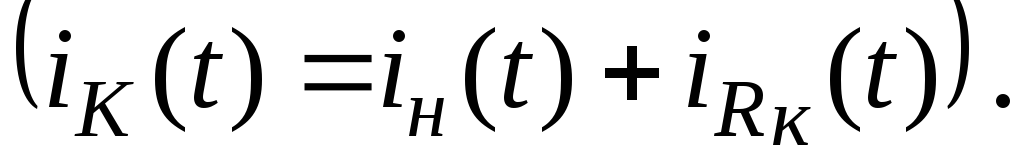 Следовательно, для переменной составляющей
коллекторного тока резисторы RК и
Следовательно, для переменной составляющей
коллекторного тока резисторы RК и 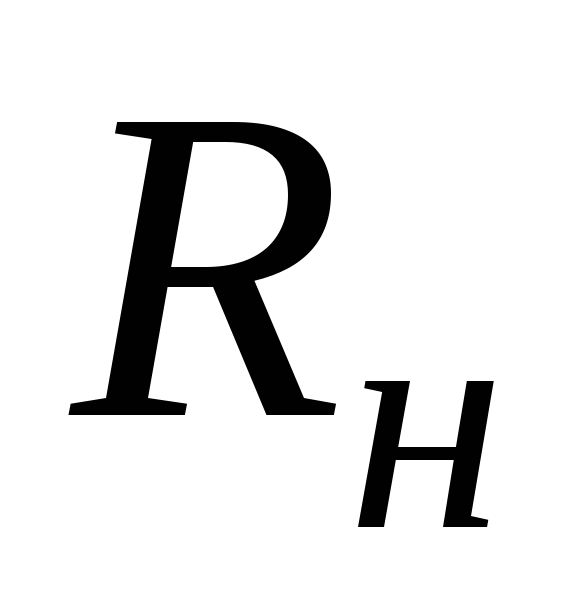 соединены параллельно. Их
параллельное соединение называют
сопротивлением выходной цепи переменному
току
соединены параллельно. Их
параллельное соединение называют
сопротивлением выходной цепи переменному
току
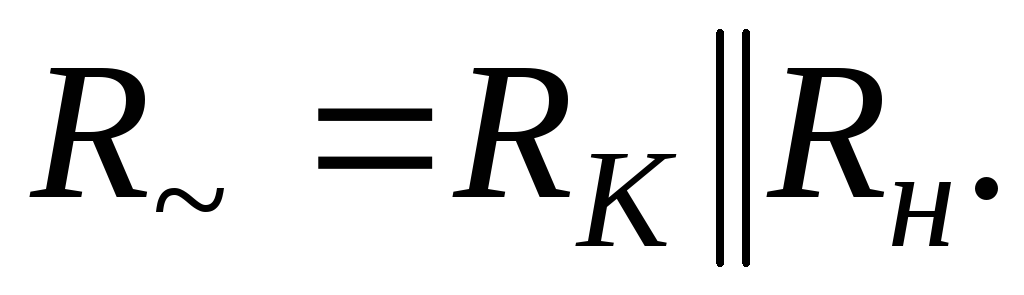 (19.12)
(19.12)
При передаче сигнала мгновенные значения тока и напряжения в коллекторной цепи транзистора определяются соотношениями
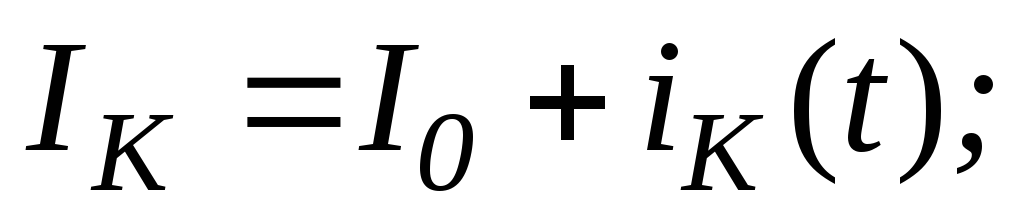 (19.13)
(19.13)
 (19.14)
(19.14)
причем переменные составляющие связаны уравнением
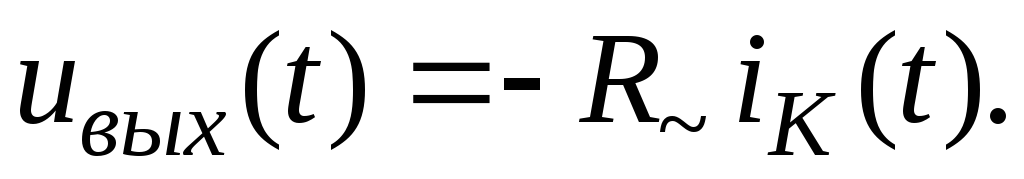 (19.15)
(19.15)
Знак минус подчеркивает тот факт, что с ростом коллекторного тока напряжение на транзисторе уменьшается.
Подставив в уравнение (19.15) значения переменных составляющих коллекторного тока и напряжения из (19.13) и (19.14), получим уравнение нагрузочной прямой переменного тока
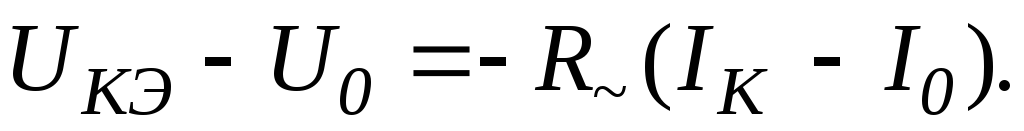 (19.16)
(19.16)
Она проходит через
точку покоя 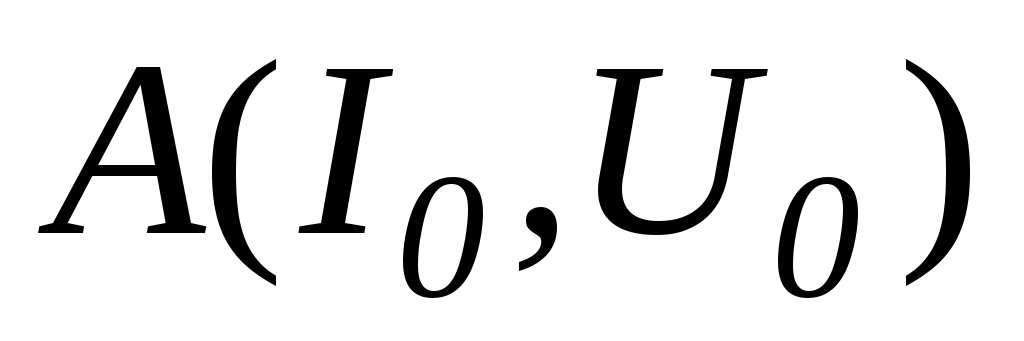 и точку на оси абсцисс с координатой
и точку на оси абсцисс с координатой  По ней совершает колебания рабочая
точка под действием сигнала, причем
По ней совершает колебания рабочая
точка под действием сигнала, причем  и
и  определяют амплитуды переменных
составляющих
определяют амплитуды переменных
составляющих 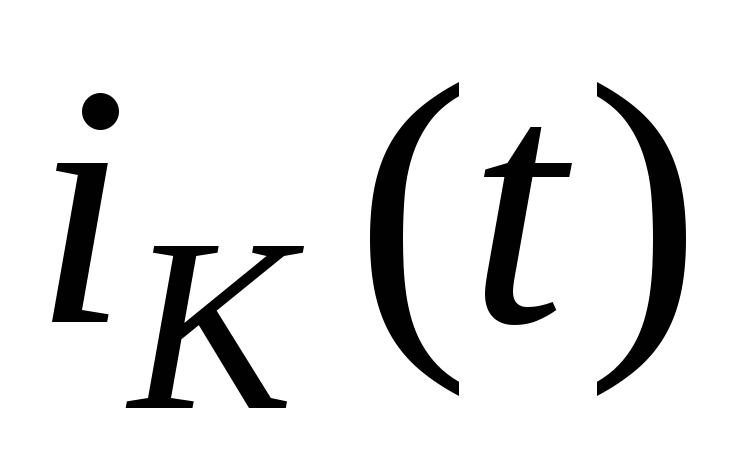 и
и 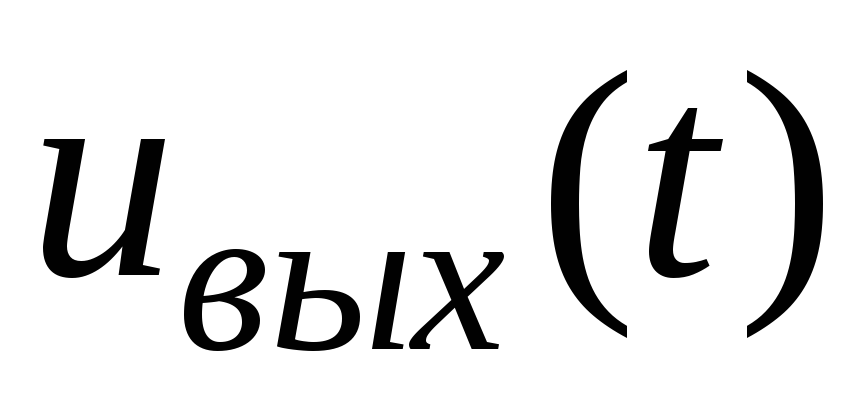 для заданной амплитуды изменения
базового тока
для заданной амплитуды изменения
базового тока 
Путем рассмотренных графических построений легко определяется коэффициент усиления по напряжению при работе каскада в режиме большого сигнала.
Для режима малого сигнала расчет проводят аналитическим путем с использованием эквивалентных схем. С целью упрощения анализа выделяют на АЧХ области нижних, средних и верхних частот и проводят анализ отдельно для каждой частотной области.
При построении эквивалентной схемы
усилительного каскада в области
средних частот рабочего диапазона
закорачиваются источник постоянного
напряжения Е, конденсаторы С1 и С2, транзистор заменяется его
эквивалентной схемой для средних частот
(не учитываются емкости переходов и
зависимость  от частоты). В схеме рис. 19.14 транзистор
заменен приближенной схемой замещения
с использованием h-параметров
для схемы включения с О
от частоты). В схеме рис. 19.14 транзистор
заменен приближенной схемой замещения
с использованием h-параметров
для схемы включения с О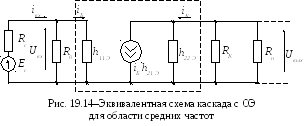 Э,
выделенной пунктирной линией.
Э,
выделенной пунктирной линией.
Входное сопротивление каскада (смотрим на входную цепь каскада со стороны источника сигнала)
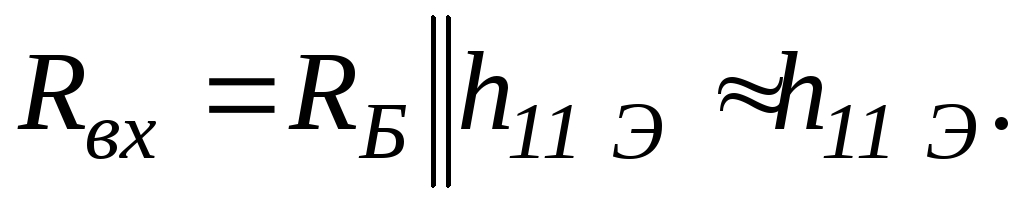 (19.17)
(19.17)
Выходное сопротивление каскада (смотрим на выходную цепь каскада со стороны нагрузки)
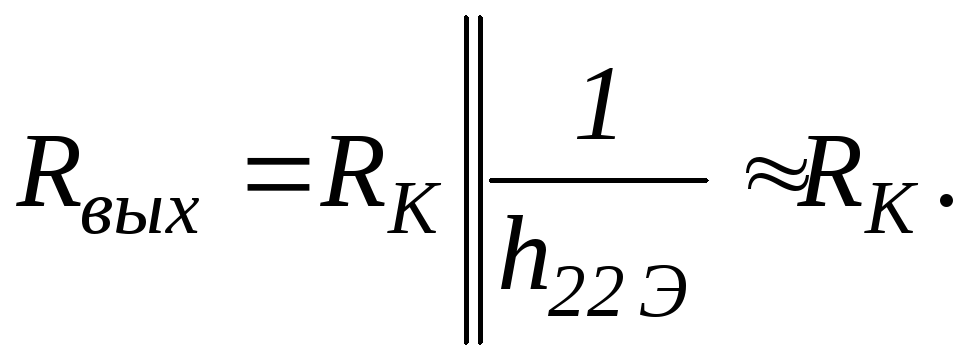 (19.18)
(19.18)
Коэффициент усиления по напряжению
 (19.19)
(19.19)
где 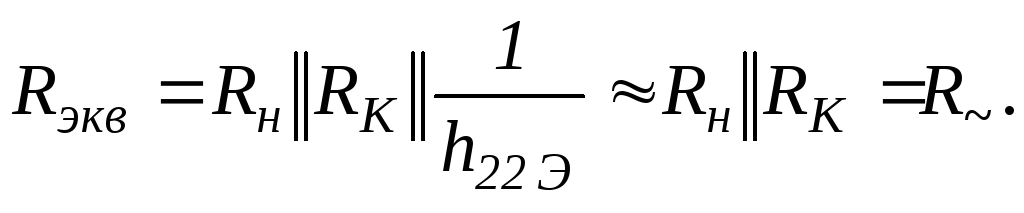
Знак минус говорит о том, что каскад с ОЭ инвертирует фазу входного сигнала.
Коэффициент усиления каскада по току
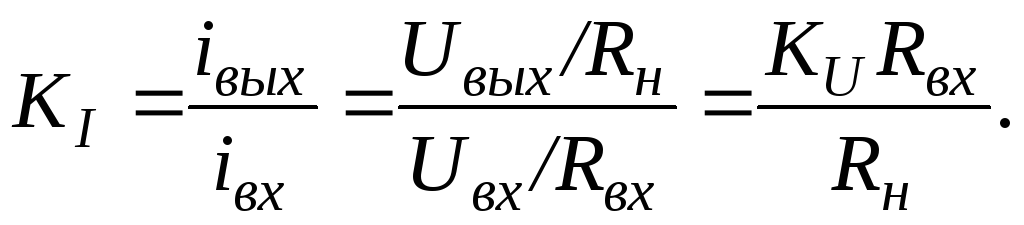 (19.20)
(19.20)
Сквозной коэффициент усиления
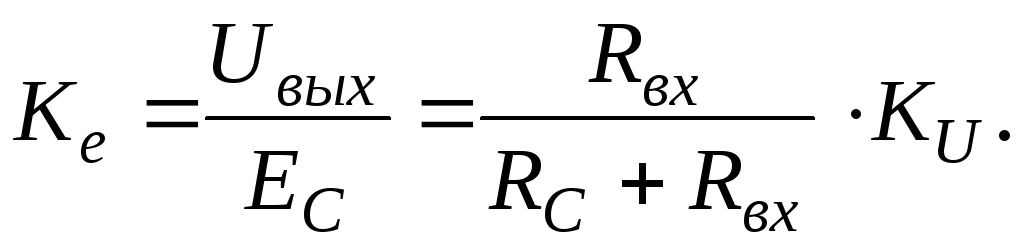 (19.21)
(19.21)
Каскад с ОЭ дает усиление и по напряжению,
и по току, обеспечивая значительное
усиление сигнала по мощности 
На нижних частотах возрастает сопротивление разделительных конденсаторов С1 и С2 (их уже нельзя считать закороченными, как на средних частотах), вследствие чего образуются делители напряжения во входной и выходной цепях усилительного каскада. Уменьшается коэффициент передачи входной цепи, не все сформированное на коллекторе напряжение сигнала доходит до нагрузки.
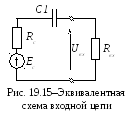 Оценим
влияние разделительного конденсатора С1, воспользовавшись эквивалентной
схемой входной цепи для области нижних
частот (рис. 19.15).
Оценим
влияние разделительного конденсатора С1, воспользовавшись эквивалентной
схемой входной цепи для области нижних
частот (рис. 19.15).
Полное сопротивление контура
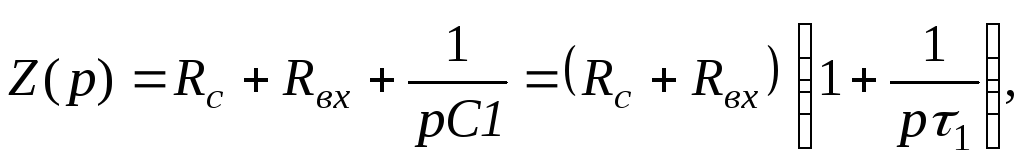
где 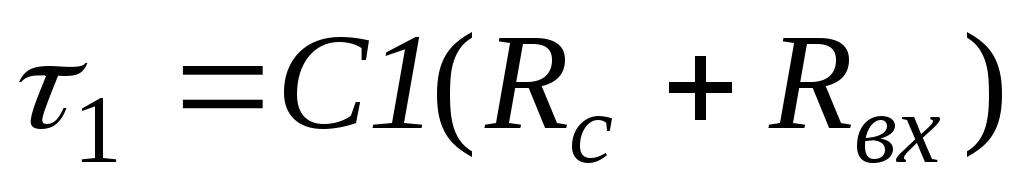 – постоянная времени
входной цепи на нижних частотах.
– постоянная времени
входной цепи на нижних частотах.
Коэффициент передачи входной цепи
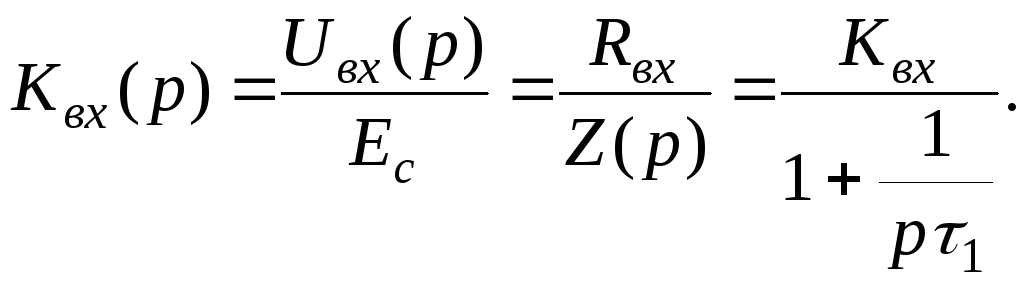 (19.22)
(19.22)
По операторному выражению (19.22) можно записать соотношения для оценки вносимых конденсатором С1 частотных и фазовых искажений:
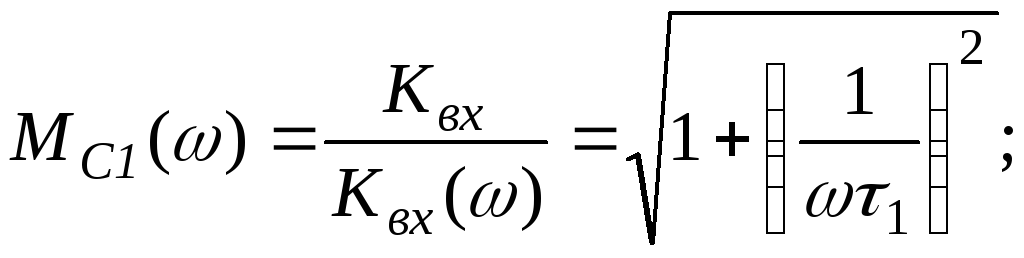 (19.23)
(19.23)
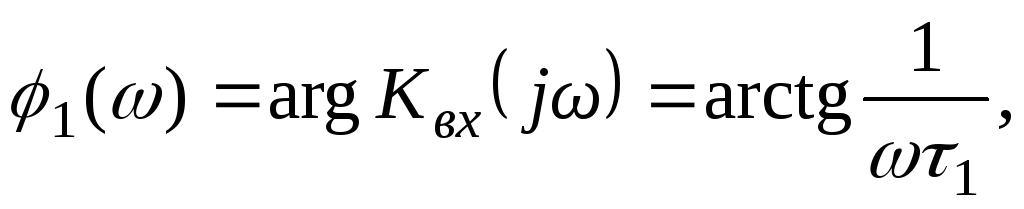 (19.24)
(19.24)
а также построить переходную характеристику
входной цепи для области больших времен
(рис. 19.16):
также построить переходную характеристику
входной цепи для области больших времен
(рис. 19.16):
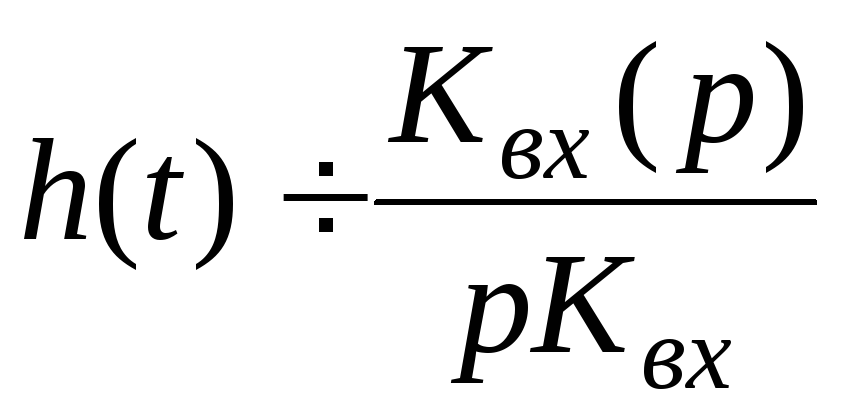 или
или 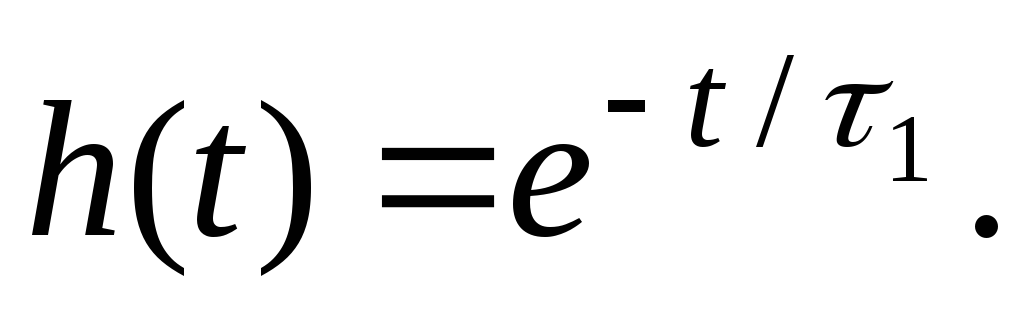 (19.25)
(19.25)
Относительный спад вершины импульса
длительностью 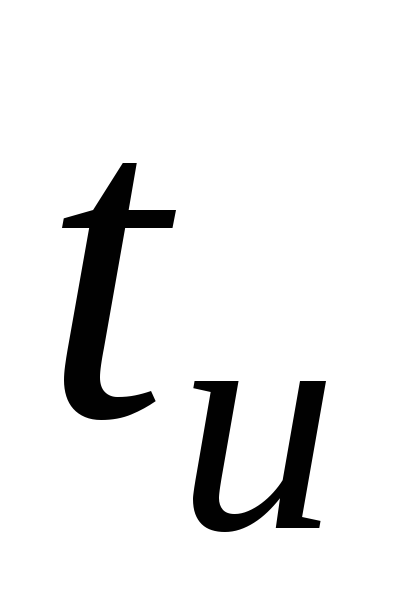 за счет заряда разделительного
конденсатора С1 определяется
соотношением
за счет заряда разделительного
конденсатора С1 определяется
соотношением
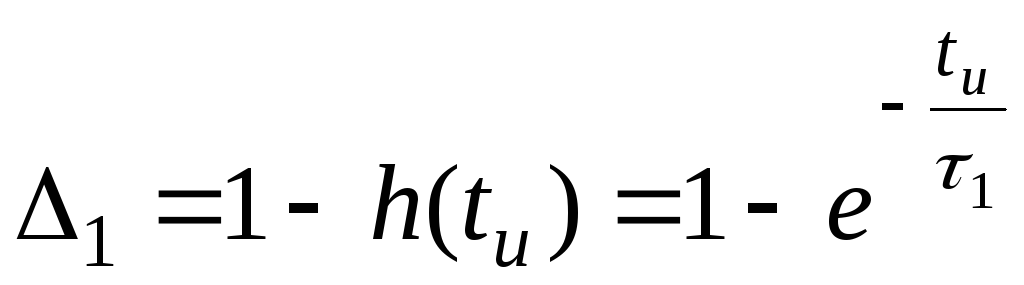 .
(19.26)
.
(19.26)
Разложив экспоненту в ряд Маклорена и
заменив при 
 начальный участок экспоненты прямой
линией, получим
начальный участок экспоненты прямой
линией, получим
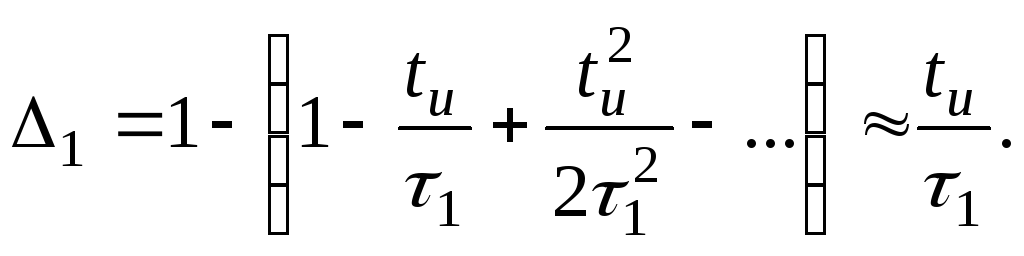 (19.27)
(19.27)
По допустимой величине частотных искажений МС1 на нижней рабочей частоте fн емкость конденсатора С1 может быть выбрана из соотношения (19.23):
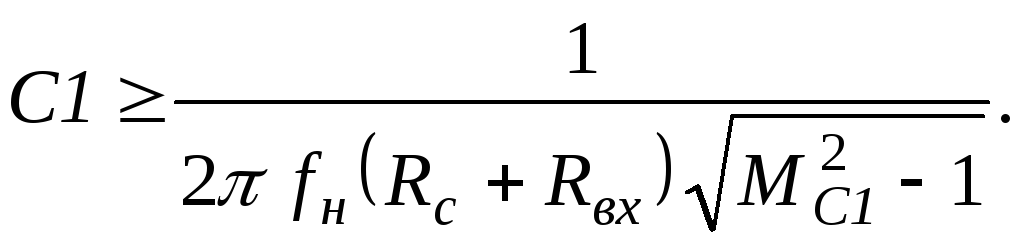 (19.28)
(19.28)
Значение МС1 в выражение (19.28) необходимо подставлять в относительных единицах (не в децибелах). После расчета емкость конденсатора округляется до ближайшего стандартного номинала в большую сторону.
При расчете линейных импульсных усилителей емкость разделительного конденсатора С1 выбирают по допустимой величине относительного спада вершины импульса из соотношения (19.27):
 (19.29)
(19.29)
Заметим, что наличие конденсатора С1 добавило в знаменатель передаточной
функции сомножитель типа  ,
дающий на ЛАЧХ спад коэффициента передачи
с наклоном 20 дБ на декаду левее частоты
сопряжения 1/.
,
дающий на ЛАЧХ спад коэффициента передачи
с наклоном 20 дБ на декаду левее частоты
сопряжения 1/.
По аналогии с этим анализ эквивалентной схемы выходной цепи для области нижних частот (рис. 19.17) позволяет получить передаточную функцию коэффициента усиления по напряжению в виде
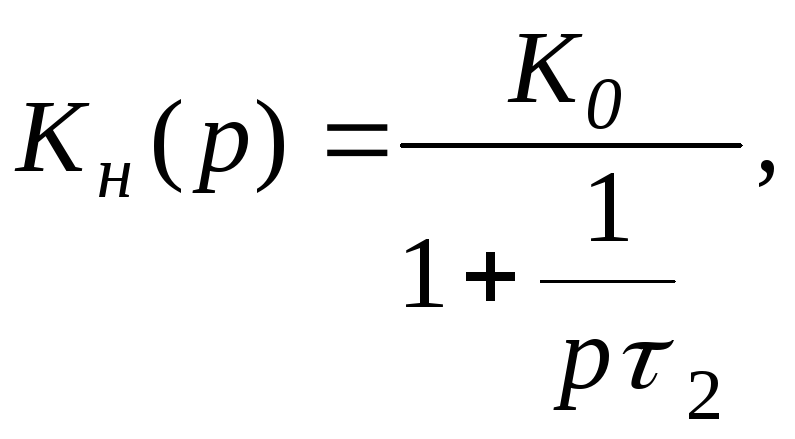 (19.30)
(19.30)
г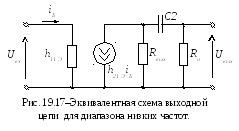 де
де 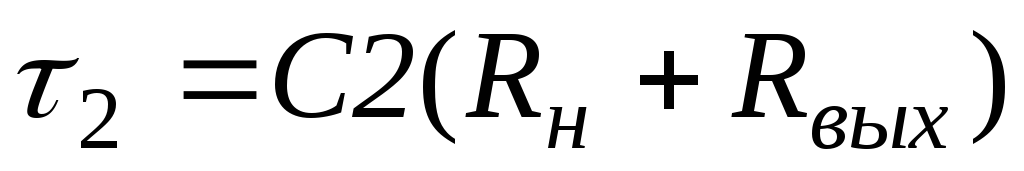 – постоянная времени выходной цепи на
нижних частотах.
– постоянная времени выходной цепи на
нижних частотах.
Подобно соотношениям (19.28) и (19.29) можно
записать выражения для расчета емкости
разделительного конденсатора С2 по
допустимой величине частотных искажений МС2 на
нижней частоте fнили по
допустимому спаду импульса длительностью 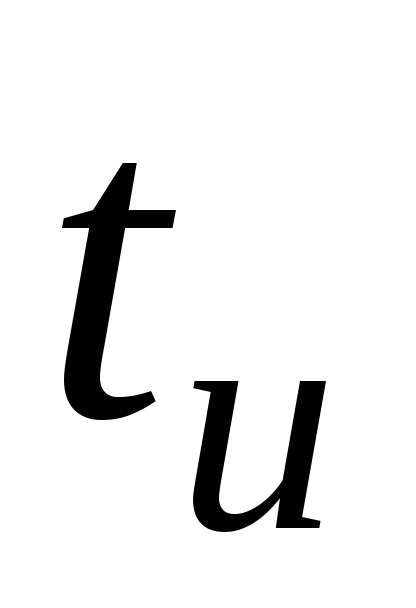 :
:
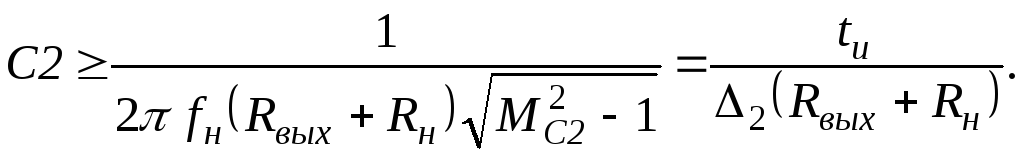 (19.31)
(19.31)
В области верхних частот учитывают влияние емкости коллекторного перехода СК и инерционность процесса рекомбинации неосновных носителей, отражаемую комплексным коэффициентом передачи тока базы
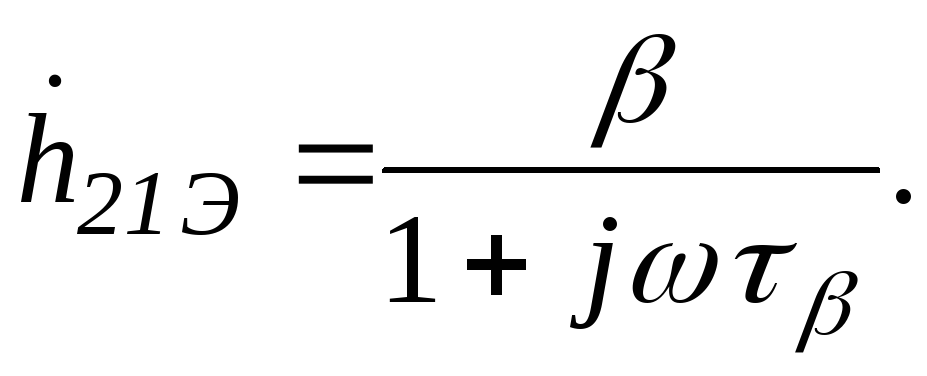
Анализ эквивалентной схемы каскада для области верхних частот (рис. 19.18) приводит в первом приближении к передаточной функции коэффициента усиления по напряжению в виде
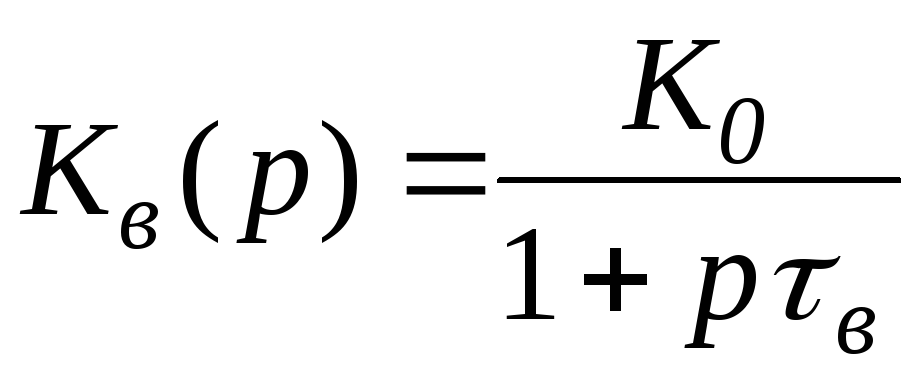 , (19.32)
, (19.32)
г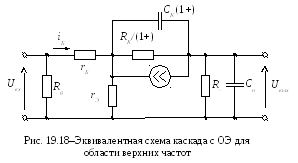 де
де 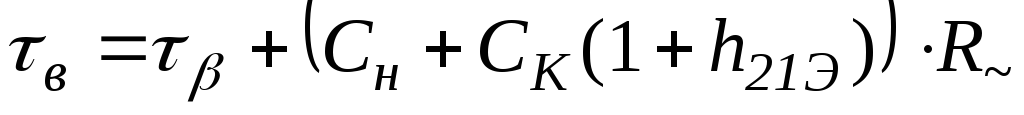 –
постоянная времени каскада в области
верхних частот.
–
постоянная времени каскада в области
верхних частот.
Рассчитав постоянную времени  ,
можно оценить частотные и фазовые
искажения на верхних частотах (в том
числе и на верхней граничной частоте
),
а также время нарастания фронта импульса
на выходе каскада по формулам
,
можно оценить частотные и фазовые
искажения на верхних частотах (в том
числе и на верхней граничной частоте
),
а также время нарастания фронта импульса
на выходе каскада по формулам
 (19.33)
(19.33)
Результирующие характеристики каскада. Объединив результаты анализа в различных диапазонах частот, можно записать выражение для передаточной функции сквозного коэффициента усиления в виде
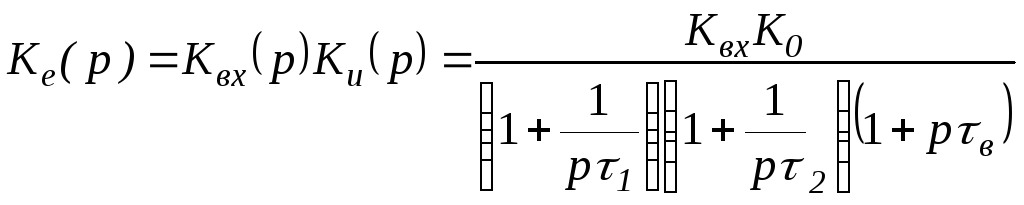 . (19.34)
. (19.34)
Амплитудно-частотная
характеристика 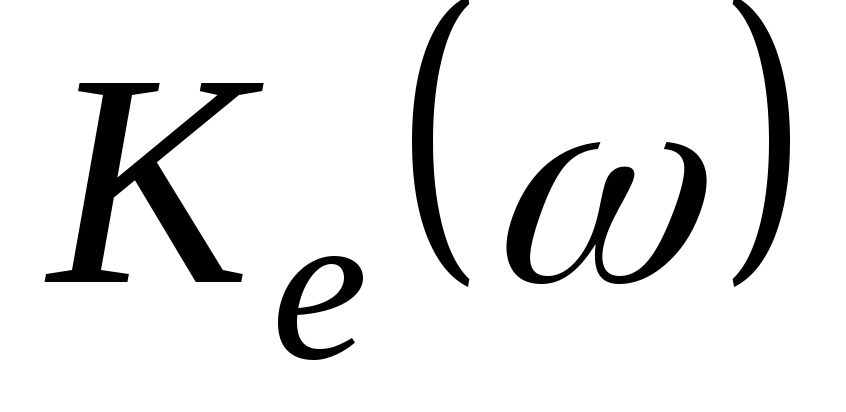 определится выражением
определится выражением
 (19.35)
(19.35)
Фазочастотная характеристика каскада
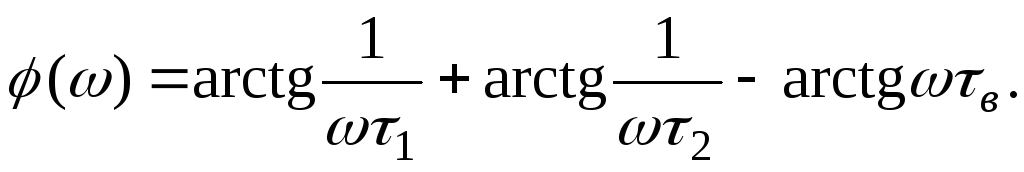 (19.36)
(19.36)
Х арактерные
искажения прямоугольного импульса
длительностью tи при его усилении каскадом с ОЭ показаны
на рис. 19.19.
арактерные
искажения прямоугольного импульса
длительностью tи при его усилении каскадом с ОЭ показаны
на рис. 19.19.
Время нарастания фронта импульса определяется соотношением
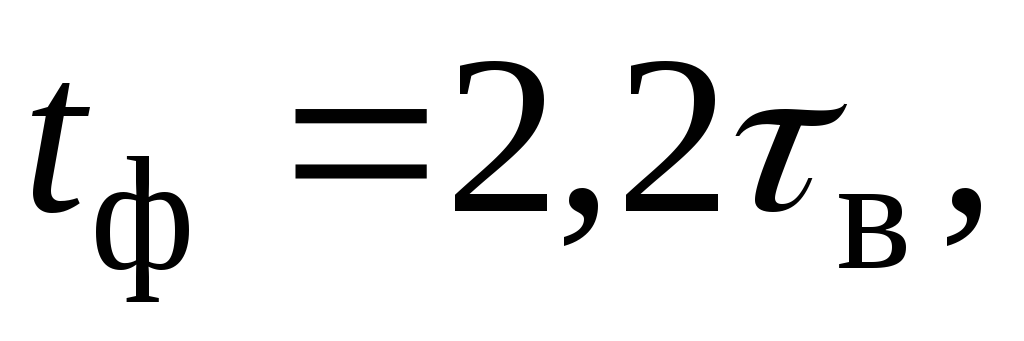 (19.37)
(19.37)
а относительный спад вершины импульса
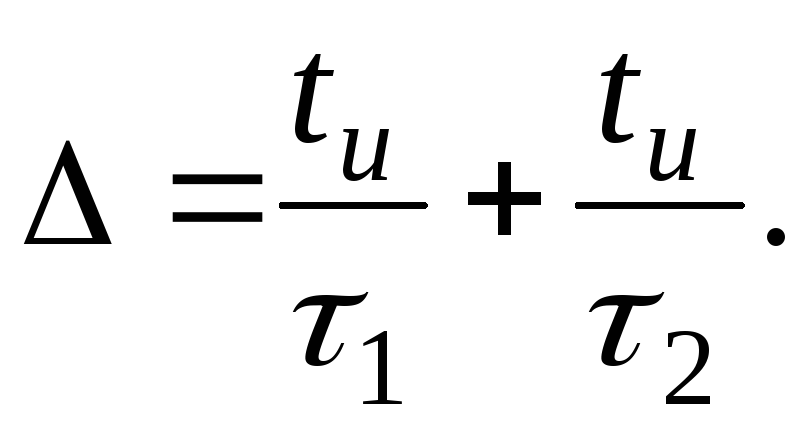 (19.38)
(19.38)
Существенным недостатком биполярных транзисторов является зависимость их параметров от температуры. При повышении температуры происходит смещение точки покоя A вверх по нагрузочной прямой постоянного тока и возможен выход ее за пределы линейного участка в область насыщения (см. рис. 19.13).
Д ля
уменьшения влияния температуры на
работу усилительного каскада с ОЭ в
цепь эмиттера включают резистор RЭ,, шунтированный конденсатором СЭ (рис. 19.20). В цепи базы для создания
начального смещения UЭБ между базой и эмиттером применен
делитель R1, R2, причем ток делителя Iд выбран значительно большим тока базы IБ.
ля
уменьшения влияния температуры на
работу усилительного каскада с ОЭ в
цепь эмиттера включают резистор RЭ,, шунтированный конденсатором СЭ (рис. 19.20). В цепи базы для создания
начального смещения UЭБ между базой и эмиттером применен
делитель R1, R2, причем ток делителя Iд выбран значительно большим тока базы IБ.
Напряжение UБЭ зависит от сопротивлений резисторов:
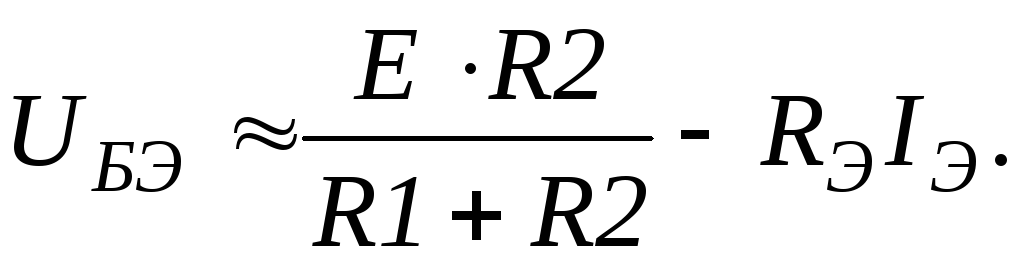
При наличии резистора RЭ увеличение эмиттерного тока IЭ = IК +IБ из-за повышения температуры приводит к возрастанию падения напряжения на резисторе RЭ. Это вызывает снижение потенциала базы по отношению к потенциалу эмиттера, и, следовательно, уменьшение токов IЭ и IК. В схеме действует ООС по постоянному току. Ясно, что уменьшение коллекторного тока под действием резистора RЭ не может полностью скомпенсировать рост его за счет температуры, но влияние температуры на ток IК при этом во много раз снижается.
Отношение нестабильности тока коллектора в точке покоя к температурному смещению выходных характеристик транзистора называют коэффициентом температурной нестабильности.
Для каскада, собранного по схеме рис. 19.20, он определяется соотношением
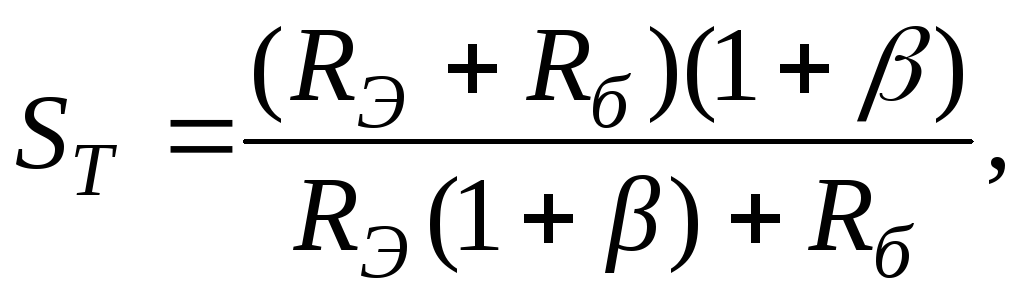 (19.39)
(19.39)
где Для каскада по схеме рис. 19.11  Обычно приемлемая температурная
стабильность обеспечивается при
Обычно приемлемая температурная
стабильность обеспечивается при 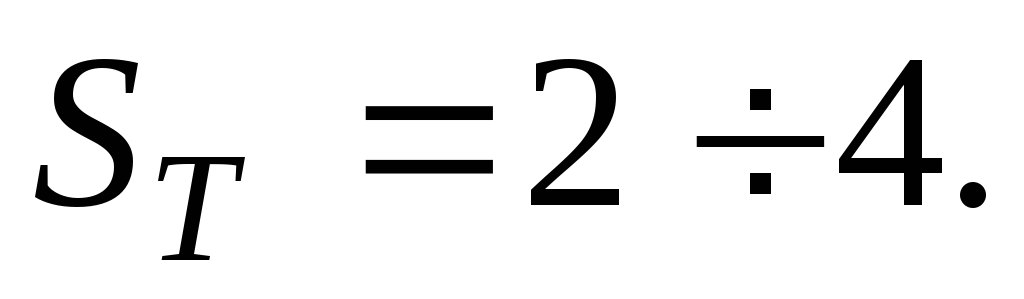
Введение резистора RЭ при отсутствии конденсатора СЭ изменяет работу усилительного каскада не только в режиме покоя, но и при наличии входного сигнала. Переменная составляющая эмиттерного тока создает на резисторе падение напряжения uЭ = RЭ iЭ , которое уменьшает усиливаемое напряжение, подводимое к транзистору

Коэффициент усиления по напряжению снижается до величины
 (19.40)
(19.40)
Для устранения ООС по переменному току резистор RЭ шунтируют конденсатором СЭ , который рассчитывают так, чтобы его сопротивление в рабочем диапазоне частот было мало. По допустимой величине частотных искажений МСэ емкость конденсатора определяют из соотношения
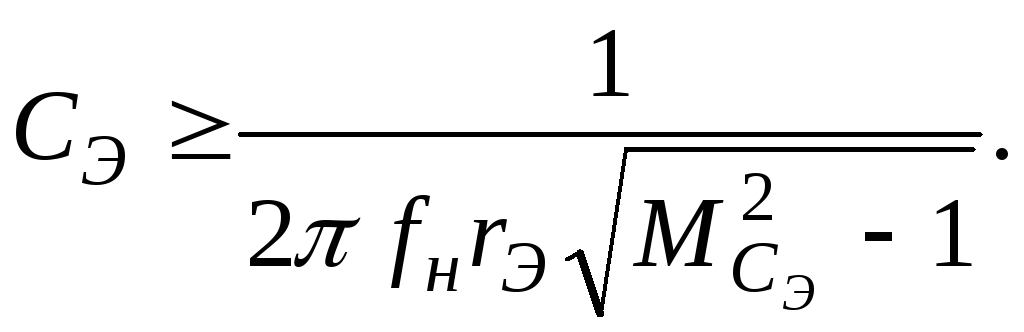
Пример 19.3. Выбрать элементы и оценить основные параметры каскада с ОЭ на транзисторе КТЗ15В при следующих исходных данных: Е =15 В, I0 = 1 мА, U0 = 5 В, fн = 20 Гц, Rн = 5 кОм, = 100, СК = 7 пФ, f = 5МГц.
Решение. Задаваясь падением напряжения на
резисторе RЭ,
равным 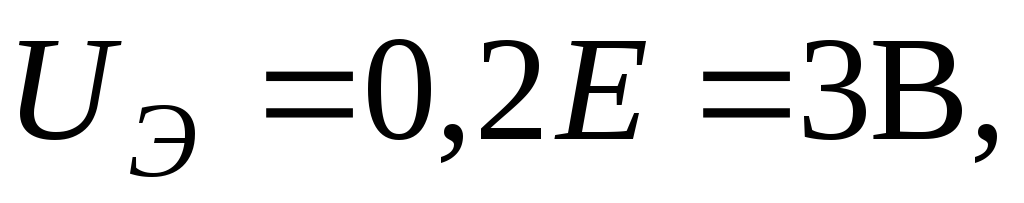 рассчитаем сопротивления
резисторов выходной цепи транзистора:
рассчитаем сопротивления
резисторов выходной цепи транзистора:

Задаваясь допустимым коэффициентом температурной нестабильности ST = 4 из соотношения (19.39) оценим параллельное соединение резисторов базового делителя:

Верхний резистор базового делителя

Нижний резистор базового делителя
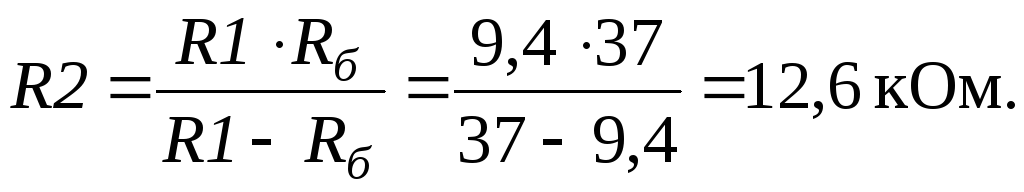
Выбираем
резисторы УЛМ или МЛТ ряда Е12 с допустимым
отклонением 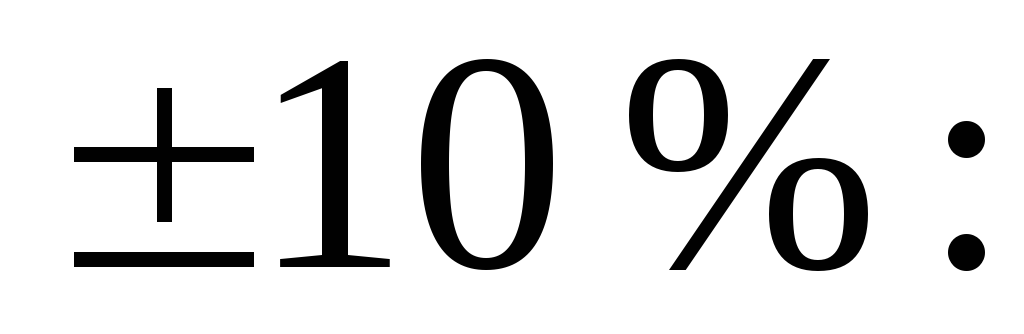
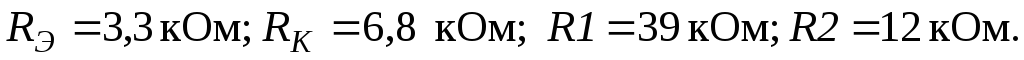
Входное сопротивление транзистора
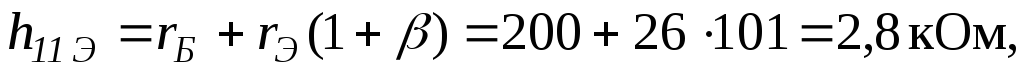
где  Ом – омическое сопротивление области
базы транзистора;
Ом – омическое сопротивление области
базы транзистора;
 – сопротивление эмиттерного перехода.
– сопротивление эмиттерного перехода.
Входное сопротивление каскада
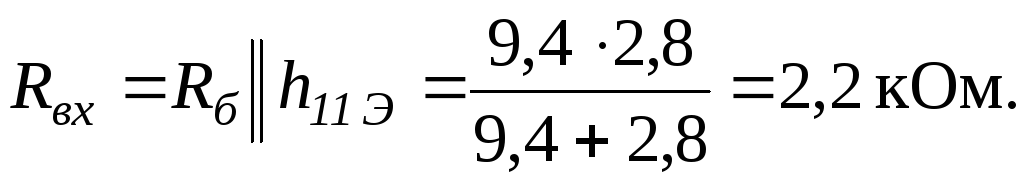
Выходное сопротивление каскада (см. выражение 19.18)

Сопротивление выходной цепи переменному току
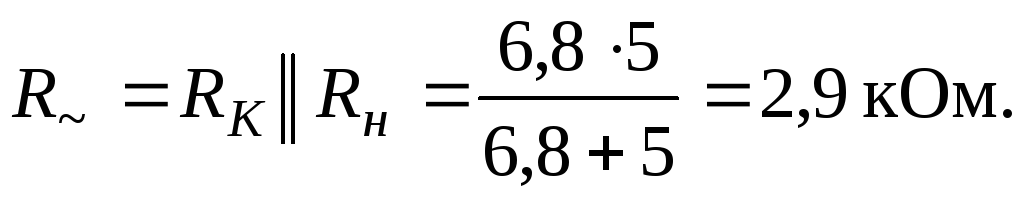
Коэффициент усиления по напряжению
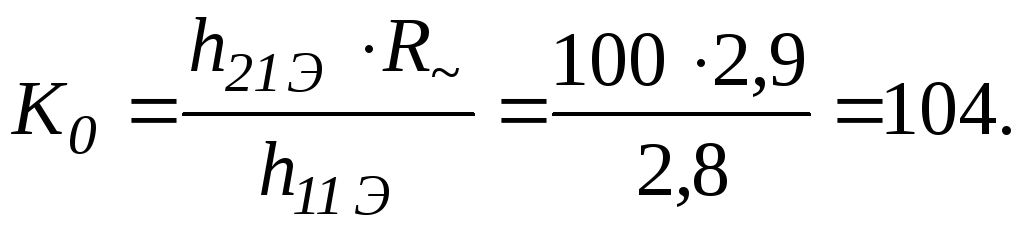
Коэффициент усиления по току
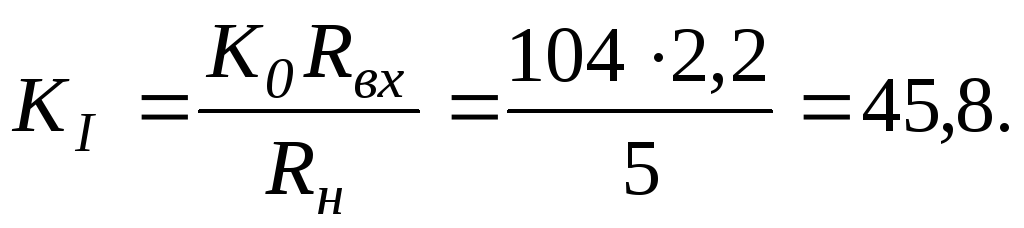
Коэффициент усиления по мощности

Результирующий
коэффициент частотных искажений на
нижней частоте  равен произведению коэффициентов
частотных искажений за счет каждого из
конденсаторов
равен произведению коэффициентов
частотных искажений за счет каждого из
конденсаторов 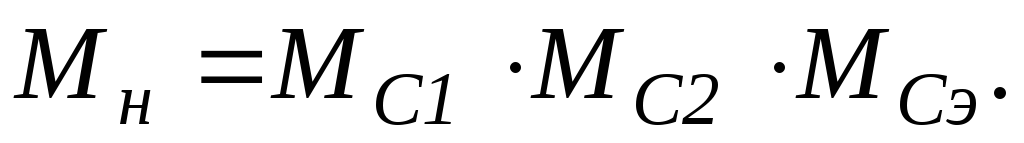 Равномерно распределяя искажения по
конденсаторам, при расчете каждого из
них будем ориентироваться на
Равномерно распределяя искажения по
конденсаторам, при расчете каждого из
них будем ориентироваться на 
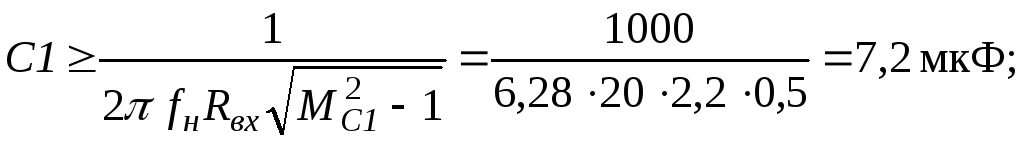
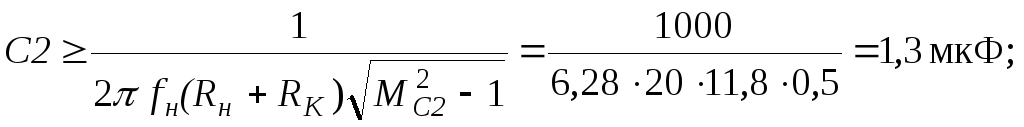
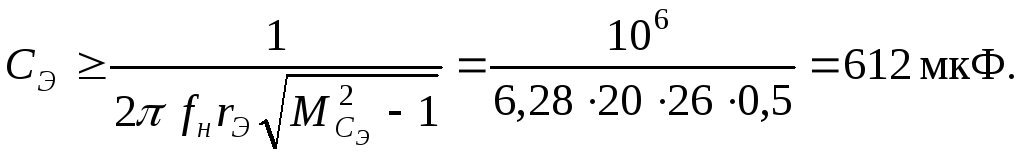
Выбираем электролитические конденсаторы из ряда Е12:
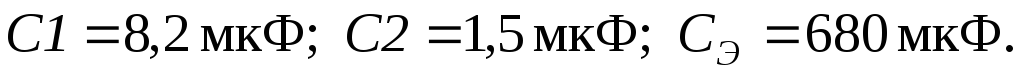
Постоянная времени каскада в области верхних частот

где 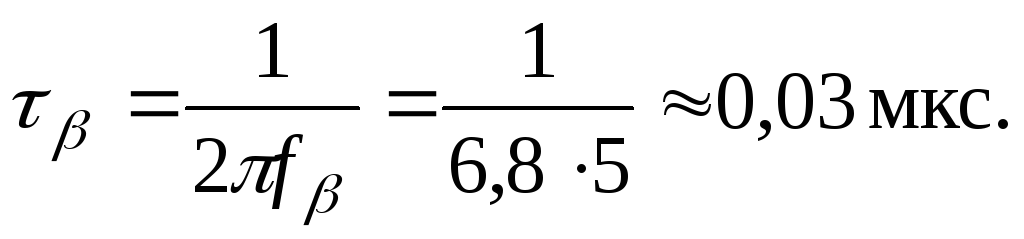
Верхняя
граница полосы пропускания каскада на
уровне 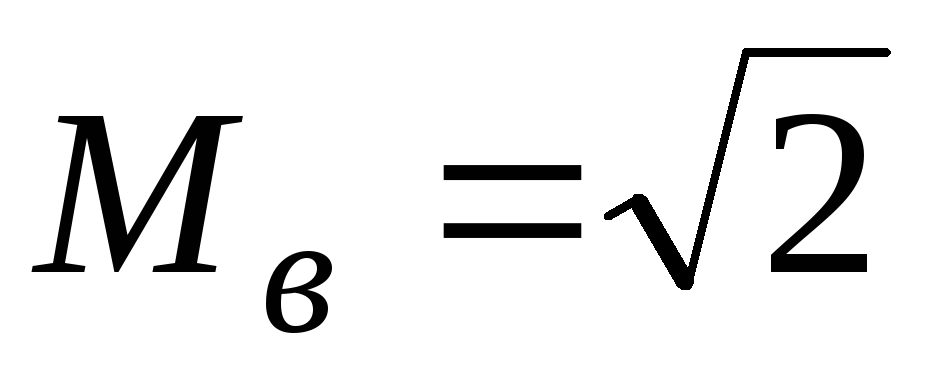
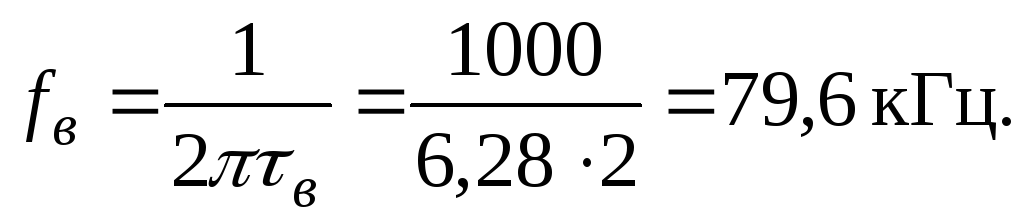
Площадь усиления

Максимальная амплитуда выходного синусоидального напряжения, которую можно получить без ограничения:
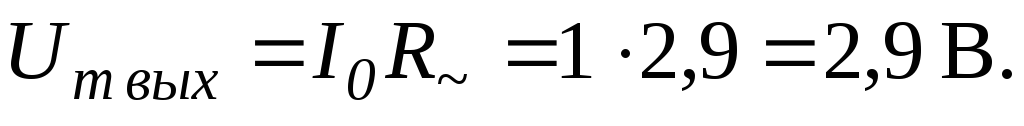
При этом коэффициент полезного действия каскада составит
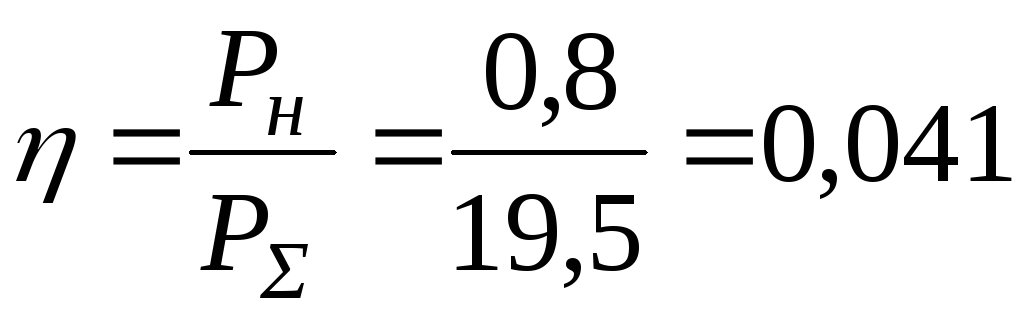 или
или 
где 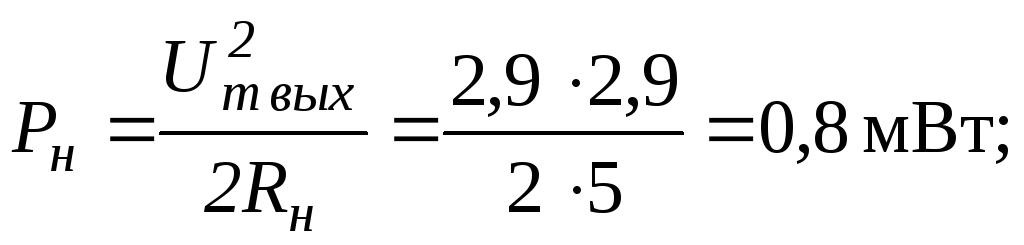
– суммарная мощность, потребляемая каскадом от источника питания.
19.4. Схемотехника резистивных усилительных каскадов
На рис. 19.21 приведен
вариант построения усилителя по схеме
с общим
коллектором (ОК). При работе в режиме малого сигнала
можно выбрать в точке покоя IЭ = I0 =(0,51)
мА, UКЭ = U0 = E/2,
ток делителя Iд = 10IБ =
10I0/ и
рассчитать сопротивления резисторов
по формулам
и
рассчитать сопротивления резисторов
по формулам
В данном каскаде сопротивления выходной
цепи по постоянному и переменному току
определяются соотношениями
данном каскаде сопротивления выходной
цепи по постоянному и переменному току
определяются соотношениями

К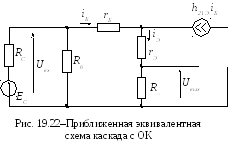 оллектор
транзистора по переменному току заземлен
(внутреннее сопротивление источника
питания Е близко к нулю). Входной
сигнал через разделительный конденсатор С1 подается в цепь базы транзистора VT1, а выходной
– снимается с эмиттера. В каскаде
действует стопроцентная ООС по напряжению,
в результате которой к участку «база —
эмиттер» транзистора прикладывается
разность входного и выходного напряжений.
оллектор
транзистора по переменному току заземлен
(внутреннее сопротивление источника
питания Е близко к нулю). Входной
сигнал через разделительный конденсатор С1 подается в цепь базы транзистора VT1, а выходной
– снимается с эмиттера. В каскаде
действует стопроцентная ООС по напряжению,
в результате которой к участку «база —
эмиттер» транзистора прикладывается
разность входного и выходного напряжений.
Эквивалентная схе-ма каскада для средних частот приведена на рис. 19.22. Транзистор заменен приближенной Т-образной схемой замещения.
Входное сопротивление со стороны базы VT1

Входное сопротивление каскада
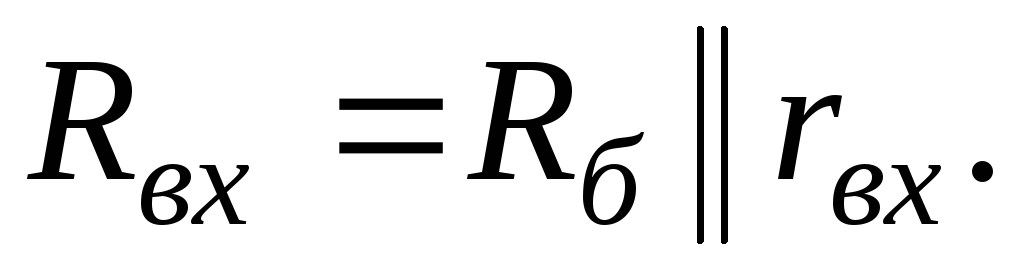 (19.41)
(19.41)
Коэффициент усиления, формула и примеры
Определение и формула коэффициента усиления
Коэффициент усиления является одним из основных параметров электронных усилителей. Исходя из требований, которые предъявляются к параметрам выхода усилителя, выделяют следующие коэффициенты усиления: по напряжению, по току, по мощности. Коэффициент усиления, обычно обозначают буквой K, внизу справа добавляют индекс, указывающий параметр усиления.
Коэффициентом усиления по току () называют физическую величину, равную отношению амплитуды переменной компоненты выходной силы тока () к амплитуде входной силы тока ():
Коэффициентом усиления по мощности ( является физическая величина, равная:
где — выходная мощность, — входная мощность.
Коэффициент усиления характеризует усилительные свойства схемы.
Действительный и комплексный коэффициенты усиления
При отсутствии реактивных элементов в схемах и исключении их влияния коэффициенты усиления — действительные величины, не зависящие от частоты переменного сигнала. При этом на выходе получают сигнал, имеющий форму такую же, что у входного сигнала, отличие состоит только в амплитуде.
Если в схеме присутствуют реактивные элементы (конденсаторы, индуктивности), то коэффициент усиления является комплексной величиной. Причем, следует учесть, что действительная и мнимая части коэффициента зависят от частоты входного сигнала.
Периодический сигнал, имеющий сложную форму можно представить как сумму гармонических составляющих, обладающих разными амплитудами, частотами и фазами. Если иметь в виду, что коэффициент усиления является комплексной величиной, то амплитуды и фазы гармонических компонент входного сигнала при прохождении через усилитель будут изменяться по-разному. Тогда выходной сигнал будет иметь форму отличную от входного.
Трансформации сигнала при прохождении через усилитель, вызванные зависимостью параметров усилителя от частоты и не зависящие от амплитуды сигнала входа, называют линейными искажениями. Их делят на частотные и фазовые. Частотные искажения характеризуют изменения модуля коэффициента усиления. Фазовые линейные искажения характеризуют связь сдвига по фазе между выходным и входным сигналами от частоты, что связано с влиянием реактивных элементов.
Коэффициент усиления считают постоянной величиной внутри полосы пропускания.
Искажения в выходном сигнале оценивают при помощи коэффициента частотных искажений (M):
где — коэффициент частотных искажений на нижних граничных частотах; — коэффициент частотных искажений на верхних граничных частотах; — коэффициент усиления на нижних частотах; — коэффициент усиления на верхних частотах; — коэффициент усиления на средних частотах.
Общий коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах. Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
Единицы измерения коэффициента усиления
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.

