47.Электромагнитное поле. Уравнение Максвелла в интегральной форме.
Введение Максвеллом понятия тока смещения привело его к завершению созданной им единой макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле (см. § 137) может быть как потенциальным (eq), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ+ЕB. Так как циркуляция вектора eq равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
Э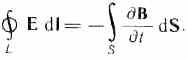 то
уравнение показывает, что источниками
электрического поля могут быть не только
электрические заряды, но и меняющиеся
во времени магнитные поля.
то
уравнение показывает, что источниками
электрического поля могут быть не только
электрические заряды, но и меняющиеся
во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
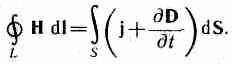
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D (см. (89.3)):
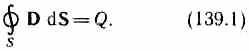
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (139.1) запишется в виде
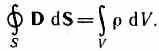
4. Теорема Гаусса для поля В (см. (120.3)):
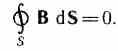
И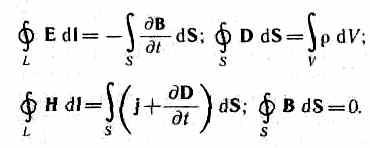 так,полная
система уравнений Максвелла в
интегральной форме:
так,полная
система уравнений Максвелла в
интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные не сегнетоэлектрические и не ферромагнитные среды):
D=0E,
В=0Н,
j=E,
где 0и 0 — соответственно электрическая и магнитная постоянные, и — соответственно диэлектрическая и магнитная проницаемости, — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Д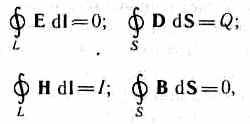 ля
стационарных полей (Е=const
и В=const) уравнения
Максвелла примут
вид
ля
стационарных полей (Е=const
и В=const) уравнения
Максвелла примут
вид
т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно
Воспользовавшись
известными из векторного анализа
теоремами Стокса и Гаусса
м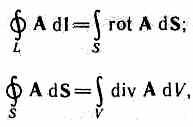 ожно
представитьполную
систему уравнений Максвелла в
дифференциальной форме (характеризующих
поле в каждой точке пространства):
ожно
представитьполную
систему уравнений Максвелла в
дифференциальной форме (характеризующих
поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная
и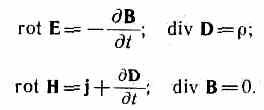
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):
D1n=D2n, E1=E2, B1n=B2n, H1= H2
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, смогла объяснить не только уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.
Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе
от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле. Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
Уравнения Максвелла в интегральной форме, с примерами
Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био – Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом. Запишем уравнения используя систему единиц Гаусса.
Система уравнений Максвелла
В состав системы уравнений Максвелла входят четыре уравнения.
Первое уравнение:
Это Закон Фарадея (Закон электромагнитной индукции).
где -напряженность электрического поля, -вектор магнитной индукции, c – скорость света в вакууме.
Это уравнение говорит, о том, что ротор напряженности электрического поля равен потоку (т.е. скорости изменения во времени) вектора магнитной индукции сквозь этот контур.
Уравнение (1.1) представляет собой первое уравнение Максвелла в дифференциальной форме.
Это же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:
или
где – проекция на нормаль к площадке dS вектора магнитной индукции,
– магнитный поток.
рис. 2.
Циркуляция вектора напряженности электрического поля вдоль замкнутого контура L (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данным контуром. Знак минус по правилу Ленца означает направление индукционного тока.
Согласно Максвеллу закон электромагнитной индукции (а это именно он), справедлив для любого замкнутого контура, произвольно выбранного в переменном магнитном поле.
Смысл этого уравнения: Переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.
Второе уравнение Максвелла:
где -вектор магнитной напряженности, — плотность электрического тока, — вектор электрического смещения.
Данное уравнение Максвелла является обобщение эмпирического закона Био- Савара о том, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения в том, что источником возникновения вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( -плотность тока смещения).
В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
или
Циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и тока смещения, сцепленных с контуром.
Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.
Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:
и
где —плотность электрического заряда.
Что в интегральном виде представляет собой следующее:
и
где -поток электрического смещения — поток магнитной индукции сквозь замкнутую поверхность, охватывающую свободный заряд q.
Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.
Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.
Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):
Полная система уравнений Максвелла в интегральном виде
Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):
Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы c величинами, описывающими электрические и магнитные свойства среды.
где – относительная диэлектрическая проницаемость, – относительная магнитная проницаемость, -удельная электропроводность, – электрическая постоянная, – магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.
На границе раздела двух сред выполняются граничные условия:
где — поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, единичный вектор, касательный к границе, — проекция вектора плотности поверхностных токов проводимости на единичный вектор.
Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.
Примеры решения задач
5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
5.1.Теория максвелла – теория единого электромагнитного поля
Теория Максвелла — это последовательная теория единого электромагнитного поля, которое создается произвольной системой электрических зарядов и токов. В теории Максвелла решается основная задача электродинамики: по заданному распределению зарядов и токов вычисляются характеристики создаваемых ими электрического и магнитного полей. Теория Максвелла – это обобщение важнейших законов, описывающих электрические и магнитные явления: теоремы Гаусса, закона полного тока, закона электромагнитной индукции.
Эта
теория не рассматривает внутренний
механизм явлений, происходящих в среде
и вызывающих появление электрических
и магнитных полей. Среда описывается с
помощью трех величин, задающих ее
электрические и магнитные свойства:
относительной диэлектрической
проницаемости  ,
относительной магнитной проницаемости
,
относительной магнитной проницаемости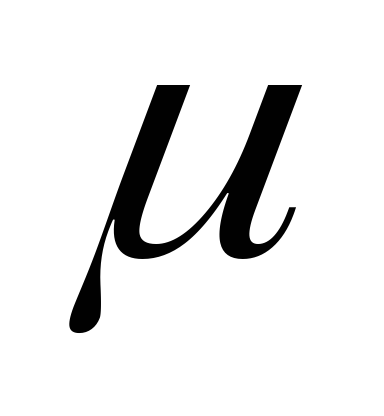 и удельной электрической проводимости
и удельной электрической проводимости .
.
Рассматриваются макроскопические поля, которые создаются макроскопическими зарядами и токами, сосредоточенными в объемах, много больших объемов атомов и молекул. Расстояния от источников полей до рассматриваемых точек пространства много больше линейных размеров атомов и молекул. Поэтому макроскопические поля изменяются заметно лишь на расстояниях, много больших размеров атомов.
Макроскопические заряды и токи являются совокупностями микроскопических зарядов и токов, которые создают свои электрические и магнитные микрополя. Эти микрополя непрерывно меняются с течением времени в каждой точке пространства. Макроскопические поля – это усредненные микрополя.
Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия осуществляются посредством электромагнитного поля и распространяются с конечной скоростью, равной скорости света в данной среде.
5.2. Первое уравнение максвелла
Первое уравнение Максвелла в интегральной форме – это обобщение закона электромагнитной индукции Фарадея:
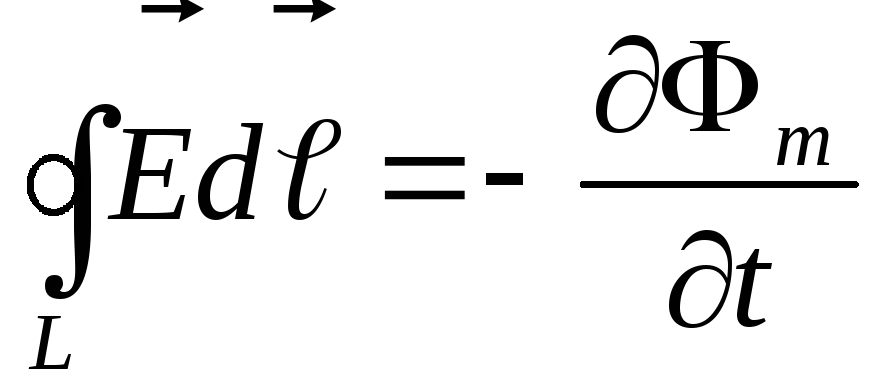 .
(5.1)
.
(5.1)
Этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, выбранного в переменном магнитном поле. Таким образом, переменное магнитное поле создает в любой точке пространства вихревое индуцированное электрическое поле независимо от того, находится в этой точке проводник, или нет.
Действительно,
рассмотрим электромагнитную индукцию
в контуре. Пусть контур, в котором
индуцируется ток, неподвижен, а изменения
магнитного потока обусловлены изменениями
магнитного поля. Возникновение
индукционного тока свидетельствует о
том, что изменение магнитного поля
вызывает появление в контуре сторонних
сил, которые действуют на носители тока.
Эти сторонние силы не могут быть
тепловыми, химическими и т.п., они не
могут также быть магнитными, так как
магнитные силы не совершают работу.
Таким образом, индукционный ток может
быть обусловлен только возникающим в
проводе электрическим полем. Обозначим
напряженность этого поля 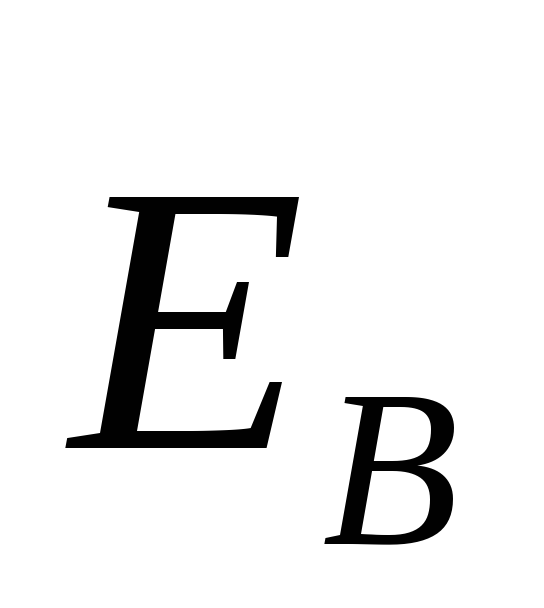 .
Электродвижущая сила равна циркуляции
векторапо данному контуру:
.
Электродвижущая сила равна циркуляции
векторапо данному контуру:
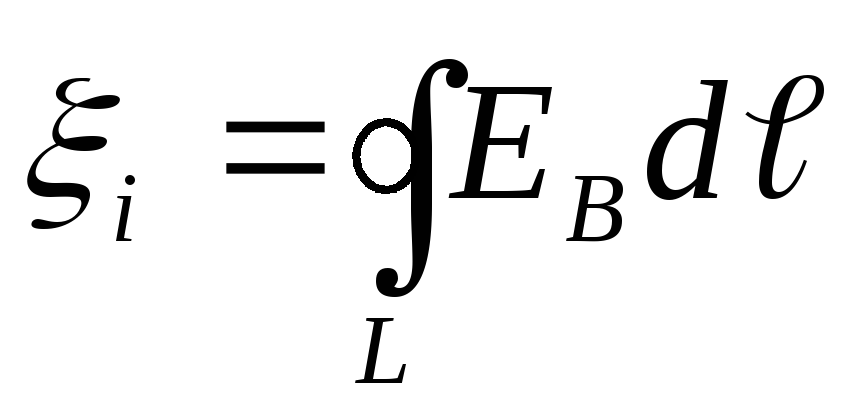 .
.
Известно,
что 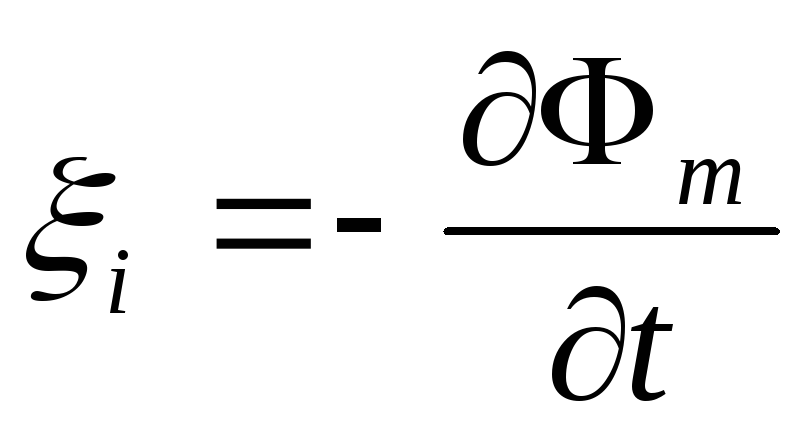 (здесь используется частная производная
т. к.
(здесь используется частная производная
т. к.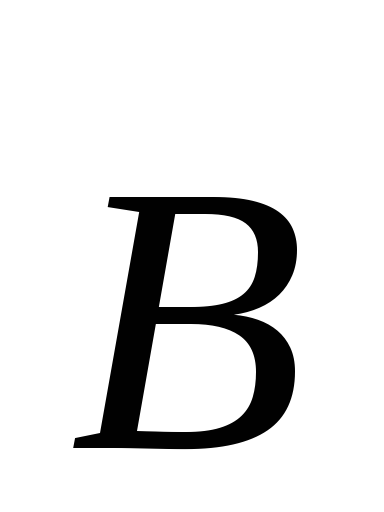 является функцией не только времени,
но и координат) . Магнитный поток
является функцией не только времени,
но и координат) . Магнитный поток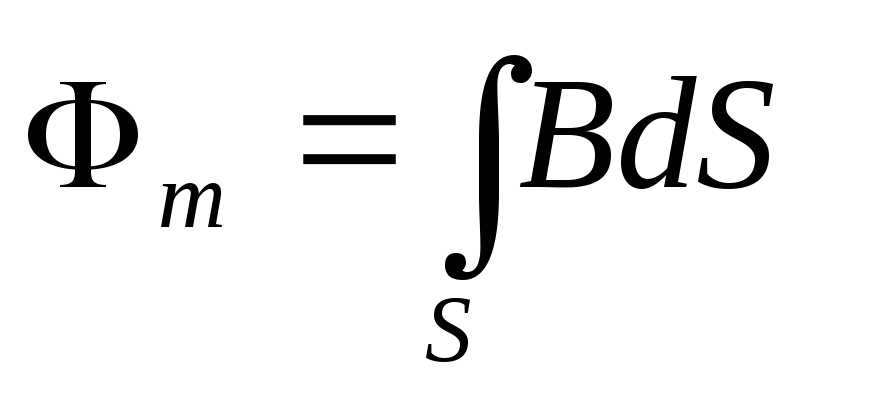 ,
поэтому
,
поэтому
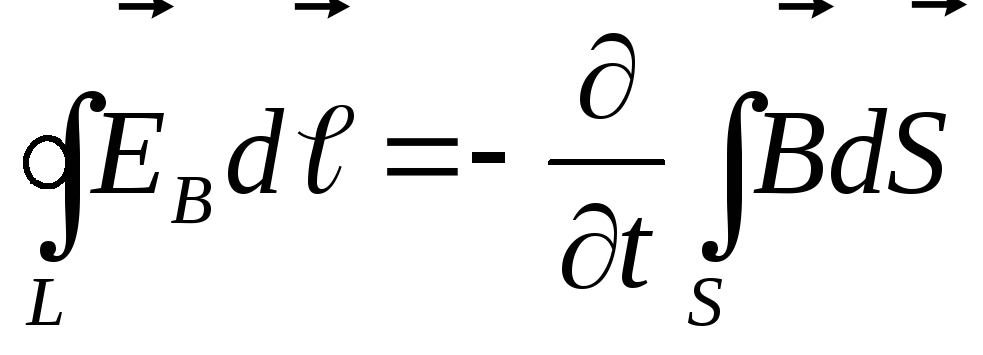 .
.
Контур L и поверхность S неподвижны, поэтому операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:
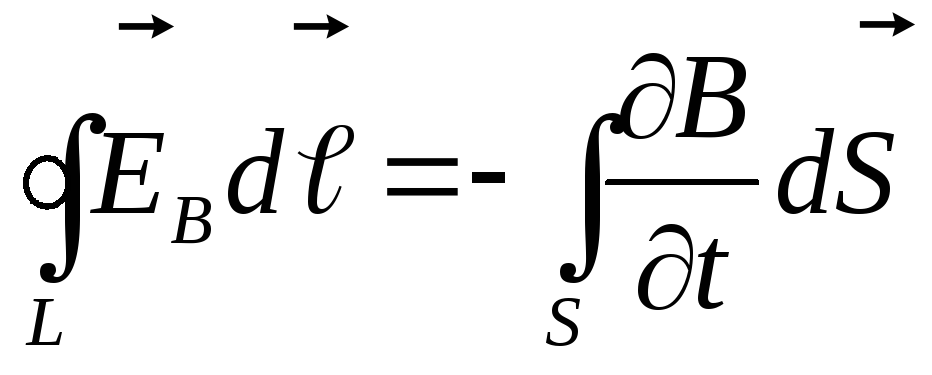 .
.
Это выражение преобразуем по теореме Стокса:
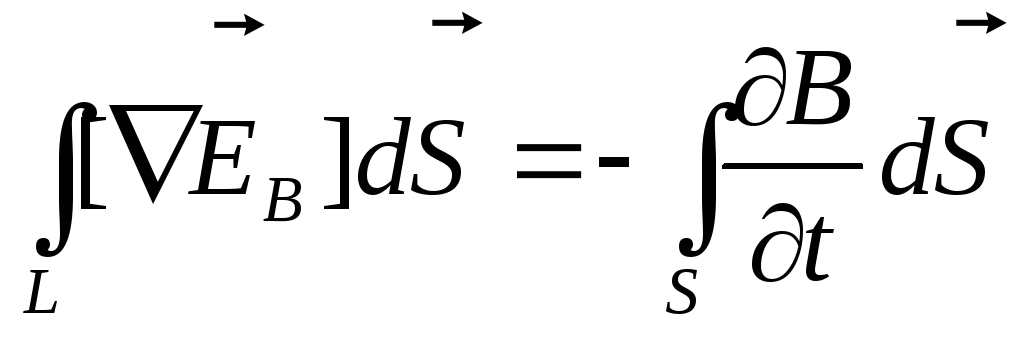 ,
,
тогда
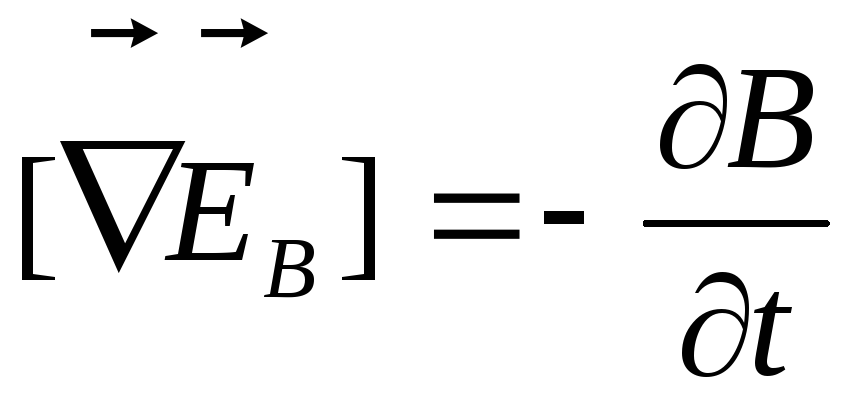 (5.2)
(5.2)
— ротор
поля  в каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора
в каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора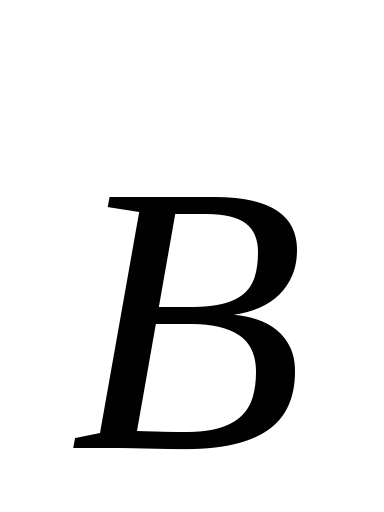 .
Это первое уравнение Максвелла в
дифференциальной форме.
.
Это первое уравнение Максвелла в
дифференциальной форме.
Таким
образом, изменяющееся во времени
магнитное поле порождает электрическое
поле. Это поле 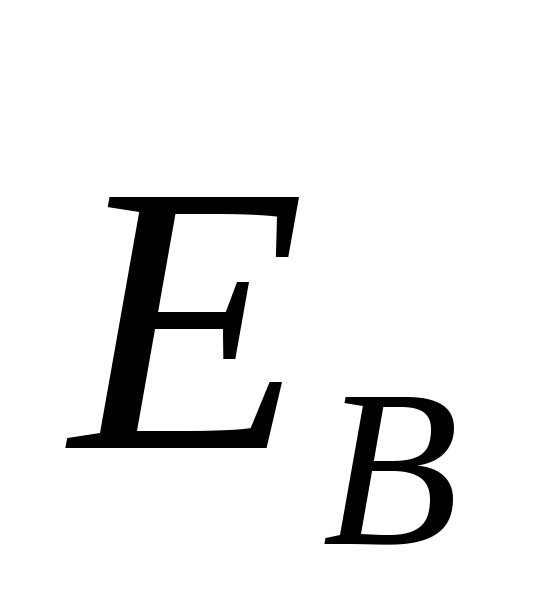 существенно отличается от поля
электростатического
существенно отличается от поля
электростатического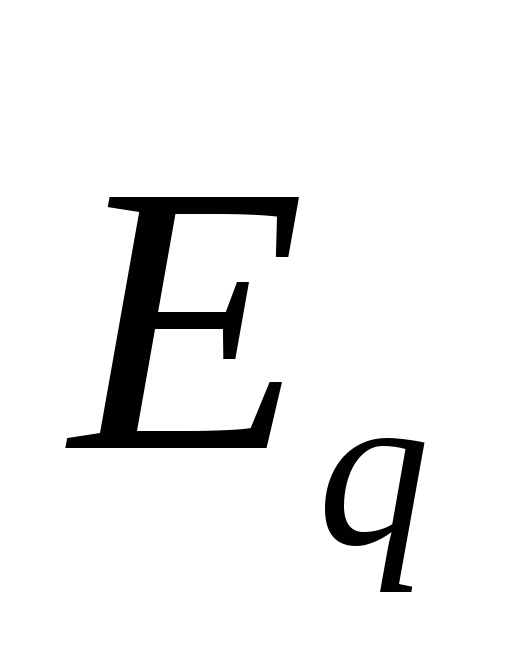 ,
создаваемого неподвижными зарядами.
Электростатическое поле потенциально,
его линии напряженности начинаются и
заканчиваются на зарядах, ротор вектора
,
создаваемого неподвижными зарядами.
Электростатическое поле потенциально,
его линии напряженности начинаются и
заканчиваются на зарядах, ротор вектора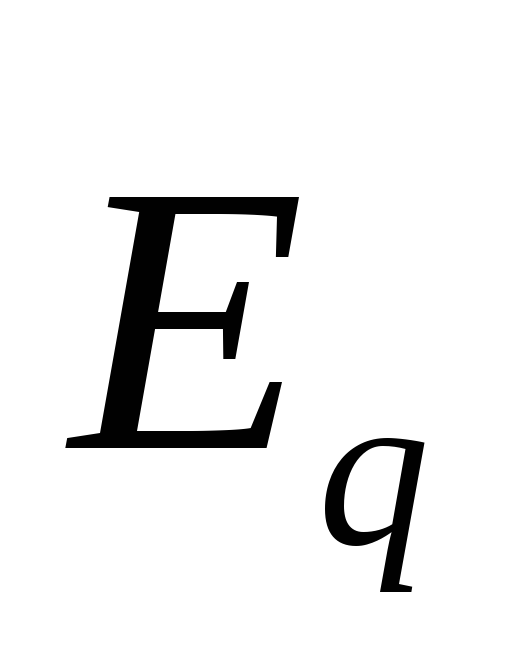 ,
в любой точке поля равен нулю. Ротор же
поля
,
в любой точке поля равен нулю. Ротор же
поля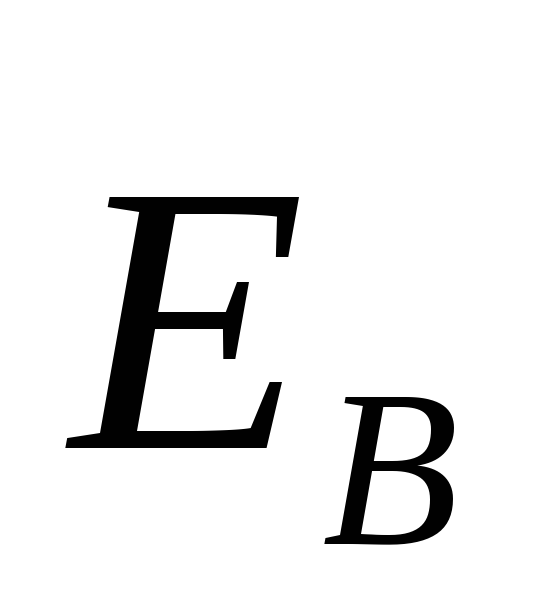 отличен от нуля, т.е. это поле является
вихревым, непотенциальным. Линии
напряженности
отличен от нуля, т.е. это поле является
вихревым, непотенциальным. Линии
напряженности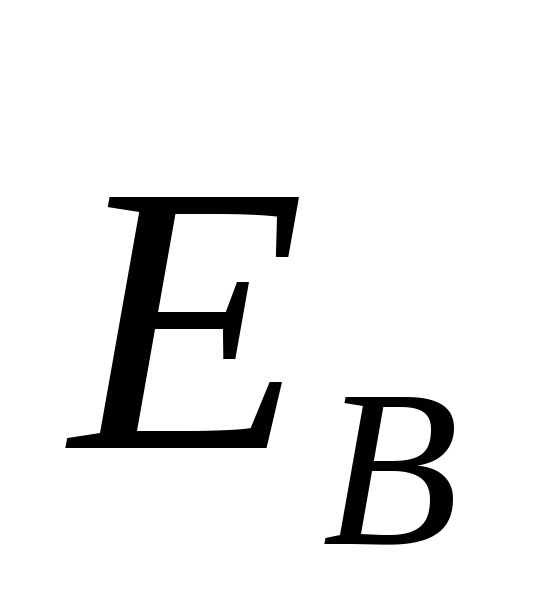 замкнуты.
замкнуты.
Итак, электрическое поле может быть как потенциальным, так и вихревым. В общем случае электрическое поле равно векторной сумме полей:
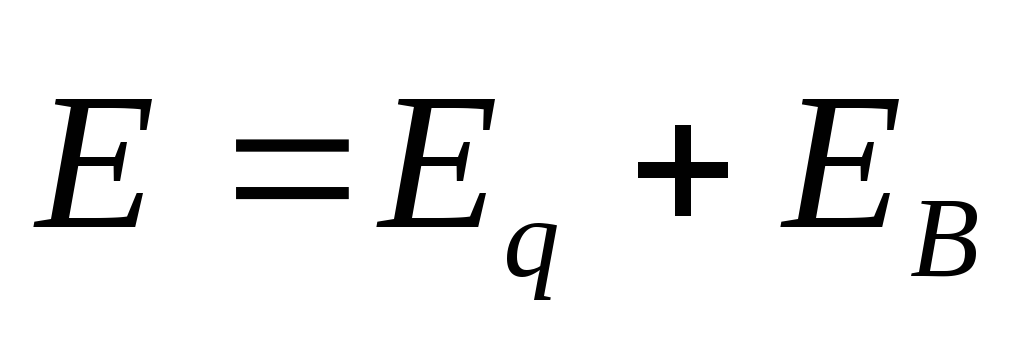 ,
,
причем 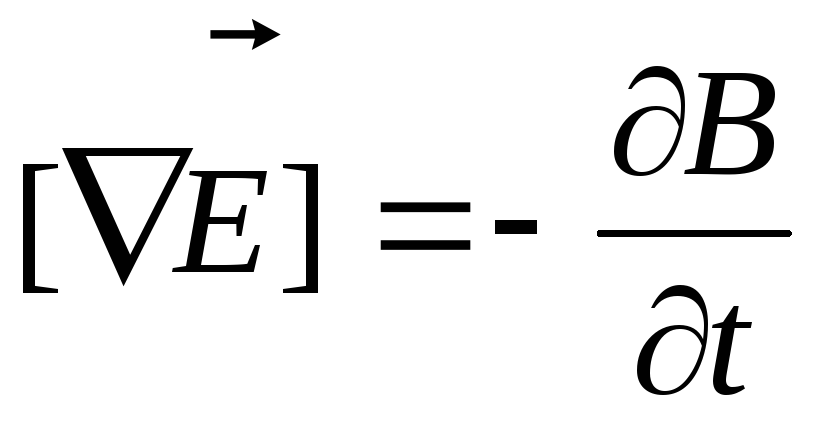 .
.
Таким образом, существует взаимосвязь электрического и магнитного полей, поэтому раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электрическое поле создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем отсчета эти заряды движутся, и, следовательно, порождают не только электрическое, но и магнитное поле. Неподвижный провод с постоянным током создает в каждой точке пространства постоянное магнитное поле. Однако относительно других инерциальных систем этот провод находится в движении. Поэтому создаваемое им магнитное поле в любой точке с координатами (х,у,z) будет меняться, и , следовательно, порождать вихревое электрическое поле. Поле, которое относительно одной системы отсчета оказывается чисто магнитным, относительно других систем отсчета будет представлять совокупность электрического и магнитного полей, образующих единое электромагнитное поле.
5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
5.1.Теория максвелла – теория единого электромагнитного поля
Теория Максвелла — это последовательная теория единого электромагнитного поля, которое создается произвольной системой электрических зарядов и токов. В теории Максвелла решается основная задача электродинамики: по заданному распределению зарядов и токов вычисляются характеристики создаваемых ими электрического и магнитного полей. Теория Максвелла – это обобщение важнейших законов, описывающих электрические и магнитные явления: теоремы Гаусса, закона полного тока, закона электромагнитной индукции.
Эта
теория не рассматривает внутренний
механизм явлений, происходящих в среде
и вызывающих появление электрических
и магнитных полей. Среда описывается с
помощью трех величин, задающих ее
электрические и магнитные свойства:
относительной диэлектрической
проницаемости  ,
относительной магнитной проницаемости
,
относительной магнитной проницаемости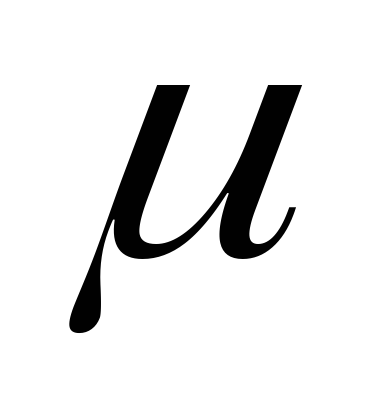 и удельной электрической проводимости.
и удельной электрической проводимости.
Рассматриваются макроскопические поля, которые создаются макроскопическими зарядами и токами, сосредоточенными в объемах, много больших объемов атомов и молекул. Расстояния от источников полей до рассматриваемых точек пространства много больше линейных размеров атомов и молекул. Поэтому макроскопические поля изменяются заметно лишь на расстояниях, много больших размеров атомов.
Макроскопические заряды и токи являются совокупностями микроскопических зарядов и токов, которые создают свои электрические и магнитные микрополя. Эти микрополя непрерывно меняются с течением времени в каждой точке пространства. Макроскопические поля – это усредненные микрополя.
Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия осуществляются посредством электромагнитного поля и распространяются с конечной скоростью, равной скорости света в данной среде.
5.2. Первое уравнение максвелла
Первое уравнение Максвелла в интегральной форме – это обобщение закона электромагнитной индукции Фарадея:
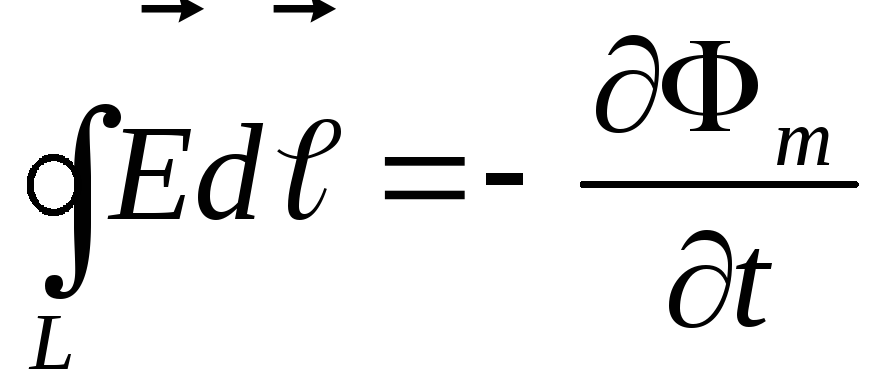 .
(5.1)
.
(5.1)
Этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, выбранного в переменном магнитном поле. Таким образом, переменное магнитное поле создает в любой точке пространства вихревое индуцированное электрическое поле независимо от того, находится в этой точке проводник, или нет.
Действительно,
рассмотрим электромагнитную индукцию
в контуре. Пусть контур, в котором
индуцируется ток, неподвижен, а изменения
магнитного потока обусловлены изменениями
магнитного поля. Возникновение
индукционного тока свидетельствует о
том, что изменение магнитного поля
вызывает появление в контуре сторонних
сил, которые действуют на носители тока.
Эти сторонние силы не могут быть
тепловыми, химическими и т.п., они не
могут также быть магнитными, так как
магнитные силы не совершают работу.
Таким образом, индукционный ток может
быть обусловлен только возникающим в
проводе электрическим полем. Обозначим
напряженность этого поля 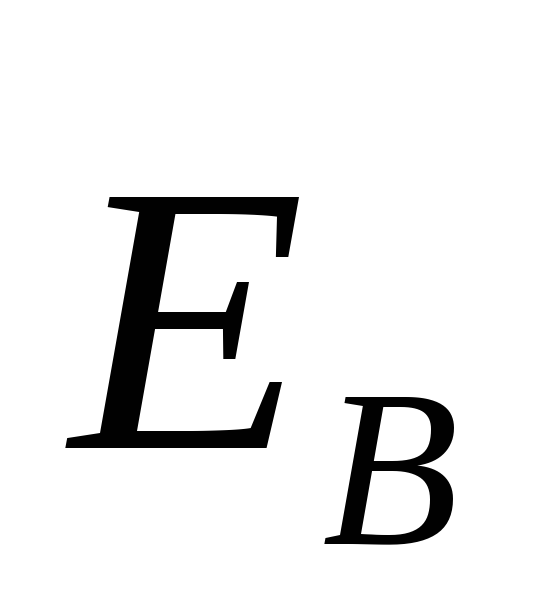 .
Электродвижущая сила равна циркуляции
вектора
.
Электродвижущая сила равна циркуляции
вектора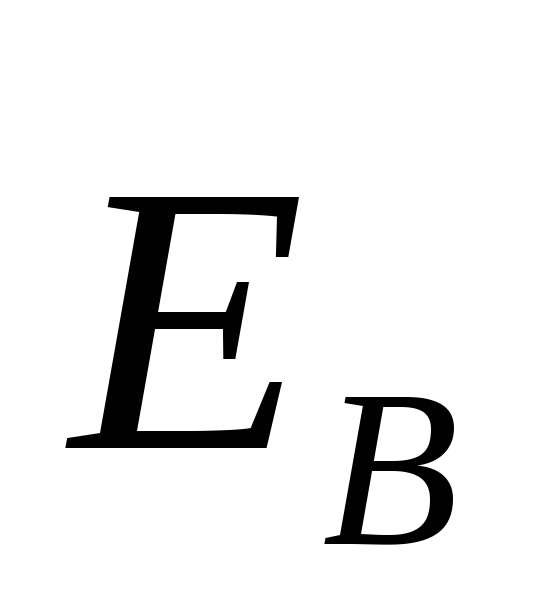 по данному контуру:
по данному контуру:
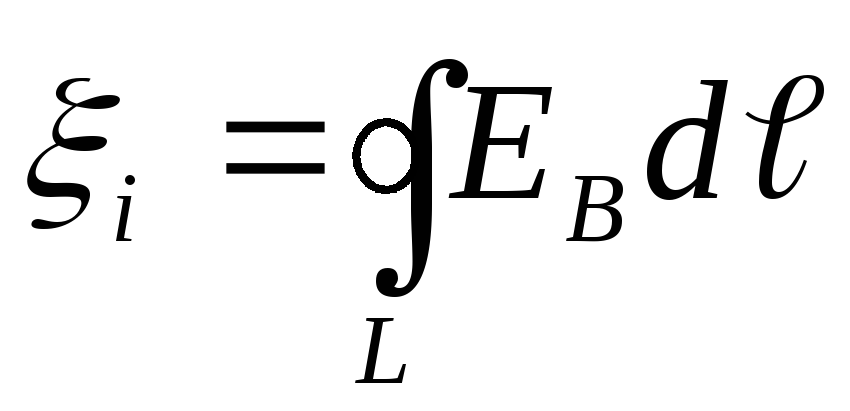 .
.
Известно,
что 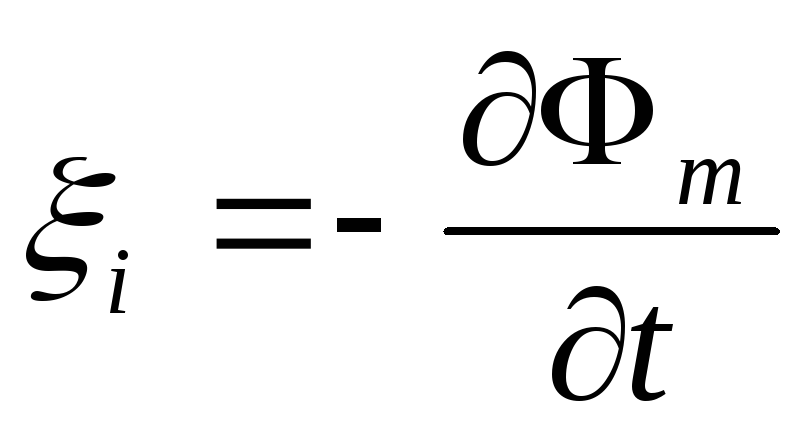 (здесь используется частная производная
т. к.
(здесь используется частная производная
т. к.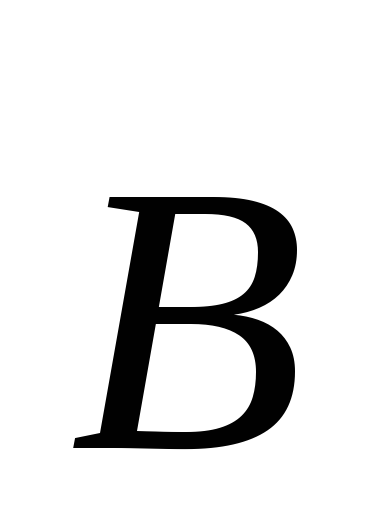 является функцией не только времени,
но и координат). Магнитный поток
является функцией не только времени,
но и координат). Магнитный поток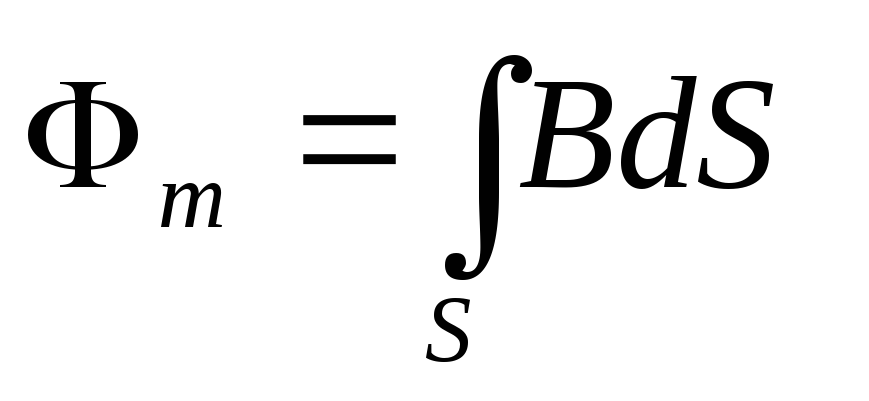 ,
поэтому
,
поэтому
.
Контур L и поверхность S неподвижны, поэтому операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:
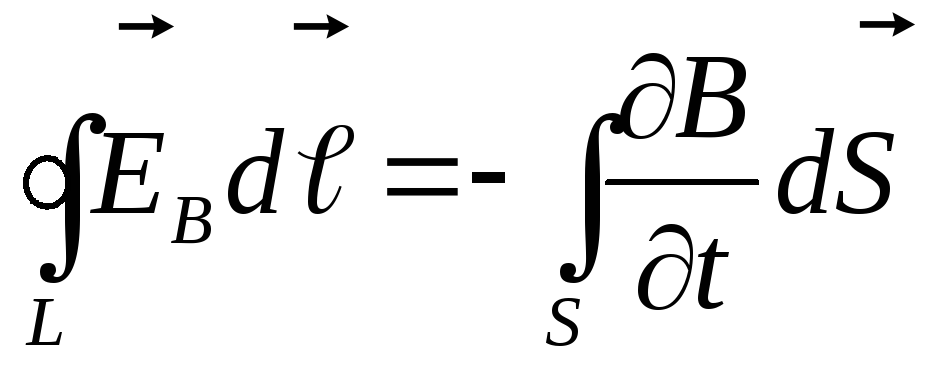 .
.
Это выражение преобразуем по теореме Стокса:
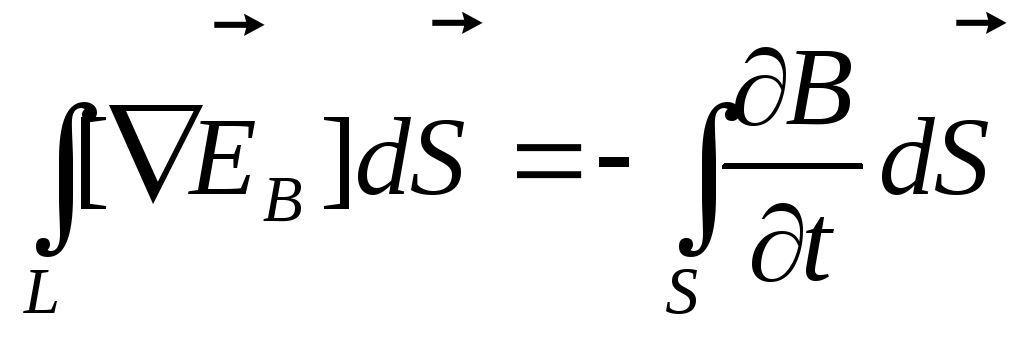 ,
,
тогда
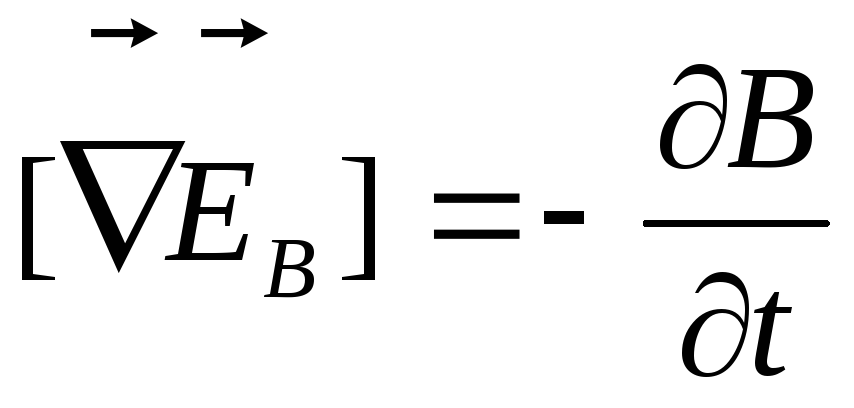 (5.2)
(5.2)
— ротор
поля 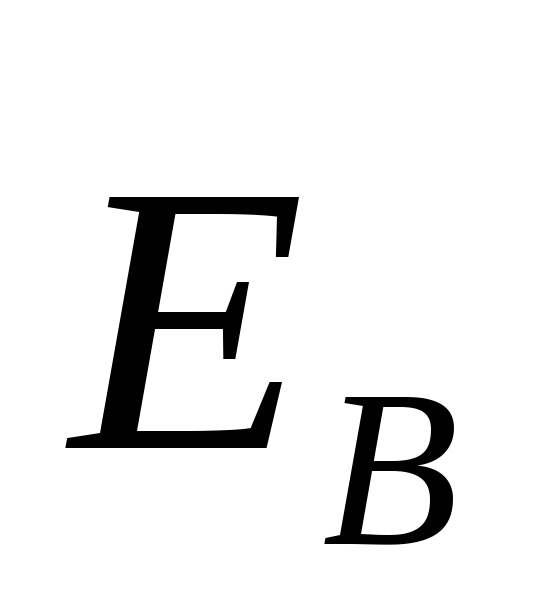 в каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора
в каждой точке пространства равен взятой
с обратным знаком производной по времени
от вектора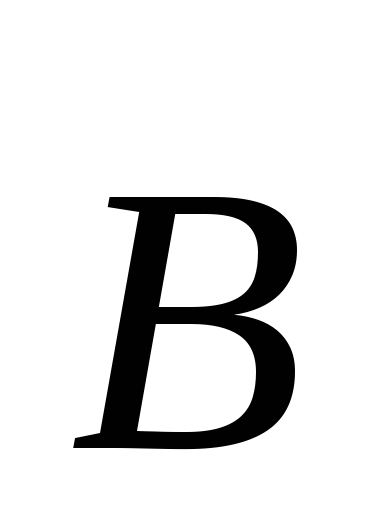 .
Это первое уравнение Максвелла в
дифференциальной форме.
.
Это первое уравнение Максвелла в
дифференциальной форме.
Таким
образом, изменяющееся во времени
магнитное поле порождает электрическое
поле. Это поле 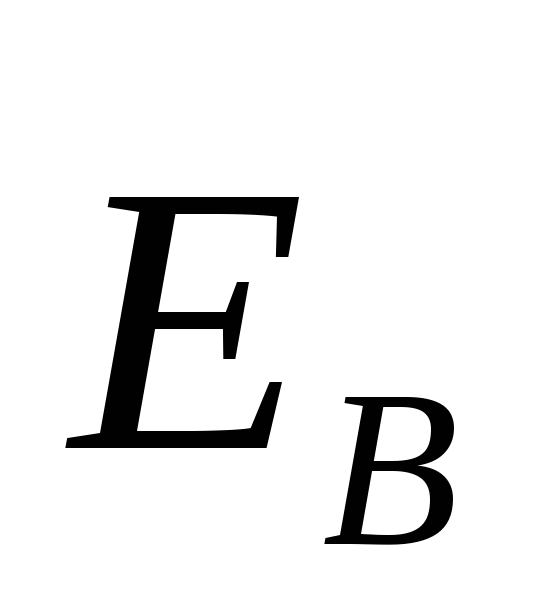 существенно отличается от поля
электростатического
существенно отличается от поля
электростатического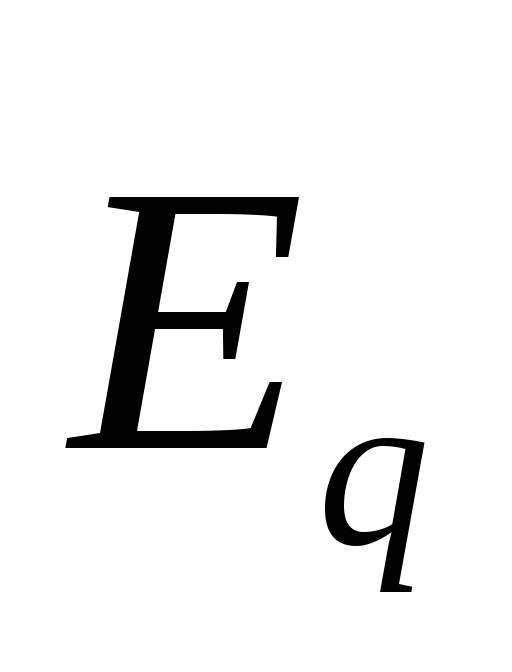 ,
создаваемого неподвижными зарядами.
Электростатическое поле потенциально,
его линии напряженности начинаются и
заканчиваются на зарядах, ротор вектора
,
создаваемого неподвижными зарядами.
Электростатическое поле потенциально,
его линии напряженности начинаются и
заканчиваются на зарядах, ротор вектора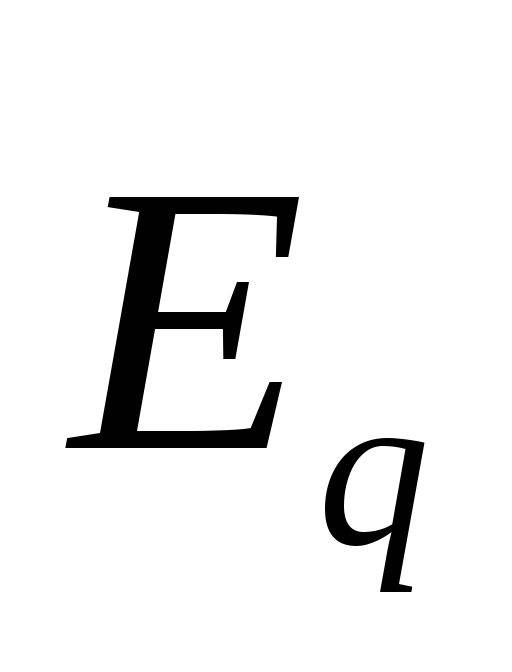 ,
в любой точке поля равен нулю. Ротор же
поля
,
в любой точке поля равен нулю. Ротор же
поля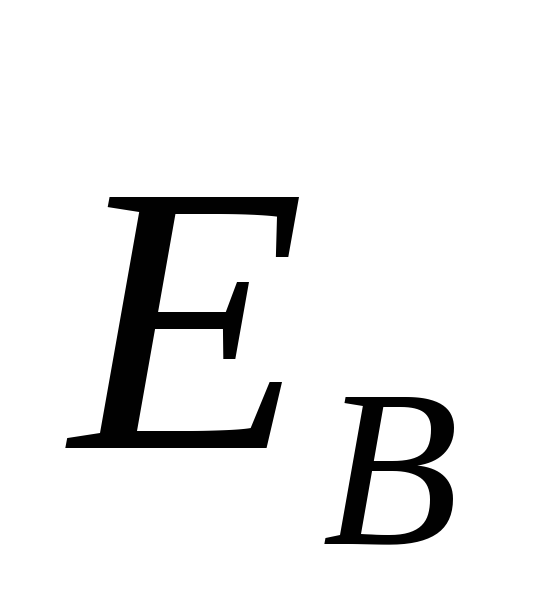 отличен от нуля, т.е. это поле является
вихревым, непотенциальным. Линии
напряженности
отличен от нуля, т.е. это поле является
вихревым, непотенциальным. Линии
напряженности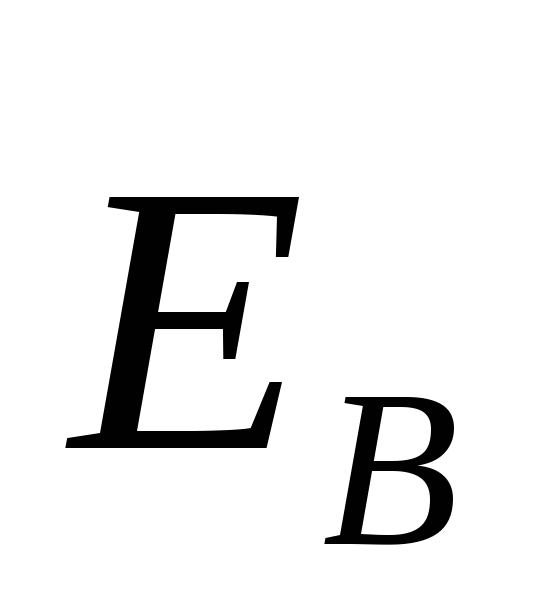 замкнуты.
замкнуты.
Итак, электрическое поле может быть как потенциальным, так и вихревым. В общем случае электрическое поле равно векторной сумме полей:
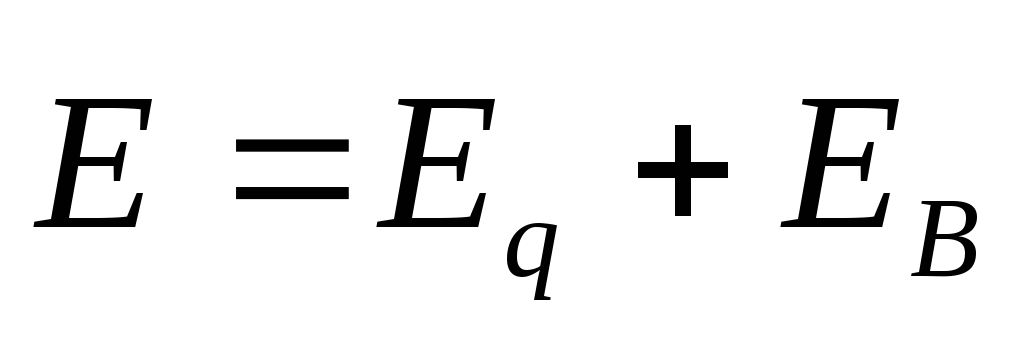 ,
,
причем 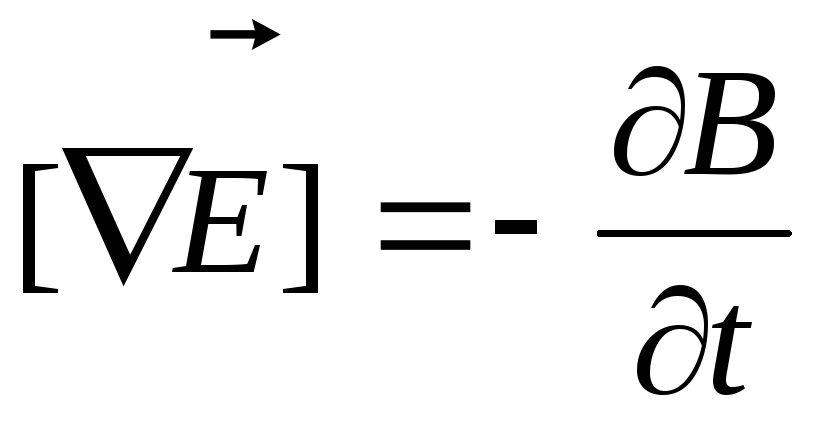 .
.
Таким образом, существует взаимосвязь электрического и магнитного полей, поэтому раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электрическое поле создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем отсчета эти заряды движутся, и, следовательно, порождают не только электрическое, но и магнитное поле. Неподвижный провод с постоянным током создает в каждой точке пространства постоянное магнитное поле. Однако относительно других инерциальных систем этот провод находится в движении. Поэтому создаваемое им магнитное поле в любой точке с координатами (х,у,z) будет меняться, и , следовательно, порождать вихревое электрическое поле. Поле, которое относительно одной системы отсчета оказывается чисто магнитным, относительно других систем отсчета будет представлять совокупность электрического и магнитного полей, образующих единое электромагнитное поле.
Уравнения Максвелла ☑️ формулы для интегральной и дифференциальной форм, физический смыл в теории электромагнитного излучения, основные условия теории
Основная идея
Если в замкнутом контуре меняется магнитный поток, то по нему течёт электрический ток. В итоге возникает электродвижущая сила магнитной индукции. Происходит это из-за изменения магнитного поля. Предположим, имеется магнит, у которого поток с течением времени увеличивается. Если в поле поместить замкнутый проводник кольцевого типа, то по правилу Ленца в нём возникнет индукционный ток, противоположный магнитной силе через контур.
Ток — это направленное движение заряженных частиц. Сила, заставляющая их перемещаться, называется электрическим полем. Появляется она при изменении магнитного потока. Отсюда можно сделать вывод, что электрическое поле существует всегда там, где есть изменяющееся магнитное, при этом оно имеет замкнутую форму. Этот вид силы и называли вихревым полем. Когда вектор магнитной силы возрастает, то увеличивается и вихревое поле, а если убывает, то, соответственно, оно уменьшается.

Джеймс Клерк Максвелл предположил, что если меняющееся магнитное поле порождает электрическое, то этот процесс может быть и обратным. Его идея заключалась в том, что если имеется проводник с током, то вокруг него существует стационарное магнитное поле. На длине этого проводника он выбрал произвольные три точки равноудалённые от него на расстояние r.
В этих точках поле будет одинаковое. Максвелл предположил, что если проводник разорвать, то для того чтобы ток продолжал движение, нужно сохранить заряды. То есть фактически использовать конденсатор. По мнению Максвелла, тогда в точке разрыва поле будет такое же, как и вокруг проводника. Между обкладками возникнет электрическая сила, так как на них происходит сохранение (накопление) зарядов. Учитывая это, физик пришёл к выводу, что изменяющееся электрическое поле приводит к возникновению магнитного потока.
Так как на обкладках имеется заряд, то сила тока будет равняться I = dq / dt. Заряд можно связать с напряжением на обкладках конденсатора и электроёмкостью: q = C * U. Ёмкость же в вакууме определяется как E0 * S/ d, а напряжение — как E * d.
Подставив значения в формулу, Максвелл получил выражение: dq / dt = E0 * S * dE / dt. Так как ток между обкладками не течёт, а перенос происходит полем, физик предложил ввести понятие фиктивный ток смещения. Плотность этого тока можно найти по формуле: j = E0 * dE / dt. Это позволило упростить вычисления магнитной силы. Ток смещения и вихревое поле стали основой для создания системы уравнений.
Физическая суть
Электромагнитное поле представляет собой материю, с помощью которой заряженные элементарные частицы взаимодействуют между собой. В вакууме явление характеризуется напряжённостью E и магнитной индукцией B. Эти параметры определяют силы, воздействующие на подвижные и неподвижные заряды. Кроме них, значение электромагнитного поля определяется скалярным и векторным потенциалами и двумя дополнительными величинами: индукцией D и напряжённостью магнитных линий H.

Открытие в 1831 году Фарадеем закона электромагнитной индукции, устанавливающего зависимость между зарядом и намагниченностью у токоведущих тел, помогло Максвеллу сформулировать ряд уравнений, после названных его именем. Главное его исследование заключалось в исследовании тока смещения, равного по магнитному действию электрическому току.
Сформулировав свою систему, физик смог связать электрическое и магнитное поле с зарядом и током. Физический смысл уравнений Максвелла заключается в том, что электромагнитное поле рассматривалось им как самостоятельный объект, в котором передача энергии происходит колебанием от точки к точке с конечной скоростью. При этом в вакууме она определяется скоростью света.
С точки зрения математики, для описания процессов учёный использовал векторный анализ, выраженный через инвариантную форму, использующую кватернионы Гамильтона. Написанные им уравнения неохотно принимались учёным советом Лондонского Королевского общества. Это происходило из-за того, что они не были похожи ни на одно из описаний известных ранее.
Тем не менее система Максвелла получила признание и стала фундаментальной в области электродинамики. При этом её справедливость получила подтверждение не только в микромире, ни и в области квантовой физики.
Основным следствием открытия стало понятие о скорости распространения электромагнитных волн и создании теории света. По сути, эта система теории волн в науке об электромагнетизме играет роль сопоставимую с законами Ньютона в области механики или с теоремами в электродинамике.
Дифференциальная запись
Открытие в проводящих телах тока смещения позволило Максвеллу вывести четыре уравнения, на основе которых была создана теория электромагнитных явлений. Обычно в физике математическая запись процессов не зависит от системы единиц, но в термодинамике это не так. Всё дело в том, что при записи в различных системах изменяются коэффициенты (постоянные).

Например, в системе единиц, используемой в описании квантовой теории поля, скорость света и электромагнитная константа равна единице. Поэтому уравнения не будут иметь ни одной постоянной. Для записи используют две системы: СГС — симметричная гауссова, и СИ — Международная система единиц.
В этих двух стандартах система уравнений Максвелла может быть описана словесно и математически следующим образом:
- В качестве источника электрической индукции выступает заряженная частица. В СГС: ∇ * D = 4*p* ρ; в СИ: ∇ * D = 4* ρ.
- В электромагнитном поле магнитных зарядов нет. В обеих системах формула выглядит одинакового: ∇ * B = 0.
- При изменении величины магнитной индукции возникает электрическое вихревое поле. В СГС: ∇ * E = — δ B / c * δ t; в СИ: ∇ * E = — δ B / δ t.
- Вихревое магнитное поле появляется из-за изменений электрической индукции и тока. В СГС: ∇ * H = 4 pj / c + δ D / c * δ t; в СИ: ∇ * H = j + δ D / δ t.
Это классические четыре закона описывающие природу и условия возникновения электромагнитного поля. Первая гипотеза связывает напряжённость с индукцией и является выражением теоремы электромагнитной индукции. Вторая доказывает отсутствие объектов, генерирующих магнитное поле. Третья устанавливает зависимость между током смещения и проводимостью, создающейся в магнитном поле. Четвёртая объясняет, что источником вектора электрической индукции служит сторонний заряд.
Указанные уравнения представляют собой запись в дифференциальной форме. При этом каждое из них эквивалентно скалярным уравнениям. В этой форме они имеют следующий вид:

- (δEy / δx) — (δEx / δy) = — δBx / δt;
- (δBx / δx) — (δEy / δy) + (δBz / δz) = 0;
- (δHy / δx) — (δHx / δy) = jz + δDx / δt;
- (δDx / δx) — (δDy / δy) + (δDz / δz) = ρ.
Для того чтобы воспользоваться этими постулатами для расчёта полей, нужно уравнения дополнить граничными правилами объединяющим электрическую индукцию (D), плотность электрического тока (j), напряжённость (E). Эти положения имеют вид: D = e0*e*E; B = m0*m*H; j = δ*E. Совокупность этих соотношений позволяет сделать вывод об основе электродинамики сред, находящихся в спокойном состоянии.
Интегральная форма
Запись уравнений Максвелла в интегральной и дифференциальной форме позволяет рассчитать электромагнитное поле в любой среде. Первые два уравнения, включающие интегралы, получаются путём преобразования дифференциальных форм по произвольной поверхности и применения теоремы Стокса, ограничивающей поверхность. Вторые же два путём интегрирования по произвольному объёму с дальнейшим их упрощением по теореме Остроградского — Гаусса, по ограниченной поверхности в замкнутом объёме.

Выглядят они следующим образом:
- ∫ D * ds = 4 pQ. Это закон Гаусса устанавливающий, что поток электрической индукции сквозь ограниченную поверхность зависит от величины свободного заряда, существующего в объёме формирующимся этой поверхностью.
- ∫ B * ds = 0. Теорема для магнитного поля сообщающая, что сила линий магнитной индукции через ограниченную поверхность равна нулю.
- ∫ E * dl = — d / dt*c ∫ B * ds. Свойство Фарадея обозначающее, что поток магнитной индукции, проходя через замкнутую поверхность пропорционален вращению электрического поля в контуре ограничивающим поверхность.
- ∫ H * dl = 4pI / c + (d / dt) ∫ D * ds. Правило циркуляции магнитного поля. Электрический ток свободных частиц и колебания электромагнитной индукции зависят от размера и движения магнитного потока, ограниченного контуром l.
В этих уравнениях буквой S обозначается замкнутое пространство двухмерной поверхности определяющей границы объёма V или контура l. При этом Q является электрическим зарядом, находящимся в замкнутом объёме площадью S и равным: Q = ∫p * dV, а I — электрическим током, протекающим сквозь S и определяющимся из уравнения: I = ∫j * ds.
Нужно отметить, что вектор потока по ограниченной поверхности считается направленным из объёма. Вращение же находится согласно правилу правого винта по незамкнутой площади. В уравнениях величины E, B, D и H являются равнозначными значениями, определяющимися в результате решения системы.
Значение уравнений
Система уравнений Максвелла для электромагнитного поля объясняет все электромагнитные явления. Её применяют при полном анализе полей при известных распределениях токов и заряженных частиц. Часто уравнения называют материальными, подчёркивая индивидуальные свойства занимающей пространство среды: D = e * e0 * E, B = m * m0 * H, J = E .
Формулы физика подтверждают существование электромагнитных волн. Иначе говоря, предпологают возможность электрического поля излучать энергию вне зависимости от присутствия электрических зарядов и токов. Из всего многообразия применения уравнений можно выделить основные четыре:


- Нахождение характеристик электрического и магнитного поля по известному распределению заряженных частиц и токов. То есть это теория электромагнитного поля (ЭМП) примирительная к любой системе зарядов и токов. Она обобщает электрические и магнитные явления.
- Изучение макроскопических полей. Уравнения Максвелла применимы к макрозарядам и макротокам. Их можно использовать в среде, где расстояния от источника излучения до зафиксированной точки намного превышает периоды внутренних явлений.
- Теоремы Максвелла раскрывают внутренний механизм процессов в среде, описываемых тремя фундаментальными характеристиками: ε, μ и σ.
- Используя теорию, являющуюся близкодейственной, можно описать электрические и магнитные взаимодействия, возникающие в электромагнитном поле распространяющимся с ограниченной скоростью.
Система включает в себя все основные законы электрического и магнитного поля с учётом такого важного параметра, как электромагнитная индукция. Теоретическое исследование физика позволило утверждать, что свет представляет собой электромагнитные волны и существования токов смещения в магнитном поле. То есть изменение ЭМП без движения электрических зарядов. Благодаря этому стало возможным находить полный ток.
Максвеллом было найдено четыре важных закономерности, заключающиеся в том, что электрический заряд образует электрическое поле, колебания магнитных волн порождает электрические вихри, магнитных зарядов быть не может, изменение индукции приводит к появлению вихревого магнитного потока. Эти теоретические суждения после были подтверждены экспериментально и позволили получить картину распространения свободной энергии электромагнитной волны в пространстве.
39. Уравнения Максвелла в интегральной форме.
Введение Максвеллом понятия полного тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения объяснить электрические и магнитный явления и предсказать новые.
В основе теории Максвелла лежат четыре уравнения, полученные нами ранее:
1.
Циркуляция вектора напряженности
суммарного поля 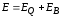 (циркуляция вектора
(циркуляция вектора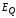 равна нулю):
равна нулю):
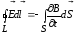 (12)
(12)
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2.
Обобщенная теорема о циркуляции вектора 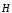 :
:
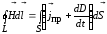 .(13)
.(13)
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3.
Теорема Гаусса для поля 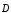 :
:
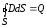 (14)
(14)
или, если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ:
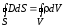 . (15)
. (15)
Это уравнение показывает, что в природе существуют электрические заряды.
4.
Теорема Гаусса для поля 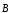 :
:
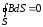 . (16)
. (16)
Это уравнение показывает, что в природе не существуют магнитные заряды.
Дополнительные уравнения, используемые с уравнениями Максвелла. Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует связь:
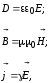
где 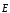 — напряженность электрического поля;
— напряженность электрического поля;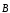 — магнитная индукция;
— магнитная индукция;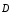 — электрическое смещение;
— электрическое смещение;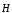 —
напряженность магнитного поля;
—
напряженность магнитного поля;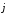 —
плотность тока проводимости; γ – удельная
проводимость вещества;
—
плотность тока проводимости; γ – удельная
проводимость вещества;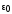 и
и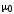 – электрическая и магнитная постоянная;
ε и μ – электрическая и магнитная
проницаемости.
– электрическая и магнитная постоянная;
ε и μ – электрическая и магнитная
проницаемости.
Совокупность этих 7 уравнений составляют основу электродинамики покоящихся сред.
Уравнения
Максвелла для стационарных полей (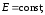
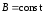 ).
).
1. ; 2.;
3. ; 4..
Источниками электрического поля являются только электрические заряды, источниками магнитного поля – только токи проводимости. В этом случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поля.
40. Уравнения Максвелла в дифференциальной форме
Теоремы векторного анализа, используемые при переходе от интегральной формы уравнения к дифференциальной
1.
Теорема Стокса: зная ротор вектора 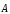 в каждой точке некоторой поверхностиS можно вычислить циркуляцию этого вектора
по контуру L,
ограничивающему S:
в каждой точке некоторой поверхностиS можно вычислить циркуляцию этого вектора
по контуру L,
ограничивающему S:
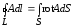 .
.
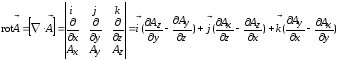 .
.
2. Теорема
Гаусса: зная
дивергенцию вектора 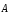 в каждой точке пространства, можно
вычислить поток этого вектора через
произвольную замкнутую поверхностьS конечных размеров.
в каждой точке пространства, можно
вычислить поток этого вектора через
произвольную замкнутую поверхностьS конечных размеров.
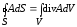 .
.
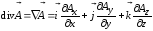 ;
;
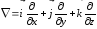 .
.
Уравнения Максвелла в дифференциальной форме характеризуют поле в каждой точке пространства. Физический смысл уравнений Максвелла в дифференциальной форме тот же, что и уравнения Максвелла в интегральной.
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла эквивалентны. Однако, если имеются поверхности разрыва (поверхности, на которых свойства среды меняются скачкообразно), то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред:
1. 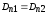 ;
(на границе раздела нет свободных
зарядов)
;
(на границе раздела нет свободных
зарядов)
2. 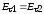 ;
;
3. 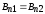 ;
;
4. 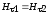 (на границе раздела нет токов проводимости).
(на границе раздела нет токов проводимости).
Некоторые следствия из уравнений Максвелла
Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в электродинамике такую же роль, как законы Ньютона в механике.
1. Согласно идеям Максвелла, переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным полем, т.е. электрические и магнитные поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.
2. Теория Максвелла не только смогла объяснить уже известные экспериментальные факты, но и предсказала новые явления: существование магнитного поля токов смещения позволило предсказать существование электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью (скоростью света). Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны.
Теория Максвелла была экспериментально подтверждена: электромагнитные волны были получены на практике немецким физиком Герцем, который доказал, что законы их возбуждения и распространения полностью подчиняются уравнениям Максвелла.
3. К электромагнитному полю применим только принцип относительности Эйнштейна, согласно которому, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т.е. описываются одинаковыми уравнениями. Из принципа относительности следует, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Так если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается чисто электрическим или чисто магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей.
Вывод: теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, основанных на представлении об электромагнитном поле
Уравнения Максвелла в интегральной форме.
Уравнения Максвелла являются основными законами классической макроскопической электродинамики, которые являются обобщением большого количества экспериментальных данных. Они в компактной форме выражают все содержимое классической электродинамики неподвижных сред.
Уравнения Максвелла принято делить на структурные и материальные,которые могут быть представлены как в интегральной, так и в дифференциальной формах. В отдельности мы уже рассматривали эти уравнения. Теперь появилась возможность обсудить эти уравнения как непротиворечивую системуосновных уравнений классической электродинамики.
Структурных уравнений Максвелла четыре:
 ;
; ;
; ;
; .
.
Материальных уравнений три:
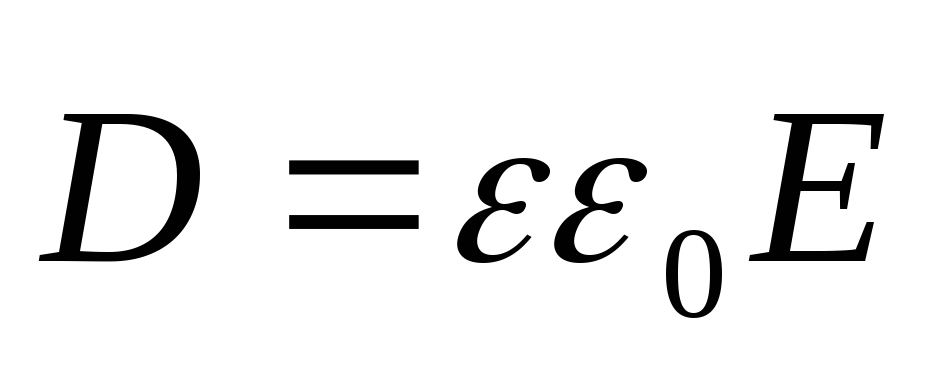 ,
,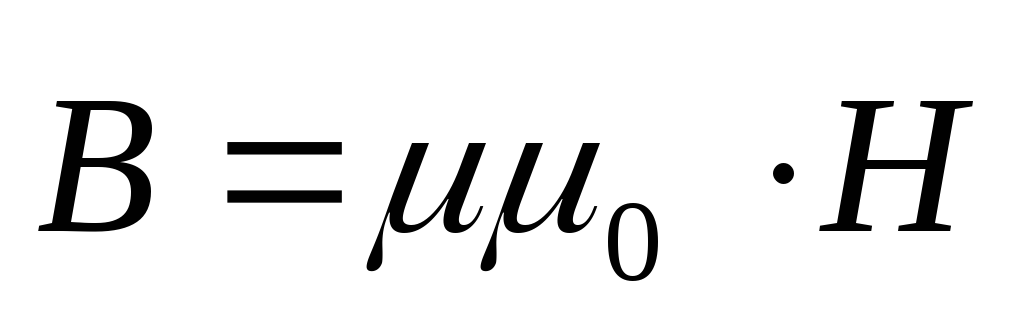 ,
,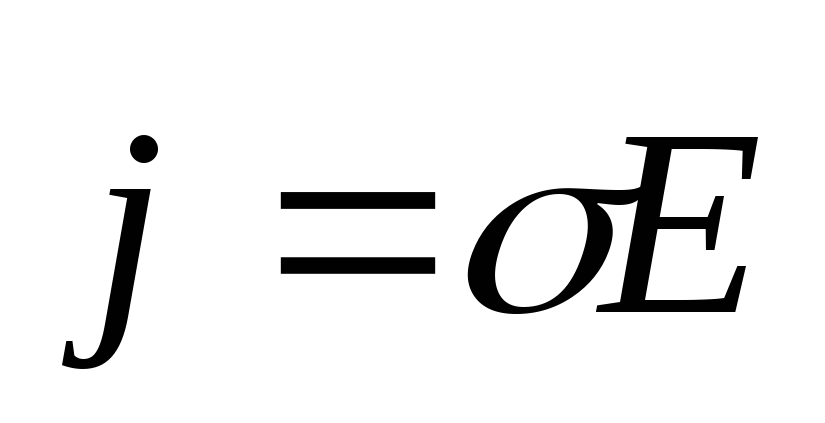 .
.
Первое структурное уравнение выражает закон создания магнитных полей действием электрического тока и переменным электрическим полем. Второе структурное уравнение выражает закон создания вихревого электрического поля переменным магнитным полем. Третье структурное уравнение выражает закон создания электрических полей действием электрических зарядов и отражает наличие свободных электрических зарядов. Четвертое структурное уравнение выражает вихревой характер магнитного поля и отражает отсутствие свободных магнитных зарядов.
Отметим, что закон сохранения электрического
заряда содержится в структурных
уравнениях Максвелла. Материальные
уравнения отражают влияние среды на
характеристики создаваемых в ней полей
и содержат параметры среды 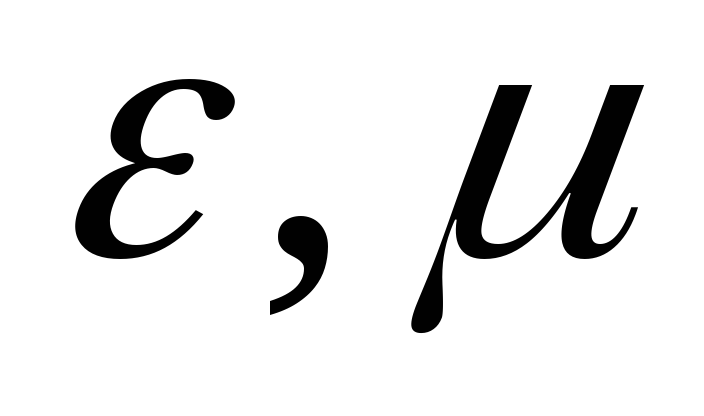 и удельную проводимость
и удельную проводимость .
В рамках максвелловской теории, параметры
среды должны быть заданы, чаще всего
они находятся опытным путем. Для линейных
сред эти величины не зависят от
характеристик полей. Поэтому для линейных
сред система уравнений Максвелла
является совокупностьюлинейных уравнений относительно характеристик
полей
.
В рамках максвелловской теории, параметры
среды должны быть заданы, чаще всего
они находятся опытным путем. Для линейных
сред эти величины не зависят от
характеристик полей. Поэтому для линейных
сред система уравнений Максвелла
является совокупностьюлинейных уравнений относительно характеристик
полей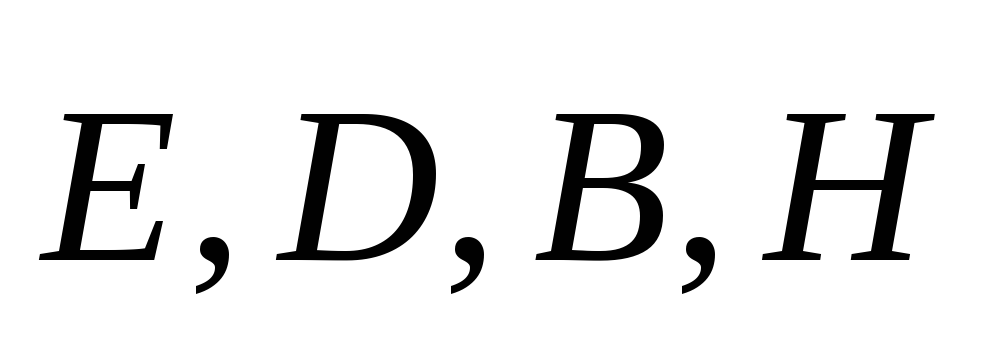 .
Эта линейность отражает физический
факт отсутствия взаимодействия
электромагнитных полей между собой
(они лишь накладываются друг на друга
без взаимного изменения своих
характеристик), что отражается в известном
принципе суперпозиции:
.
Эта линейность отражает физический
факт отсутствия взаимодействия
электромагнитных полей между собой
(они лишь накладываются друг на друга
без взаимного изменения своих
характеристик), что отражается в известном
принципе суперпозиции:
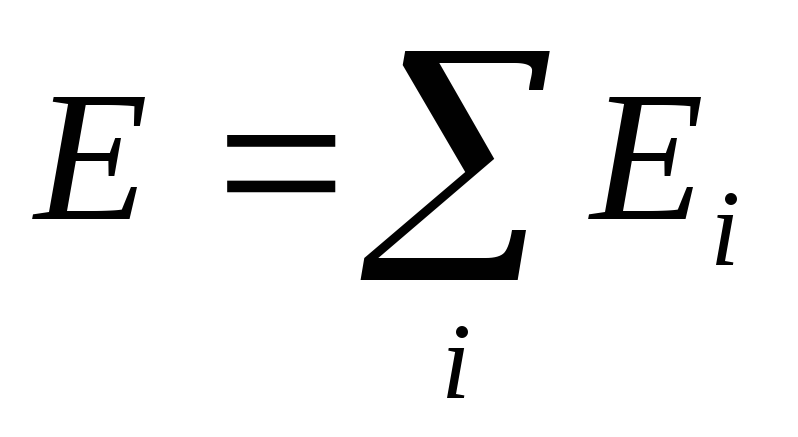 ,
,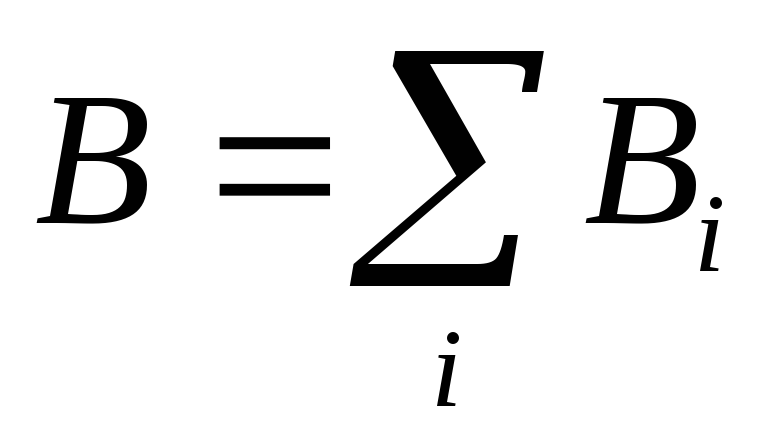 .
.
Для нелинейных сред 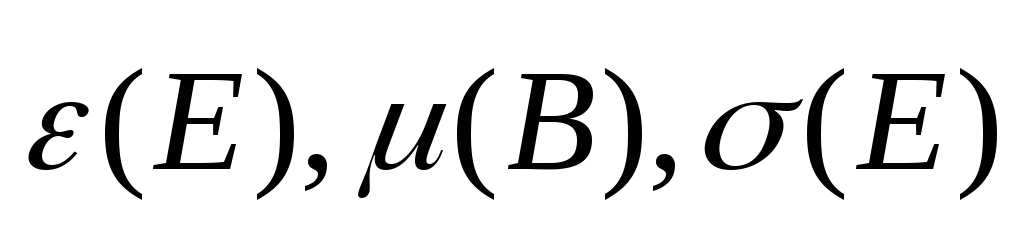 ,
являются функциями характеристик полей.
Система уравнений Максвелла для таких
сред являетсянелинейной.В нелинейных
средах возникает взаимодействие
электромагнитных полей, и принцип
суперпозиции не выполняется.
,
являются функциями характеристик полей.
Система уравнений Максвелла для таких
сред являетсянелинейной.В нелинейных
средах возникает взаимодействие
электромагнитных полей, и принцип
суперпозиции не выполняется.
Теория Максвелла находит широкое применение в различных областях науки и техники. При решении прикладных задач уравнение Максвелла необходимо дополнить начальными и граничными условиями.


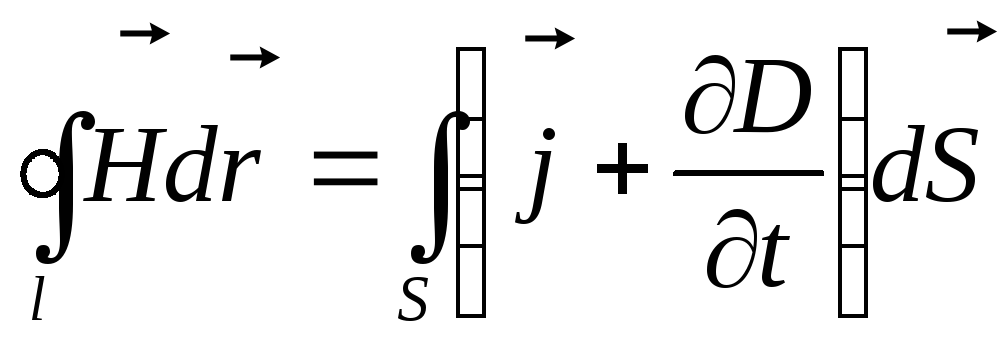 ;
;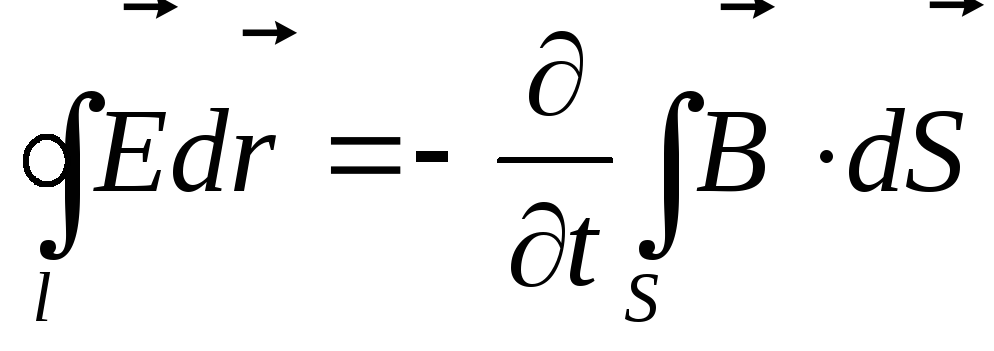 ;
;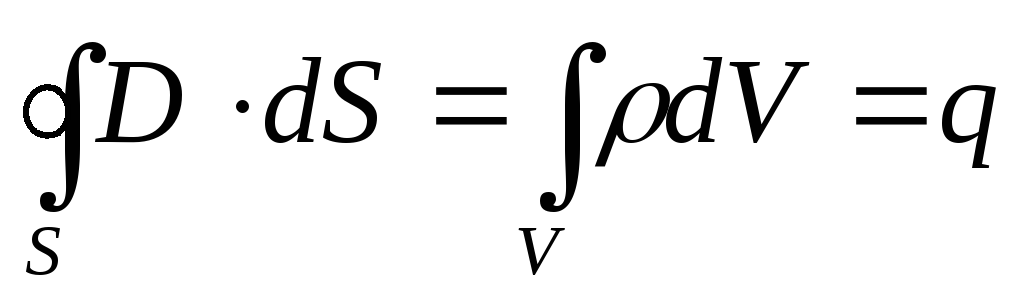 ;
;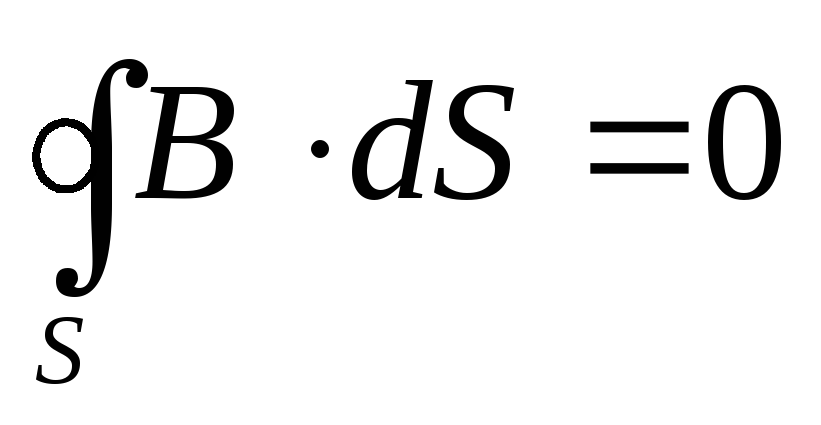 .
.